Preprint
Article
Geological Insights from Porosity Analysis for Sustainable Development of Santos Basin’s Pre-Salt Carbonate Reservoir
Altmetrics
Downloads
170
Views
175
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
12 June 2024
Posted:
13 June 2024
You are already at the latest version
Alerts
Abstract
Carbonate reservoirs, influenced by depositional and diagenetic processes and characterized by features like faults and vugs that impact storage capacity, require more than traditional Borehole Imaging logs (BHI) for accurate porosity data. This data is essential for geological assessments, production forecasting, and reservoir simulations. This work aims to address this limitation by developing methods to measure and monitor the sustainability of carbonate reservoirs and exploring the application of sustainability principles to their management. The study integrates BHI and conventional logs from two wells to classify porosity-based facies within the Barra Velha Formation (BVF) in the Santos Basin. The methodology involves four steps: (i) analyzing conventional logs; (ii) segmenting BHI logs; (iii) integrating conventional and segmented BHI logs using Self-Organizing Maps (SOM); and (iv) interpreting the resulting classes. Matrix porosity values and non-matrix pore sizes categorize the porosity into four facies (A to D). Facies A has high non-matrix porosity with 14,560 small megapores, 5,419 large megapores, and 271 gigapores (71.9%, 26.76%, and 1.34% of the 20,250 pores, respectively). Facies B shows moderate non-matrix porosity with 8,669 small megapores, 2,642 large megapores, and 33 gigapores (76.42%, 23.29%, and 0.29% of the 11,344 pores, respectively) and medium matrix porosity. Facies C exhibits low non-matrix porosity with 7,749 small megapores, 2,132 large megapores, and 20 gigapores (78.27%, 21.53%, and 0.20% of the 9,901 pores, respectively) and medium matrix porosity. Facies D has low non-matrix porosity with 9,355 small megapores, 2,346 large megapores, and 19 gigapores (79.82%, 20.02%, and 0.16% of the 11,720 pores, respectively) and low matrix porosity. The novelty of this work lies in integrating data from two sources to classify porosity across the Pre-Salt reservoir interval, serving as a proxy for preliminary litho-facies identification without core data. This study advances our understanding of carbonate reservoir sustainability and heterogeneity, offering valuable insights for robust, sustainable reservoir characterization and management in the context of global environmental and geological changes.
Keywords:
Subject: Engineering - Other
1. Introduction
Porosity analysis provides essential geological insights that significantly impact policy decisions for sustainable energy production. By measuring pore space within rocks or sediments, this technique helps understand the storage and flow of fluids like oil, gas, and water. It enables policymakers to identify suitable reservoirs for energy storage, assess carbon capture and storage potential, evaluate unconventional energy resources, manage groundwater sustainably, and conduct environmental impact assessments. Identifying formations with high porosity and permeability supports decisions on renewable energy storage projects, such as compressed air and pumped hydroelectric storage. It also assesses the capacity of geological formations to store carbon dioxide (CO2) from industrial processes, guiding decisions on carbon capture and storage projects to mitigate climate change. For unconventional energy resources like shale gas and tight oil, porosity analysis evaluates viability and environmental impact, informing regulations and policies. It also provides insights into the porosity and permeability of aquifers for sustainable groundwater management, guiding water extraction rates, recharge strategies, and resource protection. Moreover, porosity analysis contributes to environmental impact assessments by evaluating potential groundwater contamination, subsidence, and other geological hazards. This information helps develop policies to minimize environmental impacts and ensure the responsible use of energy resources. In summary, porosity analysis offers vital geological insights that aid policymakers in making informed decisions across various aspects of sustainable energy production and environmental protection ([1]).
Brazilian pre-salt carbonate reservoirs exhibit intricate heterogeneities, primarily influenced by the depositional system’s characteristics and subsequent diagenetic processes ([2,3]). Identifying and characterizing geological features such as faults, fractures, caves, conduits, and vugs in these reservoirs is imperative due to their significant impact on fluid flow behaviors, distinguishing them from siliciclastic reservoirs dominated by matrix production ([4]). Understanding these complexities is essential for improving our knowledge of the geological dynamics within carbonate reservoirs, which is crucial for their sustainable development and potential utilization in carbon capture and storage.
Recent years have seen substantial efforts directed towards comprehending the origins and impacts of primary heterogeneities, including faults, fractures, caves, and vugs, within carbonate reservoirs (e.g., [5,6]). The prediction of significant heterogeneities, such as faults (associated with tectonic processes) and caves (resulting from karstic processes), has prompted numerous studies utilizing seismic data and seismic attributes ([7,8,9,10,11]). For instance, [7] investigated anomalous bright spots known as the string of beads response () on seismic migration sections, a prevalent feature in carbonate reservoirs directly associated with caves resulting from karst processes. Similarly, [8] characterized fault systems and paleokarst features using bright spots from seismic data and formation micro-imager logs across different scales.
However, inherent resolution limitations in seismic data ([12]) underscore the challenges in achieving high-quality acquisition, given its associated costs. Addressing these resolution-related concerns, some works (e.g., [10,13]) have sought to improve seismic resolution data by developing methodologies such as spectral whitening, deconvolution, and inverse Q-filtering. By mitigating these resolution issues, the proposed methods enhance precision and confidence in seismic data interpretation, contributing to a more nuanced understanding of the complex geological features in carbonate reservoirs. Nevertheless, some significant heterogeneities related to carbonate reservoirs, such as fractures, conduits, and vugs, cannot be recognized through seismic data due to inherent scale limitations.
On the other hand, borehole image logs () have gained widespread utilization for several purposes, including detecting sub-seismic features like fractures and vugs, predicting porosities ([14]), establishing connections between acoustic facies (derived from ) and petrophysical parameters ([15]), and interpreting acoustic facies in the context of depositional settings ([16]).
Fractures and vugs, referred to in this article as non-matrix-related pores, are of paramount importance in carbonate reservoirs, driving recent studies (e.g., [9,17,18]) focused on understanding their impact on storage, fluid flow, and oil production. However, an early step in understanding the impact of non-matrix-related pores is their identification. In this sense, logs play a significant role in interpreting fractures and vugs within carbonate reservoirs.
Recognizing the critical need for expeditious assessment of fractures and vugs within carbonate reservoirs, coupled with the limited availability of for comprehensive well coverage and the high time consumption for manual interpretation, researchers (e.g., [19,20,21]) have scrutinized the response of conventional well logs to non-matrix-related pores. While conventional well logs lack the ability to provide qualitative details such as the size and shape of non-matrix-related pores, they have proven effective in offering quantitative information regarding porosity. However, detecting non-matrix-related pores solely through conventional logs poses significant challenges.
Acknowledging the inherent uncertainty associated with the nature of data, recent emphasis has been on integrating data at various scales to enhance results. Several scholars, including [18,20,22,23,24,25,26], have made considerable efforts to formulate methodologies focused on data integration to mitigate uncertainties and enhance the identification and characterization of distinct geological features.
To date, there is a notable absence of works that integrate conventional and logs for the characterization of non-matrix-related pores. The predominant focus of existing studies has been on utilizing core data, plugs, thin sections, or specialized well logs (e.g., nuclear magnetic resonance ()) to explore porosity. However, the availability and cost of such specialized data for all wells are limitations.
Nonetheless, the use of techniques has emerged as an indispensable tool for combining data and aiding in predicting reservoir characteristics, as evidenced by numerous publications (e.g., [27,28,29,30]). This widespread integration of ML techniques signifies their pivotal role in enhancing our ability to comprehend and predict crucial reservoir characteristics, especially in scenarios where conventional methods face limitations.
Recognizing the crucial sustainable role of non-matrix-related pores in carbonate reservoirs, particularly acknowledging that logs provide optimal visual interpretation of these features, and leveraging the availability of conventional well logs, this study introduces a methodology to seamlessly integrate logs and three specific conventional logs (sonic, density, and photoelectric factor) through the implementation of a self-organizing map (). The primary objective is to conduct facies classification based on porosity. This approach offers distinct advantages, including the application of a semi-automatic methodology that harmonizes data from disparate sources (borehole imaging tools for logs and well logging tools for conventional well logs) and scales (meso-scale for logs and macro-scale for well logs). This integration not only mitigates the time-consuming aspects associated with handling extensive datasets but also minimizes uncertainties inherent to each dataset. Additionally, the interpreted facies lend themselves to a meaningful interpretation in terms of depositional environments.
To establish a preliminary correlation between porosity-based facies and the principal litho-facies identified in the Barra Velha Formation (), we conducted an analysis. The dataset employed in this study comprises conventional well logs (sonic, density, and photoelectric factor) and data from two wells drilled in the Santos Basin’s . A detailed exposition of this dataset is provided in the subsequent section. Through this innovative methodology, we aim to enhance our understanding of carbonate reservoir characteristics by integrating visual insights from logs with quantitative data derived from conventional logs, contributing to a more comprehensive and nuanced interpretation of subsurface geological features. Additionally, this work aims to contribute to the development of sustainable strategies for carbon capture and storage in these carbonate reservoirs.
2. Geological Settings
The investigation undertaken in this study focuses on the meticulous examination of two wells situated within the Santos Basin, located in the southeastern margin of Brazil, as illustrated in Figure 1a. The inception of this basin can be traced back to the Late Jurassic to Early Cretaceous period, marked by the fragmentation of the Gondwana Supercontinent, consequently leading to the emergence of the South Atlantic Ocean. This geological transformation gave rise to the complex Brazilian Rift System, encompassing diverse basins, prominently featuring the Santos Basin ([27,31,32]).
As expounded by [34], the developmental trajectory of sedimentary basins along the Eastern Brazilian margin, inclusive of the Santos Basin, unfolds through three discernible tectonic stages. The initial stage, termed the Rift phase, is characterized by heightened lithospheric stretching and asthenosphere uplift, representing a pivotal intracontinental rifting episode within the South Atlantic region. The subsequent stage, denoted as the Transitional phase, denotes the cessation of syn-rift extension and is distinguished by the gradual diminution of sizable faults that rotated the rift block along with their sedimentary covert. The consequential break-up unconformity demarcates the boundary between continental lacustrine sediments and those transitioning to marine environments ([34]). In certain sedimentary basins, a significant thickness of Aptian siliciclastic and carbonate rocks is observed between this unconformity and the evaporite transitional sequence, construed as sag basin fill. Biostratigraphic and geochemical analyses provide compelling evidence that this sequence harbors hydrocarbon source rocks. During the Late Aptian, an arid climate and intermittent marine-water influx facilitated the formation of an elongated salt basin stretching between the West African and eastern Brazilian margins. The third and final stage, recognized as the Drift phase, is marked by the emergence of a mid-Atlantic ridge, accompanied by spreading processes and widespread salt tectonics ([34]).
The reservoir under scrutiny in this study pertains to the Aptian carbonates of the , strategically positioned within the aforementioned Transitional phase. The is characterized by three distinct unconformities, elucidated in Figure 1b: i) The Pre-Alagoas Unconformity situated at the summit of the Itapema Formation; ii) the Intra-Alagoas Unconformity, demarcating the division of the into Upper and Lower ; and iii) the Salt Base Unconformity, segregating the from the Ariri Formation ([33,35]).
The carbonates constituting the underwent their genesis in lacustrine environments, with their deposition intricately governed by factors such as salinity, pH, water level, topography, and variations in sediment supply ([5]). As posited by [36], the development of vugs and dissolved fractures can be ascribed to intervals of sub-aerial exposure of prominent structures termed mounds. [37], along with [38], contend that these mounds exhibit substantial vuggy and fracture porosities, hypothesized to be a consequence of the influence of elevated temperatures or hydrothermal fluids, facilitated by the interaction between Mg-silicate and the carbonates.
The predominantly comprises in-situ and reworked carbonates, encompassing diverse lithologies: (1) carbonates fashioned in the form of calcite crystal shrubs; (2) spherulites; (3) reworked carbonates consisting of intraclasts; and (4) locally extensive and laterally persistent accumulations of carbonate mud. These lithological constituents are consistently associated with a broad spectrum of pore sizes ([35,39,40]).
In conclusion, this study delves into the geological intricacies of the Santos Basin, specifically within the context of the Aptian carbonates of the . By elucidating the tectonic stages and depositional characteristics of the basin, we gain valuable insights into the geological processes that have shaped this region. Furthermore, the detailed analysis of the sheds light on the diverse lithologies and pore structures within the reservoir, offering crucial information for understanding and optimizing hydrocarbon exploration and extraction in similar geological settings.
3. Materials and Methods
In Figure 2, the mind-map illustrates the sequential progression of steps devised within the dataset and methods framework. The initial elucidation pertains to the dataset, encompassing Conventional Logs (specifically, the Density Log, Sonic Log, and Photoelectric Factor Log) and Borehole Images, featuring the Ultrasonic Borehole Imager () and Circumferential Borehole Imaging Log (). The comprehensive dataset forms the foundational basis for subsequent analytical procedures. Lastly, but of paramount importance, the articulated methods include Petrophysical analysis, Image segmentation for pore size classification, and the application of a () technique, namely the . This strategic delineation serves to underscore the systematic and structured approach undertaken in the exploration and analysis of geological data, highlighting the integral role of both dataset components and methodological processes in this scientific endeavor.
3.1. Dataset Overview
This research hinges on a meticulous examination of conventional logs and borehole images, employing advanced techniques such as image segmentation and methodologies. The meticulous nature of the examination is geared towards extracting nuanced insights from the dataset. To safeguard the confidentiality of sensitive information, the dataset is derived from two anonymized wells, denoted as A and B. This strategic anonymization ensures that the integrity of the dataset is preserved while adhering to ethical standards in research. The utilization of cutting-edge techniques, such as image segmentation and , underscores the commitment to a thorough and advanced analysis of the dataset, seeking a profound understanding of the geological characteristics within the context of the studied wells.
3.1.1. Conventional Logs
Within the dataset, a diverse array of well logs emerges, each contributing distinctive perspectives on the intricate features of subsurface formations. These encompass Density, Sonic, Photoelectric Factor (), as illustrated in Figure 3.
Density Log
The Density log assumes a pivotal role as a critical metric in determining the bulk density of geological formations ([41]). Operating as a comprehensive measure, the bulk density encapsulates both the solid matrix and fluids residing within pores ([42]). This log proves indispensable for comprehending the overall composition, with matrix density shedding light on the solid framework of rocks, devoid of porosity. Employing gamma radiation, typically emanating from sources like caesium-137 or cobalt-60, the density log meticulously gauges the return of gamma-rays, offering essential insights into the rock’s intricate composition ([42]).
Sonic Log
The Sonic log assesses the interval transit time of a compressional sound wave navigating the formation along the borehole axis. This temporal interval intricately links to the elastic properties of the matrix, thereby providing significant revelations about porosity ([20,43]). Outfitted with ultrasonic transmitters and receivers, the Sonic log furnishes indispensable data for discerning the lithological properties governing subsurface formations.
Photoelectric Factor Log
The log serves as a quantitative measurement of gamma-ray absorption by electrons. This log is extensively employed for lithological identification, offering valuable insights into subsurface rock compositions. Nevertheless, the widespread application of the log is not without challenges, particularly in scenarios involving the incorporation of barite as a mud additive. Barite, characterized by its high photoelectric absorption index, introduces a complicating factor by inducing pronounced peaks in the log readings when it infiltrates pore spaces. This phenomenon, as elucidated by [44], underscores the necessity for a nuanced interpretation of logs in settings where barite is utilized, requiring a careful consideration of the potential impact of mud additives on the log’s response. The intricate interplay between lithological characteristics and the presence of mud additives, such as barite, highlights the need for a comprehensive understanding of the log’s behavior to ensure accurate lithological recognition and interpretation in diverse geological contexts.
3.1.2. Borehole Images ()
logs were procured utilizing two distinct tools in this study. Specifically, the Circumferential Borehole Imaging Log (Dynamic from Baker) was employed for well A, while the Ultrasonic Borehole Imager (Dynamic from Schlumberger) was utilized for well B ([45]). These tools, each renowned for its unique capabilities, contributed essential data to the investigation. The Circumferential Borehole Imaging Log, provided by Baker, operates dynamically to offer a comprehensive view of the well’s surroundings. In contrast, the , supplied by Schlumberger, utilizes dynamic imaging capabilities based on high-frequency acoustic pulses, ensuring a detailed representation of the borehole conditions. The strategic selection of these tools aimed to capture nuanced geological features and provide a holistic understanding of subsurface formations in the respective wells, enhancing the overall depth and reliability of the dataset for subsequent analyses.
Ultrasonic Borehole Imager ()
The functions at elevated frequencies, providing heightened image resolution through precise measurements of amplitude and transit time. Its sensitivity to subtle variations on the borehole wall permits the to capture intricate details, wherein rugosity plays a pivotal role in influencing reflection amplitude. Notwithstanding, the effectiveness of in detecting lithological variations is intricately linked to surface effects rather than discerning changes in subsurface lithology ([45,46]). While its adeptness in delineating surface features is notable, careful consideration must be given to the interpretative limitations imposed by its reliance on surface characteristics, necessitating a nuanced understanding of its application in lithological analyses.
Circumferential Borehole Imaging Log ()
The serves a specialized purpose, meticulously designed for ultrasonic scanning operations in both open and cased hole wells. This instrument operates by transmitting acoustic pulses at high frequencies, facilitating a detailed analysis of the subsurface. Through the precise measurement of arrival times and amplitudes of echoes, the adeptly distinguishes variations in rock properties and borehole geometry, capturing the unique characteristics of the returning wave. Of particular significance is ’s noteworthy application in fracture analysis, offering insights into the structural integrity of geological formations. Moreover, it contributes to estimating the in-situ stress field by scrutinizing borehole breakouts and fractures induced during drilling activities ([46,47]).
This dataset, which seamlessly integrates conventional logs with advanced borehole images, serves as the fundamental groundwork for subsequent analytical endeavors employing sophisticated methodologies such as image segmentation and techniques. The synergistic application of these methodologies aims to yield a comprehensive and nuanced understanding of the intricate subsurface dynamics within Brazilian pre-salt carbonate reservoirs, contributing to advancements in reservoir characterization and resource management strategies.
3.2. Methodology
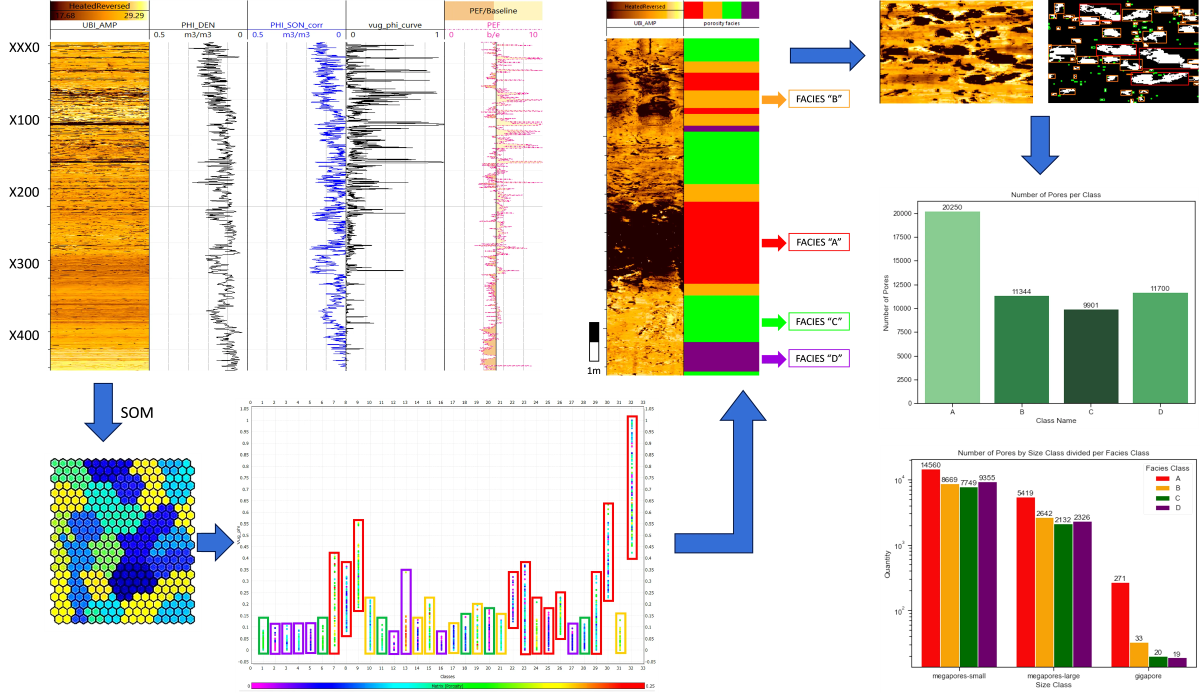
In the pursuit of advancing this research, an initial petrophysical analysis of density and sonic logs was undertaken to derive values for total and matrix porosity, respectively. A meticulous examination of values from the log was subsequently conducted to qualitatively assess the potential presence or absence of pore spaces, guided by a predetermined cutoff () established in existing literature ([27]). Intervals surpassing this threshold were construed as having a heightened likelihood of harboring pore spaces. Similarly, and logs underwent image segmentation and applications, facilitating the creation of a novel quantitative log denoted as . This log encapsulates depth-specific values of visible porosity. The ensuing step involved utilizing density, sonic, , and logs as inputs, from which derived classes with akin data patterns. These classes were subsequently juxtaposed with the and matrix porosity, culminating in the identification of facies based on porosity. The nomenclature assigned to these facies is predicated on qualitative assessments of matrix and non-matrix porosity, coupled with considerations of the predominant pore sizes.
The comprehensive methodology employed in this study is succinctly encapsulated in Figure 4, with detailed elucidation provided subsequently. This strategic amalgamation of petrophysical analyses, log assessments, and clustering techniques, as depicted in the ensuing sections, serves as the bedrock for unveiling the intricate characteristics of carbonate reservoirs.
intt=[draw,text centered,minimum size=6em,text width=5.00cm,text height=0.34cm] intl=[draw,text centered,minimum size=3em,text width=2.75cm,text height=0.34cm] int=[draw,minimum size=3em,text centered,text width=3.4cm] intg=[draw,minimum size=3em,text centered,text width=3cm] intr=[draw, minimum size=2em,text centered, text width=4cm] inta=[draw, minimum size=3em,text centered, text width=3cm] sum=[draw,shape=circle,inner sep=2pt,text centered,node distance=3.5cm] intb=[draw, minimum size=3em,text centered, text width=2cm] summ=[drawshape=circle,inner sep=4pt,text centered,node distance=3.cm]
3.2.1. Petrophysical Analysis
The examination of conventional well logs through petrophysical analysis serves as a crucial methodology for delineating fundamental physical attributes of rocks, encompassing lithology, porosity, permeability, and water saturation ([18,43,48]). Within the scope of this study, sonic and density logs served as pivotal tools for scrutinizing the isolated and synergistic behaviors of these well logs concerning porosity. The sonic log quantifies the time taken by a compressional sound wave to traverse the interval along the axis of the borehole ([43]). The computation of porosity is facilitated through the application of the Wyllie time-average equation (Equation 1), an empirical relationship correlating the velocity of the rock matrix with borehole fluids ([49]). This equation, outlined as follows, forms the cornerstone for porosity derivation:
Where, denotes the fractional porosity of the rock, v signifies the velocity of the formation (), represents the velocity of interstitial fluids (), and stands for the velocity of the rock matrix (). The subsequent sections expound upon the intricate interplay of these variables, unraveling the intricacies of porosity computation in the pursuit of comprehending the underlying geological formations.
Utilizing Equation 1, we derived Equation 2 by considering the reciprocal of velocity () as the interval transit time ().
The computation of matrix porosity becomes feasible when the values of transit time are known, achieved through Equation 3, which was extracted from Equation 2 ([43]).
In the context of the presented equation, signifies matrix porosity, represents acoustic transit time, and denote acoustic transit time of interstitial fluids () and acoustic transit time of the rock matrix (), respectively.
It is noteworthy that when the travel time (t) is a known variable, the computation of porosity becomes feasible. Drawing upon Equation 2 and substituting the acoustic transit time ( by travel time (t), we systematically derived the matrix porosity as illustrated in the subsequent formulation.
Where, represents matrix porosity, t denotes travel time (), signifies travel time of interstitial fluids () and shows travel time of the rock matrix ().
The density log provides a comprehensive portrayal of density values across the entirety of the formation, encompassing both its solid and fluid components. Employing Equation 2 as a foundation, and substituting the acoustic transit time () by the formation bulk density (), we derived Equation 5. This equation serves as a computational tool for determining the values of total porosity ().
Where, denotes the total porosity, represents the matrix density. Also, and signify formation bulk density and fluid density, respectively.
3.2.2. Image Segmentation for Pore Size Classification
Pore size classification plays a pivotal role in understanding the dynamic properties of carbonate reservoirs, as distinct behaviors emerge with varying pore sizes ([50,51]). Larger pores, for instance, exhibit correlations with fluid losses during drilling or signify intervals of heightened productivity ([51]). The intricate three-dimensional nature and irregularities of pores, as highlighted by [50], pose challenges in precisely characterizing their sizes visually. However, the application of image segmentation has proven instrumental in identifying and scrutinizing pore spaces. This analytical process involves linking the well image to an image of identical dimensions, establishing a correlation between each well region and a specific class. The execution of a meticulously devised workflow, depicted in Figure 5 and grounded in image processing techniques, facilitates the connection of each individual pore analysis to its corresponding class.
Leveraging the capabilities of the Python programming language, the methodology proposed by [52] is implemented for noise reduction and segmentation, employing the Multi-Scale Retinex with Color Preservation and Color Image Quantization method on the log. Following segmentation, the determination of pore size is conducted by adopting the porous radius representation outlined by [53]. The final size value is defined as the average of major and minor axes, calculated through the opencv library function, "boundingRect()", which provides values for the major and minor axes of a convex contour (such as porous). Initially in a 1-pixel scale, these values are subsequently converted to millimeters using the original well scale, with a conversion rate of . The resultant data undergoes classification into gigapores, large-mesopores, and small-mesopores, adhering to the nomenclature proposed by [50,54,55,56].
[50] delineated three primary size classes for regularly-shaped pores smaller than . Specifically, pores smaller than are termed micropores, and those ranging from to are identified as mesopores. Due to inherent image resolution limitations, the detection of micropores and mesopores proved unfeasible in this research. Pores spanning 4 to are designated megapores, further categorized into small megapores ( to ) and large megapores ( to ). While [50] introduced the term cavern for pores larger than , a nomenclature inconsistency led to the adoption of gigapores for sizes surpassing , aligning with the classification proposed by [54].
3.2.3. Advancements in Machine Learning Techniques for Geological Analysis
Numerous studies underscore the transformative impact of techniques across diverse domains, with particular relevance to geosciences, as exemplified in works by [57,58]. Notably, recent developments emphasize novel methodologies tailored for big data analysis, leveraging deep learning algorithms, as evidenced by the works of [59]. However, the available well dataset provides limited instances detailing the application of these state-of-the-art techniques. Traditional approaches to well log analysis typically hinge on supervised methods for classification, including Multilayer Perceptron and ensemble techniques, necessitating prior rock classification to train the algorithm. Yet, during the exploration phase, where insights into the field are minimal, and core data is unavailable, employing such techniques becomes impractical.
In response to this challenge, this study advocates a pioneering methodology that amalgamates all available data, seeking to autonomously identify patterns within the dataset and facilitate field interpretation during the exploration phase. To this end, the study presents best practices for applying an unsupervised method, opting for , a classical clustering technique. Devised by [60] in the 1980s, represents a neural network technique proficient in projecting high-dimensional data into a 2D space, forming a map, as illustrated in Figure 6. This map comprises nodes, or neurons, arranged in a network or linked mesh. The iterative process of competitive learning adjusts the positions of nodes based on computed distances between samples and nodes. During learning, the algorithm computes the distance of samples to all nodes, adjusting not only the winning node but also its neighbors to be closer to the sample. This meticulous process ensures the preservation of crucial topological relationships within the displayed data, allowing for the visual analysis of various data types through the map. The resulting map of distances, termed the U-matrix, and the component maps, which depict the distribution of each attribute used for training, provide insights into the topological organization of the data.
Given the high number of nodes in the map, an application of k-means is employed to regroup them, utilizing the Davies-Bouldin index to define the optimal number of clusters. Through the judicious use of component maps and the U-matrix, the user gains the flexibility to define clusters, grouping nodes in the map as per their preferences. This comprehensive approach underscores the efficacy of in offering an intelligent and visual means to analyze complex datasets, particularly in scenarios where traditional supervised methods face practical limitations during the exploration phase.
At the core of s lies a sophisticated array of artificial neurons, meticulously organized within a two-dimensional grid. Each neuron within this grid is associated with a weight vector, the adaptation of which forms the central thrust of the network’s learning process. The following delineates a more comprehensive exposition of the workings of s:
- Initialization: The weight vectors corresponding to each neuron are initially configured either randomly or through alternative initialization methods. These weight vectors effectively represent points within the input space.
- Competition and Cooperation: Throughout the training process, an input vector is introduced to the . Each neuron computes its resemblance to the input vector by employing a similarity metric, most commonly the Euclidean distance. The neuron with the weight vector that most closely resembles the input is deemed the winning neuron.
- Weight Adjustment: The winning neuron and its immediate neighbors within the lattice have their weight vectors adjusted to become more akin to the input vector. The extent of this adjustment is contingent upon the neighborhood function, which gradually contracts over time, allowing the to converge.
- Topology Preservation: A striking attribute of s is their ability to conserve the topological relationships inherent in the input data. Comparable input vectors are mapped to proximate neurons within the grid, thereby facilitating data visualization and clustering.
- Training Iteration: The steps delineated in points 2 through 4 are iteratively repeated for a predefined number of training cycles, progressively enhancing the mapping of input data within the .
- Final Representation: After training, the furnishes a condensed, structured representation of the input data, effectively functioning as an organized, lower-dimensional rendition of the original dataset.
- ∘
-
Similarity Metric (Euclidean Distance): The similarity (or dissimilarity) between an input vector, denoted as I, and a neuron equipped with a weight vector, denoted as W, is calculated as follows:Where and represent the components of the input vector and the weight vector, respectively.
- ∘
-
Weight Adjustment: The modification of the weight vector for the winning neuron and its neighboring neurons is executed in the following manner:Where, signifies the change in weight, corresponds to the learning rate, designates the neighborhood function, and signifies the disparity between the input vector and the weight vector.
- ∘
-
Neighborhood Function: The neighborhood function, denoted as , dictates the influence exerted by the winning neuron on its neighboring neurons, with its magnitude diminishing as a function of both time and distance from the winner:Where, c denotes the distance from the winning neuron, while represents the neighborhood radius.
In this study, was applied to perform automatic segmentation of the log, creating a new log based on porosity while recognizing patterns within conventional logs and those derived from in an automatic and hierarchical manner. The utilization of provides a valuable approach for comprehensive data analysis, particularly when traditional supervised methods prove impractical in the absence of detailed rock classifications during the exploration phase.
Utilizing for Curve Computation
Preceding any analytical procedures, it is imperative to underscore the significance of adhering to robust practices in image analysis, particularly in the identification and segregation of non-geological features. As asserted by [61], the initial phase of any interpretation should involve the meticulous recognition of non-geological features or image artifacts. Employing filters stands out as a prevalent practice to extricate image artifacts while preserving lithological features (e.g., [62]). Consequently, as a foundational step, the methodology advanced by [52] was applied to cleanse the images, ensuring their quality and mitigating potential issues linked to noise during training.
The fundamental premise underpinning the automatic recognition of porous spaces in this study hinges on their direct association with low amplitude values in the borehole image, manifested as dark brown coloration. Subsequently, the well images underwent individual classification via and k-means pre-processing. was implemented with parameters elucidated in Table 1, utilizing the three channels of the Red, Green, and Blue () image of the reservoir interval as input data, classified separately for each well.
The determination of a high number of clusters was automated through the Davies-Bouldin index. In a subsequent interactive phase, the interpreter scrutinized the clusters discerned by and k-means, ultimately defining the optimal cutoff for porous spaces and effecting the binarization of the image into porous spaces and background. The porous spaces thus identified were correlated with depth, providing the foundational data for the computation of the percentage of pores within the image diameter, referred to in this study as . This intricate methodology ensures a meticulous and automated delineation of porous spaces, contributing to the nuanced understanding of reservoir characteristics in the exploration phase.
Integration of Datasets Using (Conventional and Logs)
The prevailing consensus within the literature underscores a crucial limitation: individual conventional well logs, in isolation, often fall short in effectively discerning pore spaces arising from fractures or dissolution, as substantiated by [20,63,64,65]. Consequently, the pivotal question arises in an investigative context: What distinctive behavioral patterns should one anticipate from well logs within a porous environment, and how can the integration of datasets enhance the identification of non-matrix-related pores?
Addressing these inquiries, a tandem application of and k-means is employed once more to amalgamate the image log with the conventional well logs. The deliberate overestimation of the number of clusters, assessed by Davies-Bouldin, serves a strategic purpose—capturing a maximal spectrum of information pertaining to the variability of well logs contingent upon porosity content. This methodological fusion engenders a comprehensive synthesis of data, facilitating a nuanced exploration of the intricate interplay between image-derived porosity information and conventional well log data. The judicious integration of these disparate datasets promises to enhance the discernment of non-matrix-related pores, thereby advancing the precision of reservoir characterization in porous environments.
4. Results and Discussion
This section presents the discrete outcomes attained through the advocated methodology. The initial findings pertain to the utilization of image segmentation and techniques, culminating in the derivation of a novel log termed . Subsequently, employing petrophysical analysis, we delve into comprehending the intricacies of the logs employed as input data, facilitating an automated classification process. Ultimately, the resultant clusters from the automated classification underwent further categorization, resulting in the establishment of four distinct facies groups. These groups, meticulously described and interpreted, offer comprehensive insights into their lithological associations. The ensuing discussion unpacks the implications and significance of these findings, shedding light on the broader geological context and enhancing our understanding of the subsurface intricacies within the studied reservoirs
4.1. “ Curve” Calculation
In the meticulous undertaking of delineating the " curve", a comprehensive and intricate methodology utilizing was deployed. This involved the establishment of a neuron map for well A and a more delimited neuron map for well B The ultimate quantification of errors, pertaining to both quantization and topography, was assiduously documented. Specifically, the quantization errors for well A were precisely recorded at , while the corresponding topographic errors were meticulously noted at . Similarly, for well B, the quantization errors were detailed at , and the topographic errors were discerningly documented at . The graphical representation of these findings is eloquently portrayed in Figure 7. The intricacies of this computational analysis reveal the meticulous attention given to the nuanced characteristics of each well, providing a comprehensive insight into the intricacies of the " curve" calculation.
It is of paramount importance to emphasize the necessity for meticulous implementation within the realm of automated unsupervised image segmentation. The inherent patterns embedded in images often deviate from the precise goals of the interpreter. Consequently, it becomes essential to meticulously design and execute a systematic array of tests. These tests should be subjected to judicious evaluation, aligning with predefined benchmarks and objectives, as elucidated in the current investigation [27]. The intricacies of image segmentation demand a thorough and circumspect approach to ensure the attainment of accurate and meaningful outcomes in alignment with the study’s elucidation.
The formidable undertaking at present revolves around the discrimination of porous spaces from the ambient background. Although an instinctive approach to segmentation might incline towards a binary classification of mapped nodes, the consequences ensuing from the classification utilizing the unveil a pitfall in the segmentation of Kohonen maps through k-means into two classes. This leads to an overestimation of pore spaces, as illustrated in Figure 8. The nuanced intricacies of this process highlight the need for a more refined and nuanced segmentation strategy, considering the limitations inherent in the simplistic binary classification employed initially.
A discernible factor contributing to the overestimation of pore space in is rooted in the algorithm’s inability to achieve the optimal Davies-Bouldin index value. Additionally, in this particular scenario, the category pertaining to porous space within well B constitutes a mere 9% of the entire reservoir interval. This occurrence results in an inherent imbalance, a subtlety that becomes obscured when simplifying the image into two classes. The misalignment between the algorithmic assessment and the actual distribution of porous space in well B accentuates the significance of refining the algorithmic parameters to ensure a more accurate portrayal of subsurface characteristics. The nuanced nature of reservoir characterization demands a meticulous approach to algorithmic calibration, acknowledging the intricate heterogeneity within the geological formations under scrutiny. As such, a comprehensive understanding of these complexities is imperative for advancing the precision and reliability of Borehole Image analysis in reservoir characterization studies.
The endorsed approach encompasses the broadening of clusters examined through the lens of the Davies-Bouldin index, with particular attention directed towards scrutinizing the cluster characterized by the most minimal amplitude values within the Kohonen map. This intricate procedure, as delineated in Figure 9, underscores a nuanced and systematic examination reliant on the proportionality of input range values. By meticulously navigating this process, it is affirmed that the optimal number of classes is ascertained, thereby facilitating a more refined and precise mapping of the dataset. The visual representation in Figure 9 effectively illustrates the intricacies of this methodology, highlighting its reliance on scrutinizing amplitude values and underscoring its efficacy in enhancing the overall mapping accuracy of the dataset. This methodological refinement ensures a discerning exploration of the dataset’s inherent structure, contributing to a heightened understanding and representation of the underlying patterns and relationships within the data.
Following segmentation, the enumeration of pixels categorized as pore space becomes instrumental in deriving the percentage of this particular class at varying depths. This computational endeavor results in the generation of a non-matrix porosity percentage curve denoted as . In the context of this research, well A underwent segmentation, resulting in its division into eight distinct clusters. While well B was subjected to a similar process, leading to its partitioning into six clusters. It is noteworthy that within this classification, the cluster characterized by lower amplitude values assumes the role of representing the pore space. This meticulous approach to segmentation and subsequent cluster assignment aims to discern and quantify the distribution of pore spaces at different depths in the wells under investigation, thereby contributing valuable insights into the subsurface characteristics and porosity variations. The choice of clusters, particularly designating the one with lower amplitude values, reflects a deliberate strategy to capture and emphasize the relevant geological features related to pore space within the wells under scrutiny.
4.1.1. Responses of the Data Inputs Against Porous Environment
This section delves into the nuanced responses of data inputs within porous environments, particularly focusing on carbonate reservoirs renowned for their intricate porosity systems. These systems are categorized into porosity stemming from the matrix (interparticle porosity) and non-matrix-related porosity, encompassing features like caves, fractures, and vugs ([66]). The sonic log emerges as a key informant, furnishing insights into interval transit time and establishing a direct linkage with interparticle porosity. By applying the Wyllie time-average equation ([49]), the values of matrix porosity can be derived, offering a comprehensive understanding of the depositional and early diagenetic processes of the reservoir.
Complementary to the sonic log, the density log contributes vital information by supplying values of bulk density. This density is a composite influenced by matrix density and the fluid density within the pores, as outlined by [43]. Employing a well-established equation, the density log aids in calculating the total porosity specific to a given interval, contributing to a comprehensive assessment of the reservoir’s porosity characteristics. Differences between density and sonic log values illuminate non-matrix porosity, typically filled with mud filtrate. This filtrate, distinguished by lower density and prolonged travel time compared to the host rock, becomes a crucial indicator. Intervals exhibiting low density values and prolonged travel time, contrasted with the established background values for carbonates, are interpreted as zones with a heightened percentage of pore spaces ([20,21,66]).
Conversely, intervals demonstrating elevated density values and reduced travel time are construed as areas with underdeveloped or non-visible pores. This nuanced interpretation underscores the intricate interplay between data inputs and the porous environment, providing valuable insights into the nature and extent of porosity within carbonate reservoirs. Such meticulous analysis, supported by advanced equations and log readings, forms the foundation for a comprehensive understanding of reservoir characteristics and facilitates informed decision-making in the realm of geological exploration and resource extraction.
Despite the quantitative insights offered by density and sonic logs concerning porosity, it is imperative to meticulously record and distinguish the configurations of non-matrix related pores to enhance classification accuracy. To address this need, the utilization of image segmentation on logs emerged as a pivotal tool, significantly contributing to the characterization and delineation of shapes and sizes associated with non-matrix related pores. This aspect introduced an additional criterion for our ultimate facies classification, thereby refining our understanding of the reservoir’s geological attributes. Nonetheless, it is crucial to acknowledge the inherent limitations of logs, including challenges related to image resolution and potential confusion stemming from image artifacts that may be mistakenly identified as non-matrix features, as noted by [54].
In an effort to overcome the constraints associated with image artifacts, we employed the methodology proposed by [52] to meticulously eliminate noise from the images, preserving solely the pertinent geological features. This methodological refinement facilitated a clearer distinction between genuine geological attributes and potential artifacts, enhancing the reliability of our data. Subsequent to this refinement process, our analysis revealed the identification of three distinct categories of pore sizes: (i) small megapores, (ii) large megapores, and (iii) gigapores, as per the taxonomy introduced by [50], a visual representation of which is provided in Figure 10. This detailed categorization of pore sizes constitutes a critical step forward in our understanding of the reservoir’s intricacies, laying the groundwork for more nuanced interpretations and informed decision-making in the domain of geological exploration and resource management.
An additional well log subjected to analysis in this study is the Photoelectric Factor (). Widely recognized as a conventional log, the log serves as a direct tool for lithology determination, as evidenced by the works of [64,65,67], and [68]. Beyond its conventional application, the log also plays a crucial role in the initial identification of non-matrix related pores, as highlighted by [67,68], and [66]. In the context of our research, the primary utility of the log lies in qualitatively distinguishing intervals with non-matrix pores from those without. The response of the log to non-matrix related pores is characterized by elevated values (above ), attributable to the filling of these pores with barite-containing mud filtrate. The high photoelectric factor of barite, as elucidated by [44], contributes to these heightened values. Conversely, when intervals lack pores in direct contact with the well wall, log values closely align with the background for carbonate rocks, specifically around . A comprehensive summary delineating the applicability of each conventional well log for identifying distinct porosity is presented in Table 2.
4.1.2. Integration of Conventional and logs
Upon completion of the comprehensive petrophysical analysis and the computation of the curve, the subsequent phase involves the integration of this dataset to unveil latent patterns in an unsupervised manner. This integration is accomplished through the deployment of the , which utilizes the following logs as inputs: , , , and . The representation of these logs is visually rendered on bidimensional maps, as delineated in Figure 11.
The 2D portrayal of the log (Figure 11b) elucidates distinct groups, showcasing their values’ spatial distribution. Elevated values are concentrated in the left and bottom left corner, whereas lower values are situated in the top right corner. Intermediate values predominate based on the map’s distribution.
Upon plotting the log on the 2D map (Figure 11c), the porosity derived from sonic measurements is observed to segregate into different groups, delineated by varying colors on the map. Notably, high values are concentrated in the bottom right, while lower values are found at the top. The central area of the map is characterized by intermediate values.
Likewise, the 2D representation of (Figure 11d) manifests a distribution and behavior akin to , where higher values cluster in the bottom left, and lower values occupy the top. Intermediate values of predominate and are centralized on the map.
The 2D map of the log (Figure 11e) portrays values grouped such that higher values are concentrated in the bottom left, while lower values are positioned in the top and slightly right bottom corner. The prevalence of lower values is observable across the map.
The distinctive colors characterizing each 2D map signify groups with analogous distances between nodes or neurons, representing the values of each well log. The spatial location of each color group is intrinsically linked to the input space of the respective log.
The outcomes of the network training with the four inputs (, , , and ) are visually presented in a 2D map (Figure 11a). A noticeable variation in the color scale (ranging from blue to yellow) facilitates the visual separation into groups with comparable characteristics. Post-training, the has the potential to group high values of , , , and . To achieve precise grouping, a segmentation of the 2D map is imperative, involving the application of the Davies-Bouldin index and k-means. This segmentation is a crucial step in ensuring an accurate and meaningful classification of the dataset.
For the segmentation process, both wells underwent a joint classification. The was configured on a map, yielding quantization and topographic errors of and , respectively. Subsequently, this 2D map underwent further subdivision into 32 distinct patterns, guided by the performance of the Davies-Bouldin index in conjunction with the k-means split method, as visually represented in Figure 12.
The Davies-Boldin index functions as a critical metric for evaluating the clustering efficacy of 2D maps that encapsulate information from all well logs. Diminished values of the Davies-Boldin index signify a more proficient clustering outcome. Application of the Davies-Boldin index to the 2D map (Figure 12b) culminated in the final classification of data into thirty-two discernible groups (Figure 12c). This enumeration of groups (thirty-two) is deemed the optimal clustering solution, substantiated by the performance of the Davies-Boldin index on our trained 2D map.
4.2. Porosity-Based Facies
Within the framework of facies delineation based on porosity, an exhaustive examination of the 32 discerned classes led to the delineation of four discrete facies designated as A, B, C, and D. This systematic categorization was executed through a meticulous scrutiny of the intricate interdependencies existing among matrix and non-matrix porosities, values, and the parameter, as visually depicted in Figure 13. The intricate nature of these interrelationships was pivotal in establishing the distinct identities of the aforementioned facies. This analytical endeavor sought to uncover nuanced patterns and correlations embedded within the porosity characteristics, thereby contributing to a refined classification system. The resulting facies classification not only serves as a foundational framework for further geological interpretations but also signifies a significant advancement in our understanding of the subsurface reservoir heterogeneity. This approach underscores the importance of integrative analyses in deciphering intricate geological features and enhances the potential for accurate reservoir characterization.
4.2.1. Facies A
Within the geological context being examined, facies A emerges with distinct characteristics concerning porosity parameters gleaned from diverse well logs. Specifically, the total porosity values assigned to facies A, extrapolated from density logs, span a noteworthy spectrum ranging from to . Simultaneously, matrix porosity values, derived from sonic logs, manifest within the range of to . The values associated with this facies exhibit considerable variability, spanning from to , with a pronounced concentration surpassing the threshold of . The curve, depicting variations in vuggy porosity, showcases the highest values fluctuating between 0 and , with a predominant concentration observed within the interval of to . A meticulous examination of visible pore spaces through advanced image segmentation techniques reveals that facies A predominantly encompasses pores exceeding but falling below . Utilizing the classification proposed by [50], pores within the 4 to range are designated as small megapores. Intriguingly, despite this classification, facies A also exhibits pores surpassing the threshold. The automated enumeration of total pores within this facies underscores the prevalence of small megapores at 71.90%, large megapores at 26.76%, and gigapores at 1.34%, culminating in a total pore count of 20250, as delineated in Table 3. The amalgamation of insights from well logs and pore size analysis converges to depict facies A as a facies characterized by high non-matrix porosity, graphically elucidated in Figure 14. This nuanced exploration of facies A not only contributes to the refinement of subsurface geological interpretations but also underscores the intricate heterogeneity inherent in reservoir formations, thereby enriching our understanding of the geological complexities at play.
4.2.2. Facies B
Facies B is distinguished by a spectrum of total porosity values ranging from to , with matrix porosity values slightly exceeding those of facies A and falling within the range of to . values within this facies exhibit a dispersed distribution, fluctuating between 3.1836 b/e and . The curve also reveals varied values, spanning from a minimum of 0 to a maximum of . Notably, predominant visible pores in this classification are characterized as small megapores, with sizes ranging from to , constituting 76.46% of the total enumerated pores. Large megapores account for 23.29%, while gigapores represent a minimal 0.29%. The cumulative pores in this category amount to 11344, as detailed in Table 3. Through a comprehensive integration of data, facies B emerges as a classification demonstrating moderate non-matrix and medium matrix porosity, as illustrated in Figure 14. This meticulous analysis contributes significant insights into the nuanced characteristics of facies B, shedding light on its porosity parameters and enhancing our understanding of the heterogeneity inherent in subsurface geological formations.
4.2.3. Facies C
In the analysis of facies C, a comprehensive examination reveals a broad spectrum of total porosity values ranging from to . Notably, the matrix porosity values exhibit variability within the range of to , with average values surpassing those observed in the matrix porosity of both facies A and B. The values, albeit scattered, display a discernible range from to , with a noteworthy concentration of values closely aligning with the background levels. Moreover, facies C manifests low values of , presenting a minimum of 0 and a maximum of . The predominant pore sizes in this facies span from to , constituting small megapores, which contribute to a substantial 78.27% of the total pores enumerated. Large megapores represent 21.53%, whereas gigapores constitute a minimal 0.20%. The total number of pores identified in facies C amounts to 9901, as detailed in Table 3. Importantly, given the constraints imposed by image resolution quality, there is a heightened probability of the presence of mesopores, as inferred from the moderate values of matrix porosity. Delving into the nuances of visible pore sizes and acknowledging the pronounced significance of matrix porosity, it is plausible to characterize facies C as a facies marked by low non-matrix porosity and medium matrix porosity, a characterization substantiated by the graphical representation in Figure 14. This detailed exploration enhances our understanding of the intricate geological characteristics inherent in facies C.
4.2.4. Facies D
Facies D, as evidenced by comprehensive analysis, manifests the most diminished levels of both total and matrix porosity within the studied geological context. The range of total porosity values spans from to , while matrix porosity values exhibit a spectrum from to . Notably, when juxtaposed with the preceding three facies, facies D emerges with the lowest values, fluctuating between and . Concurrently, the values for this specific facies exhibit a noteworthy minimum, oscillating between 0 and . In parallel with the previously elucidated facies, facies D showcases a dominance of small megapores, constituting an overwhelming 79.82%, followed by large megapores at 20.02%, and gigapores at a marginal 0.16%. The automated enumeration of total pores for this facies tallies to 11720 (refer to Table 3), underscoring the intricate pore structure inherent in this geological setting. Analogous to the characteristics observed in facies C, the identification of mesopores and micropores remains elusive. However, a nuanced consideration of the conspicuously low values associated with matrix porosity prompts speculation regarding the probable occurrence of micropores. Consequently, facies D is categorically described as a geological stratum characterized by low non-matrix and low matrix porosity, a characterization visually represented in Figure 14. This multifaceted analysis delves into the intricate nuances of facies D, shedding light on its distinct porosity attributes and hinting at the potential existence of micro-scale porosity features, thereby enriching our understanding of the geological composition under investigation.
4.3. Porosity-Based Facies as Lithology Proxies
The intricate lithological composition characterizing the has spurred numerous researchers ([15,27,66,69]) to engage in comprehensive sedimentological and petrophysical investigations. [35] innovatively employed thin sections, core descriptions, and chemical data to propose a novel facies classification system grounded in the relative abundance of mud, calcite spherulites, and calcite shrubs. [69] utilized plug samples and techniques to categorize groups with analogous petrophysical behaviors, facilitating a qualitative differentiation of the Barra Velha reservoir into categories of tight, good, and excellent. [15], employing a holistic approach integrating borehole image logs, nuclear magnetic resonance, and core samples, conducted a meticulous acoustic facies classification, subsequently establishing correlations between these facies and specific lithologies. It is noteworthy that the aforementioned studies share a common reliance on specific databases, primarily comprised of cores or plugs, enabling a robust analysis of lithological aspects within the reservoir. However, the prevalent absence of cores and plug samples in most reservoirs poses a common challenge, impeding accurate lithological interpretations. In response to this challenge, recent noteworthy endeavors by [15,70], and [16] have involved the interpretation of logs to identify acoustic facies. Subsequently, these acoustic facies have been associated with the prevailing lithologies, incorporating crucial petrophysical parameters such as porosity and permeability into their analyses. This innovative approach, relying on well log data, addresses the common limitation of core scarcity and significantly contributes to advancing our understanding of the complex lithological dynamics within the .
[15] present a comprehensive analysis of five interpreted litho-facies within the geological context of the , amalgamating both depositional and post-depositional characteristics. These litho-facies include (1) shrub-dominated lithologies; (2) partially cemented shrub-dominated lithologies; (3) intraclastic/spherulitic grainstones-rudstones; (4) highly cemented lithologies; and (5) dolomudstones and marls. According to the findings of [15], shrub-dominated lithologies exhibit high visual porosity, whereas detrital carbonates, represented by grainstones and rudstones, showcase medium to high visual porosity. Partially silicified and/or dolomitized lithologies, specifically the partially silicified shrubby framestones, demonstrate medium visual porosity. In contrast, highly cemented lithologies, such as spherulite packstones, dolomudstones, and marls, exhibit low visual porosity. In a similar vein, [16] undertake a correlation between acoustic facies and the principal lithologies described in the , as per the framework proposed by [35]. The visual porosity characteristics of these lithologies can be delineated as follows: (1) shrubstone-like lithologies demonstrate high porosity, aligning with pore morphologies resembling the growth patterns of shrubs; (2) rudstones-like lithologies display high porosity attributed to subangular cobbles, whereas low porosity is linked to angular pebbles; (3) grainstones-like lithologies exhibit medium porosity, with pore spaces situated between intraclasts of silica lamina, shrub fragments, or extraformational clasts; and (4) mudstone-like lithologies manifest low porosity owing to their highly homogeneous nature and the frequent interbedding of strata. These detailed characterizations contribute significantly to our understanding of the diverse porosity attributes associated with distinct litho-facies within the .
While these studies have demonstrated efficacy in discerning vertical variation patterns and aiding in the identification of depositional facies, certain impediments, such as the challenge of low quality in data or the labor-intensive nature of their interpretation, impose limitations on the widespread application of these approaches, particularly when confronted with extensive datasets. The inherent constraints of low quality can compromise the accuracy of interpretations, while the time-consuming nature of the analysis may hinder the efficiency of the investigative process. In addition, the absence of cores or plug samples, which is a common scenario in many reservoirs, presents a notable challenge. The absence of these physical samples can complicate the establishment of a nuanced relationship between depositional character and the porosity system. In light of these challenges, this paper endeavors to navigate these constraints by presenting a preliminary correlation between porosity-based facies and lithology. This innovative approach seeks to provide insights into the lithological characteristics of the , offering a potential avenue for overcoming the limitations associated with data quality and the absence of traditional core samples in the context of extensive datasets.
The facies denoted as A, expounded upon in this article and distinguished by its heightened non-matrix porosity, can be associated with lithologies that evolve in-situ, notably shrubstones and spherulitestones ([15,16,35]). The paucity of gigapores evident in facies A finds plausible correlation with dissolution processes, as posited by [15], while the presence of megapores is attributed to the typical morphologies associated with dendritic form shrub growth. In the context of matrix porosity, the observed values fluctuating between low and intermediate levels may be attributed to the interparticle nature of the primary deposition. Subsequently, this primary deposition appears to have undergone transformations influenced by processes such as cementation and silicification, as elucidated by [69] and [15]. This nuanced understanding of facies A not only contributes to our comprehension of its porosity characteristics but also sheds light on the intricate geological processes shaping its lithological attributes, fostering a more comprehensive analysis within the framework of the .
Facies B is characterized by a moderate level of non-matrix and matrix porosity, and a correlation with rudstones lithologies is established, originating from subrounded to subangular pebbles comprising shrubstone, spherulitestone, and silicified nodules ([16,35,70]). The visual porosity within this facies primarily emanates from the morphological characteristics and particle sizes of shrubstone clasts, as well as spherulitestone components, as explicated by [69]. Concurrently, the matrix porosity predominantly results from interparticle spaces, arising from the interspersing of shrub and spherulite pores. The intermediate values of matrix porosity described in this study for facies B align cohesively with –derived porosity values reported by [15,16] for analogous rudstones-like facies. This congruence underscores the robustness of the analytical framework applied in this investigation, substantiating the consistency of our findings with established methodologies. Furthermore, this alignment with existing -derived porosity values enhances the credibility of the correlations drawn between visual and matrix porosity in facies B, providing a more nuanced understanding of its lithological attributes within the broader context of the .
Facies C is characterized by a juxtaposition of low non-matrix porosity and medium matrix porosity, revealing distinct attributes within the lithological spectrum. This facies is intricately associated with detrital carbonates, specifically grainstones lithologies, as indicated by [16]. The visual pores in facies C are notably sparse, primarily localized along the contacts of laminations or linked to the morphological remnants of shrub fragments. The observed matrix porosity values in facies C are marginally lower than those documented for facies B. This disparity in matrix porosity can be elucidated through a parallel analysis, revealing that matrix porosity in facies C is chiefly intraparticle, influenced to some extent by silicification or cementation processes, aligning with the findings of [15]. The nuanced examination of facies C thus not only refines our comprehension of its porosity characteristics but also delves into the geological processes shaping its matrix porosity, shedding light on the intricate interplay of factors contributing to the lithological framework within the broader context of the .
Lastly but not least, facies D, characterized by low non-matrix and low matrix porosity, aligns seamlessly with lithologies dominated by mudstone, as extensively elucidated by Basso et al. (2022) and Soares et al. (2023). The distinctive feature of this facies lies in its highly homogeneous nature, a quality that translates into the identification of only a minimal number of mesopores. The homogeneity observed in facies D is indicative of potential early-stage silicification or cementation processes during the deposition of mudstone-like lithologies, in accordance with the interpretations provided by [15,16]. The notably low values of matrix porosity in facies D further underscore the influence of these early-stage processes, as expounded upon and extensively detailed by [15]. A succinct comparison between the outcomes presented by [15,16] is encapsulated in Table 4, providing a concise synthesis of the congruence and variations in their findings, thus contributing to a more comprehensive understanding of the intricate lithological dynamics within the .
5. Conclusions
The study explores the effectiveness of logs and conventional well logs in identifying sub-seismic features, such as faults, fractures, and vugs, crucial in unconventional reservoirs. While logs excel in this task, their scarcity and susceptibility to interference patterns necessitate the consideration of conventional well logs. This research proposes a semi-automatic methodology integrating and conventional well logs to distinguish between matrix and non-matrix-related pore spaces, providing a preliminary classification of reservoir facies based on porosity. In summary, this study yields the following key conclusions:
- Utility of Logs: logs prove to be the superior tool for identifying sub-seismic features in unconventional reservoirs.
- Challenges with Logs: Despite their efficacy, logs may be scarce and susceptible to interference patterns, requiring additional data sources.
- Role of Conventional Well Logs: Conventional well logs, primarily used for defining physical rock characteristics, can be utilized (with limitations) for interpreting sub-seismic features.
- Complementary Nature of Conventional Well Logs: Individual conventional well logs lack sufficient information for pore space identification but combining them aids in preliminary detecting intervals with high pore space percentages.
- Integration Methodology: Proposing a semi-automatic methodology that integrates and conventional well logs using a small database and neural network.
- Neural Network Training: Using four variables (Density, Sonic, , and ) to train a Neural Network, resulting in 32 classes regrouped into four facies based on porosities and non-matrix pore size.
- Facies Characterization: Facies A exhibits high non-matrix porosity, B displays medium non-matrix and matrix porosity, C shows medium to low non-matrix and matrix porosity, and D is characterized by low non-matrix and low matrix porosity.
- Correlation with Lithologies: Facies A correlates with shrubstone-like lithologies, B with rudstones-like lithologies, C with grainstones-like lithologies, and D with mudstone-like lithologies.
- Reservoir Quality Assessment: Facies A and B are identified as excellent-quality reservoirs with significant fluid storage and transport capacity, while C is considered good-quality, and D is categorized as poor-quality reservoir facies.
- Flow Behavior Implications: The study suggests that A and B facies exhibit superior fluid storage and transport capabilities compared to C and D facies.
- Reliability of the Proposed Methodology: The semi-automatic methodology proves to be a reliable means of preliminary facies classification based on porosity, considering the limitations of the available small database and individual data types.
In conclusion, this study advances our understanding of permeability modeling in carbonate reservoirs, emphasizing the critical role of vuggy porosity and its profound impact on production rates. The proposed methodology bridges the gap between static and dynamic data, offering a comprehensive approach to permeability assessment. These insights hold immense value for reservoir management and the optimization of production strategies in complex carbonate reservoirs.
Author Contributions
Conceptualization, S.M.M., J.G.D.F. and A.I.B.G.; methodology, S.M.M., J.G.D.F. and A.I.B.G.; validation, S.M.M. and J.G.D.F.; formal analysis, S.M.M. and J.G.D.F.; investigation, S.M.M. and J.G.D.F.; resources, S.M.M., J.G.D.F. and A.I.B.G.; data curation, S.M.M. and J.G.D.F.; writing—original draft preparation, S.M.M.; writing—review and editing, S.M.M., J.G.D.F. A.I.B.G.; supervision, A.I.B.G.; project administration, J.G.D.F. and A.I.B.G.; funding acquisition, S.M.M., J.G.D.F. and A.I.B.G.
Acknowledgments
This research was carried out in association with the ongoing project registered as nº 20469-3, Desenvolvimento de reservatórios carbonáticos - SIMFRAC sponsored by Shell Brasil Petróleo Ltda under the levy as Compromisso de Investimentos com Pesquisa e Desenvolvimento. The authors would also like to thank the Institute of Geosciences, the Center of Petroleum Studies (), the Geologic Modeling of Reservoirs group (), and the Research in Reservoir Simulation and Management group () from the University of Campinas for providing support to this research. The authors are also grateful to Schumberger and Geoactive for providing the academic licenses of Techlog and Interactive Petrophysics softwares, respectively.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations and Nomenclatures
The following abbreviations and nomenclatures are used in this manuscript:
| Nuclear Magnetic Resonance | |
| Ultrasonic Borehole Image | |
| String of Beads Response | |
| Borehole Image Logs | |
| Barra Velha Formation | |
| Self Organizing Map | |
| Potential of Hydrogen | |
| Magnesium | |
| Photoelectric Factor | |
| Circumferential Borehole Imaging | |
| Fractional Porosity of the rock | |
| v | Velocity of the formation |
| Velocity of interstitial fluids | |
| Velocity of the rock matrix | |
| Matrix porosity | |
| Acoustic transit time | |
| Acoustic transit time of interstitial fluids | |
| Acoustic transit time of the rock matrix | |
| t | Travel time |
| Travel time of interstitial fluids | |
| Travel time of the rock matrix | |
| Total porosity | |
| Matrix density | |
| Formation bulk density | |
| Fluid density | |
| D | Euclidean distance |
| I | Input vector |
| W | Weight vector |
| Modification of weight vector | |
| Neighborhood function | |
| c | Distance from the winning neuron |
| Neighborhood radius | |
| Machine learning | |
| Red, Green, Blue |
References
- Gardiner, N.J.; Roberts, J.J.; Johnson, G.; Smith, D.J.; Bond, C.E.; Knipe, R.; Haszeldine, S.; Gordon, S.; O’Donnell, M. Geosciences and the energy transition. Earth Science, Systems and Society 2023, 3, 10072. [Google Scholar] [CrossRef]
- Netto, P.R.; Pozo, M.; da Silva, M.D.; Gomes, M.E.B.; Mexias, A.; Ramnani, C.W.; Parizek-Silva, Y.; Borghi, L.; Rios-Netto, A.d.M. Paleoenvironmental implications of authigenic magnesian clay formation sequences in the Barra Velha Formation (Santos Basin, Brazil). Minerals 2022, 12, 200. [Google Scholar] [CrossRef]
- de Mello, V.L.; Lupinacci, W.M. Mineralogy based classification of carbonate rocks using elastic parameters: A case study from Buzios Field. Journal of Petroleum Science and Engineering 2022, 209, 109962. [Google Scholar] [CrossRef]
- Correa, R.; Pereira, C.; Cruz, F.; Lisboa, S.; Junior, M.; Souza, V.; Rocha, C.; Araujo, F.; de Carvalho, B.M. Integrated seismic-log-core-test fracture characterization and modelling, Barra Velha Formation, Pre-Salt of Santos Basin. 2019 AAPG Annual Convention and Exhibition:, 2019.
- Correia, M.G.; Maschio, C.; Schiozer, D.J. Integration of multiscale carbonate reservoir heterogeneities in reservoir simulation. Journal of petroleum science and engineering 2015, 131, 34–50. [Google Scholar] [CrossRef]
- Guan, C.; Zeng, L.; Yao, Y.; Zhang, H.; Zhang, J.; Liang, D. Natural Fractures and Their Contribution to Natural Gas Migration and Accumulation in Marine Carbonate Reservoirs: Lower Triassic Feixianguan Formation, Northeast Sichuan Basin, China. Sustainability 2023, 15, 16155. [Google Scholar] [CrossRef]
- Xu, C.; Di, B.; Wei, J. A physical modeling study of seismic features of karst cave reservoirs in the Tarim Basin, China. Geophysics 2016, 81, B31–B41. [Google Scholar] [CrossRef]
- Yu, J.; Li, Z.; Yang, L. Fault system impact on paleokarst distribution in the Ordovician Yingshan Formation in the central Tarim basin, northwest China. Marine and Petroleum Geology 2016, 71, 105–118. [Google Scholar] [CrossRef]
- Zhang, D. Production allocation method in numerical simulation for fractured vuggy reservoirs. Geoenergy Science and Engineering 2023, 226, 211735. [Google Scholar] [CrossRef]
- Liu, B.; Yasin, Q.; Sohail, G.M.; Chen, G.; Ismail, A.; Ma, Y.; Fu, X. Seismic characterization of fault and fractures in deep buried carbonate reservoirs using CNN-LSTM based deep neural networks. Geoenergy Science and Engineering 2023, 229, 212126. [Google Scholar] [CrossRef]
- Li, W.; Yue, D.; Colombera, L.; Duan, D.; Long, T.; Wu, S.; Liu, Y. A novel method for seismic-attribute optimization driven by forward modeling and machine learning in prediction of fluvial reservoirs. Geoenergy Science and Engineering 2023, 227, 211952. [Google Scholar] [CrossRef]
- Duarte, S.B.; De Jesus, C.M.; Da Silva, V.F.; Arouca Sobreira, M.C.; Cristofaro, R.A.L.; de Lima, L.; De Mello E Silva, F.G.; Marques De Sa, C.H.; De Oliveira Berto, F.M.; Backheuser, Y. ; others. Artificial Intelligence Use To Predict Severe Fluid Losses in Pre-Salt Carbonates. SPWLA Annual Logging Symposium. SPWLA, 2018, p. D043S008R002.
- Ek-Chacón, E.; Molino-Minero-Re, E.; Méndez-Monroy, P.E.; Neme, A.; Ángeles-Hernández, H. Semi-Supervised Training for (Pre-Stack) Seismic Data Analysis. Applied Sciences 2024, 14, 4175. [Google Scholar] [CrossRef]
- Li, J.; Xu, T.; Zhang, W.; Liu, H.; Kang, Y.; Lv, W. A borehole porosity prediction method with focusing on local shape. Geoenergy Science and Engineering 2023, 228, 211933. [Google Scholar] [CrossRef]
- Basso, M.; Souza, J.P.P.; Honório, B.C.Z.; Melani, L.H.; Chinelatto, G.F.; Belila, A.M.P.; Vidal, A.C. Acoustic image log facies and well log petrophysical evaluation of the Barra Velha Formation carbonate reservoir from the Santos Basin, offshore Brazil. Carbonates and Evaporites 2022, 37, 50. [Google Scholar] [CrossRef]
- Soares, M.V.T.; da, S. Bomfim, L.; Vidal, A.C.; Avansi, M.C.K.; Cunha, O.R.; García, R.G.V.; de Paiva Medeiros, R.S. Pre-salt carbonate cyclicity and depositional environment: NMR petrophysics and Markov cyclicity of lacustrine acoustic facies (Santos Basin, Brazil). Marine and Petroleum Geology 2023, 157, 106494. [Google Scholar] [CrossRef]
- Chen, W.; Yang, J.; Li, L.; Wang, H.; Huang, L.; Jia, Y.; Hu, Q.; Jiang, X.; Tang, J. Investigation of Mechanical Properties Evolution and Crack Initiation Mechanisms of Deep Carbonate Rocks Affected by Acid Erosion. Sustainability 2023, 15, 11807. [Google Scholar] [CrossRef]
- Zhou, X.; Wei, J.; Hadavimoghaddam, F.; Gayubov, A.; Ostadhassan, M.; Chen, Y.; Wang, Y.; Yang, B.; Pu, B.; Zhang, X.; others. “Double sweet spot” identification method via cluster analysis of petrophysical properties from well logg data: A case study of a tight sandstone reservoir. Geoenergy Science and Engineering 2023, 227, 211821. [Google Scholar] [CrossRef]
- Huang, F.; Huang, L.; Zhu, Z.; Zhang, M.; Zhang, W.; Jiang, X. A Logging Data Based Method for Evaluating the Fracability of a Gas Storage in Eastern China. Sustainability 2024, 16, 3165. [Google Scholar] [CrossRef]
- Aghli, G.; Moussavi-Harami, R.; Mortazavi, S.; Mohammadian, R. Evaluation of new method for estimation of fracture parameters using conventional petrophysical logs and ANFIS in the carbonate heterogeneous reservoirs. Journal of Petroleum Science and Engineering 2019, 172, 1092–1102. [Google Scholar] [CrossRef]
- Yasin, Q.; Ding, Y.; Baklouti, S.; Boateng, C.D.; Du, Q.; Golsanami, N. An integrated fracture parameter prediction and characterization method in deeply-buried carbonate reservoirs based on deep neural network. Journal of Petroleum Science and Engineering 2022, 208, 109346. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, T.; Yang, J.; Zhang, Z.; Feng, C.; Tang, J. Approaches of Combining Machine Learning with NMR-Based Pore Structure Characterization for Reservoir Evaluation. Sustainability 2024, 16, 2774. [Google Scholar] [CrossRef]
- Xu, Z.; Lin, M.; Jiang, W.; Cao, G.; Yi, Z. Identifying the comprehensive pore structure characteristics of a rock from 3D images. Journal of Petroleum Science and Engineering 2020, 187, 106764. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, Y.; Cai, J.; Zhang, C.; Wu, S.; Zhou, X. Key factors of marine shale conductivity in southern China—Part II: The influence of pore system and the development direction of shale gas saturation models. Journal of Petroleum Science and Engineering 2022, 209, 109516. [Google Scholar] [CrossRef]
- Zhu, B.; Meng, J.; Pan, R.; Song, C.; Zhu, Z.; Jin, J.; Zhang, C.; Liu, L.; Xu, L.; Zhou, X. Multi-scale characterization of organic matter pore space in deep marine shale combined with mathematical morphology. Geoenergy Science and Engineering 2023, 223, 211539. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Santos, A.A.S.; Correia, M.G.; Schiozer, D.J. Scenario reduction methodologies under uncertainties for reservoir development purposes: distance-based clustering and metaheuristic algorithm. Journal of Petroleum Exploration and Production Technology 2021, 11, 3079–3102. [Google Scholar] [CrossRef]
- Gavidia, J.C.R.; Chinelatto, G.F.; Basso, M.; da Ponte Souza, J.P.; Soltanmohammadi, R.; Vidal, A.C.; Goldstein, R.H.; Mohammadizadeh, S. Utilizing integrated artificial intelligence for characterizing mineralogy and facies in a pre-salt carbonate reservoir, Santos Basin, Brazil, using cores, wireline logs, and multi-mineral petrophysical evaluation. Geoenergy Science and Engineering 2023, 231, 212303. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, C.; Chen, Y.; Shen, W.; Wang, Y.; Chen, H.; Geng, J. Fluid and lithofacies prediction based on integration of well-log data and seismic inversion: A machine-learning approach. Geophysics 2021, 86, M151–M165. [Google Scholar] [CrossRef]
- Xing, Y.; Yang, H.; Yu, W. An approach for the classification of rock types using machine learning of core and log data. Sustainability 2023, 15, 8868. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Q.; Li, M.; Li, X.; Zhou, K.; Tian, X.; Niu, J.; Yang, Z.; Zhang, Q.; Sun, M. Pore Pressure Prediction for High-Pressure Tight Sandstone in the Huizhou Sag, Pearl River Mouth Basin, China: A Machine Learning-Based Approach. Journal of Marine Science and Engineering 2024, 12, 703. [Google Scholar] [CrossRef]
- Gu, Y.; Li, Y.; Yang, Y.; Xiao, B.; Zhang, D.; Bao, Z. Classification pattern of lacustrine carbonate diagenetic facies and logging-based data-driven prediction via a generalized and robust ensemble learning: A demonstration of pre-salt profile, santos basin. Geoenergy Science and Engineering 2023, 223, 211543. [Google Scholar] [CrossRef]
- Junior, A.N.; Queiroz, G.N.; Godoy, M.G.; da Silva Cardoso, V.; Cedrola, S.M.L.; Mansoldo, F.R.P.; Firpo, R.M.; Paiva, L.M.G.; Sohrabi, M.; Vermelho, A.B. Assessing EOR strategies for application in Brazilian pre-salt reservoirs. Geoenergy Science and Engineering 2023, 211508. [Google Scholar] [CrossRef]
- Moreira, J.L.P.; Madeira, C.V.; Gil, J.A.; Machado, M.A.P.; others. bacia de Santos. Boletim de Geociencias da PETROBRAS 2007, 15, 531–549. [Google Scholar]
- Mohriak, W.; Nemčok, M.; Enciso, G. South Atlantic divergent margin evolution: rift-border uplift and salt tectonics in the basins of SE Brazil. Geological Society, London, Special Publications 2008, 294, 365–398. [Google Scholar] [CrossRef]
- Gomes, J.; Bunevich, R.; Tedeschi, L.; Tucker, M.; Whitaker, F. Facies classification and patterns of lacustrine carbonate deposition of the Barra Velha Formation, Santos Basin, Brazilian Pre-salt. Marine and Petroleum Geology 2020, 113, 104176. [Google Scholar] [CrossRef]
- Wright, V.P.; Barnett, A. Critically evaluating the current depositional models for the pre-salt Barra Velha Formation, Offshore Brazil. AAPG Search and Discovery, Article 2017, 51439. [Google Scholar]
- Tosca, N.J.; Wright, V.P. Diagenetic pathways linked to labile Mg-clays in lacustrine carbonate reservoirs: a model for the origin of secondary porosity in the Cretaceous pre-salt Barra Velha Formation, offshore Brazil. Geological Society, London, Special Publications 2018, 435, 33–46. [Google Scholar] [CrossRef]
- Poros, Z.; Jagniecki, E.; Luczaj, J.; Kenter, J.; Gal, B.; Correa, T.S.; Ferreira, E.; McFadden, K.A.; Elifritz, A.; Heumann, M. ; others. Origin of Silica in Pre-Salt Carbonates, Kwanza Basin, Angola. https://www.searchanddiscovery.com/pdfz/documents/2017/51413poros/ndx_poros.pdf.html, 2017. Accessed: December 11, 2023. 11 December.
- Wright, V.P.; Barnett, A.J. An abiotic model for the development of textures in some South Atlantic early Cretaceous lacustrine carbonates. Geological Society, London, Special Publications 2015, 418, 209–219. [Google Scholar] [CrossRef]
- Minzoni, M.; Cantelli, A.; Thornton, J.; Wignall, B. Seismic-scale geometries and sequence-stratigraphic architecture of Early Cretaceous syn-post rift carbonate systems, Presalt Section, Brazil. In Seismic Characterization of Carbonate Platforms and Reservoirs; Geological Society, London, Special Publications, 2021; pp. 105–126. [CrossRef]
- Pickell, J.J.; Heacock, J.G. Density logging. Geophysics 1960, 25, 891–904. [Google Scholar] [CrossRef]
- Bjorlykke, K. Petroleum geoscience: From sedimentary environments to rock physics; Springer Science & Business Media, 2010.
- Asquith, G.B.; Krygowski, D.; Gibson, C.R. Basic well log analysis; Vol. 16, American Association of Petroleum Geologists Tulsa, 2004. [CrossRef]
- Serra, O.; Serra, L. Well Logging. Data Acquisitions and Applications, 2004.
- Schlumberger. UBI: advanced borehole imaging independent of mud type. https://www.slb.com/products-and-services/innovating-in-oil-and-gas/reservoir-characterization/surface-and-downhole-logging/wireline-openhole-logging/ultrasonic-borehole-imager. Accessed: December 7, 2023.
- Shahinpour, A. Borehole image log analysis for sedimentary environment and clay volume interpretation. Master’s thesis, Institutt for petroleumsteknologi og anvendt geofysikk, 2013.
- Nian, T.; Wang, G.; Xiao, C.; Zhou, L.; Deng, L.; Li, R. The in situ stress determination from borehole image logs in the Kuqa Depression. Journal of Natural Gas Science and Engineering 2016, 34, 1077–1084. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, W.; Liu, Y. Mathematical model of artificial fracture reinitiation in vugs of carbonate reservoirs. Geoenergy Science and Engineering 2023, 221, 211366. [Google Scholar] [CrossRef]
- Wyllie, M.R.J.; Gregory, A.R.; Gardner, L.W. Elastic wave velocities in heterogeneous and porous media. Geophysics 1956, 21, 41–70. [Google Scholar] [CrossRef]
- Choquette, P.W.; Pray, L.C. Geologic nomenclature and classification of porosity in sedimentary carbonates. AAPG bulletin 1970, 54, 207–250. [Google Scholar] [CrossRef]
- de Jesus, C.M.; Compan, A.L.M.; Coêlho, J.R.P.; de Sá Silveira, A.E.; Blauth, M. Evaluation of Karst Porosity Morphological Properties through Borehole Image Logs–Correlation with Dynamic Reservoir Properties from a presalt Oil Field. Offshore Technology Conference Brasil. OTC, 2019, p. D021S026R002. [CrossRef]
- Bomfim, L.D.S.; Pedrini, H.; Vidal, A.C. A Combined Noisy Borehole Image Log Segmentation Method. 2023 30th International Conference on Systems, Signals and Image Processing (IWSSIP). IEEE, 2023, pp. 1–5.
- Jia, M.; Huang, W.; Li, Y. Quantitative Characterization of Pore Structure Parameters in Coal Based on Image Processing and SEM Technology. Energies 2023, 16, 1663. [Google Scholar] [CrossRef]
- de Jesus, C.M.; Martins Compan, A.L.; Surmas, R. Permeability estimation using ultrasonic borehole image logs in dual-porosity carbonate reservoirs. Petrophysics 2016, 57, 620–637. [Google Scholar]
- Mohammadizadeh, S.; Moghaddam, M.A.; Talebbeydokhti, N. Analysis of flow in porous media using combined pressurized-free surface network. Journal of Porous Media 2021, 24. [Google Scholar] [CrossRef]
- Malki, M.L.; Saberi, M.R.; Kolawole, O.; Rasouli, V.; Sennaoui, B.; Ozotta, O. Underlying mechanisms and controlling factors of carbonate reservoir characterization from rock physics perspective: A comprehensive review. Geoenergy Science and Engineering 2023, 226, 211793. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, X.; Lan, Z.; Wang, X.; Yao, G. Pore pressure prediction assisted by machine learning models combined with interpretations: A case study of an HTHP gas field, Yinggehai Basin. Geoenergy Science and Engineering 2023, 229, 212114. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Soltanmohammadi, R.; Heidaryan, E.; Faroughi, S.A. Geosystems risk and uncertainty: The application of ChatGPT with targeted prompting. Geoenergy Science and Engineering, 2024; 212889. [Google Scholar] [CrossRef]
- Guo, J.; Luo, Y.; Zeng, F.; Wang, R.; Yuan, C.; He, L.; Lu, C. Reconstruction of missing shear wave slowness in shale gas reservoir based on deep learning algorithm. Geoenergy Science and Engineering 2023, 227, 211865. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps; Springer Berlin, Heidelberg, 2001. [CrossRef]
- Lofts, J.; Bourke, L. The recognition of artefacts from acoustic and resistivity borehole imaging devices. Geological Society, London, Special Publications 1999, 159, 59–76. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, W.; Steinsiek, R.; Patterson, D. Ultrasonic signal noise reduction processing in borehole imaging application. 2016 IEEE International Frequency Control Symposium (IFCS). IEEE, 2016, pp. 1–6. [CrossRef]
- Aguilera, R. Analysis of naturally fractured reservoirs from conventional well logs (includes associated papers 6420 and 6421). Journal of petroleum technology 1976, 28, 764–772. [Google Scholar] [CrossRef]
- Wu, X.; Su, Y.; Zhang, C.; Xin, Y.; Chen, X.; Li, N.; Huang, R.; Tang, B.; Zhao, X. A novel evaluation method of dolomite reservoir using electrical image logs: The Cambrian dolomites in Tarim Basin, China. Geoenergy Science and Engineering 2024, 233, 212509. [Google Scholar] [CrossRef]
- Lai, J.; Bai, T.; Zhao, Y.; Xiao, L.; He, Z.; Wang, C.; Wang, G.; Qin, Z. Unusually petrophysical behavior and geological significance of mudrocks. Geoenergy Science and Engineering 2023, 230, 212171. [Google Scholar] [CrossRef]
- Fernández-Ibáñez, F.; Jones, G.D.; Mimoun, J.G.; Bowen, M.G.; Simo, J.; Marcon, V.; Esch, W.L. Excess permeability in the Brazil pre-Salt: Nonmatrix types, concepts, diagnostic indicators, and reservoir implications. AAPG Bulletin 2022, 106, 701–738. [Google Scholar] [CrossRef]
- Li, Z.; Fan, C.; Sun, B.; Han, X.; Hui, X.; Deng, X.; Wang, A.; Wang, G. Characteristics, logging identification and major controlling factors of bedding-parallel fractures in tight sandstones. Geoenergy Science and Engineering 2023, 228, 211956. [Google Scholar] [CrossRef]
- Hasan, M.L.; M. Tóth, T. Localization of potential migration pathways inside a fractured metamorphic hydrocarbon reservoir using well log evaluation (Mezősas field, Pannonian Basin). Geoenergy Science and Engineering 2023, 225, 211710. [Google Scholar] [CrossRef]
- Tamoto, H.; dos Santos Gioria, R.; de Carvalho Carneiro, C. Prediction of nuclear magnetic resonance porosity well-logs in a carbonate reservoir using supervised machine learning models. Journal of Petroleum Science and Engineering 2023, 220, 111169. [Google Scholar] [CrossRef]
- Muniz, M.; Bosence, D. Lacustrine carbonate platforms: facies, cycles, and tectonosedimentary models for the presalt Lagoa Feia Group (Lower Cretaceous), Campos Basin, Brazil. AAPG Bulletin 2018, 102, 2569–2597. [Google Scholar] [CrossRef]
Figure 1.
A) Location map of study area, B) Stratigraphy chart of the . Modified from [33].
Figure 1.
A) Location map of study area, B) Stratigraphy chart of the . Modified from [33].
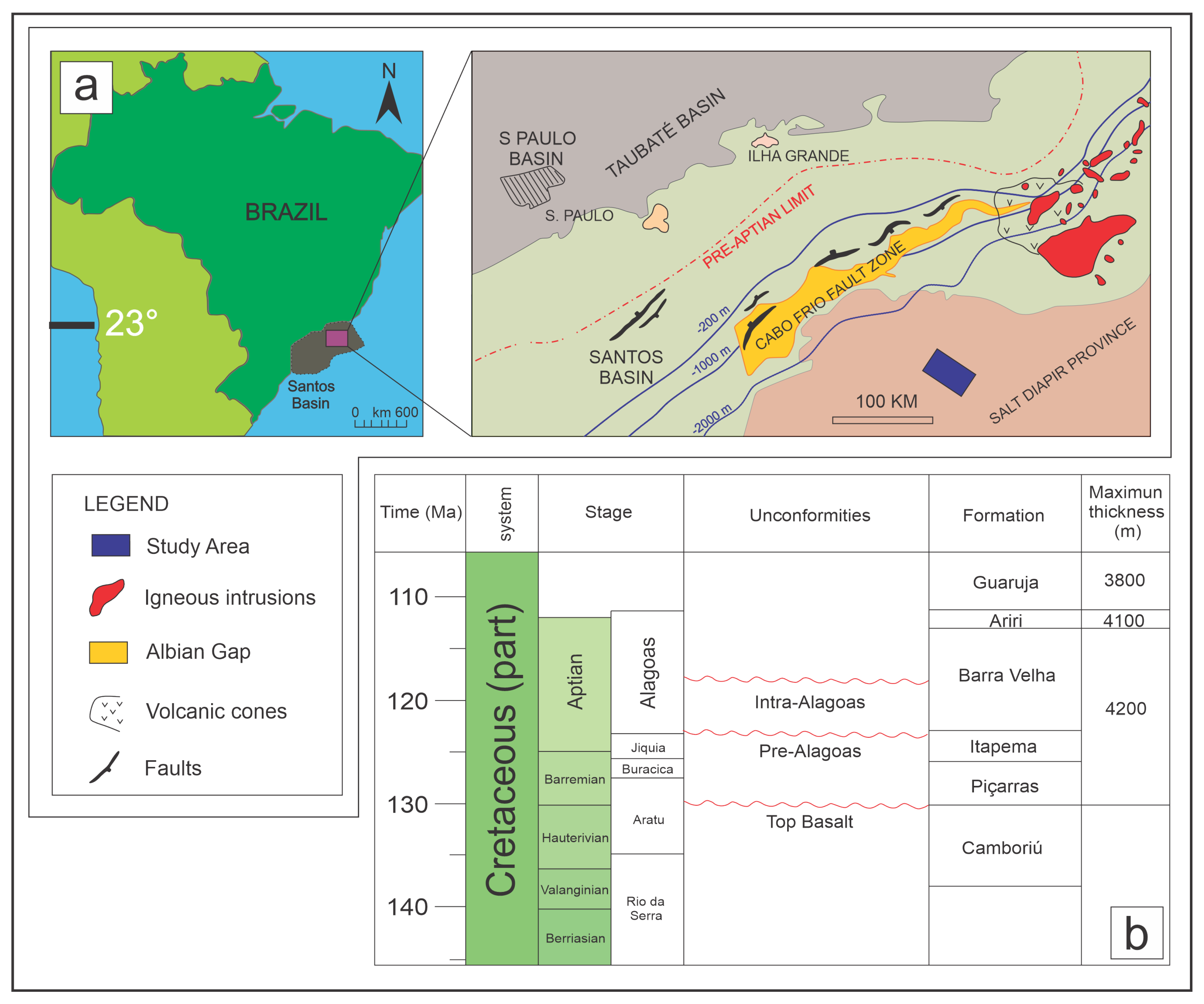
Figure 2.
Mind-map showing the dataset and methodology
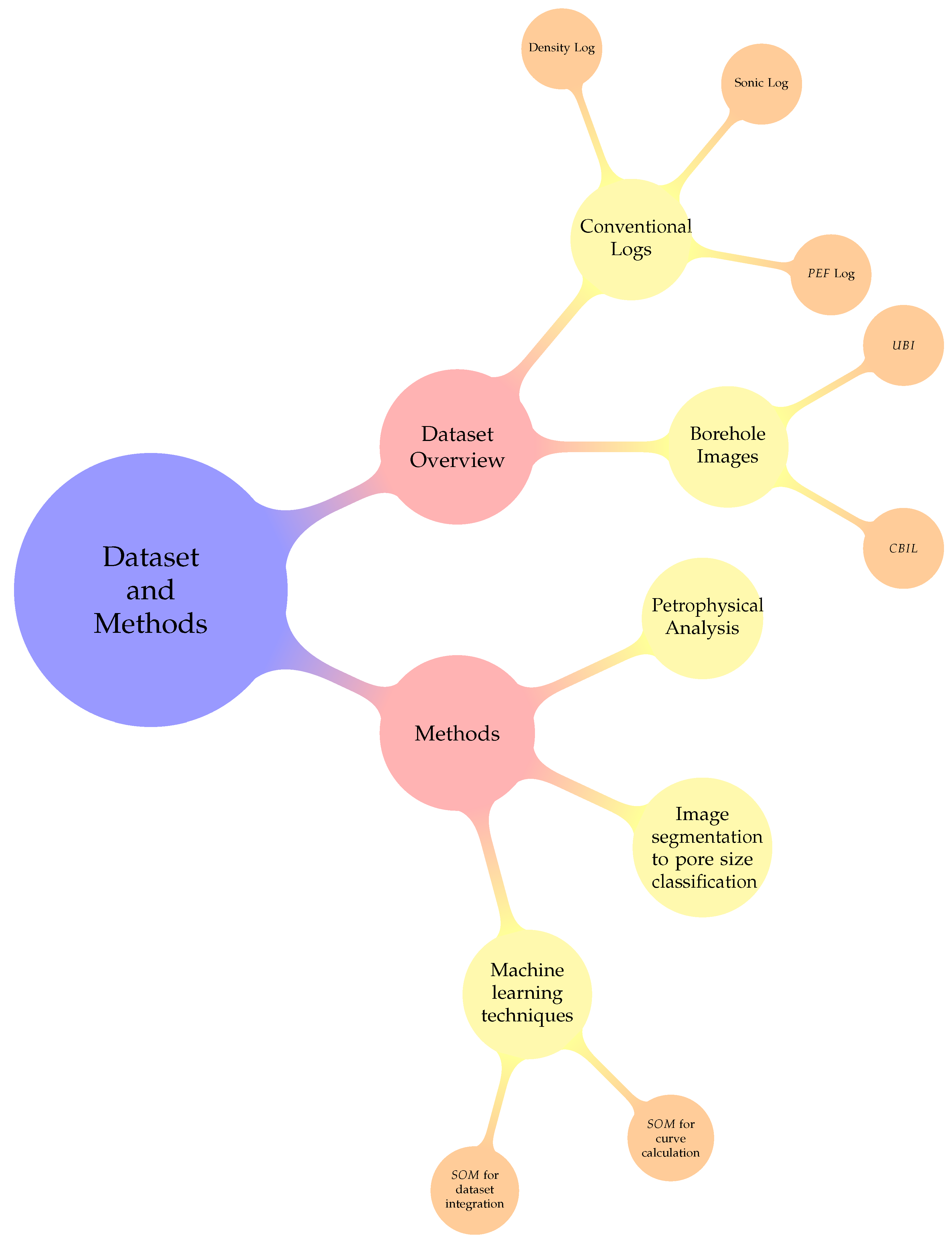
Figure 3.
Composition of the Study Dataset: Utilized data originates from two wells encompassing conventional well logs (sonic, density, and photoelectric factor) alongside logs (Dynamic and , presented at scale for well A and scale for well B).
Figure 3.
Composition of the Study Dataset: Utilized data originates from two wells encompassing conventional well logs (sonic, density, and photoelectric factor) alongside logs (Dynamic and , presented at scale for well A and scale for well B).
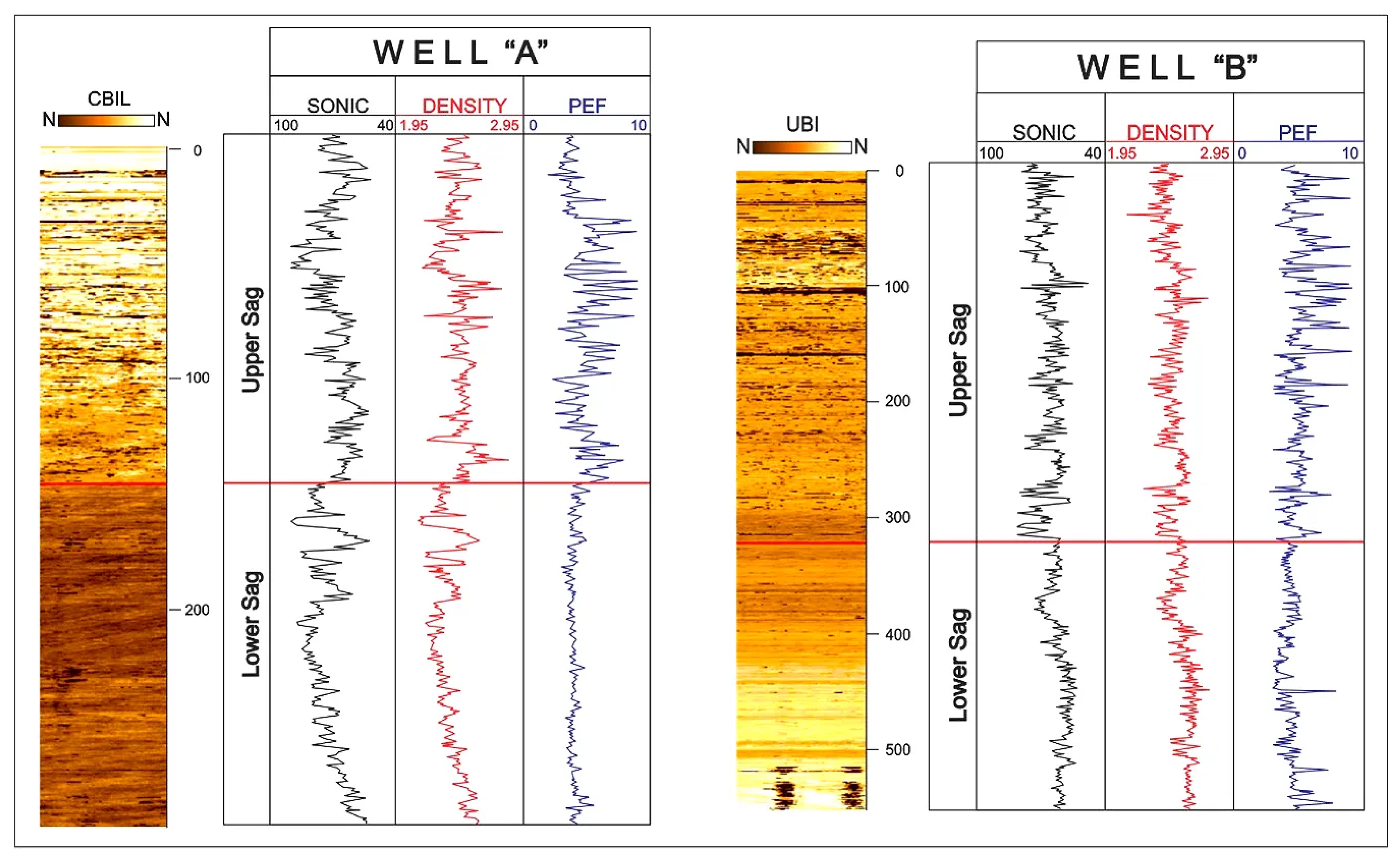
Figure 4.
Concise Overview of Methodology: Detailed depiction of petrophysical analysis, image segmentation, and self-organizing maps in the proposed approach.
Figure 4.
Concise Overview of Methodology: Detailed depiction of petrophysical analysis, image segmentation, and self-organizing maps in the proposed approach.
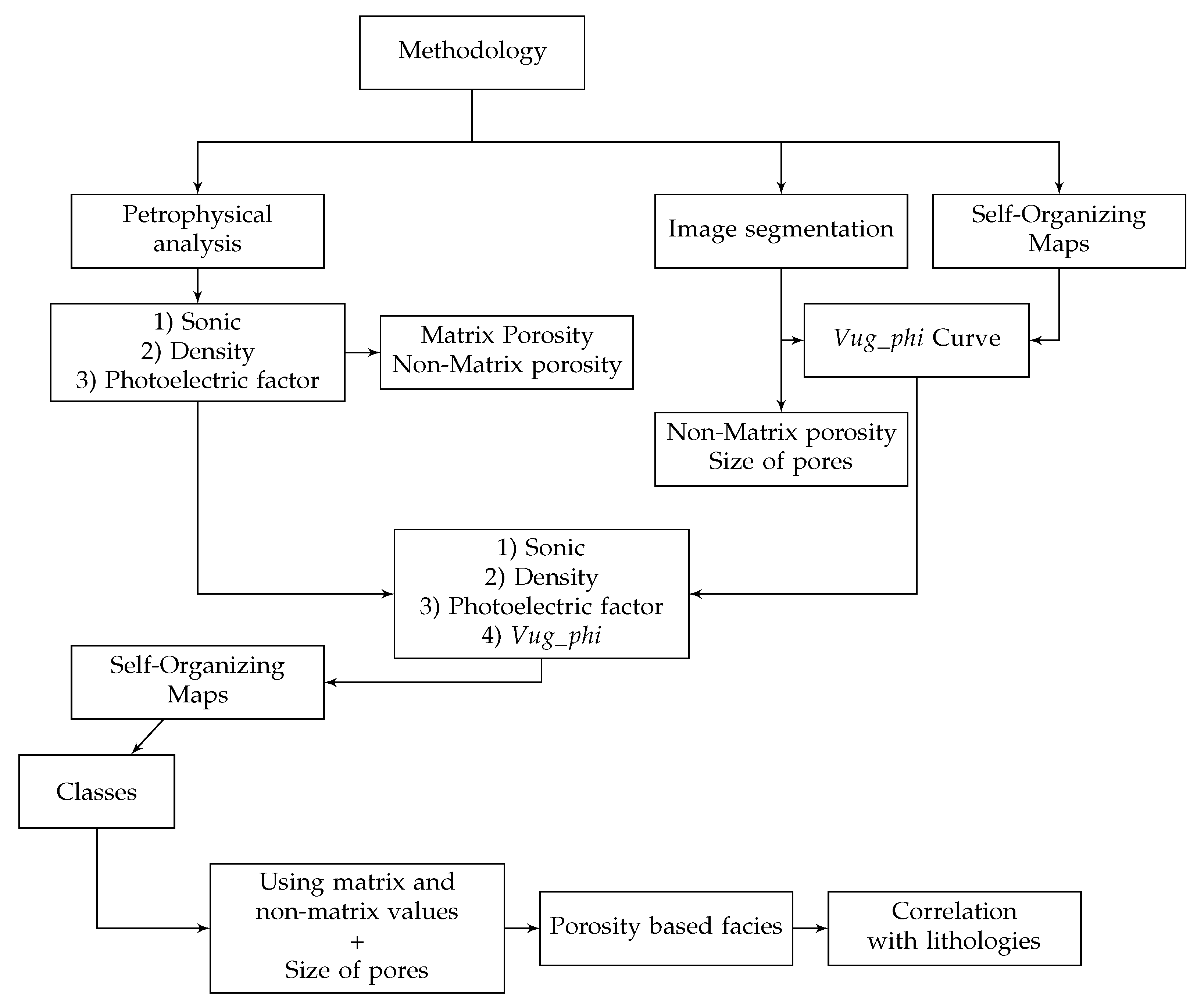
Figure 5.
Workflow to analyze the pore geometry based on image processing.
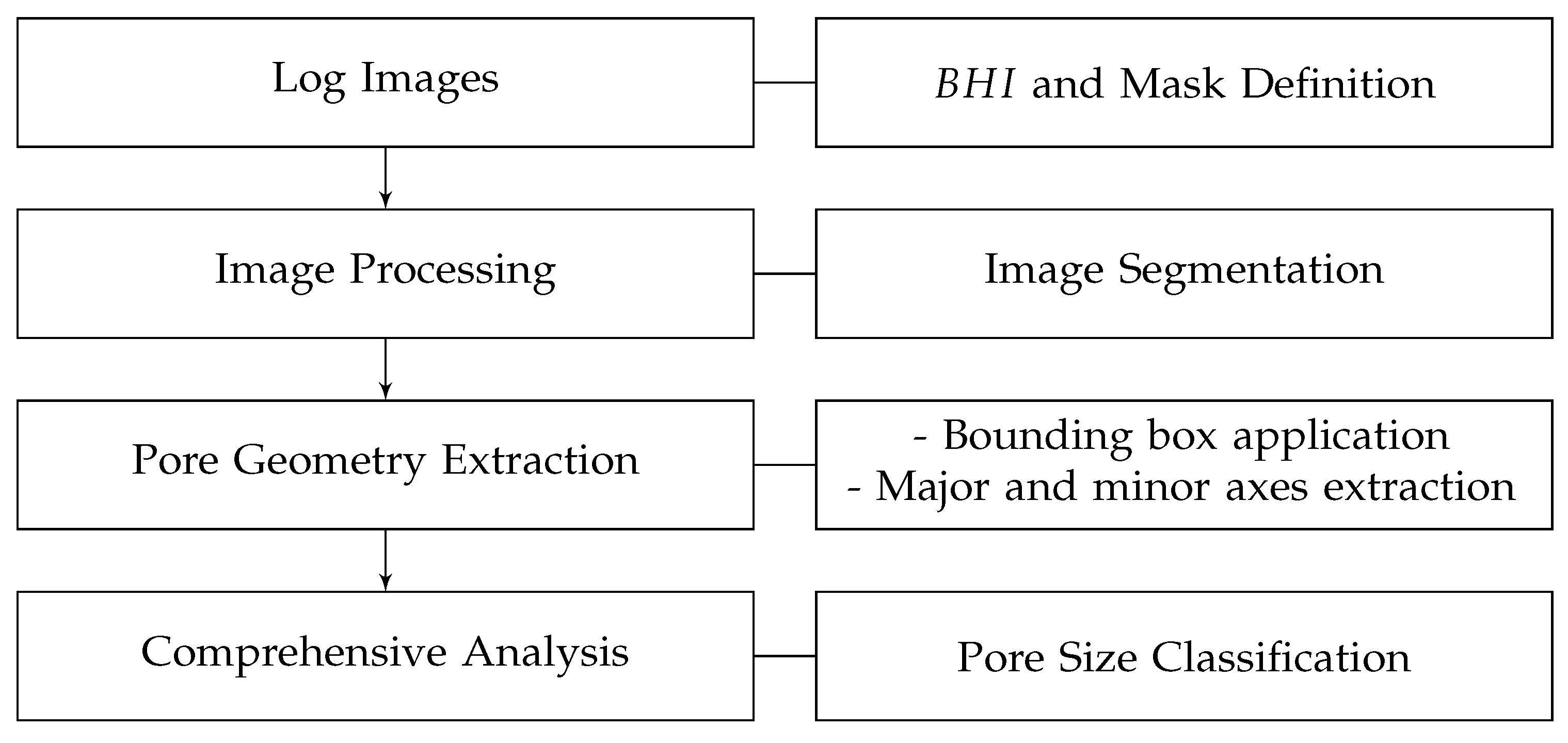
Figure 6.
Visualization of the training process using , where the arrangement is dictated by the similarity of dataset values. Subsequently, the grouped dataset undergoes further categorization through k-means clustering, providing insight into the clustering dynamics and the formation of distinct patterns.
Figure 6.
Visualization of the training process using , where the arrangement is dictated by the similarity of dataset values. Subsequently, the grouped dataset undergoes further categorization through k-means clustering, providing insight into the clustering dynamics and the formation of distinct patterns.
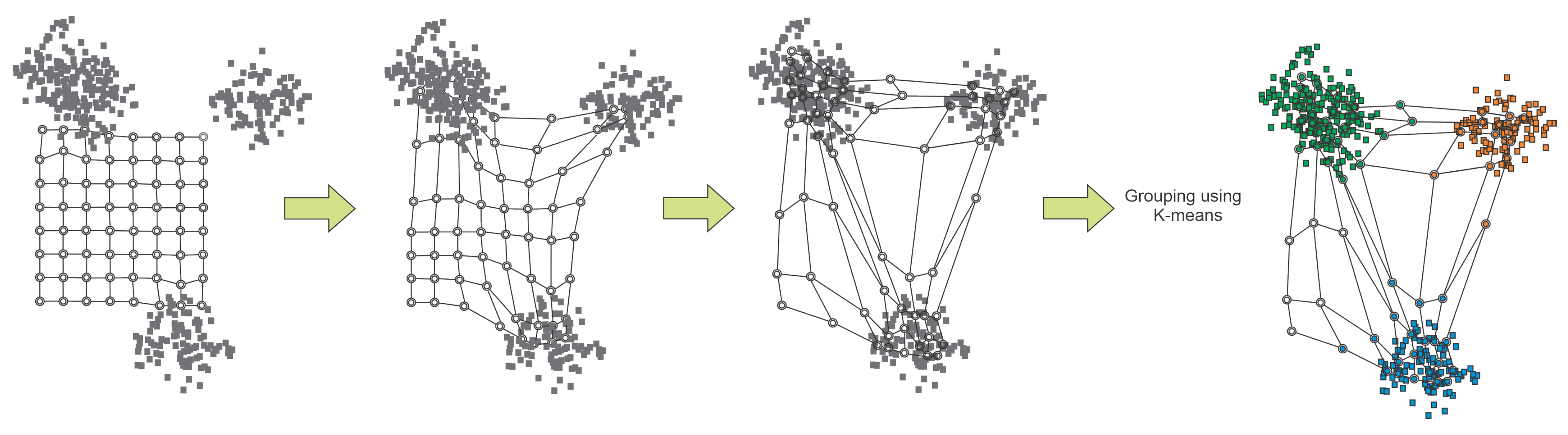
Figure 7.
2D -generated maps illustrating the U-matrix distribution of channels for A and B wells. Subfigures (a) and (e) depict the U-matrix with the overall distribution of channels for A and B wells, respectively. Further breakdowns are provided in subfigures (b) and (f) for the red channel values, (c) and (g) for the blue channel values, and (d) and (h) for the green channel values for A and B wells, respectively.
Figure 7.
2D -generated maps illustrating the U-matrix distribution of channels for A and B wells. Subfigures (a) and (e) depict the U-matrix with the overall distribution of channels for A and B wells, respectively. Further breakdowns are provided in subfigures (b) and (f) for the red channel values, (c) and (g) for the blue channel values, and (d) and (h) for the green channel values for A and B wells, respectively.
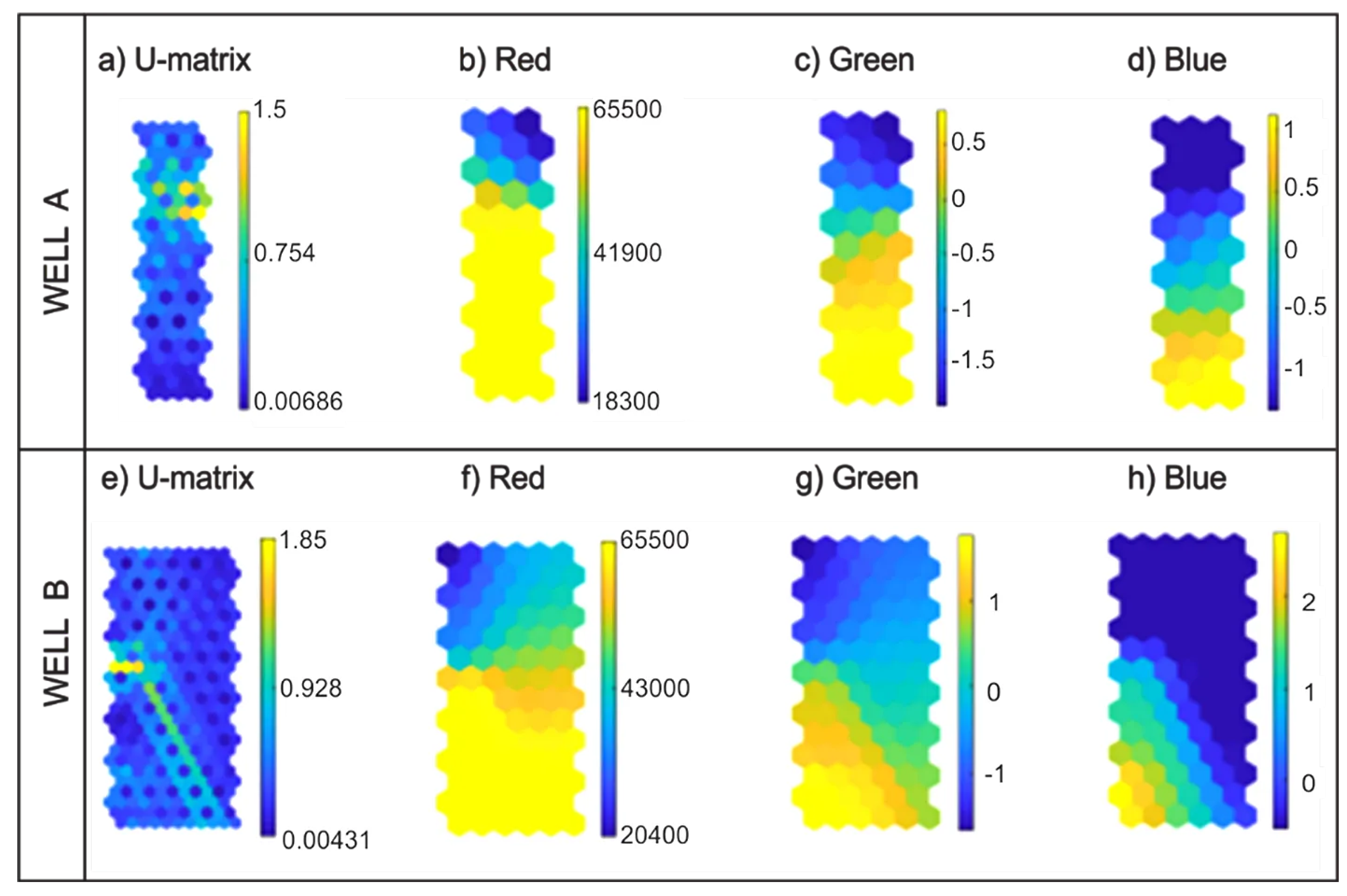
Figure 8.
Curve Calculation. (a) Representation of a 10-meter interval from the original of well B, revealing a significant porous space. (b) Initial split of the Kohonen map by k-means into two classes, displaying an overestimated porous segmentation. (c) Improved results with segmentation into six classes, offering greater flexibility and reliability. For this segmentation, one class is specifically associated with porous space, while the remaining classes represent the background. (d) The resultant curve obtained through image segmentation.
Figure 8.
Curve Calculation. (a) Representation of a 10-meter interval from the original of well B, revealing a significant porous space. (b) Initial split of the Kohonen map by k-means into two classes, displaying an overestimated porous segmentation. (c) Improved results with segmentation into six classes, offering greater flexibility and reliability. For this segmentation, one class is specifically associated with porous space, while the remaining classes represent the background. (d) The resultant curve obtained through image segmentation.
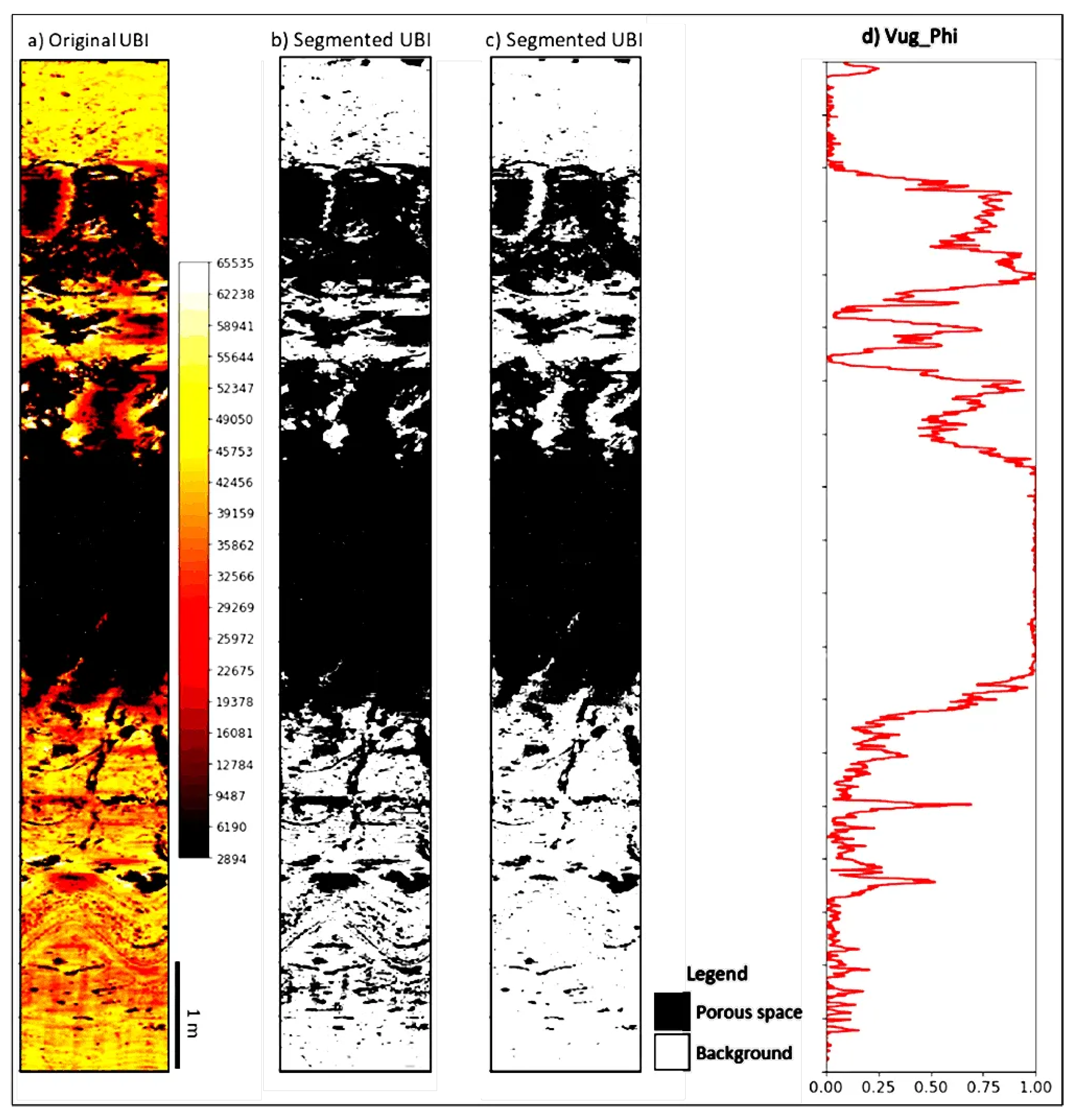
Figure 9.
Visual representation of (a) and (d) Davies-Bouldin index, (b) and (e) Kohonen map, and (c) and (f) segmented maps for well A and B, respectively. Well A exhibits division into six clusters, while well B displays separation into eight clusters. Notably, Cluster 6 in both wells corresponds to the lowest values of amplitude.
Figure 9.
Visual representation of (a) and (d) Davies-Bouldin index, (b) and (e) Kohonen map, and (c) and (f) segmented maps for well A and B, respectively. Well A exhibits division into six clusters, while well B displays separation into eight clusters. Notably, Cluster 6 in both wells corresponds to the lowest values of amplitude.
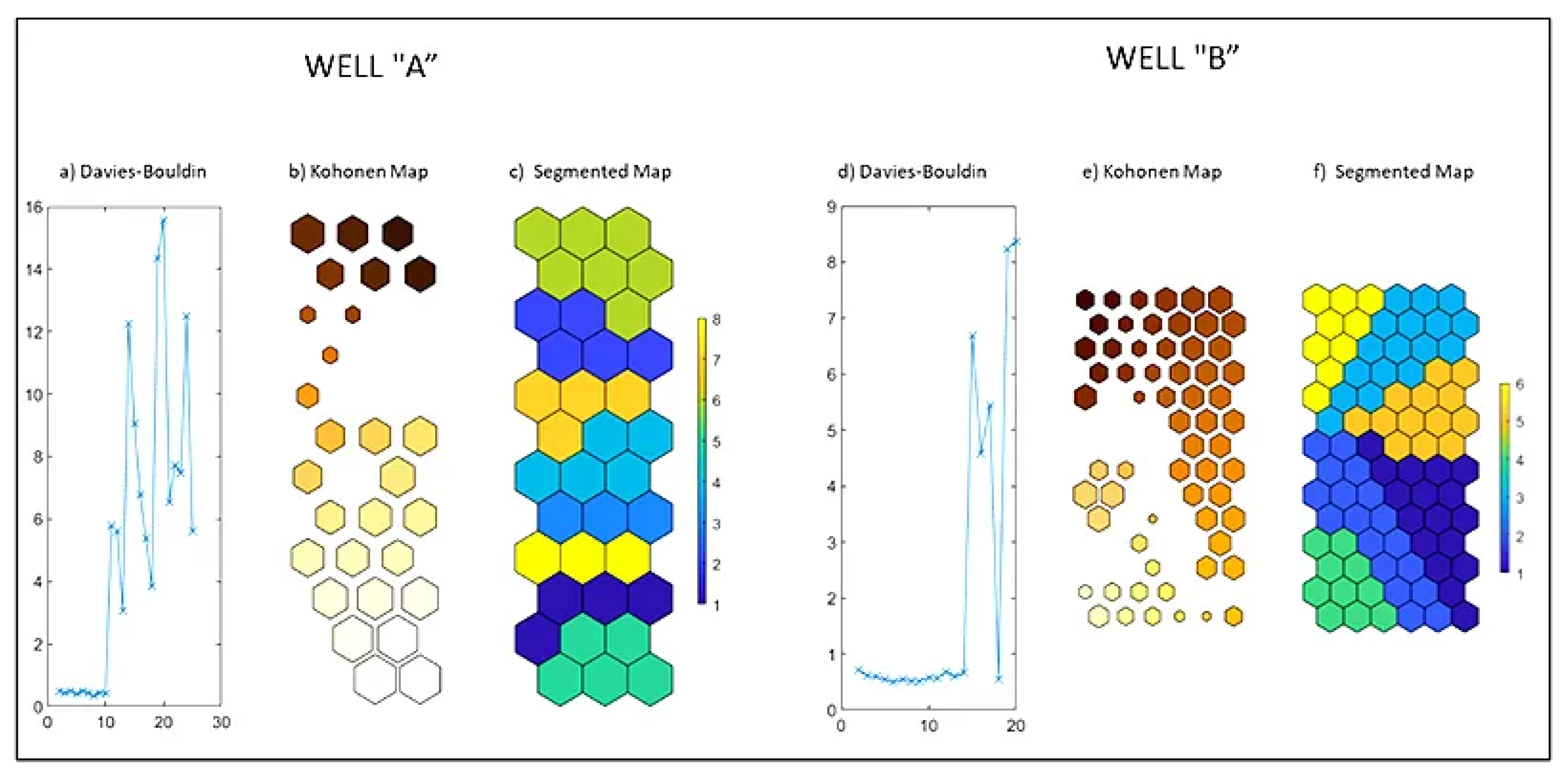
Figure 10.
Pore-size classification using image processing, adopting nomenclature proposed by [50,51]. In this representation, pore areas are depicted in white, while the background is rendered in black for image processing clarity.

Figure 11.
2D maps of the input dataset. (a) Final U-matrix map, illustrating the neural network’s training outcome using input values from (b) to (e) as a guide to differentiate groups with similar information. (b) 2D map depicting the distribution of values for . (c) 2D map depicting the distribution of values for porosity derived from the sonic log. (d) 2D map illustrating the distribution of values for total porosity. (e) 2D map showing the distribution of values for the log.
Figure 11.
2D maps of the input dataset. (a) Final U-matrix map, illustrating the neural network’s training outcome using input values from (b) to (e) as a guide to differentiate groups with similar information. (b) 2D map depicting the distribution of values for . (c) 2D map depicting the distribution of values for porosity derived from the sonic log. (d) 2D map illustrating the distribution of values for total porosity. (e) 2D map showing the distribution of values for the log.
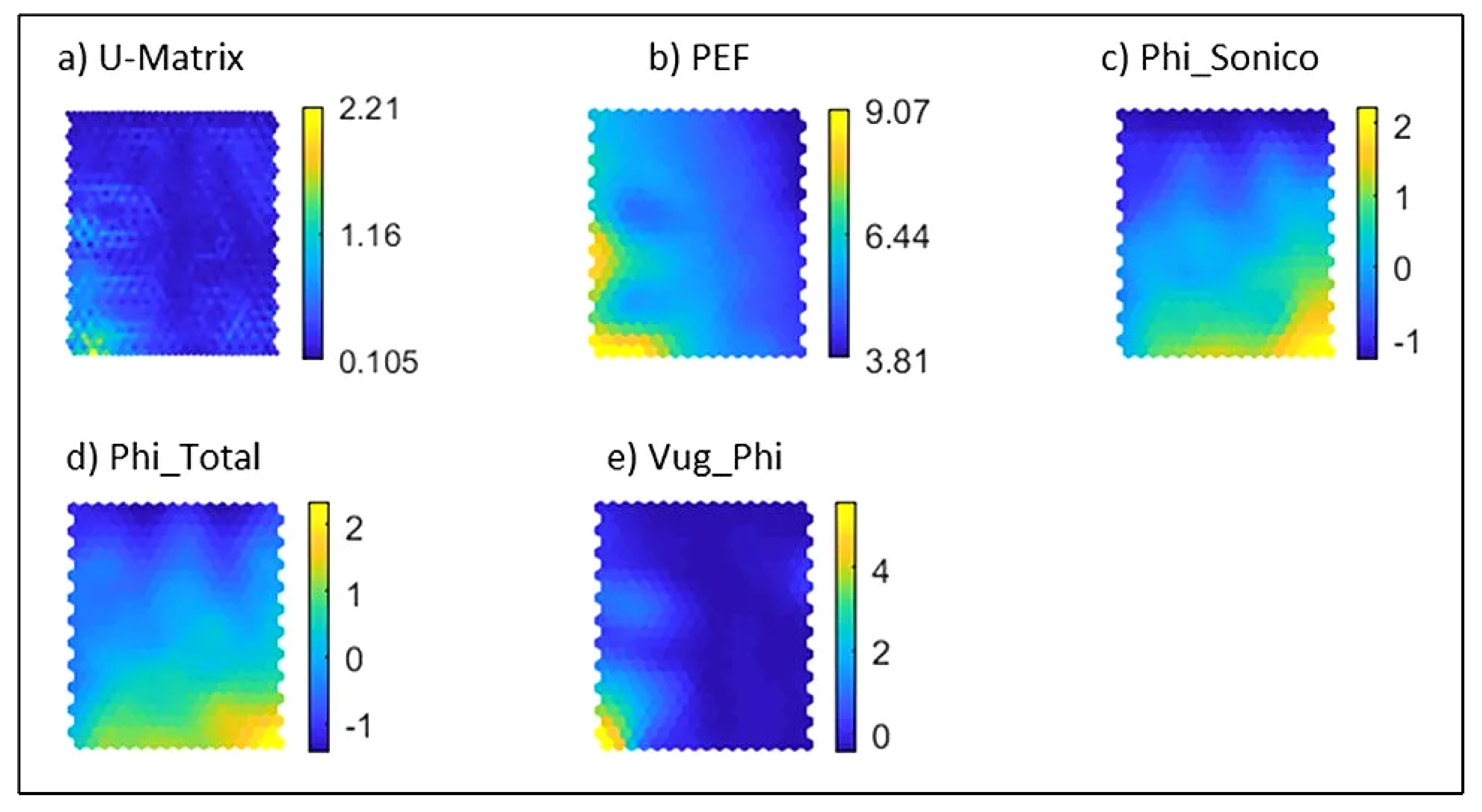
Figure 12.
(a) Visualization of the Davies-Bouldin index, (b) 2D map incorporating the entire dataset input, and (c) Segmented map into 32 groups, guided by the Davies-Bouldin index.
Figure 12.
(a) Visualization of the Davies-Bouldin index, (b) 2D map incorporating the entire dataset input, and (c) Segmented map into 32 groups, guided by the Davies-Bouldin index.
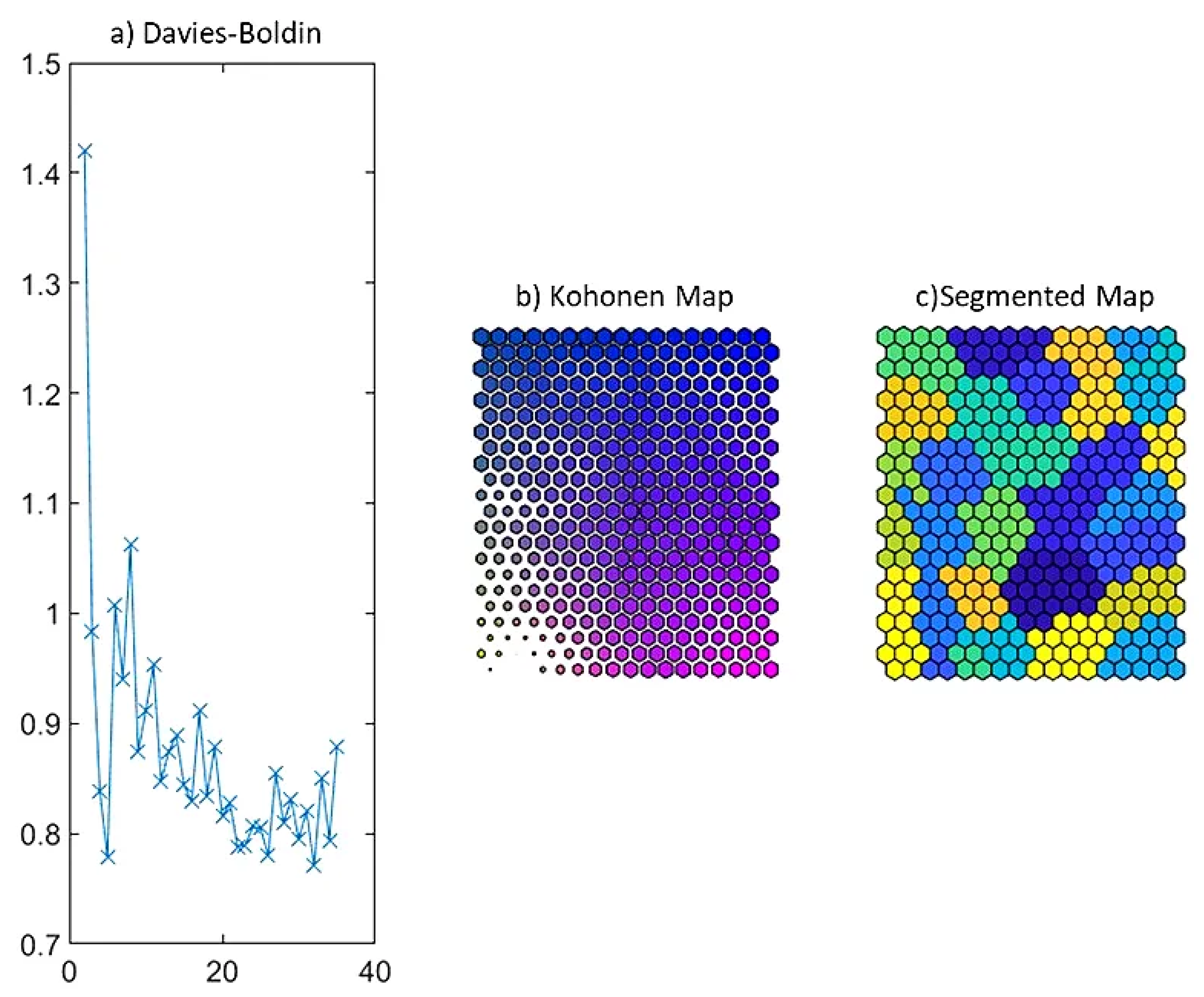
Figure 13.
Porosity-based facies classification: (a) Cross-plot depicting the relationship between , 32 classes, and matrix porosity values, (b) Cross-plot illustrating the correlation between total porosity, , and 32 classes, (c) Visualization of the 32 classes with minimum and maximum values derived from all input data.
Figure 13.
Porosity-based facies classification: (a) Cross-plot depicting the relationship between , 32 classes, and matrix porosity values, (b) Cross-plot illustrating the correlation between total porosity, , and 32 classes, (c) Visualization of the 32 classes with minimum and maximum values derived from all input data.
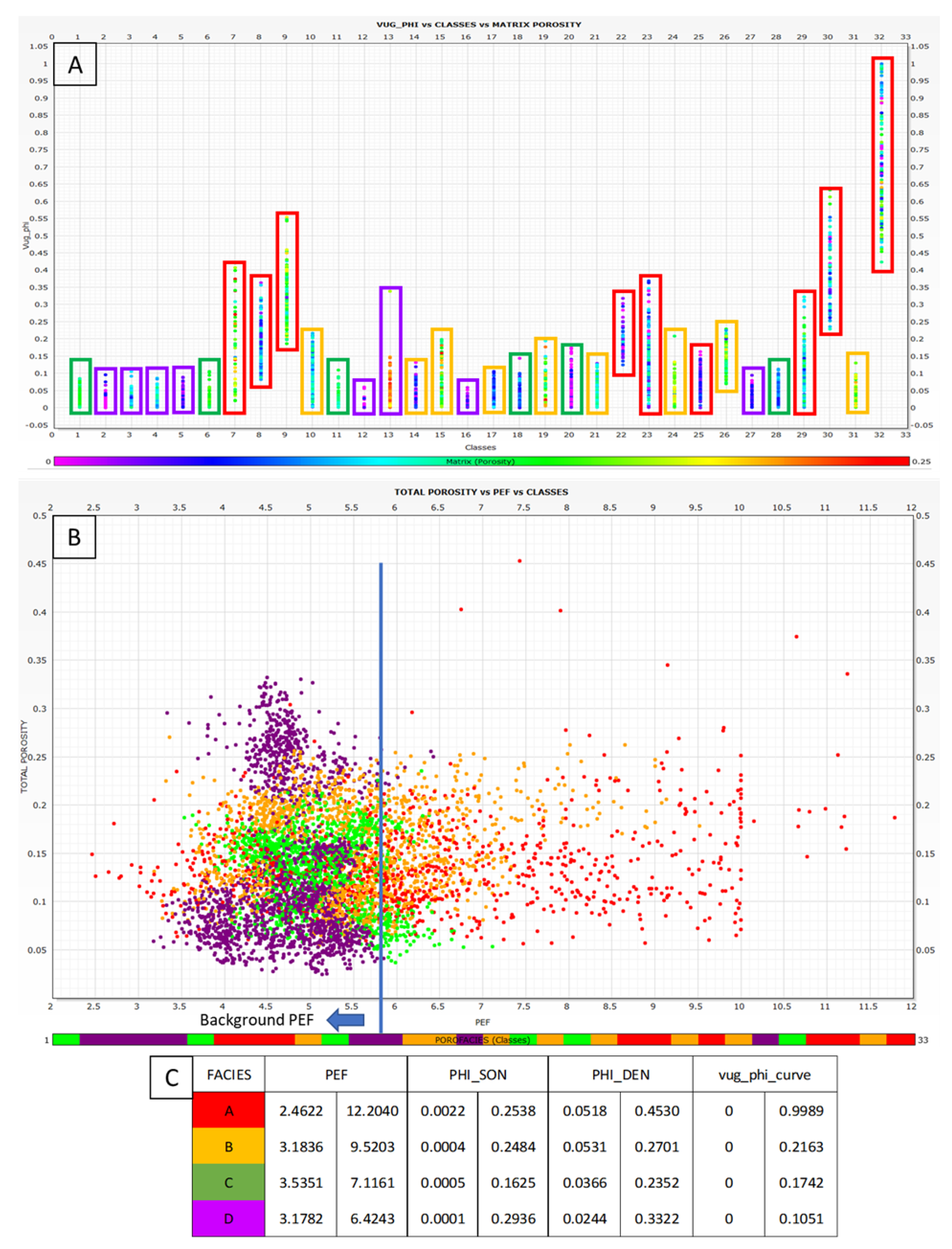
Figure 14.
Conventional and logs of a representative well, showcasing porosity facies classification. Facies A is distinguished by the presence of gigapores (), while facies B, C, and D are predominantly characterized by smaller megapores. Limitations in image resolution precluded the differentiation of pores with diameters less than , resulting in the exclusion of mesopores and micropores from the analysis.
Figure 14.
Conventional and logs of a representative well, showcasing porosity facies classification. Facies A is distinguished by the presence of gigapores (), while facies B, C, and D are predominantly characterized by smaller megapores. Limitations in image resolution precluded the differentiation of pores with diameters less than , resulting in the exclusion of mesopores and micropores from the analysis.
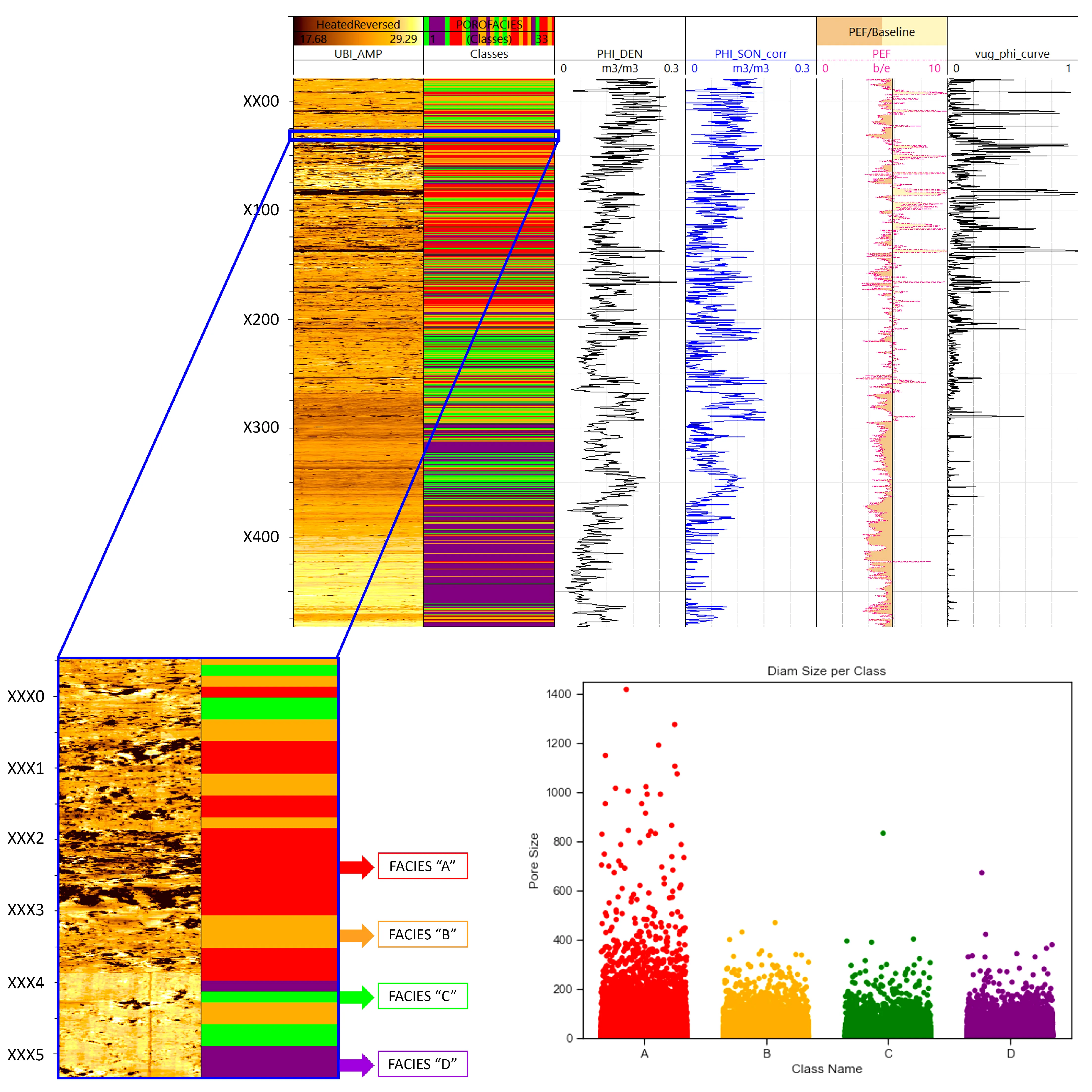
Table 1.
Input parameters for training.
| Parameter | Condition | value |
|---|---|---|
| Topology shape | 2D rectangular sheet map | |
| Map lattice | Hexagonal | |
| Normalization | Normalized variance to unity, and its mean to zero | |
| Algorithm | Initialized | Batch |
| Alpha | Always | Decreasing |
| Neighborhood | Always | Gaussian |
| Initial Alpha | Rough training phase | 0.5 |
| Final Alpha | Fine tuning phase | 0.05 |
| Initial Radius | Initialized randomly | Max (side length map)/4 |
| Initial Radius | Rough training phase | Max (1, (initial value)/4) |
| Final Radius | Fine tuning phase | 1 |
| Number of iterations | Rough training phase | 4 m/n 1 |
| Number of iterations | Fine tuning phase | 16 m/n |
The parameter m represents the count of map units, while n denotes the quantity of data samples.
Table 2.
Overview of Employed Well Logs and Corresponding Porosity Types
| Well log | Type of porosity |
|---|---|
| Density | Total porosity |
| Sonic | Matrix porosity |
| Photoelectric factor | Non-matrix porosity |
| Difference between density and sonic | Non-matrix porosity |
Table 3.
Facies-based porosity and number of pores automatically detected
| Quantity of pores | ||||
|---|---|---|---|---|
| Facies A | Facies B | Facies C | Facies D | |
| Gigapores | 271 (1.34%) | 33 (0.29%) | 20 (0.20%) | 19 (0.16%) |
| Large megapores | 5419 (26.76%) | 2642 (23.29%) | 2132 (21.53%) | 2346 (20.02%) |
| Small megapores | 14560 (71.90%) | 8669 (76.42%) | 7749 (78.27%) | 9355 (79.82%) |
| Large mesopores | non-detected | non-detected | non-detected | non-detected |
| Small mesopores | non-detected | non-detected | non-detected | non-detected |
| Micropores | non-detected | non-detected | non-detected | non-detected |
| TOTAL | 20250 | 11344 | 9901 | 11720 |
Table 4.
Comparative Analysis of Lithological Interpretations by [15,16] Utilizing Acoustic Facies and Visual Porosity, in Contrast with the Four Porosity-Based Facies Proposed in the Current Study.
| [15] | [16] | ||
| Lithology | Visual Porosity | Lithology | Visual Porosity |
| Shrubstones | High | Shrubstone-like | High |
| Grainstones and rudstones | Medium | Rudstones-like | High/Low |
| Partially silicified shrubby | Medium | Grainstones-like | Medium |
| Spherulite packstones/dolomudstones | Low | Mudstone-like | Low |
| Current Study | |||
| Posible Lithology | Non-Matrix Porosity | Porosity-facies | |
| Shrubstone | High | A | |
| Rudstones | Medium | B | |
| Grainstones | Low | C | |
| Mudstone | Low | D | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








