Prerpints.org logo
Preprint
Article

Free Surface Energy and Hansen Solubility Parameters Vector Field. Interface Thickness

Altmetrics

Downloads

94

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

13 June 2024

Posted:

13 June 2024

You are already at the latest version

Alerts
Abstract
A three-dimensional vector field model is proposed, whose dimensions are the Hansen Solubility Parameters: dispersion parameter (δD), polarity parameter (δP), and hydrogen bonding parameter (δH). The vector space that defines the field has the peculiarity of having the dispersion vector with a magnitude of 2, as its base vector, while polarity and hydrogen bonding vectors have a magnitude of 1. A substance is characterised as a position vector, and the interaction between two substances is determined by calculating the vector difference of both, known as the interaction vector. Interaction among substances may involve solubility, swelling, cracking, surface tension, interface tension, and any physical phenomena where intermolecular energies of dispersion, polarity or hydrogen bonding come into play. This paper studies free surface energy (surface and interfacial tension). It has been found that free surface energy is directly proportional to the square of the magnitude of the interaction vector. The proportionality constant, τ, is expressed in length units, has a value of 0.025 nm, and does not depend on the chemical nature of the substance or state of matter (solid, liquid or gas). Constant value τ appears universal and aligns with the thickness of interfaces, thereby supporting Guggenheim's hypothesis. This hypothesis asserts that interfaces possess actual thickness and are not merely mathematical surfaces, as originally postulated by Gibbs. Moreover, it also has been found that interface thickness, τ, is approximately equal to half of the Bohr radius, a0, which is defined by universal constants. Because the solubility parameters of thousands of substances are known and can be easily determined from molecular structure, a good approximation of the surface and interfacial tension of any given substance can now be calculated. It has also been found that contact angles of sessile droplets in three-phased systems can be calculated from the interaction vectors of the implicated substances.
Keywords: 
Subject: Chemistry and Materials Science  -   Surfaces, Coatings and Films

1. Introduction

Hildebrand and Scott suggest that the process of solubilisation is similar to the process of evaporation, as both processes involve the separation of molecules by breaking their intermolecular bonds [1]. To energetically quantify the solubilisation of a substance, Hildebrand defined the solubility parameter, δ, as the square root of the cohesive energy density of said substance:
∂ = E v
Where v is the molar volume of the pure substance (m3/mol), E is the energy of vaporization (J/mol) and E/v is the cohesive energy (J/m3).
Charles M. Hansen considers that the Hildebrand Solubility Parameter is valid when it comes to the global energy balance, but it does not include structural considerations of molecules [2]. That would explain why substances with similar heat of vaporization and different molecular structures cannot be dissolved between them. To overcome this obstacle, Hansen considers the solubility parameter to be the combination of three solubility parameters:
δ 2 = δ D 2 + δ P 2 + δ H 2
Where δD, δP and δH are the dispersion, polarity, and hydrogen bond solubility parameters, respectively. The “distance”, Ra, between two substances, called 1 and 2, is determined by the following equation:
R a = 4 δ D 2 − δ D 1 2 + δ P 2 − δ P 1 2 + δ H 2 − δ H 1 2
The coordinates of each substance are the centre of a sphere with a radius R0, termed the solubility sphere. Within the solubility sphere, the 'good solvents' for the substance are located, while outside the solubility sphere, the 'bad solvents' are found. The parameter called RED (Relative Energy Difference) is defined as:
R E D = R a R 0
When RED > 1, the substance is not soluble in the considered solvent while if RED ≤ 1 the opposite will be.
Hansen solubility parameters have been related not only to the phenomenon of solubility but to a multitude of phenomena in which surface free energy is involved. Various correlations have been found between surface and interfacial tension, σ, with solubility parameters that respond to the general expressions [1,2,3,4,5,6,7]:
σ = f a δ D α , b δ P β , c δ H γ , v d
Where v is the molar volume and the constants a, b, c, d, a, b and g are empirical adjustment constants without physical meaning.
Various correlations of surface and interfacial tension versus Hansen solubility parameters are shown in Table 1.
The present work aims to establish, both theoretically and experimentally, a vector field model for the Hansen solubility parameters. This model will allow, in the first place, the characterisation of substances as components of a vector. The coordinates of this vector will be the dispersion (δD), polarity (δP), and hydrogen bonding (δH) parameters of the substances. In the second place, it will enable the evaluation of physical processes and phenomena in which different substances interact as a function of the vectors that characterise these processes, referred to as interaction vectors. The immediate practical applications of the Hansen vector field and interaction vectors are evident in surface processes, where free surface energy is a critical factor, manifesting as surface tension, interfacial tension, and contact angle.
The hypothesis assumes that the free surface energy is proportional to the square of the magnitude of the interaction vector between the phases involved, where the proportionality constant will have an identifiable physical meaning. This interaction vector, which will be defined later, is closely related to the cohesive energy density.
This hypothesis is very reasonable as it is since free surface energy, which has units in the International System of J/m², must be proportional to the cohesive energy density, which has units of J/m³, where the proportionality constant should be a distance, with the unit being meters.
J m 2 = m J m 3

2. Materials and Methods

This work is mainly based on experimental data published on surface tensions, interfacial tensions, and contact angles bibliography.
In the case of the surface tensions of liquids we have also included values that we experimentally determined using the droplet weight method [9]. A perfect concordance has been observed between our values and the ones already published. Additional surface tension data has been published by Masakazu Murase and Daisuke Nakamura in 2023 [7].
The Hansen solubility parameters values used in this study are sourced from the solvents Table A.1 and polymers Table A.2 in the Appendix A of “Hansen Solubility Parameters. A User's Handbook” [2]. Free surface energy data of solids with air, σLG, at 25 ºC come from Weiyan Yu and Wanguo Hou, 2019 [10]. Interfacial tension of solids with liquids, σSL, at 25 ºC comes from Masakazu Murase and Daisuke Nakamura, 2023 [7]. The contact angle of diverse liquids over PMMA and n-Octacosane comes from J. Panzer, 1973 [11].

3. Data and Discussion

Before delving into specific empirical data and its discussion, the Hansen Solubility Parameters will be reformulated as a vector field. This will enable a more successful approach to the subsequent discussions.

3.1. The Hansen Solubility Parameters Vector Field

3.1.1. Concepts and Definitions

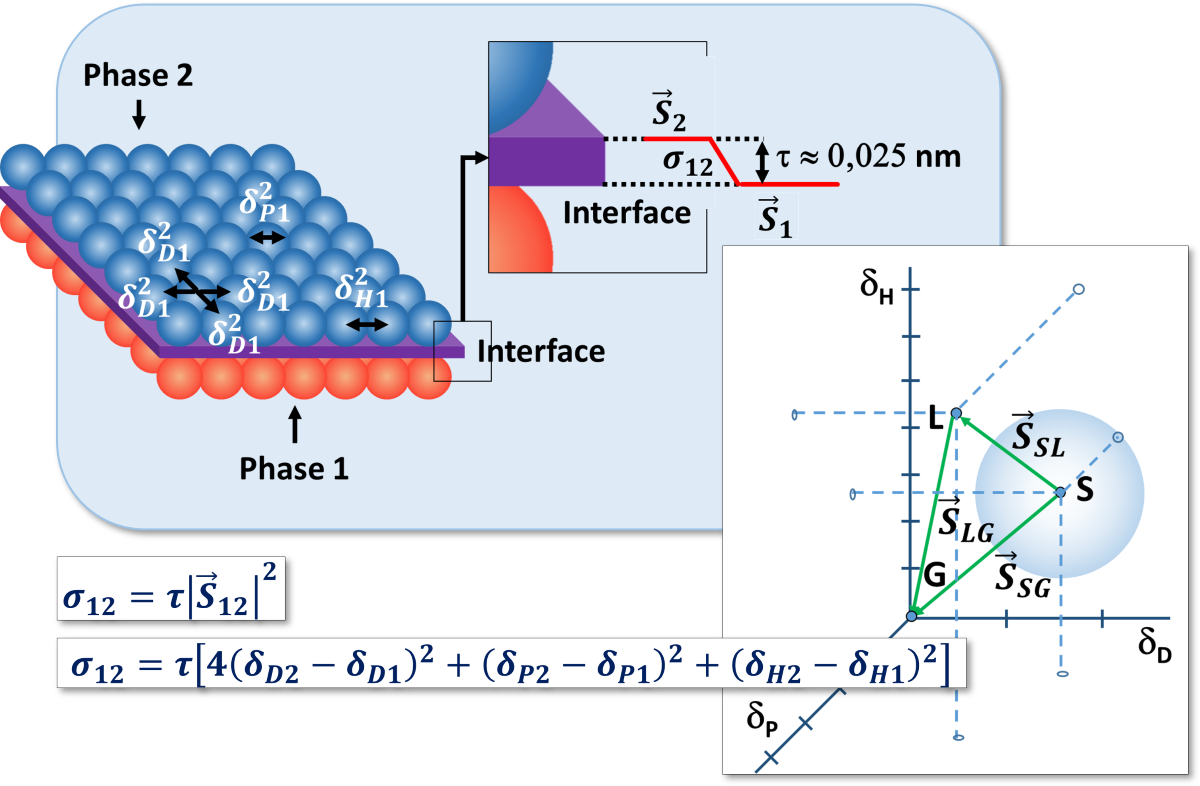
Hansen solubility parameters correspond to a three-dimensional vector field in which the dimensions are London dispersion forces, D, polarity forces due to permanent dipoles, P, and forces due to hydrogen bonding, H. Said vector field dictates the physical phenomena where intermolecular forces (like solubility, polymer swelling and cracking), or free surface energies (surface tension, interfacial tension, contact angle and others) come into play.
Inside that vector field, any given substance is a vector, S → , composed by the sum of three vectors:
S → = S → D + S → P + S → H
Where their components are the multiplication of the scalar solubility parameters by the direction vectors, i ^ , j ^ and k ^ , of the base of vector space.
S → D = δ D i ^ S → P = δ P j ^ S → H = δ H k ^
The particularity of the Hansen vector field is that the magnitude of the direction vectors of the field base, j ^ y k ^ , is 1 (like in Euclidean fields) while the magnitude of the vector of the base i ^ is two times bigger. In other words, their magnitudes are:
i ^ = 2 j ^ = 1 k ^ = 1
The vector field base is orthogonal.
The vector that represents a substance in the vector field is a position vector and it is expressed like the following:
S → = δ D i ^ + δ P j ^ + δ H k ^
Likewise:
S → = δ D , δ P , δ H
This vector starts in the origin and has its destination in a certain point of the field δ D , δ P , δ H . The magnitude of the vector S → is:
S → = δ D i ^ 2 + δ P j ^ 2 + δ H k ^ 2
Because i ^ = 2 , this leads to:
S → = 4 δ D 2 + δ P 2 + δ H 2
The coefficient 4 that goes with the dispersion component is obtained due to the squaring the direction vector i ^ .
Figure 1 shows three substances 1, 2 and 3, with their vectors S → 1 , S → 2 and S → 3 . It can be observed that, in the base of the space, the direction vector i ^ is twice as large as vectors j ^ and k ^ and therefore, the scale of δD is twice the scales of δP and δH.
The interaction between substances 1 and 2 is represented by a new vector S → 12 , called interaction vector, which is defined by the difference between both said vectors:
S → 12 = S → 2 − S → 1
S → 12 = δ D 2 − δ D 1 i ^ + δ P 2 − δ P 1 j ^ + δ H 2 − δ H 1 k ^
Vector S → 21 is directed from 2 to 1. Additionally, it is true that the magnitudes of the interaction vectors S → 12 and S → 21 are idempotent. According to Hansen, these magnitudes correspond to the distance, Ra, between 1 and 2:
S → 12 = R a 1,2 = 4 δ D 2 − δ D 1 2 + δ P 2 − δ P 1 2 + δ H 2 − δ H 1 2
Likewise, interaction vectors for substances 1 and 3, and substances 2 and 3, are defined as:
S → 13 = S → 3 − S → 1
S → 23 = S → 3 − S → 2
The interaction between substances could be referred to solubility, swelling, cracking, interfacial tension, or any other physical phenomenon in which any of the intermolecular energies of dispersion, polarity o hydrogen bonding came into play.
Let it be considered a case where the interaction consists of solubilization. In the depicted scenario, as shown in Figure 1, the sphere that surrounds substance 1 represents the volume in which good solvents are found. In this illustration a good solvent is substance 2, whereas substance 3, that is out of the solubility sphere, is a bad solvent. Therefore, RED > 1 for solvent 2, while RED < 1 for solvent 3.

3.1.2. Interaction Vectors and Free Surface Energy

As presented in the introduction above, a great deal of research work has been done to link free surface energy with Hansen solubility parameters. In all cases, δ D , δ P , and δ H parameters have been conceived as three independent magnitudes with no interdependence whatsoever. To name an example, in the Beerbower equation [3], solubility parameters are affected by a and b parameters, which change depending on the chemical family studied.
δ D 2 + a δ P 2 + b δ H 2 = 13.9 1 v 1 / 3 σ
In this paper, δ D , δ P , y δ H will be conceptualised as components of a vector in a vector space. The three-dimensional basis of this space is defined by a director vector, which has a magnitude of 2 for the dispersion forces. In contrast, the magnitudes of the director vectors for polarity and hydrogen bonding forces are set to 1.
Taking the above into account, free surface energy is regarded as directly proportional to the square of the magnitude of the interaction vector between the two phases that create the surface:
σ 12 = τ S → 12 2
That is to say:
σ 12 = τ 4 δ D 2 − δ D 1 2 + δ P 2 − δ P 1 2 + δ H 2 − δ H 1 2
If phase 1 is air, and since its cohesion energy is very weak, the solubility parameters can be considered equal to zero. In that case the surface free energy (surface tension) would be:
σ = τ 4 δ D 2 + δ P 2 + δ H 2
The proportionality constant is called τ, and its units are of length.

3.2. Surface Tension of Liquids

Surface tension is the interaction between a liquid phase and air or any other gas. It is interpreted that, because cohesion energy is very low in gases, their solubility parameters will be negligible: δ D , g a s = δ P , g a s = δ H , g a s = 0 . As such, the interaction vector of a liquid phase with a gas phase will, in general, be:
S → L G = δ D L i ^ + δ P L j ^ + δ H L k ^
Nonetheless, when a liquid interacts with air (which is non-polar), it can present the following behaviours depending on the molecular structure of the liquid (Figure 2), and these will modify the number of dimensions to be considered in the interaction vector:
(a)
The liquid is completely non-polar, and its molecules do not present any special orientation at the interface with air, since its molecules are, like the air molecules, non-polar. The only relevant parameter is δD, as δP = 0 and δH = 0. This is the case, for instance, of hydrocarbons like pentane.
(b)
The liquid is polar, but molecular size is sufficiently large to “hide” its hydrogen bonds in the inner part of the liquid preventing them from interacting with air. The electric dipole moment cannot be “hidden” because it affects the molecule itself. In this case, δH would not be relevant to the air-liquid interaction, while dispersion and polarity would. The Figure 2 shows the example of a carboxylic acid like hexanoic acid. The five-atom carbon chain creates a non-ionic barrier that would conceal the hydrogen bonds.
(c)
The liquid is polar, but molecular size is very small, and non-polar hydrocarbon chains are not able to “hide” the hydrogen bonding effect versus the air. In this case, the three solubility parameters–dispersion, polarity, and hydrogen bonding–variables would be relevant. Figure 2 shows the case of formic acid, a small ionic molecule with hydrogen bonds that cannot be concealed.
According to the suggested hypothesis, surface tension will be directly proportional to the magnitude of the interaction vector between the liquid and the gas.
σ L G = τ L G S → L G 2
In cases a) and b), the vectors of these molecules would operate in the Hansen vector space governed by dimensions D and P, since hydrogen bonding, H, is nonexistent or masked. In this instance, the vector that would represent those molecules would be two-dimensional:
S → L G = δ D L i ^ + δ P L j ^
Then, according to equation (24), the surface tension of most liquids (excluding ionic ones, such as water, glycols, glycerin, amines, amides, sulfoxides, and low molar mass carboxylic acids) can be calculated using the following expression:
σ L G = τ L G 4 δ D L 2 + δ P L 2
In case c), vectors of the small ionic molecules would operate in the full extent of the Hansen vector field governed by dimensions D, P, and H. In this instance, the vector that represents these molecules would be three-dimensional:
S → L G = δ D L i ^ + δ P L j ^ + δ H L k ^
Then, according to equation (24), the surface tension of ionic liquids, including water, glycols, amines, amides, sulfoxides, and low molar mass carboxylic acids, can be calculated using the following:
σ L G = τ L G 4 δ D L 2 + δ P L 2 + δ H L 2
To prove these hypotheses, surface tension data of 122 liquids, and values measured by the authors, using the droplet weight method [9], have been gathered and analyzed.

3.2.1. Surface Tension of Non-Ionic Liquids or Ionic with Non-Small Molecular Size as Function of the Interaction Vector

Table A1, in Appendix A, shows surface tension and Hansen solubility parameters data for liquids of very diverse chemical categories such as aliphatic hydrocarbons, cyclic hydrocarbons, aromatic compounds, chlorinated derivatives, alcohols, ketones, carboxylic acids, esters, ethers, glycol ethers, nitrogen compounds, etc. They all are liquids included in the above-mentioned cases a) and b) and represent most liquids. In Figure 3, surface tension versus the square of the interaction vector magnitude, and the linear regression for these compounds are shown. The correlation is excellent as a fitting coefficient R2 = 0.990. Standard deviation of absolute errors of the surface tension is 3.2 mN/m, and the mean is 2.9 mN/m.
It is proven that in this case, surface tension is directly proportional to the square of the magnitude of the interaction vector, with the expression:
σ L G = 0.0243 4 δ D L 2 + δ P L 2
Generalizing:
σ L G = 0.0243 S → L G 2
Where surface tension, σLG, is expressed in mN/m, vector magnitude is expressed in MPa and τ L G = 0.0243 n m . It is worthwhile to note that τ L G does not depend on the molar volume and its units are those of length.
The equation of a circle with origin as center in a plane is:
x 2 + y 2 = R 2
Where x and y are abscissa and ordinate axis coordinates, respectively, and R is the radius of the circle. If (29) is reorganized, it is found that it also fits the equation of a circle with center at the origin of coordinates within the Hansen DP plane:
4 δ D L 2 + δ P L 2 = 41 σ L G
The abscissa, being in a Hansen vectorial field, is multiplied by 2 (4 when squared), and the radius circle, Rs, is:
R σ = 41 σ L G
This expression allows to draw lines of equal tension (iso-tension lines) in a DP diagram. Knowing the solubility parameters δD and δP of any given liquid (except for low molar mass, polar ones) it can be graphically determined with ease its surface tension (Figure 4).

3.2.2. Surface Tension of Ionic or Non-Ionic Liquids with Not-Small Molecular Size as Function of the Interaction Vector

Table A2, in Appendix A, shows surface tension data of small ionic molecules including water, glycols, glycerine, nitrogen compounds and dimethyl sulfoxide. Their molecules are small and cannot hide their hydrogen bonds from air, which is why the interaction vector operates in entire Hansen space volume. The case of 1,5-Pentanediol is not an anomaly: although its molecule is not small, it has a double bond that prevents rotation around the molecule's axis, making the hydroxyl groups difficult to hide. Similarly, a similar situation occurs with 3-hydroxymethylpyridine, a flat, rigid molecule that also does not allow the reorientation of polar substituents. The square of the magnitude of the interaction vector has been calculated including the three solubility parameters: 4dD2+dP2+dH2.
Figure 5 shows surface tension versus the square of the magnitude of the interaction vector, along with the linear regression. Fitting is also excellent, with a coefficient of R2 = 0.995. The standard deviation of absolute errors of the surface tension is 3.7 mN/m, and mean is 3.0 mN/m.
For the case of small polar molecules, it is also correct that surface tension is directly proportional to the square of the module of the interaction vector that encompasses the entire Hansen vector space. It is further demonstrated that, in this instance, surface tension is directly proportional to the square of the interaction vector according to this expression:
σ L G = 0.0257 4 δ D L 2 + δ P L 2 + δ H L 2
And generalizing:
σ L G = 0.0257 S → L G 2
Surface tension, σLG, is expressed in mN/m, the units of the vector magnitude are MPa, and τ L G = 0.0257 n m , being very similar to the value obtained for non-small molecules. As such, τ L G is independent of molar volume and polarity, regardless of the molecular size.
The equation of a sphere with the origin as its centre is given by the following expression:
x 2 + y 2 + z 2 = R 2
Where x, y, z are coordinates of the three axes of the space, and R is the radius of the sphere. If equation (34) is reorganized, it is found that it also fits the equation of a sphere with the origin of coordinates as its centre in Hansen vector field:
4 δ D L 2 + δ P L 2 + δ H L 2 = 39 σ L G
The abscissa, being in a Hansen vectorial field, is multiplied by 2 (4 when squared), and the radius of the circle is Rσ:
R σ = 39 σ S G
It should be noted that surface tension spheres resemble the well-known Hansen solubility spheres. This shows that surface tension is a phenomenon closely related to solubilization: dispersion, polarity, and hydrogen bonding forces operate in both cases.

3.3. Surface Free Energy of Solids

The surface tension of a solid, commonly known as surface free energy, is the result of the interaction of a solid with air or any other gas. Because the cohesion energy of gases is negligible, their solubility parameters will be zero, or, in other words: δ D , g a s = δ P , g a s = δ H , g a s = 0 . Unlike liquids, in which molecules have mobility and can reorient themselves when interacting with a gas to show their least ionised part at the liquid-gas interface, solids cannot do that due to their limited mobility. For this reason, the interaction vector will be constituted of the three components: dispersion, polarity, and hydrogen bonding.
S → S G = δ D S i ^ + δ P S j ^ + δ H S k ^
Therefore:
σ S G = τ S G S → S G 2
And:
σ S G = τ S G 4 δ D S 2 + δ P S 2 + δ H S 2
Table A3 in Appendix A shows surface free energy data of 21 solid materials with different degrees of polarity. Additionally, interaction vector values and calculated free energy data are displayed.
Figure 6 graphically shows the surface tensions (free surface energies) of the solids included in Table A3 in Appendix A and their linear regression. The correlation is satisfactory as R2=0.9828 despite the difficulty of accurately determining experimental values of free surface energies of solids. The constant τ S G = 0.0260 n m , is very similar to the values of liquid surface tensions ( τ L G ≈ 0.0243 n m ≈ 0.0257 n m ).

3.4. Interfacial Tension between a Solid and a Liquid, or Any Given two Substances

The diagram of Figure 7 displays a ternary system comprised of a solid (S), a liquid (L) and a gas (G). It Is true that:
S → S G + S → S L = S → L G
The interaction vector between solid and liquid, S → S L , will then be:
S → S L = S → L G − S → S G
Substituting (26) and (36) in (43):
S → S L = δ D L i ^ + δ P L j ^ + δ H L k ^ − δ D S i ^ + δ P S j ^ + δ H S k ^
Operating leads to:
S → S L = δ D L − δ D S i ^ + δ P L − δ P S j ^ + δ H L − δ H S k ^
The magnitude of the interaction vector between liquid and solid will be:
S → S L = 4 δ D L − δ D S 2 + δ P L − δ P S 2 + δ H L − δ H S 2
And this matches with the Hansen distance, Ra, between S and L:
S → S L = R a
For this reason:
σ S L = τ S L S → S L 2 = τ S L R a 2
σ S L = τ S L 4 δ D L − δ D S 2 + δ P L − δ P S 2 + δ H L − δ H S 2
Table A4 shows data of experimental interfacial tension data of several liquids with a few solids: polystyrene polymers (PS), polymethylmethacrylate (PMMA), Polyamide 6,6 (PA66), polytetrafluoroethylene (PTFE), and polyvinylbutyral (PVB). Solubility parameters of polymers and various liquids, the square of the module of the interaction vector S → S L and calculated interfacial tension according to (49) are also shown.
Interfacial tensions between solid polymers and liquids, and linear regression are displayed in Figure 8:
σ S L = 0.0268 4 δ D L − δ D S 2 + δ P L − δ P S 2 + δ H L − δ H S 2
The value τ S L = 0.0268 n m is also very similar to previous values found for liquid-gas and solid-gas interactions.
The previous solid-liquid interaction equations can also be extended to the interaction between two liquids. Therefore, for a liquid L1, and a liquid L2, it can be expressed that:
σ L 1 , L 2 = t L 1 , L 2 S → L 1 , L 2 2 = τ L 1 , L 2 R a 2
σ L 1 , L 2 = τ L 1 , L 2 4 δ D L 2 − δ D L 1 2 + δ P L 2 − δ P l 1 2 + δ H L 2 − δ H L 1 2

3.4. Free Surface Energy: General Equation

Figure 9 plots the surface free energy against the square of the modulus of the interaction vector for liquid-gas interactions (large nonpolar and polar molecules, LG, and small polar molecules, LG*), solid-gas interactions (SG), and solid-liquid (SL) interactions. The linear fit for all values is of high quality, since all types of molecules, large and small, polarized, and non-polarized, solid, liquid, or gaseous, are correlated.
All of this means that the following expression can be established as a general equation for the evaluation of free surface energy between two substances:
σ 12 = τ S → 12 2
Whereτ is a general constant (τ = 0.025 nm = 25·10-12 m) and S → 12 2 is the square of the magnitude of the interaction vector between substance 1 and 2.
For most liquid-gas interactions, except for those involving low molecular mass polarised ones, the interactions occur in the DP plane, so:
S → L 2 = 4 δ D L 2 + δ P L 2
In the case of high molecular mass liquids, the interaction vector operates exclusively in the DP plane.
For polarised low molecular mass liquids, the entire Hansen field (DPH space) is used, so:
S → L 2 = 4 δ D L 2 + δ P L 2 + δ H L 2
For solid-gas interactions, DPH space is used, too:
S → S 2 = 4 δ D S 2 + δ P S 2 + δ H S 2
For the interaction of any given substance 1, with any given substance 2:
S → 12 2 = 4 δ D 2 − δ D 1 2 + δ P 2 − δ P 1 2 + δ H 2 − δ H 1 2
If substance 1 or 2 is a gas, this general expression is then transformed into (55) and (56).

3.5. Physical Meaning of τ Constant

Classical approaches in interface thermodynamics, according to Gibbs, involve conceiving interfaces as per their mathematical definition, in other words, structures with no volume, only area [12]. Each extensive property of the system, such as free energy, entropy, or the quantity of matter is divided in three contributions. The first contribution is to a bulk phase in which it is assumed that said extensive property is homogeneous until reaching maximum mathematical surface. The second is a similar contribution in the other homogeneous bulk phase, and third is formed by residues of the extensive property that get assigned to the mathematical surface. That is to say that extensive properties like free energy or entropy get assigned to the mathematical surface but do not get assigned to volume. From a mathematical point of view, this assumption can be valid; however, from a physical perspective, it does not make sense that something without volume could store free energy or entropy. Another obstacle these approximations face is that the no-volume mathematical surface can be spatially situated at will, allowing selected extensive properties to have an arbitrarily chosen value, including zero.
It must be accepted that the mathematical surface, which by definition does not have volume, does not correspond to the physical representation of an interfacial layer. Those objections where manifested by Guggenheim, who proposes a new approach in which interfaces are not a mathematical construct, but a real physical layer with volume and thickness [13]. Guggenheim uses theoretical reasoning to develop thermodynamics of interfaces in systems formed by various compounds, coming from the physical existence of the interfacial layer with thickness estimated to be less than 10 nm, he does not propose any experimental value.
Dadashev et al. have theoretically studied adsorption in binary systems of indium-tin, gallium-bismuth, and thallium-bismuth. Their aim was to determine the influence of the concentrations of the components on the distance between different positions of an interfacial surface defined according to Gibbs [14]. The obtained equations predict that said surface must be in a range that would correspond to a physical layer with thickness inferior to atoms size or, in other words, less than 0.1 nm.
It has been proposed that the pressure coefficient, which is the derivative of the interfacial tension with respect to pressure, can be used as a measurement of the interfacial layer thickness, τ:
τ = ∂ σ ∂ P
The pressure coefficient, defined as the interfacial tension divided by pressure, has units of distance and is thus a suitable candidate for determining the thickness of an interfacial layer. As such, it has been considered for a long time. However, recently, Junhan Cho et al. studied compressible polymer mixtures and found that, while this coefficient presents values compatible with a potential interfacial layer, it can exhibit negative values in some regions, rendering it incompatible with thickness [15]. They suggest that pressure by itself cannot predict thickness because interfacial tension is also strongly dependent on the Flory-Huggins theory of polymer solutions interaction parameter, χ12. In addition, there is also dependence on the density of polymer packing, η [16]. In a Monte Carlo simulation about capillary waves in homopolymer interfaces, proportionality between interfacial tension and χ12 parameter has been found [17].
The polymer-solvent interaction parameter, χ12, is defined as:
χ 12 = z Δ w k T
Where z is the coordination number (number of neighbor units occupied by either a polymer segment or a solvent molecule). Δ w is the energy increment because of the interaction between substance and solvent, k is the Boltzmann constant an T is the absolute temperature. The interaction parameter can be estimated by the expression [2]:
χ 12 = v δ 1 − δ 1 2 R T + β
Where v is the molar volume of the solvent, δ 1 is the Hildebrand solubility parameter of the solvent, δ 2 the Hildebrand solubility parameter of the polymer, R is the gas constant and T is the absolute temperature. The empirical constant, β, is used as a correction for Flory combinatorial entropy. If Hansen solubility parameters are considered, χ 12 can also be estimated using the following expression:
χ 12 = v A 12 R T
Where A12 is:
A 12 = δ D 2 − δ D 1 2 + 0.25 δ P 2 − δ P 1 2 + 0.25 δ H 2 − δ H 1 2
It can be observed that for an interaction between a polymer 2 with a solvent 1, A12 is equal to quarter of the square of the interaction vector magnitude S → 12 according to the vector field model:
A 12 = 1 4 S → 12 2
For this reason, S → 12 2 is proportional to χ 12 :
S → 12 2 = 4 R T v χ 12
Solving (53) it is obtained:
τ = σ 12 S → 12 2
If we compare this equation with the pressure coefficient (58), it can be observed that it is also a free surface energy divided by an equivalent pressure magnitude, so the units will be of length. Pressure by itself, as suggested by Junhan Cho [15,16], is not enough to exactly represent the thickness of the interface because, in some way or another, it must contain the parameter χ 12 in its formulation.
Actually, S → 12 2 is that magnitude with pressure as units (a mandatory condition) that also is related to the χ 12 parameter. Therefore, it can be concluded that expression (65) represents the thickness of the interface.
When fitting the data by regression, it has been found that τ is very close to 0.025 nm in all instances. In other words, it is less than 0.1 nm, just like Dadashev and collaborators predicted [14]. The thickness is smaller than an atom's diameter, and it must be so. Otherwise, the interface would be occupied by the atoms and molecules of one of the phases. The interface can also be visualised as a zone in which atomic and molecular orbitals of both phases get close but do not belong to either of them, acting a transition between them.
The obtained value τ is independent of whether it represents surface or interfacial tension, the chemical family of substances involved, or the state of matter, whether solid, liquid, or gas. This leads to the conclusion that τ is a dimensional characteristic of the interface by itself, rather than being dependent on the nature of the phases.
It could be due to chance or an unknown causal relationship, but the interface thickness, τ, is, approximately (and with great accuracy), half of the Bohr radius, a0 = 0.05292 nm.
τ ≈ 1 2 a 0
The Bohr radius is the radius of the orbit of the electron of the hydrogen atom in the atomic model developed by Niels Bohr in 1913 for the quantum number n = 1. According to the Schrödinger model, the Bohr radius is actually the distance to the nucleus at which the probability of finding the electron is maximum for the 1s atomic orbital of the hydrogen atom. The radius is obtained from the universal physical constants:
a 0 = 2 ε 0 h m e e
Where ε 0 is the permittivity of vacuum, h Planck constant, m e the resting electron mas, and e la elemental electric charge.
If there were an unknown but plausible causal relationship, the interface thickness would be a property of quantum nature resulting from the combination of universal physical constants, and it would follow the next expression:
τ = ε 0 h m e e = 0.02646 n m
Figure 10 shows an idealised representation of an interface located between two molecular monolayers. This interface is the boundary where properties of phase 1, especially its solubility parameters, δD1, δP1 and δH1, gradually become the values of phase 2 (δD2, δP2 and δH2). In this case, the thickness τ could also be expressed as the variation of the interfacial tension versus the variation of the square of the interaction vector magnitude:
τ = d σ 12 d S → 12 2
Figure 10 also shows that the coordination number of molecules from monolayers in contact with the interface is usually 4. This implies that the electronic dispersion of a molecule affects 4 neighbouring molecules. For this reason, δ D 2 parameter needs to be considered 4 times. However, polarity and hydrogen bonding are unidirectional, and thus should only be accounted for once. This is the molecular justification for why dispersion is assessed 4 times when calculating the magnitude of the interaction vectors. For two (1 and 2) phases:
τ = σ 12 4 δ D 2 − δ D 1 2 + δ P 2 − δ P 1 2 + δ H 2 − δ H 1 2 ≈ 0.025 n m ≈ 1 2 a 0

3.6. Contact Angle and the Solubility Parameters Vector Field

Tensions that come into play when a liquid droplet is dropped over a solid surface are shown in Figure 11. The surface tension of the droplet versus air (or any given gas) is σLG, the surface tension of the solid surface versus air is σSG, and the interfacial tension between the solid surface and the liquid droplet is σSL. The tension σLG is tangent to the surface of the droplet where the three phases come into contact. The angle formed by σLG is called the contact angle, θ.
The cosine of the contact angle is:
c o s θ = σ S G − σ S L σ L G
Substituting free surface energies with their expression as a function of the interaction vector it results in:
c o s θ = S → S G 2 − S → S L 2 S → L G 2
Or, in other words:
θ = a r c c o s S → S G 2 − S → S L 2 S → L G 2
If:
S → S G 2 − S → S L 2 > S → L G 2
This means that critical surface tension, σc, has been surpassed and values c o s θ = 1 and θ = 0 will be directly assigned.
To confirm the validity of (72) and (73), calculated values have been compared with experimental values the contact angles of various liquids on Poly(methyl methacrylate) (PMMA) and n-Octacosane surfaces (Table A5 in Appendix A). Figure 12 shows the correlation between experimental and calculated values. Experimental contact angle estimation is usually not very accurate because a variety of factors like surface roughness or impurities can distort the measurement. Even so, for the same solid-liquid-gas system there can be a wide range of contact angles. Within that range of possible contact angles, the largest is called the advancing contact angle and the smallest is known as the receding contact angle. Despite potential experimental contact angle inconveniences, and the fact that small solubility parameters biases can be amplified when squaring parameters, correlation can be classified as excellent: R2 = 0.981.

3.7. Contact Angle and Interaction Vectors Angle

Contact angles and interaction vectors angle work in two different vector spaces, but they can be linked. Figure 13 depicts a comparative image between interaction vectors angles in the Hansen field, α, β, γ, and contact angle, θ.
Inside the Hansen field, the triangle formed by the interaction vectors that link solid, S, liquid, L, and gas, G, where angles are α, β, γ, and the sides opposite to these angles are a, b, and c, respectively, the opposite sides to the angles. The law of cosines is expressed as follows:
a 2 = b 2 + c 2 − 2 b c · c o s α
Reorganizing:
c 2 − a 2 = 2 b c · c o s α − b 2
(72) can also be enunciated as:
c o s θ = c 2 − a 2 b 2
Substituting (76) in (77) and operating:
c o s θ = 2 c b · c o s − 1
c o s θ = 2 S → S G S → L G · c o s α − 1
Figure 14 shows three relevant instances where contact angle, θ, and the vectors are related.
Case a): Maximum moisturising happens when c o s θ = 1 . In this situation:
S → S G = S → L G α = 0
This means that maximum moisturisation happens when the solid and liquid Hansen solubility parameters are the same because their vectors overlap each other.
Case b): The contact angle is 90º when c o s θ = 0 , and that also implies that:
S → S G S → L G · c o s α = 1 2
According to this expression, multiple configurations of S → S G and S → L G vectors, and the angles between them, are possible. One of the potential combinations is when S → S G = S → L G and α = 60 º .
Case c) Moisturising is zero when θ = 180 º , or, in other words, c o s θ = − 1 . This happens when S → S G and S → L G vectors are perpendicular: α = 90 º .

4. Conclusions

The Hansen vector field model established in this paper allows, among other things:
(a)
To link, for the first time, the cohesion energy of substances with their free surface energy, as surface or interfacial tension.
(b)
To calculate the surface tension and free energy of thousands of substances by knowing their Hansen solubility parameters, which are easily obtained from the molecular structure of substances. Likewise, it is possible to determine the interfacial tension between them with a simple vector calculation.
(c)
To theoretically calculate and accurately estimate contact angles that would, in many cases, be hard to experimentally determine. This vector field model saves experimental work and time.
Furthermore, this model allows to empirically prove that the interface between two substances is not a mathematical surface with no thickness (as suggested by the Gibbs hypothesis), but indeed has a small-scale thickness, as proposed by Guggenheim. Said thickness is approximately half of the Bohr radius.
Further research is needed to explore the application of the Hansen vector space for other interactions such as polymer swelling, chemical resistance of coatings, cracking, suspension stability, covering penetration, biological membrane penetration, absorption, adsorption, etc.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. Formal analysis, RBM; investigation, RBM, ASAA; methodology, RBM, ASAA; resources, RBM, ASAA; visualization, RBM, MABR; writing - original draft, RBM, MABR; writing - review & editing, RBM, MABR, ASAA.

Funding

This research received no external funding.

Institutional Review Board Statement

This article does not contain any studies with human participants or animals performed by any authors.

Informed Consent Statement

Not applicable.

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.

Acknowledgments

This work has been carried out as part of the research of the doc-toral thesis of Aqeel Shaikhah Arafat Aljadiri, directed by Rafael Bailón-Moreno. The doctoral thesis belongs to the Doctoral Pro-gram in Chemistry of the University of Granada (codes ISCED 1 Chemistry and ISCED 2 Physical, Chemical, Geological Sciences). Escuela Internacional de Postgrado of Universidad de Granada.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Surface tension of liquids versus air, σLG, at 25 ºC, and solubility parameters. Medium and high molar volume and ionicity molecules in which hydrogen bonding component is not relevant to surface tension.
Table A1. Surface tension of liquids versus air, σLG, at 25 ºC, and solubility parameters. Medium and high molar volume and ionicity molecules in which hydrogen bonding component is not relevant to surface tension.
Nº Substance Ref. σLG, mN/m δD, MPa1/2 δP, Mpa1/2 δH, MPa1/2 4δD2+δP2, MPa σLG,cal., mN/m Error, mN/m
1 1,1,2,2-Tetrabromoethane 2 48,9 22,6 5,1 8,2 2069,1 51,7 2,8
2 1,2,3-Tribromopropane 2 44,8 19,6 6,3 6,4 1576,3 39,4 -5,4
3 1,3-Diiodopropane 2 46,3 19,4 5,7 4,3 1537,9 38,4 -7,9
4 1,4-Dioxane 2 32,3 19,0 1,8 7,4 1447,2 36,2 3,9
5 1-Bromonaphthalene 2 43,9 20,6 3,1 4,1 1707,1 42,7 -1,2
6 1-Butanol 1 24,7 16,0 5,7 15,8 1056,5 26,4 1,7
7 1-Chloro-2-Methylpropane 2 21,3 15,6 5,0 2,9 998,4 25,0 3,7
8 1-Chloro-3-Methylbutane 2 23,0 15,7 4,5 2,9 1006,2 25,2 2,2
9 1-Chlorobutane 2 22,5 16,2 5,5 2,0 1080,0 27,0 4,5
10 1-Chloronaphthalene 2 41,3 19,9 4,9 2,5 1608,1 40,2 -1,1
11 1-Decanol 2 28,1 16,0 4,7 10,0 1046,1 26,2 -1,9
12 1-Methyl Naphthalene 2 38,0 20,6 0,8 4,7 1698,1 42,5 4,5
13 1-Nitropropane 2 28,9 16,6 12,3 5,5 1253,5 31,3 2,4
14 1-Octanol 2 27,2 16,0 5,0 11,9 1049,0 26,2 -1,0
15 1-Propanol 2 23,7 16,0 6,8 17,4 1070,2 26,8 3,1
16 1-Propanol 1 27,5 16,0 6,8 17,4 1070,2 26,8 -0,7
17 2-Chloro-2-Methyl Propane 2 19,1 15,6 7,6 2,0 1031,2 25,8 6,7
18 2-Phenyl-ethanol 1 41,0 19,0 5,8 7,2 1477,6 36,9 -4,1
19 2-Propanol 2 22,6 15,8 6,1 16,4 1035,8 25,9 3,3
20 2-Propanol 1 27,0 15,8 6,1 16,4 1035,8 25,9 -1,1
21 3-Methylbutanenitrile 2 25,6 15,4 9,7 4,6 1042,7 26,1 0,5
22 Acetic acid 1 23,0 14,5 8,0 13,5 905,0 22,6 -0,4
23 Acetone 2 24,6 15,5 10,4 7,0 1069,2 26,7 2,1
24 Acetone 1 23,3 15,5 10,4 7,0 1069,2 26,7 3,4
25 Acetonitrile 1 28,6 15,3 18,0 15,8 1260,4 31,5 2,9
26 Aniline 2 43,1 19,4 5,1 10,2 1531,5 38,3 -4,8
27 Benzene 2 28,2 18,4 0,0 2,0 1354,2 33,9 5,7
28 Benzene 1 28,8 18,4 0,0 2,0 1354,2 33,9 5,1
29 Benzyl Alcohol 2 38,5 18,4 6,3 13,7 1393,9 34,8 -3,7
30 Benzyl Benzoate 2 45,4 20,0 5,1 5,2 1626,0 40,7 -4,7
31 Bromobenzene 2 35,9 19,2 5,5 4,1 1504,8 37,6 1,7
32 Bromoform 2 40,8 21,4 4,1 6,1 1848,7 46,2 5,4
33 Butanone 1 24,0 16,0 9,0 5,1 1105,0 27,6 3,6
34 Butyronitrile 2 27,6 15,3 12,4 5,1 1090,1 27,3 -0,3
35 Carbon Tetrachloride 2 26,3 16,1 8,3 0,0 1105,7 27,6 1,3
36 Chlorobenzene 2 33,0 19,0 4,3 2,0 1462,5 36,6 3,6
37 Chloroform 2 26,9 17,8 3,1 5,7 1277,0 31,9 5,0
38 Cis-Decahydronaphthalene 2 31,0 18,8 0,0 0,0 1413,8 35,3 4,3
39 Cloroform 1 27,2 17,8 3,1 5,7 1277,0 31,9 4,7
40 Cyclohexane 2 24,3 16,8 0,0 0,2 1129,0 28,2 3,9
41 Cyclohexane 1 28,8 16,8 0,0 0,2 1129,0 28,2 -0,6
42 Cyclohexanol 2 34,4 17,4 4,1 13,5 1227,9 30,7 -3,7
43 Cyclohexanone 1 28,2 16,8 5,7 8,0 1161,5 29,0 0,8
44 Cyclopentanol 2 32,2 17,2 5,3 12,8 1211,5 30,3 -1,9
45 Decane 2 23,4 15,7 0,0 0,0 986,0 24,6 1,2
46 Dichloromethane 1 27,0 17,0 7,3 7,1 1209,3 30,2 3,2
47 Dichloromethane 2 25,9 17,0 7,3 7,1 1209,3 30,2 4,3
48 Diethyl ether 1 18,6 14,5 2,9 5,1 849,4 21,2 2,6
49 Diethyl Fumarate 2 31,1 16,7 5,6 7,6 1146,9 28,7 -2,4
50 Diethyl Phthalate 2 36,7 17,6 9,6 4,5 1331,2 33,3 -3,4
51 Diiodomethane 2 50,1 22,0 3,9 5,5 1951,2 48,8 -1,3
52 Dimethyl Formamide 2 36,4 17,4 13,7 11,3 1398,7 35,0 -1,4
53 Dipropylene Glycol Monomethyl Ether 2 27,9 15,5 5,7 11,2 993,5 24,8 -3,1
54 Dodecane 2 24,9 16,0 0,0 0,0 1024,0 25,6 0,7
55 Ethanol 2 21,7 15,8 8,8 19,4 1076,0 26,9 5,2
56 Ethanol 1 21,6 15,8 8,8 19,4 1076,0 26,9 5,3
57 Ethyl 2-Aminobenzoate 2 39,0 18,7 8,3 7,9 1467,7 36,7 -2,3
58 Ethyl Acetate 1 24,9 15,8 5,3 7,2 1026,7 25,7 0,8
59 Ethyl Benzene 2 28,7 17,8 0,6 1,4 1267,7 31,7 3,0
60 Ethyl Bromide 2 23,6 16,5 8,4 2,3 1159,6 29,0 5,4
61 Ethylene Dichloride 2 32,6 19,0 7,4 4,1 1498,8 37,5 4,9
62 Ethylene Glycol Monoethyl Ether 2 28,1 16,2 9,2 14,3 1134,4 28,4 0,3
63 Furfural 2 41,3 18,6 14,9 5,1 1605,9 40,1 -1,2
64 Heptane 2 19,7 15,3 0,0 0,0 936,4 23,4 3,7
65 Hexachloro-1,3-Butadiene 2 35,5 19,1 5,3 0,6 1487,3 37,2 1,7
66 Hexadecane 2 27,0 16,3 0,0 0,0 1062,8 26,6 -0,4
67 Hexane 2 17,9 14,9 0,0 0,0 888,0 22,2 4,3
68 Iodobenzene 2 39,1 19,5 6,0 6,1 1557,0 38,9 -0,2
69 Isopropyl Benzene (Cumene) 2 27,7 18,1 1,2 1,2 1311,9 32,8 5,1
70 Limonene 1 26,4 17,2 1,8 4,3 1186,6 29,7 3,3
71 Mesitylene 2 28,4 18,0 0,0 0,6 1296,0 32,4 4,0
72 Methanol 2 22,3 15,1 12,3 22,3 1063,3 26,6 4,3
73 Methyl Anthranilate 2 43,7 19,1 8,9 8,7 1538,5 38,5 -5,2
74 Methyl Ethyl Ketone 2 24,0 16,0 9,0 5,1 1105,0 27,6 3,6
75 m-Nitrotoluene 2 40,8 18,9 7,3 4,0 1482,1 37,1 -3,7
76 m-Xylene 2 28,3 17,6 1,0 3,1 1240,0 31,0 2,7
77 N,N-Dimethyl Acetamide 2 36,0 16,8 11,5 9,4 1261,2 31,5 -4,5
78 n-Butyl acetate 1 27,8 15,8 3,7 6,3 1012,3 25,3 -2,5
79 n-Butylbenzene 2 28,7 17,4 0,1 1,1 1211,1 30,3 1,6
80 n-Heptane 1 19,7 15,3 0,0 0,0 936,4 23,4 3,7
81 Nitrobenzene 2 43,3 20,0 8,6 4,1 1674,0 41,8 -1,5
82 Nitroethane 2 31,3 16,0 15,5 4,5 1264,3 31,6 0,3
83 Nitromethane 2 36,0 15,8 18,8 6,1 1352,0 33,8 -2,2
84 N-Methyl-2-Pyrrolidone 2 40,2 18,0 12,3 7,2 1447,3 36,2 -4,0
85 n-Tetradecane 2 26,1 16,2 0,0 0,0 1049,8 26,2 0,1
86 Octane 2 21,1 15,5 0,0 0,0 961,0 24,0 2,9
87 o-Nitrotoluene 2 40,9 19,0 7,5 4,3 1500,3 37,5 -3,4
88 o-Xylene 2 29,5 17,8 1,0 3,1 1268,4 31,7 2,2
89 p-Cymene 2 27,6 17,3 2,4 2,4 1202,9 30,1 2,5
90 Perfluoroheptane 2 12,4 12,0 0,0 0,0 576,0 14,4 2,0
91 Perfluorohexane (PFC 5060) 2 11,4 12,1 0,0 0,0 585,6 14,6 3,2
92 Perfluorooctane 2 13,5 12,1 0,8 0,3 586,3 14,7 1,2
93 Phenyl Isothiocyanate 2 40,9 19,4 13,9 8,5 1698,7 42,5 1,6
94 Propylbenzene 2 28,5 17,3 2,2 2,9 1202,0 30,1 1,6
95 Pyridine 2 37,3 19,0 8,8 5,9 1521,4 38,0 0,7
96 Pyrrole 2 36,1 19,2 7,4 6,7 1529,3 38,2 2,1
97 Quinoline 2 42,6 19,8 5,6 5,7 1599,5 40,0 -2,6
98 Tetrachloroethylene 1 28,4 18,3 5,7 0,0 1372,1 34,3 5,9
99 Tetrahydrofuran 1 27,2 16,8 5,7 8,0 1161,5 29,0 1,8
100 Tetrahydrofuran 2 25,8 16,8 5,7 8,0 1161,5 29,0 3,2
101 Toluene 2 27,8 18,0 1,4 2,0 1298,0 32,4 4,6
102 Toluene 1 27,5 18,0 1,4 2,0 1298,0 32,4 4,9
103 Tricresyl Phosphate 2 40,5 19,0 12,3 4,5 1595,3 39,9 -0,6
104 Triethanolamine 5 45,9 17,3 22,4 23,3 1698,9 42,5 -3,4
105 Undecane 2 24,2 16,0 0,0 0,0 1024,0 25,6 1,4
106 Xylene (isomers) 1 27,8 17,7 1,0 3,1 1254,2 31,4 3,6
The “Ref” column indicates the origin of surface tension data. When the reference is 1, it means that the data have been directly measured by the authors using the Harkins and Brown droplet weight method. When the reference is 2, it indicates that the data have been published by [7]. In some cases, surface tension data of the same substance but with references 1 and 2 are shown with the intent to test the (always small) variability of both references. Moreover Hansen solubility parameters are included according to the values published in the second edition of his manual [2]. Likewise, the calculated squares of the interaction vectors like 4dD2+dP2, surface tensions calculated after linear regression and absolute error between calculated and experimental or bibliographic values are shown.
Table A2. Surface tension of liquids versus air, σLG, at 25 ºC and solubility parameters. Low molar volume and high ionicity molecules.
Table A2. Surface tension of liquids versus air, σLG, at 25 ºC and solubility parameters. Low molar volume and high ionicity molecules.
Nº Substance Ref. σLG, mN/m δD, MPa1/2 δP, Mpa1/2 δH, MPa1/2 4δD2+δP2+δH2, MPa σLG,cal., mN/m Error, mN/m
107 1,5-Pentanediol 2 42,7 17,0 8,9 19,8 1627,3 40,7 -2,0
108 Diethylene Glycol 2 44,4 16,6 12,0 20,7 1674,7 41,9 -2,5
109 Diethylene Glycol 4 44,4 16,6 12,0 20,7 1674,7 41,9 -2,5
110 Dipropylene Glycol 2 33,4 16,5 10,6 17,7 1514,7 37,9 4,5
111 Dipropylene Glycol 1 34,8 16,5 10,6 17,7 1514,7 37,9 3,1
112 Dimethyl sulfoxide 1 42,2 18,4 16,4 10,2 1727,2 43,2 0,9
113 Dimethyl sulfoxide 3 41,8 18,4 16,4 10,2 1727,2 43,2 1,4
114 Dimethylformamide 3 39,1 17,4 13,7 11,3 1526,4 38,2 -0,9
115 Ethanolamine 2 48,3 17,0 15,5 21,2 1845,7 46,1 -2,2
116 Ethylene Glycol 2 47,3 17,0 11,0 26,0 1953,0 48,8 1,5
117 Formamide 2 57,8 17,2 26,2 19,0 2230,8 55,8 -2,0
118 Formic acid 3 31,4 14,3 11,9 16,6 1235,1 30,9 -0,5
119 Glycerol 2 64,3 17,4 12,1 29,3 2215,9 55,4 -8,9
120 Glycerol 3 63,7 17,4 12,1 29,3 2215,9 55,4 -8,3
121 3-Hydroxymethylpyridine 2 47,4 19,2 9,6 14,5 1777,0 44,4 -3,0
122 Water (molecule) 2 72,0 15,5 16,0 42,3 3006,3 75,2 3,2
When reference 1 is indicated, it means that surface tension values have been determined in a laboratory by the authors using the Harkins and Brown droplet weight method. Data with reference 2 are provided by [7], those with reference 3 are taken of [18], and those with reference 4 are from [19]. Solubility parameters data obtained by [2] are also shown. Calculated surface tensions and absolute error in regard to experimental or bibliographic values is also shown.
Table A3. Surface free energy of solids with air, σLG, at 25 ºC and solubility parameters. Source: Weiyan Yu and Wanguo, 2019 [10].
Table A3. Surface free energy of solids with air, σLG, at 25 ºC and solubility parameters. Source: Weiyan Yu and Wanguo, 2019 [10].
Nº Substance σSG, mN/m δD, MPa1/2 δP, Mpa1/2 δH, MPa1/2 4δD2+δP2+δH2, MPa σSG,cal., mN/m Error, mN/m
1 Polyethylene 33,0 17,3 1,7 2,1 1204,5 31,3 -1,7
2 Poly(vinyl chloride) 40,8 18,6 5,8 9,0 1498,5 39,0 -1,8
3 Poly(vinylidene chloride) 41,6 17,6 9,1 7,8 1382,7 35,9 -5,7
4 Poly(vinyl fluoride) 36,7 17,4 13,7 11,3 1526,4 39,7 3,0
5 Poly(vinylidene fluoride) 31,4 17,0 12,1 10,2 1406,5 36,6 5,2
6 Poly(tetrafluoroethylene) 15,0 15,1 0,9 1,7 915,7 23,8 8,8
7 Poly(ethylene terephthalate) 41,9 18,2 6,4 3,7 1379,6 35,9 -6,0
8 Poly(methyl methacrylate) 40,7 17,0 4,8 5,7 1211,5 31,5 -9,2
9 PA66 43,5 18,7 5,2 8,4 1496,4 38,9 -4,6
10 Polystyrene 41,3 20,5 3,1 2,6 1697,4 44,1 2,8
11 Polychlorotrifluoroethylene 26,9 14,1 2,7 5,5 832,8 21,7 -5,2
12 Polypropylene 30,1 18,1 1,0 0,0 1311,4 34,1 4,0
13 Polyisobutylene 33,6 16,9 2,5 4,0 1164,7 30,3 -3,3
14 Poly-α-methyl styrene 39,0 18,5 2,4 2,4 1380,5 35,9 -3,1
15 Poly-n-butyl methacrylate 31,2 15,9 5,5 5,9 1076,3 28,0 -3,2
16 Polycarbonate 34,2 18,4 5,9 6,9 1436,7 37,4 3,2
17 Polyethylmethacrylate 35,9 17,6 9,7 4,0 1349,1 35,1 -0,8
18 Graphite 35,0 18,0 9,3 7,7 1441,8 37,5 2,5
19 MoS2 34,4 18,0 9,0 6,2 1415,4 36,8 2,4
20 WS2 33,1 17,0 9,5 13,2 1420,5 36,9 3,8
21 BN 30,1 18,0 7,0 7,0 1394,0 36,2 6,1
Table A4. Interfacial tension of solids with liquids, SL, at 25 ºC and solubility parameters. Source: Masakazu Murase and Daisuke Nakamura, 2023 [7].
Table A4. Interfacial tension of solids with liquids, SL, at 25 ºC and solubility parameters. Source: Masakazu Murase and Daisuke Nakamura, 2023 [7].
HSPS HSPL
Solid Liquid σSL, mN/m δDS, MPa1/2 δPS, Mpa1/2 δHS, MPa1/2 δDL, MPa1/2 δPL, Mpa1/2 δHL, MPa1/2 S → S L 2 , MPa σSL, calc., mN/m Error, mN/m
PS Water 49,4 20,6 2,5 1,5 15,5 16,0 42,3 1953,8 52,8 3,4
Formamide 26,6 20,6 2,5 1,5 17,2 26,2 19,0 914,2 24,7 -1,9
Ethylene Glycol 21,9 20,6 2,5 1,5 17,0 11,0 26,0 726,0 19,6 -2,3
Benzyl Alcohol 0,4 20,6 2,5 1,5 18,4 6,3 13,7 183,5 5,0 4,6
Nitromethane 8,1 20,6 2,5 1,5 15,8 18,8 5,1 369,8 10,0 1,9
PMMA Water 27,0 18,5 9,0 8,4 15,5 16,0 42,3 1235,6 33,4 6,4
Formamide 17,2 18,5 9,0 8,4 17,2 26,2 19,0 414,1 11,2 -6,0
Ethylene Glycol 17,9 18,5 9,0 8,4 17,0 11,0 26,0 323,7 8,7 -9,2
Benzyl Alcohol 5,3 18,5 9,0 8,4 18,4 6,3 13,7 36,0 1,0 -4,3
1-Bromonaphtalene 3,9 18,5 9,0 8,4 20,6 3,1 4,1 71,6 1,9 -2,0
Nitromethane 8,7 18,5 9,0 8,4 15,8 18,8 5,1 134,4 3,6 -5,1
PA66 Water 15,6 19,5 6,2 14,7 15,5 16,0 42,3 921,3 24,9 9,3
Formamide 9,6 19,5 6,2 14,7 17,2 26,2 19,0 438,6 11,8 2,2
Ethylene Glycol 10,4 19,5 6,2 14,7 17,0 11,0 26,0 175,4 4,7 -5,7
Benzyl Alcohol 6,0 19,5 6,2 14,7 18,4 6,3 13,7 5,7 0,2 -5,8
1-Bromonaphtalene 1,7 19,5 6,2 14,7 20,6 3,1 4,1 126,9 3,4 1,7
Nitromethane 9,9 19,5 6,2 14,7 15,8 18,8 5,1 304,4 8,2 -1,7
PTFE Water 55,8 13,6 1,7 0,0 15,5 16,0 42,3 2008,4 54,2 -1,6
Formamide 31,1 13,6 1,7 0,0 17,2 26,2 19,0 1013,6 27,4 -3,7
Ethylene Glycol 27,2 13,6 1,7 0,0 17,0 11,0 26,0 809,7 21,9 -5,3
Benzyl Alcohol 13,6 13,6 1,7 0,0 18,4 6,3 13,7 302,8 8,2 -5,4
1-Bromonaphtalene 13,8 13,6 1,7 0,0 20,6 3,1 4,1 217,5 5,9 -7,9
Nitromethane 8,1 13,6 1,7 0,0 15,8 18,8 5,1 338,0 9,1 1,0
n-Decane 2,9 13,6 1,7 0,0 15,7 0,0 0,0 21,4 0,6 -2,3
n-Hexane 2,7 13,6 1,7 0,0 14,9 0,0 0,0 10,2 0,3 -2,4
Dimethyl sulfoxide 15,0 13,6 1,7 0,0 18,4 16,4 10,2 413,6 11,2 -3,8
PVB Water 33,9 17,9 8,3 4,2 15,5 16,0 42,3 1534,2 41,4 7,5
Formamide 18,3 17,9 8,3 4,2 17,2 26,2 19,0 540,9 14,6 -3,7
Ethylene Glycol 20,0 17,9 8,3 4,2 17,0 11,0 26,0 486,0 13,1 -6,9
Benzyl Alcohol 8,4 17,9 8,3 4,2 18,4 6,3 13,7 95,6 2,6 -5,8
1-Bromonaphtalene 3,0 17,9 8,3 4,2 20,6 3,1 4,1 56,6 1,5 -1,5
Nitromethane 9,1 17,9 8,3 4,2 15,8 18,8 5,1 128,1 3,5 -5,6
Table A5. Contact angle of diverse liquids over PMMA and n-Octacosane. PMMA solubility parameters: δD = 18.64, δP = 10.52, δH = 7.51. n-Octacosane solubility parameters: δD = 16.91, δP = 0 δH = 0. Source: J. Panzer, 1973 [11].
Table A5. Contact angle of diverse liquids over PMMA and n-Octacosane. PMMA solubility parameters: δD = 18.64, δP = 10.52, δH = 7.51. n-Octacosane solubility parameters: δD = 16.91, δP = 0 δH = 0. Source: J. Panzer, 1973 [11].
Liquid Solid θexp. δD, MPa1/2 δP, Mpa1/2 δH, MPa1/2 S → L G 2 S → S G 2 S → S L 2 θcalc.
Octane n-Octacosane 0 15,5 0,0 0,0 961,0 1143,8 8,0 0
2-Propanol PMMA 0 15,8 6,1 16,4 1035,8 1556,9 130,8 0
Acetone PMMA 0 15,5 10,4 7,0 1069,2 1556,9 39,7 0
Benzyl alcohol PMMA 0 18,4 6,3 13,7 1393,9 1556,9 56,4 0
Bromobenzene PMMA 0 19,2 5,5 4,1 1504,8 1556,9 38,1 0
Ethyl acetate PMMA 0 15,8 5,3 7,2 1026,7 1556,9 59,6 0
Octane PMMA 0 15,5 0,0 0,0 961,0 1556,9 206,5 0
Tetrahydrofuran PMMA 0 16,8 5,7 8,0 1161,5 1556,9 37,0 0
Chlorobenzene PMMA 1 19,0 4,3 2,0 1462,5 1556,9 69,6 0
Dodecane PMMA 1 16,0 0,0 0,0 1024,0 1556,9 194,9 0
Pyridine PMMA 1 19,0 8,8 5,9 1521,4 1556,9 6,1 0
Ethanol PMMA 2,5 15,8 8,8 19,4 1076,0 1556,9 176,6 0
Methanol PMMA 3 15,1 12,3 22,3 1063,3 1556,9 272,0 0
o-xylene PMMA 3 17,8 1,0 3,1 1268,4 1556,9 112,9 0
Hexadecane PMMA 4 16,3 0,0 0,0 1062,8 1556,9 189,0 0
Nitroethane PMMA 7 16,0 15,5 4,5 1264,3 1556,9 61,7 0
Carbon Tetrachloride PMMA 8 16,1 8,3 0,0 1105,7 1556,9 87,1 0
Cyclohexanol PMMA 8 17,4 4,1 13,5 1227,9 1556,9 83,2 0
Carbon Tetrachloride n-Octacosane 24 17,8 0,0 0,6 1267,4 1143,8 3,5 26
Diethylene glycol PMMA 35 16,6 12,0 20,7 1674,7 1556,9 192,8 35
Cyclohexanol n-Octacosane 36 17,4 4,1 13,5 1227,9 1143,8 200,0 40
Bromoform n-Octacosane 39 21,4 4,1 6,1 1848,7 1143,8 134,7 57
Pyridine n-Octacosane 39 19,0 8,8 5,9 1521,4 1143,8 129,7 48
Nitroethane n-Octacosane 40 16,0 15,5 4,5 1264,3 1143,8 263,8 46
Nitrobenzene n-Octacosane 45 20,0 8,6 4,1 1674,0 1143,8 129,0 53
Nitromethane n-Octacosane 51 15,8 18,8 6,1 1352,0 1143,8 395,6 56
Ethylene Glycol PMMA 51 17,0 11,0 26,0 1953,0 1556,9 352,9 52
Formamide PMMA 52 17,2 26,2 19,0 2230,8 1556,9 386,2 58
Glycerol PMMA 68 17,4 12,1 29,3 2215,9 1556,9 483,5 61
Water PMMA 71 15,5 16,0 30,3 2135,1 1556,9 588,9 63
Diethylene glycol n-Octacosane 76 16,6 12,0 20,7 1674,7 1143,8 572,9 70
Dimethyl sulfoxide n-Octacosane 76 18,4 16,4 10,2 1727,2 1143,8 381,9 64
Ethylene Glycol n-Octacosane 86 17,0 11,0 26,0 1953,0 1143,8 797,0 80
Formamide n-Octacosane 95 17,2 26,2 19,0 2230,8 1143,8 1047,8 88
Glycerol n-Octacosane 95 17,4 12,1 29,3 2215,9 1143,8 1005,9 86
Water n-Octacosane 106 15,5 16,0 30,3 2135,1 1143,8 1182,0 91
Solubility parameters values from liquids and Poly(methyl methacrylate) (PMMA) are the ones published by [2]. n-Octacosane solubility parameters have been calculated by extrapolation from homologue hydrocarbons data published by Hansen, as well. Square of the module of the interaction vector for liquid-air, solid-air and solid-liquid interactions, and calculated contact angle data are as well shown in the table.

References

  1. Hildebrand, J. H.; Scott, R. L. The solubility of Nonelectrolytes; Reinhold: New York, 1950. [Google Scholar]
  2. Hansen, C.M. Hansen Solubility Parameters. A User's Handbook; CRC Press. Taylor & Francis Group: Boca Ratón, 2007. [Google Scholar]
  3. Beerbower, A. Surface Free Energy: A New Relationship to Bulk Energies. Journal of Colloid and Interface Science 1971, 35, 126–131. [Google Scholar] [CrossRef]
  4. Koenhen, D. M.; Smolders, C. A. The determination of Solubility Parameters of Solvents and Polymers by Means of Correlations with other Physical Quantities. Journal of Applied Polymer Science 1975, 19, 1163–1179. [Google Scholar] [CrossRef]
  5. Large, M. J.; Ogilvie, S. P.; King, A. A.; Dalton, A. B. Understanding Solvent Spreading for Langmuir Deposition of Nanomaterial Films: A Hansen Solubility Parameter Approach. Langmuir 2017, 33, 14766–14771. [Google Scholar] [CrossRef] [PubMed]
  6. AlQasas, N.; Eskhan, A.; Johnson, D. Hansen Solubility Parameters from Surface Measurements: A Comparison of Different Methods. Surfaces and Interfaces 2023, 36, 102594. [Google Scholar] [CrossRef]
  7. Murase, M.; Nakamura, D. Hansen Solubility Parameters for Directly Dealing with Surface and Interfacial Phenomena. Langmuir 2023, 39, 10475–10484. [Google Scholar] [CrossRef] [PubMed]
  8. Abbott, S.; Hansen, C.M.; Yamamoto, H.; Valpey, R. S. Hansen Solubility Parameters in Practice, Complete with eBook, Software and Data. 2013. [Google Scholar]
  9. Harkins, W. D.; Brown, F. E. The Determination of Surface Tension (Free Surface Energy) and the Weight of Falling Drops: The Surface Tension of Water and Benzene by the Capillary Method. Journal of the American Chemical Society 1919, 41, 499–525. [Google Scholar] [CrossRef]
  10. Yu, W.; Hou, W. Correlations of Surface Free Energy and Solubility Parameters for Solid Substances. Journal of Colloid and Interface Science 2019, 544, 8–13. [Google Scholar] [CrossRef] [PubMed]
  11. Panzer, J. Components of Solid Surface Free Energy from Wetting Measurements. Journal of Colloid and Interface Science 1973, 44, 142–161. [Google Scholar] [CrossRef]
  12. Gibbs, J. W. On the equilibrium of heterogeneus substances. American Journal of Science 1878, s3-16, 441–458. [Google Scholar] [CrossRef]
  13. Guggenheim, E. A. The Thermodynamics of Interfaces in Systems of Several Componets. Transactions of the Farady Society 1940, 35, 397–411. [Google Scholar] [CrossRef]
  14. Dadashev, R. K.; Elimkhanov, D. Z.; Kutuev, R. A.; Umarkhadzhiev, K. S. Concentration Dependence of the Distance Between Different Positions of the Gibbs Dividing Surface in Two-Component Solutions. Russian Journal of Physical Chemistry A 2021, 95, 2290–2294. [Google Scholar] [CrossRef]
  15. Cho, J. Pressure Coefficient of Interfacial Tension for Polymer Blends. Macromolecular Research 2013, 21, 1360–1365. [Google Scholar] [CrossRef]
  16. Cho, J. Superposition in Flory-Huggins X and Interfacial Tension for Compresible Polymer Blends. Macro Letters 2013, 2, 544–549. [Google Scholar] [CrossRef] [PubMed]
  17. Werner, A.; Schmid, F.; Müller, M.; Binder, K. "Intrinsic" Profiles and Capillary Waves at Homopolymer Interfaces: A Monte Carlo Study. Physical Review E 1999, 59, 728–738. [Google Scholar] [CrossRef]
  18. Singh, M. Survismeter, 2-in-1 For Viscosity and Surface Tension Measurement, an Excellent Invention for Industrial Proliferation of Surface Forces in Liquids. Surface review and Letters 2007, 14, 973–983. [Google Scholar] [CrossRef]
  19. Gaur, A. P.; Sahoo, S.; Ahmadi, M.; Dash, S. P.; Guinel, M. J. F.; Katiyar, R. S. Surface Energy Engineering for Tunable Wettability through Controlled Synthesis of MoS2. Nano Letters 2014, 14, 4314–4321. [Google Scholar] [CrossRef] [PubMed]
Preprints 109170 g001
Figure 1. Hansen solubility parameters vector space.
Figure 1. Hansen solubility parameters vector space.
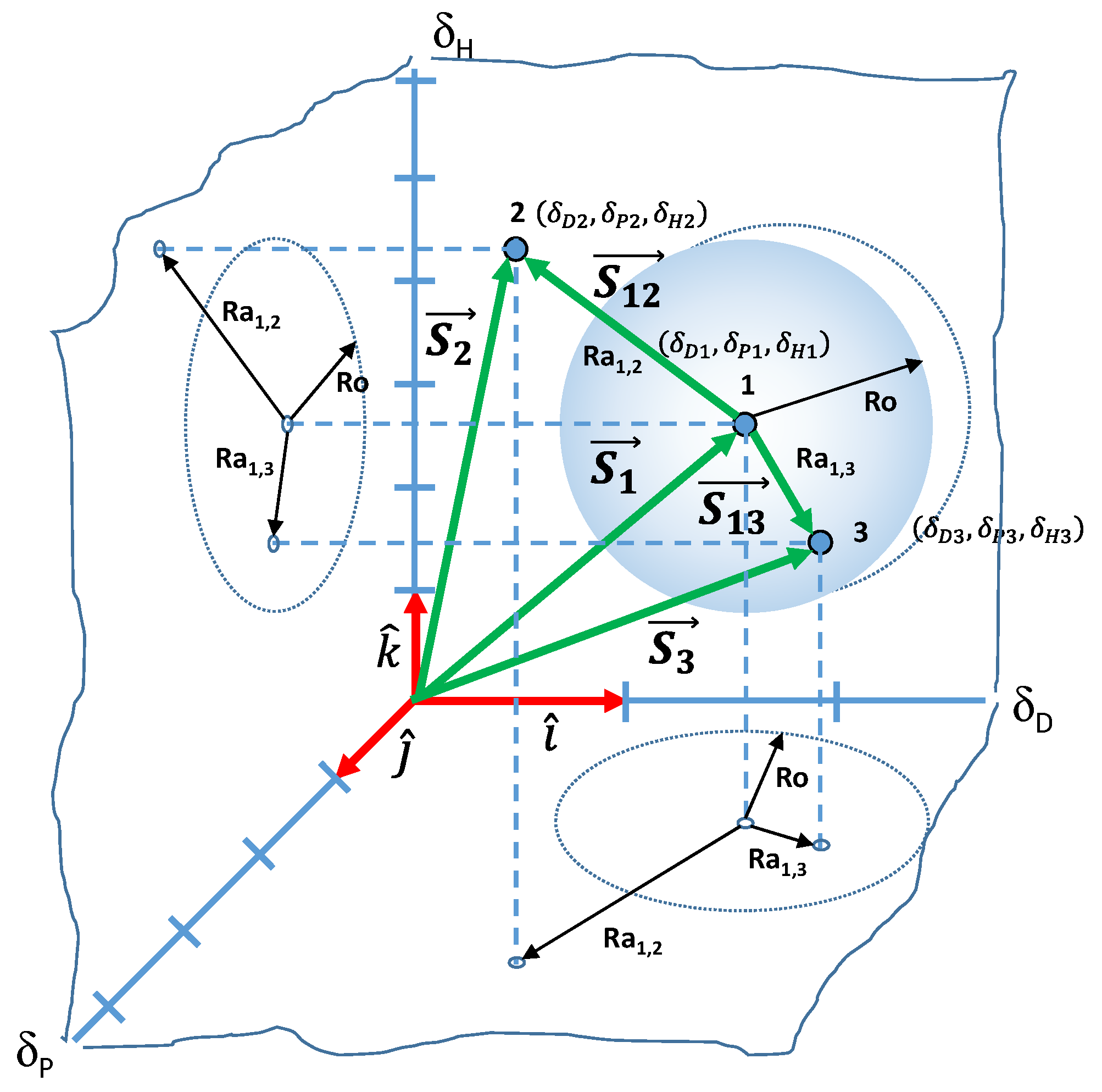
Preprints 109170 g001
Preprints 109170 g002
Figure 2. Liquid-air interface for a) pentane, b) hexanoic acid and c) formic acid.
Figure 2. Liquid-air interface for a) pentane, b) hexanoic acid and c) formic acid.
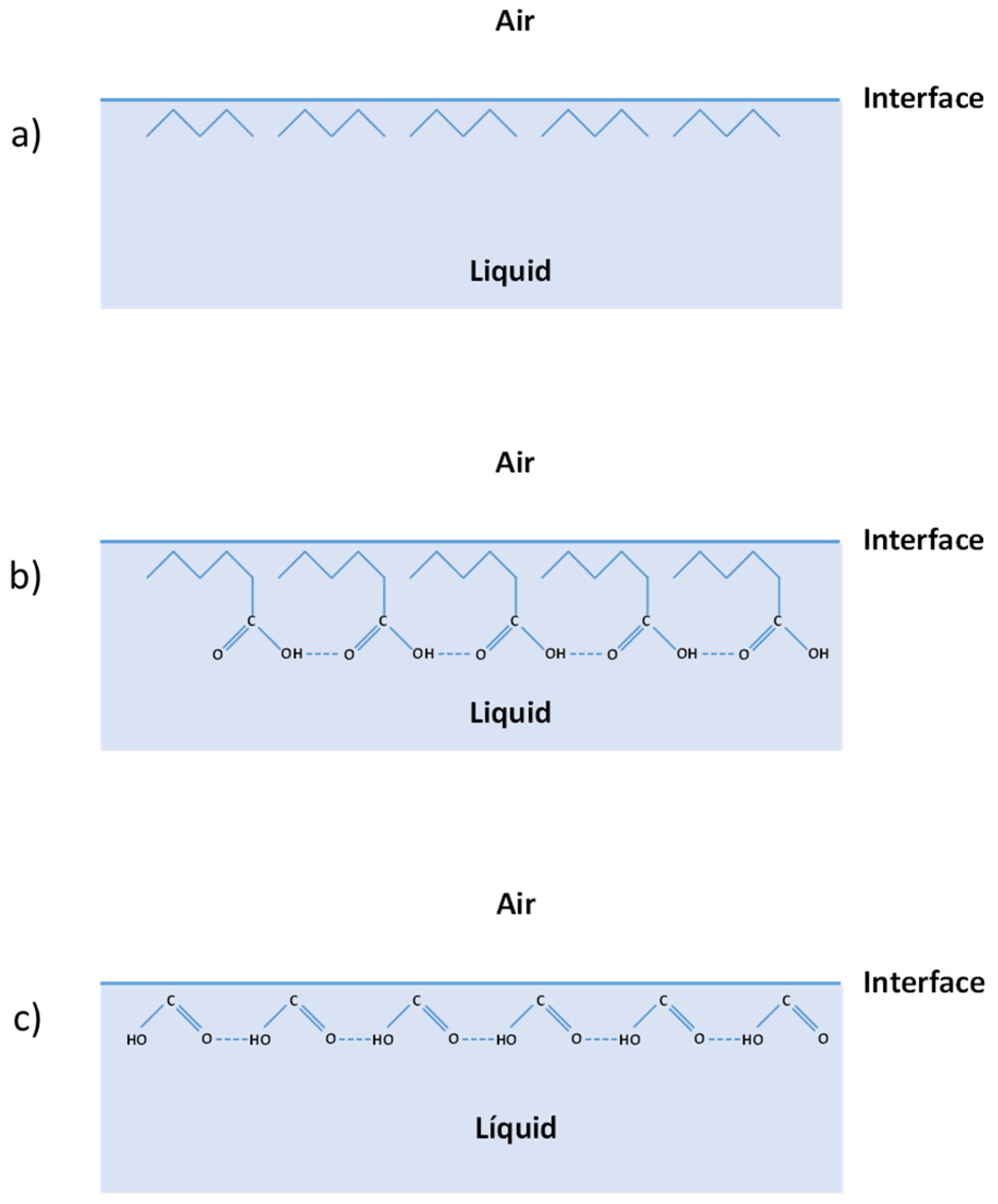
Preprints 109170 g002
Preprints 109170 g003
Figure 3. Correlation of surface tension, σLG, and 4δD2+δP2, for every molecule type except for low molecular mass ionic molecules.
Figure 3. Correlation of surface tension, σLG, and 4δD2+δP2, for every molecule type except for low molecular mass ionic molecules.
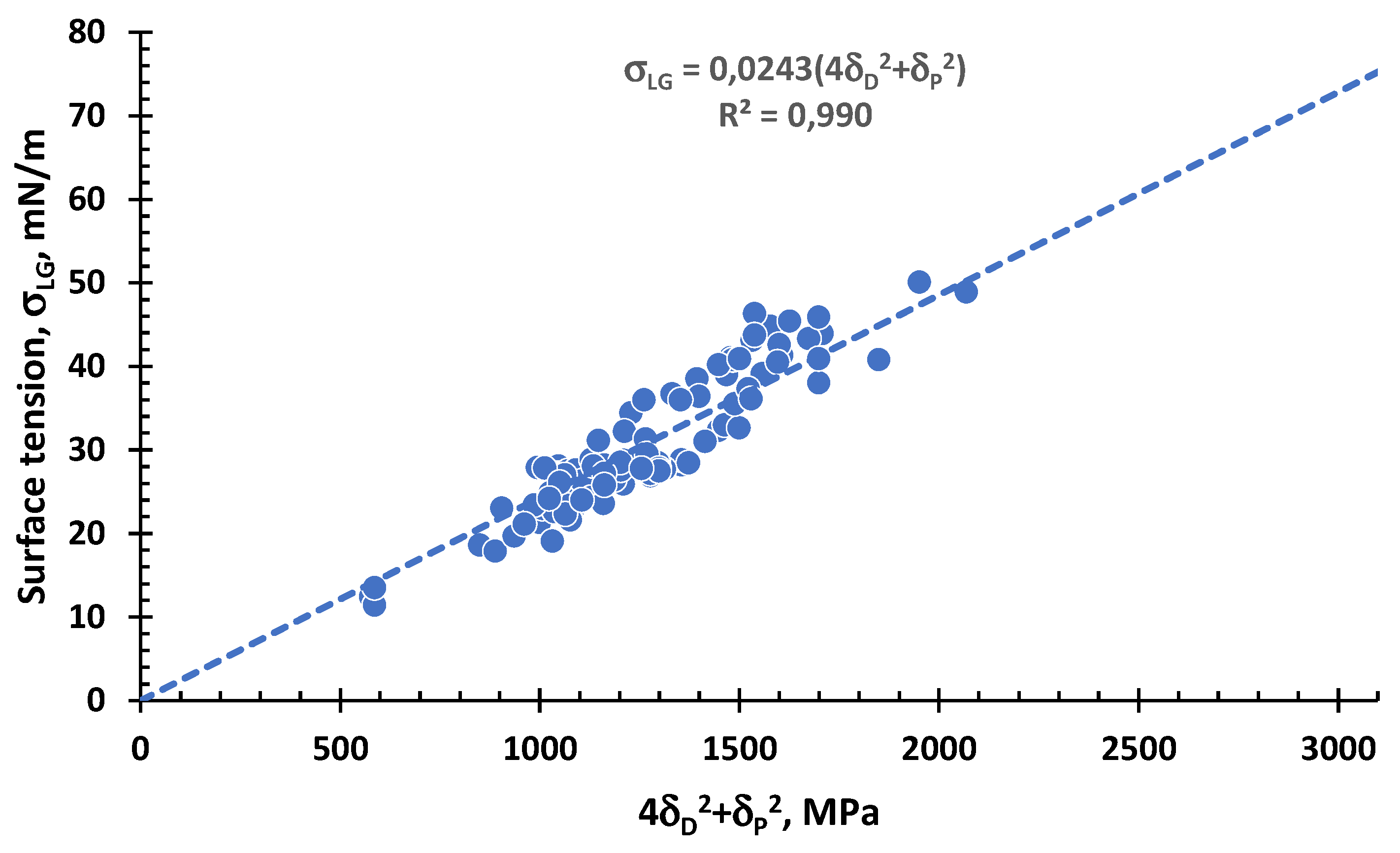
Preprints 109170 g003
Preprints 109170 g004
Figure 4. Surface Iso-tension curves, σ, in mN/m, for liquid substances with molar volume, v, equal or bigger than 100 cm3/mol, for every hydrogen bonding parameter value, δH,.
Figure 4. Surface Iso-tension curves, σ, in mN/m, for liquid substances with molar volume, v, equal or bigger than 100 cm3/mol, for every hydrogen bonding parameter value, δH,.
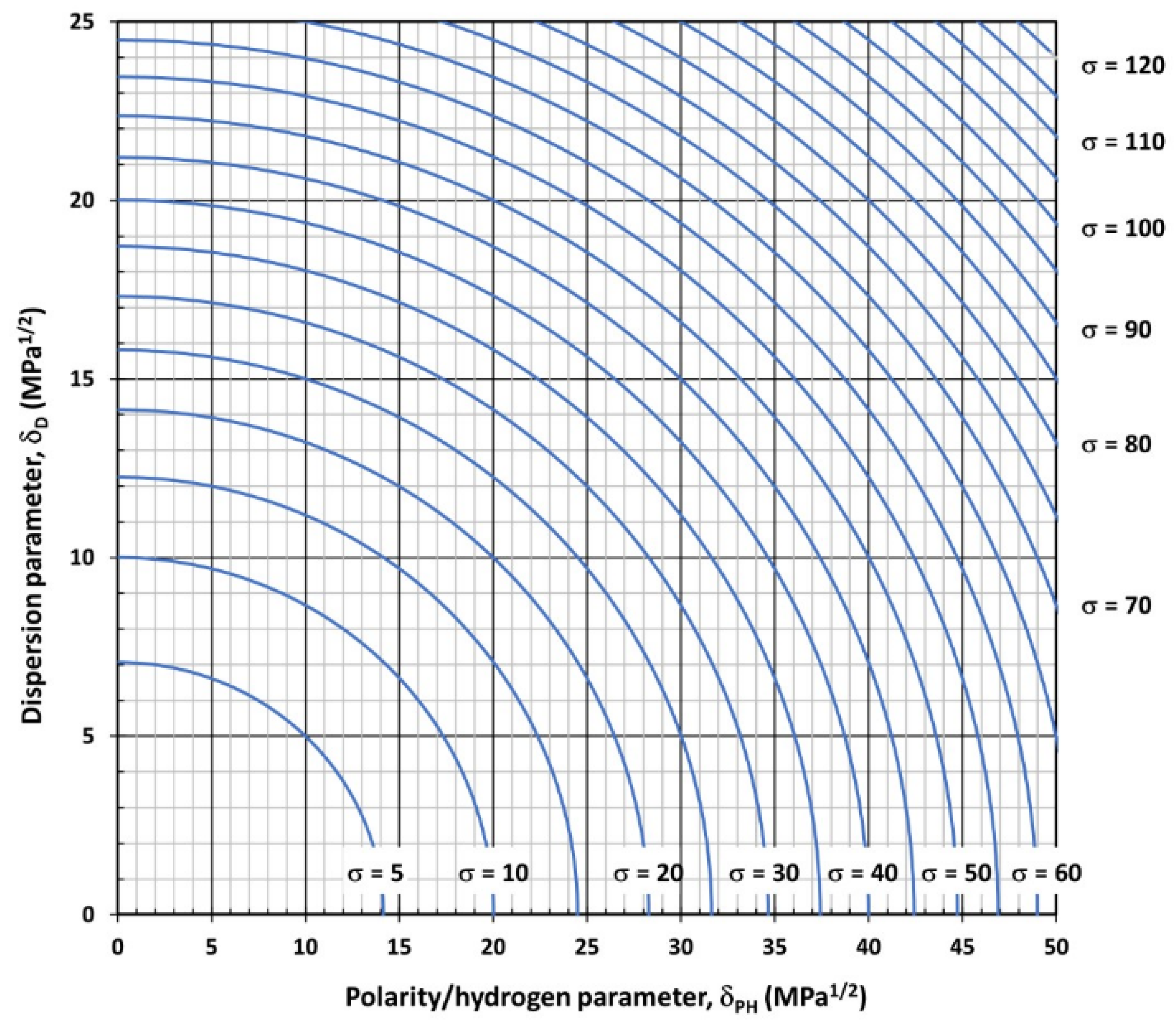
Preprints 109170 g004
Preprints 109170 g005
Figure 5. Correlation between surface tension, σLG, and 4δD2+δP2+δH2 for polar and low mass molecules.
Figure 5. Correlation between surface tension, σLG, and 4δD2+δP2+δH2 for polar and low mass molecules.
Preprints 109170 g005
Preprints 109170 g006
Figure 6. Correlation of surface free energy of solids, σSG, and 4δD2+δP2+δH2.
Figure 6. Correlation of surface free energy of solids, σSG, and 4δD2+δP2+δH2.
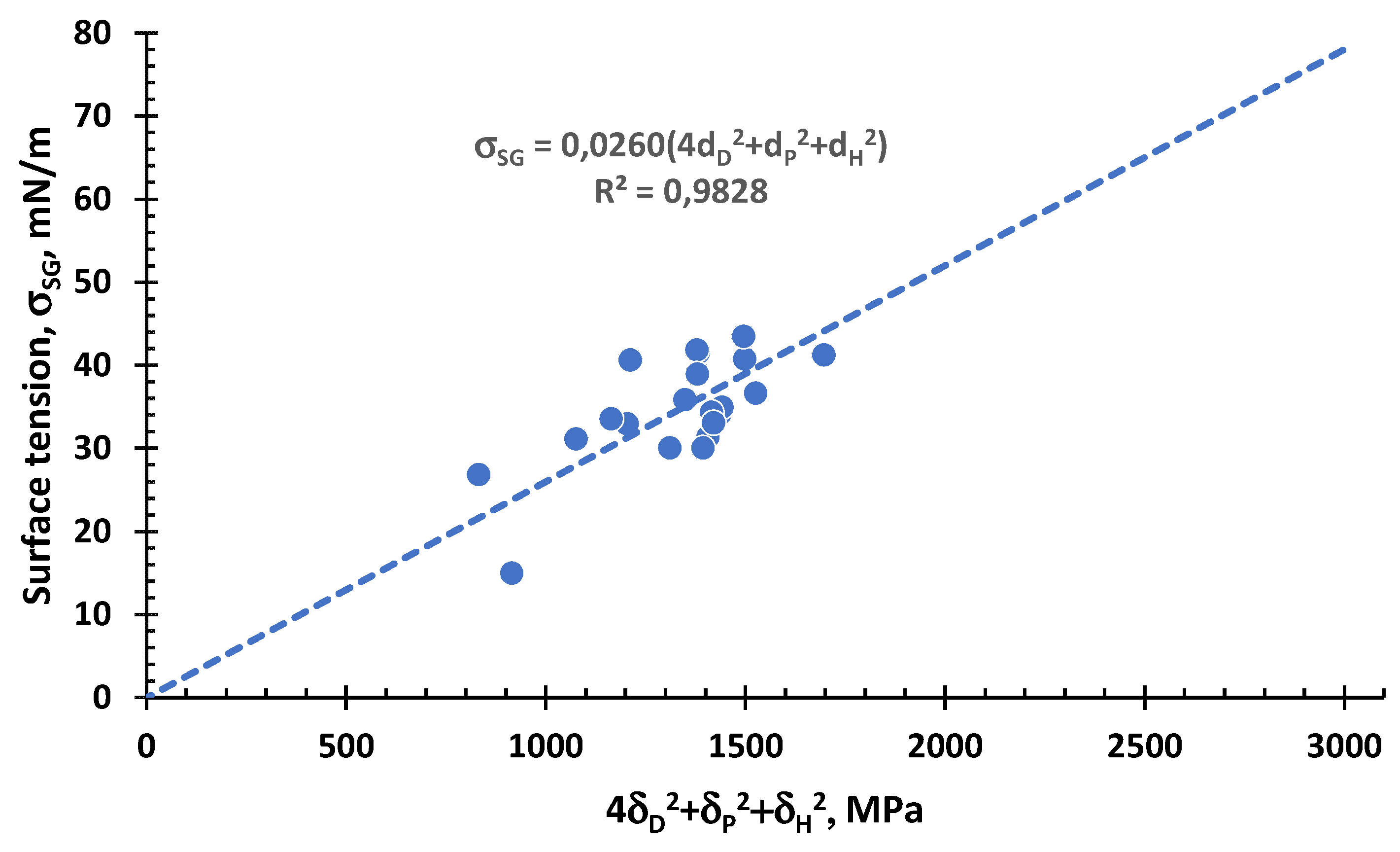
Preprints 109170 g006
Preprints 109170 g007
Figure 7. Interaction vectors of a three-phase system: solid (S), liquid (L), and gas (G).
Figure 7. Interaction vectors of a three-phase system: solid (S), liquid (L), and gas (G).
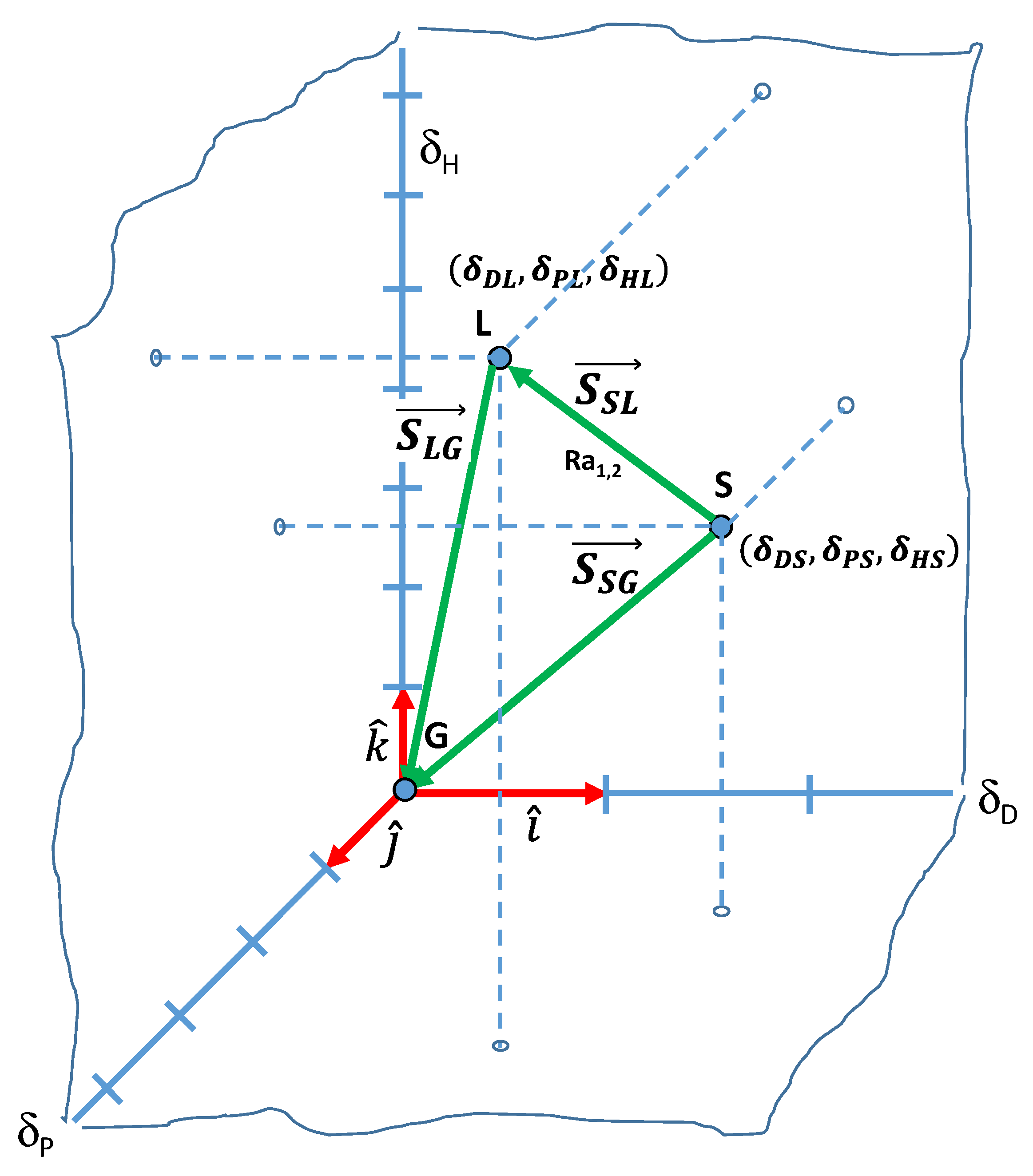
Preprints 109170 g007
Preprints 109170 g008
Figure 8. Correlation between interfacial tension of solids with liquids, sSL, and the square of the module of the interaction vector.
Figure 8. Correlation between interfacial tension of solids with liquids, sSL, and the square of the module of the interaction vector.
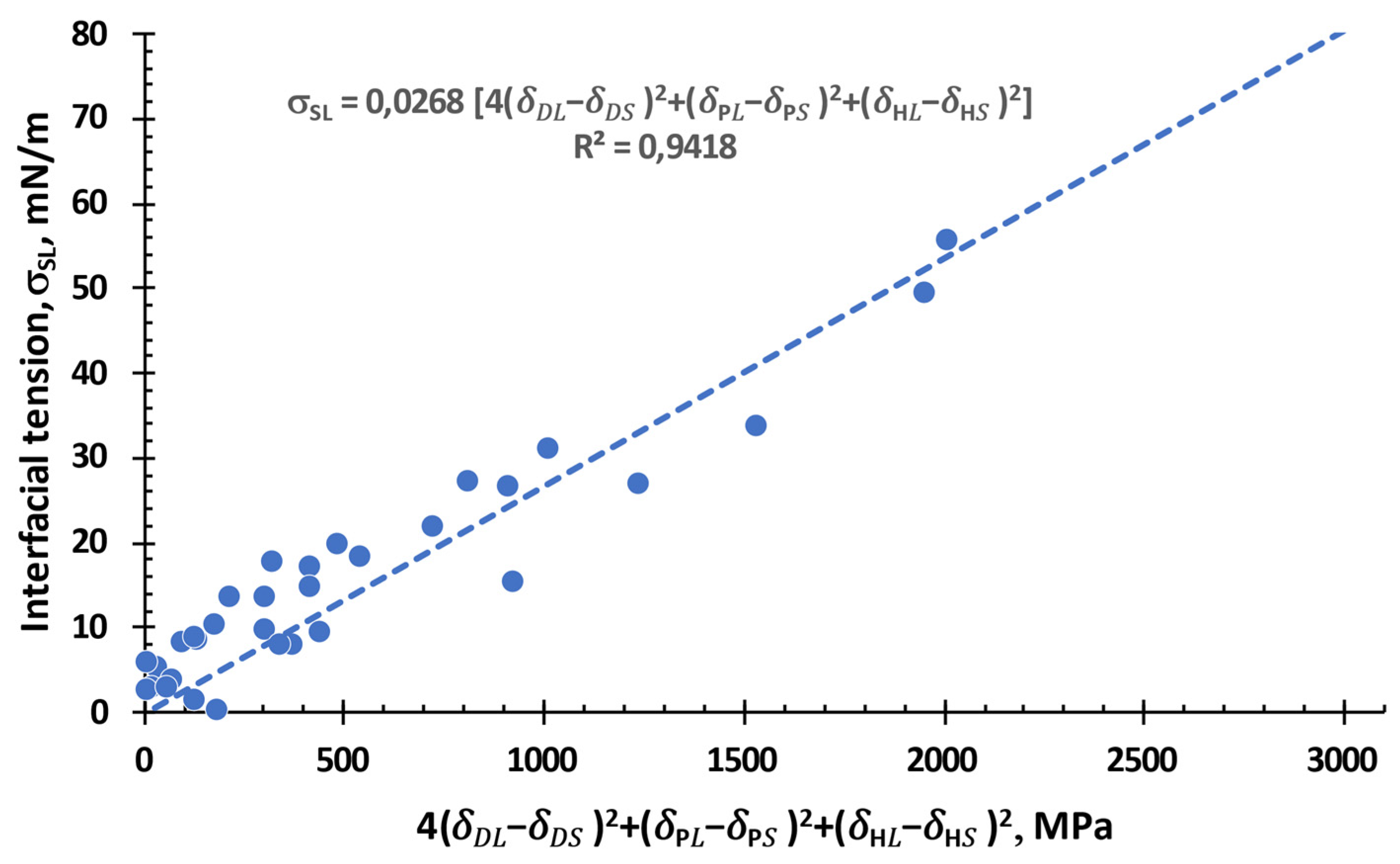
Preprints 109170 g008
Preprints 109170 g009
Figure 9. Correlation between free surface energy and the square of the magnitude of the interaction vector.
Figure 9. Correlation between free surface energy and the square of the magnitude of the interaction vector.
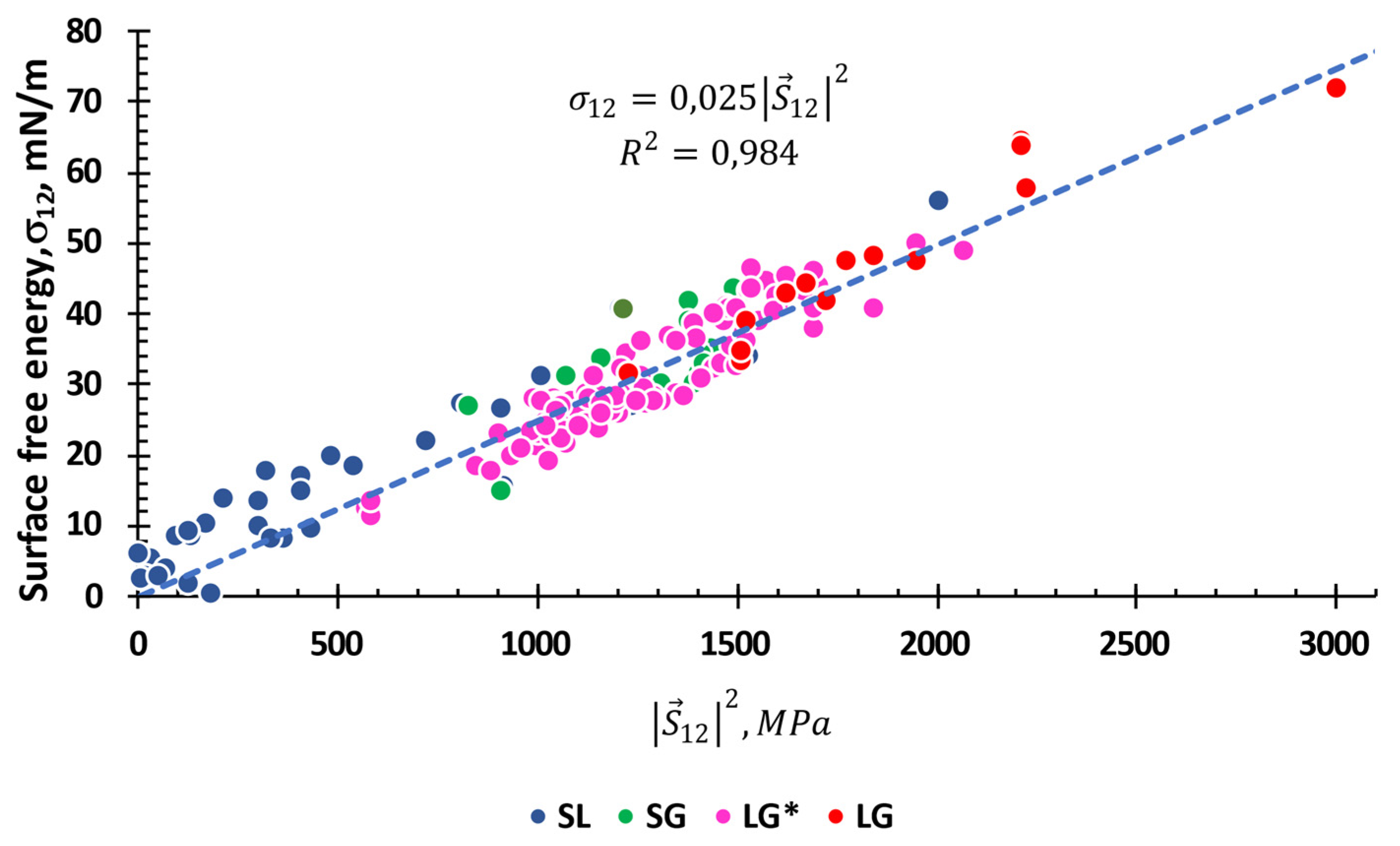
Preprints 109170 g009
Preprints 109170 g010
Figure 10. Idealized image of an interfacial layer between two phases.
Figure 10. Idealized image of an interfacial layer between two phases.
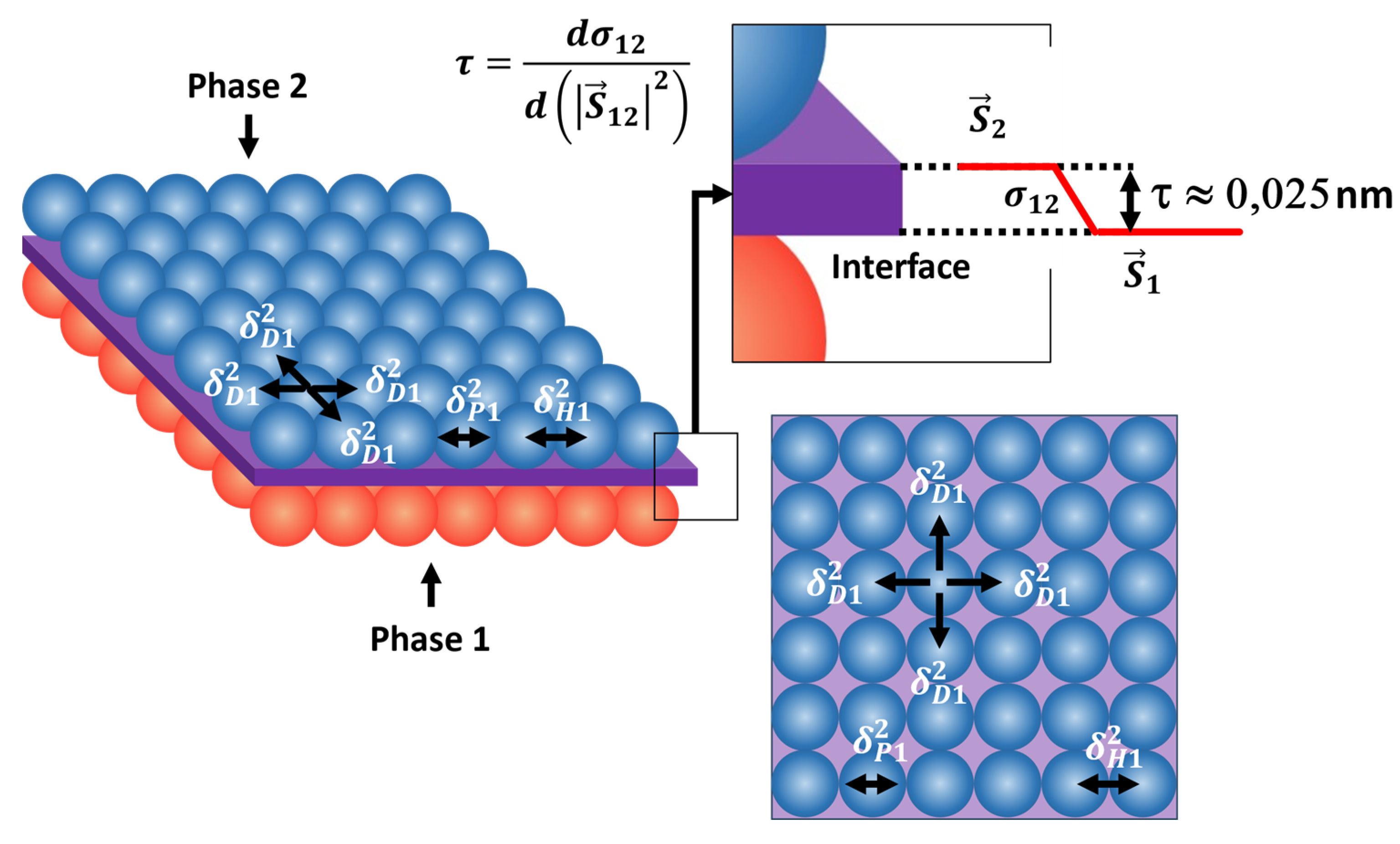
Preprints 109170 g010
Preprints 109170 g011
Figure 11. Tension balance of a liquid droplet dropped over a solid surface.
Figure 11. Tension balance of a liquid droplet dropped over a solid surface.
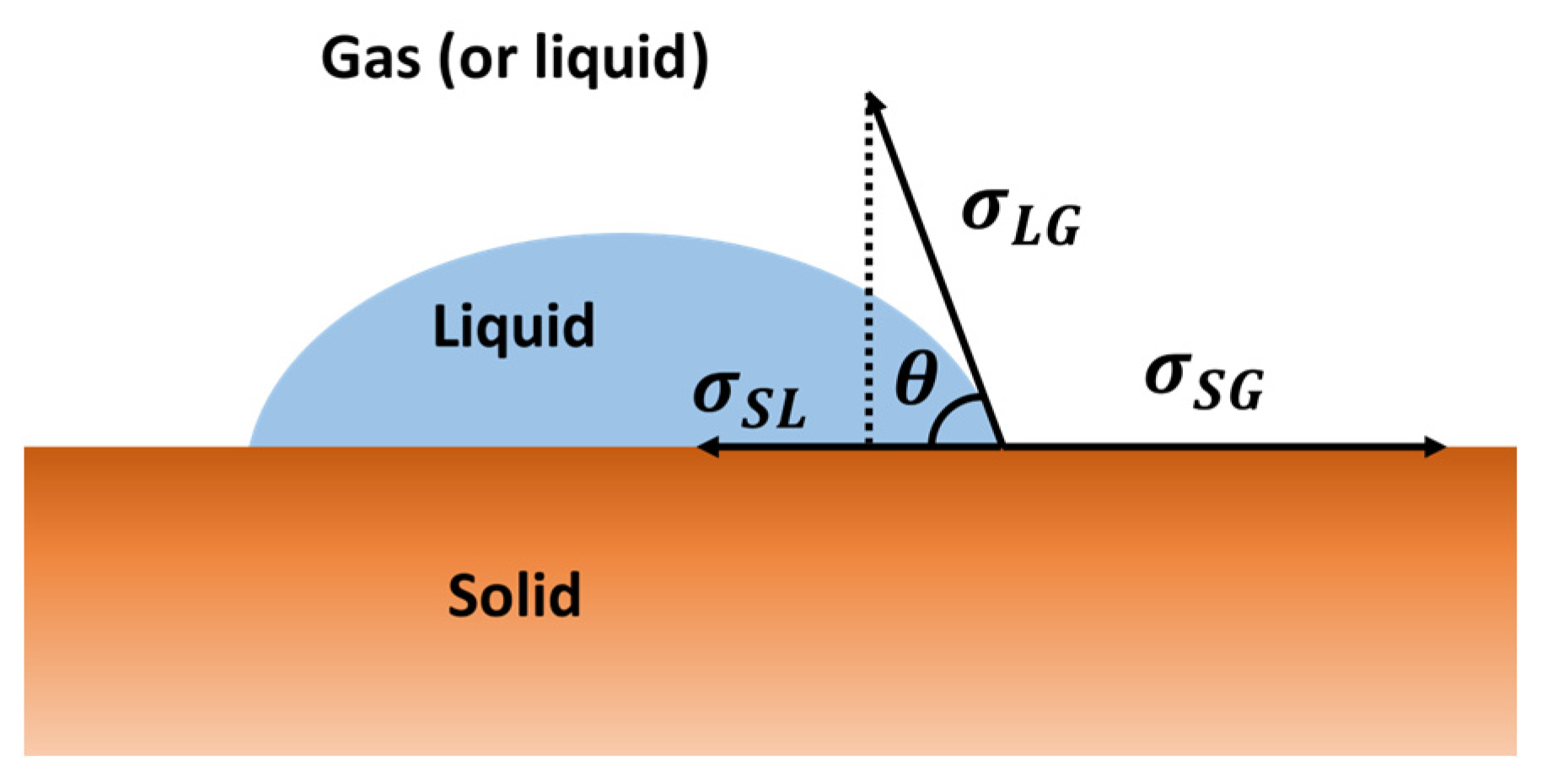
Preprints 109170 g011
Preprints 109170 g012
Figure 12. Calculated contact angle versus experimental contact angle.
Figure 12. Calculated contact angle versus experimental contact angle.
Preprints 109170 g012
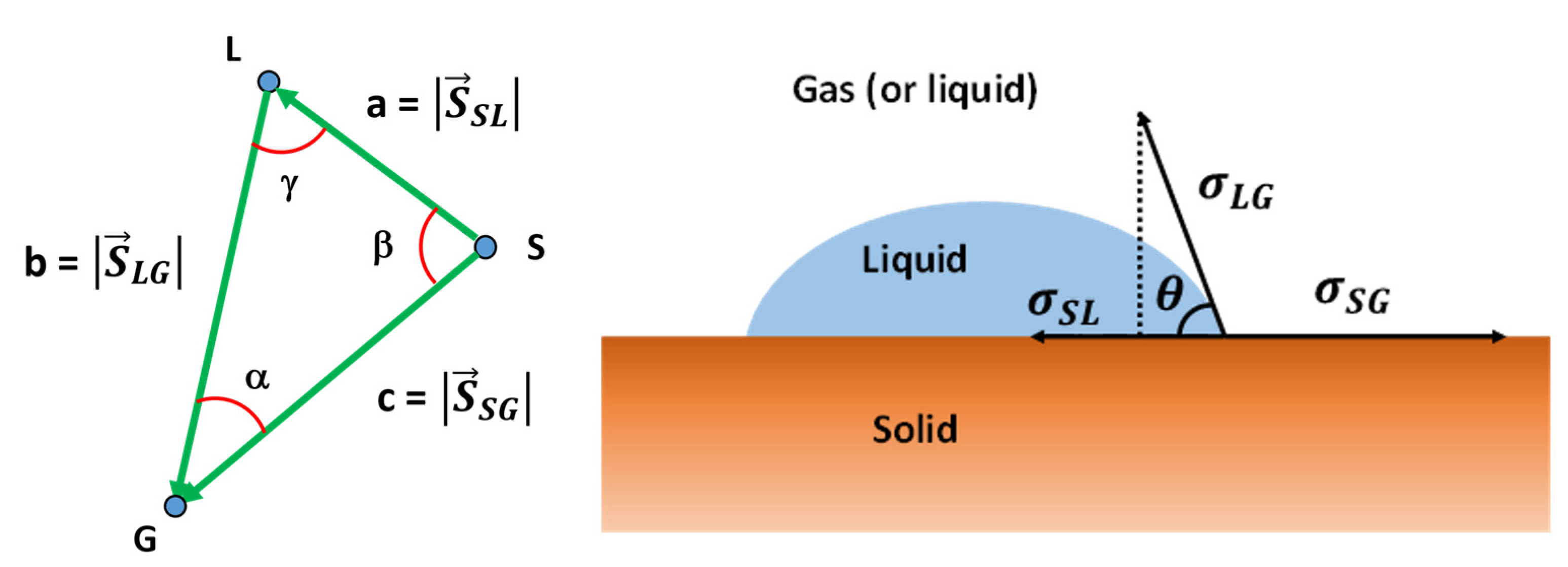
Preprints 109170 g013
Figure 13. Angles between interaction vectors and contact angle.
Figure 13. Angles between interaction vectors and contact angle.
Preprints 109170 g013
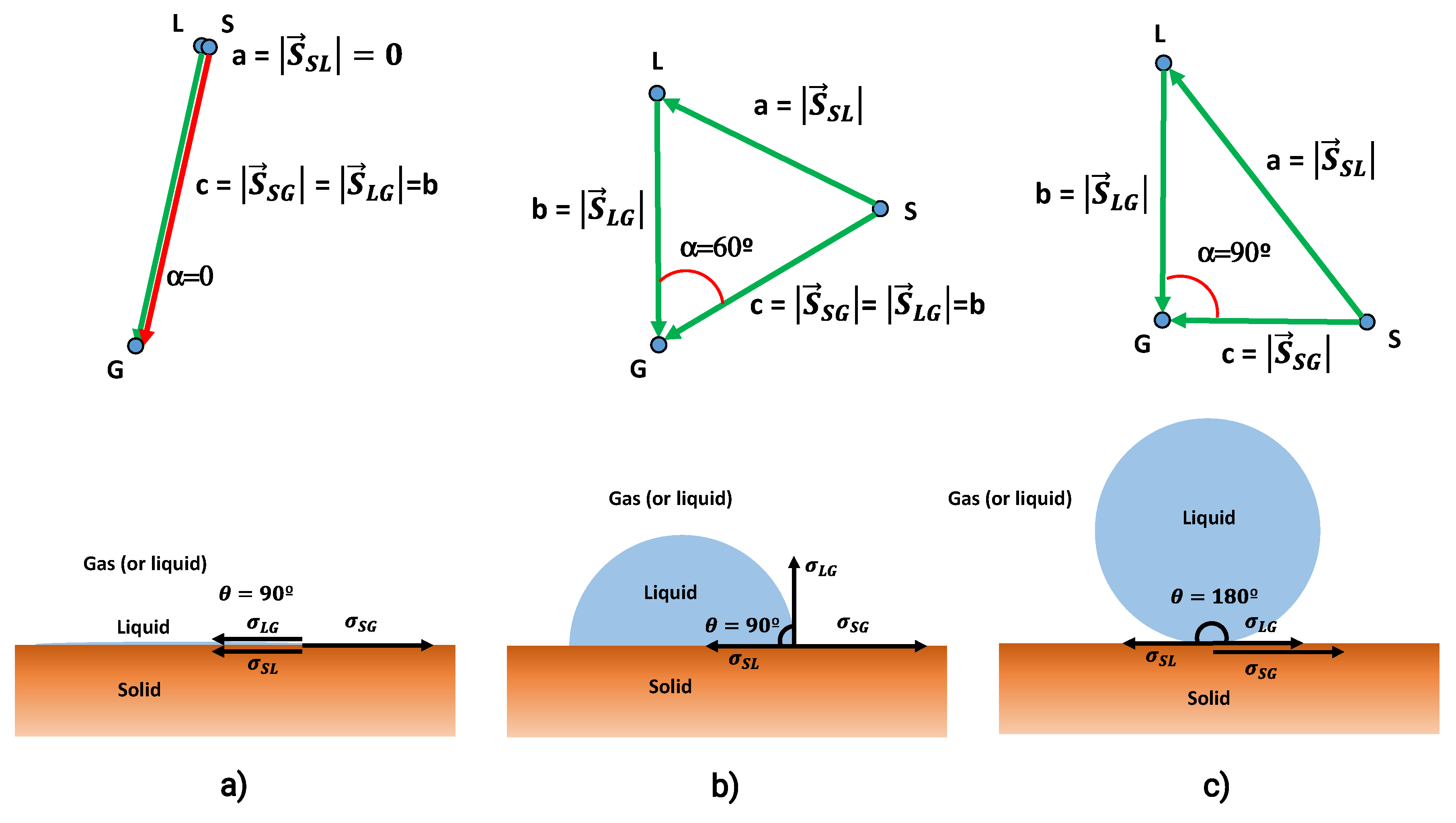
Preprints 109170 g014
Figure 14. Relation between contact angle, θ, and α angle between S → S G and S → L G vectors
Figure 14. Relation between contact angle, θ, and α angle between S → S G and S → L G vectors
Preprints 109170 g014
Table 1. Correlations of surface free energy with solubility parameters.
Table 1. Correlations of surface free energy with solubility parameters.
Preprints 109170 i001a
Preprints 109170 i001b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated