Preprint
Article
Evolutionary Reinforcement Learning of Binary Neural Network Controllers for Pendulum Task—Part2: Genetic Algorithm
Altmetrics
Downloads
71
Views
25
Comments
0
This version is not peer-reviewed
Submitted:
13 June 2024
Posted:
13 June 2024
You are already at the latest version
Alerts
Abstract
Evolutionary algorithms and swarm intelligence algorithms find applicability in reinforcement learning of neural networks due to their independence from gradient-based methods. To achieve successful training of neural networks using these algorithms, careful considerations must be made to select appropriate algorithms due to the availability of various algorithmic variations. In Part1, the author previously reported experimental evaluations on Evolution Strategy for reinforcement learning of binary neural networks, utilizing the Pendulum control task. This article constitutes Part2 of the series of comparative research. In this study, Genetic Algorithm is adopted as another evolutionary algorithm. Wilcoxon signed rank test revealed that there was no statistically significant difference between the fitness scores obtained using GA and those using ES. However, the p-value 0.11 indicated that GA worked better than ES on this training task. As the values of binary weights, {-1, 1} were significantly superior to {0, 1} (p < .01). The motion of the pendulum controlled by the binary MLP after the training showed that the binary MLP successfully swung the pendulum swiftly into an inverted position and maintained its stability after inversion.
Keywords:
Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning
1. Introduction
The author has been investigating a reinforcement learning approach for training neural networks using evolutionary algorithms. For instance, the author previously reported an experimental result of evolutionary reinforcement learning of neural network controllers for the pendulum task [1,2,3,4]. In these previous studies, a conventional multilayer perceptron was employed in which connection weights were real numbers. On the contrary, researchers are exploring neural networks in which the weights are discrete values rather than real numbers, accompanied by the corresponding learning methodologies [5,6,7,8,9,10,11,12].
An advantage of discrete neural networks lies in their ability to reduce the memory footprint required for storing trained models. For instance, when employing binarization as a discretization method, only 1 bit is needed for each connection weight, compared to 32 or 64 bits required for a real-valued weight. This results in a memory size reduction of 1/64 (1.56%) or 1/32 (3.13%) per connection. Given the presence of numerous connections in deep neural networks, the memory size reduction achieved through discretization becomes more pronounced, facilitating the implementation of large network models on memory-constrained edge devices. However, the performance of discrete neural networks on modelling nonlinear functions falls below that of real-valued neural networks with the same model size. To achieve comparable performance to real-valued neural networks, it is necessary for discrete neural networks to increase its model size. As the model size increases, so does the memory footprint, introducing a trade-off between memory size reduction through discretization. In other words, to maximize the effect of memory size reduction achieved through neural network discretization, it is essential to limit the increase in model size while simultaneously minimizing the number of bits per connection weight.
In this study, the author experimentally applies Genetic Algorithm [13,14,15,16] to the reinforcement training of binary neural networks and compares the result with the previous experimental result [17] in which, instead of GA, Evolution Strategy [18,19,20] was applied. In both studies, the same pendulum control task is utilized.
2. Pendulum Control Task
As a task that requires reinforcement learning to solve, this study employs Pendulum task provided at OpenAI Gym1. Figure 1 shows a screenshot of the system. This task is the same as that in the previous study; details on this task were described in [1]. The same method for scoring fitness of a neural network controller was employed again in this study.
3. Neural Networks with Binary Connection Weights
In a previous study [1] the author employed a three-layered feedforward neural network known as a multilayer perceptron (MLP) as the controller. An MLP with the same topology is utilized in this study and another previous study [17], where connection weights are not continuous numbers but binary. Figure 2 illustrates the topology of the MLP. The feedforward calculations are the same as those described in [1]. Note that the unit activation function is the hyperbolic tangent (tanh), which is the same as in the previous study [17]. Thus, the MLP with binary weights outputs real numbers within the range [-1.0, 1.0].
In both of this study and the previous one [17], the MLP serves as the policy function: action(t) = F(observation(t)). The input layer consists of three units (N=3 in Figure 2), each corresponding to the values obtained by an observation. The output layer comprises one unit (L=1 in Figure 2), and its output value is applied as the torque to the pendulum system. Note that the torque is the twice of the MLP output value to make the torque within the range [-2.0,2.0] [1].
4. Training of Binary Neural Networks by Genetic Algorithm
A three-layered binary perceptron, as depicted in Figure 2, includes M+L unit biases and NM+ML connection weights, resulting in a total of M+L+NM+ML parameters. Let D represent the quantity M+L+NM+ML. For this study, the author sets N=3 and L=1, leading to D=5M+1. The training of this perceptron is essentially an optimization of the D-dimensional binary vector. Let denote the D-dimensional vector, where each corresponds to one of the D parameters in the perceptron. In this study, each is a binary variable, e.g. {-1,1} or {0,1}. By applying the value of each element in to its corresponding connection weight or unit bias, the feedforward calculations can be processed.
In this study, the binary vector is optimized using Genetic Algorithm [13,14,15,16]. GA treats as a chromosome (a genotype vector) and applies evolutionary operators to manipulate it. The fitness of is evaluated based on eq. (1) described in the previous article [1]. Figure 3 illustrates the GA process. In Step 1, D-dimensional binary vectors are randomly initialized where P denotes the population size. A larger value of P promotes exploration more. In Step 2, binary values in each vector () are applied to the MLP and the MLP controls the pendulum for a single episode with 200 time steps. The fitness of is then evaluated with the result of the episode. In Step 3, the loop of evolutionary training is finished if a preset condition is met. A simple example of the condition is the maximum number of fitness evaluations.
Elites are the best E vectors among all offsprings evaluated so far, where E denotes the size of elite population. To exploit around the good solutions found so far, elite vectors are kept as parent candidates for the crossover. The elite population is empty at first. In Step 4, members in the elite population, are updated. Step 5 consists of the crossover and the mutation. In Step 5.1, new offspring vectors are produced by applying the crossover operator to the union of the elite vectors and the vectors in the current population. A single crossover with two parents produces two new offsprings, where the two parents are randomly selected from the union of and To produce new offspring vectors, the crossover is performed times. Each vector in the union of and can be selected as a parent two or more times (several vectors in the union may not be selected any time). The new offspring vectors replace the population Crossover operators applicable to binary chromosomes are a single-point crossover, a multi-point crossover and the uniform crossover. The uniform crossover is applied in this study. In Step 5.2, each element in the new offspring vectors is bit-flipped under the mutation probability pm. A greater pm promotes explorative search more.
5. Experiment
In the previous study where the binary MLPs were trained using ES, the number of fitness evaluations included in a single run was set to 5,000 [17]. The number of new offsprings generated per generation was either of (a)10 or (b)50. The number of generations for each case of (a) or (b) was 500 and 100 respectively. The total number of fitness evaluations were 10 × 500 = 5,000 for (a) and 50 × 100 = 5,000 for (b). The experiments in this study where the binary MLPs are trained using GA employ the same configurations. The hyperparameter configurations for GA are shown in Table 1. The mutation probability pm is set to 1/D where D denotes the length of a binary genotype vector.
Sets of two values such as {-1,1} or {0,1} can be used for the binary connection weights. The author first presents experimental results using {-1,1}. In the previous study using ES, the author tested three options, M=16, 32, and 64, for the number of hidden units. The same options are employed in this study using GA.
Table 2 presents the best, worst, average, and median fitness scores of the trained MLPs across the 11 runs. Each of the two hyperparameter configurations (a) and (b) in Table 1 was applied. A larger value is better in Table 2 with a maximum of 1.0.
To investigate which of the two configurations (a) or (b) is superior, the Wilcoxon signed-rank test was applied to the 122 data points presented in Table 2. This test revealed that the configuration (a) is superior to the configuration (b) with a statistical significance (p<.01). Thus, reducing the population size and increasing the number of generations is more favorable than the opposite approach. This finding is consistent with that in previous study [17] using ES; although no statistically significant difference was observed between the configurations (a) and (b), the configuration (a) was slightly superior to the configuration (b). A greater number of generations would contribute better than a greater population size in these two studies, because the length of genotype vectors (i.e., the value of D) is large and thus fine-tuning the genotype vectors repetitively in the later generations improves the MLP performance well.
Next, the author examines whether there is a statistically significant difference in the performances among the three MLPs with the different numbers of hidden units M. For each M of 16, 32, and 64, the author conducted 11 runs using the configuration (a), resulting in 11 fitness scores. The Wilcoxon rank sum test was applied to the 113 data points. The results showed that there was little difference between M=64 and M=32 (p=.47). While there was no significant difference between M=16 and either M=32 or M=64 (with p-values of 0.057 and 0.396, respectively), the proximity of the p-values to 0.05 indicated that M=16 performed much worse than M=32. Thus, M=32 exhibited superior performance to M=16 and little difference to M=64. Therefore, from the perspective of the trade-off between performance and memory size, the most desirable number of hidden units was found to be 32. This result is consistent with the previous study using ES [17].
Figure 4 presents learning curves of the best, median, and worst runs among the 11 runs where the configuration (a) was applied. Note that the horizontal axis of these graphs is in a logarithmic scale. Figure 4(i), (ii), and (iii) depict learning curves of MLPs with different numbers of hidden units (M=16, 32, 64). The curves in Figure 4(i), (ii), and (iii) exhibit similar shapes to the corresponding figures in the previous article [17]; each curve started around a fitness value of 0.1 and rose to approximately 0.5 within the first 10 to 100 evaluations. Subsequently, over the remaining approximately 4900 evaluations (roughly 490 generations), the fitness values increased from around 0.5 to around 0.8. However, in all cases (i), (ii), and (iii), the worst runs did not show an increase in fitness from around 0.5, indicating a failure to achieve the task. The reason for the significant difference between the best and worst runs would be due to the configuration (a) which promotes local search over global search, thus leading to some runs falling into local optima as a result of insufficient exploration of the search space. Particularly, when the number of hidden units M is set to 64, it can be observed that the performance of the median run (0.637) is as low as that of the worst run (0.606), indicating six or more failed runs. This can be attributed to the fact that as M increases, so does D, expanding the solution space extensively, thereby making failures due to insufficient global exploration more likely to occur.
Figure 5(a) illustrates the actions by the MLP and the errors of the pendulum to the target state (values of Error(t) defined in the previous article [1]) in the 200 steps prior to training, while Figure 5(b) displays the corresponding actions and errors after training. In this scenario, the MLP included 32 hidden units, and GA utilized the configuration (a) in Table 1. Supplementary videos are provided which demonstrate the motions of the pendulum controlled by the MLPs before/after trained2,3. Figure 5(a)(b) in this article closely resemble Figure 6(a)(b) previously published in [17]. For details on the figures, readers are referred to the previous article [17] on the study using ES. These figures showed that, regardless of whether GA or ES was employed for the evolutionary training, the trained MLPs swiftly inverted the pendulum and subsequently maintained it in an inverted position with nearly zero torque.
The above reported the experimental result where {-1,1} were used as the binary values for the connection weights. The author next presents the experimental result using {0,1} instead of {-1,1}. A connection with a weight of 0 is equivalent to be disconnected, signifying its redundancy. Therefore, the presence of numerous connections with the weight of 0 implies a lighter feedforward computation for the neural network.
Table 3 presents the best, worst, average, and median fitness scores of the trained MLPs across the 11 runs. Based on the results with {-1,1}, the number of hidden units in the MLP was set to 32 and GA utilized the configuration (a) in Table 1. Comparing Table 3 with Table 2 reveals that the values in Table 3 are consistently smaller than their corresponding values in Table 2. Thus, the performance of MLPs with {0,1} weights are inferior to those with {-1,1} weights. The Wilcoxon rank sum test to the 11 fitness scores for each case reveals that this difference is statistically significant (p < .01). This result aligns with those obtained using ES [17], which suggests that, irrespective of the evolutionary algorithm employed for training, the performance of trained binary MLPs will be better when {-1,1} is used instead of {0,1}. Verification using other algorithms and other tasks remains future work. Furthermore, evaluating the performance when using a ternary {-1,0,1} instead of binary {-1,1} or {0,1} is also a subject for future investigation.
Figure 6 illustrates the learning curves of the MLP with {0,1} weights in the same format as Figure 4. Figure 7 illustrate the actions by the {0,1} MLPs and the errors of the pendulum to the target state, in the same format as Figure 5. The MLP included 32 hidden units, and GA utilized the configuration (a) in Table 1. Theses figures are also quite similar to the corresponding figures by the previous study using ES [17]. Therefore, the insights described in the previous article [17] regarding the observations gleaned from these figures are applicable to the experimental results presented in this article. For a detailed examination of these insights, readers are encouraged to refer to the previous article [17]. Supplementary videos are provided which demonstrate the motions of the pendulum controlled by the {0,1} MLPs before/after trained4,5.
6. Statistical Test to Compare GA With ES
The author conducts the Wilcoxon signed rank test to investigate whether there is a statistically significant difference between the fitness scores obtained from the previous experiment using ES [17] and those from the experiment using GA. The data used for this test included the 11 fitness scores obtained using ES and the corresponding 11 fitness scores obtained using GA, where the same configuration (a) and the same number of hidden units (M=32) are adopted. The test revealed that there was no statistically significant difference between the two sets of fitness scores (p > .05). However, the p-value (p=0.11) indicated that GA worked better than ES on this training task. The configuration (a) is designed to promote local search over global search by having a smaller population size but a greater number of generations. While GA excels at global search, they typically lag behind ES in local search. Therefore, the configuration (a) compensates for this deficiency in local search, resulting in a better balance between global exploration and local exploitation. Consequently, the configuration (a) facilitates GA to discover superior solutions.
7. Conclusion
In this study, Genetic Algorithm was applied to the reinforcement learning of a neural network controller for the pendulum task, where the connection weights in the neural network are not continuous numbers but binary. The experimental result was compared with another result of the previous experiment [17] in which, instead of GA, Evolution Strategy was applied to the same task. The findings from this study are summarized as follows, where (1)-(4) align with the previous result [17].
- (1)
- The optimal number of hidden units for the binary MLP was found to be 32 among the choices of 16, 32, and 64.
- (2)
- The configuration (a) yielded superior results compared to the configuration (b) in Table 1. The configuration (a) involved a smaller population size and a larger number of generations compared to the configuration (b).
- (3)
- The motion of the pendulum controlled by the binary MLP after the training showed that the binary MLP successfully swung the pendulum swiftly into an inverted position and maintained its stability after inversion.
- (4)
- As the values of binary weights, {-1, 1} were significantly superior to {0, 1} (p < .01).
- (5)
- The Wilcoxon signed rank test revealed that there was no statistically significant difference between the fitness scores obtained using GA and those using ES. However, the p-value (p=0.11) indicated that GA worked better than ES on this training task.
Future studies will include evaluations of other evolutionary algorithms on the same task and evaluations of evolutionary algorithms on the reinforcement learning of binary MLPs applied to tasks other than the Pendulum task.
Acknowledgments
The author conducted this study under the Official Researcher Program of Kyoto Sangyo University.
References
- Okada, H. (2022). Evolutionary reinforcement learning of neural network controller for pendulum task by evolution strategy. International Journal of Scientific Research in Computer Science and Engineering, 10(3), 13–18.
- Okada, H. (2023). An evolutionary approach to reinforcement learning of neural network controllers for pendulum tasks using genetic algorithms, International Journal of Scientific Research in Computer Science and Engineering, 11(1), 40-46.
- Okada, H. (2023). A comparative study of DE, GA and ES for evolutionary reinforcement learning of neural networks in pendulum task, IEEE CPS Proceedings of 25th International Conference on Artificial Intelligence (ICAI'23), held jointly in 2023 World Congress in Computer Science, Computer Engineering, & Applied Computing (CSCE'23), Las Vegas, USA.
- Okada, H. (2023). An evaluative analysis of particle swarm optimization for reinforcement learning in pendulum task, Journal of Engineering and Technology for Industrial Applications (ITEGAM-JETIA), 9(42), 11-15.
- Courbariaux, M., Bengio, Y., & David, J.P. (2015). BinaryConnect: training deep neural networks with binary weights during propagations. Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS'15), 2, MIT Press, 3123–3131.
- Courbariaux, M., Hubara, I., Soudry, D., El-Yaniv, R., & Bengio, Y. (2016). Binarized neural networks: training deep neural networks with weights and activations constrained to +1 or -1. arXiv preprint arXiv:1602.02830.
- Tang, W., Hua, G., & Wang, L. (2017). How to train a compact binary neural network with high accuracy? Proceedings of the AAAI Conference on Artificial Intelligence, 31(1).
- Lin, X., Zhao, C., & Pan, W. (2017). Towards accurate binary convolutional neural network. Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), 344–352.
- Bethge, J., Yang, H., Bartz, C., & Meinel, C. (2018). Learning to train a binary neural network. arXiv preprint arXiv:1809.10463.
- 10. Qin, H., Gong, R., Liu, X., Bai, X., Song, J., & Sebe, N. (2020). Binary neural networks: a survey. Pattern Recognition, 105, 107281. [CrossRef]
- Yuan, C., & Agaian, S.S. (2023). A comprehensive review of binary neural network. Artificial Intelligence Review, 56, 12949–13013. [CrossRef]
- Sayed, R., Azmi, H., Shawkey, H., Khalil, A. H., & Refky, M. (2023). A systematic literature review on binary neural networks. IEEE Access, 11, 27546–27578. [CrossRef]
- Goldberg, D.E., Holland, J.H. (1988). Genetic algorithms and machine learning. Machine Learning 3, 95-99. [CrossRef]
- Holland, J. H. (1992). Genetic algorithms. Scientific American, 267(1), 66-73.
- Mitchell, M. (1998). An introduction to genetic algorithms. MIT press.
- Sastry, K., Goldberg, D., & Kendall, G. (2005). Genetic algorithms. Search methodologies: Introductory tutorials in optimization and decision support techniques, 97-125.
- Okada, H. (2023). Evolutionary reinforcement learning of binary neural network controllers for pendulum task — part1: evolution strategy. Preprints.org. [CrossRef]
- Schwefel, H.P. (1984). Evolution strategies: a family of non-linear optimization techniques based on Imitating some principles of organic evolution. Annals of Operations Research, 1, 165–167.
- Schwefel, H.P. (1995). Evolution and Optimum Seeking. Wiley & Sons.
- Beyer, H.G., & Schwefel, H.P. (2002). Evolution strategies: a comprehensive introduction. Journal Natural Computing, 1(1), 3–52.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] |
Figure 1.
Pendulum system1.
Figure 1.
Pendulum system1.
Figure 2.
Topology of the MLP.
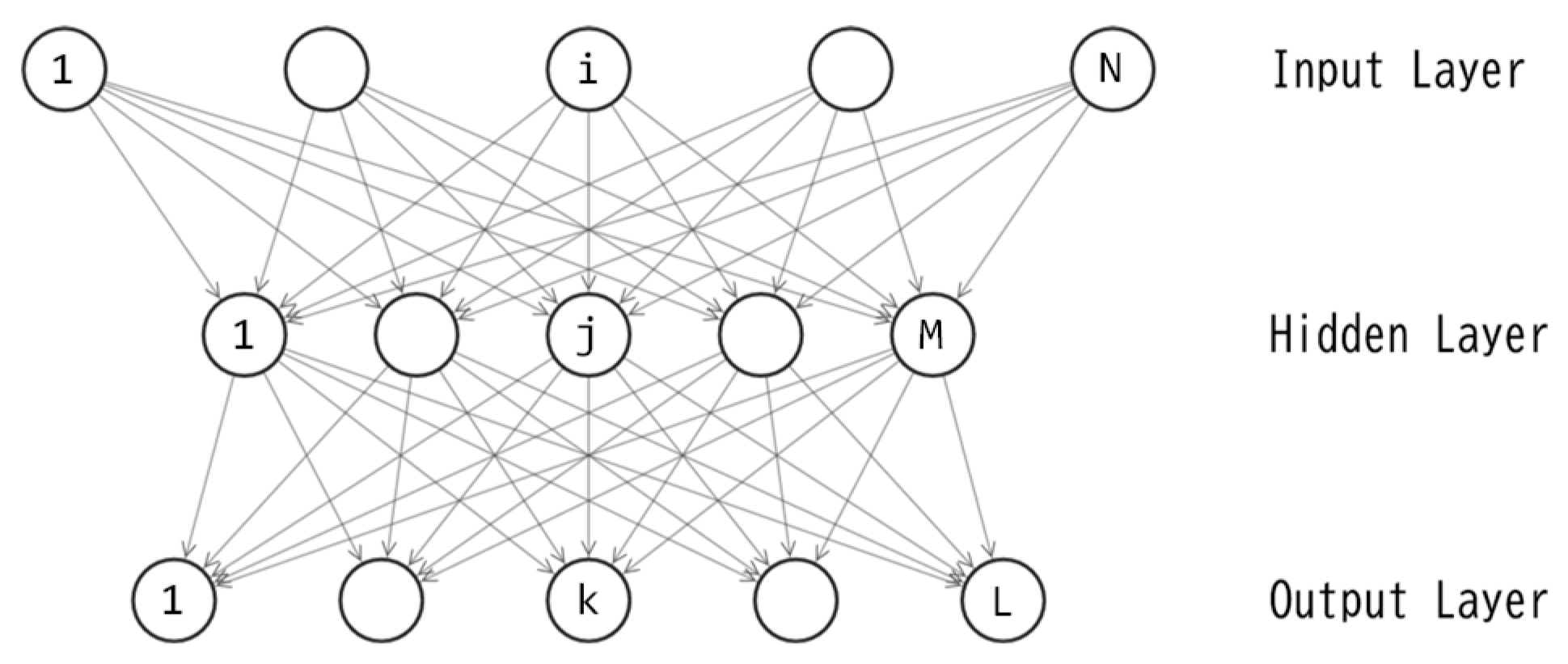
Figure 3.
Process of genetic algorithm.

Figure 4.
Learning curves of MLP with M hidden units.
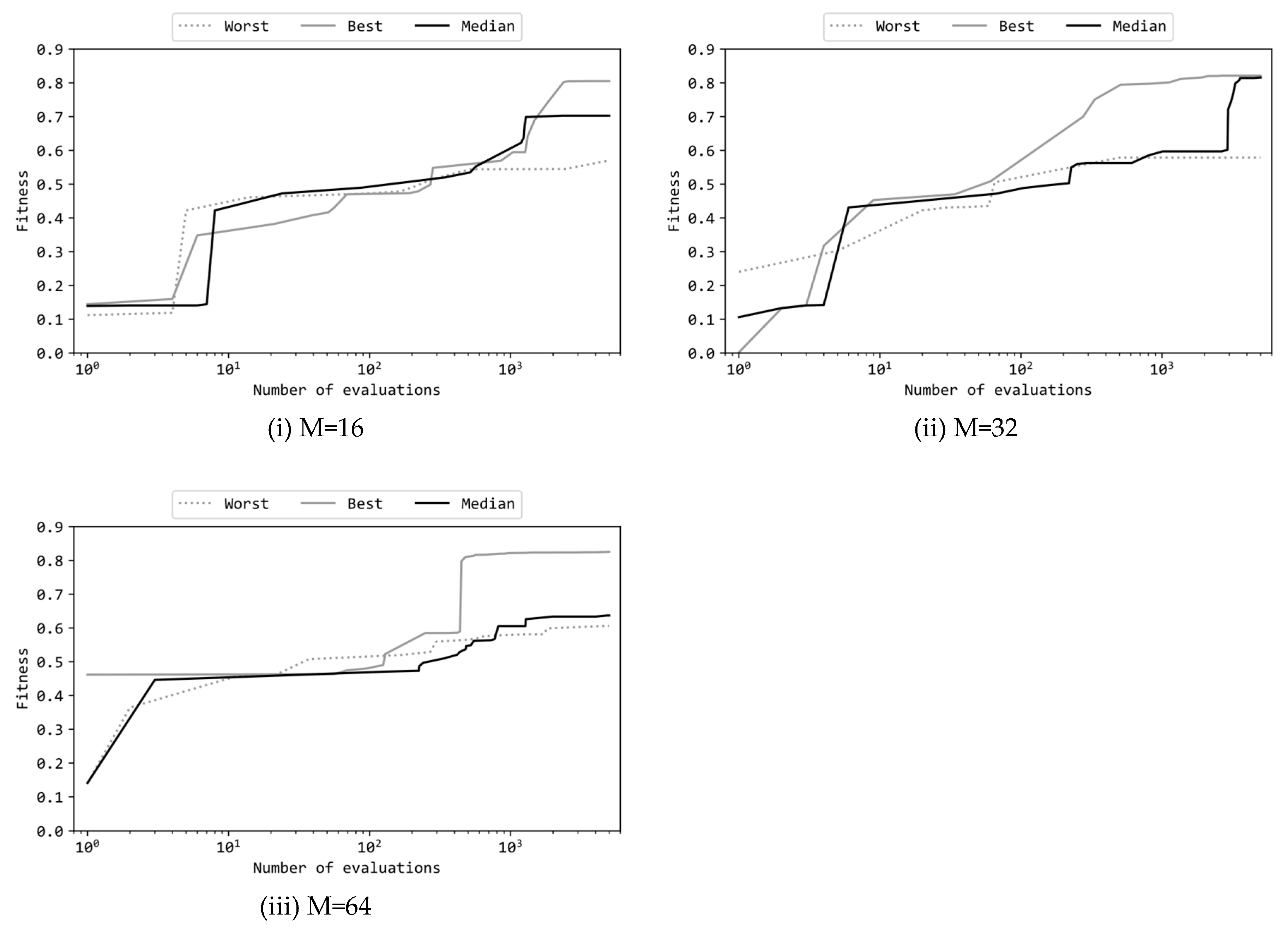
Figure 5.
MLP actions and errors in an episode.
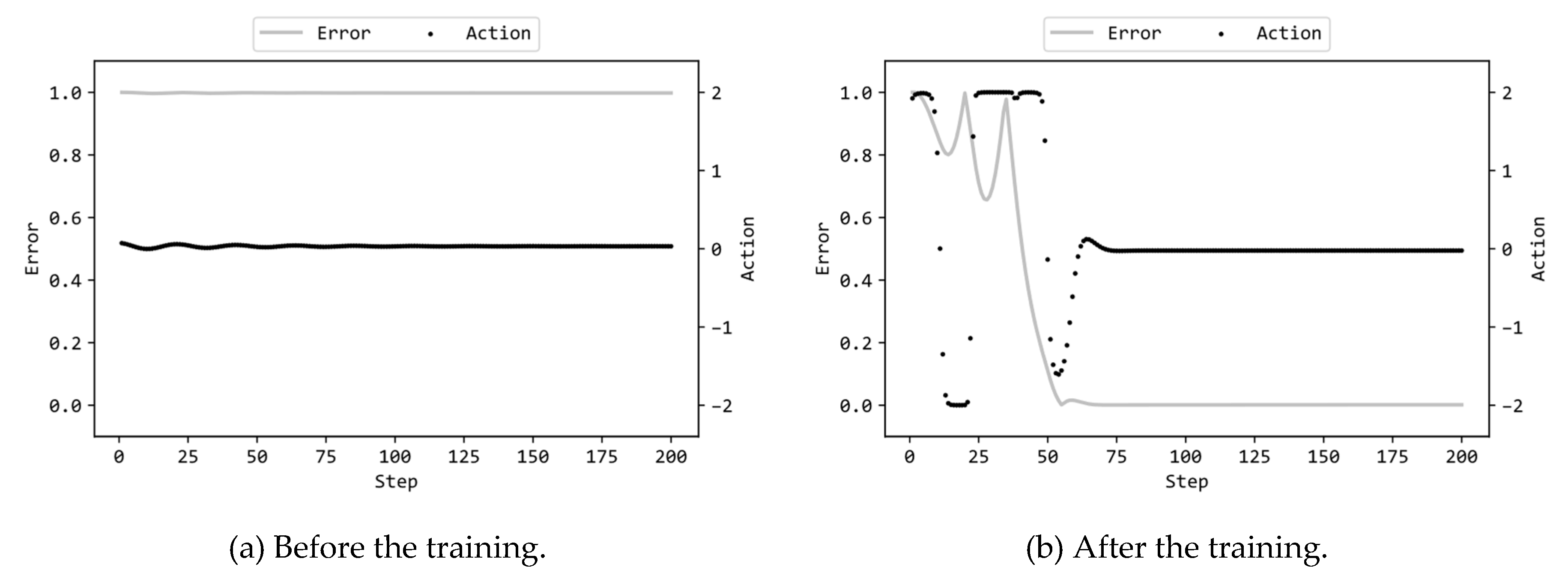
Figure 6.
Learning curves of MLP with 32 hidden units and {0,1} weights.
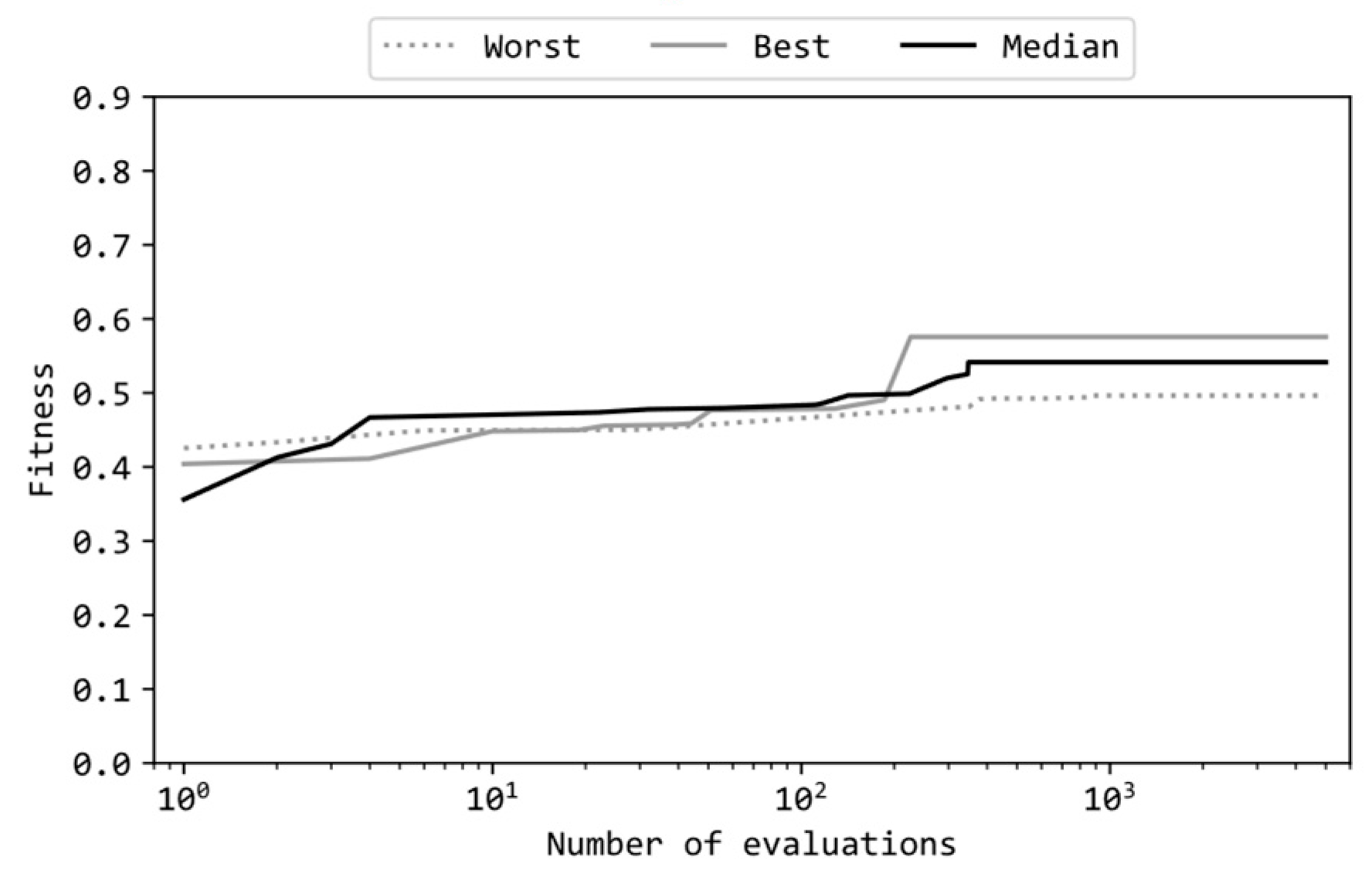
Figure 7.
Figure 7. MLP actions and errors in an episode ({0,1} weights).
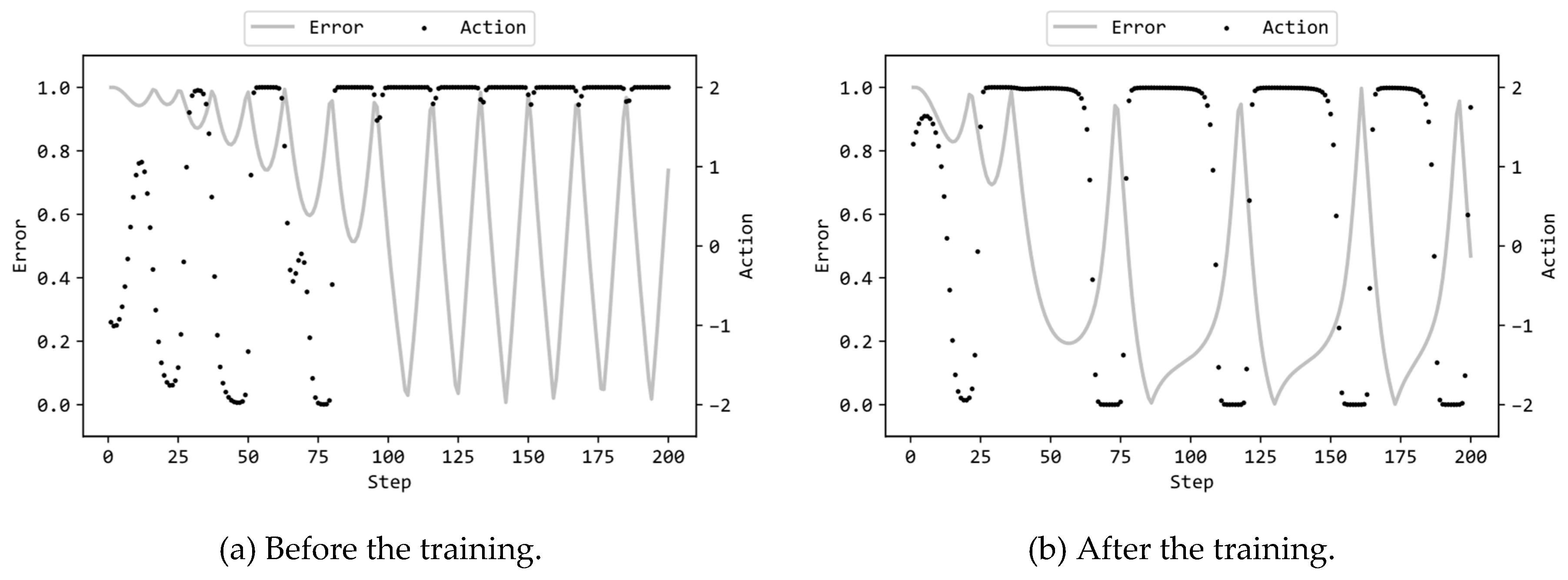
Table 1.
GA Hyperparameter Configurations.
| Hyperparameters | (a) | (b) |
|---|---|---|
| Population size (P) | 10 | 50 |
| Generations | 500 | 100 |
| Fitness evaluations | 500=5,000 | 100=5,000 |
| Number of elites (E) | 0.2=2 | 0.2=10 |
| Mutation probability (pm) | 1/D | 1/D |
Table 2.
Fitness Scores among 11 Runs.
| M | Best | Worst | Average | Median | |
|---|---|---|---|---|---|
| (a) | 16 | 0.805 | 0.545 | 0.696 | 0.703 |
| 32 | 0.821 | 0.579 | 0.741 | 0.816 | |
| 64 | 0.826 | 0.606 | 0.698 | 0.637 | |
| (b) | 16 | 0.640 | 0.551 | 0.591 | 0.584 |
| 32 | 0.710 | 0.570 | 0.624 | 0.593 | |
| 64 | 0.780 | 0.556 | 0.632 | 0.619 |
Table 3.
Fitness Scores among 11 Runs ({0,1} Weights).
| M | Best | Worst | Average | Median | |
|---|---|---|---|---|---|
| (a) | 32 | 0.576 | 0.496 | 0.537 | 0.542 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






