Prerpints.org logo
Preprint
Review

High power lasers

Altmetrics

Downloads

218

Views

72

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 June 2024

Posted:

13 June 2024

You are already at the latest version

Alerts
Abstract
High-power lasers play an important role in modern science, industry, and medicine. A signifi-cant milestone was reached on December 5, 2022, when Inertial Confinement Nuclear Fusion (ICF) achieved scientific breakeven, releasing more energy than the input laser energy. Additionally, Extreme Ultraviolet Lithography (EUVL) has enabled the development of microchips with 3 nm process nodes, marking a leap in semiconductor technology. These examples together with the recent achievement of a 10 PW (1015 W) laser output heralds remarkable advancements in technology and science soon. Laser systems are broadly classified based on their operating re-gimes into two main categories: Continuous Wave (CW) operation, where the laser is continuously pumped and emits a steady beam of light, and the pulsed regime, in which the laser pro-duces single or multiple pulses at various repetition rates. This review will primarily focus on pulsed laser systems, exploring their various types and recent technological advancements.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

It's hard to overstate the crucial role that lasers play in modern life. From welding, cutting, and drilling in subtractive manufacturing [1] to 3D printing in additive manufacturing [2], particularly in metal processing, lasers are indispensable. Besides, they accelerate charged particles to high energy [3], produce hard radiation [4] crucial for various scientific and medical applications, and have recently demonstrated breakthroughs such as achieving breakeven in Confinement Nuclear Fusion [5] and enabling Extreme Ultraviolet Lithography [6]. These are just a few examples showcasing the immense capabilities of high-power lasers.
Laser systems are broadly classified based on their operating regimes into two main categories: Continuous Wave (CW) operation, where the laser is continuously pumped and emits a steady beam of light, and the pulsed regime, in which the laser produces single or multiple pulses at various repetition rates.
 In CW regime high power fiber lasers are created from active optical fibers pumped by semiconductor laser diodes, a merger between two of the most innovative and advanced laser technologies reached the remarkable  output power up to 100s kW [7] and feature a wide range of operating wavelengths and record wall-plug efficiency up to 50% [8]. Multi-kW carbon oxide (CO2) gas lasers present another example of greater reliability, higher output consistency, which allowed them the widely spread in industry and medicine [9].
Nevertheless, this paper will primarily focus on ultrahigh power pulsed laser systems, exploring their various types and recent technological advancements. High power laser systems possess the ability to concentrate the energy into extremely small space-time volume. The laser beam with recently reached 10 petawatts (1015 Watt -PW) output pulse power was focused on the few microns spot which allowed to achieve the highest in the observable universe intensity approaches to 1024 watts per square centimeter (W/cm2) [10].  With a duration of approximately 20 femtoseconds (10-15 seconds - fs), this pulse occupies a mere ~7 μm of space during its propagation. Such a short pulse duration enables the attainment of tremendous power and intensity with a modest energy input ranging from 300 to 500 Joules. To put this into perspective, consider that the total power output of all the world's power plants is around 2 terawatts (1012 watts - TW), while the sunlight reaching the Earth amounts to approximately 90 PW. Achieving an intensity of 1024 W/cm2 is feasible by concentrating this power into a spot with a diameter of just 30 μm.
 The light produced by cutting-edge technologies boasts remarkable specifications, revolutionizing various fields of science and industry. Take, for instance, the Extreme Light Infrastructure for Nuclear Physics (ELI-NP) 20PW laser, crafted from sapphire crystals doped with titanium ions (Ti:Sa). This system generates 600J of output energy with a pulse duration of 30 fs across two converging channels [10]. In a different league, the NIF Nd: Glass laser system, pivotal in achieving thermonuclear fusion breakeven, wields a staggering 4MJ of energy at a wavelength of 1.053 μm, converted in 1.8MJ of third harmonic at 0.35 μm through 192 channels. Its pulse duration spans a nanosecond, with an output power of 0.5PW [11]. Furthermore, ASML employs a 1MW CO2 gas laser within their Extreme Ultraviolet Lithography system, revolutionizing microchip production [12], showcasing just a glimpse of the transformative capabilities of these cutting-edge light sources.
Figure 1 demonstrated the chart of historical development of the laser systems with high pulse power (intensity).
Since Richard Maiman's groundbreaking invention of the laser in 1960 [13], the power of laser technology has undergone rapid growth, fueled primarily by the discovery of two pivotal operational regimes: Q-Switching and Mode Locking (a detailed explanation follows) [14,15]. These breakthroughs, illustrated on the accompanying chart, marked a turning point in laser development. By implementing these regimes in laser oscillators, scientists and engineers achieved a remarkable feat: the gradual reduction of pulse durations from microseconds to nanoseconds, and later, to femtoseconds, all without significant energy loss. The peak power is determined by dividing the energy by the pulse duration, thus there are two primary pathways to increase peak power. The first is extensive, involving increasing the energy output of the laser by developing Master Oscillator+ Power Amplifiers (MOPA) scheme. The second is intensive, focusing on reducing the pulse duration. Intensive improvements, such as pulse duration reduction, are often favored due to their cost-effectiveness. By enhancing the efficiency and precision of laser systems, researchers can achieve higher peak powers without significantly increasing energy consumption or production costs. This approach underscores the importance of refining pulse duration technologies, which not only boosts parameters but also promotes accessibility in laser applications across various new fields.
Following the period of gradual intensity growth post-1970, a significant technological breakthrough emerged in 1985: Chirped Pulse Amplification (CPA) [16,17]. This innovation provided a substantial boost to laser capabilities, propelling the power growth trajectory forward, a trend that continues to evolve to this day and beyond. The development of Chirped Pulse Amplification (CPA) involved the collective efforts of numerous scientists over the years. While it's true that two individuals were awarded the Nobel Prize in 2018 for their contributions to CPA, namely Jerard Mourou and Dona Strickland, it's essential to recognize the collaborative nature of scientific progress. Countless researchers worldwide have dedicated their knowledge, expertise, and resources to advancing CPA technology, each playing a vital role in its development and refinement. In this paper, we will delve into a comprehensive explanation of the aforementioned technologies, elucidating their principles, applications, and contributions to the evolution of laser science and industry.

2. Ideas and Methods of Laser Power Increasing

Let's begin with a brief overview of how a laser oscillator operates. For a deeper understanding, readers can refer to [18]. In essence, a laser oscillator comprises three primary components: a resonator or cavity, typically consisting of two mirrors (one of which is usually partially transparent, serving as the output coupler), a Gain Medium (GM) that facilitates amplification of light within a specific spectral range, and a pump system responsible for energizing the gain medium to enable light amplification (refer to Figure 2a top for illustration).
Some of the spontaneous photons generated by GM and reflected by mirrors of the cavity can produce standing waves or resonance frequencies (longitude modes) which are able respectively long time exist in resonator, for example, as standing waves on the guitar string. The condition for that is the equivalence of number (q) of half-waves (λ/2) to resonator length (L) multiplied by the index of refraction (n) of the media  nL= qλ/2, similar, the resonance frequencies can also be expressed as ν = qc/2L, where (c) represents the speed of light.
Initially, the frequency amplitudes are uniform within the empty cavity, depicted in Figure 2a at the bottom, with equidistant spacing calculated by the formula Δν = c/2L, resulting in an infinite array of frequencies. However, the resonator is not truly empty; it contains a GM capable of amplifying the frequencies suitable with its luminescence spectra. In reality, the laser medium (GM) exhibits specific spectral bandwidths for light amplification, determined by its structure and condition, as illustrated in Figure 2b (blue curve). Only a handful of frequencies align with this curve, as other frequencies experience limited or no amplification. Additionally, losses occur within the cavity due to imperfections in optical surfaces, finite apertures, and output energy (R1, R2). Consequently, only a select few modes persist within the resonator under steady-state conditions, matching the amplification spectra and surpassing the losses. This condition means lasing threshold and can be found by formula R1R2 exp(-aL) exp(bL) =1, where a is the coefficient of losses in the cavity material, b-the coefficient of amplification.
The lasing threshold is shown by the green line on Figure 2b and only five mod amplitudes were bigger than it, that means the laser is able generate only these mods. So, a broader amplification spectrum of a gain medium allows generate the light with the larger spectral bandwidths (more modes). The spectral bandwidth is directly linked to the pulse duration produced by the laser, as dictated by the uncertainty principle. In this context, it can be expressed as Δν × Δτ = Const, where Δν and Δτ represent the spectral bandwidth and pulse duration typically measured at the Full Width Half Maximum (FWHM) of their intensities. Consequently, the product constant implies that a larger spectral bandwidth results in a shorter pulse duration.
In Figure 3a, three spectral widths are depicted alongside pulse durations corresponding to them. Notably, the pulse duration of 50 fs requires a much larger spectral width compared to 10 ps (10-12 seconds). Furthermore, Figure 3b,c illustrate the luminescence spectra of two laser crystals, Nd:YAG and Ti:Sa. Oscillators utilizing these crystals typically generate 4 × 103 and 3 × 105 longitudinal modes respectively, resulting in spectral bandwidths of 0.5 nm and 30 nm measured at FWHM.
Now, let's explore the practical methods of receiving laser pulses. The simplest, albeit not the most effective, method involves positioning an electromagnetic or mechanical interrupter within the CW laser output beam. In this scenario, the continuous wave power will match the pulsed power, despite losing energy. However, as evidenced by the chart in Figure 1, following the invention of the laser in 1960, its peak power experienced rapid growth over the subsequent decade, up to 1970. This advancement can be attributed to the development of two key technologies: "Q-switching" [14] and "Mode-locking" [15].
In the first method, unlike the previously discussed approach, the switcher was positioned inside the laser resonator to alter its Q-factor (quality factor), as depicted in Figure 4a (top). The Q-factor in this context can be defined as the ratio of stored energy to energy dissipated per oscillation cycle. Essentially, a high Q- factor corresponds to low energy losses in the cavity, and vice versa. When the Q-switch is closed (low Q-factor), it prevents light propagation within the cavity during the pumping of the GM, as illustrated in Figure 4a (bottom). Once sufficient energy is accumulated, the Q-switch is opened, allowing the light photons spontaneously born in GM pass between the resonator mirrors and undergo amplification in the gain medium by stimulating identical photons emission, thereby increasing pulse energy.
The duration of the generated pulses is influenced by several factors, including the resonator round-trip time, the initial gain, and the resonator losses. A higher initial gain results in a quicker buildup of pulses, leading to higher energy extraction and typically a faster decay of power after reaching the pulse maximum. Generally, the duration of pulses is at least on the order of the resonator round-trip time and often longer than 1 nanosecond (10-9 seconds - ns). Q-switch oscillators typically produce pulses with a repetition rate in the range below megahertz, boasting pulse powers up to megawatts (106 Watts - MW).
  In the resonator, longitudinal modes exhibit random phases, as depicted in Figure 4b (top). However, laser pulses can be significantly shortened by synchronizing the cavity modes, as illustrated in Figure 4b (bottom). This synchronization, known as Mod-lock operation regime in laser oscillators, ensures that the maximum amplitudes of all longitudinal modes coincide at the same point and same time within the cavity. This constructive summation results in a substantial increase in intensity at this point, manifesting as a pulse with a duration of a few optical cycles (a few fs). Furthermore, as more modes concentrate the energy in a smaller area, the pulse duration becomes even shorter (see Figure 3). As the soliton traverses between cavity mirrors, its energy escalates to the nano - microjoule level upon passing through the GM. A significant number of modes or a broad spectral bandwidth necessitates a gain medium with a large fluorescence spectrum, along with devices to compensate for dispersion in optical elements, such as pairs of prisms [19]. In practice, like Q-switching, achieving the Mode-locking regime can be realized through external driving modulators within the laser resonator (active mode locking) [20] or by exploiting nonlinear effects in the cavity elements, such as the Kerr effect or absorption saturation (passive mode locking) [21]. Advancements in these techniques, coupled with the integration of laser oscillators with amplifiers, led to a remarkable increase in output laser pulse power within a decade following the invention of lasers, achieving peak powers of up to terawatts (TW) [22]. However, further increases in power necessitated significant enlargement of the aperture of optical elements and gain media. This was due to the approaching of these elements to their damage threshold and/or the onset of undesired nonlinear effects, which can distort the laser beam and degrade pulse quality.
  An effective method for increasing pulse power involves reducing its duration rather than simply increasing energy, as expressed by the equation P=E/τ , where P is power, E is energy, and τ is pulse duration. However, it's essential to consider the damage threshold, which is proportional to the square root of pulse duration. For instance, when pulse durations approach tens of femtoseconds, the damage threshold can be as low as 100 millijoules per square centimeter (mJ/cm2) of energy fluence. Moreover, severe nonlinear effects such as self-focusing [23] can occur even earlier, typically when energy fluence approaches 1 mJ/cm2, with critical power levels reaching gigawatts (109 Watts - GW) in most cases. A direct method to mitigate these undesirable phenomena is by increasing the aperture size, as it was pointed out above. However, starting from the TW energy level, this approach becomes exceedingly expensive and even impractical. For instance, to achieve PW energy levels, a Ti:Sa crystal with a diameter of 3 meters would be necessary for the final amplifier in the laser system.
A more creative approach was proposed back in 1985. Initially, a short pulse with low energy is temporally stretched, resulting in a longer duration suitable for further amplification. This allows for a significantly reduced beam aperture. After accumulating a certain energy level in a chain of amplifiers, the long pulse is then compressed back to its original short pulse duration, yielding very high power. This groundbreaking method is known as Chirped Pulse Amplification (CPA) technique [16,17]. CPA has proven immensely fruitful in the development of ultra-high-power lasers, leading to a gradual increase in power over the years (see Figure 1). Recently, it has even enabled the achievement of power levels up to 10 petawatts. The general scheme of the CPA laser system is presented on Figure 5 a.
Initiating from the Mod-lock oscillator, which produces pulses ranging from 10s nJ to 1μJ with durations spanning from a few ps to few fs, the beam is directed towards a stretcher. This device elongates the pulse duration by several orders of magnitude, extending it up to the nanosecond level. The stretcher comprises two diffraction gratings with an optical telescope positioned between them (messed for simplicity at Figure 5 (a)). This specific configuration of the stretcher, proposed by Oscar Martinez in 1985 [24], has proven highly effective in facilitating the implementation of the CPA method. This optical setup disperses the broad spectrum of the short pulse into multiple narrow harmonics and routes them along different optical paths. Specifically, it arranges the longer wavelength harmonics (red) to travel shorter paths compared to the shorter wavelength ones (blue). Upon undergoing double passes through the stretcher, these harmonics reassemble into a single, elongated pulse with what is termed a positive chirp, where the red wavelengths precede the blue ones. In reality, the discretization of the continuous spectrum into separate harmonics was carried out for the sake of simplicity. For a more thorough understanding of the stretcher's operation, refer to [25]. As demonstrated earlier, the longer pulses possess a higher damage threshold for optics, enabling a significant reduction in the aperture of the optical elements to a reasonable level, even for high energy applications. These elongated pulses are then directed, following stretching, to a chain of multipass amplifiers where they accumulate the required energy. Subsequently, from the final amplifier, the large energy long pulses are directed to the compressor, comprised of either two or four diffraction gratings as depicted in Figure 5a. The compressor, as described in [26], executes the reverse procedure of the stretcher. It guides the red harmonics with longer wavelengths along longer paths and the blue ones with shorter wavelengths along shorter paths, culminating at the compressor output into a short pulse. Ideally, this pulse equals the initial one but now possesses significantly higher energy, leading to an exceptionally high pulse power.
Each element of this scheme has undergone modifications and improvements since 1985. Here, we'll outline the main trends of this technology. The general modifications applied to two key components of the CPA system, namely the stretcher and compressor, primarily involved enhancing pulse stretching [27], improving the quality and size of the gratings [28], and achieving better alignment and conjugation between the stretcher and compressor [29,30,31].
Concerning the oscillator and amplifiers, their initial designs were centered around Nd:glass and  Nd:YAG crystals [32,33], which typically exhibited a luminescent spectral bandwidth of 0.5 - 15nm FWHM. These oscillators could generate pulses with durations of several hundreds of femtoseconds. However, to achieve the desired output power of 1PW from these laser systems, amplification to the kilojoule energy level was necessary.
  The adoption of Ti: Sapphire crystals [34] as the gain medium for CPA brought about a significant reduction in pulse duration, thanks to their much broader luminescent spectra spanning up to 200 nm, capable of supporting pulse durations as short as 5fs. Additionally, these crystals possess several unique properties such as high thermal conductivity for effective heat extraction, low thermal expansion, and impressive hardness, rendering them suitable for use in laser oscillators and amplifiers. With the capacity to produce large-aperture crystals above 20cm [35] in diameter (Figure 6 a), they have become the workhorse for amplifiers in CPA laser systems, ultimately facilitating the achievement of the current record output power of 10PW [10].
However, achieving this extraordinary result demanded numerous technological improvements in laser amplifiers. For instance, generating the energy required for a 10PW pulse power approaches several hundreds of joules, necessitating crystal apertures of tens of centimeters in diameter. Consequently, the gain in the transverse direction far exceeds that in the longitudinal direction, considering the typical crystal thickness of a few centimeters. Thus, extracting stored energy by the amplified pulse (seed) requires a multipass optical scheme and takes considerably longer time compared to the pulse duration (approximately 100ns for a 1ns pulse). A typical scheme of a multipass Ti:Sa amplifier is illustrated in Figure 6b.
The initial method of amplification involved the full energy crystal pumping before the arrival of the seed pulse, resulting in substantial energy losses due to amplified spontaneous emission (ASE) and/or transverse parasitic generation. Figure 7a illustrates the luminescence of the pumped Ti:Sa crystal before and after the onset of parasitic generation.
  One of the methods employed to mitigate these substantial losses was the cladding of the side surface of the crystal with a material having a refractive index equal to that of the crystal, thereby preventing light reflection back into the crystal material and minimizing further losses [36]. However, this approach proved insufficient for truly large crystal apertures due to the significant transverse gain. In 2003, a new method was proposed to address this challenge, namely the optimization of timing between crystal pumping and pulse extraction [37,38,39,]. This method, known as Extraction During Pumping (EDP), enabled the optimization of the energy required for pumping before and after each seed pulse pass, thereby reducing losses. First time this method was tested with the Hercules laser system in the Centr for Ultrafast Optical Science (CUOS) of University of Michigan. Figure 7b shows the final amplifier of The Hercules during shot. The laser system reached the record intensity of 2*1022 W/cm2 in 2008 [40]. With EDP, it became possible to extract up to 0.6 kJ from large-aperture Ti:Sa crystals with diameters of up to 25cm [39].
Another type of amplifier utilized in high-power CPA systems is the Optical Parametric Amplifier (OPA) or Optical Parametric Chirped Pulse Amplifier (OPCPA) [41]. Unlike traditional laser amplifiers, OPAs leverage nonlinear interactions between pump and seed pulses within crystals. In the parametric amplification process, the high-energy quantum state of the crystal, excited by pump photons, undergoes decay stimulated by a seed photon (see Figure 8). This decay leads to the emission of another seed photon and an idler photon, facilitated by the virtual energy level between the excited and lower states. All three photons adhere to the laws of energy and momentum conservation, necessitating their efficient amplification within a certain distance of the crystal [42]. To amplify pulses with broad spectral bandwidths, the initially collinear incidence of pump and seed beams on the crystal surface has been replaced with a noncollinear approach (NOPA), enabling the maintenance of synchronization conditions for these broad spectra [43]. NOPAs offer several advantages over traditional laser amplifiers for their applications in CPA systems, such as improved temporal contrast and energetic efficiency. However, OPCPA systems face challenges, including the necessity for high-quality pump pulses and precise synchronization with the seed pulse, which can be considered disadvantages. It's worth noting that the output power of OPCPA systems now approaches that of laser CPAs [44]. Used for OPA the KDP and DKDP crystals can be grown with large size clear aperture up to 500 mm diameter, allowing amplification of nanosecond stretched broad-bandwidth laser pulses at kJ-energy-level. Looking ahead, there are ambitious plans to further increase power output, with projects aiming for up to 50 – 100 PW, as demonstrated by initiatives like the OPCPA system development project referenced in [45,46].
Industrial, medical, and numerous scientific applications of CPA lasers necessitate a substantial increase in the pulse Repetition Rate (RR), or in other words, the average power. However, the RR of existing high peak power laser systems is typically low, often limited to a few Hz or less [47]. The primary obstacle to significant RR raising is the escalating heat generation in amplifiers, attributed to the quantum defect, which creates an energy difference between pump and seed photons.
The Thin Disc (TD) geometry of laser amplifier active media, such as Yb:YAG, has proven highly effective for heat dissipation, enabling remarkable achievements in laser power. Continuous Wave (CW) regimes have achieved output powers of up to 10s kW [48], while in master oscillator - power amplifier (MOPA) systems, several Joules of energy per pulse and high average power have been attained [49].
The typical scheme of TD amplifier is shown on Figure 9 a, the heat is extracted through the largest face of the crystal for efficient and uniform cooling, in opposite to the conventional side-surface heat extraction. The very high thermal conductivity Ti:Sa crystal with combination of TD technology allows to increase this effect, preventing the overheating of the laser crystals and, thus eliminating the beam thermal distortions and possible crystal damage even for an extremely high average power operation regime [50,51,52,53,54]. Figure 9b,c demonstrate consequently TD 35*3 mm Ti:Sa crystal and holder with both large surfaces direct contact water chilling.
However, the TD crystal shape represents just one possible geometry for the final amplifier in laser systems, and it may undergo changes depending on the desired output parameters. In paper [54], simulations were conducted to determine the maximal achievable pump fluence of the amplifier crystal, which was found to depend on the repetition rate (RR). These simulations also highlighted the effect of pump fluences on the selection of crystal shape.
Figure 10 illustrates the relationship between the required output average power and the repetition rate (RR), delineating preferred areas of usage for different Ti:Sa crystal configurations such as Thin Disc (TD), Rectangular Thin Crystal Plate (RTCP), and Cross Thin Slab (XTS). As depicted, the TD crystal configuration is well-suited for systems with an RR below a few hundred Hz, especially if an output pulse energy above 10 Joules is required (red area) [50,51]. Conversely, the RTCP geometry demonstrates superiority for Ti:Sa amplifiers operating at an RR above 1 kHz, covering an energy range of 0.1–10 J (violet area). Lastly, the XTS crystal shape emerges as the preferred choice for amplifiers operating at high RR levels above 1 kHz but with a low energy per pulse below 100 mJ (blue area) [52,53].
The laser systems utilizing the CPA technique have recently achieved remarkable results and continue to show significant potential for further development. Several facilities have been constructed or are currently under construction. One of the pioneering and notable projects in this field is the Extreme Light Infrastructure (ELI).
Under this project, three laser centers were developed in Eastern Europe (see Figure 11): ELI-Beamlines in the Czech Republic [55], ELI-ALPS in Hungary [56], and ELI-NP in Romania [57]. These three pillars of ELI include several petawatt-class lasers: ELI-ALPS (HF) Ti:Sa system with a peak power of 2 PW and a pulse duration of 17 fs; ELI-BEAMLINES (L3) Ti:Sa laser with a 30 J pulse energy, 1 PW peak power and a pulse duration ~ 30 fs; ELI-BEAMLINES (L4) Nd: Glass lasers of 2kJ / 10 PW/ 130fs; and ELI-NP with two channels Ti:Sa lasers of 300 J / 10 PW each.
Two other notable high-power laser systems are the Chinese system with an output power of 10 PW [58] and the South Korean system with an output power of 5 PW. The latter recently achieved the highest intensity of 2×1023 W/cm2 [59].

4. Prospects and Conclusion

The next milestone for high-power lasers is reaching 100 PW, with several systems currently under design and development. A Chinese OPCPA system aims to achieve 100 PW by 2030 [60], and the University of Rochester system in the USA is expected to reach 50 PW [45].
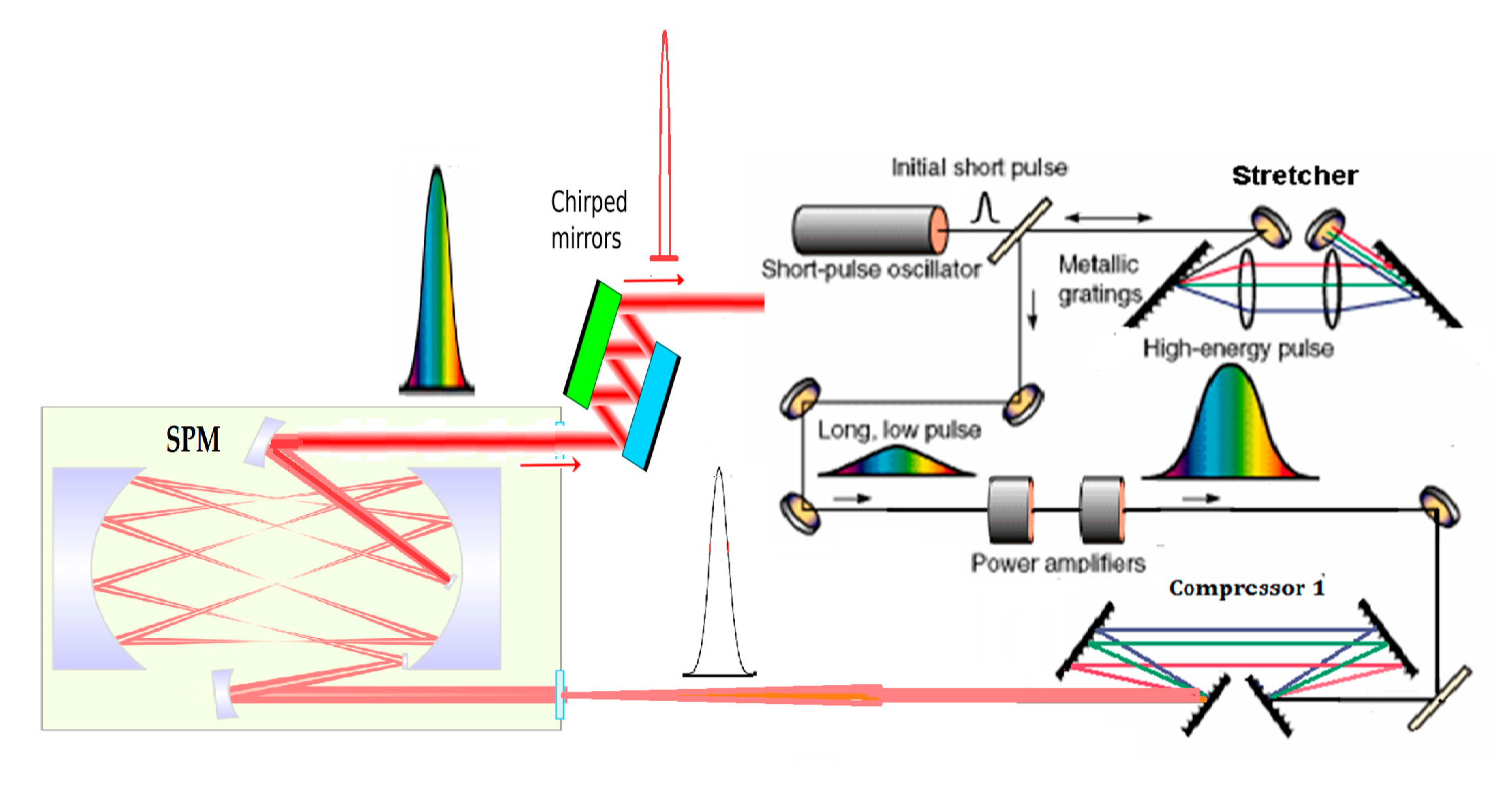
Several designs incorporating CPA techniques promise to further increase laser power to the 1018 W - exawatt (EW) and 1021 W - Zettawatt (ZW) level. One of them is the post-compression methods, where intense pulses from a standard CPA laser undergo spectral broadening via self-phase modulation (SPM) in a nonlinear material, followed by further compression (see Figure 12) [61,62].
This technique, which allows for the compression of femtosecond pulses into near single-cycle pulses lasting just a few femtoseconds, achieves spectral broadening in a variety of materials, ranging from gases to solids. In 2010, a method for compressing laser pulses with energy levels at the joule scale and higher was both proposed and demonstrated [63,64]. However, SPM in solid materials faces challenges such as low damage thresholds and potential heating problems, limiting improvements in both peak and average output power. In contrast, gas-filled Multi-Pass Cells (MPC) for spectral broadening via SPM offer a promising solution to substantially mitigate these limitations and are now under intensive development [65,66].
Another approach is an amplification method, weaving the three basic compression techniques, CPA, OPCPA and Plasma Compression by Backward Raman Amplification (BRA) in plasma. It is called C3 for Cascaded Conversion Compression. It has the capability to compress with good efficiency kilojoule to megajoule, nanosecond laser pulses into femtosecond pulses [67]. The modification of pulse compression in plasma was presented in [68]. The simulation demonstrates that laser pulse compression by a density gradient plasma allows to achieve exawatt to zettawatt pulse power.
More than five order compression from a 20 ns duration stretched pulse to a 100 fs Fourier transform-limited one after propagating through a six-grating compressor arrangement allows to produce exawatt-scale pulses. The paper [69] presents the based on simultaneous proof of this ability by an ideal spatial-temporal pulse structure that requires a chirped beam and chirped pulse amplification in a Nd: Mixed-glass laser system.
As seen from the presented review, laser technologies are experiencing rapid progress, inspired by promising recent applications such as confinement nuclear fusion, extreme ultraviolet lithography and industrial manufacturing. The deployment of these new devices and systems in industry and medicine has enabled significant advancements in technological capabilities, which can greatly enhance human life. In scientific research, these new systems will facilitate experiments in the new regime of ultra-relativistic optics and even in nonlinear quantum electrodynamics (QED), with laser intensities for matter interaction exceeding 1025 W/cm2, leading to a deeper understanding of the nature.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. J. Naresh, P. Khatak. Laser cutting technique: A literature review. Materials Today: Proceedings 2022, 56, 2484-2489.
  2. M.L. Dezaki, A. Serjouei, A. Zolfagharian, M. Fotouhi, M. Moradi, M.K. Ariffin, M. Bodaghi. A review on additive/subtractive hybrid manufacturing of directed energy deposition (DED) process Advanced Powder Materials, 2022, 1, 100054.
  3. T. Tajima, X. Q. Yan & T. Ebisuzaki. Wakefield acceleration, Reviews of Modern Plasma Physics, 2020, 4, 7.
  4. Rockwood, A.; Wang, Y.; Wang, S.; Berrill, M.; Shlyaptsev, V.N.; Rocca, J.J. Compact gain-saturated x-ray lasers down to 6.85 nm and amplification down to 5.85 nm. Optica 2018, 5, 257–262.
  5. Samuel E. Wurzel, Scott C. Hsu. Progress toward fusion energy breakeven and gain as measured against the Lawson criterion, Pys. Plasmas, 2022, 29, 062103.
  6. Nan Fu1,, Yanxiang Liu, Xiaolong Ma, Zhanfeng Chen. EUV Lithography: State-of-the-Art Review, J. Microelectron. Manuf. 2019, 2, 19020202.
  7. Jiapo Sun, Lie Liu, Lianghua Han, Qixin Zhu, Xiang Shen, Ke Yang. 100 kW ultra-high power fiber laser,Optics Continuum. 2022; 1, 1932–1938.
  8. Shaoyu Zhao, Aiyi Qi, Mingjin Wang, Hongwei Qu, Yuzhe Lin, Fengxin Dong, Wanhua Zheng. High-power high-brightness 980 nm lasers with >50% wall-plug efficiency based on asymmetric super large optical cavity Optics Express, 2018, 26, 3518.
  9. Yong Zhang, Tim Killeen. Gas Lasers: CO2 lasers - progressing from a varied past to an application-specific future. Laser Focus World, 2016, 4, 3.
  10. Christophe Radier, Olivier Chalus, Mathilde Charbonneau, Shanjuhan Thambirajah, Guillaume Deschamps, Stephane David, Julien Barbe, Eric Etter, Guillaume Matras, Sandrine Ricaud, 10 PW peak power femtosecond laser pulses at ELI-NP. High Power Laser Science and Engineering. 2022; 10, 21.
  11. John Crane, Mikael Martinez, Bryan Moran, Curt Laumann, James Davin, Joshua Rothenberg, Raymond Beach, Brad Gollock, Russ Jones, Ron Wing, John Braucht, Ken Skulina, and Scott Mitchell, High-gain, Nd-doped-glass preamplifier for the National Ignition Facility (NIP) laser system. Conference Proceedings LEOS'96 9th Annual Meeting IEEE Lasers and Electro-Optics Society, 18-21 November 1996.
  12. Andreas Thoss. EUV lithography revisited. Laser Focus World. 2019; 8, 29.
  13. Mark Wolverton. A Solution for Almost Everything, 50 Years of the Laser. Inventions and Technology, 2010, 25, 2.
  14. F. J. McClung and R. W. Hellwarth, Giant optical pulsations from ruby. J. Appl. Phys. 1962, 33 , 828.
  15. W. E. Lamb Jr., Theory of an optical laser, Phys. Rev. 1964 134, 1429.
  16. T. Damm, M. Kaschke, F. Noack, and B. Wilhelmi. Compression of picosecond pulses from a solid-state laser using self-phase modulation in graded-index fibers. Opt. Lett. 1985, 10, 176.
  17. D. Strickland and G. Mourou. Compression of amplified chirped optical pulses. Opt. Commun. 1985, 56, 219.
  18. Anthony E. Siegman, Fundamentals of Laser Oscillation. Lasers, Aidan Kelly, University Science Books, 55D Gate Five Road, Sausalito, CA 94965, 1986, pp. 457-547.
  19. R.L. Fork, O.E. Martinez, J.P. Gordon. Optics Letters, 1984, 9,150.
  20. L. E. Hargrove, R. L. Fork, and M. A. Pollack. Locking of He–Ne laser modes induced by synchronous intracavity modulation, Appl. Phys. Lett. 1964, 5, 4.
  21. E. P. Ippen, C. V. Shank, A. Dienes. Passive mode locking of the cw dye lasers, Appl. Phys. Lett. 1972, 21, 348.
  22. K. R. Manes, H. G. Ahlstrom, R. A. Haas, and J. F. Holzrichter. Light-plasma interaction studies with high- power glass laser, J. Opt. Soc. Amer. 1977, 67, pp. 717-726.
  23. P. L. Kelley. Self-focusing of optical beams, Phys. Rev. Lett. 1965, 15 (26), 1005.
  24. O. E. Martínez et al. Negative group-velocity dispersion using refraction. J. Opt. Soc. Am. (1984, 1, 1003.
  25. Zhigang Zhang, Yanrong Song, Darui Sun, Lu Chai, Hong Sun, Ching-yue Wang. Compact and material- dispersion-compatible Offner stretcher for chirped pulse amplifications. Optics Communications, 2002, 206, Issues 1–3, 7-12.
  26. E. B. Treacy. Optical pulse compression with diffraction gratings. IEEE J. Quantum Electron. 1969, 5, 454.
  27. G. Cheriaux et al. Aberration-free stretcher design for ultrashort-pulse amplification. Opt. Lett. 1996, 21, 414.
  28. N. Bonod, J. Neauport. Diffraction gratings: from principles to applications in high-intensity lasers. Advances in Optics and Photonics, 2016, 8, 156-199.
  29. C. M. Gonz´alez, O. E. Mart´ınez. Quartic phase compensation with a standard grating compressor. Optics Letters, 1997, 22, 1186.
  30. V. Bagnoud, F. Salin. Global Optimization of Pulse Compression in Chirped Pulse Amplification. IEEE J. Sel. Top. Quantum Electron. 1998, 4, 445. [Google Scholar] [CrossRef]
  31. V. Chvykov, V. Yanovsky. Precise Alignment of Large-aperture Compressor Gratings for High-power Lasers by Using Diffraction Interferometry. In Proceedings of OSA/CLEO/IQEC, JWB4, Baltimore, USA, 31/05/2009.
  32. Campbell, J.H., Hayden, J.S., Marker, A. High-power solid-state lasers: a laser glass perspective. Int. J. Appl. Glass Sci. 2011, 2, 3–29.
  33. Chi, H.; Wang, Y.; Davenport, A.; Menoni, C.S.; Rocca, J.J. Demonstration of a kilowatt average power, 1 J, green laser. Opt. Lett. 2020, 45, 6803–6806. [Google Scholar] [CrossRef]
  34. P. F. Moulton. Spectroscopic and laser characteristics of Ti:Al2O3. J. Opt. Soc. Am. B. 1986, 3, 125.
  35. D. Joyce, B. Ripley, K. Schmid, S. Cohen. High-Power Solid-State Lasers: Ti:sapphire laser crystals reach 200 mm diameter. Laser Focus World 2010, 2, 28.
  36. F. G. Patterson, J. Bonlie, D. Price, and B. White. Suppression of parasitic lasing in large-aperture Ti:sapphire laser amplifiers. Optics Letters. 1999, 24, 963-965.
  37. Chvykov, V.; Yanovsky, V.; Bahk, S.W.; Kalintchenko, G.; Mourou, G. Suppression of parasitic lasing in multi-pass Ti-sapphire amplifiers. In Proceedings of the Conference on Lasers and Electro-Optics, Munich, Germany, 2003.
  38. V. Chvykov, K. Krushelnick. Optics Communications, 2012, 285, 2134.
  39. Chvykov, V.; Krushelnik, K. Transverse amplified spontaneous emission: The limiting factor for output energy of ultra-high-power lasers. Opt. Commun. 2014, 312, 216. [CrossRef]
  40. V. Yanovsky, V. Chvykov, G. Kalinchenko1, P. Rousseau, T. Planchon, T. Matsuoka, A. Maksimchuk, J. Nees, G. Cheriaux, G. Mourou, K. Krushelnick, Optics Express. 2008, 16, 2109.
  41. R. Butkus et al. Progress in chirped pulse optical parametric amplifiers, Appl. Phys. B, 2004, 79, 693.
  42. R. A. Baumgartner and R. L. Byer, Optical parametric amplification, IEEE J. Quantum Electron. 1979, 15, 432.
  43. T. Kobayashi and A. Baltuška, Sub-5 fs pulse generation from a noncollinear optical parametric amplifier, Meas. Sci. Technol. 2002, 13, 1671.
  44. V. V. Lozhkarev et al., 200 TW 45 fs laser based on optical parametric chirped pulse amplification, Opt. Express, 2006, 14, 446.
  45. Bromage, J. et al. MTW-OPAL: a technology development platform for ultra-intense optical parametric chirped-pulse amplification systems. High. Power Laser Sci. Eng. 2021, 9, 63. [CrossRef]
  46. Li, Z. & Kawanaka, J. Possible method for a single-cycle 100-petawatt laser with wide-angle non-collinear optical parametric chirped pulse amplification. OSA Contin. 2019, 2, 1125–1137.
  47. E. Sistrunk, T. Spinka, A. Bayramian, et al. All Diode-Pumped, High-repetition-rate Advanced Petawatt Laser System (HAPLS). In Proceedings of OSA/CLEO/IQEC, STh1L.2, San Jose, California United States, 14–19 May 2017.
  48. Giesen, A. Thin Disk Lasers – Power scalability and beam quality. Laser Technik Journal, (2005), 2, 42-45.
  49. Tümmler, J.; Jung, R.; Stiel, H.; Nickles, P.V.; Sandner, W. High-repetition-rate chirped-pulse-amplification thin-disk laser system with joule-level pulse energy. Opt. Lett. 2009, 34, 1378–1380. [CrossRef]
  50. Chvykov, V.; Nagymihaly, R.S.; Cao, H.; Kalashnikov, M.; Osvay, K. Design of a thin disk amplifier with extraction during pumping for high peak and average power Ti: Sa systems (EDP-TD). Opt. Express 2016, 24, 372. [CrossRef]
  51. Chvykov, V.; Cao, H.; Nagymihaly, R.; Kalashnikov, M.P.; Khodakovskiy, N.; Glassock, R.; Ehrentraut, L.; Schnuerer, M.; Osvay, K. High peak and average power Ti: sapphire thin disk amplifier with extraction during pumping. Opt. Lett. 2016, 41, 3017 [CrossRef]
  52. Cao, H.; Nagymihaly, R.S.; Chvykov, V. Cross thin slab kW-class Ti: Sapphire amplifiers. Laser Phys.2019, 29, 065802. [CrossRef]
  53. Chvykov, V.; Chi, H.; Wang, Y.; Dehne, K.; Berrill, M.; Rocca, J.J. Demonstration of a side-pumped cross- seeded thin-slab pre-amplifier for high-power Ti:Sa laser systems. Opt. Lett. 2022, 47, 3463. [CrossRef]
  54. V. Chvykov, Ti:Sa Crystal Geometry Variation vs. Final Amplifiers of CPA Laser Systems Parameters. Crystals 2022, 12, 1127.
  55. ELI BEAMLINES FACILITY: https://www.eli-beams.eu.
  56. ELI-ALPS Research Institute: https://www.eli-alps.hu.
  57. Nuclear Physics (ELI-NP): https://www.eli-np.ro.
  58. Li W. Gan Z.; Yu L.; Wang C.; Liu Y.; Guo Z.; Xu L.; Xu M.; Hang Y.; Xu Y. 339 J high-energy Ti:sapphire chirped-pulse amplifier for 10 PW laser facility. Opt. Lett. 2018, 43, 5681–5684.
  59. Yoon J.W.; Kim Y.G.; Choi I.W.; Sung J.H.; Lee H.W.; Lee S.K.; Nam C.H. Realization of laser intensity over 1023 W/cm2. Optica 2021, 8, 630–635. [CrossRef]
  60. Wang, X. et al. 13.4 fs, 0.1 Hz OPCPA front end for the 100 PW-class laser facility. Ultrafast Sci. 2022, 1–8 (2022).
  61. G. Mourou, S. Mironov, E. Khazanov, A. Sergeev. Single cycle thin film compressor opening the door to Zeptosecond-Exawatt physics. Eur. Phys. J. Special Topics 2014, 223, 1181–1188.
  62. Efim Khazanov. Post-compression of femtosecond laser pulses using self-phase modulation: from kilowatts to petawatts in 40 years. Quantum Electronics, 2022, 52, 208-226.
  63. V Chvykov, C Radier, G Chériaux, G Kalinchenko, V Yanovsky, G Mourou, Compression of ultra-high power laser pulses, , CLEO (2010) , JThG4, San Jose, California United States, 16 May 2010.
  64. V. Ginzburg, I. Yakovlev, A. Kochetkov, A. Kuzmin, S. Mironov, I. Shaikin, A. Shaykin, E. Khazanov, 11 fs, 15 PW laser with nonlinear pulse compression. Opt. Express (2021), 29, 28297–28306.
  65. Martin Kaumanns, Dmitrii Kormin, Thomas Nubbemeyer, Vladimir Pervak, Stefan Karsch, Spectral broadening of 112 mJ, 1.3 ps pulses at 5 kHz in a LG10 multipass cell with compressibility to 37 fs, Optics Letters, 2021, 46, 929.
  66. V. Savichev , T. Tarkan, Y. Wang, J. Rocca, V. Chvykov. Free Beam Propagation Multipass Cells for Post-Compression of High-Energy Laser Pulses. CLEO 2024, In Proceedings of OSA/CLEO/IQEC, STh4I.2, 05/09/ 2024.
  67. G.A. Mourou, N.J. Fisch, V.M. Malkin, Z. Toroker, E.A. Khazanov, A.M. Sergeev, T. Tajima, B. Le Garrec. Exawatt-Zettawatt pulse generation and applications. Optics Communications 2012, 285, 720-724.
  68. M. Hur, B. Ersfeld, H. Lee, H. Kim, K. Roh, Y. Lee, H. S. Song, M. Kumar, S. Yoffe, D. A. Jaroszynski, H. Suk . Laser pulse compression by a density gradient plasma for exawatt to zettawatt lasers. Nature Photonics 2023, 17, 1074–1079.
  69. Chesnut, K. D. & Barty, C. P. J. Ideal spatio-temporal pulse distribution for exawatt-scale lasers based on simultaneous chirped beam and chirped pulse amplification. Opt. Express 2023, 31, 5687.
  70. Laser Basics: https://www.slideshare.net/slideshow/part-i-laser-basics-lorenser-2009/1245640.
  71. G. Toesko, C. Dehnert. Ultrafast Laser Optics: Femtosecond laser optics combat pulse dispersion, color errors, and reflections. Laser Focus World 2016, 03, 18. Source URL: https://www.laserfocusworld.com/optics/article/16547107/ultrafast-laser-optics-femtosecond-laser-optics-combat-pulse-dispersion-color-errors-and-reflections.
  72. Photonics Spectra: https://www.photonics.com/Articles/Understanding_Passively_Q-Switched_Solid-State/a56862 (November 2014).
  73. Photonics Encyclopedia: https://www.rp-photonics.com/q_switching.html (06/03/2024).
  74. Newport: https://www.newport.com/n/pulsed-laser-methods (06/03/2024).
  75. University of Rochester/ Laboratory for Laser Energetics: https://www.lle.rochester.edu/chirped-pulse-amplification (06/04/2024).
  76. University of Michigan/ Center for Ultrafast Optical Science (CUOS): https://cuos.engin.umich.edu/researchgroups/hfs/facilities/hercules-petawatt-laser (06/04/2024).
  77. Ple, F.; Pittman, M.; Jamelot, G.; Chambaret, J.P. Design and demonstration of a high-energy booster amplifier for a high repetition rate petawatt class laser system. Opt. Lett. 2007, 32, 238. [CrossRef]
  78. Photon picture of Optical Parametric Amplification (OPA).svg: https://upload.wikimedia.org/wikipedia/commons/9/98/Photon_picture_of_Optical_Parametric_Amplification_%28OPA%29.svg (10/09/2017).
  79. Photonics Encyclopedia:https://www.rp-photonics.com/thin_disk_lasers.html (06/05/2024).
  80. N. Nicolas, J. Neauport. Diffraction gratings: from principles to applications in high-intensity lasers. Advances in Optics and Photonics 2016, 8, 156-199.
Preprints 109145 g001
Figure 1. Historical development of the pulsed high-power laser systems. Modified from [60].
Figure 1. Historical development of the pulsed high-power laser systems. Modified from [60].
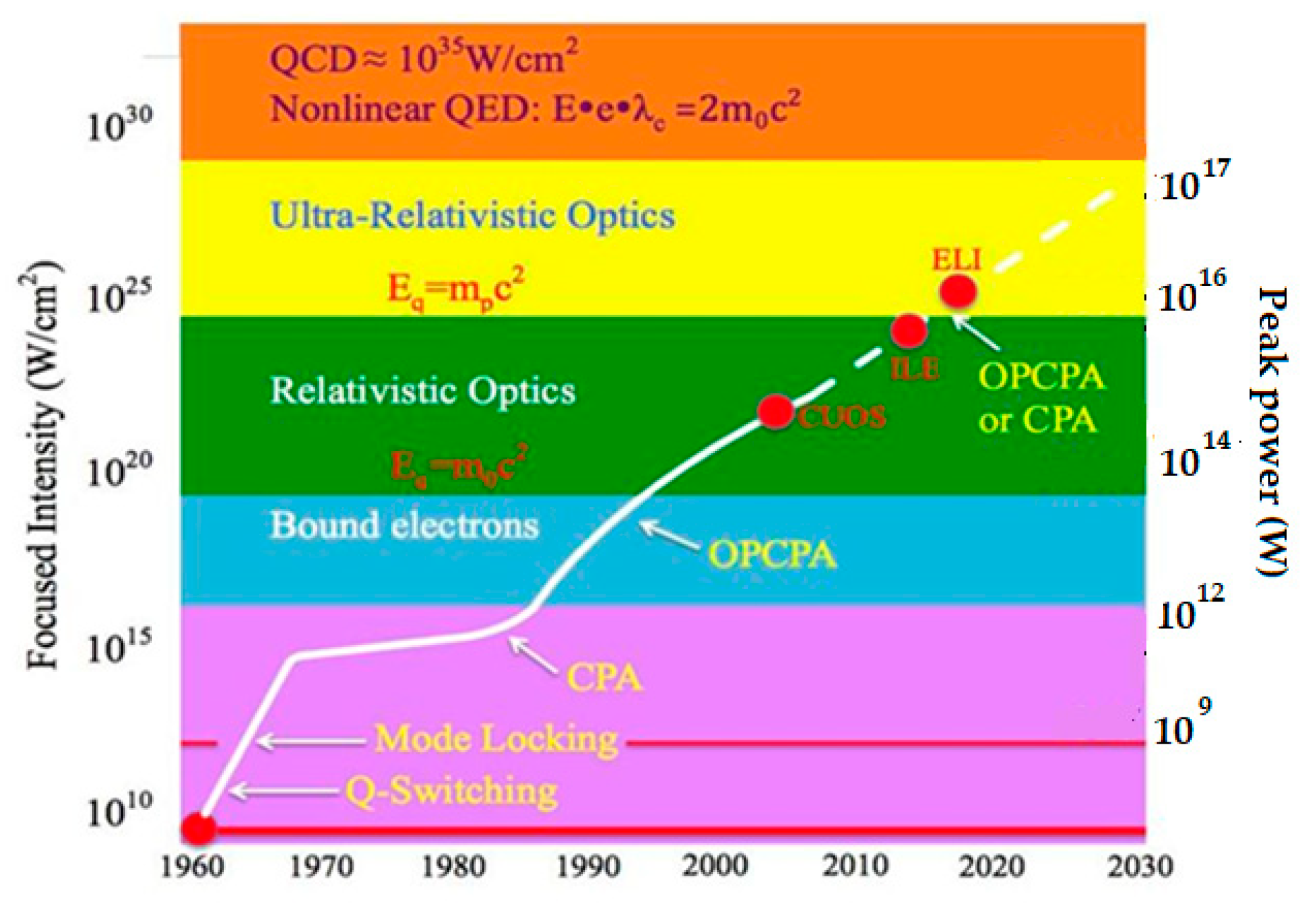
Preprints 109145 g001
Preprints 109145 g002
Figure 2. (a) Laser oscillator (top) and the longitudinal mods in cavity (bottom); (b) longitudinal mods of HeNe laser. Modified from [68].
Figure 2. (a) Laser oscillator (top) and the longitudinal mods in cavity (bottom); (b) longitudinal mods of HeNe laser. Modified from [68].
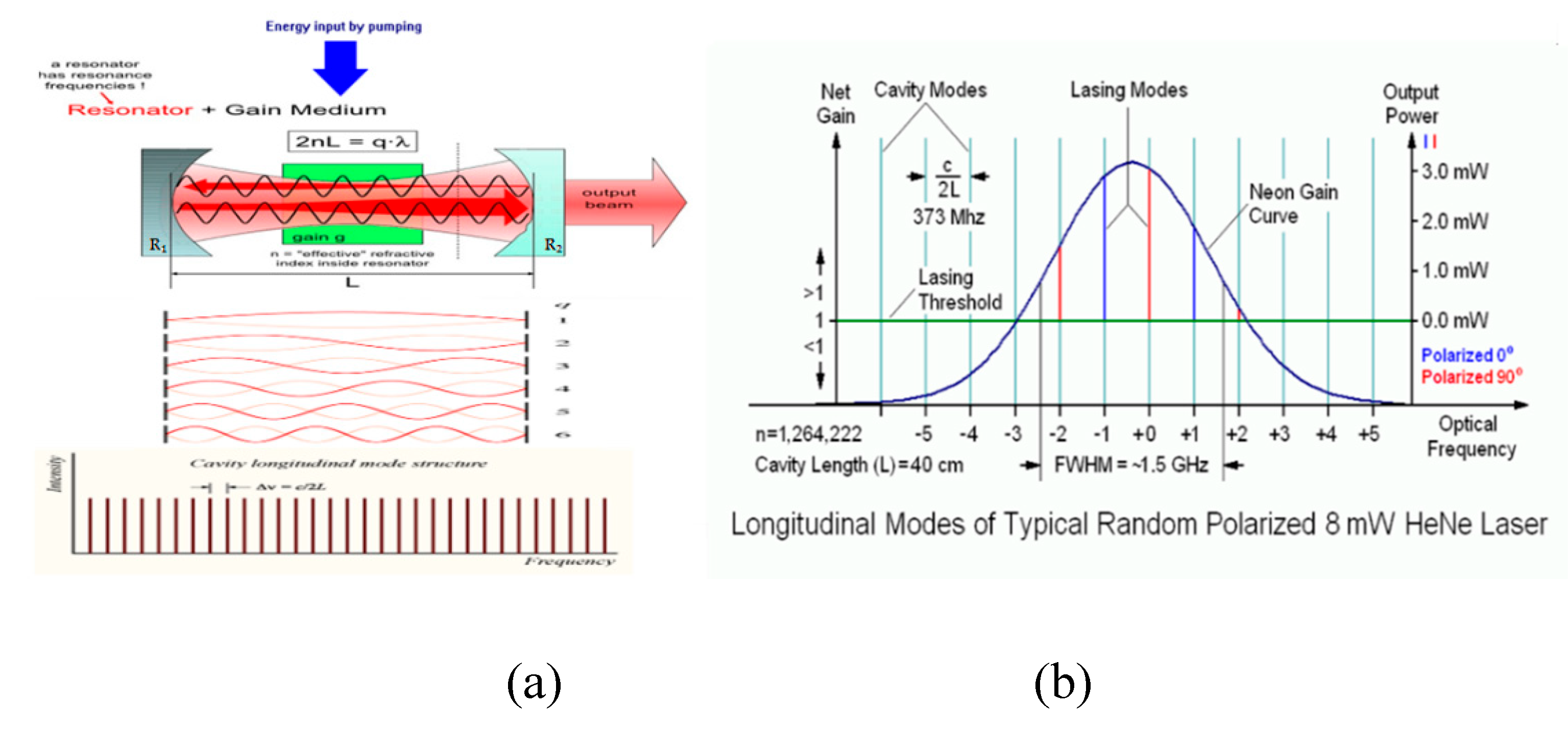
Preprints 109145 g002
Preprints 109145 g003
Figure 3. (a) Spectral widths and the corresponding pulse durations [69]; (b) Luminescence spectra of Nd :YAG laser crystal; (c) Luminescence spectra of Ti:Sa crystal. Modified from [32].
Figure 3. (a) Spectral widths and the corresponding pulse durations [69]; (b) Luminescence spectra of Nd :YAG laser crystal; (c) Luminescence spectra of Ti:Sa crystal. Modified from [32].
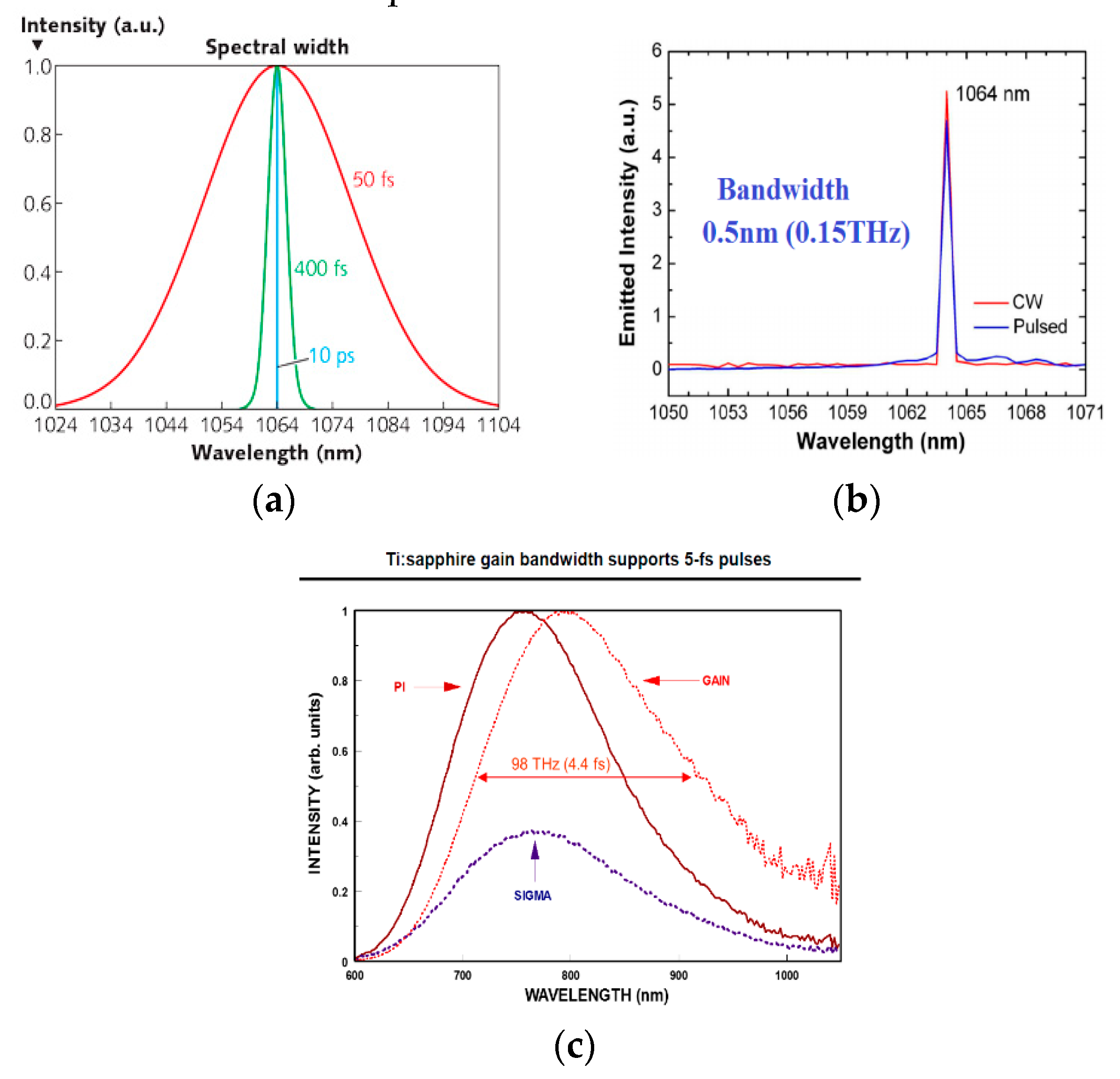
Preprints 109145 g003
Preprints 109145 g004
Figure 4. (a) Q-switch laser oscillator (top) [70] and temporal evolution of gain and losses in a passively Q-switched laser (bottom) [71]; (b) Longitudinal modes with random phases (top) and synchronizing cavity modes (bottom) [72].
Figure 4. (a) Q-switch laser oscillator (top) [70] and temporal evolution of gain and losses in a passively Q-switched laser (bottom) [71]; (b) Longitudinal modes with random phases (top) and synchronizing cavity modes (bottom) [72].
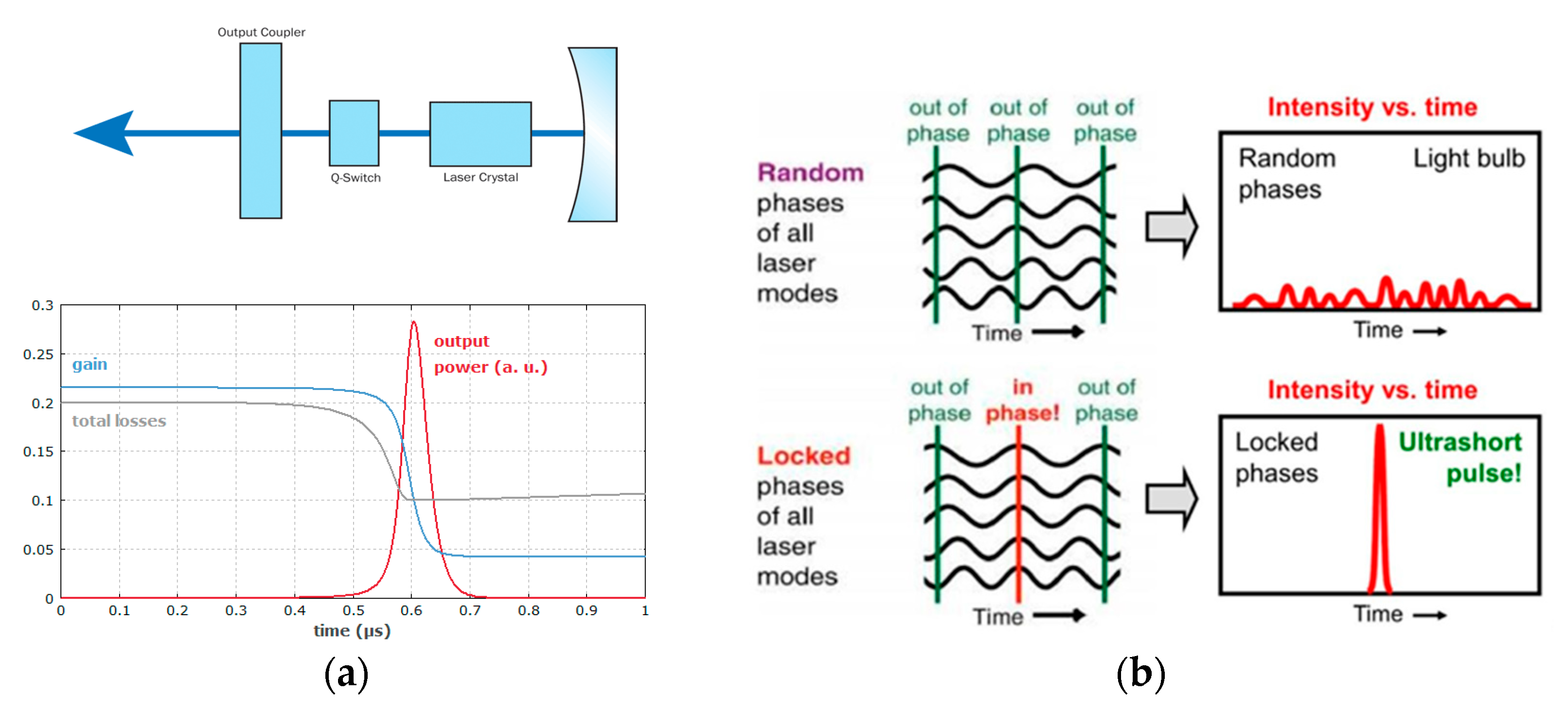
Preprints 109145 g004
Preprints 109145 g005
Figure 5. (a) General idea of CPA laser system [73]; (b) Typical block-scheme of CPA laser. Modified from [74].
Figure 5. (a) General idea of CPA laser system [73]; (b) Typical block-scheme of CPA laser. Modified from [74].
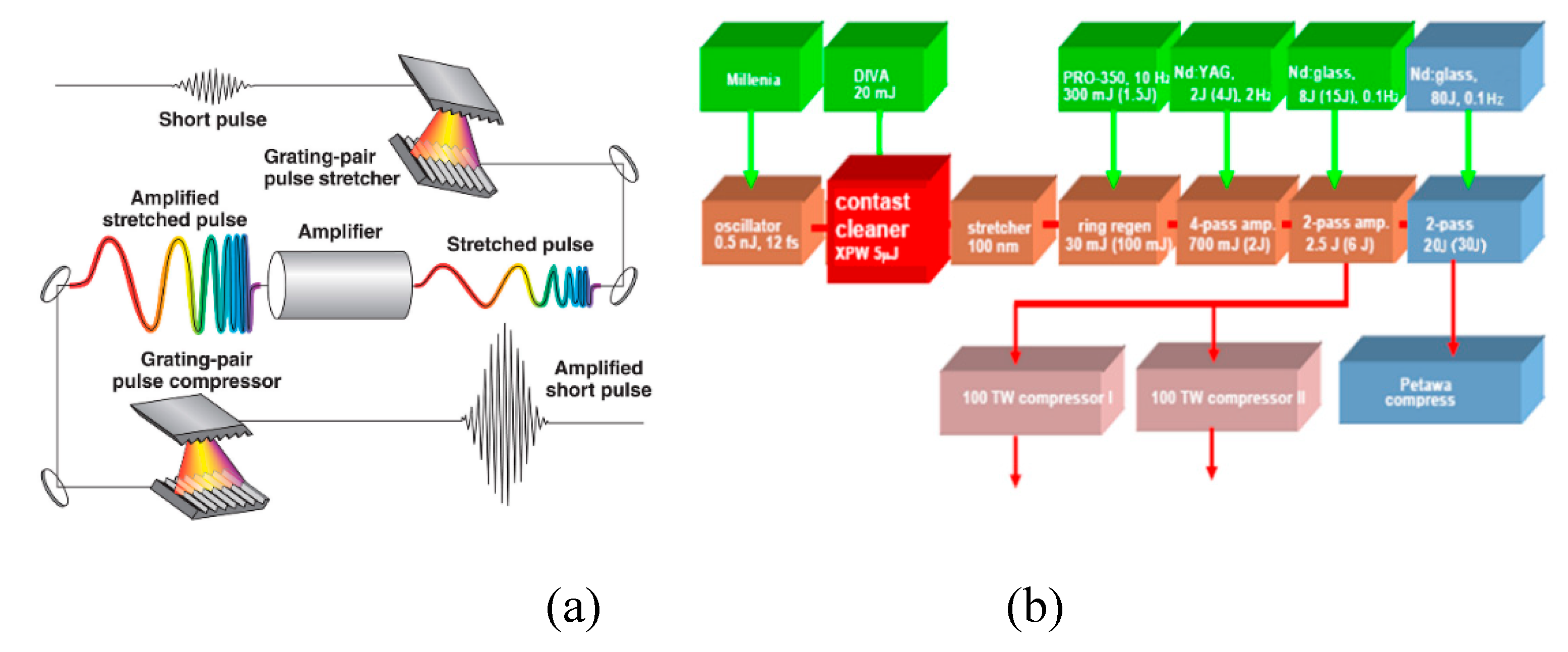
Preprints 109145 g005
Preprints 109145 g006
Figure 6. (a) Large-aperture Ti:Sa crystals [35] (b) Typical scheme of a multipass Ti:Sa amplifier [54].
Figure 6. (a) Large-aperture Ti:Sa crystals [35] (b) Typical scheme of a multipass Ti:Sa amplifier [54].
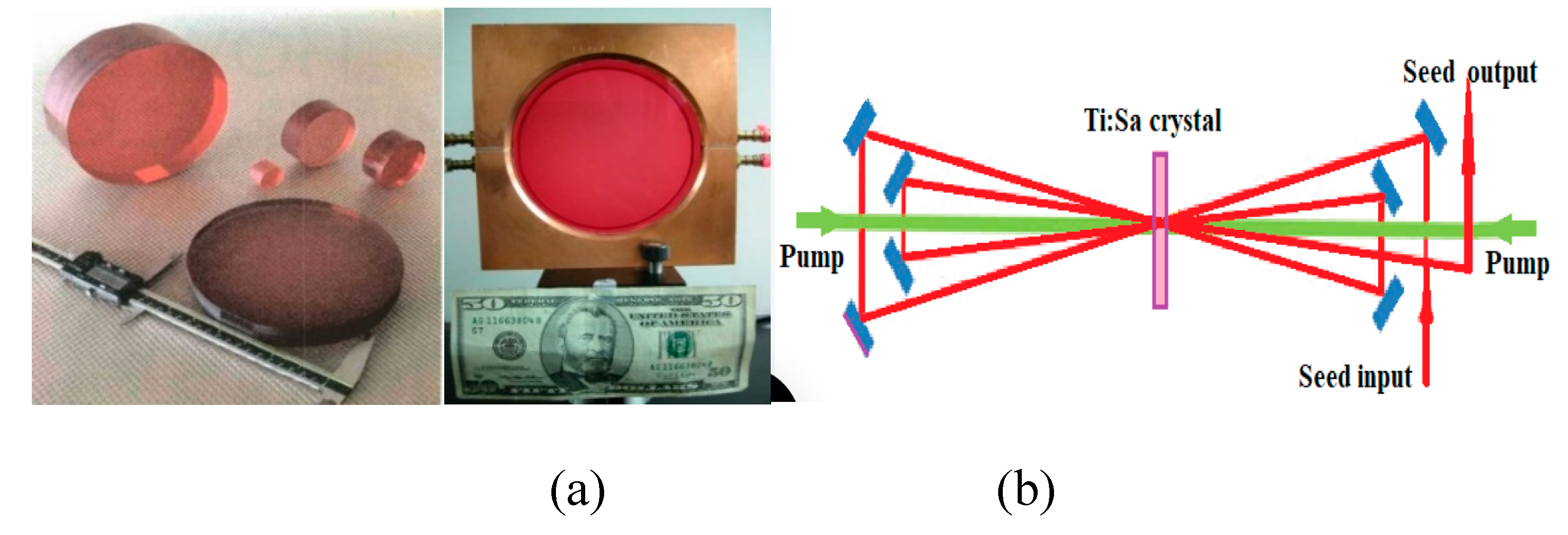
Preprints 109145 g006
Preprints 109145 g007
Figure 7. (a) Transverse parasitic generation in the large-aperture Ti:Sa crystal [77]; (b) Final amplifier of the Hercules during shot [76].
Figure 7. (a) Transverse parasitic generation in the large-aperture Ti:Sa crystal [77]; (b) Final amplifier of the Hercules during shot [76].
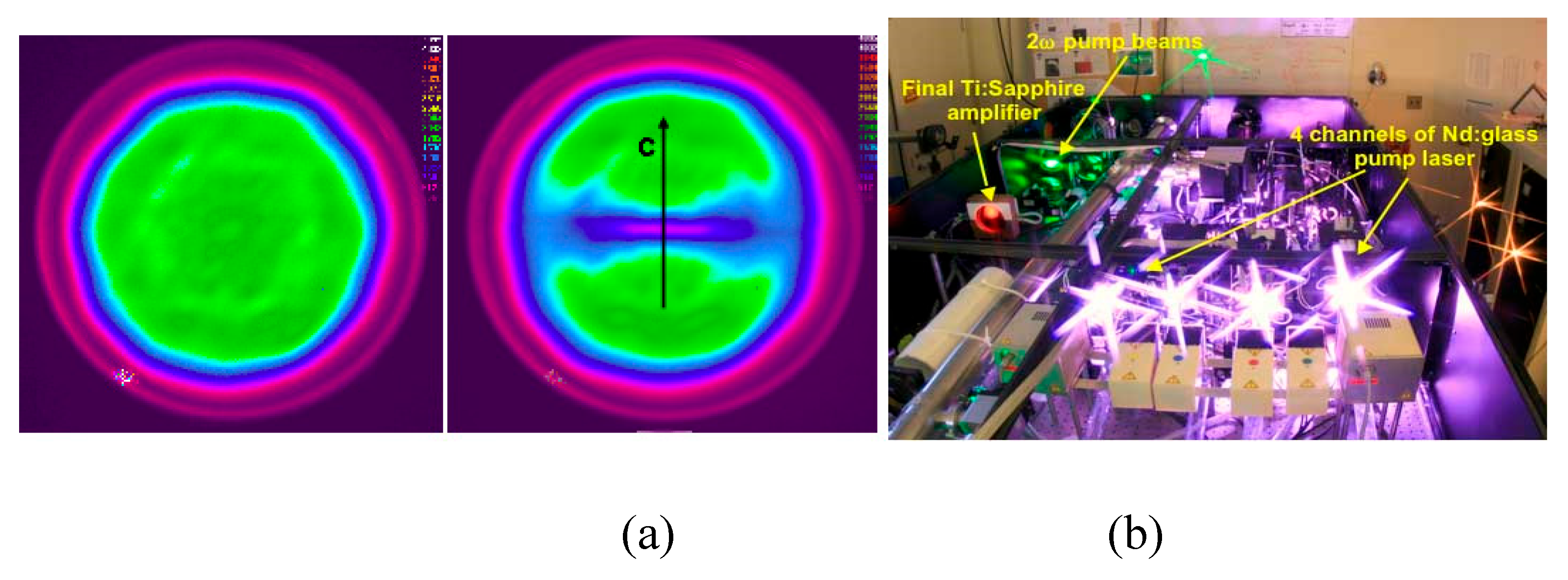
Preprints 109145 g007
Preprints 109145 g008
Figure 8. Optical Parametric Amplification (OPA) process [78].
Figure 8. Optical Parametric Amplification (OPA) process [78].
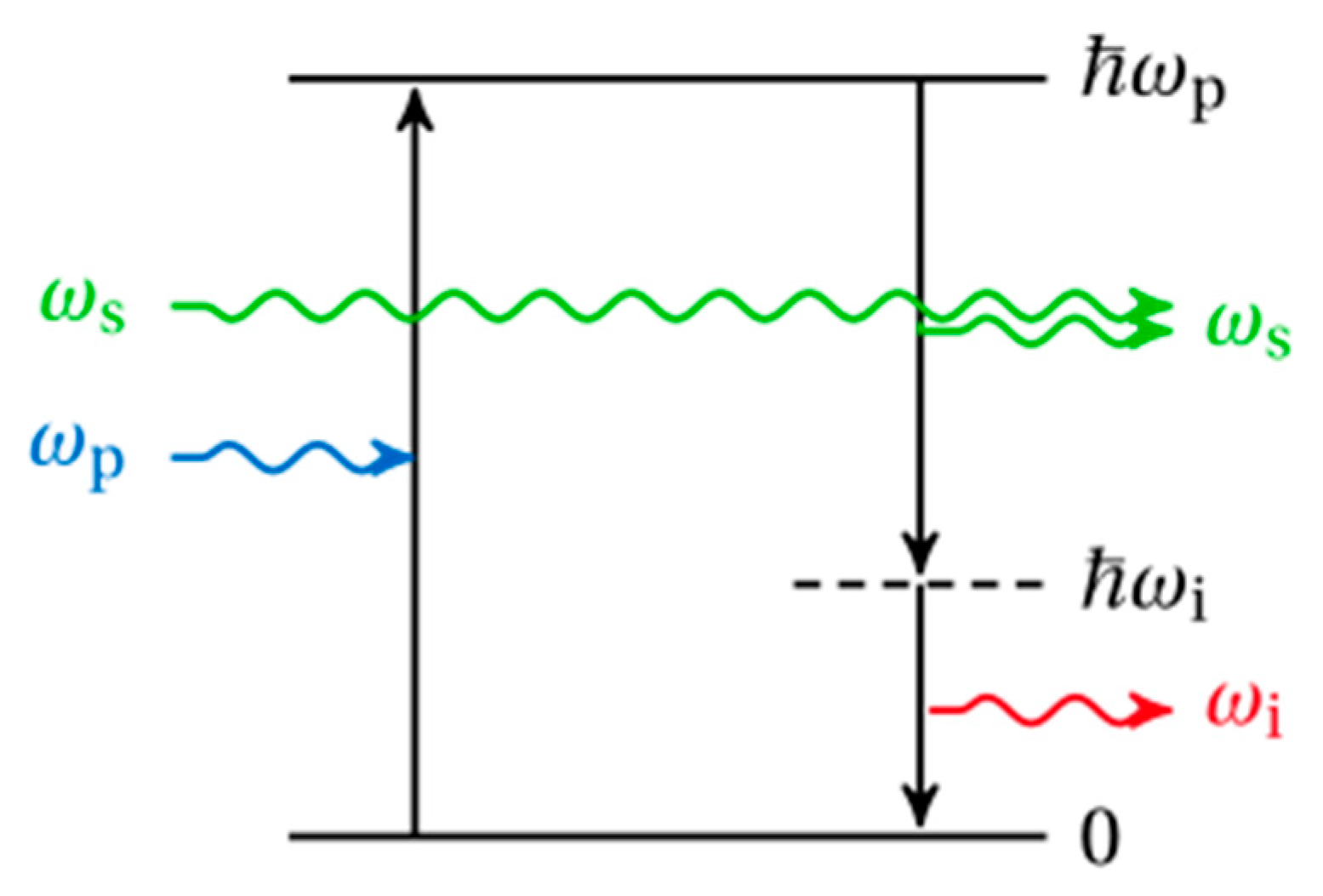
Preprints 109145 g008
Preprints 109145 g009
Figure 9. (a) Typical scheme of Thin Disc (TD) amplifier [77]; (b) TD Ti:Sa crystal [54]; (c) Ti:Sa crystal holder with both large surfaces direct contact water chilling.
Figure 9. (a) Typical scheme of Thin Disc (TD) amplifier [77]; (b) TD Ti:Sa crystal [54]; (c) Ti:Sa crystal holder with both large surfaces direct contact water chilling.
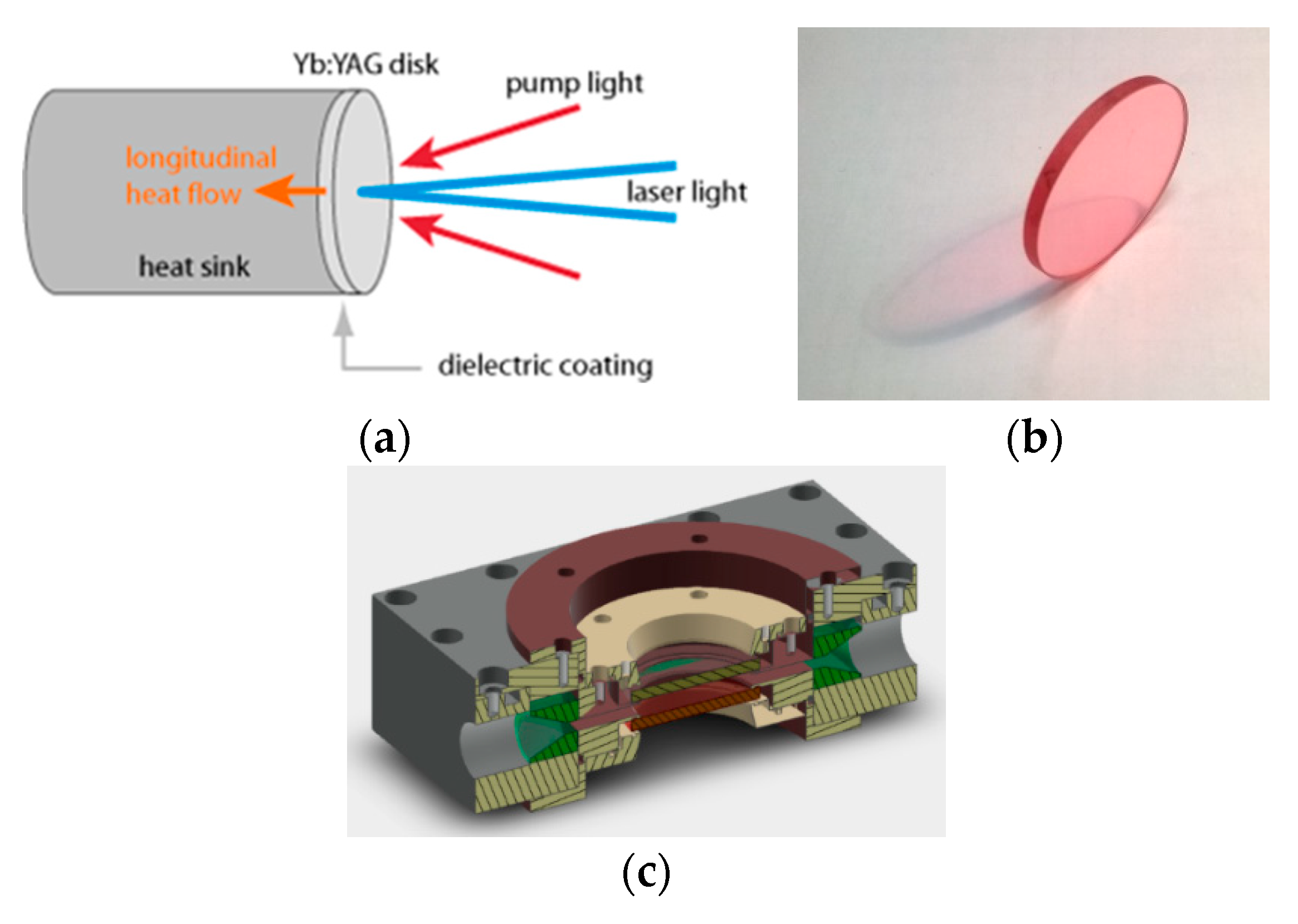
Preprints 109145 g009
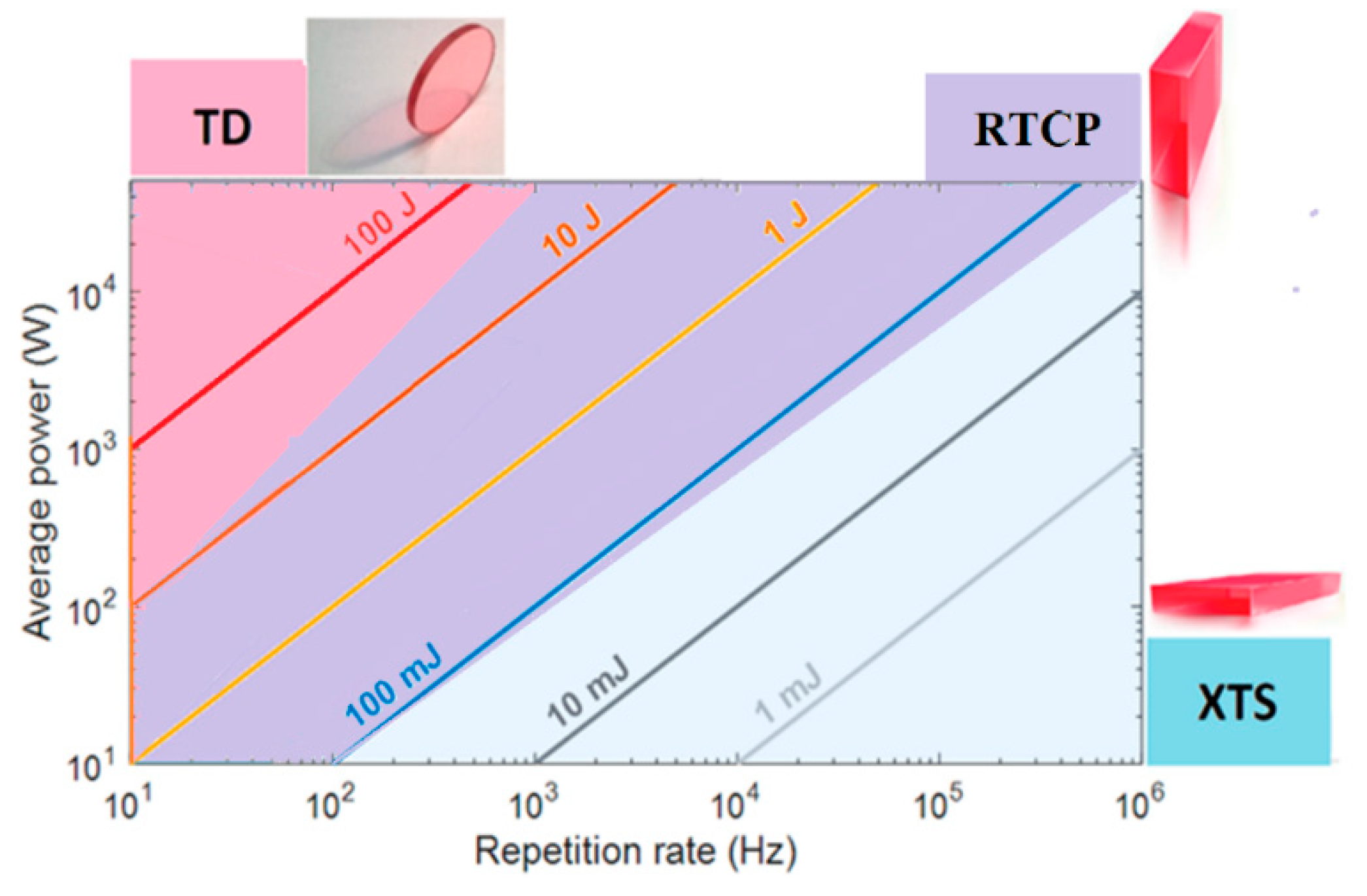
Preprints 109145 g010
Figure 10. Output average power dependence on the RR with preferable areas of TD, RTCP, and XTS Ti:Sa crystal configurations [54].
Figure 10. Output average power dependence on the RR with preferable areas of TD, RTCP, and XTS Ti:Sa crystal configurations [54].
Preprints 109145 g010
Preprints 109145 g011
Figure 11. Extreme Light Infrastructures (ELI): (a) ELI-Beamlines in the Czech Republic; (b) ELI-ALPS in Hungary; (c) ELI-NP in Romania.
Figure 11. Extreme Light Infrastructures (ELI): (a) ELI-Beamlines in the Czech Republic; (b) ELI-ALPS in Hungary; (c) ELI-NP in Romania.
Preprints 109145 g011
Preprints 109145 g012
Figure 12. General scheme of the post-compression technique. Modified from [80].
Figure 12. General scheme of the post-compression technique. Modified from [80].
Preprints 109145 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated