Preprint
Article
Effect of Flow Interference Between Cylinders Subjected to a Cross Flow Over a Cluster of Three Equally Spaced Cylinders
Altmetrics
Downloads
71
Views
14
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
14 June 2024
Posted:
18 June 2024
You are already at the latest version
Alerts
Abstract
Flow over a cluster of three equally spaced circular cylinders was studied by numerical simulation on base of the turbulent mode k-kl-ω for two incidence angles β=0° and 60°, at different Reynolds number,in this paper, flow interference pattern characteristics between cylinders, characteristics of force parameters and Strouhal number of each cylinder with different spacing ratios ranging from 1.5 to 4 at Re 8×104, 2×105and 2×106 had been obtained. At incidence angle β=0° and 60°, the wake was nearly symmetric if S/D≥2.0; at β=60°,S/D=1.5 and Re=2×105, the asymmetric periodic flow pattern occurred in the wake region which leaded to the significant effect on the surface mechanical parameters and Strouhal number which was found for the first time; the periodic flow regime of the wake region also occurred at S/D=1.35 and 1.5, without the same phenomenon at S/D=1.7 and 2.0; the phenomenon of periodic flow regime of the wake region was intrinsic and related to Reynolds number and space ratio. in addition, characteristics of force parameters of three cylinders mainly were affected by the interference between cylinders, at 1.5<S/D<4, which leaded to that the drag coefficient of three cylinders reduced with different Reynolds numbers. At incidence angle 60°, in subcritical and critical regime, the Strouhal numbers of the upstream cylinders were more than that of single cylinder, and with the enlargement of spacing ratio, the Strouhal number decreased; for the downstream cylinder , the Strouhal number is far less than that of single cylinder and with the enlargement of spacing ratio, the Strouhal number increases, which were another prominent flow inference influence. The results indicated the effect of flow interference between cylinders subjected to a cross flow over a cluster of three equally spaced cylinders on the flow pattern,surface mechanical parameters and Strouhal number.
Keywords:
Subject: Engineering - Other
1. Introduction
Interaction between fluid flow and cylindrical bodies is seen in multiple engineering applications. Therefore, there are numerous investigations on flow over uniform single circular cylinders [1,2,3,4,5,6,7,8,9]. Many of the previous studies focused on the vortex shedding phenomenon, which results in periodic loading. But, modern engineering applications usually involve fluid flow interaction with multiple cylinders, such as ocean engineering. In practical applications, pile foundations of offshore wind turbine foundations are mostly used. Pile foundation includes single pile, three piles, four piles, as well as the ring group of piles in the bearing platform structure and the multi-pile floating foundation applied to the floating foundation. So, under the action of the tidal current, the interference flow pattern occurs in the flow around the pile group of piles consequentially which affects the characteristics of surface mechanical parameters. The interference flow pattern, effect of spacing ratio, incidence angle and different Reynolds number are researched in papers [10,11,12,13,14,15,16,17] which indicates the variation rules of drag and lift coefficient, the Strouhal number and the surface pressure coefficient with spacing ratio, incidence angle and different three cylinders arrangements in subcritical regime.
The present investigation focuses on cross-flow over a cluster of three equally spaced cylinders. The flow development results in complex vortex interactions and multiple frequency-centered activities in the wake region. The previous investigations have shown that the pattern of the wake region and characteristics of surface mechanical parameters are governed primarily by the spacing ratio between the cylinders(S/D),incidence angle and Reynolds numbers. But the study above focuses in the subcritical regime, for the critical and supercritical regime, the research results are rare. In this paper, the different Reynolds numbers for different regimes (Re=3×104,8×104,2×105,5×105,2×106,4×106) are studied with different spacing ratio (S/D=1.5-4) at different incidence angles (β=0°, 20°,40°,60°), the pattern of the wake region and characteristics of surface mechanical parameters are analyzed to indicate the intrinsic laws because of the interference effect among cylinders.
2. Numerical Simulation Method and Validity Checking
2.1. Governing Equation
For the viscous incompressible fluid, the governing equations include the continuity equation and momentum equation which are written as follows:
continuity equation:
momentum equation:
In the equations, ρ,ui,p,μ,Si represent velocity component, the fluid density, the time, the pressure, the fluid dynamic viscosity and source item, respectively.
2.2. Turbulence Model and Its Selection for Numerical Simulation
2.2.1. Three Turbulence Model Selected
For simulating the flow around the cylinder, three turbulence models are selected two equation model Realizablek-ε, SSTk-ω and k-kl-ω three equation model.
(1) Realizablek-ε two equation model
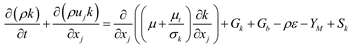
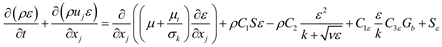
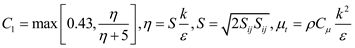
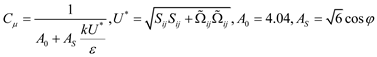
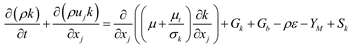
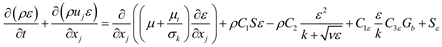
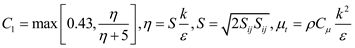
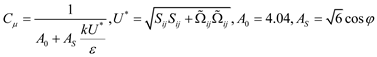
In Equations (5) and (6), the Cμ is a variable quantity rather than constant, which is decided by the shear tensor, rotation tensor, the kinetic energy and dissipation rating rather than constant 0.09. so the equation could simulate the large deformation flow.
(2) two equation model SSTk-ω considering shear rating [18]
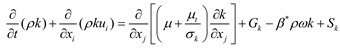
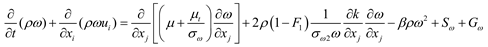
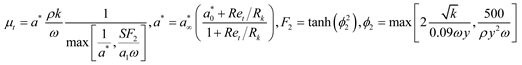In two equation model SST k-ω, the shear ratingSF2/(ɑ1ω) is leaded in the turbulence viscosity μt, which could simulate the boundary layer separation flowing across the smooth wall accurately.
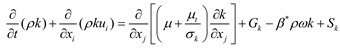
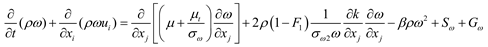
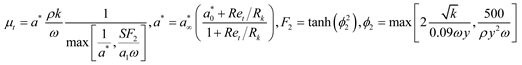
(3) three equation model k-kl-ω [19]
On base of the two equation model, the equation for describing the laminar flow kinetic energy kL is leaded in the equations depicting turbulence flow considering the transition of the boundary layer leading to the variation of the laminar flow kinetic energy
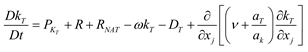
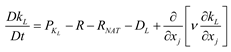
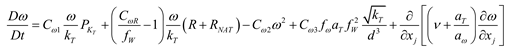
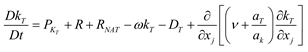
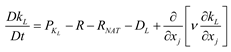
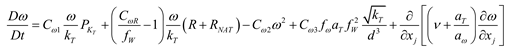
2.2.2. Comparison between Simulation Results of Different Turbulence Models
(1) Mesh generation and time step
Farrant et al. [6] indicated that a computational domain with 16D upstream, 14D downstream and 10D on either side of the cylinders could provide a better compromise between accuracy and computational costs for the flow around the cylinders. With the development of the computer techniques, the larger computational domain and more mesh quantity are adopted to simulate the flow around the cylinder more accurately. The computational domain and grid model are shown in Figure 1, the width being 31 times and length being 46 times diameter of cylinder. The inlet is defined as the velocity inlet boundary; the outlet is specified constant pressure; the left and right of the area and the surface of the cylinder are specified no-slip wall boundary. To discriminate the pressure, shear stress and separation degree of surface of cylinder for different turbulence models, the boundary layer grid is adopted near the cylinder surface( the first layer height being 10-5m, Y+=0.22), and the dimensionless time step is the value 0.01(VΔt/D=0.01)[13].
(2) Comparison of simulation results among different turbulence models
During the calculation, the Re=4×104 is adopted to simulate the flow around the cylinder for comparing the roughness efficient CD, Strouhal number St, pressure efficient Cp and boundary separation angle θs, the comparison results are shown in Table 1. N. Mulvany et al. [20], Filipe.S.Pereira.et al [9]and F.R.Meter [21] analyze the effect on the numerical results of the different turbulence model. N. Mulvany indicates Realizablek-ε model could simulate the wing boundary layer problem more accurately than the SSTk-ω model for high Re number and F.R.Meter indicates the SSTk-ω model leads to the larger shear stress of surface. In Table 1, the model drag coefficient for Realizablek-ε model is smaller (62%), the root-mean-square value of the lift coefficient pulsation is smaller (107%), the Strouhal number St is larger (45.5%), the angle of separation is larger (25%), and the basal pressure coefficient Cpb is smaller than the test value (47.5%); the drag coefficient for SSTk-ω model is larger (3%), the root-mean-square value of the lift coefficient pulsation is larger (70%), the Strouhal number St is larger (26.5%), basal pressure coefficient Cpb is larger (25.4%), and the separation angle is moderate; the drag coefficient for k-kl-ω model is close to the value 1.18[1](5%),there is less error for the root-mean-square value of the lift coefficient pulsation (0.3%[5]), the Strouhal number St is a little smaller than Unal.U result 0.186 (7.5%[7]), the basal pressure coefficient Cpb is similar with N. Mulvany and Anatol Roshko results -1.18(5%[2,20]), and the separation angle is close to the E. Achenbach.et.al result [3](0.6%). The comparison results of Table 1 shows the model k-kl-ω simulates the better results for flow around cylinder and the model is adopted to analyze the flow around three equally spaced cylinders in critical regime.
2.3. Grid and Its Validity Checking
Considering the bunching effect of the pile cluster, the larger computation domain is selected to avoid the blockage effect of flow. Figure 2 shows the computation domain and grid of three piles and Figure 3 shows the arrangement for three cylinders. The spacing between upstream of cylinder and inlet boundary is 20D; the spacing between downstream of cylinder and outlet boundary is 30D; the spacing between side wall and surface of cylinder is 10D. The inlet is defined as the velocity inlet boundary; the outlet is specified constant pressure; the left and right of the area and the surface of the cylinder are specified no-slip wall boundary. To discriminate the pressure, shear stress and separation degree of surface of cylinder for different turbulence models, the boundary layer grid is adopted near the cylinder surface(the first layer height being 10−5m, Y+=0.22), and the dimensionless time step is the value 0.01(VΔt/D=0.01)[13].
Considering the effect of number of cell, three different quantity grids are designed to analyze the impact on the mean roughness efficient CD. In Table 2, the number of cell reaches 430000, the variation of the CD satisfies the accuracy of simulation, error being 1%.
The verification of the simulation results is shown in Table 3. Analyzing the data of Table 3, At Re=8×104, the CD result of current work approaches the study of the S.G.Pouryoussefi · M. et al. [12], error being 3%; At Re=3×104, the CD and St result of current work approach the data of the A.T.Sayers [10], error being 2% and 4% respectively. From the Table 3, it can be seen that the results of this paper are basically in consistent with previous results, which proved that the numerical method and parameter settings of this paper are reasonable and feasible.
3. Results Analysis and Discussion
3.1. Flow Interference Pattern Characteristics among Cylinders
3.1.1. Effect of Spacing Ratio S/D on the Flow Pattern
The effect of interference is the fundamental characteristic distinguishing the flow through a cluster of three equally spaced cylinders from the flow past a circular cylinder, which changes with the variations of spacing ratios, incidence angles to the free stream and Reynolds number. Zdravkovich [11](60 < Re < 300) indicates that when the Re is a constant, the flow interference pattern among piles is divided into three categories: (1) The proximity interference, which takes place when the distance between the cylinders is small enough. (2). The wake interference, which generates in the downstream cylinder completely or partially submerged in the wake of others. (3). The combined interference which represents wake and proximity interference [13]. The present investigation also reveals the similar interference characteristic with the variation of spacing ratio at Re=8×104.
Figure 4 shows the instantaneous velocity contours for flow field at S/D=1.5 and Re=8×104, with four different incidence angles(β=0°, 20°,40°,60°). The wake of the upstream cylinder is suppressed by the cylinder downstream and proximity interference dominates the flow. In addition, the incidence angle affects also significantly the flow pattern:(1) the symmetrical form appears in wake of the cylinders downstream at β=0°,60° (Figure 3a,d); (2) the asymmetrical form appears in wake of the cylinders downstream at β=20°,40° (Figure 3b,c); (3) the bi-stable regime is not observed at β=0°(Figure 3a) which illustrates that Reynolds number can have a significant effect on the onset of the bi-stable flow regime, and the numerical research by Bao et al. [15] showed no bi-stable flow at Re=100 for approximately the same spacing ratios as those studied by Lam and Cheung [16].
At S/D=2.5 which is selected as a intermediate spacing ratio, the flow interference is dominated by the suppression between cylinders and interference of the wake. Figure 5 shows the instantaneous velocity contours for flow field at S/D=2.5 and Re=8×104, with four different incidence angles(β=0°, 20°,40°,60°). the suppression and the gap stream between cylinders dominates the flow field at β=0°, 40° just as Figure 5a,c display, but the interference of the wake affected the flow pattern significantly at β=20°, 60° just as Figure 5b,d display.
Enlarging the spacing ratio S/D, at S/D=4, the the interference of wake between cylinders controls the flow pattern just as Figure 6 shows. Figure 6 shows the instantaneous velocity contours for flow field at S/D=4 and Re=8×104, with four different incidence angles(β=0°, 20°,40°,60°). At β=0°,the shedding vortex appears in the wake flow over three cylinders because of the wake of cylinders downstream; the wake of the C1 cylinder is affected by the cylinders C3 primarily at β=20°; the effect of suppression between cylinders is very weak for the flow field and the interference of wake plays an important role at β=40°,60°.
The spacing ratio and incidence angle are both very important parameters affecting the flow pattern flow over three cylinders, but the Reynolds number is another factor impacting the flow regime significantly just as M.S. Bansal.et.al [14]indicate.
3.1.2. Effect of Reynolds Number
It is well known that the flow regime and force characteristics change with the Reynolds number for flow past single cylinder, which is divided into subcritical regime, critical regime, supcritical regime and postcritical regime for turbulent regime [17]. Similarly, flow through a cluster of three equally spaced cylinders also is transformed with different Reynolds numbers.
Figure 7 shows the instantaneous velocity contours for flow field at S/D=1.5 and β=0°, with six different Reynolds numbers(Re=3×104,8×104,2×105,5×105,2×106,4×106, corresponding to subcritical regime, critical regime, supcritical regime and postcritical regime respectively). At Re=3×104,8×104,2×105, the wake of the cylinders downstream(C2 and C3) exhibits symmetrical feature, and the bi-stable flow regime doesn’t appear in the present investigation. At Re=5×105,2×106,4×106 (supcritical and postcritical regime), the combined shedding vortex between two cylinders downstream appears in the wake of flow past three cylinders, but the frequency and spacing distance between vortex centers are different with Reynolds number just as Figure 7d–f display; Another obvious feature is that at Re=5×105,2×106, the vortex street is nearly symmetrical distribution in transversal direction and asymmetrical distribution at Re=4×106.
At S/D=1.5 and β=60°, with different Reynolds numbers (Re=3×104,8×104,2×105,5×105,2×106,4×106, the instantaneous velocity contours for flow field are shown in Figure 8. The figure indicates that at Re=3×104,8×104,5×105,2×106,4×106, the flow fields exhibit nearly perfect symmetry, when the cylinder(C3) downstream suppresses the wakes of the cylinders (C1 and C2) upstream. But at Re=2×105, the wake of the cylinder(C3) downstream displays the asymmetrical feature and the typical vortex appears downstream cylinder C3 just as Figure 8c shows. For the flow regime at Re=2×105, β=60° and different spacing ratios, the paper catches through the further study for its characteristics and force parameters by 2D and 3D numerical simulation, and the study indicates the flow regime exhibits the periodic feather, namely the same wake of flow over three cylinders occurs periodically(if the period is T), which is elaborated in 3.1.3 part.
3.1.3. Characteristics of Periodic Flow Regime of the Wake Region Past Three Cylinders
3.1.3.1. Verification of Three Dimensional Flow Field
At Re=2×105,β=0°, the flow pattern of the wake region is similar to that of the subcritical region at Re=8×104 . At S/D=1.5 and β=0°, there is no bi-stable flow regime in the wake region; but at β= 60°, the periodic flow regime of the wake region past three cylinders is the first time to be found, which has not yet been introduced and explained in the existing literature. In this paper, it is believed that this periodic flow regime of the wake region past three cylinders is caused by the coupling of Reynolds number-reduced wake and limited spacing ratio.
Considering the study above at Re=2×105, β=60°, S/D=1.5 being caught through by the two dimensional flow field, to verify the authenticity of the results, the study has also been done by three dimensional flow field further. In addition, whether the periodic flow regime of the wake region occurs only in particular spacing ratio range is also analyzed.
Figure 9 shows the arrangement for three cylinders for three dimensional flow field analysis:(a) geometric model; (b) grid model, the space ratios being S/D=1.35,1.5,1.7,2 and aspect ratio being L/D=10 (eliminating the influence of aspect ratio). In Figure 9b, the mesh scale near cylinders is 0.005m and the boundary layers are also adopted near the cylinder surfaces(the first layer height being 10−5m, Y+=0.22, the number of grid being 650 thousand), and the dimensionless time step is the value 0.01(VΔt/D=0.01).
Figure 10 shows the three dimensional flow velocity contour, which verifies that in three dimensional flow field, periodic flow regime of the wake region past three cylinder also occurs at S/D=1.35 and 1.5, without the same phenomenon at S/D=1.7 and 2.0, which the wake regime exhibit nearly perfect symmetry. So, the phenomenon of periodic flow regime of the wake region past three cylinders is intrinsic and related to Reynolds number and space ratio.
3.1.3.2. Evolution Process of the Periodic Flow Regime of the Wake Region
The asymmetrical gap flow between cylinder C1,C3 and C2,C3 reduces the periodic flow regime of the wake region past three cylinders directly at Re=2×105, β=60°, S/D=1.5or1.35, and the coupling coherent influence of the wake past cylinder C1,C2 and the cylinder C3 surface is the intrinsic cause.
Figure 11 shows the evolutionary process of the periodic flow regime of the wake region within a cycle. Figure 11a shows the wake region past cylinder C3 deflects to the cylinder C1 and the coherent vortex flow past three cylinders communicates with the wake region past cylinder C2; at the time t+T/8, the wake region past cylinder C3 enlarges and the wake regions of cylinders C1 and C3 communicates with each other Initially;at the moment of t+2T/8, the shedding vortex of the wake region past cylinder C1 propagates to the wake region downstream past three cylinders, the initial coherent vortex disappears, the small-scale coherent vortex is formed, the wake of cylinder C3 is gradually biased towards cylinder C2, and there is no shedding vortex structure in the wake region of cylinder C2;at the moment t+3T/8, the coherent vortex is formed downstream of cylinder C3 to which the trailing zone of cylinder C1 is connected, the wake region of cylinder C3 is fully biased towards cylinder C2 and is separated from the downstream coherent vortex by the gap flow, and the trailing zone of cylinder C2 is also separated from the downstream coherent vortex;at the moment of t+4T/8, the coherent vortex past three cylinders moves downstream, the trailing zone of cylinder C1 starts to separate from the coherent vortex, the initial fusion of trailing zones past cylinder C3 and C2 occurs, and the separation vortex forms at the end of the pile C2 trailing zone;at the moment of t+5T/8, the wake regions of cylinder C2 and C3 are fused, the shedding vortex of flow field past cylinder C2 is gradually shed and propagates downstream, and wake region of the cylinder C3 starts to deflect; at the moment of t+6T/8, the shedding vortex behind the cylinder C2 propagates downstream, the coherent vortex downstream is formed initially, and the wake region of cylinder C3 deflects to the cylinder C1; at the moment of t+7T/8, the coherent vortex scale behind three cylinders enlarges which develops gradually to maturity, and the wake region of cylinder C2 is biased toward cylinder C1, the coherent vortex behind three cylinders separates from the wake of cylinder C1, and the wake of cylinder C2 is connected with the coherent vortex.
Consequently, from the viewpoint of the evolution law within the cycle of the wake region and the coherent vortex, the emergence of the periodic alternating flow is due to the periodic shedding of the separation bubbles in the wake of cylinders C1 and C2, and the coherent vortex downstream of cylinder C3 evolves from the separation bubbles of wake regions of cylinders C1 or C2. When the separation bubbles exist in the wake region of cylinder C1, the coherent vortex evolves from the separation bubbles in the wake region behind cylinder C2 at the previous moment, and otherwise, it evolves from the separation bubbles behind cylinder C1 at the previous moment. Thus, for a certain gap ratio, Reynolds number conditions under the incidence angle of 60°, the emergence of periodic periodic flow regime of the wake region is the inevitable result because of the coherent effect of the flow field among cylinders C1,C2 and C3.
3.2. Characteristics of Force Parameters
3.2.1. Pressure Coefficient Distributions Around Cylinders
The pressure distribution around the cylinder surface under the influence of inter-cylinder gap flow for flow past three cylinders is significantly different from that in the case of flow past one cylinder. The gap flow increases the local velocity and reduces the local pressure, while the location of the stagnation point behind cylinders changes due to the presence of the gap flow.
Figure 12 and Figure 13 show variation laws of surface pressure coefficient with spacing ratio S/D at incidence angle β=0°and β=60° in subcritical regime. At incidence angle β=0°, the surface pressure distribution of cylinder C1 exhibits symmetrically, the pressure of the wake region of cylinder C1 rises and the Cp value increases due to the role of downstream cylinders C2 and C3, and with the increase of S/D, the Cp value of the wake region decreases gradually; the wake region of cylinder C1 is as the upstream of cylinders C2 and C3, and under the role of the inter-cylinder gap flow, the stagnation point of the surfaces of cylinders C2 and C3 deflects to the gap flow side, for cylinder C2 being near 350° and cylinder C3 being near 10°; when the value of S/D is smaller than four, the pressure coefficient around cylinder near the gap flow is slightly smaller and there is no controlling effect on pressure coefficient if value of S/D is larger than four. At the incidence angle β = 60 °, the gap flow occurs between cylinder C1 and C3 and also C2 and C3, and near the gap flow side, the pressure coefficient drops suddenly which leads to that the stagnation point slightly moves to the side of the gap flow; the pressure coefficient distribution around cylinder C3 at the small spacing ratio of S/D=1.5,2, exhibits basically symmetrically, and at S/D=2.5,3, because of the impact of wake region behind cylinders C1, C2, the pressure distribution exhibits asymmetrically.
In the critical regime, the characteristics of the cylinder surface pressure distribution are different from that in the subcritical regime. Figure 14 and Figure 15 plots the changing rules of cylinder surface pressure coefficient with S/D in the critical regime. At the incidence angle β=0°, enlarging the spacing ratio S/D value from 1.5 to 4, the surface pressure coefficient of the cylinder C1 is basically symmetrically distributed; for cylinders C2,C3, the pressure coefficient around cylinder near the gap flow is slightly smaller due to the role of the gap flow, and the stagnation point location is on the opposite side. When the incidence angle β being 60°, the prominent phenomenon is that at S/D=1.5, the periodic flow regime of the wake region or coherent vortex structure occurs, which is manifested by the surface pressure coefficient of the cylinder C3 near the gap flow side steeply decreasing, and at the same time, the pressure coefficient of the cylinder C2 near the gap flow side is small, and when the opposite flow pattern occurs, the cylinder C1 will show the same rule with the cylinder C2.
Figure 16 and Figure 17 plots the distribution of cylinder surface pressure coefficient with the different S/D value in supercritical regime. The cylinder surface pressure coefficient are mainly affected by the wake region behind the cylinders, and the influence of the gap flow is not obvious comparing to that in subcritical and critical regimes.
3.2.2. Characteristics of Drag and Lift Coefficients
At β=0°, Figure 18 shows the variation of the mean drag coefficients with S/D with different Reynolds number(8×104,2×105,2×106). For Re=8×104, in Figure 18a, the mean drag coefficients for three cylinders C1,C2 and C3 increases with the enlargement of S/D from two to four; at S/D=1.5, the mean drag coefficients(C1:0.666,C2:0.747,C3:0.749) are far less than the value of the single cylinder(CD=1.18) which indicates the upstream cylinder plays a significant role in reducing the mean value of the drag coefficients on the side by side downstream cylinders and also the downstream cylinders play a role in reducing the mean value of the drag coefficient upstream cylinder; with the enlargement of S/D, the interference among three cylinders attenuates, and the mean drag coefficient increases; at S/D=4, the mean drag coefficients for three cylinders are 0.884(C1),1.061(C2) and 1.128(C3) respectively, indicating that the value of the cylinders C1 and C2 is close to the value (1.18)of the single cylinder, but the downstream cylinders play a role in reducing the mean value of the drag coefficient upstream cylinder with drag coefficient of C1 being 0.884. For Re=2×105, the variation of mean drag coefficients for three cylinders C1,C2 and C3 with S/D exhibits the similar law with that for Re=8×104, because of the interference among cylinders, the value of drag coefficient being less than that of single cylinder(approximate 1.08). For Re=2×106, at 1.5<S/D<2.5, the drag coefficient for cylinder C1 increases with the enlargement of S/D, and S/D>2.5, the drag coefficient for cylinder C1 decreases with the enlargement of S/D; at 1.5<S/D<4, the drag coefficients for cylinders C2 and C3 are in a certain range 0.36~0.41 which is less than the value 0.73 as the drag coefficient of the single smooth cylinder; in addition, at 1.5<S/D<4, the the interference among cylinders still reduces the drag coefficient of three cylinders.
At β=60°, Figure 19 shows the variation of the mean drag coefficients with S/D with different Reynolds number(8×104,2×105,2×106). For Re=8×104, in Figure 19a, at 1.5<S/D<3, the drag coefficients of the side by side cylinders C1 and C2 decrease with the enlargement of S/D, at S/D=1.5, drag coefficients being both 1.15; at S/D=4, the drag coefficients for cylinders C1 and C2 are both 1.5 which is more than value(1.18) of the single smooth cylinder; for the cylinder C3, at 1.5<S/D<2.5, the drag coefficient increases with the enlargement of S/D, and at S/D=3, the drag coefficient decreases and increases if S/D >3; the upstream the side by side cylinders C1 and C2 play a significant role in reducing the mean value of the drag coefficients on downstream cylinder C3. For Re=2×105, in Figure 19b,at 1.5<S/D<4, the drag coefficients of the side by side cylinders C1 and C2 decrease with the enlargement of S/D, at S/D=1.5, the mean drag coefficients for cylinders C1 and C2 being 0.983(C1),0.969(C2) respectively and at S/D=4, the values being both 0.919; for the cylinder C3, at 1.5<S/D<3, the drag coefficient increases with the enlargement of S/D and the drag coefficient increases if S/D >3; in addition, at 1.5<S/D<4, the the interference among cylinders still reduces the drag coefficient of three cylinders, the cylinder C3 being more prominent. For Re=2×106, in Figure 19c, at 1.5<S/D<3, the drag coefficients of the side by side cylinders C1 and C2 decrease with the enlargement of S/D and slightly enlarge if S/D >3, at S/D=1.5, the mean drag coefficients for cylinders C1 and C2 being 0.567(C1),0.576(C2) respectively and at S/D=4, the values being 0.449(C1),0.456(C2);for the cylinder C3, at 1.5<S/D<3, the drag coefficient increases with the enlargement of S/D and the drag coefficient increases if S/D >3; in addition, at 1.5<S/D<4, the the interference among cylinders still reduces the drag coefficient of three cylinders.
Figure 20, Figure 21 and Figure 22 show the time-history variation of surface drag coefficient and lift coefficient (S/D=1.5,β=60°) with different Reynolds number(8×104,2×105,2×106). In Figure 20 and Figure 22, the drag and lift coefficient curves with time show the weaker fluctuating characteristic which is compatible with the flow pattern in Figure 8. At S/D=1.5,β=60°,Re=2×105, the periodic flow regime of the wake region past three cylinders is found and the drag and lift coefficient curves with time are displayed in Figure 21. In Figure 21, the drag and lift coefficient curves with time exhibit the strong fluctuating characteristic, the lift coefficient curve of cylinder C3 being more prominent. In Figure 21a, the drag coefficient curves of cylinders C1 and C2 exhibit the anisotropic phase and have the same period;there is a certain phase difference between the cylinder C3 and cylinders C1 and C2, and the phase difference is unchanged with time. In Figure 21b, there is the long period and short period signal in the lift coefficient curves with time of cylinders C1 and C2, the long period being mainly due to the coherent vortex structure in the wake region past three cylinders; For cylinder C3, lift coefficient curve with time forms due to the effect of periodic flow regime of the wake region, displaying mainly a long period signal, in which there is a strong fluctuating characteristic and the fluctuating amplitude is close to 2;
The time-history variation curves of surface drag and lift coefficient of three equally spaced cylinders compared with the single cylinder or larger S/D conditions, due to the interference among cylinders, the flow pattern and drag and lift characteristics change significantly, especially, the effect of periodic flow regime of the wake region among cylinders at S/D=1.5,β=60°,Re=2×105 leads to change the frequency of mechanical properties around cylinders and the main frequency is obviously reduced, if the mechanical data of the single cylinder is still used in the analysis of the cylinder dynamic characteristics around three or more cylinders which will bring a lot of error for St or lift or drag.
3.3. Characteristics of Strouhal Number
Due to the interference of the wake regions among cylinders, Strouhal number of the flow past three cylinders is no longer a single function of the Reynolds number and also changes with the incidence angle of the incoming flow and the pile spacing.
Table 4 lists the Strouhal number of single cylinder for different Reynolds numbers. Table 5 lists the Strouhal number for different spacing ration, Reynolds number and incidence angle of the flow past three equally spaced cylinders in present work. At Re=8×104,β=0°, the St of cylinder C1 increases with the enlargement of spacing ratio from 0.138 to 0.19 which is compatible to the result of Senlin Zheng.et.al study [13]; at S/D=2.5, the Strouhal number of three cylinders is 0.19 which is close to the value 0.185. At Re=2×105,β=0°, the Strouhal numbers of three cylinders are 0.225(C1) and 0.2(C2,C3) which is more than that of single cylinder. For Re=2×106,β=0°, the Strouhal number of cylinder C1 increases with the enlargement of spacing ratio from 0.167 to 0.213 and the Strouhal numbers of cylinders C2,C3 are both 0.3 and 0.293 for S/D=2.0,2.5 respectively which is less than the value of single cylinder. At Re=8×104,β=60°, the Strouhal numbers of cylinders C1,C2 decrease with the enlargement of spacing ratio from 0.263 to 0.212 which is far more than the value 0.185 of single cylinder, but the Strouhal number of cylinder C3 increases with the enlargement of spacing ratio from 0.075 to 0.1 which is far less than the value 0.185 of single cylinder, which indicates that the interference of wake regions behind cylinders enlarges the Strouhal number of upstream cylinders C2,C3 and reduces the Strouhal number of downstream cylinder C1. At Re=2×105,2×106,β=60°, the similar rules are displayed in Table 5; considering the effect of periodic flow regime of the wake region among cylinders at S/D=1.5,β=60° which is shown in Figure 21b, the period of lift coefficient curve for the cylinder C3 is 37.73s corresponding to the Strouhal number 0.033 which is far less than the value 0.188 of single cylinder;in addition, for cylinders C1 and C2, there are two types of cycles: a long cycle due to coherent vortex which is close to the value of cylinder C3, and a short cycle due to shedding vortex in the wake region corresponding to the more frequency and less period.
4. Conclusions
In this paper, a finite volume method with structured meshes on base of the turbulent model k-kl-ω is used to simulate the flow past three cylinders in an equilateral triangle arrangement for two incidence angles β=0° and 60°, at Reynolds number 8×104, 2×105and 2×106. Based on the present results, flow interference pattern characteristics among cylinders, characteristics of force parameters and characteristics of Strouhal number of each cylinder with different spacing ratios ranging from 1.5 to 4 at Re 8×104, 2×105and 2×106 have been obtained. The main conclusions are drawn as follows:
(1) on base of the study of comparison of simulation results among different turbulence models, the model k-kl-ω simulates the better results for flow around cylinder for the parameters of drag coefficient, root-mean-square value of the lift coefficient pulsation, Strouhal number St, basal pressure coefficient Cpb and separation angle.
(2) the interference flow pattern past equilateral triangle arrangement cylinders is related to the Reynolds number, spacing ratio and incidence angle: (a) at Re=3×104,8×104,2×105,β=0°, the wake of the cylinders downstream(C2 and C3) exhibits symmetrical feature, and the bi-stable flow regime doesn’t appear in the present investigation.at Re=5×105,2×106,4×106, the combined shedding vortex between two cylinders downstream appears in the wake of flow past three cylinders and another obvious feature is that at Re=5×105,2×106, the vortex street is nearly symmetrical distribution in transversal direction and asymmetrical distribution at Re=4×106 (b)at Re=3×104,8×104,5×105,2×106,4×106,β=60°, the flow fields exhibit nearly perfect symmetry, when the cylinder(C3) downstream suppresses the wakes of the cylinders (C1 and C2) upstream;But at Re=2×105, the wake of the cylinder(C3) downstream displays the asymmetrical feature and the typical vortex appears downstream cylinder C3.
(3) For the flow regime at Re=2×105, β=60° and different spacing ratios, the periodic flow regime of the wake region past three cylinders is the first time to be found. The periodic flow regime of the wake region past three cylinder also occurs at S/D=1.35 and 1.5, without the same phenomenon at S/D=1.7 and 2.0, which the wake regime exhibit nearly perfect symmetry. So, the phenomenon of periodic flow regime of the wake region past three cylinders is intrinsic and related to Reynolds number and space ratio.
(4) Characteristics of force parameters of three cylinders mainly are affected by the interference among cylinders, at small spacing ratio such as S/D=1.5, the pressure coefficient Cp increases and drag coefficient decreases for the upstream cylinders; in addition, at 1.5<S/D<4, the the interference among cylinders reduces the drag coefficient of three cylinders with different Reynolds numbers.
(5) At β=60°, in subcritical and critical regime, the Strouhal number of the upstream cylinders C1 and C2 is more than that of single cylinder, and with the enlargement of spacing ratio, the Strouhal number decreases; for the downstream cylinder C3, the Strouhal number is far less than that of single cylinder and with the enlargement of spacing ratio, the Strouhal number increases.
Author Contributions
Conceptualization, Jia Dong..; methodology, Jia Dong.; software, Jia Dong; validation, Jia Dong; formal analysis, Jia Dong; investigation, Jia Dong; resources, Jia Dong; data curation, Jia Dong; writing—original draft preparation, Jia Dong and Genhua Yan; writing—review and editing, Jia Dong and Xianrui Shi; visualization, Jia Dong.; supervision, Jia Dong; project administration, Genhua Yan; funding acquisition, Jia Dong and Genhua Yan. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Special Funds for Basic Research Operating Costs of Central-level Public Welfare Research Institutes(Y122006) and Jiangsu Funding Program for Excellent Postdoctoral Talent.
Data Availability Statement
no applicable.
Acknowledgments
I acknowledge the funding support of Jiangsu Funding Program for Excellent Postdoctoral Talent.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Lists of symbols | |
| Re | Reynolds number = ρVD/µ |
| S | distance between centers of two cylinders |
| D | the diameter of a cylinder |
| S/D | spacing ratio |
| β | incidence angle |
| St | Strouhal number f×D/V |
| f | vortex shedding frequency |
| V | flow velocity |
| CD | drag coefficient |
| CL | lift coefficient |
| Cpb | basal pressure coefficient |
| Cp | pressure efficient |
| Θs | separation angle |
| C′L | lift coefficient pulsation |
References
- Wieselsberger.C. New data on the laws of fluid resistance. Technical report TN 84, NACA,1921.
- Anatol Roshko. Experiments on the flow past a circular cylinder at very high Reynolds number. Fluid Mech.,1960,10: 345-356 . [CrossRef]
- E. Achenbach. Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re =5×106. J.Fluid Mech, 1968,34(4): 625-639.
- C. Norberg. Fluctuating lift on a circular cylinder: review and new measurements. Journal of Fluids and Structures, 2003,17:57–96 . [CrossRef]
- Gonter Schewe. On the force fluctuations acting on a circular cylinder in cross flow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech.,1983,133 :265-285.
- Ivette Rodriguez, Oriol Lehmkuhl.et al. LES-based study of the roughness effects on the wake of a circular cylinder from subcritical to transcritical Reynolds numbers. Flow Turbulence Combust, 2017,99:729–763 . [CrossRef]
- Unal.U, Atlar. M. An experimental investigation into the effect of vortex generators on the near-wake flow of a circular cylinder. Exp. Fluids ,2010,48:1059–1079.
- Alessandro Capone, Christian Klein.et al. Phenomenology of a flow around a circular cylinder at sub-critical and critical Reynolds numbers. Physics of fluids, 2016,28(7):1-17 . [CrossRef]
- Filipe S. Pereira, Luís Eça.et al. On the simulation of the flow around a circular cylinder at Re = 140000. International Journal of Heat and Fluid Flow, 2019,76:40–56.
- A.T.Sayers. Flow interference between three equispaced cylinders Flow interference between three equispaced cylinders when subjected to a cross flow. Journal of Wind Engineering and Industrial Aerodynamics, 1987,26: 1-19.
- Zdravkovich MM. The effects of interference between circular cylinders in cross flow. J Fluid Struct,1987,1:235–2261. [CrossRef]
- S. G. Pouryoussefi · M. Mirzaei. Force coefficients and Strouhal numbers of three circular cylinders subjected to a cross-flow. Arch Appl Mech, 2011,81:1725–1741.
- Senlin Zheng, Wei Zhang, Xiangcui Lv. Numerical simulation of cross-flow around three equal diameter cylinders in an equilateral-triangular configuration at low Reynolds numbers.Computers and Fluids, 2016,130: 94–108 . [CrossRef]
- M.S. Bansal, S. Yarusevych.Experimental study of flow through a cluster of three equally spaced Cylinders. Experimental Thermal and Fluid Science, 2017, 80:203–217. [CrossRef]
- Y. Bao, D. Zhou, C. Huang, Numerical simulation of flow over three circular cylinders in equilateral arrangements at low Reynolds number by a second order characteristic-based split finite element method. Comput. Fluids, 2010, 39: 882-899. [CrossRef]
- K.Lam, W.C.Cheung. Phenomena of vortex shedding and low interference of three cylinders in different equilateral arrangements. J. Fluid Mach, 1988,196:1-26.
- Guido Buresti. the effect of surface roughness on the flow regime around circular cylinders. Journal of Wind Engineering and Industrial Aerodynamics, 1981,8:105-114 . [CrossRef]
- F.R.Meter. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA Journal. 1994,32(8):1598-1605.
- D. Keith Walters, Davor Cokljat. a three-equation eddy-viscosity model for Reynolds-averaged Navier–Stokes simulations of transitional flow. Journal of Fluids Engineering, 2008,130(12):1-14 . [CrossRef]
- N. Mulvany, J. Y. Tu.et al. Assessment of two-equation turbulence modelling for high Reynolds number hydrofoil flows. Int. J. Numer. Meth. Fluids, 2004,45(3):275–299 . [CrossRef]
- F.R.Meter. Performance of Popular Turbulence Models for Attached and Separated Adverse Pressure Gradient Flows. AIAA journal, 2012,30(8):2066-2072.
- Farrant T, Tan M, Price WG. A cell boundary element method applied to laminar vortex-shedding from arrays of cylinders in various arrangements. J Fluid Struct, 2000,14:375–402. [CrossRef]
Figure 1.
Computational domain model and grid model.
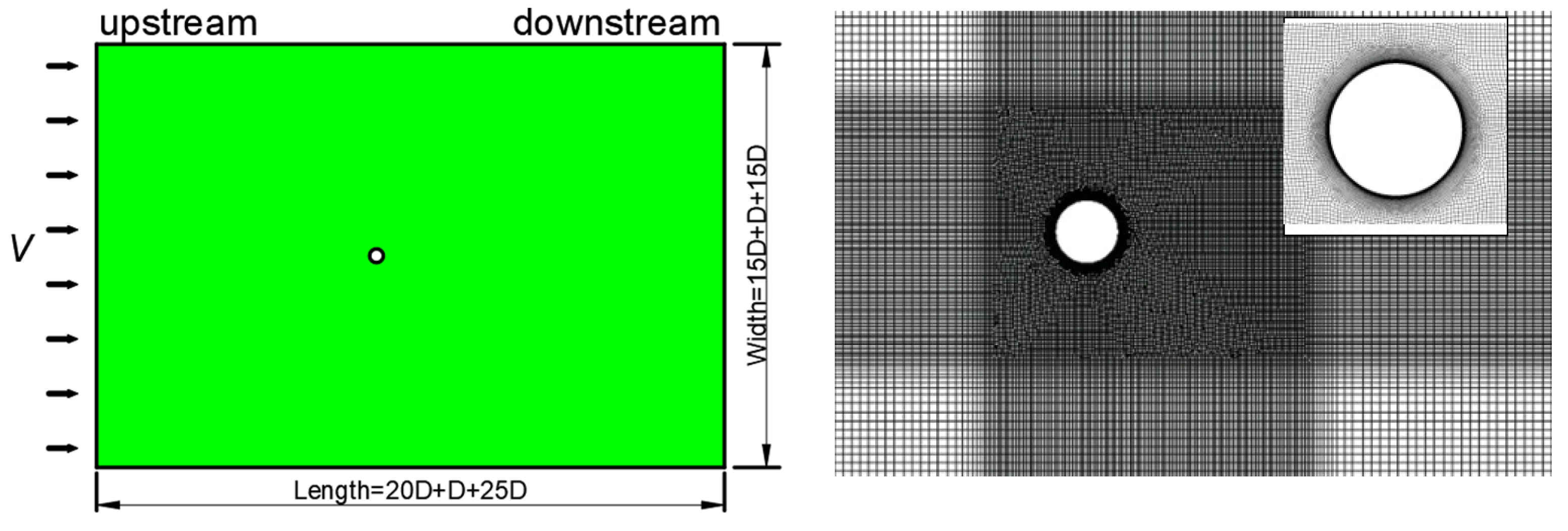
Figure 2.
Computation domain and grid of three piles:(a) diagram of computation domain for three equally spaced cylinders;(b) grid of three cylinders β=60°.
Figure 2.
Computation domain and grid of three piles:(a) diagram of computation domain for three equally spaced cylinders;(b) grid of three cylinders β=60°.
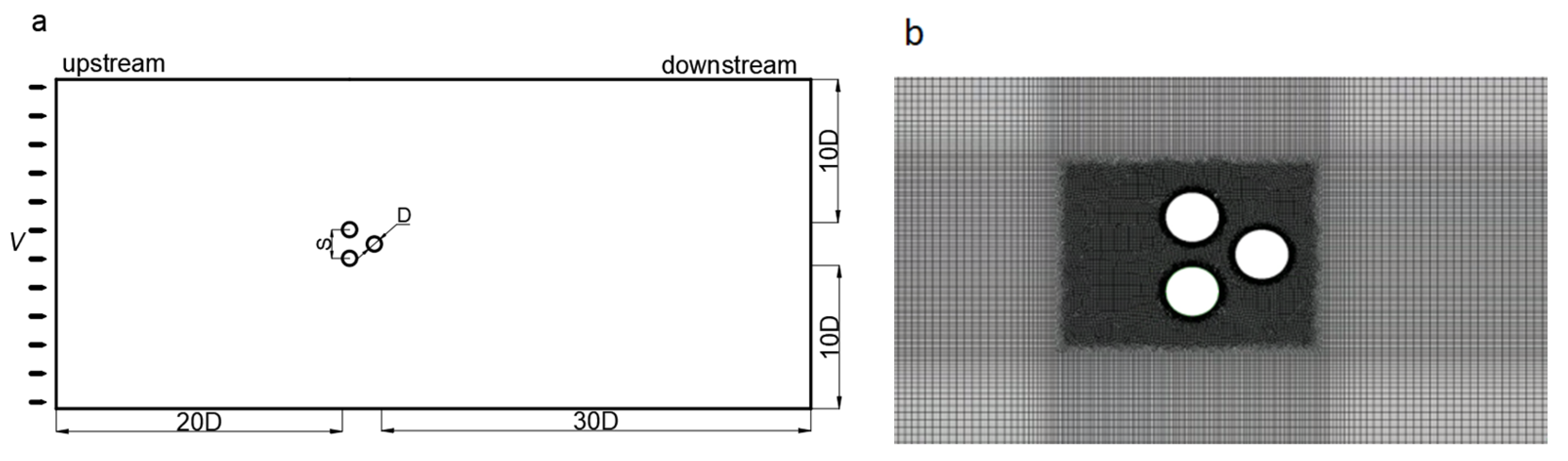
Figure 3.
Arrangement for three cylinders:(a)Position of cylinders β=60°; (b)Position of cylinders β=0°.
Figure 3.
Arrangement for three cylinders:(a)Position of cylinders β=60°; (b)Position of cylinders β=0°.
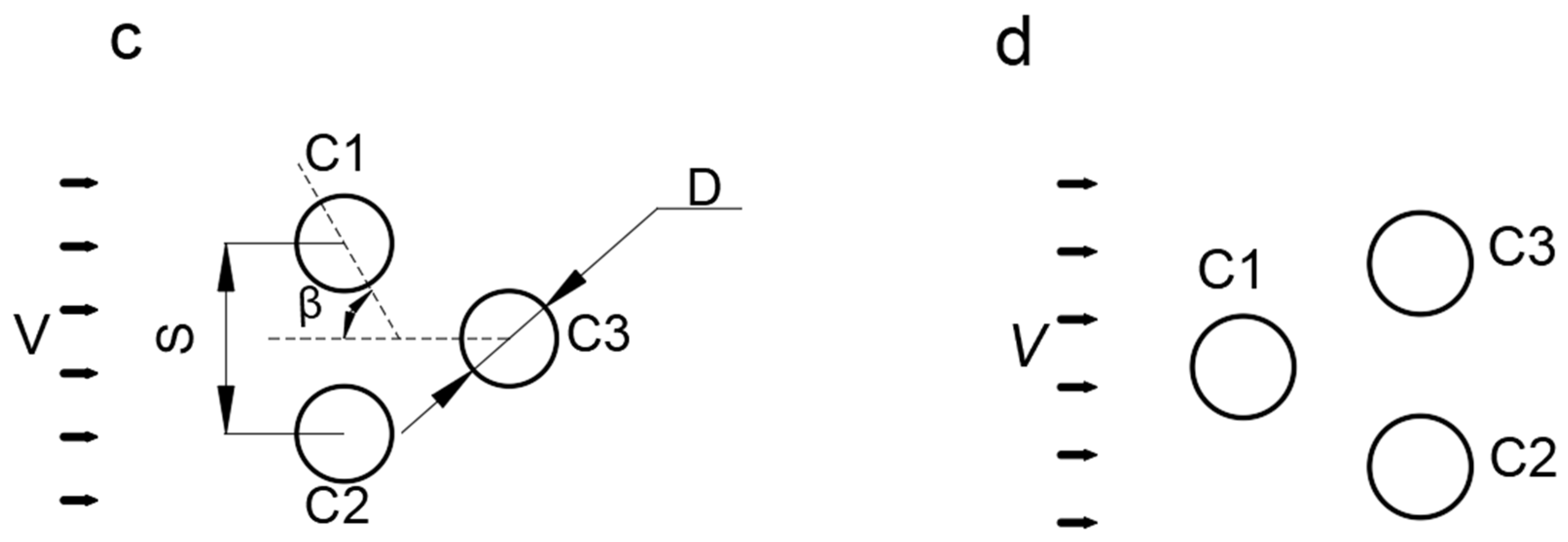
Figure 4.
Contour of velocity with different incidence angular:S/D=1.5,Re=8×104.
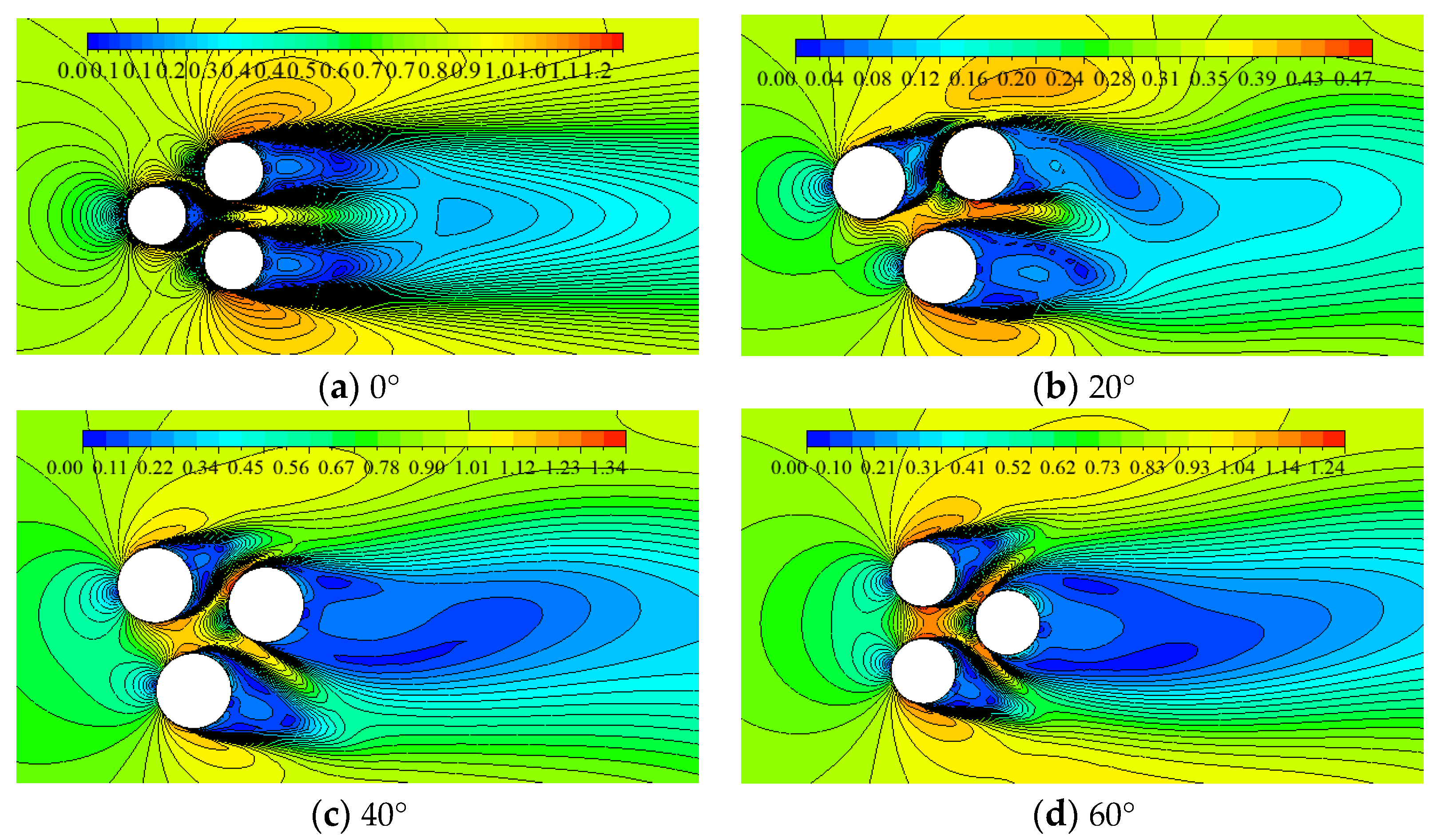
Figure 5.
Contour of velocity with different incidence angular: S/D=2.5,Re=8×104.
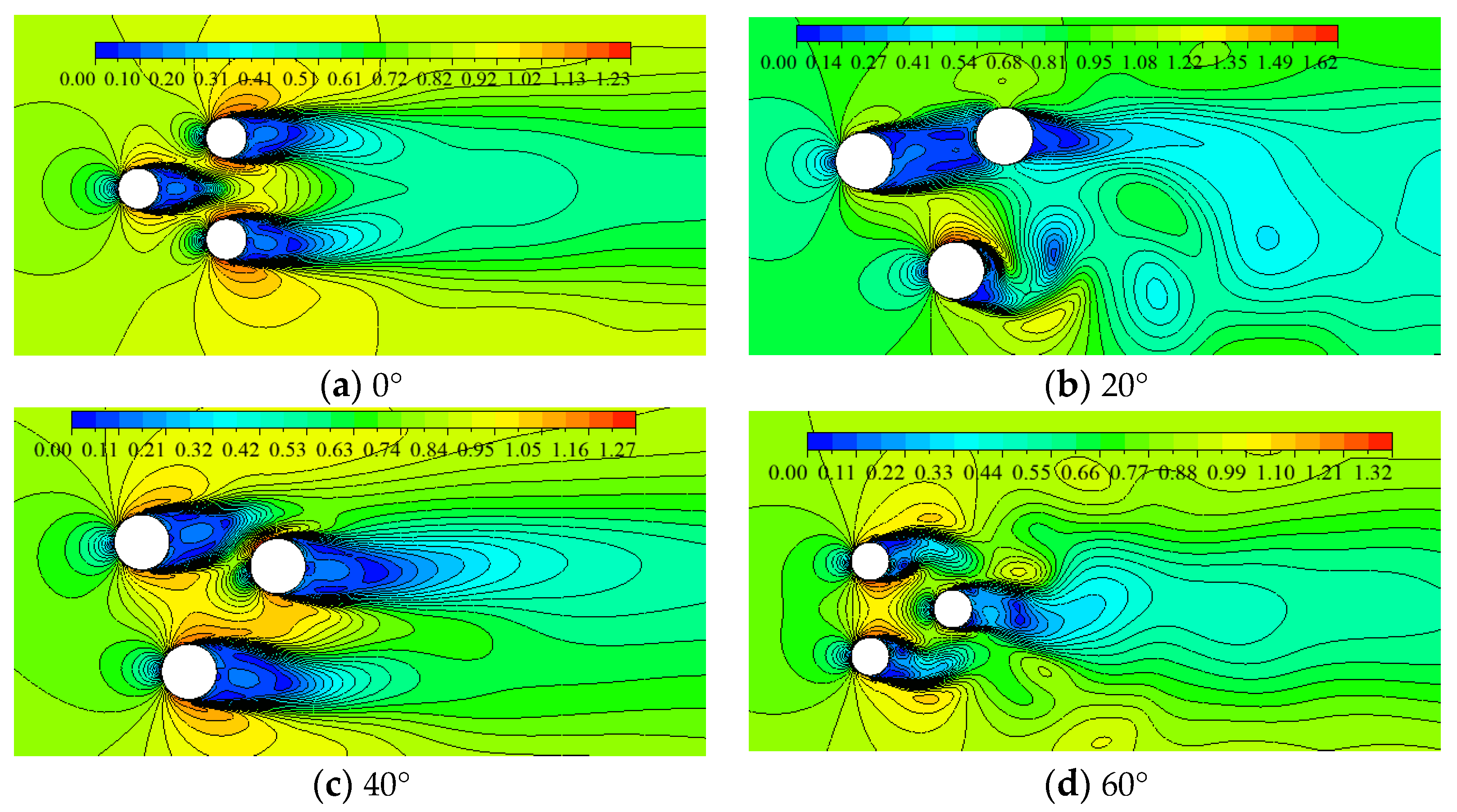
Figure 6.
Contour of velocity with different incidence angular:S/D=4,Re=8×104.
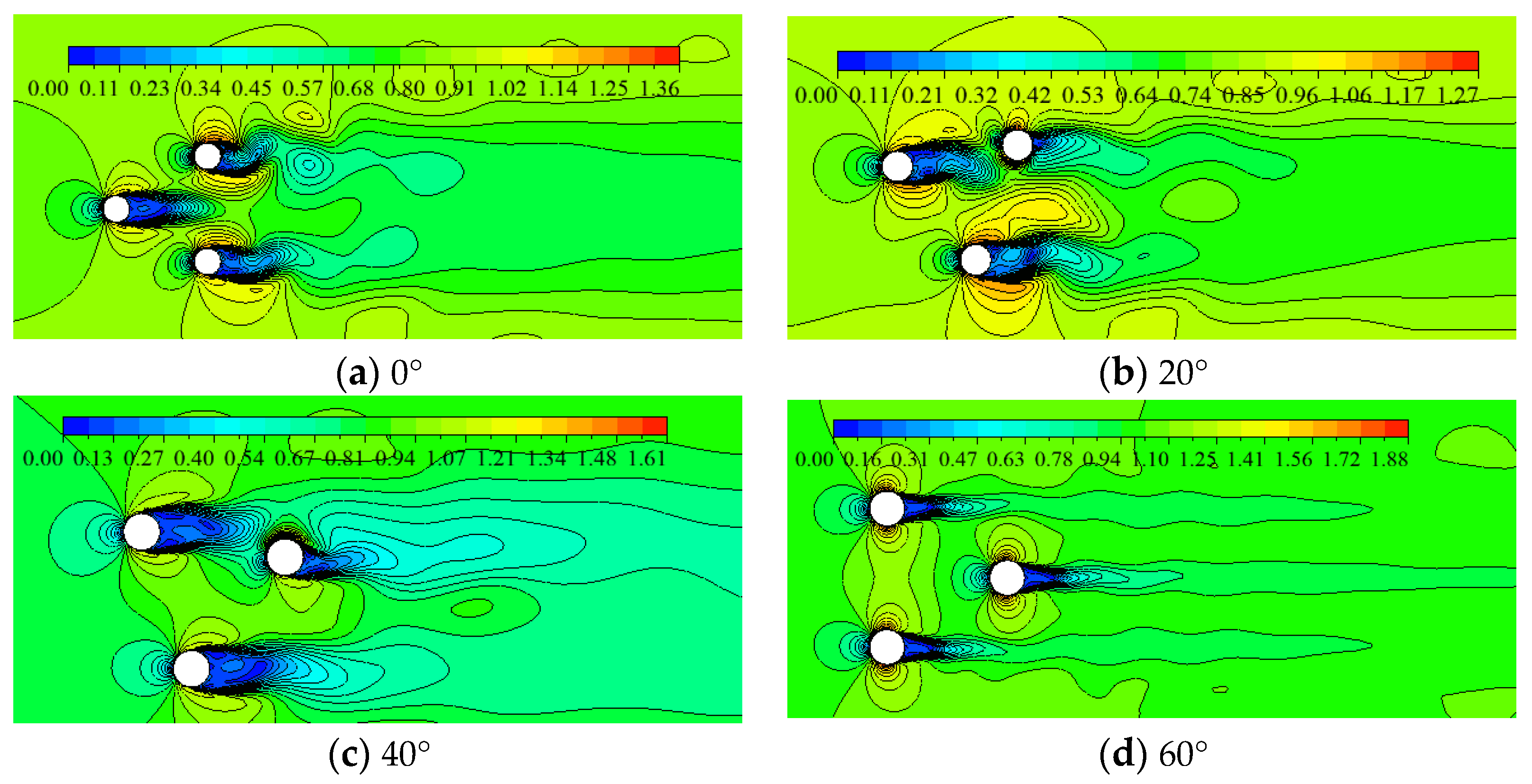
Figure 7.
Contour of velocities with Re(S/D=1.5,β=0°).
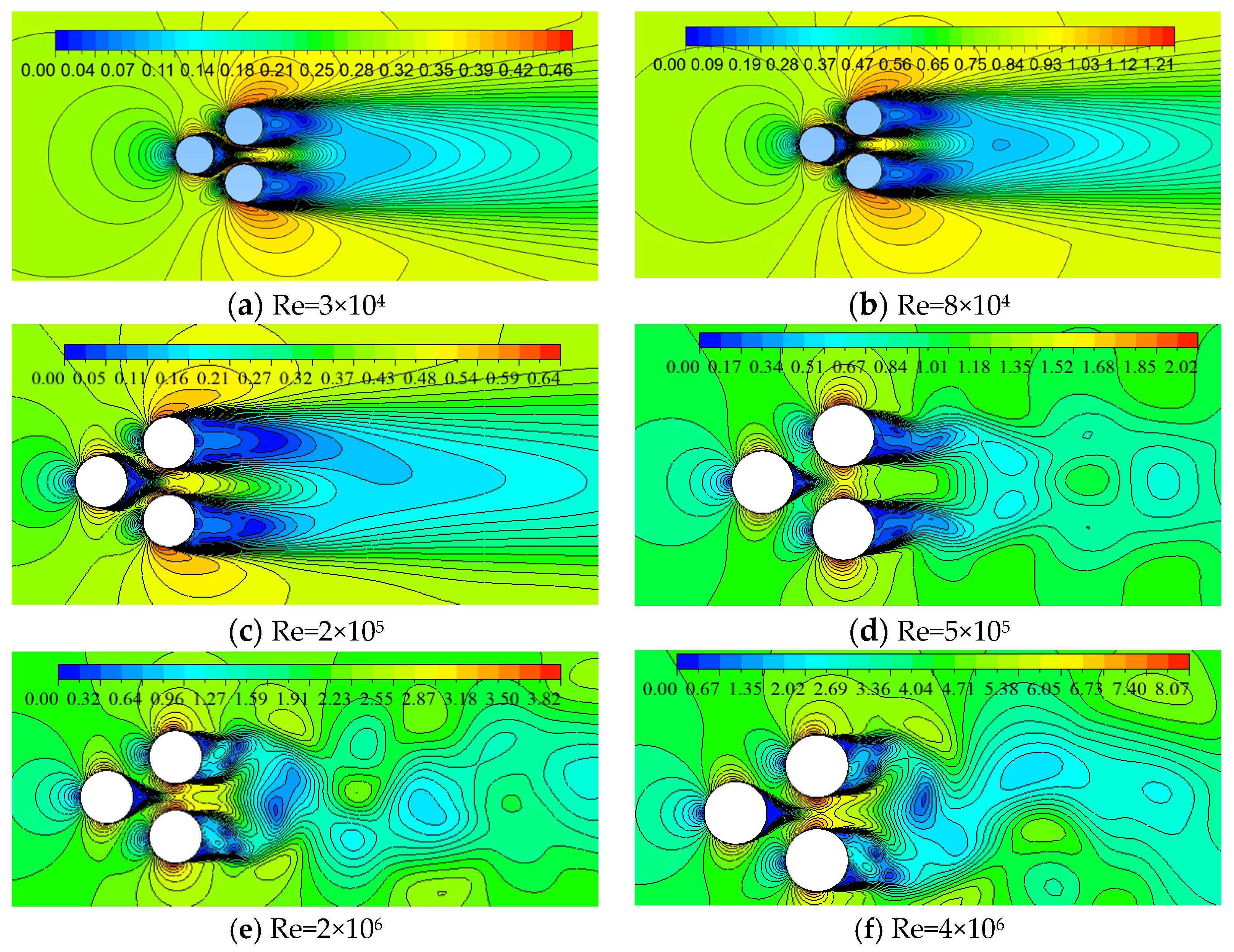
Figure 8.
Contour of velocities with Re(S/D=1.5,β=60°).
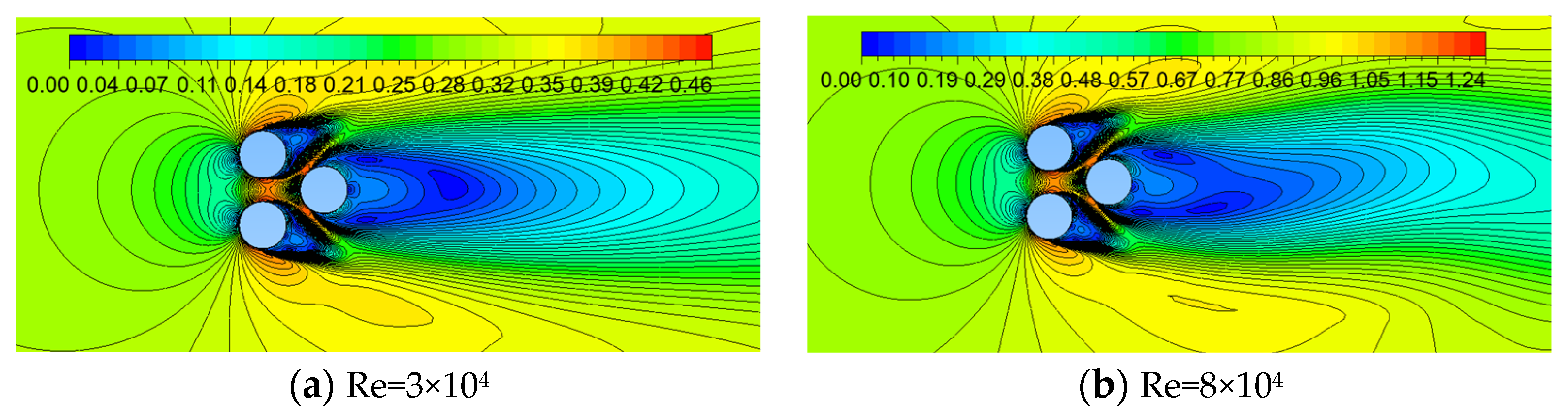
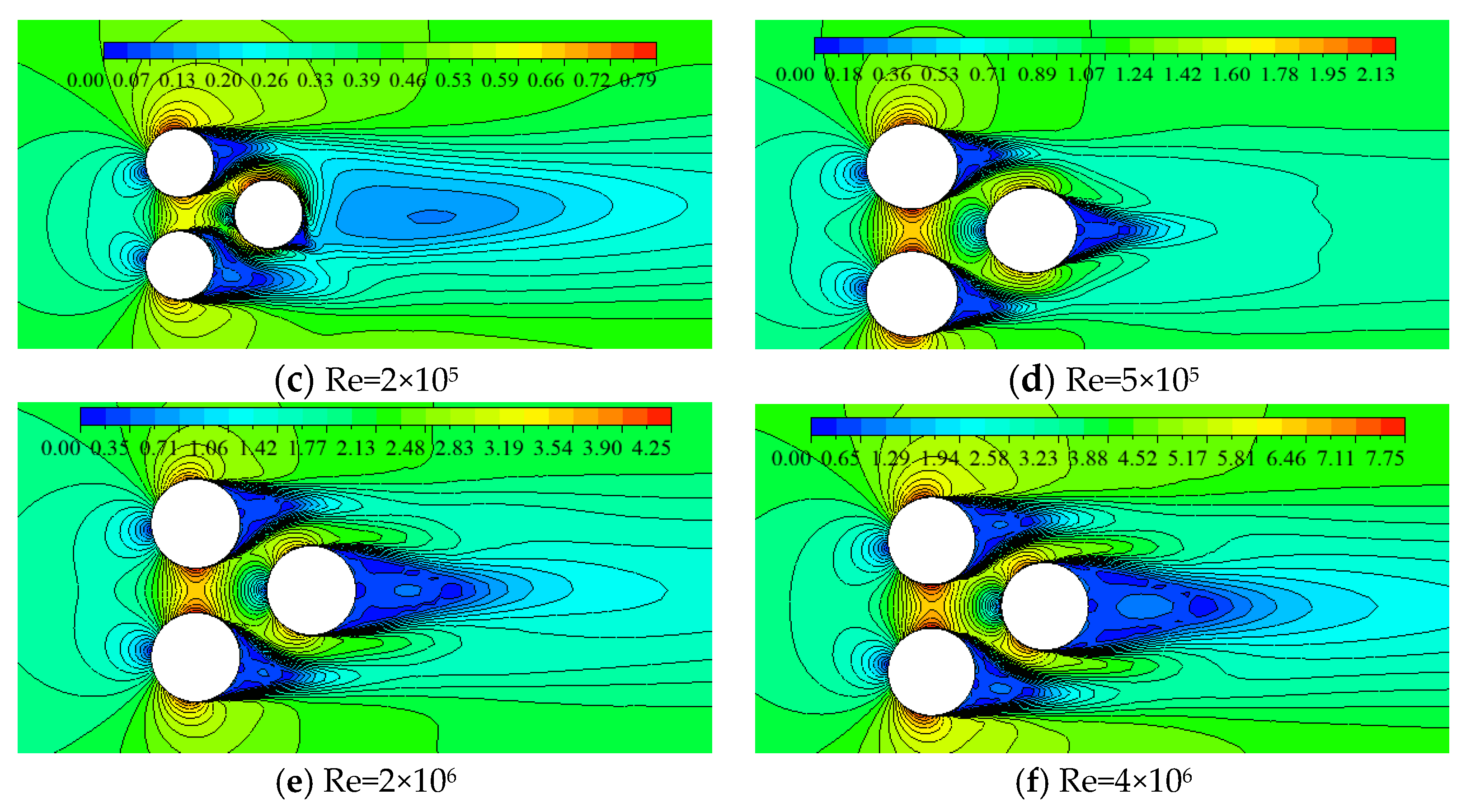
Figure 9.
Arrangement for three cylinders:(a) Geometric model; (b) grid model.
Figure 10.
three dimensional flow velocity contour past three cylinders:(a) S/D=1.35;(b)S/D=1.5;(c) S/D=1.7;(c) S/D=2.0.
Figure 10.
three dimensional flow velocity contour past three cylinders:(a) S/D=1.35;(b)S/D=1.5;(c) S/D=1.7;(c) S/D=2.0.
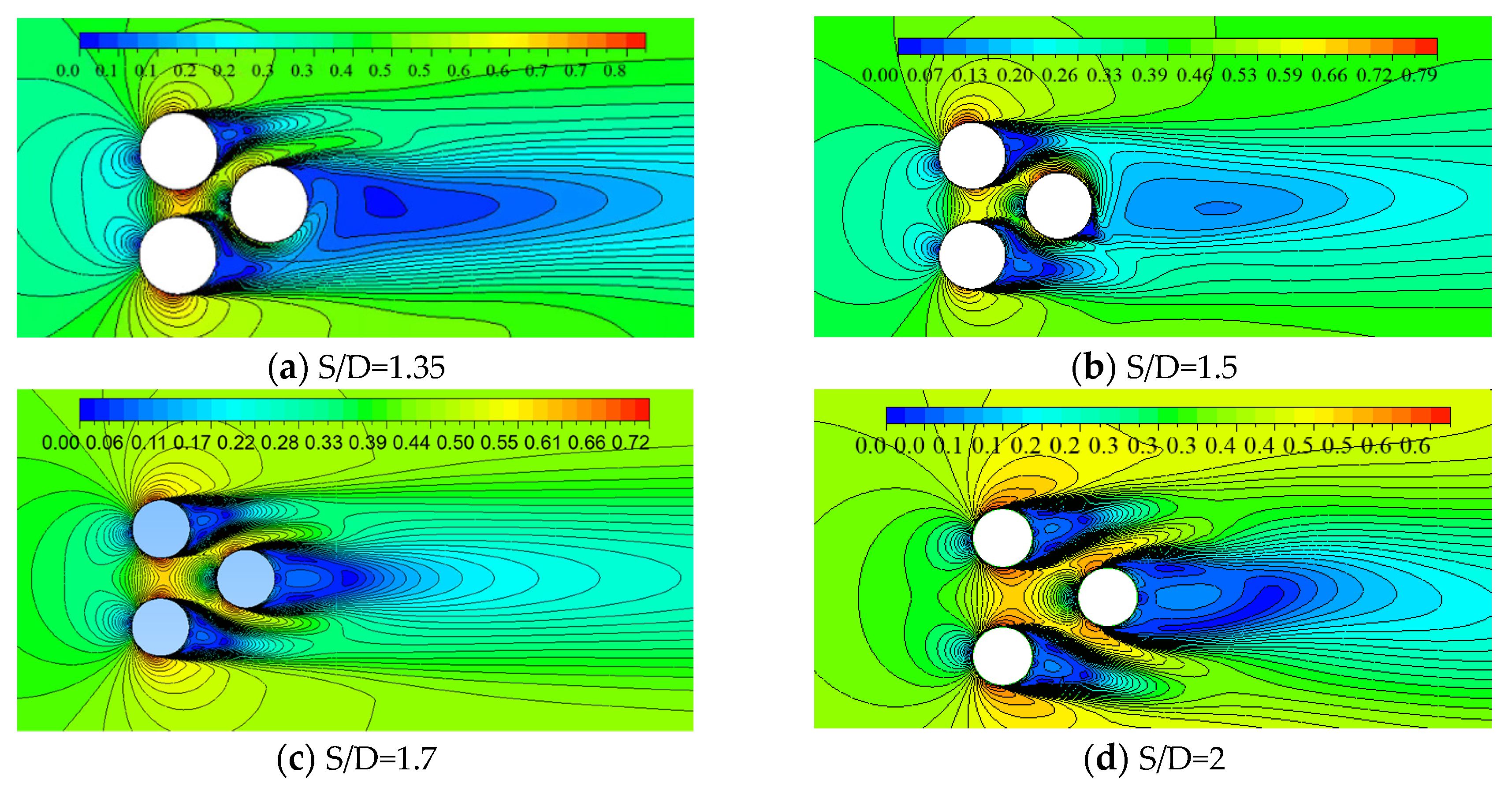
Figure 11.
Evolution of periodic flow regime during T.
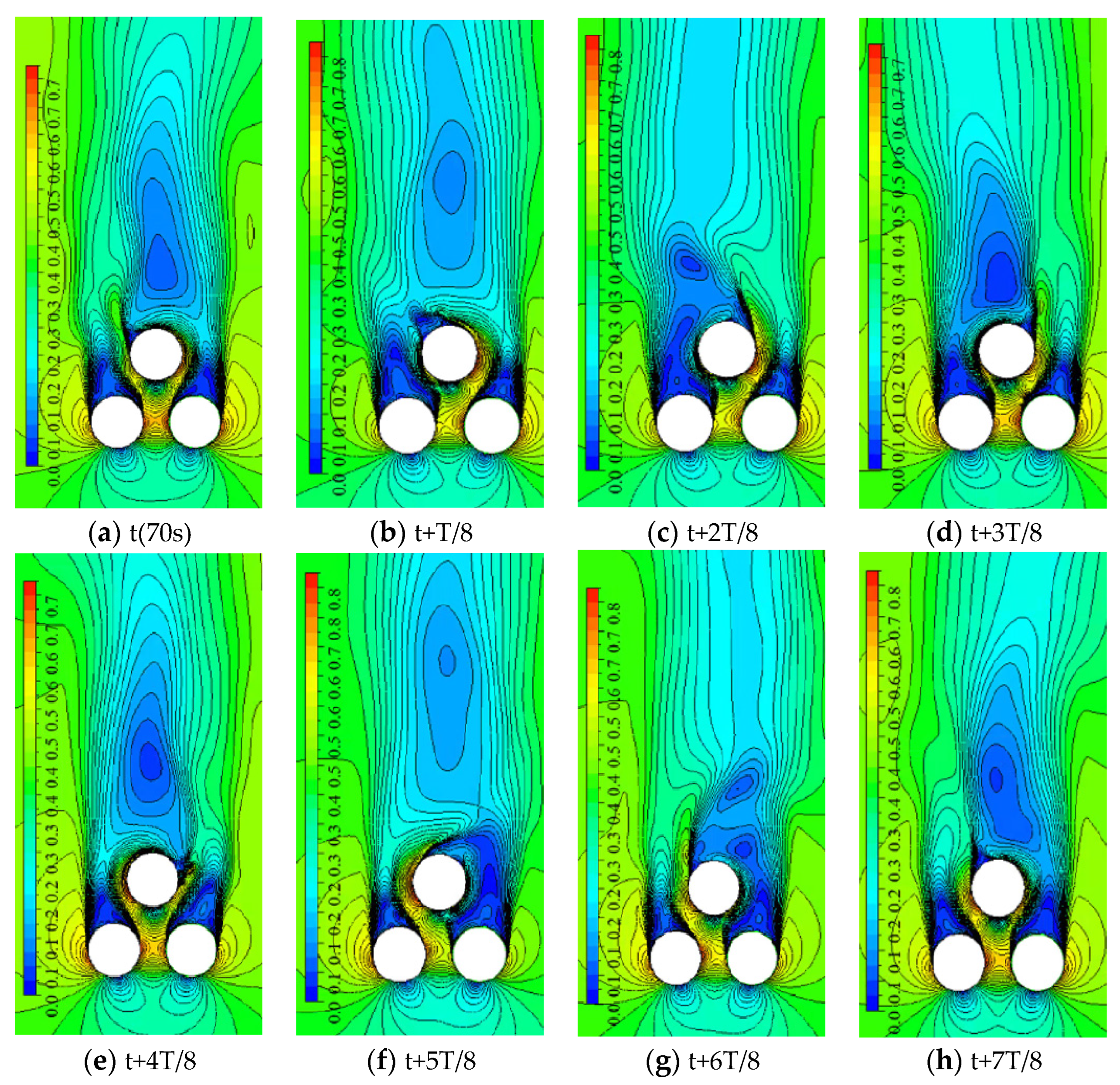
Figure 12.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=8×104,β=0°;(a) C1;(b) C2;(c) C3.
Figure 12.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=8×104,β=0°;(a) C1;(b) C2;(c) C3.
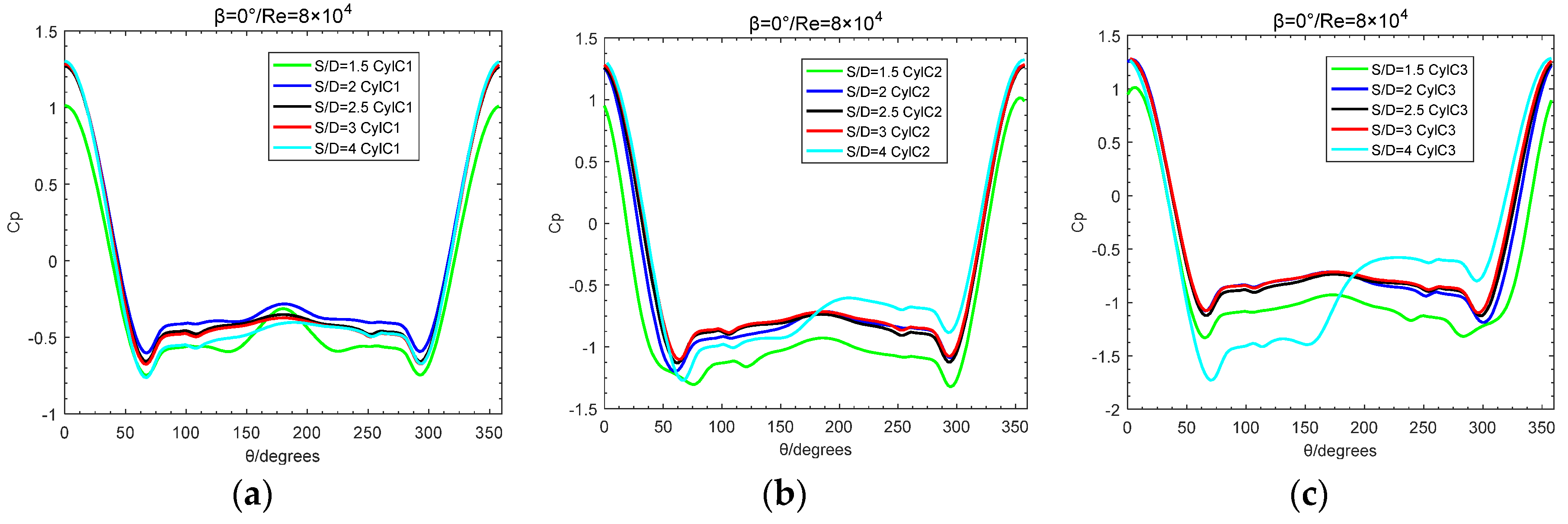
Figure 13.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=8×104,β=60°;(a) C1;(b) C2;(c) C3.
Figure 13.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=8×104,β=60°;(a) C1;(b) C2;(c) C3.
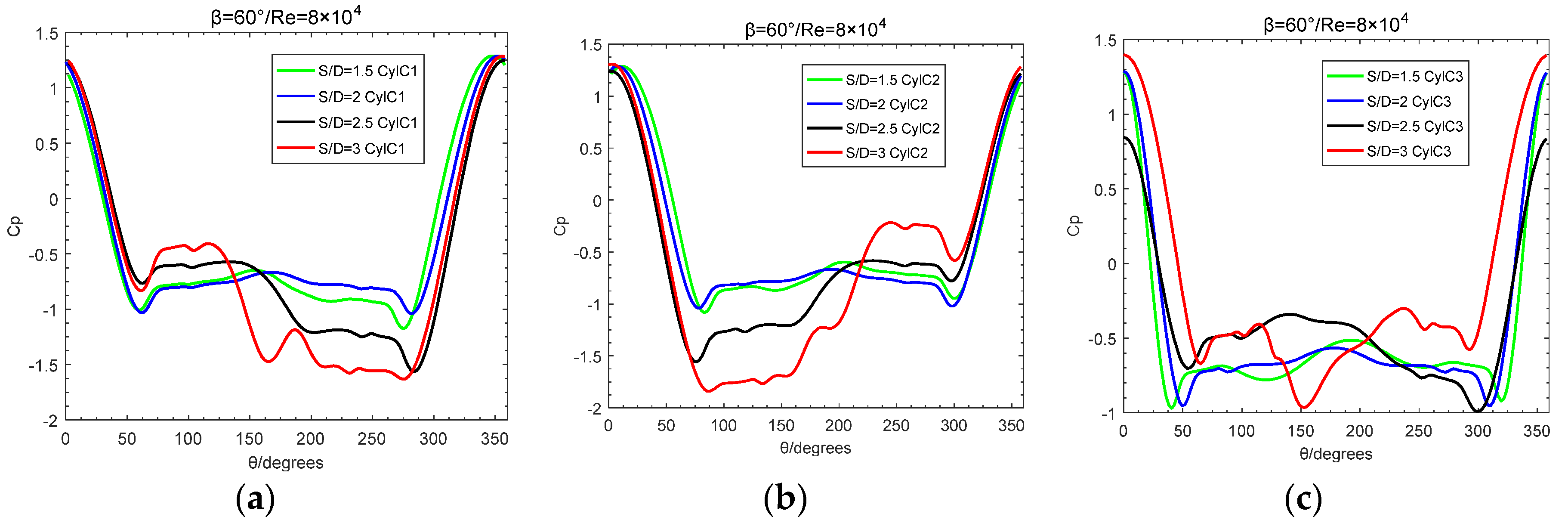
Figure 14.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×105,β=0°;(a) C1;(b) C2;(c) C3.
Figure 14.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×105,β=0°;(a) C1;(b) C2;(c) C3.
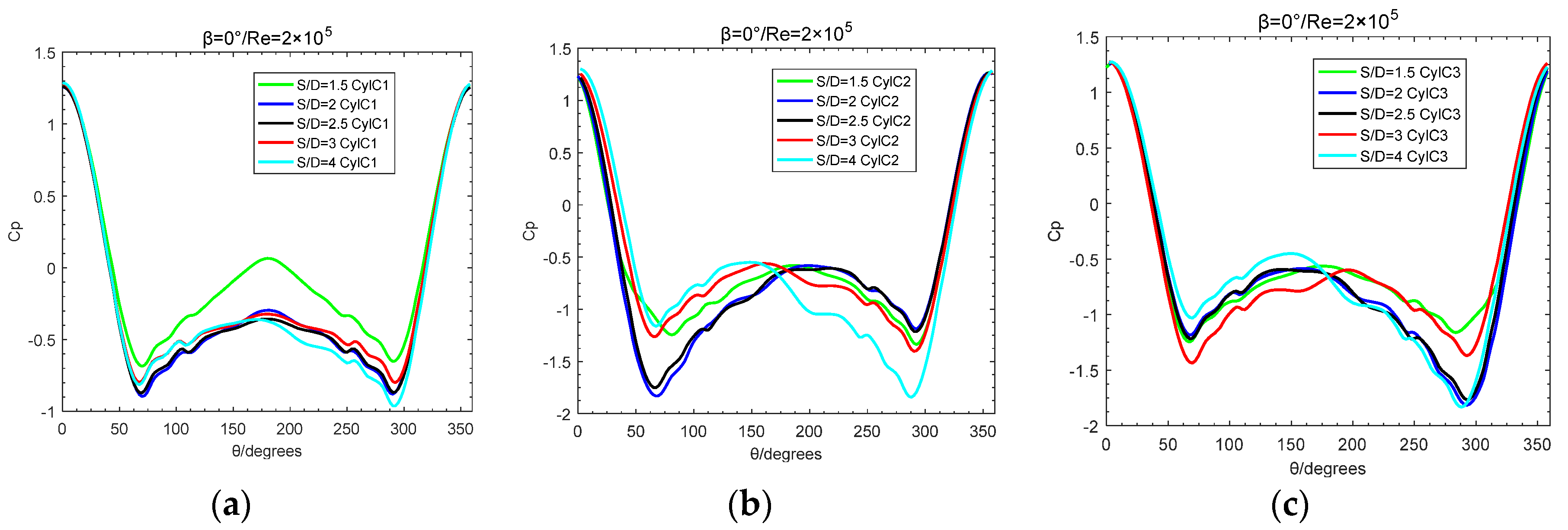
Figure 15.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×105,β=60°;(a) C1;(b) C2;(c) C3.
Figure 15.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×105,β=60°;(a) C1;(b) C2;(c) C3.
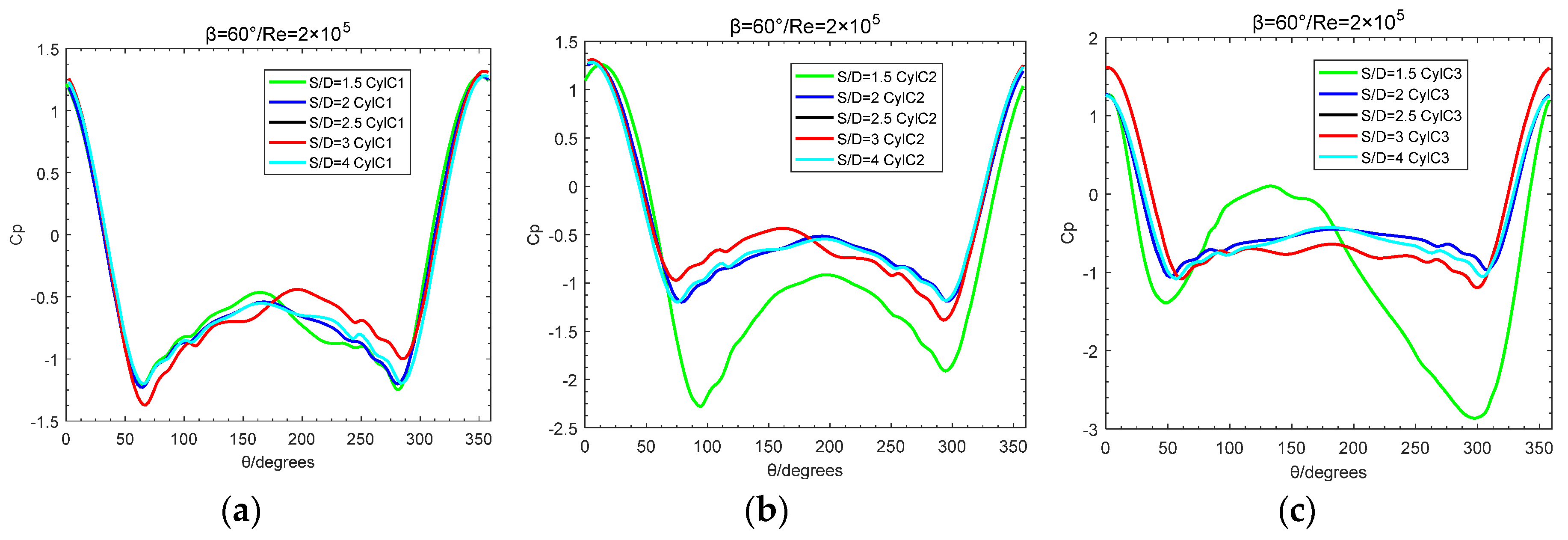
Figure 16.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×106,β=0°;(a) C1;(b) C2;(c) C3.
Figure 16.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×106,β=0°;(a) C1;(b) C2;(c) C3.
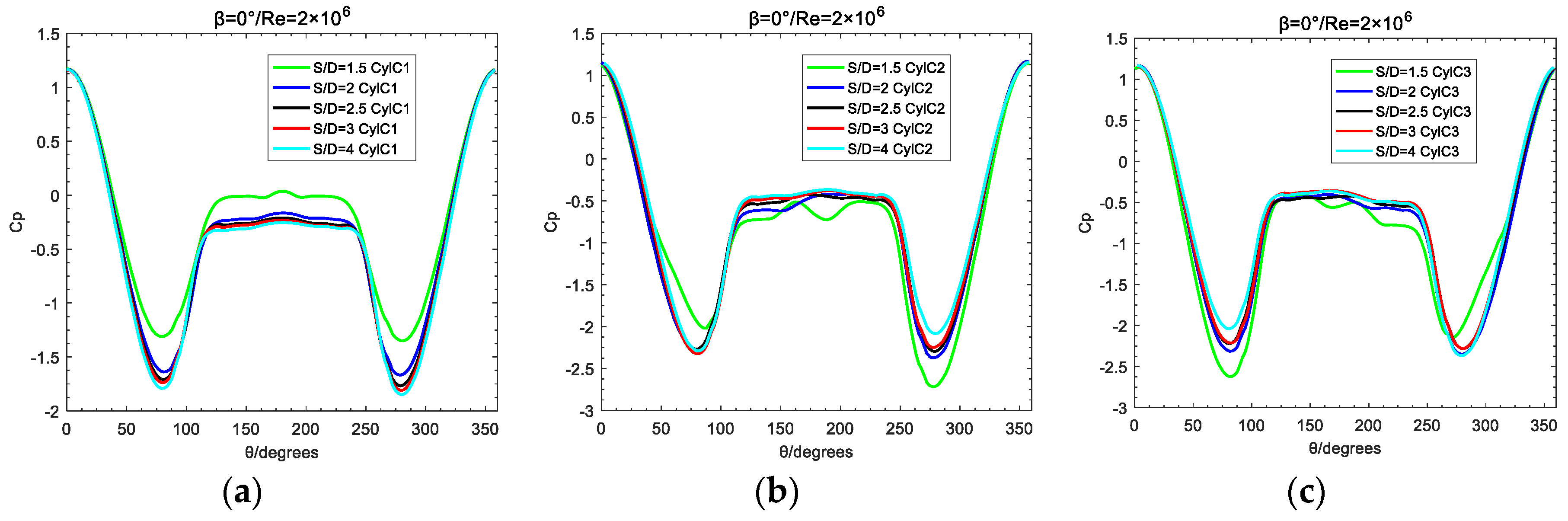
Figure 17.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×106,β=60°;(a) C1;(b) C2;(c) C3.
Figure 17.
Variation of pressure coefficient of three cylinders with spacing ratio S/D:Re=2×106,β=60°;(a) C1;(b) C2;(c) C3.
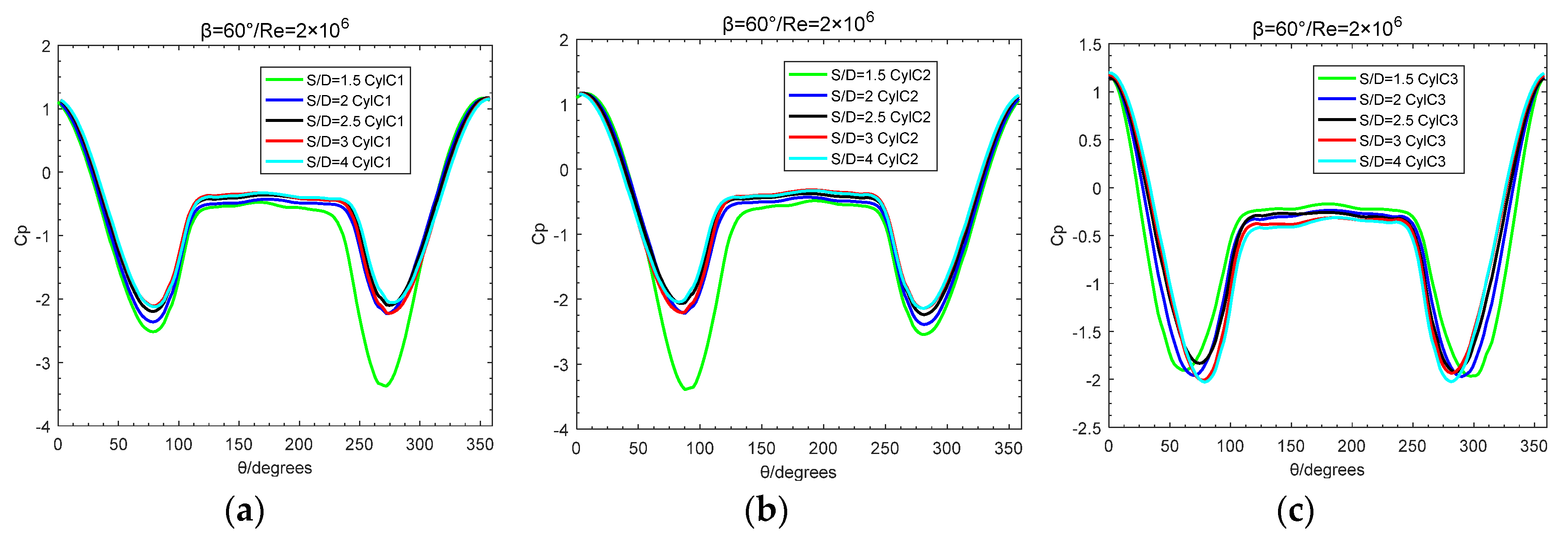
Figure 18.
the variation of the mean drag coefficients with S/D(β=0°):(a) Re=8×104; (b)Re=2×105; (c)Re=2×106;.
Figure 18.
the variation of the mean drag coefficients with S/D(β=0°):(a) Re=8×104; (b)Re=2×105; (c)Re=2×106;.
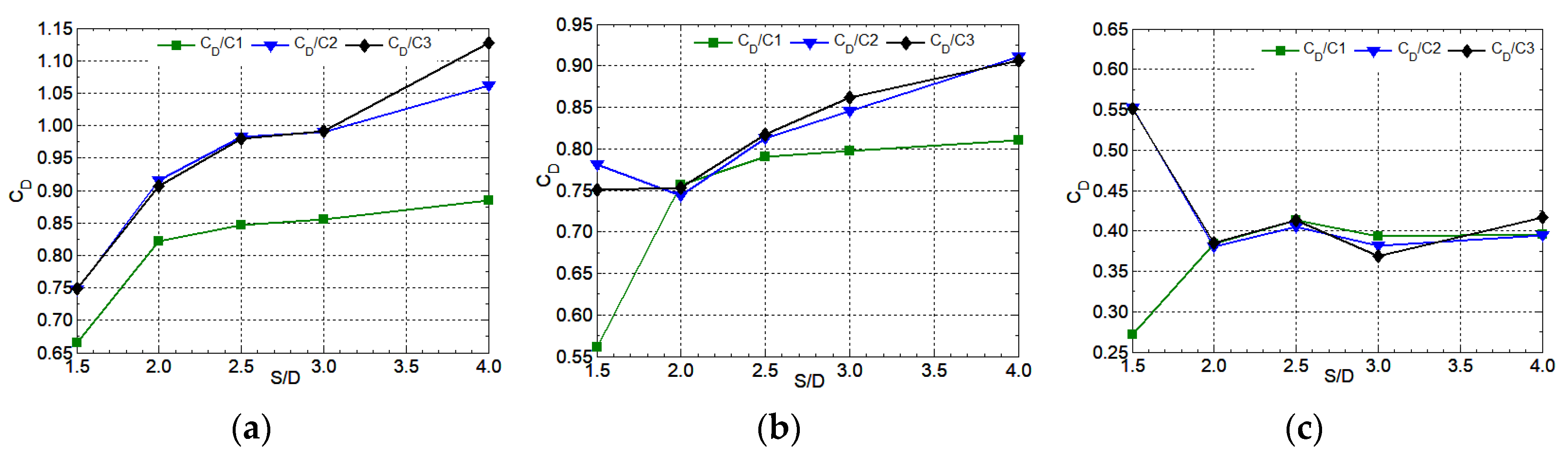
Figure 19.
the variation of the mean drag coefficients with S/D (β=60°):(a) Re=8×104; (b)Re=2×105; (c)Re=2×106;.
Figure 19.
the variation of the mean drag coefficients with S/D (β=60°):(a) Re=8×104; (b)Re=2×105; (c)Re=2×106;.
Figure 20.
Time-history variation of surface drag coefficient and lift coefficient:Re=8×104,S/D=1.5,β=60°; (a) drag coefficient; (b) lift coefficient.
Figure 20.
Time-history variation of surface drag coefficient and lift coefficient:Re=8×104,S/D=1.5,β=60°; (a) drag coefficient; (b) lift coefficient.
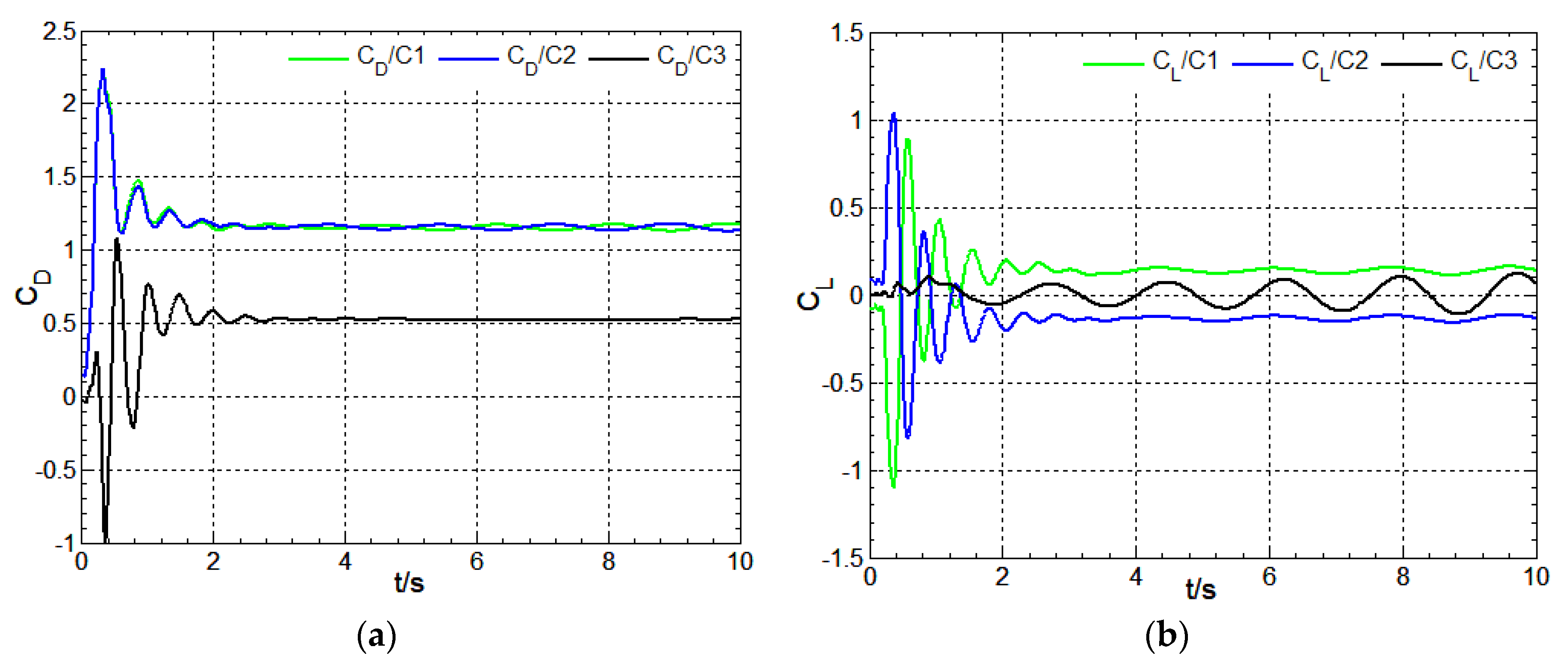
Figure 21.
Time-history variation of surface drag coefficient and lift coefficient:Re=2×105,S/D=1.5,β=60°; (a) drag coefficient; (b) lift coefficient.
Figure 21.
Time-history variation of surface drag coefficient and lift coefficient:Re=2×105,S/D=1.5,β=60°; (a) drag coefficient; (b) lift coefficient.
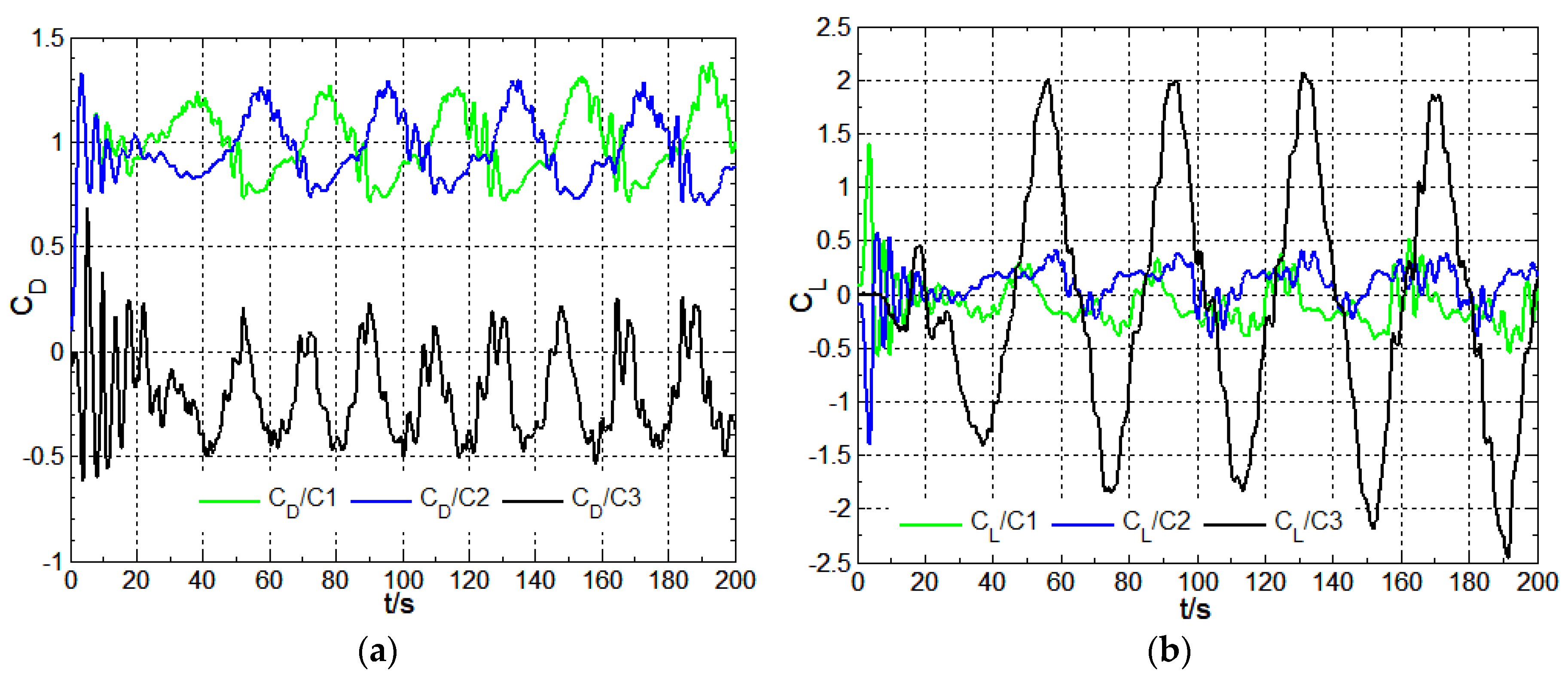
Figure 22.
Time-history variation of surface drag coefficient and lift coefficient:Re=2×106,S/D=1.5,β=60°; (a) drag coefficient; (b) lift coefficient.
Figure 22.
Time-history variation of surface drag coefficient and lift coefficient:Re=2×106,S/D=1.5,β=60°; (a) drag coefficient; (b) lift coefficient.
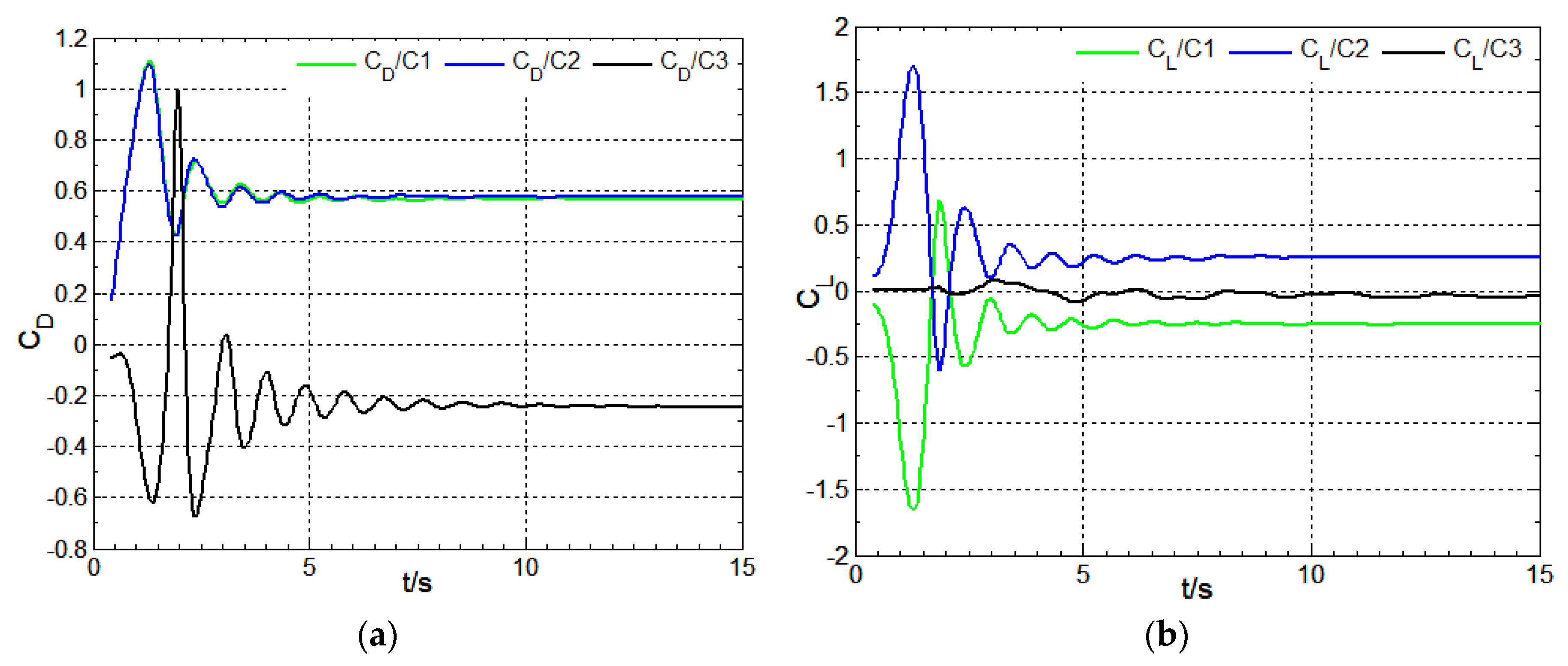
Table 1.
Comparison and verification data of turbulent model.
| Researcher | Re/104 | CD | C’L | St | Cpb | Cpmin | θs |
|---|---|---|---|---|---|---|---|
| Ivette Rodriguez [6]/LES | 4.2 | 0.994 | 0.316 | 0.214 | -1.024 | -1.548 | 87.5 |
| N. Mulvany [20]/test | 4.2 | -1.18 | -1.241 | ||||
| Unal.U [7] | 4.1 | 1.14 | 0.186 | ||||
| E. Achenbach [3] | 6 | 1.23 | 81.5 | ||||
| Wieselsberger.C.[1] | 3～4.2 | 1.18 | |||||
| Anatol Roshko [2] | 10 | -1.18 | |||||
| C. Norberg [4] | 4 | 0.495 | 0.189 | ||||
| Gonter Schewe [5] | 4 | 1.1 | 0.352 | 0.2 | |||
| Alessandro Capone [8] | 6.9 | 95～104 | |||||
| Current work | |||||||
| Realizablek-ε model | 4 | 0.722 | 0.17 | 0.275 | -0.8 | -1.85 | 102～105 |
| SSTk-ω model | 4 | 1.21 | 0.598 | 0.239 | -1.48 | -1.92 | 80～95 |
| k-kl-ω model | 4 | 1.12 | 0.353 | 0.172 | -1.12 | -1.394 | 82 |
Table 2.
Calculation results of different grid scales.
| Mesh | Re/104 | S/D | Incidence Angle /° |
Number of Cell | CD(C1,C2,C3) |
|---|---|---|---|---|---|
| Mesh 1 | 8.0 | 1.5 | 0 | 80000 | 0.68/0.747/0.749 |
| Mesh2 | 8.0 | 1.5 | 0 | 210000 | 0.727/0.812/0.811 |
| Mesh3 | 8.0 | 1.5 | 0 | 430000 | 0.735/0.811/0.807 |
Table 3.
Validation results.
| Researcher | Re/104 | S/D | Incidence Angle /° |
CD(C1,C2,C3) | StA | StB | StC |
|---|---|---|---|---|---|---|---|
| S.G.Pouryoussefi · M. et al. [12] | 6.08 | 2.5 | 0 | 0.82/1.08/1.05 | 0.336 | 0.181 | 0.181 |
| A.T.Sayers [10] | 3.0 | 1.5 | 0 | 0.75/0.769 | 0.274 | 0.175 | 0.175 |
| Current work | 3.0 | 1.5 | 0 | 0.735/0.811/0.807 | 0.263 | 0.183 | 0.183 |
| Current work | 6.08 | 2.5 | 0 | 0.846/0.982/0.98 |
Table 4.
Strouhal number under different Reynolds numbers for single cylinder.
| Reynolds Number | 8×104 | 2×105 | 2×106 | 4×106 |
|---|---|---|---|---|
| Strouhal number | 0.185[4] | 0.188[4] | 0.32 | 0.2[16] |
Table 5.
Strouhal number for cylinders for different spacing ration, Reynolds number and incidence angle.
Table 5.
Strouhal number for cylinders for different spacing ration, Reynolds number and incidence angle.
| Incidence Angle | Spacing Ratio | Cylinder | Reynolds Number | ||
|---|---|---|---|---|---|
| 8×104 | 2×105 | 2×106 | |||
| 0° | 1.5 | c1 | 0.138 | ||
| c2 | 0.181 | ||||
| c3 | 0.181 | ||||
| 2 | c1 | 0.150 | 0.225 | 0.167 | |
| c2 | 0.175 | 0.200 | 0.300 | ||
| c3 | 0.175 | 0.200 | 0.300 | ||
| 2.5 | c1 | 0.190 | 0.225 | 0.213 | |
| c2 | 0.190 | 0.200 | 0.293 | ||
| c3 | 0.190 | 0.200 | 0.293 | ||
| 60° | 1.5 | c1 | 0.263 | ||
| c2 | 0.263 | ||||
| c3 | 0.075 | 0.033 | |||
| 2 | c1 | 0.230 | 0.250 | 0.300 | |
| c2 | 0.230 | 0.250 | 0.275 | ||
| c3 | 0.092 | 0.100 | 0.075 | ||
| 2.5 | c1 | 0.212 | 0.225 | 0.273 | |
| c2 | 0.212 | 0.225 | 0.273 | ||
| c3 | 0.100 | 0.12 | 0.102 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated