Two-Tier Efficient QoE Optimization for Partitioning and Resource Allocation in UAV-Assisted MEC

1. Introduction

In recent years, Mobile Edge Computing (MEC) has emerged as a prominent computing paradigm to accommodate the rapid proliferation of Internet of Things (IoT) devices and novel application scenarios such as virtual reality (VR), augmented reality (AR), autonomous driving, and intelligent robotics [1]. However, ground-based MEC networks face inherent limitations in coverage, deployment flexibility, and the handling of hotspot issues due to the immobility of MEC servers. The limitations of stationary infrastructure present challenges in accommodating the dynamic edge network environment. Consequently, researchers have increasingly focused on UAV-assisted MEC (UAV-MEC), which offers significant advantages in terms of high mobility and low deployment costs [2,3].

The existing body of work addresses numerous challenges associated with UAV-MEC systems, including the limited computational and battery capacities of UAVs, trajectory planning, cooperative control of multiple UAVs, and data transmission security. Various optimization problems have been formulated to tackle these challenges by adjusting offloading decisions, bandwidth allocation, caching strategies, and UAV trajectories. Common optimization objectives include minimizing task execution time [4], reducing energy consumption [5,6], or balancing a weighted combination of both [7]. For instance, resource allocation and task offloading ratios are jointly optimized to minimize the total energy consumption of user devices (UDs) under partial offloading strategies [8], and the joint design of UAV trajectory, task allocation, and communication resource management aims to minimize a weighted sum of execution latency and energy consumption [9]. Similarly, maximizing computational efficiency to ensure robust system performance is another focus [10,11]. However, these objectives often emphasize system performance over the Quality of Experience (QoE) for UDs, potentially leading to unfair resource allocation.

From the users’ perspective, it is crucial to consider both waiting time and execution time to measure QoE in UAV-MEC systems. Several studies have addressed this by formulating optimization problems aimed at minimizing task response time, which encompasses both waiting and execution times [12,13]. For instance, [14] proposes a joint optimization approach that considers offloading ratios, service policies, and UAV trajectories to minimize the maximum delay of delay-sensitive tasks in each time slot. Furthermore, [15] introduces a comprehensive metric called the shrinkage ratio, balancing factors such as waiting time, execution time, task length, and UD computational capabilities, providing a straightforward and effective measure of optimization efficiency in UAV-MEC networks. However, these studies often assume that computation tasks are divisible and do not fully account for the impact of a large number of UDs in UAV-MEC systems. In reality, the increasing number of UDs and the binary offloading model for indivisible tasks present significant challenges in maintaining good QoE for users.

Optimizing user QoE in large-scale edge networks remains a challenging problem, as measuring user experience typically involves considering response latency rather than task execution latency [16]. The offloading decisions of multiple users, resource allocation strategies, and UAV trajectories often lead to tightly coupled optimization problems. A holistic metric called the shrinkage ratio has been proposed to reconcile variables such as waiting delay, processing delay, and the computational resources of edge devices [15]. However, previous work did not account for the binary offloading approach nor the impact of a growing number of nodes within expansive IoT networks on the complexity of the solution.

In this paper, we investigate the QoE-oriented computation task offloading optimization problem in a large scale UAV-MEC network with considering binary offloading mode at each UD. We aim to minimize the sum of shrinkage ratios for all UDs by jointly optimizing UAV trajectory, task offloading mode selection, network bandwidth and computation resource allocation. To handle the high complexity of large number of UDs and the coupling of drone trajectory for each coverage partition and resource allocation for computation task, we propose an efficient propose a two-tier optimization scheme to solve it. We first develop a low-complexity partition coverage algorithm algorithm based on Welzl method and determine the UAV flight trajectory by solving a TSP problem. Subsequently, for the network bandwidth and computing resource allocation sub-problem, we develop a low-complexity CD-based method for the small scale Iot network and a ADMM-based method which can leverages parallel computing to enhance solving speed, suitable for large-scale networks.

The main contributions of this paper are summarized as follows:

• We extend model in [13,15] to handle binary task offloading mode and large scale nodes in a UAV-MEC system. Our model takes into consideration the impact of UAV on the response time of UDs while leveraging the radius coverage of UAV to reduce the high complexity in large-scale node scenarios. Our model exhibits practicality and scalability in resource allocation within large-scale IoT-enabled UAV-MEC.
• We propose an two-tier optimization scheme to decouple the drone trajectory planning and resource allocation for computation task. We design a circle cover algorithm based on Welzl method to divide area into smaller partitions to reduce the scale of the problem.
• We develop a CD-based method and a ADMM-based method for the task offloading mode selection and resource allocation in UAV-MEC system. The CD-based method has a linear complexity with respect to network scale, while the ADMM-based approach can convergence fast, making it suitable for large-scale networks.
• We conduct plenty of numerical simulations to evaluate the effectiveness and practicability of our algorithm. Our algorithm outperforms all baseline algorithms and its number of iteration exhibits a linear relationship with the scale of network.

The rest of this paper is organized as follows. Section 2 discusses the related work on UAV-MEC. In Section 3, we present a system model for user QoE optimization in large-scale edge networks and formulate it as a combinatorial optimization problem. Section 4 provides the algorithm for solving this optimization problem. In Section 5, we validate the effectiveness of the algorithm through numerical experiments. Section 6 concludes this paper and discusses future work.

2. Related Work

Unmanned aerial vehicles (UAVs) have garnered significant attention in the field of mobile edge computing (MEC) due to their low cost and high flexibility, which can substantially enhance the coverage and efficiency of edge networks [3]. For instance, Xiang et al. [17] propose a joint optimization algorithm for UAV-MEC that incorporates task offloading strategies and UAV trajectory planning, demonstrating superior energy efficiency and convergence compared to other methods. Similarly, He et al. [18] focus on optimizing 3-D multi-UAV trajectories in MEC systems to ensure fairness in task allocation and minimize energy consumption. Zhang et al. [19] utilize UAVs as aerial relay platforms to forward signals from ground or air to edge servers or other edge devices. Liu et al. [5] investigate the use of UAVs as resource-constrained mobile edge nodes that provide limited computing services to terminal devices, acting as relays for computation tasks that cannot be completed locally. Gao et al. [20] address secure data transmission in UAV-relay assisted maritime MEC systems by proposing a scheme that optimizes transmit power, time slot allocation, and UAV trajectory, enhancing both system security and computation capability.

Integration of UAVs with new-generation communication technologies has also been explored. Jiao et al. [21] maximize the rate of strong users while ensuring the target rate for weak users in an intelligent reflecting surface (IRS)-based UAV-assisted NOMA downlink network by optimizing the IRS-UAV location. Wang et al. [22] propose an energy minimization scheme for UAV-based MEC and traffic offloading in broadband Terahertz (THz) mobile networks. Additionally, M. A. Baker Siddiki Abir et al. [23] introduce a digital twin-based aerial MEC architecture for 6G networks, employing UAVs as aerial base stations with MEC capabilities to deliver high network performance for real-time and latency-sensitive applications.

Recent research has also explored the synergy between UAVs and machine learning to enhance MEC systems. For example, Chen et al. [24] leverage deep reinforcement learning to optimize UAV trajectory and resource allocation in real-time, improving overall system efficiency under dynamic network conditions. Li et al. [25] use federated learning in UAV-assisted MEC to enable distributed model training while preserving data privacy, essential for sensitive applications. Xu et al. [26] develop a scalable optimization framework combining graph theory and convex optimization to manage UAV trajectories and resource allocation in dense urban environments, reducing computational complexity and adapting to the varying demands of heterogeneous IoT devices. However, these studies primarily focus on enhancing system performance and often overlook the Quality of Experience (QoE) for user devices, potentially leading to unfair resource distribution.

QoE in UAV-MEC systems is crucial that attracted some researcher attention. Tian et al. [27] design a three-tier UAV-MEC network that includes users, drones, and a cloud center, introducing an optimization metric called the response ratio based on user preferences and real-time requirements. Shen et al. [15] propose a metric called the shrinkage ratio to measure the optimization efficiency brought by the UAV-MEC network to users, transforming QoE optimization into a minimization problem of the shrinkage ratio. However, many of these studies assume divisible computation tasks and do not fully consider the challenges posed by a large number of user devices and the binary offloading model for indivisible tasks, which significantly impacts QoE.

3. System Model and Problem Formulation

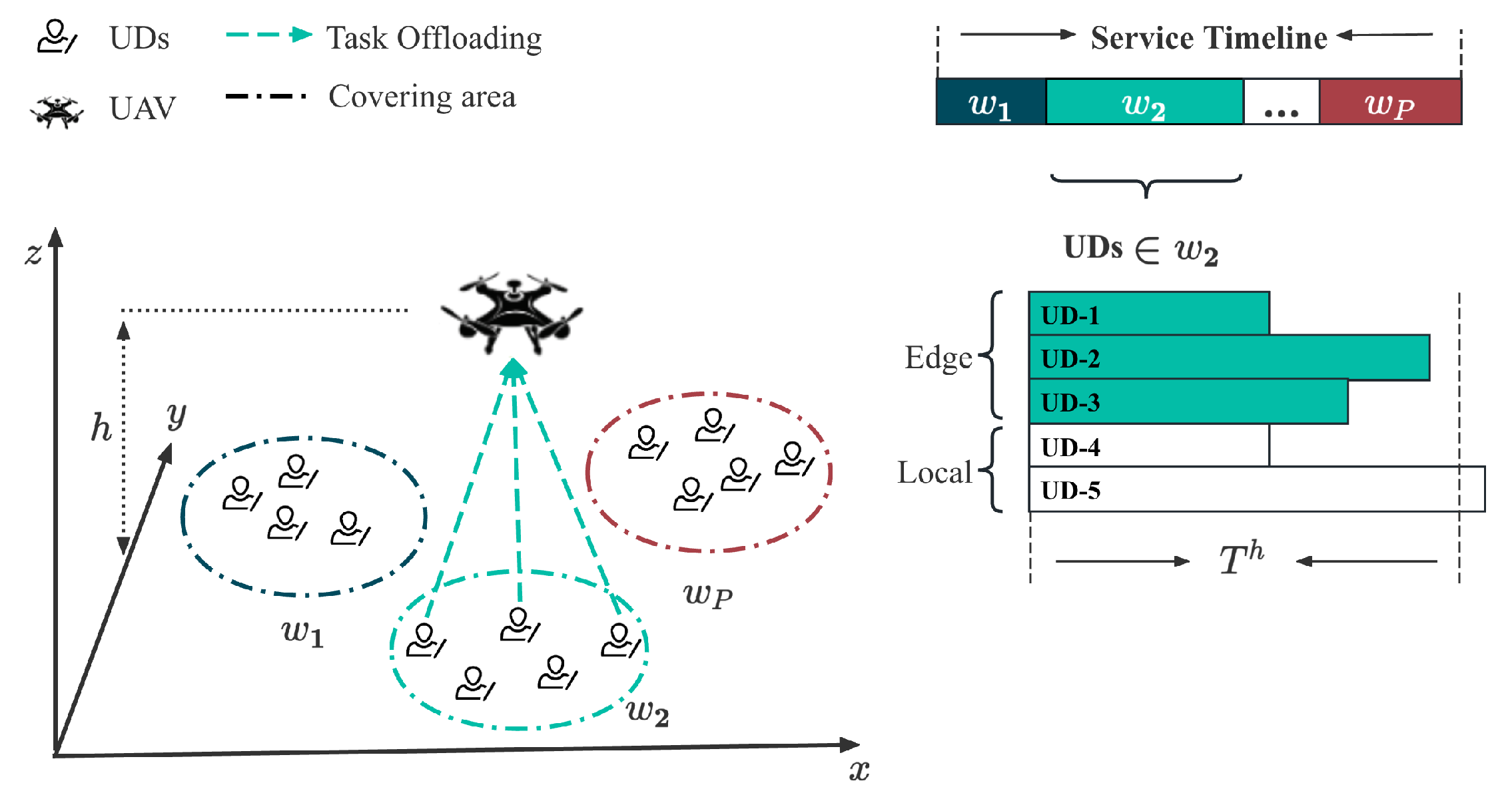
We consider the UAV-assisted MEC network as shown in Figure 1, which comprises I UDs and a UAV equipped with a lightweight edge computing server. The set of all UDs is denoted by $\mathcal{I}=\{1,2,...,I\}$. Each UD has an indivisible, computation-intensive task $o_i$ characterized by the tuple $\langle c_i,u_i\rangle$ within a time period, where $c_i$ represents the amount of computation workload (in CPU cycles), and $u_i$ denotes the data size (in bytes). It is assumed that each generated task can be completely processed in a single time period.

3.1. UAV Coverage Partition and Flight Model

In a reality Iot network, the spatial distribution of UDs usually exhibits a certain level of clustering [28], so here we partition them into multiple circles area with a same radius which equals to the coverage radius of UAV [29]. Let $\mathcal{P}=\{1,2,...,P\}$ denote all the coverage circles of UAV, where $q_p=\left(x_p,y_p,0\right)$ represents the coordinates of the center of coverage circle p, and the set ${\mathcal{I}}_p$ represents all user equipment located within coverage circle p. Let ${\mathit{q}}_m=(x_m,y_m,0)$ denote the location of UD-m, where $x_m$ and $y_m$ represent the horizontal and vertical coordinates respectively, satisfying $0\le x_m\le x^{max}$, $0\le y_m\le y^{max}$, $\forall m$.

We assume that UAV employ a hover-fly-hover mode similar to [30]. The UAV’s movement can be simplified to constant-speed linear motion between multiple coverage circles. The UAV does not perform task offloading while in transit and only provides task computing services to UDs within a coverage circle when hovering above it. The UAV starts from a designated coverage area and traverses all coverage circles along the shortest path. Let the non-repetitive ordered set $\mathit{w}=\{w_1,w_2,...,w_P\mid w_p\in \mathcal{P},\forall p=1,2,...,P\}$ represent the UAV’s trajectory. Once the partition set $\mathcal{P}$ is obtained, we can determine the UAV trajectory $\mathit{w}$ by solving a standard small scale TSP problem.

3.2. Computation Model

Due to the indivisibility of computation tasks, we adopt a binary task offloading mode for each UDs. We define a binary decision variable $d_i\in \{0,1\}$ for UD i to determine the offloading choice. If $d_i$ equals 1, the computation task is offloaded to the edge server on the UAV; otherwise, the task is processed locally.

3.2.1. Local Computing

If $d_i=0$, then UD i can process the computation task locally at the initial stage of the system without waiting for the UAV’s arrival. Let $f_i^l$ denote the local CPU frequency of UD i. Thus, the total delay of task $o_i$ in local computation mode can be expressed as:

$$\begin{array}{cc}\hfill & T_i^l=\frac{c_i}{f_i^l}\hfill \end{array}$$

(1)

3.2.2. Edge Computing

If $d_i=1$, then UD i needs to wait for the UAV to reach its partition and then offload task to the UAV for execution. When the UAV is hovering over coverage circle p, multiple user devices within the set ${\mathcal{I}}_p$ communicate with the UAV through orthogonal frequency-division multiple access (OFDMA) such that interference among multiple UDs can be neglected. During the task offloading process, the uplink bandwidth W is allocated to multiple UDs selecting the offloading computation mode, enabling parallel transmission. To ensure resources wastage, channel bandwidth should only be allocated to UDs who select the edge computation mode. Thus, we have the following bandwidth constraints:

$$\begin{array}{c}{\displaystyle \sum _{i\in {\mathcal{I}}_p}}{W}_i\le W,\forall {\mathcal{I}}_p\hfill \end{array}$$

(2)

$$\begin{array}{c}{W}_i\left\{\begin{array}{cc}=0,& d_i=0\\ >0,& d_i=1\end{array}\right.,\forall i\in \mathcal{I}\hfill \end{array}$$

(3)

Since air-to-ground communication only occurs when the UAV is in a hovering state, there is no Doppler frequency shift during communication due to the UAV’s high-speed movement [31]. Let ${\mathit{q}}_{\mathit{i}}=(x_i,y_i,0)$ represent the three-dimensional coordinates of UD i. When the UAV hovers over coverage circle p and provides task offloading services to UD i, the channel gain between them can be expressed as $h_i=\frac{g_0}{{\left(x_p-x_i\right)}^2+{\left(y_p-y_i\right)}^2+z^2}$, where $g_0$ represents the unit-distance channel gain at 1 meter. The data transmission rate can be expressed as:

$$\begin{array}{cc}\hfill & r_i=W_i·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)\hfill \end{array}$$

(4)

where $P_i$ denotes the transmission power of UD i, and $N_0$ represents the additive Gaussian white noise power. The delay of task $o_i$ offloaded to the UAV can be expressed as:

$$\begin{array}{cc}\hfill & T_i^o=\frac{u_i}{r_i}\hfill \end{array}$$

(5)

Assuming that tasks offloaded to the UAV can be executed in parallel, the UAV’s computational resources need to be allocated to multiple user tasks. Let $f^{edge}$ represent the computational frequency of the edge server, and $f_i$ represent the computational frequency allocated to UD i by the edge server. Then, in the edge computation mode, the execution time of task $o_i$ on the UAV can be expressed as:

$$\begin{array}{cc}\hfill & T_i^e=\frac{c_i}{f_i}\hfill \end{array}$$

(6)

Similar to the bandwidth allocation constraints (2) and (3), the allocation of UAV’s computational resources should also satisfy the following conditions:

$$\begin{array}{c}{\displaystyle \sum _{i\in {\mathcal{I}}_p}}{f}_i\le f^{edge},\forall {\mathcal{I}}_p\hfill \end{array}$$

(7)

$$\begin{array}{c}{f}_i\left\{\begin{array}{cc}=0,& d_i=0\\ >0,& d_i=0\end{array}\right.,\forall i\in \mathcal{I}\hfill \end{array}$$

(8)

We consider a fixed hover time, that is, the UAV hovers in each area for the same duration $T^h$, and the time required for the UAV to fly from the previous area $w_{p-1}$ to the area $w_p$ is denoted as $T_{w_p}^f$. The total time required for the area $w_p$ to wait for the UAV to reach the center of the area can be expressed as:

$$\begin{array}{cc}\hfill T_{w_p}^w& ={\displaystyle \sum _{j=1}^{p-1}}\left(T_{w_j}^f+T^h\right)+T_{w_p}^f\hfill \end{array}$$

(9)

In the edge computation mode, the total delay incurred by user i in processing its computational task within coverage area $w_p$ can be expressed as:

$$T_i^e=T_{w_p}^w+T_i^o+T_i^e,\forall i\in {\mathcal{I}}_{w_p}$$

(10)

In addition, due to the usually negligible transmission time compared to task offloading and drone computation [32], the total latency incurred by user i in processing its computing task can be expressed as:

$$T_i=d_i·T_i^e+(1-d_i)·T_i^l$$

(11)

3.3. Problem Formulation

We aim to optimize the QoE of task offloading services in UAV-edge networks, a goal achieved by minimizing the sum of all user devices’ shrinkage rates. Similar to [15], the sum of system shrinkage rates can be represented as:

$$\begin{array}{cc}\hfill \mathcal{S}& ={\displaystyle \sum _{w_p\in \mathit{w}}}{\displaystyle \sum _{i\in {\mathcal{I}}_{w_p}}}{\mathcal{S}}_i={\displaystyle \sum _{w_p\in \mathit{w}}}{\displaystyle \sum _{i\in {\mathcal{I}}_{w_p}}}\frac{T_i}{T_i^l}\hfill \end{array}$$

(12)

By jointly optimizing the partitioning strategy of coverage areas $\mathcal{P}$, the UD’s computation mode selection $\mathit{d}=\left\{d_i\right\}$, uplink bandwidth $\mathit{B}=\left\{B_i\right\}$, and UAV’s computation resource allocation strategy $\mathit{f}=\left\{f_i\right\}$, the objective is to minimize the sum of all users’ shrinkage rates. It is noteworthy that the coverage strategy $\mathcal{P}$ here includes the coordinates of each coverage circle and the set of user devices it contains. Thus, the aforementioned problem of minimizing the sum of shrinkage rates can be formulated as:

$$\begin{array}{cc}\hfill \left(\mathrm{P}1\right){\displaystyle \underset{\mathcal{P},\mathit{d},\mathit{B},\mathit{f}}{min}}& \mathcal{S}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right),\left(3\right),\left(7\right),\left(8\right)\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & d_i\in \{0,1\},\forall i\in \mathcal{I}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & {\mathcal{I}}_p\ne \varnothing ,\forall p\in \mathcal{P}\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\mathcal{I}}_{p_1}\cap {\mathcal{I}}_{p_2}=\varnothing ,\forall p_1,p_2\in \mathcal{P},p_1\ne p_2\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\mathcal{I}}_1\cup {\mathcal{I}}_2\cup ...\cup {\mathcal{I}}_P=\mathcal{I}\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & T_i^o+T_i^e\le T^h,\forall i\in \mathcal{I}\hfill \end{array}$$

(18)

Here, constraints (2), (3), (7), (8) ensure that the uplink bandwidth for task offloading and the UAV’s computation resources are allocated only to valid links, (15)-(17) restrict the feasibility of the coverage strategy, (18) ensures that each device completes the task offloading within the hover time. Due to the involvement of binary constraint (14) and a non-convex objective function, P1 is a coupled MINLP problem. Clearly, solving it directly is challenging.

4. Algorithm Design

In this section, an efficient two-tier algorithm is proposed to address the formulated non-convex problem. Firstly, a polynomial-time complexity greedy algorithm based on the Welzl method [33] for the UAV set covering problem (USCP) is proposed to obtain a feasible $\mathcal{P}$. Secondly, from the perspectives of algorithm complexity and solution quality, two different strategies are proposed in the second tier for computation mode selection and resource allocation problem. The process of the global algorithm is depicted in Figure 2.

4.1. UAV Set Covering Probelm

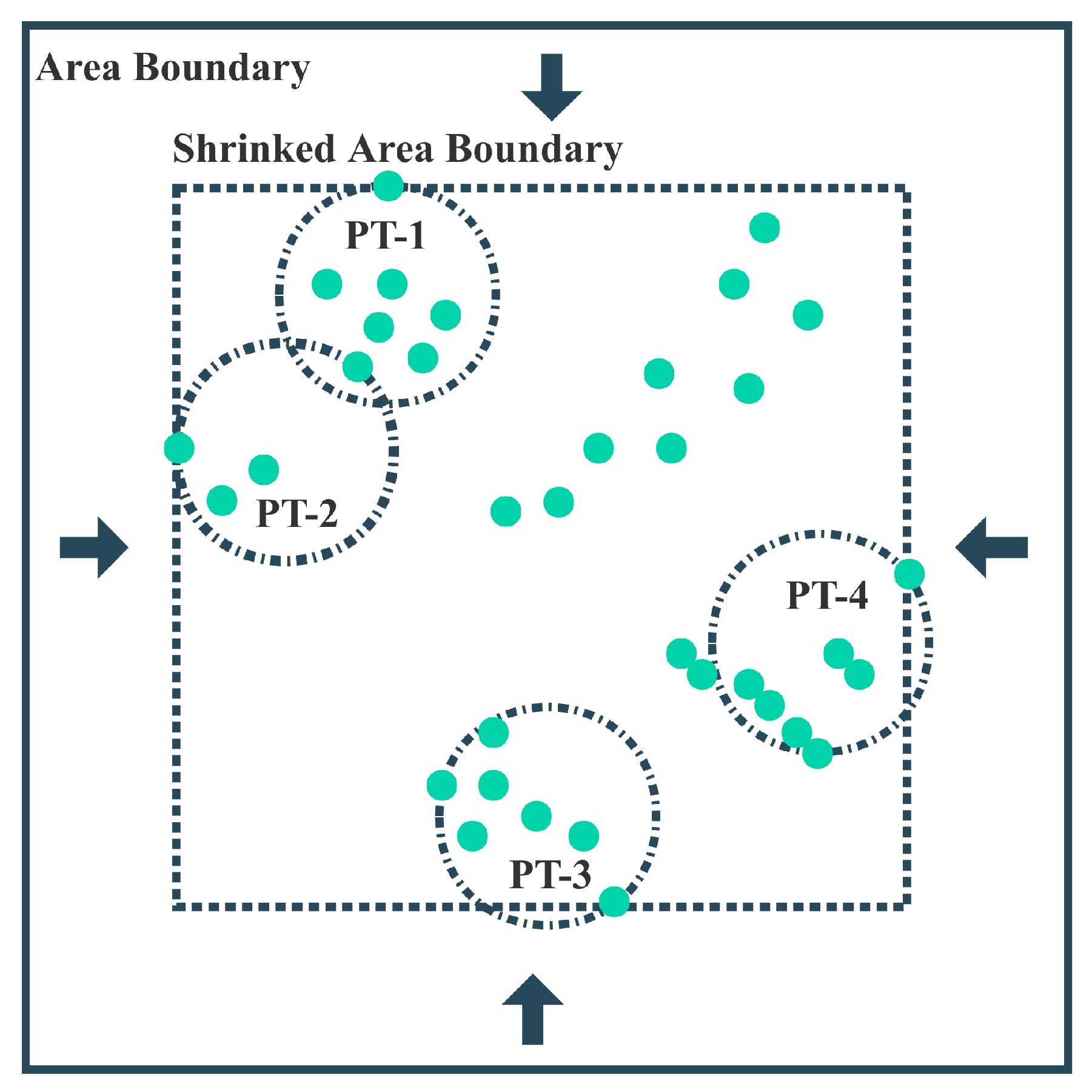
Since the user devices within a single coverage circle can concurrently receive task offloading services provided by the UAV, to enhance system efficiency, we aim to minimize the number of coverage areas, thus minimizing the time spent by UAVs in position shifting. This problem can be described as a fixed-radius circular coverage problem or an UAV set covering problem, which aims to cover all UDs within the system area using multiple circles with a fixed radius r, while minimizing the number of circles used. This is a typical NP-hard problem, for which there is no polynomial-time exact algorithm. In this section, we propose the Welzl-based UAV set covering (WUSC) algorithm, which provides an approximate solution to the coverage circle set in polynomial time.

The Welzl algorithm is an incremental algorithm used to solve the minimum enclosing circle problem. It takes all points within a circular coverage area and returns the minimum radius of the circle. We consider iteratively invoking this algorithm to solve the fixed-radius circular coverage problem. As shown in Figure 3, the boundary of the system area is continuously reduced until there exists a device exactly on the boundary. Then, starting from a point i on the boundary and initializing a coverage area ${\mathcal{I}}_p=\left\{i\right\}$, the device closest to this point within the region is added to the set ${\mathcal{I}}_p$, and it is determined using the Welzl algorithm whether the set can be completely covered by a circle with a radius not exceeding r. This process is repeated until all user devices are included in some coverage set. Algorithm 1 describes the detailed procedure of the WUSC algorithm.

Algorithm 1: WUSC algorithm

Additionally, once the coverage strategy $\mathcal{P}$ is obtained, the UAV trajectory $\mathit{w}$ can be obtained by a standard TSP model based on the partitions. Then, P1 can be reformulated as:

$$\begin{array}{cc}\hfill \left(\mathrm{P}2\right){\displaystyle \underset{\mathit{d},\mathit{W},\mathit{f}}{min}}& \mathcal{S}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right),\left(3\right),\left(7\right),\left(8\right),\left(14\right),\left(18\right)\hfill \end{array}$$

(19)

Note that P2 is still a MINLP problem. However, since the hover time is constant, there is no coupling between multiple partitions, and thus, the problem can be divided into multiple smaller sub-problems for parallel solution based on the partition dimension. We will present the algorithms for P2 as follows.

4.2. Computation Mode Selection and Resource Allocation

We can decompose P2 into P independent sub-problems in the following form according to the coverage areas:

$$\begin{array}{cc}\hfill \left(\mathrm{P}2.1\right){\displaystyle \underset{{\mathit{d}}_{\mathit{p}},{\mathit{W}}_{\mathit{p}},{\mathit{f}}_{\mathit{p}}}{min}}& {\displaystyle \sum _{i\in {\mathcal{I}}_{w_p}}}\frac{d_i·\left(T_{w_p}^w+T_i^o+T_i^e\right)+(1-d_i)·T_i^l}{T_i^l}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right),\left(3\right),\left(7\right),\left(8\right),\left(14\right),\left(18\right)\hfill \end{array}$$

(20)

For problem P2.1, we will propose two different algorithms to solve it. The first is a low-complexity CD-based algorithm, suitable for smaller-scale IoT networks. The second is a joint optimization algorithm based on ADMM technique, designed for larger-scale networks that require higher solution precision.

4.2.1. Alternating Optimization using CD Method

In this section, we consider alternating iterative optimization of discrete and continuous variables. Given the computation mode $\mathit{d}$, let ${\mathcal{I}}_p\left(0\right)$ represent the set of UDs choosing local computation mode in coverage area p, and ${\mathcal{I}}_p\left(1\right)$ represent the set of users choosing edge computation mode. Then, P2.1 can be equivalently transformed into the following form:

$$\begin{array}{cc}\hfill \left(\mathrm{P}2.1\text{’}\right){\displaystyle \underset{{\mathit{W}}_{\mathit{p}},{\mathit{f}}_{\mathit{p}}}{min}}& {\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}\frac{T_i^o+T_i^e}{T_i^l}\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right),\left(7\right),\left(18\right)\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & W_i,f_i>0,\forall i\in {\mathcal{I}}_p\left(1\right)\hfill \end{array}$$

(22)

P2.1’ is a convex problem, which can obtain the optimal closed-form solution for the problem using the KKT conditions. By introducing Lagrange multipliers $\lambda =\{{\lambda }_i,\forall i\in \mathcal{I}\},{\nu }_1,{\nu }_2$ for the inequality constraints (18), (2), (7), we can obtain the Lagrangian function as:

$$\begin{array}{cc}\hfill \mathcal{L}({\mathit{W}}_{\mathit{p}},{\mathit{f}}_{\mathit{p}};& {\lambda }_{\mathit{p}},{\nu }_1,{\nu }_2)={\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}\left\{\frac{u_i}{W_i·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)·T_i^l}+\frac{c_i}{f_i·T_i^l}+{\lambda }_i·\left[-T^h+\frac{c_i}{f_i}\right.\right.\hfill \\ \hfill & \left.\left.+\frac{u_i}{W_i·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)}\right]\right\}+{\nu }_1·\left({\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{W}_i-W\right)+{\nu }_2·\left({\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{f}_i-f^{edge}\right)\hfill \end{array}$$

(23)

The corresponding KKT conditions can be derived as:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}1+{\lambda }_i-{\nu }_1·\frac{W_i^2·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)·T_i^l}{u_i}=0,\forall i\in {\mathcal{I}}_p\left(1\right)\hfill & \left(a\right)\hfill \\ 1+{\lambda }_i-{\nu }_2·\frac{f_i^2·T_i^l}{c_i}=0,\forall i\in {\mathcal{I}}_p\left(1\right)\hfill & \left(b\right)\hfill \\ {\nu }_1·\left({\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{W}_i-W\right)=0\hfill & \left(c\right)\hfill \\ {\nu }_2·\left({\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{f}_i-f^{edge}\right)=0\hfill & \left(d\right)\hfill \\ {\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{W}_i-W\le 0\hfill & \left(e\right)\hfill \\ {\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{f}_i-f^{edge}\le 0\hfill & \left(f\right)\hfill \\ {\lambda }_i,{\nu }_1,{\nu }_2\ge 0\hfill & \left(g\right)\hfill \\ {\lambda }_i·\left[\frac{u_i}{W_i·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)}+\frac{c_i}{f_i}-T^h\right]=0,\forall i\in {\mathcal{I}}_p\left(1\right)\hfill & \left(h\right)\hfill \\ \frac{u_i}{W_i·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)}+\frac{c_i}{f_i}-T^h\le 0,\forall i\in {\mathcal{I}}_p\left(1\right)\hfill & \left(i\right)\hfill \end{array}\right.\end{array}$$

(24)

Based on the KKT system of equations (24), we can derive the following lemma:

Lemma 1.

When the optimal solution of P2.1’ is obtained, the resources are fully allocated to the users, i.e., ${\sum }_{i\in {\mathcal{I}}_p\left(1\right)}{W}_i=W,{\sum }_{i\in {\mathcal{I}}_p\left(1\right)}{f}_i=f^{edge}$ hold strictly.

Proof. 

From (a), (b), (c), (d), (g), it can be inferred that ${\nu }_1,{\nu }_2>0$. Substituting (c) and (d) into the equations yields ${\sum }_{i\in {\mathcal{I}}_p\left(1\right)}{W}_i=W$ and ${\sum }_{i\in {\mathcal{I}}_p\left(1\right)}{f}_i=f^{edge}$, which means that the bandwidth and computational resources should be allocated entirely to the users when the optimal solution is achieved.    □

We refer to the resource allocation strategy obtained without considering constraints (18) as the optimal solution ${\mathcal{S}}^{OPT}$, and the optimal solution of P2.1’ as a suboptimal solution ${\mathcal{S}}^{*}$. Based on whether ${\mathcal{S}}^{OPT}={\mathcal{S}}^{*}$, we can analyze P2.1’ in the two different cases as follows.

1) ${\mathcal{S}}^{OPT}={\mathcal{S}}^{*}$, meaning that there is no UDs violate the hovering constraint under ${\mathcal{S}}^{*}$. In this case, we have the following lemma for this optimal solution.

Lemma 2.

When ${\mathcal{S}}^{OPT}={\mathcal{S}}^{*}$ holds, both ${\mathit{W}}_{\mathit{p}}^{*}$ and ${\mathit{f}}_{\mathit{p}}^{*}$ have corresponding closed-form solutions.

Proof. 

We have ${\lambda }_{\mathit{p}}=0$ when hovering constraints are not in effect. Based on (a) and (b), we have $W_i^2=\frac{u_i}{{\nu }_1·{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)·T_i^l}$ and $f_i^2=\frac{c_i}{{\nu }_2·T_i^l}$. Then we have $\sqrt{{\nu }_1}=\frac{{\sum }_{i\in {\mathcal{I}}_p\left(1\right)}\sqrt{\frac{u_i}{{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)·T_i^l}}}{W}$ and $\sqrt{{\nu }_2}=\frac{{\sum }_{i\in {\mathcal{I}}_p\left(1\right)}\sqrt{\frac{c_i}{T_i^l}}}{f^{edge}}$. Finally, substituting ${\nu }_1$ and ${\nu }_2$ into (a) and (b) yields the following closed-form solutions for $W_i,f_i,\forall i\in {\mathcal{I}}_p\left(1\right)$:

$$\begin{array}{c}\hfill W_i=\frac{\sqrt{\frac{u_i}{{log}_2\left(1+\frac{P_i·h_i}{N_0^2}\right)·T_i^l}}}{{\sum }_{j\in {\mathcal{I}}_p\left(1\right)}\sqrt{\frac{u_j}{{log}_2\left(1+\frac{P_j·h_j}{N_0^2}\right)·T_j^l}}}·W,f_i=\frac{\sqrt{\frac{c_i}{T_i^l}}}{{\sum }_{j\in {\mathcal{I}}_p\left(1\right)}\sqrt{\frac{c_j}{T_j^l}}}·f^{edge}\end{array}$$

(25)

   □

2) ${\mathcal{S}}^{OPT}\ne {\mathcal{S}}^{*}$, which means that some UDs violate the hover constraint under ${\mathcal{S}}^{OPT}$. If the ${\mathcal{S}}^{*}$ has a solution, it indicates that the suboptimal strategy assigns additional bandwidth or computation resources to those UDs that exceed the hover time, allowing them to complete the computation within $T^h$. However, this approach simultaneously increases the time consumed for other non-violating devices. Let ${\mathcal{I}}_p^A=\{i\mid i\in {\mathcal{I}}_p\left(1\right),T_i^o+T_i^e>T^h\}$ denote the set of UDs which choose the edge computing mode and violate the hover constraint, and ${\mathcal{I}}_p^B={\mathcal{I}}_p\left(1\right)\setminus {\mathcal{I}}_p^A$ represents the others. According to (24), a complex system of equations with $\left(3\right|{\mathcal{I}}_p\left(1\right)|+2)$ variables and equalities can be derived. Enumerating $2^I$ possible closed-form solutions is impractical. Moreover, if the ${\mathcal{S}}^{*}$ has no solution, it implies the bandwidth and computation resource of the UAV is insufficient to meet the computational demands of all selected offloading UDs within the given hover time $T^h$. Therefore, these two parts $\left\{\mathit{d}\right\}$ and $\{\mathit{W},\mathit{f}\}$ cannot be fully decoupled by the CD method.

In summary, we can obtain the optimal $\{\mathit{W},\mathit{f}\}$ in $\mathcal{O}\left(1\right)$ using (25) for the first type of problem. For the second type, the corresponding KKT equations either have no solution or are challenging to solve directly. To minimize coupling and simplify the solution of the KKT equations, a greedy strategy can be adopted by converting the second type problem approximately to the first type. Additionally, for the computation mode $\left\{\mathit{d}\right\}$, we consider obtaining a locally optimal solution through a simple one-dimensional linear search. For convenience, let ${\mathit{d}}_p=(d_1,d_2,...,d_{\left|p\right|})$ represent the computation modes of all UDs within coverage area p. At the beginning of the $(l-1)$-th iteration, the initial value is defined as ${\mathit{d}}_p^{l-1}$. Each user attempts to change their computation mode based on ${\mathit{d}}_p^{l-1}$:

$$\begin{array}{c}\hfill {\mathit{d}}_p^{l-1}\left(i\right)=\left(d_1^{l-1},...,d_{i-1}^{l-1},\oplus \left(d_i^{l-1}\right),d_{i+1}^{l-1},...,d_{\left|p\right|}^{l-1}\right)\end{array}$$

(26)

where $\oplus (·)$ denotes the negation operation for binary variables, e.g., $\oplus \left(1\right)=0$, $\oplus \left(0\right)=1$. This generates $\left|p\right|$ different computation modes, and the one with the smallest shrinkage rate is selected as the return value for the $(l-1)$-th iteration. A locally optimal solution is achieved when no user can further reduce the global shrinkage rate by changing their computation mode. Algorithm 2 describes the detailed procedure of the CD-based greedy (CD-Greedy) algorithm for P2.1.

Algorithm 2: CD-Greedy Algorithm for P2.1

4.2.2. Joint Optimization Using ADMM Method

The main advantage of the CD-based algorithm lies in its simplicity and relatively high efficiency due to the closed-form resource allocation strategy. However, alternating optimization is prone to falling into local optima, and the one-dimensional search causes the number of iterations required for convergence to increase with the network scale. In this section, we will propose an ADMM-based algorithm to jointly optimize computation mode and resource allocation. The main idea is to decompose the coupled problem P2.1 into $|{\mathcal{I}}_p|$ parallel small-scale MINLP problems. First, to eliminate the coupled inequality constraints, we introduce auxiliary variables to reformulate P2.1 into the following equivalent form:

$$\begin{array}{cc}\hfill \left(\mathrm{P}2.2\right){\displaystyle \underset{{\mathit{d}}_{\mathit{p}},{\mathit{W}}_{\mathit{p}},{\mathit{f}}_{\mathit{p}},{\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}}}{min}}& {\displaystyle \sum _{i\in {\mathcal{I}}_p}}q(d_i,W_i,f_i)+g({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(14\right),\left(22\right)\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & x_i,y_i\ge 0,\forall i\in {\mathcal{I}}_p\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & x_i=W_i,y_i=f_i,\forall i\in {\mathcal{I}}_p\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{i\in {\mathcal{I}}_p}}{x}_i\le W,{\displaystyle \sum _{i\in {\mathcal{I}}_p}}{y}_i\le f^{edge}\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & \frac{u_i}{x_i·{log}_2\left(1+P_i·h_i/N_0^2\right)}+\frac{c_i}{y_i}\le T^h,\forall i\in {\mathcal{I}}_p\hfill \end{array}$$

(31)

where $q(d_i,W_i,f_i)$ is the simplified form of the original objective function:

$$\begin{array}{c}\hfill q(d_i,W_i,f_i)=\frac{d_i·\left(T_i^o+T_i^e\right)+(1-d_i)·T_i^l}{T_i^l}\end{array}$$

(32)

$g({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})$ is the equivalent form of the inequality constraints in the original problem:

$$\begin{array}{cc}\hfill g({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})& =\left\{\begin{array}{cc}0& \mathrm{if}({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})\in {\mathcal{G}}_p\\ +\infty & otherwise\end{array}\right.\hfill \end{array}$$

(33)

where ${\mathcal{G}}_p$ denotes the feasible set of $g({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})$:

$${\mathcal{G}}_p=\left\{({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})\mid {\displaystyle \sum _{i\in {\mathcal{I}}_p}}{x}_i\le W,{\displaystyle \sum _{i\in {\mathcal{I}}_p}}{y}_i\le f^{edge};\frac{u_i}{x_i·{log}_2\left(1+P_i·h_i/N_0^2\right)}+\frac{c_i}{y_i}\le T^h,\forall i\in {\mathcal{I}}_p\right\}$$

(34)

Problem P2.2 can be effectively decomposed using the ADMM method to find the optimal solution to the dual problem. By introducing Lagrange multipliers for the equality constraint (29), we can represent the augmented Lagrangian function of P2.2 as:

$$\begin{array}{cc}\hfill \mathit{L}(\mathit{u},\mathit{v},\theta )& ={\displaystyle \sum _{i\in {\mathcal{I}}_p}}q\left(\mathit{u}\right)+g\left(\mathit{v}\right)+{\alpha }_i·(W_i-x_i)+{\beta }_i·(f_i-y_i)\hfill \\ \hfill & -\frac{c}{2}·{\displaystyle \sum _{i\in {\mathcal{I}}_p}}{(W_i-x_i)}^2-\frac{c}{2}·{\displaystyle \sum _{i\in {\mathcal{I}}_p}}{(f_i-y_i)}^2\hfill \end{array}$$

(35)

where $\mathit{u}=\{{\mathit{d}}_{\mathit{p}},{\mathit{W}}_{\mathit{p}},{\mathit{f}}_{\mathit{p}}\}$, $\mathit{v}=\{{\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}}\}$, $\theta =\{{\alpha }_{\mathit{p}},{\beta }_{\mathit{p}}\}$, and $c>0$ represents the step size. The corresponding dual problem can be formalized as:

$$\begin{array}{c}\hfill \left(\mathrm{P}2.3\right){\displaystyle \underset{\theta }{max}}d\left(\theta \right)\end{array}$$

(36)

where $d\left(\theta \right)={min}_{\mathit{u},\mathit{v}}\left\{\mathcal{L}(\mathit{u},\mathit{v},\theta )\mid \mathit{u}\in \mathcal{U},\mathit{v}\in \mathcal{V}\right\}$ represents the Lagrangian dual function of $\mathcal{L}$, $\mathcal{U}=\{({\mathit{d}}_{\mathit{p}},{\mathit{W}}_{\mathit{p}},{\mathit{f}}_{\mathit{p}})\mid W_i,f_i\ge 0,d_i\in \{0,1\},\forall i\in {\mathcal{I}}_p\}$, $\mathcal{V}=\{({\mathit{x}}_{\mathit{p}},{\mathit{y}}_{\mathit{p}})\mid x_i,y_i\ge 0,\forall i\in {\mathcal{I}}_p\}$.

The ADMM method solves the dual problem P2.3 by iteratively optimizing $\{\mathit{u},\mathit{v},\theta \}$. Let the solution obtained at the l-th iteration be $\{{\mathit{u}}^l,{\mathit{v}}^l,{\theta }^l\}$. The operations required in the $(l+1)$-th iteration can be described as the following three steps:

• Step 1: Given $\{{\mathit{v}}^l,{\theta }^l\}$, minimize $\mathcal{L}$ by finding suitable $\left\{{\mathit{u}}^l\right\}$.

$$\begin{array}{c}\hfill {\mathit{u}}^{l+1}=arg{\displaystyle \underset{\mathit{u}}{min}}\mathcal{L}(\mathit{u},{\mathit{v}}^l,{\theta }^l)\end{array}$$

(37)

Since there is no coupling among multiple users, (37) can be decomposed into $|{\mathcal{I}}_p|$ identical subproblems solved in parallel. Each subproblem can be formulated as:

$$\begin{array}{cc}\hfill {\mathit{u}}_i^{l+1}& =arg{\displaystyle \underset{\mathit{u}\in \mathcal{U}}{min}}q(d_i,W_i,f_i)+{\alpha }_i·(W_i-x_i)+{\beta }_i·(f_i-y_i)-\frac{c}{2}·\left[{(W_i-x_i)}^2+{(f_i-y_i)}^2\right]\hfill \end{array}$$

(38)

When $d_i=0$, we have $B_i=f_i=0$. In this case, ${\mathit{u}}_i^{l+1}$ can be directly computed using (38). When $d_i=1$, (38) becomes a standard convex optimization problem and yields a closed-form optimal solution. For example, by separating $W_i$ and $f_i$ into two independent parts, setting the first derivative to zero and combining with the Cardano formula, we can obtain a unique optimal solution. Therefore, we consider the two possible values of $d_i$ separately. After obtaining the corresponding $W_i$ and $f_i$, they are substituted into (38), and the smaller value is chosen as the optimal solution for ${\mathit{u}}_i^{l+1}$. Note that the time complexity for solving each subproblem ${\mathit{u}}_i^{l+1}$ is $\mathcal{O}\left(1\right)$.

• Step 2: Given $\{{\mathit{u}}^{l+1},{\theta }^l\}$, minimize $\mathcal{L}$ by finding suitable $\left\{{\mathit{v}}^{l+1}\right\}$.

From (33), it is evident that to ensure the problem’s solvability, it is necessary to ensure ${\mathit{v}}^{l+1}\in {\mathcal{G}}_p$. Since the offloading decisions are known, here we only need to consider the auxiliary variables corresponding to the edge computing mode UDs. The solution for ${\mathit{v}}^{l+1}$ can be formulated as a convex problem in the following form:

$$\begin{array}{cc}\hfill \left(\mathrm{P}2.4\right)arg{\displaystyle \underset{\mathit{v}}{min}}& {\displaystyle \sum _{i\in {\mathcal{I}}_p\left(1\right)}}{\alpha }_i·(W_i-x_i)+{\beta }_i·(f_i-y_i)-\frac{c}{2}·\left[{\left(W_i-x_i\right)}^2+{\left(f_i-y_i\right)}^2\right]\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(28\right),\left(29\right),\left(30\right),\left(31\right)\hfill \end{array}$$

(39)

To obtain the optimal solution to P2.4, we consider using convex optimization solver, e.g., CPLEX, CVX. Solvers based on standard convex optimization methods like interior point methods ensure that the obtained solution is the optimal solution, thereby preventing the problem P2.4 from being infeasible due to $g\left(\mathit{v}\right)$ taking on positive infinity.

• Step 3: Given $\{{\mathit{u}}^{l+1},{\mathit{v}}^{l+1}\}$, minimize $\mathcal{L}$ by finding suitable $\left\{\theta \right\}$.

This can be achieved by updating the Lagrange multipliers ${\theta }_m^l$ according to the following rules:

$$\begin{array}{cc}\hfill & {\alpha }_i^{l+1}={\alpha }_i^l-c·(W_i^{l+1}-x_i^{l+1})\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & {\beta }_i^{l+1}={\beta }_i^l-c·(f_i^{l+1}-y_i^{l+1})\hfill \end{array}$$

(41)

Obviously, the time complexity for updating the Lagrange multipliers is $\mathcal{O}\left(I\right)$.

Repeat the above three steps until the absolute errors of $\mathit{u}$ and $\mathit{v}$ reach the desired accuracy. The absolute errors of both can be measured by the following equation:

$$\begin{array}{c}\hfill {\displaystyle \sum _{i\in {\mathcal{I}}_p}}\left(|W_i^l-x_i^l|+|f_i^l-y_i^l|\right)\le 2\delta \end{array}$$

(42)

where $\delta$ is a predefined error bound, typically a very small positive number. Due to the presence of duality gap for P2.1, the ADMM algorithm may not converge to the optimal solution. Therefore, when the algorithm terminates, the dual optimal solution $\{{\mathit{d}}^l,{\mathit{W}}^l,{\mathit{f}}^l\}$ is an approximate solution, and its performance gap will be evaluated through simulation experiments. Algorithm 3 describes the detailed procedure of the ADMM-based joint optimization algorithm for P2.1.

Algorithm 3: ADMM-based Algorithm for P2.1

4.3. Computational Complexity Analysis

The WUSC algorithm consists of nested three-level loops, where the outer loop is used to check if there are any uncovered UDs, and the remaining two loops iterate over the boundary point set and attempt to construct a new coverage area starting from each boundary point. The time complexity of implementing the minimum circle covering of n vertices using the Welzl algorithm is $\mathcal{O}\left(n\right)$, thus the time complexity of generating a coverage area in each iteration of the middle loop is $\mathcal{O}\left(\right|{\mathcal{I}}_p{|}^2)$. In addition, considering that WUSC employs sorting, the overall time complexity is $\mathcal{O}(I^2·log\left(I\right))$.

Let $L_{CD}$ denote the number of iterations, the time complexity of CD-based greedy algorithm can be expressed as $\mathcal{O}\left(L_{CD}·{\sum }_{i\in \mathcal{I}}\left|{\mathcal{I}}_p\left(i\right)\right|\right)$ = $\mathcal{O}\left(L_{CD}·{\sum }_{p\in \mathcal{P}}{\left|{\mathcal{I}}_p\right|}^2\right)\le$$\mathcal{O}\left(L·I^2\right)$, where ${\mathcal{I}}_p\left(i\right)$ represents the partition where user i located. However, due to the computation modes searching along only one dimension for each iteration, in most cases, removing the UD with the maximum timeout only needs one. Therefore, the average time complexity is closer to $\mathcal{O}(L_{CD}·I)$.

The time complexity of the ADMM method is mainly determined by Step 2. For example, using an interior point method would result in a high time complexity of the step 2 of ${\sum }_{p\in \mathcal{P}}\mathcal{O}\left(\right|{\mathcal{I}}_p{|}^{3.5})\le \mathcal{O}\left(I^{3.5}\right)$. The total computational complexity can be given by $\mathcal{O}(L_{ADMM}·I^{3.5})$.

5. Simulation Results

In this section, we evaluate the performance of two algorithms through numerical experiments. The system area is a square with a side length of 1 km, containing a UAV carrying computing equipment to provide task offloading services for all UDs. We assume all UDs are homogeneous, with the same local computing frequency and transmission power, $f_i^l=0.1$GHz, $p_i=1$W, $\forall i\in \mathcal{I}$. For the UAV, similar to [15], we set $f^{edge}=10$GHz, $W=100$MHz, $v^{max}=20$m/s, $r=150$m. Additionally, for channel conditions, we set $g_0=-50$dBm, $N_0^2=-100$dBm [9].

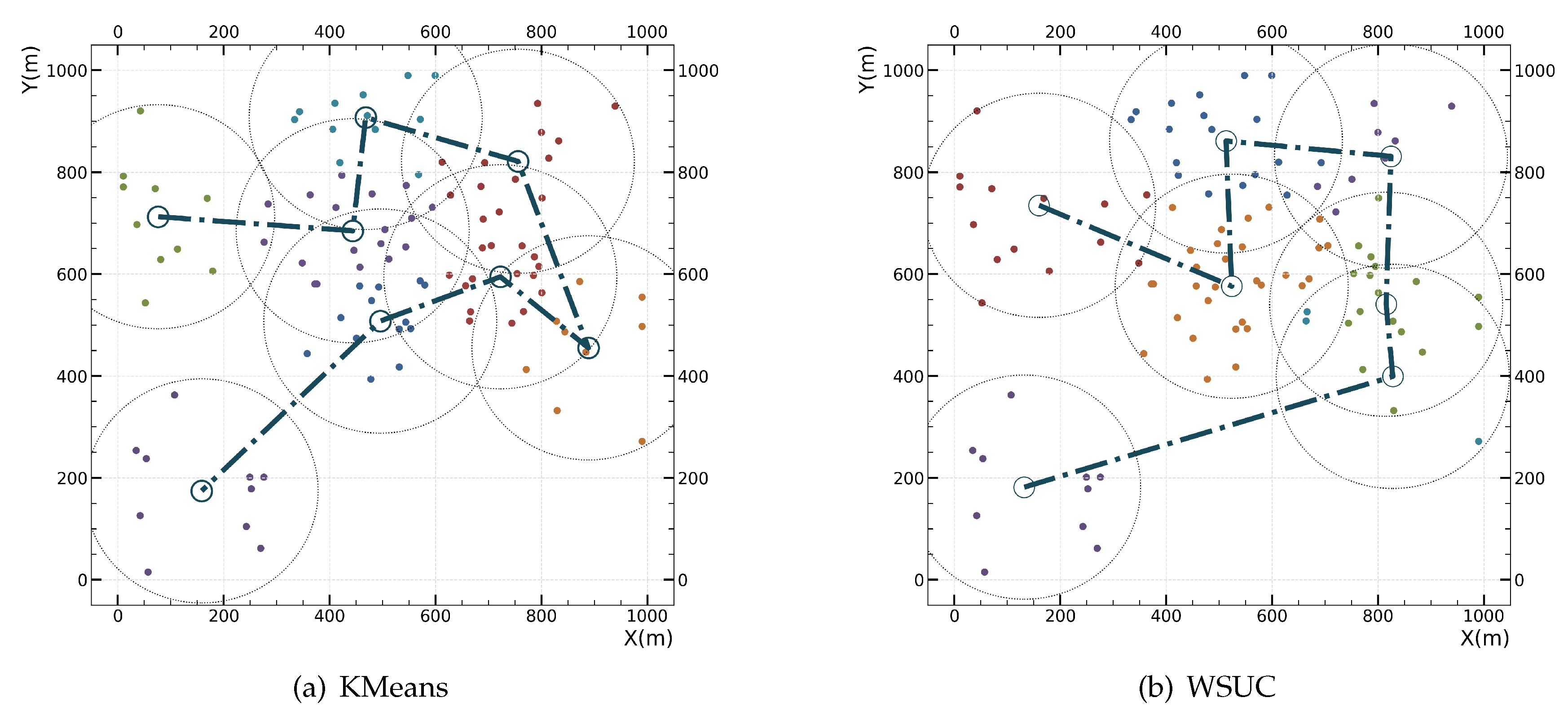
Figure 4 shows the results of performing fixed-radius circular coverage in the system area with 100 UDs using KMeans and WUSC algorithms, as well as the shortest path for the UAV departing from the specified coverage area. KMeans is a commonly used clustering algorithm in machine learning. The test results indicate that WUSC requires fewer coverage circles than KMeans, which to some extent reduces the time the UAV spends on location movement, thereby improving the utilization of bandwidth and computing resources. Experimental results show that compared to the KMeans method, WUSC reduces the time the UAV spends on location movement by 10%.

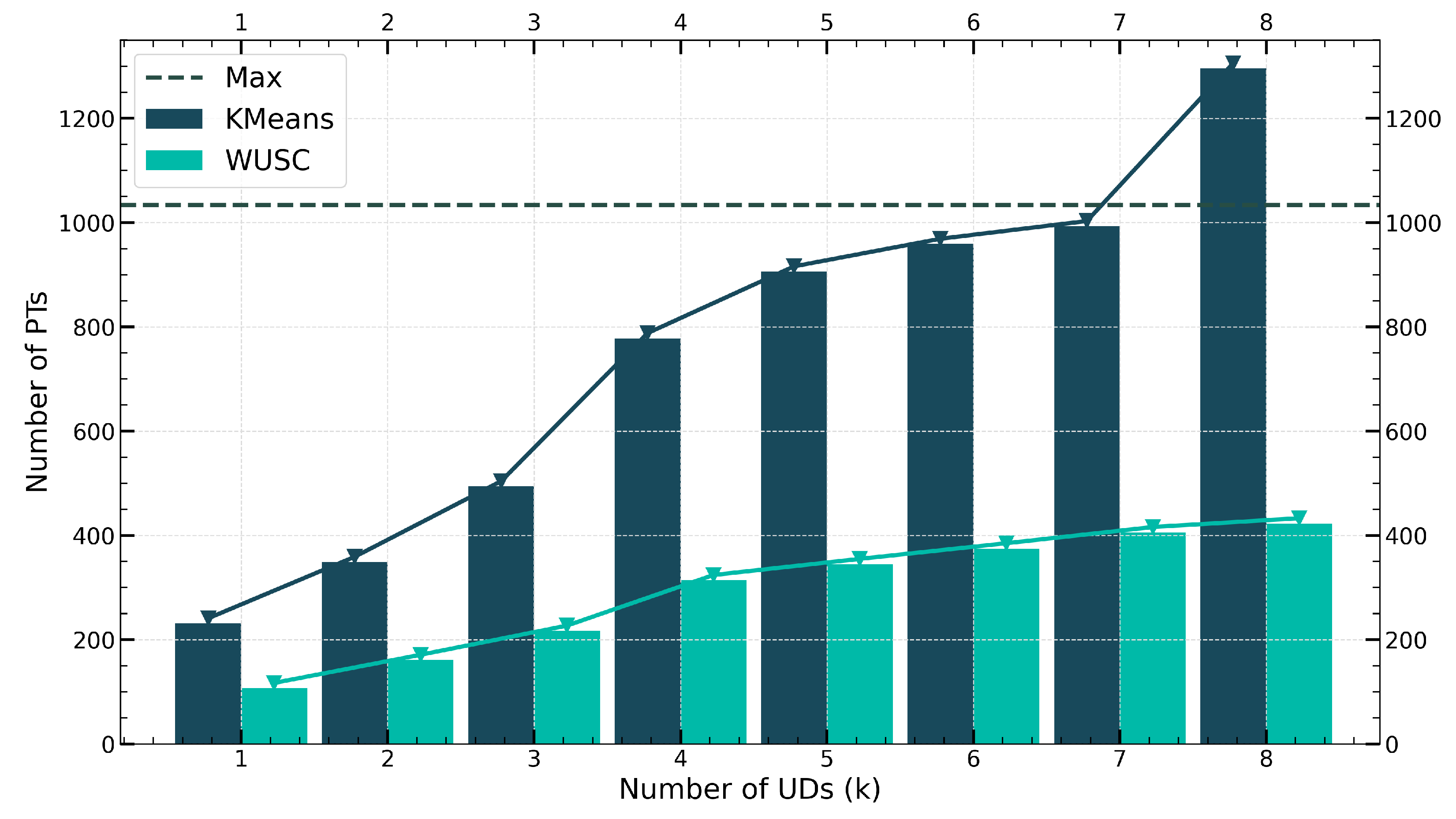
Figure 5 depicts the area coverage results for different numbers of UDs in a larger area ($10\times 10$km²). As the total number of UDs increases, the number of coverage circles required by WUSC slowly rises, while KMeans exceeds the maximum number of circles required to cover the entire area at $M=8000$. The number of coverage circles required by WUSC is close to $\frac{1}{3}$ of KMeans, indicating that in large-scale fixed-radius circular coverage problems, the solution provided by WUSC is significantly superior to clustering methods.

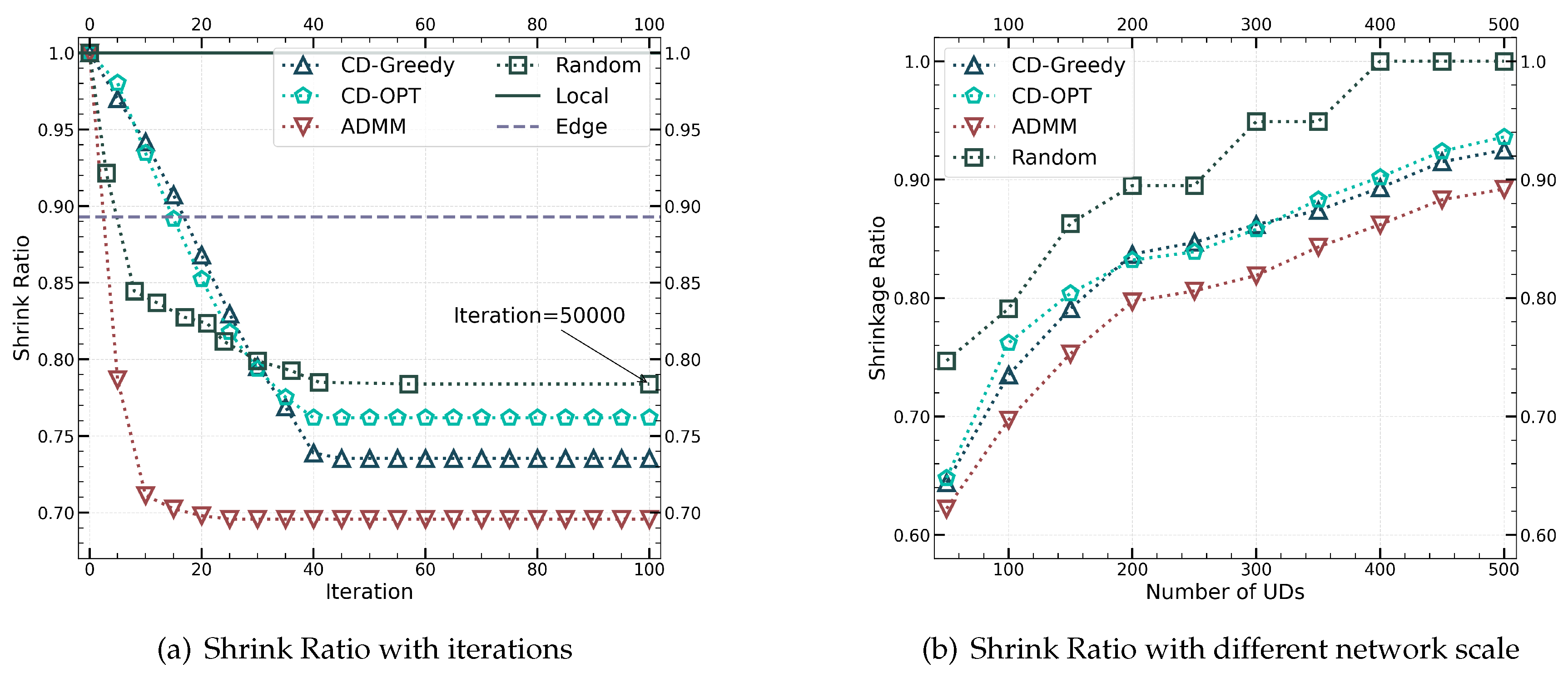
Figure 6 illustrates the trend of shrinkage ratio variation for different algorithms, where Figure 6a represents the convergence curves of shrinkage ratio with the increase of iteration numbers in a network with 100 UDs. Figure 6b shows the trend of shrinkage ratio variation as the network scale increases for different algorithms. It can be observed from Figure 6a that both CD-Greedy and ADMM methods can converge stably to a good result than CD-OPT after tens of iterations. The CD-OPT method is similar to the CD-Greedy method, with the difference that CD-OPT utilizes convex optimization to solve P2.1. In comparison, ADMM has a faster convergence rate, while CD-Greedy requires iterations close to the total number of devices finally offloaded, which is closely related to the characteristic of one-dimensional search. Compared to CD-OPT, Random, Local, or Edge methods, the two proposed algorithms demonstrate excellent performance. From Figure Figure 6b, it can be seen that both CD-Greedy and ADMM can work normally in networks with hundreds of edge nodes, with ADMM reducing the compression ratio by about $5\%$ compared to CD-Greedy. The Random method, on the other hand, can only choose the Local strategy due to its inability to obtain feasible offloading schemes.

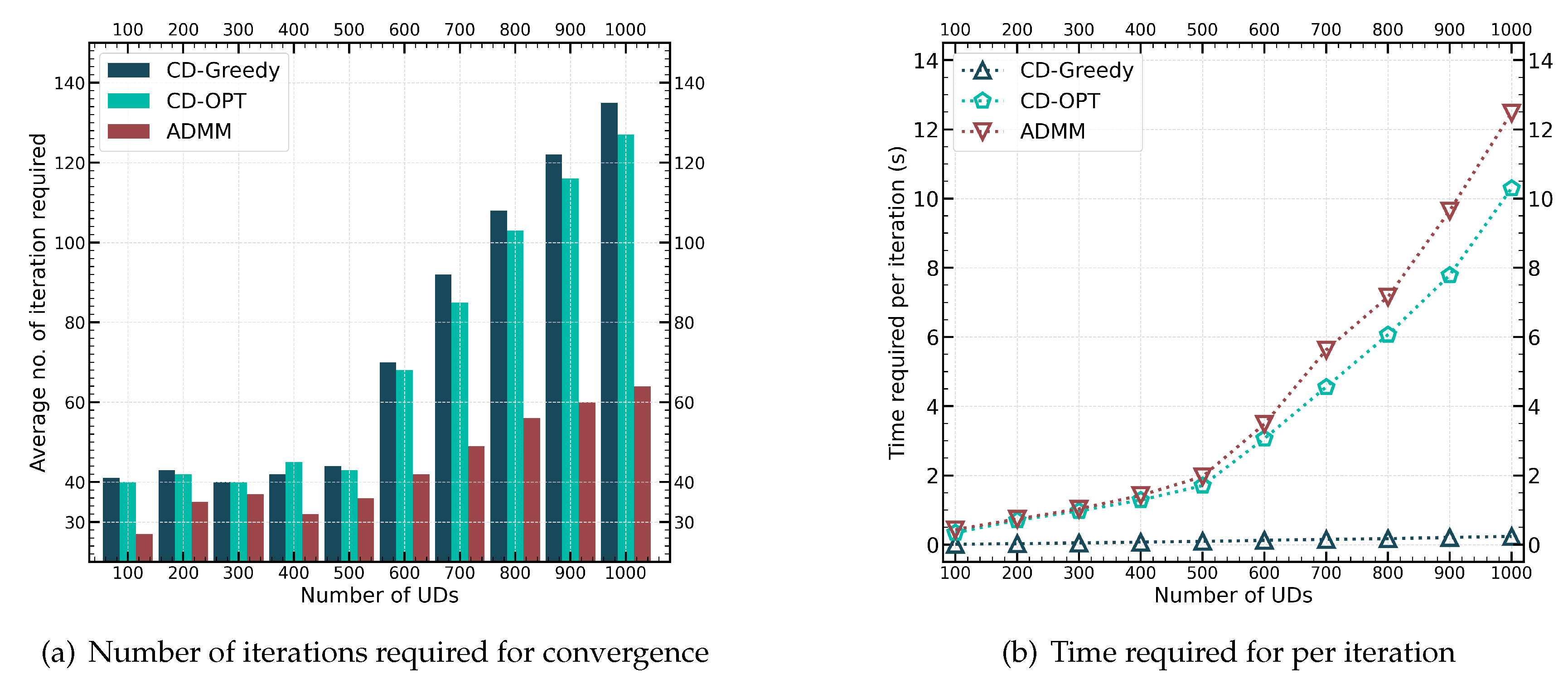
In Figure 7, we examine the convergence performance of the CD-Greedy, CD-OPT and ADMM methods. Figure 7a shows the variation of the number of iterations required for convergence of these three algorithms as the number of devices increases from 100 to 1000. When the total number of UDs increases from 100 to 500, the computing capability of the UAV remains constant. However, when the number of UDs increases from 500 to 1000, we adjust the computing performance of the UAV to 10GHz, 20GHz ..., respectively. When the computing resources of the UAV are limited, the number of iterations required for convergence of both methods remains stable, essentially equal to the total number of devices finally offloaded. However, as the computing resources of the UAV increase, more UDs are eventually selected for offloading, leading to a faster increase in the number of iterations required for convergence in CD-Greedy and CD-OPT. In contrast, the increase in iterations for the ADMM method is slower. This highlights the advantage of joint optimization algorithms over alternating optimization algorithms. Figure 7a shows the trend of the average execution time per iteration of three methods with the increase of network size. It can be seen that the execution time of the convex optimization-based method is more obviously affected by the problem size. However, since ADMM requires fewer iterations to converge, the overall convergence time is shorter compared to CD-OPT. In addition, the CD-Greedy method has significant efficiency advantages in large-scale edge networks, with only millisecond-level execution latency per iteration. This indicates that CD-Greedy and ADMM are suitable for different scenarios with high execution efficiency and higher quality solutions, respectively.

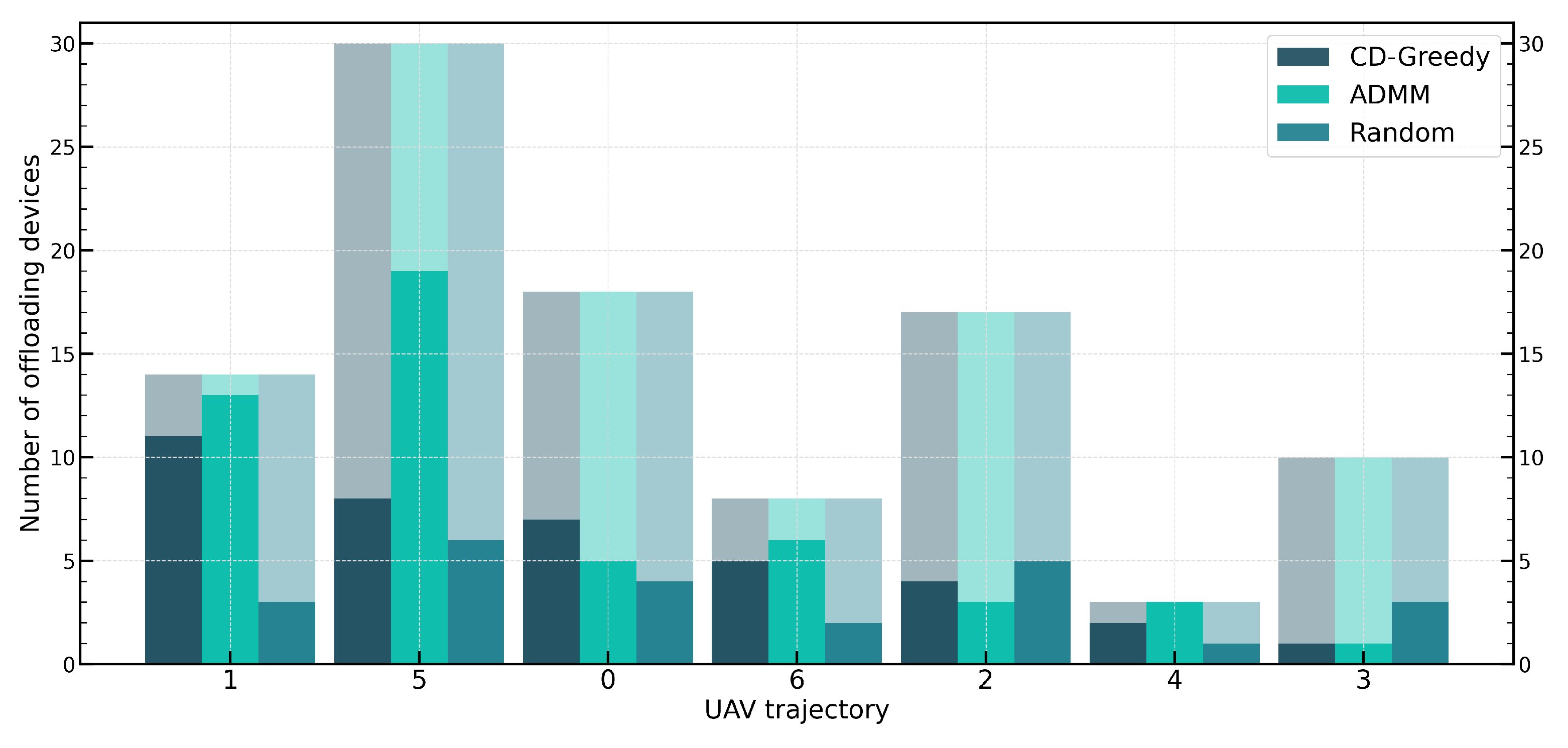
Finally, Figure 8 illustrates the proportion of UDs offloaded in different coverage areas, with the coverage areas sorted according to the UAV’s trajectory. The results of CD-OPT are similar to those of CD-Greedy, so they are not shown in the figure. From the graph, it can be observed that both CD-Greedy and ADMM tend to select coverage areas near the beginning of the trajectory for offloading. This is because the fixed hovering time ignores the decision of coverage areas’ influence on subsequent areas. Moreover, since coverage areas near the beginning of the trajectory typically have shorter waiting times, offloading more UDs in these areas will result in lower compression ratios. Additionally, due to limited resources in the system, the probability of selecting coverage areas for offloading decreases further when the number of devices selected for offloading reaches a certain threshold. Furthermore, if multiple consecutive service periods are considered, the coverage area at the end of the previous period will become the starting point for the UAV in the next period, thereby achieving relative fairness among multiple coverage areas.

6. Conclusions and Future Work

In this paper, we investigate the minimization of the shrinkage ratio in large-scale UAV-MEC networks. To achieve efficient optimization strategies in large-scale networks, we utilize a partitioning concept combined with a fixed hovering time to decouple interactions between multiple regions, resulting in two low-complexity algorithms. The CD-Greedy algorithm is simple to implement, converges stably, and is widely applicable to various mixed-decision efficient optimization scenarios. The ADMM method, while achieving better optimization results by jointly optimizing integer and continuous variables with fewer iterations, has a longer execution time due to convex optimization, making it suitable for scenarios where high-quality solutions are desired and timeliness is not critical. In our future work, we will focus on enhancing the QoE for dynamic UAV hover times, which presents greater challenges and aligns more closely with real-world scenarios.