Prerpints.org logo
Preprint
Article

A Surrogate-Assisted Symbolic Time-Series Discretization Using Multi-breakpoints and a Multi-objective Evolutionary Algorithm

Altmetrics

Downloads

89

Views

30

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 June 2024

Posted:

17 June 2024

You are already at the latest version

Alerts
Abstract
The enhanced multi-objective symbolic discretization for time series (eMODiTS) method employs a flexible discretization scheme using different value cuts for each non-equal time interval, which requires a computational cost for evaluating each objective function. Therefore, surrogate models were implemented to minimize this disadvantage. Nevertheless, each solution found by eMODiTS is a different-sized vector, so the surrogate model must be able to handle data sets under this characteristic. Consequently, this work's contribution lies in analyzing the surrogate models' implementation on the time series discretization, where each potential scheme is a real-number different-sized vector. For this reason, the surrogate model proposed was k-nearest Neighbors for regression with Dynamic Time Warping as a distance measure. Results suggest our proposal finds a suitable approximation to the final eMODiTS solutions with a functions evaluation reduction rate between 15% and 95%. However, according to Pareto front performance measures, the proposal Pareto front is competitive compared to the eMODiTS Pareto front, reaching an average Generational Distance (GD) between 0.0447 and 0.0536. Moreover, the average Hypervolume Ratio (HVR) ranges between 0.334 and 0.3891. Finally, our proposal compared against SAX-based methods presents a similar behavior regarding classification tasks and statistical tests.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Time series discretization transforms continuous values into discrete ones [1]. Symbolic discretization is one of the most widely used approaches for transforming time series due to its ability to exploit data richness and its lower bounding properties, among others, [2,3]. On the other hand, the Symbolic Aggregate Approximation (SAX) is the most widely used symbolic discretization method due to its easy conception, implementation, and low computational time [2,3].
SAX employs the well-known Piecewise Aggregate Approximation (PAA). PAA reduces the dimensionality of the time series by averaging the values falling on one of the equal-sized time intervals defined at the beginning of the SAX procedure. Finally, each average value is mapped to a set of breakpoints computed based on the Gaussian distribution to assign the corresponding symbol. Despite SAX’s advantages, SAX has been criticized for its Gaussian distribution assumption and its inevitable information loss when the dimensionality of the data is reduced [4,5,6,7].
From competitive SAX results reported in the literature, several variants were implemented to solve its drawbacks. For example, Extended SAX (ESAX) [3,8] complements the PAA average values with two more minimum and maximum values and matches each with a different symbol. Furthermore, in α SAX [9], the breakpoints computed by the Gaussian distribution are adjusted by the one-dimensional clustering algorithm of k-means (Lloyd algorithm).
On the other hand, rSAX (Random Shifting-based SAX) [10] minimizes information loss with perturbations τ of the breakpoint values generated using a uniform distribution. Similarly, 1D-SAX [11] tries to minimize information loss, considering trends or slopes along with the average value. Therefore, the symbolic representation of 1D-SAX is obtained by two values: slope and mean value ( s , a ) , and the assigned character is provided by interleaving the binary representation s and a in each time interval.
Recently, He et al. [12] proposed two new representations for symbolic time series based on the Transformable Interval Object approach (TIO), the Hexadecimal Aggregate approXimation (HAX), and the Point Aggregate approXimation (PAX). TIO employs the maximum and minimum values from a time series segment and, based on these values, computes the corresponding segment angle. PAX string is based on these TIO points, and HAX transforms the TIO points into a hexadecimal string.
Furthermore, Kegel et al. [13] proposed two representation approaches, sSAX and tSAX, using two features of time series: season and trend, respectively. Similarly, Bountrogiannis et al. [14] proposed two other representations to avoid the Gaussian assumptions of SAX: pSAX and cSAX. pSAX (probabilistic SAX) approximates the actual distribution accurately from data instead of assuming a Gaussian distribution by the Epanechnikov Kernel Distribution Estimator and Lloyd-Max Quantizer. cSAX (clustering SAX) discretizes the time series using the mean-shift clustering algorithm, automatically setting the number of breakpoints or alphabets.
All these methods use local search to find the discretization scheme. However, some methods focus on implementing a global search for this task. For example, Acosta-Mesa et al. [15] proposed a discretization scheme found by a global search algorithm called Evolutionary Programming. However, Ahmed et al. [16,17] proposed using the Harmony Search algorithm to find the best symbolic time series discretization scheme. Furthermore, Fuad et al. [18,19] implemented two well-known evolutionary algorithms, Genetic Algorithm and Differential Evolution, to search for the optimal values for the breakpoints.
Another symbolic time series discretization approach is the enhanced Multi-objective Symbolic Discretization for Time Series (eMODiTS) [20], which increases the search space by several unique breakpoints for each unequal-sized time interval. This method uses a multi-objective evolutionary algorithm to find suitable discretization schemes and obtain competitive results in the classification task. However, it implies a computational cost to evaluate each objective function, representing an essential disadvantage of the method. Therefore, several strategies have emerged to address this disadvantage. One of them is the implementation of surrogate models.
Surrogate models reduce the processing time in most complex optimization problems [21]. Although these models emerged in the 1960s, their rise in complex problems has been observed in the last ten years (Figure 1a). The areas where surrogate models are applied are diverse. According to the literature, engineering is the area with more applications of these models, followed by Information and Computing Sciences, Artificial Intelligence, and Aerospace Engineering; see Figure 1b.
In engineering and computer science, surrogate models mainly concentrate on finding suitable designs for mechanical pieces. Remarkably, they focus on optimizing antenna design [22,23,24,25], microwave components [25,26], Aerodynamic Shape [27,28], or even optimizing groundwater exploitation [29]. In addition, these works employ multi-objective evolutionary optimization and Kriging, as well as Support Vector Regression (SVR), among others, as surrogate models.
Moreover, surrogate models are employed for machine learning tasks. In this sense, an analysis of the use of surrogate models in each machine learning task is presented in Figure 2. This figure shows that the prediction task is the most recurring data mining task where an approximation model is used instead of the original prediction model. However, for tasks such as classification, the number of publications underperforms the prediction publications, resulting in an opportunity niche for researchers. Mostly, the surrogate model research applied to time series classification is focused on hyperparameter optimization [30], deep learning [31], and neuroevolution [32]. Nevertheless, as far as state-of-the-art has been reviewed, surrogate models have been scarcely implemented in time series discretization.
Márquez et al. [33] is one of the few works in which surrogate models were implemented to minimize the computational cost by identifying an appropriate discretization scheme for temporal data. The researchers applied surrogate models to the enhanced multi-objective symbolic discretization for time series (eMODiTS) [20]. eMODiTS is a temporal data mining technique that discretizes time series by a unique set of value cuts for each time cut and three objective functions. However, before obtaining the value of each objective function for an individual, the data set is discretized using the discretization scheme that represents this individual. Consequently, this process implies a computational cost to evaluate each objective function, representing an essential disadvantage of the method. Therefore, surrogate models were employed to approximate the values of the three objective functions. As the individual representation size of eMODiTS varies across instances, the k-nearest Neighbor (KNN) was employed as a surrogate model. Moreover, the Pareto front is evaluated in the original models every N generation and added to the training set to update the surrogate models. However, this results in a lessened update of the surrogate model, thereby reducing the model’s fidelity.
Consequently, our primary motivation for this research is to extend the findings of [33], modifying the model update process. The proposed methodology evaluates the Pareto front using the original objective functions at each generation (individual-based strategy) and the current population at regular intervals (generation-based strategy). Additionally, each time the generation-based update is applied, the Pareto front (evaluated on the original functions) will be incorporated into the training set.
Therefore, the objectives of this research are described below:
  • To increase the number of evaluations conducted on the original problem functions, thereby improving the fidelity of the surrogate models.
  • To maintain the accuracy of the classification task achieved by the original model (eMODiTS).
  • To analyze the surrogate model behavior compared with SAX-based discretization methods to verify whether the proposal maintains, improves, or worsens by incorporating these models regarding the well-known discretization approaches.
The organization of this document is presented as follows. First, Section 2 describes the materials and methods used in this research and the implemented methodology. On the other hand, Section 3 presents the experiments performed to reach the objectives introduced in Section 1 and the discussion of the results. Finally, Section 4 describes the conclusions from the results presented in the previous section.

2. Materials and Methods

2.1. Symbolic Aggregate approXimation (SAX)

Symbolic Aggregate approXimation (SAX) is the most famous symbolic time series discretization method. SAX is based on the dimensionality reduction method called PAA.
PAA partitions the time series into equal p intervals W , averaging the time series values within each interval. Each average value is called the PAA coefficient.
Definition 2.1.
Let T i be a time series, τ t a time series value at time t, W = { w 1 , w 2 , w 3 , … , w | W | } a set of equal-sized intervals ( w i = [ w i , w i + 1 ) , i ≠ | W | ), thePAA coefficient s ¯ of the interval w i is computed as s ¯ w i = 1 η ∑ t ∈ w i s t , where η is the number of time series values within the interval w i .
The calculation of the PAA coefficients is visually represented in Figure 3a. In this particular case, there are six intervals of equal size, denoted as | W | = 6 . For each interval w i , the coefficient s ¯ w i is determined based on the values within that interval.
SAX is a method that transforms time series into a reduced-symbolic discretization using the PAA approach. The transformation process involves mapping each PAA coefficient (referred to as word segments) to symbols. It is achieved by defining a set of intervals, known as breakpoints or alpahet cuts, in the value space based on a normal distribution. Each interval in the set represents a symbol or character, denoted as s i . The PAA coefficient that falls within a specific interval is then replaced by its corresponding symbol. The resulting collection of symbols is called string.
Definition 2.2.
Let A = { ( α 1 , s 1 ) , ( α 2 , s 2 ) , ( α 3 , s 3 ) , … , ( α | A | , s | A | ) } be a set of intervals or breakpoints in the values spaces α j = [ α j , α j + 1 ) , j ≠ | A | with their corresponding symbol s j , astring ( S )is formed as S = { s j | s ¯ w i ∈ α j } , ∀ i ∈ { 1 , 2 , … , | W | } and ∀ j ∈ { 1 , 2 , … , | A | } .
Figure 3b shows the SAX representation of the PAA coefficients shown in Figure 3a. In this example, the breakpoints are | A | = 6 . Each PAA coefficient s w i is replaced by a corresponding symbol according to the interval in which it falls. The resulting string for this example is d c b d b . It is worth mentioning that SAX requires two crucial initial parameters: the number of word segments ( | W | ) and the number of breakpoints ( | A | ). Both parameters impact the overall behavior of the approach. Normalizing the time series before discretization is also necessary, as the breakpoints are generated based on this distribution.

2.2. Multi-Objective Optimization Problem (MOOP)

The Multi-objective Optimization Problem (MOOP) involves simultaneously optimizing functions by maximizing, minimizing, or both. Furthermore, each possible solution results in a trade-off in each function [34]. Therefore, the MOOP is expressed in Definition 2.3.
Definition 2.3.
Let x → = [ x 1 , x 2 , … , x x → ] be the vector of decision variables for a problem where | x → | is the number of variables, F → the set of functions to be optimized, g ( x → ) and h ( x → ) inequality and equality constrained functions, respectively, themultiobjective optimization problem (MOOP)can be stated as Equation 1.
M i n i m i z e / M a x i m i z e F → = { f 1 ( x → ) , f 2 ( x → ) , … , f | F → | ( x → ) } S u b j e c t t o : g ( x → ) ≤ 0 h ( x → ) = 0
Instead of finding a unique solution, MOOP aims to find a set of feasible solutions. [35]. Nevertheless, locating this set of feasible solutions poses a significant challenge. The Pareto Optimality approach is widely utilized in Multi-Objective Optimization Problems (MOOP) due to its ability to produce competitive outcomes [36,37]. Furthermore, Pareto introduced a method of dominance to determine the superior solution from a given set of solutions [38]. This form of dominance is referred to as Pareto dominance and is defined in the following manner.
Definition 2.4.
Let x → 1 and x → 2 be two feasible solutions, x → 1 dominates (≺) to x → 2 based onPareto dominance, if and only if f i ( x → 2 ) ≤ f i ( x → 1 ) ∀ i ∈ { 1 , 2 , ⋯ , | F → | } and f ( x → 2 ) < f ( x → 1 ) at least in one function.
This dominance makes it possible to obtain a collection of non-dominant solutions, called the Pareto front ( F ). From this set, a final solution is chosen based on the user’s preference.

2.3. The Enhanced Multi-Objective Symbolic Discretization for Time Series (eMODiTS)

eMODiTS is a SAX-based discretization approach [20]. Thus, it employs the PAA technique to reduce dimensionality, word segment cuts, alphabet cuts, and the same symbol assignment process. However, unlike SAX, each word segment includes distinct, random, and non-normal distributed breakpoints. Therefore, it does not assume a normal distribution in time series. Graphical representation of the eMODiTS discretization scheme for the example depicted in Figure 3b is shown in Figure 4.
In addition, eMODiTS aims to determine the optimal number of word segments and breakpoints in the discretization process. The eMODiTS approach focuses on optimizing three functions at the same time: entropy, complexity, and information loss. Consequently, the search task to find a suitable discretization scheme employs the well-known Non-dominated Sorting Genetic Algorithm (NSGA-II) [39,40,41]. Nevertheless, specific NSGA-II components were modified to handle the individual representation of eMODiTS. Figure 5 depicts the general discretization procedure employed in eMODiTS. The dotted and light gray squares represent the modified steps of NSGA-II.

2.3.1. Population Generation

The population comprises individuals who represent discretization schemes, where each word break includes a distinct breakpoints scheme. The word segments and breakpoints are integer and float value arrays, respectively. As an illustration, Figure 6 displays the vector that represents Figure 4. In this representation, each word segment w i is accompanied by its corresponding breakpoints A w i , j . At the start of eMODiTS, these individuals are initialized randomly, taking into account the length and values of a temporal dataset.

2.3.2. Evaluation Process

As previously mentioned, the eMODiTS method aims to identify flexible discretization schemes that are based on entropy (E), complexity ( C X ), and information loss ( I L ). Each function is specifically targeted in the search for appropriate discretization schemes. E is employed as a method for estimating classification using a confusion matrix ( c m ) created through the discretized time series ( S ), where the rows of the confusion matrix are the unique discretized time series, and the columns represent the different classes in a database for each. The data in the matrix indicates the frequency of each class for a particular discretized time series. E is calculated using Equation 2, where P ( ( S i , c ) ) denotes the probability of a discretized time series being assigned the class c. When the measure values are close to zero, it indicates that each time series is assigned to only one class. On the contrary, values close to one suggest that a time series has multiple class labels. Therefore, values close to zero are preferred.
E = ∑ i = 1 M − ∑ c = 1 C c m ( P ( S i , c ) ) · log 2 c m ( P ( S i , c ) )
Alternatively, C X assesses the complexity of the resulting discrete database by considering the number of distinct discretized time series. This measure is used to determine the level of difficulty for classifiers in comprehending the discrete dataset. A value close to zero indicates only a few instances in the discrete dataset, making the classification task more manageable. In contrast, a value close to one suggests that the number of discretized time series is similar to the number of original time series, resulting in a more complex discriminator model for the classifier. Therefore, values close to zero are preferable. Equation 3 expresses C X , where | D | represents the number of time series in the original dataset, | S | is the number of unique discretized time series, and C denotes the total number of classes in the problem.
C X = | D | − | S | − C | D | + ( C − 1 ) | S | − C < 0 | S | − C | D | + ( C − 1 ) o t h e r w i s e
Finally, the information loss ( I L ) measure is used to evaluate the data lost during dimensionality reduction. The Mean Square Error (MSE) measure is a commonly used metric for this purpose. MSE calculates the similarity among two time series of equal size, so it is necessary to reconstruct the discretized time series to compare it with the original ( T i ). Values close to zero indicate that the time series are similar, while values close to one indicate dissimilarity. Equation 4 shows how I L is calculated. In the equation, R represents a reconstructed time series, and | R | is the number of reconstructed time series. Both series are scaled to intervals [0,1] for fair comparison.
I L = 1 | R | ∑ i = 1 | R | M S E ( R i , T i ) M S E ( R i , T i ) = ∑ ( r i − τ j ) 2 n − 1 , r i ∈ R i , τ j ∈ T i

2.3.3. Offspring’s Creation and Mutation

As previously stated, the individuals in eMODiTS consist of varying-sized vectors. Therefore, the crossover operator was modified to generate novel individuals by combining two solutions given this condition. The recombination operator used in this study was the commonly used one-point crossover. In this operator, a random cut is made for both parents, and the resulting segments are then combined [42,43,44,45,46]. However, in this particular case, a different cut is randomly applied for each parent, considering the parents’ sizes. Subsequently, each section of the parents is merged as follows. In the first child ( O 1 ), the first part of the first parent ( P 1 1 s t ) corresponds to its first part, while the second part of the second parent ( P 2 2 n d ) is copied to its last part. For the second child ( O 2 ), the first part of the second parent ( P 2 1 s t ) becomes its first part, and the second part of the first parent ( P 2 2 n d ) fills its second part. Figure 7 illustrates the adapted one-point crossover operator.
In contrast, the uniform mutation operator is utilized, selecting individual positions randomly to modify based on a mutation percentage defined by the user [44,47].

2.3.4. Population Replacement

The last process of eMODiTS consists of replacing the current population from the union of the parent and offspring sets. The fast, non-dominated sorting is applied to obtain the ranking of the parent and offspring set. Subsequently, the next generation population is filled with the first front of the joined set. If the new population ends with a size smaller than the current population, the second front is selected for the filling procedure. If the updated population size remains less than the current population, the third position is chosen, and so on.

2.3.5. Preferences Handling

The eMODiTS search mechanism utilizes NSGA-II, which results in a collection of non-dominated solutions (Pareto front) being generated upon completion of the search process rather than a singular solution. Hence, it is essential to have a preference selection mechanism in place to select a single solution from the Pareto front. The preference handling employed in eMODiTS relies on the misclassification rate achieved for each solution on the Pareto front by applying the Decision Tree classifier to the training set. The final discretization scheme is chosen based on the solution that achieves the lowest misclassification rate. It is important to note that the test set is used solely to demonstrate the final classification performance and not to select the final discretization scheme.

2.4. Surrogate-Assisted Multi-Objective Symbolic Discretization for Time Series (sMODiTS)

Due to the flexible discretization scheme integrated into eMODiTS, the search space expands, leading to a higher computational cost. The computational cost is primarily associated with evaluating every solution in the three objective functions. Consequently, a modified approach that integrates approximated models is introduced to reduce the computational cost of eMODiTS. This approach is called Surrogate-assisted Multi-objective Symbolic Discretization for Time Series (sMODiTS). A surrogate model is a substitute in optimization scenarios involving computationally intensive problems. It uses an iterative and updating approach to develop an approximate model that is simpler to manage and less computationally demanding compared to the original model [48,49,50,51]. Figure 8 illustrates the general procedure for implementing sMODiTS, highlighting the specific instances when the surrogate model needs to be established and revised.

2.4.1. Training set creation

The training set for the surrogate models was generated by applying a uniform design of the experiments. The solutions were randomly initialized within the search space following a uniform distribution [21,52,53,54]. Design is primarily motivated by the varying number of individual decision variables, making applying traditional initial sampling methods more complex.

2.4.2. Surrogate model creation

Several surrogate models have been used for multi-objective evolutionary optimization [55,56], including the Gaussian process [57,58,59,60,61,62], Support Vector Machines (SVM) [29,63,64], Kriging [29,65,66], kernel extreme learning machines [29], Radial Basis Function (RBF) [61,65,66,67,68], and Artificial Neural Networks [69,70,71], among others. However, these models are usually applied to individuals of the same size. On the other hand, another model used mainly for single objective optimization is the k-Nearest Neighbor for regression [50,72,73], which allows comparing two unequal-sized vectors by adjusting the distance measure.
Unlike the original kNN method, the K N N R method returns the average class label values of the k neighbors of an instance instead of the class label frequency. Equation 5 shows the calculation of this method [50], where y → i is a solution belonging to the training set.
K N N R ( x → i ) = ∑ i k f ( y → i ) k
Since K N N R is a distance-based classifier and eMODiTS contains solutions of different sizes, an elastic similarity measure was incorporated into K N N R to compare two individuals with sMODiTS. Due to the competitive results reported in the state of the art, the selected elastic measure was Dynamic Time Warping (DTW). However, the primary disadvantage of DTW is the computational complexity caused by the exhaustive search for all possible subsequences in the compared vectors.

2.4.3. Surrogate Model Update

The evolution control is a fundamental component of surrogate modeling in optimization tasks. Consequently, sMODiTS implements an individual- and generation-based strategy to update each surrogate model. The individual-based strategy consists of evaluating each individual of the Pareto Front in the original objective functions. It is applied to each generation of the evolutionary process. On the other hand, in the generation-based strategy, the current population is evaluated based on the original objective functions in each generation U G .
Furthermore, in this strategy, Pareto front individuals are inserted into each training set P t r a i n i and the model is re-trained. However, to avoid the growth of the training set and, thus, excessive use of computer memory, the size of the training set must be maintained. Thus, the fast, non-dominated sorting was applied to the training set for this process. First, the new training set is filled with non-dominated solutions. Then, if the new training set size is less than the previous set, the following non-dominated solutions are taken without counting the first ones until the size of the new training set is complete.
Finally, the frequency of application of the generation-based strategy is determined by the predictive power of the Pareto front, measured by the metric d j . In other words, the update process will be delayed if each surrogate model achieves prediction values greater than 90%. In contrast, if a surrogate model achieves prediction values below 90%, the update process will be executed earlier based on the obtained prediction.

2.5. Performance Metric for Surrogate Model Prediction

Evaluating surrogate models’ predictive power is essential in implementing them as it indicates their fidelity to the original models.
A metric used to evaluate the goodness of fit in regression models is the modified agreement index ( d j ) or the Willmott index [74]. The d j values range from 0 to 1, where 0 indicates total disagreement between the observed and predicted values, and 1 indicates total agreement. Unlike R 2 , which can generate negative values when comparing unrelated sets of values, d j always produces results within the defined range. Equation 6 expresses the metric d j . The observed and predicted values are denoted by Y i and Y i ^ , respectively, and the average of the observed values is represented by Y ¯ . The value of j is usually set to one.
d j = 1 − ∑ i = 1 Y Y i − Y i ^ j ∑ i = 1 Y Y i ^ − Y ¯ + Y i − Y ¯ j

2.6. Datasets

This study used 41 databases from the UCR repository [75] to test our proposal. Each database has been donated by the original authors and categorized according to the problem addressed in their respective articles. Table 1 shows the databases utilized in this document.
Each database is classified into different domains based on the type of data input. For instance, data sets classified as image types comprise time series obtained from image outlines or other methods to convert an image into time series. On the contrary, the Spectro type includes a time series extracted from spectrograms of a specific food. Additionally, the sensor type comprises time series collected from various sensors, including engine noise, motion tracking, and electrical power metrics. The UCR Repository [75] provides explanations and access to all types of datasets.

3. Results and Discussion

3.1. Experimental Design

As mentioned above, eMODiTS has proven to have competitive results regarding the classification time series task. However, the computational cost is its primary drawback. Therefore, the experiment’s goal in this document is to reduce such computational costs by using surrogate models without losing the classification power. Moreover, each experiment was designed to prove if our proposal improves the prediction power (model fidelity) regarding the proposal described in [33].
As a consequence, the experiments were planned to answer the following research questions based on the objectives set out in Section 1:
  • Can sMODiTS increase the model fidelity regarding [33]? This question arises in analyzing the prediction power of sMODiTS and the proposal introduced in [33] compared to eMODiTS (original model). The results will seek to achieve the first research objective and are presented in Section 3.2.
  • Is it possible to minimize the computational cost caused by evaluating the solutions in the eMODiTS functions without losing the ability to classify the time series? This question arises to achieve the second research objective, which seeks to find an alternative evaluation of the objective functions without losing the time series classification rate. The answer to this question will be presented in Section 3.3.
  • Is sMODiTS a competitive alternative compared to SAX-based symbolic discretization models? Finally, this question arises to analyze whether implementing the surrogate models in sMODiTS remains competitive in the task for which the tool was designed. Therefore, a comparison is made against symbolic discretization models showing competitive performance in time-series classification. In Section 3.4, the results that answer this question will be presented.
It is essential to mention that the methods compared in Section 3 were implemented under the same experimental environment. The parameters used for eMODiTS and sMODiTS are presented in Table 2. Additionally, for sMODiTS, the model update process was performed at the beginning of every 60 generations for the generation-based strategy, starting with five updates and changing according to prediction ability. The prediction measure was d j , and the prediction error threshold used to update the generation-based application was 0.9 . Regarding the DTW parameter, the window size employed for the Sakoe-Chiba constraint was 10%, an often used value when this method is implemented [76].
Moreover, the Evolutionary Programmin (EP) approach [15] was compared using the same sMODiTS experimental environment. However, since the other SAX-based approaches do not report results for all databases in the UCR repository, most databases have no parameter settings. Therefore, the word size and alphabet values for each method are obtained from the best solution found by EP. Furthermore, these symbolic discretization approaches require additional parameters, such as 1D-SAX and rSAX. For example, for 1D-SAX, the slope number used for its execution was eight, and for rSAX, the value of the parameter τ was ten. For the other methods and their parameters, the initial settings suggested by the authors were used because of the strong performance observed in their specific applications.
All methods were compared using the F measure ( F M ). This measure is one of the most robust and insensitive to class balancing. Equation 7 expresses the calculation of the measure F, where T P represents the number of true positives, F N false negatives, and F P false positives. Values close to one are preferred because they represent a suitable method performance.
F M = 2 T P 2 T P + F N + F P
Concerning statistical analysis, a normality test was applied for each data group in each comparison. The normality test used was Anderson-Darling test with a confidence level of 95%. Data groups do not present a normal distribution for the first and last comparisons. Thus, the selected statistical test was Friedman test with the post hoc test called Nemenyi at 95%-confidence for both.
Moreover, the Texas Sharpshooter plot was employed to analyze these statistical results graphically per each data set using the Wilcoxon Rank Sum test. The plot axis x represents the F measure ratio ( F m e a s u r e _ r a t i o ) between sMODiTS and eMODiTS (Equation 8), and the axis y represents the p-value obtained by the paired statistical test mentioned lines above. Each axis is divided into two regions, which form four regions in total. Values above one in the "x" axis represent that sMODiTS outperforms eMODiTS; otherwise, eMODiTS is more competitive than sMODiTS. On the other hand, values above 0.05 do not represent significant statistical differences between approaches. Therefore, the four regions are (A) when F m e a s u r e _ r a t i o is less than one and the p-value is higher than 0.05, (B) F m e a s u r e _ r a t i o is higher than one, and the p-value is higher than 0.05, (C) F m e a s u r e _ r a t i o is less than one, and the p-value is less than 0.05 (worst scenario), and (D) F m e a s u r e _ r a t i o is higher than one and the p-value is less than 0.05 (ideal scenario).
F m e a s u r e _ r a t i o = s M O D i T S _ F m e a s u r e e M O D i T S _ F m e a s u r e
One essential way to compare two Multi-Objective Evolutionary Algorithms (MOEA) is to compare the similarity among their final Pareto fronts. Consequently, a set of well-known metrics is employed to compare the Pareto fronts of eMODiTS and sMODiTS. These metrics are described below.
  • Hypervolume Ratio (HVR) [34]. This metric is based on the hypervolume (H) measure, which computes the volume in the space of objective functions covered by a set of non-dominated solutions based on a reference point. Therefore, Equation 9 expressed the computation H V R , where H F i is the hypervolume of the obtained Pareto front and H F j is the hypervolume of the true Pareto front. In this document, we take the True Pareto front the eMODiTS Pareto front and the obtained Pareto front the sMODiTS Pareto front. H V R < 1 indicates that the sMODiTS Pareto front does not reach the eMODiTS Pareto front, H V R = 1 indicates that both fronts are similar, and H V R > 1 indicates that the sMODiTS Pareto front outperforms the eMODiTS Pareto front. Therefore, the ideal value is H R V = 1
    H V R = H F i H F j
  • Generational Distance (GD) [77]. G D measures the closeness of the obtained and True Pareto front. Equation 10 shows this metric, where | F i | is the number of non-dominated solutions in the obtained Pareto front, and d i is the Euclidean distance between each solution of the obtained Pareto front and the nearest solution of the True Pareto front, measured in the space of the objective functions. Like HVR, for our purpose, the True Pareto front is taken as the eMODiTS Pareto front, and the obtained Pareto front is taken as the sMODiTS Pareto front. Values near zero indicate that the sMODiTS Pareto front is similar to the eMODiTS Pareto front.
    G D = ∑ i = 1 | F i | d i 2 | F i |
  • Coverage measure (C) [78]. This measure computes the fracción of two Pareto fronts covered or dominated by one another or vice versa. Equation 11 described this measure. C ( F i , F j ) = 1 represents that all elements of F j are dominated by the F i , otherwise C ( F i , F j ) = 0 indicates that no elements from F j are dominated by the F i . It is important to mention that C ( F i , F j ) ≠ C ( F j , F i ) and C ( F i , F j ) ≠ ( 1 − C ( F j , F i ) ) . Therefore, both scenarios must be analyzed to provide a wide panorama of this measure. Two Pareto fronts are considered similar when the coverage in both senses is zero simultaneously.
    C ( F i , F j ) = { y → ∈ F j | ∃ x → ∈ F i : x → ≺ y → } | F j |
  • Convergence index (CI) [78]. This measure is the difference between the coverage of F i over F j . Equation 12 expressed this measure. C I ( F i , F j ) ≥ 0 denotes that portion coverage of F i is higher than F j . Otherwise, the portion of F j is higher than F i .
    C I ( F i , F j ) = C ( F i , F j ) − C ( F j , F i )
Finally, for computational cost analysis, the percentage reduction of the number of evaluated performed was calculated using Equation 13, where sMODiTS_Evals is the number of evaluations performed by sMODiTS and eMODiTS_Evals is the number of evaluations performed by eMODiTS.
E v a l u a t i o n s R a t i o = | s M O D i T S _ E v a l s − e M O D i T S _ E v a l s | e M O D i T S _ E v a l s * 100

3.2. sMODiTS’ Prediction Power Analysis

The sMODiTS’ prediction power was measured based on the accumulated Pareto front obtained in each data set using the measures R M S E , d j , M A P E , and M A E . It is essential to mention that each Pareto front point is a solution estimated from the surrogate model. Therefore, each point was evaluated in the original functions to perform the approximation analysis. Moreover, sMODiTS was compared with the previous work presented by Márquez-Grajales et al. [33] due to the intention of this work to improve its prediction power. Both were executed using five configurations 1 N N D T W , 3 N N D T W , 5 N N D T W , 7 N N D T W , and 9 N N D T W for k = { 1 , 3 , 5 , 7 , 9 } of the algorithm K N N R , respectively. Figure 9 and Table 3 show this analysis.
Figure 9 shows the prediction plots in which the predicted values are compared with the original values. The color bar represents the absolute prediction error between the predicted and observed values, with a difference close to zero representing a high-accuracy prediction and a difference close to one representing a low-accuracy prediction. Moreover, a red dotted line is displayed to locate the scenario where the predicted and observed values match. Consequently, points close to or inside the red line represent a good approximation.
As we can see in this figure, sMODiTS presents a higher accuracy in the approximation of the values of the objective functions, showing differences of less than 0.6 in the function of Complexity and Information Loss (InfoLoss), being entropy, the function with a higher value in the difference. In contrast, the approach presented by Márquez-Grajales et al. [33] presents a more significant number of differences with values greater than 0.8 in predicting both entropy and complexity, with entropy producing the most favorable outcomes. However, these values do not exceed those found by sMODiTS, whose plots are mainly around the red line in this function.
Moreover, these results are confirmed in Table 3, where the highest results are found for sMODiTS in most prediction measures. For example, the values of d j using sMODiTS are highest in the 1 N N D T W version for the entropy function (0.6198) and the Information Loss function (0.5356), while the versions 3 N N D T W and 5 N N D T W obtained the best value for the Complexity function (0.6704). Regarding RMSE and MAE, only for the Entropy function, the method introduced by Márquez-Grajales et al. obtained lower values than those shown by sMODiTS (0.0748 and 0.0318 for RMSE and MAE, respectively). In contrast, the opposite is the case for the other functions, where sMODiTS is superior.
Consequently, a singular subrogated model cannot accurately represent all three functions. This situation is evidenced by distinct versions of K N N R yield disparate outcomes across all three objective functions. Therefore, it is plausible to employ an alternative machine learning approach to align with the specific requirements of each function. Moreover, the outcomes above have enabled us to achieve the initial objective proposed in Section 1 and to answer the first research question mentioned before. It allows us to conclude that a more accurate approximation of the model can be achieved by modifying how the surrogate models are updated.

3.3. Comparison between eMODiTS and sMODiTS

The second analysis compares the performance of the original method (eMODiTS) and the surrogate-assisted method (sMODiTS). This comparison is presented based on the classification performance evaluated by the F measure, the similarity of Pareto fronts, and the computational cost assessed by the number of evaluations performed.

3.3.1. Classification Performance

Figure 10 presents the outcomes of the Friedman test combined with the Nemenyi post hoc test at a 95%-confidence level to compare the original method (eMODiTS) against each surrogate model (sMODiTS). These tests were chosen because the data does not follow a normal distribution. As we can see, all the methods compared do not have significant statistical differences; that is, all have the same behavior in terms of classification. This outcome is anticipated since the surrogate model approximates the actual model rather than enhancing it. However, eMODiTS ranked better concerning the F measure, which means that in most databases, eMODiTS still reaches better classification rates than sMODiTS. This behavior may be due to the initial sampling employed by sMODiTS, which does not guarantee that the initial training set covers all search space. Nevertheless, the search space in eMODiTS is vast and complex to cover by the conventional sampling methods due to the discretization scheme used by eMODiTS.
Also, Figure 11 shows the statistical results for each dataset in which the F-measure ratio was calculated using Equation 8 and the Texas Sharpshooter plot. The statistical test used was the Wilcoxon Rank Sum Test with a confidence level of 95%. Moreover, this figure is divided into four regions, designated as A, B, C, and D. The points in Regions A and C demonstrate that eMODiTS outperforms sMODiTS in classification. The distinction between these regions is that the points in Region A indicate no significant statistical difference. In contrast, those in Region C indicate that there is a significant statistical difference. In contrast, the points in Regions B and D indicate that sMODiTS outperformed eMODiTS in classification. Notably, Region D is the one where the points located present significant statistical differences.
The results of Figure 11 show that most of the database is concentrated in Region C, which is the reason why it is placed in a better place in Figure 10. However, the F measure ratio distribution is between 0.7 and 1.3, which means that the F measure value between sMODiTS and eMODiTS is not statistically different, confirming that sMODiTS achieves a suitable approximation to the original model.

3.3.2. Analysis of Pareto Fronts

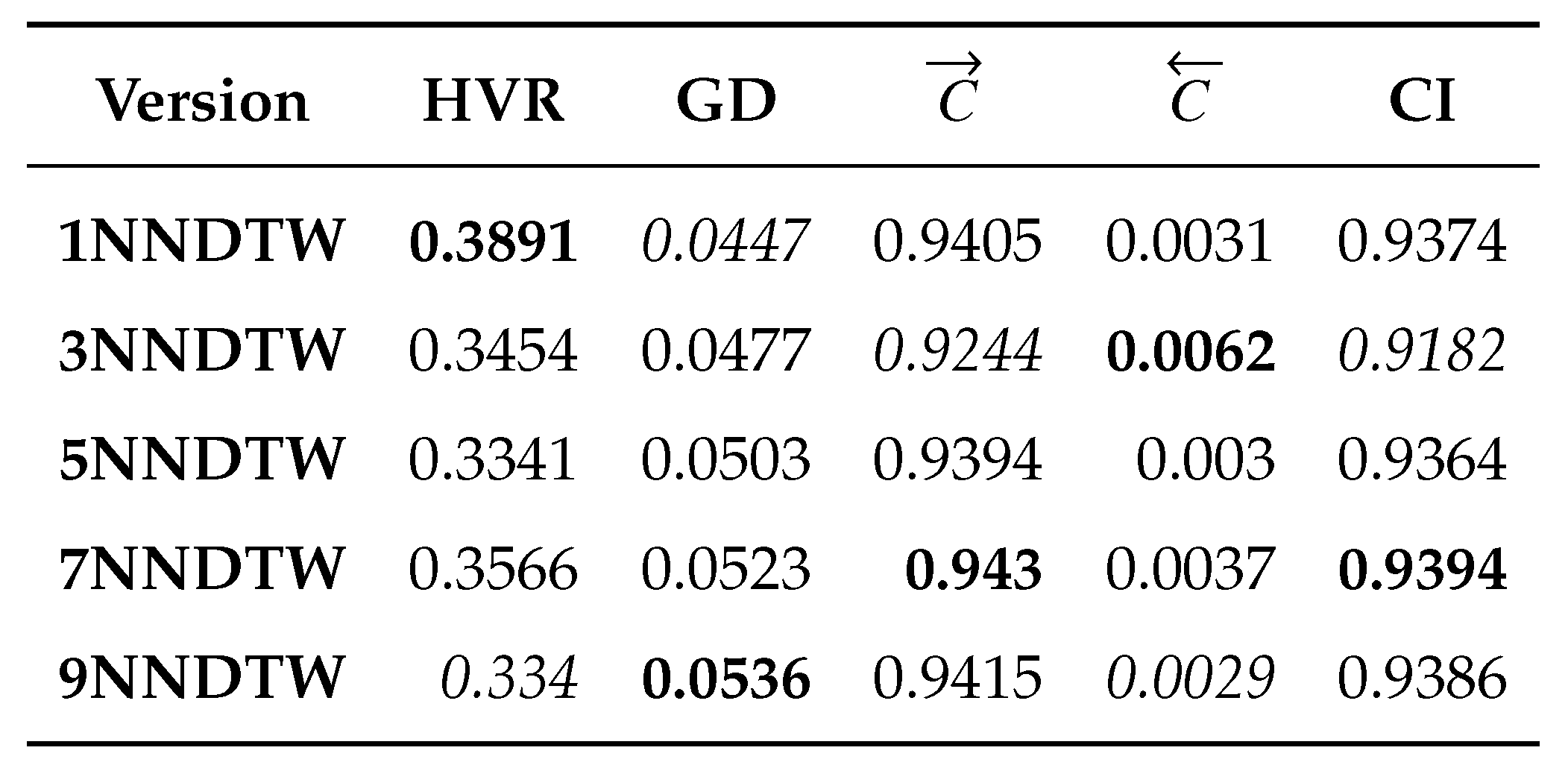
Table 4 shows the average results of applying five performance measures for Pareto front analysis in all test datasets. In this table, the analyzed Pareto fronts were obtained from eMODiTS, and each version of sMODiTS was used to compare the ability of the proposed surrogate model to approximate the solutions to the original model solutions. In addition, this analysis allows us to verify the similarity of both approaches in the objective function space.
The HVR measure indicates that the space covered by eMODiTS is more significant than that covered by each version of sMODiTS. Nevertheless, the mean value of the hypervolume ratio (HVR) for each dataset ranges between 0.334 and 0.3891 , indicating that the eMODiTS hypervolume is slightly higher than the sMODiTS in the majority of cases. Given that our MOOP is a minimization problem, the HVR results indicate that each Pareto front of the sMODiTS versions is above the eMODiTS Pareto front. These results suggest that the surrogate model approximation was not faithful to the original model.
Regarding the coverage metric, the convergence index shows that the Pareto fronts generated by eMODiTS on the test datasets outperform those produced by all versions of sMODiTS, with values between 0.9182 and 0.9394 . As with HVR, these values indicate that the eMODiTS Pareto fronts are situated below the sMODiTS fronts, which cover them in almost all databases tested. This result implies that sMODiTS failed to approximate sufficiently to obtain Pareto fronts similar to the original ones. However, it is essential to clarify that, due to its nature, sMODiTS could not improve the front obtained by eMODiTS. Its maximum performance would be to approach or equal the original fronts.
Despite the inability of sMODiTS, in all its versions, to obtain Pareto fronts comparable to the original, it does succeed in approximating them. This situation can be observed in the maximum ( 0.0447 ) and minimum ( 0.0536 ) values of the GD measure, where their average values are close to zero, indicating that the fronts are very close.
In conclusion, sMODiTS cannot generate Pareto fronts identical to eMODiTS. However, it can achieve a similar outcome, maintaining the same behavioral characteristics.

3.3.3. Computational Cost Analysis

The computational cost was measured based on the number of evaluations performed in eMODiTS and sMODiTS. Figure 12 shows the number of reduction percentages of evaluations based on Equation 13 reached by sMODiTS compared with eMODiTS. eMODiTS performs 30 , 200 calls per objective function in one execution, while sMODiTS computes an average of 18 , 389 calls per objective function, representing a reduction of 40%. It is essential to mention that the number of evaluations executed by sMODiTS varies due to the model updating process. As mentioned in Section 2.4.3, the training set update process in sMODiTS consists of evaluating the first Pareto front in original objective functions and inserting them into this set. Since the number of solutions for the first Pareto front differs, in each update, sMODiTS performs different calls of the original objective functions.
As we can see, the reduction percentages of evaluations performed by sMODiTS are between 15% and 80%. This reduction means that sMODiTS performs a lower number of the original objective function calls, reducing the computational cost of these functions. However, since sMODiTS uses a surrogate model based on DTW distance, the computational cost is transferred to this process, increasing the algorithm’s execution time.
The examination conducted in this section enables us to achieve the second goal outlined in Section 1 and address the second question mentioned in Section 3.1.

3.4. Comparison of sMODiTS among the SAX-Based Methods

The last experiment compares sMODiTS against SAX-based approaches to analyze if the surrogate model incorporated in eMODiTS is still conserving the classification performance when its discretization scheme is applied to a temporary dataset. Since all the data obtained for each method do not follow a normal distribution, the Friedman statistical test was used with the Nemenyi post hoc test with a confidence level of 95%. The SAX-based models used in this comparison were EP, SAX, α SAX, ESAX, ESAXKMeans, 1D-SAX, SAXKMeans, rSAX, pSAX, and cSAX. In the case of sMODiTS, the 3NNDTW and 5NNDTW versions were identified as the most appropriate for inclusion in this experiment based on Figure 10.
Figure 13 shows the results of the statistical tests of the comparison of sMODiTS with ten SAX-based approaches, selected by their competitive results and their novel discretization schemes. eMODiTS was used as a reference for this purpose. This figure shows no significant difference among all methods, which means that sMODiTS presents a classification behavior similar to the well-known symbolic discretization methods, preserving the characteristics of the original approach (eMODiTS). It is essential to mention that the sMODiTS is better ranked than seven (SAX, 1D-SAX, pSAX, cSAX, α SAX, ESAXKMeans, and SAXKMeans) of the SAX-Based approaches, outperforming them in classification terms. However, ESAX, EP, and rSAX outperform sMODiTS versions, ranking in a better place.
As previously mentioned, the outcomes detailed in these sections are anticipated since sMODiTS solely employs surrogate models to estimate the objective functions for identifying appropriate symbolic discretization schemes without introducing any conceptual alterations to the original eMODiTS method. Using surrogate models has proven to be a practical approach for reducing the evaluation cost of the objective functions.
These results answer the third research question described in Section 3.1, consequently, the third goal of Section 1.

4. Conclusions

Surrogate models are an alternative tool for approximating objective functions in evolutionary optimization. This document implemented a surrogate model for estimating the objective functions of eMODiTS. This research is an extension of the approach proposed by Márquez-Grajales et al. [33]. Since eMODITS employs individuals of different sizes, the kNN algorithm and DTW were incorporated as the surrogate model in eMODiTS. This surrogate-assisted eMODiTS was called sMODiTS, and its behavior was compared against the original model.
The results suggest that each version of sMODiTS implemented presents a behavior similar to the original approach (eMODiTS), which does not present a significant statistical difference. However, eMODiTS still has a low error classification rate in most datasets, unlike the sMODITS method. Moreover, regarding the prediction power of the surrogate model, the metrics suggest that sMODiTS presents a low accuracy in estimating the values of the original eMODiTS fitness functions.
On the other hand, the Pareto fronts of both approaches were compared using MOEA performance measures to evaluate the behavior of the final solutions found by each approach. These measures indicate that the performance of the sMODiTS algorithm is competitive compared to the eMODiTS algorithm since the sMODiTS Pareto front is close to the eMODiTS Pareto front.
Regarding computational cost, the number of evaluations performed by sMODiTS is lower than those achieved by eMODiTS, with reduction percentages of the use of the original objective functions between 15% and 80%, reducing the computational cost of the original algorithm.
Finally, the statistical test indicates that sMODiTS achieves competitive results compared to SAX-based symbolic discretization methods. There is no statistical difference among all the compared methods, and it ranks lower than seven of ten approaches.
In summary, the surrogate models used in this study approximated the actual model outcomes while significantly reducing the number of computationally intensive objective function evaluations. They also preserved the effectiveness of the time series discretization task compared to methods that have demonstrated competitive performance in tested problems. Furthermore, although the surrogate models’ accuracy is low, they are suitable for problems where the solutions have different lengths from each other, particularly in the time series discretization proposed by the eMODiTS approach. Consequently, the objectives set out in Section 1 have been achieved, verifying that the surrogate model maintains the original model results with a competitive approximation to the eMODiTS solutions but with a lower computational cost.
As a future work, we propose to implement other surrogate models (one different per each objective function) capable of handling different-sized solutions to increase the sMODiTS’ estimation accuracy concerning the fitness functions of the eMODiTS method. Moreover, suitable initial sampling methods can be incorporated into this solution to achieve a reliable approximation of the original model. Finally, a comparison of different training set codifications can be performed to evaluate if this feature impacts the fidelity of the original models.

Author Contributions

Conceptualization, A.M.G., E.M.M., and H.G.A.M.; Formal analysis, A.M.G. and F.S.M.; Methodology, A.M.G., E.M.M., and H.G.A.M.; Software, A.M.G.; Writing - original draft, A.M.G.; Writing - review & editing, E.M.M., H.G.A.M., F.S.M. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

The original data presented in the study are openly available in UCR Repository at [75]

Acknowledgments

The first author is grateful to the Consejo Nacional de Humanidades, Ciencias y Tecnología (CONAHCYT) for the postdoctoral grant awarded for this research under CVU number 419862.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Dimitrova, E.S.; Licona, M.P.V.; McGee, J.; Laubenbacher, R. Discretization of time series data. Journal of Computational Biology 2010, 17, 853–868. [Google Scholar] [CrossRef] [PubMed]
  2. Lin, J.; Keogh, E.; Lonardi, S.; Chiu, B. A symbolic representation of time series, with implications for streaming algorithms. In Proceedings of the Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery, 2003, pp. 2–11.
  3. Lkhagva, B.; Suzuki, Y.; Kawagoe, K. Extended SAX: Extension of symbolic aggregate approximation for financial time series data representation. DEWS2006 4A-i8 2006, 7. [Google Scholar]
  4. Sant’Anna, A.; Wickström, N. Symbolization of time-series: An evaluation of sax, persist, and aca. In Proceedings of the 2011 4th international congress on image and signal processing. IEEE, 2011, Vol. 4, pp. 2223–2228.
  5. Zhang, H.; Dong, Y.; Xu, D. Entropy-based Symbolic Aggregate Approximation Representation Method for Time Series. In Proceedings of the 2020 IEEE 9th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), 2020, Vol. 9, pp. 905–909. [CrossRef]
  6. Muhammad Fuad, M.M. Modifying the Symbolic Aggregate Approximation Method to Capture Segment Trend Information. In Proceedings of the Modeling Decisions for Artificial Intelligence; Torra, V.; Narukawa, Y.; Nin, J.; Agell, N., Eds., Cham, 2020; pp. 230–239.
  7. Hui, R.; Xiaoguang, H.; Jin, X.; Guofeng, Z. TrSAX—An improved time series symbolic representation for classification. ISA Transactions 2020, 100, 387–395. [Google Scholar] [CrossRef]
  8. Lkhagva, B.; Suzuki, Y.; Kawagoe, K. New time series data representation ESAX for financial applications. In Proceedings of the 22nd International Conference on Data Engineering Workshops (ICDEW’06). IEEE, 2006, pp. x115–x115.
  9. Pham, N.D.; Le, Q.L.; Dang, T.K. Two novel adaptive symbolic representations for similarity search in time series databases. In Proceedings of the 2010 12th International Asia-Pacific Web Conference. IEEE, 2010, pp. 181–187.
  10. Bai, X.; Xiong, Y.; Zhu, Y.; Zhu, H. Time series representation: a random shifting perspective. In Proceedings of the International Conference on Web-Age Information Management. Springer, 2013, pp. 37–50.
  11. Malinowski, S.; Guyet, T.; Quiniou, R.; Tavenard, R. 1d-sax: A novel symbolic representation for time series. In Proceedings of the International Symposium on Intelligent Data Analysis. Springer, 2013, pp. 273–284.
  12. He, Z.; Zhang, C.; Ma, X.; Liu, G. Hexadecimal Aggregate Approximation Representation and Classification of Time Series Data. Algorithms 2021, 14, 353. [Google Scholar] [CrossRef]
  13. Kegel, L.; Hartmann, C.; Thiele, M.; Lehner, W. Season-and Trend-aware Symbolic Approximation for Accurate and Efficient Time Series Matching. Datenbank-Spektrum 2021, 21, 225–236. [Google Scholar] [CrossRef]
  14. Bountrogiannis, K.; Tzagkarakis, G.; Tsakalides, P. Data-driven kernel-based probabilistic SAX for time series dimensionality reduction. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO). IEEE, 2021, pp. 2343–2347.
  15. Acosta-Mesa, H.G.; Rechy-Ramírez, F.; Mezura-Montes, E.; Cruz-Ramírez, N.; Jiménez, R.H. Application of time series discretization using evolutionary programming for classification of precancerous cervical lesions. Journal of biomedical informatics 2014, 49, 73–83. [Google Scholar] [CrossRef]
  16. Ahmed, A.M.; Bakar, A.A.; Hamdan, A.R. Harmony search algorithm for optimal word size in symbolic time series representation. In Proceedings of the 2011 3rd conference on data mining and optimization (DMO). IEEE, 2011, pp. 57–62.
  17. Ahmed, A.M.; Bakar, A.A.; Hamdan, A.R. A harmony search algorithm with multi-pitch adjustment rate for symbolic time series data representation. International Journal of Modern Education and Computer Science 2014, 6, 58. [Google Scholar] [CrossRef]
  18. Fuad, M.M.M. Differential evolution versus genetic algorithms: towards symbolic aggregate approximation of non-normalized time series. In Proceedings of the 16th International Database Engineering & Applications Sysmposium; IDEAS ’12; Association for Computing Machinery: New York, NY, USA, 2012; pp. 205–210. [Google Scholar] [CrossRef]
  19. Fuad, M.; Marwan, M. Genetic algorithms-based symbolic aggregate approximation. In Proceedings of the International Conference on Data Warehousing and Knowledge Discovery. Springer, 2012, pp. 105–116.
  20. Márquez-Grajales, A.; Acosta-Mesa, H.G.; Mezura-Montes, E.; Graff, M. A multi-breakpoints approach for symbolic discretization of time series. Knowledge and Information Systems 2020, 62, 2795–2834. [Google Scholar] [CrossRef]
  21. Jiang, P.; Zhou, Q.; Shao, X. Surrogate model-based engineering design and optimization; Springer, 2020.
  22. Koziel, S.; Pietrenko-Dabrowska, A. Rapid multi-criterial antenna optimization by means of pareto front triangulation and interpolative design predictors. IEEE Access 2021, 9, 35670–35680. [Google Scholar] [CrossRef]
  23. Koziel, S.; Pietrenko-Dabrowska, A. Rapid multi-objective optimization of antennas using nested kriging surrogates and single-fidelity EM simulation models. Engineering Computations 2020. [Google Scholar] [CrossRef]
  24. Koziel, S.; Pietrenko-Dabrowska, A. Fast multi-objective optimization of antenna structures by means of data-driven surrogates and dimensionality reduction. IEEE Access 2020, 8, 183300–183311. [Google Scholar] [CrossRef]
  25. Koziel, S.; Pietrenko-Dabrowska, A. Constrained multi-objective optimization of compact microwave circuits by design triangulation and pareto front interpolation. European Journal of Operational Research 2022, 299, 302–312. [Google Scholar] [CrossRef]
  26. Pietrenko-Dabrowska, A.; Koziel, S. Accelerated multiobjective design of miniaturized microwave components by means of nested kriging surrogates. International Journal of RF and Microwave Computer-Aided Engineering 2020, 30, e22124. [Google Scholar] [CrossRef]
  27. Amrit, A.; Leifsson, L.; Koziel, S. Fast multi-objective aerodynamic optimization using sequential domain patching and multifidelity models. Journal of Aircraft 2020, 57, 388–398. [Google Scholar] [CrossRef]
  28. Arias-Montano, A.; Coello, C.A.C.; Mezura-Montes, E. Mezura-Montes, E. Multi-objective airfoil shape optimization using a multiple-surrogate approach. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation. IEEE, 2012, pp. 1–8.
  29. Fan, Y.; Lu, W.; Miao, T.; Li, J.; Lin, J. Multiobjective optimization of the groundwater exploitation layout in coastal areas based on multiple surrogate models. Environmental Science and Pollution Research 2020, 27, 19561–19576. [Google Scholar] [CrossRef]
  30. Dumont, V.; Garner, C.; Trivedi, A.; Jones, C.; Ganapati, V.; Mueller, J.; Perciano, T.; Kiran, M.; Day, M. HYPPO: A Surrogate-Based Multi-Level Parallelism Tool for Hyperparameter Optimization. In Proceedings of the 2021 IEEE/ACM Workshop on Machine Learning in High Performance Computing Environments (MLHPC), 2021, pp. 81–93. [CrossRef]
  31. Zheng Yi, W.; Atiqur, R. Optimized Deep Learning Framework for Water Distribution Data-Driven Modeling. Procedia Engineering 2017, 186, 261–268. [Google Scholar] [CrossRef]
  32. Vijayaprabakaran, K.; Sathiyamurthy, K. Neuroevolution based hierarchical activation function for long short-term model network. Journal of Ambient Intelligence and Humanized Computing 2021, 12, 10757–10768. [Google Scholar] [CrossRef]
  33. Márquez-Grajales, A.; Mezura-Montes, E.; Acosta-Mesa, H.G.; Salas-Martínez, F. Use of a Surrogate Model for Symbolic Discretization of Temporal Data Sets Through eMODiTS and a Training Set with Varying-Sized Instances. In Proceedings of the Advances in Computational Intelligence. MICAI 2023 International Workshops; Calvo, H.; Martínez-Villaseñor, L.; Ponce, H.; Zatarain Cabada, R.; Montes Rivera, M.; Mezura-Montes, E., Eds., Cham, 2024; pp. 360–372.
  34. Coello, C.A.C.; Lamont, G.B.; Veldhuizen, D.A.V. Evolutionary algorithms for solving multi-objective problems; Springer, 2007; Vol. 5. [Google Scholar]
  35. Rangaiah, G.P. Multi-objective optimization: techniques and applications in chemical engineering; Vol. 5, world scientific, 2016.
  36. Delboeuf, J. Mathematical psychics, an essay on the application of mathematics to the moral sciences, 1881.
  37. Deb, K.; Deb, K. Multi-objective Optimization. In Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; chapter 15; Springer: Boston, MA, USA, 2014; pp. 403–449. [Google Scholar] [CrossRef]
  38. Pareto, V. Cours d’économie politique; Vol. 1, Librairie Droz, 1964.
  39. Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International conference on parallel problem solving from nature. Springer, 2000, pp. 849–858.
  40. Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE transactions on evolutionary computation 2002, 6, 182–197. [Google Scholar] [CrossRef]
  41. Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. Ieee Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
  42. Syswerda, G.; et al. Uniform crossover in genetic algorithms. Proceedings of the ICGA, 1989; Vol. 3, 2–9. [Google Scholar]
  43. Poli, R.; Langdon, W.B. Genetic programming with one-point crossover. In Soft Computing in Engineering Design and Manufacturing; Springer, 1998; pp. 180–189.
  44. Mirjalili, S. Genetic algorithm. In Evolutionary algorithms and neural networks; Springer, 2019; pp. 43–55.
  45. Zainuddin, F.A.; Abd Samad, M.F.; Tunggal, D. A review of crossover methods and problem representation of genetic algorithm in recent engineering applications. International Journal of Advanced Science and Technology 2020, 29, 759–769. [Google Scholar]
  46. Singh, G.; Gupta, N. A Study of Crossover Operators in Genetic Algorithms. In Frontiers in Nature-Inspired Industrial Optimization; Springer, 2022; pp. 17–32.
  47. Singh, A.; Gupta, N.; Sinhal, A. Artificial bee colony algorithm with uniform mutation. In Proceedings of the Proceedings of the International Conference on Soft Computing for Problem Solving (SocProS 2011) December 20-22, 2011. Springer, 2012, pp. 503–511.
  48. Koziel, S.; Ciaurri, D.E.; Leifsson, L. Surrogate-based methods. In Computational optimization, methods and algorithms; Springer, 2011; pp. 33–59.
  49. Tong, H.; Huang, C.; Minku, L.L.; Yao, X. Surrogate models in evolutionary single-objective optimization: A new taxonomy and experimental study. Information Sciences 2021, 562, 414–437. [Google Scholar] [CrossRef]
  50. Miranda-Varela, M.E.; Mezura-Montes, E. Constraint-handling techniques in surrogate-assisted evolutionary optimization. An empirical study. Applied Soft Computing 2018, 73, 215–229. [Google Scholar] [CrossRef]
  51. Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Computers & Chemical Engineering 2018, 108, 250–267. [Google Scholar]
  52. Fang, K.; Liu, M.Q.; Qin, H.; Zhou, Y.D. Theory and application of uniform experimental designs; Vol. 221, Springer, 2018.
  53. Kai-Tai, F.; Dennis K.J., L.; Peter, W.; Yong, Z. Uniform Design: Theory and Application. Technometrics 2000, 42, 237–248. [Google Scholar] [CrossRef]
  54. Yondo, R.; Andrés, E.; Valero, E. A review on design of experiments and surrogate models in aircraft real-time and many-query aerodynamic analyses. Progress in aerospace sciences 2018, 96, 23–61. [Google Scholar] [CrossRef]
  55. Díaz-Manríquez, A.; Toscano, G.; Barron-Zambrano, J.H.; Tello-Leal, E. A review of surrogate assisted multiobjective evolutionary algorithms. Computational intelligence and neuroscience 2016, 2016. [Google Scholar] [CrossRef]
  56. Deb, K.; Roy, P.C.; Hussein, R. Surrogate modeling approaches for multiobjective optimization: Methods, taxonomy, and results. Mathematical and Computational Applications 2020, 26, 5. [Google Scholar] [CrossRef]
  57. Lv, Z.; Wang, L.; Han, Z.; Zhao, J.; Wang, W. Surrogate-assisted particle swarm optimization algorithm with Pareto active learning for expensive multi-objective optimization. IEEE/CAA Journal of Automatica Sinica 2019, 6, 838–849. [Google Scholar] [CrossRef]
  58. Zhao, M.; Zhang, K.; Chen, G.; Zhao, X.; Yao, C.; Sun, H.; Huang, Z.; Yao, J. A surrogate-assisted multi-objective evolutionary algorithm with dimension-reduction for production optimization. Journal of Petroleum Science and Engineering 2020, 192, 107192. [Google Scholar] [CrossRef]
  59. Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. An adaptive Bayesian approach to surrogate-assisted evolutionary multi-objective optimization. Information Sciences 2020, 519, 317–331. [Google Scholar] [CrossRef]
  60. Ruan, X.; Li, K.; Derbel, B.; Liefooghe, A. Surrogate assisted evolutionary algorithm for medium scale multi-objective optimisation problems. In Proceedings of the Proceedings of the 2020 genetic and evolutionary computation conference, 2020, pp. 560–568.
  61. Bao, K.; Fang, W.; Ding, Y. Adaptive Weighted Strategy Based Integrated Surrogate Models for Multiobjective Evolutionary Algorithm. Computational Intelligence and Neuroscience 2022, 2022. [Google Scholar] [CrossRef] [PubMed]
  62. Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Transfer Learning Based Co-Surrogate Assisted Evolutionary Bi-Objective Optimization for Objectives with Non-Uniform Evaluation Times. Evolutionary computation 2022, 30, 221–251. [Google Scholar] [CrossRef] [PubMed]
  63. Rosales-Pérez, A.; Coello, C.A.C.; Gonzalez, J.A.; Reyes-Garcia, C.A.; Escalante, H.J. A hybrid surrogate-based approach for evolutionary multi-objective optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation. IEEE, 2013, pp. 2548–2555.
  64. Bi, Y.; Xue, B.; Zhang, M. Instance Selection-Based Surrogate-Assisted Genetic Programming for Feature Learning in Image Classification. IEEE Transactions on Cybernetics 2021. [Google Scholar] [CrossRef] [PubMed]
  65. Blank, J.; Deb, K. GPSAF: A Generalized Probabilistic Surrogate-Assisted Framework for Constrained Single-and Multi-objective Optimization. arXiv 2022, arXiv:2204.04054 2022. [Google Scholar]
  66. Wu, M.; Wang, L.; Xu, J.; Wang, Z.; Hu, P.; Tang, H. Multiobjective ensemble surrogate-based optimization algorithm for groundwater optimization designs. Journal of Hydrology, 1281. [Google Scholar]
  67. Isaacs, A.; Ray, T.; Smith, W. An evolutionary algorithm with spatially distributed surrogates for multiobjective optimization. In Proceedings of the Australian Conference on Artificial Life. Springer, 2007, pp. 257–268.
  68. Datta, R.; Regis, R.G. A surrogate-assisted evolution strategy for constrained multi-objective optimization. Expert Systems with Applications 2016, 57, 270–284. [Google Scholar] [CrossRef]
  69. Kourakos, G.; Mantoglou, A. Development of a multi-objective optimization algorithm using surrogate models for coastal aquifer management. Journal of Hydrology 2013, 479, 13–23. [Google Scholar] [CrossRef]
  70. Yan, Y.; Zhang, Y.; Hu, W.; Guo, X.j.; Ma, C.; Wang, Z.a.; Zhang, Q. A multiobjective evolutionary optimization method based critical rainfall thresholds for debris flows initiation. Journal of Mountain Science 2020, 17, 1860–1873. [Google Scholar] [CrossRef]
  71. De Melo, M.C.; Santos, P.B.; Faustino, E.; Bastos-Filho, C.J.; Sodré, A.C. Computational Intelligence-Based Methodology for Antenna Development. IEEE Access 2021, 10, 1860–1870. [Google Scholar] [CrossRef]
  72. Gatopoulos, I.; Lepert, R.; Wiggers, A.; Mariani, G.; Tomczak, J. Evolutionary Algorithm with Non-parametric Surrogate Model for Tensor Program optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020, pp. 1–8.
  73. Zhi, J.; Yong, Z.; Xian-fang, S.; Chunlin, H. A Surrogate-Assisted Ensemble Particle Swarm Optimizer for Feature Selection Problems. In Proceedings of the International Conference on Sensing and Imaging. Springer, 2022, pp. 160–166.
  74. Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resources Research 1999, 35, 233–241. [Google Scholar] [CrossRef]
  75. Keogh, E.e.a. The UCR Time Series Classification Archive, 2018. https://www.cs.ucr.edu/~eamonn/time_series_data_2018/.
  76. Ratanamahatana, C.A.; Keogh, E. Everything you know about dynamic time warping is wrong. In Proceedings of the Third workshop on mining temporal and sequential data. Citeseer, 2004, Vol. 32.
  77. Knowles, J.; Corne, D. On metrics for comparing nondominated sets. In Proceedings of the Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600), 2002, Vol. 1, pp. 711–716 vol.1. [CrossRef]
  78. Ascia, G.; Catania, V.; Palesi, M. A GA-based design space exploration framework for parameterized system-on-a-chip platforms. IEEE Transactions on Evolutionary Computation 2004, 8, 329–346. [Google Scholar] [CrossRef]
Preprints 109405 g001
Figure 1. Bibliographic analysis elaborated from https://www.dimensions.ai/. (a) Keywords used: surrogate model or approximation model. (b) Keywords used: surrogate model optimization or approximation model optimization.
Figure 1. Bibliographic analysis elaborated from https://www.dimensions.ai/. (a) Keywords used: surrogate model or approximation model. (b) Keywords used: surrogate model optimization or approximation model optimization.
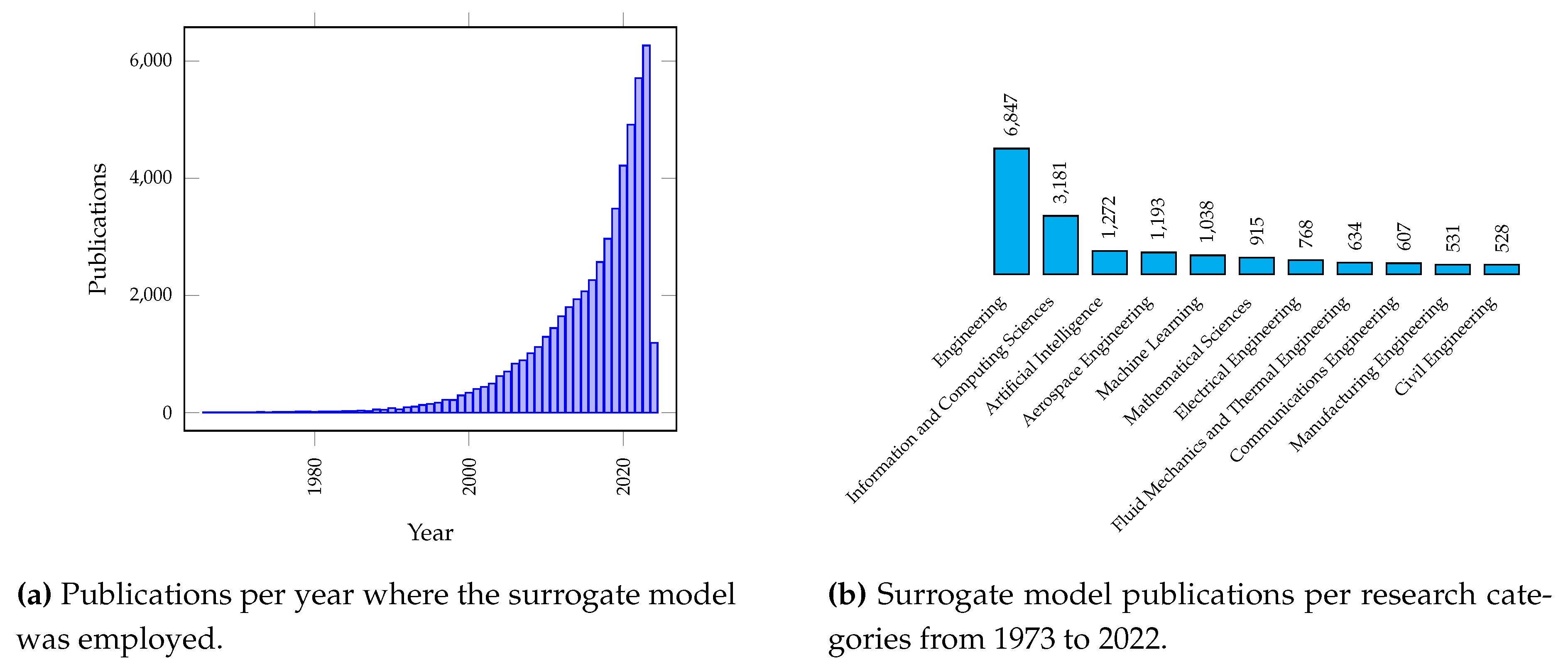
Preprints 109405 g001
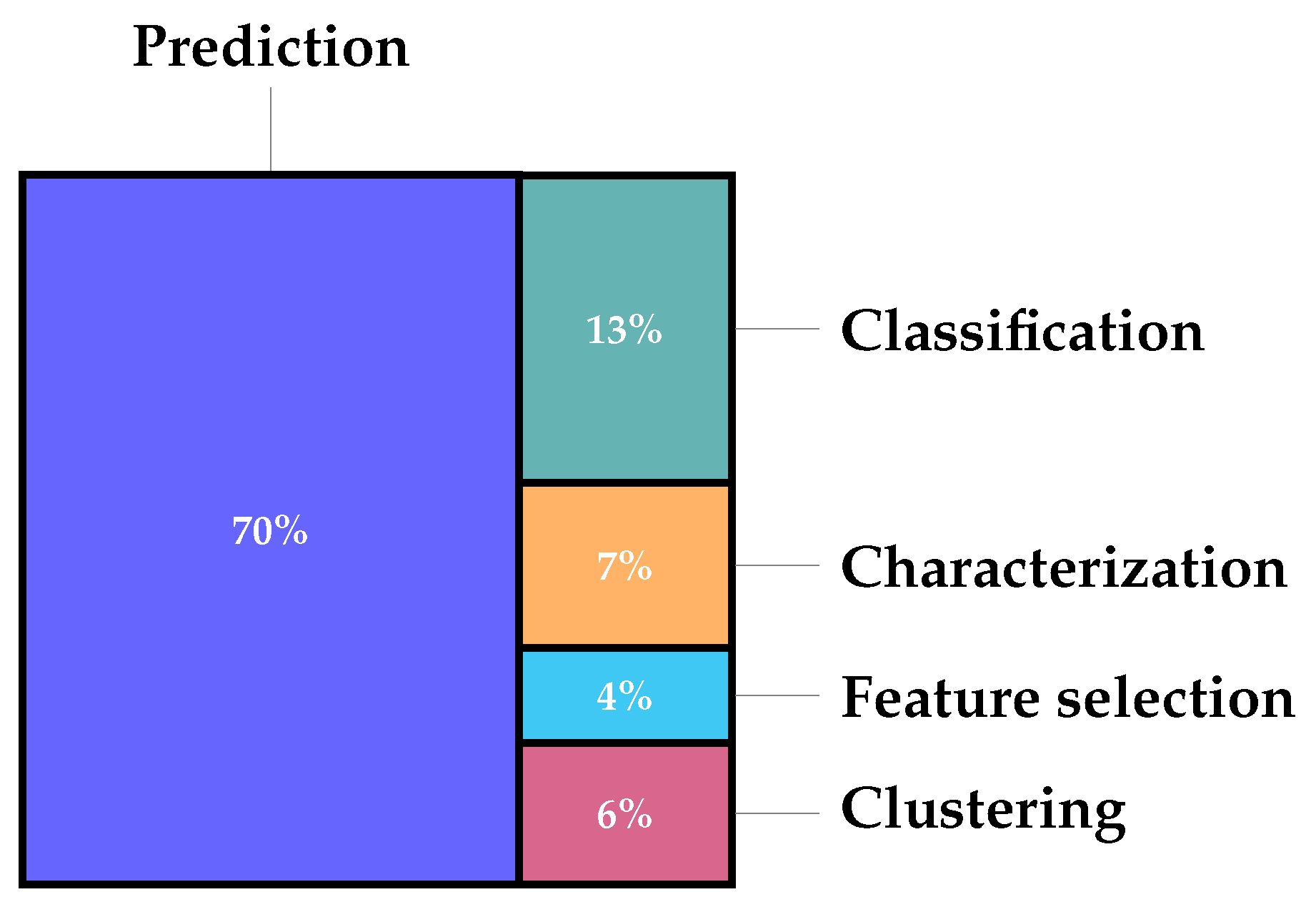
Preprints 109405 g002
Figure 2. Marimekko chart searched at https://www.dimensions.ai/ using the keywords Surrogate model optimization OR approximation model optimization and clustering, classification, prediction, associative analysis, characterization, and feature selection.
Figure 2. Marimekko chart searched at https://www.dimensions.ai/ using the keywords Surrogate model optimization OR approximation model optimization and clustering, classification, prediction, associative analysis, characterization, and feature selection.
Preprints 109405 g002
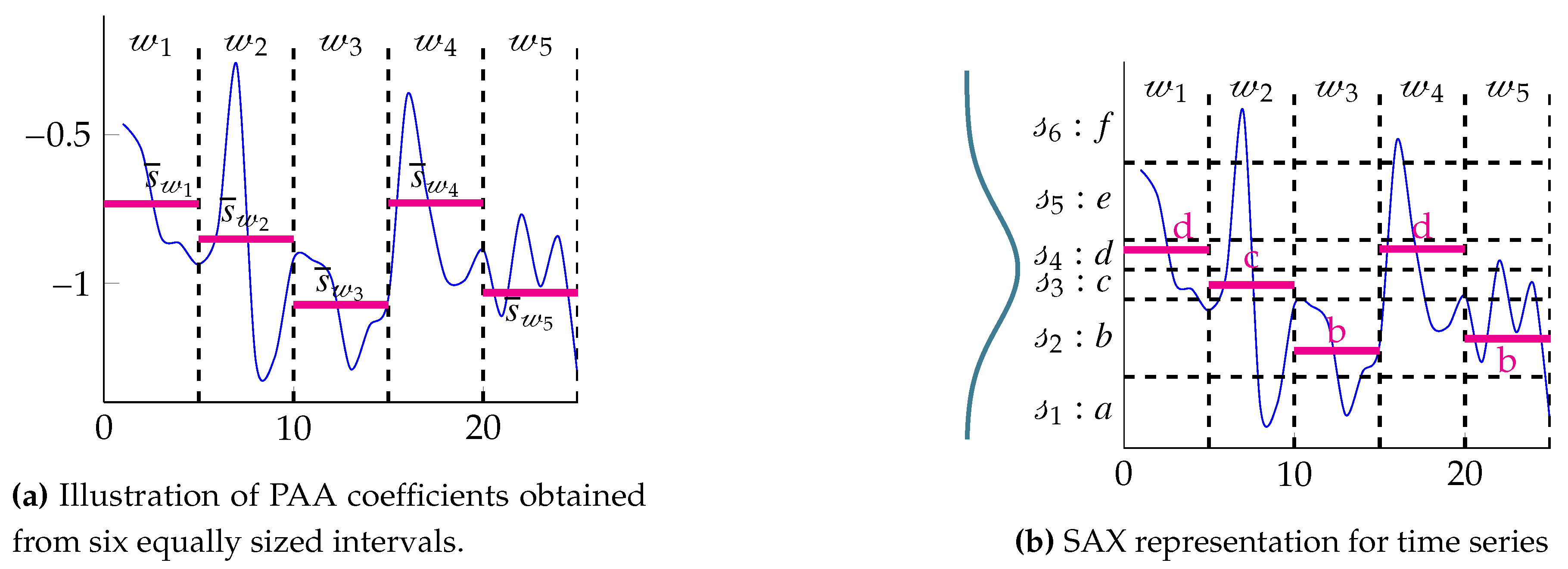
Preprints 109405 g003
Figure 3. Representations for PAA and SAX algorithms. The final string d c b d b is obtained by mapping each PAA coefficient s ¯ w i into a symbol s j .
Figure 3. Representations for PAA and SAX algorithms. The final string d c b d b is obtained by mapping each PAA coefficient s ¯ w i into a symbol s j .
Preprints 109405 g003
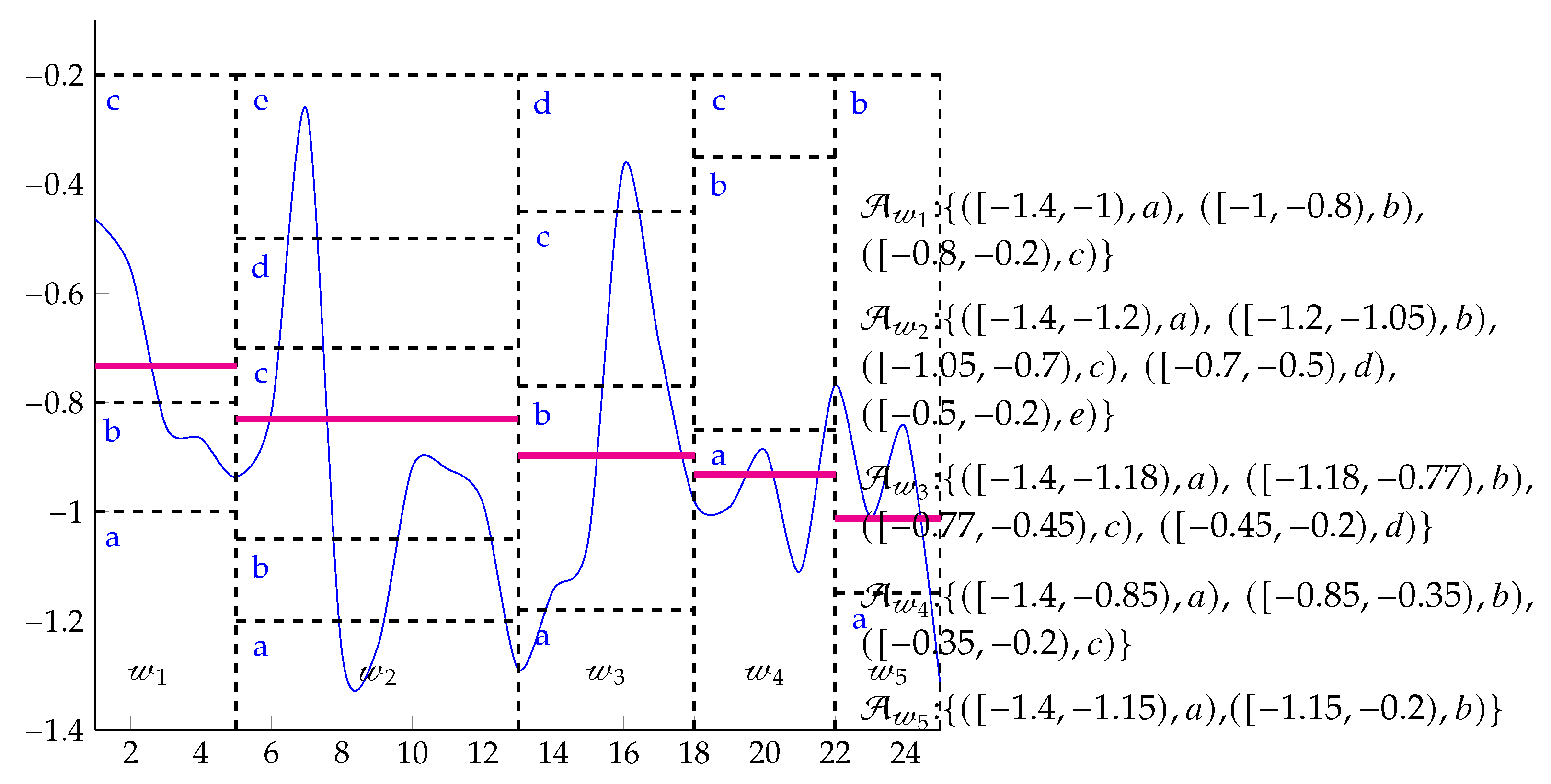
Preprints 109405 g004
Figure 4. eMODiTS scheme discretization approach where each word segment w i contains its breakpoint scheme A w i . In this example, the final string is c c b a b .
Figure 4. eMODiTS scheme discretization approach where each word segment w i contains its breakpoint scheme A w i . In this example, the final string is c c b a b .
Preprints 109405 g004
Preprints 109405 g005
Figure 5. eMODiTS’s flowchart. Dotted and light gray boxes represent the NSGA-II stages necessary to adapt them to the eMODiTS representation schemes.
Figure 5. eMODiTS’s flowchart. Dotted and light gray boxes represent the NSGA-II stages necessary to adapt them to the eMODiTS representation schemes.
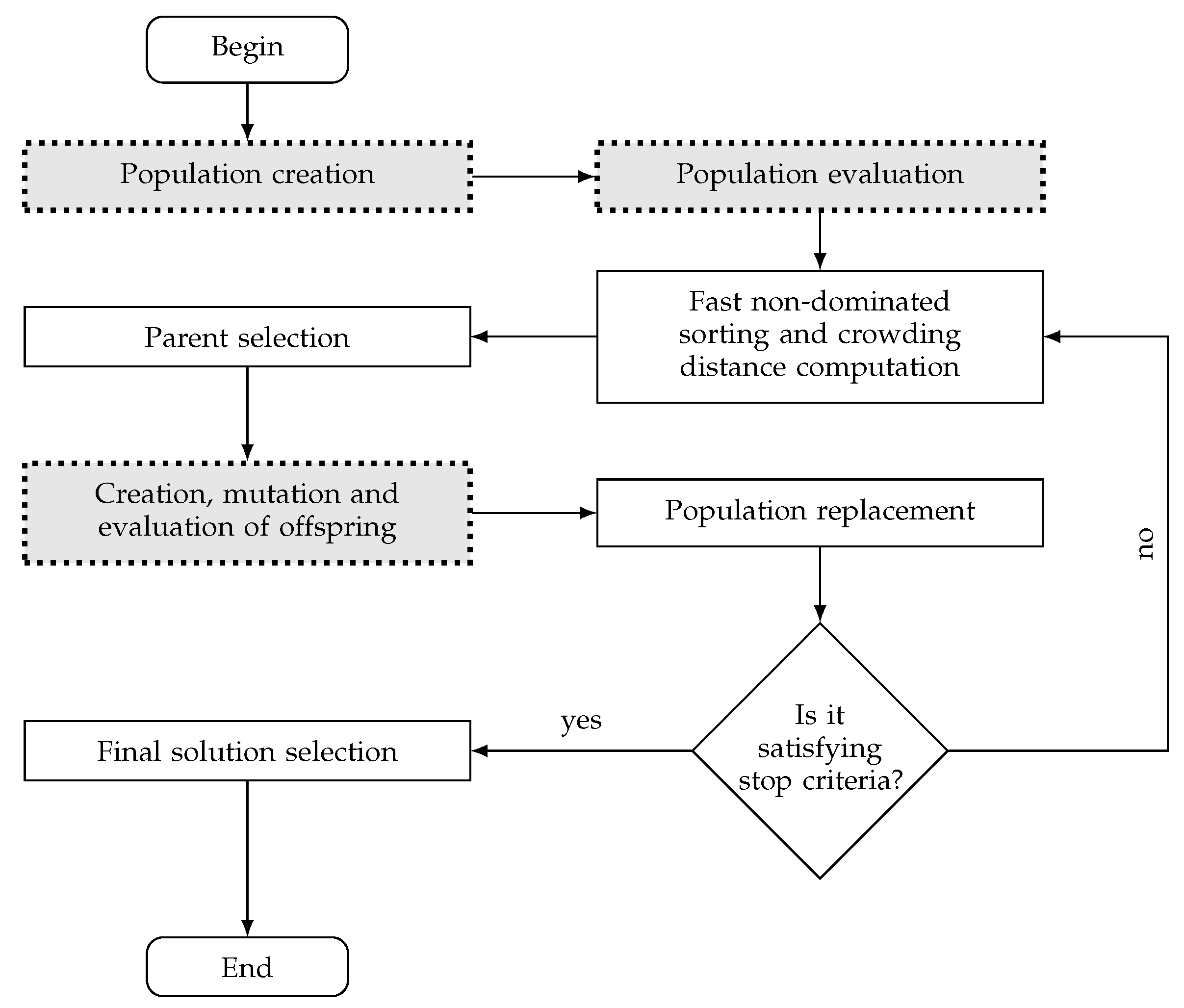
Preprints 109405 g005
Preprints 109405 g006
Figure 6. Representation of an individual in eMODiTS.
Figure 6. Representation of an individual in eMODiTS.
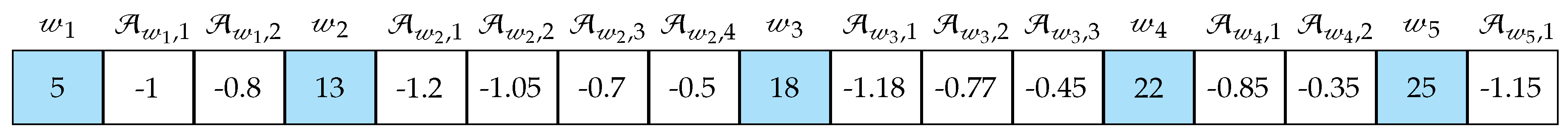
Preprints 109405 g006
Preprints 109405 g007
Figure 7. Crossover operator based on the one-point approach. The dashed line represents the cuts performed by each parent.
Figure 7. Crossover operator based on the one-point approach. The dashed line represents the cuts performed by each parent.
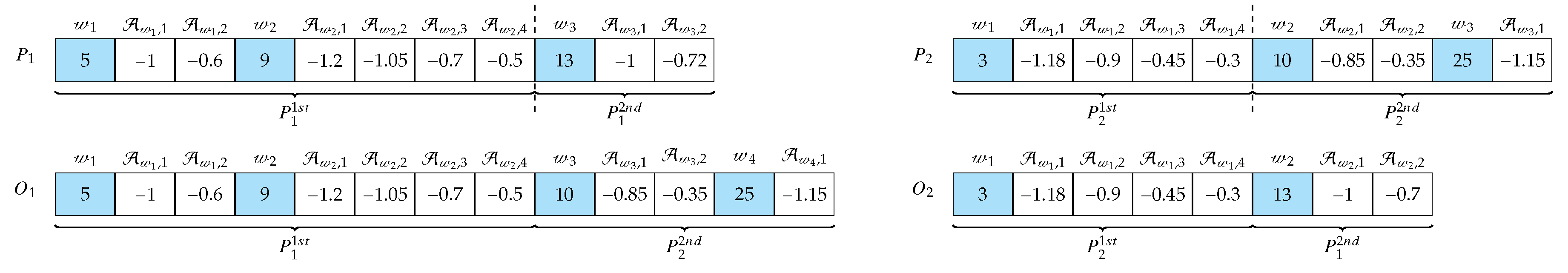
Preprints 109405 g007
Preprints 109405 g008
Figure 8. General scheme of sMODiTS. Green arrows indicate paths to follow when the conditions are satisfied. Red arrows indicate paths to follow when conditions are not satisfied. Finally, the blue arrows represent the normal flow of the diagram.
Figure 8. General scheme of sMODiTS. Green arrows indicate paths to follow when the conditions are satisfied. Red arrows indicate paths to follow when conditions are not satisfied. Finally, the blue arrows represent the normal flow of the diagram.
Preprints 109405 g008
Preprints 109405 g009
Figure 9. Prediction power reached by (a) Márquez-Grajales et al.[33] and (b) sMODiTS. The color bars represent the absolute discrepancy between the two approaches regarding prediction error.
Figure 9. Prediction power reached by (a) Márquez-Grajales et al.[33] and (b) sMODiTS. The color bars represent the absolute discrepancy between the two approaches regarding prediction error.
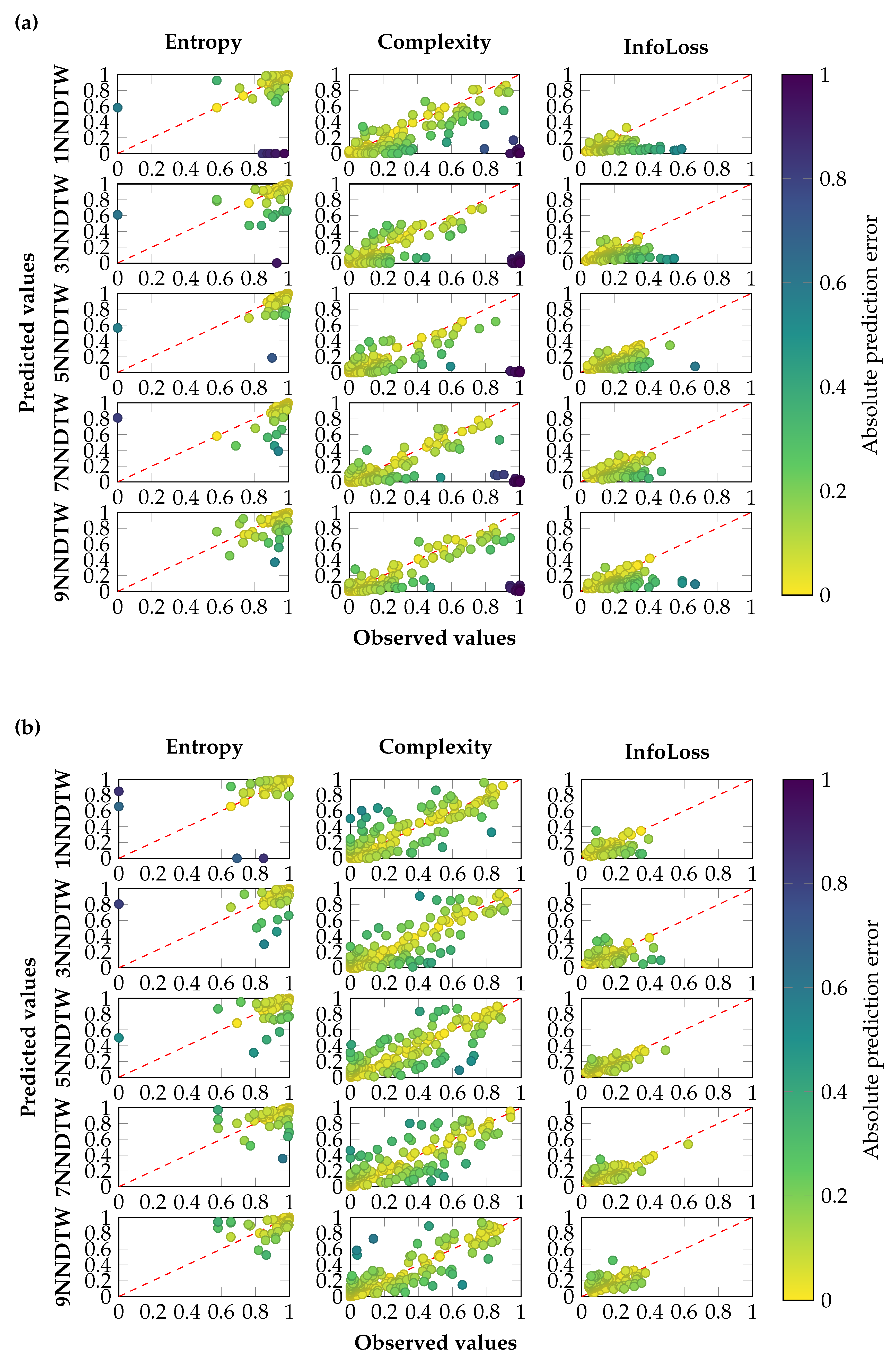
Preprints 109405 g009
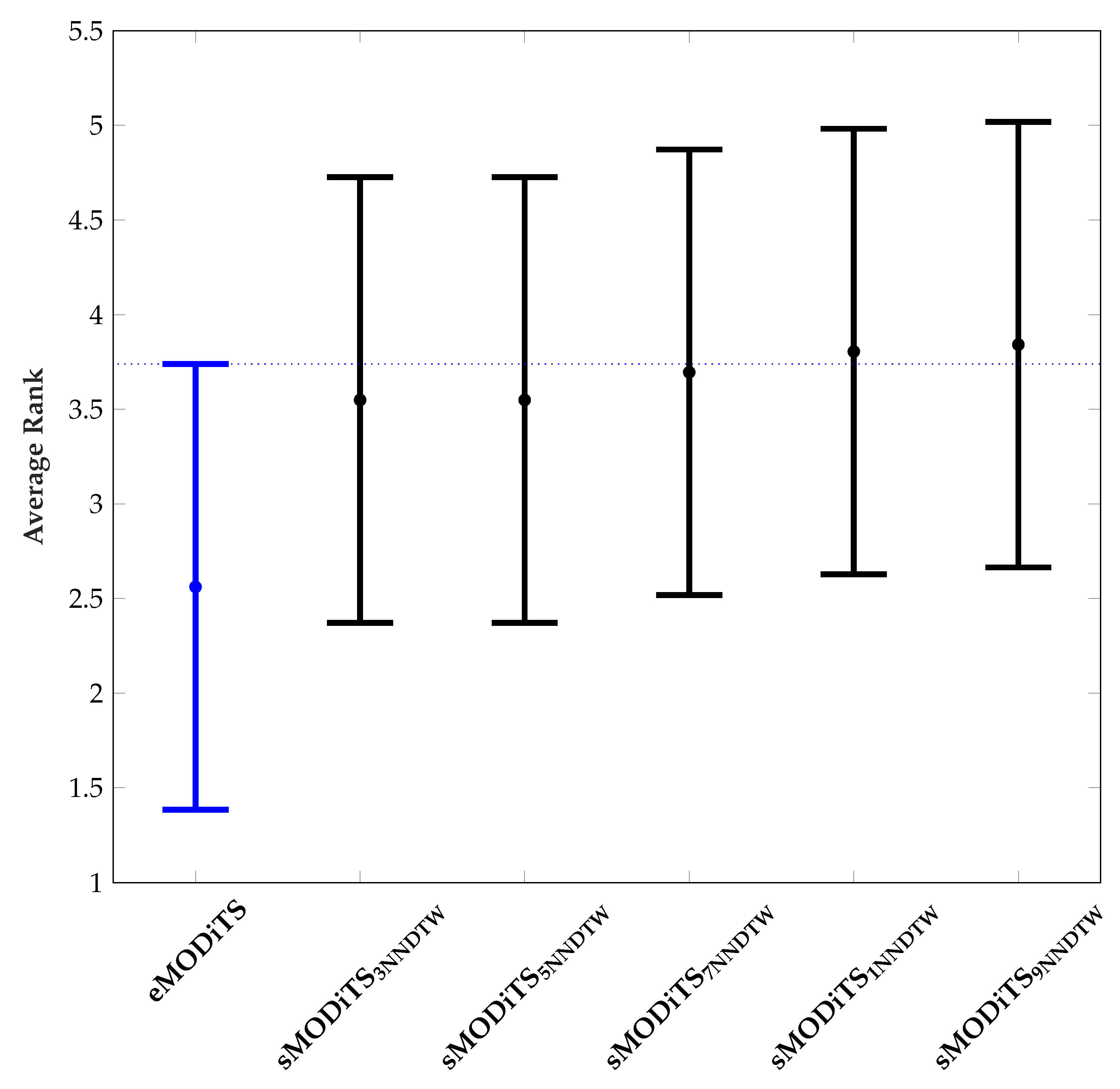
Preprints 109405 g010
Figure 10. Statistical comparison results between eMODiTS and every version of sMODiTS. Friedman test and Nemenyi post hoc were employed to perform this analysis with a 95%-confidence level.
Figure 10. Statistical comparison results between eMODiTS and every version of sMODiTS. Friedman test and Nemenyi post hoc were employed to perform this analysis with a 95%-confidence level.
Preprints 109405 g010
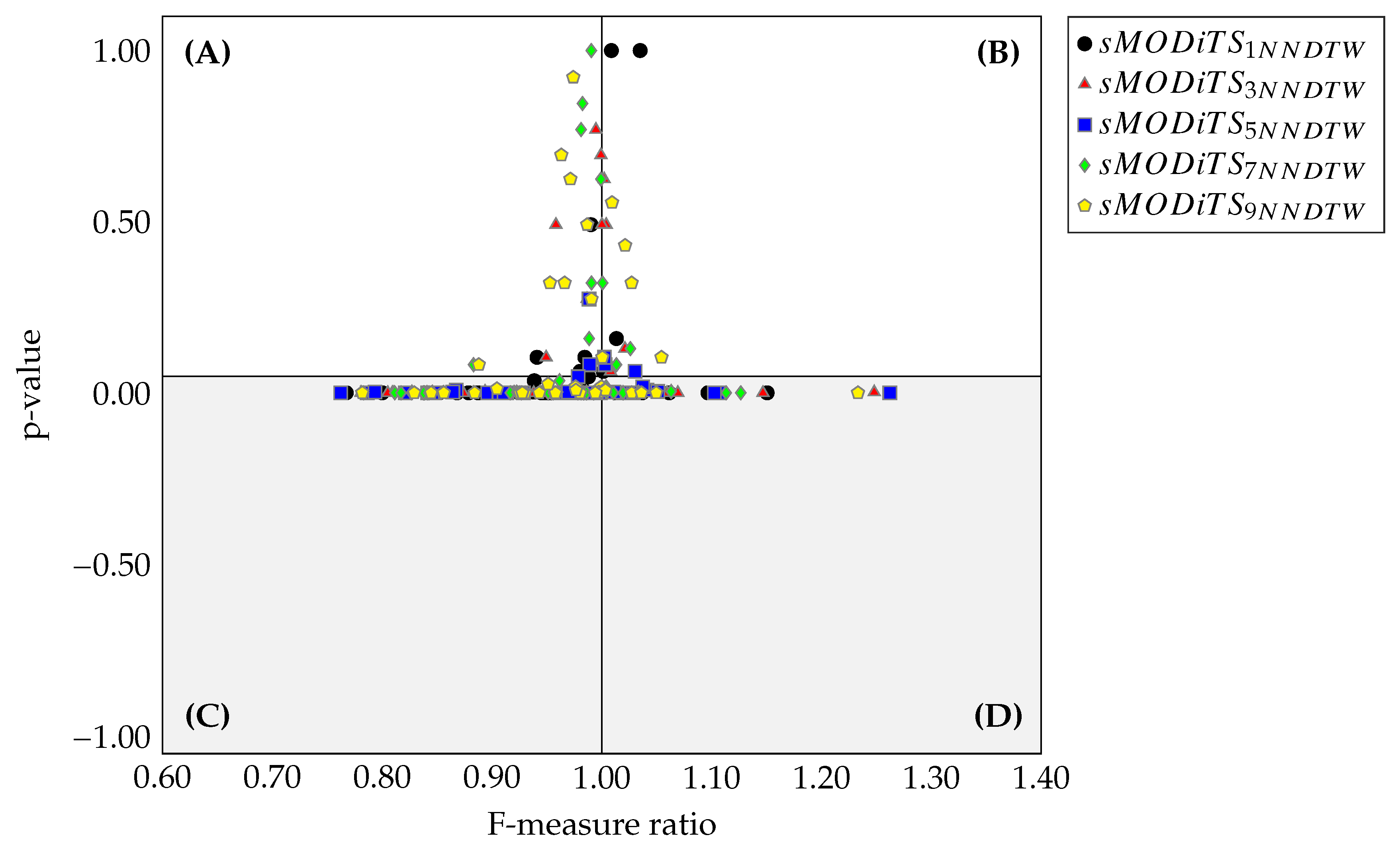
Preprints 109405 g011
Figure 11. Statistical results of comparing eMODiTS and sMODiTS by the Texas Sharpshooter plot and the Wilcoxon Rank Sum Test with a 95% confidence. Regions (A) and (C) determine the regions the eMODiTS approach outperforms sMODiTS regarding the F measure. On the other hand, regions (B) and (D) determine the regions where the sMODiTS approach outperforms eMODiTS. Finally, regions (C) and (D) are zones where the Wilcoxon Rank Sum Test showed a significant difference, and (A) and (B) are the opposite.
Figure 11. Statistical results of comparing eMODiTS and sMODiTS by the Texas Sharpshooter plot and the Wilcoxon Rank Sum Test with a 95% confidence. Regions (A) and (C) determine the regions the eMODiTS approach outperforms sMODiTS regarding the F measure. On the other hand, regions (B) and (D) determine the regions where the sMODiTS approach outperforms eMODiTS. Finally, regions (C) and (D) are zones where the Wilcoxon Rank Sum Test showed a significant difference, and (A) and (B) are the opposite.
Preprints 109405 g011
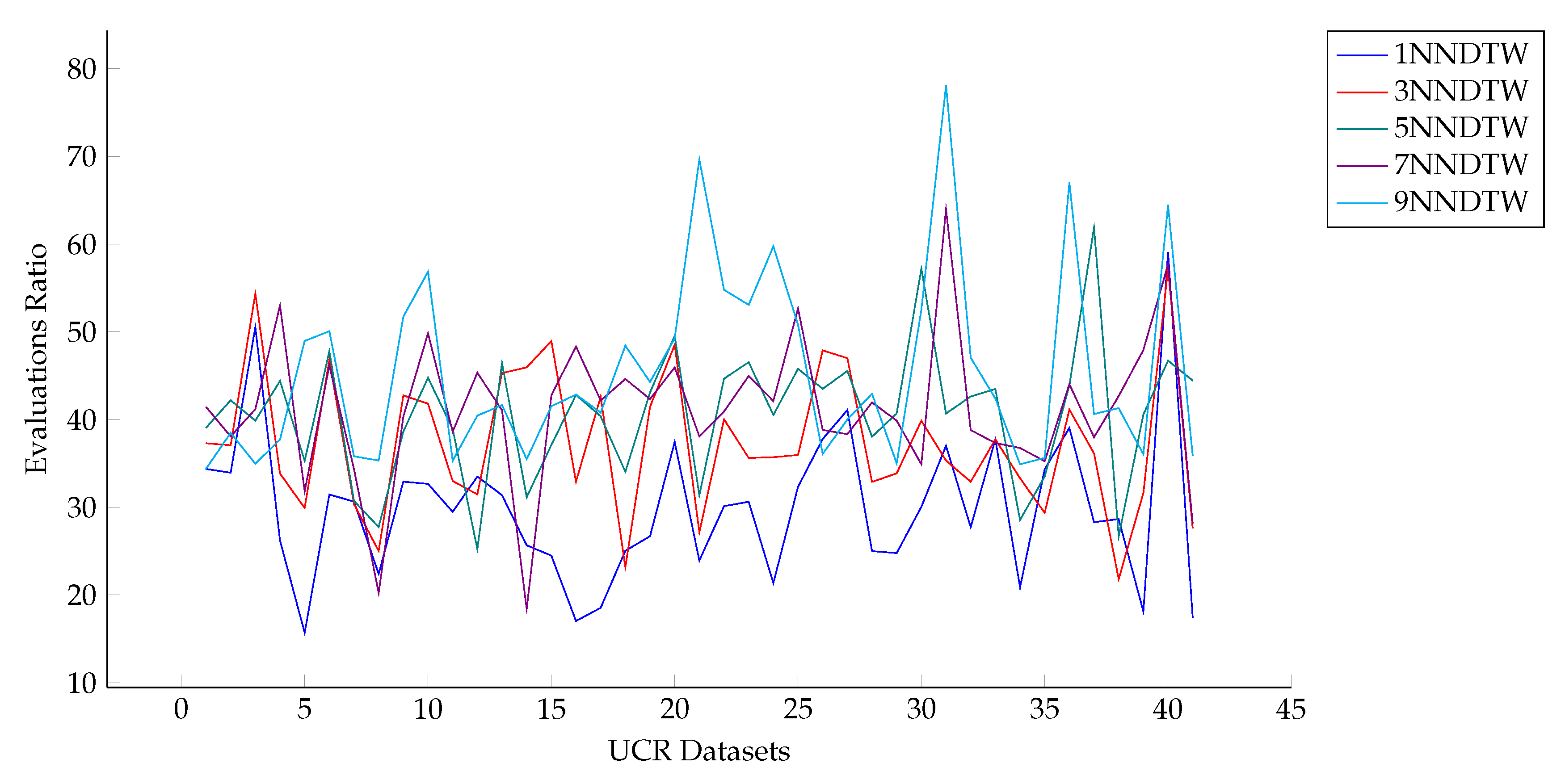
Preprints 109405 g012
Figure 12. Percentage reduction of the number of evaluations reached by sMODiTS compared to eMODiTS.
Figure 12. Percentage reduction of the number of evaluations reached by sMODiTS compared to eMODiTS.
Preprints 109405 g012
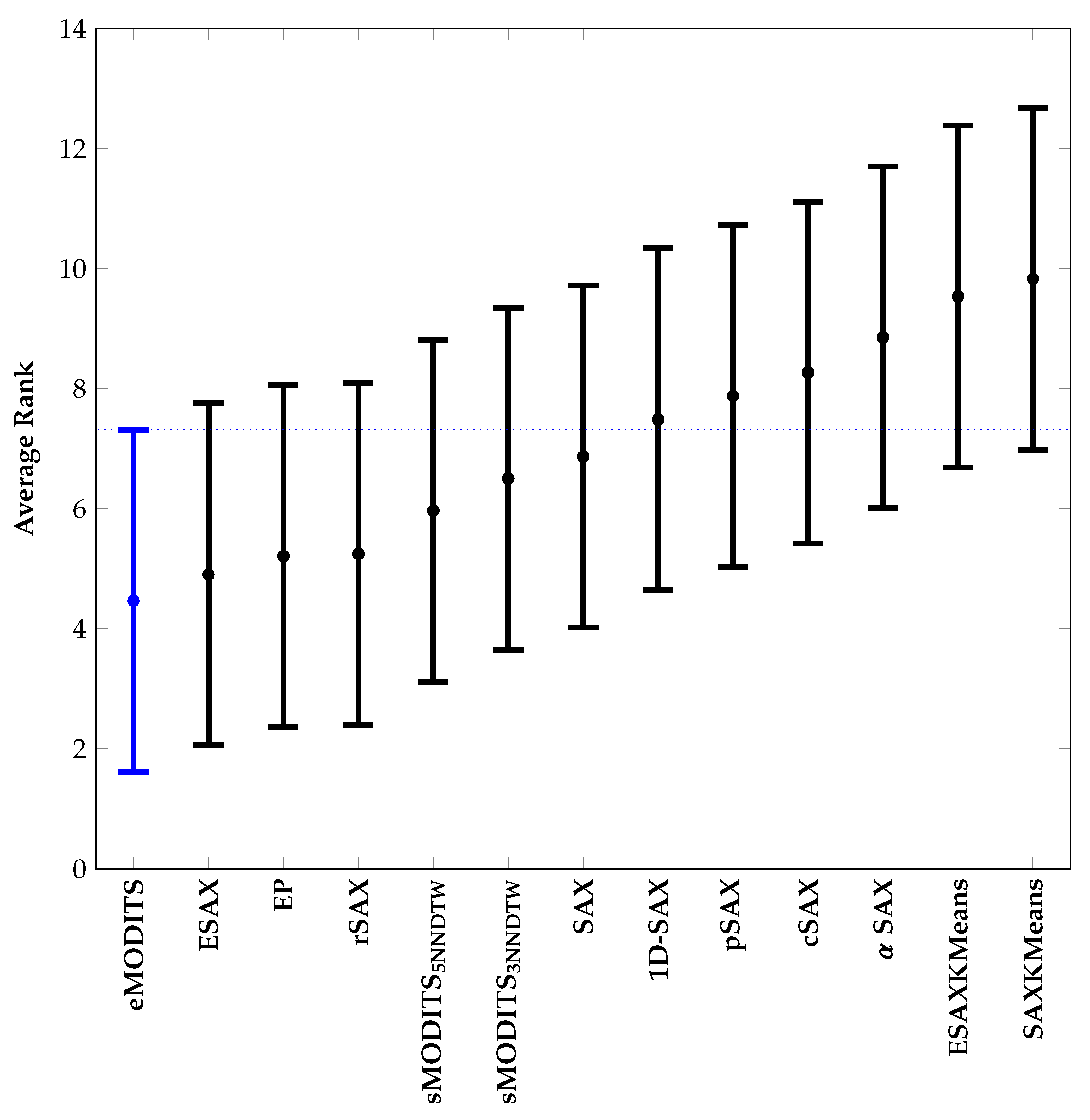
Preprints 109405 g013
Figure 13. Statistical comparison results between two versions of sMODiTS and ten SAX-based approaches. eMODiTS was used as a reference. Friedman test and Nemenyi post hoc were employed to perform this analysis with a 95%-confidence level.
Figure 13. Statistical comparison results between two versions of sMODiTS and ten SAX-based approaches. eMODiTS was used as a reference. Friedman test and Nemenyi post hoc were employed to perform this analysis with a 95%-confidence level.
Preprints 109405 g013
Table 1. Datasets used in this research. This data was obtained from [75]. The ‘Abbrev’ column is the authors’ suggested abbreviation for the database name.
Table 1. Datasets used in this research. This data was obtained from [75]. The ‘Abbrev’ column is the authors’ suggested abbreviation for the database name.
Preprints 109405 i001
Preprints 109405 i002
Table 2. Parameter setting for eMODiTS and sMODiTS. The values were selected according to the reported in [20].
Table 2. Parameter setting for eMODiTS and sMODiTS. The values were selected according to the reported in [20].
Parameter Value
Population size 100
Generation number 300
Independent executions number 15
Crossover rate 80%
Mutation rate 20%
Table 3. Average prediction metrics achieved by Márquez-Grajales et al. [33] and sMODiTS. Bold numbers represent the best values for each measure.
Table 3. Average prediction metrics achieved by Márquez-Grajales et al. [33] and sMODiTS. Bold numbers represent the best values for each measure.
Preprints 109405 i003
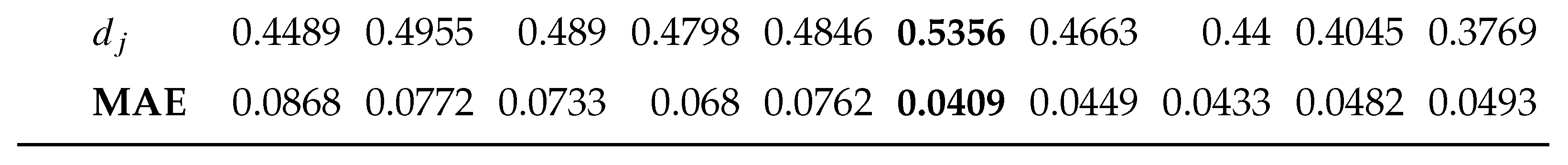
Preprints 109405 i004
Table 4. Analysis results of the Pareto fronts obtained by eMODiTS and each version of sMODiTS using the performance measures HVR, Generational Distance (GD), coverage of the eMODiTS over sMODiTS ( C → ), coverage the sMODiTS over eMODiTS ( C ← ), and convergence index (CI). The values displayed represent the average of each measure for all test databases. In addition, values in bold indicate the maximum values for each metric, while values in italics indicate the minimum values.
Table 4. Analysis results of the Pareto fronts obtained by eMODiTS and each version of sMODiTS using the performance measures HVR, Generational Distance (GD), coverage of the eMODiTS over sMODiTS ( C → ), coverage the sMODiTS over eMODiTS ( C ← ), and convergence index (CI). The values displayed represent the average of each measure for all test databases. In addition, values in bold indicate the maximum values for each metric, while values in italics indicate the minimum values.
Preprints 109405 i005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated