Submitted:
24 July 2024
Posted:
26 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
The Standard Security System
2. A Novel Security System on the Internet of Things
3. Modified Elliptic Curve Cryptography Algorithm
- Step 1. Mapping the message on the curve.
- Step 2. Generate all the points based on the first point (point doubling & point adding).
- Step 3. Calculate the private key:
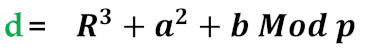
- Step 4. Calculate the public key,
- Step 5. Calculate K value:
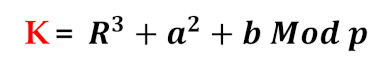
- Step 6. Apply the encryption equation.
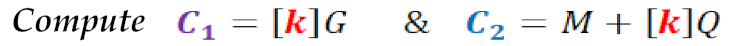
- Step 7. Send that ciphertext to the destination.
- Step 8. Receive that ciphertext.
-
Step 9. Apply the decryption equation.
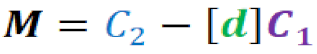
- Step 10. Mapping the message back.
Full Educational Example


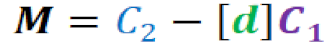
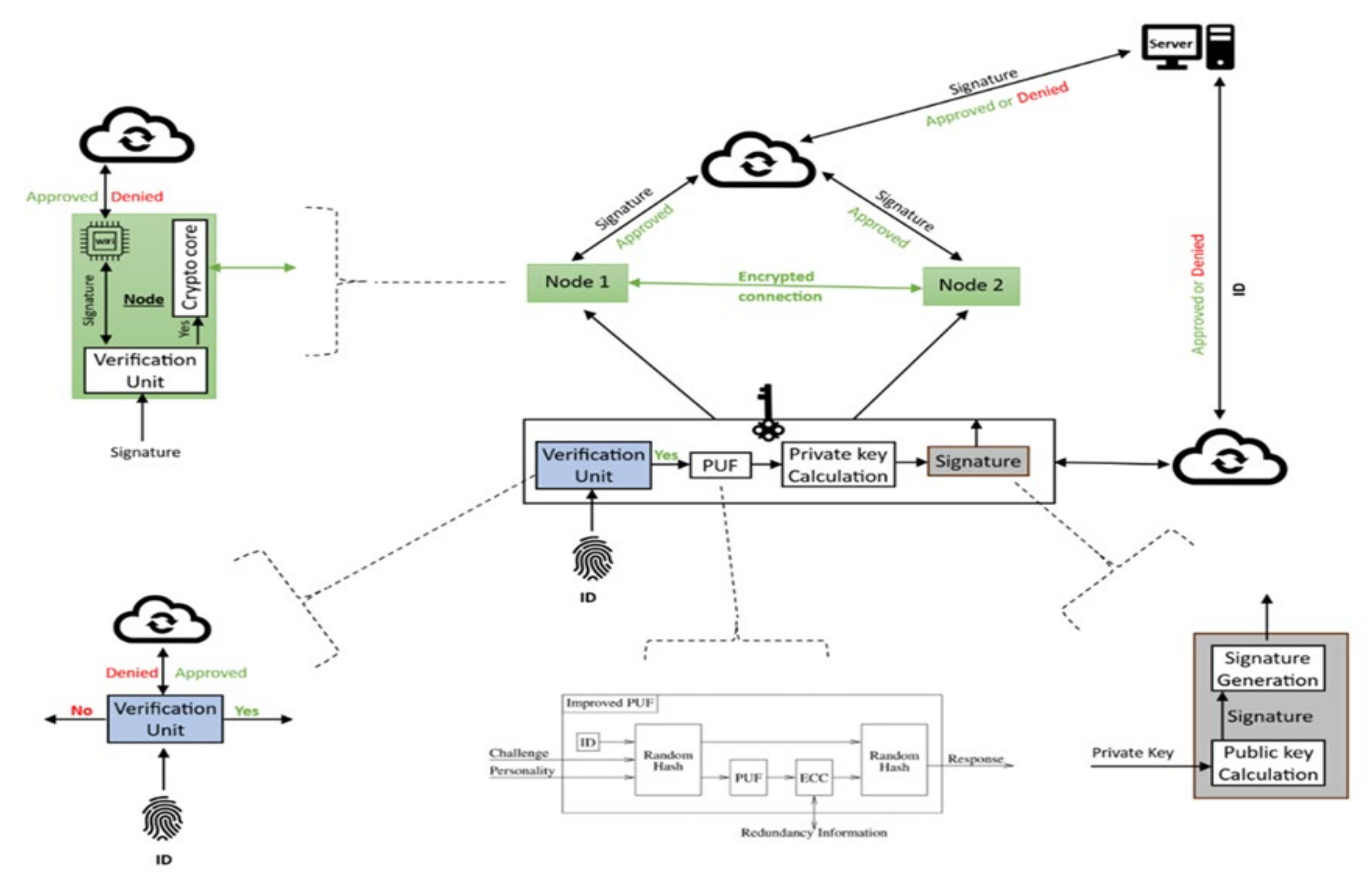
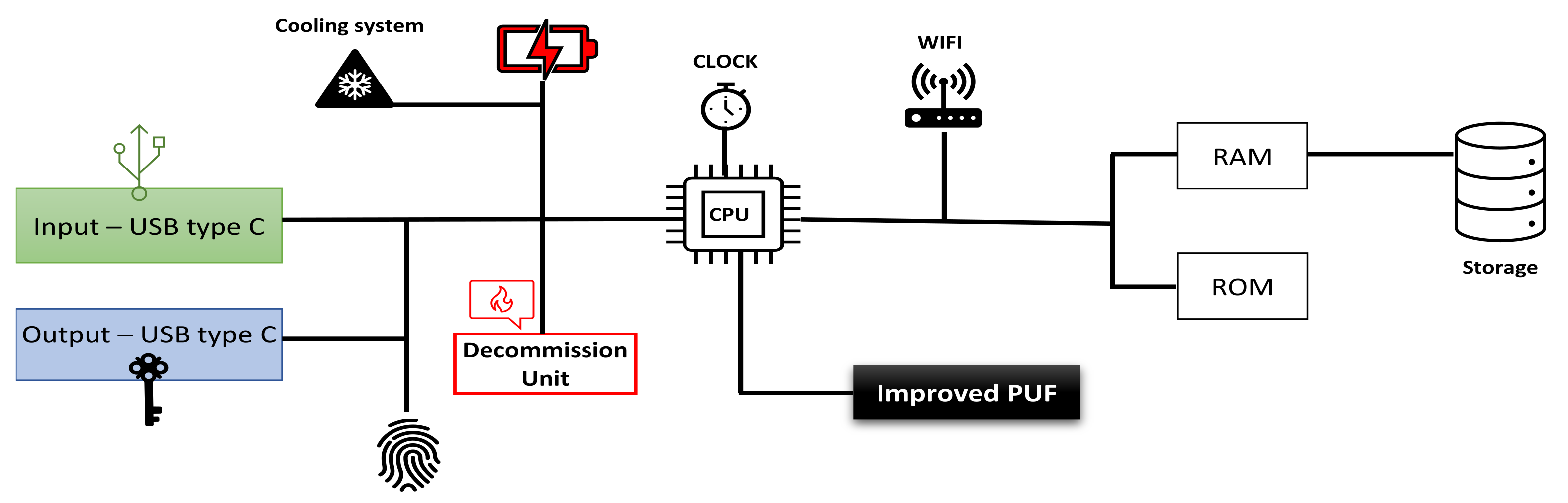
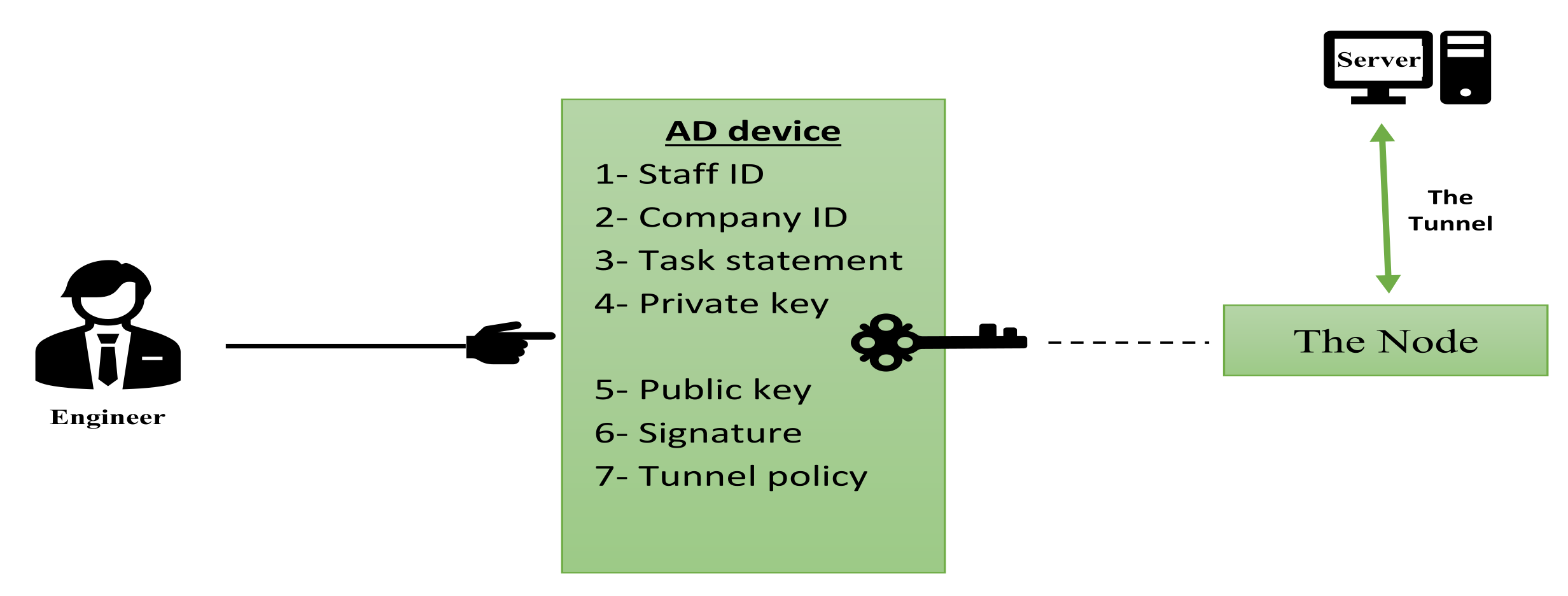
4. The Authority Device (AD)
The Authority Device Structure
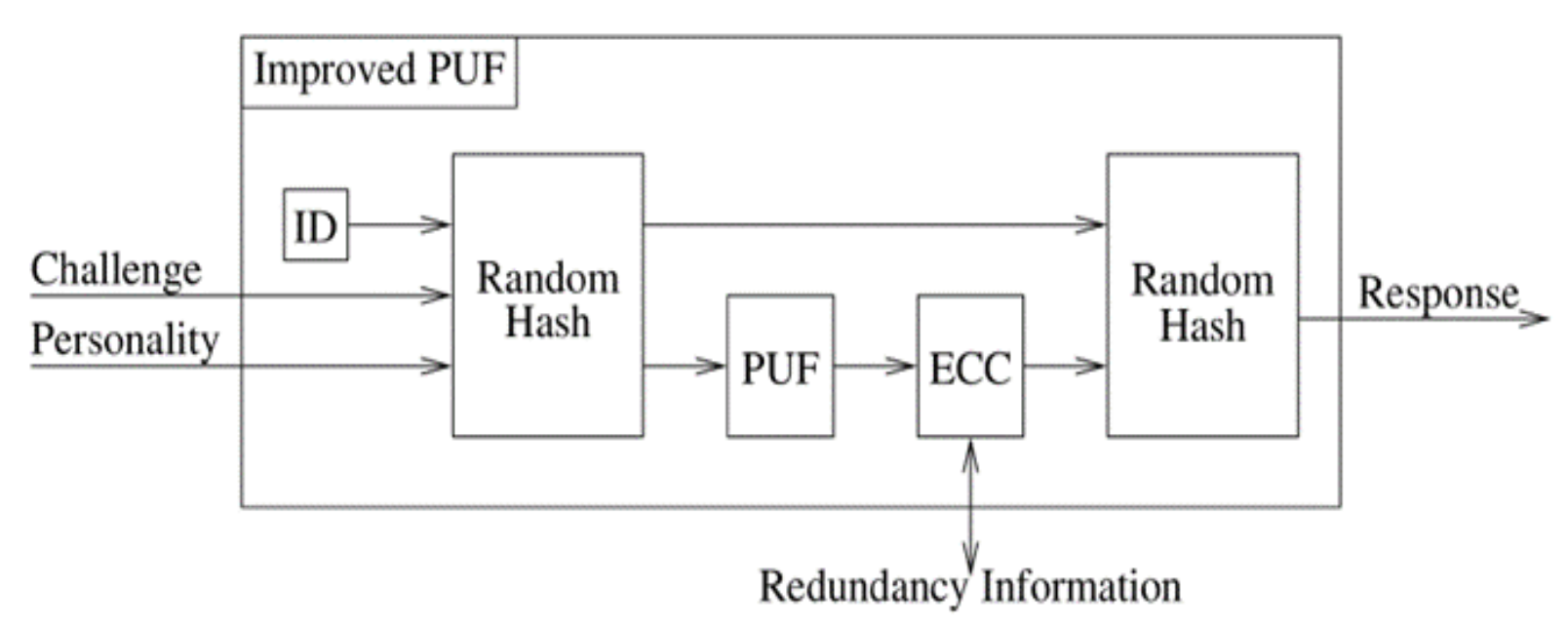
- Improved PUF device: This device was developed in the last decade to generate an advance, unclonable random number for each challenge to calculate the private key using the improved ECC algorithm. That number is significantly important on this innovative system. Because it provides an additional layer protection.
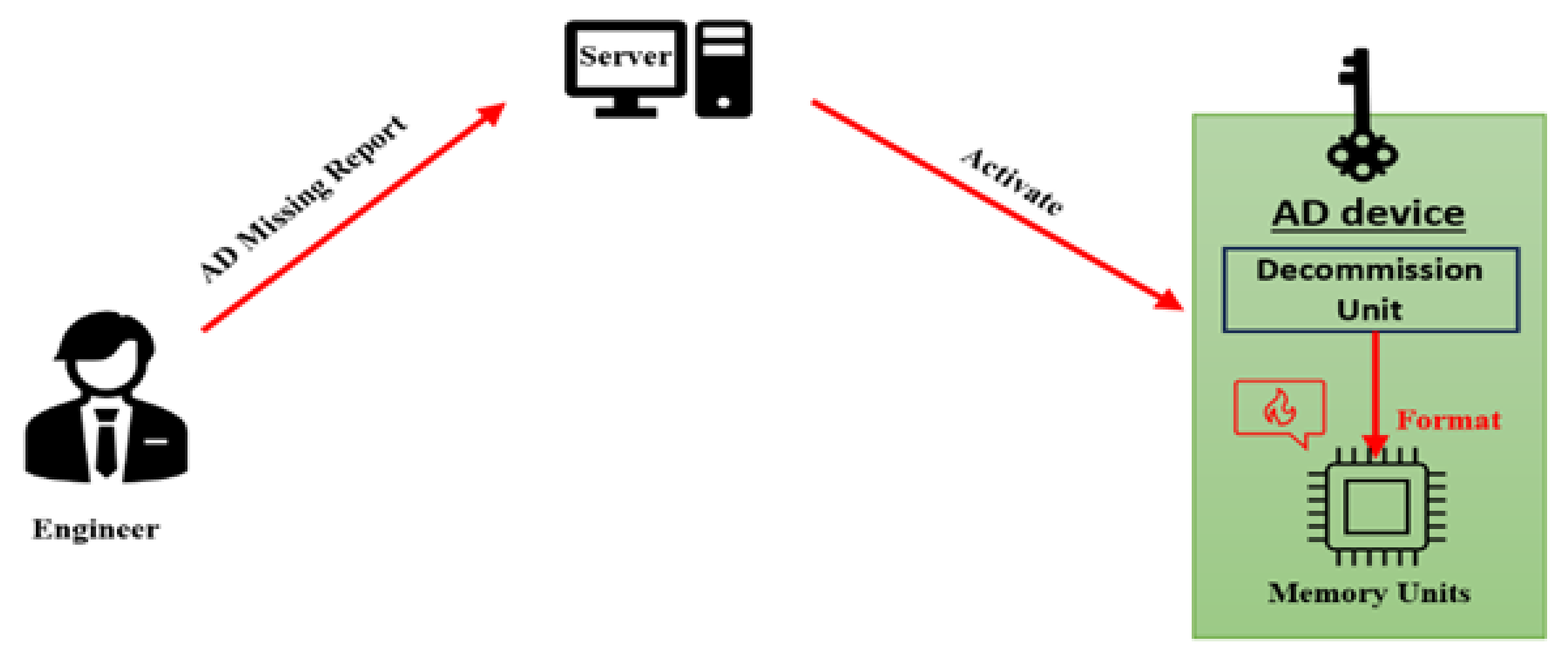
- Decommission unit: This unit’s task is destroying the whole motherboard with all other components by sending high voltage suddenly. This unit is acting in an emergency only when the AD devices is lost or intentionally hidden. It activates directly from the server or automatically once the task statement period has expired. The direct order comes from the server when the technical engineer inform his manager of the missing device; Otherwise, he should promptly return the AD device back to company once his mission has finished immediately. because if not the decommission unit will be activated from itself once the mission period has expired. For the security purposes the decommission unit will destroy all the device’s parts if the device does not return safely to company at the appropriate time.
- Fingerprint reader: This unit provides an additional protection layer on the system. The unit’s task is preventing intruder to use the AD device. Therefore, this device should verify the engineer identification first before begin activating all nodes in the system.
- Central Processing Unit CPU: It is the processor which is essential to processing the system instructions to drive the whole device. Basically, the CPU is the main crucial integrated circuitry chip in all devices. Control unit with arithmetic logical unit working together to interpreting the most of device commands.
- Storage units: Random Access Memory RAM is significant part to store the security info comes from the solid-state drive or storage on it before transmitting it to nodes system. Read only memory task is storing the system essential instructions.
- Power supply unit PSU: It is the unique power source which is needed to operate the motherboard and all other the AD device parts.
- Cooling system: That system’s mission is preserving the temperature in the desired range to prevents overheating on the device which generated by electronic components. Furthermore, the cooling system works to enhance device performance by removing overheating, which let the system operating at higher speed.
- Wi-Fi network: Wireless Fidelity is a significant part in this system using to associate AD device with the server by VPN tunnel which will be created over the internet. Figure 4 displays the AD device structure and shows all the device parts.
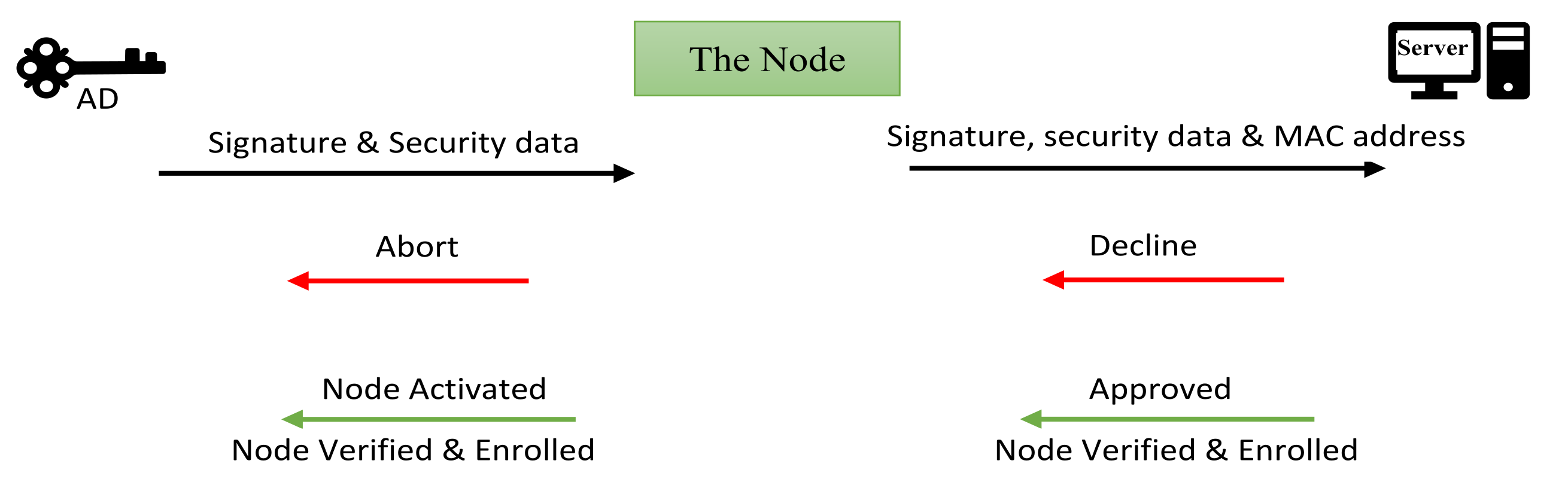
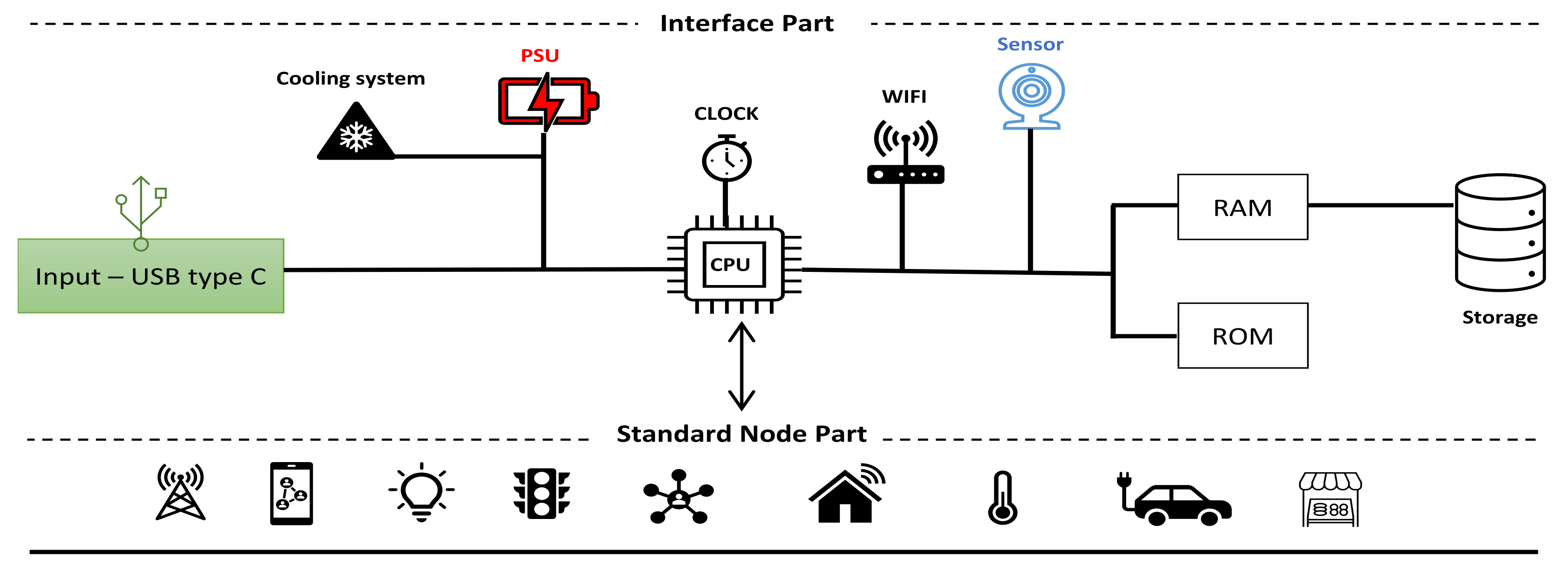
5. The Node Device
5.1. The Node Structure
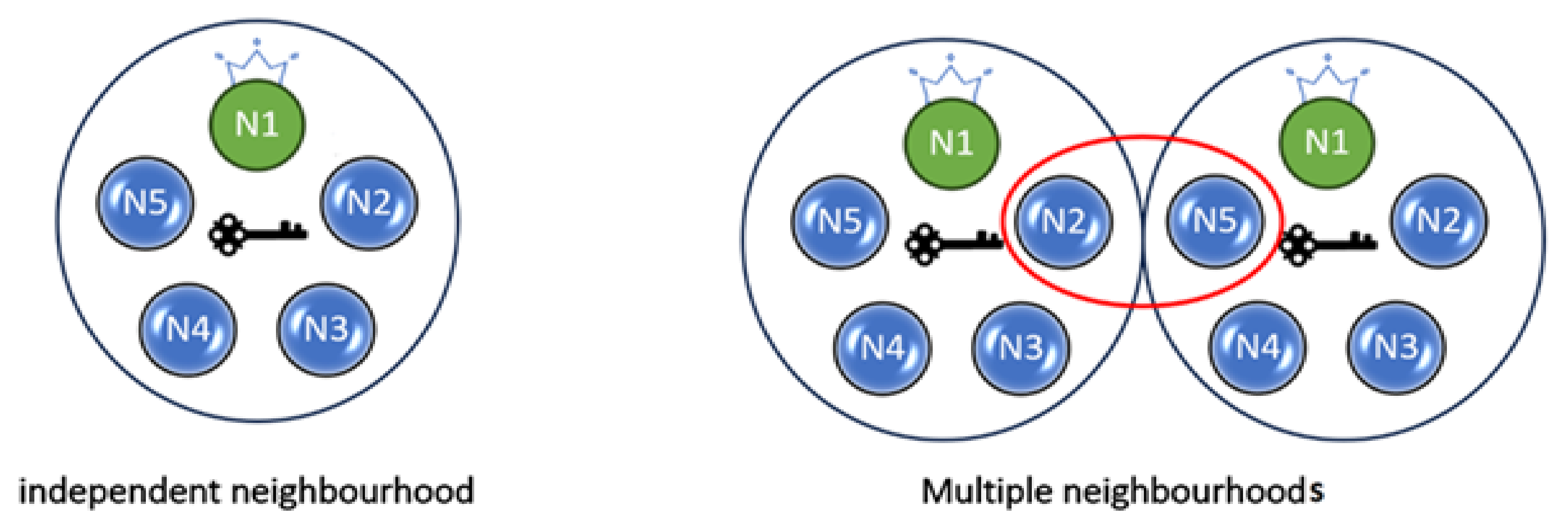
5.2. The Node Neighborhood
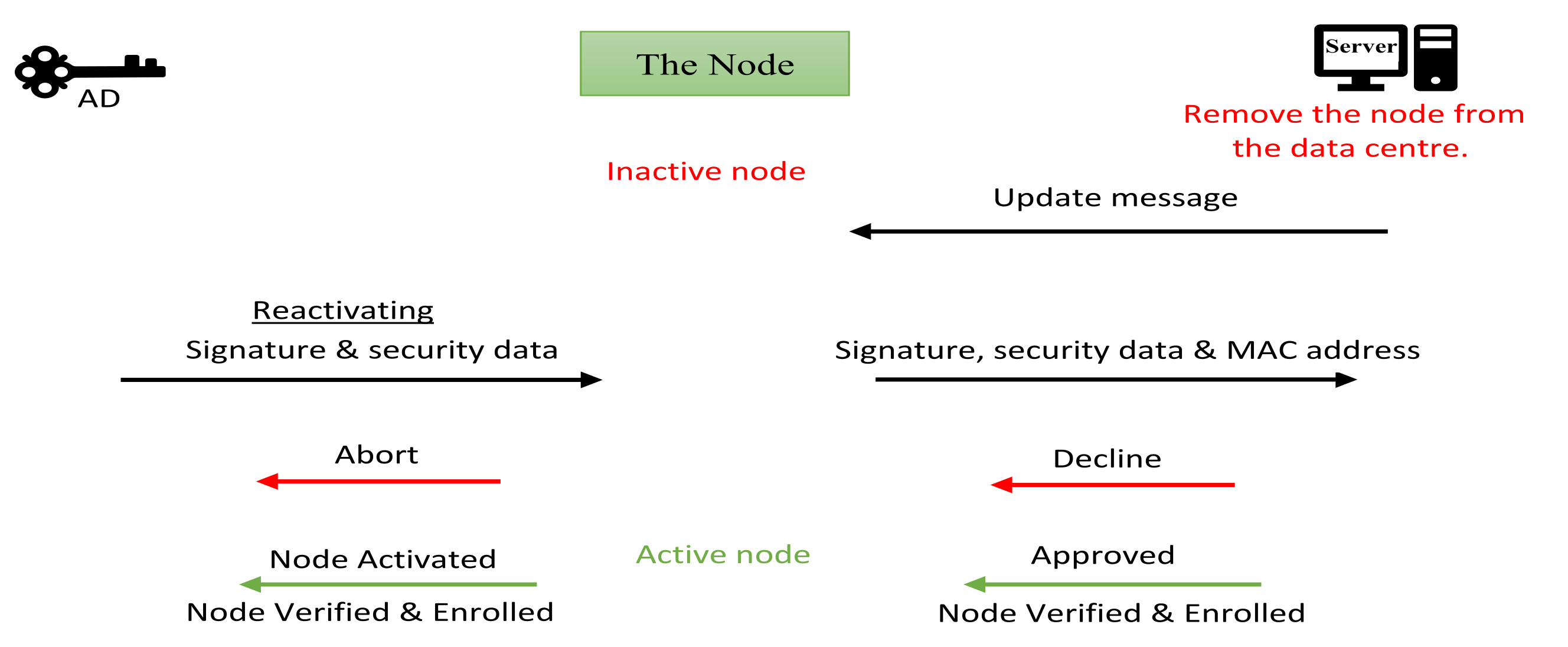
5.3. The Node Decommission
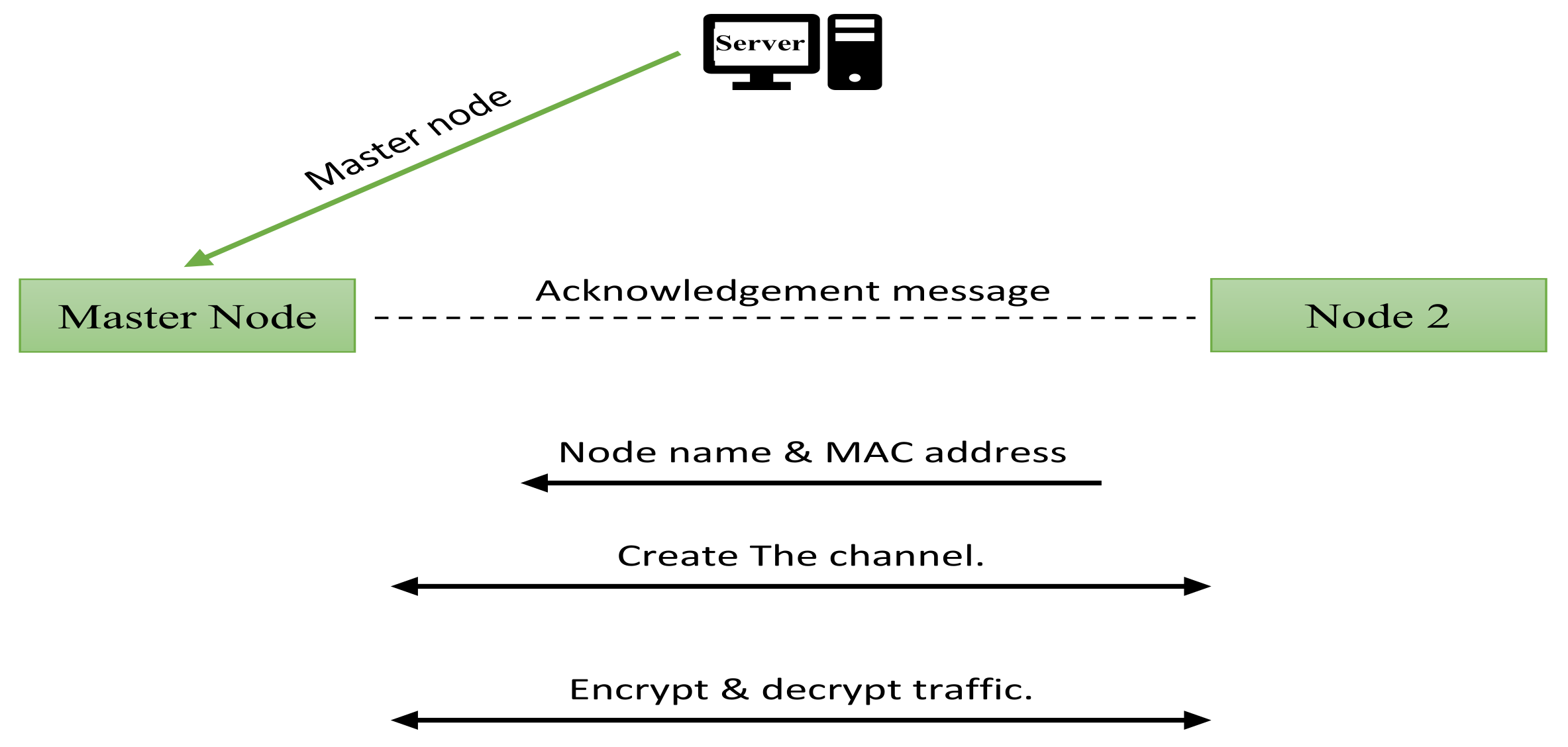
5.4. Multiple Nodes System
6. The System Reliability and Integrity
6.1. The System Reliability Features
6.2. The Authority Device, Decommission Unit
7. Implementing the Modified ECC Algorithm on Internet of Things
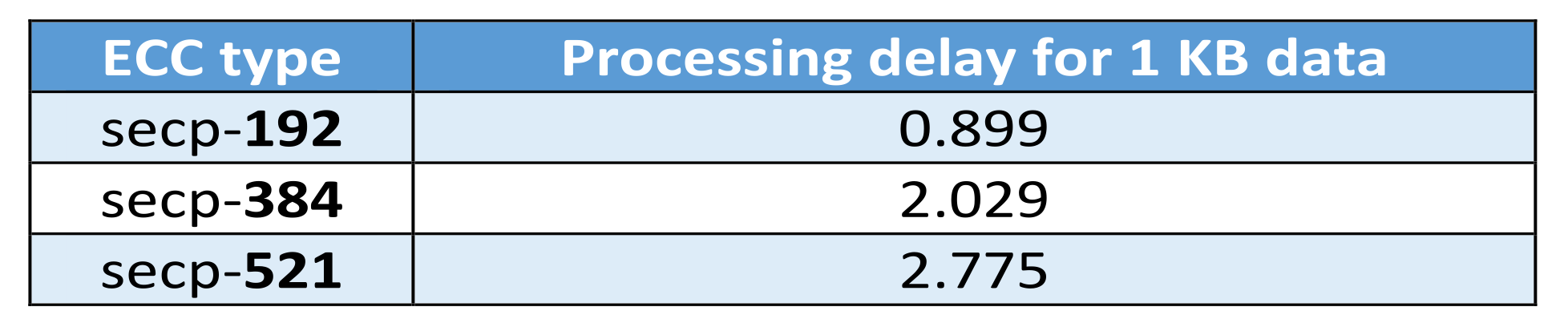
7.1. Applying Elliptic Curve Cryptography Algorithm on the Internet of Things
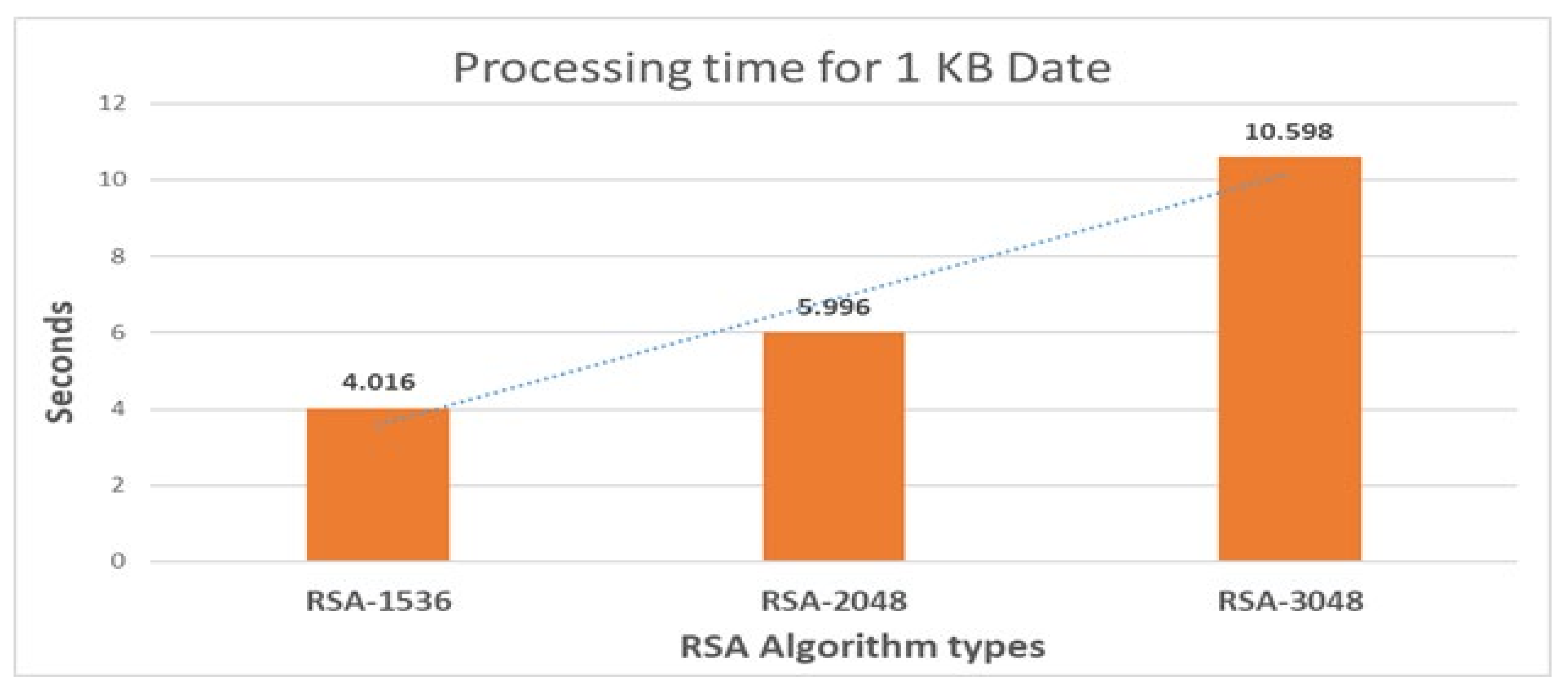
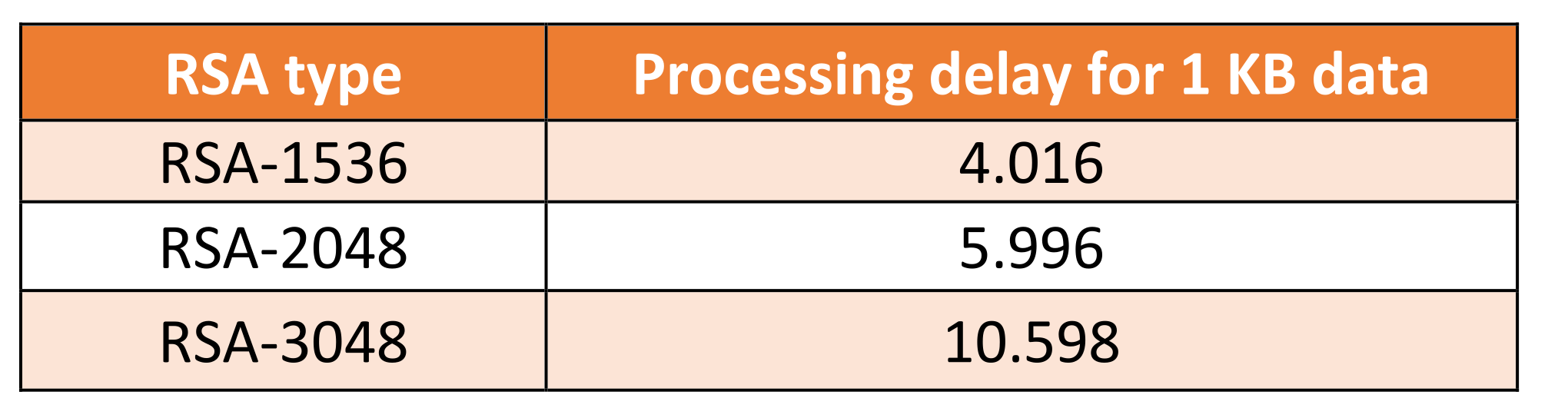
7.2. Applying Rivest Shamir Adleman Algorithm on the Internet of Things
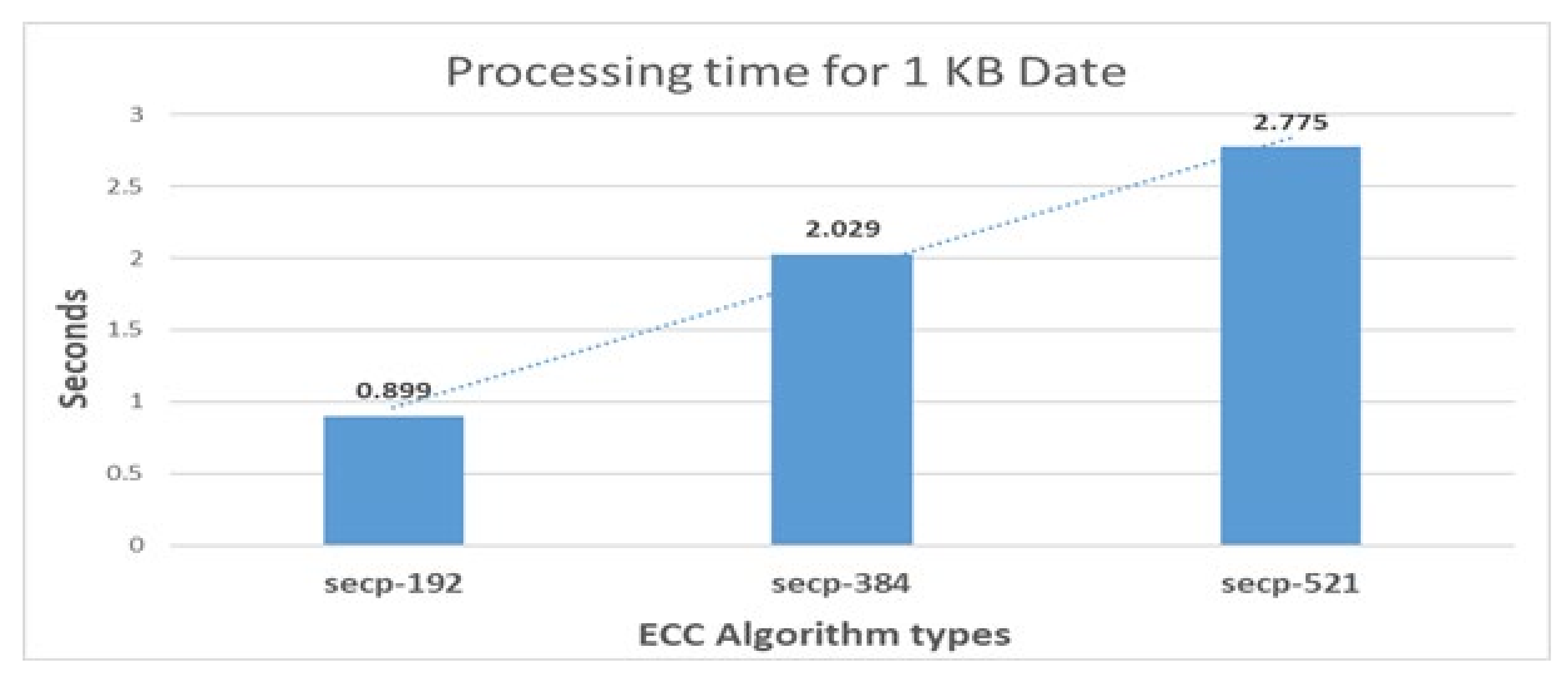
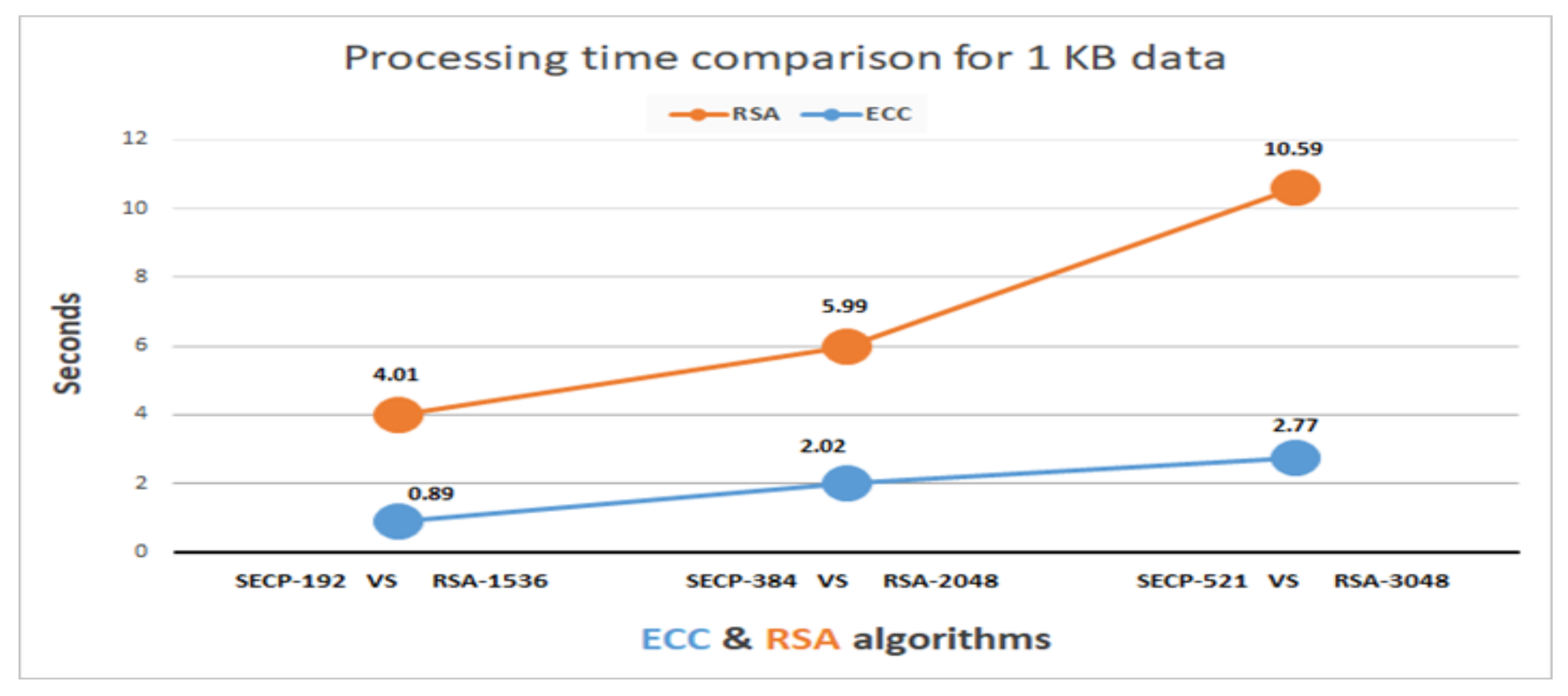
7.3. The Comparison Results between ECC and RSA Algorithms
8. A Comparison Study between the Standard and the Novel Security System
9. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Controlled Physical Random Function .Blaise Gassend, Dwaine Clarke, Marten van Dijk † and Srinivas Devadas. 13 Dec. 2002, 18th Annual Computer Security Applications Conference, 2002. Proceedings., pp. 149-160.
- Goutsos, Konstantinos.Physical Unclonability Framework forthe Internet of Things. The UK - Newcastle : Newcastle University, 2019.
- KINZA SHAFIQUE, BILAL A. KHAWAJA, FARAH SABIR, SAMEER QAZI, MUHAMMAD MUSTAQIM. Internet of Things (IoT) for Next-Generation Smart Systems: A Review of Current Challenges, Future Trends and Prospects for Emerging 5G-IoT Scenarios. s.l. : IEEE Acess, 2020.
- Internet of Things security: A survey.Fadele Ayotunde Alabaa, Mazliza Othman, Ibrahim Abaker Targio Hashem, Faiz Alotaibi. 2017, Journal of Network and Computer Applications, Vol. 88, pp. 10-28.
- András Varga, Rudolf Hornig.AN OVERVIEW OF THE OMNeT++ SIMULATION ENVIRONMENT. Budapest, Hungary : s.n., 2016.
- (Ed.), Phillip Rogaway.Advances in Cryptology – Crypto 2011. Santa Barbara, CA, USA : Springer, August 14-18, 2011.
- Niels Ferguson, Bruce Schneier, Tadayoshi Kohno.Cryptography Engineering: Design Principles and Practical Applications. s.l. : Wiley 1st edition, March 2010.
- Elliptical Curve Cryptography Design Principles.J VenkataGiri, Dr. ASR Murty. 2021. International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT).
- Analysis of Encryption Algorithms Proposed for Data Security in 4G and 5G Generations.Khalid Fadhil Jasim 1*, Kayhan Zrar Ghafoor2,3, and Halgurd S. Maghdid. 2022. ITM Web of Conferences 42, 01004 (2022).
- Analysis of Standard Elliptic Curves for the Implementation of Elliptic Curve Cryptography in Resource-Constrained E-commerce Applications. Javed R. Shaikh, Maria Nenova, Georgi Iliev and Zlatka Valkova-Jarvis. Sofia, Bulgaria : s.n., 2017. IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems (COMCAS).
- Elliptic Curve Cryptosystems.Koblitz, Neal. 1987, MATHEMATICS OF COMPUTATION, Vol. 48, pp. 203-209.
- Constandinos X. Mavromoustakis, Jordi Mongay Batalla, George Mastorakis.Internet of Things (IoT) in 5G Mobile Technologies. Switzerland : Springer International Publishing Switzerland , 2016.
- Lightweight and Secure PUF Key Storage Using Limits of Machine Learning.Meng-Day, Yu1, David M’Raihi, Richard Sowell,. 2011, International Association for Cryptologic Research, p. 16.
- Brown, Daniel R. L.SEC 1: Elliptic Curve Cryptography. s.l. : Standards for Efficient Cryptography, 2009.
- SEC 2 : Recommended Elliptic Curve Domain Parameters. s.l. : Standards for Efficient Cryptography, 2010.
- Buckley, Eoin. SEC 4 Elliptic Curve Qu-Vanstone Implicit Certificate Scheme (ECQV) - draft 2. s.l. : Standards for Efficient Cryptography, 2014.
- Silicon Physical Random Functions.Blaise Gassend, Dwaine Clarke, Marten vandijk, and Srinivas Devadas. November 2002. Proceedings of the 9th ACM conference on Computer and communications security.
- Implementation of ElGamal Elliptic Curve Cryptography Over Prime Field Using C.Debabrat Boruah, Monjul Saikia. India : s.n., 2014. ICICES2014 - S.A.Engineering College, Chennai, Tamil Nadu, India.
- The State of Elliptic Curve Cryptography.NEAL KOBLITZ, ALFRED MENEZES, SCOTT VANSTONE. 2000, Kluwer Academic Publishers, Boston. Manufactured in The Netherlands, Vol. 19, pp. 173–193.
- Towards 5G Security Analysis against Null Security Algorithms Used in Normal Communication.Run Zhang,1 WenAn Zhou ,1 and Huamiao Hu2. 2021, Hindawi Security and Communication Networks, p. 15.
- Buckley, Eoin.SEC 4: Elliptic Curve Qu-Vanstone Implicit Certificate draft - 1. s.l. : Standards for Efficient Cryptography, 2013.
- AES, DES, and RSA: A Comprehensive Study on Data Security Mechanisms.Kapoor, Aditya. 2018, IJCAM Research Consultant, Indore , India, p. 9.
- Maletsky, Kerry.RSA vs ECC Comparasion for Embedded system. s.l. : Microchip, 2020.
- Shaheen, Mai Helmy. Hybrid Encryption Algorithms Over Wireless Communication Channels. Oxon : A SCIENCE PUBLISHERS BOOK, 2022.
- Advances in Security Technology, Security Analysis of “A Novel Elliptic Curve Dynamic Access Control System”. Haeng-kon Kim, Tai-hoon Kim, Akingbehin Kiumi. China : s.n., 2008. International Conference SecTech.
- Cryptographic Analysis of DES and RSA Algorithm Using the AVISPA Tool andWSN.Shailendra Singh Gaur, Megha Gupta, and Gautam Gupta. 2021, Proceedings of 3rd International Conference on Computing Informatics and Networks, Vol. 167.
- Tom St Denis, Simon Johnson.Cryptography for Developers. s.l. : Syngress, 2006.
- Sumit Singh Dhanda, Brahmjit Singh, and Poonam Jindal.Elliptic Curve Cryptography: A Software Implementation. India : Department of Electronics and Communication Engineering, National Institute of Technology, 2021.
- Encoding And Decoding of a Message in the Implementation of Elliptic Curve Cryptography.Padma Bh, D.Chandravathi , P.Prapoorna Roja. 2010, (IJCSE) International Journal on Computer Science and Engineering, Vol. 02, p. 05.
- Burt Kaliski, Terry S. Arnold,.IEEE Standard Specifications for Public-Key Cryptography. New York : American National Standards Institute, 2000.
 |
 |
| Standard system | Novel system | |
| Secret keys | plaintext | Encrypted |
| System Safety | Trust Engineers | Zero Trust Network Access |
| Hardware component | None | Improved PUF |
| Authority device | None | Yes |
| Key generation method | Good | Advanced |
| Keys distribution | Manually (weak) | Automatically (strong) |
| Encryption | Strong | Advanced |
| Cryptography algorithm type | Ratchet (good) | Modified ECC (advanced) |
| Authentication | Manually (weak) | Automatically (strong) |
| Authorisation | Individually (weak) | Centrally (strong) |
| Nodes decommission task | Individually (weak) | Centrally (strong) |
| Algorithm speed | Fast | Faster |
| System Reliability | Strong | Advanced |
| System Installation | Slow | Speed |
| System compatibility | Matched with current technology | Matched with current & coming technology |
| Environment | 4G, 5G | 5G & 6G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





