Prerpints.org logo
Preprint
Article

CuFP: An HLS Library for Customized Floating-Point Operators

This is a preprint, it has not been peer-reviewed.

Submitted:

17 June 2024

Posted:

18 June 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
High-Level Synthesis (HLS) tools have revolutionized FPGA application development by providing a more efficient and streamlined approach, significantly impacting digital design methodologies. Despite the capability of FPGAs to customize numerical representations in data paths, most HLS projects have focused on fixed-point precision, while floating-point representations remain limited to vendor-provided single, double, and half-precision formats. This paper proposes a customized floating-point library compatible with HLS to address these limitations. This library allows programmers to define the number of exponent and mantissa bits at compile time, providing greater flexibility and enabling the use of mixed precision. Moreover, this library includes optimized implementations of common components such as vector summation (VSUM), dot-product (DP), and matrix-vector multiplication (MVM). Results demonstrate that the proposed library reduces latency and resource utilization compared to vendor IP blocks, particularly in VSUM, DP, and MVM operations. For example, the MVM operation involving a 32x32 matrix, using vendor IP requires 22 clock cycles, whereas CuFP completes the same task in just 7 clock cycles, using approximately 60% fewer DSPs, 10% fewer LUTs, and 60% fewer FFs.
Keywords: 
  -  

1. Introduction

The High-Level Synthesis (HLS) approach is pivotal in making FPGA programming more accessible and significantly enhancing design productivity. HLS tools empower developers to describe digital system behaviors through high-level programming languages like C or C++, freeing them from low-level hardware details. This abstraction allows a focus on system-level functionality, leading to faster design iterations. Moreover, HLS tools automate various optimization processes, reducing manual effort and accelerating development cycles [1].
The latest HLS tools have built-in support for single- and double-precision floating-point types and operations [2]. There are various sources of floating-point IP available for FPGA designs. One option is to use IP core generators provided by vendors, such as the floating-point libraries from Xilinx [3] and Intel [4]. However, floating-point cores are encapsulated as "black-box" entities in HLS tools, and developers encounter limitations in accessing and modifying their internal configurations, which restricts their ability to fine-tune precision for specific applications [5,6,7]. Despite advancements in intra-cycle scheduling of combinational components, which deals with the scheduling of unified pipelined blocks in HLS, internal pipeline registers within IP blocks may still impact block-level scheduling and pose efficiency challenges, particularly in coordinating diverse operations within the pipeline to maximize throughput while meeting timing constraints [8].
In the register transfer level (RTL) design, it is relatively straightforward to specify custom-precision floating-point operations, and optimizing floating-point types can effectively reduce resource usage without compromising accuracy [9,10,11,12]. One of the works at the RTL level is proposed in [13], where floating-point operator entities receive general inputs that define floating-point types, and the data-path widths are established during the elaboration phase. Flopoco [14] stands out as a significant research effort at the RTL level and serves as a foundation for numerous other researches [15,16,17,18]. It focuses on efficient floating-point arithmetic implementations. In contrast, FPGA customization for floating-point operations is less explored in many HLS methodologies, especially compared to fixed-point representations. This is evident because HLS tools typically support a limited set of vendor-provided floating-point types, such as half-, single-, and double-precision. Some works focus on high-level, customized floating-point representations [15,19] but offer little control over certain hardware optimizations, such as latency or resource utilization.
These observations highlight the need for greater customization and flexibility in floating-point operations within HLS techniques to achieve optimal scheduling, efficient resource utilization and lower latencies. In that regard, minimizing latency can be a crucial target for such applications as hardware-in-the-loop (HIL) [11]. Many applications require extensive floating-point computations but suffer from high latency and excessive resource utilization without the full precision of standard floating-point formats [20,21,22]. Customized floating-point implementations, by tailoring precision and format, were shown to be a means to improve latency [10].
This paper introduces CuFP, an HLS-based library for customized floating-point operators. A key attribute of this HLS-based library is its flexibility, allowing users to customize floating-point types for their calculations, providing users with enhanced control over precision. Another significant contribution is the provision of dedicated operators, such as vector sum, dot-product, and matrix-vector multiplication operations, which are crucial for numerous applications. This integration sets this library apart from others. The proposed library significantly reduces latency and resource utilization for the aforementioned operators. CuFP is fully compatible with Xilinx tools via a command-line interface, enabling users to specify parameters and generate corresponding IP cores seamlessly, enhancing usability and facilitating efficient integration into FPGA designs. Incorporating CuFP into other projects is straightforward, as users can simply include a header file, ensuring effortless integration and user-friendly implementation. Its platform independence and open-source nature promote transparency and ease of debugging while maintaining performance levels1
The remainder of this paper is organized as follows: Section 2 presents an overview of floating-point numbers and explains some recent works that are related to customized floating-point numbers. In Section 3, the development flow is described in detail. This section explains a detailed implementation of the proposed method and dedicated operations. Section 4 presents the results for primary operations as well as dedicated operations compared to others. A discussion and conclusion are given in Section 5 and Section 6, respectively.

2. Background

2.1. Floating-Point Format

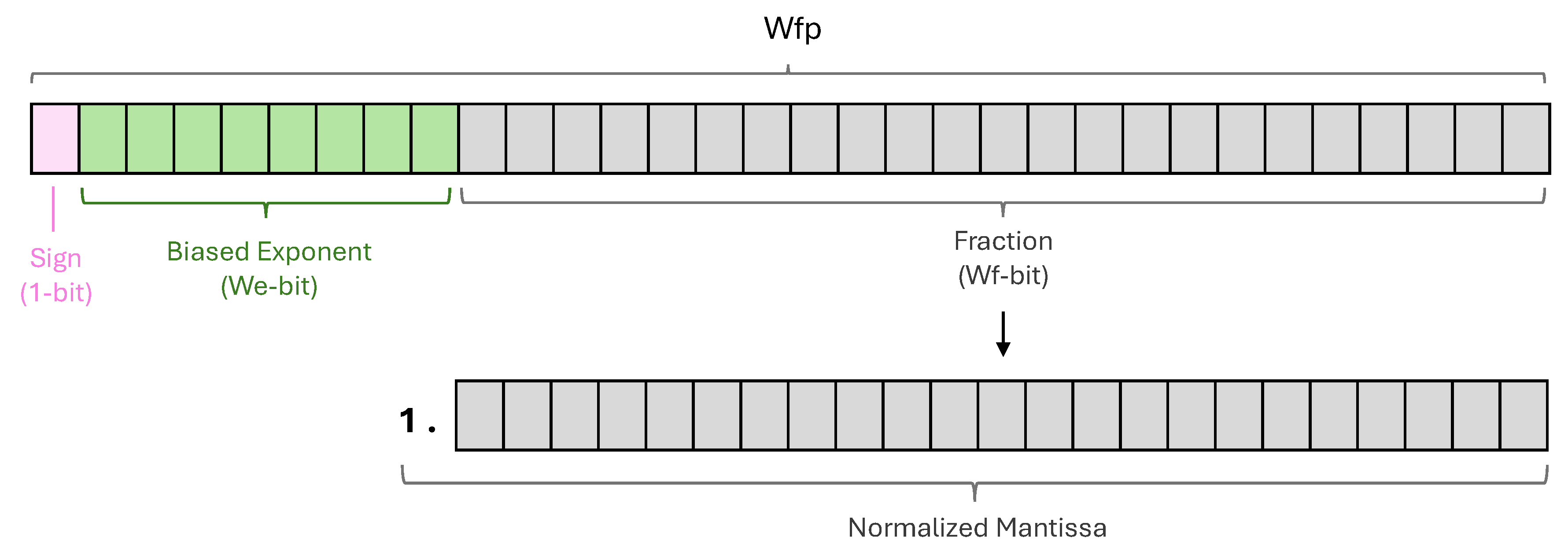
The IEEE-754 floating-point standard is widely used and recognized for representing floating-point numbers [23]. It comprises three main components: the sign bit, the exponent, and the mantissa. The value of a floating-point number is calculated using the formula:
Value = ( − 1 ) s × 2 e × m
where s indicates the sign of the number, with 0 representing positive and 1 representing negative, e is the exponent, typically stored in a biased form, which scales the number by a power of two, allowing for a wide range of values, and m is the normalized mantissa m ∈ [ 1 , 2 ) . The mantissa represents the significant digits of the number, providing the necessary precision. Figure 1 illustrates the binary floating-point representation, where a number is given on Wfp bits. The sign bit occupies one bit, the biased exponent occupies We bits, and the fraction occupies Wf bits, making Wfp = 1 + We + Wf .
The IEEE-754 standard defines various precision levels, including half-precision (16 bits), single-precision (32 bits), double-precision (64 bits), and quadruple-precision (128 bits), each with distinct bit widths, as shown in Table 1.
Allocating more bits to the exponent increases the dynamic range of representable numbers, allowing the number format to handle a wider range of magnitudes, accommodating both very large and very small numbers. Conversely, allocating more bits to the mantissa enhances precision, as more bits in the fraction allow for finer granularity of representable values.

2.2. Custom Formats

While standard formats are widely used, there are situations where bit-width customization is beneficial [24,25]. Custom floating-point formats can achieve a trade-off between dynamic range, speed, area, and numerical resolution, depending on the application’s specific requirements. Consequently, customized floating-point garners considerable attention.

2.2.1. RTL Libraries

VFLOAT [26], known as the Variable Precision Floating Point library, offers a comprehensive suite of variable-precision floating-point cores designed to perform fundamental arithmetic operations such as addition, subtraction, multiplication, and division. Additionally, it integrates conversion operators to facilitate transitions between floating-point and fixed-point representations. While VFLOAT serves as a valuable reference library for testing and validating floating-point cores, it is intended primarily for validation purposes rather than for use in actual designs.
FloPoCo [14,27], short for "FLoating Point Operator COres," is an open-source framework dedicated to producing optimized arithmetic operators specifically tailored for FPGA setups. This platform automates the generation of VHDL or Verilog code for a wide range of arithmetic functions, including addition, subtraction, and multiplication. FloPoCo creates non-encrypted VHDL cores with templates designed for integer, fixed-point, floating-point, and complex types.

2.2.2. HLS Libraries

The integration of custom floating-point implementations into HLS methodologies has been limited despite their long-standing use in FPGAs, the focus of many HLS tools on fixed-point arithmetic, and the challenge of achieving optimal performance and resource utilization. Several methods exist to address the need for soft floating-point libraries within HLS [28], but these libraries often lack the capability to generate IP cores at compile-time, restricting them to predefined operator widths. One approach explores using HLS to develop non-standard floating-point operations, such as summation [29], but it does not support heterogeneous precision.
Template HLS (THLS) [15] addresses customized floating-point operations at a high level using C++ templates. THLS allows compile-time selection of exponent and fraction widths and supports mixed precisions for input arguments and result types [8]. While it offers a unique implementation for both simulation and synthesis, it primarily focuses on basic operations, leaving room for further optimization and the inclusion of additional useful operations.
TrueFloat [19], integrated with the open-source HLS tool Bambu [30], represents another significant advancement. This integration facilitates new optimization opportunities and generates equivalent representations at a higher level of abstraction. TrueFloat simplifies the translation between different floating-point encodings and offers a straightforward process through simple command-line options.

3. Implementation Methodology

3.1. Development Flow

Developing customizable floating-point operations requires efficient, optimized C++ code adhering to HLS guidelines. Using directives and pragma annotations enhances hardware performance, area, and power consumption. Clear specifications of input/output formats, precision requirements, complex operations, and performance constraints are essential for the design and implementation phases. Once defined, the core logic is implemented in C++.
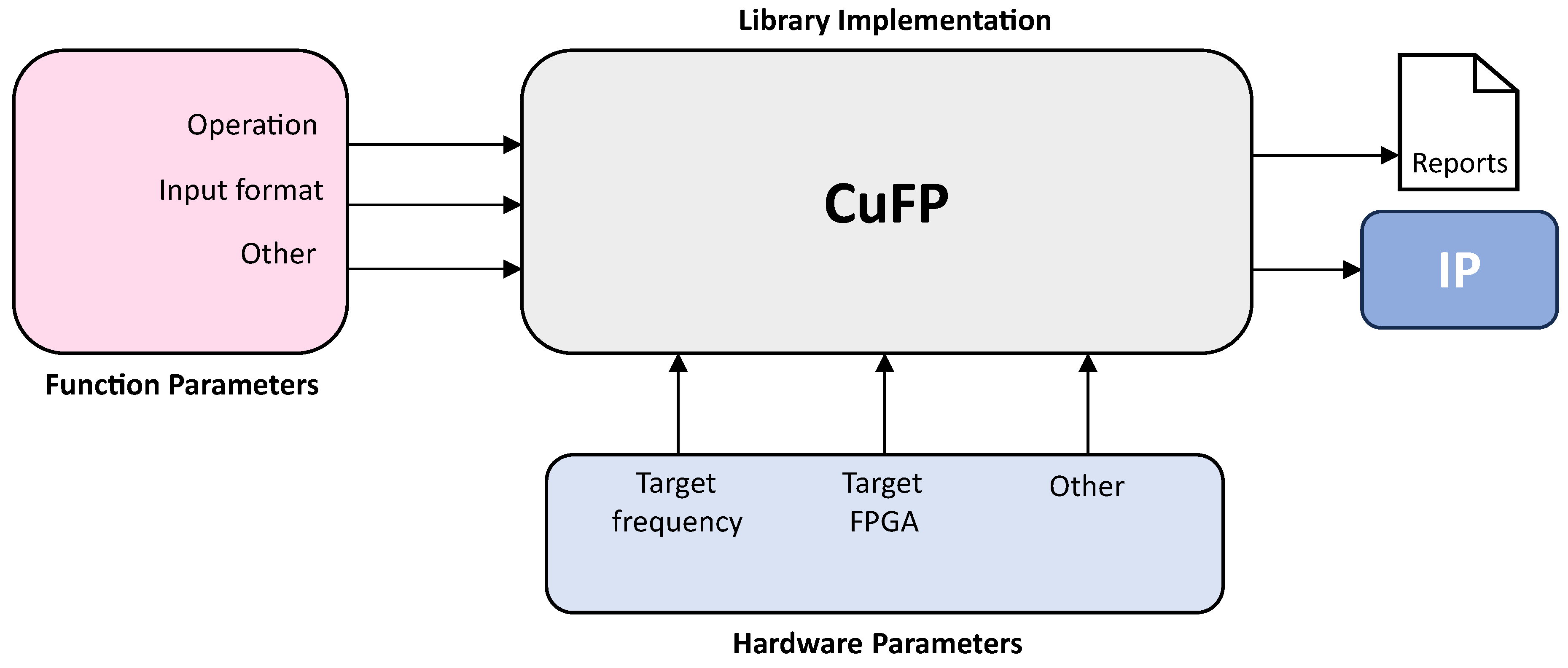
Figure 2 illustrates the HLS workflow of the CuFP framework, demonstrating user interaction to create desired IP. After compiling and debugging the C-based code, the HLS tool packages the function into hardware IP for RTL-based projects. CuFP supports heterogeneous number formats, allowing arbitrary bit-widths for inputs and outputs via a template-based interface, ensuring hardware implementation aligns with application needs, maximizing efficiency and precision.
Customizable bit-width formats benefit applications with varying precision and resource constraints. High-precision computations may require extended bit-widths to minimize errors, while real-time tasks may prioritize lower latency and reduced resource usage with narrower bit-widths. Our approach leverages the HLS tool’s built-in libraries, ensuring lightweight, independent implementations, simplifying development, and enhancing project compatibility.
A key achievement of the library is providing dedicated volumetric vector and matrix operations, specifically vector summation (VSUM), dot-product (DP), and matrix-vector multiplication (MVM), utilizing HLS built-in libraries. These operations are crucial for high-performance computing applications like scientific simulations, 3D graphics processing, and machine learning algorithms. Customizing bit-widths allows users to achieve desired precision, manage resource usage, and ensure efficient computation for various operations on large vectors.

3.2. Standard Floating-Point Operations

Contrary to fixed-point numbers, floating-point numbers offer a large dynamic range by allowing the radix point to float. However, they must be aligned for almost every arithmetic operation, requiring unpacking before computation and packing afterward. Additionally, values must be normalized after each numerical computation when stored in memory or registers.
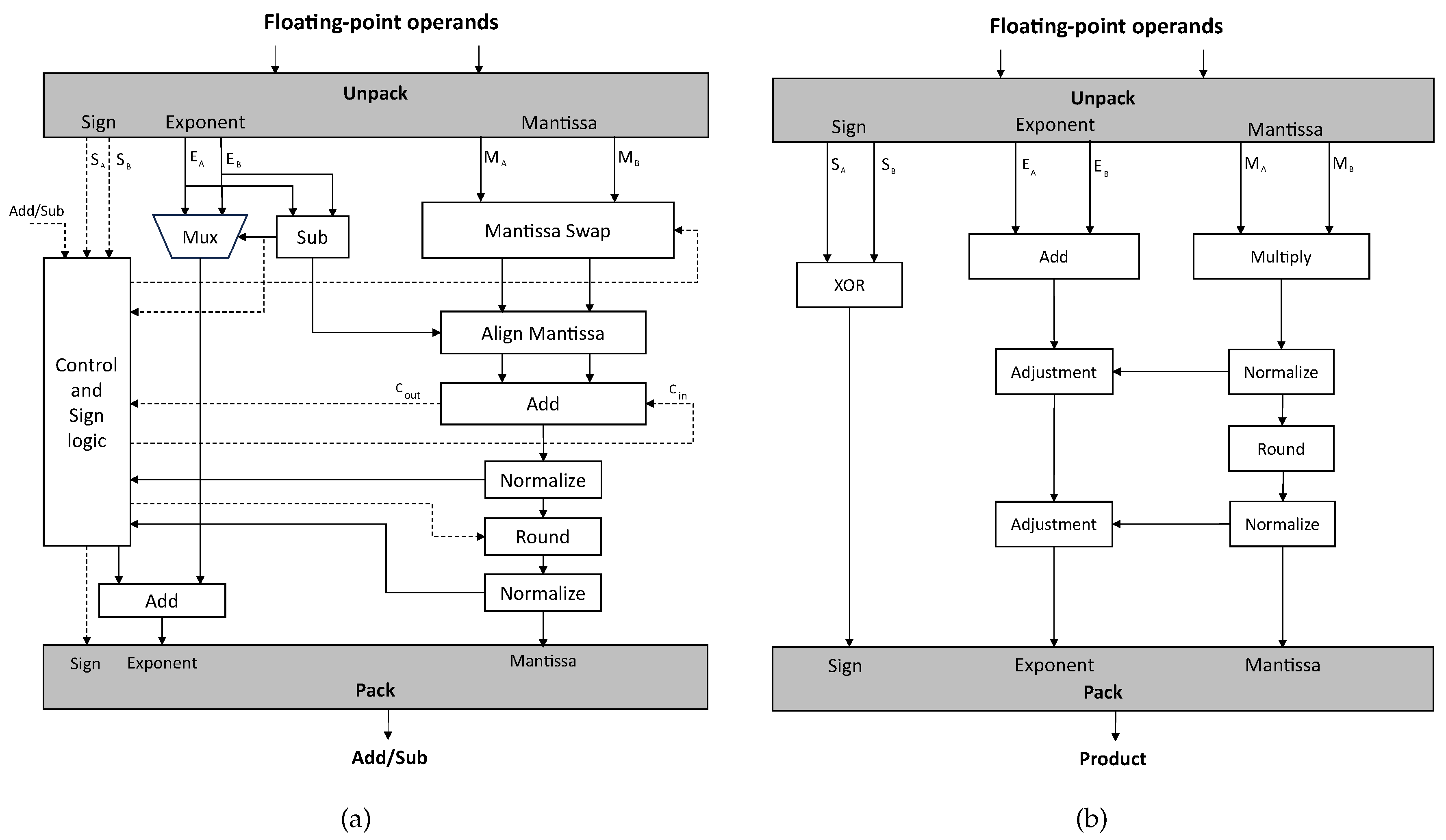
Figure 3 illustrates a block-level schematic of addition and multiplication for floating-point numbers in standard formats. For addition, the process begins by aligning the exponents of the two values, which involves shifting the smaller exponent’s mantissa and updating the exponent. Once aligned, the mantissas are added or subtracted. In multiplication, the mantissas are multiplied, and the exponents are added to determine the preliminary product and exponent.
CuFP follows these steps with modifications to enable additional capabilities. Efficient HLS development requires knowledge of the target FPGA’s resources and the HLS tool’s mapping strategies. While algorithms in high-level languages may execute efficiently on x86 CPUs, HLS tools may not generate efficient FPGA logic. FPGAs benefit from parallel architectures, so dividing algorithms into parallelizable portions and scheduling them accordingly can enhance performance. These optimizations are typically performed by the HLS tool, but developers must provide useful hints to guide the compiler.

3.3. CuFP: Detailed Implementation

The CuFP library, designed with a templated C++ format, supports a wide range of custom floating-point data types. This approach offers several advantages, including determining the optimal width for operands in each operation and using heterogeneous floating-point data types with different exponent and mantissa sizes. This flexibility is beneficial for developing algorithms focusing on efficiency or low latency.
The performance and efficiency of the final RTL generated by the HLS tool depend heavily on the coding style. While an object-oriented approach in C++ may introduce some overhead compared to a procedural C-style format, it results in cleaner, more maintainable, and extensible code. Balancing these approaches can enhance both performance and code quality. In CuFP, we utilized a mixture of both approaches to keep the latency and resources as low as possible while keeping the source code easy to use, modify, and extend. In this direction, we avoided using extra classes for different data types and instead used a templated class with various member functions that implement primary floating-point operations, allowing us to extend the library to support more complex operations.
The CustomFloat class template in the CuFP namespace shown in Listing  1 defines a custom floating-point number with customizable bit-width (WL) and mantissa size (MS). It includes member variables for the mantissa (mnts), exponent (exp), and sign (sign). The class provides several constructors and utility functions to allow users to convert different data types together and work with them easily. We deliberately omitted implementation details to concentrate on the most important code sections in this code sample and the subsequent code snippets throughout the paper.
Preprints 109560 i001

3.3.1. Primary Operations

The templated function mul performs multiplication on two custom floating-point numbers stored in the CustomFloat class. A pseudo-code of this function is given in Listing  2. It starts by multiplying the mantissas of the operands x and y, resulting in a potentially larger intermediate mantissa (line 5). The function then normalizes and rounds the resulting mantissa. It calculates the number of bits to shift based on the mantissa sizes (line 8) and performs a right shift, either rounding or truncating the mantissa based on whether EN_ROUNDING is defined (lines 9-13). Next, the function adjusts the exponent by adding the exponents of x and y along with any overflow bits detected from the normalization process (lines 16-17). It determines the sign of the result by XORing the signs of the operands (line 20). Finally, the function constructs and returns a new CustomFloat, completing the multiplication operation (line 22).
Preprints 109560 i002
The templated function sum performs addition on two custom floating-point numbers stored in the CustomFloat class. A pseudo-code of this function is given in Listing  3. It begins by comparing the exponents of the operands and swapping them if necessary, setting the result’s exponent to this larger value (lines 5-7). It calculates the difference between the exponents to align the mantissas, shifting the smaller exponent’s mantissa to the right, either rounding or truncating it based on whether EN_ROUNDING is defined (lines 10-15). Then, it extends the mantissas to the same bit-width to ensure they can be added correctly (line 18). After applying the signs to the mantissas, it sums them up and determines the sign of the resulting mantissa (lines 21-24). The function then normalizes the result; if no overflow bits are present, it finds the position of the leading one, left-shifts the mantissa to normalize it, and adjusts the exponent accordingly. If overflow bits exist, it right-shifts the mantissa by one bit and increments the exponent, again considering rounding if defined (lines 27-39). Finally, the function constructs and returns a new CustomFloat object, completing the addition operation (line 40).
The CuFP library uses flattened code or template-based recursive functions instead of loops in sub-modules and sub-functions. While this approach may demand more resources, it results in highly competitive performance. This makes CuFP ideal for applications requiring fast, adaptable floating-point operations with reasonable resource usage.
Preprints 109560 i003

3.4. Customized Vector Operations

In computation, scientific, and engineering fields, operations like matrix-vector multiplication, dot-product, and vector summation are crucial for performance. These operations underpin various algorithms and numerical computations, from simple arithmetic to complex tasks in statistical analysis, signal processing, image processing, and machine learning. Efficient execution of these operations enhances application performance, enabling faster computations and better resource utilization. We have incorporated these operations as custom blocks within the CuFP library to optimize latency and resource use, leveraging customized floating-point arithmetic.

3.4.1. Vector Summation

Vector summation is a fundamental operation in computational mathematics and data processing that entails adding whole items within a vector. Consider an N-sized vector represented as x = [ x 1 , . . . , x N − 1 , x N ] . The vector summation operation is defined as follows:
∑ i = 1 N x i = x 1 + . . . + x N − 1 + x N
The templated function vsum accumulates N elements of an array of custom floating-point numbers (CustomFloat<WR, MR>). Listing  4 provides a simplified representation of the vsum body function. It begins by determining the additional bits needed to safely sum the mantissas (line 5). The function then extracts the exponents from each array element, identifies the maximum exponent (max_exp), and assigns it as the result exponent (lines 8-10). It aligns all mantissas to this maximum exponent by computing exponent differences and shifting the mantissas accordingly (lines 13-14). After applying the signs to the mantissas, they are summed using a recursive template adder, and the resulting sign is determined (lines 17-19). The rest is quite similar to the sum operation elaborated in the previous subsection.
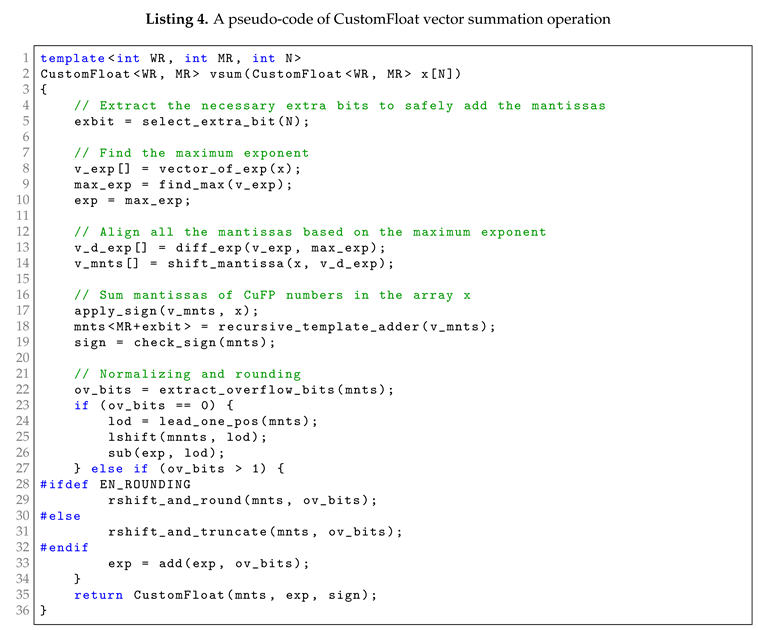
Preprints 109560 i004
A key aspect of developing generic vector summation is its ability to accumulate a variable set of customized floating-point numbers. Given that the input array can vary in size, we needed loops or similar constructs to perform essential sub-functions such as determining the maximum exponent (line 9) or summing the mantissas (line 18). A straightforward approach is to use loops with unrolling directives. However, the Vivado HLS tool typically creates an unbalanced tree structure for array-reduction operations like an accumulator when unrolling the corresponding loops. Figure 4 illustrates the difference between unbalanced and balanced tree hierarchies for executing array-reduced operations on an 8-sized array. Both consume 7 binary operators but in different cycles, resulting in the unbalanced version having a longer critical path and inefficient performance. Although there is a directive (unsafe_math_optimizations)  [32] to balance match expressions under certain conditions, we designed a template-based recursive function structure to reduce reliance on tool features and ensure the operations are consistently optimized.

3.4.2. Dot-Product Operation

The dot-product, also known as the scalar product or inner product, calculates the sum of the products of corresponding elements in two vectors. Mathematically, the dot product of two vectors x and a of size N is computed as the sum of the products of their corresponding elements:
〈 x , a 〉 = x T · a = ∑ i = 1 N x i · a i = x 1 · a 1 + x 2 · a 2 + . . . + x N · a N
As shown in Equation 3, dot-product involves multiplying two vectors and then summing these products. Therefore, Developing the generic dot-product operation was carried out by mul and vsum operations. Listing  5 demonstrates how to use these functions to complete the dot-product operation. We first multiply the array’s corresponding elements using an unrolled loop. All multiplications are executed in parallel in this stage. The produced array is then passed to the vsum operator, which computes the final result. Additionally, the inline and pipeline directives are employed to prevent component reuse and ensure that the process is fully pipelined.
Preprints 109560 i005

3.4.3. Matrix-Vector Multiplication

Matrix-vector multiplication is another fundamental operation in linear algebra that involves multiplying a matrix by a vector to produce a new vector. This operation plays a pivotal role in various mathematical and computational tasks. Conceptually, matrix-vector multiplication consists of taking each row of the matrix and performing a dot-product with the vector, resulting in the corresponding element of the resulting vector as shown in Equations 4 and  5.
X = x 11 x 12 ⋯ x 1 N x 21 x 22 ⋯ x 2 N ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 ⋯ x N N , y = y 1 y 2 ⋮ y N
The result of multiplying matrix X by vector y is calculated as follows:
z = Xy = x 11 x 12 ⋯ x 1 N x 21 x 22 ⋯ x 2 N ⋮ ⋮ ⋱ ⋮ x N 1 x N 2 ⋯ x N N y 1 y 2 ⋮ y N = x 11 y 1 + x 12 y 2 + ⋯ + x 1 N y N x 21 y 1 + x 22 y 2 + ⋯ + x 2 N y N ⋮ x N 1 y 1 + x N 2 y 2 + ⋯ + x N N y N
So, the result of the matrix-vector multiplication Xy is an N-element vector where each element is obtained by taking the dot-product of the i-th row of the matrix X with the vector y . Listing  6 represents the implementation of mvm using dot-product operation inside an unrolling loop.
Preprints 109560 i006

3.5. CuFP Automation

An automated process employing TCL and bash scripts was created to simplify the synthesis and implementation of customized floating-point operations in HLS. Users can select specific operations like sum, mul, vsum, dp, or mvm and set design parameters, including customized bit-widths. The automation compiles the HLS code, synthesizes the design, and exports the generated RTL as an IP block, ready for integration into larger projects. It also supports the Vivado Design Suite implementation with specified hardware parts and clock frequencies, as shown in Figure 2.
Encapsulating the entire process in a single bash script command allows users to quickly generate RTL designs without delving into library details, reducing errors and manual mistakes. It enables easy exploration of different configurations, facilitating the identification of the most suitable version for specific requirements. This ensures consistent quality results and accelerates the design workflow.

4. Experimental Results

This section presents the experimental results of implementing the proposed CuFP library with Vivado HLS 2019.1. The target device chosen is the Virtex UltraScale+ (xcvu13p-fhga2104-3-e). Although the design space for evaluating a generic library like CuFP is extensive, we focused on assessing it in the most common and impactful areas. We aimed to provide valuable quantitative and qualitative experimental results to help researchers select the most suitable option for their work.
The operations in the CuFP library are designed with full pipelining, allowing new input values to be fed every clock cycle for continuous data processing. However, the initiation interval can be increased by applying the appropriate directives in the code, offering flexibility in scheduling operations. This strategy may result in better resource utilization. For the sake of fairness in the comparison, the Vendor’s IPs are likewise set to be fully pipelined in the following results too.
For each circuit reported in this paper, a set of registers is present at the input and output stages to ensure accurate signal capture and readiness for subsequent stages. For illustrative purposes, a circuit with three levels of the pipeline actually has two computing stages surrounded by registers.

4.1. Primary Operations

We evaluate the impact of fraction width variation on the performance of floating-point arithmetic operations. We consider the fundamental arithmetic operations of sum and mul in both versions of rounding (CuFP (r)) and truncation (CuFP(t)).
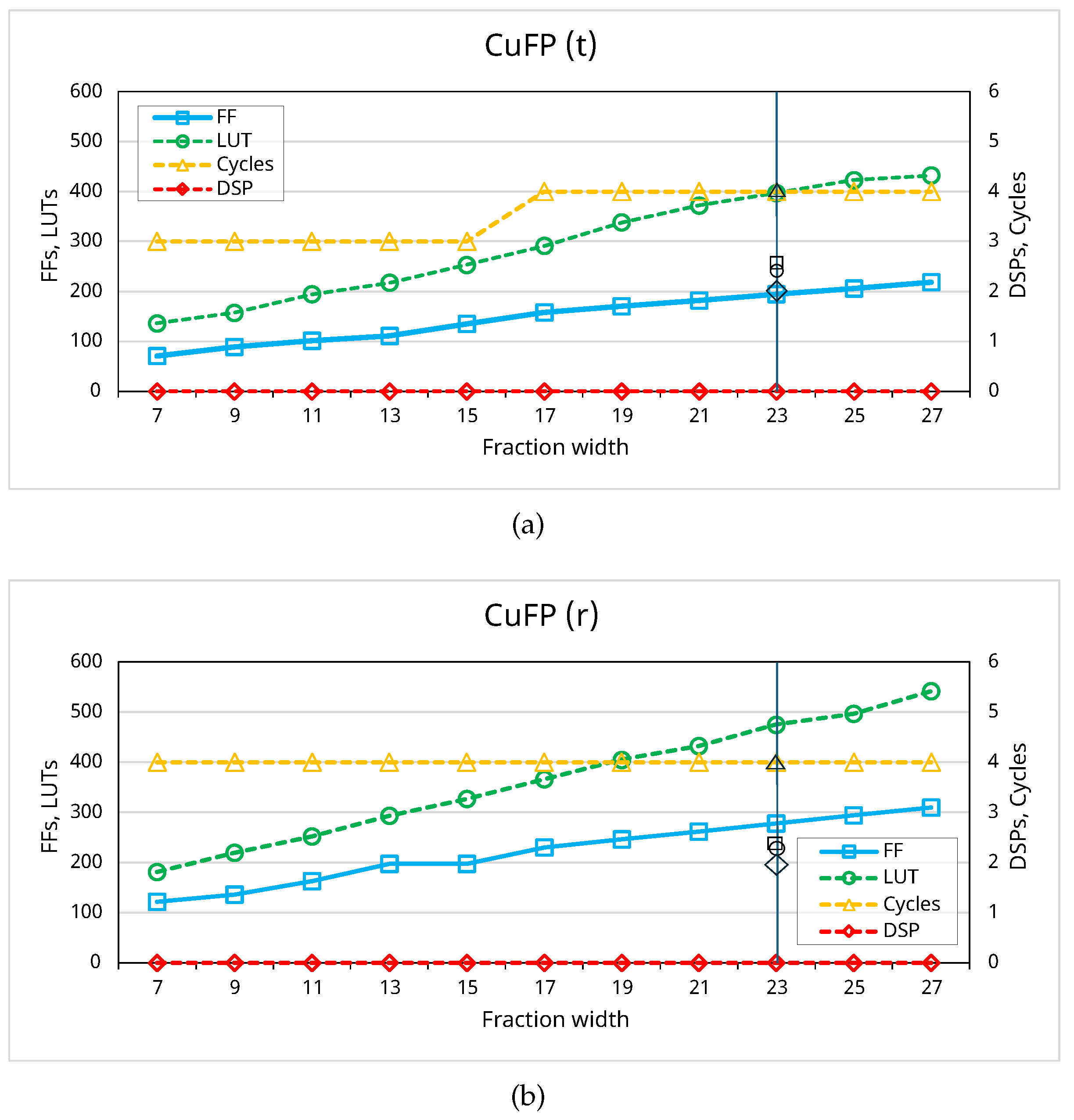
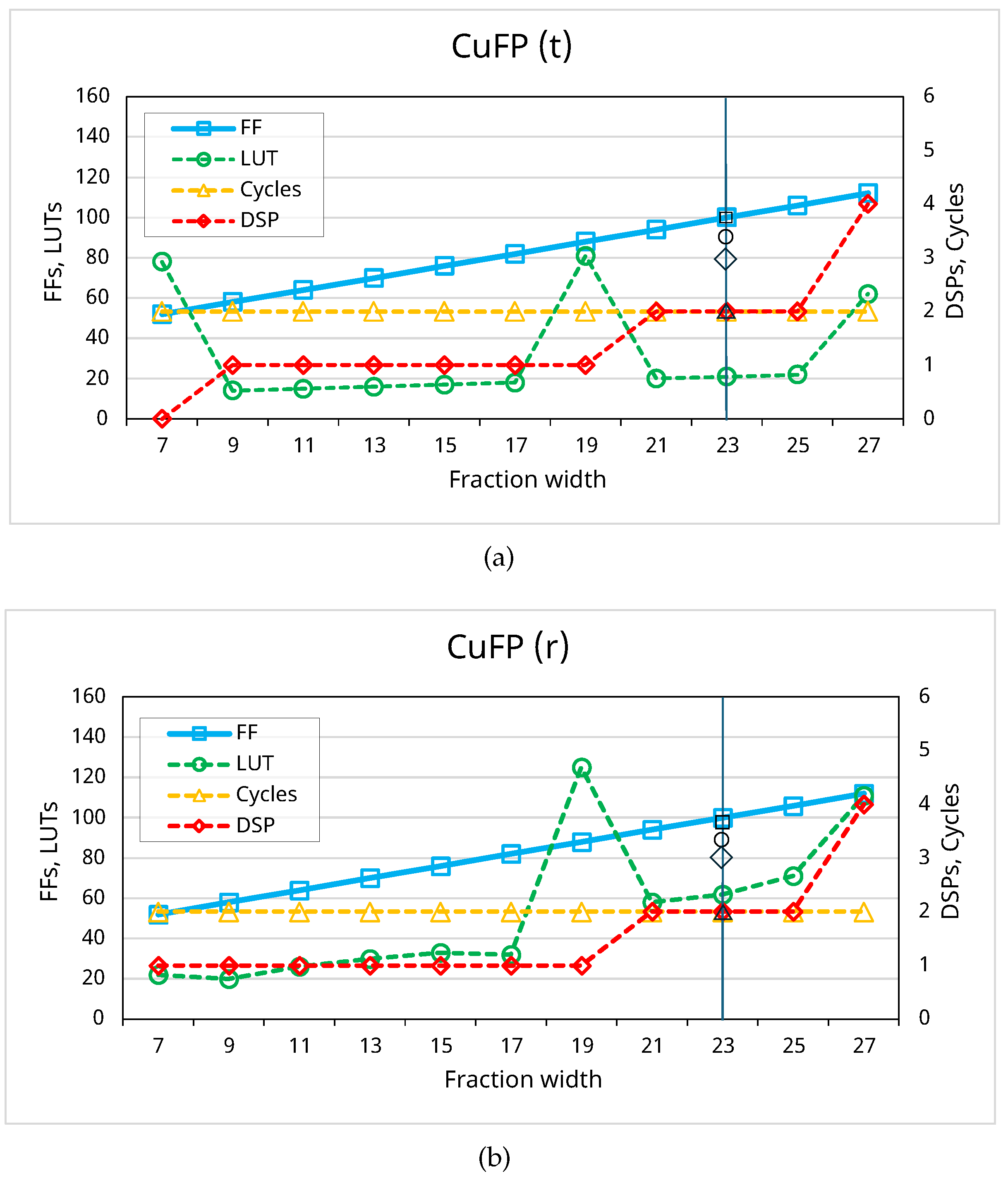
Figure 5 illustrates CuFP’s resource utilization and cycle counts for the sum operation across different fraction widths at 200 MHz. Resource utilization in truncation mode is generally lower than in rounding mode due to the absence of additional rounding logic. Look-up table (LUT) utilization increases linearly in both modes, while flip-flops (FF) utilization also rises, albeit slower. CuFP’s use of integer-based operators for adding fractions in the sum operation results in no digital signal processing (DSP) block allocation by the HLS tool. The cycle count is steady at 4 cycles in rounding mode, while truncation mode maintains 3 cycles up to 15 fraction bits, increasing by one cycle thereafter. This highlights the efficiency trade-offs between rounding and truncation modes.
The vertical line at 23 fraction bits in both charts represents the vendor IP, highlighting the corresponding results. The vendor IP consumes less LUT than CuFF with the same bit-width, while it requires slightly more FF than CuFP(t). Both CuFP and the vendor IP exhibit the same number of cycles. The most significant difference is in DSP utilization, so the vendor IP uses 2 DSPs for floating-point addition, whereas CuFP does not utilize any DSPs.
Similar visualizations in Figure 6 demonstrate the resource utilization and cycles of CuFP with different fraction widths for rounding and truncation modes in the mul operation at a clock frequency of 200 MHz. The number of FFs in both modes is almost identical, exhibiting a linear increase with the growth of fraction bits. The utilization of DSPs increases with every other increment of fraction bits and remains nearly consistent between both modes, except at the 7-bit fraction width.
Figure 6 reveals a notable peak in LUT utilization just before an increase in DSP usage, which is attributed to the oversizing of DSP operands during mantissa multiplication. Given that the input size of DSPs in the Virtex Ultrascale+ family is 18×27 [12], managing transitions beyond 18 fraction bits challenges the HLS tool in efficiently allocating logic. During these transitions, the tool initially allocates extra LUTs for fraction multiplication. As the fraction width increases further, it shifts to additional DSPs to handle larger inputs, normalizing LUT utilization. This demonstrates the HLS tool’s balance between LUT and DSP allocation to optimize resource use for the mul operation in CuFP.
Regarding the vendor IP for a single-precision floating-point multiplier, it consumes more LUTs and DSPs than CuFP in both rounding and truncation modes. The number of cycles and FFs between the vendor IP and CuFP are identical. This indicates that while the vendor IP may provide a standard implementation, CuFP offers a heterogeneous data format and achieves similar performance with more efficient utilization of resources, particularly in terms of LUT and DSP consumption.

4.2. Comparative Analysis of CuFP

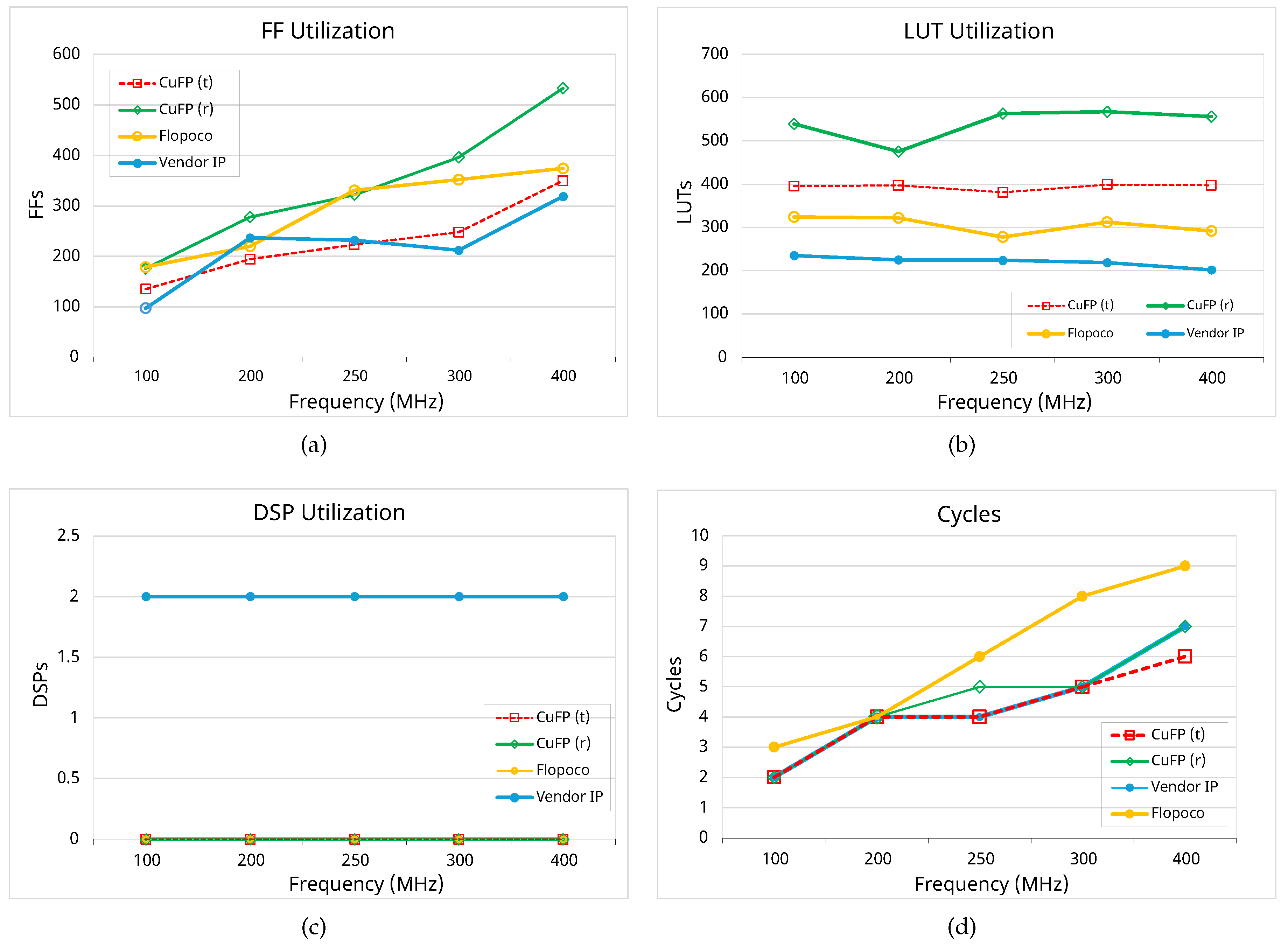
In this part of the evaluation, CuFP is compared to the existing floating-point vendor IP and Flopoco. In this experiment, the bit-width of input and output numbers is considered fixed and the same as the standard 32-bit floating-point. Figure 7 resource utilization trends for the sum operation at different clock frequencies for the two modes of CuFP, the vendor IP, and Flopoco. All the evaluated methods typically require more cycles to complete their processes as the clock frequency increases. Correspondingly, they exhibit growing FF utilization for storing internal signals and passing them to subsequent stages. Flopoco generally requires more cycles than the other methods. The vendor IP and CuFP(t) show competitive FF consumption, while Flopoco and CuFP(r) utilize more FFs than the others when the clock frequency exceeds 200 MHz. In contrast, LUT consumption is not significantly affected by changes in clock frequency. The vendor’s sum operation, Flopoco, CuFP(t), and CuFP(r) require approximately 210, 300, 400, and 490 to 570 LUTs, respectively. None of the methods consume DSPs except for the vendor IP, which requires 2 DSPs.
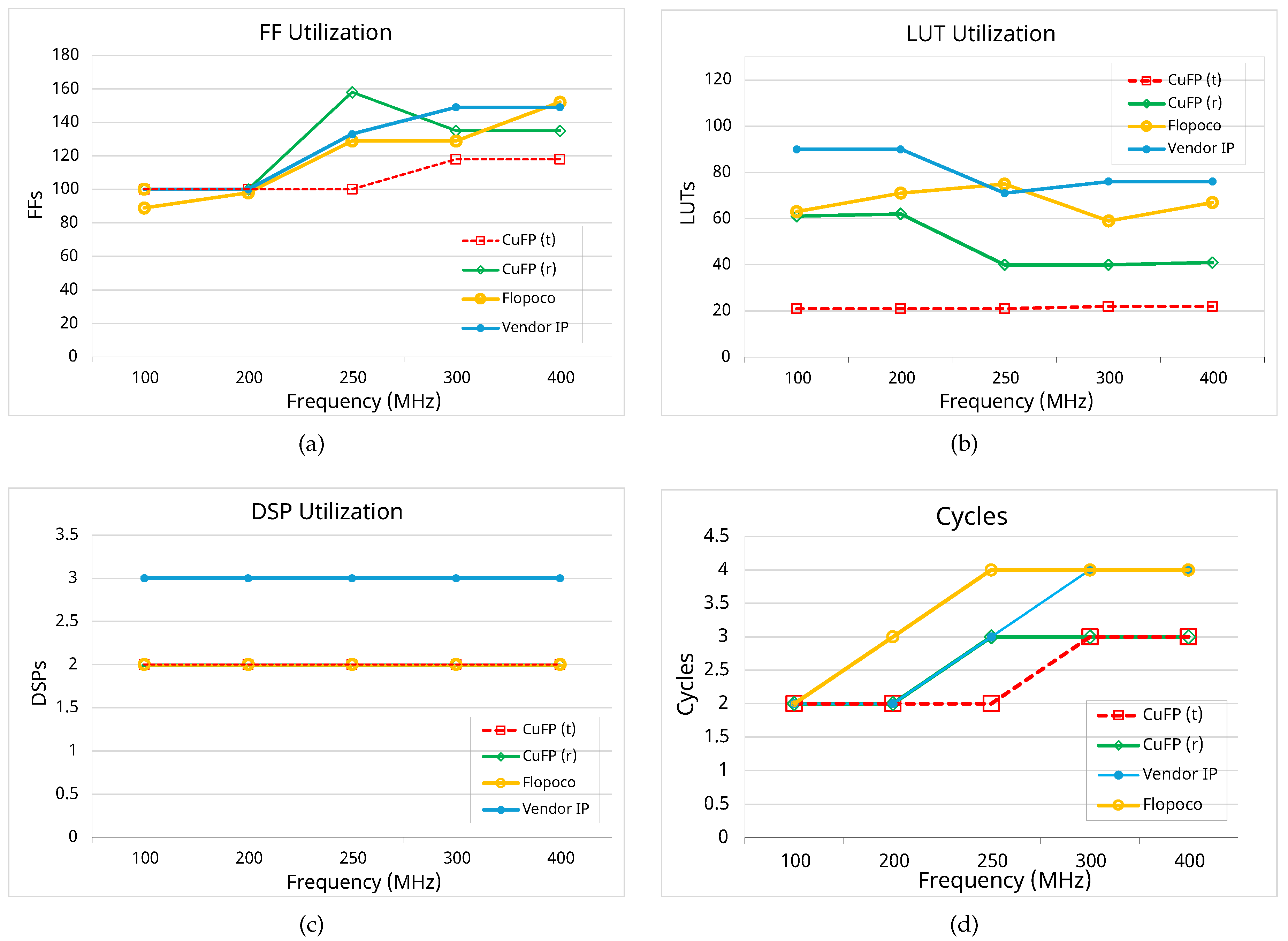
Figure 8 compares the mentioned methods for their mul operations. Unlike the sum operation, changing the clock frequency does not affect the required cycles. CuFP demonstrates superior performance in terms of clock cycles in both modes, requiring only 2 to 3 cycles. Similarly, FF consumption is competitive, ranging from approximately 95 to 160. CuFP(t) exhibits the lowest FF utilization across most clock frequencies. Regarding LUT utilization, CuFP(t) proves to be the most efficient method, consuming between 2× and 5× fewer LUTs than the vendor IP and Flopoco. As observed with the sum operation, changing the clock frequency does not significantly impact the number of LUTs used. Finally, all methods for mul operations, except for the vendor IP, utilize 2 DSPs consistently across all clock frequencies. The vendor IP requires 3 DSPs regardless of the clock frequency.
Table 2 presents a comparative analysis of the maximum clock frequencies, the number of stages, and resource utilization for sum and mul operations across CuFP (both rounding and truncation modes), Vendor IP, and Flopoco. CuFP performs better in terms of maximum clock frequency for both sum and mul operations compared to the Vendor IP and Flopoco. Specifically, CuFP(t) achieves the highest clock frequencies, reaching 436 MHz and 468 MHz for sum and mul operations, respectively. Regarding resource utilization, CuFP(t) consumes fewer FFs and LUTs than CuFP(r) and requiring no DSPs for the sum operation, unlike the Vendor IP which uses 2 DSPs. Both CuFP modes efficiently utilize 2 DSPs for the mul operation, while the Vendor IP requires 3 DSPs.

4.3. Evaluation of Dedicated Vector Operations

This subsection comprehensively evaluates dedicated vector operations implemented using CuFP compared to traditional vendor IPs. The focus is on three critical operations: vsum, dp, and mvm.

4.3.1. Vector Summation

The resource utilization and performance results of the vsum operation presented in Table 3 show improvement of CuFP over the vendor IP, particularly in terms of clock cycle efficiency. CuFP consistently requires fewer clock cycles to complete operations. For instance, CuFP handles vector sizes with 4 to 32 elements using only 4 to 6 stages, whereas the vendor IP requires 8 to 20 stages for the same operations. This substantial reduction in the number of stages translates to significantly lower clock cycles, thereby enhancing processing speed and throughput.
Moreover, CuFP achieves this clock cycle efficiency without relying on DSPs, which is a notable advantage. While the vendor IP consumes a substantial number of DSPs (ranging from 6 to 62 DSPs), CuFP operates efficiently without any DSPs. Although CuFP uses more LUTs and FFs, this trade-off is beneficial considering the reduced clock cycles and DSP independence. The clock cycle efficiency of CuFP improves computing performance while simultaneously providing flexibility in input vector size and data width.

4.3.2. Dot-Product

Table 4 presents the resource utilization and performance results of the dp operation, and reveals significant improvement of CuFP over the vendor IP, particularly in clock cycle efficiency. CuFP consistently demonstrates superior clock cycles, completing a dp operation with fewer clock cycles than the vendor IP across varying vector sizes. For example, at a vector size of 32, CuFP requires only 7 stages, while the vendor IP needs 22 stages, resulting in significantly lower clock cycles for CuFP.
This clock cycle efficiency of CuFP translates to enhanced processing speed and throughput, making it highly suitable for time-sensitive applications. CuFP exhibits efficient resource utilization, particularly evident in linear growth in DSP usage with increasing vector size. Despite consuming more LUTs than the vendor IP, CuFP’s efficient DSP and FF utilization and lower stage count contribute to its overall resource efficiency and potential for faster performance.
The efficiency of CuFP in dp operation is rooted in its implementation using a generic vsum, as discussed earlier. By leveraging the efficient architecture of vsum, CuFP minimizes the number of stages and maximizes DSP utilization, resulting in faster computation and lower latency across different vector sizes.

4.3.3. Matrix-Vector Multiplication

The resource utilization and performance results of the mvm operation are presented in Table 5. The efficiency of CuFP in mvm operations is demonstrated through its implementation leveraging the generic dp operation. The CuFP variant exhibits a consistent increase in resource utilization (DSP, LUT, and FF) with growing vector sizes while maintaining a moderate number of stages. For instance, with a vector size of 4, CuFP uses 32 DSPs, 5,230 LUTs, and 1,831 FFs over 5 stages. As the vector size increases to 32, the DSP usage scales to 2,048, with 294,019 LUTs and 120,679 FFs over 7 stages. This efficient scaling indicates CuFP’s robust architecture, which is designed to handle larger computations effectively. Comparatively, the vendor IP displays a more significant increase in both resource utilization and the number of stages. For a vector size of 4, the vendor IP requires 72 DSPs, 4,240 LUTs, and 3,960 FFs over 10 stages. At a vector size of 32, resource utilization jumps to 5,056 DSPs, 324,261 LUTs, and 297,720 FFs over 22 stages. While the vendor IP uses fewer LUTs for smaller vector sizes, it becomes less efficient as vector sizes grow, with significantly higher DSP and FF usage and a larger number of stages than CuFP.

5. Discussion

The CuFP library offers several benefits and demonstrates significant improvements over traditional vendor IP cores regarding flexibility, resource utilization, and performance, particularly in vsum, dp, and mvm operations. Its primary advantage is its flexibility in defining custom floating-point formats. By allowing users to specify the number of bits for the exponent and mantissa, the library enables a more tailored approach to precision and dynamic range based on the application’s specific needs. This customization is particularly valuable in applications where a balance between precision and resource utilization is critical, such as in FPGA-based scientific computing and real-time signal processing.
The experimental results indicate that CuFP achieves lower latency and better resource utilization than vendor-provided IP cores. For instance, the vsum operation shows a notable reduction in the number of DSP slices and LUTs used and a decrease in the number of clock cycles required for computation. These improvements are consistent across different vector sizes and operations, highlighting the efficiency of the CuFP library in handling large-scale computations. Suppose an application running at 200 MHz clock frequency, deals with floating-point numbers, and requires the multiplication of a 32x32 matrix by a 32-element vector. This task involves 32x32=1024 multiplications, which can potentially be executed in parallel, and 32x31=992 additions (as each of the 32 rows requires 31 additions) that can be done in the form of balanced tree additions for each row. If the application employs standard single-precision floating-point vendor IP cores, it would take 22 clock cycles as outlined in Table 5. However, CuFP offers a dedicated mvm operation that needs only 7 cycles to do the same calculations. Furthermore, CuFP uses approximately 60% fewer DSPs, 10% fewer LUTs, and 60% fewer FFs, making it a highly efficient and more advantageous option for such applications.

5.1. Comparison with Existing Solutions

When compared to other customizable floating-point libraries, such as FloPoCo, CuFP offers several enhancements. Using C++ templates and HLS directives allows for more efficient hardware mapping and optimization. Moreover, CuFP’s support for heterogeneous floating-point types and its integration with HLS tools streamline the development process, making it easier for developers to incorporate custom floating-point functionality into their designs. The CuFP library demonstrates superior resource utilization, especially in operations that involve extensive arithmetic computations. The library minimizes the required resources by optimizing the alignment, normalization, and rounding processes while maintaining high performance. This optimization is evident in the experimental results, where CuFP consistently uses fewer DSP slices and LUTs than vendor IP cores.
For instance, at a vector size of 32 and clock frequency of 200 MHz, CuFP utilizes 7,420 LUTs and 3,050 FFs compared to the vendor IP with 7,283 LUTs and 7,245 FFs, but the vendor IP requires significantly more DSPs and stages. The vsum operation in CuFP can add 32 single-precision floating-point numbers approximately 3x faster than the usual method using the vendor-provided IP cores thanks to elaborately customizing floating-point addition and eliminating excess processing steps in the middle like packing, unpacking, and normalizing. Given that the other vectorized operations of CuFP are implemented by leveraging vsum, they also benefit from resource efficiency and high-speed performance.

5.2. Challenges and Limitations

Despite its advantages, the CuFP library also presents some challenges. The complexity of designing and implementing custom floating-point operations can lead to increased development time and effort. Additionally, while the library offers significant performance improvements, the trade-off between resource usage and precision must be carefully managed to avoid potential issues in applications that require extremely high accuracy. Future work on the CuFP library could focus on several areas for further enhancement. One potential direction is the development of additional custom operations and optimizations for specific application domains, such as machine learning. Additionally, exploring the integration of CuFP with other high-level synthesis tools and FPGA platforms could broaden its applicability and usability. Moreover, further research into the automatic optimization of custom floating-point parameters could help ease the development process and reduce the manual effort required for fine-tuning designs. Enhancing the library’s support for mixed-precision arithmetic and expanding its compatibility with various FPGA architectures would also contribute to its versatility and performance.

6. Conclusion

This paper introduces CuFP, an efficient HLS library for custom floating-point representations using C++ templates, designed to enhance flexibility and reduce latency in FPGA applications. By allowing users to define heterogeneous floating-point types at compile time, CuFP offers a broader spectrum of precision options, surpassing traditional vendor IP cores. Experimental results demonstrate that CuFP consistently outperforms vendor IP cores, particularly in vsum, dp, mvm operations. CuFP’s dedicated mvm operation, for example, significantly reduces clock cycles and hardware resources.
Compared to other customizable floating-point libraries, CuFP leverages C++ templates and HLS directives to achieve more efficient hardware mapping and optimization. This results in superior performance in arithmetic computations while minimizing resource usage. However, the design and implementation of custom floating-point operations may require additional development time and effort.
Future enhancements to CuFP should focus on expanding its capabilities by developing additional custom operations, integrating with other high-level synthesis tools, and supporting mixed-precision arithmetic. These improvements will further solidify CuFP’s position as a versatile and high-performance tool for FPGA-based applications.

Note

1
https://github.com/FahimeHajizadeh/Custom-Float-HLS

References

  1. Uguen, Y.; Dinechin, F.D.; Lezaud, V.; Derrien, S. Application-Specific Arithmetic in High-Level Synthesis Tools. ACM Trans. Archit. Code Optim. 2020, 17. [CrossRef]
  2. Xilinx. UG902: Vivado Design Suite User Guide, 2021.
  3. Xilinx. PG060: Floating-point operator v7.1-logicore ip product guide, 2020.
  4. Intel. Floating-Point IP Cores User Guide, 2023.
  5. Cherubin, S.; Cattaneo, D.; Chiari, M.; Bello, A.D.; Agosta, G. TAFFO: Tuning Assistant for Floating to Fixed Point Optimization. IEEE Embedded Systems Letters 2020, 12, 5–8. [CrossRef]
  6. Agosta, G. Precision tuning of mathematically intensive programs: A comparison study between fixed point and floating point representations. Master’s thesis, School of Industrial and Information Engineering, Politecnico di Milano, 2021.
  7. Cattaneo, D.; Chiari, M.; Fossati, N.; Cherubin, S.; Agosta, G. Architecture-aware Precision Tuning with Multiple Number Representation Systems. 2021 58th ACM/IEEE Design Automation Conference (DAC), 2021, pp. 673–678. [CrossRef]
  8. Thomas, D.B. Compile-Time Generation of Custom-Precision Floating-Point IP using HLS Tools. IEEE Symposium on Computer Arithmetic (ARITH), 2019, pp. 192–193. [CrossRef]
  9. Langhammer, M.; VanCourt, T. FPGA Floating Point Datapath Compiler. IEEE Symposium on Field Programmable Custom Computing Machines, 2009, pp. 259–262. [CrossRef]
  10. Ould-Bachir, T.; David, J.P. Self-Alignment Schemes for the Implementation of Addition-Related Floating-Point Operators. ACM Trans. Reconfigurable Technol. Syst. 2013, 6. [CrossRef]
  11. Montaño, F.; Ould-Bachir, T.; David, J.P. A Latency-Insensitive Design Approach to Programmable FPGA-Based Real-Time Simulators. Electronics 2020, 9. [CrossRef]
  12. Xilinx. UG579: UltraScale Architecture DSP Slice, 2021.
  13. Fang, X.; Leeser, M. Open-Source Variable-Precision Floating-Point Library for Major commercial FPGAs 2016. 9. [CrossRef]
  14. de Dinechin, F.; Pasca, B. Designing Custom Arithmetic Data Paths with FloPoCo. IEEE Design & Test of Computers 2011, 28, 18–27. [CrossRef]
  15. Thomas, D.B. Templatised Soft Floating-Point for High-Level Synthesis. IEEE Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), 2019, pp. 227–235. [CrossRef]
  16. de Dinechin, Florent, K.M. Application-Specific Arithmetic; Springer International Publishing, 2023.
  17. Böttcher, A.; Kumm, M.; de Dinechin, F. Resource Optimal Truncated Multipliers for FPGAs. 2021 IEEE 28th Symposium on Computer Arithmetic (ARITH), 2021, pp. 102–109. [CrossRef]
  18. Böttcher, A.; Kumm, M. Towards Globally Optimal Design of Multipliers for FPGAs. IEEE Transactions on Computers 2023, 72, 1261–1273. [CrossRef]
  19. Fiorito, M.; Curzel, S.; Ferrandi, F. TrueFloat: A Templatized Arithmetic Library for HLS Floating-Point Operators. Embedded Computer Systems: Architectures, Modeling, and Simulation; Silvano, C.; Pilato, C.; Reichenbach, M., Eds., 2023, pp. 486–493.
  20. Perera, A.; Nilsen, R.; Haugan, T.; Ljokelsoy, K. A Design Method of an Embedded Real-Time Simulator for Electric Drives using Low-Cost System-on-Chip Platform. PCIM Europe digital days 2021; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, 2021, pp. 1–8.
  21. Zamiri, E.; Sanchez, A.; Yushkova, M.; Martínez-García, M.S.; de Castro, A. Comparison of Different Design Alternatives for Hardware-in-the-Loop of Power Converters. Electronics 2021. [CrossRef]
  22. Hajizadeh, F.; Alavoine, L.; Ould-Bachir, T.; Sirois, F.; David, J.P. FPGA-Based FDNE Models for the Accurate Real-Time Simulation of Power Systems in Aircrafts. 2023 12th International Conference on Renewable Energy Research and Applications (ICRERA), 2023, pp. 344–348. [CrossRef]
  23. IEEE Standard for Floating-Point Arithmetic. IEEE Std 754-2008 2008, pp. 1–70.
  24. Sanchez, A.; Todorovich, E.; De Castro, A. Exploring the Limits of Floating-Point Resolution for Hardware-In-the-Loop Implemented with FPGAs. Electronics 2018, 7. [CrossRef]
  25. Martínez-García, M.S.; de Castro, A.; Sanchez, A.; Garrido, J. Analysis of Resolution in Feedback Signals for Hardware-in-the-Loop Models of Power Converters. Electronics 2019, 8. [CrossRef]
  26. Wang, X.; Leeser, M. VFloat: A Variable Precision Fixed- and Floating-Point Library for Reconfigurable Hardware. ACM Trans. Reconfigurable Technol. Syst. 2010, 3. [CrossRef]
  27. de Dinechin, F. Reflections on 10 years of FloPoCo. ARITH 2019 - 26th IEEE Symposium on Computer Arithmetic; , 2019; pp. 1–3. [CrossRef]
  28. Bansal, S.; Hsiao, H.; Czajkowski, T.; Anderson, J.H. High-level synthesis of software-customizable floating-point cores. 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), 2018, pp. 37–42. [CrossRef]
  29. Uguen, Y.; de Dinechin, F.; Derrien, S. Bridging high-level synthesis and application-specific arithmetic: The case study of floating-point summations. 2017 27th International Conference on Field Programmable Logic and Applications (FPL), 2017, pp. 1–8. [CrossRef]
  30. Ferrandi, F.; Castellana, V.G.; Curzel, S.; Fezzardi, P.; Fiorito, M.; Lattuada, M.; Minutoli, M.; Pilato, C.; Tumeo, A. Invited: Bambu: An Open-Source Research Framework for the High-Level Synthesis of Complex Applications. ACM/IEEE Design Automation Conference (DAC), 2021, pp. 1327–1330. [CrossRef]
  31. Parhami, B. Computer Arithmetic: Algorithms and Hardware Designs; Oxford series in electrical and computer engineering, Oxford University Press, 2010.
  32. Xilinx. UG1399: Vitis High-Level Synthesis User Guide, 2023.
Preprints 109560 g001
Figure 1. Structure of the IEEE-754 floating-point standard.
Figure 1. Structure of the IEEE-754 floating-point standard.
Preprints 109560 g001
Preprints 109560 g002
Figure 2. HLS workflow of the CuFP framework.
Figure 2. HLS workflow of the CuFP framework.
Preprints 109560 g002
Preprints 109560 g003
Figure 3. Standard floating-point operations for (a) addition; and (b) multiplication [31].
Figure 3. Standard floating-point operations for (a) addition; and (b) multiplication [31].
Preprints 109560 g003
Preprints 109560 g004
Figure 4. (a) Unbalanced tree binary operations; (b) Balanced tree binary operations.
Figure 4. (a) Unbalanced tree binary operations; (b) Balanced tree binary operations.
Preprints 109560 g004
Preprints 109560 g005
Figure 5. Resource utilization and cycles of CuFP(8,23) for sum operation: fraction width varies from 7 to 27; (a) CuFP(t): Truncation mode; (b) CuFP(r): Rounding mode.
Figure 5. Resource utilization and cycles of CuFP(8,23) for sum operation: fraction width varies from 7 to 27; (a) CuFP(t): Truncation mode; (b) CuFP(r): Rounding mode.
Preprints 109560 g005
Preprints 109560 g006
Figure 6. Resource utilization and cycles of CuFP(8,23) for mul operation: fraction width varies from 7 to 27; (a) CuFP(t): Truncation mode; (b) CuFP(r): Rounding mode.
Figure 6. Resource utilization and cycles of CuFP(8,23) for mul operation: fraction width varies from 7 to 27; (a) CuFP(t): Truncation mode; (b) CuFP(r): Rounding mode.
Preprints 109560 g006
Preprints 109560 g007
Figure 7. Comparing the resource utilization of sum operation for CuFP (8,23) and vendor IP as the target clock constraint is swept from 100 to 400 MHz; (a) FF Utilization; (b) LUT Utilization; (c) DSP Utilization; (d) Number of clock cycles.
Figure 7. Comparing the resource utilization of sum operation for CuFP (8,23) and vendor IP as the target clock constraint is swept from 100 to 400 MHz; (a) FF Utilization; (b) LUT Utilization; (c) DSP Utilization; (d) Number of clock cycles.
Preprints 109560 g007
Preprints 109560 g008
Figure 8. Comparing the resource utilization of mul for CuFP (8,23) and vendor IP as the target clock constraint is swept from 100 to 400 MHz; (a) FF Utilization; (b) LUT Utilization; (c) DSP Utilization; (d) Number of clock cycles.
Figure 8. Comparing the resource utilization of mul for CuFP (8,23) and vendor IP as the target clock constraint is swept from 100 to 400 MHz; (a) FF Utilization; (b) LUT Utilization; (c) DSP Utilization; (d) Number of clock cycles.
Preprints 109560 g008
Table 1. Floating-Point Format Specifications.
Table 1. Floating-Point Format Specifications.
Format Word Size Exponent Width Fraction Width Bias
(Wfp) (We) (Wf)
Half-Precision 16 5 10 15
Single-Precision 32 8 23 127
Double-Precision 64 11 52 1,023
Quadruple-Precision 128 15 112 16,383
Table 2. Comparing the maximum possible clock frequency of Sum and Mul operations for CuFP (8, 23) in two modes of rounding, Vendor IP (single-precision floating-point), and Flopoco (8, 23).
Table 2. Comparing the maximum possible clock frequency of Sum and Mul operations for CuFP (8, 23) in two modes of rounding, Vendor IP (single-precision floating-point), and Flopoco (8, 23).
Operation Variant # of Stage Max Frequency
(MHz)		 Resource Utilization
DSP LUT FF
CuFP (r) 6 420 0 486 414
Sum CuFP (t) 6 436 0 410 314
Vendor 6 375 2 219 277
Flopoco 6 332 0 278 331
CuFP (r) 3 436 2 41 135
Mul CuFP (t) 3 468 2 22 118
Vendor 3 284 3 71 133
Flopoco 3 338 2 71 98
Table 3. Comparing the resource utilization of vsum with different vector sizes for CuFP (8, 23) and vendor IP (single precision floating-point), at 200 MHz clock frequency.
Table 3. Comparing the resource utilization of vsum with different vector sizes for CuFP (8, 23) and vendor IP (single precision floating-point), at 200 MHz clock frequency.
Variant Vector Size # of Stages Resource Utilization
DSP LUT FF
CuFP 4 4 0 1,071 441
8 5 0 2,110 685
16 5 0 3,675 1,277
32 6 0 7,420 3,050
Vendor IP 4 8 6 701 709
8 12 14 1,642 1,645
16 16 30 3,522 3,513
32 20 62 7,283 7,245
Table 4. Comparing the resource utilization of dp with different vector sizes for CuFP (8, 23) and vendor IP (single-precision floating-point), at 200 MHz clock frequency.
Table 4. Comparing the resource utilization of dp with different vector sizes for CuFP (8, 23) and vendor IP (single-precision floating-point), at 200 MHz clock frequency.
Variant Vector Size # of Stages Resource Utilization
DSP LUT FF
CuFP 4 5 8 1,427 562
8 5 16 2,629 1,085
16 6 32 4,736 2,350
32 7 64 9,117 4,831
Vendor IP 4 10 18 1,057 1,095
8 14 38 2,354 2,415
16 18 78 4,947 5,051
32 22 158 10,138 10,319
Table 5. Comparing the resource utilization of mvm with different vector sizes for CuFP (8, 23) and vendor IP (single precision floating-point), at 200 MHz clock frequency.
Table 5. Comparing the resource utilization of mvm with different vector sizes for CuFP (8, 23) and vendor IP (single precision floating-point), at 200 MHz clock frequency.
Variant Vector Size # of Stages Resource Utilization
DSP LUT FF
CuFP 4 5 32 5,230 1,831
8 5 128 20,393 6,759
16 6 512 80,974 29,320
32 7 2,048 294,019 120,679
Vendor IP 4 10 72 4,240 3,960
8 14 304 18,859 17,416
16 18 1,248 79,188 72,836
32 22 5,056 324,261 297,720
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated