Prerpints.org logo
Preprint
Article

Symmetry-Engineered Dual Plasmon-Induced Transparency via Triple Bright Modes in Graphene Metasurfaces

Altmetrics

Downloads

71

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 June 2024

Posted:

18 June 2024

You are already at the latest version

Alerts
Abstract
Dynamical manipulation of plasmon-induced transparency (PIT) in graphene metasurfaces is promising for optoelectronic devices such as optical switching and modulating, however, previous design approaches are limited within one or two bright/dark modes, and the realization of dual PIT windows through triple bright modes in graphene metasurfaces is rare and urgently needed. Here we demonstrate that dual PIT can be realized through a symmetry-engineered graphene metasurface, which consists the graphene central cross (GCC) and graphene rectangular ring (GRR) arrays. The GCC supports a bright mode from electric dipole (ED), the GRR supports two nondegenerate bright modes from ED and electric quadrupole (EQ) due to the C2v symmetry breaking, and the resonant coupling of these three bright modes induces the dual PIT windows. A triple coupled-oscillator model (TCM) is proposed to evaluate the transmission performances of the dual PIT phenomenon, and the results are in good agreement with the finite-difference time-domain (FDTD) method. In addition, the dual PIT windows are robust to the variation of the structural parameters of the graphene metasurface except the y-directioned length of the GRR. By changing the carrier mobility of graphene, the amplitudes of the two PIT windows can be effectively tuned. The alteration of the Fermi level of graphene enables the dynamic modulation of the dual PIT with good performances for both modulation degree (MD) and insertion loss (IL).
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

Electromagnetically induced transparency (EIT) is a physical phenomenon that occurs in three-level atomic systems, where quantum interference between atomic energy levels and excitation pathways reduces the absorption of probing light, resulting in a very narrow transparency window in the transmission spectra [1]. In order to more conveniently and flexibly study the EIT phenomenon and expand its applications, researchers have proposed numerous schemes to realize classical analogies of EIT in various model systems [2,3]. Among these, the plasmon-induced transparency (PIT) effect in metamaterial structures which combines EIT in optical systems with surface plasmon polaritons (SPPs) has been extensively studied due to its flexible design and ease of implementation [4,5]. Previous research has reported that the PIT effect is primarily achieved through the destructive interference phenomenon of bright and dark modes [6,7]. The bright mode refers to a resonant mode directly excited by incident light, while the dark mode is a mode not directly excited by incident light but indirectly activated through near-field coupling with the bright mode. The PIT effect exhibits steep dispersion (potentially leading to slow light effects), large nonlinear characteristics, and high spectral sensitivity to the local dielectric environment [8,9,10], all of which open up new avenues for designing novel devices, such as slow light devices [11], optical sensors [12], and plasmonic switches [13]. However, once nanostructures are fabricated, the performance and operating frequency of PIT in metamaterials cannot be flexibly adjusted, hindering their applications in the fields of tunable or reconfigurable devices.
In order to overcome the aforementioned issues, researchers have recently combined active media with metasurfaces to achieve dynamic control of PIT, such as through the use of micro-electro mechanical systems (MEMS) [14], phase-change materials [15], nonlinear media [16], semiconductor materials [17], two-dimensional (2D) materials [18], and others. In particular, graphene can function as an excellent platform for the active manipulation of PIT due to its excellent photoelectric characteristics [19,20,21]. In contrast to traditional metal materials with high losses, graphene exhibits high electron mobility, high modulation depth, tunable surface conductivity, and low insertion loss (IL), making it widely utilized in the design of tunable PIT devices. The combination of graphene with metamaterials or metasurfaces can be employed to achieve dynamic tunable PIT effects. For example, by the excitation of the bright mode and dark mode simultaneously in the graphene strips, the controllable PIT window can be realized [22,23]. By the excitation of two bright modes simultaneously in the graphene metasurfaces, the tunable PIT window can also be achieved [24,25,26,27]. Additionally, the dynamic control of double PITs is possible in the graphene-based metasurfaces through the coupling between one bright mode and two dark modes [28], or two bright modes and one dark mode [29,30]. However, PIT arising from the triple bright modes has not been studied in graphene-based metasurfaces.
In this work, we demonstrate that the dual PIT phenomenon can be realized in the terahertz (THz) region through the resonant coupling of triple bright modes in the graphene metasurface. The unit cell of the proposed graphene metasurface contains a graphene central cross (GCC) and a graphene rectangular ring (GRR). The dual PIT phenomenon is attributed to the resonant couplings between the bright mode in the GCC and two nondegenerate bright modes in the GRR with symmetry-breaking. The results of the proposed triple coupled-oscillator model (TCM) are highly consistent with those of the finite-difference time-domain (FDTD) method. As the structural parameters are varied, the dual PIT windows exhibit strong robustness except the length of GRR along the y direction. The transmission window of the dual PIT can be effectively modulated by the carrier mobility of graphene. Finally, we study the modulation degree (MD) and the corresponding IL at different Fermi levels, which demonstrates excellent tunability of the dual PIT windows at multiple frequencies.

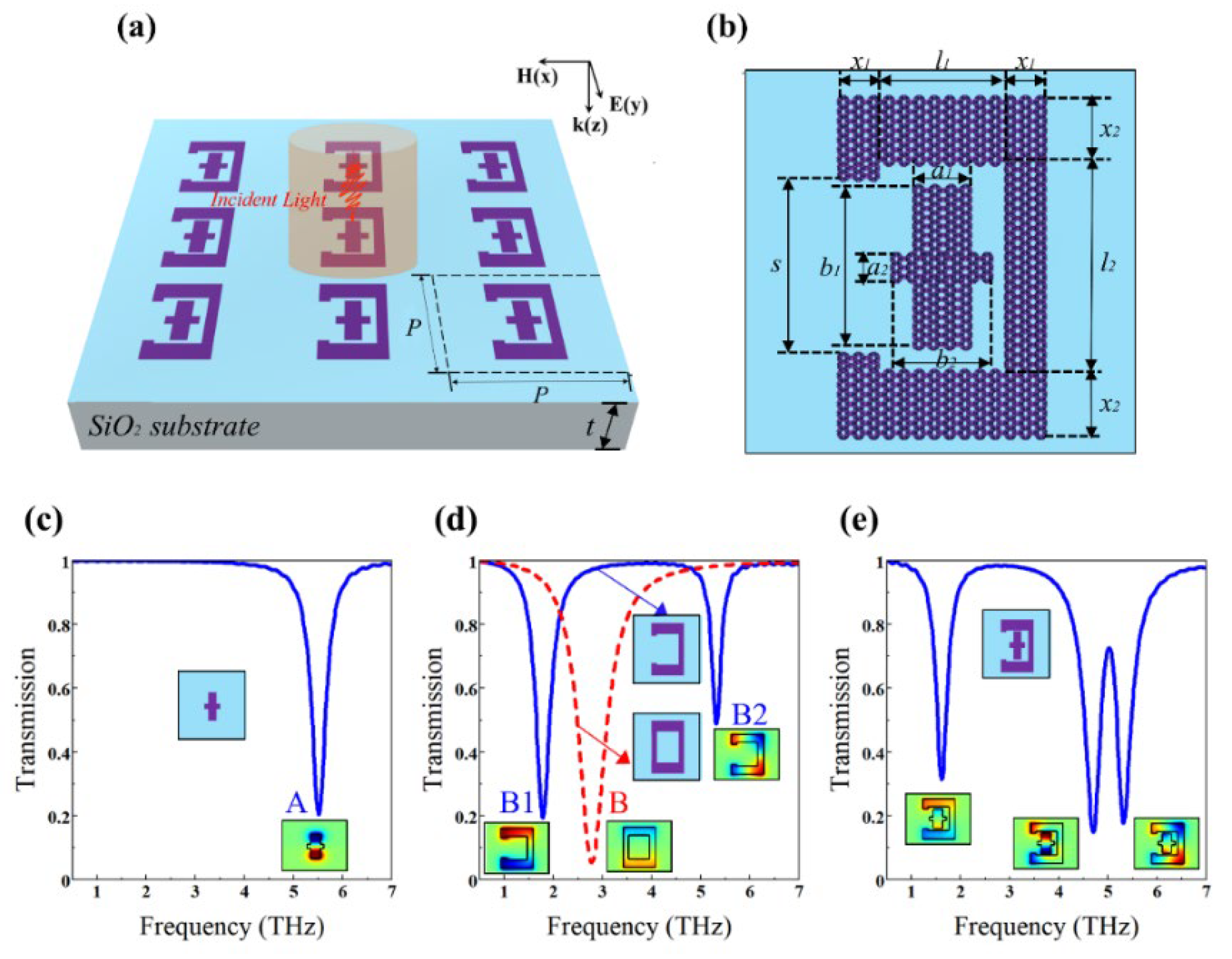
2. Structure and Method

Figure 1a shows the schematic diagram of the proposed graphene metasurface on a silica (SiO2) substrate under the illumination of a normally incident THz wave. The period of the graphene metasurface is P; the thickness of the SiO2 substrate is t, and its refractive index is 1.96 [31]. As shown in Figure 1b, the graphene metasurface consists of two resonators in its unit cell, one is the GCC with length (b1,b2) and width (a1,a2), the other is the GRR with length (l1,l2), width (x1,x2) and a cut s. In principle, the unit cell of the GCC possesses structural symmetry both in the x and y directions, while the GRR exhibits structural symmetry only along the y direction as s≠0. In this case, besides the resonant mode arising from the GCC, the resonant modes of the GRR will be nondegenerate due to the symmetry breaking with s≠0 and they can be tuned by s as well, thus symmetry-engineered PIT is possible in the proposed graphene metasurface through the interaction of the resonant modes of GCC and GRR.
In the THz wavelength region, the monolayer graphene can be regarded as a surface conductivity σ(ω) with neglectable interband component, and it can be simplified according to the random phase approximation [32,33]:
σ ( ω ) = i e 2 E F π ℏ 2 ( ω + i τ − 1 )
,
where ω is the angular frequency, e is the charge of an electron, EF is the Fermi level, ћ is the reduced Planck constant, and τ is the relaxation time. The intrinsic relaxation time satisfies the relationship τ=μEF/evF2, where vF=c/300 is the Fermi velocity and μ=10000 cm2/Vs is the measured carrier mobility. The Fermi level of graphene is set to 1 eV and the temperature is 300 K.
In the simulation, graphene is modeled as a thin layer with the relative permittivity expressed as εg=1+iσ(ω)/(ε0ωΔ), where Δ=1 nm is the thickness of graphene, and ε0 is the vacuum permittivity. We adopted a commercial software from Ansys Lumerical, in which a FDTD method had been applied to calculate the optical responses and the field distributions of the structure. Periodic boundary conditions are applied in the x and y directions, while perfectly matched layers are applied in the z direction. The grid size is chosen as 10 nm to ensure the accuracy of the calculation.
To well demonstrate the PIT properties of the proposed graphene metasurface, the transmission spectra of the GCC structure and the GRR structure are provided as a comparison, as shown in Figure 1c,d. As shown in Figure 1c, the GCC structure can be excited by the incident light directly and it exhibits a distinct transmission dip at 5.51 THz. This indicates that it is a bright mode and we labeled it as Mode A, which is associated with the excitation of the electric dipole (ED) according to the field distribution inserted in the figure. In Figure 1d, it can be seen that the GRR structure with s=0 can also be excited directly by the incident light with a resonant dip at 2.78 THz (Mode B), indicating the bright mode feature with the ED mode according to its field distribution. However, Mode B will split into two nondegenerate bright modes of Mode B1 and Mode B2 as s≠0 due to the symmetry breaking of the structure, which is associated with the cancellation of the short-circuit capacitance of the GRR according to the inductor-capacitor (LC) model [34], and the resonant locations of Mode B1 and Mode B2 are 1.78 THz and 5.31 THz, respectively. According to their field distributions inserted in the figure, Mode B1 and Mode B2 correspond to the ED and electric quadrupole (EQ) modes, respectively [35]. In Figure 1e, for the graphene metasurface consisting of the GCC and GRR in its unit cell, it can be seen two transparent windows (one broadband centered at 2.95 THz and the other narrowband centered at 5.01 THz) can be excited due to the interaction of the triple bright modes, with three dips located at 1.61, 4.70, and 5.31 THz respectively. The electric field inserted in the figures reveals that the resonant dip at 1.61 THz is associated with the resonant coupling between Mode A and Mode B1, the resonant dip at 5.31 THz is originated from the resonant coupling between Mode A and Mode B2, and the resonant dip at 4.70 THz is exhibited the hybrid mode properties among Modes A, B1 and B2. Therefore, the resonant coupling of Modes A, B1 and B2 are responsible for the occurrence of the two transparent windows.

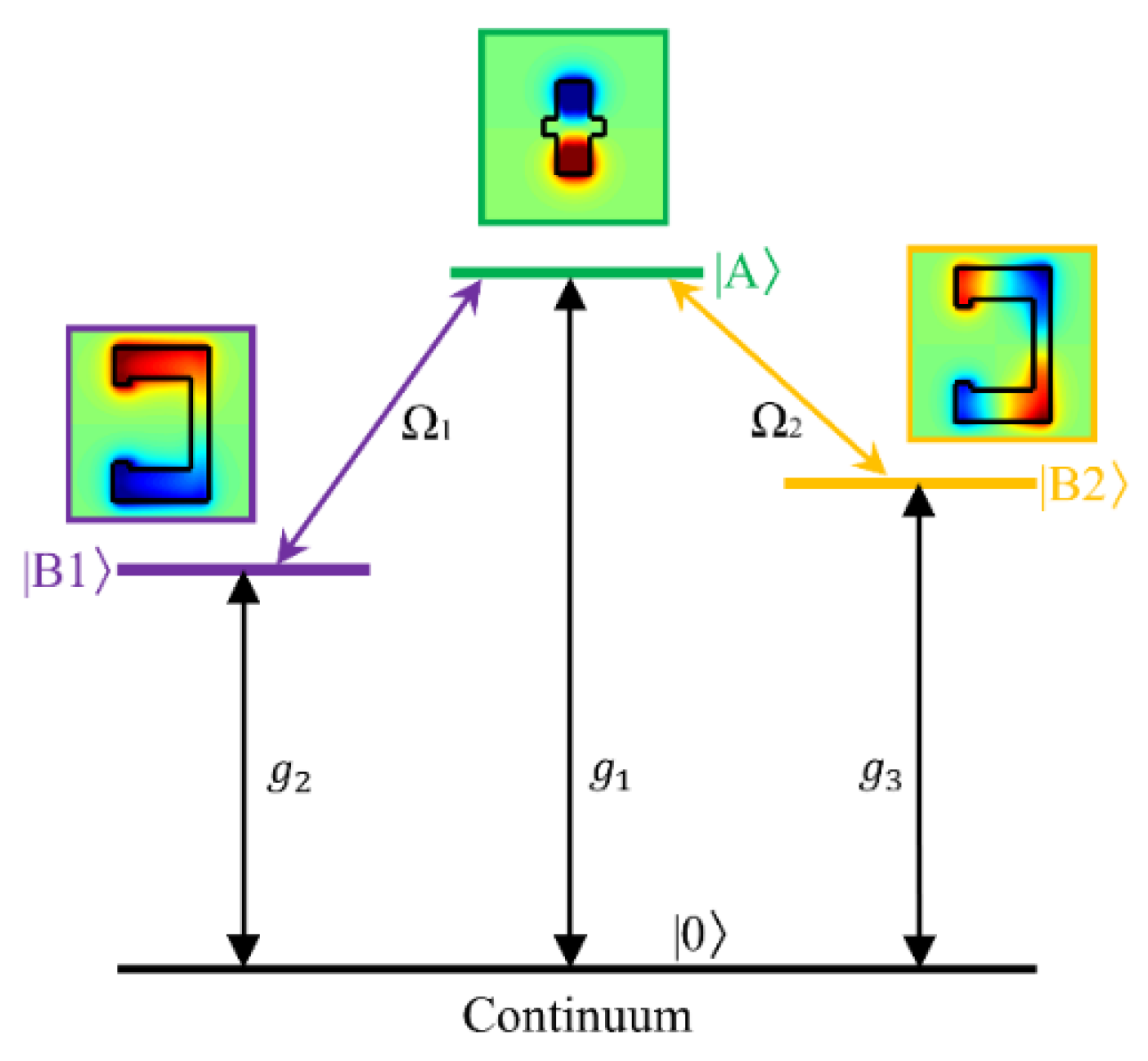
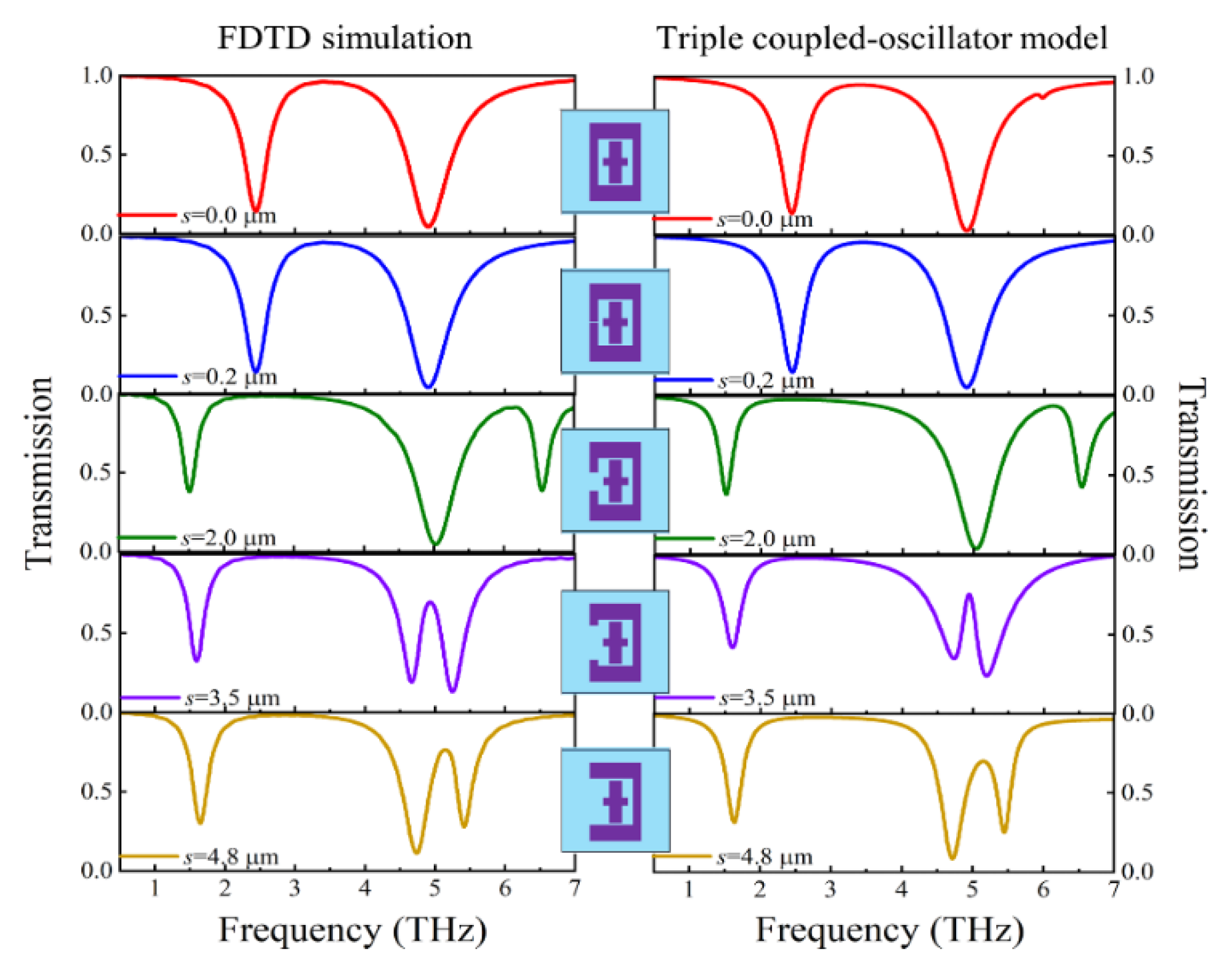
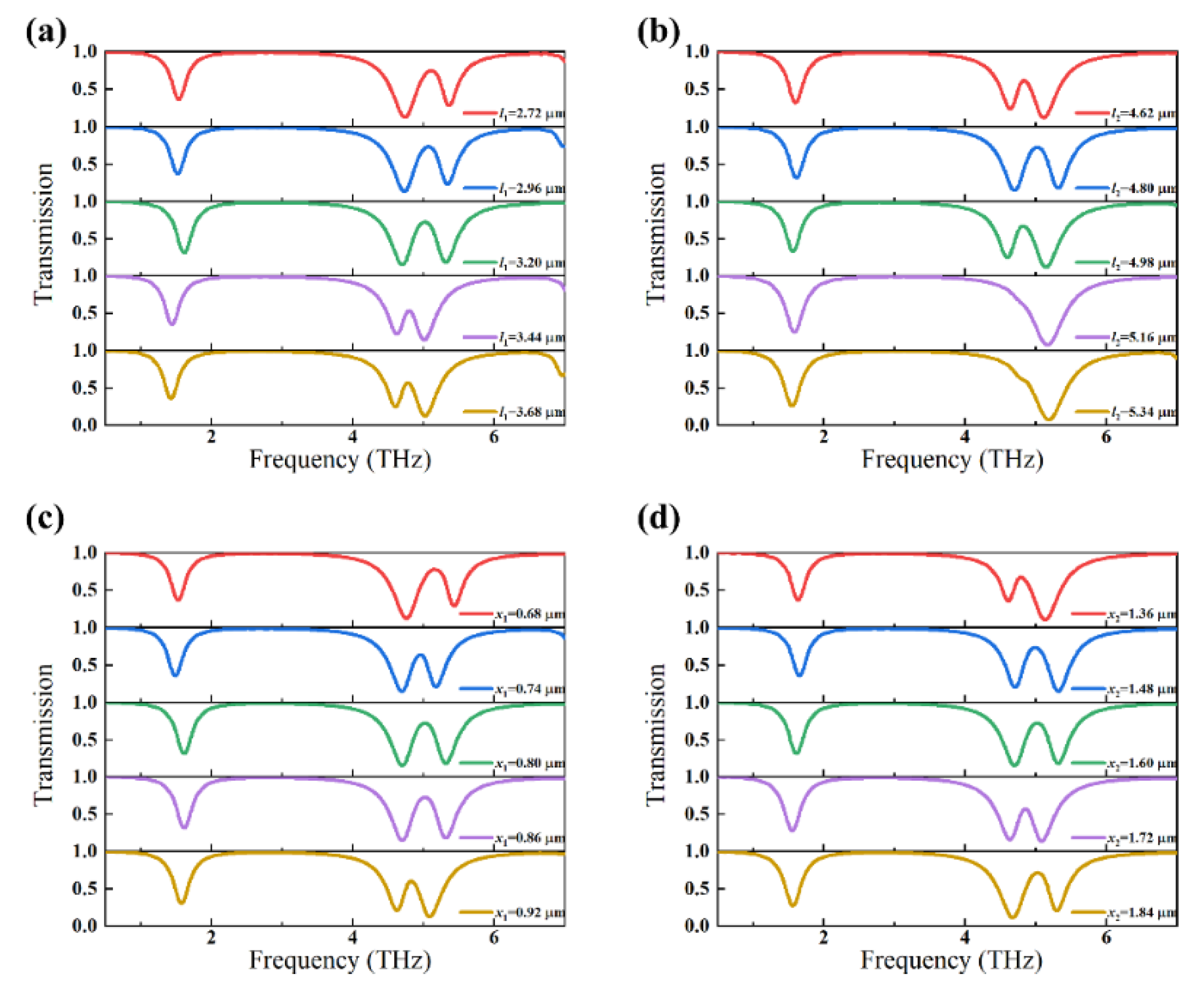
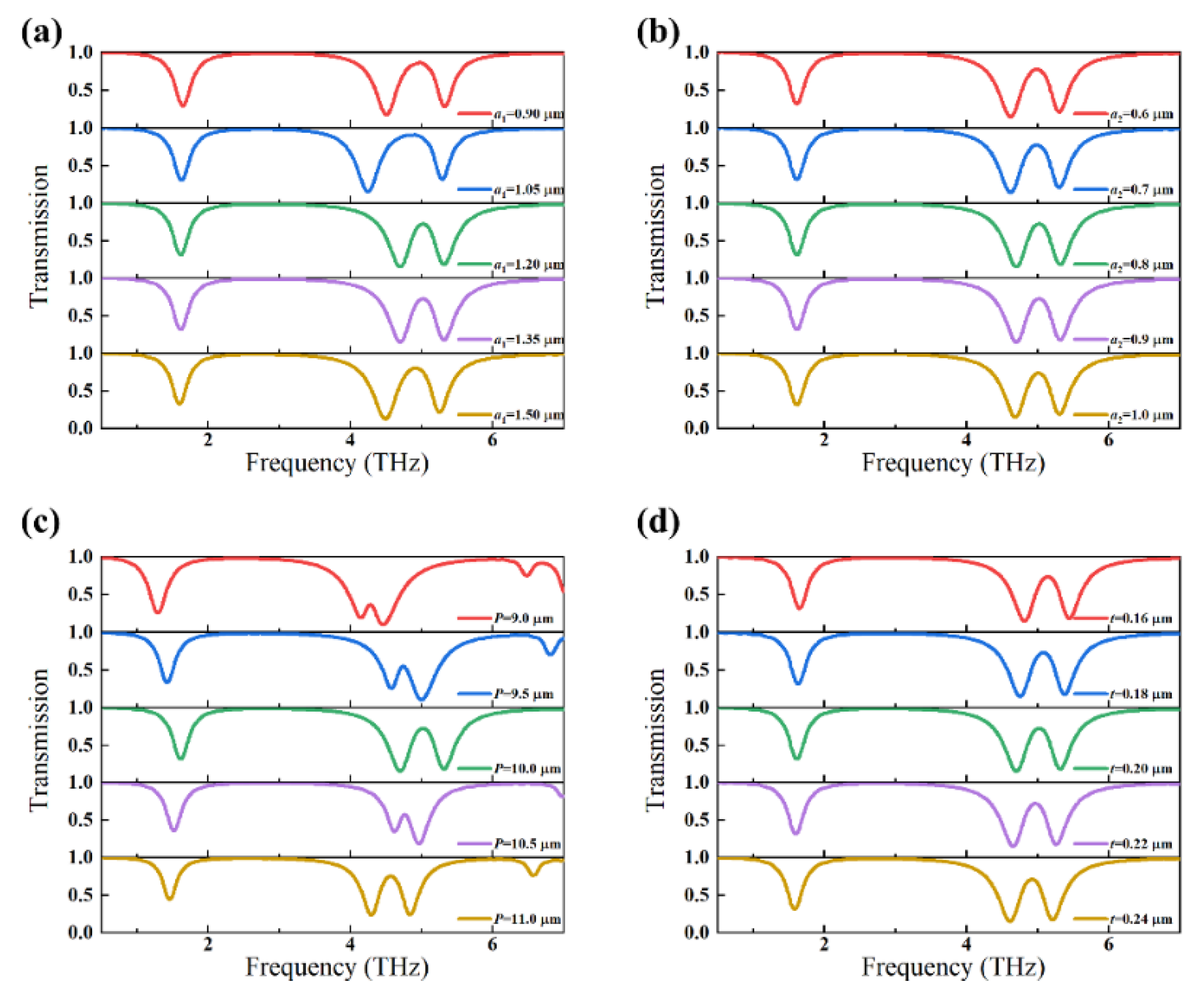
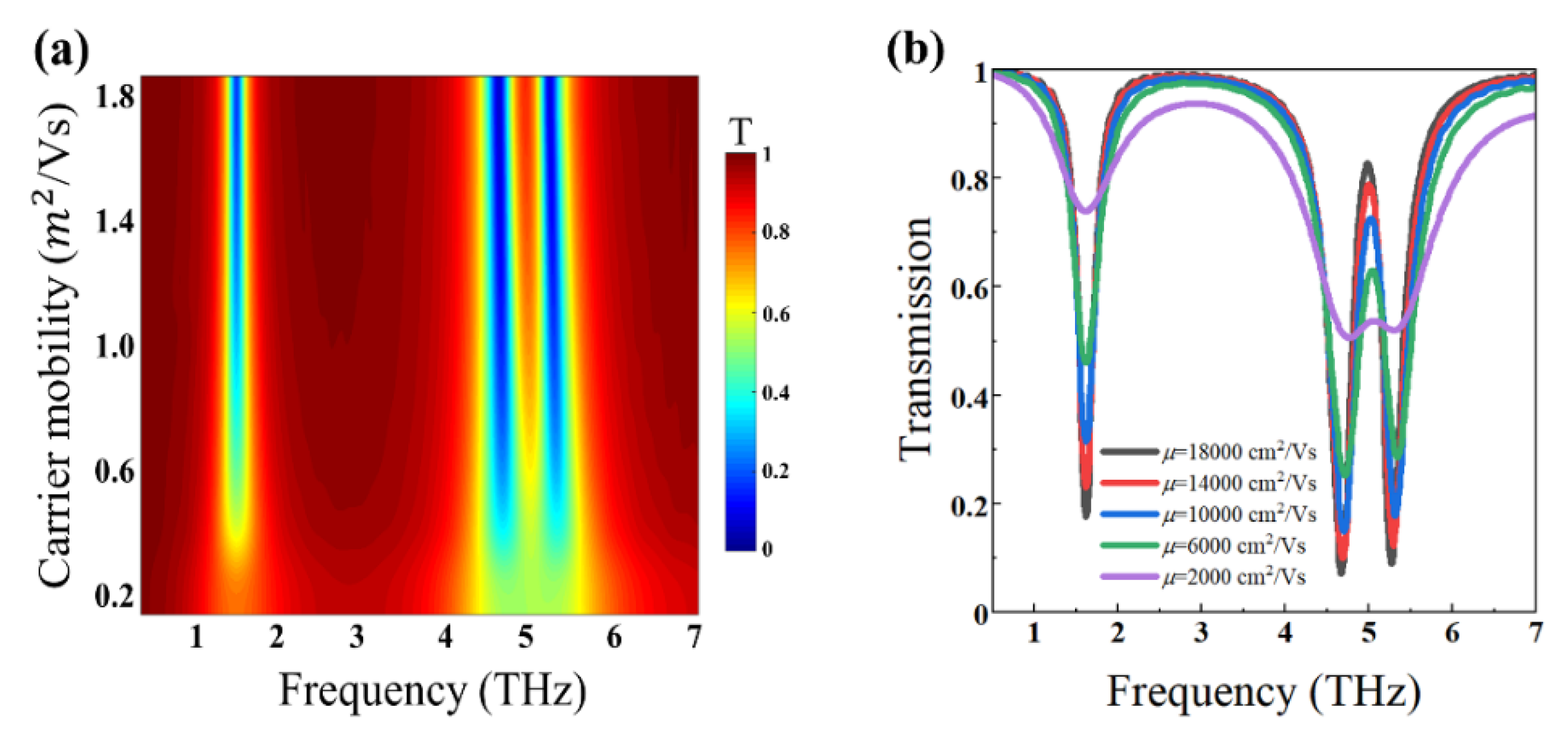
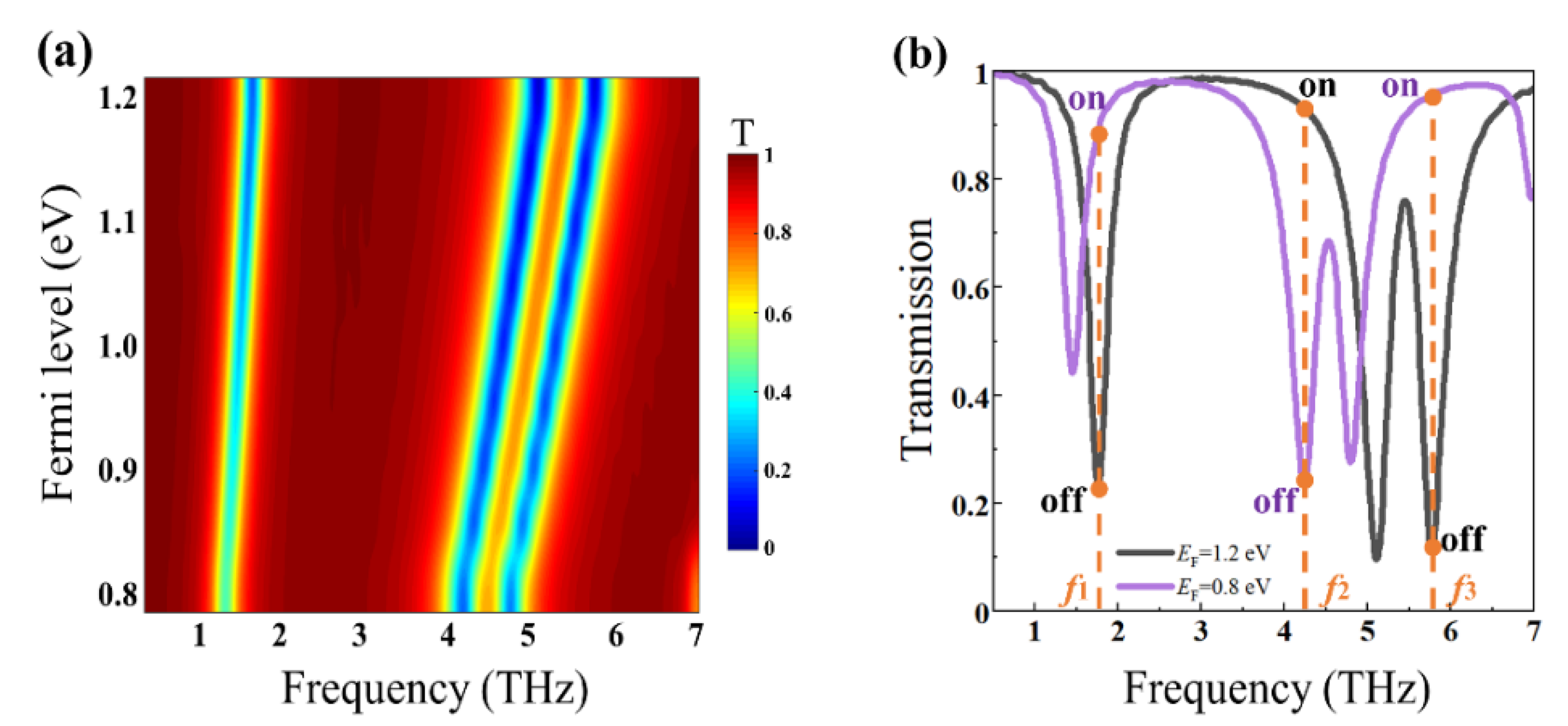
3. Results and Discussion

To gain further insights into the physical mechanism behind the two transparent windows, we propose a coupled four-level plasmonic model to describe the dual PIT phenomenon from the phenomenological perspective, as shown in Figure 2. The GCC can be regarded as the radiative plasmon state |A〉 featuring with the ED mode, and |A〉 is the bright mode as it can be efficiently excited by the incident light of the ground state |0〉. Similarly, the GRR can also be directly excited by the incident light corresponding to the degenerate bright Mode B with s=0. However, due to the symmetry breaking of the structure of the GRR as s≠0, Mode B will split into two bright modes of Mode B1 from ED (i.e., the state |B1〉) and Mode B2 from EQ (i.e., the state |B2〉). The transition of |0〉→|A〉 can be realized through a direct path of |0〉→|A〉, and two indirect paths of |0〉→|A〉→|B1〉→|A〉 and |0〉→|A〉→|B2〉→|A〉. Therefore, it is possible to create two transmission windows through the interferences between the direct path and the two indirect paths in the coupled four-level plasmonic system.
To demonstrate the validity of the underlying dual PIT phenomenon, we propose the TCM to evaluate the resonant coupling of the triple bright modes according to the two coupled-oscillator theory [36,37]. Here the TCM for triple bright modes in the proposed graphene metasurface can be described by the following equations containing three oscillators:
d 2 x 1 d t 2 + γ 1 d x 1 d t + ω 1 2 x 1 + Ω 1 2 x 2 + Ω 2 2 x 3 = g 1 E
d 2 x 2 d t 2 + γ 2 d x 2 d t + ω 2 2 x 2 + Ω 1 2 x 1 = g 2 E
d 2 x 3 d t 2 + γ 3 d x 3 d t + ω 3 2 x 3 + Ω 2 2 x 1 = g 3 E
where Mode A, Mode B1, and Mode B2 correspond oscillator 1, oscillator 2, and oscillator 3, respectively; (x1,x2,x3), (γ1,γ2,γ3), and (ω1,ω2,ω3) represent the displacement, damping factor, and resonant frequency of oscillators 1, 2, and 3, respectively. g1=Q1/M1, g2=Q2/M2, and g3=Q3/M3 are the coupling strengths of the bright modes, where (Q1,Q2,Q3) and (M1,M2,M3) represent the effective charge and mass of the oscillators. Ω1 and Ω2 represent the coupling strengths between oscillators 1 and 2, and oscillators 1 and 3, respectively. Because Mode B1 and Mode B2 are quasi-orthogonal modes (B1 is even mode while B2 is odd mode), their couplings are sufficiently small and can be ignored. The electric field of the incident terahertz radiation is denoted by E=E0eiωt, where ω represents its frequency.
To solve Equations (2)–(4) and obtain the displacements (x1,x2,x3), we assume the trial solution to be xn=Nneiωt, and the magnetization χ can be related to the polarizability P of the incident terahertz radiation as:
χ = P ϵ 0 E = Q 1 x 1 + Q 2 x 2 + Q 3 x 3 ϵ 0 E = Q 1 2 M 1 ϵ 0 ( α 1 Ω 1 4 + α 2 Ω 2 4 + α 3 Ω 1 2 + α 4 Ω 2 2 + η + β Ω 1 2 Ω 2 2 D 1 D 2 D 3 − Ω 2 4 D 2 − Ω 1 4 D 1 )
where A1=Q1/Q2, A2=Q1/Q3, B1=M1/M2, B2=M1/M3 D1=ω12-ω2+iωγ1, D2=ω22-ω2+iωγ2, D3=ω32-ω2+iωγ3. Also, we have taken there α1=-B2/A22, α2=-B1/A12, α3=-D3(1+B1)/A1, α4=-D2(1+B2)/A2, β=(B1+B2)/A1A2, η=D2D3+B1D2D3/A12+B2D1D2/A22. The transmission spectra of the proposed graphene metasurface can be obtained by using the Krammer-Koning relation T=1-image (χ).
Figure 3 shows the results of the FDTD simulation and the TCM for the graphene metasurface with different cut width s. As can be seen in Figure 3, the transmission properties can be engineered by changing the asymmetry parameter of s, and the PIT can be switched from one window to two windows with the increase of s. In addition, although s is varied in a wide range from 0-4.8 μm, the transmission responses of the TCM are in good agreement with those of the FDTD simulation, validating that the proposed model could provide a general strategy to evaluate the dual PIT phenomenon of the graphene metasurface associated with triple bright modes.
Then, we investigate the influences of the structural parameters (l1,l2,x1,x2) of the GRR on the transmission responses, as shown in Figure 4. As can be seen in Figure 4a, with l1 increasing the dual PIT phenomenon exhibits a slight red shift. According to the LC theory, the resonant frequency of the graphene metasurface can be estimated as fi∝1/(LC)∝1/Pi, where Pi is the outer side length of the GRR [38]. Consequently, the increase in l1 leads to a larger Pi, resulting in a decrease in resonant frequencies and a subsequent shift of the dual PIT phenomenon to the low-frequency region. In Figure 4b, it can be seen that the dual PIT windows will degrade into a single broad transmission window with the increase of l2. This degradation is attributed to the increasing distance between the GCC and GRR, thereby diminishing their coupling. Ultimately, the hybrid mode around 4.70 THz disappears as l2 is sufficiently large. In Figure 4c,d, it can be seen that the dual PIT windows can be maintained almost the same except a slight redshift of the resonance location with the increase of x1 or x2. As the variation of x1 or x2 is comparably small comparing with l1, the shift of the resonance locations of the two transmission windows is small comparing with l1 according to the LC theory. However, the transmission responses are very robust to the variations of the structural parameters of x1, x2, or l1, and the dual PIT phenomenon can be maintained even if they are deviated from the design values of ±15%.
Next, we investigate the influences of the structural parameters (a1,a2,P,t) on the transmission responses of the graphene metasurface, as shown in Figure 5. In Figure 5a,b, it can be seen that the transmission responses of the graphene metasurface are insensitive to the variations of a1 or a2. As shown in Figure 1e, the electric field of resonance is concentrated at the two ends of the GCC along the y direction, and the variation of a1 or a2 has negligible influence on the length of the GCC along the y direction, thus the transmission responses can be maintained almost the same as a1 or a2 is varied. In Figure 5c, it can be seen that with the increase of P, the two transmission windows are slightly blueshifted followed by a slight redshift. In Figure 5d, it can be seen that the dual PIT phenomenon can be maintained almost the same except a slight redshift of the resonance location with the increase of t, which features the Fabry-Pérot cavity modes confined in the structure [39].
Besides the influence of structural parameters on the graphene metasurface, the carrier mobility μ of graphene, which corresponds to the intrinsic loss of graphene, also plays an important role in the transmission responses, and the carrier mobility can be controlled by utilizing chemical doping or electric field tuning [40,41]. Figure 6 shows transmission responses of the graphene metasurface as μ is varied in the range from 2000 cm2/Vs to 18000 cm2/Vs. As can be seen in Figure 6a, the variation of μ has little influence on the location of the transmission windows. However, the dual PIT phenomenon is not obvious if μ<4000 cm2/Vs. This is because the intrinsic loss of graphene is sufficiently large if μ is small, resulting in the increased absorption and reduced transmission efficiency of the structure. In Figure 6b, it can be seen that the intensity of the dual PIT are reduced as μ is increased, and the two transmission windows tend to be disappeared with μ=2000 cm2/Vs.
Finally, we demonstrate that the dual PIT windows can be dynamically tuned by altering the Fermi level EF of the graphene, as shown in Figure 7. In Figure 7a, it can be seen that the frequency f of the resonant dips exhibit the noticeable blueshift with the increase of Fermi level EF, which is due to the square law of f∝EF1/2 [42]. Figure 7b shows the transmission spectra of the metasurface when EF is set as 0.8 eV and 1.2 eV. Note significant differences in the transmission amplitude can be achieved at the specified frequencies (i.e., f1=1.76 THz, f2=4.23 THz, and f3=5.77 THz), thus the on-off modulation can be realized based on the dual PIT phenomena. Here we define the MD and the corresponding IL to evaluate the tunability of modulation of the graphene metasurface:
M D = | T o n − T o f f | T o n × 100 %
I L = − 10 l g T o n
where Ton denotes the maximum transmission amplitude and Toff denotes the minimum transmission amplitude.
As can be seen in Figure 7b, when EF is set to 0.8 eV (the purple line), the transmission amplitudes at frequency f1 (1.76 THz) and f3 (5.77 THz) are 0.89 and 0.96, respectively; which can be functioned as the ‘on’ states with the IL of 0.5 dB and 0.19 dB, respectively. When EF is set to 1.2 eV (the black line), the transmission amplitudes at the frequencies of f1 and f3 are 0.22 and 0.11, respectively; which can be functioned as the ‘off’ states. Therefore, the MD at f1 (1.76 THz) and f3 (5.77 THz) are 75% and 89%, respectively. Similarly, when EF increases from 0.8 eV to 1.2 eV, the transmission amplitude at frequency f2 (4.23 THz) is increased from 0.24 to 0.93, where the MD is 74% and IL is 0.32 dB. Note the MD and IL are comparable with the multilayered graphene metasurfaces [43,44] and the hybrid metal-graphene metasurfaces [45], however, the proposed metasurface does not require the complex patterns such as the multilayered graphene patterns or the hybrid metal-graphene patterns, which may be advantageous for the optoelectric-related applications due to its comparably simple architecture.

4. Conclusions

In summary, we theoretically and numerically demonstrate a symmetry-engineered dual PIT phenomenon in a graphene-based metasurface. The unit cell of metasurface is composed of a GCC and a GRR and they both serve as bright modes that can be directly excited by incident light. By breaking the C2v symmetry of GRR with the cut width s≠0, one bright mode excited from incident light will split into two bright modes featuring with ED and EQ modes, and dual-band PIT phenomenon is realized due to the resonant coupling between the bright mode from GCC and two bright modes from asymmetric GRR. The derived formulas based on the TCM can well evaluate the transmission performances of the triple bright modes induced PIT. Dual-band PIT windows are robust to the variations of the structural parameters except the length l2 of the GRR along the y direction. The transmission of the dual PIT window can be effectively modulated by the carrier mobility of graphene. By changing the Fermi level of graphene, the dual PIT windows can be dynamically tuned with good performances for both MD and IL at different frequencies. The proposed symmetry-engineered metasurfaces provide a new design scheme for tunable PIT devices, which is promising for optical switching and modulating, selective filtering, and slow light equipment in the THz regime.

Author Contributions

Conceptualization, Y.C.; methodology, T.S.; software, Y.C.; validation, Y.C. and T.S.; formal analysis, Y.C.; investigation, Y.C. and T.S.; writing—original draft preparation, Y.C. and T.S.; writing—review and editing, Y.C. and T.S.; visualization, Y.C. and T.S.; supervision, T.S. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the by the National Natural Science Foundation of China (61975153) and Jiangsu Province Training Program of Innovation and Entrepreneurship for Undergraduates (2023CX196).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Yang, Y.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef] [PubMed]
  2. Hu, Y.; Jiang, T.; Sun, H.; Tong, M.; You, J.; Zheng, X.; Xu, Z.; Cheng, X. Ultrafast frequency shift of electromagnetically induced transparency in terahertz metaphotonic devices. Laser Photonics Rev. 2020, 14, 1900338. [Google Scholar] [CrossRef]
  3. Wang, C.; Jiang, X.; Zhao, G.; Zhang, M.; Hsu, C.W.; Peng, B.; Stone, A.D.; Jiang, L.; Yang, L. Electromagnetically induced transparency at a chiral exceptional point. Nat. Phys. 2020, 16, 334–340. [Google Scholar] [CrossRef]
  4. Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef] [PubMed]
  5. Niu, X.; Hu, X.; Yan, Q.; Zhu, J.; Cheng, H.; Huang, Y.; Lu, C.; Fu, Y.; Gong, Q. Plasmon-induced transparency effect for ultracompact on-chip devices. Nanophotonics 2019, 8, 1125–1149. [Google Scholar] [CrossRef]
  6. Xiong, C.X.; Xu, H.; Zhao, M.Z.; Zhang, B.H.; Liu, C.; Zeng, B.; Wu, K.; Ruan, B.X.; Li, M.; Li, H.J. Triple plasmon-induced transparency and outstanding slow-light in quasi-continuous monolayer graphene structure. Sci. China Phys. Mech. Astron. 2020, 64, 224211. [Google Scholar] [CrossRef]
  7. Luo, P.; Wei, W.; Lan, G.; Wei, X.; Meng, L.; Liu, Y.; Yi, J.; Han, G. Dynamical manipulation of a dual-polarization plasmon-induced transparency employing an anisotropic graphene-black phosphorus heterostructure. Opt. Express 2021, 29, 29690–29703. [Google Scholar] [CrossRef]
  8. Ge, J.H.; You, C.; Feng, H.; Li, X.; Wang, M.; Dong, L.; Veronis, G.; Yun, M. Tunable dual plasmon-induced transparency based on a monolayer graphene metamaterial and its terahertz sensing performance. Opt. Express 2020, 28, 31781–31795. [Google Scholar] [CrossRef]
  9. Liu, Y.; Weng, X.; Wang, M.; Li, W.; Ma, S.; Zhang, L.; Zhou, P.; Deng, L. Full control of Fano spectral profile with GST-based metamaterial. ACS Photonics 2022, 9, 888–894. [Google Scholar] [CrossRef]
  10. Chong, M.Z.; Zhao, J.; Yin, L.Z.; Han, F.Y.; Zhang, C.Q.; Liu, P.K. Nonlinear modulation of terahertz waves based on a MAPbI3/Gold/Si hybrid plasmon-induced transparency (PIT) metasurface. Opt. Mater. 2022, 129, 112554. [Google Scholar] [CrossRef]
  11. Zhang, B.; Li, H.; Xu, H.; Zhao, M.; Xiong, C.; Liu, C.; Wu, K. Absorption and slow-light analysis based on tunable plasmon-induced transparency in patterned graphene metamaterial. Opt. Express 2019, 27, 3598–3608. [Google Scholar] [CrossRef] [PubMed]
  12. He, Z.; Li, Z.; Li, C.; Xue, W.; Cui, W. Ultra-high sensitivity sensing based on ultraviolet plasmonic enhancements in semiconductor triangular prism meta-antenna systems. Opt. Express 2019, 28, 17595–17610. [Google Scholar] [CrossRef] [PubMed]
  13. Ono, M.; Hata, M.; Tsunekawa, M.; Nozaki, K.; Sumikura, H.; Chiba, H.; Notomi, M. Ultrafast and energy-efficient all-optical switching with graphene-loaded deep-subwavelength plasmonic waveguides. Nat. Photonics 2020, 14, 37–43. [Google Scholar] [CrossRef]
  14. Pitchappa, P.; Manjappa, M.; Ho, C.P.; Singh, R.; Singh, N.; Lee, C. Active control of electromagnetically induced transparency analog in terahertz MEMS metamaterial. Adv. Opt. Mater. 2016, 4, 541–547. [Google Scholar] [CrossRef]
  15. Mao, L.; Li, Y.; Li, G.; Zhang, S.; Cao, T. Reversible switching of electromagnetically induced transparency in phase change metasurfaces. Adv. Photonics 2020, 2, 056004. [Google Scholar] [CrossRef]
  16. Paul, S.; Ray, M. Plasmonic switching and bistability at telecom wavelength using the subwavelength nonlinear cavity coupled to a dielectric waveguide: a theoretical approach. J. Appl. Phys. 2016, 120, 203102. [Google Scholar] [CrossRef]
  17. Zhang, Z.; Yang, J.; He, X.; Han, Y.; Huang, J.; Chen, D. Tunable plasmon-induced transparency and slow light in terahertz chipscale semiconductor plasmonic waveguides. J. Phys. D: Appl. Phys. 2020, 53, 315101. [Google Scholar] [CrossRef]
  18. Xia, S.; Zhai, X.; Wang, L.; Wen, S. Plasmonically induced transparency in in-plane isotropic and anisotropic 2D materials. Opt. Express 2020, 28, 7980–8002. [Google Scholar] [CrossRef] [PubMed]
  19. Sang, T.; Dereshgi, S.A.; Hadibrata, W.; Tanriover, I.; Aydin, K. Highly efficient light absorption of monolayer graphene by quasi-bound state in the continuum. Nanomaterials 2021, 11, 484. [Google Scholar] [CrossRef]
  20. Jin, R.; Huang, L.; Zhou, C.; Guo, J.; Fu, Z.; Chen, J.; Wang, J.; Li, X.; Yu, F.; Chen, J.; Zhao, Z.; Chen, X.; Lu, W.; Li, G. Toroidal dipole BIC-driven highly robust perfect absorption with a graphene-loaded metasurface. Nano Lett. 2023, 23, 9105–9113. [Google Scholar] [CrossRef]
  21. Liu, Z.; Xie, Y.; Luo, X.; Zhou, F.; Cheng, Z.; Yi, Z. Dynamically adjustable high-Q quasi-bound state in the continuum based on Si gratings and graphene hybrid system. Opt. Laser Technol. 2024, 177, 111106. [Google Scholar] [CrossRef]
  22. He, Z.; Cui, W.; Ren, X.; Li, C.; Li, Z.; Xue, W.; Zhang, B.; Zhao, R. Ultra-high sensitivity sensing based on tunable plasmon-induced transparency in graphene metamaterials in terahertz. Opt. Mater. 2020, 108, 110221. [Google Scholar] [CrossRef]
  23. Liu, Z.; Gao, E.; Zhang, Z.; Li, H.; Xu, H.; Zhang, X.; Luo, X.; Zhou, F. Dual-mode on-to-off modulation of plasmon-induced transparency and coupling effect in patterned graphene-based terahertz metasurface. Nanoscale Res. Lett. 2020, 15, 1–9. [Google Scholar] [CrossRef] [PubMed]
  24. He, X.; Liu, F.; Lin, F.; Shi, W. Graphene patterns supported terahertz tunable plasmon induced transparency. Opt. Express 2018, 26, 9931–9944. [Google Scholar] [CrossRef] [PubMed]
  25. Fan, C.; Ren, P.; Jia, W.; Jia, Y.; Wang, J. Tunable plasmon induced transparency in patterned graphene metamaterial with different carrier mobility. Superlattices Microstruct. 2019, 136, 106295. [Google Scholar] [CrossRef]
  26. Zheng, S.; Zhao, Q.; Peng, L.; Jiang, X. Tunable plasmon induced transparency with high transmittance in a two-layer graphene structure. Results Phys. 2021, 23, 104040. [Google Scholar] [CrossRef]
  27. Tang, B.; Guo, Z.; Jin, G. Polarization-controlled and symmetry-dependent multiple plasmon-induced transparency in graphene-based metasurfaces. Opt. Express 2022, 30, 35554–35566. [Google Scholar] [CrossRef] [PubMed]
  28. Wu, T.; Wang, G.; Jia, Y.; Shao, Y.; Chen, C.; Han, J.; Gao, Y.; Gao, Y. Dual-spectral plasmon-induced transparent terahertz metamaterial with independently tunable amplitude and frequency. Nanomaterials 2021, 11, 2876. [Google Scholar] [CrossRef] [PubMed]
  29. Gao, E.; Liu, Z.; Li, H.; Xu, H.; Zhang, Z.; Luo, X.; Xiong, C.; Liu, C.; Zhang, B.; Zhou, F. Dynamically tunable dual plasmon-induced transparency and absorption based on a single-layer patterned graphene metamaterial. Opt. Express 2019, 27, 13884–13894. [Google Scholar] [CrossRef]
  30. Li, M.; Li, H.; Xu, H.; Xiong, C.; Zhao, M.; Liu, C.; Ruan, B.; Zhang, B.; Wu, K. Dual-frequency on-off modulation and slow light analysis based on dual plasmon-induced transparency in terahertz patterned graphene metamaterial. New J. Phys. 2020, 22, 103030. [Google Scholar] [CrossRef]
  31. Li, G.; Sang, T.; Qi, H.; Wang, X.; Yin, X.; Wang, Y.; Hu, L. Flexible control of absorption enhancement of circularly polarized light via square graphene disks. OSA Continuum 2020, 3, 1999–2009. [Google Scholar] [CrossRef]
  32. Horng, J.; Chen, C.F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Drude conductivity of Dirac fermions in graphene. Phys. Rev. B 2011, 83, 165113. [Google Scholar] [CrossRef]
  33. Deng, G.; Song, X.; Dereshgi, S.A.; Xu, H.; Aydin, K. Tunable multi-wavelength absorption in mid-IR region based on a hybrid patterned graphene-hBN structure. Opt. Express 2019, 27, 23576–23584. [Google Scholar] [CrossRef] [PubMed]
  34. Corrigan, T.D.; Kolb, P.W.; Sushkov, A.B.; Drew, H.D.; Schmadel, D.C.; Phaneuf, R.J. Optical plasmonic resonances in split-ring resonator structures: an improved LC model. Opt. Express 2008, 16, 19850–19864. [Google Scholar] [CrossRef] [PubMed]
  35. Papasimakis, N.; Fedotov, V.A.; Savinov, V.; Raybould, T.A.; Zheludev, N.I. Electromagnetic toroidal excitations in matter and free space. Nat. Mater. 2016, 15, 263–271. [Google Scholar] [CrossRef]
  36. Yahiaoui, R.; Manjappa, M.; Srivastava, Y.K.; Singh, R. Active control and switching of broadband electromagnetically induced transparency in symmetric metadevices. Appl. Phys. Lett. 2017, 111, 021101. [Google Scholar] [CrossRef]
  37. Wang, L.; Zhao, Z.; Du, M.; Qin, H.; Ako, R.T.; Sriram, S. Tuning symmetry-protected quasi bound state in the continuum using terahertz meta-atoms of rotational and reflectional symmetry. Opt. Express 2022, 30, 23631–23639. [Google Scholar] [CrossRef]
  38. Gong, C.; Zhan, M.; Yang, J.; Wang, Z.; Liu, H.; Zhao, Y.; Liu, W. Broadband terahertz metamaterial absorber based on sectional asymmetric structures. Sci. Rep. 2016, 6, 32466. [Google Scholar] [CrossRef] [PubMed]
  39. Mi, Q.; Sang, T.; Pei, Y.; Yang, C.; Li, S.; Wang, Y.; Ma, B. High-quality-factor dual-band Fano resonances induced by dual bound states in the continuum using a planar nanohole slab. Nanoscale Res. Lett. 2021, 16, 150. [Google Scholar] [CrossRef]
  40. Vu, T.V.; Hieuc, N.V.; Phuc, H.V.; Hieu, N.N.; Bui, H.D.; Idrees, M.; Amin, B.; Nguyen, C.V. Graphene/WSeTe van der Waals heterostructure: controllable electronic properties and Schottky barrier via interlayer coupling and electric field. Appl. Surf. Sci. 2020, 507, 145036. [Google Scholar] [CrossRef]
  41. Choi, M.S.; Nipane, A.; Kim, B.S.Y.; Ziffer, M.E.; Datta, I.; Borah, A.; Jung, Y.; Kim, B.; Rhodes, D.; Jindal, A.; et al. High carrier mobility in graphene doped using a monolayer of tungsten oxyselenide. Nat. Electron 2021, 4, 731–739. [Google Scholar] [CrossRef]
  42. Zhu, A.; Bu, P.; Cheng, L.; Hu, C.; Mahapatra, R. High-sensitivity sensor based on diametrical graphene strip plasma-induced transparency. Photonics 2023, 10, 830. [Google Scholar] [CrossRef]
  43. Liu, Z.; Zhang, X.; Zhang, Z.; Gao, E.; Zhou, F.; Li, H.; Luo, X. Simultaneous switching at multiple frequencies and triple plasmon-induced transparency in multilayer patterned graphene-based terahertz metamaterial. New J. Phys. 2020, 22, 083006. [Google Scholar] [CrossRef]
  44. Zhang, X.; Liu, Z.; Zhang, Z.; Gao, E.; Zhou, F.; Luo, X.; Wang, J.; Wang, Y. Photoelectric switch and triple-mode frequency modulator based on dual-PIT in the multilayer patterned graphene metamaterial. J. Opt. Soc. Am. A 2020, 37, 1002–1007. [Google Scholar] [CrossRef] [PubMed]
  45. Yan, R.; Arezoomandan, S.; Sensale-Rodriguez, B.; Xing, H.G. Exceptional terahertz wave modulation in graphene enhanced by frequency selective surfaces. ACS Photonics 2016, 3, 315–323. [Google Scholar] [CrossRef]
Preprints 109532 g001
Figure 1. Optical properties of the proposed graphene metasurface. The parameters are: P=10 μm, t=0.2 μm, l1=3.2 μm, l2=4.8 μm, x1=0.8 μm, x2=1.6 μm, a1=1.2 μm, a2=0.8 μm, b1=4.2 μm, b2=2.4 μm, s=4 μm. (a) Schematic diagram of the graphene metasurface on a SiO2 substrate under the illumination of a normally incident THz wave. (b) Top view of the unit cell of the graphene metasurface consisting of a GCC and a GRR. Transmission spectra of (c) GCC structure, (d) GRR structure with s=4.0 μm (blue solid line) and s=0 (red dashed line), and (e) the total structure; the z components (Ez) of the corresponding electric fields are inserted in the figures.
Figure 1. Optical properties of the proposed graphene metasurface. The parameters are: P=10 μm, t=0.2 μm, l1=3.2 μm, l2=4.8 μm, x1=0.8 μm, x2=1.6 μm, a1=1.2 μm, a2=0.8 μm, b1=4.2 μm, b2=2.4 μm, s=4 μm. (a) Schematic diagram of the graphene metasurface on a SiO2 substrate under the illumination of a normally incident THz wave. (b) Top view of the unit cell of the graphene metasurface consisting of a GCC and a GRR. Transmission spectra of (c) GCC structure, (d) GRR structure with s=4.0 μm (blue solid line) and s=0 (red dashed line), and (e) the total structure; the z components (Ez) of the corresponding electric fields are inserted in the figures.
Preprints 109532 g001
Preprints 109532 g002
Figure 2. Schematic diagram of a coupled four-level plasmonic model. |0〉 is the ground state corresponds to the incident light; |A〉 is the radiative plasmon state corresponding to the bright mode of the GCC; |B1〉 and |B2〉 are two radiative plasmon states corresponding to the nondegenerate bright modes of the GRR with s≠0. The free space coupling strength between the ground state |0〉 and |A〉, |B1〉, |B2〉 are g1, g2, g3, respectively. The coupling strengths between |A〉 and |B1〉, |B2〉 are Ω1, Ω2, respectively.
Figure 2. Schematic diagram of a coupled four-level plasmonic model. |0〉 is the ground state corresponds to the incident light; |A〉 is the radiative plasmon state corresponding to the bright mode of the GCC; |B1〉 and |B2〉 are two radiative plasmon states corresponding to the nondegenerate bright modes of the GRR with s≠0. The free space coupling strength between the ground state |0〉 and |A〉, |B1〉, |B2〉 are g1, g2, g3, respectively. The coupling strengths between |A〉 and |B1〉, |B2〉 are Ω1, Ω2, respectively.
Preprints 109532 g002
Preprints 109532 g003
Figure 3. Results of the FDTD simulation and the TCM for the proposed graphene metasurface with different cut width s. Other parameters are the same as in Figure 1e.
Figure 3. Results of the FDTD simulation and the TCM for the proposed graphene metasurface with different cut width s. Other parameters are the same as in Figure 1e.
Preprints 109532 g003
Preprints 109532 g004
Figure 4. Transmission responses of the graphene metasurface under the influences of the structural parameters of the GRR for (a) l1, (b) l2, (c) x1, and (d) x2. Other parameters are the same as in Figure 1e.
Figure 4. Transmission responses of the graphene metasurface under the influences of the structural parameters of the GRR for (a) l1, (b) l2, (c) x1, and (d) x2. Other parameters are the same as in Figure 1e.
Preprints 109532 g004
Preprints 109532 g005
Figure 5. Transmission responses of the graphene metasurface under the influences of the structural parameters for (a) a1, (b) a2, (c) P, and (d) t. Other parameters are the same as in Figure 1e.
Figure 5. Transmission responses of the graphene metasurface under the influences of the structural parameters for (a) a1, (b) a2, (c) P, and (d) t. Other parameters are the same as in Figure 1e.
Preprints 109532 g005
Preprints 109532 g006
Figure 6. Transmission responses of the graphene metasurface under the influences of the carrier mobility of graphene. Other parameters are the same as in Figure 1e. (a) Transmission 2D map as a function of the carrier mobility of graphene. (b) Transmission spectra for different carrier mobility of graphene.
Figure 6. Transmission responses of the graphene metasurface under the influences of the carrier mobility of graphene. Other parameters are the same as in Figure 1e. (a) Transmission 2D map as a function of the carrier mobility of graphene. (b) Transmission spectra for different carrier mobility of graphene.
Preprints 109532 g006
Preprints 109532 g007
Figure 7. Transmission responses of the graphene metasurface under the influences of the Fermi level of graphene. Other parameters are the same as in Figure 1e. (a) Transmission 2D map as a function of the Fermi level of graphene. (b) Transmission spectra for different Fermi levels of graphene. The on-to-off switching modulations are evaluated by the resonant frequencies of f1=1.76 THz, f2=4.23 THz, and f3=5.77 THz.
Figure 7. Transmission responses of the graphene metasurface under the influences of the Fermi level of graphene. Other parameters are the same as in Figure 1e. (a) Transmission 2D map as a function of the Fermi level of graphene. (b) Transmission spectra for different Fermi levels of graphene. The on-to-off switching modulations are evaluated by the resonant frequencies of f1=1.76 THz, f2=4.23 THz, and f3=5.77 THz.
Preprints 109532 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated