In theoretical physics, division algebras are used to represent physical phenomena via an isomorphism. Out of the four normed division algebras, the largest is the octonions [1,2]. Octonions exhibit interesting algebraic properties beyond their non-commutativity and non-associativity, like not having a multiplicative inverse for each nonzero element. A novel method is applied to study the octonion algebra, also called Cayley algebra [3], on a split basis, which discloses the quark theory [4,5]. In the same perspective, there has long been conjecture that there is a relationship between octonions and the Standard Model [6], which clarifies a lot of the issues that come with the algebraic model of the Standard Model. In mathematical physics, the SU(3) Lie group can be described by the octonion algebra. Taking into consideration the theory of octonion variables, Pushpa et al. [7,8] developed the correlations between different isospin components and quark states to the case for the SU(3) group. The octonionic structure of the exceptional groups includes the SU(3) colour group. Quantum chromodynamics (QCD) and quantum electrodynamics (QED) seem to share a lot of similarities. The QED interaction is mediated by a massless photon that corresponds to the single generator of the U(1) local gauge symmetry, while the QCD interaction is mediated by eight massless gluons that correspond to the eight generators of the SU(3) local gauge symmetry. Three conserved colour charges (R, B, and G) take the place of the single charge found in QED. In the SU(3) colour space, these colour charges serve as a label for the orthogonal states [9]. Particles only couple to gluons when their colour charge is non-zero. Because of this, the colourless leptons are immune to the powerful force. There are three orthogonal colour states for the quarks, which are charged particles. Chanyal et al. [10,11] proposed split octonions as a basis for the field equations of hot and cold dark matter in their study of the role of octonions in quark chromodynamics and the dark matter field. Furthermore, a number of phenomenological physical theories have been explained by the application of hyper-complex division algebras by different authors [12]. As a result, the quark’s colour charge has no bearing on the QCD interaction intensity. The colour group SU(3) is isomorphic to octonion. We tried to write a connection between octonion algebra and SU(3) colour group generators in light of recent advances [13]. The SU(3) colour symmetry group is based on three colours: R, B, and G. 34 colour combinations are conceivable for the four quarks that are engaged in this process. There are eight additional gluons that could be swapped. As a result, 648 different quark colour and gluon combinations are possible to contribute to the process. Thankfully, a single colour component can absorb the effect of adding up all the colour and gluon combinations. The Feynman diagram is used to illustrate how colour quark particles interact. A thorough explanation of the strong interactions among quarks is provided by QCD.

The octonions constitute an 8-dimensional unital, distributive algebra over R with basis $e_A(A=1,2,....7)$ and $e_0$ is the multiplicative unit element. A hypercomplex normed division algebra over real numbers, octonion has twice as many dimensions as quaternions. This algebra is non-associative [3]. An octonion variable may be expressed using eight real integers as

These octonion basis elements satisfy some following relations: where $(A,B,C=1,2,...,7)$, and brackets [ ] and { } indicated the commutation and the anti-commutation relations, respectively, while ${\delta }_{AB}$ is the standard Kronecker delta-Dirac symbol. For the following permutations, the structure constant $f_{ABC}$ is entirely antisymmetric and take the value 1, i.e.$f_{ABC}$$=+1$ for $ABC$= (123), (471), (257), (165), (624), (543), (736). The norm of the octonion algebra is expressed as

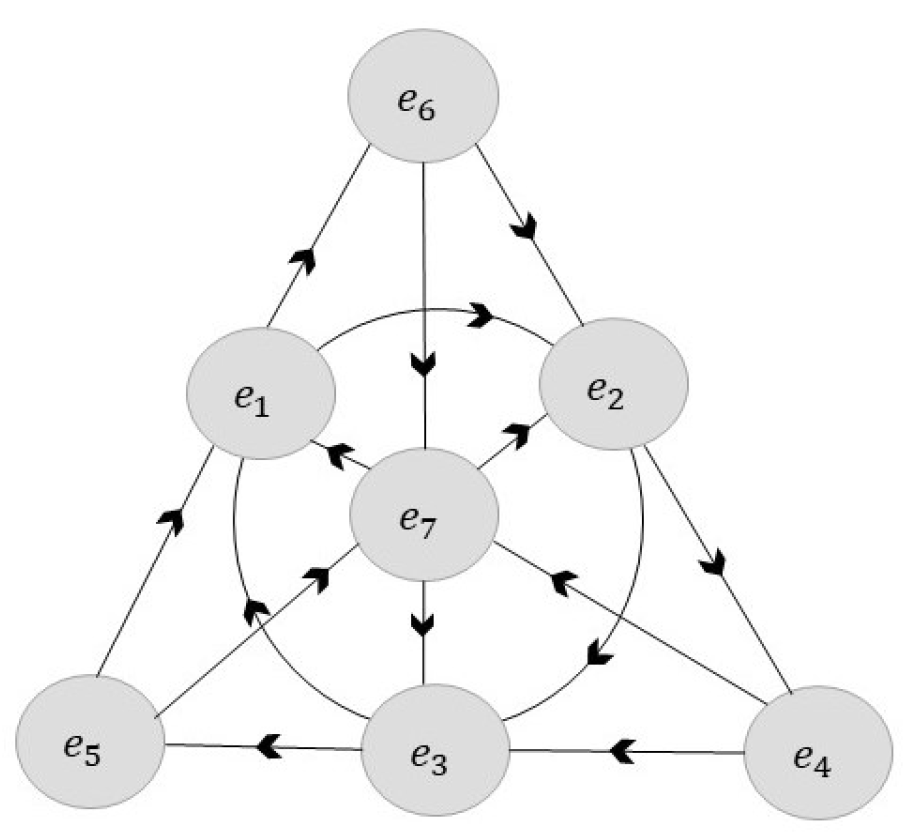
The fano plane also allows one to display the algebraic structure of octonions and their multiplications. The triangle’s three sides, the incircle, and the three altitudes are the seven quaternions subsets that are shown in Figure 1.

The new elements will not necessarily be anti-hermitian when characterising the complexified SU(3) group, the complex linear combinations of the SU(3) components, but they will be traceless, which is precisely the property of the Lie algebra of SL(3, C). The basis of SL(3, C)—group i.e., $E_{12},E_{23},E_{13},E_{21},E_{32},E_{31}$ will be equivalent of octonion operators in octonion representation as [13],

Where u${ }_{12},{\overline{u}}_{12}^{*},u_{45},{\overline{u}}_{45}^{*},u_{67},{\overline{u}}_{67}^{*}$ are the octonion shift operators. These are the complexified form of elements of SU(3) Lie algebra. The two generators may be used as Cartan generators ($u_3$$=\frac{-i{e}_3}{2},u_0=\frac{2}{3}{e}_0)$. This is a group which acts on the colour indices of quark favours described in the form of a basic triplet [14]. which transform as $\Phi ⟶{\Phi }^{{ }^{\prime }}=U\Phi$, where U are unitary matrices of unity determinant and the set of unitary matrices as follows where ${\sigma }_{\alpha }$ are the eight parameters of SU(3) group and $u_{\alpha }$ are the complex octonion matrices of SU(3) group form the fundamental representation. The Gell-Mann matrices are as follows:

It satisfy some properties

The Gell-Mann matrices of SU(3) symmetry in terms of SU(3) Lie algebra and it consists of antihermitian traceless matrices. Hence the consequence, the SU(3) group, $G_2\sim SU\left(3\right)$, is an automorphism of the octonion algebra. Colour SU(3) refers to the eight conserved charges that make up the QCD symmetry group. As is well known, quantum field theory explains how charged particle interactions are described by quantum electrodynamics (QED); in this theory, coloured particle interactions are described by quantum chromodynamics (QCD).

The evaluation of a Feynman diagram, which shows a particular decay or scattering process is done by using the Feynman rules which help to calculate the matrix element. The matrix element contains the dynamical information of particles. Feynman rule for QCD are shown in table-6 .

where $u_f^{\left(s\right)}(E,p)$ and $v_f^{\left(s\right)}(E,p)$ are Dirac spinor in terms of energy and momentum, s index $=(1,2)=$ (up, down).

The octonionic color quark states can be represented as and the octonionic anti-color quark states are given by

Since only eight gluons are coloured and the others are not, there are eight octonionic physical gluons that can be exchanged. The matrix form of the eight octonionic gluonic state is shown below.

In the complexified octonion field, these are alternatively referred to as octonionic shift operators. These octonionic gluonic states correspond to the field associated with the generator of SU(3) colour symmetry and act as a mediator for the octonionic colour quark interaction. It can be said that $u_{12}$ and ${\overline{u}}_{12}^{*}$ correspond to the exchange of $R\overline{G}$ and $G\overline{R}$, $u_{45}$ and ${\overline{u}}_{45}^{*}$ correspond to the exchange of $R\overline{B}$ and $B\overline{R}$, $u_{67}$ and ${\overline{u}}_{67}^{*}$ correspond to the exchange of $G\overline{B}$ and $B\overline{G}$, $u_3$ and $u_0$ correspond to the exchange of $R\overline{R}-G\overline{G}$ and $\frac{1}{\sqrt{3}}$$(R\overline{R}+G\overline{G}-2B\overline{B})$ gluons. The relationship between these colour states and the octonion complex operator, or space, has been derived.

These octonionic gluonic states are corresponding to field associated with generator of SU(3) color symmetry. It can be said that $u_{12}$ and ${\overline{u}}_{12}^{*}$ correspond to the exchange of $R\overline{G}$ and $G\overline{R}$, $u_{45}$ and ${\overline{u}}_{45}^{*}$ correspond to the exchange of $R\overline{B}$ and $B\overline{R}$, $u_{67}$ and ${\overline{u}}_{67}^{*}$ correspond to the exchange of $G\overline{B}$ and $B\overline{G}$, $u_3$ and $u_0$ correspond to the exchange of $R\overline{R}-G\overline{G}$ and $\frac{1}{\sqrt{3}}$$(R\overline{R}+G\overline{G}-2B\overline{B})$ gluons.

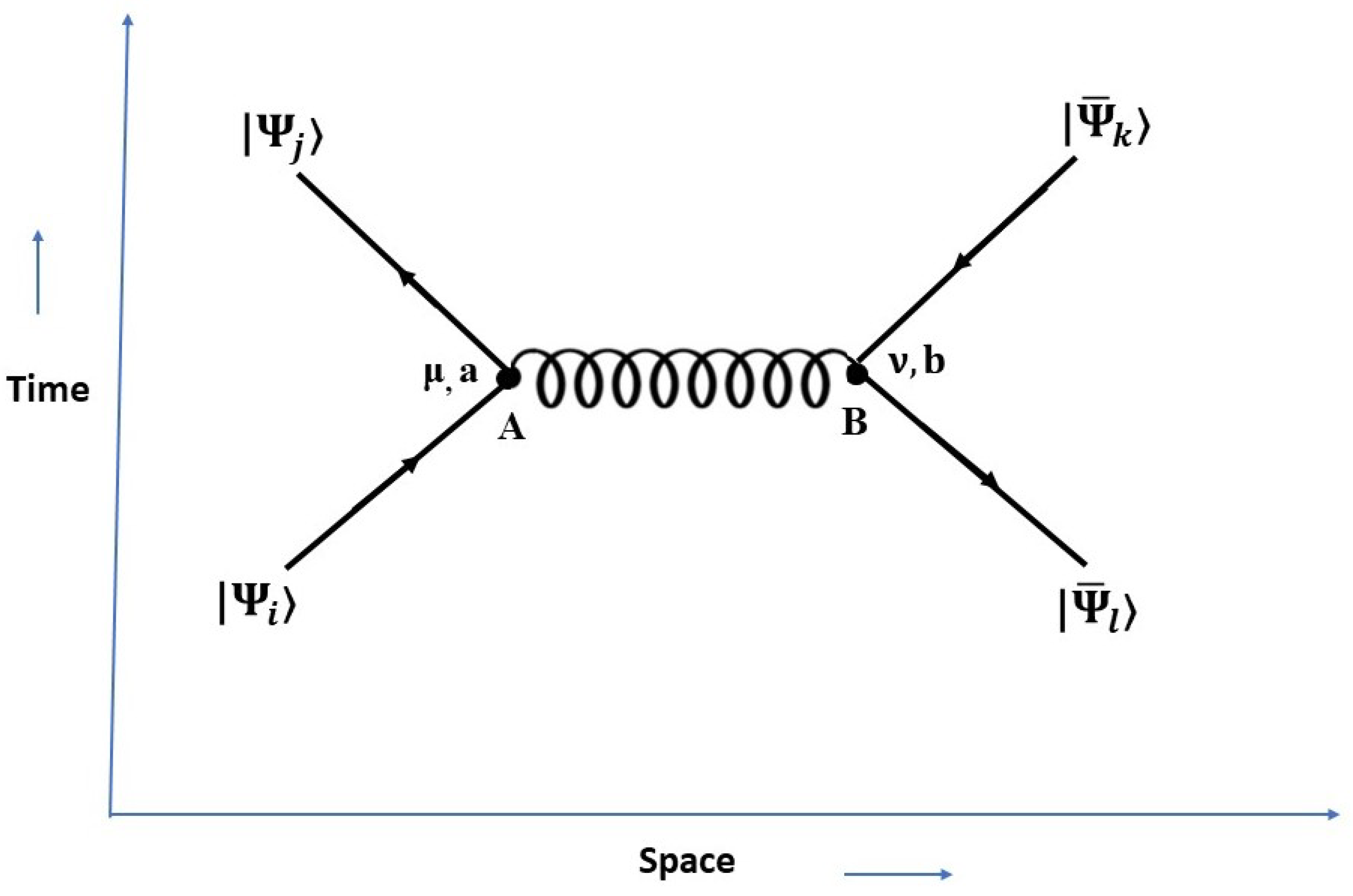
The interaction of octonionic color quark can be represented with the help of space-time diagram(Feynman diagram) as shown in fig.

where, vertex A:- $\frac{-i{g}_s{u}_3{\gamma }^{\mu }}{2}$ and $\frac{-i{g}_s{u}_0{\gamma }^{\mu }}{2}$

vertex B:-$\frac{-i{g}_s{u}_3{\gamma }^{\mu }}{2}$ and $\frac{-i{g}_s{u}_0{\gamma }^{\mu }}{2}$

Propogator:-$\frac{-i{g}_{\mu \nu }}{{(p_i-p_f)}^2}$.

The OQCD color factor can be calculated by using octonion complex shift operator or octonionic operator (u${ }_{12},{\overline{u}}_{12}^{*},u_{45},{\overline{u}}_{45}^{*},u_{67},{\overline{u}}_{67}^{*}$,$u_3$ and $u_0$). The different color indices determine which elements of octonion operators are relevant to this interaction, which in turns determines which gluons contribute. The color charge is conserved at each vertex. The octonion color factor for this interaction is $\frac{1}{2}$. Because of SU(3) color symmetry, the value of color factor for $i=j=\overline{k}=\overline{l}$ is same. We have summarized the OQCD color factor in Table 3.

Where $C_O$ are color factor and octonion color factor. $i,j,k,$and l represents different indices which are assigned to the incoming and outgoing particles in quark-quark ($qq\mapsto qq$) interaction (i.e. $R,G,$ and $B).$ Similarly, we can study the octonion color quark-antiquark and antiquark-antiquark interaction. The color factor for $R\overline{R}-R\overline{R}$ and $\overline{R}\overline{R}-\overline{R}\overline{R}$ is same as $RR-RR$. $R\overline{G}-R\overline{G}$ and $\overline{R}\overline{G}-\overline{R}\overline{G}$ is same as $RG-RG$. $R\overline{R}-G\overline{G}$ and $\overline{R}\overline{G}-\overline{G}\overline{R}$ is same as $RG-GR$.

Octonionic algebra is used to study a variety of fields. We used octonion states, propagator, vertex and interaction terms to represent the interaction of color quarks interactions. We have derived the matrix element for color quark-quark interactions. We have shown the representation of color quark-quark interaction with help of Feynman diagram. All interactions are constructed in octonion space. We have also calculated the QCD color factor. Octonion QCD of SU(3) colour group directly established the one to one mapping between the non-associativity and the theory of the strong interaction. Quark theory’s octonion analysis will provide us with a novel method in particle and theoretical physics.