Applying and Improving Pyranometric Method to Estimate Sunshine Duration for a Tropical Site

Preprint

Article

Applying and Improving Pyranometric Method to Estimate Sunshine Duration for a Tropical Site

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Tovondahiniriko Fanjirindratovo^*

,Didier Calogine,Oanh Chau,Olga Ramiarinjanahary

Tovondahiniriko Fanjirindratovo^*

,Didier Calogine,Oanh Chau,Olga Ramiarinjanahary

This version is not peer-reviewed

Submitted:

19 June 2024

Posted:

21 June 2024

You are already at the latest version

Alerts

Abstract

The aim of this paper is to apply all the existing pyranometric method, to estimate the sunshine duration from the global solar irradiation, in order to find in their original form the most suitable method for a tropical site. Then, in a second step, one of these methods will be optimized to well fit tropical sites. Five methods in the literature (Step Algorithm, Carpentras Algorithm, Slob & Monna Algorithm, Slob & Monna 2 Algorithm, and Linear Algorithm) were applied with eleven years of global and diffuse solar radiation data. As a result, in their original form, the Step Algorithm is on the first rank. But in the second step, after improving its main coefficients, the Carpentras Algorithm was found to be the best algorithm for tropical site in the southern hemisphere.

Keywords:

Subject: Physical Sciences - Other

1. Introduction

The sunshine duration (SD) for a given period is the sum of sub-period for which the direct solar beam irradiance exceeds 120 [W.m^-2]. It is an important parameter for climatology, tourism, agriculture and solar energy. According to the World Meteorological Organization (WMO) in its Guide to Instruments and Methods of Observation in [1], the following two methods can be used to measure the SD. The first is the pyrheliometric method in which a pyrheliometer installed on a two axis solar tracker measures the direct irradiance. The second is called the pyranometric method which consists to measure the global and diffuse irradiance on horizontal surface. The difference of the global and diffuse gives the direct irradiance on horizontal surface, and after dividing it by the sine of solar angle elevation, the direct solar beam irradiation can be found. It is this second method that will be used in the present paper.

Due to the purchase, installation and maintenance high cost, especially for the pyrheliometer method, several studies has been done to estimate the SD by the global radiation (G) on horizontal surface measured by pyranometer, that is the most available data. All these methods are based on the comparison of the direct solar beam irradiance measured by a pyrheliometer with the global irradiance on horizontal surface for several years. Most of these algorithms were fitted for the northern hemisphere, so the aim of this paper is first to apply them to a database for a tropical region in order to estimate their uncertainties and then to find out the most suitable method. Then, one of these algorithms was optimized, to the present database, by improving its main coefficients to well fit a tropical site. The database contains eleven years of global and diffuse irradiation on a horizontal surface data, measured at the University of Reunion Island in its center at Saint-Pierre locality (latitude -21.34°).

This paper is composed of six sections, first the introduction, then the methodology section where the following will be explained; the pyranometric method, all the existing algorithms, the details of the database, the data quality control protocol and the statistical methods to evaluate the uncertainty and quality of the different algorithms. The third section is about the result where statistical analysis about SD reference versus calculated SD by pyranometric methods, on its original form, is done. The fourth section is focused on improving one pyranometric method with its result. The fifth section is devoted to discussion and the last section deals with the conclusion.

2. Materials and Methods

2.1. The Database

The database is a measurement for eleven years (2007-2017) about time and date, global (G) and diffuse (D) irradiance on horizontal surface based on every minute average recording. The other astronomical data like solar azimuth, elevation angle (el) and declination angle (δ) are calculated by the Michalsky’s Algorithm in [2], that is the recommended method according to the World Meteorological Organization [1]. The value of the mean extra-terrestrial global irradiance is according to [3].

2.2. The pyranometric Method

The direct irradiance on a horizontal surface (

I_{h}

) is the difference between the global and diffuse

I_{h} = G - D

(1)

The direct solar beam radiation (I) is obtained by the division of the direct radiation on horizontal surface and the sine of the solar elevation angle

I = \frac{I_{h}}{s i n (e l)}

(2)

So, the sunshine duration reference (SD_ref) is estimated per minute, if I is higher or equal to the level 120W.m^-2 then SD_ref=1 minute, otherwise SD_ref =0. To avoid abnormal high value of I for low elevation angle on sunrise and sunset, a minimum value of the elevation angle is posed below which the solar beam is considered inferior than 120 [W.m^-2] so the calculus of I is not done, and SD_ref is always zero. This minimum angle is 3° and this value comes from the different pyranometric methods. The unit of SD can be hour per day [h/day] or hour per year [h/year].

2.3. Data Quality Control Protocol

This protocol was developed inside the Baseline Station Radiation Network (BSRN) community as seen in [4]. Some intervals for each parameters (G, D and I) are done and also for their combination or ratio. If the data exceed these intervals, they are considered as erroneous and excluded from the study. So, a flag is associated with each every minute recording, if the value is good according to the protocol, the flag is set to zero; otherwise the flag is set to a nonzero number. Only the data with flag equal to zero are used to estimate SD. The same protocol is repeated for algorithm using 10 minutes average of global irradiation. The average value of G for 10 minutes is calculated and then the quality control is applied to it.

2.4. Step Algorithm (SA)

This algorithm is detailed in [5] and [6]. The averaged value of global irradiance G per minute is compared with a simplified threshold G_S1.

G \geq G s 1

then SDSA=1 minute, otherwise SDSA=0 minute, where

G_{s 1} = 0,4 . I_{0} . s i n (e l)

(3)

I_{0}

is the extra-terrestrial irradiance (solar constant) that value is 1367W/m² according to [3].

The Sunshine duration of the Step algorithm (SDSA) is calculated every minute, and the sum during a day gives the hour/day sunshine duration.

2.5. Carpentras Algorithm or Meteo France Algorithm (MFA)

This method is detailed in [5,6,7]. Like the Step Algorithm, the averaged value of global irradiance per minute is compared to a threshold

G_{s 2}

I f G \geq G_{s 2} a n d e l \geq 3 °

then SD_MFA = 1 minute, otherwise SD_MFA = 0 minute

G_{s 2} = F_{C} * 1080 * {(s i n (h))}^{1,25}

(4)

F_{C} = A + B * c o s (\frac{360 * d}{365})

(5)

d

is the day number for the year, for example d=32 for February, 1st. From [8], Table 1 lists the value for A and B for some BSRN station.

As it can be seen, most of the fitting was done in the northern hemisphere, only the Momote station is situated in the southern hemisphere on the tropics but it is nearer the equator than the Reunion Island’s latitude. However, the Momote’s coefficients will be used in this study because they are the only available for the southern hemisphere. Like SA the daily SD is done by the sum of per minute SD_MFA.

2.6. Slob & Monna Algorithm (SMA)

This method detailed in [9,10,11] is based on the estimation of the direct and diffuse radiation. The daily SD is the sum of 10 minutes SD. Three values of the 10 minutes global irradiance are needed; the average G, the maximum G_max and the minimum G_min. For each 10 minutes, a fraction coefficient

f \in [0,1]

f is calculated and the SD for SMA is SDSMA= f * 10minutes. If f=0 there is no sunshine, if f=1 it is sunshine. If 0<f<1, there are intermittent clouds during the 10 minutes period. The method is based on the estimation of the direct solar beam and diffuse irradiance on horizontal surface. The direct solar beam is estimated by:

I = I_{0} {(r_{0} / r)}^{2} . e x p (- T_{L} / (0,9 + 9,4 * \sin (e l))

(6)

with

I_{0}

the solar constant 1366W/m² by [11]

r_{0}

, the mean earth-sun distance

r

, the actual value of earth-sun distance

T_{L}

, Linke turbidity factor

e l

, solar elevation angle with

μ_{0} = s i n (e l)

(7)

The extra-terrestrial global irradiance on horizontal surface is

G_{0} = I_{0} {(\frac{r_{0}}{r})}^{2} . s i n (e l)

(8)

It is the normalized value of I, G and D compared to

G_{0}

that is used. There is sunshine if the global is higher or equal than a limit that is the sum of the estimated direct and diffuse irradiance, it means if

G / G_{0} \geq {(G / G_{0})}_{l i m}

(9)

{(G / G_{0})}_{l i m} = I . s i n (e l) / G_{0} + D / G_{0} = µ_{0} I / G_{0} + D / G_{0}

(10)

µ_{0} I / G_{0} = e x p (- T_{L} / (0.9 + 9.4 * \sin (e l))

(11)

The diffuse D thereby the value of

T_{L} d e p e n d

on the solar elevation. The algorithm can be summarized as below:

μ_{0} < 0.1

then f =0 (sun too low, el<3°)

{0.1 \leq μ}_{0} < 0.3

T_{L} = 6

D / G_{0} = 0.2 + µ_{0} / 3

G / G_{0} \geq {(G / G_{0})}_{l i m}

then f =1 else f =0

μ_{0} \geq 0.3

T_{L} = 10

D / G_{0} = 0.3

G_{m a x} / G_{0} < 0.4

then f =0 else

G_{m i n} / G_{0} > {(G / G_{0})}_{l i m}

then f =1 else

(G_{m a x} / G_{0} > {(G / G_{0})}_{l i m})

and

(G_{m a x} / G_{0} - G_{m i n} / G_{0}) < 0,1

then f =1 else

T_{L} = 4

\frac{D}{G_{0}} = 1.2 G_{m i n} / G_{0}

D / G_{0} > 0,4

then

D = 0.4

and

f = (G / G_{0} - D) / (µ_{0} I / G_{0})

The last part of the algorithm that is written in bold is the estimation of intermittent clouds.

2.7. Slob & Monna Algorithm 2 (SMA2)

This is an improvement of the SMA as seen in [10]. The algorithm is summarized on the following points:

The minimum angle is brought down for $μ_{0} = 0.1$ to $μ_{0} = 0.05$
Estimate the intermittent clouds in the ${0.05 \leq μ}_{0} < 0.3$ interval
$F o r {0.05 \leq μ}_{0} < 0.3$ , $T_{L} = 4$ and $D / G_{0} = 0.02 + 1 / (20 μ_{0} + 4)$ for limit calculus, then $T_{L} = 2.5$ to estimate intermittent clouds.
For $μ_{0} \geq 0.3$ , $T_{L} = 5$ for limit calculus and $D / G_{0} = 0.01 + 1 / (20 μ_{0} + 4)$ , then $T_{L} = 4$ to estimate intermittent clouds.
$D / G_{0} = 0.3$ to estimate intermittent clouds.

2.8. Linear Algorithm (LA)

Reference [10] shows this method. Using always a 10 minutes period, this method needs only the 10 minutes average of the global. It is a direct and linear correlation.

For

μ_{0} < 0.3

G / G_{0} < l_{1}

then f =0

l_{1} \leq G / G_{0} < u_{1}

then

f = (G / G_{0} - l_{1}) / (u_{1} - l_{1})

G / G_{0} \geq u_{1}

then

f = 1

For

μ_{0} \geq 0.3

G / G_{0} < l_{2}

then f =0

l_{2} \leq G / G_{0} < u_{2}

then

f = (G / G_{0} - l_{2}) / (u_{2} - l_{2})

G / G_{0} \geq u_{2}

then

f = 1

The coefficients are in the Table 2.

2.9. Statistical Analysis of the results

The main data is the daily SD [h/day]. SDx means the SD calculated by whichever algorithm. The following parameters and tasks are calculated or performed;

N: Number of experimental points (daily SD).
totdif [h]: cumulative difference between the algorithms and the reference in hours (SD_x - SD_ref).
rtotdif [%]: relative cumulative difference between the algorithms and the reference.
mdd [h/day]: mean value of the daily differences (SD_x - SD_ref). Trueness or accuracy of the method.
sdd [h/day]: standard deviation of the daily differences. Precision and repeatability of the method.
$U 95$
[h/day]: uncertainty interval that contains 95% of daily differences.
Scatter plot SDx versus SDref with linear fitting.
Plot of cumulative differences for the eleven years with totdif and rtotdif.
Plot of the histogram of daily differences with skewness.

3. Results

3.1. Scatter Plot with Linear Fitting

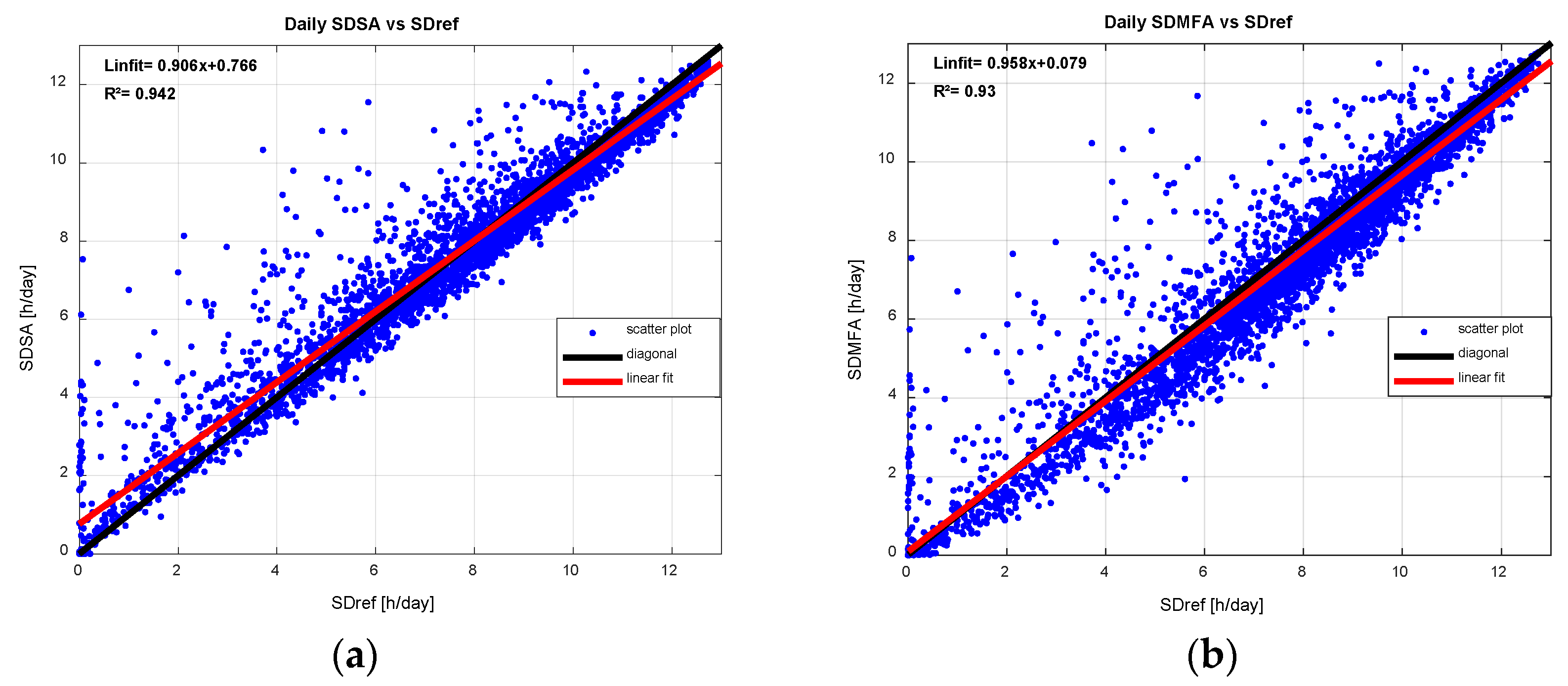
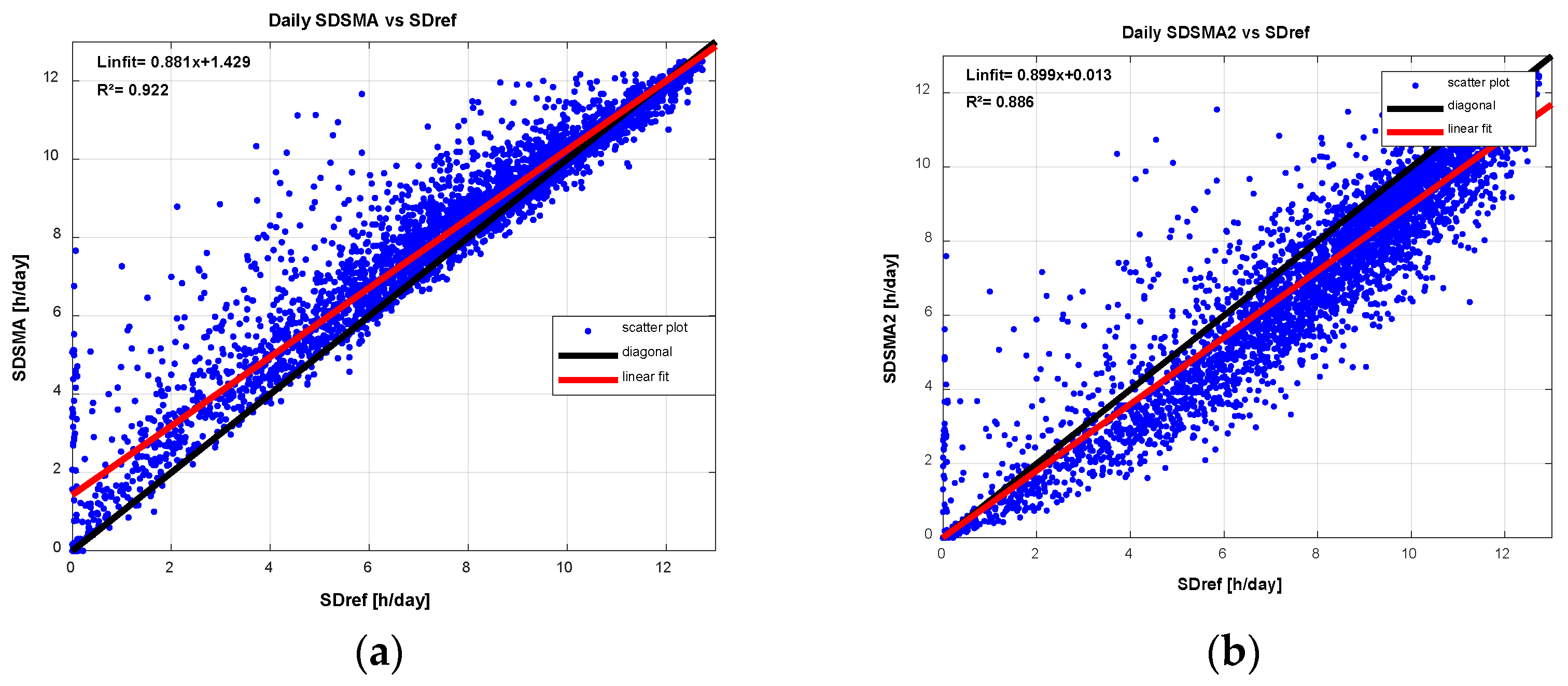
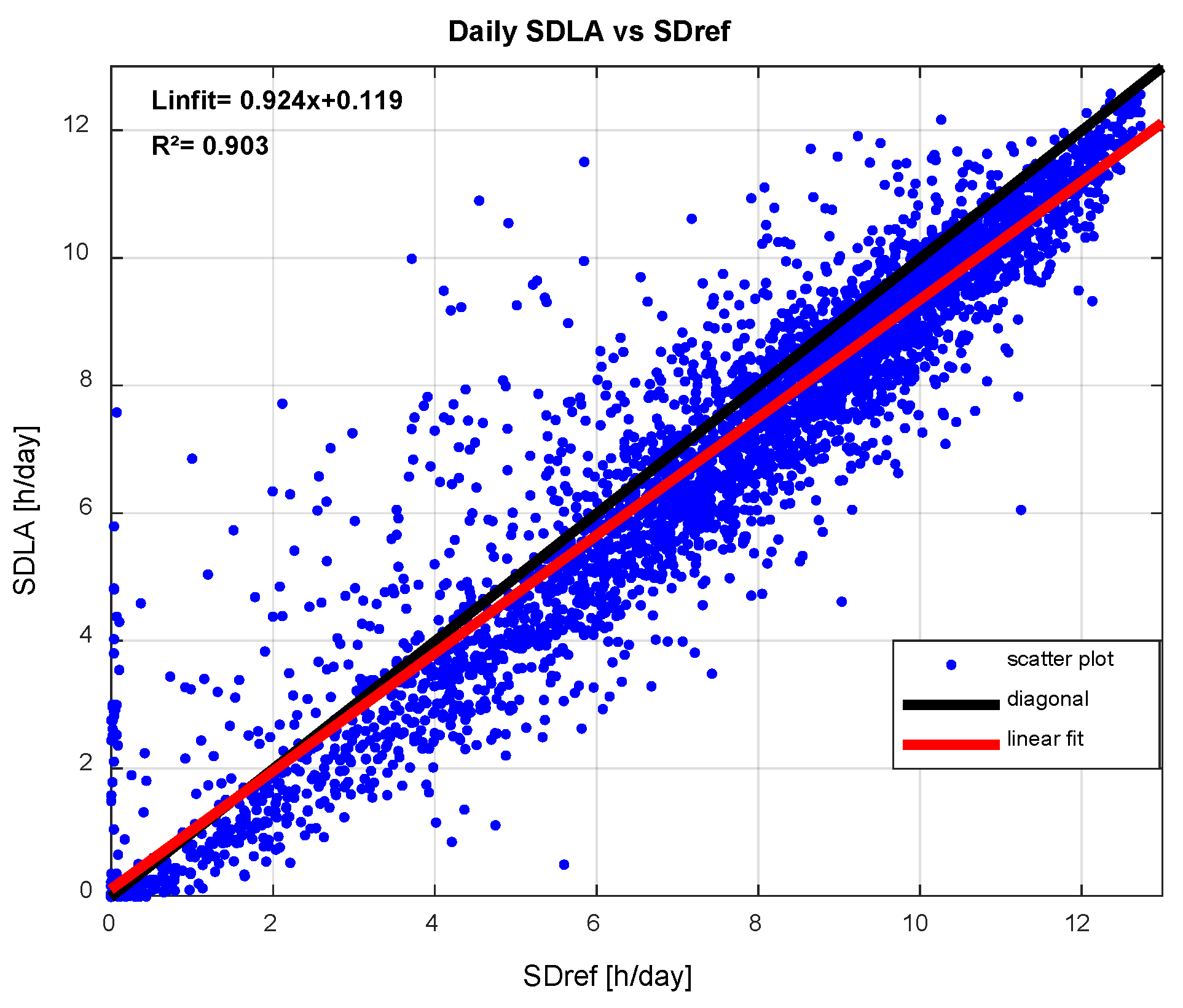
Figure 1 until Figure 3 show the scatter plot of SDx versus SDref. Linear fitting also is calculated and plotted in red line whereas the diagonal is in black line. The number of measuring point is N=4018.

By Figure 1(a), for the Step Algorithm, in average there is overestimation for sunshine duration less than 8[h/day], and conversely there is underestimation, for sunshine duration more than 8[h/day]. For Meteo France or Carpentras Algorithm as seen in Figure 1(b), the linear fitting, practically overlaps on the diagonal for SD less than 4 [h/day], and for higher value there is underestimation. So in general, the Meteo France Algorithm underestimates the sunshine duration. 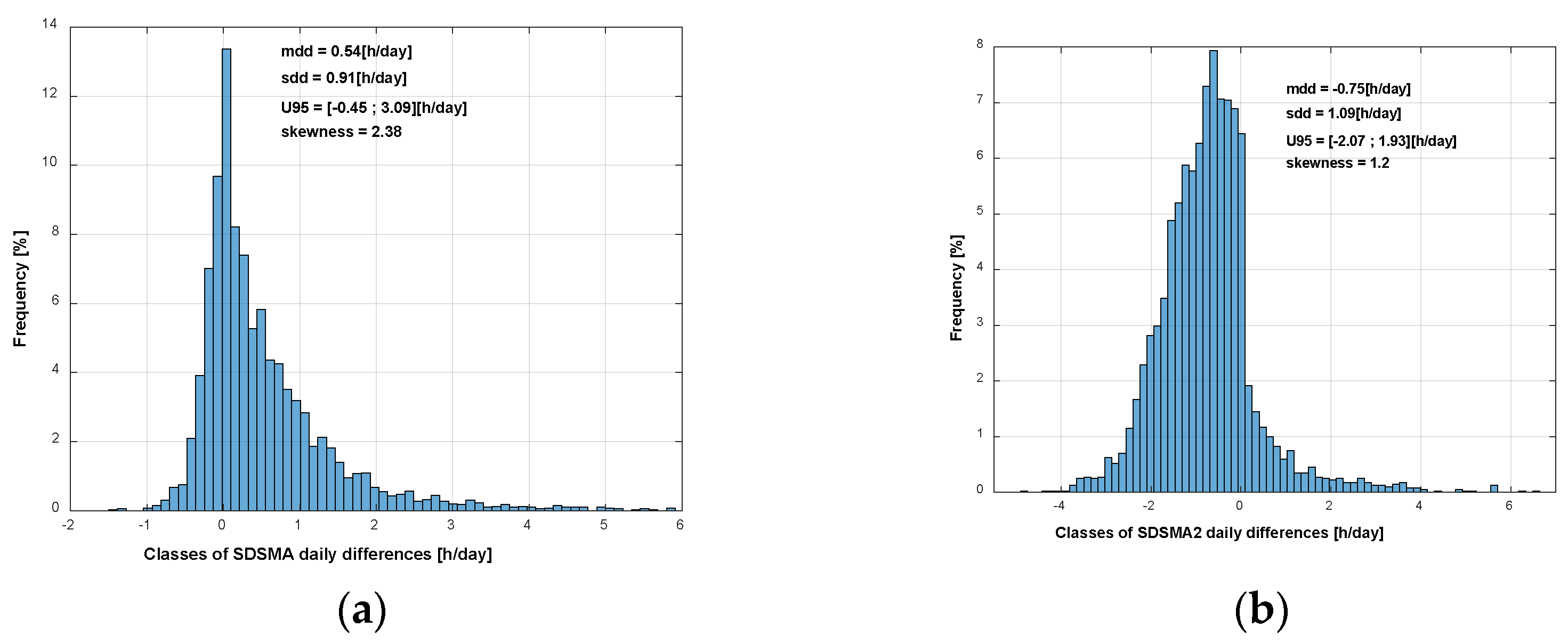Figure 2 shows for the two Slob & Monna Algorithms.

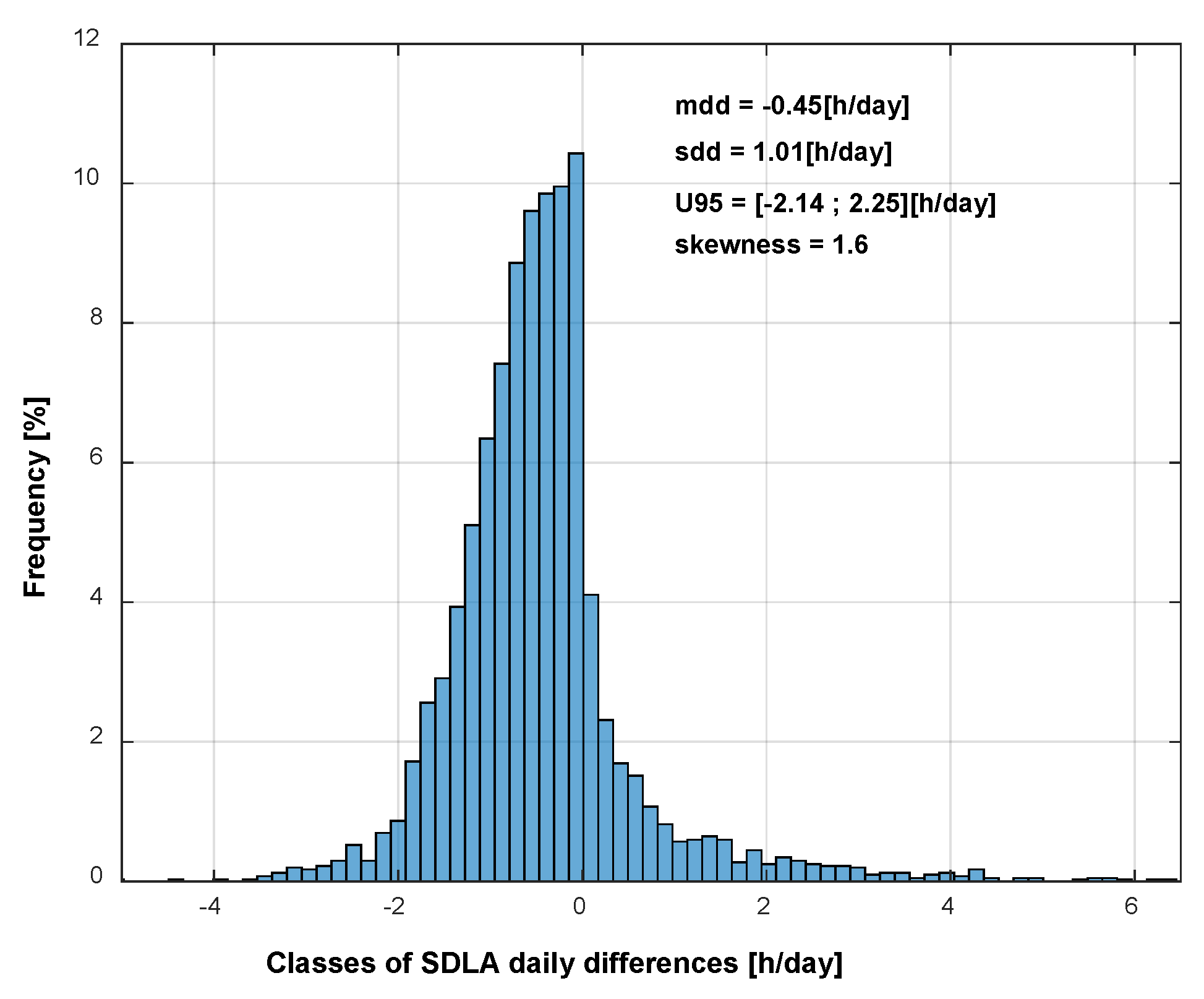
Figure 2 shows that Slob & Monna Algorithm overestimates the sunshine duration whereas the Slob & Monna 2 Algorithm underestimates. Finally, Figure 3 gives the situation for the Linear Algorithm.

By Figure 3, it can be concluded that the linear Algorithm also underestimates the Sunshine Duration.

3.1. Plot of Total and Relative Cumulative Differences

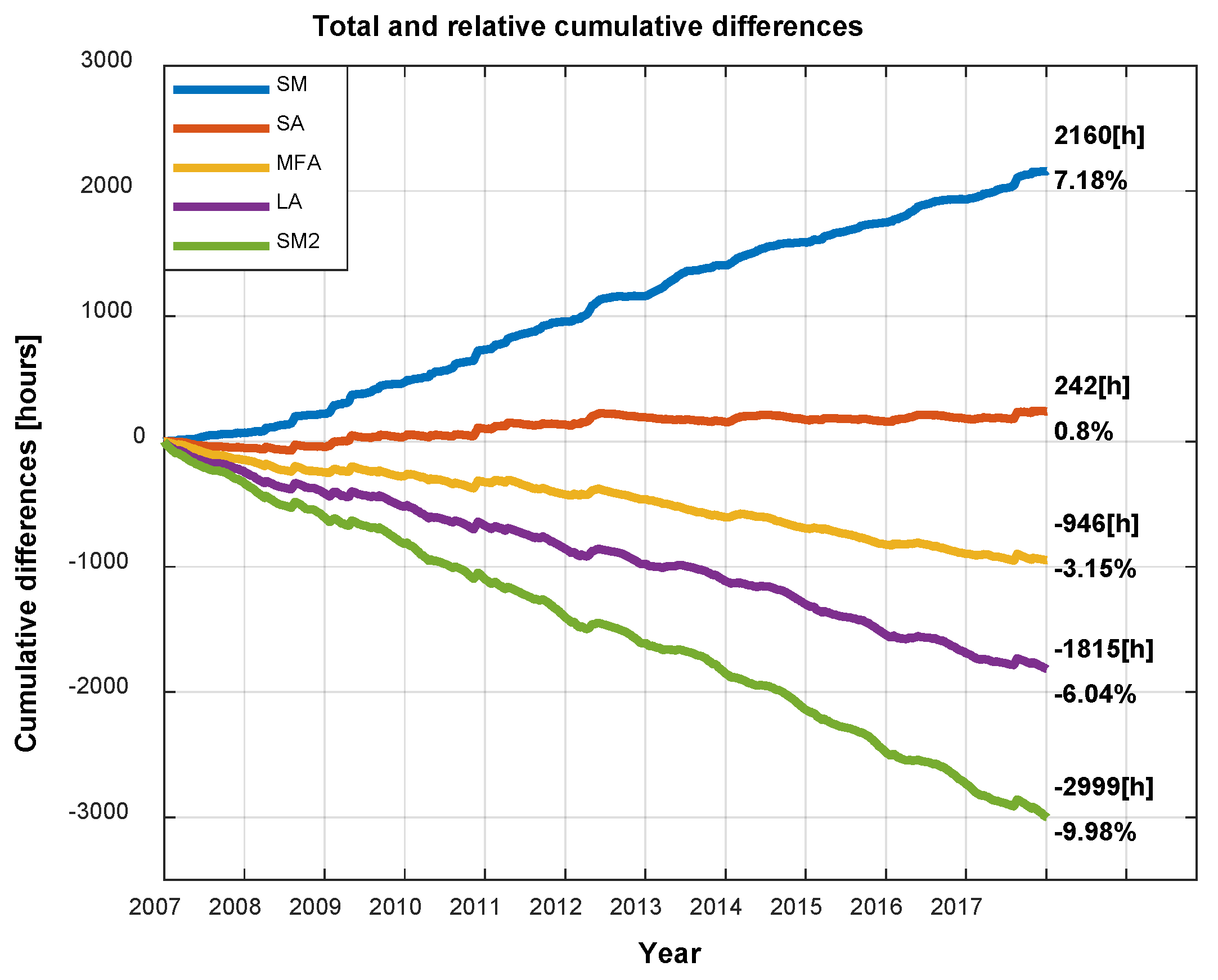
Figure 4 shows the total cumulative differences in hours (totdif), and the total relative cumulative differences in percentage (rtotdif), between algorithms and the reference for the 11 years.

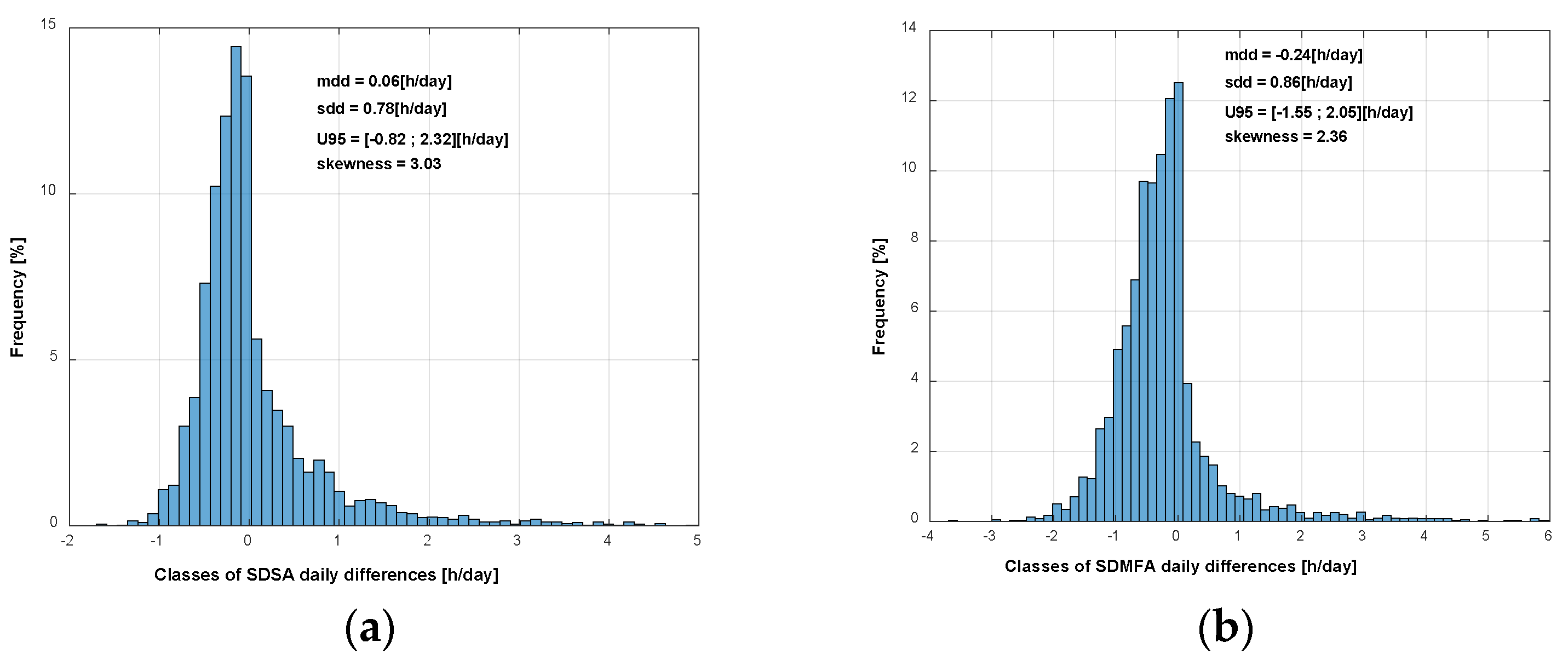
By Figure 4, the Step Algorithm gives the best result with 0.8% of total relative difference, followed by MFA with -3.15%. MFA, SMA2 and LA underestimate the SD whereas SMA overestimates, as already shown in Figure 1, 2 and 3. The following plots are for the histogram of daily differences for each method, with the experimental mean of daily differences (mdd) and standard deviation of daily differences (sdd). The skewness (skw) of the histogram is also shown and its formula is the one used in [6]. If

x_{i}

is the daily difference between SDx and SDref, the skewness is

s k w = \frac{N}{(N - 1) (N - 2)} \frac{\sum_{i = 1}^{N} {(x_{i} - m d d)}^{3}}{{s d d}^{3}}

(12)

The last information with the histogram is the U95 interval that holds 95% of the value of

x_{i}

. So, it represents the uncertainty interval for the method.

Figure 6. Histogram and statistical parameters: (a) SDSMA; (b) SDSMA2.

Figure 7. Histogram and statistical parameters for SDLA.

Table 3 summarizes the analysis of the five methods. The spanU95 datum is the length or size of the U95 uncertainty interval.

Obviously the Step Algorithm is the best among the existing methods on their original form. It has the lowest total (242[h]) and relative cumulative differences (0.8%). SA has also the mean daily differences nearest to zero (0.06[h/day]) with the lowest dispersion value because it has the smallest standard deviation for the mean (0.79[h/day]), and of course SA has the smallest length of the interval containing 95% of the daily differences values. On the second rank is the Carpentras or Meteo France Algorithm with -3.15% of relative cumulative differences. The SA method is a basic, simple and empiric method, the others that are more complicated should be better than it, but the result shows that it is SA on the first rank. The reason is that the other methods were mainly fitted for northern hemisphere or for latitude far the Reunion Island’s latitude. So, it is important to identify which method can be improved to fit tropical sites and how to do. Seen that the MFA is in the second rank and its uncertainties are not too high, it is the suitable candidate to be improved.

4. Improving the Carpentras Algorithm

The improvement is to adjust the method for the local database. Practically, it means finding the proper value for A and B coefficients. Table 1 shows already that these coefficients should be adjusted following the latitude, and the coefficients for Momote’s station are the starting points because this site is in the southern hemisphere. The computation shows that A coefficient should be in the interval [0.59, 0.65] and B coefficient in the interval [-0.09, 0]. At the end, the result shows that the most suitable coefficients are A=0.63 and B=-0.05. The notation of the improved MFA is MFAi on this paper. 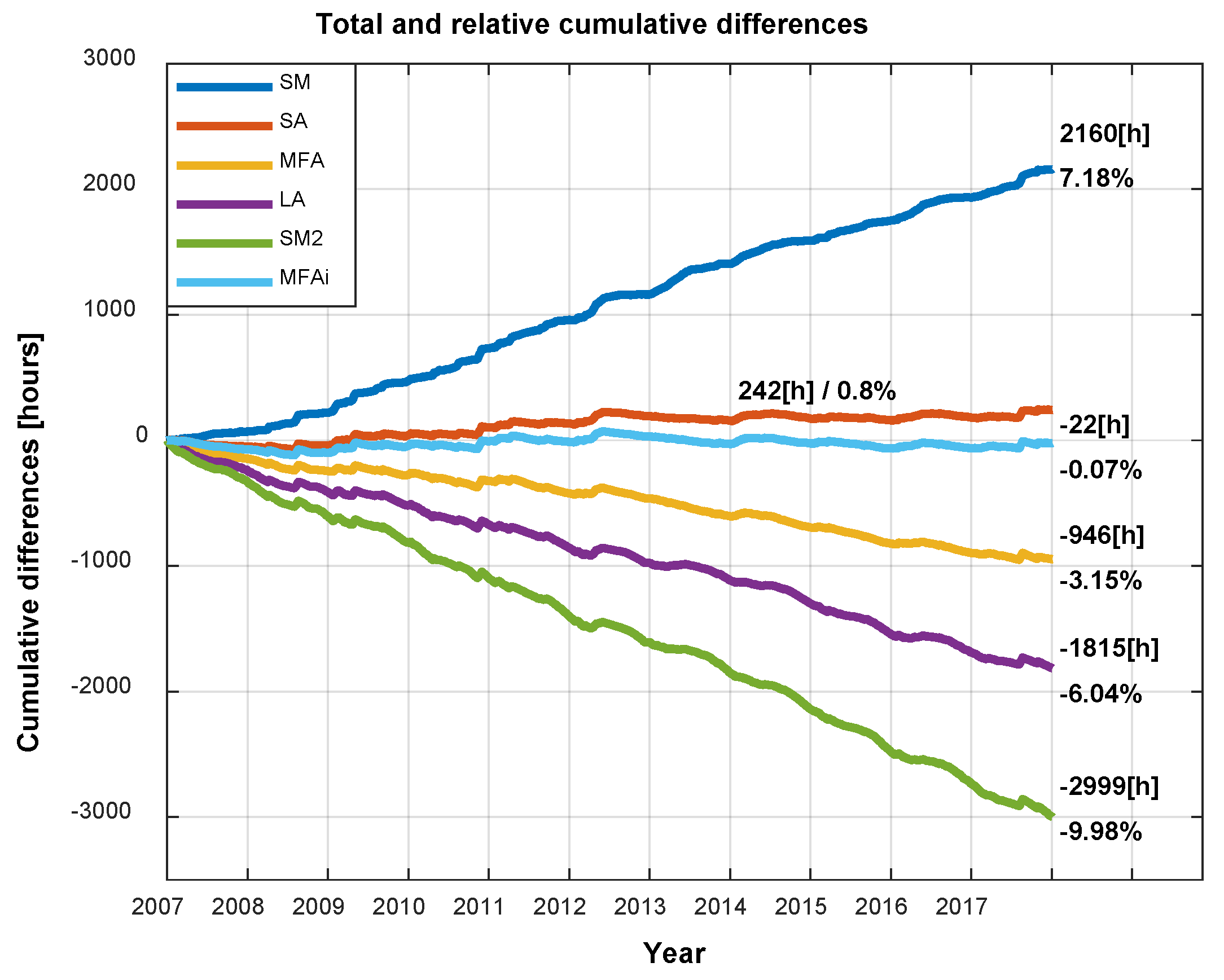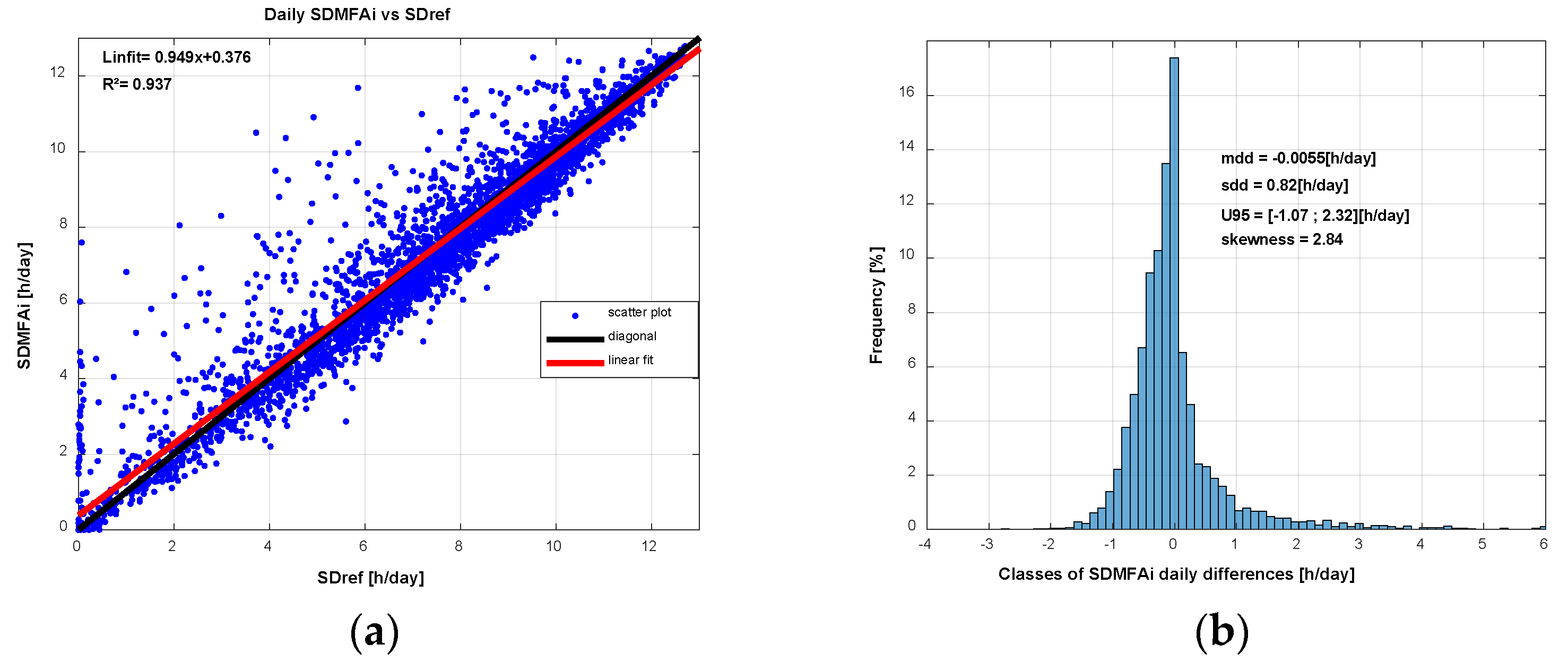Table 4 shows the result of the statistical parameters and Figure 8 gives the total and relative cumulative differences.

By Table 4 and Figure 8, it can be assumed that the MFAi gives a best result than the SA, the total and relative cumulative differences are reduced from 242 hours (0.8%) to -22 hours (-0.07%) over the eleven years. The mean daily differences is very near to zero (-0.0055 [h/day]), even the standard deviation of the mean and the length of U95 interval is little bit higher than the SA. MFAi in the long term underestimates the SD following the behavior of its origin which is the Météo France Algorithm. Figure 9 shows the scatter plot and histogram of MFAi.

The behavior of MFAi is similar to SA, for SD less to 7 [h/d] there is overestimation, and conversely there is overestimation for SD higher than 7[h/d]. But the maximum distance between the linear fit and the diagonal is less than for the SA.

5. Discussion

For the present paper, the MFA is the best method, if it is well adjusted to the local database. So by far, the best method is MFAi followed by SA. The World Meteorological Organization (WMO) recommends the MFA and SMA for the best method to get sunshine duration from global irradiation, in its Guide to Instruments and Methods of Observation in [10]. The present study validates MFA but not really SMA for the tropics, because LA is in the third position, before SMA, if looking at the total and relative cumulative differences. As reported in [5] and [6], an inter-comparison program done in France and Italy indicates that the best algorithm is MFA followed by SA and SMA in the third position, but LA was not tested in this case. Reference [8] emphasizes that if well adjusted by pyrheliometric data, MFA can give very low uncertainties.

Even SMA is recommended by the WMO, it is always in the third or fourth position, and maybe the reason comes from the fact that it was fitted in northern hemisphere outside the tropics. The present work also shows that the SA is a good, simple and worldwide suitable alternative and can give acceptable practical uncertainties without the need to adjust each time the method to the local database or latitude.

6. Conclusions

For Reunion Island, the best method to estimate the sunshine duration from global irradiation is the Carpentras or Météo France Algorithm especially with the appropriate coefficients that were computed by the present work, this method is also the easiest to improve or to adjust among the existing algorithms. The Step Algorithm in second position is a simple and suitable alternative for practical use. The other algorithms give too high uncertainties for tropical site. The present result can be applied for any tropical site whose latitude is similar to Reunion Island.

Author Contributions

Conceptualization, Tovondahiniriko Fanjirindratovo. and Didier Calogine.; methodology, Tovondahiniriko Fanjirindratovo., and Didier Calogine.; software, Tovondahiniriko Fanjirindratovo.; validation, Didier Calogine., Oanh Chau. and Olga Ramiarinjanahary.; formal analysis, Tovondahiniriko Fanjirindratovo., Didier Calogine., Oanh Chau; investigation, Tovondahiniriko Fanjirindratovo., and Didier Calogine.; resources, Tovondahiniriko Fanjirindratovo., and Didier Calogine.; data curation, Tovondahiniriko Fanjirindratovo.; writing—original draft preparation, Tovondahiniriko Fanjirindratovo.; writing—review and editing, Didier Calogine., Oanh Chau., and Olga Ramiarinjanahary; visualization, Tovondahiniriko Fanjirindratovo., and Didier Calogine.; supervision, Didier Calogine., Oanh Chau., and Olga Ramiarinjanahary; project administration, Didier Calogine.; funding acquisition, Didier Calogine. All authors have read and agreed to the published version of the manuscript.

Funding

This study was made possible thanks to cooperation between the University of Reunion Island and the University of Toliara, under the “Micro Reseau Mafate Project” that is funded by the European Regional Development Fund, the Reunion Council, and the French Government.

Data Availability Statement

Data are available from corresponding author on reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

World Meteorological Organization. Measurement of Sunshine Duration. In Guide to Meteorological Instruments and Methods of Observation, 7th ed.; World Meteorological Organization: Geneva, Switzerland, 2008; Volume 8, pp. I.8-1 - I.8-11.
Michalsky, J.J. The Astronomical Almanac’s algorithm for approximate solar position (1950-2050). Solar Energy 1988, 40, 227–235. [Google Scholar] [CrossRef]
Liou, K.N. An introduction to Atmospheric Radiation, 2nd ed.; Academic Press: Massachusetts, USA, 2002. [Google Scholar]
Long, C.N.; Dutton, E.G. BSRN global network recommended QC tests, V2.0. BSRN Tech. Rep. Available online: http://ezksun3.ethz.ch/bsrn/admin/dokus/qualitycheck.pdf.
Vuerich, E.; et al. Measurements methods for sunshine duration (SD): accuracy evaluation of pyranometric methods and SD measuring instruments. Proceedings of TECO, Helsinki, Finland, 30 August - 1 September 2010. [Google Scholar]
Vuerich, E.; et al. Updating and development of methods for worldwide accurate measurements of sunshine duration. Proceedings of TECO, Brussels, Belgium, 16 - 18 October 2010. [Google Scholar]
Oliviéri, J.C. Sunshine duration measurement using a pyranometer. In WMO, IOM Reports n°70, WMO tech doc 877,; World Meteorological Organization: Casablanca, Morocco, 1998; Volume 70, pp. 357–359. [Google Scholar]
Morel, J.P.; et al. Sunshine duration measurements using the Carpentras method. Proceedings of Baseline Surface Radiation Network meeting, Postdam, Germany; 2012. [Google Scholar]
Hinssen, Y.B.L. Comparison of different methods for the determination of sunshine duration. Royal Netherlands Meteorological Institute Report (KNMI) 2006, 6.
Hinssen, Y.B.L.; Knap, W.H. Comparison of pyranometric and pyrheliometric methods for the determination of sunshine duration. Journal of Atmospheric and Oceanic Technology 2007, 24, 835–846. [Google Scholar] [CrossRef]
Slob, W.H.; Monna, W.A. Bepaling van directe en diffuse straling en van zonneschijnduur uit 10-minuutwaarden van de globale straling. Royal Netherlands Meteorological Institute Report (KNMI) 1991, 136, 31. [Google Scholar]

Figure 1. Scatter plot with linear fitting: (a) SDSA vs SDref; (b) SDSMFA vs SDref.

Figure 2. Scatter plot with linear fitting: (a) SDSMA vs SDref; (b) SDSMA2 vs SDref.

Figure 3. Scatter plot od SDLA with linear fitting.

Figure 4. Total and relative cumulative differences between algorithms and the reference.

Figure 5. Histogram and statistical parameters: (a) SDSA; (b) SDMFA.

Figure 8. Plot of the total and relative cumulative differences for SDMFAi compared to the others models.

Figure 9. SDMFAi results: (a) Scatter plot and linear fit, and (b) Histogram.

Table 1. Coefficients for Carpentras or Meteo France Algorithm.

BSRN station	Latitude	A	B
Momote	-2	0.68	-0.06
Tamanrasset	22	0.77	0
Tateno	36	0.73	0.05
Boulder	40	0.67	0.06
Carpentras	44	0.71	0.05
Payerne	47	0.75	0.06
Palaiseau	48	0.75	0.04
Cabauw	52	0.77	0.06
Toravere	58	0.74	0.06

Table 2. Coefficients for Linear Algorithm.

$l_{1}$	$u_{1}$	$l_{2}$	$u_{2}$
0.4	0.5	0.45	0.6

Table 3. Summary of statistical analysis.

	SA	MFA	SMA	SMA2	LA
mdd [h/day]	0.06	-0.24	0.54	-0.75	-0.45
sdd [h/day]	0.79	0.86	0.91	1.09	1.01
Span U95 [h/day]	3.13	3.6	3.54	4.64	4.4
totdif [h]	242	-946	2160	-2999	-1815
rtotdif [h]	0.8%	-3.15%	7.18%	-9.98%	-6.04%

Table 4. Statistical analysis of MFAi.

	MFAi	SA	MFA
mdd [h/day]	-0.0055	0.06	-0.24
sdd [h/day]	0.81	0.79	0.86
Span U95 [h/day]	3.38	3.13	3.6
totdif [h]	-22	242	-946
rtotdif [h]	-0.07%	0.8%	-3.15%

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Applying and Improving Pyranometric Method to Estimate Sunshine Duration for a Tropical Site

Abstract

1. Introduction

2. Materials and Methods

2.1. The Database

2.2. The pyranometric Method

2.3. Data Quality Control Protocol

2.4. Step Algorithm (SA)

2.5. Carpentras Algorithm or Meteo France Algorithm (MFA)

2.6. Slob & Monna Algorithm (SMA)

2.7. Slob & Monna Algorithm 2 (SMA2)

2.8. Linear Algorithm (LA)

2.9. Statistical Analysis of the results

3. Results

3.1. Scatter Plot with Linear Fitting

3.1. Plot of Total and Relative Cumulative Differences

4. Improving the Carpentras Algorithm

5. Discussion

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe