Preprint
Article
Molecular-scale liquid density fluctuations and cavity thermodynamics
Altmetrics
Downloads
94
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
20 June 2024
Posted:
21 June 2024
You are already at the latest version
Alerts
Abstract
Molecular-scale density fluctuations at equilibrium produce cavities in a liquid and can be analyzed to shed light on the statistics of the number of molecules occupying observation volumes of increasing radius. An information theory approach led to the conclusion that these probabilities should follow a Gaussian distribution function. This prediction has been confirmed by computer simulations in different liquid models if the size of the observation volume is not large. The reversible work of cavity creation is exactly linked to the probability of finding zero molecules in a given observation volume. The Gaussian formula for the latter probability is scrutinized to arrive at the enthalpy and entropy changes associated with cavity creation. The reversible work of cavity creation has a purely entropic origin due to the solvent-excluded volume effect produced by the inaccessibility of a given region of the configurational space. The consequent structural reorganization of liquid molecules leads to exactly compensating enthalpy and entropy changes. These results are in line with those obtained in a direct statistical mechanical study by Lee.
Keywords:
Subject: Chemistry and Materials Science - Physical Chemistry
1. Introduction
A theoretical analysis of solvation (i.e., the transfer of a solute molecule from a fixed position in the gas phase to a fixed position in the liquid phase, according to the so-called Ben-Naim standard [1]) indicates the need to account for the process of cavity creation in the liquid [2,3,4,5,6,7]. The need descends from the recognition that, since a liquid is a condensed state of the matter, a suitable space (i.e., a cavity) must be created, at a fixed position, to host the solute molecule. This need is well understood by theoreticians, not so well by experimentalists. The latter claim that any liquid possesses a lot of void space, around 50% of the total volume, and so cavity creation should be un-necessary. However, the void volume in a liquid is partitioned in very small pieces whose dimensions do not allow the insertion of a real solute molecule [8,9,10,11,12] (i.e., the average dimensions of such small pieces depend on the diameter of liquid molecules, as can be soon grasped on thinking of the voids left in a box filled by tennis balls or by ping-pong balls). The process of cavity creation can be studied solely by means of theoretical approaches, or computer simulations in suitable models of the different liquids. The reversible work associated with cavity creation is a large and positive quantity in all liquids [2,3,4,5,6,7]. Moreover, it is widely recognized that the magnitude of the reversible work of cavity creation is larger in water with respect to the other common liquids [13,14,15], and is the ultimate cause of the poor solubility of nonpolar species in water [2,3,4,5,6,7].
A statistical mechanical analysis of cavity creation, performed forty years ago by Lee [16], indicates that: (a) the reversible work of cavity creation has an entropic origin because cavity creation causes a marked decrease in the number of configurations accessible to liquid molecules (i.e., one has to pick out solely the liquid configurations in which the desired cavity is present); the consequent reduction in the size of the statistical ensemble leads to an entropy decrease in all liquids, and can be described as a solvent-excluded volume effect; (b) there is a cavity enthalpy change, coming from a structural reorganization of liquid molecules (i.e., the presence of the cavity is a perturbation that pushes the liquid molecules to assume positions which render possible the cavity existence); this structural reorganization is distinct from the solvent-excluded volume effect, and produces also an entropy change that exactly compensates the cavity enthalpy change [16,17]. The purely entropic nature of cavity creation is a fundamental feature, holding for all the cavities that can be produced by molecular-scale density fluctuations at equilibrium.
A general theorem of statistical mechanics connects the reversible work of cavity creation to the logarithm of the probability of finding no liquid molecules in the volume corresponding to the desired cavity, P(0; v) [18]. In order to exploit this connection, P(0; v) must be known. Pratt and colleagues [19,20,21] devised an elegant information theory approach to arrive at P(0; v), by determining the probabilities of finding the centers of n molecules P(n; v) inside a randomly positioned volume v, whose size corresponds to the solvent-excluded volume of the desired cavity (i.e., a spherical cavity has a van der Waals radius rc, and a solvent-excluded radius Rc = rc + rs, where rs is the van der Waals radius of the spherical solvent molecules; in other words, rc is the radius of the spherical volume in which no part of the solvent molecules can be found, Rc is the radius of the spherical volume in which no center of the solvent molecules can be found [17]). Using a flat default model in an approach based on the maximum entropy principle [22] resulted in a discrete Gaussian distribution for the P(n; v) probabilities [19]. This theoretical result is in line with the fluctuation theory in statistical mechanics, where a Gaussian approximation holds for the fluctuation in the number of particles in the grand-canonical ensemble [23]. Moreover, it has been supported by computer simulations of liquid models. Indeed, the results of Monte Carlo simulations and molecular dynamics simulations on hard sphere fluids [24], Lennard-Jones liquids [25], n-hexane [26], dimethyl sulfoxide [26], and several models of water [19,27,28,29] proved that the P(n; v) probabilities are well described by Gaussian distributions for not so large observation volumes (i.e., when the ratio of observation volume radius to liquid molecule radius is smaller than two, the Gaussian distribution holds, regardless of the nature of the energetic interactions among liquid molecules). For instance, it has been shown that the so-called monoatomic water model [30] is characterized by molecular-scale density fluctuations that follow a Gaussian distribution up to a cavity radius Rc ≈ 4 Å [31]. It should be clear that there is no compelling reason to expect that the P(n; v) probabilities should obey a Gaussian distribution. Indeed, by increasing the radius of the observation volume in water models, there are large deviations from Gaussian values in the low-number tail of the distribution [27,28,29,31,32,33]. Moreover, a different distribution, called a binomial cell model, has been proposed to analyze molecular-scale density fluctuations in water models [34].
Notwithstanding the studies published on this matter, the basic relationships between the probability distribution of number density fluctuations and cavity thermodynamics have not yet spelled out in detail, except for the analysis by one of us [35]. The aim of the present study is to demonstrate that the entropic nature of the reversible work of cavity creation emerges in a direct manner by the P(0; v) formula provided by the Gaussian distribution.
2. Theoretical foundation
A liquid possesses a huge ensemble of molecular configurations and a statistical mechanical description is unavoidable. Assuming that X is a multidimensional vector accounting for the position of each of the N spherical molecules of the liquid, the probability density function associated with a specific liquid configuration, in the NPT ensemble, is [17]:
where H(X) = E(X) + P⋅V(X) is the enthalpy of the configuration X, E(X) is the total interaction energy of liquid molecules in the configuration X, V(X) is the volume of the configuration X, P is the pressure of the liquid, k is the Boltzmann constant, and the denominator is the isobaric-isothermal configurational partition function. We are interested in the probability of cavity occurrence in the liquid or better in the probability that the centers of all the N spherical molecules of the liquid are located outside the solvent-excluded volume, v, of the cavity. This probability is obtained by integrating ρ(X) of Equation (1) over all the configurations having the centers of all the N spherical molecules in the volume <V> - v [2,35]. In performing the integration, it is important to recognize that: (a) the location of the cavity, whose solvent-excluded volume is v, has to be fixed, but arbitrarily in the liquid volume because the liquid density is uniform at equilibrium; (b) even though the total volume is not strictly constant in the NPT ensemble, it is right to consider that the total volume of a macroscopic system will assume, at equilibrium, values sharply close to the ensemble average value <V>. Thus one obtains:
where the integration domain has the already clarified meaning. The calculation of P(0; v) corresponds to pick out only a very small fraction of the total liquid configurations, i.e., the ones having the cavity of the requested solvent-excluded volume. Such a selection leads to a drastic decrease in the number of molecular configurations accessible to the liquid, and so to an entropy loss for the liquid (i.e., entropy is an extensive thermodynamic function and its magnitude depends on the size of the statistical ensemble [16,18,23]). This entropy loss holds for any liquid, regardless of the energetic interactions occurring among the liquid molecules.
ρ(X) = exp[-H(X)/kT]/ ∫exp[-H(X)/kT]dX
P(0; v) = P(N; <V> - v) = ∫ρ(X) dX
<V> - v
Cavity creation at a fixed position in a liquid, keeping fixed NPT, causes an increase in the average volume of the system by a quantity equal to the van der Waals volume of the cavity, vvdW. Nevertheless, the existence of a cavity of solvent-excluded volume v implies that the spherical shell given by the difference (v - vvdW) becomes inaccessible to the centers of liquid molecules. It is a solvent-excluded volume effect (i.e., a geometric effect) because it is a constraint for all the N molecules of the liquid whose centers, during their continuous translations, cannot enter the cavity solvent-excluded volume, if the cavity is to exist (see Figure 1). The inaccessible shell can be approximated by the solvent accessible surface area of the cavity in all the solvents. It is interesting to note that a geometric entropy, linearly proportional to the surface area of the solvent-excluded volume, emerged in a theoretical approach based on a density field theory [36].
As underscored by Tolman [18], there is an exact statistical mechanical relationship between the occurrence probability of a constrained configuration of a thermodynamic system and the reversible work to produce that constrained configuration:
where W(0; v) is the reversible work (i.e., the Gibbs free energy change) to create a cavity of solvent-excluded volume equal to v, W(0; v) = ΔGc(v; Rc), where Rc is the solvent-excluded cavity radius. Now, the assumption that molecular-scale density fluctuations at equilibrium obey Gaussian statistics can be scrutinized to shed further light on the entropy loss associated with cavity creation.
P(0; v) = exp[-W(0; v)/kT]
3. Gaussian fluctuations
According to the results of computer simulations of several liquids [19,20,21,24,25,26,27,28,29,31], the probability of finding the centers of exactly n molecules inside a randomly positioned observation volume v, when the liquid number density is ρ ≡ NAv/vm (i.e., NAv is the Avogadro’s number and vm is the molar volume of the liquid), and pressure and temperature are held constant, is well described by a Gaussian distribution, if the observation volume is not large (see above): Therefore, one has:
where δn = n - <n>, <n> is the average number of molecular centers in the volume v, <n> = ρ⋅v, and σn2 = <δn2> = <n2> - <n>2 is the variance of the Gaussian distribution, i.e., the mean square fluctuation in the number of molecular centers inside the volume v. It is important to recognize that the first two moments of the Gaussian distribution are related to the number density and the radial distribution function of the liquid, respectively, quantities that are experimentally measurable [19,20,21]. Since we are interested in the probability of finding a cavity in the liquid, we need the probability P(0; v) of finding zero molecular centers in the volume v:
P(n; v) = (2π⋅σn2)-1/2 ⋅ exp(-δn2/2σn2)
P(0; v) = (2π⋅σn2)-1/2 ⋅ exp(-<n>2/2σn2) = (2π⋅σn2)-1/2 ⋅ exp(-ρ2v2/2σn2)
The probability of cavity occurrence is related to molecular-scale density fluctuations at equilibrium, underscoring that cavity creation is a special process, depending solely on the properties of the pure liquid. Introducing Equation (5) into Equation (3), one obtains:
ΔGc(v; Rc) = (kT/2)⋅ln(2π⋅σn2) + (kT⋅ρ2v2/2σn2)
Equation (6) indicates that ΔGc ∝ 1/σn2, it is inversely proportional to the variance of the Gaussian distribution. The σn2 value depends on the v size and can solely be determined by means of computer simulations on a molecularly detailed model of the liquid of interest [19,20,21]. For a cavity whose solvent-excluded volume is suitable to host methane, Rc = 3.3 Å, <n> = 5.11, σn2 = 1.39 [34], and using Equation (6), ΔGc = 26.1 kJ mol-1 at 300 K, in line with computer simulation results [19,34]. We do not want to perform calculations with Equation (6), but to deepen its thermodynamic features and consequences. When the volume of interest corresponds to the molar volume of the liquid, the variance of the Gaussian distribution is proportional to the isothermal compressibility, σn2 ∝ βT [23], and this implies that ΔGc ∝ 1/βT. The reversible work of cavity creation, measuring the entropy loss due to the solvent-excluded volume effect, is inversely proportional to the isothermal compressibility of the liquid. This relationship was originally obtained by Pratt and colleagues [19,20,21]. Water has the smallest βT value among all common liquids (i.e., at 25 °C, βT(in atm-1⋅105) = 4.58 for water, 9.80 for benzene, 11.55 for c-hexane, 16.27 for n-hexane, 10.81 for carbon tetrachloride, 14.79 for methanol, and 10.26 for ethanol [17]), and, in fact, it has the largest ΔGc value for a given van der Waals cavity radius among all common liquids, as demonstrated by computer simulation results [13,14,15]. The isothermal compressibility is a macroscopic thermodynamic quantity, and a closer scrutiny is necessary to single out the microscopic difference between water and the other liquids.
According to statistical mechanics, βT is a measure of the ensemble fluctuations in the liquid number density, βT = vm⋅σn2/<n>2⋅kT [23]. Water has the smallest βT value among all common liquids mainly because the molar volume of water is the smallest among those of all common liquids: at 25 °C and 1 atm, vm(in cm3 mol-1) = 18.07 for water [37], 89.41 for benzene, 108.75 for c-hexane, 131.62 for n-hexane, 97.09 for carbon tetrachloride, 40.73 for methanol, and 58.68 for ethanol [38]. This fact stems from the effective size of liquid molecules. The effective size of water molecules is the smallest among those of all common liquids; at 25 °C, the effective hard sphere diameter is 2.80 Å for water [12], 5.26 Å for benzene, 5.63 Å for c-hexane, 5.92 Å for n-hexane, 5.37 Å for carbon tetrachloride [38], 3.83 Å for methanol, and 4.44 for ethanol Å [17]. It is important to underscore that the effective hard sphere diameter of water molecules is smaller than their van der Waals diameter as a consequence of the bunching up effect caused by the strength of H-bonds [39].
Application of fundamental relationships of equilibrium thermodynamics to Equation (6) allows the derivation of the enthalpy and entropy changes associated with cavity creation:
and
ΔHc = -T2[∂(ΔGc/T)/∂T]P = -(kT2/2)⋅{∂[ln(2π⋅σn2) + (ρ2v2/σn2)]/∂T}P
= -(kT2/2σn2)⋅{[1 - ((ρ2v2/σn2)]⋅(∂σn2/∂T)P + 2ρv2⋅(∂ρ/∂T)P}
ΔSc = -(∂ΔGc/∂T)P = -(k/2)⋅ln(2π⋅σn2) - (kρ2v2/2σn2) +
-(kT/2σn2)⋅{[1 - ((ρ2v2/σn2)]⋅(∂σn2/∂T)P + 2ρv2⋅(∂ρ/∂T)P}
In performing the derivatives, the σn2 quantity has been considered a simple function of temperature (i.e., not a composite one), and the v quantity has been considered temperature independent [35]. Equations (7) and (8) indicate that: (a) the cavity enthalpy change is totally counterbalanced by a corresponding term in the cavity entropy change, and so there is no net enthalpic contribution to the reversible work of cavity creation; (b) the cavity entropy change has a second contribution, given by -ΔGc/T, that measures the solvent-excluded volume effect associated with cavity creation in a liquid (i.e., the entropy loss due to the reduction in the size of the statistical ensemble of the liquid for the selection of the configurations possessing the desired cavity). The above sentences may appear a circular argument [40], unless Equation (7) is identified as the enthalpy change due to cavity creation in an independent manner.
In water the σn2 quantity depends little on temperature because the isothermal compressibility of water is almost constant over the 0-100 °C temperature range [37]. Thus, the derivative (∂σn2/∂T)P should be a negligible quantity, and Equation (7) can be rearranged to:
where αP = -(1/ρ)⋅(∂ρ/∂T)P is the isobaric thermal expansion coefficient of the liquid. According to Equation (9), ΔHc ∝ αP, in line with the relationship originally derived by Pierotti [41], in the framework of scaled particle theory [42]. In the other liquids the quantity σn2 depends on temperature, but the factor [1 - (ρ2v2/σn2)] occurring in Equation (7) is expected to be small; thus, Equation (9) should be a not-bad approximation for all liquids. By assuming that v = vm and using the statistical mechanical definition of the isothermal compressibility in Equation (9), the latter becomes:
ΔHc ≅ -(kT2ρv2/σn2)⋅(∂ρ/∂T)P = kT2ρ2v2αP/σn2
ΔHc = αP⋅T⋅vm/βT
Both αP and βT are thermodynamic response functions [23], and it is reliable to associate them with a process such as cavity creation that implies a structural reorganization of the pure liquid. The liquid molecules in the configurations possessing the desired cavity must have special spatial distributions that produce changes in both enthalpy and entropy. This structural reorganization can be described by a proper function of αP and βT of the pure liquid because there is no solute molecule inserted in the liquid when the cavity is created. On the basis of Equation (10), it is correct to state that the structural reorganization (which is distinct from the solvent-excluded volume effect) associated with cavity creation is characterized by a complete enthalpy-entropy compensation.
4. Conclusions
Molecular-scale density fluctuations at equilibrium obey Gaussian statistics in several liquids when the observation volumes are not large. This makes it possible to arrive at an analytical relationship for the probability of finding zero molecules in a solvent-excluded volume corresponding to the desired cavity [19,20,21]. A careful analysis of this relationship leads to formulas for the Gibbs free energy change, the enthalpy change and the entropy change associated with cavity creation. These formulas demonstrate that: (a) the Gibbs free energy cost of cavity creation is purely entropic for the reduction in the size of the statistical ensemble caused by the solvent-excluded volume effect; (b) there is a complete enthalpy-entropy compensation associated with the structural reorganization of solvent molecules upon cavity creation. This thermodynamic scenario matches the one determined by Lee [16], with a general statistical mechanical approach.
Author Contributions
Conceptualization, G.G.; formal analysis and investigation, A.T. and G.G.; writing—original draft preparation, A.T. and G.G.; writing—review and editing, A.T. and G.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by internal funds of the University of Sannio; it has not received external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ben-Naim, A. Solvation Thermodynamics; Springer US: Boston, MA, 1987; ISBN 978-1-4757-6552-6. [Google Scholar]
- Ben-Naim, A. Water and Aqueous Solutions; Springer US: Boston, MA, 1974; ISBN 978-1-4615-8704-0. [Google Scholar]
- Lee, B. The physical origin of the low solubility of nonpolar solutes in water. Biopolymers 1985, 24, 813. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Gallicchio, E.; Kubo, M.M.; Levy, R.M. Enthalpy−Entropy and Cavity Decomposition of Alkane Hydration Free Energies: Numerical Results and Implications for Theories of Hydrophobic Solvation. J. Phys. Chem. B 2000, 104, 6271–6285. [Google Scholar] [CrossRef]
- Graziano, G. Shedding Light on the Hydrophobicity Puzzle. Pure and Applied Chemistry 2016, 88, 177–188. [Google Scholar] [CrossRef]
- Silverstein, T.P. The Hydrophobic Effect: Is Water Afraid, or Just Not That Interested? ChemTexts 2020, 6, 26. [Google Scholar] [CrossRef]
- Pohorille, A.; Pratt, L.R. Cavities in Molecular Liquids and the Theory of Hydrophobic Solubilities. J. Am. Chem. Soc. 1990, 112, 5066–5074. [Google Scholar] [CrossRef] [PubMed]
- Pratt, L.R.; Pohorille, A. Theory of Hydrophobicity: Transient Cavities in Molecular Liquids. Proceedings of the National Academy of Sciences 1992, 89, 2995–2999. [Google Scholar] [CrossRef]
- Tang, K.E.S.; Bloomfield, V.A. Excluded Volume in Solvation: Sensitivity of Scaled-Particle Theory to Solvent Size and Density. Biophysical Journal 2000, 79, 2222–2234. [Google Scholar] [CrossRef]
- STONE, M.T.; IN ’T VELD, P.J.; LU, Y.; SANCHEZ, I.C. Hydrophobic/Hydrophilic Solvation: Inferences from Monte Carlo Simulations and Experiments. Molecular Physics 2002, 100, 2773–2792. [Google Scholar] [CrossRef]
- Graziano, G. Water: Cavity Size Distribution and Hydrogen Bonds. Chemical Physics Letters 2004, 396, 226–231. [Google Scholar] [CrossRef]
- Tomás-Oliveira, I.; Wodak, S.J. Thermodynamics of Cavity Formation in Water and N-Hexane Using the Widom Particle Insertion Method. The Journal of Chemical Physics 1999, 111, 8576–8587. [Google Scholar] [CrossRef]
- Graziano, G. Comment on “Reevaluation in Interpretation of Hydrophobicity by Scaled Particle Theory. ” J. Phys. Chem. B 2002, 106, 7713–7716. [Google Scholar] [CrossRef]
- Sedov, I.; Magsumov, T. The Gibbs Free Energy of Cavity Formation in a Diverse Set of Solvents. The Journal of Chemical Physics 2020, 153, 134501. [Google Scholar] [CrossRef]
- Lee, B. A Procedure for Calculating Thermodynamic Functions of Cavity Formation from the Pure Solvent Simulation Data. The Journal of Chemical Physics 1985, 83, 2421–2425. [Google Scholar] [CrossRef]
- Graziano, G. Scaled Particle Theory Study of the Length Scale Dependence of Cavity Thermodynamics in Different Liquids. J. Phys. Chem. B 2006, 110, 11421–11426. [Google Scholar] [CrossRef] [PubMed]
- Tolman, R.C. The Principles of Statistical Mechanics, Oxford University Press, London, UK, 1938.
- Hummer, G.; Garde, S.; García, A.E.; Pohorille, A.; Pratt, L.R. An Information Theory Model of Hydrophobic Interactions. Proceedings of the National Academy of Sciences 1996, 93, 8951–8955. [Google Scholar] [CrossRef]
- Hummer, G.; Garde, S.; García, A.E.; Paulaitis, M.E.; Pratt, L.R. Hydrophobic Effects on a Molecular Scale. J. Phys. Chem. B 1998, 102, 10469–10482. [Google Scholar] [CrossRef]
- Pratt, L.R. MOLECULAR THEORY OF HYDROPHOBIC EFFECTS: “She Is Too Mean to Have Her Name Repeated.”*. Annual Review of Physical Chemistry 2002, 53, 409–436. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- McQuarrie, D. Statistical Mechanics, Harper & Row, New York, NY, USA, 1976.
- Crooks, G.E.; Chandler, D. Gaussian Statistics of the Hard-Sphere Fluid. Phys. Rev. E 1997, 56, 4217–4221. [Google Scholar] [CrossRef]
- Huang, D.M.; Chandler, D. Cavity Formation and the Drying Transition in the Lennard-Jones Fluid. Phys. Rev. E 2000, 61, 1501–1506. [Google Scholar] [CrossRef]
- Peter, C.; van der Vegt, N.F.A. Solvent Reorganization Contributions in Solute Transfer Thermodynamics: Inferences from the Solvent Equation of State. J. Phys. Chem. B 2007, 111, 7836–7842. [Google Scholar] [CrossRef]
- Gomez, M.A.; Pratt, L.R.; Hummer, G.; Garde, S. Molecular Realism in Default Models for Information Theories of Hydrophobic Effects. J. Phys. Chem. B 1999, 103, 3520–3523. [Google Scholar] [CrossRef]
- Head-Gordon, T.; Lynden-Bell, R.M.; Dowdle, J.R.; Rossky, P.J. Predicting Cavity Formation Free Energy: How Far Is the Gaussian Approximation Valid? Phys. Chem. Chem. Phys. 2012, 14, 6996–7004. [Google Scholar] [CrossRef] [PubMed]
- Cerdeiriña, C.A.; González-Salgado, D. Temperature, Pressure, and Length-Scale Dependence of Solvation in Water-like Solvents. I. Small Solvophobic Solutes. J. Phys. Chem. B 2021, 125, 297–306. [Google Scholar] [CrossRef]
- Molinero, V.; Moore, E.B. Water Modeled As an Intermediate Element between Carbon and Silicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef]
- Ashbaugh, H.S. Gaussian and Non-Gaussian Solvent Density Fluctuations within Solute Cavities in a Water-like Solvent. J. Chem. Theory Comput. 2024, 20, 1505–1518. [Google Scholar] [CrossRef] [PubMed]
- Patel, A.J.; Varilly, P.; Chandler, D.; Garde, S. Quantifying Density Fluctuations in Volumes of All Shapes and Sizes Using Indirect Umbrella Sampling. J Stat Phys 2011, 145, 265–275. [Google Scholar] [CrossRef] [PubMed]
- Rego, N.B.; Patel, A.J. Understanding Hydrophobic Effects: Insights from Water Density Fluctuations. Annual Review of Condensed Matter Physics 2022, 13, 303–324. [Google Scholar] [CrossRef]
- Alexandrovsky, V.V.; Basilevsky, M.V.; Leontyev, I.V.; Mazo, M.A.; Sulimov, V.B. The Binomial Cell Model of Hydrophobic Solvation. J. Phys. Chem. B 2004, 108, 15830–15840. [Google Scholar] [CrossRef]
- Graziano, G. Cavity Thermodynamics in the Gaussian Model of Particle Density Fluctuations. Chemical Physics Letters 2007, 446, 313–316. [Google Scholar] [CrossRef]
- Callaway, D.J.E. Surface Tension, Hydrophobicity, and Black Holes: The Entropic Connection. Phys. Rev. E 1996, 53, 3738–3744. [Google Scholar] [CrossRef]
- Kell, G.S. Density, Thermal Expansivity, and Compressibility of Liquid Water from 0.Deg. to 150.Deg.. Correlations and Tables for Atmospheric Pressure and Saturation Reviewed and Expressed on 1968 Temperature Scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
- Wilhelm, E.; Battino, R. Estimation of Lennard-Jones (6,12) Pair Potential Parameters from Gas Solubility Data. The Journal of Chemical Physics 1971, 55, 4012–4017. [Google Scholar] [CrossRef]
- Madan, B.; Lee, B. Role of Hydrogen Bonds in Hydrophobicity: The Free Energy of Cavity Formation in Water Models with and without the Hydrogen Bonds. Biophysical Chemistry 1994, 51, 279–289. [Google Scholar] [CrossRef] [PubMed]
- Lee, B. Enthalpy-Entropy Compensation in the Thermodynamics of Hydrophobicity. Biophysical Chemistry 1994, 51, 271–278. [Google Scholar] [CrossRef]
- Pierotti, R.A. A Scaled Particle Theory of Aqueous and Nonaqueous Solutions. Chem. Rev. 1976, 76, 717–726. [Google Scholar] [CrossRef]
- Reiss, H. Scaled Particle Methods in the Statistical Thermodynamics of Fluids. In Advances in Chemical Physics; John Wiley & Sons, Ltd, 1965; pp. 1–84 ISBN 978-0-470-14355-1.
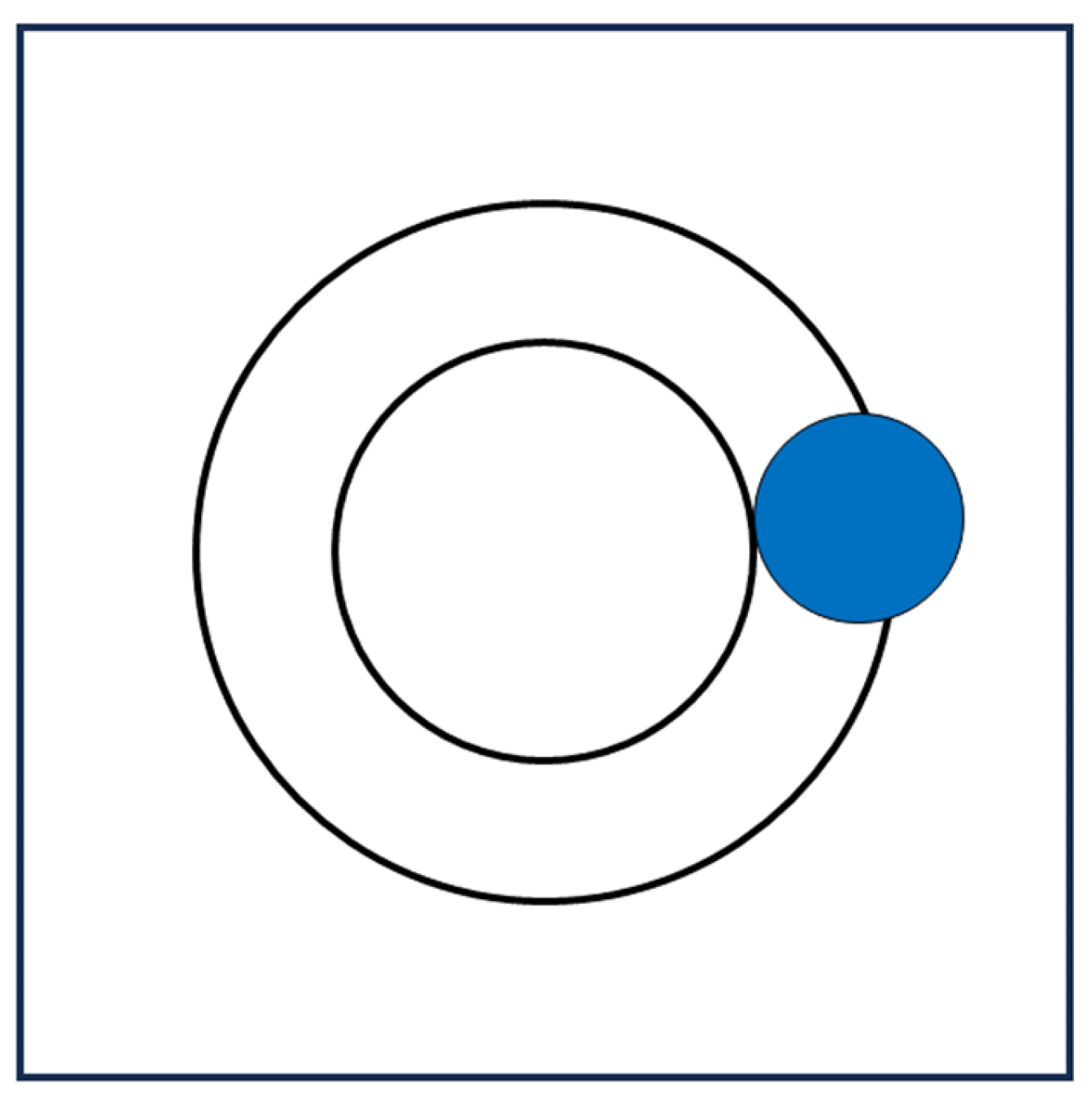
Figure 1.
Figure 1. The creation of a cavity (i.e., the inner circle), at constant NPT, causes an increase in the volume of the liquid by a quantity corresponding to the van der Waals volume of the cavity. But, a spherical shell corresponding to the difference between the solvent-excluded volume of the cavity and its van der Waals volume (i.e., the space between the outer circle and the inner one) becomes inaccessible to the center of liquid molecules (the filled blue circle represents one liquid molecule), if the cavity is to exist. This is the solvent-excluded volume effect associated with cavity creation.
Figure 1.
Figure 1. The creation of a cavity (i.e., the inner circle), at constant NPT, causes an increase in the volume of the liquid by a quantity corresponding to the van der Waals volume of the cavity. But, a spherical shell corresponding to the difference between the solvent-excluded volume of the cavity and its van der Waals volume (i.e., the space between the outer circle and the inner one) becomes inaccessible to the center of liquid molecules (the filled blue circle represents one liquid molecule), if the cavity is to exist. This is the solvent-excluded volume effect associated with cavity creation.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





