Prerpints.org logo
Preprint
Article

Unification: inflation and dark epochs from multi-field theory.

Altmetrics

Downloads

85

Views

24

Comments

0

This version is not peer-reviewed

Submitted:

12 June 2024

Posted:

21 June 2024

You are already at the latest version

Alerts
Abstract
A two scalar field model that incorporates non Riemannian Measures of integration or usually called Two Measures Theory (TMT) is introduced, in order to unify the early and present universe. In the Einstein frame, a K-essence is generated and as a consequence for the early universe, we can have an Inflation for the very early universe and then, after inflation, an early dark energy period and a late dark energy period for the present universe dark, both dark energy epochs have a consistent generation of dark energy (DE), dark matter (DM) and stiff matter. This is obtained when the scale invariance is introduced and then is spontaneously broken from the integration of the degrees of freedom associated with the modified measures. The resulting effective potentials and K-essence in the Einstein frame produce the three flat regions corresponding to the different epochs mentioned before. For the first flat region, we can associate an inflationary universe. Also assuming this first plateau, we study the inflation in the framework of the slow-roll approximation. In this scenario under the slow roll approximation, we obtain a linear combination that is a constant. The corresponding cosmological perturbations in our model are determined and we also obtain the different constraints on the parameter-space from the Planck data. The slow roll approximation can be arranged so that the transition from inflation to the next flat region can be achieved without problems. In the following two flat regions, in addition to the inflation phase, representing the Early Dark Energy and Late Dark Energy Periods, with DE and also the DM, do not need to be introduced separately, they are instead a result of a K-essence induced by the multi measures, multi field theory. Therefore the scalars generate both the DE and the DM . Also a stiff matter component is automatically generated from the K-essence theory from two scalar fields. From the perturbative analysis associated to the perturbation solution of background, we find a correlation between the two scalars. Besides, we obtain that our model during the dark epoch has a behaviour of tracking freezing mode
Keywords: 
Subject: Physical Sciences  -   Particle and Field Physics

1. Introduction

In the most popular paradigm for the early universe, it is postulated that the universe suffers a period of exponential expansion called “inflation” introduced by Guth [1] , Starobinsky [2] and others (cf. the books [3,4] and references therein). However after the discovery of the late universe the accelerating universe [7,8], we also find there a period that some common features with the inflationary period, although the relevant scales are very different.
In this framework, the late universe “standard cosmological” description for the late universe, is now the Λ CDM model [9]. This model incorporates a cosmological constant and a Dark Matter (DM) consisting of pressure-less dust and ordinary visible matter (which is also dust) and in this scenario the universe being now dominated by the Cosmological Constant Λ or Dark Energy (DE). The Λ CDM model is now being challenged by the discovery of some observational tensions, the H 0 and the σ 8 tensions [10,11].
In the inflationary period also primordial density perturbations are generated (Ref.[4] and references therein). The “inflation” is followed by particle creation, where the observed matter and radiation were generated [3], and finally the evolution arrives to a present phase of slowly accelerating universe [7,8]. In this standard model, however, at least three fundamental questions remain unanswered:
  • The inflationary epoch, although solving many cosmological puzzles, like the horizon, flatness problems etc. and also providing a mechanism for primordial density perturbations, cannot address the initial singularity problem;
  • In this model there is no reason for the existence of two (or more, like three if we want to incorporate early dark energy and late dark energy, in addition to inflation) scenarios of exponential expansion with such wildly different scales the inflationary epoch and the current era of slowly accelerated expansion of the universe.
  • There is no explanation for the existence of the Dark Matter, that represents an invisible part and most of the dust in the universe that must be different from the baryonic matter, the visible part of the dust component of our universe.
The best known mechanism for producing a phase of accelerated expansion is from some vacuum energy or a cosmological constant. In the framework of a standard scalar field theory, vacuum energy density arises when the scalar field acquires an effective potential U eff which has flat plateaus so that the field (inflaton) can “slowly roll” [12,13] and its kinetic energy can be disregarded with which the energy-momentum tensor T μ ν ≃ − g μ ν U eff , a contribution that mimics that of a cosmological constant. We will make use of this mechanism to explain the accelerated expansion of the universe associated to the inflation phase of the universe. In the late phases of the universe we will also find a contribution from an effective scalar field potential, but there will be also a contribution to the DE from a K-essence background configuration that also gives rise to a contribution that satisfies the equation of state p = − ρ . ∝ g μ ν One aspect that we have not studied more in this paper is the possibility of an emergent period or emergent universe was proposed in Refs.[5,6] In [58] in the same flat region used for the inflation, the emergent universe can also take place and the effective potential contribution also can combine with the K-essence to produce an equation of state p = − ρ / 3 which produces no acceleration and in particular a static Einstein universe, which is stable for a range of parameters, unlike the original Einstein universe. Therefore the interplay of an effective potential and K-essence will be crucial for many effects studied in this paper along many continuously connected phases of the universe.
In the present paper we will not use one of the three flat regions for obtaining an emergent phase, because we emphasize on inflation, Early DE and late DE, and to obtain the best results in this respect, we have to identify the region that must be used for inflation different to what we did in [58] , which leads to a clean evolution after the slow role inflation to the Early DE, an effect not studied and not obviously possible here now, given the choices made here are different to those in [58], for this reason, the study of a possible emergent phase is not studied here.
The connection between the inflationary epoch to a slowly accelerating universe through the evolution of a single scalar field denominated “the quintessential inflation scenario” has been first analyzed in Ref.[14]. Besides, a quintessential inflation mechanism developed on the K-essence model, was studied in Ref.[15]. Also quintessential inflation founded on the “variable gravity” model was developed in Ref.[16] and for another list of references, see Ref.[17]. Additionally other approaches founded on the so called α attractors, which utilizes non canonical kinetic terms have been analyzed in Ref.[18]. Also a quintessential inflation developed on a Lorentzian slow- roll approximation which automatically gives two flat regions was studied in [19]. In addition, the F ( R ) models can connect both periods an early time inflationary era and a late time de Sitter epoch from different values of effective vacuum energies, see Ref.[20]. For a review of f ( R ) model and another modified gravity, see Refs.[21,22].
The framework for this research is the use of the metric independent non Riemannian measures for the construction of modified gravity theories Refs.[23]-[25] (see also Refs.[26]-[29]), in some instances we have included the standard measure as well, where the standard Riemannian integration measure might also contain a Weyl-scale symmetry preserving R 2 -term [25]. Some applications have been, (i) D = 4 -dimensional models of gravity and matter fields containing the new measure of integration appear to be promising candidates for resolution of the dark energy and dark matter problems, the fifth force problem, and a natural mechanism for spontaneous breakdown of global Weyl-scale symmetry [23]-[29], (ii) To study of reparametrization invariant theories of extended objects (strings and branes) based on employing of a modified non-Riemannian world-sheet/world-volume integration measure [30,31], leads to dynamically induced variable string/brane tension and to string models of non-abelian confinement, interesting consequences from the modified measures spectrum [32], and construction of new braneworld scenarios [33], (iii) To study in Ref.[34] of modified supergravity models with an alternative non-Riemannian volume form on the space-time manifold .
Directly connected to the present research are our papers [35] where we have studied a unified scenario where both an inflation and a slowly accelerated phase for the universe can appear naturally from the existence of two flat regions in the effective scalar field potential which we derive systematically from a Lagrangian action principle. Namely, we started with a new kind of globally Weyl-scale invariant gravity-matter action within the first-order (Palatini) approach formulated in terms of two different non-Riemannian volume forms (integration measures) [36]. Also we have studied the reheating scenario in this theory assuming the curvaton field in order to decay to the hot big bang model[37,38]. In this new theory there is a single scalar field with kinetic terms coupled to both non-Riemannian measures, and in addition to the scalar curvature term R also an R 2 term is included (which is similarly allowed by global Weyl-scale invariance). Scale invariance is spontaneously broken upon solving part of the corresponding equations of motion due to the appearance of two arbitrary dimensionfull integration constants. Furthermore, in a subsequent paper we generalized this to a two-field case[39] where three flat regions appear, one for inflation and the remaining two for early DE and a late DE phase. In order to describe the early DE and DM, we have introduced a matter action defined as a scale invariant form, which is independent of the scalar fields.
In this paper we will add a new aspect, that is, without introducing any new additional matter action, therefore not introducing the DM separately, as compared to [39], we consider instead more generic scale invariant couplings, like involving R 2 and others, and we produce as a result a theory that is also able to provide a non singular emergent phase for the universe where the effective potential contribution combines with the K-essence to produce a p = − ρ / 3 equation of state which produces no acceleration and in particular a static Einstein Universe, which is stable for a range of parameters, unlike the original Einstein universe. This emergent phase is then followed by the inflationary phase as well as, in addition after the emergent and inflation eras we have a second flat region that provide an explanation for the DE and DM of the late universe. This is a consequence of the K-essence produced by the additional kinetic terms and R square terms introduced into the action. In this context, we have a contribution to the DE that comes from an effective scalar field potential and also there is a contribution to the DE from a K-essence background configuration. Additionally, we have a DM component and an additional stiff matter component which originate from the perturbation of the background K-essence configuration. Here we obtain a consistency condition that correlates the perturbations of the two fields in the late universe. Also, the different constraints from each phase are shown to be consistent with the constraints on the same parameters from the other phases.
The plan of the present article is as follows. In the next Section we discussion the general formalism for the new class of gravity-matter considering two independent non Riemannian volume forms. In Section 3 we analyze the three flat regions from the effective scalar potential in the Einstein framework.
In Section 5.1 we describe the inflationary epoch. Here we analyze the slow-roll approximation during the background scenario and also we determine the perturbations cosmological. In this context we find the constraints of the different parameters from the Planck data. In Section 5.2, we analyze how our model of K-essence can describe the late universe. From the second flat plateau we find different components assuming the perturbations K-essence background configuration. Also we determine the equation of state associated to the dark sector together with the derivative of this parameter. Similar analysis is done for the third plateau. The second and third plateaus are good candidates for the early and late dark energies. In Section 6 we end up with a discussion section concerning generalizations of the model, additional mechanisms for inducing DE and the role of the third flat region and its possible relation to early and late DE. For simplicity we will consider units where the Newton constant is taken as G Newton = 1 / 16 π .

2. Modified Theory: Two Independent Non-Riemannian Volume-Forms

We shall consider the action of the general form involving two independent alternative integration measure densities generalizing the model studied in Ref.[36] with which we have
S = ∫ d 4 x Φ 1 ( A ) R + L ( 1 ) + ∫ d 4 x Φ 2 ( B ) L ( 2 ) + ϵ R 2 + Φ ( H ) − g ,
where the following definitions are utilized:
  • The functions Φ 1 ( A ) and Φ 2 ( B ) are two densities and these are independent non-metric volume-forms given in terms of the curl of the anti-symmetric 3-index tensor gauge fields defined as
    Φ 1 ( A ) = 1 3 ! ε μ ν κ λ ∂ μ A ν κ λ , a n d Φ 2 ( B ) = 1 3 ! ε μ ν κ λ ∂ μ B ν κ λ .
  • The quantity R = g μ ν R μ ν ( Γ ) corresponds to the scalar curvature and R μ ν ( Γ ) denotes the Ricci tensor and these are defined in the first-order (Palatini) formalism, in which the affine connection Γ ν λ μ is a priori independent of the metric g μ ν .
  • The two Lagrangians L ( 1 , 2 ) use two scalar matter fields φ 1 and φ 2 and these Lagrangians are defined as
    L ( 1 ) = − g ̉ μ ν ∂ μ φ 1 ∂ ν φ 1 − g ̉ μ ν ∂ μ φ 2 ∂ ν φ 2 − V ( φ 1 , φ 2 ) ,
    L ( 2 ) = − b 1 2 e − α 1 φ 1 g μ ν ∂ μ φ 1 ∂ ν φ 1 − b 2 2 e − α 2 φ 2 g μ ν ∂ μ φ 2 ∂ ν φ 2 + U ( φ 1 , φ 2 ) ,
    where the potentials V ( φ 1 , φ 2 ) and U ( φ 1 , φ 2 ) are given by
    V ( φ 1 , φ 2 ) = f 1 exp { − α 1 φ 1 } + g 1 exp { − α 2 φ 2 } , a n d U ( φ 1 , φ 2 ) = f 2 exp { − 2 α 1 φ 1 } + g 2 exp { − 2 α 2 φ 2 } .
    Here the quantities α 1 , α 2 , f 1 , g 1 , f 2 , ϵ and g 2 are positive parameters, whereas b 1 and b 2 are dimensionless and their ranges are to be determined. Here α 1 and α 2 have dimensions of M P l − 1 , instead the quantities f 1 , f 2 , g 1 and g 2 have units of M P l 4 . Also, the parameter ϵ has units of M P l − 2 .
  • The function Φ ( H ) corresponds to the dual field strength of a third auxiliary 3-index antisymmetric tensor defined as
    Φ ( H ) = 1 3 ! ε μ ν κ λ ∂ μ H ν κ λ .
We note that the action given by Eq.(1) is invariant under the global scale transformations, such that
g μ ν → λ g μ ν ,   Γ ν λ μ → Γ ν λ μ ,   φ 1 → φ 1 + 1 α 1 ln λ , φ 2 → φ 2 + 1 α 2 ln λ A μ ν κ → λ A μ ν κ ,   B μ ν κ → λ 2 B μ ν κ ,   H μ ν κ → H μ ν κ .
The variation of the action (1) w.r.t. affine connection Γ ν λ μ and following Ref.[23], we find that its solution Γ ν λ μ becomes a Levi-Civita connection , where the Weyl-rescaled metric g ¯ μ ν results
g ¯ μ ν = ( χ 1 + 2 ϵ χ 2 R ) g μ ν , w h e r e χ 1 ≡ Φ 1 ( A ) − g , a n d χ 2 ≡ Φ 2 ( B ) − g .
Besides, the variation of the action (1) w.r.t. auxiliary tensors A μ ν λ , B μ ν λ and H μ ν λ gives
∂ μ R + L ( 1 ) = 0 , ∂ μ L ( 2 ) + ϵ R 2 + Φ ( H ) − g = 0 , ∂ μ Φ 2 ( B ) − g = 0 ,
and the solutions can be written as
Φ 2 ( B ) − g ≡ χ 2 = const , R + L ( 1 ) = − M 1 = const , L ( 2 ) + ϵ R 2 + Φ ( H ) − g = − M 2 = const .
Here the quantities M 1 and M 2 are arbitrary dimension full and the parameter χ 2 denotes an arbitrary dimensionless integration constant. We mention that the parameter χ 2 in (10) preserves global scale invariance (7) and the second and third integration constants M 1 , M 2 implies breakdown of global scale invariance under Eq.(7).
Additionally, the variation of the action (1) w.r.t. g μ ν and assuming relations (10) we have
χ 1 R μ ν + g μ ν L ( 1 ) − T μ ν ( 1 ) − 2 T μ ν ( 2 ) + g μ ν ϵ R 2 + M 2 − 2 R R μ ν = 0 ,
in which T μ ν ( 1 , 2 ) ( φ 1 , φ 2 ) = T μ ν ( 1 , 2 ) are the energy-momentum tensors defined as
T μ ν ( 1 , 2 ) = g μ ν L ( 1 , 2 ) − 2 ∂   ∂ g μ ν L ( 1 , 2 ) .
By using the trace of Eq.(11) and considering again second relation (10) we obtain
χ 1 = 2 χ 2 T ( 2 ) / 4 + M 2 L ( 1 ) − T ( 1 ) / 2 − M 1 ,
in which the trace T ( 1 , 2 ) = g μ ν T μ ν ( 1 , 2 ) .
By considering Eqs.(10) and (11) we find the Einstein-like form:
R μ ν − g ̉ μ ν R = g ̉ μ ν L ( 1 ) + M 1 + 1 2 T μ ν ( 1 ) − g μ ν L ( 1 ) + χ 2 2 χ 1 T μ ν ( 2 ) + g μ ν M 2 + ϵ ( L ( 1 ) + M 1 ) 2 ,
where the function Ω is given by
= 1 − χ 2 χ 1 2 ϵ L ( 1 ) + M 1 .
From Eqs.(8), (10) and (15), the relation between g ¯ μ ν and g μ ν can be written as
g ¯ μ ν = χ 1 g μ ν .
Thus, the Eq.(14) for the rescaled metric g ¯ μ ν (16), i.e., the Einstein-frame becomes
R μ ν ( g ¯ ) − μ ν R ( g ¯ ) = T ̉ μ ν eff ,
where the effective energy-momentum tensor in the Einstein-frame becomes
T μ ν eff = g ¯ μ ν L eff − 2 ∂   ∂ g ¯ μ ν L eff ,
in which the effective Einstein-frame scalar fields Lagrangian associated to φ 1 and φ 2 yields
L eff ( φ 1 , φ 2 ) = 1 χ 1 L ( 1 ) + M 1 + χ 2 χ 1 L ( 2 ) + M 2 + ϵ ( L ( 1 ) + M 1 ) 2 .
For the Lagrangian L eff in terms of the Einstein-frame metric g ¯ μ ν (16), we can use the short-hand notation for the scalar kinetic terms X 1 and X 2 such that
X 1 ≡ − μ ν ∂ μ φ 1 ∂ ν φ 1 , a n d X 2 ≡ − μ ν ∂ μ φ 2 ∂ ν φ 2 ,
and then the two Lagrangians L ( 1 , 2 ) can be written as
L ( 1 ) = χ 1 X 1 + X 2 − V , L ( 2 ) = χ 1 b 1 e − α 1 φ 1 X 1 + b 2 e − α 2 φ 2 X 2 + U ,
with V and U given by Eq.(5).
By considering Eqs.(13) and (15), taking into account (3), we have
1 χ 1 = ( V − M 1 ) 2 χ 2 U + M 2 + ϵ ( V − M 1 ) 2 1 − χ 2 b 1 e − α 1 φ 1 V − M 1 − 2 ϵ X 1 + b 2 e − α 2 φ 2 V − M 1 − 2 ϵ X 2 .
Replacing expression (22) into (19), we obtain at the explicit form for the Einstein-frame scalar Lagrangian given by
L eff = A 1 ( φ 1 , φ 2 ) X 1 + A 2 ( φ 1 , φ 2 ) X 2 + B 1 ( φ 1 , φ 2 ) X 1 2 + B 2 ( φ 1 , φ 2 ) X 2 2 + B 12 ( φ 1 , φ 2 ) X 1 X 2 − U eff ( φ 1 , φ 1 ) ,
where the functions A 1 ( φ 1 , φ 2 ) and A 2 ( φ 1 , φ 2 ) are defined as
A 1 ( φ 1 , φ 2 ) = 1 + b ̉ 1 e − α 1 φ 1 − ϵ ( V − M 1 ) V − M 1 U + M 2 + ϵ ( V − M 1 ) 2 = 1 +
1 2 b ̉ 1 e − α 1 φ 1 − ϵ f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 − M 1 f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 − M 1 f 2 e − 2 α φ 1 + g 2 e − 2 α φ 2 + M 2 + ϵ ( f 1 e − α φ 1 + g 1 e − α 2 φ 2 − M 1 ) 2 ,
and
A 2 ( φ 1 , φ 2 ) = 1 + b ̉ 2 e − α 2 φ 2 − ϵ ( V − M 1 ) V − M 1 U + M 2 + ϵ ( V − M 1 ) 2
= 1 + b ̉ 2 e − α 2 φ 2 − ϵ f 1 e − α φ 1 + g 1 e − α 2 φ 2 − M 1 f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 − M 1 f 2 e − 2 α φ 1 + g 2 e − 2 α φ 2 + M 2 + ϵ ( f 1 e − α φ 1 + g 1 e − α 2 φ 2 − M 1 ) 2 .
Besides, the coefficient B 1 ( φ 1 , φ 2 ) is given by
B 1 ( φ 1 , φ 2 ) = χ 2 ϵ U + M 2 + ( V − M 1 ) b 1 e − α 1 φ 1 − 1 4 b 1 2 e − 2 α φ 1 U + M 2 + ϵ ( V − M 1 ) 2 = χ 2 ϵ f 2 e − 2 α φ 1 + g 2 e − 2 α φ 2 + M 2 + ( f 1 e − α φ 1 + g 1 e − α 2 φ 2 − M 1 ) b 1 e − α 1 φ 1 − 1 4 b 1 2 e − 2 α 1 φ 1 f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 + M 2 + ϵ ( f 1 e − α 1 φ 1 + g 2 e − α 2 φ 2 − M 1 ) 2 ,
and for the coefficient B 2 ( φ 1 , φ 2 ) we have
B 2 ( φ 1 , φ 2 ) = χ 2 ϵ U + M 2 + ( V − M 1 ) b 2 e − α 2 φ 2 − 1 4 b 2 2 e − 2 α φ 2 U + M 2 + ϵ ( V − M 1 ) 2 = χ 2 ϵ f 2 e − 2 α φ 1 + g 2 e − 2 α φ 2 + M 2 + ( f 1 e − α φ 1 + g 1 e − α 2 φ 2 − M 1 ) b 2 e − α 2 φ 2 − 1 4 b 2 2 e − 2 α 2 φ 2 f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 + M 2 + ϵ ( f 1 e − α 1 φ 1 + g 2 e − α 2 φ 2 − M 1 ) 2 ,
and the function B 12 ( φ 1 , φ 2 ) we have
B 12 ( φ 1 , φ 2 ) = χ 2 E 0 [ − E 1 b 2 e − α 2 φ 2 − E 2 b 1 e − α 1 φ 1 + 2 E 0 E 1 E 2 [ ( M 2 + U ) +
ϵ ( M 1 − V ) 2 ] + 2 ϵ [ ( 1 / E 0 ) − ( E 1 + E 2 ) ( M 1 − V ) ] ] ,
and the quantities E 0 , E 1 and E 2 are given by
E 0 = ( V − M 1 ) 2 χ 2 [ U + M 2 + ϵ ( V − M 1 ) 2 ] , E 1 = χ 2 b 1 e − α 1 φ 1 V − M 1 − 2 ϵ , a n d E 2 = χ 2 b 2 e − α 2 φ 2 V − M 1 − 2 ϵ .
The effective scalar field potential as a function of the scalar fields becomes
U eff ( φ 1 , φ 2 ) = ( V − M 1 ) 2 4 χ 2 U + M 2 + ϵ ( V − M 1 ) 2 =
( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 − M 1 ) 2 4 χ 2 f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 + M 2 + ϵ ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 − M 1 ) 2 ,
in which we have considered for V and U, the expressions given by Eq.(5).

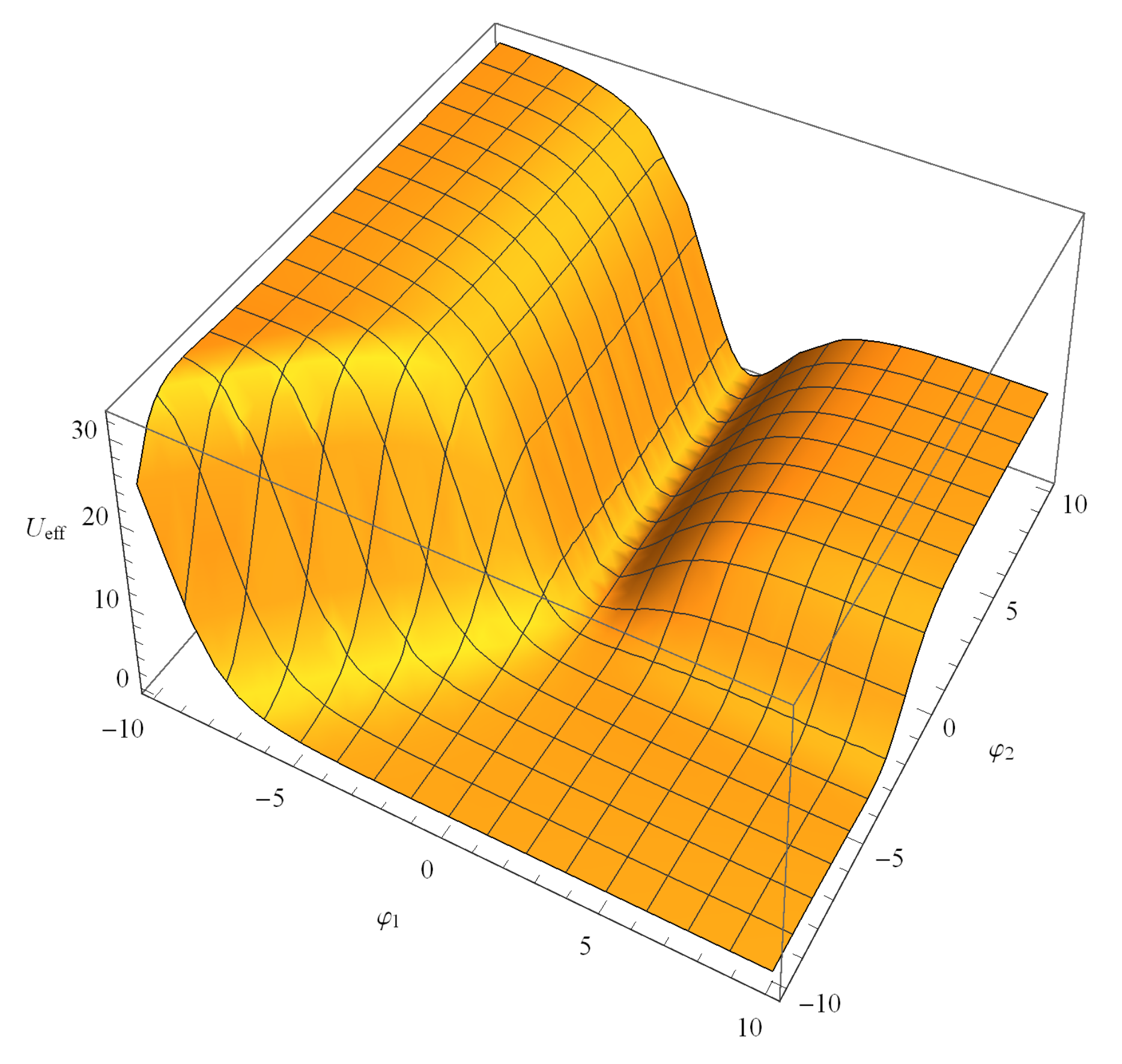
3. Three flat regions from the Effective Scalar Potential

The crucial feature of U eff ( φ 1 , φ 2 ) is the presence of three infinitely large flat regions. In this sense, we have one for large positive values of the scalar fields φ 1 and φ 2 and two others for the limits φ 1 → − ∞ and φ 2 → − ∞ .
In the first flat region for large positive φ 1 and also φ 2 , we find that the effective potential reduces to
U eff ( φ 1 , φ 2 ) ≃ U eff ( + ∞ , + ∞ ) = U eff ( + ) = M 1 2 / M 2 4 χ 2 ( 1 + ϵ M 1 2 / M 2 ) ,
and the kinetic coefficients are
A 1 ( φ 1 , φ 2 ) = A 2 ( φ 1 , φ 2 ) ≃ A ( + ) ≡ M 2 M 2 + ϵ M 1 2 , B 1 ( φ 1 , φ 2 ) = B 2 ( φ 1 , φ 2 ) ≃ B ( + ) ≡ ϵ χ 2 M 2 M 2 + ϵ M 1 2 ,
and for this limit we find that the coefficient B 12 ( φ 1 , φ 2 ) becomes
B 12 ( φ 1 , φ 2 ) = B 12 ( + ∞ , + ∞ ) = B 12 ( + ) = 2 ϵ χ 2 M 2 M 2 + ϵ M 1 2 = 2 B ( + ) .
For large negative values of φ 1 , which we will choose to describe the very early phase of the universe, meaning the emergent phase and inflation we have for the effective potential and the coefficient functions in the Einstein-frame scalar Lagrangian (23)-(29):
U eff ( φ 1 , φ 2 ) ≃ U eff ( − ∞ , φ 2 ) = U e f f = f 1 2 / f 2 4 χ 2 ( 1 + ϵ f 1 2 / f 2 ) ,
A 1 ( φ 1 , φ 2 ) ≃ A 1 ( − ∞ , φ 2 ) = A 1 = 1 + b ̉ 1 f 1 / f 2 1 + ϵ f 1 2 / f 2 , B 1 ( φ 1 , φ 2 ) ≃ B 1 ( − ∞ , φ 2 ) = B 1 = − χ 2 b 1 2 / 4 f 2 − ϵ ( 1 + b 1 f 1 / f 2 ) 1 + ϵ f 1 2 / f 2 .
For the terms A 2 and B 2 in the limit in which φ 1 → − ∞ we have
A 2 ( φ 1 , φ 2 ) ≃ A 2 ( − ∞ , φ 2 ) = A 2 = 1 1 + ϵ f 1 2 / f 2 , a n d B 2 ( φ 1 , φ 2 ) ≃ B 2 ( − ∞ , φ 2 ) = B 2 = χ 2 ϵ 1 + ϵ f 1 2 / f 2 .
For the coefficient B 12 ( φ 1 , φ 2 ) in the limit in which the scalar field φ 1 → − ∞ becomes
B 12 ( φ 1 , φ 2 ) ≃ B 12 ( − ∞ , φ 2 ) = B 12 = χ 2 E ˜ 0 − E ˜ 2 b 1 + E ˜ 0 b 2 + 2 ϵ E ˜ 0 + ϵ E ˜ 0 f 1 2 + 2 ϵ f 1 ( E ˜ 1 + E ˜ 2 ) ,
where
E ˜ 0 = f 1 2 χ 2 [ f 2 + ϵ f 1 2 ] , E ˜ 1 = χ 2 b 1 f 1 − 2 ϵ , a n d E ˜ 2 = − 2 χ 2 ϵ .
For the third flat region we will consider that the scalar field φ 2 → − ∞ such that the effective potential in the second flat region is given by
U eff ( φ 1 , φ 2 ) ≃ U eff ( φ 1 , − ∞ ) = U eff g = g 1 2 / g 2 4 χ 2 ( 1 + ϵ g 1 2 / g 2 ) ,
and the kinetic coefficients A 2 and B 2 in the limit in which φ 2 → − ∞ result
A 2 ( φ 1 , − ∞ ) = A 2 g = 1 + b ̉ 2 g 1 / g 2 1 + ϵ g 1 2 / g 2 , B 2 ( φ 1 , − ∞ ) = B 2 g = − χ 2 b 2 2 / 4 g 2 − ϵ ( 1 + b 2 g 1 / g 2 ) 1 + ϵ g 1 2 / g 2 ,
and the terms A 1 and B 1 in this limit result
A 1 ( φ 1 , φ 2 ) ≃ A 1 ( φ 1 , − ∞ ) = A 1 g = 1 1 + ϵ g 1 2 / g 2 , B 1 ( φ 1 , φ 2 ) ≃ B 1 ( φ 1 , − ∞ ) = B 1 g = χ 2 ϵ 1 + ϵ g 1 2 / g 2 .
For the coefficient B 12 ( φ 1 , φ 2 ) in the limit in which the scalar field φ 2 → − ∞ we have
B 12 ( φ 1 , φ 2 ) ≃ B 12 ( φ 1 , − ∞ ) = B 12 g = χ 2 E ˜ 3 − E ˜ 2 b 2 + E ˜ 3 g 2 + 2 ϵ E ˜ 3 + ϵ E ˜ 3 g 1 2 + 2 ϵ g 1 ( E ˜ 4 + E ˜ 2 ) ,
where
E ˜ 3 = g 1 2 χ 2 [ g 2 + ϵ g 1 2 ] , a n d E ˜ 4 = χ 2 b 2 g 1 − 2 ϵ .
The important feature of the effective potential U eff given by Eq.(29) is the presence of three infinitely large flat regions for large positive values of the fields φ 1 and φ 2 . In the following we will consider that the first flat region corresponds for large positive values of φ 1 and φ 2 . Thus, we have for the effective potential is reduced to
U eff ( φ 1 , φ 2 ) ≃ U eff ( + ∞ , + ∞ ) = U eff ( + ) = M 1 2 / M 2 4 χ 2 ( 1 + ϵ M 1 2 / M 2 ) .
For the second flat region we consider the situation in which we only have large negative φ 1 :
U eff ( φ 1 , φ 2 ) ≃ U eff ( − ∞ , φ 2 ) = U eff = f 1 2 / f 2 4 χ 2 ( 1 + ϵ f 1 2 / f 2 ) .
In the third flat region in which we only have large negative φ 2 :
U eff ( φ 1 , φ 2 ) ≃ U eff ( φ 1 , − ∞ ) = U eff g = g 1 2 / g 2 4 χ 2 ( 1 + ϵ g 1 2 / g 2 ) .
The different flat regions given by these limits, correspond to the evolution of the early inflationary universe described by the region (41) and the late dark energies given by the regions (42) and (43), respectively. Thus, from the scaling of energy densities, we can consider that the ratio of the coupling constants satisfies
M 1 2 M 2 ( 1 + ϵ M 1 2 / M 2 ) ≫ f 1 2 f 2 ( 1 + ϵ f 1 2 / f 2 ) , a n d f 1 2 f 2 ( 1 + ϵ f 1 2 / f 2 ) > g 1 2 g 2 ( 1 + ϵ g 1 2 / g 2 ) .
On the other hand, to study the evolution of the universe from of the inflationary scenario to dark epochs, we consider that the standard Friedman-Lemaitre-Robertson-Walker space-time metric is given by
d s 2 = − d t 2 + a 2 ( t ) d r 2 1 − K r 2 + r 2 ( d θ 2 + sin 2 θ d ϕ 2 ) ,
where a ( t ) denotes the scale factor and K corresponds to the space curvature.
By assuming that the matter is described by a perfect fluid with an energy density and pressure ρ and p, we have that the associated Friedmann equations are
a . . a = − 1 12 ( ρ + 3 p ) , H 2 + K a 2 = 1 6 ρ , a n d ρ ˙ + 3 H ( ρ + p ) = 0 ,
where H = a . a is the Hubble parameter. Also, here the energy density and pressure associated to the scalar fields φ 1 = φ 1 ( t ) and φ 2 = φ 2 ( t ) are defined as
ρ = A 1 ( φ 1 , φ 2 ) X 1 + A 2 ( φ 1 , φ 2 ) X 2 + 3 B 1 ( φ 1 , φ 2 ) X 1 2 + 3 B 2 ( φ 1 , φ 2 ) X 2 2 + 3 B 12 ( φ 1 , φ 2 ) X 1 X 2 + U eff ( φ 1 , φ 2 ) ,
and
p = A 1 ( φ 1 , φ 2 ) X 1 + A 2 ( φ 1 , φ 2 ) X 2 + B 1 ( φ 1 , φ 2 ) X 1 2 + B 2 ( φ 1 , φ 2 ) X 2 2 + B 12 ( φ 1 , φ 2 ) X 1 X 2 − U eff ( φ 1 , φ 2 ) .
Henceforth the dots indicate derivatives with respect to the time t and we have assumed that the scalar fields are homogeneous.
In the following chapter, we will analyze the unification of the inflation and the dark sectors in the special case in which we have a canonical form for the fields φ 1 and φ 2 in the Einstein frame, and this is achieved by considering that the parameters ϵ , b 1 and pter b 2 take the values ϵ = 0 , b 1 = 0 and b 2 = 0 .

4. Evolution of the Universe in the Situation in Which ϵ = 0 , b 1 = 0 and b 2 = 0 and Spontaneous Scale Symmetry Breaking

4.1. Flat Regions of the Effective Scalar Potential

In this section we will analyze the specific situation in which the parameters ϵ = 0 , b 1 = 0 and b 2 = 0 . In this sense, the theory is reduced to a canonical form for the two fields i.e., without k-essence terms in the Einstein frame.
From the effective potential U eff (see eq.(29)) we have three infinitely large flat regions for large values of the fields φ 1 and φ 2 .
The inflationary epoch is realized for large positive values of φ 1 and φ 2 and it corresponds to the first flat region. In this context, we have that the effective potential in the case in which ϵ = 0 reduces to
U eff ( φ 1 , φ 2 ) ≃ U ( φ 1 → + ∞ , φ 2 → + ∞ ) = U ( + + ) ≡ M 1 2 4 χ 2 M 2 .
For the second flat region we can consider the situation in which we only have large negative φ 1
U eff ( φ 1 , φ 2 ) ≃ U ( φ 1 → − ∞ ) ≡ f 1 2 4 χ 2 f 2 .
In the other flat region in which we only have large negative φ 2
U eff ( φ 1 , φ 2 ) ≃ U ( φ 2 → − ∞ ) ≡ g 1 2 4 χ 2 g 2 .
In Figure 1 we show a qualitative example for the effective potential in which is possible to appreciate the three flat regions.
The flat regions described by the potentials given by Eqs.(49), (50) and (51) are responsible of the evolution of the inflationary era and the early and late dark epochs, respectively. In order to archive this history of the universe, we choose the ratio of the coupling constants in the original scalar potentials versus the ratio of the scale-symmetry breaking integration constants to satisfy
M 1 2 M 2 ≫ f 1 2 f 2 a n d f 1 2 f 2 > g 1 2 g 2 ,
which makes the first flat region associated to the inflationary universe U ( + + ) much bigger than that of the early and late dark eras.
We note that using the tensor to scalar ratio r together with the scalar power spectrum P S , we have that the first flat region associated to the effective potential U ( + + ) is approximately [44]
U ( + + ) ∼ M 1 2 / χ 2 M 2 ∼ 6 π 2 r P S ∼ 10 − 8 ,
in units of M P l 4 . Let us recall that, since we are considering units in which the constant G Newton = 1 / 16 π , then in the present case the Planck mass M P l = 1 / 8 π G Newton = 2 .
For the situation in which the parameters ϵ = 0 and b 1 = b 2 = 0 , the total energy density and pressure of the scalar fields φ 1 = φ 1 ( t ) and φ 2 = φ 2 ( t ) , are reduced to
ρ = 1 2 + 2 2 + U eff ( φ 1 , φ 2 ) ,
p = 1 2 + 2 2 − U eff ( φ 1 , φ 2 ) ,
in which the effective potential is
U eff ( φ 1 , φ 2 ) = ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 − M 1 ) 2 4 χ 2 f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 + M 2 .
Besides, the scalar equations of motion for the scalar field φ 1 and φ 2 , can be written as
φ . . 1 + 3 H φ . 1 + ∂ U eff / ∂ φ 1 = 0 ,
and
φ . . 2 + 3 H φ . 2 + ∂ U eff / ∂ φ 2 = 0 .
In order to analyze the unification from inflation to the dark sector, we have that in the early epoch the potential begins at U ( + + ) and finishes at the lower value of the late dark energy.

4.2. Inflation: Slow Roll approximation and Perturbations

In this section we will study the dynamics and the cosmological perturbations during the inflationary scenario associated to the first flat region in which the effective potential is given by U ( + + ) , see Eq.(49).
In order to analyze the inflationary dynamics during the early universe and because of the flatness of the effective potential, we can expect that the slow roll approximation is valid. In this sense, we can introduce the standard “slow-roll” parameters defined as [40]:
ε = − H . H 2 , η 1 = − φ . . 1 H φ . 1 , a n d η 2 = − φ . . 2 H φ . 2 ,
and under the slow-roll approximation these parameters are ε , η 1 and satisfy η 2 ≪ 1. In this approximation, the φ 1 , φ 2 -equations of motion together with the flat ( K = 0 ) Friedmann Eq.(46) simplify to
3 H φ . 1 + ∂ U eff / ∂ φ 1 ≃ 0 , 3 H φ . 2 + ∂ U eff / ∂ φ 2 ≃ 0 , a n d H 2 ≃ 1 6 U eff .
During the inflationary scenario the fields φ 1 and φ 2 evolve on the first flat region of U eff = U ( + + ) for large positive values of the fields (49) and then we can assume that the effective potential during inflation can be approximated to,
U e f f ( φ 1 , φ 2 ) ≃ M 1 2 − 2 M 1 ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) 4 χ 2 M 2 ,
here we have utilized the expansion of the effective potential given by eq.(29) in the case in which ϵ = 0 .
Introducing the standard definition of the number of e − folds N = ln ( a / a f ) where a f denotes the scale factor at the end of the inflationary epoch, that is, at the end of inflation N = 0 , we can rewrite eq.(60) using eq.(61) as
d φ 1 d N = 6 M 1 α 1 f 1 e − α 1 φ 1 [ M 2 2 − 2 M 1 ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) ] ,
and
d φ 2 d N = 6 M 1 α 2 g 1 e − α 2 φ 2 [ M 2 2 − 2 M 1 ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) ] ,
respectively. From these two equations we find a relation between the scalar fields φ 1 and φ 2 given by,
e α 1 φ 1 d φ 1 = f 1 α 1 g 2 α 2 e α 2 φ 2 d φ 2 .
Note that the symmetry breaking constants M 1 and M 2 disappear from this above differential equation. The solution of this equation becomes
e α 1 φ 1 = f 1 α 1 2 g 1 α 2 2 e α 2 φ 2 + C ,
where C corresponds to a constant of integration. Notice that in the absence of the constant of integration C , the integrated relation (65) is scale invariant and should be regarded as an additional scale symmetry breaking constant. To avoid this extra scale symmetry breaking, in the following we will assume that the constant C = 0 .
Following Ref.[39], we can consider an orthogonal transformation in which φ ˙ 1 2 + φ ˙ 2 2 = ϕ ˙ 1 2 + ϕ ˙ 2 2 , where the field ϕ 1 is invariant and ϕ 2 transforms under a scale transformation. Thus, we define two new scalar fields ϕ 1 and ϕ 2 as [39]
ϕ 1 = α 1 φ 1 − α 2 φ 2 α 1 2 + α 2 2 , a n d ϕ 2 = α 2 φ 1 + α 1 φ 2 α 1 2 + α 2 2 .
We note that in this situation, the scale invariant combination α 1 φ 1 − α 2 φ 2 gets determined, which corresponds to fixing the scalar field ϕ 1 given by Eq.(66) and this scalar field is scale invariant with which
ϕ 1 = 1 α 1 2 + α 2 2 ln f 1 α 1 2 g 1 α 2 2 = c o n s t a n t .
Here we have used Eq.(65).
Nevertheless, the scalar field ϕ 2 given by Eq. (66), evolves in time. We notice that although we have broken the scale invariance, through the constants M 1 and M 2 , some of the remaining equations maintain the scale invariance. As we have noted, the integration constants M 1 and M 2 dropped from such equation. That is indeed the reason that the equation that relates the two scalars keeps the scale invariance, which is not valid for other equations. Additionally, using Eqs.(66) and (67), we find that the scalar field φ 1 in terms of the scalar field φ 2 can be written as
φ 1 = 1 α 1 α 2 φ 2 + ln f 1 α 1 2 g 1 α 2 2 .
In order to establish that the term f 1 e − α 1 φ 1 ≫ g 1 e − α 2 φ 2 for the transition from slow roll inflation to the second flat region, we need to satisfy that the ratio α 2 2 / α 1 2 ≫ 1 . This condition take places since the term f 1 e − α 1 φ 1 = g 1 ( α 2 2 / α 1 2 ) e − α 2 φ 2 from Eq.(68) and then α 2 2 / α 1 2 ≫ 1 is satisfied.
From Eqs.(63) and (68), we find that the relation between the scalar field φ 2 and the number of e − folds N results
a 2 α 2 e α 2 φ 2 + a 3 φ 2 = a 1 N + c t e ,
where the constants a 1 , a 2 and a 3 are defined as
a 1 = 6 M 1 α 2 g 1 , a 2 = M 2 2 , a n d a 3 = − 2 M 1 g 1 α 2 2 α 1 2 + g 1 ,
respectively. However, we can get φ 2 = φ ( N ) using the ProductLog function [59]. This function corresponds to a product logarithm , also called the Omega function or Lambert W function and it is a multivalued function. Thus, we obtain that the scalar field φ 2 as a function of the number of e-folds from Eq.(69) results in,
φ 2 ( N ) = ( a 1 N + C 1 ) / a 3 − α 2 − 1 P r o d u c t L o g [ ( a 2 / a 3 ) e α 2 ( a 1 N + C 1 ) / a 3 ] ,
where C 1 denotes an integration constant.
We mention that to find a real solution for the scalar field φ 2 it is required that the argument of the function ProductLog satisfies the condition ( a 2 / a 3 ) e α 2 ( a 1 N + C 1 ) / a 3   > − e − 1 , see [59].
Besides, considering Eqs.(65) and (66) we obtain that the new scalar field ϕ 2 results
ϕ 2 = α 2 α 1 2 + 1 φ 2 + C 2 ,
where C 2 is a constant given by
C 2 = α 2 α 1 α 1 2 + α 2 2 ln f 1 α 1 2 f 2 α 2 2 .
Thus, the effective potential associated to the new field ϕ 2 can be written as
U e f f ( ϕ 2 ) ≃ M 1 2 − 2 M 1 g 1 α 2 α 1 2 + 1 e − α 1 α 2 ( ϕ 2 − C 2 ) α 1 2 + α 2 2 4 χ 2 M 2 .
Here we have used Eqs.(61), (65) and (71), respectively.
Now, the inflationary stage reduces to a single field ϕ 2 , such that the new equations associated to the new field ϕ 2 are given by 6 H 2 = ϕ ˙ 2 2 2 + U e f f ( ϕ 2 ) and ϕ ¨ 2 + 3 H ϕ ˙ 2 + ∂ U e f f ( ϕ 2 ) / ∂ ϕ 2 =0, respectively.
As we have a single field ϕ 2 in our model, we can introduce the new slow roll parameters ϵ and η related to the scalar field ϕ 2 defined by
ϵ ≃ ∂ U e f f / ∂ ϕ 2 U e f f 2 , a n d η ≃ 2 ∂ 2 U e f f / ∂ ϕ 2 2 U e f f .
By using the effective potential associated to the field ϕ 2 given by Eq.(72), we find that the slow roll parameters become
ϵ ≃ 4 g 1 2 α 2 2 ( α 1 2 + α 2 2 ) M 1 2 α 1 2 e − 2 α 1 α 2 ( ϕ 2 − C 2 ) α 1 2 + α 2 2 , a n d η ≃ − 4 g 1 α 2 2 M 1 e − α 1 α 2 ( ϕ 2 − C 2 ) α 1 2 + α 2 2 .
Here we have utilized that the effective potential U e f f can be approximated to U e f f ∼ M 1 2 / ( 4 χ 2 M 2 ) .
Besides, we can find the value of ϕ 2 at the end of the inflationary epoch ϕ 2 e n d and it is characterized from the condition ϵ = 1 (or equivalently a ¨ = 0 ), which through (74) results
ϕ 2 e n d = α 1 2 + α 2 2 2 α 1 α 2 ln 4 g 1 2 α 2 2 ( α 1 2 + α 2 2 ) M 1 2 α 1 2 + C 2 .
On the other hand, in order to constraints the space-parameter in our model, we will analyze the scalar and tensor perturbations in the inflationary epoch associated to the single field ϕ 2 . In this way, from ref.[49,57] the power spectrum of the scalar perturbation P S under the slow-roll approximation for the scalar field ϕ 2 is given by
P S = H 2 2 π ϕ 2 ˙ 2 ≃ 1 96 π 2 U e f f 3 ( ∂ U e f f / ∂ ϕ 2 ) 2 ,
and the scalar spectral index n s is defined as
n s − 1 = d ln P S d ln k = − 6 ϵ + 2 η ,
where the slow roll parameters ϵ and η are given by eq.(74).
Besides, it is well known that the generation of tensor perturbations during the early universe would generate gravitational waves. In this sense, the spectrum of the tensor perturbations P T is given by[49,57]
P T = H π 2 ≃ U e f f 6 π 2 ,
and the tensor spectral index n T can be written in terms of the slow parameter ϵ as n T = d ln P T d ln k = − 2 ϵ .
An important observational quantity corresponds to the tensor-to-scalar ratio r = P T P S . We mention that these observational quantities should be fixed when the cosmological scale exits the horizon. In what follows the subscript * is used to denote the epoch in which the cosmological scale exits the horizon i.e., k = a * H * .
In this context, from Eq.(76) we find that the power spectrum of the scalar perturbation P S results
P S ( ϕ 2 = ϕ 2 * ) = P S * ≃ k 1 e 2 α 1 α 2 α 1 2 + α 2 2 ( ϕ 2 * − C 2 ) ,
in which the quantity k 1 is defined as
k 1 = 1 1536 π 2 M 1 4 χ 2 M 2 g 1 2 α 2 2 [ ( α 2 / α 1 ) 2 + 1 ] .
Also by using Eq.(77) the scalar spectral index n s becomes
n s ( ϕ 2 = ϕ 2 * ) = n s * ≃ 1 − 8 g 1 α 2 2 M 1 3 g 1 ( α 1 2 + α 2 2 ) M 1 α 1 2 e − α 1 α 2 α 1 2 + α 2 2 ( ϕ 2 * − C 2 ) + 1 e − α 1 α 2 α 1 2 + α 2 2 ( ϕ 2 * − C 2 ) .
Now, considering Eq.(79) and assuming that the constant C 1 = 0 , we obtain that the quantity χ 2 M 2 g 1 2 / M 1 4 as a function of the power spectrum and the number of e-folds can be written as
χ 2 M 2 g 1 2 M 1 4 = 1 1536 π 2 α 1 2 α 2 2 ( α 1 2 + α 2 2 ) P S * e − 6 α 2 2 [ ( α 2 2 / α 1 2 ) + 1 ] N * .
Additionally, using Eq.(80) we obtain that the ratio g 1 / M 1 has a the real and positive solution given by
g 1 M 1 = α 1 2 6 ( α 1 2 + α 2 2 ) 1 + 3 2 ( α 1 2 + α 2 2 ) α 1 2 α 2 2 ( 1 − n s ) − 1 e − 3 α 1 α 2 2 ( α 1 2 + α 2 2 ) N * .
Also, we obtain that the tensor to scalar ratio r in terms of the number of e-folds N results
r ( N = N * ) = r * = 64 χ 2 g 1 M 1 2 α 2 2 ( α 1 2 + α 2 2 ) α 1 2 e 6 α 1 2 α 2 2 ( α 1 2 + α 2 2 ) N * ,
here we have considered eqs.(78) and (79).
By combining Eqs.(80) and (83), we obtain a relation to the parameter χ 2 given by
χ 2 = 3 r * ( α 1 2 + α 2 2 ) 32 α 1 2 α 2 2 1 + 3 2 ( α 1 2 + α 2 2 ) α 1 2 α 2 2 ( 1 − n s ) − 1 − 2 ∼ 3 r * 32 α 1 2 1 + 3 2 α 1 2 ( 1 − n s ) − 1 − 2 .
Besides, using Eqs.(81) and (84) we can find an expression for the parameter g 1 given by
g 1 2 ≃ 1 1546 π 2 M 1 4 M 2 32 α 1 4 3 r * ( α 1 2 + α 2 2 ) 2 P S   * 1 + 3 2 ( α 1 2 + α 2 2 ) α 1 2 α 2 2 ( 1 − n s * ) − 1 2 e − 6 α 2 2 [ ( α 2 2 / α 1 2 ) + 1 ] N *
∼ 1 1546 π 2 M 1 4 M 2 32 α 1 4 3 r * α 2 4 P S   * 1 + 3 2 α 1 2 ( 1 − n s * ) − 1 2 e − 6 α 1 2 N * .
Here in these expressions we have used that α 2 2 / α 1 2 ≫ 1 .
In the situation in which α 1 is small, we can consider for example the limit when the parameter α 1 → 0 . In this case, we find that from Eq.(84) gives us χ 2 → r * 16 ( 1 − n s * ) ∼ 0.08 assuming r * = 0.04 and n s * = 0.967 , and from Eq.(85) we have that g 1 → 0 .

4.3. Introducing dust matter, including dark matter

In this section we will study the dynamics of the dark energy and dust matter that should include dark matter as a remnant of the inflationary epoch. At the end of the inflationary scenario there must be an epoch of particle creation that will generate dark matter as well as ordinary matter, this can be realized in different even in the case of one scalar field coupled to different measures [60]. In this context, we consider a dark matter particles contribution, given in a scale invariant form by the matter action S m given by
S m = ∫ ( Φ 1 + b m e κ 1 ϕ 2 − g ) L m d 4 x ,
in which b m corresponds to a constant that characterizes the strength to the coupling of ϕ 2 to − g , coupling to the measure Φ 2 , see Ref.[39]. In relation to the matter Lagrangian density L m we have
L m = − ∑ i m i ∫ e κ 2 ϕ 2 g α β d x i α d λ d x i β d λ δ 4 ( x − x i ( λ ) ) − g d λ ,
in which the quantities κ 1 and κ 2 are defined by the condition of scale invariance and the constant m i corresponds to the mass parameter of the “i-th" particle. Scale invariace specifies the coupling constants to be equal to κ 1 = − α 1 α 2 α 1 2 + α 2 2 and κ 2 = − 1 2 κ 1 , respectively.
By using these conditions the presence of matter generates an effective potential for the scalar field ϕ 2 . This happens since there is an exponential of the scalar field ϕ 2 which multiplies a ¨density of matter¨contribution which is ϕ 2 independent, see Eq.(87). In this way, the scalar field ϕ 2 coupling to matter contains the factor multiply L m
( e − 1 2 κ 1 ϕ 2 Φ 1 + b m e 1 2 κ 1 ϕ 2 − g ) ,
and then the potential associated to matter can be written as [39]
U m = L m ( e − 1 2 κ 1 ϕ 2 Φ 1 + b m e 1 2 κ 1 ϕ 2 − g ) .
Now, this potential is extremized in relation to the scalar field ϕ 2 and then we have
Φ 1 − b m e κ 1 ϕ 2 − g = 0 .
Different effects were found in a scale invariant two measure model of gravity, matter and one scalar field in Ref.[61] to the elimination of the Fifth Force Problem, which the ϕ 2 , the ¨dilaton¨, since it is a massless field. Here the elimination of the Fifth Force Problem is also realized and we can arrange for this to happen when the scalar field ϕ 1 satisfies itself the above equation. In this sense, using Eqs.(8) and (22), which gives the value of Φ 1 to − g in the absence of matter which is again validated in the presence of matter when (90) is satisfied, as shown in Ref.[61] , since the combination Φ 1 − b m e κ 1 ϕ 2 − g miraculously appears simultaneously in the equations of motion of the dilaton, the constrained equation and the anomalous, non canonical terms in the energy momentum tensor, that disappear when (90) is satisfied. Thus, we obtain that the equation for ϕ 1 is given by
2 χ 2 f 2 e − α 1 2 α 1 2 + α 2 2 ϕ 1 + 2 χ 2 g 2 e α 1 2 α 1 2 + α 2 2 ϕ 1 = b m f 1 + b m g 1 e α 1 2 + α 2 2 ϕ 1 .
The Eq.(91) gives the value of ϕ 1 to be constant and then solving this equation, we can obtain that the velocity of the scalar field ϕ 1 is zero i.e. ϕ ˙ 1 = 0 .
To find the value of the scalar field ϕ 1 we consider the change of variable x = e α 1 2 ϕ 1 α 1 2 + α 2 2 and then Eq.(91) becomes
2 χ 2 g 2 x 2 − b m g 1 x 2 α 1 2 + α 2 2 α 1 2 − b m f 1 x + 2 χ 2 f 2 = 0 ,
here we note that the field ϕ 2 drops from this equation. This happens since the field ϕ 2 undergoes a shift under the scale transformation. Thus, the field ϕ 2 is decoupled from matter, which implies the elimination of the 5th force.
The solution for the scalar field ϕ 1 from eq.(91) or (92) corresponds to a transcendental equation and we have not analytical solution. In order to find a solution for the scalar field ϕ 1 , we can consider that for very large value of ϕ 1 or equivalently x → ∞ the dominating terms of eq.(92) become
2 χ 2 g 2 x 2 − b m g 1 x 2 α 1 2 + α 2 2 α 1 2 ∼ 0 , a n d x ∼ 2 χ 2 g 2 g 1 b m ( α 1 / α 2 ) 2 ,
since the ratio ( α 2 / α 1 ) 2 ≫ 1 , then necessarily we have the quantity ( χ 2 g 2 / g 1 b m ) → ∞ . Thus using this value of x, we find that the scalar field ϕ 1 at this point results
ϕ 1 ( + ) ∼ α 1 2 + α 2 2 α 2 2 ln 2 χ 2 g 2 f 1 b m .
In the opposite limit in which the scalar field ϕ 1 → − ∞ or x → 0 , we have that the dominant terms of Eq.(92) become
− b m f 1 x + 2 χ 2 f 2 ∼ 0 , a n d x ∼ 2 χ 2 f 2 f 1 b m → 0 ,
and then the value of the scalar field at this point ϕ 1 ( − ) becomes
ϕ 1 ( − ) ∼ α 1 2 + α 2 2 α 1 2 ln 2 χ 2 f 2 f 1 b m .
These values of the scalar fields ϕ 1 ( + ) and ϕ 1 ( − ) correspond to the minimum of the total potential associated to the second flat region U ( φ 1 → − ∞ ) = f 1 2 / ( 4 χ 2 f 2 ) together with the matter potential U m containing coupling to the scalar fields, see Eq.(89).
In what follows of this section, we analyze the dynamics of the dark sector using the equations for the ratio of the two measures developed in Ref.[39]. We mention that we analysis in the very flat region, there is also no inconsistency with ϕ 1 being a constant.
The Friedmann equation for this scenario can be written as
6 H 2 = ρ φ 1 , φ 2 + ρ m ,
in which the energy density ρ φ 1 , φ 2 related to the scalar fields φ 1 and φ 2 becomes
ρ φ 1 , φ 2 = φ ˙ 1 2 2 + φ ˙ 2 2 2 + U e f f ( φ 1 , φ 2 ) .
For the case of the energy density of the dark matter ρ m we have
ρ ˙ m + 3 H ρ m = 0 , t h e n ρ m ( a ) ∝ 1 a 3 .
By considering Eq.(29) in which ϵ = 0 and assuming the region in which f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ≫ M 1 and f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 ≫ M 2 , then the effective potential simplifies to
U e f f ( φ 1 , φ 2 ) ≃ ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) 2 4 χ 2 ( f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 ) .
Using Eq.(66) we find that the effective potential given by Eq.(99) can be rewritten as a function of the single scalar field ϕ 1 results
U e f f ( ϕ 1 ) ≃ ( f 1 e − α 1 2 + α 2 2 ϕ 1 + g 1 ) 2 4 χ 2 ( f 2 e − 2 α 1 2 + α 2 2 ϕ 1 + g 2 ) .
Here we note that now the effective potential U e f f depends only of the scalar field ϕ 1 .
In this way, the energy density related to the dark energy becomes
ρ φ 1 , φ 2 = ρ ϕ 1 , ϕ 2 = ϕ ˙ 1 2 2 + ϕ ˙ 2 2 2 + U e f f ( ϕ 1 ) = ϕ ˙ 2 2 2 + U e f f ( ϕ 1 ) ,
where we have considered that ϕ ˙ 1 = 0 , since, the scalar field ϕ 1 has been determined to a constant because of the extremization of the ϕ 2 matter induced potential, see eq.(91).
To analyze the evolution of our model, we can assume that the first flat region after inflation takes place when ϕ 1 → − ∞ where the effective potential in this region is U e f f − = ( f 1 2 / 4 χ 2 f 2 ) , as supported by the calculation under the slow roll approximation in which α 2 2 / α 1 2 ≫ 1 .
In this form, the second flat region after the inflation is defined as ϕ 1 → + ∞ and then the effective potential given by eq.(100) reduces to U e f f + = g 1 2 / ( 4 χ 2 g 2 ) .
From Eq.(101) we note that the scalar field ϕ 2 corresponds to a massless field and then the evolution as a function of the scale factor a becomes
ϕ ¨ 2 + 3 H ϕ ˙ 2 = 0 , → ϕ ˙ 2 = b 1 a 3 = ϕ ˙ 2 − a − a 3 ,
where b 1 corresponds to an integration constant. Here the quantity b 1 = ϕ ˙ 2 − a − 3 , where a − and ϕ ˙ 2 − denote the scale factor and the speed of the scalar field in the first flat region after inflation of the effective potential defined as U e f f − = f 1 2 / ( 4 χ 2 f 2 ) .
The evolution of the scalar field ϕ 2 in terms of the scale factor in the first flat region after inflation can be found considering that ϕ ˙ 2 = a ˙ ( d ϕ 2 / d a ) = a H ( d ϕ 2 / d t ) and then from Eq.(102) we have,
d ϕ 2 d a = b 1 a 4 H ,
where the Hubble parameter H in terms of the scale factor is given by,
H = 1 6 b 1 2 2 a 6 + U e f f ( − ) + b 2 a 3 1 / 2 , w i t h b 2 = ρ m − a − 3 ,
where ρ m   − is the energy density related to the dark matter in the first flat region of the effective potential U e f f ( − ) . In this form, we obtain that the evolution of the scalar field ϕ 2 = ϕ 2 ( a ) in terms of the scale factor results
ϕ 2 ( a ) = ϕ 2 − + 2 3 A r c t a n h b 1 2 + b 2 a − 3 b 1 b 1 2 + 2 a − 3 ( b 2 + U e f f ( − ) a − 3 ) − 2 3 A r c t a n h b 1 2 + b 2 a 3 b 1 b 1 2 + 2 a 3 ( b 2 + U e f f ( − ) a 3 ) .
Besides, the total EoS parameter w T associated to dark matter and scalar fields becomes
w T = w ( 1 + ρ m / ρ ϕ 1 , ϕ 2 ) ,
where w corresponds to the equation of state (EoS) or EoS parameter associated to the scalar fields. Thus we find that the total EoS parameter in terms of the scale factor yields
w T ( a ) = 2 χ 2 f 2 b 1 2 f 1 2 a − 6 − 1 2 χ 2 f 2 b 1 2 f 1 2 a − 6 + 1 × 1 + b 2 a − 3 ( b 1 2 / 2 ) a − 6 + ( f 1 2 / 4 χ 2 f 2 ) − 1 .
Also, the eq.(107) can be rewritten as a function of the density parameter Ω by using the Friedmann equation in which 1 = Ω − + Ω m − , where Ω − and Ω m − correspond the densities parameters of different components in the first flat region and then the EoS parameter is given by
w T ( a ) = ( Ω − y − − 1 ) a ˜ − 6 − 1 ( Ω − y − − 1 ) a ˜ − 6 + 1 × 1 + y − ( 1 − Ω − ) a ˜ − 3 ( Ω − y − − 1 ) a ˜ − 6 + 1 − 1 ,
where the new scale factor a ˜ is defined as a ˜ = a / a − and the parameter y − denotes the rate y − = 6 H − 2 / U e f f ( − ) where H − corresponds to the Hubble parameter in the first flat stage after inflation. Since the kinetic energy is defined as a positive quantity, then the condition for the quantity y − is y − > 1 / Ω − .
Additionally, for our model we obtain that the density energy associated to dark energy Ω ϕ 1 , ϕ 2 = ρ ϕ 1 , ϕ 2 / 6 H 2 results
Ω ϕ 1 , ϕ 2 ( a ) = 1 + ( [ Ω − y − − 1 ] a ˜ − 6 + 1 ) a ˜ 3 y − ( 1 − Ω − ) − 1 .
On the other hand, during the second flat regime after inflation related to the effective potential U e f f ( + ) , and in analogy to the before case (in which ϕ 1 → − ∞ ), we have the Hubble parameter in terms of the scale factor in this region is given by
H = 1 6 b ˜ 1 2 2 a 6 + U e f f ( + ) + b ˜ 2 a 3 1 / 2 , w i t h b ˜ 1 = ϕ 2 ˙ + a 0 3 , b ˜ 2 = ρ m 0 a 0 3 ,
where U e f f ( + ) corresponds to the effective potential for very positive large scalar field ϕ 1 and it is given by U e f f ( + ) = g 1 2 / ( 4 χ 2 g 2 ) , from eq.(100). Here, the value ρ m 0 denotes the dark energy of the matter at the present epoch in which the scale factor a = a 0 = 1 .
As before, we find that the evolution of the scalar field in terms of the scale factor during this stage
ϕ 2 ( a ) = ϕ 20 + 2 3 A r c t a n h b ˜ 1 2 + b ˜ 2 a 0 3 b ˜ 1 b ˜ 1 2 + 2 a 0 3 ( b ˜ 2 + U e f f ( + ) a 0 3 ) − 2 3 A r c t a n h b ˜ 1 2 + b ˜ 2 a 3 b ˜ 1 b ˜ 1 2 + 2 a 3 ( b ˜ 2 + U e f f ( + ) a 3 ) .
Besides, we obtain that the total EoS parameter w T = w T ( a ) related to dark matter and scalar fields during this scenario becomes
w T ( a ) = 2 χ 2 g 2 b ˜ 1 2 g 1 2 a − 6 − 1 2 χ 2 g 2 b ˜ 1 2 g 1 2 a − 6 + 1 × 1 + b ˜ 2 a − 3 ( b ˜ 1 2 / 2 ) a − 6 + ( g 1 2 / 4 χ 2 g 2 ) − 1 ,
and as before, we can rewrite eq.(112) as a function of the density parameter at present era Ω ϕ 01 , ϕ 02 = Ω + and then the total EoS parameter becomes
w T ( a ) = ( Ω + y + − 1 ) a − 6 − 1 ( Ω + y + − 1 ) a − 6 + 1 1 + y + ( 1 − Ω + ) a − 3 ( Ω + y + − 1 ) a − 6 + 1 − 1 ,
with the scale factor a / a 0 = a and the quantity y + corresponds to the rate y + = 6 H 0 2 / U e f f ( + ) . Since the kinetic energy is a positive quantity, then we find that the condition for the parameter y + > 1 / Ω + . In particular, we have that the density parameter at the present related to dark energy Ω + ≃ 0.7 , such that y + > 10 / 7 .
On other hand, we can find some estimations from the observational values on the parameter-space of the our model. In particular, for the second flat region after inflation in which the effective potential corresponds to U e f f ( + ) , we can consider that the coupling constants g 1 ∼ M E W 4 and χ 2 g 2 ∼ M P l 4 , where M E W , M P l are the electroweak and Plank scales, respectively.
Thus, we have a very small vacuum energy density U ( ϕ 1 → + ∞ ) = U e f f ( + ) ∼ g 1 2 / χ 2 g 2 given by
U e f f ( ϕ 1 → + ∞ ) = U e f f ( + ) ∼ M E W 8 / M P l 4 ∼ 10 − 120 M P l 4 ,
where the mass M E W ∼ 10 − 15 M P l and eq.(114) corresponds to the right order of magnitude for the present epoch’s vacuum energy density[62]. Thus, we can assume that the parameter g 1 ∼ 10 − 60 (in units of Planck mass to the fourth power). In particular, considering the inflationary constraint on the parameter χ 2 ∼ 0.1 when α 1 → 0 , we estimate that value of g 2 ∼ 10 1 M P l 4 . This suggests that when the parameter α 1 → 0 is satisfied that the parameter g 2 ≫ g 1 .

5. Evolution of the Universe in the Situation in Which ϵ ≠ 0 , b 1 ≠ 0 and b 2 ≠ 0 , with a Spontaneously Broken Scale Symmetry

5.1. Inflation: Slow Roll Approximation and Perturbations

In this section we will unify the different epochs of the universe, considering the more general situation in which the parameters ϵ ≠ 0 , b 1 ≠ 0 and b 2 ≠ 0 in the framework of a spontaneously broken scale invariant two measures theory. In order to unify the different scenarios of the universe, we start with the inflationary epoch and to describe this epoch, we can consider the situation in which both scalar fields φ 1 → + ∞ and φ 2 → + ∞ , as in the previous section. Under these limits of the fields φ 1 and φ 2 , the effective potential associated to first flat region is given by Eq.(30).
Now in this situation, the full equations for the scalar fields φ 1 and φ 2 are given by
φ ¨ 1 A 1 + 6 B 1 X 1 + B 12 X 2 + 3 H φ ˙ 1 A 1 + 2 B 1 X 1 + B 12 X 2 + B 12 3 H φ 2 ˙ φ ¨ 2
= − U e f f , φ 1 + A 1 , φ 1 X 1 + A 2 , φ 1 X 2 + B 1 , φ 1 X 1 2 + B 2 , φ 1 X 2 2 + B 12 , φ 1 X 1 X 2 ,
and
φ ¨ 2 A 2 + 6 B 2 X 2 + B 12 X 1 + 3 H φ ˙ 2 A 2 + 2 B 2 X 2 + B 12 X 1 + B 12 3 H φ 1 ˙ φ ¨ 1
= − U e f f , φ 2 + A 2 , φ 2 X 2 + A 1 , φ 2 X 1 + B 2 , φ 2 X 1 2 + B 1 , φ 2 X 1 2 + B 12 , φ 2 X 1 X 2 ,
where the notation , φ 1 and , φ 2 denote ∂ / ∂ φ 1 and ∂ / ∂ φ 2 , respectively.
As before, introducing the “slow-roll” parameters for the scalar fields given by Eq.(59) and assuming that these parameters are ε , η 1 and η 2 ≪ 1 , then we can ignore the terms φ ¨ 1 , 2 and non-linear, such that the Eqs.(115) and (116) together with the Friedmann equation reduce to
3 A 1 H φ . 1 + U e f f , φ 1 ≃ 0 , 3 A 2 H φ . 2 + U e f f , φ 2 ≃ 0 , a n d H 2 ≃ 1 6 U eff ,
where the coefficients A 1 and A 2 satisfy A 1 = A 2 and they are defined by Eq.(31). In particular for the special case in which ϵ = 0 then A 1 = A 2 = 1 .
From Eq.(29) and considering the region in which f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ≪ M 1 and f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 ≪ M 2 , the effective potential is reduced to
U e f f ( φ 1 , φ 2 ) ≃ M 1 2 − 2 M 1 ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) 4 χ 2 ( M 2 + ϵ M 1 2 ) .
As in the previous section, we introduce the number of e − folds N given by N = ln ( a / a f ) in which a f denotes the scale factor at the end of the inflation, that is, at the end of inflation N = 0 . In this way, from Eqs.(117) and (118), we have
d φ 1 d N = 6 M 1 α 1 f 1 e − α 1 φ 1 A 1 [ ( M 2 + ϵ M 1 2 ) 2 − 2 M 1 ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) ] ,
and
d φ 2 d N = 6 M 1 α 2 g 1 e − α 2 φ 2 A 2 [ ( M 2 + ϵ M 1 2 ) 2 − 2 M 1 ( f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ) ] .
From these two equations we find a relation between the scalar fields φ 1 and φ 2 becomes
e α 1 φ 1 d φ 1 = f 1 α 1 g 2 α 2 e α 2 φ 2 d φ 2 .
Here we have used that in the region in which φ 1 → + ∞ and φ 2 → + ∞ , the coefficients A 1 = A 2 = A ( + ) , see Eq.(31).
We note that the scale symmetry breaking constants M 1 and M 2 together with ϵ dropped from this equation. The solution of this first order differential equation introduces a new constant of integration C
e α 1 φ 1 = f 1 α 1 2 g 1 α 2 2 e α 2 φ 2 + C .
As before, to avoid this extra scale symmetry breaking, in the following we will assume that the constant C = 0 for simplicity. Also, we note that this relation between the scalar fields is similar to the obtained in the previous section in which ϵ = 0 , b 1 = 0 and b 2 = 0 (see Eq.(65)). This similarity occurs since the coefficients A 1 = A 2 = A ( + ) and also we have ignored the terms φ ¨ 1 , 2 and the terms non-linear under the slow roll approximation.
As before, we can redefine two new scalar fields ϕ 1 and ϕ 2 , in terms of the scalar fields φ 1 and φ 2 , such that
ϕ 1 = α 1 φ 1 − α 2 φ 2 α 1 2 + α 2 2 , a n d ϕ 2 = α 2 φ 1 + α 1 φ 2 α 1 2 + α 2 2 ,
and this transformation is orthogonal, ϕ ˙ 1 2 + ϕ ˙ 2 2 = φ ˙ 1 2 + φ ˙ 2 2 , in which ϕ 1 is invariant and ϕ 2 transforms under a scale transformation. So, we see that even after spontaneous breaking of scale symmetry, this symmetry still has a role in the classification of the fields of the theory.
As before, the scale invariant combination α 1 φ 1 − α 2 φ 2 gets determined, which corresponds to fixing the scalar field ϕ 1
ϕ 1 = 1 α 1 2 + α 2 2 ln f 1 α 1 2 g 1 α 2 2 = c o n s t a n t .
In contrast, the scalar field ϕ 2 defined by Eq.(123), evolves in time. As we have noticed in particular, ϵ and the integration constants M 1 and M 2 dropped from such equation. That is indeed the reason that the equation that relates the two scalars retains the scale invariance, which is not true for other equations. In fact, the field ϕ 2 defined by Eq.(123) is the analog of what is called the Nambu Goldstone boson for the problem at hand, since they transform under the global scale transformation, unlike the scalar field ϕ 2 . In order to find a relation between the scalar field φ 2 and the number of e − folds N, we combine Eqs.(120) and (122) results
a 2 α 2 e α 2 φ 2 + a 3 φ 2 = a 1 N + c t e ,
and as before we can find φ 2 = φ ( N ) using the ProductLog function. From this definition, we obtain that the scalar field φ 2 in terms of the number of e-folds can be written as
φ 2 ( N ) = ( a 1 N + C 1 ) / a 3 − α 2 − 1 P r o d u c t L o g [ ( a 2 / a 3 ) e α 2 ( a 1 N + C 1 ) / a 3 ] ,
where C 1 denotes another integration constant and the quantities a 1 , a 2 and a 3 are defined as
a 1 = 6 M 1 α 2 g 1 A ( + ) = 6 M 1 α 2 g 1 ( M 2 + ϵ M 1 2 ) M 2 , a 2 = ( M 2 + ϵ M 1 2 ) 2 , a 3 = − 2 M 1 g 1 α 2 2 α 1 2 + 1 .
As before a real solution for the scalar field φ 2 it is necessary that the argument of the function ProductLog satisfies the condition ( a 2 / a 3 ) e α 2 ( a 1 N + C 1 ) / a 3   > − e − 1 .
Now, combining Eqs.(122) and (123) we find that the new scalar field ϕ 2 in terms of the field φ 2 is given by
ϕ 2 = α 2 α 1 2 + 1 φ 2 + C 2 ,
where C 2 is a constant defined as
C 2 = α 2 α 1 α 1 2 + α 2 2 ln f 1 α 1 2 f 2 α 2 2 .
Thus, the effective potential associated to the new field ϕ 2 results
U e f f ( ϕ 2 ) ≃ M 1 2 − 2 M 1 g 1 α 2 α 1 2 + 1 e − α 1 α 2 ( ϕ 2 − C 2 ) α 1 2 + α 2 2 4 χ 2 ( M 2 + ϵ M 1 2 ) .
In this way, we note that the inflationary scenario is reduced to a single field ϕ 2 as an exponential potential associated to this field defined by Eq.(128).
By considering the slow roll parameters ϵ U and η U related to the scalar field ϕ 2 where these are defined as before as in the standard case ϵ U ≃ ∂ U e f f / ∂ ϕ 2 U e f f 2 , a n d η U ≃ 2 ∂ 2 U e f f / ∂ ϕ 2 2 U e f f , we obtain that from the effective potential given by Eq.(128) these parameters as a function of the scalar field ϕ 2 result in,
ϵ U ≃ 4 g 1 2 α 2 2 ( α 1 2 + α 2 2 ) M 1 2 α 1 2 e − 2 α 1 α 2 ( ϕ 2 − C 2 ) α 1 2 + α 2 2 , a n d η U ≃ − 4 g 1 α 2 2 M 1 e − α 1 α 2 ( ϕ 2 − C 2 ) α 1 2 + α 2 2 .
Here we have used that the effective potential U e f f ∼ M 1 2 / ( 4 χ 2 ( M 2 + ϵ M 1 2 ) ) .
Besides, we can find the value of ϕ 2 at the end of the slow-roll regime ϕ 2 e n d and it is fixed from the condition ϵ U = 1 and from Eq.(129) yields
ϕ 2 e n d = α 1 2 + α 2 2 2 α 1 α 2 ln 4 g 1 2 α 2 2 ( α 1 2 + α 2 2 ) M 1 2 α 1 2 + C 2 .
However, from Eq.(126) we have that the value of scalar field ϕ 2 at the end of inflation takes place when the number of e-folds N = 0 then we have
ϕ 2 e n d = C 2 + α 2 2 α 1 2 2 + 1 C 1 a 3 − 1 α 2 P r o d u c L o g [ ( a 2 / a 3 ) e α 2 C 1 / a 3 ] .
On the other hand, in the following we will analyze the scalar and tensor perturbations during the inflationary epoch for our model of the single field ϕ 2 . In this context, considering Refs.[49,57], the power spectrum of the scalar perturbations P S under the slow-roll approximation is given by
P S = H 2 2 π ϕ 2 ˙ 2 ≃ 1 96 π 2 U e f f 3 ( ∂ U e f f / ∂ ϕ 2 ) 2 ,
and for the scalar spectral index n s we have
n s − 1 = d ln P S d ln k = − 6 ϵ U + 2 η U ,
in which the slow roll parameters ϵ U and η U are given by Eq.(129)
The spectrum of the tensor perturbations P T is defined P T = H π 2 ≃ U e f f 6 π 2 and the tensor spectral index n T can be written in terms of the slow parameter ϵ U as n T = d ln P T d ln k = − 2 ϵ U . Also, we have the tensor-to-scalar ratio r defined as r = P T P S as another observational parameter. We recall that these observational parameters should be evaluated when the cosmological scale exits the horizon. As before, in what follows the subscript * is utilized to denote the stage in which the cosmological scale exits the horizon.
From the slow-roll approximation, we obtain that the power spectrum of the scalar perturbation P S in terms of the field ϕ 2 using Eq.(132) becomes
P S * ≃ k 1 e 2 α 1 α 2 α 1 2 + α 2 2 ( ϕ 2 * − C 2 ) ,
in which the quantity k 1 is defined as
k 1 = 1 1536 π 2 M 1 4 χ 2 g 1 2 α 2 2 ( M 2 + ϵ M 1 2 ) [ ( α 2 / α 1 ) 2 + 1 ] .
By considering Eq.(133), we find that the scalar spectral index n s as a function of ϕ 2 , yields
n s * ≃ 1 − 8 g 1 α 2 2 M 1 3 g 1 ( α 1 2 + α 2 2 ) M 1 α 1 2 e − α 1 α 2 α 1 2 + α 2 2 ( ϕ 2 * − C 2 ) + 1 e − α 1 α 2 α 1 2 + α 2 2 ( ϕ 2 * − C 2 ) .
Thus, using Eq.(134) we obtain that the quantity χ 2 g 1 2 M 2 / M 1 4 as a function of the power spectrum and the number of e-folds N becomes
χ 2 g 1 2 M 2 M 1 4 ≃ 1 1546 π 2 α 1 2 A ( + ) α 2 2 ( α 1 2 + α 2 2 ) P S * e − 6 α 2 2 A ( + ) [ ( α 2 2 / α 1 2 ) + 1 ] N * .
Here we have considered for simplicity that the constant C 1 = 0
Also, from Eq.(135) we find that the ratio g 1 / M 1 has a real and positive solution given by,
g 1 M 1 = α 1 2 6 ( α 1 2 + α 2 2 ) 1 + 3 2 ( α 1 2 + α 2 2 ) α 1 2 α 2 2 ( 1 − n s * ) − 1 e − 3 α 1 2 α 2 2 A ( + ) ( α 1 2 + α 2 2 ) N * .
Here as before we have used C 1 = 0 .
Additionally, we get that the tensor to scalar ratio r as a function of the number of e-folds N yields
r ( N = N * ) = r * = 64 χ 2 g 1 M 1 2 α 2 2 ( α 1 2 + α 2 2 ) α 1 2 e 6 α 1 2 α 2 2 A ( + ) ( α 1 2 + α 2 2 ) N * ,
here we have used eqs.(78) and (134).
Also from eqs.(140) and (82) we find that the parameter χ 2 becomes
χ 2 = 3 r * ( α 1 2 + α 2 2 ) 32 α 1 2 α 2 2 1 + 3 2 ( α 1 2 + α 2 2 ) α 1 2 α 2 2 ( 1 − n s * ) − 1 − 2 .
Additionally, we find a constraint on the parameter g 1 replacing Eq.(139) into Eq.(136) yields
g 1 2 ≃ 1 1546 π 2 M 1 4 M 2 32 α 1 4 A ( + ) 3 r * ( α 1 2 + α 2 2 ) 2 P S   * 1 + 3 2 ( α 1 2 + α 2 2 ) α 1 2 α 2 2 ( 1 − n s * ) − 1 2 e − 6 α 2 2 A ( + ) [ ( α 2 2 / α 1 2 ) + 1 ] N * .
Here we note that while the parameter χ 2 depends on the quantities α 1 and α 2 together the observational parameters, we observe that the parameter g 1 also depends on the constants M 1 , M 2 and ϵ .

5.2. Early dark energy: First region with the generation of DM and stiff matter from non linear terms

In this section we will study the second flat region when the scalar field φ 1 → − ∞ and it corresponds to the first dark energy sector region or early dark energy. In this way, during the early dark energy we can consider that the effective potential is given by Eq.(33).
In order to analyze this stage that includes dark matter together with dark energy, we need to consider the non-standard kinetic terms associated to the theory or the k − essence theory, in which dark matter is generated naturally as was studied in Ref.[45], see also Refs.[46,58]. In contrast with we did in the Section 4.3, where we have introduced the dark matter particles contribution separately, here the dark matter is generated naturally from the scalar fields themselves.
In this context, the equation of motion for the scalar field φ 2 becomes
d d t a 3 φ ˙ 2 ( A 2 + 2 B 2 X 2 + B 12 X 1 ) = 0 .
The trivial solution is φ ˙ 2 = 0 , together with the term ( A 2 + 2 B 2 X 2 + B 12 X 1 ) ≠ 0 and then we can consider that the kinetic term associated to the scalar field φ 2 is X 2 = 0 . In this way, under a small perturbation we can consider that
X 2 = 0 + δ 2 , a n d d d t ( a 3 δ 2 1 / 2 ) = 0 ,
and then the solution for X 2 yields,
X 2 = φ 2 ˙ 2 2 = δ 02 a a 0 − 6 ,
where δ 02 denotes to a positive constant, since the kinetic term X 2 > 0 .
In addition, the equation of motion for the scalar field φ 1 becomes
d d t a 3 φ ˙ 1 ( A 1 + 2 B 1 X 1 + B 12 X 2 ) = 0 ,
where the coefficients A 1 , A 2 and B 12 are defined by Eqs.(34), (35) and (36), respectively.
In this case we do not assume the solution φ ˙ 1 = 0 , instead we consider the situation in which ( A 1 + 2 B 1 X 1 + B 12 X 2 ) = ( A 1 + 2 B 1 X 1 ) = 0 , where we have utilized that the kinetic term X 2 = 0 . In this form, the trivial solution for φ ˙ 1 becomes
X 1 = − A 1 2 B 1 = X 10 = p o s i t i v e c o n s t a n t .
In this case we must have b 1 2 > 4 f 2 ϵ ( 1 + b 1 f 1 / f 2 ) with which the term B 1 is negative and A 1 > 0 (or − 2 < b 1 f 1 / f 2 ).
From Ref.[45] we can determine that the solution given by Eq.(144) is stable under a small perturbation. Thus, we can perturb this solution as
X 1 = − A 1 2 B 1 + δ 1 = X 10 + δ 1 ,
where the perturbation δ 1 ≪ X 10 . In this way, replacing Eq.(145) into Eq.(143) and expanding to order one in δ 1 we get
d d t ( a 3 δ 1 ) = 0 , t h e n δ 1 ∝ a − 3 .
In this way, the perturbative solution as a function of the scale factor given by Eq.(145) becomes
X 1 ( a ) = X 10 1 + δ 01 ( a / a 0 ) − 3 ,
where δ 01 and a 0 correspond to two new constants. Also, as δ 1 ≪ X 10 , then we have δ 01 ( a / a 0 ) − 3 ≪ 1 .
Thus, using Eqs.(142) and (146) into the total energy density ρ we have
ρ ( a ) ≃ ρ 0 + ρ 1 a a 0 − 3 + ρ 2 a a 0 − 6 ,
where ρ 0 corresponds to the energy density associated to dark energy and it is given by
ρ 0 = A 1 X 10 + 3 B 1 X 10 2 + U eff = A 1 2 4 B 1 + U eff > 0 ,
where U eff is defined by Eq.(33). Besides, we mention that in Eq.(147) we have neglected the term ( a / a 0 ) − 12 since during the evolution of present universe this term is highly suppressed.
Now the second term of Eq.(147) represents to the dark matter and the quantity ρ 1 is defined as
ρ 1 = X 10 δ 01 [ A 1 + 6 B 1 X 10 ] = δ 01 A 1 2 B 1 .
Since B 1 < 0 , then we impose that the constant δ 01 is a negative quantity, in order to obtain that the dark matter to be positive and also | δ 01 | ≪ 1 .
Also, the last term of Eq.(147 corresponds to stiff equation of state where the quantity ρ 2 is given by
ρ 2 = A 2 δ 02 + 3 B 12 X 10 δ 02 + 3 B 1 X 10 2 δ 01 2 ,
and ρ 2 is a positive quantity.
Additionally, we write that the pressure p as a function of the scale factor becomes
p ( a ) ≃ p 0 + p 1 a a 0 − 3 + p 2 a a 0 − 6 ≃ p 0 + p 2 a a 0 − 6 ,
in which the constants p 0 , p 1 and p 2 are given by
p 0 = A 1 X 10 + B 1 X 10 2 − U eff = − A 1 2 4 B 1 − U eff = − ρ 0 , p 1 = X 10 δ 10 [ A 1 + 2 B 1 X 10 ] = 0 ,
and
p 2 = δ 02 [ A 2 + B 12 X 10 ] + δ 01 2 B 1 X 10 2 = δ 02 A 2 − B 12 g A 1 2 B 1 + A 1 2 δ 01 2 4 B 1 .
We mention that as before we have neglected the term ( a / a 0 ) − 12 in Eq.(148) and we have also considered that the matter corresponds to a dust-matter in which p 1 = 0 .
Besides, to obtain a consistent stiff equation of state, which is necessary from energy momentum conservation we have that the coefficients ρ 2 = p 2 . Thus, we get that the relation between the constants δ 01 and δ 02 assuming the condition given by stiff equation of state is given by
δ 02 = − B 1 X 10 B 12 δ 01 2 = A 1 2 B 12 δ 01 2 ,
and then we obtain that ρ 2 = p 2 = δ 02 A 2 . We note that as ρ 2 > 0 then δ 02 > 0 , and from Eq.(149) the coefficient B 12 > 0 . Therefore, we have found a relation between the δ 01 and δ 02 associated to the small perturbations during the scenario DE, DM and stiff component from multi fields dynamics.
On the other hand, from Friedmann equation 6 H 2 = ρ , we can obtain that the scale factor as a function of the cosmological time t i.e., a ( t ) results [52]
a ( t ) a 0 = Ω 1 Ω 0 + 2 ( 1 − Ω 0 − Ω 1 ) Ω 0 sinh 2 3 Ω 0 ( H 0 t + C ) 2 + ( 1 − Ω 0 − Ω 1 ) Ω 0 1 − e − 3 Ω 0 1 / 2 ( H 0 t + C ) 1 / 3 ,
where C corresponds to an integration constant. Note that in the absence of stiff matter in which ρ 2 = 0 , the scale factor a ( t ) ∝ sinh 2 / 3 ( 3 Ω 0 ( H 0 t + C ) / 2 ) , see [47].
Also, the quantities Ω 0 and Ω 1 associated to the dark energy and dark matter at the present time are given by
Ω 0 = ρ 0 6 H 0 2 , a n d Ω 1 = ρ 1 6 H 0 2 ,
where H 0 denotes the Hubble parameter at the present epoch.
Besides, we can obtain the scalar fields as a function of the scale factor. In this way, for the scalar field φ 2 we have that from Eq.(142) that the speed of the scalar field φ 2 becomes
φ ˙ 2 = H x d φ 2 d x = ± 2 δ 02 x 3 , w i t h x = a a 0 ,
and then the solution for φ 2 ( x = a / a 0 ) can be written as
φ 2 ( x ) = C ˜ 2 ∓ 2 δ 02 3 H 0 1 − Ω 0 − Ω 1 A r c t a n h Ω 1 x 3 + 2 ( 1 − Ω 0 − Ω 1 ) 2 1 − Ω 0 − Ω 1 x 3 ( Ω 1 + Ω 0 x 3 ) + ( 1 − Ω 0 − Ω 1 ) ,
where C ˜ 2 corresponds to an integration constant.
Similarly for the field φ 1 , we obtain that the solution in terms of the normalized scale factor x = a / a 0  yields
φ 1 ( x ) = C ˜ 1 ± 2 2 X 01 3 H 0 Ω ¯ − Ω 1 − 2 Ω 0 x 3 Ω ¯ g 1 ( x ) − g 2 ( x ) g 3 ( x ) ,
where C ˜ 1 is another integration constant and the functions g 1 ( x ) , g 2 ( x ) and g 3 ( x ) are defined as
g 1 ( x ) = Ω 0 ( x 3 + δ 01 ) 2 δ 01 − Ω 1 − Ω ¯ ( Ω ¯ 2 + Ω 1 Ω ¯ + Ω 0 Ω 1 x 3 + Ω 0 Ω ¯ x 3 ) F [ x ¯ , m 1 ] ,
g 2 ( x ) = δ 01 Ω 0 ( Ω 1 + Ω ¯ − 2 δ 01 Ω 0 ) ( Ω 1 + Ω ¯ + 2 Ω 0 x 3 ) 1 Ω 1 + Ω ¯ − 2 Ω 0 δ 01 ( δ 01 + x 3 ) Ω 0 2 Ω 0 δ 01 − Ω 1 − Ω ¯ Π [ m 2 , x ¯ , m 1 ] ,
and
g 3 ( x ) = Ω 0 ( Ω 1 + Ω ¯ ) δ 01 + x 3 Ω 1 + Ω ¯ + 2 δ 01 Ω 0 Ω 1 + Ω ¯ − 2 δ 01 Ω 0 ( 1 − Ω 0 − Ω 1 ) + Ω 1 x 3 + Ω 0 x 6 ,
where the quantities F and Π denote to the Elliptic functions of the first and second kind, respectively, see [48]. Also, the function x ¯ and the quantities m 1 , m 2 , and Ω ¯ are defined as
x ¯ = A r c s i n Ω 1 + Ω ¯ + 2 Ω 0 x 3 Ω 1 + Ω ¯ − 2 δ 01 Ω 0 , m 1 = Ω 1 + Ω ¯ − 2 δ 01 Ω 0 2 Ω ¯ , m 2 = Ω 1 + Ω ¯ − 2 δ 01 Ω 0 Ω 1 + Ω ¯ ,
and Ω ¯ = Ω 1 2 − 4 Ω 0 ( 1 − Ω 0 − Ω 1 ) .
We mention that in order to obtain the scalar fields as a function of the cosmological time, we need to replace the normalized scale factor given by Eq.(150) into Eqs.(151) and (152) to find φ 1 ( t ) and φ 2 ( t ) , respectively.
Additionally, the equation of state (EoS) or total EoS parameter w t = p / ρ in our model in terms of the scale factor results
w T ( a ) = − Ω 0 + ( 1 − Ω 0 − Ω 1 ) ( a / a 0 ) − 6 Ω 0 + Ω 1 ( a / a 0 ) − 3 + ( 1 − Ω 0 − Ω 1 ) ( a / a 0 ) − 6 .
From the analysis made in Ref.[58] for the EoS parameter in terms of the scale factor, we can mention that when we decrease the density parameter associated to the dark matter Ω 1 the EoS parameter w ( a ) increase with the scale factor. Also, from the analysis for w ( a ) developed in Ref.[58], we can mention that for values of the parameter Ω 1 < 0.29 (more stiff matter) and for values of the scale factor x < 0.7 , the universe does not present an accelerated stage, since the EoS parameter becomes positive. Additionally, from the analysis of w ( a ) studied in Ref.[58], we can mention that when we have a very small quantity of stiff matter, in particular for values of the parameter Ω 1 associated to the matter Ω 1 > 0.29 , the universe always has an accelerated phase, since the EoS parameter w ( a ) < 0 for these values of Ω 1 .

5.3. Late Dark Energy: Second Region with the Generation of DM and Stiff Matter from Non Linear Terms

In this section we will discuss the third flat region in which the scalar field φ 2 → − ∞ and it corresponds to the dark energy sector region in which the effective potential is defined by Eq.(37). In order to discuss this second scenario that incorporates dark matter together with dark energy, we need to replace the results of the section before by making the substitution f 1 → g 1 , f 2 → g 2 , b 1 → b 2 , together with the potential and the respective coefficients given by Eqs.(37)-(40).

6. Summary and Discussion of Possible Future Lines of Research

In this article we have studied a new approach to unify the evolution of the universe from an inflationary epoch to the dark sectors at the present, assuming a scale invariant theory with metric independent measures which considers two scalar fields. In this framework, we have analyzed in the early universe the stage of the inflationary era under the slow roll approximation. Also we have studied the dark sectors first assuming the DE and DM in the context of the a canonical theory introducing a matter Lagrangian density in order to generate the DM. However, we have also studied the unification of inflation to the dark sector in the framework of the a non-canonical theory. Here, we have analyzed the DE, DM and stiff matter during the late universe and a more elaborate model to generate DM (without considering a matter Lagrangian) with a spontaneously generated k-essence from the modified measures theory was developed. In this context, the scale invariance is spontaneously broken by the integration of the equations of motion and considering the Einstein framework, we obtain a theory with an effective potential associated to two scalar fields that displays three flat regions and corresponding k-essence terms in the more general case, see Eq.(29). In this study we have analyzed two Lagrangians, one that does not include the k-essence terms in the Einstein frame and the other that generates k-essence terms in the Einstein frame. In each Lagrangian theories, we use each of these flat regions to explain the different phases of the universe. Thus, the higher energy density corresponds to the very early universe inflationary era in which both fields φ 1 and φ 2 take large positive values. During the inflationary era, we have used the slow roll approximation and we have defined two new scalar fields ϕ 1 and ϕ 2 from an orthogonal transformation of the fields φ 1 and φ 2 .
In relation to the slow roll solutions we have found that in both Lagrangians one of these scalar fields does not depend on time, i.e., we have ϕ ˙ 1 = 0 and then the effective potential simplifies to a single scalar field ϕ 2 .
Besides, we have noted that the effective potential (29) interpolates between the vacuum with asymptotic values M 1 2 4 χ 2 M 2 , f 1 2 4 χ 2 f 2 and g 1 2 4 χ 2 g 2 for the special case in which ϵ = 0 and between the vacuum M 1 2 4 χ 2 ( M 2 + ϵ M 1 2 ) , f 1 2 4 χ 2 ( f 2 + ϵ f 1 2 ) and g 1 2 4 χ 2 ( g 2 + ϵ g 1 2 ) .
For the more general case. Here in both cases we have found that these interpolations between the different vacuums are independent of the choice of the relative signs of M 1 , g 1 , and f 1 . By using the standard expressions for the observational parameters because the model is reduced to a single field ϕ 2 , we have determined the scalar power spectrum, scalar spectral index and the upper bound of the ratio tensor to scalar. From these observational parameters we have found expressions for the parameters χ 2 and g 1 2 in terms of these observational parameters together with the number of e − folds N. In this context, we have obtained that the observational constraint on the parameter χ 2 does not depend on the ϵ and then in both Lagrangians the constraints are similar. However, we have found from the observational constraints that the parameter g 1 depends of ϵ thought A ( + ) and it implies that the value of the parameter g 1 decreases when we consider values of ϵ ≠ 0 . Additionally, we have noted that the parameter g 1 also depends on the constants M 1 and M 2 .
The second flat region describes a dark sector with DE and DM in which the DE is labeled by a large negative value of the field φ 1 in the effective potential. In the case in which the theory corresponds to the canonical form, we have introduced a matter Lagrangian density (or action) in order to account to the DM, see Eq.(87). However, in the k-essence theory the DE, DM and stiff components owe its existence to the k-essence induced by multi measure theory. It is interesting that a consistency condition for the generation of the DE, DM and stiff components which correlates the perturbations of the two scalar fields in the framework of k-essence with respect to a certain background solution is obtained in (149) from the condition found by stiff equation of state ρ 2 = p 2 .
In general for both Lagrangians we have found the evolution of the EoS parameter w versus the normalized scale factor a i.e, w = w ( a ) . Besides, we have noted that when we decrease the density parameter associated to dark matter Ω 1 , the EoS parameter increase for the same value of a. Also, for the canonical and non canonical Lagrangians, we have determined the solution for the scale factor as a function of the cosmological time and also we have obtained the solutions for the scalar fields in term of the scale factor and then ϕ 1 = ϕ 1 ( t ) and ϕ 2 = ϕ 2 ( t ) , respectively.
There is also a third flat region, in which the DE is described by a large negative value of the field φ 2 in the effective potential which could represent a future DE sector, or may be represents the present state of the universe in a scenario where there was an early dark energy region (the second flat region), during the radiation matter equality and this brings us to the issues that should be studied further. In this sense, we can describe that the universe makes use of the third flat region with asymptotic behavior as the late dark energy region, representing the universe now.
To do this, we should go back to considering eq.(29) and assuming the region in which f 1 e − α 1 φ 1 + g 1 e − α 2 φ 2 ≫ M 1 ,and f 2 e − 2 α 1 φ 1 + g 2 e − 2 α 2 φ 2 ≫ M 2 , then the effective potential simplifies to (118) for both the second and the third flat region Using eq.(66) we find that the effective potential given by eq.(118) can be rewritten as a function of the single scalar field ϕ 1 results (100) we noted that now the effective potential U e f f depends only of the scalar field ϕ 1 .
In this case, we should connect the second dark region described transition to the third dark energy region, representing the late DE era. A scenario, where two DE states are connected through bubble nucleation was considered in [54,55] to formulate a possible resolution of the H 0 problem and we could consider it also in a future research for our model. In this respect, it is interesting to notice that the presence of matter, coupled in a scale invariant way, changes the form of the effective potential for the scalar field, into an effective potential that on the matter density, which in turn depends on the scale factor a, since the density of matter gets diluted as the universe expands. The overall effective potential displays two minima, one located in the early dark energy region and the other in the late dark energy region. For a certain value of the scale factor, the tunneling from one minimum to the other becomes of the order of one, and then we can explain the sudden transition from early dark energy to late dark energy. The details of these calculations will be given in a future parer with Pedro Labraña [63].
The second subject concerning we want to discuss concerning possible future lines of research is a very simple possible variation of the model that could lead to interesting results in the unification of the early and current universe. As we have seen in the previous sections, the best results are obtained for ϵ small, so it is worthwhile to study ϵ = 0 . Furthermore, it is quite interesting that for ϵ = 0 , we can also include a term, that which when considered in Einstein frame, produces just a shift in the effective potential, that is it just produces a the same effect of a cosmological term in Einstein frame.
The slightly modified theory, where the ϵ is eliminated and a Λ 0 term is added and then the new action can be written as
S = ∫ d 4 x Φ 1 ( A ) R − 2 Λ 0 Φ 1 ( A ) − g + L ( 1 ) + ∫ d 4 x Φ 2 ( B ) L ( 2 ) + Φ ( H ) − g ,
which is still invariant under the global scale transformations (7). To see application of this type of term in questions also related to DE, applied to a Gravity-Assisted Emergent Higgs Mechanism in the Post-Inflationary Epoch in [41].
In this context now the Weyl-rescaled metric g ¯ μ ν that defines the Einstein frame is given by g ¯ μ ν = χ 1 g μ ν where χ 1 ≡ Φ 1 ( A ) − g one can indeed suspect that the extra term just induces a cosmological term in the Einstein frame, since using the previous definition we can check that − 2 Λ 0 Φ 1 ( A ) 2 − g = − 2 Λ 0 − g ¯ .
This expectation is indeed confirmed by a more detailed analysis, and we can see that the effective Lagrangian (23) is still valid, but now the corresponding A and B coefficients are evaluated for ϵ = 0 and the effective potential is shifted by 2 Λ 0 .
This has some consequences, like it is easier to guarantee a positive DE, just choose a big enough value for 2 Λ 0 . Apart from that there is not much change.
Notice also that Φ 1 ( A ) is now not just a measure of integration, since it appears also square, and the theory with Φ 1 ( A ) appearing just linearly has the highly non conventional infinite dimensional additional symmetry, valid for any regular set of four functions f δ , such that, A μ ν γ → A μ ν γ + ϵ μ ν γ δ f δ ( R + L ( 1 ) ) (where ϵ μ ν γ δ is the totally antisymmetric symbol taking values zero, one or minus one), which is absent in the theory where Φ 1 ( A ) appears also squared, i.e. for Λ 0 ≠ 0 , so that can be an argument for Λ 0 = 0 , or a symmetry that protects Λ 0 from becoming big after quantum corrections.
A stiff era, as the one obtained in this work can have interesting observational consequences. This era could occurs before the BBN or after. In both cases the stiff era can affect the light element abundances and perhaps the CMB, if the modes correspond to linear modes. Such an issue has been discussed for example in [56] and references therein. The study of this issue concerning the consequences of component with a stiff equation of state and how would be the special features that would be a consequence this stiff state in our scenario would be a very interesting subject for future research concerning our model.

Acknowledgments

E.G. want to thank the Pontificia Universidad Católica de Valparaíso, Chile, for hospitality during this collaboration, FQXi for great financial support for work on this project at BASIC in Ocean Heights, Stella Maris, Long Island, Bahamas and COSMOVERSE • COST ACTION CA21136, Addressing observational tensions in cosmology with systematics and fundamental physics for additional financial support and discussions on cosmological tensions with the members of this cost action.

References

  1. Alan, H. Guth, Phys.Rev.D 23 (1981) 347-356; Adv.Ser.Astrophys.Cosmol. 3 (1987) 139-148 (reprint).
  2. A. Starobinsky, Phys.Lett. B 91, 99-102 (1980).
  3. E.W. Kolb and M.S. Turner, “The Early Universe”, Addison Wesley (1990);A. Linde, “Particle Physics and Inflationary Cosmology”, Harwood, Chur, Switzerland (1990);
  4. V. Mukhanov, “Physical Foundations of Cosmology”, Cambridge Univ. Press (2005).
  5. G.F.R. Ellis and R. Maartens, Class. Quantum Grav. 21 (2004) 223 (gr-qc/0211082).
  6. G.F.R. Ellis, J. Murugan and C.G. Tsagas,Class. Quantum Grav. 21 (2004) 233 (arxiv:gr-qc/0307112);D.J. Mulryne, R. Tavakol, J.E. Lidsey and G.F.R. Ellis, Phys. Rev. D71 (2005) 123512 (arxiv:astro-ph/0502589);
  7. M.S. Turner, in Third Stromle Symposium “The Galactic Halo”, ASP Conference Series Vol.666, B.K. Gibson, T.S. Axelrod and M.E. Putman (eds.), (1999);N. Bahcall, J.P. Ostriker, S.J. Perlmutter and P.J. Steinhardt, Science 284, (1999) 1481;
  8. A. Riess, et al., Astronomical Journal 116 (1998) 1009-1038;S. Perlmutter et al., Astrophysical Journal 517 (1999) 565-586.
  9. A New cosmological paradigm: The Cosmological constant and dark matter Lawrence M. Krauss, AIP Conf.Proc. 444 (1998) 1, 59-69 • Contribution to: SILAFAE 98, 59-69, 5th International WEIN Symposium: A Conference on Physics Beyond the Standard Model (WEIN 98), Tropical Workshop on Particle Physics and Cosmology, PASCOS 1998 • e-Print: hep-ph/9807376 [hep-ph]; Ren-Yue Cen, Jeremiah P. Ostriker, Astrophys.J. 429 (1994) 4 • e-Print: astro-ph/9404012 [astro-ph].
  10. Jose Luis Bernal, Licia Verde, Adam G. Riess, JCAP 10 (2016)019 DOI: 10.1088/1475-7516/2016/10/019, arXiv:1607.05617 [astro-ph.CO]; José Luis Bernal, Licia Verde, Raul Jimenez, Marc Kamionkowski, David Valcin et al., Phys.Rev.D 103 (2021) 10, 103533 • e-Print: 2102.05066 [astro-ph.CO]; Leila L. Graef, Micol Benetti, Jailson S. Alcaniz, Phys.Rev.D 99 (2019) 4, 043519 • e-Print: 1809.04501 [astro-ph.CO]. [CrossRef]
  11. R. E. Keeley, S. Joudaki, M. Kaplinghat and D. Kirkby, JCAP 12 (2019), 035; K. L. Pandey, T. Karwal and S. Das, JCAP 07 (2020), 026; A. Quelle and A. L. Maroto, Eur. Phys. J. C 80 (2020) no.5, 369; A. Bhattacharyya, U. Alam, K. L. Pandey, S. Das, and S. Pal, Astrophys. J. 876, 143 (2019), arXiv:1805.04716 [astro-ph.CO]; G. Lambiase, S. Mohanty, A. Narang, and P. Parashari, Eur. Phys. J. C 79, 141 (2019), arXiv:1804.07154 [astroph.CO]; W. Lin, K. J. Mack and L. Hou, Astrophys. J. Lett. 904 (2020) no.2, L22, arXiv:1910.02978 [astro-ph.CO]; M. Berbig, S. Jana and A. Trautner, Phys. Rev. D 102 (2020) no.11, 115008; Quantifying the Sigma 8 tension with the Redshift Space Distortion data set, David Benisty, Phys.Dark Univ. 31 (2021) 100766 • e-Print: 2005.03751 [astro-ph.CO]. arXiv:1910.02978.
  12. A. Linde, Phys. Lett. 108B (1982) 389-393;A. Albrecht and P. Steinhardt, Phys. Rev. Lett. 48 (1982) 1220-1223.
  13. A.R. Liddle and D.H. Lyth, Phys. Lett. 291B (1992) 391-398 (arxiv:astro-ph/9208007);A.R. Liddle and D.H. Lyth, Phys. Reports 231 (1993) 1-105 (arxiv:astro-ph/9303019). arxiv:astro-ph/9303019.
  14. P.J.E. Peebles and A.Vilenkin, Phys. Rev. D59 (1999) 063505.
  15. R. Saitou and S. Nojiri, Eur. Phys. J. C71 (2011) 1712 (arxiv:1104.0558 [hep-th]).
  16. C. Wetterich, Phys. Rev. D89 (2014) 024005 (arxiv:1308.1019 [astro-ph]).
  17. Md. Wali Hossain, R. Md. Wali Hossain, R. Myrzakulov, M. Sami and E.N. Saridakis, Phys. Rev. D90 (2014) 023512 (arxiv:1402.6661 [gr-qc]).
  18. Konstantinos Dimopoulos, Charlotte Owen, JCAP 06 (2017) 027 • e-Print: 1703.00305 [gr-qc]; Konstantinos Dimopoulos, Leonora Donaldson Wood, Charlotte, Phys.Rev.D 97 (2018) 6, 063525 • e-Print: 1712.01760 [astro-ph.CO];R. Herrera, Eur. Phys. J. C 78, no.3, 245 (2018); R. Herrera, Phys. Rev. D 98, no.2, 023542 (2018);R. Herrera, Phys. Rev. D 99, no.10, 103510 (2019); R. Herrera, Phys. Rev. D 102, no.12, 123508 (2020); Llibert Aresté Saló, David Benisty, Eduardo I. Guendelman, Jaime d. Haro, JCAP 07 (2021) 007 • e-Print: 2102.09514 [astro-ph.CO];M. Gonzalez-Espinoza, R. Herrera, G. Otalora and J. Saavedra, Eur. Phys. J. C 81, no.8, 731 (2021);R. Herrera and C. Rios, [arXiv:2210.10080 [gr-qc]]; Llibert Aresté Saló, David Benisty, Eduardo I. Guendelman, Jaime d. Haro, Phys.Rev.D 103 (2021) 12, 123535 • e-Print: 2103.07892 [astro-ph.CO]. arXiv:2210.10080.
  19. David Benisty, Eduardo I. Guendelman, Eur.Phys.J.C 80 (2020) 6, 577 • e-Print: 2006.04129 [astro-ph.CO]; Lorentzian Quintessential Inflation, awarded 2nd prize in the 2020 Gravity Research Foundation Essays Competition, David Benisty, Eduardo I. Guendelman, Int.J.Mod.Phys.D 29 (2020) 14, 2042002 • e-Print: 2004.00339 [astro-ph.CO].
  20. S. Nojiri and S. Odintsov, Phys. Rev. D68 (2003) 123512 (arxiv:hep-th/0307288);G. Cognola, E. Elizalde, S. Nojiri, S.D. Odintsov, L. Sebastiani and S. Zerbini, Phys. Rev. D77 (2008) 046009 (0712.4017 [hep-th]), and references therein;
  21. f(R) Theories Of Gravity, Thomas P. Sotiriou, Valerio Faraoni, Rev.Mod.Phys. 82 (2010) 451-497 • e-Print: 0805.1726 [gr-qc] ; S.Nojiri and S.D.Odintsov, Phys. Rept. 505, 59-144 (2011) https://doi.org/10.1016/j.physrep.2011.04.001 [arXiv:1011.0544 [gr-qc]]; S. Capozziello and M. De Laurentis, Phys. Rept. 509, 167-321 (2011) https://doi.org/10.1016/j.physrep.2011.09.003 [arXiv:1108.6266 [gr-qc]]; R. Herrera and N. Videla, Int. J. Mod. Phys. D 23, no.08, 1450071 (2014) https://doi.org/10.1142/S0218271814500710 [arXiv:1406.6305 [gr-qc]]. [CrossRef]
  22. T. Clifton, P. G. Ferreira, A. Padilla and C. Skordis, Phys. Rept. 513, 1-189 (2012) https://doi.org/10.1016/j.physrep.2012.01.001 [arXiv:1106.2476 [astro-ph.CO]]; S. Nojiri, S. D. Odintsov and V. K. Oikonomou, Phys. Rept. 692, 1-104 (2017) https://doi.org/10.1016/j.physrep.2017.06.001 [arXiv:1705.11098 [gr-qc]]; S. D. Odintsov, V. K. Oikonomou, I. Giannakoudi, F. P. Fronimos and E. C. Lymperiadou, Symmetry 15, no.9, 1701 (2023) https://doi.org/10.3390/sym15091701 [arXiv:2307.16308 [gr-qc]]. [CrossRef]
  23. E.I. Guendelman, Mod. Phys. Lett. A14 (1999) 1043-1052 (arxiv:gr-qc/9901017);E.I. Guendelman, in “Energy Densities in the Universe”, Proc. Rencontres de Moriond, Les Arcs (2000) (arxiv:gr-qc/0004011).
  24. E.I. Guendelman and A. Kaganovich, Phys. Rev. D60 (1999) 065004 (arxiv:gr-qc/9905029).
  25. E.I. Guendelman and O. Katz, Class. Quantum Grav. 20 (2003) 1715-1728 (arxiv:gr-qc/0211095).
  26. S. del Campo. E. Guendelman, R. Herrera and P. Labrana, JCAP 1006 (2010) 026 (arxiv:1006.5734 [astro-ph.CO]).
  27. S. del Campo. E. Guendelman, A. Kaganovich, R. Herrera and P. Labrana, Phys. Lett. 699B (2011) 211 (arxiv:1105.0651 [astro-ph.CO]).
  28. E.I. Guendelman and P. Labrana, Int. J. Mod. Phys. D22 (2013) 1330018 (arxiv:1303.7267 [astro-ph.CO]).
  29. E.I. Guendelman, D. Singleton and N. Yongram, JCAP 1211 (2012) 044 (arxiv:1205.1056 [gr-qc]);E.I. Guendelman, H. Nishino and S. Rajpoot, Phys. Lett. 732B (2014) 156 (arxiv:1403.4199 [hep-th]). arxiv:1403.4199.
  30. E.I. Guendelman, Class.Quant.Grav. 17 (2000) 3673-3680 • e-Print: hep-th/0005041 [hep-th]; E.I. Guendelman, Phys.Rev.D 63 (2001) 046006 • e-Print: hep-th/0006079 [hep-th]; E. Guendelman, A. Kaganovich, E. Nissimov and S. Pacheva, Phys. Rev. D66 (2002) 046003 (arxiv:hep-th/0203024). arxiv:hep-th/0203024.
  31. H. Nishino and S. Rajpoot, Phys. Lett. 736B (2014) 350-355 (arxiv:1411.3805 [hep-th]).
  32. International Journal of Modern Physics, Implications of the spectrum of dynamically generated string tension theories E. I, e-Print: 2110.09199 [hep-th]. [CrossRef]
  33. Eduardo Guendelman, Eur.Phys.J.C 81 (2021) 10, 886 • e-Print: 2107.08005 [hep-th]; Eduardo Guendelman, Eur.Phys.J.C 82 (2022) 10, 857. [CrossRef]
  34. E. Guendelman, E.Nissimov, S. Pacheva and M. Vasihoun, Bulg. J. Phys. 40 (2013) 121-126 (arxiv:1310.2772 [hep-th]);E. Guendelman, E.Nissimov, S. Pacheva and M. Vasihoun, Bulg. J. Phys. 41 (2014) 123-129 (arxiv:1404.4733 [hep-th]). arxiv:1404.4733.
  35. Eduardo Guendelman, Ramón Herrera, Pedro Labrana, Emil Nissimov, Svetlana Pacheva, Gen.Rel.Grav. 47 (2015) 2, 10 • e-Print: 1408.5344 [gr-qc].
  36. E. Guendelman, E. Nissimov and S. Pacheva, arxiv:1407.6281 [hep-th].
  37. Eduardo, I. Guendelman, Ramon Herrera, Gen.Rel.Grav. 48 (2016) 1, 3 • e-Print: 1511.08645 [gr-qc].
  38. Eduardo, I. Guendelman, Ramon Herrera, Pedro Labrana, Phys.Rev.D 103 (2021) 123515 • e-Print: 2005.14151 [gr-qc] and references there.
  39. Eduardo Guendelman, Ramón Herrera, David Benisty, Phys.Rev.D 105 (2022) 12, 124035 • e-Print: 2201.06470 [gr-qc].
  40. A. R. Liddle and D. H. Lyth, Phys. Lett. B 291, 391-398 (1992). arXiv:astro-ph/9208007. [CrossRef]
  41. Eduardo Guendelman, Emil Nissimov, Svetlana Pacheva, Int.J.Mod.Phys.D 25 (2016) 12, 1644008 • e-Print: 1603.06231 [hep-th].
  42. D. I. Kaiser and E. I. Sfakianakis, Phys. Rev. Lett. 112, no.1, 011302 (2014). arXiv:1304.0363. [CrossRef]
  43. X. Chen, M. X. Huang, S. Kachru and G. Shiu, JCAP 0701 (2007) 002; B. A. Bassett, S. Tsujikawa and D. Wands, Rev. Mod. Phys. 78, (2006) 537-589.
  44. P. A. R. Ade et al. [BICEP and Keck], Phys. Rev. Lett. 127 (2021) no.15, 151301. arXiv:2110.00483. [CrossRef]
  45. R. J. Scherrer, Phys. Rev. Lett. 93, 011301 (2004). arXiv:astro-ph/0402316. [CrossRef]
  46. Eduardo Guendelman, Emil Nissimov, Svetlana Pacheva, Eur.Phys.J.C 76 (2016) 2, 90 • e-Print: 1511.07071 [gr-qc].
  47. J. Frieman, M. Turner and D. Huterer, Ann. Rev. Astron. Astrophys. 46, 385-432 (2008).
  48. M. Abramowitz, I.A. Stegun (eds.), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing (Dover, New York, 1972).
  49. B. A. Bassett, S. Tsujikawa and D. Wands, Rev. Mod. Phys. 78, 537-589 (2006). arXiv:astro-ph/0507632. [CrossRef]
  50. I. Zlatev, L.-M. Wang, and P. J. Steinhardt, Phys. Rev. Lett. 82, 896 (1999).
  51. P. J. Steinhardt, L.-M. Wang, and I. Zlatev, Phys. Rev. D 59, 123504 (1999); I. Zlatev and P. J. Steinhardt, Phys. Lett. B 459, 570 (1999).
  52. P. H. Chavanis, Phys. Rev. D 92, no.10, 103004 (2015).
  53. S. Nojiri, S. D. Odintsov and H. Stefancic, Phys. Rev. D 74, 086009 (2006). arXiv:hep-th/0608168. [CrossRef]
  54. Florian Niedermann, Martin S. Sloth. Phys.Lett.B 835 (2022) 137555 • e-Print: 2112.00759 [hep-ph].
  55. Juan, S. Cruz, Florian Niedermann, Martin S. Sloth • e-Print: 2209.02708 [astro-ph.CO].
  56. A Stiff Pre-CMB Era with a Mildly Blue-tilted Tensor Inflationary Era can Explain, the 2023 NANOGrav Signal, V.K. arXiv:2309.04850.
  57. X. Chen, M. x. Huang, S. Kachru and G. Shiu, JCAP 01, 002 (2007). arXiv:hep-th/0605045. [CrossRef]
  58. arXiv:arXiv:2301.10274. [CrossRef]
  59. L. Surhone, M. Timplendon and S. Marseken, “Wright Omega Function: Mathematics, Lambert W Function, Continuous Function, Analytic Function, Differential Equation, Separation or Variables", Betascript Publishing (2010).
  60. E. I. Guendelman, R. Herrera and P. Labrana, Phys. Rev. D 103, 123515 (2021). arXiv:2005.14151. [CrossRef]
  61. E. I. Guendelman and A. B. Kaganovich, Annals Phys. 323, 866-882 (2008). arXiv:0704.1998. [CrossRef]
  62. Nima Arkani-Hamed, Lawrence J. Hall, Christopher Kolda, Hitoshi Murayama, A New Perspective on Cosmic Coincidence Problems. doi 10.1103/Phys Rev Lett.85.4434 (2000) arXiv:astro-ph/0005111 [pdf, ps, other] astro-ph hep-ph hep-th.
  63. From early DE to late DE by diluting matter potential, Eduardo Guendelman, Ramon Herrera and Pedro Labraña, in preparation.
Preprints 109140 g001
Figure 1. The effective potential with three flat regions. One flat region refers to the inflationary phase and the other region refers to dark energy. The third could be another early dark energy phase.Here we have used a positive value for M 1 .
Figure 1. The effective potential with three flat regions. One flat region refers to the inflationary phase and the other region refers to dark energy. The third could be another early dark energy phase.Here we have used a positive value for M 1 .
Preprints 109140 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated