Preprint

Technical Note

Enhanced Performance of a Hydrokinetic Turbine Through a Biomimetic Design

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Submitted:

19 June 2024

Posted:

21 June 2024

You are already at the latest version

Alerts

Abstract

Hydrokinetic energy constitutes a significant promise as a renewable energy source, yet many regions experience flow velocities insufficient to support conventional turbine installations. According to this, the present work proposes a vertical axis hydrokinetic turbine aimed to environments where conven-tional turbines may not be feasible due to insufficient water velocity. This turbine is based on a biologi-cally inspired design which improves the traditional Savonius turbine. This innovative configuration is inspired by the Fibonacci spiral. The turbine's performance was analyzed through Computational Fluid Dynamics. A notable improvement was found in comparison with the traditional Savonius turbine, providing a 15.1% increment in the power coefficient.

Keywords:

Subject: Environmental and Earth Sciences - Environmental Science

1. Introduction

The utilization of renewable energy has gained significant attention in addressing the growing global energy demand while mitigating environmental impacts. Among renewable energy options, marine renewable energies have emerged as promising alternatives for sustainable power generation. Particularly, in river and tidal applications, hydrokinetic energy presents great opportunities. The development of marine renewable energy technologies, including hydrokinetic energy conversion systems, has been the focus of extensive research and technological advancements. Unfortunately, many regions of the world do not present high-flow velocities. According to this, the use of hydrokinetic turbines for energy generation in low-flow velocity environments has gained significant attention in the recent years. For small-scale power generation, vertical-axis turbines are often favored over horizontal-axis turbines due to several advantages, including design simplicity and flow direction independence [1]. Within the category of vertical-axis hydrokinetic turbines, commonly used types include Squirrel cage Darrieus, H-Darrieus, Gorlov, and Savonius turbines [1]. In this regard, the Savonius turbine, a type of vertical axis turbine, has demonstrated its suitability for harnessing energy from low-flow velocity applications, offering an interesting advantage regarding the low starting torque requirements. Kumar and Saini [2] recommend the Savonius hydrokinetic turbine for flow velocities ranging from 0.5 m/s and above. Singh and Kumar [3] calculated the suitable water velocity for the Savonius turbine at 0.65 m/s. Gunawan et al. [4] highlighted the advantage of the Savonius water turbine for relatively low-velocity water flows, emphasizing its applicability in such conditions. Katayama et al. [5] indicated that the Savonius type is suitable for utilization in open channels with ultra-low head hydropower sites, providing insights into its applicability in specific hydrokinetic environments.

While the Savonius turbine offers several advantages, it is important to highlight its low efficiency [6]. The performance parameters and design optimization of Savonius hydrokinetic turbines have been the subject of extensive research. In this sense, computational fluid dynamics (CFD), constitutes a powerful tool for simulating and understanding the complex flow phenomena associated with hydrokinetic turbines, enabling detailed investigations into their hydrodynamic characteristics and efficiency. Numerical models provide substantial benefits compared to experimental setups. Unlike the high costs and time required for conducting experimental tests on different configurations, CFD models serve as a rapid and cost-effective tool for analyzing the performance parameters of various geometries. Additionally, numerical models offer valuable insights into velocity and pressure fields that are often too complex to measure through experimental methods. Kumar and Saini [2] emphasized the importance of CFD in evaluating the performance parameters of Savonius hydrokinetic turbines, highlighting the need for further research in optimizing their design. Patel et al. [7] and Barbarić and Guzović [8] utilized CFD to investigate the influence of aspect ratio, overlap ratio, and diffuser geometrical configurations on the performance of hydrokinetic turbines, providing valuable insights into design improvements. Mejia et al. [9] underscored the significance of CFD simulations in the evaluation of vertical-axis hydrokinetic turbines, demonstrating the potential for coupling numerical methods with analytical models to assess turbine designs. Fertahi et al. [10] used CFD to analyzed a combined Savonius-Darrieus hydrokinetic turbines. Taludkar et al. [11] developed 2D CFD analyses and experimental studies in an open channel at a water velocity 0.8 m/s. Tian et al. [12] analyzed a novel blade design to improve the performance of the Savonius hydrokinetic turbine using CFD. Kumar et al. [13] numerically analyzed the effect of blade arc angle and blade shape for flow velocities from 0.5 to 2 m/s. Sarma et al. [14] compared a Savonius hydrokinetic turbine with a Savonius wind turbine using CFD for water current velocities from 0.3 to 0.9 m/s. Other authors [15,16,17] used CFD to analyze the effect of deflectors in Savonius hydrokinetic turbines.

The present study introduces a novel design of the Savonius turbine. This design is inspired by the Fibonacci spiral, which is found in various aspects of nature. The performance of this innovative design was analyzed using Computational Fluid Dynamics (CFD), offering insights into understanding the fluid flow problem and assessing the turbine's behavior. This analysis enables the evaluation of the impact of the Fibonacci spiral-inspired blade design, thereby providing valuable guidance for optimizing its efficiency and effectiveness in harnessing hydrokinetic energy.

2. Materials and Methods

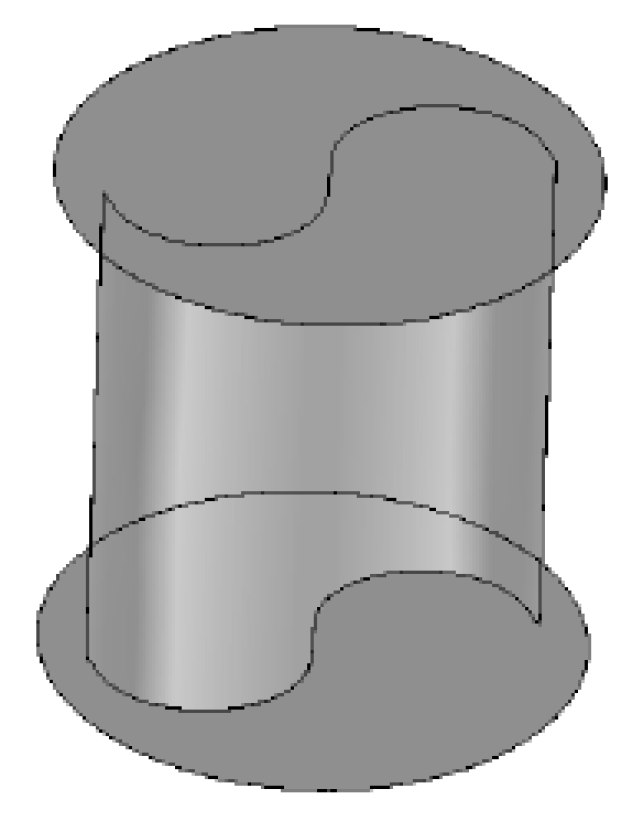
The Savonius turbine, Figure 1, is a type of vertical axis turbine characterized by its simple and robust design, consisting of curved blades arranged in a semicircular fashion around a central shaft. This distinctive configuration enables the Savonius turbine to effectively capture energy from fluid flows, including wind and water currents, regardless of the direction of the flow. The turbine operates based on the principle of drag, with the curved blades generating lift force differentials as they rotate, thereby converting the kinetic energy of the fluid flow into mechanical energy. The turbine's inherent ability to self-start at a very low fluid velocity and its simplicity of construction contribute to its versatility and potential for decentralized energy generation in various settings, specially in environments with low-speed fluid currents [18,19,20].

As indicated above, this study employs CFD to investigate a modification of the Savonius-type vertical axis turbine. This model was previously validated with experimental results. To this end, data from Blackwell et al. [21] were employed. For this purpose, an examination was conducted on a turbine 1 m height, 1 m diameter and with 2 blades. Other parameters such as overlap, separation gap and twist angle were 0. The turbine configuration thus consists of two semicircular blades and two supporting endplates.

Regarding the numerical model, the open-source software OpenFOAM was chosen for its accessibility, allowing complete access to the code for understanding and manipulation purposes. The governing equations utilized were the Reynolds-averaged Navier–Stokes equations (RANS), incorporating the principles of mass and momentum conservation. To account for the turbulence effect, the SST k-ω model was selected based on its demonstrated effectiveness in previous studies [21]. In prior investigations [22,23] several turbulence models were evaluated, with the SST k-ω model deemed the most suitable for these type of simulations despite its higher computational cost compared to commonly used models like k-ε. In what concerns the pressure-velocity coupling, the PIMPLE algorithm was employed, while a temporal treatment was conducted using an implicit method. The time step was set constant and equivalent to 1 degre of rotation. To achieve a quasi-steady state, multiple revolutions were analyzed. The results presented in this study correspond to the 6th rotation.

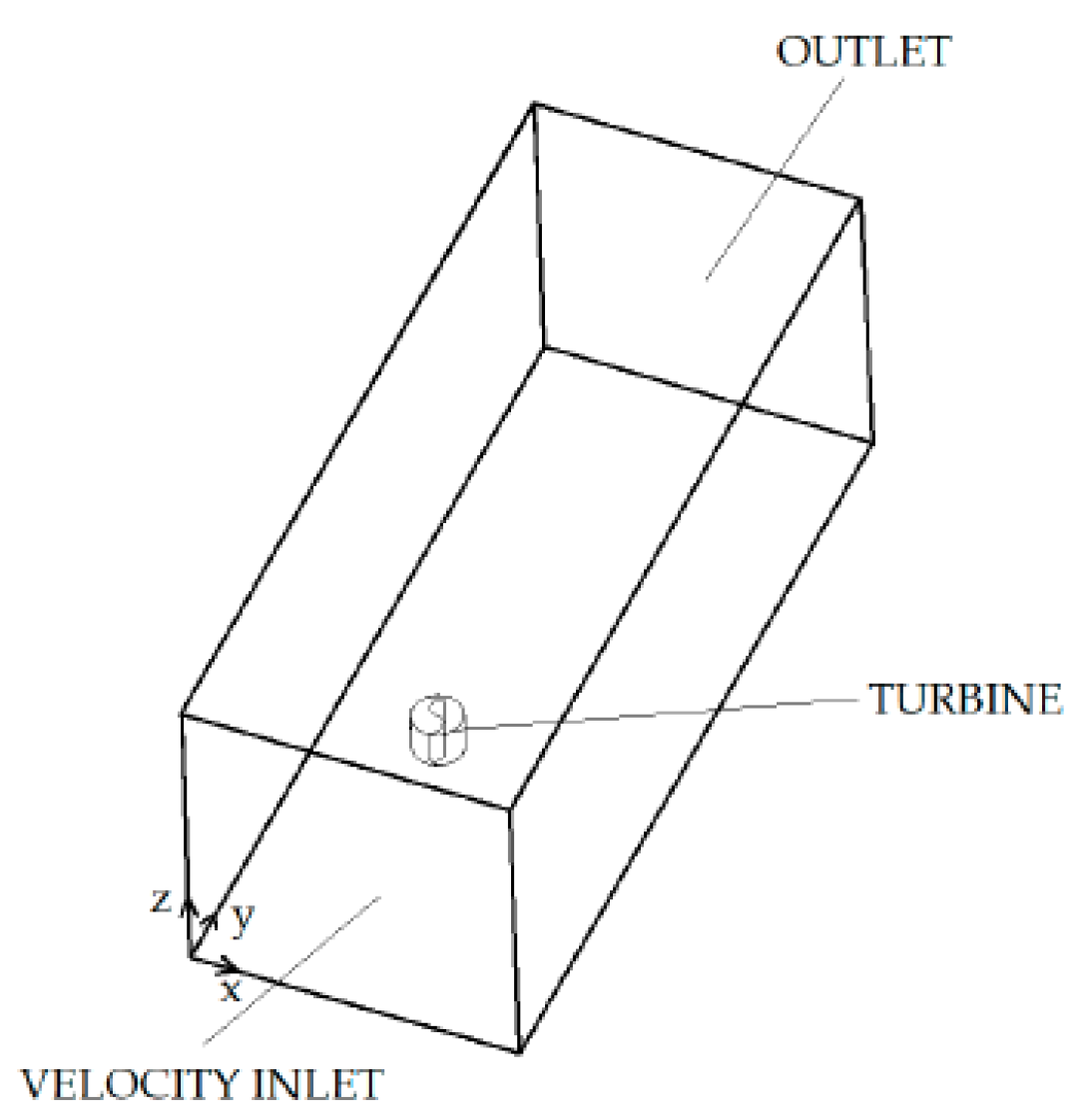
The domain utilized in the present work and its corresponding boundary conditions are depicted in Figure 2, with dimensions of 23 x 8 x 8 meters. It was confirmed that these dimensions are sufficiently large to mitigate any border effects, as verified by repeating simulations using domains of 10 x 10 x 25 meters and 12 x 12 x 30 meters, which yielded consistent results. The boundary conditions considered in the present work are also outlined in the figure. The upstream face was modeled as a velocity inlet, while the downstream face was modeled as an outlet. External faces were designated as free slip to minimize border effects, imposing zero shear stress, meaning the tangential velocity derivative normal to the boundary is zero. The turbine blades were treated as no-slip surfaces.

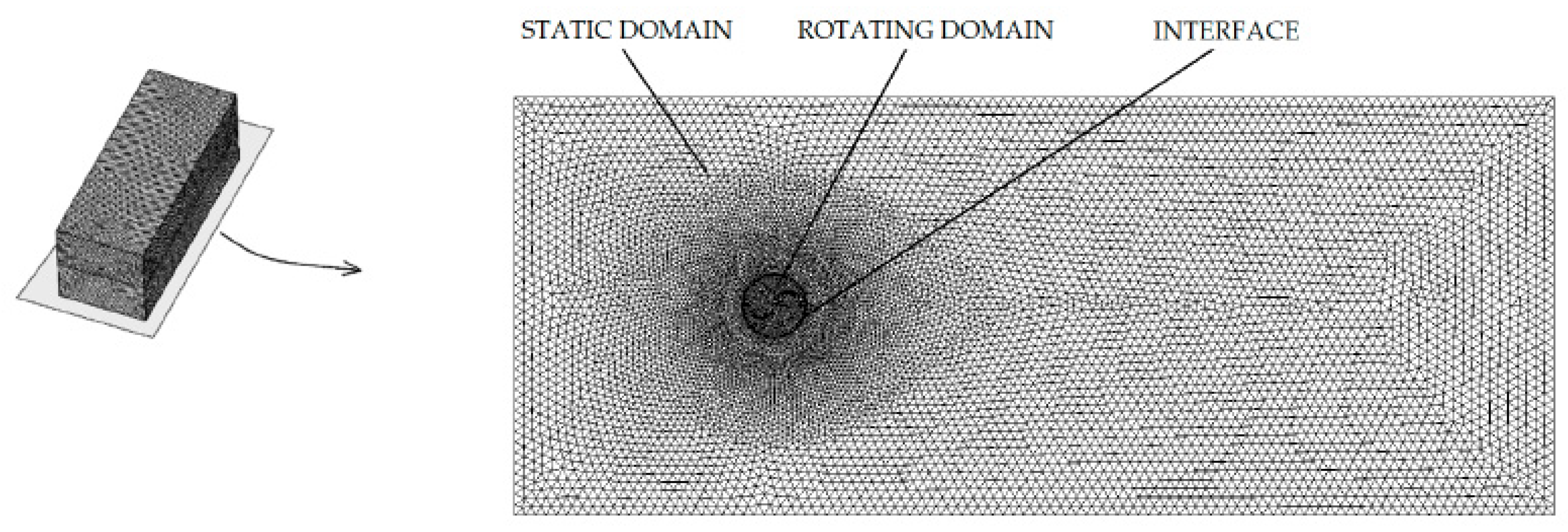
Figure 3 illustrates the mesh utilized in the study, providing both a three-dimensional view and a detailed depiction of the middle plane. The mesh comprises tetrahedral elements ranging from 0.05 to 0.2 meters in size, with finer resolution implemented around the turbine. Two distinct zones were defined: static and rotating. The rotating domain encompasses a cylinder surrounding the turbine, which rotates about the turbine axis, while the static domain encompasses the remaining stationary region. A sliding interface was established to connect the static and rotating domains, facilitating the interaction between the two zones.

To ensure the robustness and reliability of the numerical simulations, multiple meshes with varying element sizes were examined to assess the independence of the results from the mesh size. This rigorous approach helps to validate the accuracy and consistency of the computational model, ensuring that the obtained results are not unduly influenced by the mesh resolution. By systematically testing different mesh configurations and confirming the convergence of results across these variations, confidence in the accuracy and robustness of the simulation outcomes is bolstered.

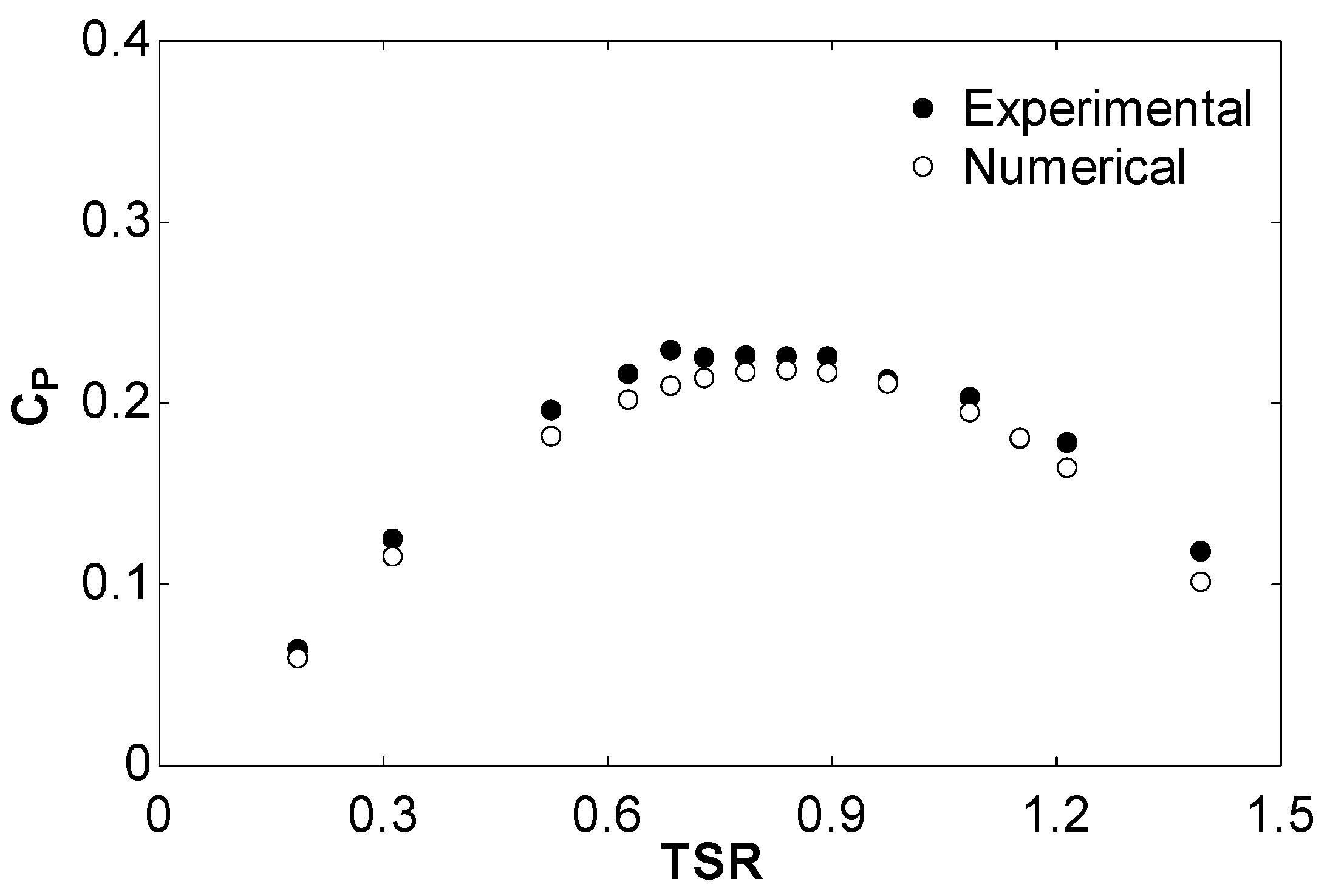
The graph in Figure 4 illustrates the comparison between the average power coefficients obtained from numerical simulations and experimental trials. The power coefficient was represented against the tip speed ration. These parameters are indicated in Eqs. (1-2), respectively. In these equations, ω is the rotational velocity, R the turbine radius, V the free-stream flow velocity, P the power, ρ the density, S the section, and D the turbine diameter.

TSR = \frac{blade tip \tan gential velocity}{wind speed} = \frac{ω R}{V}

(1)

C_{p} = \frac{power}{available power} = \frac{P}{0 . 5 ρ {SV}^{3}}

(2)

Notably, a satisfactory agreement is observed between the two sets of data in Figure 4, with an average error of 5.8%. Both datasets exhibit a similar trend, showcasing an initial increase in average power coefficients followed by a decline beyond a certain tip speed ratio. This behavior can be attributed to the phenomenon wherein increasing tip speed ratios lead to higher rotational velocities, causing the blade tips to surpass the incoming air velocity. Consequently, less power is effectively transferred from the air to the turbine, resulting in a reduction in net power output.

3. Results and Discussion

Once the CFD model was validated, the present work proposes a new blade profile based on a biologically inspired shape. In engineering, drawing inspiration from nature, a concept known as bioinspiration or biomimicry, often proves to be an apt approach. This is because natural forms and processes have undergone countless years of evolution, resulting in highly efficient and optimized solutions to various challenges [24,25].

Embracing biomimicry principles, the turbine's design is meticulously crafted to efficiently harness energy from diminished hydrokinetic currents, addressing the pressing need for effective energy extraction under such conditions. The Fibonacci spiral was proposed to this end. For comparison purposes, both Savonius and Fibonacci blade profiles are shown in Figure 5. As can be seen in this figure, the Savonius turbine is constituted by semicircunferencial profiles (red color dotted line). The Fibonacci spiral (black color dashed line), derived from the Fibonacci sequence, is a spiral characterized by a growth pattern where each number is the sum of the two preceding ones.

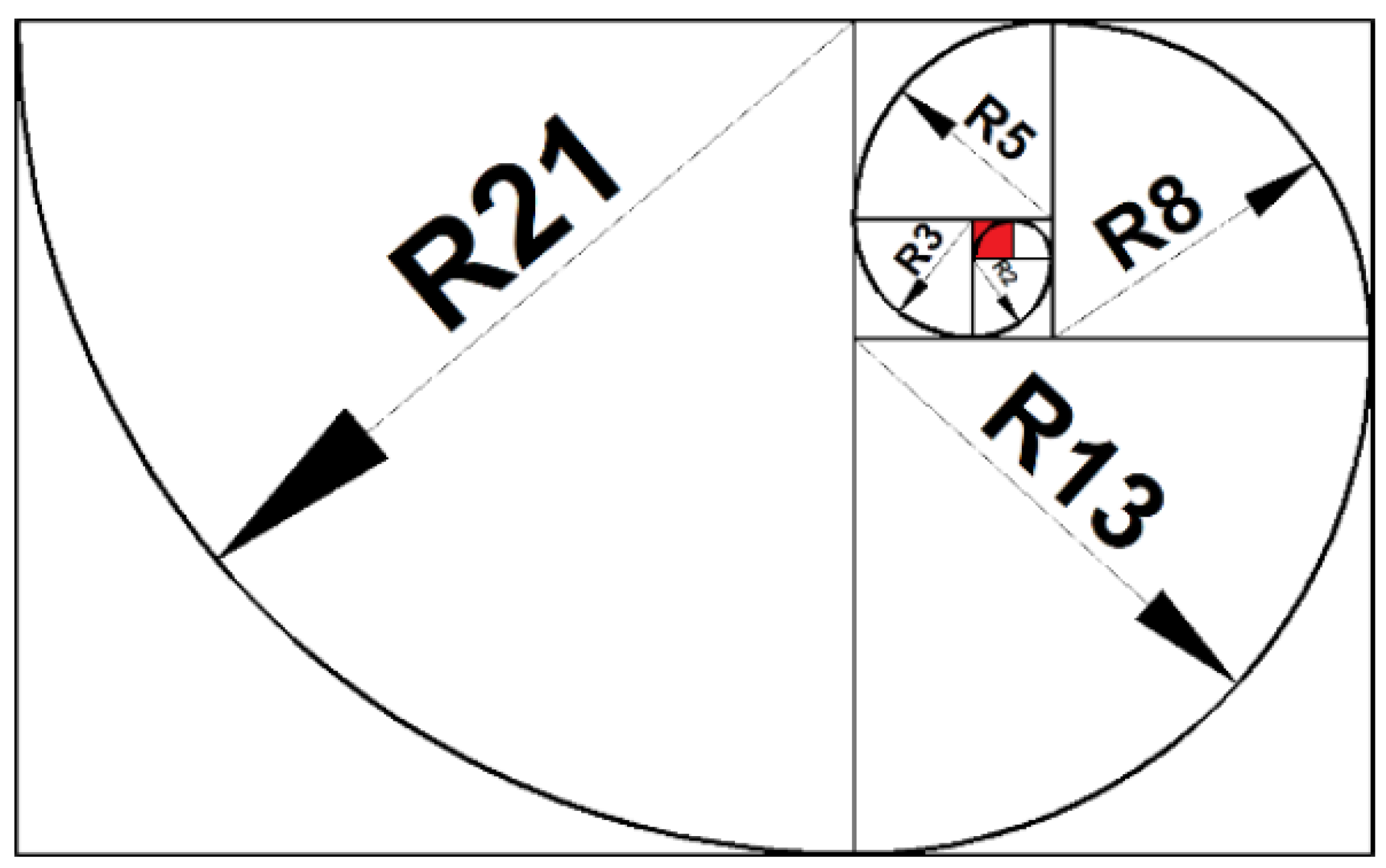
The Fibonacci spiral is a geometric pattern derived from the Fibonacci sequence, a series of numbers where each number is the sum of the two preceding ones (0, 1, 1, 2, 3, 5, 8, 13, 21, and so on). When these numbers are used to create a spiral, Figure 6, each segment of the spiral has a length proportional to a Fibonacci number, resulting in a distinctive spiral shape. The Fibonacci spiral is characterized by its unique properties, including self-similarity and the golden ratio. The golden ratio, approximately equal to 1.618, is a mathematical ratio that appears frequently in nature and art. In the Fibonacci spiral, the ratio of each successive segment's length to the previous one approaches the golden ratio as the sequence progresses.

This spiral pattern can be found in various natural phenomena, Figure 7, such as the arrangement of seeds in a sunflower, the spiral shells of certain mollusks, and the branching patterns of trees.

In engineering, the Fibonacci spiral may be utilized to improve systems. When applied to the blade profile of a Savonius hydrokinetic turbine, the Fibonacci spiral offers several advantages. Firstly, the spiral's geometric properties, such as self-similarity and the golden ratio, contribute to an efficient and aerodynamic blade design, enhancing the turbine's performance in capturing energy from low-flow velocity environments. Additionally, the Fibonacci spiral-inspired blade profile provides a larger surface area for energy capture, optimizing the turbine's efficiency in capturing kinetic energy from fluid flows. The use of the Fibonacci spiral as the blade profile for a Savonius turbine aligns with the principles of biomimicry, drawing inspiration from natural patterns to enhance the turbine's performance and energy extraction capabilities.

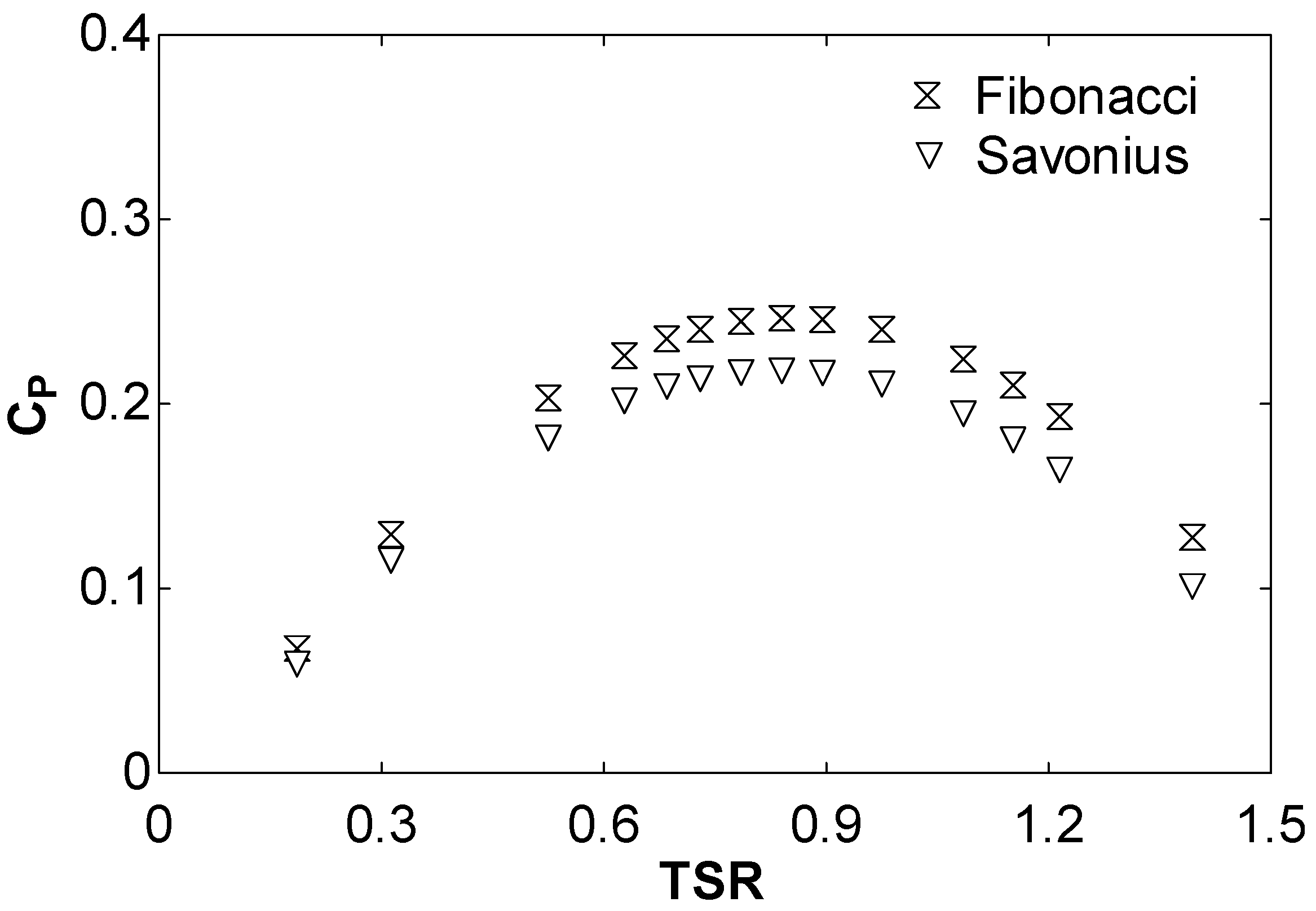
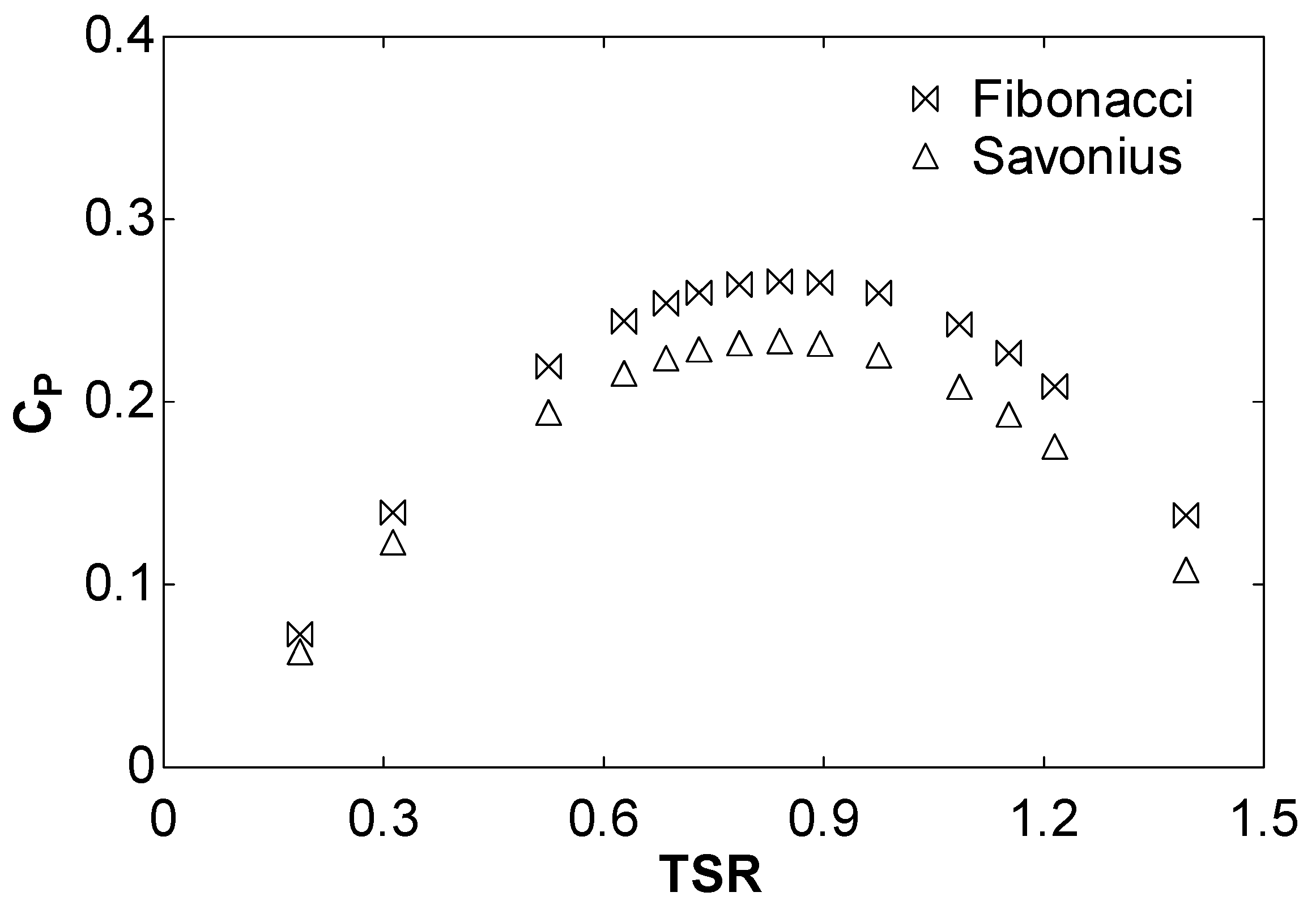
The comparison of Fibonacci and Savonius blade profiles is illustrated in Figs. 8 and 9 for air (wind turbine) and water (hydrokinetic turbine), respectively. In the simulations of Figure 8, air with 7 m/s was implemented, corresponding to the experiments of Blackwell et al. [21]. In the simulations of Figure 9, water with 1 m/s was implemented.

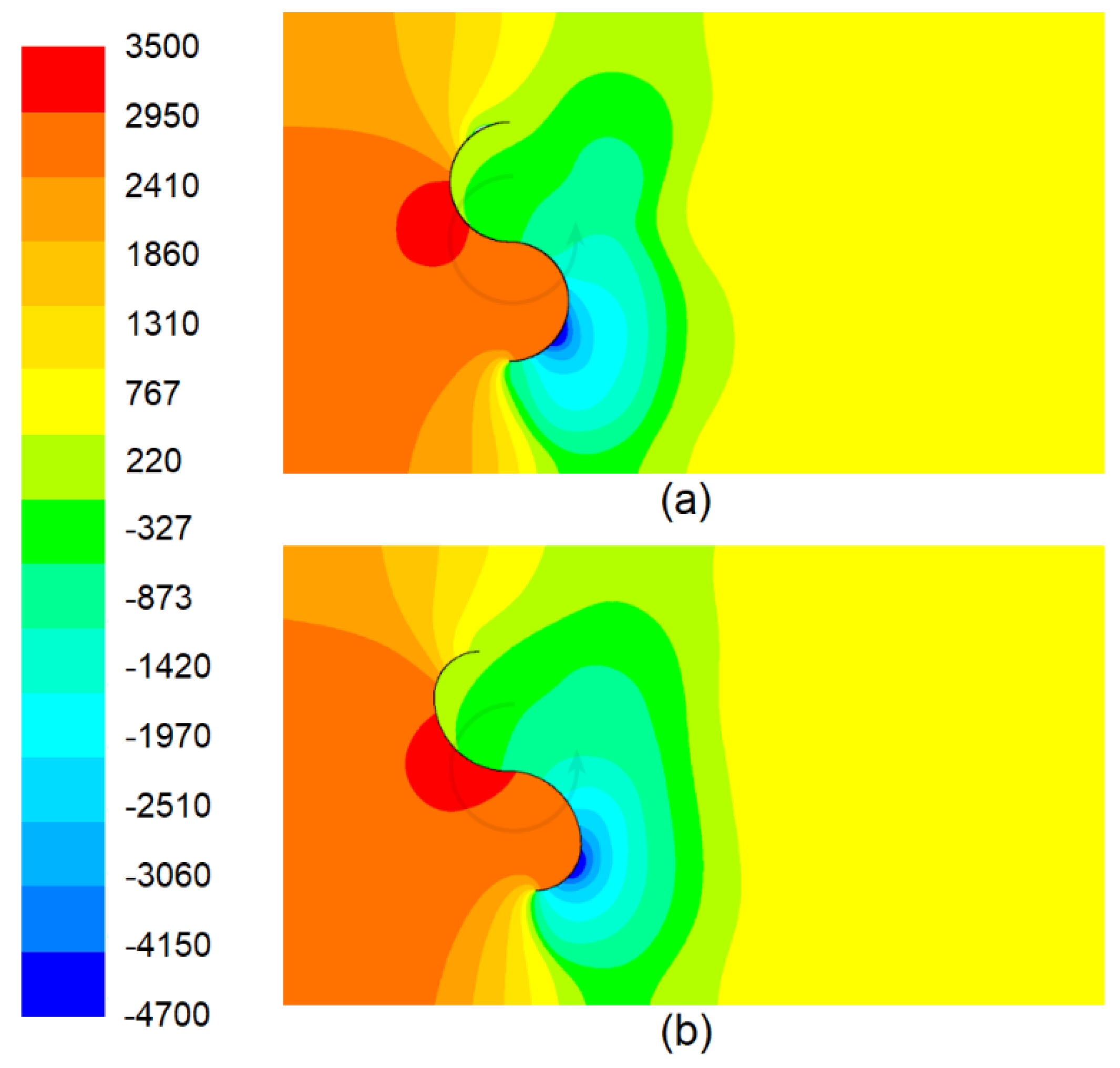
Both Figs. 8 and 9 show an improvement of the Fibonacci blade profile upon the traditional semi-circular Savonius blade profiles. The reason for this is due to the performance of the turbine. The turbine comprises the rotating blades arranged around a central shaft. In this design, one blade functions as the advancing blade, while the other acts as the returning blade. The advancing blade is characterized by a concave surface oriented towards the water flow, whereas the returning blade features a convex surface facing the water flow. In this setup, the turbine primarily rotates due to the drag force between the concave and convex sides of the blades. The advancing blade experiences greater drag force than the returning blade, resulting in positive torque production. In the Fibonacci design, the negative torque is reduced on the returning blade. 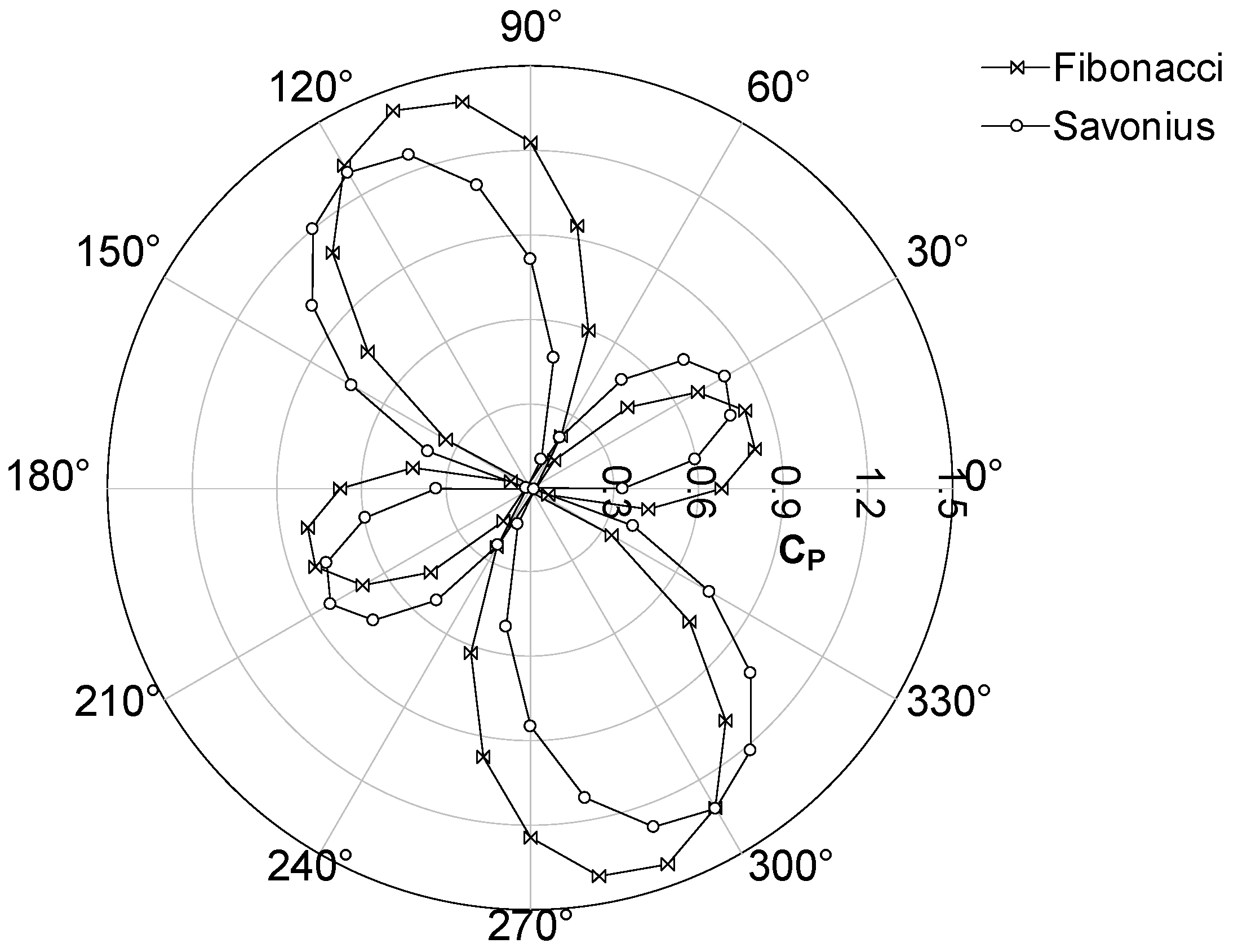This is illustrated in the pressure field shown in Figure 10. This figure compares Savonius with Fibonacci designs. As can be seen, the Fibonacci design provide a better concentration of the flow on the concave blade and removing from the convex blade. This figure corresponds to water flow field at 1 m/s free stream velocity, TSR = 0.85 and position 0º. The power coefficient in this situation is higher for Fibonacci than Savonius. The power coefficient corresponding to Fibonacci and Savonius at other positions is shown in Figure 11, which represents the power coefficient along a full rotation (from 0 to 360º). Both Savonius and Fibonacci blade profiles are illustrated in Figure 11. This figure correspond to TSR = 0.85 and Re = 996000. The average power coefficient in the rotation is 0.266 for Fibonacci and 0.231 for Savonius, thus corresponding to a 15.1% improvement. At other TSR the results are very similar and thus are not shown again.

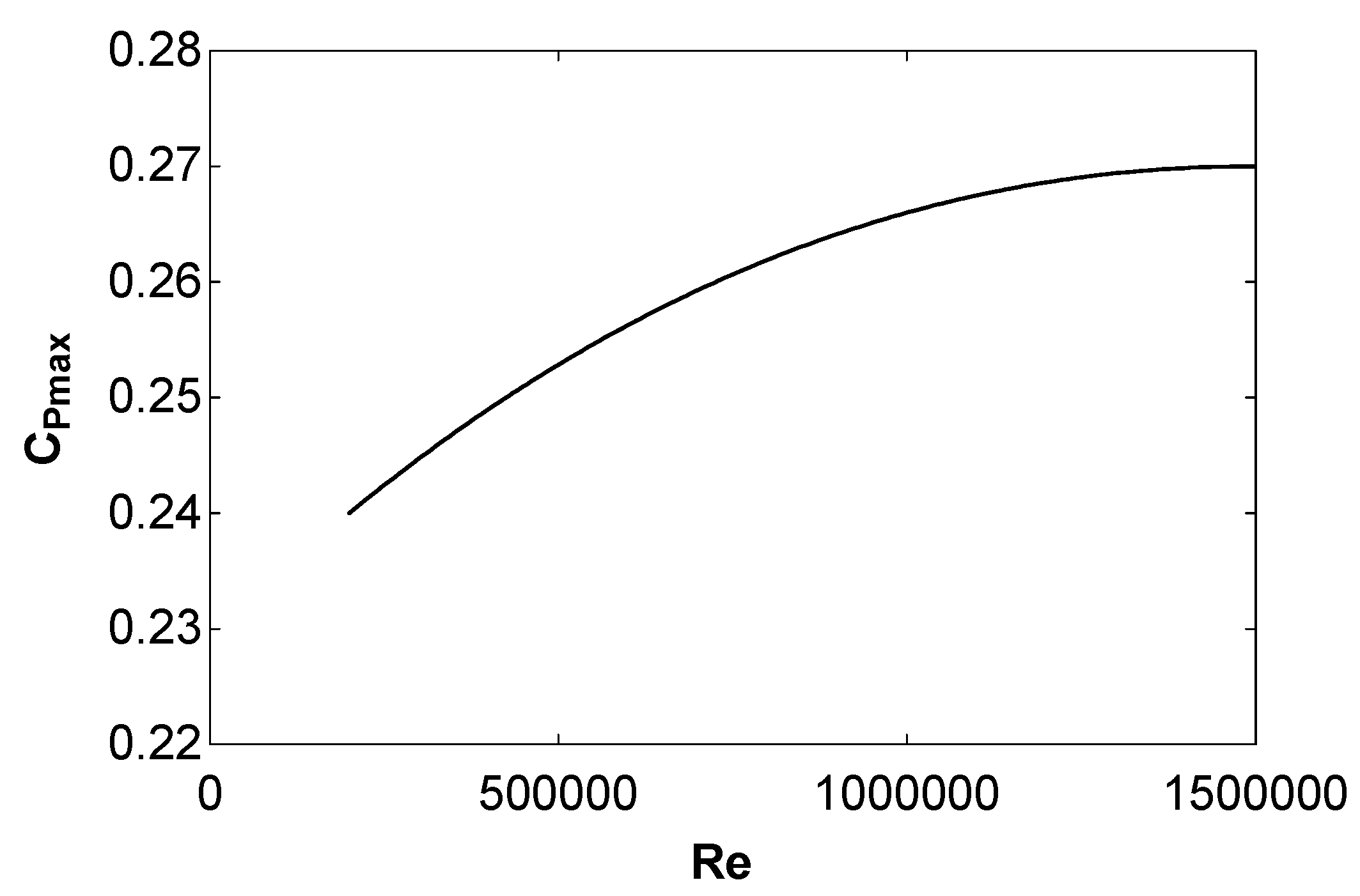
Another important conclusion that can be extracted from Figs. 8 and 9 is that the power coefficient is higher with water than air. The Reynolds number corresponding to the air case is 432000, while the corresponding one to the water case is 996000. Figure 12 illustrates the maximum power coefficient against the Reynolds number for a hydrokinetic turbine (water) under flow velocities from 0.2 to 1.5 m/s, i.e., Reynolds numbers from approximately 200000 to 1500000. As can be seen, the power coefficient increments as the Reynolds number is incremented.

5. Conclusions

The present work treats about a new design to improve the Savonius turbine for hydrokinetic purposes. These type of turbines were chosen due to their independence of the fluid direction and favorable starting characteristics. Some regions have low speed currents with much energy but poor water velocities, and specifically low-flow water environments, such as rivers, streams, and tidal channels, where conventional turbines may not be feasible due to insufficient water velocity. Savonius turbines have the capacity to self-start at very low fluid velocity. Regarding the environmental sensitivity Savonius turbines, have minimal environmental impact compared to large-scale hydroelectric dams or fossil fuel-based power generation. They do not promote significant alterations to water, making them suitable for environmentally sensitive areas where preservation of natural habitats is a priority.

Through observing and understanding biological systems, a blade design based on the Fibonacci spiral was proposed. This design was analyzed through CFD. Current velocities between 0.2 and 1.5 m/s were analyzed, and the proposed design demonstrated a promise for sustainable energy generation in this low-flow velocity conditions.

As future works, additional research must be realized to obtain additional improvements in the efficient modifying some parameters such as overlap ratio, separation gap and twist angle. Other improvements such as deflectors will also be considered.

Author Contributions

Conceptualization, J.M.R.L.; methodology, M.I.L.G. and J.B.D.; software, M.I.L.G. and J.B.D.; validation, J.d.D.R.G., C.G.C, and A.C.C.; formal analysis, J.d.D.R.G., C.G.C, and A.C.C.; investigation, J.M.R.L.; M.I.L.G., J.d.D.R.G., C.G.G., J.B.D., J.T.M., and A.C.C.; resources, J.M.R.L.; M.I.L.G., J.d.D.R.G., C.G.G., J.B.D., J.T.M., and A.C.C.; writing—original draft preparation, J.M.R.L.; M.I.L.G., J.d.D.R.G., C.G.G., J.B.D., J.T.M., and A.C.C.; writing—review and editing, J.M.R.L.; M.I.L.G., J.T.M., and A.C.C.; supervision, J.d.D.R.G., C.G.G., and J.B.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Khan, M.J.; Bhuyan, G.; Iqbal, M.T.; Quaicoe, J.E. Hydrokinetic energy conversion systems and assessment of horizontal and vertical axis turbines for river and tidal applications: A technology status review. Applied Energy 2009, 89, 1823–1835. [Google Scholar] [CrossRef]
Kumar, A.; Saini, R.P. Performance parameters of Savonius type hydrokinetic turbine – A Review. Renewable and Sustainable Energy Reviews 2016, 64, 289–310. [Google Scholar] [CrossRef]
Singh, Kumar. Study of flow characteristics of a Savonius turbine inside nozzle diffuser duct. Journal of Engineering Research 2022. [Google Scholar]
Susilo, R.D.; Gunawan, G.; Kurniawati, D.M. Testing the effect of variation of deflector shapes on the performance of the three blade vertical axis Savonius water turbine. Jurnal Teknik Energi 2022, 18, 115–118. [Google Scholar]
Katayama, Y.; Watanabe, S.; Tsuda, S. Influence of distance from water surface of a horizontally installed Savonius turbine in a rectangular open channel on turbine performance. Journal of Physics Conference Series 2022. [Google Scholar] [CrossRef]
Sood, M.; Singal, S.K. Development of hydrokinetic energy technology: A review. International Journal of Energy Research 2019, 43. [Google Scholar] [CrossRef]
Patel, V.; Bhat, G.; Eldho, T.I.; Prabhu, S.V. Influence of overlap ratio and aspect ratio on the performance of Savonius hydrokinetic turbine. International Journal of Energy Research 2016, 41. [Google Scholar] [CrossRef]
Barbarić, M.; Guzović, Z. Investigation of the possibilities to improve hydrodynamic performances of micro-hydrokinetic turbines. Energies 2020, 13, 4560. [Google Scholar] [CrossRef]
Mejia, O.D.; Mejia, O.E.; Escorcia, K.M.; Suarez, F.; Lain, S. Comparison of sliding and overset mesh techniques in the simulation of a vertical axis turbine for hydrokinetic applications. Processes 2021, 9, 1933. [Google Scholar] [CrossRef]
Fertahi, S.; Bouhal, T.; Rajad, O.; Kousksou, T.; Arid, A.; El Rhafiki, T.; Jamil, A.; Benbassou, A. CFD performance enhancement of a low cut-in speed current vertical tidal turbine through the nested hybridization of Savonius and Darrieus. Energy Conversion Management 2018, 169, 266–278. [Google Scholar] [CrossRef]
Talukdar, P.K.; Sardar, A.; Kulkarni, V.; Saha, U.K. Parametric analysis of model Savonius hydrokinetic turbines through experimental and computational investigations. Energy Conversion and Management 2018, 158, 36–49. [Google Scholar] [CrossRef]
Tian, W.; Mao, Z.; Zhang, B.; Li, Y. Shape optimization of a Savonius wind rotor with different convex and concave sides. Renewable Energy 2018, 113, 287–299. [Google Scholar] [CrossRef]
Kumar, A.; Saini, R.P. Performance analysis of a single stage modified Savonius hydrokinetic turbine having twisted blades. Renewable Energy 2017, 113, 461–478. [Google Scholar] [CrossRef]
Sarma, N.K.; Biswas, A.; Misra, R.D. Experimental and computational evaluation of Savonius hydrokinetic turbine for low velocity condition with comparison to Savonius wind turbine at the same input power. Energy Conversion and Management 2014, 83, 88–98. [Google Scholar] [CrossRef]
Samadi, M.; Hassanabad, M.G.; Mozafari, S.B. Performance enhancement of low speed current Savonius tidal turbines through adding semi-cylindrical deflectors. Ocean Engineering 2022, 259, 111873. [Google Scholar] [CrossRef]
Wahyudi, B.; Soeparman, S.; Hoeijmakers, H.W.M. Optimization design of Savonius diffuser blade with moving deflector for hydrokinetic cross flow turbine rotor. Energy Procedia 2015, 68, 244–253. [Google Scholar] [CrossRef]
Golecha, K.; Eldho, T.I.; Prabhu, S.V. Influence of the deflector plate on the performance of modified Savonius water turbine. Applied Energy 2011, 88, 3207–3217. [Google Scholar] [CrossRef]
Damota, J.; Lamas, I.; Couce, A.; Rodriguez, J. Vertical axis wind turbines: Current technologies and future trends. Renewable Energy Power Quality Journal 2015, 1, 530–535. [Google Scholar] [CrossRef]
Blanco Damota, J.; Rodriguez, J.D.; Couce, A.; Lamas, M.I. Proposal of a nature-inspired shape for a vertical axis wind turbine and comparison of its performance with a semicircular blade profile. Applied Sciences 2021, 11, 6198. [Google Scholar] [CrossRef]
Javier Blanco Damota; Juan de Dios Rodríguez García; Antonio Couce Casanova; Javier Telmo Miranda; Claudio Giovanni Caccia; María Isabel Lamas Galdo. Optimization of a nature-inspired shape for a vertical axis wind turbine through a numerical model and an artificial neural network. Applied Sciences, 2022; 12, 8037.
Blackwell, B.F.; Sheldahl, R.E.; Feltz, L.V. Wind tunnel performance data for two- and three-bucket Savonius rotors. Sandia Laboratories: Springfield, VA, USA, 1977.
Damota, J.B.; García, J.D.; Casanova, A.C.; Miranda, J.T.; Caccia, C.G.; Galdo, M.I.L. Analysis of a nature-inspired shape for a vertical axis wind turbine. Applied Sciences 2022, 12, 7018. [Google Scholar] [CrossRef]
Blanco Damota, J. Perfil de Pala de Turbina Eólica de Eje Vertical de Diseño Bioinspirado: Estudio Comparativo y Optimización Mediante Modelo CFD Parametrizado. Ph.D. Thesis, Unviersidade da Coruña, A Coruña, Spain, 2022. [Google Scholar]
Lamas, M.I.; Rodríguez, J.D.; Rodríguez, C.G.; González, P.B. Three-dimensional CFD analysis to study the thrust and efficiency of a biologically-inspired marine propulsor. Polish Maritime Research 2011, 18, 10–16. [Google Scholar] [CrossRef]
Lamas Galdo, M.I.; Rodriguez Vidal, C.G. Hydrodynamics of biomimetic marine propulsion and trends in computational simulations. Journal of Marine Science and Engineering 2020, 8, 479. [Google Scholar] [CrossRef]

Figure 1. Savonius turbine.

Figure 2. Boundary conditions.

Figure 3. Computational mesh.

Figure 4. Power coefficient corresponding to the experimental and numerical results.

Figure 5. Fibonacci and Savonius shapes.

Figure 6. Fibonacci spiral with radius.

Figure 7. Instances of the Fibonacci spiral occurring in nature; (a) vegetal; (b) animal.

Figure 8. Power coefficient against the tip speed ratio. Wind turbine (air), flow velocity 7 m/s, Re = 432000.

Figure 9. Power coefficient against the tip speed ratio. Hydrokinetic turbine (water), flow velocity 1 m/s, Re = 996000.

Figure 10. Pressure (Pa) corresponding to 0º position; (a) Savonius blade profile; (b) Fibonacci blade profile. Hydrokinetic turbine (water), flow velocity 1 m/s, Re = 996000, TSR = 0.85.

Figure 11. Power coefficient against the rotation angle. Hydrokinetic turbine (water), flow velocity 1 m/s, Re = 996000, TSR = 0.85.

Figure 12. Maximum power coefficient against Reynolds. Hydrokinetic turbine (water), flow velocity from 0.2 to 1.5 m/s.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.