Prerpints.org logo
Preprint
Article

Tunable Radiation Patterns on the Temperature-Denpendent Materials

Altmetrics

Downloads

69

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 June 2024

Posted:

24 June 2024

You are already at the latest version

Alerts
Abstract
The utilization of optical antennas for active control of far-field radiation at the subwavelength scale is crucial in various scientific and technological applications. We propose a thermally tunable disk design of indium tin oxide (ITO) and aluminum gallium nitride (Al0.18Ga0.82As), enabling a switch between absorption and scattering. Furthermore, the control of far-field radiation pattern can be easily realized by combining ITO and Al0.18Ga0.82As to enhance or suppress emission. Our results demonstrate that hybrid structure can be dynamically tuned with temperature variations. In the proposed design, a frequency is achieved at the epsilon-near-zero wavelength of 1240 nm. The thermal tunability of hybrid structure introduces new multifunctional possibilities for light manipulation, thereby enhancing the potential applications of new devices in the near-infrared range.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

0. Introduction

With the rapid advancement of miniaturized devices, antenna regulation of antennas has garnered significant attention. Dynamic modulation of the far-field to achieve versatile control is highly desirable. Specifically, negative refraction, tunable metasurfaces, optical switches, tunable cavities, and coherent perfect absorbers have been realized using indium tin oxide (ITO) as epsilon-near-zero (ENZ) materials and aluminum gallium arsenide (AlGaAs). [1,2,3,4]. However, there has been no report on temperature-controlled far-field radiation of antennas to date. Significantly, beyond purely optical considerations, the design of temperature-dependent nanoantennas must also account for their electromagnetic response. This can be addressed by solving dynamic regulation problems, such as solutions for exchange energy and anisotropies. The far-field radiation patterns are determined by the refractive index, which is temperature-dependent. By increasing the temperature of an antenna, multiople decomposition suggests that the temporal and spatial coherence of the far-field radiation can be engineered through careful material selection or dimensional adjustments. The engineering of far-field radiation is of great interest for applications in lighting, thermoregulation, energy harvesting [5,6], tagging and radiation therapy [7].
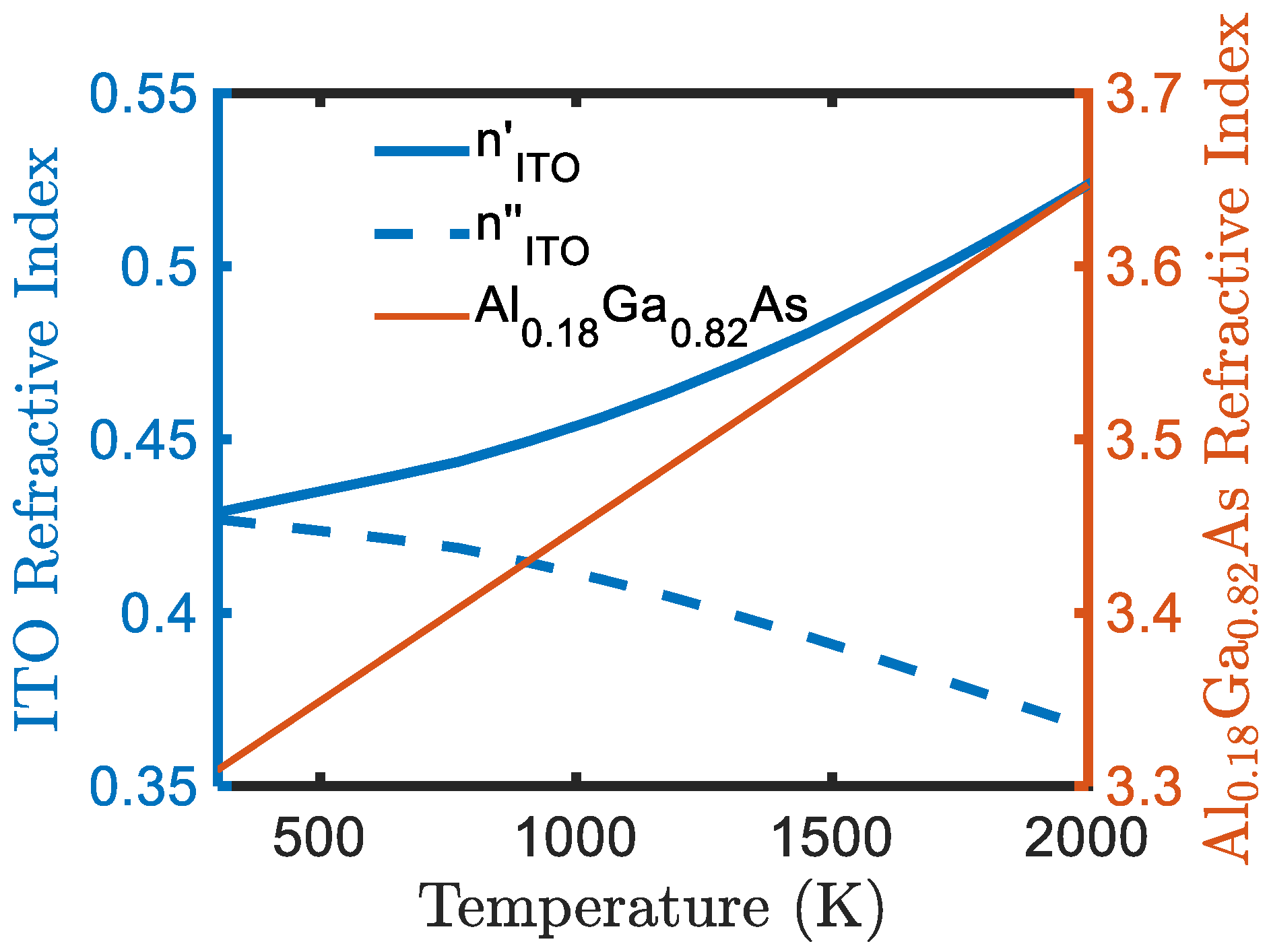
Recent studies have demonstrated that ENZ materials and AlGaAs exhibit an exceptionally large temperature-dependent refractive index (see Figure 1(a)) [8,9]. Consequently, ENZ and AlGaAs materials offer a new platform for optically tuning the material response within a subpicosecond timescale [2]. One way to increase the temperature modulation speed is to forgo heating the material to obtain hot electrons that has been demonstrated using ultrafast pump pulses with modulation speeds in the 100 s of femiseconds in graphene [10], and several picoseconds in metals such as gold and tungsten [11].
III-V semiconductors have the advantage of a short electron lifetime compared to silicon, making them suitable for switching applications. Al x Ga 1 − x As features a broad transparency windwo ranging from the near to mid-infrared, from 0.9 to 17 μ m [12]. Additionally, Al 0 . 18 Ga 0 . 82 As exhibits a high relative permittivity. The resonance of ITO disk is weaker than that of Al 0 . 18 Ga 0 . 82 As disk with the same diameter due to higher absorption losses of ITO. However, the absorption cross section of ITO disk remains evident. The electromagnetic response of the hybrid nanoantenna was further confirmed by measuring the optical Kerr effect as a function of temperature.
In this paper, we utilize ITO and Al 0 . 18 Ga 0 . 82 As to engineer the far-field control of radiation patterns. First, we present the basic formalism describing the refractive indices of ITO and Al 0 . 18 Ga 0 . 82 As , and study the scattering and far field properties to realize dynamically reconfigurable far field radiation pattern based on single nanophotonic structures. We then emphasize the hybridization of ITO and Al 0 . 18 Ga 0 . 82 As to exploit their properties for energy efficiency and sustainability, thereby engineering the far-field radiation effectively. The relevance of this study is primarily theoretical, as the relationship between far-field radiation distribution and the transition between super-absorption and super-scattering remains largely unexplored using the calibrated temperature-index models. We demonstrate that this aspect, although not explicitly accounted for, may be spatially transferable when applied to sufficiently large temperature range. Methods to achieve temperature control of far-field radiation have been implemented by heating, adjusting light intensity, or altering voltage as the refractive index changes with electron temperature. Notably, the far-field variation not only changes by half but also shifts the scattering direction from the original x-axis to the y-axis, resulting in a more significant control range. Clearly, nanoscale electromagnetics is one of the technologies with the potential to provide such functionality, including reception, emission, and more generally, the control of light at the nanoscale.

1. Materials and Methods

According to the optical properties of ITO as a function of electron temperature, the real and imaginary components of the refractive index at λ E N Z = 1240 nm are shown by the blue lines in Figure 1. The change in the real part of the refractive index with intensity is approximately 0.22, and the linear refractive index is 0.45. The calculated refractive index of Al 0 . 18 Ga 0 . 82 at λ E N Z is depicted in Figure 1 by the red line. The change in the real part of the refractive index with intensity is approximately 0.22, while the linear refractive index is 3.32.
Preprints 110074 g001
Figure 1. Temperature-dependent materials. Refractive indices of ITO and Al 0 . 18 Ga 0 . 82 as a function of temperature at a wavelength of λ = 1240 nm.
Figure 1. Temperature-dependent materials. Refractive indices of ITO and Al 0 . 18 Ga 0 . 82 as a function of temperature at a wavelength of λ = 1240 nm.
Preprints 110074 g001
The temperature-dependent refractive index of ITO is expressed as,
ϵ ( ω , T e ) = ϵ ∞ − N e 2 ϵ 0 [ m * ( T e ) ω 2 + i e ω / μ ( T e ) ] ,
where ε ∞ is the high frequency permittivity, N is the carrier density, e is the electron charge, m * ( T e ) and μ ( T E ) are the electron effective mass and mobility, which vary with electron temperature. The plasma frequency ω p = N e 2 / [ ε 0 m * ( T e ) ] with the γ = e / [ m * ( T e ) μ ( T e ) ] . The parameters for the commercial ITO are: N = 1 . 5 * 10 21 cm − 3 , m * = 0 . 3964 m e , ε ∞ = 3 . 404 , E F = 0 . 8793 eV , C = 0 . 4191 e V − 1 . The mobility μ ( T ) = 18 . 3 + 2 . 13 * 10 − 5 T 1 . 53 . The real part of the dielectric constant ε of ITO is zero at 1240 nm that is the ENZ wavelength λ E N Z [13,14]. According to the optical properties of ITO as a function of electron temperature on the model, the real and imaginary components of the refractive index are plotted in Figure 1 in blue at λ E N Z [13,15]. The change of the real part of the refractive index with intensity is about 0.22, the linear refractive index is 0.45.
While, the Sellmeier equation of Al x Ga 1 − x As with temperature dependence can be written as
n ( x , λ , T ) = 10.906 − 2.92 x + 0.97501 λ 2 + C − 0.002467 ( 1.41 x + 1 ) λ 2 1 / 2 + ( T − 26 ∘ C ) × ( 2.04 − 0.3 x ) × 10 − 4 / ∘ C
The first brackets term is the refractive index at room temperature. The second brackets represents the temperature-dependent Sellmeier coefficient. The temperature T, wavelength λ enable us to calculate the index for Al 0 . 18 Ga 0 . 82 As , where C = ( 0 . 52886 − 0 . 735 x ) 2 . This Sellmeier can be used at 1240 nm and 2000 K [16]. The calculated index of Al 0 . 18 Ga 0 . 82 As are plotted in Figure 1 in red line at λ E N Z [16]. The change of the real part of the refractive index with intensity is about 0.22, the linear refractive index is 3.32.

2. Results

2.1. Tuning the Scattering and Far Field for Temperature-Dependent Materials

The proposed structure, consisting of three-dimensional (3D) ITO disk with height H = 150 nm and diameter D = 600 nm, is schematically shown in the inset of Figure 2(a). The nonlinear material made of ITO is illuminated by a plane wave with electric field E inc r , ω = ( E 0 / 2 ) e i ( k · r − ω t ) e x + c . c . , where | k | = 2 π / λ is the wavenumber, ω is the angular frequency, E 0 is the amplitude of incident field, and c.c. means complex conjugate. I 0 = 1 2 c ε 0 | E 0 | 2 is the free-space intensity of the incident plane wave. 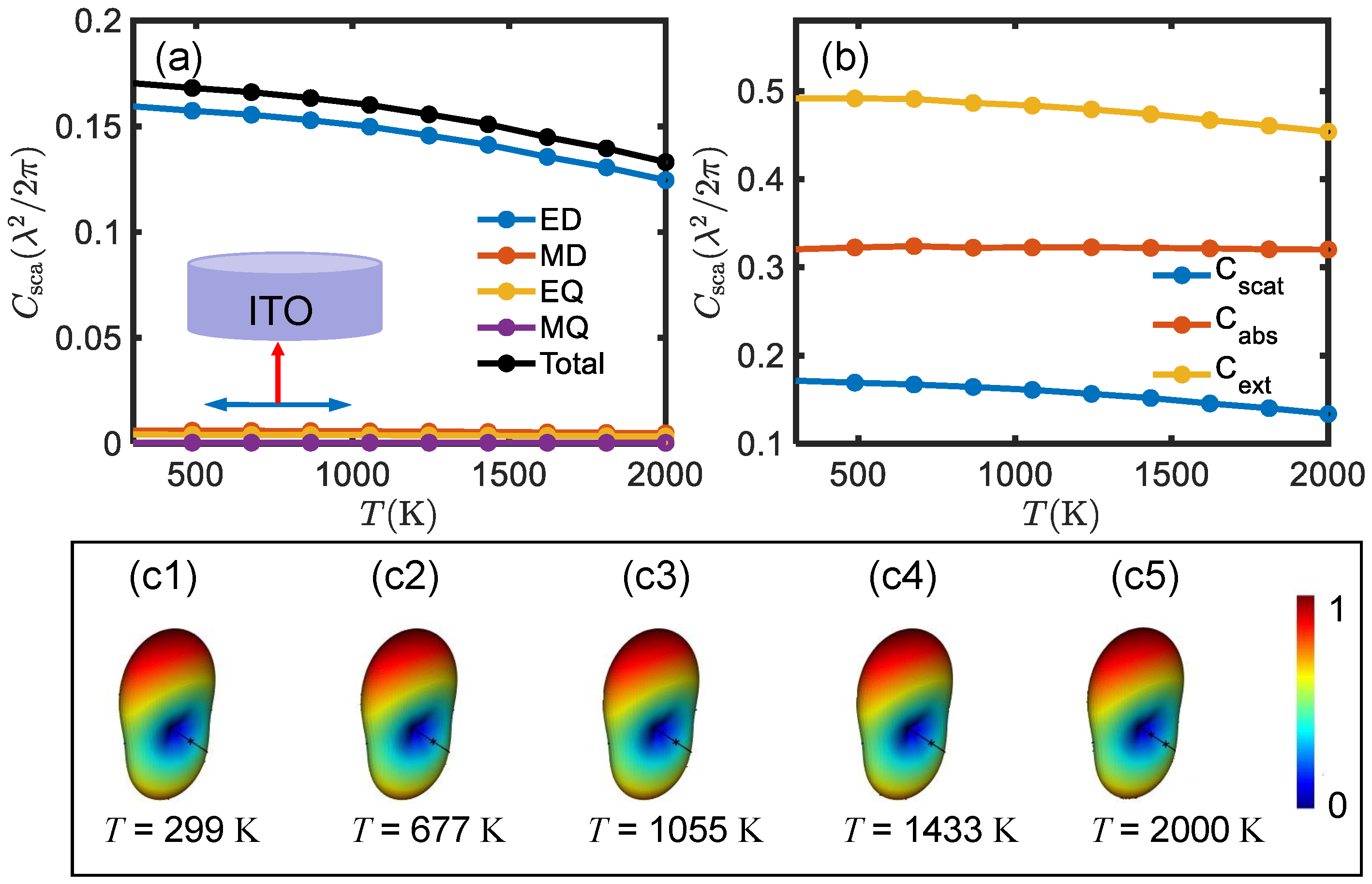E r , ω is the electric field inside the ITO. The scattering properties of the ITO nanodisk, including its electric and magnetic dipole contributions, are depicted in Figure 2(a). The nanodisk is discretized using a 10 nm hexagonal mesh following a convergence test. As shown in Figure 2(a), the scattering cross-section exhibits minimal variation with temperature. The primary contribution to the multipole scattering arises from the electric dipoles (ED), while the contributions from magnetic dipole (MD), electric quadrupole (EQ), magnetic quadrupole (MQ) are relatively minor. Consequently, the far-field radiation pattern, influenced by the interference between the multipoles, remains largely unchanged. Due to the imaginary component of ITO, the antenna also exhibits an absorption cross-section. Figure 2(b) illustrates that both the absorption and scattering cross-sections vary slightly with temperature, leading to a corresponding change in the extinction cross-section. It is evident from Figure 2(b) that the absorption cross-section is dominant, approximately twice that of the scattering cross-section.
The optical response of radiation pattern can be explained by the multipole expansion of the induced displacement current J N L ( r , ω ) = − i ω ϵ N L ( r , ω ) − ϵ 0 E ( r , ω ) [17,18]. The excited multipole can be obtained by the induced nonlinear displacement current J N L . The exact multipole expansion introduced by [19,20]
p α = − 1 i ω ∫ d 3 r J α , NL j 0 k r + k 2 2 ∫ d 3 r 3 r · J NL r α − r 2 J α , NL j 2 k r k r 2 , m α = 3 2 ∫ d 3 r r × J NL α j 1 k r k r , Q α β xz = − 3 i ω ∫ d 3 r 3 r β J α , NL + r α J β , NL − 2 r · J NL δ α β j 1 ( k r k r + 2 k 2 ∫ d 3 r [ 5 r α r β ( r · J NL ) − ( r α J β , NL + r β J α , NL ) r 2 − r 2 ( r · J NL ) δ α β ] j 3 ( k r ) ( k r ) 3 } , Q α β y z = 15 ∫ d 3 r r α r × J NL β + r β r × J NL α j 2 k r k r 2 ,
where α , β ∈ x , y , z , p α , m α , Q α β e , and Q α β m are the electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ), and magnetic quadrupole (MQ) multipole moments, respectively. j n k r is the nth spherical Bessel function. The total scattering cross section can be calculated by [19,20]
C sca = k 4 6 π ε 0 2 | E 0 | 2 ∑ α p α 2 + m α c 2 + ∑ α , β k Q α β e 2 + k Q α β m c 2 ,
which is the contribution of each multipole moment (marked ’total’ in Figs. 1(c) and 2(c)). The interference between multipoles can satisfy the generalized Kerker condition. The far field corresponding to the radiation pattern ( ∝ | E | 2 ) in space is
E ≈ k 2 4 π ε p x e i k r r − sin φ φ ^ + cos θ cos φ θ ^ − k 2 4 π ε ε r m y c e i k r r sin φ cos θ φ ^ − cos φ θ ^ − k 2 4 π ε i k Q e 6 e i k r r − sin φ cos θ φ ^ + cos 2 θ cos φ θ ^ − k 2 4 π ε i k Q m 6 c e i k r r − sin φ cos 2 θ φ ^ + cos θ cos φ θ ^ ,
where r, θ , and φ are the spherical coordinates. k is the wavenumber, c is the speed of light.
The temperature-induced change in the refractive index results in minor variations in the scattering. These variations are due to the contributions of multipoles, which remain relatively constant and exhibit an almost unchanged far-field radiation pattern, as illustrated in Figure 2(c1)-(c2). In the study of the optical properties of a single ITO nanostructure, both scattering and absorption are influenced by temperature. However, these changes are minimal, primarily because the refractive index of ITO changes by less than 1, resulting in a very small difference between the refractive index of ITO and the background refractive index (set to 1).
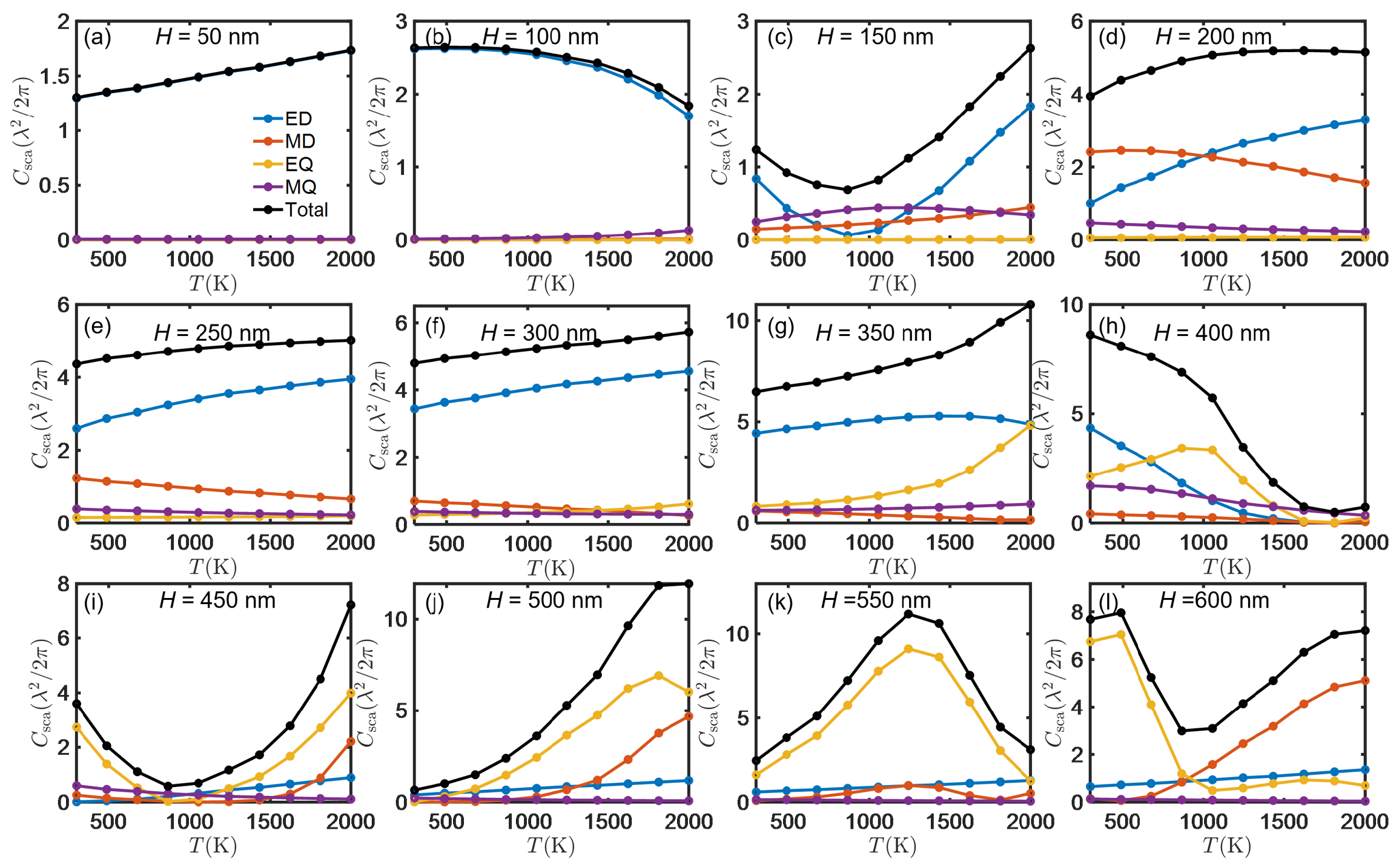
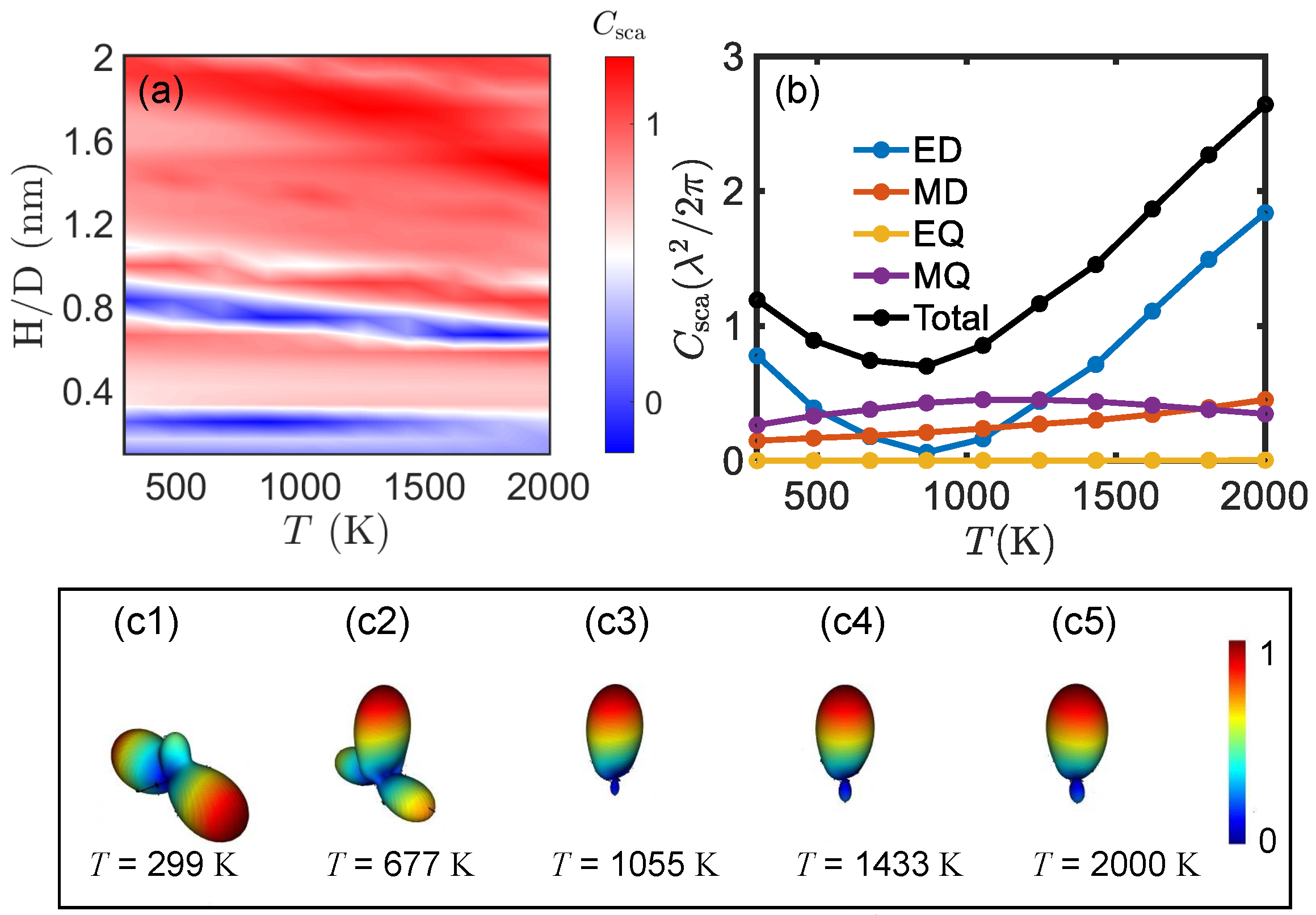
Similarly, we use an Al 0 . 18 Ga 0 . 72 As antenna of the same size to study its scattering and far-field characteristics. Al 0 . 18 Ga 0 . 72 As allows for even greater control over the scattering properties of antennas. As a lossless dielectric, we focus on the scattering cross-section. Figure 3(a) presents the scattering cross-section as a function of temperature for different height-to-diameter ratios ( H / D ). At a specific diameter and temperature, the scattering cross-section is not proportional to height variations, exhibiting irregular fluctuations. Furthermore, for a fixed size, the pattern of the scattering cross-section changing with temperature is not consistent. Taking D = 600 nm and H = 150 nm as an example, the scattering cross-section initially decreases and then increases. More diverse changes are shown in Supplementary Material Figure S2. When the temperature is below 866 K, the electric dipole contribution decreases while the magnetic dipole contribution gradually increases, leading to a reduction in far-field radiation in the ± y direction and an increase in the + z direction. Approaching 866 K, the scattering is the smallest due to the smallest contribution of electric dipole. Correspondingly, the contribution of the magnetic quadrupole is the largest. When the temperature exceeds 866 K, the electric dipole contribution steadily increases, resulting in forward scattering in the far-field radiation pattern. The significant changes in electric dipoles before and after 866 K profoundly affect the far-field radiation patterns. The radiation pattern of Al 0 . 18 Ga 0 . 82 As changes more than that of ITO due to its refractive index changing by 0.22 with temperature. Additionally, its refractive index is around 3.5, which is significantly different from the background refractive index.

2.2. Tuning the Scattering and Far Field of Hybrid Structures for Opposite Illumination

To realize the switching between tunable far-field radiation and superradiant absorption, we integrated both materials and investigated their optical characteristics under the opposite electric fields. A hybrid nonlinear antenna composed of ITO and lossless Al 0 . 18 Ga 0 . 82 As is depicted in Figure 4(a). Owing to the broken inversion symmetry, the hybrid antenna demonstrates a biaisotropic response.
In Figure 4(b), it is observed that when light illuminates a material from two opposing directions, the extinction cross-section remains identical [20]. Due to the loss characteristics of ITO, associated with optical bistability, both scattering and absorption cross-sections are contingent upon the direction of incident light. Initially, commencing from room temperature, the scattering cross-section of the hybrid structure exhibits a preference for illumination from below compared to illumination from above. However, nearing approximately 866 K, the scattering cross-sections converge, and with further temperature elevation, a reversal occurs, where the scattering cross-section for illumination from above surpasses that for illumination from below. Figure 4c,d depict the multipole decomposition. Under bottom illumination, electric dipoles consistently dominate with variations in temperature. Under top illumination, electric dipoles mainly dominate at T < 866 K and T > 1777 K, while both electric and magnetic quadrupoles contribute more at 866 K < T < 1777 K.
Preprints 110074 g005
Figure 5. Radiation patterns of hybrid antenna. (a1)-(a5) Evolution of representative radiation patterns for the bottom illumination direction, i.e., k = + k 0 e z , increases 299 to 2000 K . (b1)-(b5)The radiation patterns for the bottom illumination direction, i.e., k = − k 0 e z , increases from 299 to 2000 K .
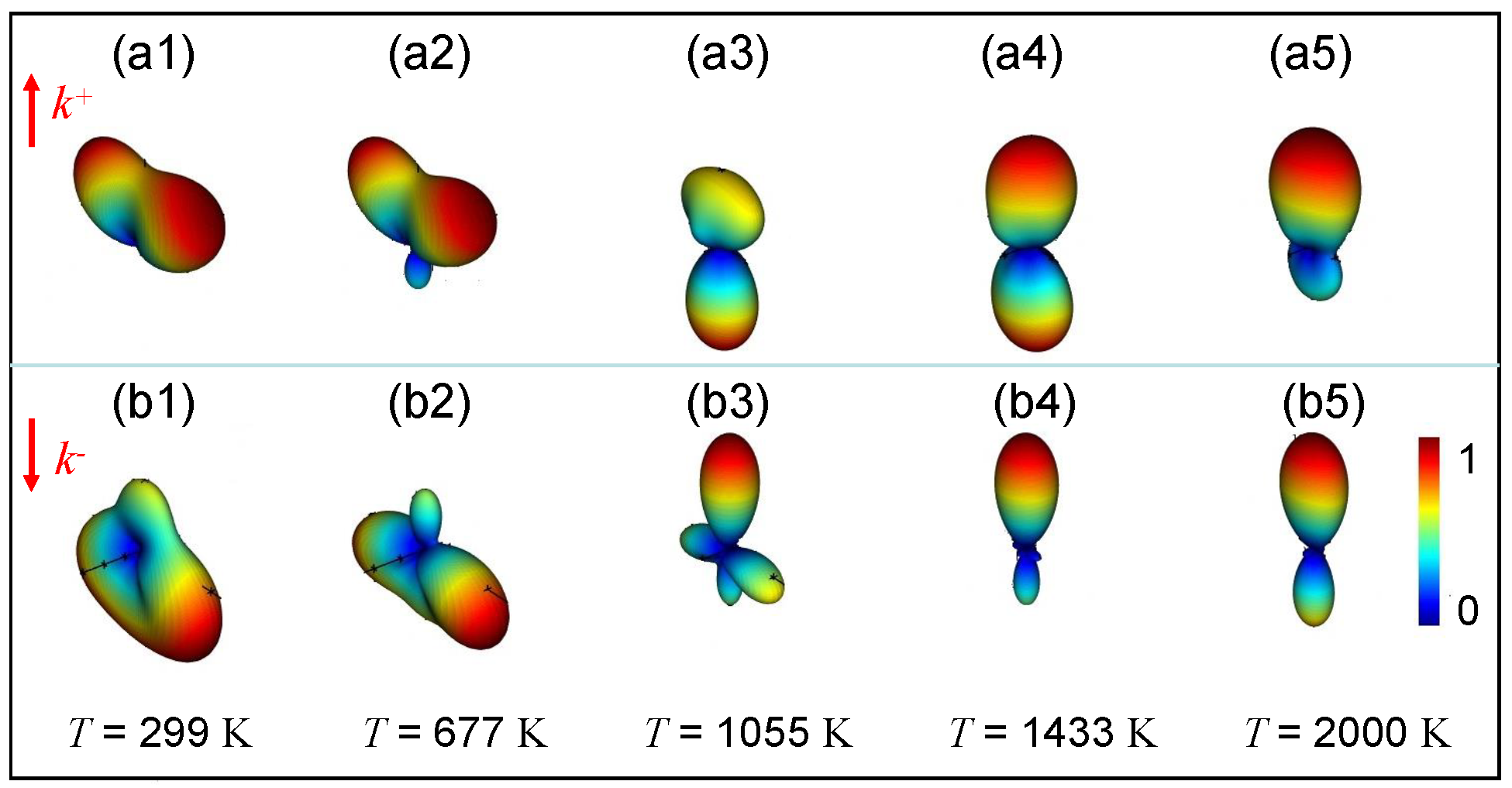
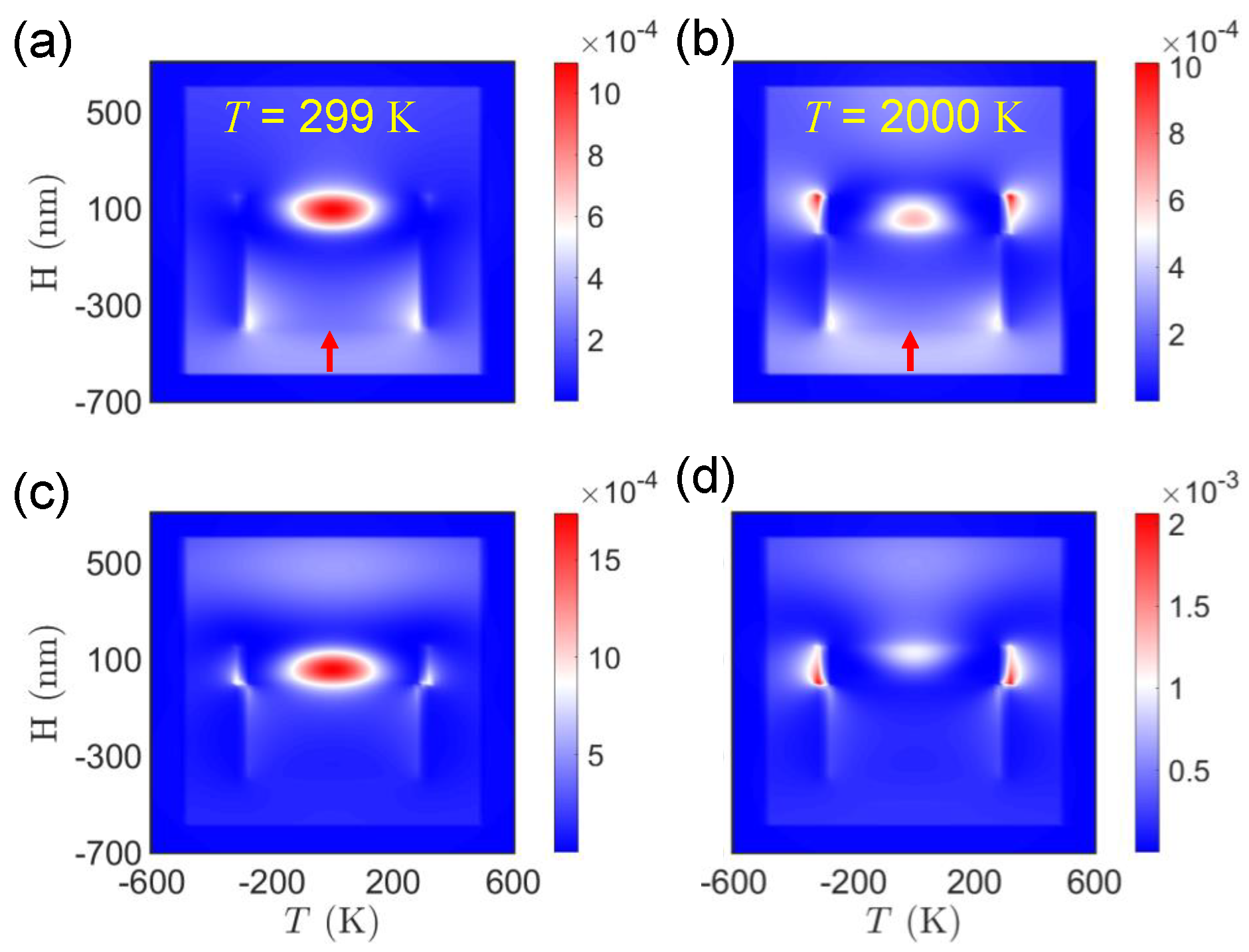
Figure 5. Radiation patterns of hybrid antenna. (a1)-(a5) Evolution of representative radiation patterns for the bottom illumination direction, i.e., k = + k 0 e z , increases 299 to 2000 K . (b1)-(b5)The radiation patterns for the bottom illumination direction, i.e., k = − k 0 e z , increases from 299 to 2000 K .
Preprints 110074 g005
The induced electric, magnetic dipoles and quadrupoles interfere constructively (destructively) in the backward (forward) direction. Under bottom illumination, the radiation pattern initially consists of two lobes distributed symmetrically about the z-axis without backward illumination at room temperature. As temperature rises, backscattering gradually emerges on the radiation map. Further temperature increase induces bidirectional changes in the radiation pattern, with backward (forward) radiation decreasing (increasing) correspondingly. Ultimately, significant tunability of the induced multipole moments in the hybrid antenna by temperature enables control over radiation patterns from a bidirectional to unidirectional pattern. Specifically, under bottom illumination, the initially omnidirectional radiation at room temperature transforms into a three-lobe pattern distributed symmetrically about the y-axis and the upper side of the z-axis. With continued temperature elevation, the radiation pattern evolves from three lobes to four, predominantly radiating from the upper side of the z-axis. Subsequently, with further temperature increase, radiation in the y-direction of the four-lobe pattern diminishes, resulting in bidirectional radiation with forward scattering. Consequently, the nonreciprocal characteristics of hybrid structures arise from the distinct electromagnetic couplings generated.

3. Conclusion

In summary, this study investigated the influence of temperature variations on far-field radiation patterns through numerical simulations employing a spatially explicit temperature-index model. A hybrid structure comprising two materials, each exhibiting temperature-dependent refractive indices, was analyzed. The refractive index change from room temperature to 2000 K was determined to be 0.22. This structure capitalizes on the temperature-induced loss in ITO to achieve switching between absorption and scattering, while also leveraging the strong scattering characteristics resulting from the high refractive index of Al 0 . 18 Ga 0 . 82 As . Temperature adjustments induce diverse far-field radiation distributions. Furthermore, the operational wavelength range can be broadened significantly, and the law of refractive index changing with temperature has been given. Moreover, the methodology employed to determine the temperature-dependent refractive indices of ITO and Al 0 . 18 Ga 0 . 82 As at 1240 nm can be extended to other wavelengths, facilitating multi-parameter control of far-field radiation and enhancing regulation replication, thereby expanding the tunable wavelength range.

Author Contributions

The following statements should be used “Conceptualization, L. C.; methodology,Lin Cheng; software, F. W.; validation, L. C.; formal analysis, F. W.; investigation, L. C.; resources, F. W.; data curation, F. W.; writing—original draft preparation, L. C.; writing—review and editing, K. H.; visualization, K. H.; supervision, L. C.; project administration, all; funding acquisition, L. C., F. W., K. H. All authors have read and agreed to the published version of the manuscript.

Funding

We would like to acknowledges the support the National Natural Science Foundation of China (62305312), the Natural Science Foundation of Shanxi Province, China (202203021222021), Research Project Supported by Shanxi Scholarship Council of China(2312700048MZ) and the fellowship of China Postdoctoral Science Foundation (2022M722923). Shanxi Provincial Teaching Reform and Innovation Project (PX-624261). Shaanxi Fundamental Science Research Project for Mathematics and Physics (23JSQ020). Shanxi Provincial Teaching Reform and Innovation Project(J20221525).

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Appendix A.1. Far fields and Radiation Patterns

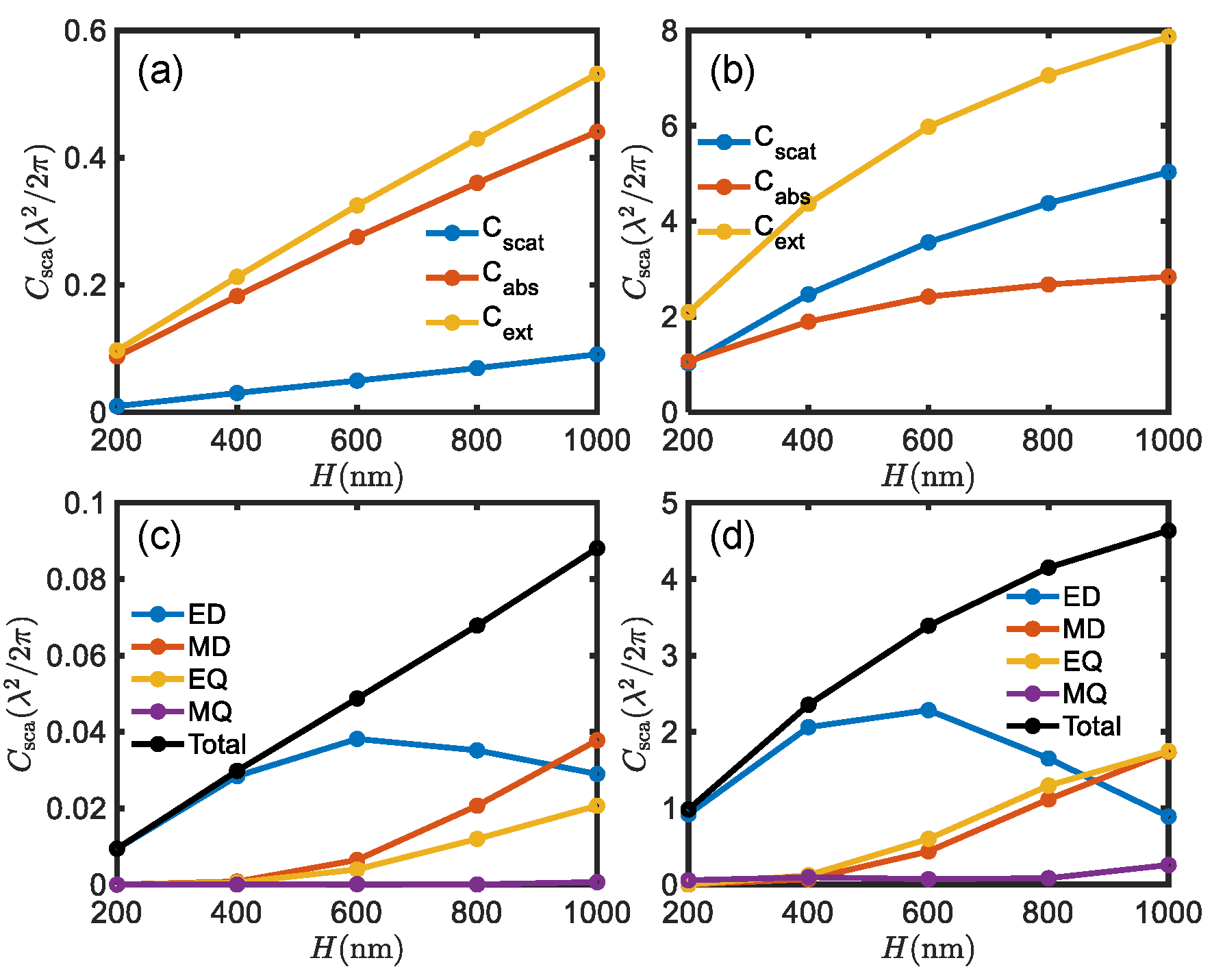
Preprints 110074 g0a1
Figure A1. The extinction, absorption and scattering cross section of the ITO antenna as a function of height H (a) with diameter D = 200 nm. (b) with diameter D = 1000 nm. (c) When diameter D = 200 nm, the contribution of different multipole moments ED, MD, EQ and MQ, respetively. (d) When diameter D = 1000 nm, the contribution of different multipole moments ED, MD, EQ and MQ, respetively.
Figure A1. The extinction, absorption and scattering cross section of the ITO antenna as a function of height H (a) with diameter D = 200 nm. (b) with diameter D = 1000 nm. (c) When diameter D = 200 nm, the contribution of different multipole moments ED, MD, EQ and MQ, respetively. (d) When diameter D = 1000 nm, the contribution of different multipole moments ED, MD, EQ and MQ, respetively.
Preprints 110074 g0a1
Using the induced multipole moments in Eq.(3), the far field can be found [21,22]
E ED = k 2 4 π ϵ 0 e i k r r p x − sin φ e φ + cos θ cos φ e θ , E MD = k 2 4 π ϵ 0 e i k r r m y c − cos θ sin φ e φ + cos φ e θ , E EQ = k 2 4 π ϵ 0 e i k r r i k 6 Q z x e cos θ sin φ e φ − 2 cos 2 θ − 1 cos φ e θ , E MQ = k 2 4 π ϵ 0 e i k r r i k 6 c Q z y m 2 cos 2 θ − 1 sin φ e φ − cos θ cos φ e θ ,
where r , θ , φ are the radial distance, polar angle, and azimuthal angle, respectively. Considering the contribution from all multipole moments (up to magnetic quadrupole), the electric field corresponding to the radiation pattern ( ∝ E 2 ) in the x z -plane, i.e., φ = 0 , can be written as
E ≈ k 2 4 π ϵ 0 e i k r r p x cos θ + m y c − i k 6 Q x z e 2 cos 2 θ − 1 − i k 6 c Q z y m cos θ e θ ,
from which, the radiation pattern ( ∝ E 2 ) can be obtained. Equations (A1) and (A2) are used to plot the radiation patterns in the main text.

Appendix A.2. Antennas Based on ENZ Materials

In this section, we discuss the temperature-dependant scattering cross sections of the ITO antenna.
We use finite difference time domain (FDTD) to analyze the two-dimensional (2D) far-field radiation patterns at H = 200 nm and H = 1000 nm, respectively. Here, Periodic boundary conditions are employed along the x and y axes; Perfectly matched layer (PMLs) are applied along the z axis. The structure is excited by a single plane wave source at 1240 nm for normal incidence. In order to obtain accuracy results, the mesh size is optimized after a converging test. 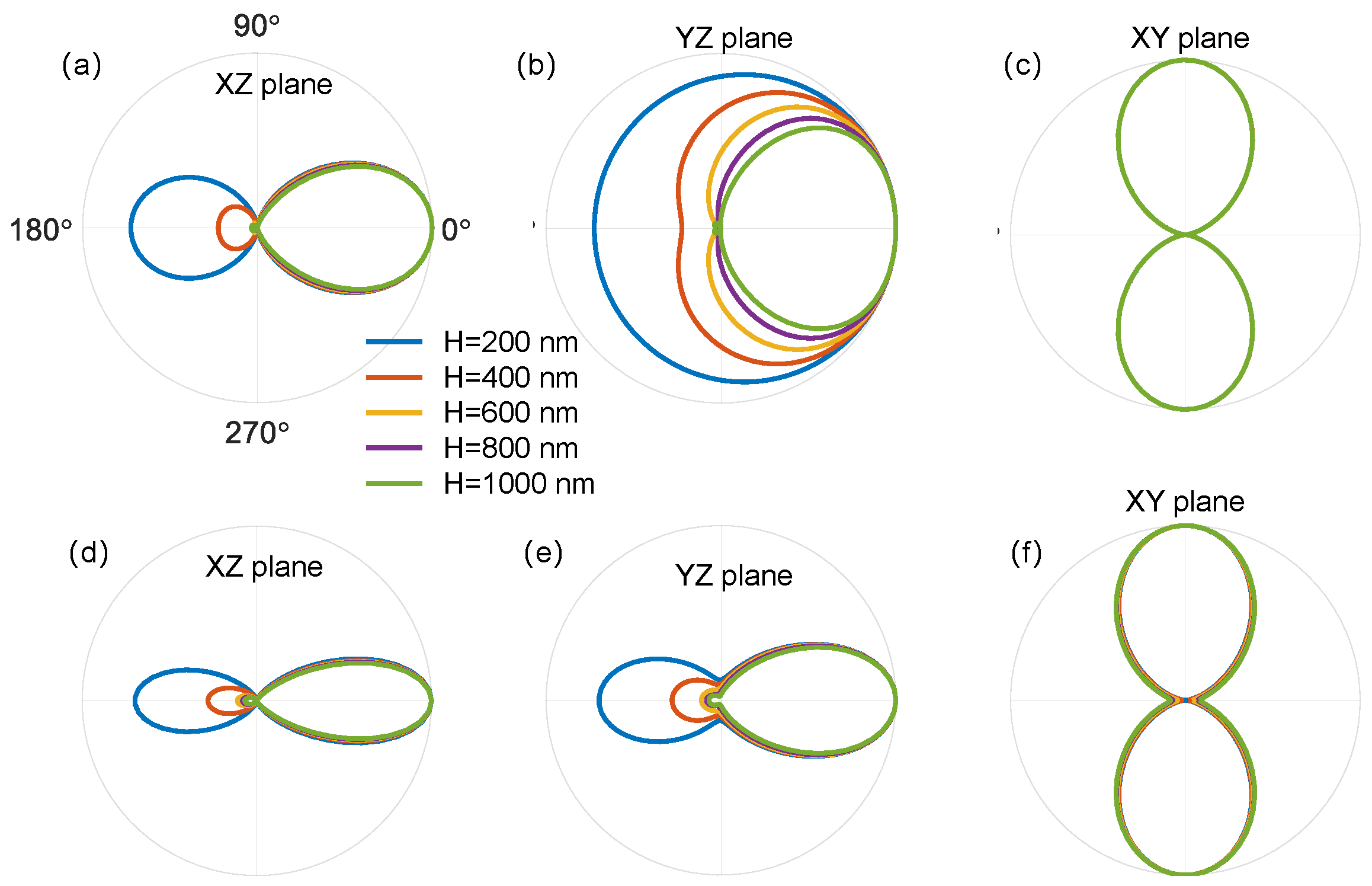The 2D radiation pattern are shown in Figure A2.
Preprints 110074 g0a2
Figure A2. (a) The radiation patterns in (a) XZ plane (b) YZ plane (c) XY plane, with the diameter D = 200 nm. (d)-(e) Same as (a)-(c) with the diameter D = 1000 nm.
Figure A2. (a) The radiation patterns in (a) XZ plane (b) YZ plane (c) XY plane, with the diameter D = 200 nm. (d)-(e) Same as (a)-(c) with the diameter D = 1000 nm.
Preprints 110074 g0a2
Figure A1(a) and Figure A1(b) shows an ITO antenna when illuminated by an x-polarized plane wave propagating in the z direction. The scattering, absorption and extinction cross section increases as the height of ITO increases. Figure A1(c) and Figure A1(d) show the contribution of different multipole moments. The proportion of the individual multipoles changes, and the coherent interference between the multipoles causes the far-field radiation to change from bidirectional to unidirectional (see Figure A2(a)-Figure A2(c)). When the D increases to 1000 nm, the angle of radiation gradually decreases (see Figure A2(d)-Figure A2(f)). Consequently, the antenna exhibits a nearly unidirectional radiation pattern with very small backscattering [see Figure A2(a)- Figure A2(d)], a phenomenon known as the generalized Kerker effect [22,23].
Preprints 110074 g0a3
Figure A3. (a)-(l) When the diameter D = 600 nm, the contribution of different multipole moments ED, MD, EQ, MQ, and the scattering cross section (normalized to λ 2 / 2 π ) as a function of the temperature for different height H.
Figure A3. (a)-(l) When the diameter D = 600 nm, the contribution of different multipole moments ED, MD, EQ, MQ, and the scattering cross section (normalized to λ 2 / 2 π ) as a function of the temperature for different height H.
Preprints 110074 g0a3

Appendix A.3. Antennas Based on Al 0.18 Ga 0.82 As

In this section, we show the temperature-dependent multipole moments for different height. The scattering cross section increases when the height at H = 50 , 200 , 250 , 300 , 350 , 500 nm. When H = 150 , 500 nm, the scattering cross section decreases and then increases. The scattering cross-section at different height changes with temperature, which is due to the obvious change of the induced multipole with the change of height. These trends provide a reference for the design of hybrid structures.

Appendix A.4. Field Distribution of the Hybrid Nonreciprocal Nonlinear Antennas

When the hybrid antenna is illuminated from the top, compared to the bottom illumination, different field distribution in the X Z plane [see Figure A4(a)- Figure A4(d).
Preprints 110074 g0a4
Figure A4. (a) The field distribution in X Z plane of the hybrid structure for opposite illumination for the bottom illumination direction when T = 299 K.(b) The field distribution in X Z plane of the hybrid structure for opposite illumination for the bottom illumination direction when T = 2000 K. (c)-(d) Same as (a)-(b) for the top illumination.
Figure A4. (a) The field distribution in X Z plane of the hybrid structure for opposite illumination for the bottom illumination direction when T = 299 K.(b) The field distribution in X Z plane of the hybrid structure for opposite illumination for the bottom illumination direction when T = 2000 K. (c)-(d) Same as (a)-(b) for the top illumination.
Preprints 110074 g0a4

References

  1. N. Kinsey, C. Devault, J. Kim and A. Boltasseva, Optica2015.
  2. M. Z. Alam, I. D. Leon and R. W. Boyd,Science, 2016, 352, 795.
  3. Argyropoulos, Christos, Chen, Pai-Yen, D’Aguanno, Giuseppe, Engheta, Nader, Alu and Andrea, Physical Review B Condensed Matter & Materials Physics,2012.
  4. E. Mobini, R. Alaee, R. W. Boyd and K. Dolgaleva,ACS Photonics, 2021, 8, 3234–3240.
  5. Jack, Ng, Huanyang, Chen, C., T. and Chan,Optics Letters, 2009.
  6. A. E. Miroshnichenko and M. I. Tribelsky, Physical Review Letters,2018,120, 033902.
  7. S. Clement, J. M. Campbell, W. Deng, A. Guller, S. Nisar, G. Liu, B. C. Wilson and E. M. Goldys,Advanced Science, 2020, 7.
  8. J. P. Kim and A. M. Sarangan,Optics Letters, 2007, 32, 536–538.
  9. J. Paul, M. Miscuglio, Y. Gui, V. J. Sorger and J. K. Wahlstrand,Optics Letters, 2020.
  10. C. H. Lui, R. F. Mak, R. Shan and R. F. Heinz, Physical Review Letters,2010,105, 127404.
  11. M. A. A. O. S. Y. C. P. A. Fortov, JETP Letters,2015,101, 598–602.
  12. S. Gehrsitz and F. K. Reinhart, Journal of Applied Physics,2000,87, 7825–7837.
  13. K. J. Russell, T. L. Liu, S. Cui and E. L. Hu, Nature Photonics,2012,6, 459–462.
  14. R. Orad, G. Enno, A. M. Zahirul, D. L. Israel, U. Jeremy and R. W. Boyd, Optics Letters,2017,42, 3225.
  15. J. Paul, M. Miscuglio, Y. Gui, V. J. Sorger and J. K. Wahlstrand, Opt. Lett.,2021,46, 428–431.
  16. J. P. Kim and A. M. Sarangan, Opt. Lett.,2007,32, 536–538.
  17. R. Alaee, C. Rockstuhl and I. Fernandez-Corbaton, Advanced Optical Materials,2019,7, 1800783.1–1800783.14.
  18. R. Alaee, C. Rockstuhl and I. Fernandez-Corbaton, Optics Communications,2017,407.
  19. R. Alaee, C. Rockstuhl and I. Fernandez-Corbaton, Opt. Commun.,2018,407, 17 – 21.
  20. R. Alaee, C. Rockstuhl and I. Fernandez-Corbaton,Adv. Opt. Mater., 2019, 7, 1800783.
  21. J. D. Jackson,Classical Electrodynamics, Wiley, 1999.
  22. R. Alaee, R. Filter, D. Lehr, F. Lederer and C. Rockstuhl, Opt. Lett.,2015,40, 2645–2648.
  23. W. Liu and Y. S. Kivshar, Opt. Express,2018, 26, 13085–13105.
Preprints 110074 g002
Figure 2. Optical response of the epsilon-near-zero (ENZ) material. (a) Total scattering cross section (normalized to λ 2 / 2 π ) and contributions from variou electric and magnetic multipole moments as a function of the temperature for the ITO antenna. (b) Scattering, absorption and extinction cross sections as functions of temperature for H = 150 nm, and D = 600 nm. (c1) -(c5) Far-field radiation patterns at five temperatures.
Figure 2. Optical response of the epsilon-near-zero (ENZ) material. (a) Total scattering cross section (normalized to λ 2 / 2 π ) and contributions from variou electric and magnetic multipole moments as a function of the temperature for the ITO antenna. (b) Scattering, absorption and extinction cross sections as functions of temperature for H = 150 nm, and D = 600 nm. (c1) -(c5) Far-field radiation patterns at five temperatures.
Preprints 110074 g002
Preprints 110074 g003
Figure 3. Optical response of the Al 0 . 18 Ga 0 . 82 material. (a) Total scattering cross section C sca (normalized to λ 2 / 2 π ) of the ITO antenna as a function of height-to-diameter ratios, H / D , and the temperature T, where the diameter of the antenna D = 600 nm. (b) Total scattering cross section (normalized to λ 2 / 2 π ) and contribution of different electric and magnetic multipole moments as a function of the temperature for the ITO antenna. (c1) -(c5) Far-field radiation patters in five temperatures.
Figure 3. Optical response of the Al 0 . 18 Ga 0 . 82 material. (a) Total scattering cross section C sca (normalized to λ 2 / 2 π ) of the ITO antenna as a function of height-to-diameter ratios, H / D , and the temperature T, where the diameter of the antenna D = 600 nm. (b) Total scattering cross section (normalized to λ 2 / 2 π ) and contribution of different electric and magnetic multipole moments as a function of the temperature for the ITO antenna. (c1) -(c5) Far-field radiation patters in five temperatures.
Preprints 110074 g003
Preprints 110074 g004
Figure 4. Scattering of hybrid antenna. (a) The hybrid structure for the top and bottom illumination directions, i.e., k = ± k 0 e z (b) Total extinction ( C ext ± ), scattering ( C sca ± ) and absorption ( C abs ± ) cross section (normalized to λ 2 / 2 π ) of the hybrid antenna as a function of the temperature for the ITO antenna. Total scattering cross section (normalized to λ 2 / 2 π ) and contribution of different electric and magnetic multipole moments as a function of the temperature (c) for the bottom illumination (d) for the top illumination. The diameter is 600 nm, H ITO = 150 nm, H Al 0 . 18 Ga 0 . 82 As = 400 nm.
Figure 4. Scattering of hybrid antenna. (a) The hybrid structure for the top and bottom illumination directions, i.e., k = ± k 0 e z (b) Total extinction ( C ext ± ), scattering ( C sca ± ) and absorption ( C abs ± ) cross section (normalized to λ 2 / 2 π ) of the hybrid antenna as a function of the temperature for the ITO antenna. Total scattering cross section (normalized to λ 2 / 2 π ) and contribution of different electric and magnetic multipole moments as a function of the temperature (c) for the bottom illumination (d) for the top illumination. The diameter is 600 nm, H ITO = 150 nm, H Al 0 . 18 Ga 0 . 82 As = 400 nm.
Preprints 110074 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated