Prerpints.org logo
Preprint
Article

New Physically-Based Mathematical Model and Experiments for a Recently Invented Solar Pot

Altmetrics

Downloads

82

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 June 2024

Posted:

24 June 2024

You are already at the latest version

Alerts
Abstract
The studied solar pot is a recent invention, which gained a utility model protection in 2021 from the Hungarian Intellectual Property Office under patent number 5489. The device is made for environmentally friendly cooking or heating (by utilizing solar energy) of foods and liquids. Its structure is similar to a double pipe heat exchanger, it has an outer mantle and an inner cooking tank. The goals of the paper are proposing a new physically-based mathematical model describing the solar pot and carrying out computer experiments with it, assembling an experimental system of the pot connected with a solar collector and performing measurements on it. Based on the results, the solar pot can successfully be used for cooking or sterilizing foods or liquids during the studied time period, in Hungary.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The thermal energy provided by the sun is used to treat food in different ways. Examples include drying [1], baking and cooking [2]. Solar food preparation devices operated with solar energy are known, in which solar energy directly heats a surface or air along it in a closed box, and the heat is transferred from there to the closed vessel placed in the box [3]. With this solution, the preparation of food by cooking cannot be solved in many cases [4]. However, there are solar cookers able to produce the temperature required for cooking, which is 73.9°C according to [5]. Typical types are the reflective panel [6], the parabolic [7] and the evacuated tube solar cooker [8]. These are the so-called direct-type food processing devices. Indirect types use a solar collector to produce the thermal energy needed for food processing.
In [9] a solar cooker with solar collector and heat storage is investigated in China that uses oil as heat transfer medium. The main elements of the system are the solar collector, the heat storage and the cooking plate, which can be converted into a traditional electric cooking plate when supplemented with a heating element, enabling cooking even when there is not enough solar energy available. The main goal of the research was to investigate the effect of the quartzite heat storage medium on the system. For this, a mathematical model describing the performance of the system was prepared. The design with heat storage was compared with a version with one and two heat storage tanks. Based on the results, the version with quartzite heat storage increases the performance of the system, and the investment cost also decreases. The specific cost of cooking was 0.3884 U S D k W h , the solar share was 71%. When using the equipment to replace an electric stove, the annual reduction in carbon dioxide emission is 1.75 tons, in the case of a gas stove, it is 0.52 tons. In [10] a research is conducted on an indirect type solar food processing device with nanofluid working medium. One of the main elements of the system is the parabolic solar collector, at the focal point of which the working medium is heated by flowing through it. The other important element is the cooking unit, which consists of a copper pot and the copper pipe that surrounds it (wrapped around it). The heated working medium flows in this pipe, thus transferring the heat to the cooking space. A separate tank was also installed between the cooking unit and the collector, through which the working medium also flows. Due to the parabolic collector, the spiral heat exchanger and the additional tank, the structure of the system is more complex and thus its implementation is obviously more expensive than the system of the solar pot of this paper, which uses a more conventional evacuated tube collector and the solar pot similar to a simple, jacketed heat exchanger. The authors investigated the effect of mixing nano-sized particles with the oil serving as the working medium, how the mass fraction of the particles and the volumetric flow rate of the medium affect the development of the system's energy efficiency. The mass fraction was varied between 0 and 0.5% by mass, and the flow rate between 0.25 and 0.55 l i t r e s m i n u t e . Based on their tests, it was found that while the efficiency of the collector increases continuously with the increase in volumetric flow rate, the highest efficiency is achieved in the case of the cooking unit at 0.25 l i t r e s m i n u t e . Increasing the mass ratio increases the energy efficiency of both main units. The energy efficiency of the entire system increases by 20.08% in the case of a particle concentration of 0.5% by mass and a flow rate of 0.25 l i t r e s m i n u t e , and 2 litres of water at 30°C could be heated to boiling point in 31.51% less time as in the case of the version using oil only. In [11] an indirect-type solar cooker is prepared in Egypt with flat plate collectors equipped with reflectors. They used phase change material, magnesium nitrate hexahydrate, mixed with steel shavings as heat storage material. The equipment is capable of cooking general meals in the midday and afternoon hours. In the evening it can be used to prepare special dishes that can be cooked at low temperatures for a long time (e.g. beans). In the night and morning hours it can be used to keep or reheat food. In [12] it was investigated how the performance of the system changes when the collector is supplemented with reflectors in an indirect solar food processing system equipped with a flat plate collector with water as working medium and supplemented with a heat storage tank containing a phase change material. They found that without a reflector, the highest average temperature of the absorber is 92°C, the highest temperature of the outlet working medium is 71°C, and the highest energy efficiency is 63%. It can be stated that the system is not suitable for cooking as the minimum safe temperature for cooking is 73.9°C according to [5]. On the other hand, thanks to the addition of reflectors, these values were respectively 130°C, 103.65°C and 79%. The device was used to cook 1 kg of rice and 1 kg of pasta in 1.5 litres of water. In both cases they were successful. It should be mentioned that the additions made in order to increase the performance of the equipment significantly increased the complexity of the system. The system examined in this paper has a simpler design and does not contain phase change material. In [13] a solar pressure cooker is investigated, which is connected to an evacuated tube solar collector to provide the necessary energy for operation. The water heated in the collector flows directly into the cooking chamber (under pressure) without the intervention of a heat exchanger. Thus, during operation, the condition of the heat-treated raw material/food must be difficult to check. The system we are examining is more practical, the cooking space is accessible during operation too, as it is hydraulically separated from the collector circuit under pressure. In [13] they used experiments to investigate the thermal behaviour of the equipment, under different weather conditions (radiation intensity, ambient temperature), regarding the boiling of different masses of water. Based on their results, a larger mass of water boils proportionally in less time, so the efficiency of the system improves when larger quantities are boiled. In [14] a large-scale cooking system was made capable of supplying energy to several cooking units at the same time. The flat plate collector system also includes a heat storage tank made of oil and stone, in addition to the cooking units. The flow of the working medium is not forced, no pump is needed. The system has been successfully used for food preparation in several developing countries (e.g. Mali, India). The system, that is the subject of this paper’s research, works with a pump, so its placement/implementation can be done in a less constrained manner, it is also simpler and does not contain heat storage.
The main elements of the system examined are the solar collector and the solar pot. In the literature, there are mathematical models for collectors and solar heating systems [15,16], however, as it is a new invention, no model has yet been worked out for the solar pot. In terms of design, the solar pot is similar to a tube-in-tube heat exchanger or a solar storage tank. Models for those are already available in the literature. There are two main types of models. One is the black-box type and the other one is the physically-based model. The physically-based model relies on the physical background of the modelled system or process, which is therefore often difficult to set up in the case of a complex system [17]. Black-box modelling does not take into account the physical background, it represents a more result-oriented approach, the creation of the model is typically simpler [18,19].
The Hottel-Whillier-Bliss physically-based mathematical model worked out for flat plate collectors [20] can be used to describe the temperature distribution of the working medium along the length of the collector as a function of place and time. In [21] a physically-based mathematical model was developed that can be used to describe the temporal behaviour of a flat plate collector. Estimation of the temperature of the outlet working medium is made possible by a differential equation formulated on the basis of the energy balance of the collector. Reference [22] presents several physically-based mathematical models describing the dynamic behaviour of unglazed flat plate collectors. In [23] the possibility of a device that can be used for heating and domestic hot water production was developed, in which the collector is equipped with a mirror. In connection with this, a physically-based model was worked out for evacuated tube solar collectors, which can be used to estimate the total solar radiation reaching the collector. In [24] a black-box type neural network model was made, which can be used to model the thermal behaviour of a flat plate collector. Knowing the intensity of solar radiation, the ambient temperature and the temperature of the working medium entering the collector, with a constant mass flow, the temperature of the outlet heat transfer medium can be predicted with the model. In [25] a black-box model based on multiple linear regression was developed for solar collectors. As a result, the appropriate temperature of the outlet working medium can be calculated. The identified and validated model was compared to the physically-based model of [21]. The results showed that the model in [25] was able to predict the temperature of the outlet working medium more accurately. The importance of the model, in addition to the appropriate accuracy (average accuracy better than 5%), is due to its simplicity. It requires little calculation and can be used for any type of collector (e.g. evacuated tube collector).
There are several mixed storage models in the literature. In [15] a physically-based mathematical model was developed. An ordinary differential equation based on the energy balance of the tank allows the temperature of the tank to be calculated. The model does not take into account the heat capacity of the solar storage material. In [26] a physically-based mathematical model for a mixed storage was worked out, based on the heat balance of the storage, which can be used to calculate the temperature of the storage. A similar model can be found in [27]. In [28] a black-box model based on multiple linear regression was developed for mixed solar storages, which can be used to determine the geometric average temperature of the storage.
When modelling tube-in-tube heat exchangers, energy balance is often assumed between the working media of the two sides, neglecting the environmental heat exchange [29,30]. In [31] various mathematical models for tube-in-tube heat exchangers similar to the solar pot examined in this paper were developed. The physically-based model takes into account the heat exchange with the environment, too. A black-box type mathematical model was also developed in [31] based on multiple linear regression, which also takes environmental heat exchange into account. The models were validated using measurements on a heat exchanger. Based on the results, the physically-based model not neglecting the heat exchange with the environment can estimate the temperature of the outlet working medium more accurately than the other model version assuming energy balance between the two sides of a heat exchanger. The black-box model proved to be more accurate than both models, in case of considerable environmental heat exchange. In [32] there are physically-based models for tube-in-tube heat exchangers. The first one is a model with distributed parameters, which can be used to calculate the temperature of the working medium on the cold and hot sides of the heat exchanger. The second one is a second-order concentrated parameter model, which can be used to determine the outlet temperature of the cold and hot side working fluids. According to the authors' conclusion, second-order concentrated parameter models based on the logarithmic mean temperature difference approach can reliably describe the dynamics of heat exchangers.
The contribution of the present paper is as follows:
1. A new physically-based mathematical model is proposed to describe the examined, recently invented solar pot. Computer simulations are made with the model, based on which conclusions are drawn regarding the practical applicability of the solar pot.
2. An experimental system of the hydraulically connected solar pot and a solar collector is physically assembled. The different variables of the system (different temperature values) are measured. Based on measured data, conclusions are drawn regarding the practical applicability of the solar pot.
The structure of the paper is the following: Section 2 contains the description of the modelled and measured system. Section 3 presents the physically-based model of the solar pot along with the simulation results. In Section 4, the measurements made on the experimental system and the measured data are shown. Section 5 serves with conclusions and future research proposals.

2. System Description

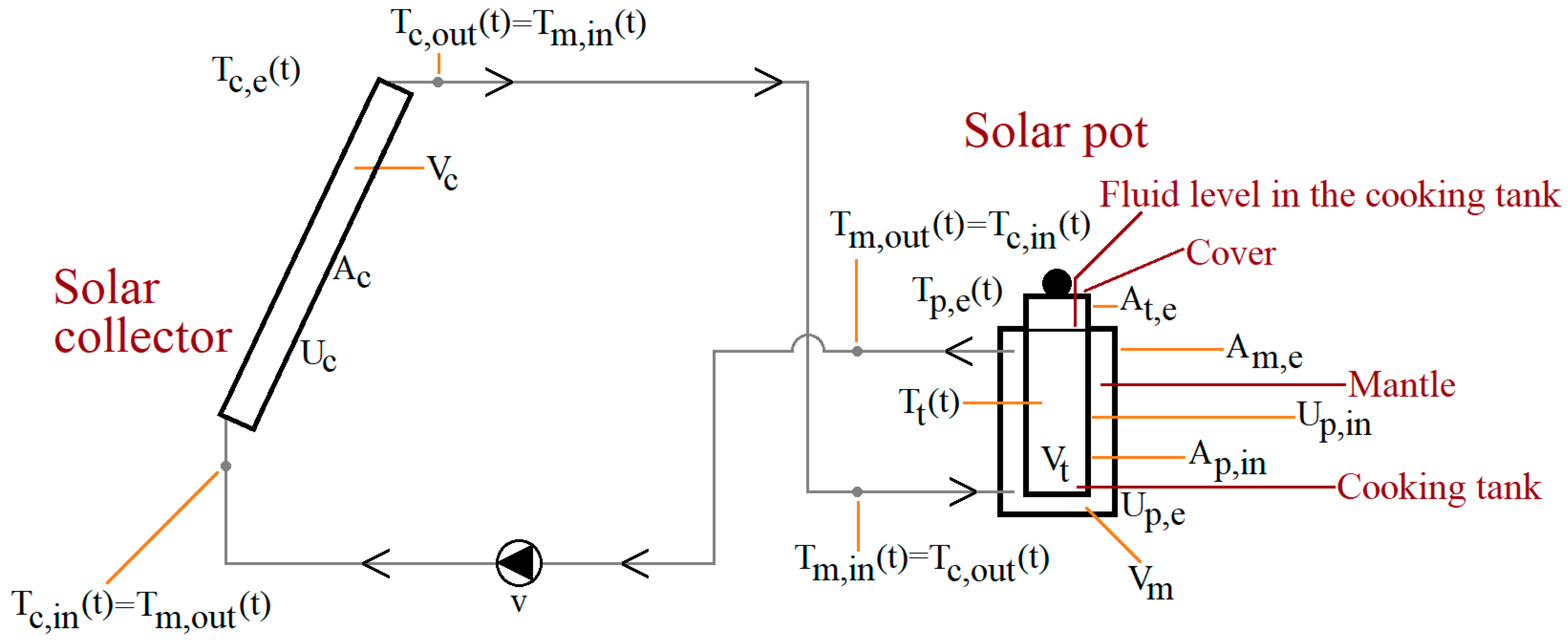
The solar pot (shown in Figure 1) is a recent invention, which gained a utility model protection in 2021 from the Hungarian Intellectual Property Office under patent number 5489 [33]. The device is made for environmentally friendly cooking or heating of foods and liquids. Its structure is similar to a double pipe heat exchanger. It has an outer mantle and an inner cooking tank. Cooking or heating is done as follows. The mantle heats the cooking tank by circulating working medium (water or else) along the cooking tank’s outer surface. The mantle forms a closed hydraulic circuit with a solar collector. The working medium in the mantle and the interior of the cooking tank are hydraulically separated from each other, which implies heating and cooking can be executed hygienically. The pot can also be used for reheating foods or heating liquids not only in connection with food preparation. Using the device, heating and cooking can be made with the utilization of renewable solar energy. The solar pot has the advantage that it can be connected to an existing solar heating system. It is an indirect-type food processing equipment, which can be used with any collector using liquid as working fluid. If there is insufficient solar energy, one can heat the pot with a stove or a cooking plate as well.
In the experimental system of this paper, the solar pot is connected to an evacuated tube solar collector. The solar heating system with the solar pot and the time-dependent variables along with the parameters of the system are shown in Figure 2.
In Figure 2, t denotes the time dependence of the variables. These variables are the following:
T c , e : temperature of the solar collectors’s environment (outdoors), °C,
T c , i n : solar collector inlet (water) temperature, °C,
T c , o u t : solar collector outlet (water) temperature, °C,
T t : temperature in the cooking tank, °C,
T p , e : temperature of the solar pot’s environment (indoors), °C,
T m , i n : mantle inlet (water) temperature, °C,
T m , o u t : mantle outlet (water) temperature, °C.
As the fluid in the mantle is considered mixed, its temperature is the same as the mantle outlet temperature. As the pipes connecting the solar pot and the collector are insulated and their volume is neglected, we consider the solar collector outlet temperature and the mantle inlet temperature equal T c , o u t = T m , i n . The same holds for the solar collector inlet temperature and the mantle outlet temperature T c , i n = T m , o u t .
The constant parameters of the system are the following:
A c : surface area of the collector (one side), m 2 ,
A m , e : surface area of the mantle to the environment, m 2 ,
A t , e : surface area of the cooking tank to the environment, m 2 ,
A p , i n : surface area between the mantle and the cooking tank, m 2 ,
U c : overall heat loss coefficient of the solar collector, W m 2 K ,
U p , e : overall heat loss coefficient of the solar pot, W m 2 K ,
U p , i n : overall heat transfer coefficient between the mantle and the cooking tank, W m 2 K ,
v: volumetric flow rate of the pump, m 3 s ,
V c : volume of the collector, m 3 ,
V m : volume of the mantle, m 3 ,
V t : volume of the cooking tank, m 3 .
During the tests, the cooking tank is filled with water up to the top of the mantle and covered by a stainless steel plate. We also circulate water between the solar pot and the solar collector as the working fluid.

3. Mathematical Modelling

The model of the solar pot is a physically-based mathematical model based on the energy balance of the pot. It consists of two submodels (due to the jacketed structure of the pot), one for the mantle temperature and the other for the cooking tank temperature, constituting a system of differential equations. Both equations are non-homogeneous linear differential equations with constant coefficients. The model uses temperature differences only, which allows the use of either Celsius or Kelvin values.

3.1. Mathematical Model

Equations (1a) and (1b) represent the model of the solar pot. Equation (1a) is for the mantle, while Equation (1b) is for the cooking tank temperature:
d T m , o u t d t = v V m · T m , i n − T m , o u t + A m , e · U p , e ρ · c · V m · T p , e − T m , o u t + A p , i n · U p , i n ρ · c · V m · T t − T m , o u t ,
d T t d t = A p , i n · U p , i n ρ · c · V t · T m , o u t − T t + A t , e · U p , e ρ · c · V t · T p , e − T t ,
where the density of water is ρ and the specific heat capacity is c.

3.2. Simulation Results

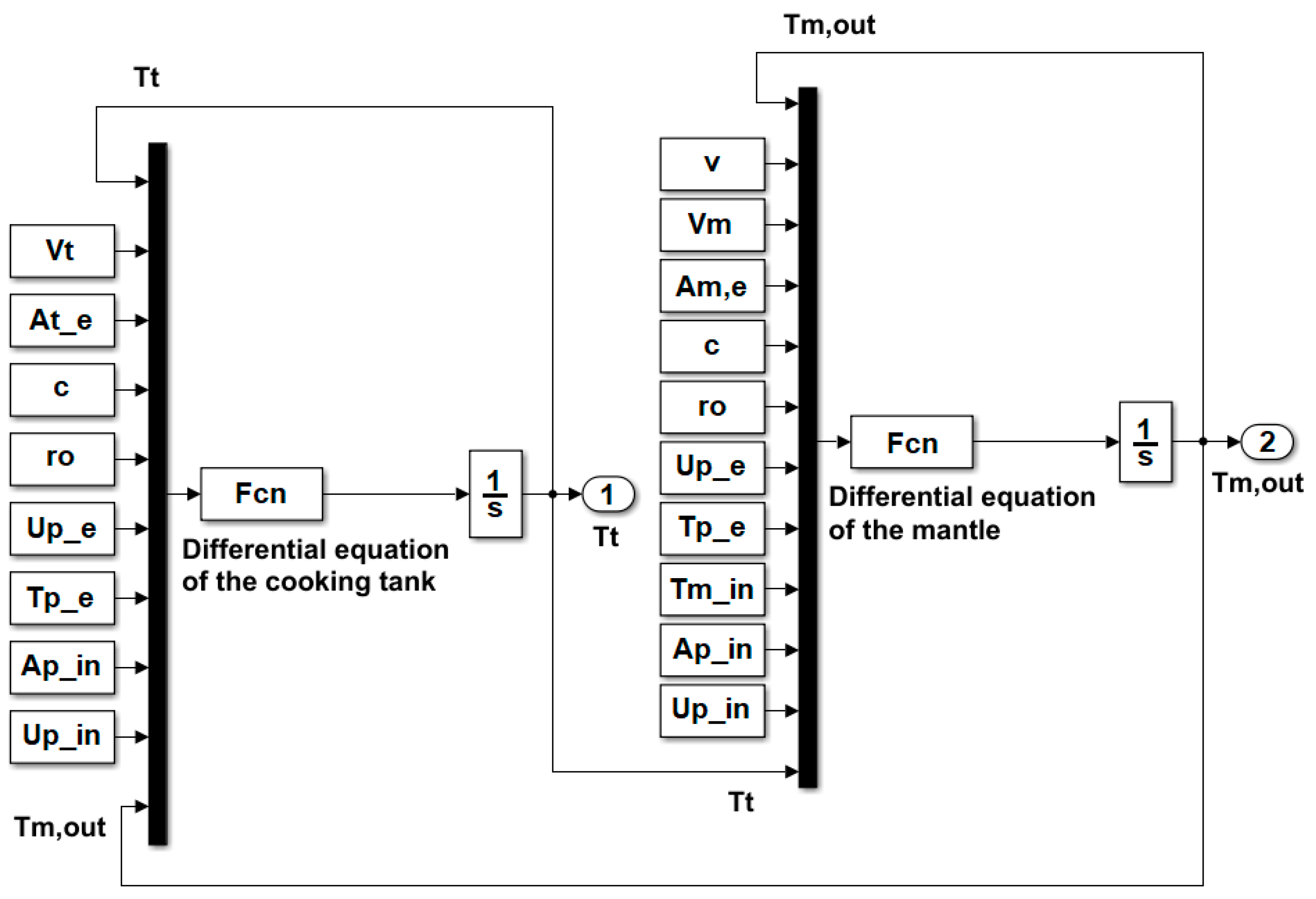
Equations (1a) and (1b) were fed into the Matlab/Simulink programming environment. The computer realization of the model can be seen in Figure 3.
To run the model, the values of the solar pot’s parameters need to be provided. A m , e = 0.19 m 2 , A t , e = 0.041 m 2 , A p , i n = 0.112 m 2 , V m = 3.691 l ( = 3.691 · 10 − 3 m 3 ) , and V t = 4.418 l ( = 4.418 · 10 − 3 m 3 ) are geometric parameters of the physically manufactured solar pot (see Figure 1 in Section 2.). The density ( ρ ) and specific heat capacity (c) of water are also needed. These values are 1000 k g m 3 and 4200 J k g K , respectively.
The determinations of U p , e = 20.4 W m 2 K (overall heat loss coefficient) and U p , i n = 351 W m 2 K (overall heat transfer coefficient) are made by calculations based on recommendations from the literature.
U p , e is the overall heat loss coefficient between the mantle and the solar pot’s environment. It is determined by considering the following:
1. Convective heat transfer between the inside of the mantle and the inner surface of the mantle’s wall. (This wall is adjacent to the environment.) Taking into account the liquid in the mantle (water) and the material of the mantle’s wall (stainless steel), and assuming forced convective heat transfer along the inner surface of the mantle’s wall, the heat transfer coefficient is 850 W m 2 K , which is an average value according to [34].
2. Thermal conduction inside the mantle’s wall. Taking into account the material of the mantle’s wall, which is stainless steel (with a thickness of 0.002 m), the thermal conductivity coefficient is 15 W m K , which is an average value according to [34].
3. Convective heat transfer between the outer surface of the mantle’s wall and the solar pot’s environment. Taking into account the material of the mantle’s wall (stainless steel) and the air surrounding the pot from outside, and assuming free convective heat transfer along the surface of the wall, the heat transfer coefficient is 21 W m 2 K , which is an average value according to [34].
The above details were fed into the [35] online program, which made the necessary calculations for the overall heat loss coefficient. The result is U p , e = 20.4 W m 2 K .
In the value of A t , e (which is the responsible surface regarding the heat loss of the cooking tank to the environment), the surface area of both the cover and that part of the tank’s wall which is above the mantle are included. Furthermore, U p , e is applied to this surface when determining the heat loss of the cooking tank to the environment. Clearly, this approach contains certain simplifications since it does not take into account that there is some air between the tank’s fluid and the cover. Nevertheless, it must underestimate the pot’s real heat performance a bit since the air has some (advantageous) thermal insulating effect.
U p , i n is the overall heat transfer coefficient between the mantle and the cooking tank. It is determined by considering the following:
1. Convective heat transfer between the inside of the mantle and the outer surface of the cooking tank’s wall. Taking into account the liquid in the mantle (water) and the material of the cooking tank wall (stainless steel), and assuming forced convective heat transfer along the surface of the wall, the heat transfer coefficient is 850 W m 2 K , which is an average value according to [34].
2. Thermal conduction inside the mantle’s wall. Taking into account the material of the mantle’s wall, which is stainless steel (with a thickness of 0.002 m), the thermal conductivity coefficient is 15 W m K , which is an average value according to [34].
3. Convective heat transfer between the inner surface of the cooking tank’s wall and the inside of the cooking tank. Taking into account the material of the wall (stainless steel) and the liquid in the cooking tank (water), and assuming free convective heat transfer along the surface of the wall, the heat transfer coefficient is 650 W m 2 K , which is an average value according to [34].
The above details were fed into the [35] online program, which made the necessary calculations for the overall heat transfer coefficient. The result is U p , i n = 351 W m 2 K .
T p , e ( t ) is assumed to be constant as the solar pot is located in an air-conditioned mobile container, so T p , e ≔ T p , e t ≔ 25 ℃ , in accordance with the temperature set inside the container. The initial values of the model are also set to this value, so T m , o u t 0 ≔ 25 ℃ and T t 0 ≔ 25 ℃ . For the sake of simplicity, T m , i n t ( = T c , o u t ( t ) ) is set constant in the simulations, 80°C. Choosing this temperature value, it was taken into consideration that it can easily be reached and maintained for a longer time on a typical day in May in Hungary (see Figure 7 in Section 4.2.), and that this inlet temperature is probably high enough for the cooking tank to reach the minimum temperature for sterilizing foods - based on our preliminary assumption. This minimum temperature is 73.9°C according to [5], but in this work 75°C is aimed due to safety purposes. The simulations were carried out with two different volumetric flow rate ( v ) values, which can be realized in the experimental system as well. 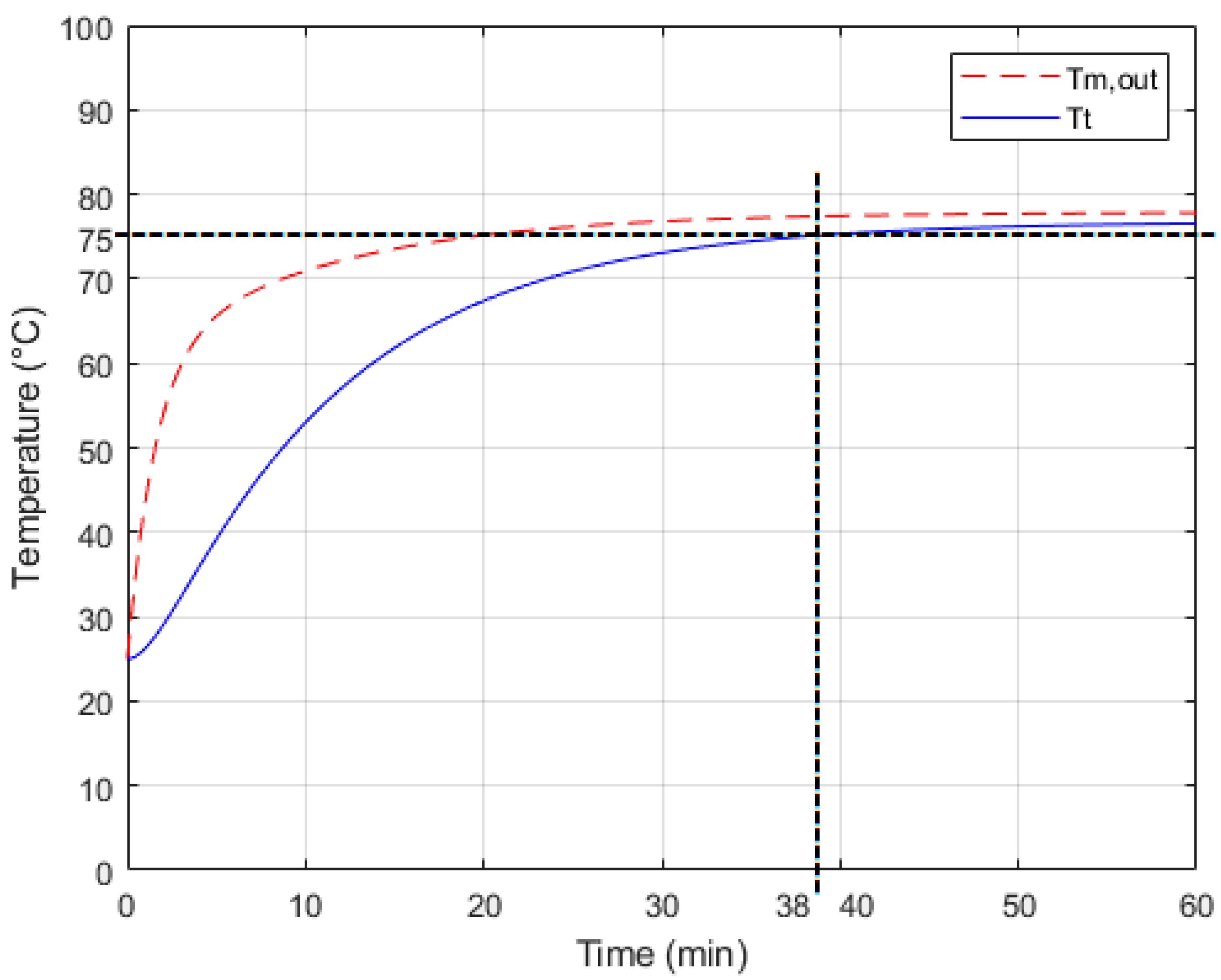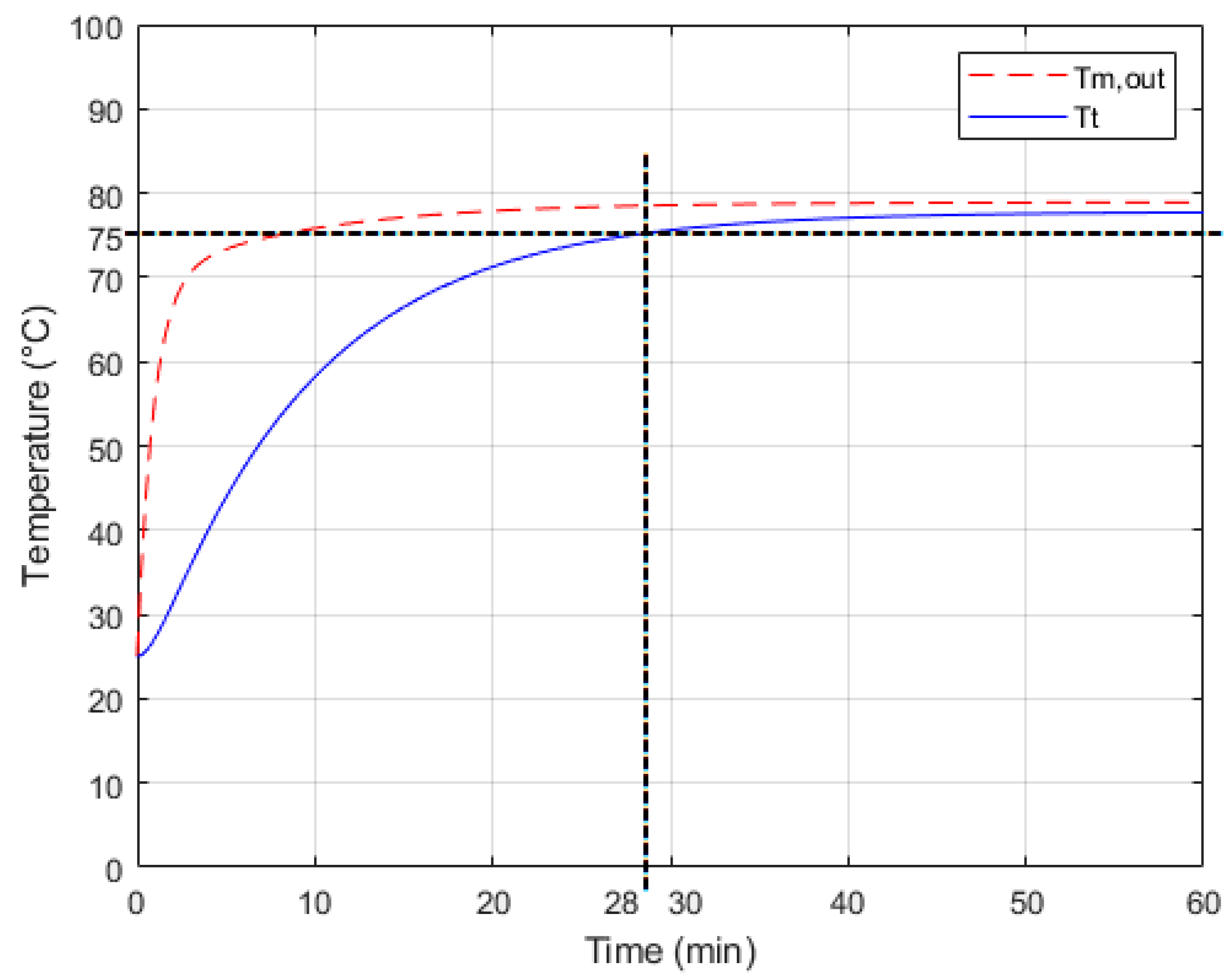The results of the simulations are presented in Figure 4 and Figure 5. More specifically, Figure 4 presents the modelled T m , o u t and T t temperatures in case of v = 100 l h ( = 2.78 · 10 − 5 m 3 s ) , while Figure 5 presents them in case of v = 200 l h ( = 5.56 · 10 − 5 m 3 s ) . The running time of the simulations was 1 hour in both cases.
.
In Figure 4 and Figure 5, it can be seen that the cooking tank temperature reaches 75°C, which is normally enough for the sterilization of foods. It can also be stated that this temperature is reached in less time with higher flow rate. With 100 l h , it took 38 minutes (see Figure 4), while with 200 l h , it required 28 minutes (see Figure 5). In addition, the maximum (final) tank temperature was 76.5°C in case of 100 l h and 77.7°C with 200 l h .

4. Experimentation

4.1. Experimental System

During the measurements, values of T c , e , T m , i n   ( = T c , o u t ) , T m , o u t   ( = T c , i n ) , T p , e , T t and v are measured. The pipes connecting the solar pot and the collector are insulated and their volume is neglected. As a result, we consider the mantle inlet water temperature and the solar collector outlet water temperature equal T m , i n = T c , o u t . The same goes for the mantle outlet water temperature and the solar collector inlet water temperature T m , o u t = T c , i n . The structure of the experimental system, installed at the campus of the Hungarian University of Agriculture and Life Sciences (Gödöllő, Hungary), is shown in Figure 2, the physically manufactured solar pot is presented in Figure 1 and the connected evacuated tube solar collector can be seen in Figure 6.

4.2. Experimental Results

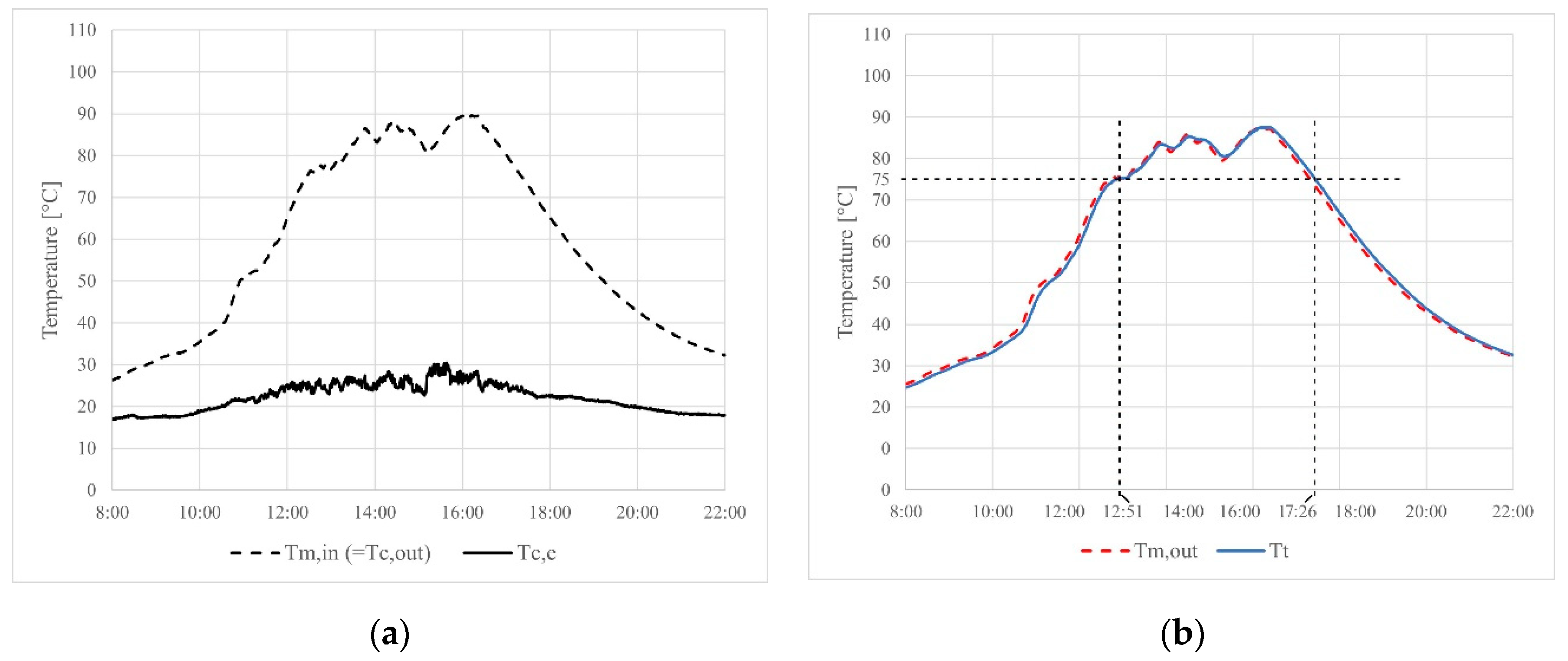
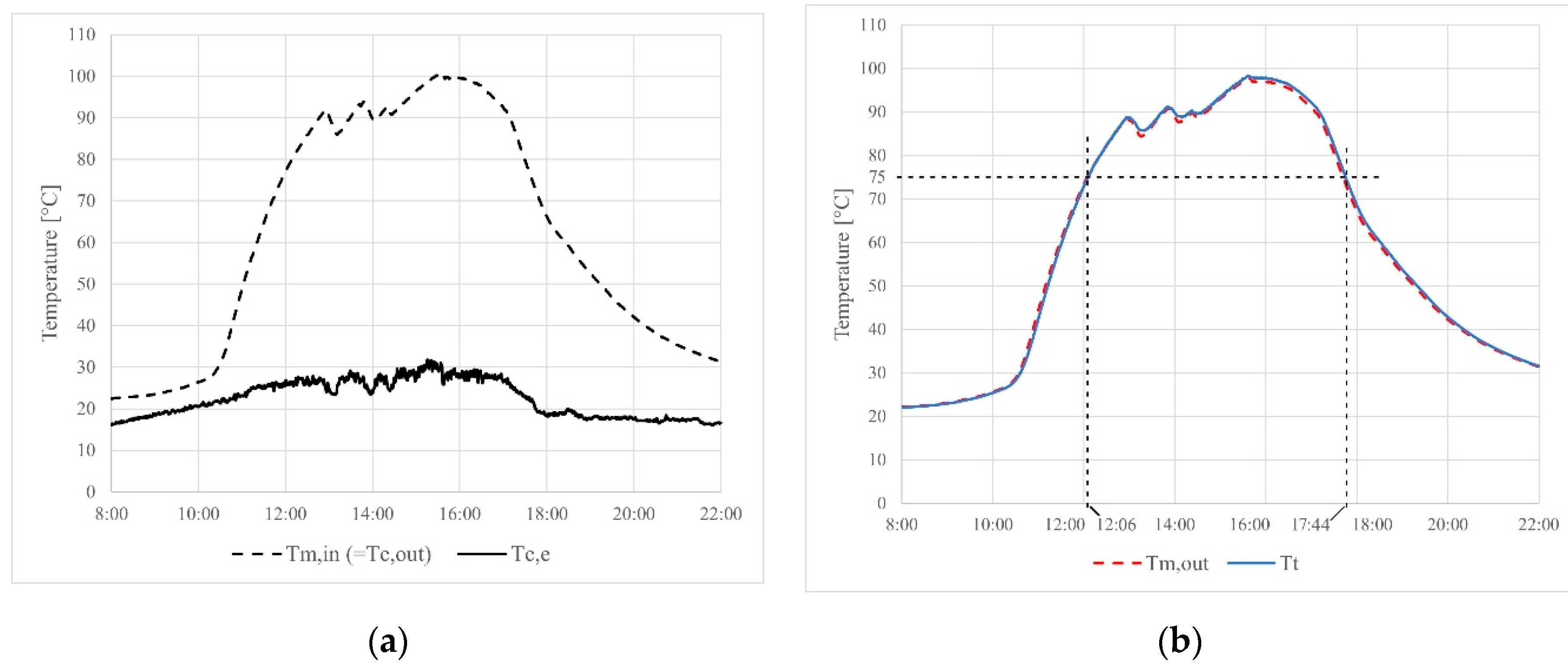
During the measurements, the same flow rates were used as in the simulations. The temperature of the solar pot’s environment ( T p , e ) was also constant 25°C as the temperature of the mobile container where the solar pot is located was set to this value with an air-conditioner. Figure 7 and Figure 8 show the measurement results of two days (26. 05. 2024. and 28. 05. 2024.) when the flow rate was set to 100 l h . 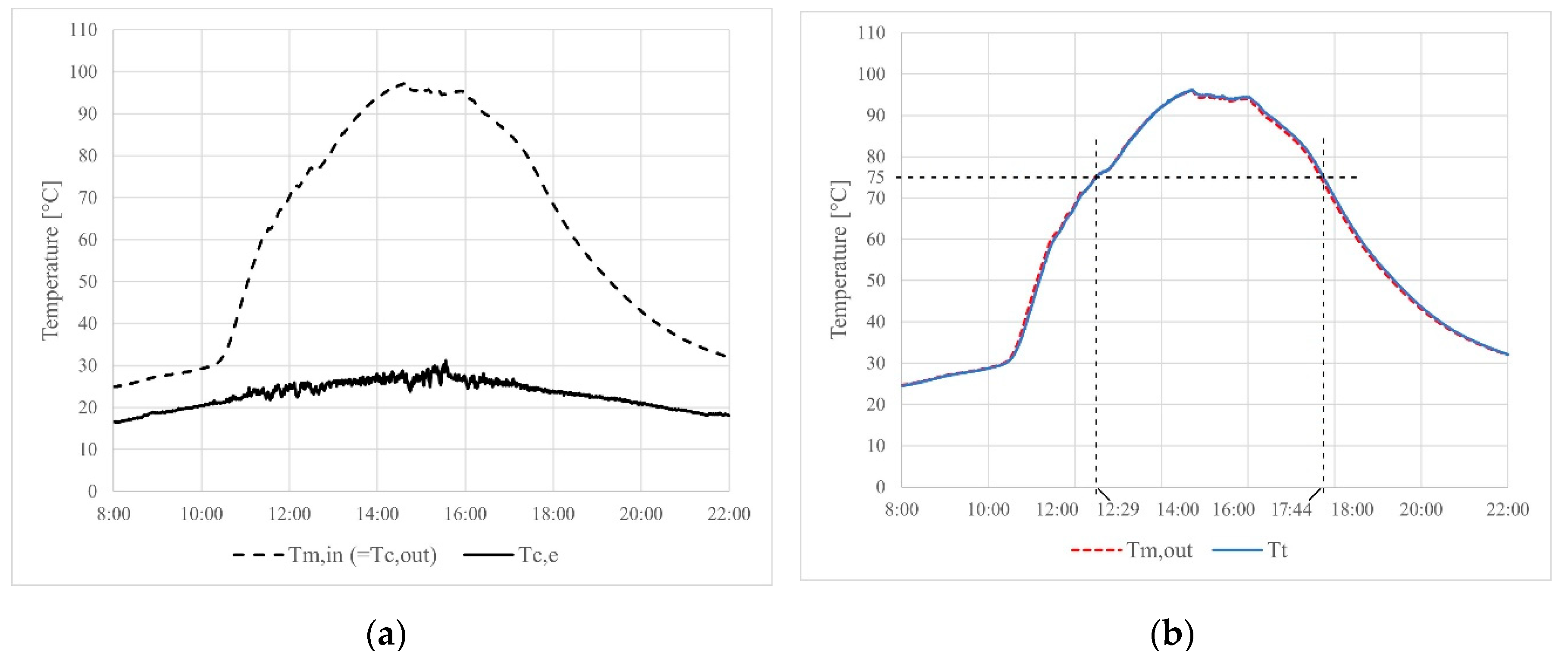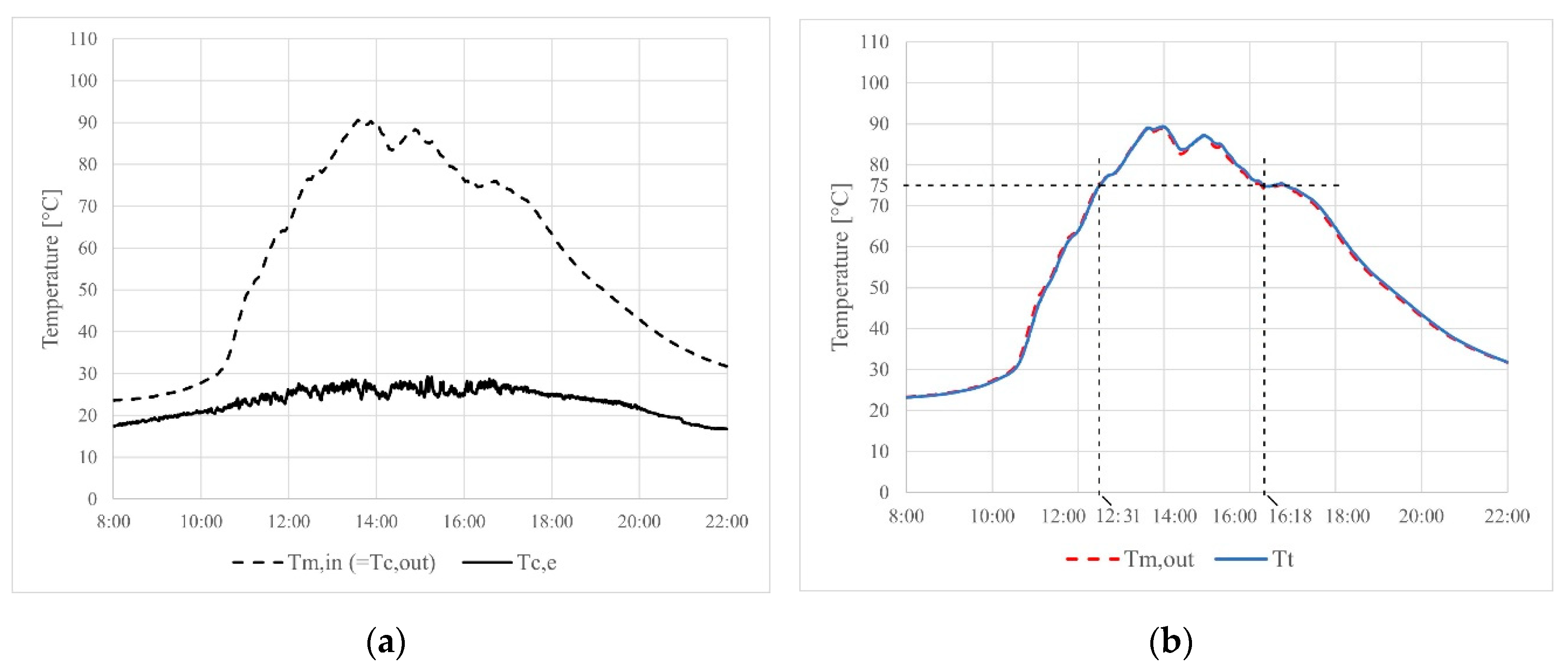In Figure 9 and Figure 10, the measured data of two days (29. 05. 2024. and 30. 05. 2024.) are presented when the flow rate was set to 200 l h . On the left side of the figures (a), the graphs of T m , i n   ( = T c , o u t ) and T c , e can be seen, on the right (b), there are the graphs of T m , o u t and T t .
Figure 7, Figure 8, Figure 9 and Figure 10 demonstrate that the cooking tank temperature reached the safe cooking temperature of 75°C during the measurements in the early afternoon, between 12:00 and 13:00. The temperature of the cooking tank was higher than this value until late afternoon, between 17:20 and 18:00. The only exception was on 30th May when the tank temperature decreased below 75°C at 16:18 due to the cloudier weather than usual. According to the measurements, it can be stated that the volumetric flow rate has no considerable influence on the heating. Both examined flow rate values made the safe cooking possible for a satisfactory time interval within each measured day. The measured values of T m , o u t and T t are almost equal, which is in accordance with the final modelled temperature values in the simulations (see Figure 4 and Figure 5).

5. Conclusions

In the paper, a new physically-based mathematical model was proposed and an experimental system was assembled for a recently invented solar pot. The solar pot, as an environmentally friendly technical tool, utilizes renewable solar heat, provided by a solar collector as the heat source, for cooking or heating foods, drinks or other liquids. Based on both the simulated and the measured results, the solar pot, containing an inner cooking tank (where the cooking or heating task is realized) and an outer mantle (connected directly to the solar collector), can be used successfully to cook or sterilize different dishes and liquids. In particular, based on measured data, the temperature level needed for heat treatment (75°C) can be maintained in the cooking tank for several hours (~5 hours, on the average) in a typical day in May in Hungary.
Future research plans include the investigation of how long does it take for the solar pot-collector system to cook different dishes (like pasta, meat etc.) in different seasons and weather conditions. The possibility and relevance of different types of auxiliary (not solar) heating solutions (in addition to the solar collector) may also be examined, in order to extend the operating period of the solar pot.

Acknowledgment: The research was supported by the project ‘The feasibility of the circular economy during national defense activities’ of 2021 Thematic Excellence Programme of the National Research, Development and Innovation Office under grant no.: TKP2021-NVA-22, led by the Centre for Circular Economy Analysis.

Author Contributions

Conceptualization, M.R. and R.K.; methodology, M.R., R.K. and L.Sz.; software, M.R.; investigation, M.R., G.G. and R.K.; resources, M.R., G.G., R.K. and L.Sz.; data curation, M.R. and G.G.; writing—original draft preparation, M.R. and R.K.; writing—review and editing, M.R., G.G., R.K. and L.Sz.; visualization, M.R. and G.G.; supervision, R.K. and L.Sz.; project administration, M.R., G.G., R.K. and L.Sz.; funding acquisition, G.G. and L.Sz. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the project ‘The feasibility of the circular economy during national defense activities’ of 2021 Thematic Excellence Programme of the National Research, Development and Innovation Office under grant no.: TKP2021-NVA-22, led by the Centre for Circular Economy Analysis.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support findings of this study are available from the corresponding author upon request.

Conflicts of Interest

The authors declare that they have no conflict of interest.

References

  1. Kalita, N.; Muthukumar, P.; Dalal, A. Performance investigation of a hybrid solar dryer with electric and biogas backup air heaters for chilli drying. Therm. Sci. and Eng. Prog. 2024, 52, 1–13. [Google Scholar] [CrossRef]
  2. Mehling, H. Use of phase change materials for food applications – state of the art in 2022. Appl. Sci. 2023, 13(5), 3354. [Google Scholar] [CrossRef]
  3. Saxena, A.; Cuce, E.; Tiwari, G. N.; Kumar, A. Design and thermal performance investigation of a box cooker with flexible solar collector tubes: An experimental research. En. 2020, 206, 1–15. [Google Scholar] [CrossRef]
  4. Bigelow, A. W.; Tabatchnick, J.; Hughes, C. Testing Solar Cookers for Cooking Efficiency. Sol. En. Advantages 2024, 4, 1–7. [Google Scholar] [CrossRef]
  5. USDA (Food Safety and Inspection Service, U.S. Department of Agriculture). Safe Minimum Internal Temperature Chart. Available online: https://www.fsis.usda.gov/food-safety/safe-food-handling-and-preparation/food-safety-basics/safe-temperature-chart (accessed on 06 June 2024).
  6. Gupta, P. K.; Misal, A.; Agrawal, S. Development of low cost reflective panel solar cooker. Materialstoday: Pro. 2021, 45, 1–4. [Google Scholar] [CrossRef]
  7. Saini, P.; Pandey, S.; Goswami, S.; Dhar, A.; Mohamed, M. E.; Powar, S. Experimental and numerical investigation of a hybrid solar thermal-electric powered cooking oven. En. 2023, 280, 1–12. [Google Scholar] [CrossRef]
  8. Hosseinzadeh, M.; Faezian, A.; Mirzababaee, S. M. Parametric analysis and optimization of a portable evacuated tube solar cooker. En. 2020, 194, 1–12. [Google Scholar] [CrossRef]
  9. Zhou, C.; Wang, Y.; Li, J.; Ma, X.; Li, Q.; Yang, M.; Zhao, X.; Zhu, Y. Simulation and economic analysis of an innovative indoor solar cooking system with energy storage. Sol. En. 2023, 263, 1–15. [Google Scholar] [CrossRef]
  10. Hosseinzadeh, M.; Sadeghirad, R.; Zamani, H.; Kianifar, A.; Mirzababaee, S. M. The performance improvement of an indirect solar cooker using multi-walled carbon nanotube-oil nanofluid: An experimental study with thermodynamic analysis. Renew. En. 2021, 165, 14–24. [Google Scholar] [CrossRef]
  11. Hussein, H. M. S.; El-Ghetany, H. H.; Nada, S. A. Experimental investigation of novel indirect solar cooker with indoor PCM thermal storage and cooking unit. En. Conv. and Man. 2008, 49, 2237–2246. [Google Scholar] [CrossRef]
  12. Getnet, M. Y.; Gunjo, D. G.; Sinha, D. K. Experimental investigation of thermal storage integrated indirect solar cooker with and without reflectors. Res. in Eng. 2023, 18, 1–14. [Google Scholar] [CrossRef]
  13. Kumar, R.; Adhikari, R. S.; Garg, H. P.; Kumar, A. Thermal performance of a solar pressure cooker based on evacuated tube solar collector. Appl. Therm. Eng. 2001, 21, 1699–1706. [Google Scholar] [CrossRef]
  14. Schwarzer, K.; Krings, T. Demonstrations- und Feldtest von Solarkochern mit temporärem Speicher in Indien und Mali. Abschlussbericht 1996 (in German).
  15. Buzás, J.; Farkas, I. Solar domestic hot water system simulation using blockoriented software. The 3rd ISES-europe Solar World Congress. CD-ROM Proceedings. København. Denmark. 2000, pp. 1-9.
  16. Castellanos, L. S. M.; Noguera, A. L. G.; Velásquez, E. I. G.; Caballero, G. E. C.; Lora, E. E. S.; Cobas, V. R. M. Mathematical modeling of a system composed of parabolic trough solar collectors integrated with a hydraulic energy storage system. En. 2020, 208, 1–16. [Google Scholar] [CrossRef]
  17. Kalogirou, S. A.; Panteliou, S.; Dentsoras, A. Modeling of Solar Domestic Water Heating Systems Using Artificial Neural Networks. Sol. En., 1999, 65, 335–342. [Google Scholar] [CrossRef]
  18. Brus, L.; Zambrano, D. Black-box identification of solar collector dynamics with variant time delay. Cont. Eng. Prac. 2010, 18, 1133–1146. [Google Scholar] [CrossRef]
  19. Zheng, J.; Febrer, R.; Castro, J.; Kizildag, D.; Rigola, J. A new high-performance flat plate solar collector. Numerical modelling and experimental validation. Appl. En. 2023, 355, 1–14. [Google Scholar] [CrossRef]
  20. Hottel, H. C.; Whillier, A. Evaluation of flat-plate collector performance, Trans. Conf. Use of Sol. En. 1955, 3. [Google Scholar]
  21. Buzás, J.; Farkas, I.; Biró, A.; Németh, R. Modelling and simulation aspects of a solar hot water system. Math. and Comp. in Sim. 1998, 48, 33–46. [Google Scholar] [CrossRef]
  22. Hilmer, F.; Vajen, K.; Ratka, A.; Ackermann, H.; Fuhs, W.; Melsheimer, O. Numerical solution and validation of a dynamic model of solar collectors working with varying fluid flow rate. Sol. En. 1999, 65, 305–321. [Google Scholar] [CrossRef]
  23. Mao, C.; Li, M.; Li, N.; Shan, M.; Yang, X. Mathematical model development and optimal design of the horizontal all-glass evacuated tube solar collectors integrated with bottom mirror reflectors for solar energy harvesting. Appl. En. 2019, 238, 54–68. [Google Scholar] [CrossRef]
  24. P. Géczyné Víg, Modelling of solar collector systems with neural network, PhD thesis, Szent István University, Gödöllő, 2007 (in Hungarian).
  25. Kicsiny, R. Multiple linear regression based model for solar collectors. Sol. En. 2014, 110, 496–506. [Google Scholar] [CrossRef]
  26. Hiris, D. P.; Pop, O. G.; Balan, M. C. Analytical modeling and validation of the thermal behavior of seasonal storage tanks for solar district heating. En. Rep. 2022, 8, 741–755. [Google Scholar] [CrossRef]
  27. Badescu, V. Optimal control of flow in solar collector systems with fully mixed water storage tanks. En. Conv. and Man. 2008, 49, 169–184. [Google Scholar] [CrossRef]
  28. Kicsiny, R. Black-box model for solar storage tanks based on multiple linear regression. Renew. En. 2018, 125, 857–865. [Google Scholar] [CrossRef]
  29. Bradley, J. Counterflow, crossflow and cocurrent flow heat transfer in heat exchangers: Analytical solution based on transfer units. Heat and Mass Trans. 2010, 46, 381–394. [Google Scholar] [CrossRef]
  30. Zohuri, B. Compact Heat Exchangers, Selection, Application, Design and Evaluation, Springer International Publishing, Switzerland, 2017. [CrossRef]
  31. Géczi, G.; Kicsiny, R. , Korzenszky, P. Modified effectiveness and linear regression based models for heat exchangers under heat gain/loss to the environment. Heat and Mass Trans. 2019, 55, 1167–1179. [Google Scholar] [CrossRef]
  32. Zavala-Río, A.; Santiesteban-Cos, R. Reliable compartmental models for double-pipe heat exchangers: An analytical study. Appl. Math. Mod. 2007, 31, 1739–1752. [Google Scholar] [CrossRef]
  33. Géczi, G.; Kicsiny, R. (inventors), Hungarian University of Agriculture and Life Sciences (owner), Apparatus for Preparing Food with Solar Energy and/or for Heating Liquid, Utility Model Protection, Hungarian Intellectual Property Office, patent number 5489, 2021 (in Hungarian).
  34. Cao, E. Heat Transfer in Process Engineering, 1st Edition, McGraw-Hill Education, ISBN: 9780071624084, 2010.
  35. Engineering toolbox. Available online: https://www.engineeringtoolbox.com/overall-heat-transfer-coefficient-d_434.html (accessed on 06 June 2024).
  36. Székely, L.; Kicsiny, R.; Hermanucz, P.; Géczi, G. Explicit analytical solution of a differential equation model for solar heating systems. Sol. En. 2021, 222, 219–229. [Google Scholar] [CrossRef]
Preprints 110095 g001
Figure 1. Photos of the solar pot.
Figure 1. Photos of the solar pot.
Preprints 110095 g001
Preprints 110095 g002
Figure 2. The solar pot and the experimental system.
Figure 2. The solar pot and the experimental system.
Preprints 110095 g002
Preprints 110095 g003
Figure 3. Computer realization of the mathematical model.
Figure 3. Computer realization of the mathematical model.
Preprints 110095 g003
Preprints 110095 g004
Figure 4. Result of the simulation in case of v = 100 l h
Figure 4. Result of the simulation in case of v = 100 l h
Preprints 110095 g004
Preprints 110095 g005
Figure 5. Result of the simulation in case of v = 200 l h
Figure 5. Result of the simulation in case of v = 200 l h
Preprints 110095 g005
Preprints 110095 g006
Figure 6. Photo of the solar collector [36].
Figure 6. Photo of the solar collector [36].
Preprints 110095 g006
Preprints 110095 g007
Figure 7. Measured values of T c , e , T m , i n ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 26. 05. 2024, between 8:00 and 22:00, when v = 100 l h .
Figure 7. Measured values of T c , e , T m , i n ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 26. 05. 2024, between 8:00 and 22:00, when v = 100 l h .
Preprints 110095 g007
Preprints 110095 g008
Figure 8. Measured values of T c , e , T m , i n   ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 28. 05. 2024, between 8:00 and 22:00, when v = 100 l h .
Figure 8. Measured values of T c , e , T m , i n   ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 28. 05. 2024, between 8:00 and 22:00, when v = 100 l h .
Preprints 110095 g008
Preprints 110095 g009
Figure 9. Measured values of T c , e , T m , i n   ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 29. 05. 2024, between 8:00 and 22:00, when v = 200 l h .
Figure 9. Measured values of T c , e , T m , i n   ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 29. 05. 2024, between 8:00 and 22:00, when v = 200 l h .
Preprints 110095 g009
Preprints 110095 g010
Figure 10. Measured values of T c , e , T m , i n   ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 30. 05. 2024, between 8:00 and 22:00, when v = 200 l h .
Figure 10. Measured values of T c , e , T m , i n   ( = T c , o u t ) on the left (a) and T m , o u t , T t on the right (b) on 30. 05. 2024, between 8:00 and 22:00, when v = 200 l h .
Preprints 110095 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated