Prerpints.org logo
Preprint
Article

Commutative Encryption and Reversible Watermarking Algorithm for Vector Maps Based on Virtual Coordinates

Altmetrics

Downloads

110

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 June 2024

Posted:

24 June 2024

You are already at the latest version

Alerts
Abstract
The combination of encryption and digital watermarking technologies is a trend to achieve full lifecycle data protection. Recently, reversible data hiding in encrypted domain (RDHED) has greatly aroused the interests of many scholars. But the fixed order of first encryption and then watermarking makes this kind of algorithms unsuitable to many applications. Commutative encryption and watermarking (CEW) technology realizes the flexible combination of encryption and watermarking, and suits more applications. However, most existing CEW schemes for vector maps are not reversible and unsuitable to high precision maps. To solve this problem, here we propose a commutative encryption and reversible watermarking (CERW) algorithm for vector maps based on virtual coordinates which are uniformly distributed on the number axis. The CERW algorithm consists of virtual interval step based encryption scheme and coordinate difference based reversible watermarking scheme. In the encryption scheme, the map coordinates are moved randomly by multiples of virtual interval step defined as distance between two adjacent virtual coordinates. In the reversible watermarking scheme, difference expansion (DE) technique is used to embed the watermark bit into the coordinate difference computed based on the relative position of a map coordinate in a virtual interval. Since the relative position of a map coordinate in a virtual interval keeps unchanged during the coordinate scrambling encryption process, the watermarking operation and the encryption operation don’t interfere with each other and the commutativity between encryption and watermarking achieves. Results show that: proposed method has high security, high capacity and good invisibility. In addition, the algorithm is not only applicable to polyline and polygon vector data, but also can be applied to sparsely distributed point data which the traditional DE watermarking algorithm often fails to watermark.
Keywords: 
Subject: Computer Science and Mathematics  -   Security Systems

1. Introduction

Vector maps are frequently used in many fields, such as navigation, land management, energy development, urban planning and public safety, which lead to an important and unique status for vector maps [1]. Protecting the privacy and integrity of vector map data is of great significance in promoting the healthy development of the geographic information industry [2]. Currently, encryption and digital watermarking technologies are the mainstream technical means to effectively protect the security of geographic information [3]. Encryption technology primarily addresses the issue of confidentiality in the process of information storage and transmission. Plaintext (the original readable information) is converted into ciphertext (the encrypted information) through specific algorithms to prevent unauthorized users from accessing and understanding the information. However, the security of encryption technology relies heavily on the management of the key; if the key is lost or stolen, then the encrypted information will be completely exposed [4]. Different from encryption technology, digital watermarking technology mainly solves the problems of copyright protection and data traceability. Normally, a specific kind of information (e.g., copyright information, identification, etc.) is embedded into digital media (e.g., images, audio, video, etc.) in an imperceptible way [5]. In particular, although digital watermarking is designed to be invisible to the human eyes or inaudible to the human ears, in reality, the watermark embedding alters the original data, and this impact needs to be kept within boundaries [6]. For vector maps, the combination of encryption and digital watermarking technologies is imperative to achieve full lifecycle data protection [7].
In recent years, algorithms for reversible data hiding in encrypted domain (RDHED) have been proposed [8,9,10,11,12], in which the plaintext data are first encrypted and then the additional information is embedded in the encrypted data. RDHED is suitable for scenarios where the data embedder is an unauthorized user and has no access to the original data. In RDHED, the original data can be recovered after additional data extraction, and this make RDHED very suitable for vector maps which have high requirements for data accuracy. However, existing RDHED mainly focus on raster images, and few RDHED algorithms for vector maps have been proposed. Peng et al [13] proposed an RDHED algorithm for 2D vector graphics based on a real-number reversible mapping model, which strikes a good balance between watermark invisibility, capacity and security. However, the watermark extraction can only be carried out in the ciphertext domain for this algorithm, while in practical applications watermark extraction in both ciphertext and plaintext domains are often required. Subsequently, Peng et al [14] proposed another RDHED algorithm for 2D vector graphics, which realizes watermark extraction in both ciphertext and plaintext domains and suits more application scenarios. Although not specially designed for vector maps, these algorithms have reference significance for encrypting and watermarking vector maps. Jang et al [15] proposed a crypto-marking technique for vector maps, which watermarks the map data at first and then encrypts the data using progressive perceptual encryption method. The watermarking and the progressive perceptual encryption are independent of each other. However, the fixed order of first marking and then encrypting in this method limits its application scenarios.
In the algorithms mentioned above, the order of encryption and watermarking is fixed, which is not flexible enough for practical applications. In order to realize flexible interchangeable operations between watermarking and encryption, some scholars further proposed commutative encryption and watermarking (CEW) schemes. These schemes can be categorized into three types according to the mechanism employed to achieve commutativity: separate domains based CEW, homomorphic encryption based CEW, and feature invariant based CEW.
Separate domains based CEW schemes achieve the commutativity by performing encryption and watermarking operations in two different domains. Jiang et al [16] proposed a CEW scheme based on orthogonal decomposition. The component coefficients of the orthogonal decomposition are independent of each other, while the composite vector is sensitive to any changes in the component coefficients. The 2D image can be orthogonally decomposed into two domains based on this property for encryption and watermarking respectively. This algorithm has no special requirements for encryption and watermarking, so it has high universality. But some plaintext information is exposed in this kind of schemes, leading to security problems.
Homomorphic encryption based CEW schemes achieve the commutativity by taking advantage of homomorphism. Lian [17] proposed a quasi-commutative watermarking scheme based on a homomorphic encryption method with an additive mechanism to encrypt the video as a whole, which can realize simple homomorphic watermarking operation but lacks robustness. For vector maps, Wu et al [18] encrypted quantized integer coordinates based on paillier homomorphic encryption and embedded the watermark by homomorphic operations in the ciphertext domain. Although homomorphic encryption algorithms can provide excellent security for the data, they suffer from the defects of computational complexity and low efficiency.
Feature invariant based CEW schemes fulfill the commutativity by embedding watermark information into a certain feature space which keeps unchanged during encryption or decryption process. Compared with the multimedia data such as images, vector maps have various spatial features, which make it more convenient to discover and construct some special invariants to realize the commutativity between encryption and watermarking. For example, Ren et al [19] constructed two feature invariants based on the sum of inner angles and the storage direction of two adjacent objects according to the inherent characteristics of vector map, and designed a CEW scheme based on these two feature invariants. But the watermark capacity of this algorithm is only half of the number of objects in a vector map. Li et al [20] proposed a new CEW algorithm for vector maps based on coordinate values which serve as feature invariants. Note that the above two algorithms are only applicable to polyline and polygon objects, unsuitable to point data. To achieve higher watermarking capacity, Ren et al [21] further proposed a vector map CEW method based on congruence relationship and geometric feature, in which the angles and the distance ratios are selected as the geometric features, and the watermark is embedded into the residuals of the congruence operations performed on the geometric features. The watermark capacity of this algorithm achieves 2 bits per vertex. For the improvement of robustness, Ren [22] went on to propose a CEW method for vector data based on singular value decomposition（SVD）, in which the singular values are selected as the feature invariants.
In literature, a few CEW schemes for vector maps have been proposed. However, most existing CEW algorithms focus on the watermark robustness. Few focus on the reversibility and suit the application scenarios that have high requirements for data accuracy. In this regard, Guo et al [23] proposed a lossless CEW algorithm for vector data, in which no data distortion is introduced after watermarking. But the watermark capacity is small. Tan et al [24] proposed a CEW algorithm based on zero watermarking and permutation encryption, and can be applied to high-precision vector maps. However, the algorithm is only applicable to vector maps represented by polylines and polygons and cannot be applied to points.
Different from the schemes mentioned above, this paper proposes a novel commutative encryption and reversible watermarking (CERW) method for vector maps, in which not only the commutativity between encryption and watermarking is achieved, but also the reversibility of watermarking is achieved. It means that the original ciphertext map without watermark can be recovered from the ciphertext map with watermark and the original plaintext map without watermark can be recovered from the plaintext map with watermark. The proposed CERW scheme is constructed based on virtual coordinates which uniformly distribute on the number axis. The commutativity between encryption and watermarking is achieved by using feature invariant which is defined as the relative position of a map coordinate in a virtual interval formed by two adjacent virtual coordinates. In the encryption part, the map coordinates are moved by random multiples of the virtual interval step. In the reversible watermarking part, the watermark bit is embedded into the difference computed based on the map coordinate’s relative position in a virtual interval using difference expansion (DE) technique. By introducing virtual coordinates, the proposed CERW scheme can achieve higher watermark capacity and better watermark invisibility than traditional DE watermarking algorithms. Furthermore, the proposed CERW scheme suits all kinds of vector maps, including point maps, such as POI map.
The remainder of this paper is organized as follows. Section 2 introduces some preliminaries involved in this paper, including the pseudo-random number generation method, difference expansion (DE) technique and principle of cosine-transform-based chaotic system (CTBCS). Section 3 describes the proposed algorithm in detail. Section 4 discusses the key parameters involved in the algorithm. Section 5 verifies the effectiveness and analyzes the performance of the proposed algorithm by implementing a series of experiments. Finally, Section 6 summarizes and outlooks the full work.

2. Preliminary

2.1. Pseudo-Random Numbers Generation Based on Hash Function and Streaming Cryptograph-y Algorithm

In cryptography, pseudo-random numbers are usually utilized to increase the unpredictability and security of the encryption process [25]. Hash function is a method that converts an input (information) of arbitrary length to an output of fixed length. In watermarking algorithms, hash function is usually chosen for data integrity checking, password storage and random number generation [26]. The common ones are MD5 (Message Digest Algorithm 5), SHA-1 (Secure Hash Algorithm) and SHA-2. SHA-256, SHA-384 and SHA-512 are algorithms subdivided under SHA-2. Among them, SHA-512 runs and processes data faster and is more secure than SHA-256 and SHA-384.
Stream cipher is a cryptographic method that generates a stream of ciphertext by performing an exclusive-or operation between a plaintext stream and a key stream, and can be used to provide high-quality, high-entropy pseudo-random number sequence with good statistical properties and randomness. Salsa 20 algorithm can realize fast encryption, which is a stream cipher algorithm with high security [27].
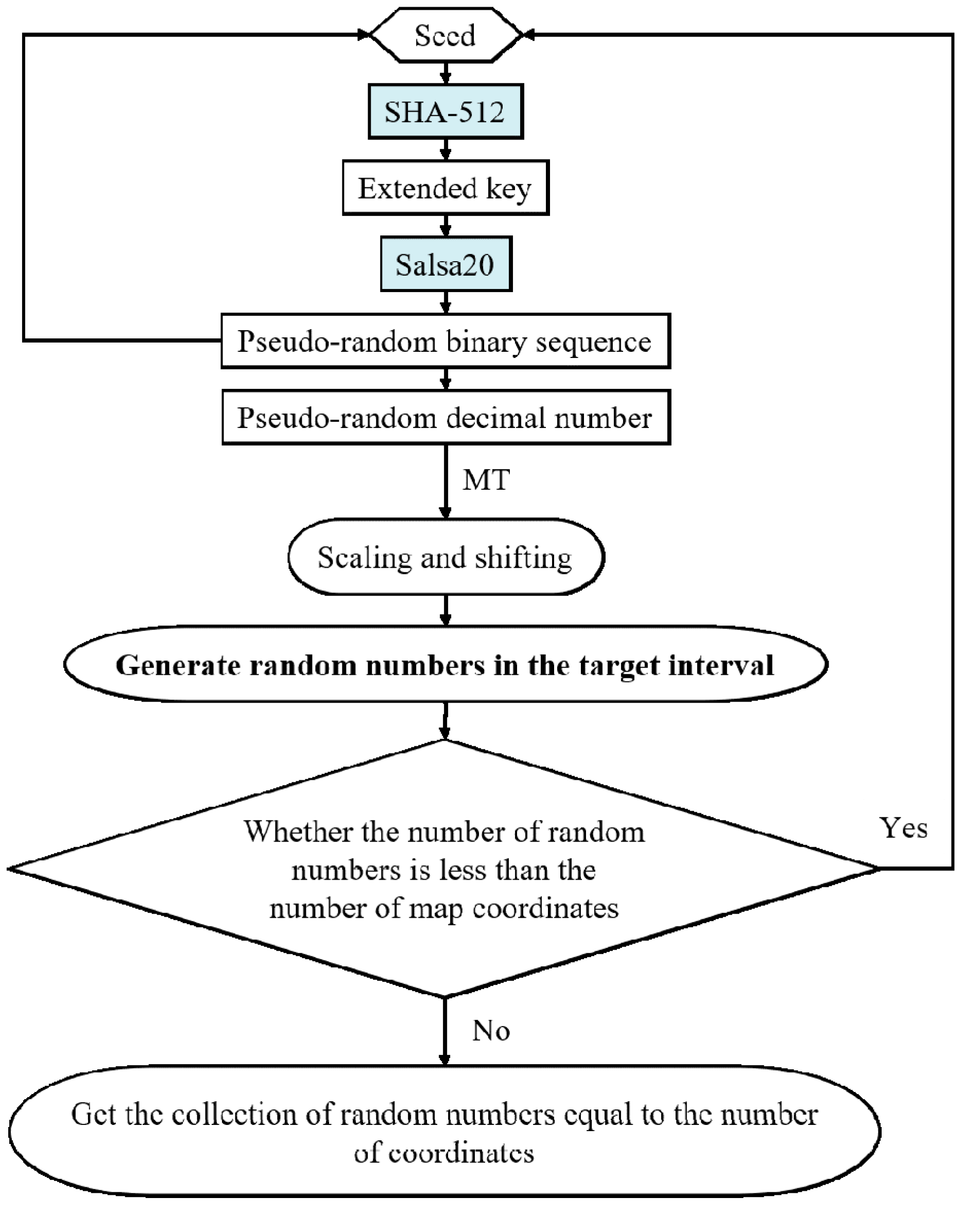
We choose SHA-512 and Salsa20 and design a SHA-512-Salsa20 generator to generate secure and reliable pseudo-random numbers. Specific steps are as follows:
Step 1: A seed is selected as the initial value input, and then the seed is input into SHA-512 to obtain the output of SHA-512 as the extended key. This extended key will be used as the key for the stream cipher.
Step 2: The Salsa20 algorithm is initialized using the extended key.
Step 3: Use the Salsa20 algorithm to generate a pseudo-random binary sequence，and then convert the sequence to a decimal number.
Step 4: Input the pseudo-random binary sequence generated in the previous step as a new seed into SHA-512 and obtain the output of SHA-512 as a new extended key. This step is to increase the randomness and enhance the security.
Step 5: In conjunction with the Mersenne Twister (MT) algorithm, the pseudo-random number generated in Step 3 is scaled and shifted using Eq. (1) in order to generate a random number within the target interval.
r_number = floor[(pr_number-a) / (b-a) * MT(c ,d)]
A pseudo-random number will be generated as a result of each run of the stream cipher algorithm. a denotes the minimum value of the generated pseudo-random numbers and b denotes the maximum value of the generated pseudo-random numbers. Here, a , b , c , d are all integers, p r _ n u m b e r is the generated pseudo-random number in the interval [ a , b ], f l o o r is the downward rounding function, M T is a function that generates random numbers based on the Mersenne Twister and r _ n u m b e r is a pseudo-random number generated by formula (1) that maps real values in the interval [ a , b ] to the interval [ c , d ] by scaling and shifting.
Step 6: Loop through Step 1 to 5 until a sufficient number of random numbers are obtained.
Preprints 110072 g001
Figure 1. Flowchart of the pseudo-random number generation
Figure 1. Flowchart of the pseudo-random number generation
Preprints 110072 g001

2.2. Difference Expansion (DE) Technique

Difference Expansion (DE) technique was earlier designed for and applied in raster image reversible watermarking, where pairs of pixel values are used to calculate the difference values, and the reversibility of the scheme is achieved by embedding the watermark bits through difference expansion [28]. Considering the low correlation and redundancy between vertices for vector data, Peng et al [29,30] explored and improved the difference expansion technique based on Wang [31], which embedded the watermark into the ratio set of the relative coordinates of all vertices of a 2D CAD engineering drawing to improve the watermarking capacity and imperceptibility. But the watermarking data integrity is destroyed if the watermark is extracted by referring to the vertices in reverse order. Subsequent algorithms based on histogram shifting, prediction error expansion, least significant bit substitution (LSB), and wavelet transform combined with difference expansion were devoted to improve the watermark capacity and visual quality.
DE is a reversible watermarking technique. The principle of watermark embedding is to calculate the difference for each pair of neighboring elements, and provide the watermark embedding space by expanding the difference to twice the original value. The smaller the difference value, the less the watermark embedding disturbs the data. Therefore, limiting the difference value to a small range can realize very small graphic distortion after watermark embedding. The fundamentals of the traditional DE technique are described in detail below.
During the watermark embedding stage, firstly, given a pair of neighboring elements of highly correlated carrier data x 1 ,   x 2 x 1   >   x 2 , an integer transformation is defined to compute their difference d and integer mean   m according to Equation (2). Then, a watermark bit w is embedded into the difference d according to Equation (3). Finally, the carrier data with embedded watermark x 1 w , x 2 w can be obtained from Equation (4).
d = x 1 - x 2 m = f l o o r x 1 + x 2 2
d ' = d   ×   2 + w
x 1 w = m + f l o o r d ' + 1 2 x 2 w = m - f l o o r d ' 2
For watermark extraction, firstly, the difference d ' and the integer mean m of the watermarked elements need to be computed according to Equation (5). Then, the original difference d is recovered and the watermark w is extracted by Equation (6). Finally, the original pair of elements x 1 , x 2 is constructed based on Equation (7).
d ' = x 1 w   - x 2 w m = f l o o r x 1 w + x 2 w 2
d = f l o o r d ' 2 w = d '   - d × 2
x 1 = m + f l o o r d + 1 2 x 2 = m - f l o o r d 2

2.3. Cosine Transform-Based Chaotic System (CTBCS)

Chaotic systems are widely used in the fields of information hiding and cryptography due to their unpredictability and initial value sensitivity. CTBCS [32] with two chaotic mappings as seed mappings is a composite chaotic system with lower computational complexity compared to high dimensional chaos, and more secure and reliable compared to low dimensional chaos. Therefore, CTBCS can be used for chaotic dislocation during watermark information generation to further enhance the security of the algorithm. Here, we use the existing Logistic mapping and Tent mapping as the seed mapping, which can be mathematically defined as:
Logistic   mapping :   x i + 1 = L ( h , x i ) = 4 h x i ( 1 - x i )
Tent   mapping   :   x i + 1 = T ( h , x i ) = 2 h x i                                     i f x i < 0.5 2 h 1 - x i                     i f x i ≥ 0.5
Here, the variable h is the control parameter of the Logistic mapping and the Tent mapping, h ∈ [ 0 , 1 ] .
CTBCS can be mathematically expressed as:
x i + 1 = cos ( π ( F ( a , x i ) + G ( b , x i ) + β ) )
where F ( a , x i ) and G ( b , x i ) are two known chaotic mappings as seed mappings, a and b are the parameters of the seed mappings, and β is the transformation constant (in this paper, we set β = - 0.5). Set parameter a = h and parameter b = 1   - h . h is the key parameter of the generated chaotic mapping.

3. The Proposed Method

3.1. Basic Idea

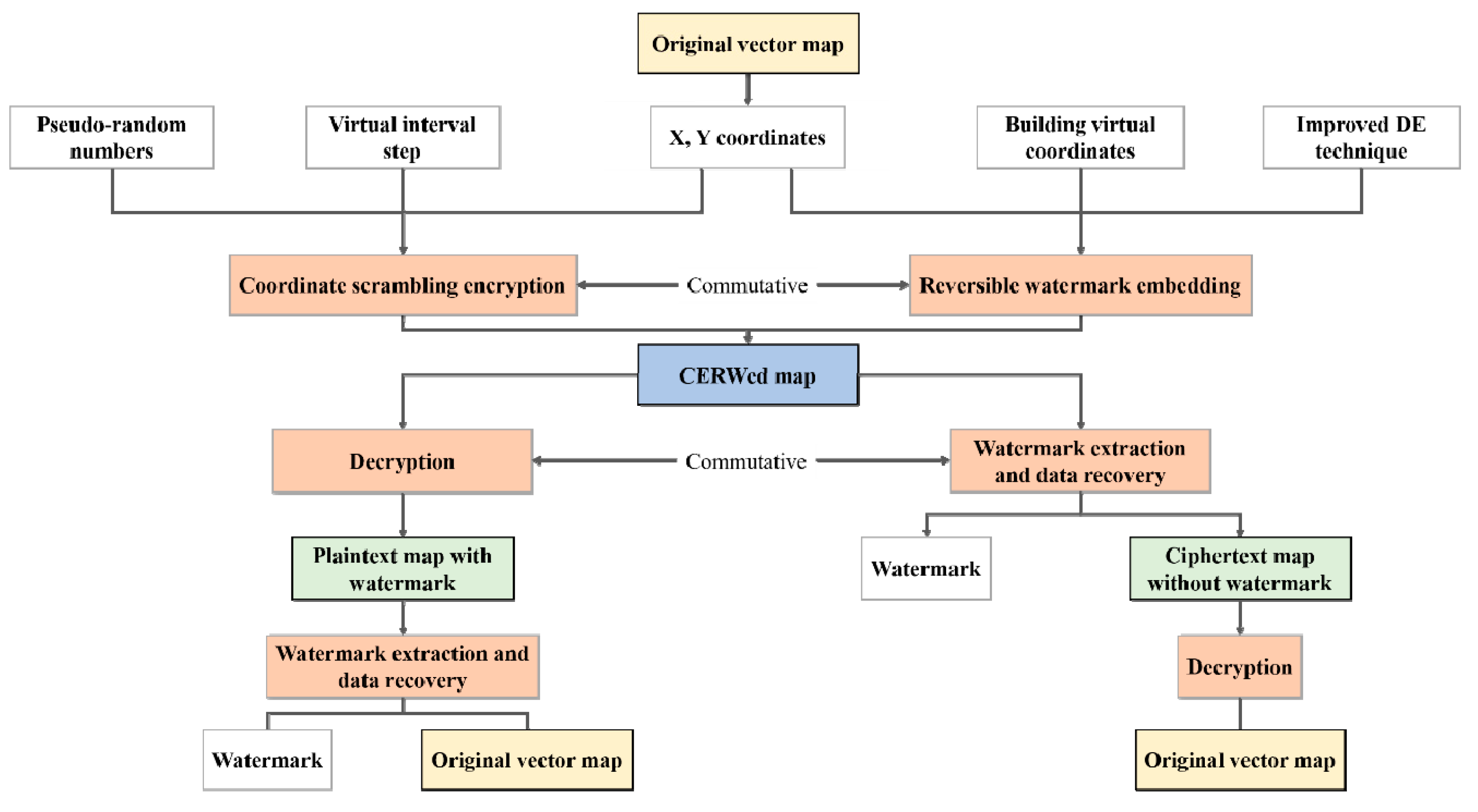
We devise a new coordinate scrambling encryption scheme and a new reversible watermarking scheme for vector map data based on virtual coordinates in the proposed CERW scheme. In the encryption scheme, we design a pseudo-random number generator by combining SHA-512 and Salsa20, and realize coordinate scrambling based on a virtual interval step and pseudo-random numbers. In the watermarking scheme, we improve the traditional DE technique based on virtual coordinates, and finally realize reversible embedding of watermark and lossless recovery of original data using improved DE technique. Since the relative position of each coordinate in the virtual interval keeps unchanged in the coordinate scrambling process, both the difference computed based on the coordinate relative position and the watermark embedded in the difference are not affected by the coordinate scrambling, so the encryption operation and the watermarking operation do not interfere with each other, and the combination of the two can build the CERW scheme. The framework of the proposed scheme is shown in Figure 2.
Preprints 110072 g002
Figure 2. Framework of the proposed CERW scheme
Figure 2. Framework of the proposed CERW scheme
Preprints 110072 g002

3.2. Coordinates Scrambling Encryption Scheme Based on Virtual Interval Step

In the map coordinates encryption scheme, we first design a pseudo-random number generator using hash function and stream cipher ideas as described in section 2.1. Then, we use geometric scrambling for all x and y coordinates respectively based on a certain integer virtual interval step and the pseudo-random numbers generated by the pseudo-random number generator, where the interval step and the seed of the pseudo-random number generator are used as the encryption key. The following subsections give the encryption method for the x-coordinates, and the encryption scheme for the y-coordinates is the same as that for the x-coordinates.

3.2.1. Coordinates scrambling based on virtual interval step

Scrambling encryption is an encryption technique that makes the original data difficult to decipher and use by changing the order or structure of the data. The underlying logic of vector map scrambling encryption is to destroy the data neighborhood correlation and spatial ordering [33]. Vector map data consists of spatial and attribute data that describe geographic entities in the form of geometric elements such as points, polylines, and polygons. The vector map scrambling encryption method is mainly used on the spatial coordinates.
Coordinates scrambling using the virtual interval step and pseudo-random numbers generated by a secure and efficient generation method is a feasible scrambling encryption method, which can achieve secure reversibility of the algorithm and smaller consumption (both in time and computation). This method moves the coordinates randomly by multiples of the virtual interval step. Take x coordinates as an example. First, virtual intervals are divided on the x-coordinate axis according to the virtual interval step l t shown as Figure 3. Then a certain pseudo-random number generation method is applied to generate random numbers r i . And finally the coordinates are dislocated using equation (11). The range of each coordinate move is a random multiple of the interval step. It is obvious that the interval step l t and the random number r i are the essential keys of the encryption scheme in the above encryption process. Equation (12) shows the process of coordinate recovery, which is the inverse operation of the disordered encryption mentioned above. The scrambling method for the y coordinates is the same as for the x coordinates.
x i * = x i + r i   l t
x i = x i *   - r i   l t

3.2.2. Encryption of the vector map

The vector map is encrypted based on the coordinates scrambling method described above. The encryption operation can be performed on both original and watermarked maps. Take the x coordinates as an example. The algorithm steps are as follows.
Step 1: Loop to obtain map coordinates. For a given map, get the set of coordinates x 1 o , … , x i o , … , x n o   ( i ∈ 1 , 2 , … , n ) .
Step 2: Adjust the position of each coordinate’s decimal points. According to Equation (13), adjust the coordinate’s decimal point to get the integer part x i and decimal part f of the adjusted coordinate. P denotes the number of digits that the decimal point moves to the right, in this paper, P m a x = 6. The decimal part of the adjusted coordinate is not involved in the encryption process, and the subsequent operations are based on the integer coordinate x i . Save the value of P as the key E _ K 0 .
x i = f l o o r x i o × 10 P                                                                         P ≤ P max f = x i o × 10 P   - f l o o r x i o × 10 P                                     P ≤ P max
Step 3: Coordinate disorder. According to Equation (11) in section 3.2.1, combine the interval step l t and the random number r i to calculate the dislocated coordinate x i * , where l t is set to an odd integer number and r i is generated by the SHA-512-Salsa20 generator described in Section 2.1. The interval step l t is saved as the key E _ K 1 , and the seed of the SHA-512-Salsa20 generator is saved as key E _ K 2 .
Step 4: Generate the final encrypted coordinate. First, integrate the dislocated integer part x i * and the original decimal part f to form a disordered float coordinate x i t as Equation (14). Then, Move the decimal point of x i t to the left by P digits to generate the final encrypted coordinate x i e as Equation (14).
x i t =   x i * + f x i e = x i t × 10 - P
Step 5: Repeat Step 2 to Step 4 until all the vertex coordinates of the vector map are encrypted.

3.2.3. Decryption of the vector map

Vector map decryption is an inverse process of encryption. The decryption operation can be performed on both the original encrypted map and watermarked encrypted map. Take the x coordinates as an example. The specific steps are as follows.
Step 1: Loop to obtain the encrypted map coordinates X e = x 1 e , … , x i e , … , x n e .
Step 2: Adjust the position of each encrypted coordinate’s decimal point based on the E _ K 0 to obtain the encrypted integer part x i * and the decimal part f as Equation (15).
x i * = f l o o r x i e × 10 E _ K 0 f = x i e × 10 E _ K 0   - f l o o r x i e × 10 E _ K 0
Step 3: Obtain the decrypted integer part x i according to Equation (12), where l t = E _ K 1 and r i is generated by the SHA-512-Salsa20 generator based on the seed E _ K 2 .
Step 4: The original coordinate is obtained according to Equation (16).
x i o = ( x i + f ) × 10 - E _ K 0
Step 5: Repeat Step 2 to Step 4 until all the encrypted coordinates are decrypted.

3.3. Reversible Watermarking Scheme Based on Improved Difference Expansion (IDE)

We utilize virtual coordinates to make improvements to traditional DE technique. In our proposed IDE watermarking scheme, the watermark embedding domain consists of the difference values with virtual coordinates as references. Although both the watermarking scheme and the encryption scheme are based on coordinate modifications, the encryption scheme does not change the watermark embedding domain, so the proposed watermarking scheme is commutative with the encryption scheme. The watermarking scheme includes watermark generation, watermark embedding, and watermark extraction and data recovery. In the watermark generation stage, the original watermark sequence is scrambled before embedding using the CTBCS mapping mentioned in Section 2.3. In the watermark embedding stage, the virtual coordinates are first generated based on the virtual interval step l t , and then the differences are calculated based on the relative positions of map coordinates in virtual intervals, and the watermark is embedded in the difference using DE technique to generate the watermark-containing map. In the watermark extraction stage, the virtual coordinates consistent with those in the embedding stage are generated with the assistance of the watermarking key, and the differences are computed as in the watermark embedding stage. The watermark bits are extracted from the differences according to DE technique to verify the data source. Data recovery is based on the inverse process of difference expansion. The following is a detailed description of the watermarking scheme for the x-coordinates as an example, and the watermarking scheme for the y-coordinates is the same as that for the x-coordinates.

3.3.1. Differences Calculation Based on Virtual Coordinates

Vector maps consist of points, polylines and polygons represented by coordinates. A prerequisite for using difference expansion is the high correlation between the neighboring coordinates in order to obtain a small coordinate difference to ensure that the data distortions introduced by DE watermarking are not significant. In practice, the neighboring coordinates of many kinds of maps are not highly correlated, leading to large coordinate differences and failed watermark embedding. So we propose to construct virtual coordinates to overcome this problem. Taking the virtual coordinates as the reference points, the differences between the actual coordinates and the neighboring virtual coordinates are calculated. In this way, the differences can be controlled by adjusting the virtual interval step which the virtual coordinates are constructed based on. The virtual coordinates construction and the coordinate differences calculation are shown in Figure 3.
Here, take the x-coordinates as an example to illustrate in detail the steps of differences calculation based on virtual coordinates.
Step 1: Construct virtual points x ^ i ( i = 0 , 1 , . . . ) on the x-coordinate axis based on the virtual interval step l t according to Equation (17). l t is set to be an odd integer.
x ^ i = l t   ×   i
Step 2: For any coordinate x i , if x i doesn’t coincide with any virtual coordinate, then calculate the left adjacent virtual coordinate x ^ left and the right adjacent virtual coordinate x ^ right , as shown in Equation (18).
x ^ left = l t × x i l t x ^ right = l t × x i l t
If x i coincides with a certain virtual coordinate, then the left adjacent virtual coordinate x ^ left and the right adjacent virtual coordinate x ^ right are computed according to Equation (19).
x ^ left = l t × ( x i l t - 1 ) x ^ right = l t × ( x i l t + 1 )
Step 3: Choose the virtual coordinate closest to x i as the reference coordinate. Then the difference between the actual coordinate x i and the reference coordinate is calculated according to Equation (20). d i is the direct carrier of the hidden watermark.
d i = 0   if   x i - x ^ left = x ^ right - x i x i - x ^ left   if   x i - x ^ left < x ^ right - x i x ^ right - x i   if   x i - x ^ left > x ^ right - x i

3.3.2. Reference Coordinate Flag Map

There exist three cases for the reference coordinate of each actual coordinate x i . Case 1: the reference coordinate is the left adjacent virtual coordinate of x i ; Case 2: the reference coordinate is the right adjacent virtual coordinate of x i ; Case 3: the reference coordinate is x i itself if x i coincides with a certain virtual coordinate. A reference coordinate flag map F is defined to record the reference coordinate of each actual coordinate.
F = f i | f i ∈ - 1 , 0 , 1 , i = 1 , … , n
f i = - 1 if the reference coordinate of x i belongs to case 1; f i = 1 if the reference coordinate of x i belongs to case 2; f i = 0 if the reference coordinate of x i belongs to case 3.

3.3.3. Watermark Generation

Given that the original watermark information W o = { b 1 , b 2 , … … , b t } is a binary sequence of length t. A one-dimensional chaotic sequence W = { w 1 , w 2 , … … , w t } is generated according to the CTBCS mapping mentioned in Section 2.3. This step is to enhance the security of the watermark information. The key parameter for saving the CTBCS mapping is recorded as W _ K 0 , which can recover the original watermark information after watermark extraction. The chaotic sequence   W is to be embedded into the map.

3.3.4. Watermark Embedding

Watermark embedding can be performed in both plaintext and ciphertext domains. The specific steps for watermark embedding are given as follows.
Step 1: Obtain all vertex coordinates of the map. For each coordinate, adjust the position of the coordinate’s decimal point to get the integer coordinate x i and the fractional part f according to Equation (13). The subsequent watermark embedding processes are all based on the integer coordinate x i . The fractional part f is not involved in the watermark embedding.
Step 2: Based on the method described in section 3.3.1, construct the virtual coordinates, determine the reference coordinate of x i , and compute the difference d i between the integer coordinate x i and the reference coordinate.
Step 3: Assign the corresponding flag to f i in F described in section 3.3.2 according to the determined reference coordinate of x i .
Step 4: Embed one watermark bit into d i using DE technique described in section 2.2 and obtain the watermark-containing difference d i w .
Step 5: The integer watermarked coordinates x i w is computed based on Equation (22).
x i w = x ^ left + d i w   if   f i = - 1 x i + d i w   if   f i = 0 x ^ right   - d i w   if   f i = 1
If f i = 0 and d i w > 0 , reassign -1 to f i after the bit insertion to amend the flag map.
Step 6: Integrate the watermarked integer part x i w and the original decimal part f to form a watermarked float coordinate x i w _ t as Equation (23). Then, Move the decimal point of x i w _ t to the left by   P digits to generate the final watermarked coordinate x i o _ w as Equation (23).
x i w _ t = x i w + f x i o _ w = x i w _ t × 10 - P
Step 7: Repeat Step 1 to Step 6 until all the coordinates are watermarked.
The interval step l t , the reference coordinate flag map F , and the value of P are kept as the watermarking key W _ K 1 for the subsequent watermark extraction and data recovery.

3.3.5. Watermark Extraction and Data Recovery

The watermark extraction and map decryption in the proposed CERW scheme are separable. The watermark extraction and data recovery can be done in both ciphertext and plaintext domains. The watermark information is extracted directly from the watermarked difference computed based on the watermarked coordinate’s relative position in a virtual interval. The original differences can be recovered based on the DE technique and then the original coordinates can be recovered using the original differences. The steps for extracting the watermark from the watermarked coordinates are described in detail below.
Watermark extraction:
Step 1: Read W _ K 1 to determine the virtual interval step l t , the reference coordinate flag map F , and the value of P.
Step 2: Obtain all the coordinates of the watermarked map. For each coordinate, get the watermarked integer part x i w and the fractional part f as Step 1 in watermark embedding does. Watermark extraction is based on the integer coordinate x i w .
Step 3: Construct virtual coordinates based on the virtual interval step l t and determine the reference coordinate of x i w based on the reference coordinate flag map F . Calculate the watermarked difference d i w between the reference coordinate and x i w .
Step 4: Extract one watermark bit from d i w according to Equation (24).
w = d i w mod   2
Step 5: Repeat Step 2 to Step 4 until all the watermarked coordinates are used to extract the watermark bits.
Step 6: Arrange all the detected bits to form the detected chaotic sequence W ' = { w 1 ' , w 2 ' … … , w t ' } . Decrypt the chaotic sequence W ' to obtain a sequence W o ' = { b 1 ' , b 2 ' , … … , b t ' } by using W _ K 0 . W o ' can be compared with the original watermark information W o to verify the map data consistency.
Data recovery:
Step 1: The original difference can be recovered according to Equation (25).
d i = floor d i w 2
Step 2: Then the original integer coordinates x i can be obtained based on Equation (26).
x i = x ^ left + d i   if   f i = - 1 x i w   if   f i = 0 x ^ rig h t   - d i   if   f i = 1
Step 3: Finally, the original float coordinate can be recovered according to Equation (27).
x i o = ( x i + f ) × 10 - P
Step 4: Repeat Step 1 to Step 3 until all the original coordinates are recovered losslessly.

4. Discussion of Some Parameters

4.1. The Interval Step l t

In the proposed scheme, the virtual interval step l t is a decisive parameter for the virtual coordinates construction and affects the magnitudes of the data distortions introduced by DE watermarking. A larger l t leads to bigger differences, resulting more significant data distortions after watermarking. In order to ensure the data distortions are within the data accuracy tolerance τ, l t mustn’t be too large.
To meet the data accuracy tolerance τ, the offset between the watermarked coordinate x i w and the original coordinate x i should be not greater than 10 P τ , namely x i w   - x i ≤ 10 P τ . In order to satisfy this inequality, according to the principle of DE watermarking, 2 d i + w - d i ≤ 10 P τ can be set up. Because w ∈ { 0 , 1 } , it is enough to satisfy only d i + 1 ≤ 10 P τ . And it is sufficient to satisfy l t   / 2 + 1 ≤ 10 P τ Since 0 < d i < l t   / 2 . So l t ≤ 2 ( 10 P τ - 1 ) is obtained. Besides this, l t is an odd integer number with the minimum value of 1. That means, as long as the value of l t is in the interval [1,   2 ( 10 P τ - 1 ) ], all the coordinate differences d i computed based on the virtual coordinates can be used for embedding the watermark without affecting the usability of the watermarked data and the data distortions introduced by watermarking are sure to be within the data accuracy tolerance τ.

4.2. Pseudo-Random Number r i

There are two considerations for the pseudo-random number r i . The first one is that the range of the ciphertext map encrypted using r i should be consistent with the range of the plaintext map for the sake of visual rationality. And the second one is that the differences between the encrypted coordinates and the original coordinates are big enough to destroy the data usability.
For the first consideration, x min ≤ x i * ≤ x max can be set up. That is x min ≤ x i + r i l t ≤ x max . And r i needs to meet x min - x i l t ≤ r i ≤ x max - x i l t . For the second consideration, the difference between x i * and x i should be greater than the data accuracy tolerance τ. That is r i   l t > 10 P τ or r i l t < - 10 P τ . In other words, r i > 10 P τ l t or r i < - 10 P τ l t needs to be satisfied. To sum up, the pseudo-random number r i generated by the SHA-512-Salsa20 generator should meet the two considerations to be used for producing an effective ciphertext map.

5. Experiments and Results

5.1. Experimental Data and Parameter Settings

The experiments were implemented in VS2013 on Windows 10 using python language. Three shapefile datasets of different types are chosen as original vector maps listed in Table 1 and shown in Figure 4a-c. The original watermark image is a binary image of 64 × 64 pixels. The experimental parameters are set as follows: CTBCS mapping parameter h = 0.5, parameter P = 6, the virtual interval step l t = 1 . In the pseudo-random number generator, the seed is set to "666".

5.2. Result Maps Visualization

The original vector maps are performed commutative encryption and reversible watermarking (CERW) operations using the proposed algorithm. The result maps are shown in Figure 5 and Figure 6. Figure 5 displays the CERWed maps. Figure 5a-c display the encrypted-watermarked (E-Wed) maps which are obtained by performing encryption operation first and reversible watermarking operation afterwards to the original vector maps. Figure 5d-f display the watermarked-encrypted (W-Eed) maps obtained by performing reversible watermarking operation first and then encryption operation to the original vector maps. Figure 6 shows the recovered plaintext maps without watermark. Figure 6a-c show the recovered-decrypted (R-Ded) maps obtained by performing watermark extraction and data recovery at first and then decryption to the CERWed maps. Figure 6d-f show the decrypted-recovered (D-Red) maps obtained by performing decryption at first and then watermark extraction and data recovery to the CERWed maps. As shown in Figure 5, there is no any clue about the original maps left in the CERWed maps. And the recovered plaintext maps shown in Figure 6 are identical with the original maps visually.

5.3. Commutativity

In order to verify that the encryption process and the reversible watermarking process in the proposed scheme are commutative, it is necessary to compare the E-Wed maps produced by the operation sequence of encryption and watermarking with the W-Eed maps produced by the operation sequence of watermarking and encryption. If the two kinds of maps are consistent correspondingly, then the commutativity between the encryption process and the reversible watermarking process is proved.
Similarly, the commutativity between the watermark extraction and data recovery process and the decryption process in the proposed scheme can be verified by evaluating the consistency between the R-Ded maps produced by watermark extraction and data recovery first and decryption afterwards and the D-Red maps produced by decryption first and watermark extraction and data recovery afterwards. Besides, the watermarks extracted before and after decryption are compared. If the R-Ded maps and the D-Red maps are consistent correspondingly, and the watermarks extracted before and after decryption are identical, then the commutativity between the watermark extraction and data recovery process and the decryption process is proved.
In order to evaluate the difference between the E-Wed map and the W-Eed map, and the difference between the R-Ded map and the D-Red map, the root mean square error (RMSE) is introduced as shown in Equation (27). The value of the RMSE is closer to 0, the two compared maps are more similar. Table 2 displays the comparison results between the E-Wed maps and the W-Eed maps. It can be found from Table 2 that all the vertices in both maps are identical, and their RMSEs are 0, which suggests the E-Wed maps are exactly the same as the W-Eed maps. Therefore, it is obvious that the encryption process and the reversible watermarking process in the proposed scheme are commutative.
RMSE = 1 n ∥ V   -   V ' ∥ = 1 n   ∑ i = 1 n [   V i   -   V i '   ] 2
Table 3 displays the comparison results between the R-Ded maps and the D-Red maps. It also can be found from Table 3 that the R-Ded maps and the D-Red maps are exactly the same. Besides, the bit error ratio (BER) of the extracted watermark information is also introduced to measure the difference between the original watermark and the extracted watermark. The definition of BER is shown in Equation (28).
BER = n e L w
where n e denotes the number of extracted wrong watermark bits and L w is the watermark length.
Table 4 displays BER results of the watermarks extracted before and after decryption. The second and third columns in Table 4 show BERs of the watermarks extracted before decryption, and the fourth column shows BERs of the watermarks extracted after decryption. All the BER values displayed in Table 4 are 0, which shows that the watermarks extracted before decryption are exactly the same as the watermarks extracted after decryption. Table 3 and Table 4 jointly prove the commutativity between the watermark extraction and data recovery process and the decryption process in the proposed scheme.

5.4. Encryption Security Analysis

5.4.1. Effectiveness of the encryption scheme

To verify the security of the proposed encryption scheme, we compare the experimental results before and after encryption. A reliable scheme needs to demonstrate the unavailability of the data after encryption as well as the availability after decryption. The encryption effect is shown in Figure 7a-c, where the spatial relationships of the original maps are totally destroyed and the encrypted maps are completely unavailable, making it difficult to obtain any plaintext information directly from the ciphertext map. Figure 7d-f shows that the decrypted maps are visually consistent with the original maps, indicating good decryption effect.
In addition to visual verification, RMSE is used as a quantitative index to illustrate the encryption and decryption effect. The encrypted maps and decrypted maps are compared with the original maps respectively, and the RMSEs between them are calculated. The results are displayed in Table 5. It can be found in Table 5 that, due to the coordinates geometrical scrambling encryption, the RMSEs between the encrypted maps and the original maps are very large, which suggests pretty good encryption effect. The RMSEs between the decrypted maps and the original maps are 0 as shown in Table 5, quantitatively proving the effectiveness of the proposed decryption algorithm. Therefore, the effectiveness of the proposed encryption scheme is proved visually and quantitatively.

5.4.2. Key Space

The key space is the set of all possible values of a key used in cryptography to encrypt and decrypt data. The size of the key space affects the security of a cryptosystem. A larger key space usually implies higher security and the size of the key space should be larger than the standard requirement (i.e., 2100)[20]. The encryption key for the proposed algorithm which is also the decryption key includes the parameter P , the virtual interval step l t , and the seed of the SHA-512-Salsa20 generator. The maximum value of the parameter P is set to 6 in this paper. So there are 7 possible values for P . The value range for l t is [1, 2 ( 10 P τ - 1 ) ] suggesting that there are 2 ( 10 P τ - 1 ) possible values for   2 ( 10 P τ - 1 ) . For the seed of the SHA-512-Salsa20 generator, its length is 512 bits indicating that there are 2 512 possible values for it. Based on the possible values for P , l t and the seed, the key space of the proposed scheme is given as: KeySpace =   7 × 2 ( 10 P τ - 1 ) × 2 512 > 2 512 , which is sufficiently larger than the standard requirement. Therefore, the key space of the proposed scheme is large enough to resist the brute force attack and has good security.

5.4.3. Key Sensitivity

High sensitivity for key is of great importance for encryption algorithms, which means that small adjustments can make a huge difference, thus making it impossible for an illegal user to decipher the unreadable data [20]. To further illustrate the impact of key changes, we experimentally verify the key sensitivity of the proposed algorithm using Key 1 and Key 2, respectively. Specifically, Key   1 = (   P = 6 , l t = 3 ,   seed = " 666 " ) ， Key   2 = (   P = 6 ,   l t = 5 ,   seed = " 666 " ) . Figure 8 a-c show the encrypted maps using different keys. Table 6 shows the RMSE and Max-R between the two encrypted maps obtained using the two keys. It can be seen from Table 6 that there is a large gap between the corresponding encrypted coordinates in the two ciphertext maps and the encryption results using the two keys are significantly different although the two keys are slightly different.
We also analyze the effect of key change on decryption results. When using Key 1 to decrypt the map encrypted with Key 2, it can be seen from Figure 8 d-f that the decryption fails. This shows that the ciphertext map can’t be decrypted correctly when the key is modified even with minimal changes.
All the experiments show that not only the encryption result is sensitive to key change, but also the decryption result is sensitive to key change. Therefore, the proposed algorithm has strong key sensitivity.

5.5. Watermarking Performance Evaluation

The watermarking performance under different interval steps l t , including watermark capacity, watermark invisibility and reversibility are discussed in this section. Some existing related algorithms are selected for watermarking performance comparison. Wang et al. [31] is a reversible watermarking algorithm for vector map based on traditional DE technique. Wang et al. [34] is a reversible vector map watermarking algorithm based on virtual coordinates, but different from the proposed algorithm in virtual coordinates construction method and watermark embedding mechanism. And Peng et al. [30] is an improved algorithm of Wang et al. [34] for 2D CAD engineering graphics.

5.5.1. Analysis of Watermark Capacity

Watermark capacity is the upper limit of the number of watermark bits that can be embedded in a dataset, and the watermark capacity can be expressed in terms of the average number of watermark bits embedded in each vertex, which is also known as the embedding rate (bits/vertex). In the proposed watermarking algorithm, as long as the value of l t is in the interval [1,   2 ( 10 P τ - 1 ) ], then each coordinate can be embedded one watermark bit. Thus the embedding rate achieves 2 bits/vertex. Moreover, the watermark capacity can be stably achieved for any type of maps, including maps with sparse vertex distribution in which many reversible watermarking algorithms often fail to embed watermark. For example, Wang et al. [31] fails to embed watermark in the POI data and Peng et al. [30] fails to embed watermark in the POI and Buildings data as can be seen in Table 7.
Table 7 demonstrates the watermarking capacity of the compared algorithms and the proposed algorithm. It can be seen that the capacity of the proposed algorithm is stabilized at 2 bits/vertex across different datasets, which is more than 7 times higher than the traditional DE method in Wang et al. [31]. Theoretically, the number of iterations in Peng et al. [30] can tend to be infinite, which makes the watermark capacity of Peng et al. [30] much higher than that of the proposed without considering other watermark performance. However, it is found that when Peng et al. [30] is applied to large-scale maps in this paper, the increase in the number of iterations will affect the watermark invisibility and the computational complexity increases significantly. So the number of iterations in the comparison experiments is set to 1.
Under the same watermark embedding strength, the number of coordinates for embedding watermark bits in Wang et al. [34] is the same as that in Peng et al. [30], and therefore the watermark capacity is the same. The watermark capacity of the proposed is slightly higher than that of Wang et al. [34] and Peng et al. [30], which is due to the fact that the method in Wang et al. [34] and Peng et al. [30] cannot embed the watermark into the reference coordinates, while the algorithm in this paper allows all vertices to participate in the watermark embedding.
In summary, we propose a watermarking algorithm that can achieve a much larger watermark capacity relative to the traditional DE method, and significantly reduces the impact of vertices correlation on the watermarking capacity.

5.5.2. Analysis of Watermark Invisibility

Invisibility means that the watermark will not be noticed by the users after it is embedded. In this experiment, the watermark invisibility is assessed visually and quantitatively. For watermark security and data usability, the coordinate offsets of the watermarked map should be invisible. In the proposed CERW scheme, the coordinate offsets of the decrypted-watermarked (D-Wed) map obtained by decrypting the CERWed map should also satisfy the invisibility property.
To assess the watermark invisibility of the proposed watermarking scheme visually, the watermarked map is compared with the original map overlay. And there is no significant data distortion and other problems found in topology checking in ArcGIS. Take the Roads as an example. Figure 9 displays the overlay effect of the watermarked data and the original data. It can be found from Figure 9 that the watermarked data and the original data are almost the same without zooming in, and zooming in the details reveals that the coordinates have a slight offset, but the overall distortion doesn’t occur, and the element topology is well maintained.
Max – R ⁡   V , V w   = max ∥ v i   - v i w ∥
RMSE and Max-R between the watermarked map and the original map are also calculated to measure the watermark invisibility quantitatively. The smaller RMSE and Max-R are, the better the watermark invisibility is. In the proposed watermarking scheme, the magnitude of RMSE and Max-R is affected by the interval step size l t and the P-value. The relationship between Max-R and l t and between RMSE and l t under different P-value is shown in Figure 10 and Figure 11 respectively.
As can be seen from Figure 10 and Figure 11, the RMSE and Max-R of all the three datasets increase with the increase of l t and decrease with the increase of P-value when l t keeps unchanged. Figure 10 shows that the Max-R curves of all the three datasets are almost the same. This is because the theoretical value of Max-R is determined only by P-value and l t and not affected by map characteristics. Consequently, although the three datasets have completely different characteristics, the Max-R curves of the three datasets present the same pattern. This is where the proposed watermarking method outperforms the traditional DE watermarking method in which the Max-R value is affected by the map characteristics. In fact, the traditional DE watermarking method is not suitable for maps with sparse vertex distribution because of the too large Max-R and RMSE values, while the proposed improved DE watermarking method in this paper suits all types of maps.
According to the RMSE curves as shown in Figure 11, the Roads dataset has the best invisibility and the POIs has the relatively worst invisibility among the three datasets. This indicates that the watermark invisibility of a map with dense vertex distribution is often better than that of a map with less dense vertex distribution if watermarked using the proposed watermarking method, which is the common characteristic of DE watermarking methods.
To comprehensively demonstrate the watermark invisibility of the proposed algorithm，some related algorithms are selected for comparison. The comparison results are listed in Table 8 and shown in Figure 12. In particular, the vertical axis in Figure 12 uses a logarithmic scale, where the longer the length of the bar, the closer it is to 0.0001, indicating a smaller value, and conversely the shorter the length of the bar, the closer it is to 1, indicating a larger value. As can be seen in Table 8 and Figure 12, the RMSE and Max-R of the proposed algorithm are significantly lower than that of the other three algorithms. Besides, the watermark invisibility of the proposed algorithm is more stable than that of the other three algorithms when applied to different types of maps, which can be proved by Table 8 and Figure 12. It can be seen in Figure 12 that the RMSE and Max-R values of Wang et al. [31] when applied to the three different datasets are significantly different. For POIs, Wang et al. [31] even fails to embed watermark in it due to the too large RMSE value. It is notable that Peng et al. [30] only succeeds to embed watermark in the dataset of Roads and fails in the other two datasets. Although Wang et al. [34] successfully embeds watermarks in the three datasets, there is a relatively big difference in the watermark invisibility in the three datasets. It is worth noting that the proposed algorithm not only succeeds to embed watermarks in the three different datasets, but also achieves approximate Max-R values for the three datasets. In summary, the proposed algorithm suits various kinds of maps, and meanwhile, has much better and more stable watermark invisibility.
In the experiment, when the map scale is 1:1000, the Max-R of the proposed algorithm is 0.00001395 <0.30 m [18], which is far below the threshold of the actual production standards. The watermarked map accuracy of other test datasets also meets the application requirements. Therefore, the data distortions caused by the watermark embedding in the proposed algorithm will not affect the usability of the vector map.

5.5.3. Analysis of Watermark Reversibility

The watermarking algorithm proposed in the CERW scheme is fully reversible. The data recovery operation to the CERWed map can be performed either before decryption or after decryption. The encrypted-recovered (E-Red) map without watermark can be obtained when data recovery operation is performed to the CERWed map before decryption, and the decrypted-recovered (D-Red) map without watermark can be obtained when data recovery operation is performed to the CERWed map after decryption. In order to verify the reversibility of the watermarking scheme, the E-Red map is compared with the original encrypted map and the D-Red map is compared with the original plaintext map. The comparison results are listed in Table 9. As Table 9 shows, all the RMSE and Max-R values of E-Red maps and D-Red maps are 0, which demonstrates the reversibility of the proposed watermarking scheme.
The reversibility of the three compared algorithms is also assessed using RMSE and Max-R computed between the recovered map and the original map. As listed in Table 9, the RMSE and Max-R values of Wang et al. [31] are all 0, and the RMSE and Max-R values of Wang et al. [34] and Peng et al. [30] are all very small floating numbers. Table 9 shows that the reversibility of Wang et al. [31] is the same as the proposed algorithm, while the reversibility of Wang et al. [34] and Peng et al. [30] is relatively worse than the proposed scheme. This is determined by the underlying watermarking mechanism. The proposed algorithm and Wang et al. [31] watermark map data using DE technique which shifts the binary form of the difference value one bit to the left to embed the watermark and shifts one bit back to the right to recover data. There is no precision loss in the binary difference shifting operations. In the algorithms of Wang et al. [34] and Peng et al. [30], the watermark embedding and data recovery are achieved by building a reversible mapping between original data and watermarked data. There is precision loss caused by floating operations during the mapping process from original data to watermarked data and the inverse mapping from watermarked data to original data. This is why the RMSE and Max-R values of Wang et al. [34] and Peng et al. [30] are not equal to 0. Besides, the three compared algorithms can only be implemented in plaintext domain, and the proposed watermarking algorithm can be implemented in both plaintext and ciphertext domains, thus has a higher practical value.

6. Conclusion

In this paper, a CERW algorithm for vector maps is proposed based on virtual coordinates. In the proposed coordinates scrambling encryption scheme, the coordinates are moved by random multiples of the virtual interval step. The random number is generated by a pseudo-random number generator designed using the hash function SHA-512 and the Salsa20 stream cipher algorithm. In the proposed reversible watermarking scheme, the coordinate differences are first calculated with virtual coordinates as references and then the DE technique is utilized to embed watermark reversibly. Because the coordinates scrambling encryption has no impact on the coordinate differences in which the watermark is embedded, the commutativity between encryption operation and reversible watermarking operation is achieved. The operation order of encryption and watermark embedding doesn’t change the final results, and the watermark extraction and data recovery can be performed before or after decryption. The main contributions of this paper are as follows:
(1) Although there are a few existing CEW algorithms for vector maps, the original map can’t be recovered from the watermarked version in these algorithms, which makes the algorithms unsuitable for applications that require high data precision. The proposed CERW algorithm not only achieves the commutativity between encryption and watermarking, but also achieves the watermark reversibility, which makes the proposed algorithm suitable for more kinds of applications than the existing CEW algorithms.
(2) Traditional DE watermarking algorithm often has small watermark capacity and big data distortions when used in vector map watermarking. Especially, the watermarking operation often fails because of the too large data distortions introduced by watermarking when used to watermark a map with sparse vertex distribution. The watermarking performance of traditional DE algorithm is affected significantly by map characteristics. The improved DE (IDE) watermarking algorithm proposed in this paper overcomes the above-mentioned problems of traditional algorithms by introducing virtual coordinates as references in the coordinate difference calculation, and significantly improves the watermark capacity, which is more than 7 times higher than that of the traditional DE methods. Meanwhile, by adjusting the virtual interval step, the proposed IDE algorithm can achieve very small data distortions after watermarking. Furthermore, the watermarking performance of the proposed IDE method is not affected by map characteristics and very stable for different kinds of maps.
(3) The encryption method of the proposed CERW scheme designs a SHA-512-Salsa20 random number generator to implement coordinates scrambling, and achieves good encryption effect and high encryption security as analyzed in section 5.4. It is worth noting that the SHA-512-Salsa20 generator can be replaced with any arbitrary existing pseudo-random number generation method in the proposed encryption scheme.
Proposed algorithm has a relatively poor performance in watermark robustness. The map translation operation has no impact on the coordinate differences, thus proposed algorithm can resist the map translation attack. However, the map scaling and rotation operations will change the coordinate differences, so the proposed algorithm can’t resist the map scaling and rotation attacks. Therefore, improving the robustness of the proposed CERW scheme will be the future work of this research.

Author Contributions

Qianyi Dai and Baiyan Wu conceived and designed the experiments; Qianyi Dai implemented the methodology; Qianyi Dai and Fanshuo Liu completed the computer code and the implementation of the supporting algorithms; Qianyi Dai performed the analyses and prepared the original draft; Baiyan Wu, Fanshuo Liu, Zixuan Bu and Haodong Zhang reviewed and edited the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Research Foundation of the Department of Natural Resources of Hunan Province, grant number 20230126XX.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to spatial sensitivity.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Da, Q.; Sun, J.; Zhang, L.; Kou, L.; Wang, W.; Han, Q.; Zhou, R. A novel hybrid information security scheme for 2D vector map. Mobile Networks and Applications, 2018, 23, 734-742. [CrossRef]
  2. Zhu, C. Research progresses in digital watermarking and encryption control for geographical data. Acta Geodaetica et Cartographica Sinica, 2017, 46(10), 1609-1619. [CrossRef]
  3. Wang, Y.; Yang, C.; Zhu, C.; Ding, K. An efficient robust multiple watermarking alg-orithm for vector geographic data. Information, 2018, 9(12), 296. [CrossRef]
  4. Broumandnia, A. Designing digital image encryption using 2D and 3D reversible modular chaotic maps. Journal of Information Security and Applications, 2019, 47, 188-198. [CrossRef]
  5. Wang, Y.; Yang, C.; Ren, N.; Zhu, C.; Rui, T.; Wang, D. An Adaptive Watermark Detection Algorithm for Vector Geographic Data. KSII Transactions on Internet & Information Systems, 2020, 14(1), 323-343. [CrossRef]
  6. Pham, G. N.; Ngo, S. T.; Bui, A. N.; Tran, D. V.; Lee, S. H.; Kwon, K. R. Vector map random encryption algorithm based on multi-scale simplification and Gaussian distribution. Applied Sciences, 2019, 9(22), 4889. [CrossRef]
  7. Higgins, S. The lifecycle of data management. Managing research data, 2012, 17-46. [CrossRef]
  8. Shi, Y. Q.; Li, X.; Zhang, X.; Wu, H. T.; Ma, B. Reversible data hiding: Advances i-n the past two decades. IEEE access, 2016, 4, 3210-3237. [CrossRef]
  9. Ma, K.; Zhang, W.; Zhao, X.; Yu, N.; Li, F. Reversible data hiding in encrypted images by reserving room before encryption. IEEE Transactions on information forensics and security, 2013, 8(3), 553-562. [CrossRef]
  10. Zhang, X. Reversible data hiding in encrypted image. IEEE signal processing letters, 2011, 18(4), 255-258. [CrossRef]
  11. Puech, W.; Chaumont, M.; Strauss, O. A reversible data hiding method for encrypted images. In Security, forensics, steganography, and watermarking of multimedia contents X. SPIE, 2008, 6819, 534-542. [CrossRef]
  12. Zhang, X.; Long, J.; Wang, Z.; Cheng, H. Lossless and reversible data hiding in encrypted images with public-key cryptography. IEEE Transactions on Circuits and Systems for Video Technology, 2016, 26(9), 1622-1631. [CrossRef]
  13. Peng, F.; Lin, Z. X.; Zhang, X.; Long, M. Reversible data hiding in encrypted 2D ve-ctor graphics based on reversible mapping model for real numbers. IEEE transactions on information forensics and security, 2019, 14(9), 2400-2411. [CrossRef]
  14. Peng, F.; Jiang, W. Y.; Qi, Y.; Lin, Z. X.; Long, M. Separable robust reversible watermarking in encrypted 2D vector graphics. IEEE Transactions on Circuits and Systems for Video Technology, 2020, 30(8), 2391-2405. [CrossRef]
  15. Jang, B. J.; Lee, S. H.; Lee, E. J.; Lim, S.; Kwon, K. R. A crypto-marking method for secure vector map. Multimedia Tools and Applications, 2017, 76, 16011-16044. [CrossRef]
  16. Jiang, L.; Xu, Z.; Xu, Y. Commutative encryption and watermarking based on orthogonal decomposition. Multimedia tools and applications, 2014, 70, 1617-1635. [CrossRef]
  17. Lian, S. Quasi-commutative watermarking and encryption for secure media content distribution. Multimedia Tools and Applications, 2009, 43(1), 91-107. [CrossRef]
  18. Wu, B.; Dai, Q.; Peng, Y.; Wang, W. Robust vector map watermarking algorithm in homomorphic encrypted domain. Journal of Geo-information Science, 2022, 24(6), 1120-1129. [CrossRef]
  19. Ren, N.; Zhu, C.; Tong, D.; Chen, W.; Zhou, Q. Commutative encryption and watermarking algorithm based on feature invariants for secure vector map. IEEE Access, 2020, 8, 221481-221493. [CrossRef]
  20. Li, Y.; Zhang, L.; Wang, X.; Zhang, X.; Zhang, Q. A novel invariant based commutative encryption and watermarking algorithm for vector maps. ISPRS International Journal of Geo-Information, 2021, 10(11), 718. [CrossRef]
  21. Ren, N.; Tong, D.; Cui, H.; Zhu, C.; Zhou, Q. Congruence and geometric feature-based commutative encryption-watermarking method for vector maps. Computers & Geosciences, 2022, 159, 105009. [CrossRef]
  22. Ren, N.; Zhao, M.; Zhu, C.; Sun, X.; Zhao, Y. Commutative encryption and watermarking based on SVD for secure GIS vector data. Earth Science Informatics, 2021, 14, 2249-2263. [CrossRef]
  23. Guo, S.; Zhu, S.; Zhu, C.; Ren, N.; Tang, W.; Xu, D. A robust and lossless commutative encryption and watermarking algorithm for vector geographic data. Journal of Information Security and Applications, 2023, 75, 103503. [CrossRef]
  24. Tan, T.; Zhang, L.; Zhang, M.; Wang, S.; Wang, L.; Zhang, Z.; ... Wang, P. Commutative encryption and watermarking algorithm based on compound chaotic systems and zero-watermarking for vector map. Computers & Geosciences, 2024, 184, 105530. [CrossRef]
  25. Deng, L. Y.; Bowman, D. Developments in pseudo-random number generators. Wiley Interdisciplinary Reviews: Computational Statistics, 2017, 9(5), e1404. https://do-i.org/10.1002/wics.1404.
  26. Coron, J. S.; Dodis, Y.; Malinaud, C.; Puniya, P. Merkle-Damgård revisited: How to construct a hash function. In Advances in Cryptology–CRYPTO 2005: 25th Annual International Cryptology Conference, Santa Barbara, California, USA, August 14-18, 2005. Proceedings 25. Springer Berlin Heidelberg, 2005, 430-448. [CrossRef]
  27. Ding, L. Improved related-cipher attack on salsa20 stream cipher. IEEE Access, 2019, 7, 30197-30202. [CrossRef]
  28. Tian, J. Reversible watermarking by difference expansion. In Proceedings of workshop on multimedia and security. 2002, 19-22.
  29. Peng, F.; Lei, Y. Z.; Long, M.; Sun, X. M. A reversible watermarking scheme for two-dimensional CAD engineering graphics based on improved difference expansion. Computer-Aided Design, 2011, 43(8), 1018-1024. [CrossRef]
  30. Peng, F.; Long, Q.; Lin, Z. X.; Long, M. A reversible watermarking for authenticating 2D CAD engineering graphics based on iterative embedding and virtual coordinates. Multimedia Tools and Applications, 2019, 78, 26885-26905. [CrossRef]
  31. Wang, X.; Shao, C.; Xu, X.; Niu, X. Reversible data-hiding scheme for 2-D vector maps based on difference expansion. IEEE Transactions on information forensics and security, 2007, 2(3), 311-320. [CrossRef]
  32. Hua, Z.; Zhou, Y.; Huang, H. Cosine-transform-based chaotic system for image encryption. Information Sciences, 2019, 480, 403-419. [CrossRef]
  33. Wang, X.; Yan, H.; Zhang, L. Vector map encryption algorithm based on double random position permutation strategy. ISPRS International Journal of Geo-Information, 2021, 10(5), 311. [CrossRef]
  34. Wang, N.; Zhang, H.; Men, C. A high capacity reversible data hiding method for 2D vector maps based on virtual coordinates. Computer-Aided Design, 2014, 47, 108-117. [CrossRef]
Preprints 110072 g003
Figure 3. Schematic diagram of the difference construction and coordinate scrambling based on virtual coordinates
Figure 3. Schematic diagram of the difference construction and coordinate scrambling based on virtual coordinates
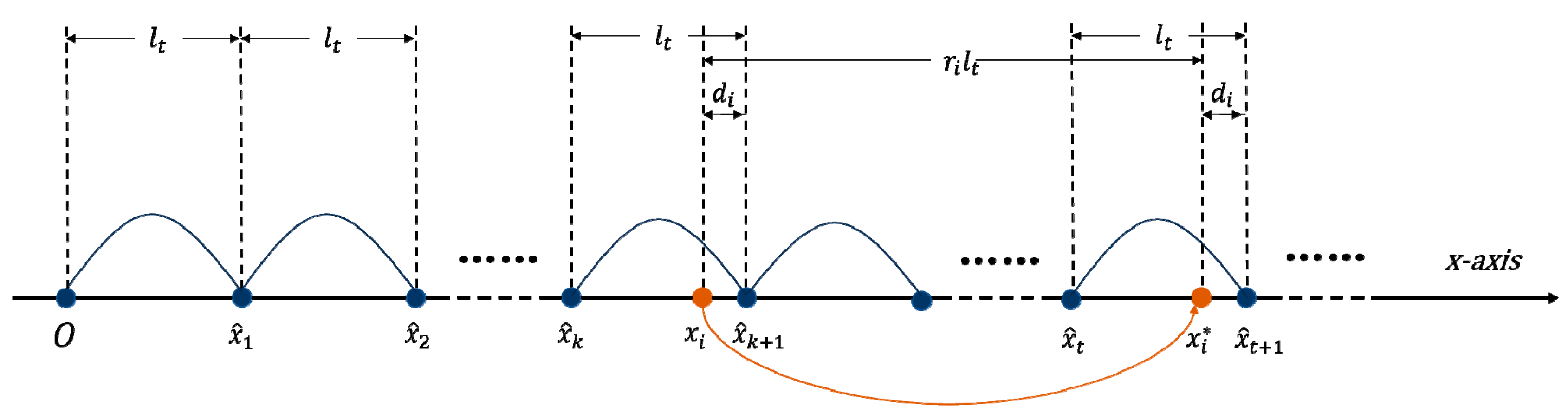
Preprints 110072 g003
Preprints 110072 g004
Figure 4. Original experimental data: (a) POIs, (b) Roads, (c) Buildings
Figure 4. Original experimental data: (a) POIs, (b) Roads, (c) Buildings
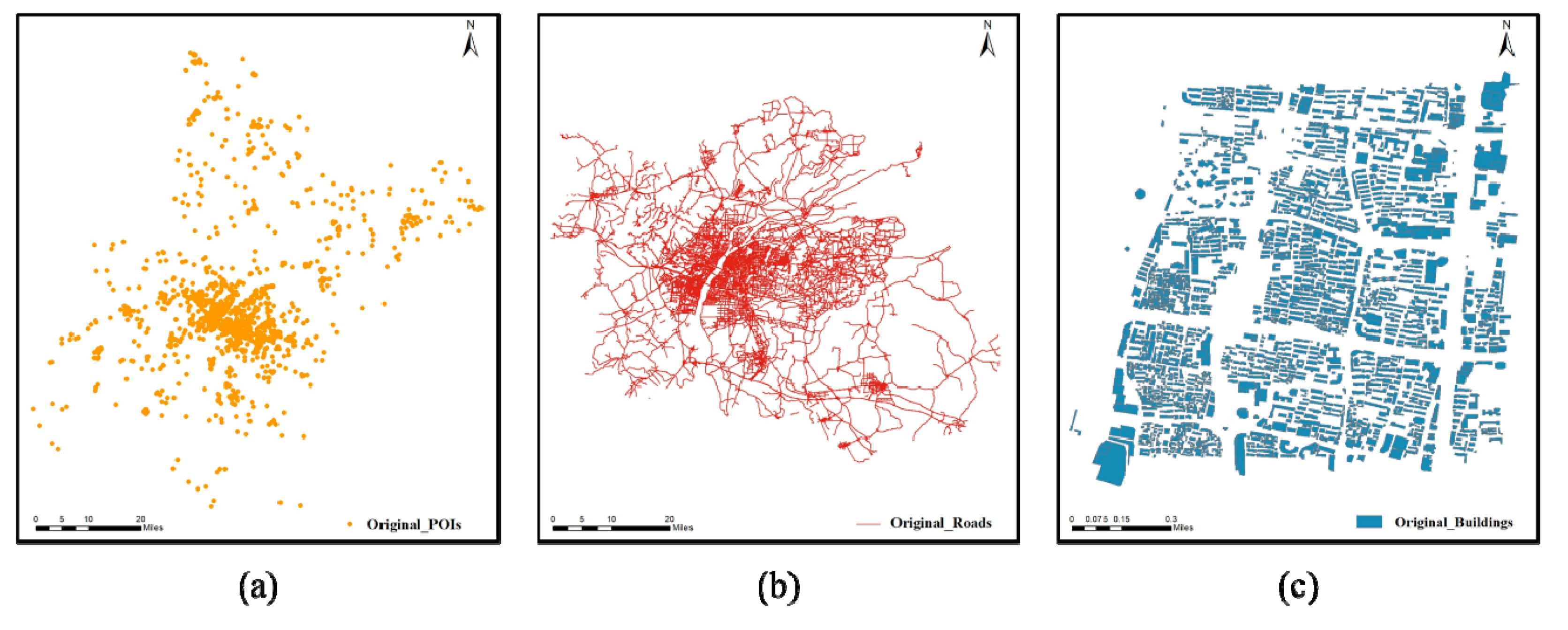
Preprints 110072 g004
Preprints 110072 g005
Figure 5. The visualization of CERWed maps: (a) E-Wed POIs; (b) E-Wed roads; (c) E-Wed buildings; (d) W-Eed POIs; (e) W-Eed roads; (f) W-Eed buildings
Figure 5. The visualization of CERWed maps: (a) E-Wed POIs; (b) E-Wed roads; (c) E-Wed buildings; (d) W-Eed POIs; (e) W-Eed roads; (f) W-Eed buildings
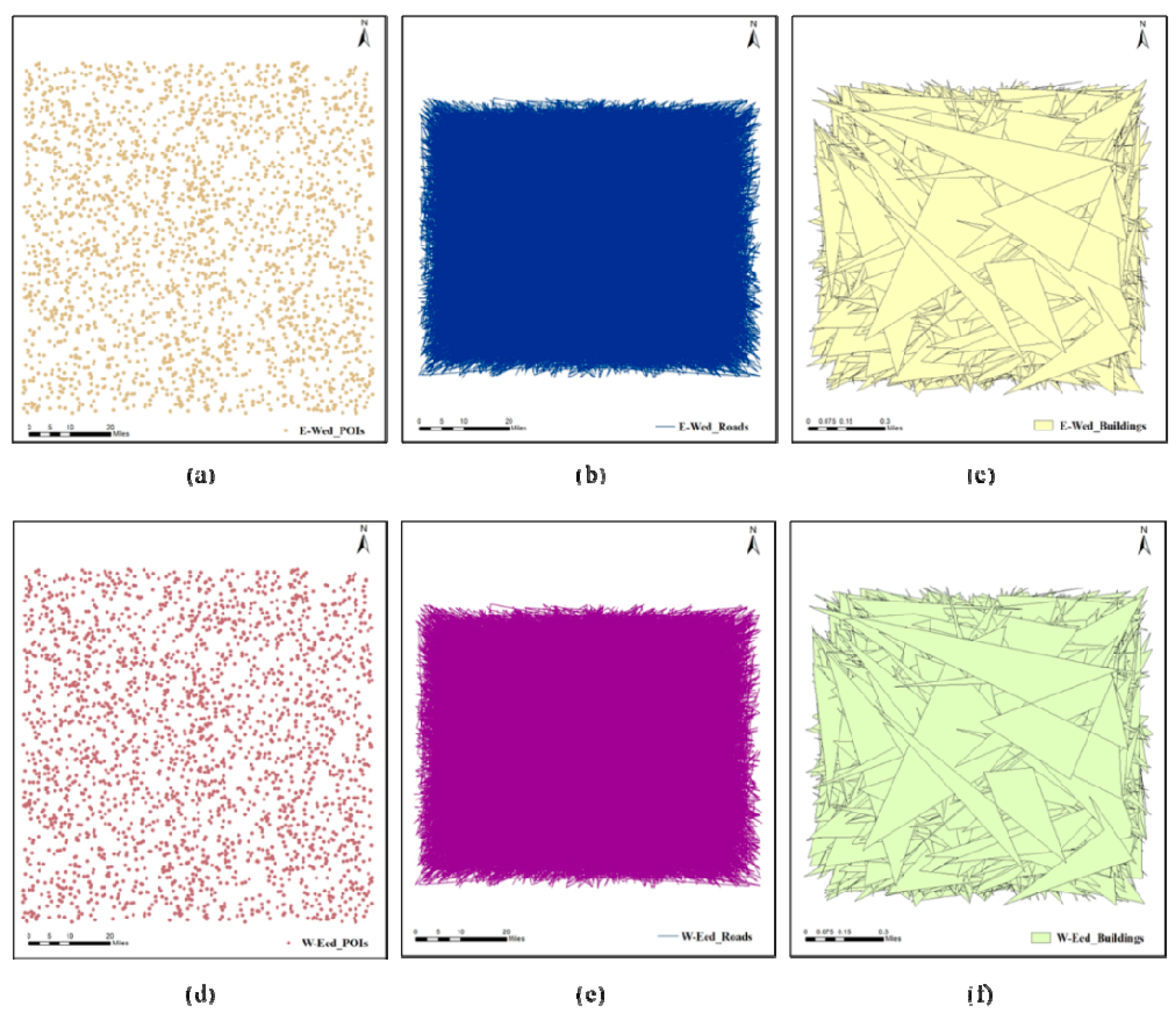
Preprints 110072 g005
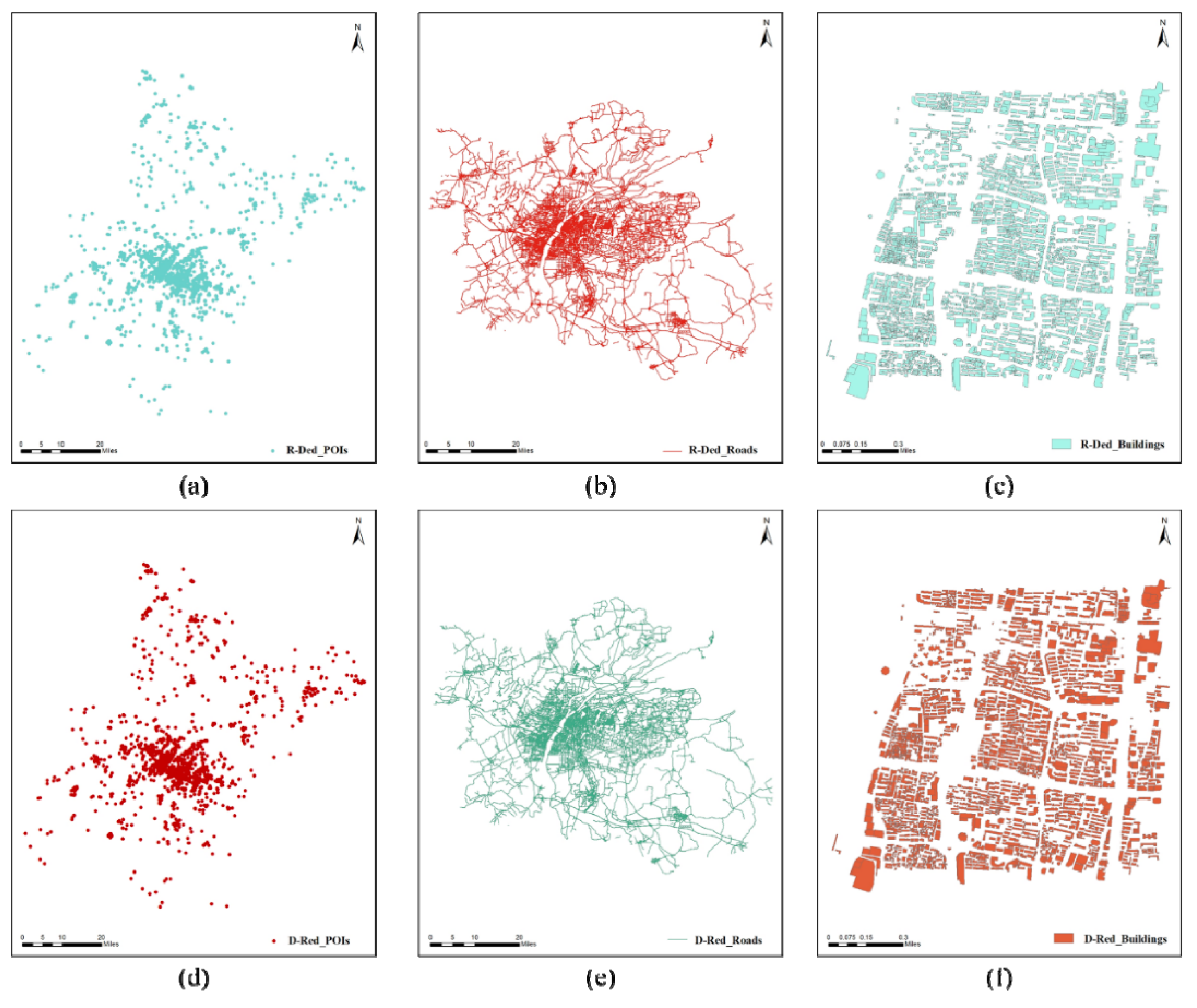
Preprints 110072 g006
Figure 6. The visualization of the recovered plaintext maps: (a) R-Ded POIs; (b) R-Ded roads; (c) R-Ded buildings; (d)D-Red POIs; (e) D-Red roads; (f)D-Red buildings
Figure 6. The visualization of the recovered plaintext maps: (a) R-Ded POIs; (b) R-Ded roads; (c) R-Ded buildings; (d)D-Red POIs; (e) D-Red roads; (f)D-Red buildings
Preprints 110072 g006
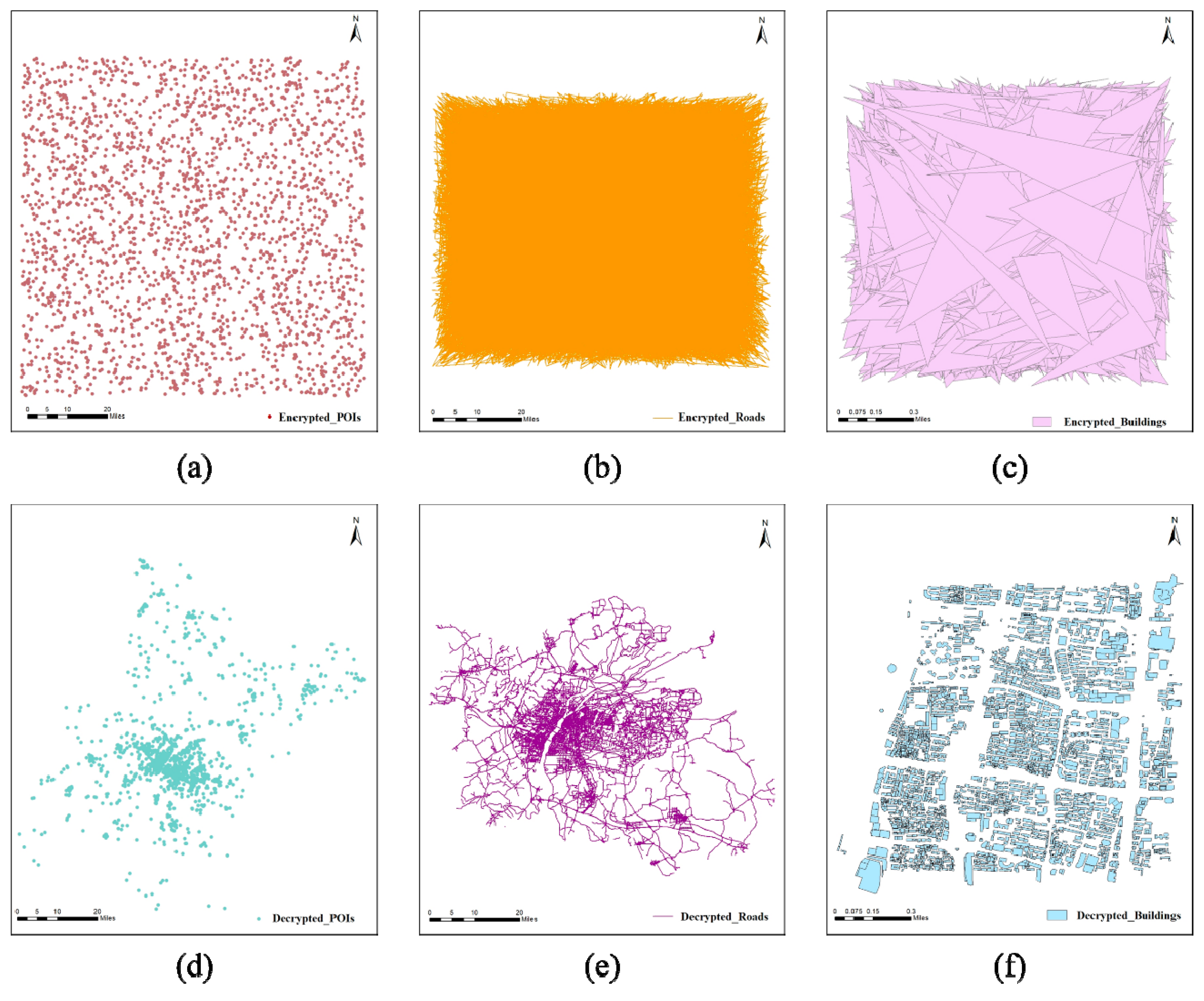
Preprints 110072 g007
Figure 7. Visualization of the encryption and decryption results: (a) Encrypted POIs; (b) Encrypted roads; (c) Encrypted buildings; (d) Decrypted POIs; (e) Decrypted roads; (f) Decrypted buildings
Figure 7. Visualization of the encryption and decryption results: (a) Encrypted POIs; (b) Encrypted roads; (c) Encrypted buildings; (d) Decrypted POIs; (e) Decrypted roads; (f) Decrypted buildings
Preprints 110072 g007
Preprints 110072 g008
Figure 8. The encrypted maps using slightly different keys and decrypted maps using slightly modified key: (a) encrypted POIs using Key 1 and Key 2; (b) encrypted roads using Key 1 and Key 2; (c) encrypted buildings using Key 1 and Key 2; (d) the result of using Key 1 to decrypt the POIs encrypted with Key 2; (e) the result of using Key 1 to decrypt the roads encrypted with Key 2; (f) the result of using Key 1 to decrypt the buildings encrypted with Key 2
Figure 8. The encrypted maps using slightly different keys and decrypted maps using slightly modified key: (a) encrypted POIs using Key 1 and Key 2; (b) encrypted roads using Key 1 and Key 2; (c) encrypted buildings using Key 1 and Key 2; (d) the result of using Key 1 to decrypt the POIs encrypted with Key 2; (e) the result of using Key 1 to decrypt the roads encrypted with Key 2; (f) the result of using Key 1 to decrypt the buildings encrypted with Key 2
Preprints 110072 g008
Preprints 110072 g009
Figure 9. Overlay of watermarked data and original data (Roads)
Figure 9. Overlay of watermarked data and original data (Roads)
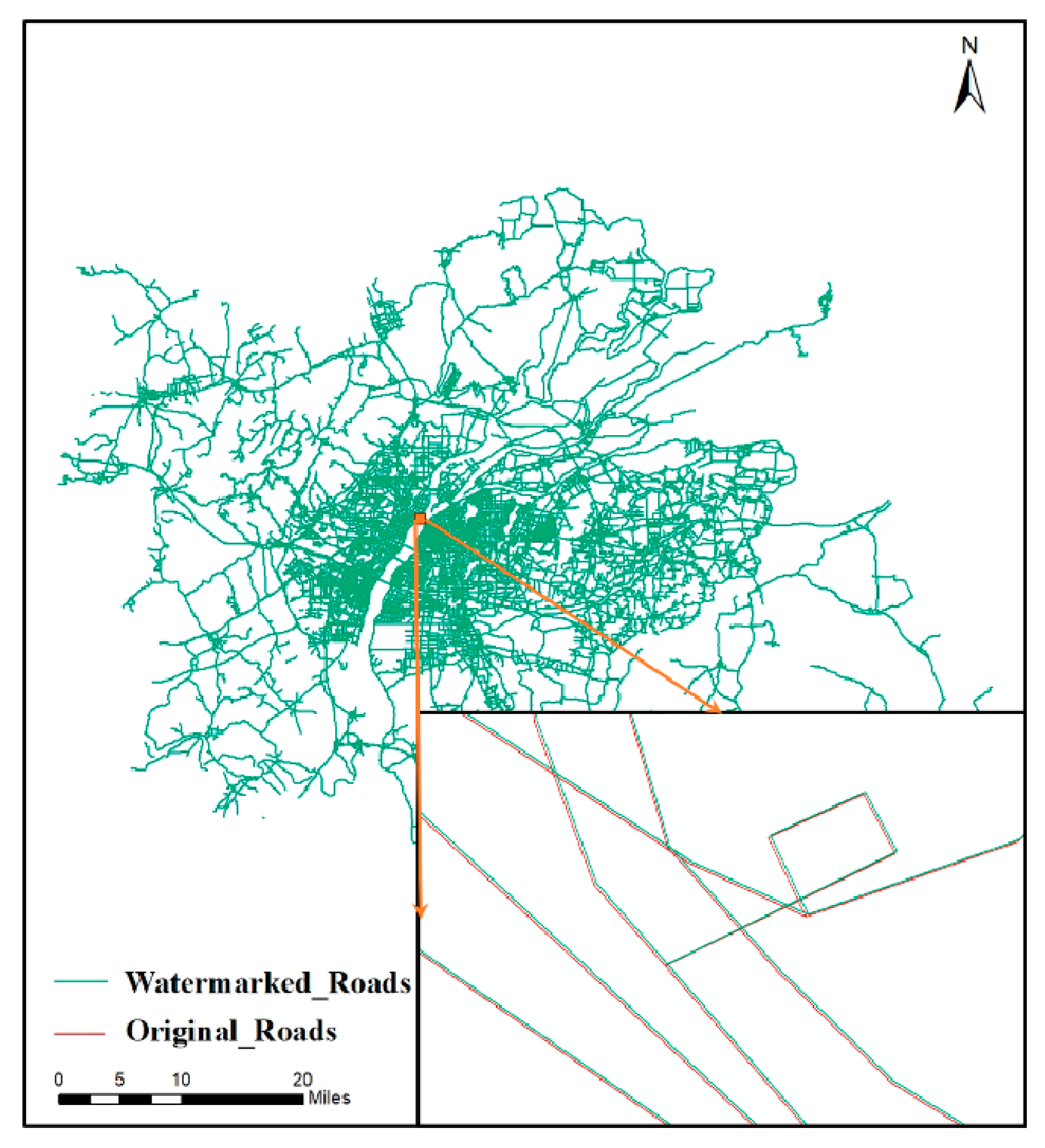
Preprints 110072 g009
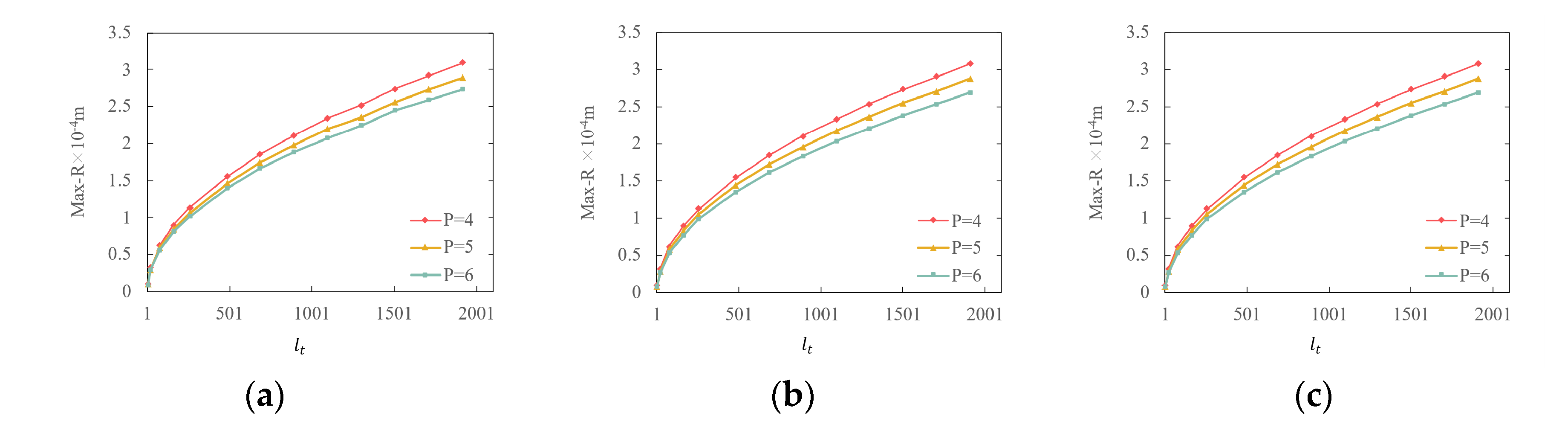
Preprints 110072 g010
Figure 10. Max-R versus interval step l t : (a) POIs; (b) Roads; (c) Buildings
Figure 10. Max-R versus interval step l t : (a) POIs; (b) Roads; (c) Buildings
Preprints 110072 g010
Preprints 110072 g011
Figure 11. RMSE versus interval step l t : (a) POIs; (b) Roads; (c) Buildings
Figure 11. RMSE versus interval step l t : (a) POIs; (b) Roads; (c) Buildings
Preprints 110072 g011
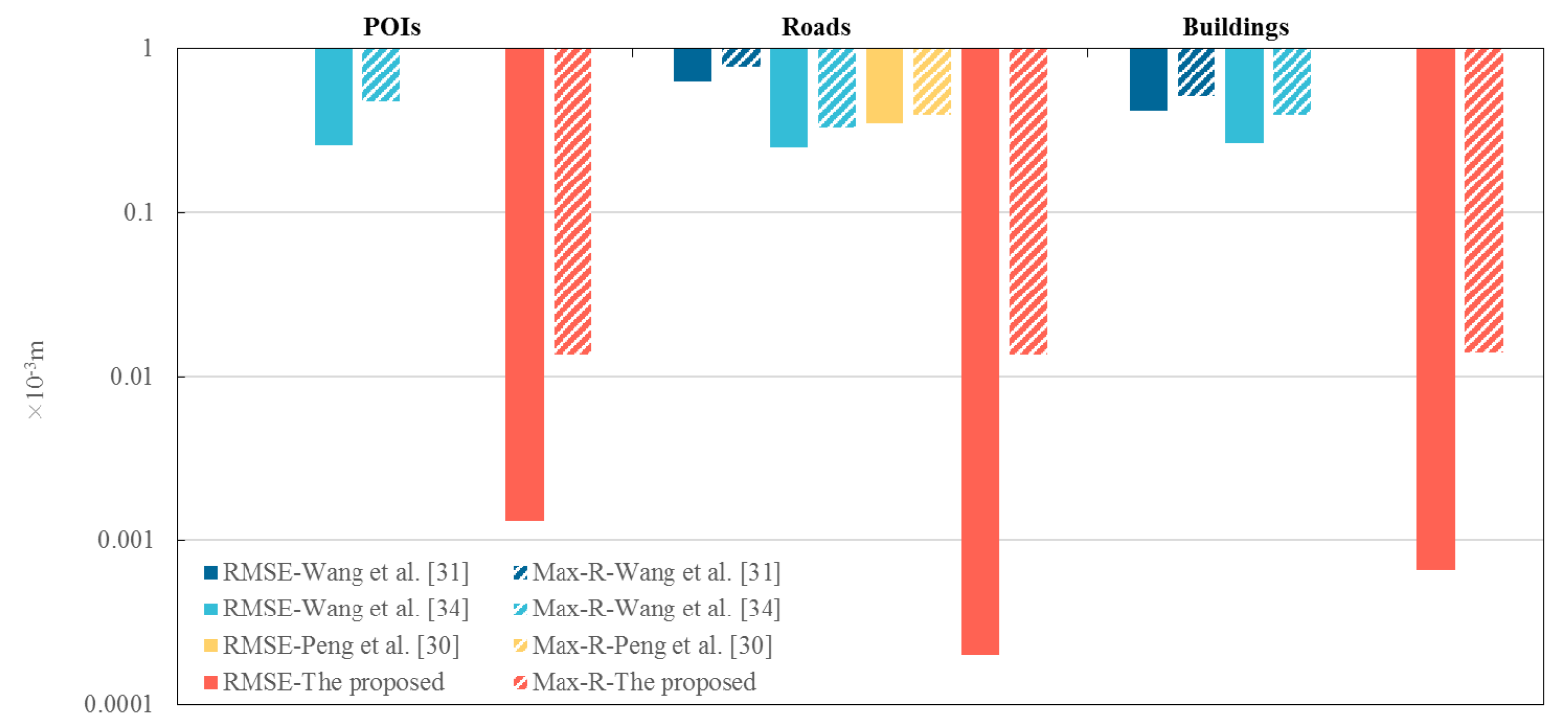
Preprints 110072 g012
Figure 12. Comparison of the RMSE and Max-R of different reversible algorithms
Figure 12. Comparison of the RMSE and Max-R of different reversible algorithms
Preprints 110072 g012
Table 1. The detailed information of the experimental data.
Table 1. The detailed information of the experimental data.
Maps Data types Features Vertices number Scale τ （m）
POIs Point 2410 2410 1:10000 1
Roads Polyline 11423 122962 1:10000 1
Buildings Polygon 5660 20325 1:1000 0.1
* τ denotes the precision tolerance.
Table 2. Comparison results between the E-Wed maps and the W-Eed maps
Table 2. Comparison results between the E-Wed maps and the W-Eed maps
Datasets Consistent vertices count Inconsistent vertices count RMSE
E-Wed and W-Eed POIs 2410 0 0
E-Wed and W-Eed roads 122962 0 0
E-Wed and W-Eed buildings 20325 0 0
Table 3. Comparison results between the R-Ded maps and the D-Red maps
Table 3. Comparison results between the R-Ded maps and the D-Red maps
Datasets Consistent vertices count Inconsistent vertices count RMSE
R-Ded and D-Red POIs 2410 0 0
R-Ded and D-Red roads 122962 0 0
R-Ded and D-Red buildings 20325 0 0
Table 4. BER results of the extracted watermarks
Table 4. BER results of the extracted watermarks
Datasets Extraction from
E-Wed maps 		Extraction from
W-Eed maps		 Extraction from
D-Wed maps
POIs 0 0 0
Roads 0 0 0
Buildings 0 0 0
Table 5. RMSE values of the encrypted and decrypted maps
Table 5. RMSE values of the encrypted and decrypted maps
Datasets RMSE between encrypted map and original map (m) RMSE between decrypted map and original map (m)
POIs 448973.8688 0
Roads 48368.7397 0
Buildings 15216.4770 0
Table 6. Difference between encryption results of Key 1 and Key 2
Table 6. Difference between encryption results of Key 1 and Key 2
Datasets RMSE(m) Max-R(m)
POIs 4322.2641 15318.6846
Roads 615.6829 2711.3073
Buildings 437.2614 1757.5051
Table 7. Comparison of watermark capacity in different algorithms (bits/vertex)
Table 7. Comparison of watermark capacity in different algorithms (bits/vertex)
Datasets Wang et al. [31] Wang et al. [34] Peng et al. [30] The proposed
POIs - 1.9887 - 2
Roads 0.2790 1.9761 1.9761 2
Buildings 0.1480 1.9568 - 2
Table 8. RMSE and Max-R values of different algorithms ( P =6) (10-3m)
Table 8. RMSE and Max-R values of different algorithms ( P =6) (10-3m)
Datasets Wang et al. [31] Wang et al. [34] Peng et al. [30] The proposed
POIs RMSE - 0.25920 - 0.00131
Max-R - 0.47274 - 0.01367
Roads RMSE 0.62505 0.25107 0.34937 0.00020
Max-R 0.78143 0.33009 0.39582 0.01373
Buildings RMSE 0.41708 0.26517 - 0.00066
Max-R 0.50781 0.39302 - 0.01395
Table 9. Comparison of reversibility of different algorithms (P = 6) (m)
Table 9. Comparison of reversibility of different algorithms (P = 6) (m)
Datasets Wang et al. [31] Wang et al. [34] Peng et al. [30] The proposed
E-Red map D-Red map
POIs RMSE - 6.90900   × 10 - 8 - 0 0
Max-R - 1.40915   × 10 - 7 - 0 0
Roads RMSE 0 4.06783   × 10 - 8 2.45678   × 10 - 8 0 0
Max-R 0 1.02359   × 10 - 7 1.04865   × 10 - 7 0 0
Buildings RMSE 0 9.89177   × 10 - 8 - 0 0
Max-R 0 2.33080   × 10 - 7 - 0 0
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated