Overturn Dynamics of a Small Moon

Preprint

Brief Report

Overturn Dynamics of a Small Moon

Altmetrics

Downloads

Views

Comments

Vladimir S. Aslanov^*

This version is not peer-reviewed

Submitted:

24 June 2024

Posted:

24 June 2024

You are already at the latest version

Alerts

Abstract

The paper considers the possibility of rotating a small moon by 180 degrees from a dynamic point of view using two rocket engines mounted on the surface of the moon. A thrust control law for the engines which allows to turn the moon over and then stabilize it relative to a new equilibrium position by parrying a gravity gradient torque is proposed. The dynamic aspects of such an experiment are discussed using the example of the Mars satellite Deimos.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

It is difficult to imagine, but in the future, it is likely that a mission that requires the overturning of one of a small moon of the planets of the solar system [1,2,3,4,5,6,7,8] will be realized. The purpose of this paper is to show the possibility of a 180-degree rotation of a small moon from a mechanical point of view, and to propose this new problem of astrodynamics for discussion. The problem is studied in a planar formulation, when the small moon is acted upon only by a gravitational torque caused by the inequality of its main moments of inertia and by a control torque induced by two rocket engines installed on the surface of the moon. The paper discusses the dynamical aspects of such an experiment using the Deimos satellite of Mars as an example. The paper has the following structure. In Section 2, an equation is given for the planar attitude motion of a satellite (moon) under the action of the gravity gradient torque. Section 3 presents the control law of the rocket engines to perform the 180-degree rotation of the small moon and its further stabilization in the inverted position. Section 4 is devoted to the numerical simulation of the Deimos overturn. Finally, the conclusions are given in Section 5.

2. Mathematical Model

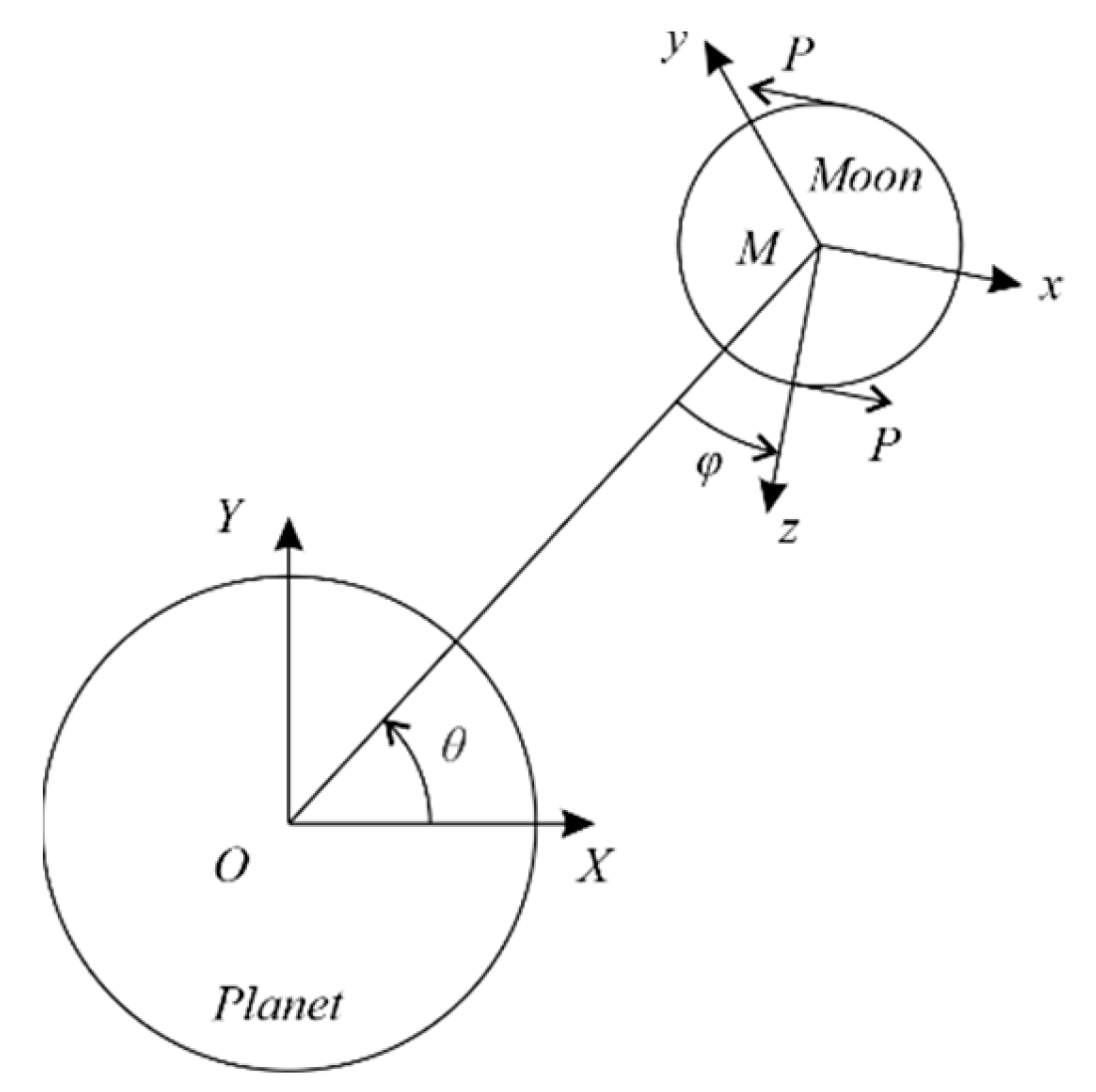
Consider the plane motion of a moon in the gravitational field of a planet. A gravity gradient torque acting on the planet's moon is written as [9], p 370

M_{G} = - \frac{3}{2} n^{2} (A - C) \sin 2 φ

(1)

where

φ

is the angle of rotation of the moon relative to the local vertical,

n

is the mean orbital rate,

A, B

are the transverse moments of inertia and

C

is the axial moment of inertia of the moon. For a circular orbit and in the plane case of the attitude motion, the equation is as follows

B (\ddot{θ} + \ddot{φ}) = - \frac{3}{2} n^{2} (A - C) \sin 2 φ

(2)

where

θ

is the true anomaly. In the case of a circular orbit (

\dot{θ} = n = c o n s t

) for the new independent variable

θ = n t

, equation (2) takes the form

φ^{″} + \frac{3}{2} σ \sin 2 φ = 0

(3)

where

φ^{″} = \frac{d^{2} φ}{d θ^{2}}

σ = \frac{A - C}{B} > 0

is the inertial parameter. The inertia tensor of most moons is not a diagonal matrix of equal elements, i.e. a scalar matrix. Their principal moments of inertia are usually not equal to each other and due to the choice of coordinate axes the following rule holds

A > B > C

(4)

Equation (3) has four equilibria. Two of them are stable

φ_{1, 2} = 0, π

(5)

and the other two are unstable

φ_{3, 4} = \pm \frac{π}{2}

(6)

If condition (4) is satisfied for planet’s satellites, then there are two stable equilibrium positions (5). This results in the satellite's longitudinal axis

O z

being oriented along the line connecting the centers of mass of the planet and its satellite. In this case, the moon is always facing one side to the planet.

3. Turning Control Law

This section is devoted to a rocket engine control law, which makes it possible to realize the turning of the small moon from one stable position (

φ_{1} = 0

) to another (

φ_{2} = π

) and its stabilization in the new stable position, i.e. to turn the previously invisible side of the moon towards the planet.

Suppose that each of the two rocket engines installed at opposite points on the moon surface (Figure 1) produces a thrust equal to

P (θ, φ, φ^{'}) = k φ^{'} sgn (\cos φ) + P_{0} δ sgn (φ)

(7)

where

φ^{'} = \frac{d φ}{d θ}

P

is engine thrust,

P_{0}

is thrust increment at the start of the turn,

r

is the moon radius, and

k > 0

is control factor,

δ

is the factor that ensures the initial swing of the moon over a period of one revolution of the moon around the planet

δ = \{\begin{cases} 1, θ \leq 2 π \\ 0, θ > 2 π \end{cases}

(8)

The first term in the control law (7) at

φ \in (- \frac{π}{2}, \frac{π}{2})

implements further rotation relative to the initial stable position (

φ_{1} = 0

), at

φ \in (\frac{π}{2}, \frac{3 π}{2})

it is provides stabilisation relative to the new stable equilibrium position (

φ_{2} = π

). The second term in the control law (7) gives the initial rotation of the moon from the initial stable position (

φ_{1} = 0

). Taking into account the control (7) Equation (3) is written as

φ^{″} + \frac{3}{2} σ \sin 2 φ = \frac{2 r}{B n^{2}} P (θ, φ, φ^{'})

(9)

4. Numerical Simulations

The Martian satellite Deimos is taken as an example to verify the proposed control law (7). The data on the pricipal moments of inertia and other parameters of Deimos are known [1,2], which allows to perform numerical simulations using Equation (9). The physical parameters of Deimos are shown in Table 1 [2]. The following parameters of the control law (7) are used in the numerical simulation:

k = 5 10^{7} N, P_{0} = 10^{7} N .

(10)

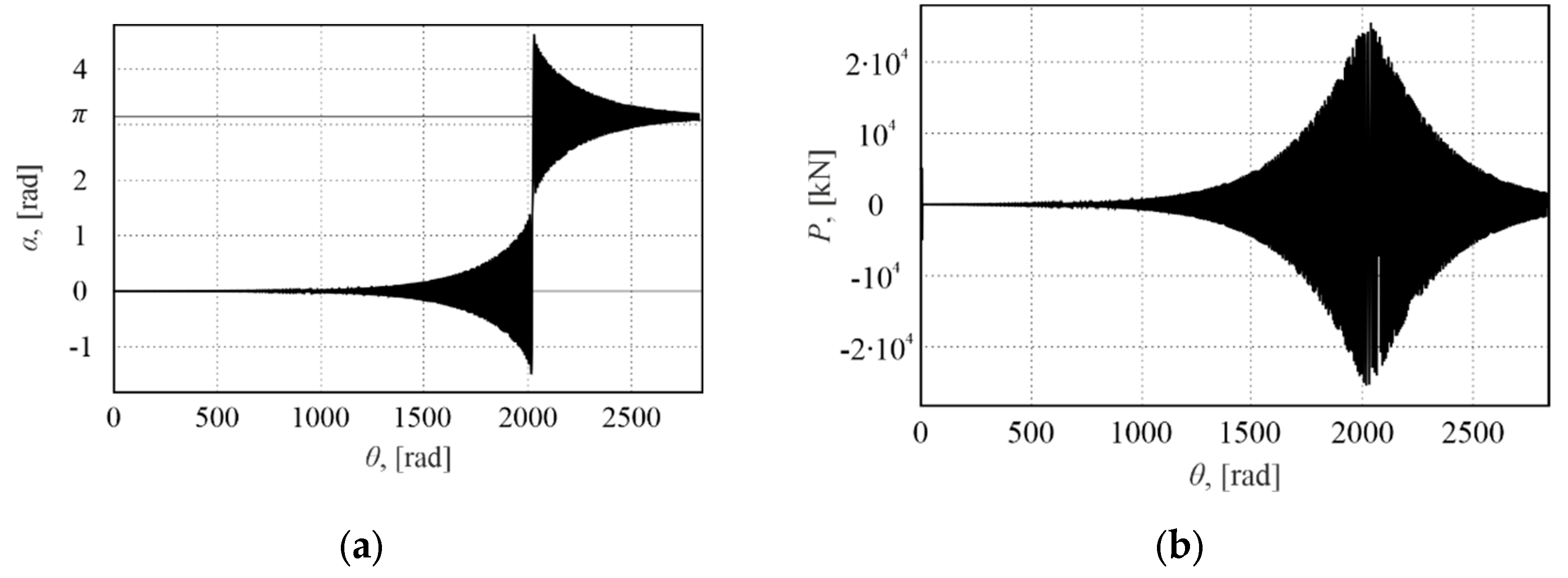
Figure 2 shows (a) the overturning and stabilisation of the moon relative to the new equilibrium position (

φ_{2} = π

) and (b) the control force required for this manoeuvre.

5. Conclusions

A new problem of astrodynamics is proposed for discussion, which may be widely discussed and realized in the future. Especially, it cannot be ruled out in the future that humanity will have a need to turn the moon reverse side in the Earth. Using the example of Deimos and a very simple control law, it is shown that the realization of its overturning requires large amounts of energy and time. If a moon has a small difference in transverse moments of inertia, then this problem would require less energy and time and might be easier to realize.

Author Contributions

Conceptualisation: V.S.A.; investigation: V.S.A.; methodology: V.S.A.; software: V.S.A; writing—original draft: A.V.S.; writing—review and editing: V.S.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The author declare no conflicts of interest.

References

Rubincam, D.P.; Chao, B.F.; Thomas, P.C. The Gravitational Field of Deimos. Icarus 1995, 114, 63–67. [Google Scholar] [CrossRef]
Huang, K.; Zhang, L.; Yang, Y.; Ye, M.; Li, Y. Dynamical Model of Rotation and Orbital Coupling for Deimos. Remote Sensing 2024, 16, 1174. [Google Scholar] [CrossRef]
Zhong, Z.; Wen, Q.; Yan, J.; Pang, L. The Mean Moment of Inertia for Irregularly Shaped Phobos and Its Application to the Constraint for the Two-Layer Interior Structure for the Martian Moon. Remote Sensing 2023, 15, 3162. [Google Scholar] [CrossRef]
Burša, M. Principal moments of inertia and secular love number of Phobos. Earth, Moon, and Planets 1988, 42, 49–53. [Google Scholar] [CrossRef]
Porco, C.C.; Thomas, P. C.; Weiss, J. W.; Richardson, D. C. Saturn's small inner satellites: Clues to their origins. Science 2007, 318, 1602–1607. [Google Scholar] [CrossRef] [PubMed]
Showalter, M. R. The rings and small moons of Uranus and Neptune. Philosophical Transactions of the Royal Society A 2020, 378, 20190482. [Google Scholar] [CrossRef] [PubMed]
Showalter, M.; Hamilton, D. Resonant interactions and chaotic rotation of Pluto’s small moons. Nature 2015, 522, 45–49. [Google Scholar] [CrossRef] [PubMed]
Stern, S.A.; Weaver, H. A.; Steffl, A. J.; Mutchler, M. J.; Merline, W. J.; Buie, M. W.; Young, E.F.; Young, L.A.; Spencer, J. R. A giant impact origin for Pluto's small moons and satellite multiplicity in the Kuiper belt. Nature 2006, 439, 946–948. [Google Scholar] [CrossRef] [PubMed]
Routh, E.J. Dynamics of a System of Rigid Bodies; Part II; Dover Publications: New York, 1860. [Google Scholar]

Figure 1. Planet and Moon.

Figure 2. (a) The angle of rotation of the moon relative to the local vertical

φ

; (b) The control force

P

Figure 2. (a) The angle of rotation of the moon relative to the local vertical

φ

; (b) The control force

P

Table 1. Major physics parameters of Deimos.

Parameters	Symbol	Vatue
Mass	$m (k g)$	$1.48 \cdot 10^{15}$
Radius	$r (m)$	$6250$
Moments of inertia	$A (k g m^{2})$	$0.508 m r^{2}$
	$B (k g m^{2})$	$0.461 m r^{2}$
	$C (k g m^{2})$	$0.338 m r^{2}$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Overturn Dynamics of a Small Moon

Abstract

1. Introduction

2. Mathematical Model

3. Turning Control Law

4. Numerical Simulations

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe