Prerpints.org logo
Preprint
Review

Review of Data-Driven Models in Wind Energy: Demonstration of Blade Twist Optimization Based on Aerodynamic Loads

Altmetrics

Downloads

145

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 June 2024

Posted:

25 June 2024

You are already at the latest version

Alerts
Abstract
With the increasing use of data-driven modeling methods new approaches to complex problems in the field of wind energy can be addressed. Topics reviewed through literature include wake modeling, performance monitoring and controls applications, condition monitoring and fault detection, and other data-driven research. Literature shows the advantages of data-driven methods reduce computational expense or complexity, particularly in the cases of wake modeling and controls, as well as various data-driven methodologies’ aptitude for predictive modeling and classification, as in the cases of fault detection and diagnosis. Significant work exists for fault detection while less work is found for controls applications. A methodology for creating data-driven wind turbine models for arbitrary performance parameters is proposed. Results are presented utilizing the methodology to create wind turbine models relating active adaptive twist to steady-state rotor thrust as a performance parameter of interest. Resulting models are evaluated by comparing root-mean-square-error (RMSE) on both the training and validation data sets, with Gaussian Process Regression (GPR), deemed an accurate model for this application. The resulting model undergoes particle swarm optimization to determine the optimal aerostructure twist shape at a given wind speed with respect to the modeled performance parameter, aerodynamic thrust load. The optimization process shows an improvement of 3.15% in thrust loading for the 10 MW reference turbine, and 2.66% for the 15 MW reference turbine.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

The wind industry is a growing market due to modern efforts to reduce fossil fuel emissions, with a growth in global capacity of 9% in 2022, up to 906 GW. Capacity is expected to continue growing, with an average of 15% per year for several years [1]. In this space, the domain of wind energy research, a foremost objective is to reduce the Levelized Cost of Energy (LCoE) [2,3,4], with many advancements in the field making wind energy more available, more productive, and cheaper. This can include many technologies or features which improve operation of the turbine, ranging from fatigue monitoring and reduction, structural improvements, aerodynamic improvements and modeling efforts, and materials technologies, and can impact onshore [5] and offshore [6] turbines [7,8].
One of the foremost avenues of investigating improvements for wind turbines is in power generation. The total available amount of capturable power is well known through the Betz’ limit [9], and efficiency improvements at many stages of turbine design allow progressively more of this theoretical limit to be captured in real systems [10]. Fatigue is also an ongoing point of interest for wind turbine research [11,12,13], as reduction of fatigue allows the system to operate for more total time, increasing the total energy generated per system, and reducing maintenance costs during that operation time. Similarly, structural and material considerations [14] also contribute to the reduction of LCoE by increasing uptime, reducing maintenance or manufacturing costs [15], and improving power output.

2. Data-Driven Methods

Data-driven methods include a variety of mathematical techniques which utilize data collection, application of data sets, or in some way deal with data as part of their use. This more general description is intentionally vague to encompass many related, yet distinct techniques which fall under the term. More narrowly, data-driven methods typically involve “learning” information from prepared data sets, through tasks such as regression, classification, and more [16,17,18,19,20,21,22,23,24,25,26], for the purposes of identifying relationships and complex patterns in data. A notable advantage of this is that, depending on the problem, such techniques may reduce computational expense or complexity over other methods. The following section includes a description of various data-driven methods which feature prominently in the literature for wind energy, as a summary of the features and advantages of such methods.
Dynamic mode decomposition (DMD). DMD, introduced by Peter J. Schmid and Joern Sesterhenn [16,17,18], is a dimension-reduction technique for time series data. DMD identifies modes with specific oscillation frequencies and decay/growth rates, which are the normal modes in linear systems or the approximations of Koopman operator modes and eigenvalues in general cases. DMD captures modes with explicit temporal behaviors and features, including damped or driven sinusoidal patterns, hence DMD differs from other dimension-reduction methods such as the principal component analysis (PCA).
Artificial Neural Networks (ANNs). ANNs are a branch of machine learning models that consist of interconnected groups of artificial neurons [19], where each connection can transmit a signal from one neuron to another and be controlled by activation functions.
Convolutional Neural Networks (CNNs). CNNs are a specialized type of artificial neural network designed for processing data that has a grid-like topology, such as images [20]. CNNs employ a mathematical operation called convolution and are particularly effective for tasks involving image recognition, classification, and analysis. CNNs can efficiently handle the spatial hierarchy in data by filtering inputs for useful information and thus reducing the dimensions of the data, making it easier to analyze.
Bidirectional Gated Recurrent Units (BiGRU). This method is a sequence processing model that consists of two Gated Recurrent Units [21,22,23], one taking the input in a forward direction, and the other in a backwards direction. It is a bidirectional recurrent neural network with only the input and forget gates.
Gaussian process regression (GPR). A method of interpolation based on Gaussian process governed by prior covariances, GPR is a non-parametric, Bayesian approach to regression that provides a probabilistic method to infer predictions [24]. It models the underlying function that generates the data as a Gaussian process, characterized by its mean and covariance functions.
The Decision Tree method. Decision Tree is a machine learning algorithm used in applied statistics for both classification and regression tasks [25,26]. It models decisions and their possible consequences by splitting data into branches at decision nodes, based on feature values. Each node represents a feature in the dataset, each branch represents a decision rule, and each leaf node represents an outcome. Decision Trees work by repeatedly partitioning the dataset into subsets based on the feature that results in the highest information gain or the biggest reduction in impurity. This process continues recursively until a stopping criterion is met.
The Random Forest method (RF). RF is a powerful ensemble learning technique for both classification and regression tasks [25,26]. It operates by constructing a multitude of decision trees at training time and outputting the mode of the classes (for classification) or mean prediction (for regression) of the individual trees. RFs improve upon the simplicity of decision trees by adding randomness and bootstrapping (sampling with replacement) to the tree-building process, which helps in reducing overfitting and ensures better generalization to unseen data.

2.1. Data Driven Modeling in Wind Turbine Applications

In wind energy, as well as aerodynamics overall, there are several avenues for data-driven modeling to provide potential benefits. Aerodynamics research is already making use of data-driven methods for the purposes of systems identification [27,28], that is, the identification of relationships between input data and output data, and feature extraction [29], the identification of features in the data [30]. Relating this back to the stated purposes and advantages of data driven methods, reduced-order data-driven modeling provides a significant reduction in computational expense over traditional methods, such as computational fluid dynamics (CFD), and provides approaches to aerodynamics problems where CFD is too expensive to accomplish.
Connecting these aerodynamic modeling advantages to wind energy, the review conducted by Pandit et al. provides a possible foundation for examining many of the applications of data-driven models in wind turbines but is narrowed to focus on the implementation of supervisory control and acquisition data (SCADA) systems and their use in data-driven models. Their paper places strong emphasis on condition monitoring as a task for these models, while also briefly discussing the importance and application of performance monitoring to pair with it. The review features a notable highlight in that, until recent years, classification-based models, in the context of SCADA data, have historically been the subject of much greater attention than regression-based models [31].
With this foundation of condition monitoring and performance monitoring as a branching-off point, there exist several groups of research efforts to examine as a way to gain insight into the present state of data-driven models in wind turbine research. The condition monitoring efforts mentioned in [31] is one such avenue, as are recent developments in the fields of wake modeling, and other efforts. With this context in mind, the following section highlights specific applications in wind turbine research and examines how various data-driven models are currently being used to conduct research on the topic.

2.2. Wake Modeling

Wake modeling [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48], in this context, involves 1) a farm-scale interaction between multiple wind turbines, where the aerodynamic wake of one turbine influences the performance of downwind turbines, and 2) a turbine-scale investigation of how the flow field of wind evolves after its interaction with a turbine. This is an interdisciplinary topic which touches on aerodynamics such as fluid-structure interactions and turbulent flow analysis. While wake modeling remains an area of interest for several different, wider topics, for the scope of this paper, its intersection with data-driven modeling efforts accommodates several notable approaches and outcomes, including flow prediction.
Naseem Ali and Raúl Bayoán utilize dynamic mode decomposition (DMD) to forecast wake states, with the intent to assist controls systems to adjust farm-scale system according to predicted power output. This particular effort currently shows an approximate 15% error between predictive and actual fluctuating velocities, and future work intends to better capture nonlinearities [32]. In a similar effort, H. Zhang et al. utilize a sparsity-promoting DMD method to improve the computational efficiency of standard DMD methodology in numerical simulations, via reduction in the number of required modes for reconstruction of the wake [33].
Guo Nai-Zhi, Zhang Ming-Ming, and Li Bo investigate wind turbine wake using an RF approach to determine the relationship between local inflow parameters and the wake expansion rate. The paper takes in SCADA data, filters it for inflow data at the upwind turbine, then utilizes that as the inflow conditions for the model. It then uses a genetic algorithm (GA) to solve an optimization problem regarding the RMSE between the measured rate and calculated rate to find the optimal wake expansion rate for the time domain. By doing so, the paper presents a data-driven model which combines machine learning and analytical models, for an improvement in RMSE of 20% [34].
S. Ashwin Renganathan et al. also attempted to model the wake flow fields of a turbine farm, utilizing wind LIDAR measurements to improve accuracy over “incomplete and noisy” experimental data. In this paper, several machine learning methods are utilized in tandem. A neural network (NN) is first used to compress the data state-space by several orders of magnitude. Then, GPR is applied, to map that state space. The paper thus presents a predictive wake model which drastically saves on computational expense, the intent being that the data-driven methods create low expense, accurate wake models that can be used in real time [35].
A novel data-driven method for reducing the computational expense of wake modeling is also presented by J. Steiner, R. Dwight, and A. Viré. The method described in their work generates data using high-fidelity Large Eddy Simulations (LES) and applies this data to a lower-fidelity Reynolds Averaged Navier-Stokes (RANS) model as a correction term derived through regression modeling. Overall, this approach is intended to take advantage of the preferable computational performance of the RANS model, while still maintaining some of the quality of data from the LES method [36].
Overall, the research presented shows a directed effort towards reduction of complexity and computational expense presented by the turbulent flow field problem. Corroborating this, research by Martin Geibel and Galih Bangga on wake reconstruction explicitly state their results reduce dimensionality of the flow data, through use of a particular ANN [37]. Generally, this feature is the one of the most advantageous to the application of wake modeling and flow data.

2.3. Performance Monitoring

Performance monitoring is another ongoing avenue of research for data-driven modeling in the wind turbine space [31,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63]. For the purposes of this paper, performance modelling is classified here as any task where data-driven models are utilized to observe, predict, control, and optimize the performance of individual turbines, or turbine farms, referencing tasks as such as in [31]. One such use case of this technology is in power capture, as an example, being used at least as early as 2011 in predictive control schemes to optimize power capture using a neural network [49]. Performance monitoring typically involves an examination of specific performance parameters of the turbine, such as power capture and vibration, often with the intent of controlling these values or otherwise manipulating turbine features. Applications here range from optimization of power capture, to accounting for changes in environmental and turbine conditions in a controls system.
R. Pandit, D. Infield and M. Santos examined the impact of a variety of environmental conditions on a GPR data-driven model describing the power curve of a turbine. They found that many known environmental factors do significantly influence the ability of a data-driven model to describe the power curve, with the strongest influence being turbulence intensity. Inclusion of this environmental feature improved model accuracy by approximately 15% [50].
Another method to improve the modeling of a turbine power curve is presented in the paper by Wang, Y. et al. for modeling power output to wind speed with a single wind speed input. The proposed method is a combination of several data-driven methods: extreme learning machines, channel attention, CNN, and Huber loss. Through the sequential application of these techniques, the method produces a power curve that outperforms traditional models. The authors of the paper note that, through the testing of several data driven methods, the ability of the CNN to fit nonlinear data is a key feature in its ability to perform above other techniques, such as artificial neural networks (ANN) [51].
A more modern effort for the active control of wind turbine parameters, as compared to [49] as aforementioned, is discussed in a paper by R. Dinkla et al. This effort uses a model predictive control method, specifically, subspace predictive control, to contribute to a closed loop controller for the blade pitch actuation. The goal of this effort is to improve performance of the blade pitch controller by reducing the total amount of pitch actuation, by incorporating detected future wind disturbances instead of traditional methods, with the added benefit of improving data efficiency of the controller through less requisite data retention [52].
Similar controls-oriented efforts can be seen in work by Yang Liu et al. [53], whom also designed a data-driven pitch controller to reduce computational expense of the system model, as well as in work by Jingjie Xie et al. [54], who use a NN-based adaptive controls algorithm to manage pitch and torque control. The efforts mentioned in [52,53,54] take advantage of the reduction in computational expense that data-driven methods provide, as does the work by M. Nouri Manzar and A. Khaki-Sedigh [55]. Their effort, too, involves the use of a data-driven model to enable active control of pitch and torque control schemes, through reduction of computational expense for the controller to operate in real-time. Data-driven models also contribute to other controls applications in wind energy due to their reduction in the complexity of problems, such as the work done by Jian Yang et al. [56], where a model for fatigue load distribution is utilized to optimize active power dispatch to a wind turbine farm, combining wake research with performance control.
Other facets of performance provide more niches for data-driven models. In the work by S. P. Mulders et al., a data-driven approach for the calibration of internal controller models is presented. The calibration algorithm uses turbine operating data to calibrate the internal model. While this effort is foremost intended to assist in ensuring the performance of the turbine is optimal by calibrating the internal model to match the actual operating parameters of turbine, it should be noted that this calibration process also accounts for turbine degradation [57].

2.4. Condition Monitoring

Condition monitoring [29,31,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90] involves a breadth of subjects, including the long-term examination of the health and integrity of the turbine, the classification of anomalies turbines experience in operation, the detection of faults as they occur, and the prediction of when and how such issues arise. For the purposes of this paper, condition monitoring is classified here as any task which involves the observation or influencing of turbine health, operational status, or anomalies in the turbine systems, referencing such as in [30].
Among the various condition monitoring applications of data-driven models in wind turbines, a common use case is that of fault detection. However, within this broader scope, a variety of more specific applications can also be delineated. Namely, this includes applications such as detection, to find issues when they occur [64,67,73,74,81], diagnosis, to classify issues [64,68,69,70,71,74,77,82], and prediction, to determine when an issue may occur [65,66,72,77,78,79,80]. The purpose of these tasks, as stated by J.-Y. Hsu et al., is “provide technicians early warnings, improve equipment efficient, and decrease system downtime of wind turbine operation [31],” or more broadly, to reduce LCoE through system maintenance cost and overall system efficiency and uptime.
In the same paper by J.-Y. Hsu et al., two data-driven models were trained to detect and classify anomalies in wind turbine operation, one decision tree model, and one random forest (RF) model. Their process to develop these models also examined machine learning algorithms including neural network (NN), support vector machine (SVM), boosting tree, and General Chi-square Automatic Interaction Detector, concluding that the random forest (RF) model produced the most accurate results. Validation tests of the final models showed 92.68 % accuracy for the decision tree model, and 91.98% accuracy for the random forest model [64].
Multiple papers by L. Xiang et al. [65,66] describe an effort to use a convolutional neural network (CNN) model with an attention mechanism (AM) in the application of fault detection. The effort in [65] implements a “long- and short-term memory network” in the CNN, with weighting influenced by the AM, to run alongside the operation of the turbine, and predict when its condition will violate set parameters that denote a fault or anomaly. In [66], the effort continues by implementing “two bidirectional gated recurrent unit[s],” and both display results through utilization of the model on SCADA datasets of real turbine operation. It is of note, the primary features these models examine is operational temperature, unlike many similar fault detection efforts.
The fault detection system described by S. Cho et al. is specific to hydraulic blade pitch subsystems. The system uses a Kalman filter to estimate the current operating conditions of the subsystem, and an artificial neural network (ANN) to diagnose fault types. Notably, while the Kalman filter is used in detection of the fault, this ANN system falls under a classification framework, and is capable of classifying six specific types of faults. Validation tests in the paper show an approximate 97% accuracy of the system [67].
Overall, data-driven efforts for fault detection applications are the most populous domain in the examined literature regarding wind, by a wide margin. In addition to the efforts described in greater detail above, the literature presents many other such works. Yanjie Guo et al. propose a data-driven method for fault diagnosis for turbine drive trains, citing robustness to “harmonic interference and background noise,” for a more efficient method than traditional methods [68]. Mengshi Li et al. also propose a data-driven model for fault diagnosis, this time examining the drive train, actuators, and sensors for faults across the turbine system, similarly citing “robustness to noise,” as well as an applicability to a wide range of turbine systems, given availability of appropriate data [69]. Similar to [68], research by Zhen Xu et al. incorporates data fusion into its approach to fault diagnosis on the drive chain [70].
Bilal, Adjallah, and Sava propose the groundwork for a fault classification method through analysis of a variety of data types for a particular wind farm [71]. J. Man, Z. Zhang, and Q. Zhou present a framework to predict wind turbine shutdowns through data-driven predictive analytics [72]. Jaclyn Solimine and Murat Inalpolat present a data-driven, acoustics-based method to detect damage to the turbine blades, reaching between 89% and 99.8% detection accuracy depending on the type of fault [73]. D. Yu et al. propose a “deep-belief network” data-driven method for fault detection and classification which is not only compared to traditional models, but also to a selection of multiple existing data-driven models as well to emphasize its accuracy over previous methods [74], a comparison illustrating just how well adapted data-driven modeling is to fault detection as an application, and how populous it has become in the space.
Despite the relative abundance of fault detection and fault classification research efforts, other niches exist in condition monitoring applications, such as health monitoring and icing prediction. For health monitoring, in work by Zhe Song et al., SCADA data is used to monitor and predict wind turbine health states. In particular, bin method, Copula method, and normal distribution method are examined and evaluated for their performance, with the examined framework showing the Copula method to be promising, despite the limited access to SCADA data by the project [75].
Another application is in icing problems [29,87,88,89,90,91]. In a paper by Y. Wu, H. Yuan and T. Wen, a hybrid data-driven and simulation method is proposed to predict icing on wind turbine blades. Physical laws regarding the growth of icing on the blade were used to set up a simulation, and then that simulation was used to generate the data for a polynomial regression model. This regression model associates a variety of parameters, such as wind speed, to the accumulation of ice. The intention of this effort, then, is for use in a predictive capacity to predict when icing will cause problems for turbines already in operation [87].

2.5. Other Data Driven Efforts

As noted, not all current research fits neatly into the above common categories. Several such articles were focused on determining operational parameters during dynamic conditions [92,93]. J. Yan et al. utilized a long-term short-term (LTSM) neural network (NN), hybridized with a database of physical, dynamic operation characteristics to assist simulation of wind turbine operations, stated by the authors to often be “physical simulation models.” The direct benefit of this research is intended to be an improvement of simulation accuracy and reduction of computational expense for these simulations, with the proposed method seeing a 99.8% accuracy in determining power output, and an 88.5% accuracy in tower root load [92]. Similarly, the efforts of Dong, X., et al. seek to assist in determining a wind turbine’s operational parameters during dynamic operating conditions through the use of a neural network. Unlike the previous effort, this is intended to augment a lack of obtainable measurements in a turbine during active dynamic operation “under severe disturbance,” rather than in simulation [93].
Unlike the previously discussed efforts, some research is directed towards improvement of the available data-driven modeling methods available in the field, rather than towards a specific application. M. Tan and Z. Zhang propose a random sampling method for wind turbine data-driven models, radially uniform sampling. The intent of the algorithm, as with most sampling algorithms, is to obtain a randomly sampled data subset which will accelerate the training process with minimum loss of accuracy. The paper goes on to compare the sampling method in five different data-driven methods, including SVM and NN, where the proposed sampling method outperforms traditional sampling methods in the accuracy of the trained models [94].
While not necessarily in the field of aerodynamics, related data-driven modeling efforts also contribute to economic considerations for the broader field of wind energy, such as site management, siting, and optimization of wind farms. A study by A. P. Reiman et al. presents data-driven turbine models for distributed wind with strong emphasis on siting and economic studies. The data-driven methodology here is a variety of regression models intended for use in economic studies relating turbine size, power generation, costs, and power storage [95].

2.6. Implications to Current Work

In previous work by the authors [96,97,98,99], adaptive aerostructures with adaptive twist capabilities were explored. In it, region 2 operation is considered for optimization of twist profile with respect to power capture, at a variety of wind speeds for a 20kW reference turbine [96]. A segmented approach is considered for implementation in a physical turbine blade, and several methods of bridging an idealized twist profile and segmented blade profile are investigated for best performance [98]. In the next stages of work by the authors, a data-driven approach is considered for modeling arbitrary performance parameters using a segmented twist profile. The efforts toward this are detailed here as an ongoing example of data-driven modeling in the space of wind turbine research.

3. Methodology

In this effort, a linear segmented approach, as detailed in [97,99], is utilized to map performance parameters of interest to twist profiles using a variety of data-driven modeling techniques. A segmented approach is chosen to reduce the number of independent variables in the cost function to a user-defined amount, which can be modulated in future work. The cost function to be examined is defined, in region 3 operation only, as:
P = f u , φ   u , { ∆ θ i } , { ∆ θ i } ,
where P is the performance parameter of interest, { ∆ θ i } are the changes in twist relative to the original twist profile at the actuation points, henceforth referred to as actuation twist, and φ is the pitch angle at the root, which is determined by the turbine controller as part of region 3 operation to constrain power capture at rated power and is assumed to be a function of relative twists. Lastly, u is the wind speed, assuming a non-turbulent, steady flow.
To acquire the data needed to build the data-driven models, in the general case, simulations are run using simulation software on a selected turbine of interest. For each simulation, a twist profile is generated using a uniform distribution for the value of each actuation twist, which is applied to the rest of the discrete points on the blade data sheet through linear interpolation. This is independently done a user-selected number of times for each given wind speed, which are randomly selected through a normal distribution. An additional value set of zero in all actuation twists is also included at each wind speed, for later comparison. Each simulation is allowed to ready a steady state, and the output values of the simulation are recorded as periodic, time-averaged data. The output must necessarily include both the performance parameter(s) of interest, and the pitch.
For the specific analysis presented here, OpenFAST is used as the modeling software, and the distribution of wind speeds uses a mean at 15 m/s and variance of 1.5 m/s. This puts the operation of the turbine in region 3, which is the focus of this effort. Furthermore, here the process is repeated using a 10MW [100] and 15MW [101] reference turbine, to ensure its generalizability, and focuses on rotor thrust load as the performance parameter to be examined, due to its relevance in fatigue research. The simulations are run using three actuation points and three randomized distributions per wind speed. Thus the cost function becomes:
T = f u , φ   u , ∆ θ 1 , ∆ θ 2 , ∆ θ 3 , ∆ θ 1 , ∆ θ 2 , ∆ θ 3
where T is the aerodynamic thrust load. For the models presented, 400 simulations were run, and 10% of data generated was set aside for validation. The data generated is then used as training data for several data-driven methods, namely, SVM, neural networks, decision tree, and gaussian process regression, which are trained through the included regression modeling software in MATLAB. Training data, here, is the subset of data which was used for initial modeling, while test data is the subset of the original data retained to evaluate the performance of the developed models, by examining predictions for data points not within the training subset. Once each model is trained, they are evaluated through set aside test data, and compared to evaluate the optimal modeling process. 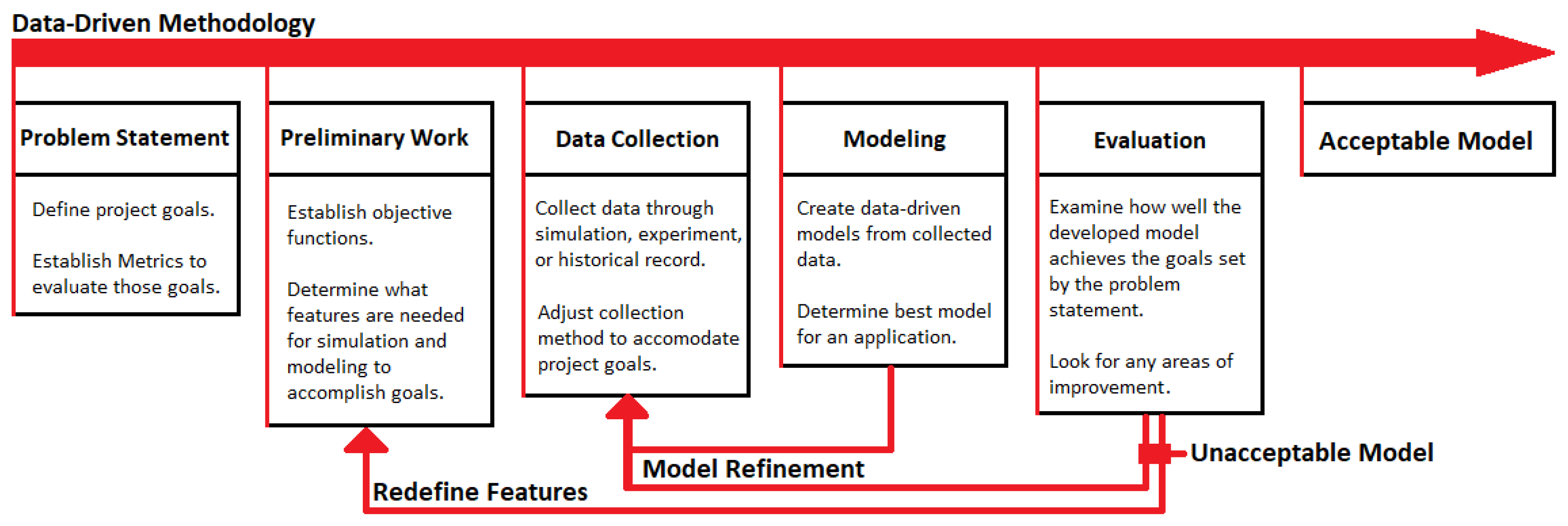The overall methodology is described in its entirety in Figure 1.

3. Results

In building the data-driven model from the data, several approaches were attempted to examine the efficacy of each in this application. Shown in Table 1 are the various approaches tested, and their relative performance as evaluated via RMSE, for the 10 MW reference turbine. This process was then repeated for the 15 MW turbine, presented in Table 2. The results show a clear advantage in accuracy of the predictions when using GPR as the modeling process. Examining the results for RMSE, the GPR method is an order of magnitude more accurate, or better, than other methods across all cases, for both target parameter and turbine examined.

3.1. Optimization of Thrust Load

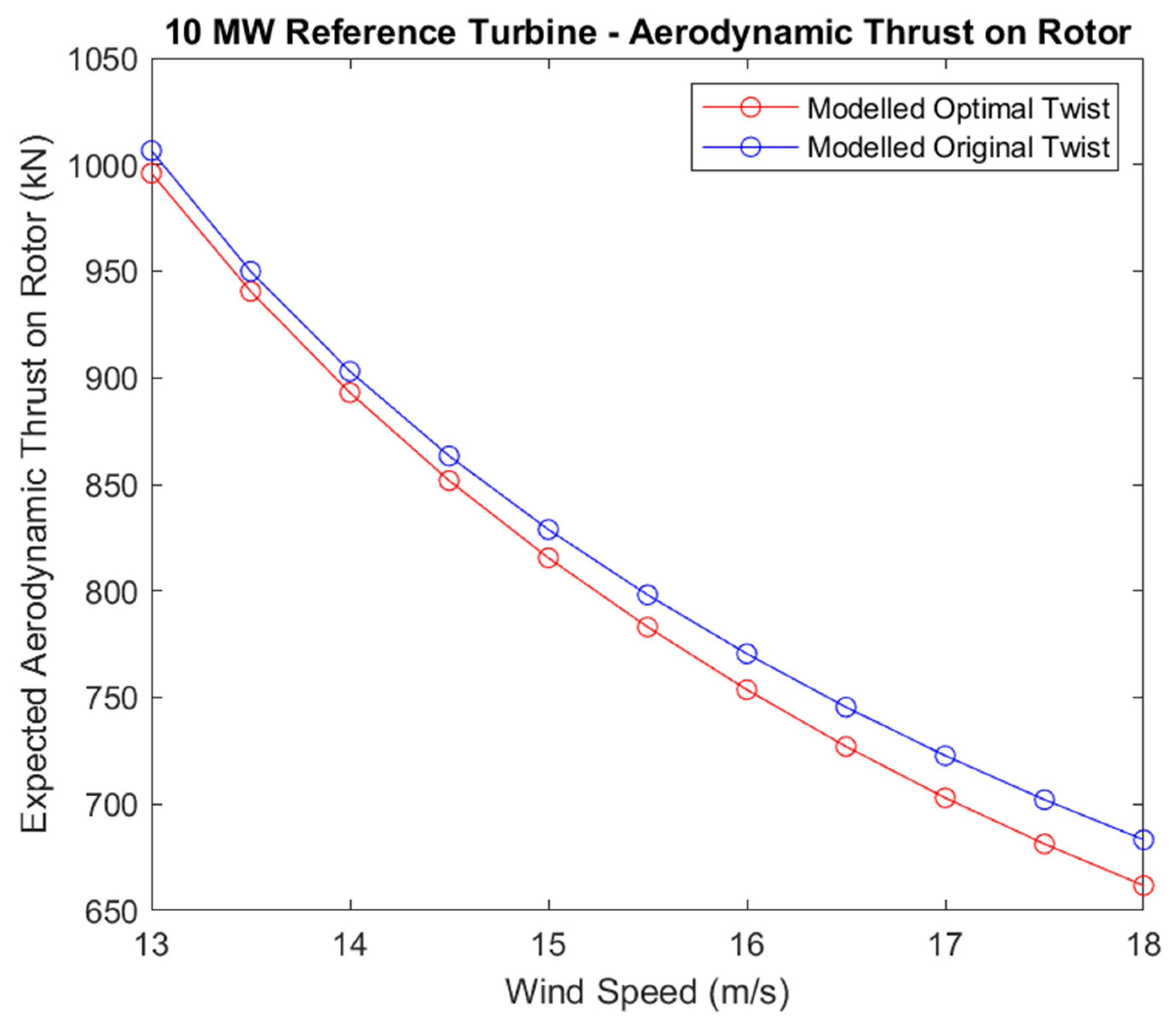
To demonstrate the application of this process, an optimization process was run using the developed models to predict optimal performance of the parameter at various wind speeds for this particular configuration of segmentation. The process utilized particle swarm optimization to find a global minimum of the objective function shown in Equation 2, using the pitch model in the input variables of the thrust model, with the actuation twist as the independent variables of the function, and wind speed held constant. The results of this optimization are shown in Figure 2 for the 10 MW turbine, and in Figure 3 for the 15 MW turbine. The optimization process showed a maximum decrease in thrust load of 3.15% in the 10 MW turbine, and a maximum decrease in thrust load of 2.66% in the 15 MW turbine.
However, closer examination of the twist profiles defined by these optimized points show that some approach the limits of interpolation possible with the models, which is set as a boundary on the optimization process to prevent predictions outside the examined region, which indicates that the global optimum may lay outside the examined region. As such, the methodology, as outlined in Figure 1, then dictates that the process should be repeated for refinement in future work to expand the applicable region in severity of possible twist, and so on until the optimum values lie within the limits of the model. Moreover, the current approach mainly focuses on learning the states of performance variables and does not take changes/evolution into account. In the future, we may use DMD or similar methods to learn the dynamics of the performance variables.
Table 3. 10 MW Turbine Model Optimization Results.
Table 3. 10 MW Turbine Model Optimization Results.
Wind Speed (m/s) 13 14 15 16 17 18
Thrust Force (kN) Original 1007 903.0 828.8 770.5 722.7 683.3
Optimized 996.0 893.1 815.5 753.7 703.0 661.8
Improvement (%) 1.09 1.10 1.60 2.18 2.73 3.15
Table 4. 15 MW Turbine Model Optimization Results.
Table 4. 15 MW Turbine Model Optimization Results.
Wind Speed (m/s) 13 14 15 16 17 18
Thrust Force (kN) Original 1489 1349 1243 1156 1085 1024
Optimized 1480 1335 1225 1136 1061 996.8
Improvement (%) 0.60 1.04 1.45 1.73 2.21 2.66

3.2. Future Work

With the preliminary results showing promising models for general modeling of arbitrary wind turbine parameters, several avenues for future work emerge. Foremost, modeling of larger variety targeted parameters of interest may assist in proving generalizability of the methodology, just as modeling among multiple reference turbines has, with the additional benefit of providing data-driven models for applications which are in need of such. When considering the limitations of the presented models, namely, exclusive operation within regions bounded by the data collected, a better understanding of what extents the domain of each input can go to without sacrificing accuracy may help reduce total simulation time by preventing unnecessary repetition of the methodology due to desired information existing outside the model, as in the case of some of the optimization results shown in Figure 2 and Figure 3.
Following other work on active morphing blades [82,83], applying optimization of the location and number of actuation points during the first steps of the methodology should improve the ability of the technology to function in desired applications, such as performance optimization, while not improving or modifying the model accuracy directly.
Of particular interest to the authors is an investigation of time-series data as training data rather than the time-averaged, periodic, steady-state data presented. The explicit reason for the use of periodic, steady-state data here is due to difficulty in having the OpenFAST simulations incorporate modifications to the overall turbine system during operation. However, with appropriate investigation, inclusion of this should be possible, and is already under preliminary examination. With this change, while the overall methodology will remain unchanged, the variety of usable data-driven methods will increase to include those that operate with consideration to time domain, such as DMD, and the objective function being investigated by the methodology can be updated to include time-varying information such as spatial derivatives of the input variables, to learn the PDE of the underlying performance variables. Such changes are warranted by the ability of data-driven models to capture nonlinear behavior of the system. In this case, the controls applications mentioned throughout the literature show what benefits can also be applied here: a reduction in computational expense and complexity that enables real-time control of a complex system.

4.0. Conclusions

Through examination of the literature on data-driven models in wind turbine applications, several points are made evident. First, the various purposes of data-driven modeling efforts are generally focused in a handful of narrow topics: reduction of computational expense [33,35,52,92,94], improvements in accuracy or other performance over existing methods [34,50,51,52,92,93,94], and leveraging the unique aspects of data driven models in novel approaches for existing problems that cannot be solved or are difficult to solve with extant methods, such as fault detection [32,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,92,94].
For condition monitoring, specifically in the case of the prominent fault detection example, the strong representation of data-driven modeling efforts [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86] is in part due to the success of many data-driven modeling techniques in classification tasks, such as NNs, SVM, and Decision Trees [16,17,18,19,20,21,22,23,24,25,26], a feature which is strongly beneficial to detection of anomalies and faults that differ from standard operating conditions.
In the cases of wake modeling, many data-driven modeling efforts are intended to reduce computational expense [32,33,36,37]. Current wake modeling techniques, such as Large Eddy Simulations (LES), are computationally expensive, and so data-driven methods are employed attempting to reduce this cost through reduced order modeling [32,33], and other techniques [36,37]. Further data-driven efforts which intersect with wake modeling are also ongoing in the wider realm of aerodynamics [30], contributing to the focus on the topic.
While a variety of performance monitoring applications are shown [31,49,50,51,52,53,54,55,56,57], the authors highlight a comparative lack of controls- and optimization-oriented efforts compared to counterparts in condition monitoring applications like fault detection. Efforts such as [52,53,54,55,56] show promise in allowing predictive, systems-identifying data-driven models to augment performance of turbines through optimizing performance parameters, improving data efficiency to enable real-time applications, and reducing computational expense, yet few sources in the literature focused on tackling this in comparison to the now more well-tread areas of fault detection.
A possible explanation for the discrepancy between volume of work directed toward controls efforts, compared to fault detection, is that fault detection has a wide applicability to many discrete elements in a wind turbine system, while controls, optimization, and performance efforts have application to select elements of the turbine system. Turbine-scale controls efforts have generally focused on pitch control systems and torque control systems [52,53,54,55], or novel methods of controls such as the work by the authors. In contrast, fault detection systems have applicability to any component of the system which sees fatigue, damages, or icing [29,87,88,89,90,91], including everything from subsystems [67], the drive chain [68,69,70], to the system as a whole [64,65,66]. Similarly, the broader category of performance monitoring takes more advantage of data-driven techniques capacity for prediction [5,54], while fault detection applications are able to take advantage of both classification and prediction [67,72,75], allowing more opportunities for data-driven techniques to permeate.
Original, preliminary work regarding data-driven modeling in the wind turbine space by the authors is also presented. A methodology to create data-driven models mapping time-averaged performance parameters to segmented adaptive twist in the blade is presented. Through examination of this process using multiple data-driven methods, on multiple reference turbines, the most effective method is shown to be Gaussian Process Regression for this application, with a noticeable improvement in RMSE over other methods in both training data and test data, for both the pitch model and the performance parameter model. An example application of this model is also present, with an optimization of thrust force at discrete wind speeds, showing a maximum 3.15% and 2.66% improvement via reduction of thrust load for the 10MW reference turbine and 15MW reference turbine respectively.

5. Patents

The work supports the development of innovation related to United States Patent # WO2019210330A1, titled, Flexible wind turbine blade with actively variable twist distribution.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: Data-Driven Design Methodology, Figure S2: 10 MW Reference Turbine Optimization Example, Figure S3: 15 MW Reference Turbine Optimization Example, Table S1: 10 MW Turbine Model RMSE Results, Table S2: 15 MW Turbine Model RMSE Results, Table S3: 10 MW Turbine Model Optimization Results, and Table S4: 15 MW Turbine Model Optimization Results.

Author Contributions

Conceptualization, Roetzer and Hall.; methodology, Roetzer, Li, and Hall formal analysis, Roetzer, Li, and Hall; investigation, Roetzer, Li, and Hall; resources, Roetzer.; data curation, Roetzer.; writing—original draft preparation, Roetzer, Li, and Hall; writing—review and editing, Roetzer, Li, and Hall; visualization, Roetzer.; supervision, Li and Hall.; project administration, Hall.; funding acquisition, Hall All authors have read and agreed to the published version of the manuscript.

Funding

Funding support for this work has been provided by the National Science Foundation (NSF), grant number 2151668.

Data Availability Statement

The data produced or examined in this study are provided within this article.

Acknowledgements

The authors express their appreciation for the support provided by the University of North Carolina at Charlotte, the Energy Production and Infrastructure Center, and the TAIMing AI Center in facilitating this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. “Global Wind Energy Report 2023.” Global Wind Energy Council, rep.
  2. T. Ashuri, M.B. Zaaijer, J.R.R.A. Martins, G.J.W. van Bussel, G.A.M. van Kuik, “Multidisciplinary design optimization of offshore wind turbines for minimum levelized cost of energy.” Renewable Energy, Volume 68, 2014, Pages 893-905, ISSN 0960-1481. [CrossRef]
  3. R. Ebenhoch, D. Matha, S. Marathe, P. C. Muñoz, C. Molins. “Comparative Levelized Cost of Energy Analysis.” Energy Procedia, Volume 80, 2015, Pages 108-122, ISSN 1876-6102. [CrossRef]
  4. P. Ziyaei, M. Khorasanchi, H. Sayyaadi, A. Sadollah. “Minimizing the levelized cost of energy in an offshore wind farm with non-homogeneous turbines through layout optimization.” Ocean Engineering, Volume 249, 2022, 110859, ISSN 0029-8018. [CrossRef]
  5. F. Bertagnolio, M. Herr, & K. D. Madsen, (2023). “A roadmap for required technological advancements to further reduce onshore wind turbine noise impact on the environment.” WIREs Energy and Environment, 12(3), e469. [CrossRef]
  6. T. Asim, S. Z. Islam, A. Hemmati, M. S. U. Khalid. “A Review of Recent Advancements in Offshore Wind Turbine Technology.” Energies, 2022, 15(2):579. [CrossRef]
  7. C. C. W. Chang, T. J. Ding, T. J. Ping, K. C. Chao, M. A. S. Bhuiyan. “Getting more from the wind: Recent advancements and challenges in generators development for wind turbines.” Sustainable Energy Technologies and Assessments, Volume 53, Part C, 2022, 102731, ISSN 2213-1388. [CrossRef]
  8. A. S. Darwish, & R. Al-Dabbagh. (2020). “Wind energy state of the art: present and future technology advancements.” Renewable Energy and Environmental Sustainability, 5(7). [CrossRef]
  9. M. De Lellis, R. Reginatto, R. Saraiva, A. Trofino. “The Betz limit applied to Airborne Wind Energy.” Renewable Energy, Volume 127, 2018, Pages 32-40, ISSN 0960-1481. [CrossRef]
  10. Johnson, K. E., Fingersh, L. J., Balas, M. J., and Pao, L. Y. (November 18, 2004). “Methods for Increasing Region 2 Power Capture on a Variable-Speed Wind Turbine.” ASME. J. Sol. Energy Eng. November 2004; 126(4): 1092–1100. [CrossRef]
  11. Bossanyi, E.A. (2003), “Wind Turbine Control for Load Reduction.” Wind Energ., 6: 229-244. [CrossRef]
  12. Ravikumar K., Subbiah R., Ranganathan N., Bensingh J., Kader A., Nayak S.K. “A review on fatigue damages in the wind turbines: Challenges in determining and reducing fatigue failures in wind turbine blades.” Wind Engineering. 2020;44(4):434-451. [CrossRef]
  13. J. Pacheco, F. Pimenta, S. Pereira, Á. Cunha, F. Magalhães. “Fatigue Assessment of Wind Turbine Towers: Review of Processing Strategies with Illustrative Case Study.” Energies. 2022, 15(13):4782. [CrossRef]
  14. X. Dong, J. Lian, H. Wang, T. Yu, Y. Zhao. “Structural vibration monitoring and operational modal analysis of offshore wind turbine structure.” Ocean Engineering, Volume 150, 2018, Pages 280-297, ISSN 0029-8018. [CrossRef]
  15. Á. M. Costa, J. A. Orosa, D. Vergara, P. Fernández-Arias. “New Tendencies in Wind Energy Operation and Maintenance.” Applied Sciences. 2021, 11(4):1386. [CrossRef]
  16. Schmid, Peter J; Sesterhenn, Joern (28 July 2008). “Dynamic mode decomposition of numerical and experimental data”. Bulletin of the American Physical Society, Sixty-First Annual Meeting of the APS Division of Fluid Dynamics. 53 (15).
  17. Schmid, P. J., Li, L., Juniper, M. P., & Pust, O. (2011). Applications of the dynamic mode decomposition. Theoretical and computational fluid dynamics, 25, 249-259.
  18. Kutz, J. N., Brunton, S. L., Brunton, B. W., & Proctor, J. L. (2016). Dynamic mode decomposition: data-driven modeling of complex systems. Society for Industrial and Applied Mathematics.
  19. Hardesty, Larry (14 April 2017). “Explained: Neural networks”. MIT News Office.
  20. Balas, Valentina E.; Kumar, Raghvendra; Srivastava, Rajshree (2019-11-19). Recent Trends and Advances in Artificial Intelligence and Internet of Things. Springer Nature.
  21. Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078.
  22. Chung, J., Gulcehre, C., Cho, K., & Bengio, Y. (2015, June). Gated feedback recurrent neural networks. In International conference on machine learning (pp. 2067-2075). PMLR.
  23. Zhao, R., Wang, D., Yan, R., Mao, K., Shen, F., & Wang, J. (2017). Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Transactions on Industrial Electronics, 65(2), 1539-1548.
  24. Dym, H., & McKean, H. P. (2008). Gaussian processes, function theory, and the inverse spectral problem. Courier Corporation.
  25. Härdle, W. K., & Simar, L. (2019). Applied multivariate statistical analysis. Springer Nature.
  26. Tinsley, H. E., & Brown, S. D. (Eds.). (2000). Handbook of applied multivariate statistics and mathematical modeling. Academic press.
  27. P. Cross, X. Ma. “Nonlinear system identification for model-based condition monitoring of wind turbines.” Renewable Energy, Volume 71, 2014, Pages 166-175, ISSN 0960-1481. [CrossRef]
  28. G. J. van der Veen, J. W. van Wingerden, P. A. Fleming, A. K. Scholbrock, M. Verhaegen. “Global data-driven modeling of wind turbines in the presence of turbulence.” Control Engineering Practice, Volume 21, Issue 4, 2013, Pages 441-454, ISSN 0967-0661. [CrossRef]
  29. X. Jin, X. Zhang, X. Cheng, G. Jiang, L. Masisi and W. Huang, “A Physics-Based and Data-Driven Feature Extraction Model for Blades Icing Detection of Wind Turbines,” in IEEE Sensors Journal, vol. 23, no. 4, pp. 3944-3954, 15 Feb.15, 2023. [CrossRef]
  30. Jiaqing Kou, Weiwei Zhang, “Data-driven modeling for unsteady aerodynamics and aeroelasticity, Progress in Aerospace Sciences,” Volume 125, 2021, 100725, ISSN 0376-0421. [CrossRef]
  31. Pandit, R., Astolfi, D., Hong, J., Infield, D., and Santos, M., “SCADA data for wind turbine data-driven condition/performance monitoring: A review on state-of-art, challenges and future trends,” Wind Engineering 2022 47:2, 422-441.
  32. 32. Naseem Ali, Raúl Bayoán Cal; Data-driven modeling of the wake behind a wind turbine array. J. Renewable Sustainable Energy 1 May 2020; 12 (3): 033304. [CrossRef]
  33. Zhang, H., Xu, C., Wei, S., Deng, Z., & Jiao, Z. (2023). Sparsity Promoting Dynamic Mode Decomposition for Data-Driven Modeling of Wind Turbine Wake. Journal of Physics: Conference Series, 012028 (10 pp.). [CrossRef]
  34. Guo Nai-Zhi, Zhang Ming-Ming, Li Bo, A data-driven analytical model for wind turbine wakes using machine learning method, Energy Conversion and Management, Volume 252, 2022, 115130, ISSN 0196-8904. [CrossRef]
  35. Ashwin Renganathan, S., Maulik, R., Letizia, S. et al. Data-driven wind turbine wake modeling via probabilistic machine learning. Neural Comput & Applic 34, 6171–6186 (2022). [CrossRef]
  36. Steiner, J., Dwight, R., & Viré, A. (2020). Data-driven turbulence modeling for wind turbine wakes under neutral conditions. Journal of Physics: Conference Series, 1618, 062051 (10 pp.). [CrossRef]
  37. Geibel, M.; Bangga, G. “Data Reduction and Reconstruction of Wind Turbine Wake Employing Data Driven Approaches.” Energies, 2022, 15, 3773. [CrossRef]
  38. Z. Ti, X. W. Deng, H. Yang. “Wake modeling of wind turbines using machine learning.” Applied Energy. Volume 257, 2020, 114025, ISSN 0306-2619. [CrossRef]
  39. N. Zehtabiyan-Rezaie, A. Iosifidis, M. Abkar. “Data-driven fluid mechanics of wind farms: A review.” J. Renewable Sustainable Energy. 1 May 2022; 14 (3): 032703. [CrossRef]
  40. D. Astolfi, F. De Caro, A. Vaccaro. “Characterizing the Wake Effects on Wind Power Generator Operation by Data-Driven Techniques.” Energies. 2023; 16(15):5818. [CrossRef]
  41. L. Wang, J. Xie, W. Luo, Z. Wang, B. Zhang, M. Chen, A. C. C. Tan. “Effectiveness of data-driven wind turbine wake models developed by machine/deep learning with spatial-segmentation technique.” Sustainable Energy Technologies and Assessments, Volume 53, Part A, 2022, 102499, ISSN 2213-1388. [CrossRef]
  42. J. Zhang, X. Zhao. “A novel dynamic wind farm wake model based on deep learning.” Applied Energy, Volume 277, 2020, 115552, ISSN 0306-2619. [CrossRef]
  43. H. Long, P. Li, W. Gu. “A data-driven evolutionary algorithm for wind farm layout optimization.” Energy, Volume 208, 2020, 118310, ISSN 0360-5442. [CrossRef]
  44. X. Yin, W. Zhang, Z. Jiang, L. Pan. “Data-driven multi-objective predictive control of offshore wind farm based on evolutionary optimization.” Renewable Energy, Volume 160, 2020, Pages 974-986, ISSN 0960-1481. [CrossRef]
  45. H. S. Dhiman, D. Deb, A. M. Foley. “Lidar assisted wake redirection in wind farms: A data driven approach.” Renewable Energy, Volume 152, 2020, Pages 484-493, ISSN 0960-1481. [CrossRef]
  46. J. Zhang, X. Zhao. “Wind farm wake modeling based on deep convolutional conditional generative adversarial network.” Energy, Volume 238, Part B, 2022, 121747, ISSN 0360-5442. [CrossRef]
  47. N. -Z. Guo, K. -Z. Shi, B. Li, L. -W. Qi, H. -H. Wu, Z. -L. Zhang, J. -Z. Xu. “A physics-inspired neural network model for short-term wind power prediction considering wake effects.” Energy, Volume 261, Part A, 2022, 125208, ISSN 0360-5442. [CrossRef]
  48. L. Gao, J. Hong. “Data-driven yaw misalignment correction for utility-scale wind turbines.” J. Renewable Sustainable Energy. 1 November 2021. 13 (6): 063302. [CrossRef]
  49. Andrew Kusiak, Zijun Zhang, Control of wind turbine power and vibration with a data-driven approach, Renewable Energy, Volume 43, 2012, Pages 73-82, ISSN 0960-1481. [CrossRef]
  50. R. Pandit, D. Infield and M. Santos, “Accounting for Environmental Conditions in Data-Driven Wind Turbine Power Models,” in IEEE Transactions on Sustainable Energy, vol. 14, no. 1, pp. 168-177, Jan. 2023. [CrossRef]
  51. Yun Wang, Xiaocong Duan, Runmin Zou, Fan Zhang, Yifen Li, Qinghua Hu, A novel data-driven deep learning approach for wind turbine power curve modeling, Energy, Volume 270, 2023, 126908, ISSN 0360-5442. [CrossRef]
  52. R. Dinkla, T. Oomen, J. -W. v. Wingerden and S. P. Mulders, “Data-Driven LIDAR Feedforward Predictive Wind Turbine Control,” 2023 IEEE Conference on Control Technology and Applications (CCTA), Bridgetown, Barbados, 2023, pp. 559-565. [CrossRef]
  53. Liu Y, Jiang Z, Hao L, Xing Z, Chen M, Zhang P. “Data-driven robust value iteration control with application to wind turbine pitch control,” Optim Control Appl Meth. 2023; 44(2): 637-646. [CrossRef]
  54. Jingjie Xie, Hongyang Dong, Xiaowei Zhao, “Data-driven torque and pitch control of wind turbines via reinforcement learning,” Renewable Energy, Volume 215, 2023, 118893, ISSN 0960-1481. [CrossRef]
  55. Nouri Manzar M, Khaki-Sedigh A. “Online data-driven control of variable speed wind turbines using the simultaneous perturbation stochastic approximation approach.” Optim Control Appl Meth. 2023; 44(4): 2082–2092. [CrossRef]
  56. Yang J, Zheng S, Song D, Su M, Yang X, Joo YH. “Data-driven modeling for fatigue loads of large-scale wind turbines under active power regulation.” Wind Energy. 2021; 24: 558–572. [CrossRef]
  57. Sebastiaan P. Mulders, Yichao Liu, Fabio Spagnolo, Poul B. Christensen, Jan-Willem van Wingerden, An iterative data-driven learning algorithm for calibration of the internal model in advanced wind turbine controllers, IFAC-PapersOnLine, Volume 56, Issue 2, 2023, Pages 8406-8413, ISSN 2405-8963. [CrossRef]
  58. Z. Lin, X. Liu. “Wind power forecasting of an offshore wind turbine based on high-frequency SCADA data and deep learning neural network.” Energy, Volume 201, 2020, 117693, ISSN 0360-5442. [CrossRef]
  59. M. Fahim, V. Sharma, T. -V. Cao, B. Canberk and T. Q. Duong. “Machine Learning-Based Digital Twin for Predictive Modeling in Wind Turbines.” in IEEE Access, vol. 10, pp. 14184-14194, 2022. [CrossRef]
  60. D. Karamichailidou, V. Kaloutsa, A. Alexandridis. “Wind turbine power curve modeling using radial basis function neural networks and tabu search.” Renewable Energy, Volume 163, 2021, Pages 2137-2152, ISSN 0960-1481. [CrossRef]
  61. H. Sun, C. Qiu, L. Lu, X. Gao, J. Chen, H. Yang. “Wind turbine power modelling and optimization using artificial neural network with wind field experimental data.” Applied Energy, Volume 280, 2020, 115880, ISSN 0306-2619. [CrossRef]
  62. M. Neshat et al. “Wind turbine power output prediction using a new hybrid neuro-evolutionary method.” Energy, Volume 229, 2021, 120617, ISSN 0360-5442. [CrossRef]
  63. Z. Lin, X. Liu, M. Collu. “Wind power prediction based on high-frequency SCADA data along with isolation forest and deep learning neural networks.” International Journal of Electrical Power & Energy Systems, Volume 118, 2020, 105835, ISSN 0142-0615. [CrossRef]
  64. J. -Y. Hsu, Y. -F. Wang, K. -C. Lin, M. -Y. Chen and J. H. -Y. Hsu, “Wind Turbine Fault Diagnosis and Predictive Maintenance Through Statistical Process Control and Machine Learning,” in IEEE Access, vol. 8, pp. 23427-23439, 2020. [CrossRef]
  65. Ling Xiang, Penghe Wang, Xin Yang, Aijun Hu, Hao Su, Fault detection of wind turbine based on SCADA data analysis using CNN and LSTM with attention mechanism, Measurement, Volume 175, 2021, 109094, ISSN 0263-2241. [CrossRef]
  66. Ling Xiang, Xin Yang, Aijun Hu, Hao Su, Penghe Wang, Condition monitoring and anomaly detection of wind turbine based on cascaded and bidirectional deep learning networks, Applied Energy, Volume 305, 2022, 117925, ISSN 0306-2619. [CrossRef]
  67. Seongpil Cho, Minjoo Choi, Zhen Gao, Torgeir Moan, Fault detection and diagnosis of a blade pitch system in a floating wind turbine based on Kalman filters and artificial neural networks, Renewable Energy, Volume 169, 2021, Pages 1-13, ISSN 0960-1481. [CrossRef]
  68. Y. Guo, Z. Zhao, R. Sun, X. Chen. “Data-driven multiscale sparse representation for bearing fault diagnosis in wind turbine.” Wind Energy. 2019; 22: 587–604. [CrossRef]
  69. M. Li, D. Yu, Z. Chen, K. Xiahou, T. Ji and Q. H. Wu, “A Data-Driven Residual-Based Method for Fault Diagnosis and Isolation in Wind Turbines,” in IEEE Transactions on Sustainable Energy, vol. 10, no. 2, pp. 895-904, April 2019. [CrossRef]
  70. Z. Xu, P. Yang, Z. Zhao, C.S. Lai, L.L. Lai, X. Wang. “Fault Diagnosis Approach of Main Drive Chain in Wind Turbine Based on Data Fusion.” Applied Sciences. 2021; 11(13):5804. [CrossRef]
  71. B. Bilal, K. H. Adjallah and A. Sava, “Data-Driven Fault Detection and Identification in Wind Turbines Through Performance Assessment,” 2019 10th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Metz, France, 2019, pp. 123-129. [CrossRef]
  72. Man, J., Zhang, Z. and Zhou, Q. (2018), “Data-driven predictive analytics of unexpected wind turbine shut-downs.” IET Renewable Power Generation, 12: 1833-1842. [CrossRef]
  73. Solimine J, Inalpolat M. “An unsupervised data-driven approach for wind turbine blade damage detection under passive acoustics-based excitation.” Wind Engineering. 2022;46(4):1311-1330. [CrossRef]
  74. D. Yu, Z.M. Chen, K.S. Xiahou, M.S. Li, T.Y. Ji, Q.H. Wu, “A radically data-driven method for fault detection and diagnosis in wind turbines,” International Journal of Electrical Power & Energy Systems, Volume 99, 2018, Pages 577-584, ISSN 0142-0615. [CrossRef]
  75. Zhe Song, Zijun Zhang, Yu Jiang, Jin Zhu, “Wind turbine health state monitoring based on a Bayesian data-driven approach,” Renewable Energy, Volume 125, 2018, Pages 172-181, ISSN 0960-1481. [CrossRef]
  76. J. Maldonado-Correa, S. Martín-Martínez, E. Artigao, E. Gómez-Lázaro. “Using SCADA Data for Wind Turbine Condition Monitoring: A Systematic Literature Review.” Energies. 2020; 13(12):3132. [CrossRef]
  77. J. Wang, Y. Liang, Y. Zheng, R. X. Gao, F. Zhang. “An integrated fault diagnosis and prognosis approach for predictive maintenance of wind turbine bearing with limited samples.” Renewable Energy, Volume 145, 2020, Pages 642-650, ISSN 0960-1481. [CrossRef]
  78. Q. He, Y. Pang, G. Jiang and P. Xie. “A Spatio-Temporal Multiscale Neural Network Approach for Wind Turbine Fault Diagnosis With Imbalanced SCADA Data.” in IEEE Transactions on Industrial Informatics, vol. 17, no. 10, pp. 6875-6884, Oct. 2021. [CrossRef]
  79. W. Chen, Y. Qiu, Y. Feng, Y. Li, A. Kusiak. “Diagnosis of wind turbine faults with transfer learning algorithms.” Renewable Energy, Volume 163, 2021, Pages 2053-2067, ISSN 0960-1481. [CrossRef]
  80. N. Huang, Q. Chen, G. Cai, D. Xu, L. Zhang and W. Zhao. “Fault Diagnosis of Bearing in Wind Turbine Gearbox Under Actual Operating Conditions Driven by Limited Data With Noise Labels.” in IEEE Transactions on Instrumentation and Measurement, vol. 70, pp. 1-10, 2021, Art no. 3502510. [CrossRef]
  81. P. Trizoglou, X. Liu, Z. Lin. “Fault detection by an ensemble framework of Extreme Gradient Boosting (XGBoost) in the operation of offshore wind turbines.” Renewable Energy, Volume 179, 2021, Pages 945-962, ISSN 0960-1481. [CrossRef]
  82. W. Tuerxun, X. Chang, G. Hongyu, J. Zhijie and Z. Huajian. “Fault Diagnosis of Wind Turbines Based on a Support Vector Machine Optimized by the Sparrow Search Algorithm.” in IEEE Access, vol. 9, pp. 69307-69315, 2021. [CrossRef]
  83. A. Bakdi, A. Kouadri, S. Mekhilef. “A data-driven algorithm for online detection of component and system faults in modern wind turbines at different operating zones.” Renewable and Sustainable Energy Reviews, Volume 103, 2019, Pages 546-555, ISSN 1364-0321. [CrossRef]
  84. H. Chen, H. Liu, X. Chu, Q. Liu, D. Xue. “Anomaly detection and critical SCADA parameters identification for wind turbines based on LSTM-AE neural network.” Renewable Energy, Volume 172, 2021, Pages 829-840, ISSN 0960-1481. [CrossRef]
  85. Z. Xu, C. Li, Y. Yang. “Fault diagnosis of rolling bearing of wind turbines based on the Variational Mode Decomposition and Deep Convolutional Neural Networks.” Applied Soft Computing, Volume 95, 2020, 106515, ISSN 1568-4946. [CrossRef]
  86. A. Kouadri et al. “Hidden Markov model based principal component analysis for intelligent fault diagnosis of wind energy converter systems.” Renewable Energy, Volume 150, 2020, Pages 598-606, ISSN 0960-1481. [CrossRef]
  87. Y. Wu, H. Yuan and T. Wen, “A Combined Data-Driven and Simulation Approach for Wind Turbine Blade Icing Prediction in Cold Regions,” 2023 13th International Conference on Power and Energy Systems (ICPES), Chengdu, China, 2023, pp. 496-502. [CrossRef]
  88. X. Cheng, F. Shi, Y. Liu, X. Liu, L. Huang. “Wind turbine blade icing detection: a federated learning approach.” Energy, Volume 254, Part C, 2022, 124441, ISSN 0360-5442. [CrossRef]
  89. X. Cheng, F. Shi, M. Zhao, G. Li, H. Zhang and S. Chen. “Temporal Attention Convolutional Neural Network for Estimation of Icing Probability on Wind Turbine Blades.” in IEEE Transactions on Industrial Electronics, vol. 69, no. 6, pp. 6371-6380, June 2022. [CrossRef]
  90. J. Xiao, C. Li, B. Liu, J. Huang, L. Xie. “Prediction of wind turbine blade icing fault based on selective deep ensemble model.” Knowledge-Based Systems, Volume 242, 2022, 108290, ISSN 0950-7051. [CrossRef]
  91. H. Yi, Q. Jiang, X. Yan, B. Wang. “Imbalanced Classification Based on Minority Clustering Synthetic Minority Oversampling Technique With Wind Turbine Fault Detection Application.” in IEEE Transactions on Industrial Informatics, vol. 17, no. 9, pp. 5867-5875, Sept. 2021. [CrossRef]
  92. J. Yan, A. Nuertayi, Y. Yan, S. Liu, Y. Liu, “Hybrid physical and data driven modeling for dynamic operation characteristic simulation of wind turbine” Renewable Energy, Volume 215, 2023, 118958, ISSN 0960-1481. [CrossRef]
  93. Dong, X., Yang, Q., & Ma, W. (2023). Data-Driven Dynamic Modeling Methods for Offshore Wind Turbine Generators. In Frontier Academic Forum of Electrical Engineering (Vol. 1054, pp. 947–956). Springer Nature Singapore. [CrossRef]
  94. M. Tan and Z. Zhang, “Wind Turbine Modeling with Data-Driven Methods and Radially Uniform Designs,” in IEEE Transactions on Industrial Informatics, vol. 12, no. 3, pp. 1261-1269, June 2016. [CrossRef]
  95. A. P. Reiman, T. Ramachandran and A. C. Orrell, “Data-Driven Generic Turbines for Distributed Wind Modeling, Optimization, and Economic Studies,” 2022 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), New Orleans, LA, USA, 2022, pp. 1-5. [CrossRef]
  96. Roetzer, J., Battaglia, F., Hall, J. (2023). A Modeling Framework to Analyze Active Adaptive Aerostructures. In: Chakrabarti, A., Singh, V. (eds) Design in the Era of Industry 4.0, Volume 2. ICORD 2023. Smart Innovation, Systems and Technologies, vol 342. Springer, Singapore. [CrossRef]
  97. Nejadkhaki, H. K., and Hall, J. F. (May 29, 2018). “Modeling and Design Method for an Adaptive Wind Turbine Blade with Out-of-Plane Twist.” ASME. J. Sol. Energy Eng. October 2018; 140(5): 051010. [CrossRef]
  98. Mou, F, Nejadkhaki, HK, Estes, A, & Hall, J. “A Weighted Least Squares Approach for the Design of Adaptive Aerodynamic Structures Subjected to an Out-Of-Plane Transformation.” Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2B: 44th Design Automation Conference. Quebec City, Quebec, Canada. August 26–29, 2018. V02BT03A043. ASME. [CrossRef]
  99. Khakpour Nejadkhaki, H, & Hall, JF. “A Design Methodology Region 2 Efficiency.” Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2A: 43rd Design Automation Conference. Cleveland, Ohio, USA. August 6–9, 2017. V02AT03A025. ASME. [CrossRef]
  100. Energy, D. W. (2017). HAWC2 Model for the DTU 10-MW Reference Wind Turbine.
  101. Gaertner, E., Rinker, J., Sethuraman, L., Zahle, F., Anderson, B., Barter, G., ... & Viselli, A. (2020). Definition of the IEA 15-megawatt offshore reference wind turbine.
Preprints 110262 g001
Figure 1. Data-Driven Design Methodology.
Figure 1. Data-Driven Design Methodology.
Preprints 110262 g001
Preprints 110262 g002
Figure 2. 10 MW Reference Turbine Optimization Example.
Figure 2. 10 MW Reference Turbine Optimization Example.
Preprints 110262 g002
Preprints 110262 g003
Figure 3. 15 MW Reference Turbine Optimization Example.
Figure 3. 15 MW Reference Turbine Optimization Example.
Preprints 110262 g003
Table 1. 10 MW Turbine Model RMSE Results.
Table 1. 10 MW Turbine Model RMSE Results.
Training Data
Decision Tree SVM Neural Network GPR
Pitch (°) 1.4327 0.12141 0.54099 0.019475
Thrust Load (N) 18881 17635 3105.6 483.04
Test Data
Decision Tree SVM Neural Network GPR
Pitch (°) 1.0738 0.12149 0.67701 0.0092139
Thrust Load (N) 19982 28100 4186.3 473.74
Table 2. 15 MW Turbine Model RMSE Results.
Table 2. 15 MW Turbine Model RMSE Results.
Training Data
Decision Tree SVM Neural Network GPR
Pitch (°) 1.4142 0.15206 0.016374 0.015752
Thrust Load (N) 30819 3012.5 6193.7 905.24
Test Data
Decision Tree SVM Neural Network GPR
Pitch (°) 1.2089 0.10908 0.016508 0.013788
Thrust Load (N) 27067 2835 5860.7 649.35
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated