Prerpints.org logo
Preprint
Article

Optimal Machine Learning Model to Predict Demolition Waste Generation for a Circular Economy

Altmetrics

Downloads

91

Views

44

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

25 June 2024

Posted:

25 June 2024

You are already at the latest version

Alerts
Abstract
A suitable waste management strategy is crucial for a sustainable and efficient circular economy in the construction sector, and requires precise data on the volume of demolition waste (DW) gen-erated. Therefore, we developed an optimal machine learning (ML) model to forecast the quantity of recycling and landfill waste based on the characteristics of DW. A dataset comprising infor-mation on the characteristics of 150 buildings, demolition equipment utilized, and volume of five waste types generated (i.e., recyclable mineral, recyclable combustible, landfill specified, and landfill mix waste, and recyclable minerals) was constructed. ML models were developed to predict the quantities of such waste. Artificial neural network, decision tree, gradient boosting machine, k-nearest neighbors, linear regression, random forest (RF), and support vector regression were applied, and optimal models were derived via hyperparameter tuning. The RF model demonstrated superior performance. In both validation and test phases, the “recyclable mineral waste” and “recyclable combustible waste” models achieved accuracies of of 0.987 and 0.972, re-spectively. The “recyclable metals” and “landfill specified waste” models achieved accuracies of 0.953 and 0.858 or higher, respectively. Moreover, the “landfill mix waste” model exhibited an accuracy of 0.984 or higher. SHapley Additive exPlanations analysis highlighted floor area as the primary input variable influencing model performance. The type of equipment employed in demolition emerged as another crucial input variable impacting the volume of recycling and landfill wastes generated. The developed model can provide precise data on waste management, thereby facilitating the decision-making process for industry professionals.
Keywords: 
Subject: Engineering  -   Architecture, Building and Construction

1. Introduction

The swift pace of industrialization and population growth has resulted in a notable surge in the production of solid waste [1,2]. Globally, the annual production of solid waste ranges from 7 to 9 trillion tons, with approximately 2 trillion tons estimated to be municipal solid waste (MSW)[3]. A recent study forecasted that the worldwide production of MSW will reach 2.59 trillion tons by 2030 and 3.4 trillion tons by 2050 [4]. Construction and demolition waste (CDW) accounts for more than 30% of the MSW generation worldwide [5,6], with Europe and the U.S. being responsible for 36% and 67% of the total generation volume, respectively [7]. The volume and composition of CDW differ across regions, with China, the U.S., and Europe being the primary contributors [8]. However, the recovery rate of CDW is not proportional to its generation volume and fluctuates significantly from 7% to 90% depending on the region [9]. Moreover, while 75% of global CDW could be recycled, approximately 35% is disposed of in landfills [10]. Given that the construction sector utilizes approximately 40% of the world’s raw materials [11], produces 40% of waste [12], and contributes to 25% of global carbon dioxide emissions [13], a low recovery rate of CDW implies that the industry lacks sustainability. Facilitated by a substantial recovery rate of CDW, recycling offers myriad benefits for sustainable development across social, environmental, and economic dimensions [14].
To achieve sustainable consumption and environmental integrity within the construction sector, stakeholders must cooperate within a circular economy framework. Such cooperation underscores the importance of acknowledging sustainable consumption and development initiatives, as well as implementing effective systems and solutions to drive efficiency and promote sustainability within the architecture, construction, and engineering industries. An example of an effective tool for such systems and solutions involves the assessment of the maximum economic and environmental benefits attainable from a structure prior to its dismantling and demolition [15]. To ensure efficient waste management (WM), precisely forecasting the volume of waste generated is essential by accurately quantifying both the quantity and composition of waste [16], which is indispensable for realizing sustainable WM practices. These endeavors will lay the groundwork for enhancing legislation pertaining to waste, conducting environmental impact assessments, assessing social and economic costs, designing WM systems, and planning the necessary infrastructure such as collection sites, recycling centers, landfills, and incinerators [17,18]. Furthermore, precise estimation of waste generation volume can serve as foundational data for effective WM practices, such as planning landfill capacity, implementing waste treatment levies or recycling incentives, and formulating comprehensive WM strategies [19]. However, owing to numerous uncertainties, accurate prediction of the quantity of waste generated is difficult [20].
Recently, owing to significant advancements in the WM domain, machine learning (ML) has emerged as an effective tool for addressing diverse challenges linked to CDW management. ML enables data-driven decision-making processes and delivers precise predictive data through the utilization of various technologies associated with data collection, processing, and information extraction [21]. In the CDW field, numerous researchers have investigated waste generation prediction models, utilizing ML as a component of WM tools. For example, Lu et al.[22] examined multi-linear regression (MLR) models to forecast the volume of renovation waste generated from renovation projects carried out in Hong Kong. Lu et al.[23] developed MLR, decision tree (DT), gray model (GM), and artificial neural network (ANN) models to predict the volume of construction waste generated within a specific region in China. Based on a deep learning model, Akanbi et al. [24] predicted the volume of waste generation destined for recycling, reuse, and burial within the context of demolition waste (DW) management. By applying random forest (RF) and gradient boosting machine (GBM) for 690 structures involved in demolition projects, Cha et al. [25] developed a model for predicting the demolition waste generation (DWG) rate. Cha et al. [26] developed a hybrid ML model that integrated principal component analysis with ANN and support vector machine (SVM) algorithms, which aimed to enhance the accuracy of predicting the DWG rate for structures undergoing demolition projects. Coskuner et al.[27] developed an ML model applied with a multilayer perceptron (MLP)-ANN for predicting the CDW of the Askar landfill site in Bahrain. Gulghane et al.[28] collected construction waste data from 134 construction sites in Nagpur, India, and developed an ML model applied with decision (DT) and k-nearest neighbors (KNN) algorithms. Hu et al.[29] gathered construction waste generation rate data from 206 construction sites and used this to develop prediction models to which SVM, ANN, and MLR algorithms are applied. The aforementioned research on CDW management introduced ML models, which primarily targeted the overall CDW generation volume of a specific project or at a regional scale, as the resulting outcome. These results can serve practical purposes such as monitoring, data collection, and devising a comprehensive waste processing strategy on a large scale, guided by the total waste generation volume. To enhance CDW management effectiveness, more comprehensive management strategies concerning detailed assessments of the environmental impact of specific waste types, evaluation of processing expenses, and the selection of appropriate recycling methods are necessary. The ML models established in previous studies seem to exhibit research gaps and limitations in achieving a sustainable construction industry. Comprehensive strategies outlining environmental impact assessments, processing costs, and recycling plans for different types of CDW can provide a broader opportunity for fostering the development of a circular economy [30]. To formulate comprehensive strategies for CDW management, comprehending the attributes of processed wastes is imperative, as well as the processing flow and categorization of CDW according to their characteristics and types. This understanding enables informed decisions regarding effective and efficient environmental impact assessments and recycling techniques for CDW.
With the surge in dismantling operations during the redevelopment projects of old buildings, an anticipated sharp increase exists in the generation of DW in Korea [31]. Therefore, managing DW poses a significant hurdle for Korea’s sustainable development. To achieve sustainable development in the Korean construction sector, it is imperative to establish comprehensive DW management strategies. These strategies should encompass aspects such as DW recovery rates, enhanced recycling rates, landfill allocation strategies, environmental impact assessments, and considerations of environmental and social costs. Such strategies should be formulated based on a thorough understanding of the flow and volume of DW generation from older structures. Accordingly, gaining insight into the processing flow and volume of DW generated from outdated structures in Korea is crucial. Therefore, this study developed an ML-based management tool to predict the volume of DW generation, along with the quantities of recyclable and discarded or landfill building materials based on their characteristics, from old structures. By identifying the characteristics of such DW, this tool can aid decision-making processes in DW management by providing data on recycling recovery rates, recyclable DW generation volumes, and landfill waste generation to support landfill allocation plans. This study presents the following specific objectives:
  • Designing a model for predicting the volumes of recycling and landfill DW, taking the characteristics of DW generated from old structures within redevelopment zones in to account.
  • Testing a variety of potential sub-prediction models by determining optimal hyperparameters (HPs) and employing different algorithms.
  • Analyzing the factors affecting the volumes of recycling and landfill DW generated.
  • Proposing an optimal ML model for forecasting the volumes of recycling and landfill DW by evaluating the performance of training, validation, and testing models.
The remainder of this paper is structured as follows: Section 2 proposes application approaches of various ML algorithms, along with the data used in model development, the theoretical basis of the applied algorithms, model optimization methods, and model evaluation techniques. In Section 3, the developed sub-prediction models are assessed, and the best-performing prediction model is proposed. Additionally, the factors influencing the models are analyzed using SHAP analysis. Section 4 offers various discussions based on the key research results, while Section 5 presents the major findings and conclusions, and also addresses the limitations of this study.

2. ML-Based Models and Application

This study examined seven ML algorithms. In waste generation studies within the WM field, the most commonly used ML algorithms are ANN, DT, KNN, RF, and SVM [32,33]. These algorithms typically demonstrate exceptional performance in supervised learning tasks, handling non-linear data, identifying faults in datasets, and managing heterogeneous output parameters and numerical target variables [34]. Accordingly, many researchers often utilize these algorithms (i.e., ANN, DT, KNN, RF, and SVM), which continue to be widely employed, and these algorithms should be prioritized during the development of prediction models. In addition, the LR algorithm is straightforward and facilitates easy interpretation of results and is thus a recurrent choice for model development in the WM domain [32,34]. Ensemble algorithms including RF, offer benefits such as improved prediction performance and enhanced generalization results compared to individual learning algorithms [35,36]. Differing from RF, the GBM algorithm is also a commonly used ensemble algorithm. Furthermore, Al Martini et al.[36] and Jayasinghe et al.[38] developed ML models with excellent prediction performance using GBM. The current study utilized ANN, DT, GBM, KNN, LR, RF, and SVR algorithms, which have demonstrated remarkable performance or are commonly employed in the WM field. The features of each algorithm and methods for enhancing their performance are described below.

2.1. Artificial Neural Network

ANN is a computing system comprising multiple layers of neurons, including input, hidden, and output layers. ANNs typically consists of three layers: input, hidden, and output. These networks incorporate non-linear transfer functions across multiple layers of neurons, thereby enabling the learning of both linear and non-linear relationships between input and output neurons. Due to their strong fault tolerance capacity, and suitability for depicting the complex relationships between variables in multivariate system, ANNs are frequently used in the WM field for developing AI models [32,39]. The architecture of ANN, such as a multilayer perceptron neural network, can achieve deep learning by expanding the hidden layer. Two fundamental HPs of an ANN model include the number of hidden layers and neurons, as well as the type of activation function. Additionally, other HPs such as epoch and regularization method (e.g., learning rate) also need to be properly selected for improving the generalization ability of the model and reducing the training time [40].

2.2. Decision Tree

As a supervised learning model for tackling classification and regression problems, the DT algorithm is used for efficiently extracting a set of rules from unfamiliar data [34] and offers numerous benefits. For example, the algorithm is particularly advantageous in terms of intuitively interpreting results, reducing computational expenses, and managing specific property data independent of omitted values. However, DT can be vulnerable to the problem of overfitting with data [32]. To construct an effective DT model with optimal performance, devising a model that avoids overfitting is crucial. Thus, the complexity of a DT model needs to be controlled by tuning HPs such as the maximum depth or segmentation criteria of the DT model [41].

2.3. Gradient Boosting Machine

Friedman [41] first proposed gradient boosting (GB) as an algorithm used for classification and regression tasks. As a boosting technique, GBM stands out as one of the most robust ML algorithms extensively utilized in the engineering domain [43]. This algorithm creates a powerful learner by continuously adding weak learners to the model. The performance of the model is enhanced while simultaneously minimizing loss or error by iteratively incorporating diverse prediction variables. As a result, the bias and variance of the prediction model can be drastically reduced [42]. As a boosting-based ensemble learning technique, GBM can enhance model efficiency and accuracy by tuning the learning rate, which reduces the influence of each classifier, and “n_estimators,” representing the maximum number of estimators at which boosting concludes [44].

2.4. K-Nearest Neighbor

The KNN algorithm is a simple and easily implementable supervised learning technique commonly employed for classification and regression purposes. This approach entails utilizing training data and computing distances for a predetermined k-value, where a set of k closest values are identified using clustering algorithms [45]. Owing to its simplicity and intuitive nature, KNN has been widely employed for regression and classification tasks across various fields. Furthermore, the algorithm is commonly considered suitable for low-dimensional data characterized by a small number of input variables [34]. KNN achieves a low error rate when managing extensive datasets and determines the optimal closest neighbors of a point using a minimal number of attributes (low dimension)[34]. The most crucial HP in KNN is the k-value, which denotes the number of nearest neighbors considered. If the k-value is too small, underfitting may occur, whereas an excessively large k-value can cause overfitting, consequently prolonging computation time. Furthermore, the enhancement of the KNN model’s performance is significantly influenced by modifying a weighted function (such as uniform and distance) and the distance metric employed for prediction [46].

2.5. Linear Regression

Combining statistical and ML techniques, the LR model is a linear equation comprising output values corresponding to specific input values. The main objective of regression analysis is to train a model using existing data and then make predictions by mapping an input value with an output value [47]. Although LR involves relatively straightforward interpretation and minimal computational expenses, it also tends to exhibit bias [34]. Despite these shortcomings, LR remains appealing due to its simplicity in terms of algorithmic design and the ease of analyzing the results [32]. Owing to these advantages, LR has been consistently used as an ML algorithm for constructing waste generation prediction models. The hyperparameters that require tuning via regularization in the LR model are penalty terms such as “L1” and “L2” to enhance the performance of the model [40,48].

2.6. Random Forest

Proposed by Breiman [49], RF is a classical bagging-based ensemble technique that creates bootstrap samples. RF creates a tree, also referred to as a weak learner, for each subset by drawing multiple subsets from the original dataset. The majority of results from each tree are aggregated to identify a strong learner, and the final prediction is derived from the average prediction of all sub-level models. Since it incorporates multiple decision trees, the RF technique delivers superior performance compared to single decision trees, reduces the risk of overfitting, and lessens the impact of outliers [50]. RF is an ensemble model that uses bagging, with the initial parameter to consider being n_estimators [44]. Subsequently, the performance of the model can be improved by tuning “max_features,” which represent the number of attributes used to create different subsets. Similar to GBM, performance can be improved in a DT-based ensemble model by tuning the split criteria and maximum depth [40].

2.7. Support Vector Machine

An SVM is an effective ML algorithm that is commonly applied for classification, regression, and anomaly detection [51]. SVM adopts the principle of structural risk minimization to address challenges such as a small number of data samples, non-linearity, high dimensionality, and local minima. SVM exhibits particularly outstanding performance in multi-class classification tasks. The basic idea is that input data are non-linearly mapped to a feature space, where an optimal linear decision function is determined. To classify the data effectively, a kernel function is used to map the data back to the original space [52]. This approach offers effective flexibility and generalization abilities, which are particularly valuable for addressing non-linear problems. In particular, SVM has the benefit of circumventing overfitting [53]. In an SVR model, the kernel type is a crucial hyperparameter that needs to be tuned first. In general, four types of kernel exist (i.e., radial basis function (RBF), and linear, polynomial, and sigmoid kernels), and selecting the appropriate kernel type is essential for improving performance. Besides kernels, the regularization parameter (C), which governs the complexity of the model, and epsilon ( ε ), which denotes the distance error of a loss function, also influence the performance enhancement of an SVR model [54].

3. Methods and Materials

As illustrated in Figure 1, this study followed a sequence comprising dataset preparation, prediction model development, performance evaluation, and ultimately the proposal and analysis of an optimal model capable of predicting the volumes of recycling and landfill DW generation (DWG).

3.1. Data Collection and Preprocessing

Data on DWG were collected from the demolition sites in redevelopment areas located in Daegu (35.88° N latitude, 128.61° E longitude) and Busan (35.87° N latitude, 128.63° E longitude), both of which are situated in the southern region of Korea. The gathered dataset comprises details on 186 buildings (102 from Project A and 84 from Project B), along with the DWG acquired during the demolition phase. The structural information encompasses the building address and characteristics such as location, structure type, usage, wall and roof types, gross floor area (GFA), and number of floors. The dataset includes details on the structure and equipment utilized for demolition, along with the volumes of recycling and landfill DW produced.
Recycling and landfill waste data were gathered in collaboration with demolition and processing companies by recording truck specifics and the volume transported to the processing company for DW treatment. Recycling and landfill wastes are categorized into three and two types, respectively. Recycling wastes consist of minerals (i.e., mortar, concrete, block, brick, roofing tile), combustibles (i.e., wood, plastics, papers), and metals. Landfill wastes consist of specified waste such as asbestos-containing materials and mixed wastes that pose challenges for recycling.
Data preprocessing was conducted to construct reliable datasets and data standardization performed to prepare datasets of identical scales as follows:
x s t a n d a r d i z a t i o n = x − x ¯ σ
where x , x ¯ , and σ is the element, mean, and standard deviation of the data, respectively.
Following data preprocessing, the dataset was resized to 150 entries (81 from Project A and 69 from Project B) to make it suitable for model development. The statistics of the data incorporated in the datasets utilized for model development, as well as the volumes of recycling and landfill waste generation are presented in Table 1 and Table 2, Figure 2. Approximately 85% of DW originating from aged structures in redevelopment areas undergo recycling, with approximately 14.5% and 0.4% of mixed and specified waste being disposed of in landfills, respectively. Specifically, minerals accounted for the majority of recycling DW, comprising 75.9% of the total, making it the largest component.

3.2. Model Development

3.2.1. Variable Selection

The datasets contain information on recycling and landfill DWG, structure characteristics (i.e., region, structure, usage, wall type, roof type, floor area, number of floors), and equipment utilized for demolition. Region, structure, usage, wall type, roof type, floor area, number of floors, and equipment type were considered as major input variables for predicting the volume of recycling and landfill DWG. Given that various input variables are anticipated to have differing impacts on the five categories of recycling and landfill DWG, devising optimal input variables based on the algorithm type and dependent variables (i.e., recycling and landfill generation by type) is essential. Thus, the correlation between the major input variables and recycling and landfill DWG was examined (Figure 3), which revealed variations among the major input variables across the recycling and landfill categories. Of the eight input variables, floor area, number of floors, equipment type, and region exhibit strong correlations across all DWG categories except for Landfill 1. Additionally, roof type was the most influential factor affecting the volume of Landfill 1 generation, ultimately displaying the strongest correlation. However, accurately predicting the DWG volume solely based on one or two input variables with strong correlations remains challenging. Therefore, various combinations of input variables were examined to forecast the generation of Recycling 1, 2, and 3, as well as Landfill 1 and 2, before tuning hyperparameters. Testing the performance of the model by sequentially adding input variables with strong correlations, according to recycling and landfill classification, revealed that the prediction accuracy was highest when eight input variables were included. Therefore, region, structure, usage, wall type, roof type, floor area, number of floors, and equipment type were selected as input variables for predicting DWG of Recycling 1, 2, and 3 as well as Landfill 1 and 2.

3.2.2. Hyperparameter Tuning

Hyperparameter (HP) tuning is considered an essential element for building an effective ML model. Before enhancing an ML model with HPs, identification of which key HPs need tuning to tailor the ML model to a particular problem or dataset is essential. As each algorithm has its own set of HPs, the process of tuning HP varies according to the ML algorithm [55]. Therefore, major HPs are tuned for developing a prediction model with optimal performance across other algorithms. All experiments were carried out utilizing Python 3.7 and Scikit-learn 1.0.
Various HPs such as activation function, the quantity of hidden layers, the number of neurons, regularization, and iteration were tuned to derive an ANN model with optimal performance. For the DP algorithms, HPs including the maximum depth, the minimum samples left, and split criteria were tuned; for the GBM model, HPs including n_estimators, learning rate, split criteria, and maximum depth were tuned for model development. HPs such as the k-value, weighted function, and distance metric were tuned to optimize the performance of the KNN model. The LR algorithm was tested using three regularization methods: ridge, lasso, and elastic. For the RF model, HPs including n_estimators, max_features, split criteria, and max depth were tuned; for the SVR model, HPs including kernel, C, and ε were tuned to derive an optimal SVR model. The types of HPs used to test different algorithms for predicting recycling and landfill waste generation are presented in Table 3, along with the results of HP tuning showing optimal prediction performance.

3.3. Performance Metrics for Model Verification

The training and test data were split in an 80:20 ratio to develop the prediction model for recycling and landfill waste generation. In addition, leave-one-out cross-validation (LOOCV) was taken into consideration for validating the developed models. As a special case of k-fold cross-validation, LOOCV is typically considered suitable for small sample sizes [56]. Since LOOCV uses all samples as both test and training data to ensure a sufficient amount of training and validation sets, this method offers the advantage of producing stable results for small-scale datasets compared to 10- or k-fold cross-validation [57,58].
As metrics for evaluating the performance of the developed models, mean absolute error (MAE) (Equation (2)), root mean squared error (RMSE) (Equation (3)), and R-squared (Equation (4)) were employed. In performance evaluation, a higher R2 result indicates a better model, while lower MAE and RMSE results are also signs of a superior model.
M A E = ∑ i = 1 n y i − x i n
R M S E = ∑ i = 1 n y i − x i 2 n
R 2 = 1 − ∑ i = 1 n y i − x i 2 ∑ i = 1 n y i − x ¯ i 2
where x i , y i , x ¯ i , and y ¯ i is the observed value, predicted, average observed, and average predicted quantity of generated DW, respectively, and n is the number of samples.

4. Results and Discussion

4.1. Assessment of Models

The eight input variables (i.e., region, structure, usage, wall type, roof type, floor area, number of floors, and equipment type) and various ML algorithms were applied to develop a prediction model for recycling and landfill DWG. The RMSE, MAE, and R-squared results are presented in Figure 4 and Table 4. Typically, low RMSE and MAE values indicate a low error rate and high prediction accuracy, while a high R-squared value signifies excellent model performance. In Figure 4, the RMSE and MAE values for R1 are higher compared to those of other models (R2, R3, L1, and L2), which is primarily due to the significantly higher waste generation volume, as depicted in Table 2 and Figure 2. ANN, GBM, and RF models demonstrate highly accurate prediction for recycling and landfill waste generation, with R-squared values higher than 0.850 in the validation and test models. The KNN model achieved a high R-squared value of 1 in all training models, as presented in Figure 4 and Table 4, while its RMSE and MAE values were notably low, as indicated in Table 4. These results suggest overfitting. The RMSE, MAE, and R-squared values of the KNN validation and test models in Table 4 reveal a decline in prediction performance. Considering the average performance results of the five models (R1, R2, R3, L1, and L2) in Table 4, the R-squared value of the ANN model is 0.977, 0.951, and 0.950 for the training, validation, and test datasets, respectively. The R-squared value of the GBM model is 0.981, 0.957, and 0.954, while that of the RF model is 0.993, 0.951, and 0.951, all indicating excellent performance. In terms of RMSE and MAE outcomes, the RF model yielded lower results compared to the ANN and GBM models, making it a superior model in terms of error reduction and accuracy. Consequently, based on the performance metrics of RMSE, MAE, and R-squared value, the RF model, which was developed using eight input variables (region, structure, usage, wall type, roof type, floor area, number of floors, and equipment type), is considered the most optimal for predicting recycling and landfill waste generation volumes.

4.2. Prediction Performance of Optimal Model and Comparison with Existing Models

The RF algorithm was utilized to develop five models (R1, R2, R3, L1, and L2) as the most optimal for predicting the generation volumes of recycling waste (recyclable minerals, combustible waste, and metals) and landfill waste (specified landfill waste and mixed waste). The performance of the five models is presented in Table 5. The models (R1, R2, R3 and L2) for predicting the generation of recyclable mineral, combustible waste, metals, and mixed waste all achieved an R-squared value of 0.95 or higher across the training, validation, and test datasets, thereby indicating a high level of accuracy. Furthermore, as illustrated in the correlation graphs of predicted and observed values in Figure 5 a–c,e, the predicted and observed values clustered closely around the center line are evidence of the accuracy of the models. The R-squared value of the L1 model is comparatively lower at 0.980, 0.858, and 0.860 in the training, validation, and test datasets (Table 5), respectively, and the predicted and observed values are relatively distant from the center line in Figure 5d). Owing to its focus on the generation of specified waste containing asbestos, the L1 model may have uneven data compared to other models. As Cha et al. [59] demonstrated, asbestos slate material was commonly utilized when updating roofs of traditional structures with asbestos roofing in Korea. The L1 model still demonstrated excellent prediction performance with R-squared values of 0.858 and 0.860 in the validation and test datasets, respectively. A graph comparing the predicted and observed values of the developed models is presented in Figure 6. The predicted and observed values of the five models that utilized the RF algorithm, and eight input variables accurately represent the actual patterns.
This study adopted various ML algorithms and eight input variables for predicting the amount of recycling and landfill demolition wastes categorized into five different types of processing methods. Ultimately, the RF model was selected as the most optimal model for its precision in predicting the volume of recycling and landfill DWG. The rationale behind the selection is the ability of the RF model to offer comprehensive insights into WM, including efficient resource allocation, cost reduction, minimal environmental impact, and support for decision-making processes. Similarly, Akanbi et al. [24] utilized deep learning (DL) to predict the volume of recyclable, reusable, and landfill DW. The R-squared value for the three DL models (recyclable, reusable, and landfill prediction models) was 0.9475, thereby indicating excellent prediction performance. Akanbi et al. [24] employed five input variables (GFA, volume, number of floors, building archetype, and usage) and presented the results of recyclable, reusable, and landfill DWG categorized by archetype. This approach proves beneficial for DW management. However, taking the distinct characteristics of each type of waste into account, their models cannot be considered prediction models for recyclable, reusable, and landfill DWG. On the other hand, the prediction models developed in this study are deemed to have distinction from those of previous research, as they are prediction models for recycling and landfill DWG considering the nature of each type of waste.
Besides the RF model proposed as the most optimal prediction model, the ANN, GBM, and SVR models also exhibit excellent prediction performance. The RF model exhibited superior performance compared to other models in terms of the average values of RMSE, MAE, and R-squared. Conversely, the L1 model demonstrated poorer performance than the R1, R2, R3, and L2 models. This could be due to the absence of reliable data or the selection of inappropriate algorithms. For the L1 model, the ANN, GBM, and SVR prediction models exhibited comparable or slightly improved prediction performance. This result implies that ANN, GBM, and SVR algorithms can be more appropriate as prediction models for DWG targeting the specified waste data. Thus, exploring a range of ML algorithms can be an advantageous approach for constructing ML models with high accuracy, particularly for data sets with limited statistics or high complexity. However, implementing such an approach requires lengthy and energy-intensive processes. Therefore, while identifying highly accurate models is vital for ML model development, a superior solution involves creating an optimal model from a comprehensive perspective.

4.3. Variable Importance

The importance of input variables was evaluated using the SHAP method. The SHAP algorithm is particularly beneficial for determining the contribution of an input variable to the final prediction of a model by quantifying the impact of input variables. In terms of such importance, a SHAP value close to 0 suggests that the input variable has minimal contribution to the outcome of a prediction model.
The SHAP analysis results of major input variables that affected the five prediction models are illustrated in Figure 6. The importance of input variables that affected the results of the R1 model is presented in Figure 6a. The most influential variable for the R1 model was floor area, with structure, number of floors, and equipment also displaying a positive correlation with the results of the model. Akanbi et al. [24] also proved that the floor area and number of floors are critical factors that affect recyclable and reusable models. The current study argues that equipment type is one of the important factors affecting recyclable mineral generation. The importance of input variables for the R2 model, a predictive tool for estimating the generation of combustible DW that can be used for energy recovery, is highlighted in Figure 6b. Region and floor area can be considered to be highly influential for the R2 model. Notably, Region B demonstrates a positive correlation with the R2 model results, whereas Region A exhibits a negative correlation. These findings suggest that the region of a structure can serve as a crucial input variable for predicting combustible DWG, leading to significantly varying outcomes based on the region. The results of the R3 model, which forecasts the volume of metal generation, are presented in Figure 6c. The importance of input variables in this model is similar to that in the R1 model. The input variable importance of the L1 model is illustrated in Figure 6d, where roof type and floor area are the important input variables for the specified waste generation. Specifically, the slate roof type, predominantly composed of asbestos, exhibits a strong positive correlation with the specified waste generation. The input variable importance of the L2 model is illustrated in Figure 6e, where floor area is the most important input variable for the mixed waste generation. Additionally, equipment, number of floors, structure, and region have a notable impact. Akanbi et al. [24] identified the number of floors and the floor area as the two most influential input variables for the landfill models. However, the current study newly suggests that equipment also has a significant impact on landfill waste generation.

5. Conclusions

Accurate information on the volume of DW generated is essential for achieving a sustainable and effective circular economy in the construction sector. In this respect, accurate data allow for the development of appropriate plans for managing the volume of recycling and landfill waste generated during demolition. Using data on structural characteristics and demolition equipment, this study created three and two models to predict recycling and landfill waste generation, respectively, based on the classification of DW properties. Various ML algorithms (including ANN, DT, GBM, KNN, LR, RF, and SVR) were tested to develop a prediction model with optimal performance. The findings indicated that the model utilizing the RF algorithm exhibited the highest performance. The average R-squared values for the training, validation, and test datasets were 0.993, 0.951, and 0.951, respectively, thus affirming its exceptional performance. In the validation and test results, the “recyclable mineral waste generation” model achieved an accuracy of 0.987, while the “recyclable combustible waste generation” model attained 0.972 accuracy. For the “recyclable metals generation” model, accuracy reached 0.953 or above, and the “landfill specified waste generation” model achieved 0.858 or higher accuracy. Lastly, the “landfill mix waste generation” model exhibited an accuracy of 0.984 or higher. The SHAP analysis established that floor area emerges as the most crucial input variable across the four models devised in this study: those for recyclable mineral waste, recyclable combustible waste, recyclable metals, and landfill mix waste. Furthermore, the type of equipment utilized in the demolition process was also revealed to be an important input variable for the generation of recycling and landfill wastes.
This study has several noteworthy implications for both academia and industry. In scholarly terms, this study suggested employing various ML algorithms to estimate the quantity of recycling or landfill waste generated from structural demolition. This approach will provide valuable insights for resource acquisition and waste handling, thereby contributing to the pursuit of sustainable and resource-efficient urban planning and construction practices. Practically, the results can aid local government officials or demolition companies in making informed decisions about resource allocation, optimizing workforce and infrastructure, maximizing recycled waste, and minimizing landfill waste.
This study has a limitation in terms of the insufficiency of data for certain types of information. For instance, the landfill specified waste generation model resulted in less accurate prediction performance than the other four models. The insufficiency of certain data can degrade the predictive capability of models. To address this limitation, data collection should be expanded through a wider range of comprehensive case studies. Consequently, the developed models can be enhanced and validated, ultimately offering detailed insights and information on WM. Continuously updating and retraining the ML algorithms employed to predict recycling and landfill waste volume generation can improve reliability and accuracy, thus offering valuable insights necessary for effective WM.

Author Contributions

Conceptualization, methodology, validation and supervision, G.-W.C.; Resources, writing—review, editing and funding acquisition, G.-W.C. and C.-W.P. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported by the Commercialization Promotion Agency for R&D Outcomes (COMPA) grant funded by the Korean Government (Ministry of Science and ICT). (RS-2023-00304695). This work was supported in part by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (NRF-2022R1F1A107517313-1-3).

References

  1. Hossein, A.H.; AzariJafari, H.; Khoshnazar, R. The role of performance metrics in comparative LCA of concrete mixtures incorporating solid wastes: a critical review and guideline proposal. Waste Manag. 2022, 140, 40–54. [Google Scholar] [CrossRef] [PubMed]
  2. Lu, W.; Chen, J. Computer vision for solid waste sorting: A critical review of academic research. Waste Manag. 2022, 142, 29–43. [Google Scholar] [CrossRef] [PubMed]
  3. Chen, D.M.-C.; Bodirsky, B.L.; Krueger, T.; Mishra, A.; Popp, A. The world’s growing municipal solid waste: trends and impacts. Environ. Res. Lett. 2020, 15, 074021. [Google Scholar] [CrossRef]
  4. Kaza, S.; Yao, L.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank Publications, 2018. [Google Scholar]
  5. Kabirifar, K.; Mojtahedi, M.; Wang, C.; Tam, V.W.Y. Construction and demolition waste management contributing factors coupled with reduce, reuse, and recycle strategies for effective waste management: A review. J. Cleaner Prod. 2020, 263, 121265. [Google Scholar] [CrossRef]
  6. Wu, H.; Zuo, J.; Zillante, G.; Wang, J.; Yuan, H. Status quo and future directions of construction and demolition waste research: A critical review. J. Cleaner Prod. 2019, 240, 118163. [Google Scholar] [CrossRef]
  7. López Ruiz, L.A.; Roca Ramón, X.; Gassó Domingo, S. The circular economy in the construction and demolition waste sector–A review and an integrative model approach. J. Cleaner Prod. 2020, 248, 119238. [Google Scholar] [CrossRef]
  8. Hao, J.; Di Maria, F.; Chen, Z.; Yu, S.; Yu, W.; Di Sarno, L. Comparative study of construction and demolition waste management in China and the European Union. Detritus 2020, 13, 114–121. [Google Scholar] [CrossRef]
  9. Duan, H.; Miller, T.R.; Liu, G.; Tam, V.W.Y. Construction debris becomes growing concern of growing cities. Waste Manag. 2019, 83, 1–5. [Google Scholar] [CrossRef]
  10. Purchase, C.K.; Al Zulayq, D.M.; O’Brien, B.T.; Kowalewski, M.J.; Berenjian, A.; Tarighaleslami, A.H.; Seifan, M. Circular economy of construction and demolition waste: A literature review on lessons, challenges, and benefits. Materials (Basel) 2021, 15, 76. [Google Scholar] [CrossRef]
  11. Darko, A.; Chan, A.P.C. Critical analysis of green building research trend in construction journals. Habitat Int. 2016, 57, 53–63. [Google Scholar] [CrossRef]
  12. Nasir, M.H.A.; Genovese, A.; Acquaye, A.A.; Koh, S.C.L.; Yamoah, F. Comparing linear and circular supply chains: A case study from the construction industry. Int. J. Prod. Econ. 2017, 183, 443–457. [Google Scholar] [CrossRef]
  13. Mahpour, A. Prioritizing barriers to adopt circular economy in construction and demolition waste management. Resour. Conserv. Recy. 2018, 134, 216–227. [Google Scholar] [CrossRef]
  14. Wei, Y.; Zhang, L.; Sang, P. Exploring the restrictive factors for the development of the construction waste recycling industry in a second-tier Chinese city: a case study from Jinan. Environ. Sci. Pollut. Res. Int. 2023, 30, 46394–46413. [Google Scholar] [CrossRef] [PubMed]
  15. Song, Y.; Wang, Y.; Liu, F.; Zhang, Y. Development of a hybrid model to predict construction and demolition waste: China as a case study. Waste Manag. 2017, 59, 350–361. [Google Scholar] [CrossRef] [PubMed]
  16. Katz, A.; Baum, H. A novel methodology to estimate the evolution of construction waste in construction sites. Waste Manag. 2011, 31, 353–358. [Google Scholar] [CrossRef] [PubMed]
  17. Hoque, M.M.; Rahman, M.T.U. Landfill area estimation based on solid waste collection prediction using ANN model and final waste disposal options. J. Cleaner Prod. 2020, 256, 120387. [Google Scholar] [CrossRef]
  18. Ma, S.; Zhou, C.; Chi, C.; Liu, Y.; Yang, G. Estimating physical composition of municipal solid waste in China by applying artificial neural network method. Environ. Sci. Technol. 2020, 54, 9609–9617. [Google Scholar] [CrossRef]
  19. Yu, Y.; Yazan, D.M.; Bhochhibhoya, S.; Volker, L. Towards circular economy through industrial symbiosis in the Dutch construction industry: A case of recycled concrete aggregates. J. Cleaner Prod. 2021, 293, 126083. [Google Scholar] [CrossRef]
  20. Abbasi, M.; El Hanandeh, A. Forecasting municipal solid waste generation using artificial intelligence modelling approaches. Waste Manag. 2016, 56, 13–22. [Google Scholar] [CrossRef]
  21. Yazdani, M.; Kabirifar, K.; Frimpong, B.E.; Shariati, M.; Mirmozaffari, M.; Boskabadi, A. Improving construction and demolition waste collection service in an urban area using a simheuristic approach: A case study in Sydney, Australia. J. Cleaner Prod. 2021, 280, 124138. [Google Scholar] [CrossRef]
  22. Lu, W.; Long, W.; Yuan, L. A machine learning regression approach for pre-renovation construction waste auditing. J. Cleaner Prod. 2023, 397, 136596. [Google Scholar] [CrossRef]
  23. Lu, W.; Lou, J.; Webster, C.; Xue, F.; Bao, Z.; Chi, B. Estimating construction waste generation in the Greater Bay Area, China using machine learning. Waste Manag. 2021, 134, 78–88. [Google Scholar] [CrossRef] [PubMed]
  24. Akanbi, L.A.; Oyedele, A.O.; Oyedele, L.O.; Salami, R.O. Deep Learning Model for Demolition Waste Prediction in a Circular Economy. J. Cleaner Prod. 2020, 274, 122843. [Google Scholar] [CrossRef]
  25. Cha, G.-W.; Moon, H.-J.; Kim, Y.-C. Comparison of random forest and gradient boosting machine models for predicting demolition waste based on small datasets and categorical variables. Int. J. Environ. Res. Public Health 2021, 18, 8530. [Google Scholar] [CrossRef] [PubMed]
  26. Cha, G.-W.; Moon, H.J.; Kim, Y.-C. A hybrid machine-learning model for predicting the waste generation rate of building demolition projects. J. Cleaner Prod. 2022, 375, 134096. [Google Scholar] [CrossRef]
  27. Coskuner, G.; Jassim, M.S.; Zontul, M.; Karateke, S. Application of artificial intelligence neural network modeling to predict the generation of domestic, commercial and construction wastes. Waste Manag. Res. 2021, 39, 499–507. [Google Scholar] [CrossRef] [PubMed]
  28. Gulghane, A.; Sharma, R.L.; Borkar, P. A formal evaluation of KNN and decision tree algorithms for waste generation prediction in residential projects: a comparative approach. Asian J. Civ. Eng. 2024, 25, 265–280. [Google Scholar] [CrossRef]
  29. Hu, R.; Chen, K.; Chen, W.; Wang, Q.; Luo, H. Estimation of construction waste generation based on an improved on-site measurement and SVM-based prediction model: A case of commercial buildings in China. Waste Manag. 2021, 126, 791–799. [Google Scholar] [CrossRef] [PubMed]
  30. Ibrahim, M.; Alimi, W.; Assaggaf, R.; Salami, B.A.; Oladapo, E.A. An overview of factors influencing the properties of concrete incorporating construction and demolition wastes. Constr. Build. Mater. 2023, 367, 130307. [Google Scholar] [CrossRef]
  31. Cha, G.-W.; Park, C.-W.; Kim, Y.-C.; Moon, H.J. Predicting Generation of Different Demolition Waste Types Using Simple Artificial Neural Networks. Sustainability 2023, 15, 16245. [Google Scholar] [CrossRef]
  32. Abdallah, M.; Abu Talib, M.A.; Feroz, S.; Nasir, Q.; Abdalla, H.; Mahfood, B. Artificial intelligence applications in solid waste management: A systematic research review. Waste Manag. 2020, 109, 231–246. [Google Scholar] [CrossRef] [PubMed]
  33. Gao, Y.; Wang, J.; Xu, X. Machine learning in construction and demolition waste management: Progress, challenges, and future directions. Autom. Constr. 2024, 162, 105380. [Google Scholar] [CrossRef]
  34. Nguyen, X.C.; Nguyen, T.T.H.; La, D.D.; Kumar, G.; Rene, E.R.; Nguyen, D.D.; …; Nguyen, V.K. Development of machine learning-based models to forecast solid waste generation in residential areas: A case study from Vietnam. Resour. Conserve. Recy. 2021, 167, 105381. [Google Scholar] [CrossRef]
  35. Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
  36. Ghimire, B.; Rogan, J.; Galiano, V.R.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GIScience Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
  37. Al Martini, S.; Sabouni, R.; Khartabil, A.; Wakjira, T.G.; Shahria Alam, M.S. Development and strength prediction of sustainable concrete having binary and ternary cementitious blends and incorporating recycled aggregates from demolished UAE buildings: Experimental and machine learning-based studies. Constr. Build. Mater. 2023, 380, 131278. [Google Scholar] [CrossRef]
  38. Jayasinghe, T.; Wei Chen, B.; Zhang, Z.; Meng, X.; Li, Y.; Gunawardena, T.; Mangalathu, S.; Mendis, P. Data-driven shear strength predictions of recycled aggregate concrete beams with/without shear reinforcement by applying machine learning approaches. Constr. Build. Mater. 2023, 387, 131604. [Google Scholar] [CrossRef]
  39. Xu, A.; Chang, H.; Xu, Y.; Li, R.; Li, X.; Zhao, Y. Applying artificial neural networks (ANNs) to solve solid waste-related issues: A critical review. Waste Manag. 2021, 124, 385–402. [Google Scholar] [CrossRef] [PubMed]
  40. Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
  41. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; …; Duchesnay, É. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  42. Friedman, J.H. Greedy function approximation: a gradient boosting machine. Ann. Statist. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
  43. Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: a comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
  44. Dietterich, T.G. Ensemble Methods in Machine Learning. In International workshop on multiple classifier systems; Springer: Berlin Heidelberg, June 2000; pp. 1–15. [Google Scholar]
  45. Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN Model-Based Approach in Classification. In On The Move to Meaningful Internet Systems 2003: CoopIS, DOA, and ODBASE.; Meersman, R., Tari, Z., Schmidt, D.C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2888, pp. 986–996. [Google Scholar]
  46. Zuo, W.; Zhang, D.; Wang, K. On kernel difference-weighted k-nearest neighbor classification. Pattern Anal. Appl. 2008, 11, 247–257. [Google Scholar] [CrossRef]
  47. Huang, J.-C.; Ko, K.-M.; Shu, M.-H.; Hsu, B.-M. Application and comparison of several machine learning algorithms and their integration models in regression problems. Neural Comput. Appl. 2020, 32, 5461–5469. [Google Scholar] [CrossRef]
  48. Ogutu, J.O.; Schulz-Streeck, T.; Piepho, H.-P. Genomic selection using regularized linear regression models: ridge regression, lasso, elastic net, and their extensions. In BMC Proc.; BioMed Central 2012, December, 6 (Suppl. 2). [CrossRef]
  49. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  50. Zhang, J.; Ma, G.; Huang, Y.; sun, J.; Aslani, F.; Nener, B. Modelling uniaxial compressive strength of lightweight self-compacting concrete using random forest regression. Constr. Build. Mater. 2019, 210, 713–719. [Google Scholar] [CrossRef]
  51. Deng, C.X.; Xu, L.X.; Li, S. Classification of Support Vector Machine and Regression Algorithm; INTECH Open Access Publisher, 2010. [Google Scholar]
  52. Cha, G.-W.; Choi, S.-H.; Hong, W.-H.; Park, C.-W. Development of machine learning model for prediction of demolition waste generation rate of buildings in redevelopment areas. Int. J. Environ. Res. Public Health 2022, 20, 107. [Google Scholar] [CrossRef]
  53. Tran, V.Q. , Dang, V.Q., & Ho, L.S.. Evaluating compressive strength of concrete made with recycled concrete aggregates using machine learning approach. Constr. Build. Mater. 2022, 323, 126578. [Google Scholar] [CrossRef]
  54. Soliman, O.S.; Mahmoud, A.S. A classification system for remote sensing satellite images using support vector machine with non-linear kernel functions. In 8th International Conference on Informatics and Systems (INFOS); IEEE Publications, 2012, May, (p BIO-181).
  55. DeCastro-García, N.; Muñoz Castañeda, Á.L.; Escudero García, D.; Carriegos, M.V. Effect of the sampling of a dataset in the hyperparameter optimization phase over the efficiency of a machine learning algorithm. Complexity 2019, 2019, 1–16. [Google Scholar] [CrossRef]
  56. Cheng, J.; Dekkers, J.C.M.; Fernando, R.L. Cross-validation of best linear unbiased predictions of breeding values using an efficient leave-one-out strategy. J. Anim. Breed. Genet. 2021, 138, 519–527. [Google Scholar] [CrossRef]
  57. Cheng, H.; Garrick, D.J.; Fernando, R.L. Efficient strategies for leave-one-out cross validation for genomic best linear unbiased prediction. J. Anim. Sci. Biotechnol. 2017, 8, 38. [Google Scholar] [CrossRef] [PubMed]
  58. Shao, Z.; Er, M.J. Efficient leave-one-out cross-validation-based regularized extreme learning machine. Neurocomputing 2016, 194, 260–270. [Google Scholar] [CrossRef]
  59. Cha, G.-W.; Kim, Y.-C.; Moon, H.J.; Hong, W.-H. New approach for forecasting demolition waste generation using chi-squared automatic interaction detection (CHAID) method. J. Cleaner Prod. 2017, 168, 375–385. [Google Scholar] [CrossRef]
Preprints 110292 g001
Figure 1. Research methodology
Figure 1. Research methodology
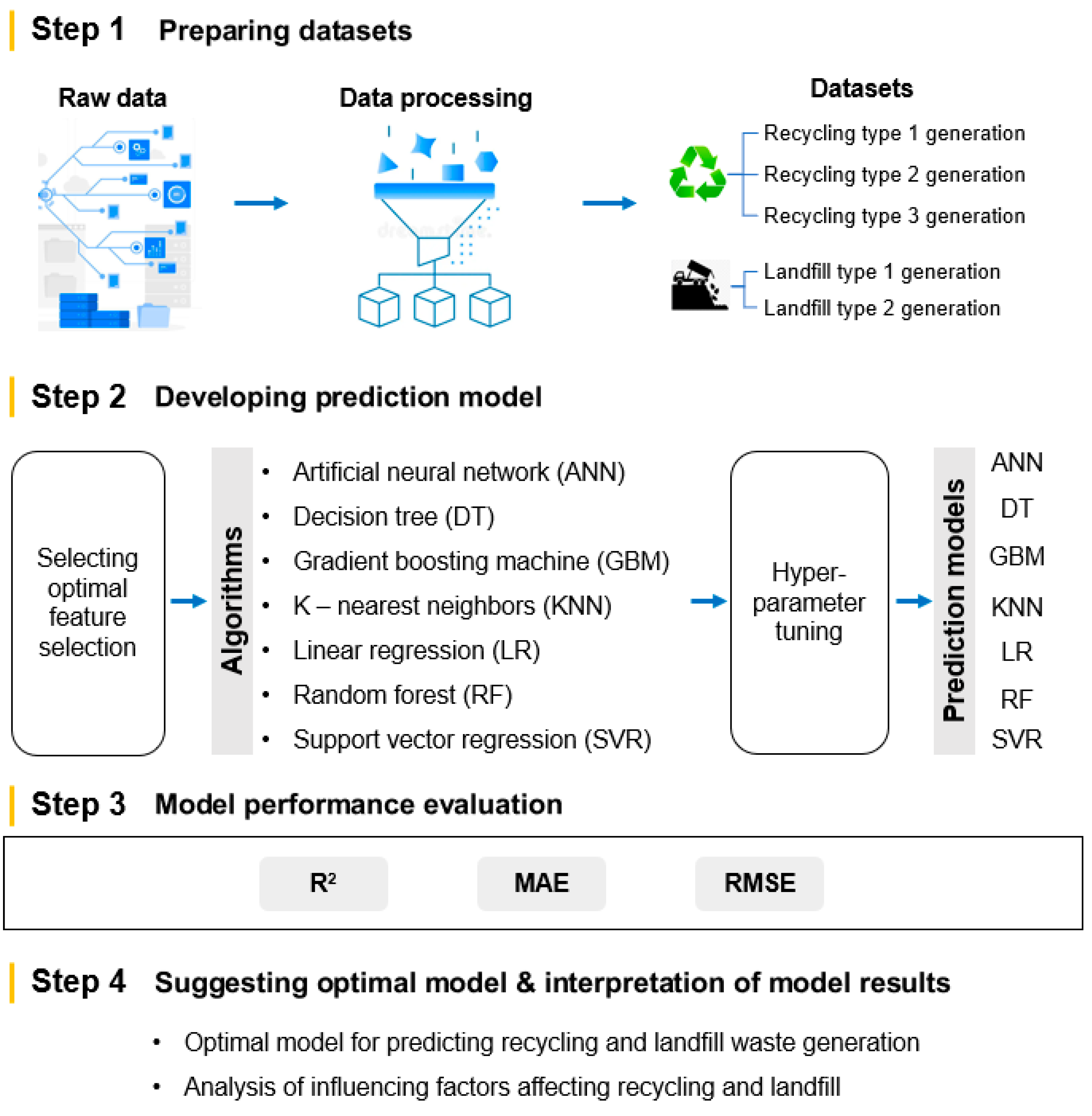
Preprints 110292 g001
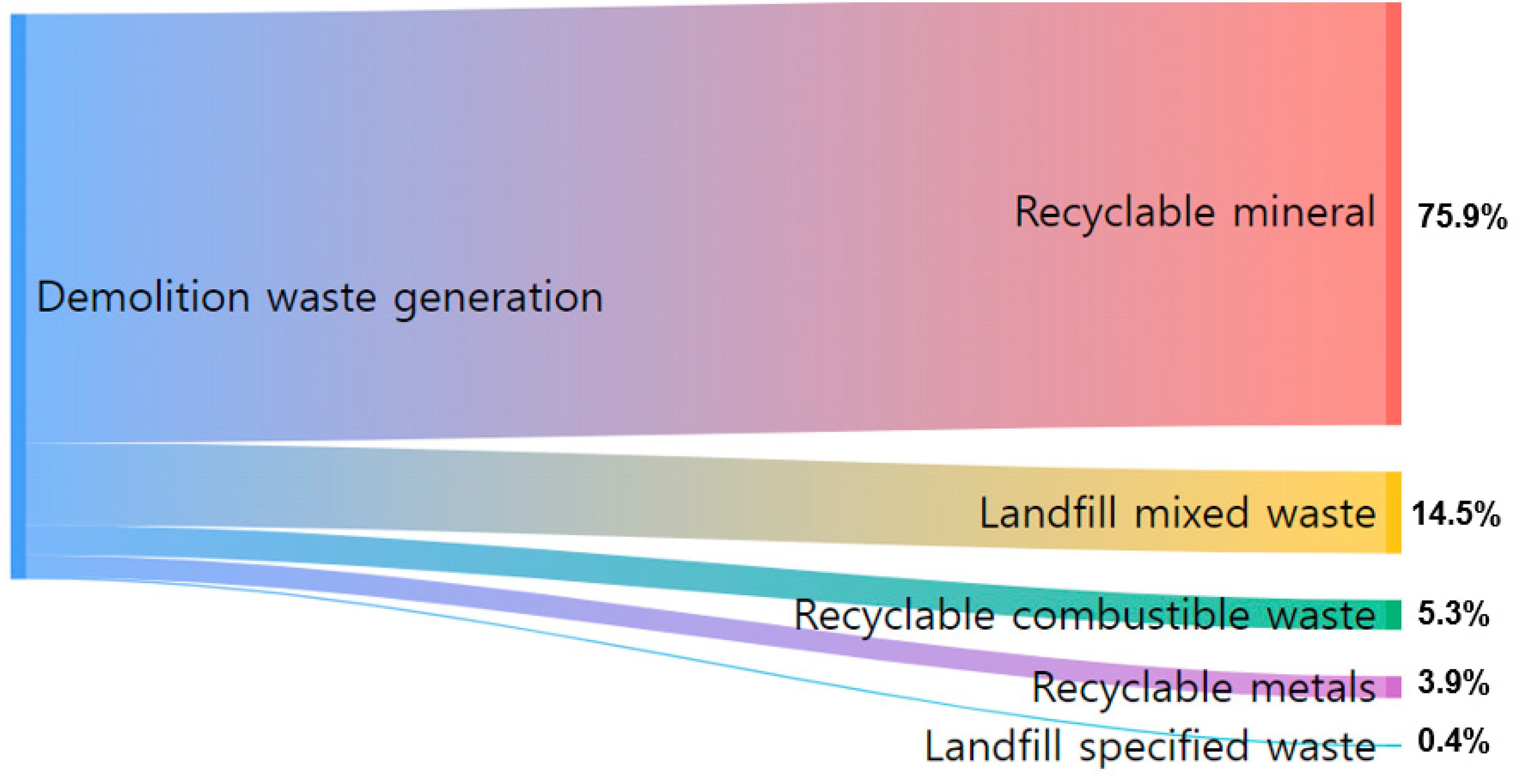
Preprints 110292 g002
Figure 2. Ratio of recycling and landfill waste generation
Figure 2. Ratio of recycling and landfill waste generation
Preprints 110292 g002
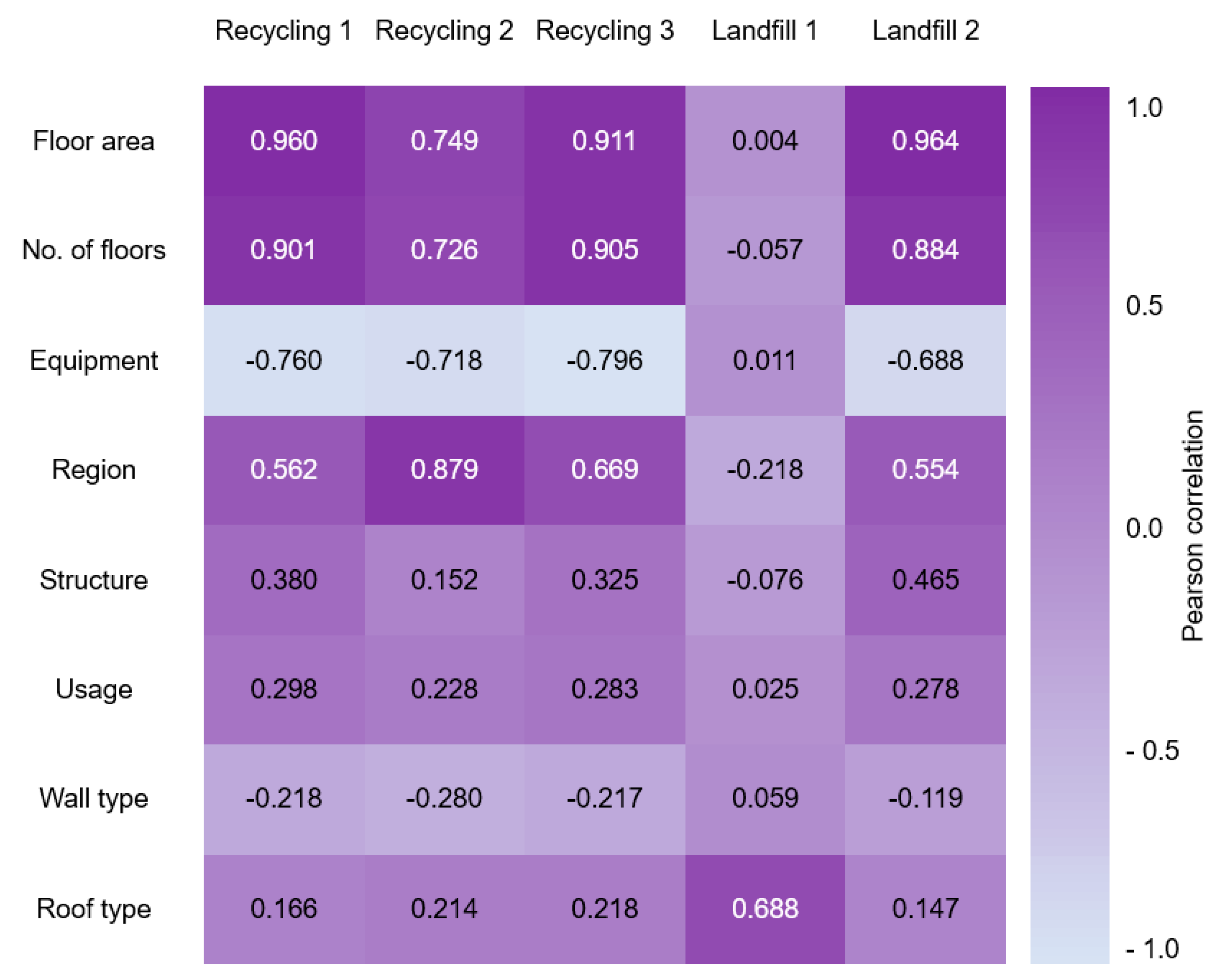
Preprints 110292 g003
Figure 3. Pearson correlation between input variables and the recycling and landfill waste generation.
Figure 3. Pearson correlation between input variables and the recycling and landfill waste generation.
Preprints 110292 g003
Preprints 110292 g004
Figure 4. Performance results for various predictive models for recycling and landfill waste generation
Figure 4. Performance results for various predictive models for recycling and landfill waste generation
Preprints 110292 g004
Preprints 110292 g005
Figure 5. Correlation between observed and predicted values of validation model by RF algorithm: (a) R1, (b) R2, (c) R3, (d) L1, and (e) L2 model.
Figure 5. Correlation between observed and predicted values of validation model by RF algorithm: (a) R1, (b) R2, (c) R3, (d) L1, and (e) L2 model.
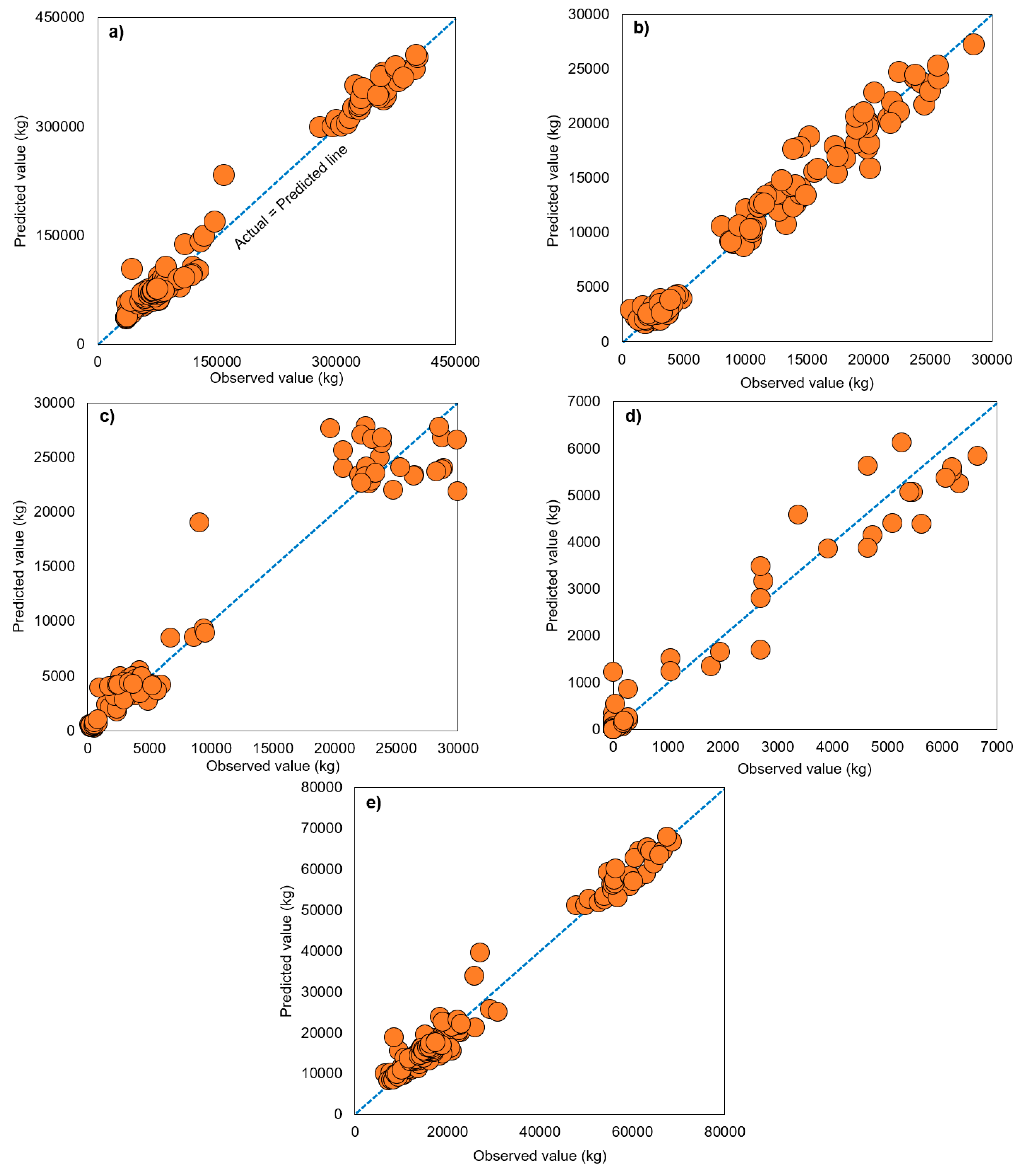
Preprints 110292 g005
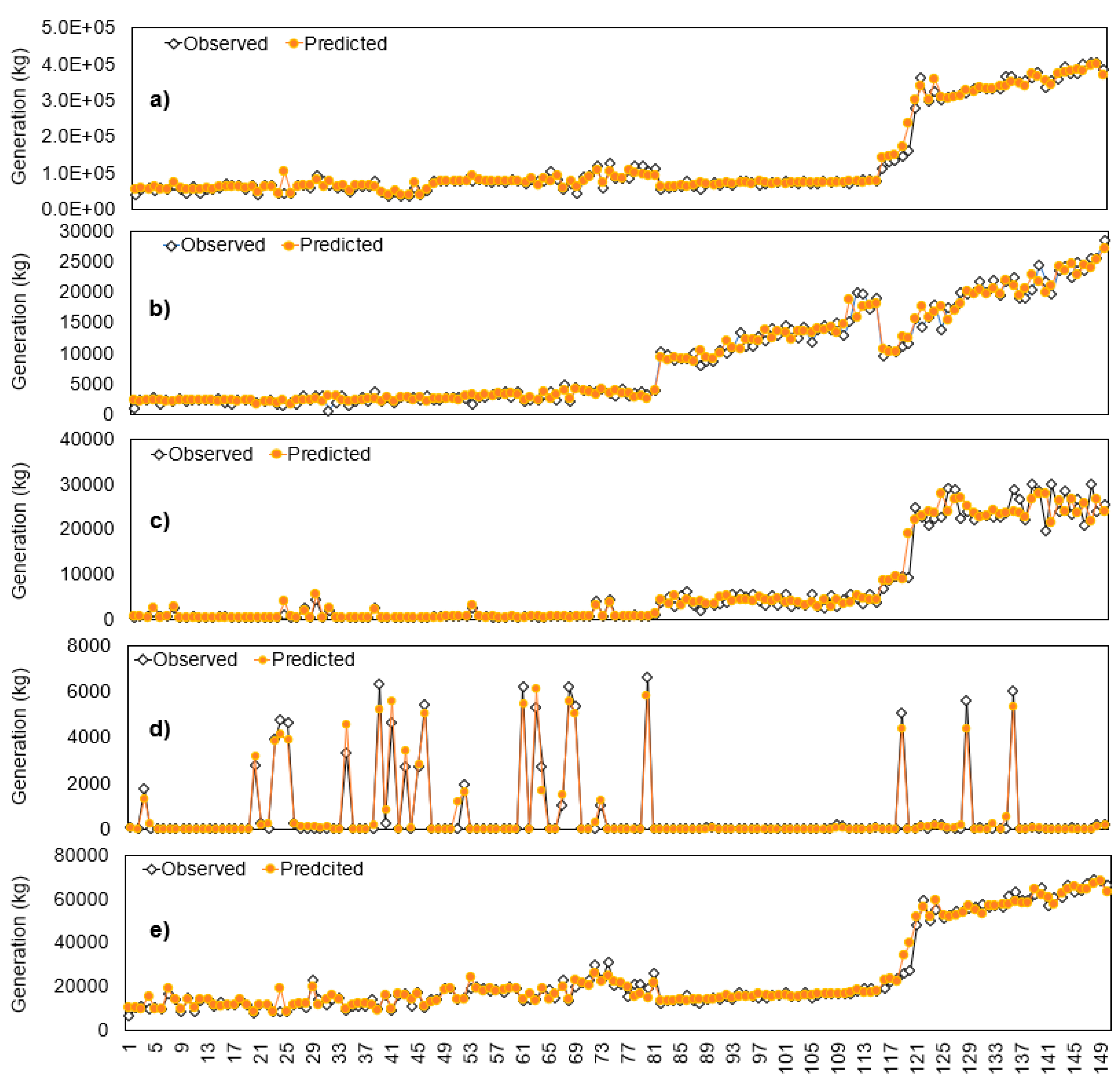
Preprints 110292 g006
Figure 6. Comparison of observed and predicted values by RF algorithm: a) R1, b) R2, c) R3, d) L1, and e) L2 model.
Figure 6. Comparison of observed and predicted values by RF algorithm: a) R1, b) R2, c) R3, d) L1, and e) L2 model.
Preprints 110292 g006
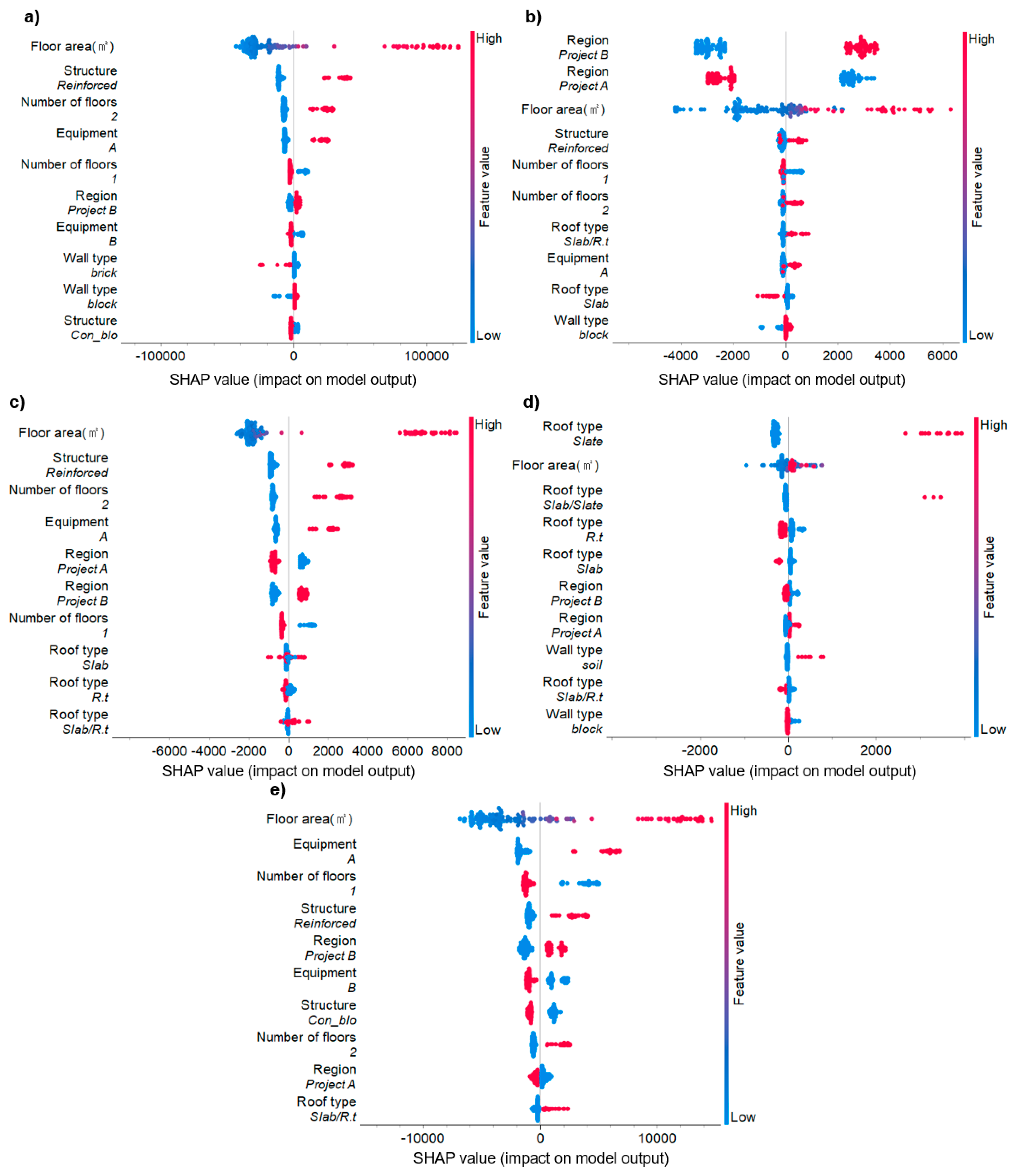
Preprints 110292 g007
Figure 6. Impact on model output of the important variables influencing demolition waste generation by waste type according to SHAP values. a) R1, b) R2, c) R3, d) L1, and e) L2 model.
Figure 6. Impact on model output of the important variables influencing demolition waste generation by waste type according to SHAP values. a) R1, b) R2, c) R3, d) L1, and e) L2 model.
Preprints 110292 g007
Table 1. Statistical analysis of information comprising the study dataset.
Table 1. Statistical analysis of information comprising the study dataset.
Building characteristics Count
Project A 81
B 69
Usage Residential 135
Residential and Commercial 15
Structure Reinforced concrete 81
Concrete block 5
Concrete brick 35
Wood 29
Wall type Block 121
Brick 22
Soil 7
Roof type Roofing tile 74
Slab 27
Slab and roofing tile 33
Slab and slate 3
Slate 13
No. of floors 1 114
2 36
Equipment type A 35
B 86
C 29
Table 2. Statistical analysis on recycling and landfill waste generation.
Table 2. Statistical analysis on recycling and landfill waste generation.
Classification Maximum Minimum Mean
Floor area (m2) 295.22 52.42 133.14
Recycling 1 (mineral) (kg) 402,040.25 35,540.20 126,319.07
Recycling 2 (combustible) (kg) 28,546.88 721.50 8834.02
Recycling 3 (metals) (kg) 30,011.73 143.90 6500.95
Landfill 1 (specified waste) (kg) 6642.72 0.00 659.86
Landfill 2 (mixed waste) (kg) 68,651.98 6421.80 24,066.29
Table 3. Hyperparameters considered for developing machine learning predictive models.
Table 3. Hyperparameters considered for developing machine learning predictive models.
Algorithms Prediction model Considered HP title Selected HP
ANN Recycling 1 (R 1) Activation function,
no. of neurons,
regularization,
iteration, 		ReLu, 12, 30, 70
Recycling 2 (R 2) ReLu, 12, 30, 70
Recycling 3 (R 3) ReLu, 12, 30, 70
Landfill 1 (L 1) ReLu, 25, 30, 40
Landfill 2 (L 2) ReLu, 20, 30, 70
DT R 1 Min_samples_split, criterion, max_depth 3, 11, 4
R 2 3, 11, 4
R 3 3, 11, 4
L 1 2, 6, 2
L 2 3, 11, 4
GBM R 1 N_estimators, criterion, max_depth, learning rate 20, 2, 2, 0.25
R 2 25, 3, 2, 0.25
R 3 15, 2, 2, 0.20
L 1 15, 2, 2, 0.25
L 2 25, 2, 2, 0.25
KNN R 1 No. of neighbors, metric, weight 3, Manhattan, distance
R 2 3, Manhattan, distance
R 3 3, Manhattan, distance
L 1 2, Manhattan, distance
L 2 3, Manhattan, distance
LR R 1 Regularization method, alpha value Ridge, 1
R 2 Ridge, 1
R 3 Ridge, 1
L 1 Ridge, 1
L 2 Ridge, 1
RF R 1 N_estimators, criterion, max_depth, max_features 35, 2, 9, 8
R 2 35, 2, 9, 8
R 3 35, 2, 9, 8
L 1 35, 2, 11, 8
L 2 35, 2, 9, 6
SVR R 1 C, epsilon, kernel type (gamma, coefficient, degree) 20, 0.35, Polynomial (2, 8, 2)
R 2 20, 0.3, Polynomial (0.9, 9.5, 2)
R 3 20, 0.35, Polynomial (1, 8, 2)
L 1 9, 0.3, Polynomial (1, 8, 2)
L 2 20, 0.35, Polynomial (1, 8, 2)
Table 4. Average performance indicators of various ML models for predicting waste generation of recycling and landfill
Table 4. Average performance indicators of various ML models for predicting waste generation of recycling and landfill
Algorithm RMSE MAE R-squared
Training Validation Test Training Validation Test Training Validation Test
ANN 2288.30 4122.32 3902.50 1615.91 4122.32 2385.03 0.977 0.951 0.950
DT 3175.80 5865.85 6063.40 2268.70 5865.85 3730.36 0.973 0.944 0.941
GBM 2245.96 4320.19 4740.58 1682.68 4320.19 2649.89 0.981 0.957 0.954
KNN 33.69 4685.90 4832.75 3.89 4685.90 2978.30 1.000 0.776 0.779
LR 5366.72 6404.70 6242.79 3874.35 6404.70 4354.99 0.944 0.926 0.927
RF 1626.83 3770.25 3838.40 1070.55 3770.25 2421.08 0.993 0.951 0.951
SVR 3560.72 4359.81 4420.18 2679.40 4359.81 3222.35 0.960 0.946 0.945
Table 5. Performance of optimal models using RF algorithm for predicting waste generation of recycling and landfill.
Table 5. Performance of optimal models using RF algorithm for predicting waste generation of recycling and landfill.
Model type Training Validation Test
RMSE MAE R-squared RMSE MAE R-squared RMSE MAE R-squared
R 1 5692.29 3838.75 0.997 13100.86 8326.42 0.987 12670.48 8158.93 0.987
R 2 486.62 350.45 0.996 1266.54 862.93 0.972 1271.18 851.98 0.972
R 3 792.42 414.48 0.993 2044.36 1119.73 0.953 2004.55 1063.50 0.954
L 1 232.78 105.66 0.980 620.71 285.36 0.858 617.64 291.14 0.860
L 2 930.01 643.42 0.997 2159.55 1510.98 0.986 2287.41 1574.08 0.984
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated