Prerpints.org logo
Preprint
Article

Biomechanical Insights and Strategic Applications in Ancient Combat Sports: Optimizing Stability, Power and Tactical Advantage

Altmetrics

Downloads

131

Views

37

Comments

0

Submitted:

25 June 2024

Posted:

26 June 2024

You are already at the latest version

Alerts
Abstract
Background: Though ancient Greece preserves many pictures of combat sports, there is research in terms of biomechanics on the principles of human motion. This research aimed to investigate Pankration postures of ancient Greek athletics, expecting to bridge the gap between historical sports practices and contemporary biomechanical applications. Methods: This study employed computational tools to analyze two images from ancient Greek Pankration, constructing a static multi-segmental model. Anthropometric models simulated postures analogous to those in historical depictions. Analysis estimated joint forces and moments, along with weight distribution and ground reaction forces for these postures. Implications for training and strength development were deduced through integration with modern scientific insights. Moreover, strategic elements of these postures were assessed using game theory to explore their correspondence with contemporary theoretical constructs. Results: The findings indicated that static postures facilitate the development of tendon stiffness, joint stability, and neuromuscular control. In the "readiness" posture, 68% of the athlete's centre of gravity (CoG) was distributed to the hind leg, enhancing stability and power generation, while the front leg promoted agility. Analysis of the kick posture revealed delivery with a dorsiflexed ankle and pronounced heel protrusion.Conclusion: The application of the proposed model suggests that ancient athletes optimized their performance using biomechanical principles, thereby gaining a competitive advantage. This study highlights the value of integrating ancient biomechanical strategies with contemporary athletic training and injury prevention, advocating for a synthesis of historical practices and modern biomechanical analysis in combat sports.
Keywords: 
Subject: Biology and Life Sciences  -   Other

Introduction

Biomechanics, as a scientific discipline, originated from a long-standing interest in human anatomy and motion principles. Its earliest roots can be traced back to Egyptian papyri around 1700-1600 BC [1]. Pioneers like Hippocrates and Galen of Pergamon furthered this curiosity, laying the groundwork for biomechanics [2]. This foundational knowledge has been of great importance across various fields, particularly in analyzing biomechanical aspects of ancient sports practices, such as those originating in Greece [3].
The ancient Greek sports have captivated researchers, who have used historical and archaeological evidence to reconstruct athletic techniques, including the long jump and discus throw [4]. These reconstructions have primarily focused on kinematics (the study of movement) without considering the forces behind it. Despite technological advancements, a detailed reconstruction of these ancient techniques remains elusive, largely due to the fragmentary nature of available sources.
Recently, researchers have explored the Centre of Gravity (CoG) in ancient sports, recognizing its critical role in biomechanical analysis. CoG is essential for maintaining balance and reducing injury risk [5]. Studies, such as those by Kiers et al. (2022), have investigated how posture maintenance relates to sports performance and injury prevention [6]. Hrysomallis (2011) emphasizes the importance of balance training for enhancing proprioceptive abilities, crucial for spatial awareness in sports [7]. This balance training helps athletes’ transition effectively between static and dynamic states, providing a competitive edge [8].
In combat sports and martial arts, mastering the control of CoG and balance is of heightened significance. Athletes adjust their CoG for stability and to execute powerful movements. Disrupting an opponent's balance is a strategic element, underscoring the mastery of CoG manipulation [9].
Therefore, statics is deeply interconnected with an athlete's, muscle functions, motor skills technical capabilities [10]. To understand optimal postures for enhancing performance, sports biomechanics researchers have increasingly turned to static optimization [11]. This technique uses optimization algorithms to determine the most efficient muscle activation patterns. It involves iterative calculations to find muscle forces that best meet an objective function, constrained by the body's biomechanics [12].
These insights from static optimization and optimal control are crucial for optimizing athletic performance, designing targeted training programs, and improving rehabilitation protocols [13]. An exhaustive biomechanical analysis of athletes also requires investigating the forces and moments acting on the legs, along with the Ground Reaction Force (GRF).
GRF is reactive to the exertions of the body and is key to understanding how athletes maintain equilibrium, orchestrate movement, and generate power in both static postures and dynamic activities [14]. Despite these advancements, the static analysis of postures of ancient athletes remains a relatively unexplored area.
While current research has enhanced our understanding of movement kinematics, the static aspects, such as the specific postures and alignments used by ancient athletes, lack comprehensive study [15]. Given the significance of posture in modern sports for performance enhancement and injury prevention, exploring this dimension in ancient athletics could provide valuable insights [16]. Static analysis could reveal how ancient athletes prepared for and executed their maneuvers, offering deeper insights into their training techniques. Therefore, this study aimed to investigate the postures of ancient Greek boxers in terms of biomechanical parameters, especially statics and the CoG. The primary objective of the present paper is to build a static multi-segmental model utilizing, computer vision techniques and investigate the biomechanical principles in ancient Greek combat sports’ postures. The secondary objective is to explore the strategic interactions and game theoretic constructs which manifest in these postures to understand their influence on opponent behaviour and their alignment with modern game theoretic principles.

Methods

The present research utilized Computer Vision, specifically OpenPose to quantify the visual information provided by the ancient depictions. OpenPose employs Convolutional Neural Networks (CNNs) for this purpose [17]. The core architecture of OpenPose utilizes a two-branch multi-stage CNN [18]. The first branch predicts a set of 2D confidence maps for body part locations, while the second branch predicts a set of 2D vector fields for part affinities, which encode the degree of association between parts [18].
In this investigation, two posture representations were used (Figure 1 and Figure 2), each exemplifying a critical phase of ancient Pankration. After the selection of these depictions, OpenPose was employed to analyze and filter the images.

Segmental and Total CoM

The determination of the centre of gravity (CoG) of each body segment and the overall CoG was achieved through a Python script. This script was developed to process keypoint data extracted from OpenPose, serving as a tool for easier interaction with OpenPose–generated files.
The script's functionality centres on the computation of the CoG within a two-dimensional Cartesian coordinate system. This computation relies on the positional data of keypoints, as detected by OpenPose. The underlying mathematical model for the CoG is encapsulated in the following formula:
CoM = ∑ m i ⋅ x ic M  
CoM = ∑ m i ⋅ y ic M
Here, m i is the mass associated with the i − t h keypoint and x ic , y ic is its position coordinates. The mass values are predetermined constants, representing the proportion of mass distributed across different body parts such as the head, trunk, and limbs [19].

Static Multi-Segmental Model of the Lower Extremity

In this study, we applied a static multi-segmental analysis to the lower extremity, structured progressively from the foot to the pelvis. The underlying assumption for each segmental analysis was the state of static equilibrium, which, in mechanical terms, is defined by the conditions that the sum of forces in the horizontal ( Σ F x = 0 ) and vertical ( Σ F y = 0 ) directions, as well as the sum of moments about any joint ( Σ M = 0 ), must be zero. These conditions are derived from the fundamental principles of statics in rigid body mechanics [20].
Given the complexity inherent in analyzing the kinetics of a large free body, a strategy of decomposition into smaller sub-free bodies is employed [21].
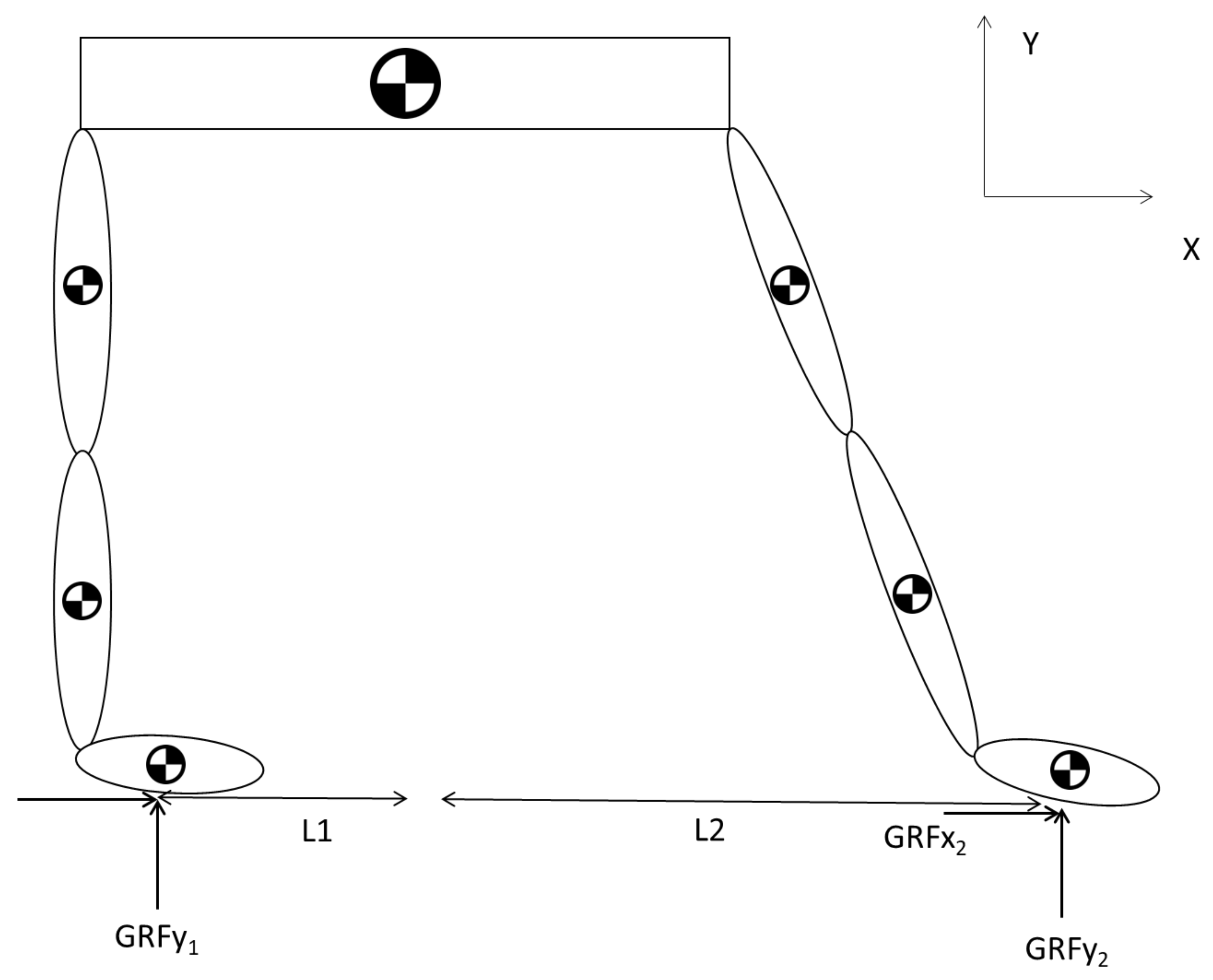
The lower extremity is divided into its constituent segments for detailed analysis. These segments typically include the thigh (upper leg), shank (lower leg), and foot. The division is based on anatomical landmarks and is crucial for isolating the forces and moments acting on each segment. For each segmented part of the lower extremity, a free-body diagram is constructed (Figure 3).
The analysis is initiated by ascertaining the Ground Reaction Force (GRF), which refers to the forces exerted at the base of the foot in response to gravitational interaction. Since the modelling was taking place in the sagittal plane (2D), we focused only on the vertical and horizontal forces. The horizontal force which is parallel to the ground is affected by the friction which is defined as:
G R F x 1 = C o × G R F y 1
Wherein 'Co' denotes the coefficient of friction, assigned a value of 0.3, a characteristic extrapolated from literature which informs us about the execution of sporting events on surfaces layered with sand [22]. The Ground Reaction Forces (GRF) for each leg can be calculated by applying the principles outlined in the free body diagram provided in Figure 3.
Therefore G R F x 2 can be calculated as:
G R F x 2 = − G R F x 1
The next step was to ascertain the individual vertical ground reaction forces (GRFy) acting on each leg, we employ the moment equilibrium equation for the system in conjunction with the horizontal ground reaction forces.
The moment equilibrium about the base of one leg provides a relation that can be used to solve for the vertical ground reaction force on the opposite leg.
Knowing that:
Σ F x = G R F x 1 + G R F x 2 = 0
Σ F y = G R F y 1 + G R F y 2 − P t o t a l = 0
We use:
Σ M = P t o t a l × L 2 − GR F y 1 × L 1 + L 2 = 0
Therefore, we have derived the necessary values to proceed with further analysis starting with the first segment i.e. the foot.
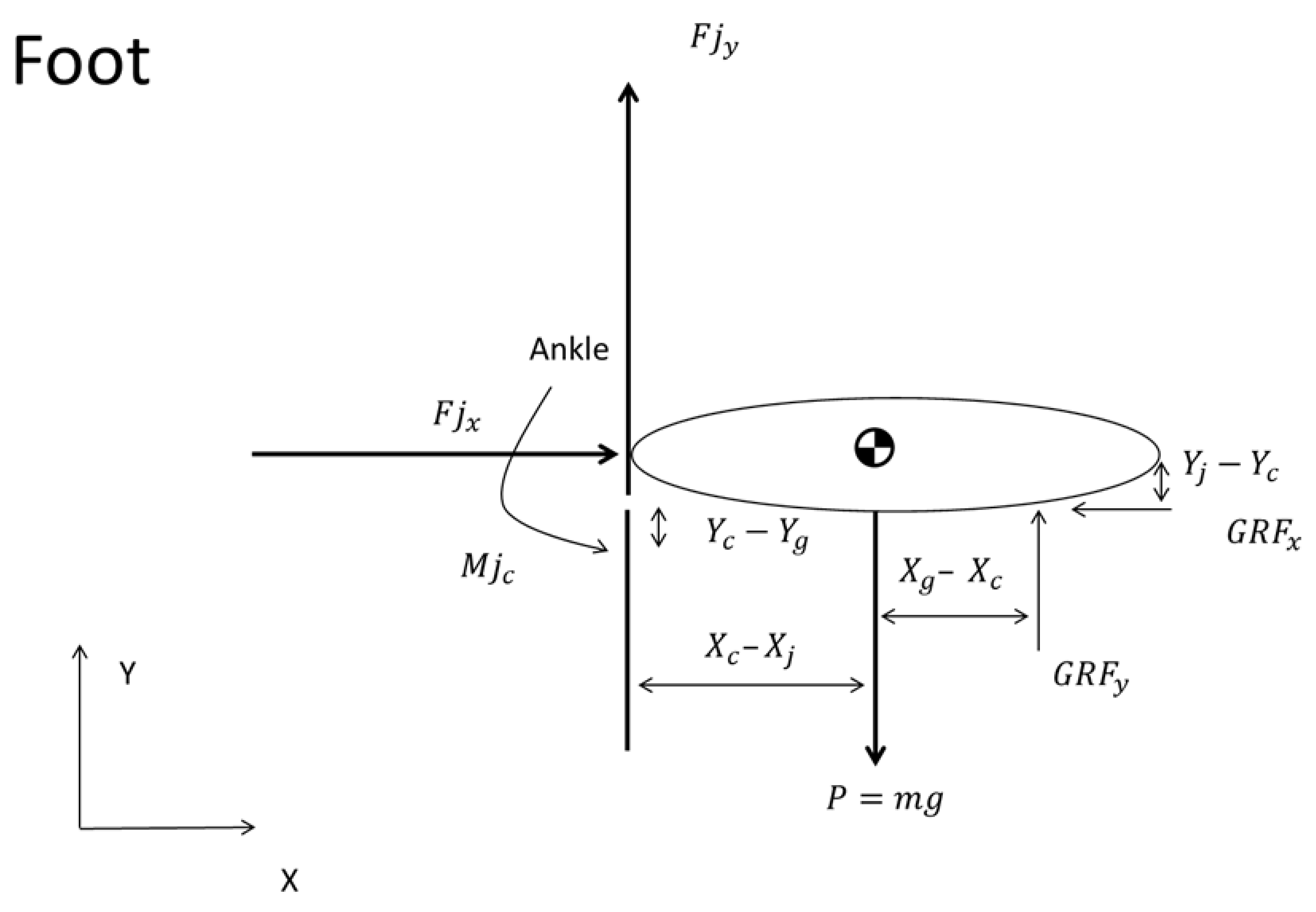
The foot, as illustrated in Figure 4, serves as a foundational tool in this analytical process. It visually represents all the forces and moments acting on the foot, which is treated as a rigid body.
For the foot segment, the equilibrium conditions are expressed by the following equations (8), (9), and (10):
Σ F a = F x a − G R F x
Σ F a = F y a + G R F y − P 1
M j c − F j y × X c − X j − F j x × y j − y c + F g y × x g − X c + F g x × y c − y g = 0
Here , M j c denotes the joint moment. The forces F j x and F j y represent the joint forces in the horizontal and vertical directions respectively. Concurrently, F g x and F g y correspond to the ground reaction forces (GRFs) in the horizontal and vertical planes. P1 is the foot weight, computed as the product of the mass of the foot and the gravitational acceleration [21].
The coordinates ( x j , y j ) mark the ankle joint's location, acting as a crucial point for the application of joint forces, whereas ( x c , y c ), indicate the foot's centre of mass. In the same manner ( x g ,   y g ) pinpoint the contact areas between the foot and the ground, where the GRFs are exerted (Figure 4).
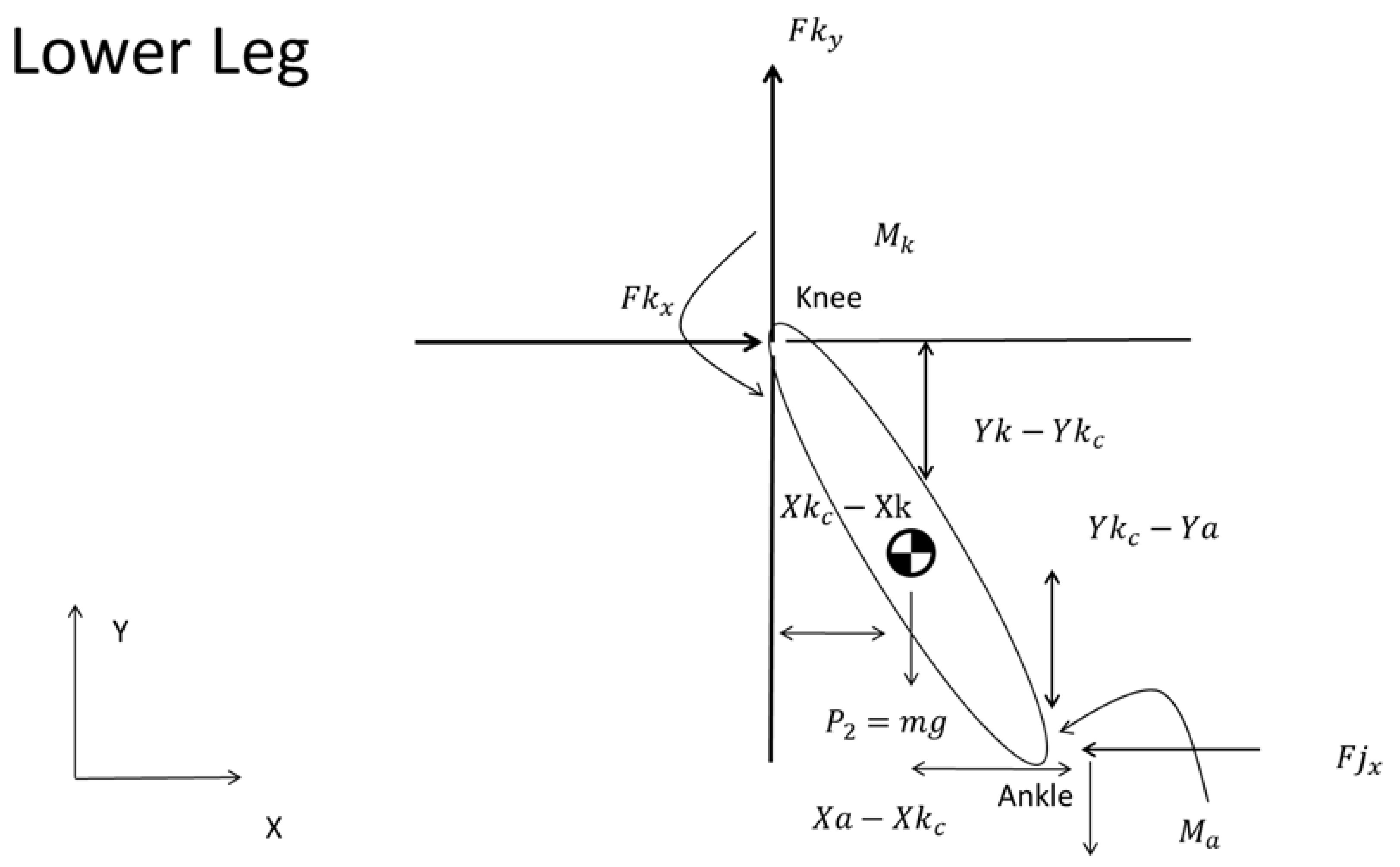
Advancing to the lower leg (ankle to knee joint), the model imposes similar equilibrium conditions, now referencing the forces and moments acting upon the ankle, articulated by equations (11), (12), and (13):
Σ F k x = F k x − F α x
Σ F k y = F k y − F   α y − P 2
− M a + M k c − F k x × y k − y k c − F k y × x k c − x k − F a y × x a − x k c − F a x × y k c − y a = 0
Within this framework, M a and M k c represent the moments at the ankle and knee, respectively, indicative of the rotational effects engendered by the forces acting on the segment.
In these equations, P 2 is the gravitational force i.e. the weight of the lower leg and m is the mass of the segment. The coordinates ( x k , y k ) and ( x a , y a ), designate the positions of the knee and ankle joints in the plane. Furthermore, ( x k c , y k c ) specifies the COM of the calf, as indicated by the literature (Figure 5).
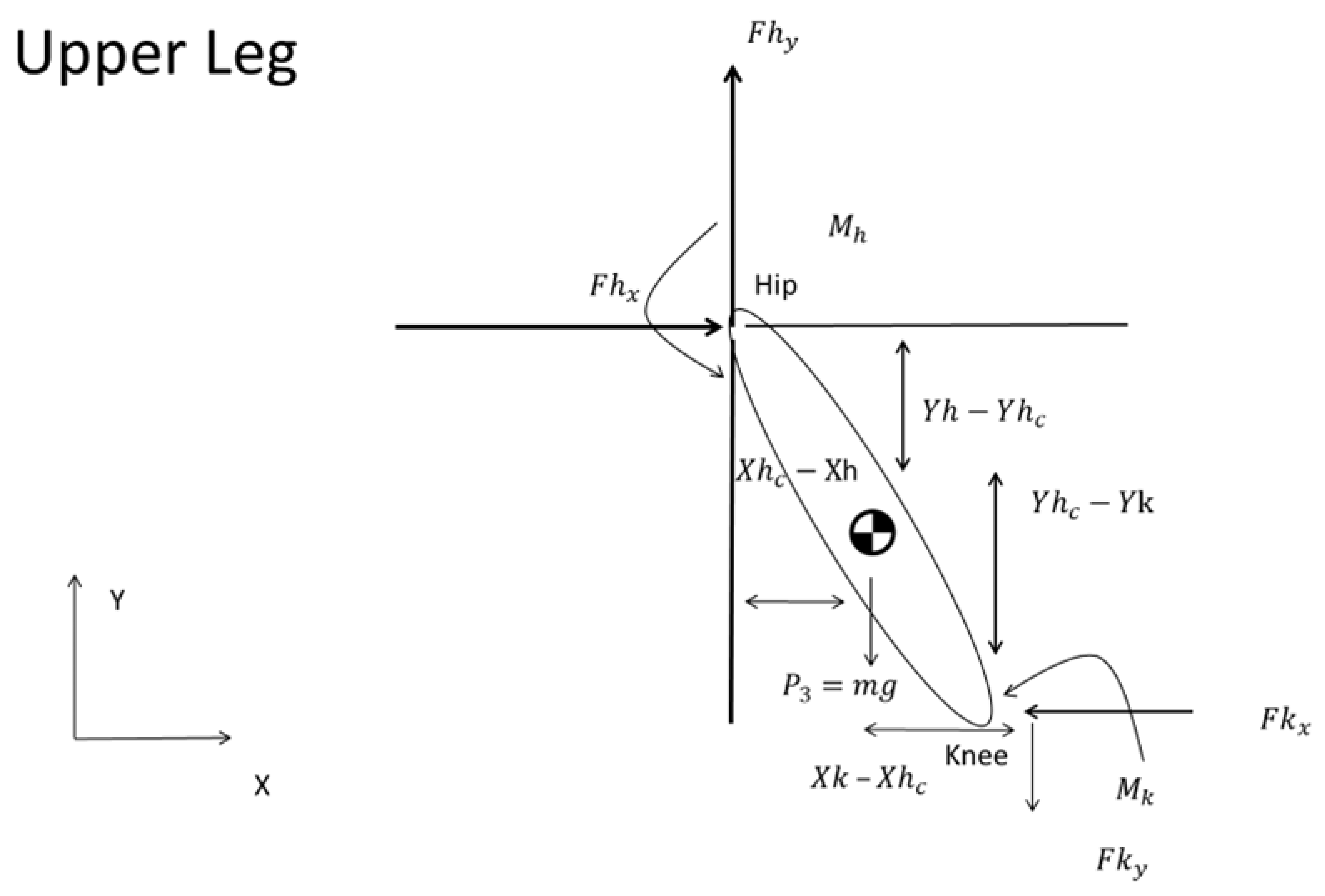
The forces and moments exerted on one segment are invariably transferred to the adjacent segment. In the same manner, the method is extended to the femur. The following diagram describes the moments and forces acting on the femur, which is the next segment where forces and moments act from the preceding segment. Therefore, we apply:
Σ F x = F h x − F k x = 0
Σ F y = F h y − F k y − P 3 = 0
− M k c + M h c − F h x × y h − y h c − F h y × x h c − x h − F k y × x k − x h c − F k x × y h c − y k = 0
Equation (14) establishes the balance of horizontal forces, denoting that the horizontal force component at the hip joint ( F h x ) is counterbalanced by the horizontal force component at the knee joint ( F k x ). Equation (15) demonstrates the vertical force equilibrium. The vertical component of the force at the hip joint ( F h y ) minus the vertical component of the knee joint force ( F k y ) and the force P3 sum to zero.
In the same manner equation (16) defines the moment equilibrium about the hip joint. M k c and M h c are the moments at the knee and hip about the centre of mass (COM) of the femur, (Figure 6). The coordinates Y h c and X h c specify the COM of the femur. Meanwhile , Y h ,   X h , pinpoint the locations of the hip and knee (Figure 6).

Anthropometric Parameters of a Hypothetical Male Athlete Model

The anthropometric model used is based on an assumed male athlete with a stature of 185 cm and a total body mass of 100 kg.
The model is divided into anatomical segments with the following specified lengths (Table 1), while the literature provides the following relationships for each segment (Table 2) [19,21]:

Results

The current analysis provided invaluable insights into the forces experienced by the athletes and the forces and moments influencing the key joints in the lower extremities.

Readiness Posture

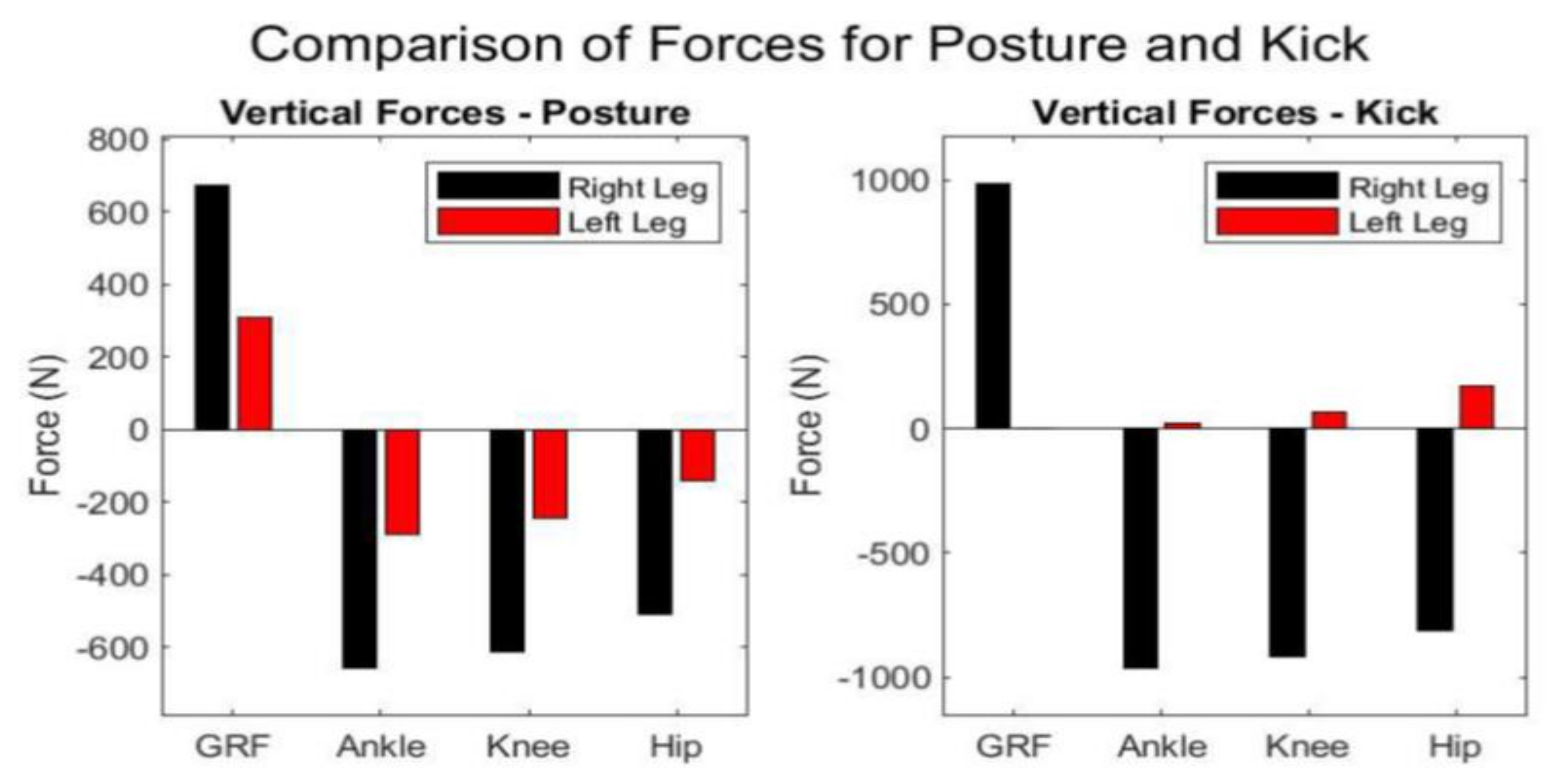
The right leg, serving as the hind leg, experiences significant forces. The horizontal ground reaction force (GRFX1) is calculated at 202.35N, however it must be noted that horizontal force is the product of friction, therefore depending on the surface it varies, but it still provides an analogous information of the magnitude of the force applied in horizontally.
The vertical ground reaction force (GRFY1) at 674.5038 N reflects the substantial load the right leg bears, corresponding to body weight and the additional biomechanical demands of maintaining posture and readiness for movement. This is further evidenced by the substantial horizontal and vertical forces at the ankle, knee, and hip joints, indicative of the right leg's involvement in power generation and absorption of impacts (Figure 7).
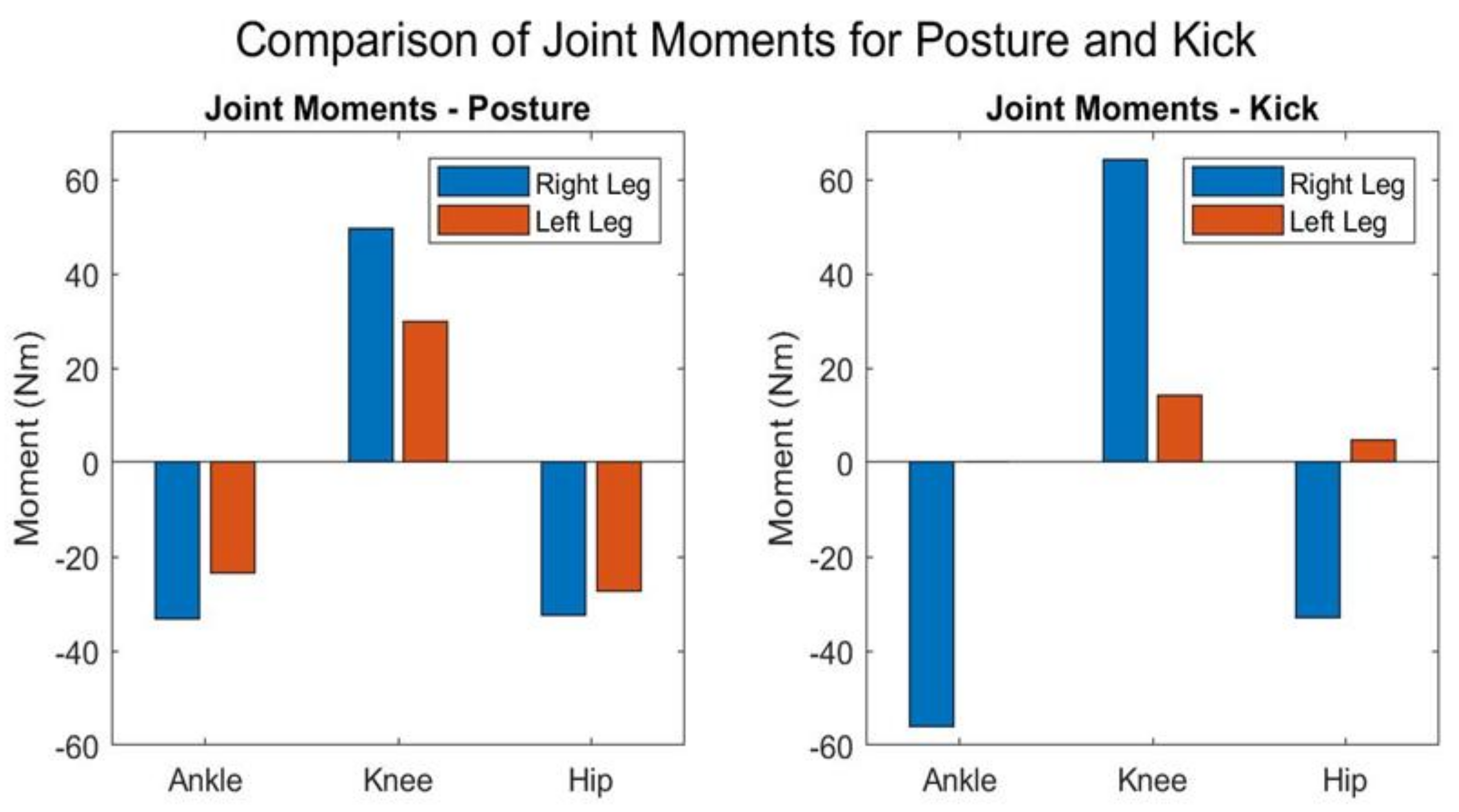
The hind leg exhibited notable torques across all joints. The ankle joint torque was estimated at -33.2249 Newton meters (Nm). The negative sign indicates the activation of the gastrocnemius muscle prompting plantar flexion. The knee joint, with a torque of 49.7192 Nm, was identified as bearing the highest load among the assessed joints which indicates the significant role in generating propulsive forces for strikes and in absorbing impacts during various combat movements. The positive sign here refers to the use of the extensor muscles and their contribution to the posture’s dynamics. The hip joint torque was registered at -32.3679 Nm with a magnitude almost identical to that of the ankle joint, causing strong activation of the glutes (Figure 8).
In contrast, the front (left) leg encounters a mirrored horizontal ground reaction force of -202.3511 N and a reduced vertical force of 306.4962 N, suggesting a lesser load-bearing role but crucial involvement in manoeuvrability and readiness for action.
The ankle joint experiences a torque of -23.3398 Nm. The knee joint torque, at 29.8407 Nm, points to its involvement in providing mobility support, enabling swift kicking actions and defensive blocks. Lastly, the hip joint showed a torque of -27.2661 Nm, indicating its role in coordinating lower and upper body movements, and in assisting force distribution during combat.
The results indicate a slightly higher reliance on the right ankle for stability and force generation, obviously due to the right leg being the hind leg in the stance.

Kick Posture

The static analysis of the kick posture provides quantified data on the power and the stability provided by the technique of the kick. The assessment specifically presents the differentiation of the loading between the kicking and supporting leg upon receiving the final kicking posture.
The supporting leg's role is to absorb the impact and providing the necessary stability and counterforce for the kick. The forces at the joints of the supporting leg, including the ankle illustrate the coordinated action across the leg to maintain posture and balance during the kick.
The torques further demonstrate its stabilizing function and the leg's contribution to resisting the kick's force and maintaining the fighter's balance. The knee joint shows the highest moment at 64.2947 Nm, along with the hip joint at 32.8831Nm which informs us about their critical role in supporting the body's weight and managing the dynamics of the kick.
The kicking leg’s results showcase its primary function in facilitating the kick. The joint forces provide the information of the leg’s tendency towards vertical lift and propulsion over horizontal stability.
The leg exhibits markedly lower torques, with a nearly negligible moment at the ankle 0.033354 Nm) and modest moments at the knee and hip. These reduced torques in the kicking leg reflect its primary engagement in executing the kick, with a focus on speed and precision, indicating the utilization of the heel as the edge of the strike.

Discussion

The exploration into the biomechanical characteristics of ancient athletics, specifically through the lens of the depicted postures and movements as exhibited in the practices of ancient Greek sports, yields insights that can be characterized as both novel and enlightening.
This study, to the best of our knowledge, represents a pioneering effort in the static biomechanical analysis of ancient athletes' postures using modern computational tools such as computer vision and static multi-segmental analysis.

Considerations of the Examined Postures Weight Distribution and Ground Reaction Forces

The first parameter examined in the present research was the weight distribution of the athlete’s body weight at the initial phase of a match.
We estimated the weight distribution of an athlete's body during the initial phase of the engagement. This analysis reveals a deliberate allocation of body mass, favouring a posterior distribution with 68% of the weight positioned on the hind leg, which can be interpreted as a biomechanical adaptation designed to optimize performance. This disparity in vertical force application between the posterior and anterior extremities represents a sophisticated approach to leveraging body mechanics for competitive advantage. The hind leg emerges as a critical element for stability and power generation [23].
On the other hand, the front leg carries a significantly smaller load, suggesting its role in manoeuvrability and providing balance during dynamic movements. This leg's reduced loading would possibly facilitate quicker, more agile adjustments in position. It must be noted that this imbalance in force distribution is indicative of a profound understanding of body mechanics, leveraging the limbs for specific functional roles: the hind leg for power and stability and the front leg for agility and balance.
The analysis of horizontal ground reaction forces (GRFs) provides an additional perspective on the dynamics of movement. Knowing that the matches used to take place in a sanded arena (palestra), the hind leg signifies the force exerted backwards against the ground, which, in turn, propels the body forward [22]. As the horizontal forces are also used for initiating movement, and producing momentum, we are able to understand one of the ancients’ approaches in power generation [24].
Additionally, it seems that the strategic postural manipulation enabled the athletes to selectively engage targeted muscle groups, resulting in a biomechanically efficient system for posture maintenance [25]. A feature we observe is the ability to generate high-magnitude forces and moments while in static equilibrium, a phenomenon derived by bodily configuration, specifically the articular angles formed at each joint throughout the kinematic chain. This is characterized as a fundamental component of effective posture manipulation [26].
As far as it concerns the kick posture obviously the full GRF is exerted on the base leg. Here, it is imperative to acknowledge the multifaceted functionality of the lower extremity, which encompasses attenuation of impact forces, alongside the provision of stability and propulsion. The analysis of the horizontal GRF elucidates the requisite lateral stabilization for equilibrium maintenance. The elevated mechanical outputs of the base leg contribute substantially to the reduction of kinetic energy during impact, which mitigates the risk of losing balance and facilitates strategic positioning and movement [27]. The suggested robust activation of the muscles is essential for pelvic stabilization and limb control at the final phase of the kick and significantly enhances the biomechanical characteristics of the kick [28].

Strategic and Tactical Considerations

The biomechanical characteristics derived from the present analysis can also inform inferences about athletes' tactical body positioning strategies [29].
The employment of biomechanical strategies that signal strength, readiness, and strategic flexibility are incorporated in the postural configurations, that we found. The athletes aimed to effectively control the pace of the engagement and influence opponent decision-making processes [29]. Joint net moments confirm the literature as they present a highly strategic distribution designed to maximize both stability and power generation [30].
The deliberate augmentation of joint moments (beyond those observed in the typical anatomical posture) introduces an element of unpredictability and dynamism to the athlete's subsequent movements and obscuring their tactical intentions from the opponent [31]. Interpreting these results through game theoretical perspectives it posited that signalling robustness, in our case provided by the posture’s configurations, serve as deterrents against careless aggression from adversaries [32].
Moreover, the stance equips athletes with the capability to execute potent counterattacks, instilling psychological hesitation and error in opponents [33]. This reflects a deliberate positioning that anticipates and reacts to the opponent's moves as it aims to control the game's flow and outcome [34].
The posture reveals a strategic manipulation of the body, enabling versatile offensive and defensive capabilities [35]. Due to its biomechanical characteristics, the athlete's next move becomes less predictable to the opponent enabling the athlete to mask his intentions and maintain versatility using mixed strategies (i.e., varying joint dynamics) effectively [31].
Our examination also asserts that a fighter’s stance transcends mere defensive positioning; it encompasses predictive and adaptive strategies facilitated by multi-muscular activations which are obviously required to counterbalance the forces and moments anticipated upon adopting such postures. This dynamic readiness not only allows for fluid transitional movements but is also important in executing preemptive strategies [36]. Hence, maintaining this posture allows the players to anticipate the opponent's moves and prepare counterstrategies. Such preparedness is integral to the athlete's ability to respond swiftly to the opponent's manoeuvres, a capability noted by Philo in his discussions on technical–tactical aspects [37].
The integration of biomechanical and strategic insights not only underscores the physical capabilities leveraged to influence opponent behaviour but also highlights how ancient athletes used techniques and tactics to dictate the engagement's development effectively [38].
The results of our static postural analysis of the kick presented at least 3 fundamental game theory-based tactics within the biomechanical setup of it.
The first tactic involves dorsiflexion of the kicking leg's foot. This specific ankle movement positions the heel as the main point of impact, thereby optimizing the force transmission and maximizing the damage potential of the kick. Dorsiflexion is selected to ensure that the area making contact with the opponent is minimised (focusing on the heel), which concentrates the force delivered and maximizes the impact, a characteristic totally aligning with the ancient descriptions of Galen [39].
The second tactic relates to the features of the supporting leg. The leg, particularly the knee joint, exhibits strong moments, indicating significant force and stability maintained during the kick which is critical not only for supporting the body during the unilateral action of kicking but also for providing a stable platform from which power can be efficiently transferred.
We observe that the fighter's posture maximizes offensive potential targeting for the highest payoff presenting a function asymmetry with varying moments at each joint., a risk–dominant tactic which potentially to a disadvantage. The high moments at the knee joint can be seen as part of a contingency plan [40], a method for ensuring that the athlete maintains stability even if the initial kicking action does not lead to the desired outcome (such as observed in the Figure 2).
The third tactic involves preparedness to adjust postures to maintain balance in case the initial kick is countered by the opponent. This is highlighted by the high ankle moments on the supporting leg, which indicate strong plantarflexion and thus stability [41]. Additionally, the position of the ipsilateral arm, which is not detailed but implied to contribute to balance and defence, supports this readiness.
In conclusion, the application of game theory principles to the analysis of the results suggests a Mixed Strategy Equilibrium for the kick, as evidenced by the functional asymmetry, the mechanical necessity, and the optimization required for executing a high-risk, devastating kick [42]. Furthermore, the aspect of Contingency Planning is adequately addressed through the stabilization mechanisms observed.

Training and Strength Implications

The forces and moments exerted on the joints of both legs represent the baseline of strength required to maintain posture and readiness for movement. While not dynamically taxing, these static loads are critical for developing tendon stiffness, joint stability, and neuromuscular control—prerequisites for executing dynamic actions with precision and power [43].
It is known that during dynamic exercises such as the vertical jump, net joint moments soar significantly higher magnitudes, however, the torques estimated from static postures, provide a method utilized to enhance maximal muscular force production and neuromuscular efficiency i.e. the static exercises [44]. The maintenance of static postures, characterized by sustained isometric tensions, augments the athlete's capacity, bolsters the integrity of joint capsules and amplify proprioceptive sensitivity [45]. These postures facilitate a methodological activation of muscle groups, achieved through the adoption of specific bodily configurations that induce significant magnitudes of force just by forming the body in a specific way [46]. This approach strategically primes the body for full activation [47]. According to Galen athletes engaged in exercises that required holding static positions, such as grappling stances without motion, to enhance muscular endurance and strength [39].
Galen identifies exercises that we would classify today as isometric, such as holding one's hands clenched as methods to increase strength [39].
As the sustained isometric contractions require continuous motor unit activation with minimal fluctuations, they enhance intramuscular coordination and muscle fibre recruitment efficiency we identify that receiving these postures contributed in developing the athletes’ strength [48]. Biochemically, isometric exercise primarily utilizes the oxidative phosphorylation pathway due to its lower, yet sustained, energy demand [49]. This constant demand for ATP, met without the cyclic rest periods characteristic of dynamic contractions, promotes mitochondrial biogenesis and efficiency within muscle cells.
Also, the persistent tension on muscle fibres during isometric holds leads to an increase in local muscular endurance and can stimulate hypertrophy through tension-induced intracellular signalling pathways [49], such as the mTOR pathway, therefore we should consider the factor of strong isometric exercises as a method of developing the extraordinary bodies developed in antiquity.
Thus, the juxtaposition of static and dynamic modalities within a training program is not merely complementary but synergistic [50]. The endurance and stability garnered from static postures provide the essential stability from which dynamic power can be launched.

Conclusions

The present research into the biomechanical characteristics of ancient Greek athletics was conducted using machine learning (Computer Vision) and static multi-segmental analysis of the lower extremity. The analysis demonstrated optimal weight distributions and effective utilization of ground reaction forces. It was found that ancient practices emphasized on strategic use of posture to influence opponents' decisions and amplify their technique’s effective both in attacking and defending, a concept fully aligning with modern game theory.
The use of strategy within the postures themselves to manipulate opponents' responses and create competitive advantages was identified. The present study elucidates how ancient athletes used their postures not as a tactical tool to influence opponents’ perceptions and actions, integrating physical and psychological strategies—a dual approach which can be adapted in sports psychology and coaching strategies in modern combat sports.
Sustained muscle tension during these postures with continuous motor unit activation is suggested, enhancing coordination and fibre recruitment for improved force production.
Historical texts confirm that isometric contractions were used to stimulate muscle growth pathways and increase muscular endurance, practices likely contributed to the robust physiques observed in ancient athletes.
Our research advocates for isometric training regimes, which strengthen muscle and joint stability, to enhance neuromuscular control. This approach aims to promote tendon stiffness, joint stability, and the acquisition of high-level coordination skills.
This study's practical implication in modern sports science lies in its application of advanced biomechanical analysis to historical athletic practices, providing new insights that were previously not quantified. The detailed examination of weight distribution, ground reaction forces, and postural strategies used by ancient athletes offers a novel perspective on how these elements can be systematically optimised for current athletic training and performance, injury prevention, and tactical strategies in contemporary sports.
Considering the foregoing arguments this study provides significant contributions to modern sports science and athletic biomechanics.

Practical Applications

This study offers practical applications for combat sports athletes and coaches leveraging insights from ancient Greek athletic practices. The main application is the use of static analysis to optimize fighting stances and techniques, allowing for enhanced power generation and strategic positioning. We emphasize isometric exercises to enhance joint stability and tendon stiffness, which is crucial for both performance enhancement and injury prevention. Athletes seeking to maximize power generation should focus on specific postural strategies, while those aiming to improve balance and agility should incorporate dynamic stability exercises. Additionally, integrating game theory principles derived from the study can be applied to develop sophisticated fight strategies when seeking to outmanoeuvre opponents, through strategic positioning, while maintaining biomechanical efficiency. Finally, the motion capture used in the research methodology can be employed to provide detailed feedback on technique refinement, enabling athletes to optimize their performance for competitive advantage.

Author Contributions

Andreas Bourantanis: Data curation, Formal analysis, Methodology, Software, Visualization, Writing – review Nomikos: Review & editing. Supervision, Biomechanical Analysis, and Project administration.

Funding

The authors declare that they have no founding sources.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. J.J. van Middendorp, G.M. Sanchez, A.L. Burridge, The Edwin Smith papyrus: a clinical reappraisal of the oldest known document on spinal injuries, European Spine Journal 19 (2010) 1815 - 1823.
  2. J. Jouanna, Egyptian Medicine and Greek Medicine, 2012.
  3. ABBREVIATIONS USED FOR WORKS OF ARISTOTLE, Aristotle's De Motu Animalium (2020).
  4. H. Friedman, P.J. Miller, Reconstruction of the Ancient Greek Long Jump - an Opportunity for Multidisciplinary Collaboration, EXARC Journal Issue 2017/3 (2017).
  5. A. G. Bourantanis, N. N. Nomikos, C. C. Trompoukis, W. W. Wang, Estimating Athletes’ Centre of Mass as Presented on Ancient Greek Pottery Depictions, American Journal of Sports Science and Medicine (2022).
  6. K. Kiers, L. Ellenberger, J. Jermann, F. Oberle, W.O. Frey, J. Spörri, Prospective Study on Dynamic Postural Stability in Youth Competitive Alpine Skiers: Test-Retest Reliability and Reference Values as a Function of Sex, Age and Biological Maturation, Frontiers in Physiology 13 (2022).
  7. C. Hrysomallis, Relationship Between Balance Ability, Training and Sports Injury Risk, Sports Medicine 37 (2007) 547-556.
  8. C. Hrysomallis, Balance Ability and Athletic Performance, Sports Medicine 41 (2011) 221-232.
  9. Sacripanti, JUDO: Biomechanical Science for IJF ACADEMY, ISBN: 978-99957-1-518-22022.
  10. C.E. Clancy, A.A. Gatti, C.F. Ong, M.R. Maly, S.L. Delp, Muscle-driven simulations and experimental data of cycling, Scientific Reports 13 (2023).
  11. B.I. Prilutsky, V.M. Zatsiorsky, Optimization-Based Models of Muscle Coordination, Exercise and Sport Sciences Reviews 30 (2002) 32-38.
  12. T. Geijtenbeek, SCONE: Open Source Software for Predictive Simulation of Biological Motion, J. Open Source Softw. 4 (2019) 1421.
  13. C.L. Dembia, N.A. Bianco, A. Falisse, J.L. Hicks, S.L. Delp, OpenSim Moco: Musculoskeletal optimal control, PLoS Computational Biology 16 (2019).
  14. S.D. Uhlrich, R.W. Jackson, A. Seth, J.A. Kolesar, S.L. Delp, Muscle coordination retraining inspired by musculoskeletal simulations reduces knee contact force, Scientific Reports 12 (2022).
  15. Bourantanis, A Static Analysis of Emblazonments Depicting Ancient Greek Pankration, University of Dundee, 2021.
  16. A. Bourantanis, Biomechanical analysis of the movement of the ancient Greek combat sports’ athletes in classical antiquity, University of Dundee, 2024.
  17. R. Pascanu, Ç. Gülçehre, K. Cho, Y. Bengio, How to Construct Deep Recurrent Neural Networks, CoRR abs/1312.6026 (2013).
  18. Z. Cao, G. Hidalgo, T. Simon, S.-E. Wei, Y. Sheikh, OpenPose: Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields, IEEE Transactions on Pattern Analysis and Machine Intelligence 43 (2018) 172-186.
  19. W. Wang, G. Arnold, T. Drew, S. Gibbs, I. Christie, Modelling Techniques, University of Dundee, Distance Learning Section, Department of Orthopaedic & Trauma Surgery, University of Dundee, 2012.
  20. W. Wang, UNIT 3 - PROPERTIES OF JOINTS AND LIMBS, Institute of Motion Analysis and Research, College of Medicine, Dentistry and Nursing, University of Dundee, Mr Ian Christie (Illustrator)2009.
  21. D.A. Winter, Biomechanics and Motor Control of Human Movement, 2009.
  22. Lucian, Anacharsis (section 2).
  23. T.J. Roberts, Contribution of elastic tissues to the mechanics and energetics of muscle function during movement, Journal of Experimental Biology 219 (2016) 266 - 275.
  24. K.C. Nishikawa, Eccentric contraction: unraveling mechanisms of force enhancement and energy conservation, Journal of Experimental Biology 219 (2016) 189 - 196.
  25. G.T. Burns, K.M. Kozloff, R.F. Zernicke, Biomechanics of Elite Performers: Economy and Efficiency of Movement, Kinesiology Review -1 (2020) 1-10.
  26. T.-W. Lu, C.-f. Chang, Biomechanics of human movement and its clinical applications, The Kaohsiung Journal of Medical Sciences 28 (2012).
  27. D. Hoelbling, A. Baca, P. Dabnichki, Sequential action, power generation and balance characteristics of a martial arts kick combination, International Journal of Performance Analysis in Sport 20 (2020) 766 - 781.
  28. D. Alexis Sobarzo Soto, E.A. Aedo-Muñoz, C. José Brito, B. Miarka, Comparisons of Motor Actions and Biomechanical Assessments of Judo Techniques Between Female Weight Categories, Journal of Human Kinetics 75 (2020) 247 - 255.
  29. Theocritus, Idylls 22: The Dioscuri.
  30. M. Poliakoff, Combat sports in the ancient world, Yale University Press1975.
  31. G.J. Székely, M.L. Rizzo, The Uncertainty Principle of Game Theory, The American Mathematical Monthly 114 (2007) 688 - 702.
  32. M. Franke, Signal to act : game theory in pragmatics, 2009.
  33. L. Brumley, Misperception and Its Evolutionary Value, Monash University, Clayton, Australia, 2014.
  34. A. Gellius, Attic Nights, Harvard University Press William Heinemann, Ltd., Cambridge, MA, London, 1927.
  35. Plutarch, De virtute morali.
  36. K.K. Trejo, J.B. Clempner, A.S. Poznyak, A Stackelberg security game with random strategies based on the extraproximal theoretic approach, Eng. Appl. Artif. Intell. 37 (2015) 145-153.
  37. Philo, Philo (10 vols. and 2 supplementary vols.), Harvard University Press, Cambridge, MA.
  38. D. Chrysostom, Orationes, Speech 8, Section 18.
  39. Galen, Galen: Selected works, Oxford University Press1997.
  40. A. Ravi, A. Gokhale, A. Nagwekar, Using Game Theory to maximize the chance of victory in two-player sports. 2021; arXiv:abs/2105.11650.
  41. W. Wang, Arnold, G., Gibbs, S., Drew, T.,, I. Christie, Inverse dynamics for the musculoskeletal system, Institute of Motion Analysis and Research, College of Medicine, Dentistry and Nursing, University of Dundee2012.
  42. K.E. Merrick, M.K.D. Hardhienata, K. Shafi, J. Hu, A Survey of Game Theoretic Approaches to Modelling Decision-Making in Information Warfare Scenarios, Future Internet 8 (2016) 34.
  43. D.M. Mulla, P.J. Keir, Neuromuscular control: from a biomechanist's perspective, Frontiers in Sports and Active Living 5 (2023).
  44. L.D.M. Mendonça, N.F.N. Bittencourt, R.L. Freire, V.C. Campos, T.V. Ferreira, P.L.P. Silva, Hip external rotation isometric torque for soccer, basketball, and volleyball athletes: normative data and asymmetry index, Brazilian journal of physical therapy 26 1 (2022) 100391.
  45. A. Moraux, A. Canal, G. Ollivier, I. Ledoux, V. Doppler, C. Payan, J.-Y. Hogrel, Ankle dorsi- and plantar-flexion torques measured by dynamometry in healthy subjects from 5 to 80 years, BMC Musculoskeletal Disorders 14 (2013) 104 - 104.
  46. E.N. Burnet, P.E. Pidcoe, Isometric gluteus medius muscle torque and frontal plane pelvic motion during running, Journal of sports science & medicine 8 2 (2009) 284-8.
  47. L.Z.F. Chiu, G.L. vonGaza, L.M.Y. Jean, Net joint moments and muscle activation in barbell squats without and with restricted anterior leg rotation, Journal of Sports Sciences 35 (2017) 35 - 43.
  48. P. Cerretelli, A. Veicsteinas, M. Fumagalli, L. Dell'orto, Energetics of isometric exercise in man, Journal of applied physiology 41 2 (1976) 136-41.
  49. D.J. Oranchuk, A.G. Storey, A.R. Nelson, J.B. Cronin, Isometric training and long-term adaptations: Effects of muscle length, intensity, and intent: A systematic review, Scandinavian Journal of Medicine & Science in Sports 29 (2019) 484 - 503.
  50. D. Lum, T.M. Barbosa, Brief Review: Effects of Isometric Strength Training on Strength and Dynamic Performance, International Journal of Sports Medicine 40 (2018) 363 - 375.
Preprints 110317 g001
Figure 1. "Readiness" Posture of athlete. The image depicts an athlete engaged in the ancient Greek sport of pankration, as illustrated on a red-figure amphora housed in the Staatliche Antikensammlungen Museum in Munich, Germany.
Figure 1. "Readiness" Posture of athlete. The image depicts an athlete engaged in the ancient Greek sport of pankration, as illustrated on a red-figure amphora housed in the Staatliche Antikensammlungen Museum in Munich, Germany.
Preprints 110317 g001
Preprints 110317 g002
Figure 2. The final posture an athlete receives upon delivering a kick, possibly aiming at the opponent’s abdomen area. The present illustrates a scene of a Pankration match depicted on a black-figure amphora from the classical period (5th century BCE), currently.
Figure 2. The final posture an athlete receives upon delivering a kick, possibly aiming at the opponent’s abdomen area. The present illustrates a scene of a Pankration match depicted on a black-figure amphora from the classical period (5th century BCE), currently.
Preprints 110317 g002
Preprints 110317 g003
Figure 3. Biomechanical model of lower limbs in the sagittal plane, used for calculating ground reaction forces.
Figure 3. Biomechanical model of lower limbs in the sagittal plane, used for calculating ground reaction forces.
Preprints 110317 g003
Preprints 110317 g004
Figure 4. Diagram illustrating the equilibrium of forces on the foot.
Figure 4. Diagram illustrating the equilibrium of forces on the foot.
Preprints 110317 g004
Preprints 110317 g005
Figure 5. Representation of lower leg forces from ankle to knee, showing equilibrium conditions.
Figure 5. Representation of lower leg forces from ankle to knee, showing equilibrium conditions.
Preprints 110317 g005
Preprints 110317 g006
Figure 6. Analysis of the femur demonstrating force and moment equilibrium, as forces are transmitted from the knee to the hip joint.
Figure 6. Analysis of the femur demonstrating force and moment equilibrium, as forces are transmitted from the knee to the hip joint.
Preprints 110317 g006
Preprints 110317 g007
Figure 7. Vertical forces on lower extremity joints during “readiness” static posture and kick posture, highlighting differences in force distribution between the right and left legs.
Figure 7. Vertical forces on lower extremity joints during “readiness” static posture and kick posture, highlighting differences in force distribution between the right and left legs.
Preprints 110317 g007
Preprints 110317 g008
Figure 8. Joint moments at the ankle, knee, and hip for "readiness" posture and kick posture.
Figure 8. Joint moments at the ankle, knee, and hip for "readiness" posture and kick posture.
Preprints 110317 g008
Table 1. Segmental Dimensions used in the Present Simulation.
Table 1. Segmental Dimensions used in the Present Simulation.
Segment Length (cm)
Foot 24
Lower Leg
Upper Leg		 48
50
Table 2. Normative data on the relative mass and Centre of mass for each anatomical segment.
Table 2. Normative data on the relative mass and Centre of mass for each anatomical segment.
Segment Relative Mass (%) Centre of Mass (% from Proximal End)
Upper Leg 10.7 43.9
Lower Leg 4.7 42.0
Foot 1.7 43.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated