Prerpints.org logo
Preprint
Article

An Insight into Perfusion Anisotropy within Solid Murine Lung Cancer Tumors

Altmetrics

Downloads

141

Views

56

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.zip (1.37MB )

Submitted:

25 June 2024

Posted:

26 June 2024

You are already at the latest version

Alerts
Abstract
Blood vessels are essential for maintaining tumor growth, progression, and metastasis, yet the tumor vasculature is under a constant state of remodeling. Since the tumor vasculature is an attractive therapeutic target, there is a need to predict the dynamic changes in intratumoral fluid pressure and velocity which occur across the tumor microenvironment (TME). The goal of this study is to get insight into perfusion anisotropy within lung tumors. To achieve this goal, we used the perfusion marker Hoechst 33342 and vascular endothelial marker CD31 to stain tumor sections from C57BL/6 mice harboring Lewis Lung Carcinoma tumors on their flank. Vasculature, capillary diameter, and permeability distribution were extracted at different time points along the tumor growth curve. A computational model was generated applying a unique modeling approach based on the smeared physical fields (Kojic Transport Model, KTM). KTM predicts spatial and temporal changes in intratumoral pressure and fluid velocity within the growing tumor. Anisotropic perfusion occurs within two domains - capillary and extracellular space. Anisotropy in tumor structure causes nonuniform distribution of pressure and fluid velocity. These results provide insights regarding local vascular distribution for optimal drug dosing and delivery to better predict distribution and duration of retention within the TME.
Keywords: 
Subject: Biology and Life Sciences  -   Other

1. Introduction

New and innovative therapeutics, such as nanoscale-based pharmaceuticals have rapidly advanced over the past decades in cancer treatment, increasing the accumulation of antitumor agents in and around tumor tissues and improving their pharmacokinetics and release profiles, while reducing the dose to normal tissues [1]. Multifunctional platforms, such as organic or metallic nanoparticles have been engineered to deliver therapeutic and diagnostic agents selectively to tumors [2], whereby tuning the size and surface properties of the nanostructure aids in overcoming physiological-pathological barriers for treatment of drug-resistant cancers and facilitating drug penetration within malignant cells [3]. However, although encouraging progress towards site-specific drug delivery [4,5] and emerging technologies for sustained and local immunotherapeutic delivery [6,7,8,9] have been investigated, the extracellular matrix constitutes a major obstacle inhibiting therapeutic success and mobility of diffusing species [10,11]. While efforts have been made to understand and model blood flow within the tumor and in vessels feeding tumors [12,13,14,15], there is still a need to predict changes in flow dynamics that occur across the tumor vessel network. Predicting changes in fluid dynamics surrounding and within the tumor would help to better screen for therapeutics capable of traversing the tumor microenvironment (TME).
One of the main reasons why current nanoscale-based pharmaceuticals fail to treat solid tumors lies within the high heterogeneity of the cancerous mass. In fact, the TME presents unique characteristics, including a high-density extracellular matrix (ECM) as well as abnormal tumor vasculature and lymphatic systems. Additionally, due to interstitial fibrosis and abnormal lymphatic vessels, the interstitial fluid pressure (IFP) in solid tumors increases to 5–130 mm Hg, compared to 0-3 mm Hg in healthy tissues [16]. All of these TME features hinder the transport of therapeutics into the tumor interstitium and its core area and, along with the rapid decrease in convection between the extravascular and intravascular spaces, create impenetrable barriers which ultimately result in ineffective drug doses to treat the target site [17]. Therefore, an enhancement in drug tumor penetration to achieve effective concentrations across the tumor mass is needed to improve therapeutic efficacy and advance novel and innovative therapeutics toward clinical translation.
To enhance the penetration and distribution of nanomaterials in solid tumors efforts have been made to engineer the nanoparticle surface [18,19] for localized delivery of the particles to site-specific areas of the tumor [20,21]. For instance, several in vivo studies demonstrate that nanoparticles with phospholipid-polyethylene glycol-derived surface functionalization show significantly increased selective and efficient internalization by target cancer cells and tissues [22,23]. In addition, the physical and chemical properties of nanoparticles, such as particle size [24,25], morphology [26], and charge [27,28] can influence their delivery and distribution across the TME [29]. Moreover, various aspects of nanoparticles, such as passivation to prevent recognition and clearance [30], size and mass considerations for transport through biological barriers [12,14,31,32,33], and composition to enhance tumor accumulation based on patient specific biomarkers [34], have all been studied to maximize drug delivery efficacy. While these efforts drive approaches towards personalized medicine, understanding TME dynamics is also critical.
Beyond considerations of particle properties to achieve better drug accumulation at the tumor site, computational and mathematical modeling of vascular flow and pressure across the tumor mass may also provide an opportunity to extract useful information for targeted delivery of diagnostic and therapeutic agents [35,36]. In fact, theoretical models offer important tools for predicting and determining a range of parameters in physiologically relevant scenarios as well as for testing potential solutions to overcome such biological barriers to reach target cells. For instance, a computational model by Frieboes et al. [37] effectively selected an optimal nanoparticle formulation in terms of particle size and vascular affinity to accumulate uniformly in the tumor mass as a function of the development stage of the malignancy. Stillman et al. [38] provided a modeling platform called the EVONANO, which is able to decrease both the time and cost required to develop nanoparticle designs by simulating tumor growth and nanoparticle transport using machine learning. However, these studies lack validation with both in vitro and in vivo experimental data. Guo et al. [39] describes a quantitative metric system to identify and evaluate new cancer targets for tumor-targeting nanomedicines using comparative flow cytometric screening and characteristics, such as tumor specificity, target expression level, cellular internalization, therapeutic function, and potential clinical impact. However, although this methodology allows for identification of parameters necessary for evaluating a potential therapeutic target to disrupt cancer pathogenesis, it was only tested in vitro with metastatic melanoma.
Computational models can also provide predictive information about therapeutic circulation and interactions with the tumor vasculature as well as tumor accumulation, payload release, efficacy, and safety [40]. For instance, Stapleton et al. [41] generated a mathematical model to describe pressure-driven fluid flow across blood vessels and through the tumor interstitium, extracting liposome accumulation curves from experimental computed tomography measurements in preclinical tumor models. A study by Caddy et al. [42] presents a three-part mathematical model to predict particle distribution after intratumoral injection, demonstrating that particles with a negative surface charge can spread farther from the injection location, occupying almost 90% more space when compared to particles with a neutral surface charge. However, this model was not validated experimentally. Finally, an in vivo biodistribution model was validated in the work by Dogra et al. [43], whereby experimental data from intravenous injection of mesoporous silica particles ranging in size from 46 to 162 nm into the plasma compartment of rats is used to develop a predictive mathematical model of whole-body nanoparticle pharmacokinetics and tumor delivery. The model was then validated with longitudinal in vivo data. Importantly, none of these models address parameters such as fluid velocity and intratumoral pressure, which can be useful predictors for developing strategies to target and retain therapeutics across the TME.
In this study, we investigated the biophysical properties of the TME, which play a major role in fluid accumulation. Parameters including tumor vasculature and permeability are extracted from pre-clinical study in lung cancer-bearing mice and results are used to model tumor fluid transport dynamics. To generate a computational model of intratumoral perfusion, we implemented the finite element (FE) methodology based on smeared physical fields (termed the Kojic Transport Model, KTM), built in the FE program PAK-BIO (Kojic et al. [44]). We believe that our computational model will be useful for predicting therapeutic outcomes across different cancers, allowing for optimized drug carrier design and improved drug delivery efficiency and retention to advance personalized medicine.

2. Materials and Methods

2.1. Animal Model of Lung Cancer

In this study, we used six-week-old female C57BL/6 mice (n = 24, 6 per timepoint) to understand the conditions over time (vasculature, capillary diameter, and perfusion) in a mouse lung cancer model (Lewis Lung Carcinoma, LLC). These parameters were used to generate a theoretical model of intratumoral perfusion. The research protocol was granted Institutional Animal Care and Use Committee (IACUC) approval (protocol # IS00005178 approved 6 May 2019) at the Houston Methodist Research Institute. The animals were purchased from Taconic Biosciences (Rensselaer, NY, USA). Female mice were chosen for study because while both naive male and female C57BL/6 mice do not present lung function differences at baseline [45], tumors grow more rapidly in female C57BL/6 mice [46]. A Lewis lung carcinoma (LLC) cell line was used in this study as a murine model of non-small cell lung cancer (NSCLC), since it is highly tumorigenic and provides a reproducible syngeneic model for lung cancer in the C57BL mouse.

2.2. Experimental Timeline of Perfusion Study

Under sedation, all mice received manual subcutaneous injection of 2 × 106 LLC cells into their right flank. Mice weight (Figure S1A) and health conditions were monitored daily, ensuring adequate nutrients (food and water ad lib.) and living conditions (clean cages, enrichment). Tumor volumes were also measured daily using a digital caliper (McMaster-Carr, Elmhurst, IL, USA, 2340A11). Tumors were palpable 4-5 days after cell injection, and after 10 days, tumor volumes reached an average of ~100 mm3. 7-, 10-, 13-, and 16-days post tumor cell inoculation, n = 6/timepoint LLC tumor bearing mice were administered the perfusion marker Hoechst 33342 (Thermo Fisher, Waltham, MA, USA, catalog number H3570) at a dose of 40 mg/kg intravenously through a lateral tail vein using insulin syringes (BD U 100 Insulin Syringe Micro Fine Needle 28G, Becton, Dickinson, Franklin Lakes, NJ, USA, 329461). We selected timepoints 7, 10, 13, and 16 days after LLC cell inoculation, identified as approximately 15%, 25%, 60%, and 80% respectively of final tumor growth to strategically capture key stages of tumor development. Experimental endpoint was based on tumor volume greater than 2 cm3, tumor interfering with normal physiological function, surgical complications, or other symptoms as outlined in the HMRI Guidelines and Policies for Determination of Humane Endpoints and Tumor Monitoring Policy, as well as the recommendation of the Comparative Medicine Program (CMP) veterinary staff and was estimated to occur ~19 days after cell inoculation, representing 100% tumor growth. Tumor volumes (V) in mm3 were calculated through daily measurements of the tumor axes using digital calipers and the following formula:
V = D * d 2 2
where D and d represent respectively the major and the minor axes of the tumor measured in mm.
All animal procedures involving injections were performed while the animals were under sedation, which was achieved by anesthetizing the mice with isoflurane. The animals were sacrificed one minute post IV injection. Tumors were excised, weighed ex vivo (Figure S1b), and fixed in 10% formalin for further analysis.

2.3. Tumor Slice Preparation

After 24 h in formalin, each tumor was sectioned using a surgical blade and divided in two halves. This dissection procedure was performed by the same investigator for consistency. Each half-tumor was paraffin embedded, and then sectioned to generate a 5 μm medial slice.

2.4. Immunofluorescence (IF) Evaluations

Tumor morphology, vasculature (Rabbit anti-CD31 antibody at a 1:50 dilution, Cat. No. ab28364, Abcam, Waltham, MA, USA followed by a Goat anti-rabbit IgG (H+L) Cross-Adsorbed Secondary Antibody, Alexa Fluor™ 594 at a 1:200 dilution, Cat. No. A-11012, Thermo Fisher Scientific, Waltham, MA, USA), and permeability (Hoechst 33342, Trihydrochloride, Trihydrate—FluoroPure Grade, Cat. No. H21492, Invitrogen, Waltham, MA, USA) were assessed in tissue sections of LLC tumors.

2.5. Tumor 2D Imaging and Heatmaps

Tumor sections were imaged in their entirety using a SLIDEVIEW VS200 research slide scanner (Olympus, Center Valley, PA) with a 10x objective. Separate images were obtained for Hoechst 33342 and CD31 staining using the OlyVia microscope software. Subsequently, the raw images were imported into ImageJ through the Bio-Formats plugin, where a 9x9 grid was systematically applied to each image. Image post-processing, involving background removal and application of an over/under threshold with a minimum below setting of 79% and 95% for Hoeschst33342 and CD31 images, respectively, was carried out in ImageJ to identify positively stained pixels.
For each tumor section, three distinct heatmaps were calculated, representing permeability (%), vasculature (%), and capillary diameter (µm). The permeability heatmaps illustrate the local density of pixels covered by Hoechst 33342 staining, expressed as the ratio of positively stained pixels to the total number of pixels in the grid cell. Vasculature heatmaps depict the local density of pixels covered by CD31 staining, expressed as the ratio of positively stained pixels to the total number of pixels in the grid cell. Finally, capillary diameter heatmaps were determined through CD31 expression and quantified using ImageJ where measurements were performed across 90 to 318 different vessels per tumor section. Specifically, six stained capillaries were randomly selected, their diameter was measured, and then averaged within each grid cell. Heatmaps were consistently generated for each tumor among the different selected timepoints (Figures S2–S5).

2.6. Computational Model

Here, we briefly give basic information about the computational model. The FE model is generated by implementation of the general concept based on the smeared physical fields (the KTM model). This methodology is adopted in several references [47,48,49,50,51,52,53,54,55], and it is well described and summarized by Kojic et al. [56,57]. The composite smeared 2D finite element used to model perfusion in a tumor is shown in Figure 1.
Fluid flow in the capillary and extracellular space is governed by Darcy’s law which in the FE format has the form (Kojic et al. [53])
K p K Δ P K = Q V p K − K p K P K
where K=1 and K=2 correspond to capillary and extracellular space, respectively, P K   is the nodal pressure vector, Δ P K are pressure increments in time step Q V p K ,is a volumetric term, and the FE matrix K is
K p I J K ( i − 1 ) = ∫ V r V K k D i j K N I , i N J , j d V ,   sum   on   i , j :   i , j = 1,2
where r V K are the volumetric fractions of the capillary (K=1) and extracellular space (K=2), k D i j K is the Darcy transport tensor (µm2/(Pa*s))—for lengths given in µm, time in seconds, and pressure in Pa, which for a capillary system represents the tensor derived from the capillary geometry (directional cosines and diameters), while for the tissue, it is a diagonal tensor of the Darcy coefficients, N I , i and N J , j are derivatives of the interpolation matrices, and V is the element volume—for the 2D model used here equal to the element surface multiplied by the unit element thickness. Regarding the nodal connectivity elements, they are 1D elements (without axial dimension—i.e., they are fictitious elements) that connect the capillary and extracellular domains at each FE node. For a FE node J, the balance equation in the form of Equation (2) is
K i j J Δ P j J = − K i j J P j J ,           i , j = 1 , 2 ;   sum   on   j
where the conductivity matrix K J is
K J = 4 d c a p J r V c a p J V J h c a p J 1 − 1 − 1 1
where d c a p J , r V c a p J , V J , and h c a p J are capillary diameter, volumetric fraction of the capillary domain (where K=1), volume of the continuum (representing a composite FE), and wall hydraulic permeability coefficient, all at node J, respectively. Since all quantities in the above expressions are assigned to nodes of the FE mesh, anisotropic characteristics of the capillary tissue system are considered in the computational model.

2.7. Statistical Analysis

All statistical analyses and graphs were obtained with GraphPad Prism (version 10.2.1; GraphPad Software, Inc., San Diego, CA, USA). Mean ± s.e.m. values were calculated and plotted in the results. The comparison of means between different groups of numerical variables was performed using a one-way ANOVA where p values (*p < 0.05, **p < 0.01) were considered statistically significant. Figures of pressure and velocity fields along with diagrams were generated using our in-house CAD software. Pressure and velocity values were obtained using measured data and an inverse-distance weighting interpolation procedure. Also, linear interpolation of geometry and other data is adopted for time points (time steps of the computational model) between the three data points.

3. Results

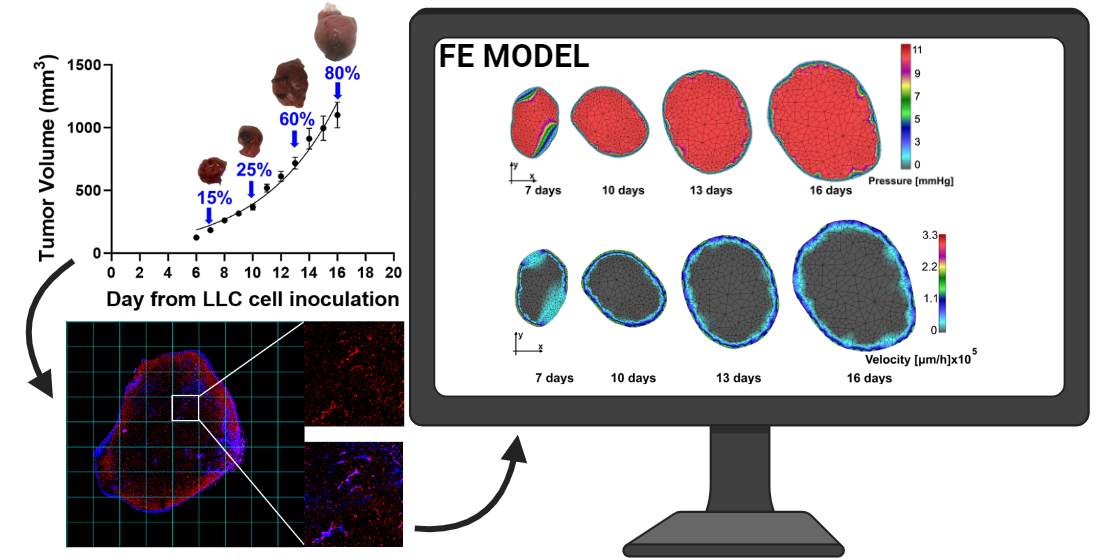
Figure 2A shows the growth curve of tumor volumes measured manually by external caliper as described in section 2.2. Tumors at 15%, 25%, 60%, and 80% of the final volume over the growth curve are indicated with a blue arrow and a representative photo of the tumor is presented. Figure 2B shows a representative fluorescence image of an entire tumor slice with overlapped channels for Hoechst (blue) and CD31 (red) as well as insets of two different grid cells. Hoechst 33342 was used specifically for staining the lung cancer cell nuclei, and CD31 was used as microvasculature marker. CD31 showed evidence of microvessels across the tumor (top inset, red channel only), and Hoechst 33342 can be visualized by a halo of blue fluorescence near the vessels (bottom inset, red and blue channels). Despite the short half-life of Hoechst 33342 [58], intravenous injections resulted in visible fluorescence across all the animals (Figures S2–S5, left columns). Figure 2C shows graphs of quantified (i) vasculature, (ii) capillary diameter and (iii) permeability over time. While the percent perfused area and capillary diameter changes were not significant as tumor growth increase, we did observe significant changes in the percent vasculature (*p < 0.05, between 15% and 80% and **p < 0.01 between 25% and 80%). Early increases in vasculature density maybe attributed to tumor angiogenesis[59] while later decreases may be attributed to necrosis [60].
To examine the local and temporal changes in tumor structure, we calculated the % vasculature, average capillary diameter in µm, and % permeability at different time points along the tumor growth curve, by applying a grid on each fluorescence image, removing the background through thresholding, quantifying the signal intensity (vasculature and permeability) or average vessel (capillary) diameter on each grid cell, and plotting them individually as heatmaps. Figure 3 illustrates this methodology, where each column represents a distinct timepoint corresponding to percent tumor growth at: 15% (A), 25% (B), 60% (C), and 80% (D). Within each column, a representative fluorescence image of a mouse tumor specimen is accompanied by heatmaps depicting average vasculature, capillary diameter, and permeability for that timepoint. The heatmaps reveal changes in vasculature (ii, vi, x, xiv), capillary diameter (iii, vii, xi, xv), and permeability (iv, viii, xii, xvi) across the four different timepoints. Additional grid images and heatmaps for each tumor sample are provided in Supplemental Figures S2–S5. By visualizing these parameters as individual heatmaps, local information is spatially preserved that would otherwise be lost by sample averaging.
Here, we briefly outline the computational procedure steps in the FE model generation. The computational model is generated from images shown in Figure 3i,v,ix,xiii (and Supplemental Figures S2–S5) where the tumor domain is divided into a 9x9 mesh. We have imposed a constant pressure of 10 mmHg within capillaries which takes into account hydrostatic and oncotic pressures and also arteriolar and venular participation within the capillary network [61,62,63,64]. This pressure is relevant for the fluid transport from capillaries to the extracellular space within tumor. Also, following the same data [64], we have imposed a zero pressure at the contour of the model as the boundary condition, assuming that there is a balance between perfusion and reabsorption between capillaries and tissue extracellular space. Using Figure S2i–vi, we extracted the contours from each of the six tumors at 15% total tumor growth and calculated an average geometry, which was used to set an initial configuration for our simulation. We then extracted contours from each of the tumors from Figues S3i–vi, S4i–vi and S5i–vi, and determined average geometries corresponding to 25%, 60%, and 80% of the total growth. During finite element simulation, we linearly interpolated boundary contours (for both geometric shape and size) between each experimental time point based on acquired average configurations.
Next, we applied the experimentally averaged vasculature, capillary diameter, and permeability to our model (Figure 3ii–iv,vi–viii,x–xii,xiv–xvi) in Equations (3) and (5). In this process, to assign all the data, equation solutions are interpolated using the inverse of the distance between two nodes as a weighting factor in accordance with the position of the final element node within the averaged heatmaps. Within each timepoint of the finite element computation, remeshing was performed, allowing for finite elements not to be fixed in space by their size or shape, since geometry is evolving during calculations. Evaluation of the capillary volumetric fraction, rVcap, is performed as follows (described here for the parameters at 15% of the tumor growth, represented as the first column in Figure 3, but broadly applicable to any time point and any node J of the FE model). The averaged vasculature displayed in Figure 3ii is first assumed to be equivalent to the capillary internal surface (Acap) divided by the total surface of the cell grid (Atot) to yield a percentage ( A c a p % ), where A c a p % = 100 A c a p / A t o t , and then expressed as
A c a p % = 100 A c a p A t o t = 100 d π L A t o t
to provide in terms of capillary diameter (d), shown in Figure 3iii, and capillary length (L). Since capillary volume can be expressed as Vcap= d2πL/4, we can then obtain capillary volumetric fraction rvcap at a point of the surface as
r V c a p = V c a p A t o t h z = d 400 h z A c a p %
where hz=1 µm is the model thickness in the direction normal to the plane (Supplemental Figure S6). Evaluation of the volumetric fraction of the extracellular space (rex), is performed as follows. The average permeability displayed in Figure 3iv is assumed to be equivalent to the area covered by the cells (Acell) divided by the total surface of the cell grid (Atot) to yield cell volumetric fraction (rvcell), where rVcell=Acell /Atot. We then express the volumetric fraction of the extracellular space (rex) as
r e x = 1 − r V c a p − r V c e l l
Finally, the wall hydraulic coefficient h c a p J in Equation (5) is obtained from the filtration coefficient (Kf) in reference [63] reduced to unit surface and expressed as 1.57x10-3 μm/(s Pa). We include perfusion anisotropy within the tumor by Equations (7) and (8) since the volumetric fractions of the capillaries and extracellular space vary over the model domain in accordance with our experimental records.
In Figure 4, pressures within the tumor at 7, 10, 13, and 16 days are presented. Pressures were determined through interpolation from the previous timepoint’s mesh to the subsequent timepoint’s mesh, ensuring that all necessary values for finite element analysis are available at the current timepoint. Figure 4A shows the pressure maps obtained using our in-house CAD software and finite element analysis, while in Figure 4B, pressure values are plotted in a 3D representation along coordinate axes x and y at the tumor center. Maximum pressure values do not vary much over the specified period. Some increase of the mean pressure is due to increase of the size of the domain with high pressure relative to the domain close to the boundary where the pressure gradient is leading to the zero value. The highest values are distributed along the model, starting from the center of the tumor, and spreading to the boundary. These results are in qualitative agreement with those reported in [65]. In Figure 4C, the mean pressure values are plotted over time for insight into pressure evolution, while spatial distribution of the pressure is displayed in Figure 4D,E. Since the model requires geometries as well as input and output boundaries, we chose to present the data in Figure 4C and Figure 5D with an x-axis starting at 7 days (15%) and ending at 16 days (80%). However, a linear interpolation can be performed for times points prior to 7 days as well as post 16 days, but performing this interpolation would require a geometry and growth trend set equal to the adjacent interval, which is an assumption not observed experimentally, and therefore, imprecise. In both the x and y directions, pressure is the highest at the middle of the tumor, decreasing to zero at the tumor boundary. It can be seen from Figure 4C–E that pressure nonuniformly changes over time, with the values at time 16 days increased with respect to the seven day configuration.
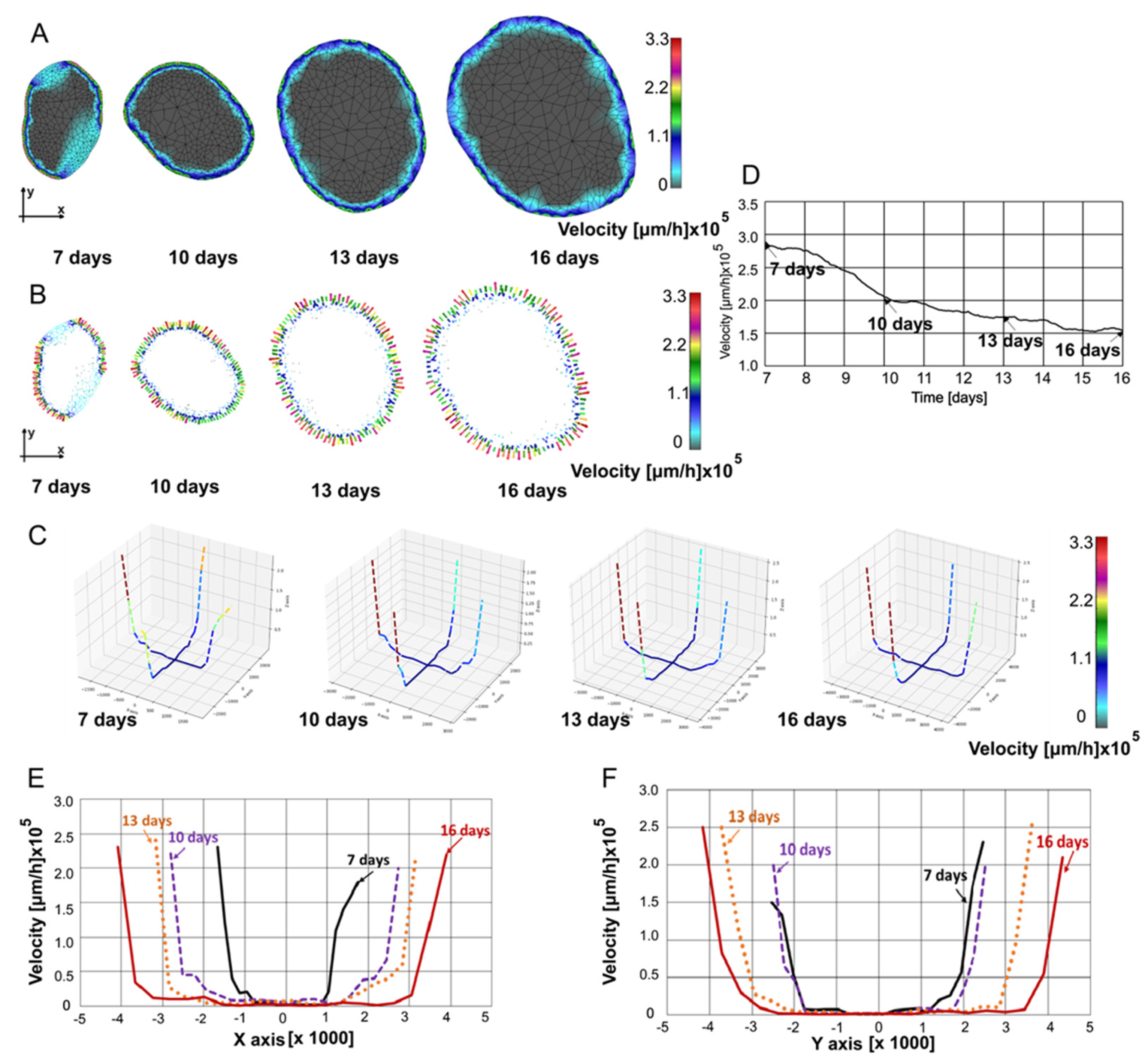
In Figure 5, fluid velocity fields at 7, 10, 13, and 16 are shown. Velocity fields were determined through interpolation from the previous timepoint’s mesh to the subsequent timepoint’s mesh, ensuring that all necessary values for finite element analysis are available at the current timepoint. Figure 5A displays the velocity maps generated using our in-house CAD software and finite element analysis, while in Figure 5B, velocities in the form of vectors are shown. In Figure 5C, velocity values are plotted in a 3D representation along the same two selected lines as in Figure 4B. It can be seen that as the tumor grows, the mean velocities slightly decrease. The velocities are always the largest at the boundary of the tumor since the pressure gradients are maximal at the boundary. In Figure 5D, the mean velocity modulus values are plotted over time to obtain insight into overall velocity values over time. Nonlinear decrease of the mean velocity is due to increase of the domain with small velocities relative to the domain close to the boundary where high pressure gradient led to high velocity values. For the spatial distribution along the x-axis, the velocities at the boundary first increase as the tumor grows, but then decrease (Figure 5E). Along the y-axis, the velocities at the boundary increased over the observed period (Figure 5F), illustrating perfusion anisotropy within the tumor.

4. Discussion

As tumor microenvironment complexity compromises therapeutic delivery, tumor-specific biophysical properties must be evaluated as a dynamic tumor growth process. This study aimed to predict intratumoral fluid pressure and velocity in three-dimensional space over time, allowing for coordinated temporal-and-spatial delivery of fluids in the intratumoral space. We used a pre-clinical model of lung cancer to generate images of tumor cross-sections, and we generated a computational model based on the smeared physical fields (Kojic Transport Model, KTM) to determine distribution of pressure and velocity within the tumor during its growth. 7-, 10-, 13-, and 16-days after tumor cell inoculation, tumor bearing mice were intravenously administered the perfusion marker Hoechst 33342 (40 mg/kg) immediately prior to euthanasia. Tumor sections were stained with the endothelial marker CD31 for vascular detection and imaged in their entirety. Image postprocessing was performed to extract vasculature, capillary diameter, and permeability distribution at different time points along the tumor growth curve. Notably, it was observed that at earlier time points along the tumor growth curve (<25%) there is an increase in vascular density which may be attributed to changes in angiogenesis, while at later time points, there is a significant decrease in percent vasculature (*p < 0.05, between 15% and 80% and **p < 0.01 between 25% and 80%), which may be attributed to necrosis in the center of advanced tumors. Necrosis and collagen content affect transport characteristics within tissue [15]. We modeled fluid flow in the capillary and extracellular space using a composite smeared 2D finite element. Outcomes from the model included fluid velocity and pressure over time as well as spatial distribution of velocity and pressure. Others have shown that IFP changes across the tumor and can reach maximum values near the tumor center with microvascular pressure as the main driving force [65] and that when limiting factors for transport of biologically useful macromolecules are known, specific measures may be taken to circumvent such difficulties [66]. We also found with the KTM model that the highest pressure values reside near the center of the tumor and reduce in strength close to the tumor boundary, while velocities are highest at the tumor boundary but illustrate spatial perfusion anisotropy when evaluated across time. This model is a first attempt to have an insight into an anisotropic view of pressure distribution in the tumor. While the subject here is perfusion, importantly the model can be extended to study drug transport by diffusion [56].
However, our study presents several limitations. First, the experimental sample size was not sufficient to highlight statistical differences in vasculature and perfusion rates over time due to the increased margin of error. Second, given that the capillary beds are numerous and highly complex [47] and precise information about capillary diameter and network geometry is confined to small areas of capture, extrapolations are necessary to larger regions to implement the model. Although our KTM model does not require modeling of each capillary as a 1D structure, data for evaluation of the transport tensor (Kojic et al. [58]) within Equation (3) are needed, such that the evaluated transport tensor can be interpolated over the model domain. Third, while the KTM model can support generation of a 3D model using stacked imaging providing information of flow patterns in the z-plane, this would require extensive tumor slicing and imaging. Therefore, we present a 2D finite element model based on the assumption that the flow pattern is the same for all layers parallel to the considered x,y plane (Supplemental Figure S6). Despite these limitations, we demonstrate the robustness of the Kojic Transport Model, and its applicability across a real physiological condition, solid lung tumor growth. Information extracted from this model regarding fluid velocity and pressure could prove useful in characterizing a tumor’s metabolic profile as well as distinguishing whether a tumor would prove amenable to certain types of therapies (i.e., radiation, chemo- and/or immune-therapy).

5. Conclusions

In summary, we investigated tumor-specific biophysical properties during a dynamic tumor growth process and used experimental data to generate a mathematical model which predicts intratumoral fluid pressure and velocity in three-dimensional space over time. Further evaluation will expand our knowledge of the tumor microenvironment to better predict therapeutic outcomes across different cancer subtypes, leading to optimized drug carrier design and more effective dosing regimens, thereby offering a more personalized approach to medicine.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1: (A) Mice and (B) ex vivo tumor weights. Dotted line (grey) represents the time point for cell inoculation (day 0). Dashed lines (blue) represent tumor harvest for the 15% group (day 7), 25% group (day 10), 60% group (day 13), and 80% group (day 16).; Figure S2: Fluorescence maps showing co-expression of Hoechst 33342 (blue) and CD31 (red) across sliced tumor area (i-vi) at 15% tumor growth for six different samples. Matrix size (width and height) are reported for each image. Heat maps showing changes in (A, D, G, J, M, P) vasculature determined by CD31 expression, (B, E, H, K, N, Q) capillary diameter determined by CD31 expression, and (C, F, I, L, O, R) permeability determined by Hoechst 33342 expression.; Figure S3: Fluorescence maps showing co-expression of Hoechst 33342 (blue) and CD31 (red) across sliced tumor area (i-vi) at 25% tumor growth for six different samples. Matrix size (width and height) are reported for each image. Heat maps showing changes in (A, D, G, J, M, P) vasculature determined by CD31 expression, (B, E, H, K, N, Q) capillary diameter determined by CD31 expression, and (C, F, I, L, O, R) permeability determined by Hoechst 33342 expression.; Figure S4: Fluorescence maps showing co-expression of Hoechst 33342 (blue) and CD31 (red) across the sliced tumor area (i-vi) at 60% tumor growth for six different samples. Matrix size (width and height) are reported for each image. Heat maps showing changes in (A, D, G, J, M, P) vasculature determined by CD31 expression, (B, E, H, K, N, Q) capillary diameter determined by CD31 expression, and (C, F, I, L, O, R) permeability determined by Hoechst 33342 expression.; Figure S5: Fluorescence maps showing co-expression of Hoechst 33342 (blue) and CD31 (red) across sliced tumor area (i-vi) at 80% tumor growth for six different samples. Matrix size (width and height) are reported for each image. Heat maps showing changes in (A, D, G, J, M, P) vasculature determined by CD31 expression, (B, E, H, K, N, Q) capillary diameter determined by CD31 expression, and (C, F, I, L, O, R) permeability determined by Hoechst 33342 expression.; Figure S6: 3D representation based on the assumption that the flow pattern is consistent across all layers parallel to the x,y plane of the 2D model.

Author Contributions

Conceptualization, R.T., M.K., and C.S.F.; methodology, A.M, R.T., B.C.F., Y.C.B., A.L.R.R., A.A.C.B. and C.S.F.; formal analysis, A.M., R.T., M.K., and C.S.F.; investigation, C.S.F.; resources, C.S.F.; data curation, A.M., R.T.; validation, A.M., R.T., M.K., and C.S.F.; software B.M., M.M., V.S., M.K.; writing—original draft preparation, A.M., R.T., M.K., B.M., and C.S.F.; writing—review and editing, R.C.W., M.K., and C.S.F.; supervision, C.S.F., R.C.W. and M.K.; funding acquisition, E.B.B., M.K., and C.S.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Golfers Against Cancer (E.B.B. and C.S.F.) and funds from Houston Methodist Research Institute (C.S.F.). The mathematical modeling work has been supported in part by funds from the NIH-National Cancer Institute (U01CA244107) (M.K.) and by the Ministry of Science of Serbia (contract numbers 451-03-68/2022-14/200378 and 451-03-68/2022-14/200107), Serbian Academy of Sciences and Arts (F- 134), and the City of Kragujevac Serbia (B.M., M.M., V.S). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Institutional Review Board Statement

All experiments conducted on the animals were approved for study (protocol no. IS00005178 approved May 6, 2019, and protocol no. IS00005819 approved March 26, 2021) by the Institutional Animal Care and Use Committee (IACUC) at the Houston Methodist Research Institute, and were performed according to the principles of the NIH Guide for the Care and Use of Laboratory Animals, the provisions of the Animal Welfare Act, PHS Animal Welfare Policy, and the policies of the Houston Methodist Research Institute. Housing and care were provided in accordance with the regulations of the Animal Welfare Act and recommendations of the Guide for the Care and Use of Laboratory Animals.

Data Availability Statement

The executable of our preprocessing and post-processing software for finite element modeling, along with the executable of our finite element analysis software, can be found in the GitHub repository https://github.com/miljanmilos/CAD-Solid-Field.

Acknowledgments

The authors are grateful to the Houston Methodist Research Institute Systems Medicine and Bioengineering (SMAB) department, the Advanced Cellular and Tissue Microscopy Core, the Houston Methodist Research Institute Comparative Medicine Program, the Houston Methodist Research Institute Research Pathology Core, and Elizabeth Eversole for their use and assistance with the fluorescence microscope, animal maintenance, histological sample preparation, and rodent handling, respectively.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Rodríguez, F.; Caruana, P.; De la Fuente, N.; Español, P.; Gámez, M.; Balart, J.; Llurba, E.; Rovira, R.; Ruiz, R.; Martín-Lorente, C.; et al. Nano-Based Approved Pharmaceuticals for Cancer Treatment: Present and Future Challenges. Biomolecules 2022, 12, 784. [Google Scholar] [CrossRef]
  2. Terracciano, R.; Demarchi, D.; Ruo Roch, M.; Aiassa, S.; Pagana, G. Nanomaterials to Fight Cancer: An Overview on Their Multifunctional Exploitability. J. Nanosci. Nanotechnol. 2021, 21, 2760–2777. [Google Scholar] [CrossRef] [PubMed]
  3. Li, Y.; Xu, X. Nanomedicine Solutions to Intricate Physiological-Pathological Barriers and Molecular Mechanisms of Tumor Multidrug Resistance. J. Control. Release 2020, 323, 483–501. [Google Scholar] [CrossRef]
  4. Anselmo, A.C.; Mitragotri, S. Nanoparticles in the Clinic: An Update. Bioeng. Transl. Med. 2019, 4, e10143. [Google Scholar] [CrossRef]
  5. Choi, M.-R.; Stanton-Maxey, K.J.; Stanley, J.K.; Levin, C.S.; Bardhan, R.; Akin, D.; Badve, S.; Sturgis, J.; Robinson, J.P.; Bashir, R.; et al. A Cellular Trojan Horse for Delivery of Therapeutic Nanoparticles into Tumors. Nano Lett. 2007, 7, 3759–3765. [Google Scholar] [CrossRef] [PubMed]
  6. Liu, H.-C.; Viswanath, D.I.; Pesaresi, F.; Xu, Y.; Zhang, L.; Di Trani, N.; Paez-Mayorga, J.; Hernandez, N.; Wang, Y.; Erm, D.R.; et al. Potentiating Antitumor Efficacy Through Radiation and Sustained Intratumoral Delivery of Anti-CD40 and Anti-PDL1. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 492–506. [Google Scholar] [CrossRef]
  7. Viswanath, D.I.; Liu, H.-C.; Huston, D.P.; Chua, C.Y.X.; Grattoni, A. Emerging Biomaterial-Based Strategies for Personalized Therapeutic in Situ Cancer Vaccines. Biomaterials 2022, 280, 121297. [Google Scholar] [CrossRef]
  8. Chua, C.Y.X.; Ho, J.; Susnjar, A.; Lolli, G.; Di Trani, N.; Pesaresi, F.; Zhang, M.; Nance, E.; Grattoni, A. Intratumoral Nanofluidic System for Enhancing Tumor Biodistribution of Agonist CD40 Antibody. Adv. Therap. 2020, 3, 2000055. [Google Scholar] [CrossRef]
  9. Chua, C.Y.X.; Jain, P.; Susnjar, A.; Rhudy, J.; Folci, M.; Ballerini, A.; Gilbert, A.; Singh, S.; Bruno, G.; Filgueira, C.S.; et al. Nanofluidic Drug-Eluting Seed for Sustained Intratumoral Immunotherapy in Triple Negative Breast Cancer. J. Control. Release 2018, 285, 23–34. [Google Scholar] [CrossRef] [PubMed]
  10. Tomasetti, L.; Breunig, M. Preventing Obstructions of Nanosized Drug Delivery Systems by the Extracellular Matrix. Adv Healthc Mater 2018, 7. [Google Scholar] [CrossRef]
  11. Lee, B.J.; Cheema, Y.; Bader, S.; Duncan, G.A. Shaping Nanoparticle Diffusion through Biological Barriers to Drug Delivery. JCIS Open 2021, 4, 100025. [Google Scholar] [CrossRef]
  12. Nizzero, S.; Ziemys, A.; Ferrari, M. Transport Barriers and Oncophysics in Cancer Treatment. Trends Cancer 2018, 4, 277–280. [Google Scholar] [CrossRef] [PubMed]
  13. van de Ven, A.L.; Wu, M.; Lowengrub, J.; McDougall, S.R.; Chaplain, M.A.J.; Cristini, V.; Ferrari, M.; Frieboes, H.B. Integrated Intravital Microscopy and Mathematical Modeling to Optimize Nanotherapeutics Delivery to Tumors. AIP Adv 2012, 2, 11208. [Google Scholar] [CrossRef]
  14. Ferrari, M. Frontiers in Cancer Nanomedicine: Directing Mass Transport through Biological Barriers. Trends Biotechnol 2010, 28, 181–188. [Google Scholar] [CrossRef] [PubMed]
  15. Yokoi, K.; Kojic, M.; Milosevic, M.; Tanei, T.; Ferrari, M.; Ziemys, A. Capillary-Wall Collagen as a Biophysical Marker of Nanotherapeutic Permeability into the Tumor Microenvironment. Cancer Res 2014, 74, 4239–4246. [Google Scholar] [CrossRef] [PubMed]
  16. Heldin, C.-H.; Rubin, K.; Pietras, K.; Ostman, A. High Interstitial Fluid Pressure—an Obstacle in Cancer Therapy. Nat. Rev. Cancer 2004, 4, 806–813. [Google Scholar] [CrossRef] [PubMed]
  17. Niu, Y.; Zhu, J.; Li, Y.; Shi, H.; Gong, Y.; Li, R.; Huo, Q.; Ma, T.; Liu, Y. Size Shrinkable Drug Delivery Nanosystems and Priming the Tumor Microenvironment for Deep Intratumoral Penetration of Nanoparticles. J. Control. Release 2018, 277, 35–47. [Google Scholar] [CrossRef] [PubMed]
  18. Terracciano, R.; Zhang, A.; Butler, E.B.; Demarchi, D.; Hafner, J.H.; Grattoni, A.; Filgueira, C.S. Effects of Surface Protein Adsorption on the Distribution and Retention of Intratumorally Administered Gold Nanoparticles. Pharmaceutics 2021, 13, 216. [Google Scholar] [CrossRef]
  19. Terracciano, R.; Sprouse, M.L.; Wang, D.; Ricchetti, S.; Hirsch, M.; Ferrante, N.; Butler, E.B.; Demarchi, D.; Grattoni, A.; Filgueira, C.S. Intratumoral Gold Nanoparticle-Enhanced CT Imaging: An in Vivo Investigation of Biodistribution and Retention. In Proceedings of the 2020 IEEE 20th International Conference on Nanotechnology (IEEE-NANO); July 2020; pp. 349–353. [Google Scholar]
  20. Terracciano, R.; Carcamo-Bahena, Y.; Royal, A.L.R.; Messina, L.; Delk, J.; Butler, E.B.; Demarchi, D.; Grattoni, A.; Wang, Z.; Cristini, V.; et al. Zonal Intratumoral Delivery of Nanoparticles Guided by Surface Functionalization. Langmuir 2022, 38, 13983–13994. [Google Scholar] [CrossRef]
  21. Terracciano, R.; Carcamo-Bahena, Y.; Butler, E.B.; Demarchi, D.; Grattoni, A.; Filgueira, C.S. Hyaluronate-Thiol Passivation Enhances Gold Nanoparticle Peritumoral Distribution When Administered Intratumorally in Lung Cancer. Biomedicines 2021, 9, 1561. [Google Scholar] [CrossRef]
  22. Zhang, D.; Zhang, J. Surface Engineering of Nanomaterials with Phospholipid-Polyethylene Glycol-Derived Functional Conjugates for Molecular Imaging and Targeted Therapy. Biomaterials 2020, 230, 119646. [Google Scholar] [CrossRef] [PubMed]
  23. Tian, H.; Zhang, T.; Qin, S.; Huang, Z.; Zhou, L.; Shi, J.; Nice, E.C.; Xie, N.; Huang, C.; Shen, Z. Enhancing the Therapeutic Efficacy of Nanoparticles for Cancer Treatment Using Versatile Targeted Strategies. J. Hematol. Oncol. 2022, 15, 132. [Google Scholar] [CrossRef] [PubMed]
  24. Perry, J.L.; Reuter, K.G.; Luft, J.C.; Pecot, C.V.; Zamboni, W.; DeSimone, J.M. Mediating Passive Tumor Accumulation through Particle Size, Tumor Type, and Location. Nano Lett. 2017, 17, 2879–2886. [Google Scholar] [CrossRef] [PubMed]
  25. Pandey, A.; Vighetto, V.; Di Marzio, N.; Ferraro, F.; Hirsch, M.; Ferrante, N.; Mitra, S.; Grattoni, A.; Filgueira, C.S. Gold Nanoparticles Radio-Sensitize and Reduce Cell Survival in Lewis Lung Carcinoma. Nanomaterials 2020, 10, 1717. [Google Scholar] [CrossRef] [PubMed]
  26. Wang, Z.; Wu, Z.; Liu, J.; Zhang, W. Particle Morphology: An Important Factor Affecting Drug Delivery by Nanocarriers into Solid Tumors. Expert Opin. Drug Deliv. 2018, 15, 379–395. [Google Scholar] [CrossRef] [PubMed]
  27. Held, K.D.; Kawamura, H.; Kaminuma, T.; Paz, A.E.S.; Yoshida, Y.; Liu, Q.; Willers, H.; Takahashi, A. Effects of Charged Particles on Human Tumor Cells. Front. Oncol. 2016, 6, 23. [Google Scholar] [CrossRef] [PubMed]
  28. Terracciano, R.; Zhang, A.; Simeral, M.L.; Demarchi, D.; Hafner, J.H.; Filgueira, C.S. Improvements in Gold Nanorod Biocompatibility with Sodium Dodecyl Sulfate Stabilization. J. nanotheranostics 2021, 2, 157–173. [Google Scholar] [CrossRef]
  29. Zhang, M.; Gao, S.; Yang, D.; Fang, Y.; Lin, X.; Jin, X.; Liu, Y.; Liu, X.; Su, K.; Shi, K. Influencing Factors and Strategies of Enhancing Nanoparticles into Tumors in Vivo. Acta Pharm. Sin. B 2021, 11, 2265–2285. [Google Scholar] [CrossRef] [PubMed]
  30. Ferrari, M. Cancer Nanotechnology: Opportunities and Challenges. Nat Rev Cancer 2005, 5, 161–171. [Google Scholar] [CrossRef]
  31. Ziemys, A.; Kojic, M.; Milosevic, M.; Ferrari, M. Interfacial Effects on Nanoconfined Diffusive Mass Transport Regimes. Phys. Rev. Lett. 2012, 108, 236102. [Google Scholar] [CrossRef]
  32. Ziemys, A.; Kojic, M.; Milosevic, M.; Kojic, N.; Hussain, F.; Ferrari, M.; Grattoni, A. Hierarchical Modeling of Diffusive Transport through Nanochannels by Coupling Molecular Dynamics with Finite Element Method. J. Comput. Phys. 2011, 230, 5722–5731. [Google Scholar] [CrossRef]
  33. Blanco, E.; Ferrari, M. Emerging Nanotherapeutic Strategies in Breast Cancer. Breast 2014, 23, 10–18. [Google Scholar] [CrossRef] [PubMed]
  34. Yokoi, K.; Tanei, T.; Godin, B.; van de Ven, A.L.; Hanibuchi, M.; Matsunoki, A.; Alexander, J.; Ferrari, M. Serum Biomarkers for Personalization of Nanotherapeutics-Based Therapy in Different Tumor and Organ Microenvironments. Cancer Lett. 2014, 345, 48–55. [Google Scholar] [CrossRef] [PubMed]
  35. Liu, Y.; Shah, S.; Tan, J. Computational Modeling of Nanoparticle Targeted Drug Delivery. Rev. Nanosci. Nanotechnol. 2012, 1, 66–83. [Google Scholar] [CrossRef]
  36. Kaddi, C.D.; Phan, J.H.; Wang, M.D. Computational Nanomedicine: Modeling of Nanoparticle-Mediated Hyperthermal Cancer Therapy. Nanomedicine 2013, 8, 1323–1333. [Google Scholar] [CrossRef] [PubMed]
  37. Frieboes, H.B.; Wu, M.; Lowengrub, J.; Decuzzi, P.; Cristini, V. A Computational Model for Predicting Nanoparticle Accumulation in Tumor Vasculature. PLOS ONE 2013, 8, e56876. [Google Scholar] [CrossRef] [PubMed]
  38. Stillman, N.R.; Balaz, I.; Tsompanas, M.-A.; Kovacevic, M.; Azimi, S.; Lafond, S.; Adamatzky, A.; Hauert, S. Evolutionary Computational Platform for the Automatic Discovery of Nanocarriers for Cancer Treatment. npj Comput. Mater. 2021, 7, 1–12. [Google Scholar] [CrossRef]
  39. Guo, P.; Yang, J.; Bielenberg, D.R.; Dillon, D.; Zurakowski, D.; Moses, M.A.; Auguste, D.T. A Quantitative Method for Screening and Identifying Molecular Targets for Nanomedicine. J. Control. Release 2017, 263, 57–67. [Google Scholar] [CrossRef] [PubMed]
  40. Kutumova, E.O.; Akberdin, I.R.; Kiselev, I.N.; Sharipov, R.N.; Egorova, V.S.; Syrocheva, A.O.; Parodi, A.; Zamyatnin, A.A.; Kolpakov, F.A. Physiologically Based Pharmacokinetic Modeling of Nanoparticle Biodistribution: A Review of Existing Models, Simulation Software, and Data Analysis Tools. Int. J. Mol. Sci. 2022, 23, 12560. [Google Scholar] [CrossRef] [PubMed]
  41. Stapleton, S.; Milosevic, M.; Allen, C.; Zheng, J.; Dunne, M.; Yeung, I.; Jaffray, D.A. A Mathematical Model of the Enhanced Permeability and Retention Effect for Liposome Transport in Solid Tumors. PLoS One 2013, 8, e81157. [Google Scholar] [CrossRef]
  42. Caddy, G.; Stebbing, J.; Wakefield, G.; Xu, X.Y. Modelling of Nanoparticle Distribution in a Spherical Tumour during and Following Local Injection. Pharmaceutics 2022, 14, 1615. [Google Scholar] [CrossRef] [PubMed]
  43. Dogra, P.; Butner, J.D.; Ruiz Ramírez, J.; Chuang, Y.; Noureddine, A.; Jeffrey Brinker, C.; Cristini, V.; Wang, Z. A Mathematical Model to Predict Nanomedicine Pharmacokinetics and Tumor Delivery. Comput. Struct. Biotechnol. J. 2020, 18, 518–531. [Google Scholar] [CrossRef] [PubMed]
  44. Kojic, M.; Filipovic, N.; Milosevic, M. 2020.
  45. Card, J.W.; Carey, M.A.; Bradbury, J.A.; DeGraff, L.M.; Morgan, D.L.; Moorman, M.P.; Flake, G.P.; Zeldin, D.C. Gender Differences in Murine Airway Responsiveness and Lipopolysaccharide-Induced Inflammation. J. Immunol. 2006, 177, 621–630. [Google Scholar] [CrossRef]
  46. Thompson, M.G.; Peiffer, D.S.; Larson, M.; Navarro, F.; Watkins, S.K. FOXO3, Estrogen Receptor Alpha, and Androgen Receptor Impact Tumor Growth Rate and Infiltration of Dendritic Cell Subsets Differentially between Male and Female Mice. Cancer Immunol. Immunother. 2017, 66, 615–625. [Google Scholar] [CrossRef] [PubMed]
  47. Kojic, M.; Milosevic, M.; Simic, V.; Koay, E.J.; Fleming, J.B.; Nizzero, S.; Kojic, N.; Ziemys, A.; Ferrari, M. A Composite Smeared Finite Element for Mass Transport in Capillary Systems and Biological Tissue. Comput. Methods Appl. Mech. Eng. 2017, 324, 413–437. [Google Scholar] [CrossRef] [PubMed]
  48. Kojic, M.; Milosevic, M.; Simic, V.; Koay, E.J.; Kojic, N.; Ziemys, A.; Ferrari, M. Extension of the Composite Smeared Finite Element (CSFE) to Include Lymphatic System in Modeling Mass Transport in Capillary Systems and Biological Tissue. J. Serbian Soc. Comput. Mech. 2017, 11, 108–119. [Google Scholar] [CrossRef] [PubMed]
  49. Kojic, M.; Simic, V.; Milosevic, M. Composite Smeared Finite Element—Some Aspects of the Formulation and Accuracy. In IPSI Transactions on Advanced Research; 2017; Vol. 13 ISBN 1820—4511.
  50. Kojic, M.; Milosevic, M.; Kojic, N.; Koay, E.J.; Fleming, J.B.; Ferrari, M.; Ziemys, A. Mass Release Curves as the Constitutive Curves for Modeling Diffusive Transport within Biological Tissue. Comput. Biol. Med. 2018, 92, 156–167. [Google Scholar] [CrossRef] [PubMed]
  51. Kojic, M.; Milosevic, M.; Simic, V.; Koay, E.J.; Kojic, N.; Ziemys, A.; Ferrari, M. Multiscale Smeared Finite Element Model for Mass Transport in Biological Tissue: From Blood Vessels to Cells and Cellular Organelles. Comput. Biol. Med. 2018, 99, 7–23. [Google Scholar] [CrossRef] [PubMed]
  52. Kojic, M.; Milosevic, M.; Simic, V.; Geroski, V.; Ziemys, A.; Filipovic, N.; Ferrari, M. Smeared Multiscale Finite Element Model for Electrophysiology and Ionic Transport in Biological Tissue. Comput. Biol. Med. 2019, 108, 288–304. [Google Scholar] [CrossRef]
  53. Kojic, M. Smeared Concept as a General Methodology in Finite Element Modeling of Physical Fields and Mechanical Problems in Composite Media. J. Serb. Soc. Comp. Mech. 2018, 12, 1–16. [Google Scholar] [CrossRef]
  54. Milosevic, M.; Simic, V.; Milicevic, B.; Koay, E.J.; Ferrari, M.; Ziemys, A.; Kojic, M. Correction Function for Accuracy Improvement of the Composite Smeared Finite Element for Diffusive Transport in Biological Tissue Systems. Comput. Methods Appl. Mech. Eng. 2018, 338, 97–116. [Google Scholar] [CrossRef] [PubMed]
  55. Milosevic, M.; Stojanovic, D.; Simic, V.; Milicevic, B.; Radisavljevic, A.; Uskokovic, P.; Kojic, M. A Computational Model for Drug Release from PLGA Implant. Materials 2018, 11, 2416. [Google Scholar] [CrossRef] [PubMed]
  56. Kojic, M.; Milosevic, M.; Ziemys, A. Computational Models in Biomedical Engineering—Finite Element Models Based on Smeared Physical Fields: Theory, Solutions, and Software; Elsevier, 2022; Vol. In Press; ISBN 978-0-323-88472-3.
  57. Kojic, M.; Milosevic, M.; Simic, V.; Milicevic, B.; Terracciano, R.; Filgueira, C.S. On the Generality of the Finite Element Modeling Physical Fields in Biological Systems by the Multiscale Smeared Concept (Kojic Transport Model). Heliyon 2024, 10, e26354. [Google Scholar] [CrossRef] [PubMed]
  58. Smith, K.A.; Hill, S.A.; Begg, A.C.; Denekamp, J. Validation of the Fluorescent Dye Hoechst 33342 as a Vascular Space Marker in Tumours. Br J Cancer 1988, 57, 247–253. [Google Scholar] [CrossRef] [PubMed]
  59. Forster, J.C.; Harriss-Phillips, W.M.; Douglass, M.J.; Bezak, E. A Review of the Development of Tumor Vasculature and Its Effects on the Tumor Microenvironment. Hypoxia (Auckl) 2017, 5, 21–32. [Google Scholar] [CrossRef] [PubMed]
  60. Nagy, J.A.; Chang, S.-H.; Dvorak, A.M.; Dvorak, H.F. Why Are Tumour Blood Vessels Abnormal and Why Is It Important to Know? Br J Cancer 2009, 100, 865–869. [Google Scholar] [CrossRef]
  61. Ganong, W.F. Review of Medical Physiology; 22nd Edition.; McGraw-Hill Medical: New York, 2005. [Google Scholar]
  62. Kurbel, S.; Flam, J. Interstitial Hydrostatic Pressure: A Manual for Students. Adv Physiol Educ 2007, 31, 116–117. [Google Scholar] [CrossRef] [PubMed]
  63. Boron, W.F.; Boulpaep, E.L. Medical Physiology; 3rd edition. 2017. [Google Scholar]
  64. Open Educational Resources (OER) Services Anatomy and Physiology II Available online:. Available online: https://courses.lumenlearning.com/suny-ap2/chapter/capillary-exchange. (accessed on 14 February 2023).
  65. Boucher, Y.; Jain, R.K. Microvascular Pressure Is the Principal Driving Force for Interstitial Hypertension in Solid Tumors: Implications for Vascular Collapse. Cancer Res. 1992, 52, 5110–5114. [Google Scholar]
  66. Jain, R.K.; Baxter, L.T. Mechanisms of Heterogeneous Distribution of Monoclonal Antibodies and Other Macromolecules in Tumors: Significance of Elevated Interstitial Pressure. Cancer Res 1988, 48, 7022–7032. [Google Scholar]
Preprints 110362 g001
Figure 1. a) Image of tumor tissue with capillary vessels stained using CD31 (red). b) Composite smeared 2D finite element with 4 nodes and 3 physical domains: capillary, extracellular space, and cells. Fluid flow from the capillaries to the extracellular space is modeled by nodal connectivity elements with the cross-sectional area equal to the surface (AJ in the figure).
Figure 1. a) Image of tumor tissue with capillary vessels stained using CD31 (red). b) Composite smeared 2D finite element with 4 nodes and 3 physical domains: capillary, extracellular space, and cells. Fluid flow from the capillaries to the extracellular space is modeled by nodal connectivity elements with the cross-sectional area equal to the surface (AJ in the figure).
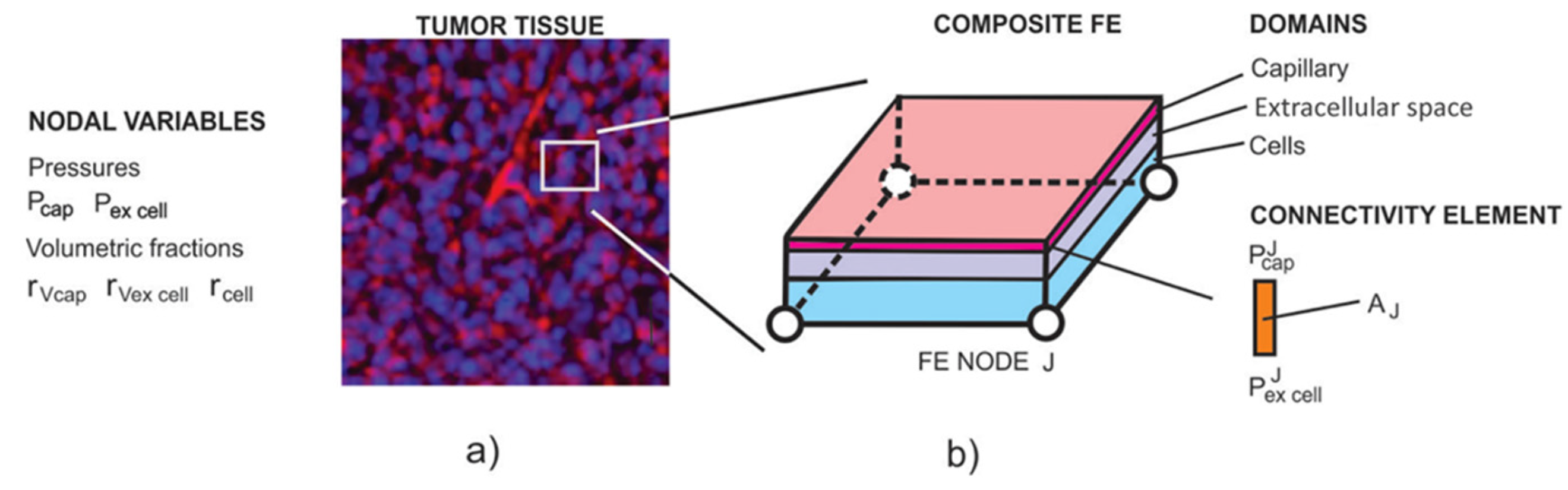
Preprints 110362 g001
Preprints 110362 g002
Figure 2. Assessments of tumor vasculature and permeability in a lung cancer mouse model. (A) LLC tumor volume growth curve. Blue arrows indicate 15% (183.4 ± 11.7), 25% (365.7 ± 23.0 mm3), 60% (717.2 ± 47.0 mm3), and 80% (1100.1 ± 102.8 mm3), of the curve where tumors were dissected after Hoechst 33342 IV injections (permeability) and CD31 (vasculature and capillary diameter) staining. (B) Representative fluorescence tumor image (10x) at 15% tumor growth: Hoechst (blue), CD31 (red). Insets show microvessels stained within the tumor (top, red channel only), and IV perfused Hoechst 33342 dye that can be visualized by a halo of blue fluorescence (white arrows) near the vessels (bottom, red and blue channels). Data is plotted and reported as mean ± s.e.m. values. (C) Quantification of (i) vasculature (ii) capillary diameter and (iii) permeability over time (*p < 0.05 and **p < 0.01). Data in (A) is fit using the exponential growth curve equation y = 59.98*exp (0.1874*x).
Figure 2. Assessments of tumor vasculature and permeability in a lung cancer mouse model. (A) LLC tumor volume growth curve. Blue arrows indicate 15% (183.4 ± 11.7), 25% (365.7 ± 23.0 mm3), 60% (717.2 ± 47.0 mm3), and 80% (1100.1 ± 102.8 mm3), of the curve where tumors were dissected after Hoechst 33342 IV injections (permeability) and CD31 (vasculature and capillary diameter) staining. (B) Representative fluorescence tumor image (10x) at 15% tumor growth: Hoechst (blue), CD31 (red). Insets show microvessels stained within the tumor (top, red channel only), and IV perfused Hoechst 33342 dye that can be visualized by a halo of blue fluorescence (white arrows) near the vessels (bottom, red and blue channels). Data is plotted and reported as mean ± s.e.m. values. (C) Quantification of (i) vasculature (ii) capillary diameter and (iii) permeability over time (*p < 0.05 and **p < 0.01). Data in (A) is fit using the exponential growth curve equation y = 59.98*exp (0.1874*x).
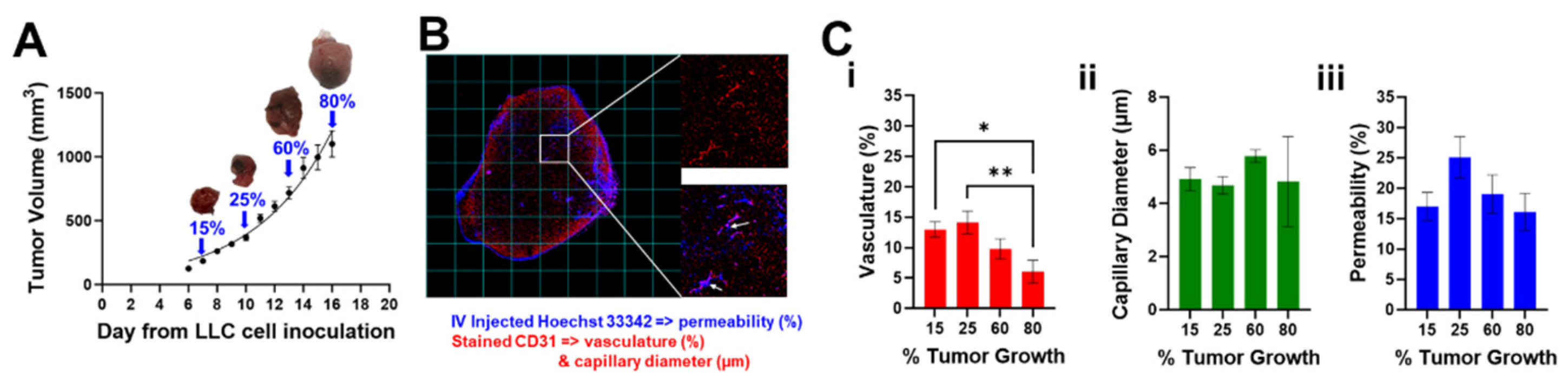
Preprints 110362 g002
Preprints 110362 g003
Figure 3. Vasculature (%), capillary diameter (µm), and permeability (%) distribution at different time points along the tumor growth curve. Tumor volume at (A) 15%, (B) 25%, (C) 60%, and (D) 80% of total growth. Representative fluorescent maps showing co-expression of Hoechst 33342 (blue) and CD31 (red) across sliced tumor area (I, v, ix, xiii). Heat maps showing local changes in the average vasculature (ii, vi, x, xiv) and capillary diameter (iii, vii, xi, xv) determined by CD31 expression and in the average permeability (iv, viii, xii, xvi) determined by Hoechst 33342 expression across the different timepoints.
Figure 3. Vasculature (%), capillary diameter (µm), and permeability (%) distribution at different time points along the tumor growth curve. Tumor volume at (A) 15%, (B) 25%, (C) 60%, and (D) 80% of total growth. Representative fluorescent maps showing co-expression of Hoechst 33342 (blue) and CD31 (red) across sliced tumor area (I, v, ix, xiii). Heat maps showing local changes in the average vasculature (ii, vi, x, xiv) and capillary diameter (iii, vii, xi, xv) determined by CD31 expression and in the average permeability (iv, viii, xii, xvi) determined by Hoechst 33342 expression across the different timepoints.
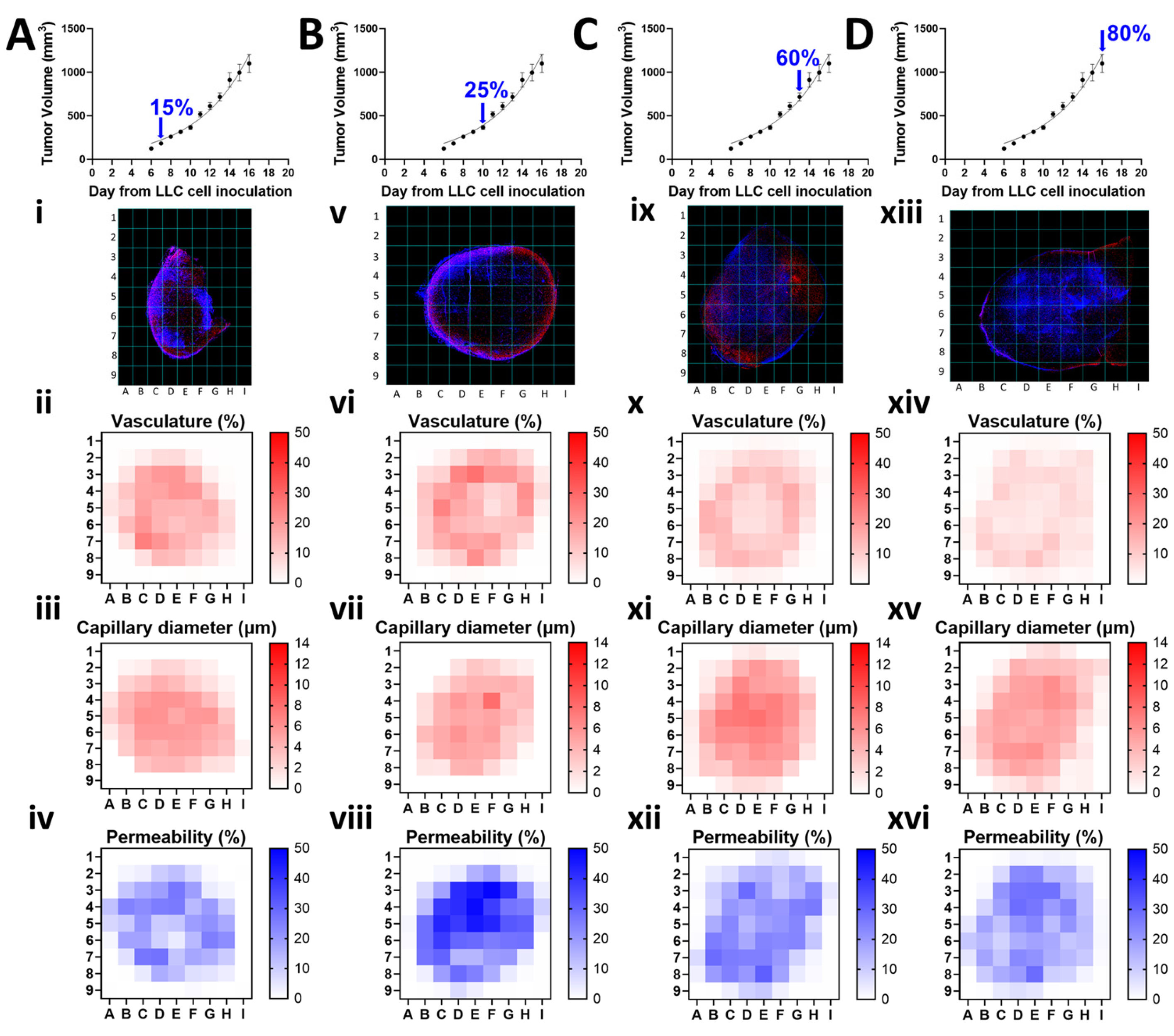
Preprints 110362 g003
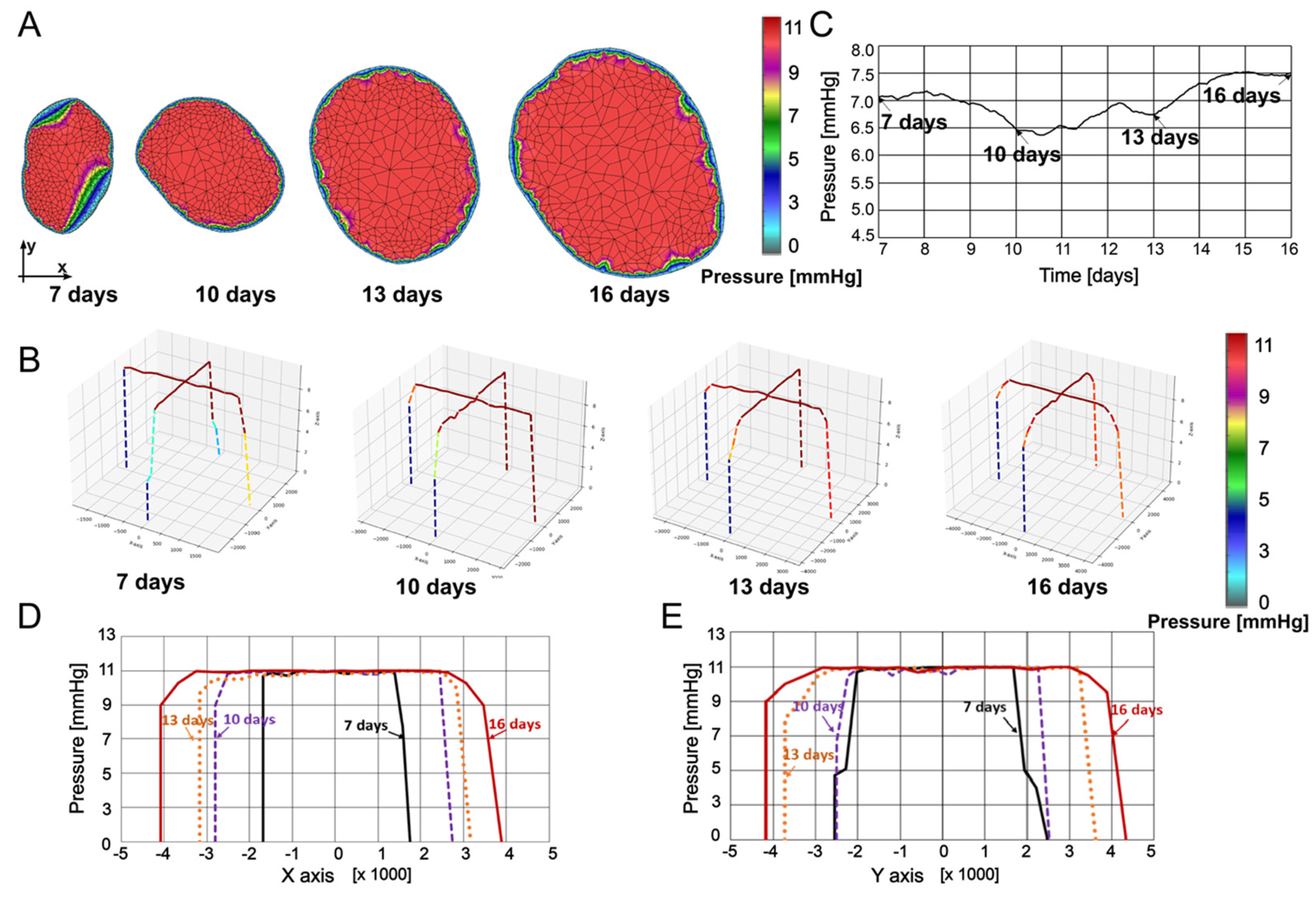
Preprints 110362 g004
Figure 4. (A) Pressure field at 7, 10, 13, and 16 days. (B) Pressure field in a 3D representation at 7, 10, 13, and 16 days. (C) Mean pressure vs time. (D) Pressure distribution along x-axis. (E) Pressure distribution along y-axis.
Figure 4. (A) Pressure field at 7, 10, 13, and 16 days. (B) Pressure field in a 3D representation at 7, 10, 13, and 16 days. (C) Mean pressure vs time. (D) Pressure distribution along x-axis. (E) Pressure distribution along y-axis.
Preprints 110362 g004
Preprints 110362 g005
Figure 5. (A) Velocity field at 7, 10, 13, and 16 days. (B) Vector velocity field at 7, 10, 13, and 16 days. (C) Velocity field in 3D representation at 7, 10, 13, and 16 days. (D) Mean velocity modulus vs. time. (E) Velocity distribution along x-axis. (F) Velocity distribution along y-axis.
Figure 5. (A) Velocity field at 7, 10, 13, and 16 days. (B) Vector velocity field at 7, 10, 13, and 16 days. (C) Velocity field in 3D representation at 7, 10, 13, and 16 days. (D) Mean velocity modulus vs. time. (E) Velocity distribution along x-axis. (F) Velocity distribution along y-axis.
Preprints 110362 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated