How can the Government Promote Sustainable Cooperation between Schools and Enterprises? A Quadrilateral Evolutionary Game Study

Preprint

Article

How can the Government Promote Sustainable Cooperation between Schools and Enterprises? A Quadrilateral Evolutionary Game Study

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Hexin Wang,Chao Liu,

Yu Dai^*

Hexin Wang,Chao Liu,

Yu Dai^*

This version is not peer-reviewed

Submitted:

26 June 2024

Posted:

27 June 2024

You are already at the latest version

Alerts

Abstract

Facilitating sustainable cooperation between schools and enterprises has become an important concern in many countries. However, there remains a gap in understanding the approaches taken by central and local governments to foster such cooperation through the lens of evolutionary game theory. Therefore, this paper aims to develop a quadrilateral evolutionary game model involving schools, enterprises, the central government, and local governments, to analyze the conditions under which governments can effectively promote school-enterprise cooperation. Our findings indicate that benefit is a decisive factor that affects the strategies of all parties. When the benefits of cooperation are sufficiently attractive, schools and enterprises are inclined to cooperate with each other independently of governmental intervention. While increasing incentives and penalties from the central government and local governments can stimulate school-enterprise cooperation, these measures are not sustainable in the long term. Additionally, the impact of the central government’s incentives and penalties on local governments in promoting school-enterprise cooperation is limited. Enhancing policy efficacy and the practical outcomes of school-enterprise cooperation is essential, which not only strengthens the bond between schools and enterprises but also ensures deep and enduring governmental involvement.

Keywords:

Subject: Social Sciences - Education

1. Introduction

The aim of school-enterprise cooperation is to align the operational mechanisms and job requirements of enterprises with the talent cultivation systems and objectives of schools. This cooperation is important for improving the quality of talent, facilitating scientific and technological innovation, promoting social responsibility, and driving economic development. Thus, school-enterprise cooperation has become a focal point of research. Various macroscopic models of school-enterprise cooperation, such as the Dual System [1,2,3,4], Cooperative Education [5,6,7,8], and Sandwich Courses [9,10,11,12], have been extensively studied, and many microcosmic training modes of school-enterprise cooperation [13,14,15,16] have also been widely discussed. Moreover, some scholars have analyzed the motivations [17,18,19], factors [20,21,22,23], and mechanisms [24,25,26] of school-enterprise cooperation in depth.

The cooperation between schools and enterprises has garnered significant governmental attention worldwide. For instance, Germany has implemented a comprehensive framework of laws, regulations, and management systems to ensure students acquire both theoretical knowledge in schools and practical skills in enterprises. Similarly, the United States the Strengthening Career and Technical Education (CTE) for the 21st Century Act was enacted to bolster partnerships between schools and enterprises. In China, the government also places significant emphasis on school-enterprise cooperation. Initiatives such as the Several Opinions on Deepening the Integration of Industry and Education highlight China’s commitment to align educational outcomes with workforce demands.

However, there are 3 shortcomings of the existing studies. Firstly, research on the role of governments remains insufficient. While some researchers have acknowledged the great influence of governments on school-enterprise cooperation [27,28], they have not considered the government as a main stakeholder of school-enterprise cooperation and conducted specialized research on it. Secondly, the distinctions between the central government and local governments have almost been ignored. It is well-known that the relationship between the central government and local governments is dynamic and complex. There is a phenomenon of information asymmetry between them [29]. Local governments have different goals and interests from the central government, so local governments submit to the unified leadership of the central government in some areas but have adversarial relationships with the central government in others [30,31,32]. Thus, it is necessary to explore the roles played by the central government and local governments in school-enterprise cooperation. Thirdly, quadrilateral evolutionary game model has not been widely adopted and studied. There are few studies using evolutionary game theory to analyze the cooperation between schools and enterprises. The evolutionary game models in previous literature are mostly bilateral and tripartite evolutionary game models [33,34,35]. Quadrilateral evolutionary game model deserves more attention.

Considering the aforementioned limitations, this paper further divides the government into central and local government and establish a quadrilateral evolutionary game model of schools, enterprises, the central government, and local governments to explore the approach of the government to promote school-enterprise cooperation.

The remainder of this paper is structured as follows: Section 2 develops the theoretical framework and constructs a quadrilateral evolutionary game model of schools, enterprises, the central government, and local governments. Section 3 examines the stability of strategies adopted by the four parties. Section 4 analyzes the stability conditions pertaining to potential equilibrium points. Finally, Section 5 presents the main conclusions drawn from the study.

2. Methodology

In this section, we first explain the game relationship between schools, enterprises, the central government, and local government in school-enterprise cooperation by building a theoretical framework. Thereafter, a quadrilateral evolutionary game model is constructed to explore the evolution of cooperative behavior among the four stakeholders.

2.1. Theoretical Framework

Schools and enterprises are the cores of this quadrilateral game. Schools benefit from cooperation with enterprises through enhancements in discipline construction, talent cultivation, and teacher development. Similarly, enterprises gain advantages such as access to cheap but high-quality labor, opportunities for technological innovation, and improved social standing through cooperation with schools. Governments play the roles of regulation and supervision in school-enterprise cooperation by promulgating relevant policies and supporting financial support to push schools and enterprises to cooperate with each other. In return, the cooperation between schools and enterprises will be more effective because of the governments’ involvement, which will provide more outstanding talents, better economic development, and higher social reputations for governments. In addition, local governments are required to implement the policies of the central government and are managed by the central government. The relationship between schools, enterprises, the central government, and local government can be shown in Figure 1.

Specifically, in this four-party game between schools, enterprises, the central government, and local governments, all parties have bounded rationality. Each party has two strategies, cooperation strategy and noncooperation strategy, and each party chooses one of the two strategies with a certain probability. We assume that the probabilities for choosing cooperation strategy for schools, enterprises, the central government, and local governments are w, x, y, and z, respectively, and the probabilities for choosing noncooperation strategy for schools, enterprises, the central government, and local governments are 1‒w, 1‒x, 1‒y, and 1‒z, respectively.

For schools, when they choose cooperation strategy, they will spend some costs C₁. In this case, if enterprises also choose cooperation strategy, schools will obtain many benefits B₁ from cooperating with enterprises. But if enterprises choose noncooperation strategy, schools will bear the losses L₁ caused by the defection from enterprises. When schools choose noncooperation strategy, if enterprises choose cooperation strategy, schools can still reap some benefits B₃, but they also need to take some losses L₁ of defecting to enterprises. When both schools and enterprises choose noncooperation strategy, schools will inevitably deserve the losses L₁ resulting from the unsuccessful cooperation with enterprises.

Similarly, for enterprises, when they choose cooperation strategy, they will spend some costs C₂. In this case, if schools also choose cooperation strategy, enterprises will obtain many benefits B₂ from cooperating with schools. But if schools choose noncooperation strategy, enterprises will bear the losses L₂ caused by the defection from schools. When enterprises choose noncooperation strategy, if schools choose cooperation strategy, enterprises can still reap some benefits B₄, but they also need to take some losses L₂ of defecting to schools. When both schools and enterprises choose noncooperation strategy, enterprises will inevitably deserve the losses L₂ resulting from the unsuccessful cooperation with schools.

For the central government, when it chooses cooperation strategy, it will spend some costs C₃. In this case, if schools, enterprises, and local governments also choose cooperation strategy, the central government will give them some rewards, denoted by G₁, G₂, and G₃, respectively, and the central government can also gain some rewards R₁ from the cooperation of them in return. If both schools and enterprises choose cooperation strategy, but local governments choose noncooperation strategy, the central government can still gain some rewards R₃ from the cooperation between schools and enterprises, which is slightly less than R₁. However, if schools, enterprises, and local governments choose noncooperation strategy, they will receive some punishments from the central government, denoted by P₁, P₂, and P₃, respectively. When the central government chooses noncooperation strategy, if schools, enterprises, and local governments choose cooperation strategy, the central government can also reap some benefits R₅ from the cooperation of them. If both schools and enterprises choose cooperation strategy, but local governments choose noncooperation strategy, the central government will gain some benefits R₇ from the cooperation between schools and enterprises, which is slightly less than R₅. Furthermore, no matter what strategy the central government chooses, as long as either schools or enterprises choose noncooperation strategy, the central government will suffer certain losses L₃ because of the unsuccessful cooperation between schools and enterprises.

Similarly, for local governments, when it chooses cooperation strategy, it will spend some costs C₄. In this case, if schools, enterprises, and the central government also choose cooperation strategy, local governments will gain some benefits R₂, and will offer some rewards to schools and enterprises, respectively denoted by G₄ and G₅. However, if schools and enterprises choose noncooperation strategy, they will receive some punishments from local governments, denoted by P₄ and P₅, respectively. If both schools and enterprises choose cooperation strategy, but the central government chooses noncooperation strategy, local governments can still gain some benefits R₆ from the cooperation between schools and enterprises, which is slightly less than R₂. When local governments choose noncooperation strategy, if schools, enterprises, and the central government choose cooperation strategy, local governments can also reap some benefits R₄ from the cooperation of the other three parties. If both schools and enterprises choose cooperation strategy, but the central government chooses noncooperation strategy, local governments will gain some benefits R₈ from the cooperation between schools and enterprises, which is slightly less than R₄. Furthermore, no matter what strategy local governments choose, as long as either schools or enterprises choose noncooperation strategy, local governments will suffer certain losses L₄ because of the unsuccessful cooperation between schools and enterprises.

The above parameters and their definitions for the four parties are listed in Table 1.

2.2. Model Construction

Based on the previous theoretical framework, the corresponding payoff matrix of schools, enterprises, the central government, and local governments is constructed and shown in Table 2.

Each entry in Table 2 contains 4 values, represent payoffs of schools, enterprises, the central government, and local governments, respectively. According to evolutionary game theory, when the expected payoff of a certain strategy for a population is higher than the average expected payoff of all other strategies for that population, the proportion of individuals who choose that strategy in that population will increase. That is, the strategy with the higher expected payoff is more likely to be imitated, replicated, and spread [36,37]. This mechanism can be expressed by the replicator dynamic equation, which is one of the most basic models in evolutionary game theory [38,39,40]. Therefore, we construct the replicator dynamic equation of schools, enterprises, the central government, and local governments by calculating expected payoffs and average expected payoffs of their cooperation and noncooperation strategies to investigate the evolution of cooperative behaviors among these four populations.

First, we use U_A1 and U_A2 to represent expected payoffs of schools’ cooperation strategy and noncooperation strategy, respectively, and use

\bar{U A}

to represent the average expected payoff. According to above payoff matrix and the probabilities of selecting different strategies, U_A1, U_A2, and

\bar{U A}

can be expressed as follows:

(1)

(2)

\bar{U_{A}} = w U_{A 1} + (1 - w) U_{A 2}

(3)

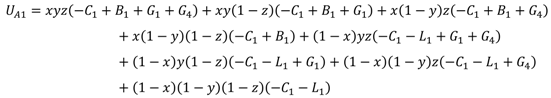
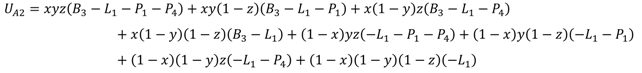
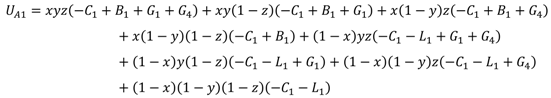
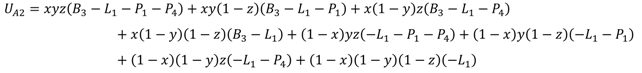
The replicator dynamic equation of schools

\frac{d w}{d t}

can be calculated as:

F (w) = \frac{d w}{d t} = w (U_{A 1} - \bar{U_{A}}) = w (1 - w) [x (B_{1} - B_{3} + L_{1}) + y (G_{1} + P_{1}) + z (G_{4} + P_{4}) - C_{1}]

(4)

In a similar way, we use U_B1 and U_B2 to represent the expected payoffs of enterprises’ cooperation strategy and noncooperation strategy, respectively, and use

\bar{U B}

to represent the average expected payoff. U_B1, U_B2, and

\bar{U B}

can be obtained as follows:

(5)

(6)

\bar{U_{B}} = x U_{B 1} + (1 - x) U_{B 2}

(7)

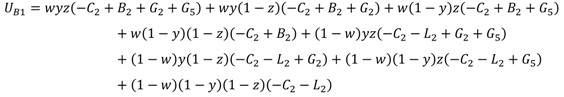
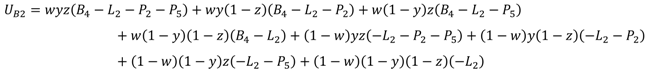
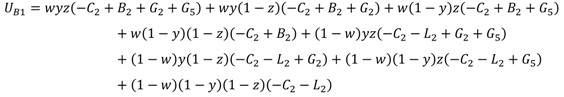
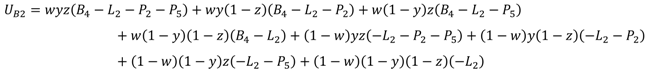
The replicator dynamic equation of enterprises

\frac{d x}{d t}

can thus be calculated as:

F (x) = \frac{d x}{d t} = x (U_{B 1} - \bar{U_{B}}) = x (1 - x) [w (B_{2} - B_{4} + L_{2}) + y (G_{2} + P_{2}) + z (G_{5} + P_{5}) - C_{2}]

(8)

Next, we use U_C1 and U_C2 to represent the expected payoff of the central government’s cooperation strategy and noncooperation strategy, respectively, and use

\bar{U C}

to represent the average expected payoff. U_C1, U_C2, and

\bar{U C}

can be obtained as follows:

(9)

U_{C 2} = w x z R_{5} + w x (1 - z) R_{7} + w (1 - x) z (- L_{3}) + w (1 - x) (1 - z) (- L_{3}) + (1 - w) x z (- L_{3}) + (1 - w) x (1 - z) (- L_{3}) + (1 - w) (1 - x) z (- L_{3}) + (1 - w) (1 - x) (1 - z) (- L_{3})

(10)

\bar{U_{C}} = y U_{C 1} + (1 - y) U_{C 2}

(11)

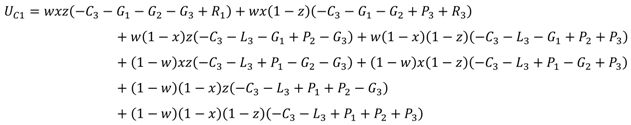
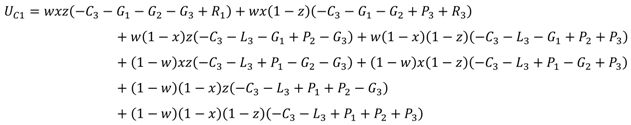
The replicator dynamic equation of the central government

\frac{d y}{d t}

can then be calculated as:

(12)

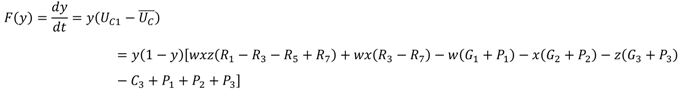
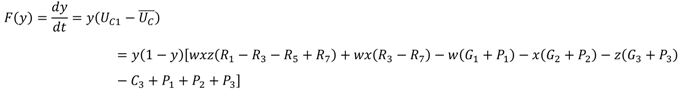
Then, we use U_D1 and U_D2 to represent the expected payoff of local governments’ cooperation strategy and noncooperation strategy, respectively, and use

\bar{U D}

to represent the average expected payoff. U_D1, U_D2, and

\bar{U D}

can be obtained as follows:

(13)

(14)

\bar{U_{D}} = z U_{D 1} + (1 - z) U_{D 2}

(15)

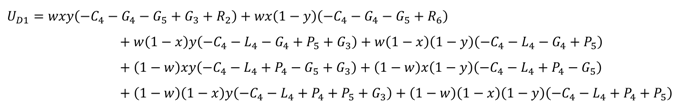
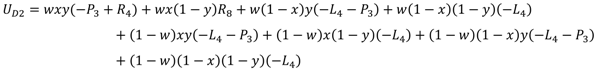
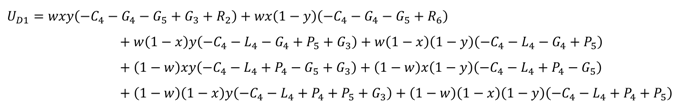
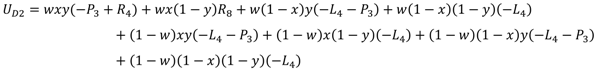
The replicator dynamic equation of local governments

\frac{d z}{d t}

can be calculated as:

(16)

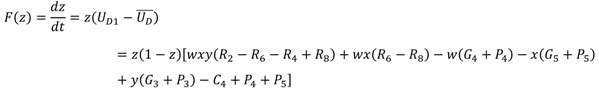
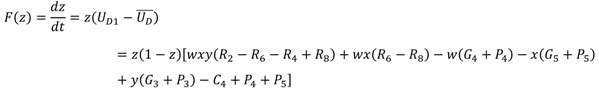
Finally, we let F(w) = 0, F(x) = 0, F(y) = 0, and F(z) = 0, and combine the replicator dynamic equations (4), (8), (12), and (16) to establish a four-dimensional dynamic system of schools, enterprises, the central government, and local governments, as shown in equation (17).

(17)

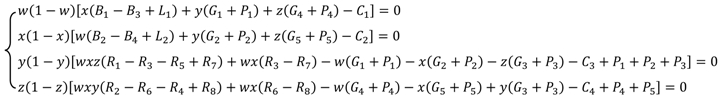
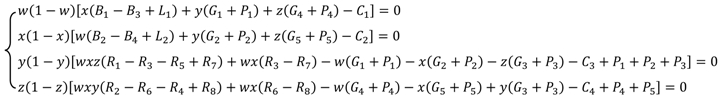
In next section, we will solve this replicator dynamic system to analyze the stability of strategies for the four parties.

3. Results

Based on the quadrilateral evolutionary game model constructed in Section 2, we find 16 four-player pure strategy equilibrium points and build a Jacobian matrix of the model to evaluate the stability of these equilibrium points.

3.1. Equilibrium Points of the Evolutionary Game Model

By solving Equation (17), 41 equilibrium points can be obtained, including 16 four-player pure strategy solutions, 24 two-player pure strategy solutions, and 1 mixed strategy solution, shown in Equations (18)–(20).

\{\begin{matrix} E_{1} (w = 0, x = 0, y = 0, z = 0) \\ \begin{matrix} E_{2} (w = 0, x = 0, y = 0, z = 1) \\ E_{3} (w = 0, x = 0, y = 1, z = 0) \\ \begin{matrix} E_{4} (w = 0, x = 0, y = 1, z = 1) \\ E_{5} (w = 0, x = 1, y = 0, z = 0) \\ \begin{matrix} E_{6} (w = 0, x = 1, y = 0, z = 1) \\ E_{7} (w = 0, x = 1, y = 1, z = 0) \\ \begin{matrix} E_{8} (w = 0, x = 1, y = 1, z = 1) \\ E_{9} (w = 1, x = 0, y = 0, z = 0) \\ \begin{matrix} E_{10} (w = 1, x = 0, y = 0, z = 1) \\ E_{11} (w = 1, x = 0, y = 1, z = 0) \\ \begin{matrix} E_{12} (w = 1, x = 0, y = 1, z = 1) \\ E_{13} (w = 1, x = 1, y = 0, z = 0) \\ \begin{matrix} E_{14} (w = 1, x = 1, y = 0, z = 1) \\ E_{15} (w = 1, x = 1, y = 1, z = 0) \\ E_{16} (w = 1, x = 1, y = 1, z = 1) \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix}

(18)

(19)

(20)

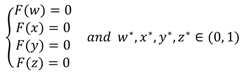
The strategy solutions of all players are certain values of 0 or 1 in Equation (18), but there are uncertain results of players’ strategy solutions in Equations (19) and (20). According to game theory, the strategy solution in a multi-agent evolutionary game must be a Nash equilibrium in pure strategies [38]. Thus, we only choose the 16 pure strategy solutions E₁, E₂, E₃, E₄, E₅, E₆, E₇, E₈, E₉, E₁₀, E₁₁, E₁₂, E₁₃, E₁₄, E₁₅, and E₁₆ as the possible stable equilibrium points.

3.2. The Stability of the Equilibrium Points

We adopt Friedman’s replication dynamics system stability analysis method [41] to evaluate the stability of the 16 equilibrium points by constructing the Jacobian matrix and calculating its eigenvalues. The Jacobian matrix of the quadrilateral evolutionary game is:

J = [\begin{matrix} \begin{matrix} \frac{\partial F (w)}{\partial w} & \frac{\partial F (w)}{\partial x} \\ \frac{\partial F (x)}{\partial w} & \frac{\partial F (x)}{\partial x} \end{matrix} & \begin{matrix} \begin{matrix} \frac{\partial F (w)}{\partial y} \\ \frac{\partial F (x)}{\partial y} \end{matrix} & \begin{matrix} \frac{\partial F (w)}{\partial z} \\ \frac{\partial F (x)}{\partial z} \end{matrix} \end{matrix} \\ \begin{matrix} \frac{\partial F (y)}{\partial w} & \frac{\partial F (y)}{\partial x} \\ \frac{\partial F (z)}{\partial w} & \frac{\partial F (z)}{\partial x} \end{matrix} & \begin{matrix} \frac{\partial F (y)}{\partial y} & \frac{\partial F (y)}{\partial z} \\ \frac{\partial F (z)}{\partial y} & \frac{\partial F (z)}{\partial z} \end{matrix} \end{matrix}] = [\begin{matrix} \begin{matrix} J_{11} & J_{12} \\ J_{21} & J_{22} \end{matrix} & \begin{matrix} J_{13} & J_{14} \\ J_{23} & J_{24} \end{matrix} \\ \begin{matrix} J_{31} & J_{32} \\ J_{41} & J_{42} \end{matrix} & \begin{matrix} J_{33} & J_{34} \\ J_{43} & J_{44} \end{matrix} \end{matrix}]

(21)

Where

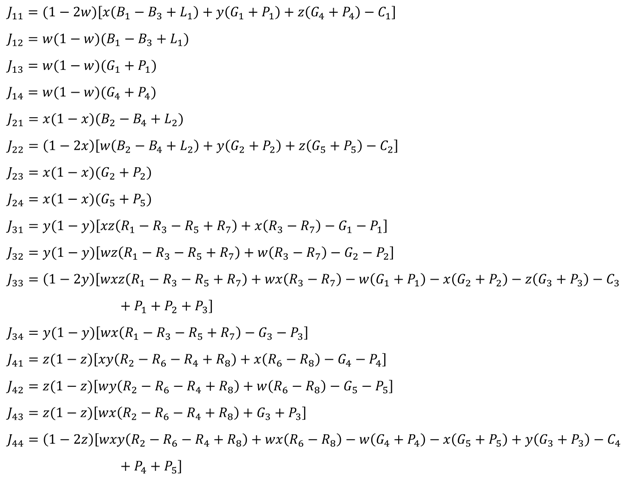
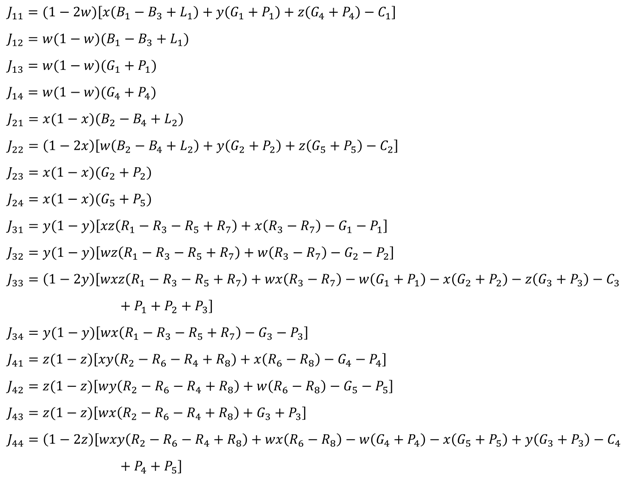
According to Lyapunov stability theory, the stability of the equilibrium point can be evaluated by analyzing the eigenvalues of the Jacobian matrix [42]. If all the eigenvalues are negative, the corresponding equilibrium point is a stable point; if there are any positive eigenvalues, the corresponding equilibrium point is an unstable point; if the signs of the eigenvalues cannot be determined, the corresponding equilibrium point is a saddle point; and if all the eigenvalues are 0, the stability of the corresponding equilibrium point is of no significance. We thus substitute each of the 16 equilibrium points into the Jacobian matrix and calculate the corresponding eigenvalues, which are shown in Table 3.

Here, “N” means that the sign of the eigenvalue cannot be determined, “+” means that the eigenvalue is positive, and “–” means that the eigenvalue is negative. As shown in Table 3, there is no stable point, which indicates that there is no stable state of cooperation between schools, enterprises, the central government, and local governments. But there are 6 saddle points, at which the quadrilateral evolutionary game has possibility to reach stable state. That is, the stable cooperation between the four parties requires conditions. Therefore, in the following section, we will discuss the conditions of the cooperation between schools, enterprises, the central government, and local governments, especially the approaches of governments to promote sustainable cooperation between schools and enterprises.

4. Discussion

As shown in Table 3, there are 6 saddle points, E₈ (0,1,1,1), E₁₂ (1,0,1,1), E₁₃ (1,1,0,0), E₁₄ (1,1,0,1), E₁₅ (1,1,1,0), E₁₆ (1,1,1,1). Next, we will assess the stability conditions of each saddle point separately.

Scenario 1 (E₈): When –B₃+L₁+P₁+P₄＜0, –G₂–G₅+C₂＜0, G₂+G₃+C₃–P₁＜0, and G₅–G₃+C₄–P₄＜0, the quadrilateral evolutionarily game reaches stable state. In this case, enterprises, the central government, and local governments all choose cooperation strategy, while only schools choose noncooperation strategy. Thus, this point is not ideal. The stability conditions of this point are not expected to be achieved. That requires P₁+P₄＞B₃–L₁, or P₁＞G₂+G₃+C₃, or P₄＞G₅–G₃+C₄, which indicates that strengthen the punishment from the central government and local governments for choosing noncooperation strategy is an important measure to prevent the emergence of schools’ noncooperative behavior.

Scenario 2 (E₁₂): It is similar to Scenario 1. When –G₁–G₄+C₁＜0, –B₄+L₂+P₂+P₅＜0, G₁+G₃+C₃–P₂＜0, and G₄–G₃+C₄–P₅＜0, the quadrilateral evolutionarily game reaches stable state. In this case, schools, the central government, and local governments all choose cooperation strategy, while only enterprises choose noncooperation strategy. This point is also not ideal. The stability conditions of this point are also not expected to be achieved. That requires P₂+P₅＞B₄–L₂, or P₂＞G₁+G₃+C₃, or P₅＞G₄–G₃+C₄, which also indicates that strengthen the punishment from the central government and local governments for choosing noncooperation strategy is an important measure to prevent the emergence of enterprises’ noncooperative behavior.

Scenario 3 (E₁₃): When –B₁+C₁＜0 and –B₂+C₂＜0, the quadrilateral evolutionarily game reaches stable state. In this case, schools and enterprises choose cooperation strategy, while the central government and local governments choose noncooperation strategy. The stability conditions can be transformed into B₁＞C₁ and B₂＞C₂. That is, when the benefits obtained by schools and enterprises through cooperating with each other are greater than their costs, even without the participation of the government, the cooperation between schools and enterprises can also reach a stable state.

Scenario 4 (E₁₄): When –B₁–G₄+C₁＜0, –B₂–G₅+C₂＜0, and –R₆+G₄+G₅+C₄＜0, the quadrilateral evolutionarily game reaches stable state. In this case, schools, enterprises, and local governments all choose cooperation strategy, while only the central government chooses noncooperation strategy. The stability conditions can be transformed into B₁+G₄＞C₁, B₂+G₅＞C₂, and R₆＞G₄+G₅+C₄, which shows that increasing rewards offered by local governments to encourage the cooperation strategy of schools and enterprises can promote their cooperation, even without direct intervention from the central government. Furthermore, just improving the incentives may not suffice. It is paramount to focus on improving the practical effect of the cooperation between schools and enterprises.

Scenario 5 (E₁₅): When –B₁–G₁+C₁＜0, –B₂–G₂+C₂＜0, –R₃+G₁+G₂+C₃–P₃＜0, and –R₄+P₃＜0, the quadrilateral evolutionarily game reaches stable state. In this case, schools, enterprises, and the central government all choose cooperation strategy, while only local governments choose noncooperation strategy. The stability conditions can be transformed into B₁+G₁＞C₁, B₂+G₂＞C₂, R₃＞G₁+G₂+C₃–P₃, and P₃＜R₄, which shows that increasing rewards provided by the central government to incentivize the cooperation strategy of schools and enterprises can facilitate their cooperation, even in the absence of active involvement from local governments. In addition, the effectiveness of punishments imposed by the central government on local governments has minimal impact on fostering school-enterprise cooperation. What really matter is improving the effectiveness of policies on school-enterprise cooperation.

Scenario 6 (E₁₆): When –B₁–G₁–G₄+C₁＜0, –B₂–G₂–G₅+C₂＜0, –R₁+G₁+G₂+G₃+C₃＜0, and –R₂+G₄+G₅–G₃+C₄＜0, the quadrilateral evolutionarily game reaches stable state. In this case, all the four parties choose cooperation strategy. This point is the most ideal. The stability conditions can be transformed into B₁+G₁+G₄＞C₁, B₂+G₂+G₅＞C₂, R₁＞G₁+G₂+G₃+C₃, and R₂＞G₄+G₅–G₃+C₄. Comparing with Scenario 4 and 5, in this scenario, increasing the rewards from the central government and local governments for choosing cooperation strategy of schools and enterprises can also have positive effect, and beyond that, since the rewards are provided jointly by the central government and local governments, the spending of them on participating in school-enterprise cooperation will be decreased. Moreover, the reward from the central government to local governments has not much influence on promoting the cooperation between schools and enterprises. What really matter is also improving the effectiveness of policies on school-enterprise cooperation.

5. Conclusions

This paper explores the stability of cooperation between schools, enterprises, the central government, and local governments, and analyzes the approaches of central and local governments to promote school-enterprise cooperation. The main conclusions are as follows:

(1) There is no stable equilibrium point of the quadrilateral game between schools, enterprises, the central government, and local governments, but there are 6 saddle points, E8 (0,1,1,1), E12 (1,0,1,1), E13 (1,1,0,0), E14 (1,1,0,1), E15 (1,1,1,0), E16 (1,1,1,1), at which the quadrilateral game has the potential to be stable. Facilitating stable and sustainable cooperation between schools and enterprises requires conditions.

(2) The primary condition for school-enterprise cooperation is benefit rather than governmental intervention. When the benefits of cooperation outweigh the costs, schools and enterprises are inclined to cooperate with each other independently of governmental intervention. Therefore, creating a robust platform for school-enterprise cooperation is crucial, providing informational support, communication channels, and ongoing evaluation.

(3) Rewards and punishments from both the central government and local governments have a profound impact on the strategy selection of schools and enterprises. Hence, appropriate enhancements to incentives and penalties by the central and local governments can effectively promote cooperation between schools and enterprises.

(4) Simply increasing rewards and punishments addresses symptoms rather than the underlying issues. Enhancing the actual outcomes of cooperation is paramount. Improving policy effectiveness, rather than merely formulating policies, is critical for promoting sustainable school-enterprise cooperation. How to make effective policies should become an essential issue for the central government and local governments to participate in school-enterprise cooperation in the future.

(5) Benefits also decisively influence the strategy choice of both the central government and local governments. When the benefits of participating in school-enterprises cooperation outweigh the costs, both the central government and local governments will choose cooperation strategy. Thus, fostering tangible outcomes derived from school-enterprise cooperation not only strengthens the relationship between schools and enterprises but also encourages deep and enduring governmental involvement. Moreover, the rewards and punishments from the central government to local governments have a limited effect on promoting school-enterprise cooperation.

These conclusions underscore the importance of aligning incentives with tangible benefits to foster effective cooperation among schools, enterprises, and governments. Moving forward, enhancing policy effectiveness and promoting meaningful outcomes will be critical for advancing school-enterprise cooperation.

Author Contributions

Conceptualization, Hexin Wang, Chao Liu and Yu Dai; Funding acquisition, Chao Liu and Yu Dai; Methodology, Hexin Wang, Chao Liu and Yu Dai; Project administration, Yu Dai; Supervision, Yu Dai; Validation, Hexin Wang and Yu Dai; Writing – original draft, Hexin Wang, Chao Liu and Yu Dai; Writing – review & editing, Hexin Wang, Chao Liu and Yu Dai. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by [Research on Promoting Common Prosperity through Education in the New Development Stage] grant number [VFA220003] and [Innovation Research on Multi-Agent Evolutionary Game Mechanism of Industry-Education Integration from the Perspective of New Quality Productivity] grant number [2024XSC-0018].

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The data presented in this study are available in the Methodology and Results sections of this article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Pritchard, R.M.O. The German dual system: Educational utopia? Comparative Education 1992, 28, 131–143. [Google Scholar] [CrossRef]
Theuerkauf, W.E.; Weiner, A. The German dual system of vocational education and implications for human resource development in America. Oxford Review of Education 2002, 1, 5373. [Google Scholar]
Remington, T.F. Business government cooperation in VET: A Russian experiment with dual education. Post Soviet Affairs 2017, 33, 313333. [Google Scholar] [CrossRef]
Pleshakova, A.Y. Dual system of education in Germany: historical context. Nauchnyi Dialog 2018, 10, 301–312. [Google Scholar] [CrossRef]
Schuurman, M.K.; Pangborn, R.N.; McClintic, R.D. Assessing the impact of engineering undergraduate work experience: Factoring in prework academic performance. Journal of Engineering Education 2008, 97, 207212. [Google Scholar] [CrossRef]
Rowe, P.M. Work experience, the scientist practitioner model, and cooperative education. Canadian Psychology Psychologie Canadienne 2018, 59, 144150. [Google Scholar] [CrossRef]
Jones, B.; Healey, M.; Matthews, H. The thick sandwich: still on the menu. Journal of Geography in Higher Education 1995, 19, 23. [Google Scholar] [CrossRef]
Chopra, S.; Golab, L. Undergraduate engineering applicants’ perceptions of cooperative education: a text mining approach. International Journal of Work-Integrated Learning 2022, 23, 95–112. [Google Scholar]
Baldwin, C.T. Sandwich courses in the universities. Physics Bulletin 1969, 20, 486. [Google Scholar] [CrossRef]
Jones, B.; Healey, M.; Matthews, H. The thick sandwich: still on the menu. Journal of Geography in Higher Education 1995, 19, 23. [Google Scholar] [CrossRef]
Santiago, A. Impact of sandwich course design on first job experience. Asia-Pacific Education Researcher 2009, 18, 205–217. [Google Scholar] [CrossRef]
Brooks, R.; Youngson, P.L. Undergraduate work placements: an analysis of the effects on career progression. Studies In Higher Education 2016, 41, 1563–1578. [Google Scholar] [CrossRef]
Wang, Y.; Bai, J. A training model of out-standing engineers: exploration of school-enterprise cooperation based on technology competition. International Journal of Engineering Education 2013, 29, 1420–1428. [Google Scholar]
Jing, C. Research on the training mode of mechanical specialty based on school enterprise cooperation. Agro Food Industry Hi-Tech 2017, 28, 399–403. [Google Scholar]
Wang, Y. Construction elements and path of practical education model in universities. Eurasia Journal of Mathematics Science and Technology Education 2017, 13, 6875–6882. [Google Scholar] [CrossRef]
Moradi, Y.; Noori, S. Entrepreneurial cooperation model between university and SMEs: a case study in Iran. Sustainability 2020, 12, 9140. [Google Scholar] [CrossRef]
Lee, J.; Win, H.N. Technology transfer between university research centers and industry in Singapore. Technovation 2004, 24, 433–442. [Google Scholar] [CrossRef]
Arza, V. Channels, Benefits and risks of public — private interactions for knowledge transfer: conceptual framework inspired by Latin America. Science and public policy 2010, 37, 473–484. [Google Scholar] [CrossRef]
Lam, A. What motivates academic scientists to engage in research commercialization: ‘Gold’, ‘ribbon’ or ‘puzzle’? Research policy 2011, 40, 1354–1368. [Google Scholar] [CrossRef]
Santoro, M.D.; Chakrabarti, A.K. Firm size and technology centrality in industry-university interactions. Research policy 2002, 31, 1163–1180. [Google Scholar] [CrossRef]
Laursen, K.; Reichstein, T.; Salter, A. Exploring the effect of geographical proximity and university quality on university-industry collaboration in the United Kingdom. Regional studies 2011, 45, 507–523. [Google Scholar] [CrossRef]
Li, Z.; Wang, D.; Li, X. Status quo and influence factors of university industry collaboration: evidence of Zhejiang Province. Science & Technology Progress and Policy 2012, 29, 150–154. (in Chinese). [Google Scholar]
Rosendo-Rios, V.; Ghauri, P.N.; Zhang, Y. Empirical analysis of the key factors that can contribute to university-industry cooperational success from a relationship marketing approach. European Journal of International Management 2016, 10, 647–677. [Google Scholar]
Zhao, J.; de Pablos, P.O. Analysis of cooperative mechanism of industry-academy R&D alliance lab and case study. Human Factors and Ergonomics in Manufacturing & Service Industries 2010, 20, 123–134. [Google Scholar]
Yang, S. Mechanism of deepening the cooperation between schools and enterprises in higher vocational education. Educational Sciences-Theory & Practice 2018, 18, 3681–3688. [Google Scholar]
Zhang, Y.; Wang, J.; Shen, X.; Song, J. Research on the influence mechanism of enterprises’ participation in school enterprise cooperation based on the analysis framework of theory of planned behavior. Frontiers in Psychology 2022, 13, 860045. [Google Scholar] [CrossRef]
Wu, W.Q.; Yu, K.X.; Ma, S.X.; Chu, C.C.; Li, S.J.; Ma, C.C.; Tsai, S.B. An empirical study on optimal strategies of industry-university-institute green innovation with subsidy. Sustainability 2018, 10, 1667. [Google Scholar] [CrossRef]
Jia, F.J.; Wang, D.D. Research on innovation decisions in industry-university-research cooperation based on differential games. Technology Analysis & Strategic Management.
Liu, G.; Wei, L.; Gu, J.; Zhou, T.; Liu, Y. Benefit distribution in urban renewal from the perspectives of efficiency and fairness: a game theoretical model and the government's role in China. Cities 2020, 96, 102422. [Google Scholar] [CrossRef]
Yang, J.; Wang, Y. Will the central-local disparity in public policy perceptions disappear? Evidence from 19 major cities in China. Government Information Quarterly 2020, 37, 101525. [Google Scholar] [CrossRef]
Lu, S.; Wang, H. Limited decentralization: understand China’s land system from the perspective of central-local relation. Land 2022, 11, 517. [Google Scholar] [CrossRef]
Zhai, Y. Government policy performance and central-local political trust in China. Journal of Public Policy 2022, 42, 782–801. [Google Scholar] [CrossRef]
Liu, C.; Wang, H.X.; Dai, Y. Sustainable cooperation between schools, enterprises, and government: An evolutionary game theory analysis. Sustainability 2023, 15, 13997. [Google Scholar] [CrossRef]
Zhang, S.Z. Educational cooperation in the perspective of tripartite evolutionary game among government, enterprises and universities. PLOS ONE 2024, 19, e0294742. [Google Scholar] [CrossRef]
Ma, J.L.; Yang, D.S. Research on the mechanism of government-industry-university-research collaboration for cultivating innovative talent based on game theory. Heliyon 2024, 10, e25335. [Google Scholar] [CrossRef]
Taylor, P.; Jonker, L. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
Hofbauer, J.; Sigmund, K. Evolutionary games and population dynamics. Cambridge University Press, 1998.
Ritzberger, K.; Weibull, J.W. Evolutionary selection in normal form games. Econometrica 1995, 63, 1371–1399. [Google Scholar] [CrossRef]
Shi, Y.; Pan, M.; Peng, D. Replicator dynamics and evolutionary game of social tolerance: The role of neutral agents. Econ. Lett. 2017, 159, 10–14. [Google Scholar] [CrossRef]
Wang, Q.; He, N.; Chen, X. Replicator dynamics for public goods game with resource allocation in large populations. Appl. Math. Comput. 2018, 328, 162–170. [Google Scholar] [CrossRef]
Friedman, D. Evolutionary games in economics. Econometrica 1991, 59, 637–666. [Google Scholar] [CrossRef]
Lyapunov, A.M. The general problem of the stability of motion. International Journal of Control 1992, 55, 531–534. [Google Scholar] [CrossRef]

Figure 1. The game relationship between schools, enterprises, the central government, and local governments.

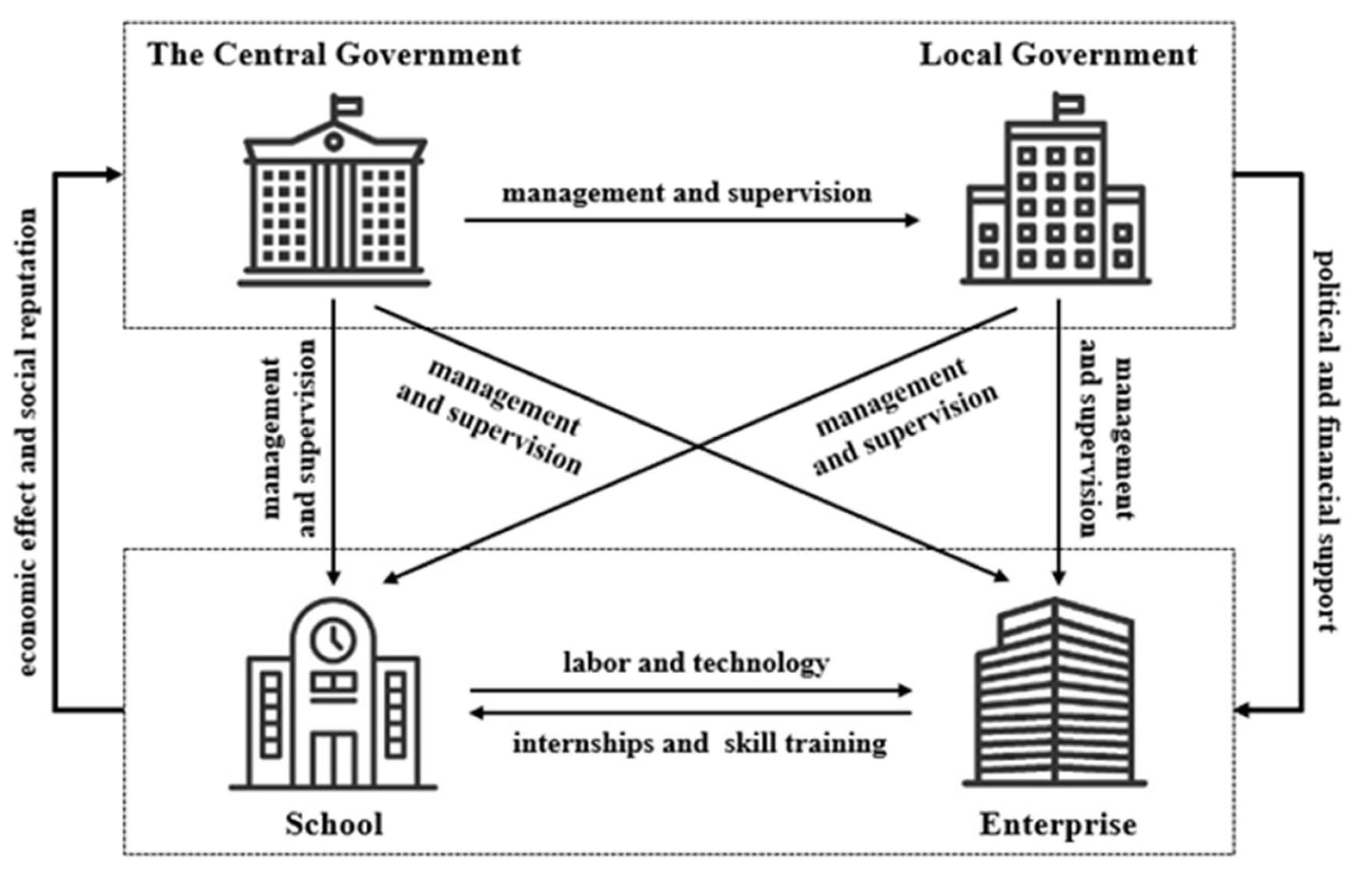
Table 1. Parameters definitions.

Party	Parameter	Definition
schools	C₁	The cost of schools’ cooperation strategy.
	B₁	The benefit of schools’ cooperation strategy for cooperating with enterprises.
	B₃	The benefit of schools’ noncooperation strategy due to the enterprises’ cooperation strategy.
	L₁	The loss suffered by schools due to the unsuccessful cooperation between schools and enterprises.
enterprises	C₂	The cost of enterprises’ cooperation strategy.
	B₂	The benefit of enterprises’ cooperation strategy for cooperating with schools.
	B₄	The benefit of enterprises’ noncooperation strategy due to the schools’ cooperation strategy.
	L₂	The loss suffered by enterprises due to the unsuccessful cooperation between schools and enterprises.
the central governments	C₃	The cost of the central government’s cooperation strategy.
	G₁	The reward from the central government for schools’ cooperation strategy.
	G₂	The reward from the central government for enterprises’ cooperation strategy.
	G₃	The reward from the central government for local governments’ cooperation strategy.
	P₁	The punishment from the central government for schools’ noncooperation strategy.
	P₂	The punishment from the central government for enterprises’ noncooperation strategy.
	P₃	The punishment from the central government for local governments’ noncooperation strategy.
	R₁	The reward for the central government’s cooperation strategy due to the cooperation of all parties.
	R₃	The reward for the central government’s cooperation strategy due to the cooperation between schools and enterprises.
	R₅	The reward for the central government’s noncooperation strategy due to the cooperation of the other three parties.
	R₇	The reward for the central government’s noncooperation strategy due to the cooperation between schools and enterprises.
	L₃	The loss suffered by the central government due to the unsuccessful cooperation between schools and enterprises.
local governments	C₄	The cost of local governments’ cooperation strategy.
	G₄	The reward from local governments for schools’ cooperation strategy.
	G₅	The reward from local governments for enterprises’ cooperation strategy.
	P₄	The punishment from local governments for schools’ noncooperation strategy.
	P₅	The punishment from local governments for enterprises’ noncooperation strategy.
	R₂	The reward for local governments’ cooperation strategy due to the cooperation of all parties.
	R₄	The reward for local governments’ noncooperation strategy due to the cooperation of the other three parties.
	R₆	The reward for local governments’ cooperation strategy due to the cooperation between schools and enterprises.
	R₈	The reward for local governments’ noncooperation strategy due to the cooperation between schools and enterprises.
	L₄	The loss suffered by local governments due to the unsuccessful cooperation between schools and enterprises.

Table 2. Payoff matrix of the quadrilateral evolutionary game between schools, enterprises, the central government, and local governments.

				the central government
				cooperation strategy		noncooperation strategy
				local governments		local governments
				cooperation strategy	noncooperation strategy	cooperation strategy	noncooperation strategy
schools	cooperation strategy	enterprises	cooperation strategy	‒C₁+B₁+G₁+G₄, ‒C₂+B₂+G₂+G₅, ‒C₃‒G₁‒G₂‒G₃+R₁, ‒C₄‒G₄‒G₅+G₃+R₂	‒C₁+B₁+G₁, ‒C₂+B₂+G₂, ‒C₃‒G₁‒G₂+P₃+R₃, ‒P₃+R₄	‒C₁+B₁+G₄, ‒C₂+B₂+G₅, R₅, ‒C₄‒G₄‒G₅+R₆	‒C₁+B₁, ‒C₂+B₂, R₇, R₈
			noncooperation strategy	‒C₁‒L₁+G₁+G₄, B₄‒L₂‒P₂‒P₅, ‒C₃‒L₃‒G₁+P₂‒G₃, ‒C₄‒L₄‒G₄+P₅+G₃	‒C₁‒L₁+G₁, B₄‒L₂‒P₂, ‒C₃‒L₃‒G₁+P₂+P₃, ‒L₄‒P₃	‒C₁‒L₁+G₄, B₄‒L₂‒P₅, ‒L₃, ‒C₄‒L₄‒G₄+P₅	‒C₁‒L₁, B₄‒L₂, ‒L₃, ‒L₄
	noncooperation strategy	enterprises	cooperation strategy	B₃‒L₁‒P₁‒P₄, ‒C₂‒L₂+G₂+G₅, ‒C₃‒L₃+P₁‒G₂‒G₃, ‒C₄‒L₄+P₄‒G₅+G₃	B₃‒L₁‒P₁, ‒C₂‒L₂+G₂, ‒C₃‒L₃+P₁‒G₂+P₃, ‒L₄‒P₃	B₃‒L₁‒P₄, ‒C₂‒L₂+G₅, ‒L₃, ‒C₄‒L₄+P₄‒G₅	B₃‒L₁, ‒C₂‒L₂, ‒L₃, ‒L₄
			noncooperation strategy	‒L₁‒P₁‒P₄, ‒L₂‒P₂‒P₅, ‒C₃‒L₃+P₁+P₂‒G₃, ‒C₄‒L₄+P₄+P₅+G₃	‒L₁‒P₁, ‒L₂‒P₂, ‒C₃‒L₃+P₁+P₂+P₃, ‒L₄‒P₃	‒L₁‒P₄, ‒L₂‒P₅, ‒L₃, ‒C₄‒L₄+P₄+P₅	‒L₁, ‒L₂, ‒L₃, ‒L₄

Table 3. The eigenvalues and stability of the equilibrium points.

equilibrium point	eigenvalues								state
equilibrium point	λ₁	symbol	λ₂	symbol	λ₃	symbol	λ₄	symbol	state
E₁ (0,0,0,0)	‒C₁	0	‒C₂	0	–C₃+P₁+P₂+P₃	0	–C₄+P₄+P₅	0	×
E₂ (0,0,0,1)	G₄+P₄–C₁	+	G₅+P₅–C₂	+	–G₃–C₃+P₁+P₂	0	C₄–P₄–P₅	N	unstable
E₃ (0,0,1,0)	G₁+P₁–C₁	+	G₂+P₂–C₂	+	C₃–P₁–P₂–P₃	N	G₃+P₃–C₄+P₄+P₅	+	unstable
E₄ (0,0,1,1)	G₁+P₁+G₄+P₄–C₁	+	G₂+P₂+G₅+P₅–C₂	+	G₃+C₃–P₁–P₂	N	–G₃–P₃+C₄–P₄–P₅	N	unstable
E₅ (0,1,0,0)	B₁–B₃+L₁–C₁	N	C₂	+	–G₂–C₃+P₁+P₃	0	–G₅–C₄+P₄	0	unstable
E₆ (0,1,0,1)	B₁–B₃+L₁+G₄+P₄–C₁	N	–G₅–P₅+C₂	N	–G₂–G₃–C₃+P₁	0	G₅+C₄–P₄	N	×/unstable
E₇ (0,1,1,0)	B₁–B₃+L₁+G₁+P₁–C₁	N	–G₂–P₂+C₂	N	G₂+C₃–P₁–P₃	N	–G₅+G₃+P₃–C₄+P₄	+	unstable
E₈ (0,1,1,1)	B₁–B₃+L₁+G₁+P₁+G₄+P₄–C₁	N	–G₂–P₂–G₅–P₅+C₂	N	G₂+G₃+C₃–P₁	N	G₅–G₃–P₃+C₄–P₄	N	saddle
E₉ (1,0,0,0)	C₁	+	B₂–B₄+L₂–C₂	N	–G₁–C₃+P₂+P₃	0	–G₄–C₄+P₅	0	unstable
E₁₀ (1,0,0,1)	–G₄–P₄+C₁	N	B₂–B₄+L₂+G₅+P₅–C₂	N	–G₁–G₃–C₃+P₂	0	G₄+C₄–P₅	N	×/unstable
E₁₁ (1,0,1,0)	–G₁–P₁+C₁	N	B₂–B₄+L₂+G₂+P₂–C₂	N	G₁+C₃–P₂–P₃	N	–G₄+G₃+P₃–C₄+P₅	+	unstable
E₁₂ (1,0,1,1)	–G₁–P₁–G₄–P₄+C₁	N	B₂–B₄+L₂+G₂+P₂+G₅+P₅–C₂	N	G₁+G₃+C₃–P₂	N	G₄–G₃–P₃+C₄–P₅	N	saddle
E₁₃ (1,1,0,0)	–B₁+B₃–L₁+C₁	N	–B₂+B₄–L₂+C₂	N	R₃–R₇–G₁–G₂–C₃+P₃	–	R₆–R₈–G₄–G₅–C₄	–	saddle
E₁₄ (1,1,0,1)	–B₁+B₃–L₁–G₄–P₄+C₁	N	–B₂+B₄–L₂–G₅–P₅+C₂	N	R₁–R₅–G₁–G₂–G₃–C₃	–	–R₆+R₈+G₄+G₅+C₄	N	saddle
E₁₅ (1,1,1,0)	–B₁+B₃–L₁–G₁–P₁+C₁	N	–B₂+B₄–L₂–G₂–P₂+C₂	N	–R₃+R₇+G₁+G₂+C₃–P₃	N	R₂–R₄–G₄–G₅+G₃+P₃–C₄	N	saddle
E₁₆ (1,1,1,1)	–B₁+B₃–L₁–G₁–P₁–G₄–P₄+C₁	N	–B₂+B₄–L₂–G₂–P₂–G₅–P₅+C₂	N	–R₁+R₅+G₁+G₂+G₃+C₃	N	–R₂+R₄+G₄+G₅–G₃–P₃+C₄	N	saddle

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

How can the Government Promote Sustainable Cooperation between Schools and Enterprises? A Quadrilateral Evolutionary Game Study

Abstract

1. Introduction

2. Methodology

2.1. Theoretical Framework

2.2. Model Construction

3. Results

3.1. Equilibrium Points of the Evolutionary Game Model

3.2. The Stability of the Equilibrium Points

4. Discussion

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe