Prerpints.org logo
Preprint
Article

Quantum-Tunnelling Deep Neural Networks for Sociophysical Neuromorphic AI

Altmetrics

Downloads

115

Views

55

Comments

0

This version is not peer-reviewed

Artificial Intelligence Models, Tools and Applications

Submitted:

27 June 2024

Posted:

27 June 2024

You are already at the latest version

Alerts
Abstract
The discovery of the quantum tunnelling effect---the transmission of particles through a high potential barrier---was one of the most impressive achievements of quantum mechanics made in the 1920s. Responding to the contemporary challenges, I introduce a novel deep neural network (DNN) architecture that processes information using the effect of quantum tunnelling. I demonstrate the ability of the quantum tunnelling DNN (QT-DNN) to recognise optical illusions like a human. Hardware implementation of QT-DNN is expected to result in an inexpensive and energy-efficient neuromorphic chip suitable for applications in autonomous vehicles. The optical illusions recognition tests developed in this paper should lay foundations for cognitive benchmarking tasks for AI systems of the future, benefiting the fields of sociophysics and behavioural science.
Keywords: 
Subject: Physical Sciences  -   Other

1. Introduction

1.1. Can AI See Optical Illusions?

How will a conscious robot [1] see us and our world? Will it understand how humans behave in natural complex environments such as oceans and space [2,3,4] and make decisions in virtual reality systems [5,6,7] and video games [8]? Speaking broadly, will a robot differentiate lie from truth in media, social networks and politics [9,10,11]?
Biological vision is enabled by physical, physiological and psychological processes [12]. In turn, AI employs machine vision [13] and neural network models [14] to recognise and classify objects. Hence, even though machine vision shares certain features with biological vision [15], in general AI and humans see two very different worlds [16,17,18].
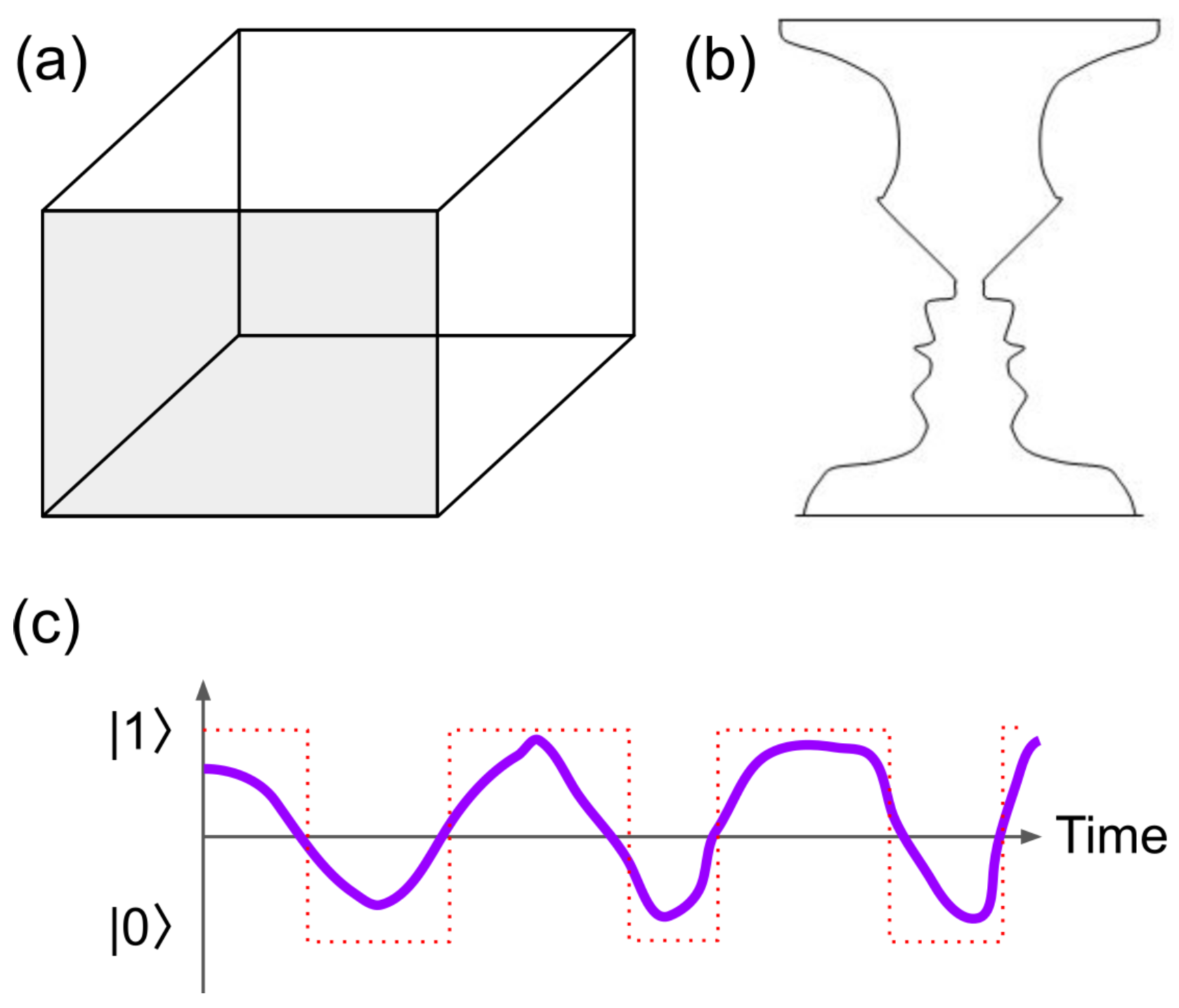
For example, how would AI see the Necker cube [19,20] and Rubin’s vase [21,22] (Figure 1a, b)? While a human looking at these paradigmatic optical illusions [19] can easily report a random switching of their perception from one possible interpretation of the figure to another [20,23] (Figure 1c), AI will struggle to produce a similar output in spite of the advances in simulation of human vision [24,25,26,27,28,29,30].

1.2. AI, Psychology and Quantum Mechanics

AI cannot see optical illusions since its algorithms do not take into account peculiar psychological and neurological aspects of human vision [19,22,31,32]. Yet, although this problem has been stressed in the literature [33,34,35,36], the relevance of visual and biological complexity of natural environments to AI has not been fully appreciated [4,37,38].
Experimental studies [39,40,41] demonstrated that the perception of the Necker cube and other ambiguous figures may not abruptly switch between the states | 0 〉 and | 1 〉 (the dotted line in Figure 1c) but continuously oscillates between them (the solid curve in Figure 1c). Those results were interpreted as the ability of humans to see a quantum-like superposition of | 0 〉 and | 1 〉 states [20,42,43,44]. Indeed, in psychological experiments humans are asked to push an electric button every time their perception of the Necker cube switches between | 0 〉 and | 1 〉 . While humans might see the cube in a superposition state [31,41], by pressing the button the observer `collapses’ the superposition to one of the possible `classical’ states [23]. This means that the ability of humans to access and use environmental information is limited, which may result in ambiguous interpretation. Subsequently, our perceptual system needs to disambiguate and interpret the available sensory information to construct stable and reliable percepts [45]. Yet, this suggests that AI can help humans to enhance their perception and gain access to information that our senses and brain cannot process naturally.
Further attempts to understand bistable perception using the methods of quantum mechanics [20,43,44] resulted in the suggestion to study the superposition of the perceptual states using a quantum oscillator model (QOM) [20]. Compared with Markov models [20], QOM accounts for multiple outcomes while processing input data with a large set of constraints, thus describing human mental states [43,44] more efficiently than classical models.
The predictions of QOM are in good agreement with a model based on the quantum Zeno effect [42]. Besides, the ability of QOM to simulate the perception of optical illusions was improved [23,46] by combining harmonic motion with the effect of quantum tunnelling (QT) through a potential barrier [47,48]. Since both QOM and quantum Zeno effect underpin quantum neural network models [49], the predictions made by QOM were additionally validated using a deep neural network (DNN) model [23] combined with a quantum generator of truly random numbers [50].

1.3. What is this article about?

In this work, I suggest and theoretically validate a novel neuromorphic DNN model (see Sect. Section 2.1 for state-of-the-art) that processes information using the physical effect of QT. I showcase the ability of the QT-DNN model to enable AI to recognise practically important optical illusions, the perception of which should pave the way for the development of machine vision system capable of recognising more complex visual effects used in fine arts and cinematography. I also demonstrate that QT-DNN can be implemented as a hardware neuromorphic chip.
My findings can be used in AI system and brain-computer interfaces aimed to enhance the performance of astronauts in long-duration spaceflight [3] and help airline pilots be aware of disorientation, loss of perspective and misinterpretation of data provided by flight instruments [51]. Interestingly enough, the algorithms proposed in this work can also help conduct research on gender since it has been demonstrated that fluidity of gender identity might be induced by optical illusions [52].
Finally, concluding the paper with a discussion of the relevance of the effect of QT to the hypothesised brain-mind link [53,54], I contribute to bridging the gap between the theories of quantum mind and decision-making [20,43] and the practically important field of sociophysics [9,11].

2. QT-DNN Architecture

2.1. Neuromorphic Quantum DNN models

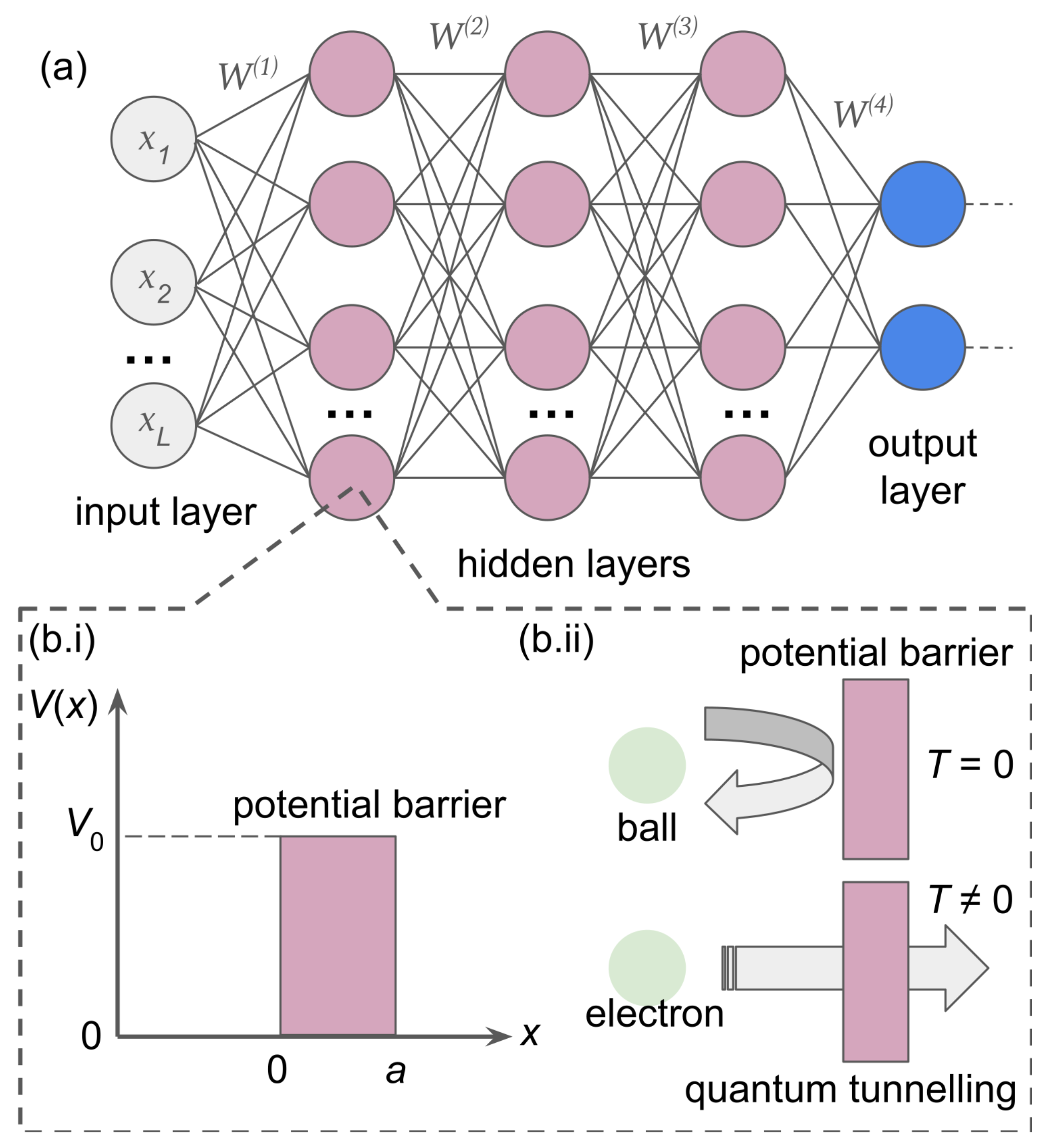
DNNs—networks composed of several layers (Figure 2a) [14]—are pivotal for machine vision and human-computer interactions [13]. Yet, they are mathematically complex [55], require considerable computational resources [56] and consume significant electric power [57].
The efficiency of DNNs can be increased by constructing the network following the principles of quantum computing [58,59,60] and optimising their algorithms using the fundamental laws of physics [61]. DNNs can also be built using the principles of neuromorphic computing [62,63].
Neuromorphic computers mimic the operation of a biological brain [62,64]. Several neuromorphic DNN models have been demonstrated [65,66], where, instead of relying on conventional Boolean arithmetic, information is processed using nonlinear dynamical properties of a physical system [63,64]. Such DNN models can be implemented as an inexpensive and low power consuming chip [65,67] suitable for applications in AI and robotics [66].

2.2. Quantum tunnelling effect

In quantum mechanics [48], the rectangular potential barrier is a computational problem that demonstrates the phenomenon of QT (Figure 2b). The problem consists in solving a one-dimensional time-independent Schrödinger equation for an electron that encounters a rectangular potential energy barrier [47]
− ℏ 2 2 m d 2 d x 2 + V ( x ) ψ ( x ) = E ψ ( x ) ,
where ψ ( x ) is a wave function, m ≈ 9.1093837 × 10 − 31 kg is the mass of the electron, ℏ ≈ 1.054571817 × 10 − 34 J·s is Plank’s constant and E is the energy of the electron. The profile of the potential barrier (Figure 2b) is
V ( x ) = 0 for x < 0 V 0 for 0 < x ≤ a 0 for x > a .
In classical mechanics, a counterpart of this physical system is a marble ball (Figure 2b). While a ball with energy E < V 0 cannot penetrate the barrier, an electron, behaving as a matter wave, has a non-zero probability of penetrating the barrier and continuing its motion on the other side. Similarly, for E > V 0 , the electron may be reflected from the barrier with a non-zero probability.
The electron tunnelling behaviour can be quantified by finding the transmission coefficient from the solution of Eq. (1) for the potential barrier given by Eq. (2). The solution of the Schrõdinger equation can be written as a superposition of left and right moving waves [47]
V ( x ) = ψ L ( x ) = A 1 e i k x + A 2 e − i k x , x < 0 ψ C ( x ) = B 1 e i κ x + B 2 e − i κ x , 0 < x ≤ a ψ R ( x ) = C 1 e i k x + C 2 e − i k x , x > a ,
where i is the imaginary unit, k = 2 m E / ℏ 2 and κ = 2 m α / ℏ 2 with α = E − V 0 (the special cases E = 0 and E = V 0 are treated separately). The coefficients A , B , C are found from the boundary conditions at x = 0 and x = a , requiring that ψ ( x ) and its derivative have to be continuous. Below, omitting the intermediate derivations [47], I present the expressions for the probability of the electron transmission through the barrier.
For electron energies smaller than the barrier height ( E < V 0 ), there is a non-zero transmission probability [47]
T | E < V 0 = 1 − β sinh 2 ( κ 1 a ) − 1 ,
where β = V 0 2 4 E α and κ 1 = − 2 m α / ℏ 2 . For E > V 0
T | E > V 0 = 1 + β sin 2 ( κ a ) − 1 ,
Finally, the expression for E = V 0 is obtained by taking the limit of T as E approaches V 0 , resulting in
T | E = V 0 = 1 + m a 2 V 0 2 ℏ 2 − 1 .

2.3. Quantum Tunnelling as an Activation Function

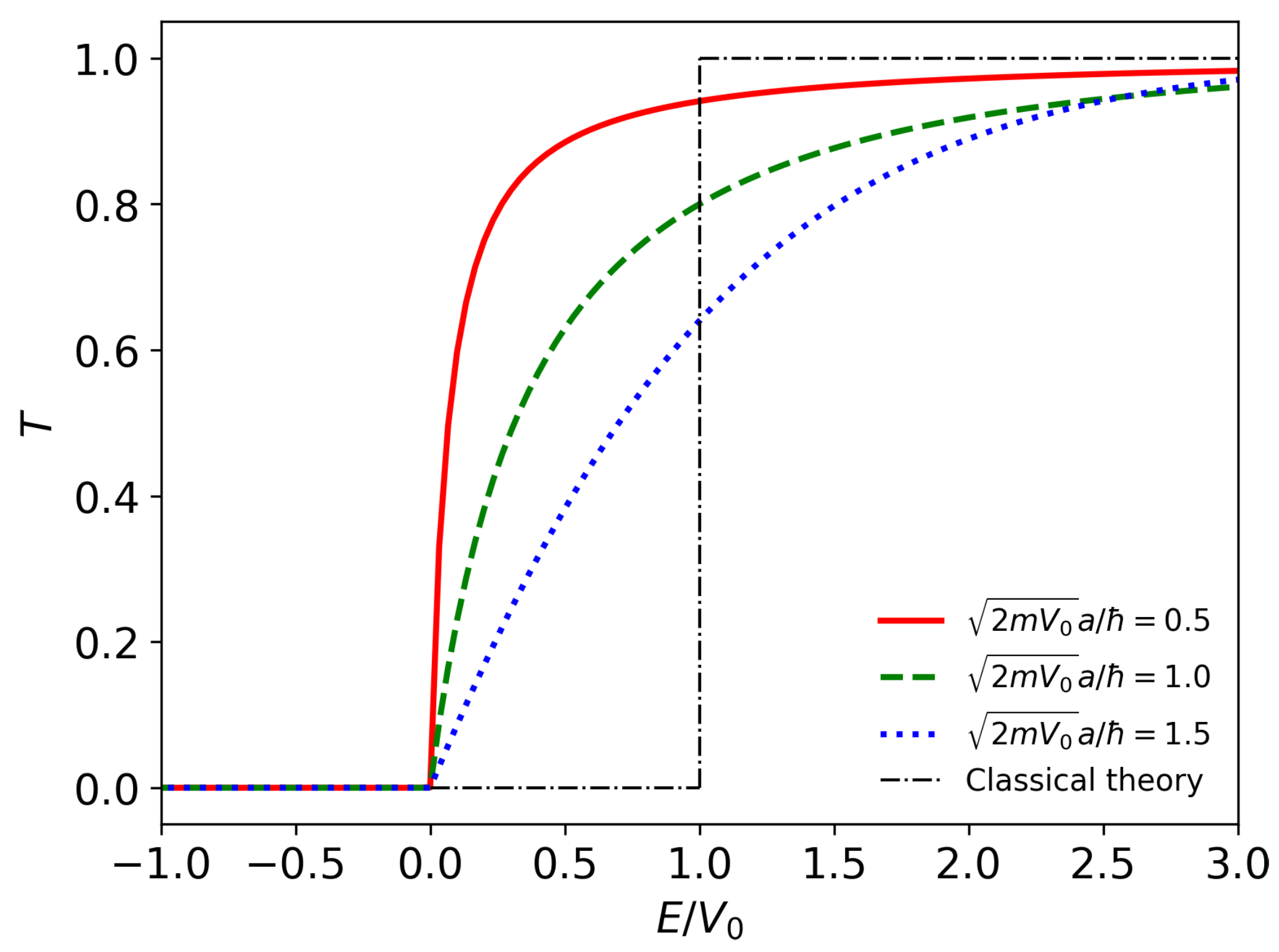
Figure 3 shows the probability of transmission of a single electron with energy E through a potential barrier with the nondimensionalised thickness 2 m V 0 a / ℏ . The result predicted by the classical theory is denoted by the straight dash-dotted lines. While physical implications of these results are well-known [47], in the following I will focus only on their meaning in the context of QT-DNN.
A close inspection of the curve plotted in Figure 3 reveals that the QT transmission function T can be employed as an activation function of the nodes of an DNN, provided that the energy of the electron E is interpreted as the input value of the node. In fact, similarly to the standard activation functions used in DNNs [14], T fulfils a number of essential mathematical criteria pertinent to the field of machine learning, including nonlinearity and differentiability, thus enabling its application with gradient-based optimisation methods [14,68]. Although the negative values of E / V 0 have no strict meaning in the framework of the physical model, in the QT-DNN model they can be interpreted as the inputs that produce a zero output. The special case E = 0 can be avoided programmatically. It is also noteworthy that the energy of the electron can be effectively amplified (see Sect. Section 4.2 for technical details), which is one of the features of the computational code that accompanies this paper.
Differentiating Eqs. (4–5) with respect to E, I obtain
T ′ | E < V 0 = − β ( sinh 2 ( δ 1 ) E + sinh 2 ( δ 1 ) − δ 1 cosh ( δ 1 ) sinh ( δ 1 ) α ) T 2 | E < V 0 , T ′ | E > V 0 = β sin 2 ( δ ) E + sin 2 ( δ ) − δ cos ( δ ) sin ( δ ) α T 2 | E > V 0 , T ′ | E = V 0 = 4 V 0 a 4 m 2 + 6 a 2 ℏ 2 m 3 V 0 2 a 4 m 2 + 12 V 0 a 2 ℏ 2 m + 12 ℏ 4 ,
where δ = κ a and δ 1 = κ 1 a .

2.4. QT-DNN Algorithm

The QT-DNN network used in this paper (Figure 2a) consists of an input layer that has L = 100 input nodes, three hidden layers each of which has N = 20 nodes and an output layer that has M = 2 output nodes that are used to classify the input dataset. The weights of the connections of the network are updated using a back-propagation training algorithm [14].
The activation function ϕ Q T of the nodes of the hidden layers and its derivative are given by Eqs. (4–7). The output nodes are governed by the Softmax function [14]
ϕ s m a x ( v i ) = exp ( v i ) ∑ k = 1 M exp ( v k ) ,
where v i is the weighted sum of input signals to the ith output node and M is the number of the output nodes.
The network is trained and exploited as follows. First, I construct the output nodes that correspond to the correct answers to the training datasets. Then, I initialise the weights of the neural network in the range from –1 to 1 using a random number generator. Entering the input data x j and the corresponding training data points d i , I calculate the error e i between the output y i and target d i as e i = d i − y i . Then, propagating the output δ i = e i in the backward direction of the network, I compute the respective parameters δ i ( n ) of the hidden nodes using the equations e i ( n ) = W ( n ) ⊤ δ i and δ i ( n ) = ϕ Q T ′ v i ( n ) e i ( n ) , where the index n denotes the sequential number of the hidden layer, prime denotes the derivative of the activation function and W ⊤ is the transpose of the matrix of weights corresponding to each relevant layer of the network. I continue the back-propagation process until the algorithm reaches the first hidden layer and then I update the weights using the learning rule w i j ( n ) ← w i j ( n ) + Δ w i j ( n ) , where w i j ( n ) are the weights between an output node i and input node j of the nth layer and Δ w i j ( n ) = α δ i ( n ) x j .
The computational steps outlined above are sequentially applied to all training data points. Typically, to obtain convergent results it suffices to complete 1000 epochs, using the learning rate parameter α = 0.01 .

2.5. Neuromorphic QT-DNN Model of Perception

A biological brain is a nonlinear dynamical system that exhibits chaotic behaviour [69]. This property has motivated the development of neuromorphic AI that mimics the operation of the brain by exploiting nonlinear dynamical properties of diverse physical systems [62,63,64].
The principal components of the human vision system, including the retina and visual cortex, also exhibit nonlinear dynamical properties that can be used to create neuromorphic computers [70]. The visual input to the retina is modulated by eye blinks and movements, which effectively converts spatial information in the temporal one [71], also playing an important role in cognition and visual perception [72,73,74]. Yet, the dynamics of eye blink is also nonlinear and it may exhibit phase changes and chaotic behaviour [75], which are the processes that underpin the perception of optical illusions [76].
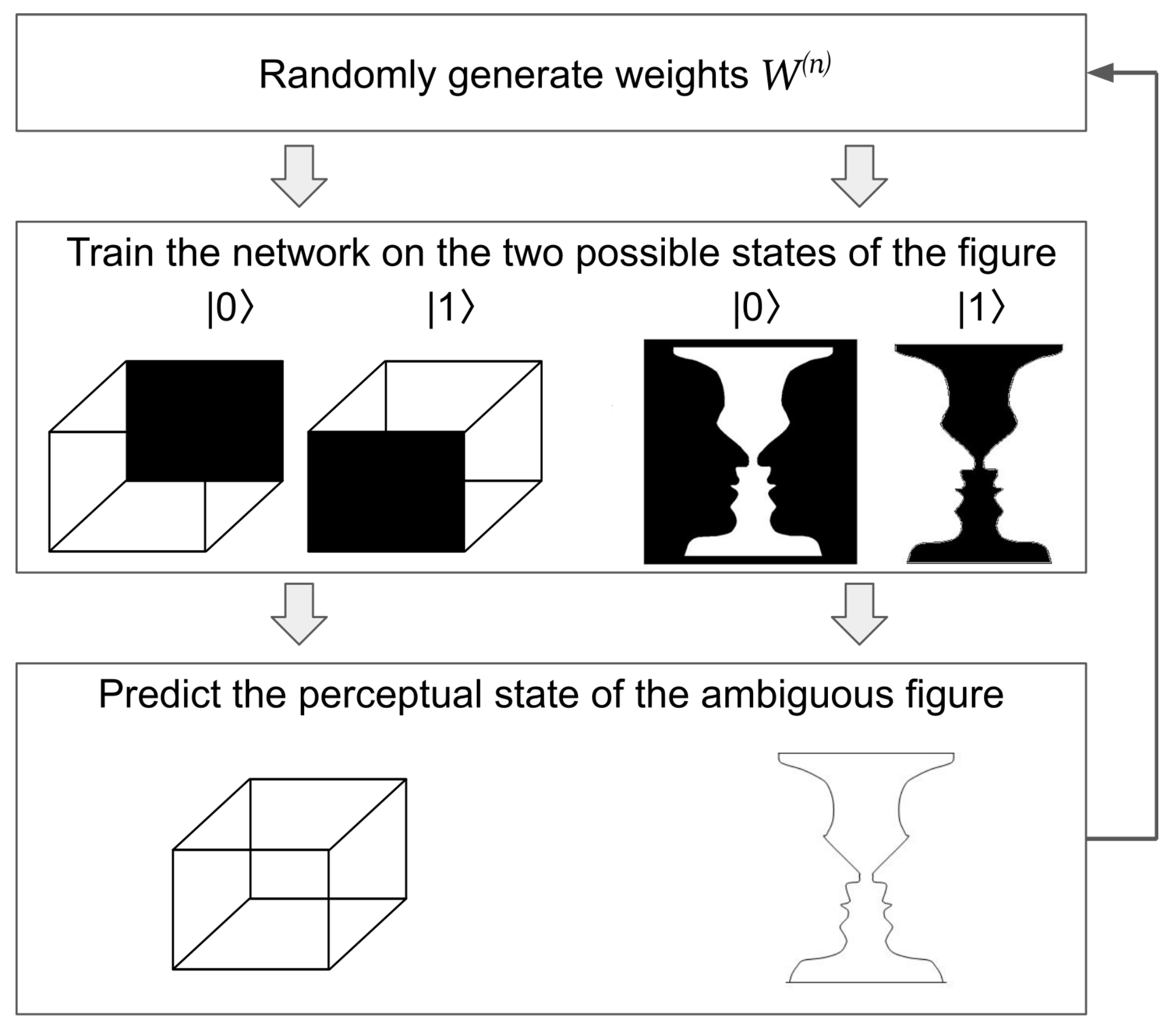
Based on these facts, it was demonstrated that the introduction of chaotic changes in the architecture of a neural network enables modelling the dynamics of information perception [23,24,25,26,27,77]. Thus, I randomly generate the weights W ( n ) , then I train QT-DNN on the 10 × 10 pixel unambiguous images of the Necker cube and then I exploit it to predict the perceptual state of the ambiguous Necker cube. This procedure is repeated in a loop to plot the dynamics of the perceived states (Figure 4).
Rubin’s vase training images had 20 × 20 pixels. Although some works studying the Necker cube claim that similar results would be obtained for Rubin’s vase [46], recent research demonstrated that Rubin’s vase has an increased contextual complexity [22]. Hence, I train QT-QNN using the figures with the shaded faces and vase, respectively, and then exploit it using a contour version of the drawing (Figure 4). Both shaded and contour versions have been used in the literature [21] and they represent an intriguing benchmarking task, especially because the shaded training images are also ambiguous.

3. Results and Discussion

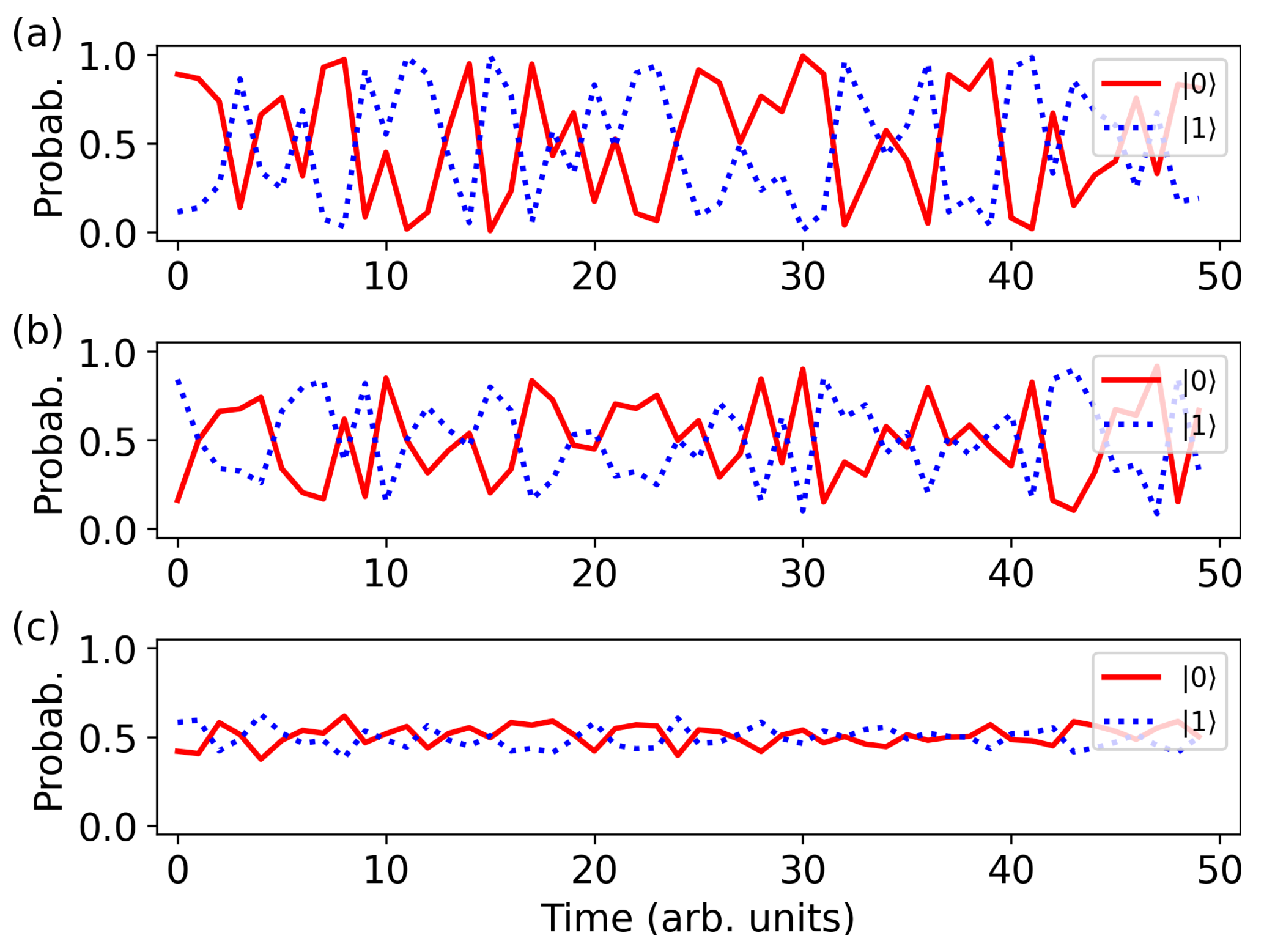
Figure 5 plots the simulated probability of perceiving | 0 〉 and | 1 〉 states of the Necker cube as a function of time (arbitrary time units are used in this work; for a relevant discussion of the cognitive timescale see Refs. [42,78]). In each panel of Figure 5, the nondimensionalised thickness of the potential barrier that is used as the activation function of QT-DNN (Figure 3) is 2 m V 0 a / ℏ = 0.5, 1 and 1.5.
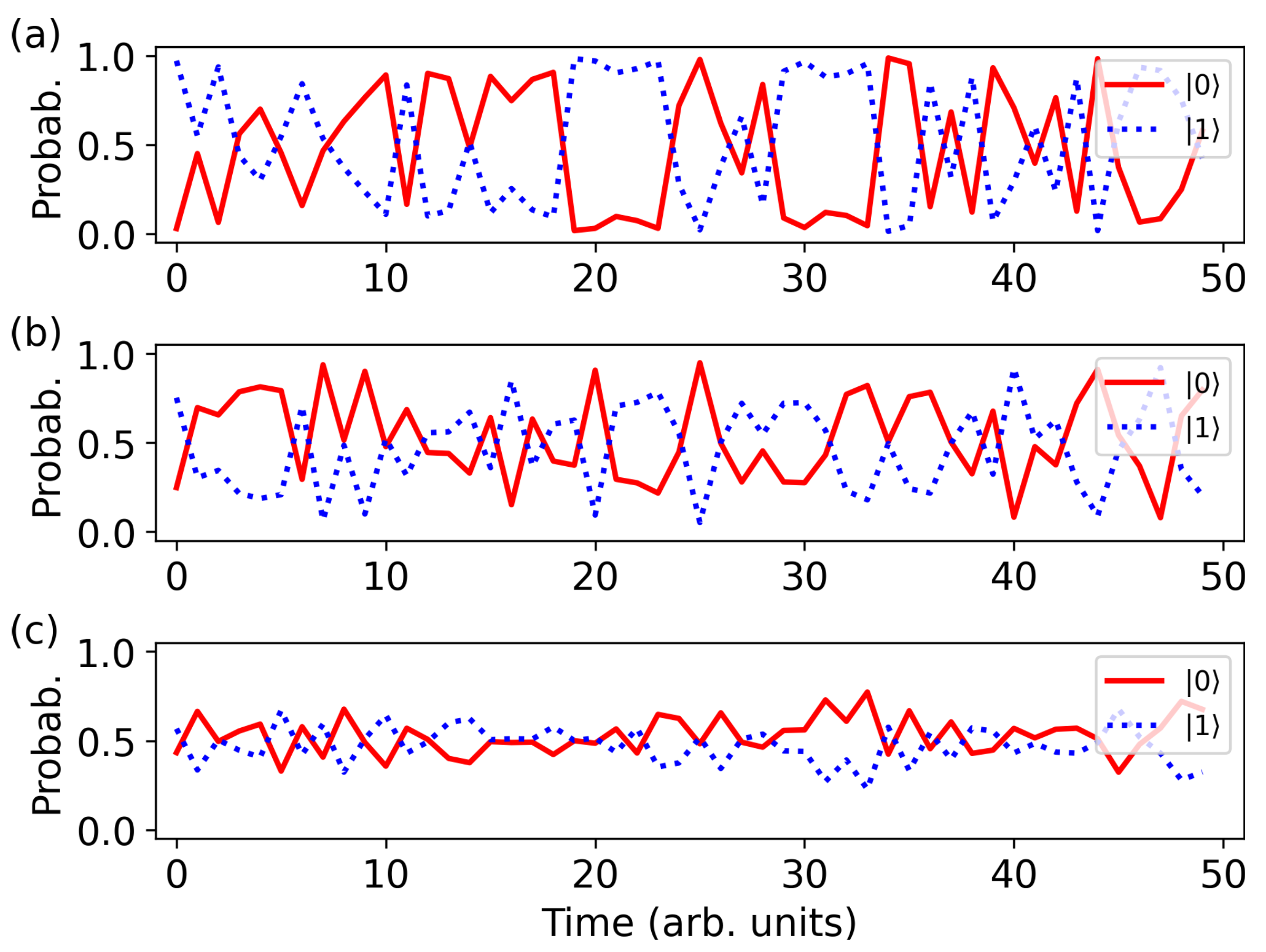
The probability curves were obtained after 50 consecutive computational runs of the algorithm outlined in Figure 4. The states of the two output nodes of QT-DNN were recorded at the end of each run. Every pair of those data points was computed using a unique set of neural weights W ( n ) . The same procedure was followed to simulate the perception of Rubin’s vase (Figure 6). The same value of barrier thickness and sets of W ( n ) were used in the respective panels of Figure 5 and Figure 6.
In Figure 5a, we can observe a time-dependent switching between the fundamental perceptual states | 0 〉 and | 1 〉 . The switching is not abrupt, as depicted in Figure 1c, but involves intermediate states that are a superposition of | 0 〉 and | 1 〉 . A similar switching pattern is observed in Figure 5b obtained for a thicker potential barrier. Although the probability of perceiving the states | 0 〉 and | 1 〉 decreases to approximately 0.85, in this case QT-DNN can readily distinguish the two states of the Necker cube.
Further increase in the thickness of the potential well (Figure 5c) results in a smaller difference between the probabilities of perceiving | 0 〉 and | 1 〉 . The so-configured QT-DNN operates similarly to perception by a human observer [78], who can quickly decode ambiguous visual information in just a few loops of recurrent biological neural activity [79], but needs much more time to decide which perceptual outcome should be reported.
In fact, I established that the same model with 2000 epochs produces a substantially more distinguishable perception pattern, which effectively means that the model requires more time to decide which perceptual state to report. Such a behaviour is beneficial for modelling the perception of illusions by different age and gender groups [80,81]. Indeed, since the dynamics of eye blink (and, therefore, the dynamics of visual information processing [71]) slows down with age [80], QT-DNN with thicker potential barriers appears to adequately model the perception of senior and visually impaired persons.
As can be seen in Figure 6, the perception switching of Rubin’s vase is similar to that of the Necker cube. Yet, QT-DNN better distinguishes the two perceptual states of Rubin’s vase, including in the case of a thick barrier (Figure 6c), without the need of increasing the number of epochs. This result is consistent with the hypothesis that states that Rubin’s vase combines an optical illusions with the perception of background [22]. Indeed, observers may interpret this figure not only as faces-vase but also as a white (black) vase on black (white) background, which gives them an additional point of reference that can be used to disambiguate the drawing.
Overall, the results presented in Figure 5 and Figure 6 are in good agreement with the predictions made by the alternative quantum cognition models [20,42,46]. Below it will also be shown that the operation of QT-DNN is consistent with the broader models of brain-mind interaction.

4. Implementation and Discussion

4.1. Software

Since one of the envisioned applications of the QT-DNN model is its integration with robotic platforms and autonomous vehicles, I implemented its algorithm in Python 3 and tested the resulting software on a Raspberry Pi 4 embedded computer (1.8 GHz CPU, 8 GB RAM, Linux Ubuntu Desktop 24.04 LTS) that is often used in onboard AI systems [82,83]. Using limited embedded computational resources, QT-DNN demonstrated the ability to be trained and exploited in less than 1 second of real time, which is an encouraging result that can be considered as on-the-fly operation. It is also worth noting that the Raspberry computer consumes just 3 W of onboard power compared with more expensive GPU-based onboard computers that are required to run traditional DNN algorithms and draw 25–30 W [82]. Therefore, QT-DNN algorithm also fulfils the criterion of energy efficiency.
The advantages of QT-DNN over the traditional neural network models amplify when software that implements it runs on a high-performance workstation computer. For example, significantly lower accuracy of neural network models trained on regular images but tested on negative ones has been reported in the previous works [84]. The nominal `vase’ state of the training images of (Figure 4) is the negative image of the `faces’ state. Subsequently, since the algorithm of QT-DNN demonstrated good performance in this image recognition scenario, it is plausible to assume that QT-based activation functions can be employed in image recognition models trained on negative images. Such models have important practical applications, including ship detection and recognition in maritime environments [85] and creative arts [86].
QT-DNN can also enhance the capabilities of models employed in the emergent field of sociophysics [9]. Indeed, since the effect of QT also underpins the operation of several physics-inspired models of human opinion formation and radicalisation in social networks [10], the algorithm of QT-DNN can be adopted in the studies of fake news [11] and research on gender and racial biases [10].

4.2. Potential Hardware Implementations

The effect of QT has been exploited in semiconductor electronic devices [87,88,89,90] and different modalities of spectroscopy [91,92] and microscopy [92,93]. It has also been demonstrated that electron devices exploiting the effect of QT can serve as a building block of neuromorphic computers [94,95]. However, in those computers QT has not been exploited directly. Instead, nonlinear dynamics of the whole QT-based electron devices and circuits formed by them has been employed as a means of computation.
In practice, the architecture of QT-DNN can be implemented using tunnelling [87] and resonant tunnelling [89] diodes. Moreover, there exist neuromorphic computing schemes that exploit negative differential resistance [96,97], a prominent feature of tunnelling diodes. Importantly, systems based on tunnelling diodes and other QT-based devices consume low electric power compared with the traditional integrated electronic circuits [94].
Alternatively, QT-DNN can be embodied using the instrumentation of scanning tunnelling microscopy (STM) [93]. For example, amplifiers developed for STM operate at microwave frequencies, enabling high signal-to-noise ratios and facilitating differential conductance spectroscopy measurements [98]. Finally, QT of individual electrons was measured in quantum dots [96]—building blocks of quantum neuromorphic systems [99].

5. Conclusions and Outlook

In this paper, I pointed out the possibility of employing the effect of quantum tunnelling as an activation function of artificial neural networks. I demonstrated that the so-constructed neural networks enable accurate modelling of human perception of optical illusions. Yet, I suggested that low power consuming, hardware neuromorphic chips built using quantum tunnelling diodes or other devices and systems based on the tunnelling effect can be employed in conscious robots and autonomous vehicles. Finally, I traced a link between quantum tunnelling and sociophysical models designed to understand human behaviour in social and political groups.
So there is just one question that needs to be clarified: how can the effect of quantum tunnelling be related to cognition? This question is important because the current works on quantum models of cognition and decision-making mostly exploit the laws and methods of quantum mechanics to create phenomenological models [10,100]. While this approach has produced practically important results [9,11], addressing this question in more detail promises to attract the attention of a larger number of experts to the emergent field of sociophysical AI.
Tunnelling can be observed in all quantum systems, which explains why many Nobel prizes in physics were awarded for research involving it [101]. This physical effect is also crucial for chemical and biological evolution [102]. Most likely, it also played an essential role in the formation of the early universe and life [101,102]. Subsequently, since quantum tunnelling remains an important topic of scientific research, there have been theoretical and experimental attempts to explain the function of biological brain neurons relying on the principles of quantum mechanics [54,103] (arguably, some of those ideas could also contribute to Nobel prize-winning discoveries [104]).
Drawing on the difference between a conscious mind and a biological brain, it was suggested that the mind and brain can interact by means of quantum tunnelling [53]. Indeed, based on the cited paper and references therein, it can be said that a mental state becomes neurally effective when a large number of biological potential barriers in neurons produce high transmission probability amplitudes, which, in turn, results in a coherent action.
If proven correct, that hypothesis justifies the design of the QT-DNN model, showing that the use of tunnelling as an activation function is more than just an phenomenological mathematical approach but a model based on the fundamental principles of cognition and brain organisation. The same should be the case of the other sociophysical and quantum mind theories.

Data Availability Statement

The computational code that implements QT-DNN can be found at https://github.com/IvanMaksymov/DeepTunnel (accessed on 26 June 2024)

References

  1. Takeno, J. Creation of a Conscious Robot: Mirror Image Cognition and Self-Awareness; CRC Press, Boca Raton, 2013.
  2. Yamamoto, S.; Yamamoto, M. Effects of the gravitational vertical on the visual perception of reversible figures. Neurosci. Res. 2006, 55, 218–121. [Google Scholar] [CrossRef] [PubMed]
  3. Clément, G.; Allaway, H.C.M.; Demel, M.; Golemis, A.; Kindrat, A.N.; Melinyshyn, A.N.; Merali, T.; Thirsk, R. Long-duration spaceflight increases depth ambiguity of reversible perspective figures. PLOS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
  4. Ni, Y.; Du, Z.; Wang, S.; Jiao, F. , Rectification of Driver’s Visual Illusion on Continuous Downhill of Urban Underwater Tunnel. In CICTP 2020; pp. 3692–3704. [CrossRef]
  5. Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; Petersen, S.; Beattie, C.; Sadik, A.; Antonoglou, I.; King, H.; Kumaran, D.; Wierstra, D.; Legg, S.; Hassabis, D. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
  6. Kuperwajs, I.; Schütt, H.H.; Ma, W.J. Using deep neural networks as a guide for modeling human planning. Sci. Rep. 2023, 13, 20269. [Google Scholar] [CrossRef]
  7. Khalid, M.N.A.; Iida, H. Objectivity and subjectivity in games: Understanding engagement and addiction mechanism. IEEE Access 2021, 9, 65187–65205. [Google Scholar] [CrossRef]
  8. Wang, P.Y.C.; Xu, C.H.; Wang, P.Y.; Huang, H.Y.; Chang, Y.W.; Cheng, J.H.; Lin, Y.H.; Cheng, L.P. Game Illusionization: A Workflow for Applying Optical Illusions to Video Games. The 34th Annual ACM Symposium on User Interface Software and Technology; Association for Computing Machinery: New York, NY, USA, 2021; pp. 1326–1344. [Google Scholar] [CrossRef]
  9. Galam, S. Sociophysics: A Physicist’s Modeling of Psycho-political Phenomena; Springer New York, 2012.
  10. Maksymov, I.S.; Pogrebna, G. Quantum-mechanical modelling of asymmetric opinion polarisation in social networks. Information 2024, 15, 170. [Google Scholar] [CrossRef]
  11. Galam, S. Fake News: “No Ban, No Spread—With Sequestration”. Physics 2024, 6, 859–876. [Google Scholar] [CrossRef]
  12. Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman lectures on physics; New millennium ed.; Basic Books: New York, NY, 2010. [Google Scholar]
  13. Kortli, Y.; Jridi, M.; Al Falou, A.; Atri, M. Face recognition systems: a survey. Sensors 2020, 20, 342. [Google Scholar] [CrossRef]
  14. Kim, P. MATLAB Deep Learning With Machine Learning, Neural Networks and Artificial Intelligence; Apress Berkeley, CA, 2017.
  15. Wencheng, W.; Ge, Y.; Zuo, Z.; Chen, L.; Qin, X.; Zuxiang, L. Visual number sense for real-world scenes shared by deep neural networks and humans. Heliyon 2023, 9, e18517. [Google Scholar] [CrossRef]
  16. Nguyen, A.; Yosinski, J.; Clune, J. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015, pp. 427–436. [CrossRef]
  17. Feather, J.; Leclerc, G.; Madry, A.; McDermott, J.H. Model metamers reveal divergent invariances between biological and artificial neural networks. Nat. Neurosci. 2023, 26, 2017–2034. [Google Scholar] [CrossRef]
  18. Cheng, F.L.; Horikawa, T.; Majima, K.; Tanaka, M.; Abdelhack, M.; Aoki, S.C.; Hirano, J.; Kamitani, Y. Reconstructing visual illusory experiences from human brain activity. Sci. Adv. 2023, 9, eadj3906. [Google Scholar] [CrossRef] [PubMed]
  19. Kornmeier, J.; Bach, M. The Necker cube–an ambiguous figure disambiguated in early visual processing. Vision Res. 2005, 45, 955–960. [Google Scholar] [CrossRef] [PubMed]
  20. Busemeyer, J.R.; Bruza, P.D. Quantum Models of Cognition and Decision; Oxford University Press, New York, 2012.
  21. Pinna, B.; Reeves, A.; Koenderink, J.; van Doorn, A.; Deiana, K. A new principle of figure-ground segregation: The accentuation. Vis. Res. 2018, 143, 9–25. [Google Scholar] [CrossRef] [PubMed]
  22. Khalil, E.L. Why does Rubin’s vase differ radically from optical Illusions? Framing effects contra cognitive illusions. Front. Psychol. 2021, 12. [Google Scholar] [CrossRef] [PubMed]
  23. Maksymov, I.S. Quantum-inspired neural network model of optical illusions. Algorithms 2024, 17, 30. [Google Scholar] [CrossRef]
  24. Inoue, M.; Nakamoto, K. Dynamics of cognitive interpretations of a Necker cube in a chaos neural network. Prog. Theor. Phys. 1994, 92, 501–508. [Google Scholar] [CrossRef]
  25. Gaetz, M.; Weinberg, H.; Rzempoluck, E.; Jantzen, K.J. Neural network classifications and correlation analysis of EEG and MEG activity accompanying spontaneous reversals of the Necker cube. Cogn. Brain Res. 1998, 6, 335–346. [Google Scholar] [CrossRef] [PubMed]
  26. Shimaoka, D.; Kitajo, K.; Kaneko, K.; Yamaguchi, Y. Transient process of cortical activity during Necker cube perception: from local clusters to global synchrony. Nonlinear Biomed. Phys. 2010, 4, S7. [Google Scholar] [CrossRef] [PubMed]
  27. Araki, O.; Tsuruoka, Y.; Urakawa, T. A neural network model for exogenous perceptual alternations of the Necker cube. Cogn. Neurodyn. 2020, 14, 229–237. [Google Scholar] [CrossRef]
  28. Sun, L.; Wang, Z.; Jiang, J.; Kim, Y.; Joo, B.; Zheng, S.; Lee, S.; Yu, W.J.; Kong, B.S.; Yang, H. In-sensor reservoir computing for language learning via two-dimensional memristors. Sci. Adv. 2021, 7, eabg1455. [Google Scholar] [CrossRef]
  29. Zhang, H.; Yoshida, S.; Li, Z. Brain-like illusion produced by Skye’s Oblique Grating in deep neural networks. PLOS ONE 2024, 19, e0299083. [Google Scholar] [CrossRef]
  30. Zhang, H.; Yoshida, S. Exploring deep neural networks in simulating human vision through five optical illusions. Appl. Sci. 2024, 14, 3429. [Google Scholar] [CrossRef]
  31. Long, G.M.; Toppino, T.C. Enduring interest in perceptual ambiguity: alternating views of reversible figures. Psychol. Bull. 2004, 130, 748–768. [Google Scholar] [CrossRef] [PubMed]
  32. Carbon, C.C. Understanding human perception by human-made illusions. Front. Hum. Neurosci. 2014, 8. [Google Scholar] [CrossRef]
  33. Watanabe, E.; Kitaoka, A.; Sakamoto, K.; Yasugi, M.; Tanaka, K. Illusory motion reproduced by deep neural networks trained for prediction. Front. Psychol. 2018, 9. [Google Scholar] [CrossRef]
  34. Mély, D.A.; Linsley, D.; Serre, T. Complementary surrounds explain diverse contextual phenomena across visual modalities. Psychol. Rev. 2018, 125, 769–784. [Google Scholar] [CrossRef] [PubMed]
  35. Kubota, Y.; Hiyama, A.; Inami, M. A Machine Learning Model Perceiving Brightness Optical Illusions: Quantitative Evaluation with Psychophysical Data. Proceedings of the Augmented Humans International Conference 2021, 2021, pp. 174–182. [Google Scholar] [CrossRef]
  36. Shahgir, H.S.; Sayeed, K.S.; Bhattacharjee, A.; Ahmad, W.U.; Dong, Y.; Shahriyar, R. IllusionVQA: A Challenging Optical Illusion Dataset for Vision Language Models, 2024, [2403. 1 5952.
  37. Paxton, A.B.; Smith, D. Visual cues from an underwater illusion increase relative abundance of highly reef-associated fish on an artificial reef. Mar. Freshwater Res. 2018, 69, 614–619. [Google Scholar] [CrossRef]
  38. Agrillo, C.; Santacà, M.; Pecunioso, A.; Petrazzini, M.E.M. Everything is subjective under water surface, too: visual illusions in fish. Anim. Cogn. 2020, 23, 251–264. [Google Scholar] [CrossRef]
  39. Piantoni, G.; Romeijn, N.; Gomez-Herrero, G.; Van Der Werf, Y.D.; Van Someren, E.J.W. Alpha power predicts persistence of bistable perception. Sci. Rep. 2017, 7, 5208. [Google Scholar] [CrossRef] [PubMed]
  40. Joos, E.; Giersch, A.; Hecker, L.; Schipp, J.; Heinrich, S.P.; van Elst, L.T.; Kornmeier, J. Large EEG amplitude effects are highly similar across Necker cube, smiley, and abstract stimuli. PLoS ONE 2020, 15, e0232928. [Google Scholar] [CrossRef]
  41. Matsumiya, K.; Furukawa, S. Perceptual decisions interfere more with eye movements than with reach movements. Commun. Biol. 2023, 6, 882. [Google Scholar] [CrossRef] [PubMed]
  42. Atmanspacher, H.; Filk, T.; Römer, H. Quantum Zeno features of bistable perception. Biol. Cybern. 2004, 90, 33–40. [Google Scholar] [CrossRef] [PubMed]
  43. Khrennikov, A. Quantum-like brain: “Interference of minds”. Biosystems 2006, 84, 225–241. [Google Scholar] [CrossRef] [PubMed]
  44. Pothos, E.M.; Busemeyer, J.R. Quantum Cognition. Annu. Rev. Psychol. 2022, 73, 749–778. [Google Scholar] [CrossRef]
  45. Liaci, E.; Fischer, A.; Atmanspacher, H.; Heinrichs, M.; Tebartz van Elst, L.; Kornmeier, J. Positive and negative hysteresis effects for the perception of geometric and emotional ambiguities. PLOS ONE 2018, 13, e0202398. [Google Scholar] [CrossRef]
  46. Benedek, G.; Caglioti, G. Graphics and Quantum Mechanics–The Necker Cube as a Quantum-like Two-Level System. Proceedings of the 18th International Conference on Geometry and Graphics; Cocchiarella, L., Ed. Springer International Publishing, 2019, pp. 161–172.
  47. McQuarrie, D.A.; Simon, J.D. Physical Chemistry – A Molecular Approach; Prentice Hall, New York, 1997.
  48. Griffiths, D.J. Introduction to Quantum Mechanics; Prentice Hall, New Jersey, 2004.
  49. Abbas, A.H.; Maksymov, I.S. Reservoir computing using measurement-controlled quantum dynamics. Electronics 2024, 13, 1164. [Google Scholar] [CrossRef]
  50. Symul, T.; Assad, S.M.; Lam, P.K. Real time demonstration of high bitrate quantum random number generation with coherent laser light. Appl. Phys. Lett. 2011, 98, 231103. [Google Scholar] [CrossRef]
  51. Dehais, F.; Ladouce, S.; Darmet, L.; Nong, T.V.; Ferraro, G.; Torre Tresols, J.; Velut, S.; Labedan, P. Dual passive reactive brain-computer interface: a novel approach to human-machine symbiosis. Front. Neuroergonomics 2022, 3. [Google Scholar] [CrossRef]
  52. Tacikowski, P.; Fust, J.; Ehrsson, H.H. Fluidity of gender identity induced by illusory body-sex change. Sci. Reps. 2020, 10, 14385. [Google Scholar] [CrossRef] [PubMed]
  53. Beck, F.; Eccles, J.C. Quantum aspects of brain activity and the role of consciousness. PNAS 1992, 89, 11357–11361. [Google Scholar] [CrossRef] [PubMed]
  54. Georgiev, D.D.; Glazebrook, J.F. The quantum physics of synaptic communication via the SNARE protein complex. Prog. Biophys. Mol. 2018, 135, 16–29. [Google Scholar] [CrossRef] [PubMed]
  55. Maji, P.; Mullins, R. On the reduction of computational complexity of deep convolutional neural networks. Entropy 2018, 20, 305. [Google Scholar] [CrossRef] [PubMed]
  56. Oh, K.S.; Jung, K. GPU implementation of neural networks. Pattern Recognit. 2004, 37, 1311–1314. [Google Scholar] [CrossRef]
  57. de Vries, A. The growing energy footprint of artificial intelligence. Joule 2023, 7, 2191–2194. [Google Scholar] [CrossRef]
  58. Wan, K.H.; Dahlsten, O.; Kristjánsson, H.; Gardner, R.; Kim, M.S. Quantum generalisation of feedforward neural networks. Npj Quantum Inf. 2017, 3, 36. [Google Scholar] [CrossRef]
  59. Beer, K.; Bondarenko, D.; Farrelly, T.; Osborne, T.J.; Salzmann, R.; Scheiermann, D.; Wolf, R. Training deep quantum neural networks. Nat. Commun. 2020, 11, 808. [Google Scholar] [CrossRef]
  60. Pan, X.; Lu, Z.; Wang, W.; Hua, Z.; Xu, Y.; Li, W.; Cai, W.; Li, X.; Wang, H.; Song, Y.P.; Zou, C.L.; Deng, D.L.; Sun, L. Deep quantum neural networks on a superconducting processor. Nat. Commun. 2023, 14, 4006. [Google Scholar] [CrossRef]
  61. Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
  62. Tanaka, G.; Yamane, T.; Héroux, J.B.; Nakane, R.; Kanazawa, N.; Takeda, S.; Numata, H.; Nakano, D.; Hirose, A. Recent advances in physical reservoir computing: A review. Neural Newt. 2019, 115, 100–123. [Google Scholar] [CrossRef] [PubMed]
  63. Marcucci, G.; Pierangeli, D.; Conti, C. Theory of neuromorphic computing by waves: machine learning by rogue waves, dispersive shocks, and solitons. Phys. Rev. Lett. 2020, 125, 093901. [Google Scholar] [CrossRef] [PubMed]
  64. Maksymov, I.S. Analogue and physical reservoir computing using water waves: Applications in power engineering and beyond. Energies 2023, 16, 5366. [Google Scholar] [CrossRef]
  65. Onen, M.; Emond, N.; Wang, B.; Zhang, D.; Ross, F.M.; Li, J.; Yildiz, B.; del Alamo, J.A. Nanosecond protonic programmable resistors for analog deep learning. Science 2022, 377, 539–543. [Google Scholar] [CrossRef] [PubMed]
  66. Ye, N.; Cao, L.; Yang, L.; Zhang, Z.; Fang, Z.; Gu, Q.; Yang, G.Z. Improving the robustness of analog deep neural networks through a Bayes-optimized noise injection approach. Commun. Eng. 2023, 2, 25. [Google Scholar] [CrossRef]
  67. Trensch, G.; Morrison, A. A system-on-chip based hybrid neuromorphic compute node architecture for reproducible hyper-real-time simulations of spiking neural networks. Front. Neuroinform. 2022, 16. [Google Scholar] [CrossRef] [PubMed]
  68. Schmidgall, S.; Ziaei, R.; Achterberg, J.; Kirsch, L.; Hajiseyedrazi, S.P.; Eshraghian, J. Brain-inspired learning in artificial neural networks: A review. APL Mach. Learn. 2024, 2, 021501. [Google Scholar] [CrossRef]
  69. Korn, H.; Faure, P. Is there chaos in the brain? II. Experimental evidence and related models. C. R. Biol. 2003, 326, 787–840. [Google Scholar] [CrossRef] [PubMed]
  70. Wang, S.; Wang, C.Y.; Wang, P.; Wang, C.; Li, Z.A.; Pan, C.; Dai, Y.; Gao, A.; Liu, C.; Liu, J.; Yang, H.; Liu, X.; Cheng, B.; Chen, K.; Wang, Z.; Watanabe, K.; Taniguchi, T.; Liang, S.J.; Miao, F. Networking retinomorphic sensor with memristive crossbar for brain-inspired visual perception. Natl. Sci. Rev 2020, 8, nwaa172. [Google Scholar] [CrossRef]
  71. Yang, B.; Intoy, J.; Rucci, M. Eye blinks as a visual processing stage. PNAS 2024, 121, e2310291121. [Google Scholar] [CrossRef]
  72. Sakai, K.; Katayama, T.; Wada, S.; Oiwa, K. Chaos causes perspective reversals for ambiguious patterns. Advances in Intelligent Computing — IPMU ’94; Bouchon-Meunier, B., Yager, R.R., Zadeh, L.A., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1995; pp. 463–472. [Google Scholar]
  73. Ang, J.W.A.; Maus, G.W. Boosted visual performance after eye blinks. J. Vis. 2020, 20. [Google Scholar] [CrossRef] [PubMed]
  74. Hershman, R.; Share, D.L.; Weiss, E.M.; Henik, A.; Shechter, A. Insights from eye blinks into the cognitive processes involved in visual word recognition. J. Cogn. 2024, 7, 14. [Google Scholar] [CrossRef] [PubMed]
  75. Harezlak, K.; Kasprowski, P. Searching for chaos evidence in eye movement signals. Entropy 2018, 20, 32. [Google Scholar] [CrossRef] [PubMed]
  76. Gladilin, E.; Eils, R. On the role of spatial phase and phase correlation in vision, illusion, and cognition. Front. Comput. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
  77. Kaneko, K. Chaotic but regular posi-nega switch among coded attractors by cluster-size variation. Phys. Rev. Lett, 1989, 63, 219–223. [Google Scholar] [CrossRef] [PubMed]
  78. Kornmeier, J.; Bach, M. Ambiguous figures – what happens in the brain when perception changes but not the stimulus. Front. Hum. Neurosci. 2012, 6. [Google Scholar] [CrossRef]
  79. Lamme, V.A.; Roelfsema, P.R. The distinct modes of vision offered by feedforward and recurrent processing. Trends Neurosci. 2000, 23, 571–579. [Google Scholar] [CrossRef] [PubMed]
  80. Sun, W.S.; Baker, R.S.; Chuke, J.C.; Rouholiman, B.R.; Hasan, S.A.; Gaza, W.; Stava, M.W.; Porter, J.D. Age-related changes in human blinks. Passive and active changes in eyelid kinematics. Invest. Ophthalmol. Vis. Sci. 1997, 38, 92–99. [Google Scholar] [PubMed]
  81. Lo, C.; Dinov, I. Investigation of optical illusions on the aspects of gender and age. UCLA USJ 2011, 24. [Google Scholar]
  82. Biglari, A.; Tang, W. A review of embedded machine learning based on hardware, application, and sensing scheme. Sensors 2023, 23, 2131. [Google Scholar] [CrossRef]
  83. Yu, Z.; Sadati, S.M.H.; Perera, S.; Hauser, H.; Childs, P.R.N.; Nanayakkara, T. Tapered whisker reservoir computing for real-time terrain identification-based navigation. Sci. Rep. 2023, 13, 5213. [Google Scholar] [CrossRef] [PubMed]
  84. Hosseini, H.; Xiao, B.; Jaiswal, M.; Poovendran, R. On the Limitation of Convolutional Neural Networks in Recognizing Negative Images. 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), 2017, pp. 352–358. [CrossRef]
  85. Gao, L.; He, Y.; Sun, X.; Jia, X.; Zhang, B. Incorporating negative sample training for ship detection based on deep learning. Sensors 2019, 19, 684. [Google Scholar] [CrossRef]
  86. Cave, A. Shooting with Soul; Quarry Books, Beverly, MA, 2013.
  87. Esaki, L. New phenomenon in narrow germanium p-n junctions. Phys. Rev. 1958, 109, 603–604. [Google Scholar] [CrossRef]
  88. Kahng, D.; Sze, S.M. A floating gate and its application to memory devices. Bell Syst. Tech. J. 1967, 46, 1288–1295. [Google Scholar] [CrossRef]
  89. Chang, L.L.; Esaki, L.; Tsu, R. Resonant tunneling in semiconductor double barriers. Appl. Phys. Lett. 1974, 12, 593–595. [Google Scholar] [CrossRef]
  90. Ionescu, A.M.; Riel, H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature 2011, 479, 329–337. [Google Scholar] [CrossRef] [PubMed]
  91. Modinos, A. Field emission spectroscopy. Prog. Surf. Sci. 1993, 42, 45. [Google Scholar] [CrossRef]
  92. Rahman Laskar, M.A.; Celano, U. Scanning probe microscopy in the age of machine learning. APL Mach. Learn. 2023, 1, 041501. [Google Scholar] [CrossRef]
  93. Binnig, G.; Rohrer, H. Scanning tunneling microscopy—from birth to adolescence. Rev. Mod. Phys. 1987, 59, 615–625. [Google Scholar] [CrossRef]
  94. Feng, Y.; Tang, M.; Sun, Z.; Qi, Y.; Zhan, X.; Liu, J.; Zhang, J.; Wu, J.; Chen, J. Fully flash-based reservoir computing network with low power and rich states. IEEE Trans. Electron Devices 2023, 70, 4972–4975. [Google Scholar] [CrossRef]
  95. Kwon, D.; Woo, S.Y.; Lee, K.H.; Hwang, J.; Kim, H.; Park, S.H.; Shin, W.; Bae, J.H.; Kim, J.J.; Lee, J.H. Reconfigurable neuromorphic computing block through integration of flash synapse arrays and super-steep neurons. Sci. Adv. 2023, 9, eadg9123. [Google Scholar] [CrossRef] [PubMed]
  96. Yilmaz, Y.; Mazumder, P. Image processing by a programmable grid comprising quantum dots and memristors. IEEE Trans. Nanotechnol. 2013, 12, 879–887. [Google Scholar] [CrossRef]
  97. Kent, R.M.; Barbosa, W.A.S.; Gauthier, D.J. Controlling chaos using edge computing hardware. Nat. Commun. 2024, 15, 3886. [Google Scholar] [CrossRef] [PubMed]
  98. Bastiaans, K.M.; Benschop, T.; Chatzopoulos, D.; Cho, D.; Dong, Q.; Jin, Y.; Allan, M.P. Amplifier for scanning tunneling microscopy at MHz frequencies. Rev. Sci. Instrum. 2018, 89, 093709. [Google Scholar] [CrossRef]
  99. Marković, D.; Grollier, J. Quantum neuromorphic computing. Appl. Phys. Lett. 2020, 117, 150501. [Google Scholar] [CrossRef]
  100. Maksymov, I.S. Quantum Mechanics of Human Perception, Behaviour and Decision-Making: A Do-It-Yourself Model Kit for Modelling Optical Illusions and Opinion Formation in Social Networks, 2024, [arXiv:physics.soc-ph/2404.10554].
  101. Merzbacher, E. The early history of quantum tunneling. Phys. Today 2002, 55, 44–49. [Google Scholar] [CrossRef]
  102. Trixler, F. Quantum tunnelling to the origin and evolution of life. Curr. Org. Chem. 2013, 17, 1758–1770. [Google Scholar] [CrossRef]
  103. Koch, C.; Hepp, K. Quantum mechanics in the brain. Nature 2006, 440, 611. [Google Scholar] [CrossRef]
  104. Eccles, J.C. The Ionic Mechanism of Postsynaptic Inhibition; Nobel Lectures, 1963.
Preprints 110484 g001
Figure 1. (a) The Necker cube: The answer to the question `Is the shaded face of the cube at the front or at the rear?’ will randomly switch between two stable perceptual states corresponding to the front ( | 0 〉 ) and rear ( | 1 〉 ) face of the cube. (b) Rubin’s vase: Do you see two people looking towards each other ( | 0 〉 ) or a vase ( | 1 〉 )?’ (c) According to the traditional psychological theories, the change from one perceptual state to another is instantaneous (the dotted line). However, current research works demonstrate that humans might see a superposition of the states | 0 〉 and | 1 〉 (the solid curve).
Figure 1. (a) The Necker cube: The answer to the question `Is the shaded face of the cube at the front or at the rear?’ will randomly switch between two stable perceptual states corresponding to the front ( | 0 〉 ) and rear ( | 1 〉 ) face of the cube. (b) Rubin’s vase: Do you see two people looking towards each other ( | 0 〉 ) or a vase ( | 1 〉 )?’ (c) According to the traditional psychological theories, the change from one perceptual state to another is instantaneous (the dotted line). However, current research works demonstrate that humans might see a superposition of the states | 0 〉 and | 1 〉 (the solid curve).
Preprints 110484 g001
Preprints 110484 g002
Figure 2. (a) Sketch of QT-DNN structure. W ( n ) with n = 1 ⋯ 4 are the matrices of the weights of the network connections. (b) QT-DNN model employs the physical effect of QT as the activation function of its nodes. Panel (b.i): one-dimensional rectangular potential barrier of thickness a and height V 0 . Panel (b.ii): unlike in classical mechanics, in quantum mechanics there is a non-zero probability for an electron with energy E < V 0 to be transmitted through the barrier.
Figure 2. (a) Sketch of QT-DNN structure. W ( n ) with n = 1 ⋯ 4 are the matrices of the weights of the network connections. (b) QT-DNN model employs the physical effect of QT as the activation function of its nodes. Panel (b.i): one-dimensional rectangular potential barrier of thickness a and height V 0 . Panel (b.ii): unlike in classical mechanics, in quantum mechanics there is a non-zero probability for an electron with energy E < V 0 to be transmitted through the barrier.
Preprints 110484 g002
Preprints 110484 g003
Figure 3. Transmission probability of an electron with energy E through a rectangular potential barrier with a nondimensionalised thickness 2 m V 0 a / ℏ . The straight dash-dotted lines denote the result predicted by the classical theory.
Figure 3. Transmission probability of an electron with energy E through a rectangular potential barrier with a nondimensionalised thickness 2 m V 0 a / ℏ . The straight dash-dotted lines denote the result predicted by the classical theory.
Preprints 110484 g003
Preprints 110484 g004
Figure 4. Neuromorphic algorithm involving the training of the network on distinguishable images of objects and its further exploitation aimed to recognise optical illusions.
Figure 4. Neuromorphic algorithm involving the training of the network on distinguishable images of objects and its further exploitation aimed to recognise optical illusions.
Preprints 110484 g004
Preprints 110484 g005
Figure 5. Perceptual switching curves produced by QT-DNN trained on the Necker cube. The data points with probability P | 0 〉 = 0 or P | 1 〉 = 1 correspond to the fundamental perceptual states of the Necker cube. The remaining data points are in a superposition of states | 0 〉 and | 1 〉 with P | 0 〉 + P | 1 〉 = 1 .
Figure 5. Perceptual switching curves produced by QT-DNN trained on the Necker cube. The data points with probability P | 0 〉 = 0 or P | 1 〉 = 1 correspond to the fundamental perceptual states of the Necker cube. The remaining data points are in a superposition of states | 0 〉 and | 1 〉 with P | 0 〉 + P | 1 〉 = 1 .
Preprints 110484 g005
Preprints 110484 g006
Figure 6. Perceptual switching curves produced by QT-DNN trained on Rubin’s vase.
Figure 6. Perceptual switching curves produced by QT-DNN trained on Rubin’s vase.
Preprints 110484 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated