Schemes for Resource-Efficient Generation of Twiddle Factors for Fixed-Radix FFT Algorithms

Preprint

Article

Schemes for Resource-Efficient Generation of Twiddle Factors for Fixed-Radix FFT Algorithms

This version is not peer-reviewed.

Keith Jones^*

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

26 June 2024

Posted:

27 June 2024

You are already at the latest version

Abstract

The paper describes schemes for the resource-efficient generation of twiddle factors for the fixed-radix version of the ubiquitous fast Fourier transform (FFT) algorithm. The schemes, which are targeted at a parallel implementation of the FFT, provide one with the facility for trading off arithmetic complexity, as expressed in terms of the required numbers of multiplications and additions (or subtractions), against the memory requirement, as expressed in terms of the amount of random access memory (RAM) required for constructing the look-up tables (LUTs) needed for the storage of the two twiddle factor components – one component being derived from the sine function and the other from the cosine function. Examples are provided which illustrate the advantages and disadvantages of each scheme – which are very much dependent upon the length of the FFT to be computed – for both the single-level and multi-level LUTs, highlighting those situations where their adoption might be most appropriate. More specifically, it is seen that the adoption of a multi‑level LUT scheme may be used to facilitate significant reductions in memory – namely, from an O(N) to an memory requirement, for the case of an N‑point FFT, where β ≥ 2 corresponds to the number of distinct angular resolutions used – at a relatively small cost in terms of increased FFT latency and arithmetic complexity.

Keywords:

Subject:

Computer Science and Mathematics - Signal Processing

1. Introduction

The fixed-radix version of the ubiquitous fast Fourier transform (FFT) algorithm [6,7] provides one with an efficient means of solving the discrete Fourier transform (DFT) [6,7], as given for the case of the N-point transform by the expression

X [k] = \frac{1}{\sqrt{N}} \sum_{n = 0}^{N - 1} x [n] . W_{N}^{n k} k = 0, 1, \dots, N - 1

(1)

where

W_{N} = \exp (- i 2 π / N), i = \sqrt{- 1},

(2)

the primitive N^th complex root of unity [4]. The complex exponential terms,

W_{N}^{n k}

, each comprise two trigonometric components – with each pair being more commonly referred to as twiddle factors – that are required to be fed into each instance of the FFT’s butterfly, this being the computational engine used for carrying out the algorithm’s repetitive arithmetic operations [6,7]. Thus, an efficient implementation of the fixed-radix FFT – particularly for the processing of large and ultra-large data sets – invariably requires an efficient mechanism for the generation of the twiddle factors which, for a decimation-in-time (DIT) type FFT design, with digit-reversed inputs and naturally-ordered outputs, are applied to the butterfly inputs, whilst for a decimation-in-frequency (DIF) type FFT design, with naturally-ordered inputs and digit-reversed outputs, are applied to the butterfly outputs [6,7]. Note that a fixed-radix FFT such as this could also be used to some effect as one component of a prime factor FFT algorithm [12], where the lengths of the individual small-FFT components are constrained to be relatively prime [4].

The twiddle factor requirement, more exactly, is that for a radix-2 FFT algorithm there will be one non-trivial twiddle factor to be applied to each butterfly. The twiddle factor possesses two components, one defined by the sine function and the other by the cosine function, which may be either retrieved directly from the coefficient memory or generated on-the-fly in order to be able to carry out the necessary processing for the FFT butterfly which is, after all, the workhorse for the fixed-radix FFT – as is used today in multiple one-dimensional and multi-dimensional digital signal processing (DSP) and image processing applications, in real-time fashion. With a radix-R version of the FFT, however, where R is an arbitrary integer greater than one, there will be R-1 non-trivial twiddle factors to be applied to each butterfly, rather than just one.

Thus, the results to be described in this paper – which are targeted, for ease of analysis, at a radix-2 formulation of the FFT – will need to be amended to cater for the increased coefficient memory needed for the generation of the R-1 non-trivial twiddle factors, particularly if a highly-parallel solution to the twiddle factor generation (whereby all the non-trivial twiddle factors are generated and applied simultaneously), and thus to the FFT, is to be achieved.

A radix-R version of the N-point FFT involves a total of

\log_{R} (N)

stages in the temporal domain – where the processing for a given stage can only commence once that of its predecessor has been completed – with each stage involving the computation of N/R radix-R butterflies in the spatial domain. 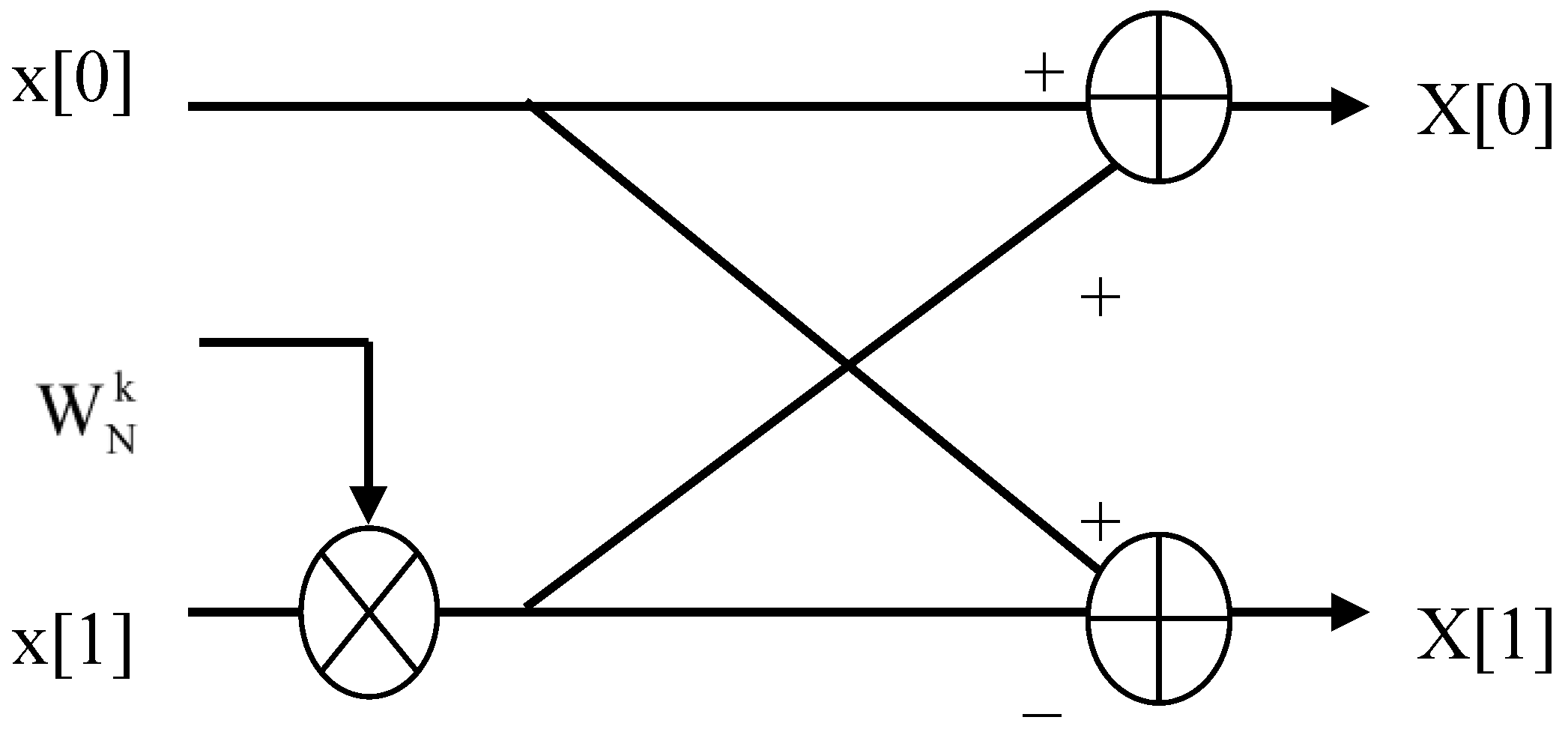Being independent, in terms of distinct input data sets, enables multiple butterflies to be computed in parallel in the spatial domain via the use of single-instruction multiple-data (SIMD) type parallel processing techniques [2]. For a fixed-radix version of the FFT such as this a single butterfly design is required, with its name deriving from the radix-2 design’s resemblance to that of a butterfly, as illustrated in Figure 1 – although for a radix-4 algorithm its design more closely resembles that of a dragonfly or, for a radix-8 algorithm, that of a spider! Clearly, a mixed-radix version of the FFT [6,7], involving a combination of different radices, such as one exploiting both radix-2 and radix-4 components, would require a commensurate number of distinct butterfly designs.

Schemes are to be described which enable a simple trade-off in computational complexity to be made between the arithmetic requirement, as expressed in terms of the number of arithmetic operations – denoted C_M for multiplications and C_A for additions (or subtractions) – required for obtaining the twiddle factors when one or more suitably sized look-up tables (LUTs) are used for their storage, and the memory requirement, as expressed in terms of the amount of random access memory (RAM) [11] – denoted C_LUT – required for constructing the one or more suitably sized LUTs. The assessment of these schemes assumes the availability of parallel computing equipment, such as that provided by means of a field-programmable gate array (FPGA) device [11], enabling the efficient mapping of the twiddle factor generation – and thus of the associated fixed-radix FFT – onto suitably defined computational pipelines [2] for optimum implementational efficiency.

Summarizing, when just one LUT is used for the storage of the twiddle factors – as is discussed in Section 2 – the scheme is said to be based upon the adoption of a single-level LUT, whereas when more than one LUT is used for their storage – as is discussed in Section 3 – the scheme is said to be based upon the adoption of a multi-level LUT, composed essentially of multiple single-level LUTs [9]. Following these descriptions of the single-level and multi-level LUT schemes, the relative advantages and disadvantages of each, which are very much dependent upon the length of the FFT to be computed, are discussed in some detail in Section 4 together with examples highlighting those situations where the adoption of the single-level, two-level and three-level LUT schemes might be most appropriate. Finally, a brief summary and conclusions is provided in Section 5.

2. Single-Level LUT Scheme

As already stated, each twiddle factor comprises two trigonometric components: one sinusoidal and the other cosinusoidal. To minimize the arithmetic requirement for the generation of the twiddle factors, a single LUT may be used whereby the sinusoidal and cosinusoidal components are read from a sampled version of the sine function with argument defined from 0 up to 2π radians. As a result, the LUT may be accessed by means of a single, easy to compute address which may be updated from one access to another via simple control logic and one addition using a fixed increment – that is, the addresses form an arithmetic sequence.

To achieve a memory-efficient implementation of the fixed-radix FFT, however, it should be noted that the coefficient memory requirement for the case of an N-point transform can be reduced from N to just N/4 memory locations by exploiting the relationship between the sine and cosine functions, as given by the expression

\cos (x) = \sin (x + \frac{1}{2} π),

(3)

as well as the periodic nature of each, as given by the expressions

\sin (x + 2 π) = \sin (x)

(4)

& \sin (x + π) = - \sin (x) .

(5)

These properties enable the twiddle factors to be obtained from a pre-computed trigonometric function defined over a single quadrant of just

π / 2

radians rather than over the full range of 2π radians.

Thus, for the case of an N-point FFT based upon the adoption of a single LUT, the arithmetic requirement is given by

C_M = 0 & C_A = 2

(6)

that is, two additions for the generation of each twiddle factor – one for the LUT address of the sinusoidal component and one for the LUT address of the cosinusoidal component – whilst the LUT needs to be of length N/4, yielding a corresponding O(N) memory requirement of

C_{L U T} = \frac{1}{4} N

(7)

words. This single-quadrant scheme, which exploits a single-level LUT, would seem to offer a reasonable compromise between the arithmetic requirement and the memory requirement, using more than the theoretical minimum amount of memory required for the storage of the twiddle factors so as to keep the arithmetic requirement, for the addressing of the LUT, to a minimum. Most FFT algorithms would invariably adopt such an approach, although as will be seen in the following sections, when the FFT is sufficiently long a multi-level scheme based upon the exploitation of multiple small LUTs might prove more attractive.

3. Multi-Level LUT Schemes

The aim of the multi-level schemes – which, essentially, involves the exploitation of multiple one-level LUTs – is to reduce the total memory requirement at the expense of increased arithmetic complexity. The twiddle factors are obtained from the contents of the multiple LUTs through the repeated application of the standard trigonometric identities

\cos (θ + ɸ) = \cos (θ) \times \cos (ɸ) - \sin (θ) \times \sin (ɸ)

(8)

\sin (θ + ɸ) = \sin (θ) \times \cos (ɸ) + \cos (θ) \times \sin (ɸ)

(9)

as will be applied directly for the two-level case, where

θ

corresponds to the angle defined over a coarse-resolution angular region and

ɸ

to the angle defined over a fine-resolution angular region. In achieving such a reduction in the memory requirement it is necessary, given ‘M_R’ different angular resolutions – where the m^th resolution is represented by LUT(s) of length S_m – that the product parameter, P, obtained from the product of the M_R LUT lengths, is such that

P = \prod_{m = 1}^{M_{R}} S_{m} = \frac{1}{4} N

(10)

as expressed by Eqtn. 7, so that the required angular resolution is achieved, whilst at the same time ensuring that the summation parameter, S, obtained from the sum of all the LUT lengths, is such that

S = \sum_{m = 1}^{M {}_{R}} α_{m} \times S_{m} is minimized,

(11)

where

α_{m}

represents the number of LUTs required by the m^th angular resolution region, so that the total coefficient memory requirement is minimized. For each LUT-based scheme, the parameter

α_{1}

is clearly equal to one, as there is only one LUT to consider for the coarse-resolution region, whilst it will be seen in this section that for the multi-level case, where m > 1, each parameter

α_{m}

is equal to two as there are two identically sized LUTs that need to be considered for each fine-resolution region – namely, one for the sine function and one for the cosine function.

3.1. Two-Level Scheme

The first multi-level scheme involves the adoption of a two-level LUT, this comprising one coarse-resolution region of length N/4L catering for both the sine and cosine functions, covering 0 up to

π / 2

radians, and one fine-resolution region of length L for each of the sine and cosine functions, covering 0 up to

π / 2 L

radians. The required twiddle factors may then be obtained from the contents of the two-level LUT through the application of the standard trigonometric identities, as given by Eqtns. 8 and 9, where

θ

corresponds to the angle defined over the coarse-resolution region and

ɸ

to the angle defined over the fine-resolution region.

By expressing the combined size of the two-level LUT for the sine function as having to cater for

f (L) = \frac{N}{4 L} + L

(12)

words, where the LUTs are assumed for ease of analysis to be each of length L, it can be seen from the application of the differential calculus [8] that the optimum LUT length is obtained when the derivative

\frac{d f}{d L} = 1 - \frac{N}{4 L^{2}}

(13)

is set to zero, giving

L = \frac{1}{2} \sqrt{N}

(14)

and resulting in a total

O (\sqrt{N})

memory requirement of

C_{L U T} = \frac{3}{2} \times \sqrt{N}

(15)

words – that is,

\sqrt{N} / 2

to cater for both the sine and cosine functions defined over the coarse-resolution region and

\sqrt{N} / 2

to cater for each of the sine and cosine functions defined over the fine-resolution region.

This scheme therefore yields a reduced memory requirement (when compared to that for the single-level scheme) for the storage of the twiddle factors at the expense of an increased arithmetic requirement, namely

C_M = 4 & C_A = 6

(16)

where four of the additions are for generating the LUT addresses – that is, two to cater for both the sine and cosine functions defined over the coarse-resolution region and two to cater for the sine and cosine functions, one per LUT, defined over the fine-resolution region.

The two-level LUT thus consists of three separate single-level LUTs, each of length

\sqrt{N} / 2

, rather than a single LUT, where an efficient parallel solution to the FFT requires that: a) two addresses need to be accessed simultaneously from the coarse-resolution LUT; and b) two addresses need to be accessed simultaneously from the two fine-resolution LUTs, one per LUT. In addition, for the efficient mapping of the FFT onto parallel computing equipment it will be necessary for the twiddle factor generation to be carried out by means of a suitably defined computational pipeline. To achieve this, the problem must first be decomposed into a number of independent tasks to be performed in the specified temporal order – the solution here involving three independent tasks, as outlined in Figure 2 – so that a new twiddle factor may be produced on the completion of the final task.

Note, however, that with a flexible computing device, such as an FPGA, each of the arithmetic operations within each task may be efficiently carried out by means of a suitably defined internal pipeline, designed around the clock cycle of the chosen computing device. This, in turn, enables each task to be carried out with a given latency, as expressed in terms of the required number of clock cycles, with a new twiddle factor being thus produced with every clock cycle at the cost of a time delay, due to the overall latency, as represented by the combined duration in clock cycles of the three short pipelines.

3.2. Three-Level Scheme

The next multi-level scheme involves the adoption of a three-level LUT, this comprising one coarse-resolution region of length N/4L² for the sine function, covering 0 up to

π / 2

radians, and two fine-resolution regions, each of length L, covering 0 up to

π / 2 L

radians and 0 up to

π / 2 L^{2}

radians, respectively, for each of the sine and cosine functions. The required twiddle factors may then be obtained from the contents of the three-level LUT through the double application of the standard trigonometric identities, as given by Eqtns. 8 and 9, so that

\cos (θ + (ɸ_{1} + ɸ_{2})) = \cos (θ) \times \cos (ɸ_{1} + ɸ_{2}) - \sin (θ) \times \sin (ɸ_{1} + ɸ_{2})

(17)

& \sin (θ + (ɸ_{1} + ɸ_{2})) = \sin (θ) \times \cos (ɸ_{1} + ɸ_{2}) + \cos (θ) \times \sin (ɸ_{1} + ɸ_{2}),

(18)

where

θ

corresponds to the angle defined over the coarse-resolution region and

ɸ_{1}

and

ɸ_{2}

to the angles defined over the first and second fine-resolution regions, respectively. These equations may be expanded and expressed as

\cos (θ + (ɸ_{1} + ɸ_{2})) = \cos (θ) \times (A - B) - \sin (θ) \times (C + D)

(19)

\sin (θ + (ɸ_{1} + ɸ_{2})) = \sin (θ) \times (A - B) + \cos (θ) \times (C + D)

(20)

where

A = \cos (ɸ_{1}) \times \cos (ɸ_{2})

(21)

B = \sin (ɸ_{1}) \times \sin (ɸ_{2})

(22)

C = \sin (ɸ_{1}) \times \cos (ɸ_{2})

(23)

D = \cos (ɸ_{1}) \times \sin (ɸ_{2}) .

(24)

By expressing the combined size of the three-level LUT for the sine function as having to cater for

f (L) = \frac{N}{4 L^{2}} + 2 L

(25)

words, where the LUTs are assumed for ease of analysis to be each of length L, it can be seen from the application of the differential calculus that the optimum LUT length is obtained when the derivative

\frac{d f}{d L} = 2 - \frac{N}{2 L^{3}}

(26)

is set to zero, giving

L = \sqrt[3]{N / 4}

(27)

and resulting in a total

O (\sqrt[3]{N})

memory requirement of

C_{L U T} = 5 \times \sqrt[3]{N / 4}

(28)

words – that is,

\sqrt[3]{N / 4}

to cater for both the sine and cosine functions defined over the coarse-resolution region and

\sqrt[3]{N / 4}

to cater for each of the sine and cosine functions defined over each of the two fine-resolution regions.

This scheme therefore yields a reduced memory requirement (when compared to that for the single-level and two-level schemes) for the storage of the twiddle factors at the expense of an increased arithmetic requirement, namely

C_M = 8 & C_A = 10

(29)

where six of the additions are for generating the LUT addresses – that is, two to cater for both the sine and cosine functions defined over the coarse-resolution region, two to cater for the sine and cosine functions, one per LUT, defined over the first fine-resolution region and two to cater for the sine and cosine functions, one per LUT, defined over the second fine-resolution region.

The three-level LUT thus consists of five separate single-level LUTs, each of length

\sqrt[3]{N / 4}

, rather than a single LUT, where an efficient parallel solution to the FFT requires that: a) two addresses need to be accessed simultaneously from the coarse-resolution LUT; and b) two addresses need to be accessed simultaneously from each of the two pairs of fine-resolution LUTs, one per LUT. In addition, for the mapping of the FFT onto parallel computing equipment it will be necessary, as with the two-level scheme, for the twiddle factor generation to be carried out by means of a suitably defined computational pipeline. To achieve this, the problem is first decomposed into five independent tasks, as outlined in Figure 3, so that a new twiddle factor may be produced on the completion of the final task. The internal pipelining of the arithmetic operations within each task then enables a new twiddle factor to be produced with every clock cycle at the cost of a time delay, due to the overall latency, as represented by the combined duration in clock cycles of the five short pipelines.

3.3. Arbitrary K-Level Scheme

Finally, the results obtained above for the two-level and three-level schemes may be straightforwardly extended to the general case of an arbitrary K-level scheme. By expressing the combined size of the K-level LUT for the sine function as having to cater for

f (L) = \frac{N}{4 L^{K - 1}} + (K - 1) L

(30)

\frac{d f}{d L} = (K - 1) (1 - \frac{N}{4 L^{K}})

(31)

is set to zero, giving

L = \sqrt[K]{N / 4}

(32)

(since K > 1) and resulting in a total

O (\sqrt[K]{N})

memory requirement of

C_{L U T} = (2 K - 1) \times \sqrt[K]{N / 4}

(33)

words – that is,

\sqrt[K]{N / 4}

to cater for both the sine and cosine functions defined over the coarse-resolution region and

\sqrt[K]{N / 4}

to cater for each of the sine and cosine functions defined over each of the K-1 fine-resolution regions.

The computational cost of adopting such a scheme, however, for K > 3 would increase to

C_M = 4K-4 & C_A = 4K-2

(34)

where 2K of the additions are for generating the LUT addresses – that is, two to cater for both the sine and cosine functions defined over the coarse-resolution region and two to cater for the sine and cosine functions, one per LUT, defined over each of the K-1 fine-resolution regions.

The K-level LUT thus consists of 2K-1 separate single-level LUTs, each of length

\sqrt[K]{N / 4}

, rather than a single LUT, where an efficient parallel solution to the FFT requires that: a) two addresses need to be accessed simultaneously from the coarse-resolution LUT; and b) two addresses need to be accessed simultaneously from each of the K-1 pairs of fine-resolution LUTs, one per LUT. In addition, for the mapping of the FFT onto parallel computing equipment it will be necessary, as with the two-level and three-level schemes, for the twiddle factor generation to be carried out by means of a suitably defined computational pipeline. To achieve this, the problem is first decomposed into 2K-1 independent tasks so that a new twiddle factor may be produced on the completion of the final task. The internal pipelining of the arithmetic operations within each task then enables a new twiddle factor to be produced with every clock cycle at the cost of a time delay, due to the overall latency, as represented by the combined duration in clock cycles of the 2K-1 short pipelines.

3.4. Discussion

Note that with each of the multi-level schemes discussed in this section, which involves the use of a suitably defined computational pipeline, there is a latency associated with the twiddle factor generation which is dependent upon the length of the FFT and thus upon the length of the pipeline. With regard to the case of a radix-R version of the N-point FFT, regardless of how it is implemented – whether via the adoption of a pipeline or a memory-based architecture [10] – the latency has to account for the computation of

\frac{N}{R} \times \log {}_{R}N

radix-R butterflies, so that the effect of the additional latency due to the twiddle factor generation on the overall latency of the fixed-radix FFT will be expected to be minimal.

Also, with each such scheme it is possible that the fixed length assigned to each LUT may not necessarily prove to be a positive integer, as is required, so that one or more of the LUT lengths may need to be modified in order for integer LUT lengths to be obtained that still satisfy the product and summation constraints of Eqtns. 10 and 11. For example, with the three-level scheme discussed in Section 3.2, if rather than constraining all LUTs to be of length

\sqrt[3]{N / 4}

(as given by Eqtn. 27), one used instead a coarse-resolution LUT, of length

\sqrt[3]{N}

, and fine-resolution LUTs, each of length

\sqrt[3]{N} / 2

, then the constraint on the product (or multiplicative) parameter, P, will still be met whilst the size of the summation (or additive) parameter, S, will actually be marginally reduced from approximately

3.16 \times \sqrt[3]{N}

(which is clearly not an integer), for the fixed-length case, to just

3 \times \sqrt[3]{N}

4. Complexity Trade-Offs for Various Parameter Sets

To illustrate the trade-off of arithmetic complexity against memory requirement, for both the single-level and multi-level LUT schemes, a set of results is provided – see Table 1 – which deal with a range of radix-2 FFT lengths: 2¹⁰ (1024), 2²⁰ (1,048,576) and 2³⁰ (1,073,741,824) which may be regarded as close approximations to 10³, 10⁶ and 10⁹, respectively, and which may ea’ch be tackled with a suitably defined radix-2^K algorithm such as a radix-2 or radix-4 FFT.

For implementation in silicon of both long and ultra-long FFTs – as are becoming of increasing interest with the trend in large scale, big data applications – such as those transforms of approximate lengths 2²⁰ (as might be encountered in processing of astronomical data) and 2³⁰ (as might be encountered in processing of cosmic microwave data [3]), respectively, considerable resources will inevitably be required, as is evidenced from the memory requirements obtained via the single-level LUT scheme listed in the table. Ways of reducing these requirements, therefore, such as via the adoption of one or other of the multi-level LUT schemes discussed here, need to be carefully considered, as the increased arithmetic complexity and pipeline delay (as will be required for a real-time parallel implementation) may be a cost worth paying for such large reductions in memory – namely, from an O(N) to an

O (\sqrt[β]{N})

memory requirement, for the case of an N-point FFT, where β ≥ 2 corresponds to the number of distinct angular resolutions used.

Note that Table 1 lists the number of arithmetic operations involved for various combinations of FFT length and LUT-based scheme. With a fully parallel hardware implementation of the FFT, however, the number of multiplications would be equivalent to the required number of hardware multipliers – which, with the availability of fast embedded multipliers as provided by an FPGA manufacturer, are particularly resource and energy efficient – namely one hardware multiplier per multiplication, whilst the number of additions (or subtractions) would, in turn, be equivalent to the required number of hardware adders, namely one hardware adder per addition (or subtraction).

Thus, with a fully parallel hardware implementation, the numbers of arithmetic operations also defines the associated hardware complexity which, with an FPGA, may be expressed very simplistically in terms of the required number of ‘slices’ of programmable logic, where a slice comprises a number of LUTs (where an LUT in this context is a collection of logic gates hard-wired on the device), flip-flops and multiplexers. With the adoption of L-bit fixed-point processing, an L-bit adder may be implemented with just L/2 slices and an (L-bit)×(L-bit) multiplier – whose size equates, essentially, to that of L adders – with approximately

L^{2} / 2

slices. With regard to memory, an L-bit word of single-port RAM (as required for the single-sample addressing of the fine-resolution LUTs) may be implemented with L/2 slices and an L-bit word of dual-port RAM (as required for the double-sample addressing of the coarse-resolution LUTs) with L slices.

Based upon these sizing figures the number of logic slices needed for the combined resource requirements of arithmetic and memory (but excluding associated control logic) may be expressed as in Table 1, for various combinations of FFT length and LUT-based scheme, where a wordlength of 24 bits has been assumed for purely illustrative purposes. The results highlight the potential benefits to be obtained through the adoption of one or other of the multi-level LUT schemes, particularly for implementation in silicon of both long and ultra-long FFTs. When compared to the single-level scheme, the two-level scheme (for the long FFT example) offers an approximate reduction in the total silicon sizing of O(10²) whilst the three-level scheme (for the ultra-long FFT example) offers a reduction of O(10⁵) – these results holding true regardless of the adopted wordlength.

5. Summary and Conclusions

The paper has described schemes for the resource-efficient generation of twiddle factors for the fixed-radix version of the FFT algorithm. The schemes, which are targeted at a parallel implementation of the FFT, provide one with the facility for trading off arithmetic complexity, as expressed in terms of the required numbers of multiplications and additions (or subtractions), against the memory requirement, as expressed in terms of the amount of RAM required for constructing the LUTs needed for the storage of the two twiddle factor components – one component being derived from the sine function and the other from the cosine function. Examples have been provided which illustrate the advantages and disadvantages of each scheme – which are very much dependent upon the length of the FFT to be computed – for both the single-level and multi-level LUTs, highlighting those situations where their adoption might be most appropriate. More specifically, it has been seen that the adoption of a multi-level LUT scheme may be used to facilitate significant reductions in memory – namely, from an O(N) to an

O (\sqrt[β]{N})

memory requirement, for the case of an N-point FFT, where β ≥ 2 corresponds to the number of distinct angular resolutions used – at a relatively small cost in terms of increased FFT latency and increased arithmetic complexity.

Note that for a radix-R version of the FFT, there will be R-1 non-trivial twiddle factors to be applied to each butterfly, rather than just one, so that the results obtained and discussed in this paper – which have been targeted, for ease of analysis, at a radix-2 formulation of the FFT – will need to be amended to cater for the increased coefficient memory, in terms of additional LUTs, needed for the generation of the R-1 non-trivial twiddle factors. This replication of resources will be necessary, regardless of the LUT-based scheme adopted, if a highly-parallel solution to the twiddle factor generation (whereby all the twiddle factors are generated and applied simultaneously), and thus to the FFT, is to be achieved.

Finally, note that such techniques as those discussed here for dealing with the fixed-radix FFT could also be used to the same effect with the design of fast solutions to other commonly used orthogonal transforms [1]. This includes the design and implementation of fast algorithms for the efficient computation of the discrete cosine transform (DCT) [13] and the discrete Hartley transform (DHT) [5] where, for the case of the DHT, the regularized version of the fast Hartley transform (FHT) [9,10] involves the design of a single large double butterfly, with eight inputs and eight outputs (making it a spider!), for its efficient parallel computation. Nearly all such fixed-radix transforms, except those based upon the adoption of non-standard arithmetic techniques – such as CORDIC arithmetic [9,14] – will rely upon the use of a pre-computed trigonometric function for their implementational efficiency.

Conflicts of Interest

The author, having been retired for some years, has no access to funding of any kind and states that there are no conflicts of interest associated with the production of this paper.

References

N. Ahmed & K.R. Rao, “Orthogonal Transforms for Digital Signal Processing”, Springer, 2012. [CrossRef]
S.G. Akl, “The Design and Analysis of Parallel Algorithms”, Prentice-Hall, 1989.
C. Bennett, “Wilkinson Microwave Anisotropy Probe”, Scholarpedia, Vol. 2, No. 10, 2007.
G. Birkhoff & S. MacLane, “A Survey of Modern Algebra”, Macmillan, 1977. [CrossRef]
R.N. Bracewell, “The Hartley Transform”, Oxford University Press, 1986.
E.O. Brigham, “The Fast Fourier Transform”, Prentice-Hall, 1974.
E. Chu & A. George, “Inside the FFT Black Box”, CRC Press, 2000.
G.H. Hardy, “A Course of Pure Mathematics”, Cambridge University Press, 1967.
K.J. Jones, “The Regularized Fast Hartley Transform: Low-Complexity Parallel Computation of FHT in One and Multiple Dimensions”, 2^nd Edition, Springer, 2022.
K.J. Jones, “A Comparison of Two Recent Approaches, Exploiting Pipelined FFT and Memory-Based FHT Architectures, for Resource-Efficient Parallel Computation of Real-Data DFT”, Journal of Applied Science and Technology (Open Source), Vol. 1, No. 2, pp. 46-55, July 2023.
C. Maxfield, “The Design Warrior’s Guide to FPGAs”, Newnes (Elsevier), 2004.
J.H. McClellan & C.M. Rader, “Number Theory in Digital Signal Processing”, Prentice-Hall, 1979.
K.R. Rao & P.C. Yip, “Discrete Cosine Transform: Algorithms, Advantages, Applications”, Academic Press, 1990.
J.E. Volder, “The CORDIC Trigonometric Computing Technique”, IRE Trans. on Electronic Computing, Vol. EC-8, No. 3, pp. 330-334, 1959. [CrossRef]

Figure 1. – illustration of butterfly for DIT version of radix-2 FFT algorithm – twiddle factor applied to butterfly input.

Figure 2. – twiddle factor generation using two-level LUT scheme.

Figure 3. – twiddle factor generation using three-level LUT scheme.

Table 1. resource requirements for different LUT-based twiddle factor generation schemes as required by radix-2 FFT algorithm.

Radix-2 FFT Length N	LUT-Based Scheme	Arithmetic Requirement		Memory Requirement (words)	Arithmetic + Memory Sizing (slices)	No Independent Tasks
Radix-2 FFT Length N	LUT-Based Scheme	No Multiplies	No Additions	Memory Requirement (words)	Arithmetic + Memory Sizing (slices)	No Independent Tasks
2¹⁰ ~ 10³	1-Level	0	2	2.56×10²	~ 6.14×10³	1
2²⁰ ~ 10⁶	1-Level	0	2	~ 2.62×10⁵	~ 6.29×10⁶	1
2²⁰ ~ 10⁶	2-Level	4	6	~ 1.54×10³	~ 2.58×10⁴	3
2³⁰ ~ 10⁹	1-Level	0	2	~ 2.63×10⁸	~ 6.44×10⁹	1
2³⁰ ~ 10⁹	3-Level	8	10	~ 3.07×10³	~ 6.16×10⁴	5

Note: wordlength adopted for silicon sizing = 24 bits.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Schemes for Resource-Efficient Generation of Twiddle Factors for Fixed-Radix FFT Algorithms

Abstract

Keywords:

Subject:

1. Introduction

2. Single-Level LUT Scheme

3. Multi-Level LUT Schemes

3.1. Two-Level Scheme

3.2. Three-Level Scheme

3.3. Arbitrary K-Level Scheme

3.4. Discussion

4. Complexity Trade-Offs for Various Parameter Sets

5. Summary and Conclusions

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe