Preprint
Article
A Structured Light 3D Reconstruction Method Based on Neural Network
Altmetrics
Downloads
158
Views
73
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
27 June 2024
Posted:
28 June 2024
You are already at the latest version
Alerts
Abstract
The monocular structured light measurement system has low cost, simple algorithms, and a wide measurement range, making it widely applicable in multiple fields. However, in practical applications, the system may be affected by various factors including noise, non-linear intensity, changes in the reflectivity of the object being measured, and the calibration method and accuracy of the system, thereby reducing the measurement accuracy. In order to solve these issues, this paper proposes a new monocular structured light measurement method, mainly comprises the following two points: (a) A denoising algorithm for phase images based on DAE is proposed, which calculates the wrapped phase of the phase-shifted fringes after initial denoising by DAE. Then, a new phase-shifted fringe pattern is generated and input into DAE for iterative denoising, achieving high-performance image denoising and high-precision wrapped phase solution. (b) A new absolute phase height calibration algorithm is proposed, which introduces camera internal and external parameters and uses a two-layer feedforward network to directly establish the relationship between phase and the 3D coordinate system. Without the need for high-precision motion platforms, high-precision phase height calibration is attainable. In general, compared to conventional methods, the experimental results indicate the effectiveness of the proposed method for low-quality phase-shifted fringe 3D reconstruction. In addition, the measurement method described in this article also demonstrates effectiveness in high-dynamic scenes.
Keywords:
Subject: Engineering - Other
0. Introduction
Structured light three-dimensional topography measurement technology[1] has been widely used in many fields due to its advantages of non-contact, highly precise, and fast. It has become one of the most widely used non-contact 3D reconstruction measurement methods in engineering[2]. The Figure 1 shows a schematic diagram of a structured light 3D measurement system based on Phase Measuring Profilometry (PMP)[3]. The system mainly consists of three parts: a computer, a digital projector, and a camera. The measurement is primarily accomplished through the following four steps: 1. The projector projects pre-coded grating fringes onto the surface of the object to be measured; 2. The camera captures the modulated grating fringe images; 3. The phase information of the object is calculated based on these images; 4. The true 3D information of the object is determined by the calibrated phase-height relationship.
Obviously, the accuracy of the measured three-dimensional information directly depends on the phase calculation of the captured phase-shift fringe images and the calibration of the measurement system. The main factors typically involved in affecting the phase calculation accuracy include three aspects[4]: (a) the quality of the phase-shifted image, which mainly depends on the noise level of the image, the intensity of the nonlinear effect, and the reflectivity of the object surface; (b) the number of phase shift steps. (c) the intensity modulation parameter. This parameter is usually affected by the system configuration and the reflectivity of the object to be measured.
Increasing the number of phase shift steps improves accuracy but slows down measurement speed. The intensity modulation parameter is usually affected by the system configuration and the reflectivity of the object to be measured. Noise directly affects phase calculation accuracy, often being the most significant and direct factor leading to errors in phase data. High-frequency noise has a severe impact, significantly reducing the accuracy of phase extraction and resulting in surface detail distortion during reconstruction. The impact of object surface reflectivity, especially on highly reflective or low-reflectivity surfaces, can be mitigated by adjusting the projection pattern, using multiple exposures, and employing polarizers to obtain clearer fringe images. However, these methods may require capturing or projecting more fringe images. Additionally, the reduction in reconstruction accuracy due to gamma mismatch can be effectively controlled through gamma calibration[5,6,7].
Moreover, for the structured light three-dimensional measurement system, the accuracy of phase height calibration determines the upper limit of the system's measurement accuracy. Calibration accuracy is often influenced by factors such as system hardware, environment, software algorithms, and configuration.
Therefore, the most common and effective measure to improve phase calculation accuracy, without projecting additional fringe images, is suppressing image noise. Filtering technology [8] can effectively reduce or suppress noise components in images, thereby improving image quality. For instance, in [9], an adaptive filtering method was employed to filter captured images, effectively removing noise while preserving image details. In [10], a new dual-domain denoising algorithm was proposed, which combines the advantages of traditional spatial and transform domain denoising algorithms. This algorithm can eliminate additive Gaussian white noise in images. In [11], a method for extracting boundary information based on smooth filtering was proposed to eliminate the influence of uneven lighting in structured light images. This method utilizes a Gaussian filtering mask of appropriate size to process the images. In [12], captured images were converted to the frequency domain for filtering processing, thereby suppressing the impact of noise and improving phase accuracy.
However, with the increasing application of deep learning in various fields, some scholars have also applied it to denoising phase shifted stripe images. Due to the good generalization and interpolation capabilities of feedforward and backpropagation neural networks, [13] proposed the application of neural networks to map distorted stripe data to non-distorted data. In [14], a model was proposed to utilize phase fringes to generate dense marker points and use backpropagation neural networks for sub-pixel calibration. In [15], a neural network-based color decoupling algorithm was proposed to address complex color coupling effects in color stripe projection systems. They utilized the generalization and interpolation capabilities of feedforward and backpropagation neural networks to map coupled color data to decoupled color data. Moreover, it can effectively compensate for the sinusoidal characteristics and phase quality of fringes. In [16], a multi-stage convolutional neural network model (FPD-CNN) based on deep learning was proposed for optical fringe pattern denoising. The architecture was designed according to the derivation of regularization theory. The residual learning technique was introduced into the network model through the solution of the regularization model. In some literature [17], a lightweight residual dense neural network based on the U-net model (LRDU Net) was also proposed for fringe pattern denoising. In [18], they investigated the application of neural network fringe calibration for a multi-channel approach.
There are primarily two methods for calibrating the correlation between absolute phase and height: implicit calibration[19] and explicit calibration[20]. In reference [21], a polynomial fitting approach was introduced to establish the phase-height relationship. Reference [22] presents a versatile new technique for calibrating the monocular system in phase-based fringe projection profilometry. This innovative algorithm features a more adaptable phase-to-height conversion model, utilizes a minimum norm solution, and concludes with a nonlinear optimization based on the maximum likelihood criterion. Additionally, an enhanced phase-height mapping approach, which involves the creation of a virtual reference plane of known height adjacent to the original reference plane, is proposed in [23].
In reference [24], a novel and flexible technique was introduced to calibrate the monocular system for panoramic 3D shape measurement. This system is based on a turntable setup consisting of a camera, projector, computer, and rotating platform. The presented algorithm primarily relies on the turntable and marker points to accomplish the calibration of the system's geometric parameters. In [25], a trained three-layer backpropagation neural network was utilized to handle the complex transformation required. Reference [26] proposed a hybrid approach that integrates geometric analysis with a neural network model. This method initially determines the phase-to-height relationship through geometric analysis for each image pixel, and subsequently employs a neural network model to identify the relevant parameters for this relationship.
Based on the proven success of deep learning in areas such as image segmentation, 3D scene reconstruction, and fringe pattern analysis, it is highly feasible to explore the utilization of deep learning techniques for precise 3D shape reconstruction from structured-light images. This is especially relevant in the denoising of fringe images and the calibration of the relationship between absolute phase and height.
Given that phase-shifting fringes are encoded using sine functions, and inspired by the application of DAE (Denoising Autoencoder) in signal processing, this paper introduces a DAE-based denoising algorithm specifically tailored for phase-shifting fringes. This algorithm aims to reduce noise in phase-shifting fringes, enabling accurate phase calculations. When compared to traditional filtering techniques, our method exhibits superior computational efficiency and is particularly adept at suppressing high-order harmonic distortions within the fringes.
Moreover, in accordance with the principle of general approximation, neural networks can serve as a "universal" function to a certain degree, capable of executing intricate feature transformations or approximating a complex conditional distribution. A multi-layer feedforward neural network (FNN) can be seen as a nonlinear composite function, and theoretically, if the hidden layer of the FNN is sufficiently deep, it can approximate any function. Therefore, by constructing an appropriate calibration model for absolute phase-to-height conversion and feeding the absolute phase as input to the FNN, with height as the output, a precise mapping relationship can be established.
Based on these concepts, this article presents the design of a neural network-based structured light 3D reconstruction measurement system. The system primarily focuses on the processing of phase fringe images and the calibration of the measurement system. The outline of this article is structured as follows: First, the measurement principle is described in Section 1. In Section 2, the implementation principles of DAE based phase-shifting fringe denoising algorithm and FNN based absolute phase height calibration algorithm are described. Then, the noise reduction and calibration accuracy verification results are discussed in Section 3. Finally, the conclusion of this article is presented in Section 4.
1. Basic Principle
1.1. Phase Measuring Profilometry (PMP) Reconstruction Principle
Compared to other phase processing methods, the phase-shifting fringe technique has been widely adopted in the field of optical 3D measurement methods, owing to its advantages such as good information fidelity, simplified calculations, and high accuracy in information recovery. The expression for a standard N-step phase-shift algorithm[27], featuring a phase shift of π/2, is as follows:
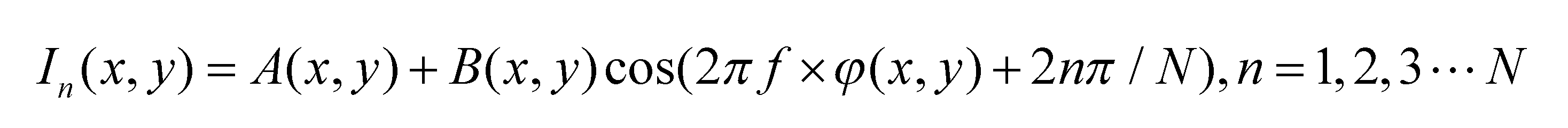
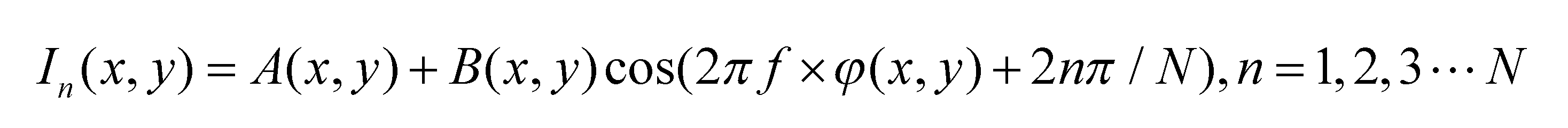
Here ƒ is the frequency of the cosine period function, A(x,y) represents the intensity of the background stripe light, B(x,y) represents the modulation intensity of this cosine function, N is the number of phase steps, φ(x,y) is the calculated wrapping phase from the equation (1).
The three-step phase shift method is employed here to determine the principal phase value of the demodulated deformed fringe image. The three captured fringe patterns are as follows:
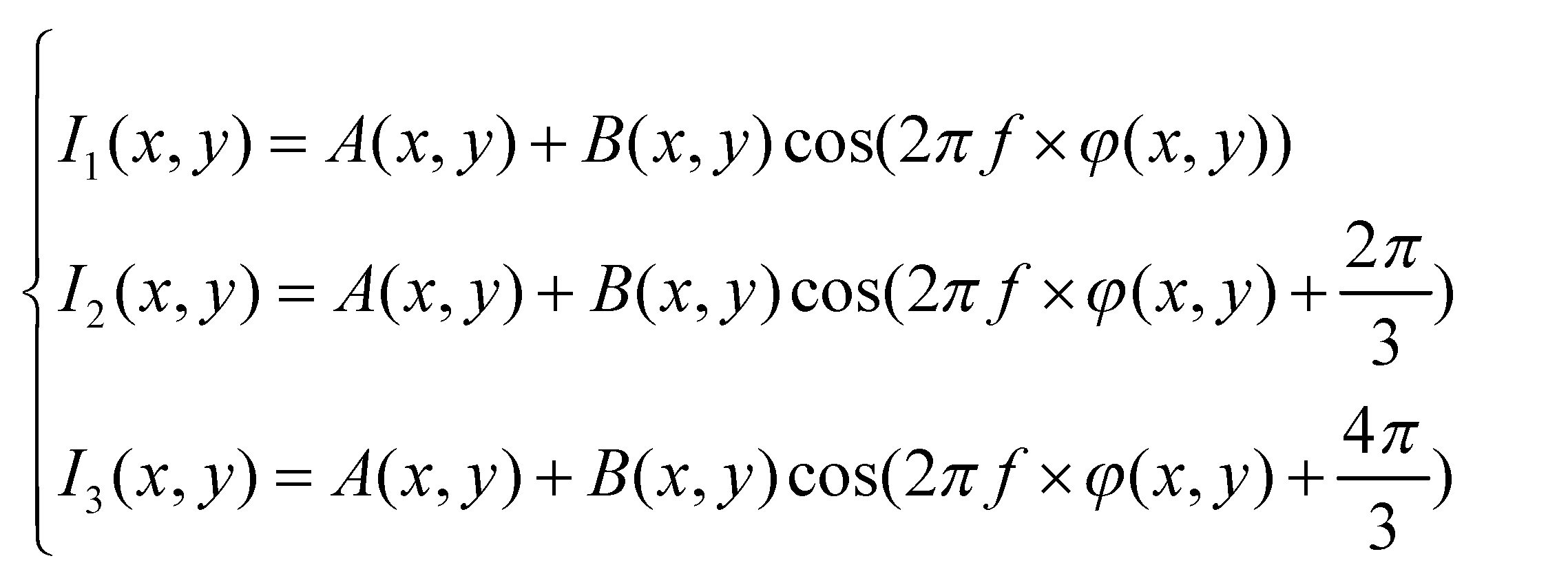
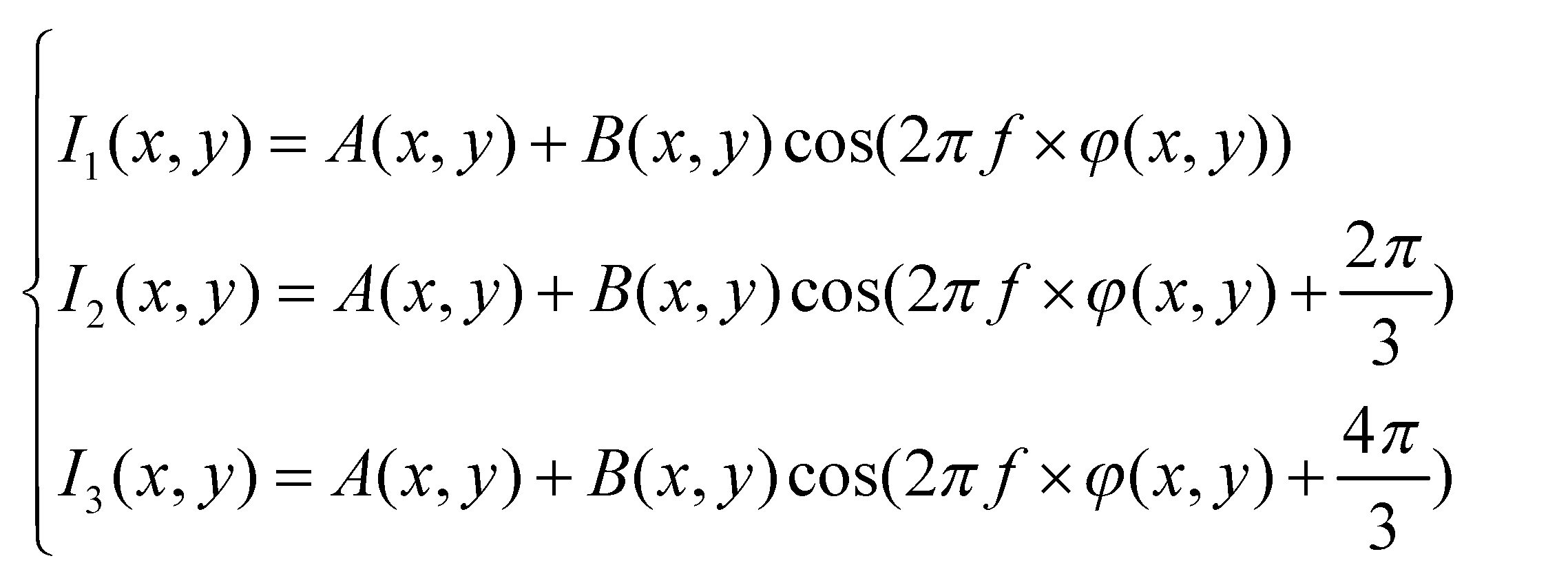
The phase can be calculated as equation (3):
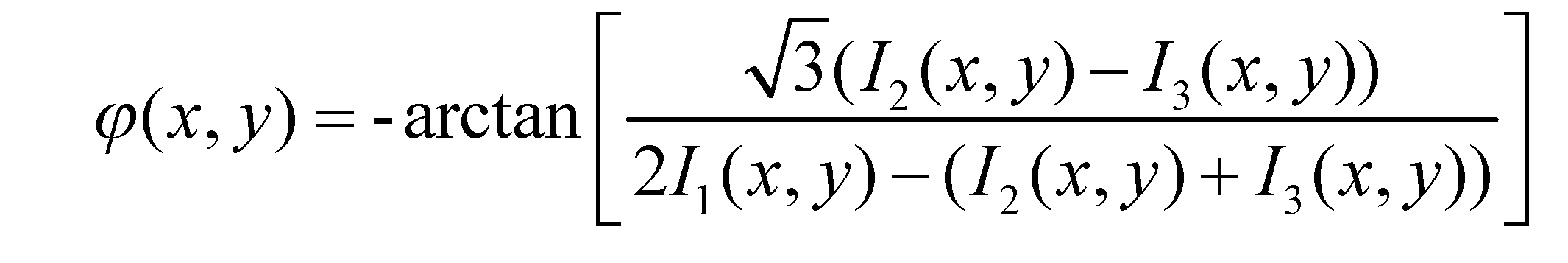
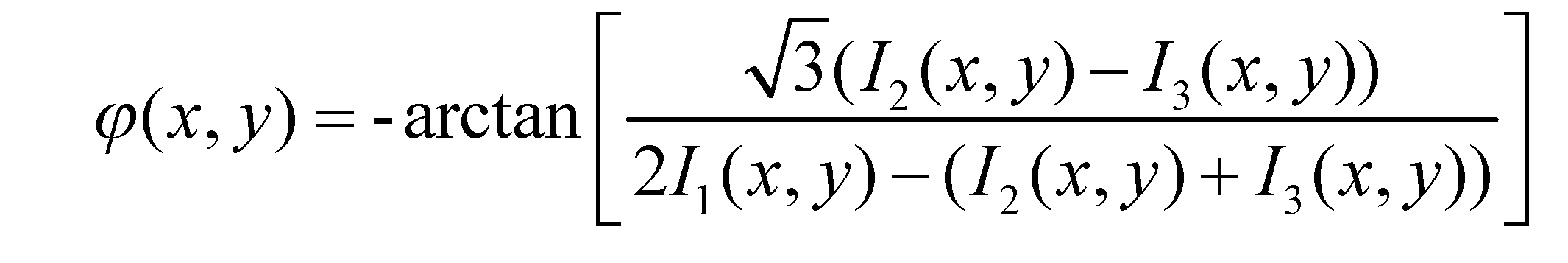
The phase principal values φ(x,y) obtained from the equation (3) are distributed in a zigzag shape in the (0,2π) interval as shown in the figure, and are referred to as the wrapped phase. It is easy to understand that the wrapped phase is uniquely determined within a single cycle, yet this value is not globally unique across the entire measurement space. Consequently, to obtain a unique phase value that spans the whole measurement range, it becomes essential to unwrap the wrapped phase, referring to the unwrapped phase φ(x,y) as the absolute phase ϕ(x,y).This article employs the three-frequency heterodyne principle for phase unwrapping calculations. Through the superposition of phase functions with distinct frequencies, a phase function of lower frequency is achieved. The phase-shift-fringe images with periods of T1, T2, and T3 determine the three wrapped phases ϕ1, ϕ2, and ϕ3(T=1/ƒ). T12 is an equivalence period determined by a heterodyne operation between T1 and T2. T23 is an equivalence period determined by a heterodyne operation between T2 and T3. T123 is an equivalence period determined by a heterodyne operation between T12 and T23.
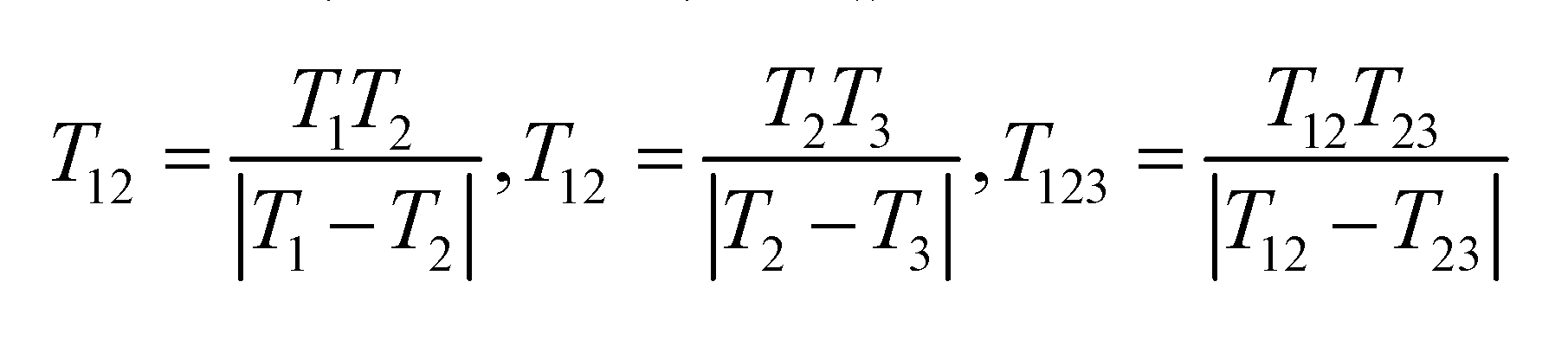
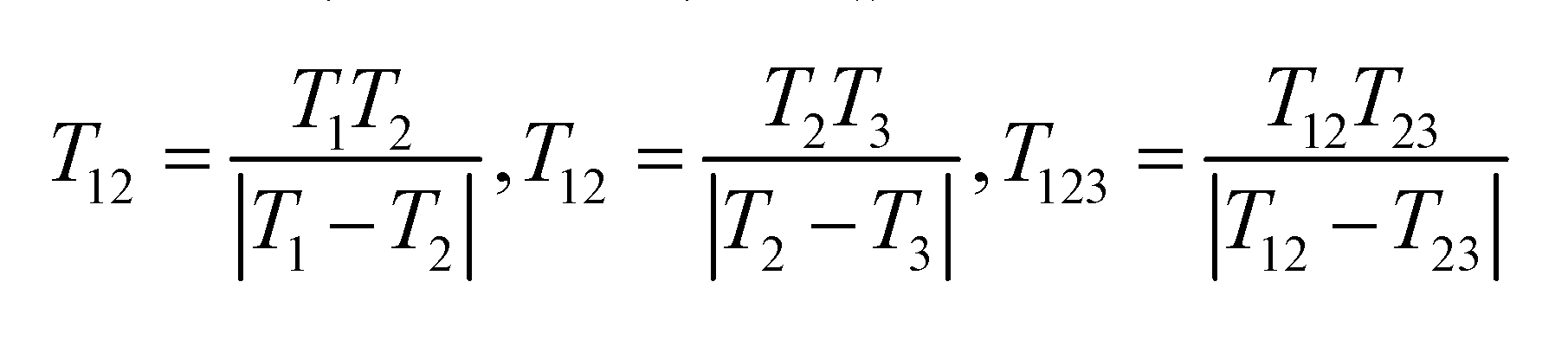
Based on the formula derived from reference [28], the superimposed phase function is calculated using the following method:
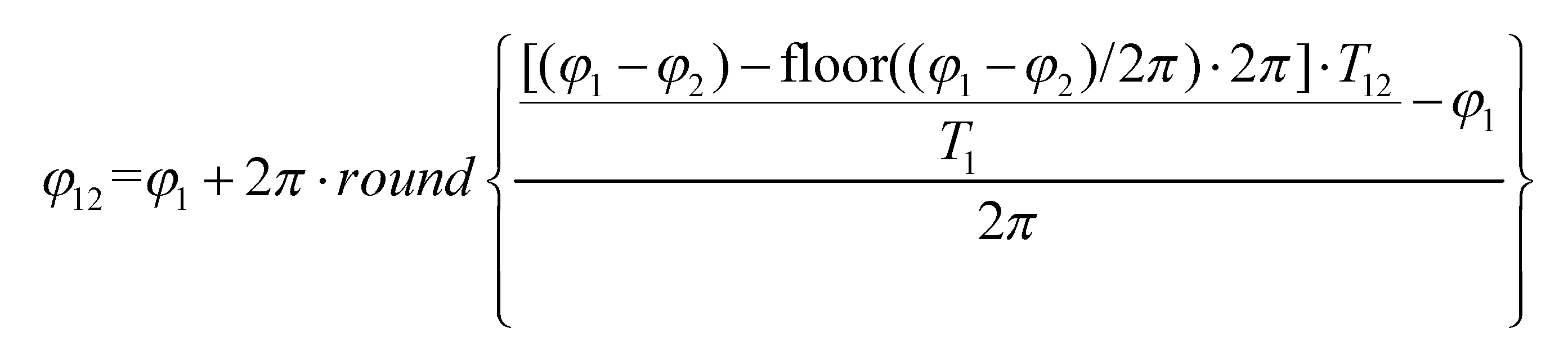
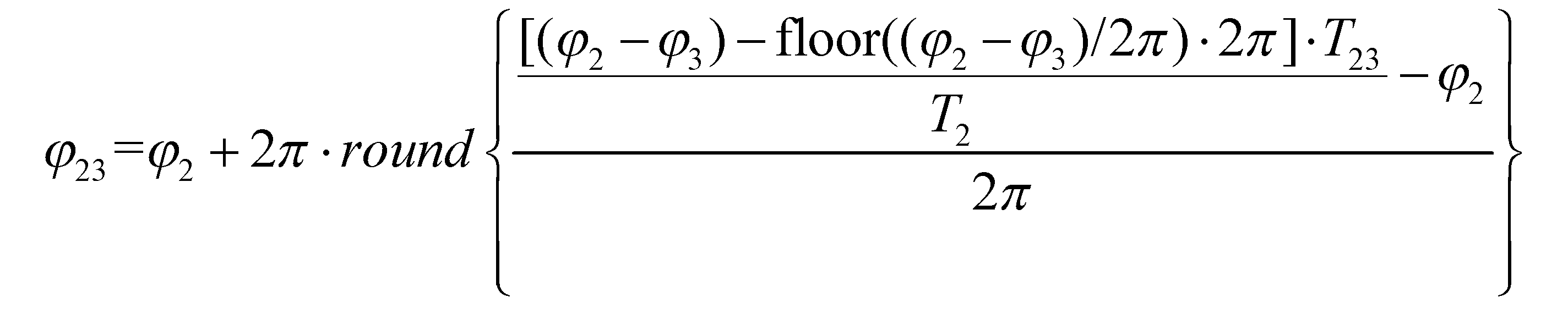
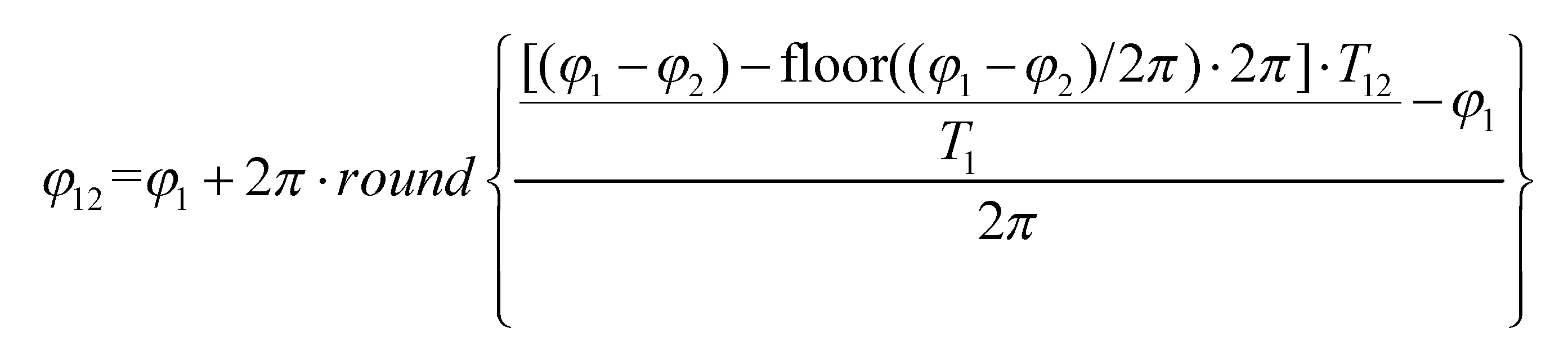
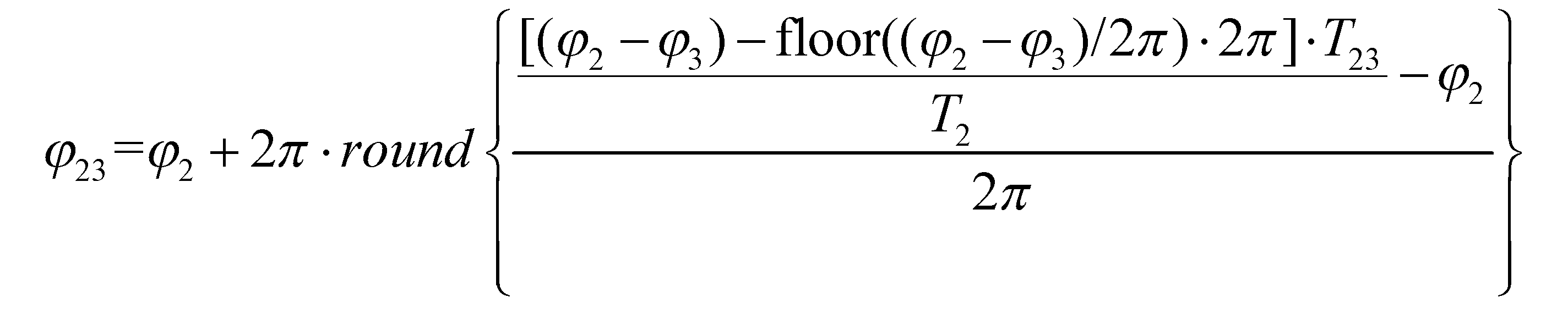
Similarly, it can be concluded that the phase of the package with an unfolding frequency of is:
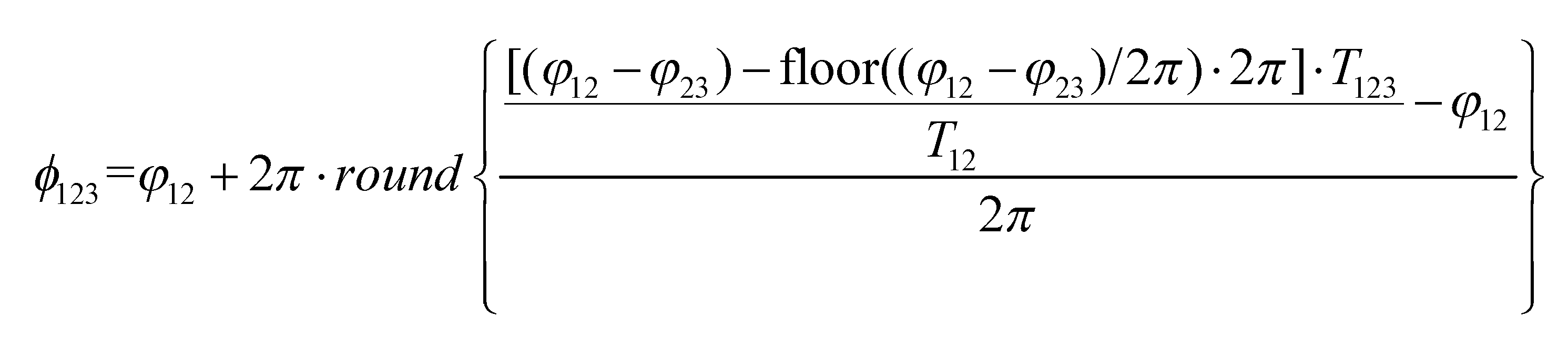
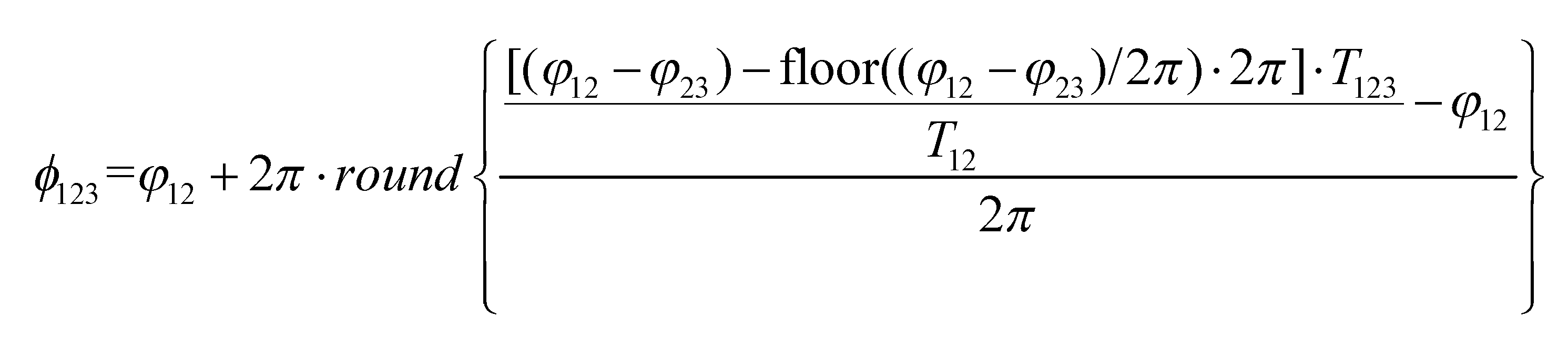
Here, ϕ123 is the final absolute phase.
After computing the absolute phase, the relationship between the absolute phase and the actual height is calibrated to determine the accurate three-dimensional information of the object.
1.2. Neural Network
A neural network[29] is a computational model that consists of numerous interconnected nodes (or neurons). Each node, excluding the input node, signifies a specific output function, referred to as the activation function. The links between nodes signify the weight, which determines the portion of the transmitted signal (representing the "memory value" considered for transmission). Variations in activation functions and weights influence the network's output, providing an approximation of a specific function or a descriptive mapping relationship.
1.2.1. Denoising Autoencoder
The Auto-Encoder[30] is a layered neural network where the input and output layers mirror each other, sharing the same number of nodes. While it learns an identity function with matching input and output, this process involves understanding the input data's inherent structure and characteristics. It condenses this information into a simplified, lower-dimensional form (encoding) and then reconstructs the original data from this condensed version (decoding).
An Auto-Encoder typically comprises three core elements: an encoder, an encoding space, and a decoder. The encoder transforms input data (like images, text, or numbers) into a condensed encoding space. This transition involves multiple hidden layers and activation functions that progressively simplify the data. The encoding space is a condensed representation of the data, highlighting its key features. The decoder then takes this condensed data and strives to recreate the original input. Through training, the autoencoder aims to minimize discrepancies between the original and reconstructed data[31].
Denoising auto-encoders[32] are a specialized variant, primarily employed in unsupervised learning for noise reduction and data restoration. Their primary goal is to derive feature representations resilient to noise. By introducing noise into the input data and then aiming to restore the original from this noisy version, they achieve noise elimination and data recovery. In comparison to standard autoencoders, denoising autoencoders exhibit superior robustness and adaptability.
1.2.2. Feed-Forward Neural Network Data Regression
Feed-forward Neural Network (FNN)[33] represents the most fundamental neural network architecture, alternatively referred to as a forward neural network or forward propagation network. In this network type, information flows strictly in one direction: from the input layer, through any hidden layers, to the output layer, without creating any loops.
Feedforward neural networks commonly comprise input layers, hidden layers, and output layers. Each layer hosts multiple neurons (or nodes) that are fully interconnected with the neurons of the adjacent layer, while neurons within the same layer remain unconnected.
Within feedforward neural networks, signals originate at the input layer, traverse one or multiple hidden layers, and terminate at the output layer. Each neuron layer receives the output from the preceding layer, which serves as input for weighted summation. Following this, an activation function is applied to produce the layer's output.
The learning process in feedforward neural networks often relies on backpropagation algorithms[34]. During training, the network initially computes an output based on the input data and compares it to the actual labels to determine the error (or loss). Subsequently, the backpropagation algorithm propagates this error backward through the network, adjusting the weights and biases of each neuron layer based on the calculated error. This iterative process continues until the discrepancy between the network's output and the actual labels falls within an acceptable range. Feedforward neural networks are prized for their simplicity, ease of implementation, and high computational efficiency, making them a popular choice in various practical applications.
2. Algorithm Design
Ideally, the captured phase shift fringes should be linear. However, the measurement system may be affected due to several factors, including environmental noise, non-linear characteristics of cameras and projectors, and the surface materials of the measured object. As a result, the measurement results can no longer be accurately represented by a simple linear formula. The collected raster image is expressed as follows:
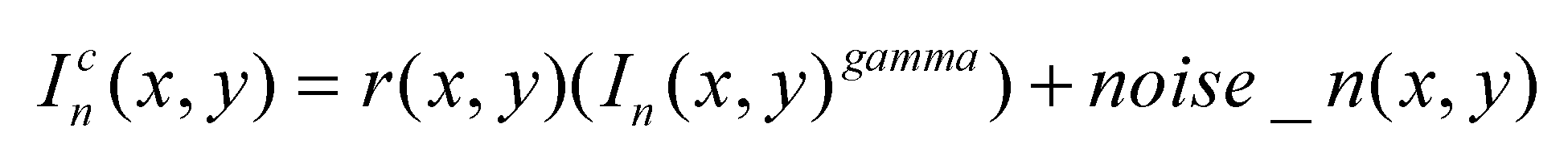
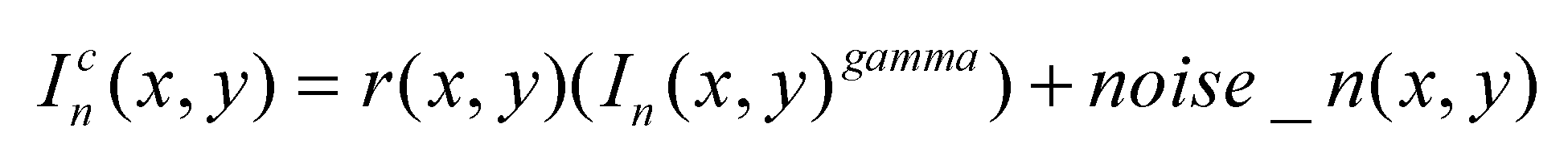
For the phase-shift-fringe images, the factors that affect fringe quality are mainly three: image noise noise_n(x,y), the non-linear intensity of the light source gamma and surface reflectivity changes r(x,y).
Although various traditional studies have shown that filtering fringe images can effectively reduce phase errors in the process of wrapping phase recovery, people may intuitively believe that directly filtering the wrapping phase can also suppress phase errors. However, experimental results indicate that directly filtering the wrapped phase is actually not feasible. This article draws inspiration from the application of Auto Encoder in signal denoising, particularly in image denoising. Using the Auto Encoder as a basis, we have designed a denoising correction algorithm tailored for Phase Measuring Profilometry images. Specifically, we train the autoencoder to reconstruct the original, noise-free phase-shifted fringe pattern from a noisy phase fringe image.
This algorithm is based on the following steps:
Step 1: Feed the noisy phase-shifted stripe image, captured by the camera, into the trained DAE for an initial noise reduction and correction.
Step 2: Compute the wrapping phase using formula (3) for the phase-shifted fringe image that has undergone preliminary noise reduction and correction.
Step 3: Using formula (9), regenerate a fresh three-step phase-shifting fringe pattern based on the wrapped phase. Subsequently, input this pattern into the DAE once again for iterative denoising.
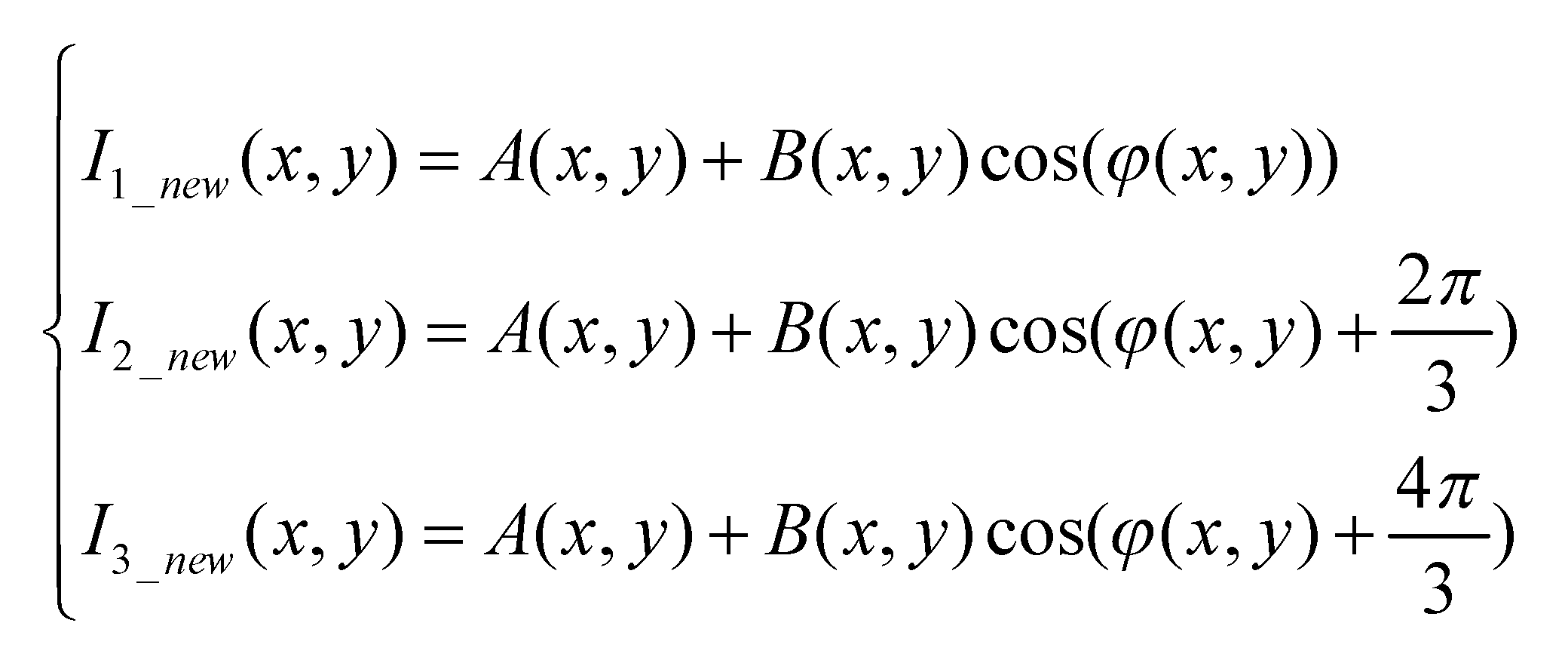
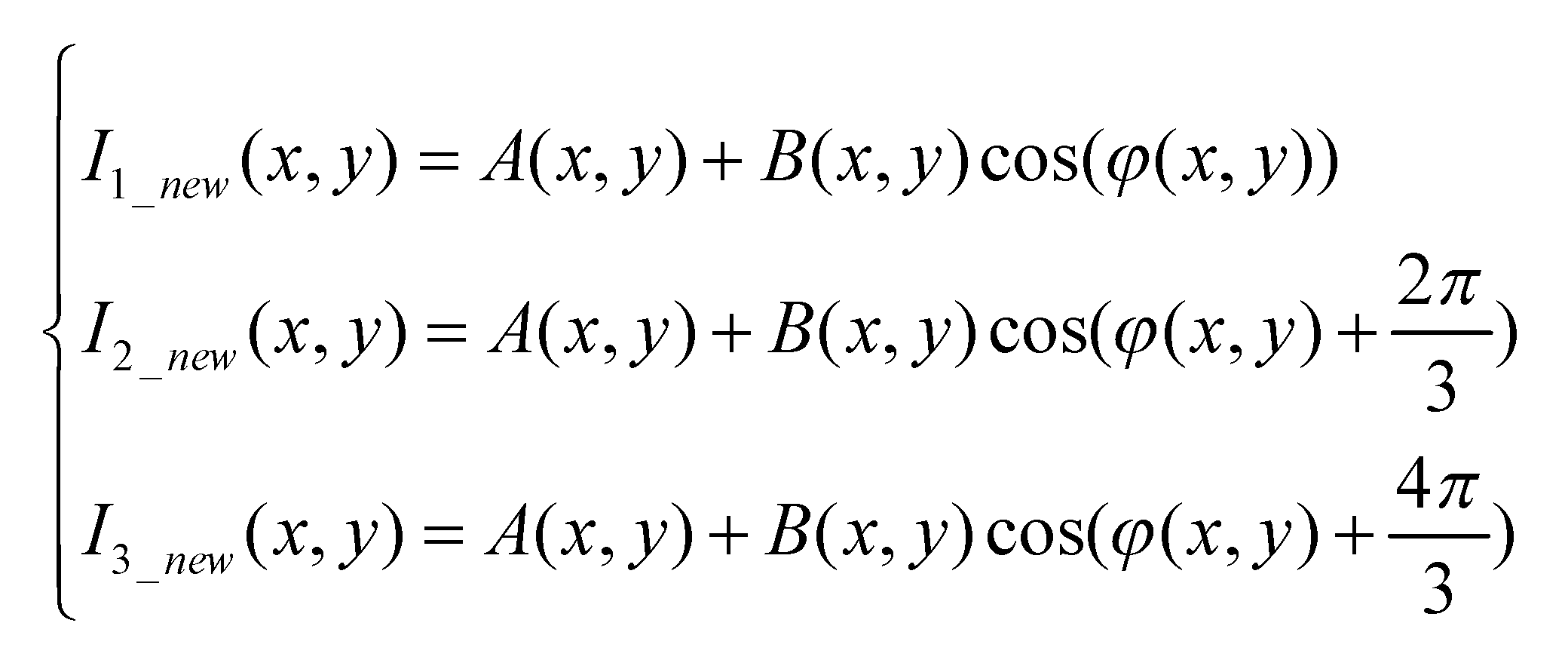
Where A(x,y) and B(x,y)represents the foreground and background encoded in the chapter 1.1, while φ(x,y) is the current calculated phase value of the wrapped phase.
Step 4: Output the iteratively generated phase-shifted stripe images after undergoing noise reduction and correction by the DAE.
It is worth noting that DAE effectively reconstructs the sine of phase-shifted stripe images without overfitting, thereby improving stripe quality. Moreover, due to the inherent characteristics of the wrapped phase, direct Gaussian filtering of the wrapped phase will result in significant distortion, leading to correction failure. This is a theoretical prerequisite for step 3 to further improve the accuracy of the wrapped phase by regenerating the phase-shifted fringe image from the wrapped phase and iteratively denoising and reconstructing it by re-inputting it into the DAE. Iterative denoising gradually refines the data, enhancing denoising performance and achieving higher accuracy.
The proposed DAE structure is shown in Figure 2. In this DAE, the encoder consists of two layers of 1D convolution: one layer has an input channel size of 1, an output channel size of 16, a convolution kernel size of 3, and an activation function of ReLU; the other layer has an input channel size of 16, an output channel size of 32, and a convolution kernel size of 3. The decoder consists of two layers of 1D deconvolution: one layer has an input channel size of 32, an output channel size of 16, a convolution kernel size of 3, and an activation function of ReLU; the other layer has an input channel size of 16, an output channel size of 1, and a convolution kernel size of 3.
After obtaining the high-precision wrapped phase, the multi-frequency heterodyne method described earlier is used to unwrap the phase φ(x,y) and obtain the absolute phase ϕ(x,y).
To further acquire the three-dimensional information of the object, calibrating the mapping relationship between the phase ϕ(x,y) and the coordinates (Xc,Yc,Zc) in the camera coordinate system is essential. In the model shown in Figure 1, the relationship between the coordinates (Xc,Yc,Zc) in the camera coordinate system and the image coordinate system (u,v) can be expressed by formula (10):
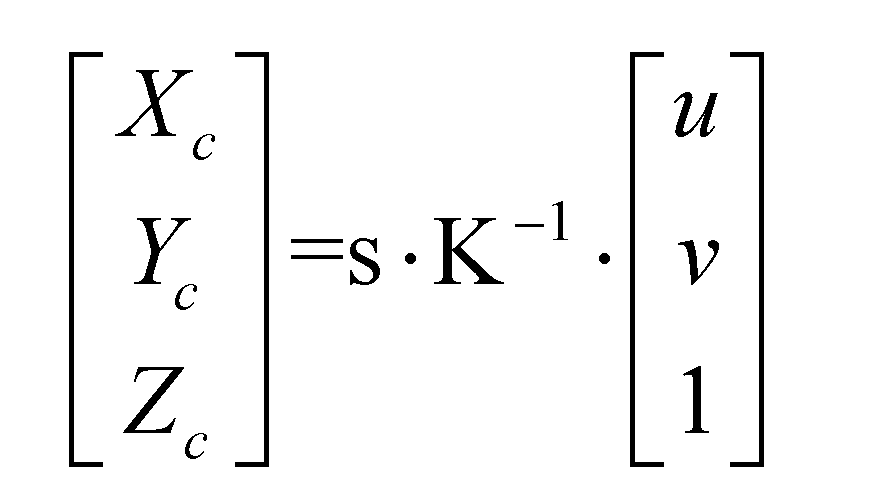
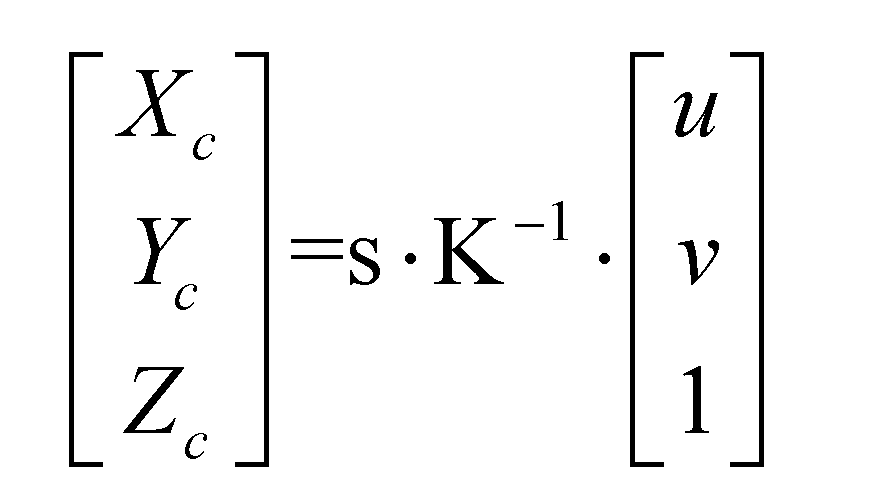
Here, K represents the camera intrinsic matrix, which can be obtained through camera calibration[35]. In the camera coordinate system, the plane equation (dot method) that is translated and perpendicular to a point can be expressed by formula (11):
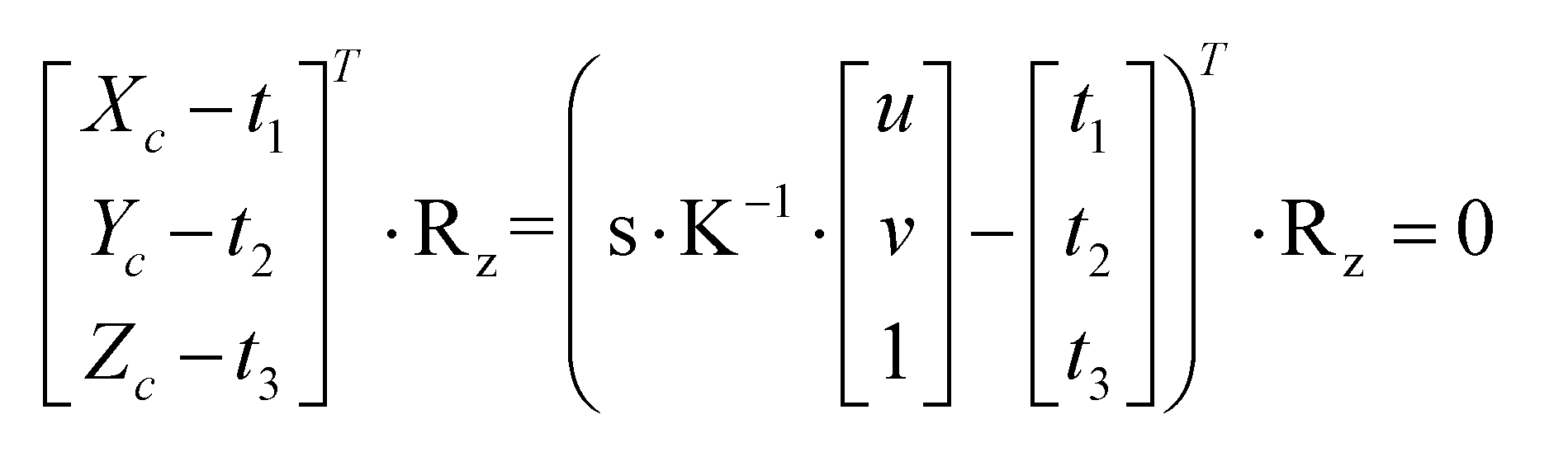
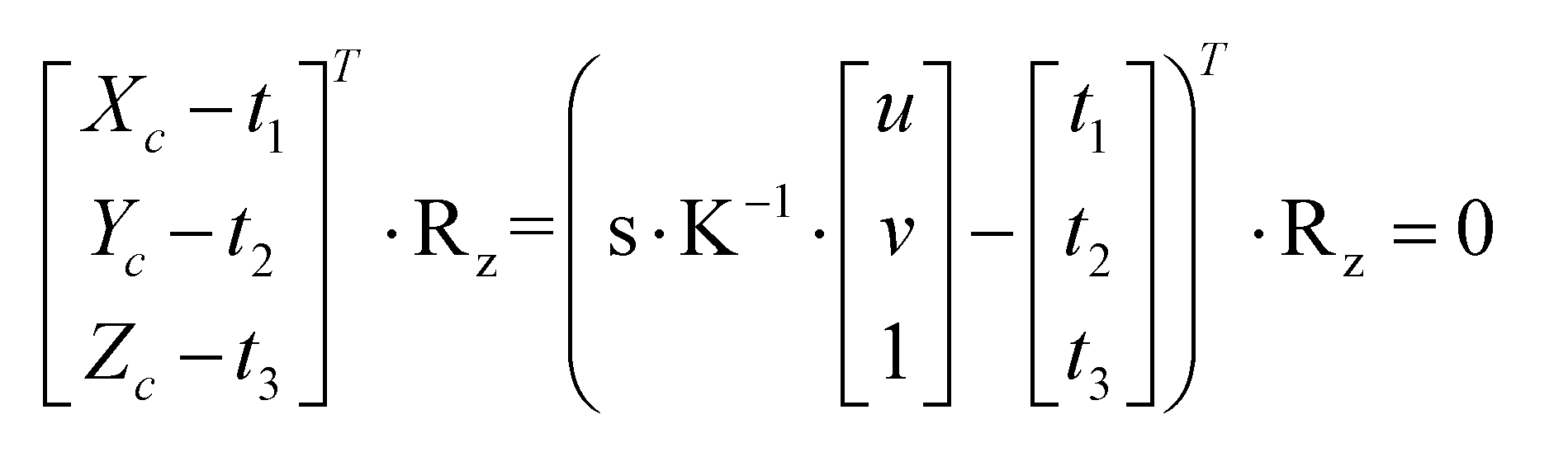
Here, Rc(3*1) denotes the z-direction component of the rotation matrix. After transformation, the scale factor from the camera coordinate system to the image coordinate system can be expressed by formula (12):
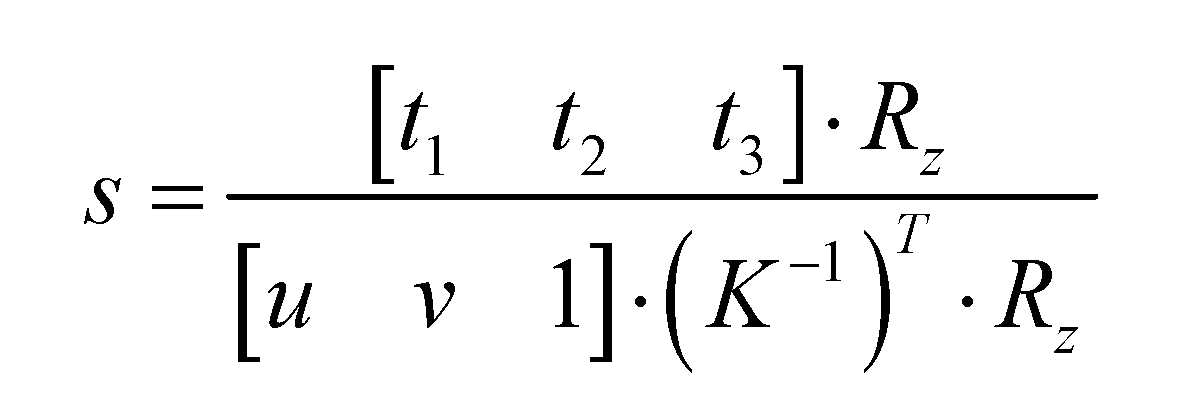
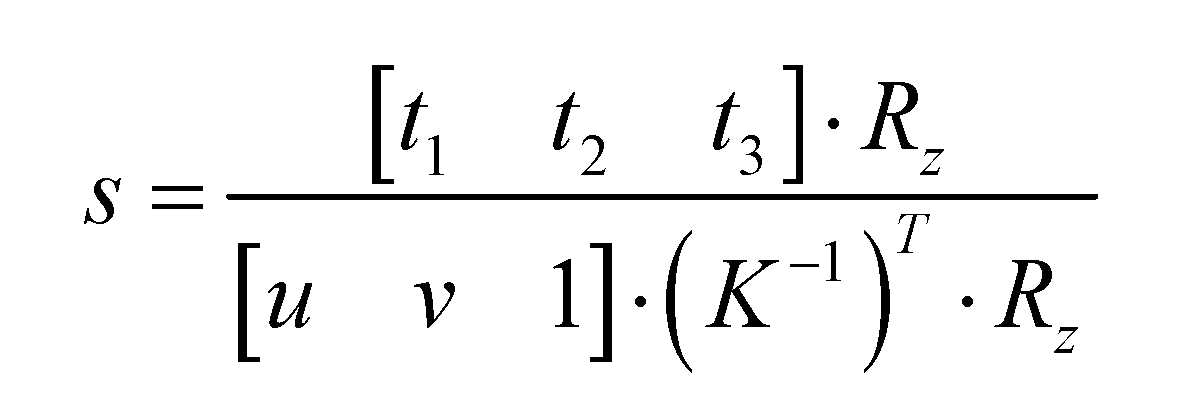
The value of s corresponding to each point (u,v) in the image coordinate system can be calculated using the aforementioned equation.
The absolute phase values corresponding to each point in the image coordinate system (u,v) can be calculated using the aforementioned method of absolute phase calculation. Based on the above relationship, this paper proposes incorporating camera intrinsic and extrinsic parameters into phase height calibration to achieve high-precision absolute phase height calibration. During the camera calibration process, as the calibration board image is captured, a phase-shifted fringe image is projected onto the surface of the calibration board. The pose of the calibration board is determined by the camera's intrinsic and extrinsic parameters, and the absolute phase value at that position is calculated to calibrate the correspondence between s and phase ϕ. Upon completing calibration, when the absolute phase information of the object to be measured is inputted, the three-dimensional coordinates of the object can be determined through formula (13):
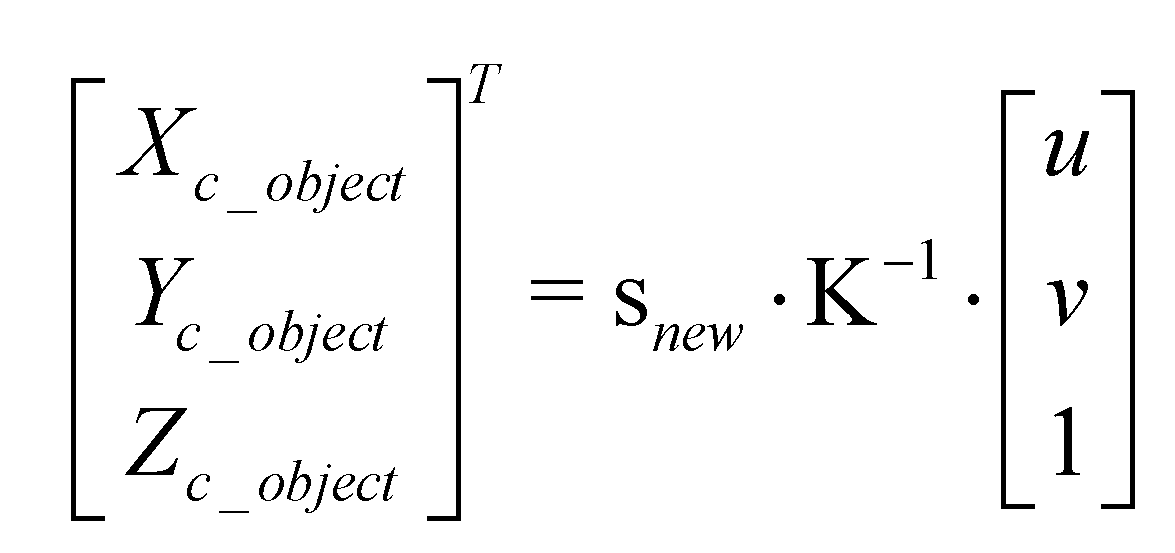
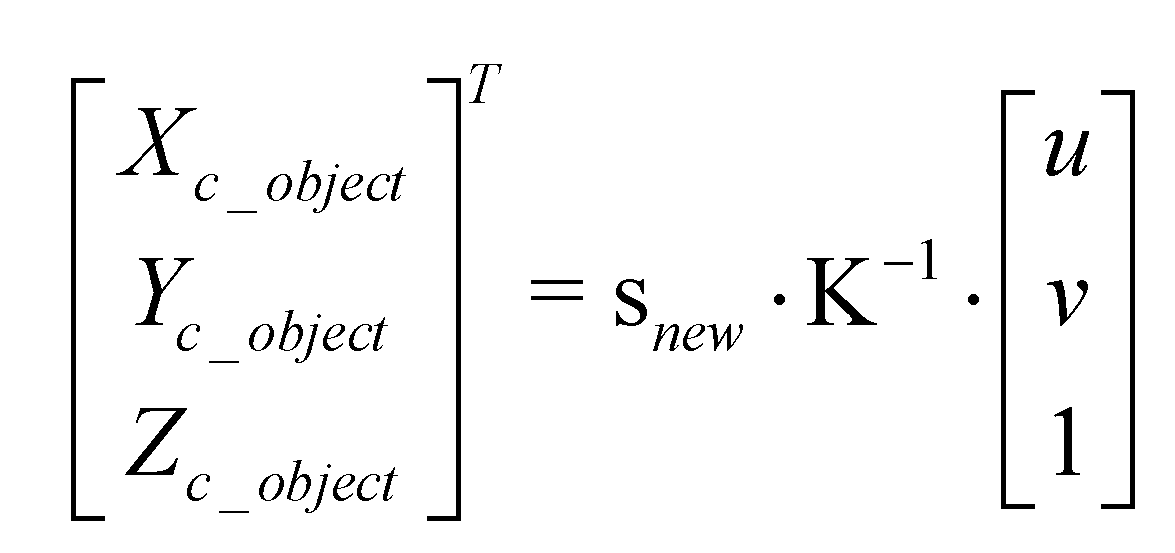
The calibration process is shown in the Figure 3.
Compared to other commonly used neural network models, the Feedforward Neural Network (FNN) demonstrates superior performance in data mapping, model flexibility, and fault tolerance. Moreover, this model boasts a simple structure, high computational efficiency, and the capability to approximate any continuous function with arbitrary precision. Drawing inspiration from this and based on the aforementioned mathematical relationship, this paper proposes using an FNN to calibrate the correspondence between s and phase ϕ. We employ a two-layer feed-forward network with sigmoid hidden neurons and linear-output neurons (fitnet) to establish the relationship between absolute phase and height. The network structure consists of ten hidden layers and one output layer. The proposed FNN structure is illustrated in Figure 4.
In summary, the overall flowchart of the measurement implementation of the 3D measurement system designed in this article is shown in Figure 5.
The Materials and Methods should be described with sufficient details to allow others to replicate and build on the published results. Please note that the publication of your manuscript implicates that you must make all materials, data, computer code, and protocols associated with the publication available to readers. Please disclose at the submission stage any restrictions on the availability of materials or information. New methods and protocols should be described in detail while well-established methods can be briefly described and appropriately cited.
3. Experiments and Results
To validate the effectiveness of the proposed algorithm, a monocular structured light 3D measurement platform was built. The system consists of a camera (resolution: 1280 × 1024 pixels) with a 12mm lens, and a DLP projector (model TJ-X23U, resolution: 1280 × 720 pixels). The absolute phase is determined by the three-frequency heterodyne method described in Section 1.1, with selected frequencies of 1/28, 1/26, and 1/24, respectively.
4.1. DAE Training
To train the DAE network, we collected a dataset consisting of 400 sets of PMP data. A digital projector was used to cast 12-step fringe patterns onto a high-precision planar surface, which were then captured and saved by a camera. The absolute phase calculated from the 12-step phase-shifting image of the object was used as the true phase reference value. Each training sample consists of a 3-step phase-shifting image (input) and a mapping between the denoised and corrected absolute phase (predicted value) and the true absolute phase (true value) calculated from the 12-step phase-shifting image. During the training process, the Adam optimizer is used to find the optimal solution, and MSELoss is employed as the loss function.
The Figure 6 shows the loss values of the training dataset. It can be seen that as the number of training sessions increases, the loss also decreases continuously during the training process of the DAE network.
4.2. Analysis of the Selection of Iterative Denoising Times for DAE
When selecting the number of iterative denoising steps, various factors such as denoising effectiveness, signal fidelity, and processing time must be taken into account. Excessive iterations can result in signal detail loss and increased computational cost and time. Thus, finding a balance point is necessary to effectively reduce noise while preserving the original signal characteristics. In this study, a set of phase-shifting fringes undergo 50 iterative denoising treatments. The mean squared error (MSE) between the predicted absolute phase value and the true 12-step phase shift value is calculated and recorded separately. The relationship between the number of iterations and MSE is plotted as shown in Figure 7.
The figure indicates that the optimal number of iterations is 6-8. To enhance computational efficiency, we choose 6 iterations of DAE denoising and correction processing.
4.3. FNN training
To train the FNN network for calibrating the relationship between absolute phase and height, we collected a dataset consisting of 100 sets of absolute phase (φ) and scale factor (s) data. First, the camera captured an image of the calibration board at a specific position. Next, phase-shifting fringe images were projected at that position through a projector, captured by the camera, and used to calculate the absolute phase at that position. However, when the camera captures a calibration board directly projecting phase-shifting stripe images, the black area of the chessboard can cause abnormal phase resolution. Therefore, when shooting a phase-shifting stripe image at that position, a high-precision ceramic board is placed before shooting. As shown in Figure 8, it displays the captured checkerboard camera calibration image and a certain phase-shifting image at the corresponding position.


Subsequently, the camera's intrinsic parameters and the RT matrix at the captured position are calculated through camera calibration. The scale factor (s) is then determined using both the intrinsic and extrinsic parameters. The calculated camera intrinsic parameters and the RT matrix at a specific position are shown in Table 1.
Finally, the FNN network uses the absolute phase (φ) as input and the scale factor (s) as output for training. Figure 9 illustrates the changes in accuracy for both the training and testing sets in a similar manner. As the number of training epochs increases, the two curves in Figure. 9 follow a similar trend and remain close to each other, indicating no significant overfitting during the FNN network's training process.
4.4. Analysis of Experimental Results
To verify the effectiveness of the proposed denoising method and evaluate the calibration approach's accuracy, experiments comparing denoising effects and accuracy were conducted.
4.4.1. Denoising Experiment
After completing DAE training, we used Gaussian filters and DAE networks to denoise and correct the phase-shifting fringe images captured by the camera, and calculated their absolute phases. To determine the absolute phase accuracy, the difference between the absolute phases obtained through two denoising and correction methods and the true absolute phase (obtained through a 12 step phase shift method) was calculated. Only the red box was considered for comparison. Figure. 10 illustrates the calculation of the absolute phase of the same high-precision diffuse reflective ceramic plate (flatness error of 1μm) after three steps of noise reduction correction, Gaussian filtering correction, DAE correction, and 12 step phase shift method. The absolute phase difference between them and the 12 step phase-shifting method is calculated separately. Figure. 10 shows the absolute phase calculated by different methods and their absolute phase difference compared to the 12 step phase-shifting method.
The DAE's accuracy is limited by the 12 step phase shift method's accuracy, as the DAE is calibrated using the absolute phase calculated by this method.
Traditional Gaussian filtering techniques can reduce phase errors caused by image noise to some extent, as shown in the figure above. However, they are more sensitive to changes in the reflectivity of the measured object. To further evaluate the DAE network's performance, phase-shifting fringe images of a highly reflective object captured by the camera were input into the network for denoising and correction.
Figure 11 illustrates the calculation of the absolute phase of the same highly reflective aluminum plane after three steps of noise reduction correction, Gaussian filtering correction, DAE correction, and the 12 step phase shift method. The absolute phase difference between them and the 12 step phase-shifting method is calculated separately.
As shown in Figure 11, traditional Gaussian filtering methods have poor processing effects due to the loss of phase shift information in reflective areas. Experimental results demonstrate that compared to direct Gaussian filtering, the DAE correction method can significantly reduce phase errors caused by image noise and has a good correction effect on phase calculation during the measurement of objects with large reflectivity changes.
4.4.2. Calibration Experiment
To test the effectiveness of the proposed phase-height calibration method, the measurement system constructed in this paper adopts inverse linear, polynomial fitting, and FNN for phase-height calibration after DAE noise reduction and correction of the collected phase-shifting fringes. Figure. 12 compares the measurement accuracy of different calibration methods for calculating standard balls with a diameter of 24.99920mm and a surface accuracy of 0.5 µm.
To verify the measurement stability of this method, 5 sets of cyclic measurements were conducted on the standard sphere, and the root mean square error (RMSE) of the mean absolute error (MAE) was calculated. The measurement results are shown in Table 2.
The results indicate that using FNN for absolute phase and height calibration results in higher accuracy and better stability compared to the other two common calibration methods.
4.4.3. Measurement Experiments in Different Scenarios
In qualitative experiments to test the object's shape recovery in different scenarios using the method in this paper, most structured light 3D measurement devices struggle to accurately measure the dimensions of black surface objects, often resulting in lost point cloud data. Figure 13 shows the reconstruction performance of a black matte plastic cover.
In addition, to verify the shape recovery of irregular free-form high-gloss objects using the method in this paper, the reconstruction performance of aluminum metal surfaces was also tested, as shown in Figure 14.
5. Conclusions
This article proposes a structured light 3D reconstruction method based on deep learning. The method utilizes DAE to denoise and correct phase-shifted fringes, obtaining high-quality fringe images for absolute phase calculation. Simultaneously, FNN is used to calibrate the relationship between absolute phase and height, achieving high-precision calibration. This method has significant application value in the field of optical 3D measurement methods. Experimental results demonstrate that, compared to traditional filtering methods, the proposed DAE denoising method has a better denoising correction effect. Moreover, compared to traditional common calibration methods, the proposed FNN-based absolute phase and height calibration method can also achieve higher calibration accuracy.
Author Contributions
The contributions of the authors are as follows. Conceptualization, C.L.; Methodology, C.L.; Software, J.C.; Formal analysis, C.L.; Part preparation for the measurement, C.L. and J.C.; Writing J.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brown, G.M. Overview of three-dimensional shape measurement using optical methods. Optical Engineering 2000, 39, 10–22. [Google Scholar] [CrossRef]
- Zhang, S.J.O.; engineering, l.i. High-speed 3D shape measurement with structured light methods: A review. Optics and lasers in engineering 2018, 106, 119–131. [Google Scholar] [CrossRef]
- Srinivasan, V.; Liu, H.C.; Halioua, M. Automated phase-measuring profilometry of 3-D diffuse objects. Appl Opt 1984, 23, 3105. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yun, J.; Xu, Z.; Huan, Z.J.M.S.; Technology. An iterative phase-correction method for low-quality phase-shift images and its application. Measurement Science and Technology 2021, 32, 065005. [Google Scholar] [CrossRef]
- Debevec, P.E.; Malik, J. Recovering high dynamic range radiance maps from photographs. In Seminal Graphics Papers: Pushing the Boundaries, Volume 2; 2023; pp. 643–652.
- Waddington, C.; Kofman, J.J.O.E. Modified sinusoidal fringe-pattern projection for variable illuminance in phase-shifting three-dimensional surface-shape metrology. Optical Engineering 2014, 53, 084109–084109. [Google Scholar] [CrossRef]
- Chen, T.; Lensch, H.P.; Fuchs, C.; Seidel, H.-P. Polarization and phase-shifting for 3D scanning of translucent objects. In Proceedings of the 2007 IEEE conference on computer vision and pattern recognition; 2007; pp. 1–8. [Google Scholar]
- Chandel, R.; Gupta, G.J.I.J.o.A.R.i.C.S.; Engineering, S. Image filtering algorithms and techniques: A review. International Journal of Advanced Research in Computer Science and Software Engineering 2013, 3. [Google Scholar]
- Takeda, H.; Farsiu, S.; Milanfar, P.J.I.T.o.i.p. Kernel regression for image processing and reconstruction. IEEE Transactions on image processing 2007, 16, 349–366. [Google Scholar] [CrossRef] [PubMed]
- Knaus, C.; Zwicker, M. Dual-domain image denoising. In Proceedings of the 2013 IEEE International Conference on Image Processing; 2013; pp. 440–444. [Google Scholar]
- Yicheng, D. ; Research on Structural Light Stripe Image Processing Technology. Zhejiang University of Technology, 2012.(in chinese).
- He, Y.; Cao, Y.; Zhong, L.; Cheng, C.J.C.J.L. Improvement on measuring accuracy of digital phase measuring profilometry by frequency filtering. Chin. J. Lasers 2010, 37, 220–224. [Google Scholar]
- Baker, M.J.; Xi, J.; Chicharo, J.F.J.A.o. Neural network digital fringe calibration technique for structured light profilometers. Applied optics 2007, 46, 1233–1243. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, S.; Jiang, H.; Zhang, Y.; Xu, Z.J.O.E. Calibration of AOTF-based 3D measurement system using multiplane model based on phase fringe and BP neural network. Optics Express 2017, 25, 10413–10433. [Google Scholar] [CrossRef]
- Rao, L.; Da, F.J.O.; Technology, L. Neural network based color decoupling technique for color fringe profilometry. Optics & Laser Technology 2015, 70, 17–25. [Google Scholar]
- Lin, B.; Fu, S.; Zhang, C.; Wang, F.; Li, Y.J.O.; Engineering, L.i. Optical fringe patterns filtering based on multi-stage convolution neural network. Optics and Lasers in Engineering 2020, 126, 105853. [Google Scholar] [CrossRef]
- Gurrola-Ramos, J.; Dalmau, O.; Alarcón, T.J.O.; Engineering, L.i. U-Net based neural network for fringe pattern denoising. Optics and Lasers in Engineering 2022, 149, 106829. [Google Scholar] [CrossRef]
- Baker, M.J.; Xi, J.; Chicharo, J.F. Multi-channel digital fringe calibration for structured light profilometers using neural networks. In Proceedings of the 2007 IEEE Instrumentation & Measurement Technology Conference IMTC 2007; 2007; pp. 1–6. [Google Scholar]
- Zhou, W.-S.; Su, X.-Y.J.J.o.m.o. A direct mapping algorithm for phase-measuring profilometry. Journal of modern optics 1994, 41, 89–94. [Google Scholar] [CrossRef]
- Mao, X.; Chen, W.; Su, X.J.A.o. Improved Fourier-transform profilometry. Applied optics 2007, 46, 664–668. [Google Scholar] [CrossRef]
- Li, Y.; Su, X.; Wu, Q.J.J.o.M.O. Accurate phase–height mapping algorithm for PMP. Journal of Modern Optics 2006, 53, 1955–1964. [Google Scholar] [CrossRef]
- Lu, J.; Mo, R.; Sun, H.; Chang, Z.J.A.O. Flexible calibration of phase-to-height conversion in fringe projection profilometry. Applied Optics 2016, 55, 6381–6388. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Liu, Y.J.O. An accurate phase-height mapping algorithm by using a virtual reference plane. Optik 2020, 206, 164083. [Google Scholar] [CrossRef]
- Yanjun, F.; Xiaoqi, C.; Kejun, Z.; Baiheng, M.; Zhanjun, Y.J. Method for phase-height mapping calibration based on fringe projection profilometry. Infrared and Laser Engineering 2022, 51, 20210403-20210401-20210403-20210409. [Google Scholar]
- Li, Z.-w.; Shi, Y.-s.; Wang, C.-j.; Qin, D.-h.; Huang, K.J.O.C. Complex object 3D measurement based on phase-shifting and a neural network. Optics Communications 2009, 282, 2699–2706. [Google Scholar] [CrossRef]
- Chung, B.-m.J.O.A. Neural network model for phase-height relationship of each image pixel in 3D shape measurement by machine vision. Optica Applicata 2014, 44, 587–599. [Google Scholar]
- Liu, Y.; Zhang, Q.; Su, X.J.O.; Engineering, L.i. 3D shape from phase errors by using binary fringe with multi-step phase-shift technique. Optics and Lasers in Engineering 2015, 74, 22–27. [Google Scholar] [CrossRef]
- Chen, L.; Deng, W.; Lou, X.J.O.T. Phase unwrapping method base on multi-frequency interferometry. Optical Technique 2012, 38, 73–78. [Google Scholar] [CrossRef]
- Orbach, J. Principles of Neurodynamics. Perceptrons and the Theory of Brain Mechanisms. Archives of General Psychiatry 1962, 7. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R.J.s. Reducing the dimensionality of data with neural networks. science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Welling, M.J.a.p.a. Auto-encoding variational bayes. arXiv preprint arXiv 2013.
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the Proceedings of the 25th international conference on Machine learning, 2008; pp. 1096–1103.
- Fine, T.L. Feedforward neural network methodology; Springer Science & Business Media: 1999.
- Rojas, R.; Rojas, R.J.N.n.a.s.i. The backpropagation algorithm. Neural networks: a systematic introduction 1996, 149-182.
- Zhang, Z.J.I.T.o.p.a.; intelligence, m. A flexible new technique for camera calibration. IEEE Transactions on pattern analysis and machine intelligence 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
Figure 1.
Structure of structured light 3D reconstruction system.
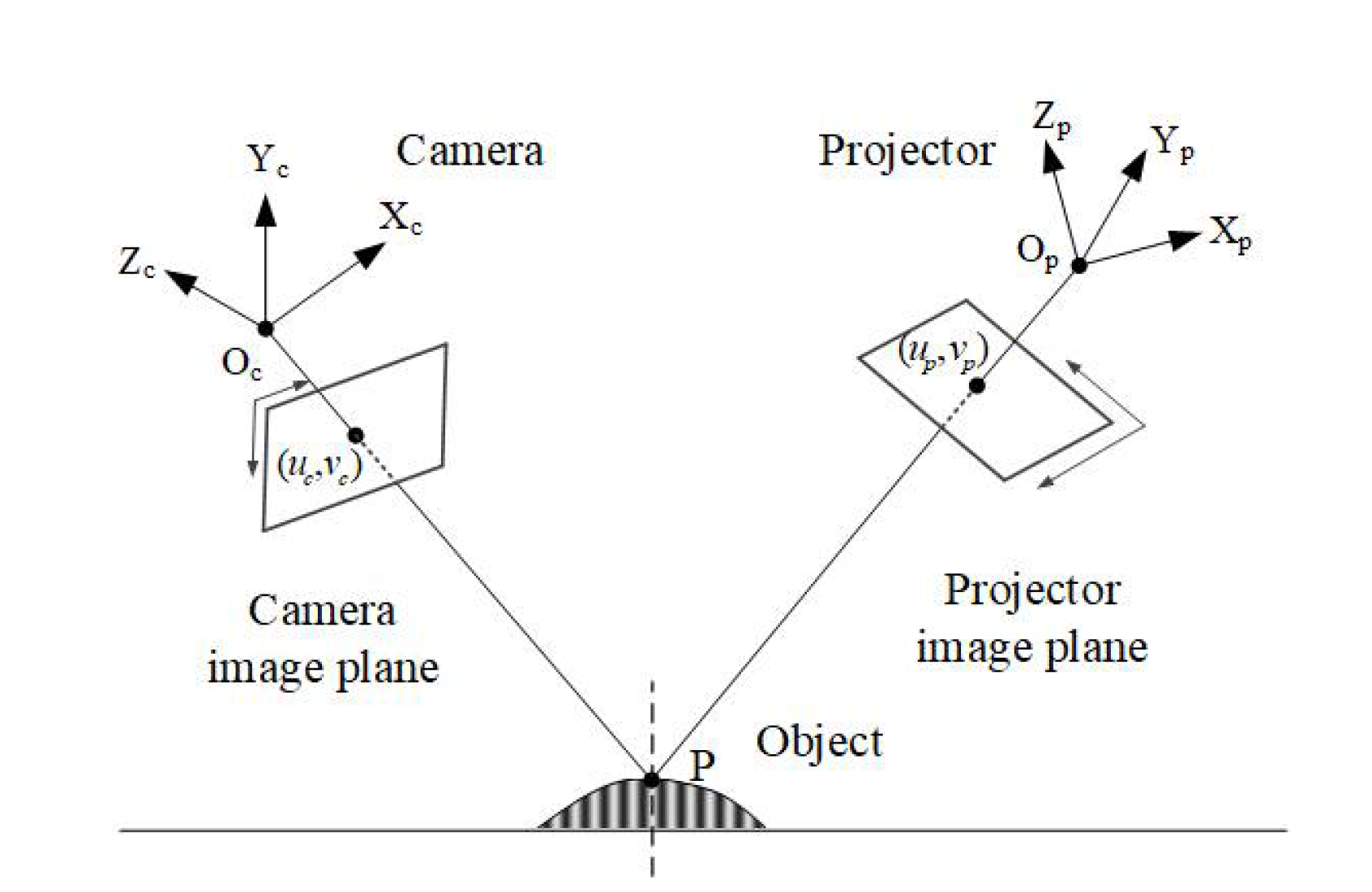
Figure 2.
The proposed DAE network architecture diagram.
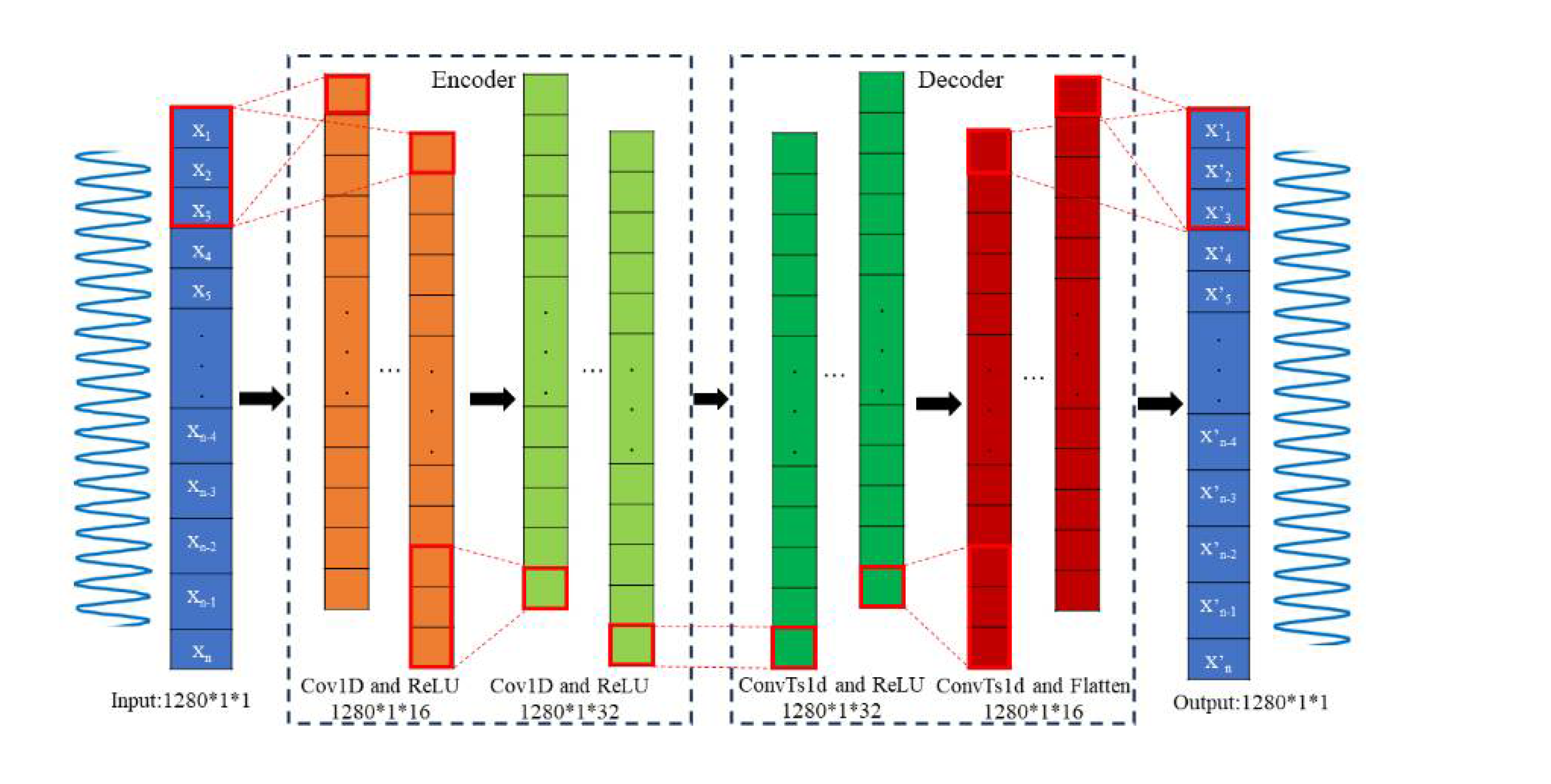
Figure 3.
Schematic diagram of phase and height calibration process.
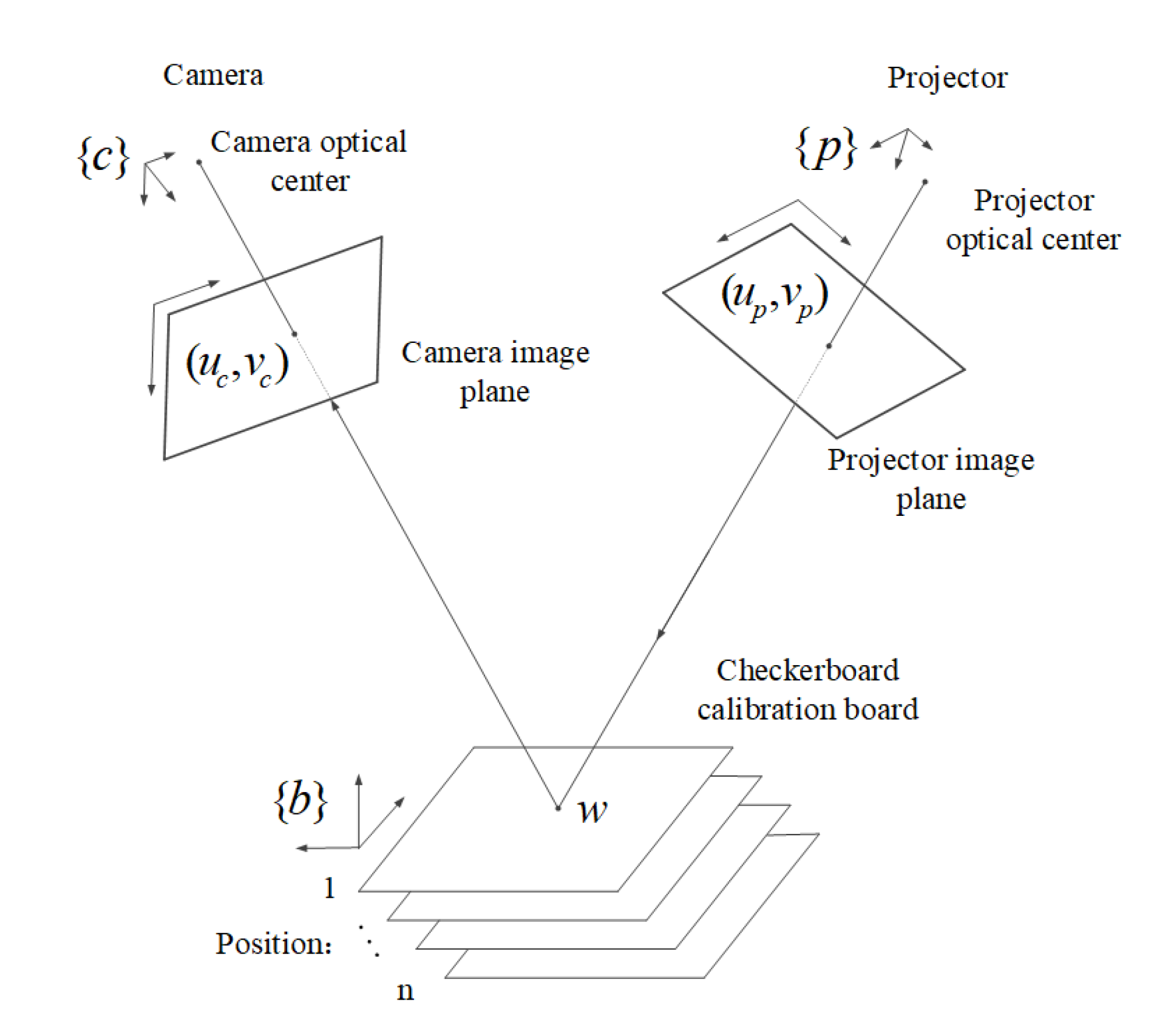
Figure 4.
The proposed FNN model structure diagram.
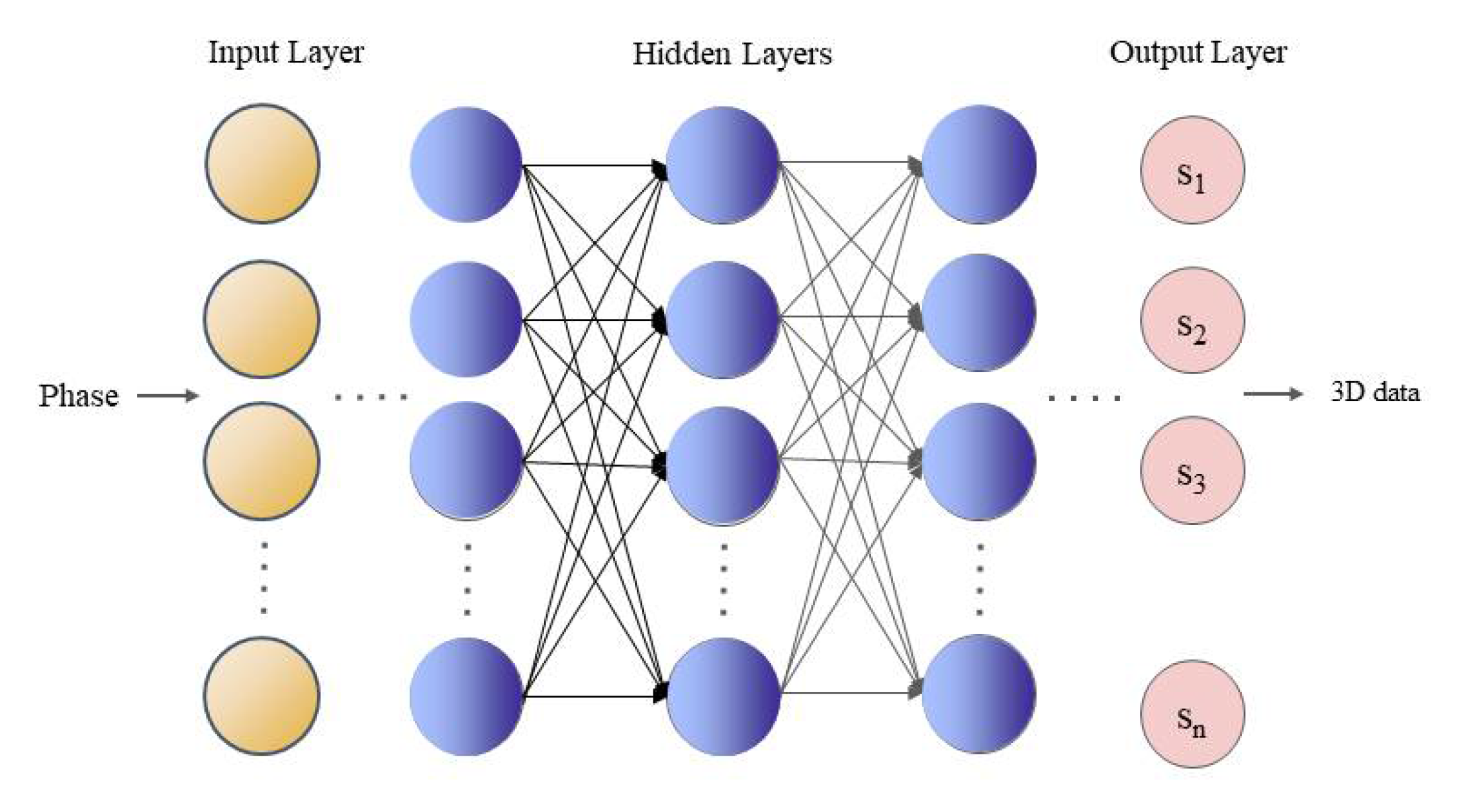
Figure 5.
Figure 5. System implementation measurement general principle diagram
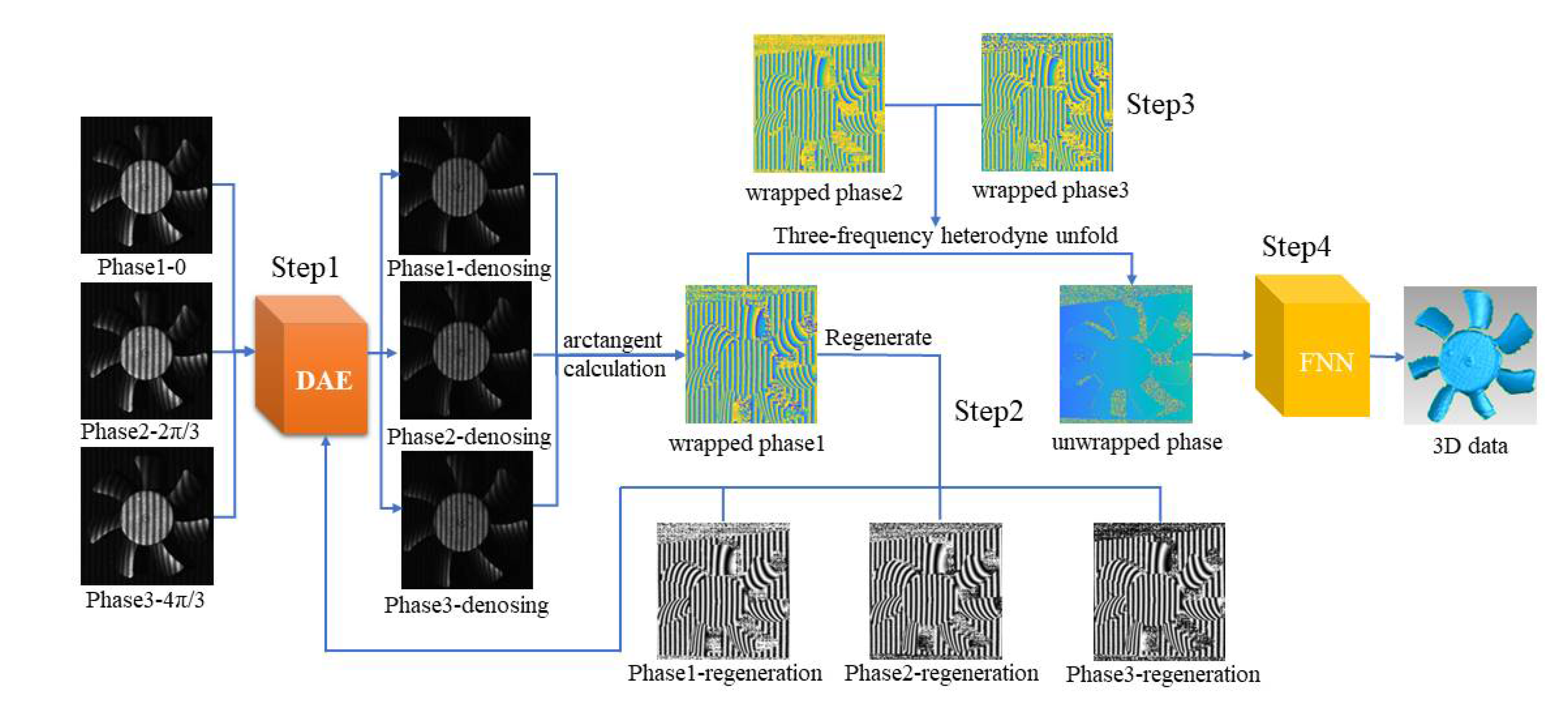
Figure 6.
The relationship between the loss values of training datasets and the number of training iterations.
Figure 6.
The relationship between the loss values of training datasets and the number of training iterations.
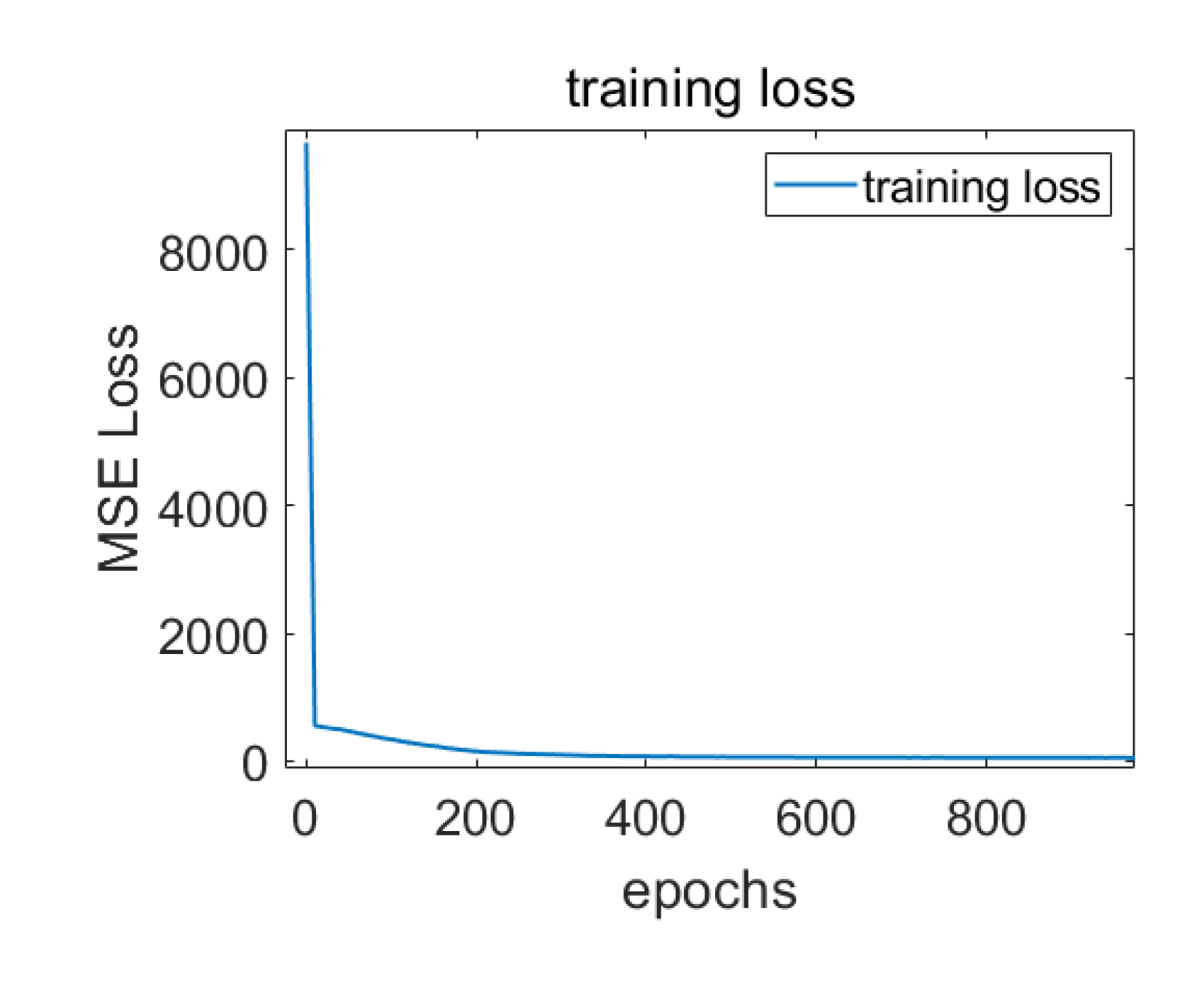
Figure 7.
Figure 7. The relationship between the number of iterations and MSE
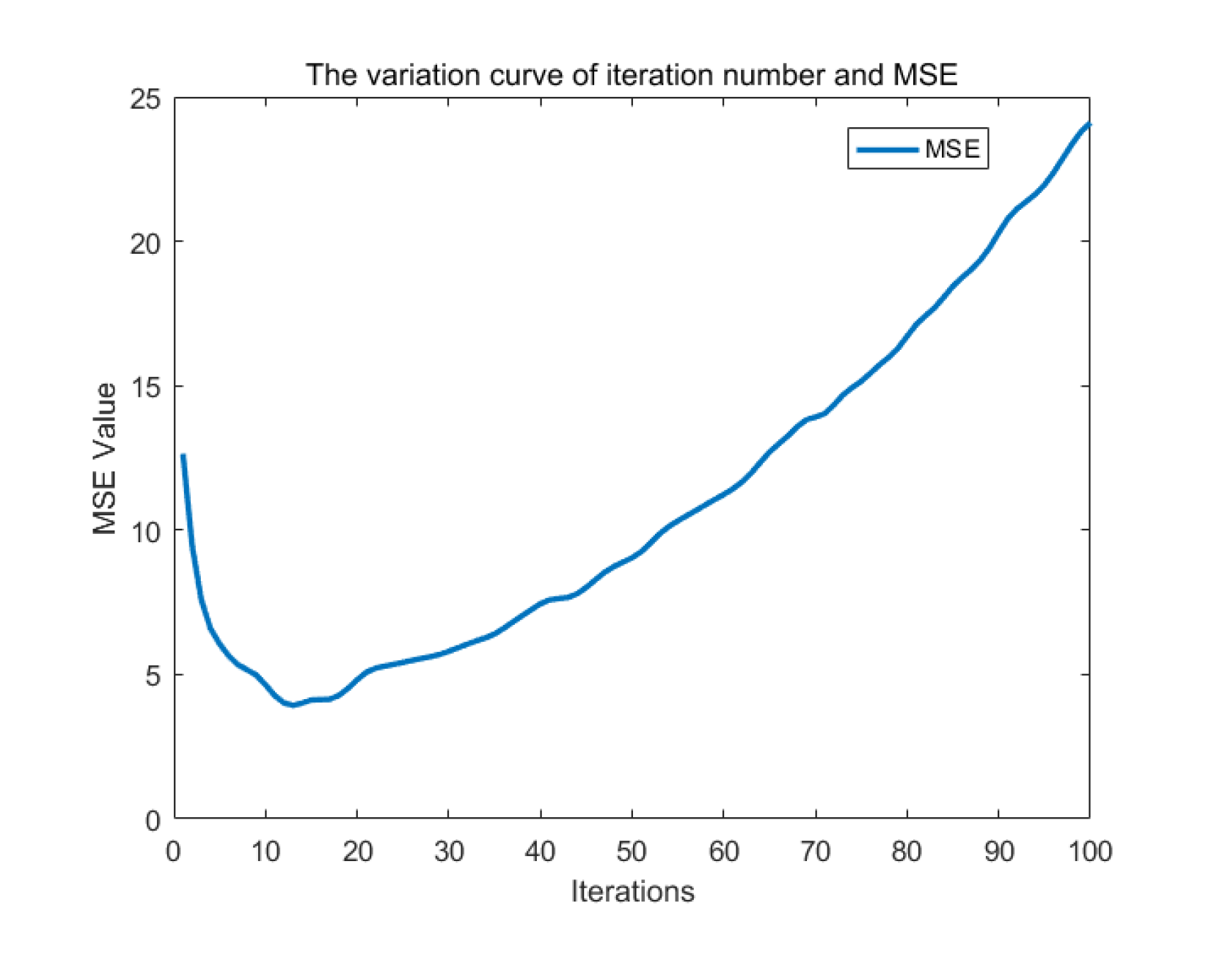
Figure 8.
Captured checkerboard camera calibration image and phase-shifting image at the corresponding position.(a)Checkerboard image taken before placing the plane; (b)Phase shift fringe pattern taken after placing the plane.
Figure 8.
Captured checkerboard camera calibration image and phase-shifting image at the corresponding position.(a)Checkerboard image taken before placing the plane; (b)Phase shift fringe pattern taken after placing the plane.

Figure 9.
The changes in accuracy for both the training and testing sets.
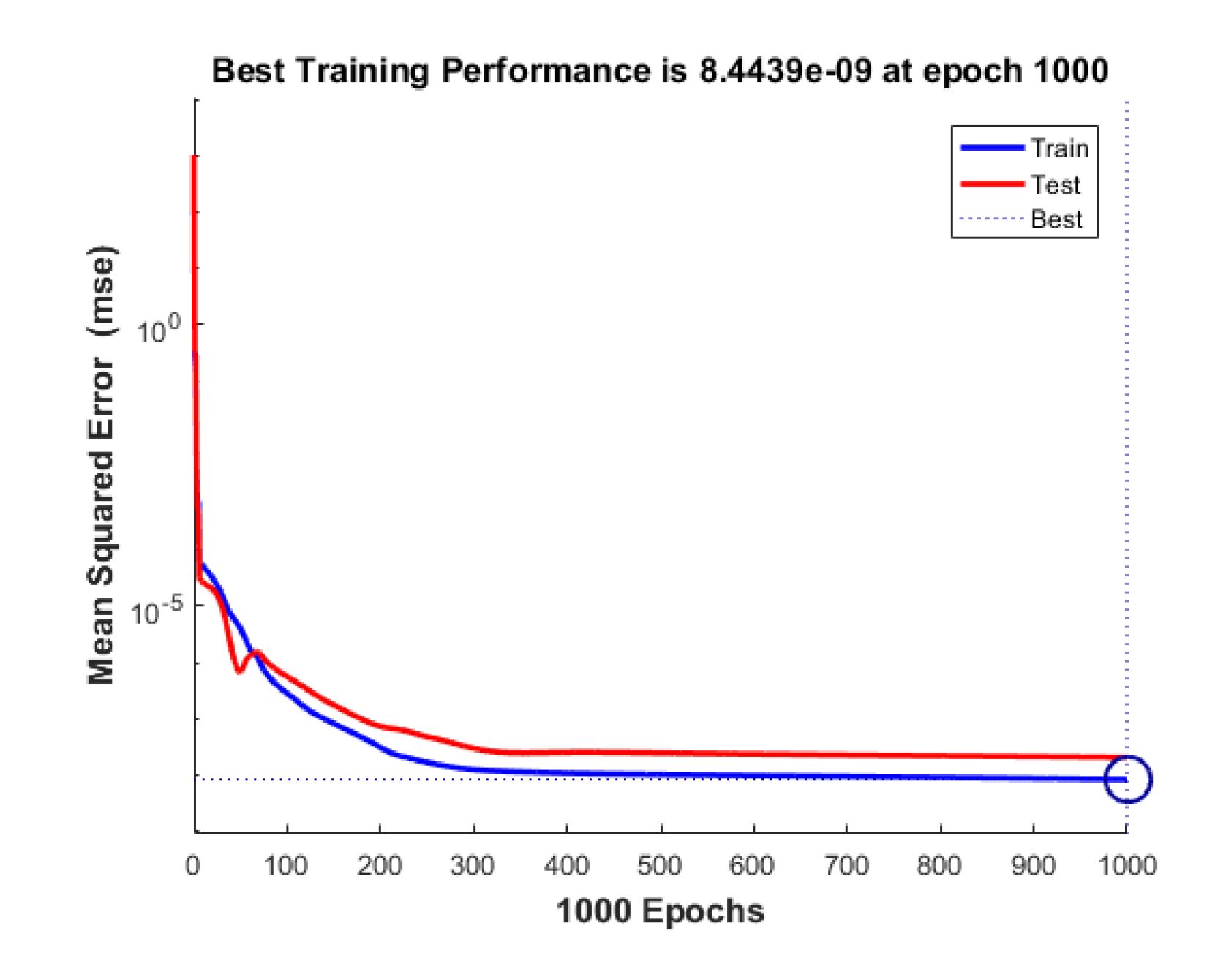
Figure 10.
the high-precision diffuse reflective ceramic plate’s absolute phase calculated by different methods and their absolute phase difference compared to the 12 step phase-shifting method. (a) Phase shift image captured; (b) Phase shifted stripe image of a certain row; (c) Absolute phase without calibration by using 3-step phase shift method; (d) Absolute phase calculated after Gaussian filtering; (e) Absolute phase calculated after DAE; (f) Absolute phase calculated by using 12-step phase shift method; (g) Absolute phase difference calculated using 3-step and 12-step phase-shifting methods; (h) Absolute phase difference calculated using gaussian filtering and 12-step phase-shifting methods; (i) Absolute phase difference calculated using DAE and 12-step phase-shifting methods;.
Figure 10.
the high-precision diffuse reflective ceramic plate’s absolute phase calculated by different methods and their absolute phase difference compared to the 12 step phase-shifting method. (a) Phase shift image captured; (b) Phase shifted stripe image of a certain row; (c) Absolute phase without calibration by using 3-step phase shift method; (d) Absolute phase calculated after Gaussian filtering; (e) Absolute phase calculated after DAE; (f) Absolute phase calculated by using 12-step phase shift method; (g) Absolute phase difference calculated using 3-step and 12-step phase-shifting methods; (h) Absolute phase difference calculated using gaussian filtering and 12-step phase-shifting methods; (i) Absolute phase difference calculated using DAE and 12-step phase-shifting methods;.
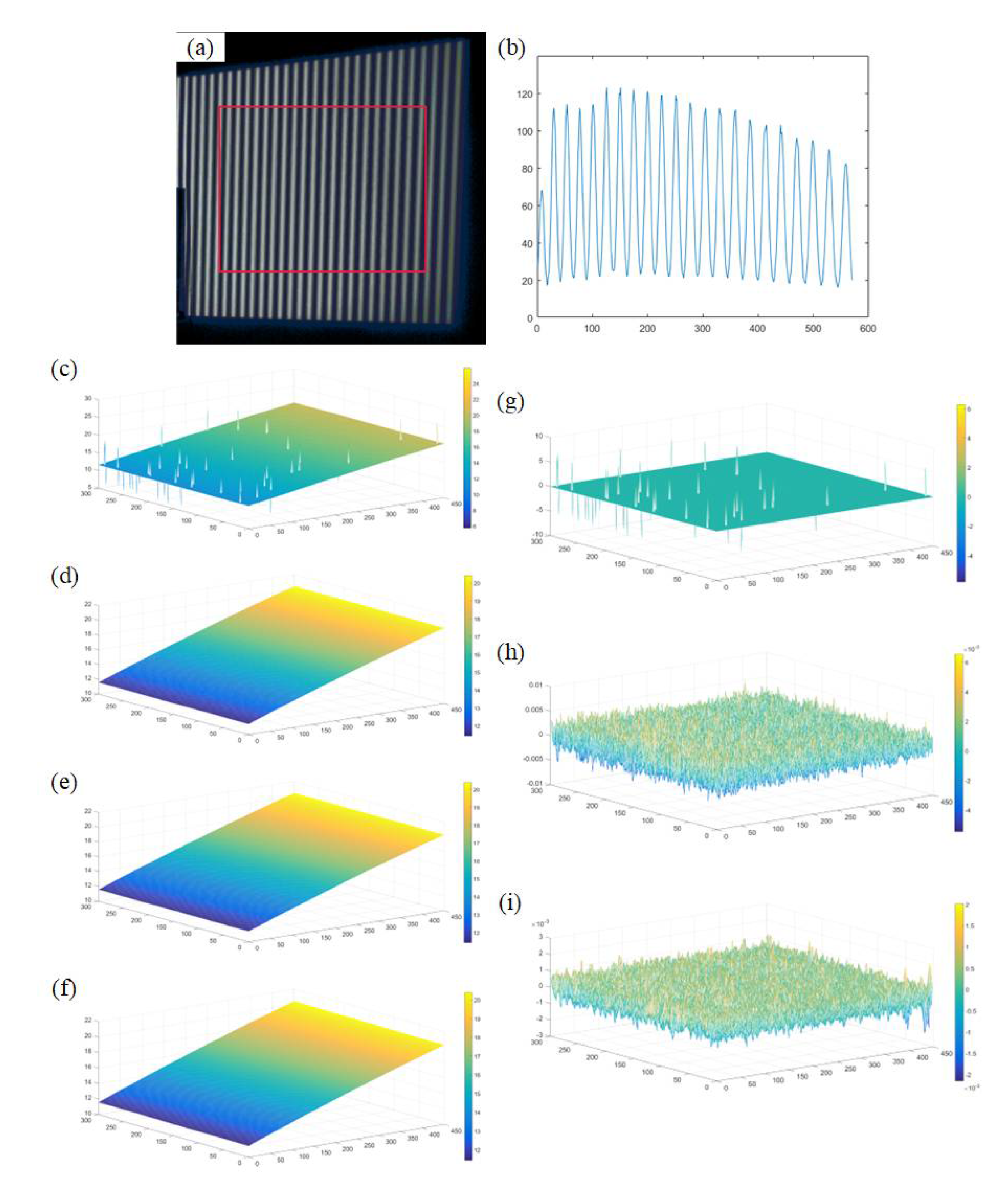
Figure 11.
the highly reflective metal aluminum plane’s absolute phase calculated by different methods and their absolute phase difference compared to the 12 step phase-shifting method. (a) Phase shift image captured; (b) Phase shift stripe pattern at high reflective red lines; (c) Absolute phase without calibration by using 3-step phase shift method; (d) Absolute phase calculated after Gaussian filtering; (e) Absolute phase calculated after DAE; (f) Absolute phase calculated by using 12-step phase shift method;(g) Absolute phase difference calculated using 3-step and 12-step phase-shifting methods; (h) Absolute phase difference calculated using gaussian filtering and 12-step phase-shifting methods; (i) Absolute phase difference calculated using DAE and 12-step phase-shifting methods;.
Figure 11.
the highly reflective metal aluminum plane’s absolute phase calculated by different methods and their absolute phase difference compared to the 12 step phase-shifting method. (a) Phase shift image captured; (b) Phase shift stripe pattern at high reflective red lines; (c) Absolute phase without calibration by using 3-step phase shift method; (d) Absolute phase calculated after Gaussian filtering; (e) Absolute phase calculated after DAE; (f) Absolute phase calculated by using 12-step phase shift method;(g) Absolute phase difference calculated using 3-step and 12-step phase-shifting methods; (h) Absolute phase difference calculated using gaussian filtering and 12-step phase-shifting methods; (i) Absolute phase difference calculated using DAE and 12-step phase-shifting methods;.
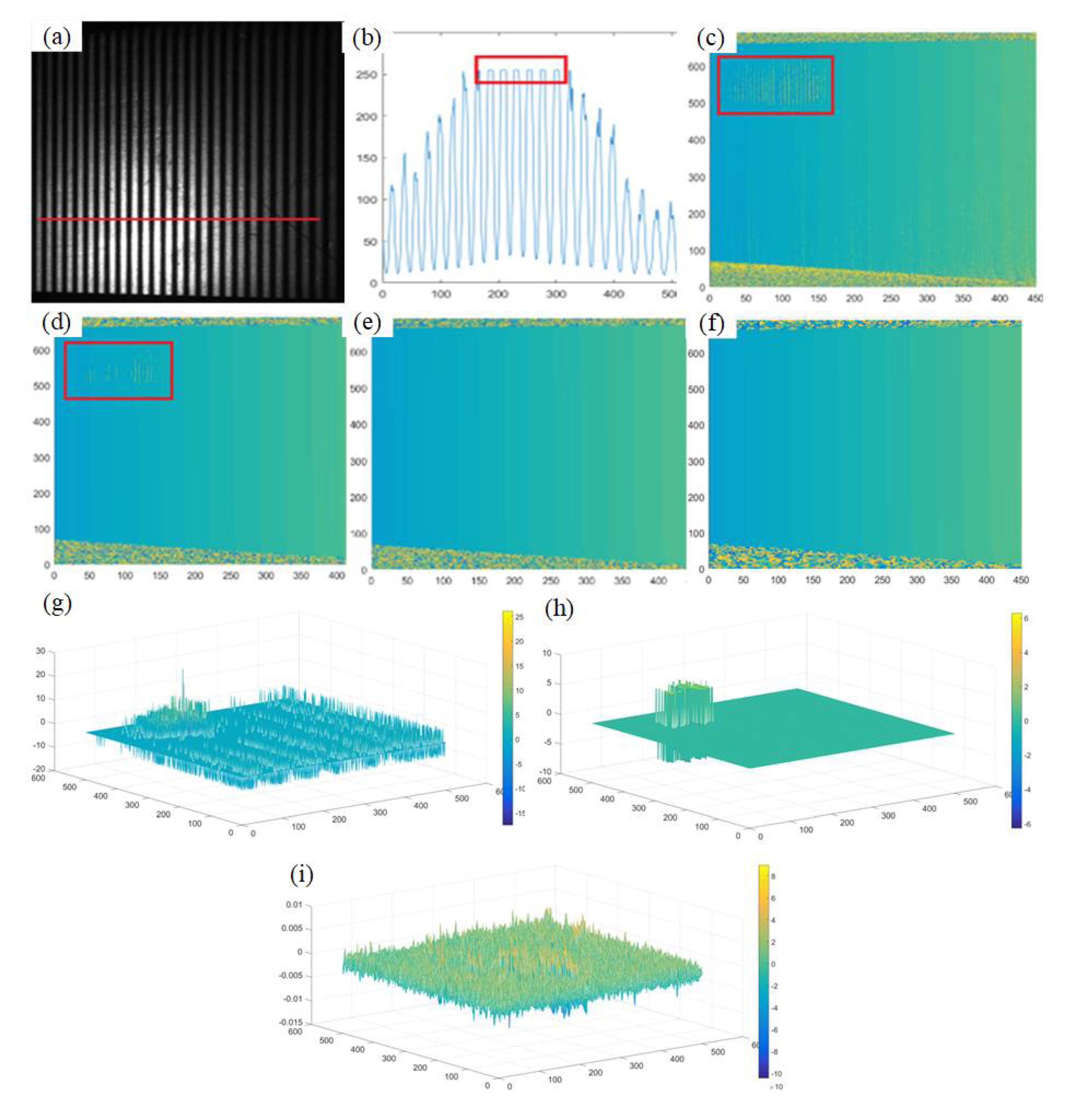
Figure 12.
The fitting of standard spherical point clouds calculated using different calibration methods. (a) Point cloud determined by the inverse linear calibration method; (b) Point cloud determined by the polynomial fitting calibration method; (c) Point cloud determined by the FNN fitting calibration method;.
Figure 12.
The fitting of standard spherical point clouds calculated using different calibration methods. (a) Point cloud determined by the inverse linear calibration method; (b) Point cloud determined by the polynomial fitting calibration method; (c) Point cloud determined by the FNN fitting calibration method;.
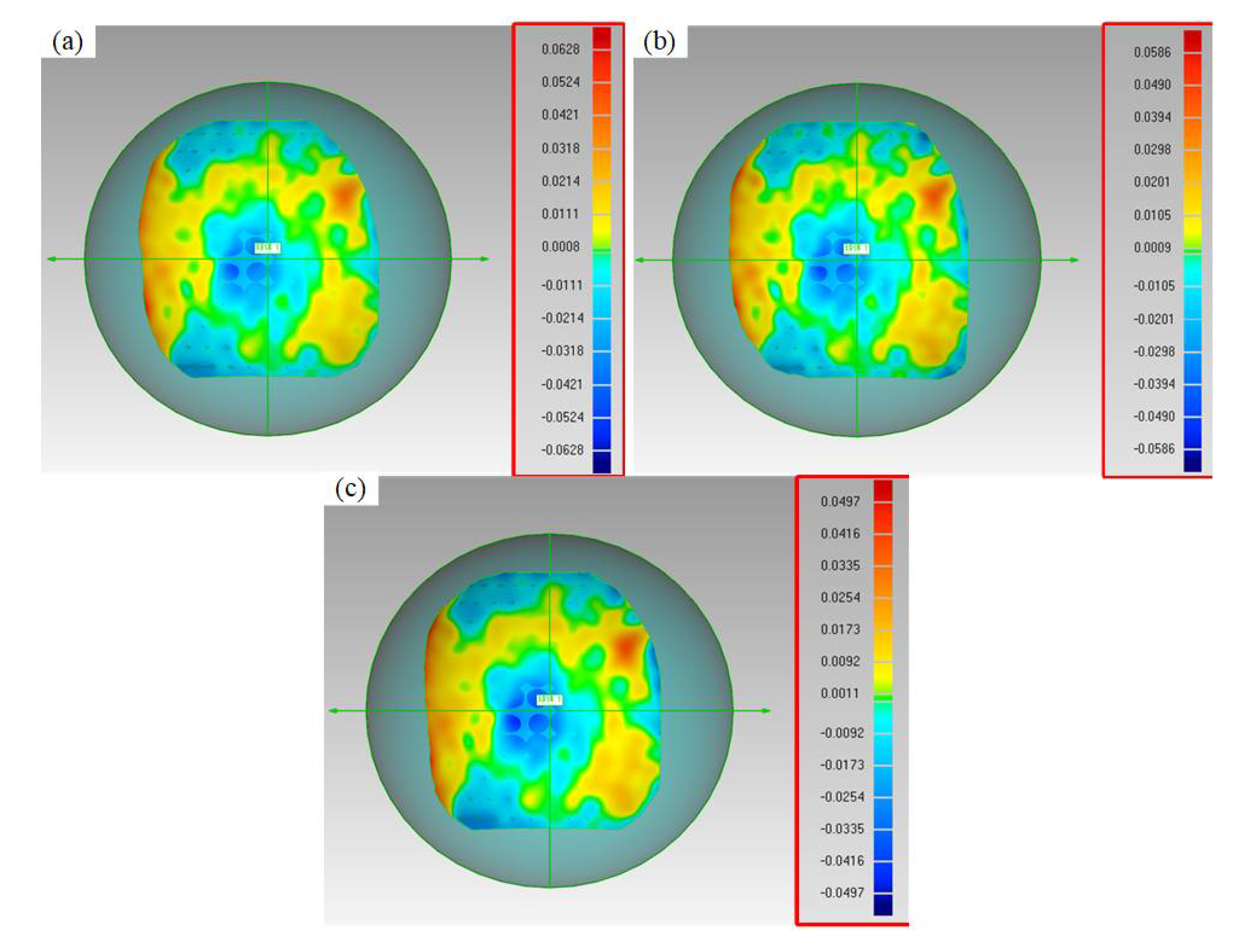
Figure 13.
The reconstruction performance of black matte plastic cover. (a)Phase shift image captured; (b) Phase shift stripe pattern at low reflective red lines; (c) Absolute phase without calibration by using 3-step phase shift method; (d) Point cloud fitting result calculated using 3-step phase shift method;(e) Absolute phase calculated after Gaussian filtering; (f) Absolute phase calculated after DAE; (g) Absolute phase calculated by using 12-step phase shift method; (h) Point cloud fitting calculated using gaussian filtering; (i) Point cloud fitting result calculated using DAE; (j) Point cloud fitting result calculated using 12-step phase shift method.
Figure 13.
The reconstruction performance of black matte plastic cover. (a)Phase shift image captured; (b) Phase shift stripe pattern at low reflective red lines; (c) Absolute phase without calibration by using 3-step phase shift method; (d) Point cloud fitting result calculated using 3-step phase shift method;(e) Absolute phase calculated after Gaussian filtering; (f) Absolute phase calculated after DAE; (g) Absolute phase calculated by using 12-step phase shift method; (h) Point cloud fitting calculated using gaussian filtering; (i) Point cloud fitting result calculated using DAE; (j) Point cloud fitting result calculated using 12-step phase shift method.
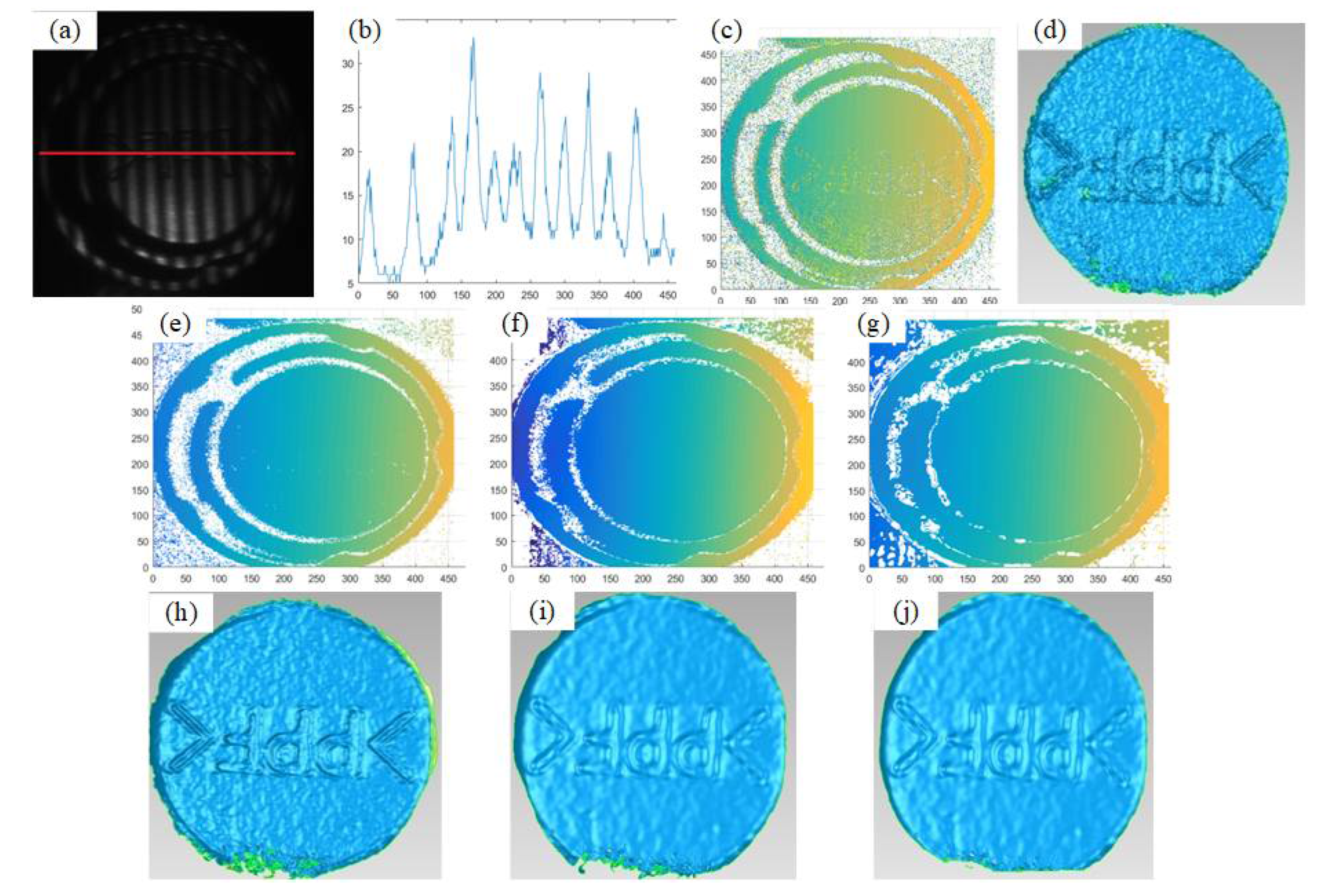
Figure 14.
Measurement results of the high reflective metal aluminum plane: (a) Point cloud fitting result calculated using 3-step phase shift method;(b) Point cloud fitting result calculated using 12-step phase shift method;(c) Point cloud fitting result calculated using method described in this article (d) Point cloud fitting result calculated using 12-step phase shift method.
Figure 14.
Measurement results of the high reflective metal aluminum plane: (a) Point cloud fitting result calculated using 3-step phase shift method;(b) Point cloud fitting result calculated using 12-step phase shift method;(c) Point cloud fitting result calculated using method described in this article (d) Point cloud fitting result calculated using 12-step phase shift method.
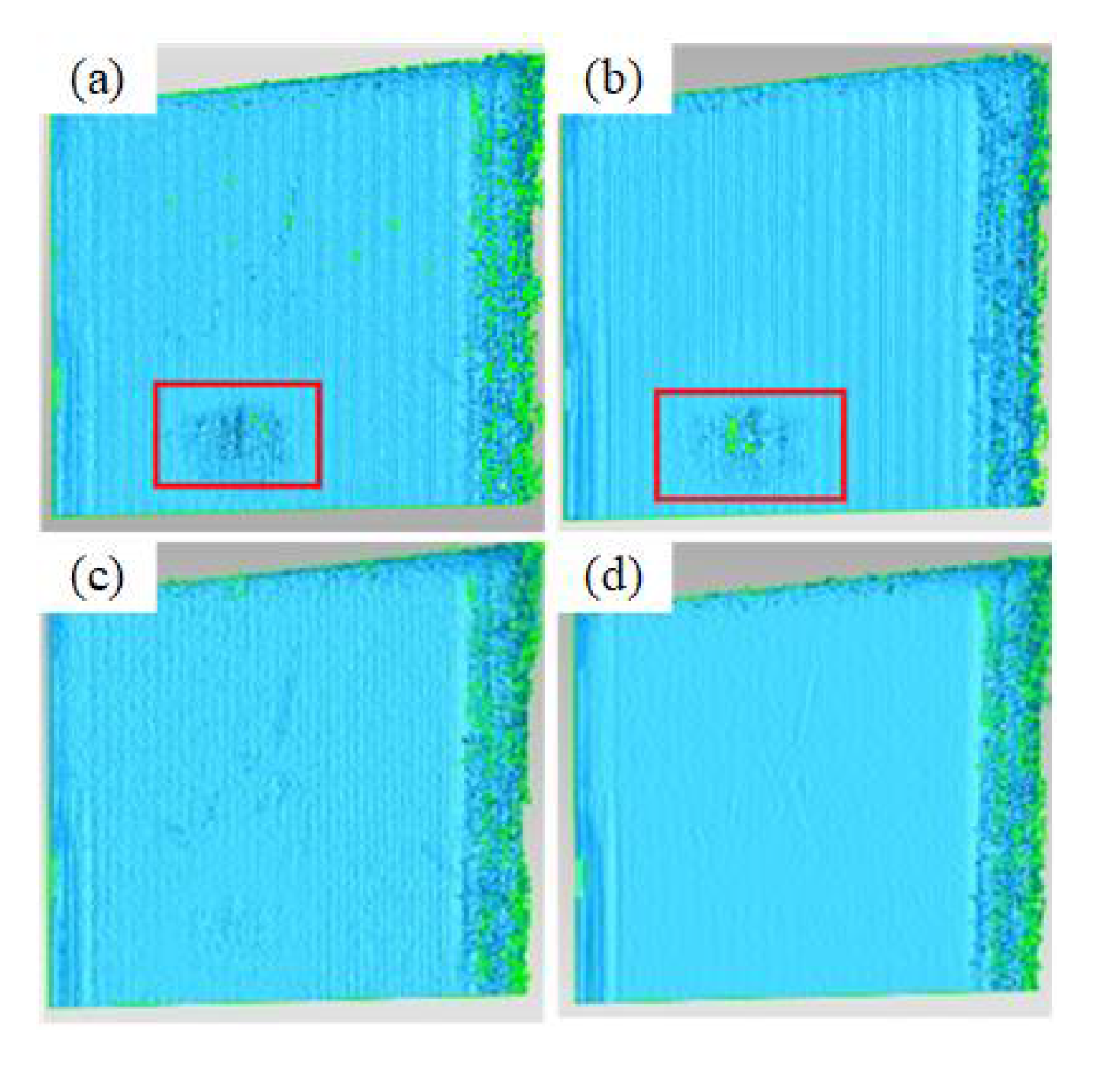
Table 1.
The intrinsic parameters of camera.
| Unit/pixel | Camera |
|---|---|
| Focal length | [3384.99, 3382.34] |
| Principal point | [645.45, 512.89] |
| Distortion | [ -0.10571, 1.46556, -0.00076, 0.00014, 0.00000] |
| Re-projection error | [ 0.03151, 0.03341 ] |
Table 2.
Measurement results of a standard ball with a diameter of 24.99920 mm.
| Method /Number |
1 | 2 | 3 | 4 | 5 | MAE (μm) |
RMSE (μm) |
|---|---|---|---|---|---|---|---|
| inverse linear | 24.935 | 25.077 | 25.064 | 25.057 | 25.066 | 66 | 66.43 |
| polynomial fitting | 24.944 | 25.061 | 25.057 | 25.05 | 25.059 | 56 | 56.12 |
| FNN | 25.042 | 24.967 | 24.962 | 24.953 | 24.951 | 44 | 44.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





