Messy Broadcasting in Grid

Preprint

Article

Messy Broadcasting in Grid

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Aria Adibi^*

Hovhannes A. Harutyunyan^*

Aria Adibi^*

Hovhannes A. Harutyunyan^*

This version is not peer-reviewed

Submitted:

27 June 2024

Posted:

28 June 2024

You are already at the latest version

Alerts

Abstract

In classical broadcast models, information is disseminated in synchronous rounds under the constant communication time model, wherein a node may only inform one of its neighbors in each time unit—also known as the processor-bound model. These models assume either a coordinating leader or that each node has a set of coordinated actions optimized for each originator, which may requiring nodes to have sufficient storage, processing power, and the ability to determine the originator. This assumption is not always ideal, and a broadcast model based on the node’s local knowledge can sometimes be more effective. Messy models address these issues by eliminating the need for a leader, knowledge of the starting time, and the identity of the originator, relying solely on local knowledge available to each node. This paper investigates the Messy broadcast time and optimal scheme in a Grid graph, a structure widely used in computer networking systems, particularly in parallel computing, due to its robustness, scalability, fault tolerance, and simplicity. The focus is on scenarios where the originator is located at one of the corner vertices, aiming to understand the efficiency and performance of Messy models in such Grid structures.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Broadcasting in computer networking means the dissemination of information, which is known initially only at some nodes, to all network members. The goal is to inform every node in the minimal time possible. There are different models for broadcasting; the simplest and the historical model is called the Classical model. In the Classical model, the dissemination happens in synchronous rounds under the constant communication time model, wherein a node may only inform one of its neighbors. This model remains popular not only for its history and graph-theoretical approach but also for its fastidious modeling of communications where small messages are exchanged, which is almost always the case in broadcasting. More information, good taxonomy, and how models are related to computer architecture are presented in [1,2,3,4,5]. The broadcast question is: What is the minimum number of rounds needed for broadcasting, and what broadcast scheme achieves it.

In the Classical model, however, for a network to know how to broadcast in minimum time, it is tacitly assumed that either

1.: an omniscient being is coordinating the actions of the nodes, or
2.: each node has a set of coordinated actions (or can compute it) optimized for each originator.

In the latter case, the nodes must have enough storage space and must also be able to determine the originator. In many situations, these assumptions are not desirable or even realistic. For instance, the network designers may want the network topology to be independently expandable, or the use of high memory or processing power may not be desirable. Some reasons for the undesirability are increased financial cost, cyber security reasons, and even susceptibility to theft, etc.

It is, therefore, natural that network nodes have local knowledge of the network rather than a global one. The exact models used in this paper are first defined in [6], named Messy models. In these models, the nodes do not know the state of the network, the originator, or the start time of the broadcasting. Moreover, they are independent agents with no coordination and a limited view of their neighbors. There are three slightly different Messy models:

Definition 1

(Model

M_{1}

). Each vertex knows the state of its neighbors at any time-unit, informed or uninformed. Each informed vertex must transmit the broadcast message to one of the uninformed neighbors, if any, in each time-unit.

Definition 2

(Model

M_{2}

). Every informed vertex knows from which neighbor (neighbors) it received the broadcast message and to which neighbors it has sent the message. Each informed vertex must transmit the broadcast message to all the neighbors except the ones it knows are informed.

Definition 3

(Model

M_{3}

). Each vertex knows to which neighbors it has sent the broadcast message. Each informed vertex must transmit the broadcast message to all the neighbors except the ones it knows are informed.

With the local knowledge, it is not natural to ask about the minimum broadcast time, but rather it is natural to ask what is the worst case time or broadcast scheme.

Definition 4

(Broadcast time of vertex u). Thebroadcast time of vertex uin graph G using model

M_{i}

, denoted

t_{i} (G, u)

or simply

t_{i} (u)

, for

i = 1, 2, 3

, is themaximumnumber of time-units required for a broadcast scheme originated from u to inform all the vertices.

Convention 1.

(Impossible to broadcast) If it is impossible to broadcast from vertex u (for example, if the graph is disconnected,) then conventionally

t_{i} (u) = \infty

for

i = 1, 2, 3

Example 1.

Figure 1 provides an example and highlights the differences between the three Messy models.

Definition 5

(

t_{i} (u, v)

). For

i = 1, 2, 3

, let

t_{i} (G, u, v)

or simply

t_{i} (u, v)

, denote the maximum number of time-units required for a broadcast scheme originated from u in graph G to inform v.

Remark 1

(Usefulness of

t_{i} (u, v)

). *Def: t(u, v) is useful since it is easy to see that

t_{i} (G, u) = {max}_{v} {t_{i} (G, u, v) | v \in V (G)}

for

i = 1, 2, 3

where

V (G)

is the vertex set of graph G.

This paper investigates the Messy Broadcast time and Optimum schemes in two-dimensional Grid graph when the originator is one of the corner vertices in subsection 3.2. The optimum broadcast time and scheme are found for Messy models

M_{1}

and

M_{3}

, which consequently gives a bound for

M_{2}

as well.

Definition 6

(Grid). A d-dimensional Grid graph of dimensions

n_{0}, n_{1}, \dots, n_{d - 1}

denoted by

G [n_{0} \times n_{1} \times \dots \times n_{d - 1}]

is a graph whose vertices are d-tuple of non-negative integers

(v_{0}, v_{1}, \dots, v_{d - 1})

where

0 \leq v_{i} \leq n_{i} - 1

for all

0 \leq i \leq d - 1

. The edges connect d-tuples which differ in exactly one coordinate by one; see Figure 2.

Definition 7.

(0 vertex) Let us call the corner vertex of a Grid with all 0 coordinates, the 0 vertex.

Our analysis will be based on vertex 0 being the originator of the broadcast. The results, however, are applicable to any corner vertex due to the existence of an automorphism that can map vertex 0 to any corner vertex.

Studying broadcasting within a Grid structure is essential due to its prevalent use in computer networking systems, especially in parallel computing. Grid topology is favored for its robustness, scalability, fault tolerance, simplicity, and efficiency.

Before delving into the Grid, this paper first examines the Messy Broadcast time and Optimum schemes under model

M_{3}

for the infinite Grid graph in subsection 3.1. Analyzing the infinite Grid is beneficial as it offers valuable insights into the broadcast problem within a borderless Grid. In this scenario, the conventional concept of broadcast time becomes irrelevant; instead, we focus on

t_{3} (0, v)

, which serves a comparable purpose to that described in Remark 1.

2. Related Work

Papers [7,8] offer a comprehensive analysis of general upper and lower bounds on Messy broadcasting, making them an excellent resource for gaining a foundational understanding of the subject. For simpler graph structures like Path, Cycle, and Complete Graph, the average (expected) Messy broadcast time has been studied instead of the worst-case scenario, as explored in [9]. Table 1 is an excerpt from a table presented in [7], highlighting a comparison between known broadcast time bounds for Classical and Messy models in various simple graph structures.

It turns out that finding the broadcast time in both Classical and Messy models is a very difficult task, in terms of NP-hardness, lower bounds of approximation algorithms, and the extremely limited classes of graphs for which the broadcast time is known. Paper [1] summarizes these difficulties for Classical models, providing the class of graphs whose broadcast time is known, though it might not be absolutely complete. Papers [10,11] offer new contributions to the study of complexity in finding broadcast time; the former investigates parameterized complexity, while the latter proves a double exponential lower bound when parameterized by the solution size. As a result, there are papers like [12,13,14,15,16,17] that focus on providing good heuristic algorithms. Meanwhile, Messy models remain less studied, highlighting the need for further research in this area.

Assumptions similar to those in Messy broadcasting are made in [18], in the context of hot-potato routing; in [19,20,21], where a similar broadcasting in a particular type of networks called radio networks is studied, and in [22,23,24] where the additional assumption that the vertices know the topology of the network is assumed, for example, a vertex would know that it is in a Hypercube. Blind broadcasting, which is similar to messy broadcasting under Model

M_{2}

, is studied in [25]. In

M_{2}

, the process ends when all the vertices are informed. In Blind broadcasting, the process continues until all of the edges are used. A related probabilistic problem is studied in [26]. In this model, each informed vertex forwards the message to a randomly chosen neighbor in a similar fashion. The goal is to determine the time by which all the vertices of an n vertex graph would know the message with the probability of

1 - \frac{1}{n}

. A list-based random model called “Quasirandom rumor spreading” is first defined in [27], which is close to the Messy model

M_{3}

. For this model, [28] have proved that if the vertices do not know the status of their neighbors, the worst broadcast time is computable from originator v to destination u in

O (m + n lg n)

-time where n is the number of vertices and m is the number of edges. Otherwise, if the status of the neighbors is known, the problem is inapproximable within a

{(\frac{1}{n})}^{0.5 - e}

multiplicative factor, for any

ϵ > 0

. Reference [29] provides a heuristic algorithm for computing universal list broadcast time using a genetic algorithm. There are other similar list-based models; one example is the Fully Adaptive model, which is studied in [30].

One might think of a more generalized version, in which instead of one-level knowledge (only neighbors), each vertex has k-level knowledge. Informally, in most cases of concern, replacing an edge with a path of length k creates graphs with similar difficulties to the original graph with one-level knowledge. Accordingly, the knowledge gained is not particularly useful. In [31], this difference was better analyzed, albeit the model there is slightly different than ours.

In the classical model, [32] computes the broadcast time and an optimum scheme for the two-dimensional Grid. It is easy to show that for a d-dimensional Grid

G = [n_{0} \times n_{1} \times \dots \times n_{d - 1}]

, the broadcast time is

\sum_{i = 0}^{d - 1} (n_{i} - 1)

. However, the broadcast time for any vertex in G remains undetermined ; [1] provides bounds for these vertices. To our knowledge, messy broadcasting has not been extensively studied in Grids, except in the context of d-dimensional Hypercubes

Q_{d}

. For

Q_{d}

[7] calculate

t_{3} (Q_{d})

and

t_{2} (Q_{d})

and providing a bound for

t_{1} (Q_{d})

In the Classical model, [32] takes a slightly different approach to study the infinite two-dimensional Grid. Let

f (n, t)

be the maximum number of vertices that can be informed after t time-units in an infinite two-dimensional Grid. They have proved that

f (2, t) \leq 2 t^{2} - 6 t + 8

for

t \geq 2

and conjectured equality. Inspired by this conjecture, papers [33,34,35] improved the results to

\begin{matrix} f (n, t) \leq \frac{2^{n}}{n!} t^{n} + \frac{2 - n 2^{n}}{(n - 1)!} t^{n - 1} \\ + \frac{1}{(n - 2)!} (4 - n - \frac{1}{3} (2^{n + 1} - n 2^{n - 2}) + n^{2} 2^{n - 1}) t^{n - 2} + O (t^{n - 3}) . \end{matrix}

Infinite two-dimensional hexagonal arrays, or triangular arrays, along with more conjectures and special case proofs have also been done; more detailed information and references can be found in [3]. No prior work has addressed the Messy models before this paper.

3. Studying and Results on Messy Broadcasting

3.1. Messy Model $M_{3}$ in Infinite d-Dimentional Grid

An infinite d-dimensional Grid is a graph similar to the definition provided in Definition 6, with the distinction that each position in the d-tuple (also referred to as a coordinate) can take any integer value. As discussed in the introduction, in infinite graphs the broadcast time becomes meaningless and the focus of this section will be on finding

t_{3} (0, v)

for any vertex v. Since there exists an automorphism that maps 0 to any other vertex, this analysis will be true for any broadcast originator.

Remark 2.

Our natural assumption is that, in any broadcast scheme, each informed vertex will inform all of its neighbors in consecutive time units. If this is not the case,

t_{3} (0, v)

can be made arbitrarily long by choosing a path with that distance and considering a scheme that only follows that path or by simply increasing the idle time of the originator.

Before diving into the details and discussions, it is helpful to provide some definitions that make describing the proof and the optimum scheme easier. First, consider the term “improving/delaying move.” Under any scheme, each message relay is referred to as a “move.” If a move reduces the distance to vertex v, we call it an “improving” move; otherwise, it is called a “delay” move. Next, let us define a k-border:

Definition 8

(Saturated coordinate). For

0 \leq i \leq d - 1

, the ith coordinate of vertex w is called saturated if

w_{i} = v_{i}

Definition 9

(k-border). A vertex w belongs to a k-border for some positive integer k if it has k saturated coordinates.

According to Definition 9, any vertex in a

(k + 1)

-border is also in a k-border. For the sake of simplicity, a 1-border is also referred to as a border.

Definition 10

(Improving path). Starting at 0, each broadcast scheme has a uniqueimproving paththat consists of the first encountered improving move for each of its vertices until it reaches v.

Definition 10 is well-defined for the following reasons: Firstly, the degree of each vertex is

2 d

. Coupled with Remark 2 and the structure of a Grid, this implies that for any vertex of this path except v, there will be an improving move. Secondly, according to the definition of an improving move, vertex v is reached in exactly

\sum_{i = 0}^{d - 1} v_{i}

improving moves. Lastly, since the first improving move is always considered for each interior vertex, the path is unique.

Theorem 1

(Infinite Grid, Messy model

M_{3}

). Consider a d-dimensional infinite Grid with 0 as the originator. Under Messy model

M_{3}

, for any vertex v

t_{3} (0, v) = \sum_{i = 0}^{d - 1} (d + i + 1) (| v_{π (i)} |)

where π is a permutation of

0, 1, \dots, d - 1

such that

| v_{π (0)} | \leq | v_{π (1)} | \leq \dots \leq | v_{π (d - 1)} |

An optimum scheme is also provided in the proof.

Proof.

For the sake of simplicity, assume that all the coordinates of v are non-negative integers. Later, the general case will be justified.

Consider an optimal scheme S, and let P be the improving path based on S. As discussed, P provides a valid route for information to be relayed from 0 to v. Consequently,

t_{3} (0, v)

is less than or equal to the maximum time required for P to reach v.

Denote 0 with

u^{0}

, and the distance of vertex x to y with

d (x, y)

. Let

G^{'}

be a finite Grid subgraph that is induced by the vertex set

V^{'} = \{w | w \in V (G), 0 \leq w_{i} \leq v_{i} for 0 \leq i \leq d - 1\}

First, consider the case where

G^{'}

is d-dimensional; i.e., for every i,

v_{i} > u_{i}^{0} = 0

Let

u^{1}

be the first vertex on P that encounters a 1-border (Definition 9) of

G^{'}

; this should happen since

u^{0}

is on no border of

G^{'}

and v is the only vertex on the d-border. The time it takes P to reach

u^{1}

is no more than

(d + 1) d (u^{0}, u^{1})

time units since each vertex in this portion of P has only d delay move options. Note that once P hits a border, it will remain on that border until it reaches v because of how an improving move is defined. Hitting the border means that for some i,

u_{i}^{1} = v_{i}

; without the loss of generality (by reindexing if necessary,) assume

u_{0}^{1} = v_{0}

. Now, let

u^{2}

be the first vertex that encounters a 2-border. It may be the case that

u^{2} = u^{1}

u^{1}

is already on a 2-border. The required time-units to travel from

u^{1}

u^{2}

on P is no more than

(d + 2) d (u^{1}, u^{2})

; one additional possible delay move for each vertex, which sends the message outside of

G^{'}

using the first coordinate. Similar to above, without the loss of generality, assume

u_{1}^{2} = v_{1}

. Generally, let

u^{k}

for

1 \leq k \leq d

be the first vertex that hits a k-border. The amount of time needed to go from

u^{k - 1}

u^{k}

does not exceed

(d + k) d (u^{k - 1}, u^{k})

; maximum

d + k - 1

delay moves before an improving move for each vertex on the path. Also,

u_{k - 1}^{k} = v_{k - 1}

is assumed. Consequently,

\begin{matrix} t_{3} (0, v) & = t_{3} (u^{0}, u^{d}) \leq \sum_{i = 1}^{d} (d + i) d (u^{i - 1}, u^{i}) \\ = ((d + 1) u_{0}^{1} - (d + 1) u_{0}^{0}) \\ + ((d + 2) u_{1}^{2} - u_{1}^{1} - (d + 1) u_{1}^{0}) \\ + ((d + 3) u_{2}^{3} - u_{2}^{2} - u_{2}^{1} - (d + 1) u_{2}^{0}) + \dots \\ + ((d + d) u_{d - 1}^{d} - u_{d - 1}^{d - 1} - \dots - (d + 1) u_{d - 1}^{0}) \\ \leq (d + 1) u_{0}^{1} + (d + 2) u_{1}^{2} + \dots + (d + d) u_{d - 1}^{d} \\ = (d + 1) v_{0} + (d + 2) v_{1} + \dots + 2 d v_{d - 1} \end{matrix}

In the above argument, some reindexing has been done for the ease of the explanation; therefore, the indices here are technically a permutation of

0, 1, \dots, d - 1

. This, then tell us that without reindexing

t_{3} (0, v) \leq max_{σ} \{(d + 1) v_{σ (0)} + (d + 2) v_{σ (1)} + \dots + (2 d) v_{σ (d - 1)}\}

where

σ

is a permutation of

0, 1, \dots, d - 1

. Hence,

t_{3} (0, v) \leq (d + 1) v_{π (0)} + (d + 2) v_{π (1)} + \dots + (2 d) v_{π (d - 1)}

, where

π

is a permutation that satisfies

v_{π (0)} \leq v_{π (1)} \leq \dots \leq v_{π (d - 1)}

. The permutation

π

signifies that the border of a shorter dimension needs to be encountered sooner than a larger one.

If, on the other hand,

G^{'}

is p-dimensional where

p < d

, the same argument as above can be made with

u^{0} = u^{1} = \dots = u^{d - p}

in mind as if the broadcast is starting at

u^{d - p}

with

2 d - p

delays available at the start. Like before, after each border is hit, the number of delays available increases by one. Note that being in this case means that (again with reindexing in mind)

v_{0} = v_{1} = \dots = v_{d - p - 1} = 0

. Accordingly, the same expression as above will work here as well.

An optimal scheme achieving this bound works as follows. Permutation

π

indicates an order on dimensions. Every vertex v, after receiving the information, sends the information to the neighbors in the negative direction of dimensions by the order indicated by

π

. After that, v uses the same order of dimensions and sends the information to the neighbors in their positive direction. It is easy to see that this scheme achieves the bound mentioned above. See Figure 3 for an example.

For a general vertex v, each coordinate may be negative. In this case, the argument remains largely the same, with a few minor nuances to consider. Firstly, in the definition of

V^{'}

, the condition for each negative coordinate will change to

v_{i} \leq w_{i} \leq 0

. Secondly, in the optimum scheme, which was described in two phases, the direction of message relay is reversed in both phases for every negative coordinate. Therefore, for any v

t_{3} (0, v) = \sum_{i = 0}^{d - 1} (d + i + 1) (| v_{π (i)} |)

where

π

is a permutation of

0, 1, \dots, d - 1

such that

| v_{π (0)} | \leq | v_{π (1)} | \leq \dots \leq | v_{π (d - 1)} |

. □

3.2. Messy Broadcasting in Grid

In this section, the term Grid refers specifically to a two-dimensional Grid. Here, the optimum broadcast time and an optimum scheme under models

M_{1}

and

M_{3}

are calculated when 0 is the originator. Since

t_{1} (0) \leq t_{2} (0) \leq t_{3} (0)

, these results provide a bound for

M_{2}

model.

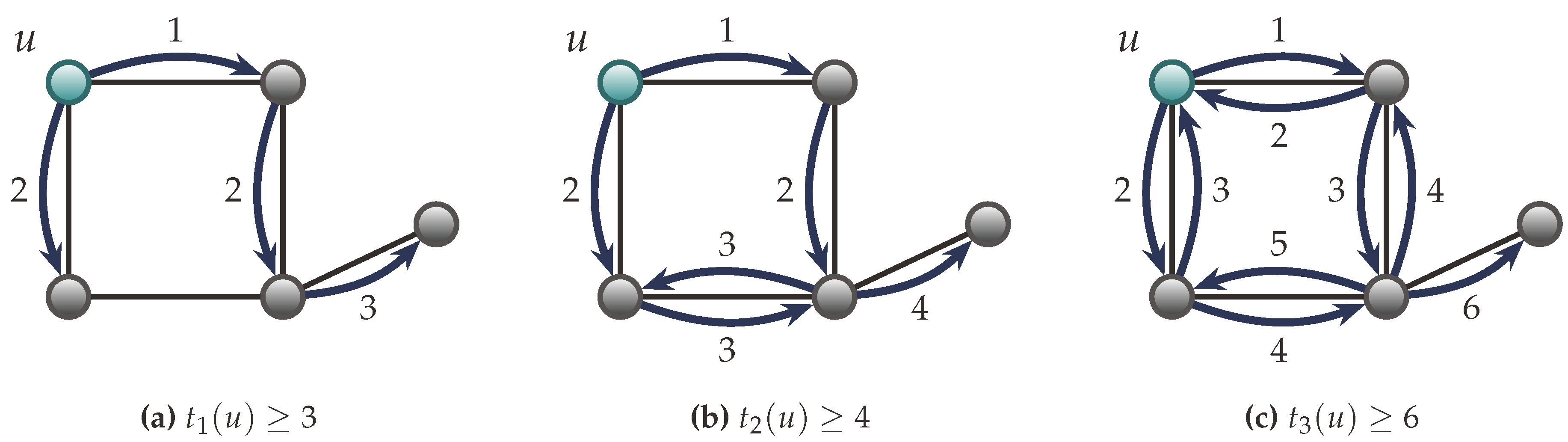
Similar to Remark 2, it is naturally assumed that in any scheme, each informed vertex will inform all of its uninformed neighbors in consecutive time units.

3.2.1. Model $M_{1}$

The messy model

M_{1}

for a d-dimensional Hypercube

Q_{d}

, a special case of a d-dimensional Grid, has been studied in [7]. It has been observed that finding

t_{1} (Q_{d})

is no trivial task, and the exact result for

Q_{d}

remains to be discovered. Thus, finding

t_{1} (G)

for any Grid G should not fare any better. For a two-dimensional Grid, however, the optimum broadcast time and scheme for Model

M_{1}

can be calculated thanks to Lemma 1.

Lemma 1.

In a two-dimensional Grid and under any optimum broadcast scheme S originated from 0, if vertex

v = (a, b)

is informed at time-unit t, then all vertices

H_{a, b} = {(x, y) | 0 \leq x \leq a, 0 \leq y \leq b}

are informed by time-unit t.

Proof.

The proof is done by induction on the time t. The claim is true for

t = 0

Assume the result is true for

t - 1

when

t \geq 1

. Let

v = (v_{0}, v_{1})

be a vertex that is informed at time t under S. Vertex v has one or two neighbors from which it can receive the broadcast message, namely

(v_{0} - 1, v_{1})

and

(v_{0}, v_{1} - 1)

. Other neighbors, if they exist, are not options because, in those cases, the induction hypothesis would apply to those neighbors, indicating that v should have been informed sooner than time t, which is not the case. Without the loss of generality, assume that the message is received from

(v_{0} - 1, v_{1})

. Therefore,

(v_{0} - 1, v_{1})

is informed by

t - 1

time units. By the induction hypothesis, it follows that all the vertices of

H_{v_{0} - 1, v_{1}}

are informed by

t - 1

time-units. Since all the vertices

(v_{0} - 1, p)

for

0 \leq p \leq v_{1}

are informed by

t - 1

time-units, based on their uninformed neighbors, it follows that all the vertices

(v_{0}, p)

for

0 \leq p \leq v_{1}

should be informed by time-unit t; concluding the induction proof. □

Theorem 2

(Two-dimensional Grid, Messy model

M_{1}

). Consider a Grid

G [n + 1, m + 1]

with 0 as the originator. Under Messy model

M_{1}

t_{1} (0) = n + m

. In this case, any scheme is an optimum scheme.

Proof.

Consider the message relaying path P from 0 to

v = (n, m)

under any broadcast scheme. Based on Lemma 1, P takes exactly

n + m

time units to relay the message, as each move increments one coordinate. Once v is informed, the entire Grid is informed. Therefore,

t_{1} (0) = n + m

. □

3.2.2. Model $M_{3}$

The presence of borders makes the problem much more complex than the analysis in subsection 3.1. It is worth noting that in this section, the use of the word “border” is similar but different from that in Definition 9. Here, in addition to a saturated coordinate (Definition 8), a 0 coordinate is also considered to define a k-border aligning with the usual intuition. Unlike in an infinite Grid, the maximum possible delay any k-border vertex could cause is smaller than that of

(k - p)

-border vertices, where

p > 0

This section provides the optimum broadcast time and an optimum broadcast scheme for a two-dimensional Grid

G [n + 1, m + 1]

for some integers

n \geq 1

and

m \geq 1

. By symmetry, without the loss of generality, assume

n \leq m

Intuitively, since the interior vertices may cause more delays, it is implied that there is an optimum broadcast scheme where, for any vertex v, the path that first informs v creeps through the borders first until it branches out in a straight line to reach v. Based on this intuition, Border-creeping paths are defined, which will be the cornerstone of our analysis.

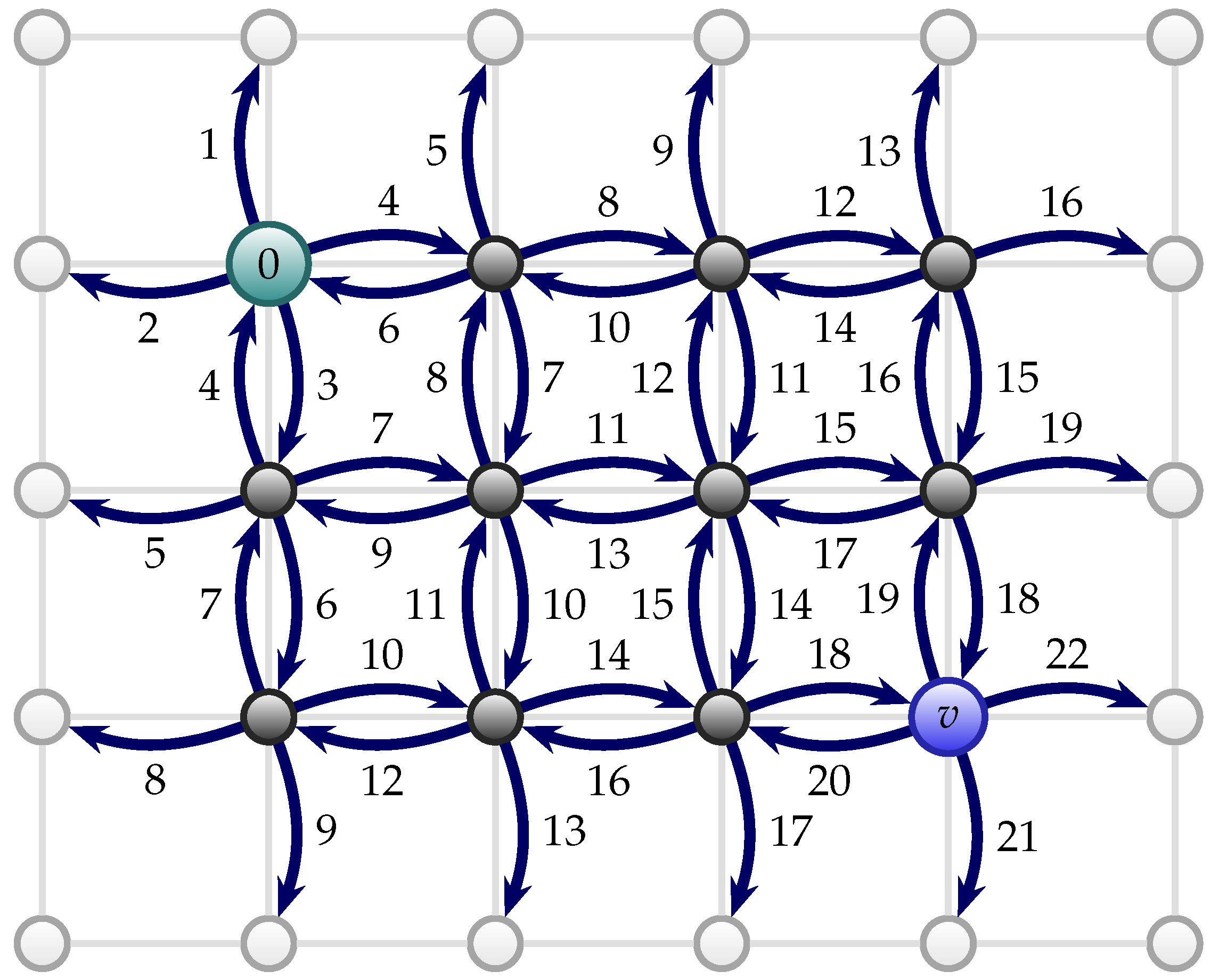
Definition 11

(Border-creeping paths). Inspired by the above motivation, for a vertex v, consider the following four border-creeping paths:

d r

-path,

d r u

-path,

r d

-path, and

r d l

-path. For example,

d r u

-path starts at 0, creeps the border downward until it reaches the bottom border, then goes right on the bottom border until it reaches the horizontal position of v, and finally, it goes up (not necessarily on any border) until v is reached. The last change of direction is the only part of these paths that may not be on any border.

Other border-creeping paths, such as the

d r u l

-path, are not considered since they are slower than another defined border-creeping path, which in this case would be the

r d l

-path.

The first move. Which direction should the originator 0 send the message first? Our intuition tells us that the shorter dimension (n, the vertical) should be informed first. The reason is as follows: As discussed, the bottleneck for delaying is the borders; therefore, the optimum scheme should delay informing them as much as possible. If the message is sent through the shorter dimension first, while it is true that the shorter border will be informed sooner, it is also true that it delays the progression of information toward the longer dimension (to the right) with the help of interior vertices and the fact that the bottom border already has significant enough delay. Based on this intuition, assume that the first move is downward along the shorter dimension. Later, we will prove that this is an optimum choice.

Based on the first move assumption, it is easy to see that for an interior vertex

v = (i, j)

the maximum time it takes each border-creeping path to reach v is:

\begin{matrix} t_{d r} (v) & = 1 + 3 (i - 1) + 3 + 4 (j - 1) \\ t_{d r u} (v) & = 1 + 3 (n - 1) + 2 + 3 (j - 1) + 3 + 4 (n - i - 1) \\ t_{r d} (v) & = 2 + 3 (j - 1) + 3 + 4 (i - 1) \\ t_{r d l} (v) & = 2 + 3 (m - 1) + 3 + 3 (i - 1) + 3 + 4 (m - j - 1) \end{matrix}

For example, let us investigate the

d r u

-path. The 1 is the maximum time it will take to reach the vertex one down of 0 (originator), the

3 (n - 1)

to reach the bottom border, the 2 for changing the direction at the corner vertex and going one to the right, the

3 (j - 1)

to reach the horizontal position of v, the 3 to change the direction upward and going one up, the

4 (n - i - 1)

to go up and reach v. See such portion of the scheme in Figure 4. These values give an easy upper bound to

t_{3} (0, v)

for interior vertices.

Lemma 2

(Upper-bound, Interior vertices). Let

v = (i, j)

be an interior vertex, then

t_{3} (0, v) \leq min \{t_{d r} (v), t_{d r u} (v), t_{r d} (v), t_{r d l} (v)\}

Similar upper bound can be given to border vertices as well; here, however, it is clear which border-creeping path has the minimum time.

Lemma 3

(Upper-bound, Border vertices). Let

v = (i, j)

be a border vertex, then

t_{3} (0, v) \leq \{\begin{matrix} 0 & i = 0 and j = 0 \\ 2 + 3 (j - 1) & i = 0 and 0 < j \leq m \\ 1 + 3 (i - 1) & j = 0 and 0 < i \leq n \\ 1 + 3 (n - 1) + 2 + 3 (j - 1) & i = n and 0 < j \leq m \\ 2 + 3 (m - 1) + 2 + 3 (i - 1) & j = m and 0 < i \leq n \end{matrix}

Comparison between the maximum time of each two border-creeping paths,

P_{1}

and

P_{2}

, separates the vertices into two groups: the vertices whose

P_{1}

maximum time is less than equal to that of

P_{2}

, and the rest. The boundary is a line; let us denote it with

L (P_{1}, P_{2})

. The equations associated with each of these six lines are as follows.

\begin{matrix} L (d r, r d) & : i = j - 1 \\ L (d r, d r u) & : i = n - (\frac{j + 1}{7}) \\ L (r d, r d l) & : i = 7 m - 7 j - 1 \\ L (d r u, r d l) & : i = (n - m) + j - \frac{1}{7} \\ L (r d, d r u) & : i = \frac{7 n - 2}{8} \\ L (d r, r d l) & : j = \frac{7 m}{8} \end{matrix}

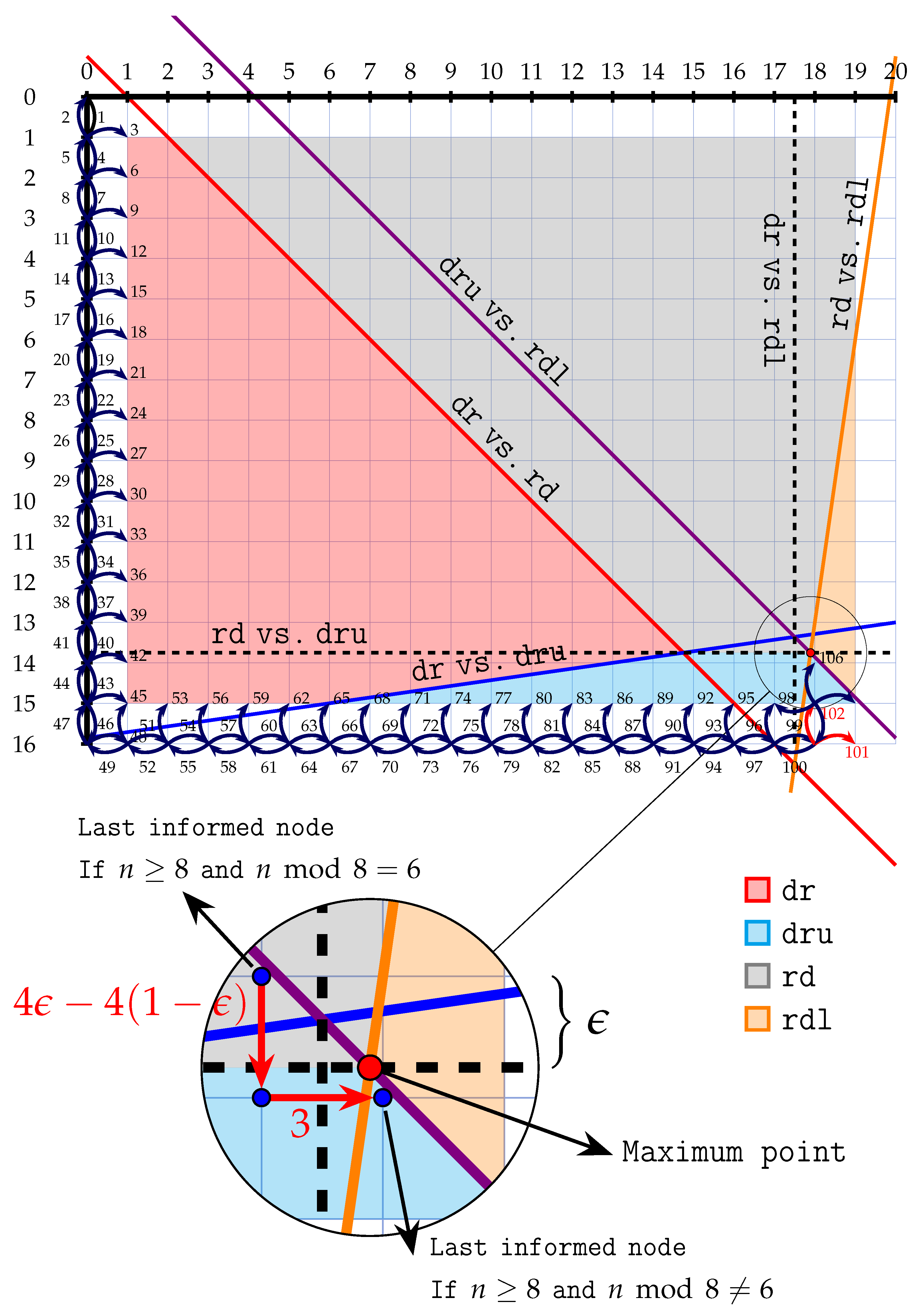
Figure 4 shows an example and also explains how to detect the regions where a particular path has the minimum. For better visualization of these regions and for the analysis to come, it is helpful to note the common intersections of some of these lines,as outlined in Lemma 4.

Lemma 4

(Common intersections). Each of the following four groups of three lines has a common intersection.

1.: $\{L (d r, r d), L (d r, d r u), L (r d, d r u)\}$
2.: $\{L (d r u, r d l), L (r d, r d l), L (r d, d r u)\}$
3.: $\{L (d r u, r d l), L (d r, d r u), L (d r, r d l)\}$
4.: $\{L (d r, r d), L (r d, r d l), L (d r, r d l)\}$

Proof.

The common point for group 1 is

(\frac{7 n - 2}{8}, \frac{7 n + 6}{8})

, for group 2 is

(\frac{7 n - 2}{8}, m - \frac{n + 6 / 7}{8})

, for group 3 is

(n - \frac{m}{8} - \frac{1}{7}, \frac{7 m}{8})

, and for group 4 is

(\frac{7 m}{8} - 1, \frac{7 m}{8})

. □

Having established an upper bound, our next step is determining a lower bound by devising an appropriate scheme. For a given scheme S, let

t_{S} (v)

be the time for S to inform v for the first time. By definition,

t_{3} (0, v) = {max}_{S} {t_{S} (v)}

for all schemes S. For any vertex v, let

x (v) \in {d r, d r u, r d, r d l}

be the type of border-creeping path which achieves the upper-bound based on Lemma 2 and Lemma 3.

In any scheme S, if

t_{S} (v) = t_{x (v)} (v)

, the behavior of S throughout the

x (v)

-path is uniquely determined. This is because only one behavior causes the vertices of

x (v)

-path to delay the information to v for this duration, and any other behavior will inform v sooner. With this understanding, we investigate whether there exists a scheme S such that for any vertex v,

t_{S} (v) = t_{x (v)} (v)

. If such a scheme exists, it would be an optimum scheme. Unfortunately, for large enough n and m, such scheme a cannot exist. This is because the final branch-out behavior is explicitly tailored to the target vertex v. If vertex v and u share the common segment of their border-creeping paths, this will result in conflicting behavior. For example, consider a Grid with

n \geq 2

and

m \geq 2

. In this case,

x ((1, 1)) = x ((2, 1)) = d r

. The

d r

-path for

(2, 1)

shares the

d r

-path for

(1, 1)

until vertex

(1, 0)

. The requirements of the described unique behavior for vertex

(1, 0)

differ depending on which of these two vertices is being considered. Therefore, such a scheme S cannot exist. However, if we relax the behavioral requirements for this final branching, we can devise a scheme we call the border-evading scheme.

Border-evading scheme. This scheme behaves as follows: For any border vertex v, the behavior of the path informing v is dictated by the

x (v)

-path informing v in

t_{x (v)} (v)

time-units. For any interior vertex v, consider the unique behavioral requirement to achieve

t_{x (v)} (v)

as described above. At the point of final branching, the requirement is to first send the message to the previous sender on the border, then to the next vertex on the border, and lastly toward v when branching out. We ease this behavior so that, at this point, the message is first sent to the previous sender on the border, then toward v, and finally to the next vertex on the border. In this way, this path conveys the information to v in

t_{x (v)} (v) - 1

time-units. It is as if the new behavior aims to evade informing the rest of the border as much as possible, hence the name border-evading scheme.

It is easy to verify that this description for each vertex v has no conflict with the description for another vertex u, which was the case before. In the border-evading scheme, for all interior vertices, the time of all four associated border-creeping paths is reduced by precisely one-time unit compared to their maximum. Accordingly, the separating lines and regions associated with the earliest reaching border-creeping paths (detected before) remain the same.

Thus far it is deduced that for border vertices

t_{3} (0, v) = t_{x (v)} (v)

and for interior vertices

t_{x (v)} (v) - 1 \leq t_{3} (0, v) \leq t_{x (v)} (v)

. Let B be the set of border vertices, then since

t_{3} (0) = {max}_{v \in V (G)} \{t_{3} (0, v)\}

we have

max \{max_{v \in B} \{t_{x (v)} (v)\}, max_{v \in V (G) - B} \{t_{x (v)} (v) - 1\}\} \leq t_{3} (0) \leq max_{v \in V (G)} \{t_{x (v)} (v)\}

Let

v^{*} =_{v \in V (G)} \{max_{v \in B} \{t_{x (v)} (v)\}, max_{v \in V (G) - B} \{t_{x (v)} (v) - 1\}\}

with a preference to be an interior vertex. In this way, if

v^{*} \in B

, then for any interior vertex v,

t_{3} (0, v^{*}) \geq t_{3} (0, v)

; consequently,

t_{3} (0) = t_{3} (0, v^{*})

and border-evading scheme is an optimum scheme. Otherwise, if

v^{*} \in V (G) - B

, if we can modify the border-evading scheme in such a way that

v^{*}

in the new scheme is informed at time-unit

t_{x (v^{*})} (v^{*})

then the new scheme will be an optimum scheme, and

t_{3} (0) = t_{x (v^{*})} (v^{*})

. To do that, first, let us find

v^{*}

Continuous view. The previously identified regions of the Grid are associated with the type of border-creeping path that reaches those areas the fastest. In the border-evading scheme, consider an edge

v u

. If

v u

is entirely within one region, the time it takes from the first moment v is inform to the first moment u is infomed is a constant based on the associated border-creeping path. For example, in the region associated with

d r

, a move to the right has +4 change while in

d r u

has +3 and in

r d l

has -4. One can change the view from discrete movements (e.g., going up by one unit) to a continuous one. In this view, define the gradient of each point within a region based on the aforementioned uniform changes; in case a point belongs to multiple regions, choose one randomly. The vector field is conservative since it can be viewed as the gradient of a function composed of unions of linear equations. To know the first informed time of a vertex v, consider a point p at the coordinate of v. For any continuous path from 0 to v (due to path independence), the line integral over the vector field is the answer. This time can be associated with any other point in the Grid. As an example, take a look at Figure 4, under the magnifying glass. As indicated, the change in the first informed time of the two vertical blue dots is

4 ϵ + (- 4) (1 - ϵ)

Using the continuous view and Lemma 4, by investigating the vector field, it is not hard to see that a point with maximum time is the intersection of

L (d r u, r d l)

L (r d, r d l)

, and

L (r d, d r u)

lines;

p^{*} = (\frac{7 n - 2}{8}, m - \frac{n + 6 / 7}{8})

. This is true even for the case

n = m

, the only case in which

L (d r u, r d l)

comes before

L (d r, r d)

. Important note: There are two latent assumptions. The placement of

p^{*}

was determined by investigating the vector field and not by directly investigating the line integrals. Take

L (d r, d r u)

, for example. Its equation was derived from

t_{d r} (v) = t_{d r u} (v)

. The latent assumption in the value of

t_{d r u} (v)

is that v’s vertical position is not n, which comes from the +2 applied for changing the direction upward. Consequently, if

\frac{7 n - 2}{8} > n - 1

m - \frac{n + 6 / 7}{8} > m - 1

are true, the above position might be problematic, and additional checks are required. The first restriction is false if and only if

n \geq 7

, and the second is false if and only if

n \geq 8

For

n \geq 8

, based on the vector fields, the choice for

v^{*}

will be limited to three possible vertices in the vicinity of

p^{*}

;

$v_{1}^{*} = (* \frac{7 n - 2}{8}, m - * \frac{n + 6 / 7}{8})$
$v_{2}^{*} = (* \frac{7 n - 2}{8} + 1, m - * \frac{n + 6 / 7}{8})$
$v_{3}^{*} = (* \frac{7 n - 2}{8} + 1, m - * \frac{n + 6 / 7}{8} + 1)$

See Figure 4 under the magnifying glass. The red point is

p^{*}

, and the possible three vertices have blue points. To understand which has the higher first informed time, the changes from

v_{1}^{*}

v_{2}^{*}

and then from

v_{2}^{*}

v_{3}^{*}

will be calculated. Let

ϵ = \frac{7 n - 2}{8} - * \frac{7 n - 2}{8}

By the slope of the lines, it is deduced that vertices

v_{2}^{*}

and

v_{3}^{*}

are in the

d r u

region (cyan color in Figure 4), and vertex

v_{1}^{*}

r d

region (gray). Note that if

n \mod 8 = 1

, then

v_{1}^{*}

is in the boundary of the

r d

and

d r

regions; in this case, we consider the

r d

region. As depicted in Figure 4, this positioning implies that the change from

v_{1}^{*}

v_{2}^{*}

4 ϵ + (- 4) (1 - ϵ)

and from

v_{2}^{*}

v_{3}^{*}

+ 3

. Consequently, vertex

v_{3}^{*}

is the sole last informed vertex except when (1)

n \mod 8 = 5

, where

v_{1}^{*}

is also the last informed; (2)

n \mod 8 = 6

, where

v_{1}^{*}

is the sole last informed vertex.

On the other hand, if

n \leq 7

, the inequality

m - \frac{n + 6 / 7}{8} > m - 1

is true, which means the latent assumption for the provided

p^{*}

is violated. In this case, by using the vector field it is not hard to see that a choice for

v^{*}

is coordinate

(n, m)

Optimum scheme, changing the border-evading scheme. Now that a possible candidates for

v^{*}

(and its time) is determined, we can describe a new similar scheme that will be completed in

t_{3} (0, v^{*})

and hence is an optimum scheme. If

n \leq 7

, no change is necessary. Otherwise, (1) if

n \mod 8 \neq 6

, change the behavior at

(n, m - * \frac{n + 6 / 7}{8} + 1)

so that at that point there is no evading of the border as described before; see Figure 4 for the modification in red. In this way, the

d r u

-path time to

v^{*}

is increased by one, and since

d r u

-path was the only path that could inform the fastest, the desired scheme is achieved. (2) If

n \mod 8 = 6

, in this case,

v^{*}

resides (only) in the

r d

region; therefore, with a similar justification modify the behavior of

(0, m - * \frac{n + 6 / 7}{8})

. Adjust the timing of the vertices whose border-evading path relied on this point, and a new valid scheme is achieved.

First move revisited. At first, it was assumed that the first move is downward, through the smaller dimension. A similar analysis can be made if the first move is toward the right. It can be seen that the new

v^{*}

will be informed sooner. Consequently, sending through the smaller dimension as the first move is an optimum choice.

To summarize all the findings:

Theorem 3

(Two-dimensional Grid, Messy model

M_{3}

). Consider a two-dimensional Grid

G [n + 1, m + 1]

, where

n \leq m

. With 0 as the originator, under the Messy model

M_{3}

\begin{matrix} t_{3} (0) = \{\begin{matrix} 3 m + 3 n - 2 & if n \leq 7 \\ 3 m + 3 n - 4 + (4 n - 3 * \frac{n + 6 / 7}{8} - 4 * \frac{7 n - 2}{8}) & if n \geq 8 and n \mod 8 = 6 \\ 3 m + 3 n - 5 + (4 n - 3 * \frac{n + 6 / 7}{8} - 4 * \frac{7 n - 2}{8}) & otherwise \end{matrix} \end{matrix}

Moreover, an optimum scheme similar to theborder-evading schemeis known, in which the sole last informed vertex is

\begin{matrix} \{\begin{matrix} (* \frac{7 n - 2}{8} + 1, m) & if n \leq 7 \\ (* \frac{7 n - 2}{8}, m - * \frac{n + 6 / 7}{8}) & if n \geq 8 and n \mod 8 = 6 \\ (* \frac{7 n - 2}{8} + 1, m - * \frac{n + 6 / 7}{8} + 1) & otherwise \end{matrix} \end{matrix}

Corollary 1.

Consider a two-dimensional Grid

G [n + 1, m + 1]

, where

n \leq m

. Under the Messy model

M_{3}

, for

n \geq 8

3 m + 3 \frac{1}{8} n - 7.322 \leq t_{3} (0) \leq 3 m + 3 \frac{1}{8} n + 0.679

Proof.

By the definitions of the floor and ceiling functions,

\frac{n + 6 / 7}{8} \leq * \frac{n + 6 / 7}{8} \leq \frac{n + 6 / 7}{8} + 1

and

\frac{7 n - 2}{8} - 1 \leq * \frac{7 n - 2}{8} \leq \frac{7 n - 2}{8}

are obtained. Using the second case for the upper bound and the third case for the lower bound, it is deduced that

3 m + 3 \frac{1}{8} n - 7.322 \leq 3 m + 3 \frac{1}{8} n - \frac{205}{28} \leq t_{3} (0) \leq 3 m + 3 \frac{1}{8} n + \frac{19}{28} \leq 3 m + 3 \frac{1}{8} n + 0.679

□

4. Discussion

This paper investigated the efficiency and performance of Messy broadcasting in Grid structures, offering valuable insights into the bottlenecks that contribute to broadcast delays in Grid graphs. By analyzing Messy models

M_{1}

and

M_{3}

, we developed an optimal broadcast scheme that identified the final informed vertex and accurately calculated the broadcast time. This provided a tight upper bound on the broadcast duration in Grid structures for these specific models. Our findings also indirectly established a bound for the

M_{2}

model. Corollary 1 offers an approximation for broadcast time and latently provides intuition of the positioning of the last informed vertices in a manner that is both easier to calculate and more intuitive. Table 2 summarizes the found Messy broadcast times in a Grid structure when the originator is one of the corner vertices.

Our work provides a more comprehensive analysis and a much tighter bound on broadcast times compared to the previous studies’ upper bounds, thereby enhancing the theoretical framework within which Messy broadcasting is understood. Provided insights on the broadcasting bottlenecks in Grids and the exact upper bound could be beneficial in the design of efficient communication protocols in distributed systems, wireless networks, and other applications reliant on rapid information dissemination that require broadcasting.

Future research directions could explore extending these models to more complex and heterogeneous network structures. Our work could serve as the foundation for determining the broadcast time for Torus and higher-dimensional Grid structures, both of which are prevalent in computer networking system designs. Since a Torus can be viewed as a Grid with “loop-back” edges, our findings on the infinite Grid may be applicable in determining the exact broadcast time for a Torus. For higher-dimensional Grids, the techniques employed in this paper, particularly our novel approach of using a continuous view, could also be utilized. In this approach, the borders of regions in higher dimensions would be represented by higher-dimensional planes described by a set of linear equations. This continuous perspective, possibly aided by linear programming, could help identify the optimum candidates. However, such analysis involves significant details and nuances, which is one reason this paper’s results were limited to two-dimensional grids. Another intriguing topology for future exploration is Hyper-cylinder graphs, as introduced in [1].

Further research could also investigate obtaining a tighter result for Model

M_{2}

. Examining the impact of dynamic changes in the network during broadcasting and developing adaptive schemes to optimize performance under varying conditions is another valuable area to explore. Additionally, empirical studies could be conducted to validate our theoretical findings in real-world network scenarios, providing a more comprehensive understanding of the practical applications of our work.

Author Contributions

Conceptualization, Aria Adibi; Formal analysis, Aria Adibi; Supervision, Hovhannes Harutyunyan; Validation, Hovhannes Harutyunyan.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Adibi, A. Broadcasting in Hyper-cylinder graphs. M.sc. thesis, Concordia University, 2021. [Google Scholar]
Fraigniaud, P.; Lazard, E. Methods and problems of communication in usual networks. Discrete Applied Mathematics 1994, 53, 79–133. [Google Scholar] [CrossRef]
Hedetniemi, S.M.; Hedetniemi, S.T.; Liestman, A.L. A survey of gossiping and broadcasting in communication networks. Networks 1988, 18, 319–349. [Google Scholar] [CrossRef]
Hromkovič, J.; Klasing, R.; Monien, B.; Peine, R. Dissemination of information in interconnection networks (broadcasting & gossiping). In Combinatorial network theory; Springer, 1996; pp. 125–212. [Google Scholar]
Harutyunyan, H.A.; Liestman, A.L.; Peters, J.G.; Richards, D. Broadcasting and gossiping. In Handbook of graph theory; 2013; pp. 1477–1494. [Google Scholar]
Ahlswede, R.; Haroutunian, H.; Khachatrian, L. Messy broadcasting in networks, Communications and Cryptography, eds. RE Blahut, DJ Costello Jr., U. Mauter, and T. Mittelholzer, 1994.
Harutyunyan, H.A.; Liestman, A.L. Messy broadcasting. Parallel Processing Letters 1998, 8, 149–159. [Google Scholar] [CrossRef]
Harutyunyan, H.A.; Hell, P.; Liestman, A.L. Messy broadcasting—Decentralized broadcast schemes with limited knowledge. Discrete applied mathematics 2011, 159, 322–327. [Google Scholar] [CrossRef]
Li, C.; Hart, T.E.; Henry, K.J.; Neufeld, I.A. Average-case" messy" broadcasting. Journal of Interconnection Networks 2008, 9, 487–505. [Google Scholar] [CrossRef]
Fomin, F.V.; Fraigniaud, P.; Golovach, P.A. Parameterized complexity of broadcasting in graphs. Theoretical Computer Science 2024, 997, 114508. [Google Scholar] [CrossRef]
Tale, P. Double Exponential Lower Bound for Telephone Broadcast. arXiv preprint 2024, arXiv:2403.03501 2024. [Google Scholar]
Scheuermann, P.; Wu, G. Heuristic algorithms for broadcasting in point-to-point computer networks. IEEE Computer Architecture Letters 1984, 33, 804–811. [Google Scholar] [CrossRef]
Beier, R.; Sibeyn, J.F. A powerful heuristic for telephone gossiping. SIROCCO 7, Proceedings of the 7th International Colloquium on Structural Information and Communication Complexity, Laquila, Italy, -22, 2000; Flammini, M.; Nardelli, E.; Proietti, G.; Spirakis, P.G., Eds. Carleton Scientific, 2000, pp. 17–35. 20 June.
Fraigniaud, P.; Vial, S. Approximation algorithms for broadcasting and gossiping. Journal of Parallel and Distributed Computing 1997, 43, 47–55. [Google Scholar] [CrossRef]
Fraigniaud, P.; Vial, S. Comparison of heuristics for one-to-all and all-to-all communications in partial meshes. Parallel Processing Letters 1999, 9, 9–20. [Google Scholar] [CrossRef]
Harutyunyan, H.A.; Shao, B. An efficient heuristic for broadcasting in networks. Journal of Parallel and Distributed Computing 2006, 66, 68–76. [Google Scholar] [CrossRef]
Lima, A.; Aquino, A.L.; Nogueira, B.; Pinheiro, R.G. A matheuristic approach for the minimum broadcast time problem using a biased random-key genetic algorithm. International Transactions in Operational Research 2024, 31, 246–273. [Google Scholar] [CrossRef]
Ben-Dor, A.; Halevi, S.; Schuster, A. On greedy hot-potatoe routing; Laboratory for Parallel Computing Research, Technion-Israel Institute of Technology, 1993.
Bagchi, A.; Hakimi, S.L. Data transfers in broadcast networks. IEEE Computer Architecture Letters 1992, 41, 842–847. [Google Scholar] [CrossRef]
Bagchi, A.; Hakimi, S.L.; Schmeichel, E.F. Gossiping in a distributed network. IEEE Transactions on Computers 1993, 42, 253–256. [Google Scholar] [CrossRef]
Bar-Yehuda, R.; Israeli, A.; Itai, A. Multiple communication in multihop radio networks. SIAM Journal on Computing 1993, 22, 875–887. [Google Scholar] [CrossRef]
Diks, K.; Dobrev, S.; Kranakis, E.; Pelc, A.; Ružička, P. Broadcasting in unlabeled hypercubes with a linear number of messages. Information Processing Letters 1998, 66, 181–186. [Google Scholar] [CrossRef]
Diks, K.; Kranakis, E.; Pelc, A. Broadcasting in unlabeled tori. Parallel Processing Letters 1998, 8, 177–188. [Google Scholar] [CrossRef]
Diks, K.; Kranakis, E.; Pelc, A. Perfect broadcasting in unlabeled networks. Discrete applied mathematics 1998, 87, 33–47. [Google Scholar] [CrossRef]
Gargano, L.; Pelc, A.; Perennes, S.; Vaccaro, U. Efficient communication in unknown networks. Networks: An International Journal 2001, 38, 39–49. [Google Scholar] [CrossRef]
Feige, U.; Peleg, D.; Raghavan, P.; Upfal, E. Randomized broadcast in networks. Random Structures & Algorithms 1990, 1, 447–460. [Google Scholar]
Doerr, B.; Friedrich, T.; Sauerwald, T. Quasirandom rumor spreading. ACM Transactions on Algorithms (TALG) 2014, 11, 1–35. [Google Scholar] [CrossRef]
Baumann, H.; Fraigniaud, P.; Harutyunyan, H.A.; de Verclos, R. The worst case behavior of randomized gossip protocols. Theoretical Computer Science 2014, 560, 108–120. [Google Scholar] [CrossRef]
Gholami, S.; Harutyunyan, H.A. HUB-GA: A heuristic for universal lists broadcasting using genetic algorithm. Journal of Communications and Networks 2023, 25, 88–110. [Google Scholar] [CrossRef]
Gholami, S.; Harutyunyan, H.A. A Note to Non-adaptive Broadcasting. Parallel Processing Letters 2024, 34, 2340017. [Google Scholar] [CrossRef]
Awerbuch, B.; Goldreich, O.; Peleg, D.; Vainish, R. A tradeoff between information and communication in broadcast protocols. Aegean Workshop on Computing. Springer, 1988, pp. 369–379.
Farley, A.M.; Hedetniemi, S.T. Broadcasting in grid graphs. Proc. 9th SE Conf. Combinatorics, Graph Theory, and Computing, Utilitas Mathematica, 1978, pp. 275–288.
Cockayne, E.; Hedetniemi, S. A conjecture concerning broadcasting in m-dimensional grid graphs. Technical report, Technical Report CS-TR-78-14, University of Oregon, 1978.
Ko, C.S. On a conjecture concerning broadcasting in grid graphs. AMS Notices, 1979; A196–A197. [Google Scholar]
Ko, C. Broadcasting, Graph homomorphisms and chord intersections. 1980: 5705-5705.

Figure 1. An example that shows the differences between Messy models. The drawn schemes are optimum. It is easy to verify that

t_{1} (u) = 3

t_{2} (u) = 4

t_{3} (u) = 6

Figure 1. An example that shows the differences between Messy models. The drawn schemes are optimum. It is easy to verify that

t_{1} (u) = 3

t_{2} (u) = 4

t_{3} (u) = 6

Figure 2. Grid graph

G [4 \times 5]

and

G [3 \times 4 \times 3]

Figure 2. Grid graph

G [4 \times 5]

and

G [3 \times 4 \times 3]

Figure 3. An optimum broadcast scheme for vertex

v = (3, 2)

in a two-dimensional infinite Grid. Vertex v is informed at time-unit

(2 + 0 + 1) \times 2 + (2 + 1 + 1) \times 3 = 18

Figure 3. An optimum broadcast scheme for vertex

v = (3, 2)

in a two-dimensional infinite Grid. Vertex v is informed at time-unit

(2 + 0 + 1) \times 2 + (2 + 1 + 1) \times 3 = 18

Figure 4. Broadcasting under Messy model

M_{3}

G [17, 21]

Figure 4. Broadcasting under Messy model

M_{3}

G [17, 21]

Table 1. Comparison of Messy and Classical broadcast time bounds, as illustrated by a partial table adapted from [7].

	$M_{3}$	$M_{1}$ and $M_{2}$	Classical	Classical
Graph	upper bound	upper bound	lower bound	upper bound
$K_{n}$	$n - 1$	$n - 1$	$log n$	$log n$
$P_{n}$	$2 n - 3$	$n - 1$	$n - 1$	$n - 1$
$C_{n}$	$n - 1$	$\frac{n}{2}$	$\frac{n}{2}$	$\frac{n}{2}$
$Q_{d}$	$\frac{d (d + 1)}{2}$	$\frac{d (d - 1)}{2} + 1$	d	d
$T_{d, h}$	$(d + 1) (2 h - 3)$	$d (2 h - 3)$	$(d + 1) (h - 1) - 1$	$(d + 1) (h - 1) - 1$

Table 2. Comparison of the Messy broadcast times in

G [n + 1, m + 1]

where

n \leq m

. The exact result for Model

M_{3}

is detailed in Theorem 3.

Table 2. Comparison of the Messy broadcast times in

G [n + 1, m + 1]

where

n \leq m

. The exact result for Model

M_{3}

is detailed in Theorem 3.

Model $M_{1}$	Model $M_{2}$	Model $M_{3}$
$n + m$	$n + m \leq t_{2} \leq 3 m + 3 \frac{1}{8} n + 0.68$	$3 m + 3 \frac{1}{8} n - 7.33 \leq t_{3} \leq 3 m + 3 \frac{1}{8} n + 0.68$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Messy Broadcasting in Grid

Abstract

1. Introduction

2. Related Work

3. Studying and Results on Messy Broadcasting

3.1. Messy Model M 3 in Infinite d-Dimentional Grid

3.2. Messy Broadcasting in Grid

3.2.1. Model M 1

3.2.2. Model M 3

4. Discussion

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.1. Messy Model $M_{3}$ in Infinite d-Dimentional Grid

3.2.1. Model $M_{1}$

3.2.2. Model $M_{3}$