Preprint
Article
Is Dark Matter a Misinterpretation of a Perspective Effect?
Altmetrics
Downloads
81
Views
39
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
26 June 2024
Posted:
28 June 2024
You are already at the latest version
Alerts
Abstract
Very recently, a straightforward way was proposed in order to understand the galaxy and
galactic cluster world without using the very elusive dark matter concept. This way was called
κ-model [1, 2, 3, 4]. The main idea is to save the form of the usual physical laws, especially the
Newton’s laws of motion when gravity is weak, but only by applying a local renormalization
procedure for the lengths, distances and velocities. This local renormalization appears as a
correspondance principle in the κ-model. In this model the fundamental physical constants
remain universal, i.e. are independent of the point and of time. The κ-model is Newtonian
in essence but a relativistic extension can easily be built. The aim of the present paper is to
detail the mathematical formalism supporting i
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
The classical laws of physics (for instance the Newtonian dynamics) have been defined at the meter scale. This scale goes from the sub-micrometric dimension to the scale of the solar system. However, we know that at the scale of the nanoscopic world these classical laws are no longer valid and the quantum field theory has to be used. Let us note that the ratio between the radius of an atom and the base unit length (meter) is . Despite this statement, when we go now in the opposite direction, i.e. the macrocosmos world, the physicists use the same physical laws than those valid at the meter scale, with no changes, whereas the ratio between one meter and one parsec is . The -model relies on the very simple suggestion that the matter does no longer behave on the same manner when the characteristic dimension of the region under study is very large (of the order of one parsec or more). The perception of an observer must then necessarily be changed [1, 2, 3, 4]. Our aim is also to reduce the modification compared to the Newtonian law at the minimal level. The main idea is that the environment of the observer modifies his perception, a bit like when this one or the observed object are immersed in different media with various refractive indices (even though the analogy can strongly be misleading). Furthermore the lengths and the velocities which are measured by him are differently renormalized following the mean densities surrounding him and the observed object. Let us note that it relates only to apparent effects, the unit of length (for instance the radius of a hydrogen atom) is obviously the same everywhere in the Universe. The renormalization coefficient, labelled , is linked to the local mean density by a simple relationship assuming with appropriate normalization [2, 3]. In section 2 some basic mathematical concepts are recalled, section 3 develops the framework of the -model, in section 4 the -structure for Minkowski space is presented, Eventually in section 5 a few illustrative applications to astrophysics are supplied. A few didactic figures have also been added.
2. Some Basic Structures on
2.1. Algebraic Structures
2.1.1. Affine and Vectorial Structure
When endowed with its usual vector space structure the set of the real n-tuples will be noted and when endowed with its affine structure it will be denoted simply by . The affine structure being a 1-transitive action of the additive group on :
When we will sometimes write .
2.1.2. Euclidean Structures
The vector space is equipped with a Euclidean structureonce a scalar producton has been selected. A scalar product is a definite positive bilinear symmetric form, in other words it is an application
linear in each variable, symmetric and satisfying , the cancellation hapenning only when .
This means that in some base of the matrix representing the bilinear form i.e.the matrix where is which means that , the Kronecker symbol.
If and we have then
Such a base of is an orthonormalbase (with respect to the particular scalar product considered).
The application
is a normon in other words it fullfills the conditions :
- Positivity ()
- Separation ()
- Homogeneity ()
- Subadditivity ()
To a scalar product is also associated a way to measure angles :
The linear transformations f of respecting the scalar product in other words such that
are called (vectorial) isometries.The set of vectorial isometries is a sub-group of the linear group called the orthogonal groupand denoted 1.
When the vectorial space is equipped with a Euclidean structure, the affine space is endowed with a distancedefined by
In other words we have
- Symmetry (),
- Separation (),
- Triangle inequality ().
Furthermore this distance will be compatible with the affine structure :
- Invariance by translation :
,
- Homogeneity :
.
The affine transformations with linear part in are the (affine) isometries.
2.1.3. Minkowski Structure
A structure of Minkowski space on is the choice of some symmetric bilinear form, on with signature , that means that in some base of the matrix associated to is . In other words, if and we have then
It is common to refer to vectors of a Minkowski space as "quadrivectors" and to as a Minkowki product.
According to the sign of , a quadrivector is
time-likewhen .
light-likewhen , the isotropy cone of .
space-likewhen .
Figure 1.
Minkowski space.
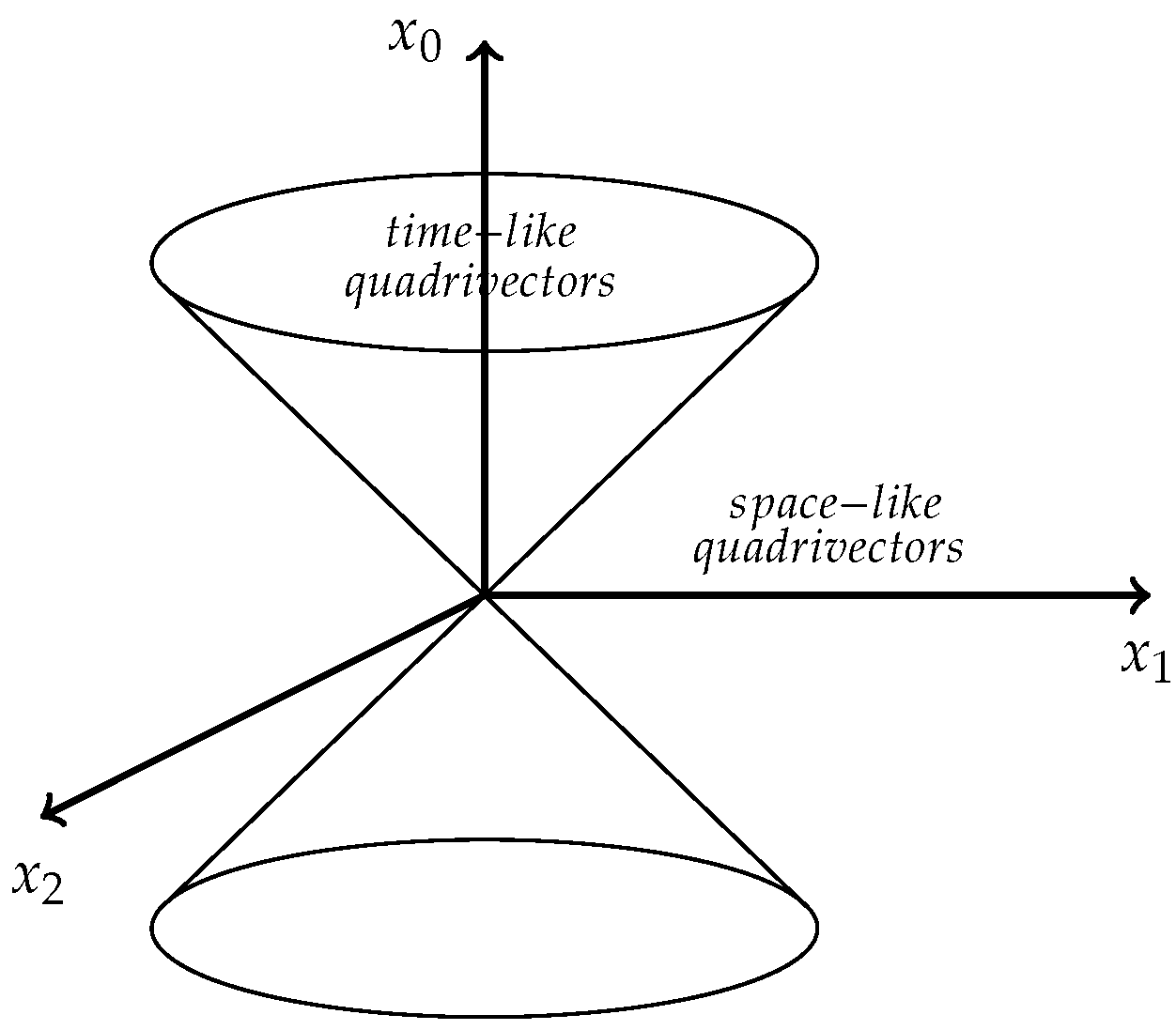
The linear transformations f of respecting the Minkowski product M in other words such that
are called Lorentz transformations.The Lorentz transformation is a sub-group of called the Lorentz groupand denoted , it is straightforward to see that Lorentz transformation f respect quadrivector’s types.
When the space is equipped with a Minkowski structure the points of the affine space are usually called events.
Two events and are time-orientedwhen the unique quadrivector such that is time-like.
2.2. Topological Structure of
A topologyon a set E is a way to give a meaning to expressions like "x and y are close" without having a way to measure a distance between x and y.
A standard way to do so is to select for each point x of E a set of parts of E, , called the set of the neighborhoodsof x. The sets fullfilling the conditions expected for such a notion :
† The set E must contain whatever is "close" to x : .
† The point x is among what is close to x : .
† If two sets contain whatever is close to x their intersection too :
.
† If V contains whatever is close to x and W contains V, W contains whatever is close to x :
if then
† If V contains whatever is close to x then there exists W, containing also whatever is close to x, and such that V contain whatever is close to whatever points in W :
Once a topology on E has been chosen an open setof E is a part O of E such that .
Different topologies can be defined on , the usual one is defined using the distance d defined in . The set is the open ballwith center at and radius r. A neighborhood of x is any subset of containing an open ball centered at x. We will also use this topology on when equipped with its Minkowski affine structure even though, in that case, there is no distance directly linked to the topologic stucture.
The notion of topology allows correct definition of some very usefull "local" notions in particular the notion of continuity at a point for a function between two topological spaces and , f is continuous at xwhen The affine orthogonal transformations (and the affine Lorentz transformations) are continuous on (and on )
In the Minkowsi space the set of light-like quadrivectors has two path connected components2. A Lorentz transformation is orthochronewhen the path connected components are respected, and antichronewhen the components are exchanged.
2.3. Differentiable Structure of
being equipped with a scalar product and the associated norm defined in and with the distance defined in .
2.3.1. Differential of a Function, Tangent Vectors at a Point
An application is differentiable at whenever
where is continuous and linear from to 3and with such that and .
The linear application
is the differentialat x of f.
The application
is the differential of f.
At first glance, the definition of the differentiability of f at a point x, suggests that the vectors are picked in the "same" space independantly of the point x we are looking at, but this point of view would be barren if we want to go further.
To each point is associated a copy of , called the tangent space to at xand denoted , its elements are called tangent vectors to at x.
With those definitions in mind, the definition of differentiability becomes
where is linear and with
satisfying and .
We have to clarify the status of the differential application , for its arrival set had became unclear.
Set
and
The set is the tangent bundle of , it identifies to and then the projection p becomes the first projection of on . The tangent bundle identifies also with the affine space .
Now let be an application differentiable at each point of , the application
is called the tangent applicationor differential applicationof f.
Furthermore the projection
is a (trivial) "fiber bundle", in that very simple case it just means that p is differentiable on .
The bitangent space to at , identifies with the product vector space then
and .
The process of differentiation can be repeted indefinitelly, applications admitting differential at all orders are said of class , the set of functions from to of class is denoted .
2.3.2. Tangent Vector Fields on
A vector field on is a section of the tangent fiber bundle i.e. an application
As the first factor of a tangent vector fields is always known, in the sequels, we will note the tangent vector field by its second factor .
Let be the canonical base of the tangent vector field will be denoted so that any tangent vector field on has a unique expression
with some functions from to .
The set of tangent vector fields of class is
We clarify now the notation :
The set , is endowed with a structure of real algebra by
- Addition defined by
- Multiplication by a real scalar defined by
- Inner multiplication defined by
.
The set is endowed with a structure of -modulus by
- Vector fields addition defined by
- The multiplication by a real scalar defined by
- Multiplication by a function defined by
A derivation on the real algebra is a linear application
satisfying
To correspond a derivation on where
Indeed we have
and
can be seen as the directional derivative of f in the direction of at x.
The notations introduced previously for a tangent vector field are now clear :
If the expression of a tangent vector field is and
for :
The Lie bracket of two tangent vector fields and is defined by
we have
Endowed with this bracket the vector space is a Lie algebra.
2.3.3. Covariant Derivation
A covariant derivationon is an application
satisfying
A covariant derivation, ∇, on is entirely defined by the family of tangent vector fields If
the functions are called Christoffelsymbols of ∇.
For and we have
2.3.4. Flat Covariant Derivation
The flat covariant derivation ∇ is the covariant derivation whose Christoffel symbols are all null, in that case we have
can be seen as the derivative of in the direction of .
2.3.5. Covariant Derivation Along a Curve, Parallel Transport
Let
be a class function.
A tangent vector field of along is an application
such that
The set of tangent vector fields of class along is denoted , it is a -modulus.
The velocity is the tangent vector field along defined by
Where . Its value depends only on the differential structure of and .
Let ∇ be a covariant derivation on . There is exactly one operator 4 on the -modulus of tangent vector fields along such that
and if is the restriction to of a tangent vector field on
For we have
When is equipped with the flat covariant derivative 5, the covariant derivative of with along is the tangent vector field along defined by
A tangent vector field along is said parallelwith respect to the covariant derivation ∇ whenever . General results on differential equations insure that a parallel tangent vector field along is determined by its value at one point of the trajectory of . For the application
where is parallel along is called the parallel transport along between time and .
When ∇ is the flat covariant derivation for any class curve the parallel vector fields along are simply the constant vector fields.
2.3.6. Acceleration
Let be a class function.
The covariant derivative of the vector field along is the covariant accelerationof it is denoted , note that unlike the velocity, depends on the choice of a covariant derivation on .
When a curve satisfies it is called a geodesiccurve of the covariant derivation ∇, for the flat covariant derivation the geodesics are the parametrizations with constant velocity of straight lines.
2.4. Riemannian Structures on
A Riemannian metricon is an application G associating to each point a scalar product on with the condition that
The general expression of a Riemannian metric on is
Where the coefficients are such that the matrix is symmetric definite positive and is defined on by
Let G be a Riemannian metric G and be a class application defined on some interval of , the real
is the speedof at instant t with respect to the Riemannian metric G or G-speed,the application
is a scalar field along .
The G-lengthof is
The G-kinetic energyof is
The G-length does not depend on the parametrization but the G-kinetic energy does.
We obtain a distance on setting for
Though is in general not associated to any norm on , the topology of induced by is always the usual topology of .
For the G-angle, , of and is defined by
2.4.1. Levi-Civita Connection
Let G be a Riemannian metric on , a covariant derivation ∇ on is compatible with G when
For any Riemannian metric G on there is exactly one torsion-free 6 covariant derivation compatible with G called the Levi-Civita connectionof G.
The Christoffel symbols of the Levi-Civita connection have expressions
where is the inverse matrix of .
2.4.2. Some Riemannian Metrics
1) The usual affine Euclidean structure of can be seen as a Riemannian structure on :
When is equipped with the metric the Levi-Civita connection is the flat covariant derivation ∇ defined previously. The distance is the usual Euclidean distance and the angle measurement is the usual angle measurement. The geodesics are parametrizations of straightlines with constant velocities.
2) For we put
The Levi-Civita connection of is also the flat covariant derivation.
The distance associated is
The angles measurement associated satisfies
The application from to is a scaling.
The geodesics are straightlines parametrized with constant velocities.
For as well as for the parallel transport is trivial, the parallel tangent vector fields are of the form where are constants.
3) For such that we put
The Levi-Civita connection is not anymore the flat covariant derivation, a straightforward computation gives the expressions of the Christoffel symbols
The geodesics are not anymore straightlines. The application from to is conformal.
2.5. Pseudo-Riemannian Structure on
A pseudo-Riemannian metricon is an application G associating to each point a Minkowski product on with the condition that
The general expression of a pseudo-Riemannian metric on is
where the coefficients are such that the matrix is symmetric with signature .
Let be the coefficient of the matrix . The usual affine Minkowski structure of is a pseudo-Riemannian structure :
It will be practical to limit the summation to . With this convention we have
As in the Riemannian case, for any pseudo-Riemannian structure on the Levi-Civita connection is the unique torsion-free covariant derivation satisfying
The Levi-Civita connection of is once again the flat covariant derivation.
For we will consider later the pseudo-Riemannian metric defined by
For this pseudo-Riemannian metric the Levi-Civita connection is still the flat covariant derivation.
3. Framework for the -Model
3.1. -Structure on a Riemannian Metric
A κ-structureon or a Riemannian metric affected with a κ-effectis a couple where
is a fixed Riemannian metric on .
is an application of class from to with .
Then, when is a -structure on we have :
1) On one hand two Riemannian metrics on :
where , is a metric conformal to G.
2) On the other hand to each point is associated the Riemannian metric which is a rescaling of G.
A point in endowed with a -structure will be called a sitting-observer.
We can think of this situation as the trivial bundle where each constant section is equipped with the Riemannian metric , the function associating to each point a of the constant section .
3.2. -Structure on the Euclidean Metric
Let us equip with a -structure , and choose once and for all a global system of coordinates such that . The distance associated is the Euclidean distance, .
Each sitting-observer is equipped via with the flat Riemannian metric defined by
from which a distance on is deduced :
However there should be no confusion between the collection of flat Riemannian metrics which are rescalings of and the non-flat Riemannian metric .
Figure 2.
Circles with same radii and centers in and with .
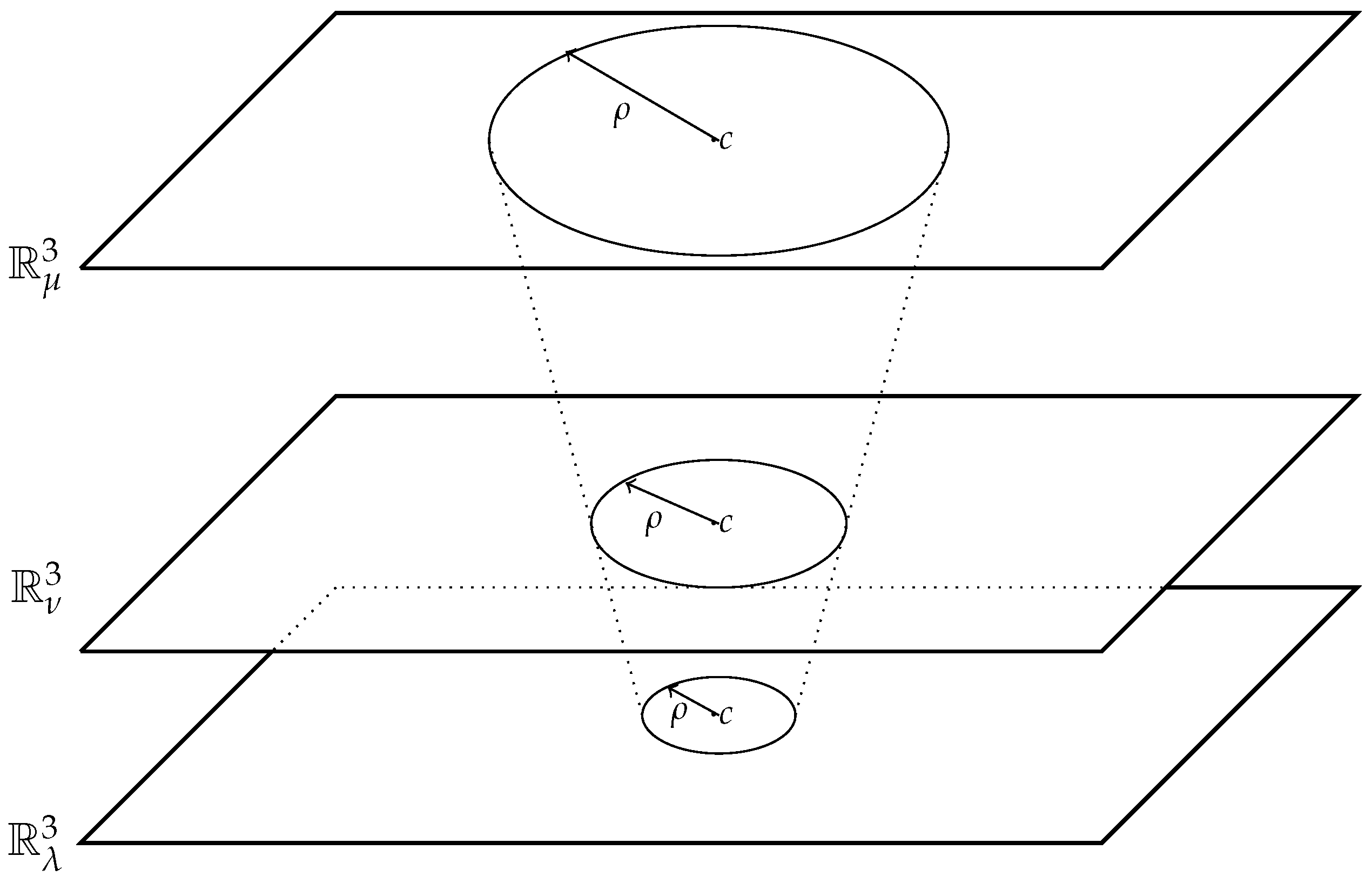
Any information retrieved using the flat Riemannian metric on will be called an observation made by the sitting-observera.
The application is not an isometry but it is nevertheless a scaling.Observations made by two sitting observers are linked, for example
while
This means that two sitting-observers will agree on angles measurements but not on length measurements. If they exchange their measurements two sitting-observers would desagree.
3.2.1. Speed Fields
Let be the euclidean metric on affected with a -effect, let be a smooth curve and be its velocity.
† The Euclidean-speedof is the scalar field along defined by
† The a-speedof is the speed observed by a sitting-observer at a, it is the scalar field
along defined by
The a-velocityof is the tangent vector field along defined by
so that the a-speed at time t is .
† The κ-speedof at time t is the speed observed by the sitting-observers coincident with
, it is the scalar field defined by
The -velocity of is the tangent vector field along defined by
so that the -speed at time t is .
The relations between the different speeds is
and
A smooth curve is κ-uniformwhen its -speed is constant, in other words when
or
3.2.2. -Uniform Straight Lines
Let and be two distinct points of . For any sitting-observer a the parametrization
is the geodesic passing through at time 0 and at time 1 with constant a-speed
.
Since is not a constant function, the smooth curve is not -uniform (unless is constant along it).
Nevertheless we can reparametrize the support of in a -uniform way.
Consider defined by
where
is some class function with
.
The -speed of c is .
The parametrization c is -uniform with constant -speed V if and only if
Then so the derivative never cancels. If c is to reach at some positive time we have .
Let be the function defined by
as is a strictly positive function, K is a strictly increasing bijective function from to itself, let be its reciprocal.
The curve defined by
is -uniform with -speed V.
Indeed its -speed
3.2.3. Velocity Fields and Covariant Accelerations
Let be a smooth curve.
For a given sitting-observer a, is equipped with , the Levi-Civita connection is flat and the solutions of the equation of cancellation of covariant derivation of the a-velocity
are the parametrizations with constant a-speed of straight lines, those are the a-geodesics.
Two sitting-observers a and b will agree on saying that a given curve is a geodesic but will observe two different speeds.
A straightforward computation gives the equation of cancellation of the flat covariant derivation of the -velocity
The flat covariant derivation is not the Levi-Civita of the metric so the equation is not the equation of geodesics of . The solution curves are the parametrizations of straightlines with constant -speed.
This can be checked easily : admits one unique solution with given initial conditions . Using an adapted frame we can assume that and is colinear to .
We have seen that the -uniform parametrization of the straight line such that and -speed 1 is
where is the reciprocal of the function K defined by
The velocity of writes
,
then
From where we find again relation .
3.2.4. Laser Distance
Let be two distinct points of and . Consider
we have
and as is the Euclidean-unit tangent vector the -speed .
The laser distance is defined by -length of between and is
This laser-distance can also be obtained with the -uniform parametrization of with -speed equal to 1.
where with .
is the "distance" obtained by compiling the observations of the speed made by sitting-observers along the straightline segment (which is not a -geodesic).
In general, the application is not a distance for it fails to satisfy the triangle inequality, but nevertheless
The positivity
The separation .
The symmetry .
are satisfied.
3.2.5. Circular Motions
Let be a parametrization of class of some Euclidean circle of , in a well chosen orthonormal coordinates system we have
with and some class function.
For , let us define the tangent vector fields
For a sitting-observer a, the apparent radius is , the a-velocity at time t is
While the -velocity at time t is given by
The (covariant) a-acceleration of is
The (covariant) -acceleration of writes
3.2.6. a-Uniform and -Uniform Circular Motions
When a circular motion is a-uniform, in other words when for a sitting observer a the a-speed is a constant, the expression of has the form with and some constants. Changing the origin of time we may assume that , and changing the orientation we may assume that .
Then
(in polar coordinates )
For any sitting-observer the motion will also be circular a-uniform with angular speed but with apparant radius of the trajectory .
The a-speed and the -speed writes
The derivative of the -speed is
where g is defined by
Of course if happens to have radial symmetry, in other words if the motion is also -uniform.
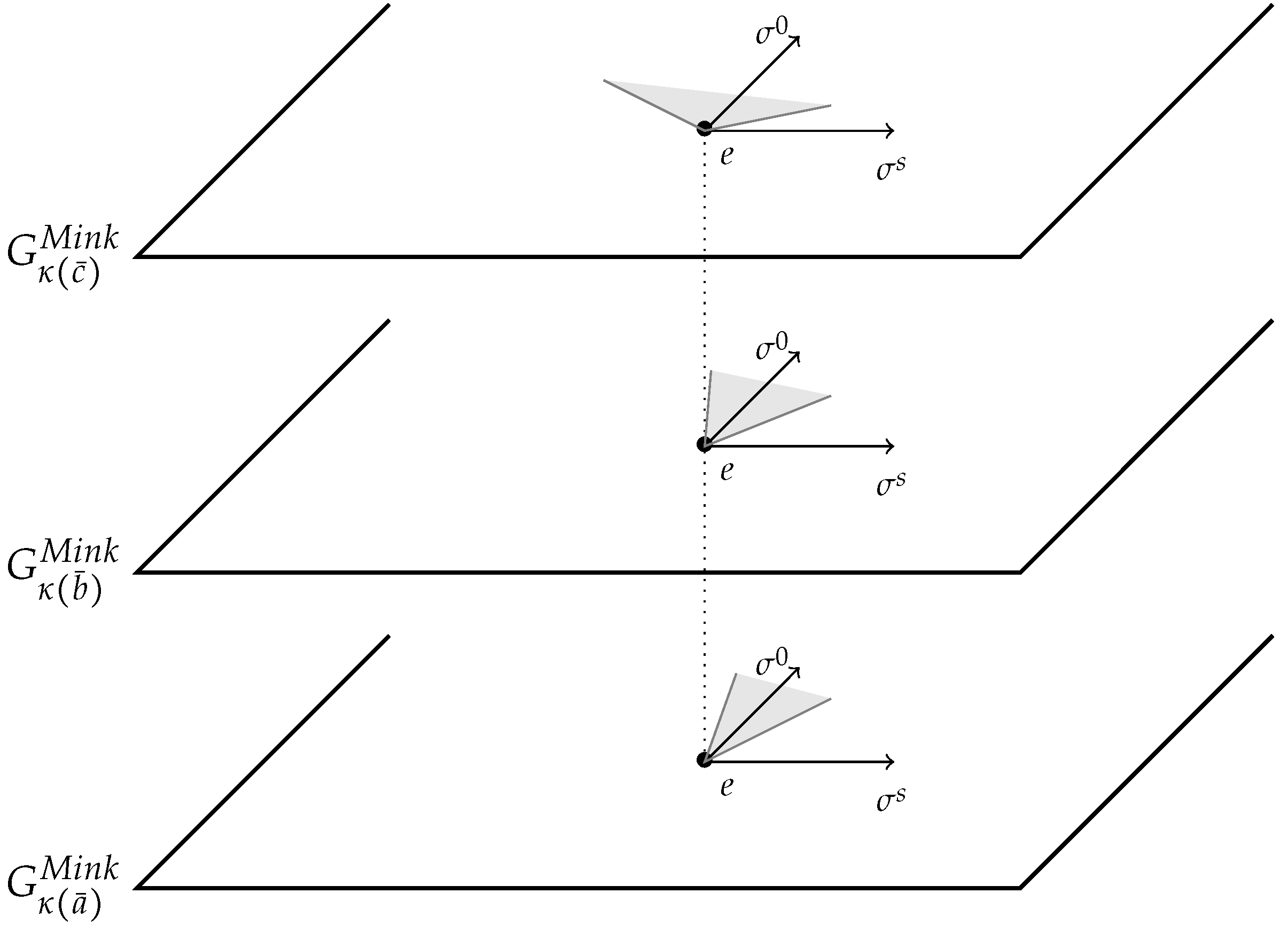
3.3. -Structure on a Minkowski Metric
Let us equip with the Minkowski metric . We choose once and for all a global system of coordinates such that the expression of the pseudo-metric is
Then
The choice of the global coordinates system provides a trivial foliation of which leaves are the equivalence classes of the relation when . Each leaves of that foliation will be called a sitting-observer relative to the chosen global coordinate system.To each point a in is associated a unique sitting-observer .
Changing the choice for the coordinate system will of course change the sitting-observers.
A Minkowski metric affected with a -effect is a couple where
is a global coordinates system such as has expression
with is a class function.
When is a Minkowski metric affected with a -effect we have
On one hand two pseudo-metrics on :
· The Minkowski metric
defined at .
· The non-flat pseudo-metric defined by
On the other hand a collection of Minkowski metrics on ,
defined by
Any information retrieved using the pseudo-metric on is an observation made by a sitting-observer . For example, let e and be two events, if is the unique quadrivector such that the sitting observer will interpret e and separated by a time-like gap when . Another sitting-observer may interpret e and separated by a space-like gap.
Figure 5.
Deformation of the ℌfuture-coneℍ at e with the ℌspace-componentℍ, represented in dimension 1.
Figure 5.
Deformation of the ℌfuture-coneℍ at e with the ℌspace-componentℍ, represented in dimension 1.
3.3.1. Quadrivelocities
Let
be a smooth worldline expressed in the coordinates system , the triplet
will be denoted . The sitting-observer associated is .
The quadrivelocity at proper time is
where the dot is the derivation with respect to the proper time , and the summation is on indexes .
The quadrivelocity observed by a sitting observer , the -quadrivelocityis defined by
so that
The quadrivelocity observed by the family of sitting-observers is the κ-quadrivelocity
so that
We have
If we put
we get the equivalence
When we say that is a Minkowski-particle worldline.
Let be a sitting-observer we have
we get the equivalence
When we say that is a -particle worldline.
We also have
we get the equivalence
When we say that is a -particle worldline.
Let us put
for two sitting-observers and we have
and
Any of the Minkowskian metrics is flat, so their Levi-Civita connexions are all equal to the trivial covariant derivative. Therefore we have
For any metric the geodesic worldlines are where the coordinate functions are affine functions.
3.3.2. Changing Coordinate Systems
Without κ-effect :
The choice of a "reference frame" where is an event and is a base of such that for and two tangent vectors at O, we have
determines a global system of coordinates on . For example we can choose for .
Consider , with , be a geodesic worldline. If we adjust a base of so that the global coordinate system generated by the frame fullfills the conditions
(1) The coordinates functions of a geodesic worldline are
affine functions
(2) If has coordinates satisfying
its coordinates satisfy
We obtain
where
Then if e has coordinates in , its coordinates in are
This is the -boost.
With the κ-effect :
Let be an event and be the sitting-observer associated. We can choose a base of such that for and two tangent vectors we have
Such a base is, for example, given by and . Let be the frame
As previously, if we consider an inertial observer passing at by a point of adjusting the coordinates system will give
where
We get the --boost.
3.3.3. Observation of a Far Away Geodesic Worldline
Let be a geodesic worldline.
Each sitting-observer interprets as a geodesic worldline, the support of is rectilinear and the quadrivelocity is a constant vector field along .
Let be a reparametrization of this geodesic worldline in such a way that there exists a strictly positive constant such that
The support is still rectilinear but the quadrivelocity field is no longer constant neverthless the -quadrivelocity is constant.
As is a reparametrization of the geodesic worldline , there exists a function , such that we have
so we have
so condition reformulates into
which can be fullfilled only when
We also get for the worldline
Let us remark that
To a distant sitting-observer the worldline appears rectilinear, even though it is not a a-geodesic worldline. For example, this means that if along a geodesic worldline the function is decreasing we may get a reparametrization of such that is constant while is not. It is then possible that a distant sitting-observer a observes the -quadrivelocity of -particle worldline being time-like on some portion of the trajectory and space-like on some other portion.
4. Applications
Let us specify that these applications are just given here for illustrative purposes. Concrete and much more complex situations in the case of spiral galaxies and galactic clusters have been discussed elsewhere [2, 3, 4].
We need to clarify "where" the objects we will be considering and "where" the observers actually are. A -structure is conceived as the trivial bundle where each constant section is equipped with the metric and the base space is equipped with the metric . Each leaf of the bundle is accessible to sitting-observers a such that , those sitting-observers are subject to an illusion (associated to the surrounding density). The real space is the base space where the objets are, but no real observer can see the geometry of that space per se. Rather these observers see the base through the magnifying glass provided by both their own environment and that of the perceived object. Any potential observer in the base space accessing to would be a "shadow-observer".
4.1. What a Sitting-Observer Sees, Size Measurement
Let a and b be two sitting-observers, as the Levi-Civita connections of and are both equal to the trivial covariant derivation, a and b will agree on which tangent vector fields along a smooth curve joining them are parallel : the constant vector fields. Assume that and let and be two constant tangent vector fields along such that
we have
Figure 3.
Discrepancy in size measurement: , while .
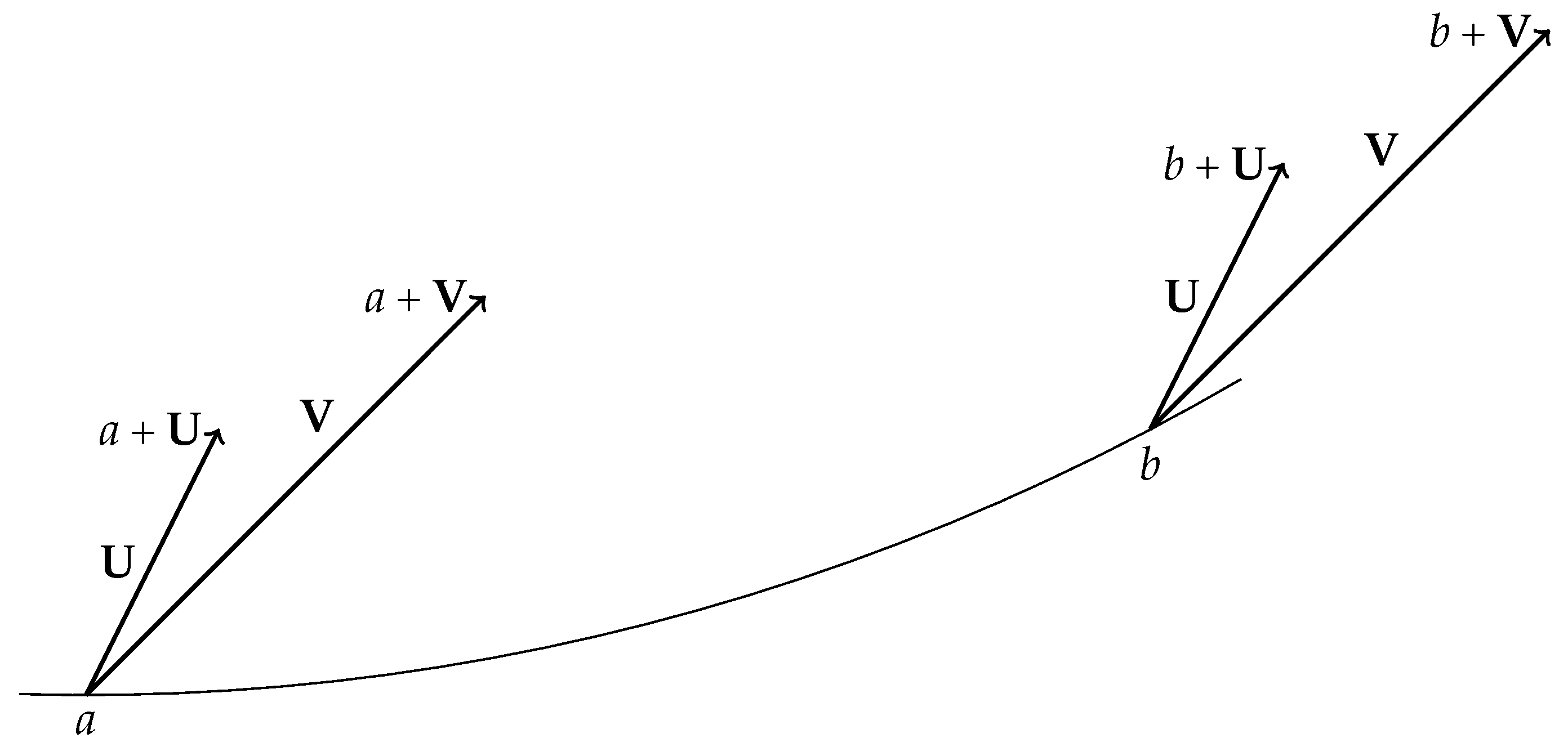
Practically, this means that two different sitting-observers, each one holding a stick, could agree on saying that the two sticks have the same length when they exchange their observations on their own stick, but if one of them use his own measurement system to measure both stick he would say that the two sticks have different lengths.
This can be illustrated on the following figure, two sitting-observers compare the radii of their own unit ball, a sees the unit ball hold by b bigger than his own.
Figure 4.
Discrepancy in size measurement for a disk.
Another illustrative point of view appears very interesting. We assume here that there is no gravity. The base is equipped with an Euclidean metric. Consider a free particle emitted at some instant from the point a (Figure 5). Arrived at b the particle emits a photon in the direction of the observer A. Then the observer A sees the particle at the position b’. He measures the spectroscopic velocity (shown in orange). Likewise the observer B sees the particle starting from a at the position a’ and he measures the spectroscopic velocity 7.
-aberration
In Figure 5 a linear variation of as a function of is assumed. Then the image of the straight line ab taken in the base (the real trajectory of the particle P) is represented by a multiplet of parallel straight lines ab’, a’b, ..., each of these lines being attached to a real observer. Let us note that the real trajectory of the particle P in the base space does not seem to be parallel to the corresponding multiplet of its images in the bundle. In fact there is no reason why this should be so. The base space is linked to the bundle by a projection which can diversely tilt any small portion of a trajectory, even though this tilt is fictitious (see also Figure 15, where the fictitious trajectory is shown as composed of a series of infinitesimal segments, each one of these segments being parallel to the real trajectory). Moreover the base space is not accessible to the real observers present in the bundle. Then an unreflected comparison of a vector in the base to the "same" vector in the bundle makes no sense regarding its apparent direction. In the base the vector (denoted by ) is constant for a free particle, while in the bundle it is that is a constant vector. In the sheet of the observer A, we have, respectively for the radial (spectroscopic) and (apparent) tangential components of the velocity, as seen by this observer ()
the dot over denotes the Lagrangian time derivative of . We can verify that if , then the tangential velocity cancels out.
Overlapping images.
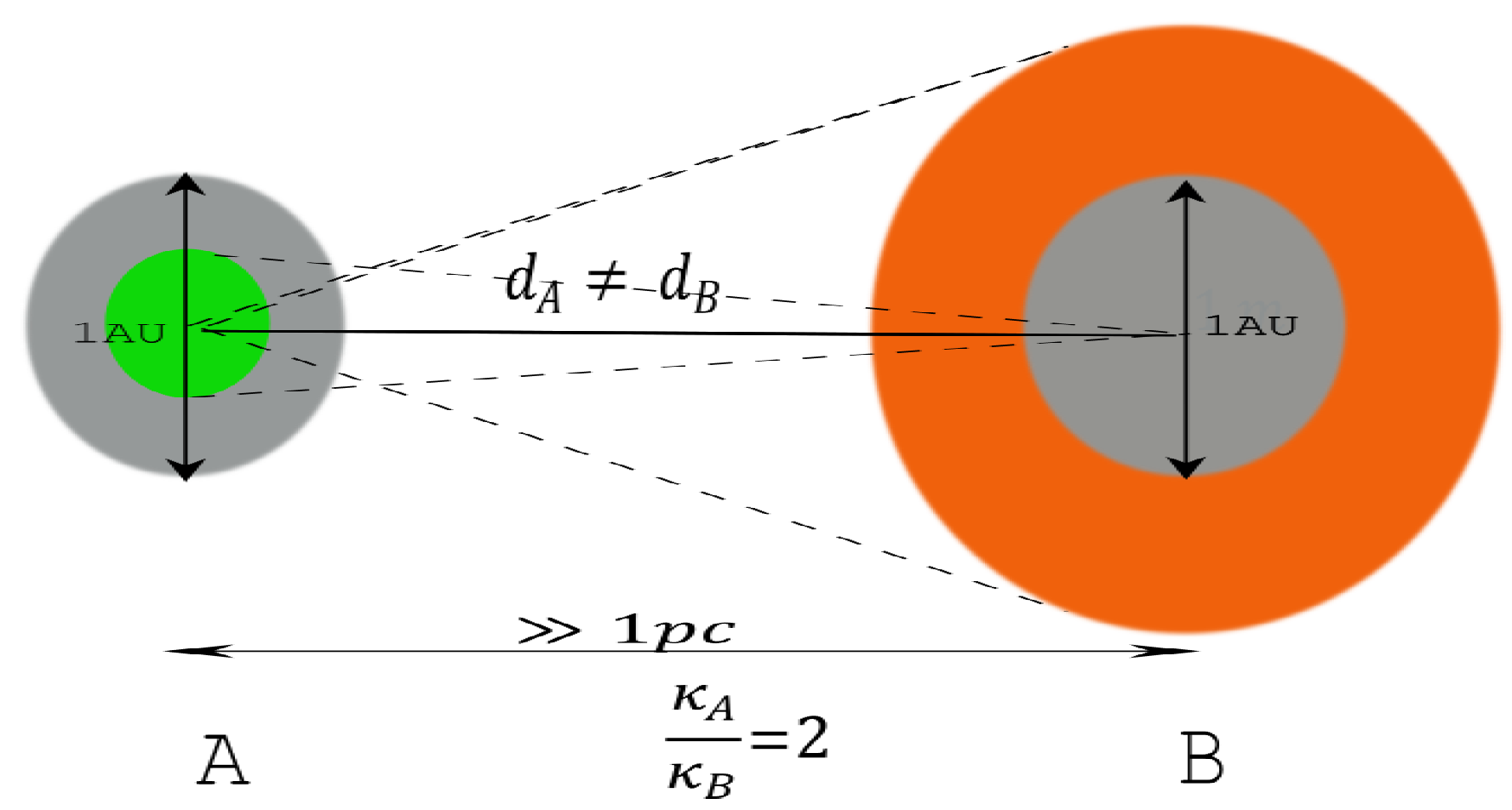
Let a be a sitting-observer, be a straight line passing through a, and be two planes orthogonal to , B be a disk and C a small concentric flattened annulus both in and centered at . Assume that , where is the radius of B and the thickness of C, for example and a few meters.
The points of B are all affected with a coefficient and the points of C are all affected with a coefficient .
We have . Let and , we have and . Photons are emitted by b and c in direction of a, but of course each emitter estimates the direction of a with its own tools, the ratio induces a magnification of the image received by a on a screen in the plane , as shown in Figure 5.
To illustrate this phenomenon let us consider three cases, in the first case (Figure 6.a) , in the second case (Figure 5.b) we assume that (3 in the Figure 6.b), in the third case (Figure 6.c) we assume the ( in Figure 6.c)
If there is no -effect, the observer a perceives an image with no magnification as shown on Figure 6.a. The second case is represented in Figure 5.b. it shows the modification of the image received by a, the image of the flattened annulus is stretched. The third case is represented in Figure 5.c, the image of the central disk is stretched and overlaps the image of the flattened annulus8.
4.2. The Circular Motion of a Test Mass Around a Motionless MassM
4.2.1. Without -Effect
Without -effect, in other words for any observer considering endowed with the Euclidean metric , the motion is the usual Newtonian motion.
Let us consider the elementary situation of a very massive point of mass M, located at the origin O of coordinates and surrounded by a spherical gas cloud of very weak density with radial symmetry. Limiting us to the examination of a circular motion of a test mass around this point, the dynamic equation is (assuming the gravitational constant )
where is the radial -unit vector at and R is the constant -distance from to O and .
It is a very simple affair to show that the Newtonian speed is that which would be measured by a fictive observer using the metric . We find the trivial result
The index 0 indicating that this is what is measured by the fictive observer. In the -model framework the Newtonian speed as defined above (103) is fictive, it cannot be measured by any real sitting-observer.
4.2.2. With -Effect
Consider a local sitting-observer , situated on the trajectory of the test mass. He sees the whole space endowed with the metric , but of course this observer has access neither to nor to . As the -effect affects the distances but does not affect the masses, the apparent radius of the trajectory is , while the mass M remains unchanged. Applying the Newtonian dynamics with this modified metric, the sitting-observer a measures the speed
where is the Newtonian velocity calculated (but not measured) by a terrestrial observer .
We are aware that in astrophysics the radial velocity (the velocity component directed along the line of sight) is measured by spectroscopy while the component of the velocity projected on the sky plane is deduced from the measurement of the proper motions. Thus within the -model framework, a clear distinction must be made between these two components. We will call spectroscopic velocity the (radial) velocity measured by any observer. This velocity is independent of the sitting observer and is defined by
where is the projection angle along the line of sight.
It is very commonly observed in the outskirts of the spiral galaxies that the density where r is the distance to the center of a galaxy, measured by a terrestrial observer, i.e. . If we assume that 9, we get for . In this case we can conclude that becomes constant and by consequence becomes constant too. In other words, the observed flatness of the rotational curves of the spiral galaxies is correlated to the variation of the density in the disk as a decreasing exponential function of the radius r. A few concrete examples are given in Figure 8.
In contrast, the tangential velocity measured by a terrestrial observer is
4.3. An Analysis of the Spiral Substructure
The spiral galaxies are dominant in the Universe. It is therefore most interesting to understand the link existing between the observation of a tight spiral substructure as it would be seen by a fictive Newtonian observer (i.e. located in the Euclidean space without -effect), compared to the point of view of a sitting-observer, affected by the -effect. If the -effect is now taken into account (each real observer lives in the bundle and not in the base which is for them an unreachable place). In a spiral galaxy the density varies as and .
Without the -effect the equation supporting the spiral substructure is that of a tight logarithmic spiral of maximal extension equal to the unit
With the -effect the equation becomes
or
For any siting-observer a
While a hypothetical Newtonian observer would see a tightly coiled spiral, any sitting-observer sees a grand design spiral. Two distinct sitting-observers a and b see the same grand design spiral, but differing by a homothety ratio .
Figure 9.
A toy example : A well-developed conservative spiral substructure seen in the bundle as opposed to its counterpart living in the base (a tightly coiled spiral).
Figure 9.
A toy example : A well-developed conservative spiral substructure seen in the bundle as opposed to its counterpart living in the base (a tightly coiled spiral).
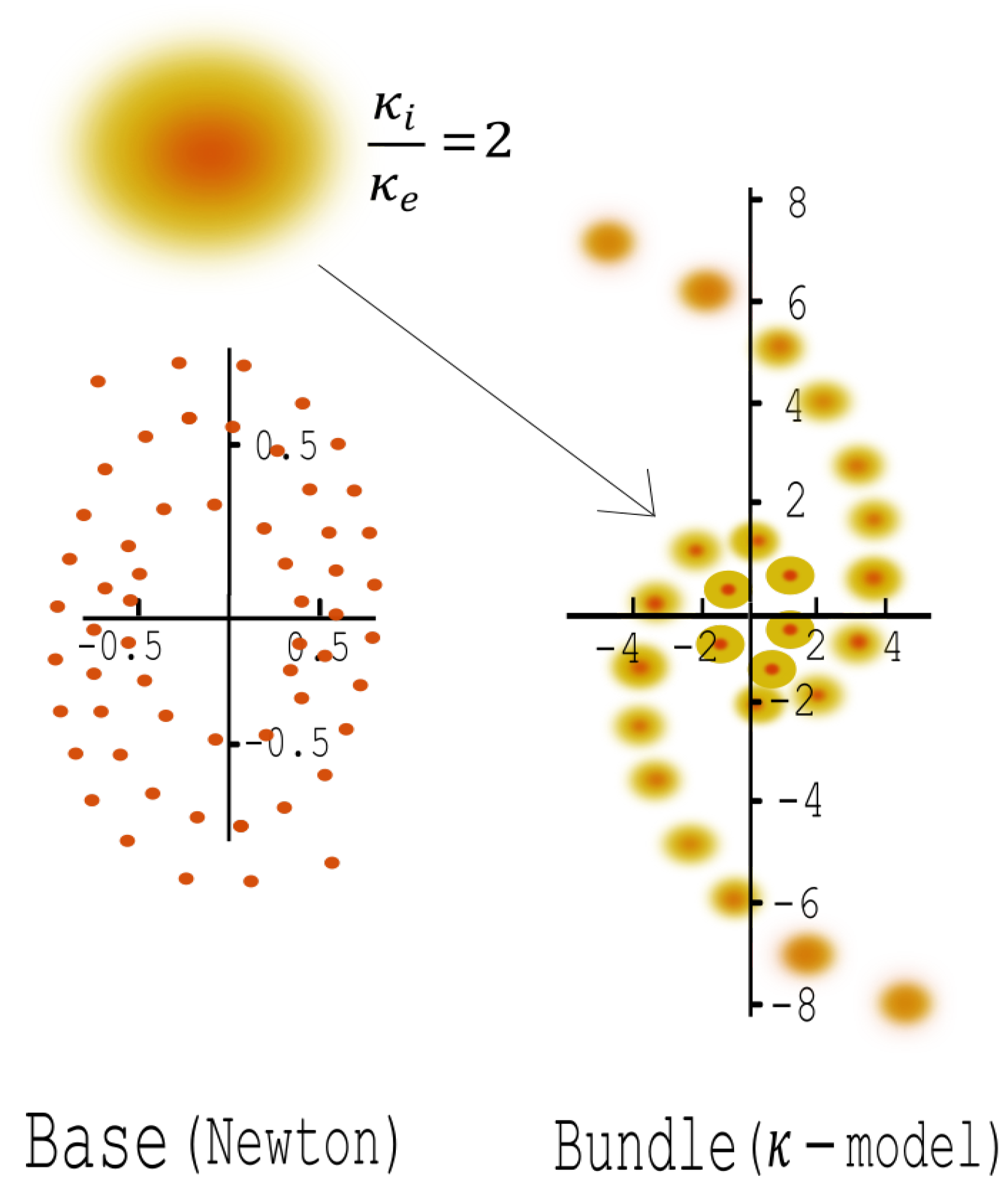
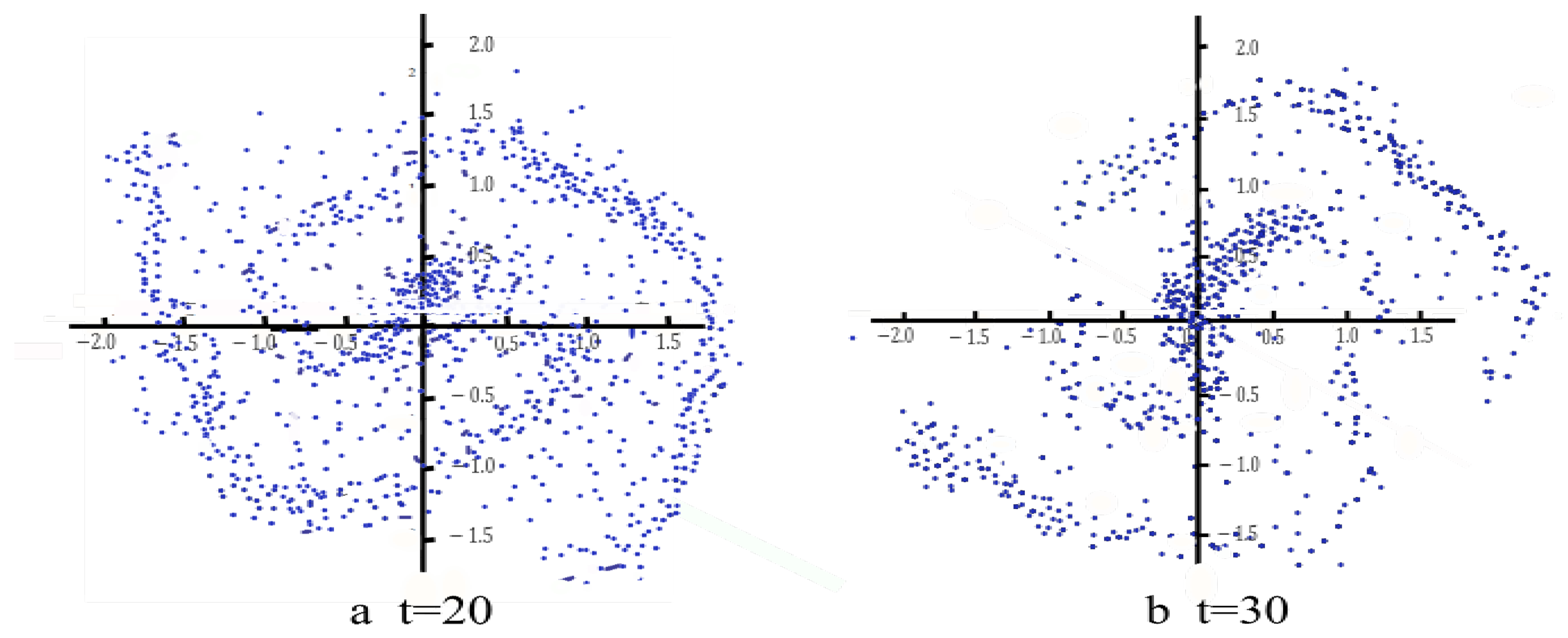
Figure 10.
A conservative grand design spiral produced by a numerical simulation in the -model framework (for the details see [2]). The elapsed time is given in the unit of 100 Myr. The Newtonian equivalent would be a much tighter spiral with a larger number of turns.
Figure 10.
A conservative grand design spiral produced by a numerical simulation in the -model framework (for the details see [2]). The elapsed time is given in the unit of 100 Myr. The Newtonian equivalent would be a much tighter spiral with a larger number of turns.
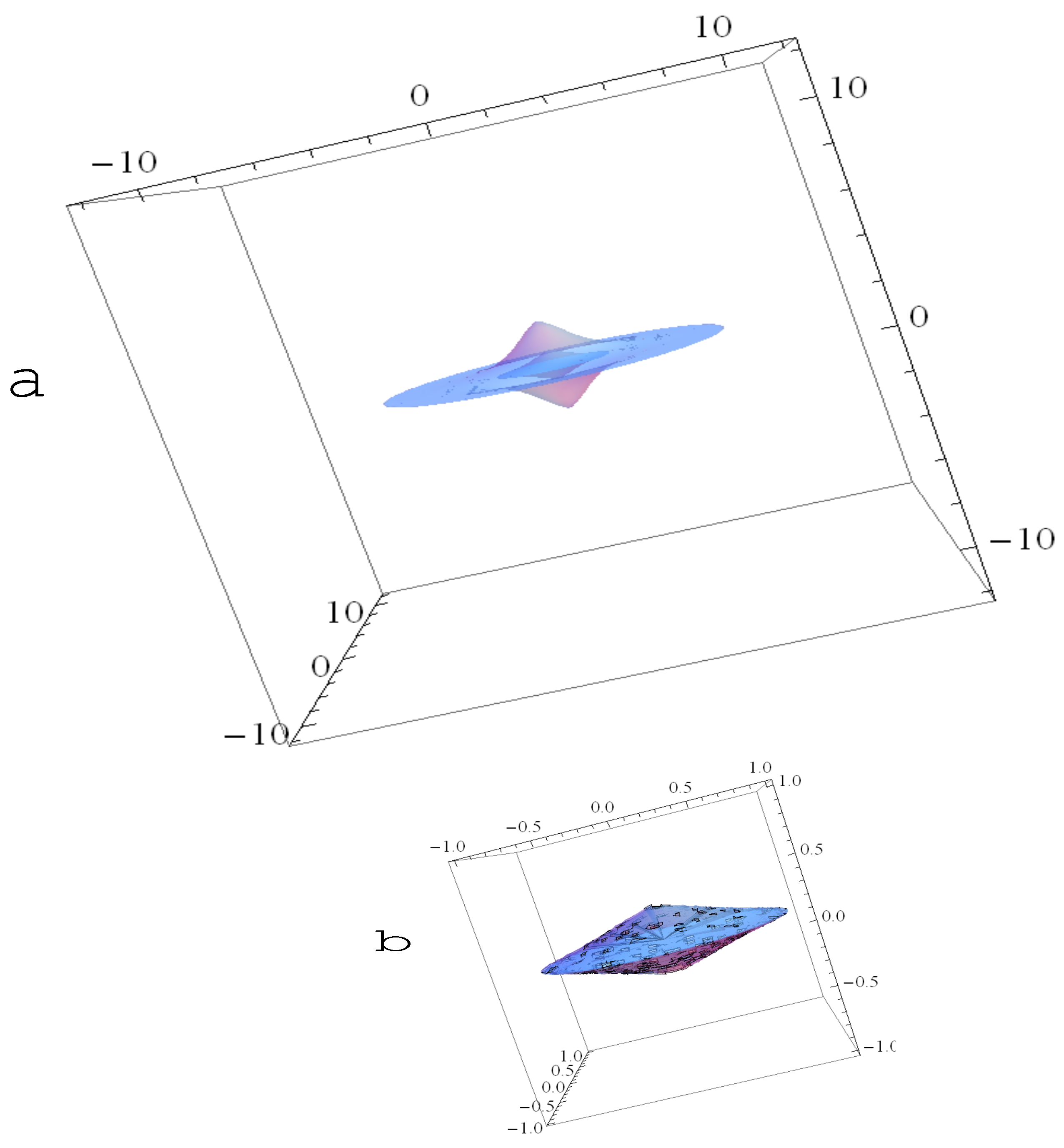
A side-on galaxy
If we assume for simplicity that a terrestrial observer measures a constant thickness for a disk galaxy, then
In addition we have
Then the local thickness is
Without -effect a side-on galaxy, seen as a very extended flat disk of constant thickness by a terrestrial observer, would appear as a much more compact object (for .
Figure 11.
A side-on galaxy seen by a terrestrial observer (a) as opposed to its compact counterpart living in the base (b). On this illustrative example the terrestrial observer measures the density .
Figure 11.
A side-on galaxy seen by a terrestrial observer (a) as opposed to its compact counterpart living in the base (b). On this illustrative example the terrestrial observer measures the density .
4.4. Galaxy Clusters
The application of the -model to the galaxy clusters has been examined in the reference [3]. We have shown that the -model can greatly lower the major part of the dark matter content in the galaxy clusters. The current dark matter/baryons mass ratio amounts to approximately 10 in the outskirts of these objects, and the -model can strongly reduce this ratio within the much more acceptable range between 0 and 1. The fits are not optimal in the inner regions of the galaxy clusters, but by lowering the gas temperature in these regions, the problem can also be easily solved. An example is the well-studied COMA cluster (Figure 12).
4.5. The Bullet Cluster
The Bullet Cluster (1E 0657-56) consists of two colliding clusters of galaxies, where a clear separation appears between the stars (compact matter) and the hot gas (diffuse matter). It is a relatively rare situation, even though other cases exhibiting very similar properties are also known (for instance MACS J0025.4-1222). The Bullet Cluster is claimed to provide strong evidence for the existence of dark matter and, on the other hand, seems to severely challenge MOND. Yet the -model validates the test, when a comparison is made between the gravitational lensing diagrams coming from both dark matter and -model paradigms (Figure 13).
4.6. Translation of an Extended Object and -Effect
We have assumed that the coefficient is linked to the average mass density, , by the relationship
where the index E designates the values associated to any baseline observer (for instance the terrestrial observer). The way we carry out this averaging operation at a given point, may depend on what we are observing. If we observe the inner motion of a little part of a galaxy, the observed zone must be affected with a coefficient deduced from an averaging of on a "small" ball with radius ; now if we observe a galaxy as a whole, taken in a galaxy cluster, we need to affect this galaxy with a coefficient , deduced from an average of on a ball , containing the whole galaxy with radius .
Let us consider a unit gaussian distribution, , centered on (Figure 12)
The convolution with any quantity gives the mean value of this quantity. For instance for the mean mass density
Figure 14.
Averaging over a ball surrounding a star or a galaxy.
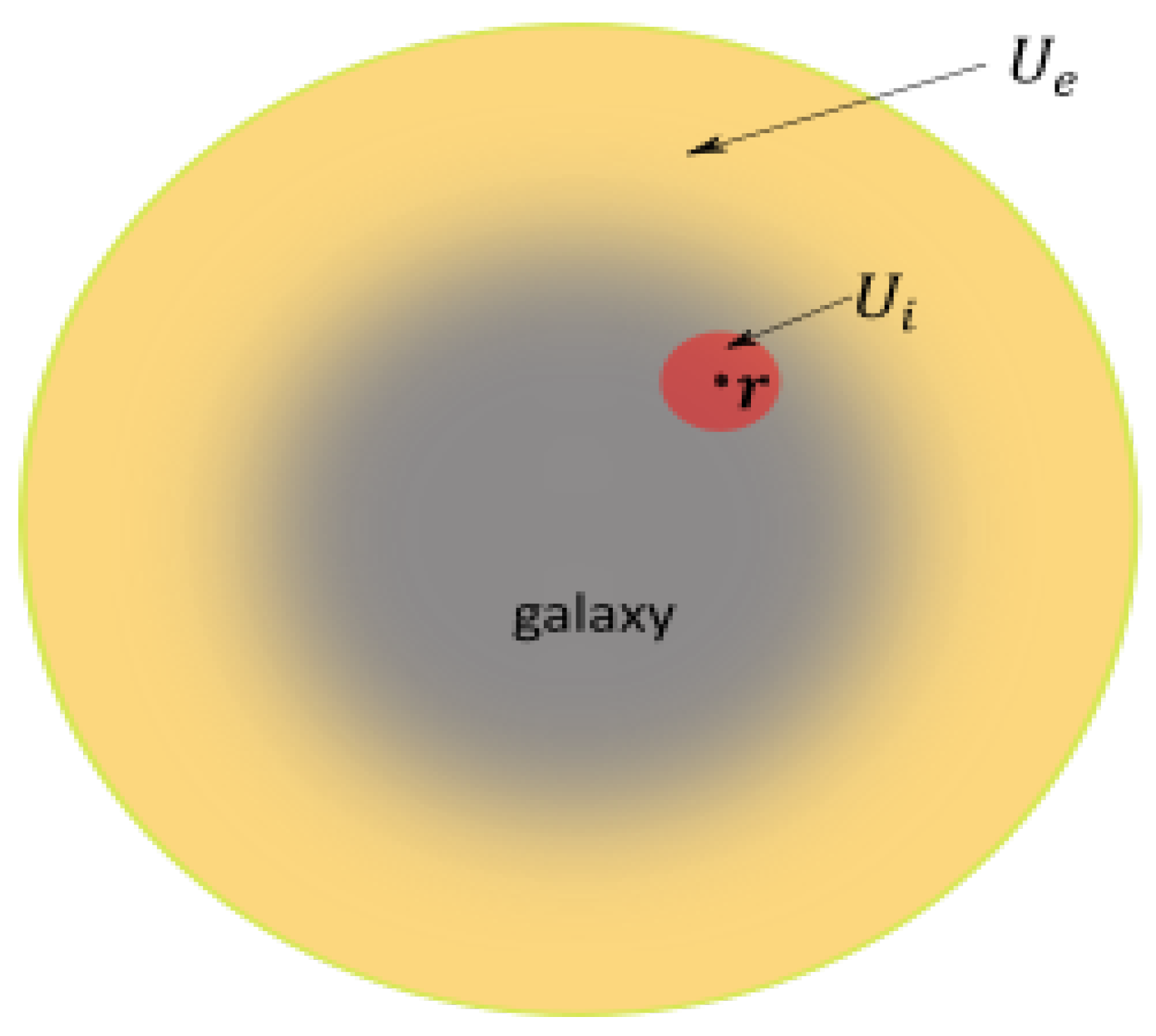
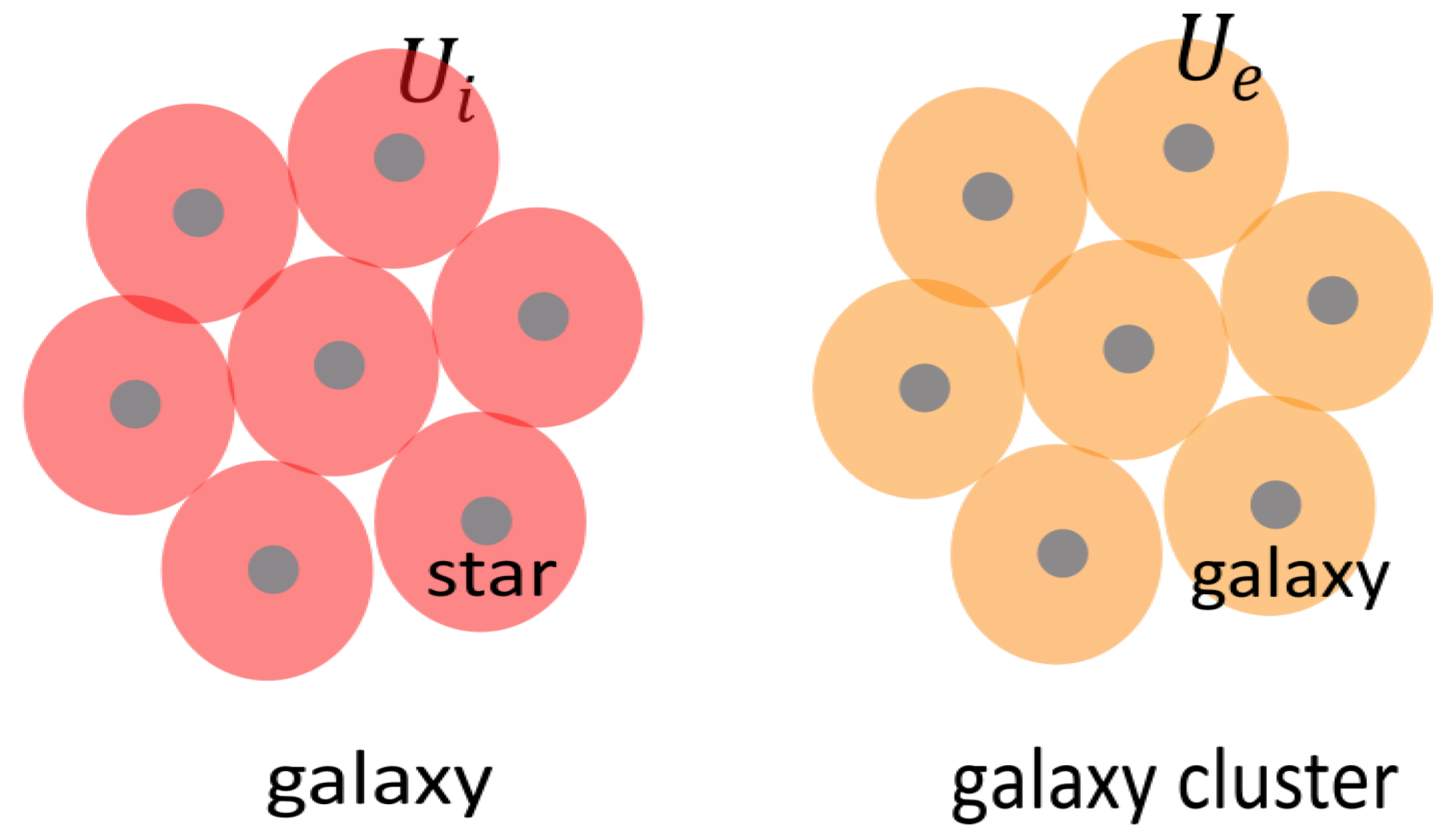
Figure 15.
Stacking of balls covering a galaxy or a galaxy cluster.
The simultaneous consideration of both inner motions in a galaxy and global motion of the galaxy, as a whole in a galaxy cluster, will necessitate the consideration of two values of .
A sitting-observer in the observed galaxy correspond to the selection of two sheets in the bundle or two different ways of measuring distances : and .
As previously the spectroscopic velocities, whether they are associated with internal motions in the galaxy or with global movement of the galaxy, are universally accessible, that means that spectroscopic velocities can therefore slide along a fiber without change.
Let us consider a galaxy moving in a cluster, and two small regions I and J of that galaxy moving into that galaxy.
Figure 16.
Point of view of different observers.
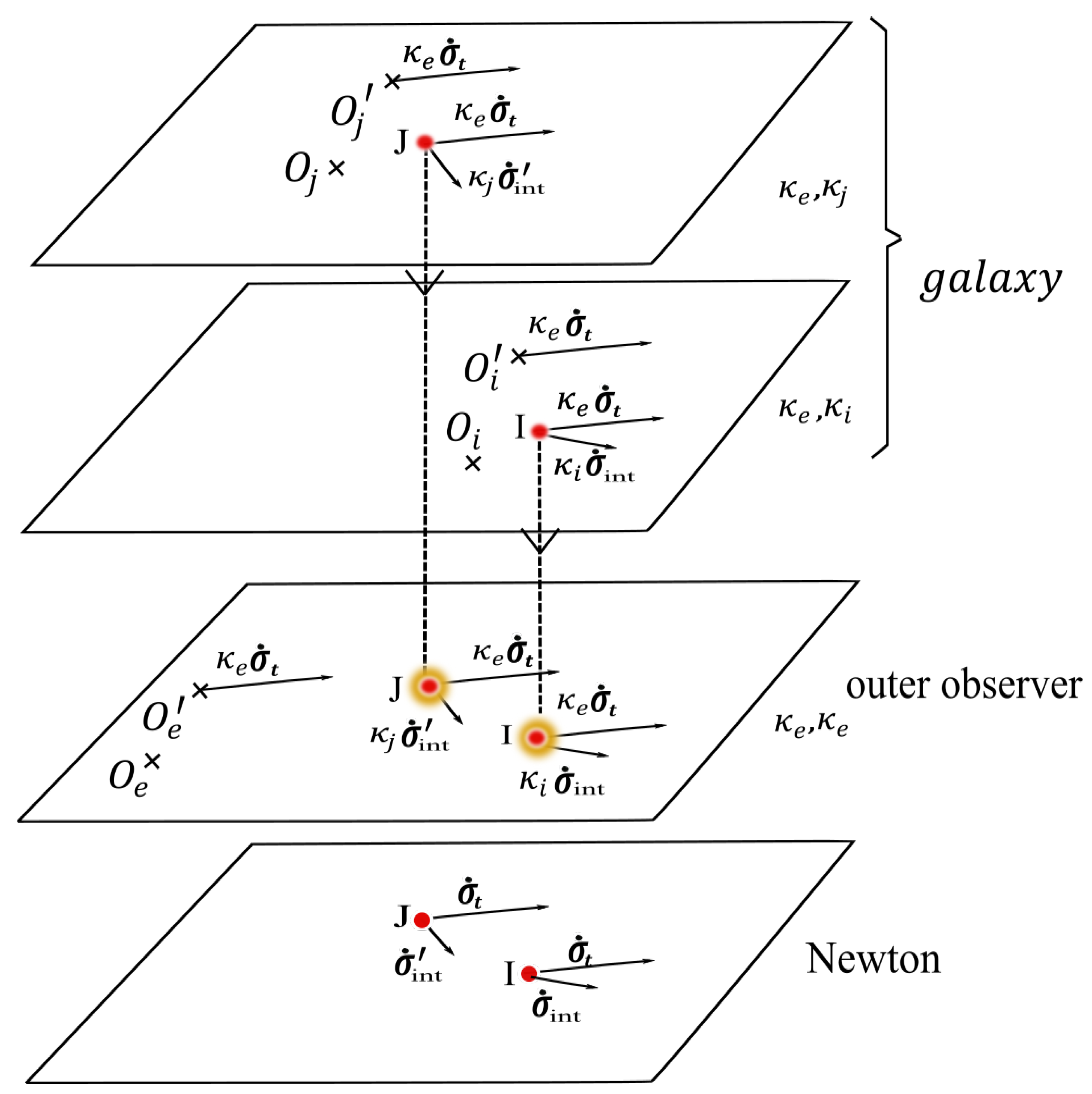
With no κ-effect
The velocities of I and J decompose in sums
and
With κ-effect inside the galaxy
At I the coefficients are for translational movement and for internal movements. An observer travelling with the galaxy coinciding with I only perceives the internal movements, i.e. at I that observer measures . The fixed observer measures the speed of the observer which is . Finally, the observer transmits to the internal velocity of I. The observer makes then the sum to get the speed
At J the coefficients are for the translation motion and for the inner motions. The fixed observer measures the speed
With κ-effect outside the galaxy
For a sitting observer a out of the galaxy the coefficient is locally computed . Cancelling the translation velocity of the galaxy, this observer only perceives the internal motions, resp. at I and at J. The fixed observer measures the speed of the observer which is obviously unique, i.e. . On the other hand the observer transmits to the values of the internal velocities of I and J. The observer then makes the respective sums :
at I
at J
4.7. The Relativistic Extension
In the world of galaxies and galaxy clusters, as both gravity and velocities are weak, a relativistic extension may not appear very useful. However this extension is needed at the cosmological level.
In general relativity, the background, i.e. , is equipped with a pseudo-Riemannian metric. In some local coordinate system , the expression of the metric at point has the form
where are some functions of with and for .
Hence the background is equipped with a pseudo-distance. An ideal observer having access to this pseudo-metric would use this metric for measurement of the space-time interval between two events, and , in other words, the pseudo-length of the -geodesic segment joining to .
For distinct, the Christoffel symbols are
For and distinct (with no summation over i)
In the -model each sitting-observer a associates to the background a modified pseudo-metric. The modification is a rescaling of the spatial coordinates of tangent quadrivectors with no change of time coordinate. Then the general form of modified pseudo-metric is
Each current sitting-observer a is provided with a value for .
The modification of the pseudo-metric induces a modification of the Christoffel symbols. If we note the coefficients of the modified metric we have
then
the Christoffel symbols of the modified metric and the initial metric are linked
This means that the supports of geodesic curves may differ from one observer to another.
The full background is also equipped with a modified pseudo-metric.
If we note the coefficients of the modified metric we have
then
the Christoffel symbols of this modified metric and the initial metric are linked (with no summation over i)
The geodesics of this pseudo-metric are not geodesics for any metric used by sitting-observers
4.7.1. Without Gravity
Without gravity the metric is Minkowskian, we have
In this special case the -effect does not affect the Christoffel symbols, and then the geodesic equation has been considered in paragraph 3.3.3.
4.7.2. With Weak Gravity
Without -effect
In the case of weak gravitational fields, the metric coefficients are slightly modified
With functions of the position and , then we have .
Furthermore if we assume that the weak gravitation field is stationary, we have
In this situation, for distinct, the Christoffel symbols are
For and distinct (with no summation over i)
If is a geodesic we have
where .
For the first component we get
In the case of low velocities, i.e. , the spatial components of the geodesic equation reduces to
For .
With -effect
The metric coefficients are changed : for . With the same hypothesis of weak stationary gravity and low speed, the geodesic equation simplifies (for eq. 117, see eq. 60)
for with . Using the variable , for ,
and
Eventually becomes
Let the Schwarzschild metric (with the attractive mass M situated at the origin of the coordinates and very far from the singularity). We have then .
For any sitting-observer a, equipped with his own coordinates and located along the trajectory of the test mass, the motion equation is ( with the speed of light )
where the right side of this equation can be compared to eq. . Especially for a terrestrial observer equipped with his usual coordinates ()
The motions perceived by two sitting-observers are homothetic to each other. All observers are equivalent and there is no priviliged observer.
Gravitational Tide
Let A and be two particles submitted to the gravitational action of a massive particle of mass M and located at the origin of coordinates. The two particles are assumed to be very close to each other. Let and their respective position vectors. Putting , the relative motion is given by the equation
Let us note that when , the self-interaction is strengthened.
Two "paradoxes" that emerge from the motion of free particles
For a free motion the equation is
or
i. A free particle (not submitted to any force) may exhibit an (apparent) auto-accelerated (or auto-decelerated) motion for a terrestrial observer. This result seems to be inconsistent with the first law of Newton. In fact the motion perceived by a terrestrial observer is fictitious. This motion is the image of a real motion taking place in the base. In the base the first law of Newton is obviously respected.
ii. Let two free particles A and , sufficiently close to each other to share the same , moving along parallel straight lines in the base. Paradoxically enough, for a terrestrial observer these particles can now appear to move toward and away from each other (Figure 17), following the sign of .
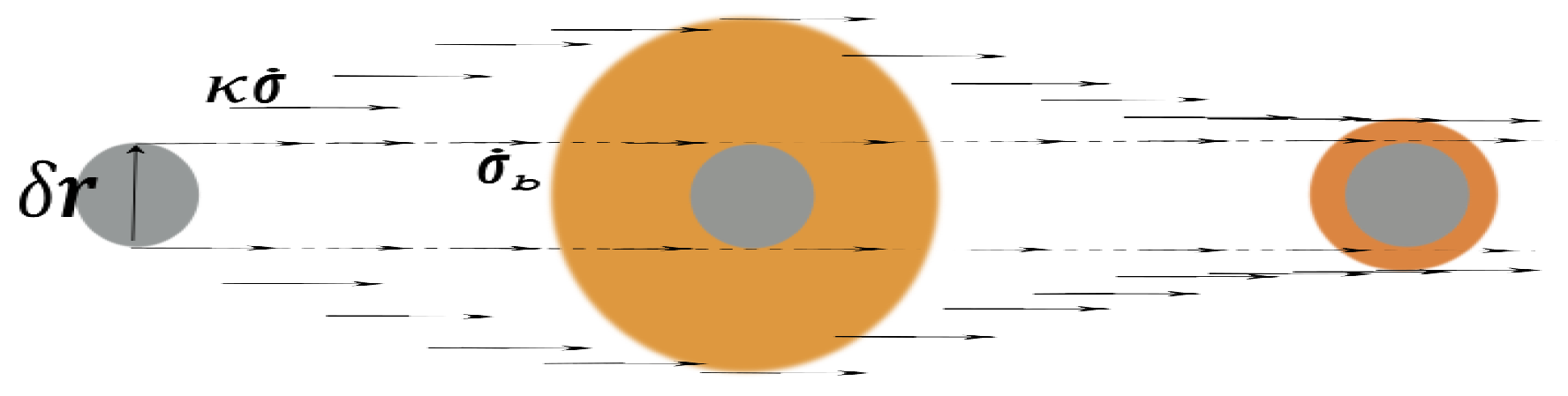
In other words the trajectories of these particles no longer appear as two absolutely continuous parallel lines. Each of these lines rather appears as a kind of Devil’s Staircase. The relative motion of these two particles reflects the apparent variation of the size of any astronomical object (a planetary system in a galaxy or a galaxy in a galaxy cluster), represented by a gray disk on Figure 15. The variation represented on the latter figure has been artificially magnified. In reality such a variation is very slow and it cannot be detected on the scale of a few hundred of millennia. In the base the velocity (denoted on Figure 17), measured by a fictitious observer, obeys to the equation (free particle)
and , whereas in the bundle the velocity (measured by a local observer), obeys to the equation
and in this case . If Figure 17 displays the projection of a moving disk on the sky plane, for instance as seen by a terrestrial observer E, then the measured velocity is . For him the size of the disk (shown in orange) increases in a first phase and then decreases in a second phase. Likewise the velocity of the disk varies as (increasing in a first phase and decreasing in a second phase). In fact the motion perceived by the terrestrial observer is fictitious, the real velocity is constant (free particle).
We have presented in this paper the formalism of the -model. Astonishingly this formalism is fairly straightforward when compared to other formalisms which try to modify the standard general relativity [5, 6, 7]. The -model is thus characterized by its relative simplicity. Furthermore any type of modified gravity necessarily leads to the introduction of new fields and surreptitiously to new particles. Thus all the various versions of modified gravity, with their lot of new unknown particles, even seems much more complex compared to the dark matter paradigm (Newtonian in essence), apparently for a very limited gain in the understanding. However the number of parameters in
5. Conclusion
We have presented in this paper the formalism of the -model. The basic hypotheses of this new paradigm are reasonably simple, and the -model exhibits some common points with the MOND theory [8, 9]. Thus, at least in its original form, MOND, relying on an unique universal parameter, , also constitutes a straigthforward way to predictively generate the rotational curves of individual galaxies. Unfortunately some issues persist for MOND at the scale of the galactic clusters, even though some solutions have been proposed to circumvent the problem [7]. The -model has the same level of efficiency as MOND to fairly predict the profiles of the rotational curves of individual spiral galaxies [4], but moreover can also help to understand the physics of galactic clusters [3]. Other interesting ways have also been suggested to circumvent the dark matter conundrum [8, 9, 10, 11,12]. We have already noticed that the latter theories share some common points with the -model [4]. Eventually we can report that, in parallel, a study focusing on the cosmological implications of the -model is in progress.
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article and the reference list.
Acknowledgments
the authors wish to thank the anonymous reviewers for useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pascoli, G., and Pernas, L., 2020, hal.archives-ouvertes.fr/hal-02530737.
- Pascoli, G. Astrophys. Space Sci. 2022; 367, 121.
- Pascoli, G. Can. J. Phys. 2023; 101, 11.
- Pascoli, G, 2024, Universe, 10(3), 151. [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophysical Journal 1983, 270, 365. [Google Scholar] [CrossRef]
- Milgrom, M. Studies in History and Philosophy of Modern Physics 2020, 7, 170. [CrossRef]
- Hodson, A.O., and Zhao, H., A&A, 2017, 598, A127. 2017, 598, A127. [CrossRef]
- Varieschi, G.U., J.Appl.Math.Phys., 2018 06, 1247. [CrossRef]
- Varieschi, G.U., Found.Phys., 2020, 50 11, 1608. [CrossRef]
- Cesare V., Diaferio A., Matsakos T., and Angus, G., 2020, A&A, 637, A70. [CrossRef]
- Varieschi, G.U. Universe 2021, 10, 387 r. [CrossRef]
- Varieschi, G.U. Eur. Phys. J. Plus 2021, 136, 183. [CrossRef]
| 1 | It is not relevant to note the particular scalar product one considers because the orthogonal groups of two different scalar products on are isomorphic. |
| 2 | A part C of a topological space E is said path connected when for any points a and b of C there is a continuous application such that and in other words a pathin C with source a and goal b
|
| 3 | It is well-known linear applications between two finite dimensional normed vector spaces are always continuous, so the condition of continuity of can be omited in the definition. |
| 4 | The usual notation can be somehow tricky because the dependance on the curve is not noted. |
| 5 | The application can be seen as a section of the trivial vector bundle over with fibers the covariant derivation along is then the flat covariant derivative of relative to the tangent field over . |
| 6 |
. |
| 7 | Let the action for a free particle
|
| 8 | We have consider a non-continuous function for a better visualisation of the overlapping, but if we had considered a continuous function we would have found a "smooth" overlapping with three layers. |
| 9 | The detailed relationship is where denotes the maximal density in the galaxy (galaxy center). Here we assume that and the density is normalized to this value. |
Figure 5.
Two observers A and B separated by a very large distance . Very close to each of them an universal "atom" of small size is represented. The dashed straight line ab’ (resp. a’b) is a geodesic of the sheet of the observer A (resp. B) equipped with (resp. ). Let us note that the norm of the vector is a constant in the base, but this norm varies as in the respective sheets of the observers. On the other hand the curve ab" displayed in blue is a geodesic of the bundle equipped of a variable .
Figure 5.
Two observers A and B separated by a very large distance . Very close to each of them an universal "atom" of small size is represented. The dashed straight line ab’ (resp. a’b) is a geodesic of the sheet of the observer A (resp. B) equipped with (resp. ). Let us note that the norm of the vector is a constant in the base, but this norm varies as in the respective sheets of the observers. On the other hand the curve ab" displayed in blue is a geodesic of the bundle equipped of a variable .
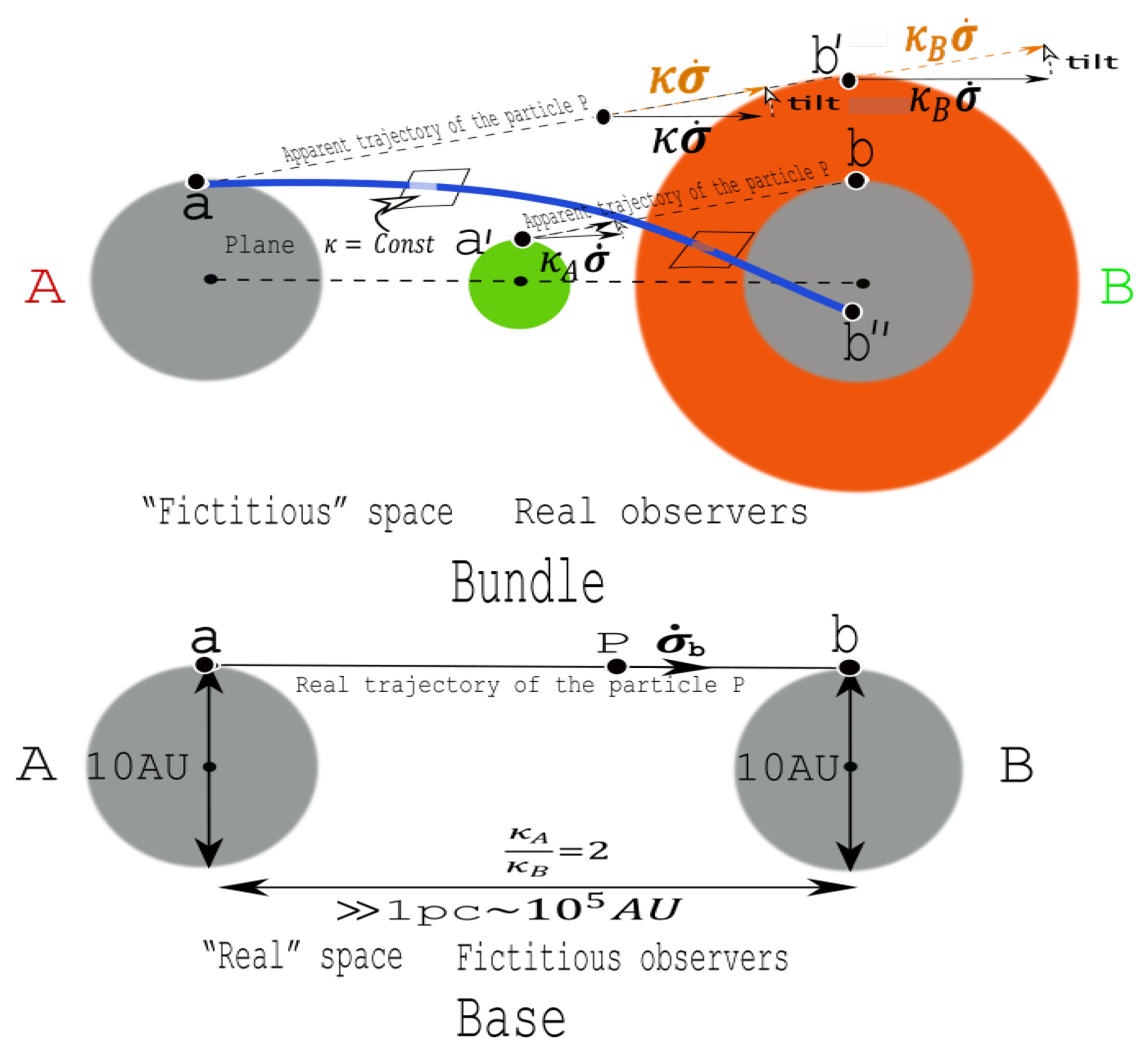
Figure 6.
a : Images obtained without -effect, the annulus is represented in yellow; the central disk is represented in red. b : Images obtained with -effect, the emitter in the annulus sees the observer a, three time closer. The gap in the image is a consequence of discontinuity at, the border between the annulus and the central disk. c : Images obtained with -effect, emiter in the central disk see a three time closer, The image of the central disk overlaps the image of the annulus, the overlapping, region is colored in orange.
Figure 6.
a : Images obtained without -effect, the annulus is represented in yellow; the central disk is represented in red. b : Images obtained with -effect, the emitter in the annulus sees the observer a, three time closer. The gap in the image is a consequence of discontinuity at, the border between the annulus and the central disk. c : Images obtained with -effect, emiter in the central disk see a three time closer, The image of the central disk overlaps the image of the annulus, the overlapping, region is colored in orange.
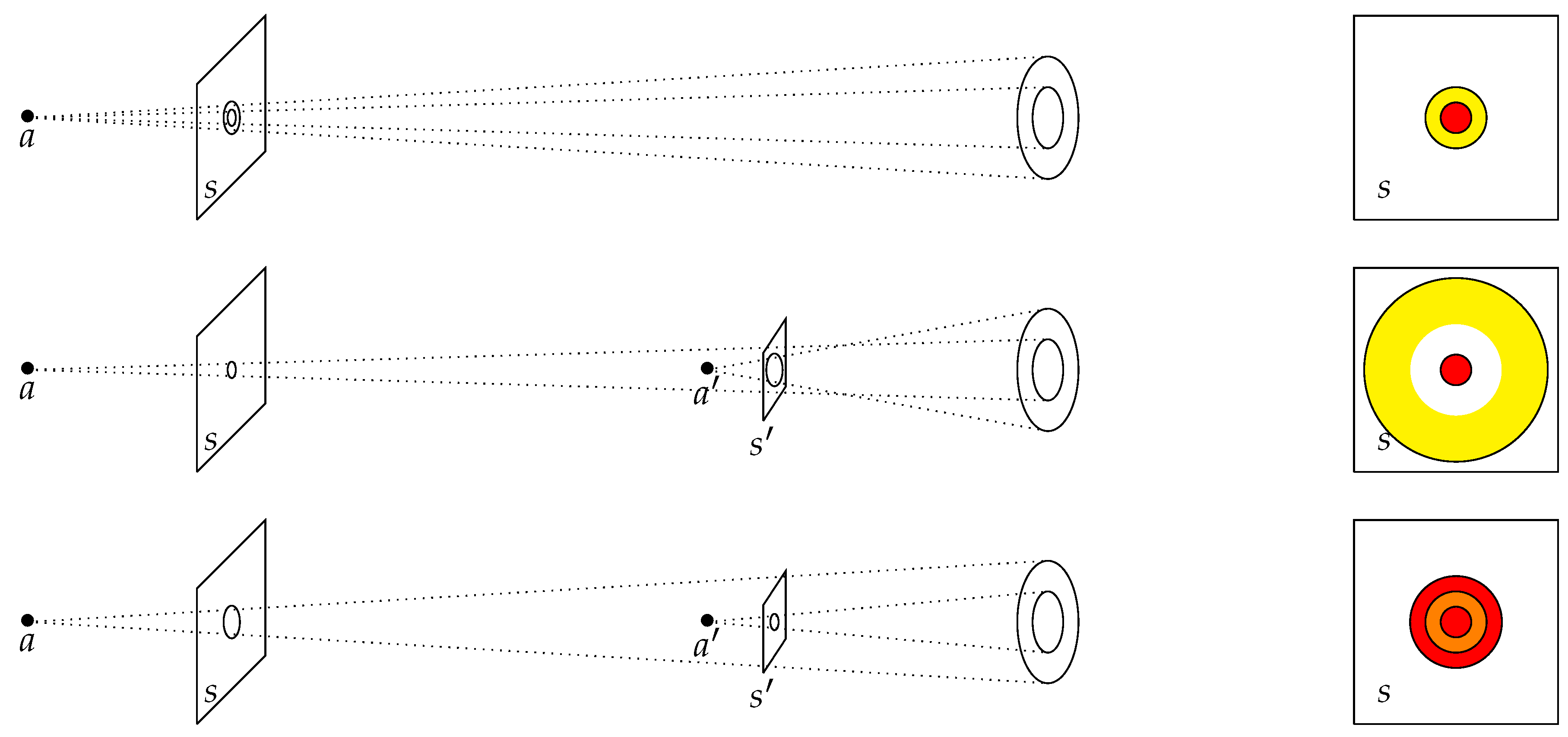
Figure 7.
Circular Newtonian motion
Figure 8.
Galaxy rotation velocity profiles: a. The Milky Way in the vicinity of the Sun, b. M33, c. NGC 1560, d. NGC6946. For the details see [2].
Figure 8.
Galaxy rotation velocity profiles: a. The Milky Way in the vicinity of the Sun, b. M33, c. NGC 1560, d. NGC6946. For the details see [2].
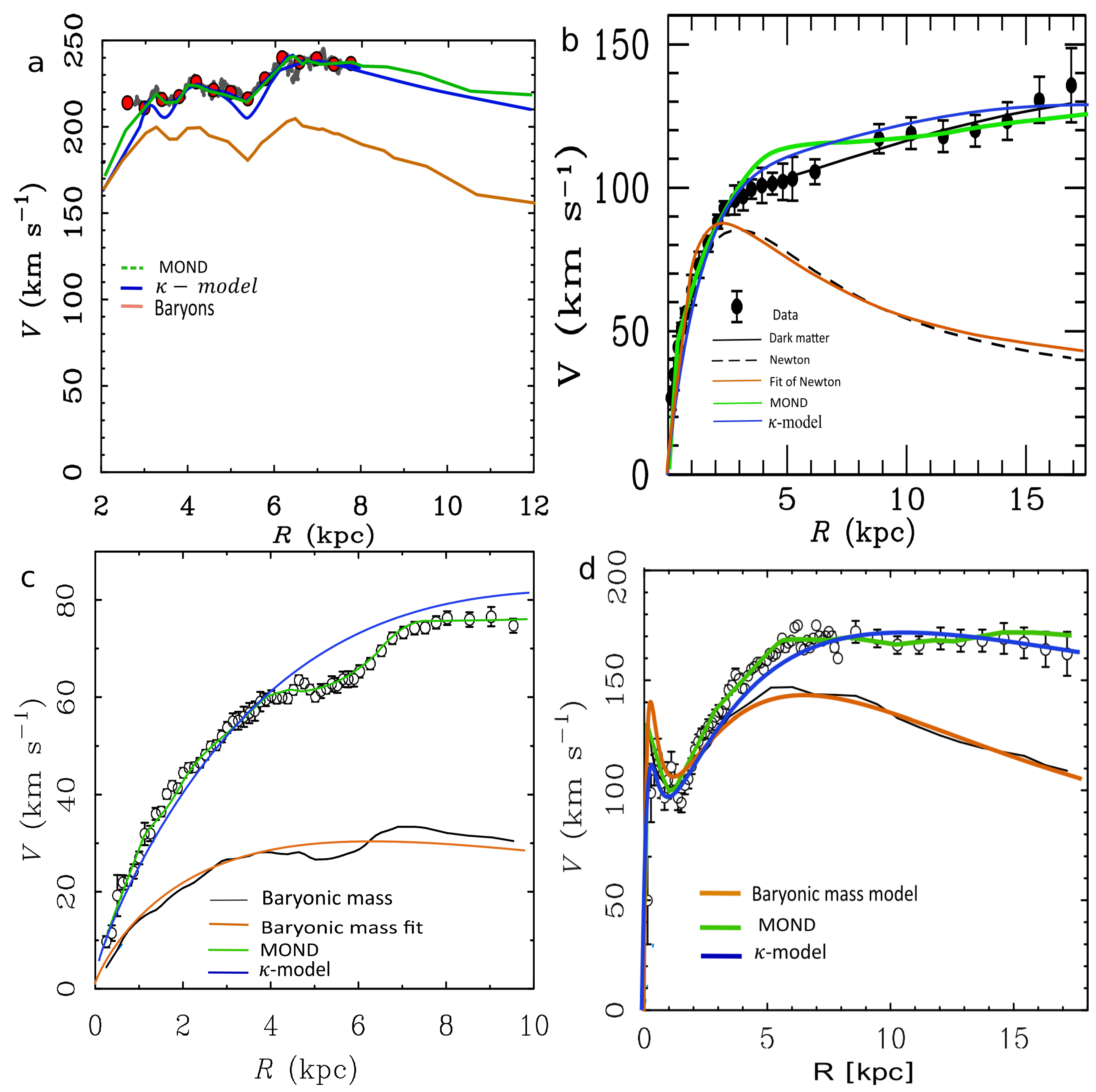
Figure 12.
The short dashed blue curve is the Newtonian dynamic mass; the dashed-dotted cyan curve is the MOND dynamic mass. The dynamic mass for -model is displayed as the amber curve (dynamic mass with constant temperature ) and green curve (assuming a non-isothermal temperature profile. The red long dashed curve is the ICM gas mass derived from X-ray observations (for the details see [3]).
Figure 12.
The short dashed blue curve is the Newtonian dynamic mass; the dashed-dotted cyan curve is the MOND dynamic mass. The dynamic mass for -model is displayed as the amber curve (dynamic mass with constant temperature ) and green curve (assuming a non-isothermal temperature profile. The red long dashed curve is the ICM gas mass derived from X-ray observations (for the details see [3]).
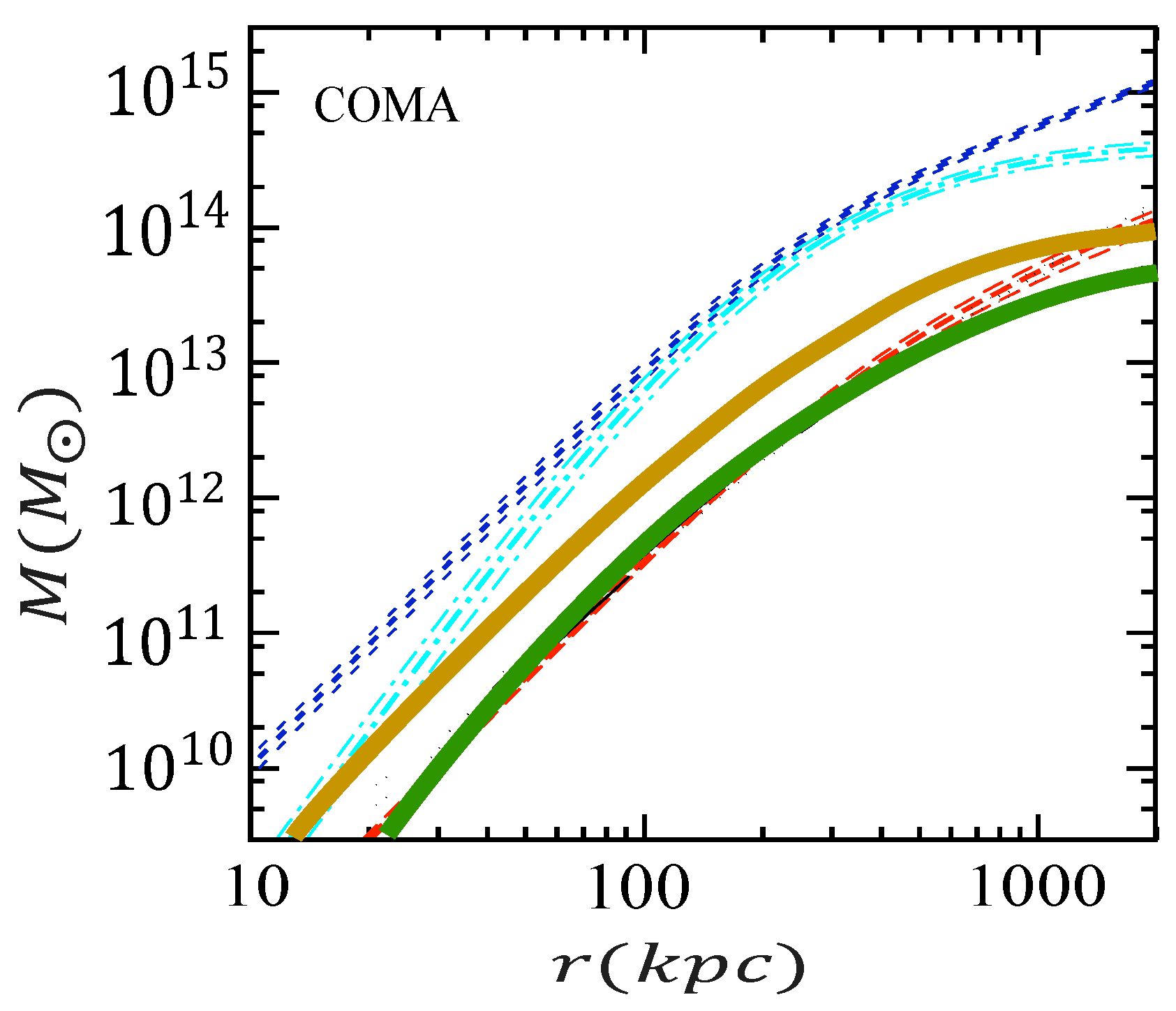
Figure 13.
A comparison between the gravitational lensing diagrams resulting from the application of both dark matter and -model paradigms in the case of the Bullet Cluster (for the details see [3]).
Figure 13.
A comparison between the gravitational lensing diagrams resulting from the application of both dark matter and -model paradigms in the case of the Bullet Cluster (for the details see [3]).
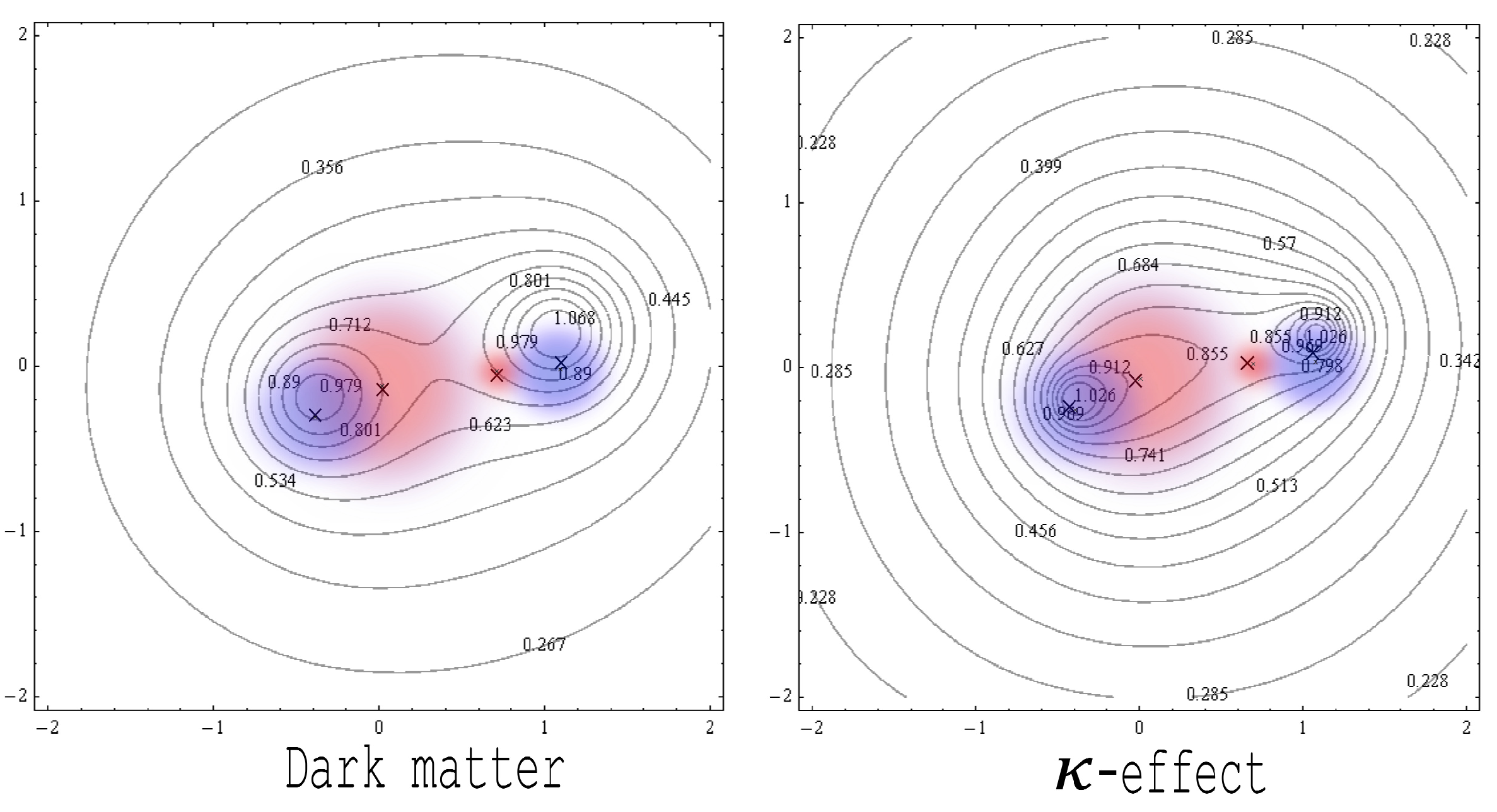
Figure 17.
Apparent variation of a disk of constant size seen from the point of view of a terrestrial observer. The real size is the disk shown in gray.
Figure 17.
Apparent variation of a disk of constant size seen from the point of view of a terrestrial observer. The real size is the disk shown in gray.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated




