Prerpints.org logo
Preprint
Article

Thermo-Mechanical and Thermo-Electric Properties of a Carbon-Based Epoxy Resin: An Experimental, Statistical and Numerical Investigation

Altmetrics

Downloads

77

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 June 2024

Posted:

28 June 2024

You are already at the latest version

Alerts
Abstract
Due to their remarkable intrinsic physical properties, carbon nanotubes (CNTs) can enhance mechanical properties and confer electrical and thermal conductivity to polymers currently investigated for use in advanced applications based on thermal management. An epoxy resin filled with varying concentrations of CNTs (up to 3 wt.%) was produced and experimentally characterized. The electrical percolation curve identified two critical filler concentrations: 0.5 wt%, near the electrical percolation threshold, suitable for exploring mechanical and piezoresistive properties, and 3 wt% for investigating thermo-electric properties due to the Joule effect with applied voltages ranging from 70V to 200V. Numerical models were developed using multiphysics simulation software. Once validated with experimental data, these models were used to investigate additional physical properties of the composites. Furthermore, a statistical approach based on the design of experiments (DoE) was employed to examine the influence of certain thermal parameters on the final performance of the materials. The purpose of this research is to promote the use of contemporary statistical and computational techniques alongside experimental methods to enhance understanding of materials science. New materials can be identified through these integrated approaches, or existing ones can be more thoroughly examined.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

Composite materials are increasingly attracting significant interest in the research community due to their ability to provide substantial weight savings in production processes, thus broadening the possibilities for designers in every engineering field [1]. These materials are favored because they exhibit remarkable strength-to-weight and stiffness-to-weight ratios, which are much higher than conventional metals [2]. This advantage not only reduces the overall mass of products but also enhances their performance and efficiency. Consequently, the adoption of composite materials is expanding across various industries, including aerospace, automotive, and civil engineering, where reducing weight without compromising other physical properties is a critical factor [3].
Epoxy polymers are widely utilized as matrices due to their excellent mechanical characteristics and compatibility with various fillers, giving rise to materials with outstanding properties, including high modulus and exceptional chemical resistance [4]. Challenges persist in addressing polymer-based composites’ limited thermal and electrical properties, traditionally acknowledged as insulating materials.
Carbon nanotubes (CNTs) possess remarkable electrical, thermal, and mechanical characteristics, making them highly appealing as fillers in developing nanocomposites to enhance the overall properties of the resulting materials [5]. In fact, technological progress has driven a growing demand for advanced composites possessing exceptional attributes not present in classic materials. Currently, carbon-based nanocomposites with improved electrical and thermal conductivity are increasingly investigated for potential thermal management applications such as heating elements, heat exchangers, or heat sinks, driven by a range of potential advantages including cost, weight, and size reduction of systems, improved chemical resistance, design flexibility, manufacturing process enhancements, and more [6,7].
Heat transfer in materials can occur through phonons or a combination of phonons and electrons. In particular, carbon nanotubes or graphene, with their free-moving electrons, offer dual heat conduction, enhancing thermal conductivity compared to other reinforcements that rely solely on phonon transmission. The percolation theory explains the conduction in composites: once the filler concentration hits the percolation threshold, continuous conductive networks form, allowing efficient heat and current flow through lower resistance pathways [8]. Therefore, carbon nanotubes (CNTs) not only improve mechanical characteristics but also impart electrical conductivity to polymers. Consequently, when electrical current or voltage is applied to these conductive materials, Joule heating occurs (self-heating), raising the temperature significantly and potentially causing the heating of the CNT-based composite. Of course, the quality of the morphological arrangement of the filler is essential, as nanoparticles can become defects if the dispersion state is inadequate [9]. Additionally, the particle concentration, aspect ratio, and waviness play critical roles in determining the final performance of the nanocomposites [10]. Carbon nanoparticles usually result in a substantial rise in the nanocomposite’s viscosity, depending on the filler type and loading, which is a crucial factor for the processability of polymers [11,12]. All these factors underscore the significance of continued research endeavors to add knowledge and pursue customized design in the realm of composite materials.
The electric heating behavior of epoxy-based composite films as a function of the applied voltage, as well as the graphene/CNT composition dispersed as fillers, has been investigated by Jeong and An [13]. Isaji et al. [14] presented findings on the self-regulating heating properties of polyethylene films infused with carbon nanotubes. From the viewpoint of potential application as highly efficient flat heaters, the researchers demonstrated that the maximum surface temperature at the equilibrium state of the composite film could be easily managed by adjusting the composite ratio of ultra-high molecular weight polyethylene (UHMWPE) to low molecular weight polyethylene (LMWPE). Chatterjee et al. [15] have documented the enhancement of mechanical properties in epoxy composites due to the combined effects of mixed fillers consisting of CNTs and graphene nanoplatelets.
Despite the promising results achieved due to their unique properties, nanocomposites present significant challenges stemming from their inherent heterogeneity. Simulation studies are particularly valuable in addressing the gaps in understanding the actual performance of nanocomposites, which often deviates from expected or desired outcomes.
In our previous research [16], a structural epoxy resin filled with varying amounts of carbon nanotubes (up to 3 wt%) was extensively characterized experimentally in terms of mechanical behavior under tensile stress and thermo-electric properties under Joule heating. To further investigate, a Design of Experiments (DoE) approach has been adopted here to explore the influence of various thermal features, such as thermal conductivity, heat transfer coefficient in air, and heat capacity, on the overall performance of the nanocomposites. This methodology was crucial in identifying the optimal parameter settings for our numerical model. Starting from preliminary and partial investigations presented in [17], this study aims to complement our experimental findings with a modeling approach based on the finite element method, validated by experimental data. The focus is on examining further thermo-mechanical and thermo-electric effects resulting from strain-stress and Joule heating at different voltage levels applied to specific formulations of the nanocomposites.

2. Materials and Methods

In the current investigation, nanocomposites for experimental tests were prepared by blending the subsequent components, according to a procedure detailed in Spinelli et al. [18]: i) an epoxy matrix, specifically 3,4-epoxycyclohexylmethyl-3’,4’-epoxycyclohexane carboxylate (ECC), serving as the precursor; ii) a curing agent based on methyl hexahydrophthalic anhydride (MHHPA); iii) multiwall carbon nanotubes (commercially known as Arkema Graphistrength® C100) acting as a conductive nanofiller. These constituents were appropriately combined to produce samples with varied concentrations, i.e., [0.3, 0.5, 1, 1.5, 2 and 3] wt%. The essential physical and chemical characteristics of the precursor, hardener agent, filler, and the dimensions of the parallelepiped-shaped test specimens are concisely outlined in Figure 1. Further details can be found in Guadagno et al. [16].
The specimens designated for mechanical characterization were manufactured according to the specifications outlined in ASTM D638 standards (American Society for Testing and Materials, ASTM) [19]. The mechanical tests were conducted using a Dual Column Tabletop Testing System (INSTRON, series 5967-INSTRON, Norwood, MA, USA) configured with a crosshead speed of 1 mm/min for both loading and unloading phases. The resulting force was converted into axial stress (σ), and mechanical strain (ε) was calculated as the crosshead displacement of the machine normalized by the gage length of the specimen under test. Local elongation was monitored using a commercial strain gauge (RS632-180, RS PRO, Corby, UK) affixed to one side of the specimen to prevent slipping phenomena. Changes in its gauge resistance were recorded with a Multimeter 3458A (Agilent, Santa Clara, CA, USA). The current-voltage (I-V) characteristics were measured using a two-probe method on electrical contacts established on the sample surface with silver paint (RS 196-3600, RS PRO, Corby, UK), employing an electrometer Keithley 6517A (Keithley Instruments, Cleveland, OH, USA) acting as both the power supply and ammeter. This measurement approach has been deemed suitable in the literature for electromechanical characterization [20,21]. The contact resistance can be disregarded, as it is lower than the overall electrical resistance of the specimens (several kΩ).
To experimentally investigate the Joule heating effect, silver paint (brand name: RS 196-3600, RS PRO, Corby, UK) was deposited to the short sides of the test specimens to establish ohmic contacts between the power supply EA-PSI 8360-10T (Elektro-Automatik, 0–360 V, 0–10 A, 1 kW max) and the HP34401A ammeter (min current 0.1 μA) using the 2-probe method. The surface temperature increase over time was then monitored under various applied voltage values (specifically 70V, 80V, and 90V) using a T-type thermocouple positioned at the center of the upper surface of the sample. The temperature values were automatically recorded by a data acquisition board (Data Logger TC-08 supplied by Pico Technology) with the assistance of the PicoLog software (version 6.2.5). The schematic diagrams of the experimental setups used to investigate the thermo-electric phenomenon due to the Joule effect and the thermo-mechanical properties are illustrated in Figure 2a) and b). The geometric specifications of the corresponding samples are also provided.
For simulation studies on mechanical properties and strain-induced heating, as well as for thermo-electric aspects related to the Joule effect, the commercial software COMSOL Multiphysics® based on the Finite Element Method (FEM) was adopted. This allowed the authors to perform a numerical/experimental comparison of the results with the aim of validating the numerical models for reliable use in further physical investigations on the analyzed samples.
Figure 3 and Figure 4, respectively, present the schematic representations and essential model definitions for the thermo-mechanical and thermo-electric case studies investigated in the current work, in parts a) and b) of each figure.
In brief, in both cases, the models are defined in a three-dimensional (3D) space, allowing for a comprehensive analysis of the physical properties of the samples evaluated with a time-dependent study to capture the dynamic response of the materials. A coupled physics by combining solid mechanics and heat transfer, is adopted to simulate the coupled thermo-mechanical behavior of the composite material. The physics module solid mechanics is used to simulate the mechanical behavior of the composite material under tensile loading. It helps in analyzing stress, strain, and deformation. Otherwise, the module heat transfer in solid state is used to model the heat generation and distribution within the material due to strain-induced heating and thermal expansion.
A coupled physics by combining Joule heating and heat transfer is adopted instead to numerically investigate the coupled thermo-electric behavior of the composite material. The physics module Joule heating is used to simulate the heating of an electrical nature due to the application of a current or voltage, whereas the module heat transfer in solid state is used to analyze the consequent thermal aspects that are triggered in the sample.
Referring to a differential volume ∆x∆y∆z, the equation (at constant pressure) governing heat transfer in a solid utilized in the simulations can be formulated in Cartesian coordinates as follows:
Preprints 110697 i001 ∂ ∂ x λ ∂ T ∂ x + ∂ ∂ y λ ∂ T ∂ y + ∂ ∂ z λ ∂ T ∂ z + Q Strain ​  heating ​  Q Joule ​  heating ​  = ρ c p ∂ T ∂ t (1)
where λ represents the thermal conductivity [Wm-1K-1], ρ is the density [kgm-3] and cp is the specific heat [Jkg-1K-1] of the materials. The term QJoule heating =J⋅E is the electrical power [Wm-3] generated by the electrical current for the Joule effect in the parallelepiped volume. In particular, J denotes the current density [Am-2] equal to current (I) divided by the effective cross-section area (A) of the sample and E is the electric field strength [WA-1m-1] caused by several voltage values (70V, 80V, 90V, 120V, 150V and 200V).
Similarly, Q S t r a i n   h e a t i n g = η ​∙ σ ​∙ ε ∙ p l a s t i c is the power per unit volume of the dogbone sample [Wm-3], generated by plastic deformation that can be expressed as the product of stress (σ, [Nm-2]) and the rate of plastic strain ( ε ∙ p l a s t i c , [s-1] ). The term η (dimensionless) is the so-called mechanical dissipation factor or in other terms the fraction of mechanical energy converted into heat.
Table 1 compiles the initial and boundary criteria necessary for accurately resolving the thermal equilibrium described by equation (1) for both parallelepiped and dogbone geometry.
Additionally, in the numerical analysis, an electrical conductivity of 6.8⋅10-2 [Sm-1] and a density of 1180 [kgm-3] were utilized based on our experimental findings, while thermal conductivity, heat transfer coefficient, and heat capacity were adopted in alignment with the results obtained from the DoE study.
The Design of Experiments (DoE) methodology falls within the realm of applied statistics and analyzes cause-and-effect relationships. This approach identifies how different factors influence a process or product and subsequently affect its output or performance function (P.F.).
In summary, as illustrated in Figure 5, controllable variables (Xi) and uncontrollable ones (Ni) can be considered during the design stage, which often includes noise and tolerances on Xi. The collective influence of these controllable (X = (X1, X2, …, Xp)) and noise (N = (N1, N2, …, Nq)) variables impacts the performance function of interest (P.F. = f(X, N)). Through the Design of Experiments (DoE), the most influential variable on the chosen P.F. can be identified, and the controllable input variables can be appropriately selected to optimize the performance. Consequently, optimal parameter settings can be determined to enhance the desired performance.
In this study, the Design of Experiments (DoE) is employed to evaluate the impact of three thermal variables on the temperature distribution of the nanocomposites. These variables are the heat transfer coefficient in still air (h, natural convection), thermal conductivity (λ), and thermal capacity (C). In particular, the surface temperature is evaluated at time t=240 s (T-240s) during the transient phase and at t=3600 s (T-3600s), which corresponds to the steady-state temperature (plateau value).
Therefore, both these temperatures serve as the focal performance metrics in this DoE study. To facilitate this analysis, a dedicated Matlab® routine has been developed. For a successful application of DoE, it is essential to establish an appropriate discretization level for the input variables. Initially, a uniformly distributed set of parameter values is recommended, with the possibility of incorporating additional intermediate points later to enhance model refinement [22]. In our study, the input variable vector x ¯ has been defined as follows:
x ¯ = h , ​  λ , ​  C ​  ϵ ​  ℝ 3
where a discretization on 3-levels is applied to the selected input factors within the following intervals: [5, 7.5], [0.100, 0.150] and [9.21, 14.5], for h,   λ , and C, respectively.
More in details, the considered values are
h 1 = 5 ,   h 2 = 6.25 , ​  h 3 = 7.5 ​ 
λ 1 = 0.100 ,   λ 2 = 0.125 , ​  λ 3 = 0.150 ​ 
C 1 = 9.21 , C 2 = 11.8 , ​  C 3 = 14.5
Consequently, the compact D that describes the variable space is mathematically expressed as follows:
D = h × λ × C ⊂ ℜ 3 ​ 
whereas the P.F. is evaluated for each ordered tern x 1 , x 2 , x 3 of the input variable vector, i.e.,:
x 1 , x 2 , x 3 = h ,   λ , ​  C ϵ D . ​ 

3. Results

The next subsections present the comprehensive results of our investigation into the thermo-mechanical and thermo-electric properties of composite materials. Both experimental data and theoretical models are analyzed to provide a thorough understanding of the behavior of these materials under various conditions. A comparative analysis between the experimental results and theoretical predictions was performed to validate the accuracy and reliability of the models used.

3.1. Experimental Results on Percolation Curve

Percolation refers to the process by which at least a continuous pathway of conductive filler particles forms within an insulating matrix as the filler concentration increases. Individual filler particles are isolated within the matrix at low filler concentrations, resulting in poor electrical conductivity. Otherwise, as the filler concentration (p) exceeds a critical threshold (the so-called percolation threshold, hereafter, pc), the filler particles begin to connect, forming a percolating network that allows for efficient electron transport and a significant increase in electrical conductivity (σel). Experimental determination of the percolation threshold and the overall percolation curve involves measuring the electrical conductivity (see Figure 6a) of nanocomposite samples prepared with varying filler amounts. As it is expected, the relationship between the filler concentration and the electrical conductivity of the nanocomposite material can be mathematical described by a power law equation that takes the form:
σ e l = σ 0 ​∙ p − p c t         f o r     p > p c .
Here, σ0 represents a pre-factor related to the intrinsic electrical conductivity of filler, whereas t is the critical exponent, i.e., a dimensionless parameter that characterizes the steepness of the conductivity increase as the filler concentration approaches and exceeds the percolation threshold.
It can be observed that thanks to the good dispersion of carbon nanotubes within the epoxy matrix, the electrical percolation threshold is reached at low filler concentrations in the range [0-0.3] wt.%. An electrical conductivity value of 15.65x10-3 S/m is measured for a concentration of 0.3 wt.% of MWCNTs which is significantly higher than that exhibited by the pure resin (order of 10-10 S/m). Further increasing the concentration of MWCNTs results in a slight increase in electrical conductivity, which reaches a maximum value of 0.13 S/m at the highest concentration investigated in this study (3 wt.%). In nanocomposite materials, tunneling is the primary mechanism for electric transport, where electrons traverse potential barriers through quantum mechanical tunneling rather than conventional conduction pathways. The validation of the tunneling mechanism in nanocomposite materials can be achieved by analyzing (see Figure 6b) the natural logarithm of conductivity as a function of concentration at p-1/3.
The investigation of the percolation phenomenon provides valuable insights into the electrical, and other behaviors of nanocomposite materials, guiding their design and optimization for various engineering applications. Based on the discussed results, composites with a filler concentration of 0.5 wt.% were selected for mechanical tests, while those with a concentration of 3 wt.% were chosen for thermo-electrical tests.
This is because a concentration near the percolation threshold (i.e., 0.5 wt.%) is ideal for exploring the strain-sensor properties of composites. At this concentration, the percolation network is just formed, and it is more sensitive to imperceptible variations due to applied strain, unlike the well-established network achieved at higher filler concentrations.
Differently, the higher concentration (3 wt.%) is recommended to analyze the thermo-electric properties of the composites due to the Joule heating effect which requires adequate conductivity values. The results of these investigations are presented in the next subsections.

3.2. Mechanical and Piezoresistive Properties: Experimental Results

The mechanical response of nanocomposite materials under axial tensile load is a crucial aspect of their characterization. Figure 7a) depicts the mechanical behavior, due to axial tensile stress, of the specimen containing 0.5 wt.% of MWCNTs, observed until failure that is occurred at a strain value of approximately ε = 2%.
For clarity, the strain ε is defined as the change (expressed in %) in length Δl divided by the initial length L0, i.e., ε =Δl/L0. Having said that, a linear response is observed up to a strain value of approximately ε = 1%. Beyond this point, a deviation from the linear response indicates the onset of plastic deformation and permanent damage.
This transition threshold is critical for the material’s structural design: below it, the material maintains its structural integrity (elastic region), whereas, beyond this threshold, the nanocomposite undergoes non-recoverable deformation (plastic regime), due to irreversible changes in the morphology of the resin network.
Similar considerations can be drawn by observing (see Figure 7b) the change in electrical resistance (ΔR/R0, in percentage), mainly due to the percolation network, as it varies with mechanical strain (ε). Here, R0 represents the electrical resistance of the unloaded specimen (i.e., ε = 0), and ΔR = R - R0 represents the change in resistance due to the applied load.
In particular, within the material’s elastic region (i.e., ε < 1%), an initial linear relationship between ΔR/R0 and applied strain ε was observed, with a fitting curve of the experimental data characterized by a slope of 4.1. As the strain increases, an elevated slope of 5 is revealed for this curve. This change is most likely attributed to plastic deformation as the material exceeds its elastic limit.
These variations are electrically noticeable because a nanocomposite with a concentration (0.5 wt%) of filler near the percolation threshold was considered, thus having a morphological structure highly sensitive to small deformations. Finally, it is worth noting that applying mechanical stress to a material generates heat due to the conversion of mechanical energy into thermal energy. In fact, when a material is subjected to mechanical stress, the internal structure of the material is deformed, resulting in frictional forces between its molecules. This friction generates heat, causing an increase in temperature within the material. Such aspects will be numerically investigated in the next sub-section.

3.3. Thermo-Mechanical Properties: Simulation Results

3.3.1. Validation Model

As the initial step in validating the numerical model for mechanical investigations, Figure 8 compares experimental and simulation results for the stress-strain behavior of the selected nanocomposite material. The inset illustrates the 50 mm gauge length used for stress evaluation, as the standard requires. In fact, the load vs. strain curve for a composite material with a dog-bone structure can vary significantly at different points along the length of the sample. This variation is due to the different distribution of stresses and strains in the sample, which is influenced by its variable geometry [23].
It is interesting to note that there is a strong correlation between the experimental and simulation results. The data points from both methods closely follow the same trend, indicating that the simulation model is well-calibrated and accurately predicts the material’s behavior. The transition from elastic to plastic regime (yield point) is clearly marked at around 1% strain. Both experimental and simulation results align well at this transition point, further validating the accuracy of the simulation. Beyond this point, the curve continues to rise but at a reduced slope, indicating that plastic deformation occurs, and the material does not return to its original shape when the load is removed.

3.3.2. z-Axis Displacement

When a tensile force is applied, the material experiences elongation along the z-axis, typically the applied load’s direction. Figure 9 illustrates the z-axis displacement versus the length along the z-axis of symmetry (see the red line of the inset) for the considered dogbone-shaped sample at different time instants (t = 0, 50, 100, 150, and 200 seconds). The
The initial displacement is zero, serving as a baseline for subsequent measurements. It is possible to note that the z-axis displacement increases with time, indicating progressive deformation of the sample and, therefore, the time-dependent strain behavior of the composite material. At each given time, the displacement is larger as we move towards the higher z-axis length, suggesting a non-uniform deformation along the length of the sample. The gauge zone, marked between approximately 60 mm and 110 mm along the z-axis, is the region of interest where deformation measurements are most relevant. The displacement within this zone is notably higher, indicating that this region experiences the most significant strain during the test. At t = 50 seconds, the related curve shows a small but noticeable increase in displacement, suggesting the beginning of strain in the material. The curve at t=100 s indicates further displacement, with a more pronounced increase than the previous times. Strain is more evident, especially in the gauge zone. A significant increase in displacement, reflecting accelerated deformation over time, is observable a t t=150 s. The gauge zone continues to display substantial strain, with displacement values considerably higher than at 100 seconds. Finally, the last curve (at t= 200 s) shows the maximum observed displacement, indicating continuous strain accumulation. The deformation is most pronounced within the gauge zone, suggesting that the material is experiencing progressive failure or significant plastic deformation.
Figure 10 shows the 3D-displacement profiles of the dogbone sample made of composite materials at different times: t=0 sec, t=50 sec, t=100 sec, t=150 sec, and t=200 sec. The displacement is measured on the central slice of the zx-plane passing through the axis of symmetry in the z-direction. The color bar indicates the magnitude of displacement in millimeters (mm).
At the initial state (t = 0 sec) there is no load applied to the sample, so the displacement is uniformly zero across the entire dogbone length, as indicated by the black color. As time progresses, the dogbone sample starts to experience displacement. The reported plots illustrate a progressive increase in displacement over time, with the maximum displacement reaching 3.33 mm at 200 seconds. The color bar effectively highlights the differences in displacement magnitude, providing a clear visual representation of the deformation behavior of the composite material under tensile stress over time.

3.3.3. Von Mises Stress

The Figure 11 illustrates the distribution of Von Mises stress recorded on the total length (165 mm) of dogbone alongside the axis of simmetry in the z-direction (see the schematic on the right part) at the selected time instants (t = 0, 50, 100, 150, and 200 seconds).
From the analysis of these plots, it is worth noting that the Von Mises stress increases with time, indicating progressive stress accumulation in the material.
For each time, the stress profile shows a peak within the gauge zone, which is the region most subjected to stress concentration. This indicates that it is the critical region for assessing the material’s stress response.
Of course, at time t = 0, the initial stress distribution shows a baseline with null stress, as expected at the start of the test.
The curve at time t=50 s shows an increase in Von Mises stress, with a noticeable peak forming in the gauge zone. This indicates the beginning of significant stress development within the material that decreases moving away from this particular area. At the time t = 100 s, the representative curve shows a further increase in stress, with the peak in the gauge zone becoming more pronounced.
Stress levels outside the gauge zone also rise but remain lower compared to the peak region. The curve at time t= 150 s presents a substantial increase in stress, especially within the gauge zone. The stress distribution is more symmetric, with the highest stress values of about 5x107 N/m2 reached in the mid-length of the sample.
The last curve relating to the time t= 200s indicates the maximum observed stress, with the peak stress in the gauge zone exceeding 5x107 N/m2.
This suggests significant stress accumulation, likely approaching the material’s failure threshold.
In all cases, the stress distribution suggests that the composite material undergoes significant stress accumulation over time, with the highest stress concentrations occurring in the central gauge zone. This behavior is typical for materials subjected to tensile loading, where the narrowest section experiences the greatest stress.
Figure 12 illustrates, with a 3D cross-section, the Von Mises stress distribution in the dogbone sample at the usual time instants.
The color bar represents the stress values in units of 107 N/m2 providing a clear visualization of the stress distribution at each time instant.
At t=0 seconds, there is no applied load, and consequently, no stress is observed in the sample. The entire sample is uniformly black, indicating a null Von Mises stress. As the tensile load is applied and time progresses, the stress in the sample increases, with the maximum stress concentrated in the gauge section and a maximum peak (7.04 x107 N/m2) reached at time t=200 s.
Regardless of the time instant, the central portion of the specimen experiences the highest stress, shown in the red region.
This is typical in tensile tests, where the narrower section (gauge zone) of the specimen bears the maximum load.
The choice to report a 3D cross-section view effectively allows observation of the distribution and evolution of Von Mises stress at various points in the specimen and at different time intervals, highlighting the regions of highest stress concentration and their temporal progression

3.3.4. Strain-Induced Heating: Thermal Expansion

The relationship between heat generated and applied strain in a material is often described by the concept of “strain-induced heating.
When a composite material is subjected to mechanical loading, part of the mechanical work done on the material is converted into heat.
This phenomenon is particularly evident in materials exhibiting viscoelastic behavior or undergoing plastic deformation.
In our case study, it is possible to numerically investigate it even though the effect is not large due to the low thermal coefficient exhibited by the epoxy resin (about 60∙10-6/K) and the limited level of plastic strain investigated according to the experimental mechanical test (from 1% up to 2%). Figure 13 illustrates the temperature increase in our dogbone-shaped composite material sample under tensile strain at different time intervals: t=0 s up to 99 seconds corresponding to strain levels in the elastic region, t=100 s at which ε is about 1% (yield point), t=150 seconds (ε ≃1.5%) and t=200 seconds (ε ≃ 2%) conforming to strain levels in the plastic region.
The temperature distributions are graphically displayed for each case, and their values are provided by the color bar. Of course, up to 99 seconds, the sample remains in the linear elastic region. There is no significant temperature increase, as the uniform black color indicates a base temperature of 293.150 K. The sample has not yet entered the plastic deformation zone, and no thermal heating is observed.
As the strain level increases above the yield point entering the plastic deformation zone, the temperature within the sample also starts to increase. This is because, in this region, the mechanical work is no longer stored as elastic potential energy; instead, some of it is converted into heat due to internal friction.
At 200 seconds, the sample is well into the plastic deformation zone, and the temperature increase is evident.
The heat distribution becomes more concentrated and localized in the gauge region subjected to higher strain levels, indicating potential hotspots that could affect the material’s mechanical properties and performance. The temperature in the central gauge section reaches a maximum of approximately 293.213 K.
The cross-head speed ​ʋ ∙ impacts the temperature distribution within a composite material during deformation. Higher strain rates generally lead to increased heat generation due to more intense mechanical work on the material in a shorter period.
This is evident from the progressively higher maximum temperatures as the cross-head speed increases.
Coherently, Figure 14 presents the thermal expansion recorded in the dogbone sample at the end of the deformation process (200 s) for three different cross-head speeds: ​ʋ ∙ =1mm/min, ​ʋ ∙ =2 mm/min, and ​ʋ ∙ =3 mm/min. The temperature distribution is illustrated using a color gradient, with corresponding maximum temperature values indicated for each strain rate.
At the lowest cross-head speed ( ​ʋ ∙ =1 mm/min), the temperature rise is minimal, as the slow deformation allows for better heat dissipation.
At moderate cross-head speed ( ​ʋ ∙ =2 mm/min), the temperature increases more, reflecting the increased energy input into the material.
The highest cross-head speed ( ​ʋ ∙ =3 mm/min) results in the maximum temperature observed, indicating that the heat generated by rapid deformation starts to exceed the rate at which it can be dissipated.
By performing additional numerical simulations at further cross-head speeds (i.e ​ʋ ∙ =0.5 mm/min and ​ʋ ∙ =1.5 mm/min), it is possible to plot a graph of the strain-induced temperature variation with respect to the cross-head speed, as shown in Figure 15. A parabolic trend relates the two considered quantities.

3.3.5. Plastic Dissipation Density

Density dissipation typically refers to the distribution and rate of energy loss in a material due to plastic deformation and other internal processes during mechanical loading. In the context of composites under tensile stress, it encompasses the conversion of mechanical work into heat and other forms of internal energy dissipation. Figure 16 shows the plastic dissipation densitiy (J/m3) over the time (up to 200 s) evaluated on the total dogbone volume.
During the initial phase, from 0 to approximately 100 seconds, the plastic dissipation density is close to inexistent. This suggests that there is minimal plastic deformation occurring within the specimen during this period: the composite material is undergoing elastic deformation initially, where the energy is stored rather than dissipated as plastic deformation.
Exceeded 100 seconds, there is a noticeable increase in the plastic dissipation density. The curve begins to rise more steeply, indicating the onset of plastic deformation within the material. More in details, as time progresses, the curve exhibits an exponential-like rise, reaching up to 8.0×104 J/m3 at 200 s.
The stress distribution in the dogbone specimen is not uniform. The gauge region (central narrow part) typically experiences the highest stress concentration and thus the most significant plastic deformation. This leads to higher plastic dissipation densities in this region where the material dissipates energy through mechanisms such as dislocation movement, microstructural changes and internal friction. The ends of the dogbone, where the specimen is clamped, experience different stress states. These areas might show lower dissipation density due to the constraints imposed by the fixtures and possible compressive stresses.
To appreciate this, the Figure 17 presents 3D views of plastic dissipation density (measured in J/m³) evaluated at different time instants and strain levels during the deformation process. Each subfigure corresponds to a specific time and strain level, with color bars indicating the range and magnitude of the plastic dissipation density. For t ≤ 99 s corresponding to a strain: ε ≤ 1 the 3D model appears entirely black, indicating that there is no plastic dissipation density in this initial stage or that it is negligible. During this phase, the material behaves elastically, meaning the deformation is reversible or, in other words, energy is stored in the material as elastic strain energy. As the time/load increases, the material enters the plastic region, where permanent deformation occurs.
At the time t = 100 s (ε ≈ 1) the 3D model shows areas of blue and orange colors. The blue regions represent lower values of dissipation density, while the orange regions represent higher values, up to 2.19 x 10⁴ J/m³.
This indicates the beginning of plastic deformation in specific areas. At the time: t = 150 s (ε ≈ 1.5) the 3D model has more pronounced blue and orange regions compared to the previous time instant. The orange regions are more extensive and intense, indicating an increase in plastic dissipation density with a maximum value of 9.89 x 10⁴ J/m³. This suggests the progression of plastic deformation as time and strain increase.
Finally, at the time t = 200 s (ε ≈ 2), it is possible to note even more extensive areas of orange and blue. The maximum dissipation density has increased to 19.5 x 10⁴ J/m³. This indicates further progression and intensification of plastic deformation. Therefore, Figure 17 effectively illustrates the dynamic changes in plastic dissipation density during the deformation process, highlighting how both time and strain contribute to the evolving material response.

3.4. Thermo-Electric Properties: Experimental Results

Figure 18 a) shows the experimental variation of the top surface temperature over time (up to 3600 s) for nanocomposites including 3 wt.% of MWCNTs, subjected to diverse voltage levels (from a minimum of 70 V to a maximum of 200 V).
Physically, it is evident that heat transfer in solid starts as transient and then reaches a steady-state, indicating a thermal equilibrium condition.
Specifically, during the transient interval, when the heat flow rate is changing, the temperature is time-dependent, T = T(t), for a brief period (t* marked in the figure). The temperature rises rapidly, then gradually approaches constant steady-state values of approximately 324.8 K and 439.2 K for 70V and 200V, respectively.
In the same figure, the corresponding electrical power dissipation (in Watt) is shown for each experimental temperature curve. Increasing the voltage from 70V to 200V increases the power from 1.15W to 9.35W, respectively.
During steady-state transfer, marked by a consistent and specific heat transfer rate, the temperature remains constant over time.
This equilibrium occurs because the total heat generated by Joule heating is balanced by natural convection dissipating heat to the surrounding environment. Referring to Figure 18 b), it is feasible to compute the heat rates (HR) as slopes of the respective temperature curves at the initial moments of the transient stage.
Specifically, as depicted in Figure 19 (right axis), these temperature values at steady-state (t=3600 s) exhibit a linear relationship (with the coefficient of determination R2 approaching 1) with the voltage levels applied. This finding aligns with theoretical expectations, as the Joule effect, akin to thermal power dissipation P, varies linearly with voltage V, following the equation P=V⋅I, where I represents the electric current. Contrarily, as depicted in Figure 19 (left axis), an almost flawless exponential interpolation (alternatively, R2 =0.973 or R2 =0.981 is achieved with linear and power-law fitting curves, respectively) is observed in the experimental data relating to the heat rate, HR [K/min], in relation to the applied voltage.
For quick reference, these experimental thermal and electrical data depicted in their respective graphs are summarized in Table 2.

3.5. Design of Experiment (DoE) for a Selected Temperature during the Transient and Steady-State Phase

The DoE method results in the Dex Scatter Plot (DSP) and Main Factor Plot (MfP) illustrated for nanocomposites subjected to 70 V and 200 V in Figure 20 and Figure 21, respectively. More specifically, in Figure 20 the DsP is shown in a) and in b) the corresponding MfP at time t = 240s, while the related graphs evaluated at time t = 3600s are displayed in c) and d), respectively. Similarly, in the case of DoE conducted with an applied voltage of 200V, as shown in Figure 21, the DsP and associated MfP evaluated at time t = 240 s are presented in a) and b), respectively, whereas the corresponding results at time t = 3600 s are shown in c) and d).
In summary, a DSP chart displays the scattered data of the performance function (P.F.), such as the upper surface temperature at the instant of time t=240 s and at t=3600 s in our study (indicated as T-240s and T-3600s), on the vertical axis, against the independent variable displayed on the horizontal axis i.e., the thermal conductivity (λ), the heat transfer coefficient (h), and the thermal capacity (C) in the current study. Graphically speaking, the DSP highlights how the P.F. responds to fluctuations of these independent factors [24,25]. Technically, their influence on the P.F. can be assessed by examining the MfP graphics and, in particular, the slope of the line connecting the average points of the performance function’s range values at the minimum and maximum levels of each factor. For a single factor, a horizontal line (parallel to the x-axis) signifies no effect on the P.F., while a sloped line indicates some level of influence, which can be measured and compared to the effects of other investigated factors. [26].
According to these guidelines, it is possible to emphasize the distinct and joint effect of each thermal factor on the surface temperature due to Joule heating, at the two selected time instants (240s and 3600s). Both the temperature values at t= 240s, regardless of the applied voltage, are impacted by all three factors, albeit to varying entities and in different manners. An increase in thermal conductivity, within the range explored in this study, leads to a slight rise in the analyzed temperature values. This impact is quantifiable through the slopes highlighted by the MfP graphs, which amount to 0.0475 and 0.4875 for the respective applied voltages of 70 V and 200 V. (see Figure 20b and Figure 21b).
On the other hand, an increase in both the heat transfer coefficient and thermal capacity results in a more significant reduction in the recorded temperature value at the time instant t=240s compared to the influence exerted by thermal conductivity. Specifically, these reductions are quantified at -1.4100 and -1.4450 for C and h, when 70V is applied. These values increase to -14.5100 and -11.3675, respectively, when 200V is applied.
Referring to the equilibrium temperature values (t=3600s), the situation undergoes significant changes. Specifically, it’s interesting to observe that the influence of thermal capacity becomes null (α = 0, see Figure 20d and Figure 21d) regardless of the voltage level. Conversely, the impact of thermal conductivity is reversed, since now an its increase leads to a slight decrease in the maximum recorded temperature. This finding aligns with theoretical principles, where higher thermal conductivity corresponds to a lower temperature gradient in a solid. Notably, the dominant effect of the heat transfer coefficient persists: in both scenarios (V= 70V and V= 200V), an increase significantly reduces (α = -4.1825 and α = -34.1475, respectively) the plateau temperature value This outcome is consistent with theoretical expectations, as a higher heat transfer coefficient results in the heated sample remaining cooler by transferring more heat to its surrounding environment
Table 3 summarizes, for the two voltages under consideration, the estimated (with the statistical DoE approach) slope values indicating the influence of the three thermal parameters on the two temperatures of interests (t=240s and t=3600s).

3.6. Response Surface Methodology (RSM) for the Investigated Temperature Values

Response Surface Methodology (RSM), initially introduced by Box & Wilson [27] in the early 1950s, continues to be a widely used mathematical tool based on Design of Experiments. It is employed to predict the relationship between multiple design parameters and experimental outcomes. Given the unknown form of the performance function (P.F.), Response Surface Methodology (RSM) aims to predict the response surface (R.S.), identifying optimal response regions amidst design input changes. The R.S. is typically expressed as follows:
R . S . = f   X 1 ,   X 2 ,   … X n + ε
where f is the mathematical relation between the R.S. and the independent input parameters (Xi) and ε is the experimental error which follows a normal distribution with a mean of zero and constant variance. Polynomial models are commonly used for surface prediction: first-order (linear) or second-order (quadratic) models as used in the present study, are typically adequate for evaluating the performance of different problems in several contexts, particularly when it dependent on two/three input parameters (e.g., thermal conductivity λ, thermal capacity C, and heat transfer coefficient h, in our case) [28,29].
Mathematical speacking, the quadratic polynomial model (n=3) can be described by the following equation:
R . S . = β 0 + ∑ i = 1 n β i x i + ∑ i = 1 n β i i x i 2 + ∑ i = 1 n − 1 ∑ j = i + 1 n β i j x i x j
where xi, xj represent the independent input parameters, β0 is the intercept coefficient whereas βi, βii and βij are the linear, quadratic and interaction regression coefficients, respectively. These variables are evaluated using the least squares method.
With reference to the temperature values T at 240s and that at 3600s (i.e., T-240s and T-3600s, respectively), the intention is to find an analytical function relating these selected temperature values with the thermal parameters taken into consideration in the current study, i.e.,   T − 240 s = f λ , C , ​  h = f x 1 , x 2 ,   x 3 - for a more appropriate mathematical representation and T − 3600 s = f λ , ​  h = f x 1 ,   x 3 .
Based on equation (16), the quadratic polynomial approximating the dependent variable T is expressed as follow:
T − 240 s = f ( x 1 , x 2 , x 3 ) = β 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + β 12 x 1 x 2 + β 13 x 1 x 3 + β 23 x 2 x 3 + β 11 x 1 2 + β 22 x 2 2 + β 33 x 3 2
T − 3600 s = f ( x 1 , x 3 ) = β 0 + β 1 x 1 + β 3 x 3 + β 13 x 1 x 3 + β 11 x 1 2 + β 33 x 3 2
The analysis is conducted with reference to the two extreme values of applied voltage, namely 70V and 200V. All coefficients of the RSM are stated in Table 4.
Figure 22 show in a) the 3D graphics of the two response surfaces at t=3600s for the two voltage levels selected for this investigation (70V and 200V) and in b) the exclusive 2D-view of the surface temperature T as function of the heat transfer coefficient (h).
Figure 22 a) demonstrates that the response surface (R.S.) closely matches the experimental data (indicated by black markers). This strong correlation confirms the accuracy of the regression model (RSM) in estimating physical properties and performance in relation to conditioning parameters also in the field of nanocomposites. From the 2D view in Figure 22b), the influence of the heat transfer coefficient on the surface temperature can be better appreciated. While the curve corresponding to 70 V appears mostly flat due to the low heating of the solid by the Joule effect, the curve obtained with a voltage of 200 V shows a decrease following a power law (see equation and corresponding R2 in the figure) of the temperature as the h factor increases with the combined effect of the thermal conductivity variation. This is due to the more efficient heat exchange between the solid and the surrounding environment that avoids the sample’s overheating.
Figure 23 displays all three-dimensional response surface plots for any pair of the three variable thermal factors. Each plot features a vertical line (z-axis) representing the upper surface temperature [K], and two horizontal lines (x and y axes) showing the actual values of the selected explanatory factors within their respective ranges. More in detail, Figure 23 shows a) the effect of thermal conductivity and heat transfer coefficient, b) the effect of thermal conductivity and thermal capacity, and c) the effect of heat transfer coefficient and thermal capacity, respectively. In each plot, the factor not represented on the horizontal axes was held constant to its minimum, average and maximum value (first, second, and third row, respectively).
From the comparison of these plots, it is once again possible to confirm the analysis derived from the DoE. It is evident (with particular reference to the applied voltage of 200 V) that the thermal capacity C plays a dominant role in determining the temperature T reached on the sample’s surface during the transient heating phase (specifically at t = 240s). Thermal conductivity has a negligible influence, whereas a contribution of the heat transfer coefficient h is appreciable (as seen from the different values of the corresponding color bars).

3.7. Thermo-Electric Properties: Simulation Results

Utilizing the DoE and RSM results, as well as the related considerations presented in the previous sections, it was possible to easily identify the thermal parameters λ, C, and h to be adopted in the various simulations. This ensured that the experimental curves regarding the surface temperature evolution of the sample at different applied voltage values could be accurately reproduced (see Figure 24) in the simulation environment of COMSOL Multiphysics used in this study.
It is worth noting that, for each applied voltage level, the experimental and simulated curves of the sample’s surface temperature perfectly overlap in the transient and steady-state phases. Table 5 summarizes the values of the thermal parameters used in the simulations that fit the experimental data for the different voltage levels.

3.7.1. Joule Heating Effect: Simulation Results

Figure 25 illustrates the effects of different electric potentials on the surface temperature distribution due to the Joule heating effect. It includes two subfigures, a) and b), each representing a different applied voltage (70 V and 200 V, respectively), and shows both the electric potential distribution and the corresponding surface temperature distribution, in the first and second row, correspondingly. The 3D plot shows a linear gradient in the electric potential from one end of the material (0 mm) to the other (80 mm), indicating a steady increase in voltage, from 0 V to 70 V in one case and from 0 V to 200 V in the other, across the length in the x-direction. The particular sectional views allow us to verify that, as expected, the electric potential assumes constant values in each transverse cross-section.
The black arrows indicate the current density, which, given the constant area, is greater for the sample subjected to a voltage of 200V than for the one powered at 70V.
The Joule effect (Joule heating) is evident as the electric potential applied to the material generates heat, causing a temperature rise. The amount of heat generated is proportional to the square of the applied voltage (P = V²/R where R is the electric resistance of the sample in Ohm), which explains the higher temperatures observed at 200 V (T ≃ 440 K at the time t= 3600s) respect to that recorded at 70 V (≃ 324 K at the same considered time). Regardless of the voltage, the temperature distribution plots show a surface temperature increase, with the central region reaching the highest temperature, whereas it is noticeably lower near the borders and edges, highlighting significant heat dissipation due to natural convection with the surrounding air.
This aspect is better investigated in Figure 26, which illustrates the multislice temperature distribution in the analyzed sample subjected to the Joule heating effect at the two different voltages, 70V, and 200V, in a) and b), respectively, both evaluated at steady-state conditions (t = 3600 s). The multislice temperature plots show how the temperature varies within the sample, emphasizing the central and edge regions.
In both cases, the central region of the samples reaches the maximum temperature of approximately 323 K and 440 K for 70V and 200V, as indicated by the corresponding orange and red areas in the plots. These result from significant Joule heating, where the electrical energy is converted into heat, causing the central part to heat up more than the edges. In fact, moving from the center toward the edges, there is a clear temperature gradient. The temperatures decrease from the central orange/red areas to the blue areas near the edges, which are around 314 K and 378 K for the sample subjected to 70V and 200V, respectively. This gradient indicates effective heat dissipation at the boundaries due to natural convection with the surrounding air. In brief, both voltage levels show a central region with the highest temperatures and lower temperatures towards the edges, highlighting the effect of natural convection in cooling the sample periphery. Natural concoction plays a crucial role here, as it removes heat from the sample edges more efficiently, preventing the outer regions from reaching the same high temperatures as the center. Higher voltages result in higher central temperatures and more pronounced gradients towards the edges.

3.7.2. Spatial Temperature Distribution Simulation Results

Exploring the spatial temperature distribution in a solid due to Joule heating is essential for understanding how temperature varies throughout the solid and for predicting the material’s performance under operational conditions. Excessive localized heating can lead to thermal stresses, deformation, or even material failure.
Figure 27 shows the temperature distribution along different spatial profiles. More in detail, each subfigure from a) to e) shows the temperature distribution along a specific cutline at two different time points (t=240 s and t=3600 s) for voltage values 70V, 120V, and 200V.
The cutlines are represented in subfigure (f) as follows:
- cut line 1: parallel to the x-axis, on the top surface, at the midpoint of the sample’s width;
- cut line 2: parallel to the y-axis, on the top surface, at the midpoint of the sample’s length;
- cut line 3: another line parallel to the x-axis, at a different position along the z-axis (at the midpoint of the sample’s thickness);
- cutline 4: also parallel to the y-axis but at a different z-coordinate (at the midpoint of the sample’s thickness);
- cut line 5: a vertical line, parallel to the z-axis passing through the centroid of the sample along its thickness.
By analyzing these plots, it is possible to observe that for the sample powered with 70 V at t= 240 s and t= 3600s, the temperature profiles are the lowest across all cut lines. The temperatures gradually increase along the length of the sample until they reach a maximum in the central area and then decrease again. Concerning 120V, the temperature profiles show moderate heating, which becomes significant in the case of 200 V. At t=3600s, the temperature stabilizes at the highest values, reaching about 440K. By comparing the results for cut lines 1 and 2 with those for cut lines 3 and 4, which differ only in their position along the thickness, it is worth noting that, although the trends are similar, the numerical values differ due to the varying Joule heating and the role played by convective heat exchange with the external environment. In particular, cut lines 3 and 4, located in the midpoint of the z-coordinates, exhibit higher temperature profiles than cut lines 1 and 2, indicating a stronger effect of Joule heating at these positions. The heat remains trapped inside the solid, without exchanging it with the external environment. For example, in the sample subjected to 200V, the temperature recorded on the surface is approximately 440K, while at the midpoint of its thickness, it reaches a value of about 448K. This particularity is more clearly evident when referring to cut line 5, which allows for exploring the vertical temperature distribution along the z-axis. The trend shows higher temperatures at higher voltages, with significant differences between the initial and steady-state times. Notably, the maximum temperature value is recorded at the midpoint of the thickness (at the centroid). The lack of convective heat transfer on the solid’s inner surfaces prevents effective heat dissipation, leading to the accumulation of thermal energy in the central region. As electrical energy is converted into heat through Joule heating, the heat generated in the core of the material cannot be efficiently transferred to the outer surfaces due to the relatively lower thermal conductivity and absence of external convection. As a result, the temperature rises significantly in this area, reaching its peak at the midpoint of the thickness, where the material’s thermal resistance is greatest. This phenomenon underscores the critical role of thermal conductivity, heat capacity, and convective boundary conditions in determining the temperature distribution within composite materials subjected to electrical heating.

3.7.3. Convective Heat Flux: Simulation Results

Effective thermal management is essential for the performance and longevity of devices designed for thermal applications. Convective heat flux, the transfer of heat from a surface to a surrounding fluid (usually air), plays a crucial role in dissipating heat and preventing overheating, and therefore, its investigation is essential. Figure 28 presents the boundary convective heat flux for the sample subjected to Joule heating at two extreme voltage levels, 70V and 200V, both evaluated at steady-state conditions (t = 3600 s), in a) and b), respectively. The color bars show the numerical values of the heat flux in W/m² while the arrows indicate the magnitude and direction of the heat flux.
It is possible to note a relatively uniform distribution across the surface, but with a slightly higher concentration of arrows in the central region, indicating a more intense heat flux there because of the greater exchange area compared to the other sides that show less heat flux. At 70V, the convective heat flux ranges from -75.4 W/m² to -127 W/m², indicating a moderate heat flux level across the sample. At 200V, the convective heat flux ranges from -585.9 W/m² to -1048 W/m², showing a significantly higher heat flux level. This is due to the increased heating effect from the higher voltage, which results in more heat being dissipated through convection. The 3D views of the sample clearly demonstrate the impact of different voltages on the convective heat flux distribution on the samples subjected to Joule heating as well as emphasize the role of natural convection in dissipating heat from the sample, especially from the central regions where the heating is most intense.

4. Discussion

The study focuses on the experimental characterization, statistical and numerical investigation of an epoxy resin composite loaded with varying concentrations of carbon nanotubes (CNTs) up to 3% by weight. These new nanocomposites, with enhanced mechanical, electrical, and thermal properties, are of significant interest for their potential use in practical applications for which, in the past, they were not taken into consideration due to their electric/thermal insulating nature. Actually, carbon-based-reinforced epoxy resins represent a promising class of materials for advanced engineering applications, including thermal management aspects. A preliminary characterization in terms of electrical conductivity as a function of filler concentration (percolation curve) allowed the identification of two optimal concentrations for further investigation. Notably, the concentration of 0.5 wt.% CNTs, corresponding to an electrical conductivity of 0.06 S/m, was selected for detailed studies on thermomechanical and piezoresistive properties. Concentrations near the electrical percolation threshold (EPT) are particularly suited for this type of analysis because the percolative network is just formed and, thus, more susceptible to deformations. It was experimentally observed that the sample exhibits elastic behavior up to strain levels of about 1% (yield point), beyond which it enters the plastic zone, leading to permanent deformations. This elastic-plastic transition is critical for understanding the mechanical properties of the nanocomposite. The slope of the linear region gives the Young’s modulus, indicating the material’s stiffness. Beyond the yield point, the material deforms plastically. Stress increases at a slower rate compared to the elastic region. The material undergoes significant permanent deformation in this region. The investigation of the variation in electrical resistance of the sample under applied strain (piezoresistive response) revealed that at the yield point, a distinct change in the slope of the resistance-strain curve was observed, confirming, once again, the transition from elastic to plastic behavior. This change is attributed to significant morphological alterations in the percolation network of CNTs under stress. The CNT network becomes disrupted in the plastic deformation region, leading to increased electrical resistance. This behavior underscores the sensitivity of the composite’s electrical properties to mechanical deformation, which is crucial for applications in sensors and structural health monitoring.
A numerical model based on the finite element method (FEM) using COMSOL Multiphysics® was adopted to predict the thermomechanical properties of the material by accurately reproducing (with CAD software) the dog-bone-shaped sample, as required by measurement standards. As a first step, the proposed model was validated against experimental measurements (load as a function of strain).
The validation process involved comparing simulated load-strain curves with experimental data. This step ensured that the numerical model accurately represented the material behavior. Upon validation, the model was used to investigate the z-displacement in the direction of the applied force, providing insights into the deformation behavior under tensile loading. Both 3D visualizations and 2D plots were generated to illustrate these displacement behaviors of a dogbone composite material under prolonged loading. The increasing displacement over time and the significant strain within the gauge zone are key observations for understanding the material’s mechanical response and potential applications or limitations in structural contexts. The progressive increase in displacement indicated that the material does not immediately recover, which could indicate permanent deformation or damage accumulation over time.
Additionally, the distribution of Von Mises stress was analyzed to identify regions of high-stress concentration. The results indicated that the maximum stresses are concentrated in the central region of the dog-bone sample, which is critical for understanding potential failure points. In the initial elastic region, as the material is strained, the stress increases linearly according to Hooke’s Law: σ=Y⋅ε where σ is the stress, Y is the Young’s modulus, and ε is the strain. This linear relationship means that as strain increases, the stress also increases proportionally, leading to a higher Von Mises stress.
Contrarily, in the plastic deformation area, the material’s resistance to further deformation increases according to a physical phenomenon known as strain hardening. The Von Mises stress in the plastic region can be described by: σ = σy + Y⋅(ε−εy) where σy is the yield stress, ε is the total strain, and εy is the strain at yielding. This equation shows that the Von Mises stress increases as strain continues to accumulate beyond the yield point.
In brief, as the material deforms elastically and plastically over time, the internal resistance to deformation increases, necessitating higher stresses to continue the deformation process. This results in an overall increase in Von Mises stress, as numerically observed.
The thermal expansion of the sample under tensile testing was also examined. Heat dissipation during deformation may result from various mechanisms, such as internal friction between the material’s molecules, disordered movements of polymer chains, or plastic deformations involving sliding and dislocations in the material’s crystalline lattice.
In our case, the epoxy resin loaded with carbon nanotubes exhibited a low coefficient of thermal expansion (approximately 60µ /K) and experienced minor plastic deformations (from 1% to 2% strain). Nonetheless, it was possible to graphically and quantitatively appreciate the overheating in the central region of the specimen. Although the recorded heating was not significant, this aspect should not be overlooked in other materials that experience more substantial plastic deformations
The effect of strain rate on strain-induced heating was also studied. Higher strain rates resulted in greater induced temperatures. This is because higher strain rates increase the rate of internal friction and mechanical energy dissipation, which converts more mechanical energy into heat. Understanding the thermal response of the material under different strain rates is crucial for applications where the material is subjected to varying mechanical loads, as excessive heating could lead to material degradation or failure.
Finally, to complete this thermomechanical numerical study, the plastic energy dissipation was analyzed, which, as expected, only appears in the plastic zone and is not observed in the elastic zone. This is because plastic energy dissipation is associated with irreversible deformations, which do not occur in the elastic region. In brief, in the elastic region, mechanical energy is stored in the material as elastic strain energy, which can be fully recovered upon unloading. Consequently, there is no plastic dissipation in this region. However, in the plastic region, the material undergoes irreversible deformations, and the mechanical energy is dissipated as heat. This distinction was evident in the numerical simulations, where plastic energy dissipation was observed only in the plastic zone. At the time t = 100 s (ε ≈ 1), the 3D model showed a plastic dissipation of about 2.19 x 10⁴ J/m³ that indicated the beginning of plastic deformation, whereas a maximum value of 9.89 x 10⁴ J/m³ is measured at t = 200 s (ε ≈ 2) thus suggesting the progression of plastic deformation over the time and strain increase.
Furthermore, as indicated in the title, this study also delved into the surface heating dynamics of composite materials driven by Joule heating at varying voltage levels. Joule heating, a fundamental process where electrical energy dissipates as heat in the material, forms the cornerstone of our experimental investigation. Voltage levels ranging from 70 V to 200 V were systematically applied to evaluate their impact on surface temperature evolution. Beyond experimental observation, our approach integrated advanced Design of Experiments (DOE) techniques, employing Dex Scatter Plot (DsP) and Main Factor Plot (MfP) analyses. These methods allowed precise comprehension of how thermal parameters—thermal conductivity, thermal capacity, and heat transfer coefficient—affect temperature profiles during transient and steady-state heating phases. Through Response Surface Methodology (RsM), we derived analytical relationships that explicitly correlate temperature variations with these thermal variables. Such statistical analyses revealed critical insights: within the studied voltage range, thermal conductivity exhibits minimal influence on temperatures during the heat transfer phase, such as 240 seconds, and during equilibrium (3600 seconds) plateau phases. Conversely, thermal capacity significantly affects temperatures during the initial heating phase but has a null impact on equilibrium temperatures. The heat transfer coefficient by natural convection h [W/m-2∙K-1] emerges as a pivotal factor governing overall heating rates and plateau temperatures, adhering to the physical relationship known as Newton’s law of cooling: Q = h ​∙ S ​∙   ​Δ T where Q [W] is heat flow, ΔT [K] is the temperature difference (TSolid- Troom) which give rises the convective transport between a heated solid surface S [m2] and the surrounding environment.
A further rigorous numerical model has been developed in COMSOL Multiphysics®. This model not only replicated experimental data accurately (this consistency served as its validation) but also facilitated a deeper exploration of thermo-electric properties, including the effects of natural convection at material edges, which induce localized cooling effects.
Future research aims to extend these insights by exploring modifications in heat sink geometries, such as edge smoothing, to optimize heat dissipation for cooling applications further or recover wasted heat for heating elements.
Therefore, insights gleaned from this integrated approach provide actionable strategies for optimizing heat exchanger designs and enhancing thermal management efficiency in various engineering applications.
In essence, this study establishes a robust framework for understanding and optimizing the thermal behavior of composite materials under mechanical stress and Joule heating, integrating advanced statistical analyses with validated numerical models to advance engineering design and innovation.
Creating new advanced hybrid materials using simulation studies and statistical techniques such as DoE and RSM can streamline the optimization process without requiring physical specimen testing. This approach cuts down on development time and the high costs of trial-and-error experiments. Additionally, the ideal composition and structure of new materials can be determined by integrating simulation methods with statistical tools. This combination also helps pinpoint the most influential controllable input factors, supporting design decisions during the manufacturing stage

5. Conclusions

This study focused on the development and characterization of epoxy resins filled with varying concentrations of multi-walled carbon nanotubes (MWCNTs), up to 3 wt%. The experimental results highlighted the importance of the electrical percolation curve in identifying critical filler concentrations. Specifically, 0.5 wt% MWCNTs around the electrical percolation threshold were found suitable for exploring mechanical and piezoresistive properties. In contrast, a concentration of 3 wt% was optimal for investigating thermo-electric properties due to the Joule effect, with applied voltages ranging from 70V to 200V. Numerical models developed using multiphysics simulation software were validated against experimental data, providing a robust framework for further investigation of the composites’ physical properties. Additionally, a statistical approach based on the design of experiments (DoE) was employed to understand the influence of thermal parameters on the final performance of the materials. Overall, the integration of experimental characterization with numerical modeling and statistical analysis has provided comprehensive insights into the behavior and potential use of MWCNT-epoxy composites in thermal management applications. This multidisciplinary approach not only enhances our understanding of these advanced materials but also paves the way for their optimized use in various industrial sections, particularly where enhanced thermomechanical and thermo-electric properties are crucial. Future research will continue to refine these models and explore additional parameters to optimize further the performance and applicability of these promising composite materials.

Author Contributions

Conceptualization G.S., R.G., L.G.; Supervision G.S.; Writing-original draft G.S.; Test samples: L.V.; Investigation of mechanical and electrical properties L.V; G.S.; Modelling software R.G.; Multiphysics simulation studies: R.G. and V. R.; Data analysis: G.S., R.G. and V. R.; Writing—review—L.G. and V.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by private fund of University ‘’Giustino Fortunato’’. The authors also gratefully acknowledge the Prin 2022 project “Integration of Continuous Fibers and Self-healing agents in 3D printed thermoplastic composites (INFINITE)” (Prot. 2022AKTCPH) and Prin 2022 project “Alternative Manufacturing Approach to Recycling Fiber- Reinforced Composites (AMORFIC)” (Prot: P20227NYXH)”, both founded by the Italian Ministry of University and Research, for financial support.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Harris, Bryan. Engineering composite materials, 2nd edition, CRC press, London, UK 1999.
  2. Kerns, Jeff. Replacing metal with plastic. Machine design 2016, 88, 34-42.
  3. Nicolais, L.; Meo, M.; Milella, E. Composite materials: a vision for the future. Springer Science & Business Media, London. UK 2011.
  4. 4. J. Mark, K. Ngai, W. Graessley, L. Mandelkern, E. Samulski, G. Wignall, J. Koenig. Physical properties of polymers, Cambridge University Press, Cambridge, UK 2004.
  5. Allaouia, A.; Baia, S.; Cheng, H.; Bai, J. Mechanical and Electrical Properties of MWNT/Epoxy Composite. Compos. Sci. Technol. 2002, 62, 1993–1998. [Google Scholar] [CrossRef]
  6. Meeuw, H.; Körbelin, J.; Wisniewski, V.K.; Nia, A.S., Vázquez, A.R.; Lohe, M.R.; Fiedler, B. Carbon Nanoparticles’ Impact on Processability and Physical Properties of Epoxy Resins—A Comprehensive Study Covering Rheological, Electrical, Thermo-Mechanical, and Fracture Properties (Mode I and II). Polymers. 2019, 11, 231.
  7. Moisala, A.; Li, Q.; Kinloch, I.A.; Windle, A.H. Thermal and electrical conductivity of single-and multi-walled carbon nanotube-epoxy composites. Compos. Sci. Technol. 2006, 66, 1285–1288. [Google Scholar] [CrossRef]
  8. Nan, C.-W.; Yang, S.; Jing, M.A. Physical properties of composites near percolation. Ann. Rev. Mater. Res., 2010, 40, 131-151.
  9. Nadiv, R.; Vasilyev, G.; Shtein, M.; Peled, A.; Zussman, E.; Regev, O. The multiple roles of a dispersant in nanocomposite systems. Compos. Sci. Technol. 2016, 133, 192–199. [Google Scholar] [CrossRef]
  10. Deng, F.; Zheng, Q.S. An analytical model of effective electrical conductivity of carbon nanotube composites. Appl. Phys. Lett. 2008, 92, 071902. [Google Scholar] [CrossRef]
  11. Rahatekar, S.S.; Koziol, K.K.K.; Butler, S.A.; Elliott, J.A.; Shaffer, M.S.P.; Mackley, M.R.; Windle, A.H. Optical microstructure and viscosity enhancement for an epoxy resin matrix containing multiwall carbon nanotubes. J. Rheol. 2006, 50, 599–610. [Google Scholar] [CrossRef]
  12. Fan, Z.; Advani, S.G. Rheology of multiwall carbon nanotube suspensions. J. Rheol. 2007, 51, 585–604. [Google Scholar] [CrossRef]
  13. Jeong, Y.G., An, J-E., Effects of Mixed Carbon Filler Composition on Electric Heating Behavior of Thermally-cured Epoxy-based Composite Films, Compos. Part A, 2014, 57, 1-7.
  14. Isaji, S.; Bin, Y.; Matsuo, M. Electrical conductivity and self-temperature-control heating properties of carbon nanotubes filled polyethylene films. Polymer 2009, 50, 1046–1053. [Google Scholar] [CrossRef]
  15. Chatterjee S, Nafezarefi F, Tai NH, Schlagenhauf L, Nusech FA, Chu BTT. Size and synergy effects of nanofiller hybrids including graphene nanoplatelets and carbon nanotubes in mechanical properties of epoxy composites. Carbon 2012, 50, 5380-6.
  16. Guadagno, L.; Longo, R.; Aliberti, F.; Lamberti, P.; Tucci, V.; Pantani, R.: Spinelli, G.; Catauro, M.; Vertuccio, L. Role of MWCNTs loading in designing self-sensing and self-heating structural elements. Nanomaterials 2023, 13, 495.
  17. Spinelli, G.; Guarini, R.; Kotsilkova, R.; Ivanov, E.; Vertuccio, L.; Romano, V.; Guadagno, L. Joule heating effect in carbon-based epoxy resin: an experimental and numerical study. Bulgarian Chemical Communications, 2023, 55, 335-343.
  18. Spinelli, G.; Lamberti, P.; Tucci, V.; Guadagno, L.; Vertuccio, L. Damage monitoring of structural resins loaded with carbon fillers: Experimental and theoretical study. Nanomaterials, 2020, 10, 434.
  19. Standard, A. D638: Standard Test Method for Tensile Properties of Plastics; ASTM International: West Conshohocken, PA, USA, 2010.
  20. Ku-Herrera, J.; Aviles, F. Cyclic tension and compression piezoresistivity of carbon nanotube/vinyl ester composites in the elastic and plastic regimes. Carbon 2012, 50, 2592–2598. [Google Scholar] [CrossRef]
  21. Oliva-Avilés, A.; Avilés, F.; Sosa, V. Electrical and piezoresistive properties of multi-walled carbon nanotube/polymer composite films aligned by an electric field. Carbon, 2011, 49, 2989–2997.
  22. Vicario, G. Computer experiments: Promising new frontiers in analysis and design of experiments. Stat. Appl. 2006, 18, 231–249. [Google Scholar]
  23. King, M.; Rahimi, S. Optimisation of sample geometry for thermo-mechanical testing of precipitation hardenable nickel-based superalloys with an ETMT machine. Strain, 2024, 60, e12458.
  24. White, C.C.; Hunston, D.L.; Tan, K.T.; Filliben, J.J.; Pintar, A.; Schueneman, G. A Systematic Approach to the Study of Accelerated Weathering of Building Joint Sealants. J. ASTM Int. 2012, 9, 1–17. [Google Scholar]
  25. Croarkin, C.; Tobias, P.; Filliben, J.J.; Hembree, B.; Guthrie, W. Handbook 151: NIST/SEMATECH e-Handbook of Statistical Methods; NIST Interagency/Internal Report (NISTIR); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2002.
  26. Kuehl, R.O. Design of Experiment: Statistical Principles of Research Design and Analysis, 2nd ed.; Duxbury Press: Pacific Grove, CA, USA, 1999. [Google Scholar]
  27. Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 270–310. [Google Scholar]
  28. Khuri, A.I. Multiresponse surface methodology. In Design and Analysis of Experiments. Handbook of Statistics 13; Ghosh, S., Rao, C.R., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1996; pp. 377–406. [Google Scholar]
  29. Draper, N.R.; Lin, D.K.J. Response surface designs. In Design and Analysis of Experiments. Handbook of Statistics 13; Ghosh, S., Rao, C.R., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1996; pp. 343–375. [Google Scholar]
Preprints 110697 g001
Figure 1. Key features of the components of nanocomposites and test specimens.
Figure 1. Key features of the components of nanocomposites and test specimens.
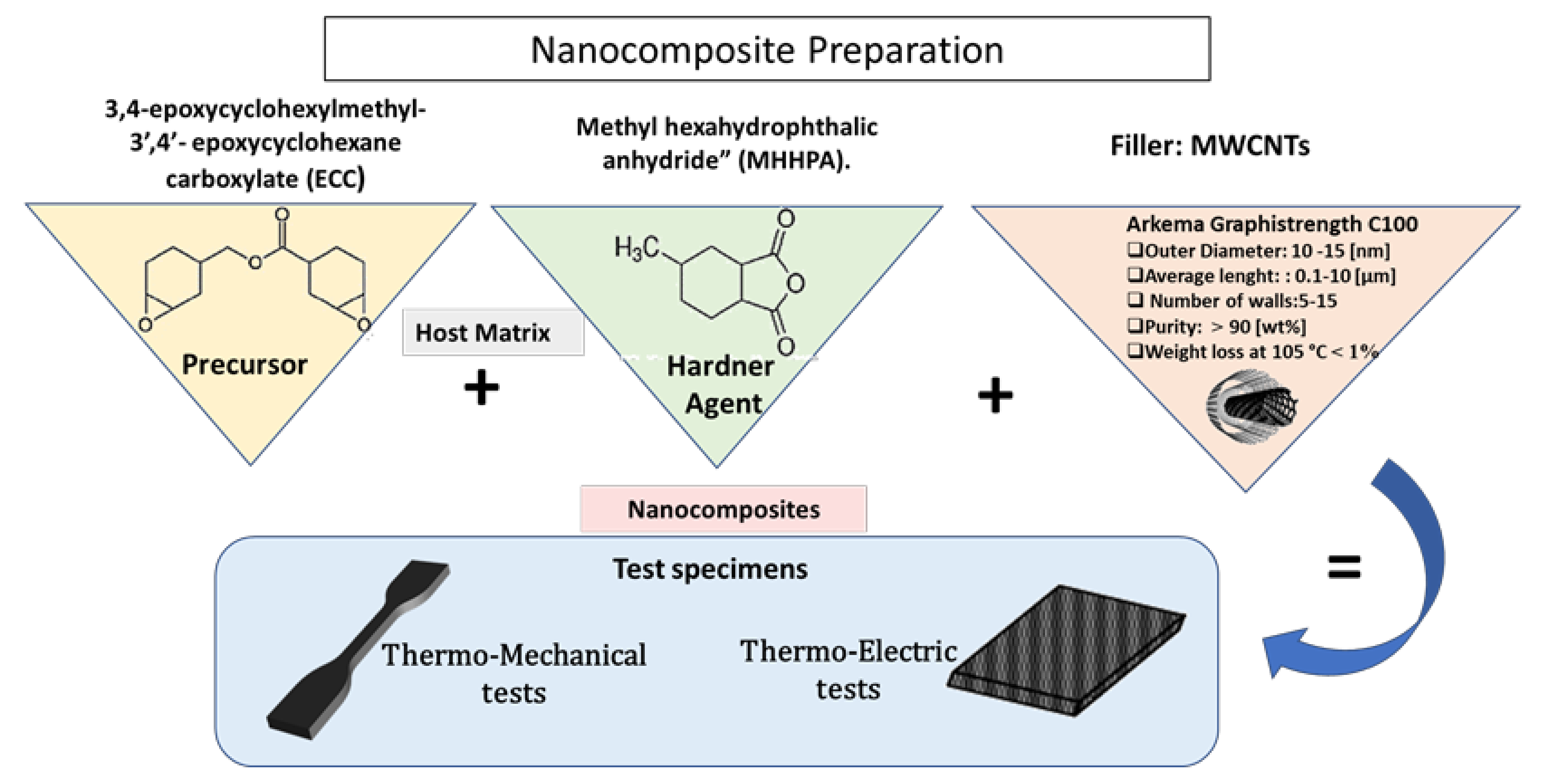
Preprints 110697 g001
Preprints 110697 g002
Figure 2. Set-up adopted for the experimental thermo-electric and thermo-mechanical measurements, including the geometrical features of the test specimens in a) and b), respectively.
Figure 2. Set-up adopted for the experimental thermo-electric and thermo-mechanical measurements, including the geometrical features of the test specimens in a) and b), respectively.
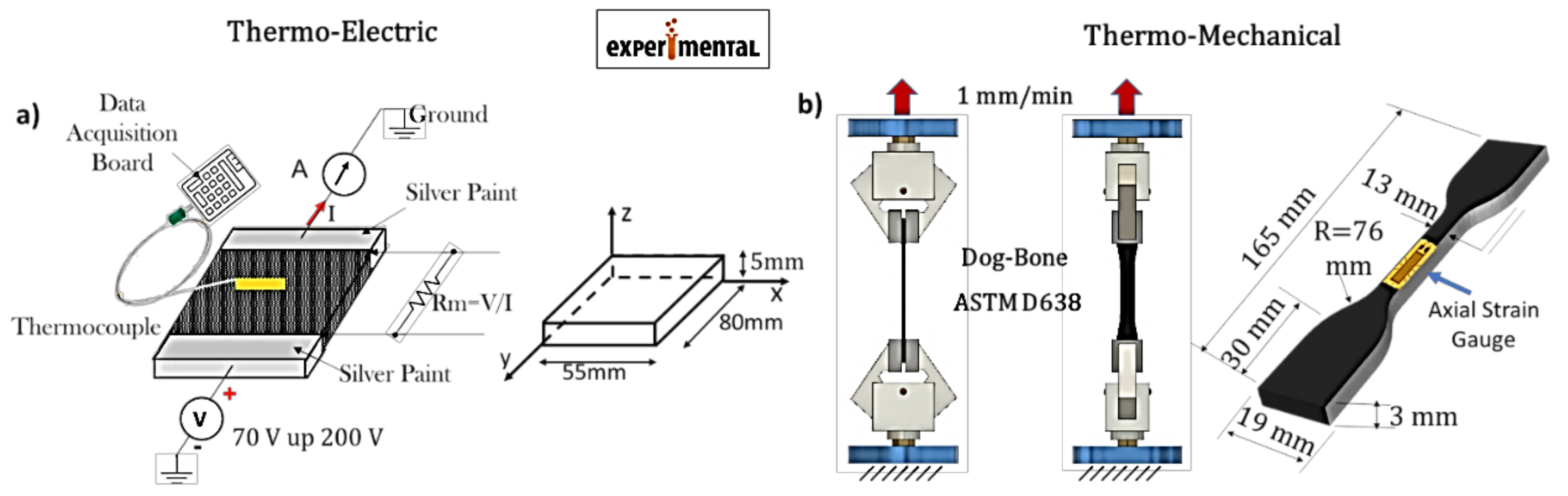
Preprints 110697 g002
Preprints 110697 g003
Figure 3. a) Thermo-mechanical case study addressed in the present study; b) Main model definitions for the numerical investigation adopted in COMSOL Multiphysics®.
Figure 3. a) Thermo-mechanical case study addressed in the present study; b) Main model definitions for the numerical investigation adopted in COMSOL Multiphysics®.
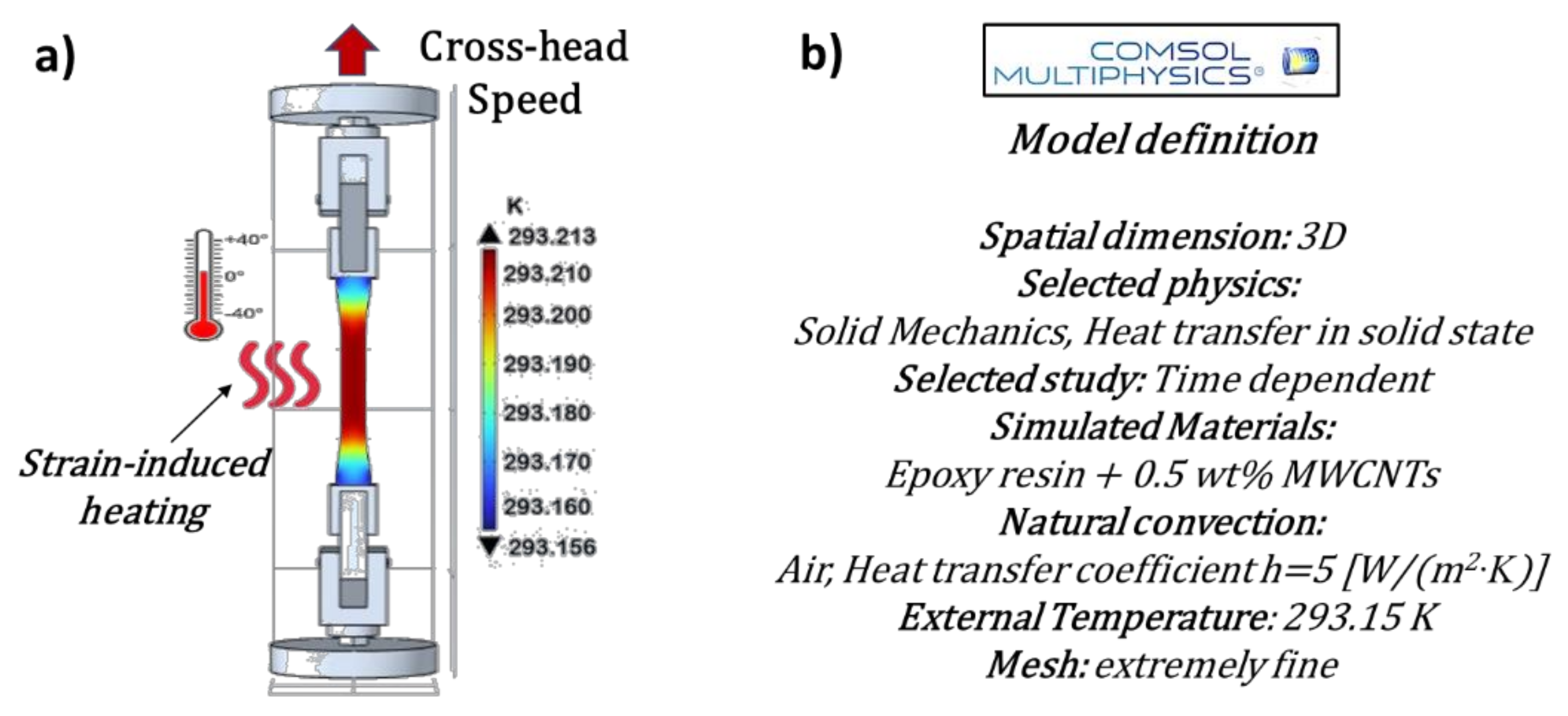
Preprints 110697 g003
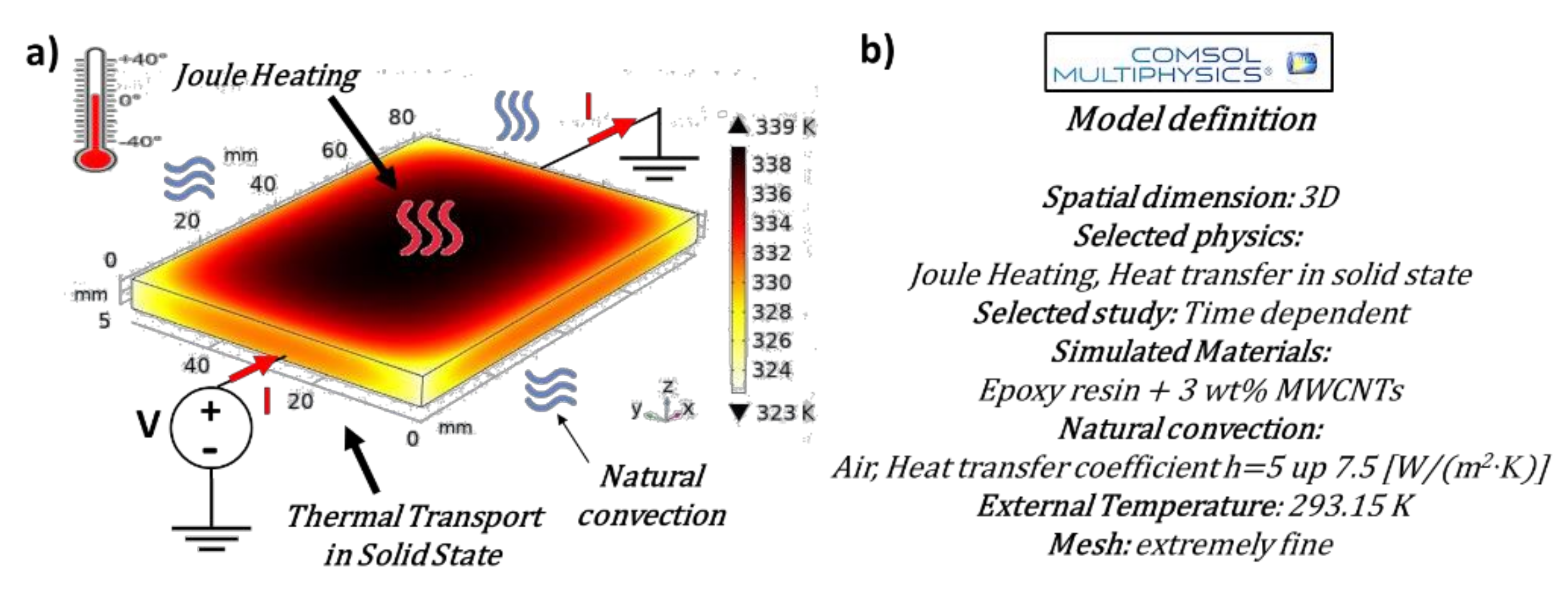
Preprints 110697 g004
Figure 4. a) Thermo-electric case study addressed in the present study; b) Main model definitions for the numerical investigation adopted in COMSOL Multiphysics®.
Figure 4. a) Thermo-electric case study addressed in the present study; b) Main model definitions for the numerical investigation adopted in COMSOL Multiphysics®.
Preprints 110697 g004
Preprints 110697 g005
Figure 5. Diagrammatic representation of a system (product or process) during the design phase.
Figure 5. Diagrammatic representation of a system (product or process) during the design phase.
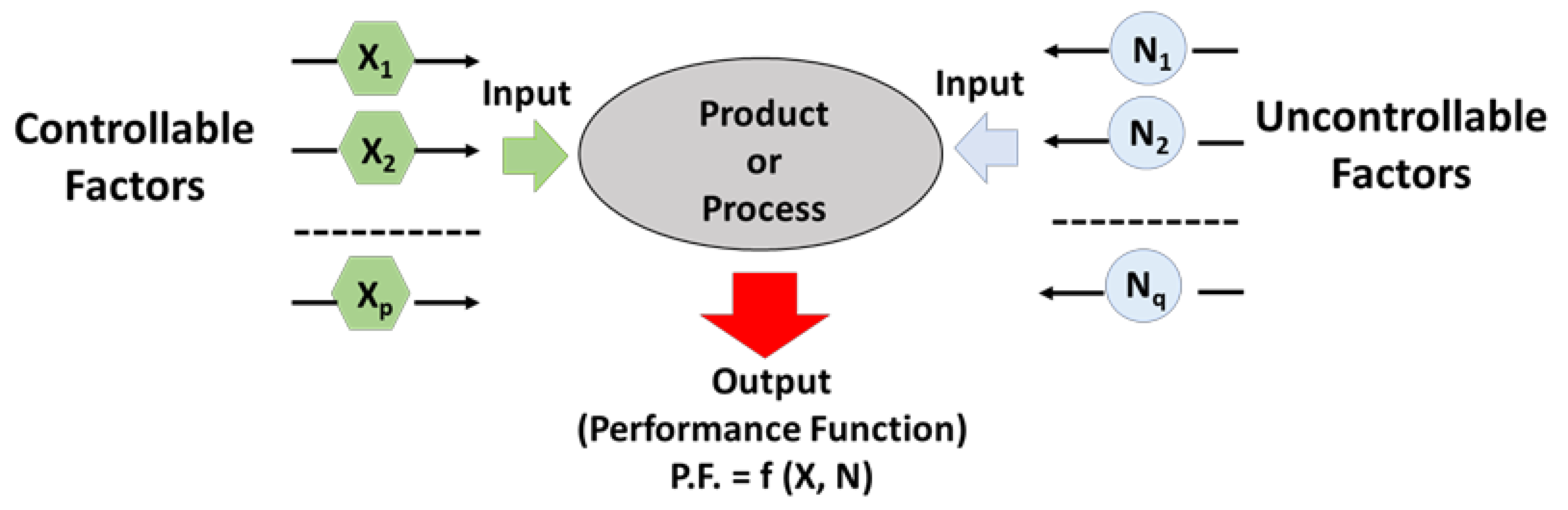
Preprints 110697 g005
Preprints 110697 g006
Figure 6. Electrical conductivity as a function of filler concentrations in a); tunneling verification in nanocomposite systems in b).
Figure 6. Electrical conductivity as a function of filler concentrations in a); tunneling verification in nanocomposite systems in b).
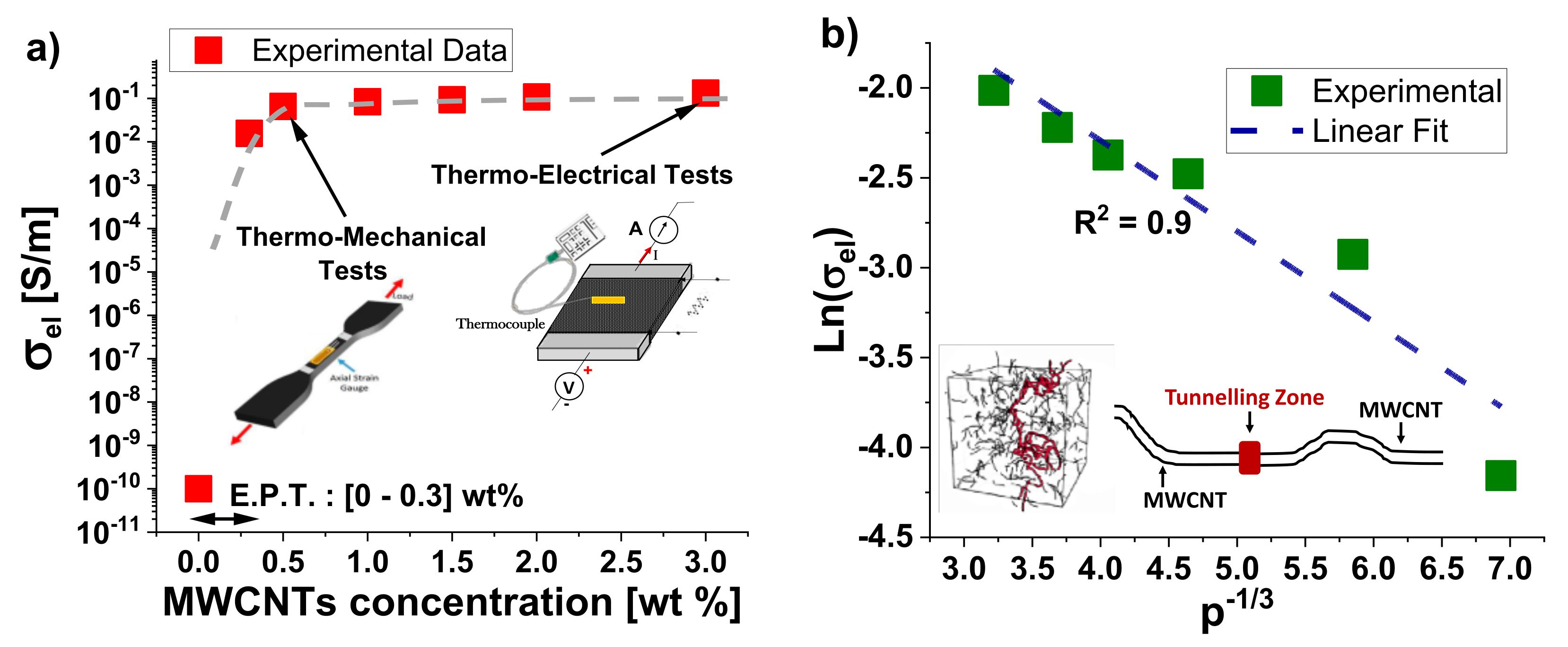
Preprints 110697 g006
Preprints 110697 g007
Figure 7. (a) Mechanical behavior and (b) resistance change ratio versus axial strain for samples reinforced with 0.5 wt.% of MWCNTs.
Figure 7. (a) Mechanical behavior and (b) resistance change ratio versus axial strain for samples reinforced with 0.5 wt.% of MWCNTs.
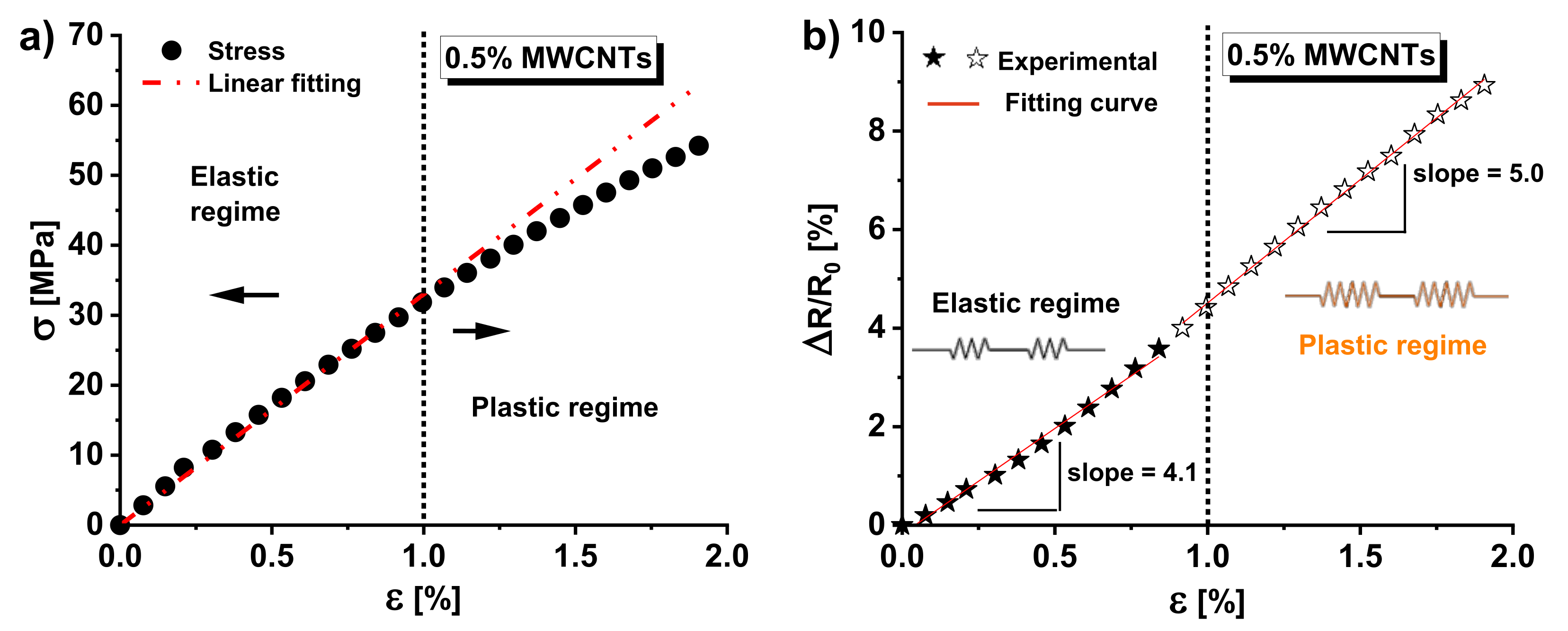
Preprints 110697 g007
Preprints 110697 g008
Figure 8. Comparison between experimental and simulated data for model validation.
Figure 8. Comparison between experimental and simulated data for model validation.
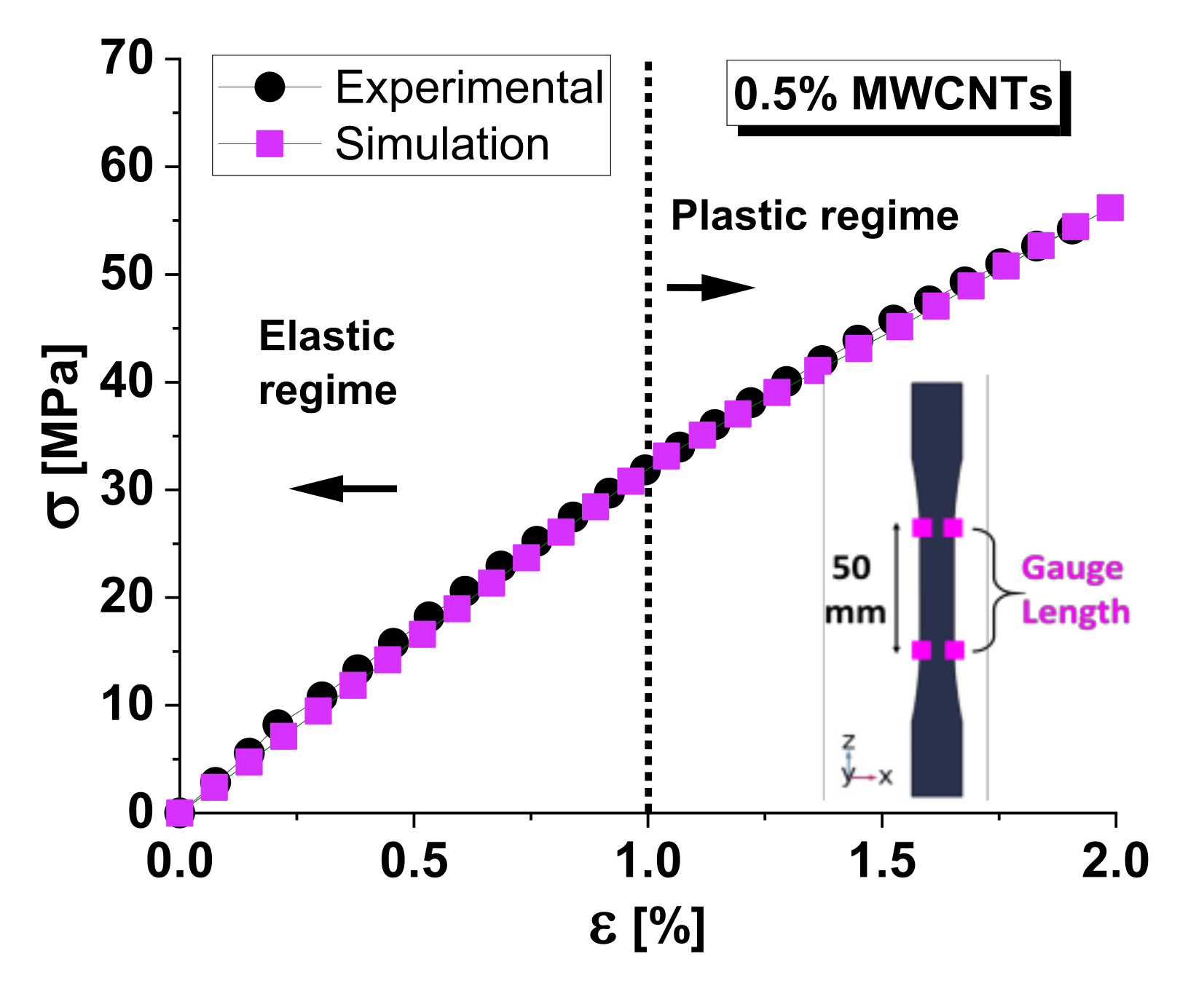
Preprints 110697 g008
Preprints 110697 g009
Figure 9. Z-axis displacement versus the dogbone length along the z-symmetry axis.
Figure 9. Z-axis displacement versus the dogbone length along the z-symmetry axis.
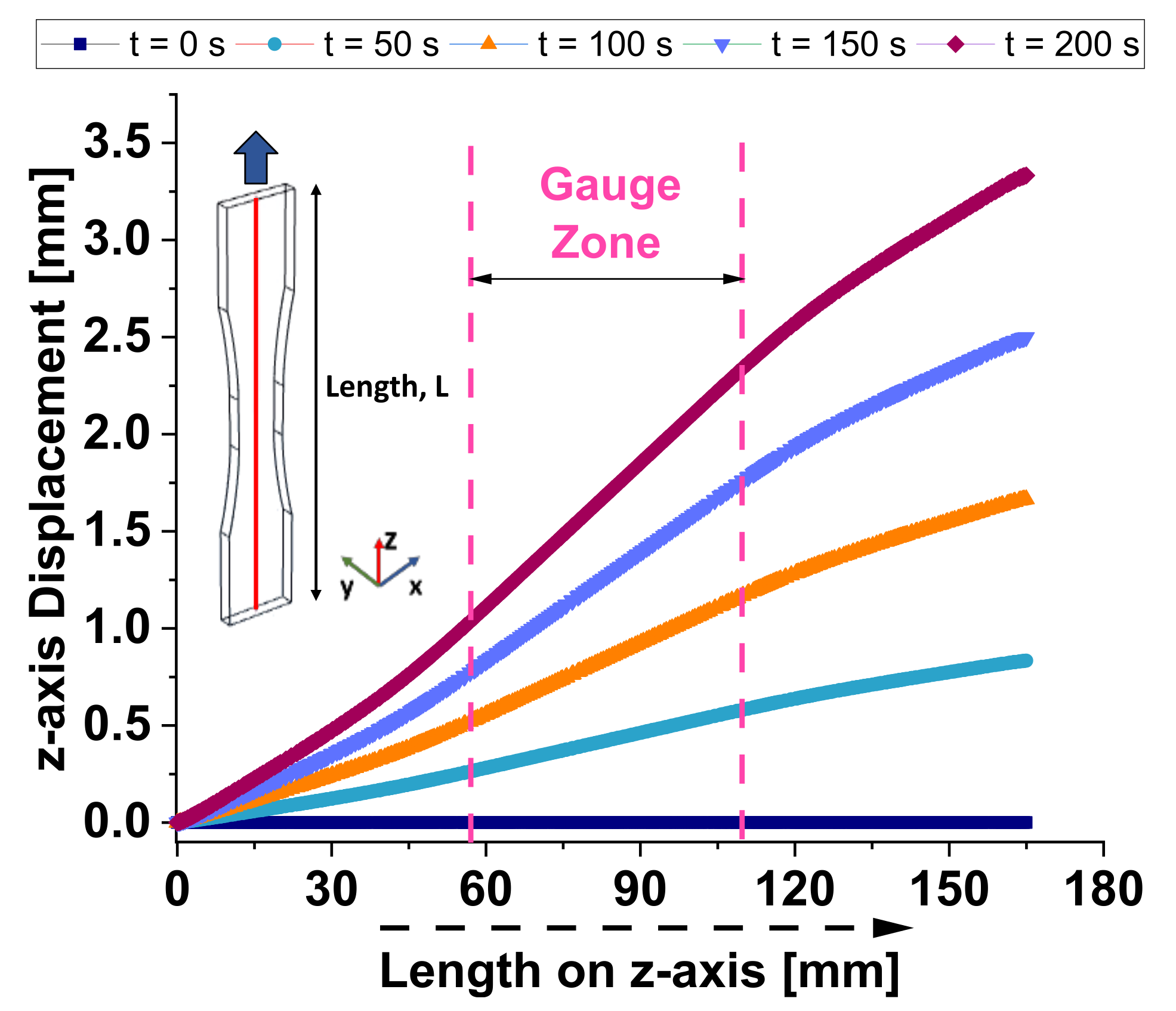
Preprints 110697 g009
Preprints 110697 g010
Figure 10. 3D z-axis displacement versus the dogbone length on the central slice of the zx-plane passing through the axis of symmetry in the z-direction.
Figure 10. 3D z-axis displacement versus the dogbone length on the central slice of the zx-plane passing through the axis of symmetry in the z-direction.
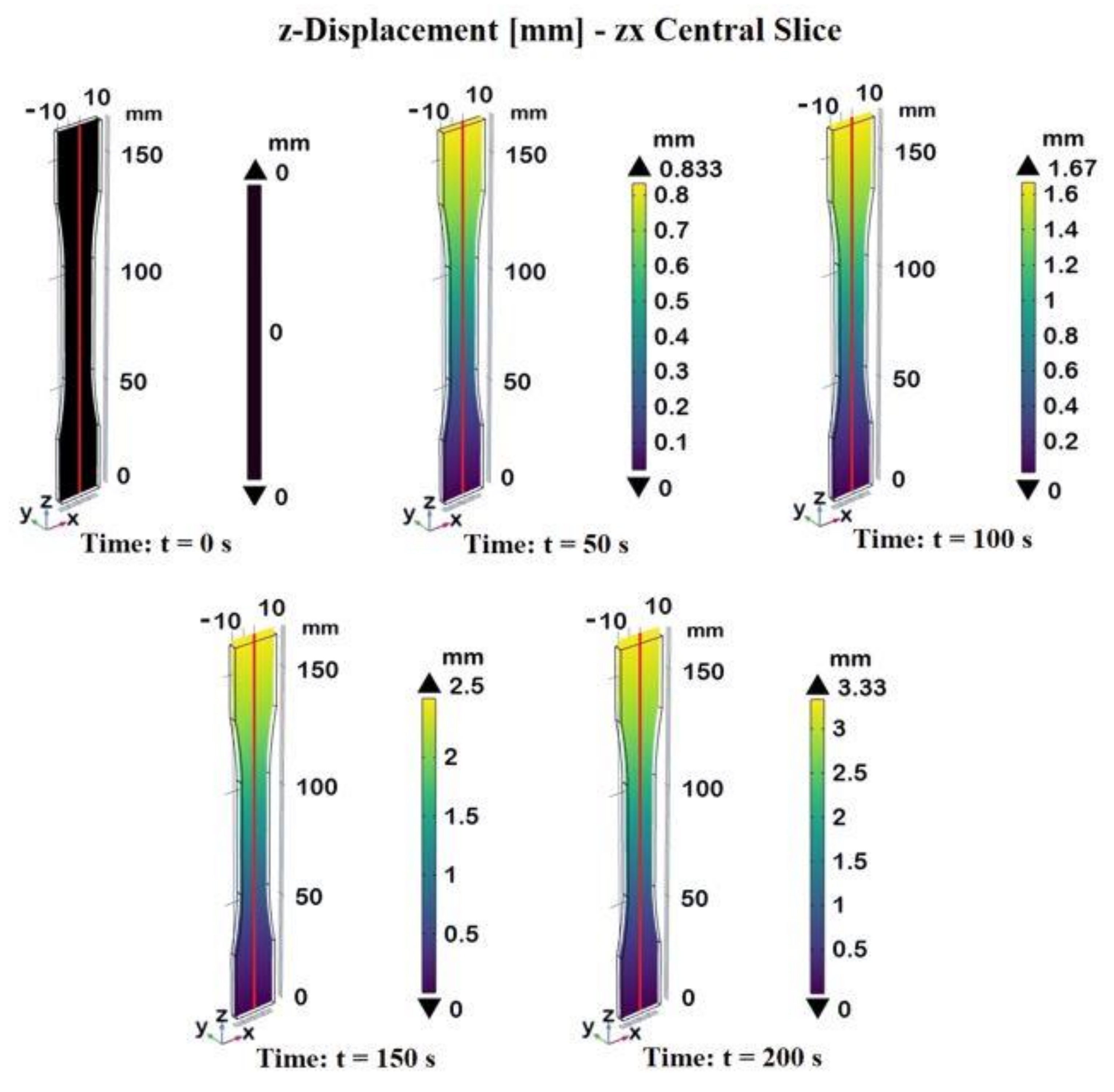
Preprints 110697 g010
Preprints 110697 g011
Figure 11. Von Mises stress profiles versus the dogbone length along the z-axis of symmetry.
Figure 11. Von Mises stress profiles versus the dogbone length along the z-axis of symmetry.
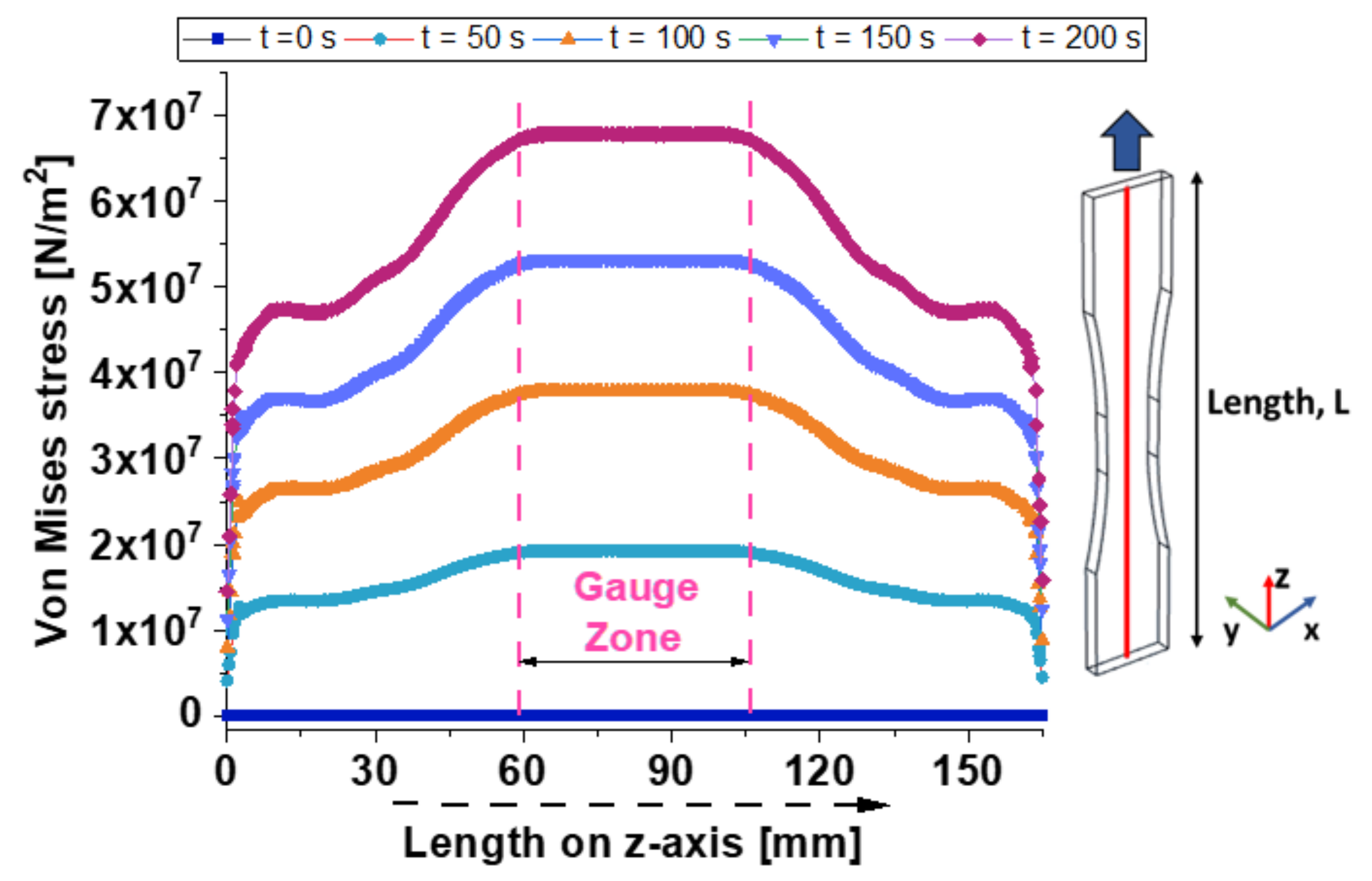
Preprints 110697 g011
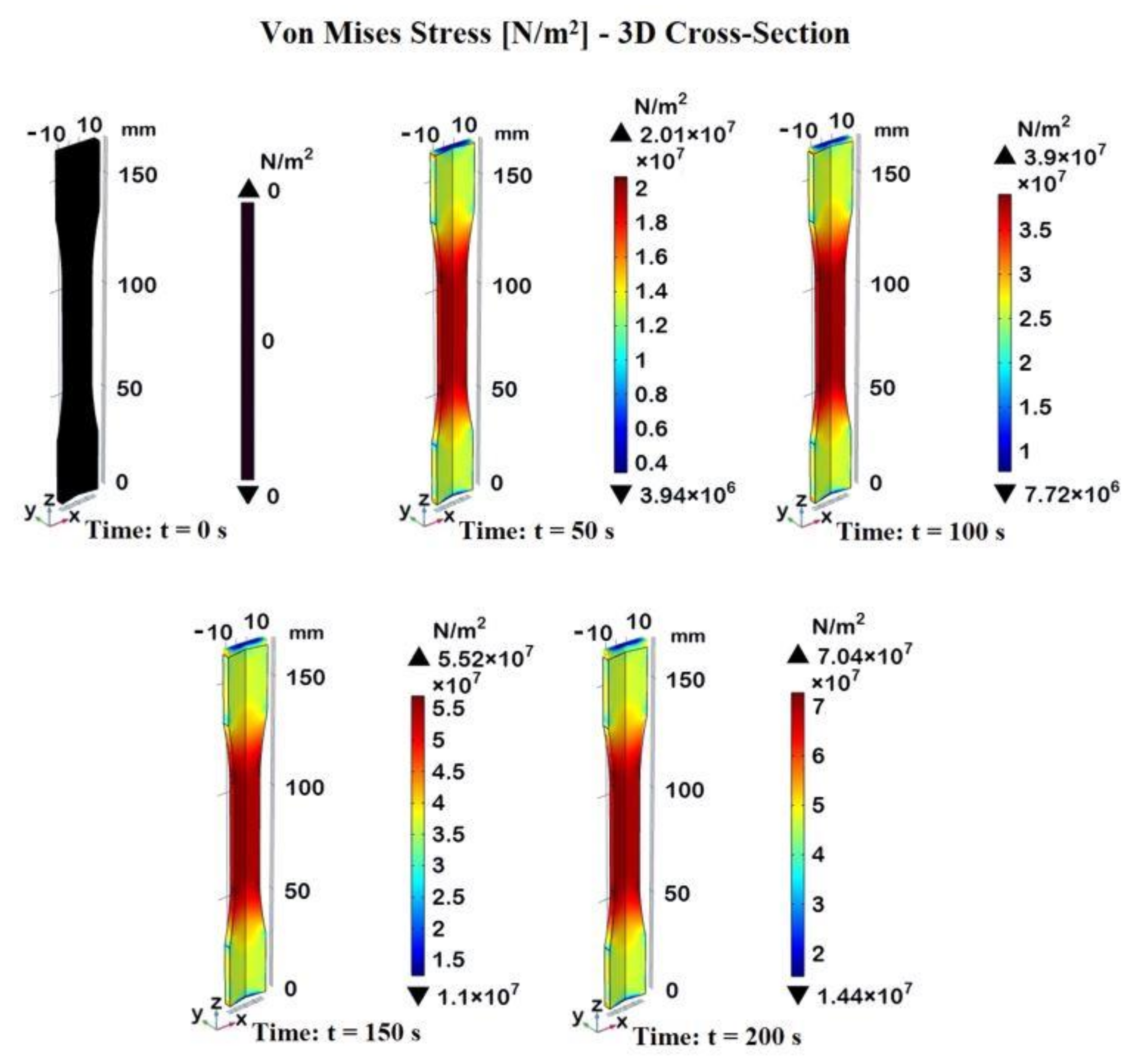
Preprints 110697 g012
Figure 12. Von Mises stress profiles (3D cross-sections) versus the dogbone’ s length. The profile along the symmetry axis in the z-direction is clearly visible.
Figure 12. Von Mises stress profiles (3D cross-sections) versus the dogbone’ s length. The profile along the symmetry axis in the z-direction is clearly visible.
Preprints 110697 g012
Preprints 110697 g013
Figure 13. Temperature distribution in the dogbone sample at different time instants corresponding to different strain levels.
Figure 13. Temperature distribution in the dogbone sample at different time instants corresponding to different strain levels.
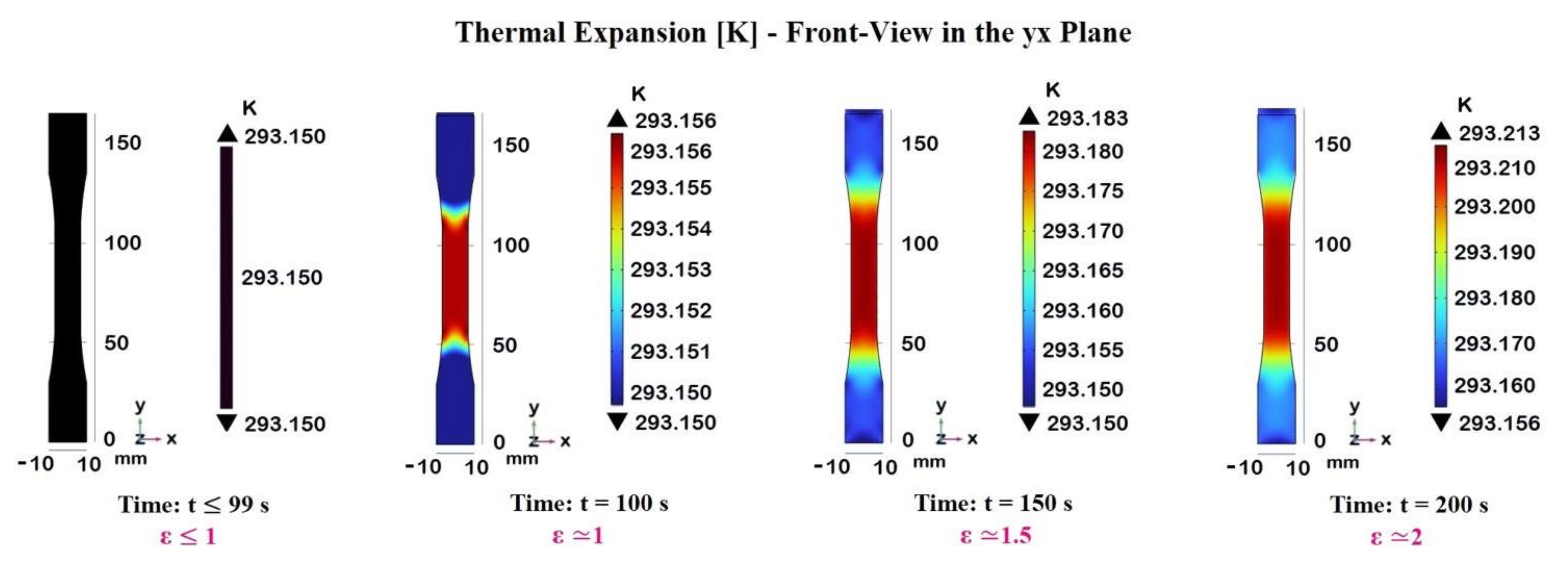
Preprints 110697 g013
Preprints 110697 g014
Figure 14. Thermal expansion in the dogbone sample for different cross-head speeds.
Figure 14. Thermal expansion in the dogbone sample for different cross-head speeds.
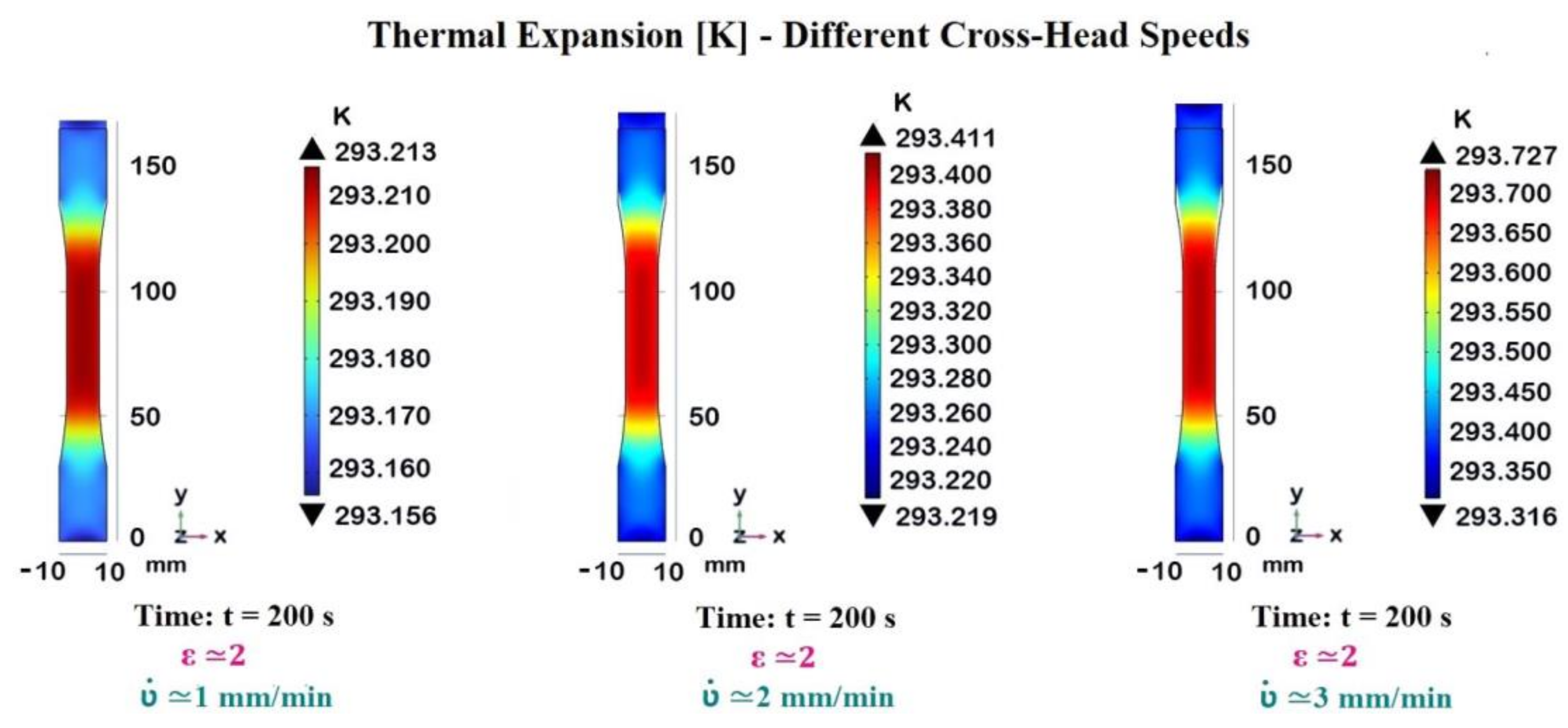
Preprints 110697 g014
Preprints 110697 g015
Figure 15. Temperature as function of the cross-head speed.
Figure 15. Temperature as function of the cross-head speed.
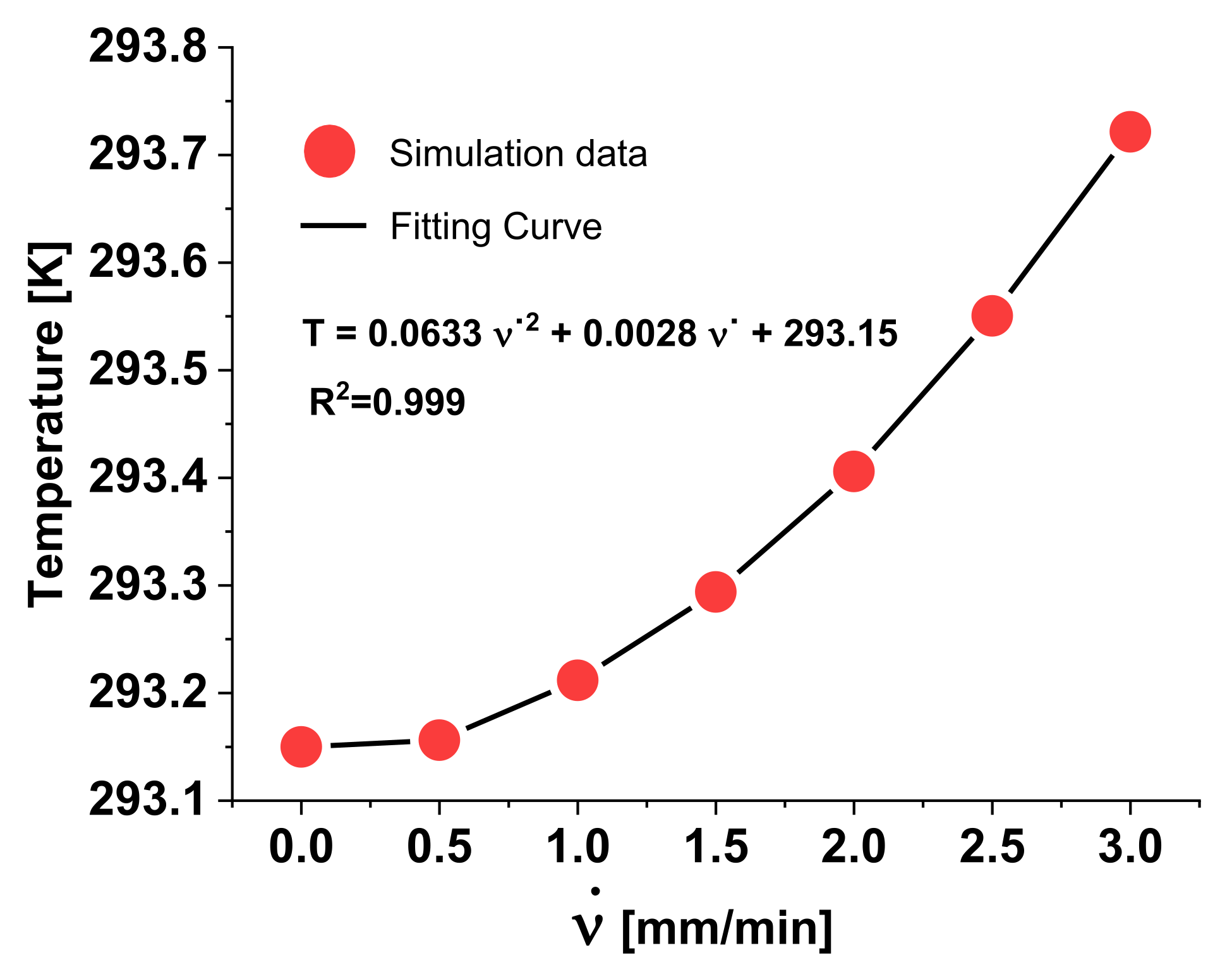
Preprints 110697 g015
Preprints 110697 g016
Figure 16. Plastic dissipation energy (average value) over the time.
Figure 16. Plastic dissipation energy (average value) over the time.
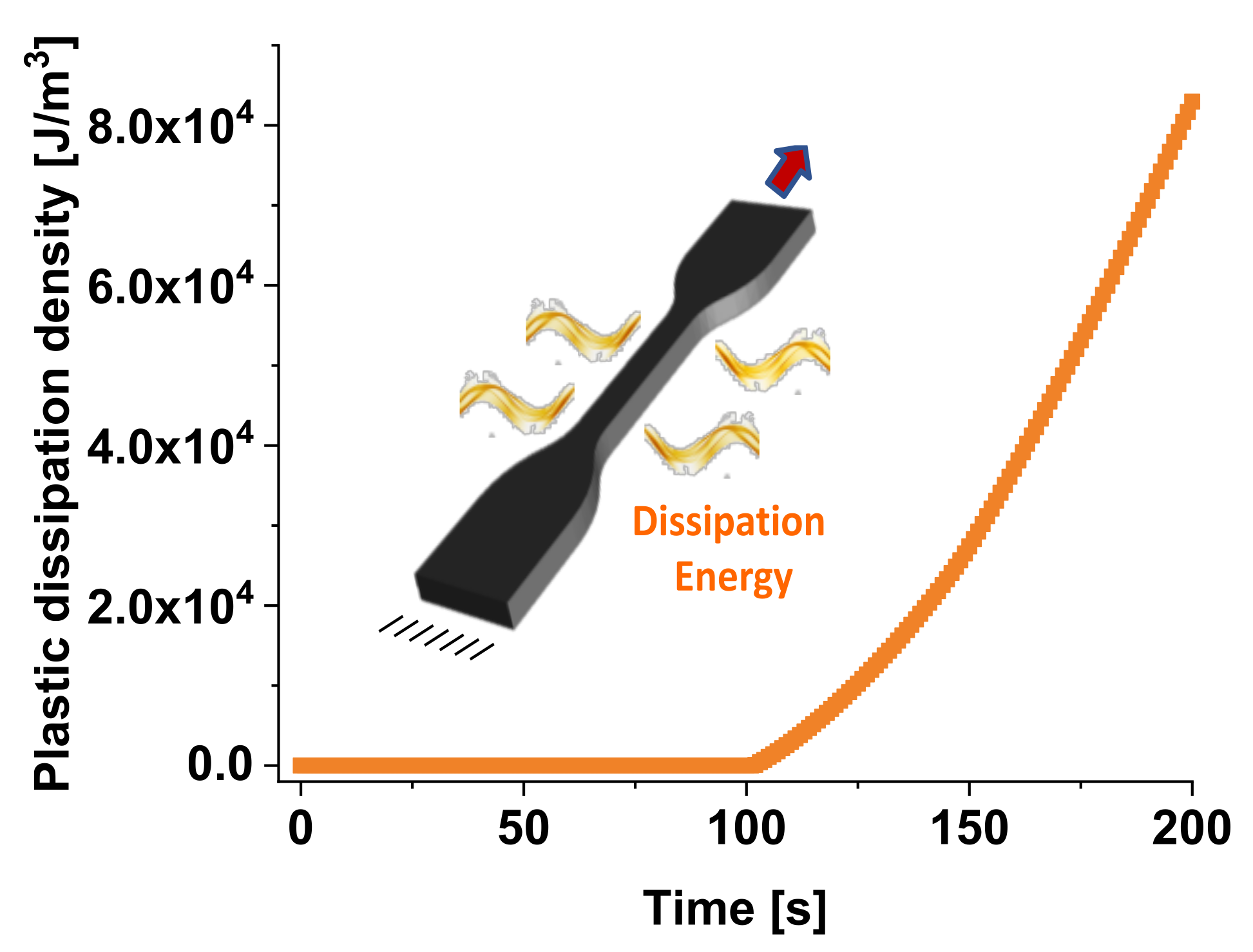
Preprints 110697 g016
Preprints 110697 g017
Figure 17. 3D-views of plastic dissipation density at different time instants/strain levels.
Figure 17. 3D-views of plastic dissipation density at different time instants/strain levels.
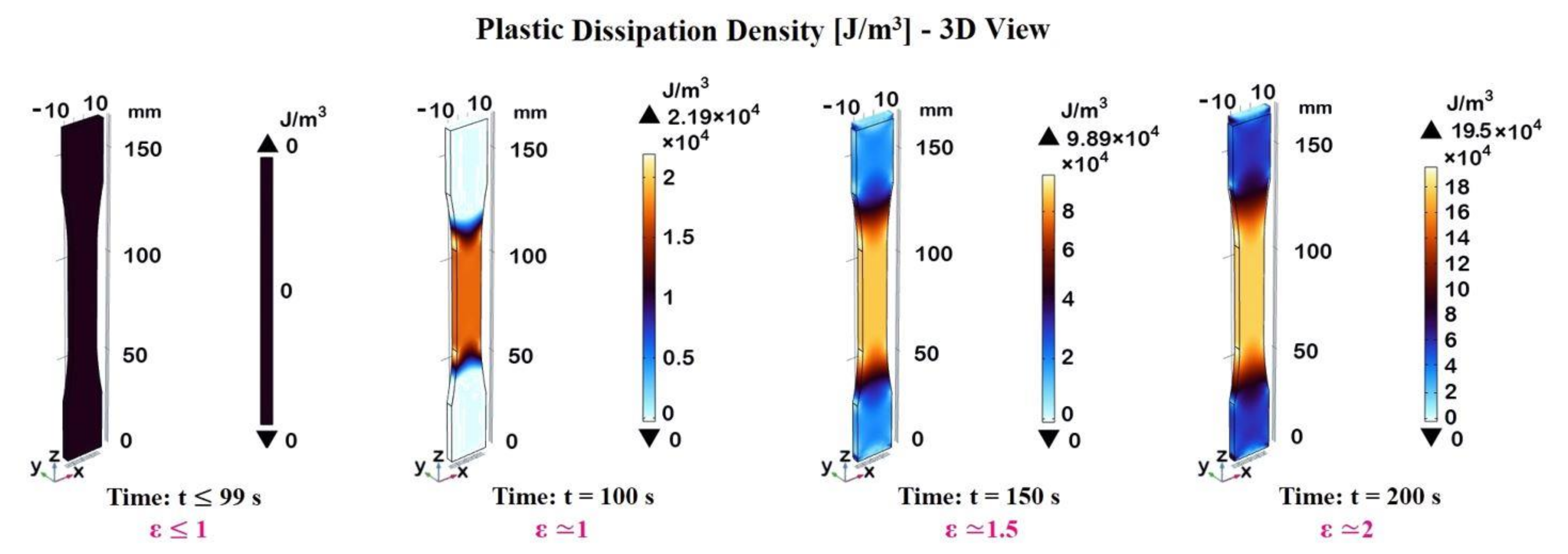
Preprints 110697 g017
Preprints 110697 g018
Figure 18. a) Temperature patterns resulting from Joule heating at various applied voltage levels (from 70V up to 90 V); b) timeframe zoom of transient heat transfer for determining the heat-rates for each voltage value.
Figure 18. a) Temperature patterns resulting from Joule heating at various applied voltage levels (from 70V up to 90 V); b) timeframe zoom of transient heat transfer for determining the heat-rates for each voltage value.
Preprints 110697 g018
Preprints 110697 g019
Figure 19. Experimental data and corresponding curve fitting of the temperature values recorded at t=3600s and heat rate as a function of the voltage levels in right and left axis, respectively.
Figure 19. Experimental data and corresponding curve fitting of the temperature values recorded at t=3600s and heat rate as a function of the voltage levels in right and left axis, respectively.
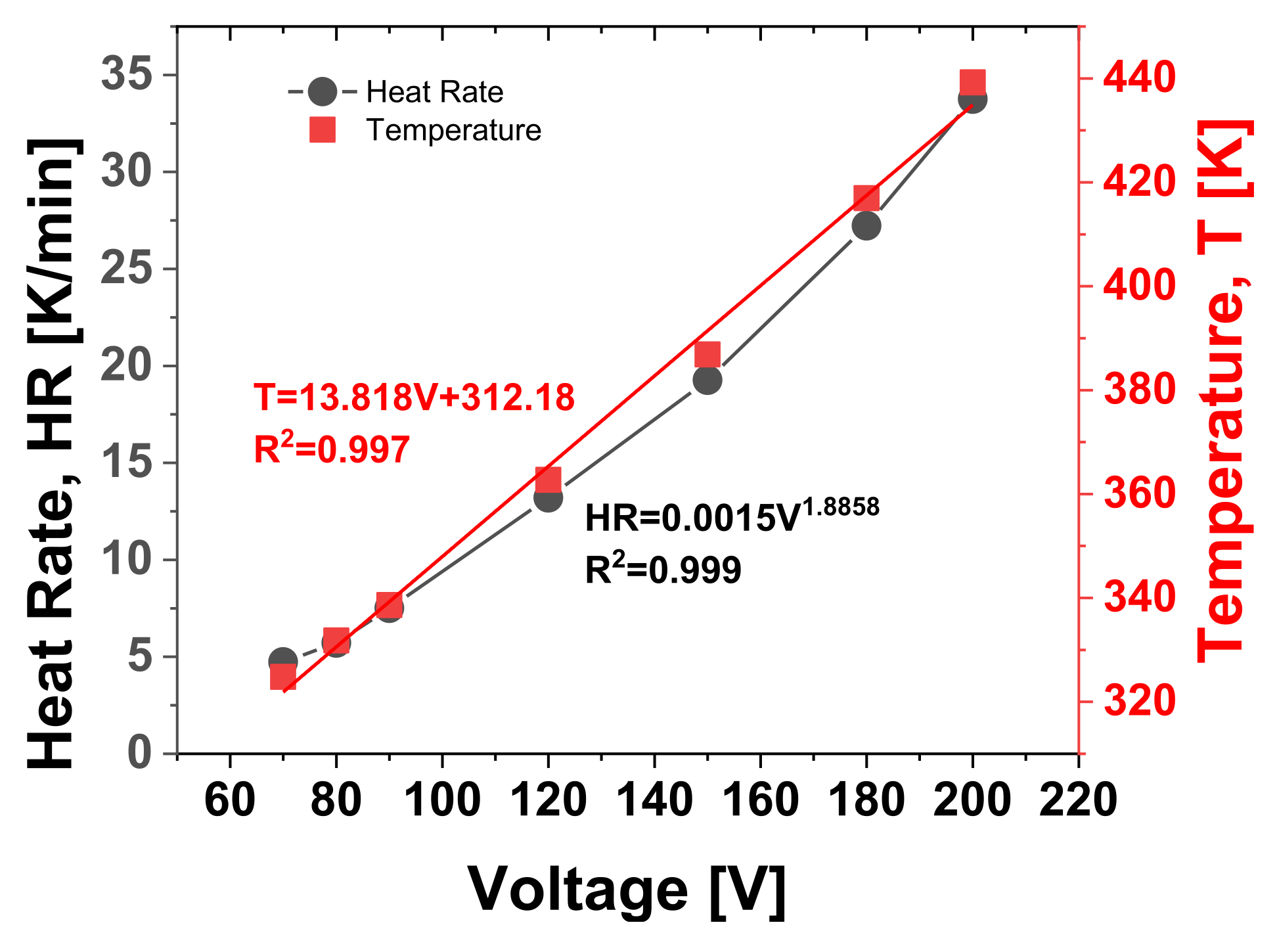
Preprints 110697 g019
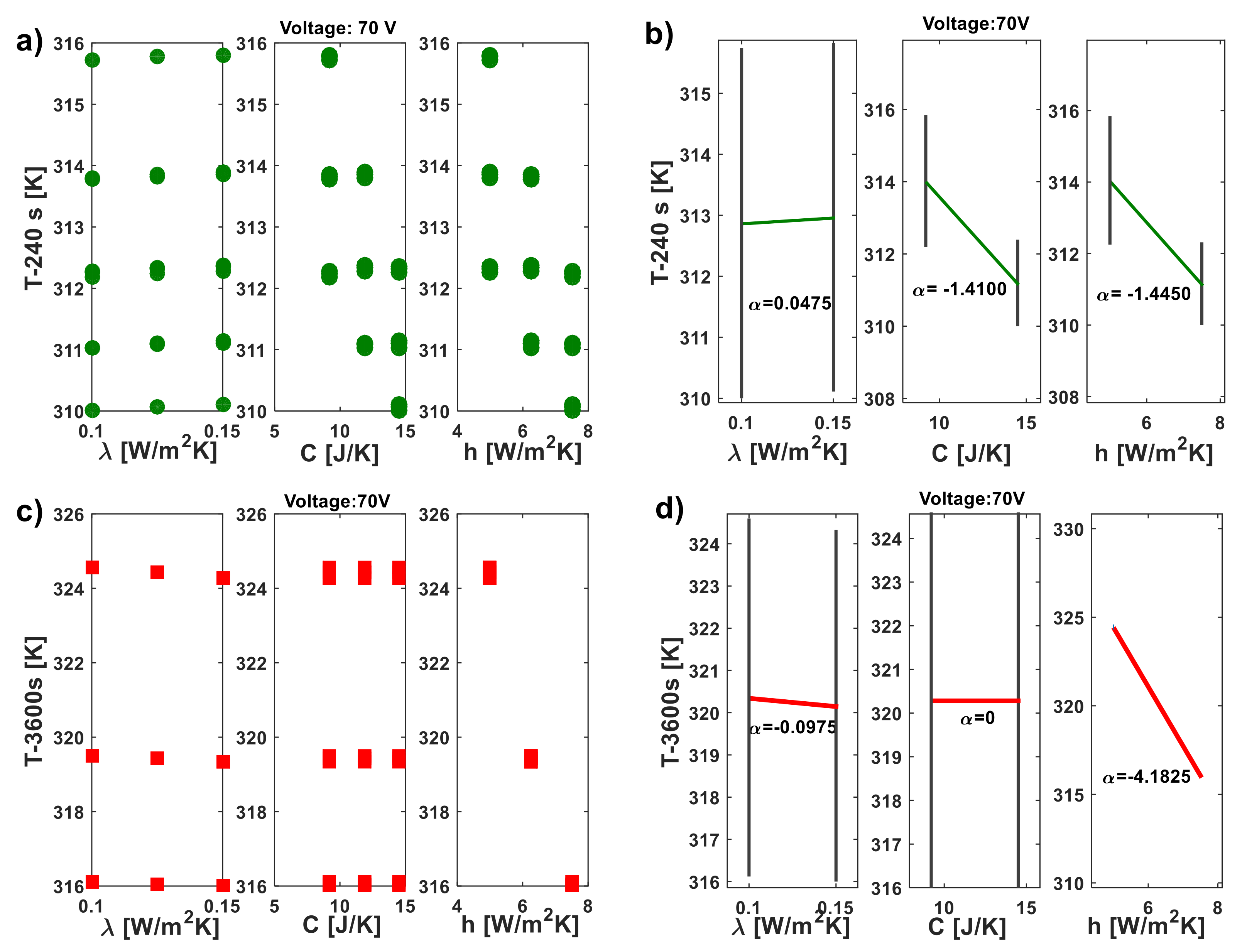
Preprints 110697 g020
Figure 20. DSP and MfP for the upper surface temperature related to sample powered with 70 V. More specifically: a) DSP at 240 s; b) MfP at t=240 s; c) DSP at 3600 s; d) MfP at t=3600 s, respectively.
Figure 20. DSP and MfP for the upper surface temperature related to sample powered with 70 V. More specifically: a) DSP at 240 s; b) MfP at t=240 s; c) DSP at 3600 s; d) MfP at t=3600 s, respectively.
Preprints 110697 g020
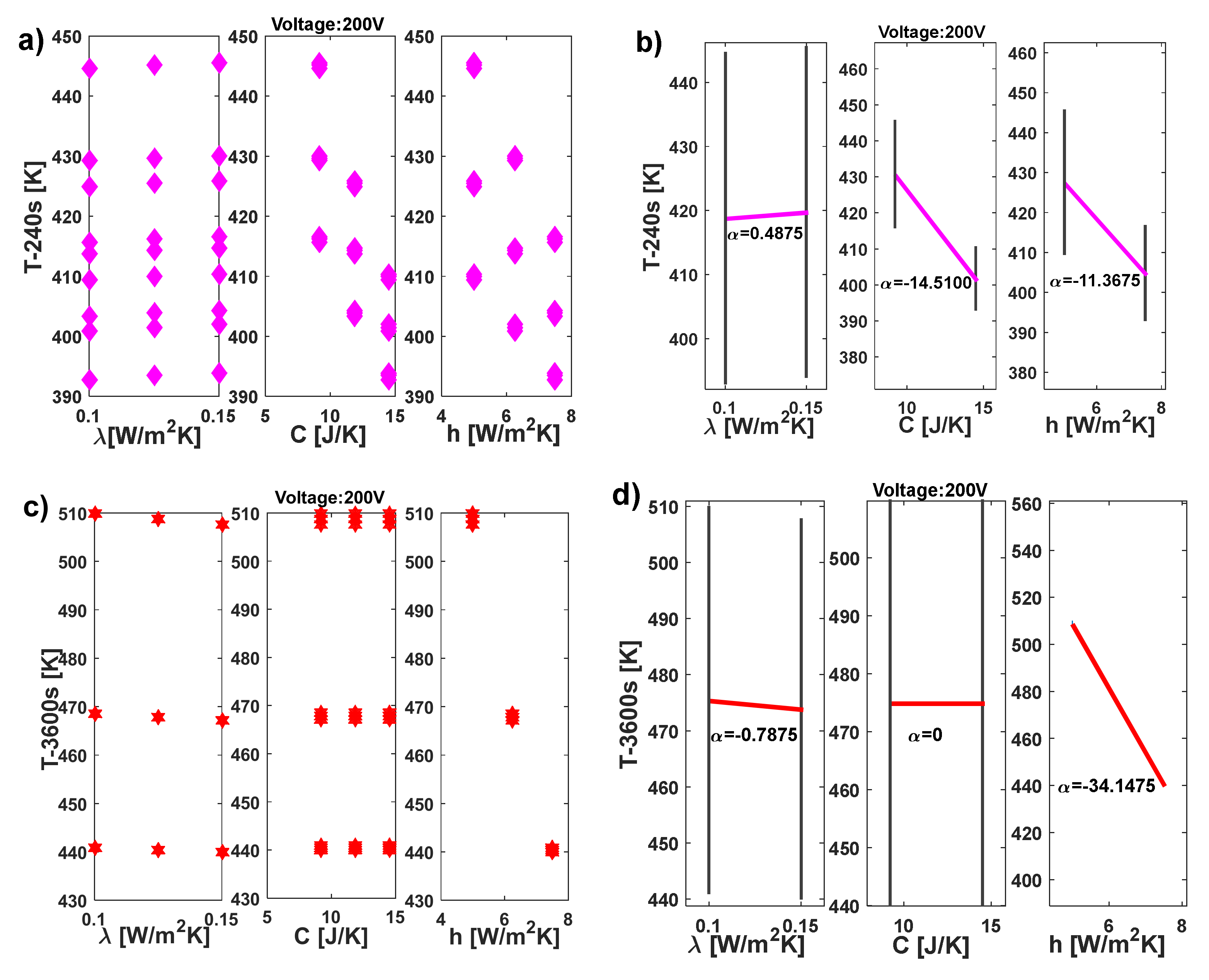
Preprints 110697 g021
Figure 21. DSP and MfP for the upper surface temperature related to sample powered with 200 V. More specifically: a) DSP at 240 s; b) MfP at t=240 s; c) DSP at 3600 s; d) MfP at t=3600 s, respectively.
Figure 21. DSP and MfP for the upper surface temperature related to sample powered with 200 V. More specifically: a) DSP at 240 s; b) MfP at t=240 s; c) DSP at 3600 s; d) MfP at t=3600 s, respectively.
Preprints 110697 g021
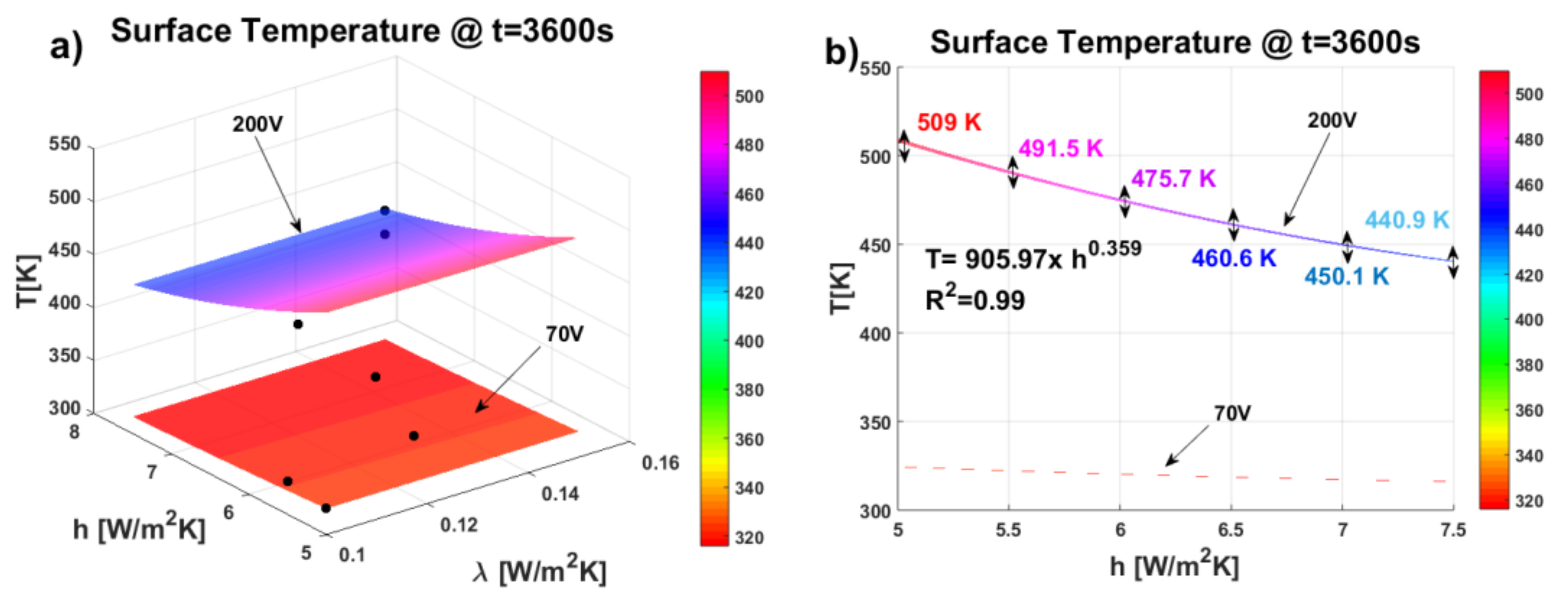
Preprints 110697 g022
Figure 22. a) 3D response surface graphics (full quadratic model) for the temperature depending on thermal conductivity and heat exchange coefficient. The black markers represent the experimental thermal data; b) 2D-view of the interpolating surfaces as a function of the exclusive heat exchange coefficient.
Figure 22. a) 3D response surface graphics (full quadratic model) for the temperature depending on thermal conductivity and heat exchange coefficient. The black markers represent the experimental thermal data; b) 2D-view of the interpolating surfaces as a function of the exclusive heat exchange coefficient.
Preprints 110697 g022
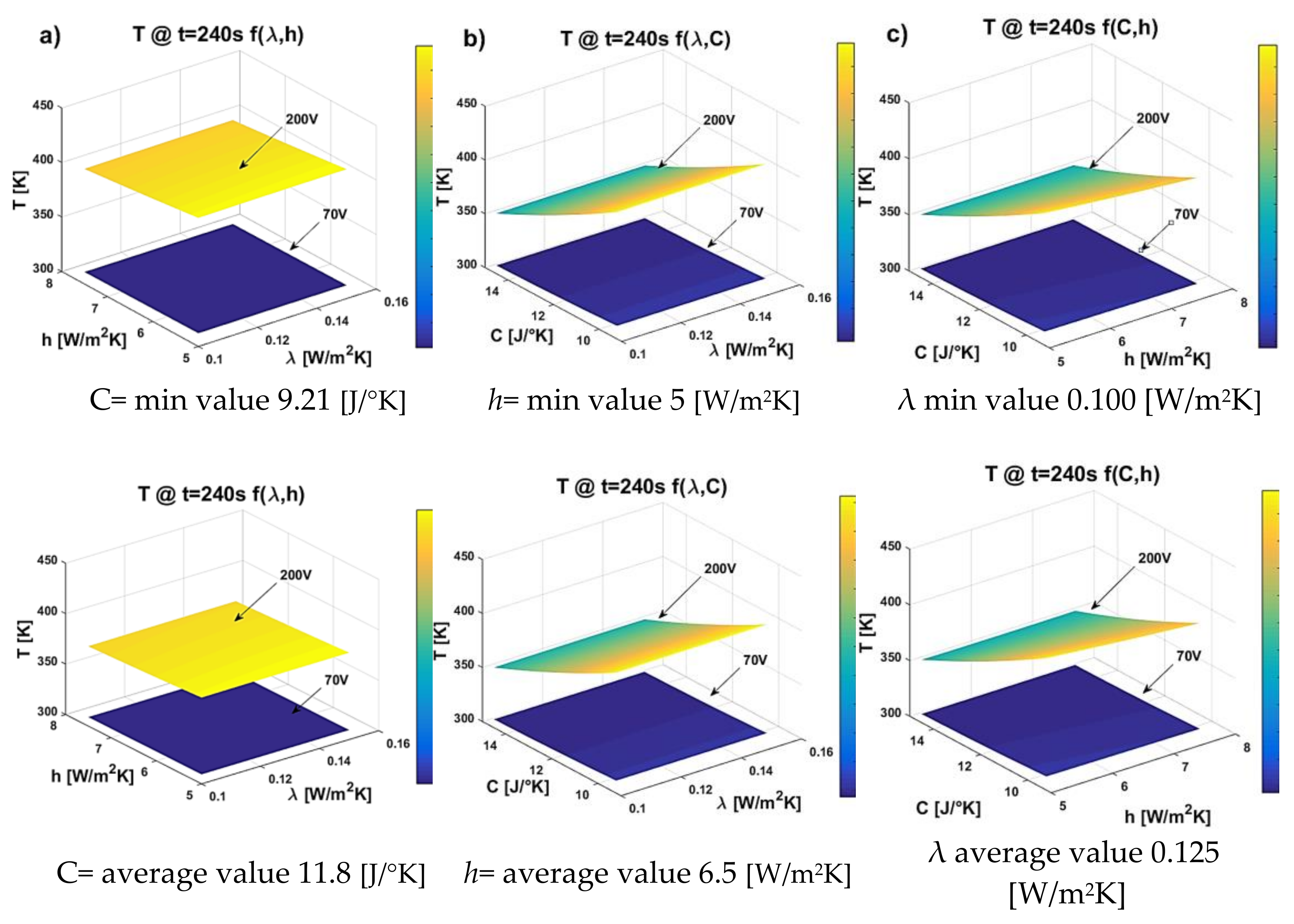
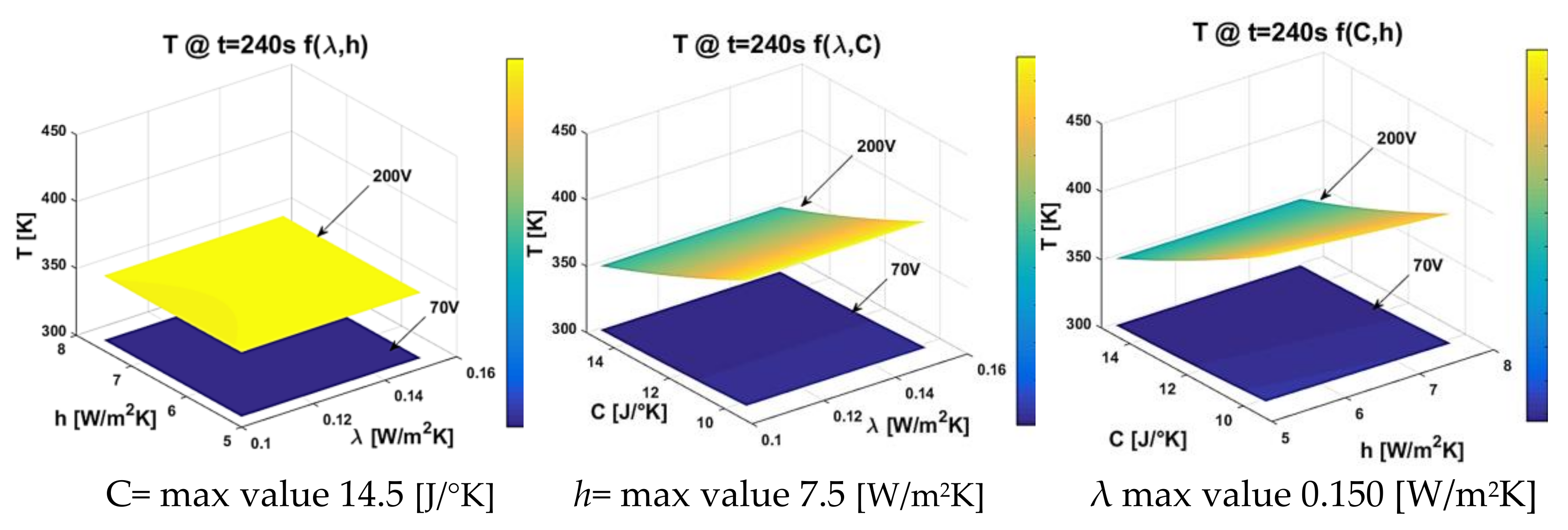
Preprints 110697 g023aPreprints 110697 g023b
Figure 23. Response surface graphics presenting the effect of the three thermal factors on the surface temperature value recorded at the time instance of 240 s: a) effect of thermal conductivity and heat transfer coefficient, b) effect of thermal conductivity and thermal capacity and c) effect of heat transfer coefficient and thermal capacity. In each plot, the unconsidered factor was held constant to its minimum, average and maximum value (first, second and third row, respectively).
Figure 23. Response surface graphics presenting the effect of the three thermal factors on the surface temperature value recorded at the time instance of 240 s: a) effect of thermal conductivity and heat transfer coefficient, b) effect of thermal conductivity and thermal capacity and c) effect of heat transfer coefficient and thermal capacity. In each plot, the unconsidered factor was held constant to its minimum, average and maximum value (first, second and third row, respectively).
Preprints 110697 g023aPreprints 110697 g023b
Preprints 110697 g024
Figure 24. Simulation fitting for the temperature patterns for each applied voltage value.
Figure 24. Simulation fitting for the temperature patterns for each applied voltage value.
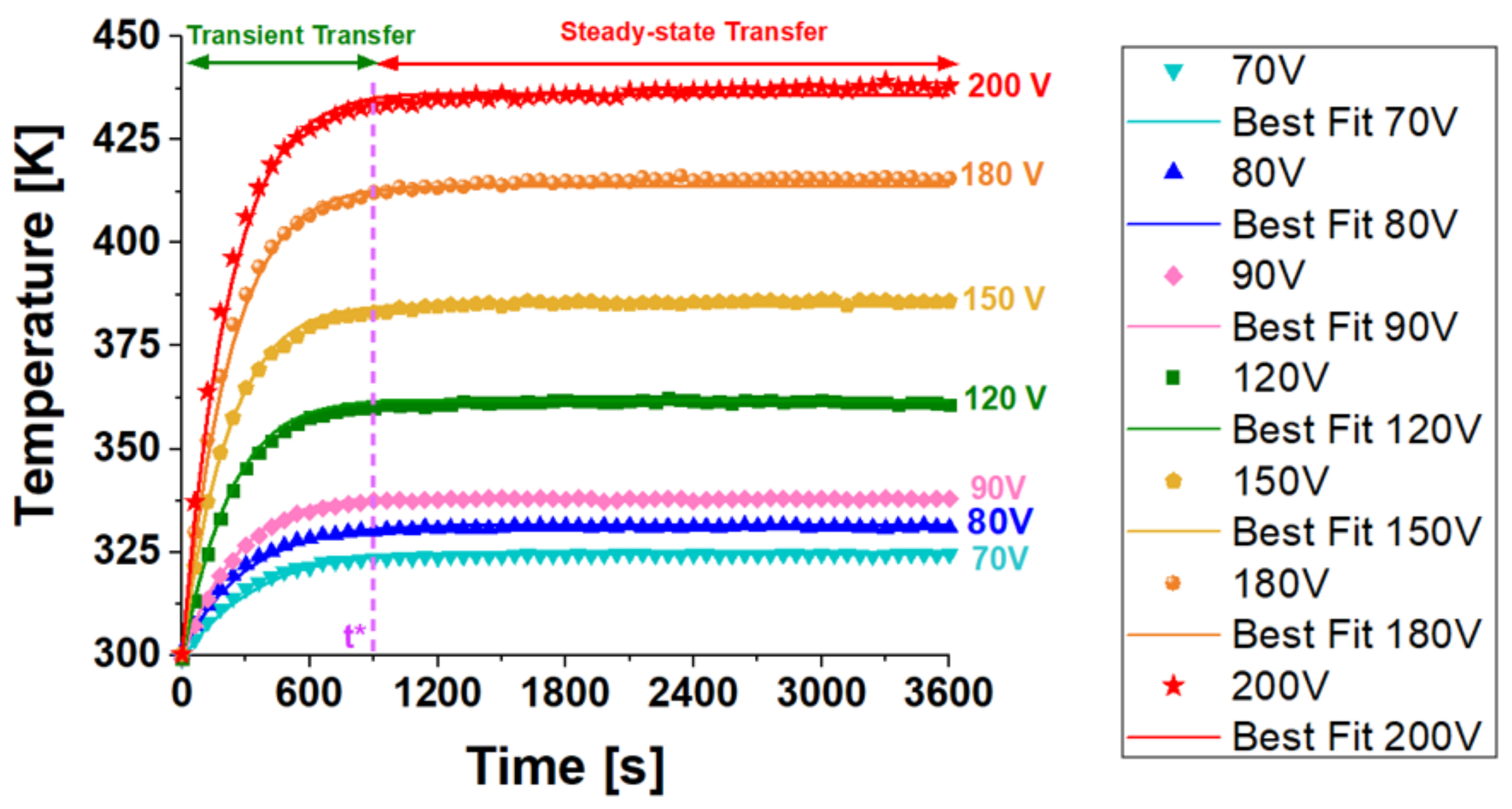
Preprints 110697 g024
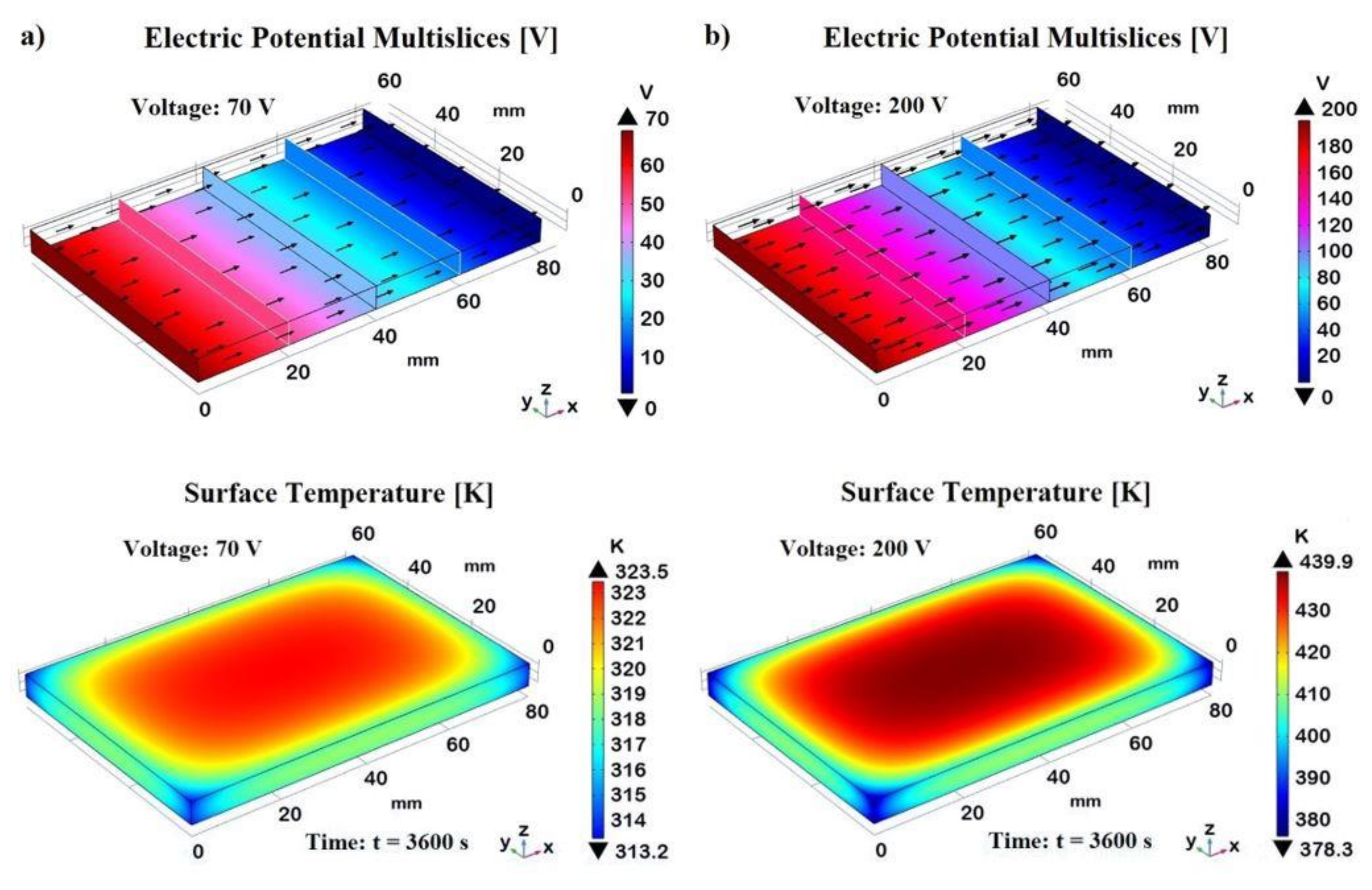
Preprints 110697 g025
Figure 25. Electric potential distributions (first row) along the x-axis direction to which the two voltage (70V and 200V, in a), and b), respectively) are applied. The second row reports the 3D views of the corresponding surface temperature (evaluated at steady-state condition, t= 3600s) due to the Joule effect.
Figure 25. Electric potential distributions (first row) along the x-axis direction to which the two voltage (70V and 200V, in a), and b), respectively) are applied. The second row reports the 3D views of the corresponding surface temperature (evaluated at steady-state condition, t= 3600s) due to the Joule effect.
Preprints 110697 g025
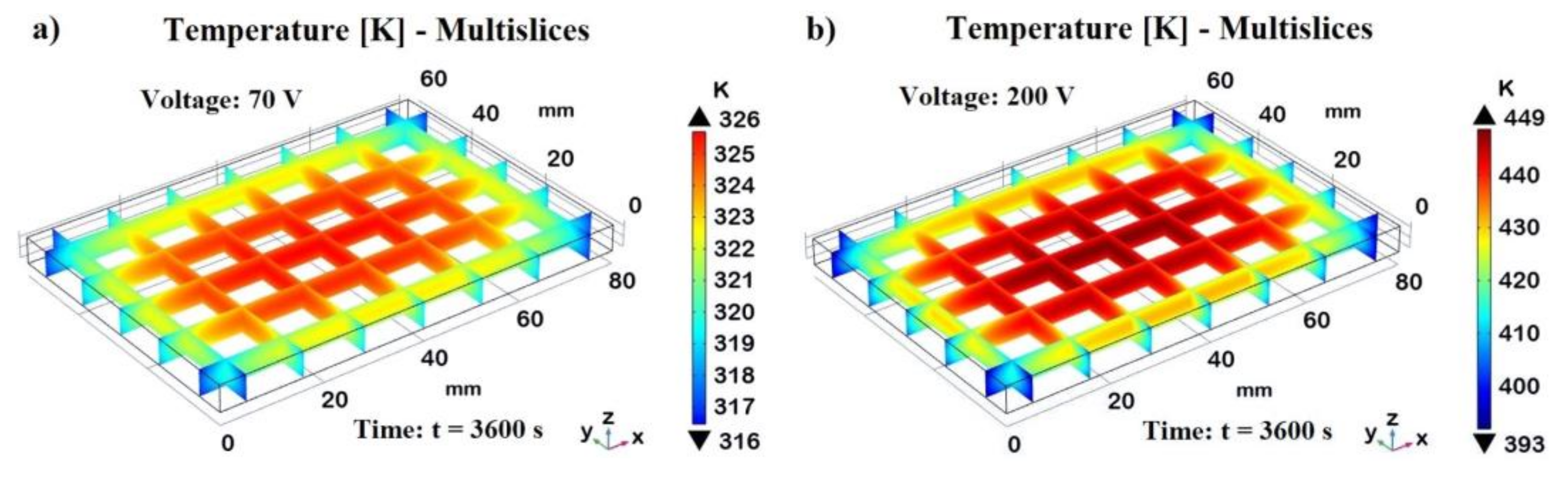
Preprints 110697 g026
Figure 26. Multislices temperature distribution (evaluated at steady-state condition, t= 3600s) due to the Joule effect for sample powered with 70V in a) e 200V in b).
Figure 26. Multislices temperature distribution (evaluated at steady-state condition, t= 3600s) due to the Joule effect for sample powered with 70V in a) e 200V in b).
Preprints 110697 g026
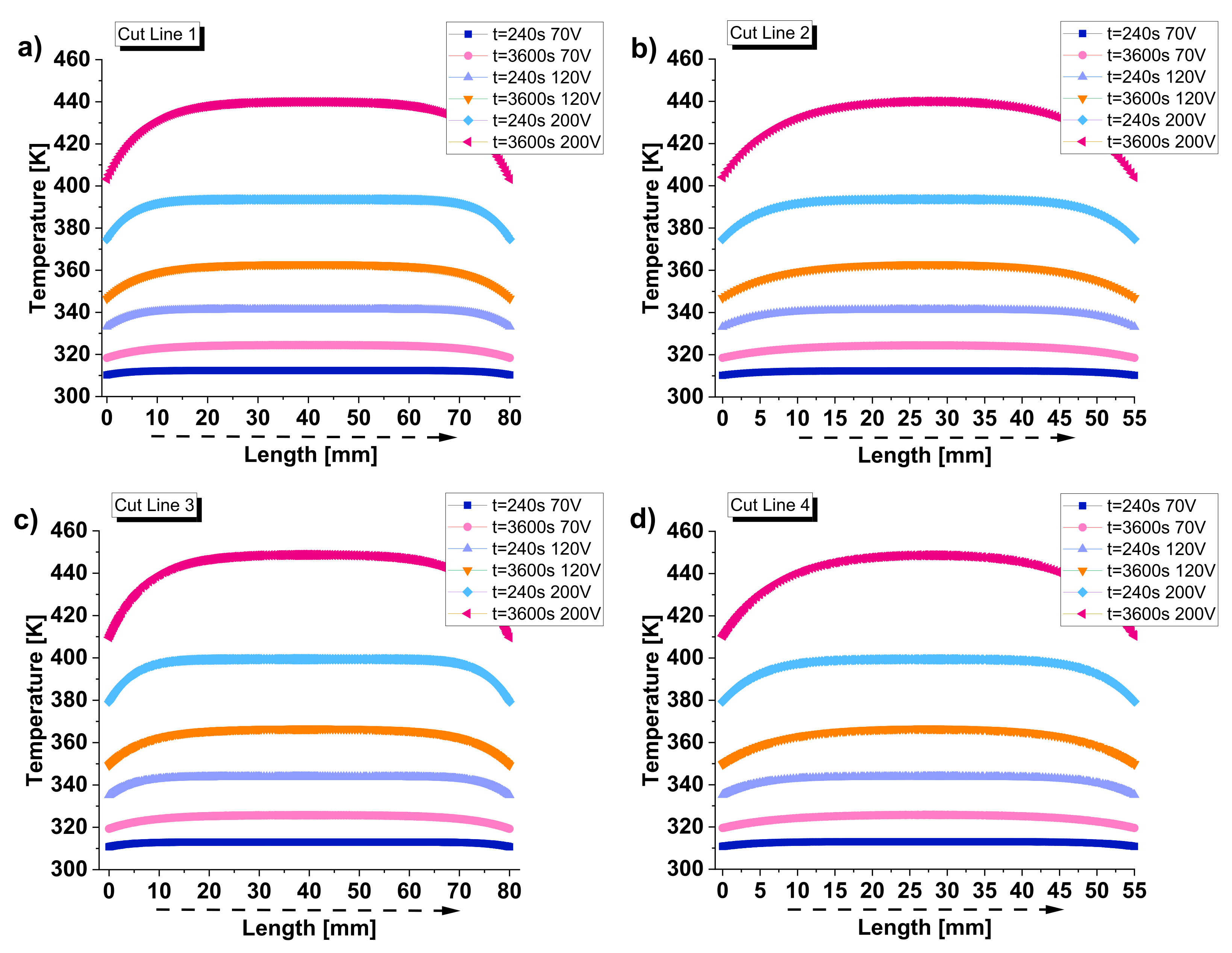
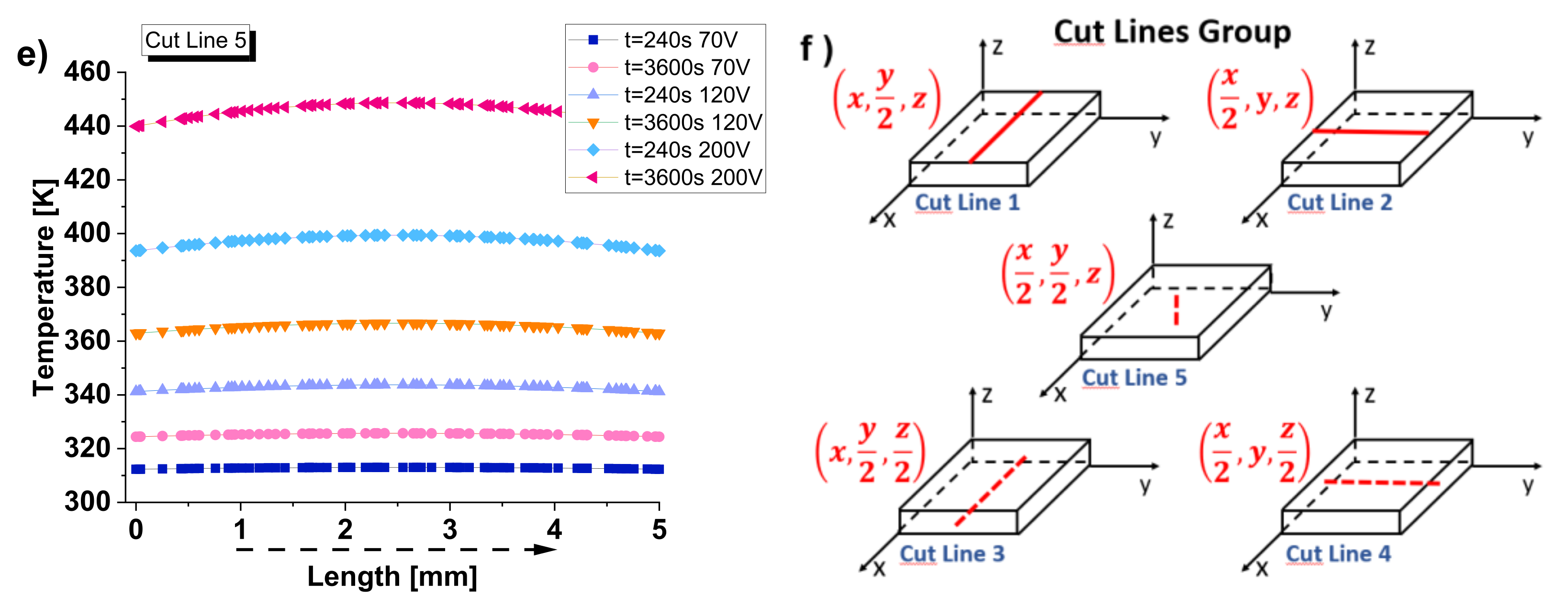
Preprints 110697 g027aPreprints 110697 g027b
Figure 27. Temperature distribution along different spatial profiles: a) cut line 1; b) cut line 2; c) cut line 3; d) cut line 5. The cut lines collection is schematized in f).
Figure 27. Temperature distribution along different spatial profiles: a) cut line 1; b) cut line 2; c) cut line 3; d) cut line 5. The cut lines collection is schematized in f).
Preprints 110697 g027aPreprints 110697 g027b
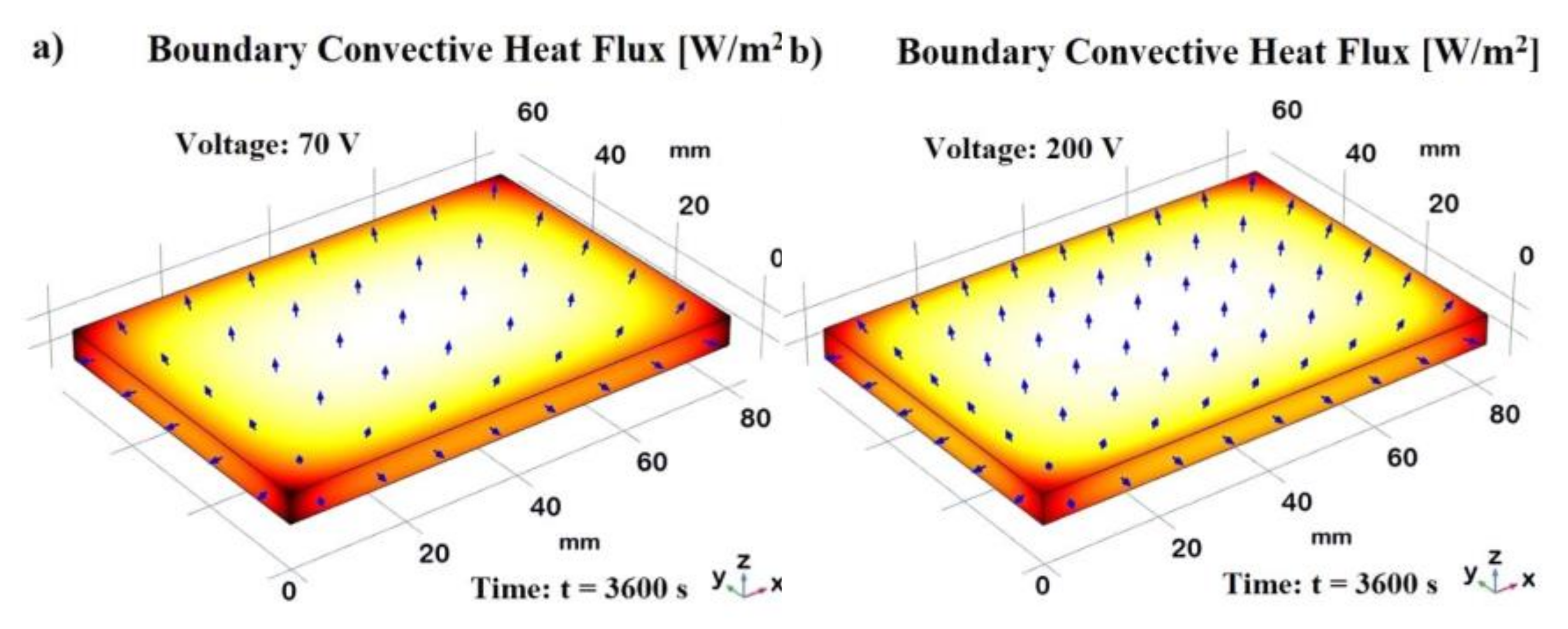
Preprints 110697 g028
Figure 28. Comparison of the convective flux at t=3600s in case of applied voltage of 70 and 200V in a) and b), respectively.
Figure 28. Comparison of the convective flux at t=3600s in case of applied voltage of 70 and 200V in a) and b), respectively.
Preprints 110697 g028
Table 1. Initial (I.C.) and boundary conditions (B.C.) for computing the eq. 1.
Table 1. Initial (I.C.) and boundary conditions (B.C.) for computing the eq. 1.
I.C. and B.C. conditions Equations Applicability
I. C. t=0 T=Room Temperature (T0) ∀ x , ∀ y , ∀ z
B. C. Top and Down Surfaces − λ ∂ T ∂ z = h ​∙ T − T ∞ ( ∀ x , ∀ y , t > 0 )
B. C. Lateral Surfaces − λ ∂ T ∂ y = h ​∙ T − T ∞ ( ∀ x , ∀ z , t > 0 )
B. C. Front and Back Surfaces − λ ∂ T ∂ x = h ​∙ T − T ∞   ( ∀ y , ∀ z , t > 0 )
Table 2. Thermal and electrical experimental data determined for each voltage value.
Table 2. Thermal and electrical experimental data determined for each voltage value.
70 Volt 80 Volt 90 Volt 120 Volt 150 Volt 180 Volt 200 Volt
Power [W] 1.15 1.40 1.89 3.37 5.26 7.57 9.35
T-3600s [K] 324.8 331.8 338.6 362.7 386.9 416.9 439.2
HR [K/min] 4.7 5.7 7.5 13.2 19.3 27.2 33.8
Table 3. Slope values for the thermal parameters λ, C and h.
Table 3. Slope values for the thermal parameters λ, C and h.
λ C h
α (T-240 s 70V) 0.0475 -1.4100 -1.4450
α (T-3600 s 70V) -0.0975 0 -4.1825
α (T-240 s 200V) 0.4875 -14.5100 -11.3675
α (T-3600 s 200V) -0.7875 0 -34.1475
Table 4. Coefficients for the quadratic response of the upper surface temperature as determined by RSM.
Table 4. Coefficients for the quadratic response of the upper surface temperature as determined by RSM.
Coefficient β0 β1 β2 β3 β11 β22 β33 β12 β13 β23
T-240s –70V +338.478 +5.560 -1.585 -3.368 -19.555 +0.018 +0.086 +0.100 -5.978x10-13 +0.097
T-3600s –70V +817.118 -91.299 0 -82.011 -2.666 0 +4.277 0 +9.839 0
T-240s –200V +640.033 +57.822 -16.136 -23.972 -174.222 +0.202 +0.321 +0.592 -0.320 +0.321
T-3600s–200V +362.323 -11.966 0 -10.068 +2.666 0 +0.5258 0 +1.199 0
Table 5. Thermal parameters for the simulation fitting.
Table 5. Thermal parameters for the simulation fitting.
70 Volt 80 Volt 90 Volt 120 Volt 150 Volt 180 Volt 200 Volt
C [J/°K] 14.5 14.5 9.21 11.8 11.8 14.5 14.5
Λ [W/m2K] 0.100 0.100 0.100 0.125 0.125 0.125 0.150
h [W/m2K] 5 5.5 5 6 7 7.5 7.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated