Prerpints.org logo
Preprint
Article

Nonturbulent troposphere of Supper Lorentz Gaussian Seed ‎Mathematically of Receiver Field and Intensity Fluctuation

Altmetrics

Downloads

62

Views

22

Comments

0

This version is not peer-reviewed

Submitted:

27 June 2024

Posted:

01 July 2024

You are already at the latest version

Alerts
Abstract
In recent studies, the circulation of a (SLG) super-Lorentz-Gaussian beam in a non-turbulent ‎troposphere has been investigated and used for laser applications. This method uses the extended ‎Huygens-Fresnel integral technique and refers to the multiplication of the Gaussian beam by the ‎Lorentz function. Formulas are derived for the normal density and approximate field of the Lo-‎Rentz-Gaussian beam in a non-turbulent troposphere. The average density power and the propagation characteristics of the SLG jet in the non-turbulent troposphere are numerically represented. ‎The characteristics of the beam boundaries at atmospheric non-turbulence for the propagation ‎distance of an SLG beam in a non-turbulent troposphere are also discussed in detail. They are ‎practical in an optical communication system used in lasers.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

In modern studies, the propagation of SLG in FSO is the understanding of the nature of ray propagation such as intensity, scintillation index, source size, and many factors that can be calculated and analyzed, the sharp dispersion of a Lorentz-Gaussian delivery is a higher order than that of a Gaussian ray propagation. As a result, Lorentz-Gaussian beams have been used as long as with more appropriate reproductions G(Gaussian) and to explain the propagation of SLG in (FSO) free-space optics [1], also to illustrate the digital phase shifter and its application in communication circuits for design and comparison with Gaussian propagation in FSO [2]. In addition, the oblique propagation of the Gaussian laser in a turbulent atmosphere was investigated and the Huygens-Fresnel integration process was studied [3]. In other words, the static model of ITU-R turbulence construction was applied and the mean SLVGB intensity was calculated in the oblique beam propagation at different perpendicular distances [4], which corresponds to the mean aperture receiver. We once checked the parameters such as the source size factor that affect the energy propagation profile. In addition, the analysis showed that the mean aperture is inflated with increasing distance of the scattering length [5]. In addition, the study of paraxial propagation in the tropospheric layer according to the width of the beam and the size of the source of the initial profile spread over space, also the structure of constant parameters that explain the wave prefiltration by using SLG beam Kolmogorov [6,7,8] free space, the paraxial propagation of Lorentz was studied such as Lorentz Gauss beams [9]. The factorial formulations of the Lorentz function and the long-range Lorentz beam were unanimously confirmed [10,11]. Moreover, the long-range propagation of the Gaussian beam, although the fractional Fourier transform was trained to the accuracy of Lorentz [12]. To numerically explore the focal oscillation, the Lorentz-Gaussian beam occupied by the pinhole lens structure was derived [13]. In addition, the second-order beam propagation for Lorentz or Lorentz-Gauss beam effects was investigated as described in [14,15]. the SLG beam was invented by using Lorentz beams as a basis in reference [16]. Due to these requirements in the area of remote detection and optical transport in free space, extensive studies on the propagation of different laser types in a turbulent atmosphere were also modified. [17,18,19,20,21,22,23]. Finally, in this paper, we use new modelling and apply the mathematical technique to improve the non-turbulent SLG on beam propagation and its application in optical communication systems.

2. Propagation of an SLG Jet in a Non-Turbulent Troposphere

The super-Lorentz G-beam in the transmitter plane at L = 0 revenue for the formulation, transmitter field of SLG illustrated in the Cartesian coordinate system, the L-axis is latched and the axis propagates as follows:
U a , b ( x t , y t ) = x t a 1 + x t 2 w l s x − 2 y t b 1 + y t 2 w l s y − 2 exp   − π λ ( w g x x t 2 + w g y y t 2 )
U a , b ( x t , y t ) denotes the transmission field of the SLG beam x t a , y t a is the oblique synchronised structure position on the source side, and, beam widths ( w l s x , w l s y ) that correspond to the parameters of SLG and λ are the wavelength of the SLG beam in the following, let us understand what we have understood by the beam according to Equation (2). If you set the beam order a, and b to 1, and 0, is likely that you will hit the vital beam and the original order of Supper LG beams. This has already been explained in this reference [3,6,24].
w g y = 0.5 π λ w g s y 2 + j F g y − 1 w g x = 0.5 π λ w g s x 2 + j F g x − 1
Wherever the beam widths of the Gaussian part w g s x , w g s y are denoted by their position and the focal length constant parameter F g x , F g y over the x and y directions [6,25], the next point in Equation (3) can be found. The limits of the C 2 p ( α ) constants with the quantity of α=1, are posted in a straight line from the organised standards in ref [26] and are Hermite polynomial H 2 p ( , ) . Notwithstanding the first impression that the overhead process might cause a theatrical increase in the sum of calculations as
x t a 1 + x t 2 w l s x − 2 = 2 − 0.5 x t i π 0.5 α − 1 ∑ n = 0 ∞ C 2 p ( α ) H 2 p x t ( α   w l s x ) − 1 exp   − 0.5 x t 2 ( α   w l s x ) − 2
Where Hermite polynomial H 2 p ( , ) , the field basis in equation (1) acts and presents the Huygens-Fresnel integral method in a nonturbulent atmosphere, moreover, L means the propagation distance between the transducer plane, the receiver field U a , b ( p , z ) evolves in a cartesian coordinate system which is studied in equation (4), [27]
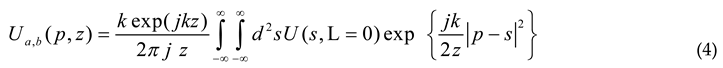
Preprints 110565 i001
For the update of the SLG beam via the formula of the extended Huygens-Fresnel integral for the start of the synchronization observed in Eq. (5). Our information is a little from Eq. (1) and Eq. (3, 4) given the new expression to follow in Eq. (5) follow and z = L .
U a , b ( p , z ) = k exp ( j k z ) j 2 π z ∫ − ∞ ∞ ∫ − ∞ ∞ d 2 s x t a 1 + x t 2 w l s x − 2 y t b 1 + y t 2 w l s y − 2 exp   − π λ ( w g x x t 2 + w g y y t 2 ) × exp   j k 2 z p − s 2    
To p − s 2 evaluate the expansion as shown in the equation (6) as shown
Preprints 110565 i002
The lower solution of this extension can be seen in equation (7)
p − s 2 = p x t 2 − 2 p x t s x t + s x t 2 + p y t 2 − 2 p y t s y t + s y t 2
By substitution, the above equations containing a number (3, 6, 7) are replaced in equation (8), resulting in a new equation that reads as follows
U a , b ( p , z ) = k exp ( j k z ) j 2 π z ∫ − ∞ ∞ ∫ − ∞ ∞ d s y t d s x t 2 − 0.5 s x t a π 0.5 1 α ∑ n = 0 ∞ C 2 p ( α ) H 2 p s x t α − 1 (   w l s x ) − 1 exp   − 0.5 s x t 2 ( α   w l s x ) − 2
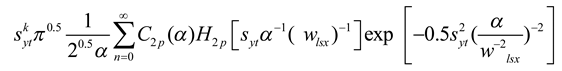
Preprints 110565 i005
exp   − π λ − 1 ( s x t 2 w − 1   g x + w g y s y t 2 ) exp   j k 2 z ( p x t 2 − 2 p x t s x t + s x t 2 + p y t 2 − 2 p y t s y t + s y t 2 )
Eq. (8) describes the receiver field and the determination of the subexpression by substituting Eq. (9) into Eq. (8). It has been observed that it can then be simplified into Eq. (8) as below
∑ n = 0 ∞ C 2 p ( α ) H 2 p s y t α ( w l s x ) − 1 = 1 4 ( 2 ) ! π ( − 1 ) 2 α w l s x 4 Γ ( 2 ) α 4 w l s x 4 − 2 Γ ( 1 ) α 3 w l s x 3
We have used approximate statements that solve equation (9a) as shown, but the Γ(.)refers to a gamma function, p is the ray order of the SLG ray, and now is the solution of equation (9) that appears in ref [24], first equation (9a), and erroneously the imitation exclusively of the synopsis, thus in refs [24,26] as obtained equations (9b, 9c, 9d) as below
f s y t α − 1 w l s x = ∑ n = 0 ∞ C p ( α ) H p s y t ( α w l s x ) − 1 − ∞ 〈 s y t α w l s x 〈 ∞
C p ( α ) = 1 2 n ( n ) ! π ∫ − ∞ ∞ exp − s y t α w l s x 2 f s y t α w l s x H p α − 1 s y t w l s x d s y t       p = 0,1,2,3,
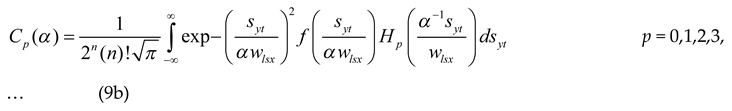
Preprints 110565 i003
We use equation (9c) and place the formulation (22.1.1) above it for the same thing to which it refers.
H p α − 1 s y t w l s x = ( − 1 ) n exp α − 1 s y t w l s x 2 d n d s y t   n exp − s y t α w l s x 2 p = 0 , 1 , 2 , 3 , 4.....
− ∞ 〈 s y t α w l s x 〈 ∞
We are about to engrave the equations via Eq.(9a,9b,9c). Moreover, the order of the original life is connected to the order of the equations, as you can see
f s y t α − 1 w l s x = ∑ n = 0 ∞ C 2 p ( α ) H 2 p s y t ( α w l s x ) − 1
C 2 p ( α ) = 2 − 2 p ( 2 n ) ! π ∫ − ∞ ∞ exp − s y t α w l s x 2 f s y t α w l s x H 2 p s y t α w l s x d s y t
H 2 p s y t α w l s x = ( − 1 ) 2 p exp α − 1 s y t w l s x 2 d 2 p d s y t   2 p exp − α − 1 s y t w l s x 2
To illustrate and replace equation (9f) with equation (9g), the results of these equations are then flattering, as shown below and converted as
C 2 p ( α ) = 1 2 2 p ( 2 p ) ! π ∫ − ∞ ∞ exp − α − 1 s y t w l s x 2 s y t α w l s x ( − 1 ) 2 p exp s y t α w l s x 2 d 2 p d s y t   2 p exp − α − 1 s y t w l s x 2 d s y t
We obtain equation (9h) by subtracting the variable constant from equation (9g) as traces
C 2 p ( α ) = 1 2 2 p ( 2 p ) ! π ( − 1 ) 2 n α w l s x ∫ − ∞ ∞ exp − α − 1 s y t w l s x 2 + s y t α w l s x 2 s y t d 2 p d s y t   2 p exp − α − 1 s y t w l s x 2 d s y t
We set p = 1, 2, as shown in Eq.(9i), and in what way we evaluate the derivative of Eq.(9i) to originally use an undeveloped Eq.(9h), as scream
C 2 p ( α ) = 1 2 2 p ( 2 n ) ! π ( − 1 ) 2 α w l s x ∫ − ∞ ∞ s y t d 2 p d s y t   2 n exp − α − 1 s y t w l s x 2 d s y t
By setting a ray order n = 1 and calculating a subsequent copy of Eq.(9i), which first gives the result for calculating the first derivative of Eq.(9j) and becomes the result for recalculating the next derivative of Eq.(9k), as shown below
d d s y t exp − s y t α w l s x 2 = − 2 α − 1 s y t w l s x exp − α − 1 s y t w l s x 2
d 2 d s y t 2 − 2 s y t α w l s x exp − s y t α w l s x 2 = − 2 s y t α w l s x × − 2 s y t α w l s x exp − s y t α w l s x 2 + exp − s y t α w l s x 2 × − 2 α w l s x
You can get the result in equation(9m) and then develop equation(9k) through the influence and as follows
s y t d 2 d s y t 2 − 2 s y t α w l s x exp − s y t α w l s x 2 = 4 s y t 3 α 2 w l s x 2 × exp − s y t α w l s x 2 + exp − s y t α w l s x 2 × − 2 s y t α w l s x
In addition, the result of innovative production is clarified in equation(9n) and then equation(9m) is substituted into equation(9i) so that equation(9i) reads as follows
C 2 p ( α ) = 1 2 2 p ( 2 p ) ! π ( − 1 ) 2 α w l s x ∫ − ∞ ∞ 4 s y t 3 α 2 w l s x 2 × exp − s y t α w l s x 2 + exp − s y t α w l s x 2 × − 2 s y t α w l s x d s y t
The expression of Eq.(9n) was improved holistically and from the basic Eq.(9n) later Eq.(9p) results as follows
C 2 p ( α ) = 1 2 2 p ( 2 p ) ! π ( − 1 ) 2 α w l s x 4 α 2 w l s x 2 ∫ − ∞ ∞ s y t 3 exp − s y t α w l s x 2 d s y t − 2 α w l s x ∫ − ∞ ∞ s y t exp − α − 1 s y t w l s x 2 d s y t
Solve the integral of equation (9q) and the integral of equation (9p) using the formula (3.381.11) of this reference [24] and substitute equation (9q) as follows
∫ − ∞ ∞ x 2 p e − B x 2 r d x = Γ ( v ) r B v , Re r 〉 0 , Re B 〉 0 , v = 2 p + 1 2 r
Equation (9p) is the solution key of the integral associated with equation (9i) and can be obtained in equation (10) as follows
∑ p = 0 ∞ C 2 p ( α ) H 2 p s y t α ( 1 w l s x ) = 1 4 ( 2 ) ! π ( − 1 ) 2 α w l s x 4 Γ ( 2 ) α 4 w l s x 4 − 2 Γ ( 1 ) α 3 w l s x 3
To obtain the new equation (11), you must change equation (8) in [27] as follows.
U a , b ( p , z ) = k exp ( j k z ) j 2 π z ∫ − ∞ ∞ ∫ − ∞ ∞ d s y t d s x t 2 − 0.5 s x t i π 0.5 α − 1 exp   − 0.5 s x t 2 ( α   w l s x ) − 2
1 4 ( 2 ) ! π ( − 1 ) 2 α w l s x 4 Γ ( 2 ) α 4 w l s x 4 − 2 α − 3 Γ ( 1 ) w l s x 3 2 2 − 0.5 s y t k π 0.5 α − 1 exp   − 0.5 s y t 2 α − 2 ( w l s x ) − 2
exp   − π λ − 1 ( w g x s x t 2 + w g y s y t 2 ) + j k z − 1 2 ( 1 p x t − 2 − 2 p x t s x t + s x t 2 + p y t 2 − 2 p y t s y t + s y t 2 )
To be back sequences of Eq. (11), we are applying the factor fixed is an out of the integral and then gets extra Eq. (12) as below
U a , b ( p , z ) = k exp ( j k z ) j 2 π z 1 4 ( 2 ) ! π ( − 1 ) 2 α w l s x 4 Γ ( 2 ) α 4 w l s x 4 − 2 Γ ( 1 ) α 3 w l s x 3 2 π 0.5 α − 1 2 − 0.5 2 − 0.5 π 0.5 α − 1 ∫ − ∞ ∞ ∫ − ∞ ∞ d s y t d s x t s x t a s y t b
exp   − π λ − 1 ( w g x s x t 2 + w g y s y t − 2 ) + j k 2 z ( p x t 2 − 2 p x t s x t + s x t 2 + p y t 2 − 2 p y t s y t + s y t 2 ) − 0.5 s x t 2 α − 2 (   w l s x ) − 2 − 0.5 s y t 2 α − 2 (   w l s x ) − 2
By using the formulation (3.462.2.8) to resolve Eq. (12) we effort to put Eq. (13) into Equation (12) of ref [24] as verified in Eq. (14) as beneath
∫ − ∞ ∞ x p e − p x 2 + 2 q x d x = p ! e q 2 / p π n 0.5 q n p ∑ k = 0 n / 2 1 ( n − 2 k ) ! k ! n 4 q 2 k
p = − π λ w g x + j k 2 z − 0.5 α − 2 ( w l s x ) 2 q = − z − 1 j k p x t
If you use equation (14) and equation (14) to solve equation (12), you get the new equation (15), which you can see below
U a , b ( p , z ) = k exp ( j k z ) j 2 π z 1 2 2 ( 2 ) ! π ( − 1 ) 2 α w l s x 4 Γ ( 2 ) α 4 w l s x 4 − 2 Γ ( 1 ) α 3 w l s x 3 2 π 0.5 α − 1 2 − 0.5 2 − 0.5 π 0.5 α − 1 f 1 ∫ − ∞ ∞ d s y t s y t k
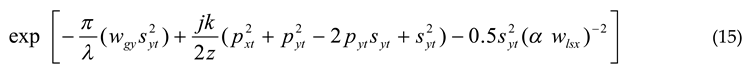
Preprints 110565 i004
To obtain the solution of the second integral of Eq. (15), which was previously solved in the same way, obtain Eq. (16) as follows
p = − π λ w g y + j k 2 z q = − j k p y t z
On the other hand, replace equation(16) with equation(15) to solve the second integral with the same formula as in equation(16), and you will get the final result of the receiver field of SLG as given in equation(17), as shown below
U a , b ( p , z ) = k exp ( j k z ) j 2 π z 1 4 ( 2 ) ! π α − 1 ( − 1 ) 2 w l s x 4 α − 4 Γ ( 2 ) w l s x 4 − 2 Γ ( 1 ) α 3 w l s x 3 2 π 0.5 α − 1 2 − 0.5 2 − 0.5 π 0.5 α − 1 f 1 2 exp   j k 2 z ( p x t 2 + p y t 2 )
The systematic equations derived above for the average intensity and the receptive field appear very complex. But n is the ray order of SLG, which is set to 0.1. As you increase n and gamma, the values drop dramatically when you set n = 5. For the results, the mean density and operational beam size calculations are done quickly by using the formulations that are now derived as described in reference [28]. As surveys
I p , z = U a , b ( p , z ) × U ∗   a , b ( p , z )
Although the direction of the receiving plane influences the intensity I p , z embodies the intensity of SLG of SLG and U a , b ( p , z ) is definite as a receiver field.

3. Numeric Computations and Outcomes Analysis

To summarize, the above formula can be used to calculate and derive the propagation of the SLG jet and the average intensity of a non-turbulent atmosphere. In addition, the standardized intensity of the SLG in Figures (4,8,11,13) is dented in different orders of magnitude, so a non-turbulent atmospheric environment of this jet dictates the positions of the jet order (00,01,10,11), scientifically at static propagation distances. Since the x and y directions in Eq. (18) are divisible, the unit of mean intensity in the x path is considered in the figures above. However, the factors used for the calculations are chosen as traces: and λ = 0.8μm. In addition, the standardized intensity power of a Gaussian beam with similar source size is shown in each figure for easy comparison. Since the sharp propagation of the super-LG jet in the basal plane is more advanced than the propagation of the Gaussian jet, the propagation of the SLG jet in a non-turbulent troposphere is less demanding than the propagation of the Gaussian jet. In addition, the difference between the propagation of the SLG beam and the Gaussian beam is increased by specifying the propagation distance z. Therefore, the measured 2D receiver field change between the hypothetical and the mathematical propagation in the x-direction of the SLG beam is shown in Figures (1, 5, 9, 15). In each figure of this receiver plane, the propagation distance is given as z = 2000 m to illustrate the same parameter constant. However, the 2D source field measured with the same parameters is shown in Figures (3,7,10,14). Gaussian part and the smaller Lorentz function The SLG beam is dominated. Therefore, the intensity distribution of the SLG beam in a non-turbulent atmosphere is closest to the Gaussian distribution observed in Figures (1,3,4,5,8,9,11,13,14,15). Accordingly, the effects of the super-Lorentz and Gaussian components are the same and the intensity of the SLG jet has been scattered. To illustrate the propagation of the SLG beam in a turbulent troposphere, the effective receiving field of the SLG beam against the transverse axis in a non-turbulent troposphere is described in each figure. Also, the same control variation of the result for the receiving field in the x and y directions only assumes that the result shown is the same as that observed in each figure. Moreover, the velocity of the SLG beam is the same as that of the smaller beam. As we have already mentioned, these figures (2, 6, 7, 10, 12) refer to the source sizes and propagation distances in different beam orders. To summarize, a hypothetical SLG beam in a non-turbulent troposphere radiates faster at a higher structure constant and is practical in an optical communication system used in lasers. In particular, the comparison with the numerical intensity values is shown in the figures of the receiver field. Finally, we point out symbolically in the figures that the beam has an order in all figures.
Preprints 110565 g001
Figure 1. The x-side of an SLG beam at propagation distances in a non-turbulent troposphere is observed in the standardized receiver field of the computational and theoretical deliveries in, z = 2km.
Figure 1. The x-side of an SLG beam at propagation distances in a non-turbulent troposphere is observed in the standardized receiver field of the computational and theoretical deliveries in, z = 2km.
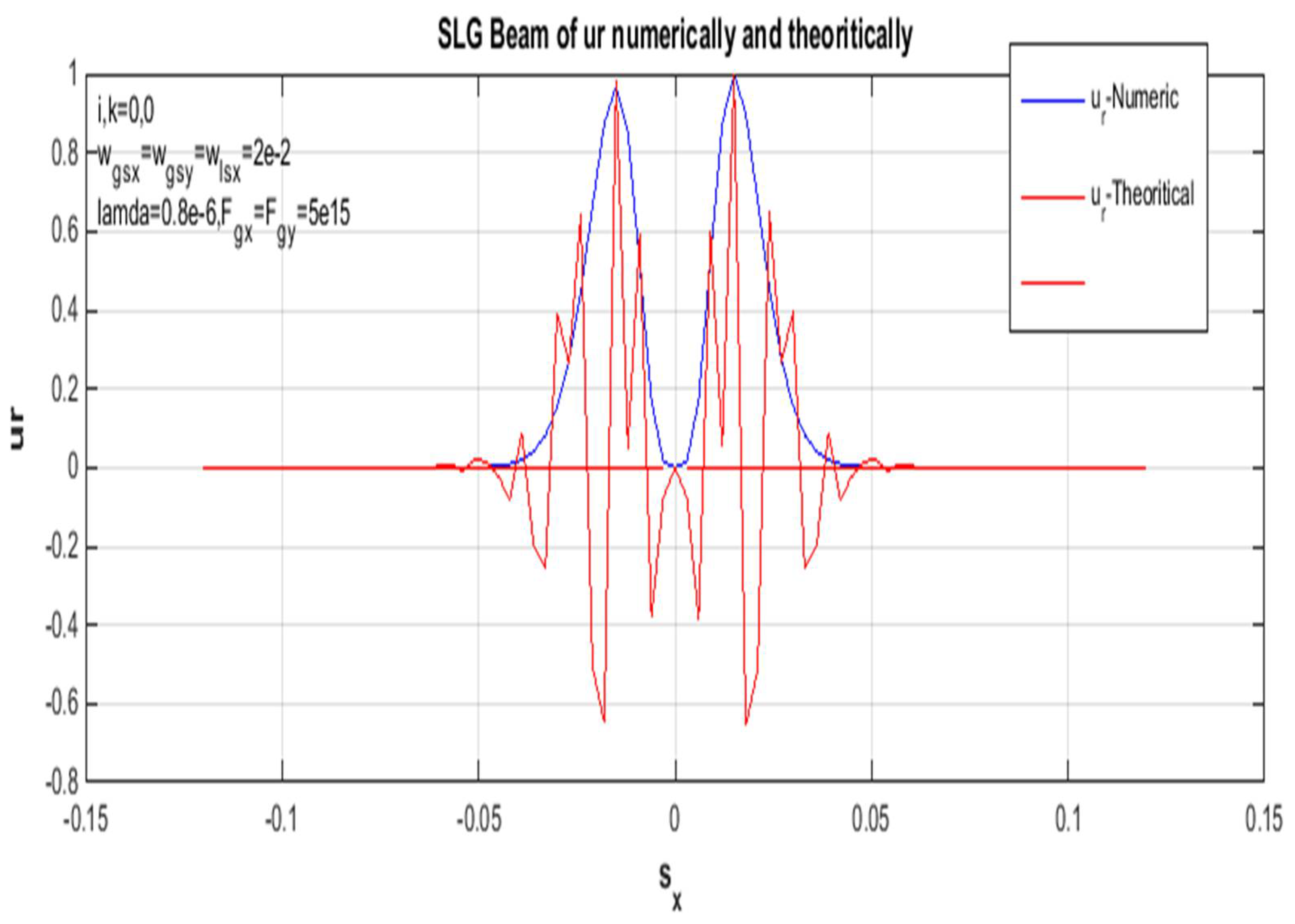
Preprints 110565 g001
Preprints 110565 g002
Figure 2. SLG beam at propagation distances in a non-turbulent atmosphere, z = 2 km. Stabilized receiver field of the hypothetical propagation on the x-side.
Figure 2. SLG beam at propagation distances in a non-turbulent atmosphere, z = 2 km. Stabilized receiver field of the hypothetical propagation on the x-side.
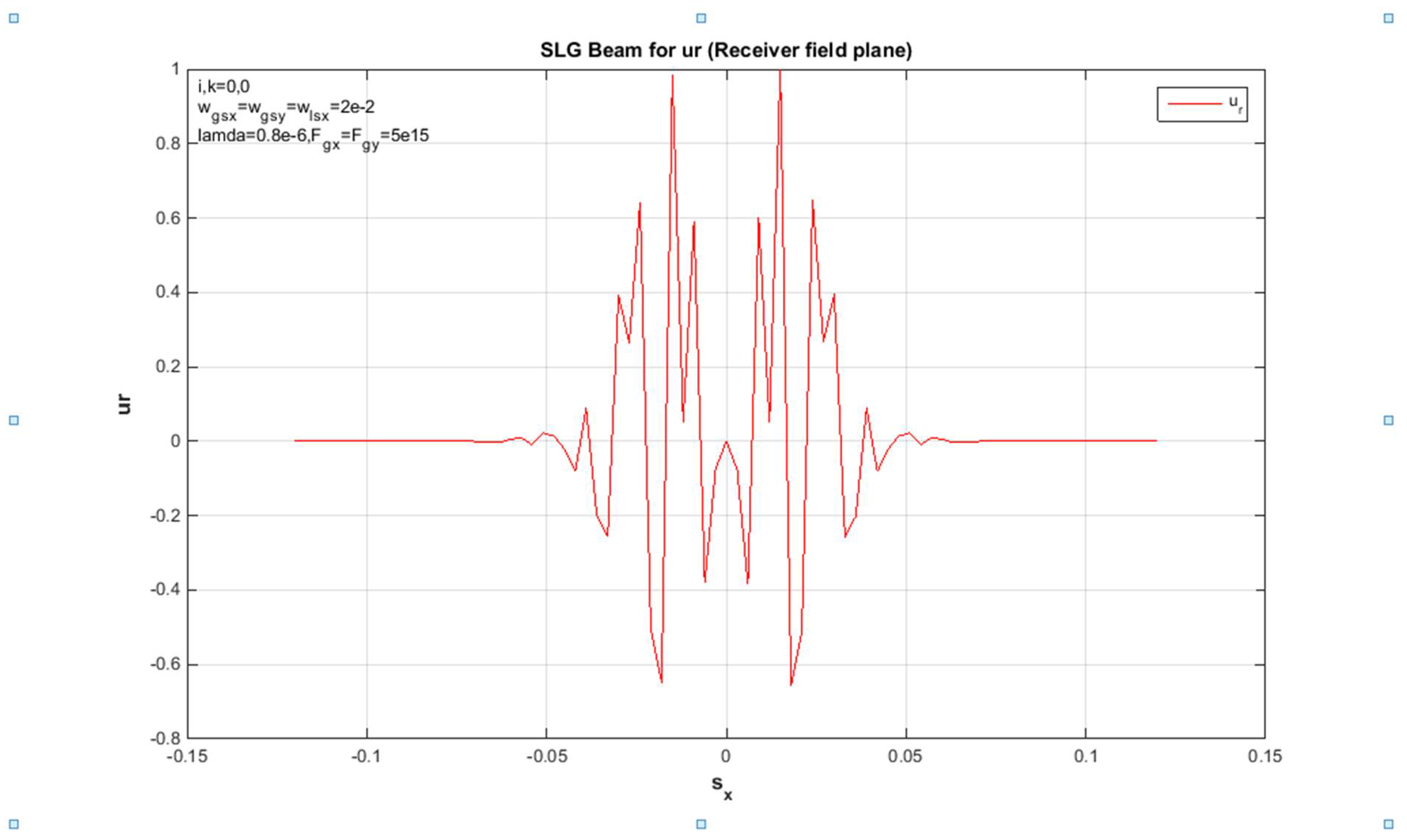
Preprints 110565 g002
Preprints 110565 g003
Figure 3. Proliferation reserves in a non-turbulent troposphere, z = 2000 m. Standardized source field supply in the x-guideless of an SLG jet.
Figure 3. Proliferation reserves in a non-turbulent troposphere, z = 2000 m. Standardized source field supply in the x-guideless of an SLG jet.
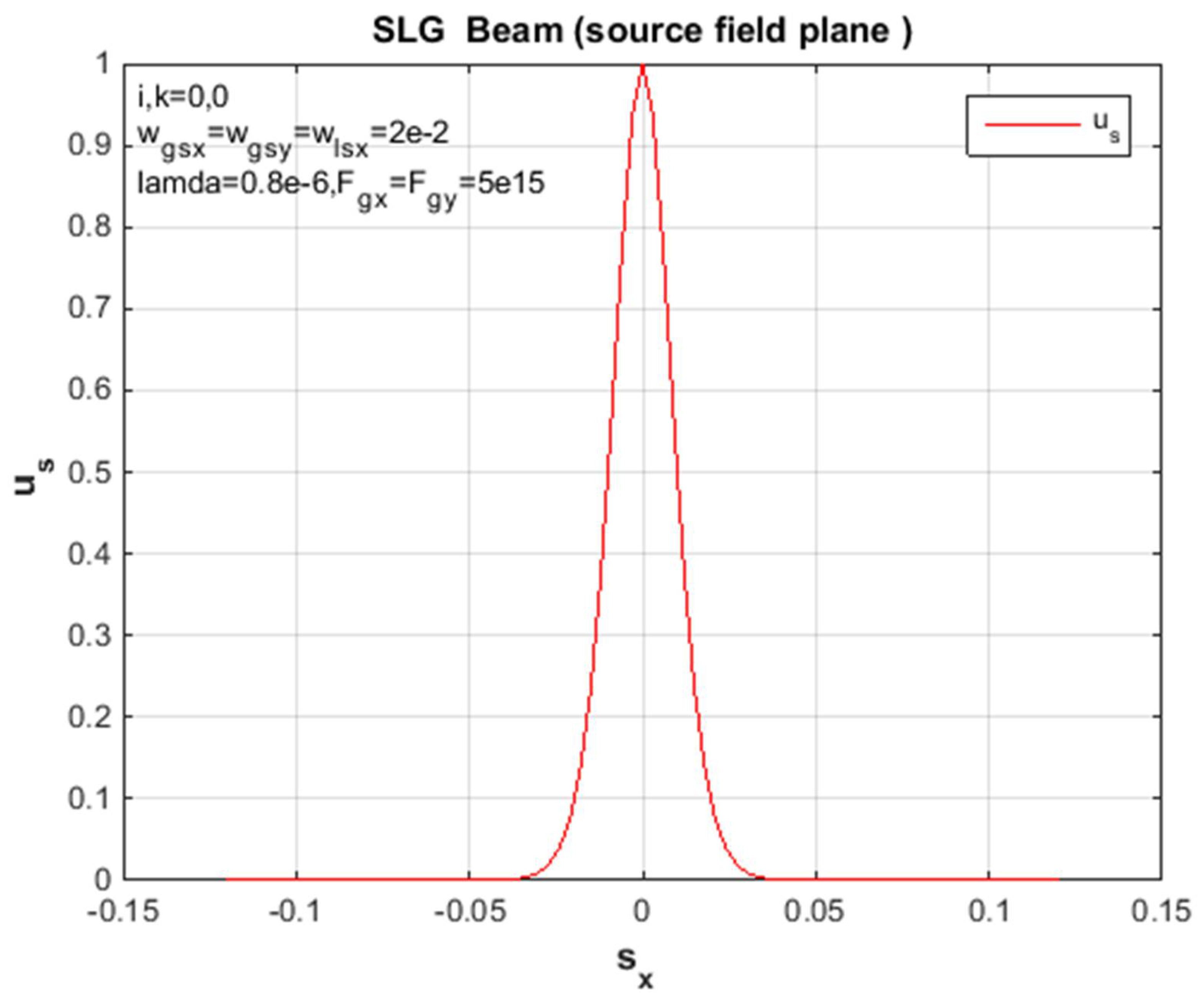
Preprints 110565 g003
Preprints 110565 g004
Figure 4. Propagation distances in a non-turbulent troposphere, z = 2000m for Standardized Intensity supplies in the x-side of an SLG beam.
Figure 4. Propagation distances in a non-turbulent troposphere, z = 2000m for Standardized Intensity supplies in the x-side of an SLG beam.
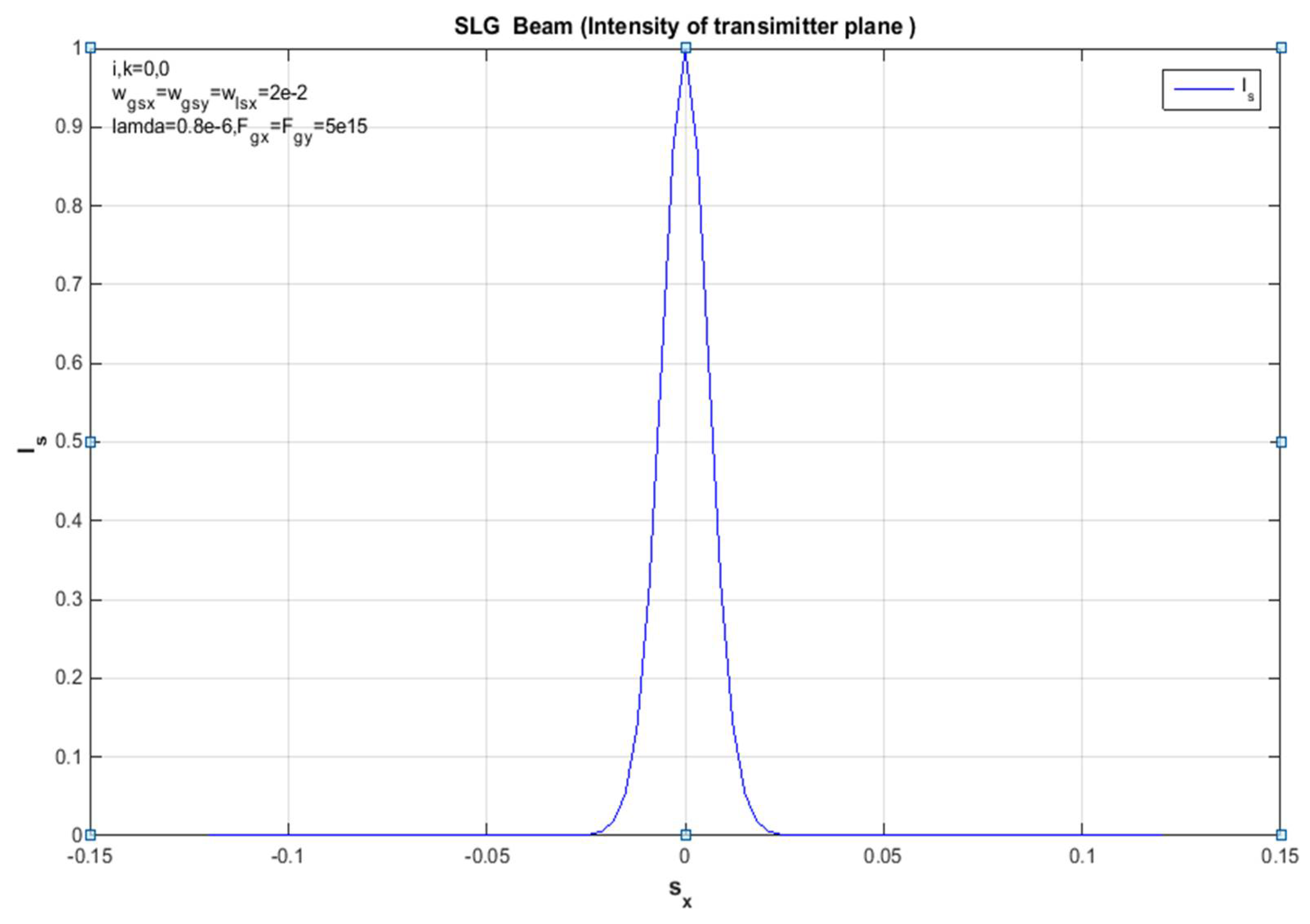
Preprints 110565 g004
Preprints 110565 g005
Figure 5. The x-side of an SLG beam at spread distances z =2000 m in a nonturbulent troposphere for Regularized receiver field numerical and theoretical distributions.
Figure 5. The x-side of an SLG beam at spread distances z =2000 m in a nonturbulent troposphere for Regularized receiver field numerical and theoretical distributions.
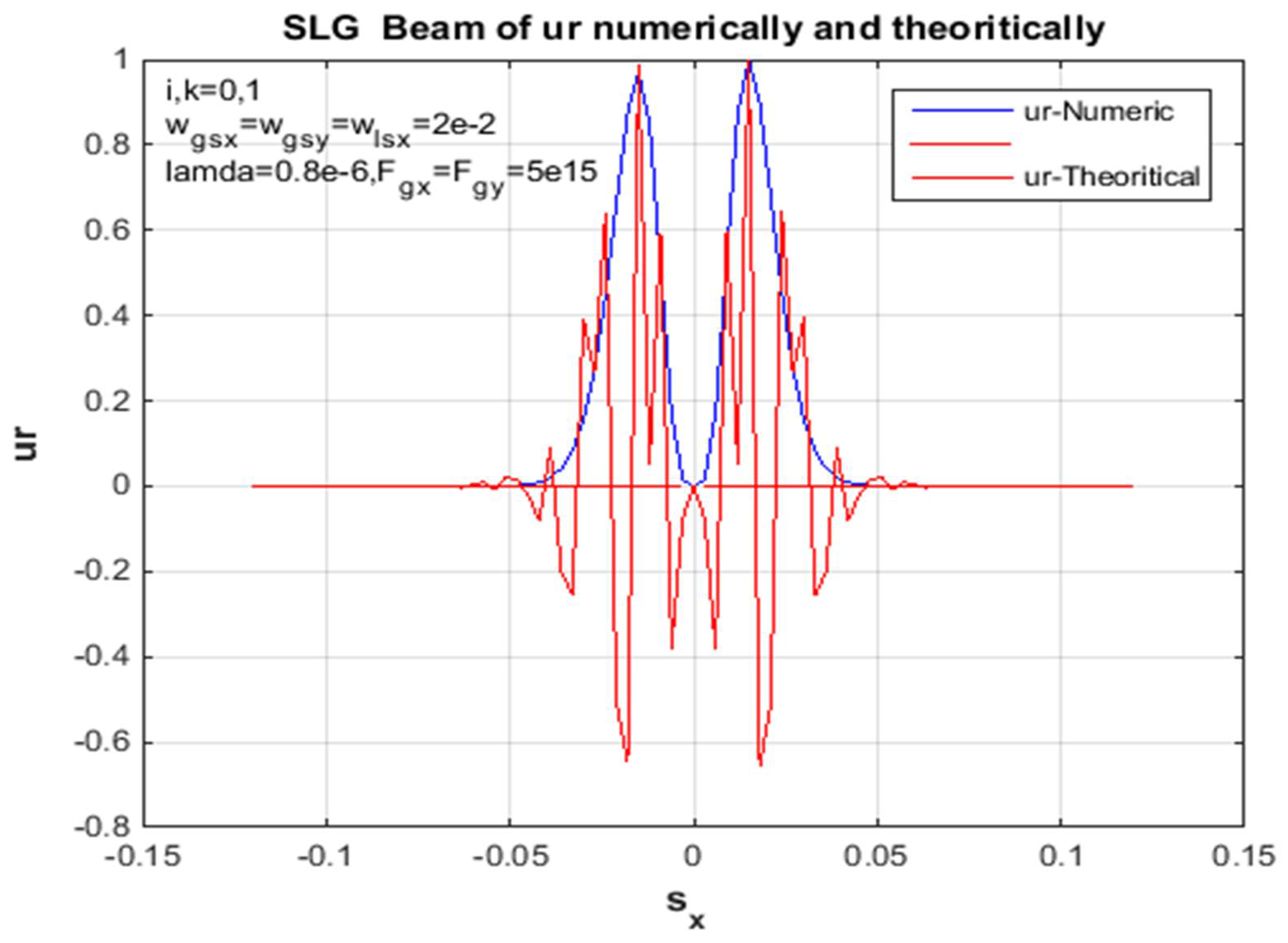
Preprints 110565 g005
Preprints 110565 g006
Figure 6. Propagation distances z = 2000 m in a non-turbulent troposphere for the standardized receiver field of a hypothetical coverage on the x-side of an SLG beam.
Figure 6. Propagation distances z = 2000 m in a non-turbulent troposphere for the standardized receiver field of a hypothetical coverage on the x-side of an SLG beam.
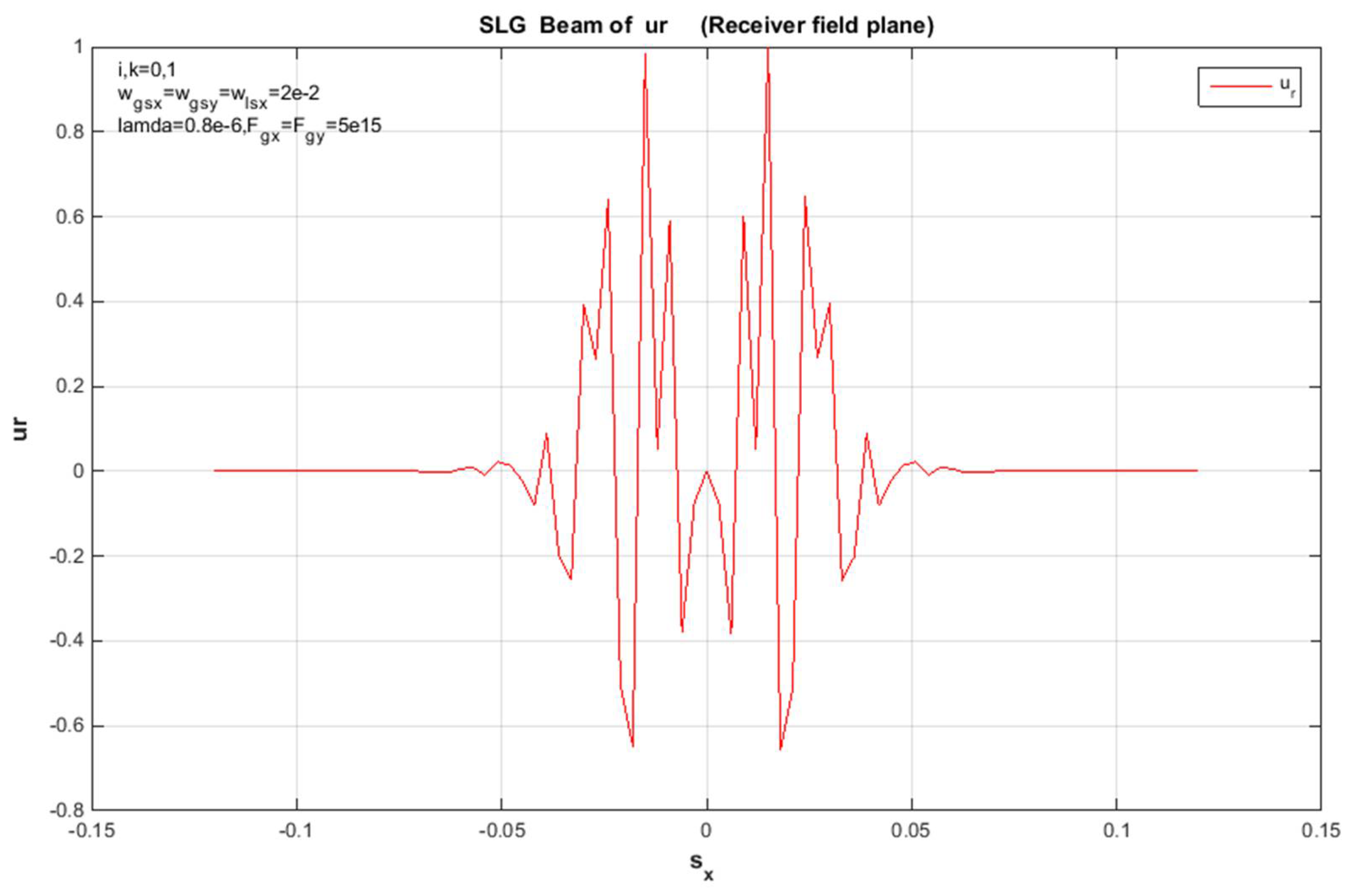
Preprints 110565 g006
Preprints 110565 g007
Figure 7. Propagation distance z = 2000 m in the turbulent troposphere for a standardized source field and deliveries on the x-side of an SLG jet.
Figure 7. Propagation distance z = 2000 m in the turbulent troposphere for a standardized source field and deliveries on the x-side of an SLG jet.
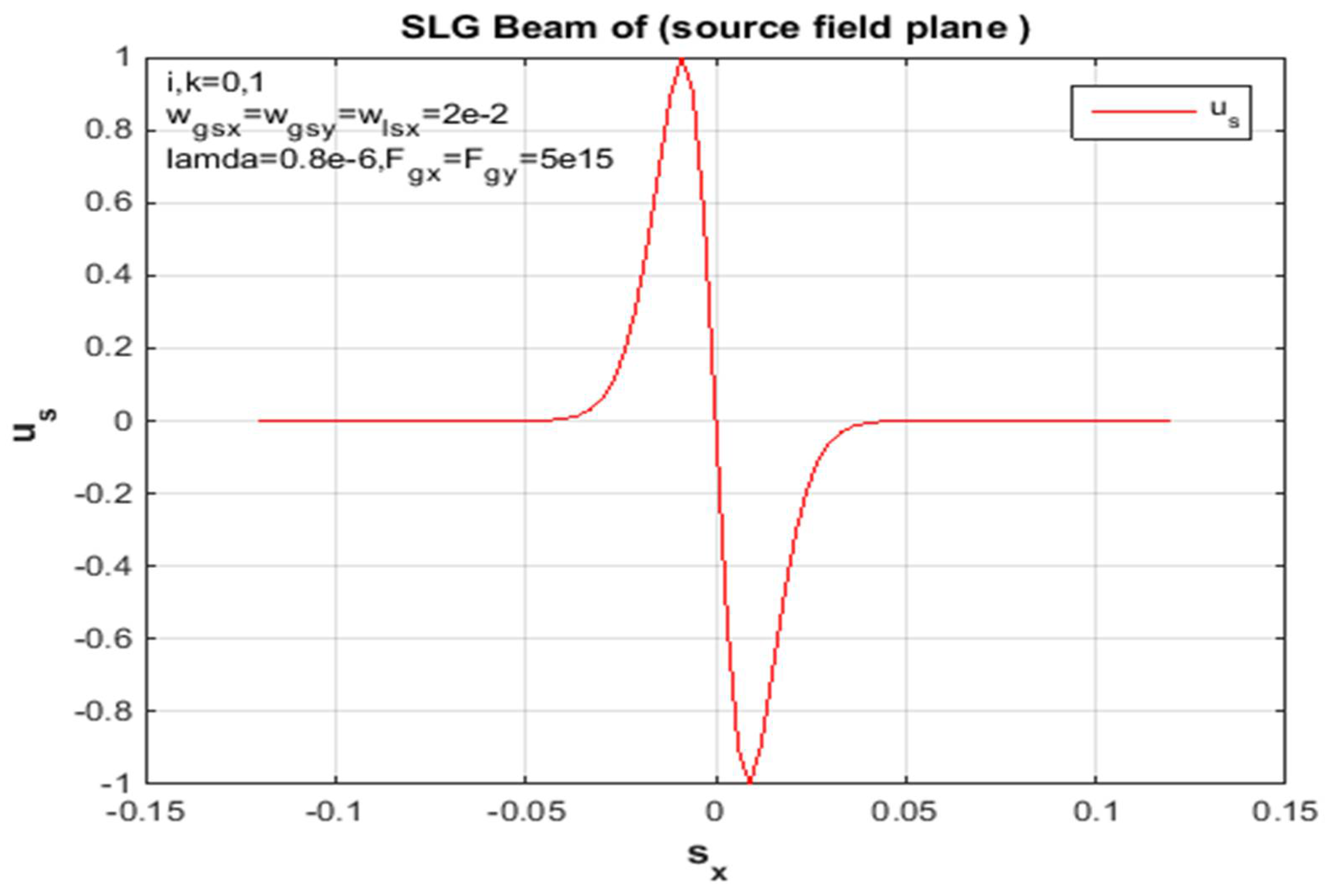
Preprints 110565 g007
Preprints 110565 g008
Figure 8. Dispersion distances z = 2000 m in a non-turbulent troposphere for Standardized Concentration supplies in the x-side of an SLG beam.
Figure 8. Dispersion distances z = 2000 m in a non-turbulent troposphere for Standardized Concentration supplies in the x-side of an SLG beam.
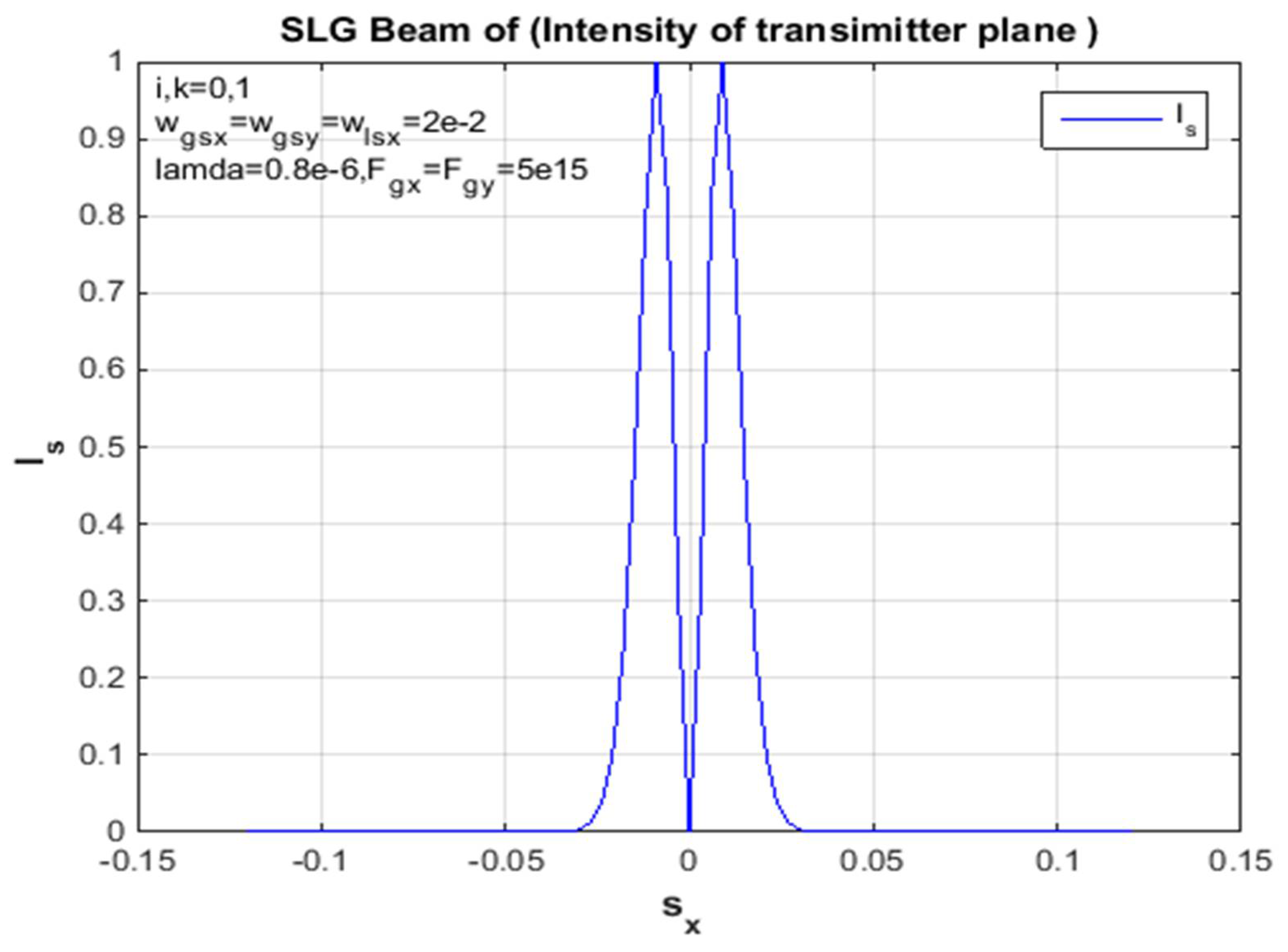
Preprints 110565 g008
Preprints 110565 g009
Figure 9. SLG jet at proliferation distances z =2000 m in the turbulent troposphere for the mathematical field of the regulated receiver and hypothetical deliveries on the x-side.
Figure 9. SLG jet at proliferation distances z =2000 m in the turbulent troposphere for the mathematical field of the regulated receiver and hypothetical deliveries on the x-side.
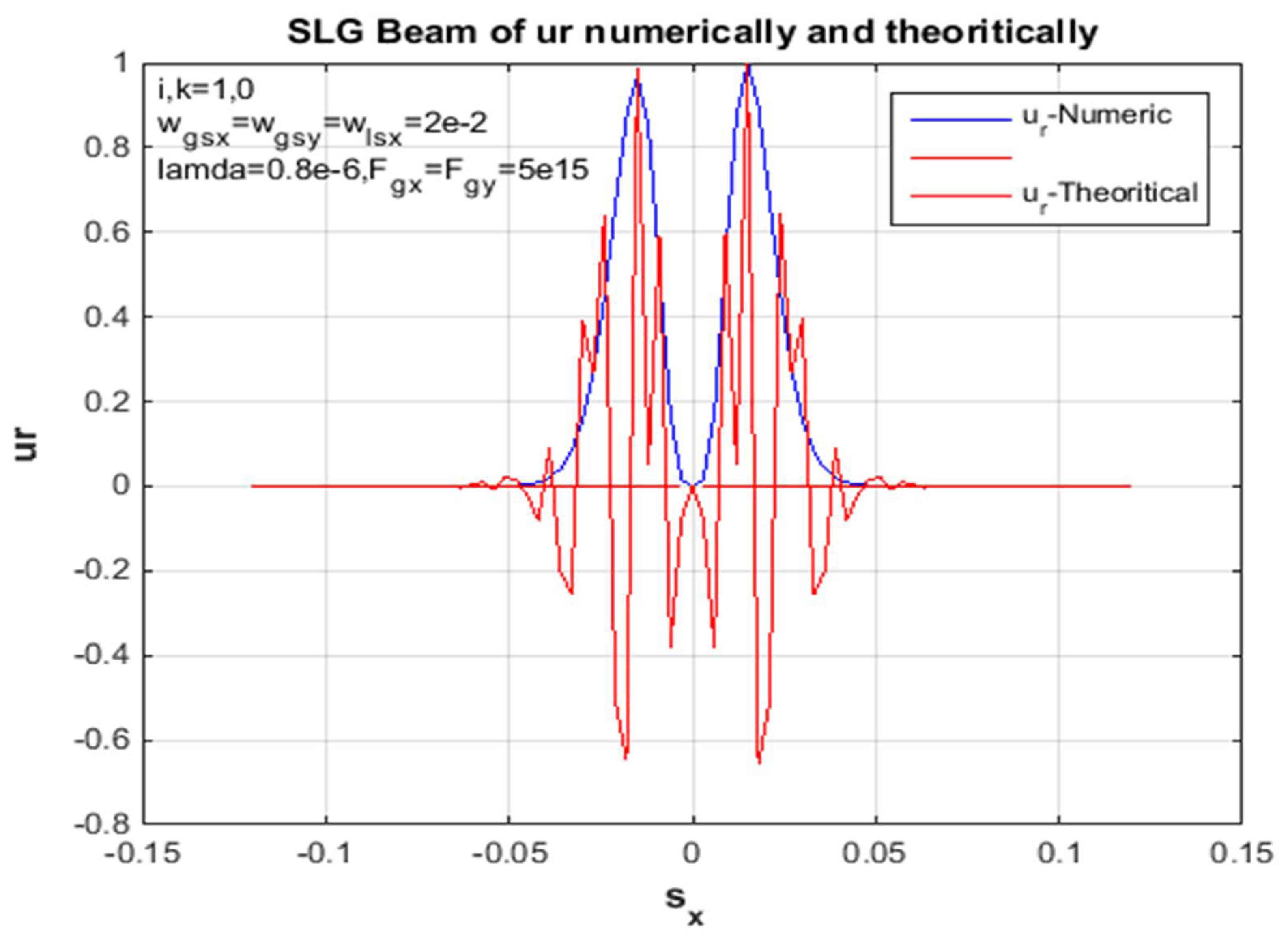
Preprints 110565 g009
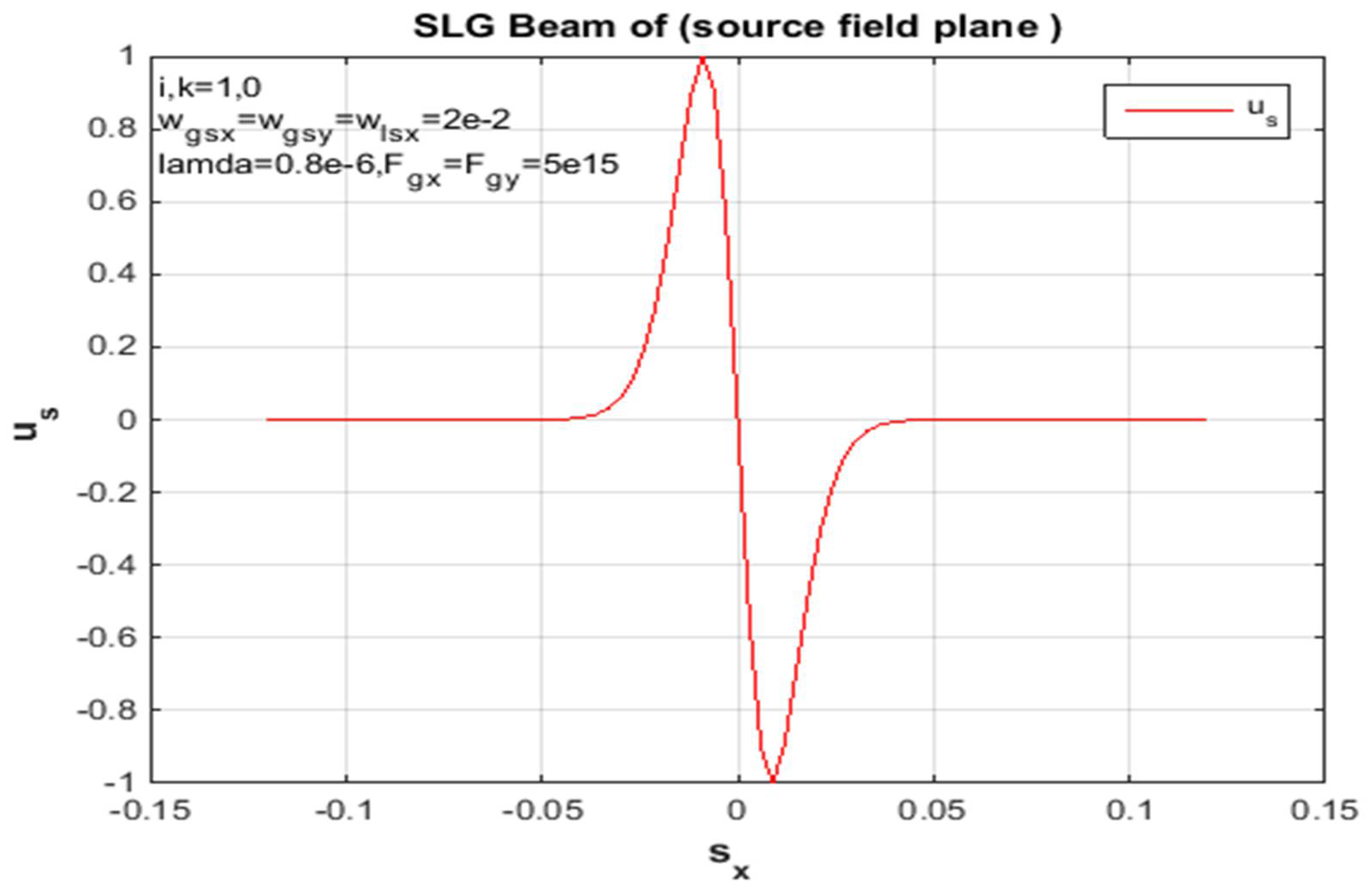
Preprints 110565 g010
Figure 10. Propagation of the source size in the turbulent troposphere z = 2000 m for a regulated source field and deliveries on the x-side of an SLG jet.
Figure 10. Propagation of the source size in the turbulent troposphere z = 2000 m for a regulated source field and deliveries on the x-side of an SLG jet.
Preprints 110565 g010
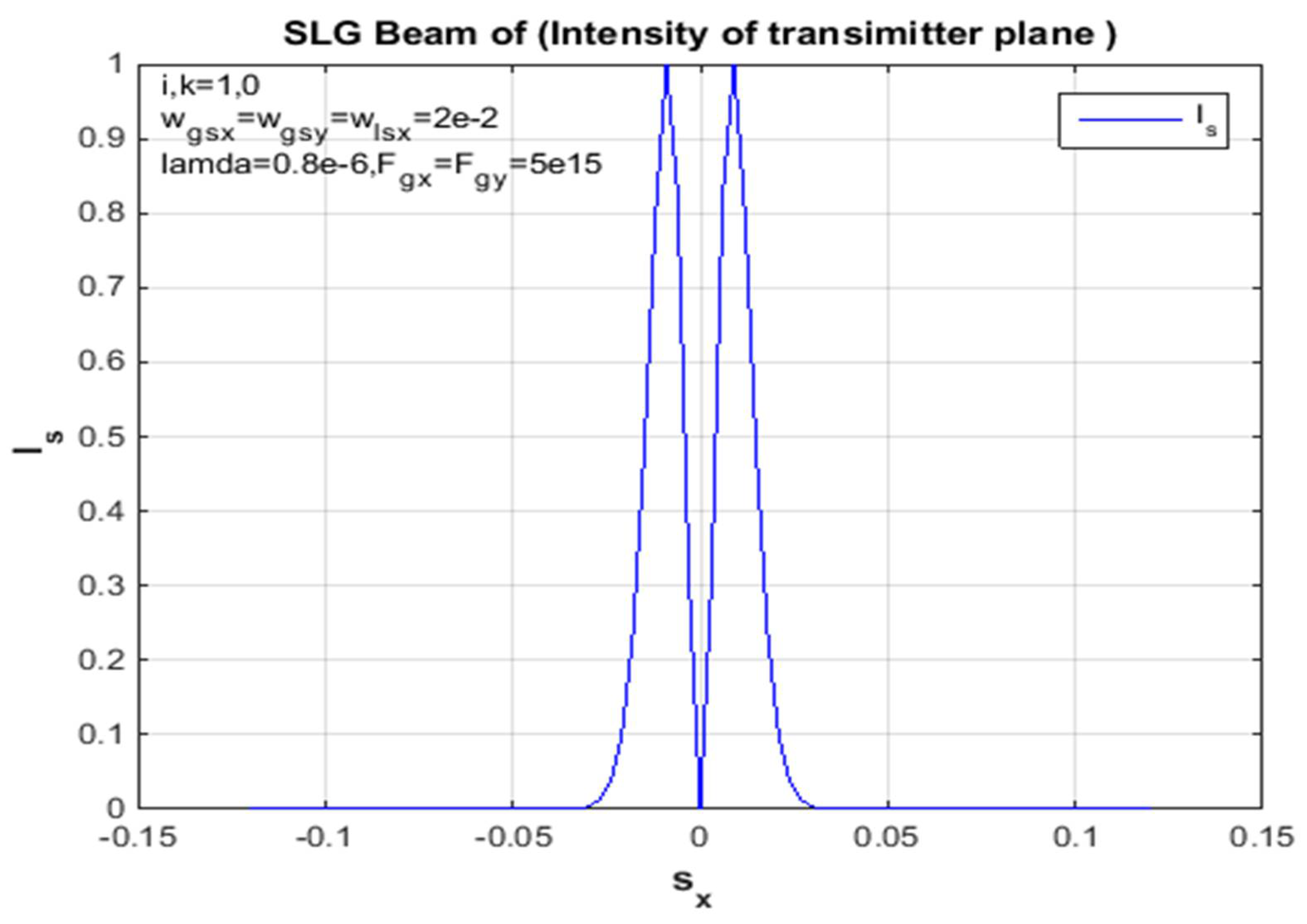
Preprints 110565 g011
Figure 11. Size of the proliferation source in a raging troposphere z = 2000 m Normalized intensity deliveries in the x-side of an SLG beam.
Figure 11. Size of the proliferation source in a raging troposphere z = 2000 m Normalized intensity deliveries in the x-side of an SLG beam.
Preprints 110565 g011
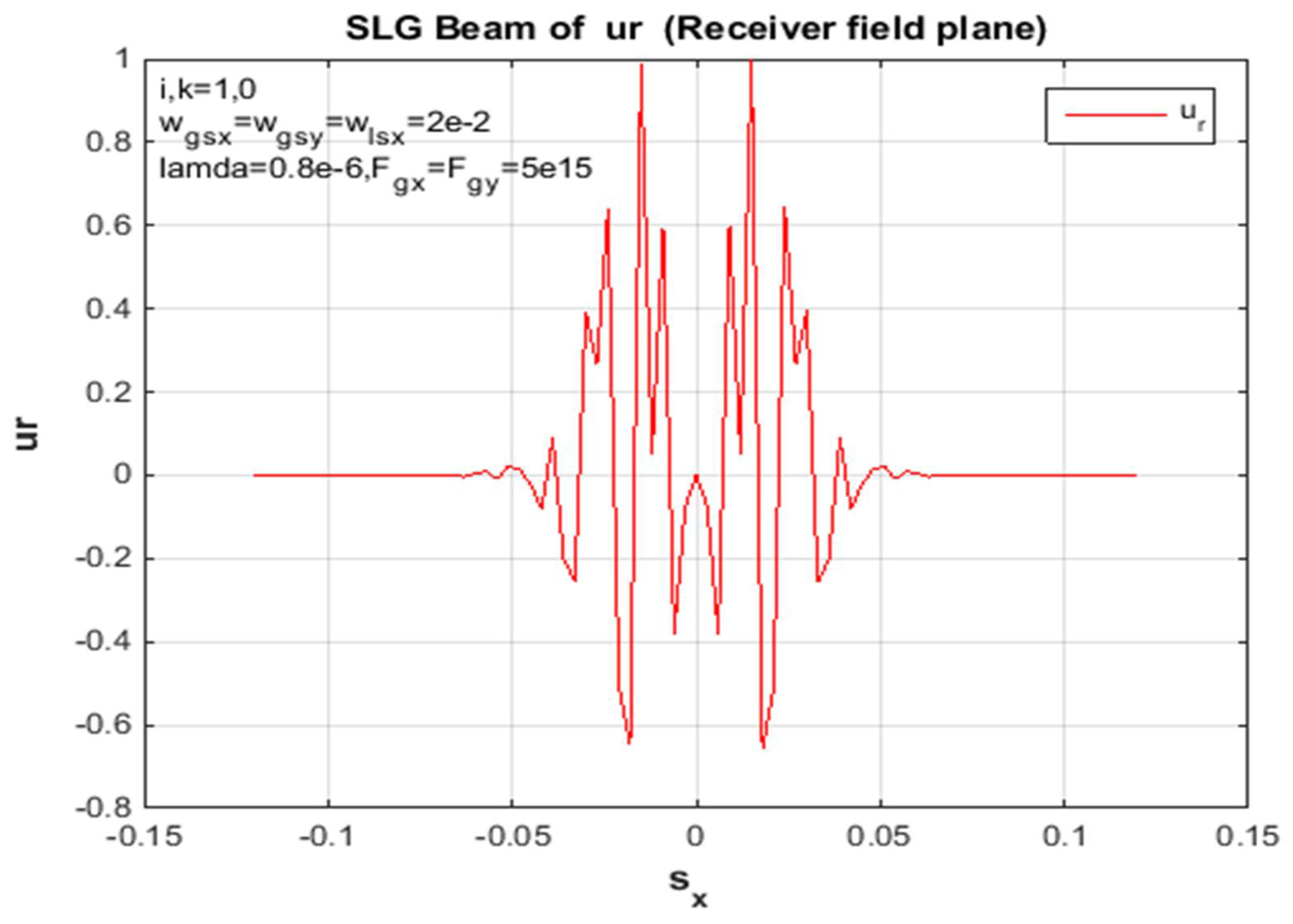
Preprints 110565 g012
Figure 12. SLG beam with scattered source size, z =2000 m in the moving troposphere for standardized receiver field, mathematical and hypothetical deliveries in x-direction.
Figure 12. SLG beam with scattered source size, z =2000 m in the moving troposphere for standardized receiver field, mathematical and hypothetical deliveries in x-direction.
Preprints 110565 g012
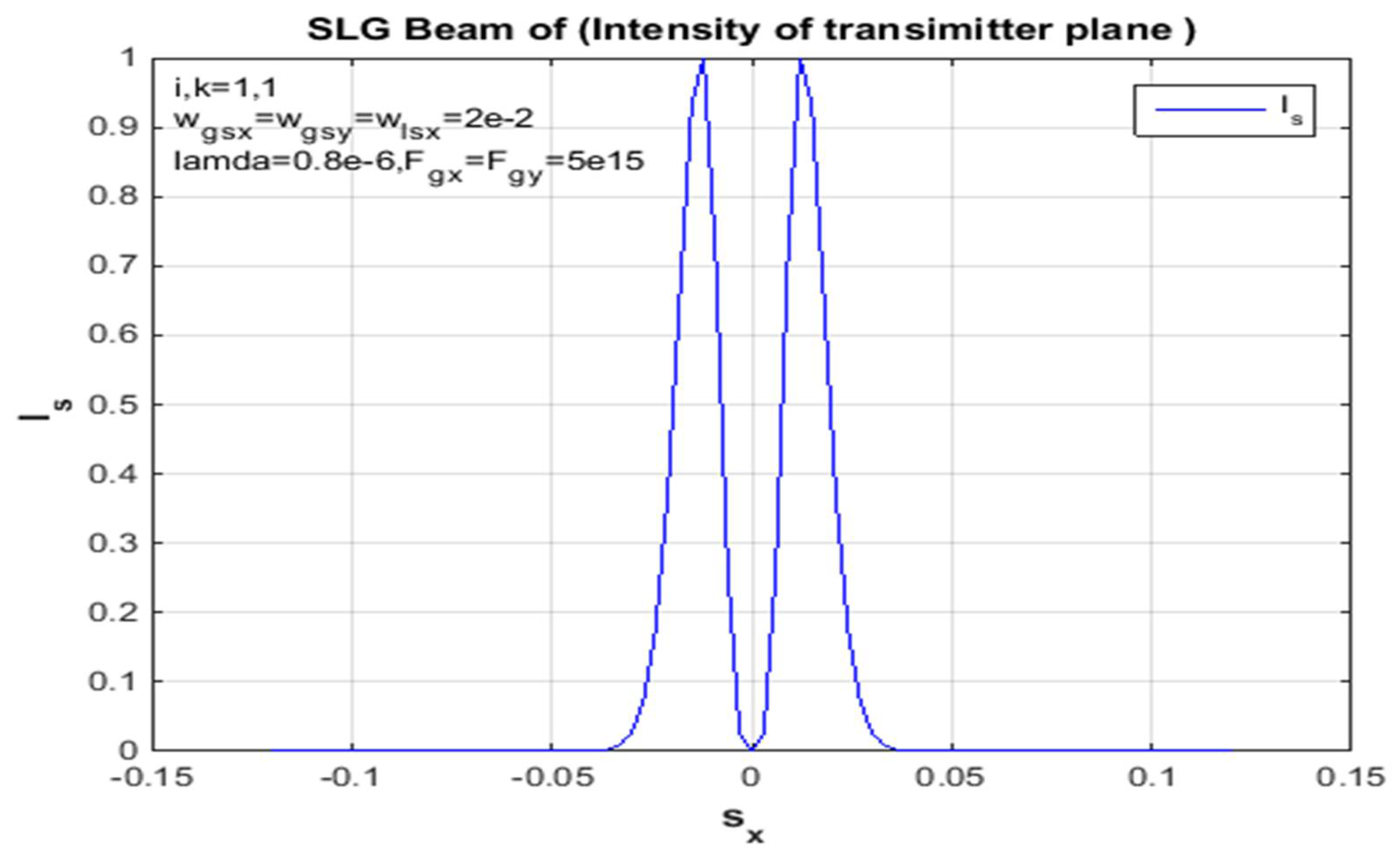
Preprints 110565 g013
Figure 13. SLG beam at proliferation source size, z = 2000 m in the turbulent atmosphere for Standardized Strength deliveries in the x-side.
Figure 13. SLG beam at proliferation source size, z = 2000 m in the turbulent atmosphere for Standardized Strength deliveries in the x-side.
Preprints 110565 g013
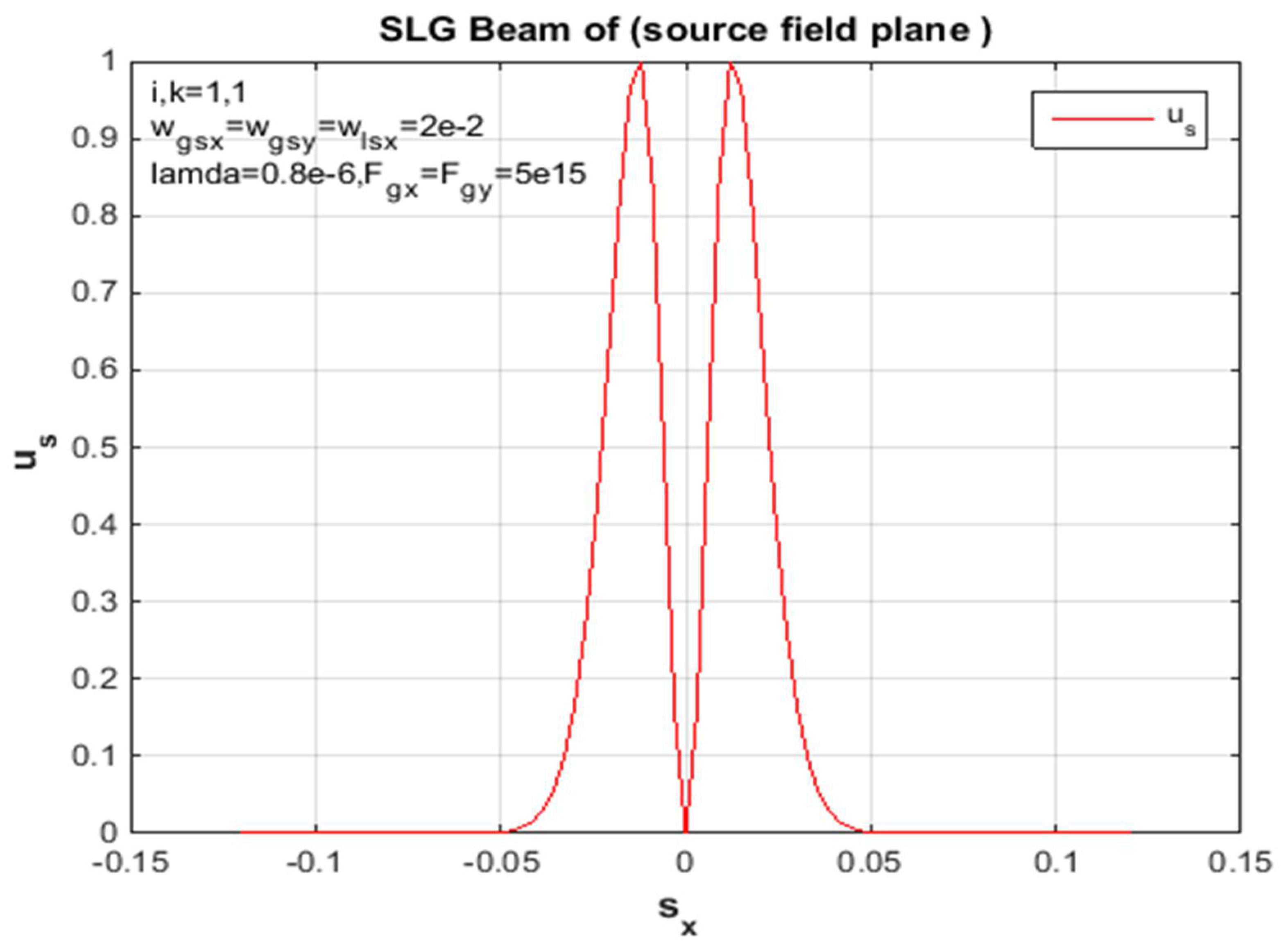
Preprints 110565 g014
Figure 14. SLG jet at proliferation source sizes at a distance z = 2000 m in the raging troposphere for the standardized source field and the supply in the x-side.
Figure 14. SLG jet at proliferation source sizes at a distance z = 2000 m in the raging troposphere for the standardized source field and the supply in the x-side.
Preprints 110565 g014
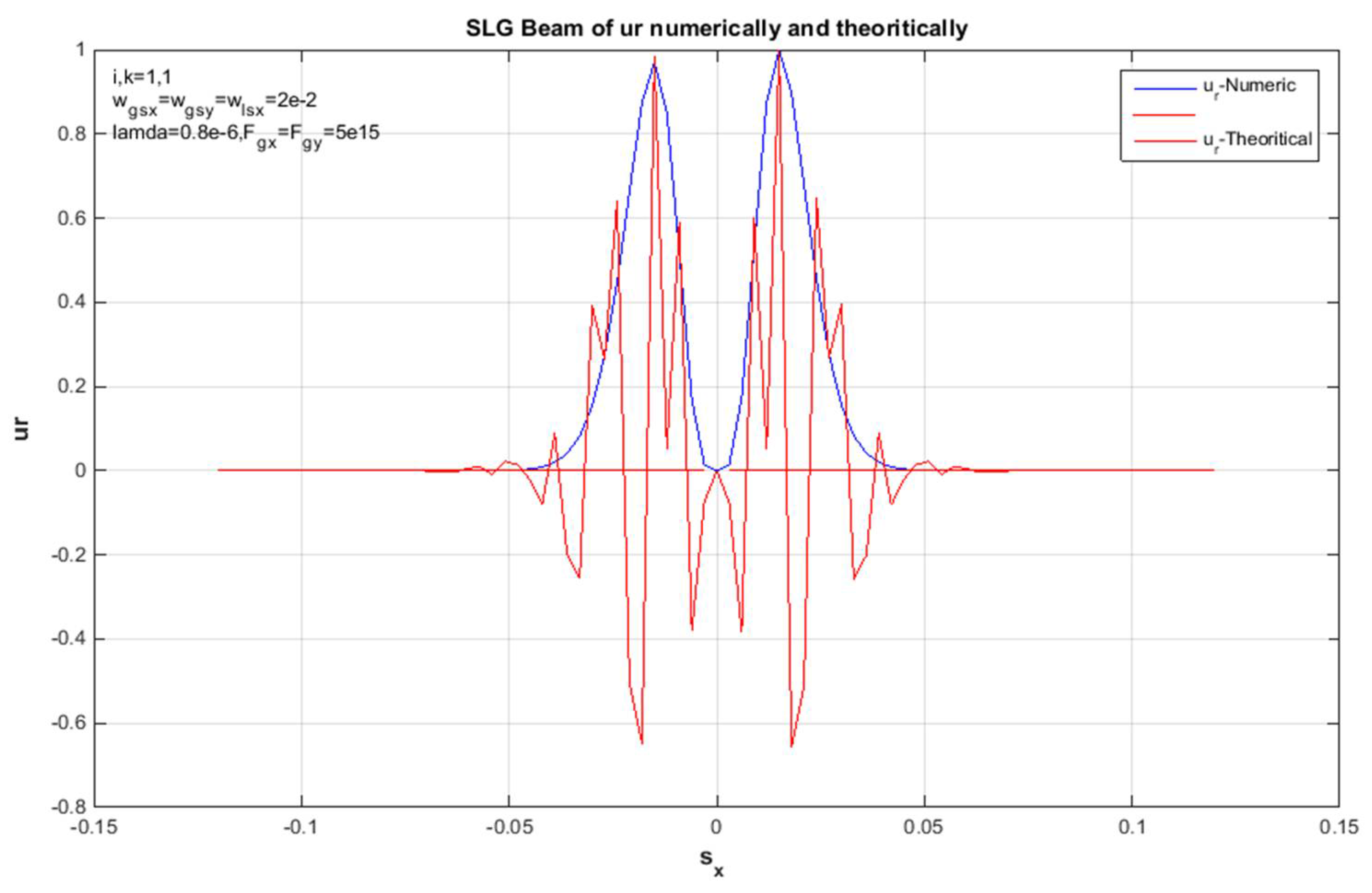
Preprints 110565 g015
Figure 15. SLG beam at propagation distances z =2000 m in the turbulent troposphere for stabilized receiver field mathematical and hypothetical deliveries on the x-side.
Figure 15. SLG beam at propagation distances z =2000 m in the turbulent troposphere for stabilized receiver field mathematical and hypothetical deliveries on the x-side.
Preprints 110565 g015

4. Conclusions

Finally, the average analytical density and numerical receiver field of the SLG beam in a raging troposphere are mathematically derived to illustrate these equations from (1 - 18), and Figures (1 - 15) are related to the super-Lorentz beam supply based on the expansion method of the extended Huygens-Fresnel integral. It is noteworthy that the Gaussian beam in a raging troposphere obtains a smaller beam order than the super-Lorentz beam during profile propagation. Therefore, we have obtained a smaller beam size for the parameters. As a result, the SLG jet propagates in a turbulent troposphere with a better jet order. Finally, this work offers advantages for use in laser applications and for use in optical communication systems

Declarations

I hereby certify that the information in this article is true and correct and that the contents and value of this shipment are as stated.

Ethical Approval

The authors are authorized for ethical publication

Acknowledgement

Thanks to Al-Nahrain University / College, College of Engineering, Department of Laser and Optoelectronics Engineering from the authors

Data available

All data generated or analyzed in this study are original data and were returned to the author based on the data contained in this published article.

Interests Competing

The personal relationships and financial interests of the authors are not in competition with each other or could give the impression that they influence the work in this article.

Finance

In this paper, no backing was established to contribute to the research

Contributions of Authors

The concept of the study and the design, data collection, analysis and interpretation of the results as well as the paper for which the authors take sole responsibility.

Competing Interests

No opposing monetary benefits or personal affairs of these authors announce that they have that could affect the effort offered in this article.

Funding

The creation of this article is explained. No conventional funds were used to finance this article.

Authors’ contributions

The author confirms sole responsibility for the conception and design of the study, the data collection, the interpretation of the results and the preparation of the manuscript.

References

  1. Khamees, H.T.; Algburi, S. Laser beam blink propagation: Evaluation BER in free space resembled dual SLG. Opt. Lasers Eng. 2023, 171. [Google Scholar] [CrossRef]
  2. Khamees, H.T.; Hussein, A.S.; Abdulkhaleq, N.I. An evaluation of scintillation index in atmospheric turbulent for new super Lorentz vortex Gaussian beam. TELKOMNIKA (Telecommunication, Comput. Electron. Control. 2023, 21, 1–7. [Google Scholar] [CrossRef]
  3. Khamees, H.T. Laser Gaussian beam analysis of structure constant depends on Kolmogorov in turbulent atmosphere for a variable angle of wave propagation. J. Laser Appl. 2022, 34. [Google Scholar] [CrossRef]
  4. Khamees, H.T. Average Intensity of SLVGB for Slant Path Propagation in Atmospheric Turbulent. Results Opt. 2021, 5, 100159. [Google Scholar] [CrossRef]
  5. Khamees, Hussein Thary, Assad H. Thary Al-Ghrairi, and Ali Abdulwahhab Mohammed. "Switched-line network with digital phase shifter." International Journal of Nonlinear Sciences and Numerical Simulation 0 (2021).
  6. Khamees, H.T.; Al-Ghrairi, A.H.T.; Suffer, K.H.; Thary, H.H. "Structure constant analyzing of SLG beam Kolmogorov in atmospheric slant path propagation." AIP Conference Proceedings. Vol. 2129. No. 1. AIP Publishing, 2019.
  7. Khamees, H.T. "Atmospheric propagation model and affecting on laser beam propagation via free space." Frontiers in optics, OSA technical digest (2017).
  8. Zhou, G. Nonparaxial propagation of a Lorentz-Gauss beam. J. Opt. Soc. Am. B 2008, 26, 141–147. [Google Scholar] [CrossRef]
  9. Zhou, G. Fractional Fourier transform of Lorentz-Gauss beams. J. Opt. Soc. Am. A 2009, 26, 350–355. [Google Scholar] [CrossRef] [PubMed]
  10. Zhou, G. Focal shift of focused truncated Lorentz-Gauss beam. J. Opt. Soc. Am. A 2008, 25, 2594–2599. [Google Scholar] [CrossRef] [PubMed]
  11. Zhou, G. The beam propagation factors and the kurtosis parameters of a Lorentz beam. Opt. Laser Technol. 2009, 41, 953–955. [Google Scholar] [CrossRef]
  12. G. Zhou, “Beam propagation factors of a Lorentz-Gauss beam,” Appl. Phys. B 96 (1), 149–153 (2009).
  13. Elgawhary, and S. Severini, “Lorentz beams as a basis for a new class of rectangular symmetric optical fields,” Opt. Commun. 269(2), 274–284 (2007).
  14. Baykal, Y. Correlation and structure functions of Hermite–sinusoidal-Gaussian laser beams in a turbulent atmosphere. J. Opt. Soc. Am. A 2004, 21, 1290–1299. [Google Scholar] [CrossRef] [PubMed]
  15. Eyyuboğlu, H.T. Hermite-cosine-Gaussian laser beam and its propagation characteristics in turbulent atmosphere. J. Opt. Soc. Am. A 2005, 22, 1527–1535. [Google Scholar] [CrossRef] [PubMed]
  16. Cai, Y.; He, S. Propagation of various dark hollow beams in a turbulent atmosphere. Opt. Express 2006, 14, 1353–1367. [Google Scholar] [CrossRef] [PubMed]
  17. Chu, X. Propagation of a cosh-Gaussian beam through an optical system in turbulent atmosphere. Opt. Express 2007, 15, 17613–17618. [Google Scholar] [CrossRef] [PubMed]
  18. Cai, Y.; Chen, Y.; Eyyuboglu, H.T.; Baykal, Y. Scintillation index of elliptical Gaussian beam in turbulent atmosphere. Opt. Lett. 2007, 32, 2405–2407. [Google Scholar] [CrossRef] [PubMed]
  19. Cai, Y.; Korotkova, O.; Eyyuboglu, H.T.; Baykal, Y. Active laser radar systems with stochastic electromagnetic beams in turbulent atmosphere. Opt. Express 2008, 16, 15834–15846. [Google Scholar] [CrossRef]
  20. Zhu, Y.; Zhao, D.; Du, X. Propagation of stochastic Gaussian-Schell model array beams in turbulent atmosphere. Opt. Express 2008, 16, 18437–18442. [Google Scholar] [CrossRef] [PubMed]
  21. Yuan, Y.; Cai, Y.; Qu, J.; Eyyuboğlu, H.T.; Baykal, Y. Average intensity and spreading of an elegant Hermite–Gaussian beam in turbulent atmosphere. Opt. Express 2009, 17, 11130–11139. [Google Scholar] [CrossRef] [PubMed]
  22. Zhao, D.; Du, X. Polarization modulation of stochastic electromagnetic beams on propagation through the turbulent atmosphere. Opt. Express 2009, 17, 4257–4262. [Google Scholar] [CrossRef] [PubMed]
  23. P. P. Schmidt, “A method for the convolution of line shapes which involve the Lorentz distribution,” J. Phys. B9(13), 2331–2339 (1976).
  24. S. Gradshteyn, and I. M. Ryzhik, Table of integrals, series, and products (Academic Press, New York, 1980).
  25. Gökçe, M.C.; Eyyuboğlu, H.T. Irradiance fluctuations of partially coherent super Lorentz Gaussian beams. Opt. Commun. 2011, 284, 4857–4861. [Google Scholar] [CrossRef]
  26. Abramowitz, M. and I. S. Stegun, Handbook of Mathematical Functions, Dover Publications, Inc., NewYork, NY, 1965.
  27. Khamees, H.T. Design Advanced Algorithm of the Single Dimension for Resolve the Electrostatic problem by Using the MoM Method. IOP Conf. Series: Mater. Sci. Eng. 2019, 518, 052015. [Google Scholar] [CrossRef]
  28. Khamees, Hussein Thary, Majeed, Munaf Salih," A receiver intensity for Super Lorentz Gaussian beam (SLG) propagation via the moderate turbulent atmosphere using a novelty mathematical model ", Journal of Optical Communications, Vol. 41, Issue. 1, pp.1-8, 2020.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated