Prerpints.org logo
Preprint
Article

Credit Card Fraud Detection with Machine Learning and Big Data Analytics: A PySpark Framework Implementation

Altmetrics

Downloads

468

Views

505

Comments

0

supplementary.xlsx (16.07KB )

Submitted:

27 June 2024

Posted:

01 July 2024

You are already at the latest version

Alerts
Abstract
This paper presents a comprehensive study on applying machine learning (ML) techniques for real-time credit card fraud detection. With the increasing prevalence of credit card fraud, financial institutions face the challenge of detecting fraudulent transactions promptly and accurately. This research evaluates various ML models, including Logistic Regression, Decision Trees, Random Forests, XGBoost, and Deep Convolutional Neural Networks, for their effectiveness in identifying fraudulent activities. Utilizing PySpark for processing large-scale transaction data, the study highlights the importance of real-time analysis, adaptive learning, and handling imbalanced datasets. Key findings reveal that XgBoost, with its balance of accuracy and complexity, emerged as the most promising model, achieving an accuracy rate of 98% in detecting fraudulent transactions. The paper further discusses the potential of ensemble methods, graph-powered systems, and intelligent sampling in enhancing fraud detection capabilities. Challenges such as overfitting, data access, and the need for real-time analysis are addressed. Future research directions include implementing models in live transaction environments, expanding model applicability across financial platforms, and developing advanced anomaly detection methodologies. This study underscores the pivotal role of machine learning in safeguarding financial transactions against fraud, offering significant implications for consumers, financial institutions, and the broader financial ecosystem.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Machine learning has demonstrated its ability to significantly revolutionize decision-making processes in various domains, particularly in tasks that require high levels of precision, effectiveness, and adaptability, such as detecting fraud in transactions, diagnosing healthcare conditions, and enhancing customer experiences.
Traditional decision-making typically relies on empirical methods, the expertise of a specialist, or rigid, outdated algorithms that cannot adapt to new information or intricate patterns found in modern data. Although the methods above may yield positive results in specific domains, they are often constrained by inherent human cognitive biases and the sheer impossibility or difficulty of analyzing such immense volumes of incoming data. Consequently, decisions made using conventional methods instead of ML techniques may experience delays in response, considerably higher rates of errors, and a general incapability to handle large datasets to uncover accurate and valuable information.
Machine learning algorithms are being used to automate the analysis of large and complex datasets, enabling the discovery of patterns and relationships that human analysts or experts may not notice. By continuously learning and adapting, machine learning algorithms greatly enhance decision-making accuracy. They accomplish this by iteratively improving their models’ using data, thereby minimizing errors in tasks such as fraud detection. This improves the quality of decisions and accelerates the decision-making process, allowing for immediate analysis and responses.
The prevalence of credit card fraud is increasing in modern economies, paralleling the advancements in digital transactions. With the advent of artificial intelligence, machine learning, and big data, innovative tools are being developed to combat fraud. According to the literature [1], a machine-learning algorithm can use past transactions to develop highly intricate features that detect fraud in real-time. This algorithm has the potential to outperform even the most skilled human investigators.
Nevertheless, despite technological advancements, the progress of fraud detection algorithms encounters substantial impediments [2]. Significant challenges arise from the imbalanced nature of fraud-related data, the requirement for benchmarks and standards to assess classifiers, and the complexity of obtaining confidential transaction data for research purposes.
Researchers have proposed several machine learning methods to tackle the issue, including employing genetic algorithms to select features, integrating the spatiotemporal attention mechanism with graphical neural networks, and utilizing Apache Spark with machine learning to analyze extensive data [3]. Nevertheless, detecting credit card fraud remains a significant challenge due to the constantly evolving characteristics of fraudulent patterns and behaviors and the imbalanced nature of the datasets.
This research study contributes significantly by introducing a novel framework for detecting fraud using machine learning methods tailored to handle large datasets. It aims to introduce novel methodologies or enhancements to existing ones to tackle the challenges associated with detecting fraud in extensive datasets. The research study also offers guidance on implementing algorithms in real-time settings, enabling banking and financial institutions to respond to fraudulent activities promptly. Moreover, it explains the difficulties and possibilities of utilizing machine learning to identify credit card fraud. Finally, the study enhances the development of payment security technologies, resulting in a more secure and reliable consumer environment.

2. Literature Review

2.1. Introduction to Credit Card Fraud Detection

Financial institutions nowadays face significant problems with digital transactions, especially fraud detection, specifically fraud detection regarding credit cards. While the digitization of financial services is increasing daily, so does online transactions, thus increasing the risk of fraudulent activities.
Recent research [4,5,6] has underscored the rise in credit card fraud, necessitating the use of machine learning methods to swiftly identify suspicious transactions. Financial organizations and businesses are investing heavily in the development of advanced fraud detection systems, demonstrating their commitment to safeguarding customers and their personal interests. Their primary goal is to identify and halt potentially fraudulent activities, ensuring the security of all parties involved.
One of the main problems that needs to be addressed in detecting credit card fraud is the imbalance discerned in the datasets. Legitimate transactions seem to outnumber fraudulent ones, which baffles experts who detect fraud. For this reason, generative adversarial networks (GANs) have emerged. They are used as a powerful solution, generating synthetic data to balance the datasets and improve the accuracy of detection rates [8]. Machine learning techniques provide a plethora of algorithms suitable for such tasks. Techniques such as logistic regression, decision trees, random forests, and the XGBoost algorithm are some of the most applied algorithms [9]. The deep convolutional neural network (DCNN) design has shown improved detection accuracy, especially when handling large volumes of data [10].

2.2. The Importance of Detecting Credit Card Fraud

Fraud detection, credit cards, machine learning, data security, decision-making. Detecting credit card fraud serves several important purposes. It protects consumers by shielding them from fake transactions, identity theft, and financial harm. Additionally, it helps protect financial institutions from losses caused by suspicious or fraudulent behavior, thereby supporting the stability of the broader financial system. Detecting and preventing fraud on time can also potentially lower costs linked to the investigation and resolution of such incidents. Ensuring legal compliance, it makes sure the right regulations and standards are being followed, depending on the market or the country. Efficient fraud detection helps consumers trust more in the credit card system, promoting more frequent usage of credit cards. Lastly, successful fraud detection offers a significant boost to the reputation of organizations that issue credit cards and provide payment services by showcasing their dedication to security and customer safety.
Fraud detection systems utilize various techniques to detect and prevent fake transactions in time [11]. These are machine learning algorithms, anomaly detection algorithms, and various behavioral analysis techniques. These techniques and systems remain involved in the rise and further complexity of the different forms fraudulent activities can take. Big data and AI have played an equally important role in improving fraud detection systems since they allow real-time analysis of vast volumes of data with great precision [12]. If we want to prevent fraudulent activities and protect the interests of customers and financial institutions, we need to continue upgrading and evolving detection algorithms and methods.
2.3 Role of Machine Learning in Improving Decision-Making Processes in Fraud Detection
Machine learning (ML) has revolutionized the methods used by organizations to detect, analyze, and combat fraudulent behaviors [13]. Consequently, this directly affects organizations' decision-making processes, particularly in the area of fraud detection, leading to substantial improvements. They can implement and utilize advanced machine learning algorithms to analyze the constant influx of extensive datasets, uncover concealed patterns, and predict potential fraudulent transactions with exceptional precision and speed. Below, we examine the concept of machine learning and its significance in facilitating efficient decision-making in the context of fraud detection.

2.3.1. Automated Pattern Recognition

When it comes to the identification of fraudulent activities, machine learning’s unique ability to recognize patterns automatically is unmatched and of the utmost importance. Machine learning algorithms, especially unsupervised learning models, seem to perform exceptionally well when it comes down to identifying complicated patterns within vast datasets, that could potentially lead to fraud detection of any kind. This capability of ML becomes a very important asset in this war of detection and interception of fraud, especially when fake operations formulate some kind of anomaly or divergence from what is considered normal behavior patterns within the data [14]. Furthermore, the process of continuous learning is what further enhances machine learning models’ abilities of adaptation and change, which are both important in identifying new fraud patterns.

2.3.2. Predictive Modelling

Machine learning algorithms also support predictive modelling which can significantly improve an organization’s decision-making processes. This can be achieved through the use of historical data in order to predict future fraudulent transactions or other similar activities. In addition, supervised learning models also have the ability to develop predictive qualities by being trained on existing fraudulent and legitimate datasets, thus being able to be applied on invisible data in order to effectively estimate probability rates of frauds [15]. Through this predictive power of ML, organizations can detect, even at a proactive level, possible frauds, which allows them to set appropriate measures in place and prevent fraud altogether. By using predictive models, decision-making processes’ accuracy is considerably improved and a proactive approach to fraud detection and management is promoted within the organization [16].

2.3.3. Dynamic Risk Scoring

Decision-making can also be improved by machine learning algorithms using a tool called risk scoring system. Unlike traditional static risk assessment models, these systems work by updating the risk scores for transactions, based on available data, patterns and behaviors of detected fraud [17]. Thus, decision-making can become diversified and takes context into consideration, through this real-time evaluation. This can make it much easier to distinguish between high-risk and low-risk activities [18]. Having detailed risk scoring is vital for resource allocation and minimizing as much as possible the impact on legitimate transactions.

2.3.4. Anomaly Detection

Anomaly detection, a specialized application of machine learning, plays a very important role in identifying outliers that may indicate fraudulent activity. By establishing a normative baseline from historical data, ML algorithms can flag transactions that deviate significantly from established patterns [19]. This capability is particularly useful in detecting novel or sophisticated fraud schemes that do not match known fraud signatures. Anomaly detection through machine learning thus contributes to a more adaptable and resilient fraud detection system.

2.3.5. Natural Language Processing (NLP)

Natural language processing, powered by machine learning, improves decision-making skills by examining textual information to detect fraudulent activities. NLP can assess customer interactions, feedback and complaints to pinpoint possible signs of fraud [20]. Through this procedure, NLP can extend the reach of fraud detection beyond just numbers, integrating qualitative observations into decision-making processes. The capacity to swiftly process and evaluate textual information in real-time, enhances the complexity of the tactics used in fraud detection.

2.3.6. Integration with Existing Systems

Machine learning techniques do not need to be solely used as standalone methods. They can work equally well by being integrated into existing business information systems and decision-making frameworks, thus boosting their overall effectiveness [21]. This integration of traditional fraud detection techniques and machine learning algorithms can result in a more robust and detailed fraud detection strategy.

2.4. Credit Card Fraud Detection: Machine Learning Applications

Nowadays, technology has permeated even the most superficial aspects of our lives, making credit card fraud detection a critical area for both consumers and financial institutions. Fraud can have severe financial and psychological effects on consumers. A closer look at the machine learning methods predominantly used in this field reveals two primary techniques. Logistic Regression is a statistical method valued for its simplicity and effectiveness in predicting categorical outcomes like the likelihood of a transaction being fraudulent. Decision Trees simplify decision-making by dividing data into subsets based on their characteristics, creating a hierarchical structure that helps determine the type of transaction. These methods exemplify the application of machine learning in enhancing the security and reliability of financial transactions.
The problem of credit card fraud prevention has become a matter of concern in the domain of online transactions. Machine learning models are necessary in detecting this kind of activities and preventing them. Several machine learning approaches, like neural networks, decision trees, support vector machines, and deep learning models, have been used to identify credit card fraud through the assessment and evaluation of different data patterns [22]. Most of the fraud detection systems suffer from this problem as it is quite common for datasets to be imbalanced [23]. Various resampling techniques can balance the data in order to mitigate the problem and increase the accuracy of fraud detection [24]. The most effective algorithms can be gauged using AUC, recall, and F1 index.
In this regard, the best performance was obtained from the AllKNN-CatBoost model with an AUC of 97.94%, a recall of 95.91%, and an F1 index of 87.40% [25]. From another recent development, a new method has been proposed to fix up the problem of credit card fraud detection. This technique combines swarm technique with machine learning in a firefly cluster search algorithm. This is a technique of tuning for support vector machines, extreme learning machines, extreme gradient-boosting machine-learning models.

2.5. Credit Card Fraud Detection Using Apache Spark

One of the almost optimal solutions for more efficient and far-reaching fraud detection based on credit cards is by making use of Apache Spark in data analysis. With high processing speeds offered by Spark, the tool works well with large datasets and provides a fast way of identifying probable fraud transactions. Spark, incorporates machine learning algorithms in it that provide real-time data analysis, making the detection of fraud rather very timely and accurate. Besides, Spark supports integration with all kinds of data sources, from banking systems to online chalks—such is needed for representing a fuller view of transactional behaviors. This ability of cross-platform detection proves to be of paramount importance for the effective prevention of fraud; therefore, it becomes very instrumental for most financial institutions and charge card companies to deter digital fraudulent activities.
Severe threats to the financial sector are from credit-card fraud. Some solutions have been proposed in which rigid analysis of data and complex machine learning algorithms are used for fraud detection in real time. Apache Spark emerged as a tool in this domain, and numerous studies have investigated its effectiveness in detecting credit card fraud [30]. These research studies have employed diverse machine learning algorithms like K-Means, C5.0 decision tree, Naive Bayes, Random Forest, and Multilayer Perceptron, showcasing accuracy rates in identifying fraudulent activities. The proposed models are assessed using authentic and fraudulent credit card datasets, demonstrating enhanced classification accuracy compared to existing methodologies. The utilization of Apache Spark has proven to be more efficient in deploying fraud detection systems than other methods.

2.6. How Machine Learning Algorithms Enhance Decision Quality in Detecting Fraud

Machine learning has proved to be an invaluable tool in regard to the identification of online fraudulent activities, making a significant contribution in the fields of financial integrity and security. These algorithms have the ability to learn and anticipate outcomes, based on vast datasets, which is impossible to do while using traditional analysis methods. That’s why we can accept the fact that there is an increase in the quality of the decisions being made by the organizations [31]. Below, we investigate the various ways in which the decision quality is being improved, regarding fraud detection, by utilizing machine learning algorithms.

2.6.1. Improved Detection Accuracy

Machine learning algorithms enhance detection accuracy by utilizing complex data patterns and relationships that cannot be tracked through manual analysis or traditional computational techniques [32,33]. By using techniques such as supervised learning [34], machine learning models can be trained on historical data that is made of both fraudulent and legitimate transactions. This kind of training enables models to identify subtle and complex indicators of fraud, thereby significantly reducing the instances of false negatives (missed fraud) and false positives (legitimate transactions being flagged as fraudulent). The ability to learn from new data ensures that the models’ accuracy improves over time, adapting to new fraud tactics and patterns.

2.6.2. Real-time Processing and Analysis

The ability of machine learning algorithms to process data in real time plays a vital role in detecting frauds promptly. Unlike approaches that involve processing data in batches, which can cause delays in spotting and addressing fraudulent behavior, ML algorithms can swiftly analyze transactions as they occur, quickly identifying suspicious activities. This feature not only improves decision quality, by minimizing the time for fraudulent transactions to slip through unnoticed, but also enables immediate intervention to prevent potential financial losses [35].

2.6.3. Handling Big Data and Complex Variables

When it comes to detecting fraudulent activity, the emergence of big data has brought up both new obstacles and possibilities. The algorithms that are used in machine learning are designed in such a way to be able to deal with large amounts of datasets that contain a great number of variables [36]. They have the ability to collect and evaluate data from a wide variety of sources, including transaction histories, consumer behavior patterns and external databases, in order to reach well-structured conclusions. With such extensive analytical capabilities, machine learning algorithms are able to examine a wider variety of elements that influence fraud, which ultimately results in decision-making that is more complex and accurate.

2.6.4. Adaptive Learning for Evolving Threats

Fraudulent schemes are continuously evolving, requiring adaptive mechanisms for effective detection. Machine learning algorithms excel in this aspect through their ability to learn from new data perpetually. As they are exposed to the latest fraudulent techniques, ML models adjust their parameters and improve their predictive capabilities [37]. This ongoing learning process ensures that the decision-making process remains robust against evolving threats, maintaining high detection rates over time.

2.6.5. Cost Efficiency through Automation

Using machine learning models to automate fraud detection processes results in cost efficiency for organizations [38]. Businesses can now better allocate their resources for more critical tasks by implementing automation techniques for data analysis and fraud detection, at least during their initial stages, where a first general screening is required. This task reallocation reduces operational costs and improves the overall quality of the decision-making processes by redirecting human expertise to other key areas within the organization.

2.6.6. Enhanced Scalability

Traditional fraud detection systems may find it challenging to increase their scaling abilities without an equivalent increase in costs and computational resources. Machine learning algorithms offer such scaling capabilities, which have been proven essential in the growing volumes of digital transactions and data management [39,40]. By using these machine learning models, organizations can maintain consistent decision quality without the burden of increasing costs or resources [41].
Machine learning algorithms improve accuracy, real-time analysis, adaptation to new threats, and cost-effectiveness, significantly changing the quality of decision-making processes regarding fraud detection [42]. The capability of machine learning to absorb and learn from enormous datasets, recognize intricate patterns, and adapt to ever-evolving fraud schemes places it at the forefront of contemporary fraud detection strategies [43]. It is anticipated that these algorithms' role in improving decision quality regarding fraud detection will become increasingly more prominent as they continue to develop. This will signal the beginning of a new era in the overall battle against financial fraud.
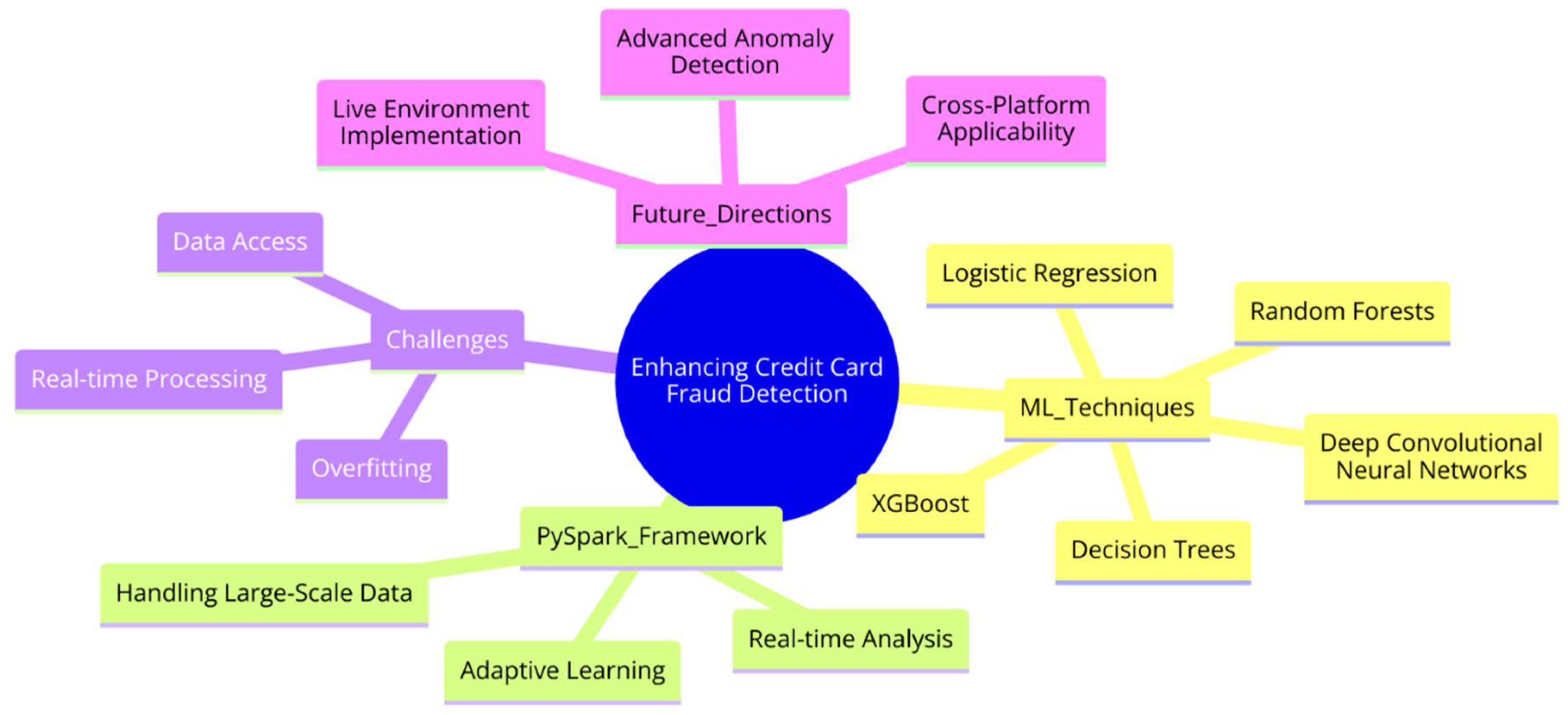
Preprints 110557 g001
Figure 1. Credit Card Fraud Detection Mindmap
Figure 1. Credit Card Fraud Detection Mindmap
Preprints 110557 g001

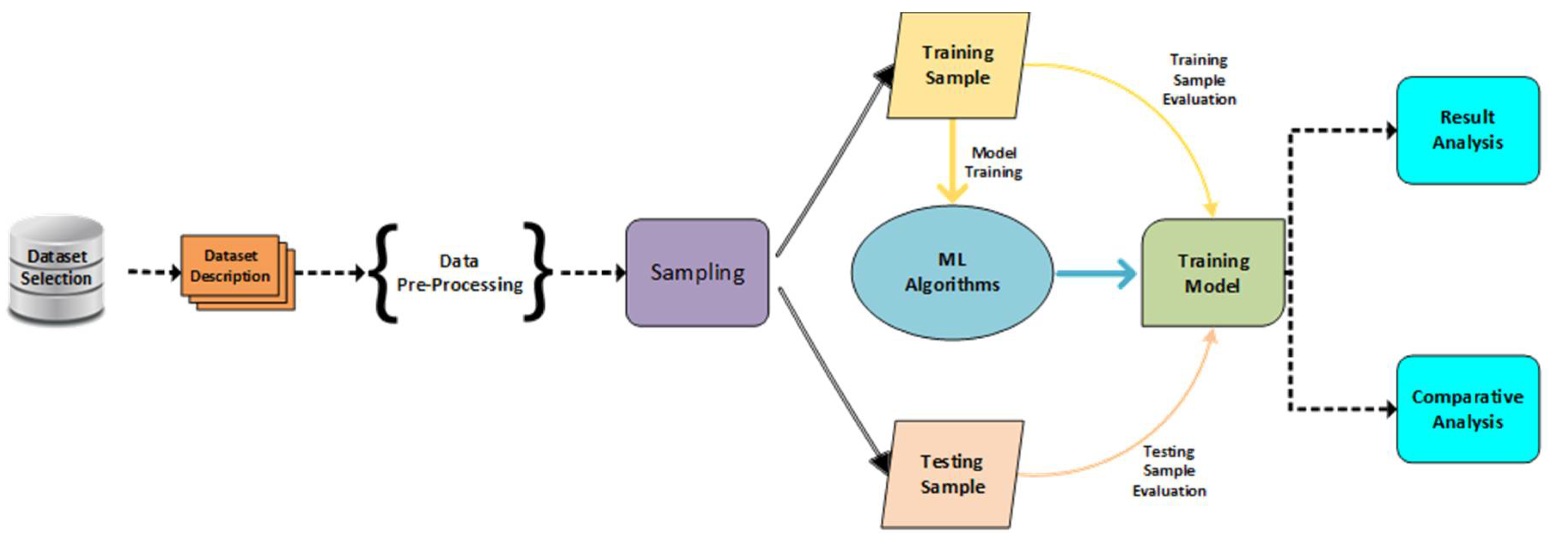
3. Materials and Methods

In this section, we will present the methods and techniques used to predict credit card fraud. We used the dataset “Credit Card Fraud Detection”, from kaggle.com, which contains anonymized data from credit card transactions with a size of more than 200 MB. We will create four training and prediction models: Logistic Regression, Decision Trees, Random Forests, and the complex XGBOOST method.
Preprints 110557 g002
Figure 2. Methodology framework
Figure 2. Methodology framework
Preprints 110557 g002
3.1 Performance Evaluation
  • Logistic Regression:
Logistic Regression is a statistical model often used for classification. Instead of predicting the exact value of a variable, as in linear Regression, logistic Regression estimates the probability of an outcome based on one or more independent variables. It is ideal for binary classification, such as predicting whether a transaction is fraudulent.
  • DecisionTrees
Decision Trees are a widely used algorithm in machine learning that utilizes a tree-like structure for decision-making. Each node in the tree represents a question or property, and each branch is a possible answer to that question. Decision Trees are easy to understand and interpret but can be sensitive or perform poorly in training with new, unseen data.
  • Random Forest
Random Forest is a machine learning algorithm that utilizes predictions from multiple machine learning algorithms, most notably Decision Trees, to improve performance and reduce overfitting. Each tree in the forest is trained on a random subset of the data, and the predictions from all the trees are combined to give one final result. This method is very effective in classification and Regression.
  • XGBoost
XGBoost (eXtreme Gradient Boosting) is an optimized machine-learning algorithm that boosts decision trees. It uses a series of models built sequentially, each new model focusing on correcting errors found in the previous models. XGBoost is known for its high performance, ability to handle large datasets effectively, and flexibility in parameter tuning.

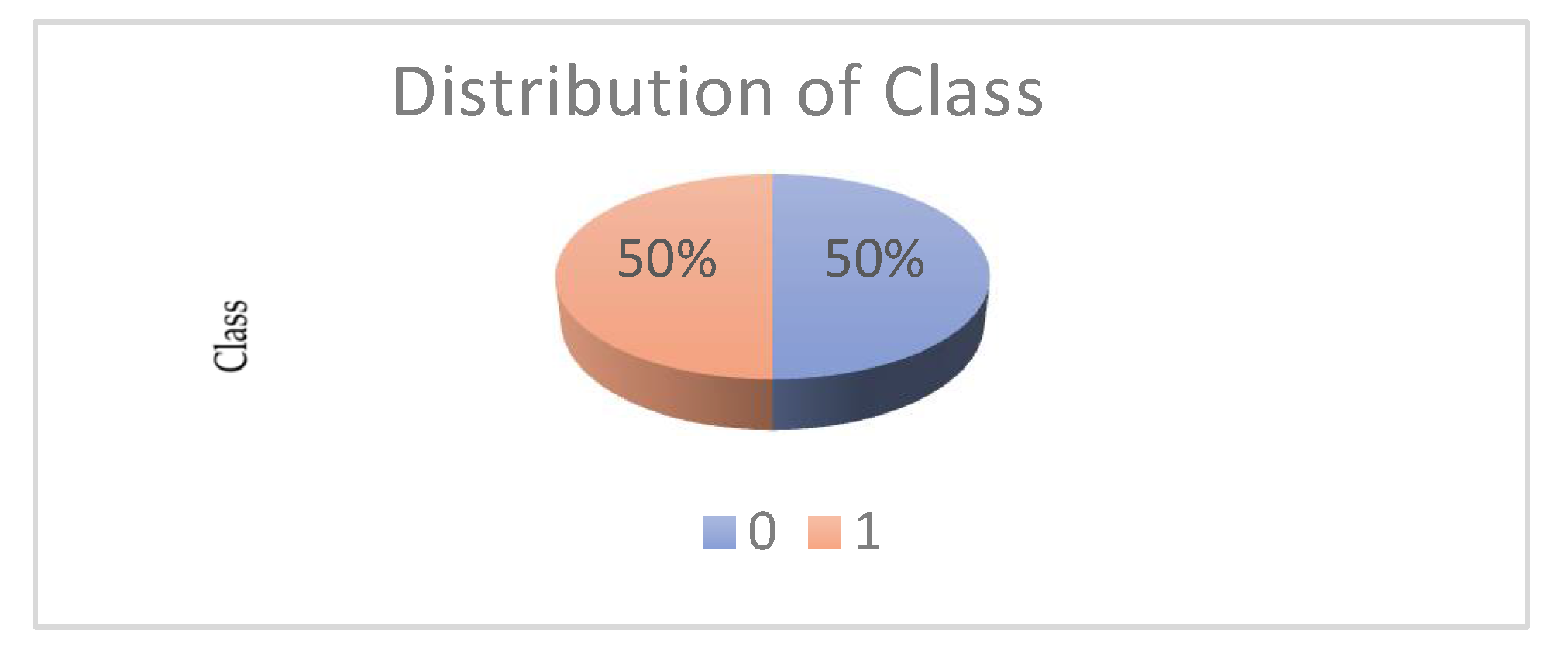
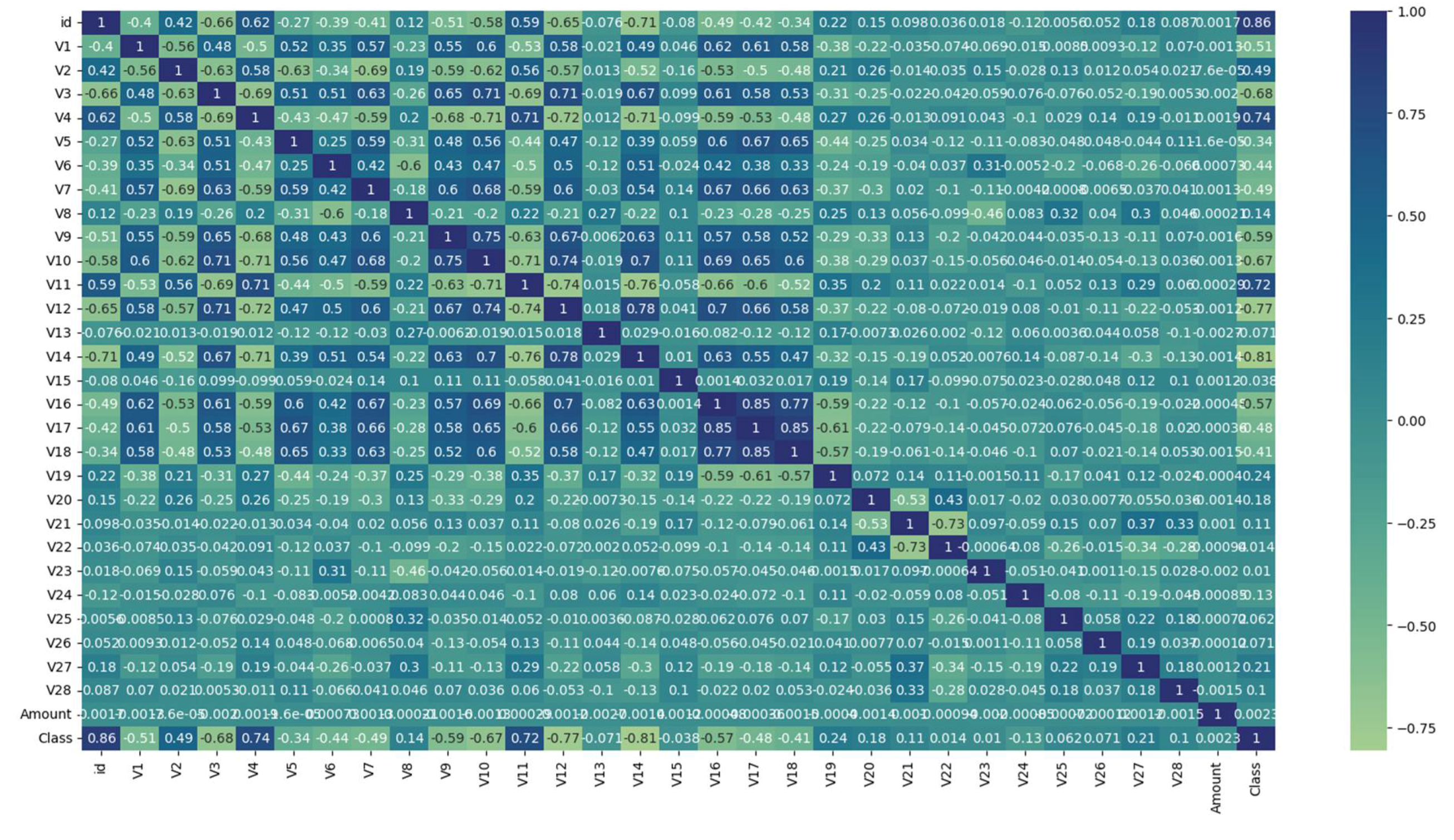
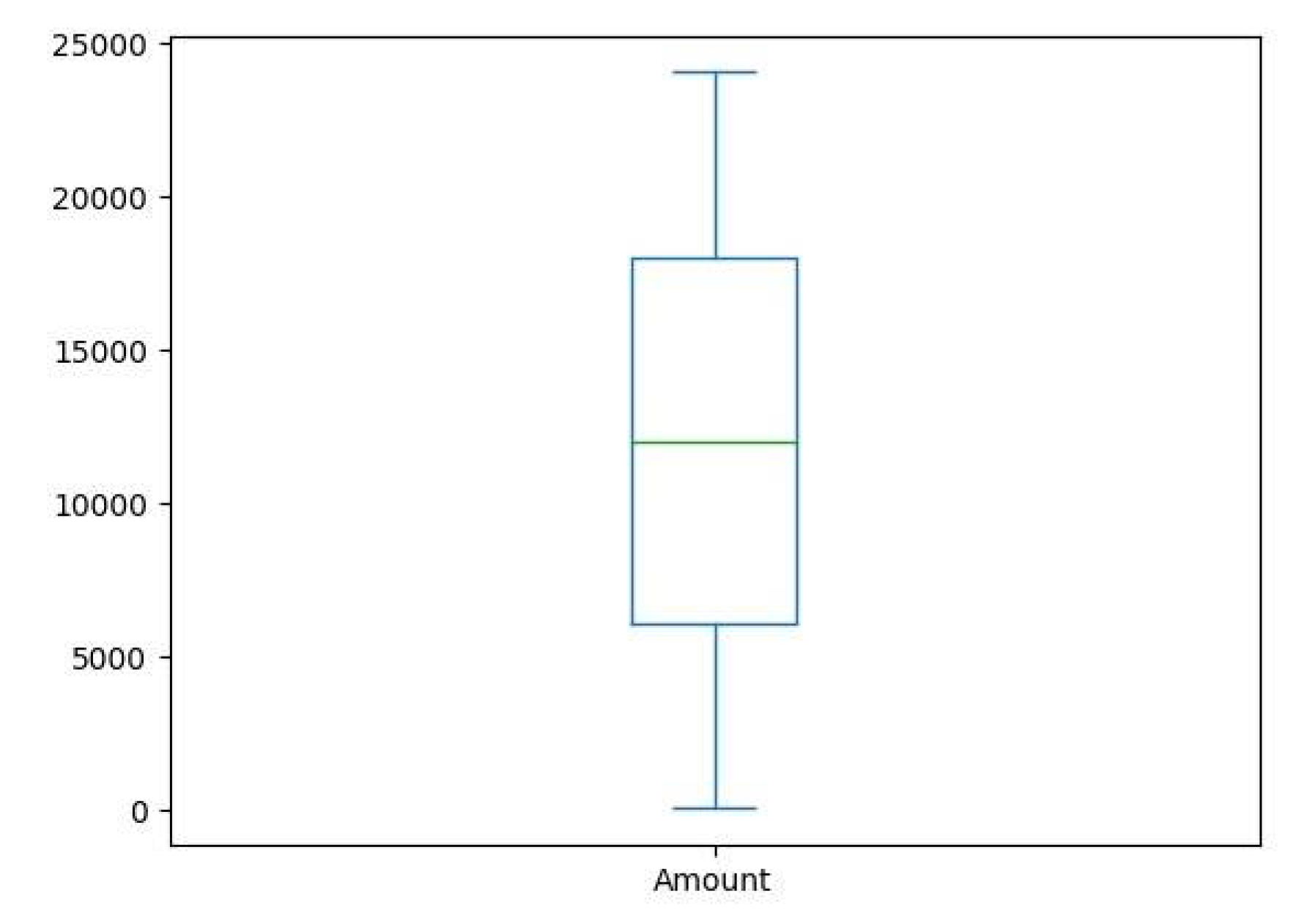
3.1. Dataset Description

To describe the dataset, we first need to study some of the data from it. Specifically, we import the dataset with the following command:
→data=pd.read_csv(‘creditcard_2023_dataset.csv’)
This command imports the dataset into our project and creates a data frame called “data”. Then, with data.head() we print some information about the dataset that we will need later. The result of running the above command is shown below (Table 1):
As shown above, we have the classes of data (v1,v2,v3 etc.) and other classes such as the amount of the transaction, as shown in the image below (Table 2).
The classes, as mentioned earlier, have been anonymized for privacy reasons. The issue here is to identify class correlation to predict the potential for fraud in electronic credit card transactions. Next, by running data.info(), we print the class types contained in our dataset. The result is shown below (Table 3).
As shown in the image above (Figure 3), we have the classes and their type. The type →float64 indicates that this class contains elements with decimal numbers while the ID, which is the odd number of each transaction, is an integer. By running data.describe(), we can see more details about our data and in particular some important statistics (Table 4).
As shown above, we have the sum (number of numbers) via count for each feature of our dataset, the mean, the standard deviation, the minimum number, the maximum and other important statistics. From the above analysis we can conclude that we have 568630 rows of observations with 31 columns. The Class row is our output attribute that indicates whether the transaction is fraudulent (1) or not (0) and that no missing data was observed in our Dataset. And finally, the data type of all the attributes seems quite satisfactory.

3.2. Dataset Pre-Processing

We continue with the pre-processing of our data. First, it is important to check if there are any missing values for each feature in our dataset. We do this by running data.isna().sum(). The result is shown below (Table 5).
As you can see from the image above, no feature contains any missing values. Therefore, we can continue with the pre-processing of our data. It is also important to check if there are duplicate entries. This is achieved by using the following command: data.duplicated().any(). The result of the execution is False, which means that there are no duplicate records, as shown below.
→ In 12 data.duplicated().any()
→ Out 12 False
Next, we want to investigate the correlation of classes with each other. We do this by running a command to create a heatmap graph. Specifically by executing the following command:
→heatmap = plt.figure(figsize=[20,10])
→sns.heatmap(data.corr(),cmap=’crest’,annot=True)
→plt.show()
The result of the command is the heatmap below.
The information deduced from the heatmap indicates that there are several notable correlations among different characteristics. V17 and V18 display a high correlation with each other, as do V16 and V17. V14 shows a negative correlation with V4, while V12 is negatively correlated with both V10 and V11. Additionally, V11 is negatively correlated with V10 but positively correlated with V4. V3 is positively correlated with both V10 and V12, and V9 and V10 also show a positive correlation.
Next, we want to investigate the transaction amounts in order to be able to draw conclusions. By executing data['Amount'].plot.box(), we can print a box plot type graph that shows us roughly where the transactions are moving in terms of amount. The result of running the above command is shown in the graph below.
Next, we want to check the distribution of the feature amount to see if the distribution of our feature amount data is normal. By executing the following command, we can create a graph, known as kdeplot which shows us the curvature of the data:
→sns.kdeplot(data=data[‘Amount’], shade=True)
→plt.show()
The result of running the above command is what is shown in the graph below (Figure 9).
Preprints 110557 g005
Figure 5. Kdeplot of transaction amount distribution to examine data curvature and normality.
Figure 5. Kdeplot of transaction amount distribution to examine data curvature and normality.
Preprints 110557 g005
As the graph shows, our data is fairly well distributed. Next, we want to study some features, which as shown by the heatmap earlier, illustrate high correlation. These features are V1, V10, V12 and V23. To see the correlation of the above features, we will need to create histograms. This is achieved by using the following command:
→paper, axes = plt.subplots(2, 2, figsize=(10,6))
→data[‘V1’].plot(kind=’hist’, ax=axes[0,0], title=’Distribution of V1’)
→data[‘V10’].plot(kind=’hist’, ax=axes[0,1], title=’Distribution of V10’)
→data[‘V12’].plot(kind=’hist’, ax=axes[1,0], title=’Distribution of V12’)
→data[‘V23’].plot(kind=’hist’, ax=axes[1,1], title=’Distribution of V23’)
→plt.suptitle(‘Distribution of V1,V10,V12 and V23’, size=14)
→plt.tight_layout()
→plt.show()
The result of running the above command is different histograms showing features V1,V10,V12 and V23 (Figure 10).
Preprints 110557 g006
Figure 6. Printing histograms of features V1, V10, V12, and V23.
Figure 6. Printing histograms of features V1, V10, V12, and V23.
Preprints 110557 g006
As shown in the graph above, we have successfully printed the features that are highly correlated with each other, and in particular, the distribution of data in them. Based on these features, we want to study what percentage of our data constitutes credit card fraud (class 1) or not (class 0). To achieve the above, we execute the command:
→data[‘Class’].value_counts().plot.pie(explode=[0,1,0],autopct=’%3.1f%%’,shadow=True,legend= True,startangle=45)
→plt.title(‘Distribution of Class’, size=14)
→plt.show()
The result of the execution of the above command is the following pie which shows us that 50% of the transactions are fraud, while the other 50% are not fraud (Figure 11).
Preprints 110557 g007
Figure 7. Data pie representing the fraud rate in credit card transactions.
Figure 7. Data pie representing the fraud rate in credit card transactions.
Preprints 110557 g007
Next, we need to divide our data into dependent and independent. So, we run the following command:
→x=data.drop([‘id’,’Class’],axis=1)
→y=data.Class
The above command removes the class "class" which indicates whether the transaction is valid or a fraud. At this point we should note that this class is the specific one we are trying to predict, which is why we “drop” it. Next, we print the head (representation) of the X dataframe we created. That is the dataset that does not contain the fraud class. The result is shown below.
x.head()
Next, we want to study the number of numbers contained in our X and Y dataset. Note that our data must be equally distributed.
→print(‘Shape of x’, x.shape)
→print(‘Shape of y’, y.shape)
→Shape of x (568630, 29)
→Shape of y (568630, )
As shown above, the data is equally distributed for the two subsets of the dataset. Next, we will need, in order to train our model on prediction, to scale the data, a step useful for correct prediction. We accomplish this by running the following commands:
→sc = StandardScaler()
→x_scaled = sc.fit_transform(x)
→x_scaled_df = pd.DataFrame(x_scaled,colomns=x.colomuns)
We then study our data again to see if the transformation has been successful. This is accomplished with x_scaled_df.head(). The result is shown below.
Preprints 110557 g008
Figure 7. Checking transformed data after scaling application.
Figure 7. Checking transformed data after scaling application.
Preprints 110557 g008
As the graph shows, our data seems to have been converted correctly. We then split our data into train/test subsets. This is accomplished with the following command:
→x_train,x_test,y_train,y_test =
train_test_split(x_scaled_df,y,test_size=0.25,random_state=15,stratify=y)
Next, we want to examine whether the subset splitting has been done successfully and the subset shapes are correct. This is achieved with the following commands:
→print(x_train.shape)
→print(x_test.shape)
→print(y_train.shape)
→print(y_test.shape)
The result is the elements contained in each subset:
→ (426472, 29)
→ (142158, 29)
→ (426472,)
→ (142158,)
Based on these subsets, we start training our first model, namely the logistic regression. We execute the command:
→1r=LogisticRegression()
Next, we run the command:
→1r.fit(x_train,y_train)
Our two commands above are responsible for loading the appropriate libraries and to make our data fit. Next, we need to create a function which is subservient to do quality evaluation of the prediction model we are building.
→def model_eval(actual,predicted):
→acc_score = accuract_score(actual, predicted)
→conf_matrix = confusion_matrix(actual, predicted)
→clas_rep = classification_report(actual, predicted)
→print(‘Model Acurracy is: ‘, round(acc_score, 2))
→print(conf_matrix)
With the above function we evaluate the model. Specifically, we want to predict the actual values based on what we have predicted. The classification report class shows us the actual values with the predicted values while the accuracy score is how well our model was able to predict transactions and classify them as either normal or fraudulent. Finally, we print the confusion matrix and the prediction class.

3. Results

For the logistic regression model, and specifically for the train subset, the results are shown below.
Table 8. Prediction model accuracy by comparing actual and predicted values, presenting an analytical classification reference, and displaying a confusion matrix.
Table 8. Prediction model accuracy by comparing actual and predicted values, presenting an analytical classification reference, and displaying a confusion matrix.
Training Accuracy
Model Accuracy is: 0,97
[[208643 4593]
[ 10330 202906]]
precision recall f1-score support
0 0,95 0,98 0,97 213236
1 0,98 0,95 0,96 213236
accuracy 0,97 426472
macro avg 0,97 0,97 0,97 426472
weighted avg 0,97 0,97 0,97 426472
Specifically, as shown above, the prediction accuracy is 0.97 or 97%. The evaluation metrics are detailed further as follows: Precision is a measure that reflects the percentage of correct positive predictions relative to the total number of positive predictions made by the model. Recall indicates the percentage of correct positive predictions relative to the total number of true positive cases in the data. The F1 score is a combination of accuracy and recall and is used to give an overall assessment of model performance, particularly when there is a class imbalance in the data. Support refers to the number of observations in the data for each class considered in the model, essentially representing the sample size for each class. These metrics were used to evaluate the performance of a ranking or classification model in machine learning and statistical analysis.
For the same model, and for the subset of tests (test), the results are presented below (Table 9).
For decision trees, we create a similar training model once the partitioning of the dataset has been done and investigate the performance again. Specifically for the training subset, the results are shown below (Table 10):
As shown above (Table 10), the accuracy of this model is 100% or 1.00. For the test subset the results are shown below (Table 11).
In this case, the model also performs better than the regression model, achieving 100% performance on all evaluation metrics. Therefore, this model is much better at detecting and predicting credit card fraud. Then, we proceed with the creation of a random forest model. For subset creation and training we use the same procedure as before.
We insert the following library:
→from sklearn.ensemble import RandomForestClassifier
We set a variable → rf = RandomForestClassifier() and fit our data → rf.fit(x_train, y_train). For the predictions we use the following:
→: preds_rf_train =rf.predict(x_train)m preds_rf_test = rf.predict(x_test)
The performance of the training subset is as follows:
While the performance of the test subset is as follows.
Table 13. Performance results of the random forest model for the test subset.
Table 13. Performance results of the random forest model for the test subset.
Training Accuracy
Model Accuracy is: 1,0
[[71060 19]
[ 0 71079]]
precision recall f1-score support
0 1,00 1,00 1,00 71079
1 1,00 1,00 1,00 71079
accuracy 1,00 142158
macro avg 1,00 1,00 1,00 142158
weighted avg 1,00 1,00 1,00 142158
We then create another machine learning model for prediction called XgBoost. This model is complex compared to the others and we want to see if it performs better than the previous ones.
We run the model import again. This time our model is as follows: import xgboost as xgb. We set up the model loading as follows:
→xgclf = xgb.XGBRFClassifier()
→xgclf.fit(x train, y train)
We initiate the prediction with the following commands:
→preds_xgb_train =xgclf.predict(x_train)
→preds_xgb_test = xgclf.predict(x_test)
The result in the training subset is as follows:
Table 14. Performance results of the XgBoost model for the training subset.
Table 14. Performance results of the XgBoost model for the training subset.
Training Accuracy
Model Accuracy is: 0,97
[[209470 3766]
[ 9686 203550]]
precision recall f1-score support
0 0,96 0,98 0,97 213236
1 0,98 0,95 0,97 213236
accuracy 0,97 426472
macro avg 0,97 0,97 0,97 426472
weighted avg 0,97 0,97 0,97 426472
While the result in the test subset is the following:
Table 15. Performance results of the XgBoost model for the test subset.
Table 15. Performance results of the XgBoost model for the test subset.
Training Accuracy
Model Accuracy is: 0,97
[[69837 1242]
[ 3280 67799]]
precision recall f1-score support
0 0,96 0,98 0,97 71079
1 0,98 0,95 0,97 71079
accuracy 0,97 142158
macro avg 0,97 0,97 0,97 142158
weighted avg 0,97 0,97 0,97 142158
As can be seen from the classification reports above, this model, although more complex, showed lower performance than the previous ones. Therefore, we will try to improve its performance further. We enter the following command:
→from sklearn.model_selection import RandomizedSearchCV
We go through the parameters we want to improve:
→param_dist_xgb = {
‘n_estimators’:[50,100,150,200,300,400],
‘learning_rate’: [0.01, 0.1, 0.2, 0.3],
‘max_depth’: [3, 4, 5, 6}
}
We import our model with the following command:
→ xgb_clf.fit(x_train,y_train)
And the training of the model with improved parameters begins. The result is shown in the image below.
Table 16. Improved XgBoost model training with custom parameters for better performance.
Table 16. Improved XgBoost model training with custom parameters for better performance.
[CV] END ..learning_rate=0,01 max_depth=4 n_estimators=400 total time= 8,1s
[CV] END ..learning_rate=0,01 max_depth=4 n_estimators=400 total time= 7,9s
[CV] END ..learning_rate=0,01 max_depth=4 n_estimators=400 total time= 8,2s
[CV] END ..learning_rate=0,01 max_depth=4 n_estimators=400 total time= 7,9s
[CV] END ..learning_rate=0,01 max_depth=5 n_estimators=300 total time= 6,5s
[CV] END ..learning_rate=0,01 max_depth=5 n_estimators=300 total time= 6,9s
[CV] END ..learning_rate=0,01 max_depth=5 n_estimators=300 total time= 7,0s
[CV] END ..learning_rate=0,01 max_depth=5 n_estimators=300 total time= 6,6s
[CV] END ..learning_rate=0,01 max_depth=5 n_estimators=300 total time= 6,8s
[CV] END ...learning_rate=0,1 max_depth=5 n_estimators=300 total time= 6,8s
[CV] END ...learning_rate=0,1 max_depth=5 n_estimators=300 total time= 7,2s
[CV] END ...learning_rate=0,1 max_depth=5 n_estimators=300 total time= 6,7s
[CV] END ...learning_rate=0,1 max_depth=5 n_estimators=300 total time= 6,5s
[CV] END ...learning_rate=0,1 max_depth=5 n_estimators=300 total time= 6,5s
The goal here is to find the best parameters for this model. By printing the best parameters for the XgBoost model, we can achieve better prediction performance. Specifically, the result is as follows:
Best Parameters for XG Boost:
→{‘n_estimators’: 400, ‘max_depth’: 6, ‘learning_rate’: 0.1}
Based on the improved parameters, we retrain our model and print the results again. The results for the training subset are shown below.
Table 17. Training the XgBoost model with the improved parameters and printing the results for the training subset.
Table 17. Training the XgBoost model with the improved parameters and printing the results for the training subset.
Training Accuracy
Model Accuracy is: 0,97
[[209366 3870]
[ 9538 203698]]
precision recall f1-score support
0 0,96 0,98 0,97 213236
1 0,98 0,96 0,97 213236
accuracy 0,97 426472
macro avg 0,97 0,97 0,97 426472
weighted avg 0,97 0,97 0,97 426472
The results for the test subset are the following:
As shown above (Table 18), there was an improvement in the model using the new parameters but not a significant improvement. Overall, the model reached 98% prediction whereas before the improvement it was still 98%. The only noticeable difference is in class 1, which is credit card fraud. Therefore, the improvement here is in the second class of data and not in the data that are normal transactions.

3.2. Comparative Analysis

As shown above (Table 19), for the training sample the Accuracy of Logistic Regression, Decision Trees, Random Forest and XGBoost are 0.97, 1.00, 1.00 and 0.97 respectively. For the testing sample, the Accuracy of Logistic Regression, Decision Trees, Random Forest and XGBoost are 0.96, 1.00, 1.00 and 0.97. As we can see, the Accuracy of Logistic Regression changes in the testing sample by +1%, while the rest 3 of the algorithms retain an unchanged percentage of Accuracy.
As we can see in Table 20 above, in the training dataset, the Precision-Recall-F1–Score for the Logistic Regression and XGBoost algorithms is 97%. The algorithms of Decision Trees and Random Forest, however, demonstrated 100% Precision, Recall and F1–Score.
Lastly, as we can see in Table 21 above, in the testing dataset, the Precision, Recall and F1–Score for the Logistic Regression is 96% and for the XGBoost is 97%. The algorithms of Decision Trees and Random Forest, demonstrated 100% Precision, Recall and F1–Score, as they also did in the training sample.

4. Discussion & Conclusions

The Logistic Regression model showed significant efficiency with an accuracy of 97%, demonstrating its usefulness in scenarios where simplicity and interpretability are key. The However, these flawless 100% accuracy scores attained by both the Decision Tree and Random Forest models have sparked worries about overfitting, considering the ever-changing nature of the real-world economic data. XGBoost, on the other hand, while maintaining a balance between efficiency and predictive capability, demonstrated a commendable 98% accuracy, showcasing its proficiency in tackling complex classification challenges.
This research methodology drew much support from PySpark, which was of great help in managing computational requirements to be met for large-scale transaction data processing. The models used here, from the simplest logistic regression to most complex ensemble methods like XGBoost, gave insight into the wholesome different approaches and methodologies applicable to fraud detection.
These summaries also prove the collective research efforts on the role of machine learning in credit card fraud detection and prevention. These modernization researchers implement advanced algorithms relevant to Logistic Regression, Decision Trees, Random Forest, and XGBoost to ensure great accuracy and efficiency compared to traditional techniques in fraud detection systems. These algorithms are further complemented by tools such as Apache Spark and Python libraries that would allow the handling of vast data sets involved in fraud transaction detection in real-time.
Though high accuracy rates have been realized and the high benefits of machine learning in this domain are observed, some challenges like data imbalance, model overfitting, and real-time processing capability remain. These present future research topics on how to come up with models that will dynamically learn to adapt to new patterns of fraud and techniques.
Future research shall be pamphleteering the collaborative efforts and sharing of insights across the financial sector. A network of fraud patterns and strategies shared among them will further fortify this collective defense against credit card fraud, thereby increasing the strength of any single machine learning model. Future improvements in machine learning models engaged in fighting credit card fraud are accomplished through continued research and collaboration. In the future, real-time detection, scalability, and continuous improvement of algorithms to stay at the very top in securing financial transactions against fraudulent activities will be the focus.
Other emerging smart city platforms can also be related to security and privacy issues in credit card fraud detection, where advanced technologies are embedded to enhance all aspects relating to citizens' security and privacy [44]. In the same way, sophisticated machine learning methods and data security measures are applied in credit card fraud detection over the sensitive financial information in such a way that complete compliance is maintained with privacy laws like the GDPR.
Individual research efforts summarized here underline the important role of machine learning in credit card fraud detection and prevention. Advanced algorithms that include logistic regression, decision trees, random forest, and XGBoost have gone a long way in improving the accuracy and efficiency of fraud detection systems over traditional methods. These are then supported by tools such as Spark Apache and Python libraries, which can manipulate huge data sets—clearly vital in finding, in real time, fraudulent transactions.
Although high rates of accuracy have been hit, and the large benefits of machines in this particular domain are already being procured, some of the other challenges still persist, especially in the areas of data imbalance, model overfitting, and real-time processing capabilities. These challenges pose opportunities for future research, especially in building models that can adapt dynamically to new patterns and techniques of fraud.
Moreover, it cannot be emphasized enough how important collaborative efforts and intelligence exchange are across the financial industry. Building a system to share such patterns and approaches will strengthen the collective defense of credit card fraud, hence positive amplification on the effectiveness of disparate machine learning models.
On the other side, machine learning has shown itself to be quite a powerful tool against credit card fraud today; still, further research and collaboration have to be done towards their model development. Bounds in real-time detection, scalability of models, and improvement in algorithms will truly stand for the continuous sustenance of machine learning at the very forefront in securing financial transactions from fraud.
  • Future Work
The research comprehensively investigates machine learning (ML) applications in detecting credit card fraud. It demonstrates the potential to improve the accuracy and adaptability of fraud detection systems. In future work, it is essential to integrate models into live financial transaction systems in real time to evaluate their feasibility and efficiency in real-world operating conditions. This involves improving machine learning models to ensure their ability to adapt to the ever-changing nature of fraudulent tactics and integrating advanced anomaly detection techniques that encompass the analysis of user behavior, potentially providing a more sophisticated capability to detect anomalies beyond just transactional ones. In addition, investigating the potential of emerging technologies, such as blockchain for secure data sharing and quantum computing for processing capabilities, could lead to significant advancements in fraud detection methodologies. Implementing this would bolster consumers' confidence in digital financial transactions and conform to worldwide movements towards heightened financial security and transparency, akin to the progress examined by researchers [45,46,47] in cloud storage.
Furthermore, it is imperative to comprehend and anticipate consumer behavior in the context of credit card fraud detection in order to identify anomalies that could potentially signify fraudulent actions. Fraud detection systems can enhance their understanding of typical versus unusual user behaviors by utilizing social signal processing techniques, which involve analyzing transactional behavior patterns and contextual data [48]. This can result in the creation of more sophisticated and flexible models, such as Kolmogorov complexity, which can identify and forecast possible instances of fraud by analyzing deviations from established patterns of behavior [49].
  • Limitations
The research is currently focused mainly on credit card transactions. However, it is recommended that its scope be broadened to include other financial platforms, such as digital wallets and online banking systems. This will create a more comprehensive framework for detecting fraud. One limitation of the research is its narrow focus on specific ML models and technologies, such as PySpark and XGBoost. This limited scope may only partially represent the capabilities of other emerging or established technologies and algorithms. The difficulties of integrating in real-time, such as dealing with delays and the ability to handle large amounts of data, while also protecting user privacy and managing the complexities of global data collaboration for the purpose of detecting fraud, are essential aspects that require thoughtful analysis and strategic preparation. Addressing these constraints and exploring the identified areas for future research could significantly enhance the efficiency, dependability, and range of fraud detection systems, rendering them more adaptable and potent in countering the ever-changing realm of financial fraud.

Author Contributions

Conceptualization, L.T., A.T. and F.Z.; methodology, L.T., A.T., F.Z. and C.H.; software, L.T. and C.H.; validation, L.T., A.T., F.Z. and C.H.; formal analysis, L.T., A.T., F.Z. and C.H.; investigation, L.T., A.T., F.Z. and C.H.; resources, L.T., A.T., F.Z. and C.H.; data curation, L.T., A.T., F.Z. and C.H.; writing—original draft preparation, L.T., A.T. and F.Z.; writing—review and editing, L.T. and C.H.; visualization, L.T., A.T., F.Z. and C.H.; supervision, L.T. and C.H.; project administration, L.T. and C.H.; funding acquisition, L.T. and C.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Data Availability Statement

The data used in this study are obtained from kaggle.com (https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud, accessed on 27 June 2024)

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Boutaher, N.; Elomri, A.; Abghour, N.; Moussaid, K.; Rida, M. (2020, November). A review of credit card fraud detection using machine learning techniques. In 2020 5th International Conference on cloud computing and artificial intelligence: technologies and applications (CloudTech) (pp. 1-5). IEEE.
  2. Minastireanu, E.A.; Mesnita, G. An Analysis of the Most Used Machine Learning Algorithms for Online Fraud Detection. Informatica Economica 2019, 23. [Google Scholar] [CrossRef]
  3. Alnafessah, A.; Casale, G. Artificial neural networks based techniques for anomaly detection in Apache Spark. Cluster Computing 2020, 23, 1345–1360. [Google Scholar] [CrossRef]
  4. Priscilla, C.V.; Prabha, D.P. (2020). Credit card fraud detection: A systematic review. In Intelligent Computing Paradigm and Cutting-edge Technologies: Proceedings of the First International Conference on Innovative Computing and Cutting-edge Technologies (ICICCT 2019), Istanbul, Turkey, October 30-31, 2019 1 (pp. 290-303). Springer International Publishing.
  5. Shirodkar, N.; Mandrekar, P.; Mandrekar, R.S.; Sakhalkar, R.; Kumar, K.C.; Aswale, S. (2020, February). Credit card fraud detection techniques–A survey. In 2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE) (pp. 1-7). IEEE.
  6. Kasa, N.; Dahbura, A.; Ravoori, C.; Adams, S. (2019, April). Improving credit card fraud detection by profiling and clustering accounts. In 2019 Systems and Information Engineering Design Symposium (SIEDS) (pp. 1-6). IEEE.
  7. Sadgali, I.; Sael, N.; Benabbou, F. Detection of credit card fraud: State of art. Int. J. Comput. Sci. Netw. Secur 2018, 18, 76–83. [Google Scholar]
  8. Fiore, U.; De Santis, A.; Perla, F.; Zanetti, P.; Palmieri, F. Using generative adversarial networks for improving classification effectiveness in credit card fraud detection. Information Sciences 2019, 479, 448–455. [Google Scholar] [CrossRef]
  9. Abdulghani, A.Q.; Uçan, O.N.; Alheeti, K.M.A. (2021, December). Credit card fraud detection using XGBoost algorithm. In 2021 14th International Conference on Developments in eSystems Engineering (DeSE) (pp. 487-492). IEEE.
  10. Karthika, J.; Senthilselvi, A. Smart credit card fraud detection system based on dilated convolutional neural network with sampling technique. Multimedia Tools and Applications 2023, 1–18. [Google Scholar] [CrossRef]
  11. Darwish, S.M. A bio-inspired credit card fraud detection model based on user behavior analysis suitable for business management in electronic banking. Journal of Ambient Intelligence and Humanized Computing 2020, 11, 4873–4887. [Google Scholar] [CrossRef]
  12. Tyagi, N.; Rana, A.; Awasthi, S.; Tyagi, L.K. (2022). Data Science: Concern for Credit Card Scam with Artificial Intelligence. In Cyber Security in Intelligent Computing and Communications (pp. 115-128). Singapore: Springer Singapore.
  13. Velasco, R.B.; Carpanese, I.; Interian, R.; Paulo Neto, O.C.; Ribeiro, C.C. A decision support system for fraud detection in public procurement. International Transactions in Operational Research 2021, 28, 27–47. [Google Scholar] [CrossRef]
  14. Kannagi, A.; Mohammed, J.G.; Murugan, S.S.G.; Varsha, M. Intelligent mechanical systems and its applications on online fraud detection analysis using pattern recognition K-nearest neighbor algorithm for cloud security applications. Materials Today: Proceedings 2023, 81, 745–749. [Google Scholar] [CrossRef]
  15. Patil, S.; Nemade, V.; Soni, P.K. Predictive modelling for credit card fraud detection using data analytics. Procedia computer science 2018, 132, 385–395. [Google Scholar] [CrossRef]
  16. Karthik VS, S.; Mishra, A.; Reddy, U.S. Credit card fraud detection by modelling behaviour pattern using hybrid ensemble model. Arabian Journal for Science and Engineering 2022, 1–11. [Google Scholar] [CrossRef]
  17. Vanini, P.; Rossi, S.; Zvizdic, E.; Domenig, T. Online payment fraud: from anomaly detection to risk management. Financial Innovation 2023, 9, 1–25. [Google Scholar] [CrossRef]
  18. Nascimento, D.C.; Barbosa, B.; Perez, A.M.; Caires, D.O.; Hirama, E.; Ramos, P.L.; Louzada, F. (). Risk management in e-commerce—a fraud study case using acoustic analysis through its complexity. Entropy 2019, 21, 1087. [Google Scholar]
  19. Alazizi, A.; Habrard, A.; Jacquenet, F.; He-Guelton, L.; Oblé, F.; Siblini, W. (2019, November). Anomaly detection, consider your dataset first an illustration on fraud detection. In 2019 IEEE 31st international conference on tools with artificial intelligence (ICTAI) (pp. 1351-1355). IEEE.
  20. Sood, P.; Sharma, C.; Nijjer, S.; Sakhuja, S. Review the role of artificial intelligence in detecting and preventing financial fraud using natural language processing. International Journal of System Assurance Engineering and Management 2023, 14, 2120–2135. [Google Scholar] [CrossRef]
  21. Xu, X.; Xiong, F.; An, Z. Using machine learning to predict corporate fraud: evidence based on the gone framework. Journal of Business Ethics 2023, 186, 137–158. [Google Scholar] [CrossRef]
  22. Esenogho, E.; Mienye, I.D.; Swart, T.G.; Aruleba, K.; Obaido, G. A neural network ensemble with feature engineering for improved credit card fraud detection. IEEE Access 2022, 10, 16400–16407. [Google Scholar] [CrossRef]
  23. Ludera, D.T. (2021). Credit card fraud detection by combining synthetic minority oversampling and edited nearest neighbours. In Advances in Information and Communication: Proceedings of the 2021 Future of Information and Communication Conference (FICC), Volume 2 (pp. 735-743). Springer International Publishing.
  24. Abd El-Naby, A.; Hemdan EE, D.; El-Sayed, A. An efficient fraud detection framework with credit card imbalanced data in financial services. Multimedia Tools and Applications 2023, 82, 4139–4160. [Google Scholar] [CrossRef]
  25. Alfaiz, N.S.; Fati, S.M. Enhanced credit card fraud detection model using machine learning. Electronics 2022, 11, 662. [Google Scholar] [CrossRef]
  26. Singh, A.; Jain, A. An efficient credit card fraud detection approach using cost-sensitive weak learner with imbalanced dataset. Computational Intelligence 2022, 38, 2035–2055. [Google Scholar] [CrossRef]
  27. Krishna Rao, N. V. , Y., Shalini, N., Harika, A., Divyavani, V., & Mangathayaru, N. (2021). Credit card fraud detection using spark and machine learning techniques. In Machine Learning Technologies and Applications: Proceedings of ICACECS 2020; Springe: Singapore; pp. 163–172.
  28. Madhavi, A.; Sivaramireddy, T. (2021). Real-Time Credit Card Fraud Detection Using Spark Framework. In Machine Learning Technologies and Applications: Proceedings of ICACECS 2020 (pp. 287-298). Springer Singapore.
  29. Zhou, H.; Sun, G.; Fu, S.; Wang, L.; Hu, J.; Gao, Y. Internet financial fraud detection based on a distributed big data approach with node2vec. IEEE Access 2021, 9, 43378–43386. [Google Scholar] [CrossRef]
  30. Chouiekh, A.; Ibn El Haj, E.H. (2022). Towards Spark-Based Deep Learning Approach for Fraud Detection Analysis. In Proceedings of Sixth International Congress on Information and Communication Technology: ICICT 2021, London, Volume 3 (pp. 15-22). Springer Singapore.
  31. El Hajjami, S.; Malki, J.; Berrada, M.; Mostafa, H.; Bouju, A. (2021, January). Machine learning system for fraud detection. a methodological approach for a development platform. In International Conference on Digital Technologies and Applications (pp. 99-110). Cham: Springer International Publishing.
  32. Vlachou, E.; Karras, A.; Karras, C.; Theodorakopoulos, L.; Halkiopoulos, C.; Sioutas, S. Distributed Bayesian Inference for Large-Scale IoT Systems. Big Data and Cognitive Computing 2023, 8, 1. [Google Scholar] [CrossRef]
  33. Karras, A.; Giannaros, A.; Karras, C.; Theodorakopoulos, L.; Mammassis, C.S.; Krimpas, G.A.; Sioutas, S. TinyML Algorithms for Big Data Management in Large-Scale IoT Systems. Future Internet 2024, 16, 42. [Google Scholar] [CrossRef]
  34. Khalid, A.R.; Owoh, N.; Uthmani, O.; Ashawa, M.; Osamor, J.; Adejoh, J. Enhancing credit card fraud detection: an ensemble machine learning approach. Big Data and Cognitive Computing 2024, 8, 6. [Google Scholar] [CrossRef]
  35. Li, Z.; Wang, B.; Huang, J.; Jin, Y.; Xu, Z.; Zhang, J.; Gao, J. A graph-powered large-scale fraud detection system. International Journal of Machine Learning and Cybernetics 2024, 15, 115–128. [Google Scholar] [CrossRef]
  36. Singh, K.; Kolar, P.; Abraham, R.; Seetharam, V.; Nanduri, S.; Kumar, D. (2024). Automated Secure Computing for Fraud Detection in Financial Transactions. Automated Secure Computing for Next-Generation Systems, 177-189.
  37. Chen, C.T.; Lee, C.; Huang, S.H.; Peng, W.C. (2024). Credit Card Fraud Detection via Intelligent Sampling and Self-supervised Learning. ACM Transactions on Intelligent Systems and Technology.
  38. Aburbeian, A.M.; Fernández-Veiga, M. Secure Internet Financial Transactions: A Framework Integrating Multi-Factor Authentication and Machine Learning. AI 2024, 5, 177–194. [Google Scholar] [CrossRef]
  39. Zhao, Y.; Zheng, G.; Mukherjee, S.; McCann, R.; Awadallah, A. (2023, June). Admoe: Anomaly detection with mixture-of-experts from noisy labels. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 37, No. 4, pp. 4937–4945).
  40. Koutras, K.; Bompotas, A.; Halkiopoulos, C.; Kalogeras, A.; Alexakos, C. Dimensionality Reduction on IoT Monitoring Data of Smart Building for Energy Consumption Forecasting. 2023 IEEE International Smart Cities Conference (ISC2). 2023. [CrossRef]
  41. Antonopoulou, S.; Stamatiou, Y.C.; Vamvakari, M. An asymptotic expansion for theq-binomial series using singularity analysis for generating functions. Journal of Discrete Mathematical Sciences and Cryptography 2007, 10, 313–328. [Google Scholar] [CrossRef]
  42. Zehra, S.; Faseeha, U.; Syed, H.J.; Samad, F.; Ibrahim, A.O.; Abulfaraj, A.W.; Nagmeldin, W. Machine Learning-Based Anomaly Detection in NFV: A Comprehensive Survey. Sensors 2023, 23, 5340. [Google Scholar] [CrossRef] [PubMed]
  43. Antonopoulou, H.; Theodorakopoulos, L.; Halkiopoulos, C.; Mamalougkou, V. Utilizing Machine Learning to Reassess the Predictability of Bank Stocks. Emerging Science Journal 2023, 7, 724–732. [Google Scholar] [CrossRef]
  44. Stamatiou, Y.; Halkiopoulos, C.; Antonopoulou, H. (2023). A Generic, Flexible Smart City Platform focused on Citizen Security and Privacy. Proceedings of the 27th Pan-Hellenic Conference on Progress in Computing and Informatics. [CrossRef]
  45. Gousteris, S.; Stamatiou, Y.C.; Halkiopoulos, C.; Antonopoulou, H.; Kostopoulos, N. Secure Distributed Cloud Storage based on the Blockchain Technology and Smart Contracts. Emerging Science Journal 2023, 7, 469–479. [Google Scholar] [CrossRef]
  46. Karras, A.; Giannaros, A.; Theodorakopoulos, L.; Krimpas, G.A.; Kalogeratos, G.; Karras, C.; Sioutas, S. FLIBD: A Federated Learning-Based IoT Big Data Management Approach for Privacy-Preserving over Apache Spark with FATE. Electronics 2023, 12, 4633. [Google Scholar] [CrossRef]
  47. Karras, A.; Karras, C.; Bompotas, A.; Bouras, P.; Theodorakopoulos, L.; Sioutas, S. SparkReact: A Novel and User-friendly Graphical Interface for the Apache Spark MLlib Library. Proceedings of the 26th Pan-Hellenic Conference on Informatics. 2022. [CrossRef]
  48. Gkintoni, E.; Kakoleres, G.; Telonis, G.; Halkiopoulos, C.; Boutsinas, B. A Conceptual Framework for Applying Social Signal Processing to Neuro-Tourism. Springer Proceedings in Business and Economics 2023, 323–335. [Google Scholar] [CrossRef]
  49. Antonopoulou, H. Kolmogorov complexity based upper bounds for the unsatisfiability threshold of random k-SAT. Journal of Discrete Mathematical Sciences and Cryptography 2020, 23, 1431–1438. [Google Scholar] [CrossRef]
Preprints 110557 g003
Figure 3. Generation of a heatmap to examine the correlations between classes.
Figure 3. Generation of a heatmap to examine the correlations between classes.
Preprints 110557 g003
Preprints 110557 g004
Figure 4. Amount of Transactions.
Figure 4. Amount of Transactions.
Preprints 110557 g004
Table 1. Printing the first rows of the dataset with data.head() in Python.
Table 1. Printing the first rows of the dataset with data.head() in Python.
id V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14
0 -0,260648 -0,469648 2,496266 -0,083724 0,129681 0,732898 0,519014 -0,130006 0,727159 0,637735 -0,987020 0,293438 -0,941386 0,549020
1 0,985100 -0,356045 0,558056 -0,429654 0,277140 0,428605 0,406466 -0,133118 0,347452 0,529808 0,140107 1,564246 0,574074 0,627719
2 -0,260272 -0,949385 1,728538 -0,457986 0,074062 1,419481 0,743511 -0,095576 -0,261297 0,690708 -0,272985 0,659021 0,805173 0,616874
3 -0,152152 -0,508959 1,746840 -1,090178 0,249486 1,143312 0,518269 -0,065130 -0,205698 0,575231 -0,752581 0,737483 0,592994 0,559535
4 -0,206820 -0,165280 1,527053 -0,448293 0,106125 0,530549 0,658849 -0,212660 1,049921 0,968045 -1,203171 1,029577 1,439310 0,241454
Table 2. Display the data classes and transaction amount in the dataset.
Table 2. Display the data classes and transaction amount in the dataset.
V15 V16 V17 V18 V19 V20 V21 V22 V23 V24 V25 V26 V27 V28 Amount
1,804879 0,215598 0,512307 0,333644 0,124270 0,091202 -0,110552 0,217606 -0,134794 0,165999 0,126280 -0,434824 -0,081230 -0,151045 17982,10
0,706121 0,789188 0,403810 0,201799 -0,340687 -0,233984 -0,231984 -0,194936 -0,605761 0,073469 -0,577395 0,296503 -0,248052 -0,064512 6531,37
3,060253 -0,577514 0,885536 0,239442 -2,366079 0,361652 -0,005020 0,702906 0,945045 -1,154666 -0,605564 -0,312895 -0,300258 -0,244718 2513,54
-0,697664 -0,030669 0,242629 2,178616 -1,345060 -0,378223 -0,378223 -0,146927 -0,038212 -1,893131 1,003963 -0,511950 -0,165316 0,048324 5384,44
0,153008 0,224358 0,366466 0,291782 0,445317 0,247237 -0,106984 0,729727 -0,161666 0,312561 -0,141416 1,071126 0,023712 0,419117 14278,97
Table 3. Presentation of class types in the credit card dataset with data.info() command.
Table 3. Presentation of class types in the credit card dataset with data.info() command.
<class ‘pandas.core.frame.DataFrame’>
RangeIndex: 568630 entries, 0 to 568629
Data columns (total 31 columns):
# Column Non-Null Count Dtype
0 id 568630 non-null int64
1 V1 568630 non-null float64
2 V2 568630 non-null float64
3 V3 568630 non-null float64
4 V4 568630 non-null float64
5 V5 568630 non-null float64
6 V6 568630 non-null float64
7 V7 568630 non-null float64
8 V8 568630 non-null float64
Table 4. Presentation of credit card dataset statistics.
Table 4. Presentation of credit card dataset statistics.
id V1 V2 V3 V4 V5 V6 V7 V8 V9
count 568630,000000 5,686300E+05 5,686300E+05 5,686300E+05 5,686300E+05 5,686300E+05 5,686300E+05 5,686300E+05 5,686300E+05 5,686300E+05
mean 284314,500000 -5,638058E-17 -1,319545E-16 -3,518788E-17 -2,879008E-17 7,997245E-18 -3,958636E-17 -3,198898E-17 2,109273E-17 3,998623E-17
std 164149,486122 1,000001E+00 1,000001E+00 1,000001E+00 1,000001E+00 1,000001E+00 1,000001E+00 1,000001E+00 1,000001E+00 1,000001E+00
min 0,000000 -3,495584E+00 -4,099666E+01 -3,183760E+00 -4,951222E+00 -9,952786E+00 -2,111111E+01 -4,351839E+00 -1,075634E+01 -3,751919E+00
25% 142157,500000 -5,652859E-01 -4,866777E-01 -6,492987E-01 -6,560203E-01 -2,934955E-01 -4,458712E-01 -2,835329E-01 -1,922572E-01 -5,687446E-01
50% 284314,500000 -9,363846E-02 -1,358939E-01 3,528579E-04 -7,376152E-02 8,108788E-02 7,871758E-02 2,333659E-01 -1,145242E-01 9,252647E-02
75% 426471,750000 8,326582E-01 3,435552E-01 6,285380E-01 7,070074E-01 4,397368E-01 4,977881E-01 5,259548E-01 4,729905E-02 5,592621E-01
max 568629,000000 2,229046E+00 4,361865E+00 1,412583E+01 3,201536E+00 4,271689E+00 2,616840E+01 2,178730E+02 5,958040E+00 2,027006E+01
Table 5. . Verification of the presence of missing values in the dataset with data.isna().sum().
Table 5. . Verification of the presence of missing values in the dataset with data.isna().sum().
Preprints 110557 i001
Table 6. Removing the “class” class from the dataset to create an independent dataset X.
Table 6. Removing the “class” class from the dataset to create an independent dataset X.
V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15
0 -0,260648 -0,469648 2,496266 -0,083724 0,129681 0,732898 0,519014 -0,130006 0,727159 0,637735 -0,987020 0,293438 -0,941386 0,549020 1,804879
1 0,985100 -0,356045 0,558056 -0,429654 0,277140 0,428605 0,406466 -0,133118 0,347452 0,529808 0,140107 1,564246 0,574074 0,627719 0,706121
2 -0,260272 -0,949385 1,728538 -0,457986 0,074062 1,419481 0,743511 -0,095576 -0,261297 0,690708 -0,272985 0,659021 0,805173 0,616874 3,060253
3 -0,152152 -0,508959 1,746840 -1,090178 0,249486 1,143312 0,518269 -0,065130 -0,205698 0,575231 -0,752581 0,737483 0,592994 0,559535 -0,697664
4 -0,206820 -0,165280 1,527053 -0,448293 0,106125 0,530549 0,658849 -0,212660 1,049921 0,968045 -1,203171 1,029577 1,439310 0,241454 0,153008
Table 9. Analytical evaluation of prediction model performance using Precision, Recall, F1-Score and Support methods for the test subset.
Table 9. Analytical evaluation of prediction model performance using Precision, Recall, F1-Score and Support methods for the test subset.
Training Accuracy
Model Accuracy is: 0,96
[[69545 1534]
[ 3520 67559]]
precision recall f1-score support
0 0,95 0,98 0,96 71079
1 0,98 0,95 0,96 71079
accuracy 0,96 142158
macro avg 0,96 0,96 0,96 142158
weighted avg 0,96 0,96 0,96 142158
Table 10. Evaluation of a decision tree training model for the training subset.
Table 10. Evaluation of a decision tree training model for the training subset.
Training Accuracy
Model Accuracy is: 1,0
[[213236 0]
[ 0 213236]]
precision recall f1-score support
0 1,0 1,0 1,0 213236
1 1,0 1,0 1,0 213236
accuracy 1,0 426472
macro avg 1,0 1,0 1,0 426472
weighted avg 1,0 1,0 1,0 426472
Table 11. Decision tree model performance results for the test subset.
Table 11. Decision tree model performance results for the test subset.
Training Accuracy
Model Accuracy is: 1,0
[[70864 215]
[ 92 70987]]
precision recall f1-score support
0 1,00 1,00 1,00 71079
1 1,00 1,00 1,00 71079
accuracy 1,00 142158
macro avg 1,00 1,00 1,00 142158
weighted avg 1,00 1,00 1,00 142158
Table 12. Performance results of the random forest model for the training subset.
Table 12. Performance results of the random forest model for the training subset.
Training Accuracy
Model Accuracy is: 1,0
[[213236 0]
[ 0 213236]]
precision recall f1-score support
0 1,00 1,00 1,00 213236
1 1,00 1,00 1,00 213236
accuracy 1,00 426472
macro avg 1,00 1,00 1,00 426472
weighted avg 1,00 1,00 1,00 426472
Table 18. Training the XgBoost model with the improved parameters and printing the results for the test subset.
Table 18. Training the XgBoost model with the improved parameters and printing the results for the test subset.
Training Accuracy
Model Accuracy is: 0,97
[[69810 1269]
[ 3214 67865]]
precision recall f1-score support
0 0,96 0,98 0,97 71079
1 0,98 0,95 0,97 71079
accuracy 0,97 142158
macro avg 0,97 0,97 0,97 142158
weighted avg 0,97 0,97 0,97 142158
Table 19. Accuracy results of models used in this research.
Table 19. Accuracy results of models used in this research.
Training Sample for 4 algorithms
Log. Regression Decision Trees RF XGBoost
Accuracy 0,97 1,00 1,00 0,97
Testing Sample for 4 algorithms
Accuracy 0,96 1,00 1,00 0,97
Table 20. Precision, Recall and F1-Score for all 4 models, for the Training sampling.
Table 20. Precision, Recall and F1-Score for all 4 models, for the Training sampling.
Log. Regression Decision Trees RF XGBoost
Precision 0,97 1,00 1,00 0,97
Recall 0,97 1,00 1,00 0,97
F1-Score 0,97 1,00 1,00 0,97
Table 21. Precision, Recall and F1-Score for all 4 models, for the Testing sampling.
Table 21. Precision, Recall and F1-Score for all 4 models, for the Testing sampling.
Log. Regression Decision Trees RF XGBoost
Precision 0,96 1,00 1,00 0,97
Recall 0,96 1,00 1,00 0,97
F1-Score 0,96 1,00 1,00 0,97
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated