Prerpints.org logo
Preprint
Article

Strip Adjustment of Multi-Temporal LiDAR Data - A Case Study at the Pielach River

Altmetrics

Downloads

125

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

28 June 2024

Posted:

01 July 2024

You are already at the latest version

Alerts
Abstract
With LiDAR (Light Detection and Ranging) time series being used for various applications, optimal realisation of a common geodetic datum over many epochs is a highly important prerequisite with direct impact on accuracy and reliability of derived measures. In our work, we develop and define several approaches to the adjustment of multi-temporal LiDAR data in a given software framework. These approaches ranging from pragmatic to more rigorous solutions are applied to an 8 year time series with 21 individual epochs. The analysis of the respective results suggests that a sequence of bi-temporal adjustments brings the best results while being more flexible and computationally viable than the most extensive approach of using all epochs in one single multi-temporal adjustment. With a combination of sparse control patches measured in the field and one selected reference block, we obtain relative datum discrepancies in the range of 1-2 cm for the complete time series. Based on our findings, we formulate design criteria for setting up and adjusting future time series with the proposed method.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

LiDAR and specifically Airborne Laser Scanning (ALS) has emerged as the technique of choice for a diversity of mapping and change detection tasks in various fields of application. Amongst others, its provision of accurate 3D measurements with high spatial resolution, its minimal requirements concerning accessibility of a scene and its penetration capabilities through vegetation are widely utilized in earth sciences [1], natural hazard management such as flood applications [2], natural resource management [3], object change detection in urban environments ([4,5]) and animal species diversity assessment [6].
Change detection with LiDAR relies on repeated surveys in suitably spaced time epochs ([1,4,7,8]). Numerous exemplary studies applying such multi-temporal ALS data can be found in Table 1.
While the sensor properties and surrounding conditions of each data acquisition epoch are extensively discussed, the data orientation and registration procedure is often depicted as an independent epoch-wise preprocessing task or not even mentioned. Most of the studies in Table 1 trust that data providers and standard processing workflows sufficiently account for potential systematic discrepancies between separate epochs. Notably, the significance of comparisons between different epochs crucially depends on whether the respective datasets are consistent in terms of sharing a common coordinate frame. Even if the individual accuracy and precision of the datasets are clearly sufficient for a given task, change detection may be hindered by systematic discrepancies between the datasets ([1,23]).
In this paper, we investigate the impact of temporal decorrelation, varying sensor characteristics and varying environmental conditions on the orientation of multi-temporal ALS data based on a state-of-the-art strip adjustment procedure [40]. Our aim is to optimize the workflow with respect to these additional challenges and answer the following questions:
  • What are the most important issues for the conceptualization, acquisition and orientation of multi-temporal ALS datasets?
  • Which criteria define an optimal workflow and how can these be achieved in practice? The presumably most rigorous method for the improvement of multi-temporal ALS data would be one simultaneous strip adjustment of all epochs combined. However, certain drawbacks can be associated with this approach. The number of observations and unknowns increases with each epoch leading to a high demand of computational resources. An integration of new epochs is elaborate and implicates datum changes for all old epochs. The central question thus is: Do the adjustment results justify these drawbacks or can they be matched by a more efficient approach?
  • What accuracy can be realistically achieved with the proposed methods?
The remainder of this article is structured as follows. In Section 2 we discuss related contributions from the literature. Section 3 introduces the study area and gives an overview of all relevant datasets. In Section 4, the methodology is presented including the basic strip adjustment approach, the proposed workflows for strip adjustment of multi-temporal datasets and the criteria for quality assessment. The results are presented and discussed in Section 5. The article is concluded in Section 6 by summarizing our findings and deducing recommendations for the design of future LiDAR time series.

2. Related Work

The questions we are addressing in this paper are approached from different directions in the literature.
The aspect of ALS data registration with strip adjustment is for instance treated in [41] and [42]. Recently, many publications specifically adapt the workflow to UAV-borne sensors, such as [40,43,44,45] and [46]. Due to its kinematic acquisition characteristics, the georeferencing of ALS data crucially depends on trajectory estimation [47] in order to achieve optimal accuracy. This can either be solved in two separate steps (1. trajectory estimation - 2. strip adjustment with additional trajectory correction) or by directly integrating trajectory estimation and strip adjustment [48]. An extensive review of integrated georeferencing approaches is provided in [49] while [50] propose an alternative approach in case of missing or unusable trajectory data. In the cited articles, evaluation is usually carried out by applying the proposed methods to datasets with rather homogeneous characteristics compared to the multi-temporal case. ALS data and reference data are typically acquired within a short time period resulting in comparable field conditions. Even then, some precautions have to be made in order to eliminate the influence of highly dynamic surfaces such as water bodies and vegetation canopy. However, it is not clear whether slow decorrelation of wider areas over several years or in the seasonal cycle can be handled. Another major difference to multi-temporal datasets is the fact that typically data from one specific sensor constellation are adjusted. Several data characteristics may still be fairly dissimilar, especially when combining the adjustment of ALS data with the adjustment of (aerial) images, as in [51,52] and [53]. But also in this case, the respective configuration is explicitly taken into account by using different suitable functional models for LiDAR and image data, respectively. Compared to that, issues may arise if a dataset acquired over many years with various LiDAR sensors is treated in a uniform manner despite divergent properties such as point density, beam divergence, measurement accuracy, wavelength, pulse length, scan pattern etc.
Contrariwise, there is the application-driven view on multi-temporal Lidar data which has already been outlined in Section 1. In an abundant number of studies, heterogeneous datasets are analyzed in detail and all sorts of conclusions are drawn. However, the question about orientation and geometric accuracy over different epochs is rarely discussed in depth. Publications such as [1] and [7] point out concerns about heterogeneous multi-temporal data in their respective fields of application. [11] take into account the aspect of similar survey configurations during selection of suitable epochs. Furthermore, they provide an explicit workflow to ensure vertical co-registration of epochs and an uncertainty estimation for the resulting application, in this case tree growth assessment. [26] conduct thorough uncertainty analysis for glacier extent analysis with DTMs interpolated from multi-temporal ALS data. The DTMs are registered using known stable areas in vicinity of the glacier. A similar approach is developed by [54]. After epoch-wise strip adjustment of multi-temporal ALS data, a rigid body transformation is estimated for each epoch in order to share the datum of one reference block. The significance of remaining DTM differences is assessed with means of error propagation in order to separate actual changes from measurement noise. More recently, [23] discuss the reliability of change detection using multi-temporal LiDAR and point out the importance of the registration procedure.
We summarize that none of the reviewed approaches performs an integrated strip adjustment for an extensive multi-temporal ALS dataset. If discovered, potential datum discrepancies are usually compensated in a separate step with significantly less rigorous approaches.

3. Study Area and Data

Due to its characteristics and the availability of an extensive multi-temporal ALS dataset, we chose our study area around the town Loosdorf in the Lower Austrian Alpine foothills (c.f. Figure 1). To the North-West, it extends through a wide and flat section of the Pielach valley surrounded by hilly terrain on both sides. It also contains "Neubacher Au", a river section investigated in numerous studies, mainly with focus on optical bathymetry (e.g. [55,56]). Residential areas are limited to the village and surroundings of Loosdorf as well as some small settlements along the margins of the Pielach valley. The rest of the study area is dominated by agricultural land along with forests and grassland.

3.1. ALS Data

Since 2013, the area around Loosdorf has seen more than 20 independent data acquisition flights with airborne LiDAR. While showing somewhat similar block layouts throughout this time series, the epoch-wise datasets differ in terms of scanner properties and phenology, c.f. Table 2. Also, the detailed flight planning varies from epoch to epoch as indicated by the respective number of strips and the average flying height above ground.

3.2. Field Measurements

In order to obtain proper reference information for the adjustment, a field measurement campaign was conducted on the 18. and 21.06.2021. A total of 60 surface patches in 12 groups were measured with a Spectra Precision SP80 GNSS receiver and a Leica TS 16 Total Station. The distribution of groups was planned to cover the core area as evenly as possible given the limited availability of buildings near the borders. Each group consists of several stable and planar surfaces, mainly building roofs, with varying slope and exposition (c.f. Figure 2).
Measurements were conducted by first determining the coordinates of auxiliary points for each group using the GNSS receiver. The total station was then mounted in a suitable place and oriented based on these auxiliary points before measuring the actual reference patches.
Depending on its shape, one planar patch was captured with at least four (triangular) or six (rectangular) total station measurements. The relevant area is limited by 3-4 corner points while the additional measurements inside serve as checks whether the assumption of planarity holds. Finally, the resulting planes are densely sampled at a point spacing of 20 cm leading to 60 individual control point clouds for the strip adjustment.
The results of an independent field measurement campaign from 02.02.2023 were available for validation purposes. Thereby, around 60 single points on horizontal surfaces such as manhole covers were measured with a GNSS receiver throughout the whole block (c.f. [49,56]). These were reduced to a sample of about 40 check points based on reliability (on stable surfaces) and unambiguousness (not occluded by vegetation and other objects).

3.3. Ancillary Data

Several land cover types were manually digitized as supplementary information for the adjustment and for the interpretation of the results. Based on a comparison of Digital Surface Models (DSMs) from several LiDAR epochs, all presumably stable road and building surfaces were identified. Additionally, all forests and some selected areas of interest such as individual agricultural fields, playgrounds etc. were delineated (c.f. Figure 2).

4. Methodology

4.1. Adjustment Concept Following the Gauss-Markov Model

The framework for multi-temporal strip adjustment was implemented using the Python bindings of the point cloud processing software OPALS ([57,58]). The OPALS module stripAdjust dedicated to LiDAR strip adjustment is based on the approach introduced in [42] and [40].
Starting from point clouds in the Sensor’s Own Coordinate System (SOCS) and the trajectory after Kalman filtering, the parameters of the direct georeferencing equation are iteratively improved.
The approach bases on the Iterative Closest Point (ICP, [59]) method in establishing observations using point correspondences, i.e. nearest neighbours in object space between overlapping point clouds: As the point density is typically not high enough to directly compare individual points of overlapping flight strips, the points of one strip are compared against the tangent plane of the corresponding point in the overlapping strip. In an analogous way, correspondences between control point clouds and flight strips are obtained. These point-to-plane distances are minimized in a least squares adjustment. Notably, a rejection step aims at higher robustness by eliminating correspondences, e.g. due to differing or unreliable (roughness) local normal vectors.
Given the amount of data collected with LiDAR, it is computationally inefficient if not impossible to run through this procedure for every single point. Thus, the locations for potential correspondences are initially reduced, e.g. via uniform sub-sampling in object space.
For parameter estimation, strips are grouped into sessions following the principle that one session (i) holds strips from one non-stop flight and (ii) is acquired with the same scanner and wavelength. Most of the key parameters can thereby be assigned to specific parts of the LiDAR multi-sensor system:
  • Scanner parameters: Session-wise constant and linear corrections can be estimated for the range and direction measurements of the laser scanner. While this is rarely necessary for survey-grade scanners, it may offer the potential to compensate for other error sources (e.g. atmospheric effects).
  • Mounting parameters: The estimation of lever arm and boresight misalignment is usually unproblematic as they can be assumed constant during one session.
  • Trajectory parameters: Correcting the trajectory is often the most crucial part of the adjustment process. Trajectory quality depends on multiple factors and is thus subject to short-term variations. It is therefore possible to choose between more conservative (bias, linear) strip-wise correction models or time-dependent corrections within a flight line using splines of arbitrary length. The selection of the correction model has to be a well-balanced trade-off between the required relative accuracy on the one hand and the risk of overfitting on the other hand.
  • Datum corrections: With proper reference data available, a global datum shift (X, Y, Z) can be estimated for each session. Such an offset may originate from the reference station placement. The explicit datum correction avoids that these discrepancies influence the estimation of other parameters or lead to deformations of entire blocks.
To achieve a better balancing between partly correlated parameters, it is furthermore possible to introduce pseudo-observations setting correction parameters to zero with a certain standard deviation. This attenuates the magnitude of corrections, e.g. in case of flexible spline trajectory correction models.

4.2. Multi-Temporal Strip Adjustment

Before addressing the various multi-temporal approaches, the individual epochs were pre-processed. All relevant information (e.g. SOCS orientation, time lag between scanner and trajectory) was acquired and empirically verified. Epoch-wise strip adjustments and quality controls were carried out in order to determine suitable settings for the automatic detection of corresponding points (observations) as well as a meaningful choice of correction parameters (unknowns), c.f. Section 4.1. Furthermore, this procedure enables the introduction of improved parameter approximations and thus saves computational resources in the multi-temporal adjustment.
When it comes to adjusting the whole multi-temporal dataset to a common datum, several strategies were developed and tested. The most relevant ones are briefly described in this section.

4.2.1. Epoch-Wise Adjustment with Control Point Clouds (CPC)

The easiest approach in terms of computational effort is the separate epoch-wise adjustment. The datum is defined by stable control patches, in this case the densified control point clouds (CPC) described in Section 3.2. As a consequence, no direct correspondences between different epochs are established, the only link to ensure a consistent datum are the CPCs. Due to their rather sparse coverage compared to the full block area, a conservative trajectory correction model is preferred.
For cases where a more flexible trajectory correction model is necessary to cope with dynamic trajectory-related discrepancies, a slightly more elaborate two-step approach was developed: Firstly, a block-wise strip adjustment with bias trajectory corrections is conducted in order to set a stable datum for the whole block. Secondly, a height model is interpolated from the adjusted point clouds and masked to areas with low discrepancies between all overlapping strips and low roughness. This height model is created for each block individually to enhance the sparse original control point clouds. The increased coverage with reference data enables strip adjustment using time-dependent spline trajectory corrections in order to minimize the relative differences in the remaining areas.

4.2.2. Block-Wise Adjustment with CPC and Stable Areas (CPC+)

Instead of enhancing the CPCs with data from the adjusted block itself (c.f. Section 4.2.1), a common extended reference dataset for all blocks can be derived using the stable areas introduced in Section 3.3. The height model of one reference block (2014-10-14, c.f. Section 4.2.3) adjusted with CPCs and bias trajectory corrections is trimmed to the stable areas and added to the measured CPCs. The resulting control information is potentially extensive enough to enable direct block-wise adjustment, also with spline trajectory corrections.

4.2.3. Bi-Temporal Adjustment with a Reference Block (REF)

While the extended reference data (CPC+) already ensure a decent coverage of the block, this approach also has immanent disadvantages. On the one hand, data from an ALS block are treated the same way as control point clouds measured with superior accuracy. On the other hand, the coverage strongly depends on the presence of sealed surfaces. This locally leads to a weak datum definition and overfitting when using flexible correction models.
Both points can be addressed by individually combining each epoch flight with a whole reference block to form a bi-temporal strip adjustment. Important criteria for choosing a suitable reference block are:
  • Coverage: The block has to cover all relevant areas in order to avoid extrapolation.
  • Stability: Time-dependent quality variations should be low enough to allow for a conservative trajectory correction model.
  • Accuracy: Relative and absolute accuracy need to be comparable or better than the overall expected values.
  • Comparability: As the very same epoch serves as reference block in all bi-temporal strip adjustments, it is important to depict a representative state of the covered area. Epochs containing particularly extensive decorrelated areas due to (i) large construction sites, (ii) the influence of natural disasters (e.g. floods, landslides) and (iii) divergent phenology should be avoided.
For the datasets at hand, the 2014-10-14 block turned out to be the best option as a reference according to these points.
First of all, the reference block is adjusted with a conservative correction model only using the measured CPC. If the quality of this block has been verified beforehand and good parameter approximations (e.g. mounting) are available, this step can be omitted. One by one, each other block (with a trajectory correction model according to Table 2) then participates in a pairwise adjustment with the reference block. The conservative trajectory correction of the reference block (bias) is thereby expected to stabilize the datum in areas where this otherwise would not be the case due to flexible trajectory correction and sparse CPC coverage.

4.2.4. Combined Multi-Temporal Adjustment off All Blocks (FULL)

As the reference block is not fully fixed in the REF approach (Section 4.2.3), it will end up with a slightly different orientation in each pairwise adjustment also potentially leading to small systematic datum discrepancies between the remaining blocks.
This can be solved by adjusting the data from all epochs simultaneously. Each block is set up according to the parameter configuration and the approximations from pre-processing (c.f. Section 4.2). Correspondences are determined between all spatially overlapping strip pairs, no matter which block they belong to. While this is expected to ensure minimal datum differences between overlapping blocks, it also leads to a vast number of highly correlated observations. Besides obvious implications such as high computational costs, another consequence is that convergence massively depends on strong attenuation of correction parameters with pseudo-observations (c.f. Section 4.1) due to the near-singular equation system.

4.3. Quality Control

Quality control is mainly based on pairwise strip differences in object space: Every single strip is interpolated after adjustment and difference models between all sufficiently overlapping strip pairs are calculated. After masking out unreliable differences (high roughness, extrapolation), mosaics are created by computing the largest signed absolute difference in each raster cell. Color-coded visualisations serve to evaluate and interpret potential systematic residuals. Since a complete mosaic for any multi-temporal dataset also contains a significant amount of explainable differences due to temporal decorrelation, an additional "stable mosaic" is created by masking out everything except for the stable areas (c.f. Section 3.3). Examples for both mosaics are provided in Figure 3.
These strip difference mosaics and stable mosaics are mainly derived for single epochs individually or for pairs of epochs. Integrating more than two epochs into one mosaic often leads to the occlusion of potentially interesting systematic effects. An appropriate overview of the complete multi-temporal dataset can be obtained by combining all pairwise difference mosaics (each represented by one characteristic statistical value) into one matrix, the "blockpair-difference matrix". For the matrices in this article we use the robust estimator σ M A D , which is defined as the "median absolute deviation to median" multiplied with the scale factor 1.4826 (c.f. documentation of module "Histo" in [58]).

4.3.1. Evaluation Criteria

When comparing the various multi-temporal strip adjustment procedures, the first and foremost question is about meaningful quality criteria. Of course, the specific priorities depend on several factors such as study area characteristics, intended application and available resources. In this section, we highlight some generic quality criteria for our dataset. These criteria are:
  • Consistency within one epoch: By adding additional observations and constraints, multi-temporal strip adjustment always slightly compromises the relative accuracy within single epochs. It is thus a sign of quality, if an approach is capable of adjusting various epochs together without significantly compromising the individual strip differences of the involved epochs compared to their single-epoch strip adjustment results.
  • Consistency with independent validation data.
  • Consistency across epochs: The main goal of multi-temporal adjustments is to minimize orientation-related discrepancies between different epochs. However, this somewhat contradicts other quality criteria in practice and is thus subject to trade-offs. The accomplishment of this criterion mainly manifests itself in multi-temporal strip difference mosaics and in the blockpair-difference matrix, both masked to stable areas.
  • Robustness with respect to decorrelation: Data acquisition with different sensors and block layouts over several months or years necessarily leads to surfaces being represented differently. Ideally, the adjustment preserves these justified differences while avoiding any impact on stable areas in the close vicinity. A high robustness is achieved, if discrepancies in presumably stable areas (roads, roofs) are not influenced by changed areas (vegetation, agricultural land) nearby.
  • Demand of resources: When it comes to practical application, efficiency is another highly important factor. This includes aspects such as manpower requirements, appropriate equipment for survey and computation as well as the total duration from data acquisition to receiving final results.
  • Expandability: As a time series is developed sequentially, efficiency considerations must not be limited to one single conclusive run of the workflow. It is just as important that new epochs can be included at any point with reasonable effort.
As anticipated in the Introduction (Section 1), there is a clear advantage of the approaches treating one or few blocks separately, i.e. CPC, CPC+ and REF (c.f. Section 4.2.1 to Section 4.2.3) with regard to the efficiency-related quality criteria "expandability" and "demand of resources" (Section 4.3.1). Processing typically takes less than a few hours per block and can be accomplished on a modern consumer-grade computer. New blocks can be added with the same effort and without causing changes to already adjusted blocks. There is only one limitation concerning the REF approach, which requires a suitable reference block a priori. Compared to that, the FULL approach (Section 4.2.4) is clearly less practicable. The computational demands increase with every epoch added. The adjustment of all blocks in our study required a random access memory (RAM) of more than 300 GB with settings comparable to the other approaches. The adjustment procedure took several weeks and was prone to unintended crashes in the process. Any addition to the time series requires a repetition of the full adjustment enhanced by new blocks and implies changes to all previously adjusted data.

5. Results and Discussion

Coming to the adjustment results, we first investigate the individual block-wise adjustment with control patches (CPC, Section 4.2.1), which is a typical solution in practice. The blockpair-difference matrices for the CPC approach (Figure 4) clearly show the disadvantages. Many of the explainable differences in matrix A also translate into discrepancies in stable areas (matrix B) - for example epoch 2016-06-16. Additionally, even blocks separated only by days (e.g. 2014-10-14 and 2014-10-16) show high differences which can not be explained with actual changes on the ground.
The small values in the diagonal compared to the rest of the matrix indicate a strong bias of the CPC approach towards minimizing relative differences in individual blocks. The absolute datum definition with sparse control patches is rather weak leading to poor consistency across epochs as well as little robustness with respect to decorrelation.
Similar results were obtained for the expanded control areas (CPC+, Section 4.2.2, Figure 5). In this study area, the coverage with stable areas is apparently not sufficient to support consistent datum definition, especially if their wide distribution encourages the use of more flexible correction models (c.f. Section 4.1).
The stable areas (Figure 5 B) show slightly smaller differences than in the CPC approach (Figure 4 B). This is not surprising as CPC+ is the only approach explicitly using these stable areas for strip adjustment. In contrast, the full blockpair difference matrix (Figure 5 A) indicates higher discrepancies than CPC and all other approaches (Figure 4 A and Figure 6 A) which suggests overfitting towards the sparse control areas.
Compared to these single-block approaches, massive improvements can be observed for the bi-temporal adjustment (REF, Section 4.2.3, Figure 6). There are still striking discrepancies in the area-wide matrix (Figure 6 A), mainly for the blocks under leaf-on conditions (May-October). But as opposed to Figure 4 and Figure 5, most of these blocks are hardly recognizable in the stable-area differences (Figure 6 B). This indicates high robustness in terms of decorrelated areas not significantly influencing the orientation of unchanged surfaces nearby. The diagonal representing the σ M A D for each individual block is comparable between CPC and REF, however, the deviations from the rest of the matrix are much smaller in the latter approach. Notably, the reference block (2014-10-14) appears similar to several other blocks in Figure 6 B. This suggests that the good overall datum does not come at the cost of strong overfitting.
When it comes to the stable blockpair-difference matrix resulting from the FULL approach (Figure 7 A, c.f. Section Figure 7), the values have a similar order of magnitude as for the REF approach. However, their distribution is somewhat different. Figure 7 B provides a direct comparison of discrepancies in stable areas between REF and FULL. The following observations can be made:
  • The REF approach tends to deal better with single blocks differing from others in key properties (e.g. phenology). This is especially obvious for block 2016-06-16, but also for 2014-10-16 and 2013-10-26.
  • In the FULL approach, accumulations of blocks with similar properties seem to produce datum clusters in the orientation procedure. As an example, the three blocks from February 2014 act as a huge aggregated reference block which pulls other blocks towards its datum, resulting in consistently green rows and columns. Another cluster seems to be formed by the first six blocks (2013-04-15 to 2014-02-21) all acquired with the same scanner.
  • The row/column of the reference block (2014-10-14) predominantly is white or light green in Figure 7 B, i.e. similar or even slightly better discrepancies in the FULL approach. This encourages the assumption that the global datum is not exceedingly biased towards the explicitly defined reference block in the REF approach. Note: As each bi-temporal adjustment leads to a (slightly) different variant of the the reference block datum, its CPC result is used for this comparison.
  • Later blocks, i.e. 2016-11-04 to 2021-03-09, seem to be more indifferent concerning the choice between FULL and REF as they show similar difference patterns between each other in both approaches. One possible explanation is the state-of-the-art equipment and the higher point density used for these blocks. But also their sparser distribution over time could play a role as it avoids any major cluster aggregation in the FULL approach. Thus, they share comparably weak influence on the global datum in both variants and are fit to an externally defined datum in a similar manner.
  • The diagonal is predominantly close to zero with only few exceptions. This suggests that the relative orientation within single epochs is not significantly influenced by the choice of orientation procedure.
A synopsis of these points suggests clear advantages of the REF approach compared to FULL. However, the mean of all values in Figure 7 B is -0.7 mm, i.e. slightly in favor of FULL. In order to clarify this apparent contradiction, several strip difference mosaics were analyzed in depth. As an example, Figure 8 compares the two approaches by means of the full strip difference mosaic for blocks 2013-05-24 and 2014-02-13.
Differences are in general comparably high for this block pair, which is not surprising due to the late May block 2013-05-24 effectively having full leave-on conditions in contrast to most other blocks. Apart from that, the distribution of differences strongly varies between the two approaches. The FULL approach (Figure 8 A) shows several areas with distinct systematic datum discrepancies. These are situated around agricultural areas in the block center where many blocks overlap. Notably, surrounding stable areas (e.g. roads, building roofs in the close-up map) are equally affected. Only the town center which predominantly consists of stable areas comes close to the results of the REF approach (Figure 8 B). In comparison, the results from the REF approach seem clearly better for most of the block. However, the quality significantly drops in vicinity of the reference block boundary where the sparse control patches remain the only link to ensure a consistent datum definition.
Several other block pairs show a similar pattern leading to the assumption that the blockpair difference matrix in Figure 6 does not reflect the full potential of the REF approach. It is disadvantageously biased by the limited coverage of the reference block, which is significantly smaller than the total area covered by all blocks combined (Figure 1).
As a result of this analysis, Table 3 rates the different approaches with respect to the quality criteria formulated earlier.
The overall view of the various criteria clearly favors the REF approach for the given dataset. This will be further supported by quantitative summaries of the blockpair-difference matrices (Figure 4 to Figure 7), an analysis of DSMs computed for each block and a comparison to check points in Table 4.
Using a DSM allows to show the full potential of the resulting data. A DSM was calculated for the REF results of each epoch following the methodology of [60]. In comparison to the models of individual LiDAR strips and their differences, the DSMs filter random noise to a higher extent.
Figure 9 visualizes the differences between epoch-wise DSMs in the style of blockpair difference matrices. The full differences (Figure 9 A) hereby also include forests as the DSM calculation contains no roughness masking. Thus, the difference patterns are massively influenced by phenology and vegetation growth. More importantly, the stable DSM differences (Figure 9 B) proof a consistent common datum definition with discrepancies of less than 2 - 3 cm ( σ M A D ) for all DSM pairs without notable outliers.
Independent validation was carried out using the point measurements from 02.02.2023 (Section 3.2). Therefore, the height measured in these points was compared to the DSM height for every ALS epoch. Figure 10 illustrates the spatial distribution of differences (mean and standard deviation) for each check point. After an analysis of these differences at the individual check points, we will look at the distribution of these differences w.r.t. each epoch.
The consistently small standard deviation (2 cm and smaller) for all check points in Figure 10 confirms the high relative accordance of all epochs. Apart from that, the exclusively positive mean differences between 0 and 8 cm are remarkable. One possible explanation is a combination of (i) a biased global datum of ALS data or check points and (ii) local datum deformations of the ALS data leading to the varying order of magnitude. A more likely reason is the difference in data acquisition: For the check points, single terrestrial measurements were carried out, mostly on manhole covers. The DSM is a result of interpolating an ALS point cloud. It is thus also influenced by a certain neighbourhood which predominantly contains slightly (e.g. road surface) or significantly (e.g. curbstone, low vegetation) higher points.
Table 4 provides a statistical comparison of all major results discussed in this section by listing quantitative measures for each epoch. The first columns show the mean σ M A D of blockpair-wise strip discrepancies for each epoch relative to all other epochs. These strip difference measures underline the assumption illustrated in Figure 4, Figure 5, Figure 6 and Figure 7 that the approaches CPC and CPC+ fall short of REF and FULL in terms of across-epoch accuracy. The overall average differences are slightly smaller for the FULL approach (4.47 cm) in comparison to REF (4.54 cm). When comparing DSM based differences to individual strip based differences (again each epoch is compared to all others), it is notable that the average over all σ M A D differences reduces from 4.5 cm to 1.7 cm. Furthermore, the range of values is 2.1 cm to only 1.2 cm (Column "DSM diff." in Table 4). This relative accuracy demonstrates the high precision and consistency airborne LiDAR measurements can provide. The differences between each DSM and independent check points confirm an absolute accuracy in the range of few centimeters while also showing the positive bias of mean differences already discussed in the context of Figure 10.
As a specific example, Figure 11 provides a DSM difference model between two blocks separated by nearly seven years. Despite the long time span and differing phenology, roads and building roofs are consistently white, i.e. less than 2 cm difference. Notably, this is also the case in direct vicinity of agricultural land and vegetation. Agricultural land is mostly negative (red), meaning 2014-06-10 is higher than 2021-03-09 due to leaf-on conditions. Positive differences (blue) show new objects such as photovoltaic panels (west of A) or new buildings (north-east of B). Vegetation gives a mixed image, depending on whether growth/plantation (blue) or phenology/clearance (red) is the dominant effect over the given time span. The grassland around (C) had been mowed in 2014-06-10 and not yet overgrown in 2021-03-09 resulting in effectively no height difference except for the hay deposited to dry in 2014. Due to the datum accordance of the two epochs, also more subtle changes such as slight degradation of the soccer field north-east of (D) can be observed. Only the differences in the river channel (south to north through D) are not meaningful as refraction corrections for the bathymetric data have not been applied.

6. Conclusions

In this paper, we compared various strip adjustment approaches to achieve a common datum for 21 LiDAR blocks distributed over a time span of approximately 8 years. The results proved that the seemingly most rigorous approach of combining all epochs into one large adjustment is not necessarily the optimal solution. Besides the high computational costs, the resulting common datum is potentially compromised by clusters of similar blocks.
Compared to that, the much more flexible pairwise adjustment of each epoch with one reference block (Section 4.2.3) showed exceptionally consistent results within the area covered by the reference block. Relative discrepancies of the derived height models were below 2-3 cm for all involved epochs with a mean of 1.7 cm. In this bi-temporal adjustment of two independent epochs, the utilized adjustment concept (Section 4.1) demonstrated high robustness with respect to short- or long-term surface changes such as vegetation or construction sites. Without the explicit application of masks, the automated matching and rejection of correspondences efficiently avoided impact on stable areas nearby.
For setting up a new time series following this approach, especially the design of the reference block plays a key role:
  • Chronology: Due to practical reasons, the reference block is presumably acquired in the very beginning of a time series since all earlier epochs would have a preliminary datum prior to its availability. Notably, our results suggest no decrease in accuracy related to an increasing temporal offset from the reference block.
  • Coverage: In order to ensure ideal datum consistency, the reference block should cover the entire designated study area. All datasets protruding beyond this area have to be supported by additional control data.
  • Point density: It is not necessary that the reference block has the highest point density of the time series. At minimum, it needs to be high enough to allow the reliable computation of local surface normal vectors for relevant surface patches (e.g. small roofs) during strip adjustment.
  • Accuracy: While we found no extreme overfitting to the reference block in our work, its quality decisively determines the achievable accuracy for the whole time series. In order to give stability to other more volatile blocks, the original trajectory estimation for the reference block has to be of high quality so that rigid trajectory correction models are sufficient for the reference block in the adjustment process. The interior and especially the borders of the reference block have to be covered with control patches varying in slope and exposition. In order to support more blocks in the time series, permanent surfaces (e.g. building roofs) for these control patches are preferred. If this is not possible, temporary targets should be placed in some distance from the permanent surface (e.g. ground) nearby. This avoids the establishment of erroneous correspondences for blocks acquired after the removal of these targets.
All other blocks of the time series need to cover an area within the reference block which is interspersed with stable patches as extensively as possible. In terms of decorrelation, vegetation is less problematic due to the robustness of the adjustment procedure. However, large areas with slow changes over time (e.g. sliding slopes) have the risk of systematically compromising datum estimation and are ideally eliminated using explicit masking.
For future work, a meaningful next step is to test this approach under changed circumstances. This includes a stronger variation of flying heights, the combination of airborne and UAV-borne sensors, flatter or more mountainous terrain characteristics etc. Furthermore, a close look into the effect of different scanner systems is worthwhile, especially when differing in scanner wavelengths and beam characteristics (c.f. [56]). Finally, working with classified data could bring benefits in terms of a broader quality control, e.g. using terrain points only, but may also help improve the adjustment procedure in challenging areas such as large forests.

Author Contributions

Conceptualization, M.W.; methodology, M.W.; software, M.W.; validation, M.W. and G.M.; formal analysis, M.W.; investigation, M.W.; resources, N.P.; data curation, G.M. and M.W.; writing—original draft preparation, M.W.; writing—review and editing, M.W., N.P., C.R., and G.M.; visualization, M.W.; supervision, N.P.; project administration, N.P. and G.M.; funding acquisition, N.P. All authors have read and agreed to the published version of the manuscript.

Funding

Michael Wimmer was partly funded within the SEHAG project (Sensitivity of High Alpine Geosystems to Climate Change Since 1850) by the Austrian Science Fund (grant no. 4062-N29).

Acknowledgments

The authors wish to thank RIEGL Laser Measurement Systems GmbH for acquisition and provision of all LiDAR datasets used in this study. Furthermore, the contribution of Sebastian Mikolka-Flöry and Lucas Dammert in field data acquisition is acknowledged.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Okyay, U.; Telling, J.; Glennie, C.L.; Dietrich, W.E. Airborne lidar change detection: An overview of Earth sciences applications. Earth-Science Reviews 2019, 198, 102929. [Google Scholar] [CrossRef]
  2. Muhadi, N.A.; Abdullah, A.F.; Bejo, S.K.; Mahadi, M.R.; Mijic, A. The use of LiDAR-derived DEM in flood applications: A review. Remote Sensing 2020, 12, 1–20. [Google Scholar] [CrossRef]
  3. Hudak, A.T.; Evans, J.S.; Smith, A.M.S. LiDAR utility for natural resource managers. Remote Sensing 2009, 1, 934–951. [Google Scholar] [CrossRef]
  4. Xiao, W.; Cao, H.; Tang, M.; Zhang, Z.; Chen, N. 3D urban object change detection from aerial and terrestrial point clouds: A review. International Journal of Applied Earth Observation and Geoinformation 2023, 118, 103258. [Google Scholar] [CrossRef]
  5. Stilla, U.; Xu, Y. Change detection of urban objects using 3D point clouds: A review. ISPRS Journal of Photogrammetry and Remote Sensing 2023, 197, 228–255. [Google Scholar] [CrossRef]
  6. Simonson, W.D.; Allen, H.D.; Coomes, D.A. Applications of airborne lidar for the assessment of animal species diversity. Methods in Ecology and Evolution 2014, 5, 719–729. [Google Scholar] [CrossRef]
  7. Riofrío, J.; White, J.C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Harmonizing multi-temporal airborne laser scanning point clouds to derive periodic annual height increments in temperate mixedwood forests. Canadian Journal of Forest Research 2022, 52, 1334–1352. [Google Scholar] [CrossRef]
  8. Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review, 2012. [CrossRef]
  9. Dalponte, M.; Jucker, T.; Liu, S.; Frizzera, L.; Gianelle, D. Characterizing forest carbon dynamics using multi-temporal lidar data. Remote Sensing of Environment 2019, 224, 412–420. [Google Scholar] [CrossRef]
  10. Hollaus, M.; Eysn, L.; Maier, B.; Pfeifer, N. Site index assessment based on multi-temporal ALS data Highlights : Based on multi-temporal ALS data the site index of forest stands was assessed for a mountainous study area in Austria. The applied approach is based on derived tree top heights. The pro. Proceedings of the Silvilaser, 2015.
  11. Hopkinson, C.; Chasmer, L.; Hall, R.J. The uncertainty in conifer plantation growth prediction from multi-temporal lidar datasets. Remote Sensing of Environment 2008, 112, 1168–1180. [Google Scholar] [CrossRef]
  12. Karna, Y.K.; Penman, T.D.; Aponte, C.; Hinko-Najera, N.; Bennett, L.T. Persistent changes in the horizontal and vertical canopy structure of fire-tolerant forests after severe fire as quantified using multi-temporal airborne lidar data. Forest Ecology and Management 2020, 472, 118255. [Google Scholar] [CrossRef]
  13. Lin, Y.C.; Habib, A. Quality control and crop characterization framework for multi-temporal UAV LiDAR data over mechanized agricultural fields. Remote Sensing of Environment 2021, 256, 112299. [Google Scholar] [CrossRef]
  14. Lin, Y.C.; Shao, J.; Shin, S.Y.; Saka, Z.; Joseph, M.; Manish, R.; Fei, S.; Habib, A. Comparative Analysis of Multi-Platform, Multi-Resolution, Multi-Temporal LiDAR Data for Forest Inventory. Remote Sensing 2022, 14. [Google Scholar] [CrossRef]
  15. Nyström, M.; Holmgren, J.; Olsson, H. Change detection of mountain birch using multi-temporal ALS point clouds. Remote Sensing Letters 2013, 4, 190–199. [Google Scholar] [CrossRef]
  16. kseter, R.; Bollandsås, O.M.; Gobakken, T.; Næsset, E. Modeling and predicting aboveground biomass change in young forest using multi-temporal airborne laser scanner data. Scandinavian Journal of Forest Research 2015, 1–12. [Google Scholar] [CrossRef]
  17. Pinagé, E.R.; Keller, M.; Duffy, P.; Longo, M.; Dos-Santos, M.N.; Morton, D.C. Long-term impacts of selective logging on amazon forest dynamics from multi-temporal airborne lidar. Remote Sensing 2019, 11, 1–21. [Google Scholar] [CrossRef]
  18. Sofonia, J.; Shendryk, Y.; Phinn, S.; Roelfsema, C.; Kendoul, F.; Skocaj, D. Monitoring sugarcane growth response to varying nitrogen application rates: A comparison of UAV SLAM LiDAR and photogrammetry. International Journal of Applied Earth Observation and Geoinformation 2019, 82, 101878. [Google Scholar] [CrossRef]
  19. Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Spatially explicit characterization of boreal forest gap dynamics using multi-temporal lidar data. Remote Sensing of Environment 2008, 112, 2326–2340. [Google Scholar] [CrossRef]
  20. Abermann, J.; Fischer, A.; Lambrecht, A.; Geist, T. On the potential of very high-resolution repeat DEMs in glacial and periglacial environments. Cryosphere 2010, 4, 53–65. [Google Scholar] [CrossRef]
  21. Anders, N.S.; Seijmonsbergen, A.C.; Bouten, W. Geomorphological change detection using object-based feature extraction from multioral lidar data. IEEE Geoscience and Remote Sensing Letters 2013, 10, 1587–1591. [Google Scholar] [CrossRef]
  22. Bollmann, E.; Sailer, R.; Briese, C.; Stotter, J.; Fritzmann, P. Potential of airborne laser scanning for geomorphologie feature and process detection and quantifications in high alpine mountains. Zeitschrift fur Geomorphologie 2011, 55, 83–104. [Google Scholar] [CrossRef]
  23. Cucchiaro, S.; Maset, E.; Cavalli, M.; Crema, S.; Marchi, L.; Beinat, A.; Cazorzi, F. How does co-registration affect geomorphic change estimates in multi-temporal surveys? GIScience and Remote Sensing 2020, 57, 611–632. [Google Scholar] [CrossRef]
  24. Fleischer, F.; Haas, F.; Piermattei, L.; Pfeiffer, M.; Heckmann, T.; Altmann, M.; Rom, J.; Stark, M.; Wimmer, M.H.; Pfeifer, N.; Becht, M. Multi-decadal (1953-2017) rock glacier kinematics analysed by high-resolution topographic data in the upper Kaunertal, Austria. Cryosphere 2021, 15, 5345–5369. [Google Scholar] [CrossRef]
  25. Ghuffar, S.; Székely, B.; Roncat, A.; Pfeifer, N. Landslide displacement monitoring using 3D range flow on airborne and terrestrial LiDAR data. Remote Sensing 2013, 5, 2720–2745. [Google Scholar] [CrossRef]
  26. Joerg, P.C.; Morsdorf, F.; Zemp, M. Uncertainty assessment of multi-temporal airborne laser scanning data: A case study on an Alpine glacier. Remote Sensing of Environment 2012, 127, 118–129. [Google Scholar] [CrossRef]
  27. Johnson, C.L.; Chen, Q.; Ozdemir, C.E. Lidar time-series analysis of a rapidly transgressing low-lying mainland barrier (Caminada Headlands, Louisiana, USA). Geomorphology 2020, 352, 106979. [Google Scholar] [CrossRef]
  28. Montreuil, A.L.; Moelans, R.; Houthuys, R.; Bogaert, P.; Chen, M. Characterization of intertidal bar morphodynamics using a bi-annual lidar dataset. Remote Sensing 2020, 12, 1–14. [Google Scholar] [CrossRef]
  29. Mora, O.E.; Gabriela Lenzano, M.; Toth, C.K.; Grejner-Brzezinska, D.A.; Fayne, J.V. Landslide change detection based on Multi-Temporal airborne LIDAR-derived DEMs. Geosciences (Switzerland) 2018, 8, 6–8. [Google Scholar] [CrossRef]
  30. Piermattei, L.; Heckmann, T.; Betz-Nutz, S.; Altmann, M.; Rom, J.; Fleischer, F.; Stark, M.; Haas, F.; Ressl, C.; Wimmer, M.H.; Pfeifer, N.; Becht, M. Evolution of an Alpine proglacial river during 7 decades of deglaciation. Earth Surface Dynamics 2023, 11, 383–403. [Google Scholar] [CrossRef]
  31. Reddy, A.D.; Hawbaker, T.J.; Wurster, F.; Zhu, Z.; Ward, S.; Newcomb, D.; Murray, R. Quantifying soil carbon loss and uncertainty from a peatland wildfire using multi-temporal LiDAR. Remote Sensing of Environment 2015, 170, 306–316. [Google Scholar] [CrossRef]
  32. Vehling, L.; Baewert, H.; Glira, P.; Moser, M.; Rohn, J.; Morche, D. Quantification of sediment transport by rockfall and rockslide processes on a proglacial rock slope (Kaunertal, Austria). Geomorphology 2017, 287, 46–57. [Google Scholar] [CrossRef]
  33. Wu, Q.; Lane, C.R.; Li, X.; Zhao, K.; Zhou, Y.; Clinton, N.; DeVries, B.; Golden, H.E.; Lang, M.W. Integrating LiDAR data and multi-temporal aerial imagery to map wetland inundation dynamics using Google Earth Engine. Remote Sensing of Environment 2019, 228, 1–13. [Google Scholar] [CrossRef] [PubMed]
  34. Zelaya Wzia̧tek. ; Terefenko.; Kurylczyk. Multi-Temporal Cliff Erosion Analysis Using Airborne Laser Scanning Surveys. Remote Sensing 2019, 11, 2666. [Google Scholar] [CrossRef]
  35. Haala, N.; Kölle, M.; Cramer, M.; Laupheimer, D.; Zimmermann, F. Hybrid georeferencing of images and LiDAR data for UAV-based point cloud collection at millimetre accuracy. ISPRS Open Journal of Photogrammetry and Remote Sensing 2022, 4, 100014. [Google Scholar] [CrossRef]
  36. Hu, F.; van Leijen, F.J.; Chang, L.; Wu, J.; Hanssen, R.F. Monitoring deformation along railway systems combining Multi-temporal InSAR and LiDAR data. Remote Sensing 2019, 11, 1–19. [Google Scholar] [CrossRef]
  37. Xi, Y.; Luo, Q. A morphology-based method for building change detection using multi-temporal airborne LiDAR data. Remote Sensing Letters 2018, 9, 131–139. [Google Scholar] [CrossRef]
  38. Yadav, R.; Nascetti, A.; Ban, Y. Building Change Detection Using Multi-Temporal Airborne Lidar Data. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives 2022, 43, 1377–1383. [Google Scholar] [CrossRef]
  39. Zhou, Z.; Gong, J.; Hu, X. Community-scale multi-level post-hurricane damage assessment of residential buildings using multi-temporal airborne LiDAR data. Automation in Construction 2019, 98, 30–45. [Google Scholar] [CrossRef]
  40. Glira, P.; Pfeifer, N.; Mandlburger, G. Rigorous strip adjustment of UAV-based laserscanning data including time-dependent correction of trajectory errors. Photogrammetric Engineering and Remote Sensing 2016, 82, 945–954. [Google Scholar] [CrossRef]
  41. Kager, H. Discrepancies between overlapping Laser Scanner Strips - Simultaneous fitting of Aerial Laser Scanner Strips. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 35, 555–560. [Google Scholar]
  42. Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. Rigorous strip adjustment of airborne laserscanning data based on the icp algorithm. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2015, 2, 73–80. [Google Scholar] [CrossRef]
  43. Pentek, Q.; Kennel, P.; Allouis, T.; Fiorio, C.; Strauss, O. A flexible targetless LiDAR–GNSS/INS–camera calibration method for UAV platforms. ISPRS Journal of Photogrammetry and Remote Sensing 2020, 166, 294–307. [Google Scholar] [CrossRef]
  44. Chen, Z.; Li, J.; Yang, B. A strip adjustment method of uav-borne lidar point cloud based on dem features for mountainous area. Sensors 2021, 21, 1–20. [Google Scholar] [CrossRef] [PubMed]
  45. dos Santos, D.; Filho, L.; de Oliveira, P.; de Oliveira, H. Attitude Mounting Misalignment Estimation Method for the Calibration of UAV LiDAR System by using a TIN-based Corresponding Model. Journal of Applied Science and Technology Trends 2020, 1, 162–168. [Google Scholar] [CrossRef]
  46. Yang, B.; Li, J. A hierarchical approach for refining point cloud quality of a low cost UAV LiDAR system in the urban environment. ISPRS Journal of Photogrammetry and Remote Sensing 2022, 183, 403–421. [Google Scholar] [CrossRef]
  47. Colomina, I. On Trajectory Determination for Photogrammetry and Remote Sensing: Sensors, Models and Exploitation. In Photogrammetric Week 2015; pp. 131–142.
  48. Brun, A.; Cucci, D.A.; Skaloud, J. Lidar point–to–point correspondences for rigorous registration of kinematic scanning in dynamic networks. ISPRS Journal of Photogrammetry and Remote Sensing 2022, 189, 185–200. [Google Scholar] [CrossRef]
  49. Pöppl, F.; Neuner, H.; Mandlburger, G.; Pfeifer, N. Integrated trajectory estimation for 3D kinematic mapping with GNSS, INS and imaging sensors: A framework and review. ISPRS Journal of Photogrammetry and Remote Sensing 2023, 196, 287–305. [Google Scholar] [CrossRef]
  50. Ressl, C.; Pfeifer, N.; Mandlburger, G. Applying 3D Affine Transformation and Least Squares Matching for Airborne Laser Scanning Strips Adjustment Without Gnss/Imu Trajectory Data. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2012, XXXVIII-5, 67–72. [Google Scholar] [CrossRef]
  51. Glira, P.; Pfeifer, N.; Mandlburger, G. Hybrid Orientation of Airborne Lidar Point Clouds and Aerial Images. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2019, 4, 567–574. [Google Scholar] [CrossRef]
  52. Zhou, T.; Hasheminasab, S.M.; Habib, A. Tightly-coupled camera/LiDAR integration for point cloud generation from GNSS/INS-assisted UAV mapping systems. ISPRS Journal of Photogrammetry and Remote Sensing 2021, 180, 336–356. [Google Scholar] [CrossRef]
  53. Yogender, Y. Hybrid adjustment of UAS-based LiDAR and image data. PhD thesis, University of Twente, 2022.
  54. Mandlburger, G.; Hauer, C.; Wieser, M.; Pfeifer, N. Topo-bathymetric LiDAR for monitoring river morphodynamics and instream habitats-A case study at the Pielach River. Remote Sensing 2015, 7, 6160–6195. [Google Scholar] [CrossRef]
  55. Mandlburger, G.; Pfennigbauer, M.; Pfeifer, N. Analyzing near water surface penetration in laser bathymetry - A case study at the River Pielach. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2013, 2, 175–180. [Google Scholar] [CrossRef]
  56. Mandlburger, G.; Pfennigbauer, M.; Schwarz, R.; Pöppl, F. a Decade of Progress in Topo-Bathymetric Laser Scanning Exemplified By the Pielach River Dataset. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences 2023, 10, 1123–1130. [Google Scholar] [CrossRef]
  57. Pfeifer, N.; Mandlburger, G.; Otepka, J.; Karel, W. OPALS - A framework for Airborne Laser Scanning data analysis. Computers, Environment and Urban Systems 2014, 45, 125–136. [Google Scholar] [CrossRef]
  58. TU Wien. OPALS Homepage: https://opals.geo.tuwien.ac.at/html/stable/index.html, 2024.
  59. Besl, P.J.; McKay, N.D. A Method for Registration of 3-D Shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence 1992, 14, 239–256. [Google Scholar] [CrossRef]
  60. Hollaus, M.; Mandlburger, G.; Pfeifer, N.; Mücke, W. Land cover dependent derivation of digital surface models from airborne laser scanning data. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences - ISPRS Archives 2010, 38, 221–226. [Google Scholar]
Preprints 110690 g001
Figure 1. Cartographic model showing the study area and its location in Austria. The red line marks the outer boundary of all LiDAR datasets combined, the blue line delimits the core area which is covered by a majority of airborne data acquisitions.
Figure 1. Cartographic model showing the study area and its location in Austria. The red line marks the outer boundary of all LiDAR datasets combined, the blue line delimits the core area which is covered by a majority of airborne data acquisitions.
Preprints 110690 g001
Preprints 110690 g002
Figure 2. Overview of field measurements and ancillary data with a shading of the Digital Terrain Model.
Figure 2. Overview of field measurements and ancillary data with a shading of the Digital Terrain Model.
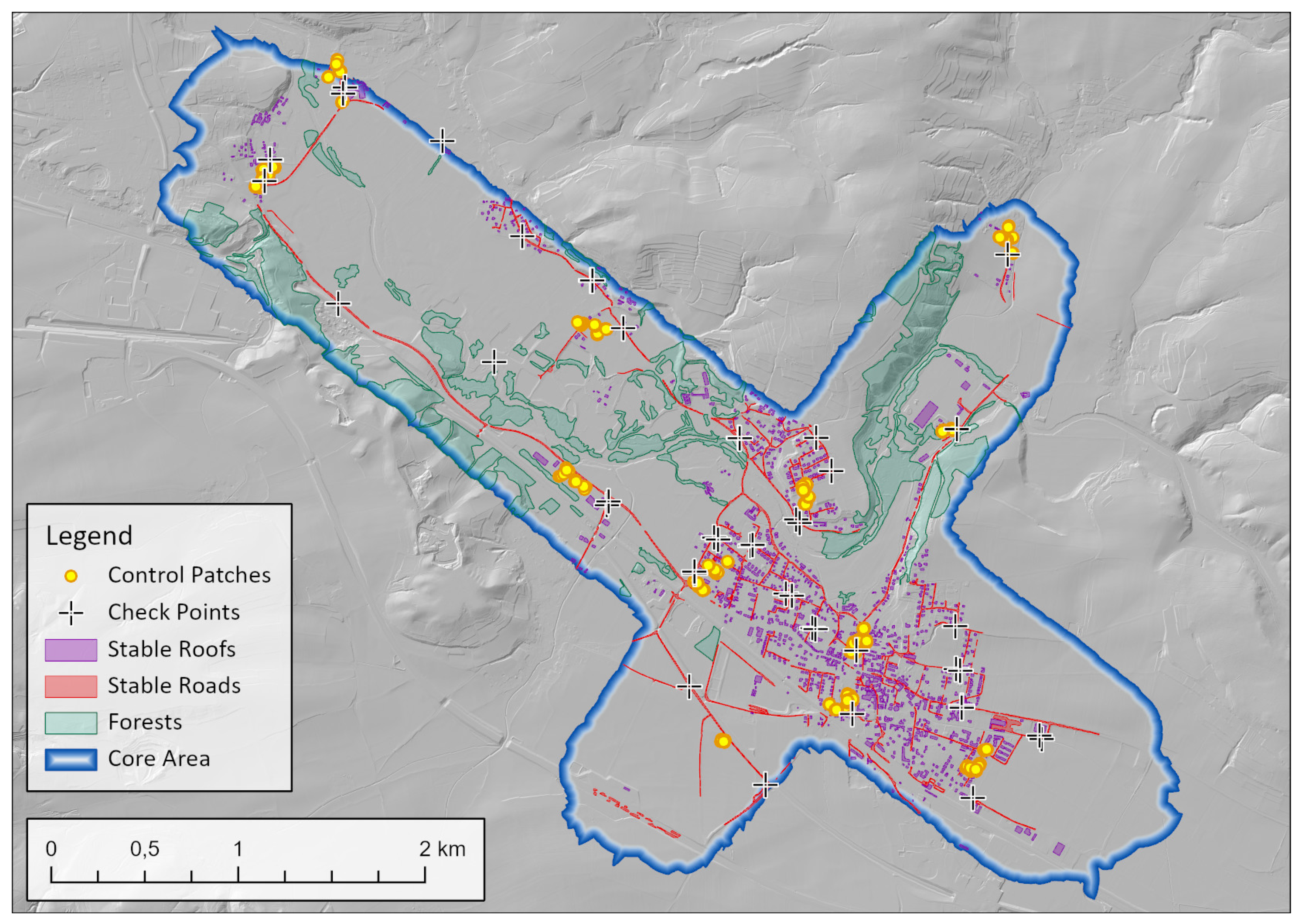
Preprints 110690 g002
Preprints 110690 g003
Figure 3. Comparison of (A) the full strip difference mosaic (largest signed absolute difference) and (B) the stable mosaic for epochs 2014-02-06 and 2014-10-14 on the background of a DSM. The unit of the differences is [m]. For the full mosaic (A), masking mainly eliminates forests based on their roughness. Thus, it still contains numerous areas affected by changes between the epochs, such as agricultural land. The stable mosaic (B) is limited to stable building roofs and road sections only, making it a better means to assess relative accuracy. Here, this assumption is relativized by the low point density of 2014-02-06 which causes a considerably stronger smoothing of edges and further leads to apparent differences, e.g. on roofs
Figure 3. Comparison of (A) the full strip difference mosaic (largest signed absolute difference) and (B) the stable mosaic for epochs 2014-02-06 and 2014-10-14 on the background of a DSM. The unit of the differences is [m]. For the full mosaic (A), masking mainly eliminates forests based on their roughness. Thus, it still contains numerous areas affected by changes between the epochs, such as agricultural land. The stable mosaic (B) is limited to stable building roofs and road sections only, making it a better means to assess relative accuracy. Here, this assumption is relativized by the low point density of 2014-02-06 which causes a considerably stronger smoothing of edges and further leads to apparent differences, e.g. on roofs
Preprints 110690 g003
Preprints 110690 g004
Figure 4. Blockpair difference matrices ( σ M A D ) for the CPC approach. Matrix (A) was created from the full strip difference mosaics, whereas matrix (B) represents the stable mosaics, c.f. Section 4.3.
Figure 4. Blockpair difference matrices ( σ M A D ) for the CPC approach. Matrix (A) was created from the full strip difference mosaics, whereas matrix (B) represents the stable mosaics, c.f. Section 4.3.
Preprints 110690 g004
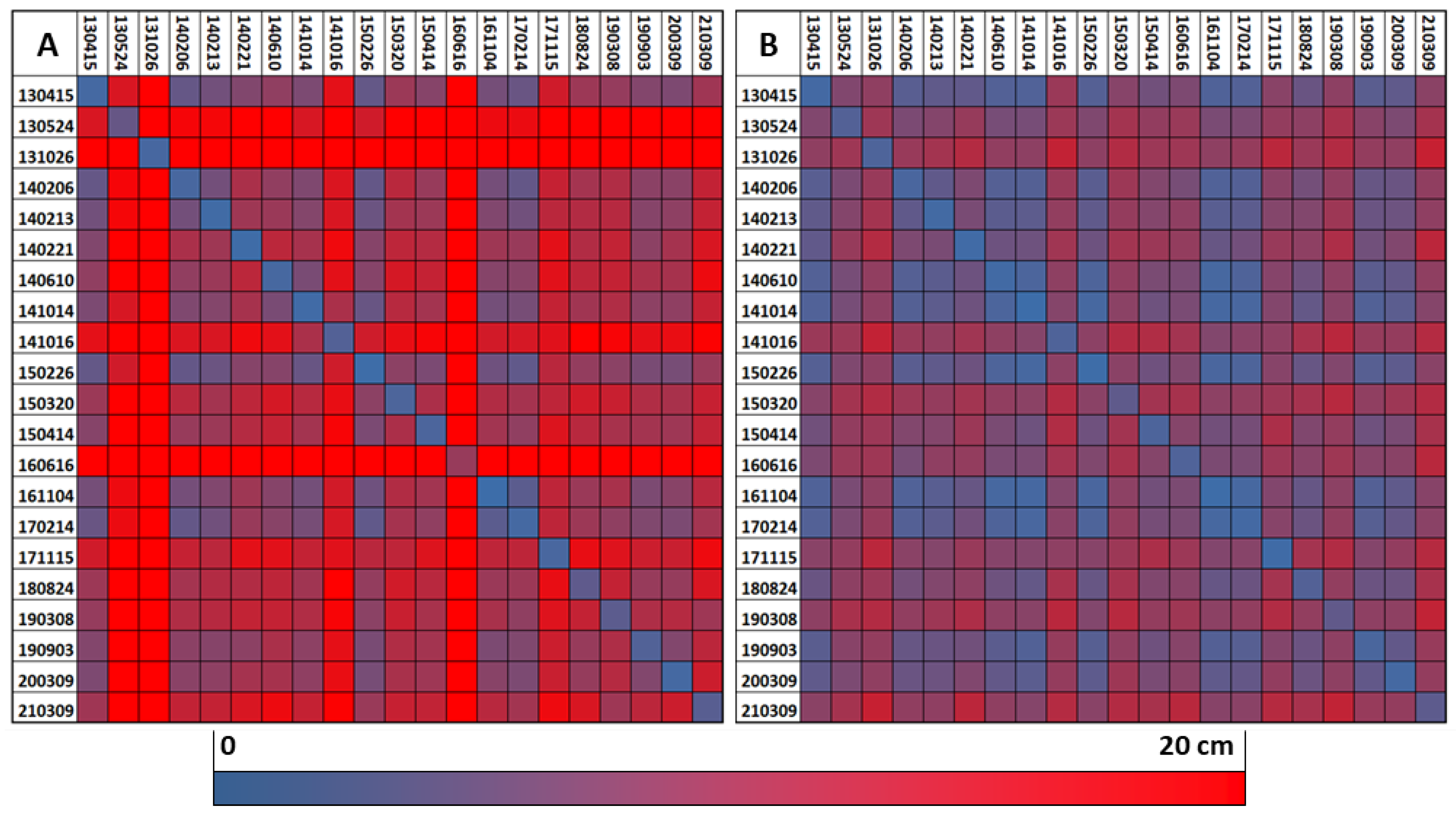
Preprints 110690 g005
Figure 5. Full (A) and stable (B) blockpair difference matrix ( σ M A D ) for the CPC+ approach.
Figure 5. Full (A) and stable (B) blockpair difference matrix ( σ M A D ) for the CPC+ approach.
Preprints 110690 g005
Preprints 110690 g006
Figure 6. Full (A) and stable (B) blockpair difference matrix ( σ M A D ) for the REF approach.
Figure 6. Full (A) and stable (B) blockpair difference matrix ( σ M A D ) for the REF approach.
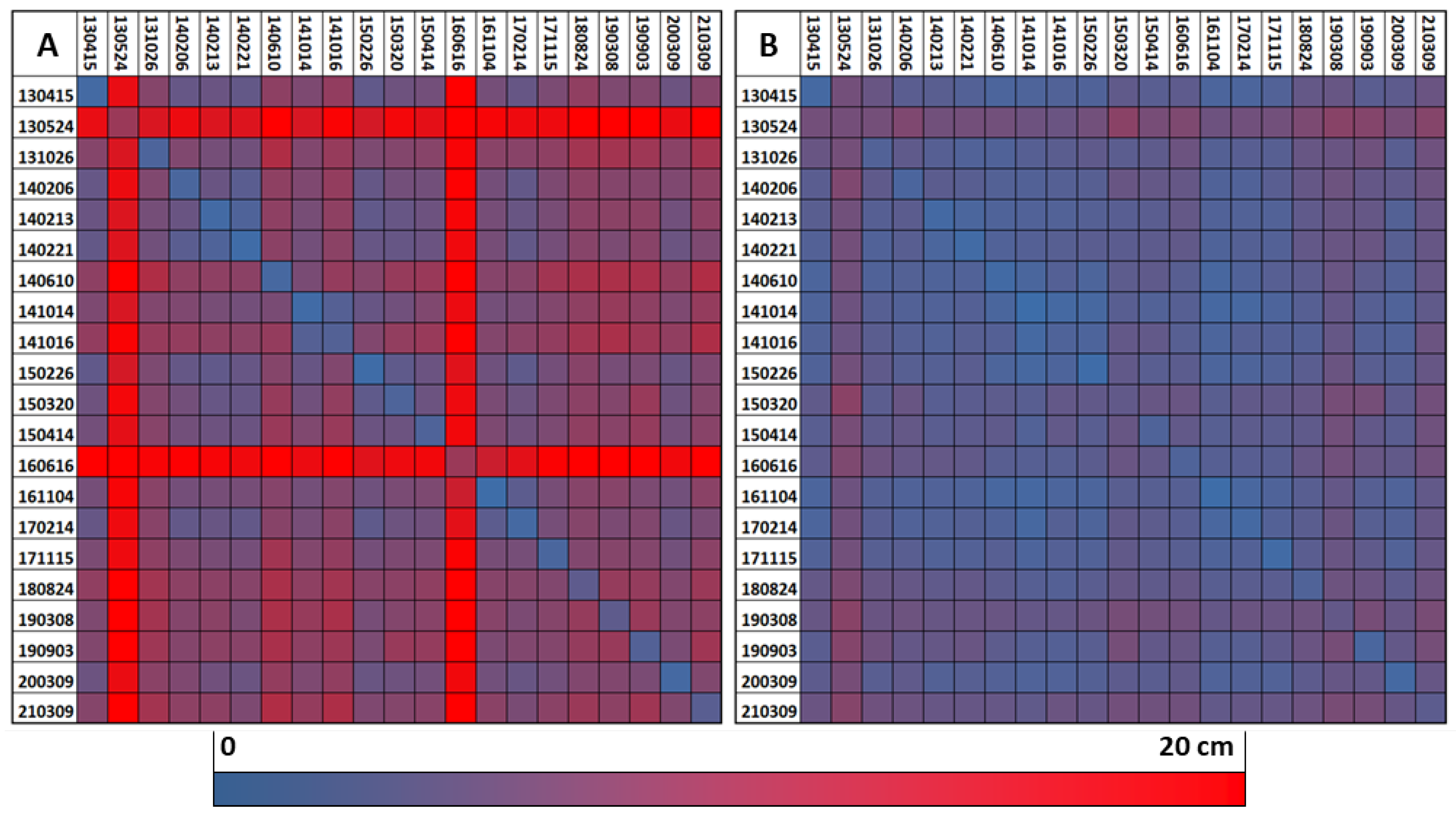
Preprints 110690 g006
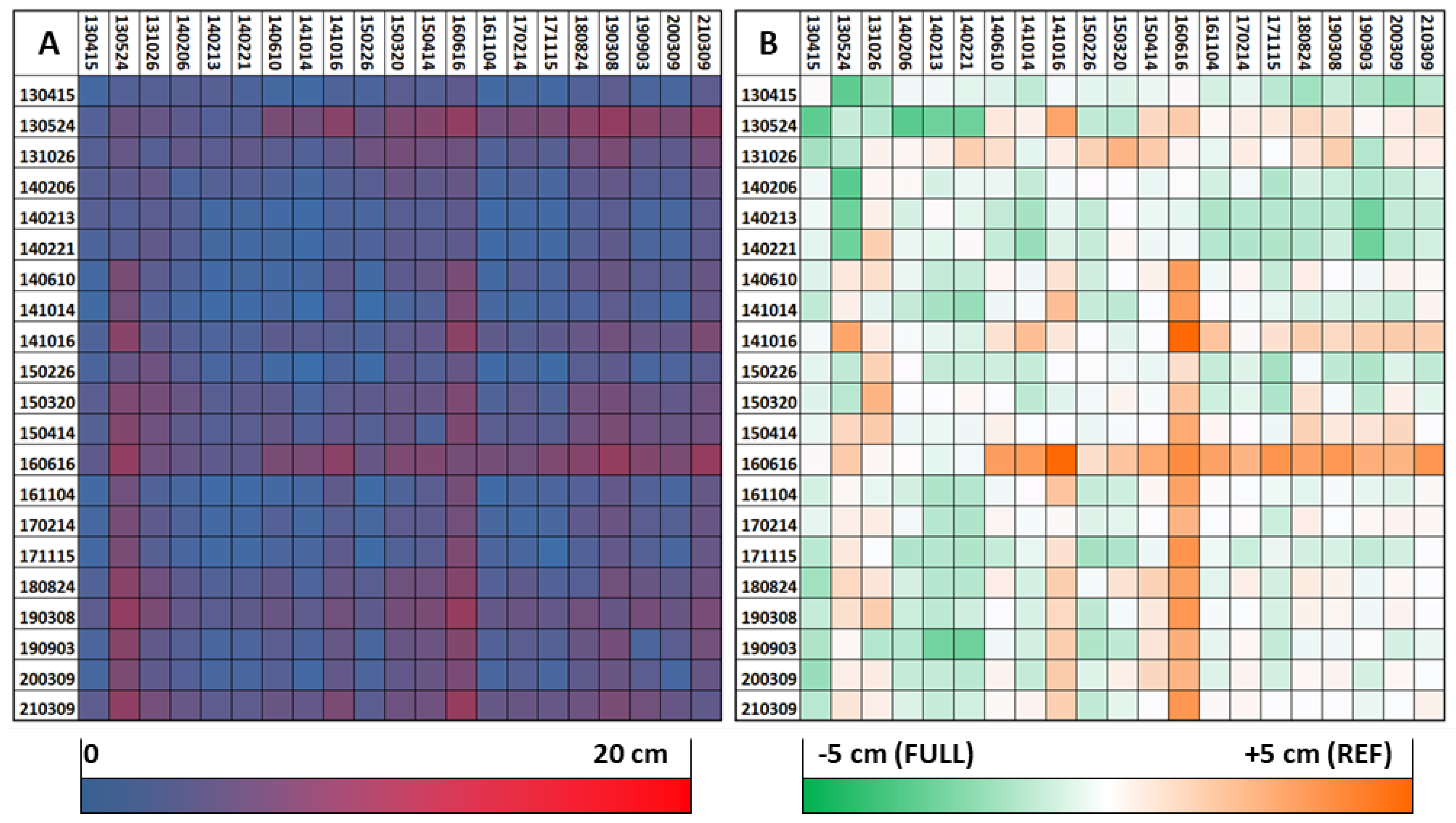
Preprints 110690 g007
Figure 7. (A) Stable blockpair difference matrix ( σ M A D , only stable areas) for the FULL approach. (B) Difference of the stable FULL-matrix from (A) minus the stable REF-matrix (Figure 6). Green fields represent better values for the FULL approach whereas orange depicts advantages of the REF approach.
Figure 7. (A) Stable blockpair difference matrix ( σ M A D , only stable areas) for the FULL approach. (B) Difference of the stable FULL-matrix from (A) minus the stable REF-matrix (Figure 6). Green fields represent better values for the FULL approach whereas orange depicts advantages of the REF approach.
Preprints 110690 g007
Preprints 110690 g008
Figure 8. Mosaic of the highest absolute across-epoch strip differences between 2013-05-24 and 2014-02-13. A cutout showing a residential area in the center of the block is enlarged on the left. The results of the FULL approach (A) are compared to the REF approach (B). For the latter, the boundary of the reference block is marked in red.
Figure 8. Mosaic of the highest absolute across-epoch strip differences between 2013-05-24 and 2014-02-13. A cutout showing a residential area in the center of the block is enlarged on the left. The results of the FULL approach (A) are compared to the REF approach (B). For the latter, the boundary of the reference block is marked in red.
Preprints 110690 g008
Preprints 110690 g009
Figure 9. (A) Differences ( σ M A D ) between the full DSMs derived from REF results. (B) DSM Differences masked to stable areas only.
Figure 9. (A) Differences ( σ M A D ) between the full DSMs derived from REF results. (B) DSM Differences masked to stable areas only.
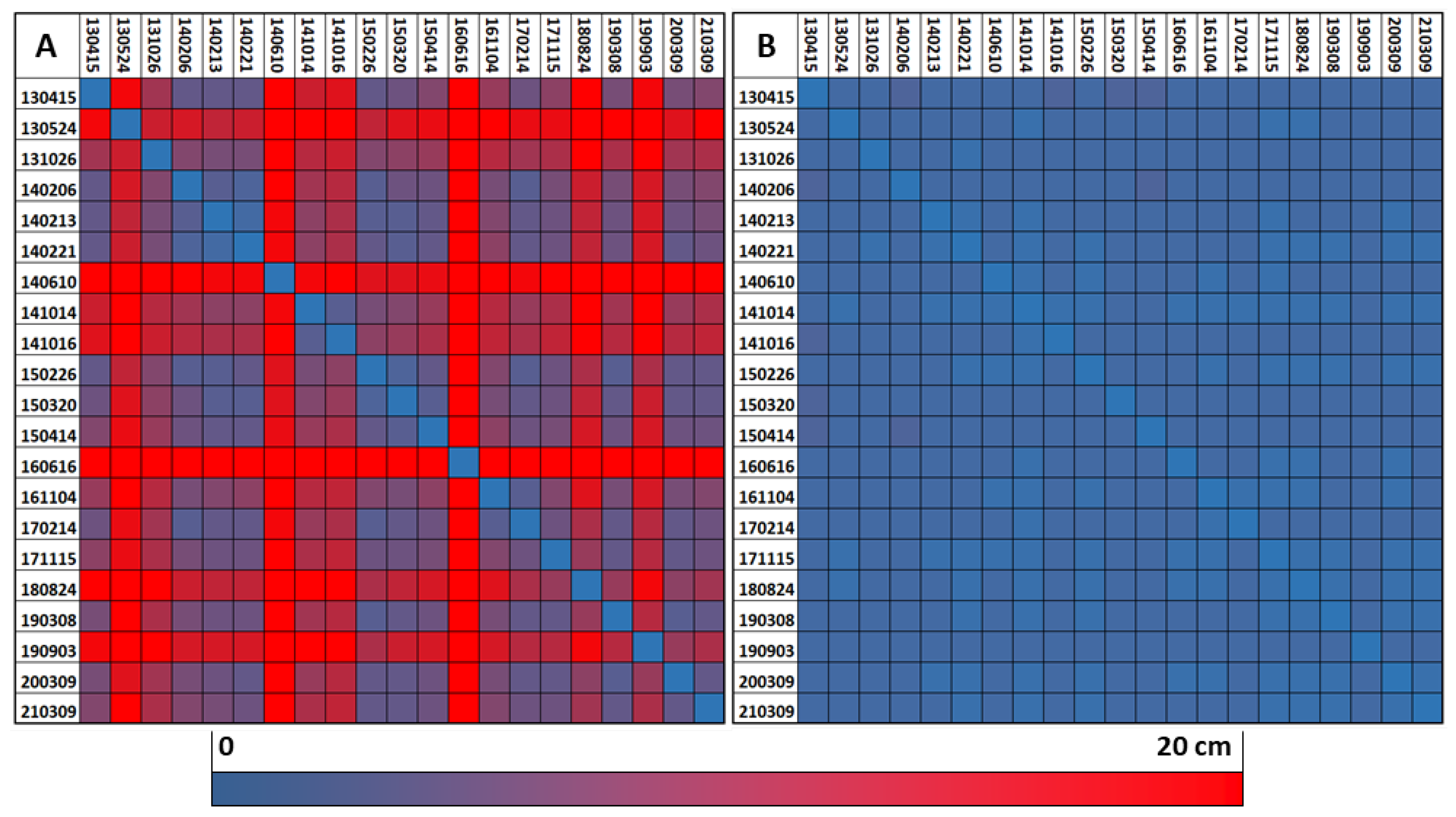
Preprints 110690 g009
Preprints 110690 g010
Figure 10. Validation results: For each check point, Mean and Standard deviation of the differences to all DSM models are visualized. In order to improve readability, nearby check points with similar values were combined to one in this Figure. A statistic based on all check points can be found in Table 4.
Figure 10. Validation results: For each check point, Mean and Standard deviation of the differences to all DSM models are visualized. In order to improve readability, nearby check points with similar values were combined to one in this Figure. A statistic based on all check points can be found in Table 4.
Preprints 110690 g010
Preprints 110690 g011
Figure 11. Top: Difference model of the DSMs from 2021-03-09 (leaf-off) and 2014-06-10 (leaf-on); bottom: Digital Orthophoto from 2020 covering the same area.
Figure 11. Top: Difference model of the DSMs from 2021-03-09 (leaf-off) and 2014-06-10 (leaf-on); bottom: Digital Orthophoto from 2020 covering the same area.
Preprints 110690 g011
Table 1. Applications of multi-temporal airborne LiDAR data in various scientific fields.
Table 1. Applications of multi-temporal airborne LiDAR data in various scientific fields.
Publication Short description of LiDAR application
Forestry and Agriculture
[9] Analysis of above-ground carbon density based on canopy height differences
[10] Site index assessment for mountainous forests
[11] Vegetation growth prediction
[12] Assessment of persistent canopy structure changes resulting from wildfires
[13] Crop characterization and row/alley localization in agricultural fields
[14] Comparison of LiDAR systems for forest inventory applications
[15] Vegetation change monitoring
[16] Estimation and prediction of above-ground forest biomass changes
[17] Impact of selective logging on rain forest canopy and understory structure
[7] Forest growth estimation using periodic annual increment
[18] Sugar cane growth cycle monitoring
[19] Analysis of forest gap dynamics
Geomorphology and Glaciology
[20] Delineation of glacial and periglacial features
[21] Classification and change detection of geomorphological features
[22] Detection of geomorphologic/glacial features and processes
[23] Impact of dataset registration quality on geomorphic change estimation
[24] Analysis of active rock glacier morphodynamics
[25] Motion estimation of an active landslide
[26] Volumetric glacier change estimation
[27] Monitoring of natural coastal barriers and their response to natural disasters
[28] Assessing morphology and dynamics of intertidal bars for coastal management
[29] Mapping of surface changes due to active landslides
[30] Long-term observation of proglacial river channel morphology
[31] Estimation of soil carbon loss from peatland wildfires
[32] Quantification of sediment transport on a rock slope
[33] Mapping of wetland inundation areas and their dynamic changes
[34] Analysis of rock cliff erosion
Infrastructure and building inspection
[35] Subsidence monitoring around a ship lock
[36] Localization and monitoring of railway deformations
[37] Building change detection
[38] Urban change detection with focus on buildings
[39] Assessment of building damage resulting from natural disasters
Table 2. Overview of the available epochs with respective LiDAR specifications. For each epoch, one basic trajectory correction model was used throughout all approaches described in Section 4.2.
Table 2. Overview of the available epochs with respective LiDAR specifications. For each epoch, one basic trajectory correction model was used throughout all approaches described in Section 4.2.
Flight date Scanner (Riegl) Wavelength
in [nm]		 # Lines Height
AGL [m]		 Points/m2
(full block)		 Trajectory
correction
2013-04-15 VQ-820-G 532 7 610 12.5 Bias
2013-05-24 VQ-580 & VQ-820-G 1064 & 532 20 570 11.7 Spline: 20 s
2013-10-26 VQ-820-G 532 11 650 16.5 Spline: 30 s
2014-02-06 VQ-820-G 532 9 810 3.6 Bias
2014-02-13 VQ-820-G 532 16 530 18.9 Spline: 30 s
2014-02-21 VQ-820-G 532 16 640 16.8 Spline: 30 s
2014-06-10 VQ-820-G 532 9 630 14.0 Bias
2014-10-14 LMS-Q680i 1550 7 520 13.1 Bias
2014-10-16 VQ-880-G 532 8 700 27.8 Spline: 10 s
2015-02-26 LMS-Q1560 1064 6 680 21.9 Bias
2015-03-20 VQ-880-G 532 11 710 34.1 Spline: 10 s
2015-04-14 VQ-880-G 532 7 750 27.4 Spline: 10 s
2016-06-16 VQ-880-G 532 & 1064 12 630 47.7 Spline: 10 s
2016-11-04 VQ-820-G 532 9 710 11.8 Bias
2017-02-14 VQ-820-G 532 7 750 12.4 Bias
2017-11-15 VQ-880-G 532 & 1064 8 640 38.6 Spline: 10 s
2018-08-24 VQ-880-G 532 & 1064 14 590 54.3 Spline: 10 s
2019-03-08 VQ-880-G 532 & 1064 12 730 48.2 Spline: 12 s
2019-09-03 VQ-880-G 532 & 1064 2 780 29.1 Bias
2020-03-09 VQ-880-G 532 & 1064 8 810 40.8 Spline: 20 s
2021-03-09 VQ-880-G 532 & 1064 8 800 38.6 Spline: 08 s
Table 3. Rating of the investigated approaches from very favorable (++) to not favorable (∼).
Table 3. Rating of the investigated approaches from very favorable (++) to not favorable (∼).
Approach Consistency
within epoch		 Consistency
between epochs		 Robustness wrt.
changed areas		 Required
Resources		 Expandability
(new blocks)
CPC ++ ∼ ∼ + ++
CPC+ ++ ∼ ∼ ++ ++
REF + + ++ + ++
FULL + + + ∼ ∼
Table 4. Epoch-wise accuracy measures for the discussed results: Columns 2-5 hold the mean σ M A D for all stable strip difference mosaics (largest signed absolute difference, c.f. Section 4.3) with participation of a certain epoch. This corresponds to line-wise mean values of the stable blockpair-difference matrices for each approach (Figure 4 B, Figure 5 B, Figure 6 B, Figure 7 A). The following column contains the mean σ M A D of DSM differences, c.f. lines in Figure 9 B. The final two columns show the distribution of height differences of the interpolated DSM minus the measured check points.
Table 4. Epoch-wise accuracy measures for the discussed results: Columns 2-5 hold the mean σ M A D for all stable strip difference mosaics (largest signed absolute difference, c.f. Section 4.3) with participation of a certain epoch. This corresponds to line-wise mean values of the stable blockpair-difference matrices for each approach (Figure 4 B, Figure 5 B, Figure 6 B, Figure 7 A). The following column contains the mean σ M A D of DSM differences, c.f. lines in Figure 9 B. The final two columns show the distribution of height differences of the interpolated DSM minus the measured check points.
All values in [cm] Mean σ M A D of blockpair-wise diff. DSM diff. DSM - Check Points
Flight date CPC CPC+ REF FULL REF Mean Std.Dev.
2013-04-15 6.7 5.6 4.1 3.2 2.1 3.4 2.8
2013-05-24 9.7 8.7 7.0 6.8 1.8 3.7 2.6
2013-10-13 7.8 10.6 4.6 5.0 1.9 4.2 2.9
2014-02-06 6.2 6.5 4.6 3.9 2.0 4.5 2.6
2014-02-13 6.1 6.9 4.0 3.1 1.7 4.1 2.4
2014-02-21 6.9 8.4 4.1 3.2 1.5 3.9 2.3
2014-06-10 5.8 5.8 3.8 3.9 1.7 3.6 2.1
2014-10-14 5.5 5.4 3.4 3.1 1.2 3.7 2.0
2014-10-16 10.5 10.2 3.9 4.9 1.9 2.4 2.3
2015-02-26 6.0 5.7 3.9 3.3 1.5 3.7 2.1
2015-03-20 10.0 10.3 5.2 5.1 2.0 3.2 2.2
2015-04-14 8.2 8.4 4.7 5.1 2.0 2.8 2.5
2016-06-16 11.0 8.9 4.9 7.1 1.7 3.0 2.6
2016-11-04 5.6 5.4 3.5 3.3 1.6 3.7 2.5
2017-02-14 5.8 5.8 3.8 3.8 1.8 3.5 2.2
2017-11-15 10.6 9.5 4.0 3.5 1.3 3.4 2.2
2018-08-24 13.0 7.8 4.8 5.0 1.4 3.7 2.3
2019-03-08 10.3 10.3 6.0 6.0 1.6 3.4 2.3
2019-09-03 8.9 6.4 5.1 4.6 1.9 2.9 2.8
2020-03-09 6.3 6.8 4.2 4.1 1.4 4.1 2.5
2021-03-09 11.2 10.7 5.8 5.9 1.6 4.1 2.8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated