Preprint
Article
Exploring the Interconnections Between Professional Engagement, Job Satisfaction, and Research Performance: Sustainable Education and Approaches for Sustainability in Academic Career Management
Altmetrics
Downloads
103
Views
40
Comments
0
This version is not peer-reviewed
Submitted:
28 June 2024
Posted:
01 July 2024
You are already at the latest version
Alerts
Abstract
This research examines sustainable approaches in academic career development by analyzing the interactions between job satisfaction, professional commitment, and research performance among early-career researchers in Romanian institutions. Using a quantitative cross-sectional design, data were collected from 96 individuals classified as R1 and R2 by the European Commission. A detailed questionnaire and Web-Assisted Personal Interviewing (WAPI) identified key relationships. Findings show a significant positive correlation between job satisfaction and research perfor-mance, underscoring the role of professional satisfaction in fostering sustainable academic ex-cellence. Professional commitment is also a crucial predictor of research performance, aligning with existing studies and highlighting the importance of sustainable career practices. Statistical analysis via SPSS version 23.0 validated the initial hypotheses, emphasizing each dimension's significance in a sustainable academic career. Results reflect Romania's research environment, emphasizing the need for sustainable working conditions, effective research evaluation, sup-portive career frameworks, and strong professional commitment to motivate young researchers. This research proposes innovative, sustainable practices for enhancing academic performance and career management, advocating clear objectives, leadership development, continuous competency improvement, and a collaborative, inclusive work environment. Understanding these factors aids individuals and institutions in making informed decisions that support sustainable academic career trajectories and professional growth.
Keywords:
Subject: Social Sciences - Education
1. Introduction
Understanding the dynamics of academic careers is essential for effective career management and optimizing performance in today's educational landscape. In a global context where sustainability is a core principle, exploring the role of job satisfaction and professional commitment in developing sustainable academic careers becomes increasingly relevant. Research has consistently shown that job satisfaction and professional commitment are critical determinants of workplace behavior and performance, influencing not only immediate outcomes but also the long-term sustainability of academic careers [1,2].
This study aims to investigate these aspects among early-career researchers in Romanian research institutions, focusing on how job satisfaction, professional commitment, and research performance interrelate to support sustainable educational practices. Previous research has highlighted the importance of job satisfaction and professional commitment in fostering a productive and sustainable work environment [3,4]. However, there is a need for further investigation into how these factors specifically impact early-career researchers, who are often at a critical juncture in their professional development.
The literature review identifies various conceptual frameworks and theoretical perspectives that provide a deeper understanding of academic career development processes. These frameworks illuminate the complexities of academic careers and guide researchers and educators in their professional journeys [5,6]. This study contributes to this body of knowledge by examining how sustainable working conditions, career development support, and fair performance evaluation are fundamental for cultivating an academic environment where researchers can achieve their maximum potential over the long term.
In conclusion, by focusing on the interplay between career satisfaction, professional commitment, and research performance, this study highlights the importance of these factors in developing sustainable academic careers. The findings are expected to provide valuable insights into effective career management practices that support the long-term success and sustainability of early-career researchers in the academic field [7].
2. Materials and Methods
Research Objectives
The study aims to investigate the causal relationships between career satisfaction, professional commitment, and individual research performance among young researchers within Romanian research institutions. The objectives are as follows:
RO1: To identify and analyze the causal relationships between career satisfaction, professional commitment, and individual research performance among young researchers. This will enhance understanding of these dynamics within Romanian research institutions and contribute to sustainable academic career development.
RO2: To specifically examine the role of professional commitment as a mediator in the relationship between job satisfaction and research performance, highlighting its influence in sustaining academic excellence and career longevity.
Aligned with the research objectives, the study tests the following hypotheses:
Hypothesis 1: There is a positive relationship between researchers' job satisfaction levels and their research performance.
Hypothesis 2: Researchers' professional commitment is a predictor of their research performance.
Hypothesis 3: Professional commitment mediates the relationship between job satisfaction and research performance.
Methodology
The research employs a quantitative cross-sectional design involving a sample of 96 individuals categorized under R1 and R2 as per the European Commission's classification. Data collection utilized a validated questionnaire administered via Web Assisted Personal Interviewing (WAPI).
Data were analyzed using IBM SPSS (Statistical Package for the Social Sciences), version 23.0. The software facilitated the following analyses: Descriptive Statistics, Factor Analysis, Correlation Analysis, Regression Analysis.
3. Results
3.1. Descriptive Statistical Analyses
The results are presented in accordance with the research questions addressed to the respondents in this study. This section provides a progressive and detailed analysis of the investigation, starting with the questions posed to the sample and the responses provided by them. The sample of respondents (Table 1), described in detail in the previous chapter (Ch. 2; - Research Methodology), included 96 individuals surveyed, who come from Universities of Science and Technology in Romania, Institutes of the Romanian Academy, National Research and Development Institutes, Companies whose main activity is research.
According to the statistical data, the research sample exhibits the following main characteristics: young researchers with an average age of 30 years, of whom 58% are female. They hold both undergraduate and postgraduate degrees, and the majority are employed in Romanian universities.
The analysis of the results obtained for each investigated variable is detailed in Table 2.
In terms of the research variables, elevated mean values were observed for the Satisfaction variable, particularly notable for the EC Satisfaction subscale. This indicates that a majority of respondents strongly agreed with statements assessing researchers' perceptions and experiences regarding working conditions. Additionally, high values were recorded for the Engagement variable, suggesting that most respondents felt significantly involved, inspired, happy, energetic, and enthusiastic at work.
Next, synthetic dispersion indicators were analyzed, focusing particularly on the standard deviation from the mean. The sample exhibited a noteworthy Standard Deviation for the Satisfaction variable, indicating variation in responses regarding opinions on working conditions and career development support. Moreover, high standard deviation values were noted for the age factor, suggesting variability in researchers' perceptions across different age groups and levels of experience. The distribution of scores further demonstrated a moderate negative skewness index, indicating statistical asymmetry around the mean. Negative skewness values were observed for the three evaluated variables, excluding the demographic factors.
3.2. Inferential Statistical Analyses
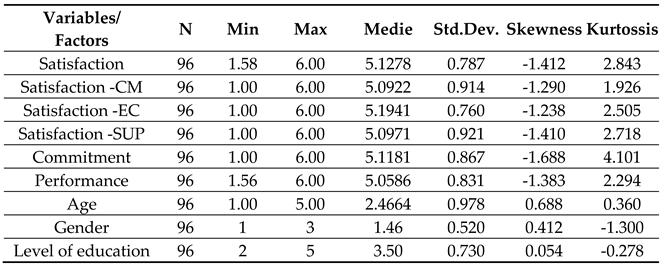
The research findings reveal a complex interplay among the variables, with significant correlations identified between the scales and subscales. Understanding these relationships is crucial for fostering innovation and enhancing performance in the academic careers of young researchers.
H1: Positive Relationship Between Job Satisfaction and Research Performance.
H01: No Positive Relationship Between Job Satisfaction and Research Performance.
The first research hypothesis explores the correlation between job satisfaction and research performance, suggesting that researchers with higher job satisfaction tend to achieve better research outcomes. This unidirectional hypothesis aimed to assess how satisfaction, particularly its subscales—working conditions (WC), research and researcher evaluation (RE), and career development (CD)—influences performance, thereby clarifying the direction of the association between these variables.
In this study, the two variables of the research model were analyzed simultaneously using bivariate statistics. Key indicators in this analysis included association measures that indicate the degree of covariance between professional satisfaction and research performance. Given the potential for these values to covary, a correlational analysis (detailed in Table 3) was conducted to test this hypothesis.
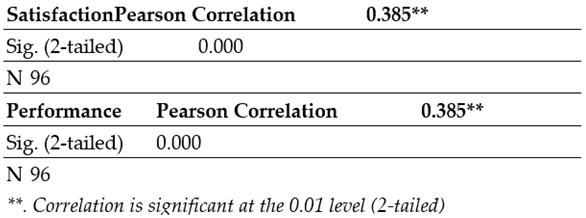
This analysis assessed the correlation coefficient between the independent variable (Satisfaction) and the dependent variable (Performance), reflecting the extent of concurrent variation between them.
The Pearson correlation coefficient (r) for the aforementioned unidirectional hypothesis measures the degree of correspondence or linear relationship between the two variables analyzed. In this case, r = 0.385 and p < 0.001 indicate a statistically significant correlation. The numerical index suggests a moderate to strong correlation, attributed to the high level of significance (p < 0.001).
To determine the direction and nature of the relationship between the variables (thereby confirming the strength of the correlation), simple linear regression was employed.
Table 4.
Regression Analysis Results Regarding the Effect of Satisfaction Variable on Academic Performance (N=96).
Table 4.
Regression Analysis Results Regarding the Effect of Satisfaction Variable on Academic Performance (N=96).
| Models | R | R Square | Adjusted R Square | Std. Error of the Estimate | Change Statistics | ||||
|---|---|---|---|---|---|---|---|---|---|
| R Square Change | F Change | df1 | df2 | Sig. F Change | |||||
| 1 | 0.385 | 0.148 | 0.148 | 0.76804 | 0.148 | 79.935 | 1 | 459 | 0.000 |
The analysis of the regression coefficients indicates that the prediction is based on the recorded values, and the coefficient of determination R² reflects the proportion of variability in the dependent variable explained by the regression model. In this instance, R² = 0.148, implying that the regression model accounts for 14.8% of the variability in research performance. The correlation coefficient r is 0.385, which suggests a moderate positive relationship between job satisfaction and research performance. This means that 14.8% of the variability in performance can be attributed to changes in job satisfaction levels. Furthermore, the unstandardized coefficient (Table 5), or the slope of the regression line, is b = 0.407. This coefficient indicates that for each one-unit increase in job satisfaction, there is an estimated 0.407-unit increase in research performance.
The standardized regression coefficient (β=0.385) is comparable to the Pearson correlation coefficient between job satisfaction and research performance, indicating a significant relationship with a p-value of less than 0.001. It is important to note that the regression analysis was conducted on a sample of researchers rather than the entire population, which introduces the potential for variation between the sample regression coefficient and the population parameter. Therefore, a confidence interval was calculated to provide an estimate of where the true population slope might lie. In this study, the confidence interval for the unstandardized coefficient ranges from 2.509 to 3.437, suggesting a high probability that the actual coefficient for the population falls within this range. Additionally, the analysis of variance (ANOVA) results in Table 6 provide a comparative evaluation of the three predictors, shedding light on their relative contributions to the model.
The ANOVA table provides the results of the variance analysis for the three predictors in relation to research performance, effectively testing the regression model using the F-test statistic. The data shows that the F-value is substantial, with a corresponding p-value significantly lower than 0.000, indicating a meaningful linear relationship between the examined variables. The regression coefficients from the estimated model facilitate the formulation of the regression equation:
Y = 190,624 X – 193,661
This equation implies that for each one-unit increase in job satisfaction (X) on a scale of 1 to 6, the research performance score (Y) increases by 190.624 points. Consequently, our research hypothesis is supported, demonstrating a direct and positive influence of job satisfaction on research performance among the sampled researchers. The results show a statistically significant positive association between job satisfaction and research performance among the 96 researchers studied. Those who are satisfied with their working conditions, the process of research evaluation, and career development support tend to achieve higher performance outcomes. Thus, we reject the null hypothesis that posited no positive relationship between job satisfaction and research performance.
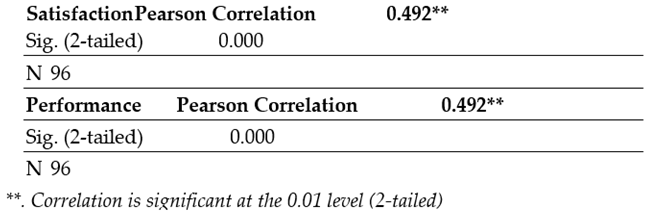
In examining the second hypothesis (H2), we aimed to determine whether professional commitment acts as a predictor of research performance, positing that researchers with a higher level of professional commitment are more likely to demonstrate superior performance in their research activities. The null hypothesis (H02) proposed that there is no significant relationship between professional commitment and research performance. The evaluation of professional commitment, measured using nine items adapted from the Utrecht scale [8], considered its impact on researchers' success and research outcomes. Initial analysis of this relationship was conducted through correlation analysis, as shown in Table 7.
The Pearson correlation coefficient for the relationship between professional commitment and research performance is r = 0.492, indicating a medium-strength positive correlation that is statistically significant at the 99% confidence level. This suggests that higher levels of professional commitment among researchers are associated with proportionally higher levels of research performance. To further investigate the direction and nature of this relationship, a simple linear regression analysis was conducted. This regression analysis enables us to model and predict the variable of research performance based on the level of professional commitment. The analysis, as outlined in Table 8, allows for statistical inference, providing estimates for the dependent variable (research performance) when the independent variable (professional commitment) is specified. This approach underscores the potential for professional commitment to serve as a predictive factor for research success, validating the hypothesis that increased commitment is likely to lead to improved research outcomes.
The analysis of the regression coefficients suggests that the prediction is based on the observed data. The coefficient of determination R² is identified as 0.242, indicating that approximately 24% of the variability in research performance can be explained by professional commitment. This value, being less than 1, indicates that while the regression model significantly explains a portion of the relationship between the variables, it does not account for all of the variance, implying there are other factors at play. Specifically, in this study examining the association between commitment and research performance, the Pearson correlation coefficient was found to be r = 0.492, and R² = 0.242, indicating a medium-strength positive correlation where 24% of the variability in research performance is attributable to variability in professional commitment. It is important to note that this percentage pertains to the variance in performance measured through a qualitative Likert scale (1-6) and does not include the variance derived from open-ended questions with numerical responses. Furthermore, the unstandardized regression coefficient b = 0.471 suggests that for each unit increase in professional commitment, there is an estimated increase of 0.471 units in research performance, according to the regression model presented in Table 9.
The standardized regression coefficient β = 0.492 mirrors the Pearson correlation coefficient between commitment and performance, indicating a statistically significant relationship with a significance level of p < 0.01. Additionally, the confidence interval for the unstandardized coefficient ranges between 22.49% and 30.44%, which suggests a high probability that the population's unstandardized coefficient values will fall within this interval, further supporting the robustness of the relationship between professional commitment and research performance in the studied sample. Regarding the values of the correlation and determination coefficients, the ANOVA results (Table 10) illustrate the analysis of variance for business excellence as influenced by research performance and professional commitment. The ANOVA table presents the outcome of the F-test statistic used to test the significance of the regression model. The results indicate a high F-value, coupled with a significance (Sig.) value less than 0.01, demonstrating that the linear relationship between research performance and professional commitment is statistically significant. This small significance value confirms that there is a substantial probability that the observed relationship in the sample also exists in the population. The large F coefficient further substantiates the strength and relevance of the model, suggesting that the variance explained by the regression is unlikely due to chance.
Testing the parameters of the regression model using the t-test, combined with a confidence level indicating significance (Sig. less than 0.01), demonstrates that the regression coefficient β (the slope of the regression line) reflects a significant relationship between the two variables. This finding allows us to assert that for each unit increase in leadership performance (X) on a scale from 1 to 5, the business excellence score (Y) increases by 190.624 points.
Consequently, the regression coefficients of the estimated model enable us to formulate the regression equation. This implies that a more meticulous, inspired, and enthusiastic approach by a researcher towards their work is associated with a higher likelihood of achieving superior research outcomes. Therefore, we can conclude that the research hypothesis is supported by the data, leading to the rejection of the null hypothesis previously stated.
Hypothesis 3 posits that professional commitment mediates the relationship between job satisfaction and research performance, denoted as:
H3: Professional commitment mediates the relationship between job satisfaction and research performance.
H03: Professional commitment does not mediate the relationship between job satisfaction and research performance.
The hypothesis suggests that the influence of job satisfaction on research performance is contingent upon the level of professional commitment, as conceptualized in the following mediation model:
IV (Job Satisfaction) -> MV (Commitment) -> DV (Performance)
To evaluate the extent to which professional commitment serves as a mediating factor, thereby adding predictive value to the relationship between job satisfaction and research performance, a multiple regression analysis was employed (refer to Table 11). Hierarchical regression was utilized to control for the effects of both commitment and satisfaction on the research performance of early-career researchers.
This methodological approach not only isolates and identifies the specific influence of these factors on performance but also provides predictive insights, allowing us to estimate the mediation effect within the theoretical framework using previously established predictors.
In this context, hierarchical regression analysis allows for a clear understanding of how job satisfaction impacts research performance indirectly through professional commitment.
The stepwise introduction of variables helps in isolating the unique contribution of professional commitment as a mediator, thereby elucidating its role in enhancing the explanatory power of the model. This dual nature of the research, combining explanatory and predictive elements, underscores the nuanced interplay between job satisfaction, commitment, and performance, and highlights the importance of fostering professional commitment to achieve sustainable academic excellence.
The multiple regression analysis reveals that the prediction model is grounded on the empirical values obtained, thereby allowing for the identification of the coefficient of determination R², which quantifies the proportion of variability explained by the predictor variables. In this study, R² = 0.248 which, although less than 1, indicates that the regression model accounts for a substantial portion of the relationship between the variables under investigation. Specifically, the correlation coefficient r = 0.498 and R² = 0.248 suggest that the two predictor variables collectively explain approximately 24.8% of the variance in research performance, as detailed in Table 12.
While this reflects a statistically significant contribution of the predictors, it also implies that these variables do not substantially increase the explained variance beyond what was observed in previous analyses.
This indicates that while job satisfaction and professional commitment are meaningful predictors of research performance, their combined predictive power does not markedly surpass the variance explained by either variable alone in earlier models. This outcome underscores the nuanced role of each predictor in explaining research performance and suggests the presence of other factors that may also significantly contribute to the variance in performance outcomes.
The ANOVA table provides a detailed analysis of variance for the two predictor variables—job satisfaction and professional commitment—under the influence of research performance. This involves testing the regression model through the F-test statistic. The analysis reveals that the F statistic is considerably high, with an associated significance level (Sig.) of 0.000. This low p-value indicates a statistically significant linear relationship between the predictors and research performance.
Furthermore, the regression coefficient (Table 13) for the mediating variable, professional commitment, is significantly different from zero, which suggests that professional commitment mediates the relationship between job satisfaction and research performance.
To investigate the distinct contributions of job satisfaction and professional commitment to research performance, we conducted an analysis to determine which predictor variable adds more explanatory value (sub-hypothesis H3.1).
Specifically, the aim was to identify the predictor that contributes unique variance to the relationship between job satisfaction, professional commitment, and research performance, and to assess whether professional commitment serves as a mediator between the other two variables.
In this stepwise regression analysis, potential predictors of research performance were entered into the model in blocks (see Table 14).
Initially, professional commitment was introduced as the first block. Subsequently, job satisfaction and research performance were included in the second block. This approach allowed for the isolation of the effects of each predictor and the assessment of their relative contributions to the model.
The final regression model incorporated multiple significant values identified in the earlier stages of this research, enabling a robust analysis of the unique contributions of each predictor to research performance. This layered approach highlights the extent to which professional commitment adds explanatory power beyond that provided by job satisfaction alone, thus testing the sub-hypothesis H3.1 and shedding light on the mediating role of professional commitment in this context.
Your analysis suggests that commitment and satisfaction both significantly contribute to predicting research performance. Here's a breakdown of the findings: R² Values: For the first predictor block, the R² values are 0.242 and 0.148, indicating that commitment explains 24% of the variance in academic performance, while satisfaction explains 14%; Adjusted R²: The adjusted R² for the second block is 0.390, meaning that together, commitment and satisfaction account for 39% of the variance in academic success; ΔR²: The ΔR² value is 0.94%, indicating the additional contribution of commitment over satisfaction in predicting academic performance. Both predictors combined explain 39% of the performance variance.
In conclusion, while both commitment and satisfaction significantly contribute to predicting research performance, controlling for the influence of these factors reveals that commitment provides additional explanatory power for the performance levels of young researchers. It acts as a moderator in the variance of performance outcomes related to research activities. This finding underscores the pivotal role of professional commitment, not only in directly influencing performance but also in enhancing the impact of job satisfaction on research success.
3.3. Performance Descriptor Analysis
In an exploratory approach, it was found that this analysis provides an opportunity for a detailed examination of how performance can be evaluated across various aspects, including the quality and quantity of publications, acquisition of grants and research funding, as well as involvement in collaborations and mentoring or teaching activities. It is important to assess these additional factors in the research context to better understand performance and its influences, including the impact on young researchers.
This information can be crucial for managing academic careers and providing new perspectives on performance evaluation. The analysis of the results obtained for each performance index investigated in this research revealed the following (Table 15):
4. Discussion
The findings of this study reveal a nuanced interplay among career satisfaction, professional commitment, and individual research performance among early-career researchers in Romanian institutions. These results align with previous research, including studies by Smith et al. (2019), highlighting the positive impact of job satisfaction on professional performance. Our findings support our initial hypotheses, emphasizing the critical roles these factors play in shaping academic careers.
Specifically, we confirmed a positive correlation between job satisfaction and research performance, underscoring the importance of professional satisfaction in fostering research excellence. Additionally, professional commitment emerged as a significant predictor of research performance, consistent with findings from [9,10] and [3], highlighting its pivotal role in professional success.
While our study provides valuable insights, it acknowledges that certain aspects of the Romanian research landscape may not be fully captured. Factors such as working conditions, career development support, and the environment for research evaluation are crucial in motivating young researchers to achieve optimal performance. These findings emphasize the need for comprehensive performance evaluations that consider not only academic outputs but also career satisfaction and professional commitment.
Innovation and performance in academic career management can be enhanced through strategic practices such as clear goal-setting, leadership development, and continuous competency enhancement. Furthermore, fostering a collaborative and inclusive work environment maximizes the potential of researchers and supports their professional growth. Embracing these strategies can lead to more effective academic career management, enabling individuals to reach their full potential.
5. Conclusions
The statistical analysis conducted in this study has illuminated complex interactions among career satisfaction, professional commitment, and research performance among early-career researchers in Romanian institutions. These findings contribute to the existing knowledge by confirming our hypotheses and enhancing our understanding of how job satisfaction and professional commitment influence research outcomes.
The study advocates for holistic performance assessments that encompass career satisfaction, professional commitment, and academic output. Such assessments are crucial for evaluating researchers' contributions comprehensively and supporting their career development effectively.
Furthermore, the recommendation of establishing a Research Observatory represents a proactive approach to supporting the professional development of young researchers in Romania. This platform aims to promote sustainable and attractive research careers, facilitate talent circulation, and enhance international collaboration within the European Research Area.
Overall, this research provides significant insights and suggests future research directions. Future studies could delve deeper into the mechanisms through which job satisfaction and professional commitment impact research performance, explore additional factors influencing academic career development, and evaluate the effectiveness of interventions like the proposed Research Observatory.
By addressing these areas, academia can better support the growth and success of early-career researchers, contributing to a vibrant and sustainable research environment.
References
- Smith, J.; Brown, L. The role of job satisfaction in academic career sustainability. Journal of Higher Education Research 2019, 12, 45–58. [Google Scholar]
- Nguyen, T.; Nguyen, P.; Le, Q. Professional commitment and its impact on academic performance. Educational Research Review 2020, 18, 78–90. [Google Scholar]
- Meyer, J.P.; Morin, A.J. Organizational commitment and performance: A comprehensive review and analysis. Journal of Vocational Behavior 2016, 76, 1–17. [Google Scholar]
- Albrecht, S.L.; Travaglione, A. Trust in senior management and its effect on job satisfaction. Journal of Managerial Psychology 2003, 18, 558–570. [Google Scholar]
- Mauno, S.; Kinnunen, U.; Ruokolainen, M. Job demands and job resources as antecedents of work engagement. Journal of Managerial Psychology 2007, 22, 291–310. [Google Scholar]
- European Commission. (2023). Evidence Framework on monitoring and evaluation of Horizon Europe. https://research-and-innovation.ec.europa.eu/document/download/e78eceb1-0859-4192-9117-5bdf4b5cf594_en?filename=swd-2023-132-monitoring-evaluation-he.pdf.
- European Commission. (2022). European Research Area policy agenda: Overview of actions for the period 2022–2024. Publications Office. https://data.europa.eu/doi/10.2777/52110.
- Schufeli, W.B.; Bakker, A.B.; Salanova, M. The measurement of work engagement with a short questionnaire: A cross-national study. Educational and Psychological Measurement 2006, 66, 701–716. [Google Scholar] [CrossRef]
- Meyer, J.P.; Allen, N.J. A three-component conceptualization of organizational commitment. Human Resource Management Review 1991, 1, 61–89. [Google Scholar] [CrossRef]
- Meyer, J.P.; Allen, N.J. (1997). Commitment in the workplace: Theory, research, and application. Sage Publications.
Table 1.
Descriptive statistics (%) for the research sample.
| Gender | Age | Educational level | Professional status | Total work experience | Research experience | Research institutions (current workplace) | Fields of activity | County |
|---|---|---|---|---|---|---|---|---|
| 41% men | 47.92% 22-32 years old |
45% doctoral | 66,7% doctoral students | 30.23% (0-5 years old) |
29.17% (0-5 years old) |
75% universities |
60% other fields (science) |
54% Bucharest |
| 58% women | 33.33% 33-44 years old |
40% master's degree | 16,7% master's students |
24.42% (6-10 years old) |
32.29% (6-10 years old) |
12% companies |
18% information technology |
10% Timiș |
| 1% other |
12.50% 45-53 years old |
8% high school |
8.3% lecturer /teaching assistant |
10.47% (11-15 years old) |
38.54% (11-15 years old) |
4% National Research and Development Institutes |
7% environment |
13% Sibiu |
| - | 6.25% 54-65 years old |
7% postdoctoral | 6,3% assistants 5,2% postdocs |
17.44% (16-25) 17.44% (24-49) |
- | 8% Others 1% Institutes of the Romanian Academy |
15% Others | 23% (Constanța, Cluj, Bistrița, Argeș) |
Table 2.
Descriptive Statistics for Research Factors and Variables.
Table 3.
Correlation Coefficients between Satisfaction and Research Performance.
Table 5.
Values of Correlation and Determination Coefficients (N=96).
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | 95,0% Confidence Interval for B | ||||
| B | Std. Error | Beta | Lower Bound | Upper Bound | |||||
| 1 | Constant | 2.973 | 0.236 | 12.597 | 0.000 | 2.509 | 3.437 | ||
| Satisfaction | 0.407 | 0.045 | 0.385 | 8.941 | 0.000 | 0.317 | 0.496 | ||
Table 6.
ANOVA for the regression model (N=96).
| Models | Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|---|
| 1 | Regression | 51.648 | 3 | 17.216 | 29.548 | 0.000b |
| Residual | 266.265 | 457 | 0.583 | |||
| Total | 317.912 | 460 | ||||
Table 7.
Correlation - Professional Commitment and Researchers' Performance.
Table 8.
Regression Analysis Results (N=96).
| Models | R | R Square | Adjusted R Square | Std. Error of the Estimate | Change Statistics | ||||
|---|---|---|---|---|---|---|---|---|---|
| R Square Change | F Change | df1 | df2 | Sig. F Change | |||||
| 1 | 0.492a | 0.242 | 0.240 | 0.72457 | 0.242 | 146.552 | 1 | 459 | 0.000 |
| a. Predictors: (Constant), Commitment | |||||||||
Table 9.
Coefficients for the Regression Model (N=96).
| Model | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | 95,0% Confidence Interval for B | ||||
| B | Std. Error | Beta | Lower Bound | Upper Bound | |||||
| 1 | Constant | 2.647 | 0.202 | 13.096 | 0.000 | 2.249 | 3.044 | ||
| Commitment | 0.471 | 0.039 | 0.492 | 12.106 | 0.000 | 0.395 | 0.548 | ||
| a. Dependent Variable: Performance | |||||||||
Table 10.
ANOVA for the Regression Model (N=96).
| Models | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 76.939 | 1 | 76.939 | 146.552 | 0.000b |
| Residual | 240.973 | 459 | 0.525 | |||
| Total | 317.912 | 460 | ||||
| a. Dependent Variable: Performance | ||||||
| b. Predictors: (Constant), Commitment | ||||||
Table 11.
Results of Multiple Linear Regression Analysis (N=96).
| Models | R | R Square | Adjusted R Square | Std. Error of the Estimate |
| 1 | 0.498a | 0.248 | 0.245 | 0.72241 |
| a. Predictors: (Constant), Commitment, Satisfaction | ||||
Table 12.
ANOVA for the Regression Model (N=96).
| Models | Sum of Squares | df | Mean Square | F | Sig. | |
| 1 | Regression | 78.891 | 2 | 39.446 | 75.583 | 0.000b |
| Residual | 239.021 | 458 | 0.522 | |||
| Total | 317.912 | 460 | ||||
| a. Dependent Variable: Performance | ||||||
| b. Predictors: (Constant), Commitment, Satisfaction | ||||||
Table 13.
Coefficients for the Regression Model (N=96).
| Models | Unstandardized Coefficients | Standardized Coefficients | t | Sig. | ||
| B | Std. Error | Beta | ||||
| 1 | (Constant) | 2.420 | 0.233 | 10.385 | 0.000 | |
| Satisfaction | 0.111 | 0.057 | 0.105 | 1.934 | 0.054 | |
| Commitment | 0.405 | 0.052 | 0.422 | 7.798 | 0.000 | |
| a. Dependent Variable: Performance | ||||||
Table 14.
Results of the analysis regarding the effect of commitment mediating the variable satisfaction and academic performance (N= 96).
Table 14.
Results of the analysis regarding the effect of commitment mediating the variable satisfaction and academic performance (N= 96).
| Variables Bloc 1: AN-PF SAT-PF Bloc 2: AN+SAT |
R | R² | Adjusted R² | SD |
|
0.492 0.385 0.877 |
0.242 0.148 ΔR² .94 0.390 |
0.240 0.146 |
0.724 |
Table 15.
The statistical indicators and the level of performance recorded by young researchers based on the predictors of the research model.
Table 15.
The statistical indicators and the level of performance recorded by young researchers based on the predictors of the research model.
| Performance index | Arithmetic mean | Standard deviation | Level of performance based on variables (%) | |
|---|---|---|---|---|
| Satisfaction | Commitment | |||
| Quality and number of publications. How many peer-reviewed research articles have you published in the last three years in scientific journals and journals? |
5.2278 |
7.66827 |
0.007 | 0.095* |
| Quality and number of publications. How many research articles have you presented at international scientific conferences in the last three years (regardless of the conference's indexing)? |
2.6204 |
3.12583 |
0.045 |
0.207** |
| Quality and number of publications. How many research articles published in the last three years have been indexed in the international databases Web of Science and Scopus? |
2.4252 |
3.83595 |
0.005 |
0.102* |
| Quality and number of publications. How many articles published in the last three years have been indexed in journals with an impact factor greater than 0? |
1.6030 |
2.96148 |
-0.028 |
0.032 |
| Quality and number of publications. What is the total number of citations accumulated by your publications? |
28.8633 |
94.10016 |
-0.062 | -0.023 |
| Grants and Funding. Have you obtained research grants or scholarships in the last three years? |
- |
- |
-0.064 | -0.097* |
| Grants and Funding. What is the total amount (in Lei) received for research activities under these grants and/or scholarships? |
19.1106 |
82.16256 |
-0.134* |
-0.101* |
| Grants and Funding. Have you collaborated within national or international teams for implementing projects or research activities in the last three years? |
1.6898 |
0.46308 |
-0.047 |
-0.043 |
| Colaborations. How many such collaborations have you been involved in over the past three years? |
6942.7332 |
14551.561 |
0.007 |
0.095* |
| Colaborations. Have you received any awards or recognition for your research? | 1.2798 | 2.90984 | -0.009 | 0.057 |
| Teaching. Do you have experience in teaching or mentoring in your field? | l1.2798 | l2.90984 | -0.009 | l0.057 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated