Modified Liu Parameter in Scaling Options of the Multiple Regression Model with Multicollinearity Problem

Preprint

Article

Modified Liu Parameter in Scaling Options of the Multiple Regression Model with Multicollinearity Problem

Altmetrics

Downloads

102

Views

Comments

Autcha Araveeporn^*

This version is not peer-reviewed

Submitted:

01 July 2024

Posted:

01 July 2024

You are already at the latest version

Alerts

Abstract

The statistical technique, the multiple regression model, is employed to analyze the relationship between the dependent variable and several independent variables. The multicollinearity problem is one of the assumptions in the multiple regression model that occurred in the relationship among independent variables. The ordinal least square is the standard method to evaluate parameters in the regression model, but the multicollinearity problem affects the unstable estimator. The Liu regression is proposed to approximate the Liu estimators based on the Liu parameter to overcome multicollinearity. For this paper, we have proposed the modified Liu parameter to estimate the biasing parameter in scaling options to compare the ordinal least square estimator with two modified Liu parameters and six standard Liu parameters. The performance of the modified Liu parameter is considered with the generating independent variables from the multivariate normal distribution in the Toeplitz correlation pattern as the multicollinearity data, where the dependent variable is obtained from the independent variable multiplied with a coefficient of regression and with the error from the normal distribution. The mean absolute percentage error is computed as an evaluation criterion of estimation. For application, the Hepatitis C patients dataset is a real dataset to investigate the benefit of the modified Liu parameter. Through the simulation and real dataset, it can be seen from the results that the modified Liu parameter outperforms the other Liu parameters and the ordinal least square estimator. It can recommend the user for estimating parameters by using the modified Liu parameter when the independent variable exits the multicollinearity problem.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

Regression analysis is a potent statistical tool that illuminates the connection between one or more independent variables and a dependent variable. Essential in data analysis and predictive modeling, it finds broad application across fields such as economics, finance, healthcare, and social sciences. However, regression models must meet certain assumptions to provide reliable and valid results. These assumptions form the foundation of regression analysis and guide researchers in interpreting the results accurately. One problematic assumption to avoid is the linear relationship among the independent variables called multicollinearity, which occurs when two or more independent variables are correlated, increasing the standard error of the coefficients. This escalation in standard errors can render the coefficients of certain independent variables statistically insignificant despite their potential significance. In essence, multicollinearity distorts the interpretation of variables by inflating their standard errors [1]. Shrestha [2] discussed the primary techniques for investigating multicollinearity using questionnaires for survey data to support customer satisfaction.

Traditional regression techniques often struggle to handle multicollinearity effectively, leading to biased results and unreliable predictions. Researchers have developed various methods to mitigate these challenges, including Liu Regression. Liu Regression is a technique developed to address multicollinearity in regression analysis. It combines the principles of Ridge Regression with orthogonalization to effectively mitigate the effects of multicollinearity. Dawoud et al. [3] devised a novel modified Liu estimator to employ multicollinearity in a regression model with a single parameter, incorporating two biasing parameters, with at least one designed to mitigate this issue. Jahufer [4], on the other hand, employed the Liu estimator to alleviate the impact of multicollinearity and the influence of specific observations, devising approximate deletion formulas for identifying influential points.

Searching for accurate models that can efficiently handle complex datasets while offering robust predictions is perpetual in predictive analytics. Among the array of methodologies, the Liu Regression Model is a game-changer, heralding a new era in predictive modeling. The Liu Regression Model introduces novel techniques that address the limitations of traditional regression methods. Unlike conventional approaches that rely solely on linear relationships between variables, Liu Regression leverages advanced algorithms to capture non-linear patterns and intricate interactions within the data. Karlsson et al. [5] introduced a Liu estimator tailored for the beta regression model with a fixed dispersion parameter, applicable in various practical scenarios where the correlation level among the regressors varies.

Liu Regression [6] involves selecting a Liu estimator to balance the bias-variance trade-off. The optimal value of the Liu estimator is typically chosen through techniques such as cross-validation. The Liu estimator, named after its developer, is essential in managing multicollinearity. It is particularly associated with methodologies like Ridge Regression with Orthogonalization, often abbreviated as Liu Regression. Liu [7] enhanced the Liu estimator within the linear regression model by considering the biasing parameter under the prediction sum of squares criterion. Yang and Xu [8] proposed an alternative stochastic restricted Liu estimator for the parameter vector in a linear regression model, incorporating additional stochastic linear restrictions. Hubert and Wijekoon [9] investigated a novel Liu-type biased estimator, termed the stochastic restricted Liu estimator, and examined its efficiency.

The improvement of the Liu estimator transformed the multiple regression model to canonical form [10] to select the biasing parameter called the Liu parameter. The appropriate Liu parameters have been developed to make minimum mean squares error in the estimation. Liu [6,7] applied the iterative method to estimate the Liu parameter as the minimum mean square error in the smallest of the Liu estimator. Özkale and Kaçiranlar [11] proposed the new restricted Liu parameter by computing the predicted residual error sum of squares to determine the biasing parameter. Dawoud et al.[12] proposed a new Liu estimator using the known mean squares error criterion to handle the multicollinearity problem. Suhail et al. [13] developed a new method of biasing parameters to mitigate the multicollinearity data. Lukman et al. [14] introduced a modified Liu estimator to address multicollinearity issues within the linear regression model.

In this paper, we propose two competing Liu parameters, following mean squares error and R-squared, to estimate the Liu estimator via multiple regression model with the multicollinearity problem. We measure this performance in terms of minimum average of mean absolute percentage errors for the simulation and real dataset. We also consider the scale option of independent variables as the center, correlation form, and standardizes.

The paper is structured as follows: Section 2 presents the multiple regression estimators and discusses the Liu estimator through the reparameterization of Liu regression into canonical form, then compared with the OLS estimator. Section 3 generates the independent and dependent variables to evaluate the performance estimators. Section 4 applies a real dataset to validate the simulation results. Section 5 discusses the findings, followed by the conclusion in Section 6.

2. The Liu Regression

The multiple regression model is expressed in matrix form as:

y = X β + ε,

(1)

where

y

is the

n \times 1

column vector of dependent variable, and

X

is the

n \times (p + 1)

independent variable matrix,

β

is the

(p + 1) \times 1

multiple regression parameter vector, and

ε

is the

n \times 1

error vector. The following assumptions of error are made:

E (ε) = 0

E (ε ε') = σ^{2} I_{n}

, and

V a r (ε) = σ^{2} I_{n} .

The efficient parameters (

β

) in (1) are common estimated to obtain the ordinary least squares (OLS) estimator in (2) as follows:

{\hat{β}}_{O L S} = {(X' X)}^{- 1} X' y .

(2)

The estimation error of

{\hat{β}}_{O L S}

is evaluated by computing

\begin{array}{l} {\hat{β}}_{O L S} - β = {(X' X)}^{- 1} X' y - β \\ = {(X' X)}^{- 1} X' (X β + ε) - β \\ = {(X' X)}^{- 1} X' ε . \end{array}

(3)

The bias, variance (Var), and mean squares error (MSE) of the OLS estimator are computed from (3) as follows:

B i a s ({\hat{β}}_{O L S}) = E ({\hat{β}}_{O L S} - β) = E [{(X' X)}^{- 1} X' ε] = 0,

\begin{array}{l} V a r ({\hat{β}}_{O L S}) = E ({\hat{β}}_{O L S} - β) ({\hat{β}}_{O L S} - β)' = E [{(X' X)}^{- 1} X' ε ε' X {(X' X)}^{- 1}] \\ = σ^{2} {(X' X)}^{- 1}, \end{array}

\begin{array}{l} M S E ({\hat{β}}_{O L S}) = V a r ({\hat{β}}_{O L S}) + {[B i a s ({\hat{β}}_{O L S})]}^{2} \\ = σ^{2} {(X' X)}^{- 1} . \end{array}

From the above computation, the OLS estimator presents the unbiased estimator, which reduces the performance in estimating parameters on the multicollinearity of independent variables.The diagonal matrix of

{(X' X)}^{- 1}

is caused the multicollinearity and inflated, increasing the estimated variance and mean squares error. To overcome this problems, Liu [6] proposed the Liu esitimator which provides the better performance than the OLS estimator [11,15]. The Liu estimator based on the

{\hat{β}}_{O L S}

is defined by

{\hat{β}}_{L i u} = {(X' X + I)}^{- 1} (X' X + d_{L i u} I) {\hat{β}}_{O L S}, 0 < d_{L i u} < 1,

(4)

where

d_{L i u}

is the Liu parameter in term of the biasing parameter and

I

is the identity matrix. The OLS form (1) and Liu estimators from (4) are related to the independent variables that are affected to the multicollinearity problem because they depend on the OLS estimator.

The estimation error of

{\hat{β}}_{O L S}

is evaluated as the OLS estimator by comparing the Liu estimator and the parameter of the multiple regression model

{\hat{β}}_{L i u} - β = {(X' X + I)}^{- 1} (X' X + d_{L i u} I) {\hat{β}}_{O L S} - β .

(5)

The bias [16], variance (Var), and mean square error (MSE) of the Liu estimator from (5) are proposed in following:

B i a s ({\hat{β}}_{L i u}) = {(X' X + I)}^{- 1} (d_{L i u} - I) β,

V a r ({\hat{β}}_{L i u}) = {(X' X + I_{p})}^{- 1} (X' X + d_{L i u} I_{p}) σ^{2} {(X' X)}^{- 1} (X' X + d_{L i u} I_{p}) {(X' X + I_{p})}^{- 1},

\begin{array}{l} M S E ({\hat{β}}_{L i u}) = V a r ({\hat{β}}_{L i u}) + {[B i a s ({\hat{β}}_{L i u})]}^{2} \\ = {(X' X + I_{p})}^{- 1} (X' X + d_{L i u} I_{p}) σ^{2} {(X' X)}^{- 1} (X' X + d_{L i u} I_{p}) {(X' X + I_{p})}^{- 1} \\ + {[{(X' X + I)}^{- 1} (d_{L i u} - I) β]}^{2} . \end{array}

The Liu estimator is shown as the bias estimator, and its varaince is greater than that of the OLS estimator when

d_{L i u}

lies on the range of zero to one. Then, Liu [7] developed the shrinkage factor [17] to create the Liu parameter that may lie outside the range between zero and one. In the following subsection, the multiple regression model can be transformed into a canonical form to estimate the OLS and Liu estimators.

2.1. The Reparameterization of Liu Regression

The reparameterization of Liu Regression transforms a multiple regression model into a canonical form, offering valuable insights into variable relationships and enhancing predictive accuracy [17]. The optimal Liu parameter is determined by minimizing the mean squares error. Akdeniz and Kacįranlar [18] introduced a new biased estimator and assessed its performance against a restricted least squares estimator regarding mean squares error. The comparison of the Liu estimator’s performance in canonical form is expressed as follows:

y = Z α + ε,

(6)

where

Z = X G

α = G' β

Z' Z = G' X' X G = Λ

, and

Λ

is a diagonal matrix such that

(λ_{1}, λ_{2}, ..., λ_{p})

. The OLS estimator of canonical form can be difined as

{\hat{α}}_{O L S} = Λ^{- 1} Z' y .

(7)

Similarly, the Liu estimator [19] can be written as

\begin{array}{l} {\hat{α}}_{L i u} = {(Λ + I_{p})}^{- 1} (Z' y + d_{R . L i u} {\hat{α}}_{O L S}) \\ = {(Λ + I_{p})}^{- 1} (Λ + d_{R . L i u} I) {\hat{α}}_{O L S} \\ = [I - (1 - d_{R . L i u}) {(Λ + I_{p})}^{- 1}] {\hat{α}}_{O L S} . \end{array}

(8)

The bias, variance (Var), and mean square error (MSE) of the reparameterization of OLS estimator from (7) are expresses as:

B i a s ({\hat{α}}_{O L S}) = E ({\hat{α}}_{O L S} - α) = E [{(Z' Z)}^{- 1} Z' ε] = 0,

\begin{array}{l} V a r ({\hat{α}}_{O L S}) = E ({\hat{α}}_{O L S} - α) ({\hat{α}}_{O L S} - α)' = E [{(Z' Z)}^{- 1} Z' ε ε' Z {(Z' Z)}^{- 1}] \\ = σ^{2} {(Z' Z)}^{- 1} = σ^{2} Λ^{- 1}, \end{array}

\begin{array}{l} M S E ({\hat{α}}_{O L S}) = V a r ({\hat{α}}_{O L S}) + {[B i a s ({\hat{α}}_{O L S})]}^{2} \\ = σ^{2} Λ^{- 1} . \end{array}

The bias, variance (Var), and mean square error (MSE) of the reparameterization of Liu estimator from (8) are proposed in following:

B i a s ({\hat{α}}_{R . L i u}) = (d_{R . L i u} - 1) {(Λ + I_{p})}^{- 1} α,

V a r ({\hat{α}}_{R . L i u}) = {(Λ + I_{p})}^{- 1} (Λ + d_{R . L i u} I_{p}) σ^{2} {(Λ)}^{- 1} (Λ + d_{R . L i u} I_{p}) {(Λ + I_{p})}^{- 1},

\begin{array}{l} M S E ({\hat{α}}_{R . L i u}) = {(Λ + I_{p})}^{- 1} (Λ + d_{R . L i u} I_{p}) σ^{2} {(Λ)}^{- 1} (Λ + d_{R . L i u} I_{p}) {(Λ + I_{p})}^{- 1} \\ + {(1 + d_{R . L i u})}^{2} {(Λ + I_{p})}^{- 1} {\hat{α}}_{O L S} {\hat{α}}_{O L S}^{'} {(Λ + I_{p})}^{- 1} . \end{array}

The comparison among the OLS and Liu estimator of canonical form by considering of the variance and MSE.

Given the

{\hat{α}}_{O L S}

and

{\hat{α}}_{R . L i u}

, if the

{\hat{α}}_{R . L i u}

is the better estimator than

{\hat{α}}_{O L S}

that is

M S E ({\hat{α}}_{O L S}) - M S E ({\hat{α}}_{R . L i u}) > 0

if and only if,

V a r ({\hat{α}}_{O L S}) - V a r ({\hat{α}}_{R . L i u}) > 0.

Recall that

V a r ({\hat{α}}_{O L S}) = σ^{2} Λ^{- 1}

and

V a r ({\hat{α}}_{R . L i u}) = {(Λ + I_{p})}^{- 1} (Λ + d_{R . L i u} I_{p}) σ^{2} {(Λ)}^{- 1} (Λ + d_{R . L i u} I_{p}) {(Λ + I_{p})}^{- 1} .

Then,

\begin{array}{l} V a r ({\hat{α}}_{O L S}) - V a r ({\hat{α}}_{R . L i u}) = σ^{2} Λ^{- 1} - {(Λ + I_{p})}^{- 1} (Λ + d_{R . L i u} I_{p}) σ^{2} {(Λ)}^{- 1} (Λ + d_{R . L i u} I_{p}) {(Λ + I_{p})}^{- 1} \\ = σ^{2} d i a g [\frac{1}{λ_{j}} - \frac{{(λ_{j} + d_{R . L i u})}^{2}}{λ_{j} {(λ_{j} + 1)}^{2}}] > 0, j = 1, ..., p . \end{array}

It can observe

\frac{1}{λ_{j}} > \frac{{(λ_{j} + d_{R . L i u})}^{2}}{λ_{j} {(λ_{j} + 1)}^{2}}

when

0 < d_{R . L i u} < 1

.It can conclude that

V a r ({\hat{α}}_{O L S}) - V a r ({\hat{α}}_{R . L i u}) > 0,

and the Liu estimator outperforms the OLS estimator.

2.2. Liu Parameter

From the above subsection, we compare the two estimators. The reparameterization of Liu regression provides the performance estimator. However, the existing Liu estimator is to select the appropriate Liu parameter that has been started by Liu [6] and developed into another model by Suhail et al. [13], Lukman et al. [14], Abdelwahab et al. [20], and Babar et al. [21]. The optimal Liu parameter is one reason to make the minimum of mean squares error (MSE) that is excessed to affect the estimation of the Liu estimator of collinearity on independent variables. However, the trace of a diagonal matrix of transformation is useful for calculating the optimal Liu parameter. For this article, we suggest the original Liu parameter, which is proposed by Liu [6], which is defined as the minimum MSE (mm), optimum (opt), and Cl criterion (cl), respectively following:

d_{m m} = ​ ​ (1 - {\hat{σ}}^{2}) [\frac{\sum_{j = 1}^{p} [\frac{1}{λ_{j} (λ_{j} + 1)}]}{\sum_{j = 1}^{p} [\frac{{\hat{α}}_{j}^{2}}{λ_{j} {(λ_{j} + 1)}^{2}}]}]

d_{o p t} = ​ ​ [\frac{\sum_{j = 1}^{p} [\frac{α_{j}^{2} - {\hat{σ}}^{2}}{{(λ_{j} + 1)}^{2}}]}{\sum_{j = 1}^{p} [\frac{{\hat{σ}}^{2} + λ_{j} {\hat{α}}_{j}^{2}}{λ_{j} {(λ_{j} + 1)}^{2}}]}]

, and

d_{c l} = ​ ​ (1 - {\hat{σ}}^{2}) [\frac{\sum_{j = 1}^{p} [\frac{1}{(λ_{j} + 1)}]}{\sum_{j = 1}^{p} [\frac{λ_{j} {\hat{α}}_{j}^{2}}{λ_{j} {(λ_{j} + 1)}^{2}}]}]

Furthermore, Liu [7] improved the Liu parameter in the multiple linear regression under the approximation of the predicted residual error sum of squares criterion by calling improved Liu estimator (ILE) as

d_{I L E} = ​ ​ \frac{\sum_{i = 1}^{n} [\frac{{\tilde{e}}_{i}}{1 - g_{i i}} (\frac{{\tilde{e}}_{i}}{1 - h_{1 - i i}} - \frac{{\hat{e}}_{i}}{1 - h_{i i}})]}{\sum_{j = 1}^{p} [\frac{{\tilde{e}}_{i}}{1 - g_{i i}} - \frac{{\hat{e}}_{i}}{1 - h_{i i}}]},

where

\begin{array}{l} \hat{e} = y_{i} - x_{i}^{'} (X' X - x_{i} x_{i}^{'}) (X' y - x_{i} y_{i}), \tilde{e} = y_{i} - x_{i}^{'} (X' X + I_{p} - x_{i} x_{i}^{'}) (X' y - x_{i} y_{i}), \\ G = X {(X' X + I_{p})}^{- 1} X', H ≅ X {(X' X)}^{- 1} X' . \end{array}

Özkale and Kaçiranlar [11] introduced a new two-parameter approach by incorporating the contraction estimator, encompassing well-known methods such as restricted least squares, restricted ridge, restricted contraction estimators, and a novel modified, restricted Liu estimator (RLE). It can be written by

d_{R L E} = ​ ​ {\sum_{i = 1}^{n} [\frac{{\hat{e}}_{d i}}{1 - h_{1 - i i}} - \frac{e_{i}}{(1 - h_{1 - i i}) (1 - h_{i i})} (h_{1 - i i} - {\tilde{H}}_{d - i i})]}^{2}

where

h_{i i} = X {(X' X)}^{- 1} X', h_{1 - i i} = X {(X' X + I)}^{- 1} X'

{\tilde{H}}_{d - i i}

is the diagonal elements from Liu hat matrix, and

{\hat{e}}_{d i}

is the ith residual at specific value of

d

Mallows [22] discussed the interpretation of Cp-plots by using the display as a basis for formally selecting a subset-regression model and extending to estimate the Liu estimator. The Liu parameter is defined to be

d_{C p} = ​ ​ \frac{S S R}{{\hat{σ}}^{2}} + 2 t r a c e ({\tilde{H}}_{d - i i}) - (n - 2),

where

S S R = ​ ​ {\sum_{i = 1}^{n} [\frac{{\hat{e}}_{d i}}{1 - h_{1 - i i}} - \frac{e_{i}}{(1 - h_{1 - i i}) (1 - h_{i i})} (h_{1 - i i} - {\tilde{H}}_{d - i i})]}^{2} .

In this paper, we modify the Liu parameter from Mallows [22] to introduce the mean squares error, which is obtained by the mean of sum squares residual (SSR) in the range between zero and one as follows:

d_{M S E} = ​ ​ \frac{{\sum_{i = 1}^{n} [\frac{{\hat{e}}_{d i}}{1 - h_{1 - i i}} - \frac{e_{i}}{(1 - h_{1 - i i}) (1 - h_{i i})} (h_{1 - i i} - {\tilde{H}}_{d - i i})]}^{2}}{p} .

Furthermore, the correlation coefficient often denoted as R-squared (

R^{2}

), is a critical metric in regression analysis. It quantifies the proportion of the variance in the dependent variable that can be predicted from the independent variables. From the significance of R-squared, we propose the new Liu parameter by computing the correlation coefficient as 1-

R^{2} = 1 - S S R / S S T

which is rewritten by

d_{R 2} = ​ ​ 1 - \frac{{\sum_{i = 1}^{n} [\frac{{\hat{e}}_{d i}}{1 - h_{1 - i i}} - \frac{e_{i}}{(1 - h_{1 - i i}) (1 - h_{i i})} (h_{1 - i i} - {\tilde{H}}_{d - i i})]}^{2}}{{\sum_{i = 1}^{n} [\frac{{\hat{e}}_{d i}}{1 - g_{1 - i i}} - \frac{e_{i}}{(1 - g_{1 - i i}) (1 - g_{i i})} (g_{1 - i i} - {\tilde{G}}_{d - i i})]}^{2}} .

Scaling options are utilized to standardize the independent variables and assess their performance via the Liu estimator. The initial method, introduced by Liu [6], is centered, standardizing independent variables to have zero mean and unit variance. The scaled option further standardizes independent variables. Lastly, the sc option scales independent variables in correlation form, a concept explored by Belsley [23].

3. Simulation Study

As the previous section’s theoretical comparison among the Liu estimator, a simulation study covers the Monte Carlo simulation using the R 4.2.1 programming languages. The objective of the simulation study is to estimate and compare the Liu parameter to grasp the better performance of the Liu parameter on the multiple regression model. The independent variables (

{\underset{˜}{x}}_{i}

) are generated from the multivariate normal distribution in five, ten, and fifteen independent variables based on Toeplitz correlation (

ρ

) values of 0.1 and 0.9. The multivariate normal distribution based on parameter means (

\underset{˜}{μ}

) and covariance matrix (

\sum

) is simulated as multicollinearity between independent variables. The probability distribution is defined by

f ({\underset{˜}{x}}_{i} | \underset{˜}{μ}, Σ) = \frac{\exp {- \frac{1}{2} {({\underset{˜}{x}}_{i} - \underset{˜}{μ})}^{T} Σ^{- 1} ({\underset{˜}{x}}_{i} - \underset{˜}{μ})}}{\sqrt{{(2 π)}^{p} | Σ |}}

(7)

, where

{\underset{˜}{x}}_{i} = [\begin{array}{l} x_{i 1} \\ x_{i 2} \\ ... \\ x_{i p} \end{array}]

\underset{˜}{μ} = [\begin{array}{l} μ_{1} \\ μ_{2} \\ ... \\ μ_{p} \end{array}], i = 1, 2, ..., n .

The type of covariance matrix is mentioned in the Toeplitz correlation model, which implies that closely located independent variables have a high correlation, and the correlation decreases as independent variables are farther apart. A matrix with the following pattern characterizes the relationship:

Σ = [\begin{array}{r} 1 & ρ & ρ^{2} & \dots & ρ^{p - 1} \\ ρ & 1 & ρ & \dots & ρ^{p - 2} \\ ρ^{2} & ρ & 1 & \dots & ρ^{p - 3} \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ ρ^{p - 1} & ρ^{p - 2} & ρ^{p - 3} & \dots & 1 \end{array}]

where the correlation coefficient or level of multicollinearity is given by 0.1 and 0.9.

The observations on the dependent variable are obtained from the multiple regression model as

y_{i} = β_{0} + x_{i 1} β_{1} + x_{i 2} β_{2} + ... + x_{i p} β_{p} + ε_{i}, i = 1, 2, ..., n,

(8)

where

ε

is generated from the normal distribution to be mean zero and variance one, the regression coefficients (

β_{0}, β_{1}, ..., β_{p}

) are defined the constant values.

The performance criterion is used to judge the performance of different Liu parameters in estimating the Liu estimator. Evaluated mean absolute percentage error (MAPE) is defined as:

Mean Absolute Percentage Error = \frac{1}{n} \sum_{i = 1}^{n} | \frac{y_{i} - {\hat{y}}_{i}}{y_{i}} | \times 100,

(9)

where

y_{i}

is the real dataset and

{\hat{y}}_{i}

is the estimated dataset. The average of mean absolute percentage error of the OLS and eight Liu parameters for five, ten, and fifteen variables are presented in Table 1, Table 2 and Table 3 according to their correlation coefficient (0.1 and 0.9). Table 4 presents the Liu parameter values to estimate the Liu estimator. The average of over 1,000 replications is employed to approximate the average of mean absolute percentage error. The minimum average of mean absolute percentage error is shown in bold letters.

Table 1, Table 2 and Table 3 describe the simulated average of mean absolute percentage error for two levels of Toeplitz correlation. In Table 1, Table 2 and Table 3 , the smallest value of the MAPE is highlighted in bold letters. The simulation results show that the modified Liu parameter in terms of R-squared (dR2) has the smallest values of MAPE, so it outperforms the other methods, especially in the SC option in Table 3. However, the dILE, dRLE, and dCp have the weakest performance in all cases. Furthermore, the MAPE of dmm, dcl, and dopt equals the dR2 in the center and scaled options in Tables 1 and 2. The behavior of sample sizes can be observed in the sample impact on estimation since the MAPE decreases when sampling sizes decrease. The MAPE of independent variables is reduced when the independent variables increase. The Liu parameter of the estimate Liu estimator is presented in Table 4 and is varied by sample sizes, independent variables, and the level of correlation.

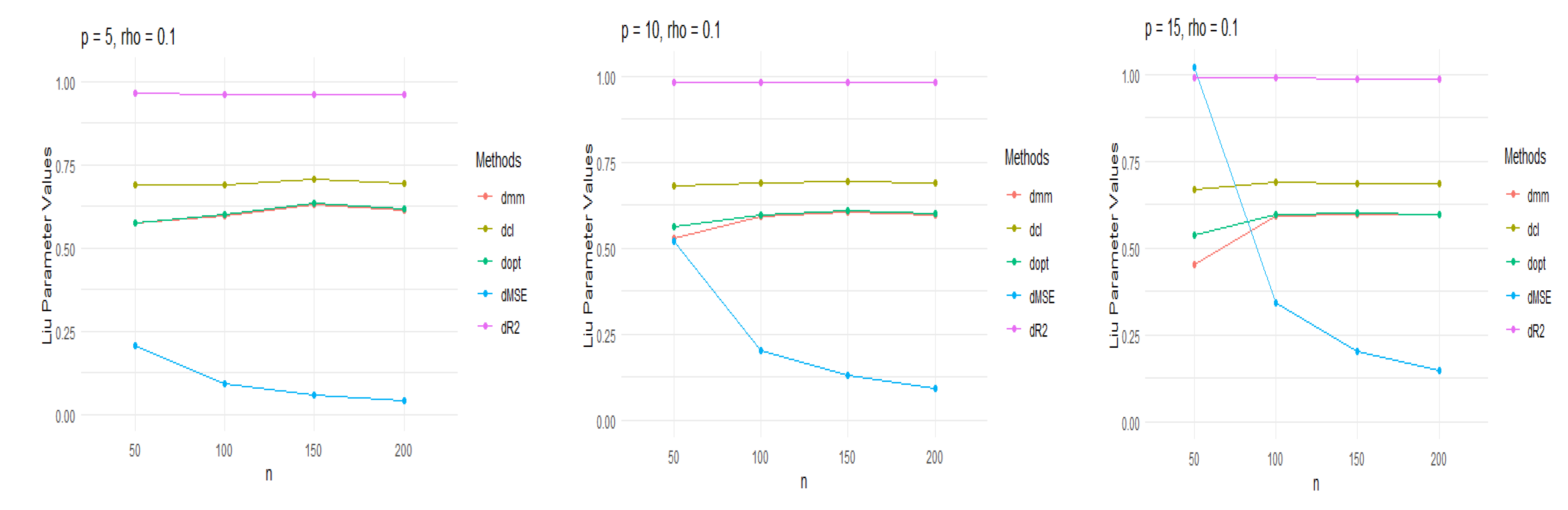
From Table 4, the level of the correlation coefficient has a significant effect in computing the Liu parameter. The dmm, dcl, and adopt are shown a positive, small correlation, but the large correlation has exhibited a negative. The dMSE is stanned from zero to one for small correlation, but the dMSE is more significant than one for large correlation. The excellent performance in Liu estimation, dR2, is approximated in the range of zero to one in all cases. Furthermore, the dILE, dRLE, and dCp have large Liu parameters and show the lowest performance in Tables 1–3. For a better understanding, we have plotted the Liu parameter just dmm, dcl, dopt, dMSE, dR2 for multicollinearity 0.1 and 0.9 in Figure 1 and Figure 2, respectively.

4. Application in Actual data

We employed Liu regression to distinguish between blood donors’ laboratory values and patients’ age using the Hepatitis C patients dataset sourced from the UCI Machine Learning. This dataset was retrieved from the https://archive.ics.uci.edu/ml/datasets/HCV+data. The dependent variable was the age of patients and independent variables included Albumin (ALB), Total Protein (PROT), Cholinesterase (CHE), Cholesterol (CHOL), Alkaline Phosphatase (ALP), Alanine Aminotransferase (ALT), Creatinine (CREA), Bilirubin (BIL), Aspartate Aminotransferase (AST), and Gamma-Glutamyl Transferase (GGT). The dataset comprised 589 records displayed the descriptive statistics about the Hepatitis C dataset in Table 5.

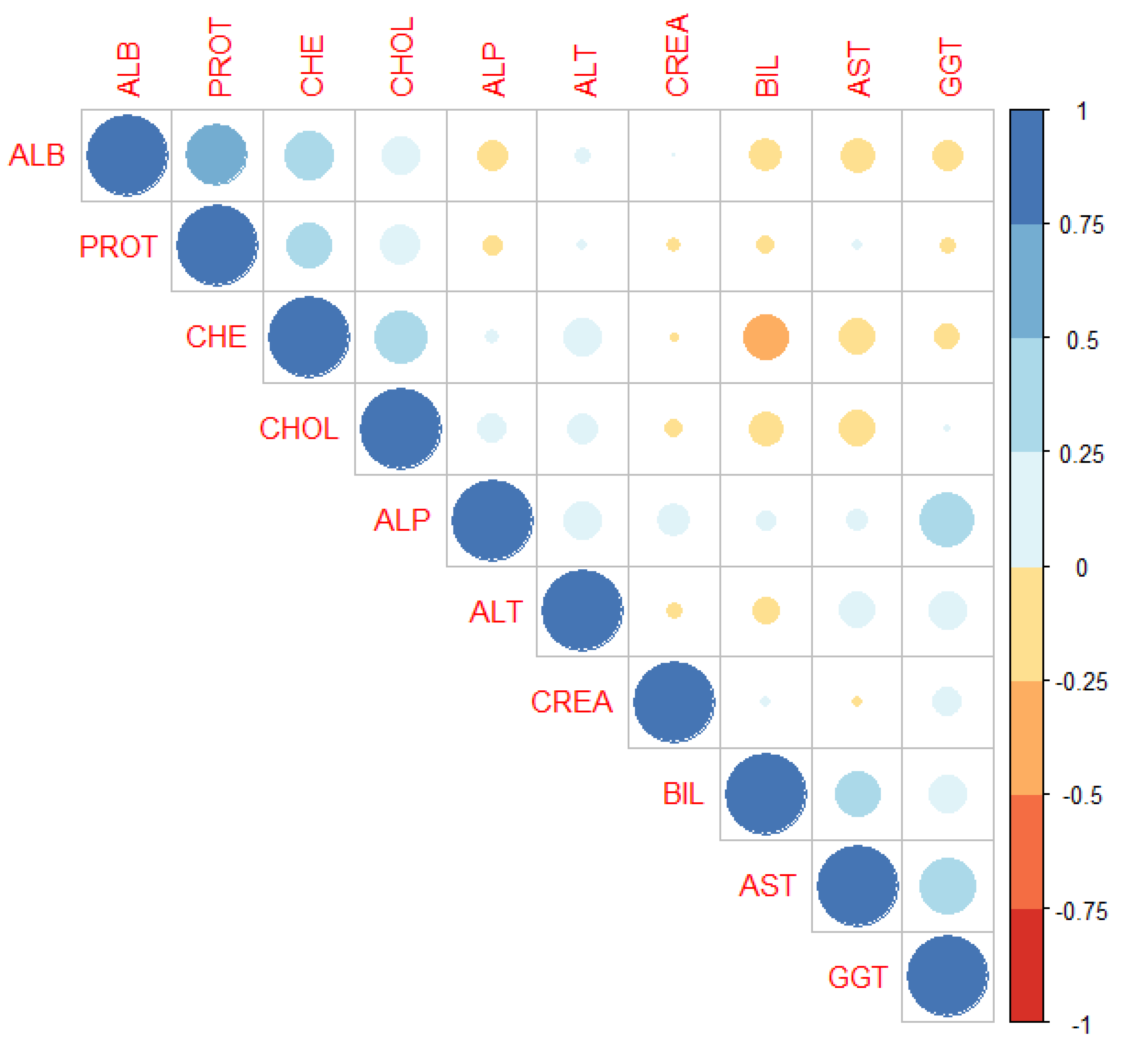
For checking multicollinearity data, Pearson’s correlation analysis was employed to ascertain any potential relationship among the ten continuous independent variables. The formula utilized for computing the correlation between two variables was:

r = \frac{n \sum_{i = 1}^{n} x_{i} y_{i} - (\sum_{i = 1}^{n} x_{i}) (\sum_{i = 1}^{n} y_{i})}{\sqrt{[n \sum_{i = 1}^{n} x_{i} - {(\sum_{i = 1}^{n} x_{i})}^{2}] [n \sum_{i = 1}^{n} y_{i} - {(\sum_{i = 1}^{n} y_{i})}^{2}]}}

From above formula, the correlation coefficients for the independent variables are outlined in Table 6. and Figure 3. The null hypothesis stated the no relationship between two variables and the alternative hypothesis assessed the significance of these relationships. The t-statistics were evaluated for hypothesis testing of Pearson’s correlation by

t = r \sqrt{\frac{n - 2}{1 - r^{2}}}

with a degree of freedom (df) n-2. Ultimately, a p-value below 0.05 for the t-statistics signified a rejected null hypothesis and mean significant relationship between the two variables as demonstrated in Table 6.

Our findings showed that a moderately significant relationship, such as between 0.41-0.6, was observed in most cases. The weak level of significant relationship was evident in some instances, such as between 0.2 and 0.4. Most of the independent variables exhibited a significant relationship, with the exceptions being between Total Protein (PROT) and Alkaline Phosphatase (ALP), Alanine Aminotransferase (ALT), Creatinine (CREA), Bilirubin (BIL), Aspartate Aminotransferase (AST), and Gamma-Glutamyl Transferase (GGT).

The computing Pearson correlation matrix displayed a different color in Figure 3, derived from Table 6, utilizes varying shades to enhance clarity. Light shading indicates moderate correlations, while dark shading represents strong correlations. Most independent variables are depicted with moderate and light shadings, suggesting inter-variable correlations or multicollinearity issues. The average of mean absolute percentage error Table 7was computed using OLS and eight Liu parameters with three scale options by generating 1,000 replications from all dataset. The selection of 50, 100, 150, and 200 sample sizes mirrored those in the simulation data.

Table 8 reveals that modified Liu parameters (dMSE and dR2) exhibited consistent and often superior accuracy prediction across all scenarios. The dCp, dMSE, and dR2 methods notably demonstrated commendable estimation in all sample sizes that better the original method as OLS. Consequently, the Liu parameter adjustment using the dCp, dMSE, and dR2 methods for ten independent variables consistently surpassed expectations and aligned closely with simulation outcomes. Although there were slight discrepancies in estimation when the sample sizes increased, substantial performance enhancements were evident with small sample sizes within the Hepatitis C dataset.

5. Discussion

The simulated results, presented in Table 1, Table 2, Table 3 and Table 4, revealed that the mean of average percentage error was affected by the number of independent variables and sample sizes. The modified Liu estimator (dR2) exhibited superior performance with all independent variables and all sample sizes, whereas dMSE slightly differed from dR2. However, the average mean of average percentage error for significant independent variables was lower than that for small independent variables. The increase in the correlation coefficient was weak impact estimation in most methods, as indicated by the slight variation in the mean of average percentage error. Moreover, as the sample size increased, the performance estimation of all methods improved consistently.

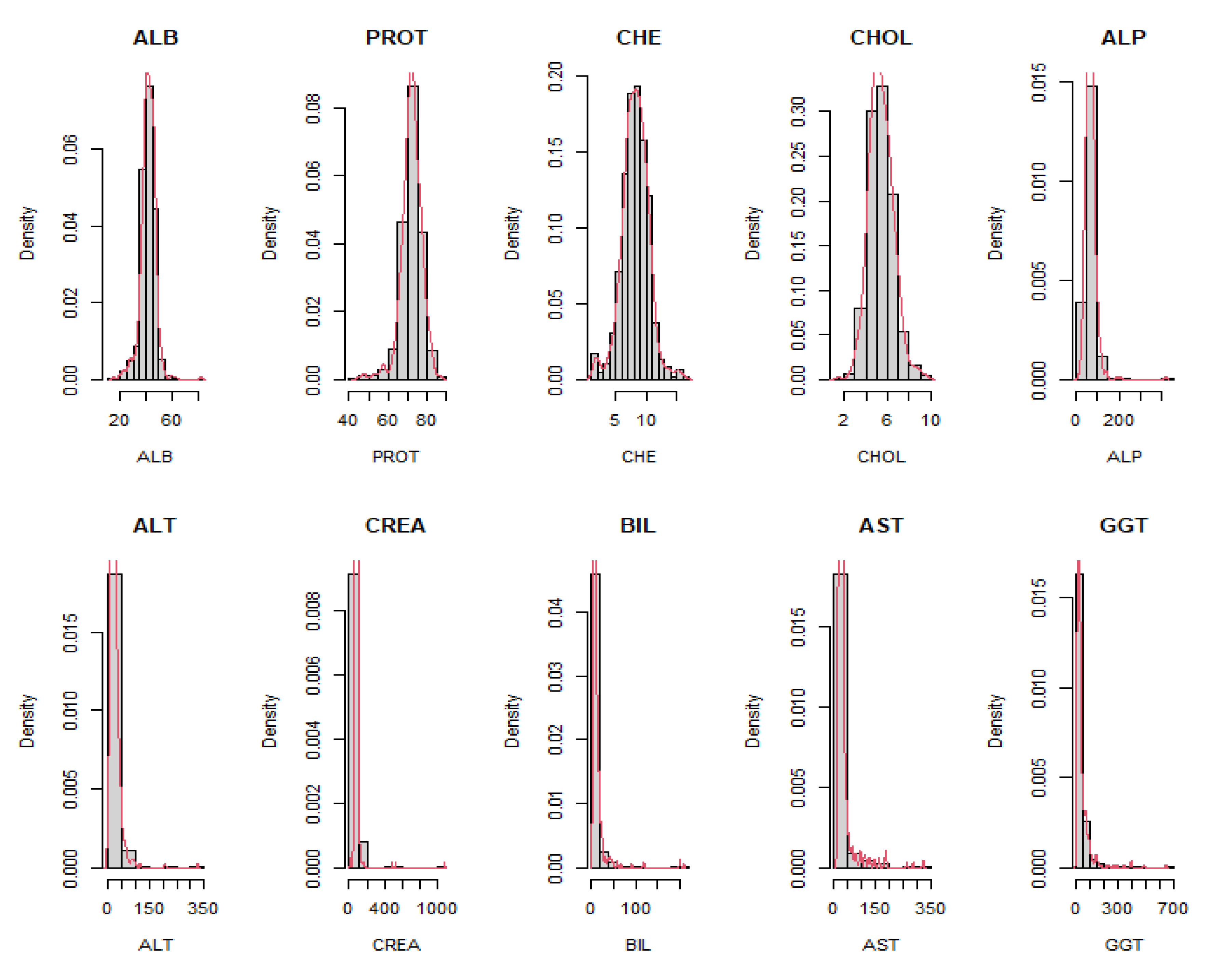
In the same direction, the real data results in Table 7 showcased that the proposed Liu parameters (dMSE and dR2) achieved the minor mean of average percentage error for datasets with eight independent variables. It was observed that the real data’s independent variables exhibited skewed distributions, as illustrated in Figure 4, confirmed by the Shapiro-Wilk test [24], indicating non-normality. So, the dCp effectively estimated large sample sizes using the center option. Notably, the discrepancy between the simulated and real data results emphasized the importance of considering the data source when selecting the Liu parameter.

The proposed Liu parameters (dMSE and dR2) emerged as the most suitable for the Liu estimator. The medical dataset is widely used to predict medical diagnosis enhancement for classification patients. However, the Hepatitis C dataset is a medical dataset used to predict the patient’s age in the multiple regression model with multicollinearity problem among the independent variables. Oladapo et al. [25] introduced a novel modified Liu Ridge-type estimator for estimating parameters in the general linear model, employing Portland cement data as a case study akin to medical data. Their proposed estimator demonstrates superior performance under certain conditions. Baber et al. [21] adapted Liu estimators to address multicollinearity issues in linear regression, utilizing tobacco data. They advocate for adopting these new estimators by practitioners facing high to severe multicollinearity among independent variables. Hammond et al. [26] employed a Liu estimator in inverse Gaussian regression, tackling multicollinearity in chemistry datasets. While considering the Liu estimator in multicollinearity based on multiple regression, the proposed Liu estimator outperforms the other. In summary, we always recommend that the Liu estimator user modify the Liu parameter in high multicollinearity.

6. Conclusions

This paper proposes a Liu parameter to estimate the Liu estimator in a multiple regression model correlated among independent variables, called multicollinearity. The selection of the Liu parameter is investigated and compared to the best performance. According to the simulation studies, the dR2 is always superior in terms of the mean of average percentage error for all levels of correlation, sample sizes, and dependent variables. For application in real data, the dCp, dMSE, and dR2 show the best performance, especially dR2. Moreover, the modified Liu parameter performs better than the OLS method in simulation and real data. The Liu parameter can significantly improve the estimator in terms of the regression model when the independent variables have the multicollinearity problem in low and high correlation. Therefore, the recommendation is to use a Liu parameter in the zero range and one that gives the best estimation. 6. Patents

Supplementary Materials

The following supporting information can be downloaded at: https://archive.ics.uci.edu/ml/datasets/HCV+data.

Acknowledgments

This research is supported by King Mongkut’s Institute of Technology Ladkrabang.

References

Daoud, J.I. Multicollinearity and regression analysis. J. Phys. Conf. Ser. 2017, 949, 1–7. [Google Scholar] [CrossRef]
Shrestha, N. Detecting multicollinearity in regression analysis. Am. J. Appl. Math. 2020, 8, 39–42. [Google Scholar] [CrossRef]
Dawoud, I.; Abonazel, M.R.; Awwad, F.A. Modified Liu estimator to address the multicollinearity problem in regression models: a new biased estimation class. Sci. Afr. 2022, 17, 1–12. [Google Scholar] [CrossRef]
Jahufer, A. Detecting global influential observations in Liu regression model. Open J. Stat. 2013, 3, 1–7. [Google Scholar] [CrossRef]
Karlsson, P.; Månsson, K.; Golam Kibria, B.M. A Liu estimator for the beta regression model and its application to chemical data,” J. Chemom. 2020, 24, 2–16. [Google Scholar] [CrossRef]
Liu, K. A new class of biased estimate in linear regression. Commun. Stat-Theor. M. 1993, 22, 393–402. [Google Scholar]
Liu, X. -Q. Improved Liu Estimation in a linear regression model. J. Stat. Plan. Inference. 2011, 141, 189–196. [Google Scholar] [CrossRef]
Yang, H.; Xu, J. An alternative stochastic restricted Liu estimator in linear regression. Stat. Pap. 2009, 50, 639–647. [Google Scholar] [CrossRef]
Hubert, M.H.; Wijekoon, P. Improvement of the Liu estimator in linear regression model. Stat. Pap. 2006, 47, 471–479. [Google Scholar] [CrossRef]
Akdeniz, F.; Erol, H. Mean squared error matrix comparison of some biased estimators in linear regression. Commun. Stat-Theor. M. 2003, 32, 2389–2413. [Google Scholar] [CrossRef]
Özkale, M.R.; Kaçiranlar, S. The restricted and unrestricted two-parameter estimators. Commun. Stat-Theor. M. 2007, 36, 2707–2725. [Google Scholar] [CrossRef]
Dawoud, I.; Abonazel, M.R.; Awwad, F.A. Modified Liu estimator to address the multicollinearity problem in regression model: A new biased estimation class. Sci. Afr. 2002, 17, 1–12. [Google Scholar] [CrossRef]
Suhail, M.; Babar, I.; Khan, Y.A.; Imran, M.; Nawaz, Z. Quantile-based estimation of Liu parameter in the linear regression model: Applications to Portland cement and US crime data. Math. Probl. Eng. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
Lukman, A.F.; Golam Kibria, B.M.; Ayinde, K.; Jegede, S.L. Modified one-parameter Liu estimator for the linear regression model. Mod. Sim. Eng. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
Lukman, A.F.; Ayinde, K.; Kun, S.S.; Adewuyi, E.T. A Modified new two-parameter estimator in a linear regression model,” Mod. Sim. Eng. 2019, 2019, 1–10. [Google Scholar]
Filzmoser, P.; Kurnaz, F.S. A robust Liu regression estimator. Commun. Stat. Simul. Comput. 2018, 47, 432–443. [Google Scholar] [CrossRef]
Druilhet, P.; Mom, A. Shrinkage Structure in Biased Regression. J. Multivar. Anal. 2008, 99, 232–244. [Google Scholar] [CrossRef]
Akdeniz, F.; Kacįranlar, S. More on the new biased estimator in linear regression. Sankhya: Indian J. Stat., Series B (1960-2002). 2001, 63, 321–325. [Google Scholar]
Duran, E.R.; Akdeniz, F.; Hu, H. Efficiency of a Liu-type estimator in semiparametric regression models. J. Comput. Appl. Math. 2011, 235, 1418–1428. [Google Scholar] [CrossRef]
Abdelwahab, M.M.; Abonazel, M.R.; Hammad, A.T.; El-Masry, A.M. Modified two-parameter Liu estimator for addressing multicollinearity in the Poisson regression model. Axioms. 2024, 13, 1–22. [Google Scholar] [CrossRef]
Babar, I.; Ayed, H.; Chand, S.; Suhail, M.; Khan, Y.A.; Marzouki, R. Modified Liu estimators in the linear regression model: An application to Tobacco data. Plos One. 2021, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
Mallows, C.L. Some Comments on Cp. Technometrics. 2012, 42, 87–94. [Google Scholar]
Belsley, D.A. A Guide to using the collinearity diagnostics. Com. Sci. Eco. Mana. 1991, 4, 33–50. [Google Scholar] [CrossRef]
Shapiro, S.S.; Wilk, M.P. An analysis of variance test for normality (complete samples). Biometrika. 1965, 52, 591–611. [Google Scholar] [CrossRef]
Oladapo, O.J.; Owolabi, A.T.; Idowu, J.I.; Ayinde, K. A new modified Liu Ridge-Type estimator for the linear regression model: Simulation and application. Int. J. Clin. Biostat. Biom. 2022, 8, 1–14. [Google Scholar]
Hammood, N.M.; Jabur, D.M.; Algamal, Z.Y. A Liu estimator in inverse Gaussian regression model with application in chemometrics. Math. Stat. Eng. Appl. 2022, 71, 248–266. [Google Scholar]

Figure 1. Estimated Liu parameter values for p = 5, 10, and 15; and the level correlation at 0.1.

Figure 2. Estimated Liu parameter values for p = 5, 10, and 15; and the level correlation at 0.9.

Figure 3. The correlation graph between ten independent variables.

Figure 4. The histogram of ten independent variables.

Table 1. The average of mean absolute percentage error of Liu estimators for Toeplitz correlation of center option.

p	Methods	$ρ = 0.1$				$ρ = 0.9$
p	Methods	$n = 50$	$n = 100$	$n = 150$	$n = 200$	$n = 50$	$n = 100$	$n = 150$	$n = 200$
5	OLS	0.810	0.722	0.758	0.747	0.815	0.766	0.760	0.752
	dmm	0.600	0.671	0.694	0.700	1.470	1.370	1.190	1.040
	dcl	0.596	0.671	0.694	0.700	0.737	0.725	0.726	0.718
	dopt	0.599	0.671	0.694	0.700	0.650	0.700	0.720	0.719
	dILE	5.970	2.360	2.090	5.980	1.490	1.440	1.260	4.720
	dPRESS	5.810	5.240	4.870	4.860	4.910	4.250	3.930	3.650
	dCp	1.150	0.823	0.761	0.737	0.901	0.753	0.733	0.721
	dMSE	0.611	0.674	0.696	0.700	0.599	0.672	0.697	0.704
	dR2	0.593	0.670	0.694	0.700	0.596	0.671	0.696	0.703
10	OLS	0.842	0.740	0.713	0.698	0.859	0.753	0.726	0.715
	dmm	0.465	0.570	0.604	0.619	1.130	0.938	0.864	0.862
	dcl	0.450	0.569	0.604	0.619	0.766	0.713	0.688	0.684
	dopt	0.461	0.570	0.604	0.619	0.520	0.617	0.641	0.656
	dILE	13.90	3.270	2.210	1.550	4.000	3.090	2.460	6.730
	dPRESS	10.80	7.830	7.030	6.680	8.010	6.470	5.510	4.970
	dCp	2.580	1.320	0.969	0.833	1.630	1.020	0.811	0.737
	dMSE	0.460	0.575	0.607	0.620	0.572	0.577	0.614	0.631
	dR2	0.439	0.567	0.604	0.619	0.448	0.576	0.614	0.631
15	OLS	0.884	0.722	0.685	0.665	0.910	0.746	0.707	0.687
	dmm	0.337	0.478	0.530	0.552	0.905	0.804	0.801	0.798
	dcl	0.286	0.476	0.529	0.552	0.706	0.681	0.688	0.657
	dopt	0.315	0.478	0.530	0.552	0.375	0.535	0.582	0.599
	dILE	19.30	4.300	2.880	1.890	5.040	5.340	3.670	4.460
	dPRESS	18.20	10.50	8.900	8.200	11.20	8.570	7.230	6.170
	dCp	4.690	2.130	1.410	1.100	2.790	1.520	1.090	0.861
	dMSE	0.288	0.483	0.533	0.554	1.150	0.505	0.546	0.570
	dR2	0.255	0.474	0.528	0.551	0.262	0.488	0.545	0.570

Table 2. The average of mean absolute percentage error of Liu estimators for Toeplitz correlation of scaled option.

p	Methods	$ρ = 0.1$				$ρ = 0.9$
p	Methods	$n = 50$	$n = 100$	$n = 150$	$n = 200$	$n = 50$	$n = 100$	$n = 150$	$n = 200$
5	OLS	0.810	0.722	0.758	0.747	0.815	0.766	0.760	0.752
	dmm	0.599	0.671	0.694	0.700	1.440	1.350	1.180	1.050
	dcl	0.595	0.671	0.694	0.700	0.728	0.724	0.726	0.718
	dopt	0.599	0.671	0.694	0.700	0.645	0.699	0.720	0.719
	dILE	5.500	2.310	2.030	6.360	1.450	1.420	1.260	5.040
	dPRESS	5.470	5.110	4.790	4.800	4.670	4.150	3.900	3.640
	dCp	1.100	0.816	0.758	0.736	0.878	0.749	0.732	0.721
	dMSE	0.609	0.674	0.696	0.700	0.599	0.672	0.697	0.704
	dR2	0.593	0.670	0.694	0.699	0.596	0.671	0.696	0.703
10	OLS	0.842	0.740	0.713	0.698	0.859	0.753	0.726	0.715
	dmm	0.463	0.570	0.604	0.619	1.100	0.913	0.864	0.861
	dcl	0.449	0.569	0.604	0.619	0.754	0.705	0.689	0.684
	dopt	0.459	0.570	0.604	0.619	0.516	0.615	0.641	0.656
	dILE	14.20	3.220	2.190	1.520	3.930	3.140	2.460	6.890
	dPRESS	10.40	7.600	6.900	6.570	7.800	6.320	5.500	4.990
	dCp	2.480	1.290	0.959	0.827	1.590	1.000	0.812	0.739
	dMSE	0.458	0.574	0.607	0.620	0.570	0.577	0.614	0.631
	dR2	0.439	0.567	0.604	0.619	0.448	0.576	0.614	0.631
15	OLS	0.884	0.722	0.685	0.665	0.910	0.746	0.707	0.687
	dmm	0.335	0.478	0.530	0.552	0.880	0.799	0.794	0.799
	dcl	0.285	0.476	0.529	0.552	0.695	0.677	0.666	0.658
	dopt	0.313	0.477	0.530	0.552	0.373	0.534	0.581	0.600
	dILE	18.50	4.170	2.790	1.870	4.840	5.370	3.420	4.660
	dPRESS	17.80	10.30	8.730	8.090	10.90	8.470	7.130	6.200
	dCp	4.570	2.080	1.390	1.090	2.730	1.510	1.080	0.865
	dMSE	0.287	0.482	0.532	0.554	1.130	0.505	0.546	0.570
	dR2	0.255	0.474	0.528	0.551	0.262	0.488	0.545	0.570

Table 3. The average of mean absolute percentage error of Liu estimators for Toeplitz correlation of SC option.

p	Methods	$ρ = 0.1$				$ρ = 0.9$
p	Methods	$n = 50$	$n = 100$	$n = 150$	$n = 200$	$n = 50$	$n = 100$	$n = 150$	$n = 200$
5	OLS	0.810	0.722	0.758	0.747	0.815	0.766	0.760	0.752
	dmm	0.955	0.950	0.929	0.944	10.30	19.30	24.80	28.70
	dcl	0.784	0.840	0.847	0.858	3.220	4.720	5.710	6.150
	dopt	0.931	0.944	0.927	0.942	1.960	3.540	5.160	6.330
	dILE	45.10	40.30	50.10	272.0	10.70	20.80	24.60	256.0
	dRLE	51.80	102.0	147.0	200.0	40.00	80.70	120.0	160.0
	dCp	8.770	9.300	9.470	9.560	5.470	6.420	6.830	7.070
	dMSE	1.380	1.590	1.670	1.690	0.726	0.937	1.090	1.170
	dR2	0.596	0.673	0.697	0.702	0.596	0.671	0.696	0.703
10	OLS	0.842	0.740	0.713	0.698	0.859	0.753	0.726	0.715
	dmm	1.060	1.030	1.030	1.050	6.440	9.680	13.50	18.70
	dcl	0.785	0.856	0.882	0.900	3.800	5.650	7.260	8.910
	dopt	0.997	1.020	1.020	1.040	1.670	3.030	4.400	6.060
	dILE	115.0	57.90	56.50	49.00	23.60	37.00	56.10	194.0
	dRLE	83.10	142.0	205.0	268.0	51.90	95.50	141.0	183.0
	dCp	19.60	21.70	22.20	22.40	10.20	12.30	13.40	13.90
	dMSE	1.060	1.720	1.900	1.980	2.090	0.695	0.691	0.829
	dR2	0.441	0.569	0.605	0.620	0.448	0.576	0.614	0.631
15	OLS	0.884	0.722	0.685	0.665	0.910	0.746	0.707	0.687
	dmm	1.220	1.060	1.090	1.110	4.440	7.550	11.40	16.40
	dcl	0.763	0.858	0.901	0.924	3.350	5.730	7.780	10.10
	dopt	1.040	1.050	1.080	1.100	1.350	2.680	4.150	5.810
	dILE	121.0	69.50	71.50	63.90	26.30	73.30	74.20	140.0
	dRLE	116.0	176.0	245.0	317.0	59.10	110.0	156.0	204.0
	dCp	29.80	34.70	36.10	36.70	14.60	18.60	20.20	21.30
	dMSE	0.737	1.570	1.920	2.070	5.810	1.540	0.772	0.613
	dR2	0.256	0.475	0.529	0.552	0.262	0.488	0.545	0.570

Table 4. The mean of Liu parameters for Toeplitz correlation in multiple regression model.

p	Methods	$ρ = 0.1$				$ρ = 0.9$
p	Methods	$n = 50$	$n = 100$	$n = 150$	$n = 200$	$n = 50$	$n = 100$	$n = 150$	$n = 200$
5	dmm	0.577	0.598	0.633	0.616	-6.730	-13.90	-18.10	-20.80
	dcl	0.690	0.692	0.707	0.695	-1.430	-2.600	-3.370	-3.690
	dopt	0.574	0.602	0.635	0.618	-0.432	-1.680	-2.940	-3.820
	dILE	-0.297	5.660	0.240	106.0	1.450	7.810	-1.300	-161.0
	dRLE	34.10	65.20	92.70	125.0	32.00	63.50	93.50	124.0
	dCp	6.590	6.810	6.880	6.910	5.220	5.940	6.250	6.410
	dMSE	0.206	0.094	0.059	0.044	0.906	0.500	0.356	0.281
	dR2	0.964	0.961	0.960	0.960	0.990	0.989	0.989	0.989
10	dmm	0.529	0.593	0.606	0.599	-3.220	-5.760	-8.340	-12.00
	dcl	0.680	0.692	0.693	0.689	-1.540	-2.920	-4.010	-5.170
	dopt	0.562	0.599	0.609	0.601	-0.079	-1.070	-2.020	-3.180
	dILE	30.70	-1.720	3.520	-2.090	3.510	-13.70	20.60	67.40
	dRLE	43.40	70.50	100.0	130.0	36.20	67.30	98.40	128.0
	dCp	11.00	11.60	11.70	11.80	7.940	9.560	10.30	10.70
	dMSE	0.520	0.205	0.129	0.093	2.370	1.160	0.821	0.637
	dR2	0.984	0.982	0.981	0.981	0.997	0.997	0.997	0.997
15	dmm	0.451	0.591	0.596	0.595	-1.860	-3.900	-6.490	-9.660
	dcl	0.669	0.690	0.688	0.686	-1.150	-2.700	-4.080	-5.540
	dopt	0.536	0.599	0.600	0.598	0.153	-0.701	-1.690	-2.760
	dILE	-0.136	7.580	1.560	-2.120	-5.300	29.40	16.10	-28.60
	dRLE	55.80	78.40	107.0	137.0	38.90	72.10	103.0	134.0
	dCp	15.10	16.30	16.60	16.70	10.40	13.00	14.20	14.90
	dMSE	1.020	0.343	0.205	0.147	4.720	1.940	1.320	1.020
	dR2	0.991	0.989	0.988	0.988	0.999	0.999	0.999	0.998

Table 5. Descriptive statistics of the Hepatitis C dataset.

Variables	Mean	Median	Std. Dev.	Min	Max
ALB	41.62	41.90	5.76	14.90	82.20
PROT	71.89	72.10	5.31	44.80	86.50
CHE	8.20	8.26	2.19	1.42	16.41
CHOL	5.39	5.31	1.12	1.43	9.67
ALP	68.12	66.20	25.92	11.30	416.60
ALT	26.58	22.70	20.86	0.90	325.3
CREA	81.67	77.00	50.69	8.00	1079.10
BIL	11.02	7.10	17.40	0.80	209.00
AST	33.77	25.70	32.86	10.60	324.0
GGT	38.20	22.80	54.30	4.50	650.90

Table 6. Pearson correlation matrix for the relationship between ten independent variables.

Variables	ABL	PROT	CHE	CHOL	ALP	ALT	CREA	BIL	AST	GGT
ABLp-value	1.00	0.57*<0.05	0.36*<0.05	0.21*<0.05	-0.15*0.01	0.041.00	0.001.00	-0.17* <0.05	-0.18* <0.05	-0.15* 0.01
PROT p-value	-	1.00	0.31* <0.05	0.25*<0.05	-0.061.00	0.021.00	-0.031.00	-0.051.00	0.02 1.00	-0.04 1.00
CHE p-value	-	-	1.000	0.43*<0.05	0.031.00	0.22* <0.05	-0.011.00	-0.32*<0.05	-0.20* <0.05	-0.10 0.36
CHOL p-value	-	-	-	1.000	0.13 0.05	0.15*0.01	-0.051.00	-0.18* <0.05	-0.20*<0.05	0.01 1.00
ALP p-value	-	-	-	-	1.000	0.22* <0.05	0.15* <0.05	0.061.00	0.07 1.00	0.46* <0.05
ALT p-value	-	-	-	-	-	1.000	-0.041.00	-0.11 0.18	0.20 <0.05	0.22 <0.05
CREA p-value	-	-	-	-	-	-	1.000	0.021.00	-0.02 1.00	0.13 0.05
BIL p-value	-	-	-	-	-	-	-	1.00	0.31* <0.05	0.21* <0.05
AST p-value	-	-	-	-	-	-	-	-	1.00	0.14* <0.05
GGT p-value	-	-	-	-	-	-	-	-	-	1.00

Note. *, The multicollinearity between two variables.

Table 7. The estimated average of mean absolute percentage error on 50, 100, 150, and 200 sample sizes.

Sample sizes	OLS	Scale Option	Liu Parameters
Sample sizes	OLS	Scale Option	dmm	dcl	dopt	dILE	dRLE	dCp	dMSE	dR2
n = 50	24	Liu parameter	-155	-74.7	8.27	-12.3	4397	11.8	6.63	0.436
		Centered	89.3	43.8	12.30	313	2311	12.2	11	10.4
		Scaled	329	179	27.3	1609	10895	29.5	18.4	10.5
		SC	1219	598	78	4806	35798	88.6	47.5	11.8
n= 100	19.8	Liu parameter	-203	-122	-17.4	-118	7756	11.9	2.69	0.271
		Centered	37.9	28.3	14.6	101	1141	13.8	13.8	13.8
		Scaled	149	97.2	21.4	477	5567	16.3	13.8	13.8
		SC	1220	774	116	4187	46859	67.7	17.4	14.9
n =150	18.7	Liu parameter	-105	-101	-21.1	-81.7	10462	12	1.63	0.215
		Centered	22.5	21.7	15.3	57.6	815	14.9	15	15
		Scaled	45.4	42.8	18	20	6464	18	15	15
		SC	587	555	115	3176	52339	56.8	15.2	15.8
n= 200	18.2	Liu parameter	-175	-100	-25.9	588	13156	12	1.19	0.185
		Centered	26.3	20.1	15.8	53.6	692	15.4	15.4	15.5
		Scaled	45.6	32	17.5	229	2689	15.5	15.4	15.5
		SC	773	462	125	4743	58533	50.9	15.4	16.2

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Modified Liu Parameter in Scaling Options of the Multiple Regression Model with Multicollinearity Problem

Abstract

1. Introduction

2. The Liu Regression

2.1. The Reparameterization of Liu Regression

2.2. Liu Parameter

3. Simulation Study

4. Application in Actual data

5. Discussion

6. Conclusions

Supplementary Materials

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe