Gait-and-Balance Assessments with Augmented-Reality Glasses in People with Parkinson’s Disease: Concurrent Validity and Test-Retest Reliability

State-of-the-art augmented-reality (AR) glasses record their position and orientation in space, enabling measurements and analyses of clinical gait-and-balance tests. This study’s objective was to evaluate concurrent validity and test-retest reliability for common clinical gait-and-balance tests in people with Parkinson’s disease: the Five Times Sit-To-Stand (FTSTS) and Timed Up-and-Go (TUG) tests. Position and orientation data was collected in 22 participants with Parkinson's disease using HoloLens 2 and Magic Leap 2 AR glasses, from which test-completion durations and durations of distinct sub-parts (e.g., sit-to-stand, turning) were derived and compared to reference systems and over test repetitions. Regarding concurrent validity, for both tests an excellent between-systems agreement was found for position and orientation time series and test-completion durations. Between-systems agreement for FTSTS (sub-)durations were all excellent, while TUG turning sub-durations were excellent (turn 1) and moderate (turn 2). Regarding test-retest reliability, the within-system test-retest variation in test-completion times and sub-durations was always much greater than the between-systems variation, implying that these (sub-)durations may be derived interchangeably from AR and reference-system data. In conclusion, AR data are of sufficient quality to evaluate gait and balance in people with Parkinson's disease, with valid quantification of test-completion durations and sub-durations of distinct FTSTS and TUG sub-parts.

Keywords:

Subject: Public Health and Healthcare - Physical Therapy, Sports Therapy and Rehabilitation

1. Introduction

Impaired posture, gait, and balance control are motor symptoms commonly observed in people with Parkinson’s disease [1]. Assessing such motor symptoms may offer healthcare professionals valuable insight into disease progression and patients’ daily life challenges, which may inform tailored treatment strategies. To this end, the Five Times Sit To Stand (FTSTS) and Timed Up and Go (TUG) tests are commonly performed. In the FTSTS, the test person is asked to stand up and sit down from a chair five times as quickly as possible with their arms crossed. Longer FTSTS completion times are associated with reduced leg muscle strength, impaired balance, and increased fall risk [2]. The TUG is probably the most used clinical gait-and-balance test, combining distinct gait-and-balance aspects in a single test like transfers, gait initiation, walking, and turning. In the TUG, the test person is asked to stand up from a chair, walk 3m, turn around, walk 3m back, and sit back in the chair. Longer TUG completion times are associated with poorer muscle strength, poorer balance, slower gait speed, and increased fall risk [3].

The standard outcome of both the FTSTS and TUG is the duration of test completion, as measured by the clinician with a stopwatch. The drawback of this method is that handling the stopwatch may hinder the clinician from fully concentrating on observing the patient for safety and visual assessment. Moreover, the stopwatch score only provides an indication of overall test-completion durations while remaining blind for specific limitations in distinct sub-parts of the test, like turning or sit-to-stand parts. To alleviate such inherent drawbacks, (automated) instrumented tests have been introduced, using sensor technology such as body-worn IMU sensors and external marker-based or markerless 3D motion-registration systems (e.g., [4,5]) providing information about the execution of (sub-parts of) the tests that may allow for a more specific assessment and treatment of motor impairments.

Augmented-reality (AR) glasses, like Microsoft’s HoloLens 2 and Magic Leap 2, represent a promising emerging technology in that regard for two reasons: 1) as a movement registration system, uniquely providing both position and orientation data in 3D, and 2) as an instrument to potentially (self-)administer tests in a standardized manner, using 3D holographic AR content to set test constraints (e.g., present a holographic pylon at 3m from the chair indicating where the test person should turn in the TUG test) and to provide standardized instructions (e.g., ‘stand up from the chair and complete the test in 3-2-1-go’). Early research with healthy adults by Sun and colleagues [6] has already explored the potential of 3D position and orientation data of HoloLens 1 for deriving TUG test-completion durations in comparison to stopwatch-based durations (with excellent between-systems agreement) and durations derived from IMU data (with good between-systems agreement). More recent work with healthy adults by Koop and colleagues [7] demonstrated statistical equivalence between TUG turning parameters derived from HoloLens 2 AR data and 3D motion-registration data as a reference. Despite their apparent potential, AR glasses have not been validated for assessing TUG and FTSTS in clinical populations like people with Parkinson’s disease.

The objective of this study was to evaluate concurrent validity and test-retest reliability of FTSTS and TUG tests in people with Parkinson’s disease using HoloLens 2 and Magic Leap 2 AR glasses. Specifically, we first examined the agreement between AR position and orientation time series and counterparts from reference motion-registration systems, for which a good-to-excellent agreement is expected. Subsequently, we derived test-completion durations as well as sub-durations for distinct sub-parts of the tests from these time series, and evaluated concurrent validity in terms of between-systems absolute-agreement statistics (i.e., intraclass correlation coefficient (ICC), bias, limits of agreement) of test-completion durations derived from AR data and the stopwatch (as clinical gold standard) as well as the between-systems absolute agreement of AR (sub-)durations with counterparts from reference systems. Finally, to help interpret the so-obtained between-systems absolute-agreement statistics, we determined within-system test-retest reliability in terms of ICC, bias and limits of agreement: we expected that (sub-)durations can be validly and reliably derived from AR data in people with Parkinson’s disease, with better between-systems than within-system absolute-agreement statistics.

2. Materials and Methods

2.1. Subjects

In total, 22 subjects (16 males, 6 females; age (mean [range]): 66.3 [51–82] years; weight 79.1 [59.0-92.9] kg; height 176.1 [154–191] cm, diagnosed with Parkinson’s disease (Hoehn and Yahr stage 2-2.5) who were capable of walking independently for over 30 minutes participated in this study. Participants did not have any other neurological or orthopedic conditions that would significantly affect their walking ability. Their cognitive function was sufficient to understand the instructions provided by the researchers. Participants did not report experiencing hallucinations and had no visual or hearing impairments.

2.2. Experimental Set-Up and Procedures

Participants performed the FTSTS and TUG tests in a fixed order during one measurement session in the gait laboratory of the Vrije Universiteit Amsterdam (VU), while wearing either HoloLens 2 or Magic Leap 2 AR glasses, block-randomized over participants. Participants initiated the FTSTS and TUG tests from a seated position with their backs touching the chair and concluded the test in the same position. A stopwatch was used to register the durations of FTSTS and TUG test completion. For the FTSTS, participants were instructed to stand up and sit down five times in a sequential manner as quickly as possible, while keeping their arms crossed on their chest, without touching the backrest of the chair for all but the last sit-down movement (Figure 1a). For the TUG, participants were asked to perform the following sequence of actions: transfer from a sitting to standing position, walk 3m, turn around, walk back to the chair, and finally, transfer from a standing to a sitting position with a turn (Figure 1b). Additionally, two reference motion-registration systems were used to evaluate concurrent validity of the AR time series and of AR data derived (sub-)duration outcomes: 1) Microsoft Kinect v2 sensor (Kinect) as part of the Interactive Walkway (Tec4Science, VU Amsterdam, [8,9,10]) to record 3D position data of various body points of which we used head, sternum and spine-base and 2) an Inertial Measurement Unit (IMU; McRoberts B.V., The Hague) worn on the lower-back to record trunk orientation. The instrumented FTSTS and TUG tests were performed twice to evaluate test-retest reliability of from AR data derived (sub-)durations.

2.3. Data Acquisition

HoloLens 2 and Magic Leap 2 are state-of-the-art AR glasses registering their 3D position and orientation with regard to their surroundings at a sampling rate of 30 and 60 Hz, respectively. Specific 3D position and orientation time series contain features that are informative for distinguishing various sub-parts of the tests, like standing up, sitting down and turning (as detailed in section 2.4). In the Supplementary Material, videos are provided of the TUG and FTSTS tests performance, including a synchronized visualization of pertinent AR data. As a reference, we acquired data from IMU and Kinect sensor systems. Specifically, the IMU captured at 100 Hz the 3D accelerations and trunk rotation velocity time series, from which reference turning sub-durations of the TUG were derived (as detailed in section 2.4). The Microsoft Kinect computer-vision sensor captured at 30 Hz in a markerless manner the 3D positions of various bodily points, including the head, sternum and spine-base, from which reference (sub-)durations of the FTSTS test were derived (as detailed in section 2.4).

2.4. Data (Pre)Processing

The time series from each of the three motion-registration systems was resampled to a constant rate of 60 Hz using linear interpolation and low-pass filtered using a fourth-order Butterworth filter with a cut-off frequency of 2 Hz. Temporal alignment in between-systems time series was obtained by incorporating the time lag of their maximal cross-correlation. The initial starting positions and orientations were subtracted from the time series.

2.4.1. Deriving (Sub-)Durations of the FTSTS Test

The AR and Kinect vertical position time series were used to determine the start and end of the FTSTS test (standing up and sitting down in a chair; Figure 2, vertical dashed lines). Specifically, we calculated zero-crossings in the vertical velocity time series to obtain an initial indication of the start and end of the test. It is important to realize that standing up and sitting down are not strict upward and downward movements, as the initial standing-up movement typically involves a forward bow [1,11] while the final sitting-down movement involves a backward bow associated with placing the back against the backrest of the chair. Hence, to obtain a more representative start and end of the FTSTS test, we determined characteristic transition points in the vertical position data (instead of simply their minima), using a mathematical model consisting of the following piece-wise linear function to find the definite start (Equation 1):

y (x; b) = b_{1} + b_{2} x + b_{3} (x - b_{4}) H (x - b_{4})

(1)

where H(x−b4) is the step function defined as:

H (x - b_{4}) = ├_{1 i f x > b_{4}}^{0 i f x \leq b_{4}}

In this model, b₁ represents the initial offset of the vertical position, b₂ represents the first slope (set to 0 for identifying the start frame), b₃ represents the second positive slope, and b₄ represents the breakpoint. To obtain the start of the test (frame number corresponding to b₄), we fitted the function (y) on the vertical position time series (x) from the first frame of the recording to the frame corresponding to the initial indication of the start of the test, using a subspace trust-region based, nonlinear, least-squares optimization method. A similar method was used to find the end of the test, where the breakpoint was found by fitting a piece-wise linear function, starting with a positive slope and ending with a constant, to the vertical position time series from the initial indication of the end of the test to the end of the recording. With these frames numbers, the time series were trimmed from start to end, from which we determined i) the between-systems agreement in time series, ii) test-completion durations for further statistical analyses.

From the trimmed data, each sit-to-stand cycle of the FTSTS was divided into four phases: sitting, sit-to-stand, standing, and stand-to-sit. Sitting and standing phases were first identified from the vertical position data from each system by means of finding zero-crossings in the vertical velocity. Since a zero-crossing gives a single time point and not the duration of the sitting and standing phases, we applied an empirically found threshold of 2 cm to obtain the start and end frame numbers of standing and sitting phases [5], from which sitting, sit-to-stand, standing, and stand-to sit sub-durations were derived (Figure 2). To reduce the influence of potential outliers in within-test repetitions of the so-obtained sub-durations (e.g., due to for example a participant taking a brief sitting rest during the test), the median of the 4 (for sitting sub-durations) or 5 (for standing, sit-to-stand, stand-to-sit sub-durations) within-test sub-durations was determined prior to further statistical analyses.

2.4.2. Deriving (Sub-)Durations of the TUG Test

The TUG test-completion duration was determined from AR vertical position time series, as described for the FTSTS test. Sub-durations for the two turns (turn 1 and turn 2) were derived from the AR orientation time series, specifically the yaw angle (Figure 3). For the IMU also yaw-angle time series were used, obtained after integrating the associated rotational velocity time series. Determining the start and end of a turn during the TUG is not straightforward, as it is characterized by a rather slow transition from one state (~0° yaw) to another (~180° yaw). We modelled this transition with the following sigmoid function y (Equation 2):

y (t; p) = p_{1} \tanh (\frac{t - p_{2}}{p_{3}}) + p_{1} + p_{4}

(2)

where tanh is the hyperbolic tangent function defined as:

\tanh (z) = \frac{e^{z} - e^{- z}}{e^{z} + e^{- z}}

In this model, p₁ represents the amplitude of the transition (usually ~180°), p₂ represents the timing (or center) of the transition, p₃ represents a scaling factor that adjusts the duration of the transition and p₄ represents the (potential) starting offset (in °). The sigmoid function y was fitted to the yaw-angle time series t using a subspace trust-region based, nonlinear, least-squares optimization method. The fitted model y was then used to determine the start and end of turning (Figure 3) by applying an empirically found threshold of 10° from the start of the transition to the end for each turn as determined by p₄ and p₄ + p₁, respectively. Turning sub-durations were derived from these indicators of the start and end of turns and used for further statistical analyses.

Concurrent validity (i.e., consistency agreement between AR and reference system time series and absolute between-systems agreement for all (sub-)durations of the FTSTS and TUG tests) and test-retest reliability (i.e., within-system absolute agreement between repetitions for all (sub-)durations of the FTSTS and TUG) were evaluated with the ICC_(C,1) and ICC_(A,1) [12]. ICC-values greater than 0.50, 0.75 and 0.90 represent, respectively, moderate, good and excellent agreement between systems or over repetitions [13]. As ICC-values alone may give misleading impressions of agreement when there is a large between-subject variation, we complemented them with two Bland-Altman analysis statistics: 1) bias, indicating a systematic difference between systems or over repetitions and 2) limits of agreement, indicating the precision of differences between systems or over repetitions [14]. All processed data used for the statistical analyses are provided in the Supplementary Material, from which missing values become apparent. Missing values mostly resulted from inaccurate Kinect data (i.e., storing 3D kinematics of the guarding researcher instead of the participant). Other reasons for missing values were: 1) one participant did not perform the FTSTS, 2) one participant was excluded from the between-systems comparisons because of an error in IMU recording, 3) two participants were removed from test-retest analyses because of incomplete data for one of the two repetitions. For concurrent validity analyses, the second trial was generally used and, when this was not possible (e.g., due to the abovementioned issues with Kinect recordings), occasionally the first trial was used to keep as many participants in the analyses.

3. Results

3.1. Concurrent Validity

3.1.1. Agreement in Time Series between AR and Reference Systems

Figure 4a shows representative examples of the AR vertical position data versus the three vertical Kinect body points of the FTSTS. At a group level, the consistency agreement between AR and Kinect time series for FTSTS was excellent (ICC_(C,1) [95% CI] for AR vs. Kinect Head: 0.992 [0.987 – 0.996], Sternum: 0.976 [0.962 – 0.989], Spine base: 0.933 [0.916 – 0.951]). Figure 4b shows a representative example of AR and IMU orientation data (yaw angle) of the TUG. At a group level, the consistency agreement between AR and IMU time series for TUG was again excellent (ICC_(C,1) [95% CI], AR vs. IMU trunk: 0.986 [0.981 – 0.990]).

3.1.2. Agreement in (Sub-)Durations Derived from AR and Reference-System Data

The absolute agreement between AR derived test-completion durations and stopwatch counterparts was excellent for both FTSTS and TUG tests (ICC_(A,1) > 0.984), with a small-but-significant bias (~2% and ~4% of the mean, respectively) and narrow limits of agreement (Table 1).

The absolute-agreement statistics between derived (sub-)durations from AR and reference-system time series are presented in Table 1. For FTSTS, the between-systems agreement (AR vs. Kinect Head data) for derived total and sub-durations was excellent (ICC_(A,1) > 0.921, with three related small-but-significant biases for sitting, sit-to-stand, and stand-to-sit sub-durations and narrow limits of agreement). A similar pattern of between-systems agreement statistics was observed for the comparisons of AR (sub-)durations with those derived from Kinect Sternum and Spine base data, with slightly worsening statistics for body points farther away from the head (see Table S1 in the Supplementary Material).

For TUG, the between-systems agreement for sub-durations were excellent for turn 1 (ICC_(A,1) = 0.913, without bias and narrow limits of agreement) and moderate for turn 2 (ICC_(A,1) = 0.589, with a substantial bias of ~22% and wide limits of agreement; Table 1).

3.2. Test-Retest Reliability for (Sub-)Durations of FTSTS and TUG

The absolute agreement between trial 1 and trial 2 for the AR data of the FTSTS-test was excellent for total durations (ICC_(A,1) = 0.914) and good to excellent for sub-durations (ICC_(A,1) > 0.830). Only the standing sub-durations showed moderate absolute agreement between repetitions (ICC_(A,1) = 0.695; Table 2). All biases were small and non-significant, while limits of agreement between test and retest trials were all greater than those seen between systems (i.e., compared to Table 1). The test-retest statistics for the reference-systems data were similar or slightly worse (see Table S2 in Supplementary Material).

The absolute agreement for TUG test-completion durations between trial 1 and trial 2 for the AR data was good (ICC_(A,1) > 0.75, no bias, wider limits of agreement than those seen between systems) and moderate for turn 1 and turn 2 sub-durations (ICC_(A,1) < 0.75, no bias and again wider limits of agreement than those seen between systems; cf. Table 2 vs. Table 1). The test-retest statistics for the reference-system data were again similar (see Table S2 in Supplementary Material).

4. Discussion

The aim of this study was to evaluate concurrent validity and test-retest reliability of AR-instrumented FTSTS and TUG tests in people with Parkinson’s disease. Here we discuss the findings associated with the three specific objectives outlined in the Introduction. The first objective was to examine the agreement between AR position and orientation time series and counterparts from reference motion-registration systems. An excellent concurrent validity was observed, better than expected, as evidenced by excellent ICC-values between AR and Kinect vertical position data and between AR and IMU yaw orientation data. As can be appreciated from the data depicted in Figure 2, Figure 3 and Figure 4, as well as from the data visualization alongside videos of TUG and FTSTS performance in the Supplementary Material, AR 3D position and orientation data contain rich information from which indicators of various distinct sub-parts of the tests can be validly derived, as discussed further below. Although we focused on temporal aspects of TUG and FTSTS test performance, there are ample opportunities for an even finer-grained parameterization of identified sub-parts given that state-of-the-art AR glasses (i.e., HoloLens 2, Magic Leap 2) are in principle 3D position sensors, a unique asset compared to other wearable sensor systems [6]. Specifically, features in the vertical position time series, in the horizontal displacement time series and in the orientation around the vertical axis (i.e., yaw-angle time series) seem informative for demarcating the various sub-parts of the TUG test (Figure 5). As can be appreciated from Figure 5, the yaw-angle time series (dashed line) clearly show the two ~180° turns while the change in slope in the horizontal displacement time series (dotted line) may be indicative of deceleration and acceleration phases demarcating turning and walking phases. Deriving spatiotemporal gait parameters like cadence and step lengths from TUG walking parts seems well feasible using the characteristic oscillations in the vertical (and non-depicted mediolateral) position time series associated with midstance (peaks) and foot strikes (valleys) [9]. Gait-parameter quantification was already successfully explored previously for healthy adults [7,15] and people with Parkinson’s disease [9] and is deemed worth studying further for standard clinical tests like for instance the 10-meter walk test and the 6-minute walk test.

The second objective was to derive, from these valid time series, TUG and FTSTS test-completion durations and sub-durations for distinct sub-parts of the tests like turning and sit-to-stand durations and to evaluate their concurrent validity against reference systems. For TUG and FTSTS test-completion durations we found an excellent agreement between AR data and the stopwatch, albeit with a small-but-significant bias (<4%), and with narrow limits of agreement, indicating that the systems can be used interchangeably. Likewise, between-systems agreement statistics were excellent for all (sub-)durations for the FTSTS, with high ICCs and narrow limits of agreement, yet with three small-but-significant biases (~ 6%) for sitting, sit-to-stand and stand-to-sit sub-durations, annulling each other subsequently given that they were in absolute terms similar in magnitude but opposite in direction, indicative of an interconnected between-systems bias in identification of frame numbers for the start and end of the sitting phase, demarcating stand-to-sit, sitting and sit-to-stand sub-durations. For the TUG, the sub-durations of the two turns showed different agreement statistics: while the between-systems agreement for sub-durations for the first turn were excellent (see also Koop and colleagues [7]), the agreement scores for the second turn were moderate. This difference between the two turns may be explained by our observation that the second turn is not a distinct sub-part but overlaps with the sitting down part of the TUG in a combined sitting-down-whilst-turning movement. Also, while turning participants sometimes looked for the location of the chair and therefore turned their head (as captured with AR yaw data) before they actually turned around with their trunk (as captured with IMU yaw data). Finally, there is an ordered sequence during turning, which generally starts with the head and is followed by the trunk and is enclosed by the head again [16], which may all have affected between-systems differences in sub-durations to some extent.

The third objective was to determine within-system test-retest reliability to help interpret abovementioned between-systems absolute-agreement statistics. An interesting observation from a statistical point of view was that the within-system test-retest variation in completion times and sub-durations (cf. Table 2) was always much greater than the between-systems variation (cf. Table 1). This was reflected in the limits of agreement, being much wider for the test-retest evaluation (for AR and reference systems alike, see also Table S2) than for the between-systems evaluation (i.e., compare limits of agreement between Table 2 and Table 1). On the one hand, this is positive, as test-completion durations and sub-durations may then be derived interchangeably from AR and reference-system data. On the other hand, the fairly large variation seen over repeated measurements, for both AR and reference systems (see also [17,18,19]), may limit their sensitivity for detecting longitudinal changes with disease progression, medication or rehabilitation intervention [20].

Overall, it seems fair to conclude that AR 3D position and orientation data are valid and contain rich features from which (sub-)durations of TUG and FTSTS performance can be validly derived in people with Parkinson’s disease, with – for both AR and reference systems – a better between-systems than within-system absolute-agreement. What are the future prospects of these findings? We envision a scenario where AR data is used to not only quantify test-completion durations (similar to the stopwatch), but, given the rich information in the data and the excellent time series concurrent validity results presented here, also to provide a more comprehensive quantitative assessment of clinically relevant sub-durations, like the turn in the TUG [4]. With AR, such quantitative tests may also be automatized, as test instructions (e.g., ‘3-2-1-go’) and test constraints (AR visual indicator for the TUG turn at 3m from the chair) can readily be provided. Automated test administration resulting in valid and reliable test scores is much needed and provides opportunities to improve care. That is, physical therapy is increasingly given remotely at home with AR [20,21], for which (self-)monitoring of treatment progress becomes key. Because such home-based AR gait-and-balance exergaming intervention programs will typically be remotely prescribed by the therapist [20,21], in principle also AR TUG and FTSTS assessments may be prescribed as part of the intervention program. Insight into progress can so be obtained at higher intervals than the standard pre-post intervention assessment in clinical practice or clinical research. This is relevant as multiple longitudinal assessments may help mitigate the effect of confounding factors like daily fluctuations, thus ensuring more reliable assessment of change over time and thereby enhancing the quality of clinical and research findings. It may also provide unique insight into dose-response relationships of prescribed AR interventions and/or concomitant medication in a time-effective and patient-friendly manner. Ultimately, remote parameterization of progress could help reduce the number of contact moments between patient and healthcare provider and also change those consults. That is, instead of administering tests, the session may be used to discuss the patient's test results and any further needs for intervention moving forward, which is expected to increase care efficiency and patient satisfaction. Our ongoing research will proceed along those lines.

5. Conclusions

From this study, it can be concluded that AR data is valid and informative for quantifying TUG and FTSTS test-performance outcomes. TUG and FTSTS test-completion durations, as well as various sub-durations of distinct sub-parts of the test, can be determined interchangeably from AR data and reference-system data in a cross-sectional assessment in persons with Parkinson’s disease. However, the relatively poorer within-system test-retest reliability (for AR and reference systems alike) than between-systems agreement should be kept in mind when performing longitudinal assessments with either system.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org., Table S1: Concurrent validity statistics for FTSTS (sub-)durations (in s): between-systems absolute agreement statistics for (sub-)durations derived from AR and Kinect sternum and Spine-base data. Table S2: Test-retest reliability: absolute agreement statistics for (sub-)durations (in s) derived from reference-systems data. Video S1: FTSTS test example, with visualization of vertical AR position data. Video S2: TUG test example, with visualization of AR 3D position and orientation data. Datafile S1: FTSTS between repetitions comparison. Datafile S2: FTSTS between systems comparison. Datafile S3: FTSTS ICC for consistency. Datafile S4: TUG between repetitions comparison. Datafile S5: TUG between systems comparison. Datafile S6: TUG ICC for consistency.

Author Contributions

Conceptualization, D.G. and M.R.; methodology, J.B., P.D., E.H., D.G., and M.R.; software, J.B. and P.D.; validation, M.R.; formal analysis, J.B. and P.D.; investigation, J.B. and E.H.; resources, M.R.; data curation, J.B. and P.D.; writing—original draft preparation, J.B. and M.R.; writing—review and editing, J.B., P.D., E.H., D.G. and M.R.; visualization, J.B., P.D. and E.H.; supervision, D.G. and M.R.; project administration, D.G. and M.R.; funding acquisition, D.G. and M.R. All authors have read and agreed to the published version of the manuscript.

Funding

This project is funded by the EMIL project financial support to third parties, which is funded by the European Union (Grant ID E115506). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union. Neither the European Union nor the granting authority can be held responsible for them.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Medical research Ethics Committees United, the Netherlands (R22.076, NL82441.100.22, 21 November 2022).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Data supporting reported results can be found in the Supplementary Material.

Acknowledgments

We would like to thank Lotte Hardeman, Annelotte Geene and Annejet van Dam for their help with performing the measurements.

Conflicts of Interest

M.R. is scientific advisor with share options for Strolll Ltd., a digital therapeutics company building AR software for physical rehabilitation. The other authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Baer, G.D.; Ashburn, A.M. Trunk movements in older subjects during sit-to-stand. Arch Phys Med Rehabil 1995, 76, 844–849. [Google Scholar] [CrossRef] [PubMed]
Lord, S.R.; Murray, S.M.; Chapman, K.; Munro, B.; Tiedemann, A. Sit-to-stand performance depends on sensation, speed, balance, and psychological status in addition to strength in older people. J Gerontol A Biol Sci Med Sci 2002, 57, M539–543. [Google Scholar] [CrossRef] [PubMed]
Schoene, D.; Wu, S.M.; Mikolaizak, A.S.; Menant, J.C.; Smith, S.T.; Delbaere, K.; Lord, S.R. Discriminative ability and predictive validity of the timed up and go test in identifying older people who fall: systematic review and meta-analysis. J Am Geriatr Soc 2013, 61, 202–208. [Google Scholar] [CrossRef] [PubMed]
Bottinger, M.J.; Labudek, S.; Schoene, D.; Jansen, C.P.; Stefanakis, M.E.; Litz, E.; Bauer, J.M.; Becker, C.; Gordt-Oesterwind, K. "TiC-TUG": technology in clinical practice using the instrumented timed up and go test-a scoping review. Aging Clin Exp Res 2024, 36, 100. [Google Scholar] [CrossRef] [PubMed]
Ejupi, A.; Brodie, M.; Gschwind, Y.J.; Lord, S.R.; Zagler, W.L.; Delbaere, K. Kinect-Based Five-Times-Sit-to-Stand Test for Clinical and In-Home Assessment of Fall Risk in Older People. Gerontology 2015, 62, 118–124. [Google Scholar] [CrossRef] [PubMed]
Sun, R.; Aldunate, R.G.; Sosnoff, J.J. The Validity of a Mixed Reality-Based Automated Functional Mobility Assessment. Sensors (Basel) 2019, 19. [Google Scholar] [CrossRef]
Miller Koop, M.; Rosenfeldt, A.B.; Owen, K.; Penko, A.L.; Streicher, M.C.; Albright, A.; Alberts, J.L. The Microsoft HoloLens 2 Provides Accurate Measures of Gait, Turning, and Functional Mobility in Healthy Adults. Sensors (Basel) 2022, 22. [Google Scholar] [CrossRef] [PubMed]
Geerse, D.J.; Coolen, B.H.; Roerdink, M. Kinematic Validation of a Multi-Kinect v2 Instrumented 10-Meter Walkway for Quantitative Gait Assessments. PLoS One 2015, 10, e0139913. [Google Scholar] [CrossRef] [PubMed]
Geerse, D.J.; Coolen, B.; Roerdink, M. Quantifying Spatiotemporal Gait Parameters with HoloLens in Healthy Adults and People with Parkinson's Disease: Test-Retest Reliability, Concurrent Validity, and Face Validity. Sensors (Basel) 2020, 20. [Google Scholar] [CrossRef]
Geerse, D.J.; Roerdink, M.; Marinus, J.; van Hilten, J.J. Walking adaptability for targeted fall-risk assessments. Gait Posture 2019, 70, 203–210. [Google Scholar] [CrossRef] [PubMed]
Yoshida, K.; An, Q.; Yozu, A.; Chiba, R.; Takakusaki, K.; Yamakawa, H.; Tamura, Y.; Yamashita, A.; Asama, H. Visual and Vestibular Inputs Affect Muscle Synergies Responsible for Body Extension and Stabilization in Sit-to-Stand Motion. Front Neurosci 2018, 12, 1042. [Google Scholar] [CrossRef] [PubMed]
McGraw, K.O. , & Wong, S. P. Forming inferences about some intraclass correlation coefficients. Psychological Methods 1996, 1, 30–46. [Google Scholar] [CrossRef]
Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J Chiropr Med 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed]
Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat Methods Med Res 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
Miller Koop, M.; Rosenfeldt, A.B.; Owen, K.; Zimmerman, E.; Johnston, J.; Streicher, M.C.; Albright, A.; Penko, A.L.; Alberts, J.L. The Microsoft HoloLens 2 Provides Accurate Biomechanical Measures of Performance During Military-Relevant Activities in Healthy Adults. Mil Med 2023, 188, 92–101. [Google Scholar] [CrossRef]
Kim, K.; Fricke, M.; Bock, O. Eye-Head-Trunk Coordination While Walking and Turning in a Simulated Grocery Shopping Task. J Mot Behav 2021, 53, 575–582. [Google Scholar] [CrossRef] [PubMed]
Lim, L.I.; van Wegen, E.E.; de Goede, C.J.; Jones, D.; Rochester, L.; Hetherington, V.; Nieuwboer, A.; Willems, A.M.; Kwakkel, G. Measuring gait and gait-related activities in Parkinson's patients own home environment: a reliability, responsiveness and feasibility study. Parkinsonism Relat Disord 2005, 11, 19–24. [Google Scholar] [CrossRef] [PubMed]
Paul, S.S.; Canning, C.G.; Sherrington, C.; Fung, V.S. Reproducibility of measures of leg muscle power, leg muscle strength, postural sway and mobility in people with Parkinson's disease. Gait Posture 2012, 36, 639–642. [Google Scholar] [CrossRef] [PubMed]
Spagnuolo, G.; Faria, C.; da Silva, B.A.; Ovando, A.C.; Gomes-Osman, J.; Swarowsky, A. Are functional mobility tests responsive to group physical therapy intervention in individuals with Parkinson's disease? NeuroRehabilitation 2018, 42, 465–472. [Google Scholar] [CrossRef] [PubMed]
Hardeman, L.E.S.; Geerse, D.J.; Hoogendoorn, E.M.; Nonnekes, J.; Roerdink, M. Remotely prescribed and monitored home-based gait-and-balance therapeutic exergaming using augmented reality (AR) glasses: protocol for a clinical feasibility study in people with Parkinson's disease. Pilot Feasibility Stud 2024, 10, 54. [Google Scholar] [CrossRef] [PubMed]
Hsu, P.Y.; Singer, J.; Keysor, J.J. The evolution of augmented reality to augment physical therapy: A scoping review. J Rehabil Assist Technol Eng 2024, 11, 20556683241252092. [Google Scholar] [CrossRef] [PubMed]

Figure 1. (a) Participant performing the Five Times Sit To Stand (FTSTS) test; data is recorded with a stopwatch, AR glasses and a Microsoft Kinect v2 sensor. (b) Participant performing the Timed Up and Go (TUG) test; data is recorded with a stopwatch, AR glasses and an Inertial Measurement Unit (IMU) worn on the lower back.

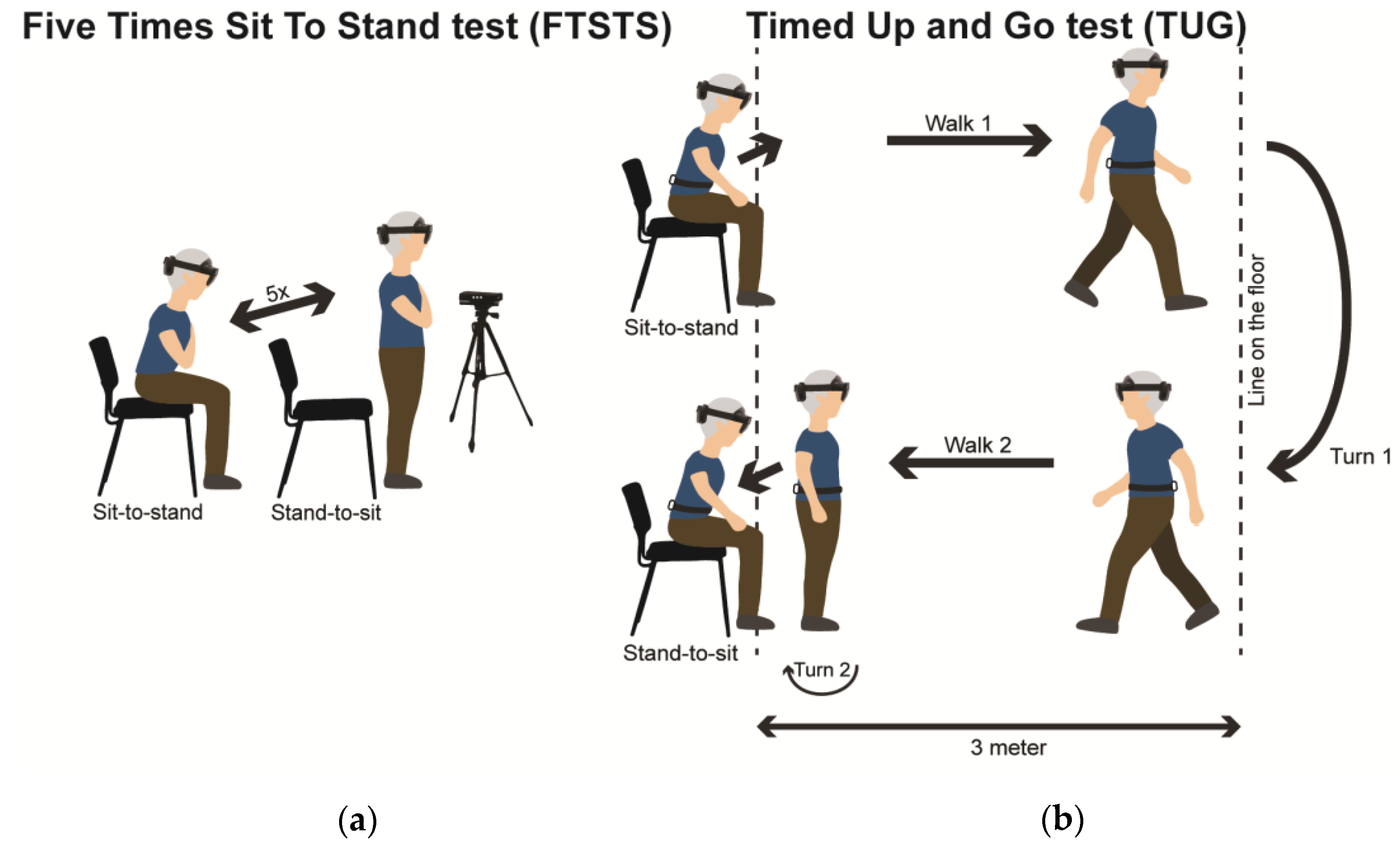
Figure 2. Representative AR vertical position time series of a participant performing the FTSTS, with vertical dashed lines indicating the start and end of the test (from which test-completion duration was derived) and with specific markers (see legend) indicating the start and end of the sit-to-stand, standing, stand-to-sit and sitting sub-parts of the test (from which sub-durations were derived).

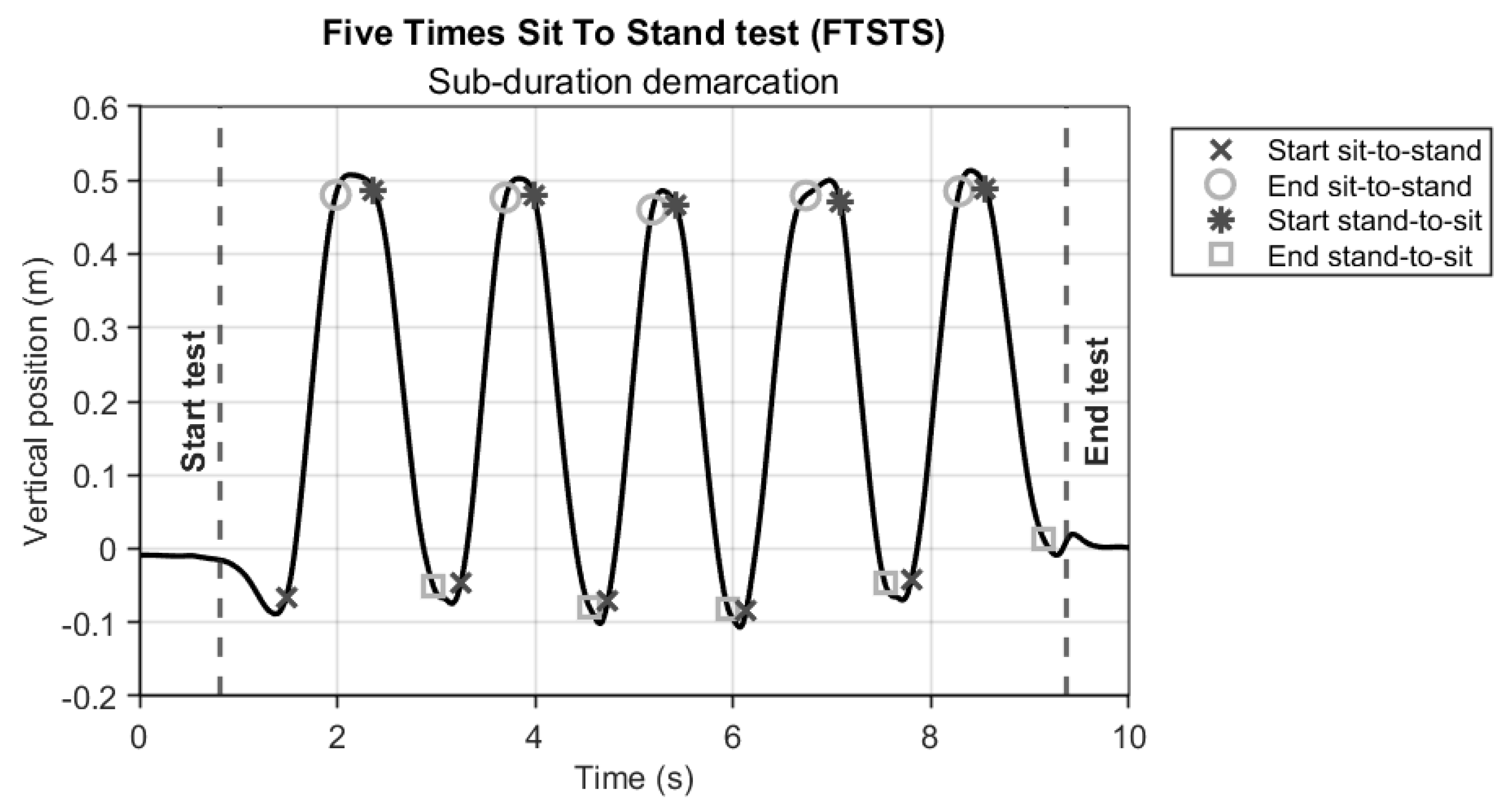
Figure 3. Representative AR yaw-angle time series (dashed line) of a participant performing the TUG, with the gray solid line representing the fitted sigmoid model y that was used to derive turning sub-durations. Statistical analysis.

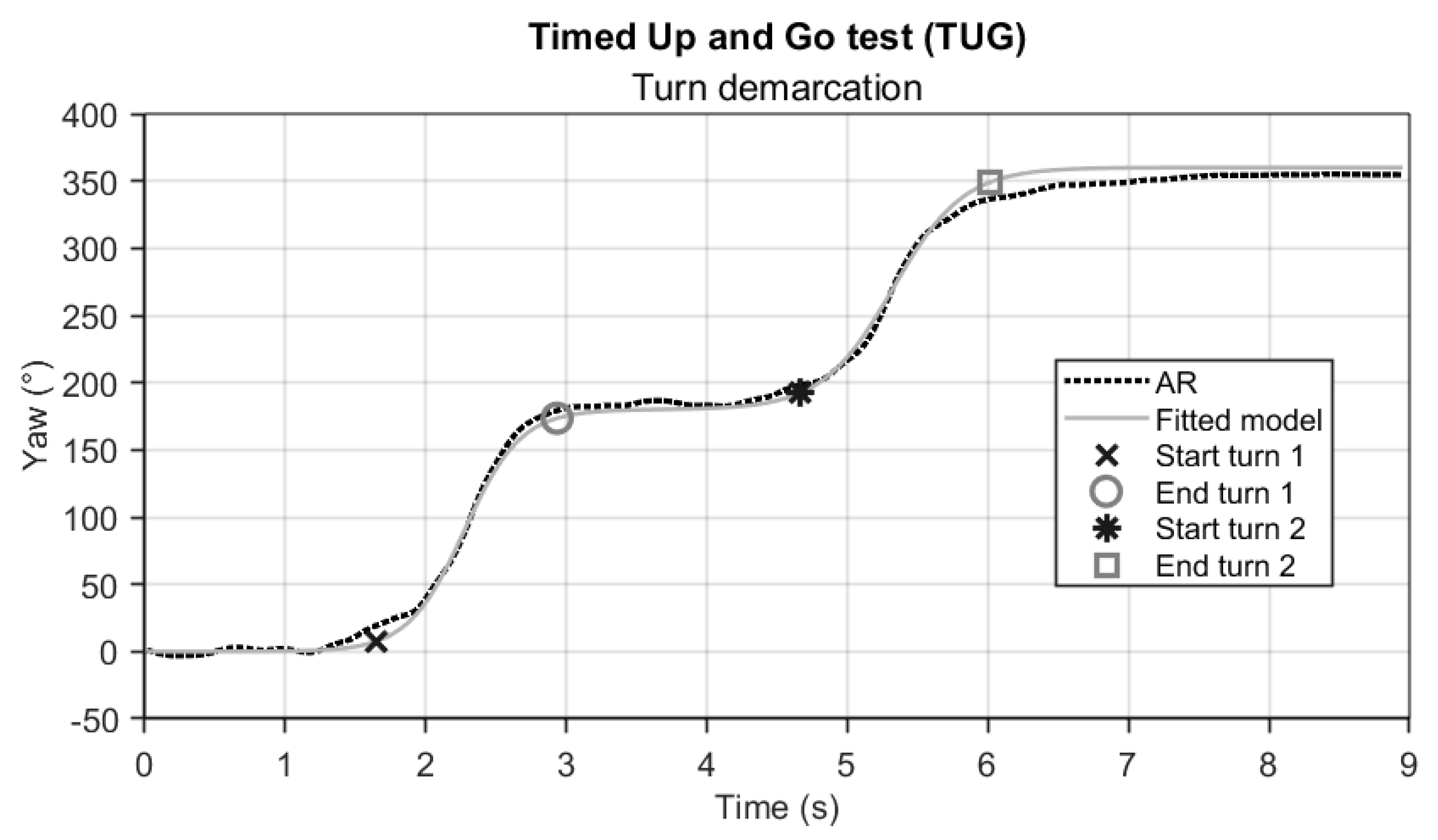
Figure 4. (a) Representative examples of AR vertical position data vs. Kinect vertical position data during the FTSTS. (b) Representative example of AR yaw orientation data vs. IMU trunk yaw data during the TUG.

Figure 5. Illustration of relevant AR data time series of a participant performing the TUG, with apparent features to identify distinct sub-parts of the test like standing up, walking and turning, from which various spatiotemporal parameters may be derived.

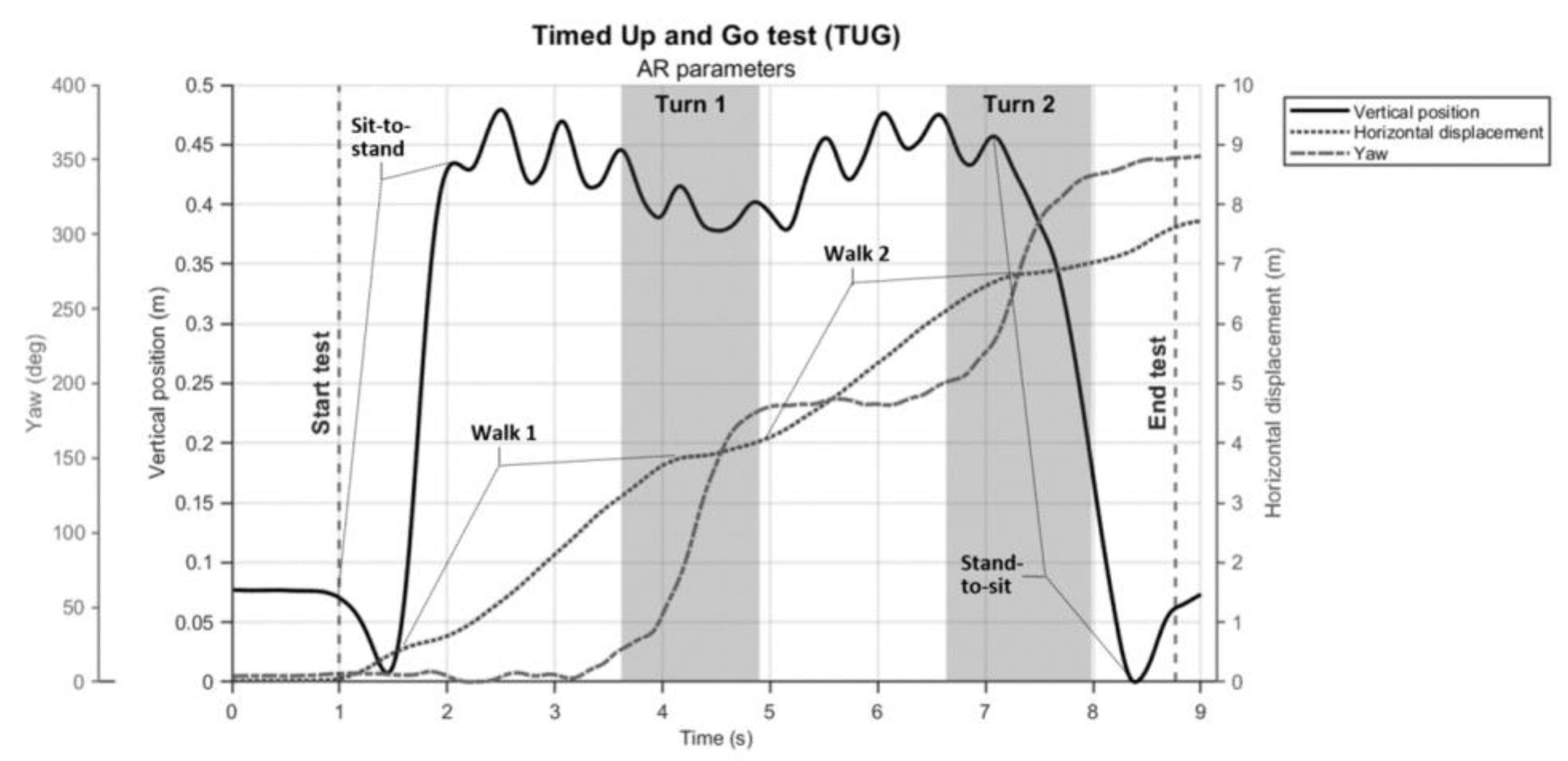
Table 1. Concurrent validity statistics for FTSTS and TUG (sub-)durations (in s): between-systems absolute agreement statistics for (sub-)durations derived from AR and reference-systems data.

		Mean ± SD	Mean ± SD	Bias (95% Limits of Agreement)	t-statistics	ICC_(A,1)
		AR	Stopwatch
FTSTS	Completion duration	12.3 ± 3.7	12.1 ± 3.7	-0.25 (-0.66 0.17)	t(20) = -5.28, p < 0.001	0.996
TUG	Completion duration	10.3 ± 3.1	9.9 ± 3.2	-0.44 (-1.19 0.31)	t(21) = -5.37, p < 0.001	0.984
		AR	Kinect Head
FTSTS^*	Completion duration	11.9 ± 3.91	11.91 ± 3.81	-0.04 (-0.38 0.3)	t(17) = -1.09, p = 0.293	0.999
	Sitting sub-duration	0.69 ± 0.49	0.62 ± 0.46	-0.07 (-0.25 0.11)	t(16) = -3.13, p = 0.006	0.971
	Sit-to-stand sub-duration	0.58 ± 0.16	0.62 ± 0.16	0.04 (-0.03 0.12)	t(16) = -4.49, p < 0.001	0.943
	Standing sub-duration	0.34 ± 0.15	0.32 ± 0.16	-0.02 (-0.09 0.06)	t(16) = 1.82, p = 0.087	0.965
	Stand-to-sit sub-duration	0.61 ± 0.16	0.65 ± 0.16	0.04 (-0.07 0.14)	t(16) =-3.05, p = 0.008	0.921
		AR	IMU Trunk
TUG	Turn 1 sub-duration	1.75 ± 0.64	1.8 ± 0.70	-0.09 (-0.4 0.6)	t(20) = -1.51, p = 0.146	0.913
TUG	Turn 2 sub-duration	2.01 ± 0.71	1.61 ± 0.62	-0.40 (-1.44 0.64)	t(20) = 3.44, p = 0.003	0.589

Significant biases are presented in bold. *One outlier participant (p4 in the supplementary data files) was excluded from the sub-duration results due to insufficient peaks in the Kinect time series only, preventing our peak-detection algorithm to accurately identify the frame numbers start and end indices.

Table 2. Test-retest reliability for FTSTS and TUG: absolute agreement statistics for (sub-)durations (in s) derived from AR data.

		Mean ± SD	Mean ± SD	Bias (95% Limits of Agreement)	t-statistics	ICC_(A,1)
		AR Trial 1	AR Trial 2
FTSTS	Completion duration	12.82 ± 4.33	12.28 ± 3.83	-0.54 (-3.78 2.70)	t(19) = 1.45, p = 0.163	0.914
	Sitting sub-duration	0.78 ± 0.45	0.75 ± 0.48	-0.03 (-0.28 0.22)	t(19) = 1.04, p = 0.314	0.964
	Sit-to-stand sub-duration	0.61 ± 0.19	0.59 ± 0.15	-0.02 (-0.21 0.17)	t(19) = 1.02, p = 0.322	0.830
	Standing sub-duration	0.37 ± 0.15	0.38 ± 0.18	0.01 (-0.25 0.26)	t(19) = -0.32, p = 0.756	0.695
	Stand-to-sit sub-duration	0.61 ± 0.16	0.62 ± 0.15	0.01 (-0.13 0.14)	t(19) = -0.54, p = 0.598	0.903
TUG	Completion duration	10.83 ± 2.71	10.32 ± 3.21	-0.51 (-3.33 2.32)	t(20) = 1.62, p = 0.122	0.874
	Turn 1 sub-duration	1.82 ± 0.73	1.78 ± 0.63	-0.04 (-1.05 0.98)	t(20) = 0.34, p = 0.740	0.721
	Turn 2 sub-duration	2.18 ± 0.76	2.04 ± 0.71	-0.14 (-1.28 1.00)	t(20) = 1.07, p = 0.295	0.684

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer