Prerpints.org logo
Preprint
Article

Two Phases GC-LDPC Decoding Aided with Early Termination and Forced Convergece

Altmetrics

Downloads

94

Views

33

Comments

0

This version is not peer-reviewed

Submitted:

29 June 2024

Posted:

02 July 2024

You are already at the latest version

Alerts
Abstract
The fast decoding of low-density parity-check (LDPC) is crucial for its future applications. In this paper, we propose to use Early Termination (ET) and Force Convergence (FC) techniques to accelerate the decoding of two new local/global two-phases decoding algorithms to reduce the Globally Coupled (GC) LDPC codes. Specifically, ET is applied in the local decoding phase of two- phases decoding of GC-LDPC codes to skip the local decoding which is highly likely to fail and avoid the unnecessary iterations. FC is applied in global decoding phase where converged variable nodes are identified and removed from Tanner graph and the decoding can be speed up shrinking parity check matrices. Two variants are proposed for the ET operation in local decoding phase. ET-1 merely stops iteration if it meets the stopping criterion while in ET-1, the iteration number saved in local decoding is added up in global decoding to improve the decoding performance. The simulation results show that the ET-1-FC scheme can save up to 42% decoding time complexity in the low SNR region while keeping the error rate performance nearly unchanged, the ET-2-FC can improve the error rate performance by 0.18dB at bit error rate 0.001 or 0.23dB at frame error rate 0.1. In the waterfalling region of BER/FER curves, both schemes can save about 25% decoding time complexity.
Keywords: 
Subject: Engineering  -   Telecommunications

1. Introduction

In recently years, the Globally-Coupled (GC) Low-Density-Parity-Check (LDPC) code attracts the many attention for its special structure and decoding algorithm [1,2,3,4]. This code performs well in both AWGNC and BEC. The GC-LDPC code consists of several individual local LDPC codes and the global coupling part. The global coupling part connects these local codes, enlarging the size of the code and improving connectivity. These local codes can be decoding individually, which is called local phase decoding. If the local decoding cannot makes the local codes convergence, the global decoding should step in the final decoding process. This kind of decoding algorithm is called local/gloabl two-phases decoding[1]. Thanks to the two-phases decoding algorhtm, the decoding time delay can be reduced by parallel local decoding. In the hardware implement, the GC-LDPC code leads the system more efficient and larger throughput [5,6,7]. In MIMO system, GC-LDPC code improves throughput by 4 and 5 times for code rates of 0.49 and 0.66[8]. To make GC-LDPC code design more flexible, many paper provide several constructions[9,10,11,12,13]. To design the GC-LDPC code with better performance, [14] gives the protograph-based construction by P-Extrinsic Information Transfer (EXIT) chart, performs better than previous GC-LDPC code, converts the general global coupling part to the tail-biting structure can also improve the code’s performance[15]. The free-ride code is utilized as the implicit global coupling part [16]. This kind of GC-LDPC code gets same code rate as the local codes, and gets more than 0.8dB gain than the local codes. In most cases, finite fields or finite geometry is used to build the QC-GC-LDPC code, and the girth is limited to 6. The short cycles always produce the trapping sets, which leads the e r r o r − f l o o r phenomenon to LDPC codes with the m e s s a g e − p a s s i n g decoding[17]. The girth of GC-LDPC code is extended from 6 to 8 with Greatest Common Divisor (GCD) criterion[18].
The Early Termination (ET) algorithm is the conventional method to save the decoding complexity[19,20,21,22,23,24]. The ET technology is consisted by Early Give Up (EGU) and Early Success (ES)[22]. The main propose of EGU is stopping the nonconvergent code early to save the decoding complexity. The ES stops the decoding process if it is converged to a valid result. The method of determining whether the code converges is very important, which decides the final performance of the code. [21,22] study the decision theory of ET. The Receiver Operating Characteristic (ROC) curve is a useful tool to analyze the sensitivity of detector to build a accuracy judge condition [22].
Same as ET, the Force Convergence (FC) algorithm is utilized as a conventional method to save decoding complexity[25,26,27,28,29,30]. By monitoring the nodes in real time, FC determines the node satisfying the convergence condition in advance and removes the node in the rest iterations. In most cases, the amplitude of each node is utilized to judge the reliability.
This paper firstly adopted the ET algorithm into the local phase decoding. The proposed ET-1 decoding scheme saves 40 − 42 % decoding time complexity compared with the conventional two- phases decoding scheme in low SNR region, without performance degradation. The ET-2 decoding scheme improves the code’s performance with the same decoding time complexity with the conventional two-phases decoding. Then, the FC scheme is used to the global phase decoding to further save the decoding time complexity. In the ET-1-FC decoding algorithm, the FC scheme saves more time complexity in the waterfall region, with the same final performance as other decoding algorithm. The ET-2-FC decoding algorithm improves 1.8dB in waterfall region in BER and 2.3dB in FER. Meanwhile, in this algorithm, the FC scheme saves 25 % decoding time complexity in the waterfall region.

2. GC-LDPC Code

Let the GC-LDPC code is consisted by t local codes H L i , i ∈ [ 0 , t − 1 ] , and the global coupling part is H X .The general structure of GC-LDPC code is shown as equation (1).
H G C = H L 0         H L 1         ⋱         H L t − 1 ̲       H X   .
In this paper, we consider H L i with same size. Setting n as the code length of H G C , the local code length is n / t . The global coupling part make the global code rate r G is lower than the local code rate r L .

2.1. Construct Method

The main construction idea of GC-LDPC code is to form the code structure H G C by deformation of the matrix with good girth. Therefore, the design method of the matrix is the most important step in the construction process.
The first construction method of GC-LDPC code is based on finite fields. Let α be a prime element in GF ( q ) . The non-zero elements in GF ( q ) constitute the sequence α 0 = 1 , α 1 . . . α q − 2 , α q − 1 = α 0 = 1 . A ( q − 1 ) × ( q − 1 ) cyclic matrix B 1 can be constructed from this cyclic sequence [1]:
B 1 = α 0 − 1 α − 1 ⋯ α q − 3 − 1 α q − 2 − 1 α q − 2 − 1 α 0 − 1 ⋯ α q − 4 − 1 α q − 3 − 1 ⋮ ⋮ ⋱ ⋮ α − 1 α 2 − 1 ⋯ α q − 2 − 1 α 0 − 1 .
Any two rows 0 ≤ i < j ≤ q − 1 and two columns 0 ≤ k < l ≤ q − 1 can be related to a 2 × 2 a sub-matrix M 1 = α i − k − 1 α j − k − 1 α i − l − 1 α j − l − 1 . At the same time, a matrix B 2 satisfy the 2 × 2 -SM constraint can be constructed as
B 2 = 1 1 1 ⋯ 1 1 β β 2 ⋯ β p − 1 1 β 2 ( β 2 ) 2 ⋯ ( β 2 ) p − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 β p − 1 ( β p − 1 ) 2 ⋯ ( β p − 1 ) p − 1 .
The method based on RS (Reed-Solomn) code can also design GC-LDPC code with girth of at least 6[10,12]. This code has remarkable performance for correcting random errors, random short phased bursts of erasures and long bursts of erasures. Let α be the prime factor of GF ( 2 s ) . If 2 s − 1 is not a prime number and n is a factor of it, 2 s − 1 = c n . Let β = α c , there is an n ordered sequence S = { 1 , β , β 2 , ⋯ , β d } , called the multiplicative group of GF ( 2 s ) . Take S as the root to get the following matrix,
B RS ( d , n ) = 1 β β 2 ⋯ β n − 1 1 β 2 ( β 2 ) 2 ⋯ ( β 2 ) n − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 β d ( β d ) 2 ⋯ ( β d ) n − 1 .
Let p s be the smallest prime factor of n and d be a positive integer less than or equal to p s , 1 ≤ d ≤ p s . When c = 1 , B R S ( d , n ) primitive RS code, otherwise it is nonprimitive RS code, and B RS ( d , n ) is a matrix that satisfies the 2 × 2 -SM constraint. Now, the matrix (1) can be constructed by B 1 , B 2 or B RS ( d , n ) through PEM (partition, edge-spreading, mask) operations. A special design scheme is proposed in [13], namely the RS-liked construction method. In this scheme, the local code and the global part can be designed independently. The RS-liked construction method simplifies the search for design parameters in algebraic construction, making it easier to determine parameters such as p and the t. This construction method can be based on any GF ( γ s ) , γ is prime, breaking the traditional RS code based on GF ( 2 s ) setting. Local code set RS 1 ( t , p , d 1 ) global part for RS 2 ( 1 , t p , d 2 ) .
RS ( a , b , d ) = β 0 β a β 2 a ⋯ β a ( b − 1 ) β 0 β 2 a β 4 a ⋯ β 2 a ( b − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ β 0 β a d β 2 a d ⋯ β a d ( b − 1 ) .
This design can flexibly design local codes of different sizes. Suppose you want to construct two different size of local code RS 1 , 1 and RS 1 , 2 . Decomposing γ s − 1 as γ s − 1 = t 1 t 2 p e . Constructed of two local codes respectively RS 1 , 1 = RS ( t 1 , p , d 1 , 1 ) and RS 1 , 2 = R S ( t 2 , p , d 1 , 2 ) , The global part is RS code RS 2 = R S ( 1 , t 1 t 2 p , d 2 ) . d 1 , 1 < ⌊ p / t 1 ⌋ , d 1 , 2 < ⌊ p / t 2 ⌋ , and d 2 < m i n { t 1 , t 2 } .
The previous construction methods can only ensure the girth 6 for GC-LDPC code. In [18], we propose the GCD-based construction method to rasie the girth to 8. The ( J , L ) GCD-based full-length row multiplier (FLRM) matrix is :
E = a 0 b 0 a 0 b 1 ⋯ a 0 b L − 1 a 1 b 0 a 1 b 1 ⋯ a 1 b L − 1 ⋮ ⋮ ⋱ ⋮ a J − 1 b 0 a J − 1 b 1 ⋯ a J − 1 b L − 1 ,
where a i , and b i are integers with 0 ≤ a 0 < a 1 < ⋯ < a J − 1 and 0 ≤ b 0 < b 1 < ⋯ < b L − 1 . Each a i , b j , i ∈ [ 0 , J ) , j ∈ [ 0 , L ) is exponential factor for P × P sized CPM. The row coefficient vector is a = ( a 0 , a 1 , ⋯ , a J − 1 ) , and in common way the column coefficients vector is b = ( b 0 , b 1 , ⋯ , b L − 1 ) = ( 0 , 1 , ⋯ , L − 1 ) . In conventional GCD-based LDPC code, the minimum bound of P is P min * = ( a J − 1 − a 0 ) ( L − 1 ) + 1 . We discover the new lower bound of the GCD-FLRM to make the design of GC-GCD-LDPC code more flexible[31]. For the GC-GCD-LDPC code have better performance than other kinds, this paper takes GC-GCD-LDPC code as the main analysis object.

2.2. Local/Global Two-Phases Decoding

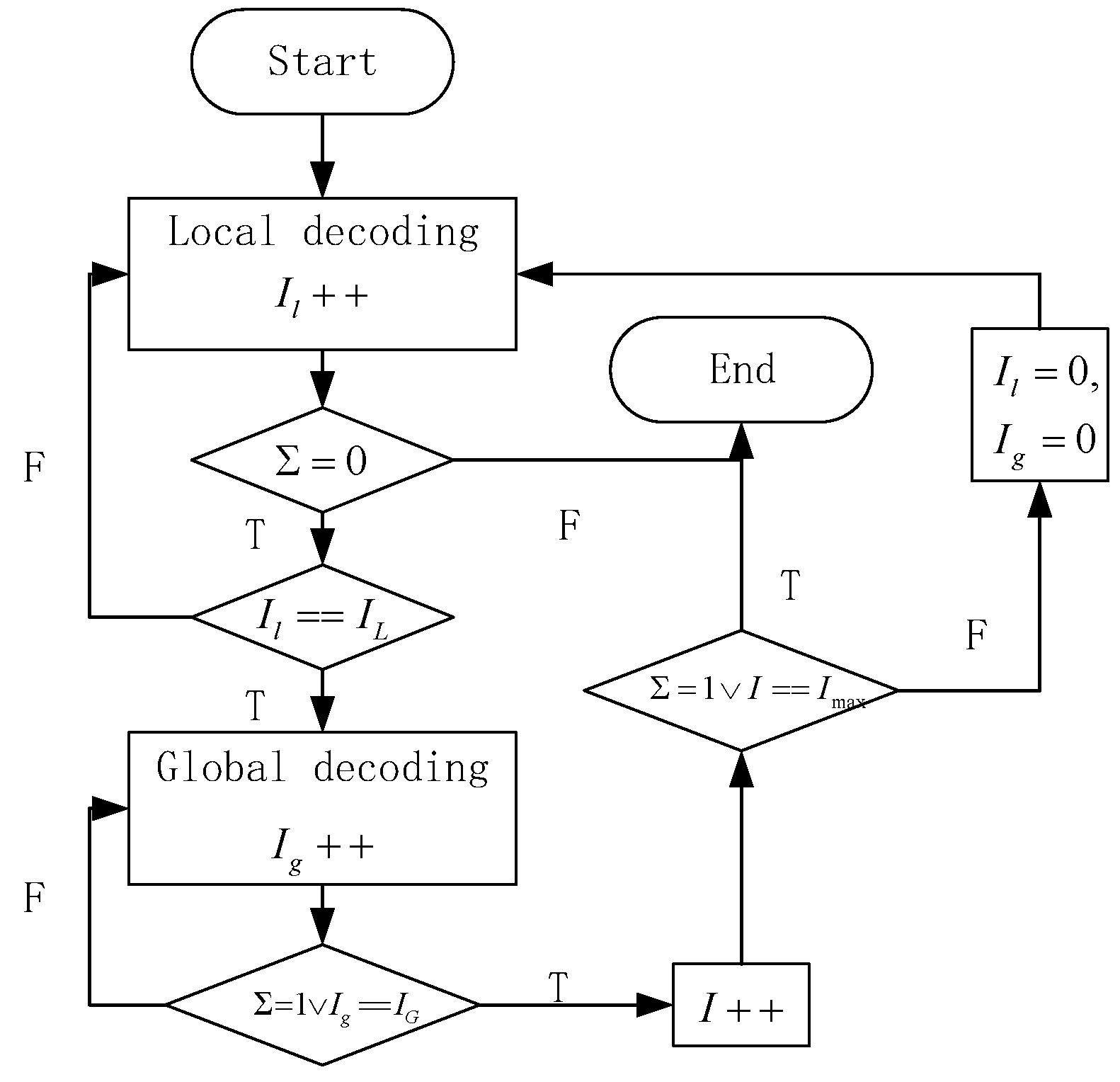
The local/global two-phases decoding scheme is the most interest characteristic of GC-LDPC code. Each bit in the codeword belongs to the local code as well as the global code. Therefore, decoding and parity-check can be processed within the local code, also in the global code. The decoding flow chart is shown Figure 1.
I L and I G defines maximum number of iterations for local and global decoding, respectively. And I m a x defines the maximum times of switch between two phases. ( I L , I G , I m a x ) defines a two-phases decoding process. If the global decoding does not back to local decoding, I m a x = 0 , the scheme is called global/local two levels decoding[2], which is determined by ( I L , I G ) . These two kind of decoding algorithm have similar limit performance. The decoding complexity can be effectively reduced by the reasonable design of two-phases decoding. For simplicity, this paper considers the local/global two level decoding as the decoding scheme. In the high SNR region, local decoding can carry out independent decoding so as to reduce the amount of computation in the process of decoding. It is foreseeable that, designing different levels of local code can be applied to techniques such as unequal protection and multilevel code.
For the local codes are mutually independent, the codes in the local phase decoding can be decoded in parallel. Therefore, the time complexity of the local decoding iteration can be regarded as the decoding complexity of the largest local code. In this paper, the local codes have the same size. The time complexity of local decoding is defined as L t = L c / t , which L c is the decoding complexity of all local codes. Defining g c as the decoding complexity of global coupling part, the global decoding complexity is G c = L c + g c , provided that the nodes are not deleted or frozen during iterations. For per-iteration, the local decoding costs less than 1 / t time of the global decoding.

3. Early Termination Algorithm

3.1. Decision Theory

In the initial ET scheme, the variable node reliability (VNR) is defined as equation 7[23].
V N R = ∑ ∀ i | L i |
The L i is the log-likelihood ratios (LLR) of i t h variable node. In [22] gives three indicators of judgment, which is defined as v 0 − v 2 in 8, to monitor convergence behavior of iterative decoding.
v 0 = ∥ L ∥ 1 / n v 1 = 1 − ∥ s ∥ 0 / ( n − k ) v 2 = | { L i : | L i | > θ } | / n
v 0 is the mean magnitude of LLR of all variable nodes. v 1 is the fraction of satisfied check nodes, s = x ^ · H T , and x ^ is the hard judge value of L . v 2 is the fraction of large amplitude of variable nodes, and the judgment threshold is θ .
Through the above three indicators, the respective criterion is designed as C 0 − C 2 .
  • C 0 if v 0 l < v 0 l − 1 appears T times, terminate decode, l < I L .
  • C 1 if v 1 l < v 1 , m i n , I l > l 1 , m i n ,the v 1 , m i n is the v 1 value in l 1 , m i n iteration, terminate decode. Or, when successive v 1 l ≤ v 1 l − 1 occur T times, stop decode.
  • C 2 if v 2 l < v 2 , m i n occurs when I l ≥ l 2 , m i n , terminate decode. v 2 , m i n is the v 2 value in l 2 , m i n iteration.
C 0 and C 2 are both limitations of variable nodes, and C 2 works better than C 0 . Thus, in this paper, C 1 and C 2 are utilized in the local decoding in the meantime.
To choose the proper parameters in C 1 and C 2 ,22] use the ROC curve to select these parameters. Let Σ = 0 , 1 represents decoding nonsuccess or success, respectively. And Σ ^ = 0 , 1 represents the predict result of decoding nonsuccess or success, respectively. Thus, the False-Positive Rate (FPR) P F P and True-Positive Rate (TPR) P T P are
P F P = P r { Σ ^ = 1 | Σ = 0 } P T P = P r { Σ ^ = 1 | Σ = 1 }
ROC curve is the relation of P F P and P T P is defined as
P T P : = f T P ( P F P )
The area under ROC curve A R O C = ∫ 0 1 f T P ( p ) d p is an effective quantitative judgment index. A larger A R O C indicates a more accurate prediction and a more reasonable setting of parameters. If the parameters are set perfectly, A R O C = 1 .

3.2. ET-Two-Phases Decoding

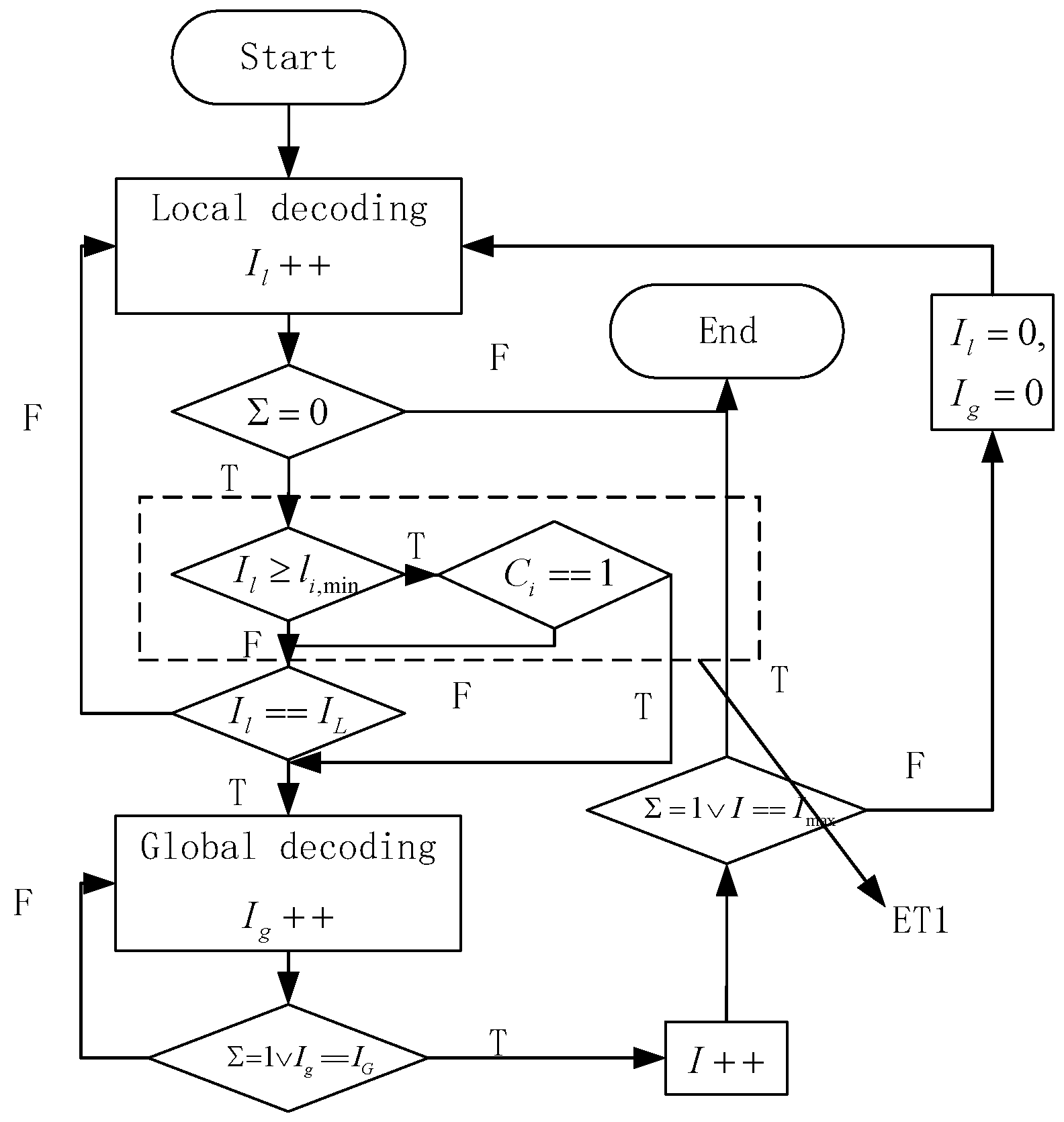
The purpose of introducing ET scheme to GC-LDPC decoding in this paper is to reduce the unnecessary iteration complexity of local decoding at low SNR. Therefore, the ET scheme is only used to local decoding process. Thus, we propose the ET-1 scheme as Figure 2.
The processes in dotted box is the ET decision. An well designed parameters save lot of unnecessary iteration of local decoding. In C 1 , l 1 , m i n or T is the key parameter. To facilitate the simulation, this paper adopts the second way. In C 2 , l 2 , m i n and v 2 , m i n should be selected to optimize the ET scheme.
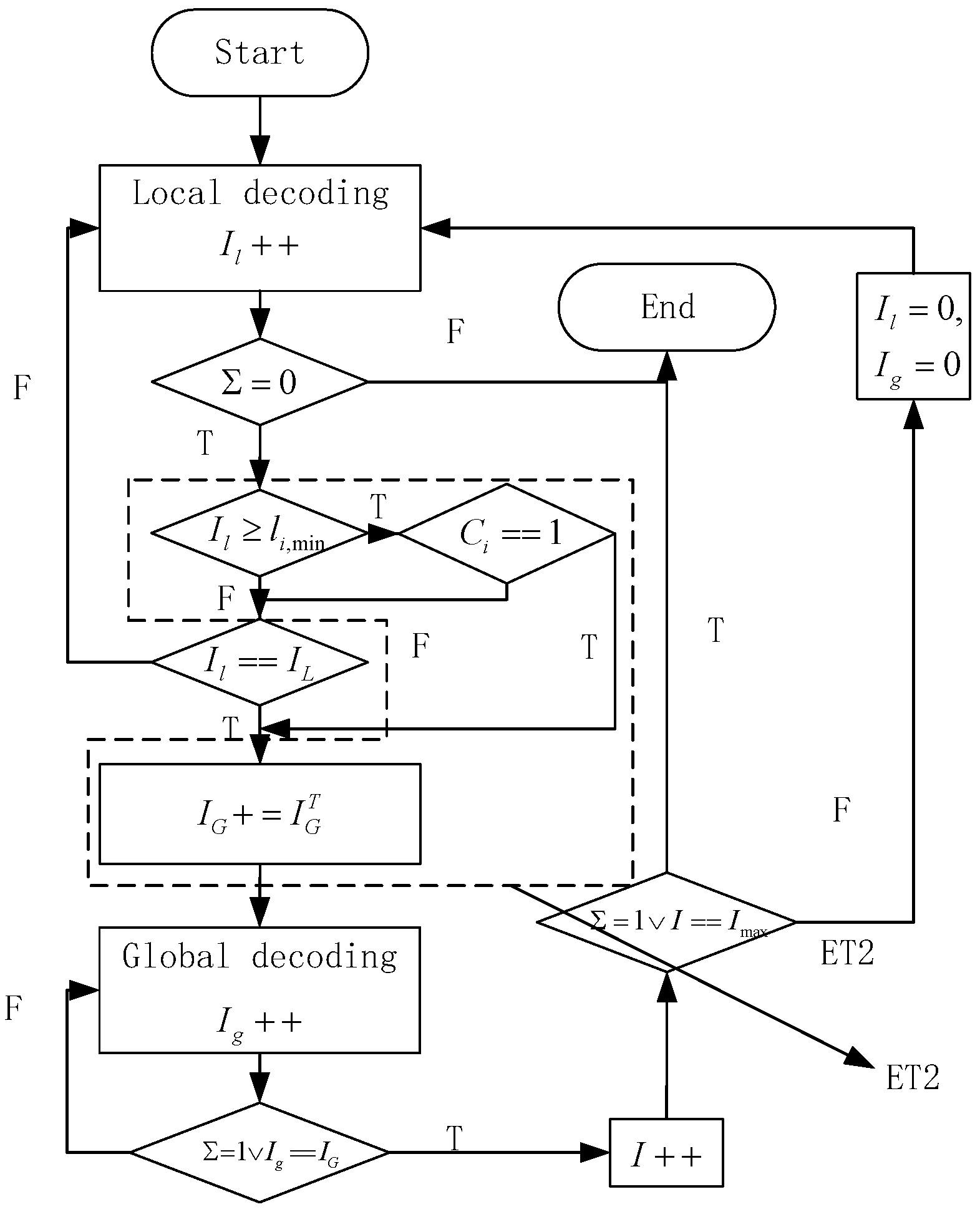
To allocate the decoding complexity more reasonably, We propose ET-2 to assign the decoding complexity adaptively. The number of decoding iterations saved by ET1 translates into I G T , which is the additional number of global decoding iterations. The process of ET-2 is show in Figure 3.
In low SNR region, the ET-2 two-phases decoding adaptively increases the number of iterations in global decoding. Thus, the performance if GC-LDPC code in low SNR region has been effectively improved. It is worth to mention, the ET scheme is aim to improve the GC-LDPC code’s performance in low SNR region. With the SNR increase, the impact of ET-1 and ET-2 decreases gradually.

4. Force Convergence Algorithm

To further save the decoding, FC scheme is introduced into the two-phases decoding to save bit-level complexity. In modern communication system, the high order Quadrature Amplitude Modulation (QAM) is a popular method to improve the throughput. For example, the 5G communication has expanded 256QAM from 64QAM in 4G. However, the reliability difference between bits becomes larger as the modulation order increases. The actual communication system is more complex and the reliability difference between bits inevitably becomes larger. In the iteration of LDPC code, the higher reliability converge earlier than others. Stopping the node iteration corresponding to the convergent bit in time can effectively reduce the decoding complexity. The well designed FC scheme can not only save decoding complexity, but also slightly improve the code’s performance.

4.1. Basic of FC algorithm

The original conception of FC, the reliability of variable and check nodes are defined as equation (11).
R j , i = ∏ i ′ , i ′ ≠ i s g n ( Q i ′ , j ) Φ ∑ i ′ , i ′ ≠ i Φ ( Q i ′ , j )
The Φ ( x ) = l o g e x + 1 e x − 1 , and Q i , j is the message exchanged through i t h check node to j t h variable node in log domain. The "aggregate messages" B i for variable node and C j for check node.
B v i = L i + ∑ R j , i C c j = ∑ Φ ( | Q i ′ , j | )
The judgement threshold of variable and check nodes are t v and t c . When B v i > t v and C c j < t c , the node is deactivated for the rest of the iteration. To simplify the judgment process, [18] uses the adjacent deactivated variable nodes to judge the check node instead of directly judging the check node information. This scheme is called Simplified Forced Convergence (SFC). In MinSum decoding scheme, the check nodes’ operation in SFC is shown as equation (13).
C c i , j = ∏ j ′ ∈ Ψ i ∖ j s i g n ( Q i , j ′ ) min j ′ ∈ Ψ i ∖ ( j , k ) ( | Q i , j ′ | )
The Ψ i denotes the set of variable nodes adjacent to i t h check node, and k is the freezed variable node. The i t h check nodes only be deactivated when the nodes in Ψ i are all freezed. Comparing with the original FC, using the method of judging only variable nodes can significantly reduce the computational complexity and memory accesses resulting in low power consumption[31], which is called Simplified Force Convergence (SFC). [29] propose an Adaptive Forced Convergence (AFC) algorithm. The dynamic threshold value is set as equation (14).
t v = t 0 − ( Δ t × i )
Where Δ t is the constant dynamic value of threshold, i is the index of iteration and t 0 is the initial threshold. To forbid the wrong judgement of nodes, the freezed check nodes, which is unsatisfied the rest iterations, should be re-active.

5. Simulation and Analysis

5.1. Code Construction

Firstly, we construct a GCD-based GC-LDPC code, which is called GC-1[18]. Building a GCD-FLRM sized 4 × 13 , the first three rows consist the exponential matrix of local code, and the global part is built with three replication of last row. The Z-factor of the exponential matrix is P = 169 . The code length is n = 6591 , and the code rate is r = 0.751934 .
In order to reflect the advantages of the proposed decoding, the 5G-LDPC code is used as the comparison code in this paper. The code rate of 5G-LDPC code is r = 0.751 , and the information length is k = 4956 . In these parameters, the BG-2 matrix should be selected as the exponential matrix, and the Z-factor is P = 240 . The transmission code length of 5G-LDPC is n = 6600 . However, the channel source should be unrate matching before the decoder. Thus, in decoder the length of the code participating in the iteration is N = 16320 . The 5G-LDPC code in this paper is called 5G-1.

5.2. ET-Two-Phases Decoding

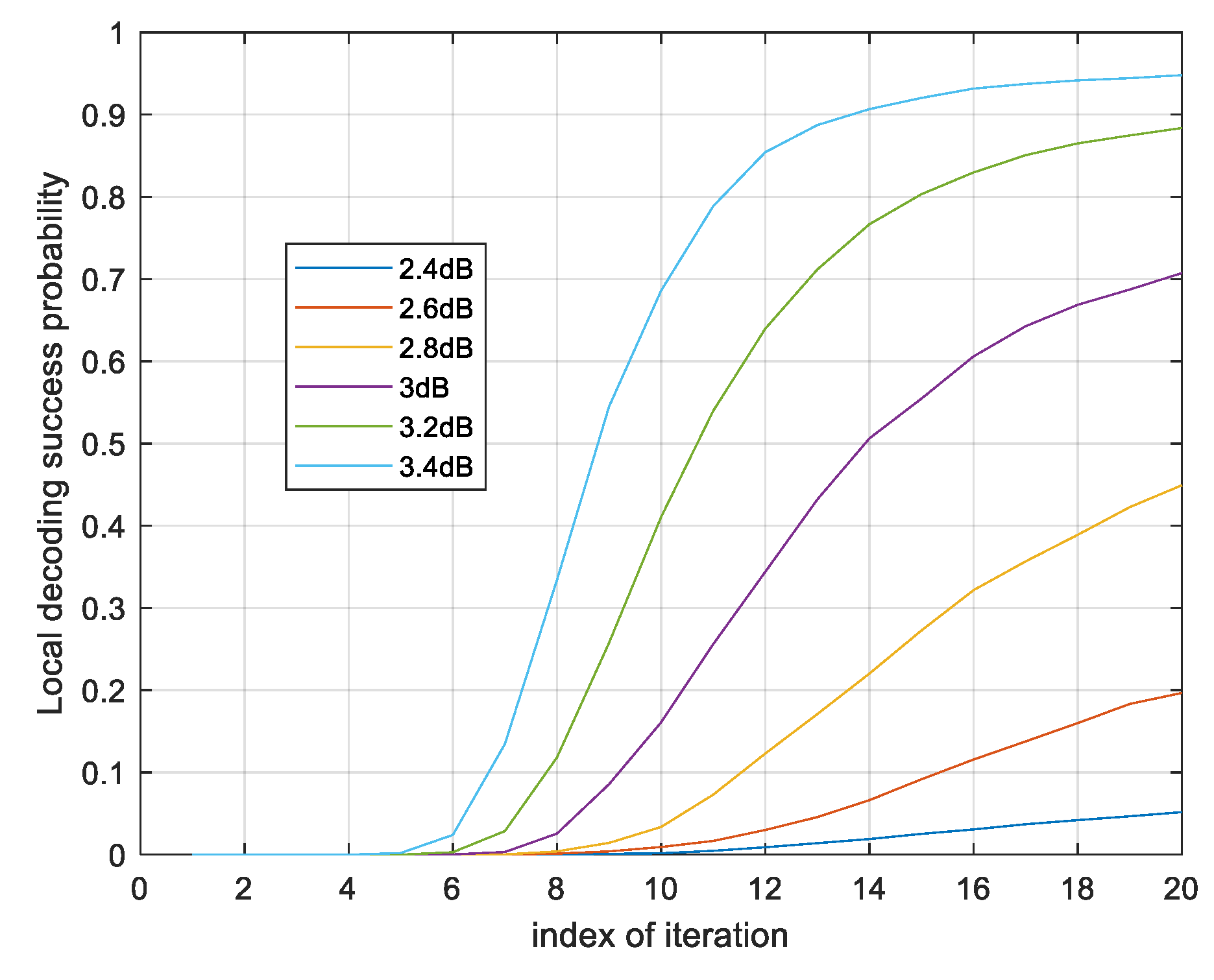
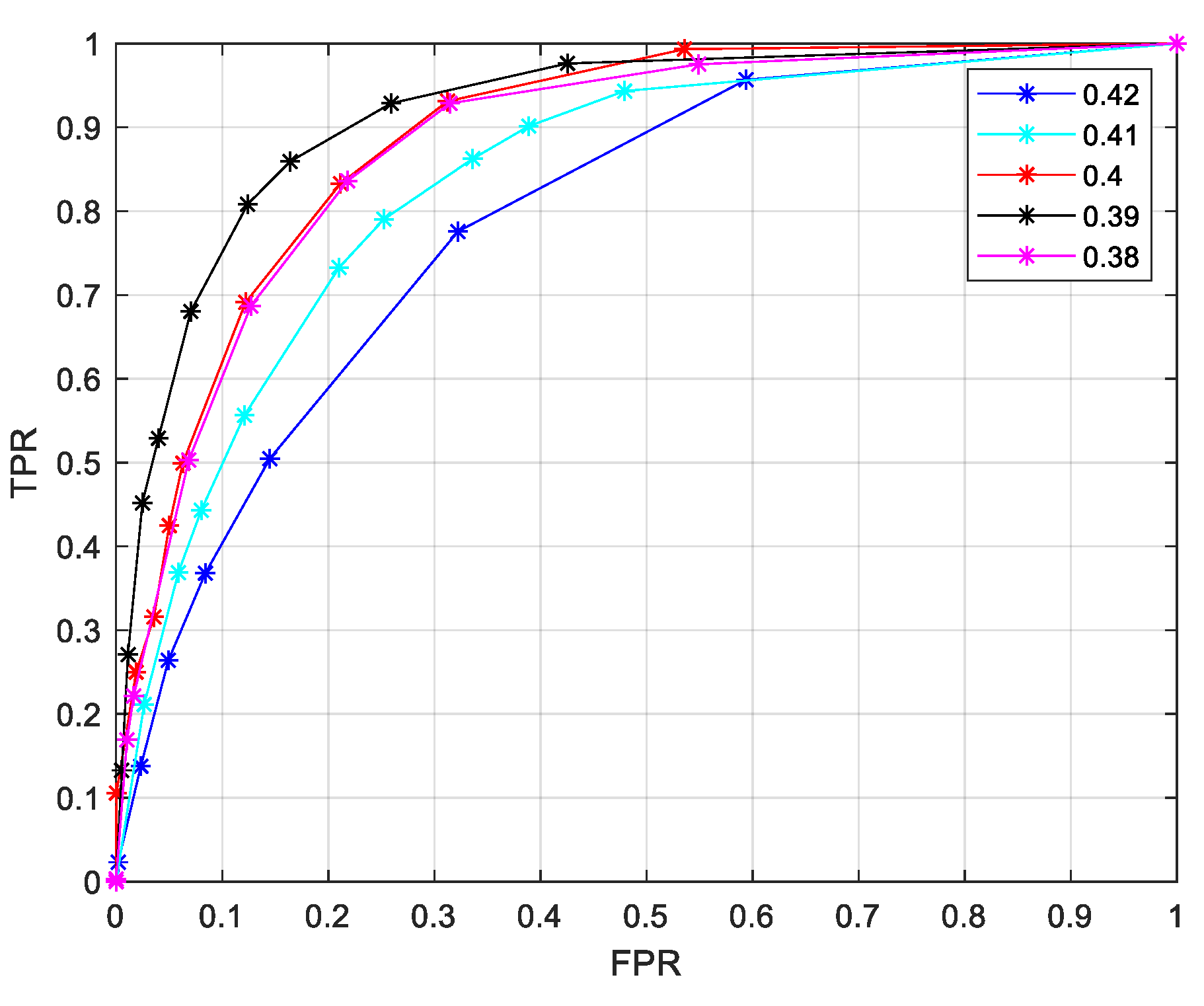
Firstly, we use the ROC curve to optimize the parameters in ET scheme.
From Figure 4 the local code of GC-1 cannot decode successful in 4 iterations. The C 2 is used in local decoding in 4 iterations. When the SNR is lower than 2.4dB, the local code can hardly decode successfully by itself. The local phase decoding in this region is almost unnecessary. When the SNR is higher than 3dB, the curve of success probability of the local decoding is flattens out at 20 iterations.
The local decoding has a probability of convergence after 10 iterations. Therefore, C 1 works with a large probability after 10 iterations. The ROC curves of v 2 , m i n in Figure 5. The threshold of the hard decision is predefined as θ = 5 .
In Figure 5, it is easy to see v 2 , m i n = 0.39 is the best selection because it maximized A R O C . v 1 , m i n and v 2 , m i n is optimized in the same way. To avoid repeating the elaboration of the optimization process, we give the Table 1 as the summation of ET schemes.
The GC-1 is simulated in AWGNC with QPSK modulation. For the sake of statistics, each time of the node participate the iterations is account to 1 time complexity. As front mentioned, the local codes are decoded in parallel, the time complexity of local decoding is L t = L c / t . The maximum number of the local iterations is set as I L = 40 . To make the global decoding has equally decoding time complexity, the maximum number of global iterations is set as I G = 10 .
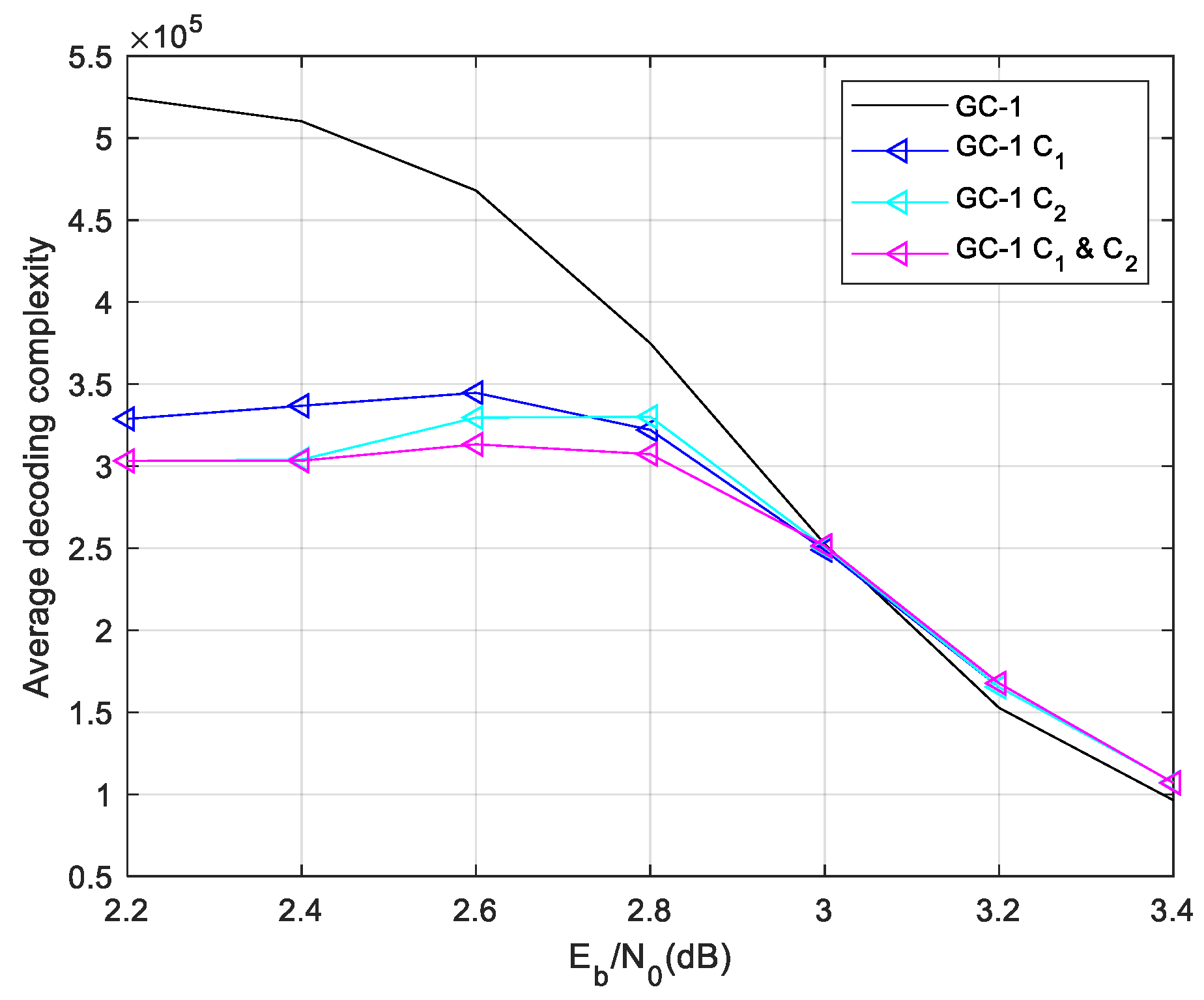
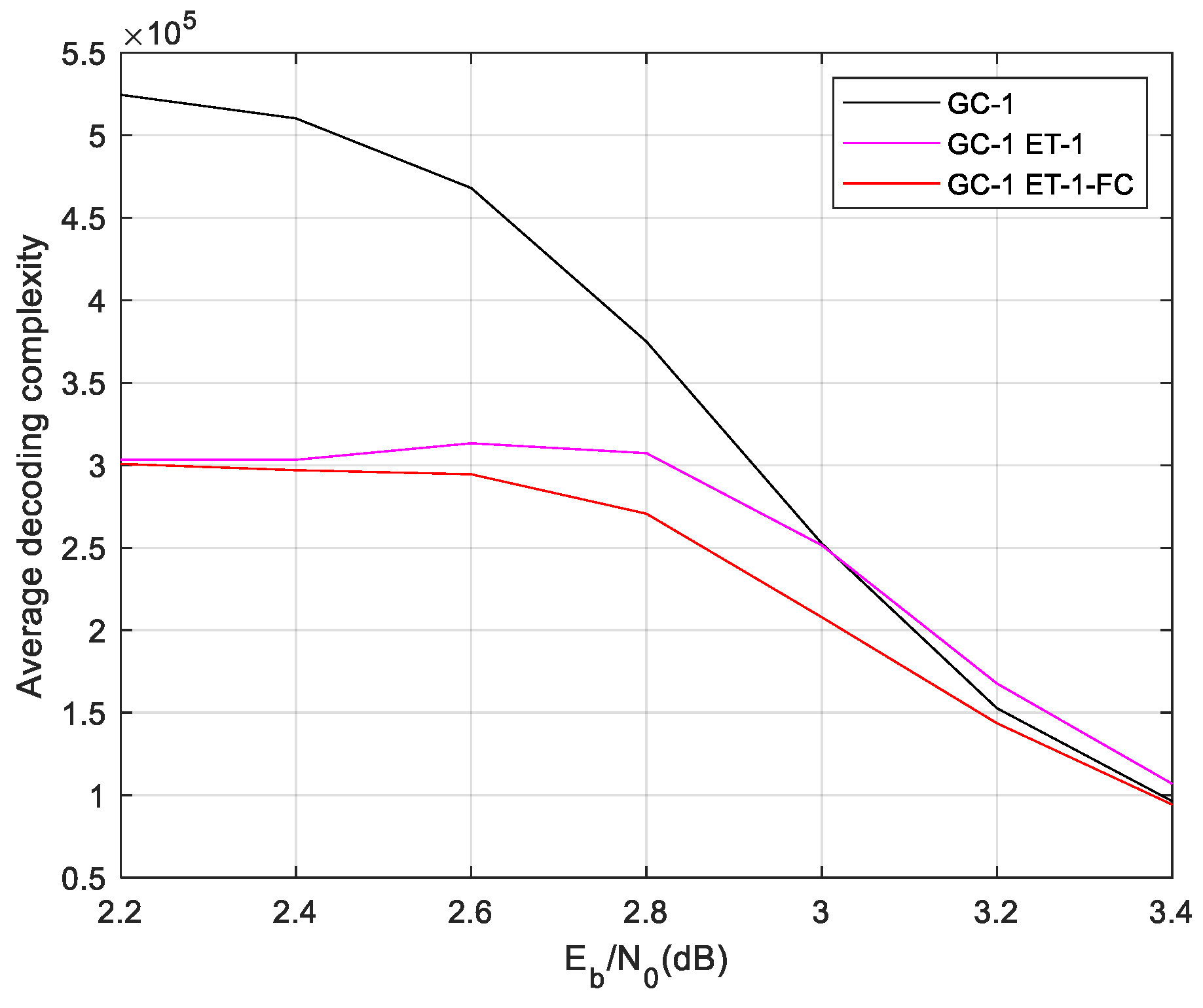
Firstly, the ET-1 schemes are used to GC-1. The comparison result of the complexity of ET-1 is given in Figure 6.
The result shows the ET-1 schemes saves much complexity in lower SNR region. In higher SNR region, the ET-1 schemes have similar time complexity with the normal local/global two level decoding. This result demonstrate the misjudgment probability of the designed ET scheme is extremely low. While the ET schemes misjudgment leads early termination of the data, thus entering the global decoding, it will lead to a large increase in the decoding time complexity. The C 1 & C 2 scheme saves more decoding time complexity than others. While SNR is 2.2dB, C 1 & C 2 scheme save 42.19 % time complexity than regular two level decoding.
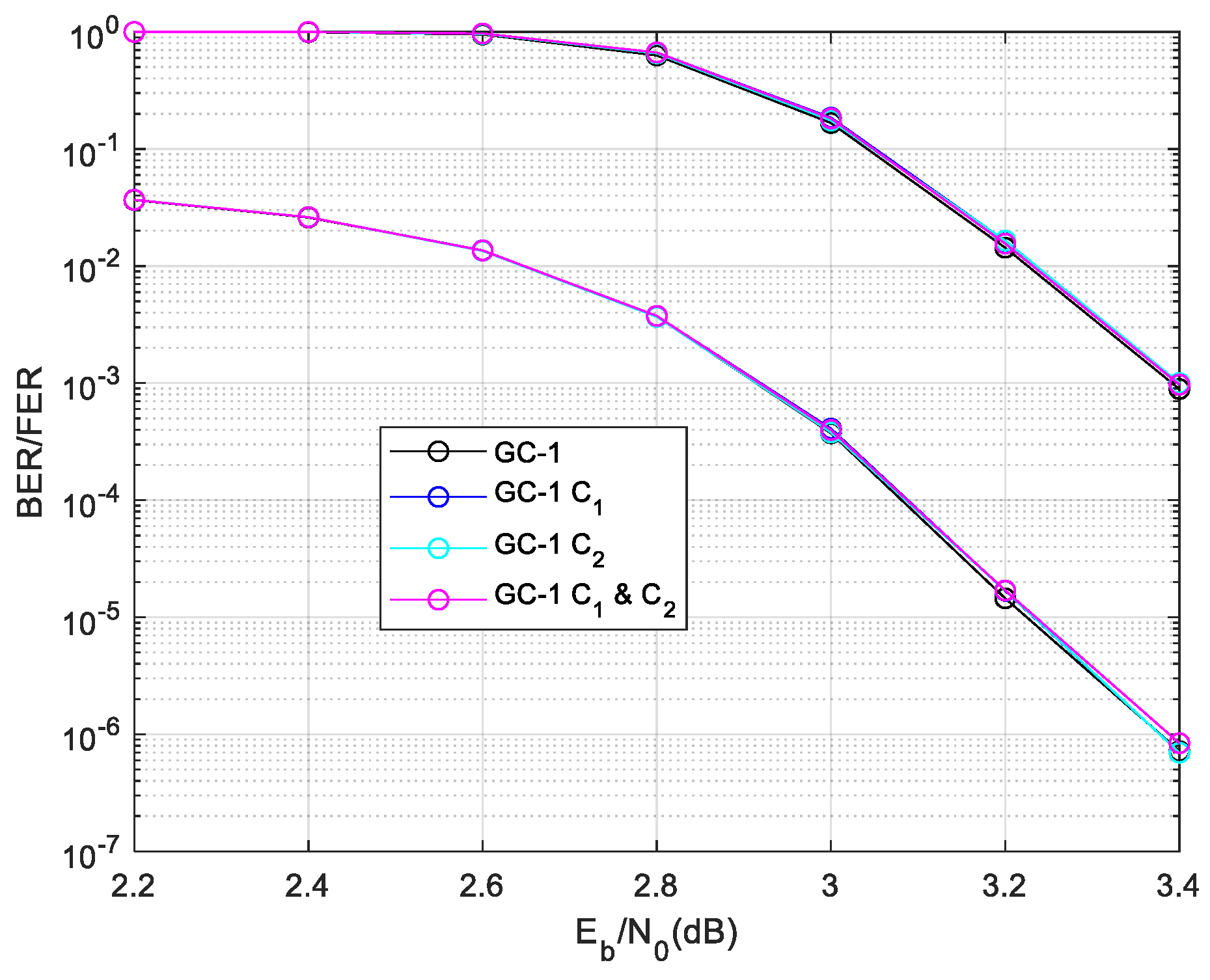
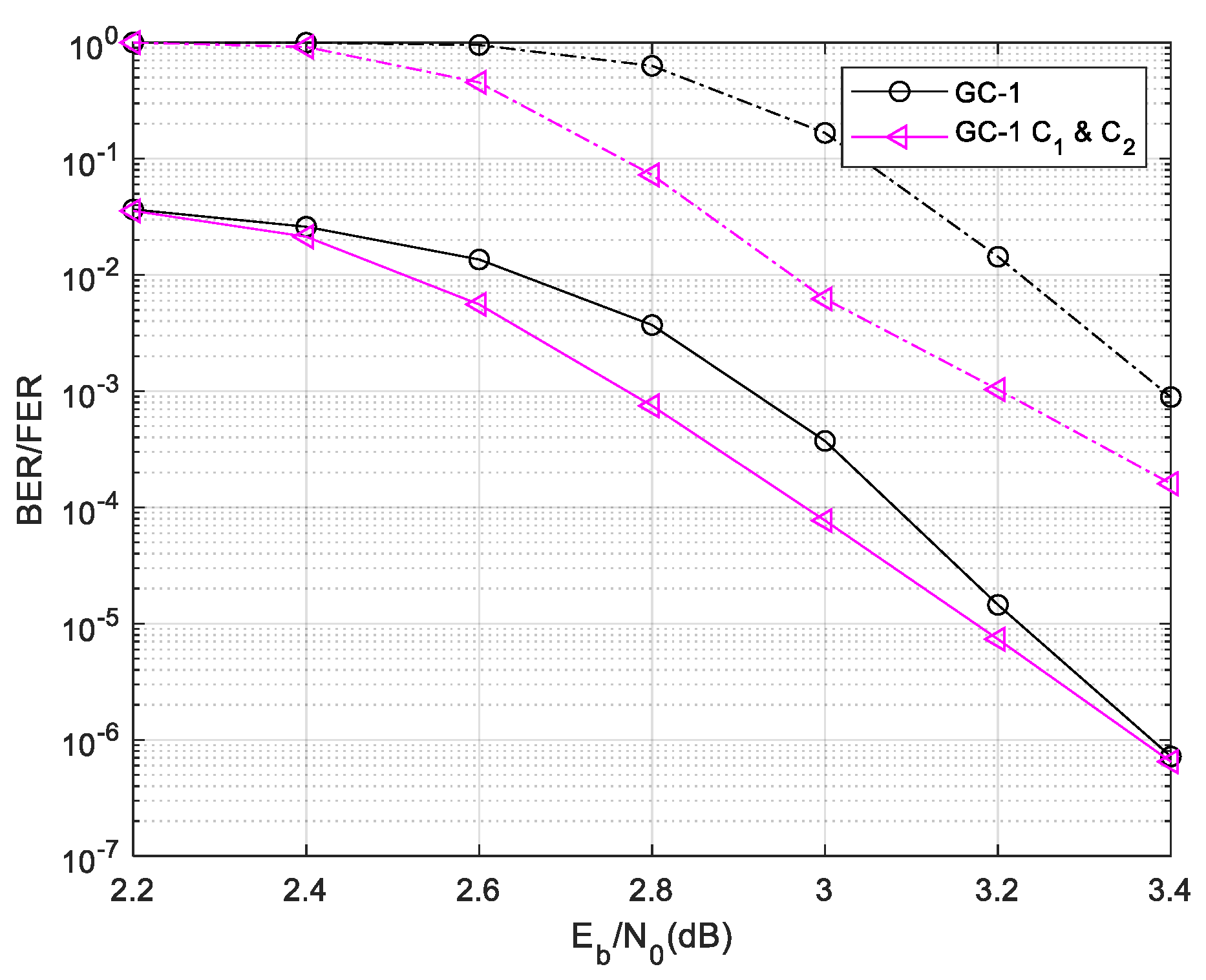
Then we give the performance of GC-1 as the Figure 7. The designed ET-1 schemes have similar BER and FER performance with the normal local/global two level decoding.
The complexity statistic and performance demonstrate the proposed C 1 & C 2 ET-1 scheme saves lot of decoding time complexity in lower SNR region without perform degradation.
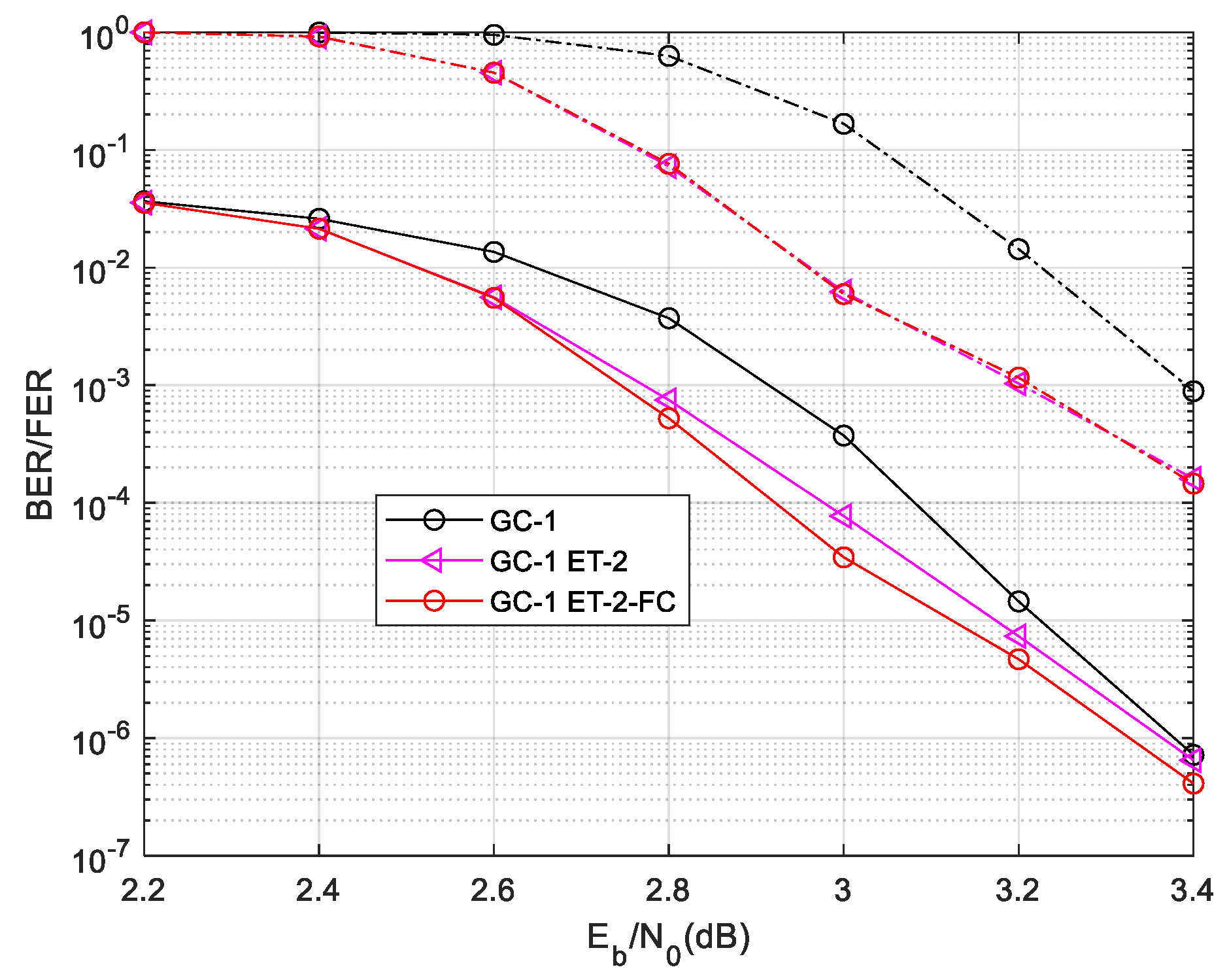
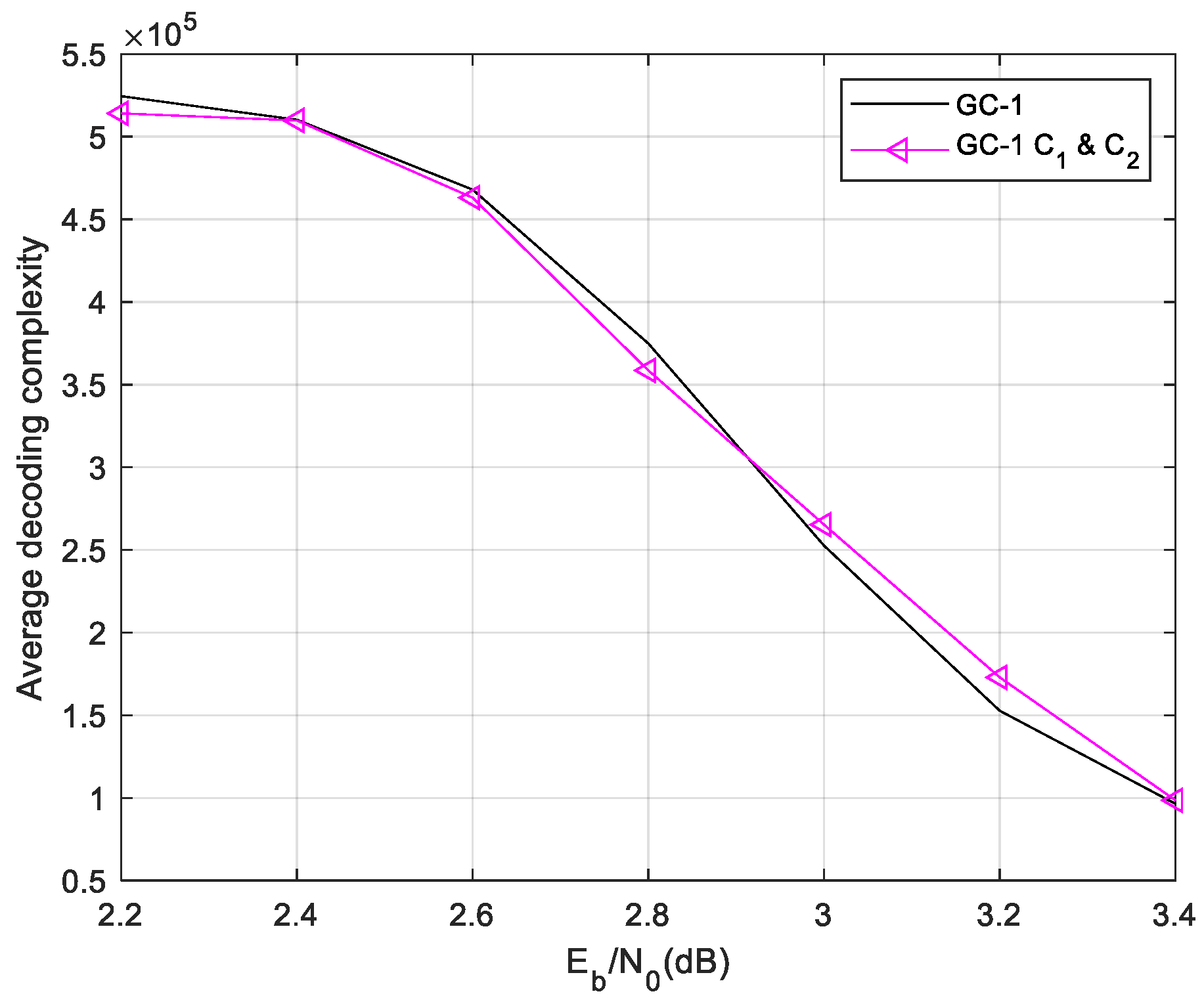
Afterward, the we use the ET-2 in these codes. For the proposed C 1 & C 2 scheme performs better than others, the C 1 and C 2 schemes are no longer simulated in follow cases. The complexity of ET-2 decoding scheme is shown as the Figure 8 .
The result shows the ET-2 scheme does not save the decoding complexity. The performance result is showing as the Figure 9.
The result proves that, the ET-2 scheme makes the GC-1’s 0.18dB gain in BER and 2.3dB gain in FER. In the low SNR region, the failure probability of local decoding is higher. The average of I G T is higher. However, with the SNR increase the average of I G T decreasing. The performance of ET-2 based GC-1 gradually approaching the conventional decoding performance. The premise of improving the performance is that the decoding complexity and the number of global decoding is limited. If the number of global decoding I G is set high enough, ET-2 scheme is difficult to bring performance gain.
Overall, the ET-1 scheme saves lots of decoding time complexity without performance degradation. The ET-2 scheme improves decoding performance without increasing the decoding complexity, when I G is limited.

5.3. ET-FC-Two-Phases Decoding

To get a better decoding performance, we combine the ET and FC schemes in the two-phases decoding of GC-LDPC code. In global phase decoding, the nodes converge better than the shorter local codes. So the FC scheme is more suitable to utilized in the global phase decoding process. In the proposed decoding algorithm, the ET-1 C 1 & C 2 scheme is utilized to the local phase decoding process and the AFC scheme is used to the global decoding process. The parameters of FC scheme is optimized by ROC curve as before. The final FC parameters are t 0 = 20 δ = 0.75 . 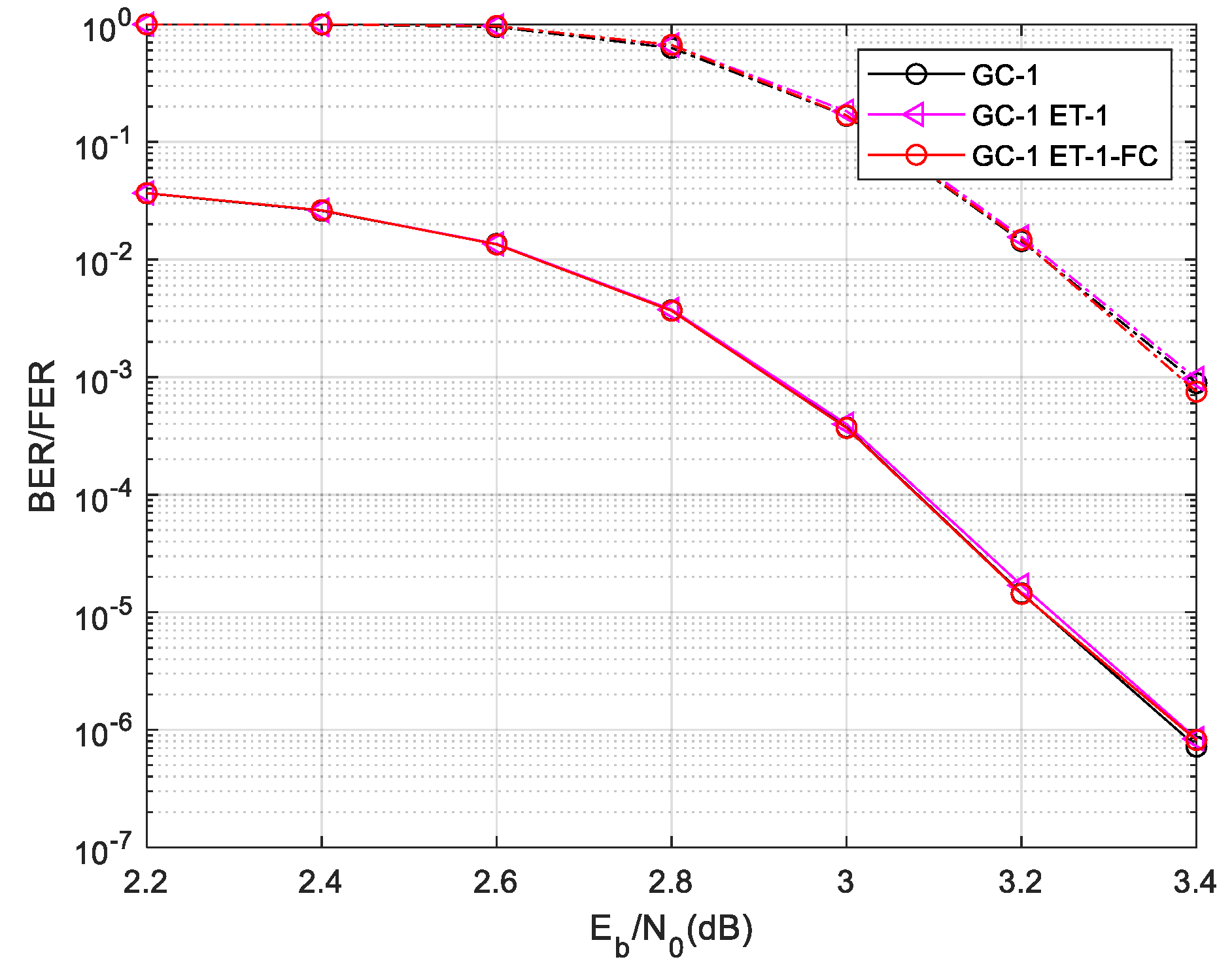The performance and decoding complexity is shown as the Figure 10 and Figure 11.
The ET-1-FC decoding scheme further saves the complexity than the ET-1 scheme in most situations. In lower SNR region, the speed of convergence is slower, the effect of the FC scheme is weaker. In the waterfall region the probability of nodes’ convergence is higher, the FC scheme saves lot of decoding complexity. And the ET-1-FC two-phases decoding algorithm does not bring any performance degradation in BER/FER, as well as the ET-1 scheme.
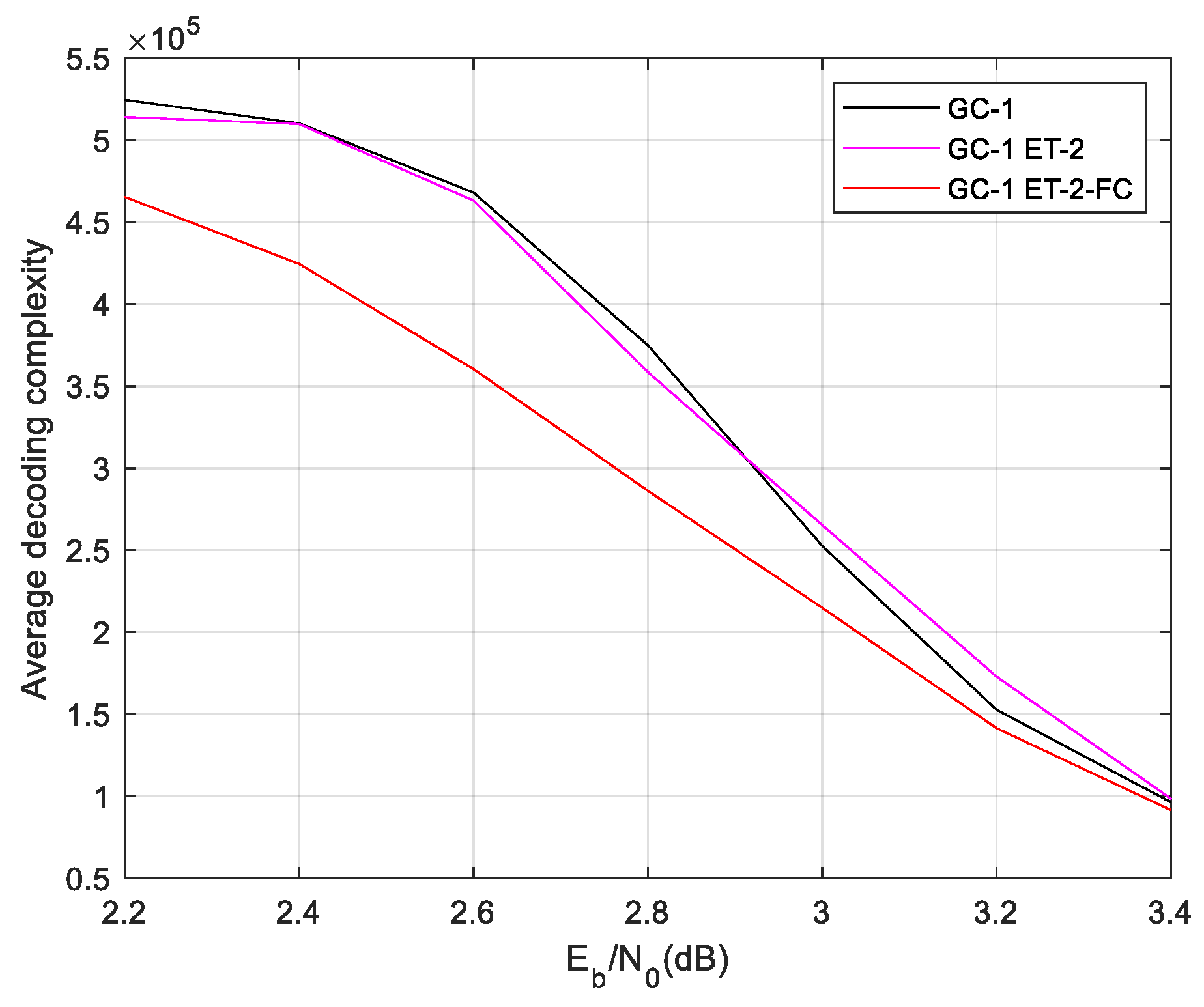
Then, the FC scheme is also used in the ET-2 two-phases decoding algorithm. The complexity and performance of ET-2-FC two-phases decoding is shown as the Figure 12 and Figure 13.
The ET-2 scheme extend the iterations of the globally decoding, which leads the FC scheme saves more complexity than the ET-1 based two-phases decoding. In the waterfall region, the ET-2-FC two- phases decoding algorithm saves about 25 % decoding time complexity. And the FC scheme also slightly improve the BER performance.

6. Conclusions

This paper gives two new two-phases decoding algorithms aiming to further save the decoding time complexity of GC-LDPC code. The ET and FC scheme is used into the decoding algorithm to save the decoding complexity. With the reasonable application of ET and FC techniques, the decoding results of GC-LDPC codes can reduce the complexity of GC-LDPC codes with almost no performance loss. The proposed ET-1-FC decoding algorithm saves 42 % decoding time complexity in the low SNR region, without performance degradation. The ET-2-FC improves the BER/FER performance when the number of global iterations with the decoding complexity is constrained. In the papers’ case, the ET-2-FC decoding algorithm improve 1.8dB in BER and 2.3dB in FER, with 25 % decoding time complexity reduction in the waterfall region.

Author Contributions

Conceptualization, K.Z.; methodology, K.Z.; investigation K.Z.; software, K.Z; supervision, H,Y; writing—original draft, K.Z.; writing—review and editing, H.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The model of the subjects was public.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. J. Li, S. Lin, K. Abdel-Ghaffar, W. E. Ryan and D. J. Costello, “Globally coupled LDPC codes," 2016 Information Theory and Applications Workshop (ITA), La Jolla, CA, USA, 2016, pp. 1-10.
  2. Y. -C. Liao, C. Lin, H. -C. Chang and S. Lin, “A (21150, 19050) GC-LDPC Decoder for NAND Flash Applications," in IEEE Transactions on Circuits and Systems I: Regular Papers, 2018, vol. 66, no. 3,pp. 1219-1230. [CrossRef]
  3. M. Nasseri, X. Xiao, B. Vasic and S. Lin, “Globally Coupled Finite Geometry and Finite Field LDPC Coding Schemes," in IEEE Transactions on Vehicular Technology, 2021, vol. 70, no. 9, pp. 9207-9216. [CrossRef]
  4. H. Liu and Q. Yu, “Matryoshka Globally-Coupled LDPC Code," in IEEE Transactions on Communications, 2023, vol. 71, no. 6,pp. 3191-3206. [CrossRef]
  5. Bao, Binhao, Wu Guan, Liping Liang, and Xin Qiu. “An efficient GC-LDPC encoder architecture for high-speed NAND flash applications." IEICE Electronics Express 21, no. 2 (2024): 20230477-20230477. [CrossRef]
  6. Hsu, Yu-Lun, Li-Wei Liu, Yen-Chin Liao, and Hsie-Chia Chang. "GC-Like LDPC Code Construction and Its NN-Aided Decoder Implementation." IEEE Open Journal of Circuits and Systems (2024). [CrossRef]
  7. Bao, Binhao, Qianhui Li, Wu Guan, Qi Wang, Liping Liang, and Xin Qiu. "Adaptive Granularity Progressive LDPC Decoding for NAND Flash Memory." IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems (2023).
  8. Fang, Jian, Baoming Bai, Ruimin Yuan, Rongchi Xu, Xiao Ma, and Chung-Li Wang. "Superposition Construction of Globally-Coupled LDPC Codes for MIMO Communication." In 2023 12th International Symposium on Topics in Coding (ISTC), pp. 1-5. IEEE, 2023. [CrossRef]
  9. J. Li, K. Liu, S. Lin and K. Abdel-Ghaffar, “Reed-Solomon based globally coupled quasi-cyclic LDPC codes," 2017 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 2017, pp. 1-10. [CrossRef]
  10. J. Li, K. Liu, S. Lin and K. Abdel-Ghaffar, “Reed-solomon based nonbinary globally coupled LDPC codes: Correction of random errors and bursts of erasures," 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 2017, pp. 381-385. [CrossRef]
  11. Y. -C. Liao, H. -C. Chang and S. Lin, “Scalable Globally-Coupled Low-Density Parity Check Codes," 2018 IEEE 10th International Symposium on Turbo Codes & Iterative Information Processing (ISTC), Hong Kong, China, 2018, pp. 1-5.
  12. J. Li, K. Liu, S. Lin and K. Abdel-Ghaffar, “Reed-Solomon based globally coupled quasi-cyclic LDPC codes," 2017 Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 2017, pp. 1-10.
  13. Y. -C. Liao, H. -C. Chang and S. Lin, “Generalized Globally-Coupled Low-Density Parity-Check Codes," 2018 IEEE Information Theory Workshop (ITW), Guangzhou, China, 2018, pp. 1-5.
  14. J. Zhang, B. Bai, M. Zhu, S. Li and H. Li, “Protograph-Based Globally-Coupled LDPC Codes Over the Gaussian Channel With Burst Erasures," in IEEE Access, vol. 7, pp. 153853-153868, 2019. [CrossRef]
  15. J. Zhang, B. Bai, S. Li, M. Zhu and H. Li, “Tail-Biting Globally-Coupled LDPC Codes," in IEEE Transactions on Communications, 2019, vol. 67, no. 12, pp. 8206-8219. [CrossRef]
  16. Q. Wang, S. Cai and X. Ma, “Free-Ride Coding for Constructions of Coupled LDPC Codes," in IEEE Transactions on Communications, 2023, vol. 71, no. 3, pp. 1259-1270. [CrossRef]
  17. L. Song, S. Yu and Q. Huang, "Low-density parity-check codes: Highway to channel capacity," in China Communications, vol. 20, no. 2, pp. 235-256, Feb. 2023. [CrossRef]
  18. Zhu, Kun, and Hongwen Yang. "Constructing Grith Eight GC-LDPC Codes Based on the GCD FLRM Matrix with a New Lower Bound" Sensors, 2022, vol 22, no. 19: 7335. [CrossRef]
  19. J. Li, G. He, H. Hou, Z. Zhang and J. Ma, “Memory efficient layered decoder design with early termination for LDPC codes," 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 2011, pp. 2697-2700.
  20. Y. -H. Chen, Y. -J. Chen, X. -Y. Shih and A. -Y. Wu, “A Channel-Adaptive Early Termination strategy for LDPC decoders," 2009 IEEE Workshop on Signal Processing Systems, Tampere, Finland, 2009, pp. 226-231.
  21. M. Ferrari, S. Bellini and A. Tomasoni, “Safe Early Stopping for Layered LDPC Decoding," in IEEE Communications Letters, 2015, vol. 19, no. 3, pp. 315-318. [CrossRef]
  22. J. Frenzel, S. Muller-Weinfurtner, J. B. Huber and R. R. Muller, “Convergence Behavior of LDPC Decoding and Application to Early Termination," 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, 2018, pp. 1-6.
  23. F. Kienle and N. Wehn, “Low complexity stopping criterion for LDPC code decoders," 2005 IEEE 61st Vehicular Technology Conference, Stockholm, Sweden, 2005, pp. 606-609 Vol. 1.
  24. M. Ferrari, S. Bellini and A. Tomasoni, "Safe Early Stopping for Layered LDPC Decoding," in IEEE Communications Letters, 2015, vol. 19, no. 3, pp. 315-318. [CrossRef]
  25. J. Fan and H. Yang, “A new forced convergence decoding scheme for LDPC codes," 2009 IEEE International Conference on Communications Technology and Applications, Beijing, China, 2009, pp. 576-580.
  26. M. Sarajlic, L. Liu and O. Edfors, “Modified forced convergence decoding of LDPC codes with optimized decoder parameters," 2015 IEEE 26th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Hong Kong, China, 2015, pp. 440-445.
  27. R. Aoyama and Y. Kaji, “Improvement of the forced-convergence decoding for LDPC codes," 2008 International Symposium on Information Theory and Its Applications, Auckland, New Zealand, 2008, pp. 1-6.
  28. E. Zimmermann, W. Rave and G. Fettweis, “Forced Convergence Decoding of LDPC Codes - EXIT Chart Analysis and Combination with Node Complexity Reduction Techniques," 11th European Wireless Conference 2005 - Next Generation wireless and Mobile Communications and Services, Nicosia, Cyprus, 2006, pp. 1-8.
  29. J. Bae, B. J. Choi and M. H. Sunwoo, “Special session: Low power LDPC deocder using adaptive forced convergence algorithm," 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 2017, pp. 309-312.
  30. B. J. Choi and M. H. Sunwoo, “Efficient Forced Convergence algorithm for low power LDPC decoders," 2013 International SoC Design Conference (ISOCC), Busan, Korea (South), 2013, pp. 372-373.
  31. B. J. Choi and M. H. Sunwoo, "Simplified forced convergence decoding algorithm for low power LDPC decoders," 2014 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Ishigaki, Japan, 2014, pp. 663-666.
Preprints 110726 g001
Figure 1. Local/global two-phases decoding
Figure 1. Local/global two-phases decoding
Preprints 110726 g001
Preprints 110726 g002
Figure 2. flow chart of ET-1
Figure 2. flow chart of ET-1
Preprints 110726 g002
Preprints 110726 g003
Figure 3. flow chart of ET-2
Figure 3. flow chart of ET-2
Preprints 110726 g003
Preprints 110726 g004
Figure 4. Probability of successful local decoding in 20 iterations with different SNR
Figure 4. Probability of successful local decoding in 20 iterations with different SNR
Preprints 110726 g004
Preprints 110726 g005
Figure 5. ROC curves in different value of v 2 , m i n
Figure 5. ROC curves in different value of v 2 , m i n
Preprints 110726 g005
Preprints 110726 g006
Figure 6. complexity of GC-1 in different ET-1 schemes
Figure 6. complexity of GC-1 in different ET-1 schemes
Preprints 110726 g006
Preprints 110726 g007
Figure 7. performances of GC-1 in different ET-1 schemes
Figure 7. performances of GC-1 in different ET-1 schemes
Preprints 110726 g007
Preprints 110726 g008
Figure 8. complexity of GC-1 in different ET-2 scheme
Figure 8. complexity of GC-1 in different ET-2 scheme
Preprints 110726 g008
Preprints 110726 g009
Figure 9. performance of GC-1 in different ET-2 scheme
Figure 9. performance of GC-1 in different ET-2 scheme
Preprints 110726 g009
Preprints 110726 g010
Figure 10. performance of GC-1 in ET-1-FC decoding scheme
Figure 10. performance of GC-1 in ET-1-FC decoding scheme
Preprints 110726 g010
Preprints 110726 g011
Figure 11. complexity of GC-1 in ET-1-FC decoding scheme
Figure 11. complexity of GC-1 in ET-1-FC decoding scheme
Preprints 110726 g011
Preprints 110726 g012
Figure 12. performance of GC-1 in ET-2-FC decoding scheme
Figure 12. performance of GC-1 in ET-2-FC decoding scheme
Preprints 110726 g012
Preprints 110726 g013
Figure 13. complexity of GC-1 in ET-2-FC decoding scheme
Figure 13. complexity of GC-1 in ET-2-FC decoding scheme
Preprints 110726 g013
Table 1. optimized parameters of C 1 and C 2
Table 1. optimized parameters of C 1 and C 2
C 1 C 2
T=1 θ = 5
l 1 t h r = 10 l 2 t h r = 4
v 1 t h r = 0.8 v 2 t h r = 0.39
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated