The Muon g-2 in a Regularized Electrodynamics

Preprint

Article

The Muon g-2 in a Regularized Electrodynamics

Altmetrics

Downloads

145

Views

205

Comments

Miroslav Georgiev^*

This version is not peer-reviewed

Submitted:

30 June 2024

Posted:

02 July 2024

Read the latest preprint version here

Alerts

Abstract

The present paper reports exact results for the muon self-energy and anomalous g-factor. A unique to the muon cut-off terms that remove the radial singularity in the system and regularize the corresponding electrodynamics are presented. Equations of motion and a transcendental equation satisfied by the muon anomalous g-factor are derived, with solution a_m=0.001165920162(198). The obtained value matches the latest experimental one found in the literature to about 0.43 ppb ruling out a possible tension between theory and experiment.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

The study of the electron’s anomalous magnetic dipole moment have played an essential role in the development of quantum theory [1,2,3,4]. After its successful theoretical description it was expected that the followed calculation of the anomalous component in the muon’s magnetic dipole moment will strengthen and crystallize the established knowledge [5,6,7,8]. Over the decades, however, with the improvement of the experimental setup and the consequent highly precise measurements the gap between the measured and calculated values not only remained but thickened [9,10,11,12,13]. The difference between the most recent experimental result [14] and the most recent consensus for the theoretical value [15] is about

2.49

ppb, a value that is greater than the relevant uncertainty. In the light of the seeming discrepancy many efforts to revise and improve the hadronic vacuum polarization corrections [16,17,18,19,20] and the hadronic light-by-light scattering one [19,20,21,22,23] have been considered. It is believed that these contributions have the prospect to reduce the obtained tension. On the other hand, the regularization procedure [24,25,26,27,28,29,30] within the classical and semi-classical methods have recently demonstrated great potential in quantifying the self-interaction and electron’s anomalous magnetic moment.

The present study implements the regularization procedure proposed in Ref. [30] (see also Ref. [31]) to quantify the anomalous component in the muon’s magnetic dipole moment and to study the seeming tension between theory and experiment. The used approach represents a regularized electrodynamics that is tightly bound to the quantum theory beyond the corresponding principle. Accordingly, exact results for the muon’s self-energy, anomalous g-factor and all intrinsic characteristics underlying the dynamics of its self-interaction are reported. Improved accuracy in the calculation of the muon anomalous g-factor is obtained (

0.43

ppb), overcoming the existing gap between the average value predicted by the quantum theory [15] and the measured one [14]. An essential outcome of the obtained accuracy is an exact bound on the sum of the muon and electron neutrinos’ rest masses.

2. Theoretical Framework

Thereunder, the used mathematical framework follows closely the one introduced in Ref. [30].

2.1. Generalities

Let

R

be the rest frame of reference of a free muon, with rest mass and electric charge denoted by

m_{μ}

and

\bar{e} = - e

, where e is the elementary charge. Let

r_{c μ} = α {\bar{λ}}_{c μ}

be the muon’s electromagnetic radius in

R

, where

α

and

{\bar{λ}}_{c μ}

are the fine structure constant and associated reduced Compton wavelength, respectively. Let

r_{μ}

be the intrinsic field vector of the muon, with magnitude

r_{μ}

, and

{\tilde{u}}_{μ}

be the magnitude of the tangential velocity

{\tilde{u}}_{μ}

related to its rotation about the origin of

R

in the plane perpendicular to the muon’s relative velocity

u_{μ} = u_{μ} κ

, where

κ

is the respective unit vector. The corresponding oscillation is characterized by an angular velocity

ω_{μ}

, with magnitude

ω_{μ} = {\tilde{u}}_{μ} r_{μ}^{- 1}

representing the muon’s intrinsic angular frequency. For more details the reader may consult Ref. [30]. The quantities

r_{μ}

and

{\tilde{u}}_{μ}

are conjugate and satisfy

r_{μ} {\tilde{u}}_{μ} = {\bar{λ}}_{c μ} c,

(1)

where c is the light speed in vacuum.

The charge

ρ_{e}

and mass

ρ_{m_{μ}}

densities are defined within the spherically symmetric spatial domain

Ω_{c μ} \in R^{3}

, with radius

r_{c μ}

, boundary

\partial Ω_{c μ}

and volume

V_{c μ}

. They satisfy the relation

ρ_{e} ρ_{m_{μ}}^{- 1} = e m_{μ}^{- 1}

. Moreover,

ρ_{M_{μ}}

is the muon’s effective mass density and

M_{μ} = m_{μ} (1 + a_{μ})

is the corresponding effective rest mass defined within

\partial Ω_{c μ}

, where

a_{μ}

is the muon’s anomalous g-factor. Here,

ρ_{M_{μ}} = ρ_{M_{μ}} (r)

is a smooth function of the radial parameter r, with

r \in (0, + \infty)

and

ρ_{M_{μ}} > ρ_{m_{μ}}

for all r. Note that if

∄ e

, then

ρ_{M_{μ}} = ρ_{m_{μ}}

The inherent dynamics of

r_{μ}

underpin the occurrence of intrinsic magnetic moment

μ_{μ} = - \frac{1}{2} g_{μ} μ_{B} κ

, where

g_{μ} = 2 (1 + a_{μ})

is the g-factor of the muon and

μ_{B}

is the Bohr magneton. We further have

g_{μ} = \frac{2}{V_{c μ}} \int_{Ω_{c μ}} G_{μ} d v, G_{μ} = \frac{e ρ_{M_{μ}}}{m_{μ} ρ_{e}} .

(2)

2.2. Electromagnetic Field Scalar Potential and Energy

Within the considered approach the electromagnetic field related to the self-interacting muon is time independent and does not propagate in space independently from the particle. The Lorenz gauge is trivially satisfied and the radial singularity is removed by a regularization. For the corresponding electromagnetic field scalar potential, we have

φ_{μ} (r) = γ_{μ} η_{μ} ψ_{μ} (r), η_{μ} = 1 + \frac{u_{μ}^{2}}{c^{2}},

(3)

where

γ_{μ}

is the Lorentz factor,

ψ_{μ} (r) = \frac{\bar{e}}{4 π ε_{o} r} (2 - e^{- χ_{μ} r} - e^{- {\tilde{χ}}_{μ} r}),

(4)

ε_{o}

is the electric constant. Here, the scaling constants of both cutoff terms in eq. (4) read

χ_{μ} = \frac{γ_{μ} m_{μ} c}{(1 + a_{e}) h}, {\tilde{χ}}_{μ} = \frac{γ_{μ} (m_{e} + δ m_{ν}) c}{(1 + a_{μ}) h},

where

a_{e}

and

m_{e}

denote the electron’s anomalous g-factor and rest mass, respectively. Furthermore, we have

δ m_{ν} = m_{ν_{μ}} + m_{{\bar{ν}}_{e}}

, where

m_{ν_{μ}}

is the muon neutrino rest mass and

m_{{\bar{ν}}_{e}}

is the electron anti-neutrino rest mass. Both neutrinos emerge from a decay of the self-interacting muon, with

δ m_{ν} > 0

for all

r \in (0, + \infty)

. We would like to point out that the two Yukawa terms in eq. (4) do not represent an on shell massive photon [32]. The photons are massless and from the perspective of quantum physics

χ_{μ}

and

{\tilde{χ}}_{μ}

will represent the wave numbers of effectively massive off shell photons, with total effective mass

m_{μ} {(1 + a_{e})}^{- 1}

and

(m_{e} + δ m_{ν}) {(1 + a_{μ})}^{- 1}

, respectively.

The field equation satisfied by the function in Equation (4) reads

Δ_{r} ψ_{μ} (r) - χ_{μ}^{2} ϕ_{μ} (r) - {\tilde{χ}}_{μ}^{2} {\tilde{ϕ}}_{μ} (r) = 0,

where

Δ_{r}

represents the radial Laplace operator in spherical symmetry,

ϕ_{μ}

and

{\tilde{ϕ}}_{μ}

are the cut-off terms implying the following boundary conditions

ψ_{μ} (r) = \{\begin{matrix} 0, & r \to \infty, & u_{μ} < c \\ (χ_{μ} + {\tilde{χ}}_{μ}) \frac{\bar{e}}{4 π ε_{o}}, & r \to 0, & u_{μ} < c \end{matrix} .

For the corresponding vector potential representation the reader is encouraged to consult Ref. [30].

The energy of the electromagnetic field in the considered system,

W_{μ} (r)

, is also regularized. Integrating the corresponding energy density

ε_{o} {| \nabla_{r} φ_{μ} (r) |}^{2}

over

R^{3}

, we obtain

\begin{matrix} W_{μ} (r) & = C_{μ} \frac{r_{c μ}}{2 r} (8 (e^{2 (χ_{μ} + {\tilde{χ}}_{μ}) r} - e^{(2 χ_{μ} + {\tilde{χ}}_{μ}) r} - e^{(χ_{μ} + 2 {\tilde{χ}}_{μ}) r}) + (2 + χ_{μ} r) e^{2 {\tilde{χ}}_{μ} r} \\ + (2 + {\tilde{χ}}_{μ} r) e^{2 χ_{μ} r} + 4 \frac{(χ_{μ} + {\tilde{χ}}_{μ} + χ_{μ} {\tilde{χ}}_{μ} r)}{χ_{μ} + {\tilde{χ}}_{μ}}) e^{- 2 (χ_{μ} + {\tilde{χ}}_{μ}) r}, \end{matrix}

where

C_{μ} = γ_{μ}^{2} η_{μ}^{2} m_{μ} c^{2}

. At the origin of

R

and for

u_{μ} < c

the electromagnetic field energy is finite. Thus, we have

lim_{r \to 0} W_{μ} (r) = C_{μ} r_{c μ} \frac{χ_{μ}^{2} + 6 χ_{μ} {\tilde{χ}}_{μ} + {\tilde{χ}}_{μ}^{2}}{2 (χ_{μ} + {\tilde{χ}}_{μ})} .

It is worth noting that in contrast to the non-regularized electrodynamics, here for all values of r the electromagnetic field constrained to the particle vanish when the particle’s rest mass equals zero. Thus, hypothetically, a particle of zero rest mass will appear as electrically neutral even in the case it possess electric charge.

3. Self-Energy

To represent the self-energy of the muon we take into account the Hamiltonian formalism.

3.1. The Hamiltonian

By analogy to the case of self-interacting electron (see Ref. [30]), the energy of a self-interacting muon is spatially independent and the corresponding Hamiltonian do not depend explicitly on time. We have

H_{μ} = γ_{μ} m_{μ} c^{2} + Σ_{μ},

(5)

where

Σ_{μ}

is the self-energy term. The latter is not a potential energy of a gradient field and equals the spatial average over the domain

Ω_{c μ}

of the interaction energy

\bar{e} φ_{μ}

. In particular, with respect to Equation (3), we have the representation

Σ_{μ} = γ_{μ} c^{2} \int_{Ω_{c μ}} (ρ_{M_{μ}} - ρ_{m_{μ}}) d v,

(6)

where the effective mass density reads

\begin{matrix} ρ_{M_{μ}} = ρ_{m_{μ}} (1 + η_{μ} \frac{r_{c μ}}{r} (2 - e^{- χ_{μ} r} - e^{- {\tilde{χ}}_{μ} r})) . \end{matrix}

(7)

3.2. The Hamiltonian Density

The information about the muon’s intrinsic dynamics is embedded in the Hamiltonian density

H_{μ}

associated to Equation (5). Taking into account Equation (1) for

r \equiv r_{μ}

we get

H_{μ} = c^{2} ρ_{m_{μ}} (γ_{μ} + \frac{α}{m_{μ} c} P_{μ}),

where

P_{μ} = γ_{μ} η_{μ} m_{μ} {\tilde{u}}_{μ} (2 - e^{- χ_{μ} r_{μ}} - e^{- {\tilde{χ}}_{μ} r_{μ}})

is the corresponding generalized momentum. Accordingly, we have the equations of motion

{\tilde{u}}_{μ} = \int_{Ω_{c μ}} \frac{\partial H_{μ}}{\partial P_{μ}} d v, {\dot{P}}_{μ} = 0

and subsequently the exact values

{\tilde{u}}_{μ} = α c, η_{μ} = 1 + α^{2}, γ_{μ}^{- 1} = \sqrt{1 - α^{2}} .

(8)

According to the applied formalism the magnitude of the tangential velocity is invariant with respect to the particles mass and hence

{\tilde{u}}_{μ} = {\tilde{u}}_{e}

, where

{\tilde{u}}_{e}

is associated to the electron.

3.3. Effective Mass-Energy Equivalence

Accounting for Equation (2), from Equations (6) and (7) we obtain

Σ_{μ} = a_{μ} γ_{μ} m_{μ} c^{2} .

As a result, from Equation (5) we get the effective rest energy

E_{μ} = γ_{μ} M_{μ} c^{2} .

(9)

Therefore, it appears that as a result of the self-interaction the muon’s energy would be

γ_{μ} (1 + a_{μ})

times higher that its rest energy.

4. The Anomalous g-Factor

In addition to the quantum field theory approach [11,15] in calculating the muon’s anomalous g-factor, we have a classical one yielding a unique transcendental equation for its calculation. In particular, accounting for Equations (2), (7) and (8), we obtain

a_{μ} = a_{e} + 3 η_{μ} (\frac{1}{2} - (\frac{1 - e^{- \frac{α γ_{μ} ξ_{μ}}{2 π (1 + a_{μ})}} (1 + \frac{α γ_{μ} ξ_{μ}}{2 π (1 + a_{μ})})}{{(\frac{α γ_{μ} ξ_{μ}}{2 π (1 + a_{μ})})}^{2}})),

(10)

where

ξ_{μ} = \frac{m_{e} + δ m_{ν}}{m_{μ}} .

(11)

The value of

a_{μ}

calculated from Equation (10) is given in the second row of Table 1, where the values of

a_{e}

and

α

are taken from Ref. [30]. The obtained accuracy regarding the most recent experimental measurements [14] is about

0.43

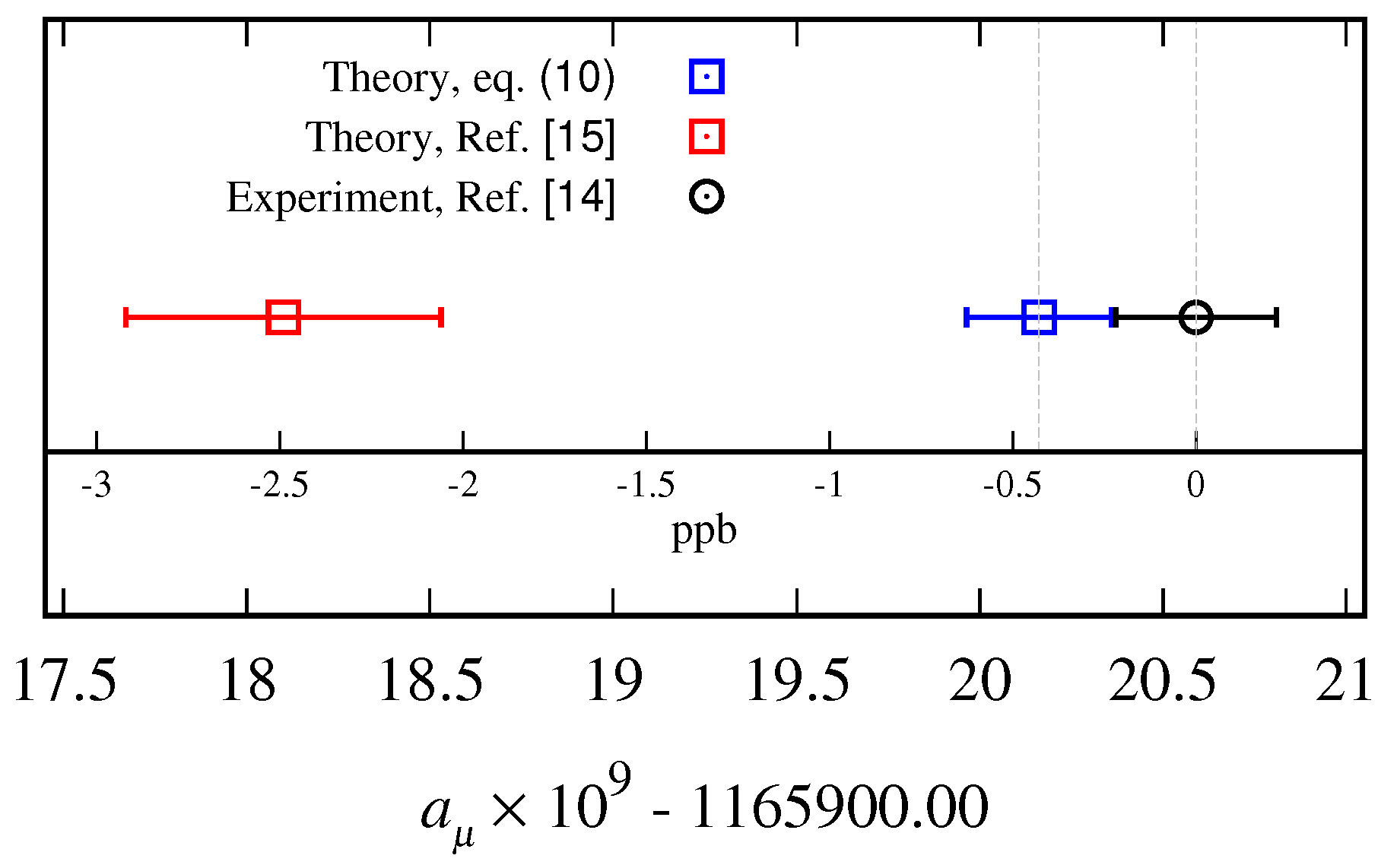
ppb, see Figure 1. On the same figure, a comparison with the latest known prediction of the quantum theory is also depicted. The value of mass ratio in Equation (11) is given in the third column of Table 1. We have

δ m_{ν} = 3.57763 \times 10^{- 38}

kg, where the values of electron’s and muon’s rest masses are taken from NIST [33]. This result suggest that the sum of the muon neutrino and electron anti-neutrino rest energies is approximately

0.02013

eV, which is consistent with the reported upper bound on the sum of the three flavor neutrino rest energies of about

0.120

eV (see Ref. [34]). Moreover, it suggests that the electron anti-neutrino mass satisfies the inequality

m_{{\bar{ν}}_{e}} < 3.57763 \times 10^{- 38}

kg. This bound is approximately 40 times lower than the one set by KATRIN collaboration [35], see also Ref. [36].

5. Summary and Conclusions

The present paper demonstrates the potential of regularized classical theory in describing qualitatively and quantitatively the self-energy, spin and anomalous magnetic moments of the muon. It also uncovers a key aspects from the elusive interrelationship between the classical and quantum theory that may reshape our understanding of their frontiers.

In particular, all observables characterizing the muon’s self-interaction are calculated exactly including those underlying its wave-like behavior. The muon’s anomalous g-factor is computed with high accuracy, improving the one obtained from the latest quantum theory calculations (see Figure 1 and Table 1) suggesting a possible ground for weakening the tension between the quantum theory and experiment. The obtained accuracy implies that the muon and electron neutrinos have a non-zero rest mass contributing to the elector-muon mass ratio, with upper bound of their sum equal to

3.57763 \times 10^{- 38}

kg, see Equations (10) and (11).

The used approach can be further applied to quantify the intrinsic dynamics of the tau lepton and fix the range of values taken by the corresponding anomalous g-factor determined by the multiplicity of branching fractions.

Author Contributions

Not applicable.

Funding

Not applicable.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data generated within this research is included in the paper.

Acknowledgments

Not applicable.

Conflicts of Interest

Not applicable.

References

Vogel, M. The anomalous magnetic moment of the electron. Contemp. Phys. 2009, 50, 437–452. [Google Scholar] [CrossRef]
Laporta, S.; Remiddi, E. Analytic QED Calculations of the Anomalous Magnetic Moment of the Electron. In Advanced Series on Directions in High Energy Physics; WORLD SCIENTIFIC, 2009; Vol. 20, pp. 119–156. [Google Scholar] [CrossRef]
Aoyama, T.; Kinoshita, T.; Nio, M. Theory of the Anomalous Magnetic Moment of the Electron. Atoms 2019, 7, 28. [Google Scholar] [CrossRef]
Fan, X.; Myers, T.; Sukra, B.; Gabrielse, G. Measurement of the Electron Magnetic Moment. Phys. Rev. Lett. 2023, 130, 071801. [Google Scholar] [CrossRef] [PubMed]
Farley, F. The 47 years of muon g-2. Prog. Part. Nucl. Phys. 2004, 52, 1–83. [Google Scholar] [CrossRef]
Jegerlehner, F.; Nyffeler, A. The muon g-2. Phys. Rep. 2009, 477, 1–110. [Google Scholar] [CrossRef]
Jegerlehner, F. The Anomalous Magnetic Moment of the Muon; Vol. 274, Springer Tracts in Modern Physics; Springer International Publishing: Cham, 2017. [Google Scholar] [CrossRef]
Solovtsova, O.P.; Lashkevich, V.I.; Kaptari, L.P. Lepton anomaly from QED diagrams with vacuum polarization insertions within the Mellin-Barnes representation. Eur. Phys. J. Plus 2023, 138, 212. [Google Scholar] [CrossRef]
De Conto, G.; Pleitez, V. Electron and muon anomalous magnetic dipole moment in a 3-3-1 model. J. High Energ. Phys. 2017, 2017, 104. [Google Scholar] [CrossRef]
Logashenko, I.B.; Eidelman, S.I. Anomalous magnetic moment of the muon. Phys.-Usp. 2018, 61, 480–510. [Google Scholar] [CrossRef]
Keshavarzi, A.; Khaw, K.S.; Yoshioka, T. Muon g-2: A review. Nucl. Phys. B 2022, 975, 115675. [Google Scholar] [CrossRef]
Dinh, D. Muon anomalous magnetic dipole moment in a low scale type I see-saw model. Nucl. Phys. B 2023, 994, 116306. [Google Scholar] [CrossRef]
Winter, P. Status of the Muon g - 2 experiment. EPJ Web of Conf. 2023, 289, 01001. [Google Scholar] [CrossRef]
Aguillard, D.P.; Albahri, T.; Allspach, D.; Anisenkov, A.; Badgley, K.; Baeßler, S.; Bailey, I.; Bailey, L.; Baranov, V.A.; Barlas-Yucel, E.; et al. Measurement of the Positive Muon Anomalous Magnetic Moment to 0.20 ppm. Phys. Rev. Lett. 2023, 131, 161802. [Google Scholar] [CrossRef]
Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Carloni Calame, C.; Cé, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Phys. Rep. 2020, 887, 1–166. [Google Scholar] [CrossRef]
Morte, M.D.; Francis, A.; Gülpers, V.; Herdoíza, G.; Von Hippel, G.; Horch, H.; Jäger, B.; Meyer, H.B.; Nyffeler, A.; Wittig, H. The hadronic vacuum polarization contribution to the muon g-2 from lattice QCD. J. High Energ. Phys. 2017, 2017, 20. [Google Scholar] [CrossRef]
Westin, A.; Kamleh, W.; Young, R.; Zanotti, J.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.; Schierholz, G.; Stüben, H. Anomalous magnetic moment of the muon with dynamical QCD+QED. EPJ Web Conf. 2020, 245, 06035. [Google Scholar] [CrossRef]
Borsanyi, S.; Fodor, Z.; Guenther, J.N.; Hoelbling, C.; Katz, S.D.; Lellouch, L.; Lippert, T.; Miura, K.; Parato, L.; Szabo, K.K.; et al. Leading hadronic contribution to the muon magnetic moment from lattice QCD. Nature 2021, 593, 51–55. [Google Scholar] [CrossRef]
Gérardin, A. The anomalous magnetic moment of the muon: status of lattice QCD calculations. Eur. Phys. J. A 2021, 57, 116. [Google Scholar] [CrossRef]
Nedelko, S.; Nikolskii, A.; Voronin, V. Soft gluon fields and anomalous magnetic moment of muon. J. Phys. G: Nucl. Part. Phys. 2022, 49, 035003. [Google Scholar] [CrossRef]
Blum, T.; Christ, N.; Hayakawa, M.; Izubuchi, T.; Jin, L.; Jung, C.; Lehner, C. Hadronic Light-by-Light Scattering Contribution to the Muon Anomalous Magnetic Moment from Lattice QCD. Phys. Rev. Lett. 2020, 124, 132002. [Google Scholar] [CrossRef]
Melo, D.; Reyes, E.; Fazio, R. Hadronic Light-by-Light Corrections to the Muon Anomalous Magnetic Moment. Particles 2024, 7, 327–381. [Google Scholar] [CrossRef]
Leutgeb, J.; Mager, J.; Rebhan, A. Holographic QCD and the muon anomalous magnetic moment. Eur. Phys. J. C 2021, 81, 1008. [Google Scholar] [CrossRef]
Groenewold, H.J. Regularized models in electrodynamics. Physica 1962, 28, 1265–1293. [Google Scholar] [CrossRef]
Barut, A.O.; Van Huele, J.F. Quantum electrodynamics based on self-energy: Lamb shift and spontaneous emission without field quantization. Phys. Rev. A 1985, 32, 3187–3195. [Google Scholar] [CrossRef]
Ibison, M. Some Properties of a Regularized Classical Electromagnetic Self-Interaction. In Causality and Locality in Modern Physics; Hunter, G., Jeffers, S., Vigier, J.P., Eds.; Springer Netherlands: Dordrecht, 1998; pp. 477–489. [Google Scholar] [CrossRef]
Galakhov, D. Self-interaction and regularization of classical electrodynamics in higher dimensions. JETP Letters 2008, 87, 452–458. [Google Scholar] [CrossRef]
Perlick, V. On the Self-force in Electrodynamics and Implications for Gravity. In Equations of Motion in Relativistic Gravity; Puetzfeld, D., Lämmerzahl, C., Schutz, B., Eds.; Springer International Publishing: Cham, 2015. [Google Scholar] [CrossRef]
Hale, T.; Kubizňák, D.; Svítek, O.; Tahamtan, T. Solutions and basic properties of regularized Maxwell theory. Phys. Rev. D 2023, 107, 124031. [Google Scholar] [CrossRef]
Georgiev, M. Exact classical approach to the electron’s self-energy and anomalous g-factor. Europhys. Lett. 2024. [Google Scholar] [CrossRef]
Georgiev, M. Self-Interactions, Self-Energy and the Electromagnetic Contribution to the Anomalous g-Factor. preprint. Phys. Sci. 2023. [Google Scholar] [CrossRef]
Tu, L.C.; Luo, J.; Gillies, G.T. The mass of the photon. Rep. Prog. Phys. 2005, 68, 77–130. [Google Scholar] [CrossRef]
2018 CODATA Value: electron mass and muon mass. The NIST Reference on Constants, Units, and Uncertainty. NIST 2019.
Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results: VI. Cosmological parameters. A & A 2020, 641, A6. [Google Scholar] [CrossRef]
The KATRIN Collaboration; Aker, M.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Bieringer, B.; Block, F.; Bobien, S.; Böttcher, M.; et al. Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat. Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
Schweiger, C.; Braß, M.; Debierre, V.; Door, M.; Dorrer, H.; Düllmann, C.E.; Enss, C.; Filianin, P.; Gastaldo, L.; Harman, Z.; et al. Penning-trap measurement of the Q value of electron capture in 163Ho for the determination of the electron neutrino mass. Nat. Phys. 2024, 20, 921–927. [Google Scholar] [CrossRef]

Figure 1. Comparison between the most recent experimental result (black circle) for the muon’s anomalous g-factor and its value obtained from Equation (10) (blue square). In addition the latest result predicted by the quantum theory (red square) is also shown. The depicted data is further provided in Table 1.

Table 1. Theoretical and experimental data for the muon’s anomalous g-factor (second column). The classical electrodynamics (CED) and quantum field theory (QFT) results are given in the second and third rows, respectively. Fourth row represents the summary of the most recent measurements. The value of mass ratio

ξ_{μ}

follows from Equation (11). For additional details see Figure 1.

ξ_{μ}

follows from Equation (11). For additional details see Figure 1.

	$a_{μ}$	$ξ_{μ}$	Ref.
CED	$0.001165920162 (198)$	$0.00483633188245 (30)$	Eq. (10)
QFT	$0.00116591810 (43)$	−	[15]
Experiment	$0.00116592059 (22)$	−	[14]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

The Muon g-2 in a Regularized Electrodynamics

Abstract

1. Introduction

2. Theoretical Framework

2.1. Generalities

2.2. Electromagnetic Field Scalar Potential and Energy

3. Self-Energy

3.1. The Hamiltonian

3.2. The Hamiltonian Density

3.3. Effective Mass-Energy Equivalence

4. The Anomalous g-Factor

5. Summary and Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe