On the Quantum Origin of the Periodic Table - The Role of Electron Dynamics and Energy Degeneracy in Atomic Reactivity and Chemical Bonding

Preprint

Article

On the Quantum Origin of the Periodic Table - The Role of Electron Dynamics and Energy Degeneracy in Atomic Reactivity and Chemical Bonding

Altmetrics

Downloads

Views

Comments

Sture Nordholm^*

This version is not peer-reviewed

Submitted:

01 July 2024

Posted:

02 July 2024

You are already at the latest version

Alerts

Abstract

Abstract: A perspective is provided which illustrates the central role of quantum mechanics in the structure and periodically varying properties of atoms and in the formation of molecules. Despite having only about one hundred basic building blocks for all substances, chemistry is a subtle discipline due to it’s fundamentally quantum mechanical origin. The atoms, and their behavior as systematized in the Periodic Table, intimately reflect mechanisms natural to quantum mechanics but foreign to classical mechanics. Given their very small mass, the electrons form atomic structures only predictable by the use of quantum mechanics. Thereby the foundation of chemistry is totally dominated by quantum effects which are generally known only empirically, e.g. as in the Periodic Table. Recently these quantum effects have increasingly become known computationally, but not necessarily understood physically and therefore still challenge students and users of chemistry. In order to provide physical insight we extract here, from known facts and relations of quantum mechanics, but without reliance on detailed mathematics or numerical analysis, a simplest, yet fully consistent, physical explanation of atomic structure and periodically variable reactivity. Atomic reactivity is found to arise due to dynamical constraints on electron motion which lead to degeneracy in the atomic energy spectrum. There is a strong correlation between energy degeneracy and reactivity with the inert gas atoms found to display no degeneracy. Chemical bonding follows as a means of atomic reactivity relaxation and reduction of energy degeneracy, achieved by permanent electron rearrangement (ionic bonding) or by oscillatory electron motion between atoms (covalent bonding). Ionic bonding is directly related to the variable stability of atomic structures which extends from neutral atoms to atomic ions. These stable ions then form molecular structures by electrostatic attraction in neutral ionic clusters. The covalent bonding mechanism is fundamentally dynamical and interatomic since it depends directly on the facility with which electrons can move between atomic centers in a molecule. Both the ionic and the covalent mechanism, interatomic displacement and oscillation of electrons, are active in any bond between atoms of different species.

Keywords:

Subject: Chemistry and Materials Science - Theoretical Chemistry

Introduction

The long history of chemistry clearly shows an early focus on the atoms as independent elements and building blocks of molecules and substances. With the advent of the Periodic Table about 150 years ago [1], it became possible to understand atomic properties as periodically variable with the atomic number of the atom [2]. Most atoms are individually reactive and rarely found in nature in gaseous form but sometimes in the form of pure elementary substances and more often as molecules in multi-atomic substances stabilized by some form of chemical bonding. There are, however, a small set of inert (or noble) atoms that are nearly always found in such gaseous form with independently moving particles. Thus it was clear from the early years of chemistry, after the composition of atoms of central nuclei and surrounding electrons had been determined [Thomson [4], Rutherford [5]], that some electronic structures of atoms, those of the inert gas atoms, were exceptionally stable while all others were reactive to a generally strong but very variable degree. Before the arrival of quantum mechanics, atomic structures and their periodically varying properties could not be understood by first principle, but an empirical rule was deduced and drawn upon in early modelling of chemical bonding.

e.g. by Lewis [6], Langmuir [7]]: Inert-gas-like electronic structures of atoms are particularly stable. This rule, and its corollary, electronic structures of atoms which are not inert-gas-like are reactive, became, in a retrospective view, a form of “empirical quantum mechanics of atoms” that was extracted from the Periodic Table and used to understand chemical bonding and molecule formation.

The early models of chemical bonding and molecule formation could be rationalized by the use of this stability rule which singled out neutral atoms of nuclear charge +Ze with Z = 2 (helium), 10 (neon), 18 (argon), 36 (krypton) … as particularly stable. One simply noted that the stability must be related to the number of electrons N_e (= 2, 10, 18, 36 … for the inert gas atoms) more than to the charge of the nucleus. The special electronic stability applies to atomic ions as well if the number of electrons is 2, 10, 18 etcetera. Thus one could achieve stability by forming molecules such that, by transfer of electrons between atoms, a cluster of atomic ions would form where all ions had 2, 10, 18, … electrons. Valence numbers, indicating how many electrons an atom would need to gain or lose to reach an inert gas electronic structure, were found to explain a major part of the specificity of the chemical bonding in molecule formation. This empirical quantum mechanics of atoms suffices to provide a fundamental understanding of ionic bonding. This electron transfer mechanism works well to explain many stable molecules but not for some of the most important, e.g. H₂, N₂, O₂. In such molecules the valence numbers are not summing to zero, as +1 and -1 in HF, but are by symmetry the same, i.e. covalent.

The early notion of covalency was that it reflected, not a transfer of electrons between atomic centers, but a sharing of electrons [Lewis [8]]. It became popular (and still is) to graphically represent the two electrons in H₂ not to permanently transfer between the protons to form either H⁺H^- or H^-H⁺, but to form H:H, where the two electrons (as dots) are taken to be shared equally between the two protons. Thus both hydrogen atoms have equal claim to the stable helium electronic structure. Similarly, the electronic structures of N₂ and O₂ were taken to display 6 and 4 shared electrons, respectively, allowing these N and O -atoms to take on some of the stability of Ne.

Without the use of any formal quantum mechanics it was in this way possible to develop an understanding of two mechanisms of chemical bonding, the ionic (electron transfer) and the covalent (electron sharing), which had great predictive power for molecule formation. The arrival and rapid development of quantum mechanics in the early 1900’s caused the very simple models above to be refined and extended with increasing input of quantum mechanics. Lewis [6,8,9] incorporated the idea of electron pairing which led, with the help of Langmuir [7,10], to the famous octet rule, Lewis electron dot diagrams and later to geometry prediction by the valence shell electron pair repulsion (VSEPR) method [11] popularized by Gillespie and Nyholm [12,13]. After the arrival of quantum mechanics to chemistry, Pauling [14,15,16] introduced an empirical form of the quantum-mechanical valence bond (VB) theory, first used by Heitler and London for H₂ [17], wherein local bonds are formed between pairs of atoms. These bonds are represented by small wave functions involving only the bonding electrons while the other electrons (for molecules larger than H₂) remain represented by atomic configurations. The interatomic molecular wave functions serve to bridge and bond atoms while the other nonbonding electrons contribute a repulsion between bonded atoms. The atomic orbital geometries and the hybridization of them to extend in new directions contributed greatly to the success of Pauling’s empirical VB theory [18]. To a comforting degree the more empirical octet rule-VSEPR and the semi-empirical VB models agree, showing that intuitive and approximate forms of quantum mechanics can be found to help chemists understand fundamental aspects of chemical bonding and molecule formation. These models remain in general use.

The relatively great success, and corresponding longevity, of these simple intuitive (octet rule, VSEPR and VB) models of bonding, molecular stability and geometry, has now been complemented by an even greater success of computational quantum chemistry [19] in providing first principle predictions of molecular ground states and properties. It would be reasonable to expect quantum chemistry to produce better understanding and more refined physical models of bonding but, unfortunately, this development has lagged behind high expectations. The access to rigorous and accurate quantum chemical methods has certainly helped understand [20,21], but not greatly elucidated and improved, the simple models above, nor resolved the historical debate over the best physical interpretation of the computational results, or overcome the inherent subtlety of the quantum effects. The Schrödinger equation clearly “knows about” chemical, and in particular covalent, bonding but its numerical answers rarely come with clear-cut physical explanations. The old bonding models are still used in essentially unchanged form. There is much discussion and disagreement over whether energy analysis or dynamical analysis (or both, as we suggest) should be the chosen way to understand chemical bonding. With rare exceptions energy analysis is chosen, given its dominant role in main-stream quantum chemistry, but there is still a lingering question whether the electrostatic interactions [22] or the kinetic energy variations should be regarded as the key to bonding. The answer must account for the paradoxical role of the virial theorem [23] which at first inspection seems to clearly favour electrostatics but on closer inspection does not. Further debate relates to whether electron densities are the natural vehicles [24] for a bonding analysis or wave functions are essential.

Here we shall try to resolve, or at least mitigate, these uncertainties and difficulties by drawing on important qualitative features of quantum mechanics while using only simple intuitive arguments from the full quantum mechanical theory of atoms and molecules. The emphasis will be on atoms, the periodic table and the origin of the periodicity of atomic reactivity. In our view, understanding the nature of the strain of the electronic structure of reactive atoms, and the reason why this strain appears to be absent for inert gas atoms, will help us better understand the mechanisms of both ionic and covalent bonding. Our reasoning will be qualitative and explanatory rather than numerically predictive. No deeper mathematical or computational experience with quantum chemistry will be required. We hope to take the empirical models of atoms and their bonding to molecules into quantum mechanics by physical reasoning. Clarifying this link between quantum mechanics and atomic properties and molecule formation should afford the reader a more fundamental understanding of atomic and molecular chemistry.

Understanding the Quantum-Mechanical Hydrogen Atom

Quantum mechanics applied to the electronic structure, particularly of the ground states, of atoms and molecules, is a deep and complex subject. Fortunately, there is a helpful ladder of simple and very useful systems and approximations which take us to the important chemical concepts of atomic periodicity and to chemical bonding. Much of what we need to know is already illustrated by the simple hydrogen atom H which is long since solved and understood by analytical mathematics.

The Key Role of Quantum Diffusivity

The hydrogen atom H is composed of a proton and an electron which are charged +e and -e, respectively. The Coulomb interaction between these particles is

V (r) = - C / r

, where

r

is the separation between particles and

C = 1389 kj / mol \times Å

. Generally we shall use atomic units au in which the charge-charge interaction of two particles in vacuum of charge

Z_{1} e

and

Z_{2} e

V (Z_{1}, Z_{2}; r) = C \times \frac{Z_{1} Z_{2}}{r} in Å and kJ / mol; = \frac{Z_{1} Z_{2}}{r} in au (0 . 529 Å and 2625 . 6 kJ / mol) .

(1)

Classically a model of two point charges (they are both small enough that we can neglect any individual particle size) would have a collapsed ground state - about like a neutron. In reality a hydrogen atom has a spherical ground state with the radius of the electron distribution around the nucleus being about half an Ångström or 0.5×10^-10 m. The existence of a hydrogen atom ground state of this small but still very considerable size must be understood as a quantum effect. Classically the “internal atomic states” would be phase space points of given positions

x, y, z

of the electron with respect to the proton at the origin and momenta p_x, p_y, p_z , but in quantum mechanics states are described by wave functions

ψ (x, y, z)

and they are diffuse in both coordinate and momentum. How diffuse must they be? This can be appreciated from the Heisenberg uncertainty principle for a one-dimensional particle motion:

Δ x \times Δ p \geq h / 4 π

(2)

Here

Δ x

and

Δ p

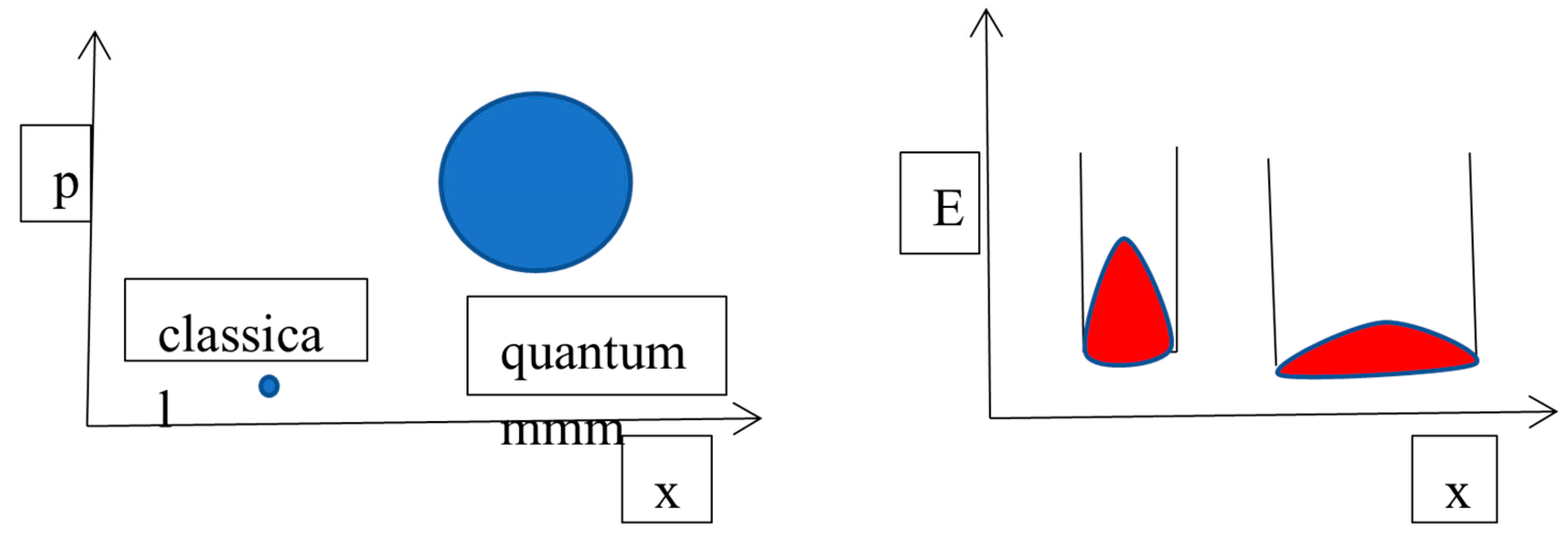
are uncertainty intervals in the coordinate

x

and momentum

p

. This principle tells us that a quantum state of a one-dimensional particle motion does not correspond to a classical phase space point

x, p

but to an area in

x, p

-space roughly proportional to the minimum uncertainty area,

\approx Δ x \times Δ p

, and to

h

. Similarly the electron moving in three dimensions has a ground state corresponding to a six-dimensional phase space volume

\approx Δ x Δ y Δ z \times Δ p_{x} Δ p_{y} Δ p_{z}

which is proportional to

h^{3}

. Not surprisingly this diffusivity also applies to excited energy eigenstates so the first lesson of quantum mechanics is that states in general, and our energy eigenstates in particular, acquire the form of space filling volumes in phase space. In an everyday metaphor “If classical mechanics builds a system from point-like grains of sand then quantum mechanics builds it from bricks”. This requirement of state diffusivity in quantum mechanics is absolutely fundamental in the understanding of atomic structure and chemical bonding.

Figure 1. On the left the classical state is a point in phase space (

x, p

) while the quantum state is covering an area

h

. On the right the quantum ground state is of higher energy when more confined by “hard walls” in some potential well.

Figure 1. On the left the classical state is a point in phase space (

x, p

) while the quantum state is covering an area

h

. On the right the quantum ground state is of higher energy when more confined by “hard walls” in some potential well.

Now we note that the uncertainty in momentum

Δ p

is directly related to the kinetic energy

K E

as follows:

{(Δ p)}^{2} = {(p - < p >)}^{2} = < p^{2} >, K E = < p^{2} / 2 m > = < {(Δ p)}^{2} > / 2 m .

(3)

Here

m

is the mass of the particle (e.g. the electron) and we used the fact that the average momentum vanishes,

< p > = 0

. It follows that localization of the electron in space forces up the kinetic energy so the diffusivity of the ground state of hydrogen is a compromise between localization in

x, y, z

to minimize electrostatic energy and delocalization in the same variables to minimize kinetic energy. The condition that quantum states must be diffuse, spread in phase space, explains why the hydrogen atom, and all other atoms, do not collapse to points. We note that increased diffusivity in coordinate space tends to lower the kinetic energy while localization tends to raise it. The rise in kinetic energy as the localization of an electron around the nucleus is increasingly tight eventually overwhelms the lowering of potential energy achieved. We note also that the cost of localization in kinetic energy is inversely proportional to the mass of the particle. Thus the light electron is far more affected by the “drive to diffuse” than the proton which is 1836 times heavier. This mass ratio is even greater for heavier atomic nuclei. It is therefore customary in quantum chemistry to use the “clamped nuclei approximation” (widely known as the Born-Oppenheimer (BO) approximation) which takes the nuclei in atoms and molecules to be stationary when determining the ground or excited states of the electron motion [25]. The small mass of the electron is the most important reason for the “quantum character of chemistry” but it is not the only reason. As we shall see below the quantum character is of a very particular kind.

The Origin of Periodic Atomic Properties - The Shell Structure of Hydrogenic Atoms

The quantum mechanical requirement of diffusivity prevents electronic structures around atoms from collapsing. Next we consider the origin of atomic reactivity. Again the simple hydrogen atom tells the story rather well [26]. According to analytical quantum mechanics the hydrogen atom has a spectrum of bound energy eigenstates (of energy less than zero) which can be identified by five quantum numbers

n, l, m, s, m_{s}

. The energies

ε_{n}

of the corresponding atomic orbitals (AOs) only depend on the principal quantum number

n

which goes from 1, 2, … to infinity:

ε_{n} = - 1 / 2 n^{2} au

(4)

where the atomic unit (au) of energy is the Hartree equal to 2625.6 kJ/mol. The quantum number

l

is the total angular momentum number and

m

is the quantum number describing the orientation of the angular momentum, both of which refer to the rotation of the electron around the proton. Their ranges are

l = 0, 1, ... n - 1, m = - l, - l + 1, ..., + l

. Finally,

s

is the spin angular momentum quantum, which is

½

, and

m_{s}

refers to the two available directions of the electron spin around its own axis, often called spin up and down (

m_{s} = \pm ½

) , respectively. We note the huge amount of degeneracy (number of states of the same energy) in the hydrogen spectrum. The degeneracy in each shell

d_{n}

is 2 for

n = 1

(

m_{s} = \pm 1

), 8 for

n = 2

(

l = 0, m_{s} = \pm 1, l = 1, m_{l} = - 1, 0, 1 and m_{s} = \pm 1

) and in general we find

d_{n} = 2 n^{2}

Degeneracy is a major feature of the spectrum of the hydrogen atom H. As we shall see below degeneracy is associated with reactivity and molecule formation is closely associated with “reduction of degeneracy”. The inert gas atoms are different from other atoms in that they have nondegenerate ground states and no excited states close in energy to the ground state, i.e. there is no near-degeneracy. In quantum mechanics energy eigenstates are related directly to particle dynamics and degeneracy means that the particle dynamics is hindered. Eigenstates of the same energy are then dynamically separable and decoupled. Eigenstates which are near-degenerate are generally coupled but motion between them occurs on a timescale proportional to the inverse of the energy difference between them. If there is no degeneracy and no near-degeneracy then the system is expected to be dynamically fully connected (ergodic) and stable. See the illustration in Figure 2 below.

Thus degeneracy and reactivity are related to constrained particle dynamics in quantum mechanics. We shall see below that chemical bonding takes free atoms towards less degeneracy and more fully coupled and global dynamics.

Hydrogenic Atoms

If we imagine atoms constructed of noninteracting electrons, so-called hydrogenic atoms, then this great degree of degeneracy for the smallest atom H would persist and may even multiply as we, by the Aufbau ansatz, can place two or more electrons in the shells defined by

n

and composed of

2 n^{2}

degenerate states adhering to the Pauli exclusion principle that each electron shall occupy a unique one-electron state. The one-electron states obtained for a nucleus of charge

+ Z e

are the same as those of the hydrogen atom but the energies are scaled by a factor

Z^{2}

and the physical extent is decreased by the factor

1 / Z

. It can be seen that degeneracy signals reactivity since multiple states of equal energy can be both filled and unfilled in the same shell of given

n

allowing an external symmetry breaking perturbation to strongly influence the ground state structure. This responsiveness to external perturbation can then facilitate interactions with external fields or other atoms. The structure would thereby be unstable and reactive.

We immediately realize that there are a few nondegenerate ground states among the “hydrogenic atoms”. For electron numbers

N_{e} = 2, 10, 28...

, in the notation

n^{N_{n}}

where

n

denotes the shell and

N^{n}

the number of electrons occupying subshells

n, l = n s, n p, ...

, we have closed shell structures

1^{2}, 1^{2} 2^{8}, 1^{2} 2^{8} 3^{18}

… with

d = 1

, i.e. we get hydrogenic helium and neon but then we miss argon because the 10 3d-electrons are for hydrogenic atoms of the same energy as the 3s and 3p-electrons. Nickel (Ni) would in the hydrogenic approximation be inert,

1^{2} 2^{8} 3^{18}

, but is not in reality.

Thus hydrogenic atoms would show “periodicity” similar, but not identical, to our periodic table for small atoms but increasingly different for higher atomic number. We also note that “inert gas character” can arise despite the system being decoupled by spin- and angular momentum-conservation, i.e. ergodic (fully coupled) dynamics is not a prerequisite for stable states to appear. Such states can appear also due to uniform occupation of degenerate states. Although they are of interest theoretically, hydrogenic atoms are, for higher atomic number

Z

, bound unrealistically strongly. For better understanding of real atoms we need to account for electron-electron repulsion which introduces a very important “screening mechanism”.

The Aufbau Model - An Empirical Mean-Field Model of Atoms

What is meant by “the Aufbau model”? - Aufbau means “build-up” and the model retains a shell structure of states related to, but significantly different from, that of the hydrogenic atoms discussed above [27,28]. Here we shall extend the model to include the one-electron character of hydrogenic atoms but predict realistic one-electron structures of many-electron atoms including the effect of electron screening. The Aufbau model thus accounts empirically and qualitatively for repulsion among the electrons and tells us which of these spin-orbital states, named by hydrogenic quantum numbers

n, l, m_{l}, s, m_{s}

, are occupied by electrons in the ground states of the neutral atoms. These “Aufbau rules” deviate significantly from the rules of the hydrogenic atoms since the orbital energies now include an account for the electron-electron repulsion. While these “Aufbau orbital energies” are not predicted quantitatively, physical reasons are often provided for the order in which they are filled, i.e., from lowest to higher energies in a given atom. We shall show that these Aufbau rules will also allow us to determine “Aufbau degeneracy” and sometimes also indicate “near-degeneracy” which, as noted above, plays an important role in understanding the properties of the atom. We have recently explored the possibility of obtaining a “measure of atomic reactivity” and included a measure based on “ground state degeneracy” as estimated by use of the Aufbau model [29]. It was found to agree well with other measures based on atomic first ionization energies or hydride atomization energies.

The hydrogenic atoms above are “periodic” with respect to reactivity-stability due to the variable degeneracy of their ground states. As we now turn to consider real interacting electrons we may at first expect all of the simplicity and periodicity of the atoms to disappear due to strong and complex electron-electron repulsion but, remarkably, most of it remains, but in modified form allowing us to use the strong simplifications of the Aufbau model without encountering disabling errors. Apparently, the electron-nucleus interaction still dominates and spherical symmetry is still a good approximation for the motion of individual electrons. In its simplest form, the “mean-field” approximation replaces the detailed interactions arising with electrons at different specific locations by an assumption that each electron can be taken to interact with the average electron density (the mean field) formed by all other electrons. This approximation was brought into quantum chemistry by Hartree and then refined by Fock to include an exact account of the Pauli principle which forces the full wave function to be antisymmetric with respect to interchange of two electrons. In this way a beautiful “Hartree-Fock theory” of electronic structure [19] was formed which has become the foundation of modern quantum chemistry. In the presence of two or more electrons of the same spin the form of the Hartree-Fock wave function includes an “exchange correlation effect” which is fundamentally related to wave functions rather than densities. It leads to significant reductions in atomic energies and a preference for “high spin Aufbau configurations”. We shall keep this in mind but leave the treatment of the corresponding “Hund’s rules” out of our simplified Aufbau model. Similarly, the spin dependence of electron-electron interactions, and the construction of atomic states of given total spin, is an important topic worthy of further study but not fundamental to our discussion due to the weakness of the spin-spin interaction, in particular for the lighter atoms. In our empirical mean-field model of atoms we thus leave aside both the treatment of total spin states and the treatment of spin dependent “exchange correlation” and use a simpler one-electron approximation of “electron screening” as follows below. Similarly we do not account for coupling of orbital angular momentum states into many-electron states of given total angular momentum, nor for the spin-orbit coupling of such many-electron states. They correspond to small energy splittings compared to the energies related to atomic reactivity and chemical bonding mechanisms that we are focusing on here.

Simple Representation of Screening in an Atom

The elaborated Aufbau model of atomic structure that we employ here is inherently of “qualitative mean-field” type. The key idea is that a given electron experiences the “other electrons” as a spherically symmetric “shield” around the nucleus effectively reducing the charge of the nucleus. The “electronic countercharge” inside the radial position

r

of the given electron can be directly subtracted from the nuclear charge while the countercharge outside the given electron is much less effective in reducing the nuclear charge. Ignoring correlations we assume that the electrons in an atom move independently as if they were in a potential of the form

V_{m f} (Z; r) = - Z_{e f f} (Z; r) / r in au

(5)

where the effective atomic number

Z_{e f f}

is decreased from the atomic number

Z

by screening (electron-electron repulsion) so that it goes from the atomic number

Z

r = 0

Z - N_{e} + 1

r = \infty

, i.e. from unscreened to fully screened nuclear charge with increasing separation. In the case of a neutral atom the number of electrons

N_{e}

is equal to the atomic number, i.e.

N_{e} = Z

, so the effective charge approaches the value in the hydrogen atom at large

r

Z_{e f f} (r) \to + 1, as r \to \infty (neutral atom) .

(6)

This shows that the orbital energies return towards values for the hydrogen atom for the outermost electrons in the neutral atom, but never all the way, as we shall see below. One reasonable, but in no way unique, form of

Z_{e f f}

is “exponential screening” as follows:

Z_{e f f} (Z, N_{e}; r) = Z - (N_{e} - 1) (1 - \exp (- k r)),

(7)

where

k

is adjusted to fit data, such as orbital energies and the inverse of the atomic radius. Note that the second term in the potential accounts for “screening” by the

N_{e} - 1

”other” electrons which goes between

0

at the center of the atom to

- (N_{e} - 1)

asymptotically outside the atom. This “single exponential” representation of screening in atoms can be made more accurate by going to multiple exponential representations where, for example, each shell of electrons is represented by an individual exponential with

k

decreasing as we go from inner towards outer shells. For the helium atom there is only a single screening electron in the inner most shell so the single exponential representation should be good. Figure 3 below illustrates the two components of the potential, Coulomb and screened Coulomb, in this case. The main point is to demonstrate that the screened component, which increasingly dominates for larger atoms, makes the total potential of shorter range, thereby increasing the energy of high

l

orbitals relative to lower

l

orbitals. Much of the empirically known behavior of atoms can be related to this effect of the screened component of the one-electron potential. The s-orbitals reach in close to the nucleus and get an added attraction from the less screened nucleus, while p-, d- and higher

l

orbitals get increasingly pushed away from this inner region and attraction from the screened component of the potential is correspondingly diminished.

We shall use this “screened atomic potential” for the purpose of understanding the effects of electron-electron repulsion on the Aufbau orbital energies. This potential has simplified “mean-field character” but it does exclude “self-interaction” (of an electron with itself) in a global approximate way. If we don’t specifically say otherwise, we shall take the atom to be neutral in our discussion below. Recalling the hydrogenic orbital energies

ε_{H, n} (Z)

we assume that the mean-field orbitals in a real atom are given by an average (

average A is < A >

) over the corresponding screened energy expression, i.e.

ε_{H, n} (Z) = - ½ \frac{Z^{2}}{n^{2}} a . u . \Rightarrow ε_{n, l} (Z) \approx - ½ \frac{< Z_{e f f}^{2} >}{n^{2}} a . u . .

(8)

The precise form of this average will not be specified but we expect it to be an average over electron-nucleus separation

r

reflecting the distribution of an electron in an orbital of type

n, l

For the moment we need not specify the optimal form of the function

Z_{e f f} (Z; r)

any further. We expect it to change smoothly in a monotonic fashion between its two limits as related to the electron density around the nucleus. Its decrease in magnitude with

r

describes the increasing screening of the nucleus due mainly to inner electrons. The gist of it is that for small

r

the potential is “hydrogenic” and unscreened while for larger

r

screening sets in and it approaches the potential in the hydrogen atom. Generally, as we go to heavier atoms, this means that the outermost populated orbitals have roughly the same energy since

Z_{e f f} (r)

for the outermost region of the neutral atoms have approached the limiting value

1

. The reasonable validity of such a simple model as we have proposed brings with it degeneracy related to the spherical symmetry of the potential and the lack of dependence on spin (Hund’s rules excepted at the moment). Thus periodicity of properties follows from the model. The model is good, but not perfect, so deviations are expected but, as we shall see, the perfect Aufbau degeneracies turn into “near-degeneracies” in reality, which bring much the same consequences. In this way the model will be able to explain the periodicity of reactivity displayed in our celebrated empirical forms of the Periodic Table.

The deviation of the order of the one-electron energies of our mean-field model (M-FM) from the corresponding hydrogenic energies is due to the screening represented in our effective atomic potential by the variable atomic number

Z_{e f f} (r)

, which in turn depends on how the electron is positioned with respect to the distance to the nucleus

r

. Here it is important to note that since the energy contribution should go like

- Z_{e f f}^{2} (r)

, i.e. proportional to the square of the effective charge number, it is particularly sensitive to electron presence at small

r

where the effective charge number is largest. This is the reason for an

l -

dependence of the mean-field energies such that for the same principal quantum number

n

the energies go like

n s < n p < n d ....

. The more rotation (higher

l

) we have, the more the electrons are withdrawn from small and large

r -

values and concentrated at intermediate distances from the nucleus. For a pure Coulomb potential

- Z / r

the interchange of radial and rotational motion in orbitals of the same principal quantum number

n

allows the total energy to be the same but with screening the variable effective charge number favors radial motion over rotation and higher

l

brings higher orbital energy. For a fixed

n

the orbital energy will grow with increased

l

, since the electron density will increasingly be pushed away from large and small

r

and centered at intermediate separations from the nucleus. In this way we can understand the empirical population order

1 s < 2 s < 2 p < 3 s < 3 p < 4 s < 3 d < 4 p < 5 s ...

of the Aufbau model. The “average” in the average effective atomic number in equation (8) must clearly be dependent on both

n

and

l

< Z_{e f f}^{2} >_{n, l}

and decrease with

l

for a fixed

n

. Moreover, the variation in

Z_{e f f} (r)

from

Z

1

increases with the atomic number and the outermost occupied

n

so the

l

-dependence of orbital energy increases with the size

Z

of the atom. This is a key insight with many important consequences.

Example of Coupling between Degeneracy and Reactivity

It is important to note that the screening mechanism accounted for empirically in the Aufbau model breaks the full

l, m_{l}, s, m_{s}

-degeneracy of the pure Coulomb potential in the hydrogenic model but retains

m_{l}, m_{s}

-degeneracy. In doing so it should decrease the atomic reactivity according to our analysis above. Is there any evidence of this in known behaviors of atoms and molecules? There is, if we add the effect of “near-degeneracy” and consider the change in character of molecules formed from first and second row central atoms. It is clear from our effective charge analysis of

l

-dependent orbital energies that the variation of the effective charge number

Z_{e f f} (Z; r)

for neutral atoms becomes greater with increasing atomic number

Z

and the increase in number of screening electrons

N_{e} - 1 = Z - 1

. Thus the

l

-dependence starts out weak for small atoms and grows as we go to heavier atoms, e.g. by going from the 2nd row (Li - Ne) to the 3rd row (Na - Ar). Similarly the reactivity should generally decrease with increasing

Z

. We can see this in the prevalence of hybridized molecular structures such as sp, sp² and sp³ when the central atom is light and the valence orbitals nearly degenerate, while with heavier central atoms the structures revert towards pure p-character since the valence s-orbital is too far below the valence p-orbital in energy. Familiar examples are H₂O with bond angel 105° indicating mainly sp³ character (109.5°) while H₂S has bond angle 92° indicating mainly p² character (90°). Similarly NH₃ with bond angle 97° and PH₃ with bond angle 94° indicate a shift from hybridized to unhybridized structures as we go from 2nd to 3rd row central atoms. The increased splitting between 3s and 3p orbital energies as compared 2s and 2p is a reason for this reduction in mixing of orbitals to achieve hybridization. This increased splitting of orbitals of the same principal quantum number

n

but different orbital angular momentum

l

is also a reason why d-orbitals play a lesser, but still important, role in molecular structure. They only arise in the valence shell for the atoms heavier than neon at

Z = 10

where the splitting of ns, np and nd -energies is already relatively large. There are clearly other factors at work, e.g. increasing presence of nonbonding electrons, but we expect and see evidence of decreased reactivity with increased principal quantum number of the outer electrons of atoms. This is in accord with our analysis of the influence of degeneracy on reactivity.

Another related feature is the reactivity bestowed on “low-

l

-electrons” due to their presence at relatively large

r

compared to their energy. Thus the outermost electrons in the inert gas atoms, except helium (

1 s

), are generally of

n s, n p

-character with the highest populated

n

-value, assuring low energy and presence at the surface of the atom. When some, or nearly all, such outermost

n s, n p

-orbitals are unfilled we have an open valence shell ready to receive, or lose, electrons to approach the nearest inert gas configuration. We conclude that both energies and spatial distributions selects outermost

n s, n p

-orbitals to be the chemically operative part of the electronic structure of the atom.

The Normal Aufbau Rules for Orbital Population

We recall first that in the hydrogenic atoms (without electron-electron interaction) only the shells defined by a given principal quantum number

n

are of different one-electron energies rising uniformly with

n

- Z^{2} / (2 n^{2})

. Accounting for electron-electron repulsion screens the nuclear potential and yields orbital energies which depend on both

n

and

l

. We don’t have simple expression for these realistic orbital energies but we have well known empirical rules allowing us to order the subshell energies - with one proviso: the rules apply to the valence electrons of neutral atoms. For positive atomic ions, as we may consider in a process of building up the neutral atom by adding one electron at a time, we expect the rules to revert back towards the hydrogenic rules, since the screening mechanism is weaker. The Aufbau rules, first proposed by Madelung [30], for the choice of outermost occupied

n, l

-subshell can be formulated as follows:

Minimize $n + l$ among as yet not fully occupied subshells;
Minimize $n$ among the available subshells $n, l$ all of the same minimal $n + l$ -value.

These rules are in full accord with what we have learned about the

l

-dependence of the Aufbau orbital energies but we should note that, despite their elegance and utility, they have not been derived and their status is mostly that of a convenient mnemonic for the observed order of the outermost

n, l

-subshells in the neutral atom ground state (see [3]).

There are a few exceptions to these normal Aufbau rules. The most notable exceptions relate to the strength of Hund’s rule exchange or a weakened

l

-dependence and return towards hydrogenic ordering. They are of interest as illustrations of competing mechanisms at work but the Madelung rules, or the corresponding graphical version of them, generally apply for the reasons discussed.

We see that, in our mean-field model, the periodicity is to a significant degree retained from the hydrogenic model of atoms but altered to account for the screening mechanism due to electron-electron repulsion so that the energies become

l

-dependent. We can now see that the existence and periodic variation in reactivity of atoms can be ascribed to two physical facts:

The diffusivity of the quantum states of electrons;
The good (but not perfect) validity of a mean-field model of the atoms with independent electrons in a spherically symmetric potential of screened Coulomb type.

Both these facts are of quantum-mechanical nature. The first prevents the collapse of atoms predicted classically and the second produces the Periodic Table as a consequence of the coupling of quantization to the dynamics of the electrons. The high symmetry of the model means that not only energy, but also angular momentum and spin, are exactly conserved quantities for each electron in the Aufbau model, but only approximately conserved in reality where the total angular momentum of all electrons is rigorously conserved but not the individual contributions from each electron. Thus the “Aufbau dynamics” is highly constrained and “nonergodic” in the sense that the quantum motion of individual electrons is decomposable into subspaces of different angular momentum and spin. This kind of “dynamical decomposability” is the origin of the reactivity of the model atoms as reflected also in the degeneracies of the energy eigenstates. Such decomposability is present in all atoms, also in the inert gas atoms, but it is associated with an energy strain (reactivity) which is strongly dependent on the electron population of the different subspaces. If the highest occupied states in each subspace are of much the same energy, and the gaps to unoccupied states are large, then the atom will be stable (inert) while if these highest energies in each subspace (subspace Fermi energies or chemical potentials) are showing large variation then the atom will be correspondingly reactive. Since the atomic orbital energies in the screened Aufbau model depend on the quantum numbers

n, l

we expect the atom to be stable if it contains only filled or empty such subshells in its ground state Aufbau population. Presence of open such subshells indicates degeneracy and atomic instability which in turn make the atom ready for molecule formation.

The Periodic Table According to Our Quantum Aufbau Model

Given that our Aufbau model and the long established Periodic Table agree in known essential features it is reasonable to see how our quantum-mechanical mechanisms of the Aufbau model impact issues of interpretation of the Periodic Table. The connection is broad and some of the impact, is obvious, so we focus on a single, perhaps most important, issue at present: The role of energy degeneracy in determining the reactivity of an atom or atomic ion. Our Aufbau analysis above suggests that the reactivity present is directly related to the degree of degeneracy present in the ground state structure. Recall that this relationship has recently been explored in connection with a search for a “measure of atomic reactivity” and found to agree very well with experimental realities [29].

Here we shall focus on one key aspect of this general reactivity issue, i.e. the least reactive inert gas structures and their placement in the orderly design of the Periodic Table [2]. From the point of view of periodicity of properties it would seem logical to have a group (column) with He at the top followed by Ne, Ar, Kr, Xe, Rn below. This is put in question by the known electronic structures of the valence shells which are of type

n s^{2} n p^{6}, n = 2, 3, 4, 5, 6

for all the heavier inert gas atoms but

1 s^{2}

for helium. Thus with respect to orbital structure helium is at the top of Group 2 followed below by the alkaline earth atoms. This may well seem unacceptable to many devotees of the Periodic Table in its more empirical and “chemical” forms.

The analysis of the quantum origin of atomic structure by the Aufbau model above tells us unequivocally that structural inertness of atoms is related to “strong non-degeneracy” of the ground state, i.e. to the uniqueness of the ground state and its separation from any excited states by a “chemically large” energy not readily recouped in various chemical bonding mechanisms. This is then the defining criterion of “inert gas” and it happens that different valence shell structures can produce such inertness, i.e. 1s² and ns²np⁶, n=2,3,4,5,6. The smallest inert gas atom He is different because it does not have access to p-orbitals in its valence shell. In a sense the property “reactivity” is thereby not fully periodic. It seems most reasonable to let the two atoms H and He be at top of Groups 1 and 2 but mark the uniqueness of the K-shell atoms some way, e.g. by lifting this first short row one empty row above the remaining longer rows. These two first elements are by necessity different since the valence shell has only two available orbital-states and cannot therefore reproduce behaviors involving eight outermost

n s

and

n p

-states as seen for all other elements. In this way of presenting the Periodic Table the inert gas position is always at the end of the regular row and the inertness is to be associated with the jump in largest principal quantum number

n

that occurs in the populated subshells as we go from the inert gas atom at the end of the row and the alkali-atom at the start of the next row below. It so happens that these inert “end-of-row atoms” do not fall in a single column due to the oddity of the first row with only two atoms. This seems a small price in graphical elegance to pay for the closer adherence of the Periodic Table to underlying electronic structure.

Our Aufbau analysis of the Periodic Table leads us to the dominant importance of the nature of the electronic ground state. Not only the energy is important but also the energy degeneracy, which can be strongly nondegenerate, near-degenerate or degenerate to variable degree. See a related discussion by Schwarz and Rich on page 437 in [3]. We conclude that both hydrogen and helium should be understood as fundamentally different from all following elements for which normal forms of the Periodic Table are more consistent with the underlying electronic structures. Hydrogen can be seen as the first alkali atom as well as the first halogen atom, i.e. one electron less than an inert gas structure. If it seems odd to see helium placed above beryllium, even with one empty row to the heavier elements, we must remember that beryllium and other alkaline earths below are much different from helium since they have six empty spin-orbitals of

p

-type in the valence shell. They are higher in energy but not “chemically separated”. Thus bonding mechanisms can draw upon their presence with the result that alkaline earth atoms are not inert despite their nondegenerate ground state structures.

Chemical Bonding Mechanisms

The historical development of chemistry, and the central role of the Periodic Table in it, leaves no doubt that chemical bonding is tightly bound to the properties of the atoms. The explanatory picture of the atoms presented above suggests that degeneracy or near-degeneracy of atomic ground states creates reactivity and leads immediately to two mechanisms available for stabilization by molecule formation:

Redistribution of electrons among atoms to form molecules composed of stable (inert gas like) atomic ions held together by Coulomb attraction between unlike charges. (Ionic bonding)
Achieving ground state non-degeneracy by removal of dynamical constraints to relax the “decomposability” of the electron dynamics and facilitate delocalization of electron motion over bonded atoms. (Covalent bonding)

These two, purely ionic and purely covalent, mechanisms have strikingly different dynamical character of permanent electron displacement and oscillatory electron motion between bonded atoms, respectively. Nevertheless they both reduce degeneracy in the molecular structures formed. Generally bonds between atoms of different species will show partial presence of both these bonding mechanisms.

Ionic Bonding

The ionic bonding mechanism is familiar and has long been understood to have a clear atomic basis. It is entirely dependent on quantum effects but, in its most basic form, only on atomic quantum mechanics as represented in the Periodic Table and the corresponding variation of atomic properties. The variation in atomic stability systematically described in the periodic table is simply recognized to extend to atomic ions of low charge, e.g. H^- and Li⁺ (He-like), O^2-, F^-, Na⁺ and Mg²⁺ (Ne-like). Ionic bond energies can be estimated reasonably, at least for singly charged ions, by atomic ionization energies

I_{1} (A)

and electron affinities

E_{a} (A)

for relevant atoms

A

and Coulomb interaction energies combined with ionic radii

r_{A}^{+}

and

r_{A}^{-}

of cations and anions, respectively. Multiply charged ions also arise with unstable doubly negative anions like O^2-, but, in its simplest form described here, the physical understanding of the ionic bond is unchanged in principle. At great separation we “promote” (excite electronically) the neutral atoms, e.g. Na and Cl, to corresponding inert gas like ions, Na⁺ and Cl^-. The cost in energy is

\begin{array}{l} Δ I E (N a^{+}, C l^{-}) = I_{1} (N a) - E_{a} (C l) = 147 kJ / mol . \\ I_{1} (N a) = 502 kJ / mol; E_{a} (C l) = 355 kJ / mol . \end{array}

A standard table (SI Chemical Data, 6th ed., Wiley) suggests that the ionic radii are

r_{h} (N a^{+}) = 102 \times 10^{- 12} m; r_{h} (C l^{-}) = 181 \times 10^{- 12} m .

The simplest interpretation is that the ions are hard spheres. The Coulomb interaction between two spherical and non-overlapping singly charged ions at this distance is obtained as

\begin{array}{l} R_{e} (N a^{+} C l^{-}) ≃ 2.83 \times 10^{- 10} m; - \frac{C}{R_{e}} = - \frac{1389}{2.83} = - 491 kJ / mol . \\ Δ E_{b} (N a^{+} C l^{-}) = 147 - 491 = - 344 kJ / mol . \end{array}

It is clear that the ionic bonding mechanism provides a very significant binding energy and will stabilize the ion pair at separations up to about 6 Å. For a structure including an O^2- ion one would have to include an extra promotion cost in energy to optimally confine the second added electron.

It follows from the analysis above that in simple, but reasonable, terms there is an ionic bonding mechanism that can be understood to be a consequence of the periodically varying properties of atoms. If we allow electrons to be transferred among reactive atoms to form pairs or small clusters of ions of inert gas electronic structure then these “ionic molecules” can be stabilized by the Coulomb interaction between the ions. In order for such stability to arise the atoms must be complementary, i.e. such that the cost of creating the positive ions is not too much greater than the electron affinities of the anions. With such complementarity the cost of ion creation at great separation can be repaid in lowered (more negative) Coulomb interaction energy so as to stabilize the equilibrium structure. We note that this mechanism can be extended from monovalent ions, as in our example above, to multiply charged ions where the “promotion” in the case of an ion like O^2- would include its confinement to a finite physical size.

We conclude that there is an ionic bonding mechanism of “atomic character” in the sense that all the quantum effects responsible are found already in the Periodic Table and the interaction mechanism is of electrostatic character. Note also that this mechanism takes reactive atoms of degenerate ground states and turns them into atomic ions of non-degenerate ground states and then, by Coulomb interaction, into a non-degenerate “ionic molecule”.

Seen in this way the ionic bonding mechanism is both simple and intuitive and it fits well with early bonding models drawing upon the concept of valency and electron redistribution. At an introductory level of discussion there is no pressing need to consider electron dynamics between ions in such structures. The empirical quantum mechanics of the Periodic Table suffices to understand the ionic mechanism of bonding. No great disputes about the nature of ionic bonding have, to our knowledge, a significant presence in the literature. A problem of another sort should be recognized: the ionic molecules discussed above are not very prominent in nature since they are inherently reactive to form larger ionic clusters and ionic crystals, as illustrated in the case of NaCl by the fact that we primarily know of it in its solid crystal form as table salt. In order to understand the species and stabilities of the molecular universe of chemistry we have to turn to the other, more subtle, form of chemical bonding.

Covalent Bonding

The covalent bonding mechanism, on the other hand, has confronted chemists with the need for a molecular form of quantum mechanics not readily extracted from the Periodic Table or the quantum mechanics of atoms. It can in small molecules, like H₂⁺ and H₂, immediately be seen to be associated with electron motion between the nuclei. In the normal energy analysis of quantum chemistry this interatomic motion is reflected in the delocalization of the molecular wave function over the two nuclei. In a one-electron model there is a splitting of the atomic ground state orbitals into a bonding and antibonding pair of molecular orbitals with the energy splitting proportional to the frequency of interatomic oscillation. This “dynamical view” of the covalent bonding mechanism, adopted by R. Feynman in a “two-state analysis of bonding” in 1965 [31], is closely related to the kinetic energy analysis of Hellmann and Ruedenberg (1933 [32] and 1962 [23]) but avoids the apparent paradox of the virial theorem encountered in the latter. The alternative dynamical interpretation of covalent bonding has also been used to understand the “non-bonding theorem” of the Thomas-Fermi density functional theory [33] and recommended as a complement to energy analysis in a series of studies of covalent bonding [34,35,36,37,38].

In an energy analysis the virial theorem seems, at first, to prove conclusively that the electrostatic interactions must be the source of the covalent bonding, since, by comparison with the far separated atoms, the kinetic energy change is positive at equilibrium separation and the potential energy change is negative and twice as large. Closer inspection shows [23], however, that the energy analysis is confused by the presence of a second mechanism, a contraction of the electron density around the nuclei, which is a corollary of covalent bonding for Coulomb interacting electrons and nuclei, but not the mechanism of bonding. The dynamical view of bonding has no such interference from the virial theorem. For H₂⁺, for example, it has been recently shown [38] that if the electron is prevented from interatomic motion then the localized ground state has the energy of the antibonding molecular orbital (MO) and the delocalization energy associated with interatomic electron motion accounts for the full drop in energy from the antibonding to the bonding MO. We emphasize that this view of covalent bonding in H₂⁺ is independent of whether we use a fixed exponent minimal basis set which cannot account for the “orbital contraction mechanism” or the optimized exponent version of the basis which accounts for the contraction. The latter basis gives better bonding mainly by reducing the Pauli repulsion associated with atomic basis overlap. In a “dynamical analysis” the covalent bonding is the result of interatomic electron motion and the need to distinguish “interatomic delocalization” and “atomic contractive” mechanisms of kinetic energy change does not arise.

Understanding covalent bonding involves three concepts, i.e. interatomic electron motion, wave function delocalization and Pauli repulsion. The first two are intimately connected. Interatomic motion is associated, in Hartree-Fock theory (or DFT), with orbital delocalization but in order to make the connection precise we must remove the overlap from the atomic orbitals we invariably start from. The process of localizing the atomic orbitals to their own half spaces raises the energy by the Pauli repulsion energy. It is possible also to make contact with the “localized” ionic mechanism of bonding by noting that, by the lifting of the constraint of electron localization to only one atom, the electron can approach the limit of being, in one quantum state, one-half at each atom with corresponding contraction of electron density around the nuclei. For large separation

R

between the nuclei the interatomic motion is so slow that the electron appears to be either at one or the other nucleus. In this view it is clear that, for homogeneous diatomic molecules, it is the frequency of the interatomic oscillation that determines how the electron goes from “at-either-or” (0 - 1 or 1 - 0) at large separation (low frequency oscillation) to “half-at-each” (½ - ½) at small separation (high frequency oscillation) and thereby turns on the stabilization. Note also that the latter “fully covalent” configuration replaces two degenerate localized configurations, i.e. the bonding reduces degeneracy. Moreover, it explains the origin of the “orbital contraction” which can be understood to arise from having only half an electron in each atomic potential well.

As we go from H₂⁺ to H₂ the complication of electron correlation must be accounted for. If we ignore it and use Hartree-Fock theory in simplest form then the molecule is well described around the equilibrium bond length but then dissociates incorrectly. The quantum-chemical Valence Bond (VB) theory recovers a sound and accurate bond energy curve by simply eliminating the so-called ionic configurations H⁺H^- and H^-H⁺ from the Hartree-Fock determinant. The remaining covalent configurations describe a molecule where two electrons correlate their oscillation between atoms so as to reduce the probability of both being at one of them. The interatomic motion is still the source of bonding but it is in the form of correlated two-electron motion. The VB theory may seem “fully correlated” in keeping the electrons at different atoms but the overlap of the atomic basis functions allow them to coexist spatially enough to account for interatomic motion. It is well known (e.g. by configuration interaction (CI) calculations) that not only are both angular and in-out (atomic) correlations completely neglected in the VB theory, but the degree of left-right (interatomic) correlation present is overestimated. A more accurate (e.g. CI) calculation shows that this correlation is in reality somewhere between the Hartree-Fock and VB proposals but tending towards the VB model in the large bond length limit [37].

The detailed resolution of the covalent bonding mechanism is an active field of research with most studies performed for wide ranges of molecules within the “energy decomposition analysis” (EDA) which dominates quantum chemistry [39,40,41]. We believe there is much to recommend the alternative dynamical analysis, particularly as a complement to the normal focus on energy and other apparently “static” properties. While the roles played by potential and kinetic forms of energy, as coupled by scaling laws reflected in the virial theorem, continue to be debated, the idea that covalent bonding requires valence electrons to be able to move between bonded atoms, and molecular segments, is yet unopposed, if possibly by not being at all considered. Moreover, the dynamical picture has clear physical implications in terms of extra stability implied when the electrons are able to move not only between pairs of atoms but in chains and rings of atoms as in aromatic hydrocarbon molecules. Finally, the metallic binding in solid metal structures bears witness that stabilization may follow from interatomic electron mobility on a macroscopic scale. The quantum dynamics of electronic motion in molecular structures may seem to present quantum chemistry with new computational challenges but the connection between already familiar energy analysis and the alternative dynamical analysis is very close in quantum mechanics and the rewards in terms of the clarification of the origin of bonding should readily justify the efforts.

The Interatomic Repulsion - Equilibrium Geometries of Molecules

The discussion of bonding above has focused on the key attractive mechanisms which do indeed dominate and cause the formation of stable molecules. The geometries of these molecules can only be understood if we also account for the repulsive mechanisms which prevent the collapse of the molecule to a larger atom (the united atom limit). The numerical methods of quantum chemistry [19] generally do a very good job of representing these repulsions. Our limited aim here is to extract some physical insight into their nature to complement the focus on attractions above.

Interatomic Electrostatic Interactions

The intramolecular electrostatic interactions play a crucial role in determining molecular geometries and also in the computations of molecular quantum chemistry. There are three different types of such interactions: i) electron-nucleus (e-n) attraction, ii) electron-electron (e-e) repulsion and iii) nucleus-nucleus (n-n) repulsion. This is also in the order of their importance. The e-n attraction is the sole reason for the existence of atoms and the only form of potential energy in a hydrogen atom. For larger atoms the e-e repulsions are added with important consequences (screening and correlation) as discussed above. We note that it is the e-e interaction of “two-body” type that turns electronic structure determination into a complex many-body problem dominated by approximations meant to reduce the full complexity. The now dominant use of Gaussian basis sets in the variational search for ground states was introduced in the 1960’s in order to exploit analyticity to reduce the burden of numerically calculating and storing the needed electron repulsion integrals. The n-n repulsions only arise for molecules or other multi-atomic systems. They prevent the collapse of the molecule in the united atom limit but otherwise, for molecules expanded beyond their equilibrium geometry, play a less important role due to “screening”. This term refers to the fact that individual atoms in the expanded molecule are surrounded by neutralizing electrons and the electrostatic interactions between thus neutralized atoms are quite small except at quite small atomic separations.

Another way to look at the electrostatic interactions in a molecule is to subdivide them into “interatomic subsets” by associating subsets of the electrons with corresponding atoms so that the e-n and e-e interactions can be similarly subdivided into “within atom” and “between atom” components. This is natural to do for expanded molecular geometries but less so for near equilibrium geometries of stable molecules. The “atoms in molecules” are not uniquely definable and the interatomic forces are not of simple pairwise form. Nevertheless the perspective of molecules as interacting atoms is intuitively appealing and frequently used [21,24]. It leads, e.g., to an understanding of the relatively short range of electrostatic interactions in an expanding neutral molecule due to the predominance of the atomic screening mechanism. An exception must be made here for ionic and highly polar covalent molecules. The total repulsions between nuclei in a molecule, and between electrons associated with different atomic centers, are normally rather precisely cancelled by interatomic e-n attraction, particularly at expanded molecular geometry. This cancellation can be hard to reproduce in quantum chemistry where the individual terms are more or less difficult to calculate (e-e being the most difficult) and correlated methods are generally needed to correctly reproduce the far separated atom limit. For equilibrium and more compressed molecular geometries the internuclear (n-n) repulsions will become predominant. It is clear therefore that intramolecular electrostatic interactions have an important role in the representation of the repulsions that determine the geometry of the molecule at equilibrium (minimal energy) but, as we discuss below, most likely not the leading role.

The Pauli Repulsion

The concept of Pauli repulsion is associated with the effect of the Pauli principle which states that permissible many-electron wave functions must be antisymmetric with respect to pairwise particle exchange. The Pauli principle forces electrons in the Aufbau model, or similar orbital-based quantum chemical theories, to be assigned unique spin-orbitals

n, l, m_{l}, m_{s}

for each electron. This requirement drives the hydrogenic or Aufbau or Hartree-Fock orbital energies occupied by additional electrons upward in energy in the one-electron spectrum of states. This process is completely fundamental in the modeling of atomic structure, being the backbone of the Aufbau model, but it also gives rise to an interatomic repulsion in molecules. It is often said that this type of Pauli repulsion is dominant in the interaction of inert gas atoms, e.g. in the case He-He. We can understand this suggestion if we note that in the “united atom limit” of the helium dimer, He-He → Be, two electrons have had to go from a 1s helium orbital to a 2s - orbital of beryllium. This increases energy and is reflected in a Pauli repulsion between the helium atoms. This repulsion is directly related to the overlap of the He 1s - orbital of the two atoms. This type of “overlap repulsion” is not only present for inert gas atoms but for atoms and molecules in general. From a physical point of view it is important to note that the Pauli principle is associated with two distinct type of effects:

Rising orbital energies (or kinetic energy) when electrons of equal spin are physically coincident;
Steric repulsion (or excluded volume) when geometrically separated electrons of equal spin approach.

The rising orbital energy effect is dominant in the Aufbau model of ground state atoms while the steric repulsion is exemplified in the interaction of ground state helium or other inert gas atoms, which basically serves to keep them apart.

We note that the Pauli principle can be satisfied by raising kinetic energy of electrons or by keeping them apart. Typically both these effects are present. These two repulsive mechanisms are both of “many-electron type”, i.e. only arising when at least two electrons of the same spin are present. We include here a third mechanism of the same general character but operating already on a single electron described by two or more atomic basis functions which are orthogonal when the atoms are far apart but overlapping and non-orthogonal when they approach: “The overlap correction”. This effect enters when the basis functions from different atomic centers are orthogonalized. Note that if this overlap correction is ignored the quantum states generated for it by Hamiltonian diagonalization will not satisfy the quantum diffusivity requirement of a certain phase space associated with a quantum state. The proper state definition has been compromised by the basis function overlap. To account for this type of “basis overlap Pauli repulsion” we add a third Pauli repulsion mechanism.

3.: Atomic space contraction - Basis function overlap correction.

We claim all three of these mechanisms belong together since they relate to the satisfaction of the rules of quantum state construction in quantum mechanics. Moreover, they tend to have similar repulsive effects in the construction of molecules from atoms.

We illustrate the role of Pauli repulsion for the simplest case of the smallest molecule H₂⁺. It may surprise to hear of Pauli repulsion for a one-electron system where no antisymmetry constraint applies to the wave function. We include here the constriction related to overlapping atomic spaces, as in mechanism 3 above, in the concept of Pauli repulsion. It is of the same mathematical nature as the antisymmetry requirement for electrons of the same spin. In the case of the single electron in H₂⁺ we must account explicitly for fact that the two atomic orbitals from different protons are still, at finite proton separation, partially representing the same phase space. The mathematics of eliminating this “double counting” forces an increase in energy.

In a simplest realistic approximation for the bonding, i.e. in a minimal atomic basis (two H1s atomic orbitals

(k^{3 / 2} / π^{1 / 2}) \exp (- k r)

) treatment, the Hamiltonian matrix and its two energy eigenvectors are

H = (\begin{matrix} α & β \\ β & α \end{matrix}) and ψ_{0} = \frac{1}{\sqrt{2 + 2 S}} (\begin{matrix} 1 \\ 1 \end{matrix}), ψ_{1} = \frac{1}{\sqrt{2 - 2 S}} (\begin{matrix} 1 \\ - 1 \end{matrix}) .

(9)

Here

α

is the atomic orbital energy in H₂⁺ , i.e.

- ½

au if the ground state hydrogen atom orbital is used and the protons are far separated. The total energy of H₂⁺ is the sum of the electronic orbital energy and the proton-proton repulsion,

1 / R

. The parameter

β

is the off-diagonal matrix element of the one-electron Hamiltonian, i.e. the kinetic energy operator and electron-proton potential, between the two atomic orbitals, which is negative. Finally

S

is the overlap (scalar product) of the two atomic basis functions. The electronic energy of the ground state orbital

ε_{0}

and the Pauli repulsion energy

Δ ε_{\Pr e p}

are given by

ε_{0} = \frac{α + β}{1 + S}, Δ ε_{\Pr e p} = \frac{α + β}{1 + S} - (α + β) = - \frac{S}{1 + S} (α + β) .

(10)

Here we note that the energy

α

contains all the electron-nucleus energy and the atomic component of the kinetic energy while

β

is the kinetic energy coupling representing interatomic motion plus an interorbital potential term both of which are negative and small at large separation. As

R

goes to zero α and β both become equal to the energy of He⁺ in the single atomic orbital basis. Neglecting the overlap S gives us twice that energy while including it as

S = 1

produces the correct united atom limit. The overlap parameter S is dimensionless and increases exponentially from zero at infinite proton separation towards 1 in the united atom limit. The range of the overlap S is greater than that of the total electrostatic effects. Thus the Pauli repulsion is likely to be more important than electrostatic repulsion as the molecule forms but eventually, at small enough separation, the nucleus-nucleus repulsion takes over and prevents molecular collapse to a “united atom”. The interatomic coupling in

β

also goes from a large negative energy in the united atom limit towards zero at infinite separation. The kinetic part can be expected to have the same range as the overlap S. In the case of H₂⁺ the attraction associated with

β

is larger than the repulsion related to S so the molecule reaches a stable minimum bond energy before the shorter range electrostatic repulsion kicks in to raise the energy. In order of importance the bonding in H₂⁺ is due to: 1. Attraction due to interatomic electron motion (

β

), 2. repulsion due to spatial constriction and orbital overlap (

S

) and 3. proton-proton repulsion (

1 / R

) at close range. The first two of these mechanisms are fundamentally quantum mechanical and related to the “size of a quantum state”. The interatomic motion opens up more phase space for the ground state while the second lessens available phase space for the state to be fitted in. The bond energy curve mainly reflects a balance between these two opposing effects on the motion of the electron in the ground state with the proviso that for small bond lengths

R \leq R_{e}

the electrostatic interaction, in particular the proton-proton repulsion, enters and dominates the approach to the united atom limit.

Suppose now we consider also the excited state orbital formed in this minimal basis treatment of H₂⁺. This will allow us to see how the interaction influences the full orbital space of the lowest bonding and first excited molecular orbitals. With and without the overlap correction (

S > 0

) their energies are

ε_{0} = \frac{α + β}{1 + S}, \to α + β for S = 0; ε_{1} = \frac{α - β}{1 - S}, \to α - β for S = 0 .

(11)

We see that without account for overlap the interatomic coupling (

β

) splits the degeneracy of the localized atomic ground states symmetrically into bonding and antibonding states so that equal population of both with non-interacting electrons will leave no resultant electronic bond interaction. The attraction of interatomic electron motion is perfectly cancelled by the repulsion of spatial restriction (Pauli repulsion) in the excited orbital. The presence of overlap

S > 0

both widens the gap and increases the average orbital energy:

\begin{array}{l} Gap : ε_{1} - ε_{0} = 2 β for S = 0, = 2 \times \frac{β + S α}{1 - S^{2}} for S > 0; \\ Average : \frac{ε_{0} + ε_{1}}{2} = α for S = 0, = \frac{α - S β}{1 - S^{2}} for S > 0 . \end{array}

(12)

At least for small overlap (equilibrium and expanded geometry) we expect the average orbital energy to rise in energy so that symmetrical occupation of both orbitals will lead to kinetic and overlap contributions which sum to a repulsion when the

n - n

interaction is included. We see that accounting for atomic orbital overlap

S

plays a fundamental role in establishing realistic repulsion between atoms due to spatial congestion. This is entirely a quantum effect. The total electrostatic interactions are repulsive for this simplest analysis of H₂⁺. They reflect quantum effects through the diffuseness of the electron distribution while the protons in this Clamped Nuclei (BO) picture are classical and therefore not diffuse. Thus the proton-proton repulsion rises to infinity like

1 / R

as they approach to eventually dominate at small

R

. More correctly, outside the BO approximation, the protons are also quantized and diffuse such that the repulsion would be softened by an additional “protonic Pauli repulsion”, but this effect is very small compared to the effects of diffuse electrons.

Recalling how the hydrogen atom gave us insight into the nature of the orbital spectrum of larger atoms we can similarly note what a hydrogenic spectrum of molecular orbitals of H₂ would bring. The analysis above, extended to more electrons by ignoring the electron-electron repulsion, suggests that H₂ would be twice (a little more due to a shorter bond length at equilibrium) as strongly bound as H₂⁺ but then H₂^- would be about half as stable again and a fourth electron would completely destabilize the molecule. Despite our neglect of electron-electron repulsion, we are not far from the truth. Pauli repulsion is known to play a major role in the interatomic repulsion that opposes bonding of, e. g., the helium dimer. This picture is, of course, just the reason why we refer to the two orbitals formed (

ψ_{0}, ψ_{1}

) as “bonding” and “antibonding”. We expect the qualitative character of these orbitals to remain after the electron-electron repulsion has been accounted for. Thus we expect occupation of the excited orbital to be unfavorable for the bonding eliminating it altogether when it is symmetrically occupied as in He₂.

This picture of covalent bonding as composed of a kinetic attraction opposed by Pauli repulsion, and for compressed geometries increasingly by electrostatic repulsion, should remain valid in essence for stable covalent bond formation also in larger molecules with symmetrical bonds. In the presence of ionic bonding, in the form of charge transfer among the bonded atoms, the electrostatic interactions will play a different, and more significant, role and contribute to the attraction. Further mechanisms do contribute, such as exchange and Coulombic correlation, “resonance effects” (generalizations of the interatomic orbital delocalization discussed here to include individual many-electron configurations, e.g. as the covalent and ionic configurations in the VB theory of H₂) in larger molecules etcetera, but the simple picture above in terms of molecular orbitals should remain the backbone of the bonding mechanism.

Summary: The covalent bonding mechanism is most fundamentally related to the ability of valence electrons to move between bonded atoms. A condition for this to be possible is that the ground state wave function is delocalized over the covalently bonded atoms. The strength of the bonding is related to the downward shifts in energy of these delocalized wave functions. Such downward level shifts are associated with upward shifts of neighboring excited levels bringing the energy spectrum to a less degenerate (more evenly spaced) form. The spacings between energy levels are proportional to the corresponding rates of interatomic electron motion (delocalization) and to the bond strength. The attraction associated with interatomic electron motion is always accompanied by repulsion of two types: i) Pauli repulsion associated with overlap of atomic orbitals and ii) electrostatic repulsion mainly associated with charge-charge repulsion between nuclei. The latter is generally of shorter range due to the electron screening mechanism so the Pauli repulsion dominates for larger separations while the electrostatic repulsion sets in around the equilibrium geometry and then rises.

This mechanistic understanding of covalent bonding is entirely of quantum mechanical origin arising from the required diffuseness of a quantum state and the lowering of kinetic energy associated with increasing diffuseness as the bonding electrons move faster between two or more atoms in the molecule. Interatomic electron motion allows electrons, at least for geometries close to equilibrium, to contract their motion around the atomic nuclei, thereby converting the kinetic energy lowering to potential energy lowering in accord with the virial theorem. The formation of a molecule also reduces available space for orbital motion causing repulsion while the electrostatic interactions both favour (n-e) and resist (n-n and e-e) the formation. The resultant bonding is a balance of effects but it is safe to conclude that the requirement of diffuse quantum states is the key to the balance and the ability of electrons to move interatomically is indispensible to the presence of resultant covalent stability.

Conclusions

Quantum mechanics made its way into chemistry, without chemists knowing it, first around 1870 in an empirical form when the atoms were found to show predictable properties as systematized by the Periodic Table. About 50 years later it became understood how the Periodic Table could in principle and, with time, modern methods and computers, increasingly in practice, be derived from the newly discovered quantum mechanics. Atomic and molecular quantum mechanics was over the last 100 years developed first mainly by physicists, but then also by chemists who have produced a form of “quantum chemistry” of great accuracy and applicability. The numerical methods are now extremely refined and available in comprehensive program packages. Our analysis above of atomic reactivity and molecule formation is meant to be complementary to the results of modern quantum chemistry, i.e. by focusing on the physical and mechanistic interpretation of the empirically or computationally obtained results. We have tried to show that the required space-momentum uncertainty, or diffuseness, of quantum states and the inherent dynamical nature of quantization leads to systematic behaviors of atoms individually and of the bonds they form in molecules. These inherent quantum mechanisms are related to the character of the energy eigenstates of the system (local or delocalized?) and the character of the spectrum of energy eigenvalues (degeneracy, near-degeneracy or chemically separated?). Thus the atomic properties are related not only to the ground state but to the nature of the energy spectrum just above it. This casts new light on the basis of periodicity in atomic electronic structure.

The atomic structure and the property variations in the Periodic Table are related to the persistence of one-electron decoupling of electron dynamics due to spherical symmetry of the whole atom. This is the origin of the one-electron Aufbau model of atoms. This decoupling due to spherical symmetry leads to degeneracies in the Aufbau model, changed in many cases to near-degeneracies in experimental reality. The ground state electron populations of some atoms will nevertheless, despite assumed decoupling, lead to some nondegenerate Aufbau ground states with exceptional stability (inert gas atoms), but in general the ground states will show degeneracy and thereby reactivity in accord with empirical reality systematized in the Periodic Table.

Molecule formation of two or more atoms relaxes reactivity and lowers degeneracy of bonded atoms generally to produce a nondegenerate molecular ground state. This is achieved by electron redistribution among the atoms or by interatomic electron motion in the ionic and covalent bonding mechanisms, respectively. These two mechanisms are both of atomic and quantum-mechanical origin but different in their dynamical character. The essence of ionic bonding can be seen by extending the Periodic Table from neutral atoms to atomic ions but covalent bonding takes us fundamentally to the properties atomic clusters where the electrons can move between atomic centers. In general heterogeneous molecules these mechanisms are both present.

Our analysis above should be seen as a way to look at and understand the physical mechanisms of atoms and their formation of molecules. It seems to capture the fundamental facts and mechanisms, which are of quantum-mechanical origin, without need of detailed mathematics or numerical calculation. Hopefully more chemists will with this analysis see the foundation of atomic and molecular chemistry more clearly. Quantum chemists have the tools to probe the validity of our analysis. There are important questions to answer by quantum-chemical computation such as: Can new computational results for not only ground states, but also their degeneracy, near-degeneracy or strong non-degeneracy, provide the claimed insight into reactivity versus stability of atoms and molecules? Can it be verified that covalent bonding fundamentally relates to relaxation of dynamical constraints seen computationally in reduction of degeneracy, and physically in electron mobility between bonded atoms?

Acknowledgement

I wish to thank George B. Bacskay for generous support in the form of discussion and many helpful suggestions.

Conflicts of interest

The author declares no conflict of interest.

References

Kaji, M.D.I. Mendeleev’s Concept of Chemical Elements and The principles of Chemistry. Bull. Hist. Chem. 2002, 27, 4–16. [Google Scholar]
Scerri, E.R. The Periodic Table—A Very Short Introduction, 2nd ed.; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
Schwarz, W.H.E.; Rich, R.L. Theoretical basis and Correct Explanation of the Periodic System: Review and Update. Journal of Chemical Education 2010, 87, 435–443. [Google Scholar] [CrossRef]
Thomson, J.J. On the Structure of the Atom: An investigation of the stability and periods of oscillation of a number of corpuscles arranged at equal intervals around the Circumference of a Circle: With Application to the theory of Atomic Structure. Phil. Mag. Ser. 1904, 6, 237–265. [Google Scholar] [CrossRef]
Rutherford, E. The Scattering of α and β Particles by Matter and the Structure of the Atom. Philos. Mag. 1911, 21, 669–688. [Google Scholar] [CrossRef]
Lewis, G.N. The Atom and the Molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
Langmuir, I. The Arrangement of Electrons in Atoms and Molecules. J. Am. Chem. Soc. 1919, 41, 868–934. [Google Scholar] [CrossRef]
Lewis, G.N. Valence and the Structure of Atoms and Molecules; American Chemical Society Monograph Series: New York, NY, USA, 1923. [Google Scholar]
Zhao, L.; Hermann, M.; Schwarz, W.H.E.; Frenking, G. The Lewis Pair Bonding Model: The physical background a century later. Nat. Rev. Chem. 2019, 3, 35–47. [Google Scholar] [CrossRef]
Langmuir, I. Types of Valence. Science 1921, 54, 54–67. [Google Scholar] [CrossRef] [PubMed]
Sidgwick, N.V.; Powell, H.M. Bakerian Lecture: Stereochemical Types and Valency Groups. Proc. Roy. Soc. A. 1940, 176, 153–180. [Google Scholar]
Gillespie, R.J.; Nyholm, R.S. Inorganic Stereochemistry. Q. Rev. Chem. Soc. 1957, 11, 339. [Google Scholar] [CrossRef]
Gillespie, R.J. Fifty Years of the VSEPR Model. Coord. Chem. Rev. 2008, 252, 1315–1327. [Google Scholar] [CrossRef]
Pauling, L. The Shared-Electron Chemical Bond. Proc. Natl. Acad. Sci. USA 1928, 14, 359–362. [Google Scholar] [CrossRef] [PubMed]
Pauling, L. The Nature of the Chemical Bond. II. The One-Electron Bond and the Three-Electron Bond. J. Am. Chem. Soc. 1931, 53, 3225–3237. [Google Scholar] [CrossRef]
Pauling, L.; Wheland, G.W. The Nature of the Chemical Bond. V. The Quantum-Mechanical Calculation of the Resonance Energy of Benzene and Naphthalene and the Hydrocarbon Free Radicals. J. Chem. Phys. 1933, 1, 362–374. [Google Scholar] [CrossRef]
Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach den Quantenmechanik. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
Helgaker, T.; Jörgensen, P.; Olsen, J. Molecular Electronic Structure Theory; Wiley: Chichester, UK, 2000. [Google Scholar]
Zhao, L.; Pan, S.; Holzmann, N.; Schwerdtfeger, P.; Frenking, G. Chemical Bonding and Bonding Models of Main-Group Compounds. Chem. Rev. 2019, 119, 8781–8845. [Google Scholar] [CrossRef] [PubMed]
Frenking, G.; Shaik, S. The Chemical Bond-Fundamental Aspects of Chemical Bonding; Wiley-VCH: Weinheim, Germany, 2014. [Google Scholar]
Burdett, J.K. Chemical Bonds: A Dialog; Wiley: Chichester, England, 1997. [Google Scholar]
Ruedenberg, K. Physical Nature of Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: USA, 1994. [Google Scholar]
Grinter, R. The Quantum in Chemistry: An Experimentalist’s View; Wiley: Chichester, England, 2005. [Google Scholar]
Keeler, J.; Wothers, P. Chemical Structure and Reactivity: An integrated approach, 2nd ed.; Oxford University Press: Oxford, 2014. [Google Scholar]
Kragh, H.S. Niels Bohr and the Quantum Atom—The Bohr Model of Atomic Structure 1913-1925; Oxford University Press: Oxford, 2012. [Google Scholar]
Scerri, E.S. The Periodic Table. Its Story and Its Significance; Oxford University Press: Oxford, 2007. [Google Scholar]
Nordholm, S. From Electronegativity towards Reactivity—Searching for a Measure of Atomic Reactivity. Molecules 2021, 26, 3680–3704. [Google Scholar] [CrossRef] [PubMed]
Madelung, E. Die Mathematische Hilfsmittel der Physikers, 3rd ed.; Springer: Berlin, 1936; p. 359. [Google Scholar]
Feynman, R.P.; Leighton, R.B.; Sands, M. The Feynman Lectures on Physics, Quantum Mechanics; Addison-Wesley Publishing Company: Reading, MA, USA, 1965; Volume III, pp. 10-1–10-12. [Google Scholar]
Hellmann, H. Zur Rolle der Kinetischen Elektronenergie für die zwischen Atomäre Kräfte. Z. Phys. 1933, 85, 180–190. [Google Scholar] [CrossRef]
Nordholm, S. Analysis of Covalent Bonding by Non-Ergodic Thomas-Fermi Theory. J. Chem. Phys. 1987, 86, 363–369. [Google Scholar] [CrossRef]
Nordholm, S.; Bäck, A.; Bacskay, G.B. The mechanism of Covalent Bonding: Analysis within the Hückel Model of Electronic Structure. J. Chem. Ed. 2007, 84, 1201–1203. [Google Scholar] [CrossRef]
Nordholm, S.; Eek, W. Ergodicity and Rapid Electron Delocalization—The Dynamical Mechanism of Atomic Reactivity and Covalent Bonding. Int. J. Quant. Chem. 2011, 111, 2072–2088. [Google Scholar] [CrossRef]
Nordholm, S.; Bacskay, G.B. The Role of Quantum Dynamics in Covalent Bonding—A Comparison of Thomas-Fermi and Hückel Models. In Advances in Quantum Theory; Cotaescu, I.I., Ed.; InTech: Rijeka, Croatia, 2012; pp. 107–152. [Google Scholar]
Nordholm, S.; Bacskay, G.B. The Basics of Covalent Bonding in Terms of Energy and Dynamics. Molecules 2020, 25, 2667–2701. [Google Scholar] [CrossRef] [PubMed]
Nordholm, S. Analysis of Bonding by Quantum Chemistry—Resolving Delocalization Stabilization in a Mechanistic Basis and New Hückel Model. J. Phys. Chem. A 2023, 127, 3449–3471. [Google Scholar] [CrossRef]
Esterhuysen, C.; Frenking, G. The Nature of the Chemical Bond Revisited. An Energy Partitioning Analysis of Diatomic Molecules E2 (E=N-Bi, F-I), CO and BF. Theor. Chem. Acc. 2004, 111, 381–389. [Google Scholar] [CrossRef]
Levine, D.S.; Head-Gordon, M. Clarifying the quantum mechanical origin of the covalent bond. Nat. Commun. 2020, 11, 4893–4900. [Google Scholar] [CrossRef]
Bacskay, G.B. Orbital Contraction and Covalent Bonding. J. Chem. Phys. 2022, 156, 204122. [Google Scholar] [CrossRef]

Figure 2. A spectrum of six energy eigenvalues is shown with, on the left, two energy levels of degeneracy 2 and 4, respectively. In the middle we have added a weak coupling splitting the degenerate states but leaving a near-degeneracy. On the right we have strengthened the coupling to produce a fully coupled (ergodic) system with a smooth progression of energy levels showing no tendency towards degeneracy. Since relaxation rates are proportional to energy eigenvalue spacings they are maximal on the right, slow in the middle case and absent within the degenerate states on the left.

Figure 3. The Coulombic potential

ϕ_{C} (r) = - 1 / r

(diamonds) and the screened Coulombic component

ϕ_{S C} (r) = - \exp (- k r) / r

(squares) for the helium atom (assuming

k = 3

as an average of 2 for H and 4 for hydrogenic He for simplicity) are shown. The sum of these components form our one-electron-potential for helium. Note that for

r < 1 / k

the two components are similar while for

r > 1 / k

the Coulomb potential persists while the screened potential rapidly approaches zero, i.e. the two components are long and short ranged in

r

, respectively. For larger atoms (larger

Z

) the screened component is multiplied by

Z - 1

and the total one-electron potential becomes increasingly dominated by its innermost (small

r

) part.

Figure 3. The Coulombic potential

ϕ_{C} (r) = - 1 / r

(diamonds) and the screened Coulombic component

ϕ_{S C} (r) = - \exp (- k r) / r

(squares) for the helium atom (assuming

k = 3

as an average of 2 for H and 4 for hydrogenic He for simplicity) are shown. The sum of these components form our one-electron-potential for helium. Note that for

r < 1 / k

the two components are similar while for

r > 1 / k

the Coulomb potential persists while the screened potential rapidly approaches zero, i.e. the two components are long and short ranged in

r

, respectively. For larger atoms (larger

Z

) the screened component is multiplied by

Z - 1

and the total one-electron potential becomes increasingly dominated by its innermost (small

r

) part.

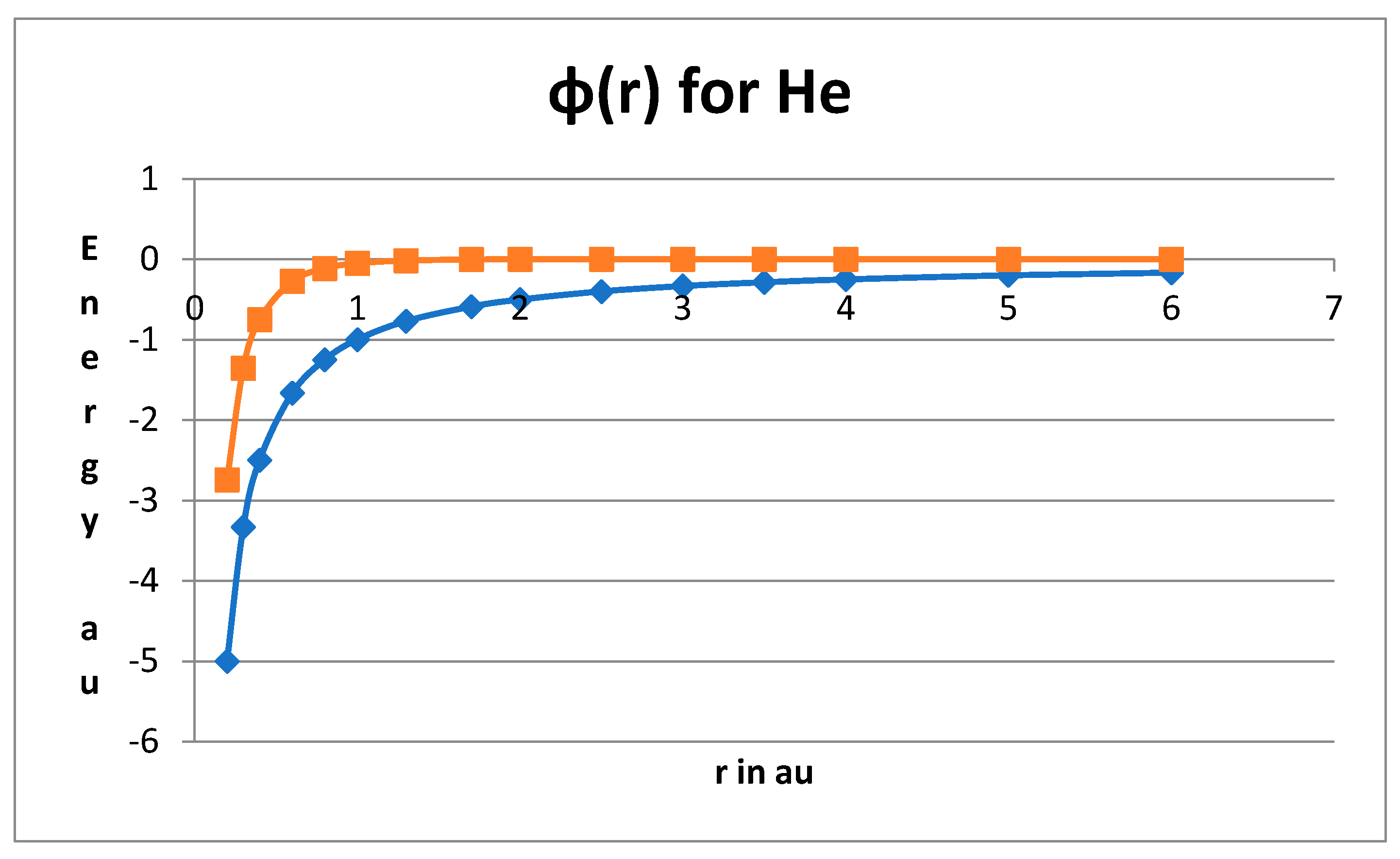
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Quantum Origin of the Periodic Table - The Role of Electron Dynamics and Energy Degeneracy in Atomic Reactivity and Chemical Bonding

Abstract

Introduction

Understanding the Quantum-Mechanical Hydrogen Atom

The Key Role of Quantum Diffusivity

The Origin of Periodic Atomic Properties - The Shell Structure of Hydrogenic Atoms

Hydrogenic Atoms

The Aufbau Model - An Empirical Mean-Field Model of Atoms

Simple Representation of Screening in an Atom

Example of Coupling between Degeneracy and Reactivity

The Normal Aufbau Rules for Orbital Population

The Periodic Table According to Our Quantum Aufbau Model

Chemical Bonding Mechanisms

Ionic Bonding

Covalent Bonding

The Interatomic Repulsion - Equilibrium Geometries of Molecules

Interatomic Electrostatic Interactions

The Pauli Repulsion

Conclusions

Acknowledgement

Conflicts of interest

References

MDPI Initiatives

Important Links

Subscribe