Prerpints.org logo
Preprint
Article

Correlating the Segmental-Relaxation Time of Polystyrene

Altmetrics

Downloads

63

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 July 2024

Posted:

02 July 2024

You are already at the latest version

Alerts
Abstract
A previous related paper dealing with the density relaxation of polystyrene (PS) has shown that the equilibrium relaxation time (eq) has a purely exponential temperature dependence (ETD) below ≈ 100ºC. Such an ETD is now also confirmed based upon available dielectric-spectra data for PS. By combining the ETD behavior of eq (or aT) at low temperatures with a VFTH behavior at higher temperatures (based mainly on available recoverable-shear-compliance data), a composite correlation for eq (or aT) is developed which is continuous with continuous slope at a crossover temperature which is found to be 99.22ºC, where eq = 92.15 sec. This composite representation is shown to describe (without any adjustable parameters) available independent data for the segmental-relaxation time over a finite range both above and below Tcrossover (i.e. the glass-transition temperature).
Keywords: 
Subject: Physical Sciences  -   Other

1. Introduction

In a recent paper by Hieber [1], based upon density relaxation of polystyrene at atmospheric pressure, it has been shown that the equilibrium relaxation time is characterized by a purely exponential temperature dependence over the experimental range available in the literature, reaching down (under equilibrium) to about 16ºC below the nominal glass-transition temperature. Such results were shown (in the same paper) to be compatible with the stress-relaxation data for polycarbonate of O’Connell and McKenna [2] as well as the equilibrium dielectric-compliance data for PVAc of Zhao and McKenna [3]; in both of these cases, the equilibrium state could again be reached down to about 16 or 17ºC below the nominal glass-transition temperature. {It is noted that “Tg,nominal” for PS is typically taken as 373ºK (i.e., essentially 100ºC), as has been done, for example, by Roland & Casalini [4] and He, et al. [5].}
In the present paper, it will be shown for polystyrene that the equilibrium relaxation time τeq(T) from Hieber [1] can be extended to temperatures above the nominal glass-transition temperature by making use of the temperature shift factor (aT) in the glass-rubber transition obtained from available independent data (in terms of recoverable-shear-creep compliance as well as stress relaxation) from the literature. It will be shown that this composite representation for τeq(T) describes (without any adjustable parameters) available data for the segmental-correlation time of PS over a temperature range extending both above and below the (nominal) glass-transition temperature.

2. Extending τeq(T) to above Tg

Based on the results from fitting the cumulative density-relaxation data for PS from Hieber [1], the resulting equilibrium relaxation time (at atmospheric pressure) is given by
τ e q T = A A exp ⁡ { − α 3 T − 100 ° C }
where
A A = 49.18 s e c , α 3 = 0.805 / ° C .
Combining this with the results from Appendix A & Appendix B below, we arrive at the plot in Figure 1 in which the ordinate is a measure of the temperature sensitivity in terms of τeq(T) or a T, namely
Ω   ≡ − d ln ⁡ τ e q   ( T ) d T
or
Ω   ≡ − d ln ⁡ a T d T
In particular, based upon the density-relaxation data for PS from Hieber [1], we have that
Ω = 0.805 / ° C
over the interval between 83.87°C and 100°C.
On the other hand, the three curves in Figure 1 are all based upon the VFTH model [6,7,8], namely,
a T = B B exp ⁡ CC T − T ∞
such that
Ω = CC ( T − T ∞ ) 2 .
Preprints 110932 g001
Figure 1. Results for Ω versus T. Curves based upon VFTH fits for flow regime (curve 1, from Appendix A) or glass-rubber transition (curves 2 and 3, from Appendix B). Dashed line based upon Equations (1) and (2).
Figure 1. Results for Ω versus T. Curves based upon VFTH fits for flow regime (curve 1, from Appendix A) or glass-rubber transition (curves 2 and 3, from Appendix B). Dashed line based upon Equations (1) and (2).
Preprints 110932 g001
In particular, curve 1 in Figure 1 is based upon cumulative data from 5 sources [9,10,11,12,13] for the “flow regime” reported in Appendix 1, with the measured temperatures ranging between 104.5°C and 290°C, and (CC, T∞) = (1793.8°C, 42.27°C), as given in Equation (A.2). On the other hand, curves 2 and 3 are based upon results for the “glass-rubber transition” from Appendix B involving cumulative data from 6 sources [9,14,15,16,17,18] in the temperature range from 100°C to 135°C, with curve 2 corresponding to (CC, T∞) = (669.8°C, 71.60°C) from Eqn. (B.1) of Appendix B and curve 3 to (CC, T∞) = (714.4°C, 69.43°C) from Equation (B.2).
Clearly, all three curves in Figure 1 have been extended to temperatures below that of the underlying data (as presented in Figures A and B). Furthermore, it is expected that the present density-relaxation results should be directly related to the “glass-rubber transition” results, both reflecting local molecular behavior, whereas the “flow-regime” results reflect long-range molecular motion. In addition, as documented in Appendix B, there is a basis for judging that curve 3 is more representative than curve 2. Accordingly, of especial interest in Figure 1 is the intercept of curve 3 with the dashed result given by Eqn. (5), which occurs at T = 99.22°C.
These results seem to strongly indicate that the VFTH behavior of the “glass-rubber transition” given by curve 3 in Figure 1 gets replaced by the constant value, given by Eqn. (5), at temperatures below the intersection point at 99.22°C. In turn, this indicates that the singularity (at T ≡ T∞) in the VFTH equation is only an apparent singularity.
Making use of the results in Figure 1, it seems appropriate to introduce the term “Tcrossover” to denote where the dashed line and curve 3 intersect. Accordingly,
Tcrossover = 99.22°C
where τeq(T) is based on Eqns. (1, 2) for T ≤ Tcrossover and is extended above Tcrossover by making use of curve 3 from Figure 1. That is, the resulting composite representation for τeq (T) is then given by
τeq(T) = 49.18 sec exp{−(0.805/°C)(T−100°C)}
for T ≤ Tcrossover, such that, from Eqns. (8, 9),
τeq(Tcrossover) = 92.15 sec
whereas, based upon curve 3 in Figure 1, for T > Tcrossover we have that
τ eq ( T ) = 92.15   sec   exp   714.4 ℃ T − 69.43 ℃ − 714.4 ℃ 99.22 ℃ − 69.43 ℃ .
It is noted that the composite representation for τeq(T), given by Eqns. (9) & (11), is continuous with a continuous slope at Tcrossover {which follows from the definition of Ω in Eqn. (3)}. Furthermore, the value of Tcrossover in Eqn. (8) is close to the “nominal Tg” of PS, namely 100º C. Accordingly, the result in Eqn. (10) is compatible with a convention typically associated with Angell [19], namely that Tg,nominal is where τeq is on the order of 102 sec.

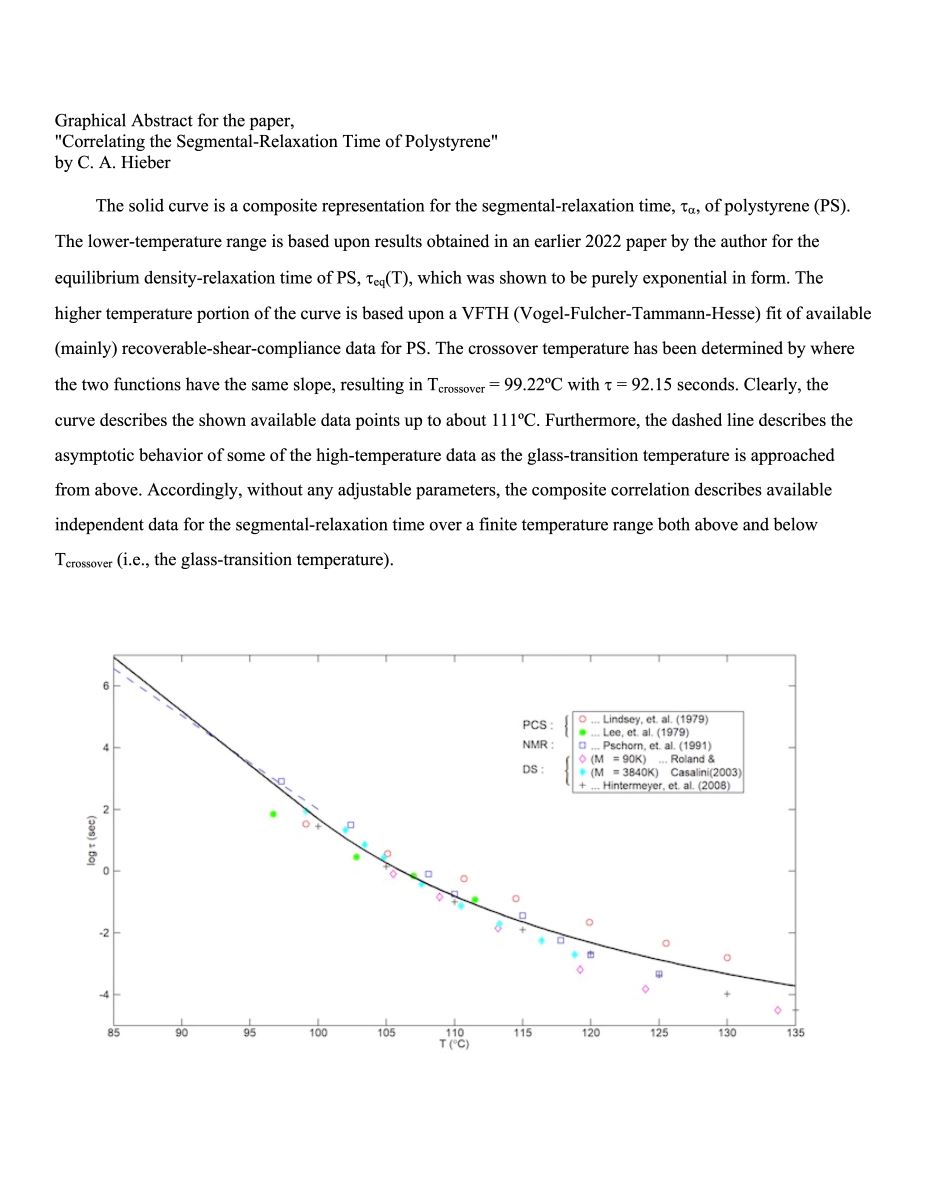
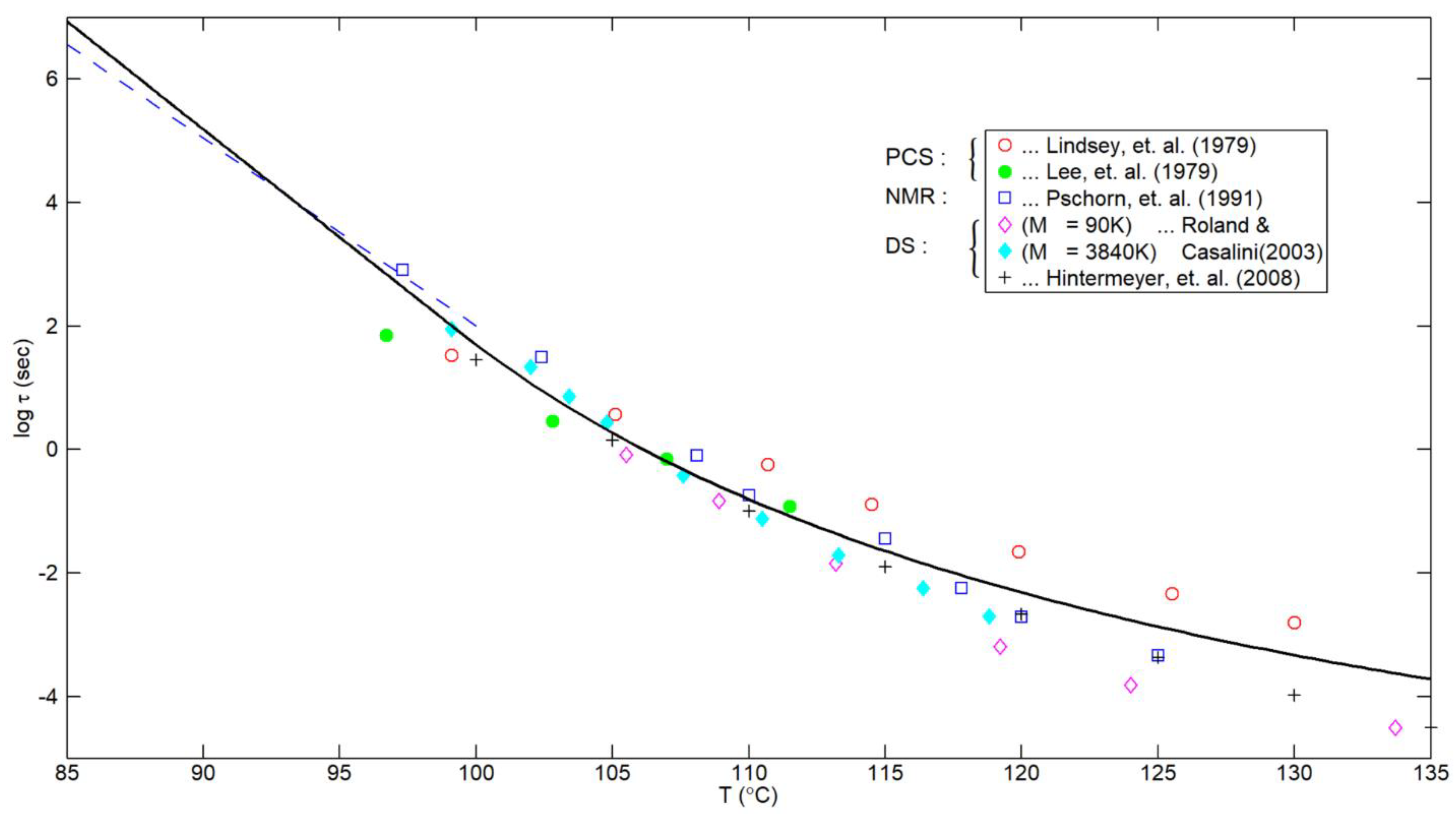
3. Comparison with Experimental Results for the Segmental-Relaxation Time

A resulting plot for τeq(T) based upon Eqns. (9) and (11) is shown plotted in Figure 2, together with corresponding data for PS based upon various experimental techniques. Despite evident scatter, a definite correlation between the data and the composite curve (with no adjustable parameter) seems apparent.
It is worth stressing that the actual level of the τeq(T) curve in Figure 2 is based upon the density-relaxation results obtained in the earlier paper, Hieber [1]. On the other hand, the extension of the curve to higher temperatures (i.e., above Tcrossover) is based upon fitting cumulative results for aT in the glass-rubber-transition region, as presented in Appendix B of the current paper.
In observing Figure 2, it is noted that the experimental results from Roland & Casalini [4] are for two PS of significantly different Mw, differing by a factor of 43, but that the corresponding results for τeq differ by no more than a half decade. For comparison, if we were dealing with viscous flow, the characteristic time would be proportional to η0 which, for these large values of Mw, would be proportional to Mw raised to the 3.4 power. Accordingly, the respective values for the viscous-flow characteristic time for these two polymers would differ by a factor of 43 raised to the 3.4 power, i.e., 3.6 × 105. Clearly, on such a scale, the present results in Figure 2 for the two PS are essentially coincident. Stated differently, these results indicate the dramatic difference in behavior of the current results in Figure 2, relating to the local-segmental motion of PS, in contrast to the global molecular motion associated with viscous flow.
As a still further confirmation that the results in Figure 2 are independent of molecular weight (if sufficiently large), the results for PS in Figure 2(b) of Hintermeyer, et al. [23] are striking, in which the curves for “lg τα (sec) versus T(ºK)” are essentially coincident for the three highest molecular weights (all of NMWD), namely 96K, 243K and 546K. In fact, the corresponding data points from Hintermeyer, et al. [23] shown in the current Figure 2 have been taken from the right-most solid curve in their Figure 2(b), which is representative of the high-Mw asymptote. It is noted that Hintermeyer, et al. (23) have determined “Tg” for each of their polymers as the temperature at which τα equals 100 seconds. From their Table 2, the corresponding values for the above three high molecular weights were 372.6ºK (99.45ºC), 373.3ºK (100.15ºC) and 372.0ºK (98.85ºC), respectively.

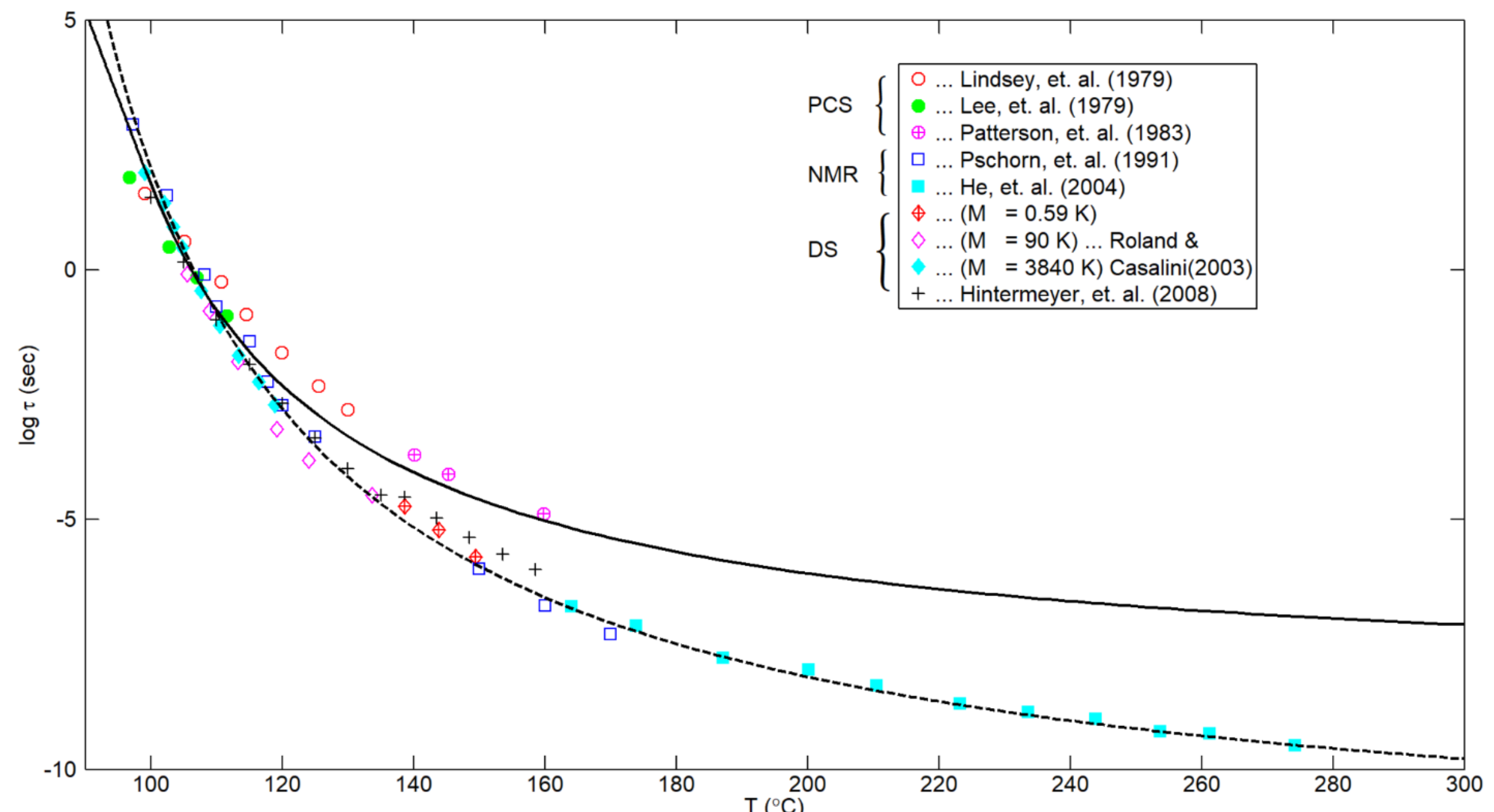
4. Behavior at Higher Temperatures

Whereas Figure 2 extends to only 135ºC (reflecting the underlying related data from Appendix B), Figure 3 extends the plot to higher temperatures. In particular, the solid curve is based upon Eqns. (9) and (11), as in Figure 2, whereas the dashed curve is based upon the empirical fit obtained by He, et al. [5], namely
τ s e g , c ( T ) = 0.87 × 10 − 12 s e c e x p ( 1248 ° C T − 61.55 ° C )
for the segmental-correlation time.
As noted in Figure 9 of He, et al. [5], their data, based upon three PS of low Mw (namely 2.05K, 2.31K and 11.45K), have been “horizontally shifted by ΔTg, taking Tg = 373ºK for high molecular weight PS”. In particular, the highest-temperature data point from He, et al. [5], as shown at 274ºC in the current Figure 3, corresponds to Mw = 2.05K and ΔTg = 54ºK/ºC. Similarly, the three data points for Mw = 0.59K from Roland & Casalini [4] are taken from their Figure 4 with a ΔTg of 119ºC. Furthermore, the five right-most data points from Hintermeyer et al. [23] shown in Figure 3 correspond to Mw = 1.350K, as presented in their Figure 11, with a ΔTg of 59ºC.
Evidently, with the exception of the data from Patterson et al. [24], the dashed curve clearly describes the high-temperature data in Figure 3 quite well. (It should be noted that the data from Lindsey et al. [20] and Patterson et al. [24] are from the same laboratory.) As indicated in Figure 9 of He, et al. [5], their higher-temperature NMR data merge well with the lower-temperature NMR data of Pschorn et al. [22]. Furthermore (as seen in Figure 3), the correlation given by Eqn. (12) seems to be substantiated by the DS measurements obtained independently by Roland & Cassalini [4] and by Hintermeyer et al. [23].
It should be noted that Eqn. (12) gives a value of about 102 sec at 100ºC (often taken as the nominal glass-transition temperature for PS). This is consistent with a convention typically associated with Angell [19] which has been explicitly employed by Roland & Casalini [4] and by Hintermeyer, et al. [23].
In closing this section, one might also consider the limiting behavior of the relaxation time at a hypothetically high temperature (i.e., as T→ ∞), namely “τ∞”. In particular, from Eqns. (11) and (12) above we get respective values of 3.546 x 10-9 sec and 0.87 x 10-12 sec. On the other hand, Boyd & Smith [25] note that the limiting behavior (as T→ ∞) of various modes all seem to converge on a time scale of picoseconds (10-12 sec), corresponding to intramolecular and torsional oscillations. Hence, it would seem that Eqn. (12) would be more appropriate than Eqn. (11). But this is complicated by the generally accepted idea [26,27] that the WLF (or VFTH) model should get replaced by an Arrhenius behavior at sufficiently high temperatures. If that is done in the case of Eqn. (11), supposing that the VFTH in Eqn. (11) gets replaced by an Arrhenius at T = T*, with their values & first derivatives being continuous, it can be verified that τ ∞   ≅   10 − 13   s e c if T * ≅   222 ° C (495ºK) and 10-12 sec if T * ≅   242 ° C (515ºK). That is, these values reflect that the Arrhenius would decay more rapidly than the VFTH at these higher temperatures and indicate that the resulting values for τ∞ based upon such a composite VFTH/Arrhenius model would not be unreasonable.
Further consideration of the temperature dependence in Eqn. (12), compared with the correlations for aT in Appendix A and Appendix B, is given in Appendix C.

5. An Unanticipated Corroboration

It is noted that Ngai [28] indicates (on p. 263) that the segmental-relaxation time (τα) has the same temperature dependence as the creep compliance up to 384ºK (111ºC); indeed, this agrees with the present results shown in Figure 2, in which there is excellent agreement with the curve, based upon Eqns. (8, 9, 11), up to about 111ºC. On the other hand, there is also evidence that Eqn. (8, 9, 11) describes τα (T) even below Tg. This is based upon results from Hintermeyer, et al. [23], as follows...
In Figure 11 of Hintermeyer, et al. [23], based on dielectric-spectra data for PS, results are plotted in terms of “lg τα (sec)”, versus “z ≡ m (T/Tg − 1)”, in which “m” is the non-dimensional “fragility index”. Of specific interest here is the fact that the data (all of which lie essentially above Tg) coalesce asymptotically onto a straight line as one approaches Tg (identified with where τα ≡ 102 sec) from above. In particular, the straight line in their Figure 11 corresponds to
log   τ α   = 2 − m T g ( T − T g )
where τα is in seconds and T & Tg in ºK. From their Figure 6, m ≈ 122 for the three largest Mw and Tg ≅ 373ºK. Hence, Eqn. (13) becomes
τα (T) = 102 sec exp{ − (0.75/ºC) (T − Tg)}
for the PS polymers of high Mw. Indeed, the value of Ω = 0.75/ºC in Eqn. (14) agrees well (within 7%) with the value of 0.805/ºC in Equation (5). This is evidenced by the dashed line in Figure 2, which is based upon Eqn. (14) with Tg = 100ºC.
Hence, there is the strong implication that the present correlation, corresponding to Eqns. (8, 9, 11) and plotted as the curve in Figure 2 above, describes τα (T) for PS not only up to 111ºC but also down to perhaps 83ºC, based on the density-relaxation results for PS presented by Hieber [1], upon which the value of 0805/ºC is based.
In a similar manner, based upon the DS data of Hintermeyer, et al. [23] for polydimethylsiloxane (PDMS) and polybutadiene (PB), one obtains respective values for Ω of 1.83/ºC and 1.19/ºC, based upon the higher-Mw samples. However, since this relates to the segmental-relaxation time, the same values for Ω also pertain (essentially) to the polymers of lower Mw, as is demonstrated in Appendix D.

6. Conclusions

Main results that have been obtained in the present paper include the following:
(i) It has been shown, making use of the extensive DS data of Hintermeyer, et al. [23] for PS {as well as for Polydimethylsiloxane (PDMS) and 1, 4-Polybutadiene (PB)}, that the temperature dependence of the local segmental-relaxation time, τα, is purely exponential below Tg, thus confirming previous results for PS obtained by Hieber [1], based on density-relaxation considerations.
(ii) The fact that the values of 0.805/ºC in Eqn. (5) and 0.75/ºC in Eqn. (14) are in such close agreement strongly suggests that τeq (T), obtained from density-relaxation considerations, and τα (T), obtained from segmental-relaxation considerations, are directly related.
(iii) The results shown in Figure 2 indicate that the smooth composite correlation (with no adjustable parameters) given by Eqns. (9) and (11) describes available experimental results for the segmental-relaxation time of PS encompassing a definite temperature range both above and below the glass-transition temperature.
(iv) Based upon the results in Appendix C, there is strong evidence that, contrary to some results in the literature, the temperature dependence of τα(T), as given in Eqn. (12), and of aT for the viscosity, as given in Eqns. (A.1) and (A.2), do not become coincident at higher temperatures.

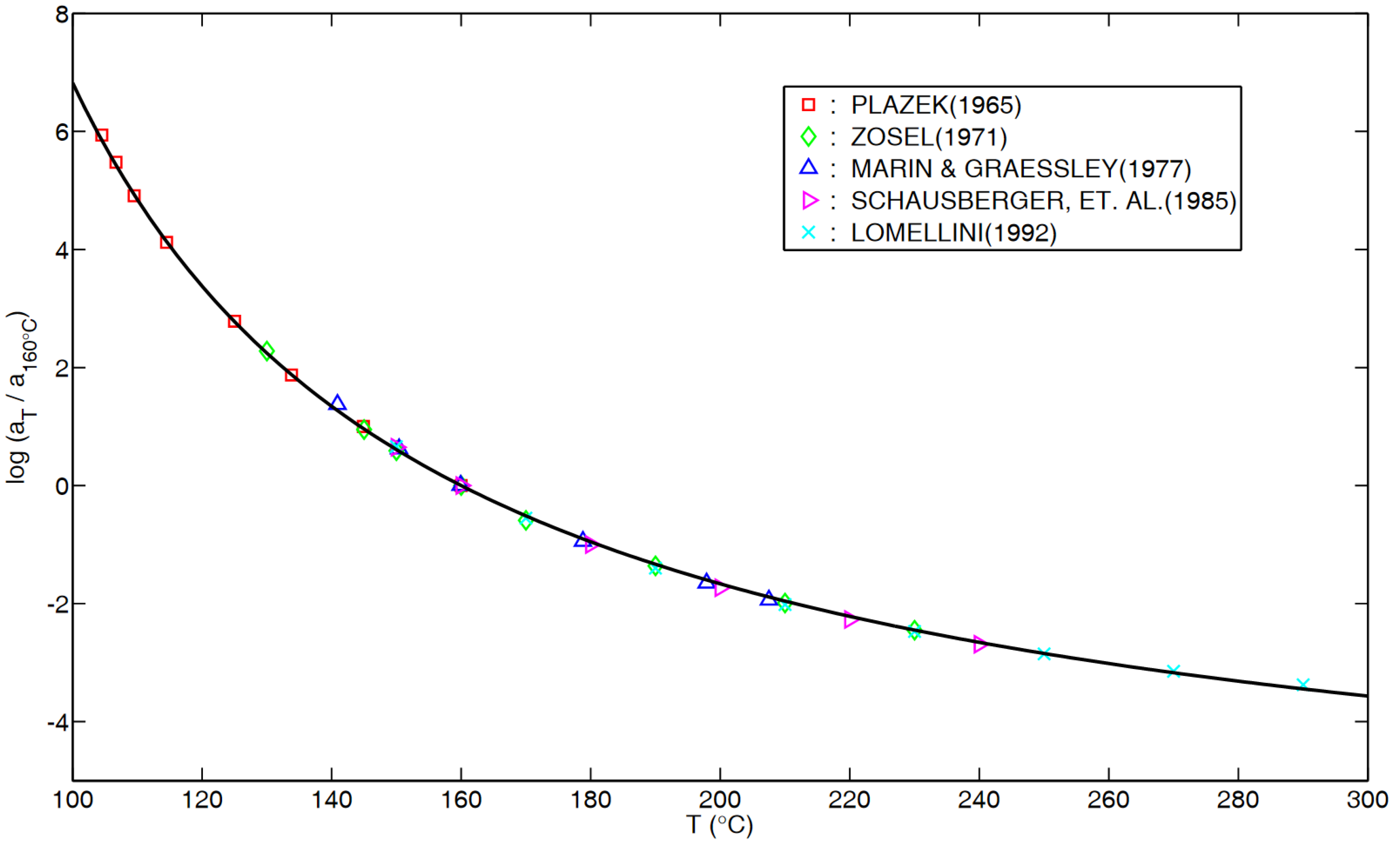
Appendix A: a T for PS in “Flow Regime”

Shown in Figure A are results for the temperature-shift factor aT/a160°C for the “flow regime” of PS based on available data. In particular, the results from Plazeck [9] are based on (long-time) shear-creep compliance whereas the remaining data are all based upon dynamic measurements in the low-frequency limit. The results from Zosel [10] are significant in that they include some eleven different PS (all with Mν>150K, of both narrow and broad molecular-weight distribution) for which aT was essentially the same. In similar manner, Marin & Graessley [11] found that, within experimental uncertainties, their results for aT were the same for their five PS (all of NMWD, with Mw between 37K and 670 K). Similarly, Schausberger et al. [12] found that, for five PS of NMWD (with Mw ranging between 70K and 3000K), aT was the same within the accuracy of the measurements. In turn, the experimental results from these three investigations have been complemented in Figure A by results from Plazek [9] and Lomellini [13], extending the results to lower and higher temperatures, respectively.
Also shown in Figure A is the corresponding curve fit based upon the VFTH model [6,7,8]:
a T / a T R E F = e x p CC T - T ∞ / e x p CC TREF - T ∞
with TREF = 160ºC. The best-fit values for (CC, T∞) have been determined by employing a simplex method (Nelder and Mead [29]), resulting in
CC = 1793.8°C, T∞ = 42.27°C, RMSDEV = 0.03994.
Preprints 110932 g0a1
Figure A. Cumulative data for the temperature sensitivity of aT for the flow regime of PS. Solid curve corresponds to VFTH model, Equations (A.1) and (A.2).
Figure A. Cumulative data for the temperature sensitivity of aT for the flow regime of PS. Solid curve corresponds to VFTH model, Equations (A.1) and (A.2).
Preprints 110932 g0a1
For comparison, it should be noted that McKenna et al. [30] have done a similar analysis of mostly different data for PS. The only viscosity measurements common to the earlier 1987 paper and the present investigation are those from Plazek [9] and Marin & Graessley [11]. Based upon fitting an extensive set of measurements, the resulting best-fit values based upon the VFTH model were found by McKenna et al. [30] to be given by
CC = 1794°C, T∞ = 42.8°C .
The remarkably close agreement between the model parameters in Eqns. (A.2) and (A.3) thus serves as a confirmation of the two separate investigations.

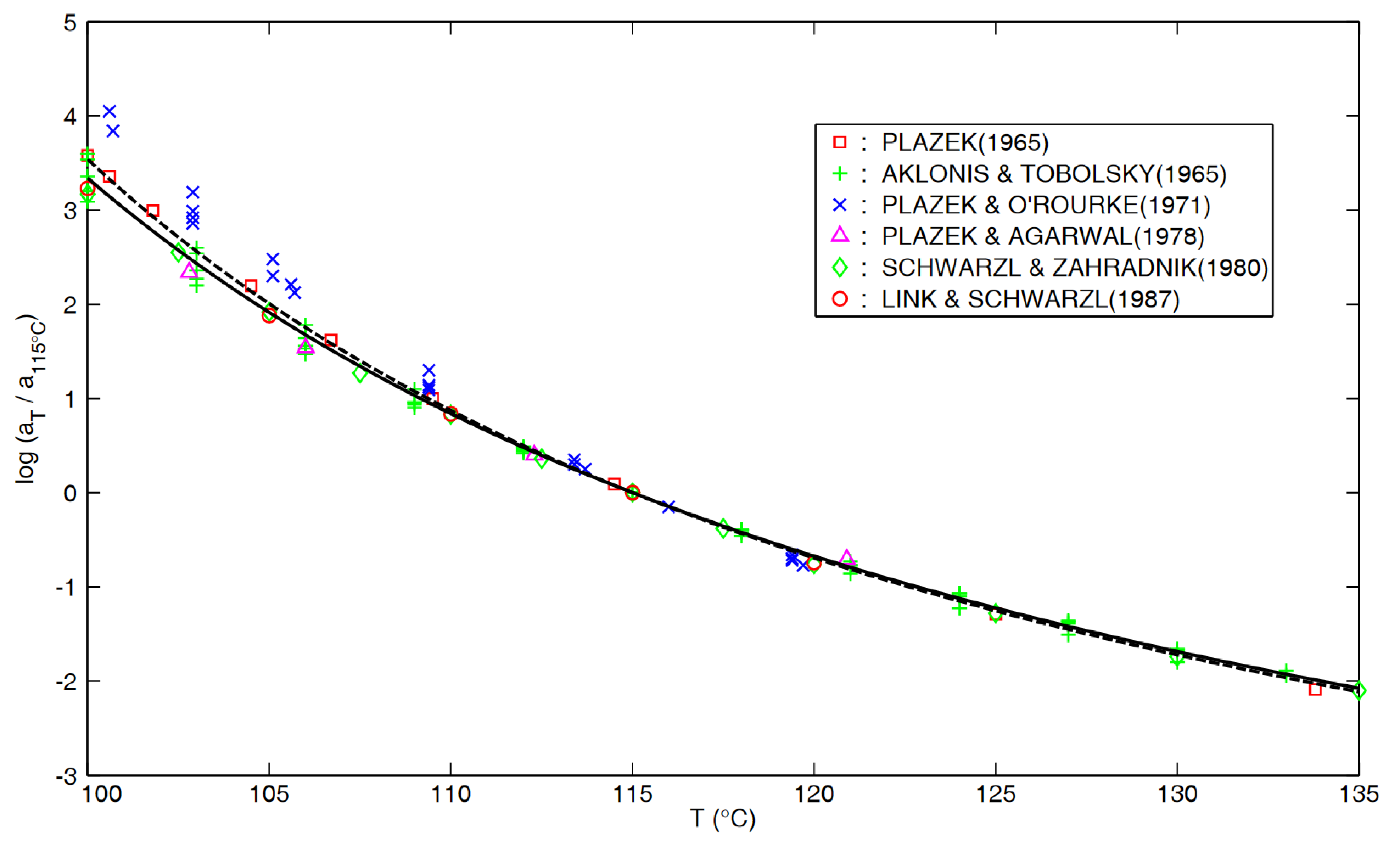
Appendix B: aT for PS in “Glass-Rubber Transition”

Shown in Figure B are results for the temperature-shift factor, aT/a115°C, for the “glass-rubber-transition” regime of PS based upon available data. In particular, the results from Aklonis and Tobolsky [14] are based upon stress-relaxation measurements whereas the remaining data are all based upon recoverable-shear-creep results.
Preprints 110932 g0a2
Figure B. Cumulative data for the temperature sensitivity of aT for the glass-rubber transition of PS. Both curves are based upon VFTH model with dashed corresponding to Eqn. (B.1) and solid to Eqn. (B.2).
Figure B. Cumulative data for the temperature sensitivity of aT for the glass-rubber transition of PS. Both curves are based upon VFTH model with dashed corresponding to Eqn. (B.1) and solid to Eqn. (B.2).
Preprints 110932 g0a2
The two curves in Figure B are both based upon the VFTH model, as given in Eqn. (A.1), now with TREF = 115°C, with the dashed curve being the best fit of all indicated data, with
CC = 669.8°C, T∞ = 71.60°C, RMSDEV = 0.1869
whereas the solid curve is the best fit when the data from Plazek and O’Rourke [15] are omitted, resulting in
CC = 714.4°C, T∞ = 69.43°C, RMSDEV = 0.09965.
It is noted that the RMSDEV is almost halved by omitting the data from Plazek and O’Rourke [15], indicating that the latter data are anomalous.
Although Plazek and O’Rourke [15] present tabulated results for nine PS of NMWD, only the four of highest molecular weight (94K, 189K, 600K and 800K) have been included in Figure B. (A fifth polymer, of molecular weight 47K, is actually from Plazek [9] and has been plotted in Figure B accordingly.) It is noted that the shift factor for recoverable compliance in Table II of Plazek and O’Rourke [15] is all relative to 100ºC. However, when expressed relative to 115ºC (which has been chosen as a representative value, given the temperature range of the data in Figure B), the results from Plazek and O’Rourke [15] become clearly anomalous in the lower temperature range because those data decay much more rapidly between 100 and 115ºC (as can be seen from Figure B) than the remaining experimental results from the other five sources.

Appendix C: Further Considerations

Figure C compares results based upon the VFTH fits in Eqns. (B.2), (12) and (A.2) expressed in terms of Ω(T), a measure of temperature sensitivity, as evaluated via Equation (7). It is noted that curve 1 is based upon the fit obtained in Appendix B based (mainly) upon recoverable-shear-creep data between 100 and 135ºC. On the other hand, curves 2 and 3 should both be applicable up to 300ºC, based upon related results in Figure 3 and Figure A, respectively. It is noted that curve 2 lies consistently above curve 1; that is, with increasing temperature, τ seg , c in Eqn. (12) consistently decays faster (on a fractional basis) than a T in Equation (B.2). On the other hand, it is noted from Figure C that curve 3, corresponding to a T for the flow regime in Appendix A, intersects curves 1 and 2 at respective temperatures of 115.9ºC (as can also be seen from Figure 1 above) and 158.5ºC.
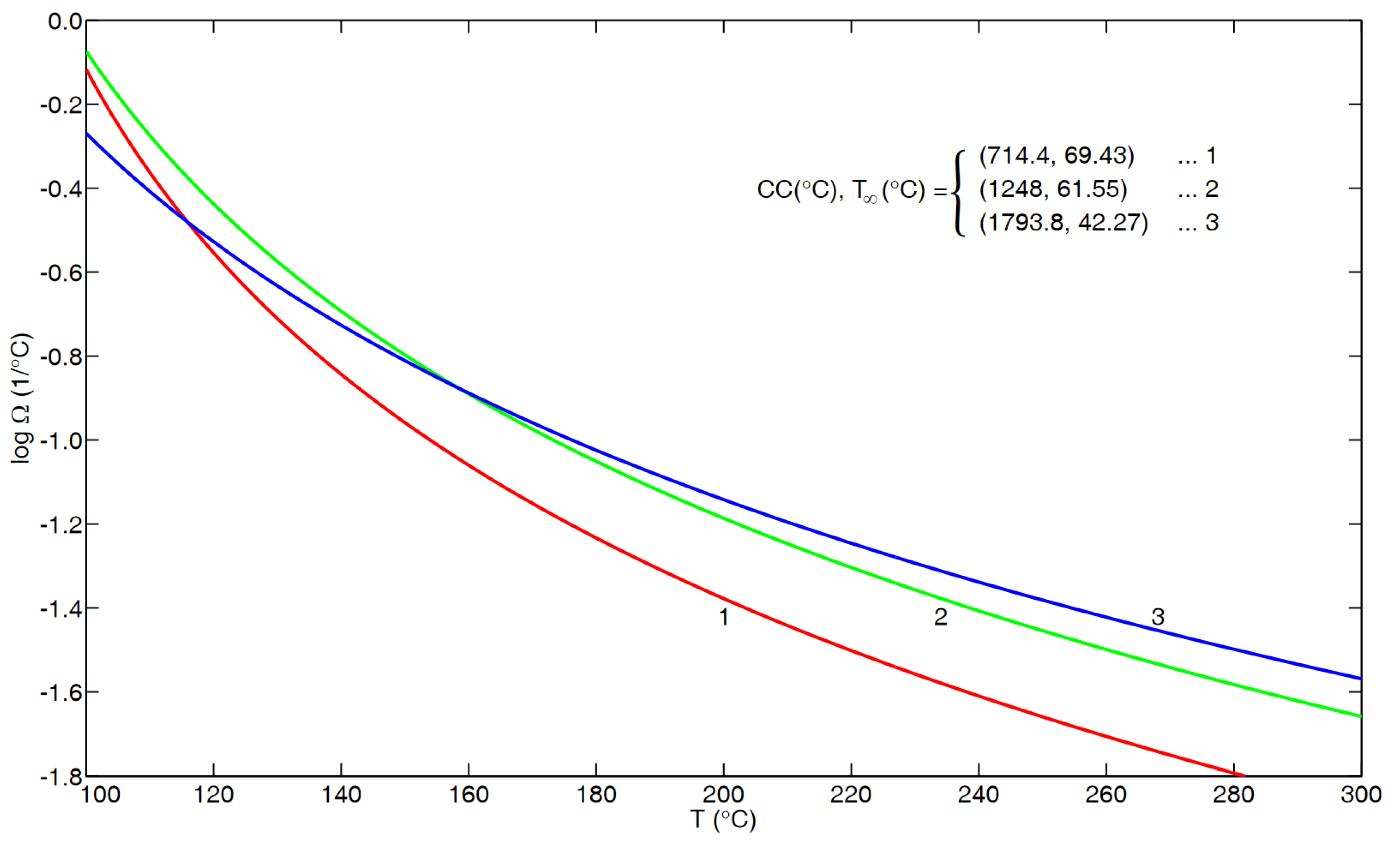
Preprints 110932 g0a3
Figure C. Results for Ω versus T based upon three VFTH fits, namely Eqn. (B.2) from Appendix B (“Glass-Rubber Transition”): curve 1 ; (12) from He, et al. [5]: curve 2 ; Eqn. (A.2) from Appendix A (“Flow Regime”): curve 3.
Figure C. Results for Ω versus T based upon three VFTH fits, namely Eqn. (B.2) from Appendix B (“Glass-Rubber Transition”): curve 1 ; (12) from He, et al. [5]: curve 2 ; Eqn. (A.2) from Appendix A (“Flow Regime”): curve 3.
Preprints 110932 g0a3
Making use of the three curves in Figure C, one might address some related results in the literature. For example, Figure 3 of He, et al. [5] seems to convincingly indicate that the segmental-correlation time and the viscosity have the same temperature dependence. In particular, the most extensive viscosity results in their Figure 3 is for the “PS-2” polymer, in terms of eight (solid square) data points which range between 1000/T ≅ 2.046/ºK at left and 2.493/ºK at right. Adjusting these points by ΔTg (= 373ºK − 331ºK = 42ºK, according to their Figure 9 and Table 1) to account for a small Mw of 2310, we are then dealing (in terms of ºC) with respective temperatures of about 257ºC and 170ºC, respectively. Based on Eqns. (A.1) and (A.2) of Appendix A above, it follows that curve 3 in Figure C corresponds to
a 170 ° C a 257 ° C = 2.960 x 10 2
whereas, from Eqn. (12), curve 2 in Figure C corresponds to
τ seg , c   ( 170 ° C ) τ seg , c   ( 257 ° C ) = 1.678 x 10 2
In particular,
2.960 x 102/1.678 x 102 = 1.764 = 100.246.
That is, according to the tight correlation for the viscosity of PS given by Eqns. (A.1 and A.2) above, the result in (C.3) indicates that the total variation of aT between the left-most and right-most solid squares in Figure 3 of He, et al. [5] exceeds that of τseg,c(T), as given in (12) above, by a factor of 1.764. On a logarithmic basis, as in their Figure 3, this becomes a difference of 0.246 decade. {Note: if aT in Eqns. (A.1) and (A.2) is replaced by Eqns. (A.1) and (A.3), namely the fit obtained by McKenna et al. [30], the difference becomes 0.263 decade.} Accordingly, such results call into question the correlation for the viscosity and τseg,c of polymer d8PS-2 shown in Figure 3 of [5].
Another concern relates to the relative behavior of the creep compliance and viscosity at higher temperatures. In this regard, one might refer to the work of Ngai [29,32], namely pp. 117/118 from [32] and pp. 262/263 from [29]. In both cases, Ngai first states that, above ≈ 407ºK (134ºC), the (recoverable) creep compliance and viscosity have the same aT. However, Ngai then qualifies this by indicating that extrapolating creep-compliance data to higher temperatures indicates a weaker temperature dependence than for the viscosity. Unlike in [32], Ngai’s corresponding plot in [29], namely Figure 101 (left panel, for PS), explicitly includes a curve for the (recoverable) creep compliance which decays more slowly than that for the viscosity. In turn, this is in agreement with the present results, as shown in Figure C, where curve 1 (corresponding to recoverable-creep compliance) lies below curve 3 (viscous flow) at higher temperatures, namely, above 115.9ºC. Since Ω characterizes the temperature sensitivity, the lower value for curve 1 indicates a slower decay with increasing temperature.

Appendix D: Calculating Ω(1/ºC) at Moderate Mw

Based upon Eqns. (3) {with “τeq” replaced by “τα“} and (13), it follows that
Ω = l n 10 × m T g ( ° K )
where Ω(1/ºK) or, equivalently, Ω(1/ºC). Hence, based on the values for m (fragility index) presented by Hintermeyer, et al. [23] in their Figures 5(c), 6(c) and 7(c) for PDMS, PS and PB, respectively, with corresponding values for Tg(ºK) from their Table 1, Table 2 and Table 3, resulting values are presented in Table D-1, Table D-2 and Table D-3 below for Ω(1/ºC) as a function of Mw.
Table D-1. Ω(1/ºC) results for PDMS, based on Eqn. (D.1) and Table 1 & Figure 5(c) of Hintermeyer, et al. [23].
Table D-1. Ω(1/ºC) results for PDMS, based on Eqn. (D.1) and Table 1 & Figure 5(c) of Hintermeyer, et al. [23].
Mw Tg(ºK) m Ω(1/ºC)
311 126.3 107.1 1.95
311 126.3 116.1 2.12
860 133.6 100.9 1.74
1600 138.2 108.0 1.80
1600 138.2 110.0 1.83
2490 139.9 110.0 1.81
3510 141.5 111.0 1.81
4560 142.4 111.4 1.80
5940 143.0 113.2 1.82
11.0K 144.0 115.1 1.84
21.6K 144.2 113.6 1.81
41.4K 144.5 114.1 1.82
128K 144.4 116.1 1.85
232K 144.6 115.0 1.83
Table D-2. Ω(1/ºC) results for PS based upon Eqn. (D.1) and Table 2 & Figure 6(c) of Hintermeyer, et al. [23].
Table D-2. Ω(1/ºC) results for PS based upon Eqn. (D.1) and Table 2 & Figure 6(c) of Hintermeyer, et al. [23].
Mw Tg(ºK) m Ω(1/ºC)
106 114.7 81.6 1.64
162 138.9 76.8 1.27
370 231.9 78.0 0.77
690 261.4 72.1 0.64
1350 314.2 97.0 0.71
3250 347.0 107.5 0.71
8900 356.9 105.4 0.68
19.1K 367.9 116.2 0.73
33.5K 369.0 119.6 0.75
96.0K 372.6 120.9 0.75
243K 373.3 122.6 0.76
546K 372.0 122.0 0.76
Table D-3. Ω(1/ºC) results for PB based upon Eqn. (D.1) and Table 3 & Figure 7(c) of Hintermeyer, et al. [23].
Table D-3. Ω(1/ºC) results for PB based upon Eqn. (D.1) and Table 3 & Figure 7(c) of Hintermeyer, et al. [23].
Mw Tg(ºK) m Ω(1/ºC)
355 140.9 70.0 1.14
466 161.2 71.1 1.02
575 162.1 73.0 1.04
777 165.3 78.0 1.09
1450 170.7 81.1 1.09
2020 173.6 83.0 1.10
2760 174.5 88.0 1.16
4600 174.0 90.9 1.20
19.9K 175.3 90.0 1.18
35.3K 174.5 90.9 1.20
87.0K 174.4 90.5 1.19

References

  1. Hieber, C.A. Modelling the Density Relaxation of Polystyrene. Rheol Acta 2022, 61, 523–538. [Google Scholar] [CrossRef]
  2. O’Connell, P.A.; McKenna, G.B. Arrhenius-type Temperature Dependence of the Segmental Relaxation Below Tg. J. Chem Phys 1999, 110, 11054–11060. [Google Scholar] [CrossRef]
  3. Zhao, J.; McKenna, G.E. Temperature Divergence of the Dynamics of a Poly (vinyl acetate) Glass: Dielectric vs. Mechanical Behaviors. J. Chem Phys 2012, 136, 154901. [Google Scholar] [CrossRef]
  4. Roland, C.M.; Casalini, R. Temperature Dependence of Local Segmental Motion in Polystyrene and its Variation with Molecular Weight. J. Chem Phys 2003, 119, 1838–1842. [Google Scholar] [CrossRef]
  5. He, Y.; Lutz, T.R.; Ediger, M.D.; Ayyagari, C.; Bedrov, D.; Smith, G.D. NMR Experiments and Molecular Simulations of the Segmental Dynamics of Polystyrene. Macromolecules 2004, 37(13), 5032–5039. [Google Scholar] [CrossRef]
  6. Vogel, H. Das Temperatur-Abhangigklitsgersetz der Viskosität von Flüssigkeiten. Phys Z 1921, 22, 645–646. [Google Scholar]
  7. Fulcher, G.S. Analysis of Recent Measurements of the Viscosity of Glasses. J Am Ceram Soc 1925, 8(6), 339–355. [Google Scholar] [CrossRef]
  8. Tammann, G.; Hesse, W. Die Abhängegkeit der Viskosität von der Temperatur bei Unterkühlten Flüssigkeiten. Z Anorg Allg Chem 1926, 156, 245–257. [Google Scholar] [CrossRef]
  9. Plazek, D.J. Temperature Dependence of the Viscoelastic Behavior of Polystyrene. J. Phys Chem 1965, 69(10), 3480–3487. [Google Scholar] [CrossRef]
  10. Zosel, J. Der Einfluss von Molekulargewicht und Molekulargewichtsverteilung auf die Viskoelastischen Eigenschaften von Polystyrolschmelzen. Rheol Acta 1971, 10(2), 215–224. [Google Scholar] [CrossRef]
  11. Marin, G.; Graessley, W. Viscoelastic Properties of High Molecular Weight Polymers in the Molten State; 1: Study of Narrow Molecular Weight Distribution Samples. Rheol Acta 1977, 16(5), 527–533. [Google Scholar] [CrossRef]
  12. Schausberger, A.; Schindlauer, G.; Janeschitz-Kriegl, H. Linear Elastico-Viscous Properties of Molten Standard Polystyrenes; I: Presentation of Complex Moduli; Role of Short Range Structural Parameters. Rheol Acta 1985, 24(3), 220–227. [Google Scholar] [CrossRef]
  13. Lomellini, P. Williams-Landel-Ferry Versus Arrhenius Behavior: Polystyrene Melt Viscoelasticity Revised. Polymer 1992, 33(23), 4983–4989. [Google Scholar] [CrossRef]
  14. Aklonis, J.J.; Tobolsky, A.V. Stress Relaxation and Creep Master Curves for Several Monodisperse Polystyrenes. J. Appl Phys 1965, 36(11), 3483–3486. [Google Scholar] [CrossRef]
  15. Plazek, D.J.; O’Rourke, V.J. Viscoelastic Behavior of Low Molecular Weight Polystyrene. J. Polym Sci, part A2 1971, 9, 209–243. [Google Scholar] [CrossRef]
  16. Plazek, D.J.; Agarwal, P. Comparison of Similar Narrow Molecular Weight Polystyrenes. J. Appl Polym Sci 1978, 22(8), 2127–2135. [Google Scholar] [CrossRef]
  17. Schwarzl, F.R.; Zahradnik, F. The Time Temperature Position of the Glass-Rubber Transition of Amorphous Polymers and the Free Volume. Rheol Acta 1980, 19(2), 137–152. [Google Scholar] [CrossRef]
  18. Link, G.; Schwarzl, F.R. Shear Creep and Recovery of a Technical Polystyrene. Rheol Acta 1987, 26(4), 375–384. [Google Scholar] [CrossRef]
  19. Angell, C.A. Relaxation in Liquids, Polymers and Plastic Crystals – Strong/Fragile Patterns and Problems. J. Non-Cryst Solids 1991, 131-133, 13–31. [Google Scholar] [CrossRef]
  20. Lindsey, C.P.; Patterson, G.D.; Stevens, J. Photon Correlation Spectroscopy of Polystyrene Near the Glass-Rubber Relaxation. J. Polym Sci (Polym Phys Ed) 1979, 17, 1547–1555. [Google Scholar] [CrossRef]
  21. Lee, H.; Jamieson, A.M.; Simha, R. Photon Correlation Spectroscopy of Polystyrene in the Glass Transition Region. Macromolecules 1979, 12(2), 329–332. [Google Scholar] [CrossRef]
  22. Pschorn, U.; Rössler, E.; Sillescu, H.; Kaufmann, S.; Schaefer, D.; Spiese, H.W. Local and Cooperative Motions at the Glass Transition of Polystyrene: Information from One- and Two-Dimensional NMR as Compared with Other Techniques. Macromolecules 1991, 24(2), 398–402. [Google Scholar] [CrossRef]
  23. Hintermeyer, J.; Herrmann, A.; Kahlau, R.; Goiceanu, C.; Rössler, E.A. Molecular Weight Dependence of Glassy Dynamics in Linear Polymers Revisited. Macromolecules 2008, 41(23), 9335–9344. [Google Scholar] [CrossRef]
  24. Patterson, G.D.; Carroll, P.J.; Stevens, J.R. Photon Correlation Spectroscopy of Polystyrene as a Function of Temperature and Pressure. J. Polym Sci (Phys) 1983, 21(4), 605–611. [Google Scholar] [CrossRef]
  25. Boyd, R.H.; Smith, G.D. Polymer Dynamics and Relaxation; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
  26. Ferry, J.D. Viscoelastic Properties of Polymers, 3rd Ed ed; Wiley: New York, NY, USA, 1980. [Google Scholar]
  27. Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am Chem Soc 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
  28. Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: New York, NY, USA, 2011. [Google Scholar]
  29. Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput J 1965, 7(4), 308–313. [Google Scholar] [CrossRef]
  30. McKenna, G.B.; Hadziioannou, G.; Lutz, P.; Hild, G.; Strazielle, C.; Straupe, C.; Rempp, P.; Kovacs, A.J. Dilute Solution Characterization of Cyclic Polystyrene Molecules and Their Zero-Shear Viscosity in the Melt. Macromolecules 1987, 20(3), 498–512. [Google Scholar] [CrossRef]
  31. Ngai, K.L. Physical Properties of Polymers, 3rd ed.; Mark, J., Ngai, K., Graessley, W., Mandelkern, L., Samulski, E., Koenig, J., Wignall, G., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 72–152. [Google Scholar]
Preprints 110932 g002
Figure 2. Predicted curve for τeq(T) based upon Eqns. (8, 9, 11) compared with PS data based on photon-correlation spectroscopy [20,21], NMR [22], and dielectric spectroscopy [4,23]. The dashed line will be described later.
Figure 2. Predicted curve for τeq(T) based upon Eqns. (8, 9, 11) compared with PS data based on photon-correlation spectroscopy [20,21], NMR [22], and dielectric spectroscopy [4,23]. The dashed line will be described later.
Preprints 110932 g002
Preprints 110932 g003
Figure 3. Predictions for the relaxation time τ(T) based on Eqns. (8, 9, 11): solid curve ; or upon Eqn. (12): dashed curve. Data based on photon-correlation spectroscopy, NMR and dielectric spectroscopy.
Figure 3. Predictions for the relaxation time τ(T) based on Eqns. (8, 9, 11): solid curve ; or upon Eqn. (12): dashed curve. Data based on photon-correlation spectroscopy, NMR and dielectric spectroscopy.
Preprints 110932 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated