Preprint
Communication
Generalized n-dimensional Effective Temperature for Cryogenic Systems in Accelerator Physics
Altmetrics
Downloads
123
Views
105
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
02 July 2024
Posted:
02 July 2024
You are already at the latest version
Alerts
Abstract
Investigations into the properties of generalized effective temperature are conducted across arbitrary dimensions. Maxwell-Boltzmann distribution is displayed for one, two, and three dimensions, with effective temperatures expressed for each dimension. The energy density of blackbody radiation is examined as a function of dimensionality. Effective temperatures for non-uniform temperature distributions in one, two, three, and higher dimensions are presented, with generalizations extended to arbitrary dimensions. Furthermore, the application of generalized effective temperature is explored not only for linearly non-uniform temperature distributions but also for scenarios involving the volume fraction of two distinct temperature distributions. Finally, the effective temperature is determined for a cryogenic system supplied with both liquid nitrogen and liquid helium.
Keywords:
Subject: Physical Sciences - Quantum Science and Technology
1. Introduction
The temperature of a body is commonly assessed through the utilization of blackbody radiation. The exploration of Stefan-Boltzmann’s law in n-dimensional space has been pursued [1]. It has been observed that thermal radiation exhibits notable deviations from blackbody radiation when considering bodies of small size. Investigations into the size effect of thermal radiation in one, two, and three dimensions have been conducted [2,3,4]. Techniques for correcting camera and infrared detector errors have been developed to enhance temperature measurement accuracy [5,6,7,8], while investigations into minimum resolvable temperature have been conducted in the realm of thermal imaging sensing [9]. Furthermore, calculations of effective temperature for non-uniform temperature distributions have been investigated [10,11]. Additionally, research across various fields has delved into the fractal dimensions of natural phenomena and their applications [12,13,14,15,16,17]. Integer dimensions are idealized constructs, whereas fractional dimensions manifest in natural phenomena. The evaluation of fractal dimensions on the thermal and hydrodynamic properties of micro-channel rough surface structures was conducted using computational fluid dynamic simulations [18]. The heat capacity of liquid helium, which exhibits a fractal dimension between two and three dimensions, was calculated. The results showed a significant dependence on this fractal dimension [19]. The fractional dimension of a body can be discerned through the measurement of the maximum frequency of thermal radiation. A study explored how the most probable frequency of emitted radiation relates to thermal energy across arbitrary dimensions [20]. Furthermore, the study of temperature-independent thermal radiation—where the color remains constant despite temperature variations—was investigated through insulator-to-metal phase transitions [21]. To construct high-energy accelerators, superconducting cavities are essential for accelerating high-energy beams. Cryogenic systems were constructed, superconducting cavities were developed, and the surface resistance of these cavities was investigated [22,23,24,25].
In this study, we investigate the properties of generalized effective temperature across arbitrary dimensions. We examine the energy density of blackbody radiation in relation to dimensionality. Generalized effective temperatures for non-uniform temperature distributions are derived for one, two, and three dimensions, with extensions to fractional dimensions and arbitrary higher dimensions. We explore the effective temperature for linearly non-uniform temperature distributions across arbitrary dimensions, as well as its variation with volume fraction. Additionally, we estimate the effective temperature when a low-temperature test system is supplied with liquid nitrogen and liquid helium.
2. Maxwell-Boltzmann Distribution for One, Two and Three Dimensions
One-dimensional Maxwell-Boltzmann distribution for a gas is
where is the velocity in x-direction and m is the mass. The one-dimensional mean speed is , the mean magnitudes of the one-dimensional speed is, and the root-mean-squared speed for the one-dimension velocity distribution is .
The velocity distribution for two different temperature regions in one dimension is
where is the number of particles in the temperature region and is the number of particles in the temperature region.
Effective temperature for the two different temperature distribution is
The velocity distribution in terms of the effective temperature in one dimension is
Two-dimensional Maxwell-Boltzmann distribution is
where . For two-dimensional velocity distribution, the most probable velocity is , the average velocity is , and the root-mean-square velocity is .
The velocity distribution for two different temperature regions in two dimension is
where is the number of particles in the temperature region and is the number of particles in the temperature region.
Effective temperature for the two different temperature distribution in two dimension is
The velocity distribution in terms of the effective temperature in two dimension is
Three-dimensional Maxwell-Boltzmann distribution is
where .
For three-dimensional velocity distribution, the most probable velocity is , the average velocity is , and the root-mean-square velocity is .
The velocity distribution for two different temperature regions in three dimension is
where is the number of particles in the temperature region and is the number of particles in the temperature region.
Effective temperature for the two different temperature distribution in three dimension is
The velocity distribution in terms of the effective temperature in three dimension is
3. Blackbody Radiation in Arbitrary Dimensions
While blackbody radiation in integer dimensions is well-understood, we can extend this concept to arbitrary dimensions. For comparison, the energy density of one-dimensional blackbody radiation is given by [4]
where represents the Boltzmann constant, T denotes the absolute temperature, stands for the Planck constant, and c denotes the speed of light. The energy density of two-dimensional blackbody radiation becomes [3]
where stands for the Riemann zeta function. The energy density for blackbody radiation in three dimensions is [2]
The energy density in equations (13), (14), and (15) is proportional to the temperature raised to a power that reflects the total dimensionality. This total dimension incorporates both spatial and temporal components. While the spatial dimension can be arbitrary, time remains one-dimensional.
Dimension which includes integer dimension as well as fractional dimension can be calculated as
where D is the dimension, S is the scaling factor, and N is the number of the pieces. The dimension of an object can be determined using an arbitrary scaling factor. Eq. (16) allows us to calculate the arbitrary dimension for any given geometry. Figure 1(a) shows one-dimension for and , Figure 1(b) shows two-dimension for and and Figure 1(c) shows three-dimension for and by using Eq.(16). Fractals is non-integer dimension and shows self-similarity in which a small piece of an object looks like whole object. Figure 1(d), Figure 1(e) and Figure 1(f) represent D=1.062 for S=1/12 and N=14. The surface area and the volume for arbitrary dimension in Euclidean space are and , respectively in which R means the radius of Euclidean plane and D means the dimension. Figure 1(g) and Figure 1(h) refer to the surface area and the volume as a function of dimension for the radius of 1 m in Euclidean space. The volume and surface area of an object increase as the dimension are increased.
The energy density of the blackbody radiation in arbitrary dimensions is given by [1,20]
where Γ is the gamma function and D denotes the space dimension. The energy density increases with temperature as T(D+1), where D represents the spatial dimensions and the additional power of 1 accounts for the time dimension.
4. Effective Temperature for One, Two and Three Dimensions
The total energy density of one-dimensional thermal radiation is defined as:
Here, represents the effective temperature of the entire body. For a one-dimensional blackbody with uniform temperature distribution, the effective temperature remains constant throughout the body. Using Eq. (13) and Eq. (18), we can derive the effective temperatures for three different temperature distributions, denoted as T1, T2, and T3
where L represents the total length of the body, with L1, L2, and L3 denoting the length corresponding to temperatures T1, T2 and T3, respectively. It’s important to note that the effective temperature of the body always surpasses the average temperature when dealing with more than two different temperature regions. For a one-dimensional non-uniform temperature distribution, the effective temperature of n segments can be generalized as
where . The effective temperature is defined for discrete non-uniform temperature distribution in Eq. (20). For continuously changing temperature distribution in one dimension, the effective temperature can be expressed as
The total energy density of two-dimensional thermal radiation is calculated as
The effective temperature represents the uniform temperature across a two-dimensional body. Using equations (14) and (22), we can calculate the effective temperatures for three different temperature distributions
where A represents the total surface area of the body, with A1, A2, and A3 denoting the surface areas corresponding to temperatures T1, T2, and T3, respectively. It’s important to note that the average temperature is lower than the effective temperature for three different temperatures. In two dimensions, the effective temperature for n segments with varying temperature distributions can be generalized as
where represents the total surface area of the two-dimensional body. Eq. (24) provides the definition of the effective temperature for discrete non-uniform temperature distribution in two dimensions. For continuously non-uniform temperature distribution in two dimensions, the effective temperature can be expressed as
The total energy density for thermal radiation in three dimensions is given by
From Eqs. (15) and (26), the effective temperature of a body with three different temperature distributions can be expressed as
where V represents the total volume of the body, with V1, V2, and V3 denoting the volume corresponding to temperatures T1, T2, and T3, respectively. The effective temperature of the body for the n segments of different temperature distribution in three-dimensional thermal radiation can be generalized as
where V represents the total volume of the body, given by . The effective temperature is defined for discrete non-uniform three-dimensional temperature distribution in Eq. (28), where many small bodies have different temperatures.
The effective temperature of continuously non-uniform temperature distribution in three-dimension is expressed as
5. Effective Temperature for Arbitrary Dimension
Many natural physical systems exhibit fractional dimensions, which often deviate from regular geometric shapes. For instance, while a line is typically considered one-dimensional, the dimension of a curved line exceeds one dimension. Similarly, while a perfectly smooth surface is typically two-dimensional, the dimension of a surface with roughness surpasses two dimensions. This study investigates thermal radiation properties across arbitrary dimensions, shedding light on the correlation between maximum radiation frequency and these dimensions [20].
The total energy density of the thermal radiation for both fractional dimension and arbitrary dimension is given by
Here, h represents the Planck constant, c denotes the speed of light, D signifies the space dimension, and Teff stands for the effective temperature of the body.
Combining Eqs (17) and (30), the effective temperature of a body with three different temperature distributions in D-dimension can be formulated as
Here, v denotes the total volume of the body, while , , and represent the volumes corresponding to temperatures T1, T2 and T3, respectively. For n segments exhibiting different temperature distributions, the generalized effective temperature of the body in arbitrary-dimensional thermal radiation is given by
where and D represents the space dimension. The generalized effective temperature of continuously changing temperature distribution in arbitrary D-dimension can be expressed as
.
Eq. (33) represents the most generalized effective temperature for continuously changing temperature distributions in D-dimension, applicable to both fractional and arbitrary dimensions.
6. Results and Discussion
The effective temperature of a cryogenic system is of utmost importance as it dictates the required cooling power and associated costs for achieving desired temperatures. Figure 2 depicts the cryogenic system designed for a quarter-wave resonator cryomodule, where the superconducting cavity is cooled using both liquid nitrogen and liquid helium. These cryogenic liquids, with boiling points at 77 K and 4.2 K respectively, are widely employed in cryogenic applications due to their effectiveness in cooling systems.
Figure 3 illustrates the effective temperature of linearly non-uniform temperature distribution for both liquid nitrogen and liquid helium. It serves as a valuable reference when examining thermal contact from room temperature to cryogenic temperatures. The effective temperatures for one, two, and three dimensions can be derived using Eq. (21), Eq. (25), and Eq. (29) respectively. The linearly non-uniform temperature distribution between liquid nitrogen and room temperature is given by T(x)=77+(300-77)x/L, where L represents the total length of the body.
For the linearly non-uniform temperature distribution ranging from 77 K to 300 K, the effective temperatures for one, two, and three dimensions are 199.2 K, 208.3 K, and 216.0 K, respectively. The average temperature is calculated as 188.5 K. Additionally, for the linearly non-uniform temperature between liquid helium and room temperature, the equation is given by T(x)=4.2+(300-4.2)x/L, where L represents the total length of the body.
For the linearly non-uniform temperature distribution ranging from 4.2 K to 300 K, the effective temperatures for one, two, and three dimensions are 174.4 K, 189.9 K, and 201.3 K, respectively. These values are obtained using Eq. (21), Eq. (25), and Eq. (29) to calculate the effective temperature for one, two, and three dimensions, respectively. The average temperature is determined to be 152.1 K. Notably, the effective temperature of a body exceeds its average temperature, and it increases with higher dimensions.
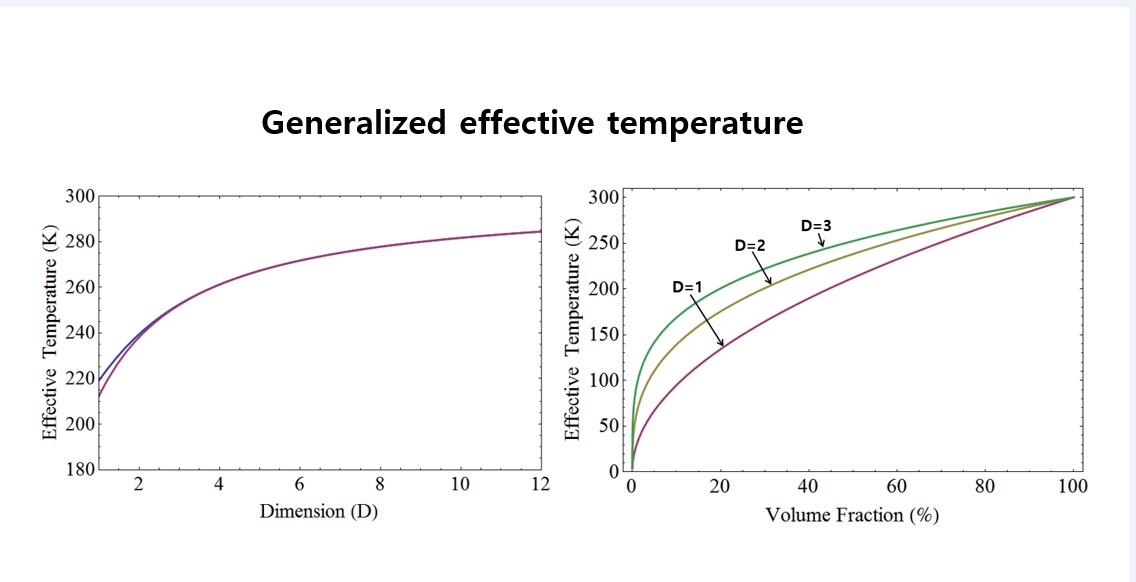
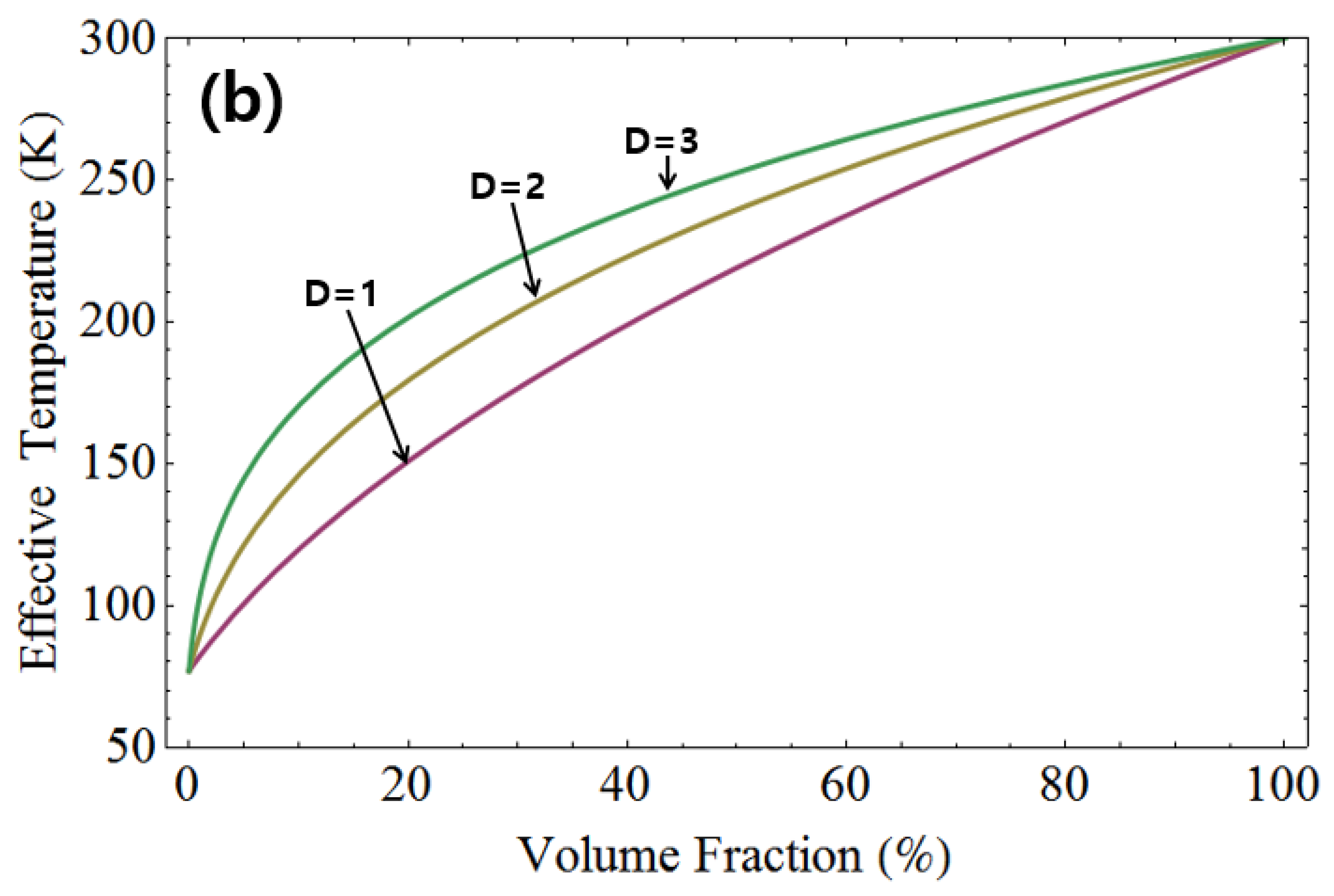
Figure 4 depicts the effective temperature with identical volume ratios for liquid helium and room temperature, as well as for liquid nitrogen and room temperature. In the top graph of Figure 4, the effective temperature is shown with the same volume ratio for 77 K and 300 K, while in the bottom graph, it is shown for 4.2 K and 300 K. It’s observed that the effective temperature increases with higher dimensions. Furthermore, the disparity in effective temperature between the two cases decreases as the dimensionality is increased.
In Figure 5, the effective temperature is presented as a function of the volume ratio for liquid helium and room temperature. Specifically, the graph illustrates the effective temperature with respect to the volume ratio of the 300 K volume to the 4.2 K volume. As anticipated, the effective temperature rises as the volume ratio increases. Moreover, it is noted that the effective temperature also escalates with increasing dimensionality while maintaining the same volume ratio.
Figure 6 illustrates the effective temperature as a function of the volume ratio, specifically the ratio of 300 K volume to 77 K volume. It is evident that the effective temperature increases with both increasing dimensionality and volume ratio.
The effective temperature of a cryogenic system holds significant importance, as it directly influences the cooling temperature of the body and the volume of the cryogenic system, particularly when using liquid helium and liquid nitrogen. These factors are closely tied to the overall cost of the system. Therefore, this research provides valuable insights into understanding the effective temperature of cryogenic systems, offering potential applications and benefits in this field.
The effective temperature represents the global temperature concept of a body, particularly useful when the local temperature distribution across the body is non-uniform. When seeking to determine the overall temperature of the body, calculating the effective temperature becomes essential. This paper offers valuable insights into computing the effective temperature for both integer and fractional dimensions, providing a useful resource for obtaining the effective temperature of a body across various dimensional spaces.
7. Conclusions
We have demonstrated the characteristics of the generalized effective temperature across both fractional and arbitrary dimensions. Additionally, we present the energy densities of blackbody radiation across one, two, three, and higher dimensions. The Maxwell-Boltzmann distribution is displayed for one, two, and three dimensions, with effective temperatures expressed for each dimension. The generalization of effective temperature for non-uniform temperature distributions in various dimensions, from one to high dimensions, is provided. Furthermore, we compute the effective temperature for cryogenic liquids, including liquid nitrogen and liquid helium, and express the effective temperature of linearly non-uniform temperature distributions as a function of arbitrary dimension. We also illustrate the effective temperature for two different temperature distributions in terms of arbitrary dimension and volume fraction. This generalized effective temperature framework is applicable across fractional and higher dimensions.
Author Contributions
H.K.: Conceptualization, investigation, writing—original draft, writing—review and editing. C.-S.P.: investigation, validation, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Research Foundation of Korea (NRF) and funded by the Ministry of Science and ICT under grant RS-2022-00214790.
Data Availability Statement
The data supporting this study’s conclusions are available from the corresponding author upon reasonable request.
Acknowledgments
The authors thank the researchers who contributed to discussions on effective temperature at IRIS.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Landsberg, P.T.; De Vos, A. The Stefan-Boltzmann constant in n-dimensional space. J. Phys. A: Math. Gen. 1989, 22, 1073–1084. [Google Scholar] [CrossRef]
- Yu, S.-J.; Youn, S.J.; Kim, H. Size effect of thermal radiation. Phys. B: Condens. Matter 2010, 405, 638–641. [Google Scholar] [CrossRef]
- Kim, H.; Lim, S.C.; Lee, Y.H. Size effect of two-dimensional thermal radiation. Phys. Lett. A 2011, 375, 2661–2664. [Google Scholar] [CrossRef]
- Kim, H.; Youn, S.J.; Yu, S. J. Generalized Thermionic Emission for Arbitrary Dimension, J. Kor. Phys. Soc. 2010, 56, 554. [Google Scholar] [CrossRef]
- Schulz, M.; Caldwell, L. Nonuniformity correction and correctability of infrared focal plane arrays. Infrared Phys. Technol. 1995, 36, 763–777. [Google Scholar] [CrossRef]
- Orżanowski, T.; Madura, H. Test and evaluation of reference-based nonuniformity correction methods for microbolometer infrared detectors. Opto-Electronics Rev. 2010, 18, 91–94. [Google Scholar] [CrossRef]
- X. Bao, X. ; Webb, D. J. ; D. A. Jackson, D. A. Combined distributed temperature and strain sensor based on Brillouin loss in an optical fiber, Opt. Lett., 1994, 19, 141. [CrossRef]
- Ji, J. K.; Yoon, J. R.; Cho, K. Nonuniformity correction scheme for an infrared camera including the background effect due to camera temperature variation, Opt. Eng. 2000, 39, 936. [Google Scholar] [CrossRef]
- Vollmerhausen, R.H. Representing the observer in electro-optical target acquisition models. Opt. Express 2009, 17, 17253–17268. [Google Scholar] [CrossRef]
- Kim, H.; Han, M.-S.; Perello, D.; Yun, M. Effective temperature of thermal radiation from non-uniform temperature distributions and nanoparticles. Infrared Phys. Technol. 2013, 60, 7–9. [Google Scholar] [CrossRef]
- Kim, H.; Park, C.-S.; Han, M.-S. Effective temperature of two-dimensional material for non-uniform temperature distribution. Opt. Commun. 2014, 325, 68–70. [Google Scholar] [CrossRef]
- Coniglio, A.; De Arcangelis, L.; Herrmann, H. Fractals and multifractals: Applications in physics. Phys. A: Stat. Mech. its Appl. 1989, 157, 21–30. [Google Scholar] [CrossRef]
- Theiler, J. Estimating fractal dimension, J. Opt. Soc. Am. A, 1990, 7, 1055. [Google Scholar] [CrossRef]
- Clarke, K.C.; Schweizer, D.M. Measuring the Fractal Dimension of Natural Surfaces Using a Robust Fractal Estimator. Cartogr. Geogr. Inf. Syst. 1991, 18, 37–47. [Google Scholar] [CrossRef]
- Draves, S.; Abraham, R.; Viotti, P.; Abraham, F. D.; Sprott, J. C. Int. J. Bifurcat. Chaos 2008, 18, 1243. [CrossRef]
- la Torre, F.C.-D.; I González-Trejo, J.; A Real-Ramírez, C.; Hoyos-Reyes, L.F. Fractal dimension algorithms and their application to time series associated with natural phenomena. J. Physics: Conf. Ser. 2013, 475, 012002. [Google Scholar] [CrossRef]
- Garg, A.; Agrawa, A.; Negi, A. A Review on Natural Phenomenon of Fractal Geometry, International Journal of Computer Applications (0975 – 8887) Volume 86 – No 4, 14, Article in International Journal of Computer Applications · May 2014. 20 January. [CrossRef]
- Chen, Y.; Zhang, C.; Shi, M.; Peterson, G.P. Optimal surface fractal dimension for heat and fluid flow in microchannels. Appl. Phys. Lett. 2010, 97, 084101. [Google Scholar] [CrossRef]
- Nam, S. T. Heat Capacity of Liquid Helium II in a Fractal Dimension, J. Korean Phys. Soc., 2004, 44, 464. [Google Scholar]
- Kim, H.; Kim, W.K.; Park, G.-T.; Shin, I.; Choi, S.; Jeon, D.-O. Generalized thermal radiation from arbitrary fractional dimension. Infrared Phys. Technol. 2014, 67, 600–603. [Google Scholar] [CrossRef]
- Shahsafi, A.; Roney, P.; Zhou, Y.; Zhang, Z.; Xiao, Y.; Wan, C.; Wambold, R.; Salman, J.; Yu, Z.; Li, J.; et al. Temperature-independent thermal radiation. Proc. Natl. Acad. Sci. 2019, 116, 26402–26406. [Google Scholar] [CrossRef]
- Sakai, H.; Cenni, E.; Enami, K.; Furuya, T.; Sawamura, M.; Shinoe, K.; Umemori, K. Field emission studies in vertical test and during cryomodule operation using precise x-ray mapping system. Phys. Rev. Accel. Beams 2019, 22, 022002. [Google Scholar] [CrossRef]
- Tan, J. Field emission studies at Saclay and Orsay, Part. Accel. 1996, 53, 1. [Google Scholar]
- Vines, J.; Xie, Y.; Padamsee, H. Systematic Trends for the Medium Field Q-Slope. In Proceedings of the SRF2007, Peking Univ., Beijing, China, 14-19 October 2007; TUP27; p. 178, (2017). [Google Scholar]
- Weingarten, W.; Eichhorn, R. Field-dependent surface resistance for superconducting niobium accelerating cavities: The case of N doping. In Proceedings of the 17th International Conference on RF Superconductivity (SRF2015), Whistler, BC, Canada, 13–18 September 2015; MOPB010; p. 95. [Google Scholar]
Figure 1.
Integer and fractional dimensions. Subfigure (a) displays one-dimension for S=1/5 and N=5, while subfigure (b) depicts two dimensions for S=1/5 and N=25. Subfigure (c) shows three dimensions for S=1/5 and N=125. Subfigures (d), (e), and (f) illustrate D=1.062 for S=1/12 and N=14. Subfigures (g) and (h) depict the surface area and volume as a function of dimension for a radius of 1 m in Euclidean space.
Figure 1.
Integer and fractional dimensions. Subfigure (a) displays one-dimension for S=1/5 and N=5, while subfigure (b) depicts two dimensions for S=1/5 and N=25. Subfigure (c) shows three dimensions for S=1/5 and N=125. Subfigures (d), (e), and (f) illustrate D=1.062 for S=1/12 and N=14. Subfigures (g) and (h) depict the surface area and volume as a function of dimension for a radius of 1 m in Euclidean space.
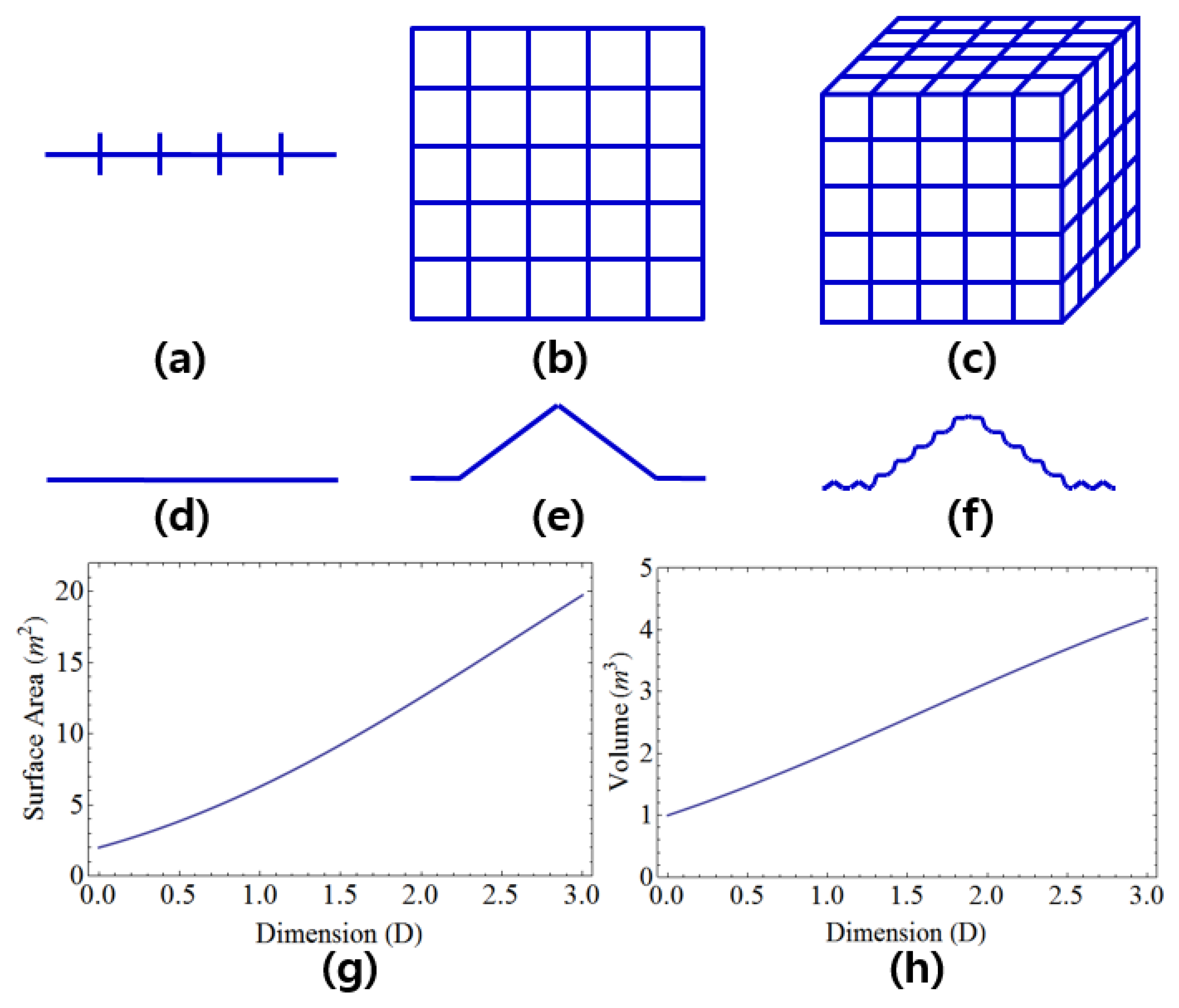
Figure 2.
A cryogenic system for a quarter-wave resonator cryomodule. The superconducting cavity within the cryomodule is cooled using a combination of liquid nitrogen and liquid helium.
Figure 2.
A cryogenic system for a quarter-wave resonator cryomodule. The superconducting cavity within the cryomodule is cooled using a combination of liquid nitrogen and liquid helium.
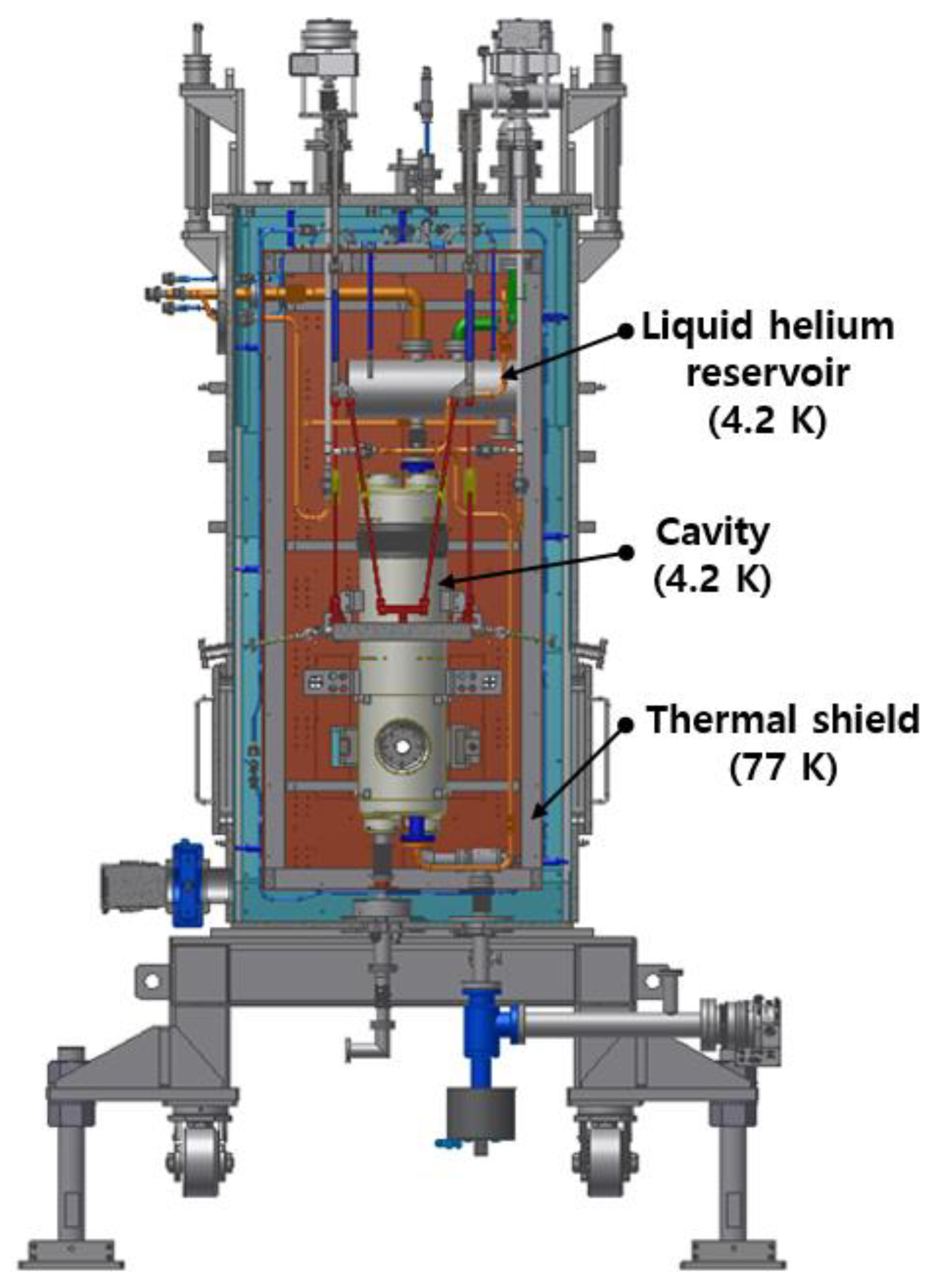
Figure 3.
The effective temperature of a linearly non-uniform temperature distribution for both liquid nitrogen and liquid helium. In the top graph, the effective temperature ranges from 77 K to 300 K. For one, two, and three dimensions, the respective effective temperatures are 199.2 K, 208.3 K, and 216.0 K. The bottom graph displays the effective temperature ranging from 4.2 K to 300 K. In this range, the effective temperatures for one, two, and three dimensions are 174.4 K, 189.9 K, and 201.3 K, respectively.
Figure 3.
The effective temperature of a linearly non-uniform temperature distribution for both liquid nitrogen and liquid helium. In the top graph, the effective temperature ranges from 77 K to 300 K. For one, two, and three dimensions, the respective effective temperatures are 199.2 K, 208.3 K, and 216.0 K. The bottom graph displays the effective temperature ranging from 4.2 K to 300 K. In this range, the effective temperatures for one, two, and three dimensions are 174.4 K, 189.9 K, and 201.3 K, respectively.
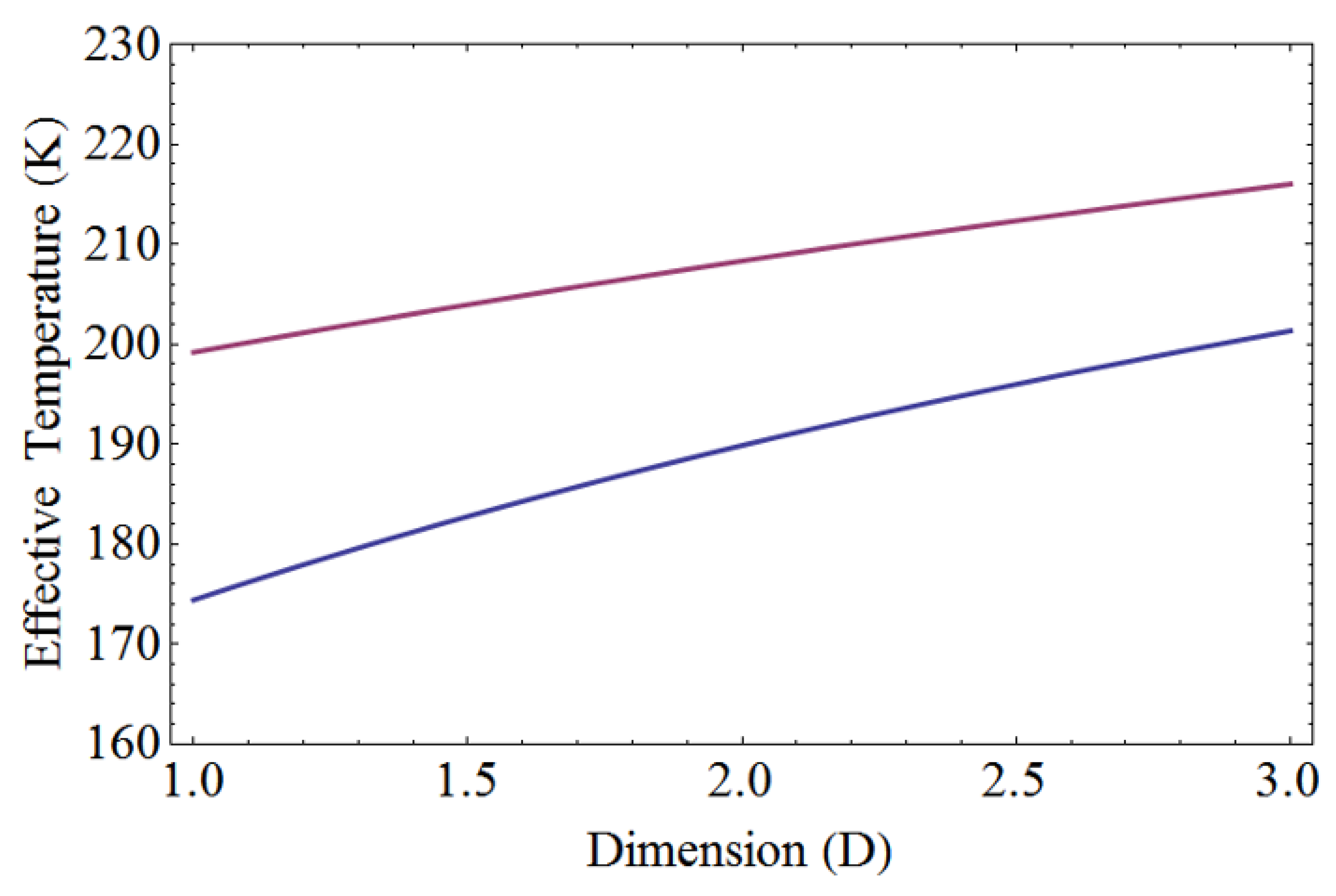
Figure 4.
The effective temperature illustrated for liquid helium and room temperature, as well as for liquid nitrogen and room temperature, maintaining the same volume ratio. In the top graph, the effective temperature is plotted for 77 K and 300 K. Similarly, the bottom graph displays the effective temperature for 4.2 K and 300 K. Notably, the effective temperature shows an increase with higher dimensions.
Figure 4.
The effective temperature illustrated for liquid helium and room temperature, as well as for liquid nitrogen and room temperature, maintaining the same volume ratio. In the top graph, the effective temperature is plotted for 77 K and 300 K. Similarly, the bottom graph displays the effective temperature for 4.2 K and 300 K. Notably, the effective temperature shows an increase with higher dimensions.
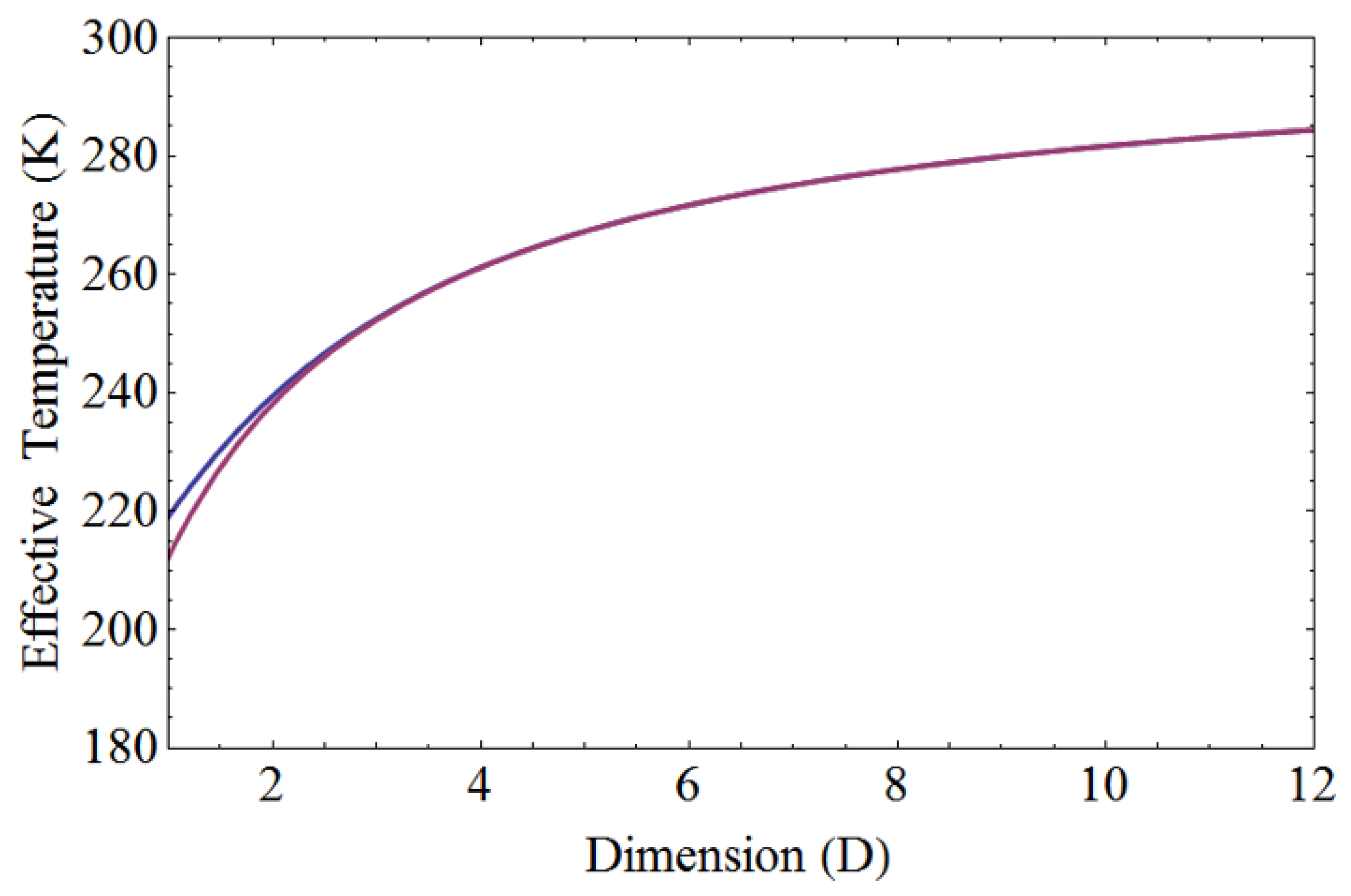
Figure 5.
The effective temperature depicted as a function of the volume ratio for liquid helium and room temperature. Specifically, the effective temperature is presented with respect to the volume ratio of the 300 K volume to the 4.2 K volume. Notably, the effective temperature demonstrates an increase with higher dimensions or increased volume ratios.
Figure 5.
The effective temperature depicted as a function of the volume ratio for liquid helium and room temperature. Specifically, the effective temperature is presented with respect to the volume ratio of the 300 K volume to the 4.2 K volume. Notably, the effective temperature demonstrates an increase with higher dimensions or increased volume ratios.
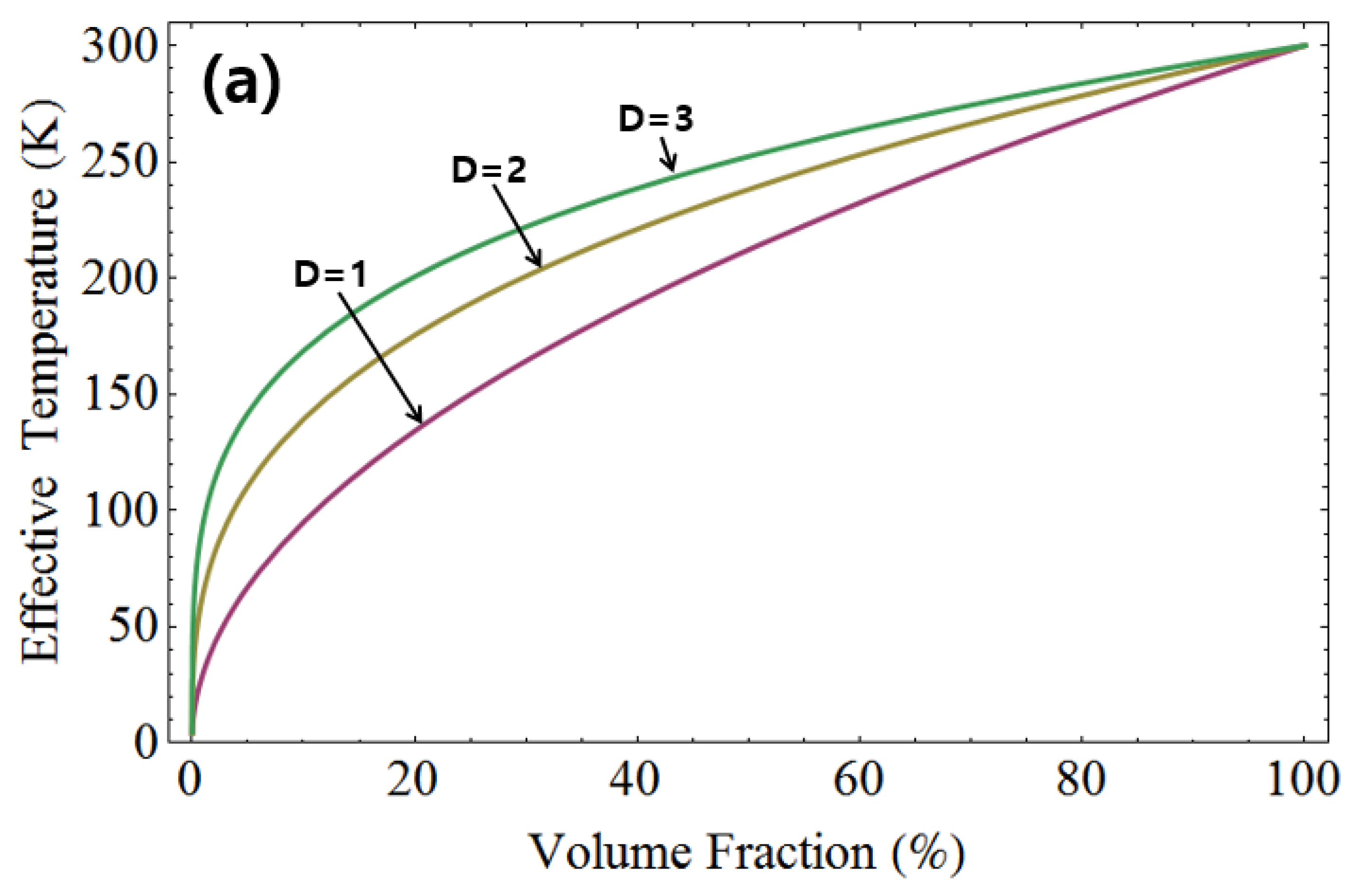
Figure 6.
The effective temperature portrayed as a function of the volume ratio for liquid nitrogen and room temperature. Specifically, the effective temperature is depicted with respect to the volume ratio of the 300 K volume to the 77 K volume. Notably, the effective temperature demonstrates an increase with higher dimensions or increased volume ratios.
Figure 6.
The effective temperature portrayed as a function of the volume ratio for liquid nitrogen and room temperature. Specifically, the effective temperature is depicted with respect to the volume ratio of the 300 K volume to the 77 K volume. Notably, the effective temperature demonstrates an increase with higher dimensions or increased volume ratios.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





