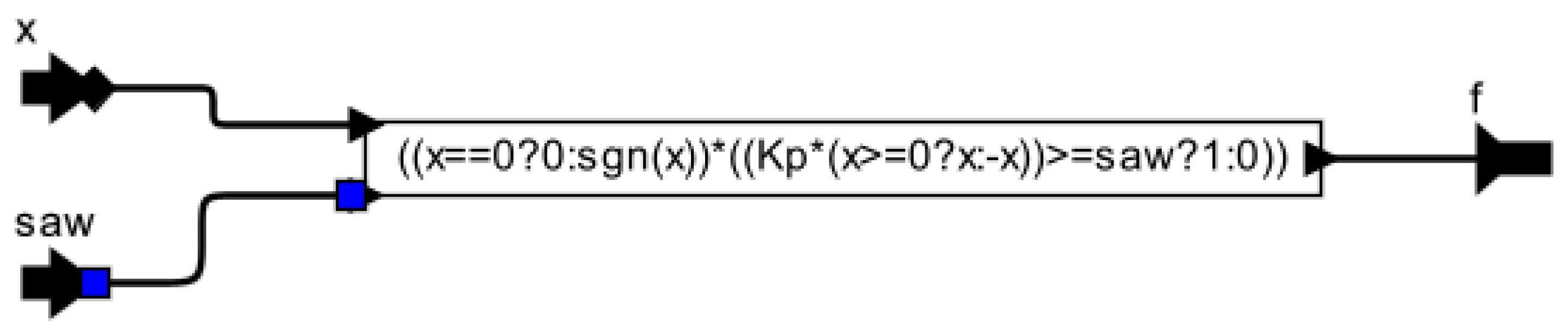Modeling and Simulation of Event Systems

1. Introduction

The PWM controllers are widely used in advanced industrial systems for efficient engine controlling [1,2]. Objective designing and adequate stable planning the functioning modes of controlling systems for servo drives within the Industry 4.0 technologies is impossible without applying computer modeling and simulation. The article considers modeling the dynamics of driving gears with the pulse-width modulation (PWM) controllers using Russian and foreign software tools. Traditionally, the presented illustrative example of the servo drive with the PWM controller is defined as a continuous system with a software model in the form of the schematic diagram in Matlab/Simulink [3] and SimInTech [4] platforms. On the other hand, the same control object is considered as an event-driven continuous or hybrid system, defined by the advanced finite state machine formalism as statecharts or the Harel diagrams [5]. Such a specification is performed using ISMA [6] and Ptolemy II [7] tools. The conclusion about software models with the specification applied to be appropriate in terms of the domain-driven adequacy is made. Efficient simulating and computer analysis of the hybrid systems requires not only specific integration techniques, considering discontinuities in the right side of the differential equation, as well as modes stiffness [8,9], but also original event detection methods, which are responsible for correct mode switching [10]. The developed algorithm for asymptotic detection in ISMA is presented.

Applying Matlab, SimInTech, Ptolemy II and ISMA libraries with numerical schemes and algorithms for event detection in numerical analysis of the illustrative example model of the servo drive with the PWM controller is discussed. The general computational algorithm for the finite state machine approach to hybrid systems studying is presented.

2. Event-Driven Systems and the Harel Diagrams

An event-driven system is a multi-mode dynamic system with continuous (С) or discrete (D) behavior, and modes of the system are determined by certain events (E).

Event-driven discrete or event-discrete systems (ED) are defined by the state vector $d\in W^r$, $W=R\cup \Im \cup B$, $\Im$ is a set of non-negative integer numbers; $B=\left\{false,\hspace{0.17em}\hspace{0.17em}true\right\}$ – a set of Boolean values; $R$ – a set of real numbers. The discrete behavior of the event system is determined by the mapping $D:R\times W^r\to W^r$, $r\in \Im$.

Event-continuous systems (EC), defined in a time interval $[t_0,t_k]$, are specified by the state vector $y\left(t\right)\in R^N\hspace{0.17em}$ and determined by the mapping $C:\hspace{0.17em}R{\hspace{0.17em}}^m\to R{\hspace{0.17em}}^m$, m – the number of system modes.

The modes of the EC system are defined by the state vector $x\left(t\right)\in R^n\hspace{0.17em}$with local behaviors $c_j$, $1\le j\le m$, which range of permissible values is defined on a set of continuously differentiable event functions [8,10] $g\left(t,\hspace{0.17em}x\right):\hspace{0.17em}R\times R^n\to R^s$, $s\le n$, and these values exist in the half-interval $\left[t_j^0,\hspace{0.17em}{t}_j^{*}\right)\subseteq \left[t_0,\hspace{0.17em}{t}_k\right]$ in a local region $g_j$, $g_j\in G$, which is the range of permissible values for the local states vector$x\left(t\right)\in R^n\hspace{0.17em}$.

An event mode function$g_j\left(t,x\right)$ [10] works in such a way, that the corresponding predicate of the mode behavior $p{r}_j:$ $g_j\left(t,x\right)<0$, $p{r}_j\in B$, is true ($p{r}_j=true$) in the entire half-interval of the mode solution $\left[t_j^0,\hspace{0.17em}{t}_j^{*}\right)\subseteq \left[t_0,\hspace{0.17em}{t}_k\right]$. Therefore, the moment $t=t_j^{*}$, when the next event $E_j,1\le j\le m$, occurs and the mode behavior changes, is determined by the moment of time, when the predicate $p{r}_j\left(t,x\right)\in B$ changes its value from $false$ to $true$.

Let’s change phase variables $x\left(t\right)=y_j\left(t\right)\hspace{0.17em}$ and constrain the mapping $C$ by the class of ordinary differential equations systems in the Cauchy form. Then local modes are presented as

$$y_j{ }^{\prime }=f_j\left(y_j,t\right), y_j\left(t_0\right)=y_j{ }_0, t\in \left[t_j^0,\hspace{0.17em}{t}_j^{*}\right),$$

(1)

where $y_j\left(t\right)\in R^n\hspace{0.17em}$; $f_j:R\times R^n\to R^n$ is a non-linear vector function, satisfying the Lipschitz conditions in a local mode; $y_j{ }_0\in \hspace{0.17em}{R}^n$ – the initial conditions vector for the local mode.

The sequence of continuous system modes generates a cause-and-effect chain of events

$$s_0=\left(t_0,y_0\right)\to E_1=\left(t_1^{*},y_{10}\right)\to \mathrm{...}\to E_m=\left(t_m^{*},y_{m0}\right),$$

that are defined on a solution of (1) with initial conditions $s_0=\left(t_0,y_0\right)$. The set of discrete behaviors is determined by the non-empty set of event functions $g=\left\{g_j\right\}$, $1\le j\le m$. In moments $t_j^{*}$, when the next event $E_j$ occurs, the right side of (1) meets discontinuity points. The Lipschitz conditions are broke at discontinuity points. In this case, taking into account discontinuities of phase variables, obtaining the only solution requires the Caratheodory conditions to be satisfied [8]. As a result, the global behavior of the entire event-continuous system is determined by solving the Cauchy problem with constraints of the event function

$$y^{\prime }=f\left(y,t\right),y\left(t_0\right)=y_0,g\left(y,t\right)<0, t\in [t_0,t_k],$$

(2)

where $y\left(t\right)\in R^N\hspace{0.17em}$; $f:R\times R^N\to R^N$ is a piecewise continuous vector function, satisfying the Caratheodory conditions [8]; $g\left(y,\hspace{0.17em}t\right):\hspace{0.17em}R\times R^N\to R^S$, $S\le N$ – a continuously differentiable event vector function (event function).

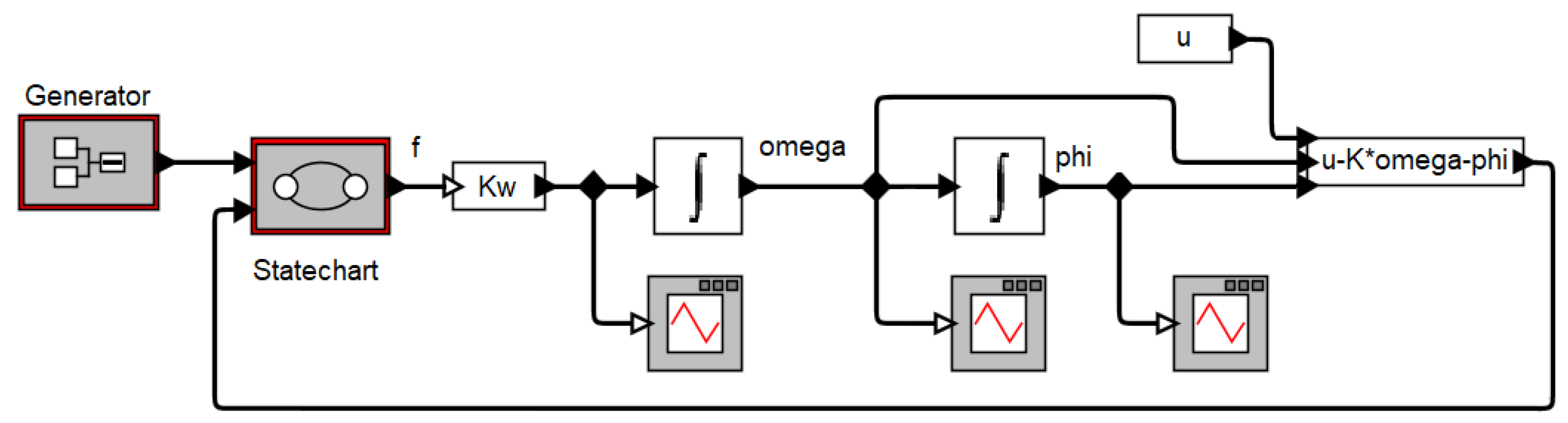
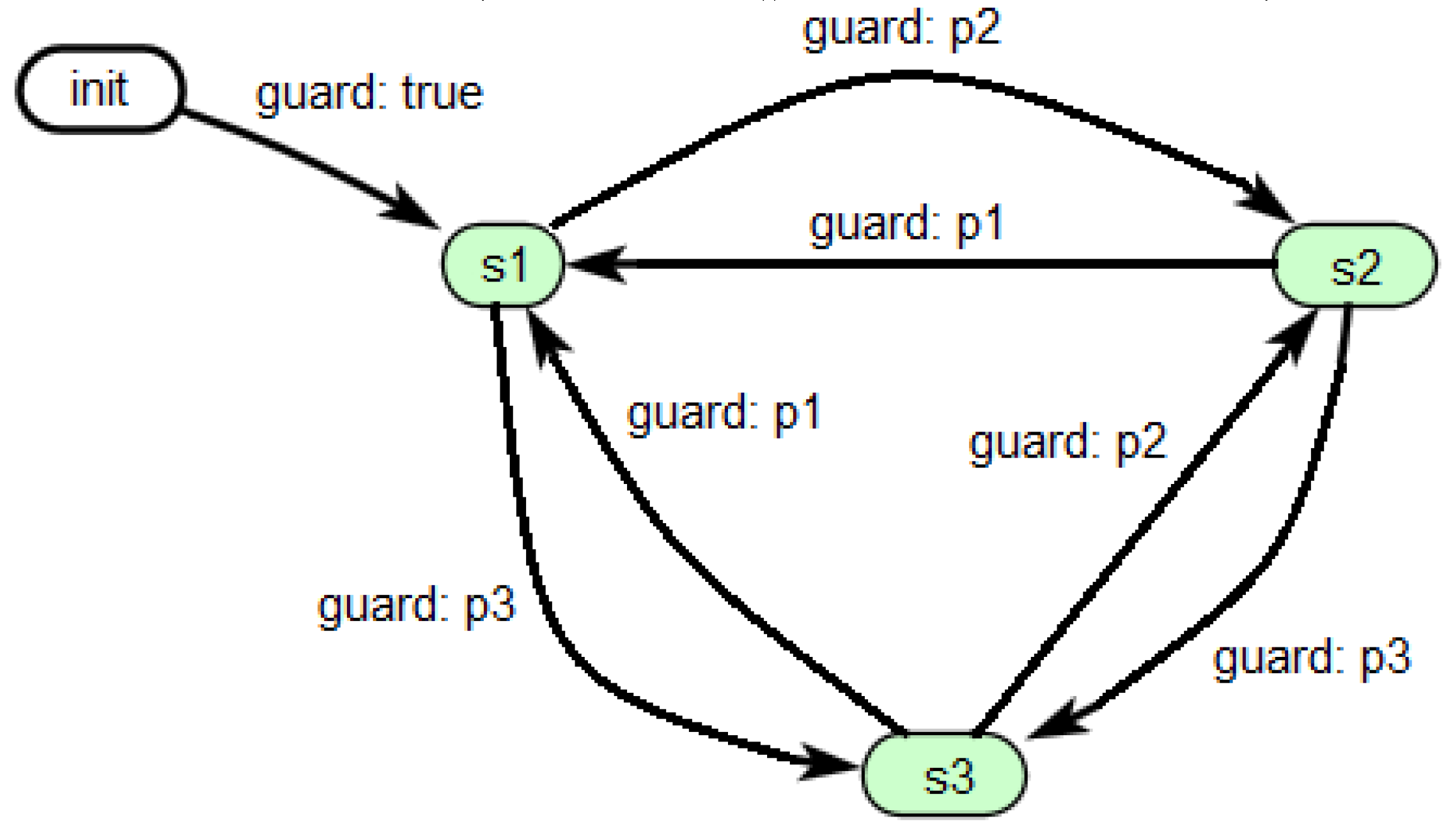
Designing multi-mode event-continuous systems (2) is based on the advanced finite state specification of the model (2) in the form of the Harel diagrams or statecharts [5,11]. The event-continuous system behavior changing from $c_i$, $1\le i\le m$, to a new one $c_j$, $1\le j\le m$, $j\ne i$, taking into account equations (1) – (2), will be determined by a new predicate

$$p_k=\neg p{r}_i\wedge p{r}_j, 1\le k\le m^2,$$

(3)

On the analogy of graph theory [12], let a pair of behaviors $(c_i,c_j)$ be adjacent behaviors of an event system, if the following condition is met: $p_k=true$, $1\le k\le m^2$. If a non-empty set of behaviors C is presented as vertices or nodes, a non-empty set of predicates $P=\{p_k,\hspace{0.33em}k=1,2,\mathrm{...}\}$ is presented as a set of directed edges, connecting adjacent nodes $(c_i,c_j)$, then a directed graph $G(s_0,C,P)$ is a chart of discrete behavior. Finally, considering the fact, that both continuous $c_i$and discrete$d_i$ behaviors take places in corresponding states $s_i\in S$, $1\le i\le m$, the directed graph $G(s_0,S,P)$ can be called a statechart or a Harel diagram.

In the modern traditional terminology, event-continuous systems are usually called hybrid systems (HS) [8,13,14]. The study of hybrid systems is based on numerical analysis of the equations (2) by the advanced tools with libraries for numerical integration and event detection algorithms to identify discrete moments of mode switching [8,10,15].

3. Problem Statement

The model of a basic servo drive with symmetrical pulse width modulation can be described by the following system of equations [16]

$$\left\{\begin{array}{l}\frac{d\omega }{dt}=k_{\omega }f\left(u-k\omega -\phi ,t\right),\\ \frac{d\phi }{dt}=\omega ,\\ \omega \left(0\right)={\omega }_0,\\ \hspace{0.33em}\phi \left(0\right)={\phi }_0,\end{array}\right.$$

(4)

where $\omega$ is the angular velocity with the initial value ${\omega }_0$; $k_{\omega }$ is the speed reinforcing coefficient; $u$is the control action or setpoint; $k$is the damping ratio; $\phi$ is the angle of rotation with the initial value ${\phi }_0$; $f:R^2\times R\to R$ is the PWM function.

Let the PWM modulating signal be defined as

$$x=u-k\omega -\phi ,$$

(5)

then

$$f\left(x,t\right)=sign\left(x\right)\cdot z\left(x,t\right),$$

(6)

where

$$sign\left(x\right)=\left\{\begin{array}{l}-1,\hspace{0.33em}if\hspace{0.33em}x<0,\\ 0,\hspace{0.33em}if\hspace{0.33em}x=0,\\ 1,\hspace{0.33em}if\hspace{0.33em}x>0.\end{array}\right.$$

(7)

The function $z\left(x,t\right)$from (6) is given as

$$z\left(x,t\right)=\left\{\begin{array}{l}1,\hspace{0.33em}if\hspace{0.33em}{k}_p\left|x\right|\ge saw\left(t\right),\\ 0,\hspace{0.33em}if\hspace{0.33em}{k}_p\left|x\right|<saw\left(t\right),\end{array}\right.$$

(8)

where $k_p=T_p^{-1}$ is the PWM coefficient, $saw\left(t\right)$ is the reference sawtooth signal.

It's clear from (6) – (8), that can be equal to three values. Accordingly, the right side of the first equation in (4) changes depending on conditions (7), (8). The mathematical model (4) – (8) can be presented as an event-continuous or hybrid system, identified by the directed graph with three nodes (states) $s_i\in S,\hspace{0.33em}i=\overline{1,3}$and directed edges (transitions from a state to another one), in this case, can be determined by the predicates in accordance to equations (7), (8). Such a directed graph $G(s_0,S,P)$ is called a Harel diagram or a statechart [5]. A hybrid system specification in the form of a statechart is a widely used advanced universal method to describe an event-continuous system [13]. The specification by the finite state machine with predicates, defining transitions, is implemented and developed in many advanced frameworks and platforms [7,14]. In Figure 1 the Harel diagram for a hybrid system, defined by (4) – (8) with the following predicates $p_i\in P,\hspace{0.33em}i=\overline{1,3}$ and $s_0=init$, is presented:

$$\begin{array}{l}{p}_1:\hspace{0.33em}\left(x\ge 0\right)\wedge \left(saw\left(t\right)-k_p\left|x\right|\le 0\right);\\ p_2:\hspace{0.33em}\left(x<0\right)\wedge \left(saw\left(t\right)-k_p\left|x\right|\le 0\right);\\ p_3:\hspace{0.33em}{k}_p\left|x\right|-saw\left(t\right)\le 0.\end{array}$$

(9)

4. Model Specification in ISMA

The source of the reference sawtooth signal in ISMA software [6] is implemented as an integrator with a reset in the following form

$$saw\left(t\right)=\left\{\begin{array}{l}u\left(0\right)+{\displaystyle \underset{0}{\overset{t}{\int }}u\left(\tau \right)d\tau ,\hspace{0.33em}if\hspace{0.17em}saw\left(t\right)\le sa{w}^{*},}\\ 0,\hspace{0.33em}\mathit{otherwise}.\end{array}\right.$$

(10)

where $sa{w}^{*}$ is the value of the integrator reset to 0.

A software model for a servo drive with a PWM controller (4) – (8) by the LISMA language [8,17] in the form of structural and text specification (STS) is presented in Figure 2.

The textual part of the specification (the "PWM" unit in Figure 2) in LISMA is illustrated in Figure 3 and, up to the operation signs (lines 1 - 4), replicates the mathematical notation of the Cauchy problem for the system of differential equations in the form (4). The software model is given the following parameters:$k_{\omega }=100$; $k=0.1$; $k_p=0.1$. Zero initial conditions for the ordinary differential equations system (4) are set by default.

Lines 1 – 4 define the initial state init, which determines the initial function $f:R^2\times R\to R$ and the system of algebraic-differential equations (4). Lines 6 – 8 present the chart with three states $s_i\in S,\hspace{0.33em}i=\overline{1,3}$, with corresponding transition predicates (8), indicated in square brackets, and actions (is) or behaviors, that were obtained by the resolving the system of differential equations (4), which was delivered to each state $s_i\in S,\hspace{0.33em}i=\overline{1,3}$ from the initial state init with the determined value$f$.

5. Model Specification in Simulink

The model implementation by schematic diagrams in MATLAB/Simulink [3] is presented in Figure 4 and Figure 5. The main structural scheme in Figure 4 is adjusted to equations (4) – (5) and the parameters values. In addition to built-in units from the platform libraries, the model includes a PWM macro-structure with the input $x\left(t\right)$, defined in (5), and the output modulating signal $out\left(t\right)$, defined by the structure, associated to expressions (6) – (9).

The presented approach to built schematic diagrams using the ‘input-output’ paradigm, unlike the advanced state machine specification, doesn’t allow applying relevant description and, consequently, a new technique for hybrid systems analysis, based on the paradigm with states, predicates and event functions. As a result, designing the PWM submodel becomes more complicated, since the specification of logical and arithmetical expressions (6) – (9) traditionally can be represented much easier not by the diagram, but by the expression, a symbol string including operands and logical and/or arithmetical operations. Applying expressions to hybrid systems definition and specification is used not only in the LISMA language, as was shown earlier, but also is accepted in the advanced software platforms for hybrid computer modeling and simulation [7,14,18,19]. It should be noticed, that even if the advanced platform implies designing continuous processes as in (4), the expressions, in case there are some of them, are presented via text units with symbol form for logical and arithmetical formulas as in (6) – (9), rather than by structural submodels [7,20].

6. Model Specification in SimInTech

A software model for a servo drive with PWM, applying statecharts of the finite state machine, is presented in Figure 6. The PWM model was built as a compound representation of the finite state machine statecharts with instantaneous determining the following state and calculating the state function values in the form of conditionally executing submodels.

The schematic diagram of the PWM submodel is presented in Figure 7. It includes the following structures: calculating transition predicates P1, P2, P3 (the left part in Figure 7); the statechart with 3 states designed as controlled submodels (the right part in Figure 7). The behaviors in states are determined by the numerical solution of the corresponding schematic diagram. The transition from the current state to another is defined by the specific transition unit (denoted at each state submodel on the right side).The transition unit generates the output of the state submodel, which can be connected to the input of another state submodel. The transition unit input gets a logical value, which is obtained by the calculating the transition predicate. The calculating can be conducted both inside and outside the state submodel. The data, obtained by the block diagram in each state, are sent to the unit for data selecting from the active state (DATA SELECTOR).

STATE1 is a submodel for $f=0$. The schematic diagram of this state is presented in Figure 8. Submodels for other states look similar.

This specification, combining two approaches, state machine and structural paradigms, is the most unsuccessful. It includes both all the disadvantages and contradictions of the structural approach applied in MATLAB/Simulink, that were discussed earlier, and confusion, associated with the finite state machine model. The SimInTech developers, aiming at applying advanced trends in hybrid systems definition, i.e. finite state machine paradigm, include the PWM finite state unit into the top level structure, corresponding to the system of equations (4). But this quite inefficient option is the only implementation of the declared finite state approach. The following process of the PWM submodel designing is carried out using structural techniques and the ‘input-output’ paradigm instead of the directed graph approach. The developers unsuccessfully try to construct the state of the directed graph using schematic diagram, but inputs and ouptuts of the structural diagram, when the output has functional dependency on the input, are not equivalent to the edges with predicates of the digraph. As a result, instead of a compact and transparent digraph, i.e. the Harel diagram (Figure 1), the model in SimInTech is presented as a lengthy tedious structure, including inexplicit embedded submodels (6 units), which hardly can be allied to the finite state paradigm. Therefore, the structural approach is not applied to hybrid systems definition. And that explains the fact, that for hybrid systems describing and analysis in Matlab, the Stateflow tool is used [21].

7. Model Specification in Ptolemy II

The specification for the servo drive in Ptolemy II [7] also combining two approaches. Top-level structural model, shown in Figure 9, include two integrators for first and second equations form (4). Sawtooth signal formed by Generator block and the PWM modulating signal (5) are sent to the input of Statechart block, which generates a control action.

The Statechart block is shown in Figure 10. It replicates the Harel diagram according to Figure 1.

The transition predicates (8) named guard and defined according to (9). The blocks for three states $s_i\in S,\hspace{0.33em}i=\overline{1,3}$, describe the rules for generating the output signal f, as shown in Figure 11.

The output f is calculated according to formula (6). The first part of expression in Figure 11 defines the function sign in accordance with (7). Hereinafter the ternary operator (like as C programming language) is used. The second part of expression corresponds to function $z\left(x,t\right)$ from (8). The modulus of x is obtained using a ternary operation (x>=0?x:-x). The result is multiplied by Kp and compared with the sawtooth signal.

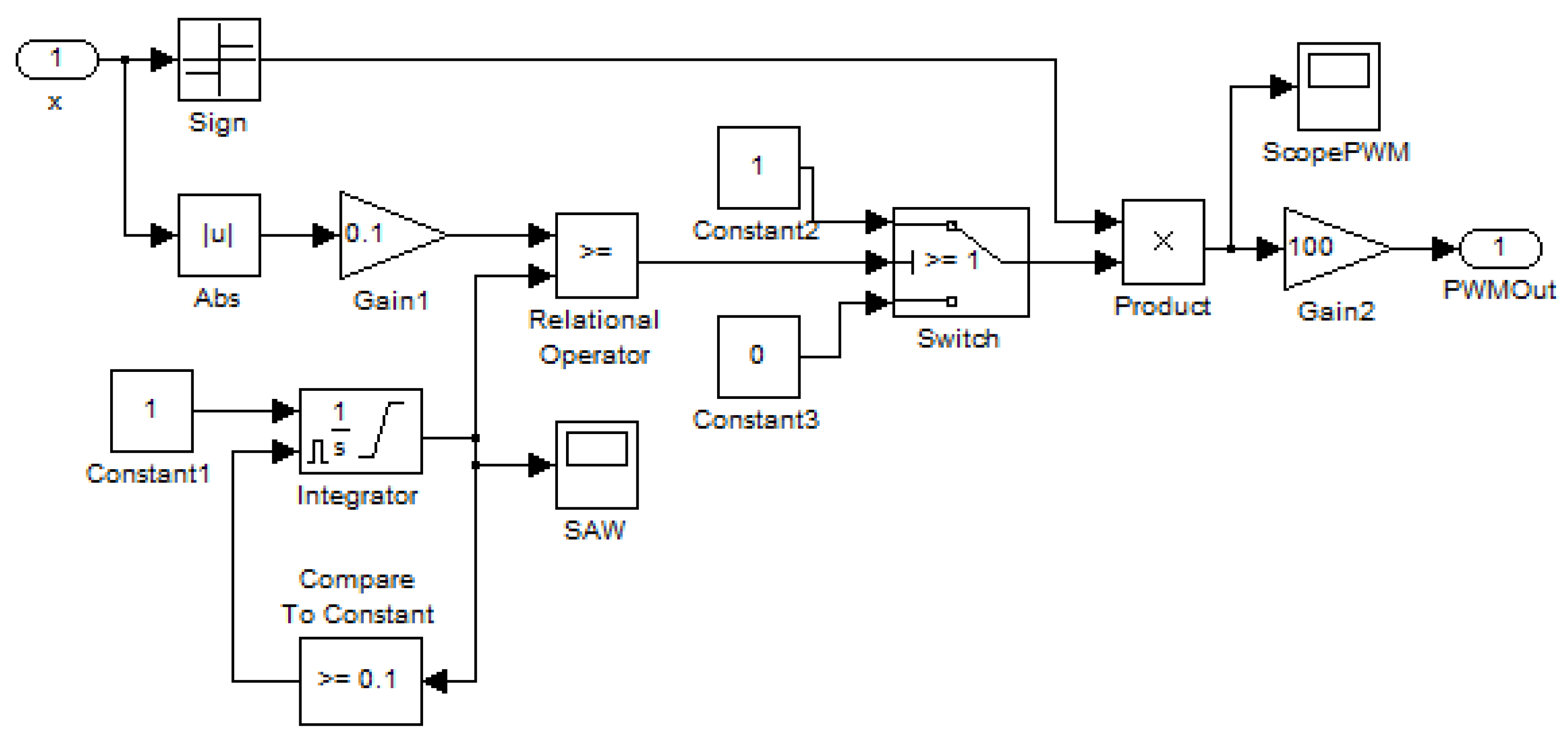
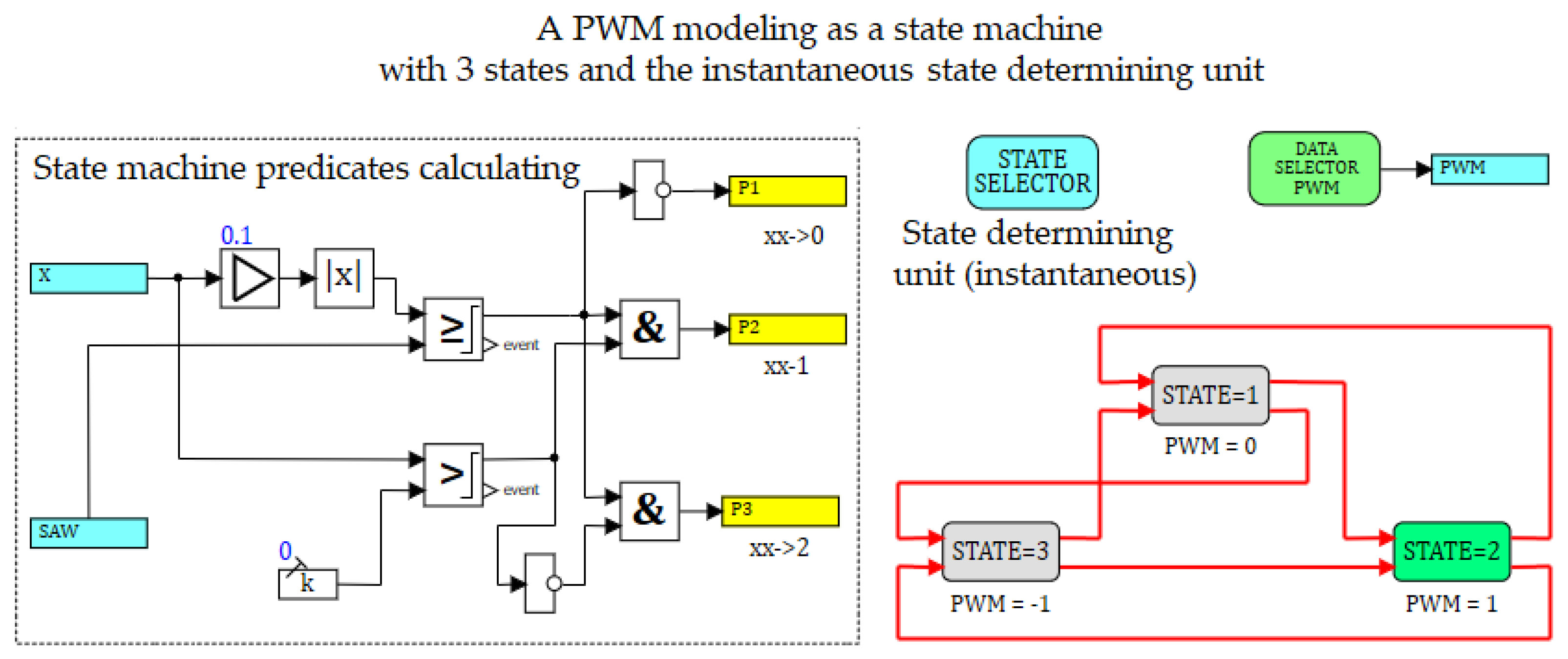
8. Event Detection Algorithms in ISMA

Let’s consider the algorithms for obtaining the event mode function $g\left(y,\hspace{0.17em}t\right)$ as in (2), implemented in the ISMA software tool. The LISMA grammar [17] is presented in the extended Backus–Naur form for the top-dawn parsers generator ANTLR4 [22]. The fragment of the grammar for conditional expressions in the software model is the following:

conditionalExpression: conditionalOrExpression;
conditionalOrExpression: conditionalAndExpression ( '||' conditionalAndExpression )*;
conditionalAndExpression: conditionalNotExpression: ( '&&' conditionalNotExpression: )*;
conditionalNotExpression: relationalExpression | '!' relationalExpression
relationalExpression: inequalityExpression | '(' conditionalExpression ')'

(11)

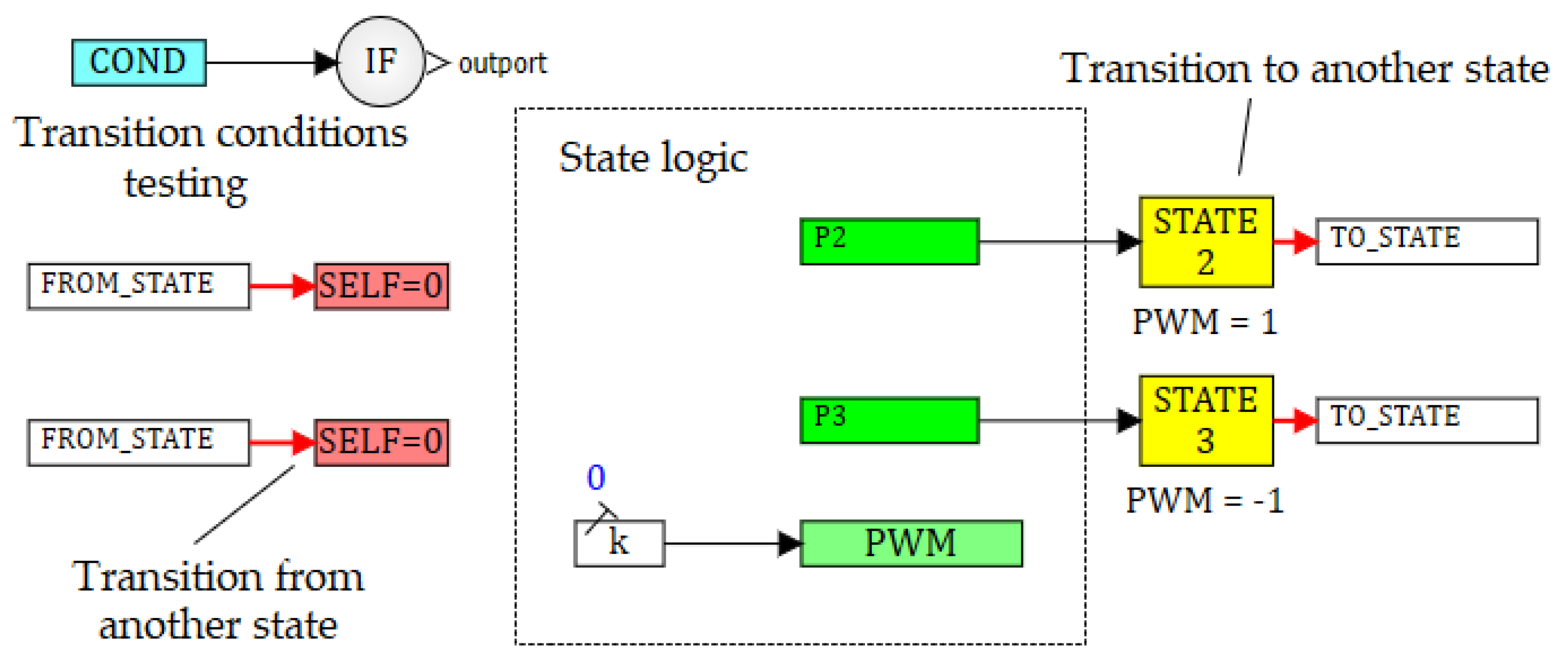
In accordance to the rules in (11), the software model includes conditions for the transition to a state $s_i\in S$. For example, the condition expression for the predicate $p_1$ from the system (9) is written down in square brackets in the line 6 (Figure 3). Taking into account the condition (3), let’s find the predicate $p{r}_i$ for the state $s_i$ in the following form:

$$p{r}_i=\underset{j\in J}{\wedge }\left(\neg p_j\right),$$

(12)

where J is the adjacent states for the state $s_i$.

Based on the syntactic tree, which was built while analyzing the software model, and its semantic attributes, the syntactic trees for the predicates $p{r}_i$ in every state of the system are constructed in the ISMA. An n-ary tree is built with the root corresponding to the conjunction operation. The root has n descendant nodes, where n is the number of adjacent states for the current mode of the hybrid system. All outgoing branches contain a vertex, corresponding to the logical negation (inversion). This vertex is the root of the syntactic tree, built for the predicate $p{r}_i$. Next, the syntactic tree is modified in a way that inversion operations are applied only to inequalities (11). De Morgan's rules for transforming logical expressions are applied here. The syntactic tree is top-down traversed, and for every node the transformations are applied according to the following recursive rules (Algorithm 1):

Algorithm 1. The mode behavior predicate transformation.

Step 1. If the tree node matches the inequality (inequalityExpression), the traverse is stopped. If the inversion operation indicator was set, the inequality sign is replaced by the opposite one.

Step 2. If the tree node matches the logical negation operation (‘!’), the inversion operation indicator is set to the descendant vertex. Resetting the indicator reverses the inversion, if negations are consecutive. The current node is excluded from the tree, the connection between a parent node and descendant one is built.

Step 3. If the tree node matches the conjunction operation (‘&&’) and the inversion operation indicator is set, the conjunction operation is replaced by the disjunction (‘||’). A new vertex with logical negation (‘!’) is added to all outgoing branches. The inversion indicator is reset.

Step 4. If the tree node matches the disjunction operation (‘||’) and the inversion indicator is set, the disjunction is replaced by the conjunction (‘&&’). A new vertex with logical negation (‘!’) is added to all outgoing branches. The inversion indicator is reset.

Computation expressions for event functions $g_i\left(y,\hspace{0.17em}t\right)$ are formed based on the trees. More specifically, these structures define the rules for determining an integration step based on the event functions dynamics.

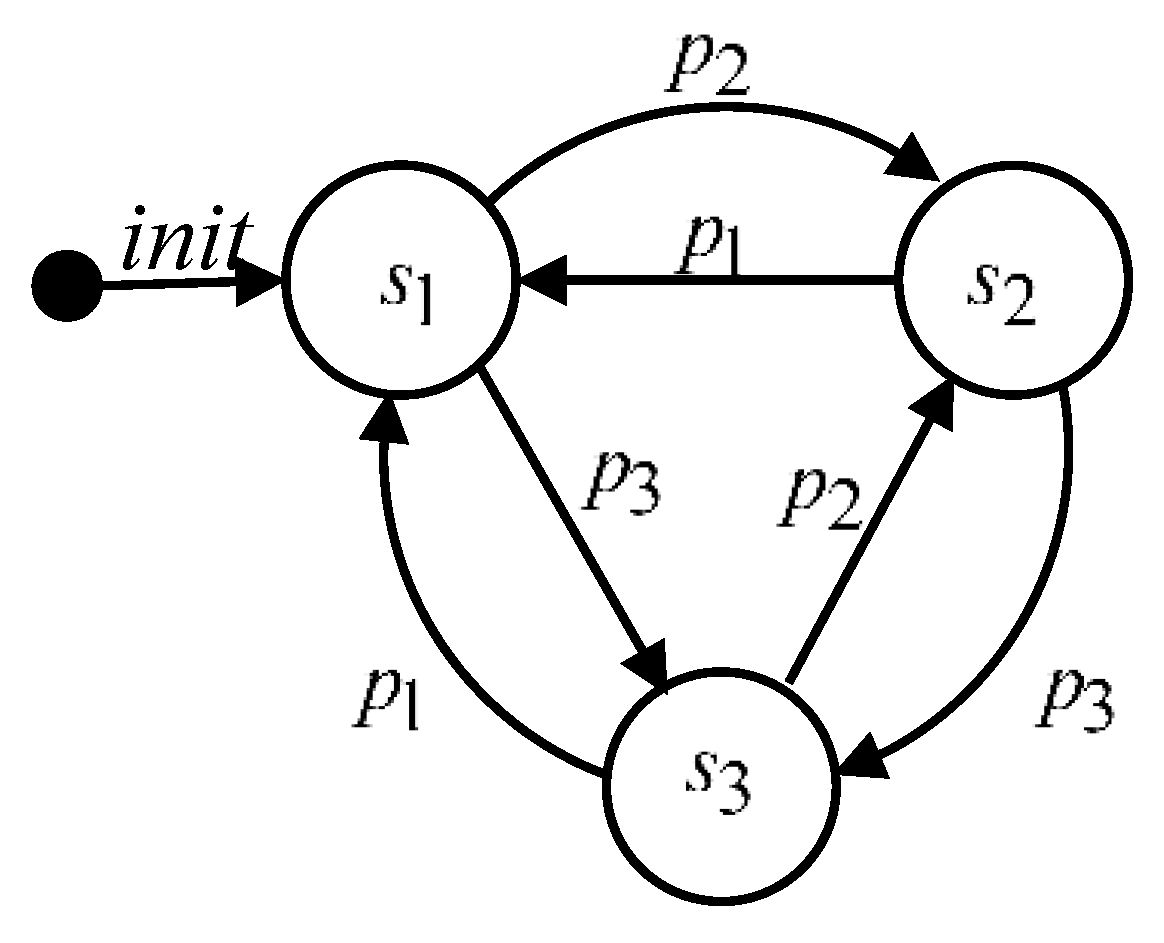
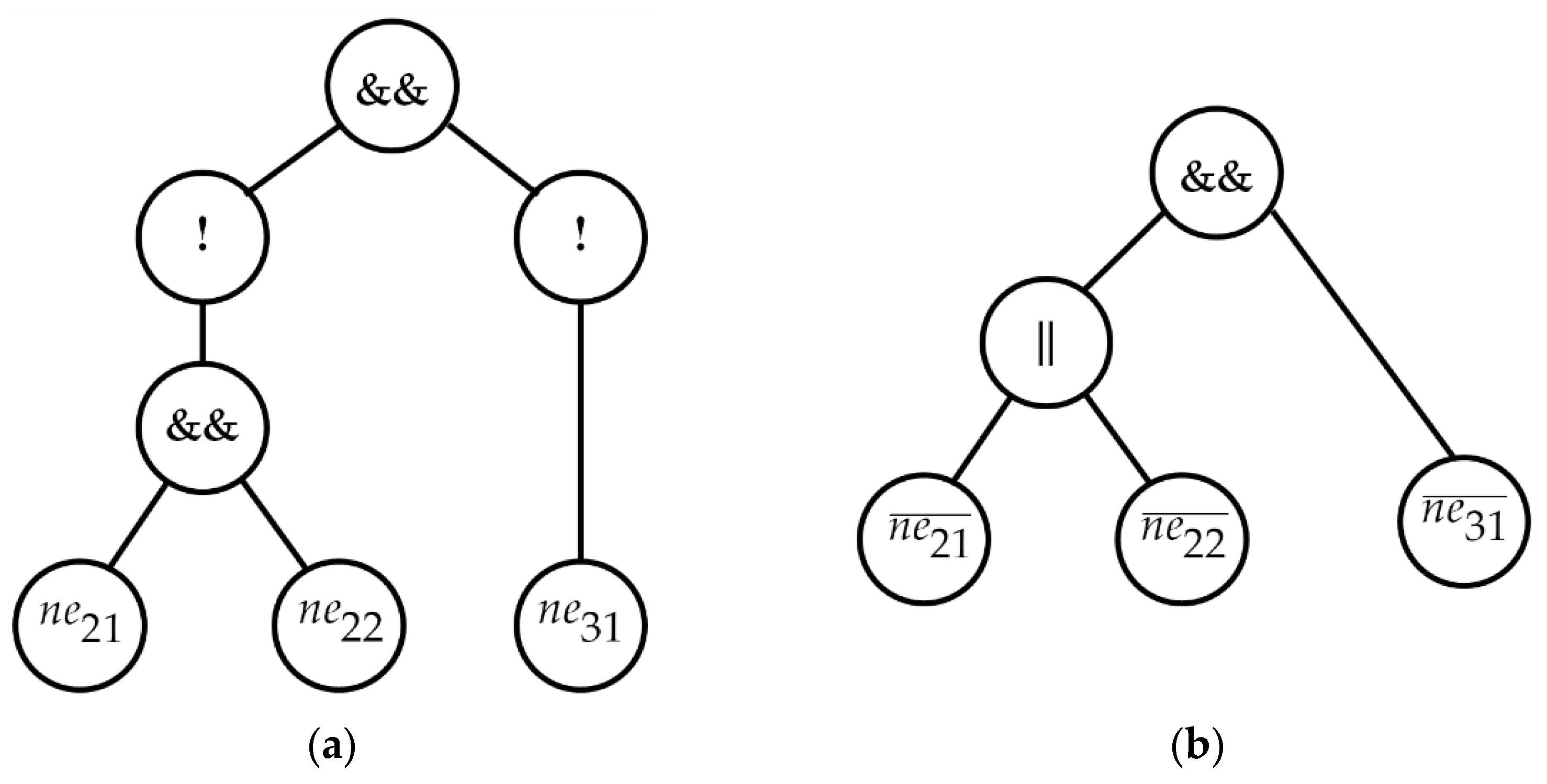
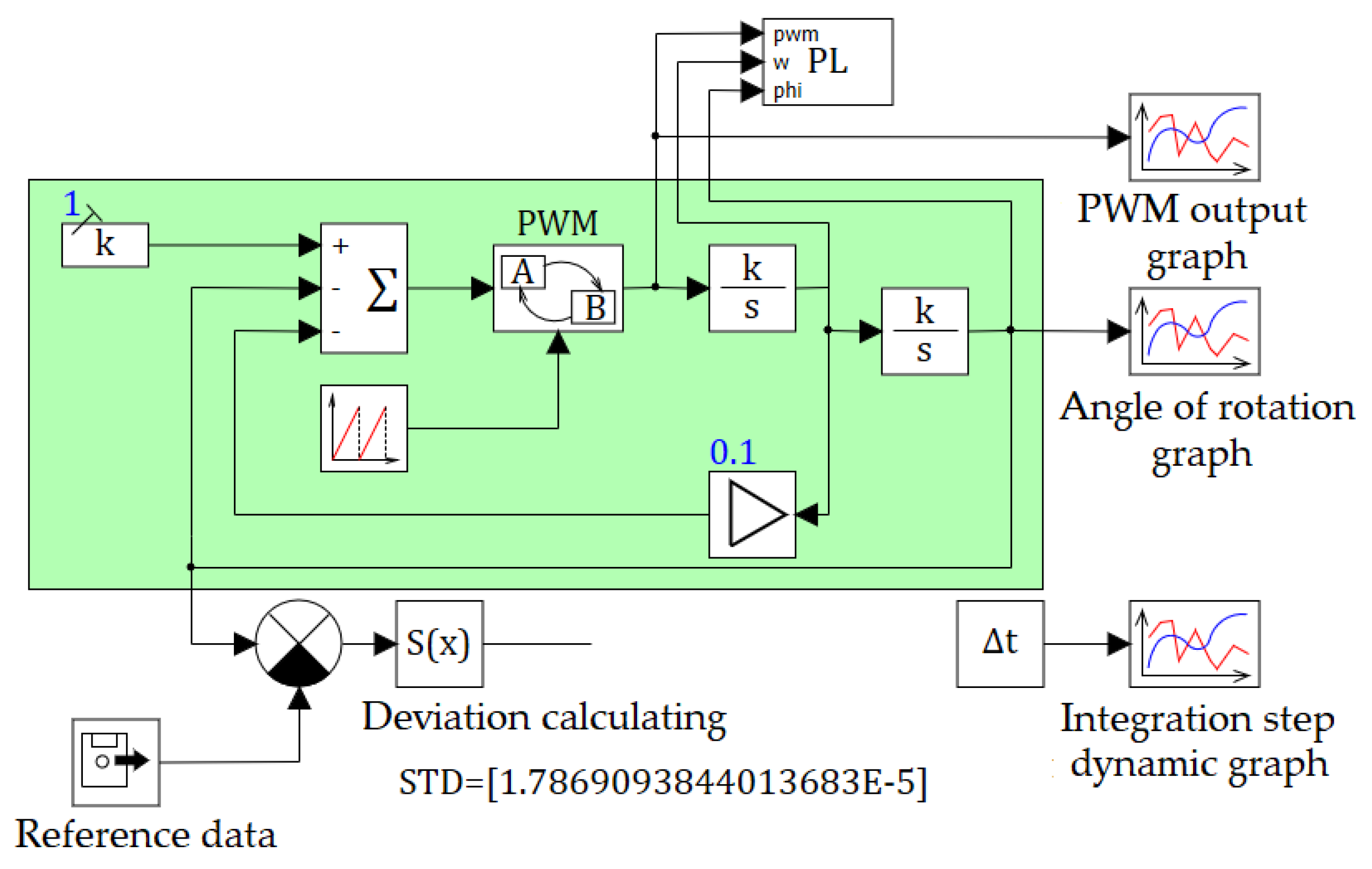
Let’s build and transform a syntactic tree for the mode behavior predicate $p{r}_1$, corresponding to the state $s_1$ (Figure 1) of the servo drive with the PWM controller model. Applying equations (12), we get $p{r}_1=\neg p_2\wedge \neg p_3$. Let inequalities be denoted as:

$$n{e}_{21}:x<0, n{e}_{22}:saw\left(t\right)-k_p\left|x\right|\le 0, n{e}_{31}:k_p\left|x\right|-saw\left(t\right)\le 0,$$

then $p{r}_1=\neg \hspace{0.33em}\left(n{e}_{21}\wedge n{e}_{22}\right)\wedge \neg n{e}_{31}$. The basic syntactic tree is shown in Figure 12, a. After the transforming process, according to the Algorithm 1, the tree presented in Figure 12, b is formed, where

$$\overline{n{e}_{21}}:x\ge 0, \overline{n{e}_{22}}:saw\left(t\right)-k_p\left|x\right|>0, \overline{n{e}_{31}}:k_p\left|x\right|-saw\left(t\right)>0.$$

The following algorithms are connected with the integration step determining, which is dependent on event functions dynamics. Let the mode behavior predicate for the state $s_i$ be like $p{r}_i:$ $g_i\left(y,t\right)<0$, i.e. the syntactic tree consists of the only inequality $n{e}_i$. And the n^th step of numerical resolving the Cauchy problem (2) is performed, the value for the right side of the differential equation $f_n=f\left(y_n,t_n\right)$ is calculated. Besides, the value of the next integration step $h_{n+1}^m$ is determined by the numerical integration algorithm. Then, according to the theorem of calculating the integration step for asymptotic approaching to the mode limit [8], the integration step can be limited by the value, determined by the following algorithm.

Algorithm 2. Determining an integration step for one-sided events detection.

Step 1. Calculate $g_n=g\left(y_n,t_n\right)$.

Step 2. Calculate $\frac{\partial g_n}{\partial y}=\frac{\partial g\left(y_n,t_n\right)}{\partial y}$.

Step 3. Calculate $\frac{\partial g_n}{\partial t}=\frac{\partial g\left(y_n,t_n\right)}{\partial t}$.

Step 4. Calculate ${g^{\prime }}_n=\frac{\partial g_n}{\partial y}\cdot f_n+\frac{\partial g_n}{\partial t}$.

Step 5. If ${g^{\prime }}_n<0$, let $h_{n+1}=h_{n+1}^m$ and go to the next integration step.

Step 6. Calculate the ‘event step size’ $h_{n+1}^{ev}$ as $h_{n+1}^{ev}=\left(\gamma -1\right)\frac{g_n}{{g^{\prime }}_n}$.

Step 7. Compute the step size $h_{n+1}=\min \left(h_{n+1}^m,h_{n+1}^{ev}\right)$ and go to the next integration step.

In Step 5 the event function derivative is determined. As the event function approaches the event surface, ${g^{\prime }}_n$ is positive, and, as it moves away from the boundary $g_i\left(y,t\right)=0$, ${g^{\prime }}_n$ becomes negative. Then, once the event function course has been determined, no additional constraints on the integration step value have to be imposed, if the event function moves away from the mode surface.

Let $h^{ev}\left(g\right)$ be the value of the integration step determined by the discussed algorithm. In general, as it was shown earlier, the condition $p{r}_i$ for the system staying to the $s_i$ might be a complex logical function depending on the set of inequalities $n{e}_{jk}$, where $j\in J$ and $k=1,2,\mathrm{...}$. If each of the inequalities has the form $n{e}_{jk}:g_{jk}\left(y,t\right)<0$, the Algorithm 2 allows to obtain a set of values for the integration step $h_{jk}^{ev}\left(g_{jk}\right)$.

Let the syntactic tree be built using Algorithm 1. Then the value of the integration step can be determined at each stage of the calculating the mode behavior by the following recursive Algorithm 3, while traversing the tree nodes.

Algorithm 3. Determining the integration step in case of a set of event functions.

Step 1. If the tree node matches an inequality (inequalityExpression), the tree traversing is stopped. The integration step value, obtained by the Algorithm 2, is returned.

Step 2. If the tree node matches the conjunction operation (‘&&’), the algorithm for the step determining is called for descendant nodes. The minimal value from all those calculated is returned.

Step 3. If the tree node matches the disjunction operation (‘||’), the algorithm for the step determining is called for descendant nodes. The maximum value from all those calculated is returned.

The Algorithm 2 is justified by the requirement of the event function for the mode behavior having negative value. Using the Algorithm 3, it may turn out that event functions, evaluated at the step 1, are non-negative. It means, that at the current moment the corresponding predicate does not cause changing the system state, therefore there is no need to call the Algorithm 2. In this case, the Algorithm 3 does not limit the step value.

Let’s illustrate the Algorithm processing while calculating the ‘event’ step in the state 1 of the servo drive with the PWM controller model. There are the following conditions: $\overline{n{e}_{21}}:x\ge 0$, $\overline{n{e}_{22}}:saw\left(t\right)-k_p\left|x\right|>0$, $\overline{n{e}_{31}}:k_p\left|x\right|-saw\left(t\right)>0$. The event functions, corresponding to the conditions, are $g_{21}=-x$, $g_{22}=saw\left(t\right)-k_p\left|x\right|$, $g_{31}=k_p\left|x\right|-saw\left(t\right)$. Then the step value is determined by the formula $h_1^{ev}=\min \left(\max \left(h_{21}^{ev}\left(g_{21}\right),h_{22}^{ev}\left(g_{22}\right)\right),h_{31}^{ev}\left(g_{31}\right)\right)$.

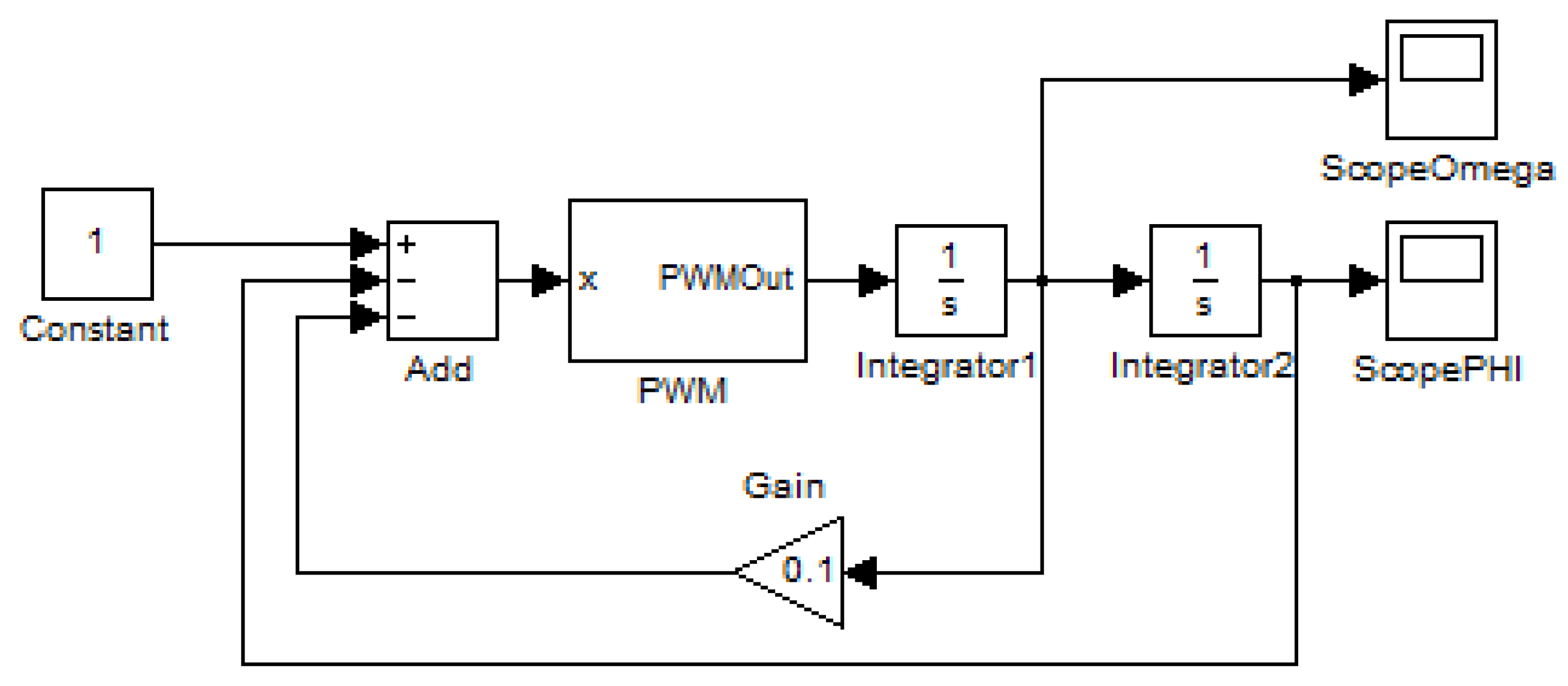
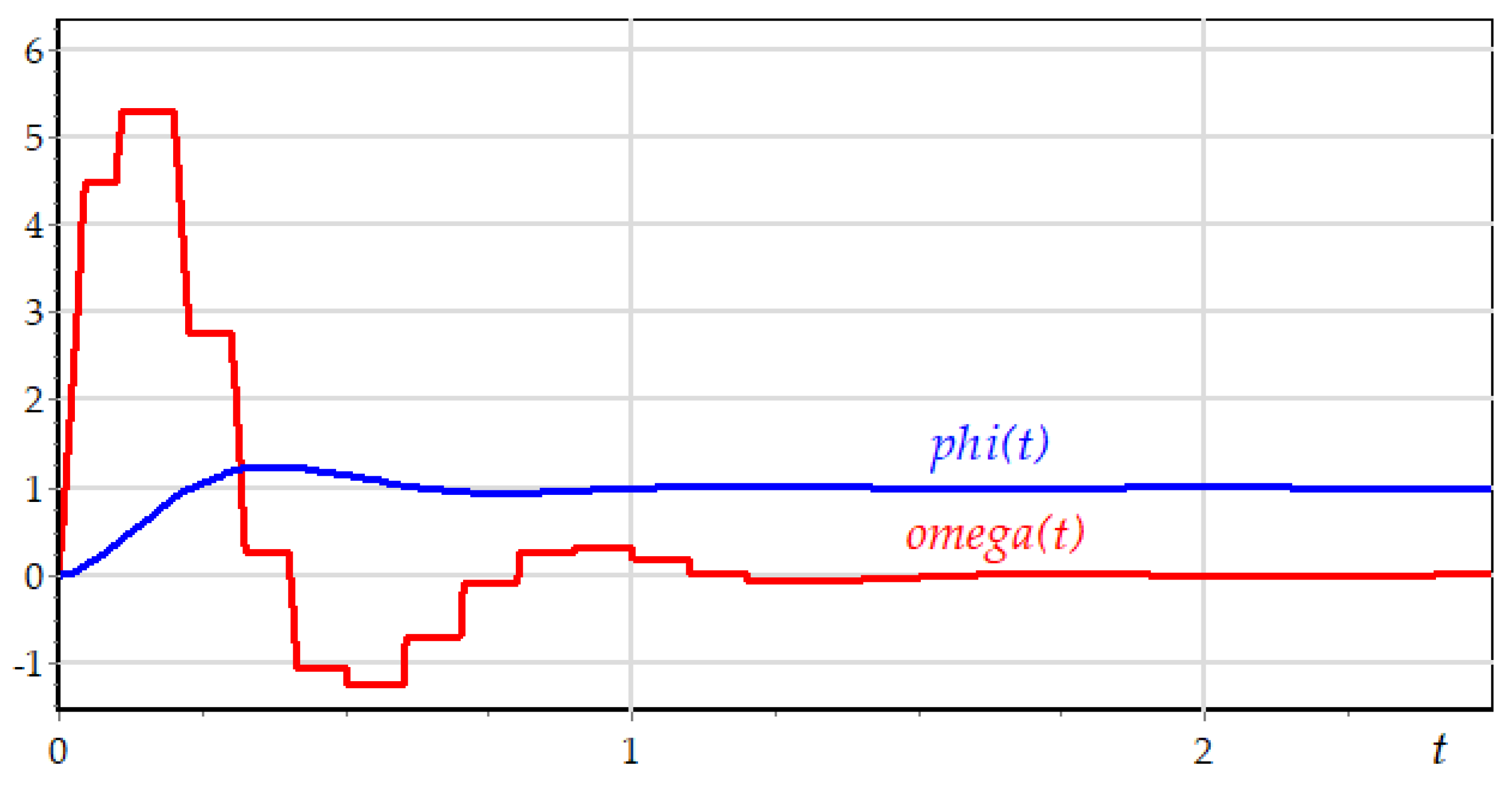
9. Calculation and Simulation

The second stage in computer modeling is implementing software models, designed at the first stage of specification. Applying various integration techniques and developed event detection algorithms, included into the libraries with numerical methods in the considered simulation platforms, for numerical computing (4) – (8) resulted in qualitatively identical solutions for phase variables $\omega \left(t\right)$ and $\phi \left(t\right)$, as presented in Figure 13.

The STEKS (5,4) technique [23] combined with the algorithm for asymptotic event detection, the parameter $\gamma =0.6$ [8], was used for calculations in ISMA. The adaptive algorithm ARK [24] and the invented technique for intersections detecting [15] with the step value refining for the signal sources and discrete units were applied in SimInTech. The integration method ode45 (Dormand-Prince) [3,9] with the algorithm for switching detection for all of the model units [25] was applied in MATLAB. The integration technique Explicit RK23 Solver [13] with double-sided event detecting was used in Ptolemy II.

Let’s evaluate the accuracy of the problem solutions in ISMA, SimInTech, MATLAB and Ptolemy II, taking into account using original libraries with numerical techniques and detection algorithms. Before the experiments, the exact moments of events generating and corresponding values of phase variables${\phi }^{*}=\phi \left(t_i^{*}\right)$ and ${\omega }^{*}=\omega \left(t_i^{*}\right)$ for the initial system of equations (4) were obtained by the analytical fitting the initial conditions. The summary data on the calculating error for the first and seventh events are presented in Table 1, where $t_i^{*}$ is the exact time of the event $i$, ${\tilde{t}}_i$ is the obtained time, ${\omega }_i^{*}$ – the exact value of the angular velocity, ${\tilde{\omega }}_i$ – the calculated value of the angular velocity, ${\phi }_i^{*}$ – the exact value of the angle of rotation, ${\tilde{\phi }}_i$ – the calculated value of the angle of rotation. Computing was carried out with the given accuracy $\epsilon ={10}^{-4}$, that is commensurable with the error of the integration techniques applied.

The model in MATLAB demonstrates the most accurate results. But it does not comply with the condition of the event one-sidedness [10], as it is presented in the table. The values of phase variables in detection points are calculated with the comparable accuracy using tools in SimInTech and ISMA. The largest calculating error is obtained in Ptolemy II by the double-sided detection method [13]. The detection technique in ISMA differs from the others mentioned, since it meets the requirement of one-sidedness [8,10], and the integration step is calculated in accordance to the condition of asymptotic approaching to the mode limit. The algorithm is based on linear extrapolation of the event function and limiting the event function dynamics at the next step, the function can change its value not more than in $\gamma$ times [8]. As a result, the discreteness of the system behavior representation in the vicinity of the mode limits is increasing. The accuracy of this representation is defined by the minimal value of the integration step, which in this case is equal to $h_{\min }={10}^{-6}$.

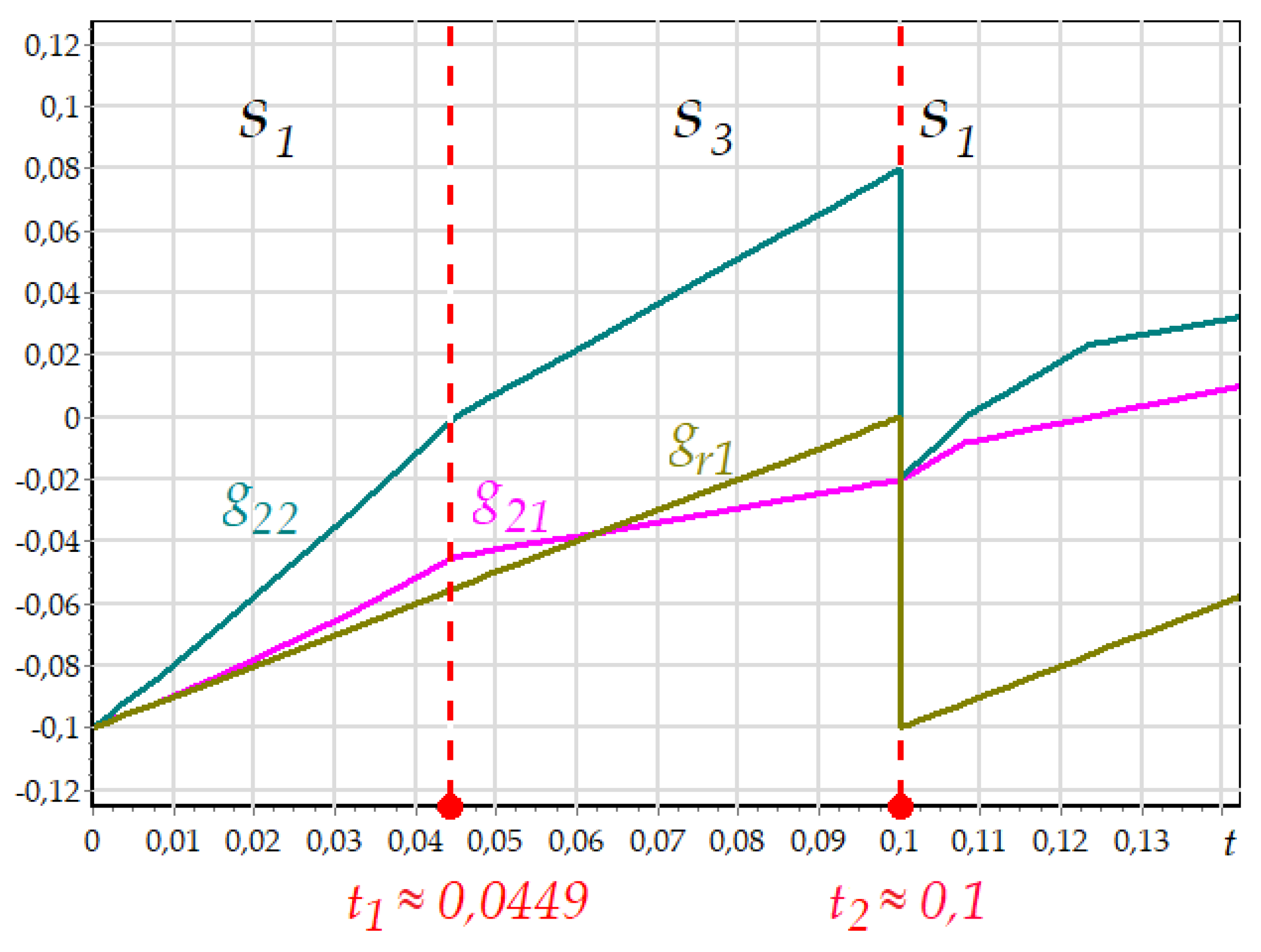
Let’s analyze the dynamics of event functions. Figure 14 demonstrates the graphs of event functions $g_{jk}$, that determine mode shifting in the interval $t\in \left[0,0.1\right)$. At first, the system is in the state 1 ($s_1$), then, in $t\approx 0.0449$, the transition to the mode (state) $s_3$ is made, after that, in $t\approx 0.1$, the system returns to $s_1$. The further transitions and state changing are not considered, although two more shifting can be seen in Figure 14.

There are three event functions for the first state: $g_{21}=-x$, $g_{22}=saw\left(t\right)-k_p\left|x\right|$, $g_{31}=k_p\left|x\right|-saw\left(t\right)$. The system is in the state $s_1$in the interval $t\in \left[0,0.0449\right)$, but the event function $g_{31}$ does not affect the mode shifting, since $g_{31}>0$. This graph is not presented in the figure above. As a result, the integration step calculating is dependent on the dynamics of the functions $g_{21}$ and $g_{22}$. 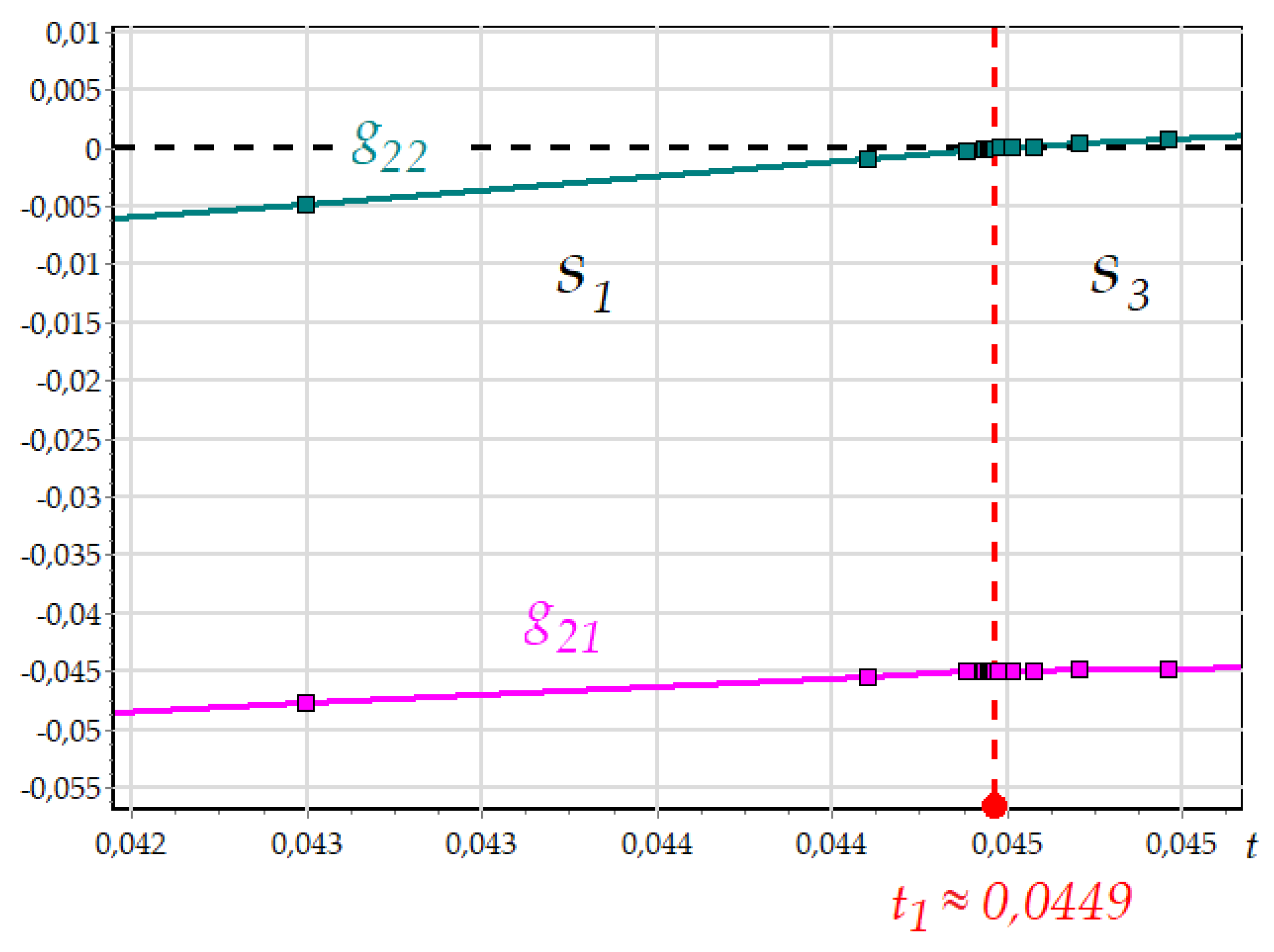The Figure 15 shows the enlarged fragment of the graph in the vicinity of the moment $t\approx 0.0449$.

Since the event function $g_{22}$ changes faster than $g_{21}$, the algorithm for the integration step determining uses the value $h_{22}^{ev}\left(g_{22}\right)$ for asymptotic approaching to the mode limit. The step decreasing, while approaching to the mode limit, is shown in Figure 15. As soon as $g_{22}=0$, the condition $p_3$ from (9) is met, the system switch to the mode $s_3$. After the transition, the integration step is increased, but the detection algorithm does not limit its value: the step can be limited only by the numerical integration method.

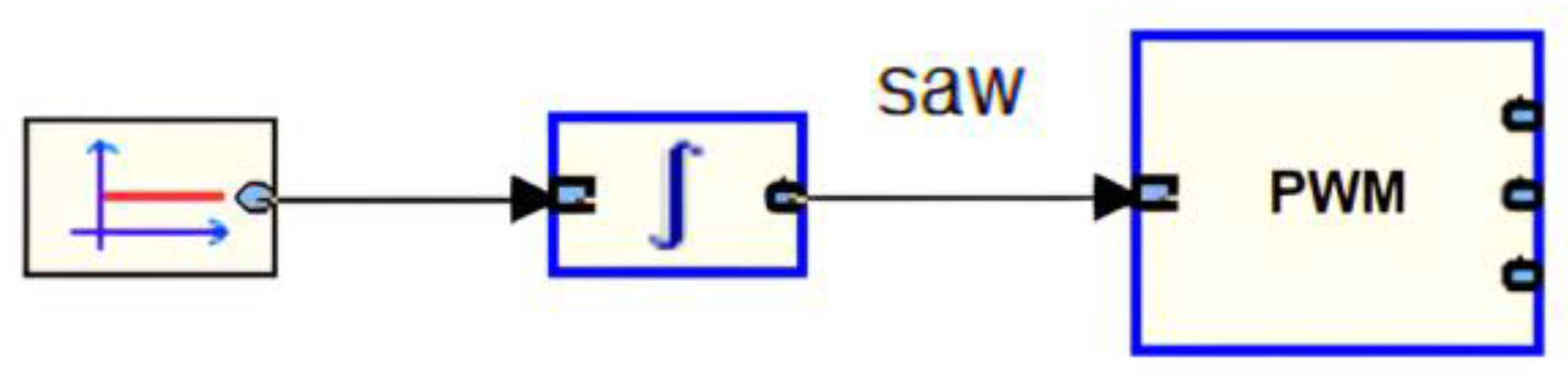
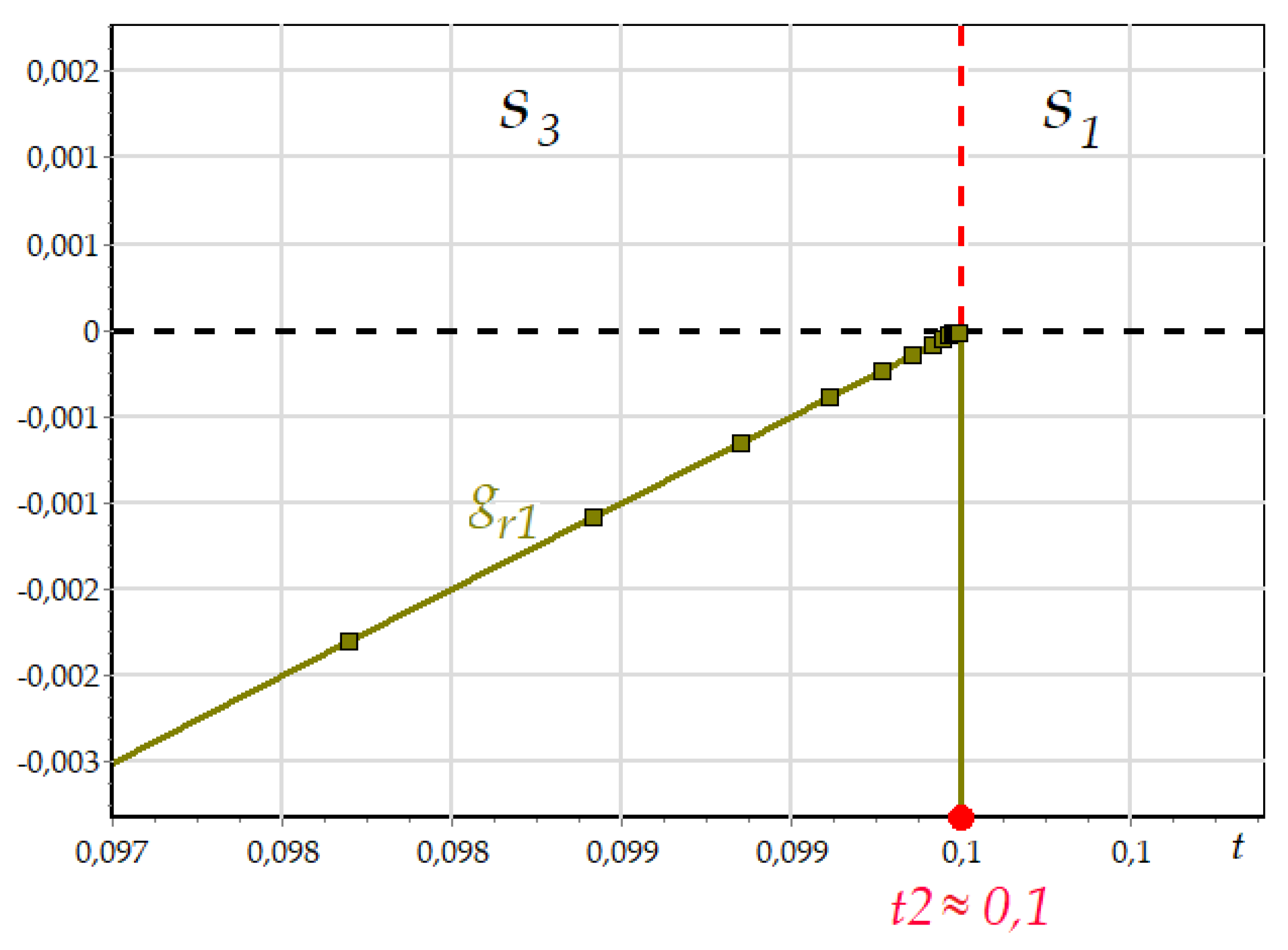
The third state has the resulting condition for the mode $g_{r1}<0$, where the function $g_{r1}=saw\left(t\right)-0.1$ is obtained from the condition of the integrator reset (Figure 2). The graphs of this event function are presented in Figure 14 and Figure 16. The enlarged fragment of the graph in the vicinity of the moment $t\approx 0.1$also demonstrates the step decreasing while approaching to the mode limit. After the modes switching, the event function changes its value instantly, since the variable saw is reset to 0. The condition $p_1$ from (9) is met, and the system switches to the mode $s_1$.

10. Conclusions

The analysis of software platforms for simulating event systems is performed. The model of a simple servo drive with the PWM controller was tested. The system is considered as a hybrid dynamic system with event-driven continuous processes, which implies applying corresponding techniques for the model definition and numerical analysis. The specification of such systems in advanced international practice is based on the finite state machine paradigm with the handy domain-driven graphical interpretation in the form of the Harel diagrams or statecharts. Two of the considered simulation platforms, ISMA and Ptolemy II, comply with the finite state methodology, having appropriate, as close to natural mathematical as possible, description for the event-continuous processes. The SimInTech tries to use the finite state approach with structural diagrams, which is unacceptable by definition. The specification results in a complex, hard to understand software model, including hierarchical submodels, which significantly complicate, rather than simplify the event processes definition, causing the contradiction with the accepted finite state paradigm. MATLAB/Simulink, unlike SimInTech, applies only the structural approach without mentioning the finite state machine. But the structural paradigm, as the engineering practice demonstrates, is intended for continuous processes specification and is very limited in case of applying to define multi-mode hybrid systems. Numerical experiments with software models show qualitatively identical results. Quantitative differences are connected with applying certain integration techniques and detection algorithms. The presented results demonstrate the smallest error of the model in MATLAB and the relatively large one of the model in Ptolemy II. ISMA and SimInTech have the intermediate results in the comparative analysis of the calculation errors. It should be noticed, that the ISMA model is the only one, that complies with the requirement of the event one-sidedness due to the developed algorithm for asymptotic detection, applied to determining the optimal integration step value, considering the event functions dynamics (Algorithm 1 – Algorithm 3). This property is the necessary condition for the model results adequacy in simulating physical processes with the requirement of non-negativity of phase variables, for example processes of chemical kinetics.