Prerpints.org logo
Preprint
Article

Combine Deep Learning and Artificial Intelligence to Optimize the Application Path of Digital Image Processing Technology

Altmetrics

Downloads

315

Views

183

Comments

0

Submitted:

02 July 2024

Posted:

03 July 2024

You are already at the latest version

Alerts
Abstract
Artificial intelligence provides a new research concept for digital image processing. However, at present, artificial intelligence is rarely introduced into the teaching of digital image processing in colleges and universities, and there are problems such as obsolete teaching content, single teaching methods, and simple course experiments, which affect the teaching effect and are not conducive to the cultivation of comprehensive and innovative talents. Digital image processing technology brings more possibilities to communication engineering and makes communication more convenient. For example, video calls and photo transmission make people's communication methods in daily life more and more diversified. Time and space limitations allow people to meet online, creating more communication possibilities. However, there are still many problems and methods worthy of in-depth exploration. Therefore, this paper has a comprehensive understanding and mastery of the traditional and deep learning methods of digital image processing to improve the relevant project practice and scientific research exploration ability and refer for similar research conclusions.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

I. Introduction

Image processing encompasses two primary categories: Analog Image Processing and Digital Image Processing. Digital image processing, in particular, involves the conversion of image information signals into digital signals. These digital signals are then subject to computer-based analysis, processing, and manipulation before being stored in computer-readable form. The primary advantage of this approach is that computers cannot process analog image information directly, and converting images to a digital format allows for data compression and efficient image transmission [1,2,3].
To facilitate this conversion, a two-dimensional array is often used to represent the shape of a digital image. This array consists of a grid of pixels, each pixel defined by its coordinates (x, y) within the grid. The values associated with each pixel, typically in the RGB (red, green, blue) color space, determine the color and intensity of that pixel within the image. Signal processing techniques allow us to calculate and interpret these pixel coordinates and their corresponding values within the two-dimensional plane space.
By applying specific algorithms, we can pinpoint the location of pixels with particular shapes or find pixels that meet certain criteria. This technology is known as signal processing technology. One example of this is the Roberts gradient method, which can be used to detect edges within an image. This edge detection technique involves convolving an image matrix with two specific convolution kernels [4]. The concept of convolution appears in many fields, such as signals and systems, digital signal processing, image classification, and so on. So, what is convolution? What is the use of convolution? How do you compute convolution? In order to fully understand convolution, this paper will study the convolution algorithm of digital image processing technology from the physical sense.
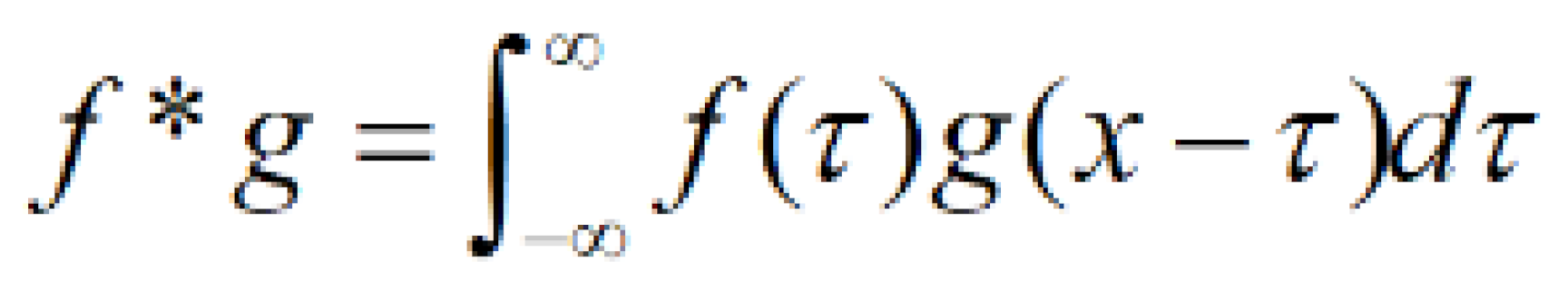
Preprints 110958 i001
In general, in order to calculate the convolution of an image, it is necessary to rotate the convolution kernel by 180° and then align the centre of the convolution kernel with the centre of the calculated pixel. If the image size is exceeded, 0 is added at the edge.
Preprints 110958 g001
Figure 1. Image convolution operation principle.
Figure 1. Image convolution operation principle.
Preprints 110958 g001
The convolution kernel is used as a set value template matrix, and the input image to be processed is used as the prototype matrix. The image convolution operation is mainly carried out by overcovering the central pixel of the template matrix (called anchor point) on the prototype matrix elements to be calculated. The central pixel points are aligned with the pixels on the prototype matrix one by one (the edge pixels cannot align the anchor points, so the convolution calculation cannot be performed. Convolution can only be performed after processing by edge pixels), and then compute the sum of the product of the element values and the values in the convolution kernel being covered. Assign this sum to the current anchor, and that's how convolution works.

II. Related Theoretcal Knowledge

A. Medical Digital Image Processing Technology

Digital image processing technology, based on current digital development, gradually derived a network processing technology, which can achieve a more real display of the picture [5,6,7]. In medicine, with the penetration of digital image processing technology, digital images will present the relevant diseases, and through processing technology to process the relevant data on the screen, this medical means can significantly improve the cure rate of related diseases and achieve more accurate treatment. In medicine, medical imaging is widely used in several areas, including CT (computed tomography), PET (positron emission tomography), MRI (nuclear magnetic resonance imaging), and UI (ultrasonic imaging). On the basis of the development of digital image processing technology, the scope of its application will be gradually expanded, and the application effect will be further improved [8,9,10,11].
Table 1. Medical digital image processing technology classification.
Table 1. Medical digital image processing technology classification.
Technical Application scenario
Image acquisition In the digital image detection, the relevant image obtained, after obtaining the relevant image, through the transformation of the computer, the image is processed in the form of data, and finally the processing result is presented.
Image processing The relevant codes are processed, such as model-based coding processing, neural network coding processing, etc.
Image recognition and reconstruction After the image restoration, the image is transformed, the relevant image is segmented after the image analysis, and the regional features of the image are measured
At the same time, the demand for digital image processing talents in enterprises and scientific research institutions has increased dramatically. Being able to master the traditional digital image processing methods and related artificial intelligence technologies at the same time can lay a solid foundation for students to engage in related work, further study and research related topics after graduation. As a professional course or elective course of computer and electronic information, digital image processing has the characteristics of strong comprehensiveness, many pilot courses, high practice requirements and fast algorithm update [12]. There are higher requirements for teachers' knowledge reserve, teaching ability and students' professional foundation. Although artificial intelligence has been widely used in the field of image processing, it is rarely involved in the teaching of colleges and universities at present, and the training of talents lags behind the development of advanced technologies and cannot adapt to the characteristics of The Times [13].

III. Application of Digital Image Processing Technology

Digital image processing courses have strong comprehensiveness and intersectionality. Visual information, as an essential source of information, plays a vital role in human development [12]. Digital image processing is an important required course and core course for computer science and technology majors, as well as an essential elective course for related majors such as communication engineering. Of course, there are many methods of digital image processing (nearest neighbour method, bilinear interpolation method, more neighboring points interpolation method); the following focus on the analysis of the bilinear interpolation method and combined with the effect of the nearest neighbour method for comparative analysis.
In daily life, digital image processing algorithms combined with deep learning are applied more and more widely. There are many forms of algorithms, such as 256 colour transformation gray level map, Walsh transform, binarisation, threshold transform, Fourier transform, discrete cosine transform, etc., in which the binary change and threshold transform are relatively high in utilisation.
f(x,y) represents the output image, and g(u,v) represents the input image. The geometric operation of enlarging or reducing an image can be defined as:
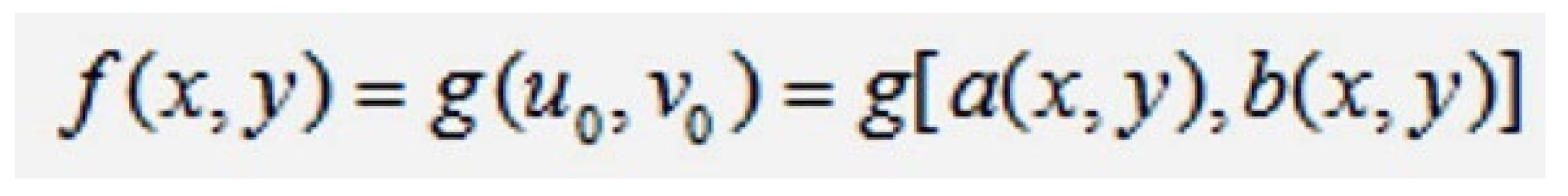
Preprints 110958 i002
If: u0=a(x,y)=x/c; v0=b(x,y)=y/d. This enlarges the image c times in the X-axis and d times in the Y-axis.
For example, if you enlarge a 200×200 image g(u,v) by 1.5 times, you will get a new image f(x,y) of 300×300. The process of producing a new image is actually the process of assigning values to 300×300 pixels.
If f(150,150) is assigned:
F (150150) = g (150/1.5, 150/1.5) = g (100100);
If f(100,100) is assigned:
F (100100) = g (100/1.5, 100/1.5) = g (66.7, 66.7).
Assuming we know the coordinates (x0,y0) and (x1,y1), we want to find the value of x on the line at some point in the interval [x0,x1]. As shown in the figure:
Preprints 110958 g002
Figure 2. One-dimensional linear interpolation model for digital image.
Figure 2. One-dimensional linear interpolation model for digital image.
Preprints 110958 g002
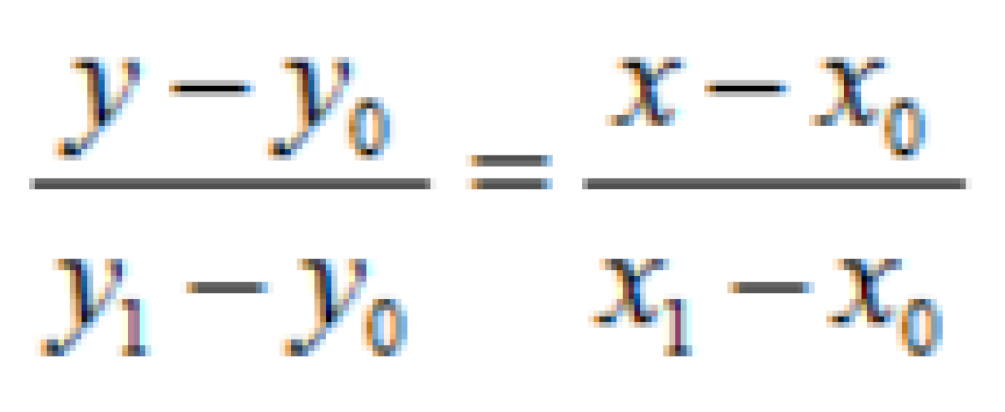
Preprints 110958 i003
If such models and formulas are applied in image processing, the final result should be:
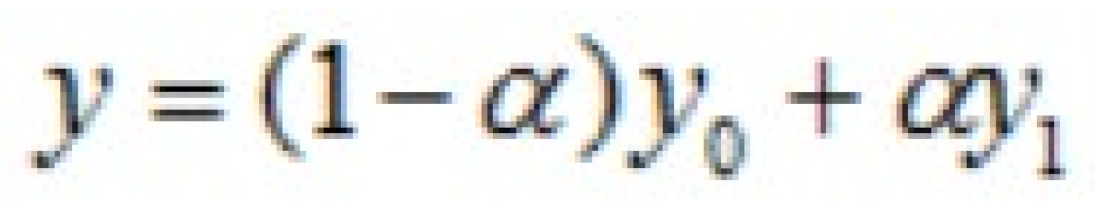
Preprints 110958 i004
The second is the bilinear digital image processing model. We calculate that the point (0,1) in g should correspond to the end (0,0.67) in f, but there is no such coordinate in f, so we use linear interpolation to calculate the pixel value at (0,0.67).
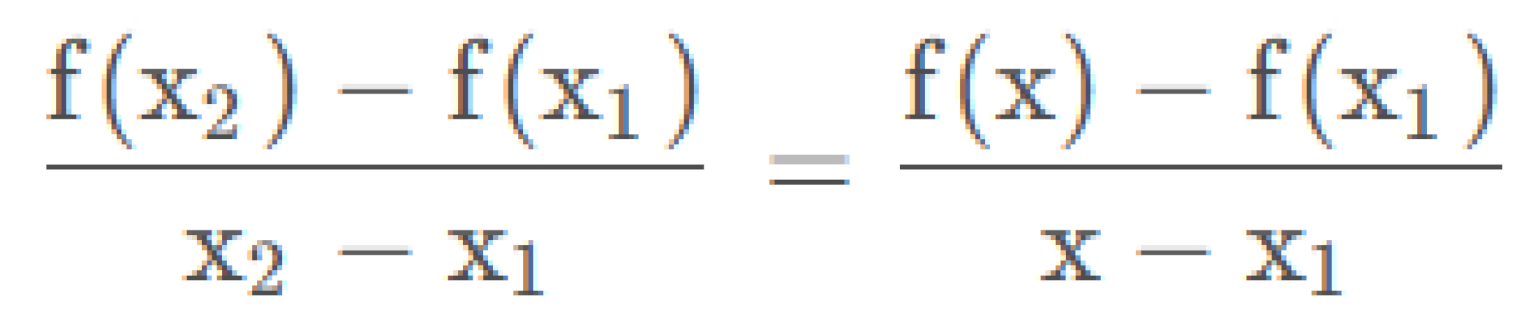
Preprints 110958 i005
The two-line value of the image processing algorithm is realised by the weight formula above.
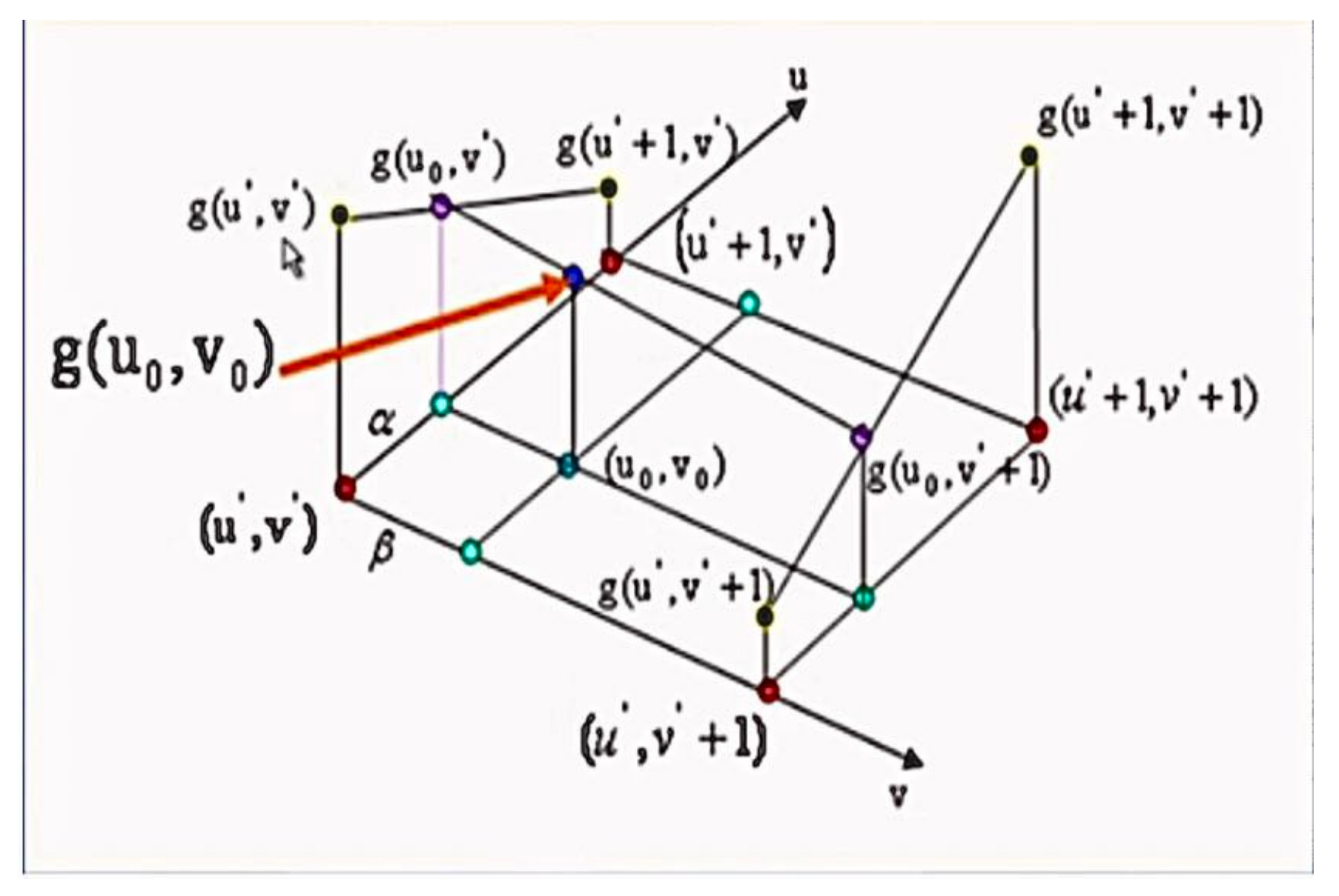
Preprints 110958 g003
Figure 3. Bilinear interpolation image processing model.
Figure 3. Bilinear interpolation image processing model.
Preprints 110958 g003
The so-called bilinear interpolation, that is, continuous use of three-dimensional linear interpolation, and finally obtain g(u0,v0).
First: g(u0,v ') by g(u ',v ') and g(u '+1,v') one-dimensional linear interpolation.
Second time: g(u0,v '+1) by g(u',v '+1) and g(u' +1,v '+1) one-dimensional linear interpolation.
Third: g(u0,v0) by g(u0,v ') and g(u0,v '+1) one-dimensional linear interpolation.
There are two main algorithmic ideas in bilinear interpolation: the first is double, which refers to the value of (x, y) in two directions, generally taking two values in the x direction and two values in the y direction; The second is linear, the two values taken in each direction are calculated as linear functions, and the actual value is generally calculated with the weights in the x and y directions, similar to the first function, the closer the mapping point is, the higher the weight is, and the overall weight sum =1.
According to the above algorithm idea, by mapping 4 points around the points, the colour of the new pixel can have a simple colour change that is different from that of the nearest neighbour interpolation algorithm. Therefore, the image interpolation algorithm can be improved.
However, the bilinear interpolation algorithm still has its shortcomings; simple linear changes will lead to edge blurring, and it will be obvious that the interpolation data is inconsistent at the edge where the color changes are large. In addition, due to the multiplication of linear weights and pixel values, there will be a certain low-pass filtering, the high-frequency component will be weakened, and the correct pixel value may not be obtained in places with large colour changes.

IV. Conclusions

Digital image processing technology is a highly applied field, offering advantages not found in analogue image processing. This article delves deeper into the basic concepts and principles of digital image processing technology, examining its strengths and exploring its potential applications in communication engineering [14]. Currently, digital image processing technology faces a number of challenges that require further investigation. Communication engineering stands to benefit greatly from this technology, improving efficiency and enhancing the overall quality of work. However, there are still technical challenges that need to be overcome as we continue to push the boundaries of science and technology [15]. Digital image processing technology is a vital auxiliary tool in various fields such as communication engineering, and both the algorithm form and the practical application mode are more in line with People's Daily life forms. Therefore, with the rapid development of the era of big data, it is crucial to invest more resources in digital image processing technology combined with deep learning to conduct deeper research on this technology. Doing so can not only expand its scope of application, but also improve the quality of life. With the continuous progress of science and technology, digital image processing technology will become the biggest helper in people's life, medical, mathematics, automation, physics and other fields [16].

References

  1. OEHLERSWALKER DAssessment of deep learning ability for problem solvers [J]. The international journal of engineering education, 2006,22(6):1261-1268.
  2. WILLIAM AND FLORA HEWLETT FOUNDATION. Deep leaing competencies (EB/0L1 2023-03-23. Available online: https://www.hewlet.org/wp-content/uploads/2016/08/DeeperLearningDefinedApril2013.pdf.
  3. Zhan, X., Shi, C., Li, L., Xu, K., & Zheng, H. (2024). Aspect category sentiment analysis based on multiple attention mechanisms and pre-trained models. Applied and Computational Engineering, 71, 21-26.
  4. Wu, B., Xu, J., Zhang, Y., Liu, B., Gong, Y., & Huang, J. (2024). Integration of computer networks and artificial neural networks for an AI-based network operator. Applied and Computational Engineering, 64, 115-120.
  5. Shi, Y., Li, L., Li, H., Li, A., & Lin, Y. (2024). Aspect-Level Sentiment Analysis of Customer Reviews Based on Neural Multi-task Learning. Journal of Theory and Practice of Engineering Science, 4(04), 1-8.
  6. Shi, Y.; Yuan, J.; Yang, P.; Wang, Y.; Chen, Z. Implementing intelligent predictive models for patient disease risk in cloud data warehousing. Appl. Comput. Eng. 2024, 67, 34–40. [Google Scholar] [CrossRef]
  7. Zhan, T.; Shi, C.; Shi, Y.; Li, H.; Lin, Y. Optimization techniques for sentiment analysis based on LLM (GPT-3). Appl. Comput. Eng. 2024, 67, 41–47. [Google Scholar] [CrossRef]
  8. Li, Huixiang, et al. "AI Face Recognition and Processing Technology Based on GPU Computing." Journal of Theory and Practice of Engineering Science 4.05 (2024): 9-16.
  9. Liang, P.; Song, B.; Zhan, X.; Chen, Z.; Yuan, J. Automating the training and deployment of models in MLOps by integrating systems with machine learning. Appl. Comput. Eng. 2024, 67, 1–7. [Google Scholar] [CrossRef]
  10. Li, A., Yang, T., Zhan, X., Shi, Y., & Li, H. (2024). Utilising Data Science and AI for Customer Churn Prediction in Marketing. Journal of Theory and Practice of Engineering Science, 4(05), 72-79.
  11. Wu, B., Gong, Y., Zheng, H., Zhang, Y., Huang, J., & Xu, J. (2024). Enterprise cloud resource optimization and management based on cloud operations. Applied and Computational Engineering, 67, 8-14.
  12. Xu, J.; Wu, B.; Huang, J.; Gong, Y.; Zhang, Y.; Liu, B. Practical applications of advanced cloud services and generative AI systems in medical image analysis. Appl. Comput. Eng. 2024, 64, 83–88. [Google Scholar] [CrossRef]
  13. Yuan, J., Lin, Y., Shi, Y., Yang, T., & Li, A. (2024). Applications of Artificial Intelligence Generative Adversarial Techniques in the Financial Sector. Academic Journal of Sociology and Management, 2(3), 59-66.
  14. Lin, Y., Li, A., Li, H., Shi, Y., & Zhan, X. (2024). GPU-Optimized Image Processing and Generation Based on Deep Learning and Computer Vision. Journal of Artificial Intelligence General science (JAIGS) ISSN: 3006-4023, 5(1), 39-49.
  15. Chen, Zhou, et al. "Application of Cloud-Driven Intelligent Medical Imaging Analysis in Disease Detection." Journal of Theory and Practice of Engineering Science 4.05 (2024): 64-71.
  16. Wang, B., Lei, H., Shui, Z., Chen, Z., & Yang, P. (2024). Current State of Autonomous Driving Applications Based on Distributed Perception and Decision-Making.
  17. Choudhury, M., Li, G., Li, J., Zhao, K., Dong, M., & Harfoush, K. (2021, September). Power Efficiency in Communication Networks with Power-Proportional Devices. In 2021 IEEE Symposium on Computers and Communications (ISCC) (pp. 1-6). IEEE.
  18. Xiao, J., Wang, J., Bao, W., Deng, T. and Bi, S., Application progress of natural language processing technology in financial research.
  19. Zhang, Y.; Liu, B.; Gong, Y.; Huang, J.; Xu, J.; Wan, W. Application of machine learning optimization in cloud computing resource scheduling and management. Appl. Comput. Eng. 2024, 64, 17–22. [Google Scholar] [CrossRef]
  20. Huang, J.; Zhang, Y.; Xu, J.; Wu, B.; Liu, B.; Gong, Y. Implementation of seamless assistance with Google Assistant leveraging cloud computing. Appl. Comput. Eng. 2024, 64, 170–176. [Google Scholar] [CrossRef]
  21. Liang, P.; Song, B.; Zhan, X.; Chen, Z.; Yuan, J. Automating the training and deployment of models in MLOps by integrating systems with machine learning. Appl. Comput. Eng. 2024, 67, 1–7. [Google Scholar] [CrossRef]
  22. Zhou, Y.; Zhan, T.; Wu, Y.; Song, B.; Shi, C. RNA secondary structure prediction using transformer-based deep learning models. Appl. Comput. Eng. 2024, 64, 95–101. [Google Scholar] [CrossRef]
  23. Liu, B., Cai, G., Ling, Z., Qian, J., & Zhang, Q. Precise Positioning and Prediction System for Autonomous Driving Based on Generative Artificial Intelligence.
  24. Cui, Z., Lin, L., Zong, Y., Chen, Y., & Wang, S. Precision Gene Editing Using Deep Learning: A Case Study of the CRISPR-Cas9 Editor.
  25. Wang, B., He, Y., Shui, Z., Xin, Q., & Lei, H. (2024). Predictive Optimization of DDoS Attack Mitigation in Distributed Systems using Machine Learning. Applied and Computational Engineering, 64, 95-100.
  26. Huo, Mingda, et al. "JPX Tokyo Stock Exchange Prediction with LightGBM." Proceedings of the 2nd International Conference on Bigdata Blockchain and Economy Management, ICBBEM 2023, May 19–21, 2023, Hangzhou, China. 2023.
  27. Tian, J.; Li, H.; Qi, Y.; Wang, X.; Feng, Y. Intelligent medical detection and diagnosis assisted by deep learning. Appl. Comput. Eng. 2024, 64, 116–121. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated