Prerpints.org logo
Preprint
Article

Consensus for Linear Time-Varying Multi-agent Systems via Event-Triggered Communication

Altmetrics

Downloads

106

Views

25

Comments

0

Submitted:

03 July 2024

Posted:

03 July 2024

You are already at the latest version

Alerts
Abstract
This paper represents the first investigation into the consensus problem of linear time-varying multi-agent systems utilizing an event-triggered communication scheme. First, a general event-triggered consensus control scheme is proposed for a general category of linear time-varying multi-agent systems. Under some suitable assumptions, it is demonstrated that all agents’ states will converge exponentially, with Zeno behaviour being ruled out. Second, the consensus problem in a network of linear time-varying multi-agent systems with a spanning tree is investigated using the proposed control strategy. It demonstrates that the consensus issue for the specified system can be reformulated as a stabilization problem for an error system through a time-varying linear transformation. Then, the event-triggered consensus problem is just a special instance of the general event-triggered consensus problem mentioned above. Finally, to illustrate the efficacy of the event-triggered method proposed in this study, simulation results are shown.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

The event-triggered communication and control strategy requires systems to communicate each other and then update the control law only at the necessary instants instead of continuously. This strategy has been the subject of increasing interest among researchers and engineers due to its advantages in saving the energy or reducing the computation loads [1,2]. Recently, this approach has quickly become a main point of attention within the multi-agent systems field and is used to overcome the consensus problem in multi-agent systems. However, from our understanding, almost all controllers that are triggered by events are made to handle the time-invariant multi-agent systems. This work aims to address the consensus problem in linear time-varying multi-agent systems by means of an event-triggered communication strategy. It is not a simple extension and needs some novel analysis method developed by us.
In the early stage of control theory, analog control equipments require that controllers are executed continuously. Thus, the field of control systems design and analysis is primarily concerned with the continuous-time systems [3]. As computer technologies advance swiftly, the implement manner of controllers are changed to be in digital platforms instead of analog platforms, where the controller is executed periodically at fixed sampling instants. A significant challenge is to identify an appropriate sampling period. In general, as stated in [4], the selection of such a period is predicated on a worst-case scenario, with the objective of ensuring the efficacy of the control task across the full range of operational conditions. Consequently, the control task is executed at a uniform rate, irrespective of the state of the plant. This control scheme is called as a time-triggered control scheme. Its merit lies in the simplicity in analysis and design, but its drawback is also obvious, that is, this results in the unnecessary consumption of energy and the accelerated wear and tear of the actuators since frequent changes of the actuator state.
To overcome the above disadvantage of time-triggered control, as an alternative approach, there exist certain known strategies for event-trigger control [5,6,7,8,9,10,11,12,13,14,15,16,17]. In contrast to the time-triggered control strategy, the event-triggered control strategy engage the actuators only under specific conditions. Thus, one notable benefit of these schemes is their capacity to ensure both reliable operation and improve energy utilization efficiency across the target systems. Specifically, in [5], Tabuada proposes an event-triggered stabilizer based on Lyapunov for a particular category of nonlinear systems, where the continuous and centralized monitoring is needed but the inter-section time is more than a constant. Then, the continuous and decentralized monitoring scheme is further addressed in [6] and [7]. The findings of [5] are further extended upon in [4] to encompass the self-triggered case, and in [8] to address the tracking problem. For linear systems with continuous time, an event-trigger control approach that occurs periodically is displayed in [9], and in [10], discrete-time systems as a means of reducing the frequency of monitoring. To mitigate the impact of network characteristics like delay and quantization, networked systems are regulated using the event-triggered control technique in [11,12,13,14]. The discussion of deterministic equivalence within event-triggered control systems is addressed in [15]. The estimate of states and parameters is studied based on event-triggered scheme in [16] and [17], respectively. Up to now, the event-triggered control scheme is currently a focal point of interest within the control field. It have been extended to a variety of area, and lots of interesting results are emerging. Because multi-agent systems have so many applications in the military and business, there has been a lot of interest in this field. Up until this point, there have been many noteworthy achievements, see, e.g, [18,19,20,21,22,23], simply to mention a few. In general, multi-agent systems are characterized as distributed networks of interconnected agents. Thus, two issues should be considered, i.e., control and communication.
The study of the event-triggered consensus problem in multi-agent systems has been spurred due to the applicability of applying event-triggered techniques to networked systems, and numerous intriguing findings have been made [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. In [24], authors study the centralized/distributed event-triggered consensus problem for first-order multi-agent systems, in scenarios where distributed event-triggered is implemented, it is guaranteed that no Zero behavior occurs for a minimum of one agent. The issue of consensus in distributed event-triggered systems is further explored in [25], specifically for multi-agent systems utilizing combinational measurements, with each agent autonomously deciding the moment of its event, and the Zeno behavior cannot appear before each agent reaches consensus. In [26,27], for a category of general linear multi-agent systems, two consensus protocols utilizing distributed event-triggered are presented, and it is assured that the bounded consensus error can rule out the Zeno behavior.
The event-triggered scheme in [27] has been expanded upon to the case of leader-following in [28]. In the context of general linear multi-agent systems, reference [29] presents a distributed observer-driven output-feedback event-triggered consensus framework. Furthermore, the output-feedback event-triggered consensus technique tailed for a passive multi-agent systems is also explored in reference [30]. To naturally prevent the Zeno behavior, the papers [31] and [32] present distributed event-triggered consensus schemes utilizing a sampling technique for both first-order multi-agent systems and general linear multi-agent systems. The similar idea is used in [33]. Different from [31,32,33], a decentralised event-triggered consensus scheme is formulated in [34] for first/second-order systems where the time between events is limited by a positive constant. The study presented in paper [42] examines the consensus problem among high-order multi-agent systems, focusing particularly on the impact of event-triggered control. Recently, the event-triggered consensus/synchronization scheme is further designed for nonlinear multi-agent systems in [31,45,46,47,48,49] and discrete-time multi-agent systems in [35,36,37,38,50]. However, the emphasis of these studies is on multi-agent systems that are not subject to time variation.
In practice, the system parameters or models might vary with different setting. Unfortunately, up to now, a limited number of studies have addressed the consensus issue in multi-agent systems that vary over time. The reason lies in that there are fewer methods and tools can be used to deal with such systems comparing with the linear time-invariant systems. The synchronization of outputs among a collection of linear and time-varying multi-agent systems is the subject of inquiry in [39]. However, the requirement of continuous communication limits its execution in practice. Thus, motivated by this observation and the development of event-triggered consensus of time-invariant multi-agent systems, we are particularly interested in researching the event-triggered consensus problem within a category of generic linear time-varying multi-agent systems. The main highlights of our contributions are outlined subsequently.
(i) We establish a general framework of event-triggered consensus control that is applicable to a broad category of linear time-varying multi-agent systems over networks. Exponential convergence of consensus errors is demonstrated, along with the prevention of any Zeno behavior within the system. Despite the existence of several studies concerning event-triggered consensus schemes of linear time-invariant multi-agent systems [24,25,26,27,28,29,30,31,32,33,35,36,37,39,51], in light of the information we have, this study marks the first instance of examining the event-triggered scheme within linear time-varying multi-agent systems.
(ii) We further apply the established general results to analyze the event-triggered consensus among a group of specific linear time-varying multi-agent systems by using the system transformation matrix that under assumption of the network with a spanning tree structure. It is assured that the consensus error of the systems will exponentially converge to zero.
This work’s remaining content is presented in the following manner. A few introductions to the algebra of graph theory, linear time-varying systems and two essential lemmas are given in Section II. The scheme to consensus using event-triggered control for a general category of linear time-varying multi-agent systems is discussed in Section III. we discuss our proposed scheme to tackle the event-triggered consensus problem among a collection of linear time-varying multi-agent systems in Section IV. In Section V, we provide a summary of the research findings.
Notations: Throughout this paper, R is used to represented the collection of real numbers; R n stands for the set of n × 1 real vectors; R n × n refers to the set of n × n real matrices; 1 N represents an N × 1 column vector filled with ones; I denotes the identity matrix with the appropriate dimensions; A T refers to the transpose of a matrix A ; max { ⋯ } indicates the maximum value among the elements; sup ( · ) stands for the supremum, which refers to the least upper bound of a set; ⊗ represents the Kronecker product; σ max ( P ) and σ min ( P ) refer to the biggest and lowest eigenvalue of a positive definite matrix P; diag A 1 , ⋯ , A m , where A i , i = 1 , 2 , ⋯ , m , are p i × q i matrices, is a Σ i = 1 m p i × Σ i = 1 m q i block diagonal matrix; The symbol | z | indicates the modulus of a real number z; ∥ · ∥ denotes the Euclidean norm; A ≥ B means that A − B is a positive semi-definite matrix.

2. Preliminary

In this section, we give some knowledge on algebraic graph theory, linear time-varying systems, and some important lemmas. The subsequent research will be bulit upon these foundational elements.

2.1. Algebraic Graph Theory

We model a communication network among agents by means of a graph in this research. A digraph of order N is specified as a pair G = ( V , E ) , where V = { 1 , 2 , ⋯ , N } signifies a finite and nonempty set of agents and a collection of ordered pairs of agents comprising the edges is indicated with E ⊆ V × V . It is important to motion that G is considered undirected if ( i , j ) ∈ E implies ( j , i ) ∈ E for arbitrary i ∈ V and j ∈ V . The neighbors of agent i are indicated with N i = { j ∈ V : ( j , i ) ∈ E } , and j ∈ N i signifies that node i has the ability to directly obtain the information from agent j. A sequence i 0 , i 1 , ⋯ , i l forms a path in a digraph. In a directed tree inside a digraph, every node except the root has precisely one parent, which is the only node without a parent and is connected to every other node directly through pathways. A graph’s directed spanning tree is a tree structure that uses its directed edges to span every node. The graph is considered to contain a directed spanning tree if a portion of a graph’s edges can form one.
In the adjacency matrix B = b i j N × N of the digraph G , each entry b i j is assigned a positive weight if the v j , v i belongs to the edge set E ; and b i j = 0 , otherwise. Assume that each node doesn’t have its own edge, i.e., b i i = 0 . The Laplacian matrix, represented by L : = d i j ∈ R N × N , is defined with elements such that d i j = − b i j when i ≠ j and d i i = ∑ j = 1 N b i j ; L is a zero row sum matrix, that is, L 1 N = 0 . Let r ∈ R N × 1 satisfy r T L = 0 and r T 1 N = 1 , then for a diagraph having a spanning tree, r exists and is unique. For the Laplacian matrix of a network having a spanning tree, the subsequent lemma is introduced to support our discussion.
Lemma 1. 
[39]: Given that a graph G possesses a spanning tree. It can be seen that there is a symmetric positive definite matrix P that meets the condition of
− L − 1 N r T T P + P − L − 1 N r T = − I .
The proof of this Lemma is similar to that of Lemma 1 in [37], and omitted here.

2.2. Linear Time-Varying System

We will analyze a linear time-varying system
x ˙ = A ( t ) x + B ( t ) u , x t 0 = x 0 ,
in this scenario, x ∈ R n denotes the state and u ∈ R m represents the control input; The matrices A ( t ) ∈ R n × n and B ( t ) ∈ R n × m are system matrices that depends on time t, t 0 is the initial time and x 0 ∈ R n is the initial state vector.
We define Φ A t 0 , t as the state transition matrix associated with system (1), this represents the sole solution to the matrix differential equation Φ ˙ A t , t 0 = A ( t ) Φ A t , t 0 with Φ A t 0 , t 0 = I n . The controllability syntax of pair ( A ( t ) , B ( t ) ) is defined as
W c t 0 , t : = ∫ t 0 t Φ A t 0 , υ B ( υ ) B ( υ ) T Φ A t 0 , υ T d υ .
Definition 1. 
[52]: A pair ( A ( t ) , B ( t ) ) is classified as uniformly controllable if it is possible to find a positive pair ( ε , T ) such that σ min W c ( t , t + T ) ≥ ε for all t ≥ 0 .
In the realm of time-varying systems, the persistently exciting (PE) condition is a pivotal element in stability analysis, defined as detailed below.
Definition 2. 
(PE condition) [52]: To characterize a time-varying symmetric matrix Δ ( t ) as PE , it must satisfy the following condition: two positive constants T and ε, are presented such that
∫ t t + T Δ ( υ ) d υ ≥ ε I , ∀ t ∈ t 0 , + ∞ .
By adhering to the argumentation outlined in the proof of Theorem 1 from reference [37], we arrive at the lemma.
Lemma 2. 
Given that ( A ( t ) , B ( t ) ) is uniformly controllable, then Φ A t 0 , t B ( t ) B ( υ ) T Φ A t 0 , t T exhibits PE , implying the existence of a pair ( T , ε ) such that
σ min ∫ t t + T Φ A t 0 , υ B ( υ ) B ( υ ) T Φ A t 0 , υ T d υ ≥ ε .
The cooperative PE is also an important concept which is used in DCA system identification shown in [39].
Definition 3. 
[53]: A series of matrix-valued functions Δ i ( t ) , i = 1 , 2 , ⋯ , N , is identified as satisfying the cooperative PE condition provided that two positive constants T and ε can be located to satisfy
∫ t t + T ∑ i = 1 N Δ i ( υ ) d υ ≥ ε I .
According to definition 3, the subsequent lemma is demonstrated within [53].
Lemma 3. 
Let Δ ( t ) = diag Δ 1 , ⋯ , Δ N . If Δ i ( t ) is cooperative PE, and L corresponds to the Laplacian matrix of a graph that is both undirected and connected, then there exists a pair ( T , ε ) such that
∫ t t + T [ Δ ( υ ) + L ] d υ ≥ ε I .

2.3. Several Inequalities

The subsequent inequalities are instrument in establishing the proof of primary theorems within this paper.
Lemma 4. 
[54]: Given any two vectors m ∈ R n , n ∈ R n , along with a positive constant μ > 0 , we can establish that
∥ m + n ∥ 2 ≥ μ 1 + μ ∥ m ∥ 2 − μ ∥ n ∥ 2 .
Lemma 5. 
[54]: (Cauchy-Schwartz inequality): For any pair of integrable vector-valued functions f ( t ) ∈ R n and g ( t ) ∈ R n , the subsequent inequality is valid:
∫ t t + T f ( υ ) T g ( υ ) d υ 2 ≤ ∫ t t + T ∥ f ( υ ) ∥ 2 d υ ∫ t t + T ∥ g ( υ ) ∥ 2 d υ .
Lemma 6. 
Given that the function φ ( t ) : t 0 , + ∞ → [ 0 , + ∞ ) is non-negative and that t 0 ≥ 0 . Assume the following conditions hold for a real number 0 < σ < 1 and positive constants T, ν, and γ:
φ ( t ) ≤ ν , t ∈ t 0 , t 0 + T
φ ( t + T ) ≤ σ φ ( t ) + γ e − α t , t ∈ t 0 , + ∞
with α ∈ 0 , − ln σ T , then
φ ( t ) ≤ b 1 e − β t + b 2 e − α t
where β = − ln σ T , b 1 = max ν e β t 0 + T , ν σ e β t 0 and b 2 = γ e α T 1 − σ e α T .
Proof. 
See Appendix A. □

3. Event-Triggered Consensus for General Linear Time-Varying Multi-Agent Systems

This section will give the overall framework for event-triggered control design methods. It may be applied to a collection of identical linear time-varying multi-agent systems, and the convergence of their consensus error systems will be analyzed.

3.1. Event-Triggered Consensus Control

Consider a team of linear time-varying multi-agent systems in the following form
χ ˙ i = Λ ( t ) χ i + Ξ ( t ) u i , t ∈ [ 0 , ∞ ) , i = 1 , 2 , ⋯ , N
where the control input is represented by u i ∈ R m and the state of the ith agent is indicated by χ i ∈ R n ; Λ : [ 0 , ∞ ) → R n × n and Ξ : [ 0 , + ∞ ) → R n × m are two time-varying matrices.
To optimize the use of communication resources, the paper adopts an event-triggered communication scheme among agents. To particularize, we set a decentralized function, termed H i t , χ i ( t ) , t k i i , χ i t k i i , to act as the trigger function for agent i , i = 1 , 2 , ⋯ , N , where t k i i is the k i th communication instant of agent i. After t k i i , agent i continuously monitors its own state χ i ( t ) to see if the trigger condition
H i t , χ i ( t ) , t k i i , χ i t k i i > 0
is satisfied. If satisfied, the current instant is denoted by t k i + 1 i + 1 , and agent i transmits t k i + 1 i + 1 and χ i t k i + 1 i + 1 to its neighboring agents immediately. At this time instant, it is said that an event occurs for agent i. Note that t k i i , i = 1 , ⋯ , N , are characterised by being independent with respect to all nodes, and does not need to be synchronized.
Definition 4. 
The Zeno behavior is confirmed to be present in the system if an event happens in an infinite times over some finite time interval.
We aim to design a distributed control u i = ν t , ∪ j ∈ { i } ∪ N i t k j j , χ j t k j j based on the event-triggered communication described above, where t k j j is the time instant of the most recent event occurring for agent i prior to the current time t, such that χ i ( t ) − χ j ( t ) → 0 for all agents while avoiding the Zeno behavior.
Considering the information above, the event-triggered control law can be generally expressed as
u i = K ( t ) ∑ i ∈ N i a i j ψ t k j j χ j t k j j − ψ t k i i χ i t k i i t ∈ t k i i , t k i + 1 i
where a i j refers to the elements of the adjacent matrix A within network topology; K ( t ) and ψ ( t ) are two bounded time-varying matrices which need to be designed. The trigger function is defined as
H i t , χ i ( t ) , t k i i , χ i t k i i = e χ i ( t ) 2 − c e − α t , t > t k i i
where e χ i ( t ) = ψ ( t ) χ i ( t ) − ψ t k i i χ i t k i i , and c , α > 0 are two positive design parameters.
Remark 1. 
The consensus control law (6) is different from that in general linear time-invariant systems such as [55]. First, the control gain matrix is time-varying. Second, an extra term ψ i ( t ) appears in the consensus term. Thus, how to design K ( t ) and ψ ( t ) is a key issue. Moreover, the trigger function (7) is inspired by that in [32], where c and α are two design parameters. To achieve the objective, K ( t ) , ψ ( t ) and α are designed by following the conditions of the Theorem 1 next.
For convenience of denotations, let χ = χ 1 T , ⋯ , χ N T and e χ ( t ) = e χ 1 T ( t ) , ⋯ , e χ N T ( t ) T . The closed-loop system is given by
χ ˙ = I N ⊗ Λ ( t ) + L ⊗ ( Ξ ( t ) K ( t ) ) χ + L ⊗ ( Ξ ( t ) K ( t ) ) e χ ( t ) .
The following consensus analysis will be based on this closed loop system.

3.2. Consensus Analysis

In the consensus analysis, to tackle the consensus problem, it is usually transformed into a stabilization issue through a fitting nonsingular transformation. As a result, we establish the subsequent assumptions regrading the system (8).
Assumption 1. 
Under the nonsingular transformation z i ( t ) = ψ ( t ) χ i ( t ) + ζ , there are two time-varying matrices Υ ( t ) and Θ ( t ) , a positive semi-definite matrix Ψ ( t ) , and a constant vector ζ that satisfy the described conditions:
z ˙ ( t ) = Υ ( t ) Ψ ( t ) z ( t ) + Θ ( t ) e z ( t )
z = z 1 T , ⋯ , z N T T , and e z ( t ) = e χ ( t ) with e z i ( t ) = z i ( t ) − z i t k i i = ψ ( t ) χ i ( t ) + ζ − ψ t k i i χ i t k i i + ζ = e χ i ( t ) . Furthermore, ψ − 1 ( t ) is uniformly bounded.
Assumption 2. 
There exists a function V ( x ) such that κ 1 z T z ≤ V ( z ) ≤ κ 2 z T z and d V ( z ) d t ≤ − z T Ω ( t ) z + ϱ e − α t where Ω ( t ) is a positive semi-definite matrix, ϱ and κ are two constants.
Assumption 3. 
There exist constants ϖ Υ , ϖ Ψ , ϖ Θ and ϖ Ω such that ∥ Υ ( t ) ∥ ≤ ϖ Υ , ∥ Ψ ( t ) ∥ ≤ ϖ Ψ , ∥ Θ ( t ) ∥ ≤ ϖ Θ , and ∥ Ω ( t ) ∥ ≤ ϖ Ω for all t ≥ 0 . Moreover, assume that Ω ( t ) ≥ Ψ ( t ) and Ω ( t ) is PE, implying the existence of two constants T and ε such that σ min ∫ t t + T Ω ( υ ) d υ ≥ ε is valid.
With the preliminaries out of the way, we can now introduce our foremost result.
Theorem 1. 
Take into consideration the closed-loop system given by Equation (8), which integrates the system (4), operates under the event-triggered control law presented in (6) and is governed by the triggered condition stated in (7). Under Assumptions 1-3, if α is designed such that α ∈ ( 0 , β ) with
β = − 1 T ln 1 − ε 2 ε + κ 2 ε + 2 κ 2 ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ,
then we have:
(i) the existence of two positive constants ζ 1 and ζ 2 , ensuring ∑ i = 1 N x i ( t ) + ψ − 1 ( t ) ζ 2 ≤ ζ 1 e − β t + ζ 2 e − α t ;
(ii) Zeno behavior is absent.
Proof of Theorem 1: 
(i) In accordance with Assumption 2, we derive that
d V ( t ) d t ≤ − z T Ω ( t ) z + ϱ e − α t .
Then, by performing integration on both sides of (10) from t to t + T , one gets
V ( t + T ) − V ( t ) ≤ − ∫ t t + T Ω 1 2 ( υ ) z ( υ ) 2 d υ + ϱ α e − α t − e − α ( t + T )
where Ω 1 2 is derived from the decomposition of the positive semi-definite matrix Ω , i.e., Ω = Ω 1 2 Ω 1 2 , and based on (9), it is concluded that
z ( υ ) = z ( t ) + ∫ t υ Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) d s .
Substituting (12) in (11) yields
V ( t + T ) − V ( t ) ≤ − ∫ t t + T ∥ Ω 1 2 ( υ ) z ( t ) + ∫ t υ ( Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) d s ∥ 2 d υ + ϱ α e − α t − e − α ( t + T ) .
According to Lemma 4 with m = Ω 1 2 ( υ ) z ( t ) and n = Ω 1 2 ( υ ) ∫ t υ Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) d s , we have
V ( t + T ) − V ( t ) ≤ − μ 1 + μ ∫ t t + T Ω 1 2 ( υ ) z ( t ) 2 d υ + μ ∫ t t + T ∥ Ω 1 2 ( υ ) ∫ t υ ( Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) d s ∥ 2 d υ + ϱ α e − α t − e − α ( t + T )
where μ is an arbitrary positive constant. From Assumption 3, one gets
V ( t + T ) − V ( t ) ≤ − μ ε 1 + μ ∥ z ( t ) ∥ 2 + μ ϖ Ω ∫ t t + T ∫ t υ Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) d s 2 d υ + ϱ α e − α t − e − α ( t + T ) ≤ − μ ε 1 + μ ∥ z ( t ) ∥ 2 + μ ϖ Ω ∫ t t + T ∫ t υ ∥ Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) ∥ 2 d s 2 d υ + ϱ α e − α t − e − α ( t + T )
Using Lemma 5 with f ( s ) = 1 and g ( s ) = ∥ Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) ∥ , combining with υ − t ≤ T , we conclude that
V ( t + T ) − V ( t ) ≤ − μ ε 1 + μ ∥ z ( t ) ∥ 2 + μ ϖ Ω T ∫ t t + T ∫ t υ ∥ Υ ( s ) Ψ ( s ) z ( s ) + Θ ( s ) e z ( s ) ∥ 2 d s d υ + ϱ α e − α t − e − α ( t + T )
After altering the integration order for the second term in inequality (16), in conjunction with t + T − s ≤ T , we derive
V ( t + T ) − V ( t ) ≤ − μ ε 1 + μ ∥ z ( t ) ∥ 2 + μ ϖ Ω T 2 ∫ t t + T ∥ Υ ( υ ) Ψ ( υ ) z ( υ ) + Θ ( υ ) e z ( υ ) ∥ 2 d υ + ϱ α e − α t − e − α ( t + T ) ≤ − μ ε 1 + μ ∥ z ( t ) ∥ 2 + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ∫ t t + T z ( υ ) T · Ψ ( υ ) z ( υ ) d υ + 2 μ ϖ Ω T 2 ϖ Θ 2 ∫ t t + T e z ( υ ) T e z ( υ ) d υ + ϱ α e − α t − e − α ( t + T )
where the known inequality ∥ m + n ∥ 2 ≤ 2 ∥ m ∥ 2 + 2 ∥ n ∥ 2 to vectors m and n is applied to generate the final inequality. From e z ( t ) T e z ( t ) ≤ N c e − α t , it implies that
V ( t + T ) − V ( t ) ≤ − μ ε 1 + μ ∥ z ( t ) ∥ 2 + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ∫ t t + T z ( υ ) T · Ψ ( υ ) z ( υ ) d υ + 2 μ ϖ Ω T 2 ϖ Θ 2 N c α e − α t − e − α ( t + T ) + ϱ α e − α t − e − α ( t + T ) .
According to Assumptions 2 and 3, we have − ∥ z ( t ) ∥ 2 ≤ − κ 2 − 1 V ( t ) and Ψ ( t ) ≤ Ω ( t ) . Then,
V ( t + T ) − V ( t ) ≤ − μ ε ( 1 + μ ) κ 2 V ( t ) + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ∫ t t + T z ( υ ) T · Ω ( υ ) z ( υ ) d υ + 2 μ ϖ Ω T 2 ϖ Θ 2 N c α e − α t − e − α ( t + T ) + ϱ α e − α t − e − α ( t + T ) .
By substituting (11) into (19) leads to
V ( t + T ) − V ( t ) ≤ − μ ε ( 1 + μ ) κ 2 V ( t ) + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ( V ( t ) − V ( t + T ) ) + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ϱ α e − α t − e − α ( t + T ) + 2 μ ϖ Ω T 2 ϖ Θ 2 N c α e − α t − e − α ( t + T ) + ϱ α e − α t − e − α ( t + T ) .
After that, one receives
V ( t + T ) ≤ κ 3 V ( t ) + κ 4 e − α t
where
κ 3 : = 1 − μ ε κ 2 ( 1 + μ ) 1 + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ , κ 4 : = 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ϱ + ϖ Θ 2 N c + ϱ α 1 + 2 μ ϖ Ω T 2 ϖ Υ 2 ϖ Ψ .
Let μ be κ 2 ε , and then we have
κ 3 = 1 − ε 2 ε + κ 2 ε + 2 κ 2 ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ∈ ( 0 , 1 ) , κ 4 = 2 κ 2 ϖ Ω T 2 ϖ Υ 2 ϖ Ψ ϱ + ϖ Θ 2 N c + ϱ ε α ε + 2 κ 2 ϖ Ω T 2 ϖ Υ 2 ϖ Ψ .
Based on Equation (10), this implies that V ( t ) ≤ ϱ T + V ( 0 ) , t ∈ [ 0 , T ) . Thus, utilizing Lemma 6, we can conclude
V ( t ) ≤ η 1 e − β t + η 2 e − α t
if α ∈ ( 0 , β ) , where β = − ln κ 3 T , η 1 = max { ( ϱ T + V ( 0 ) ) e β T , ρ T + V ( 0 ) κ 3 , and η 2 = κ 4 e α T 1 − κ 3 e α T .
(i) From z i ( t ) = ψ ( t ) χ i ( t ) + ζ and κ 1 z T z ≤ V ( t ) , it is simple to ascertain
∑ i = 1 N x i ( t ) + ψ − 1 ( t ) ζ 2 ≤ V ( t ) ψ 0 2 κ 1
where ψ 0 as the upper bound of ψ − 1 ( t ) . Substituting (22) in (23), it results in
∑ i = 1 N χ i ( t ) + ψ − 1 ( t ) ζ 2 ≤ ζ 1 e − β t + ζ 2 e − α t
where ζ 1 = η 1 ψ 0 2 κ 1 and ζ 2 = η 2 ψ 0 2 κ 1 .
(ii) Starting with e χ i ( t ) = e z i ( t ) = z i ( t ) − z i t k i i , it is discovered that e ˙ z i ( t ) = z ˙ i ( t ) for t ∈ t k i i , t k i + 1 i , and e z i t k i i = 0 . Thus, based on (9), we conclude that
e χ i ( t ) ≤ ∫ t k i i t z ˙ i ( υ ) d υ ≤ ∫ t k i i t Υ ( υ ) Ψ ( υ ) z ( υ ) + Θ ( υ ) e z ( υ ) d υ .
Based on κ 1 z T z ≤ V ( t ) and (22), we have
∥ z ( t ) ∥ ≤ η 1 κ 1 e − β 2 t k i i + η 2 κ 1 e − α 2 t k i i .
From (5) and (7), we obtain that
∥ e ( t ) ∥ ≤ N c e − α 2 t k i i .
Substituting (26) and (27) back into (25), together with Assumption 3, leads to
e χ i ( t ) ≤ μ 1 e − β t k i i + μ 2 e − α t k i i t − t k i i
where μ 1 = ϖ Υ ϖ Ψ η 1 κ 1 and μ 2 = ϖ Υ ϖ Ψ η 2 κ 1 + ϖ Θ N c . The subsequent event will occur once e i ( t ) 2 = c e − α t . Therefore, the value of υ = t − t k i i that satisfies equation
μ 1 e α 2 − β 2 t k i i + μ 2 υ = N c e − α 2 υ
serves as a minimum limit for the time intervals between events. Because of 0 < α < β , the inequality μ 2 ≤ μ 1 e α 2 − β 2 t k i i + μ 2 ≤ μ 1 + μ 2 holds. For all t k i i ≥ 0 , the solution υ t k i i is the greater or equal to υ given by μ 1 + μ 2 υ = N c e − α i 2 υ , which is strictly positive. Consequently, it is clear that the system is free from Zeno behavior. □
Remark 2. 
Assumptions 1-3 are crucial elements in establishing the proof of Theorem 1. In applications, how to choose the transformation and the Lyapunov function is key for the event-triggered consensus analysis. In the next section, we will illustrate how to identify a proper transformation and Lyapunov function for a specific linear time-varying multi-agent system within a network that includes a spanning tree.

4. Applications to Event-Triggered Consensus of Linear Time-Varying Multi-Agent Systems Having a Spanning Tree

This section utilizes the findings from Section III to engineer an event-triggered consensus control strategy for a collective of identical linear time-varying multi-agent systems over a network having a spanning tree.

4.1. Event-Triggered Control Design

Take into account a collective of identical multi-agent systems
x ˙ i = A ( t ) x i + B ( t ) u i , t ∈ [ 0 , ∞ ) , i = 1 , 2 , ⋯ , N
that are linear and change over time, where the control input is represented by u i ∈ R m and the state of the ith agent is indicated by x i ∈ R n ; A : [ 0 , ∞ ) → R n × n and B : [ 0 , + ∞ ) → R n × m are two time-varying matrices.
Based on the control law (6), we design K ( t ) = B ( t ) T Φ A ( 0 , t ) T and ψ t k j j = Φ A 0 , t k j j . Then, the detailed control law for agent i is expressed by
u i = B ( t ) T Φ A ( 0 , t ) T ∑ j ∈ N i γ i j Φ A 0 , t k j j x j t k j j − Φ A 0 , t k i i x i t k i i
where γ i , j are the entries of the adjacency matrix Γ corresponding to the graph G , and Φ A ( · , · ) is the state transformation matrix for A ( t ) . The design of trigger function is as
H i t , x i ( t ) , t k i i , x i t k i i = e x i T ( t ) e x i ( t ) − c e − α t , t > t k i i
where e x i ( t ) = Φ A ( 0 , t ) x i ( t ) − Φ A 0 , t k i i x i t k i i , and c , α > 0 are two positive design parameters.
To provide context of our main result, we must first detail the subsequent assumptions.
Assumption 4. 
There exist m ¯ ≥ 1 and n ¯ ≥ 1 such that Φ A t 1 , t 2 ≤ m ¯ and ∥ B ( t ) ∥ ≤ n ¯ for all t 1 , t 2 , t ≥ 0 .
Assumption 5. 
The pair ( A ( t ) , B ( t ) ) is uniformly controllable meaning a pair of positive numbers ( ε , T ) can be found to ensure σ min W c ( t , t + T ) ≥ ε for all t ≥ 0 .
Now that the foundation has been laid, we are prepared to introduce our primary result.
Theorem 2. 
Given that Assumptions 4 and 5 are met and the graph under consideration features a spanning tree. If the constant α satisfies 0 < α < β with
β = − 1 T ln 1 − ε 2 ε + σ max ( P ) ε + 2 σ max ( P ) m ¯ 4 n ¯ 4 l 2 T 2
where l is sup L + 1 N r T . Then,
(i) there exist two positive constants ζ 1 and ζ 2 such that
∥ x − x ¯ ∥ ≤ ζ 1 e − β 2 t + ζ 2 e − α 2 t
i.e., all agents reach consensus;
(ii) Zeno behavior is absent in the linear time-varying system, which implies that there is a fixed positive constant that severs as a lower bound for all time intervals t k i i + 1 − t k i i , i = 1 , ⋯ , N , k i = 1 , 2 , ⋯ . The complete proof is scheduled to be detailed in the next section.

4.2. Proof of Theorem 2

The problem of consensus is altered into a stabilization problem through the introduction of a new variable z = z 1 ( t ) T , ⋯ , z N ( t ) T T with z i = Φ A ( 0 , t ) x i ( t ) − ∑ i = 1 N r i x i ( 0 ) , where r i > 0 is defined as in subsection 2.1. We also let e x ( t ) = e x 1 ( t ) , ⋯ , e x N ( t ) T . Then, we have the following lemma which gives the dynamic of z ( t ) .
Lemma 7. 
The dynamic of the variable z ( t ) is governed by
z ˙ ( t ) = − L − 1 N r T ⊗ G ( t ) z ( t ) − ( L ⊗ G ( t ) ) e x ( t )
where G ( t ) = Φ A ( 0 , t ) B ( t ) B ( t ) T Φ A ( 0 , t ) T , and L is the Lapalacian matrix of graph G .
Proof. 
See Appendix B. □
Proof of Theorem 2: To employ Theorem 1, we need to check Assumptions 1-3.
1) Let Υ ( t ) = − L − 1 N r T ⊗ I , Ψ ( t ) = I ⊗ G ( t ) , Θ ( t ) = − ( L ⊗ G ( t ) ) , and ζ = − ∑ i = 1 N r i x i ( 0 ) . Obviously, Ψ ( t ) is a positive semi-definite matrix and under a nonsingular transition z i ( t ) = ψ ( t ) x i ( t ) + ζ = Φ A ( 0 , t ) x i ( t ) − ∑ i = 1 N r i x i ( 0 ) , the dynamic described in (34) suggests that Assumption 1 is satisfied.
2) As the network includes a spanning tree, a positive matrix P that meets the Lemma 1 can be determined. With the Lyapunov function defined as V = z T P ⊗ I n z ,
d V d t = z ˙ ( t ) T P ⊗ I n z ( t ) + z ( t ) T P ⊗ I n z ˙ ( t ) = z T − L − 1 N r T ⊗ Ψ ( t ) T P ⊗ I n z + z T P ⊗ I n − L − 1 N r T ⊗ Ψ ( t ) z + 2 z T P ⊗ I n ( ( − L ) ⊗ Ψ ( t ) ) e x ( t ) = − 2 z T I n ⊗ Ψ ( t ) z − 2 e x ( t ) T P L ⊗ Ψ 1 2 ( t ) I n ⊗ Ψ 1 2 ( t ) z ≤ − z T I n ⊗ Ψ ( t ) z + e x T ( t ) P L ( P L ) T ⊗ Ψ ( t ) e x ( t ) ≤ − z T I n ⊗ Ψ ( t ) z + ρ N c e − α t
where ρ = σ max 2 ( P L ) m ¯ 2 n ¯ 2 . Let κ 1 = σ min ( P ) , κ 2 = σ max ( P ) , ϱ = ρ N c and Ω ( t ) = I n ⊗ G ( t ) . Obviously, Assumption 2 holds.
3) Let ϖ Υ = l , ϖ Ψ = m ¯ 2 n ¯ 2 , ϖ Θ = ∥ L ∥ m ¯ 2 n ¯ 2 and ϖ Ω = m ¯ 2 n ¯ 2 . It can be seen from Assumptions 4 and 5 that Assumption 3 holds.
The proof has been completed according to Theorem 1 .

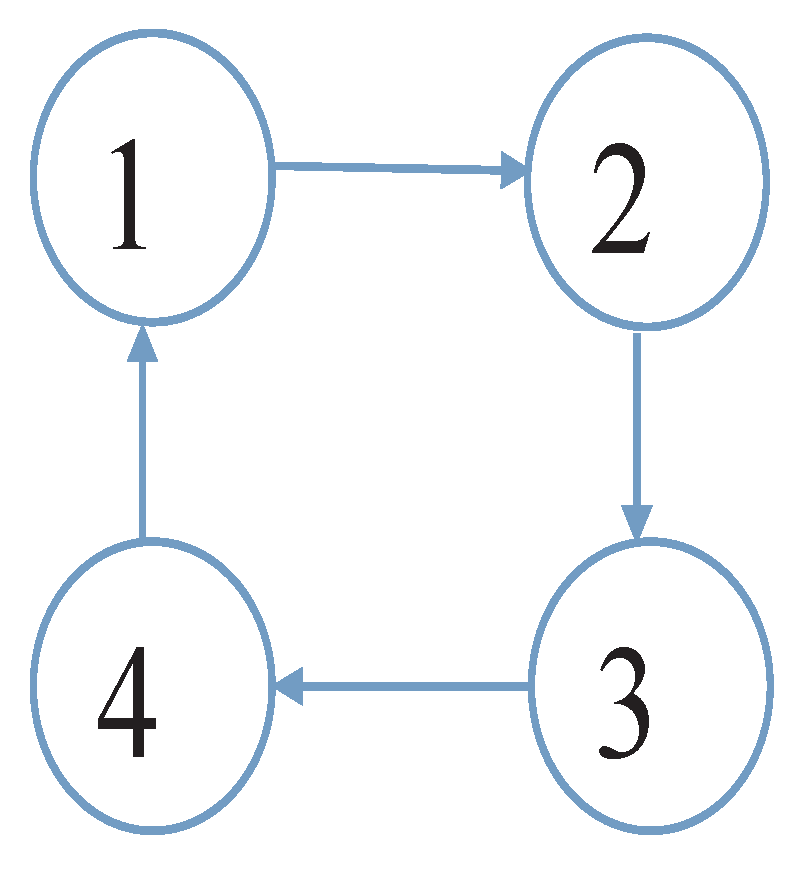
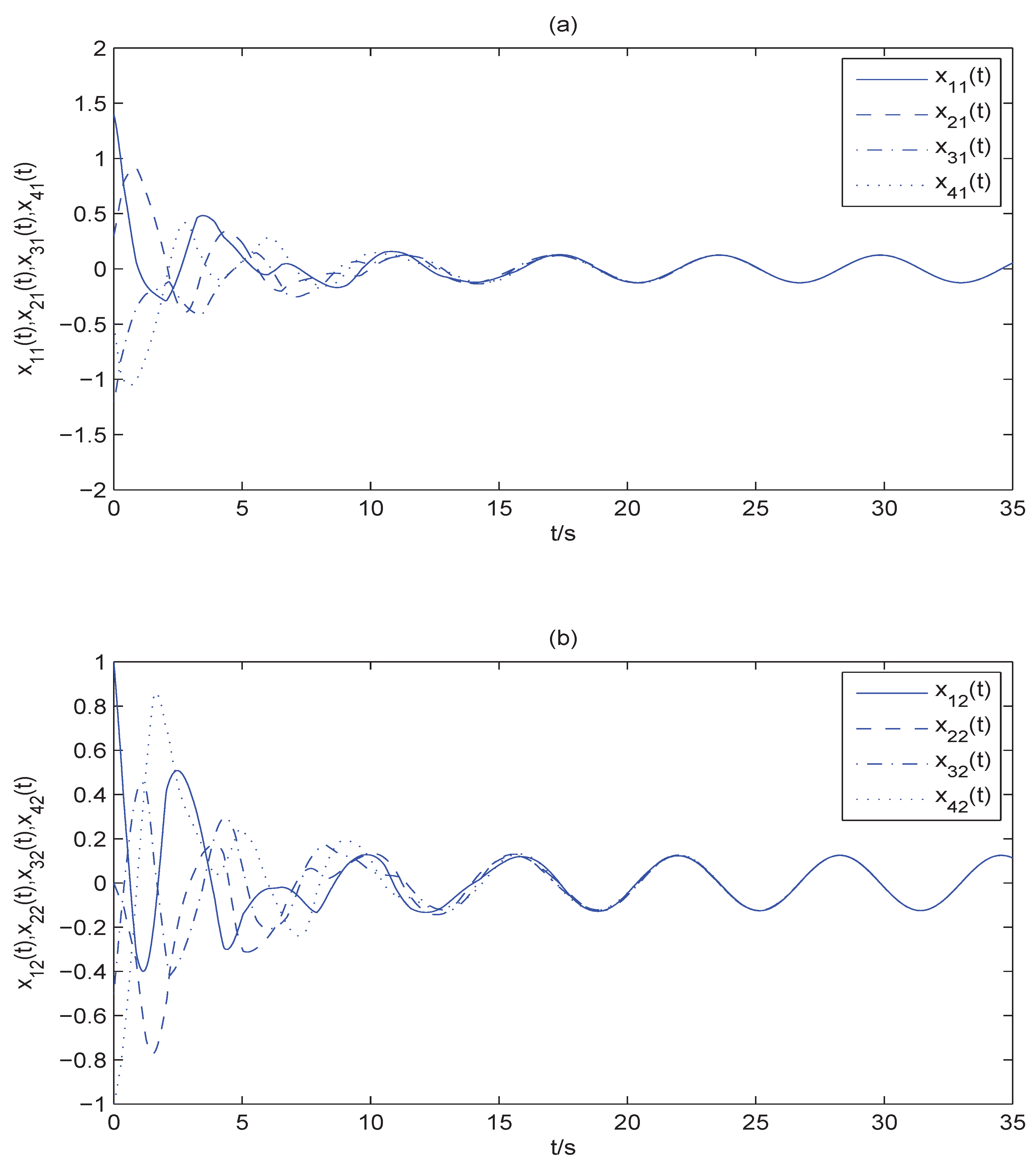
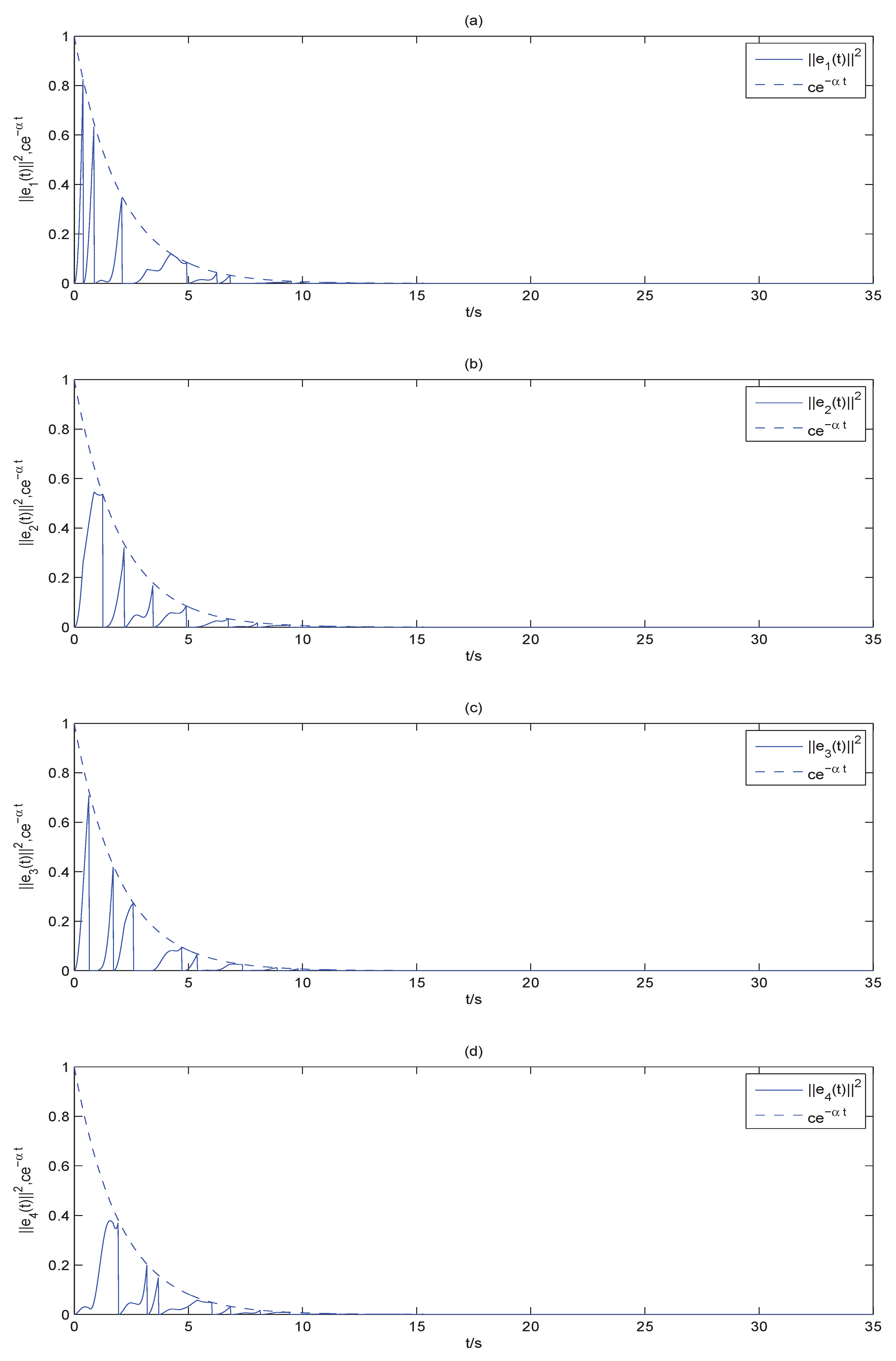
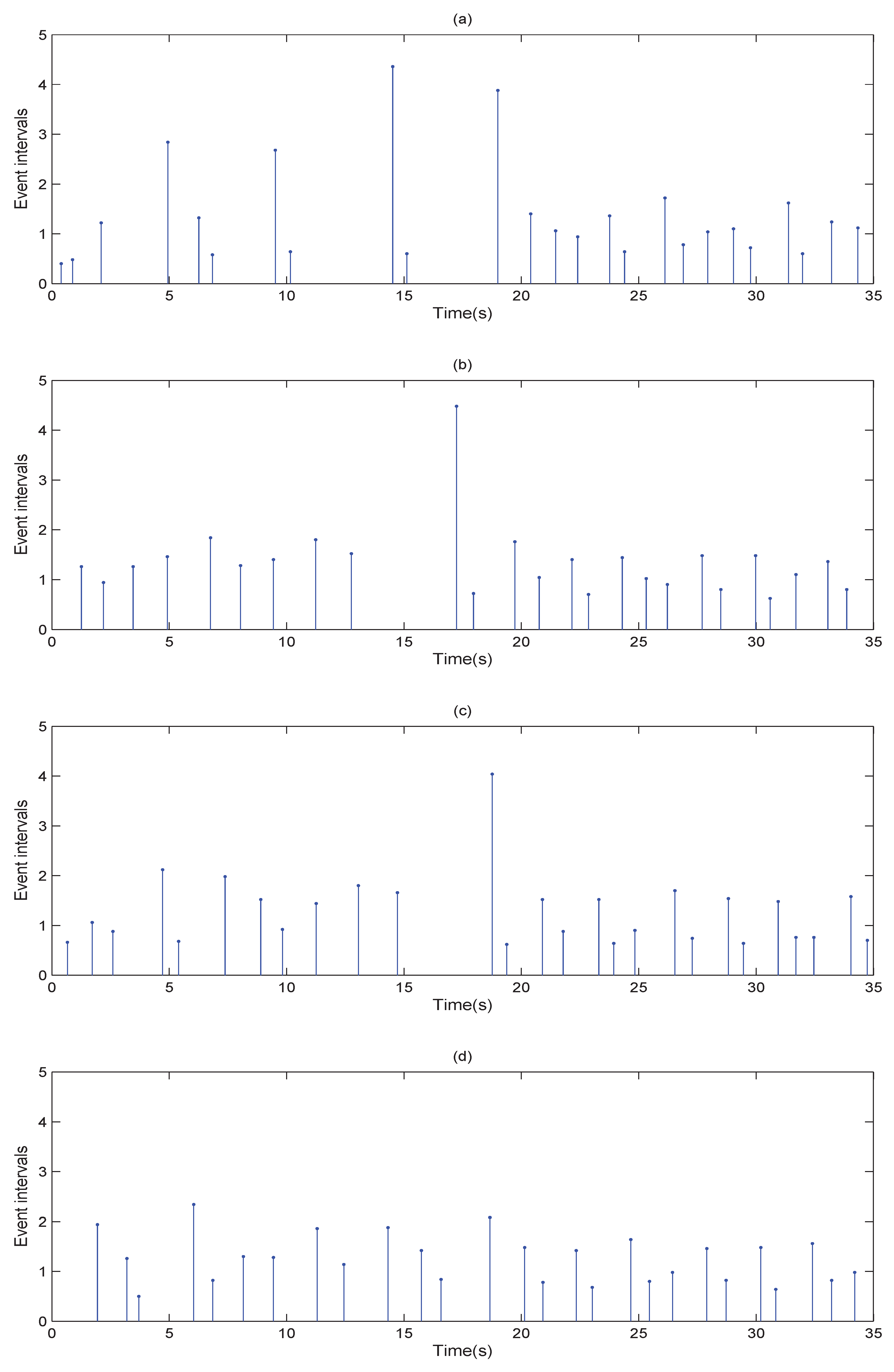
4.3. Simulation Example

In this section, We consider an example to demonstrate the efficacy of our consensus control method. Consider the subsequent agent model (30) with i = 1 , 2 , 3 , 4 , where
A ( t ) = 0 1 − 1 0 , B ( t ) = cos ( t ) sin ( t )
The transmition matrix for A ( t ) is
Φ ( 0 , t ) = cos ( t ) − sin ( t ) sin ( t ) cos ( t )
It is easily shown that Assumptions 4 and 5 hold, where m ¯ = 1 , n ¯ = 1 , T = 2 π and ε = 1.2 . Moreover, the network configuration is illustrated in Figure 1.
It is evident that a spanning tree exists, and the adjacency matrix is given by
Γ = 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0
In the simulation, we use the control law (31) along with the trigger function (32), and set the design parameter c = 1 and α = 0.5 ∈ ( 0 , 0.68 ) , and the initial states are given by x 1 = [ 1.4 , 1 ] , x 2 = [ 0.3 , 0 ] , x 3 = [ − 1.2 , − 0.5 ] , x 4 = [ − 0.5 , − 1 ] . Figure 2, Figure 3 and Figure 4 display the outcomes of the simulation. The states of all agents presented in Figure 2 confirm the achievement of state consensus. The curves of the supervised errors and the threshold function are shown in Figure 3, and the time vs event interval is shown in Figure 4. It is evident that there is no occurrence of Zeno behavior in the closed-loop system. This also accords with the results that presented in Theorem 2.

5. Conclusions

Our goal in this study is to establish a general framework for the design of consensus control in a set of linear time-varying multi-agent systems using an event-triggered communication approach. Based on certain assumptions, we proved the exponential convergence of all states of systems, and the occurrence of Zeno behavior is also precluded. The event-triggered scheme is used in communication process. Thus, our scheme can save the communication resource. Moreover, we implement the proposed event-triggered scheme to address the issue of event-triggered consensus within specific linear time-varying multi-agent systems.

Author Contributions

Conceptualization, Chi, W. S. and Hai, W.; methodology, Chi, W. S. and Peng, Z.; software, Xie, W. J.; validation, Chi, W. S.; formal analysis, Chi, W.S. and Zhang, X. Z.; investigation, Chi, W. S.; resources, Peng, Z.; data curation, Chi, W. S. and Xie, W. J.; writing—original draft preparation, Chi, W. S. and Zhang, X. Z.; writing—review and editing, Chi, W. S., Zhang, X. Z. and Peng, Z.; visualization, Xie, W. J.; supervision, Hai, W.; project administration, Hai, W. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A. PROOF OF LEMMA 6

For all t ≥ t 0 , consider N to be the positive number that satisfies t 0 + ( N − 1 ) T ≤ t ≤ t 0 + N T . Then,
Case ( i ) : t ≥ t 0 + T . From (3), it can be inferred that
φ ( t ) ≤ σ φ ( t − T ) + γ e − α ( t − T ) ≤ σ 2 φ ( t − 2 T ) + σ γ e − α ( t − 2 T ) + γ e − α ( t − T ) ⋮ ≤ σ N − 1 φ ( t − ( N − 1 ) T ) + σ N − 2 γ e − α ( t − ( N − 1 ) T ) + ⋯ + γ e − α ( t − T ) ≤ σ N − 1 φ ( t − ( N − 1 ) T ) + σ N − 2 e ( N − 1 ) α T + ⋯ + σ e 2 α T + e α T γ e − α t .
It follows from t 0 + N T ≥ t that N ≥ t − t 0 T and t − ( N − 1 ) T ∈ t 0 , t 0 + T . Together with (2), we have
σ N − 1 φ ( t − ( N − 1 ) T ) ≤ ν σ σ t − t 0 T = ν σ e − − ln σ T t − t 0 = ν σ e − β t − t 0
where β = − ln σ T . For 0 < α < − ln σ T , the inequality σ e α T < 1 holds. Therefore,
σ N − 2 e ( N − 1 ) α T + ⋯ + σ e 2 α T + e α T γ e − α t ≤ γ e − α t e α T 1 − σ e α T N − 1 1 − σ e α T ≤ γ e α T 1 − σ e α T e − α t .
Substituting (A1) and (A2) into (A3) yields
φ ( t ) ≤ ν σ e β t 0 e − β t + γ e α T 1 − σ e α T e − α t
Case (ii): t 0 ≤ t ≤ t 0 + T . It is easy to get
φ ( t ) ≤ ν ≤ ν e β t 0 + T e β t
Definite b 1 : = max ν e β t 0 + T , ν σ e β t 0 and b 2 : = γ 1 e α T 1 − σ e α T . Then, from (A4) and (A5), one gets
φ ( t ) ≤ b 1 e − β t + b 2 e − α t , t ∈ t 0 , + ∞ .
This complete this proof.

Appendix B. PROOF OF LEMMA 7

Differentiating both sides of Φ A ( 0 , t ) Φ A ( t , 0 ) = I n results into
Φ ˙ A ( 0 , t ) = − Φ A ( 0 , t ) Φ ˙ A ( t , 0 ) Φ A ( 0 , t ) = − Φ A ( 0 , t ) A ( t ) .
Then, one gets
z ˙ i ( t ) = Φ ˙ A ( 0 , t ) x i ( t ) + Φ A ( 0 , t ) x ˙ i ( t ) = Φ A ( 0 , t ) B ( t ) B ( t ) T Φ A ( 0 , t ) T × ∑ j ∈ N i r i j Φ A 0 , t k j j x j t k j j − Φ A 0 , t k i i x i t k i i .
Considering e x i = Φ A 0 , t k i i x i t k i i − Φ A ( 0 , t ) x i ( t ) and z i ( t ) = Φ A ( 0 , t ) x i ( t ) − ∑ i = 1 N r i x i ( 0 ) , we further have
z ˙ i ( t ) = Φ A ( 0 , t ) B ( t ) B ( t ) T Φ A ( 0 , t ) T × ∑ j ∈ N i r i j z j ( t ) − z i ( t ) + Φ A ( 0 , t ) B ( t ) B ( t ) T Φ A ( 0 , t ) T × ∑ j ∈ N i r i j e x j ( t ) − e x i ( t )
z ˙ ( t ) = ( ( − L ) ⊗ G ( t ) ) z ( t ) + e x ( t ) .
Observe that 1 N r T ⊗ I n z ˙ ( t ) = 0 and 1 N r T ⊗ I n z ( 0 ) = 0 . From this, we deduce that
z ˙ ( t ) = − L − 1 N r T ⊗ G ( t ) z ( t ) − ( L ⊗ G ( t ) ) e x ( t ) .
The proof comes to an end.

References

  1. Liu, Q.; Wang, Z.; He, X.; Zhou, D. A survey of event-based strategies on control and estimation. Systems Science & Control Engineering: An Open Access Journal 2014, 2, 90–97. [Google Scholar]
  2. Luo, Y.; Xiao, X.; Cao, J.; Li, A.; Lin, G. Event-triggered guaranteed cost consensus control for second-order multi-agent systems based on observers. Information Sciences 2021, 546, 283–297. [Google Scholar] [CrossRef]
  3. Phillips, C. L.; Harbor, R. D. Feedback control systems, Simon & Schuster: 1995.
  4. Anta, A.; Tabuada, P. To sample or not to sample: Self-triggered control for nonlinear systems. IEEE Transactions on Automatic Control 2010, 55, 2030–2042. [Google Scholar] [CrossRef]
  5. Tabuada, P. Event-triggered real-time scheduling of stabilizing control tasks. Journal Abbreviation 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
  6. Cai, J.; Yu, R.; Wang, B.; Mei, C.; Shen, L. Decentralized event-triggered control for interconnected systems with unknown disturbances. Journal of the Franklin Institute 2020, 357, 1494–1515. [Google Scholar] [CrossRef]
  7. Xiao, X.; Zhou, L.; Ho, D. W. C.; Lu, G. Event-triggered control of continuous-time switched linear systems. IEEE Transactions on Automatic Control 2019, 64, 1710–1717. [Google Scholar] [CrossRef]
  8. Tallapragada, P.; Chopra, N. On event triggered tracking for nonlin- ear systems. IEEE Transactions on Automatic Control 2013, 58, 2343–2348. [Google Scholar] [CrossRef]
  9. Heemels, W. P. M. H.; Donkers, M. C. F.; Teel, A. R. Periodic event- triggered control for linear systems. IEEE Transactions on Automatic Control 2013, 58, 847–861. [Google Scholar] [CrossRef]
  10. Liu, T.; Jiang, Z. P. A small-gain approach to robust event-triggered control of nonlinear systems. IEEE Transactions on Automatic Control 2015, 60, 2072–2085. [Google Scholar] [CrossRef]
  11. Garcia, E.; Antsaklis, P. J. Model-based event-triggered control for systems with quantization and time-varying network delays. IEEE Transactions on Automatic Control 2013, 58, 422–434. [Google Scholar] [CrossRef]
  12. Wang, X.; Lemmon, M. D. Event-triggering in distributed networked control systems. IEEE Transactions on Automatic Control 2011, 56, 586–601. [Google Scholar] [CrossRef]
  13. Dolk, V. S.; Tesi, P.; De Persis, C.; Heemels, W. P. M. H. Event-triggered control systems under denial-of-service attacks. IEEE Transactions on Control of Network Systems 2017, 4, 93–105. [Google Scholar] [CrossRef]
  14. Li, Y. X.; Yang, G. H. Model-based adaptive event-triggered control of strict-feedback nonlinear systems. IEEE transactions on neural networks and learning systems 2017, 29, 1033–1045. [Google Scholar] [CrossRef] [PubMed]
  15. Molin, A.; Hirche, S. On the optimality of certainty equivalence for event-triggered control systems. IEEE Transactions on Automatic Control 2013, 58, 470–474. [Google Scholar] [CrossRef]
  16. Liu, Y.; Yang, G. H. Event-triggered distributed state estimation for cyber-physical systems under dos attacks. IEEE Transactions on Cybernetics 2020, 52, 3620–3631. [Google Scholar] [CrossRef]
  17. Li, Y. X.; Yang, G. H. Event-triggered adaptive backstepping control for parametric strict-feedback nonlinear systems. International Journal of Robust and Nonlinear Control 2018, 28, 976–1000. [Google Scholar] [CrossRef]
  18. Ren, W.; Beard, R. Distributed Consensus in Multi-vehicle Cooperative Control: Theory and Applications; Springer: London, UK, 2008. [Google Scholar]
  19. Olfati-Saber, R.; Fax, J. A.; Murray, R. M. Consensus and cooperation in networked multi-agent systems. Proceedings of the IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
  20. Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
  21. Yu, C.; Wang, X.; Xu, X.; Zhang, M.; Ge, H.; Ren, J.; Sun, L.; Chen, B.; Tan, G. Distributed multiagent coordinated learning for autonomous driving in highways based on dynamic coordination graphs. IEEE Transactions on Intelligent Transportation Systems 2019, 21, 735–748. [Google Scholar] [CrossRef]
  22. Jin, L.; Li, S.; Luo, X.; Li, Y.; Qin, B. Neural dynamics for cooperative control of redundant robot manipulators. IEEE Transactions on Industrial Informatics 2018, 14, 3812–3821. [Google Scholar] [CrossRef]
  23. Li, W.; Zhang, H.; Wang, W.; Cao, Z. Fully distributed event-triggered time-varying formation control of multi-agent systems subject to mode-switching denial-of-service attacks. Applied Mathematics and Computation 2022, 414, 126645. [Google Scholar] [CrossRef]
  24. Dimarogonas, D. V.; Frazzoli, E.; Johansson, K. H. Distributed event-triggered control for multi-agent systems. IEEE Transactions on Automatic Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
  25. Fan, Y.; Feng, G.; Wang, Y.; Song, C. Distributed event-triggered control of multi-agent systems with combinational measurements. Automatica 2013, 49, 671–675. [Google Scholar] [CrossRef]
  26. Garcia, E.; Cao, Y.; Casbeer, D. W. Decentralized event-triggered consensus with general linear dynamics. Automatica 2014, 50, 2633–2640. [Google Scholar] [CrossRef]
  27. Zhu, W.; Zhang, Z.; Feng, G. Event-based consensus of multi-agent systems with general linear models. Automatica 2014, 50, 552–558. [Google Scholar] [CrossRef]
  28. Zhu, W.; Jiang, Z. P. Event-based leader-following consensus of multi-agent systems with input time delay. IEEE Transactions on Automatic Control 2015, 60, 1362–1367. [Google Scholar] [CrossRef]
  29. Zhang, H.; Feng, G.; Yan, H.; Chen, Q. Observer-based output feedback event-triggered control for consensus of multi-agent systems. IEEE Transactions on Industrial Electronics 2014, 61, 4885–14894. [Google Scholar] [CrossRef]
  30. Yu, H.; Antsaklis, P. J. Output synchronization of networked passive systems with event-driven communication. IEEE Transactions on Automatic Control 2014, 59, 750–756. [Google Scholar] [CrossRef]
  31. Meng, X.; Chen, T. Event based agreement protocols for multi-agent networks. Automatica 2013, 49, 2125–2132. [Google Scholar] [CrossRef]
  32. Guo, G.; Ding, L.; Han, Q. L. A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems. Automatica 2008, 10, 142–149. [Google Scholar] [CrossRef]
  33. Cao, M.; Xiao, F.; Wang, L. Second-order leader-following consensus based on time and event hybrid-driven control. Systems & Control Letters 2014, 50, 1489–1496. [Google Scholar] [CrossRef]
  34. Seyboth, G. S.; Dimarogonas, D. V.; Johansson, K. H. Event-based broadcasting for multi-agent average consensus. Automatica 2013, 49, 245–252. [Google Scholar] [CrossRef]
  35. Elahi, A.; Alfi, A.; Modares, H. H∞ consensus control of discrete-time multi-agent systems under network imperfections and external disturbance. IEEE/CAA Journal of Automatica Sinica 2019, 6, 667–675. [Google Scholar] [CrossRef]
  36. Li, L.; Ho, D.; Xu, S. A distributed event-triggered scheme for discrete-time multi-agent consensus with communication delays. IET Control Theory and Applications 2014, 8, 830–837. [Google Scholar] [CrossRef]
  37. Jetto, L.; Orsini, V. A new event-driven output-based discrete-time control for the sporadic mimo tracking problem. International Journal of Robust and Nonlinear Control 2014, 24, 859–875. [Google Scholar] [CrossRef]
  38. Mahmoud, M. S.; Karaki, B. J. Output-synchronization of discrete-time multiagent systems: A cooperative event-triggered dissipative approach. IEEE Transactions on Network Science and Engineering 2021, 8, 114–125. [Google Scholar] [CrossRef]
  39. Tuna, S. E. Sufficient conditions on observability grammian for synchronization in arrays of coupled linear time-varying systems. IEEE Transactions on Automatic Control 2010, 55, 2586–2590. [Google Scholar] [CrossRef]
  40. Wu, Y.; Meng, X.; Xie, L.; Lu, R.; Su, H.; Wu, Z. G. An input-based triggering approach to leader-following problems. Automatica 2017, 75, 221–228. [Google Scholar] [CrossRef]
  41. Cheng, T. H.; Kan, Z.; Klotz, J. R.; Shea, J. M.; Dixon, W. E. Event- triggered control of multiagent systems for fixed and time-varying network topologies. IEEE Transactions on Automatic Control 2017, 62, 5365–5371. [Google Scholar] [CrossRef]
  42. Wu, Z. G.; Xu, Y.; Lu, R.; Wu, Y.; Huang, T. Event-triggered control for consensus of multiagent systems with fixed/switching topologies. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2018, 48, 1736–1746. [Google Scholar] [CrossRef]
  43. Yang, R.; Zhang, H.; Feng, G.; Yan, H.; Wang, Z. Robust cooperative output regulation of multi-agent systems via adaptive event-triggered control. Automatica 2019, 102, 129–136. [Google Scholar] [CrossRef]
  44. Koike, R.; Endo, T.; Matsuno, F. Output-based dynamic event-triggered consensus control for linear multiagent systems. Automatica 2021, 133, 109863. [Google Scholar] [CrossRef]
  45. Adaldo, A.; Alderisio, F.; Liuzza, D.; Shi, G.; Dimarogonas, D. V.; di Bernardo, M.; Johansson, K. H. Event-triggered pinning control of switching networks. IEEE Transactions on Control of Network Systems 2015, 2, 204–213. [Google Scholar] [CrossRef]
  46. Xie, D.; Xu, S.; Chu, Y.; Yun, Z. Event-triggered average consensus for multi-agent systems with nonlinear dynamics and switching topology. Journal of the Franklin Institute 2015, 352, 1080–1098. [Google Scholar] [CrossRef]
  47. Yang, Q.; Li, X.; Li, J. Output consensus for networked heterogeneous nonlinear multi-agent systems by distributed event-triggered control. International Journal of Control 2021, 1–14. [Google Scholar] [CrossRef]
  48. Wang, Y.W.; Lei, Y.; Bian, T.; Guan, Z. H. Distributed control of nonlinear multiagent systems with unknown and nonidentical control directions via event-triggered communication. IEEE Transactions on Cybernetics 2020, 50, 1820–1832. [Google Scholar] [CrossRef]
  49. Liuzza, D.; Dimarogonas, D. V.; di Bernardo, M.; Johansson, K. H. Distributed model based event-triggered control for synchronization of multi-agent systems. Automatica 2016, 73, 1–17. [Google Scholar] [CrossRef]
  50. Wang, L.; Wang, Z.; Wei, G.; Alsaadi, F. E. Observer-based consen- sus control for discrete-time multiagent systems with coding-decoding communication protocol. IEEE Transactions on Cybernetics 2008, 10, 142–149. [Google Scholar]
  51. Yuan, S.; Yu, C.; Sun, J. Adaptive event-triggered consensus control of linear multi-agent systems with cyber attacks. Neurocomputing 2019, 12, 4335–4345. [Google Scholar] [CrossRef]
  52. Ioannou, P.; Fidan, B. Adaptive Control Tutorial(P. Ioannou et al.; 2006) [Bookshelf]; SIAM: Philadelphia, USA, 2004. [Google Scholar]
  53. Chen, W.; Wen, C.; Hua, S.; Sun, C. Distributed cooperative adaptive identification and control for a group of continuous-time systems with a cooperative pe condition via consensus. IEEE Transactions on Automatic Control 2014, 59, 91–106. [Google Scholar] [CrossRef]
  54. Loria, A.; Panteley, E. Uniform exponential stability of linear time- varying systems: revisited. Systems & Control Letters 2002, 47, 13–24. [Google Scholar] [CrossRef]
  55. Li, Z.; Duan, Z.; Chen, G.; Huang, L. Consensus of multiagent systems and synchronization of complex networks: A unified viewpoint. IEEE Transactions on Circuits & Systems I: Regular Papers 2010, 57, 213–224. [Google Scholar] [CrossRef]
Preprints 111111 g001
Figure 1. The network topology
Figure 1. The network topology
Preprints 111111 g001
Preprints 111111 g002
Figure 2. (a) Curves of states x 11 ( t ) ; x 21 ( t ) ; x 31 ( t ) and x 41 ( t ) ;(b) Curves of states x 12 ( t ) ; x 22 ( t ) ; x 32 ( t ) and x 42 ( t ) .
Figure 2. (a) Curves of states x 11 ( t ) ; x 21 ( t ) ; x 31 ( t ) and x 41 ( t ) ;(b) Curves of states x 12 ( t ) ; x 22 ( t ) ; x 32 ( t ) and x 42 ( t ) .
Preprints 111111 g002
Preprints 111111 g003
Figure 3. Supervised error | | e 1 ( t ) | | 2 , | | e 2 ( t ) | | 2 , | | e 3 ( t ) | | 2 , | | e 4 ( t ) | | 2 and threshold c e α t .
Figure 3. Supervised error | | e 1 ( t ) | | 2 , | | e 2 ( t ) | | 2 , | | e 3 ( t ) | | 2 , | | e 4 ( t ) | | 2 and threshold c e α t .
Preprints 111111 g003
Preprints 111111 g004
Figure 4. Time vs event interval.
Figure 4. Time vs event interval.
Preprints 111111 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated