Prerpints.org logo
Preprint
Article

Bio-Inspired Energy Efficient Cluster-based Routing Protocol for IoT in Disaster Scenarios

Altmetrics

Downloads

138

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 July 2024

Posted:

04 July 2024

You are already at the latest version

Alerts
Abstract
The Internet of Things (IoT) is a promising technology for sensing and monitoring the environment to reduce disaster impact. Energy is one of the major concerns for IoT devices, as sensors used in IoT devices are battery-operated. Thus, it is important to reduce energy consumption, especially during data transmission in disaster-adverse situations. Clustering-based communication helps reduce a node’s energy decay during data transmission and enhances the network’s lifetime. Many hybrid combination algorithms are proposed for clustering and the routing protocol to improve the network lifetime in disaster scenarios. However, the performance of these protocols is widely varied based on the underlying network configuration and the optimisation parameters considered. In this research, we have used the clustering parameters that are most relevant to disaster scenarios, such as the node’s residual energy, distance to sink, and network coverage. Then, we proposed a bio-inspired hybrid (BAO-PSO) algorithm where the Butterfly Optimisation Algorithm (BOA) is used for clustering and Particle Swarm Optimisation (PSO) is used for the routing protocol. The performance of the proposed algorithm is compared with the benchmark protocols LEACH, DEEC, PSO, PSO-GA, and PSO-HAS. Residual energy, network throughput, and network lifetime are considered performance matrices. The simulation result showed that the proposed algorithm increases network lifetime by 10%-20% by comparison with the benchmark algorithm.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Networks and Communications

1. Introduction

The number of natural disasters escalates due to global warming, environmental pollution, urbanisation, etc. According to the statistics, an average of 60000 people died due to disaster [1]. The faster detection of disasters can save many lives. To achieve this, it is required to monitor the environmental parameters (temperature, wind pressure, gas or chemical compositions, etc.) by implementing a wide range of sensors. The Internet of Things (IoT) focuses on an emerging paradigm to provide scalable solutions for a wide range of disaster problems [2]. The objects (e.g. 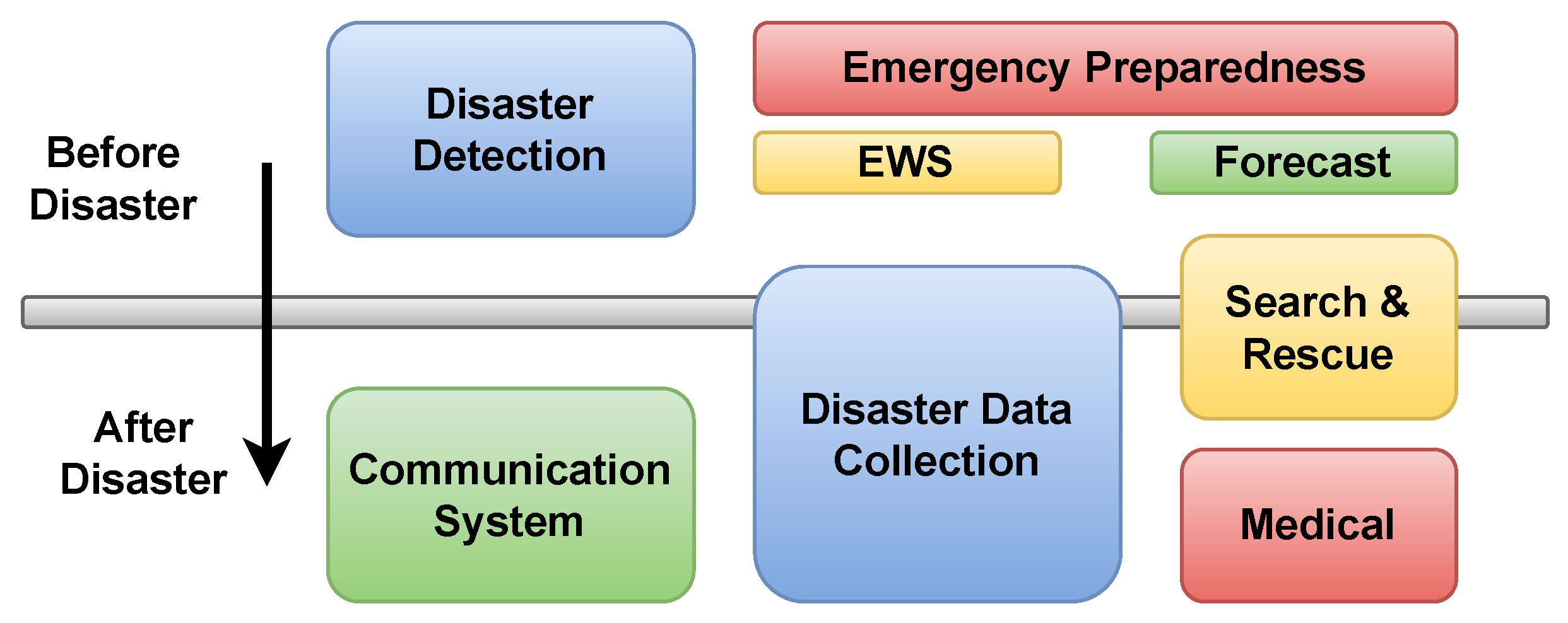mobile phones, RFID tags, sensors, etc.) in IoT networks can communicate with each other to perform a complex task by collecting data and processing it without human intervention [3]. The WSN, which acts as a virtual layer of the IoT network, covers a range of IoT applications for disaster management which includes pre-disaster environment monitoring [4,6], disaster preparedness[7], Early Warning System (EWS) [8], post-disaster response [9]. Figure 1 shows the WSN applications for the disaster management.
In WSN-based IoT applications, sensor nodes collect data from the operating environment and send it to the sink or base station[5], which is then further processed to evaluate the situation. However, there are limitations to using the WSN-based IoT network in disaster situations: limited battery life, power outage, limited memory, etc. [10]. The fundamental paradigm of the network, such as sensing the environment, data collection, and transmission, minimises the energy level of a node, which may result in the breakdown of the Communication link between the sensing nodes and the sink and disrupt the whole process. Moreover, during the 4disaster time, replacing the sensors or batteries may not be possible. As a result, the entire network may collapse, causing a delay in the response system. Hence, many researchers are working towards energy-efficient communication to increase the network’s longevity.
Clustering-based communication addresses the power-conserving issue by providing energy-efficient communication [11]. The clustering algorithm creates a group of sensor nodes and decides which cluster head (CH) to associate with among various choices. In every cluster, there is a CH, and the CH will be responsible for collecting data inside the cluster from nodes known as cluster members. CH also directly manages communication with the other CH, external gateway, or sink. Transferring data to the base station (BS) or other CH requires high energy. Therefore, it is important to select or design an energy-efficient routing protocol to reduce the energy consumption of the CH nodes. An energy-efficient routing protocol identifies the best route to transfer data between BS and the CH, which reduces the energy consumption to enhance the lifetime of the network [12]. Several energy-efficient routing protocols have been studied to select the CH dynamically and jointly optimise the energy efficiency. However, these protocols cannot be directly applied to disaster scenarios because of sudden peak network traffic, power outages, and delay sensitivity. Thus, using an efficient algorithm to find the optimal CH and best routing protocol is essential for the WSN-based IoT network in case of disaster management.
This paper aims to prolong the network lifetime by minimising the node’s energy consumption during communication between the node and sink. This paper proposes a bio-inspired energy-efficient cluster and routing (BICR) algorithm to enhance the network lifetime in disaster scenarios. The Butterfly Optimisation Algorithm (BOA) with a modified fitness function is used for cluster formation due to its high stability and lower computational complexity. The objective of the modified fitness is to prolong the network lifetime and extend connectivity in a disaster scenario. The network’s lifetime is further increased by optimising the routing path generation using particle swarm optimisation (PSO). The PSO algorithm is dynamic, prompts convergence, provides the highest throughput and reduces energy consumption compared to the other heuristic and mathematical approaches.
The main contributions of this paper are summarised below:
  • Proposed an improved BOA algorithm for the optimal cluster by utilising the search parameters critical to a disaster scenario, including residual energy, distance to the neighbours, distance to the BS, and degree of connectivity.
  • Proposed a shortage path multi-hop routing protocol using the PSO algorithm. Here, the PSO is optimised with residual energy, the distance between source and destination, and the number of relay nodes involved in the path.
  • Improved the state-of-the-art method to enhance average energy consumption, network coverage, and network lifetime by dynamically adjusting the sink position in different locations.

2. Literature Review

It is important to note that numerous researchers have made significant contributions to the field of WSN by proposing algorithms that enhance performance in terms of energy consumption, network coverage, and network availability. As energy is a critical factor in measuring WSN performance, extensive research has been conducted on clustering and routing algorithms to enhance energy efficiency. Swarm-based optimisation methods are widely studied in the literature as one of the search strategies to find the global minimum. Finding an IoT node from a group of competitive nodes and identifying the best routing path from source to destination can be described as a searching problem where the objective is to minimise energy consumption and maximise network lifetime. Many researchers have focused on swarm-based methods to solve global optimisation problems, using single meta-heuristic algorithms or hybrid models. This section will delve into some notable previous research works, providing a comprehensive overview of the existing knowledge. A plethora of optimisation algorithms have been developed that are fundamentally inspired by nature, such as the intelligent behaviours of birds, bees, fireflies, pigeons, etc. Some of the existing nature-inspired algorithms are Ant Colony Optimisation (ACO) [13], Firefly Optimisation Algorithm (FFA) [14], Artificial Bee Colony (ABC) [15] , Roach Infestation Optimisation (RIO) [16], Cuckoo Search Algorithm (CSA) [17], Honey Bee Mating Optimisation (HBMO) [18], Particle Swarm optimisation (PSO) [19], Pigeon Inspired Optimisation (PIO) [20], Bat Algorithm (BA) [21], Lion Pride Optimiser (LPO) [22], Butterfly Optimisation algorithm (BOA) [23], Lion Optimisation Algorithm (LOA) [24], and many more. ACO and PSO are extensively used for clustering and routing in WSN.
The authors in[25][26] proposed ACO based clustering and routing algorithm for the IoT network. The author [25] proposed a routing algorithm using ACO to obtain the best routing benefits by categorising the IoT environment depending on network types and applying the most suitable ACO to the concerned network. Multiple network types in an IoT environment result in overlapping areas between completely different networks. To optimise the routing for the overlapped areas, authors in [26] proposed a dual agent-based ACO algorithm to avoid overlapped intersections.
Furthermore, the authors in [27] proposed an integrated ACO and PCA-based clustering method to optimise energy dissipation and data transmission rate by formulating the fitness function with residual energy and inter-cluster distance for data aggregation. In [28], authors proposed a Harmony search algorithm (HSA) for clustering and routing in WSN and optimised it by considering the residual energy and distance between node to CH and CH-BS. An integrated PSO and HAS based algorithm is proposed in [29] to achieve global search with a rapid convergence rate. The result showed that the consumption energy and throughput were increased when using the standalone algorithm PSO and HAS.
A Genetic Algorithm (GA) based clustering and routing algorithm is presented [30] to improve the energy efficiency in WSNs. It showed sufficient improvement in the energy consumption and network lifetime when using the residual energy, distance, and routing phase in the fitness function.
Another bio-inspired energy efficient CH selection algorithm is proposed by the author using an Artificial bee colony (ABC)[31]. The result showed that the optimal number of clusters improves network performance but only for the single hop to communicate with the CH to sink.
To increase the network coverage, a multihop communication between the sink and the CH is considered in [32] and proposed an energy efficient cluster based routing protocol by integrating ABC with the firefly algorithm. Lalwani et al. [33] proposed a biogeography-based optimisation (BBO) algorithm for the CH selection; however, it suffers from single node failure as all the traffic is forwarded by the CH to sink, resulting in faster battery depletion. The Integrated Cuckoo Search (CS) method is used for the clustering and HAS for the routing in [34]. The proposed protocol considered uniform distribution of the energy consumption, though the node near the sink consumed more energy due to the traffic load.
Gao et al.[35] proposed a PSO-based clustering and routing algorithm to optimise the energy consumption in WSN. The higher residual energy of a node is considered the CH candidate during the clustering process. Morteza et. Al [36] proposed a novel fitness function using energy efficiency, cluster closeness and improved PSO-HSA.
From the above literature, it can be summarised that the hybrid metaheuristic algorithm performs better than the single metaheuristic model for the clustering and routing algorithm in terms of energy efficiency. No research is conducted using a hybrid model of BOA with the PSO for the clustering and routing algorithm. The performance of BOA and PSO algorithms is highly dependent on the fitness function. In this study, we have considered the fitness parameters that can best in a disaster scenario. This study uses this hybrid model to measure the performance of the network.

3. Network Model

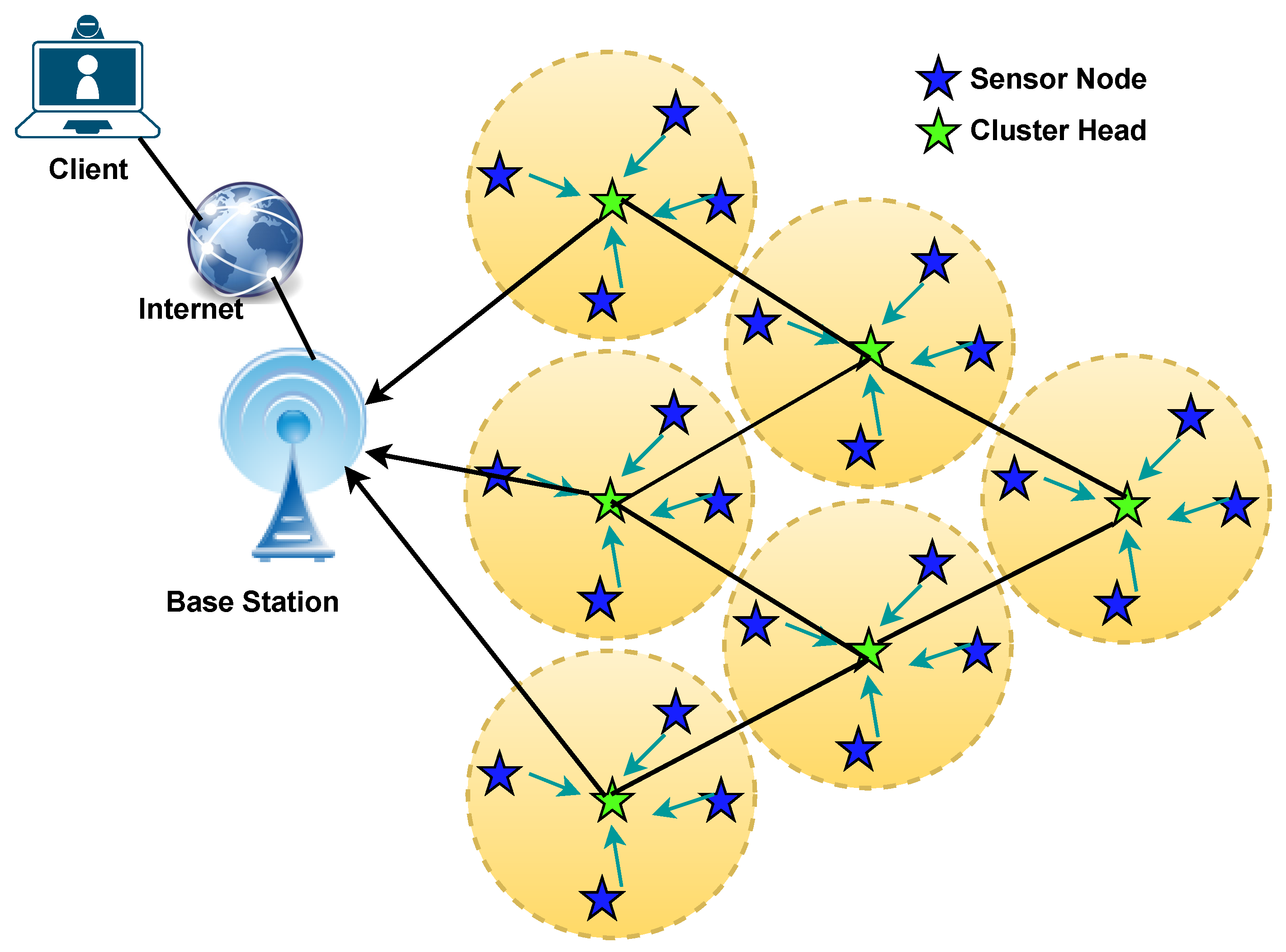
The network model used in this study is shown in Figure 2 based on the assumption mentioned below:
  • The network is considered a homogeneous network. At the time of the IoT-based sensor deployment, all the nodes are isomorphic, which means all the nodes have the same energy at the time of deployment.
  • The sensor node is operated by the battery, and there is no energy harvesting method applied or replenished used.
  • The area covered by the IoT-based sensors is randomly distributed. The location of the sensors is fixed, and each of the sensor nodes has a unique network identifier.
  • The entire sensor node perceives its location. The distance between other nodes can be calculated using the Euclidean distance equation.
  • The base station has unlimited energy and computational power.
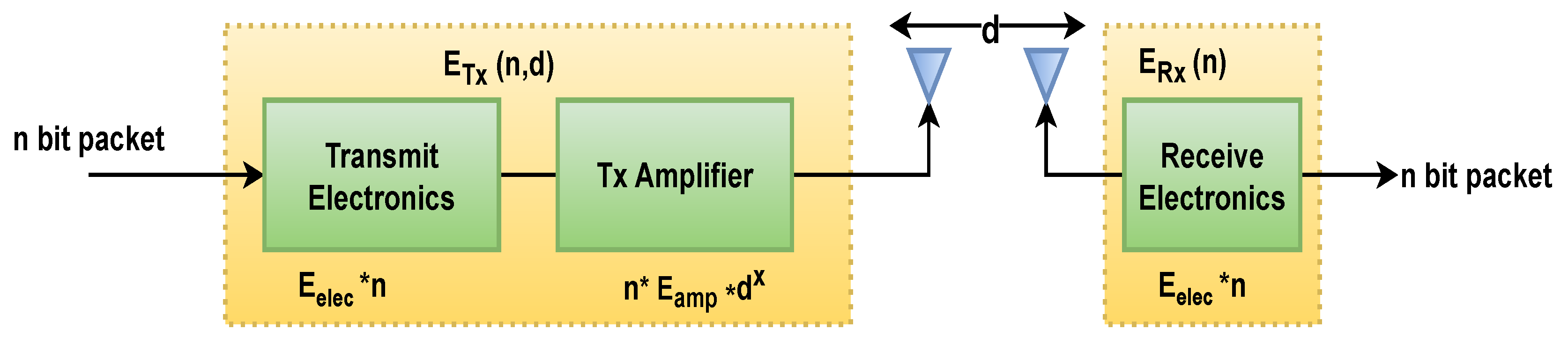
The first-order radio model is considered in this study, presented by the author [37]. The ratio of the energy consumption model is based on the distance between the sender and receiver. Figure 3 shows the ratio of energy consumption mode where the energy consumption to send a message is calculated by sender and receiver distance and the total length of the message.
E T x ( n , d ) = n * E e l e c + n * ε f s * d 2 , d ≤ d 0 n * E e l e c + n * ε m p f * d 4 , d > d 0
In Equation (1), E T x ( n , d ) is the required energy to transmit n bit over the distance d, E e l c is the energy required to transmit a bit. ε f s is the amplification factor over free space model and ε m p f is for the multipath fading model. d 0 is the distance threshold which is d 0 = ε f s ε m p f . When the distance is less than the threshold, the free space model is considered, and when the distance is greater than the threshold, consider the multipath fading model. In addition, to receive n bit of data energy required E R X = E e l e c * n .

4. CH Formation

The butterfly uses chemo-receptors to sense fragrance. While the butterfly moves to random places, it spreads intense labels of fragrance. This fragment helps to guide the butterfly agent to search for a butterfly and also helps to find a mating partner. If any given butterfly fails to get fragmented, it searches within the area in a random position, known as local exploitation. If the butterfly gets intensely fragmented, then it moves toward the butterfly known as global exploration. The fragrance of a butterfly can be defined by the f = C I α . Where f is the fragrance emitted by a butterfly, c is the sensory modality range [0,1], and I is the intensity of the fragmented, and α is the power exponent. Equations (2) and (3) represent the local search and global search [38]
x i t + 1 = x i t + ( r 2 X x j t − x k t ) X f i
x i t + 1 = x i t + ( r 2 X g * − x i t ) X f i
where x i t is the solution vector for the i number of butterfly at t number iteration, r is random number
[ 0 , 1 ]
, x j t and x k t are j butterfly and k bitterly, g * are the best solution is the current iteration. According to our network, each butterfly is initialised with an ID from 1 to N. N is the total number of sensors. Every butterfly position is denoted by the ( B i , p ) that belongs with (1≤p≤O) where O is the optimal number of CH.
Assume that N is the total no of sensors in the A ( a x a ) area. considering the free space energy consumption model, the energy consumption of a CH per round is denoted as:
E C H = n * E e l e c ( N O − 1 ) + n * E D A * N + n * E e l e c + n * ε f s * d b s 2
The energy consumption of a cluster member per round is denoted by:
E m = n * E e l e c + n * ε f s * d C H 2
Energy consumption of the cluster per round is denoted by:
E C P R = E C H + ( N o − 1 ) * E M
The total energy consumption of the network for the O number of CH per round is denoted by:
E t o t a l = E C P R * O = n ( 2 N * E e l e c + N * E D A + ε f s ( O B S 2 + N * d C H 2 ) )
The optimal number of CH can be found by the differentiating of O is denoted by [39]:
O o p t = N * n 2 π d B S 2
Similarly, for the multipath fading model, the optimum number of CH is denoted by:
O o p t = N 2 π ε f s * n ε m p * d B S 4

4.1. Fitness Function

The cluster head (CH) selection will be based on the residual energy ( R S ), node distance N D , and network coverage ( N C ).
Residual energy: Residual energy is one of the vital factors in selecting CH, as CH requires more energy to perform tasks. CH is responsible for receiving data from the node member and passing it to another CH or BS. Because of that, the node with higher residual energy has a high chance of becoming CH.
R S = ∑ i = 1 O o p t 1 E C H i
From the Equation (10), E C H i is the residual energy of the i t h cluster
Node Distance: This is also an essential factor for energy consumption. The less distance node between the CH dissipation, the less energy for the transmission. The equation for the distance between the node and the CH is:
N D = ∑ j = 1 O o p t ( ∑ i = 1 N j d i s t a n c e ( C H j , X i ) / I j )
Network coverage: The higher network coverage by assigning the CH of the node that node did not include with any other CH. This will provide higher scalability and increase the lifetime of the network[39]. The network coverage is denoted as [36]:
N C = ( N * − D ) − ∑ D = 1 D C * M D ∑ D = 1 D C * M D
The fitness function used for the BOA algorithm for this study is as follows:
F i t n e s s C H = R S * β 1 + N D * β 2 + N C β 3
where ∑ i = 1 3 1 , β i ∈ ( 0 , 1 ) . For this study, we assume, β 1 is consider . 50 , β 2 is . 30 and β 3 is consider . 20 .
The optimal CH selection process is given in Algorithm 1.
Algorithm 1 CH selection algorithm process using BOA
  • Define the objective function from Equation (13)
  • Create a population of butterfly
  • Stimulus sensor modalityc, switch probability p and power exponent α
  • while i t e r a t i o n < m a x i m u m  do
  •     for each butterfly in population: do
  •         calculate fragrance using
  •         update optimal butterfly population
  •     end for
  •     for each butterfly in population: do
  •         generate r (random number[0,1])
  •         if r<p then
  •            move towards best butterfly using Equation (3)
  •         else
  •            moves randomly using Equation (2)
  •         end if
  •     end for
  •     update power exponent value α
  • end while
  • the optimal solution for selecting the CH

5. Routing Protocol

The Cluster Head (CH) collected data from the cluster member and sent it to the BS. We assume that CH maintains a list for the BS route. The main objective of this routing algorithm is to minimise overall distance travel from source to destination as the distance is proportionally related to the energy decay and the network lifetime. The fitness function evaluates the quality of the routing protocol.
For this study, we have considered an improved PSO algorithm for the routing protocol. PSO algorithm [19] is a bio-inspired swarm of birds or fish moving in a multidimensional space for the food search. CH node is considered each of the particles, and each of the CH was initialised of a random velocity and position.
let P i = P i , 1 , P i , 2 , P i , 3 , . . . . . P i , D where D is equal to the optimal number of CH. The particles update the position based on the intensity of movement and the deviation. Particle’s observes the ( L b e s t ) and ( g b e s t ) and then adjust the position and velocity as follows [19]:
V i t + 1 = ω * V i t + C 1 * r a n d 1 * ( L b e s t − P i t ) + C 2 * r a n d 2 * ( g b e s t − P i t )
P i t + 1 = P i t + V t + 1
where, t is the current iteration, ω is the inertia weight ω m a x = 0.9 and ω m i n = 0.2 . rand1 and rand2 are a random numbers
[ 0 , 1 ]
.
Each of the CHs is assigned a random number
[ 0 , 1 ]
from a uniform random distribution. This number is then used to connect the CH with a random destination, known as the nearest relay node. We assume that each of the CHs is connected within the range of the CH or the BS.The P i , D is assigned to the final destination node C H D , which is connected with the BS. This process ensures that the data sent from the source CH C H S is routed to the BS via C H D , thereby optimising the routing process.
The improved fitness function for the PSO algorithm is considered for the residual energy, the distance between source and destination, and the total number of relay nodes. The fitness function is as follows:
F i t n e s s P S O = β 1 * ∑ i = 1 D D i s t a n c e ( C H S , C H d ) + β 2 * ∑ i = 1 D E r a v g E + β 3 * ∑ i = 1 D r e l a y ( C H S , D e s t d )
where, E r is the residual energy, A v g E is the average energy of all alive node
and D i s t a n c e ( C H S , C H d ) is the distance between source and destination node.
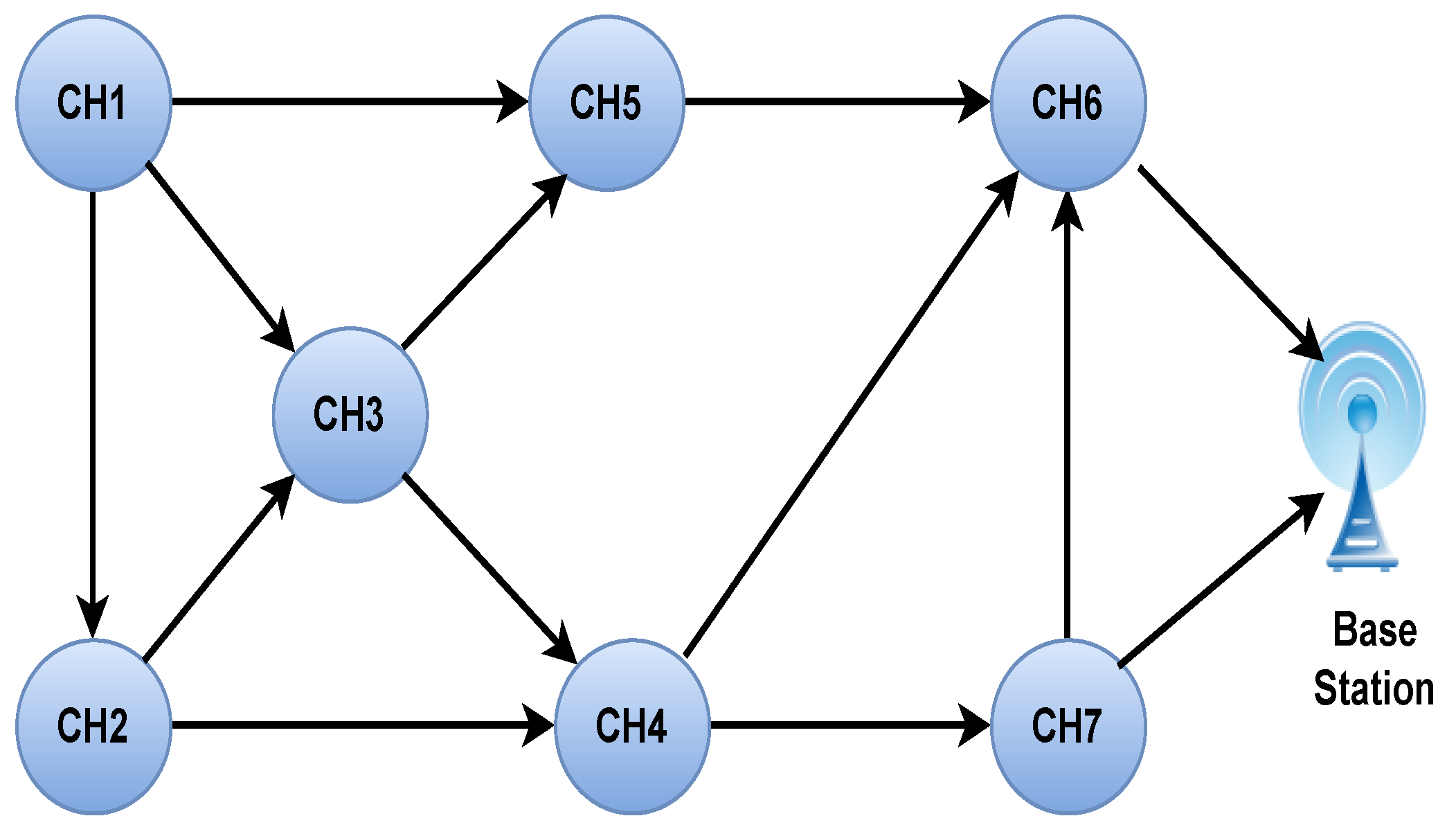
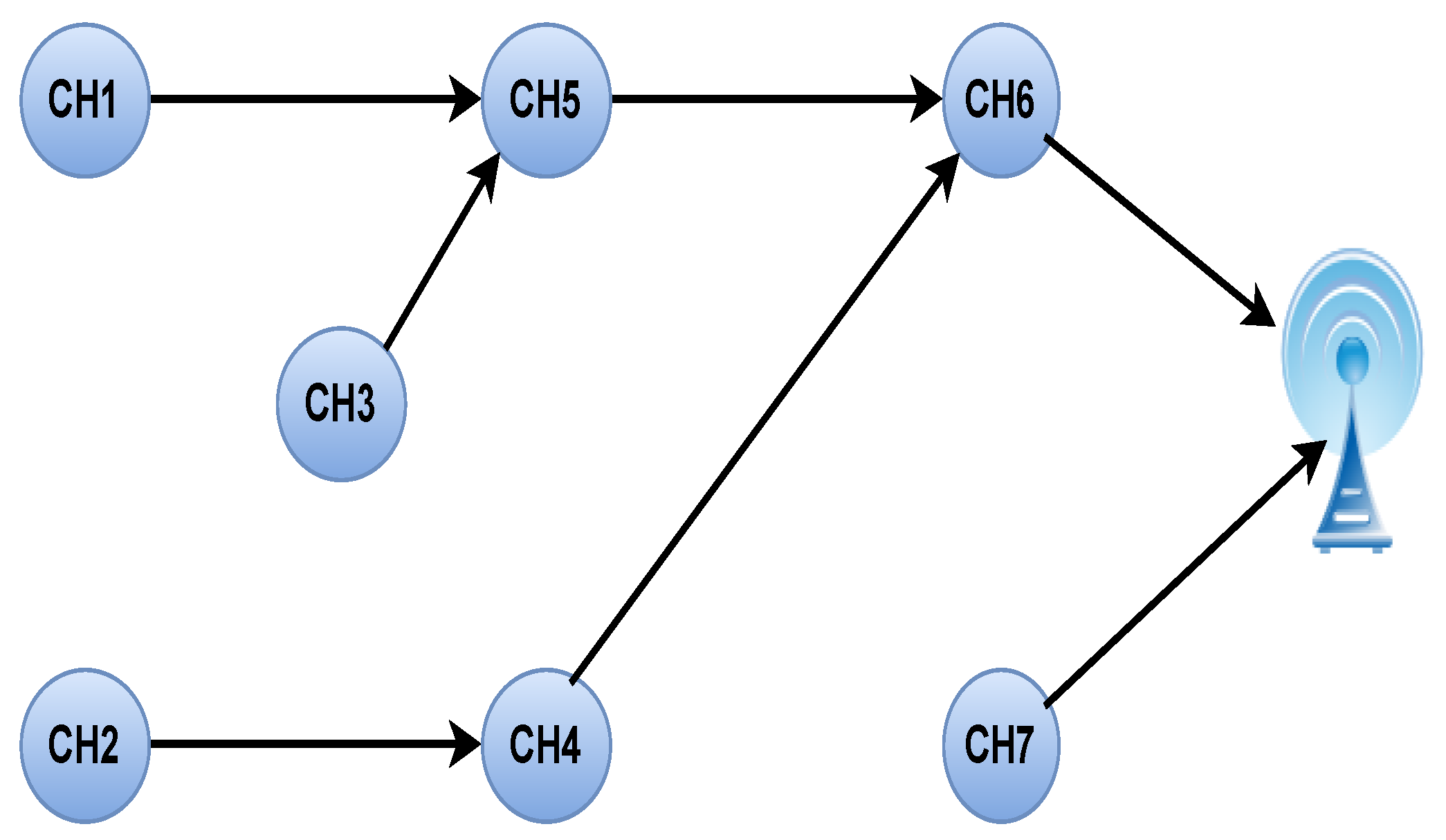
Let’s consider the network according to Figure 4 where graph G ( V , E ) shows the vertex, which is the CH acts as a gateway, and E is the edge. Table 1 shows nodes within the range of a particular CH and the total number of the relay nodes. According to Figure 4, there are 7 CHs ( C H 1 , C H 2 , C H 3 , … , C H 7 ) connected with each other in the communication range. We assign every CH with a random number P ( i , d ) ϵ [ 0 , 1 ] , mapped to a random relay node destination. Some of the CHs are connected with the BS. When the CH1 wants to send data to the BS, it can send through CH2, CH3, CH5 nodes.
After the optimization process is completed with the fitness function, CHs have information about their members and the different routes to send the other CH. The TDMA scheduler is used to solve congestion and collision issues. Each and every node has a dedicated slot to send data to the CH. The cluster member sends the data according to the specific time slot CH. The collected data is aggregated by the CH and sent by the optimized route according to the proposed model to the BS.
After every iteration, according to Equations (14) and (15), the particle position and velocity will update with respect to P b s e t and G b e s t . The updated new position value might get ≤ 0 or ≥ 1 because of algebraic addition and subtraction. To solve this issue, we regulate positions used [40]:
P ( i , d ) = 1 if P ( i , d ) > 1 m i n ( r → ) if P ( i , d ) < 0
r → is a vector of random numbers [ 0 , 1 ] .
Table 2 shows the optimization details route for the network. Figure 5 shows the optimization route for each of the CHs to aggregate data and send it to the BS.
The Algorithm 2 shows the method to select the optimal routing path.
Algorithm 2:Optimal routing path selection algorithm for the PSO
  • Define the objective function from Equation (16)
  • Input: Optimal number of CH ( C H 1 , C H 2 , C H 3 , . . . . . , C H N )
  • Initialise of particles ( P i )
  • Initialise swarm S n
  • for i = 1 to S n  do
  •     compute fitness value using equation-16
  •      L b e s t ← P i
  • end for
  • while i t e r a t i o n > M a x i m u m do
  •     for  i = 1 to S n  do
  •         update the velocity and position of each particle
  •         Evaluate the value of P i using equation 16
  •         if  L b e s t > c u r r e n t v a l u e  then
  •             L b e s t ← P i
  •         else G b e s t ← L b e s t
  •            select the best fitness value
  •         end if
  •     end for
  • end while
  • Optimal routing path by finding the optimal relay node

6. Simulation Results

The simulation was conducted to validate the proposed model. Matlab 2019b is used to perform the simulation. The properties of the Matlab installation environment are as follows: Windows 10 64-bit operating system, Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz, 16GB RAM. To validate the model, our proposed model’s simulation result is compared with the traditional model LEACH [41], DEEC [42] and state-of-the-art meta-heuristic algorithm based on PSO[43] and hybrid models PSO-GA[45] and PSO-HSA [46]. The parameters used for this simulation are given in Table 3.
The simulation considers two scenarios for the 200 X 200 m area.
Scenario-1: This scenario is considered a normal situation where BS/Sink is located in (100,100) locations. All the sensors are around the BS for short-length communication.
Scenario-2: This scenario is considered a disaster situation where BS/sink is located in a (0,0) location. All the sensors are far from the BS for long-range communication.
This simulation will help to understand and compare the proposed model stability in different situations with different models.
The following performance matrices are considered to validate the proposed model:
  • Residual Energy: The sum of all the alive sensors’ node remaining energy is considered as a performance matrix to evaluate the model. The residual energy is directly related to the energy utilisation within the network and influences the network lifetime.
  • Throughput: This is another important performance factor to evaluate the protocol. Throughput defines how much information the client gets from a monitoring area that the sensors collect and send. It measures how many packets the BS receives from the sensor node.
  • Network lifetime: The main objective of this proposed model is to maximise the network lifetime. This is to measure how much node is alive and able to send information to the sink. As mentioned above this matrix is directly related to the residual energy of a node.
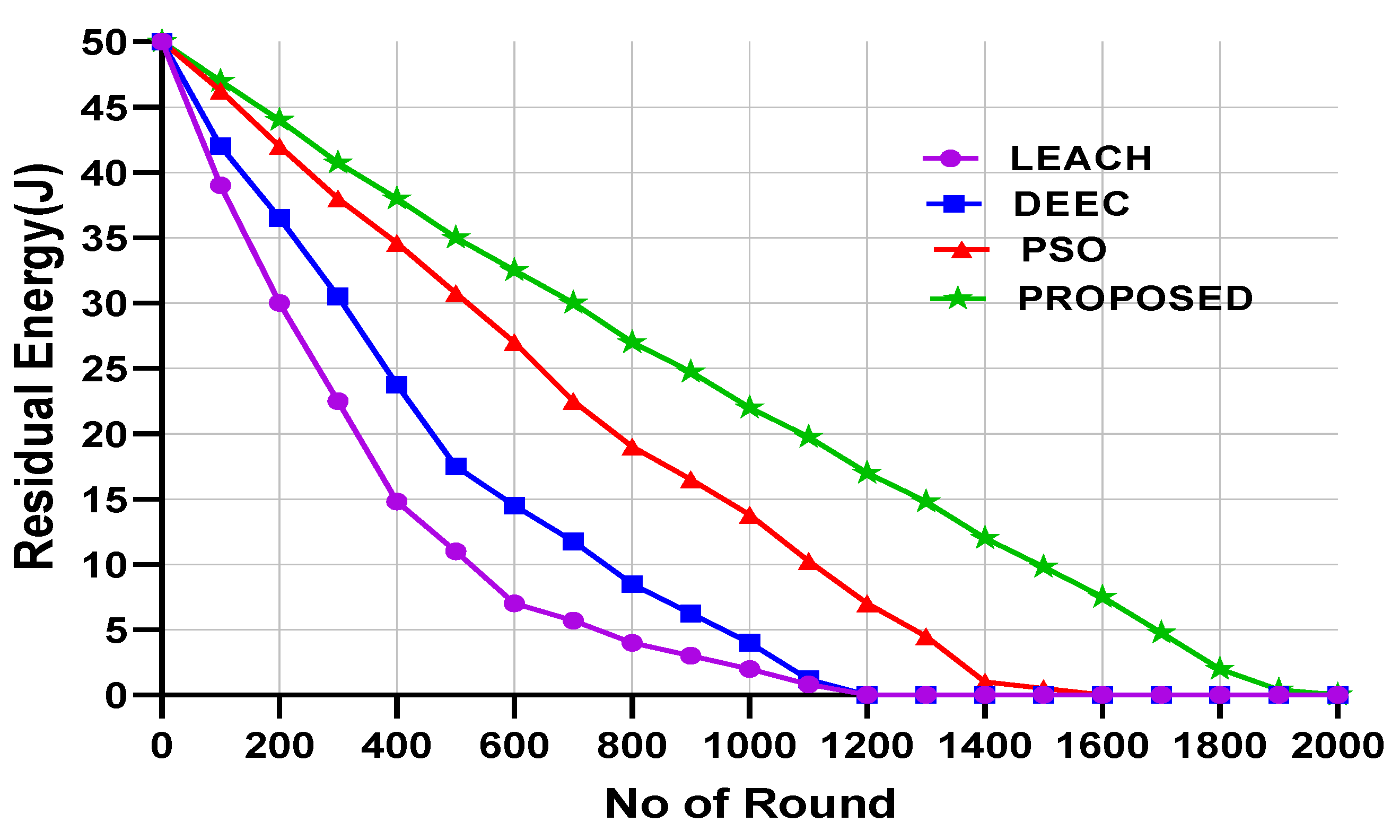
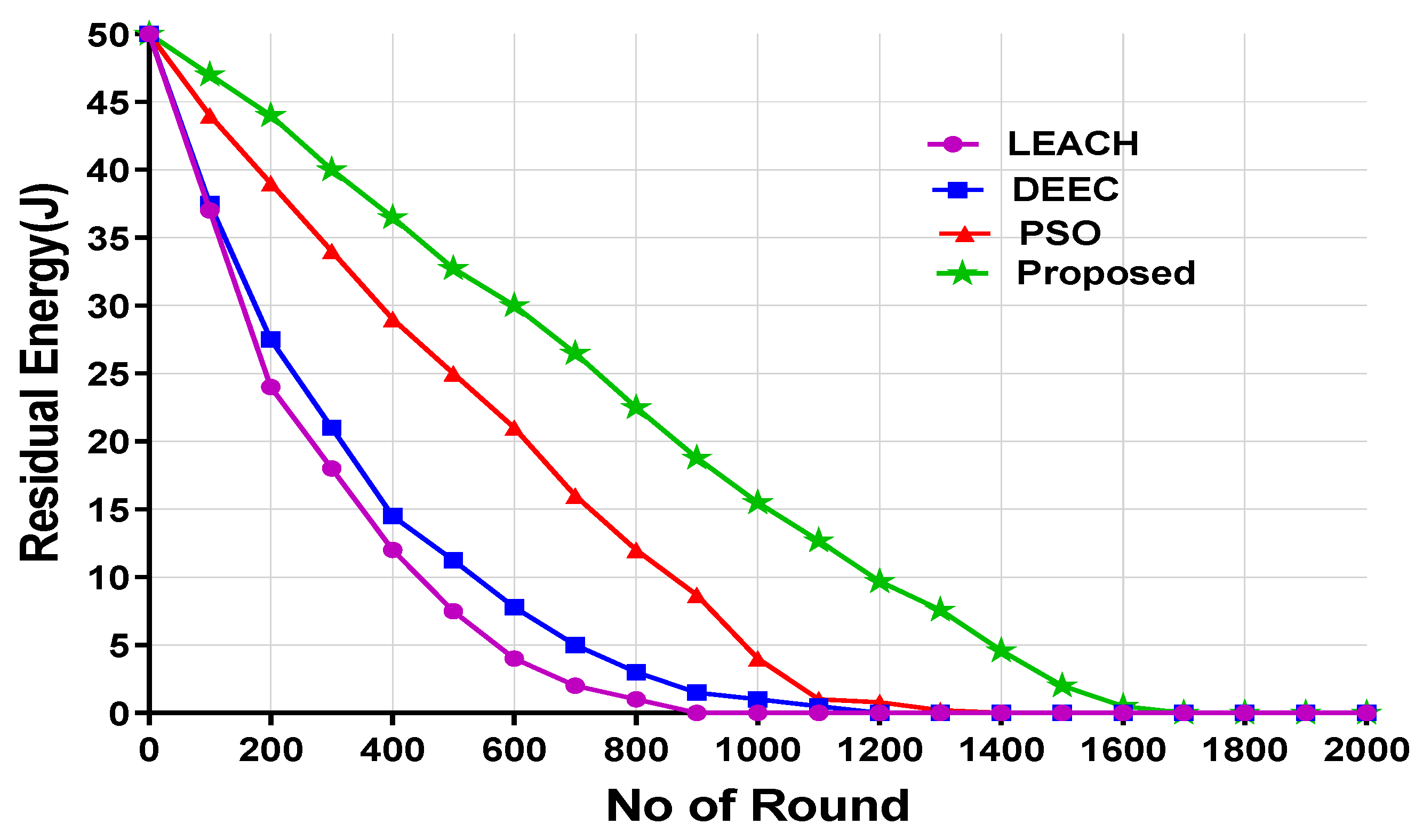
Figure 6 and Figure 7 presented the average residual energy of all the nodes for scenario 1 and scenario 2, respectively. The residual energy of the proposed model is compared with the LEACH, DEEC, and PSO models. For the calculation of the residual energy, 200 nodes are considered for both scenarios. According to the figures, the proposed model achieved the higher residual energy for all the nodes with the different numbers of rounds.
For scenario-1 (Figure 6), For the LEACH and DEEC model, all node’s residual energy is empty after 1200 rounds. PSO performs better than the LEACH and DEEC. The residual energy became low around 1450 rounds. However, the proposed model performs much better than LEACH and DEEC, the residual energy finish after 1957 rounds.
On the other hand, for scenario 2, LEACH, DEEC, and PSO’s residual energy died at 967,1187 and 1325 rounds, respectively. However, the proposed model finishes after 1600 rounds. The reason for finishing residual energy for the LEACH was higher energy consumption for the selection of random CH and single-hop data transmission. For the DEEC algorithm, the optimal distance was not considered when selecting the CH. The PSO considered the residual and distance of BS but did not consider the distance between two CH and orphan nodes. The proposed model performs better as it considered higher residual energy, distance as well and orphan nodes for the extent of network lifetime.
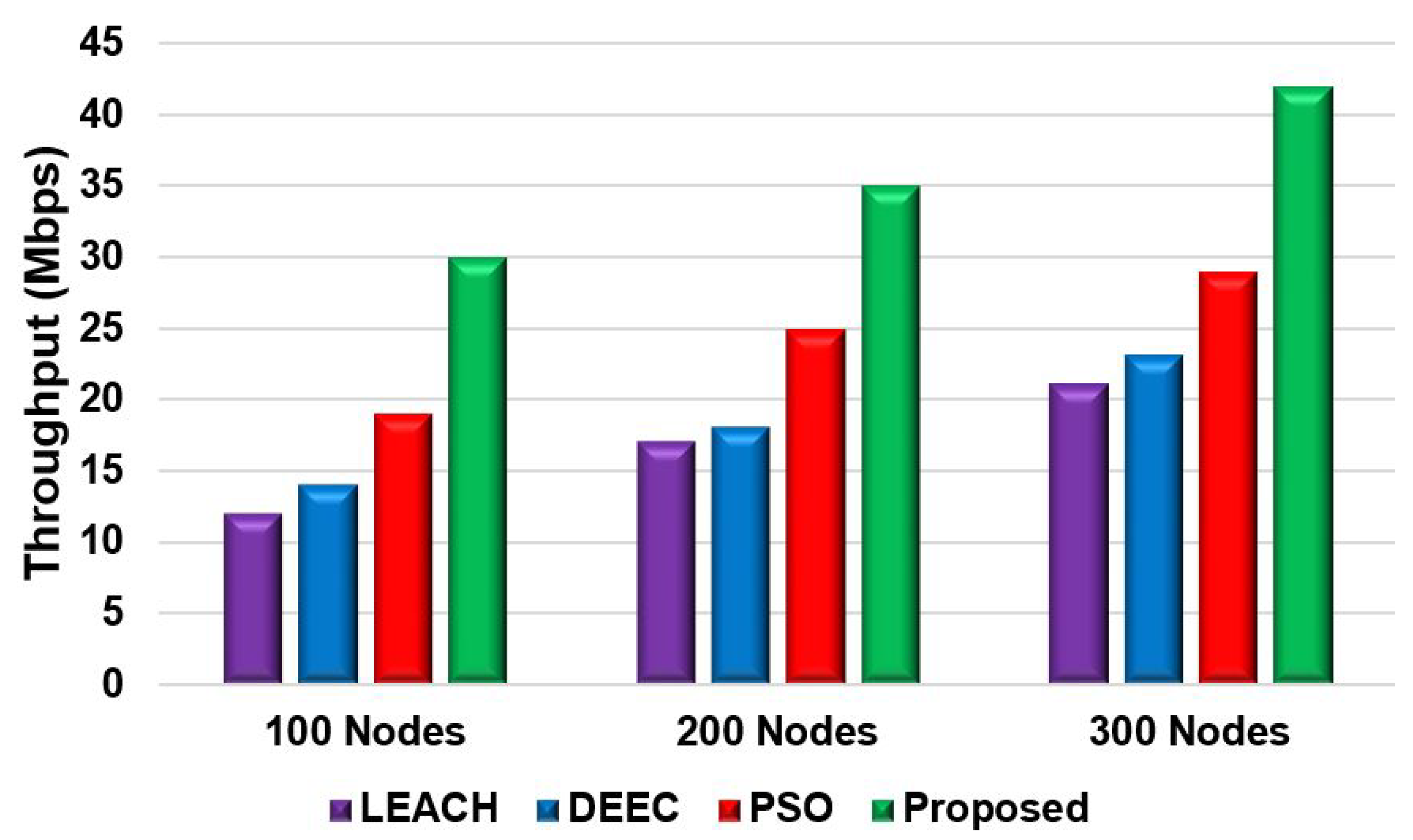
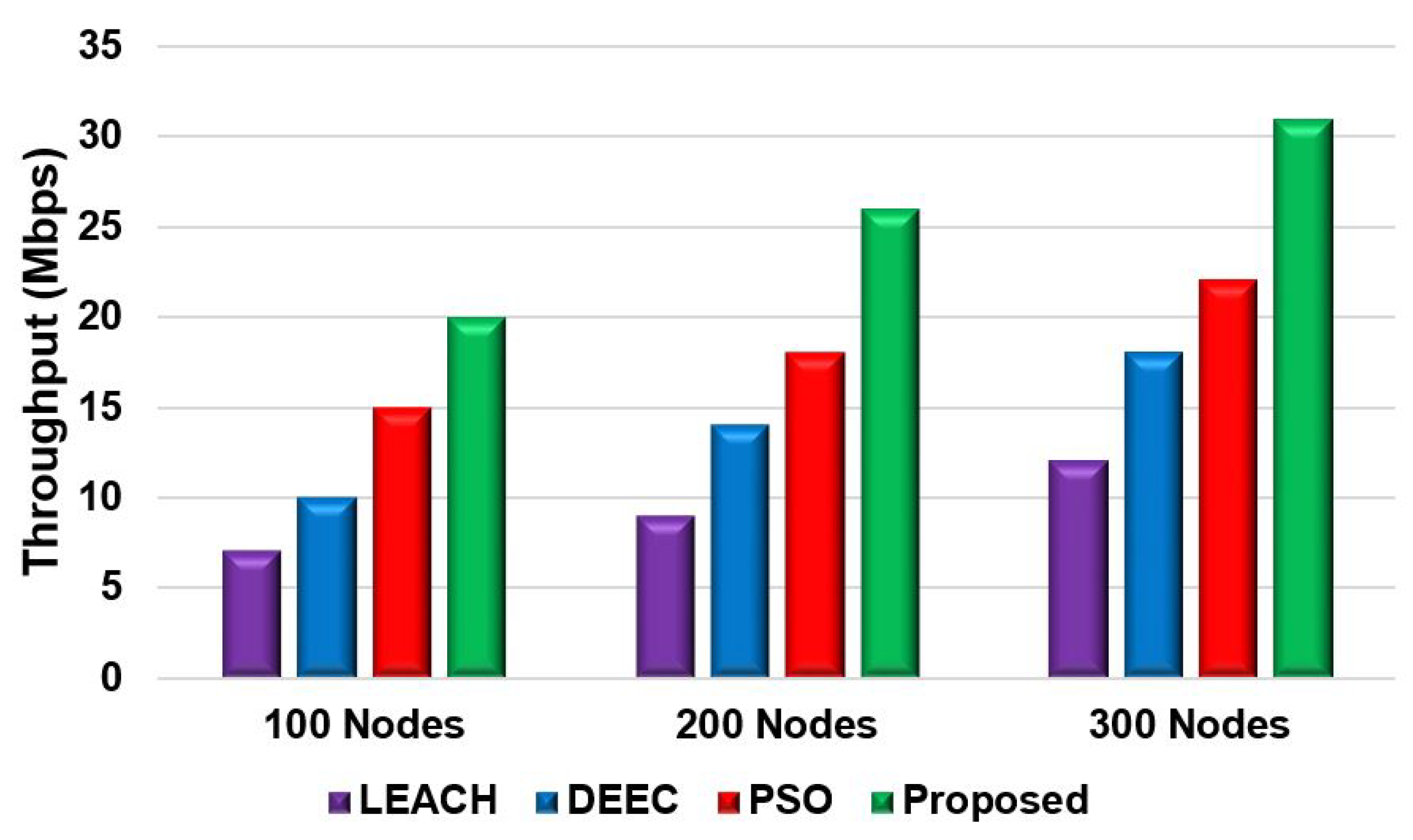
Figure 8 and Figure 9 show the network performance throughput for the proposed model and compare it with the LEACH, DEEC, and PSO for scenario 1 and scenario 2, respectively. The throughput was also measured by changing the different nodes. For both scenarios, the network throughput for the proposed model is significantly higher compared with the other protocol. The proposed model has a higher throughput from 10%-20% than the other models. The reason behind the proposed model fitness function is to use less energy consumption during data transmission to achieve a higher network throughput.
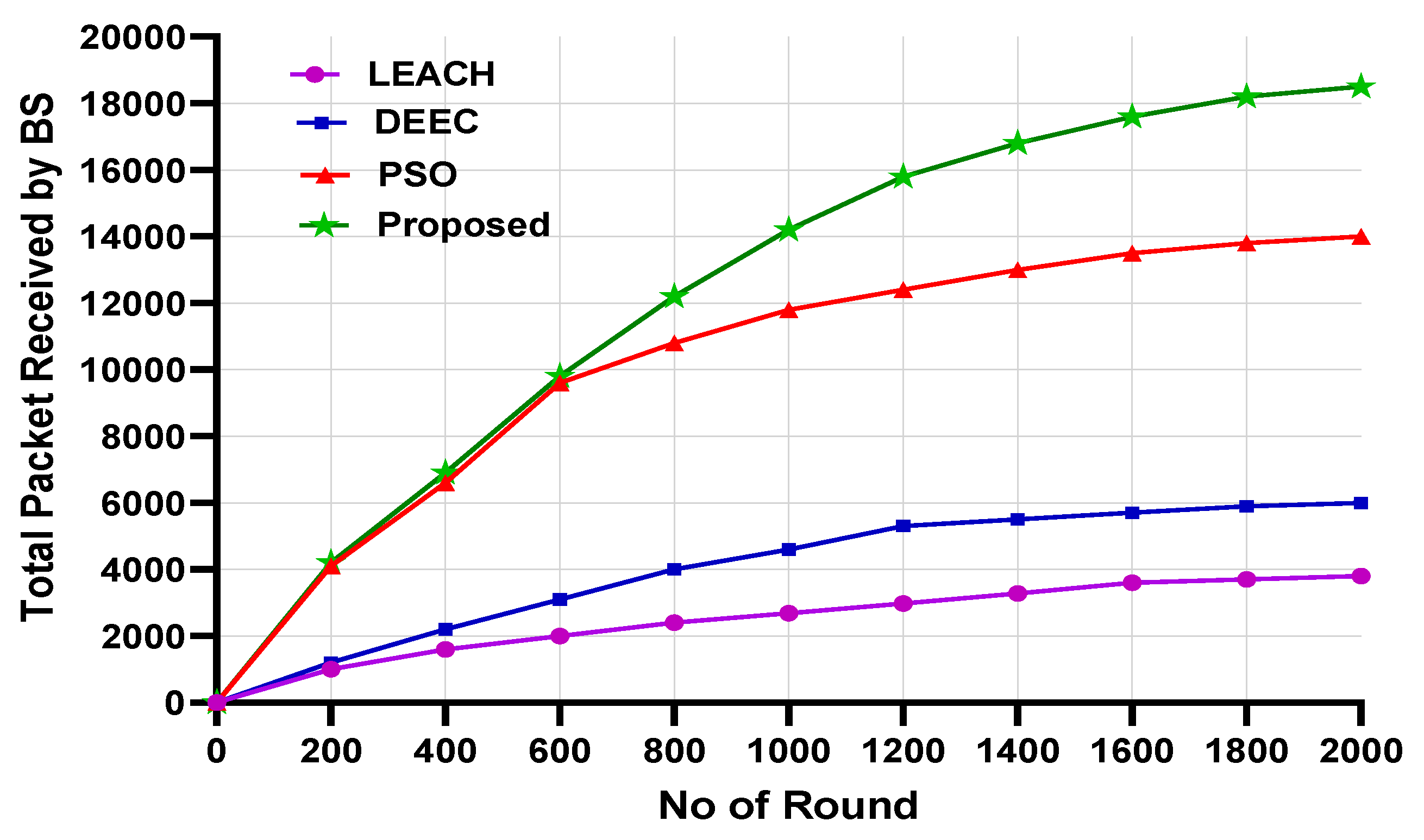
Figure 10 shows the total packet received by the BS. Scenario 2 considered 200 nodes for this evaluation. More than 18000 packets were received by the BS for the proposed model. However, the LEACH and DEEC could not send enough packets compared with the PSO. The proposed model sends more than 12000 packets to compare with the LEACH and DEEC, and 4000 packets higher than PSO. The reason behind that is that the proposed model fitness function preserves the residual energy for the nodes, which increases the nodes ’ lifetime. This will help to enhance the network lifetime and also increase the number of packets that are transmitted to the BS.
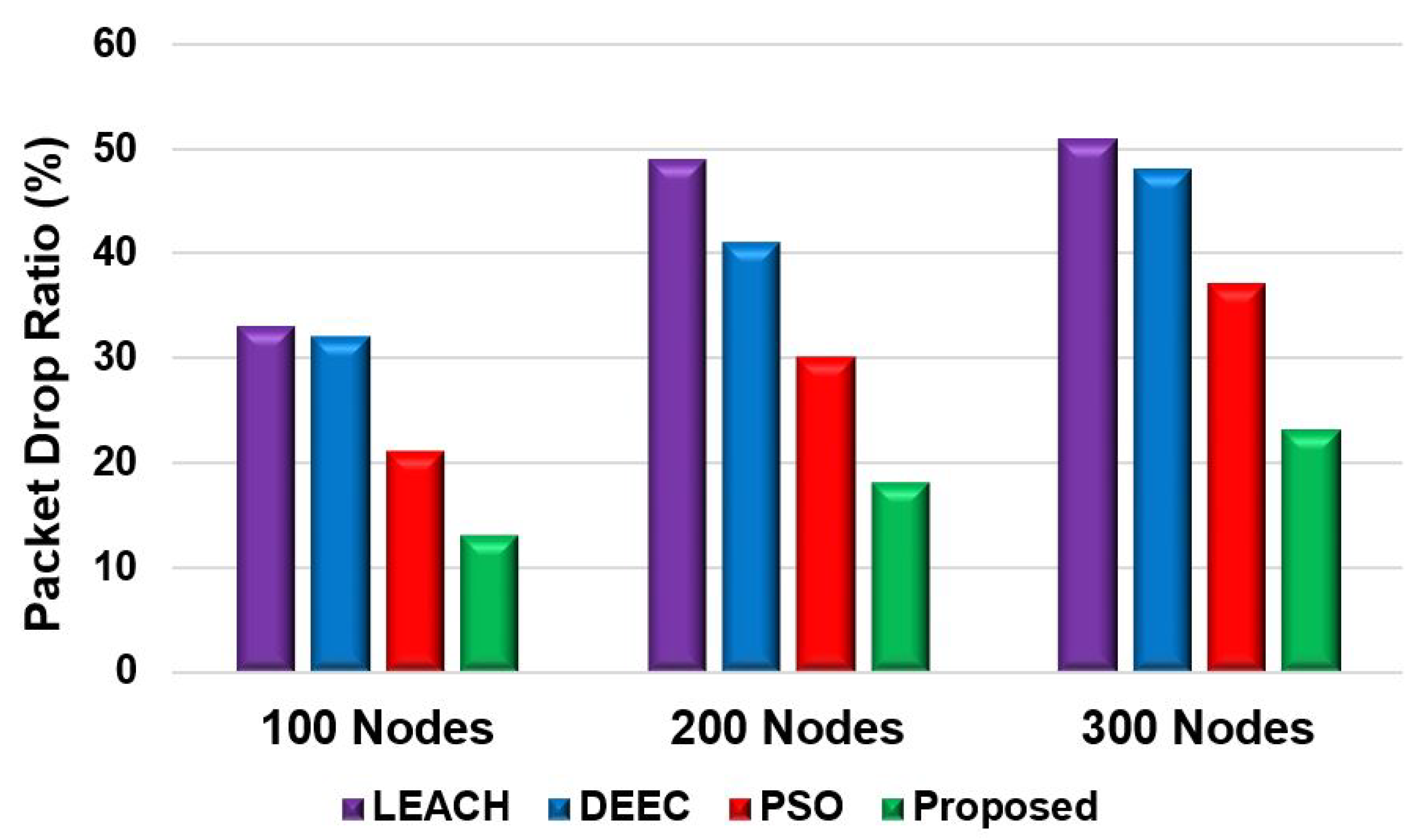
Figure 11 shows the packet drop ratio for scenario 2 with the different nodes. The proposed model achieved a lower packet drop ratio compared with the other models. LEACH and DEEC have significantly higher packet drop ratios for the different node numbers than the proposed model. The packet drop ratio in the proposed model increased by approximately 5% with the increase of 100 nodes. The proposed fitness function helps to minimise the drop of the data transfer as the model selects the energy-efficient shortage path to send the data. However, the PSO model achieves less percentage of drop ratio because of the routing efficiency. Nevertheless, due to the inefficient selection of CH and routing path, LEACH and DEEC have higher packet drop ratios.
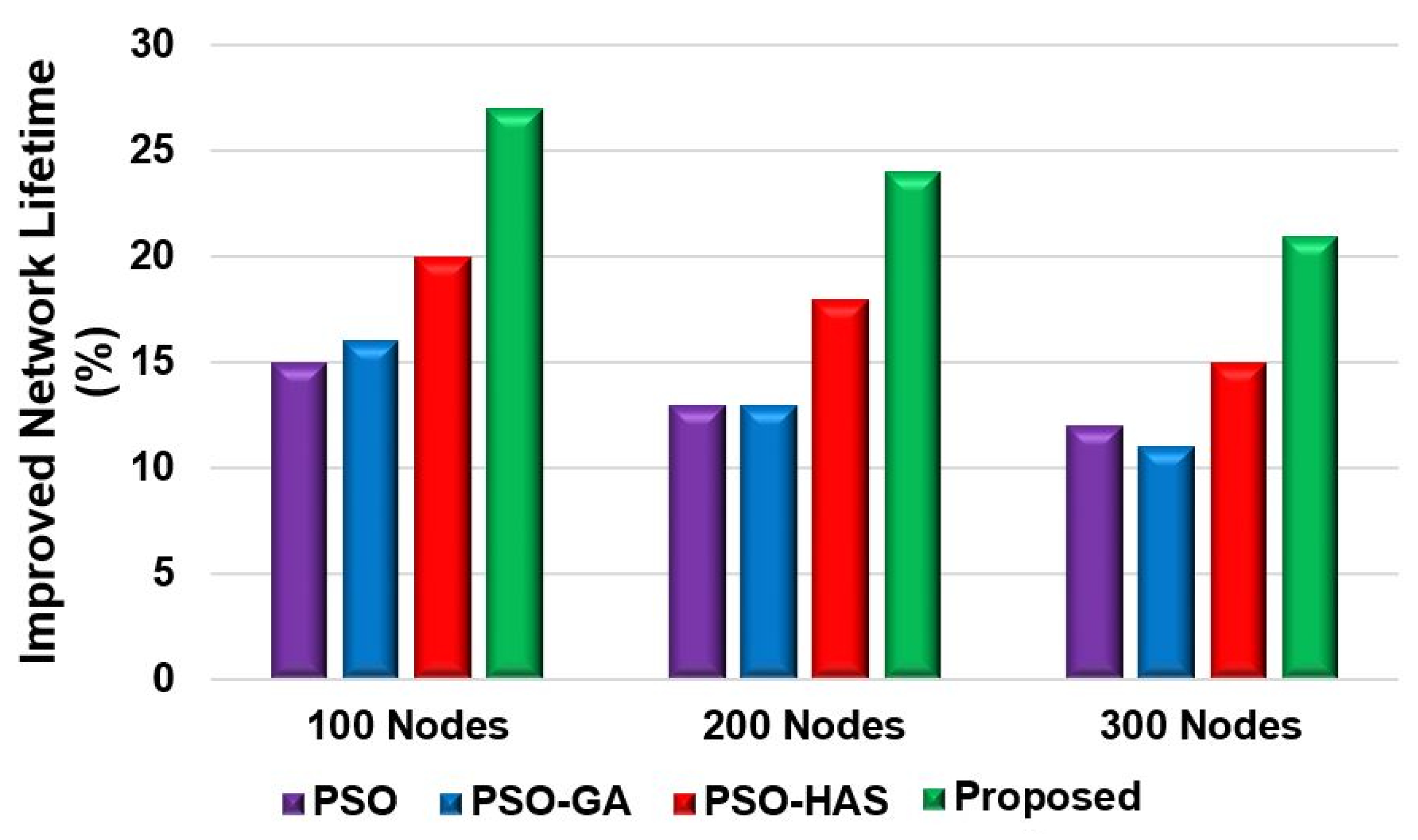
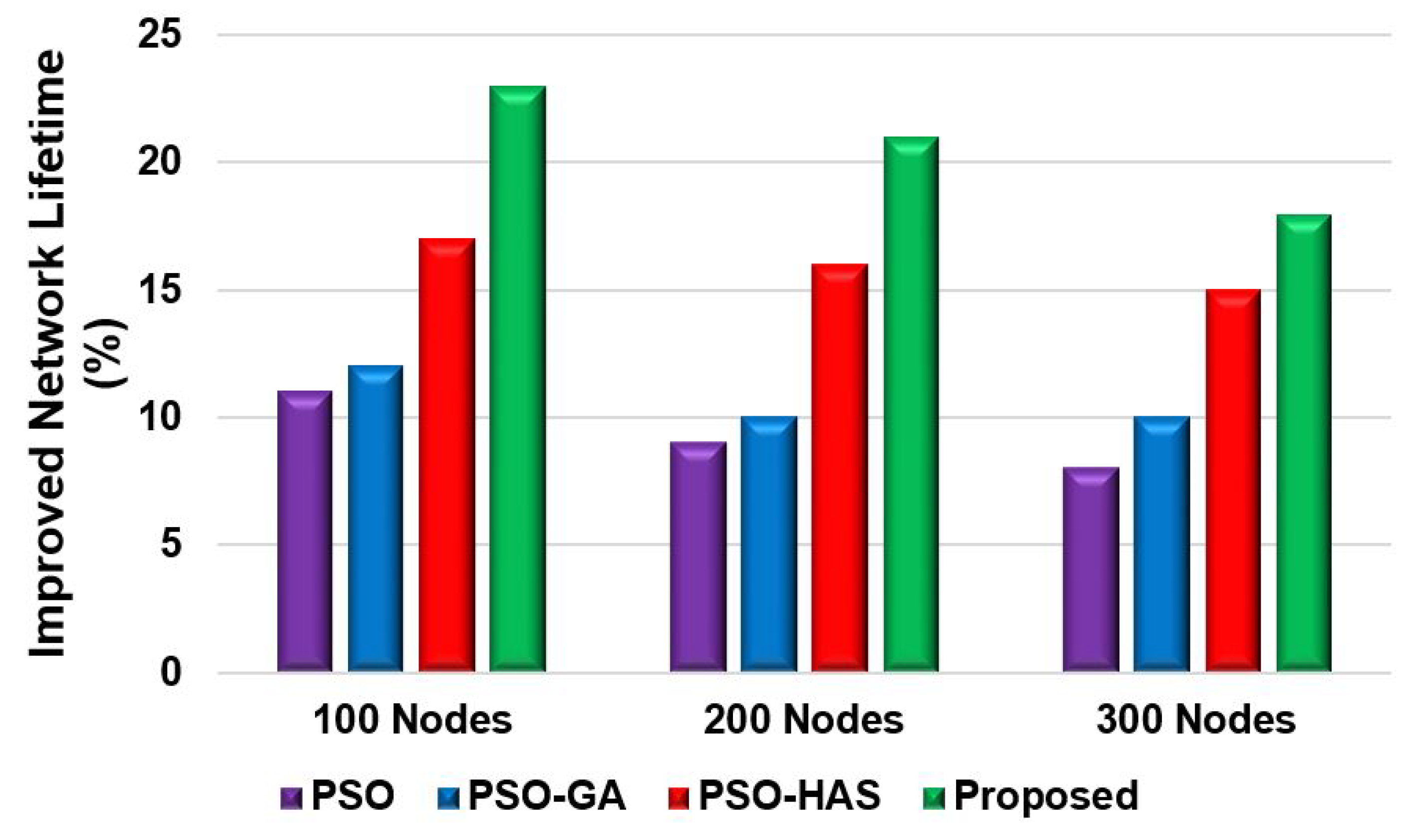
Figure 12 and Figure 13 show the percentage of improvement of the network lifetime of the proposed model for scenario 1 and scenario 2, respectively. The proposed model also compares with the state-of-the-art PSO and Hybrid models. The proposed model has significantly improved the network lifetime and increased from 27%,24%, and 21% for scenario-1 for the 100 nodes, 200 nodes, and 300 nodes, respectively. Scenario 2 (Figure 13) shows the proposed model increased by 23%, 21%, and 17% for the 100,200 and 300 nodes. The proposed model achieved a higher network lifetime compared with the other state of art models, the network lifetime increases by approximately 10%. The reason is due to the significant CH selection process, preventing energy consumption of the node during packet transmission, and finding the optimised route for the packet delivery.

7. Conclusions and Future Direction

This paper proposes a bio-inspired optimisation algorithm model for selecting the energy-efficient cluster head and optimal routing protocol. The proposed model targets increasing the network lifetime and reducing energy consumption, vital parameters for the IoT network in a disaster. For selection, the CH and routing algorithm’s effective fitness functions are used, ensuring the model’s performance enhancement. The analysis assumes a different situation by placing the BS in a different location. The proposed model is compared and evaluated with the benchmark models that use CH-based routing protocol for the IoT network. The performance matrix considers residual energy, network throughput, packet delivery, and network lifetime to evaluate the proposed model. The experimental result evaluates that the proposed model significantly enhanced the residual energy and network throughput and increased network lifetime by 10%-20% compared with the LEACH, DEEC, PSO, and hybrid PSO.
In the future, a more comprehensive scenario needs to be considered to extend the simulation models. It is also required to validate the proposed model with the broader range of the bio-inspired proposed models.

References

  1. statista. Available online: https://www.statista.com/statistics/510952/number-of-deaths-from-natural-disasters-globally/ (accessed on 26 January 2023).
  2. Dhanvijay, M.M.; Patil, S.C. Internet of Things: A survey of enabling technologies in healthcare and its applications. Comput. Netw. 2019, 153, 113–131. [Google Scholar] [CrossRef]
  3. A.A. Mutlag, M.K.A. Ghani, N.A. Arunkumar, M.A. Mohammed, O. Mohd, Enabling technologies for fog computing in healthcare IoT systems, Future Gener. Comput. Syst. 90 (2019) 62–78.
  4. T. M. Behera, S. K. Mohapatra, U. C. Samal, M. S. Khan, M. Daneshmand and A. H. Gandomi, "I-SEP: An Improved Routing Protocol for Heterogeneous WSN for IoT-Based Environmental Monitoring," in IEEE Internet of Things Journal, vol. 7, no. 1, pp. 710-717, Jan. 2020. [CrossRef]
  5. R. Yarinezhad, S.N. Hashemi, Distributed faulty node detection and recovery scheme for wireless sensor networks using cellular learning automata, Wirel. Netw. 25 (5) (2019) 2901–2917.
  6. Ohbayashi R, Nakajima Y, Nishikado H, Takayama S (2005) Monitoring system for landslide disaster by wireless sensing node network. Joint Intl IMEKO TC1 & TC7 Symposium, pp 1645–1651.
  7. Bond J, Kim D, Chrzanowski A, Szostak-Chrzanowski A (2007) Development of a fully automated, gps based monitoring system for disaster prevention and emergency preparedness: Ppms+rt. Sensors 7(7):1028–1046.
  8. Balis B, Kasztelnik M, Bubak M, Bartynski T, Gubala T, Nowakowski P, Broekhuijsen J (2011) The urbanflood common information space for early warning systems.ProcediaComputSci4(0):96–105.
  9. Kansala K, Korkalainen M, Mayra A (2011) A versatile sensor network for urban search and rescue operations. In: Proceedings of the conference on unmanned/unattended sensors and sensor networks VIII, pp 81, 840H–81, 840H–10.
  10. Shah, I. K., Maity, T., & Dohare, Y. S. (2020). Algorithm for energy consumption minimisation in wireless sensor network. IET Communications 2020, 14, 1301–1310.
  11. P.S. Mann, S. Singh, Improved metaheuristic based energy-efficient clustering protocol for wireless sensor networks. Eng. Appl. Artif. Intell. 2017, 57, 57–152.
  12. Guleria, K.; Verma, A.K. Comprehensive review for energy efficient hierarchical routing protocols on wireless sensor networks. Wirel. Netw. 2019, 25, 1159–1183. [Google Scholar] [CrossRef]
  13. Dorigo, M. , Birattari M., Stutzle T. Ant colony optimization IEEE Comput. Intell. Mag., 1 (4) (2006), pp. 28-39, 10.1109/MCI.2006.329691.
  14. Yang, X.S. , He X. Firefly algorithm: recent advances and applications Int. J. Swarm Intell., 1 (1) (2013), p. 36, 10.1504/IJSI.2013.055801.
  15. Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization, Technical report-tr06 Erciyes University, Engineering Faculty, Computer Engineering Department. 2005. [Google Scholar]
  16. Havens, T.C. , Spain C.J., Salmon N.G., Keller J.M. Roach infestation optimization 2008 IEEE Swarm Intelligence Symposium, IEEE (2008), pp. 1-7, 10.1109/SIS.2008.4668317.
  17. Yang, X.S. , Deb S. Engineering optimisation by cuckoo search Int. J. Math. Model. Numer. Opt., 1 (4) (2010), p. 330, 10.1504/IJMMNO.2010.035430.
  18. Rani, B. , Kumar C.A. Multi-Objective Swarm Intelligence Studies in Computational Intelligence, Springer Berlin Heidelberg, Berlin, Heidelberg (2015), pp. 1-25, 10.1007/978-3-662-46309-3.
  19. Kennedy, J. Swarm intelligence Handbook of Nature-Inspired and Innovative Computing, Kluwer Academic Publishers, Boston (2001), pp. 187-219, 10.1007/0-387-27705-6˙6.
  20. Duan, H. , Qiao P. Pigeon-inspired optimization: A new swarm intelligence optimizer for air robot path planning Int. J. Intell. Comput. Cybern., 7 (1) (2014), pp. 24-37, 10.1108/IJICC-02-2014-0005.
  21. Yang, X.-S. A new metaheuristic bat-inspired algorithm Studies in Computational Intelligence, vol. 284 (2010), pp. 65-74, 10.1007/978-3-642-12538-6˙6.
  22. Wang, B. , Jin X., Cheng B. Lion pride optimizer: An optimization algorithm inspired by lion pride behavior Sci. China Inf. Sci., 55 (10) (2012), pp. 2369-2389, 10.1007/s11432-012-4548-0.
  23. S. Arora, S. Singh, Butterfly optimization algorithm: a novel approach for global optimization,Softcomput. 2019; 23, 715–734.
  24. Yazdani, M. , Jolai F. Lion optimization algorithm (LOA): A nature-inspired metaheuristic algorithm J. Comput. Des. Eng., 3 (1) (2016), pp. 24-36, 10.1016/j.jcde.2015.06.
  25. Said, O. Analysis, design and simulation of internet of things routing algorithm based on ant colony optimization Int. J. Commun. Syst., 30 (8) (2016), 10.1002/dac.3174.
  26. Mahalaxmi, G. , Rajakumari K.E. Multi-agent technology to improve the Internet of Things routing algorithm using ant colony optimization Indian J. Sci. Technol., 10 (31) (2017), pp. 1-8, 10.17485/ijst/2017/v10i31/112338.
  27. S. Kaur, R. Mahajan Hybrid meta-heuristic optimization based energy efficient protocol for wireless sensor networks Egypt. Inf. J., 19 (3) (2018), pp. 145-150.
  28. P. Lalwani, S. Das, H. Banka, C. Kumar, CRHS: clustering and routing in wireless sensor networks using harmony search algorithm, Neural Computing and Applications 30 (2) (2018) 639–659.
  29. Shankar, T.; Shanmugavel, S.; Rajesh, A. Hybrid HSA and PSO algorithm for energy efficient cluster head selection in wireless sensor networks. Swarm Evol. Comput. 2016, 30, 1–10. [Google Scholar] [CrossRef]
  30. S.K. Gupta, P.K. Jana, Energy efficient clustering and routing algorithms for wireless sensor networks: GA based approach, Wirel. Pers. Commun. 83 (3) (2015) 2403–2423.
  31. Wang, Z., Ding, H., Li, B., Bao, L., & Yang, Z. (2020). An energy efficient routing protocol based on improved artificial bee colony algorithm for wireless sensor networks. IEEE Access, 8, 133577–133596.
  32. Wang, Z. , Ding, H., Li, B. et al. Energy Efficient Cluster Based Routing Protocol for WSN Using Firefly Algorithm and Ant Colony Optimization. Wireless Pers Commun 125, 2167–2200 (2022). [CrossRef]
  33. P. Lalwani, H. Banka, C. Kumar, BERA: a biogeography-based energy saving routing architecture for wireless sensor networks, Soft comput. 22 (5) (2018) 1651–1667.
  34. G.P. Gupta, S. Jha, Integrated clustering and routing protocol for wireless sensor networks using Cuckoo and harmony search based metaheuristic techniques, Eng. Appl. Artif. Intell. 68 (2018) 101–109.
  35. F. Gao, W. Luo, X. Ma, Energy constrained clustering routing method based on particle swarm optimization, Cluster Comput. 22 (3) (2019) 7629–7635.
  36. Biabani, M.; Fotouhi, H.; Yazdani, N. An Energy-Efficient Evolutionary Clustering Technique for Disaster Management in IoT Networks. Sensors 2020, 20, 2647. [Google Scholar] [CrossRef] [PubMed]
  37. Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; p. 10. [Google Scholar]
  38. M. Tubishat, M. Alswaitti, S. Mirjalili, M. A. Al-Garadi, M. T. Alrashdan and T. A. Rana, "Dynamic Butterfly Optimization Algorithm for Feature Selection," in IEEE Access, vol. 8, pp. 194303-194314, 2020. [CrossRef]
  39. A. S. Raghuvanshi, S. Tiwari, R. Tripathi and N. Kishor, "Optimal number of clusters in wireless sensor networks: An FCM approach," 2010 International Conference on Computer and Communication Technology (ICCCT), Allahabad, India, 2010, pp. 817-823. [CrossRef]
  40. Elhabyan, R.S.; Yagoub, M.C. Two-tier particle swarm optimization protocol for clustering and routing in wireless sensor network. J. Netw. Comput. Appl. 2015, 52, 116–128. [Google Scholar] [CrossRef]
  41. Heinzelman, W.R.; Chandrakasan, A.; Balakrishnan, H. Energy-efficient communication protocol for wireless microsensor networks. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; p. 10. [Google Scholar]
  42. Li Qing, Qingxin Zhu, Mingwen Wang,Design of a distributed energy-efficient clustering algorithm for heterogeneous wireless sensor networks, Computer Communications, Volume 29, Issue 12,2006, Pages 2230-2237,ISSN 0140-3664. [CrossRef]
  43. H. Qabouche, A. Sahel, A. Badri and I. El Mourabit, "Energy Efficient PSO-based routing protocol for large WSN," 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 2022, pp. 1-7. [CrossRef]
  44. Zhou, Y. , Wang, N., & Xiang, W. (2017). Clustering hierarchy protocol in wireless sensor networks using an improved PSO algorithm. IEEE Access, 5, 2241–2253.
  45. Elhabyan, R.S.; Yagoub, M.C. Two-tier particle swarm optimization protocol for clustering and routing in wireless sensor network. J. Netw. Comput. Appl. 2015, 52, 116–128. [Google Scholar] [CrossRef]
  46. A. Agnihotri and I. K. Gupta, "A hybrid PSO-GA algorithm for routing in wireless sensor network," 2018 4th International Conference on Recent Advances in Information Technology (RAIT), Dhanbad, India, 2018, pp. 1-6. [CrossRef]
Preprints 111102 g001
Figure 1. Different types of disaster applications for the pre and post-disaster.
Figure 1. Different types of disaster applications for the pre and post-disaster.
Preprints 111102 g001
Preprints 111102 g002
Figure 2. Cluster based sensors in WSN.
Figure 2. Cluster based sensors in WSN.
Preprints 111102 g002
Preprints 111102 g003
Figure 3. First order radio energy model.
Figure 3. First order radio energy model.
Preprints 111102 g003
Preprints 111102 g004
Figure 4. WSN topology for the 5 cluster head and one BS.
Figure 4. WSN topology for the 5 cluster head and one BS.
Preprints 111102 g004
Preprints 111102 g005
Figure 5. Optimisation path for the IoT network.
Figure 5. Optimisation path for the IoT network.
Preprints 111102 g005
Preprints 111102 g006
Figure 6. Residual Energy for the scenario-1.
Figure 6. Residual Energy for the scenario-1.
Preprints 111102 g006
Preprints 111102 g007
Figure 7. Residual Energy for the scenario-2.
Figure 7. Residual Energy for the scenario-2.
Preprints 111102 g007
Preprints 111102 g008
Figure 8. Throughput comparison of different nodes for the scenario-1.
Figure 8. Throughput comparison of different nodes for the scenario-1.
Preprints 111102 g008
Preprints 111102 g009
Figure 9. Throughput comparison of different nodes for scenario-2.
Figure 9. Throughput comparison of different nodes for scenario-2.
Preprints 111102 g009
Preprints 111102 g010
Figure 10. Number of packets received by the BS.
Figure 10. Number of packets received by the BS.
Preprints 111102 g010
Preprints 111102 g011
Figure 11. Packet drop ratio for the different nodes in WSN.
Figure 11. Packet drop ratio for the different nodes in WSN.
Preprints 111102 g011
Preprints 111102 g012
Figure 12. Percentage of improved network lifetime for the scenario-1.
Figure 12. Percentage of improved network lifetime for the scenario-1.
Preprints 111102 g012
Preprints 111102 g013
Figure 13. Percentage of improved network lifetime for the scenario-2.
Figure 13. Percentage of improved network lifetime for the scenario-2.
Preprints 111102 g013
Table 1. Possible relay node of the CH.
Table 1. Possible relay node of the CH.
Cluster Head Relay Node No of Relay Node
CH1 { CH2,CH3,CH5 } 3
CH2 {CH3,CH4} 2
CH3 {CH4,CH5} 2
CH4 {CH6,CH7} 2
CH5 {CH6} 1
CH6 {BS} 1
CH7 {CH6,BS} 2
Table 2. Optimised relay path of the CH.
Table 2. Optimised relay path of the CH.
Cluster Head Relay Node No of Relay Node P ( i , d ) Relay Node
CH1 { CH2,CH3,CH5} 3 .65 CH5
CH2 {CH3,CH4} 2 .73 C4
CH3 {CH4,CH5} 2 .96 C5
CH4 {CH6,CH7} 2 .52 CH6
CH5 {CH6} 1 .87 CH6
CH6 {BS} 1 .29 BS
CH7 {CH6,BS} 2 .18 BS
Table 3. Possible relay node of the CH.
Table 3. Possible relay node of the CH.
Parameters Value
Initial Energy E o 0.5j
Transmission and Receive Energy ( E e l e c ) 50(nj/bit)
Multipath Fading ( E a m p ) 0.0013pj/bit/ m 4
Free space transmitter amplifier energy ( E f s ) 10 pj/bit/ m 2
Power exponent 0.1
Sensory modality 0.01
Particle Position ( X m i n , X m a x ) 0,200
particle Velocity ( V m i n , V m a x ) m/s 0,200
No of Round 2000
No of Iteration 5
Swarm Size 15
Accelartion Constant 2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated