Prerpints.org logo
Preprint
Article

SDF2Net: Shallow to Deep Feature Fusion Network for PolSAR Image Classification

Altmetrics

Downloads

115

Views

16

Comments

0

Submitted:

03 July 2024

Posted:

04 July 2024

You are already at the latest version

Alerts
Abstract
Polarimetric Synthetic Aperture Radar (PolSAR) images encompass valuable information that can facilitate extensive land cover interpretation and generate diverse output products. Extracting meaningful features from PolSAR data poses challenges distinct from those encountered in optical imagery. Deep Learning (DL) methods offer effective solutions for overcoming these challenges in PolSAR feature extraction. Convolutional Neural Networks (CNNs) play a crucial role in capturing PolSAR image characteristics by leveraging kernel capabilities to consider local information and the complex-valued nature of PolSAR data. In this study, a novel three-branch fusion of complex-valued CNN named Shallow to Deep Feature Fusion Network (SDF2Net) is proposed for PolSAR image classification. To validate the performance of the proposed method, classification results are compared against multiple state-of-the-art approaches using the Airborne Synthetic Aperture Radar (AIRSAR) datasets of Flevoland, San Francisco, and ESAR Oberpfaffenhofen dataset. The results indicate that the proposed approach demonstrates improvements in OA, with 1.3% and 0.8% enhancement for the AIRSAR datasets and 0.5% improvement for the ESAR dataset. The analyses conducted on the Flevoland data underscore the effectiveness of the SDF2Net model, revealing a promising OA of 96.01% even with only 1% sampling ratio.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Polarimetric Synthetic Aperture Radar (PolSAR) images offer a specialized perspective in microwave remote sensing by capturing the polarization properties of radar waves, which provides detailed insights into Earth’s surface features, such as vegetation [1], water bodies [2], and man-made structures [3]. PolSAR images tackle the limitations of optical remote sensing images, which are susceptible to changes in illumination and weather conditions. Unlike optical systems, PolSAR is capable of functioning under all weather conditions and possesses a robust penetrating capability [4]. Moreover, PolSAR outperforms conventional SAR systems by comprehensively capturing extensive scattering information through four different modes. This enables the extraction of a wide range of target details, including scattering echo amplitude, phase, frequency characteristics, and polarization attributes [5]. Nowadays, PolSAR imagery has numerous applications in environmental monitoring [6], disaster management [7], military monitoring [8,9], crop prediction [10,11], and land cover classification [12].
PolSAR image classification is the task of classifying pixels into specific terrain categories. It involves analyzing the polarization properties of radar waves reflected from the Earth’s surface. This classification helps automate the identification and mapping of land cover for many applications. Conventional approaches to PolSAR image classification primarily rely on extracting distinctive features through the application of target decomposition theory [13]. The Krogager decomposition model, for instance, segregates the scattering matrix into three components, corresponding to helix, diplane, and sphere scattering mechanisms [14]. Another widely used method, the Freeman decomposition [15], dissects the polarimetric covariance matrix into double-bounce, surface, and canopy scattering components. Building upon the Freeman decomposition, [16] introduced a fourth scattering component, helix scattering power, which proves more advantageous in the classification of PolSAR images. Additionally, the Cloude decomposition [17] stands as a common algorithm for PolSAR image analysis. Despite the popularity of traditional classifiers like Support Vector Machine (SVM) [18] and decision trees [19] for PolSAR classification, challenges arise when dealing with PolSAR targets characterized by complex imaging mechanisms. This complexity often leads to inadequacies in representing these targets using conventional features, resulting in diminished classification accuracy.
Recently, Deep Learning (DL) technology has shown remarkable effectiveness in PolSAR image classification [20,21]. Specifically, Convolutional Neural Networks (CNNs) have exhibited impressive performance in this domain [4,22]. Chen et al. [23] successfully harnessed the roll-invariant features of PolSAR targets and the concealed attributes within the rotation domain to train a deep CNN model. This approach contributes to an enhanced classification performance. Zhou et al. [22] derived high-level features from the coherency matrix using a deep neural network comprising two convolutional and two fully connected layers, specifically tailored for the analysis of PolSAR images. Radman et al. [24] discussed the fusion of mini Graph Convolutional Network (miniGCN) and CNN for PolSAR image analysis. Spatial features from Pauli RGB and Yamaguchi were fed into CNN, and polarimetric features were utilized in miniGCN. The study aims to address the limitations of traditional PolSAR image classification methods and presents a dual-branch architecture using miniGCN and CNN models. Dong et al. [25] introduced two lightweight 3D-CNN architectures for fast PolSAR interpretation during testing. It applies two lightweight 3D convolution operations and global average pooling to reduce redundancy and computational complexity. The focus is on improving the fully connected layer, which occupies over 90% of model parameters in CNNs. The proposed architectures use spatial global average pooling to address the computational difficulties and over-fitting risks associated with a large number of parameters.
Phase information, a unique trait to SAR imagery, plays a vital role in various applications like object classification and recognition. Several research studies have explored the application of Complex-valued CNNs (CV-CNNs) for PolSAR data classification Owing to the difficulties encountered in this domain [26,27,28]. Unlike traditional CNNs, CV-CNNs handle complex-valued input data using complex-valued filters and activation functions, enabling effective capture of both phase and amplitude information. This capability is crucial for accurate PolSAR data classification.
Training CNNs usually demands a substantial volume of data, and acquiring an ample amount of high-quality ground reference data can be both costly and intricate. The scarcity of training samples often results in the generation of unreliable parameters and the risk of overfitting. Hence, it becomes crucial to attain high classification performance with a limited set of training data.
Shallow networks excel at capturing simple features but struggle when confronted with more intricate ones. On the contrary, deep neural network structures excel at extracting complex features. The integration of information from various depths in a network facilitates efficient learning, even when working with a small number of training samples. This combination greatly improves the network’s ability to unravel the complex details of the dataset.
In recent years, attention-based techniques have also been widely employed in PolSAR image classification to enhance the model’s ability to emphasize informative features and suppress less relevant ones by allocating more attention to the most important features rather than treating the entire input uniformly, which in turn improve the classification performance [29].
The main contributions of this paper are demonstrated as follows:
  • A proposed novel model called Shallow to Deep Feature Fusion Network (SDF2Net), which incorporates feature extraction at various depths to enhance the classification performance of PolSAR images effectively.
  • A feature-learning network with multiple depths and varying layers in each stream is developed. This design enables filters to simultaneously capture shallow, medium, and deep properties, enhancing the utilization of complex information in PolSAR. Experimental results indicate that the proposed model exhibits superior feature-learning capabilities compared to existing models in use.
  • The model we propose surpasses current methods not only when dealing with a limited number of samples but also attains higher accuracy with an ample training dataset. This conclusion is drawn from statistical outcomes obtained through thorough trials on three PolSAR datasets, which will be further elaborated and discussed in the subsequent sections.
The article’s structure is outlined as follows: Section 2 provides an introduction to the related work, Section 3 provides a detailed presentation of the proposed network SDF2Net, Section 4 reports the experimental results and analysis on three PolSAR datasets. The article concludes with a summary of conclusions and an outlook on future work in Section 5.

2. Related Work

This section offers a concise examination of the relevant literature on CNNs and Attention mechanisms, with a particular focus on the squeeze and excitation module.

2.1. Overview CNNs

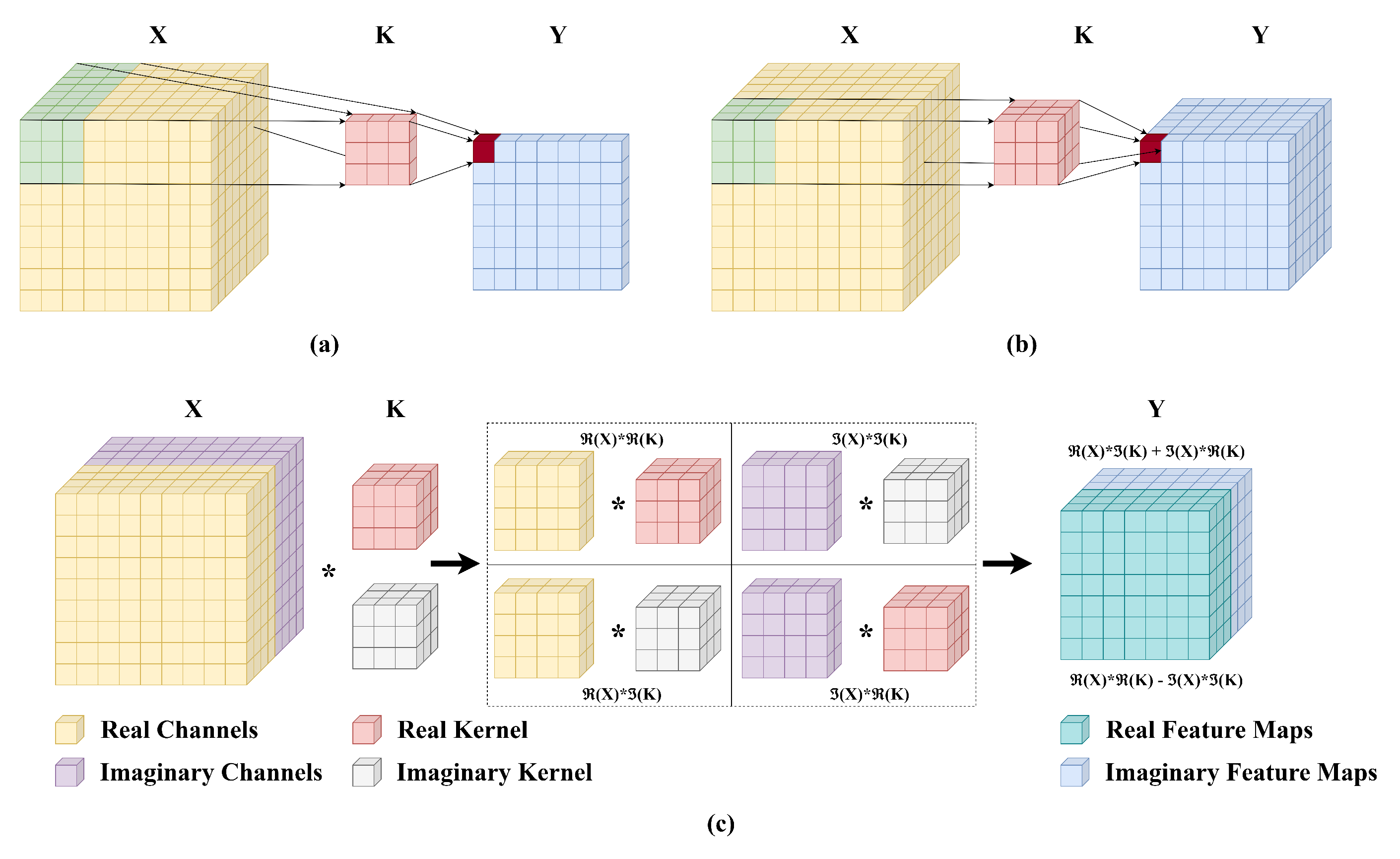
A standard CNN consists of an input layer, convolutional layers, activation layer, and an output layer. The initial input layer receives features from the image. Subsequently, convolutional layers employ convolutional kernels (illustrated in Figure 1) to extract the input features. These kernels operate by taking into account neighboring pixels, considering spatially correlated pixels within a close range (as depicted by the 3 × 3 grid in Figure 1(a)). This approach enhances the network’s capacity to capture spatially related features. However, 2D-CNNs process each band individually and fail to extract the polarimetric information provided by PolSAR images. To better process PolSAR images, researchers often turn to more advanced architectures, such as Three-dimensional CNNs (3D-CNNs).
The application of convolution operations can be expanded into three dimensions, wherein calculations are conducted across all channels concurrently instead of handling each channel separately. Figure 1(b) visually depicts the concept of 3D convolution. In 3D convolution, the process encompasses height, width, and channels, making it a suitable approach for incorporating channel context. For an image represented as X with dimensions N × N × B and a kernel denoted as K with dimensions M × M × C , the expression for 3D convolution at position ( x , y , z ) is given by Equation 1.
F ( x , y , z ) = ∑ i = 1 M ∑ j = 1 M ∑ k = 1 C K ( i , j , k ) X ( x + i , y + j , z + k ) + b
Although 3D-CNNs can capture features in a better fashion when compared to 2D-CNNs [30], the complex nature of PolSAR images, represented by complex-valued data, adds an extra layer of complexity when considering the use of 3D-CNNs for their processing. Compared to traditional CNNs, CV-CNNs have proven their superiority in PolSAR classification tasks. To fully explore the complex values in PolSAR data, we utilized CV-3D-CNN. For an image X = ℜ ( X ) + i ℑ ( X ) and a kernel k = ℜ ( K ) + i ℑ ( K ) , the result of the complex convolution Y can be expressed in Equation (2).
Y = X * K = ℜ ( X ) * ℜ ( K ) − ℑ ( X ) * ℑ ( K ) + i . ( ℜ ( X ) * ℑ ( K ) ) + i . ( ℑ ( X ) * ℜ ( K ) )
where ℜ ( . ) and ℑ ( . ) represent the real and the imaginary parts of a CV number, respectively, i is the imaginary number − 1 , and Y can be expressed as ℜ ( Y ) + i . ℑ ( Y ) . This is also illustrated in Figure 1(c).

2.2. Attention Mechanism

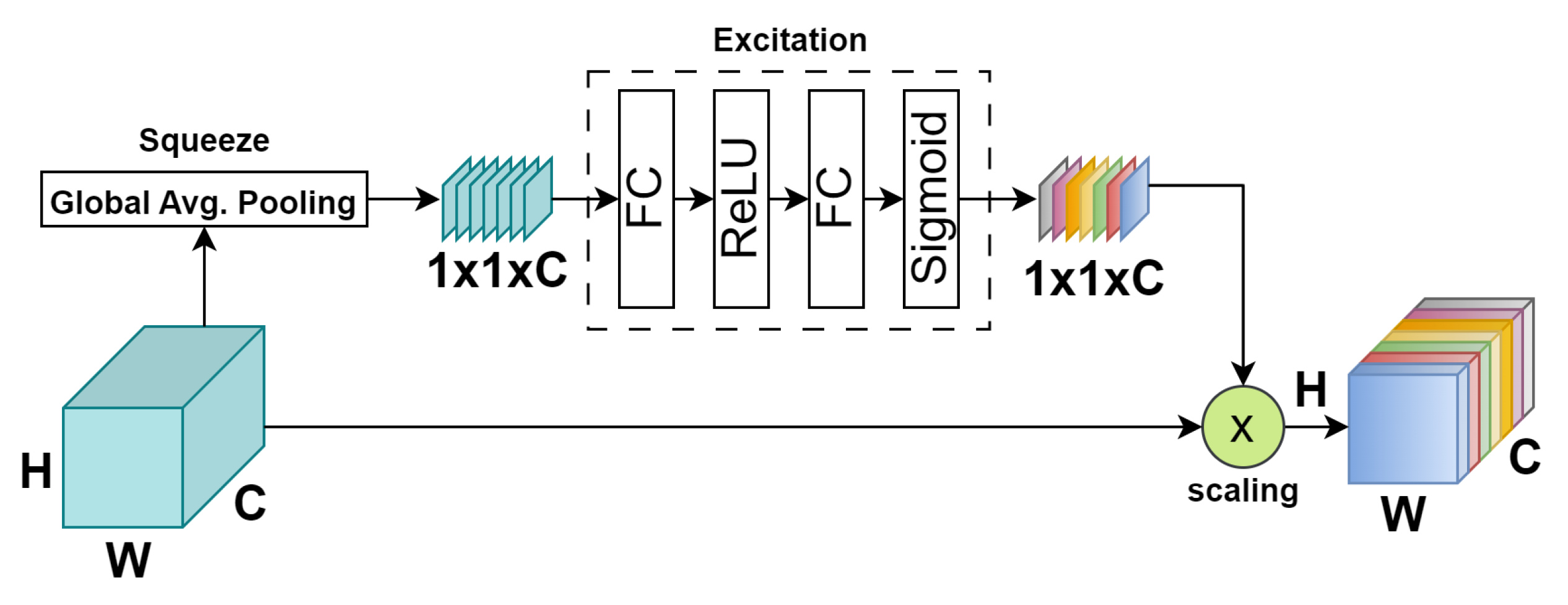
While CNNs have demonstrated promising outcomes in the classification of PolSAR images, there is limited research work regarding the enhancement of input identifiability when developing CNNs. To address this issue, the authors in [31] proposed the use of Squeeze-and-Excitation module (SE) [32] to enhance the performance of CNNs by selectively emphasizing crucial features in the input data. Also, SE improves channel interdependencies with almost no additional computational cost. Figure 2 shows the block diagram of SE.
In the SE process [34], given any transformation (e.g., convolution) F t r that maps the input X to feature maps u c , where u c ∈ R H × W × C , and u c represents the c-th H × W matrix in u, with the subscript c denoting the number of channels. In the Squeeze procedure F s q ( . ) , global average pooling is employed to transform the input of H × W × C into an output of 1 × 1 × C . The squeeze function is defined in Equation (3).
z c = F s q ( u c ) = 1 H × W ∑ i = 1 H ∑ j = 1 W u c ( i , j )
The equation reveals that the input data is transformed into a column vector during the squeeze process. The length of this vector corresponds to the number of channels. Subsequently, the excitation operation is conducted to autonomously discern the significance of each feature. This process amplifies features that exert a substantial influence on classification results while suppressing irrelevant features. The excitation function is expressed in Equation (4).
s = F e x ( z , W ) = σ ( g ( z , W ) ) = σ ( W 2 R e L U ( W 1 z ) ) ,
where σ represents the Sigmoid activation function, and W 1 ∈ R C r × C and W 2 ∈ R C × C r denote the two fully connected layers. Here, W 1 functions as the dimensionality reduction layer with a reduction ratio of r, while W 2 serves as the proportionally identical data-dimensionality increase layer. The variable z corresponds to the output from the preceding squeeze layer, and W 1 z signifies a fully connected layer operation. The Sigmoid function processes the final output of the excitation process, resulting in a value between zero and one. Following the squeeze and excitation steps, an attention vector s is obtained, which can be employed to adjust the channels of u.

3. Methodology

Within this section, a comprehensive description of the SDF2Net architecture is provided. Initially, the processing of polarimetric data from PolSAR images is showcased, followed by an exposition of the SDF2Net network architecture.

3.1. PolSAR Data Preprocessing

The construction of a polarimetric feature vector serves as a fundamental step in PolSAR imagery classification process. In PolSAR imagery, the description of each pixel is defined by a 2 × 2 complex scattering matrix, denoted as S, as given in Equation (5) [35].
S = S H H S H V S V H S V V ,
where S A B ( A , B ∈ H , V ) represents the backscattering coefficient of the polarized electromagnetic wave in emitting A direction and receiving B direction. H and V represent the horizontal and vertical polarization channels, respectively. In the context of the data acquired by a monostatic PolSAR radar system, the assumption S V H = S H V holds, indicating that the scattering matrix S is symmetric. This enables the simplification and reduction of the matrix to the polarization scattering vector k → . Employing the Pauli decomposition method, the expression for t k → can be represented as [5].
k → = 1 2 [ S H H + S V V , S H H − S V V , 2 S H V ] T .
In general, multi-look processing is essential for PolSAR data. Following the processing step, the obtained coherency matrix serves as the most commonly used representation for PolSAR data, as given in Equation (7) [5].
T = 1 n ∑ j = 1 n k j → k j → H = T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33 ,
where the operator ( . ) H stands for complex conjugate operation and n is the number of looks. It is worth mentioning that T is a Hermitian matrix with real-valued elements on the diagonal and complex-valued elements off-diagonal. As a result, the three real-valued and three complex-valued elements of the upper triangle of the coherency matrix (i.e. T 11 , T 12 , T 13 , T 22 , T 23 , T 33 ) are used as the input features of the models.
Data pre-processing is an essential step for achieving higher classification accuracy. Initially, the mean T ¯ and standard deviation T s t d of each channel are computed. Subsequently, normalization is applied to each channel, ensuring optimal data preparation for classification. By taking T 11 as an example, each channel will be normalized as in Equation (8).
T 11 = T 11 − T ¯ 11 T 11 s t d ,

3.2. Feature Extraction Using CV-3D-CNN

As explained in Section 2.1, CV-3D-CNNs are more suitable to process PolSAR data due to their complex nature. Each layer of CV-3D-CNN is followed by a ReLU activation function, and since the output features are complex, we propose the use of Complex Valued ReLu ( C ReLU(.)). It is obtained by applying the well-known ReLU(.) to both the real and imaginary parts separately, such that C ReLU(x) = ReLU(ℜ(x)) + i.ReLU(ℑ(x)).

3.3. Architecture of the Proposed SDF2Net

Currently, the predominant approach in PolSAR classification tasks involves the utilization of 2D-CNN architectures. While 2D-CNNs effectively capture spatial information, they fall short in exploiting the intricate interchannel dependencies inherent in PolSAR images. On the other hand, a 3D-CNN exhibits superior feature extraction capabilities when compared to 2D-CNN architecture [30].
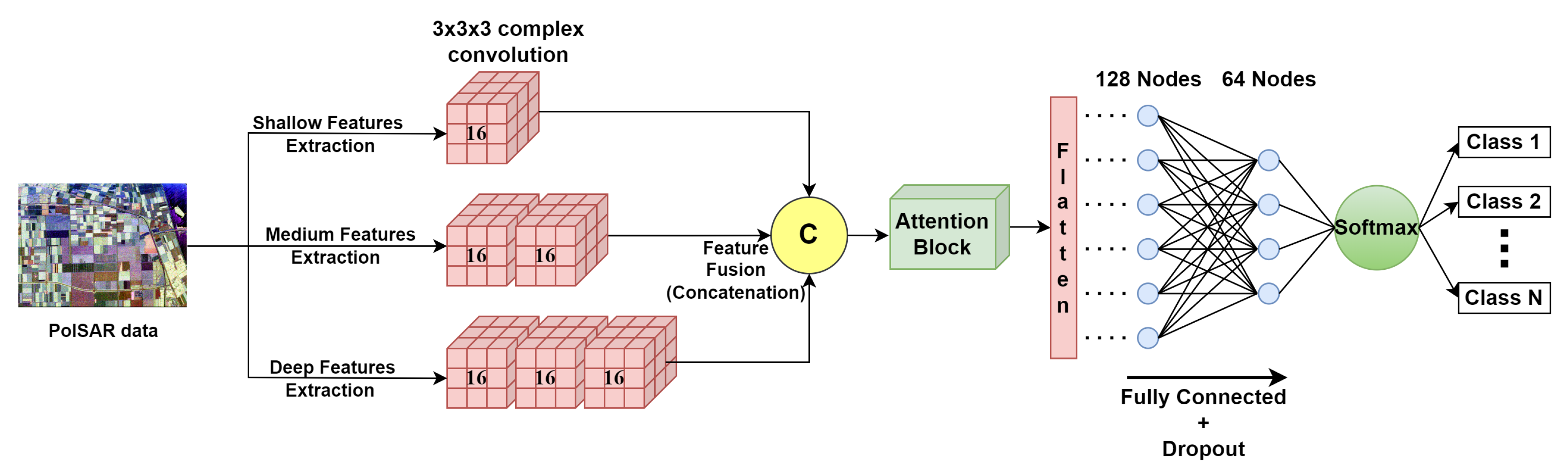
Figure 3 shows the comprehensive framework of the complete process of the proposed methodology. The model processes the data through a three-branch network, extracting features at different levels (shallow, medium, and deep), which are later concatenated. The concatenated features then pass through the Attention block to enhance the channel dependencies. The flattening layer is employed to transform the concatenated features into a one-dimensional vector. For the final classification, two fully-connected layers are employed, incorporating dropout to mitigate overfitting and a softmax layer for generating the final prediction. The detailed distribution of parameters of each layer is shown in Figure 3. The first branch incorporates a single layer of complex CV-3D-CNN with 16 filters, employing a 3×3×3 kernel size to capture shallow features. In contrast, the second branch focuses on medium features with two CV-3D-CNN layers, each maintaining a 3×3×3 kernel size. Meanwhile, the third branch is tailored to extract deep features through the utilization of three layers of CV-3D-CNN, employing 16 filters at each layer, and configuring the kernel size of each filter as 3×3×3. Due to the information loss caused by the pooling layer, it has not been utilized in this network architecture.

3.4. Loss Function

The training of the proposed SDF2Net involves the computation of Cross-entropy (CE) loss on the training samples. A softmax classifier is utilized to produce the predicted probability matrix for the samples, as shown in Equation (9).
y ^ l m = S o f t m a x ( | x o u t | ) ,
where x o u t is the output of the last fully connected layer, and | . | is the magnitude operator. It is worth noting that x o u t is complex, while the value of | x o u t | = ( ℜ ( x o u t ) ) 2 + ( ℑ ( x o u t ) ) 2 is real, and hence the value of y ^ l m will also be real. Subsequently, the presentation of the loss L o s s C E is depicted as given in Equation (10).
L o s s C E = − ∑ m = 1 M ∑ l = 1 L y l m log ( y ^ l m ) ,
where y l m and y ^ l m are the reference and predicted labels, respectively, and L and M are the land cover categories and the overall number of small batch samples, respectively.

4. Experiments and Results

In this section, three prevalent datasets in PolSAR classification, namely Flevoland, San Francisco, and Oberpfaffenhofen have been used in our experiments to validate the effectiveness of the proposed approach under various experimental configurations of the suggested framework. For a comprehensive demonstration, both visualized classification results and quantitative performance metrics are reported, in addition to comparisons with state-of-the-art approaches.

4.1. Polarimetric SAR Datasets

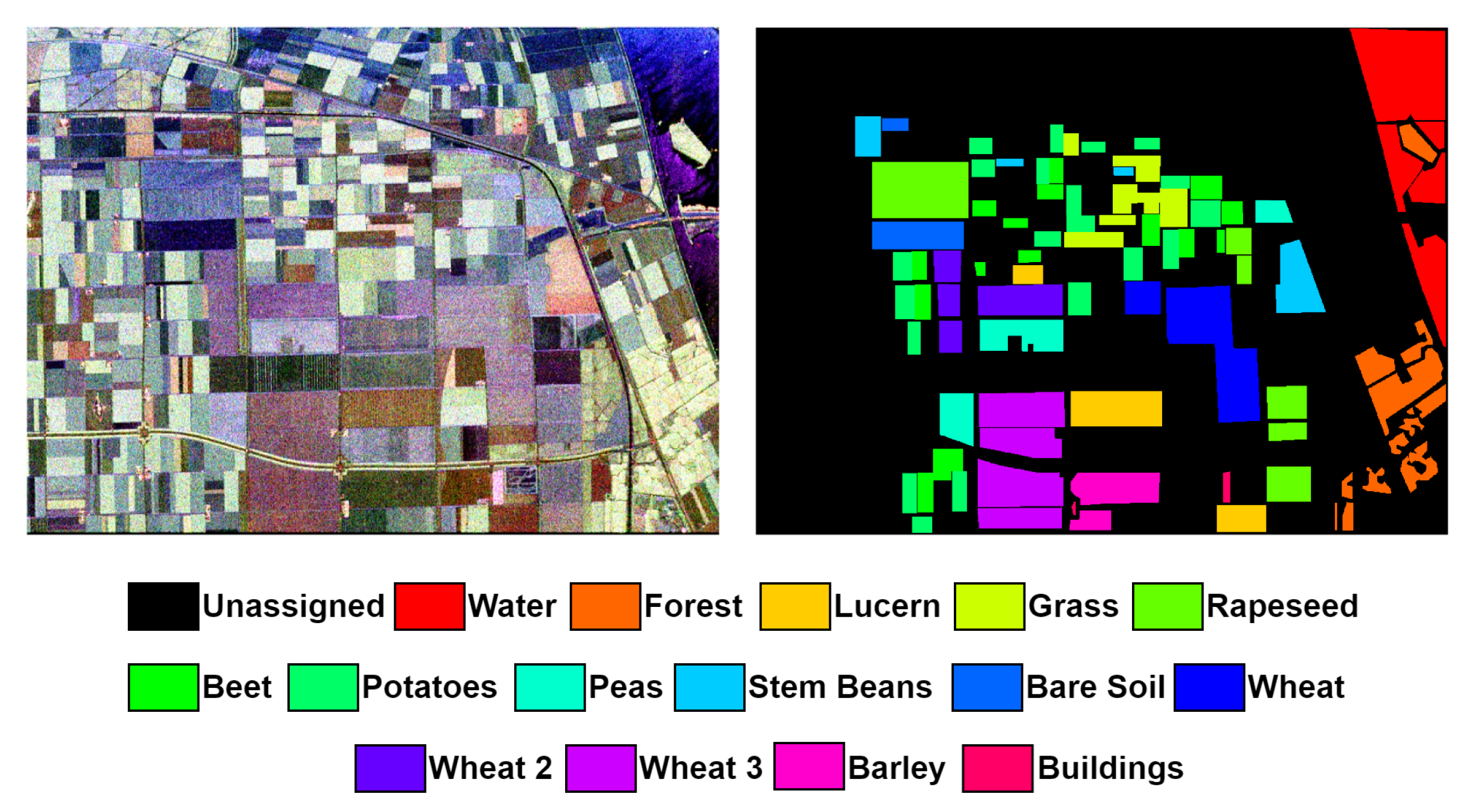
  • Flevoland Dataset: The dataset consists of L-band four-look PolSAR data with dimensions 750 × 1024 pixels with 12 meters. It was acquired by the NASA/JPL AIRSAR system on August 16, 1989 for Flevoland area in the Netherland. It has 15 distinct classes: stem beans, peas, forest, lucerne, wheat, beet, potatoes, bare soil, grass, rapeseed, barley, wheat2, wheat3, water, and buildings [36]. Figure 4 shows the Pauli pseudo-color image (Left) and ground truth map (right). Table 1 shows the number of pixels per each class in the dataset.
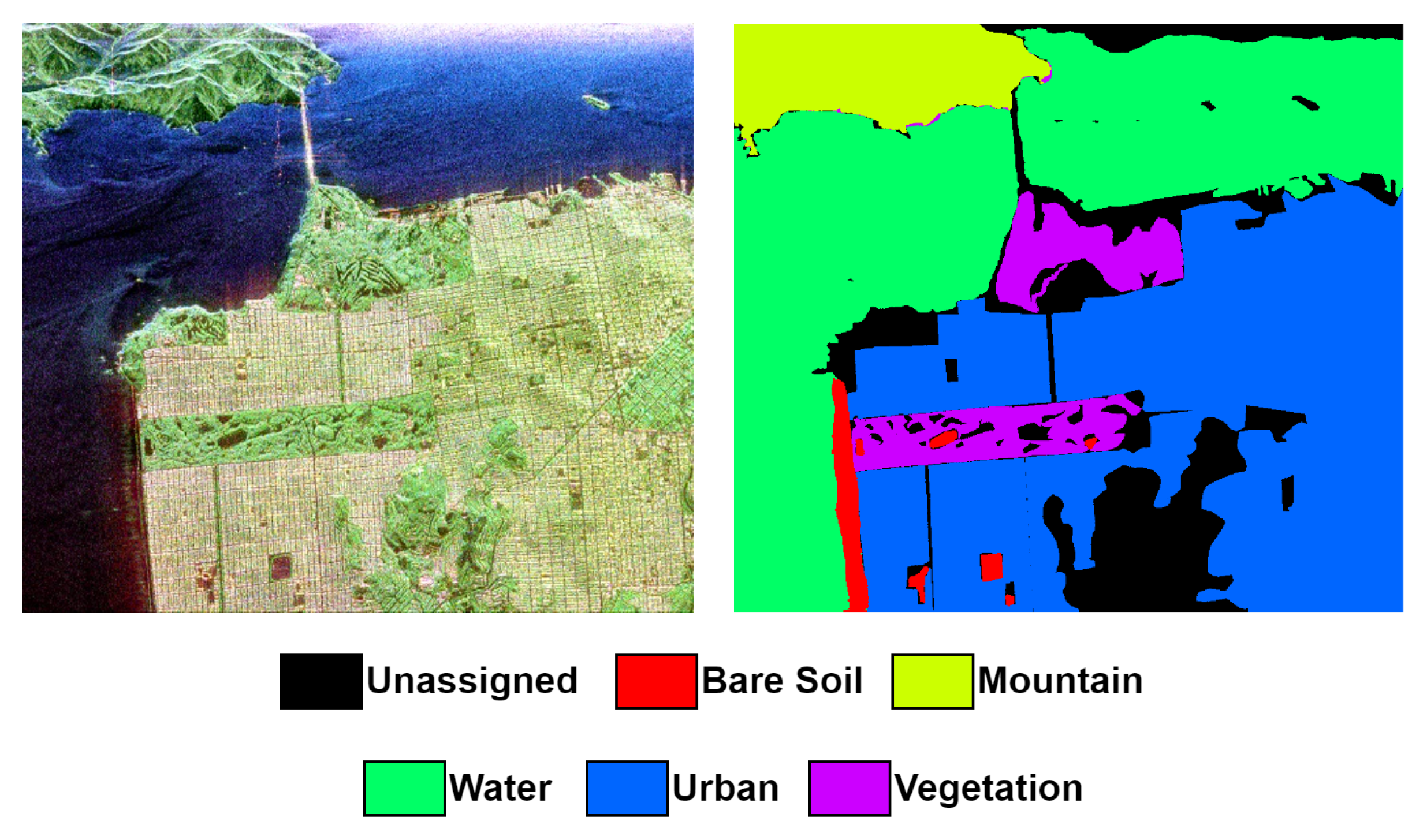
  • San Francisco Dataset: The San Francisco dataset, obtained from the L-band AIRSAR, covers the San Francisco area in 1989. The image size is 900 × 1024 pixels and has a spatial resolution of 10 meters. It comprises of five categorized terrain classes: mountain, water, urban, vegetation and bare soil [37]. Figure 5 shows a colored image formed by PauliRGB decomposition (left), and the reference class map (right). Table 2 shows the number of pixels per each class in the data set.
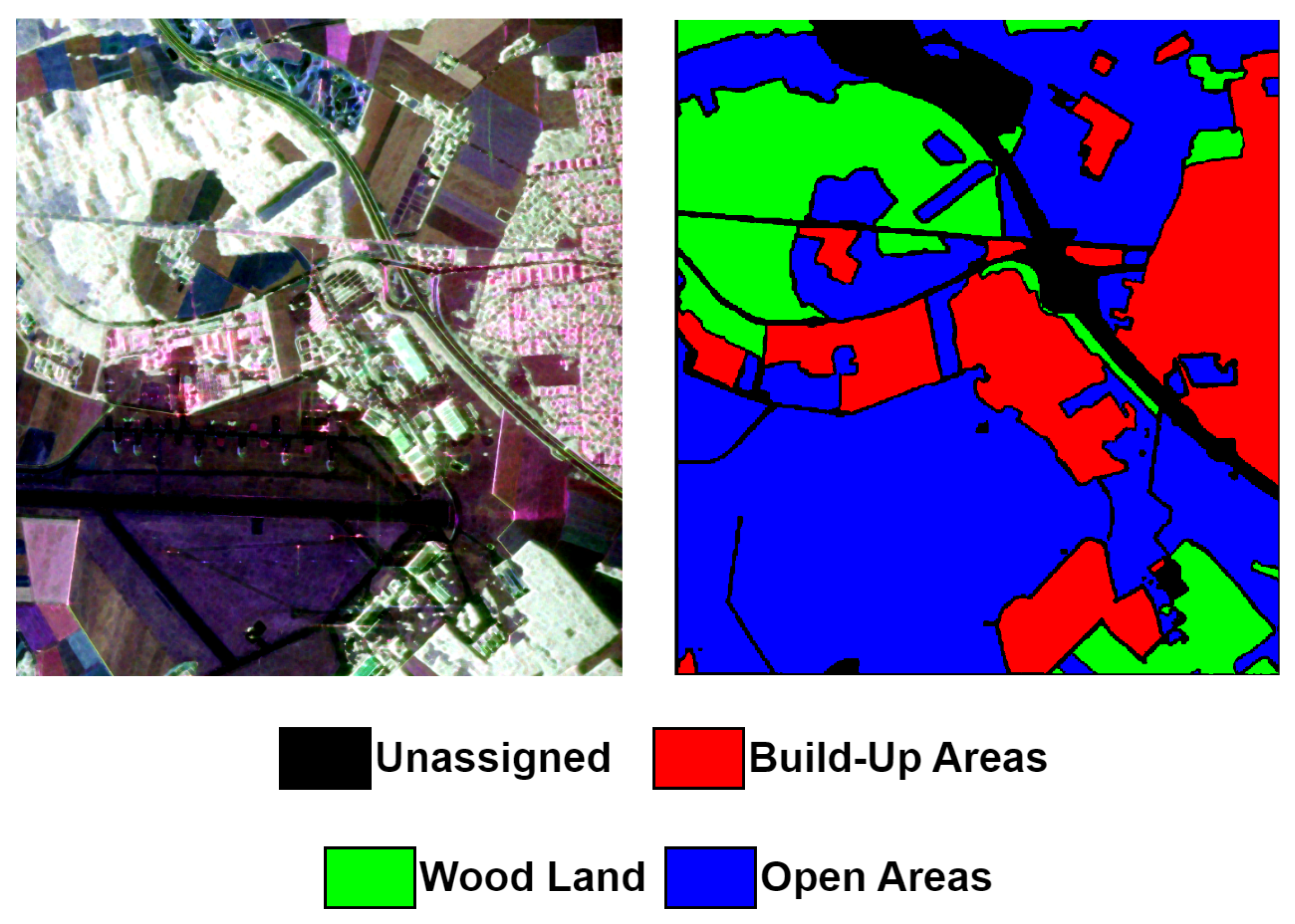
  • Oberpfaffenhofen Dataset: The Oberpfaffenhofen dataset is captured by L-band ESAR sensor in 2002, encompassing the area of Oberpfaffenhofen in Germany. It includes a PolSAR image with dimensions of 1300 × 1200 pixels and a spatial resolution of 3 meters, annotated with three land cover classes: Built-up Areas, Wood Land, and Open Areas [38]. Figure 6 shows the PauliRGB composite (left) and the reference class map (right). Table 3 shows the number of pixels per each class in the data set.

4.2. Evaluation Metrics

Assessing the effectiveness of classification results involves comparing predicted class maps with the provided reference or ground truth data. Depending solely on visual inspection for confirming pixel accuracy in the image is subjective and may lack comprehensiveness. Therefore, adopting a quantitative evaluation approach is more reliable. In this context, three metrics are employed: Overall Accuracy (OA), Average Accuracy (AA), and the Kappa score (k).
OA calculates the ratio of correctly assigned pixels to the total number of samples. AA computes the mean classification accuracy across all categories or classes. The Kappa score assesses the agreement between the predicted classified map and the ground truth, with values ranging from 0 to 1. A value of 1 indicates perfect agreement, while 0 suggests complete disagreement. Typically, a Kappa value equal to or greater than 0.80 signifies substantial agreement, whereas a value below 0.4 indicates poor model’s performance [39].

4.3. Experimental Configuration

All the tests were conducted utilizing Python 3.9 compiler and TensorFlow 2.10.0 framework. Adam optimizer is adopted with a learning rate of 1 × 10 − 3 , the batch size is 64, and the training epoch is set to 250. In the course of model training, an early stopping strategy is implemented. Specifically, if there is no improvement in the model’s performance over a consecutive span of 10 epochs, the training process halts, and the model reverts to its optimal weights. The network configuration of the proposed model using Flevoland dataset is shown in Table 4. The number of samples used for training the model is set to 1 % for all three datasets to guarantee a fair comparison.

4.4. Experimental Results

In this section, we assess the classification performance of the suggested model both quantitatively and qualitatively, utilizing the three previously mentioned datasets: Flevoland, San Francisco, and Oberpfaffenhofen. To mitigate the impact of sample selection randomness on classification outcomes, the experiments were iterated 10 times, and the final result is presented as the average value of these repetitions. Furthermore, detailed classification outcomes for each category are provided.

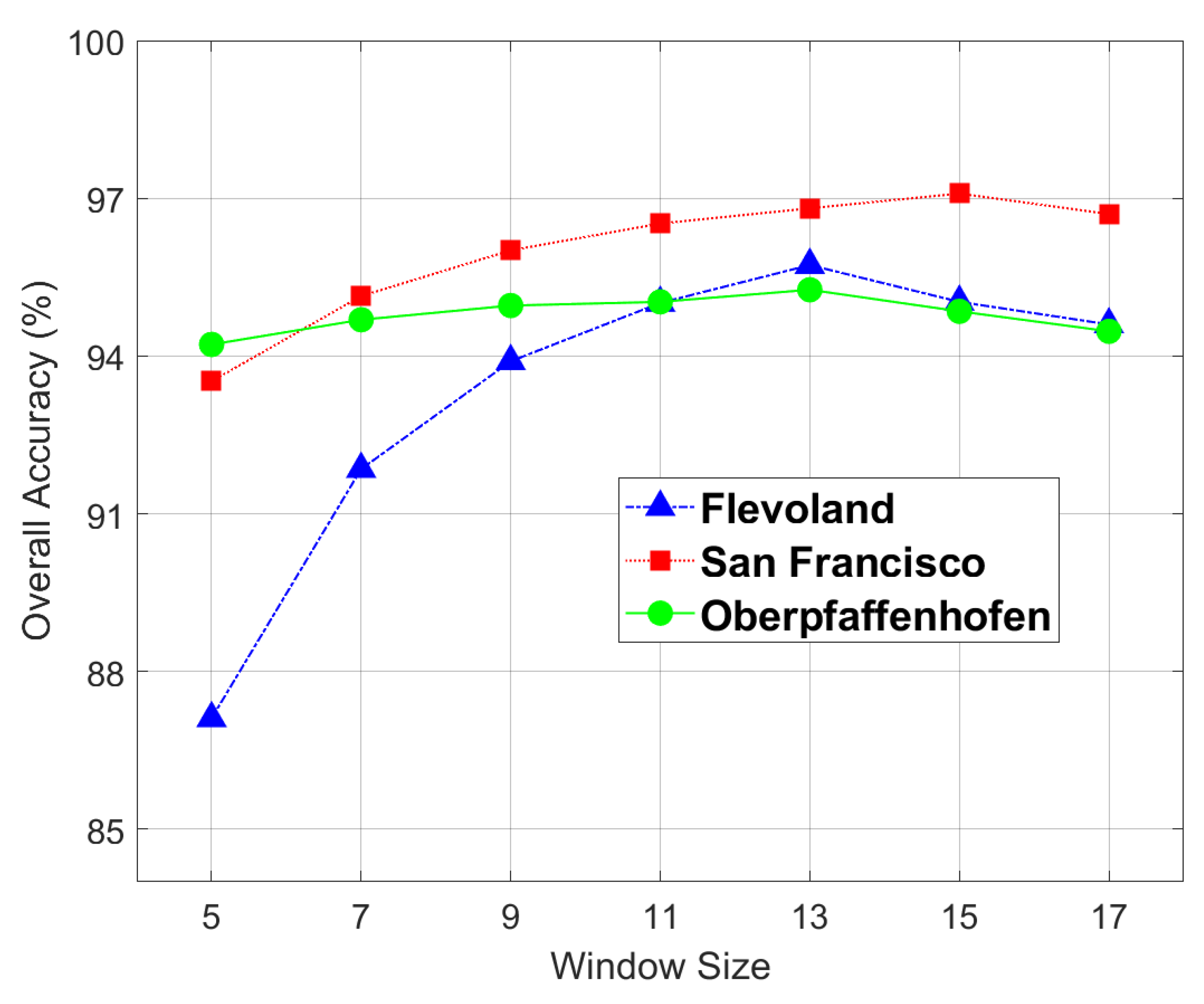
4.4.1. Determining Optimal Window Size

In this part, we investigate the effect of the spatial characteristics of the aforementioned diverse datasets on the proposed model’s capability to categorize PolSAR data and identify the optimal window size for each dataset. The window size signifies the extent of the retrieved spatial information from the 3D patch that is utilized for assigning a label to the extracted patch. A larger window may encompass a significant amount of neighborhood data, potentially containing information from other classes, thereby impeding the feature extraction process. Conversely, if the chosen window is too small, the model’s capacity to extract features will be compromised by a notable loss of spatial information. This study validates the influence of window size on model performance across the three aforementioned datasets. In the experiment, the spatial sizes were configured as { 5 × 5 , 7 × 7 , 9 × 9 , 11 × 11 , 13 × 13 , 15 × 15 , and 17 × 17 }. It is evident from Figure 7 that for the Flevoland, San Francisco, and Oberpfaffenhofen datasets, the suitable window size for the proposed model is 13 × 13 , 15 × 15 and 13 × 13 , respectively.

4.4.2. Ablation Study

This section is divided into two parts for the ablation study. The initial part focuses on assessing the influence of diverse combinations of network components. We conducted comprehensive experiments on the Flevoland dataset, as outlined in Table 5. The results demonstrate that our proposed fusion technique outperforms other combinations or fusion methods, such as Shallow (S), Medium (M), Deep (D), Shallow and Medium (S+M), Shallow and Deep (S+D), Medium and Deep (M+D), in terms of AA, OA, and Kappa metrics.
The second part examines the impact of incorporating the attention mechanism. Initially, we experimented with the model without any attention mechanism, followed by placing attention at each stream before feature fusion, and finally applying attention after feature fusion. Table 6 presents the outcomes for various attention locations on the same dataset. It is evident that the optimal location is immediately after the feature fusion step.

4.4.3. Comparison with Other Methods

Several techniques have been chosen for comparison with the SDF2Net model, such as SVM [40], 2D-CVNN [41], 3D-CVNN [42], Wavelet CNN [43], and our previously proposed method in [44], namely CV-CNN-SE. The specific experimental configurations for these methods are outlined below.
  • SVM: The SVM employs the Radial Basis Function (RBF) kernel, with the parameter γ set to 0.001 to regulate the local scope of the RBF kernel.
  • 2D-CVNN: The model consists of two Complex-Valued CNN layers, with 6 and 12 kernels of size 3 × 3 in each layer, and two fully connected layers. The input patch size is specified as 12 × 12 in [41].
  • Wavelet CNN: The proposed model utilizes the Haar wavelet transform for feature extraction to improve the classification accuracy of PolSAR imagery. It consists of three branches, each utilizing different concepts and advantages of CNNs. The model parameters were configured based on the values given in [43]
  • CV-CNN-SE: This model utilizes the use of 2D-CVNNs at different scales to extract features from PolSAR data. Extracted features are then fused and passed to SE block to enhance classification performance.
  • 3D-CVNN: In this model, four Complex-Valued convolutional layers, with 16, 16, 32 and 32 kernels of size 3 × 3 × 3 in each layer, and one fully connected layer. The input patch size is specified as 12 × 12 in [42].
As mentioned earlier, the experiments were conducted through 10 iterations, and the outcome is presented as the mean value of these repetitions. The quantitative assessments of these compared methods are presented in Table 7, Table 8 and Table 9, with the best results in each table highlighted in bold.
Based on the findings presented in Table 7, Table 8 and Table 9, it is evident that the proposed SDF2Net model surpasses other methods in performance. Examining the datasets utilized in this study, the Flevoland dataset is composed of 207,832 labeled samples, with 1% (2,078 samples) reserved for training, spanning across 15 classes. In contrast, the San Francisco dataset boasts a larger pool of labeled samples, with 8,023 allocated for training, explaining the higher classification performance observed in San Francisco.
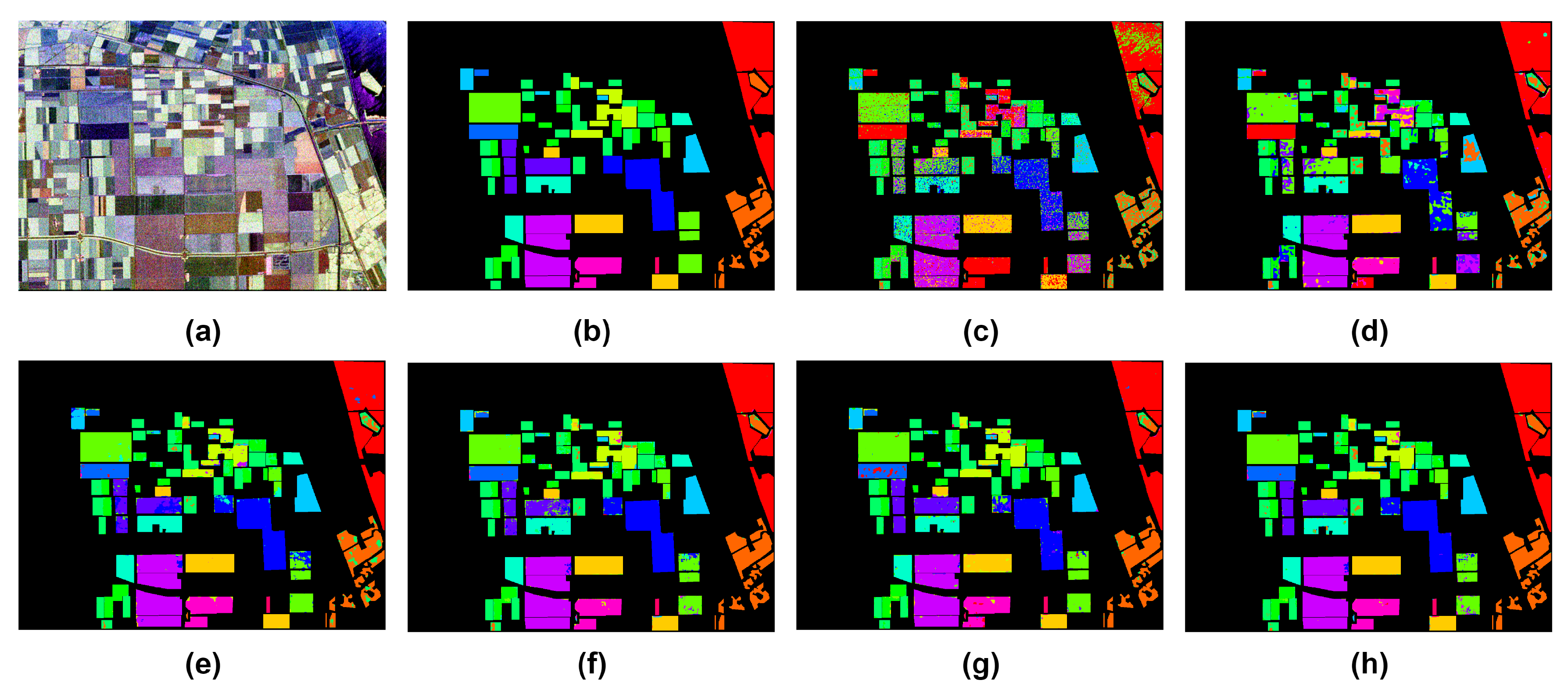
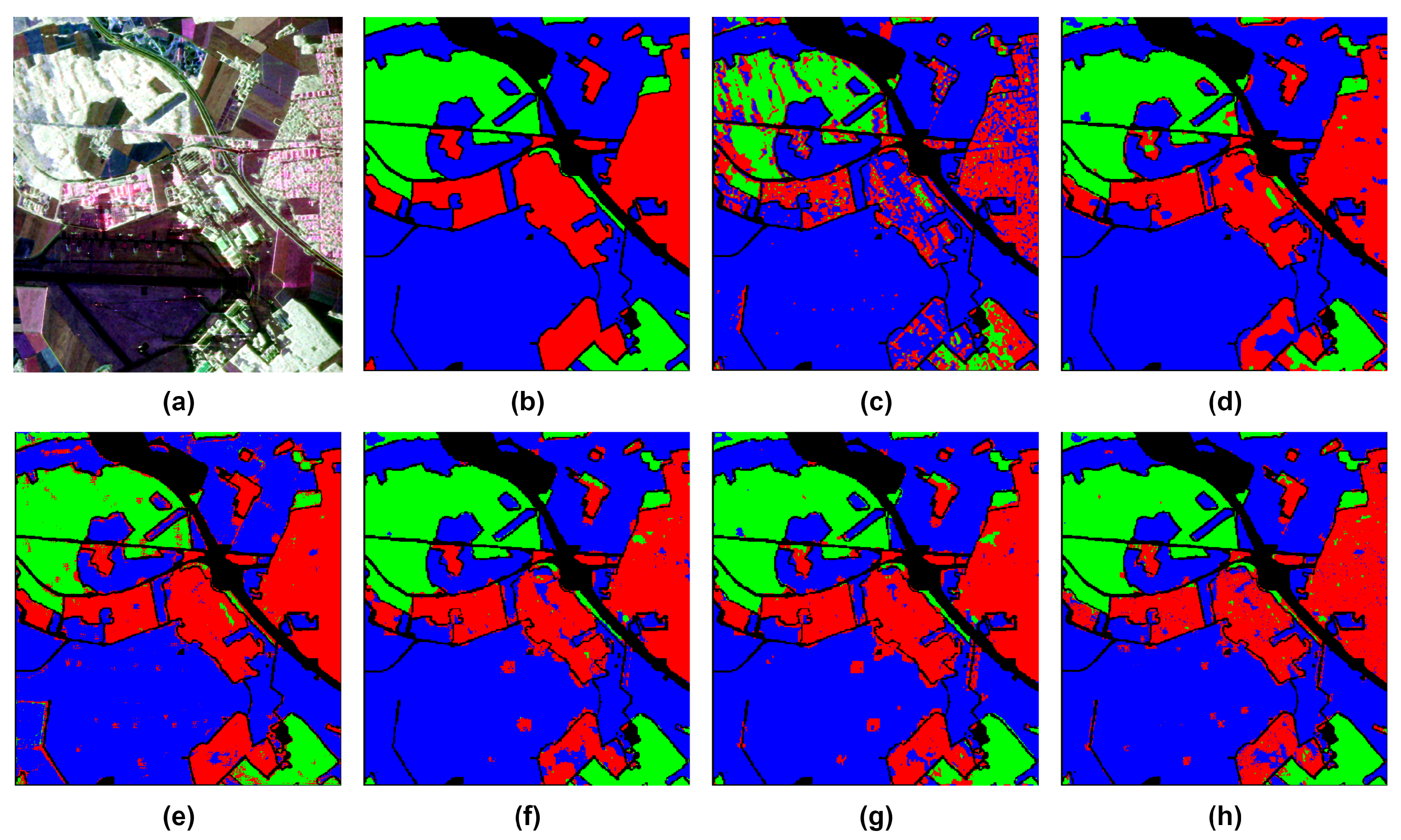
The results on Flevoland dataset are reported in Table 7, SVM demonstrated the least OA, primarily because it heavily depends on 1-dimensional information. Additionally, classes with a low number of training samples, such as Grass, Bare Soil, Wheat 2, Barley, and Buildings, were hardly detected by SVM. This suggests that SVM is an unsuitable option for datasets with a limited number of training samples, a limitation evident in the quantitative metrics associated with each class. The metrics of the 2D-CVNN exhibited an enhancement, approximately 10% greater than that of SVM. Unlike SVM, the 2D-CVNN utilizes 2D filters for spatial information extraction, resulting in a moderate increase in accuracy. Nevertheless, certain classes with a limited number of training samples, like Grass and Bare Soil, recorded lower accuracy metrics, influencing the overall performance of the model. The Wavelet CNN achieved substantial improvement to the accuracy with 91.73%, utilizing Wavelet decomposition for feature extraction, thereby enhancing classification accuracy. CV-CNN-SE, employing three parallel branches of two-dimensional kernels, demonstrated an improvement over Wavelet CNN. The 3D-CVNN, using 3D filters for three-dimensional information extraction, did not surpass CV-CNN-SE in accuracy, but did outperform other methods used in this research. Our proposed SDF2Net method outperformed CV-CNN-SE by approximately 1.5% in OA and outperformed other methods in seven categories, as detailed in the Table 7. 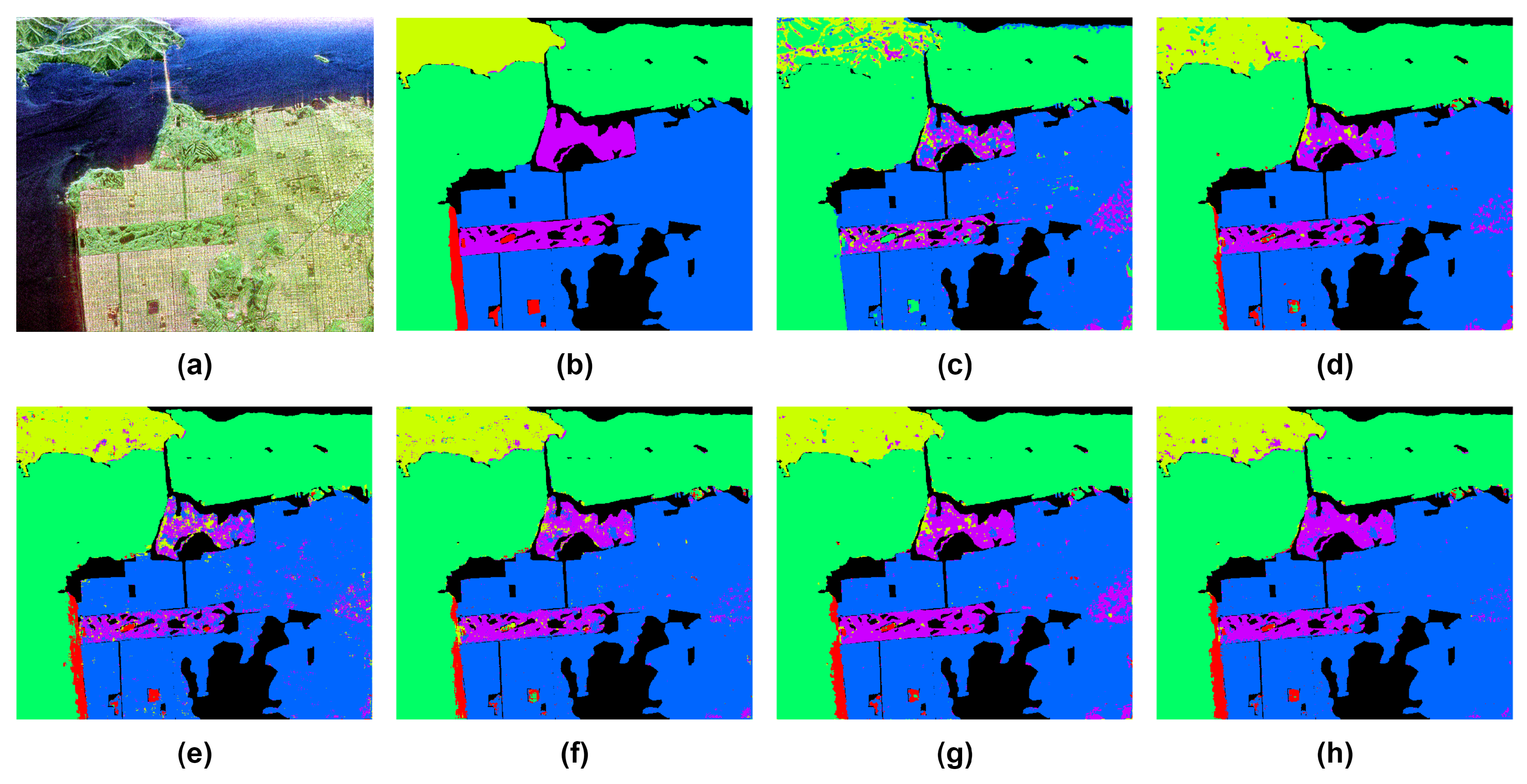For a visual representation, Figure 8 illustrates the classification results for the six approaches alongside the reference map. It is clearly shown from Figure 8(c) that SVM had numerous incorrectly assigned pixels, while the classification map generated by SDF2Net closely aligned with the reference map, showcasing superior performance.
Regarding the San Francisco dataset, Table 8 displays the classification outcomes obtained from various models. In contrast to the Flevoland dataset, this dataset comprises only five target categories. SVM yields relatively poor classification results, suggesting that the original polarimetric features lack effective discrimination. The models 2D-CVNN and CV-CNN-SE show unsatisfactory performance on this dataset, particularly in the Bare Soil category. Conversely, the Wavelet CNN and 3D-CVNN methods prove more adept at handling the intricate polarimetric features, especially in the Bare Soil category. SDF2Net achieves the highest OA at 97.13%, Average Accuracy (AA) at 91.31%, and Kappa coefficient at 95.50%. In Figure 9, the classification maps generated by the methods employed in this research are presented alongside the reference map. The classification maps produced by our method closely align with the ground truth map, especially when observing the Urban class (Blue).
The classification results of Oberpfaffenhofen dataset are shown in Table 9. SDF2Net once again achieves the best performance in terms of OA, AA and Kappa metrics when compared to the other methods. The model also achieves the highest accuracy for all classes. Figure 10 shows the classification results of the methods used in this research, which asserts that our proposed method produces the closest classification map to the ground truth one.
According to the experimental findings, the proposed SDF2Net model, outperforms other classification methods. SVM exhibits the poorest classification performance due to its reliance on 1-dimensional features, leading to a loss of spatial information. In contrast, 2D-CVNN, Wavelet CNN, and CV-CNN-SE consider spatial information, resulting in enhanced OA compared to SVM. The 3D-CVNN method extracts hierarchical features in both spatial and scattering dimensions through 3-D Complex-Valued convolutions, effectively capturing physical properties from polarimetric adjacent resolution cells. Our proposed SDF2Net demonstrates superior results across the three datasets utilized in this research, leveraging the strengths of each branch to extract features at various levels and thereby enhancing the overall classification performance.

4.5. Post-Processing with Median Filtering

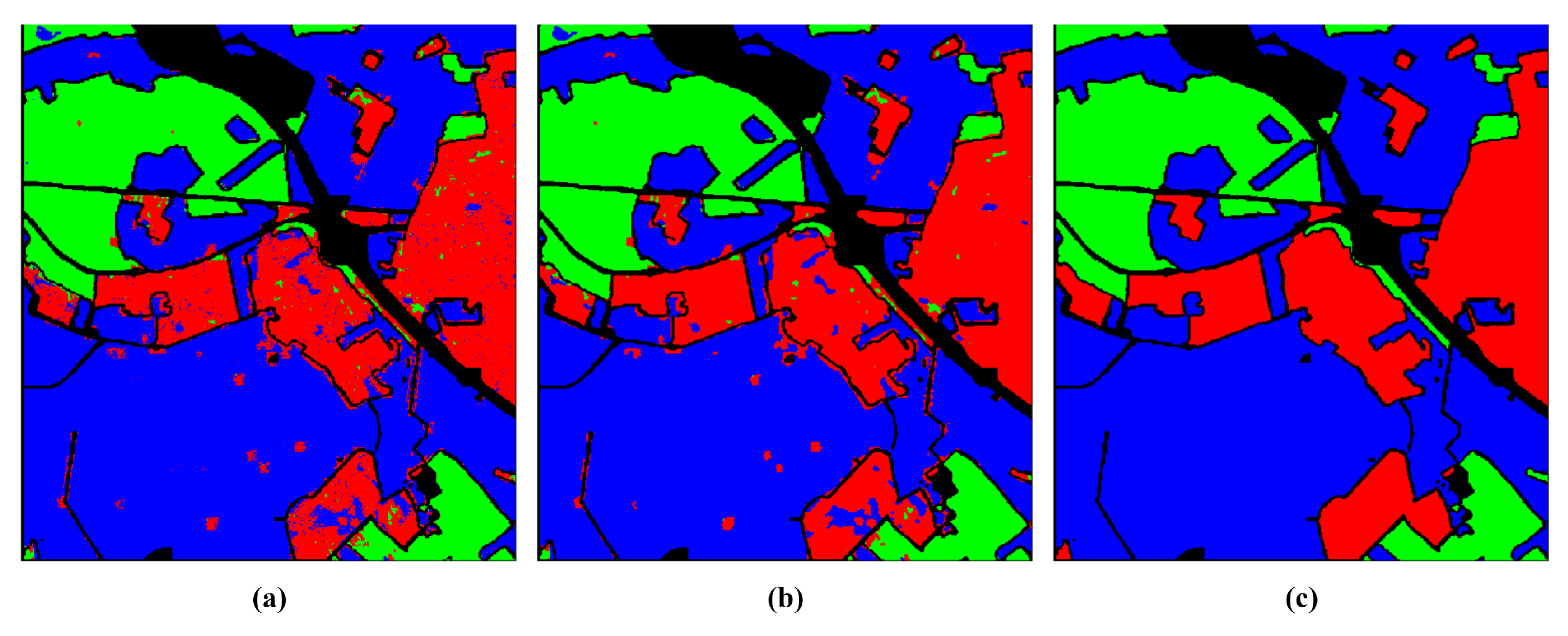
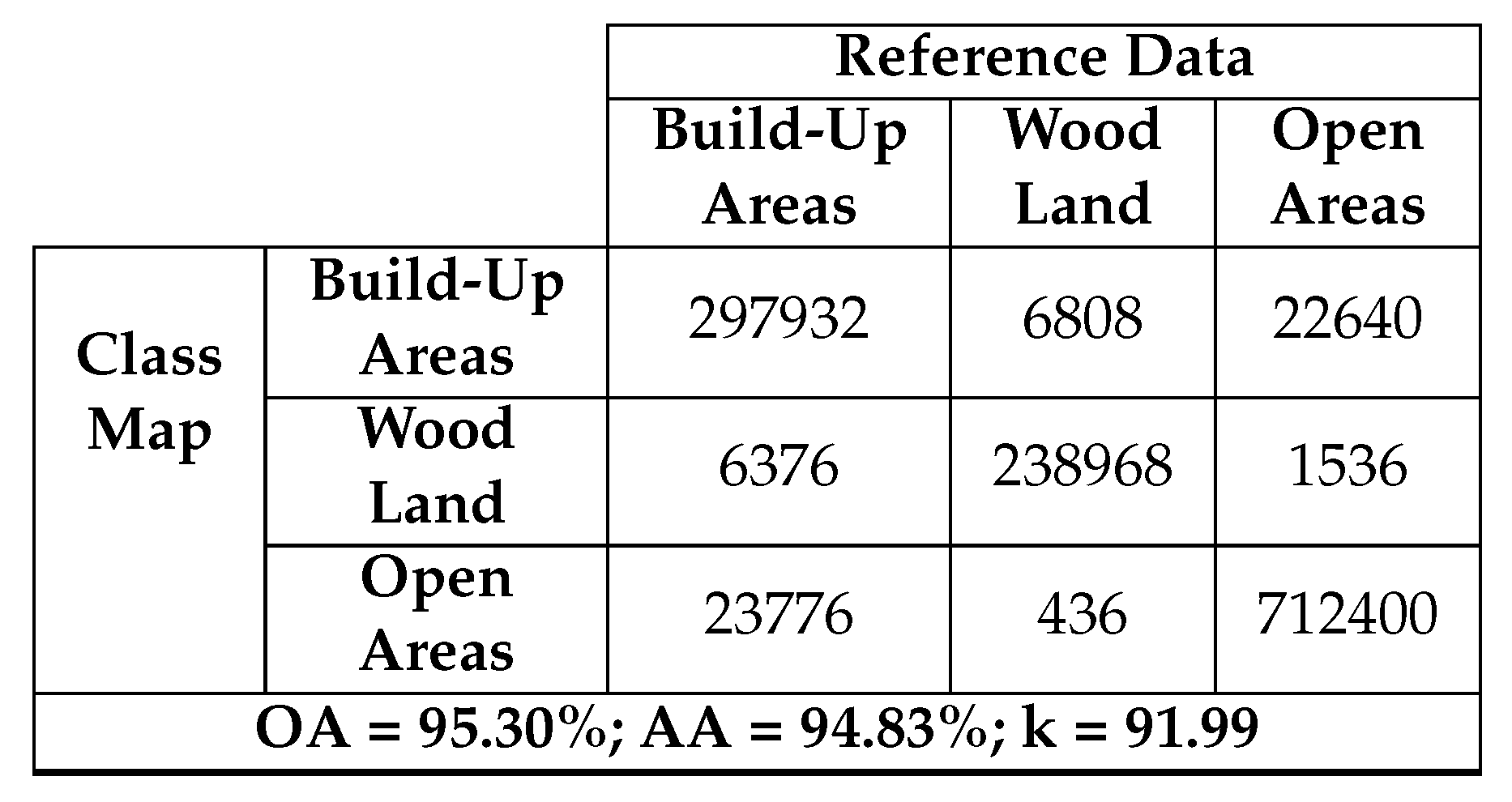
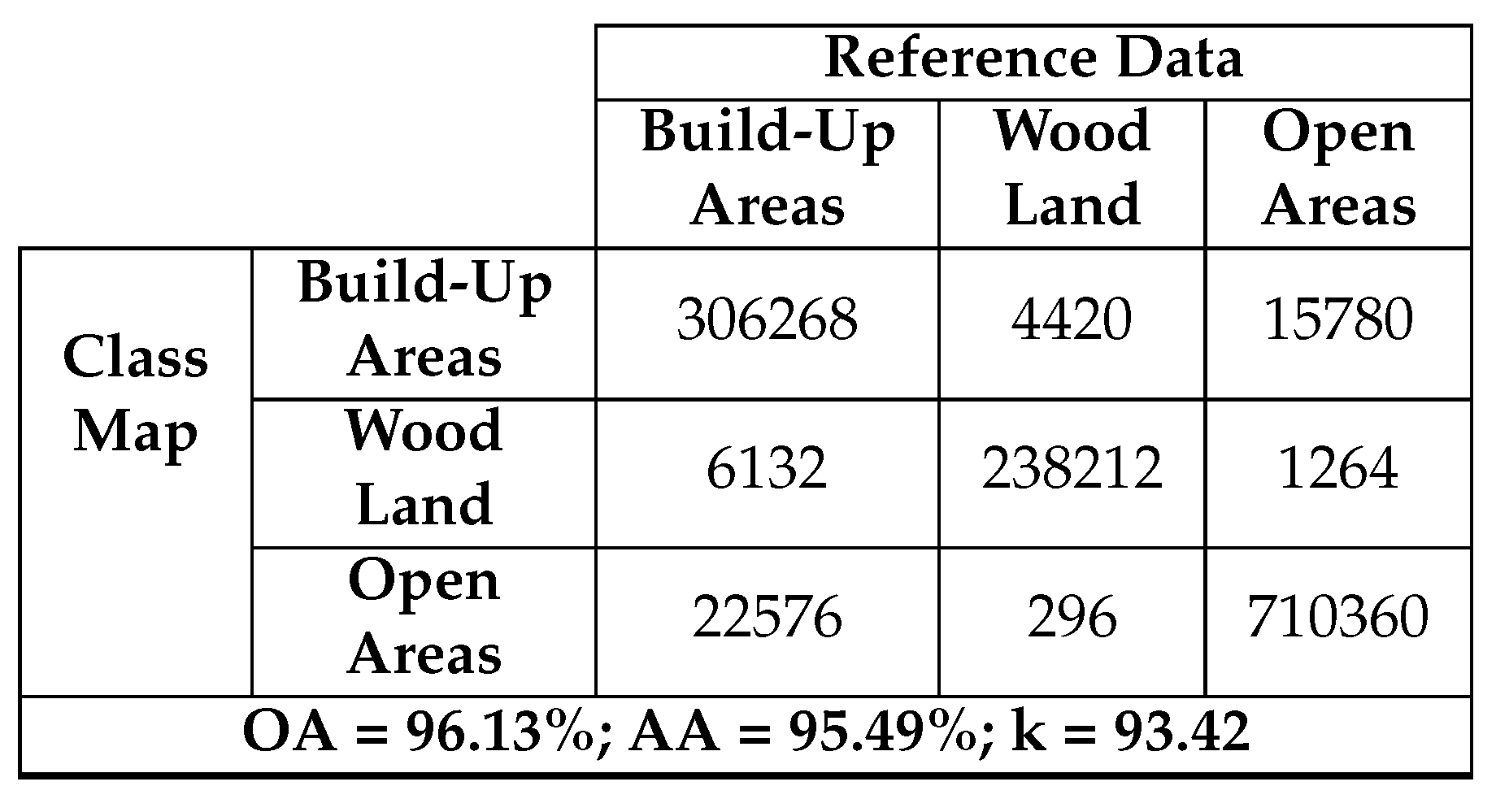
To further boost the classification accuracy, an additional spatial post-processing strategy employs a 3 × 3 median filter to eliminate isolated misclassified pixels within the assigned class. The underlying assumption is that information classes tend to occupy spatial regions of relatively uniform characteristics, typically larger than a few pixels [45]. The application of median filtering yields a more refined version of the class map with smoother transitions. To showcase the effectiveness of this process, the smoothed classification map is compared with the reference map through the confusion matrix. For illustrative purposes, the Oberpfaffenhofen dataset will be utilized as an exemplar.
Figure 11 displays classification maps for Oberpfaffenhofen. In Figure 11(a), the map is generated using the proposed model. Figure 11(b) depicts the same map after smoothing with a median filter. Figure 11(c) represents the reference data classification map. Table 10 exhibits the confusion matrix comparing the generated classification map with the reference, while Table 11 shows the confusion matrix for the filtered generated classification map in comparison to the reference one.
The diagonal of the confusion matrix demonstrates the agreement between the predicted class map and the reference class map, while discrepancies are indicated by the non-diagonal elements. Table 10 and Table 11 display a decline in the values of these non-diagonal components, signaling a decrease in the number of misclassified pixels. As a result, there is an enhancement in OA. This improvement is noticeable, particularly in the Build-Up Areas class (depicted in red). Figure 11(a) highlights numerous pixels initially classified as Open Areas. However, a substantial correction is observed after applying the median filter. This correction is corroborated by Table 10 and Table 11, revealing an initial misclassification of 22,640 Build-Up Areas pixels as Open Areas, which reduces to 15,780 after the application of the median filter. In fact, the reduction appears on all non-diagonal values. 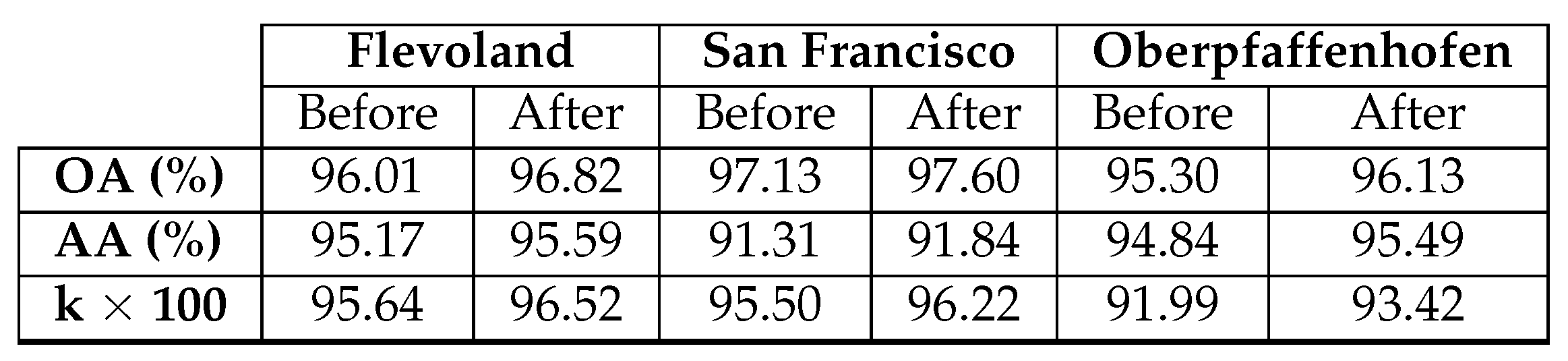Table 12 provides a summary of the enhancement achieved by applying the median filter to the resulting class map of each dataset.

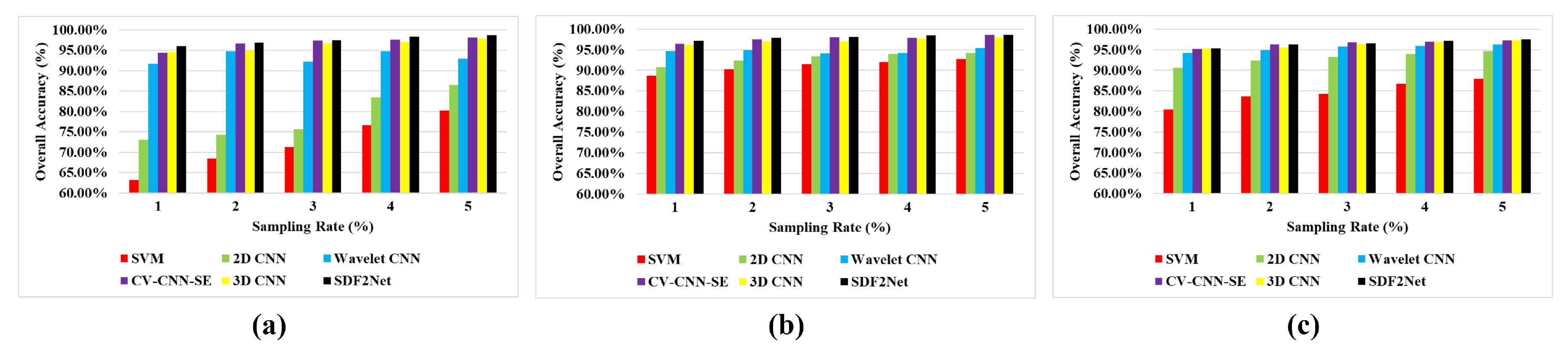
4.6. Performance of Different Models at Different Percentages of Training Data

The model’s performance can be effectively assessed by examining the classification accuracy across different percentages of training data. We randomly chose 1%, 2%, 3%, 4%, and 5% of labeled samples for training, using the remaining samples for testing the model’s performance. The classification results for each dataset are depicted in Figure 12. It is evident that, across all methods employed in this study, the classification accuracy shows improvement with an increase in the number of training samples. Notably, the proposed model consistently outperforms others across all proportions of training samples on the three datasets.

5. Conclusion

This paper introduces a novel model called SDF2Net designed for PolSAR image classification. The model addresses existing challenges in PolSAR classification by incorporating a three-branch feature fusion structure and optimizing the creation of a complex-valued CNN-based model. The data is processed through three branches of CV-3D-CNN, and the generated features from each branch are combined. Then, the fused features undergo enhancement through an attention SE block to improve model performance, followed by the application of fully connected and dropout layers to yield the final classification result. Experimental results demonstrate the effectiveness of the proposed model in terms of OA, AA, and Kappa metrics. Notably, even with a limited number of training samples, the model produces classification results almost identical to the reference or ground truth data.
As part of future work, we plan to explore a lightweight architecture with fewer training parameters to reduce computational complexity without compromising model performance. Furthermore, our objective is to explore the potential of integrating Real-Valued CNNs and CV-CNNs to enhance classification accuracy across various datasets.

Author Contributions

Conceptualization, Mohammed Alkhatib and M. Sami Zitouni; Formal analysis, Mohammed Alkhatib; Funding acquisition, Hussain Al Ahmad; Methodology, Mohammed Alkhatib and M. Sami Zitouni; Project administration, Hussain Al Ahmad; Software, Mohammed Alkhatib; Supervision, Mohammed Alkhatib and Hussain Al Ahmad; Validation, Mohammed Alkhatib; Writing – original draft, Mohammed Alkhatib; Writing – review & editing, Mina Al-saad and Nour Aburaed.

References

  1. Yin, Q.; Hong, W.; Zhang, F.; Pottier, E. Optimal combination of polarimetric features for vegetation classification in PolSAR image. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2019, 12, 3919–3931. [Google Scholar] [CrossRef]
  2. Zhang, W.; Hu, B.; Brown, G.S. Automatic surface water mapping using polarimetric SAR data for long-term change detection. Water 2020, 12, 872. [Google Scholar] [CrossRef]
  3. Xiang, D.; Tang, T.; Ban, Y.; Su, Y. Man-made target detection from polarimetric SAR data via nonstationarity and asymmetry. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2016, 9, 1459–1469. [Google Scholar] [CrossRef]
  4. Shang, R.; Wang, J.; Jiao, L.; Yang, X.; Li, Y. Spatial feature-based convolutional neural network for PolSAR image classification. Applied Soft Computing 2022, 123, 108922. [Google Scholar] [CrossRef]
  5. Ren, Y.; Jiang, W.; Liu, Y. A New Architecture of a Complex-Valued Convolutional Neural Network for PolSAR Image Classification. Remote Sensing 2023, 15, 4801. [Google Scholar] [CrossRef]
  6. Brisco, B.; Mahdianpari, M.; Mohammadimanesh, F. Hybrid compact polarimetric SAR for environmental monitoring with the RADARSAT constellation mission. Remote Sensing 2020, 12, 3283. [Google Scholar] [CrossRef]
  7. Yamaguchi, Y. Disaster monitoring by fully polarimetric SAR data acquired with ALOS-PALSAR. Proceedings of the IEEE 2012, 100, 2851–2860. [Google Scholar] [CrossRef]
  8. Hou, B.; Guan, J.; Wu, Q.; Jiao, L. Semisupervised classification of PolSAR image incorporating labels’ semantic priors. IEEE Geoscience and Remote Sensing Letters 2019, 17, 1737–1741. [Google Scholar] [CrossRef]
  9. Lupidi, A.; Greiff, C.; Brüggenwirth, S.; Brandfass, M.; Martorella, M. Polarimetric radar technology for european defence superiority-the polrad project. In Proceedings of the 2020 21st International Radar Symposium (IRS). IEEE; 2020; pp. 6–10. [Google Scholar]
  10. Mandal, D.; Rao, Y. SASYA: An integrated framework for crop biophysical parameter retrieval and within-season crop yield prediction with SAR remote sensing data. Remote Sensing Applications: Society and Environment 2020, 20, 100366. [Google Scholar] [CrossRef]
  11. Silva-Perez, C.; Marino, A.; Lopez-Sanchez, J.M.; Cameron, I. Multitemporal polarimetric SAR change detection for crop monitoring and crop type classification. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2021, 14, 12361–12374. [Google Scholar] [CrossRef]
  12. Datcu, M.; Huang, Z.; Anghel, A.; Zhao, J.; Cacoveanu, R. Explainable, Physics-Aware, Trustworthy Artificial Intelligence: A paradigm shift for synthetic aperture radar. IEEE Geoscience and Remote Sensing Magazine 2023, 11, 8–25. [Google Scholar] [CrossRef]
  13. Yang, Z.; Fang, L.; Shen, B.; Liu, T. PolSAR ship detection based on azimuth sublook polarimetric covariance matrix. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 8506–8518. [Google Scholar] [CrossRef]
  14. Krogager, E. New decomposition of the radar target scattering matrix. Electronics letters 1990, 18, 1525–1527. [Google Scholar] [CrossRef]
  15. Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE transactions on geoscience and remote sensing 1998, 36, 963–973. [Google Scholar] [CrossRef]
  16. Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Transactions on geoscience and remote sensing 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
  17. Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE transactions on geoscience and remote sensing 1996, 34, 498–518. [Google Scholar] [CrossRef]
  18. Qin, J.; Liu, Z.; Ran, L.; Xie, R.; Tang, J.; Guo, Z. A target sar image expansion method based on conditional wasserstein deep convolutional GAN for automatic target recognition. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 7153–7170. [Google Scholar] [CrossRef]
  19. Qi, Z.; Yeh, A.G.O.; Li, X.; Lin, Z. A novel algorithm for land use and land cover classification using RADARSAT-2 polarimetric SAR data. Remote Sensing of Environment 2012, 118, 21–39. [Google Scholar] [CrossRef]
  20. Wang, H.; Xu, F.; Jin, Y.Q. A review of polsar image classification: From polarimetry to deep learning. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2019; pp. 3189–3192. [Google Scholar]
  21. Parikh, H.; Patel, S.; Patel, V. Classification of SAR and PolSAR images using deep learning: A review. International Journal of Image and Data Fusion 2020, 11, 1–32. [Google Scholar] [CrossRef]
  22. Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR image classification using deep convolutional neural networks. IEEE Geoscience and Remote Sensing Letters 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
  23. Chen, S.W.; Tao, C.S. PolSAR image classification using polarimetric-feature-driven deep convolutional neural network. IEEE Geoscience and Remote Sensing Letters 2018, 15, 627–631. [Google Scholar] [CrossRef]
  24. Radman, A.; Mahdianpari, M.; Brisco, B.; Salehi, B.; Mohammadimanesh, F. Dual-Branch Fusion of Convolutional Neural Network and Graph Convolutional Network for PolSAR Image Classification. Remote Sensing 2022, 15, 75. [Google Scholar] [CrossRef]
  25. Dong, H.; Zhang, L.; Zou, B. PolSAR image classification with lightweight 3D convolutional networks. Remote Sensing 2020, 12, 396. [Google Scholar] [CrossRef]
  26. Barrachina, J.; Ren, C.; Vieillard, G.; Morisseau, C.; Ovarlez, J.P. Real-and Complex-Valued Neural Networks for SAR image segmentation through different polarimetric representations. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP). IEEE; 2022; pp. 1456–1460. [Google Scholar]
  27. Asiyabi, R.M.; Datcu, M.; Nies, H.; Anghel, A. Complex-Valued Vs. In Real-Valued Convolutional Neural Network for Polsar Data Classification. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2022; pp. 421–424. [Google Scholar]
  28. Hänsch, R.; Hellwich, O. Complex-valued convolutional neural networks for object detection in PolSAR data. In Proceedings of the 8th European Conference on Synthetic Aperture Radar. VDE; 2010; pp. 1–4. [Google Scholar]
  29. Fang, Z.; Zhang, G.; Dai, Q.; Xue, B.; Wang, P. Hybrid Attention-Based Encoder–Decoder Fully Convolutional Network for PolSAR Image Classification. Remote Sensing 2023, 15, 526. [Google Scholar] [CrossRef]
  30. Zhang, L.; Chen, Z.; Zou, B.; Gao, Y. Polarimetric SAR terrain classification using 3D convolutional neural network. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2018; pp. 4551–4554. [Google Scholar]
  31. Dong, H.; Zhang, L.; Lu, D.; Zou, B. Attention-based polarimetric feature selection convolutional network for PolSAR image classification. IEEE Geoscience and Remote Sensing Letters 2020, 19, 1–5. [Google Scholar] [CrossRef]
  32. Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp.; pp. 7132–7141.
  33. Alkhatib, M.Q.; Al-Saad, M.; Aburaed, N.; Zitouni, M.S.; Al Ahmad, H. Attention Based Dual-Branch Complex Feature Fusion Network for Hyperspectral Image Classification. In Proceedings of the 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS); 2023; pp. 1–5. [Google Scholar] [CrossRef]
  34. Zhang, J.; Ma, P.; Jiang, T.; Zhao, X.; Tan, W.; Zhang, J.; Zou, S.; Huang, X.; Grzegorzek, M.; Li, C. SEM-RCNN: a squeeze-and-excitation-based mask region convolutional neural network for multi-class environmental microorganism detection. Applied Sciences 2022, 12, 9902. [Google Scholar] [CrossRef]
  35. Ni, J.; Xiang, D.; Lin, Z.; López-Martínez, C.; Hu, W.; Zhang, F. DNN-based PolSAR image classification on noisy labels. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing 2022, 15, 3697–3713. [Google Scholar] [CrossRef]
  36. Cao, Y.; Wu, Y.; Li, M.; Liang, W.; Zhang, P. PolSAR image classification using a superpixel-based composite kernel and elastic net. Remote Sensing 2021, 13, 380. [Google Scholar] [CrossRef]
  37. Liu, X.; Jiao, L.; Liu, F.; Zhang, D.; Tang, X. PolSF: PolSAR image datasets on san Francisco. In Proceedings of the International Conference on Intelligence Science. Springer; 2022; pp. 214–219. [Google Scholar]
  38. Hochstuhl, S.; Pfeffer, N.; Thiele, A.; Hinz, S.; Amao-Oliva, J.; Scheiber, R.; Reigber, A.; Dirks, H. Pol-InSAR-Island-A benchmark dataset for multi-frequency Pol-InSAR data land cover classification. ISPRS Open Journal of Photogrammetry and Remote Sensing 2023, 10, 100047. [Google Scholar] [CrossRef]
  39. Cohen, J. A coefficient of agreement for nominal scales. Educational and Psychological Measurement 1960, 20, 37–46. [Google Scholar] [CrossRef]
  40. Lardeux, C.; Frison, P.L.; Tison, C.; Souyris, J.C.; Stoll, B.; Fruneau, B.; Rudant, J.P. Support vector machine for multifrequency SAR polarimetric data classification. IEEE Transactions on Geoscience and Remote Sensing 2009, 47, 4143–4152. [Google Scholar] [CrossRef]
  41. Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Transactions on Geoscience and Remote Sensing 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
  42. Tan, X.; Li, M.; Zhang, P.; Wu, Y.; Song, W. Complex-valued 3-D convolutional neural network for PolSAR image classification. IEEE Geoscience and Remote Sensing Letters 2019, 17, 1022–1026. [Google Scholar] [CrossRef]
  43. Jamali, A.; Mahdianpari, M.; Mohammadimanesh, F.; Bhattacharya, A.; Homayouni, S. PolSAR image classification based on deep convolutional neural networks using wavelet transformation. IEEE Geoscience and Remote Sensing Letters 2022, 19, 1–5. [Google Scholar] [CrossRef]
  44. Alkhatib, M.Q.; Al-Saad, M.; Aburaed, N.; Zitouni, M.S.; Al-Ahmad, H. PolSAR Image Classification Using Attention Based Shallow to Deep Convolutional Neural Network. In Proceedings of the IGARSS 2023-2023 IEEE International Geoscience and Remote Sensing Symposium. IEEE; 2023; pp. 8034–8037. [Google Scholar]
  45. Alkhatib, M.Q.; Velez-Reyes, M. Improved spatial-spectral superpixel hyperspectral unmixing. Remote Sensing 2019, 11, 2374. [Google Scholar] [CrossRef]
Preprints 111162 g001
Figure 1. Illustration of different types of convolution on images with multiple channels. (a) 2D Convolution; (b) 3D Convolution; (c) Complex Valued 3D Convolution.
Figure 1. Illustration of different types of convolution on images with multiple channels. (a) 2D Convolution; (b) 3D Convolution; (c) Complex Valued 3D Convolution.
Preprints 111162 g001
Preprints 111162 g002
Figure 2. Squeeze and Excitation Block [33].
Figure 2. Squeeze and Excitation Block [33].
Preprints 111162 g002
Preprints 111162 g003
Figure 3. Block diagram of the proposed SDF2Net.
Figure 3. Block diagram of the proposed SDF2Net.
Preprints 111162 g003
Preprints 111162 g004
Figure 4. Flevoland PolSAR data (left) Pauli RGB composite (right) Reference class map.
Figure 4. Flevoland PolSAR data (left) Pauli RGB composite (right) Reference class map.
Preprints 111162 g004
Preprints 111162 g005
Figure 5. San Francisco PolSAR data (left) Pauli RGB composite (right) Reference class map.
Figure 5. San Francisco PolSAR data (left) Pauli RGB composite (right) Reference class map.
Preprints 111162 g005
Preprints 111162 g006
Figure 6. Oberpfaffenhofen PolSAR data (left) Pauli RGB composite (right) Reference class map.
Figure 6. Oberpfaffenhofen PolSAR data (left) Pauli RGB composite (right) Reference class map.
Preprints 111162 g006
Preprints 111162 g007
Figure 7. Overall Accuracy (OA) of the proposed model employing varying window sizes across the three datasets.
Figure 7. Overall Accuracy (OA) of the proposed model employing varying window sizes across the three datasets.
Preprints 111162 g007
Preprints 111162 g008
Figure 8. Classification results of the Flevoland dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) 2D-CVNN; (e) Wavelet CNN; (f) CV-CNN-SE; (g) 3D-CVNN; (h) Proposed SDF2Net
Figure 8. Classification results of the Flevoland dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) 2D-CVNN; (e) Wavelet CNN; (f) CV-CNN-SE; (g) 3D-CVNN; (h) Proposed SDF2Net
Preprints 111162 g008
Preprints 111162 g009
Figure 9. Classification results of the San Francisco dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) 2D-CVNN; (e) Wavelet CNN; (f) CV-CNN-SE; (g) 3D-CVNN; (h) Proposed SDF2Net
Figure 9. Classification results of the San Francisco dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) 2D-CVNN; (e) Wavelet CNN; (f) CV-CNN-SE; (g) 3D-CVNN; (h) Proposed SDF2Net
Preprints 111162 g009
Preprints 111162 g010
Figure 10. Classification results of the Oberpfaffenhofen dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) 2D-CVNN; (e) Wavelet CNN; (f) CV-CNN-SE; (g) 3D-CVNN; (h) Proposed SDF2Net
Figure 10. Classification results of the Oberpfaffenhofen dataset. (a) PauliRGB; (b) Reference Class Map; (c) SVM; (d) 2D-CVNN; (e) Wavelet CNN; (f) CV-CNN-SE; (g) 3D-CVNN; (h) Proposed SDF2Net
Preprints 111162 g010
Preprints 111162 g011
Figure 11. Oberpfaffenhofen Image: (a) classification map resulted from the proposed model; (b) classification map after applying median filtering; (c) reference data classification map
Figure 11. Oberpfaffenhofen Image: (a) classification map resulted from the proposed model; (b) classification map after applying median filtering; (c) reference data classification map
Preprints 111162 g011
Preprints 111162 g012
Figure 12. Classification accuracy at different percentages of training data (a) Flevoland; (b) San Francisco; (c) Oberpfaffenhofen.
Figure 12. Classification accuracy at different percentages of training data (a) Flevoland; (b) San Francisco; (c) Oberpfaffenhofen.
Preprints 111162 g012
Table 1. Groundtruth classes for Flevoland scene and their respective samples number.
Table 1. Groundtruth classes for Flevoland scene and their respective samples number.
Class Name Labeled Samples
1 Water 29249
2 Forest 15855
3 Lucerne 11200
4 Grass 10201
5 Rapeseed 21855
6 Beet 14707
7 Potatoes 21344
8 Peas 10396
9 Stem Beans 8471
10 Bare Soil 6317
11 Wheat 17639
12 Wheat 2 10629
13 Wheat 3 22022
14 Barley 7369
15 Buildings 578
Total 207832
Table 2. Groundtruth classes for San Francisco scene and their respective samples number.
Table 2. Groundtruth classes for San Francisco scene and their respective samples number.
Class Name Labeled Samples
1 Bare Soil 13701
2 Mountain 62731
3 Water 329566
4 Urban 342795
5 Vegetation 53509
Total 802302
Table 3. Groundtruth classes for Oberpfaffenhofen scene and their respective samples number.
Table 3. Groundtruth classes for Oberpfaffenhofen scene and their respective samples number.
Class Name Labeled Samples
1 Build-Up Areas 328051
2 Wood Land 246673
3 Open Areas 736894
Total 1311618
Table 4. Parameter Settings of SDF2Net on each Dataset with N classes
Table 4. Parameter Settings of SDF2Net on each Dataset with N classes
Shallow Features
Extraction Path		 Medium Features
Extraction Path		 Deep Features
Extraction Path
Input:(13 × 13 × 6 × 1)
1 × Complex Convolution
(3,3,3,16), Stride = 1,
Padding = ’same’		 2 × Complex Convolution
(3,3,3,16), Stride = 1,
Padding = ’same’		 3 × Complex Convolution
(3,3,3,16), Stride = 1,
Padding = ’same’
Output1:(13 × 13 × 6 × 16) Output2:(13 × 13 × 6 × 16) Output3:(13 × 13 × 6 × 16)
Concat(Output1, Output2, Output3)
Output4:(13, × 13 × 6 × 48)
Attention Block
Flatten
Output5:(48,672)
FC-(48,672:128)
Dropout(0.25)
FC-(128:64)
Dropout(0.25)
FC-(64:N)
Output:(N)
Table 5. Results of ablation studies on different combination of model branches over the Flevoland dataset.
Table 5. Results of ablation studies on different combination of model branches over the Flevoland dataset.
Combination OA (%) AA (%) k × 100
S 93.01±0.59 91.38± 0.68 92.46±0.64
M 93.87±0.77 93.76±0.54 93.49±0.84
D 94.69±0.33 93.52±0.47 94.37±0.36
S+M 93.35±0.45 93.56±0.46 93.76±0.63
S+D 94.71±0.26 93.49±0.63 94.29±0.36
M+D 95.57±0.24 94.59±0.24 95.30±0.37
Proposed 96.01±0.40 95.17±0.62 95.64±0.44
Table 6. Impact of Attention mechanism over the Flevoland dataset.
Table 6. Impact of Attention mechanism over the Flevoland dataset.
Attention Location OA (%) AA (%) k × 100
Without Attention 95.14±0.26 94.27±0.37 94.69±0.28
Before Fusion 95.84±0.21 94.86±0.68 94.91±0.32
After Fusion 96.01±0.04 95.17±0.62 95.64±0.44
Table 7. Experimental Results of different methods on Felvoland Dataset.
Table 7. Experimental Results of different methods on Felvoland Dataset.
Class Train Test SVM 2D-CVNN Wavelet CNN CV-CNN-SE 3D-CVNN SDF2Net
Water 292 28957 81.91 97.05 99.09 99.32 99.33 99.81
Forest 159 15696 71.71 81.44 85.39 98.80 95.11 99.23
Lucerne 112 11088 82.04 93.40 98.29 96.32 90.48 97.46
Grass 102 10099 0.24 5.62 83.90 86.19 91.57 85.10
Rapeseed 219 21636 68.99 71.88 88.25 93.87 97.31 94.05
Beet 147 14560 68.10 67.92 74.78 77.65 91.51 91.59
Potatoes 213 21131 79.40 79.11 95.93 95.39 94.69 91.30
Peas 104 10292 68.33 92.72 99.19 97.65 92.76 95.80
Stem Beans 85 8386 73.01 68.48 91.45 95.90 93.20 99.00
Bare Soil 63 6254 0.00 0.00 95.06 94.08 84.88 94.49
Wheat 176 17463 73.97 69.24 96.41 98.78 89.55 98.16
Wheat 2 106 10523 0.05 22.04 72.03 81.86 95.50 97.34
Wheat 3 220 21802 83.86 95.94 97.53 98.62 97.72 98.86
Barley 74 7295 0.00 73.08 96.51 96.76 94.19 98.51
Buildings 6 572 1.04 80.97 84.60 86.33 100.00 86.85
OA (%) 63.22 ± 0.86 73.09 ± 2.53 91.73 ± 4.15 94.78 ± 1.42 94.51 ± 0.74 96.01 ± 0.40
AA (%) 50.18 ± 0.59 66.59 ± 1.47 90.56 ± 5.30 93.17 ± 2.12 93.85 ± 0.72 95.17 ± 0.62
k × 100 59.18 ± 1.67 70.38 ± 4.31 90.96 ± 5.43 93.92 ± 1.61 94.00 ± 0.79 95.64 ± 0.44
Table 8. Experimental Results of different methods on San Francisco Dataset.
Table 8. Experimental Results of different methods on San Francisco Dataset.
Class Train Test SVM 2D-CVNN Wavelet CNN CV-CNN-SE 3D-CVNN SDF2Net
Bare Soil 137 13564 0.04 47.49 78.97 57.81 73.13 79.98
Mountain 627 62104 40.61 91.27 94.62 94.82 96.31 94.49
Water 3295 326270 98.37 99.37 99.26 99.11 99.24 98.70
Urban 3428 339367 95.65 97.78 96.21 98.47 95.52 98.94
Vegetation 535 52974 64.21 78.87 60.25 77.71 86.44 87.42
OA (%) 88.73 ± 0.12 95.80 ± 0.37 94.65 ± 2.00 96.37 ± 0.22 96.19 ± 0.32 97.13 ± 0.20
AA (%) 59.77 ± 0.86 82.95 ± 3.23 85.86 ± 4.28 85.58 ± 1.78 90.33 ± 1.3 91.31 ± 1.54
k × 100 81.75 ± 0.21 93.38 ± 0.60 91.58 ± 3.08 94.28 ± 0.35 94.07 ± 0.31 95.50 ± 0.31
Table 9. Experimental Results of different methods on Oberpfaffenhofen Dataset.
Table 9. Experimental Results of different methods on Oberpfaffenhofen Dataset.
Class Train Test SVM 2D-CVNN Wavelet CNN CV-CNN-SE 3D-CVNN SDF2Net
Build-Up Areas 3281 324770 56.33 89.35 93.09 90.49 92.58 91.01
Wood Land 2467 244206 57.21 92.24 90.73 96.44 94.99 96.80
Open Areas 7369 729525 95.98 96.20 94.10 96.14 94.43 96.71
OA (%) 80.46 ± 1.29 94.35 ± 0.72 94.21 ± 0.49 94.86 ± 0.24 94.33 ± 0.55 95.30 ± 0.08
AA (%) 70.84 ± 2.10 93.01 ± 2.92 93.97 ± 1.47 94.49 ± 0.31 94.32 ± 1.27 94.84 ± 0.08
k × 100 64.20 ± 2.71 90.31 ± 3.64 90.26 ± 1.61 91.25 ± 0.30 90.41 ± 1.43 91.99 ± 0.13
Table 10. Confusion matrix between reference and generated classification maps for Oberpfaffenhofen dataset.
Table 10. Confusion matrix between reference and generated classification maps for Oberpfaffenhofen dataset.
Preprints 111162 i001
Table 11. Confusion matrix between reference and filtered classification maps for Oberpfaffenhofen dataset.
Table 11. Confusion matrix between reference and filtered classification maps for Oberpfaffenhofen dataset.
Preprints 111162 i002
Table 12. Impact of Median Filtering on the classification maps of different datasets
Table 12. Impact of Median Filtering on the classification maps of different datasets
Preprints 111162 i003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated