Fractional Calculus Meets Neural Networks For Computer Vision: A Survey

Preprint

Review

Fractional Calculus Meets Neural Networks For Computer Vision: A Survey

Altmetrics

Downloads

147

Views

Comments

A peer-reviewed article of this preprint also exists.

C. Coelho^*

M. Fernanda P. Costa,

Luís L. Ferrás

C. Coelho^*

M. Fernanda P. Costa,

Luís L. Ferrás

This version is not peer-reviewed

Submitted:

03 July 2024

Posted:

04 July 2024

You are already at the latest version

Alerts

Abstract

Traditional computer vision techniques aim to extract meaningful information from images but often depend on manual feature engineering, making it difficult to handle complex real-world scenarios. Fractional Calculus (FC), which extends derivatives to non-integer orders, provides a flexible way to model systems with memory effects and long-term dependencies, making it a powerful tool for capturing fractional rates of variation. Recently, Neural Networks (NNs) have demonstrated remarkable capabilities in learning complex patterns directly from raw data, automating computer vision tasks and enhancing performance. Therefore, the use of fractional calculus in neural network-based computer vision is a powerful method to address existing challenges by effectively capturing complex spatial and temporal relationships in images and videos. This paper presents a survey of Fractional Calculus Neural Network-based (FC NN-based) computer vision techniques for denoising, enhancement, object detection, segmentation, restoration, and NN compression. The survey compiles existing FFC NN-based approaches, elucidates underlying concepts, and identifies open questions and research directions. By leveraging FC's properties, FC NN-based approaches offer a novel way to improve the robustness and efficiency of computer vision systems.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Computer vision has become a transformative field with significant impact across various industries. Using computers to interpret visual information has been crucial for enhancing surveillance systems and aiding medical imaging for disease diagnosis.

Traditional computer vision involves many algorithms and methods to extract meaningful information from images. These techniques typically include steps like image preprocessing, feature extraction, and classification or inference.

One of the fundamental tasks in computer vision is image segmentation, where traditional techniques such as thresholding, edge detection, and region-based methods are commonly employed to partition images into semantically meaningful regions or objects. Object detection, another important task, was traditionally addressed using techniques such as Haar cascades, Histogram of Oriented Gradients (HOG), and feature-based classifiers. These methods relied on manually designed features and classifiers to detect objects within images, often requiring careful tuning of parameters and heuristics to achieve optimal performance. Similarly, image denoising, restoration, and enhancement were tackled using conventional filtering techniques, such as median filtering, Gaussian blurring, and wavelet transforms, aimed at removing noise, restoring lost details, and improving overall image quality [1].

Fractional Calculus (FC) is a powerful mathematical framework that extends integer-order derivatives and integrals to non-integer orders. This generalisation allows for more degrees of freedom and provides a more nuanced and flexible way to model systems with memory effects, long-range dependencies, and anomalous behaviours, which are prevalent in real-world phenomena [2]. In recent years, FC has gained attention across various fields, including physics [3], engineering [4], biology [5], finance [6] and medicine [7], due to their ability to capture complex dynamics that cannot be adequately described by classical integer-order derivatives.

Due to proven advantages, several FC-based approaches have been introduced in the literature to improve performance in computer vision tasks [8,9,10,11]. Although the traditional FC-based approaches have been instrumental in enabling various applications, they often struggle with complex, real-world scenarios and lack the ability to generalise well across different domains. These approaches rely heavily on manual feature engineering and human knowledge or assumptions on the ground-truth image (prior). Furthermore, FC-based approaches often face challenges in handling variability in lighting conditions, viewpoint changes, and occlusions, which are prevalent in real-world images [1].

FC has also been attracting increasing attention from researchers in the field of deep learning algorithms. The inherent ability to capture complex dynamics and temporal relationships is closely aligned with the objectives of ML, particularly in tasks that involve sequential data analysis, such as time-series forecasting, natural language processing, and sequential decision-making [12,13,14].

Recently, Neural Networks (NNs) have demonstrated remarkable capabilities in learning complex patterns and features directly from raw data. In the context of computer vision, NNs have enabled breakthroughs in image denoising, enhancement, segmentation and restoration, and object detection. Moreover, constant efforts by the research community have also lead to reducing the computational cost of these tasks. By leveraging large datasets and powerful computational resources, NNs have surpassed traditional computer vision approaches, achieving state-of-the-art performance across a wide range of tasks. Furthermore, the ability of NNs to automatically learn and extract features from data has eliminated the need for manual feature engineering and enabled systems to adapt and generalise to diverse and complex visual environments [1].

More recently, FC has emerged in NN-based computer vision, offering a compelling approach to enhance the performance of NN architectures. By incorporating non-integer orders derivatives, FC makes it possible to account for the intricate spatial and temporal relationships, combining local and global features inherent in images and videos [15]. For instance, NNs have been used to leverage the power of fractional-order differential mask operators, enabling the discovery of optimal mask orders to improve their performance in achieving specific image goals, such as denoising and enhancement [16]. Additionally, the introduction of fractional-order convolutional kernels has facilitated the compression of NN architectures, resulting in significant reductions in the number of trainable parameters [17]. These advancements underscore the versatility and efficacy of fractional derivatives in not only enhancing the performance of computer vision systems but also streamlining computational processes, thereby propelling the field towards more efficient and scalable solutions.

Based on the above, this work aims to conduct a survey of the FC NN-based computer vision techniques presented in the literature, focusing on the tasks of denoising, enhancement, object detection, segmentation, restoration, and NN compression. The aim is to compile various approaches and provide a concise yet intuitive explanation of the underlying concepts. Additionally, we aim to identify open questions and research directions that stem from each paper covered in this survey.

This paper is organised as follows. In Section 2, we provide a brief background to understand the basics of FC. Section 3 starts with a concise overview of computer vision and the various tasks it encompasses, namely denoising, enhancement, segmentation, object detection, restoration, and compression of NN architectures. Subsequently, for each task, we present the methods in the literature that combine FC and NN-based computer vision, concluding with a brief discussion of open questions and potential research directions arising from each method. Finally, the paper ends in Section 4 with the summary of the findings and conclusions drawn.

Table 1. List of symbols.

Symbol	Meaning
$α, β, γ$	Fractional-orders of the the derivatives
$D^{α} f (x)$	Fractional derivative of order $α$ of function $f (x)$
$D^{2} f (x)$	Second-order derivative of function $f (x)$
h	Step size
$t_{0}$	Arbitrary initial time
$t_{f}$	Arbitrary final time
$y (s)$	Input image
s	Pixel
$Φ (\cdot), Ψ (\cdot)$	Linear transformations
$u (t, s)$	Control input
$θ$	NN learnable parameters
$w_{k}$	Weight of layer k
$T_{↑}, T_{↓}$	Pooling and unpooling operation
$σ$	Non-linear operation
$l_{i}$	FOCNet of level i
$θ_{i}$	Learnable parameters of level i
$u_{t}^{l_{i} \pm 1}$	Upper-level and lower-level features
$I, J, K$	Pixel-wise width, length and depth of an image
$i, j, k$	Coordinates of a pixel
$X^{'}$	Denoised image
$L (θ)$	Loss function
$λ$	Hyperparameter
$S$	Sobel filter
$L$	Laplace filter
$A$	AFD mask
$M (i, j)$	Average gradient of a pixel
$t_{g}$	Gradient threshold
Q	Mean gradient of an image
$A G_{e d}, A G_{t e x}$	Average gradients of edges and textures
$R_{α}$	Rényi entropy
$p_{s}$	Normalised histogram of pixel intensities
M	Image moment
$μ$	Central moment
$\bar{x}, \bar{y}$	Image centroid
P	Legendre polynomial
L	Legendre moment
$\tilde{Y}$	Generated image
$S_{n}$	ScatNet layer
$S_{p o o l}$	ScatNet pooling
$Θ_{α}$	Fractional convolution operator
$ψ_{λ} (t)$	Wavelet function at scale $λ$
$ω$	Weighting hyperparameter
$G (i, j)$	Gaussian operator
$s t d$	Standard deviation
$F (i, j)$	Fractional convolutional filter
$i_{o}, j_{o}, k_{o}$	Parameters of a filter
l	Pixel-wise dimension of a filter
$I_{i n}, J_{i n}, D_{i n}$	Width, height and channels of the input feature map
$I_{o u t}, J_{o u t}, D_{o u t}$	Width, height and channels of the output feature map
$P_{i, j}$	Pooling region
$I n$	Input feature map
$O u t$	Output feature map
$a_{i}, b_{j}$	Hyperparameters for computing pooling windows

Table 2. List of abbreviations.

Abbreviation	Meaning
HOG	Histogram of Oriented Gradients
FC	Fractional Calculus
NN	Neural Network
ML	Machine Learning
CNN	Convolutional Neural Network
FDE	Fractional Differential Equation
FPDE	Fractional Partial Differential Equation
FOCNet	Fractional Optimal Control Network
F-ODE	Fractional Ordinary Differential Equations
TV	Total Variation
FTV	Fractional-order Total Variation
LDD	Left Down Direction
RUD	Right Up Direction
LUD	Left Up Direction
RDD	Right Down Direction
AFD	Adaptive Fractional-order Differential
AFDA	Adaptive Fractional-order Differential Algorithm
RCNN	Region-based Convolutional Neural Network
YOLO	You Only Look Once
SSD	Single-Shot Detector
FrOLM-DNN	Fractional-Order Lagrange Moments Deep Neural Network
LSF	Level-Set Function
PDE	Partial Differential Equation
CeNN	Cellular Neural Network
VAE	Variational Autoencoder
GAN	Generative Adversarial Network
GSN	Generative Scattering Network
ScatNet	Wavelet Scattering Network
PCA	Principal Component Analysis
GFRSN	Generative Fractional Scattering Networks
FrScatNet	Fractional Wavelet Scattering Network
FMF	Feature-Map Fusion
FMP	Fractional Max-Pooling

2. Fractional Calculus

Contrary to popular belief, fractional differential calculus is not a recent subject. For example, the symbol

d^{n} y / d x^{n}

was first proposed by Leibniz, and, in 1695, L’Hôpital asked Leibniz about the meaning of

d^{1 / 2} y / d x^{1 / 2}

, effectively asking, "What if n is fractional?". Leibniz responded:

"Although infinite series and geometry are distant relations, infinite series admits only the use of exponents that are positive and negative integers and does not, as yet, know the use of fractional exponents."

He continued, "This is an apparent paradox from which, one day, useful consequences will be drawn."

This correspondence can be seen as the beginning of fractional differential calculus. The term "fractional" comes from L’Hôpital’s question about the fraction

1 / 2

, although the order of differentiation can be any real or complex number. From this letter, we learn that classical and fractional differential calculus were conceived almost simultaneously [2,18,19,20]. In 1716, Leibniz died, but the interest in understanding derivatives of fractional (non-integer) order increased. Several other authors devoted their time to this subject, and the well-known Leonard Euler also contributed to the understanding and generalisation of fractional differential calculus. He extended the notion of the factorial,

n!

, to non-integer values. This extension was later named the Gamma function,

Γ (.)

, by Adrien-Marie Legendre around 1811,

Γ (z) = \int_{0}^{\infty} t^{z - 1} e^{- t} d t

where

ℜ (z) > 0

. The Gamma function plays a crucial role in defining generalised derivatives, as shown next.

The idea of generalising derivative and integral operators to an order n seems simple because one only needs to obtain operators that can be defined for non-integer n values and that match the classical operators when n is an integer. Consequently, several definitions have been proposed in the literature by different authors. Since this work is not a survey on fractional calculus, only three definitions of fractional derivatives will be considered here: the Riemann-Liouville and Caputo definitions (often used in applications to physics and engineering), and the Grünwald-Letnikov definition, which seems to be preferred in NN-based computer vision.

The Riemann-Liouville and Caputo fractional derivatives will now be introduced. However, before defining these derivatives, we will first provide the definition of a fractional integral. For that, recall the Fundamental Theorem of Calculus:

Theorem 1. 1.

Fundamental Theorem of Calculus:Let

f : [a, b] \to R

be a continuous function, and let

F : [a, b] \to R

be defined by

F (x) = \int_{a}^{x} f (t) d t .

Then, F is differentiable and

F^{'} = \frac{d F}{d t} = f .

In order to write in a more compact way some of the results to come, we now define the following differential and integral operators.

Definition 1.

Derivative and Integral Operators:We denote by D the differential operator that maps a function f into its derivative

D f (x) = f^{'} (x)

and by

J_{a}

the integral operator that maps a funtion

f (x)

into its primitive (whenever the integration can be performed on the compact interval

[a, b]

J_{a} f (x) = \int_{a}^{x} f (t) d t, x \in [a, b]

These operators can be generalized to perform n-fold iterates:

D^{n} f (x) = \frac{d}{d t} . . . \frac{d}{d t} \frac{d f}{d t} = D^{1} D^{n - 1} f (x),

J_{a}^{n} f (x) = \int_{a}^{x} . . . \int_{a}^{x} \int_{a}^{x} f (t) d t = J_{a}^{1} J_{a}^{n - 1} f (x) .

The following Lemma introduces a way to write the n-fold integral using only one integral symbol:

Lemma 1.

n-fold Integration:Let f be Riemann integrable on

[a, b] .

Then, for

a \leq x \leq b

and

n \in N

, we have

J_{a}^{n} f (x) = \frac{1}{(n - 1)!} \int_{a}^{x} {(x - t)}^{n - 1} f (t) d t .

To generalise the previous integral to non-integer orders, one simply needs to replace

(n - 1)!

with the Gamma function defined earlier,

Γ (n)

, taking into account that

Γ (n) = (n - 1)!, n \in N

Definition 2.

Riemann-Liouville Fractional IntegralLet

n \in R_{+}

and

J_{a}^{n}

be the operator defined on

L_{1} [a, b]

J_{a}^{n} f (x) = \frac{1}{Γ (n)} \int_{a}^{x} {(x - t)}^{n - 1} f (t) d t, x \in [a, b] .

Then

J_{a}^{n}

is called the Riemann-Liouville fractional integral operator of order n.

The fractional derivative is obtained by performing a derivative (of a certain integer order) of the fractional integral just defined. This implies that fractional derivatives may depend on integral operators.

Recall that in the classical case (integer orders), we have the following lemma:

Lemma 2.

n-fold Integration:Let

m, n \in N

with

m > n

, and let f be a function with a continuous

n^{th}

derivative on the interval

[a, b]

. Then,

D^{n} f = D^{m} J_{a}^{n - n} f .

Therefore, a generalisation of this lemma leads to the definition of a Riemann-Liouville Fractional Derivative [19]:

Definition 3.

Riemann-Liouville Fractional Derivative:Let

α \in R_{+}

and

m = ⌈ α ⌉

. The Riemann-Liouville fractional derivative of order α (

{}_{a}^{R}D_{t}^{α} f

) is given by

{}_{a}^{R}D_{x}^{α} f (x) = D^{m} J_{a}^{m - α} f (x) = \frac{D^{m}}{Γ (m - α)} \int_{a}^{x} {(x - t)}^{m - α - 1} f (t) d t .

For

n = 0

we have

{}_{a}^{R}D_{t}^{0} : = I

This definition of the fractional derivative generalises the classical case of integer order derivatives. However, it may lead to properties that could be seen as less appealing. For instance, the Riemann–Liouville derivative of a constant is not zero. Although, if we exchange the order of integration and differentiation, this less appealing characteristic can be easily supressed, and we obtain a new definition of fractional derivative, proposed by M. Caputo [21]:

Definition 4.

Caputo Fractional Derivative:Let

α \in R_{+}

m = ⌈ α ⌉

and

D^{m} f (t) \in L_{1} ([a, b])

. The Caputo fractional derivative of order α

({}_{a}^{C}D_{t}^{α} f)

is given by

{}_{a}^{C}D_{x}^{α} f (x) = J_{a}^{m - α} D^{m} f (x) = \frac{1}{Γ (m - α)} \int_{a}^{x} {(x - t)}^{m - α - 1} D^{m} f (t) d t .

Note the resemblance with the Riemann-Liouville fractional derivative.

These two definitions of fractional derivatives have expressions that depend on integrals. Therefore, besides the property of order generalisation, they are often used in modelling physical problems where memory is an important factor. At each instant, the integral computes the past history. The range of applications for generalised derivatives is immense. Consequently, many recent works have used these general operators.

There is another definition of fractional derivative that has captured the attention of many researchers. This definition is based on classical differentiation and seems to be more intuitive. Grünwald (1867 [22]), Post (1930 [23]) and Letnikov (1872 [24]) presented the idea of the fractional derivative as the limit of a sum.

It is well known that a classical derivative can be approximated as a limit of difference quotients. For example,

f^{'} (x) = D^{1} f (x) = lim_{h \to 0} \frac{f (x) - f (x - h)}{h}

We know that:

\begin{matrix} \nabla_{h}^{1} f (x) = & f (x) - f (x - h) \\ \nabla_{h}^{2} f (x) = & \nabla_{h}^{1} f (x) - \nabla_{h}^{1} f (x - h) = f (x) - 2 f (x - h) + f (x - 2 h) \\ ⋮ & ⋮ \\ \nabla_{h}^{n} f (t) = & \sum_{k = 0}^{n} {(- 1)}^{k} (\begin{matrix} n \\ k \end{matrix}) f (x - k h) . \end{matrix}

where

(\begin{matrix} n \\ k \end{matrix}) = \frac{n (n - 1) \dots (n - k + 1)}{k!}

is the binomial coefficient. Therefore, we can state the following:

Theorem 2. 1.

Let

n \in N

f \in C^{n} ([a, b])

and

a < t \leq b

, then:

D^{n} f (t) = lim_{h \to 0} \frac{\nabla_{h}^{n} f (t)}{h^{n}}

For example, a second order derivative can be written as:

D^{2} f (x) = lim_{h \to 0} \frac{f (x) - 2 f (x - h) + f (x - 2 h)}{h^{2}} .

Grünwald and Letnikov, performed a generalization of this result to non-integer n values, leading to the following definition of fractional derivative:

Definition 5.

Let

α \in R_{+}

f (t) \in C^{⌈ α ⌉} ([a, b])

and

h_{N} = (t - a) / N

. The Grünwald–Letnikov fractional derivative of order α (

{}_{a}^{GL}D_{x}^{α} f

) is given by

{}_{a}^{GL}D_{x}^{α} f (x) = lim_{N \to \infty} \frac{\nabla_{h_{N}}^{α} f (t)}{h_{N}^{α}} .

with

\begin{matrix} \nabla_{h}^{α} f (x) = & \sum_{k = 0}^{\infty} {(- 1)}^{k} (\begin{matrix} α \\ k \end{matrix}) f (x - k h) . \end{matrix}

Note that

(\begin{matrix} α \\ k \end{matrix}) = \frac{Γ (α + 1)}{Γ (k + 1) Γ (α - k + 1)}

is the fractional binomial coefficient, a generalisation of the classical binomial coefficient to non-integer values [18].

To simplify the notation, we will drop the GL, and the Grünwald–Letnikov fractional derivative will be simply represented by

D^{α} f (x)

. It is also common to represent the derivative by making

h_{N} \to 0

, that is:

D^{α} f (x) = lim_{h_{N} \to 0} \frac{1}{h_{N}^{α}} \sum_{k = 0}^{\infty} {(- 1)}^{k} \frac{Γ (α + 1) f (x - k h)}{Γ (k + 1) Γ (α - k + 1)} .

This definition allows for the discretisation of fractional derivatives, enabling their computation using simple finite differences. Note that there are various definitions of fractional derivatives, each with its own advantages and disadvantages (the interested reader should consult [20]).

In computer vision, integer-order calculus plays a pivotal role. Techniques such as gradient-based edge detection use derivatives to identify abrupt changes in intensity, forming the foundation of edge detection algorithms. Furthermore, integral calculus finds applications in image processing tasks such as convolution and filtering, where convolution operations are analogous to computing the integral of a function over a given region. The mathematical principles of diferential and integral calculus also form the foundation for numerous algorithms in feature extraction, object recognition, and image segmentation, allowing computers to effectively interpret and analyze visual information [25]. Therefore, in the following chapters, we present various works that use fractional calculus to enhance neural network-based computer vision. By fractional calculus, we mean works involving fractional derivatives or generalising integer-order operations (e.g., using the Gamma function instead of the factorial, or employing non-polynomials or polynomials of non-integer order instead of classical polynomials, etc). While some studies use fractional optimisation algorithms to optimise neural network parameters for computer vision tasks, this survey focuses exclusively on methods that leverage fractional calculus to modify or contribute to the architecture, such as in feature extraction or image enhancement.

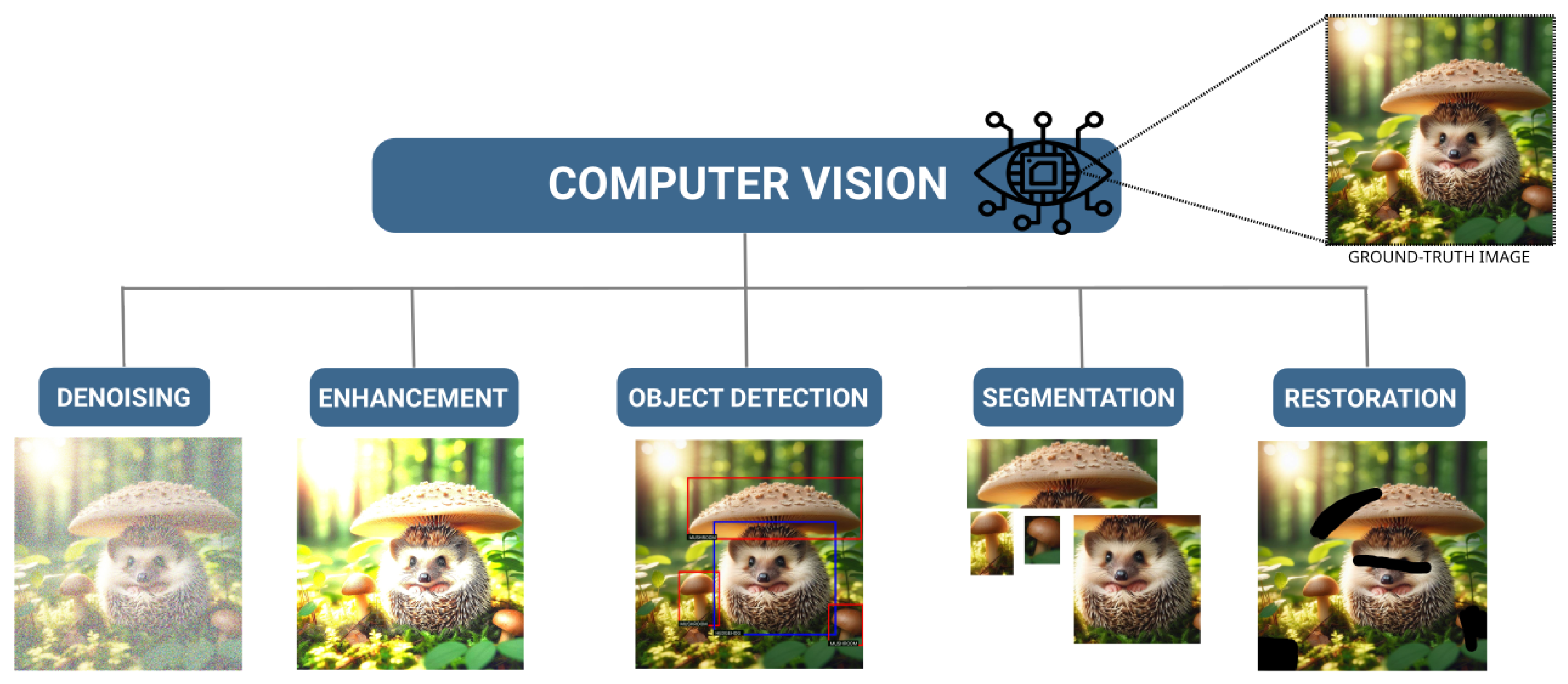
3. Computer Vision

Computer vision encompasses a diverse range of tasks, ranging from denoising and enhancement to object detection, segmentation, and restoration, Figure 1.

Recent advancements in literature have shown significant performance improvements in computer vision, and therefore, in this section we introduce and elaborate on neural network architectures and techniques that use fractional calculus to enhance computer vision tasks. These innovative approaches not only improve tasks’ performance but also contribute to reducing the computational cost associated with NN-based computer vision systems, making them more practical and scalable for real-world applications.

Ground-truth image generated by DALL-E 3.

3.1. Denoising

Image denoising is the process of removing unwanted noise from digital images to enhance their visual quality and improve the accuracy of subsequent analysis or processing tasks. Noise in images can arise from various sources, including sensor limitations, transmission errors, or environmental factors during image capture. The goal of denoising algorithms is to distinguish between the true signal representing the underlying scene and the undesirable noise components, then attenuate or eliminate the noise while preserving important image features. This typically involves applying filters or statistical techniques tailored to suppress noise, thus resulting in cleaner and more visually appealing images suitable [26].

Image denoising using FC has emerged as a promising approach to address the challenges posed by noise in digital images, offering advantages over traditional methods. By leveraging the memory effects and long-range interactions inherent in fractional calculus, researchers have developed novel denoising algorithms capable of preserving image details while effectively suppressing noise. Several works in the literature have explored this approach, with more contributions continuously being made [27,28,29,30,31,32,33].

Due to their approximation capabilities, NNs have emerged as powerful tools in image denoising by learning the underlying structure of clean images and effectively differentiating between noise and true image features. These NNs are normally trained on pairs of noisy and clean images, where they learn to map noisy inputs to their corresponding clean versions. Convolutional Neural Networks (CNNs) are particularly well-suited for image denoising tasks due to their ability to automatically extract hierarchical features from images. Through iterative training processes, NNs find the optimal parameters that minimise the difference between the denoised output and the clean ground-truth image [34]. This approach has shown remarkable success in various applications, such as medical imaging [35], surveillance systems [36] and ocean biodiversity monitorisation [37], and others.

In the literature, only two works proposing the combination of fractional calculus (FC) and NN-based techniques for image denoising were found [38,39]. In [38], the authors propose formulating denoising as a variational problem, aiming to minimise a functional that incorporates fidelity to the observed noisy image and smoothness of the denoised image. Fractional-order derivatives are integrated into the regularisation term of the variational model, facilitating the preservation of edges and textures while reducing noise, denoted as Fractional-order Total Variation. In [39], the authors use weights given by FDEs to propagate the feature maps from one layer to the next, giving rise to the Fractional Optimal Control Network.

3.1.1. Fractional-Order Total Variation

Total Variation (TV) regularisation is a core technique for image denoising that preserves important features such as edges and textures, having the ability to effectively reduce noise while maintaining sharp transitions between regions of an image. Unlike simpler techniques, such as linear smoothing or median filtering, which can blur edges and details, TV regularisation exploits the inherent sparsity in the gradient of the image, penalising rapid changes in pixel intensity.

The TV regularisation can be formulated, using

L_{2}

norm, as [38]:

L_{TV} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sqrt{{(X^{'} (i + 1, j) - X^{'} (i, j))}^{2} + {(X^{'} (i, j + 1) - X^{'} (i, j))}^{2}}

or using the

L_{1}

norm:

L_{TV} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} | X^{'} (i + 1, j) - X^{'} (i, j) | + | X^{'} (i, j + 1) - X^{'} (i, j) |

where I and J are the width and length (number of pixels in the horizontal and vertical directions) of the image, respectively, i and j are the coordinates of a pixel in the image, and

X^{'}

is the denoised image [38]. The difference

X^{'} (i + 1, j) - X^{'} (i, j)

calculates the finite horizontal gradient, corresponding to the change in pixel value along the horizontal direction. Similarly,

X^{'} (i, j + 1) - X^{'} (i, j)

is the finite vertical gradient, representing the difference between adjacent pixels along the vertical direction.

The idea is straightforward. In addition to the classical loss function, which measures the difference between the ground truth and the result obtained from the Neural Network -

L_{error}

, a new loss function is introduced to aid in image denoising and artifact reduction. This new loss function is defined as:

L_{total} = L_{error} + λ L_{TV},

where

λ

is the regularisation hyperparameter. This parameter balances the fit of the model to the observed data (data fidelity term) with the smoothness or sparsity enforced by the regularisation term. A small regularisation parameter might lead to overfitting, where the model closely matches the training data but does not generalise well to new data. Conversely, a large regularisation parameter could overly smooth or simplify the solution, potentially causing the loss of important features or details. In essence,

λ

controls the significance of the TV loss in the optimisation process. This exploits the inherent sparsity in the gradient of the image, penalising rapid changes in pixel intensity [40].

TV fails to fully use the information from neighbouring pixels, which can lead to artifacts in images. To address this limitation, fractional-order differences have been proposed for processing this gradients. The fractional variations inherently incorporate information from neighbouring pixels, allowing them to draw data not only from adjacent pixels but also from more distant ones. Consequently, fractional-order differences can theoretically capture richer pixel information and reduce artifacts.

Taking this into account, in [38] the authors proposed a new NN-based denoising model that incorporates Fractional-order TV (FTV) regularisation into the loss function. To the best of our knowledge, this was the first time FTV was used in conjunction with a NN, however, multiple studies have compared NN-based methods to FTV filters [41,42,43]

FTV is therefore an extension of TV regularisation proposed in [44], by introducing a fractional exponent

α

to the TV term.

In [38], the authors proposed a modified FTV regularisation that that computed the fractional gradient in eight directions around each pixel, namely

x^{-}, y^{-}, x^{+}, y^{+}

, Left Down Direction (LDD), Right Up Direction (RUD), Left Up Direction (LUD) and Right Down Direction (RDD):

\begin{matrix} L_{FTV} = & \sum_{i = 1}^{I} \sum_{j = 1}^{J} | D_{x^{+}}^{α} X^{'} | + | D_{y^{+}}^{α} X^{'} | + | D_{x^{-}}^{α} X^{'} | + | D_{y^{-}}^{α} X^{'} | + | D_{L D D}^{α} X^{'} | + \\ | D_{R U D}^{α} X^{'} | + | D_{L U D}^{α} X^{'} | + | D_{R D D}^{α} X^{'} |, \end{matrix}

where each term

D^{α}

corresponds to applying a fractional differential mask (using an approximation to the Grünwald-Letnikov derivative) in the corresponding direction,

x^{-}, y^{-}, x^{+}, y^{+}

, LDD, RUD, LUD, RDD. For example, in the horizontal direction x, we have that:

D_{x^{+}}^{α} X^{'} = [\begin{matrix} \dots & \dots & \dots & \dots \\ 0 & 0 & 0 \\ C_{S_{- 1}} & C_{S_{0}} & \dots & C_{S_{n}} \\ 0 & 0 & \dots & 0 \\ \dots & \dots & \dots & \dots \end{matrix}], D_{x^{-}}^{α} X^{'} = [\begin{matrix} \dots & \dots & \dots & \dots \\ 0 & 0 & 0 \\ C_{S_{n}} & C_{S_{n - 1}} & \dots & C_{S_{- 1}} \\ 0 & 0 & \dots & 0 \\ \dots & \dots & \dots & \dots \end{matrix}] .

Here, n is the last entry, with entries derived from the Grünwald-Letnikov derivative, being given by:

C_{S_{k}} = \frac{1}{Γ (- α)} [\frac{Γ (k - α + 1)}{(k + 1)!} \cdot (\frac{α}{4} + \frac{α^{2}}{8}) + \frac{Γ (k - α)}{k!} \cdot (1 - \frac{α^{2}}{4}) + \frac{Γ (k - α - 1)}{(k - 1)!} \cdot (- \frac{α}{4} + \frac{α^{2}}{8})],

with k the entry of the fractional differential mask being computed [38].

The FTV regularisation is then added to the loss function of deep learning methods with the aim of preserving texture and enhancing details [38].

L_{total} = L_{error} + λ L_{FTV},

The method of adding FTV to the loss function of NN-based models for image denoising is still very new and there hasn’t been much research in this area yet. One significant study that used this method is found in [45], which focused on classifying environmental sounds. This shows that the field has many unexplored areas, such as understanding how the choice of the

α

value affects the results and whether it’s possible to include more than one FTV regularisation term with different

α

values in the loss function.

3.1.2. Fractional Optimal Control Network

Fractional Optimal Control Network (FOCNet) is a NN architecture designed for denoising tasks, leveraging the principles of Fractional Ordinary Differential Equations (F-ODEs) to propagate features depth-wise within the network. This architecture exploits the memory persistence inherent in F-ODEs, enabling enhanced denoising performance compared to traditional NN approaches. The underlying methodology of FOCNet involves solving a Fractional Optimal Control problem [39]:

\begin{matrix} \min_{θ (t)} & \frac{1}{2} \int_{ω} (Φ (u (T, s)) - x (s))^{2} d s \\ s . t . & D_{t}^{α} u (t, s) = f (u (t, s), θ (t)), \\ u (0, s) = Ψ (y (s)), t \in [0, T] \end{matrix}

where

y (s)

represents the input image to be denoised, with s a pixel,

x (s)

denotes the corresponding ground-truth image,

Φ (\cdot)

and

Ψ (\cdot)

denote linear transformations (such as convolutions) that are predefined, and

u (t, s)

represents the control input. The function

f (u (t, s), θ (t))

describes the dynamics of the system, parameterised by a NN [39].

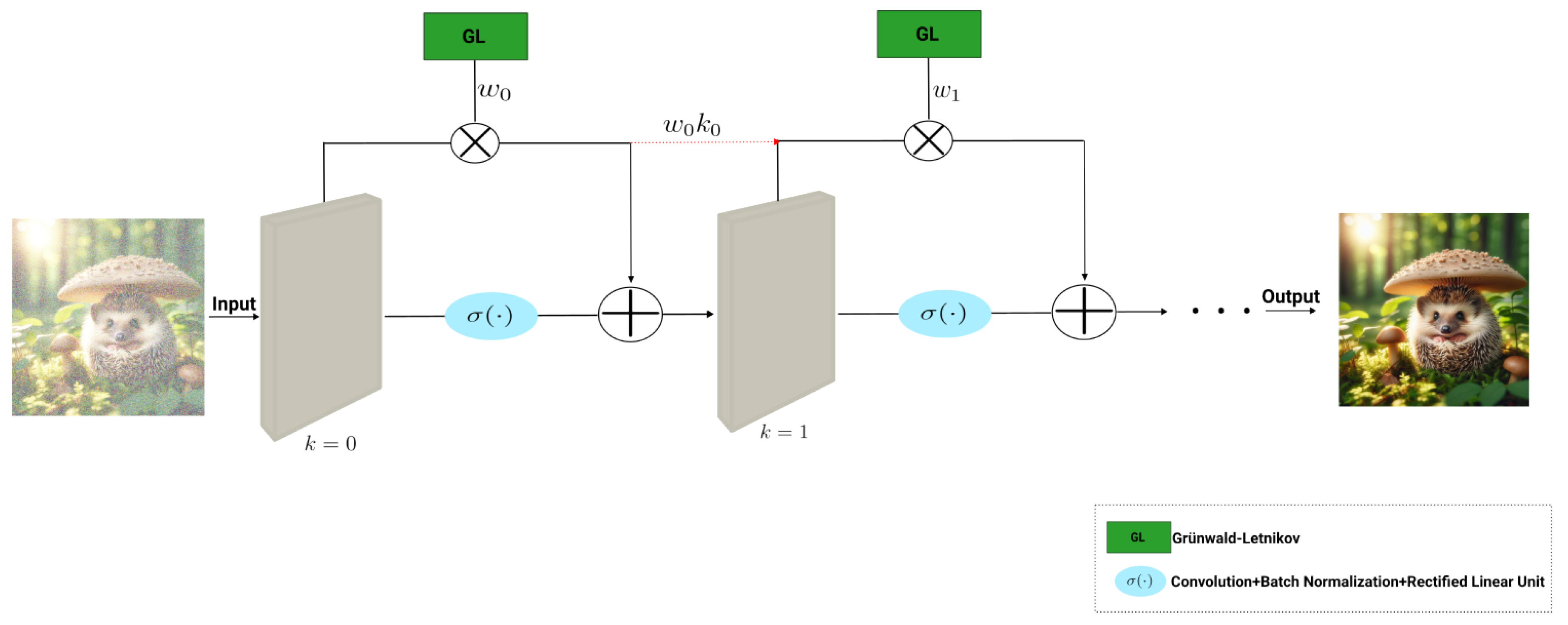
FOCNet conceptualises the NN as an infinite-depth architecture, where to each layer’s output the previous layers’ outputs are added, multiplied by a weight

w_{k}

given by discretising an F-ODE using Grünwald-Letnikov [39], Figure 2:

u_{t + 1} = \sum_{k = 0}^{t} w_{k} u_{k} + σ (θ_{t} u_{t}), with w_{k} = {(- 1)}^{t - k + 2} (\binom{α}{t - k + 1}) .

where

u_{t + 1}

is the output of layer

t + 1

, k denotes all previous layers

0 < k < t

and

σ

is a nonlinear operation given by convolution followed by batch normalisation and Rectified Linear Unit [39].

This approach enables the propagation of features from one layer to another throughout the network, enabling effective feature extraction and denoising. Thus, the usage of F-ODE allows to give weights to each layers contribution to the end result [39].

The goal of FOCNet is to optimise the denoising process by minimising the difference between the denoised image and the ground-truth image. This is achieved by iterative adjustment of the parameters

θ (t)

of the NN, guided by the solutions to the Fractional Optimal Control problem, (Section 3.1.2). To discretize the fractional-order dynamics system inherent in FOCNet, the Grünwald-Letnikov fractional derivative definition is employed [39].

In comparison to traditional denoising NNs (not FC-based), the FDE enables the NN to assign weights to each layer’s contribution to the end result. This is because F-ODEs provide a mathematical framework for describing the dynamics of the system (denoising process), including the propagation of features and the influence of different network layers on the final output [39].

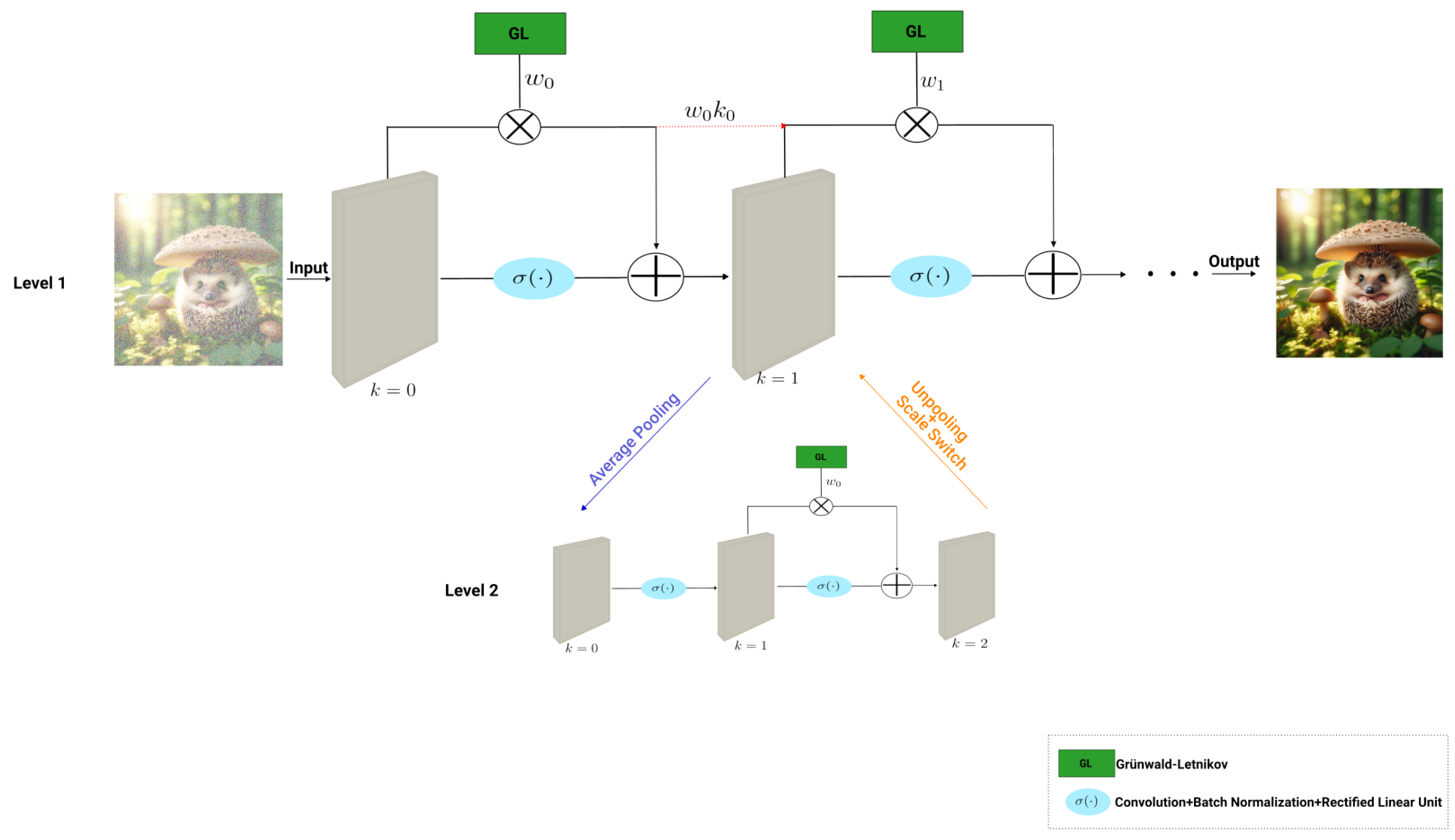
The literature has extensively demonstrated the benefits of using multiple scales of the same image to extract diverse features, thus enhancing the NN’s capacity for feature extraction. Building upon this, in [39], the authors extended FOCNet to incorporate multi-scale representations given rise to a multi-level architecture.

The Multi-scale FOCNet architecture comprises multiple hierarchical levels, with each level representing a distinct scale and containing a dedicated FOCNet, (Section 3.1.2). This modification enables the network to capture and retain both previous features and features across different scales, facilitating the long-term memory mechanisms inherent in FDEs. Unlike the standard FOCNet (Section 3.1.2), the denoising process in the multi-scale version incorporates an additional step. This step involves the application of a function

g (x) = w T (x)

, where

w \in 0, 1

and

T (\cdot)

represents a pooling or unpooling operation, enabling the propagation of contributions from lower-level layers to higher-level layers. The denoising process within the multi-scale FOCNet can be formulated as [39]:

\{\begin{matrix} D_{t}^{α} u (t, s, l_{1}) = f (u (t, s, l_{1}), g (u (t, s, l_{1 + 1}), θ_{1} (t))) \\ D_{t}^{α} u (t, s, l_{2}) = f (u (t, s, l_{2}), g (u (t, s, l_{2 \pm 1}), θ_{2} (t))) \\ \dots \\ D_{t}^{α} u (t, s, l_{i}) = f (u (t, s, l_{i}), g (u (t, s, l_{i + 1}), θ_{i} (t))) \\ u (0, s, l_{1}) = Ψ y (s) \\ u (0, s, l_{i}) = T_{↓} u (1, s, l_{i - 1}) \\ 1 \leq l_{i} \leq k \\ 0 \leq t \leq T, \end{matrix}

where

l_{i}

represents the FOCNet level i (with

l_{1}

denoting the original level),

θ_{i}

denotes the parameters of the corresponding level,

u_{t}^{l_{i} \pm 1}

denotes either the upper-level feature

u_{t}^{l_{i} + 1}

or the lower-level features

u_{t}^{l_{i} - 1}

, and

T ↓

is a pooling operation [39].

The computation to get the result of each layer is now more complex,

u_{t + 1}^{l_{i}} = \sum_{k = 0}^{t} w_{k} u_{k}^{l_{i}} + σ (θ_{i} (u_{t}^{l_{i}} + g (u_{t}^{l_{i} \pm 1}))),

aiming at strengthening the NN by promoting cross-level feature interactions[39], Figure 3.

The work presented in [39] prompts several research questions and potential directions for further investigation. Firstly, the choice of fractional derivative definition remains largely unexplored and warrants discussion or justification to provide insight into why a particular definition was selected over others. Moreover, considering that FOCNet extracts scaling features at various levels and combines them, there’s potential for enhancing its performance by employing different strategies for combining these features. Currently, in FOCNet, each level’s features contribute equally, but introducing weighting factors could be an intriguing avenue to explore. Adjusting the contribution of features at different levels could potentially improve the network’s ability to capture and leverage hierarchical information effectively.

3.2. Enhancement

Image enhancement is the process of improving the visual quality or perception of digital images by manipulating their attributes such as brightness, contrast, sharpness, and colour balance. Unlike denoising, which specifically targets noise reduction, image enhancement aims to enhance the overall appearance of images to make them more visually appealing or suitable for specific applications. Enhancement techniques can range from simple adjustments like histogram equalisation or contrast stretching to more advanced algorithms such as image fusion or super-resolution. These techniques can be used to highlight important features, improve visibility in low-light conditions, or adapt images for specific display or analysis requirements [46].

Image enhancement using FC is a well explored field with several works showing the advantages over traditional methods that rely on integer calculus. The construction of masks and filters with fractional orders has opened the possibility of attaining in-between behaviours of traditional masks, offering enhanced flexibility and performance in image enhancement tasks [8,47,48,49,50,51,52,53].

In image enhancement, NNs learn from image datasets to understand what constitutes an enhanced or improved version of an image. CNNs are a very popular architecture that by analysing these image pairs, it learns to identify patterns and relationships between low-quality features and their desired improvements. During image enhancement, the CNN takes a low-quality image as input and processes it through its layers, making adjustments to brightness, contrast, noise levels, and other visual aspects. Furthermore, NNs have also shown high efficacy in learning masks and filters to perform tasks such as edge enhancement, texture synthesis, and artefact removal [46]. The use of NNs for image enhancement has emerged as a powerful tool in several applications, such as the detection of diseases in plants [54], downsampling of temperature climatic maps [55], and the enhancement of medical imaging [56].

The authors could only find two works leveraging NNs for improving image enhancement can be found in the literature, which will be herein discussed [16,57].

In [16], the authors propose using NNs to learn the best fractional order for the masks, demonstrating promising results in image enhancement tasks.

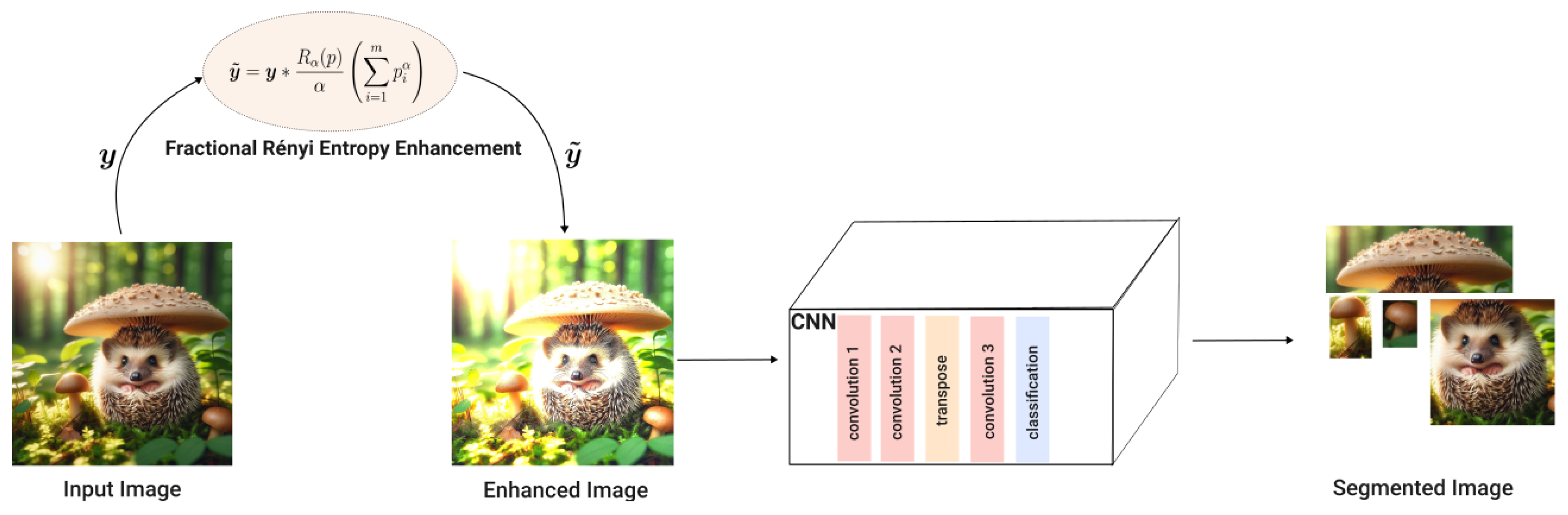
In [57], the authors propose using fractional Rényi Entropy to enhance images before feeding them into a NN for image segmentation purposes. The results show higher performance on segmentation is achieved when compared with other methods.

3.2.1. Neural Fractional-order Adaptive Masks

Masks (or kernels) and filters are mathematical operators applied to images that enhance the quality of images easing the extraction of relevant features such as patterns and structures. Masks are matrices that are applied to the pixels in an image to perform a specific operation, such as edge detection and convolution, two very popular masks are Sobel and Lapalace [25].

The Sobel mask consists of two

3 \times 3

convolution masks, one to detect horizontal changes and the other to detect vertical changes in intensity within an image [25]:

S_{x} = [\begin{matrix} + 1 & 0 & - 1 \\ + 2 & 0 & - 2 \\ + 1 & 0 & - 1 \end{matrix}] * y (s)

S_{y} = [\begin{matrix} + 1 & + 2 & - 1 \\ 0 & 0 & 0 \\ + 1 & - 2 & - 1 \end{matrix}] * y (s)

where

y

is the input image,

S_{x}

and

S_{y}

are the image with the horizontal and vertical gradients, respectively, and * is a convolution operation. The resulting gradient magnitude image is obtained by combining the horizontal and vertical gradient images using the Euclidean norm [25]:

S = \sqrt{S_{x}^{2} + S_{y}^{2}}

This operation highlights regions of significant intensity variation, effectively detecting edges in the image. The Sobel mask is commonly used in edge detection and various other image processing tasks due to its simplicity and effectiveness. Sobel masks belong to the category of first-order masks since they compute the first-order derivative of image intensity with respect to spatial coordinates [25].

In contrast, Laplace mask computes the second-order spacial derivative of image intensity, having the same mask for vertical and horizontal convolution [25]:

L_{x} = [\begin{matrix} 0 & + 1 & 0 \\ + 1 & - 4 & + 1 \\ 0 & 1 & 0 \end{matrix}] * y (s)

The Sobel and Laplace masks are both widely used for edge detection, however their approach and characteristics differ, each offering unique advantages and disadvantages. The Sobel mask, which consists of a separate mask for horizontal

S_{x}

and vertical gradients

S_{y}

, excels at detecting edges with a clear orientation, providing detailed information about the direction of intensity changes within an image. Its structured design makes it robust to noise and suitable for detecting edges in noisy environments. However, the Sobel mask struggles to detect edges at corners or junctions accurately, as it only emphasises the dominant direction of change at each pixel. In contrast, the Laplace mask detects edges regardless of their orientation and is sensitive to abrupt intensity changes, making it effective in this case. Yet, it is more sensitive to noise compared to the Sobel mask, leading to potential false edges detections in noisy images [8,25].

Due to the advantages and disadvantages inherent in the first- and second-order masks, coupled with the established theoretical foundations of fractional calculus, the exploration and refinement of fractional-order masks has been an active and growing field of research [8,58]. These masks offer a balance, leveraging the precision of higher-order derivatives while retaining the adaptability and noise resilience typically associated with lower-order operators.

A problem that persists in fractional-order masks lies in their uniform treatment of the entire image with the same fractional order. This approach can lead to the excessive enhancement of low spatial frequency content, potentially overshadowing the subtler details within the image, while simultaneously failing to adequately boost high-frequency components [16].

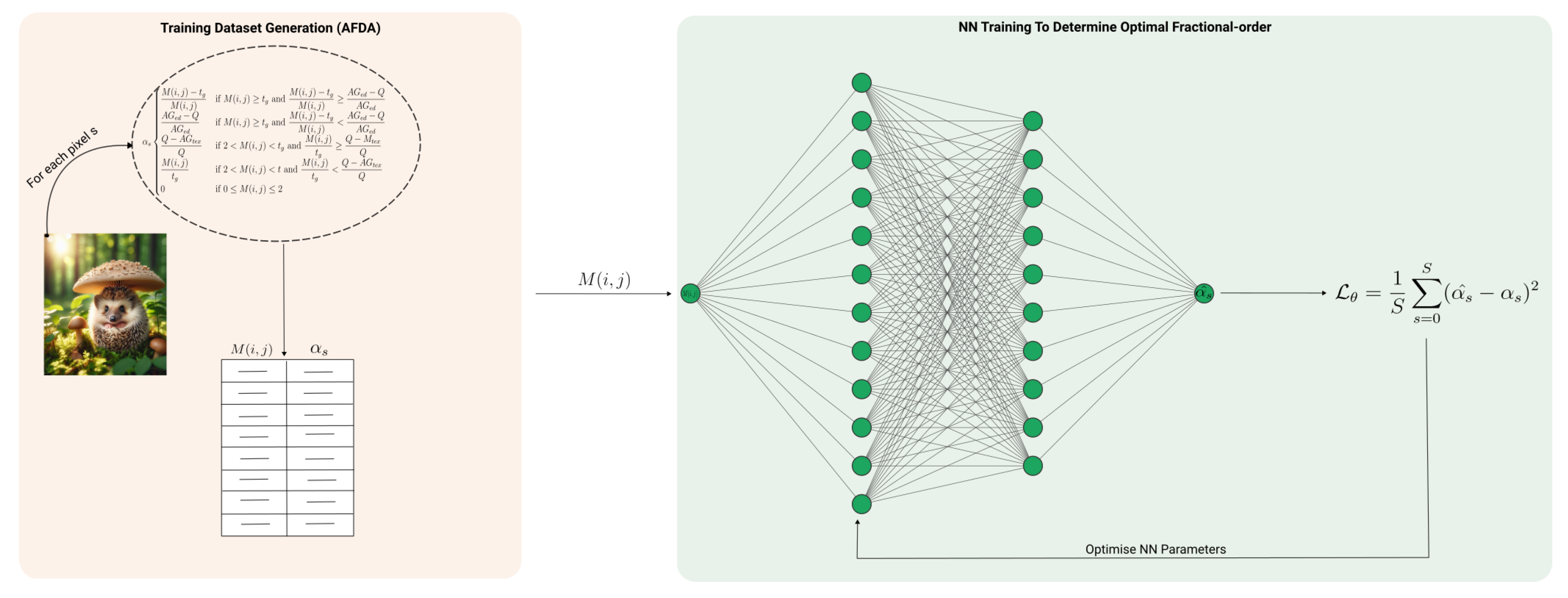
Keeping this in mind, in [16] the authors propose the Adaptive Fractional-order Differential (AFD) mask. This approach uses a NN to dynamically determine the optimal order of differentiation

α

. The goal is to train a NN to optimise the orders of the mask for any given image.

The AFD mask comprises two

3 \times 3

convolutional matrices, horizontal

A_{x}

and vertical

A_{y}

, derived from the Grünwald-Letnikov derivative definition (see [16] for details on the derivation process):

A_{x} (s) = [\begin{matrix} 0 & \frac{α_{s}^{2} - α_{s}}{2} & 0 \\ 0 & - α_{s} & 0 \\ 0 & 0 & 0 \end{matrix}] * y (s)

A_{y} (s) = [\begin{matrix} 0 & 0 & 0 \\ \frac{α_{s}^{2} - α_{s}}{2} & - α_{s} & 1 \\ 0 & 0 & 0 \end{matrix}] * y (s) .

The

α_{s}

values for each pixel of the image are determined by a NN with learnable parameters

θ

. These values are computed from the average gradient of the pixel in eight directions

M (i, j)

. To train the NN, the authors propose using a training dataset generated by employing a piece-wise function that dictates the

α_{s}

order of each pixel. This function is specified by the AFD Algorithm (AFDA) [16]:

α_{s} = \{\begin{matrix} \frac{M (i, j) - t_{g}}{M (i, j)} & if M (i, j) \geq t_{g} and \frac{M (i, j) - t_{g}}{M (i, j)} \geq \frac{A G_{e d} - Q}{A G_{e d}} \\ \frac{A G_{e d} - Q}{A G_{e d}} & if M (i, j) \geq t_{g} and \frac{M (i, j) - t_{g}}{M (i, j)} < \frac{A G_{e d} - Q}{A G_{e d}} \\ \frac{Q - A G_{t e x}}{Q} & if 2 < M (i, j) < t_{g} and \frac{M (i, j)}{t_{g}} \geq \frac{Q - M_{t e x}}{Q} \\ \frac{M (i, j)}{t_{g}} & if 2 < M (i, j) < t_{g} and \frac{M (i, j)}{t_{g}} < \frac{Q - A G_{t e x}}{Q} \\ 0 & if 0 \leq M (i, j) \leq 2 \end{matrix}

where

t_{g}

is a hyperparameter for the gradient threshold for edges, Q is the mean gradient of the image

y

A G_{e d}, A G_{t e x}

are the average gradients of edges and textures, respectively. The computation of

M (i, j)

is as follows [16]:

M (i, j) = \frac{| 8 y (i, j) - y (i - 1, j - 1) - y (i - 1, j) - y (i - 1, j + 1) - y (i, j - 1) - y (i, j + 1) - y (i + 1, j - 1) - y (i + 1, j) - y (i + 1, j + 1) |}{8} .

So, to generate the NN training dataset, the AFDA is used to compute the NN’s input values,

M (i, j)

, and their corresponding

α_{s}

orders, which serve as the ground-truth output. Subsequently, the NN is trained to minimise the error between these ground-truth

α_{s}

values and the predicted

{\hat{α}}_{s}

values, for example using the Mean Squared Error [16], Figure 4.

Upon completion of training, the NN is capable of outputting the

α_{s}

orders of the masks to treat each corresponding pixel in the target image, providing the average gradient of the pixel as input [16].

The experimental results presented in [16] demonstrate that the proposed masks yield higher contrast, clearer edges, and enhance smooth areas and texture within the images. Additionally, it is observed that after training the NN to compute the mask orders, the computational requirements for determining these orders are reduced, leading to improved performance compared to using the AFDA by itself.

Although the approach presented in [16] demonstrates improvements over manual computation of derivative orders, there remains considerable scope for enhancement and exploration. Firstly, the authors employ a relatively simple NN architecture, leaving room for experimentation with more complex architectures that could potentially yield better results. Additionally, the rationale behind the choice of the Grünwald-Letnikov definition is not explicitly addressed by the authors, which poses an open question for further investigation. Furthermore, the learnt derivative orders may be constrained due to the training dataset being generated by the AFDA, which could limit the NN’s ability to learn optimal orders without extensive prior knowledge input. This suggests a need to explore alternative approaches to dataset generation and NN training to broaden the capabilities and flexibility of the model.

3.2.2. Fractional Rényi Entropy

Rényi entropy

R_{α} (y)

[59] is a measure of uncertainty or randomness within a probability distribution, commonly employed in information theory and computer vision to quantify diversity and uncertainty in pixel intensities or image features. For a greyscale image

y

, the Rényi entropy is defined as [60]:

R_{α} (y) = \frac{1}{1 - α} log (\sum_{s = 0}^{255} p_{s}^{α}), α \in [0, \infty]

where

p_{s}

is a normalised histogram of pixel intensities and

α \in N

is a parameter governing the focus on different parts of the probability distribution. When

α \to 1

, Rényi entropy reduces to Shannon entropy [61], indicating overall uncertainty in the image. For

α \neq 1

, Rényi entropy highlights various aspects of the distribution’s structure. As

α \to 0

, it emphasises the most frequent pixel intensities akin to min-entropy [62], suitable for capturing dominant image features. Conversely, as

α \to \infty

, it emphasises rare pixel intensities akin to max-entropy [62], valuable for detecting subtle textures or anomalies in the image [60].

Fractional Rényi Entropy extends the concept of Rényi entropy by extending

α

to non-integer values, allowing for a more refined characterisation of the uncertainty and complexity within a probability distribution. This generalisation enables a spectrum of entropy measures between the limit cases of

α = 1

and

α = 0

[57].

In [57], the authors point out that image contrast and quality are major factors in the quality of image segmentation techniques. To address this, the authors propose using Fractional Rényi Entropy for image enhancement before employing a CNN for segmentation, Figure 5.

The enhanced image

\tilde{y}

is obtained from the input image

y

through pixel-wise multiplication formulated as (for details see [57]):

\tilde{y} = y * \frac{R_{α} (p)}{α} (\sum_{i = 1}^{m} p_{i}^{α}) .

The fractional-order

α

is determined experimentally on the training dataset [57].

The findings in [57] suggest that employing Fractional Rényi Entropy enhances the robustness of the model against inhomogeneous intensity values and preserves spatial relationships between image pixels. Although promising, several questions remain unanswered, such as whether there are less time-consuming strategies for selecting the

α

value and whether the

α

value could be adaptively chosen for each image region. Addressing these questions could further improve the effectiveness and efficiency of the proposed approach.

3.3. Object Detection

Object detection is the process of locating and classifying objects within digital images or video frames. The primary objective of object detection is to accurately identify and locate instances of predefined object classes within the image, using bounding boxes or outlines delineating their positions. Then, a label or category is assigned to each detected object [63].

FC for object detection remains a relatively unexplored frontier, with limited research available in this area. Existing work focuses on exploiting fractional-order moments for feature extraction [64] and employing fractional-order populational and evolutionary optimisation strategies to refine the localisation of objects within images [65].

The field of object detection has undergone a revolutionary transformation with the widespread adoption of NNs, enabling the autonomous identification and location of objects. Numerous research efforts have propelled the development of several NN architectures with enhanced accuracy, faster inference speeds, or reduced computational costs. Among the most widely used architectures is the region-based convolutional neural network (RCNN) family [66], which includes variants such as Fast RCNN [67] and Faster RCNN [68]. These leverage a blend of convolutional layers for feature extraction and region proposal algorithms to pinpoint potential object locations. By scrutinising these regions individually, they are able to classify objects and predict bounding boxes. Moreover, the emergence of one-stage detectors, such as YOLO (You Only Look Once) [69] and SSD (Single-Shot Detector) [70] has enabled real-time object detection by directly predicting object classes and bounding boxes in a single pass. Through the usage of extensive datasets annotated with object labels, NNs acquire the ability to generalise across diverse object categories and accommodate variations in scale, orientation, and occlusion, thereby solidifying their indispensable role across applications spanning satellite surveillance [71,72], public parking management [73], robotics [74] and pest management [75].

The application of FC in NN-based techniques for object detection is still relatively new but shows promising results [64,76,77,78].

In [76], inspired by previous work [64], the authors propose leveraging fractional-order Legendre moments for feature extraction. These features are then used by a NN for object detection based on the extracted feature maps.

Additionally, in [77,78], the authors propose fractional-order population-based and evolution-based optimisation algorithms to improve the optimisation process of NN parameters. However, since this survey paper only focuses on methodologies that directly modify the NN architecture or preprocess input images before feeding them into the NNs, these works won’t be covered.

3.3.1. Fractional-Order Legendre Moment Invariants

Image moments are mathematical descriptors that are used to characterise the spatial distribution and properties of intensity values within an image. They are computed by integrating the intensities of the pixels in an image

y (i, j)

, where

i, j

are the spatial coordinates. The image moment

M_{p, q}

is defined as [79]:

M_{p, q} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} i^{p} j^{q} y (i, j),

where

p, q

are non-negative integers representing the order of the moment. These moments provide insights into various image attributes, such as centroid, area, orientation, and higher-order shape characteristics. Since these are translation dependent, central moments

μ_{p, q}

are often preferred as they are invariant to translation [79]:

μ_{p, q} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} {(i - \bar{i})}^{p} {(j - \bar{j})}^{q} y (i, j),

where

\bar{i}, \bar{j}

are the centroid of an image computed as

\bar{i} = \frac{M_{10}}{M_{00}}

and

\bar{j} = \frac{M_{01}}{M_{00}} .

Image moments are widely used for shape analysis and object recognition, as they provide valuable information about the location, size, and centre of objects within an image.

There are several moments commonly used in image analysis, each with unique properties and applications. Integer-order moments, such as Zernike, Legendre, and Chebyshev moments, are among the most widely employed due to their effectiveness in capturing different aspects of image content [79].

Legendre moments are a class of orthogonal moments used in image analysis to capture shape information and structural features within an image. These moments are derived from Legendre polynomials and are computed by integrating the pixel intensities of the image weighted by Legendre polynomials of integer degree, mathematically formulated as [79]:

L_{p q} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} P_{p} (i) P_{q} (j) y (i, j),

where

P_{p} (i)

and

P_{q} (j)

are Legendre polynomials of degree p and q, respectively. Legendre moments offer advantages such as orthogonality, compactness, and rotational invariance, making them well-suited for tasks such as pattern recognition, shape analysis, and image retrieval. Additionally, their robustness to noise and illumination variations enhances their utility in real-world applications. Legendre moments also provide a concise representation of image content while preserving important geometric and structural information, contributing to the development of efficient and effective image-processing techniques [80]. The Legendre polynomials

P_{p} (i)

can be computed using a recurrence formula given by:

P_{p + 1} (i) = \frac{(2 p + 1) (2 i - 1)}{p + 1} L_{p} (i) - \frac{p}{p + 1} L_{p - 1} (i), p \geq 1,

with

P_{0} (i) = 1, P_{1} (i) = 2 i - 1

P_{q} (j)

can be computed reciprocally.

Although integer-order moments offer valuable insights into overall shape and spatial distribution, they may lack the sensitivity required to accurately represent intricate features [64,80].

Fractional-order moments extend the concept of integer-order moments to non-integer values of

α

and

β

, offering a more refined characterisation of image properties. These moments

M_{α, β}

are formulated as:

M_{α, β} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} i^{α} j^{β} y (i, j),

where

α

and

β

are non-integer values. Fractional-order moments offer enhanced sensitivity to subtle variations in image structure and texture, enabling more precise analysis and interpretation. This heightened sensitivity allows for improved accuracy in locating Regions of Interest within the image [64].

Fractional-order Legendre moments are an extension of integer-order Legendre moments (Section 3.3.1). By allowing non-integer values for the degree of Legendre polynomials, these moments provide a more flexible and adaptive framework for image analysis. The fractional Legendre moment

L_{α, β}

is formulated as [64]:

L_{α, β} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} P_{α} (i) P_{β} (j) y (i, j),

where the Legendre polynomials

P_{α} (i)

can be computed using a generalisation of the recurrence formula (Section 3.3.1) and introducing the change of variable

i = 2 t^{a} - 1

(for details see [76]):

P_{α + 1}^{a} (t) = \frac{(2 α + 1) (2 t^{a} - 1)}{α + 1} L_{α}^{a} (t) - \frac{α}{α + 1} P_{α - 1}^{a} (t), α \geq 1,

with

P_{0}^{α} (t) = 1, P_{1}^{α} (t) = 2 t^{α} - 1 .

P_{q + 1}^{β} (t)

can be computed reciprocally.

The Fractional-order Legendre moments can be extended to be used in 3-dimensions enabling the representation of the features of 3-dimensional (3D) images much used in medical imaging. Thus, the 3d fractional Legendre moment

L_{α, β, γ}

can be formulated as:

L_{α, β, γ} = \sum_{i = 1}^{I} \sum_{j = 1}^{J} \sum_{k = 1}^{K} P_{α} (i) P_{β} (j) P_{γ} (k) y (i, j, k),

where

P_{α} (i), P_{β} (j), P_{γ} (k)

are the fractional-order Legendre polynomials of degrees

α, β, γ

along the

i, j, k

axis, respectively, and

y (i, j, k)

is a 3D image.

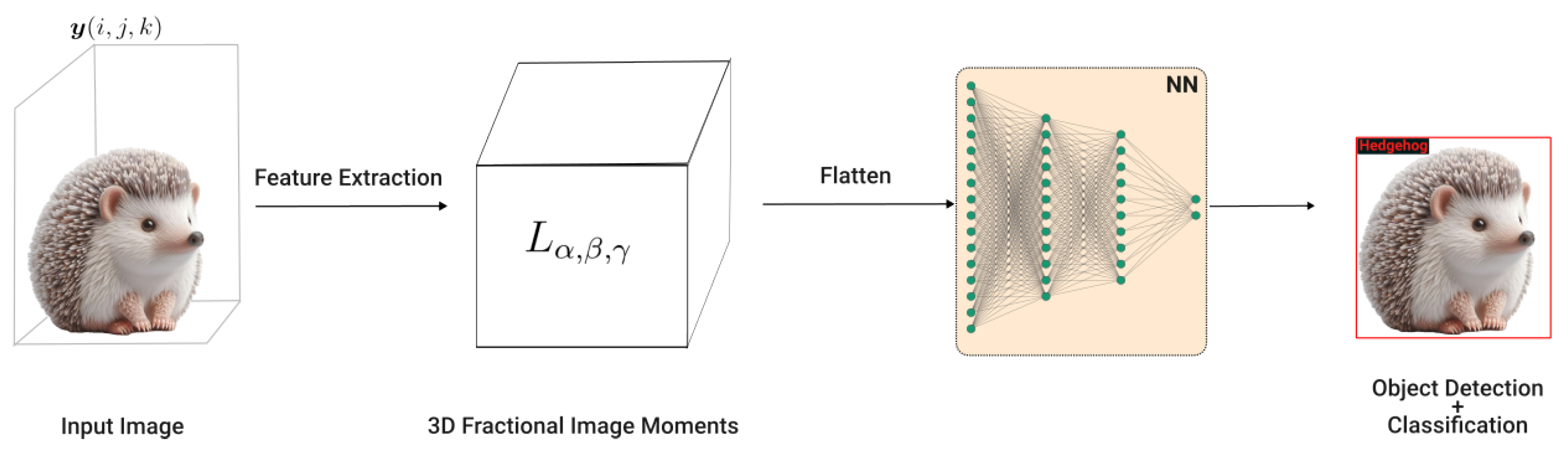
Motivated by the application of fractional-order moments for the classification of 2D objects, in [76] the authors propose using 3D fractional-order moments (for formulation details see [76]) as an input descriptor of a NN, thus giving rise to a new NN architecture, the Fractional-Order Lagrange Moments Deep NN (FrOLM-DNN).

The 3D fractional-order Legendre moments serve as an input descriptor for a NN. For each image, the moments are computed, forming a descriptor vector containing moments up to order r, where r is a user-selected hyperparameter. Subsequently, this descriptor vector is fed into the input layer of a NN, enabling the network to learn and classify the object within the image accurately. In this way, the 3D fractional-order Legendre moments function as a feature extractor, facilitating effective object classification [76], Figure 6.

Input image generated by DALL-E 3.

The main motivation for employing fractional-order moments lies in their additional parameters, which offer the potential for improved results tailored to specific use cases. The experimental results described in [76] demonstrate that the integration of 3D fractional-order moments with NN leads to improved classification accuracy compared to using them in isolation.

However, an open question raised in [76] is the impact of selecting the moments order r on the results and how to effectively determine the value of this hyperparameter. One potential avenue for future research involves devising a strategy to automate and optimise the selection of this parameter. By developing such a strategy, researchers can streamline the process of hyperparameter tuning and potentially improve the overall performance of the classification system.

3.4. Segmentation

Image segmentation is the process of partitioning a digital image into multiple segments or regions based on certain criteria such as colour, intensity, texture, or spatial proximity. The goal is to break an image into smaller parts, these segments often correspond to objects or regions of interest within the image, allowing for further analysis or manipulation at a more granular level.

The development of FC methods for image segmentation is a well-explored and rising field, with various approaches explored in recent literature. Some methods employ fractional-order optimisation algorithms to refine segmentation accuracy, while others introduce novel loss functions incorporating fractional orders. Additionally, established segmentation algorithms have been extended to accommodate fractional-order operations, enhancing performance on images with intricate textures [10,81,82,83,84,85].

CNNs are particularly well-suited for segmentation tasks due to their ability to effectively capture spatial dependencies and hierarchies of features within images. One of the most well-known architectures is the U-Net, which employs an encoder-decoder structure with skip connections to preserve spatial information and enhance segmentation accuracy [86]. Through training on annotated datasets, NNs learn to delineate boundaries and assign pixel-level labels to different regions within an image, effectively segmenting objects from the background or distinguishing between different object classes. Several successful applications can be found in the literature, from medical analysis of chest scans [87] to fingerprint security devices [88] and detection of road cracks [89].

While some research endeavours have incorporated FC into NN-based methods for image segmentation, the majority have primarily relied on fractional-order population-based optimisation algorithms to enhance the optimisation process of NN parameters [90,91,92]. However, this survey paper focuses on methodologies that directly modify the NN architecture or preprocess input images before feeding them into the NNs. In light of this, we highlight two notable works [15,92].

In [15], the authors use FOCNet [39] for image segmentation. In contrast, [92] propose the use of fractional-order differentiation active contour models for segmentation, employing a NN to solve fractional-order PDEs and thereby reducing the computational complexity associated with fractional-order active contour models.

3.4.1. Active Contour Detection With Fractional-Order Regularisation Term

Active contour models are tools particularly useful for segmenting objects with complex or ambiguous boundaries. These models are represented as a parametric curve or contour that evolves over time to minimise an energy functional. The contour is attracted to features of interest in the image while being constrained by factors such as smoothness and shape.

level-set Functions (LSF) are improved active contours that implicitly represent the contour as the zero level-set of a higher-dimensional function defined over a larger domain that includes the entire image. The evolution of the contour is described by the evolution of the level-set function, governed by a fractional-order partial differential equation (FPDE). The level-set methods evolve smoothly over the entire domain, and the contour is extracted as the zero level-set at each time step. level-set methods offer advantages in handling topological changes and complex contour deformations, making them suitable for tasks where the object boundaries are ill-defined or undergo significant changes over time [92].

Despite their differences, level-set methods and active contour models share the goal of accurately segmenting images by evolving contours to capture object boundaries. Level-set methods can be seen as a generalisation of active contour models, where the contour evolution is described implicitly through the evolution of a level-set function. This connection allows for the incorporation of active contour energy terms into level-set formulations, enhancing their versatility, robustness, and adaptability [92].

Variational level-set methods extend basic level-set techniques by incorporating variational principles into the formulation, enabling the optimisation of a variational energy functional to evolve contours over time. By formulating the segmentation problem as an optimisation task, variational level-set methods provide a systematic framework for integrating various constraints, prior knowledge, and image features into the segmentation process. This approach offers improved convergence, stability, and flexibility, having been successfully applied to challenging segmentation problems involving complex object shapes, noisy images, and topological changes [93].

The first instance of combining FDEs with active contour methods was introduced in [94]. In this work, a fractional-order differentiation active contour model was proposed, employing variational level-set methods. The energy function proposed in this model comprises three terms: a fractional-order fitting term, a regularisation term, and a penalty term. The fractional-order term enables a more precise representation of the image and improves the robustness to noise, while the penalty term ensures stable evolution [92,94].

Despite these advantages, this method incurs a significant computational burden [92]. To address computational cost, [92] proposes using Cellular Neural Networks (CeNNs) [95] to solve FPDEs instead of finite difference numerical schemes (see [92] for the mathematical formulation). CeNNs, composed of locally connected neurons arranged in a grid-like structure, offer stability, noise robustness, and time efficiency in computing solutions to FPDEs for active contour methods [92].

Due to the usage of FPDEs, that describe the temporal evolution of a system, an open area of research is the application of this approach for object tracking in temporal image sequences. Additionally, considering the popularity of physics-informed neural networks [96], it would be interesting to explore replacing CeNNs with this architecture in future studies.

3.4.2. FOCNet For Segmentation

In [15], the authors recognise the potential of FOCNet beyond denoising tasks. They propose to use the weighted skip connections of FOCNet to improve image segmentation performance, Figure 2. To facilitate segmentation using FOCNet, the authors suggest employing the Dice Coefficient as the loss function, which quantifies the similarity between the ground-truth and predicted segmentation masks. Hence, the distinction between FOCNet as proposed in [39] and in [15] lies in the choice of loss function and the nature of the training data. For denoising tasks, the input comprises a noisy image, with the corresponding ground-truth being the denoised version of the image [39]. Conversely, in segmentation tasks, the input consists of the original image, while the ground-truth represents the segmented image [15].

The usage of FOCNet for segmentation has demonstrated computational efficiency and outperformed other segmentation methods. The presence of fractional derivatives that determine the weights of the connections enables the propagation of information from shallower layers [15].

3.5. Restoration

Image restoration is the process of recovering an undistorted version of a digital image from a damaged or corrupted input. Degradation in images can occur due to various factors such as sensor limitations, time degradation or environmental factors. The goal is to complete the degraded images, making them suitable for analysis, interpretation, or presentation purposes. Restoration/inpainting techniques aim to reverse or mitigate the effects of degradation by applying mathematical models, filters, or learning-based algorithms to estimate and recover the original image underlying.

The usage of FC for enhancing image restoration and inpainting has received considerable attention in the literature, with numerous studies showcasing its performance advantages. These works demonstrate the efficacy of FC in modelling the intricate spatial and temporal variations present in image structures, leveraging information from surrounding areas to achieve more accurate restoration and inpainting results. By seamlessly integrating fractional-order techniques, these approaches effectively capture the nuanced in-between behaviours often overlooked by traditional integer-order methods [97,98,99,100,101].

The field of restoration has risen in popularity mostly due to architectures based on Variational Autoencoders (VAEs) [102] and Generative Adversarial Networks (GANs) [103] that offer novel approaches to image reconstruction. VAEs are renowned for their ability to learn rich probabilistic models of data, enabling them to effectively capture complex distributions in image space. By encoding input images into a latent space and then decoding them back to their original form, VAEs can learn to inpaint images while also providing uncertainty estimates [104]. On the other hand, GANs introduce a competitive training scheme between a generator network and a discriminator network, resulting in the generation of highly realistic images. In the context of restoration, GANs excel in producing visually convincing results by learning intricate details and textures from training data [105]. The success of NN architectures in image restoration has sparked various applications including restoring damaged historical texts [106], removing unwanted objects [107] and completion of medical scans [108].

The combination of FC and NN-based methods for image restoration/inpainting is almost not explored with only one work available [109]. Given the potential already demonstrated in the literature with the several works that are not using NNs, it comes easily that this is a promising field.

In their work [109], the authors introduce an innovative approach that leverages fractional-order wavelet transforms to enhance feature extraction within a NN encoder. Their methodology extends beyond traditional techniques by integrating fractional-order operations into the encoding process, enabling more nuanced and comprehensive feature representation. Moreover, the authors propose a novel strategy for image generation, where multiple fractional-order encoders are employed to produce different representations of the same image. These representations are subsequently merged to create a single composite image, with enhanced detail and richness.

3.5.1. Fractional Wavelet Scattering Networks

GANs [103] and VAEs [102] represent two influential paradigms in the realm of generative modelling, a field aiming to understand and replicate the underlying structure of data. GANs operate on a game-theoretic framework where a generator network competes against a discriminator network, iteratively improving the generation of data until it becomes indistinguishable from real data. On the other hand, VAEs adopt a probabilistic approach, aiming to encode and decode data by modelling the underlying probability distribution. While GANs excel in generating high-quality, realistic samples, VAEs offer a principled way to learn latent representations of data and perform tasks such as data compression and synthesis. Both methods have witnessed tremendous advancements and applications across various domains, revolutionising tasks like image generation, data augmentation, and anomaly detection.

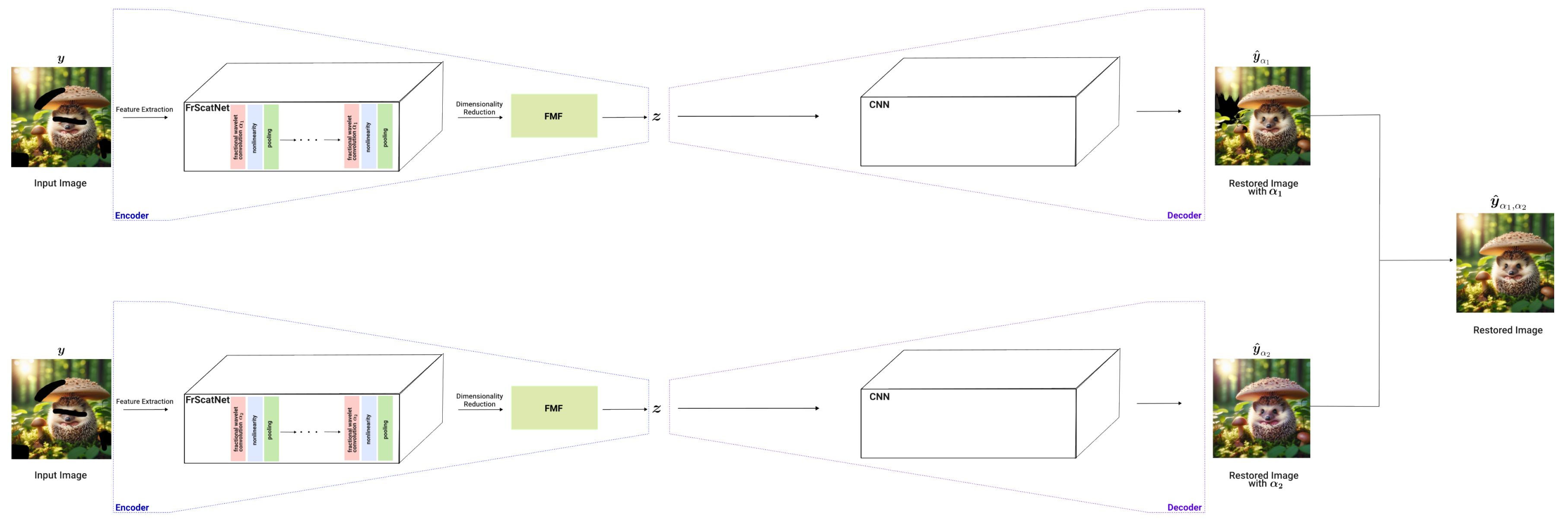
GANs and VAEs are notorious for their challenging training dynamics, including unstable training and issues like blurred images or model collapse. To address these challenges, Generative Scattering Networks (GSNs) were introduced, leveraging wavelet scattering networks (ScatNets) as encoders and CNNs as decoders [110].

ScatNets are mathematical models designed to extract meaningful features from signals, particularly in the domain of generative modelling. They operate by performing a cascade of operations on the input signal

y (t)

in each layer of the ScatNet

S_{n}

: wavelet transform in which

y (t)

is convolved with wavelet function

ψ_{λ} (t)

at different scales

λ

S_{1} y (t) = | y (t) ψ_{λ} (t) |

; modulus non-linearity in which after each wavelet transform the modulus operation is applied element-wise

S_{n} y (t) = | S_{n - 1} y (t) |

; pooling in which pooling operations are performed to aggregate information across scales

S_{p o o l} y (t) = T_{↑} | S_{n} y (t) |

. Through this hierarchical process, ScatNets create a series of increasingly invariant and abstract representations of the input signal, capturing both local and global structures.

After extracting the features with a ScatNet, Principal Component Analysis (PCA) is applied to reduce the dimensional resulting in the latent space vector

z

. Then the decoder uses a CNN to deconvolution and output the predicted image

\tilde{y}

, Figure 7.

GSNs simplify training by avoiding the need to learn ScatNet parameters, yet they may suffer from reduced image quality due to limitations in ScatNets’ expressiveness and overfitting induced by PCA in dimensionality reduction [109].

In response to these limitations, Generative Fractional Scattering Networks (GFRSNs) were proposed as an extension of GSNs in [109]. GFRSNs aim to address the overfitting issue by introducing a more suitable dimensional reduction method, thus enhancing GSN performance.

GFRSN includes an encoder made of novel components, a Fractional Wavelet Scattering Network (FrScatNet) and a Feature-Map Fusion (FMF) dimensional reduction method [109].

FrScatNet extends the concepts of ScatNets to non-integer order wavelet transforms by introducing a fractional convolution operator

Θ_{α}

to the wavelet transform operation formulated as [109]:

S_{1} y (t) = | x (t) Θ_{α} ψ_{λ} | = e^{- \frac{j}{2} t^{2} cot (θ) [y (t) e^{\frac{j}{2} t^{2} cot (θ)} ψ_{λ} (t)]},

where

α

is the fractional-order and

θ = \frac{α π}{2}

is the rotation angle. Note that FrScatNet can be reduced to a ScatNet when

α = 1 .

In [109], after employing FrScatNet for feature extraction, the authors propose using a FMF method instead of PCA, as used in ScatNets. The rationale behind this choice is that PCA fails to consider the semantic differences present in the features extracted by FrScatNets across different layers, thus overlooking the hierarchical information contained within the features. The reduced dimensional feature map after applying FMF to the features extracted by FrScatNet is the latent space

z

(for more details on FMF see [109]).

FrScatNets are equipped with a hyperparameter

α

that determines the fractional-order of the convolution. Since

α

can be chosen arbitrarily, different

α

values lead to the extraction of distinct features. Consequently, using FrScatNets with varying

α

values results in the generation of multiple feature vectors. To fully exploit this diversity in feature extraction, the authors propose merging the image predictions obtained from different

α

values using an image fusion technique. This approach allows for embedding the input in different fractional-order domains to enhance the quality of the generated images. The image fusion method proposed can be formulated as [109]:

{\tilde{y}}_{α_{1}, α_{2}} = ω {\tilde{y}}_{α_{1}} + (1 - ω) {\tilde{y}}_{α_{2}},

where

{\tilde{y}}_{α_{1}}

and

{\tilde{y}}_{α_{2}}

are image predictions generated by feature extraction using a FrScatNet with fractional-orders

α_{1}

and

α_{2}

, respectively. The hyperparameter

ω

acts as a weighting factor that determines the contribution of each predicted image [109].

The introduction of GFRSN in [109] opens up several research gaps that warrant further investigation. First, there is a need to explore the methodologies to select the appropriate

α

value for FrScatNets. Identifying which

α

values yield the most distinct features would be beneficial, as combining such features could potentially enhance the completion of the predicted output. Furthermore, while the proposed FMF method takes the average of the third-layer’s feature maps, there is room for exploring more sophisticated weighting strategies. Using alternative weight strategies could potentially improve the efficacy of the dimensionality reduction technique used in GFRSNs.

3.6. Compression

Contemporary advancements in deep learning have propelled the field to achieve remarkable performance across a spectrum of tasks, encompassing image classification, semantic segmentation, object detection, pose detection, and beyond. This progress is underpinned by the evolution of increasingly complex architectures, housing millions, and even billions of trainable parameters, thereby augmenting model efficacy. However, the proliferation of such massive architectures poses challenges concerning memory and computational resources, hindering seamless deployment in edge computing devices and other resource-constrained environments.

Reducing the computational cost of NN architectures for denoising, image restoration, segmentation, object detection, and enhancement is a critical endeavour in computer vision research. Given the increasing demand for real-time and resource-efficient solutions, optimising these architectures for computational efficiency is essential for practical deployment in various applications. Techniques for reducing computational cost typically focus on minimising the number of operations, parameters, or memory footprint required by the models while maintaining satisfactory performance.

In our survey of the literature, we uncovered two works that harness FC to alleviate the computational burden associated with NN-based computer vision tasks [17,111].

In [111], the authors introduce Fractional Max-Pooling (FMP), a novel technique designed to address the limitations of traditional max-pooling methods. By incorporating fractional-order principles, Fractional Max-Pooling allows for overlapping windows and mitigates information loss during the pooling process, thereby enhancing feature preservation while reducing the reduction size. Conversely, in [17], the authors present a groundbreaking approach by deriving fractional convolutional filters tailored for popular integer-order filters such as Gaussian, Sobel, and Laplacian. This innovative formulation not only improves filter performance but also offers a compelling advantage: a reduction in the number of parameters required, which remain constant regardless of filter size. Moreover, these fractional filters exhibit intermediate behaviours, providing a versatile tool for capturing nuanced features within the image data.

3.6.1. Fractional Max-Pooling

Max-pooling is a fundamental operation in CNNs used for down-sampling feature maps, reducing computational complexity, and extracting dominant features. Given an input feature map with dimensions

I_{i n} \times J_{i n} \times D_{i n}

, where

I_{i n}

J_{i n}

and

D_{i n}

are the width, height and number of channels, respectively, max-pooling partitions the input into non-overlapping regions and computes the maximum value within each region to produce the output [111].

Let

l \times l

denote the size of the pooling window, where l is typically a small integer, usually

l = 2

is used as default. The output dimensions of the feature map after max-pooling are given by

I_{o u t} = ⌊\frac{I_{i n}}{l}⌋

and

J_{o u t} = ⌊\frac{J_{i n}}{l}⌋ .

The pooling regions

P_{i, j}

are computed by dividing the input feature map

I_{i n} \times I_{i n}

by the size of the output feature map

I_{o u t} \times I_{o u t}

(considering

J_{i n} = I_{i n}

and

J_{o u t} = I_{o u t}

) [111]:

P_{i, j} \subset {1, 2, \dots, I_{i n}}^{2} with (i, j) \in {1, \dots, I_{o u t}}^{2},

where the size of the pooling windows can be computed as:

P_{i, j} = [2 i - 1, 2 i] \times [2 j - 1, 2 j] .

Then, for each pooling region the maximum pixel value of the input feature map

I n_{P_{i, j}}

will be kept and compose the output feature map

O u t_{i, j}

O u t_{i, j} = max (I n_{P_{i, j}}) .

Max-pooling introduces translation invariance and reduces the spatial dimensions of the feature maps, which helps in controlling overfitting and improving computational efficiency. By retaining only the maximum activations within each pooling region, max-pooling focuses on preserving the most salient features while discarding less relevant information, facilitating hierarchical feature learning in CNNs [111].

The limitations of max-pooling in CNNs are indeed well-recognised in the literature [112,113,114]. One major drawback is its fixed pooling window size, which may not adequately capture diverse spatial patterns within feature maps, especially in scenarios where objects vary significantly in scale or orientation. Additionally, the non-overlapping nature of max-pooling leads to a loss of spatial information between adjacent pooling regions, potentially discarding valuable details crucial for tasks like object localisation. Moreover, the default max-pooling results in a rapid reduction in the size of hidden layers

\frac{I_{i n}}{I_{o u t}} \approx 2

, necessitating the use of multiple stacked convolutional layers to achieve significant depth. While some methods have been proposed to address this issue [112,113], they still result in a halving of the size of hidden layers, highlighting the need for a gentler approach to spatial pooling [111].

A potential solution lies in adopting a more flexible approach to pooling that reduces the size of hidden layers by a smaller factor. By incorporating additional layers of pooling, each with a smaller reduction factor, we can observe the input image at different scales, potentially leading to easier recognition of distinctive features indicative of specific object classes. This approach could lead to more effective feature extraction and improve the performance of CNNs in various computer vision tasks [111].

In [111], the authors introduce FMP to address the issue of controlling the reduction of the spatial size of images by a fractional-order

1 < α < 2

. Additionally, FMP introduces flexibility by allowing overlapping pooling regions, thus preserving spatial information more effectively. The pooling regions

P_{i, j}

in FMP can either be overlapping squares or disjoint collections of rectangles. To generate

P_{i, j}

, two hyperparameters are needed:

a_{i}

and

b_{j}

, with

i, j \in 0, \dots, I_{o u t}

. Considering

a_{i}

and

b_{j}

as two increasing sequences with a step of 1 ending at

I_{i n}

, then the overlapping pooling regions can be computed as [111]:

P_{i, j} = [a_{i - 1}, a_{i} - 1] \times [b_{j - 1}, b_{j} - 1],

and the disjoint pooling regions as:

P_{i, j} = [a_{i - 1}, a_{i}] \times [b_{j - 1}, b_{j}] .

The output dimensions of the feature map after FMF are given by

I_{o u t} = ⌊\frac{I_{i n}}{α}⌋

and

J_{o u t} = ⌊\frac{J_{i n}}{α}⌋

, where

α

is the fractional-order of reduction

\frac{I_{i n}}{I_{o u t}} \in (1, 2)

[111].

FMP holds promise in enhancing the performance of CNNs as well as reducing their computational cost without losing information. Several research directions stemming from this work [111] could be pursued. For instance, investigating optimal combinations of reduction ratios and overlap factors in FMF could lead to improved feature representation while minimising information loss. Additionally, exploring the integration of FMF with other techniques, such as attention mechanisms or adaptive pooling strategies, may result in synergistic improvements in both model performance and efficiency.

3.6.2. Fractional Convolutional Filters

In [17], authors propose learning reduced representations of convolutional filters through combining fractional calculus and NNs, originating fractional convolutional filters.

As seen previously, convolutional filters are used in NNs to extract features from images being the most popular filters the Gaussian, Sobel and Laplacian. These are intimately connected through the derivatives of a Gaussian filter. The first derivative of the Gaussian corresponds to the Sobel operator, emphasising edges in a particular direction, while the second derivative of the Gaussian, known as the Laplacian of Gaussian, enhances areas of rapid intensity change regardless of direction. Mathematically, the relationship can be expressed as follows [17]:

G (i, j) = \frac{1}{2 π s t d^{2}} e^{- \frac{i^{2} + j^{2}}{2 s t d^{2}}}, \frac{\partial G (i, j)}{\partial i} \propto j e^{- \frac{i^{2} + j^{2}}{2 s t d^{2}}}, \frac{\partial^{2} G (i)}{\partial i^{2}} = 4 i^{2} e^{- i^{2}} - 2 e^{- i^{2}},

where

s t d

is the standard deviation.

Mathematically, using the Grünwald-Letnikov definition and considering the first 15 terms of the Taylor series, the authors extend this to fractional-order derivative of order

α

of the Gaussian

D^{α} G (i, j)

[17]:

D^{α} G (i) = \frac{A}{h^{α}} \sum_{m = 0}^{15} \frac{Γ (α + 1) G (i)}{{(- 1)}^{m} Γ (m + 1) Γ (1 - m + α)},

where

Γ

is the Gamma function.

The fractional derivative of a Gaussian provides a versatile framework for deriving a range of filters, including Gaussian, Sobel, Laplacian, and more. By selecting specific values for the fractional order

α

, we can directly obtain the corresponding traditional filters:

α = 0

yields the Gaussian filter,

α = 1

the Sobel filter, and

α = 2

the Laplacian filter. Remarkably, by varying

α

, we can interpolate between these filters, creating a continuum of filter behaviours that smoothly transition between them. This flexibility enables the creation of general customised filters whose behaviour ranges between the previous referred filters [17]. A 2D fractional convolutional filter is thus defined as:

F (i, j) = A D^{α} D^{β} e^{- \frac{{(i - i_{o})}^{2} + {(j - j_{o})}^{2}}{s t d^{2}}},

where

D^{α} D^{β} G (i, j) = D^{α} G (i) \times D^{β} G (j)

. The 3D fractional convolutional filter is given by:

F (i, j, k) = A D^{α} D^{β} D^{γ} e^{- \frac{{(i - i_{o})}^{2} + {(j - j_{o})}^{2} + {(k - k_{o})}^{2}}{s t d^{2}}},

where

α, β, γ

are the orders of the fractional derivatives and

s t d, A, i_{o}, j_{o}, k_{o}

are the parameters that define the filter.

One significant computational benefit of fractional convolutional filters is that the number of parameters required to describe them remains constant, regardless of the filter size, offering a substantial reduction in the number of parameters compared to integer-order filters. For instance, instead of needing

l \times l

parameters for an

l \times l

pixel-wise dimension filter, fractional convolutional filters require only a maximum of 6 (2d) or 9 (3d) parameters. This reduction in parameter count simplifies the model and enhances computational efficiency, making fractional convolutional filters an attractive option for various applications in image processing and computer vision [17].

An important result from [17] is that the introduction of fractional convolutional filters in CNNs allowed to achieve a record for the smallest model that could achieve an accuracy greater than

99 %

on the MNIST dataset [17]. Building upon this milestone, several promising research directions emerge. Firstly, exploring the applicability of fractional convolutional filters across diverse datasets and domains can unveil their generalisability and robustness. Furthermore, delving into the theoretical foundations and mathematical properties of fractional convolutional filters may lead to deeper insights into their underlying mechanisms and ease the development of more sophisticated variants.

4. Conclusion

In this survey paper, we have conducted an extensive exploration of the integration of fractional calculus with neural network-based computer vision methodologies, focusing on denoising, enhancement, object detection, segmentation, restoration, and neural network compression tasks. While fractional calculus’s application in computer vision is well-established, its incorporation into neural network-based approaches is still in its early stages, with limited works in the literature. Nonetheless, the results from existing studies demonstrate notable performance improvements, indicating the potential for further advancements in this area. Through our investigation, we have identified several research gaps and outlined potential directions for future exploration in each of the studied works.

In real-world conditions, image capture often occurs under less-than-ideal circumstances, resulting in complex artefacts and challenges such as corruption and varying light conditions. Addressing these challenges has spurred the development of numerous methods aimed at enhancing neural network performance in computer vision tasks. The versatility of fractional calculus methods, with their increased degrees of freedom capable of modelling nuanced behaviours, holds promise in overcoming the hardships encountered in computer vision tasks.

The goal of this survey is to provide an overview of the current research and to offer intuitive explanations of the proposed methods. We aim to demystify fractional calculus and motivate its usage over integer-order methods by providing accessible explanations. We understand that fractional calculus can appear daunting, but we hope that this survey serves to dispel misconceptions and inspire researchers to contribute to the incorporation of fractional calculus into neural network-based computer vision.

In addition to the identified research gaps, we suggest investigating the influence of fractional-order derivatives on additional aspects of convolutional neural networks architectures, such as regularisation techniques, attention mechanisms, and transfer learning. Exploring these avenues could yield novel strategies for model optimisation and performance enhancement. Additionally, given the time-dependence inherent in fractional calculus, we envisage that leveraging the memory capabilities could advance video object detection and generation tasks.

Furthermore, it is imperative to explore the interpretability and explainability of fractional calculus in neural network-based computer vision models. Understanding how fractional-order operations affect feature representations and decision-making processes within the network can provide valuable insights into model behaviour and foster trust among researchers and field experts. Furthermore, investigating the generalisability and robustness of fractional calculus-enhanced neural networks across diverse datasets and real-world scenarios is crucial to ensure their practical applicability. Finally, the scalability and computational efficiency of fractional calculus-based methods merit further investigation, particularly in resource-constrained environments and large-scale applications.

Acknowledgments

The authors acknowledge the funding by Fundação para a Ciência e Tecnologia (Portuguese Foundation for Science and Technology) through CMAT projects UIDB/00013/2020 and UIDP/00013/2020 and the funding by FCT and Google Cloud partnership through projects CPCA-IAC/AV/589164/2023 and CPCA-IAC/AF/589140/2023. C. Coelho would like to thank FCT the funding through the scholarship with reference 2021.05201.BD. This work is also financially supported by national funds through the FCT/MCTES (PIDDAC), under the project 2022.06672.PTDC - iMAD - Improving the Modelling of Anomalous Diffusion and Viscoelasticity: solutions to industrial problems.

References

Dey, S. Hands-On Image Processing with Python: Expert techniques for advanced image analysis and effective interpretation of image data; Packt Publishing Ltd, 2018.
Herrmann, R. Fractional calculus: an introduction for physicists; World Scientific, 2011.
Abdou, M.A. An analytical method for space–time fractional nonlinear differential equations arising in plasma physics. Journal of Ocean Engineering and Science 2017, 2, 288–292. [Google Scholar] [CrossRef]
Alquran, M. The amazing fractional Maclaurin series for solving different types of fractional mathematical problems that arise in physics and engineering. Partial Differential Equations in Applied Mathematics 2023, 7, 100506. [Google Scholar] [CrossRef]
Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J.H. The role of fractional calculus in modeling biological phenomena: A review. Communications in Nonlinear Science and Numerical Simulation 2017, 51, 141–159. [Google Scholar] [CrossRef]
Ma, Y.; Li, W. Application and research of fractional differential equations in dynamic analysis of supply chain financial chaotic system. Chaos, Solitons & Fractals 2020, 130, 109417. [Google Scholar]
Jan, A.; Srivastava, H.M.; Khan, A.; Mohammed, P.O.; Jan, R.; Hamed, Y. In vivo HIV dynamics, modeling the interaction of HIV and immune system via non-integer derivatives. Fractal and Fractional 2023, 7, 361. [Google Scholar] [CrossRef]
Zhang, Y.; Pu, Y.; Zhou, J. Construction of fractional differential masks based on Riemann-Liouville definition. Journal of Computational Information Systems 2010, 6, 3191–3199. [Google Scholar]
Yang, Q.; Chen, D.; Zhao, T.; Chen, Y. Fractional calculus in image processing: a review. Fractional Calculus and Applied Analysis 2016, 19, 1222–1249. [Google Scholar] [CrossRef]
Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A.; Ferreira, N.M. An efficient method for segmentation of images based on fractional calculus and natural selection. Expert Systems with Applications 2012, 39, 12407–12417. [Google Scholar] [CrossRef]
Tian, D.; Xue, D.; Wang, D. A fractional-order adaptive regularization primal–dual algorithm for image denoising. Information Sciences 2015, 296, 147–159. [Google Scholar] [CrossRef]
Coelho, C.; Costa, M.F.P.; Ferrás, L. Neural Fractional Differential Equations. arXiv preprint 2024. arXiv:2403.02737 2024.
Alsaade, F.W.; Al-zahrani, M.S.; Yao, Q.; Jahanshahi, H. A Model-Free Finite-Time Control Technique for Synchronization of Variable-Order Fractional Hopfield-like Neural Network. Fractal and Fractional 2023, 7, 349. [Google Scholar] [CrossRef]
Boroomand, A.; Menhaj, M.B. Fractional-order Hopfield neural networks. Advances in Neuro-Information Processing: 15th International Conference, ICONIP 2008, Auckland, New Zealand, November 25-28, 2008, Revised Selected Papers, Part I 15. Springer, 2009, pp. 883–890.
Arora, S.; Suman, H.K.; Mathur, T.; Pandey, H.M.; Tiwari, K. Fractional derivative based weighted skip connections for satellite image road segmentation. Neural Networks 2023, 161, 142–153. [Google Scholar] [CrossRef] [PubMed]
Krouma, H.; Ferdi, Y.; Taleb-Ahmedx, A. Neural adaptive fractional order differential based algorithm for medical image enhancement. 2018 International Conference on Signal, Image, Vision and their Applications (SIVA). IEEE, 2018, pp. 1–6.
Zamora, J.; Vargas, J.A.C.; Rhodes, A.; Nachman, L.; Sundararajan, N. Convolutional filter approximation using fractional calculus. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 383–392.
Diethelm, K.; Ford, N.J. Analysis of fractional differential equations. Journal of Mathematical Analysis and Applications 2002, 265, 229–248. [Google Scholar] [CrossRef]
Ross, B., A brief history and exposition of the fundamental theory of fractional calculus. In Fractional Calculus and Its Applications; Springer Berlin Heidelberg, 1975; p. 1–36. [CrossRef]
Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Communications in Nonlinear Science and Numerical Simulation 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent–II. Geophysical Journal International 1967, 13, 529–539. [Google Scholar] [CrossRef]
Grünwald, A. Ueber, Begrenzte, Derivationen und Deren Anwendung. Z. Math. Phys 1867, 12, 441–480. [Google Scholar]
Post, E.L. Generalized differentiation. Transactions of the American Mathematical Society 1930, 32, 723–781. [Google Scholar] [CrossRef]
Letnikov, A. An explanation of the concepts of the theory of differentiation of arbitrary index. Moscow Matem. Sbornik 1872, 6, 413–445. [Google Scholar]
Jain, R.; Kasturi, R.; Schunck, B.G.; others. Machine vision; Vol. 5, McGraw-hill New York, 1995.
Komatsu, R.; Gonsalves, T. Comparing U-Net based models for denoising color images. AI 2020, 1, 465–486. [Google Scholar] [CrossRef]
Liu, Y.; Pu, Y.; Zhou, J. Design of image denoising filter based on fractional integral. Journal of Computational Information Systems 2010, 6, 2839–2847. [Google Scholar]
Liu, Y. A digital image denoising method based on fractional calculus. Journal of Sichuan University: Engineering Science Edition 2011, 43.
Azerad, P.; Bouharguane, A.; Crouzet, J.F. Simultaneous denoising and enhancement of signals by a fractal conservation law. Communications in Nonlinear Science and Numerical Simulation 2012, 17, 867–881. [Google Scholar] [CrossRef]
Zheng, W.; Xianmin, M. Fractional-Order Differentiate Adaptive Algorithm for Identifying Coal Dust Image Denoising. 2014 International Symposium on Computer, Consumer and Control. IEEE, 2014, pp. 638–641.
Pan, X.; Liu, S.; Jiang, T.; Liu, H.; Wang, X.; Li, L. Non-causal fractional low-pass filter based medical image denoising. Journal of Medical Imaging and Health Informatics 2016, 6, 1799–1806. [Google Scholar] [CrossRef]
Li, D.; Jiang, T.; Jin, Q.; Zhang, B. Adaptive fractional order total variation image denoising via the alternating direction method of multipliers. 2020 Chinese Control And Decision Conference (CCDC). IEEE, 2020, pp. 3876–3881.
Al-Shamasneh, A.R.; Ibrahim, R.W. Image denoising based on quantum calculus of local fractional entropy. Symmetry 2023, 15, 396. [Google Scholar] [CrossRef]
Ilesanmi, A.E.; Ilesanmi, T.O. Methods for image denoising using convolutional neural network: a review. Complex & Intelligent Systems 2021, 7, 2179–2198. [Google Scholar]
Jifara, W.; Jiang, F.; Rho, S.; Cheng, M.; Liu, S. Medical image denoising using convolutional neural network: a residual learning approach. The Journal of Supercomputing 2019, 75, 704–718. [Google Scholar] [CrossRef]
Singh, P.; Shankar, A. A novel optical image denoising technique using convolutional neural network and anisotropic diffusion for real-time surveillance applications. Journal of Real-Time Image Processing 2021, 18, 1711–1728. [Google Scholar] [CrossRef]
Chandra, I.S.; Shastri, R.K.; Kavitha, D.; Kumar, K.R.; Manochitra, S.; Babu, P.B. CNN based color balancing and denoising technique for underwater images: CNN-CBDT. Measurement: Sensors 2023, 28, 100835. [Google Scholar] [CrossRef]
Bai, Y.C.; Zhang, S.; Chen, M.; Pu, Y.F.; Zhou, J.L. A fractional total variational CNN approach for SAR image despeckling. Intelligent Computing Methodologies: 14th International Conference, ICIC 2018, Wuhan, China, August 15-18, 2018, Proceedings, Part III 14. Springer, 2018, pp. 431–442.
Jia, X.; Liu, S.; Feng, X.; Zhang, L. Focnet: A fractional optimal control network for image denoising. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2019, pp. 6054–6063.
Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica D: nonlinear phenomena 1992, 60, 259–268. [Google Scholar] [CrossRef]
Yang, X.; Zhang, J.; Liu, Y.; Zheng, X.; Liu, K. Super-resolution image reconstruction using fractional-order total variation and adaptive regularization parameters. The Visual Computer 2019, 35, 1755–1768. [Google Scholar] [CrossRef]
Wang, Q.; Gao, Z.; Xie, C.; Chen, G.; Luo, Q. Fractional-order total variation for improving image fusion based on saliency map. Signal, Image and Video Processing 2020, 14, 991–999. [Google Scholar] [CrossRef]
Zhang, X.; Yan, H. Medical image fusion and noise suppression with fractional-order total variation and multi-scale decomposition. IET Image Processing 2021, 15, 1688–1701. [Google Scholar] [CrossRef]
Jun, Z.; Zhihui, W. A class of fractional-order multi-scale variational models and alternating projection algorithm for image denoising. Applied Mathematical Modelling 2011, 35, 2516–2528. [Google Scholar] [CrossRef]
Yazgaç, B.G.; Kırcı, M. Fractional-order calculus-based data augmentation methods for environmental sound classification with deep learning. Fractal and Fractional 2022, 6, 555. [Google Scholar] [CrossRef]
Lepcha, D.C.; Goyal, B.; Dogra, A.; Sharma, K.P.; Gupta, D.N. A deep journey into image enhancement: A survey of current and emerging trends. Information Fusion 2023, 93, 36–76. [Google Scholar] [CrossRef]
Pu, Y. Fractional calculus approach to texture of digital image. 2006 8th international Conference on Signal Processing. IEEE, 2006, Vol. 2.
Huang, G.; Xu, L.; Chen, Q.; Men, T. Image Enhancement Using a Fractional-Order Differential. Proceedings of the 4th International Conference on Computer Engineering and Networks: CENet2014. Springer, 2015, pp. 555–563.
Saadia, A.; Rashdi, A. Fractional order integration and fuzzy logic based filter for denoising of echocardiographic image. Computer methods and programs in biomedicine 2016, 137, 65–75. [Google Scholar] [CrossRef]
Lei, J.; Zhang, S.; Luo, L.; Xiao, J.; Wang, H. Super-resolution enhancement of UAV images based on fractional calculus and POCS. Geo-spatial information science 2018, 21, 56–66. [Google Scholar] [CrossRef]
AbdAlRahman, A.; Ismail, S.M.; Said, L.A.; Radwan, A.G. Double fractional-order masks image enhancement. 2021 3rd Novel Intelligent and Leading Emerging Sciences Conference (NILES). IEEE, 2021, pp. 261–264.
Aldawish, I.; Jalab, H.A. A Mathematical Model for COVID-19 Image Enhancement based on Mittag-Leffler-Chebyshev Shift. Computers, Materials & Continua 2022, 73. [Google Scholar]
Miah, B.A.; Sen, M.; Murugan, R.; Gupta, D. Developing Riemann–Liouville-Fractional Masks for Image Enhancement. Circuits, Systems, and Signal Processing 2024, pp. 1–30.
Yogeshwari, M.; Thailambal, G. Automatic feature extraction and detection of plant leaf disease using GLCM features and convolutional neural networks. Materials Today: Proceedings 2023, 81, 530–536. [Google Scholar] [CrossRef]
Accarino, G.; Chiarelli, M.; Immorlano, F.; Aloisi, V.; Gatto, A.; Aloisio, G. Msg-gan-sd: A multi-scale gradients gan for statistical downscaling of 2-meter temperature over the euro-cordex domain. AI 2021, 2, 600–620. [Google Scholar] [CrossRef]
He, C.; Li, K.; Xu, G.; Yan, J.; Tang, L.; Zhang, Y.; Wang, Y.; Li, X. Hqg-net: Unpaired medical image enhancement with high-quality guidance. IEEE Transactions on Neural Networks and Learning Systems 2023.
Jalab, H.A.; Al-Shamasneh, A.R.; Shaiba, H.; Ibrahim, R.W.; Baleanu, D. Fractional Renyi entropy image enhancement for deep segmentation of kidney MRI 2021.
Ferdi, Y. Some applications of fractional order calculus to design digital filters for biomedical signal processing. Journal of Mechanics in Medicine and Biology 2012, 12, 1240008. [Google Scholar] [CrossRef]
Rényi, A. On measures of entropy and information. Proceedings of the fourth Berkeley symposium on mathematical statistics and probability, volume 1: contributions to the theory of statistics. University of California Press, 1961, Vol. 4, pp. 547–562.
Karmeshu. Entropy measures, maximum entropy principle and emerging applications 2003.
Bromiley, P.; Thacker, N.; Bouhova-Thacker, E. Shannon entropy, Renyi entropy, and information. Statistics and Inf. Series (2004-004) 2004, 9, 2–8. [Google Scholar]
Zhu, S.C.; Wu, Y.N.; Mumford, D. Minimax entropy principle and its application to texture modeling. Neural computation 1997, 9, 1627–1660. [Google Scholar] [CrossRef]
Ibraheam, M.; Li, K.F.; Gebali, F.; Sielecki, L.E. A performance comparison and enhancement of animal species detection in images with various r-cnn models. AI 2021, 2, 552–577. [Google Scholar] [CrossRef]
Xiao, B.; Li, L.; Li, Y.; Li, W.; Wang, G. Image analysis by fractional-order orthogonal moments. Information Sciences 2017, 382, 135–149. [Google Scholar] [CrossRef]
Kumar, S.P.; Latte, M.V. Modified and optimized method for segmenting pulmonary parenchyma in CT lung images, based on fractional calculus and natural selection. Journal of Intelligent Systems 2019, 28, 721–732. [Google Scholar] [CrossRef]
Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. Proceedings of the IEEE conference on computer vision and pattern recognition, 2014, pp. 580–587.
Girshick, R. Fast r-cnn. Proceedings of the IEEE international conference on computer vision, 2015, pp. 1440–1448.
Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Advances in neural information processing systems 2015, 28. [Google Scholar] [CrossRef]
Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 779–788.
Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11–14, 2016, Proceedings, Part I 14. Springer, 2016, pp. 21–37.
Coelho, C.; Costa, M.F.P.; Ferrás, L.L.; Soares, A.J. Object detection with retinanet on aerial imagery: The algarve landscape. International Conference on Computational Science and Its Applications. Springer, 2021, pp. 501–516.
Tang, Z.; Liu, X.; Chen, H.; Hupy, J.; Yang, B. Deep learning based wildfire event object detection from 4K aerial images acquired by UAS. AI 2020, 1, 166–179. [Google Scholar] [CrossRef]
Albuquerque, L.; Coelho, C.; Costa, M.F.P.; Ferrás, L.; Soares, A. Improving public parking by using artificial intelligence. AIP Conference Proceedings. AIP Publishing, 2023, Vol. 2849.
Gunturu, S.; Munir, A.; Ullah, H.; Welch, S.; Flippo, D. A spatial AI-based agricultural robotic platform for wheat detection and collision avoidance. AI 2022, 3, 719–738. [Google Scholar] [CrossRef]
Barbedo, J.G.A. Detecting and classifying pests in crops using proximal images and machine learning: A review. Ai 2020, 1, 312–328. [Google Scholar] [CrossRef]
El Ogri, O.; Karmouni, H.; Sayyouri, M.; Qjidaa, H. 3D image recognition using new set of fractional-order Legendre moments and deep neural networks. Signal Processing: Image Communication 2021, 98, 116410. [Google Scholar] [CrossRef]
Zhou, M.; Li, B.; Wang, J. Optimization of Hyperparameters in Object Detection Models Based on Fractal Loss Function. Fractal and Fractional 2022, 6, 706. [Google Scholar] [CrossRef]
Mahaveerakannan, R.; Anitha, C.; Thomas, A.K.; Rajan, S.; Muthukumar, T.; Rajulu, G.G. An IoT based forest fire detection system using integration of cat swarm with LSTM model. Computer Communications 2023, 211, 37–45. [Google Scholar] [CrossRef]
Castleman, K.R. Digital image processing; Prentice Hall Press, 1996.
Deepika, C.L.; Kandaswamy, A.; Vimal, C.; Satish, B. Palmprint authentication using modified legendre moments. Procedia Computer Science 2010, 2, 164–172. [Google Scholar] [CrossRef]
Kamaruddin, N.; Abdullah, N.A.; Ibrahim, R.W. IMAGE SEGMENTATION BASED ON FRACTIONAL NON-MARKOV POISSON STOCHASTIC PROCESS. Pakistan Journal of Statistics 2015, 31. [Google Scholar]
Tang, Q.; Gao, S.; Liu, Y.; Yu, F. Infrared image segmentation algorithm for defect detection based on FODPSO. Infrared Physics & Technology 2019, 102, 103051. [Google Scholar]
Kamaruddin, N.; Maarop, N.; Narayana, G. Fractional Active Contour Model for Edge Detector on Medical Image Segmentation. Proceedings of the 2020 2nd International Conference on Image, Video and Signal Processing, 2020, pp. 39–44.
Vivekraj, A.; Sumathi, S. Resnet-Unet-FSOA based cranial nerve segmentation and medial axis extraction using MRI images. The Imaging Science Journal 2023, 71, 750–766. [Google Scholar] [CrossRef]
Geng, N.; Sheng, H.; Sun, W.; Wang, Y.; Yu, T.; Liu, Z. Image segmentation of rail surface defects based on fractional order particle swarm optimization 2D-Otsu algorithm. International Conference on Algorithm, Imaging Processing, and Machine Vision (AIPMV 2023). SPIE, 2024, Vol. 12969, pp. 56–59.
Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18. Springer, 2015, pp. 234–241.
De Silva, M.S.; Narayanan, B.N.; Hardie, R.C. A patient-specific algorithm for lung segmentation in chest radiographs. AI 2022, 3, 931–947. [Google Scholar] [CrossRef]
Chhabra, M.; Ravulakollu, K.K.; Kumar, M.; Sharma, A.; Nayyar, A. Improving automated latent fingerprint detection and segmentation using deep convolutional neural network. Neural Computing and Applications 2023, 35, 6471–6497. [Google Scholar] [CrossRef]
Zhang, T.; Wang, D.; Lu, Y. ECSNet: An accelerated real-time image segmentation CNN architecture for pavement crack detection. IEEE Transactions on Intelligent Transportation Systems 2023.
Marques, F.; De Araujo, T.P.; Nator, C.; Saraiva, A.; Sousa, J.; Pinto, A.M.; Melo, R. Recognition of simple handwritten polynomials using segmentation with fractional calculus and convolutional neural networks. 2019 8th Brazilian Conference on Intelligent Systems (BRACIS). IEEE, 2019, pp. 245–250.
Nirmalapriya, G.; Agalya, V.; Regunathan, R.; Ananth, M.B.J. Fractional Aquila spider monkey optimization based deep learning network for classification of brain tumor. Biomedical Signal Processing and Control 2023, 79, 104017. [Google Scholar] [CrossRef]
Lakra, M.; Kumar, S. A fractional-order PDE-based contour detection model with CeNN scheme for medical images. Journal of Real-Time Image Processing 2022, 19, 147–160. [Google Scholar] [CrossRef]
Li, C.; Xu, C.; Gui, C.; Fox, M.D. Level set evolution without re-initialization: a new variational formulation. 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05). IEEE, 2005, Vol. 1, pp. 430–436.
Ren, Z. Adaptive active contour model driven by fractional order fitting energy. Signal Processing 2015, 117, 138–150. [Google Scholar] [CrossRef]
Chua, L.O.; Yang, L. Cellular neural networks: Theory. IEEE Transactions on circuits and systems 1988, 35, 1257–1272. [Google Scholar] [CrossRef]
Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational physics 2019, 378, 686–707. [Google Scholar] [CrossRef]
Zhang, Y.; Pu, Y.; Hu, J.; Zhou, J. A class of fractional-order variational image inpainting models. Appl. Math. Inf. Sci 2012, 6, 299–306. [Google Scholar]
Bosch, J.; Stoll, M. A fractional inpainting model based on the vector-valued Cahn–Hilliard equation. SIAM Journal on Imaging Sciences 2015, 8, 2352–2382. [Google Scholar] [CrossRef]
Li, D.; Tian, X.; Jin, Q.; Hirasawa, K. Adaptive fractional-order total variation image restoration with split Bregman iteration. ISA transactions 2018, 82, 210–222. [Google Scholar] [CrossRef] [PubMed]
Ammi, M.R.S.; Jamiai, I. FINITE DIFFERENCE AND LEGENDRE SPECTRAL METHOD FOR A TIME-FRACTIONAL DIFFUSION-CONVECTION EQUATION FOR IMAGE RESTORATION. Discrete & Continuous Dynamical Systems-Series S 2018, 11. [Google Scholar]
Gouasnouane, O.; Moussaid, N.; Boujena, S.; Kabli, K. A nonlinear fractional partial differential equation for image inpainting. Mathematical modeling and computing 2022, pp. 536–546.
Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv preprint 2013, arXiv:1312.6114 2013. [Google Scholar]
Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Communications of the ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
Peng, J.; Liu, D.; Xu, S.; Li, H. Generating diverse structure for image inpainting with hierarchical VQ-VAE. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 10775–10784.
Chen, Y.; Zhang, H.; Liu, L.; Chen, X.; Zhang, Q.; Yang, K.; Xia, R.; Xie, J. Research on image inpainting algorithm of improved GAN based on two-discriminations networks. Applied Intelligence 2021, 51, 3460–3474. [Google Scholar] [CrossRef]
Farajzadeh, N.; Hashemzadeh, M. A deep neural network based framework for restoring the damaged persian pottery via digital inpainting. Journal of Computational Science 2021, 56, 101486. [Google Scholar] [CrossRef]
Cai, X.; Song, B. Semantic object removal with convolutional neural network feature-based inpainting approach. Multimedia Systems 2018, 24, 597–609. [Google Scholar] [CrossRef]
Wang, Q.; Chen, Y.; Zhang, N.; Gu, Y. Medical image inpainting with edge and structure priors. Measurement 2021, 185, 110027. [Google Scholar] [CrossRef]
Wu, J.; Zhang, J.; Wu, F.; Kong, Y.; Yang, G.; Senhadji, L.; Shu, H. Generative networks as inverse problems with fractional wavelet scattering networks. arXiv preprint 2020, arXiv:2007.14177 2020. [Google Scholar]
Angles, T.; Mallat, S. Generative networks as inverse problems with scattering transforms. arXiv preprint 2018, arXiv:1805.06621 2018. [Google Scholar]
Graham, B. Fractional max-pooling. arXiv preprint 2014, arXiv:1412.6071 2014. [Google Scholar]
Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems 2012, 25. [Google Scholar] [CrossRef]
Zeiler, M.D.; Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. arXiv preprint 2013, arXiv:1301.3557 2013. [Google Scholar]
Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 1–9.

Figure 1. Different tasks in computer vision: denoising for removing unwanted noise, enhancement for ground-truth image’s quality improvement, object detection for identification and labelling, segmentation for image partitioning for further analysis, and restoration for missing parts inpainting1

Figure 2. Architecture of a FOCNet.2

Figure 3. Schematic representation of a multi-scale FOCNet with two levels.

Figure 4. Training process of Neural Fractional-Order Adaptive Masks

Figure 5. Image enhancement with Fractional Rényi Entropy before using a CNN for image segmentation.

Figure 6. Architecture of a FrOLM-DNN for object detection and classification of a 3D image.

Figure 7. Architecture of a GSN with a ScatNet and PCA encoder, and a CNN decoder.

Figure 8. Architecture of a GFRSN with a FrScatNet and FM encoder, and a CNN decoder. By using two GFRSNs with different fractional-orders, one can enhance the predicted image

\tilde{y}

by merging the outputs from both orders,

{\tilde{y}}_{α_{1}}

and

{\tilde{y}}_{α_{2}}

Figure 8. Architecture of a GFRSN with a FrScatNet and FM encoder, and a CNN decoder. By using two GFRSNs with different fractional-orders, one can enhance the predicted image

\tilde{y}

by merging the outputs from both orders,

{\tilde{y}}_{α_{1}}

and

{\tilde{y}}_{α_{2}}

Notes

1	Ground-truth image generated by DALL-E 3.
2	Input image generated by DALL-E 3.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Fractional Calculus Meets Neural Networks For Computer Vision: A Survey

Abstract

1. Introduction

2. Fractional Calculus

3. Computer Vision

3.1. Denoising

3.1.1. Fractional-Order Total Variation

3.1.2. Fractional Optimal Control Network

3.2. Enhancement

3.2.1. Neural Fractional-order Adaptive Masks

3.2.2. Fractional Rényi Entropy

3.3. Object Detection

3.3.1. Fractional-Order Legendre Moment Invariants

3.4. Segmentation

3.4.1. Active Contour Detection With Fractional-Order Regularisation Term

3.4.2. FOCNet For Segmentation

3.5. Restoration

3.5.1. Fractional Wavelet Scattering Networks

3.6. Compression

3.6.1. Fractional Max-Pooling

3.6.2. Fractional Convolutional Filters

4. Conclusion

Acknowledgments

References

Notes

MDPI Initiatives

Important Links

Subscribe