Prerpints.org logo
Preprint
Article

Performance of Linear and Spiral Hashing

Altmetrics

Downloads

96

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 July 2024

Posted:

04 July 2024

You are already at the latest version

Alerts
Abstract
Linear Hashing is an important algorithm for many key-value stores. Spiral Storage was invented to overcome the poor fringe behavior of Linear Hashing, but after an influential study by Larson, seems to have been discarded. Since almost 50 years have passed, we repeat Larson’s comparison with in-memory implementation of both to see whether his verdict still stands. Our study shows that Spiral Storage has slightly better look-up performance, but slightly poorer insert performance.
Keywords: 
Subject: Computer Science and Mathematics  -   Data Structures, Algorithms and Complexity

1. Introduction

Key-value stores have become a main-stay of data organization for Big Data. For instance, Amazon DB is a pioneering NoSQL database built on this concept. A key-value store implements a map or dictionary. They can be implemented in different ways. B-tree like structures allow for range queries, whereas dynamic hash tables have simpler architectures and have better asymptotic performance of O ( 1 ) for inserts, updates, and reads. For instance, Linear Hashing, the best known version of dynamic hash tables, is used internally by both Amazon’s DynamoDB and BerkeleyDB. These data structures were originally conceived to implement indices for database tables and continue to be used for this purpose. They were developed in a world of anemic CPU performance and slow and small storage systems, but they have been successfully used in the world of Big-Data.
In this article, we compare Linear Hashing (LH) with a competitor proposed at roughly the same time in the late eighties. Both store key-value pairs in containers, the so-called buckets. Originally, each bucket resided in a page or several pages of storage, i.e. in those days exclusively in a magnetic hard drive. However, in-memory implementations of LH are common. Hash based structures can also be employed in distributed systems. The key together with the current state of the file is used to calculate the bucket to which the key-value pair belongs. A file usually accomodates to an increase in the number of records by splitting a single bucket into two or more buckets. It can also react to a decrease in the number of records by merging buckets.
LH adjusts to growth in the number of records by splitting a predetermined bucket, following a constant ordering of buckets. Thus, the state of an LH-file is determined entirely by the number of buckets, N. The last ⌊ log 2 ( N ) ⌋ or ⌊ log 2 ( N ) ⌋ + 1 bits of the hash of a key determines where the record – the key value pair – is located. The main criticism of LH is the cyclic worst case performance for inserts and lookups. The ingenious addressing mechanism of Spiral Storage or Spiral Hashing (SH) as we prefer to call it, avoids this cyclic behavior. Like LH and other hash based schemes, stores key-value pairs in buckets. It uses a more complex address calculation to even out worse-case performance. In a well-received study, [6], P.-A. Larsen compared the performance of LH, SH, an unbalanced binary tree, and a scheme built on double hashing, and came to the conclusion that LH always outperforms SH (and the other two schemes). This reflects the cost of the more complex addressing scheme in SH. However, the environment has changed considerably for both schemes. More data is stored in memory or in the new NVRAM technologies. Processor speed have increased much faster than memory access times or storage access times. We decided to test whether Larsen’s verdict still stands. It does not!
In the following, we first review the the standard versions of LH and SH. We then perform a theoretical Fringe analysis for bulk insertions into both data structures. Even if a large bulk of data is inserted, and thus a large number of splits occur, LH’s performance is still cyclic. Then, we explain our implementations for LH and SH as main memory tables. The next section gives our experimental results and conclusions.

2. Background

Hashing schemes implement key-value stores and provide the key-based operations of insert, update, delete, and read. A hash record consists of a key and a value. Hashing places the record in a location calculated from the key. Typically, the location can contain more than a single record in which case it is called a bucket. Dynamic hashing schemes adjust to changes in the number of records by increasing the number of buckets where a record can be placed. With this strategy, the computational complexity of a key-based operation can be made independent of the number of records, provided that the expected number of records in a bucket is limited by some constant and provided that the calculation of the address (i.e. the bucket where a record is located) takes time independent of the current state of the hash file.
While most dynamic hashing scheme place records into buckets, often implemented a linked lists or arrays, they differ in the organization and behavior of the buckets. Originally, the classic dynamic hashing schemes like extensible hashing [4], LH [7], and SH [9,10] stored records in blocks in a hard disk drive. Nowadays, they are also used to distribute data in a distributed system or to store records in NVRAM, flash memory, or in main memory.

2.1. Linear Hashing

Linear Hashing (LH) is a dynamic hashing scheme that provides stable performance and good space utilization. An LH file allows expansions and contractions to adjust to the growth or decline in the number of records. It stores records in buckets, which could be, but not have to be pages in a storage device. In this case, the bucket capacity is limited and overflow records would be stored in an overflow bucket associated with the overflowing bucket. LH has been widely used in disk-based database systems such as Berkeley DB and PostgreSQL [12].
The number of buckets in an LH file increases linearly with the number of records inserted. LH allows for various ways in which the number of buckets is increased (or decreased) as the number of inserted records changes. There are several variants of LH depending on the criteria for incrementing the number of buckets. The first possibility is to maintain the number of inserted records r together with the number n of buckets and keep the ratio β = r / n above a threshold. The main alternative is to set a bucket capacity. For each bucket, we then either maintain or recalculate the number of records in the bucket on an insert. Whenever an insert increments the number of records in a bucket, then the LH file grows by increasing the number of buckets. Like Fagin’s extendible hashing [4], the number of buckets increases through splits where the records in one bucket are divided into the existing and a newly created bucket. Unlike extendible hashing, the bucket to split is predetermined and independent of the number of records in the bucket that is split [7].
Internally, LH maintains a file state that in principle consists only of the current number b of buckets. Buckets are numbered starting with zero. From b, we calculate the levell and the split pointer s as
l = ⌊ log 2 ( b ) ⌋ , s = b − 2 l
so that
b = 2 l + s , s < 2 l .
The original paper by Litwin [7] also had an option for starting out an LH-file with more than one bucket, in which case these formulae need to be adjusted. In practice, most LH-File start with one bucket. If the number of bucket is incremented, then Bucket s splits into Bucket s and Bucket s + 2 l . The split pointer s is then incremented. If s is equal to 2 l , then the level is incremented and s is reset to zero. Thus the equations we used to define split pointer s and level l is not used directly.
To calculate the bucket in which a record with key c resides, LH uses a family of consistent hash functions. For this purpose we use a long hash function h of the key. We then define a partial hash function h i by
h i ( c ) = h ( c ) ( mod 2 i ) ,
so that h i ( c ) is made up of the last i bits of h ( c ) . If the LH file has level l, then the partial hash functions h l and h l + 1 are used. To be more precise, the address a of a record with key c is the bucket in which the record should be placed, and it is first calculated as a = h l ( c ) , but if a < s it is recalculated as a = h l + 1 ( c ) .
The key difference between extendible hashing and LH is the selection of the bucket to be split. Extendible hashing always splits the bucket that overflows, but needs to maintain now a special directory structure that reflects the history of splits. LH always splits the bucket with number given by the split pointer s. Thus, the series of bucket numbers to split is
0 ; 0 , 1 ; 0 , 1 , 2 , 3 ; 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 ; 0 , 1 , … ,
which is made up of ranges from 0 to 2 l − 1 . The advantage of LH is the almost trivial file state that an LH file has to maintain, but an overflowing bucket might need to wait before a split remedies the overflow. During a split, all records in the bucket to split are rehashed with the new partial hash function h l + 1 and accordingly either remain in the same bucket or are moved to the new bucket. We can also implement merges to adjust to a decrease in the number of records. A merge always undoes the last split.

2.2. Spiral Hashing

A drawback to LH is the existence of buckets that are already split and not yet split at the same time. The former buckets tend to have twice as many records than the latter. As we will see below, Section 3, the number of records rehashed when a file is split depends on the split pointer and varies between B / 2 and B, where B is the maximum expected number of records in a yet-to-be-split bucket. To avoid this type of behavior, Spiral Hashing (SH) was invented by Martin [2,9,10]. 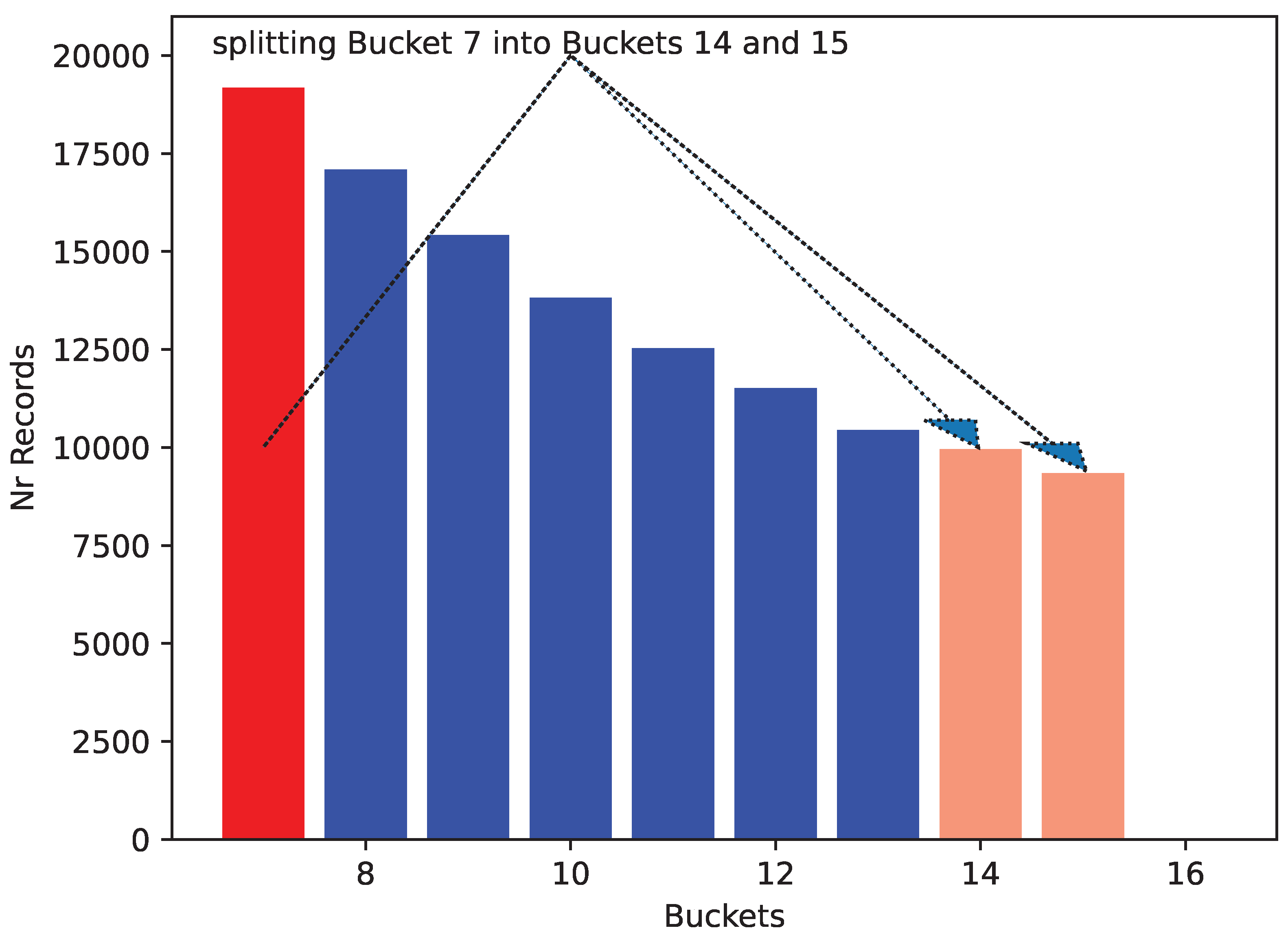SH intentionally distributes the records unevenly into Buckets S, S + 1 , S + 2 , …, 2 S − 1 , where S is the file state, Figure 1. If desired, a simple address translation keeps the buckets in the range 1, 2, …, s . We will not be using this final translation step here. When the file grows, the contents of bucket S are distributed into the new buckets Bucket 2 S and Bucket 2 S + 1 . Afterwards, Bucket S is deleted. If the hash used is completely uniform, then the probability that a record is allocated to Bucket i is p i = log 2 ( 1 + 1 / i ) . This remarkable feat is achieved with the logarithmic address calculation given in Figure 2. SH can be easily modified to generate d new buckets for each freed one. It is also possible to use an approximate address calculation. However, modern chip architectures with their efficient floating point units obviate the need for speeding up the address calculation.

3. Fringe Analysis

Fringe Analysis [1] analyzes the behavior of a data structure under mass insertion. For instance, Glombiewski, Seeger, and Graefe showed that a steady stream of inserts into a B-tree can create “waves of misery”, where restructuring in the B-tree can leads to surges in the amount of data moved [5]. While Linear Hashing is attractive because of its conceptual and architectonic simplicity, the average number of records per bucket varies between buckets already split in the epoch and those yet to split. 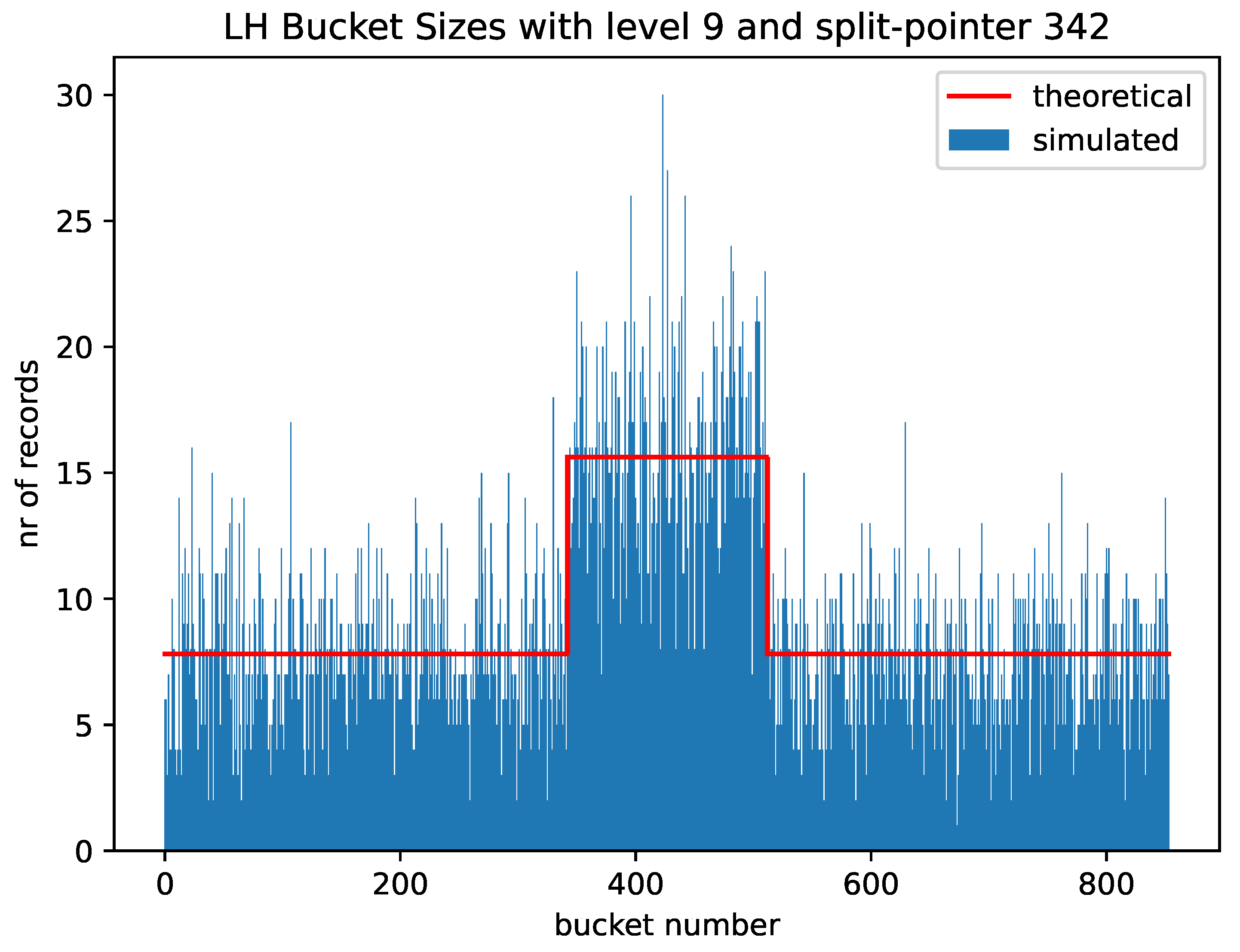Figure 3 gives an example with level 9 and split pointer 342 and a total of 8,000 records. Buckets 0 to Bucket 341 on the left and Buckets 512 to Bucket 853 on the right have on average about half the records than the Buckets 342 to Bucket 511. These numbers were obtained by using random numbers as the keys. Only if the split pointer is zero will all buckets have the same expected number of keys. In general, with level l and split pointer s, the buckets with numbers 0 to s − 1 and 2 l to 2 l + s − 1 have already split and have on average half as many records as the remaining ones.
We can analyze the fringe behavior of Linear Hashing analytically. We assume that the LH structure maintains a maximum ratio of records over buckets. If the number of records is r and B is this ratio, i.e. the average number of records per bucket, then the number of buckets is r / B . The level of the LH file is then λ = ⌊ log 2 ( r / B ) ⌋ . The expected number of records in an unsplit bucket is then r 2 λ . Every B inserts, a split happens, so
r B · 2 ∗ λ
on average are rehashed. About half of them are rehashed. The average number of records rehashed follows a saw-tooth curve increasing from 1 to 2 starting at B times a power of two and being reset at the next power of two. Figure 4 gives the result. We give an example of an experiment with bucket capacity 10 in Figure 5.
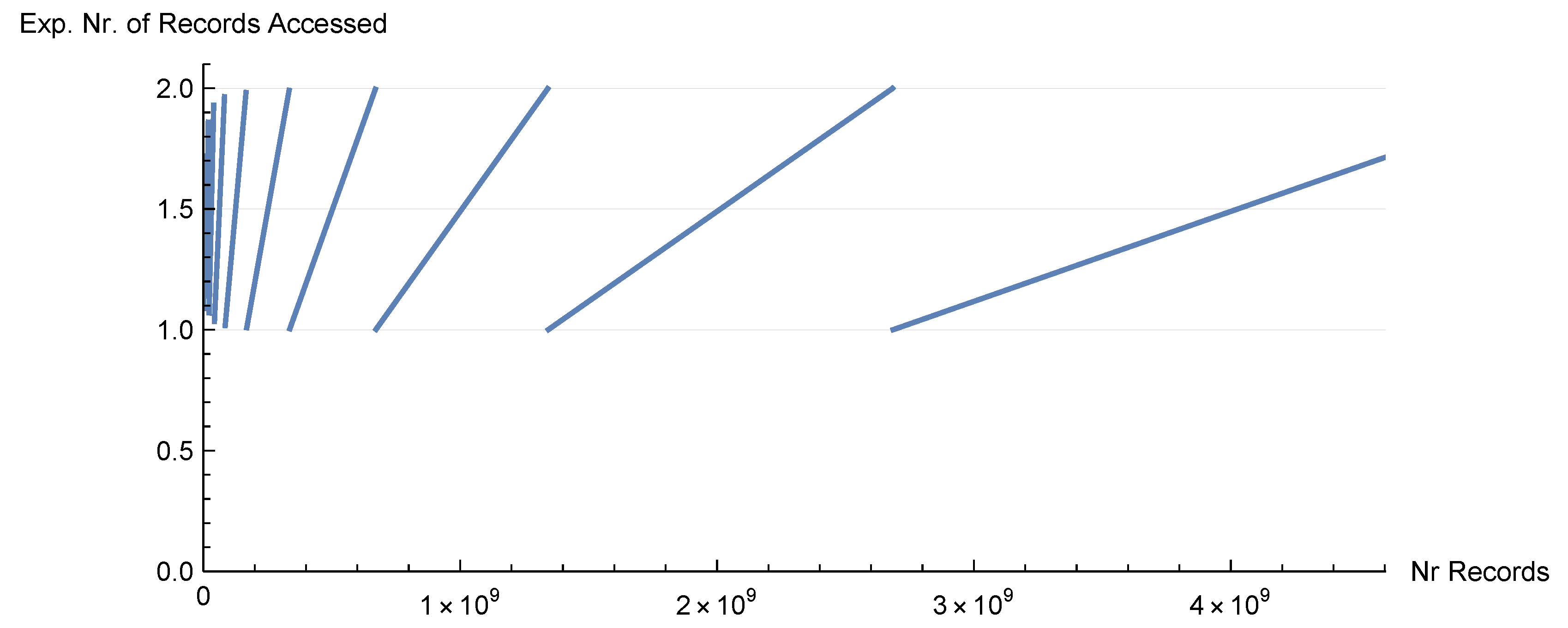
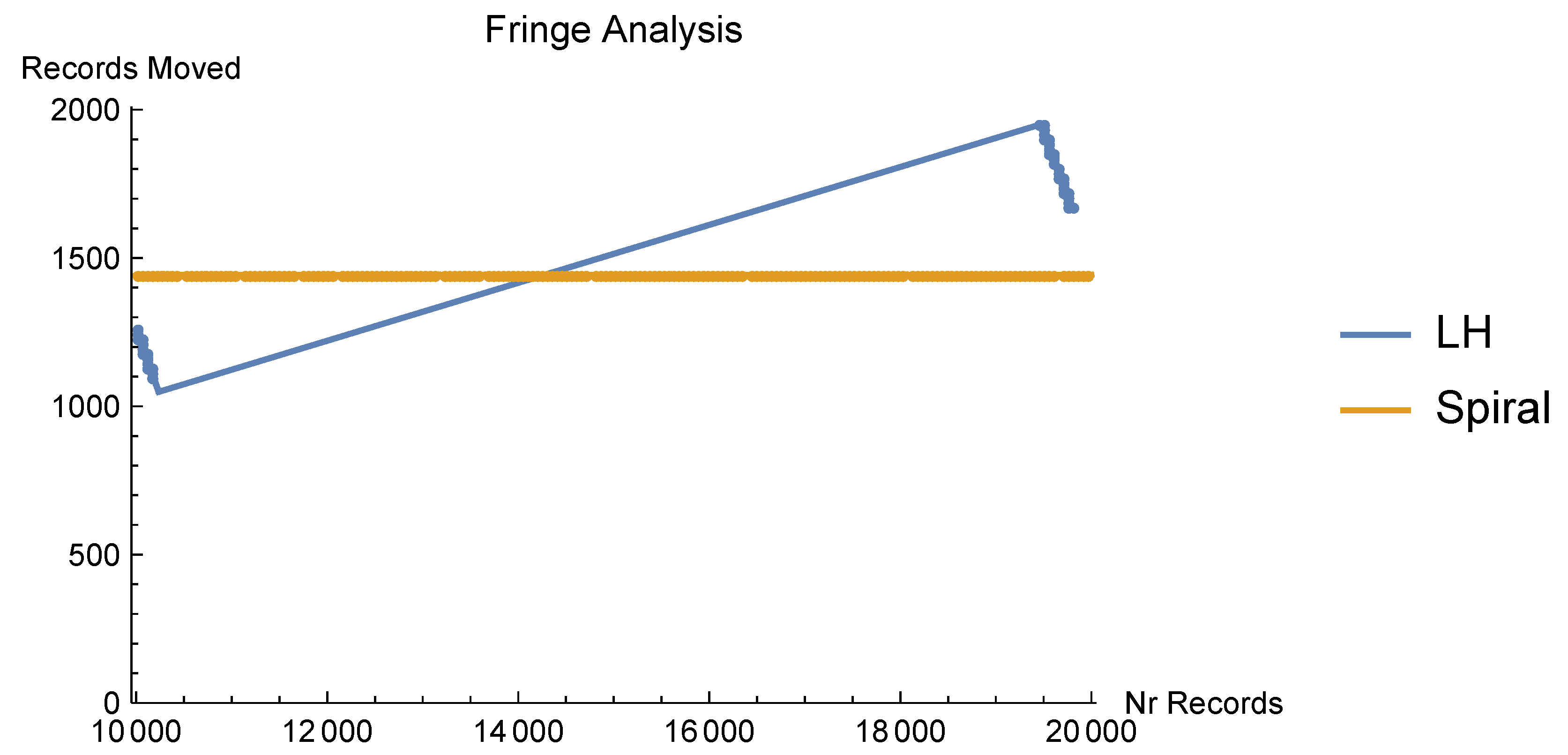
In Figure 6, we show the number of records in an LH file starting at n records, n ∈ [ 10000 , 20000 ] , that are evaluated when 1000 records (a growth between 5% and 10%) are added.
Spiral Hashing’s selling point is the avoidance of this fringe behavior. The probability of a record belonging to Bucket i is log 2 ( 1 + 1 / i ) . The size of the bucket that is split is always rather close to 1.44. Thus, instead of a cyclic fringe behavior, Spiral Hashing shows close to constant movement, independent of the number of records, Figure 6.
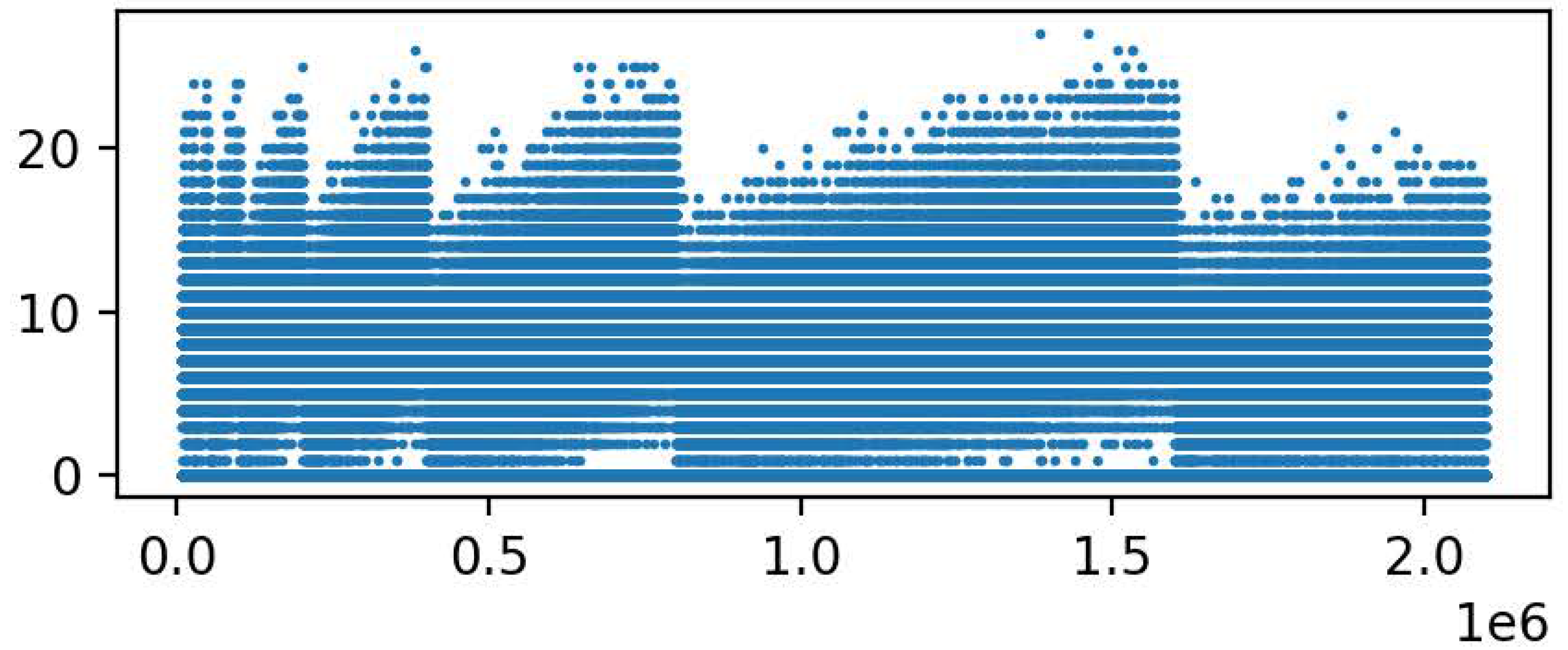
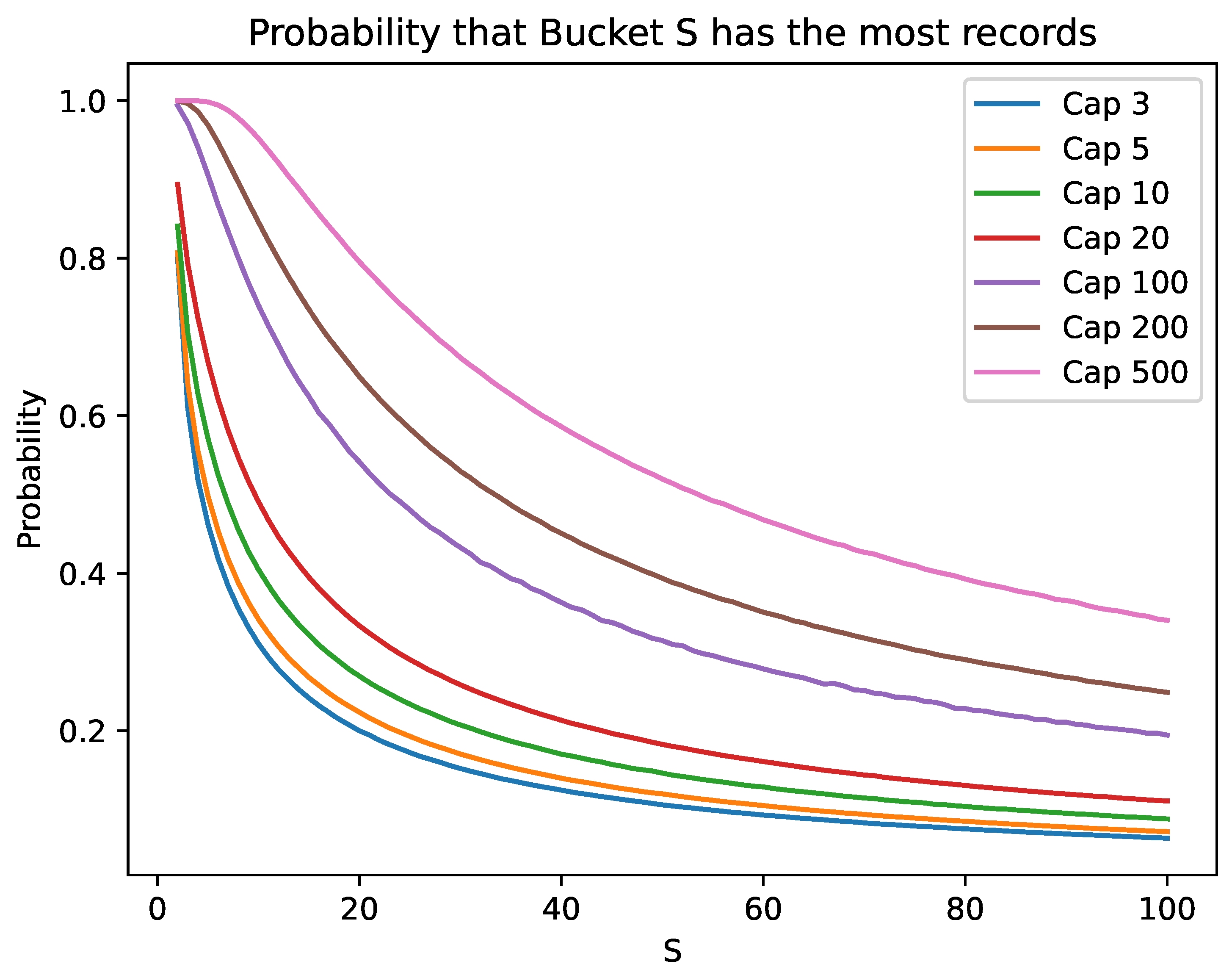
Spiral Hashing assigns a record to Bucket i with probability p i = log 2 ( 1 + 1 / i ) for i between S and 2 S − 1 . The smallest numbered bucket has the largest expected number of records and is always the next one to be split. However, it is often not the bucket with the actual largest number of buckets. The number of records in a bucket is given by a binomial distribution and we can therefore calculate the probability that one bucket contains more records than another exactly. There does not seem however a simple, closed formula for this probability. Instead of using the Central Limit Theorem and approximating with the normal distribution, we used the Las Vegas method to determine the probability that the next bucket to split actually has the largest number of records, as we would prefer. However, this is not the case as our results in Figure 7 show. As the nominal bucket capacity increases and as the number of buckets remains small, the probability that Bucket S has the most records increases, but for larger structures, that probability diminiushes quickly.

4. Implementations

We want to compare the efficiency of the two data structures. The advantage of Linear Hashing is its simplicity and elegance, and, in comparison with SH, its simpler addressing mechanism. The advantage of SH is better fringe behavior, but SH is burdened with a more complex addressing function. In fact, we discovered one key (an unsigned int in C++) and one file state where the addressing function when implemented in a straight-forward manner with C++ functions gave a wrong address because of a rounding error. This single instance forced us to include an additional check in the SH-addressing mechanism. Because we want to compare the relative merits of both data structures, we decided to implement a threaded, in-memory data structure with short records. Alternatives would be a distributed data structure (such as LH*) [8], and more prominently, an in-storage data structure. Our choice should highlight the relative differences.
Instead of following Larsen’s and Ellis Schlatter’s basic structure [3,6], we relied on the the efficiency of the implementations of containers in the C++ standard library. Our buckets are C++ vectors and they are organized inside another C++ vector. For concurrency, we used locks. There is a global lock for the file-state, which becomes a bottleneck under a load of heavy inserts. Each bucket has a lock.
An LH insert or lookup gains a non-exclusive lock on the file state. After determining the address of the bucket, the operation gains an exclusive lock on the bucket. It then inserts or retrieves a pointer to the record depending on its nature. An insert can trigger a split. The split operation first gains an exclusive lock on the file state. It then acquires another exclusive lock on the bucket to split. After rehashing the bucket into a new bucket and a new old bucket, we replace the old bucket with the new old bucket, add the new bucket, delete the old bucket and release the lock on the file state. The SH inserts and lookups follow along the same lines.

5. Experimental Results

We tested the efficiency of the two data structures varying two parameters, namely the number of threads and the bucket capacity, i.e. the average number of records per bucket. Using threads and locking generates of course quite a bit of overhead, but this because we do not do any other work within a thread. As each thread only accesses the data structure, lock contentioned is maximized.
We loaded our data structure with 1,000,000 records. For the first experiment, we then inserted another 1,000,000 records consisting of a random unsigned integer as the key and a short string. These records were stored in a C++ Standard Library vector and each thread is given an equal-sized region of this vector to insert. This write-only workload leads to many splits and contention on the file-state. For the second experiment, we again preloaded the data structure with 1,000,000 records with random keys. Then we filled a vector with 1,000,000 random keys. Each thread then performed lookup operations for regions of the same size in this vector. This operation does not acquire exclusive locks on the file state and the timing is much better. However, most of the time, the lookup operation will access all records in a bucket. Each experiment was performed 100 times (in a new process).
We performed our experiments on a Powerbook Mac with the M2 Max processor and 64 GB memory. Results on an earlier Powerbook Mac with an Intel processor had the same behavior. In both cases, the OS assigns only one CPU to the process.
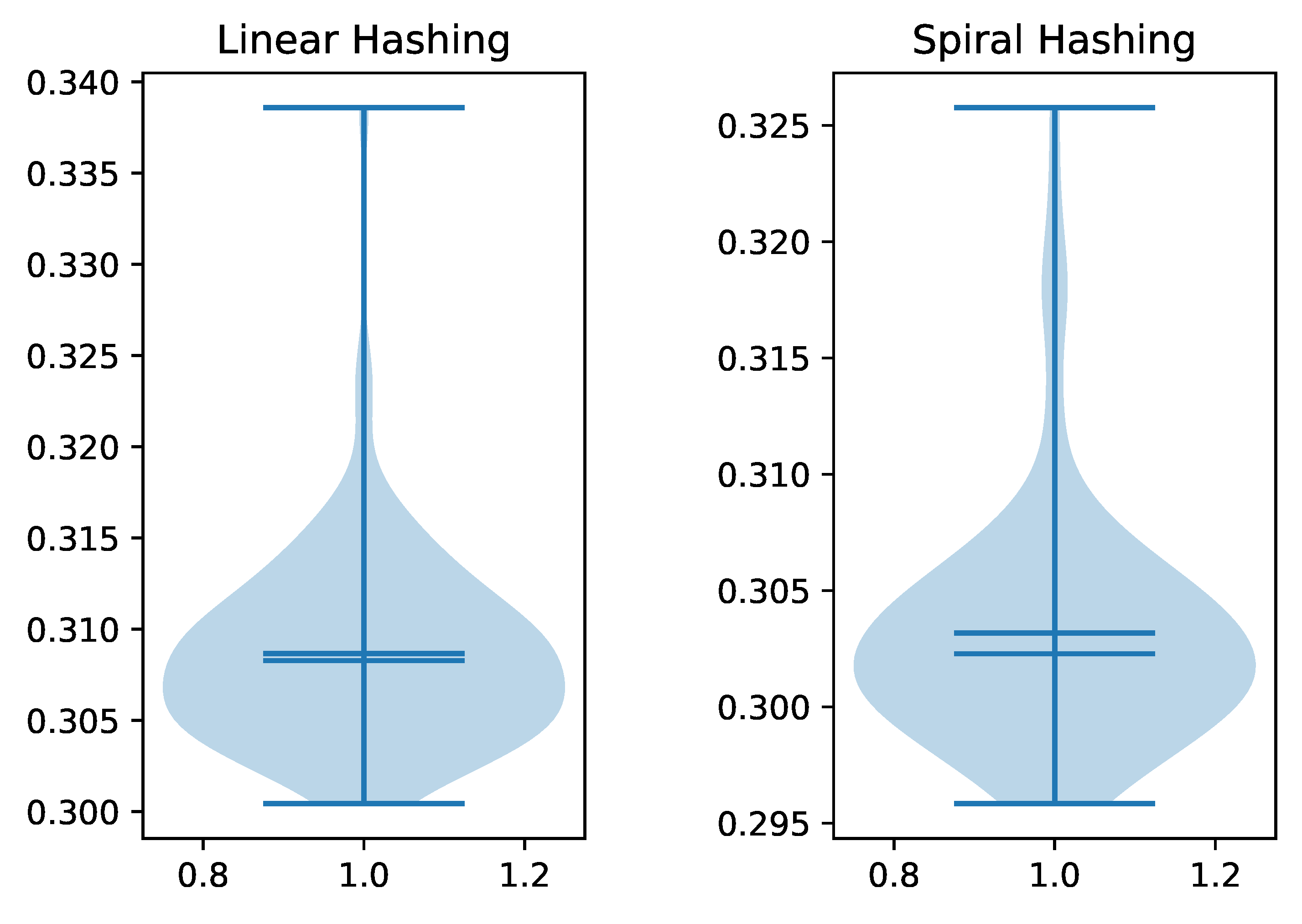
Because we are using random keys, each run of the program had a unique workload. This seems to be the dominant factor in the variation of the execution time, as the violin plots in Figure 8 indicate. We can see that the distribution of execution times have a long tail, but otherwise resemble that of a normally distributed random variable. While the run times are definitely not normally distributed, they justify the use of the mean in reporting of our results.
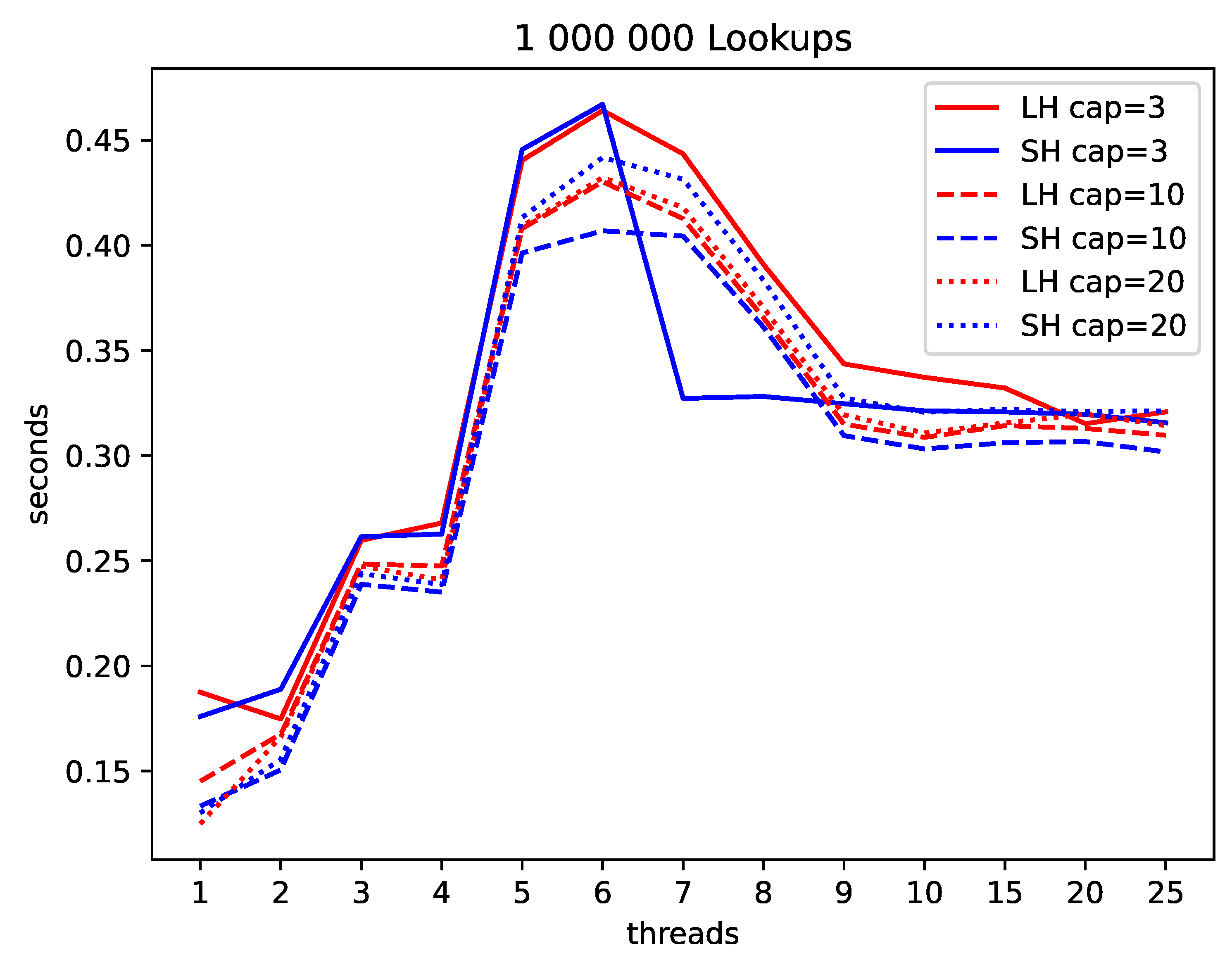
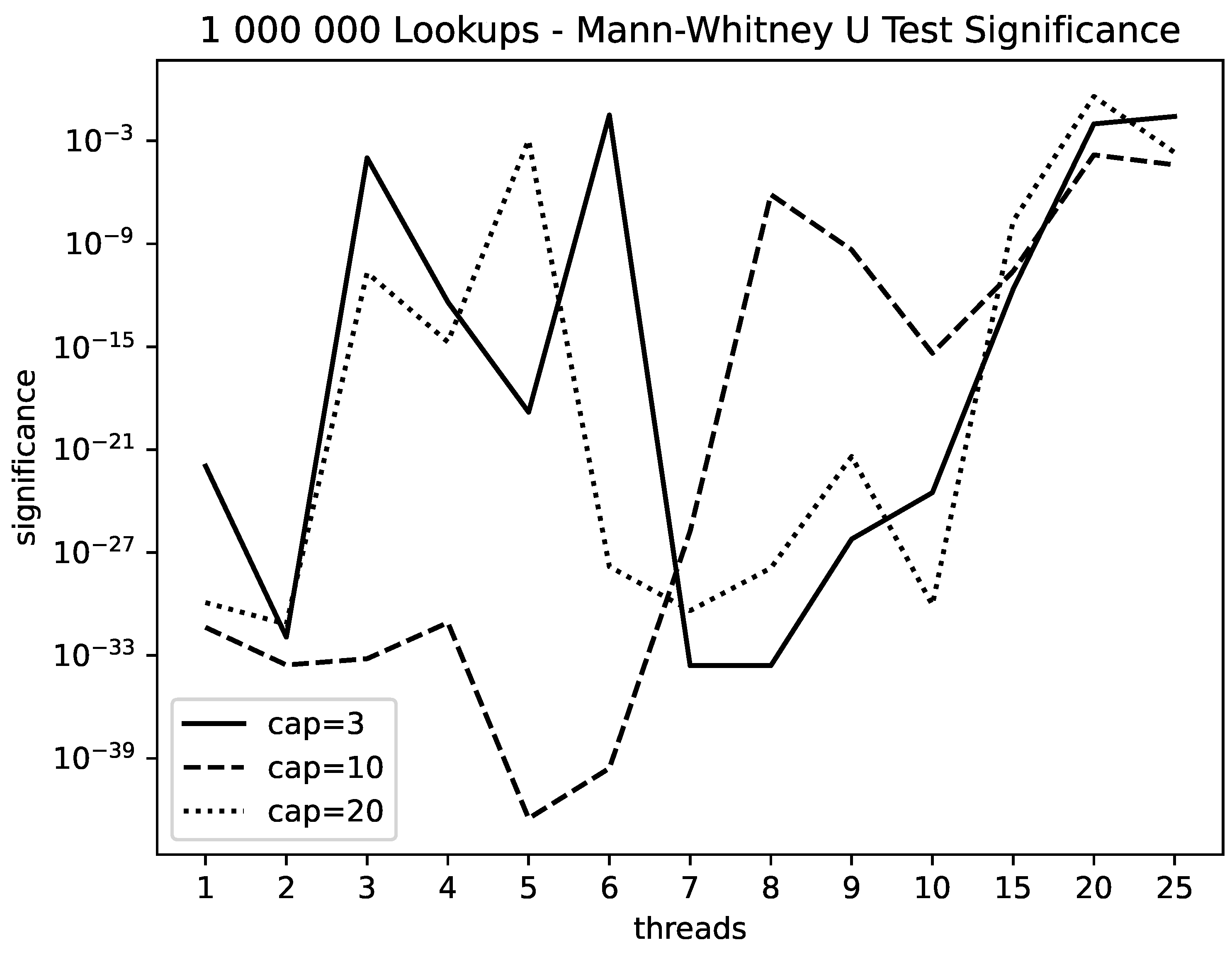
We give these results in Figure 10 and Figure 9. We also used the non-parametric Mann Whitney U-test to ascertain the significance of the observed differences. Not surprisingly, they are highly significant, as Figure 11 shows. The values shown give the probability that the differences in the run times for LH and for SH are by chance.
Our experiments show that Linear Hashing is faster than Spiral Hashing under a write load whereas usually, Spiral Hashing is faster under lookups. The different complexity of the addressing mechanisms do not seem to be relevant.

6. Conclusions and Future Work

Performance based judgements need to be revised whenever the underlying technology has changed. A reassessment of Spiral Hashing and Linear Hashing was overdue and we undertook it in this article. As a result, Spiral Hashing now provides a viable alternative to Linear Hashing even as an in-memory structure. Its more complicated addressing mechanism is balanced by its better fringe behavior.
If the buckets are stored in pages in storage, the better fringe behavior should be even more attractive. In Spiral Hashing, the biggest bucket is often the next bucket to be split. This behavior avoids page overflows, which are usually handled by adding overflow pages. The same observation applies to distributed systems.
Our implementation used locks. Lock-free implementations of Linear Hashing exit [11,13]. Shalev’s implementation realizes that an in-memory LH hash file is essentially a single, linked list and buckets form sublists. The list is ordered by the keys in reverse order. Thus, we can simply adjust a lock-free linked-list implementation. A bucket split results from the insertion of a new pointer to the leading record in the bucket, dividing the previous sub-list corresponding to the bucket. A similar observation holds for SH. An implementation is left to future work.

References

  1. Baeza-Yates, R. A. “Fringe analysis revisited,” ACM Computing Surveys (CSUR), vol. 27, no. 1, pp. 109–119, 1995. [CrossRef]
  2. Chu, J.-H. and Knott, G. D. “An analysis of spiral hashing,” The Computer Journal, vol. 37, no. 8, pp. 715–719, 1994. [CrossRef]
  3. Schlatter Ellis, C. “Concurrency in linear hashing,” ACM Transactions on Database Systems (TODS), vol. 12, no. 2, pp. 195–217, 1987. [CrossRef]
  4. Fagin, R., Nievergelt, J., Pippenger, J. and Strong, H. R. “Extendible hashing —- a fast access method for dynamic files,” ACM Transactions on Database Systems (TODS), vol. 4, no. 3, pp. 315–344, 1979. [CrossRef]
  5. Glombiewski,N. Seeger, B. and Graefe, G. “Waves of misery after index creation,” Datenbanksysteme für Business, Technologie und Web, Lecture Notes in Informatics, Gesellschaft für Informatik, Bonn, pp. 77–96, 2019.
  6. Larsen, P.-A. "Dynamic hash tables", Communications of the ACM, vol. 31, no. 4, pp. 446-457, 1988.
  7. Litwin, W. “Linear hashing: a new tool for file and table addressing.” in Proceedings, Conference on Very Large Database Systems, 1980.
  8. Litwin, W., Neimat, M. A., and Schneider, D. A. "LH*—a scalable, distributed data structure." ACM Transactions on Database Systems (TODS), vol. 21(4), p. 480-525, 1996. [CrossRef]
  9. Martin, G. N. N. “Spiral storage: Incrementally augmentable hash addressed storage,” Theory of Computation Report - CS-RR-027, University of Warwick, 1979.
  10. Mullin J. K. “Spiral storage: Efficient dynamic hashing with constant performance,” The Computer Journal, vol. 28, no. 3, pp. 330–334, 1985. [CrossRef]
  11. Shalev, O. and Shavit, N. "Split-ordered lists: Lock-free extensible hash tables", Journal of the ACM (JACM), vol. 53, no. 3, pp. 379-405, 2006. [CrossRef]
  12. Wan, H., Li, F, Zhou, Z., Zeng, K., Li, J., and Xue, C.J. "NVLH: crash consistent linear hashing for non-volatile memory", in 2018 IEEE 7th Non-Volatile Memory Systems and Applications Symposium (NVSMA), IEEE, pp. 117-118, 2018.
  13. Zhang, D. and Larson, P.-A. “Lhlf: lock-free linear hashing,” (poster paper) in Proceedings of the 17th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, pp. 307– 308, 2012.
Preprints 111029 g001
Figure 1. Spiral Hashing with S=7, before and after splitting.
Figure 1. Spiral Hashing with S=7, before and after splitting.
Preprints 111029 g001
Preprints 111029 g002
Figure 2. Address calculation in Spiral Hashing for key key and file state S.
Figure 2. Address calculation in Spiral Hashing for key key and file state S.
Preprints 111029 g002
Preprints 111029 g003
Figure 3. Theoretical and expected number of records per buckets in an LH file.
Figure 3. Theoretical and expected number of records per buckets in an LH file.
Preprints 111029 g003
Preprints 111029 g004
Figure 4. Number of records rehashed during a split in LH. Theoretical result for Linear Hashing when buckets split based on the ratio of records over buckets.
Figure 4. Number of records rehashed during a split in LH. Theoretical result for Linear Hashing when buckets split based on the ratio of records over buckets.
Preprints 111029 g004
Preprints 111029 g005
Figure 5. Number of records rehashed during a split in LH. Experimental results for random keys in case splits are triggered by an overflowing bucket.
Figure 5. Number of records rehashed during a split in LH. Experimental results for random keys in case splits are triggered by an overflowing bucket.
Preprints 111029 g005
Preprints 111029 g006
Figure 6. Number of records rehashed when adding 1000 records to a Linear Hashing and Spiral Hashing file with n records, n ∈ [ 10000 , 20000 ] .
Figure 6. Number of records rehashed when adding 1000 records to a Linear Hashing and Spiral Hashing file with n records, n ∈ [ 10000 , 20000 ] .
Preprints 111029 g006
Preprints 111029 g007
Figure 7. Probability that the smallest numbered bucket under Spiral Hashing has indeed the largest number of records.
Figure 7. Probability that the smallest numbered bucket under Spiral Hashing has indeed the largest number of records.
Preprints 111029 g007
Preprints 111029 g008
Figure 8. Violin Plot of the run times of LH and SH under inserts with 10 threads and a bucket capacity of 10.
Figure 8. Violin Plot of the run times of LH and SH under inserts with 10 threads and a bucket capacity of 10.
Preprints 111029 g008
Preprints 111029 g009
Figure 9. Run time means for the insert experiment for various numbers of threads and bucket capacities
Figure 9. Run time means for the insert experiment for various numbers of threads and bucket capacities
Preprints 111029 g009
Preprints 111029 g010
Figure 10. Run time means for the lookup experiment.
Figure 10. Run time means for the lookup experiment.
Preprints 111029 g010
Preprints 111029 g011
Figure 11. P-values for the null hypothesis of equal lookup times using the Whitney-Mann U test.
Figure 11. P-values for the null hypothesis of equal lookup times using the Whitney-Mann U test.
Preprints 111029 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated