Prerpints.org logo
Preprint
Article

An ANFIS-Based Strategy for Autonomous Robot Collision-Free Navigation in Dynamic Environments

This version is not peer-reviewed.

Submitted:

02 July 2024

Posted:

04 July 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Autonomous navigation in dynamic environments poses a significant challenge in the field of ro-botics with the primary goals of ensuring both smooth and safe movement. This study introduces control strategy based on an Adaptive Neuro-Fuzzy Inference System (ANFIS) to enhance au-tonomous robot navigation in dynamic environments, emphasizing on collision-free path plan-ning. This strategy employs, a path planning technique to develop a trajectory that allows the ro-bot to navigate smoothly while avoiding collisions with both static and dynamic obstacles. The developed control system incorporates four ANFIS controllers: two are tasked with guiding the robot toward its end point, and the other two are activated for obstacle avoidance. The experi-mental setup conducted in CoppeliaSim involves a mobile robot equipped with ultrasonic sensors navigating in an environment with static and dynamic obstacles. Simulation experiments are conducted to demonstrate the model's capability in ensuring collision-free navigation, employing a path planning algorithm to ascertain the shortest route to the target destination. The simulation results highlight the superiority of the ANFIS-based approach over conventional methods, partic-ularly in terms of computational efficiency and navigational smoothness.
Keywords: 
Subject: 
Engineering  -   Mechanical Engineering

1. Introduction

The robotics research community has a strong focus on autonomous navigation in dynamic environments, particularly for the development of intelligent autonomousguided robots with significant industrial applications. The use of mobile robots in manufacturing, warehousing, and construction is on the rise. Real-world scenarios pose challenges when robots and humans share the same environment, necessitating effective human-robot interaction mechanisms. For example, in manufacturing, autonomous guided vehicles may encounter human obstructions and need to implement collision avoidance measures. Researchers in this field have explored a range of methodologies incorporating various sensor types, including laser measurement systems [1], lidar sensors [2,3], cameras [4], among others.
Artificial intelligence (AI) techniques show significant potential in addressing complex challenges within dynamic and uncertain environments. Robots capable of demonstrating complex behaviors by interpreting their environment and adapting their actions through sensors and ANFIS control mechanisms are commonly referred to as behavior-based systems. The application of fuzzy logic and neural networks has shown effectiveness in the field of autonomous robot navigation. [5,6,7,8,9,10,11].
Al-Mayyahi et al. [5] present a novel approach that utilizes an Adaptive Neuro-Fuzzy Inference System (ANFIS) to address navigation challenges encountered by an Autonomous Guided Vehicle (AGV). The system is comprised of four ANFIS controllers; two regulate the AGV's angular velocities for reaching the target and two for optimal heading adjustments to avoid obstacles. For low-level motion control, the velocity controllers receive input from three sensors, including front distance, right distance and left distance. For the target reaching mission, the heading controllers consider only one input, which is the angle difference between the AGV's current heading and the target point in order to determine the optimal direction. This work primarily emphasizes on the optimal heading adjustment to ensure collision avoidance, but does not consider any path planning method for trajectory optimization.
Miao et al. [6] presented a novel obstacle avoidance fuzzy controller utilizing fuzzy control algorithms. This controller utilized operational data to establish an AGV adaptive neuro-fuzzy network system, capable of providing precise behavioral commands for AGV's dynamic obstacle avoidance.
Haider et al. [7] introduced a solution that leverages an Adaptive Neuro-Fuzzy Inference System (ANFIS) in conjunction with a Global Positioning System (GPS) for control and navigation, effectively addressing issues such as low performance in cluttered and unknown environments, high computational costs and multiple controller models for navigation. The proposed approach automates mobile robot navigation in densely cluttered environments, integrating GPS and heading sensor data fusion for global path planning and steering. A fuzzy inference system (FIS) is employed for obstacle avoidance, incorporating distance sensor data as fuzzy linguistics. Furthermore, a type-1 Takagi–Sugeno FIS is utilized to train a five-layered neural network for local robot planning, with ANFIS parameters fine-tuned through a hybrid learning method.
Farahat et al. [8] focuses on an extensive analysis and investigation into AI algorithm techniques for controlling the path planning of a four-wheel autonomous robot, enabling it to autonomously reach predefined objectives while intelligently circumventing static and dynamic obstacles. The research explores the viability of employing Fuzzy Logic, Neural Networks, and the Adaptive Neuro-Fuzzy Inference System (ANFIS) as control algorithms for this intricate navigation task.
Jung et al. [9] explores a vision guidance system for Automated Guided Vehicles (AGVs) that leverages an ANFIS. The vision guidance system is founded on a driving method capable of recognizing salient features such as driving lines and landmarks, providing a data-rich alternative to other induction sensors in AGVs. Due to the camera’s sensitivity to lighting variations, a "dark-room environment" was developed to ensure consistent lighting conditions, minimizing brightness disturbances that affect camera performance. This controlled environment limits external light interference, stabilizing illumination to enhance the reliability of the vision system. Although this approach restricts the camera's viewing angle and presents control challenges at high speeds or sudden changes in direction, it proves effective with ANFIS-enhanced steering control, offering an improvement over traditional Proportional–Integral–Derivative (PID) methods. This specialized setup acknowledges the challenges of camera-only systems and contrasts with broader autonomous driving technologies that integrate multiple sensors to adapt to diverse environmental conditions.
Khelchandra et al. [10] introduced a method for path planning considering mobile robot navigation within environments with static obstacles, which combines neuro-genetic-fuzzy techniques. This approach involves training an artificial neural network to select the most suitable collision-free path from a range of available paths. Additionally, a genetic algorithm is employed to enhance the efficiency of the fuzzy logic system by identifying optimal positions within the collision-free zones.
Faisal et al. [11] presented a technique for fuzzy logic-based navigation and obstacle avoidance in dynamic environments. This method integrates two distinct fuzzy logic controllers: a tracking fuzzy logic controller, which steers the robot toward its target, and an obstacle avoidance fuzzy logic controller. The principal aim of this research is to demonstrate the utility of mobile robots in material handling tasks within warehouse environments. It introduces a notable departure from the traditional colored line tracking approach, replacing it with wireless communication methods.
A thorough review of recent literature highlights various control strategies employed for obstacle avoidance in robotic systems, which are centered around ANFIS [12,13,14,15,16,17,18,19] and fuzzy logic [20,21,22,23,24,25]. Various artificial intelligence techniques including reinforcement learning, neural networks, fuzzy logic and genetic algorithms enhance the reactive navigation capabilities of mobile robots. Particularly, fuzzy logic is notable for its capacity to articulate linguistic terms and make reliable decisions amidst uncertainty and imprecise data, proving invaluable in control systems. Fuzzy control systems, which are rule-based and draw on domain knowledge or expert insights, use fuzzy if-then rules to simplify decision-making without needing detailed computations. These systems are widely recognized for their ability to handle a broad range of tasks effectively. Fuzzy logic excels in dynamic or unknown environments by mimicking human reasoning and decision-making processes, thus facilitating robust and quick-responsive navigation. This approach not only adapts to the unpredictable nature of real-world settings but also does not require precise environmental models for effective navigation [26].
A notable limitation of fuzzy controllers is the absence of a systematic design methodology, frequently resulting in labor-intensive tuning of membership function parameters. The integration of neural network learning techniques with fuzzy logic has enabled the development of neuro-fuzzy controllers, significantly accelerating the design process and enhancing performance. This hybrid approach has become a prominent area of research within the field of robot navigation in uncertain environments [14].
Significant progress has been made in applying fuzzy control and ANFIS to mobile robotics, enhancing adaptability in dynamic environments. Despite these advances, traditional systems still struggle with rapid adaptability to new or evolving conditions and exhibit computational inefficiencies in complex scenarios. This underscores the necessity for further research aimed at developing simpler, more efficient control models. Simplifying these systems would not only expedite response times but also decrease computational demands, thereby advancing the capabilities of autonomous navigation technologies.
In our present work, we employ a combination of four Adaptive Neuro-Fuzzy Inference Systems (ANFIS) to facilitate mobile robot navigation towards a desired destination while ensuring collision avoidance capabilities for both stationary and mobile obstacles. This approach focuses on the application of a path planning algorithm to establish an efficient route from the start point to the end point, ensuring a smooth path within a static environment. During this initial phase, two ANFIS controllers are dedicated to tracking and guiding the robot towards the end point. However, if the robot encounters a mobile obstacle during its trajectory, another pair of ANFIS controllers is activated, specifically designed for obstacle avoidance maneuvers. Once the obstacle avoidance action is executed, the robot smoothly resumes its original planned path.
In our experimental evaluations, we conduct a comparative analysis between the ANFIS controllers and fuzzy logic controllers. Significantly, our ANFIS controllers exhibit improved operational efficiency, employing fewer rules compared to the fuzzy logic controllers, emphasizing a simpler approach. The proposed control algorithm, with ANFIS at its core, is proved to be both simple yet effective, providing valuable insights into robotic navigation in dynamic environments within the existing literature.
The innovation of this work is summarized around four key points:
  • Development of a novel control strategy that employs the ANFIS model's capabilities to simplify and facilitate the decision-making process, thereby enhancing the system’s computational efficiency.
  • Application of four Adaptive Neuro-Fuzzy Inference Systems (ANFIS) that are expertly optimized to minimize the rule set of fuzzy controllers, while maintaining system efficiency.
  • Enabling efficient navigation in environments cluttered with obstacles through a simplified rule structure.
  • Integration of a path planning algorithm that adds a layer of sophistication, enhancing the determination of optimal trajectories and significantly improving the efficiency and effectiveness of autonomous robot navigation.
The paper is organized as follows: Section 2 provides a concise overview of the kinematics of Autonomous Guided Vehicles, essential for understanding the subsequent development of the control system. Section 3 introduces the novel path planning strategy, crucial for autonomous navigation. Section 4 presents a comparative analysis of ANFIS and PID controllers, underscoring the advantages of ANFIS in dynamic environments. Section 5 presents the design of the ANFIS controllers, explaining their roles in tracking and avoidance within the robotic control system. In Section 6, the simulation experiments conducted in CoppeliaSim are presented. Finally, conclusions and directions for future advancements in robotic navigation are presented in Section 7.

2. Kinematics of a Two-Wheel Drive Robot

The core focus of this research is to design a control system that ensures safe and reliable navigation for a mobile robot in dynamic environments, a process that necessitates a thorough consideration of the robot's kinematic and geometric properties. To this end, the kinematics of two-wheel differential-drive robot, such as Pioneer p_3dx used in this work, are presented in the following.
Figure 1 illustrates two critical frames of reference that describe the robot's movement: a stationary global reference frame (I), denoted by X I and Y I , and a moving local reference frame (R), denoted by X R and Y R , fixed to the robot. Establishing these frames is fundamental for developing a robust control strategy that can dynamically adapt to the environment. It is also noted that θ represents the robot’s orientation, and P marks its position.
The kinematic model for the wheeled robot's motion builds upon three foundational assumptions: each wheel maintains perpendicularity to its respective plane; there's a singular contact point between the wheel and the plane and the wheel rolls without slippage. Integrated into this model are two key constraints: firstly, the wheel's translational motion along the plane corresponds directly with its rotational velocity; secondly, no translational motion occurs perpendicularly to the wheel plane.
In accordance with [22], the differential drive configuration is characterized by two wheels placed on the same axis, each independently driven by separate motors. The motion of the robot is a cumulative outcome of the contributions from each of these wheels, and understanding this dynamic is essential for implementing precise control. The model is mathematically described as follows:
u = r 2 ω r i g h t + ω l e f t
ω = r L ω r i g h t − ω l e f t
where u denotes the linear velocity of the robot, ω its angular velocity, r the radius of the wheels, ω r i g h t and ω l e f t the angular velocities of the right and left wheels respectively, and L the distance between the two wheels.

3. Strategy for Path Planning

3.1. Path Planning Concepts

Path planning is a crucial and essential issue in autonomous mobile robot navigation. Over the past two decades, extensive research, as presented in [23], has been dedicated to the domain of path planning for mobile robots in various environments. This procedure involves the identification of a collision-free path that connects two points while minimizing the associated route cost. In online path planning, the robot utilizes sensor data to gather information about its surroundings and construct an environmental map. Conversely, offline path planning entails the robot independently acquiring environmental information without dependence on sensors. This process plays a crucial role in enabling effective autonomous navigation.

3.2. The Bump-Surface concept

In the present study, we implement the Bump-Surface concept [27] as a strategic approach to path planning. This method offers a solution to the path-planning challenges encountered by mobile robots operating within 2D static environments. The development of the Bump-Surface method involves the utilization of a control-point network, the density of which can be adjusted to fulfill specific path-planning precision requirements. In summary, increased grid density results in enhanced precision. Moreover, leveraging the flexibility of B-Spline surfaces enables us to achieve the desired level of accuracy, utilizing their features for both local and global control. Subsequently, a genetic algorithm (GA) is employed to explore this surface, aiming to find an optimal collision-free path that aligns with the objectives and constraints of motion planning.

4. Basic Concepts on the Adaptive Neuro-Fuzzy Inference System (ANFIS)

The Adaptive Neuro-Fuzzy Inference System [28] represents a versatile computational framework that integrates the merits of fuzzy logic and neural networks. This fusion equips ANFIS to handle intricate problems that might pose challenges for conventional mathematical methodologies. Essentially, ANFIS combines the human-like, intuitive reasoning of fuzzy logic with the data-driven capabilities of neural networks. It serves as a valuable tool for tasks involving modeling, prediction, and rule-based decision-making. ANFIS models encompass fuzzy logic membership functions that collaborate with adaptive neural network nodes. These nodes undergo learning and enhancement through training. The integration of fuzzy and neural components renders ANFIS adaptable and robust, making it a powerful tool for addressing real-world issues, ranging from system control to pattern recognition.
The ANFIS method features a structure that combines a fuzzy inference system with a neural network, utilizing input and output data pairs. This configuration acts as a self-adapting and flexible hybrid controller with embedded learning algorithms. Fundamentally, this method enables fuzzy logic to dynamically adjust the parameters of membership functions, aligning the fuzzy inference system with the input and output data of the ANFIS model. Adapting neural networks to manage fuzzy rules necessitates specific modifications in the conventional neural network structure, enabling the integration of these two vital components.
ANFIS combines the strengths of fuzzy logic and neural networks, making it highly effective for complex problems that challenge standard mathematical methods. While PID controllers are effective for environments with linear and nonlinear characteristics, ANFIS exhibits superior performance particularly in dynamically evolving environments without necessitating a complex mathematical model, allowing it to handle unpredictably changing conditions more effectively. This capability allows ANFIS to navigate through unpredictably changing conditions more effectively, as it fuses the intuitive, human-like reasoning of fuzzy logic with the learning power of neural networks, enhancing its adaptability and overall effectiveness.
ANFIS models use fuzzy logic membership functions and adaptive neural network nodes that learn and improve through training. This allows ANFIS to adjust automatically to unexpected changes, such as obstacles or varying terrain—something PID controllers struggle with. The system integrates fuzzy and neural elements to become both adaptable and robust, making it ideal for real-world applications like system control and pattern recognition. ANFIS features a unique setup that merges a fuzzy inference system with a neural network, using data pairs to guide adjustments. This setup forms a flexible, self-learning hybrid controller that can adjust fuzzy rules dynamically, a necessary feature for integrating fuzzy logic with neural networks.

5. Designing the ANFIS Controllers for the Automated Guided Vehicle

In this section, we conduct a comprehensive analysis of the proposed ANFIS controllers, which have been designed and implemented using the ANFIS Toolbox in MATLAB R2019b. Notably, we have devised four individual ANFIS controllers, each serving a distinct role: initially, two ANFIS controllers are designed to facilitate reaching the end point by following a predefined path, while the remaining two ANFIS controllers are created to manage obstacle avoidance tasks.

5.1. ANFIS Tracking Controllers

The primary goal of our robot is to navigate towards a specified end point within its environment, utilizing sensor feedback for real-time adjustments. The tracking controller's role is to align the robot's orientation with the desired point. It operates based on two inputs: the position error and the heading error. The position error is calculated using the Euclidean distance between the current position of the mobile robot and its target point along the planned trajectory. This error is measured in meters and normalized within the range of [0,1]. The heading error, measured in degrees, represents the angular discrepancy between the robot's current heading and the direct line to the target. It is normalized between [-1, 1].
To achieve the goal of reaching the end point, two ANFIS tracking controllers are introduced. One controller manages the right motor velocity, while the other is responsible for the left motor velocity. Both controllers have two inputs: the position error and the heading error, which collectively determine the motors velocity (right and left), as shown in Figure 2. Importantly, when the position error reaches zero, indicating that the robot has reached its target, the robot stops moving to prevent further unnecessary motion.

5.1.1. Data Set for ANFIS Tracking Controllers

To create the dataset for training the ANFIS tracking controllers, we first developed a fuzzy logic tracking controller. Following that, we utilized this fuzzy logic tracking controller to generate the dataset required for training the ANFIS tracking controllers.
The fuzzy logic tracking controller has two inputs and two outputs. The first input is the position error, and the second is the heading error. The first output controls the velocity of the right motor, and the second output controls the velocity of the left motor.
The position error range is set to [0, 1] and the heading error range is [-1, 1]. The fuzzy sets expressing the position error use trapezoid membership functions to define linguistic terms, namely "small", "medium" and "large" (Figure 3). These terms are employed to represent position error values as follows:
To analyze position errors more thoroughly within the range of 0 to 1, we've categorized them into three fuzzy sets: 'small,' 'medium,' and 'large.' (Figure 3). Each fuzzy set represents a different degree of error.
  • 'small' represents values from 0 to 0.13, indicating that the robot is very close to the target.
  • 'medium' ranges from 0.05 to 0.3, suggesting a moderate distance from the target.
  • 'large' encompasses values from 0.15 to 1, indicating that the robot is far from the target.
The same approach is applied to heading error, as shown in Figure 4: Five fuzzy sets, namely 'negative big,' 'negative small,' 'zero,' 'positive small,' and 'positive big,' represent different ranges of heading deviations. This approach helps us better understand and manage the AGV's orientation during navigation tasks.
  • 'negative big' represents values ranging from -1 to -0.3, indicating a significant deviation in the negative direction.
  • 'negative small' spans values from -0.55 to -0.07, suggesting a moderate negative deviation.
  • 'zero' encompasses values from -0.15 to 0.15, indicating no deviation from the desired heading.
  • 'positive small' extends from 0.07 to 0.55, representing a moderate positive deviation.
  • 'positive big' ranges from 0.3 to 1, indicating a significant deviation in the positive direction.
In this study, the output velocity (m/s) of both the left and right motors, play a crucial role in the performance of our AGV navigation system. For better understanding of the velocity output, we have categorized this range into three fuzzy sets: "slow", "medium" and "fast" (Figure 5), as follows:
  • 'slow': covering values from 0 to 0.4, representing slower motor speeds.
  • 'medium': ranging from 0.27 to 0.6, indicating intermediate motor speeds.
  • 'fast': extending from 0.47 to 1, denoting higher motor speeds.
Based on our knowledge of the AGV navigation system, a set of 15 expert rules is defined guiding the AGV's actions across various scenarios, effectively establishing a fuzzy tracking controller. This set of rules is a crucial component of our navigation control strategy (Table 1).
The training dataset has been generated in accordance with the expert logical rules described previously. These rules define the connections between position error, heading error, and motor velocities within the AGV navigation system. Following these rules ensures that the training data thoroughly encompasses a wide spectrum of scenarios and behaviors, accurately capturing the AGV's responses to various error conditions. This dataset is fundamental for training the AGV navigation system and optimizing its performance. A sample of training data for the ANFIS tracking controller is presented in Table 2.

5.1.2. Training ANFIS For Tracking Controllers (left and right)

In this work, a dataset consisting of 228 data points is generated using the fuzzy logic tracking controller to train the ANFIS tracking controllers (left and right). In the proposed ANFIS system setup, three membership functions have been used for each input for each controller. These functions are of the trapezoidal type, contribute to capturing complex patterns effectively. For the output, linear membership functions are chosen, ensuring straightforward mapping of rules. The system is generated using a grid partition approach for efficient input organization and a hybrid optimization method is applied during training to improve performance. Finally, the system is trained over 200 iterations (epochs). The training error is calculated as the root mean square error (RMSE) between the predicted motor velocities (outputs of the ANFIS controller) and the actual motor velocities (target outputs). These settings enhance the precision and adaptability of our system for various robotics applications. Figure 6 presents the training data for the left motor ANFIS tracking controller and while Figure 7 depicts the training error for the same controller through 200 epochs.
Figure 8 displays the training and FIS output data for the Left Motor ANFIS tracking controller after the ANFIS is trained. The proposed ANFIS model performed well during training with a minimal error of 0.045806. It has a total of 35 components, consisting of 27 linear and 24 nonlinear parameters. These components work together to make the model accurate and capable of handling complex data patterns. The ANFIS controller features 9 rules, demonstrating a decrease of 6 rules compared to the fuzzy tracking controller, which contained 15 rules (refer to Section 5.1.1).
Figure 9 displays the training data for the right motor ANFIS tracking controller and Figure 10 displays the training error for the right motor ANFIS tracking controller.
Figure 11 shows the training and FIS output data for the right motor ANFIS tracking controller after completion of the ANFIS training process. The proposed ANFIS model performed well during training with a minimal error of 0.046201. It uses a combination of 35 components, including 27 linear and 24 nonlinear parameters. The ANFIS tracking controller for the right motor follows a similar pattern, employing 9 rules, which is a reduction of 6 rules compared to the previous fuzzy controller with 15 rules.
This ANFIS model is versatile and can be useful for various robotics applications.

5.2. ANFIS Avoidance Controllers

The primary objective of the robot's obstacle avoidance controller is to navigate safely within its environment by avoiding collisions with obstacles. This controller is composed of two ANFIS avoidance controllers, one specifically governing the left motor and the other the right motor. Each controller takes two crucial inputs: the left sensor reading and the right sensor reading. These sensor values provide information about the proximity of obstacles on either side of the robot, with a range scaled from 0 to 1.
The output of each ANFIS avoidance controller corresponds to the velocity (m/s) of the respective motor (left and right) as shown in Figure 12. These controllers collaboratively work to dynamically adapt motor velocities, enabling the robot to navigate around obstacles and maintain a collision-free path. By processing sensor data, the ANFIS avoidance controllers are capable of making real-time decisions regarding motor speeds, ensuring effective obstacle avoidance in the robot's navigation process. This mechanism enhances the robot's safety and reliability.

5.2.1. Data Set for ANFIS Avoidance Controllers

To create the dataset for training the ANFIS avoidance controllers, we first developed a fuzzy avoidance controller. Following that, we utilized this fuzzy avoidance controller to generate the dataset required for training the ANFIS avoidance controllers. The fuzzy avoidance controller has two inputs: the left sensor value and the right sensor value as shown in Figure 12. The controller also features two outputs: the left motor velocity and the right motor velocity. For the two inputs (left and right sensors), trapezoidal membership functions are defined for the linguistic terms " very close" , " close" , " medium"," far" , and " very far", as shown in Figure 13.
The membership functions for the outputs (left and right motor velocity) are shown in Figure 14 and are characterized by the linguistic terms 'slow' and 'fast'.
Afterwards, a set of 25 expert rules shown in Table 3 is established that governs the behavior of the AGV in different situations.
This process effectively forms a fuzzy avoidance controller providing the foundation for generating training data for our ANFIS avoidance controller. The training dataset follows the expert logical rules outlined in Table 3. These rules precisely define how the AGV's sensors relate to its motor velocities. By following these rules, a diverse dataset is generated encompassing a wide range of scenarios and behaviors. This systematic approach guarantees that the AGV is ready to navigate and adapt to real world situations ensuring efficient and reliable performance. A sample of training data for the ANFIS avoidance controllers is presented in Table 4.

5.2.2. Training ANFIS for Avoidance Controllers (Left and Right)

In this study, 32 datasets are generated using the fuzzy logic avoidance controller to train the ANFIS avoidance controllers (left and right). In the proposed ANFIS model, four membership functions are established for each input (left and right sensor), characterized by trapezoidal shapes. The output membership functions are linear. The Fuzzy Inference System is constructed employing grid partitioning and the hybrid optimization method is applied. The model was trained over 50 epochs. The training error is calculated as the root mean square error (RMSE) between the predicted motor velocities (outputs of the ANFIS controller) and the actual motor velocities (target outputs).
Figure 15 displays the training data for the left motor ANFIS avoidance controller and Figure 16 depicts the training error for the left motor ANFIS avoidance controller.
Figure 17 displays the training and FIS output data for the left motor ANFIS avoidance controller after the ANFIS is trained. In this ANFIS model, a minimal training RMSE of 0.001669 is achieved. The model utilizes 53 nodes with a combination of 48 linear and 32 nonlinear parameters, totaling 80 parameters. Notably, this model is built upon 16 fuzzy rules, demonstrating a notable decrease when compared to the fuzzy avoidance controller, which is comprised of 25 rules (see Section 5.2.1).
The same approach is applied for the right motor. Figure 18 displays the training data for the right motor ANFIS avoidance controller and Figure 19 displays the training error for the right motor ANFIS avoidance controller.
Figure 20 displays the training and FIS output data for the right motor ANFIS avoidance controller, after ANFIS is trained. In this ANFIS model, a minimal training RMSE of 0.001670 is attained. The model employs 53 nodes, comprising 48 linear and 32 nonlinear parameters, summing up to 80 parameters in total. As before, this ANFIS integrates 16 fuzzy rules, which is a reduction of 9 rules compared to the 25 rules in the fuzzy avoidance controller.

6. Simulation Experiments

The experiments were conducted in a simulated environment configured using CoppeliaSim, a robot simulator that provided the necessary robustness and versatility for preliminary validation. The use of CoppeliaSim was crucial in overcoming the practical limitations of real-world experimentation, such as time and cost constraints, enhancing both the thoroughness and efficiency of the proposed control strategy.

6.1. Robot System and Kinematics

The mobile robot chosen for this research is the Pioneer p_3dx, a compact two-wheel differential-drive robot, notable for its integration of 16 ultrasonic sensors. The maximum sensing range of the ultrasonic sensors used on the Pioneer p_3dx robot is set to 1 meter. This setting standardizes the measurement scale, ensuring that all distance readings are directly comparable and appropriately scaled for input into our ANFIS controllers. In this study, an effort is made to simplify the complexity of the ANFIS obstacle avoidance controller by exclusively utilizing the six frontal sensors, organized into two sets, as shown in Figure 21.
The determination of the right and left sensor values is computed as follows:
Right Sensor Value = ((Measurement from Sensor 1 + Measurement from Sensor 2 + Measurement from Sensor 3)) / 3
Left Sensor Value = ((Measurement from Sensor 4 + Measurement from Sensor 5 + Measurement from Sensor 6)) / 3

6.2. Simulation Results

Simulations have been conducted in three environmental setups including different obstacle arrangements with varying numbers, sizes, and both static and dynamic obstacles. To test the robustness of our navigation method, 10 test cases were conducted for each environment, each featuring varied start and end points which led to different paths determined by the path planning algorithm and obstacles that originated from different locations and moved into various directions. Due to space limitations, two representative test cases conducted from different environmental setups, illustrating the robot's ability to successfully navigate to the endpoint, effectively handling different numbers, shapes, and sizes of both dynamic and static obstacles.
Firstly, a scene is established using CoppeliaSim, where both the start and end points are specified for the robot’s navigation. Our primary objective is to guide the robot towards its designated end point while avoiding any obstacles, either static or dynamic. This scene includes five warehouse racks, four boxes in the lower left corner and a control room in the upper right corner, as shown in Figure 22.
Based on this scene, the Bump-Surface concept is employed to determine the shortest and optimal path for the robot to traverse from its start position to the designated end point. The resulting optimal path, computed using a path planning algorithm, is depicted in green color in Figure 23. This path serves as a visual representation of the route the robot is intended to follow within the simulated environment.
For the robot tracking process, a vector P is formulated containing the (x, y) coordinates necessary for the robot's path to the end point. To this end, the ANFIS tracking controller is deployed. This controller facilitates the robot's movement from one point to another within vector P. As the robot reaches each point within the vector, it proceeds towards the next point. This process continues until the robot reaches the final end point represented by a green circle in Figure 23.
In the examined scenario, apart from the obstacles handled using the Bump-Surface concept to find the shortest path for the robot towards the end point while avoiding them, three additional obstacles have been incorporated into the scene. These include two static obstacles, represented by paper boxes, and one dynamic obstacle, represented by a human moving in the environment, as shown in Figure 24. These obstacles obstruct the path planning process, requiring the robot to maneuver around them to reach the end point.
The robot navigation starts by following the predefined path using the ANFIS tracking controllers. The ANFIS tracking controller is employed to guide the robot along the predefined path (green line). When the robot senses that there is an obstacle blocking its way, the obstacle avoidance controller is enabled. The robot then executes a maneuver, temporarily diverting from its pre-established path to evade a collision with the obstacle. Once the obstacle is avoided, the robot returns back to the predefined path.
The first obstacle encountered is the dynamic obstacle (human); thus, prompting the activation of the ANFIS avoidance controllers. The robot then executes a maneuver to avoid the human moving close to the robot, as illustrated in the Figure 25. In all Figures, the green line depicts the path generated by the path planning algorithm, whereas the yellow line indicates the actual path taken by the robot to maneuver around obstacles and reach the end point.
Following the robot's maneuver to avoid the human, it resumes its path along the predefined path. However, it encounters the first static obstacle, represented by paper boxes, obstructing its trajectory. Consequently, the robot executes a second maneuver to navigate around this obstacle, as depicted in Figure 26.
After navigating around the first static obstacle (paper boxes), the robot encounters a second static obstacle of the same type. In response, it executes a third maneuver to avoid this obstacle, as depicted in Figure 27.
Figure 28 illustrates the entire path that the robot follows to reach the end point, encompassing the maneuvers made to navigate around obstacles encountered along the way.
After the simulation test is completed, the robot's performance is evaluated, revealing a completion time of 71.4 seconds and a total of 13 turns, as depicted in Figure 29. In this study, a targeted approach is implemented to simplify paths and detect turns, aiming to enhance computational efficiency and the significance of our findings in robotic navigation. Specifically, a 'significant turn' in the robot's path is defined as a directional change of 0.2 radians or more. This threshold is established through extensive preliminary experimentation, which assessed the impact of various turn magnitudes on path efficiency and navigational accuracy. Our findings indicate that turns measuring under 0.2 radians generally had negligible impacts on the overall path trajectory, making them insignificant for our analysis.
Aiming to compare the ANFIS strategy and the fuzzy logic controller strategy, Table 5 provides a summary of key performance indicators. These indicators include the time taken to reach the end point (in seconds), the number of turns executed, and the count of rules for each strategy: ANFIS and fuzzy logic controller.
The comparison shows that the ANFIS strategy outperforms the fuzzy logic strategy in several aspects. ANFIS strategy takes a shorter time to reach the end point with 71.4 seconds compared to 73.2 seconds for fuzzy logic controller. Furthermore, the ANFIS strategy exhibits fewer turns, totaling only 13 compared to 18 observed in the fuzzy logic controller (Figure 30), leading to a rule reduction of 33.3%. Additionally, the ANFIS strategy employs simpler rules, with 9 rules for tracking controller and 16 for avoidance controller (a rule reduction of 40%), while fuzzy logic uses 15 rules for tracking and 25 for avoidance (a rule reduction of 36%). These results indicate that the ANFIS strategy provides smoother navigation paths, making it more effective for robotic navigation tasks.
Reducing the number of rules offers several key benefits that enhance the system's overall performance and efficiency. Firstly, a smaller number of rules leads to a simpler fuzzy model, which is generally easier to understand, interpret, and manage. This simplification is crucial for maintaining the transparency of the system, particularly valuable in control applications where understanding the logic behind decision-making processes is important. Secondly, reducing the number of rules decreases the necessary computations required for decision making, thereby lowering the overall computational load [29]. This is especially beneficial in real-time applications where decision speed is critical, allowing the ANFIS controller to operate more efficiently and respond faster in dynamic environments typically encountered by mobile robots. Lastly, models with fewer rules are easier to maintain and update, offering better scalability in practical applications, where the environment or operational conditions may evolve over time, necessitating model adjustments or updates.
Next, another scene is established, as shown in Figure 31, depicting both the provided path after using the path planning algorithm (green line) and the actual path (yellow line). Figure 31 also illustrates the static and two dynamic obstacles (humans) in the environment. The obstacles are positioned to intersect the planned path, requiring the robot to change its direction to avoid them. The robot navigates following the path succeeding to reach the end point avoiding collisions with both static and dynamic obstacles.
Figure 32 provides snapshots where the robot effectively maneuvers around obstacles. The robot consistently follows the planned path, adjusting its trajectory as needed to avoid collisions. It is worth noting that the success rate of the proposed system was 100% across all test cases, demonstrating full reliability for reaching the end point without collisions with static and dynamic obstacles. This success rate is critical for assessing the effectiveness of the developed navigation algorithms.
A limitation identified concerns sensor position and range. Obstacles located beyond the sensor's effective range were occasionally not detected early enough, resulting in potential collisions or sudden maneuvers. It mainly occurs in rare scenarios, where a moving object approaches from beyond the sensor range without altering its path. However, such scenarios are unlikely to occur in real-world applications, as humans would notice the robot and either stop or change direction, while other robots would use their sensors to avoid collisions. Despite this limitation, the robot successfully navigated around both static and dynamic obstacles to reach its endpoint in all tested scenarios. Although a few instances involved late detection of objects, leading to sudden maneuvers, the robot consistently managed to reach the end point successfully.
To compare the CPU times, 10 test cases are executed in each of the three environments both using ANFIS controllers and fuzzy controllers for comparison. Figure 33 presents the average computation times (CPU times) for all test cases conducted within the three environments. It is clear that the average CPU time using the ANFIS strategy is lower than its counterpart using the fuzzy system strategy. Consequently, the reduction in the number of rules, not only maintains the systems performance but also achieves less computational time.
As a concluding remark, the primary advantage of using the ANFIS model over a fuzzy strategy model lies in its adaptive learning capabilities. ANFIS refines and adjusts the initial rules, which is particularly important as some rules may be weakly fired, contributing minimally to the decision-making process under certain conditions. By adapting the rules, ANFIS ensures that only the most effective rules are applied, enhancing the system's overall efficiency and accuracy.

7. Conclusions

In this study, we introduce an innovative ANFIS-based control strategy, representing a notable advancement in robotics, especially concerning autonomous mobile robot navigation within dynamic environments. The core issue of our research work lies in the integration of the Adaptive Neuro-Fuzzy Inference System (ANFIS) with a path planning algorithm. This integration establishes a new standard for realizing collision-free navigation, simultaneously enhancing both the safety and efficiency of the process.
Our method focuses on a sophisticated combination of four ANFIS controllers, each one designed to handle specific aspects of the navigation process. Two of these controllers are responsible guiding the robot towards its end point, ensuring precise and reliable path planning. The remaining two controllers are activated in the presence of obstacles, enabling the robot to perform avoidance maneuvers without deviating from its designated path to the end point.
Our strategy was rigorously tested using the Pioneer p_3dx mobile robot equipped with 16 ultrasonic sensors in a simulation environment utilizing the CoppeliaSim platform. The simulation results demonstrated the robot's capability to navigate through an environment cluttered with both static and dynamic obstacles, utilizing ultrasonic sensors to detect and react to these challenges in real-time.
The simulation outcomes highlight the superiority of the ANFIS-based approach over the conventional fuzzy logic methods, demonstrating not only improved computational efficiency but also enhanced navigational smoothness. The robot successfully completed its paths, successfully avoiding obstacles and reaching its end point in a shorter time frame and with fewer turns compared to strategies employing conventional fuzzy logic controllers.
This study presents a novel ANFIS-based control strategy and also paves the way for future research in autonomous robot navigation. Our approach's adaptability and efficiency in dynamic environments hold vast potential for a wide array of applications. A noted limitation was the sensor range; obstacles beyond the effective range sometimes weren't detected early enough, leading to collisions or abrupt maneuvers. This highlights the need for future improvements in sensor capabilities and processing power for earlier obstacle detection and smoother navigation adjustments.
Our future work will be dedicated to enhancing the robustness and intelligence of the ANFIS-based navigation framework using machine learning models. We aim to extend the system's efficacy across diverse and challenging operational scenarios, including outdoor terrains and dynamically changing environments. A significant focus will also be placed in sectors like autonomous delivery systems, search and rescue operations, and smart mobility solutions, ensuring a broader societal impact and real-world utility.

Author Contributions

Conceptualization, S.S. and P.Z.; methodology, S.S.; software, S.S.; validation, S.S.; formal analysis, S.S. and P.Z.; investigation, S.S. and P.Z.; resources, S.S.; data curation, S.S.; writing—original draft preparation, S.S. and P.Z.; writing—review and editing, S.S. and P.Z.; visualization, S.S. and P.Z.; supervision, P.Z. All authors have read and agreed to the published version of the manuscript

Funding

“This research received no external funding”

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pratama, P.S.; Jeong, S.K.; Park, S.S.; Kim, S.B. Moving Object Tracking and Avoidance Algorithm for Differential Driving AGV Based on Laser Measurement Technology. Int. J. Sci. Eng. 2013, 4, 11–15. [Google Scholar] [CrossRef]
  2. Ito, S. ; Hiratsuk,a S. ; Ohta, M.; Matsubara, H.; Ogawa, M. Small Imaging Depth LIDAR and DCNN-Based Localization for Automated Guided Vehicle. Sensors 2018, 18, 177. [Google Scholar] [CrossRef]
  3. Rozsa, Z.; Sziranyi, T. Obstacle Prediction for Automated Guided Vehicles Based on Point Clouds Measured by a Tilted LIDAR Sensor. IEEE T Intell Transp 2018, 19, 2708–2720. [Google Scholar] [CrossRef]
  4. Lee, J.; Hyun, C.-H.; Park, M. A Vision-Based Automated Guided Vehicle System with Marker Recognition for Indoor Use. Sensors 2013, 13, 10052–10073. [Google Scholar] [CrossRef] [PubMed]
  5. Al-Mayyahi, A.; Wang, W.; Birch, P. Adaptive Neuro-Fuzzy Technique for Autonomous Ground Vehicle Navigation. Robotics 2014, 3, 349–370. [Google Scholar] [CrossRef]
  6. Miao, Z.; Zhang, X.; Huang, G. Research on Dynamic Obstacle Avoidance Path Planning Strategy of AGV, J. Phys.: Conf. Ser. 2006 012067. [CrossRef]
  7. Haider, M.H.; Wang, Z.; Khan, A.A.; Ali, H.; Zheng, H.; Usman, S.; Kumar, R.; Usman Maqbool Bhutta, M.; Zhi, P. Robust mobile robot navigation in cluttered environments based on hybrid adaptive neuro-fuzzy inference and sensor fusion. Journal of King Saud University - Computer and Information Sciences 2022, 34, 9060–9070. [Google Scholar] [CrossRef]
  8. Farahat, H.; Farid, S.; Mahmoud, O.E. Adaptive Neuro-Fuzzy control of Autonomous Ground Vehicle (AGV) based on Machine Vision. Engineering Research Journal 2019, 163, 218–233. [Google Scholar] [CrossRef]
  9. Jung, K.; Lee, I. ; Song,H.; Kim, J.; Kim, S. Vision Guidance System for AGV Using ANFIS. Proceedings of the 5th International Conference on Intelligent Robotics and Applications - Volume Part I, 2012; [CrossRef]
  10. Khelchandra, T.; Huang, J.; Debnath, S. Path planning of mobile robot with neuro-genetic-fuzzy technique in static environment. International Journal of Hybrid Intelligent Systems 2014, 11, 71–80.
  11. Faisal, M. ; Hedjar, R; Al Sulaiman, M.; Al-Mutib, K. Fuzzy Logic Navigation and Obstacle Avoidance by a Mobile Robot in an Unknown Dynamic Environment. Int J Adv Robot Syst 2013, 1–7. [Google Scholar]
  12. Anish, P; Abhishek, K. K; Dayal, R. P; Patle,B.K Autonomous mobile robot navigation between static and dynamic obstacles using multiple ANFIS architecture. World Journal of Engineering 2019, 275–286; [CrossRef]
  13. Brahim, H; Mohammed, R; Abdelwahab, N An intelligent ANFIS mobile robot controller using an expertise-based guidance technique. 14th International Conference on Intelligent Systems: Theories and Applications (SITA) 2023. IEEE; [CrossRef]
  14. Singh, M. K.; Parhi, D. R.; Pothal, J. K. ANFIS approach for navigation of mobile robots. International Conference on Advances in Recent Technologies in Communication and Computing. 2009, IEEE. [Google Scholar] [CrossRef]
  15. Muhammad, H. H.; Hub, A.; Abdullah, A. K.; Hao, Z.; Usman, M. B.; Shaban, U.; Pengpeng, Z.; Zhonglai, V. Autonomous mobile robot navigation using adaptive neuro fuzzy inference system. International Conference on Innovations and Development of Information Technologies and Robotics (IDITR). 2022, IEEE. [Google Scholar] [CrossRef]
  16. Malika, L.; Nacéra, B. ; Intelligent system for robotic navigation using ANFIS and ACOr. Applied Artificial Intelligence. 2019, 33, 399–419. [Google Scholar] [CrossRef]
  17. Muhammad, H. H.; Zhonglai, W.; Abdullah, A. K.; Hub, A.; Hao, Z.; Shaban, U.; Rajesh, K.; Usman, M. B.; Pengpeng, Z. Robust mobile robot navigation in cluttered environments based on hybrid adaptive neuro-fuzzy inference and sensor fusion. Journal of King Saud University - Computer and Information Sciences. 2022. [CrossRef]
  18. Marichal, G.; Acosta, L.; Moreno, L.; Méndez, J.A.; Rodrigo, J.; Sigut, M. Obstacle avoidance for a mobile robot: A neuro-fuzzy approach. Fuzzy Sets and Systems, 2001, 124, 171–179.
  19. Vaidhehi, V. The role of dataset in training ANFIS system for course advisor. International Journal of Innovative Research in Advanced Engineering (IJIRAE), 2014, 1, 249–253. ISSN: 2349–2163.
  20. Sy-Hung, B.; Soo-Y, Y. ; An efficient approach for line-following automated guided vehicles based on fuzzy inference mechanism. Journal of Robotics and Control (JRC), 2022, Volume 3, Issue 4, ISSN: 2715-5072. [CrossRef]
  21. Kovács, Sz. , Kóczy, L.T. Application of an approximate fuzzy logic controller in an AGV steering system, path tracking and collision avoidance strategy. Fuzzy Set Theory and Applications, Tatra Mountains Mathematical Publications, Mathematical Institute Slovak Academy of Sciences, 1999, vol. 16, pp. 456–467, Bratislava, Slovakia.
  22. Dudek, G.; Jenkin, M. Computational Principles of Mobile Robotics (2nd ed.). Cambridge University Press, USA, 2010.
  23. Gul, F.; Rahiman, W.; Sahal Nazli Alhady, S. A comprehensive study for robot navigation techniques. Cogent Engineering, 2019, 6, 1–25. [Google Scholar] [CrossRef]
  24. Al-Mallah, M.; Ali, M.; Al-Khawaldeh, M. Obstacles Avoidance for Mobile Robot Using Type-2 Fuzzy Logic Controller, Robotics 2022, 11, 130. [CrossRef]
  25. Al-Mahturi, A.; Santoso, F.; Garratt, M.A.; Anavatti, S.G. A Novel Evolving Type-2 Fuzzy System for Controlling a Mobile Robot under Large Uncertainties. Robotics 2023, 12, 40. [Google Scholar] [CrossRef]
  26. Hong, T.S.; Nakhaeinia, D.; Karasfi, A. Application of Fuzzy Logic in Mobile Robot Navigation. Fuzzy Logic - Controls, Concepts, Theories and Applications; 2012. [CrossRef]
  27. Azariadis, P.; Aspragathos, N. Obstacle representation by Bump-Surfaces for optimal motion-planning, Journal of Robotics and Autonomous Systems 2005, 51, 129–150.
  28. Jang J.-S., R. ANFIS Adaptive-Network-based Fuzzy Inference System. IEEE T Syst Man Cyb 1993, 23, 665–685. [Google Scholar] [CrossRef]
  29. Hung, C.-C.; Fernandez, B. Minimizing rules of fuzzy logic system by using a systematic approach. Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 1993, pp. 38–44 vol.1. [CrossRef]
Preprints 111045 g001
Figure 1. A visual depiction of the robot within both the global and local reference frames.
Figure 1. A visual depiction of the robot within both the global and local reference frames.
Preprints 111045 g001
Preprints 111045 g002
Figure 2. ANFIS Tracking Controllers: inputs: position and heading errors – outputs motor velocities for path tracking.
Figure 2. ANFIS Tracking Controllers: inputs: position and heading errors – outputs motor velocities for path tracking.
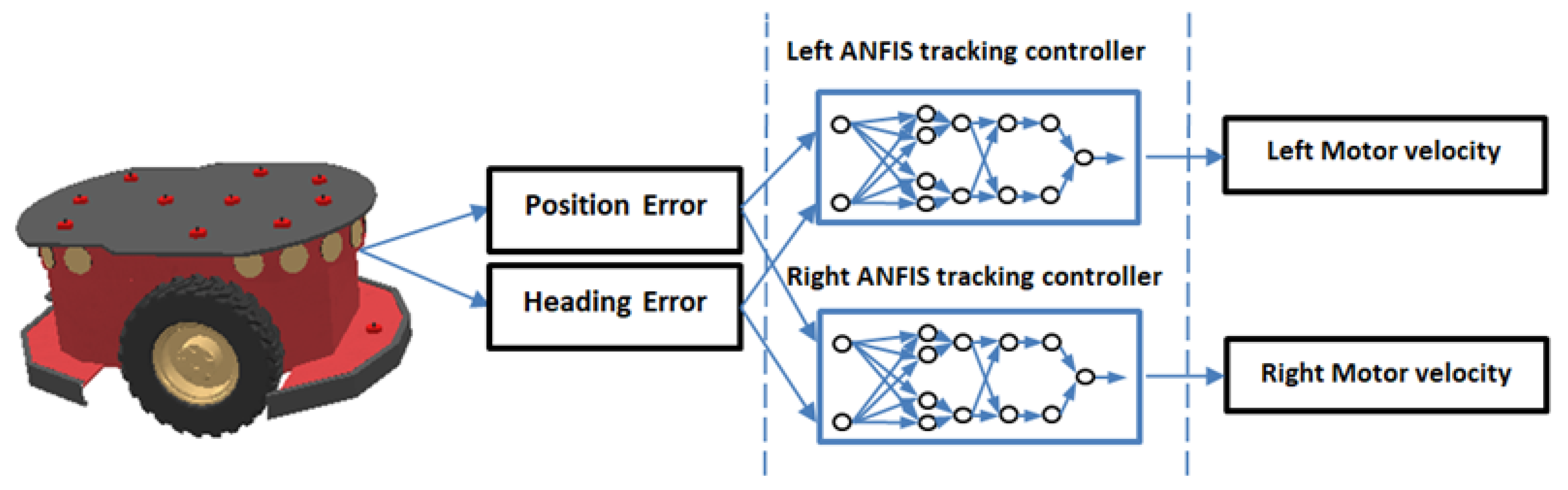
Preprints 111045 g002
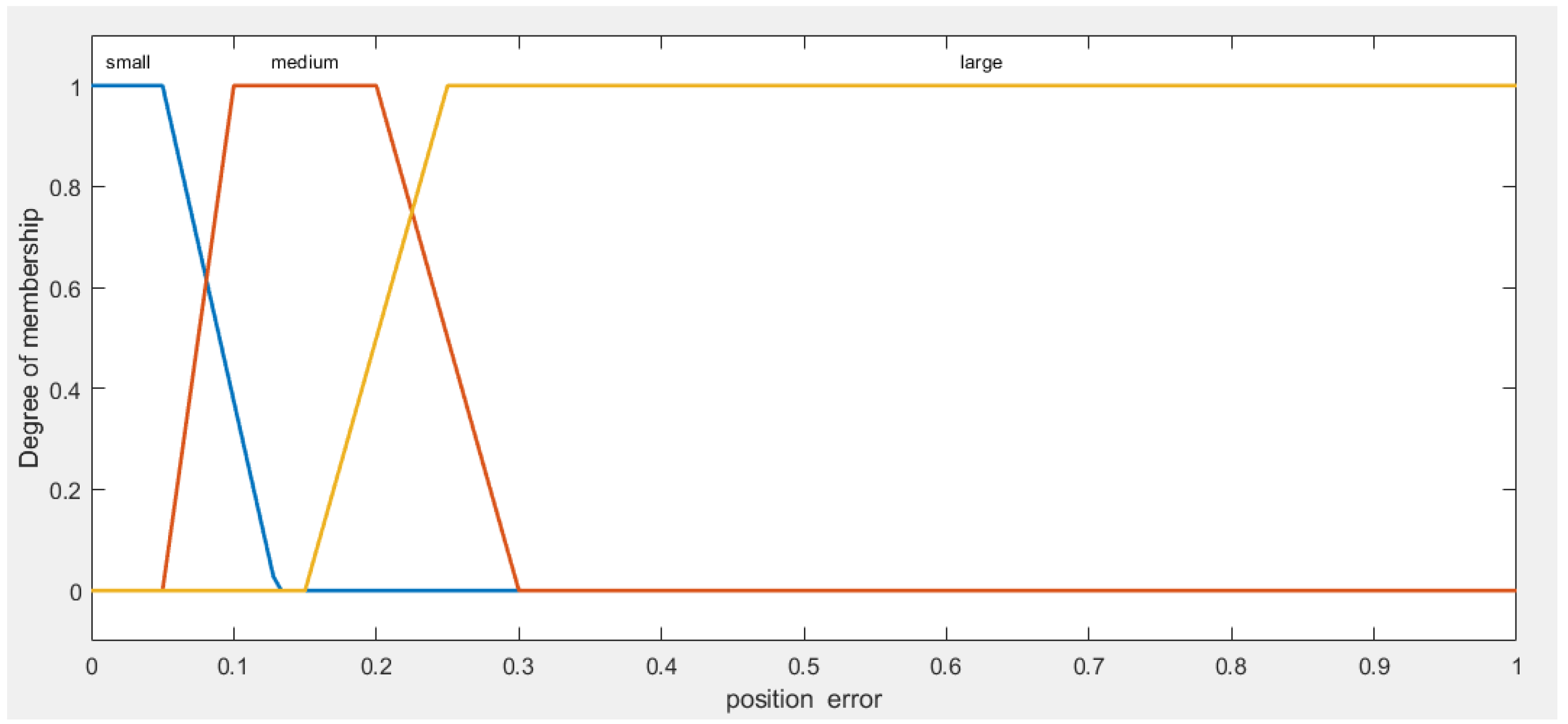
Preprints 111045 g003
Figure 3. Fuzzy logic tracking controller position error fuzzy sets.
Figure 3. Fuzzy logic tracking controller position error fuzzy sets.
Preprints 111045 g003
Preprints 111045 g004
Figure 4. Fuzzy logic tracking controller heading error fuzzy sets.
Figure 4. Fuzzy logic tracking controller heading error fuzzy sets.
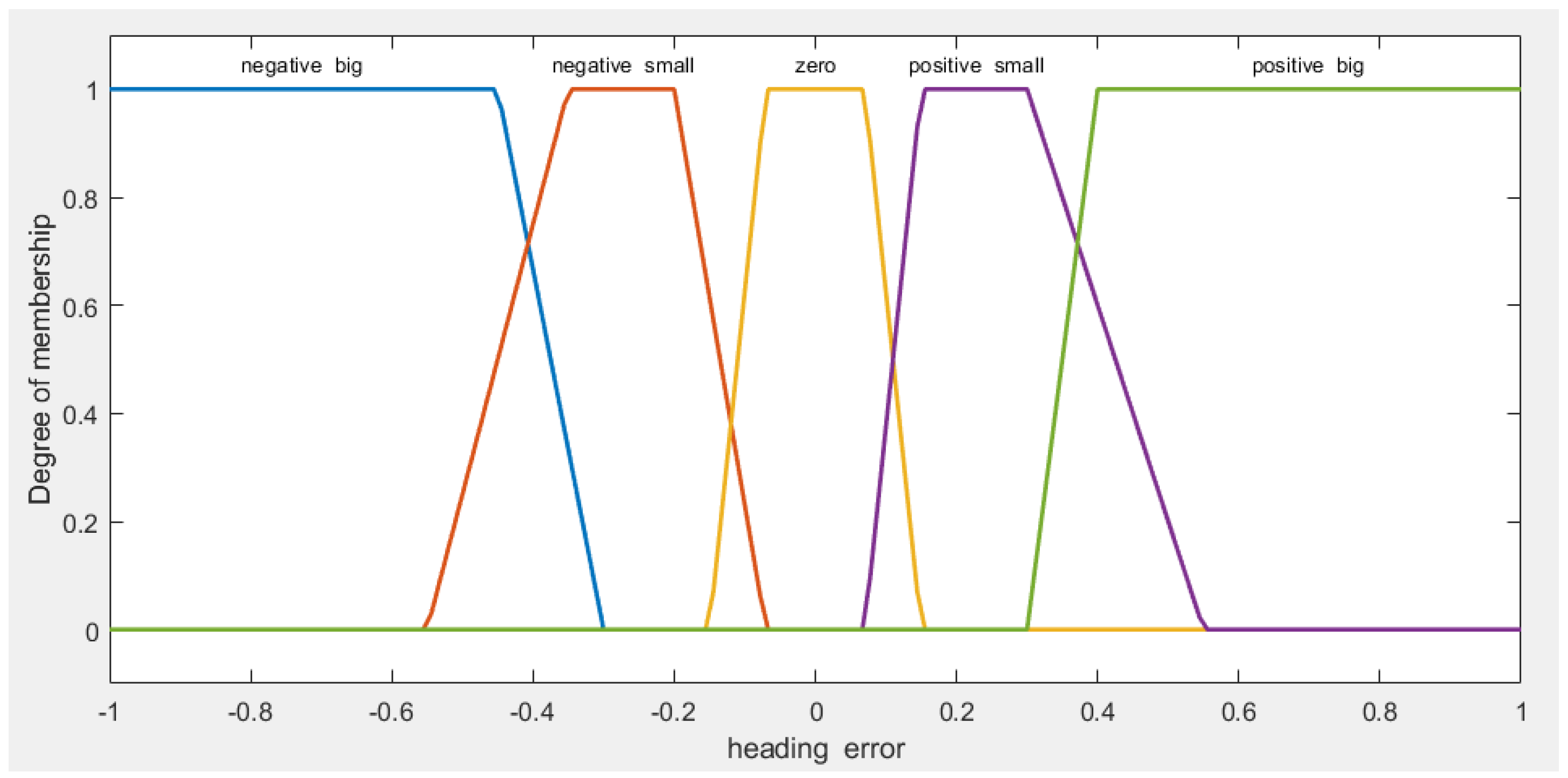
Preprints 111045 g004
Preprints 111045 g005
Figure 5. Fuzzy logic tracking controller output velocity fuzzy sets (right and left motors).
Figure 5. Fuzzy logic tracking controller output velocity fuzzy sets (right and left motors).
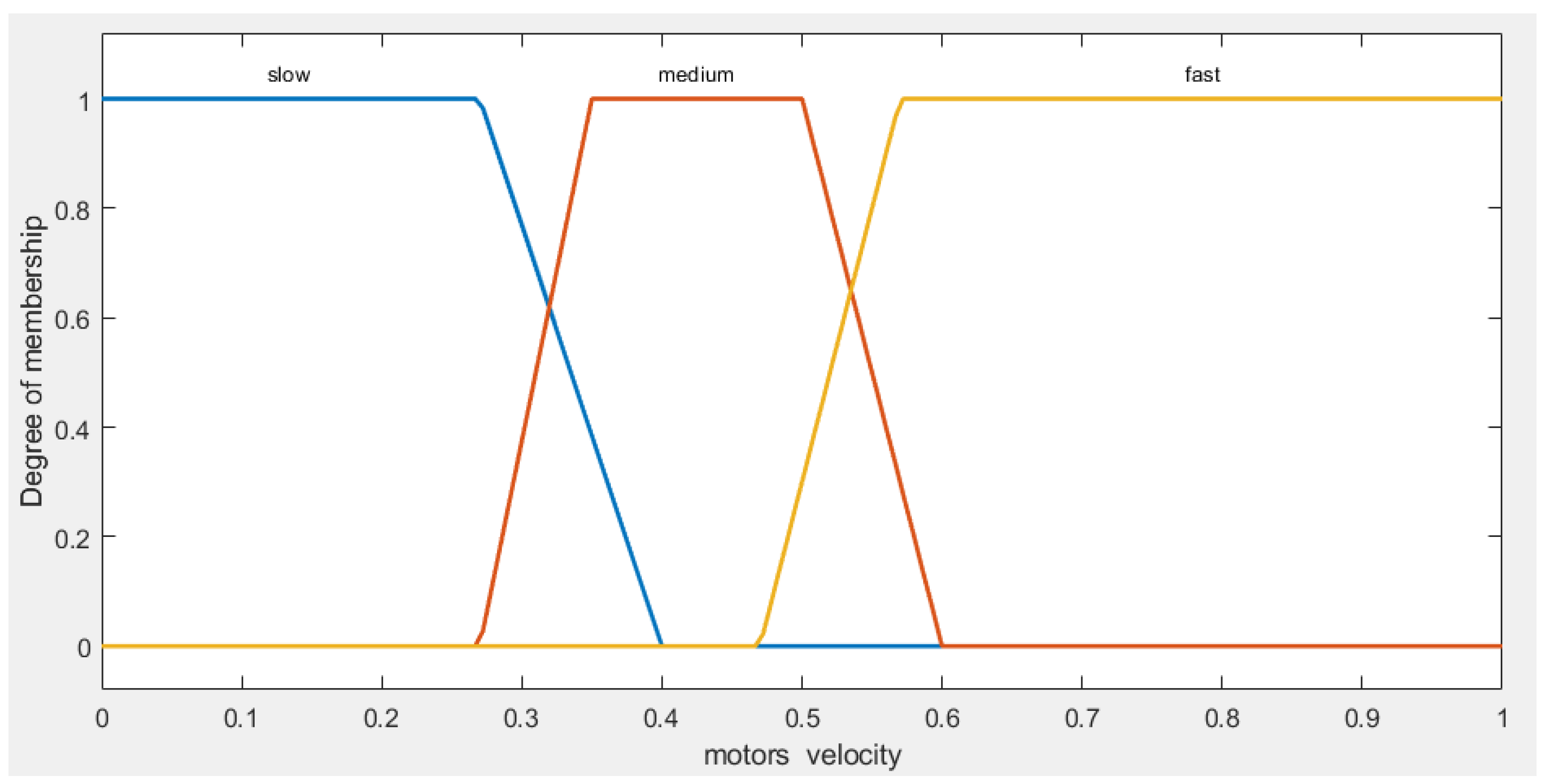
Preprints 111045 g005
Preprints 111045 g006
Figure 6. Training Data for the Left Motor ANFIS Tracking Controller.
Figure 6. Training Data for the Left Motor ANFIS Tracking Controller.
Preprints 111045 g006
Preprints 111045 g007
Figure 7. Training Error for Left Motor ANFIS Tracking Controller.
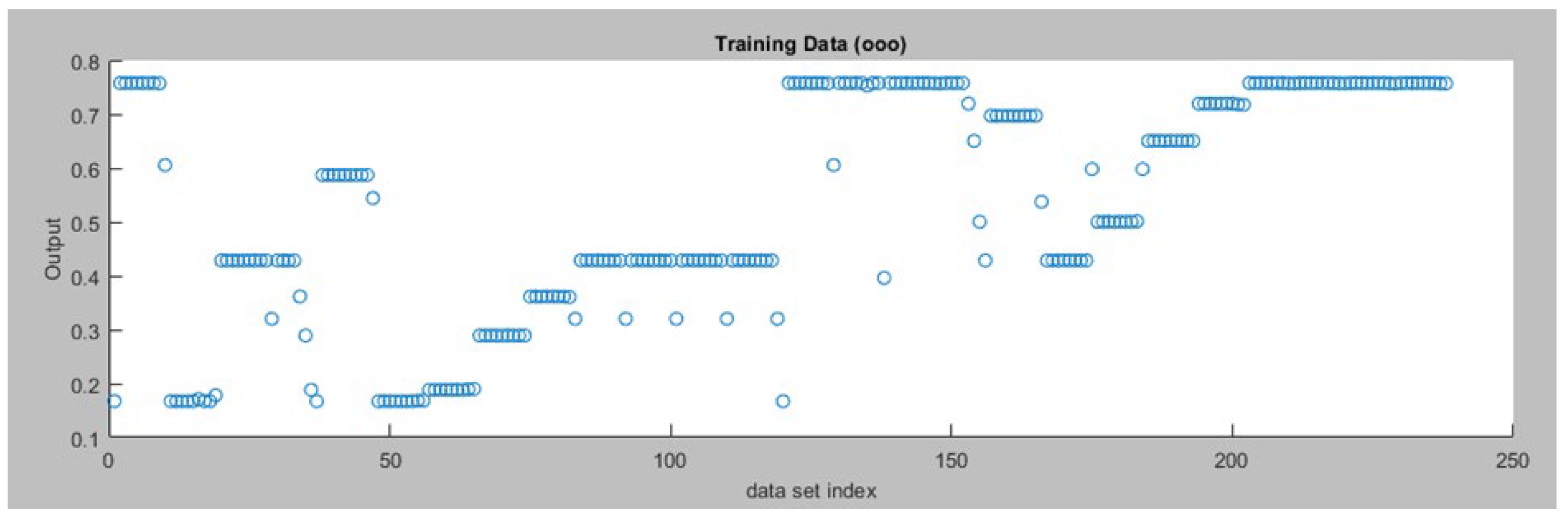
Figure 7. Training Error for Left Motor ANFIS Tracking Controller.
Preprints 111045 g007
Preprints 111045 g008
Figure 8. Data after the ANFIS is trained (Left Motor ANFIS Tracking Controller).
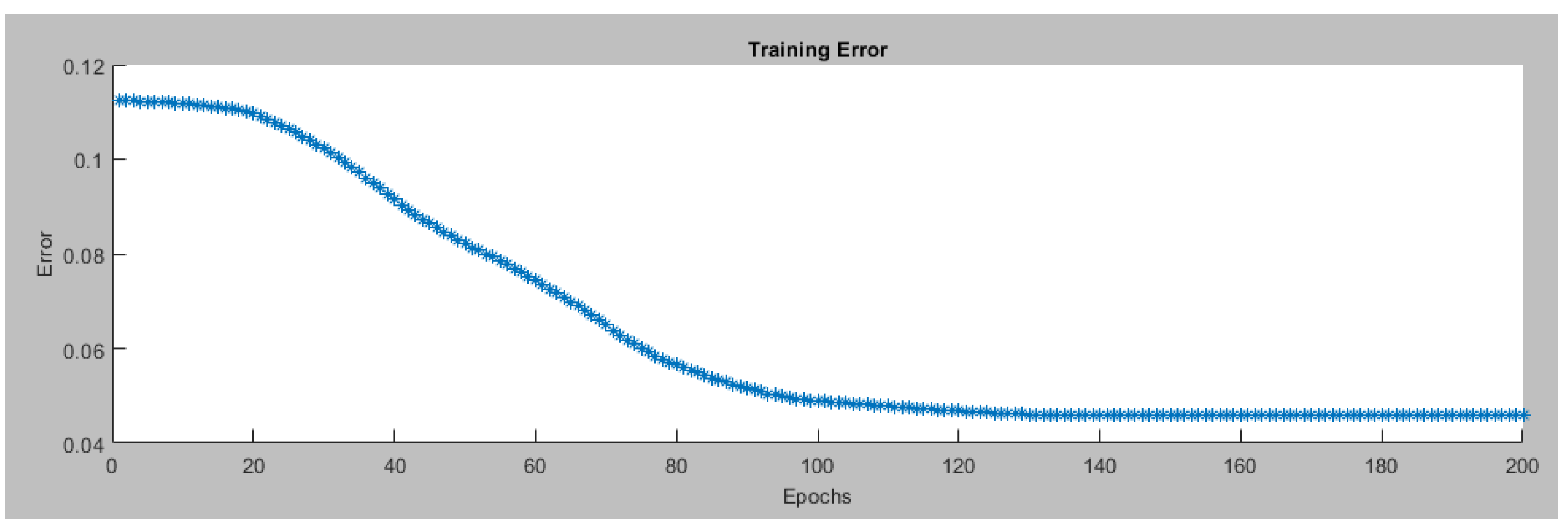
Figure 8. Data after the ANFIS is trained (Left Motor ANFIS Tracking Controller).
Preprints 111045 g008
Preprints 111045 g009
Figure 9. Training Data for the Right Motor ANFIS Tracking Controller.
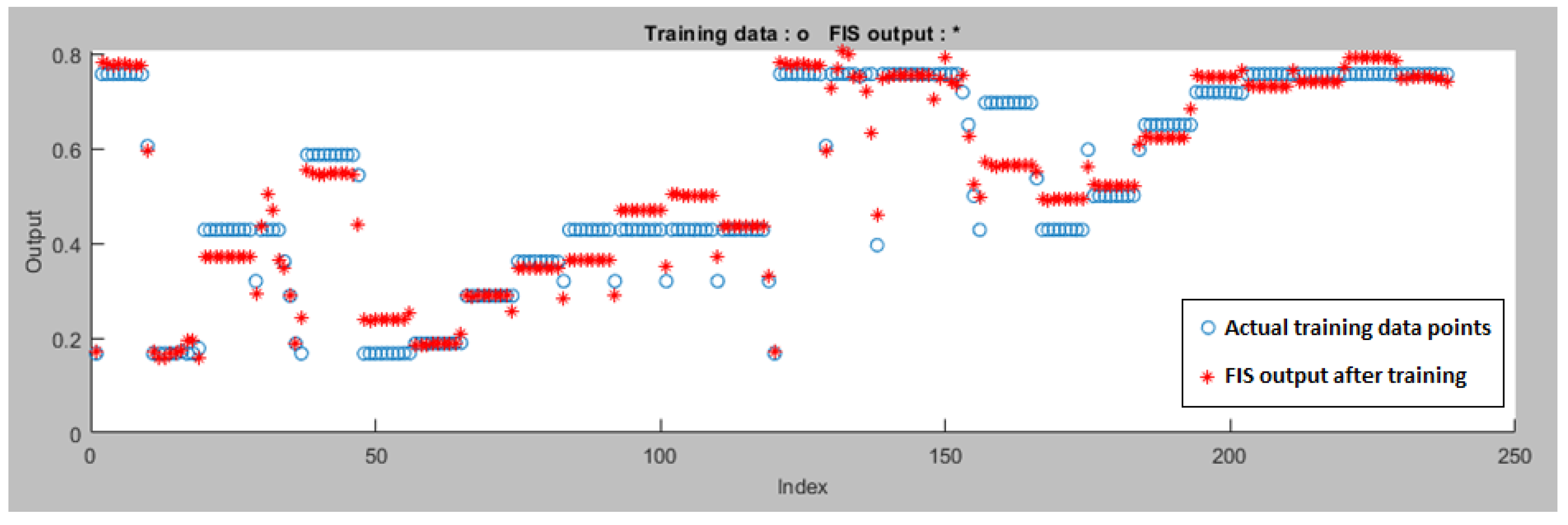
Figure 9. Training Data for the Right Motor ANFIS Tracking Controller.
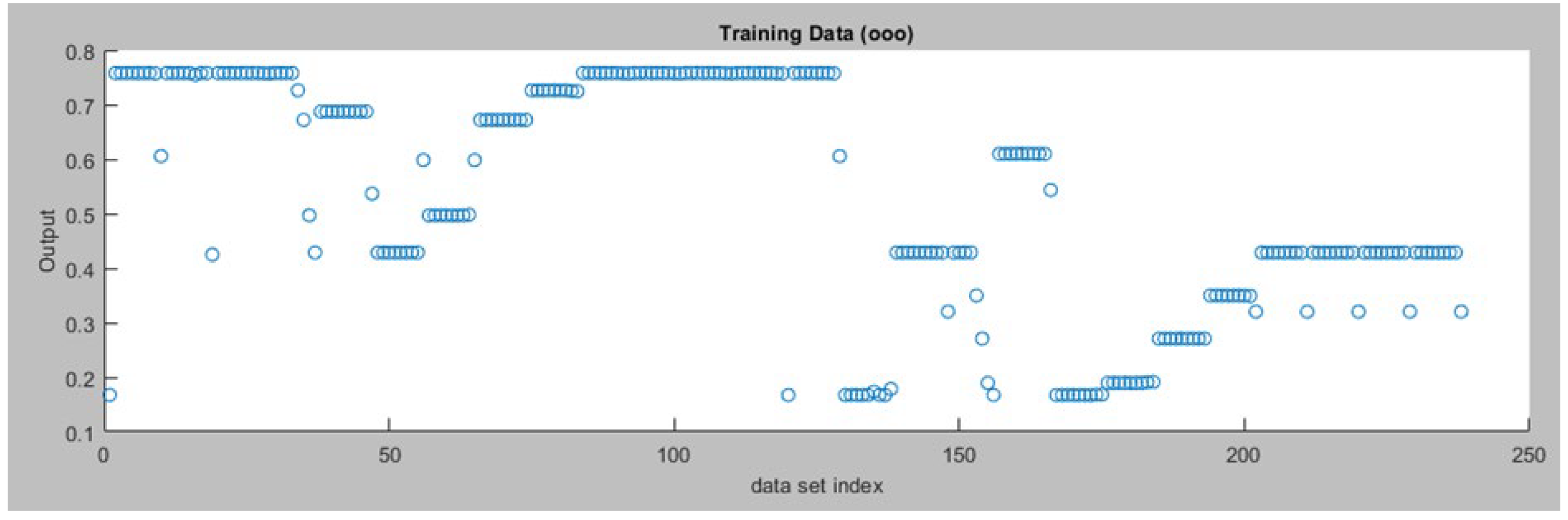
Preprints 111045 g009
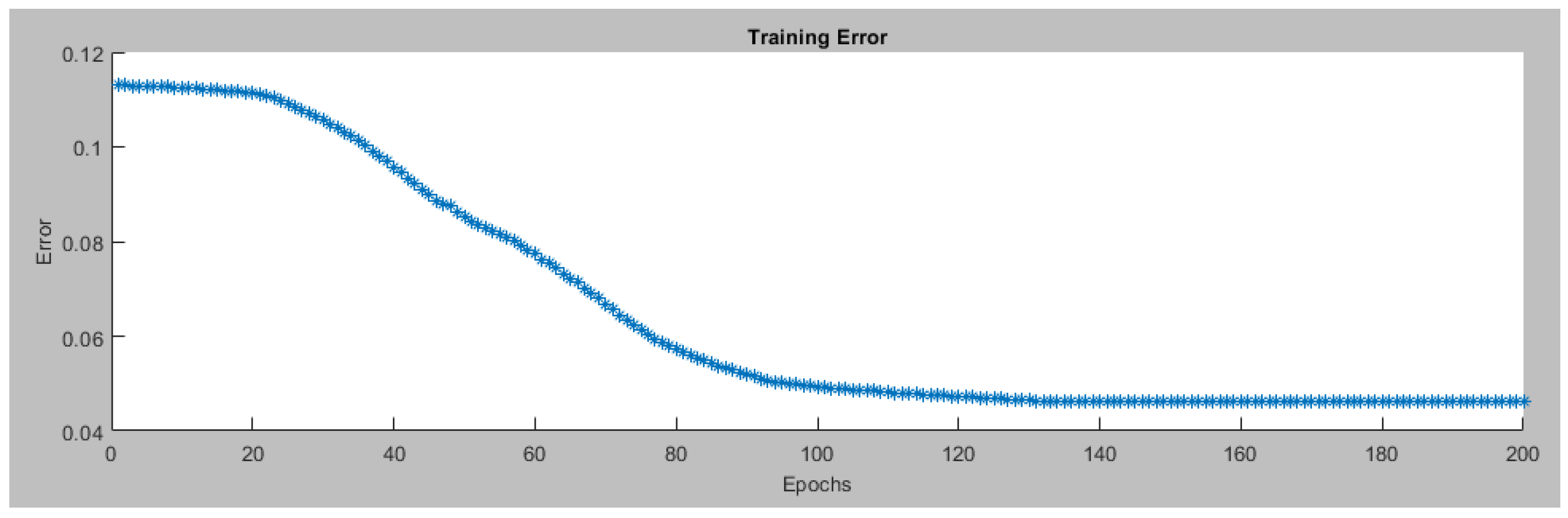
Preprints 111045 g010
Figure 10. Training Error for Right Motor ANFIS Tracking Controller.
Figure 10. Training Error for Right Motor ANFIS Tracking Controller.
Preprints 111045 g010
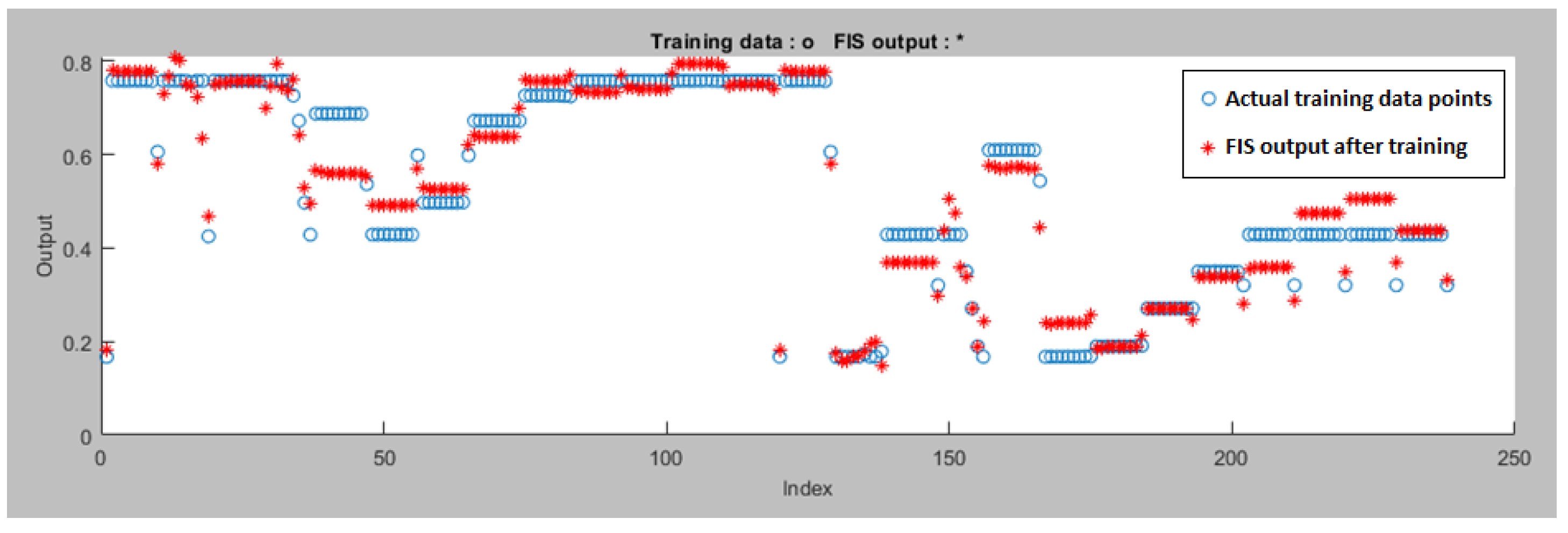
Preprints 111045 g011
Figure 11. Data after the ANFIS is trained (Right Motor ANFIS Tracking Controller).
Figure 11. Data after the ANFIS is trained (Right Motor ANFIS Tracking Controller).
Preprints 111045 g011
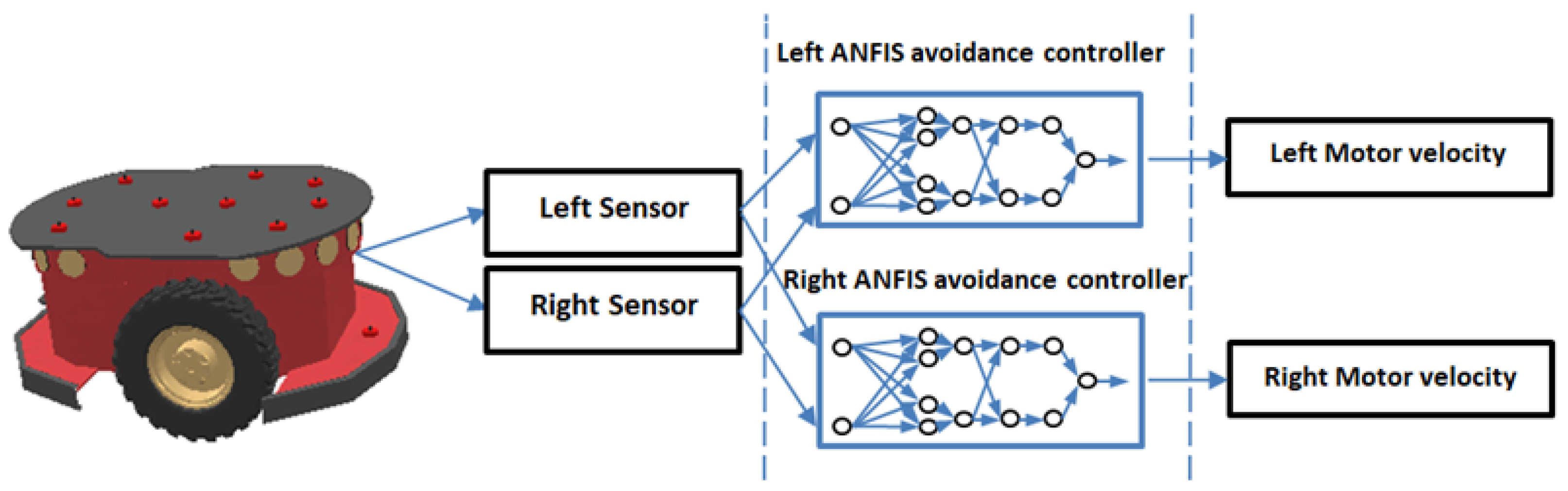
Preprints 111045 g012
Figure 12. ANFIS Avoidance Controllers: inputs: sensor readings – outputs: motor velocities for obstacle navigation.
Figure 12. ANFIS Avoidance Controllers: inputs: sensor readings – outputs: motor velocities for obstacle navigation.
Preprints 111045 g012
Preprints 111045 g013
Figure 13. Fuzzy logic avoidance controller inputs (left and right sensor) fuzzy sets.
Figure 13. Fuzzy logic avoidance controller inputs (left and right sensor) fuzzy sets.
Preprints 111045 g013
Preprints 111045 g014
Figure 14. Fuzzy logic avoidance controller output velocity fuzzy sets (right and left motors).
Figure 14. Fuzzy logic avoidance controller output velocity fuzzy sets (right and left motors).
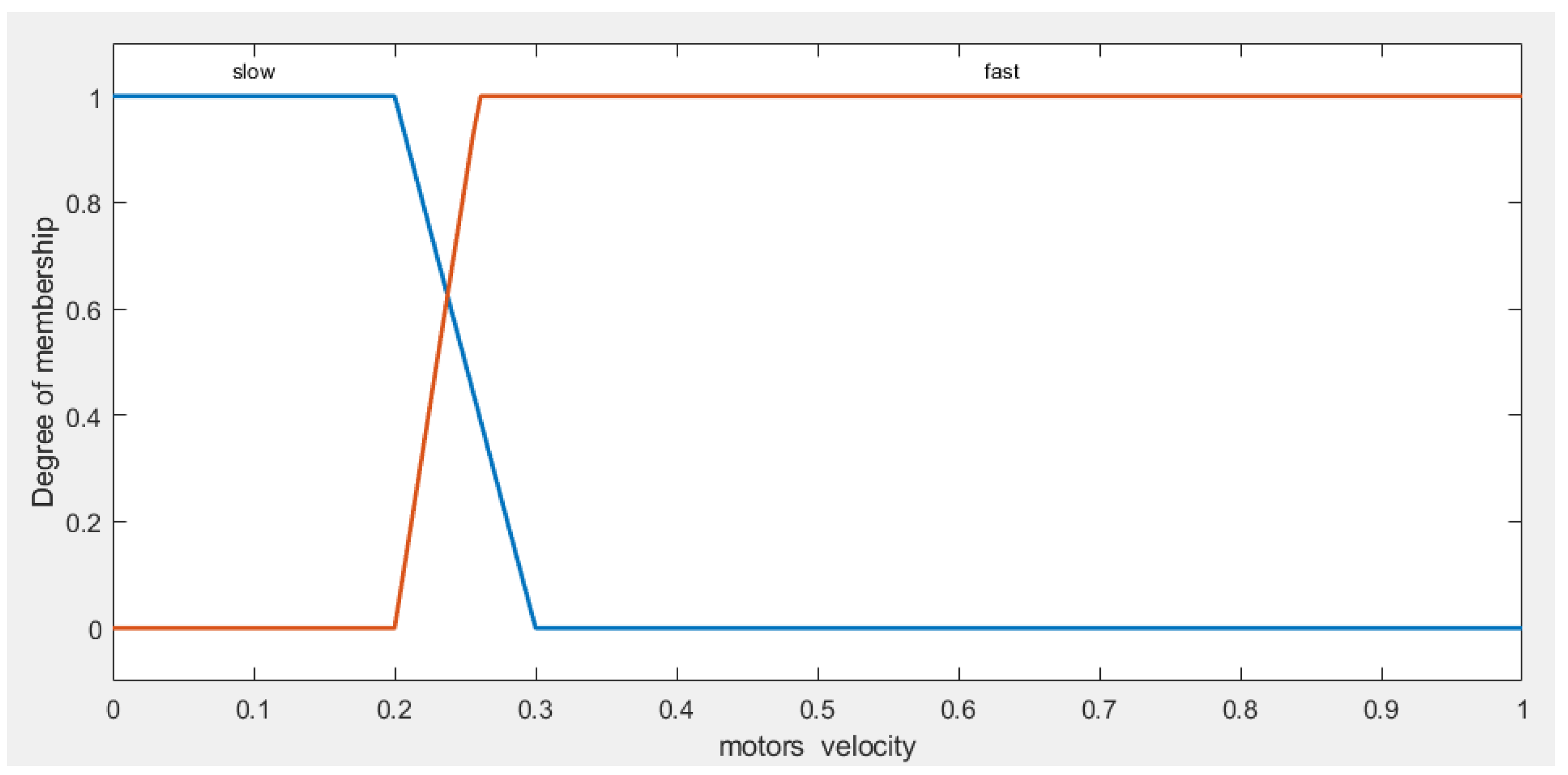
Preprints 111045 g014
Preprints 111045 g015
Figure 15. Training Data for the Left Motor ANFIS Avoidance Controller.
Figure 15. Training Data for the Left Motor ANFIS Avoidance Controller.
Preprints 111045 g015
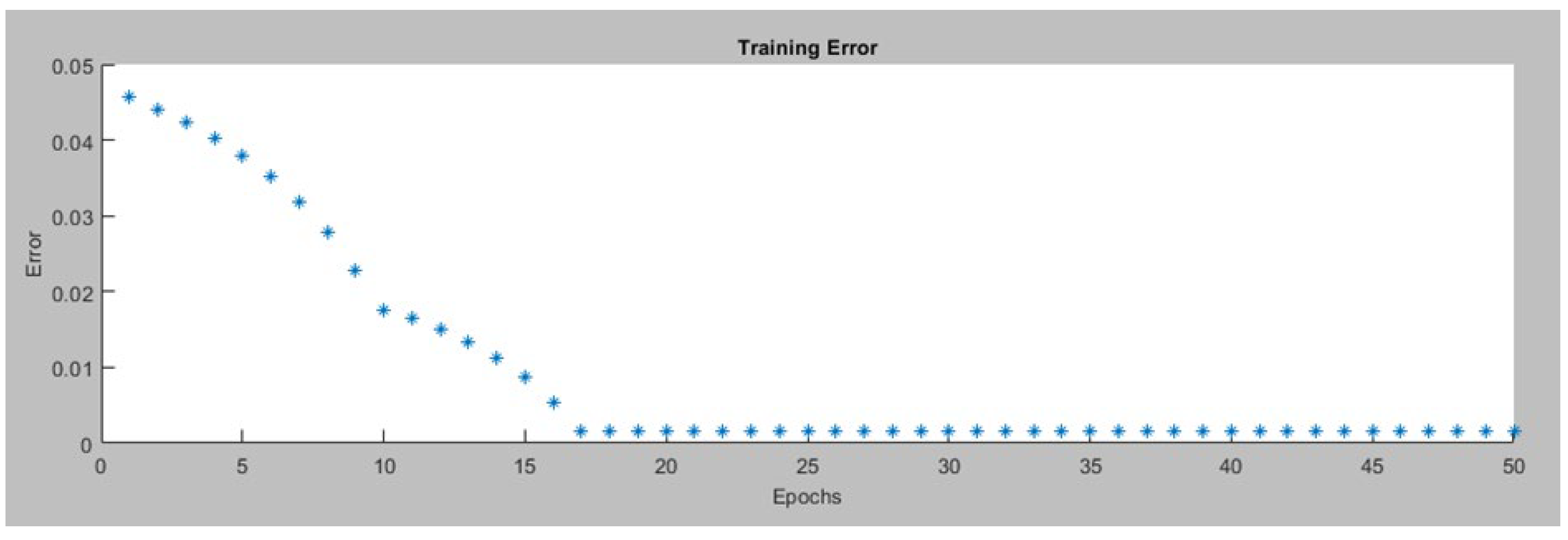
Preprints 111045 g016
Figure 16. Training Error for Left Motor Velocity ANFIS Avoidance Controller.
Figure 16. Training Error for Left Motor Velocity ANFIS Avoidance Controller.
Preprints 111045 g016
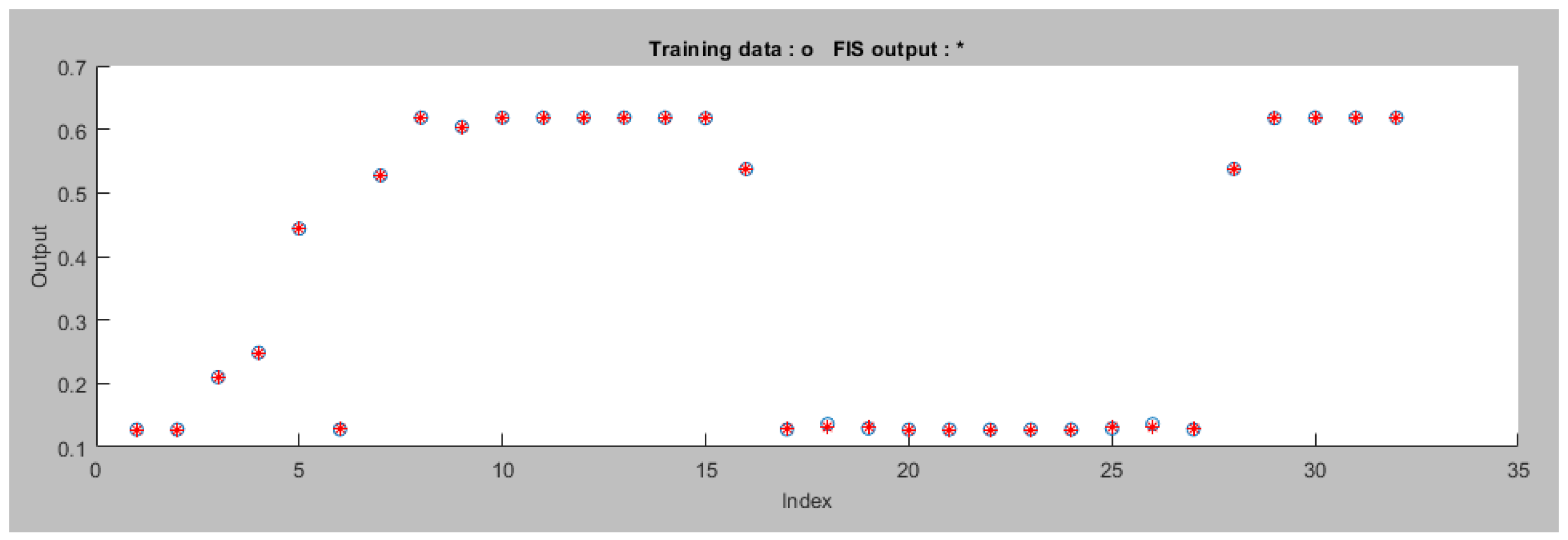
Preprints 111045 g017
Figure 17. Data after the ANFIS is trained (Left Motor ANFIS Avoidance Controller).
Figure 17. Data after the ANFIS is trained (Left Motor ANFIS Avoidance Controller).
Preprints 111045 g017
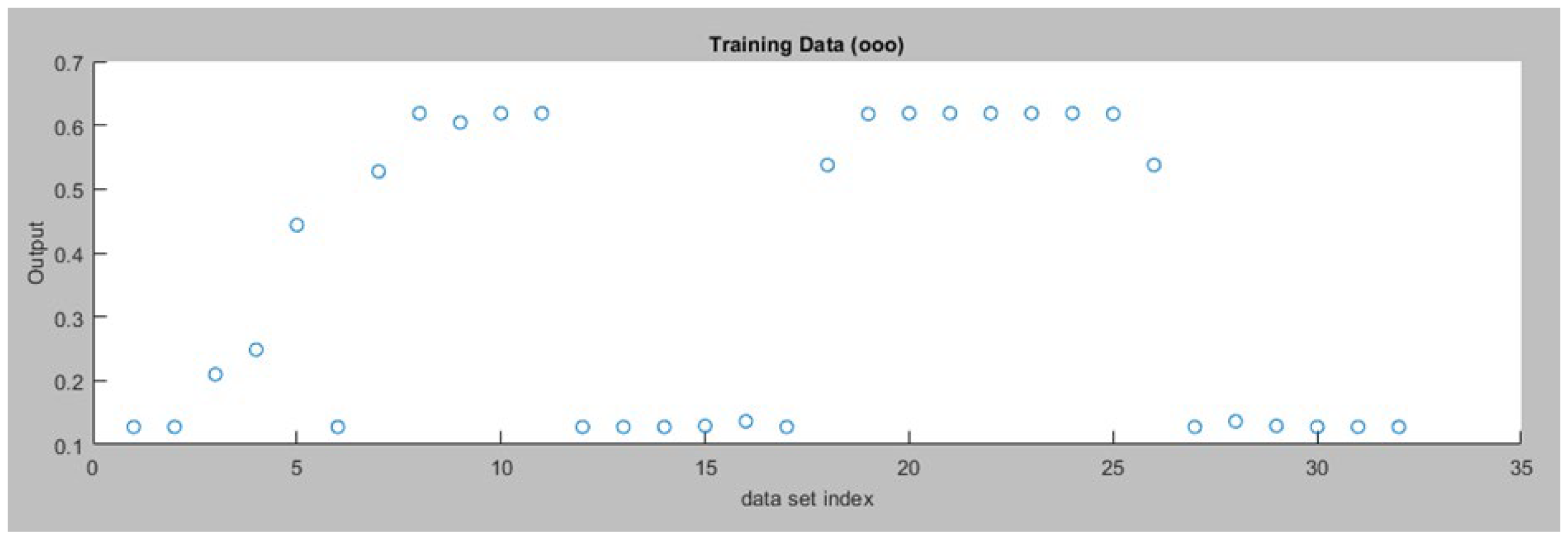
Preprints 111045 g018
Figure 18. Training Data for the Right Motor ANFIS Avoidance Controller.
Figure 18. Training Data for the Right Motor ANFIS Avoidance Controller.
Preprints 111045 g018
Preprints 111045 g019
Figure 19. Training Error for Right Motor ANFIS Avoidance Controller.
Figure 19. Training Error for Right Motor ANFIS Avoidance Controller.
Preprints 111045 g019
Preprints 111045 g020
Figure 20. Data after the ANFIS is trained (Right Motor ANFIS Avoidance Controller).
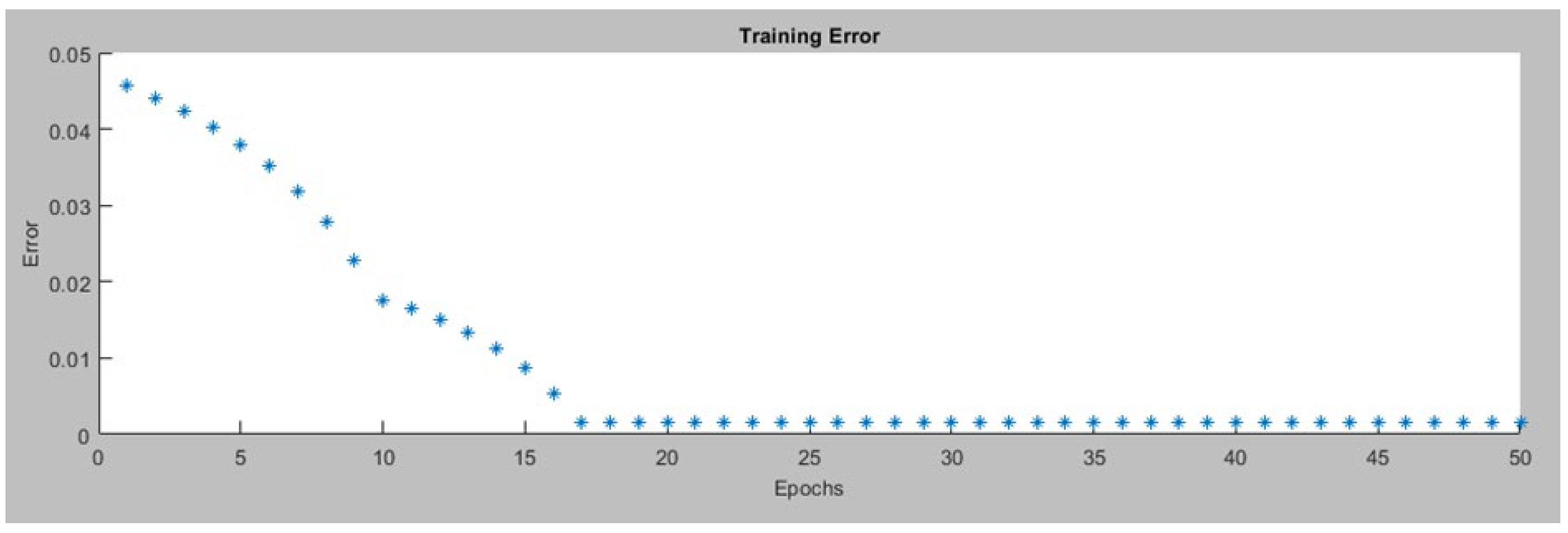
Figure 20. Data after the ANFIS is trained (Right Motor ANFIS Avoidance Controller).
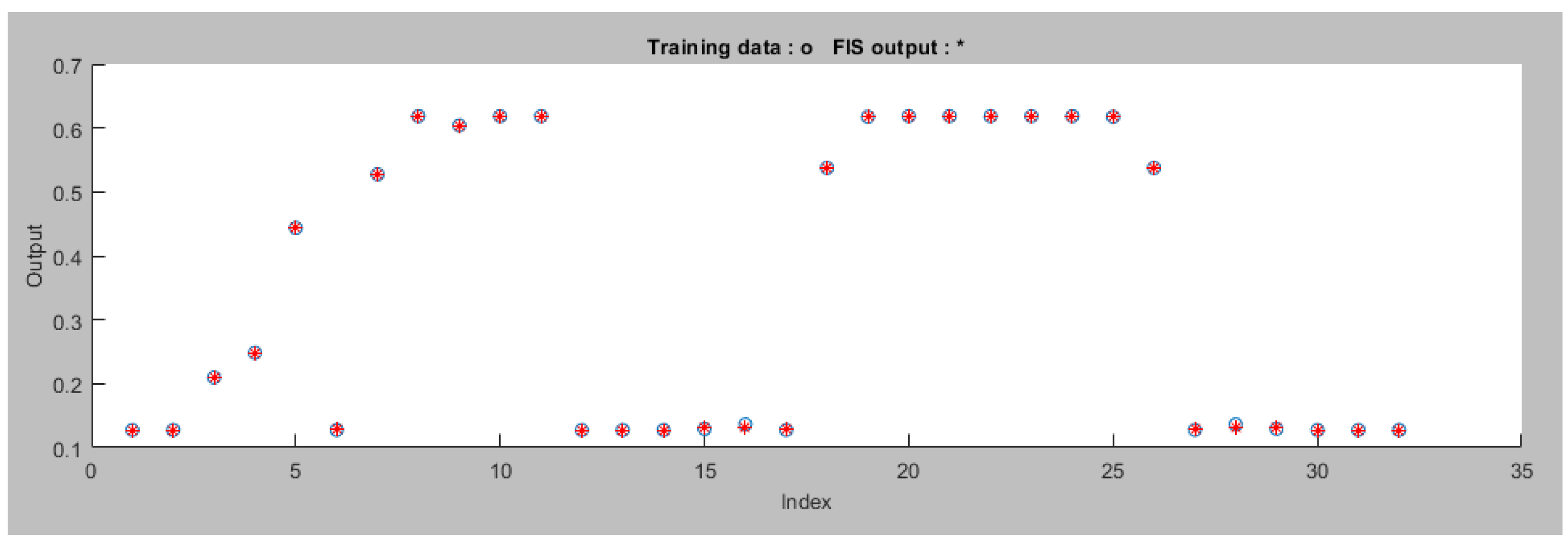
Preprints 111045 g020
Preprints 111045 g021
Figure 21. Left and Right Sensor.
Figure 21. Left and Right Sensor.
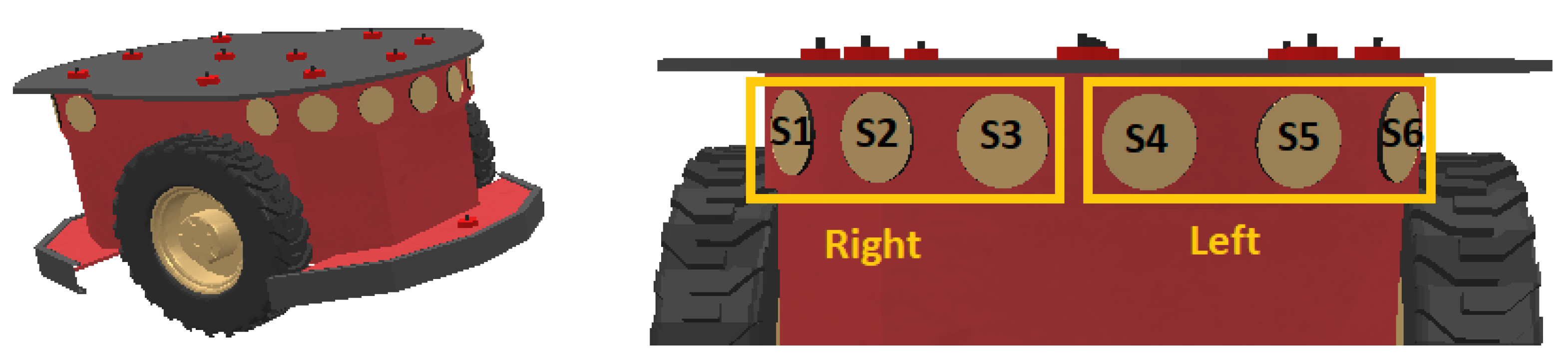
Preprints 111045 g021
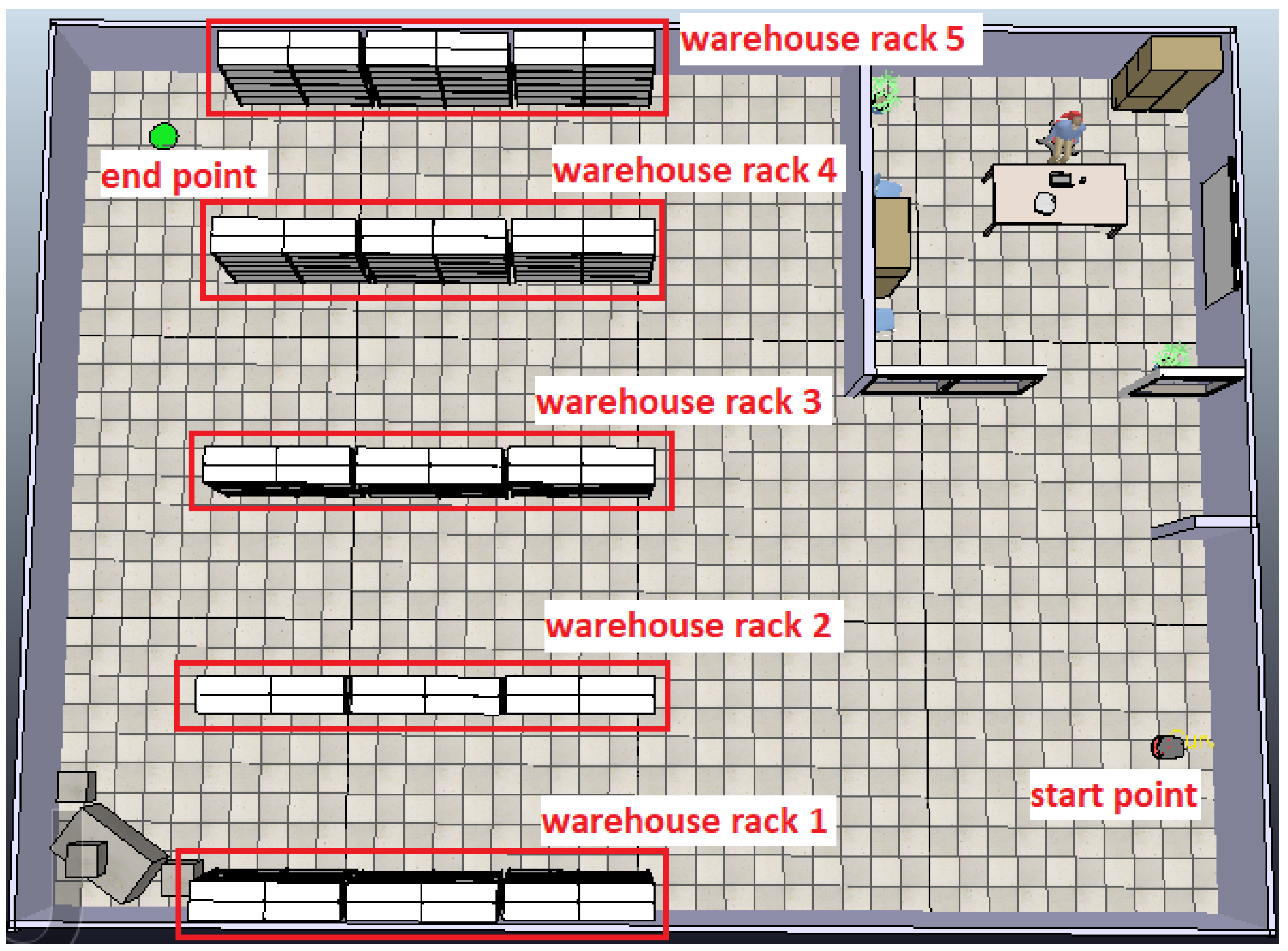
Preprints 111045 g022
Figure 22. CoppeliaSim scene and static obstacles.
Figure 22. CoppeliaSim scene and static obstacles.
Preprints 111045 g022
Preprints 111045 g023
Figure 23. Optimal path computed using a path planning algorithm.
Figure 23. Optimal path computed using a path planning algorithm.
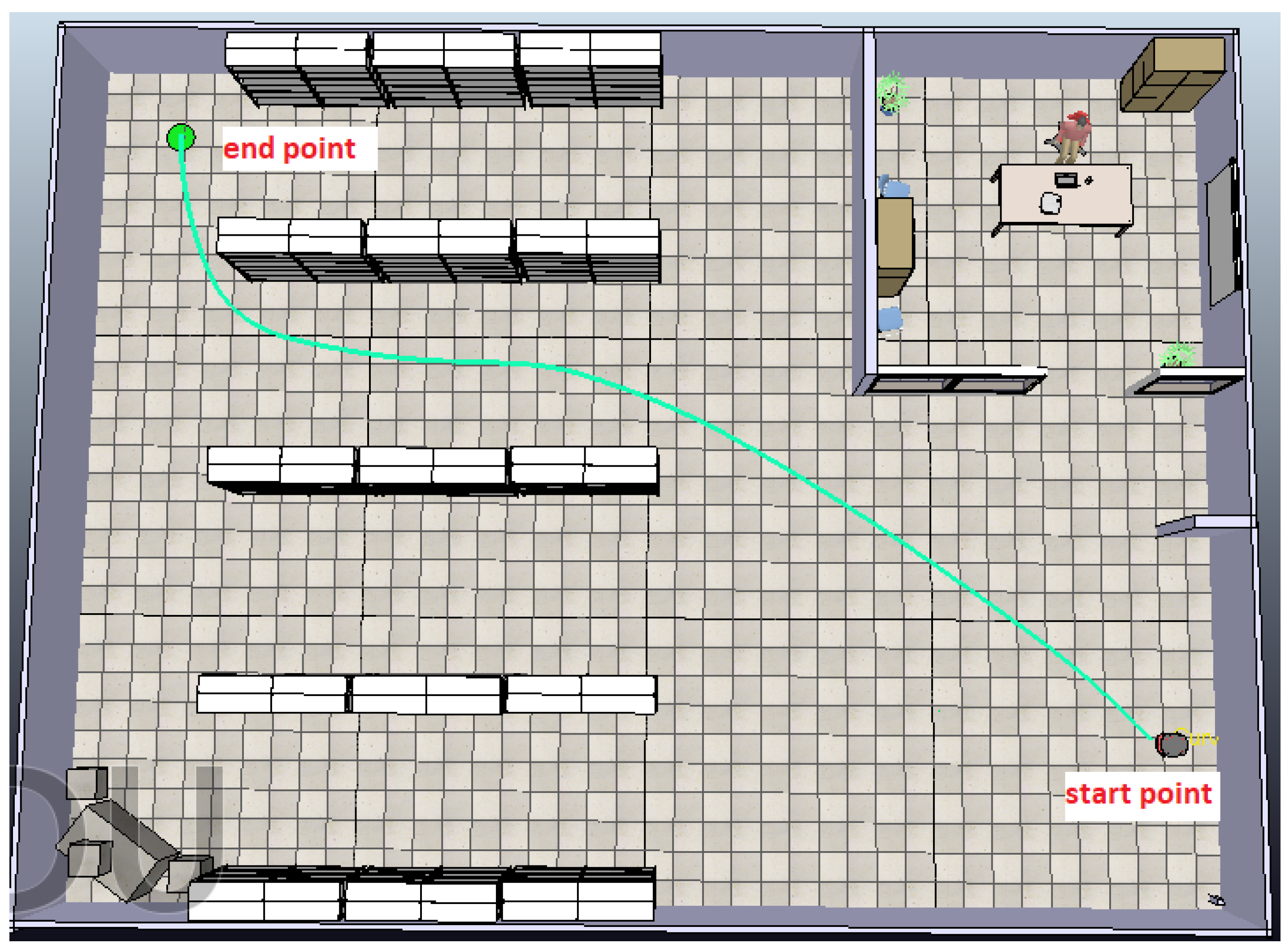
Preprints 111045 g023
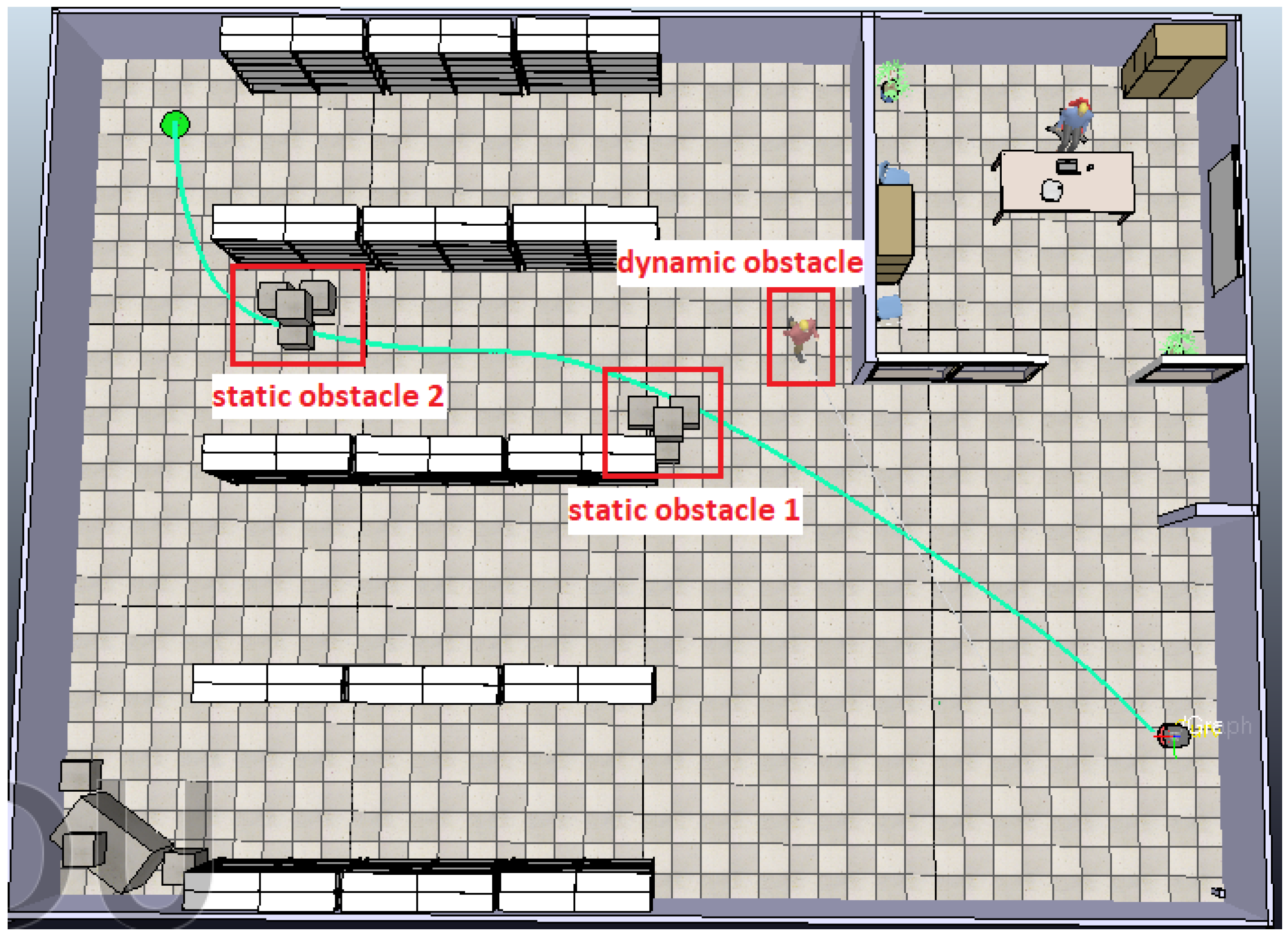
Preprints 111045 g024
Figure 24. A scene with static obstacles and a dynamic obstacle.
Figure 24. A scene with static obstacles and a dynamic obstacle.
Preprints 111045 g024
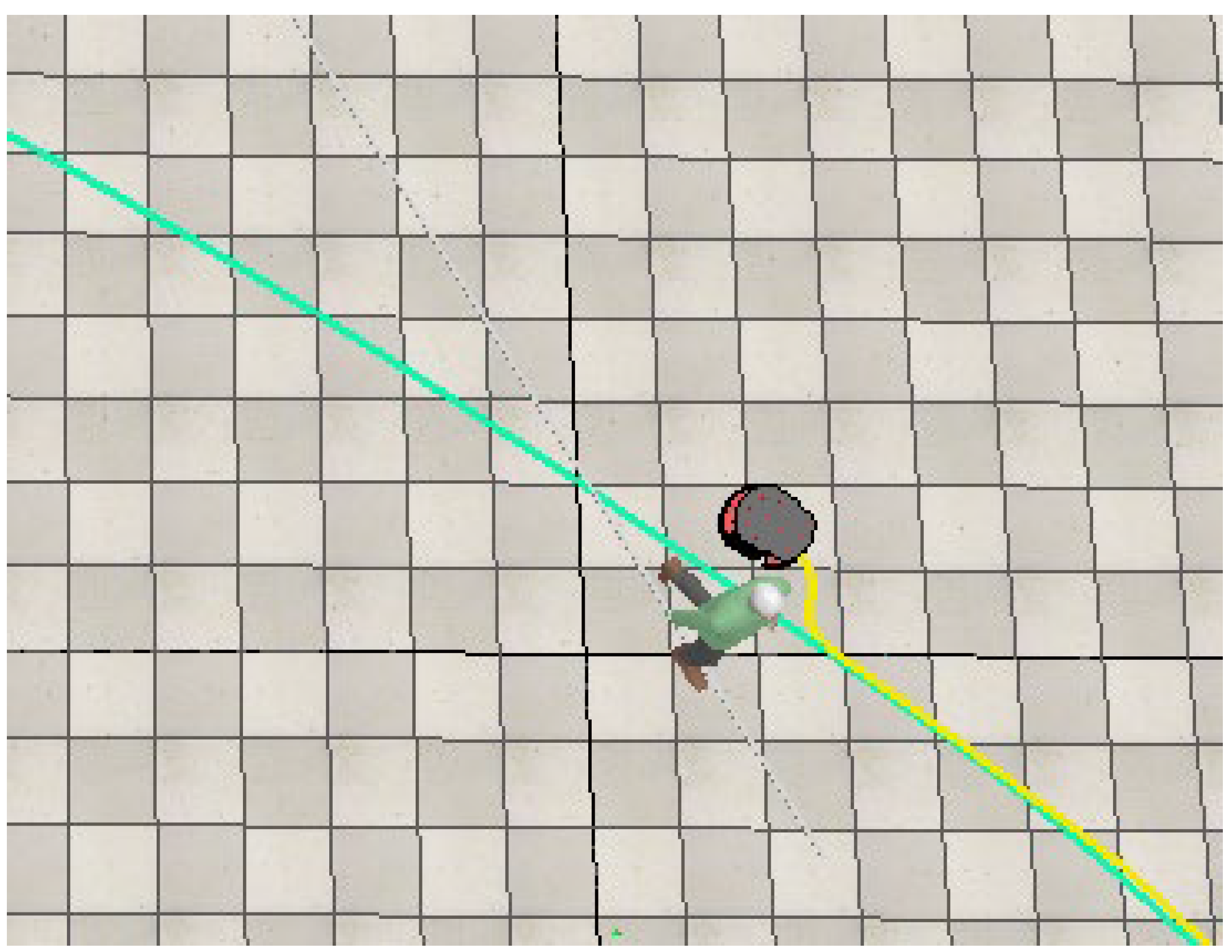
Preprints 111045 g025
Figure 25. The robot executes a maneuver to avoid the dynamic obstacle.
Figure 25. The robot executes a maneuver to avoid the dynamic obstacle.
Preprints 111045 g025
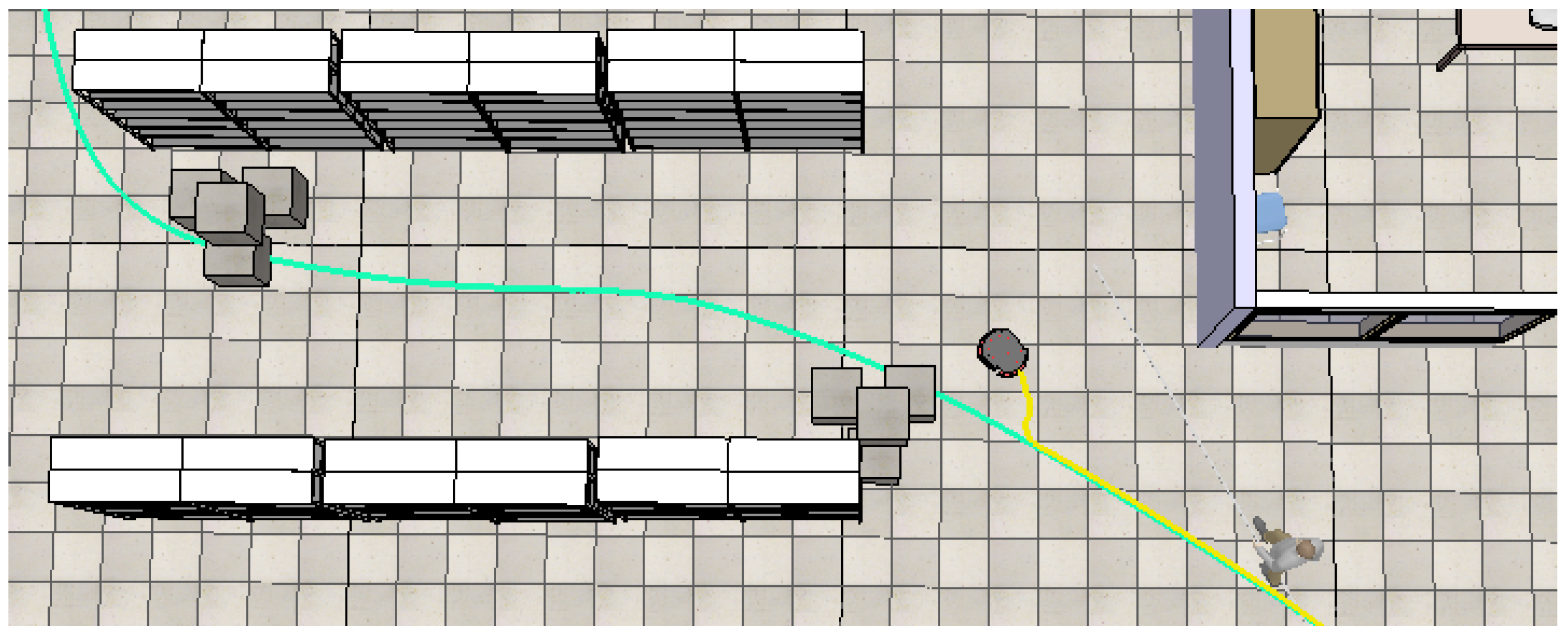
Preprints 111045 g026
Figure 26. The robot executes a maneuver to avoid the first static obstacle.
Figure 26. The robot executes a maneuver to avoid the first static obstacle.
Preprints 111045 g026
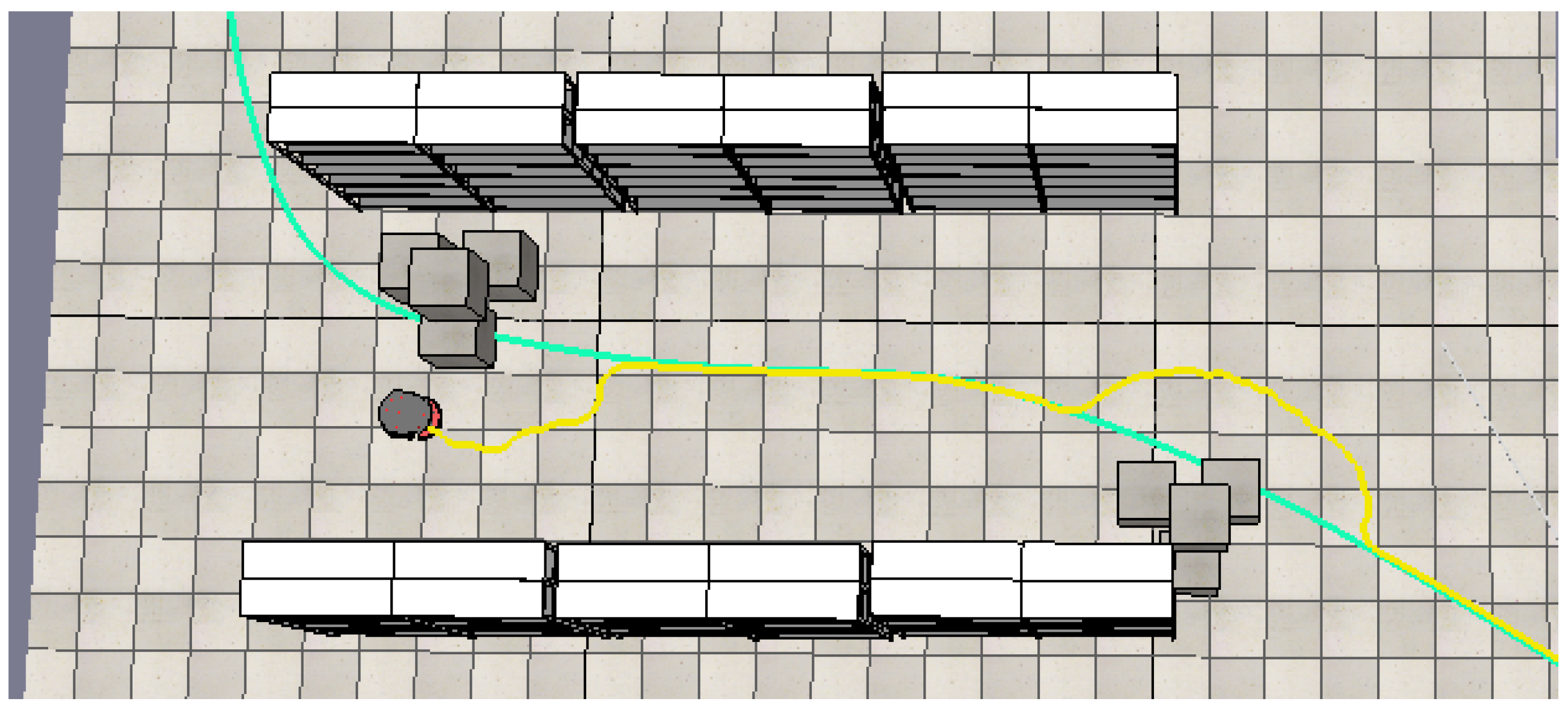
Preprints 111045 g027
Figure 27. The robot executes a maneuver to avoid the second static obstacle.
Figure 27. The robot executes a maneuver to avoid the second static obstacle.
Preprints 111045 g027
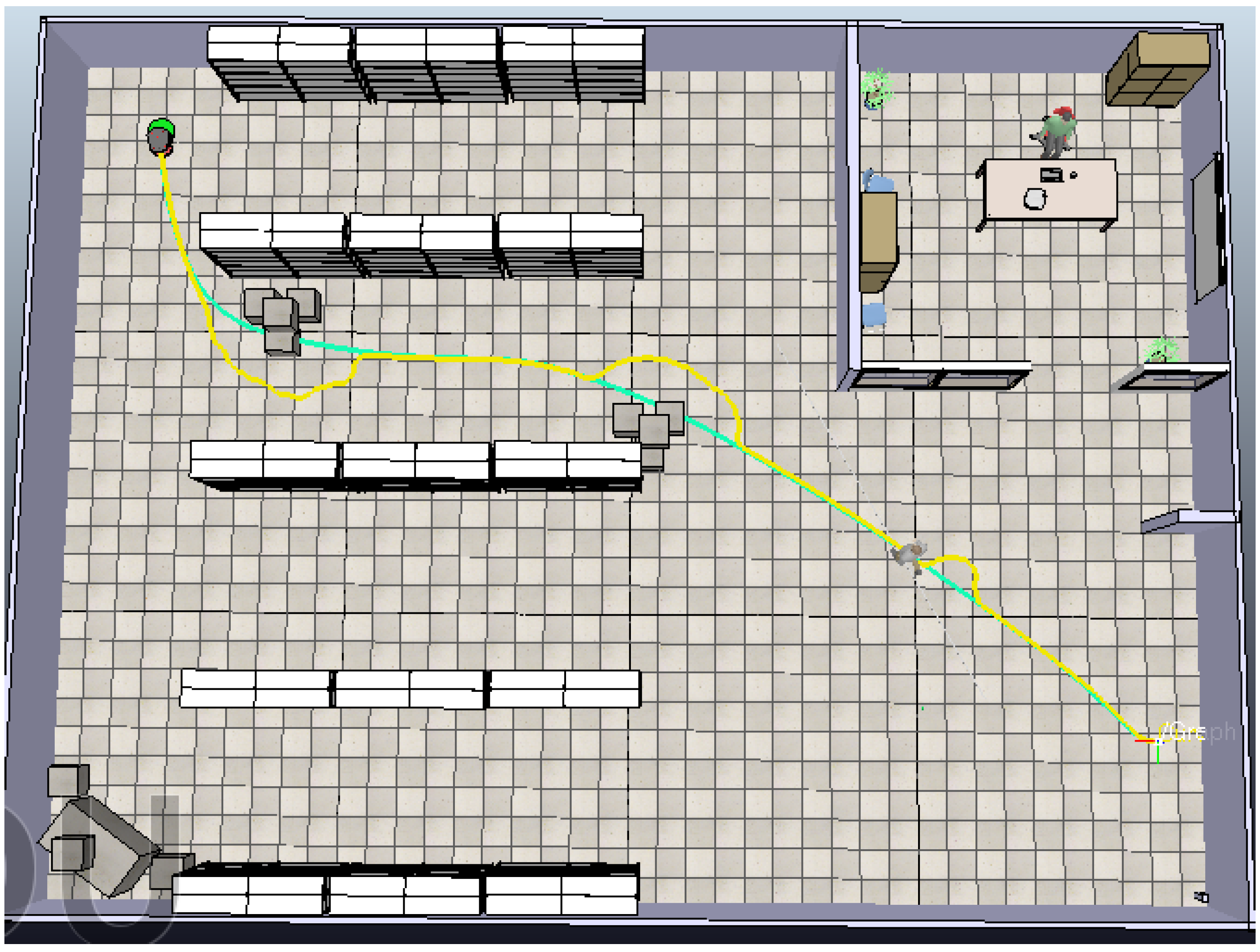
Preprints 111045 g028
Figure 28. The robot effectively navigates by avoiding all encountered obstacles to successfully reach its designated end point.
Figure 28. The robot effectively navigates by avoiding all encountered obstacles to successfully reach its designated end point.
Preprints 111045 g028
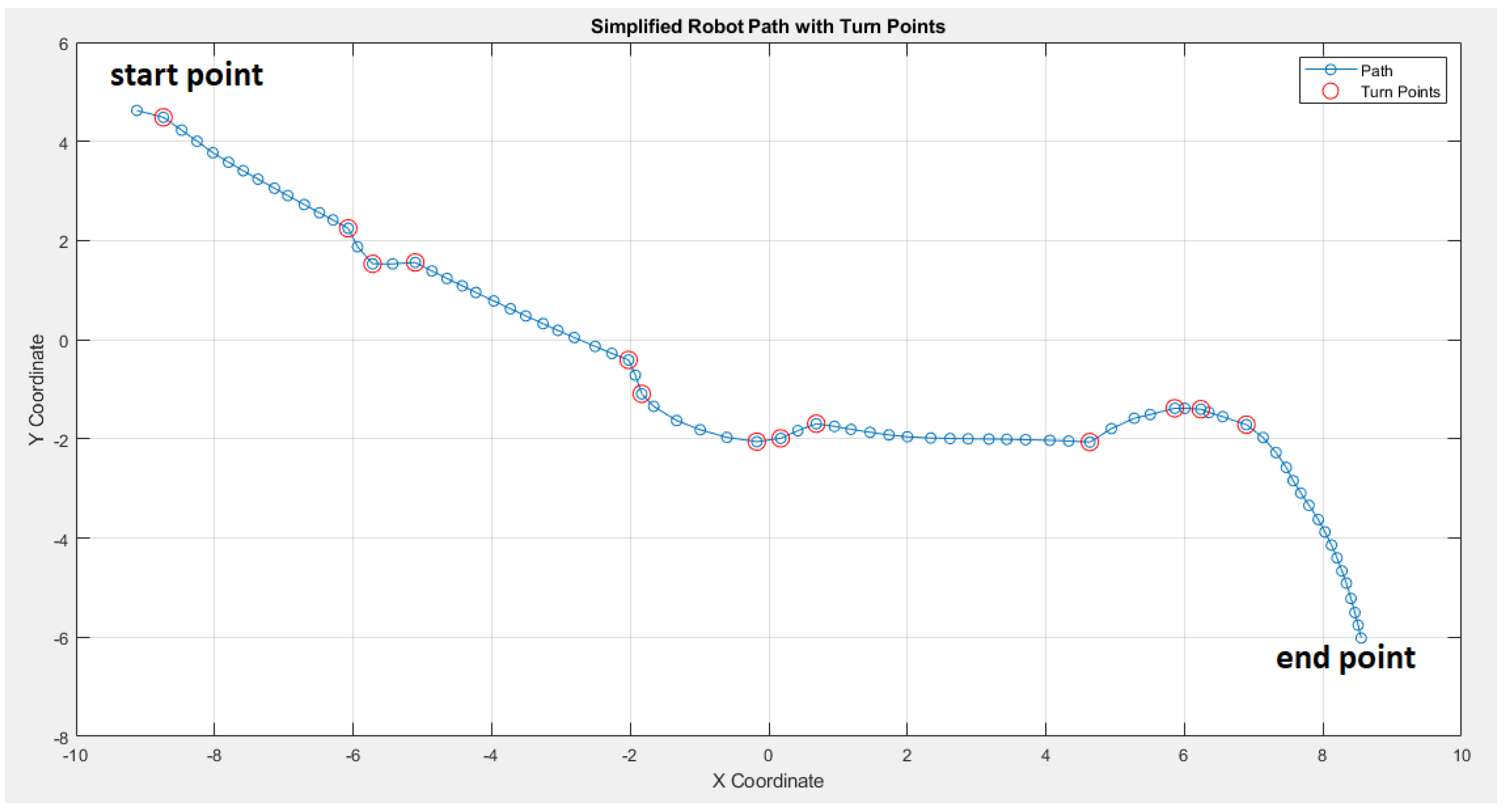
Preprints 111045 g029
Figure 29. Number of turns using ANFIS controllers.
Figure 29. Number of turns using ANFIS controllers.
Preprints 111045 g029
Preprints 111045 g030
Figure 30. Number of turns using fuzzy logic controllers.
Figure 30. Number of turns using fuzzy logic controllers.
Preprints 111045 g030
Preprints 111045 g031
Figure 31. Another scene including static and dynamic obstacles.
Figure 31. Another scene including static and dynamic obstacles.
Preprints 111045 g031
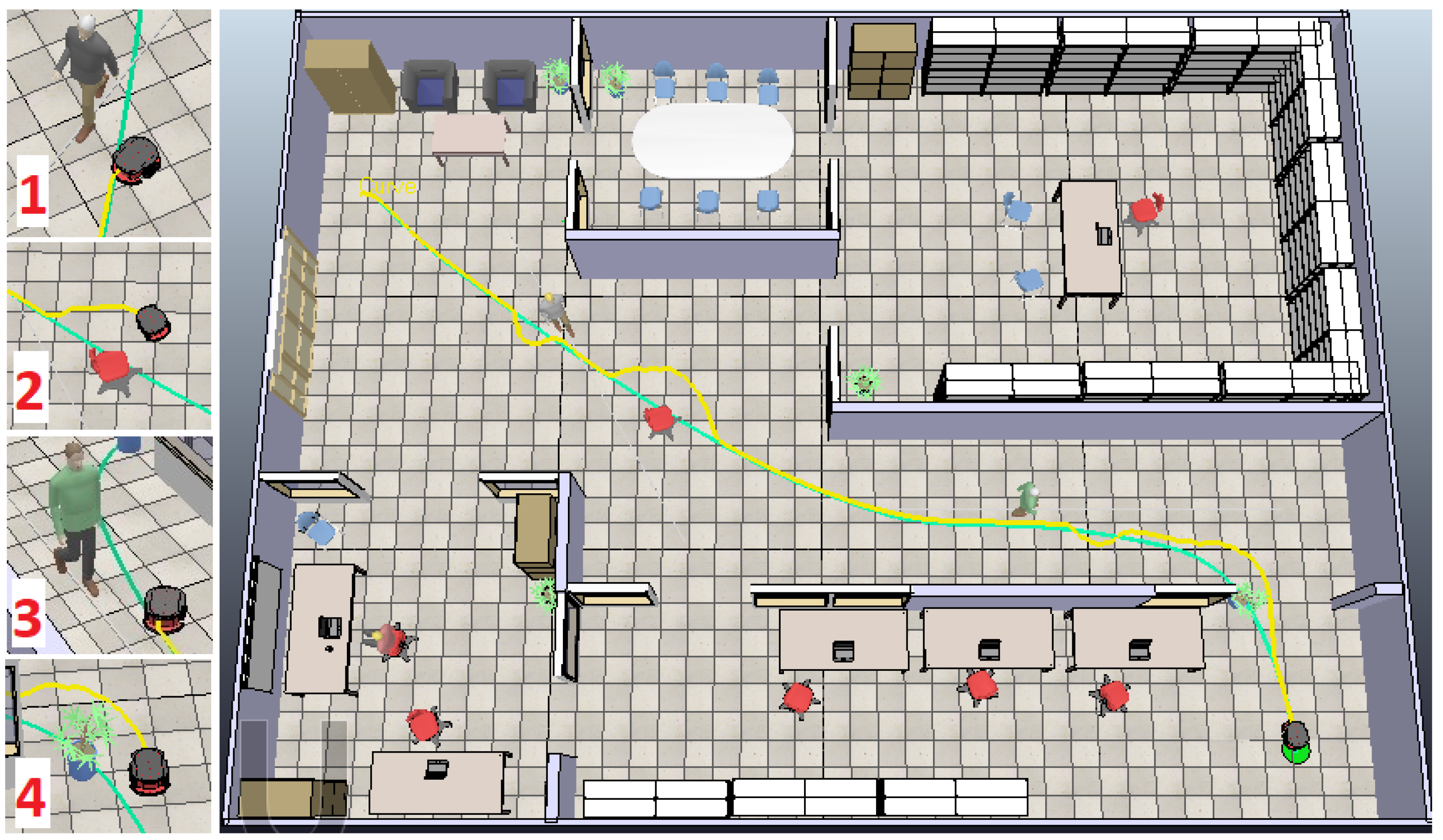
Preprints 111045 g032
Figure 32. Detailed snapshots of the robot navigating around obstacles.
Figure 32. Detailed snapshots of the robot navigating around obstacles.
Preprints 111045 g032
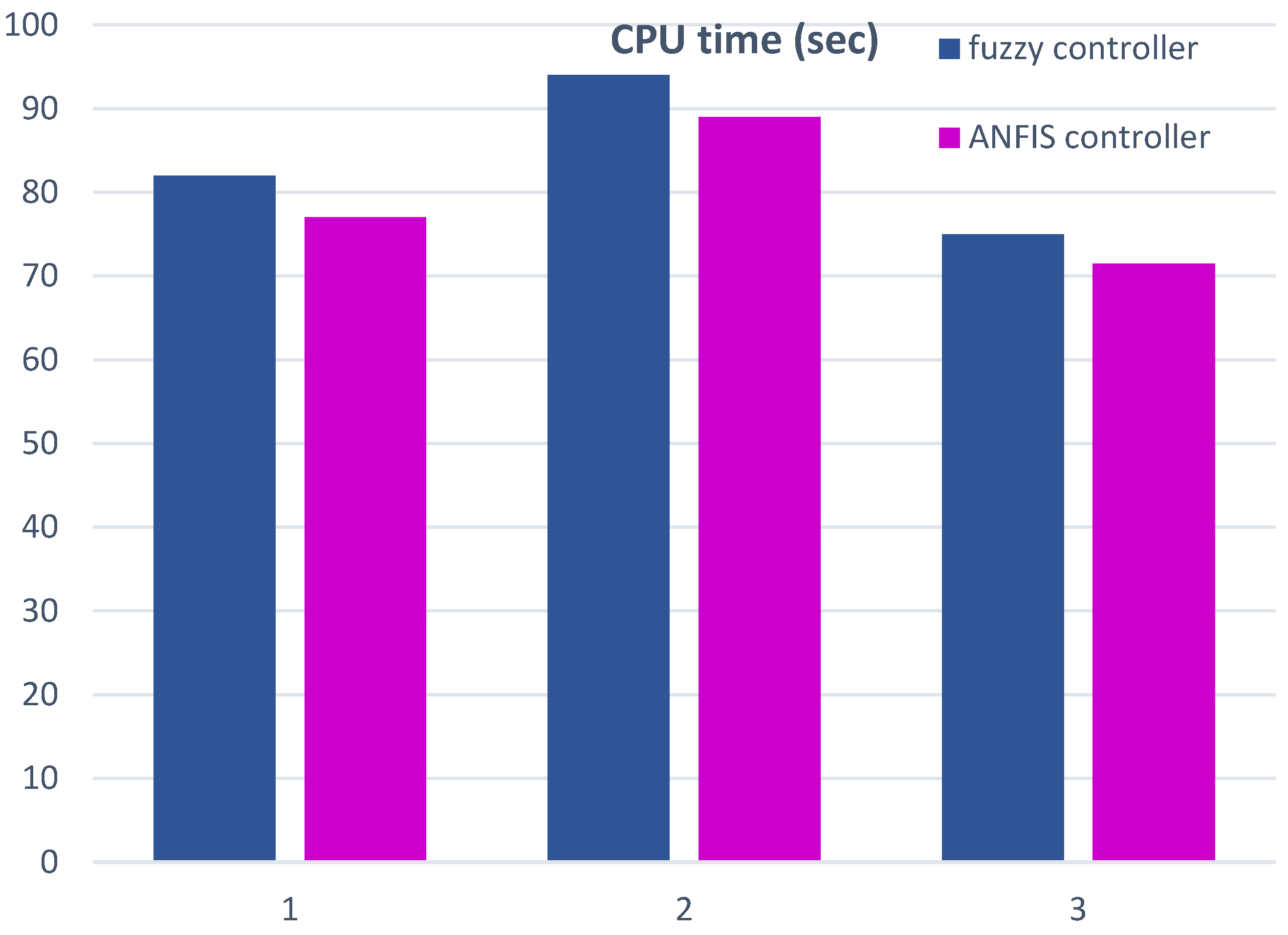
Preprints 111045 g033
Figure 33. The average CPU times for all test cases within the three environments.
Figure 33. The average CPU times for all test cases within the three environments.
Preprints 111045 g033
Table 1. Rule set for fuzzy tracking controller.
Table 1. Rule set for fuzzy tracking controller.
rule position error heading error right motor velocity left motor velocity
1 large negative big medium fast
2 large negative small slow medium
3 large zero fast fast
4 large positive small medium slow
5 large positive big fast medium
6 medium negative big medium fast
7 medium negative small slow medium
8 medium zero fast fast
9 medium positive small medium slow
10 medium positive big fast medium
11 small negative big slow fast
12 small negative small slow fast
13 small zero slow slow
14 small positive small fast slow
15 small positive big fast slow
Table 2. Sample of training data generated by the fuzzy tracking controller.
Table 2. Sample of training data generated by the fuzzy tracking controller.
position error heading error expected right motor velocity expected left motor velocity
0.9 0 0.7578 0.7578
0.8 0 0.7578 0.7578
0.7 0 0.7578 0.7578
0.6 0 0.7578 0.7578
0.5 0 0.7578 0.7578
0.4 0 0.7578 0.7578
0.3 0 0.7578 0.7578
0.2 0 0.7572 0.7572
0.1 0 0.6055 0.6055
0 0.9 0.7578 0.1674
0 0.8 0.7578 0.1674
0 0.7 0.7578 0.1674
0 0.6 0.7578 0.1674
0 0.5 0.7578 0.1674
0 0.4 0.7546 0.1713
Table 3. Rule set for fuzzy avoidance controller.
Table 3. Rule set for fuzzy avoidance controller.
rule left sensor right sensor right motor velocity left motor velocity
1 very close very close slow slow
2 very close close slow fast
3 very close medium slow fast
4 very close far slow fast
5 very close very far slow fast
6 close very close fast slow
7 close close slow slow
8 close medium slow fast
9 close far slow fast
10 close very far slow fast
11 medium very close fast slow
12 medium close fast slow
13 medium medium slow slow
14 medium far slow fast
15 medium very far slow fast
16 far very close fast slow
17 far close fast slow
18 far medium fast slow
19 far far fast fast
20 far very far slow fast
21 very far very close fast slow
22 very far close fast slow
23 very far medium fast slow
24 very far far fast slow
25 very far very far fast fast
Table 4. Sample of training data for the ANFIS avoidance controllers.
Table 4. Sample of training data for the ANFIS avoidance controllers.
left sensor right sensor expected right motor velocity expected left motor velocity
0 1 0.6186 0.1276
0.1 0.9 0.6186 0.1276
0.2 0.8 0.6186 0.1276
0.3 0.7 0.6175 0.1292
0.4 0.6 0.5377 0.1364
0.5 0.5 0.1276 0.1276
0.6 0.4 0.1363 0.5377
0.7 0.3 0.1292 0.6175
0.8 0.2 0.1276 0.6186
0.9 0.1 0.1276 0.6186
1 0 0.1276 0.6186
Table 5. Performance comparison between ANFIS and fuzzy logic controller strategies.
Table 5. Performance comparison between ANFIS and fuzzy logic controller strategies.
strategy time to reach the end point (sec) number of turns number of rules for tracking controller number of rules for avoidance controller
ANFIS 71.4 13 9 16
Fuzzy system 73.2 18 15 25
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated