Finite-Time Control Design for the Discrete-Time Chaotic Logistic Equation

Preprint

Article

Finite-Time Control Design for the Discrete-Time Chaotic Logistic Equation

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 July 2024

Posted:

05 July 2024

You are already at the latest version

Alerts

Abstract

Finite-time control theory has been widely used as a mathematical tool to design robust controllers. By manipulating the finite-time convergence proof of this theory, we developed a new control design appropriately tuned for the finite-time control of the chaotic logistics system. In our experimental setup, the logistic equation is programmed into a PIC microcontroller, and a part of the controller was conceived using analog electronics. Because the system to be controlled is in the discrete-time domain, and the finite-time stability proof is stated in the continuous-time representation, our finite-time control approach is a good example for designing control algorithms in both time domain schemes. Hence, our experimental results support our main contribution. Pulse Width Modulation (PWM) is the signal format used to translate digital signals into continuous-time fields.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Finite-time control theory is a well-established method to develop robust controllers applied to dynamical systems [2,9]. An important feature of the finite-time control approach is its ability to guarantee that there exists a finite time in which the trajectories of the closed-loop system have reached an equilibrium point [3]. This control approach was originally conceived in the continuous-time domain [2,3,9], although there are some contributions on the topic in the discrete-time domain [4,5]. However, if we want to design a mixed combination of digital and analog controllers, one option is to use the continuous-time domain framework to then translate a designed control system into the discrete-time format. We follow this idea to develop a mixed analog-discrete finite-time controller for the chaotic logistic equation. In our experimentation, the chaotic logistic system is implemented into a PIC microcontroller, the PIC16F84A. This microcontroller has been used for a long time, and it can be considered obsolete, but it is still useful. We invoke the chaotic logistic equation because is a good reference for control design in chaotic systems and its applications [6,7]. Therefore, our main objective and contribution is to design a new finite-time controller for the chaotic logistic equation by using analog and discrete-time algorithms. Lyapunov’s theory is employed for our closed-loop stability in finite time, and pulse-width-modulation (PWM) is employed for manipulating digital signals into the continuous-time domain. In addition, a low-cost experimental platform was also conceived. Experimental results support our findings.

The rest of this document is structured as follows. Section 2 describes our main result on finite-time stability for continuous systems followed by our main contribution on the topic. Section 3 is a brief on the chaotic logistic equation. Section 4 and 5 show our designed experimental platform and control realization along with experimental results. Finally, Section 6 gives the closing remarks.

2. Finite-Time Stability

Hereafter, we will concentrate our discussion on scalar non-linear and time-invariant systems. Globally finite-time stability consists of any solution to the systems for

x (0) \neq 0

and given by 1:

\dot{x} = f (x), x \in R,

(1)

where

f : R \to R

is a continuous function and assumed that

f (0) = 0

is the unique equilibrium point of the system, reach its equilibrium point in finite-time [9]. Therefore, a settling-time function depends on the system’s initial condition [8]. We have the next result [8]:

Theorem 1.

Let the system’s origin (1) be its unique equilibrium point. The origin is globally finite-time stable if for all

x \in R ∖ {0}

, we have:

$\dot{v} (x) < 0$ ;
$\int_{x}^{0} \frac{d z}{f (z)} < + \infty$ ;

where

v (x) = \frac{1}{2} x^{2}

is its Lyapunov function, and the corresponding settling-time function,

T_{0} (x)

, is given by

T_{0} (x) = \int_{x}^{0} \frac{d z}{f (z)}

Also, the above Theorem is also true if

\dot{v} (x) < - a {| v (t) |}^{b}; a, b \in R_{> 0}

, and

b \in (0, 1)

[8]. Using the above Theorem, we have our main contribution as a Corollary to this Theorem:

Corollary 1.

Let the system’s origin (1) be its unique equilibrium point. The origin is globally finite-time stable if for all

x \in R ∖ {0}

, we have:

$\dot{v} (x) < - a v (t) - b a, b \in R_{> 0}$ ;
$\int_{x}^{0} d v < + \infty$ ;

where

v (x)

is its Lyapunov function, and the corresponding settling-time function,

T_{0} (x)

, is given by

T_{0} (x) = \int_{x}^{0} d v

Proof of Corollary 1.

First observe that

\dot{v} (x) < - a v (t) - b < - a v (t)

, which assures that the equilibrium point is globally asymptotically stable. Then

\dot{v} (x) < - a v (t) - b \to \dot{v} (x) < - b

, implying that

T_{0} (x) = \int_{x}^{0} d v \leq - b t_{s}

, being

t_{s}

the settling-time, yielding

t_{s} \leq \frac{v (x (0))}{b}

. □

3. Chaotic Logistic Equation

A one-dimensional chaotic logistic equation or chaotic logistic map can be represented as [7]:

z (k + 1) = 3.6 z (k) [1 - z (k)], z (0) \in (0, 1) .

(2)

A sample of the chaotic trajectory using

z (0) = 0.5

is shown in Figure 1, where a line joins each data point generated by the logistic map.

Finally, recall that the logistic system’s discrete solution is inside the open interval between zero and one.

4. Control Design and Experimentation

This section is dedicated to obtaining a continuous-time dynamic model of the logistic map based on the first Euler method. As an initial step, let us add the control input

u (k)

as follows:

z (k + 1) = 3.6 z (k) [1 - z (k)] + u (k), z (0) \in (0, 1) .

(3)

The above expression can be re-written as (

h = 1

z (k + 1) = z (k) + h [2.6 z (k) - 3.6 z^{2} (k) + u (k)] . z (0) \in (0, 1),

(4)

Then, and according to the Euler’s first method that says:

\dot{x} (t) = f (x, u) \to x (k + 1) = x (k) + h [f (x (k), u (k))],

(5)

where the parameter h is the step integration, we conclude that a feasible model for the control design of the logistic map may be:

\dot{x} (t) = f (x (t), u (t)) = 2.6 x (t) - 3.6 x^{2} (t) + u (t) .

(6)

Linearization of the above system around the origin equilibrium point of the non-actuated system, yields:

\dot{x} (t) = 2.6 x (t) + u (t) .

(7)

Given the Lyapunov function

v (x) = \frac{1}{2} x^{2}

, and using:

u (t) = - 2.6 x (t) - s g n (x (t)),

(8)

we obtain that

\dot{v} (t) = - \sqrt{2} v^{1 / 2} (t)

. This concludes that the closed-loop linearized system ( 7)-( 8) is globally finite-time stable. Here,

s n g (x) = 1

for

x > 0

s g n (x) = - 1

for

x < 0

, and

s g n (x) = 0

for

x = 0

. Figure 2 shows a picture of the obtained control algorithm.

On the other hand, if we select

v (x) = | x |

, we have

\dot{v} (t) = - v - 1

if the control law is:

u (t) = - 3.6 x (t) - s g n (x (t)) .

(9)

From the above Corollary, we conclude that the closed-loop linearized system ( 9)-( 7) is globally finite-time stable too. Observe that both controllers ( 8) and ( 9) are too similar.

For chaotic logistic experimental realization, we will use PWM (Pulse-Width-Modulation). This is a technique for getting analog results with digital means. Actually, this is a well-known technique in electronics. We want to implement the chaotic logistic map into a PIC microcontroller of 8 bits, the PIC16F84A microcontroller, the PWM duty cycle should be from "0" to "255" digital count. Hence, we are required to scale the logistic equation using the following scale transformation

x (k) = K z (k)

, yielding:

x (k + 1) = 3.6 x (k) [K - z (k)] / K, x (0) \in (0, K) .

(10)

Therefore, for our case, we have

K = 255

. After that, we have to add the control input:

x (k + 1) = 3.6 x (k) [K - z (k)] / K + u (k), x (0) \in (0, K) .

(11)

Hence, our PWM duty cycle will be

x (k)

, and the PWM period will be the count of a value bigger than 255. In programming, we use 258. Additionally,

x (k) \in [0, 255]

. This PMW signal is then sent out of the microcontroller unit followed by an

R C

low pass filter. See Figure 3. The comparator used in the given circuit through an operational amplifier is an analog-to-digital conversion stage before feedback to the microcontroller. The reference of

2.5

V given by the trimmer

P_{1}

is due to the logical threshold level between the 0 and 1 logical values corresponding to 0V and 5V, respectively. In this way, the average value at the output of this comparator corresponds to the analog value of

V_{a} : = v_{a} (t)

2 seen by the microcontroller. A photo of the experimental platform is shown in Figure 4.

To conclude this section, and due to the used PMW format and the fact the initial and the solution to the chaotic map equation presents positive solutions, from the control law given ( 8) (or ( 9)), we can observe that this control action has negative derivative for the system’s output signal. Therefore, by using digital programming in the microcontroller unit

u = u + 1

3 or

u = u - 1

4 means positive or negative control variation for the digital control signal to the logistic system, respectively. See Figure 5. In this way, if the time activation of

u^{+} (u = u + 1)

is less than the time activation of

u^{-} (u = u - 1)

means negative feedback and asymptotic stability of the closed-loop system.

5. Experimental Results and Discussion

This section is dedicated to experimental results and discussions on the main contribution of this paper. Using the program displayed in Figure 5, Figure 6 shows the expected result. On the other hand, if the locations of

u^{+}

and

u^{-}

are exchanged, we hope the closed-loop system be unstable. This is the case shown in Figure 7. On the other hand, the most obvious question is why not

u^{+} = 0 (u = 0)

. Well, this is the experimental result shown in Figure 8. Once again, if we exchange the control location as before, we expect that the closed-loop system will be unstable. This is shown in Figure 9.

Additional, in comparison to the chaotic circuit using a microcontroller presented in [10], our design is simpler because we use a few microcontroller pins to produce an analogical chaotic signal.

6. Conclusions

This article presents some background on finite-time stability and then applied it to stabilize the chaotic logistic map. In our control realization, we have also developed a novel and low-cost experimental platform for practicing academic control theory and digital and analog electronics.

Author Contributions

Conceptualization, L.A. and G.P.; methodology, L.A. and P.B.; software, L.A.; validation, L.A., P.B., and G.P.; formal analysis, G.P.; investigation, L.A. and G.P.; resources, P.B.; data curation, P.B.; writing—original draft preparation, L.A., G.P., and P.B.; writing—review and editing, L.A., G.P., and P.B.; visualization, L.A., G.P., and P.B.; supervision, L.A., G.P., and P.B.; project administration, L.A.; funding acquisition, L.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Moulay, E. , W. Finite-Time Stability and Stabilization. In Advances in Variable Structure and Sliding Mode Control. Lecture Notes in Control and Information Science, vol 334.; Edwards, C., Fossas Colet, E., Fridman, L., Eds.; Springer: Berlin-Heidelberg, Germany, 2006; pp. 23–41. [Google Scholar]
Liu, Yang and Li, Hongyi and Lu, Renquan and Zuo, Zongyu and Li, Xiaodi. An overview of finite/fixed-time control and its application in engineering systems. IEEE/CAA Journal of Automatica Sinica 2022, 9, 2106–2120. [CrossRef]
Hong, Yiguang; Jiang, Zhong-Ping; Feng, Gang. Finite-time input-to-state stability and applications to finite-time control design. SIAM Journal on Control and Optimization 2010, 48, 4395–4418. [CrossRef]
Amato, Francesco; Ariola, Marco. Finite-time control of discrete-time linear systems. IEEE Transactions on Automatic control 2005, 50, 724–729. [CrossRef]
Haddad, Wassim M.; Lee, Junsoo. Finite-time stabilization and optimal feedback control for nonlinear discrete-time systems. IEEE Transactions on Automatic Control 2022, 68, 1685–1691.
Kashchenko, Sergey A. Dynamics of the logistic equation with delay and delay control. International Journal of Bifurcation and Chaos 2014, 24, 1440017. [Google Scholar] [CrossRef]
De La Hoz, Mauricio Zapateiro; Acho, Leonardo; Vidal, Yolanda. A secure communication design based on the chaotic logistic map: An experimental realization using arduino microcontrollers. Computation, Cryptography, and Network Security 2015, 737–756.
Moulay, Emmanuel; Perruquetti, Wilfrid. Finite time stability conditions for non-autonomous continuous systems. International Journal of control 2008, 81, 797–803. [CrossRef]
Zuppa, Leonardo Acho. Chaotic logistic map implementation in the PIC12F629 microcontroller unit. IFAC Proceedings Volumes 2010, 43(24), 167–170. [Google Scholar] [CrossRef]
Chiu, R. , Mora-Gonzalez, M., and Lopez-Mancilla, D. (2013). Implementation of a chaotic oscillator into a simple microcontroller. IERI Procedia 2013, 4, 247–252. [Google Scholar] [CrossRef]

1	The dot notation means: $\dot{(\cdot)} = \frac{d (\cdot)}{d t}$ .
2	The notations $: =$ means defined as
3	Programming line meaning that the content of register u is increased by one
4	Programming line meaning that the content of register u is decreased by one

Figure 1. A chaotic trajectory generated by the logistic map using lines to join adjacent chaotic data.

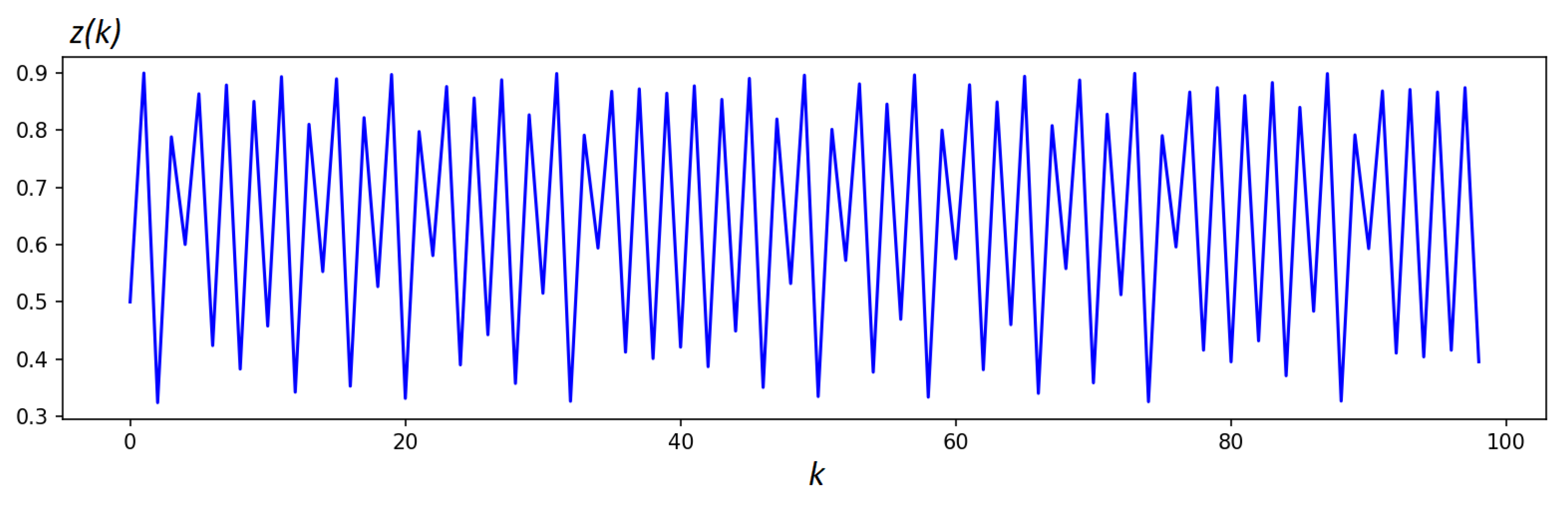
Figure 2. A plot of the control law ( 8).

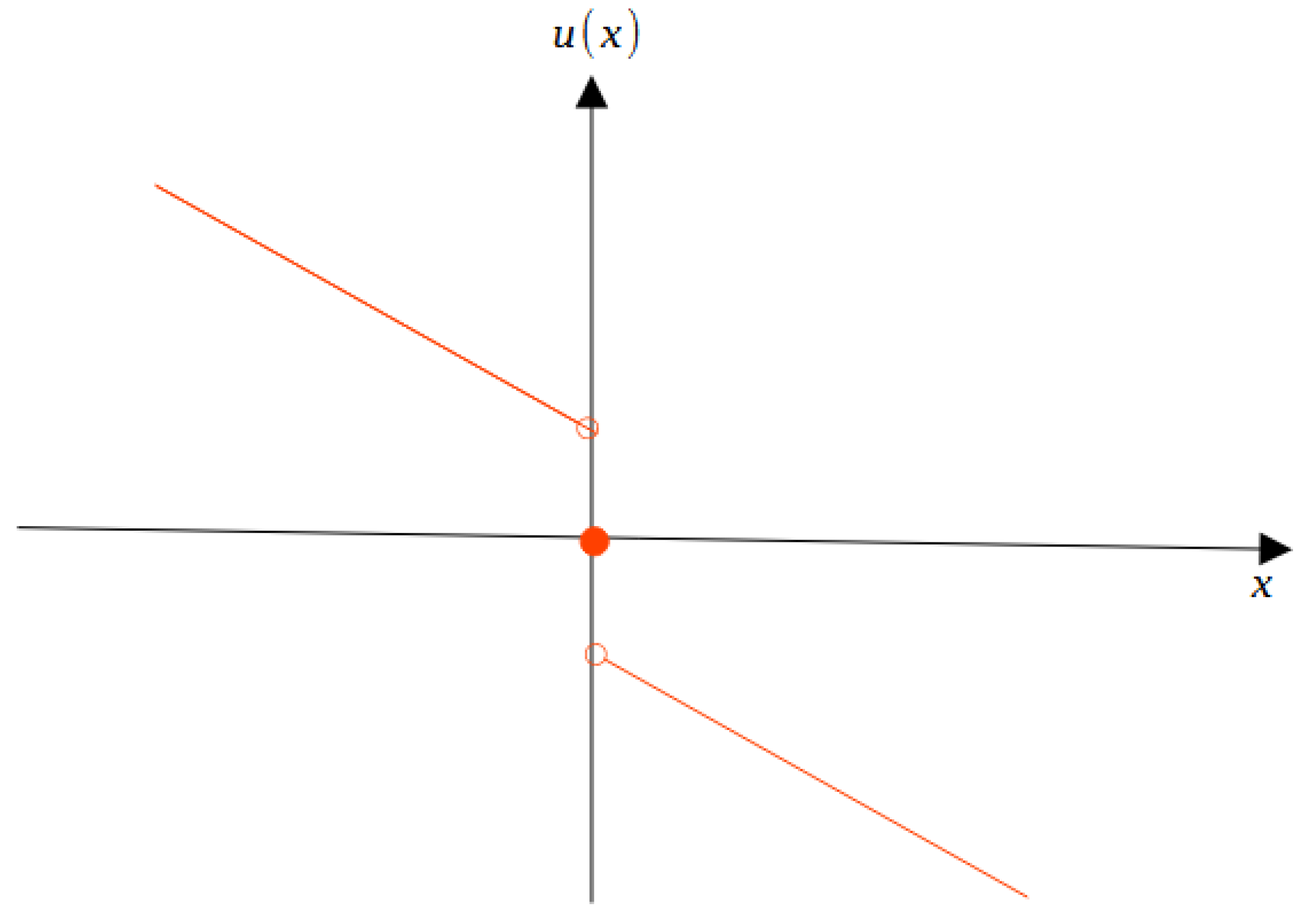
Figure 3. Electronic circuit of our experimental platform. A computer reads the voltage

V_{a} : = V_{a} (t)

via a digital oscilloscope. This value corresponds to the analog version of

x (k)

. The LED receives the microcontroller’s clock operation and is used here to visualize that this unit is working. The switch

S W

is employed to reset the PIC unit. Finally, the entire system operates on a single supply voltage of 5 volts.

Figure 3. Electronic circuit of our experimental platform. A computer reads the voltage

V_{a} : = V_{a} (t)

via a digital oscilloscope. This value corresponds to the analog version of

x (k)

. The LED receives the microcontroller’s clock operation and is used here to visualize that this unit is working. The switch

S W

is employed to reset the PIC unit. Finally, the entire system operates on a single supply voltage of 5 volts.

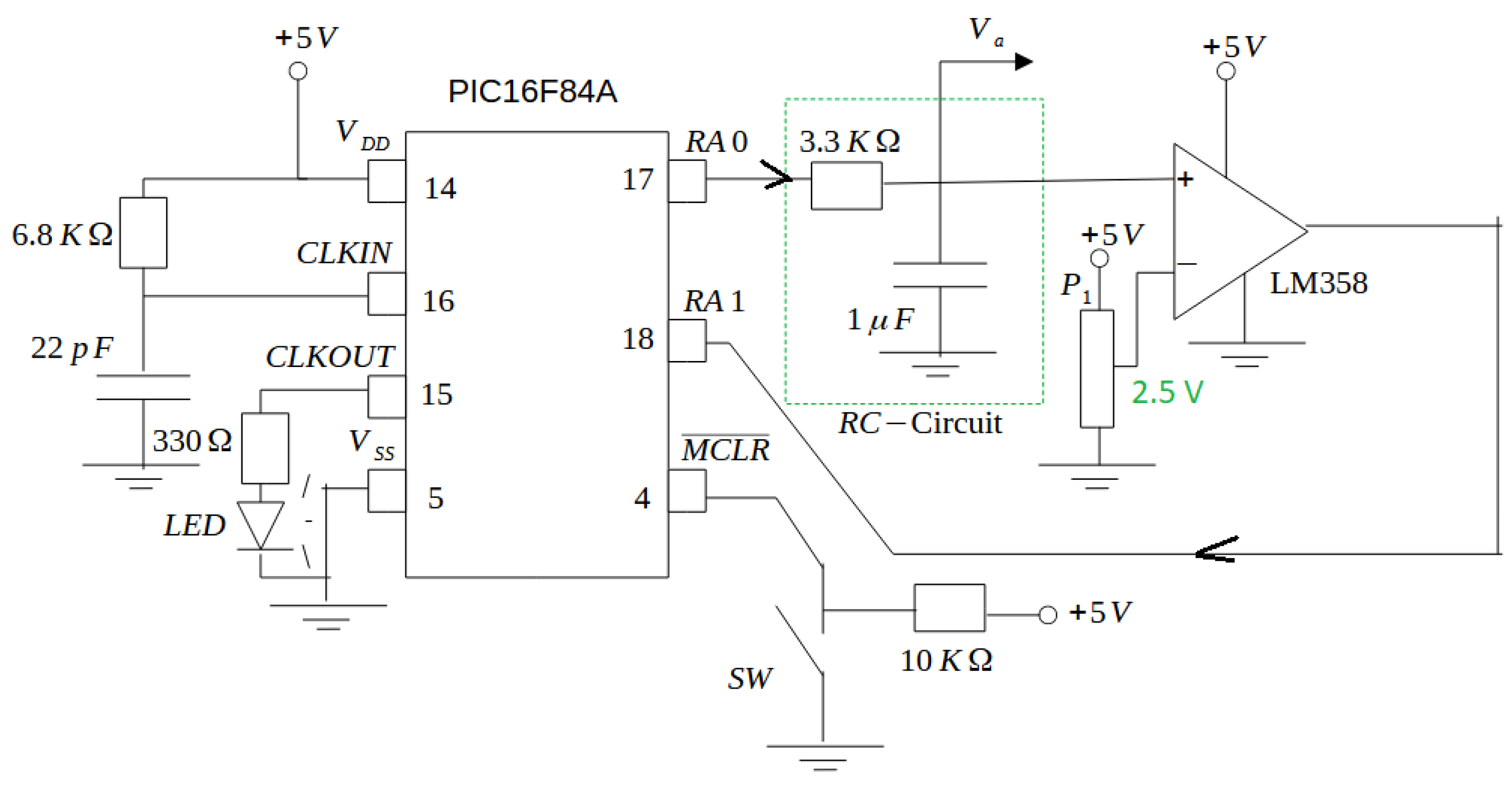
Figure 4. A photo of our experimental platform.

Figure 5. PIC program. At pin

R A 1

is the input feedback signal.

Figure 5. PIC program. At pin

R A 1

is the input feedback signal.

Figure 6. Closed-loop response

V_{a} (t)

by using a stable controller. Horizontal axis in seconds. At point "A" the experimental platform is activated for the uncontrolled logistic map, and at point "B", the control algorithm is activated.

Figure 6. Closed-loop response

V_{a} (t)

by using a stable controller. Horizontal axis in seconds. At point "A" the experimental platform is activated for the uncontrolled logistic map, and at point "B", the control algorithm is activated.

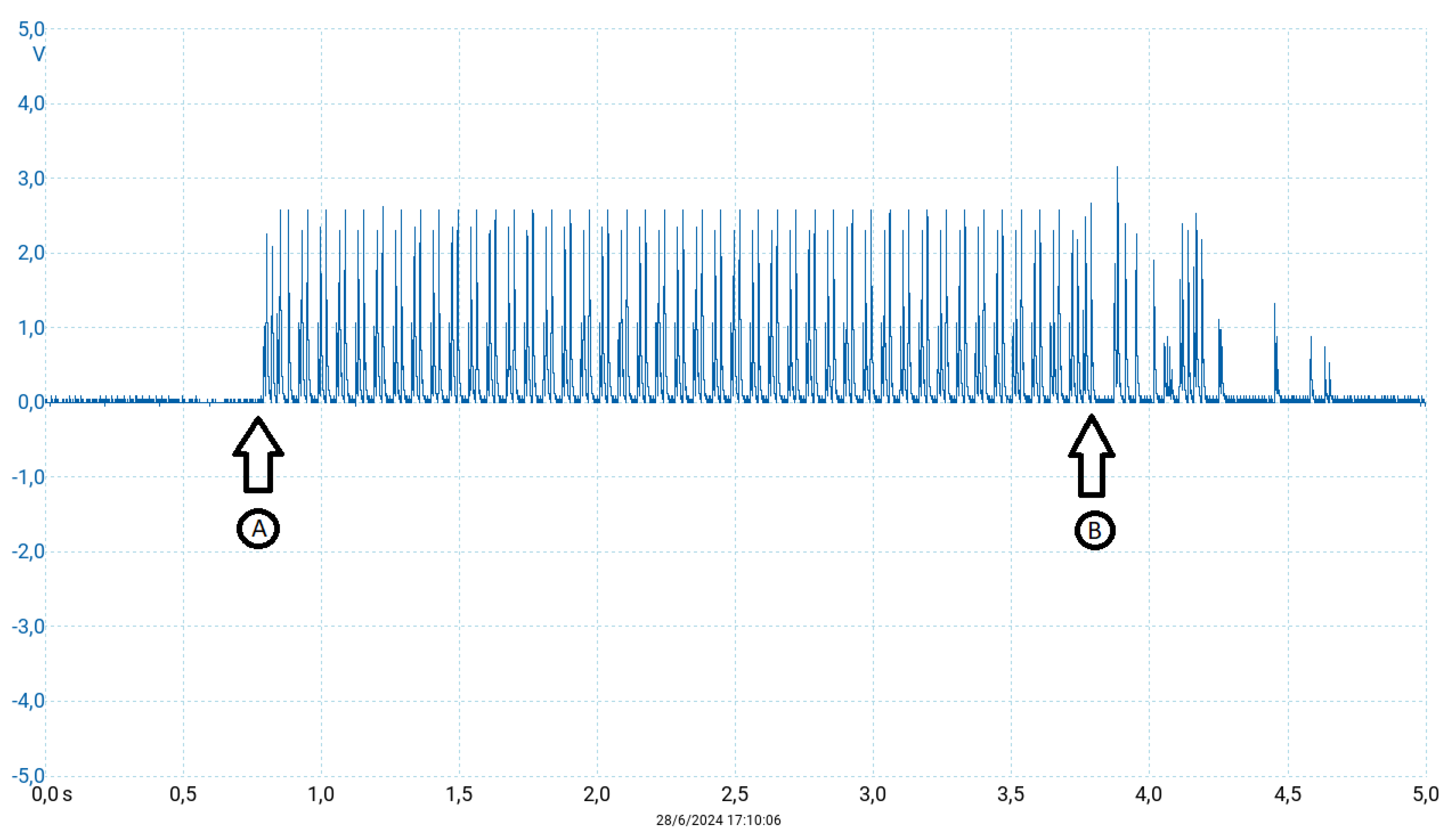
Figure 7. Closed-loop response

V_{a} (t)

by using an unstable controller. Horizontal axis in seconds. At point "A" the experimental platform is activated for the uncontrolled logistic map, and at point "B", the control algorithm is set on. Here,

u^{+}

and

u^{-}

are exchanged showing instability.

Figure 7. Closed-loop response

V_{a} (t)

u^{+}

and

u^{-}

are exchanged showing instability.

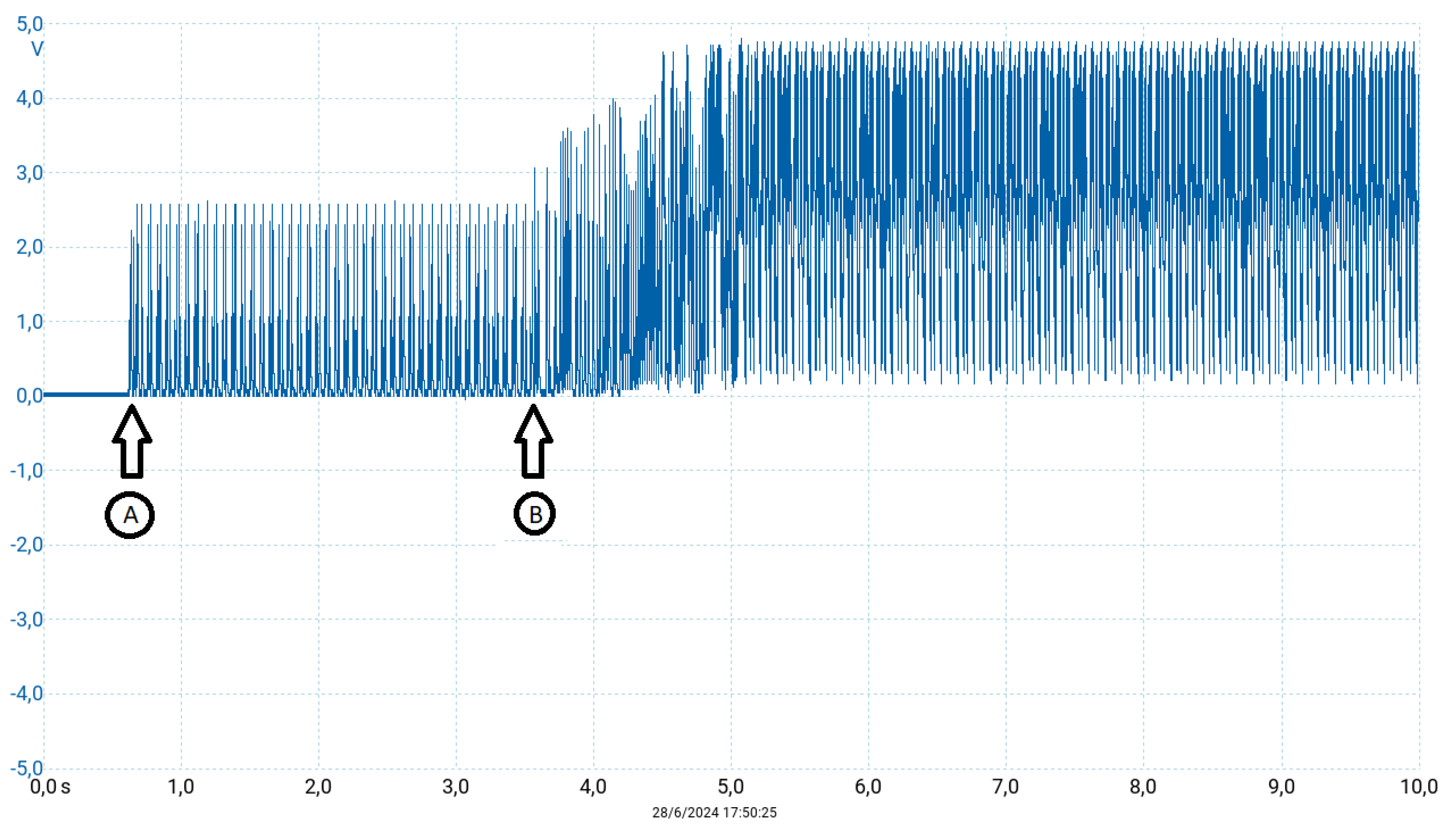
Figure 8. Closed-loop response

V_{a} (t)

by using an stable controller. Horizontal axis in seconds. At point "A" the experimental platform is activated for the uncontrolled logistic map, and at point "B", the control algorithm is set on. Here

u^{+} = 0

showing stability.

Figure 8. Closed-loop response

V_{a} (t)

u^{+} = 0

showing stability.

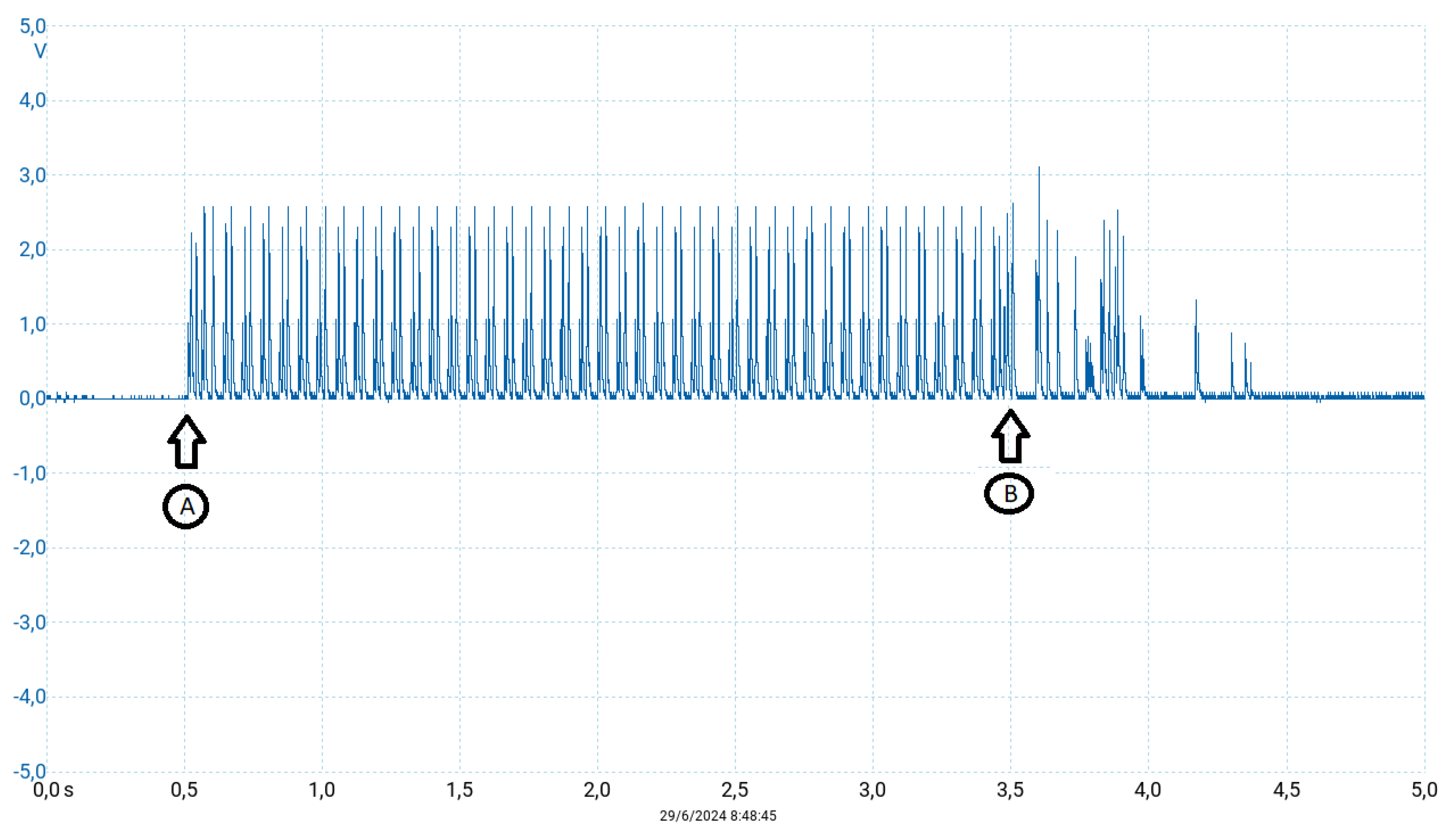
Figure 9. Closed-loop response

V_{a} (t)

u^{+} = 0

Figure 9. Closed-loop response

V_{a} (t)

u^{+} = 0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Finite-Time Control Design for the Discrete-Time Chaotic Logistic Equation

Abstract

1. Introduction

2. Finite-Time Stability

3. Chaotic Logistic Equation

4. Control Design and Experimentation

5. Experimental Results and Discussion

6. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe